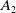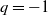1. Introduction
Let
![]() $A=(A,m,\Delta)$
be a Hopf algebra over a field
$A=(A,m,\Delta)$
be a Hopf algebra over a field
![]() $\Bbbk$
. A Hopf cocycle
$\Bbbk$
. A Hopf cocycle
![]() $\sigma$
with coefficients in
$\sigma$
with coefficients in
![]() $\Bbbk$
for A is a linear map
$\Bbbk$
for A is a linear map
![]() $\sigma\colon A\otimes A\to \Bbbk$
which is convolution invertible and satisfies
$\sigma\colon A\otimes A\to \Bbbk$
which is convolution invertible and satisfies
This condition allows to deform the multiplication
![]() $m\rightsquigarrow m_\sigma=\sigma\ast m\ast \sigma^{-1}$
into a new associative product, so that the cocycle deformation
$m\rightsquigarrow m_\sigma=\sigma\ast m\ast \sigma^{-1}$
into a new associative product, so that the cocycle deformation
![]() $A_\sigma=(A,m_\sigma,\Delta)$
is again a Hopf algebra. Introduced by Doi and Takeuchi in [Reference Doi and Takeuchi11], Hopf cocycles have evolved in recent years from a technical device to an inescapable and key tool in the classification program for non-semisimple Hopf algebras.
$A_\sigma=(A,m_\sigma,\Delta)$
is again a Hopf algebra. Introduced by Doi and Takeuchi in [Reference Doi and Takeuchi11], Hopf cocycles have evolved in recent years from a technical device to an inescapable and key tool in the classification program for non-semisimple Hopf algebras.
Indeed, the classification of finite-dimensional pointed Hopf algebras over abelian groups is completely determined by Hopf cocycles. Each such Hopf algebra is a cocycle deformation of the bosonization
![]() $B\# H$
, where
$B\# H$
, where
![]() $B=\mathfrak{B}(V)$
is a finite-dimensional Nichols algebra of diagonal type and
$B=\mathfrak{B}(V)$
is a finite-dimensional Nichols algebra of diagonal type and
![]() $H=\Bbbk\Gamma$
is a commutative group algebra. This was first observed by Masuoka in [Reference Masuoka21], see also [Reference Grunelfelder and Mastnak18], for the Hopf algebras classified in [Reference Andruskiewitsch and Schneider3], and proved in full generality in [Reference Angiono and García Iglesias7]. A similar statement is true for every known example of a finite-dimensional pointed Hopf algebra over
$H=\Bbbk\Gamma$
is a commutative group algebra. This was first observed by Masuoka in [Reference Masuoka21], see also [Reference Grunelfelder and Mastnak18], for the Hopf algebras classified in [Reference Andruskiewitsch and Schneider3], and proved in full generality in [Reference Angiono and García Iglesias7]. A similar statement is true for every known example of a finite-dimensional pointed Hopf algebra over
![]() $H=\Bbbk G$
, G non-necessarily abelian, cf. [Reference García and Mastnak13, Reference García Iglesias and Mombelli14, Reference García Iglesias and Vay16, Reference García Iglesias and Vay17]. Moreover, the same holds for copointed Hopf algebras over
$H=\Bbbk G$
, G non-necessarily abelian, cf. [Reference García and Mastnak13, Reference García Iglesias and Mombelli14, Reference García Iglesias and Vay16, Reference García Iglesias and Vay17]. Moreover, the same holds for copointed Hopf algebras over
![]() $H=\Bbbk^G$
, see [Reference Andruskiewitsch and Vay4, Reference Fantino, García and Mastnak12, Reference García Iglesias and Vay17].
$H=\Bbbk^G$
, see [Reference Andruskiewitsch and Vay4, Reference Fantino, García and Mastnak12, Reference García Iglesias and Vay17].
It is important to remark that, despite the name, Hopf cocycles do not arise from a cohomology setup (unless the Hopf algebra is cocommutative, in which case there are no deformations in this sense). In fact, the set
![]() $Z^2(A)$
of Hopf cocycles in A is not a group. This is a major obstruction for a systematic construction of cocycles. There is, however, a notion of cohomologous cocycles, via an action of the group of convolution units in
$Z^2(A)$
of Hopf cocycles in A is not a group. This is a major obstruction for a systematic construction of cocycles. There is, however, a notion of cohomologous cocycles, via an action of the group of convolution units in
![]() $A^\ast$
.
$A^\ast$
.
As a matter of fact, the classification results bypass an explicit description of the cocycles involved and work with the algebraic counterpart of cleft objects. These are certain comodule algebras C endowed with a convolution invertible comodule isomorphism
![]() $\gamma\colon A \to C$
. Any pair
$\gamma\colon A \to C$
. Any pair
![]() $(C,\gamma)$
defines a Hopf cocycle via
$(C,\gamma)$
defines a Hopf cocycle via
There is a more cohomological alternative to compute Hopf cocycles, rooted in the Hochschild cohomology
![]() $\textrm{H}^{\bullet}(A,\Bbbk)$
of A, as some Hopf cocycles can be obtained as exponentials of Hochschild 2-cocycles in
$\textrm{H}^{\bullet}(A,\Bbbk)$
of A, as some Hopf cocycles can be obtained as exponentials of Hochschild 2-cocycles in
![]() $\textrm{Z}^2(A,\Bbbk)$
. We also investigate this approach, which turns out to be rather limited. We say that a Hopf cocycle is pure when it is not cohomologous to an exponential.
$\textrm{Z}^2(A,\Bbbk)$
. We also investigate this approach, which turns out to be rather limited. We say that a Hopf cocycle is pure when it is not cohomologous to an exponential.
We propose to explicitly compute the Hopf cocycles involved in the classification by writing down the section for each cleft object and calculating the values of
![]() $\sigma$
using (1.1). Also, we determine which of these cocycles are pure and which are exponentials.
$\sigma$
using (1.1). Also, we determine which of these cocycles are pure and which are exponentials.
1.1. Setting
Motivated by the state-of-the-art of the classification program just described, we restrict ourselves to the following context
-
 $A=B\# H$
, where H is a semisimple Hopf algebra and
$A=B\# H$
, where H is a semisimple Hopf algebra and
 $B\in{}^{H}_{H}\mathcal{YD}$
is a (braided) graded Hopf algebra
$B\in{}^{H}_{H}\mathcal{YD}$
is a (braided) graded Hopf algebra
 $B=\bigoplus_{n\geq 0} B_n$
with
$B=\bigoplus_{n\geq 0} B_n$
with
 $B_0=\Bbbk$
and generated by
$B_0=\Bbbk$
and generated by
 $V\,:\!=\, B_1$
. That is, B is a pre-Nichols algebra.
$V\,:\!=\, B_1$
. That is, B is a pre-Nichols algebra. -
The Hopf cocycles
 $\sigma$
for A belong to the set
In particular, they are determined by the set
$\sigma$
for A belong to the set
In particular, they are determined by the set \begin{equation*} Z^2_0(A)\,:\!=\,\left\{\sigma\in Z^2(A) | \sigma_{|H\otimes H}=\epsilon\right\}. \end{equation*}
of H-linear cocycles
\begin{equation*} Z^2_0(A)\,:\!=\,\left\{\sigma\in Z^2(A) | \sigma_{|H\otimes H}=\epsilon\right\}. \end{equation*}
of H-linear cocycles \begin{equation*} Z^2(B)^H\,:\!=\,\left\{\sigma_B\in Z^2(B) | \sigma\!\left(h_{(1)}\cdot x,h_{(2)}\cdot y\right)=\epsilon(h)\sigma(x,y), \ h\in H, x,y\in B\right\} \end{equation*}
\begin{equation*} Z^2(B)^H\,:\!=\,\left\{\sigma_B\in Z^2(B) | \sigma\!\left(h_{(1)}\cdot x,h_{(2)}\cdot y\right)=\epsilon(h)\sigma(x,y), \ h\in H, x,y\in B\right\} \end{equation*}
 $\sigma_B$
for B, as a braided bialgebra, see (2.3), so that
(1.2)Thus,
$\sigma_B$
for B, as a braided bialgebra, see (2.3), so that
(1.2)Thus, \begin{align} \sigma(ah,bk)=\sigma_B(a,h\cdot b)\epsilon(k), \qquad a,b\in B, \ h,k\in H. \end{align}
\begin{align} \sigma(ah,bk)=\sigma_B(a,h\cdot b)\epsilon(k), \qquad a,b\in B, \ h,k\in H. \end{align}
 $\sigma_B=\sigma_{|B\otimes B}$
and
$\sigma_B=\sigma_{|B\otimes B}$
and
 $\sigma$
is determined by its values on a basis of B. We write
$\sigma$
is determined by its values on a basis of B. We write
 $\sigma=\sigma_B\# \epsilon$
, so
$\sigma=\sigma_B\# \epsilon$
, so
 $Z^2_0(A)\simeq Z^2(B)^H$
. See [Reference Andruskiewitsch and García Iglesias1] for details on braided cocycles.
$Z^2_0(A)\simeq Z^2(B)^H$
. See [Reference Andruskiewitsch and García Iglesias1] for details on braided cocycles.
We develop some tools that reduce the number of calculations we need to perform to compute the cocycles, see Lemma 3.2.
Ştefan shows in [Reference Ştefan25] that there is an action of H on
![]() $\textrm{Z}^\bullet(B,M)$
, that descends to
$\textrm{Z}^\bullet(B,M)$
, that descends to
![]() $\textrm{H}^{\bullet}(B,M)$
,
$\textrm{H}^{\bullet}(B,M)$
,
![]() $M\in B\textrm{-bimod}$
, in such a way that
$M\in B\textrm{-bimod}$
, in such a way that
![]() $\textrm{H}^\bullet(A,M)\simeq \textrm{H}^\bullet(B,M)^H$
. This action is not explicit in loc.cit. We write down Ştefan's Theorem in our context as Theorem 4.4: we present an element-based proof of it and show that the action is:
$\textrm{H}^\bullet(A,M)\simeq \textrm{H}^\bullet(B,M)^H$
. This action is not explicit in loc.cit. We write down Ştefan's Theorem in our context as Theorem 4.4: we present an element-based proof of it and show that the action is:
for
![]() $h\in H$
,
$h\in H$
,
![]() $f\in \textrm{Z}^q(B,M)\subset\textrm{Hom}_\Bbbk(B^{\otimes\,q}, M)$
and
$f\in \textrm{Z}^q(B,M)\subset\textrm{Hom}_\Bbbk(B^{\otimes\,q}, M)$
and
![]() ${\textbf{x}}\in B^{\otimes\,q}$
;
${\textbf{x}}\in B^{\otimes\,q}$
;
![]() $\mathcal{S}$
denotes the antipode of H. See also [Reference Căldăraru, Giaquinto and Witherspoon9] for H a group algebra. As well, we show that we can restrict the study of
$\mathcal{S}$
denotes the antipode of H. See also [Reference Căldăraru, Giaquinto and Witherspoon9] for H a group algebra. As well, we show that we can restrict the study of
![]() $\eta\in\textrm{Z}^2(A,\Bbbk)$
to cocycles in
$\eta\in\textrm{Z}^2(A,\Bbbk)$
to cocycles in
![]() $\eta_B\in \textrm{Z}^2(B,\Bbbk)^H$
, cf. (1.2). Finally, we show in Proposition 5.5 that
$\eta_B\in \textrm{Z}^2(B,\Bbbk)^H$
, cf. (1.2). Finally, we show in Proposition 5.5 that
![]() $e^\eta\in Z^2(B)^H$
if and only if
$e^\eta\in Z^2(B)^H$
if and only if
![]() $\eta\in \textrm{Z}^2(B,\Bbbk)^H$
.
$\eta\in \textrm{Z}^2(B,\Bbbk)^H$
.
Now, the cleft objects in the classification arise as
![]() $C=E\# H$
, for E a cleft object for B in
$C=E\# H$
, for E a cleft object for B in
![]() $H\textrm{-mod}$
. In particular the section
$H\textrm{-mod}$
. In particular the section
![]() $\gamma$
is given by
$\gamma$
is given by
![]() $\gamma=\gamma_B\#\textrm{id}_H$
,
$\gamma=\gamma_B\#\textrm{id}_H$
,
![]() $\gamma_B\colon B\to E$
. Formula (1.1) extends to this context, see [Reference Andruskiewitsch and García Iglesias1].
$\gamma_B\colon B\to E$
. Formula (1.1) extends to this context, see [Reference Andruskiewitsch and García Iglesias1].
In this setting, our strategy runs as follows.
-
(a) Compute the section
 $\gamma_B\colon B\to E$
in a basis
$\gamma_B\colon B\to E$
in a basis
 $\mathbb{B}$
of B.
$\mathbb{B}$
of B. -
(b) Write down the table of values of
 $\sigma$
as in (1.1) in terms of
$\sigma$
as in (1.1) in terms of
 $\mathbb{B}^2$
.
$\mathbb{B}^2$
. -
(c) Compute the space
 $\textrm{Z}^2(B,\Bbbk)^H$
of H-invariant Hochschild 2-cocycles and find necessary and sufficient conditions so that
$\textrm{Z}^2(B,\Bbbk)^H$
of H-invariant Hochschild 2-cocycles and find necessary and sufficient conditions so that
 $e^\eta$
is a Hopf cocycle.
$e^\eta$
is a Hopf cocycle. -
(d) Determine those Hopf cocycles that are cohomologous to exponentials
 $e^\eta$
and those that are pure.
$e^\eta$
and those that are pure.
1.2. An example of diagonal type
We perform all of these steps for a braiding
 \begin{equation*}\mathfrak{q}=\left(\begin{array}{c@{\quad}c}-1&q_{12}\\[5pt]
q_{21}&-1\end{array}\right)\end{equation*}
\begin{equation*}\mathfrak{q}=\left(\begin{array}{c@{\quad}c}-1&q_{12}\\[5pt]
q_{21}&-1\end{array}\right)\end{equation*}
of Cartan type
![]() $A_2$
, with parameter
$A_2$
, with parameter
![]() $q=q_{12}q_{21}=-1$
, and a principal YD-realization, see (2.10), in
$q=q_{12}q_{21}=-1$
, and a principal YD-realization, see (2.10), in
![]() ${}^{H}_{H}\mathcal{YD}$
for a semisimple Hopf algebra H. We recall that
${}^{H}_{H}\mathcal{YD}$
for a semisimple Hopf algebra H. We recall that
is a PBW basis for the Nichols algebra
![]() $B=\mathfrak{B}_{\mathfrak{q}}$
and that the deformations
$B=\mathfrak{B}_{\mathfrak{q}}$
and that the deformations
![]() $\mathfrak{u}_\mathfrak{q}(\boldsymbol\lambda)$
of
$\mathfrak{u}_\mathfrak{q}(\boldsymbol\lambda)$
of
![]() $A=B\# H$
are classified by triplets
$A=B\# H$
are classified by triplets
![]() $\boldsymbol\lambda=(\lambda_1,\lambda_2,\lambda_{12})\in\Bbbk^3$
, subject to certain restrictions (depending on H), see Section 6. Our main results are Theorems 6.5 and 6.13, which can be summarized as follows.
$\boldsymbol\lambda=(\lambda_1,\lambda_2,\lambda_{12})\in\Bbbk^3$
, subject to certain restrictions (depending on H), see Section 6. Our main results are Theorems 6.5 and 6.13, which can be summarized as follows.
Theorem. Let
![]() $\mathfrak{q}$
, H be as above. Any Hopf cocycle
$\mathfrak{q}$
, H be as above. Any Hopf cocycle
![]() $\sigma\in Z^2\!\left(\mathfrak{B}_{\mathfrak{q}}\right)^H$
is cohomologous to a cocycle
$\sigma\in Z^2\!\left(\mathfrak{B}_{\mathfrak{q}}\right)^H$
is cohomologous to a cocycle
![]() $\sigma_{\boldsymbol\lambda}$
,
$\sigma_{\boldsymbol\lambda}$
,
![]() $\boldsymbol\lambda=(\lambda_1,\lambda_2,\lambda_{12})$
, as in the following table:
$\boldsymbol\lambda=(\lambda_1,\lambda_2,\lambda_{12})$
, as in the following table:

In particular,
In turn, the cocycle
![]() $\sigma_{\boldsymbol\lambda}$
is cohomologous to an exponential if and only if at most one of the parameters
$\sigma_{\boldsymbol\lambda}$
is cohomologous to an exponential if and only if at most one of the parameters
![]() $\lambda_1,\lambda_2,\lambda_{12}$
is nonzero.
$\lambda_1,\lambda_2,\lambda_{12}$
is nonzero.
This table was computed by the second author in his Tesis de Licenciatura [Reference Sánchez23].
1.3. About the exponential
The theorem above shows in particular that the exponential approach is far from optimal. Up to cohomology, only three non-trivial cocycles are exponentials, namely
![]() $\sigma_{(1,0,0)}, \sigma_{(0,1,0)}$
and
$\sigma_{(1,0,0)}, \sigma_{(0,1,0)}$
and
![]() $\sigma_{(0,0,1)}$
.
$\sigma_{(0,0,1)}$
.
On the other hand, it is unclear which conditions on
![]() $\eta$
are necessary to imply that the exponential
$\eta$
are necessary to imply that the exponential
![]() $e^\eta$
is a Hopf cocycle. There are well-known sufficient commutation conditions (5.1) and (5.2) in the convolution algebra
$e^\eta$
is a Hopf cocycle. There are well-known sufficient commutation conditions (5.1) and (5.2) in the convolution algebra
![]() $\textrm{Hom}(A^{\otimes 3},\Bbbk)$
. As a byproduct of our calculations, we obtain in Lemma 6.11 that
$\textrm{Hom}(A^{\otimes 3},\Bbbk)$
. As a byproduct of our calculations, we obtain in Lemma 6.11 that
-
There are Hochschild cocycles
 $\eta$
that fail (5.1), (5.2) but still
$\eta$
that fail (5.1), (5.2) but still
 $e^\eta$
is a Hopf cocycle.
$e^\eta$
is a Hopf cocycle. -
However, we show that in our examples such cocycles
 $\eta$
are cohomologous to a cocycle satisfying those conditions. We are not aware if this a general fact.
$\eta$
are cohomologous to a cocycle satisfying those conditions. We are not aware if this a general fact.
An important comment worth making is that, depending on the realization and certain normalization conditions, a pure cocycle deformation
![]() $A_\sigma$
can be isomorphic to an exponential deformation
$A_\sigma$
can be isomorphic to an exponential deformation
![]() $A_{e^\eta}$
, see Remark 6.2. Nevertheless, the corresponding cleft objects are not isomorphic.
$A_{e^\eta}$
, see Remark 6.2. Nevertheless, the corresponding cleft objects are not isomorphic.
Some of these observations have already been implicitly pointed in [Reference García and Mastnak13], for cocycles related to pointed Hopf algebras over
![]() $\mathbb{S}_4$
. Nevertheless, the exponential Hopf cocycles obtained in loc.cit. considered a restricted class of Hochschild cocycles, namely those that are concentrated in degree one. We hope to obtain a full description of the missing pure cocycles in future work.
$\mathbb{S}_4$
. Nevertheless, the exponential Hopf cocycles obtained in loc.cit. considered a restricted class of Hochschild cocycles, namely those that are concentrated in degree one. We hope to obtain a full description of the missing pure cocycles in future work.
On the other hand, those restrictions are enough to find all cocycles for pointed Hopf algebras over
![]() $\mathbb{S}_3$
ibid., as deformations of the Fomin-Kirillov algebra
$\mathbb{S}_3$
ibid., as deformations of the Fomin-Kirillov algebra
![]() $\mathcal{FK}_3$
and copointed Hopf algebras over the dihedral groups
$\mathcal{FK}_3$
and copointed Hopf algebras over the dihedral groups
![]() $\mathbb{D}_{4m}$
in [Reference Fantino, García and Mastnak12]. In a forthcoming work [Reference García Iglesias and Sánchez15], we show that pure cocycles are indeed needed for pointed deformations of
$\mathbb{D}_{4m}$
in [Reference Fantino, García and Mastnak12]. In a forthcoming work [Reference García Iglesias and Sánchez15], we show that pure cocycles are indeed needed for pointed deformations of
![]() $\mathcal{FK}_3$
over more general groups
$\mathcal{FK}_3$
over more general groups
![]() $G\twoheadrightarrow\mathbb{S}_3$
, or for copointed deformations over
$G\twoheadrightarrow\mathbb{S}_3$
, or for copointed deformations over
![]() $\Bbbk^{\mathbb{S}_3}$
.
$\Bbbk^{\mathbb{S}_3}$
.
It is also worth mentioning that, under certain conditions, some families of cocycles for the pointed Hopf algebras in [Reference Andruskiewitsch and Schneider3] were described in [Reference Mastnak and Witherspoon20]. The example we treat in this article escapes those restrictions.
1.4. Organization
The paper is organized as follows. In Section 2, we recall some preliminaries on Hopf algebras and deformations. In Section 3, we develop some tools and techniques to compute the cocycles. In Section 4, we study the Hochschild cohomology of the algebras in our setting Section 1.1, in particular the structure of the set of H-invariant 2-cocycles. We also investigate the H-invariance introduced in [Reference Ştefan25] and give an explicit description of the action. We combine these analysis to study the exponential cocycles in Section 5. Finally, we apply all of these steps in Section 6 where we compute in detail the cocycles associated to a deformation of Cartan type
![]() $A_2$
.
$A_2$
.
2. Preliminaries
We work over an algebraically closed field of characteristic zero
![]() $\Bbbk$
. All tensor products, vector spaces and maps are assumed to be defined over
$\Bbbk$
. All tensor products, vector spaces and maps are assumed to be defined over
![]() $\Bbbk$
. If
$\Bbbk$
. If
![]() $\theta\in\mathbb{N}$
, we set
$\theta\in\mathbb{N}$
, we set
![]() $I_\theta=\{1,\dots,\theta\}\subset \mathbb{N}$
.
$I_\theta=\{1,\dots,\theta\}\subset \mathbb{N}$
.
We let
![]() $(H,m,\Delta)$
be a Hopf algebra; we use Sweedler’s notation
$(H,m,\Delta)$
be a Hopf algebra; we use Sweedler’s notation
![]() $\Delta(h)=h_{(1)}\otimes h_{(2)}$
for the comultiplication, similarly for comodules over H and the coaction. We set
$\Delta(h)=h_{(1)}\otimes h_{(2)}$
for the comultiplication, similarly for comodules over H and the coaction. We set
![]() $\Delta^{(2)}=(\Delta\otimes\textrm{id})\Delta(=(\textrm{id}\otimes\Delta)\Delta)$
. We write G(H) for the set of group-like elements on H,
$\Delta^{(2)}=(\Delta\otimes\textrm{id})\Delta(=(\textrm{id}\otimes\Delta)\Delta)$
. We write G(H) for the set of group-like elements on H,
![]() $\textrm{P}(H)$
for the primitive elements and U(H) for the units. We denote by
$\textrm{P}(H)$
for the primitive elements and U(H) for the units. We denote by
![]() $H_0$
the coradical of H. Recall that H is pointed when
$H_0$
the coradical of H. Recall that H is pointed when
![]() $H_0=\Bbbk G(H)$
and copointed when
$H_0=\Bbbk G(H)$
and copointed when
![]() $H_0=k^G$
for some (finite) non-abelian group G.
$H_0=k^G$
for some (finite) non-abelian group G.
A (right) cleft object for H is a right comodule algebra C endowed with a convolution invertible comodule isomorphism
![]() $\gamma\colon H\to C$
. This map is called a section when
$\gamma\colon H\to C$
. This map is called a section when
![]() $\gamma(1)=1$
. We let
$\gamma(1)=1$
. We let
![]() $\textrm{Cleft}(H)$
denote the set of cleft objects up to isomorphism. Left, and bi-cleft, objects are defined similarly.
$\textrm{Cleft}(H)$
denote the set of cleft objects up to isomorphism. Left, and bi-cleft, objects are defined similarly.
2.1. Hopf cocycles
A Hopf 2-cocycle
![]() $\sigma\,:\, H\otimes H \to \Bbbk$
is a convolution-invertible linear map
$\sigma\,:\, H\otimes H \to \Bbbk$
is a convolution-invertible linear map
![]() $x\otimes y\mapsto\sigma(x,y)$
satisfying
$x\otimes y\mapsto\sigma(x,y)$
satisfying
It follows that
![]() $\sigma(1,1)\neq 0$
and
$\sigma(1,1)\neq 0$
and
![]() $\sigma(x, 1) = \sigma(1, x) = \epsilon(x)\sigma(1,1)$
,
$\sigma(x, 1) = \sigma(1, x) = \epsilon(x)\sigma(1,1)$
,
![]() $x\in H$
, so by
$x\in H$
, so by
we can always assume that
![]() $\sigma(x, 1) = \sigma(1, x) = \epsilon(x)$
. Such cocycles are called normalized. We shall denote by
$\sigma(x, 1) = \sigma(1, x) = \epsilon(x)$
. Such cocycles are called normalized. We shall denote by
the set of normalized Hopf 2-cocycles in H.
We will use a coordinate-free version of (2.1), namely
This allows us to consider a braided version of Hopf cocycles for any bialgebra in a braided category; see [Reference Andruskiewitsch and García Iglesias1] for details.
2.1.1. Cocycle deformations
Let
![]() $\sigma\in Z^2(H)$
. Then
$\sigma\in Z^2(H)$
. Then
![]() $\cdot_{\sigma}\,:\,H\otimes H\rightarrow H$
, given by
$\cdot_{\sigma}\,:\,H\otimes H\rightarrow H$
, given by
defines an associative product on the vector space H. Moreover, the collection
![]() $(H,\cdot_\sigma, \Delta)$
is a Hopf algebra with antipode
$(H,\cdot_\sigma, \Delta)$
is a Hopf algebra with antipode
![]() $\mathcal{S}_{\sigma} = f*\mathcal{S}*f^{-1}$
, for
$\mathcal{S}_{\sigma} = f*\mathcal{S}*f^{-1}$
, for
![]() $f =\sigma\circ(\textrm{id}\otimes\,\mathcal{S})\circ\Delta$
. This Hopf algebra is denoted
$f =\sigma\circ(\textrm{id}\otimes\,\mathcal{S})\circ\Delta$
. This Hopf algebra is denoted
![]() $H_\sigma$
and referred to as a cocycle deformation of H.
$H_\sigma$
and referred to as a cocycle deformation of H.
If
![]() $\sigma\in Z^2(H)$
, then there is another deformation of the multiplication in H. Namely,
$\sigma\in Z^2(H)$
, then there is another deformation of the multiplication in H. Namely,
![]() $\cdot_{(\sigma)}\,:\,H\otimes H\rightarrow H$
, given by
$\cdot_{(\sigma)}\,:\,H\otimes H\rightarrow H$
, given by
also defines an associative product on the vector space H; we denote this new algebra by
![]() $H_{(\sigma)}$
. In this case, the comultiplication
$H_{(\sigma)}$
. In this case, the comultiplication
![]() $H\to H\otimes H$
defines coactions
$H\to H\otimes H$
defines coactions
![]() $H_{(\sigma)}\to H_{(\sigma)}\otimes H$
and
$H_{(\sigma)}\to H_{(\sigma)}\otimes H$
and
![]() $H_{(\sigma)}\to H_{\sigma}\otimes H_{(\sigma)}$
in such a way that
$H_{(\sigma)}\to H_{\sigma}\otimes H_{(\sigma)}$
in such a way that
![]() $C=H_{(\sigma)}$
becomes a
$C=H_{(\sigma)}$
becomes a
![]() $(H_{\sigma},H)$
-bicleft object.
$(H_{\sigma},H)$
-bicleft object.
Moreover, any (right) cleft object C for H (and hence any cocycle deformation
![]() $H_{\sigma}$
) arises in this way. If C is a cleft object with a normalized section
$H_{\sigma}$
) arises in this way. If C is a cleft object with a normalized section
![]() $\gamma\,:\,H\to C$
, then
$\gamma\,:\,H\to C$
, then
![]() $C\simeq H_{(\sigma)}$
; for the cocycle
$C\simeq H_{(\sigma)}$
; for the cocycle
![]() $\sigma\colon H\otimes H\to \Bbbk$
determined by the formula
$\sigma\colon H\otimes H\to \Bbbk$
determined by the formula
We stress that formula (2.6) extends to cleft objects in braided categories, see [Reference Andruskiewitsch and García Iglesias1].
Furthermore, it is possible to recover
![]() $H_{\sigma}$
completely in terms of the cleft object C, as the so-called Schauenburg left Hopf algebra L(C, H); in particular, no cocycles are explicitly involved. See [Reference Schauenburg24] for further details.
$H_{\sigma}$
completely in terms of the cleft object C, as the so-called Schauenburg left Hopf algebra L(C, H); in particular, no cocycles are explicitly involved. See [Reference Schauenburg24] for further details.
2.1.2. Cohomologous Hopf cocycles
The group
![]() $U(H^*)$
of convolution units in
$U(H^*)$
of convolution units in
![]() $H^\ast$
acts on
$H^\ast$
acts on
![]() $Z^2(H)$
via
$Z^2(H)$
via
We write
![]() $\sigma\sim_\alpha\sigma^{\prime}$
when
$\sigma\sim_\alpha\sigma^{\prime}$
when
![]() $\sigma^{\prime}=\alpha\rightharpoonup\sigma$
and set
$\sigma^{\prime}=\alpha\rightharpoonup\sigma$
and set
Moreover, if
![]() $\sigma^{\prime}=\alpha\rightharpoonup\sigma$
, then
$\sigma^{\prime}=\alpha\rightharpoonup\sigma$
, then
![]() $H_\sigma\simeq H_{\sigma^{\prime}}$
as Hopf algebras. However, the converse is not true, see Remark 2.1 below.
$H_\sigma\simeq H_{\sigma^{\prime}}$
as Hopf algebras. However, the converse is not true, see Remark 2.1 below.
The equivalence does hold for H-cleft objects, namely
![]() $(C,\gamma)\simeq (C^{\prime},\gamma^{\prime})$
if and only if
$(C,\gamma)\simeq (C^{\prime},\gamma^{\prime})$
if and only if
![]() $[\sigma]=[\sigma^{\prime}]$
, for
$[\sigma]=[\sigma^{\prime}]$
, for
![]() $\sigma,\sigma^{\prime}$
the Hopf 2-cocycles associated to
$\sigma,\sigma^{\prime}$
the Hopf 2-cocycles associated to
![]() $\gamma,\gamma^{\prime}$
, respectively, as in (2.6), so that
$\gamma,\gamma^{\prime}$
, respectively, as in (2.6), so that
![]() $C\simeq H_{(\sigma)}$
and
$C\simeq H_{(\sigma)}$
and
![]() $C^{\prime}\simeq H_{(\sigma^{\prime})}$
, see [Reference Doi10, Theorem 2.2]. That is, there is an equivalence
$C^{\prime}\simeq H_{(\sigma^{\prime})}$
, see [Reference Doi10, Theorem 2.2]. That is, there is an equivalence
We may always assume that such
![]() $\alpha$
as in (2.7) is such that
$\alpha$
as in (2.7) is such that
![]() $\alpha(1)=1$
. Indeed,
$\alpha(1)=1$
. Indeed,
![]() $c=\alpha(1)\neq 0$
as
$c=\alpha(1)\neq 0$
as
![]() $\alpha$
is convolution invertible and
$\alpha$
is convolution invertible and
Remark 2.1. Two cocycle deformations
![]() $H_{\sigma}$
and
$H_{\sigma}$
and
![]() $H_{\sigma^{\prime}}$
may be isomorphic for two non-equivalent cocycles
$H_{\sigma^{\prime}}$
may be isomorphic for two non-equivalent cocycles
![]() $\sigma,\sigma^{\prime}\in Z^2(H)$
.
$\sigma,\sigma^{\prime}\in Z^2(H)$
.
We briefly develop an example. Let
![]() $H=\Bbbk\big\langle x,g\,:\,x^2=0, g^2=1, gx=-xg\big\rangle$
be the Taft algebra and let
$H=\Bbbk\big\langle x,g\,:\,x^2=0, g^2=1, gx=-xg\big\rangle$
be the Taft algebra and let
![]() $\sigma_\lambda$
,
$\sigma_\lambda$
,
![]() $\lambda\in\Bbbk$
, be the cocycle determined by
$\lambda\in\Bbbk$
, be the cocycle determined by
![]() $\sigma_\lambda(x,x)=\lambda$
and
$\sigma_\lambda(x,x)=\lambda$
and
for
![]() $a,b,i,j\in\{0,1\}$
. It follows that
$a,b,i,j\in\{0,1\}$
. It follows that
![]() $H_{\sigma_{\lambda}}\simeq H$
for every
$H_{\sigma_{\lambda}}\simeq H$
for every
![]() $\lambda\in\Bbbk$
. If
$\lambda\in\Bbbk$
. If
![]() $\lambda\neq 0$
, then
$\lambda\neq 0$
, then
![]() $\sigma_{\lambda}\not\sim \sigma_1$
, but
$\sigma_{\lambda}\not\sim \sigma_1$
, but
![]() $\sigma_{1}\not\sim \sigma_0=\epsilon$
. Indeed, they determine the (non-isomorphic) cleft objects
$\sigma_{1}\not\sim \sigma_0=\epsilon$
. Indeed, they determine the (non-isomorphic) cleft objects
![]() $C_\lambda=\Bbbk\big\langle y,g\,:\,y^2=\lambda, g^2=1, gy=-yg\big\rangle$
,
$C_\lambda=\Bbbk\big\langle y,g\,:\,y^2=\lambda, g^2=1, gy=-yg\big\rangle$
,
![]() $\lambda=0,1$
.
$\lambda=0,1$
.
2.2. Yetter–Drinfeld modules and Nichols algebras
We recall that the category
![]() ${}^{H}_{H}\mathcal{YD}$
of Yetter–Drinfeld modules over H is the category of all simultaneously left modules and left comodules M such that the action
${}^{H}_{H}\mathcal{YD}$
of Yetter–Drinfeld modules over H is the category of all simultaneously left modules and left comodules M such that the action
![]() $\cdot$
and the coaction
$\cdot$
and the coaction
![]() $\rho$
are subject to
$\rho$
are subject to
When the antipode
![]() $\mathcal{S}$
of H is bijective this is a braided category, with braiding
$\mathcal{S}$
of H is bijective this is a braided category, with braiding
![]() $c_{M,N}\colon M\otimes N\to N\otimes M$
,
$c_{M,N}\colon M\otimes N\to N\otimes M$
,
![]() $m\otimes n\mapsto m_{({-}1)}\cdot n\otimes m_{(0)}$
;
$m\otimes n\mapsto m_{({-}1)}\cdot n\otimes m_{(0)}$
;
![]() $M,N\in{}^{H}_{H}\mathcal{YD}$
,
$M,N\in{}^{H}_{H}\mathcal{YD}$
,
![]() $m\in M$
,
$m\in M$
,
![]() $n\in N$
.
$n\in N$
.
A braided vector space is a pair (V, c), where V is a vector space together with an invertible linear map
![]() $c\colon V\otimes V\to V\otimes V$
that satisfies the braid equation
$c\colon V\otimes V\to V\otimes V$
that satisfies the braid equation
![]() $(c\otimes\textrm{id})(\textrm{id}\otimes\, c)(c\otimes\textrm{id})=(\textrm{id}\otimes\, c)(c\otimes\textrm{id})(\textrm{id}\otimes \,c)$
. In particular, any
$(c\otimes\textrm{id})(\textrm{id}\otimes\, c)(c\otimes\textrm{id})=(\textrm{id}\otimes\, c)(c\otimes\textrm{id})(\textrm{id}\otimes \,c)$
. In particular, any
![]() $M\in{}^{H}_{H}\mathcal{YD}$
is a braided vector space with
$M\in{}^{H}_{H}\mathcal{YD}$
is a braided vector space with
![]() $c=c_{M,M}$
. Conversely, a realization of (V, c) over H is a structure of Yetter–Drinfeld module on V so that
$c=c_{M,M}$
. Conversely, a realization of (V, c) over H is a structure of Yetter–Drinfeld module on V so that
![]() $c=c_{V,V}\in{}^{H}_{H}\mathcal{YD}$
.
$c=c_{V,V}\in{}^{H}_{H}\mathcal{YD}$
.
If
![]() $B\in{}^{H}_{H}\mathcal{YD}$
is an algebra, then one may use the braiding to define an algebra structure on
$B\in{}^{H}_{H}\mathcal{YD}$
is an algebra, then one may use the braiding to define an algebra structure on
![]() $B\otimes B\in{}^{H}_{H}\mathcal{YD}$
. A bialgebra, resp. Hopf algebra, in
$B\otimes B\in{}^{H}_{H}\mathcal{YD}$
. A bialgebra, resp. Hopf algebra, in
![]() ${}^{H}_{H}\mathcal{YD}$
is defined under this convention. In this case, the bosonization
${}^{H}_{H}\mathcal{YD}$
is defined under this convention. In this case, the bosonization
![]() $B\# H$
becomes a (Hopf) algebra. We recall that in this case the multiplication is defined via
$B\# H$
becomes a (Hopf) algebra. We recall that in this case the multiplication is defined via
We write bh for an element
![]() $b\#h$
of
$b\#h$
of
![]() $B\# H$
. Notice that this is coherent with the multiplication just defined as
$B\# H$
. Notice that this is coherent with the multiplication just defined as
as algebras and
![]() $(b\otimes 1)(1\otimes h)=b\otimes h$
. As well, notice that, for
$(b\otimes 1)(1\otimes h)=b\otimes h$
. As well, notice that, for
![]() $h\in H$
,
$h\in H$
,
![]() $b \in B$
:
$b \in B$
:
In turn, the comultiplication is given by the rule
See [Reference Andruskiewitsch and Schneider2] for details.
A Nichols algebra is a connected graded Hopf algebra
![]() $B=\oplus_{n\geq 0} B_n$
in
$B=\oplus_{n\geq 0} B_n$
in
![]() ${}^{H}_{H}\mathcal{YD}$
generated by
${}^{H}_{H}\mathcal{YD}$
generated by
![]() $V=B_1$
and such that
$V=B_1$
and such that
![]() $\textrm{P}(B)=V$
. We say that such a Hopf algebra is pre-Nichols when this last condition is not satisfied, so that
$\textrm{P}(B)=V$
. We say that such a Hopf algebra is pre-Nichols when this last condition is not satisfied, so that
![]() $V\subsetneq \textrm{P}(V)$
. We denote such Nichols algebra by
$V\subsetneq \textrm{P}(V)$
. We denote such Nichols algebra by
![]() $\mathfrak{B}(V)$
, as it is completely determined by the braided vector space (V, c), independently of the realization in
$\mathfrak{B}(V)$
, as it is completely determined by the braided vector space (V, c), independently of the realization in
![]() ${}^{H}_{H}\mathcal{YD}$
.
${}^{H}_{H}\mathcal{YD}$
.
A finite-dimensional braided vector space is of diagonal type when there is a basis
![]() $\left\{x_1,\dots,x_\theta\right\}$
of V and a matrix
$\left\{x_1,\dots,x_\theta\right\}$
of V and a matrix
![]() $\mathfrak{q}=(q_{ij})_{i,j\in\mathbb{I}_\theta}$
so that the braiding
$\mathfrak{q}=(q_{ij})_{i,j\in\mathbb{I}_\theta}$
so that the braiding
![]() $c=c^{\mathfrak{q}}$
is given by
$c=c^{\mathfrak{q}}$
is given by
![]() $c\!\left(x_i\otimes x_j\right)=q_{ij}x_j\otimes x_i$
,
$c\!\left(x_i\otimes x_j\right)=q_{ij}x_j\otimes x_i$
,
![]() $i,j\in \mathbb{I}_\theta$
. In this setting
$i,j\in \mathbb{I}_\theta$
. In this setting
![]() $\mathfrak{B}(V)$
is also denoted
$\mathfrak{B}(V)$
is also denoted
![]() $\mathfrak{B}_{\mathfrak{q}}$
.
$\mathfrak{B}_{\mathfrak{q}}$
.
A principal YD-realization of V over H is a family
![]() $(\chi_i,g_i)_{i\in \mathbb{I}_\theta}$
with
$(\chi_i,g_i)_{i\in \mathbb{I}_\theta}$
with
![]() $g_i\in G(H)$
and
$g_i\in G(H)$
and
![]() $\chi_i\colon H\to \Bbbk$
algebra maps so that
$\chi_i\colon H\to \Bbbk$
algebra maps so that
![]() $i,j\in \mathbb{I}_\theta$
,
$i,j\in \mathbb{I}_\theta$
,
![]() $g\in G(H), h\in H$
. This determines a realization
$g\in G(H), h\in H$
. This determines a realization
![]() $V\in{}^{H}_{H}\mathcal{YD}$
via
$V\in{}^{H}_{H}\mathcal{YD}$
via
Remark 2.2. Diagonal braided vector spaces
![]() $(V,c^{\mathfrak{q}})$
, or equivalently matrix braidings
$(V,c^{\mathfrak{q}})$
, or equivalently matrix braidings
![]() $\mathfrak{q}$
, with finite-dimensional associated Nichols algebra, are classified in [Reference Heckenberger19] in terms of decorated Dynkin diagrams. On top of that, the Nichols algebras
$\mathfrak{q}$
, with finite-dimensional associated Nichols algebra, are classified in [Reference Heckenberger19] in terms of decorated Dynkin diagrams. On top of that, the Nichols algebras
![]() $\mathfrak{B}_{\mathfrak{q}}$
are presented by generators and relations in [Reference Angiono5, Reference Angiono6] as quotients of the tensor algebra T(V). In turn, if H is a semisimple Hopf algebra with a principal YD-realization
$\mathfrak{B}_{\mathfrak{q}}$
are presented by generators and relations in [Reference Angiono5, Reference Angiono6] as quotients of the tensor algebra T(V). In turn, if H is a semisimple Hopf algebra with a principal YD-realization
![]() $V\in{}^{H}_{H}\mathcal{YD}$
, then all deformations of
$V\in{}^{H}_{H}\mathcal{YD}$
, then all deformations of
![]() $A=\mathfrak{B}_{\mathfrak{q}}\# H$
are classified in [Reference Angiono and García Iglesias7], by defining an exhaustive family of cleft objects
$A=\mathfrak{B}_{\mathfrak{q}}\# H$
are classified in [Reference Angiono and García Iglesias7], by defining an exhaustive family of cleft objects
![]() $(C_{\boldsymbol\lambda})_{\boldsymbol\lambda\in\Lambda}$
for A in such a way that every deformation arises as the associated Schauenburg left Hopf algebra
$(C_{\boldsymbol\lambda})_{\boldsymbol\lambda\in\Lambda}$
for A in such a way that every deformation arises as the associated Schauenburg left Hopf algebra
![]() $L(C_{\boldsymbol\lambda},A)$
, which is presented by generators and relations as a quotient
$L(C_{\boldsymbol\lambda},A)$
, which is presented by generators and relations as a quotient
![]() $\mathfrak{u}_{\mathfrak{q}}(\boldsymbol\lambda)$
of
$\mathfrak{u}_{\mathfrak{q}}(\boldsymbol\lambda)$
of
![]() $T(V)\# H$
. In particular,
$T(V)\# H$
. In particular,
![]() $\mathfrak{u}_{\mathfrak{q}}(\boldsymbol\lambda)$
is a cocycle deformation of A.
$\mathfrak{u}_{\mathfrak{q}}(\boldsymbol\lambda)$
is a cocycle deformation of A.
For any connected
![]() $B=\bigoplus_{n\geq 0} B_n$
bialgebra and
$B=\bigoplus_{n\geq 0} B_n$
bialgebra and
![]() $b\in B^+\,:\!=\,\bigoplus_{n\geq 1} B_n$
, we shall consider the restricted comultiplication:
$b\in B^+\,:\!=\,\bigoplus_{n\geq 1} B_n$
, we shall consider the restricted comultiplication:
Also, we set
![]() $\underline{\Delta}(1)=1\otimes 1$
; and write
$\underline{\Delta}(1)=1\otimes 1$
; and write
![]() $\underline{\Delta}(b)=b_{\underline{{(1)}}}\otimes b_{\underline{{(2)}}}$
,
$\underline{\Delta}(b)=b_{\underline{{(1)}}}\otimes b_{\underline{{(2)}}}$
,
![]() $b\in B.$
We will use a similar notation
$b\in B.$
We will use a similar notation
![]() $\underline{\rho}$
for coactions. A restricted version of coassociativity holds:
$\underline{\rho}$
for coactions. A restricted version of coassociativity holds:
As usual, we write
![]() $b_{\underline{{(1)}}{\underline{{(1)}}}}\otimes b_{\underline{{(1)}}{\underline{{(2)}}}}\otimes b_{\underline{{(2)}}}=b_{\underline{{(1)}}}\otimes b_{\underline{{(2)}}{\underline{{(1)}}}}\otimes b_{\underline{{(2)}}{\underline{{(2)}}}}=b_{\underline{{(1)}}}\otimes b_{\underline{{(2)}}}\otimes b_{\underline{{(3)}}}$
.
$b_{\underline{{(1)}}{\underline{{(1)}}}}\otimes b_{\underline{{(1)}}{\underline{{(2)}}}}\otimes b_{\underline{{(2)}}}=b_{\underline{{(1)}}}\otimes b_{\underline{{(2)}}{\underline{{(1)}}}}\otimes b_{\underline{{(2)}}{\underline{{(2)}}}}=b_{\underline{{(1)}}}\otimes b_{\underline{{(2)}}}\otimes b_{\underline{{(3)}}}$
.
3. Some tools to compute the cocycles
Recall our setting from Section 1. Namely, H is a semisimple Hopf algebra,
![]() $B\in{}^{H}_{H}\mathcal{YD}$
,
$B\in{}^{H}_{H}\mathcal{YD}$
,
![]() $A=B\# H$
and we consider Hopf cocycles
$A=B\# H$
and we consider Hopf cocycles
so
![]() $\sigma=\sigma_B\#\epsilon$
,
$\sigma=\sigma_B\#\epsilon$
,
![]() $\sigma_B\in Z^2(B)^H$
, see (1.2). We let
$\sigma_B\in Z^2(B)^H$
, see (1.2). We let
![]() $\mathbb{B}$
be a homogeneous basis of B, set
$\mathbb{B}$
be a homogeneous basis of B, set
![]() $V\,:\!=\, B_1$
and fix
$V\,:\!=\, B_1$
and fix
![]() $\{x_1,\dots,x_\theta\}\subset \mathbb{B}$
a basis of V.
$\{x_1,\dots,x_\theta\}\subset \mathbb{B}$
a basis of V.
In this section, we collect some ideas that reduce the number of computations necessary to calculate the values
We also investigate the orbit of
![]() $\sigma$
under the action of
$\sigma$
under the action of
![]() $U(A^\ast)$
in Section 3.1.
$U(A^\ast)$
in Section 3.1.
The first result is straightforward.
Lemma 3.1. Let
![]() $(E,\gamma)$
be a cleft object for B in
$(E,\gamma)$
be a cleft object for B in
![]() $H\textrm{-mod}$
and let
$H\textrm{-mod}$
and let
![]() $\sigma$
the associated cocycle as in (2.1). For each
$\sigma$
the associated cocycle as in (2.1). For each
![]() $x\in \textrm{P}(B), b\in B^+$
, we have
$x\in \textrm{P}(B), b\in B^+$
, we have
Proof. Indeed, we have that
Hence, we get
by (2.1).
Next lemma drastically reduces the number of computations, showing that the values
![]() $\{\sigma(b,b^{\prime})\,:\,b,$
$\{\sigma(b,b^{\prime})\,:\,b,$
![]() $b^{\prime}\in\mathbb{B}\}$
rely on the bialgebra structure of B in
$b^{\prime}\in\mathbb{B}\}$
rely on the bialgebra structure of B in
![]() ${}^{H}_{H}\mathcal{YD}$
and the set:
${}^{H}_{H}\mathcal{YD}$
and the set:
Let
![]() $\left(c_{i,j}^{p,q}\right)_{ \begin{smallmatrix} i,j,\\ p,q \end{smallmatrix} \in\mathbb{I}_\theta}$
be the matrix coefficients of the braiding
$\left(c_{i,j}^{p,q}\right)_{ \begin{smallmatrix} i,j,\\ p,q \end{smallmatrix} \in\mathbb{I}_\theta}$
be the matrix coefficients of the braiding
![]() $c\,:\,V\otimes V\to V\otimes V$
, so
$c\,:\,V\otimes V\to V\otimes V$
, so
Lemma 3.2. Let
![]() $a=xa^{\prime},b\in B^+$
,
$a=xa^{\prime},b\in B^+$
,
![]() $x\in V$
,
$x\in V$
,
![]() $\deg a^{\prime}>0$
. If a is a monomial, then
$\deg a^{\prime}>0$
. If a is a monomial, then
 \begin{align} \begin{split} \sigma\!\left(a,b\right) & = \sigma\!\left(x,a^{\prime}b\right)+\sigma\!\left(a^{\prime},b_{\underline{{(1)}}}\right)\sigma\!\left(x,b_{\underline{{(2)}}}\right)+\sigma\!\left(a^{\prime}_{\underline{{(1)}}},a^{\prime}_{\underline{{(2)}}({-}1)}\cdot b\right)\sigma\!\left(x,a^{\prime}_{\underline{{(2)}}(0)}\right)\\
&\quad +\sigma\!\left(a^{\prime}_{\underline{{(1)}}},a^{\prime}_{\underline{{(2)}}({-}1)}\cdot b_{\underline{{(1)}}}\right)\sigma\!\left(x,a^{\prime}_{\underline{{(2)}}(0)}b_{\underline{{(2)}}}\right)-\sigma\!\left(x,a^{\prime}_{\underline{{(1)}}}\right)\sigma\!\left(a^{\prime}_{\underline{{(2)}}},b\right). \end{split} \end{align}
\begin{align} \begin{split} \sigma\!\left(a,b\right) & = \sigma\!\left(x,a^{\prime}b\right)+\sigma\!\left(a^{\prime},b_{\underline{{(1)}}}\right)\sigma\!\left(x,b_{\underline{{(2)}}}\right)+\sigma\!\left(a^{\prime}_{\underline{{(1)}}},a^{\prime}_{\underline{{(2)}}({-}1)}\cdot b\right)\sigma\!\left(x,a^{\prime}_{\underline{{(2)}}(0)}\right)\\
&\quad +\sigma\!\left(a^{\prime}_{\underline{{(1)}}},a^{\prime}_{\underline{{(2)}}({-}1)}\cdot b_{\underline{{(1)}}}\right)\sigma\!\left(x,a^{\prime}_{\underline{{(2)}}(0)}b_{\underline{{(2)}}}\right)-\sigma\!\left(x,a^{\prime}_{\underline{{(1)}}}\right)\sigma\!\left(a^{\prime}_{\underline{{(2)}}},b\right). \end{split} \end{align}
In particular, for each
![]() $a,b\in\mathbb{B}^+$
there is a subset
$a,b\in\mathbb{B}^+$
there is a subset
![]() $S_\sigma^{a,b}\subseteq S_\sigma$
such that
$S_\sigma^{a,b}\subseteq S_\sigma$
such that
for some
![]() $\left(c_{s_1\dots s_\ell}\right)_{s_i\in S_\sigma^{a,b}}\in\mathbb{Z}\!\left[c_{i,j}^{p,q}\right]_{\begin{smallmatrix} i,j,\\ p,q \end{smallmatrix} \in\mathbb{I}_\theta}$
.
$\left(c_{s_1\dots s_\ell}\right)_{s_i\in S_\sigma^{a,b}}\in\mathbb{Z}\!\left[c_{i,j}^{p,q}\right]_{\begin{smallmatrix} i,j,\\ p,q \end{smallmatrix} \in\mathbb{I}_\theta}$
.
Proof. We proceed by induction on the degree
![]() $\deg(a)$
of a monomial
$\deg(a)$
of a monomial
![]() $a\in B$
. If
$a\in B$
. If
![]() $\deg(a)=1$
, this is clear. Fix
$\deg(a)=1$
, this is clear. Fix
![]() $n>1$
and assume that such decomposition exists for elements of degree
$n>1$
and assume that such decomposition exists for elements of degree
![]() $\leq n-1$
. If
$\leq n-1$
. If
![]() $a\in B$
is of degree n, then there exists
$a\in B$
is of degree n, then there exists
![]() $x\in V$
such that
$x\in V$
such that
![]() $a=xa^{\prime}$
, where
$a=xa^{\prime}$
, where
![]() $\deg(a^{\prime})=n-1$
. Hence, we have
$\deg(a^{\prime})=n-1$
. Hence, we have
![]() $\Delta(x)=x\otimes 1+1\otimes x$
and
$\Delta(x)=x\otimes 1+1\otimes x$
and
cf. (2.11). In this case, (2.1) becomes:
Now, the left hand side can be developed further and we get
 \begin{align*} \sigma(x_{(1)},a^{\prime}_{(1)})\sigma\!\left(x_{(2)}a^{\prime}_{(2)},b\right)& = \sigma(x,a^{\prime})\sigma(1,b)+\sigma(x,1)\sigma\!\left(a^{\prime},b\right)+\sigma\!\left(x,a^{\prime}_{\underline{{(1)}}}\right)\sigma\!\left(a^{\prime}_{\underline{{(2)}}},b\right)\\
& \quad +\sigma\!\left(1,x_{({-}1)}\cdot a^{\prime}\right)\sigma\!\left(x_{(0)},b\right)+\sigma(1,1)\sigma\!\left(xa^{\prime},b\right)+\sigma\!\left(1,x_{({-}1)}\cdot a^{\prime}_{\underline{{(1)}}}\right)\sigma\!\left(x_{(0)}a^{\prime}_{\underline{{(2)}}},b\right)\\
&=\sigma(a,b)+\sigma\!\left(x,a^{\prime}_{\underline{{(1)}}}\right)\sigma\!\left(a^{\prime}_{\underline{{(2)}}},b\right), \end{align*}
\begin{align*} \sigma(x_{(1)},a^{\prime}_{(1)})\sigma\!\left(x_{(2)}a^{\prime}_{(2)},b\right)& = \sigma(x,a^{\prime})\sigma(1,b)+\sigma(x,1)\sigma\!\left(a^{\prime},b\right)+\sigma\!\left(x,a^{\prime}_{\underline{{(1)}}}\right)\sigma\!\left(a^{\prime}_{\underline{{(2)}}},b\right)\\
& \quad +\sigma\!\left(1,x_{({-}1)}\cdot a^{\prime}\right)\sigma\!\left(x_{(0)},b\right)+\sigma(1,1)\sigma\!\left(xa^{\prime},b\right)+\sigma\!\left(1,x_{({-}1)}\cdot a^{\prime}_{\underline{{(1)}}}\right)\sigma\!\left(x_{(0)}a^{\prime}_{\underline{{(2)}}},b\right)\\
&=\sigma(a,b)+\sigma\!\left(x,a^{\prime}_{\underline{{(1)}}}\right)\sigma\!\left(a^{\prime}_{\underline{{(2)}}},b\right), \end{align*}
that is,
![]() $\sigma(a,b)=\sigma\!\left(x_{(1)},a^{\prime}_{(1)}\right)\sigma\!\left(x_{(2)}a^{\prime}_{(2)},b\right)-\sigma\!\left(x,a^{\prime}_{\underline{{(1)}}}\right)\sigma\!\left(a^{\prime}_{\underline{{(2)}}},b\right)$
.
$\sigma(a,b)=\sigma\!\left(x_{(1)},a^{\prime}_{(1)}\right)\sigma\!\left(x_{(2)}a^{\prime}_{(2)},b\right)-\sigma\!\left(x,a^{\prime}_{\underline{{(1)}}}\right)\sigma\!\left(a^{\prime}_{\underline{{(2)}}},b\right)$
.
Now we can develop the right hand side, and obtain:
 \begin{align*} \sigma\!\left(a^{\prime}_{(1)},b_{(1)}\right)\sigma\!\left(x,a^{\prime}_{(2)}b_{(2)}\right) & = \sigma\!\left(a^{\prime},b\right)\sigma(x,1)+\sigma\!\left(a^{\prime},1\right)\sigma(x,b)+\sigma\!\left(a^{\prime},b_{\underline{{(1)}}}\right)\sigma\!\left(x,b_{\underline{{(2)}}}\right)\\
&\quad +\sigma\!\left(1,a^{\prime}_{({-}1)}\cdot b\right)\sigma\!\left(x,a^{\prime}_{(0)}\right)+\sigma(1,1)\sigma\!\left(x,a^{\prime}b\right)+\sigma\!\left(1,a^{\prime}_{({-}1)}\cdot b_{\underline{{(1)}}}\right)\sigma\!\left(x,a^{\prime}_{(0)}b_{\underline{{(2)}}}\right)\\
&\quad +\sigma\!\left(a^{\prime}_{\underline{{(1)}}},{a^{\prime}_{\underline{{(2)}}({-}1)}}\cdot b\right)\sigma\!\left(x,a^{\prime}_{\underline{{(2)}}(0)}\right)+\sigma\!\left(a^{\prime}_{\underline{{(1)}}},1\right)\sigma\!\left(x,a^{\prime}_{\underline{{(2)}}}b\right)\\
&\quad +\sigma\!\left(a^{\prime}_{\underline{{(1)}}},{a^{\prime}_{\underline{{(2)}}({-}1)}}\cdot b_{\underline{{(1)}}}\right)\sigma\!\left(x,{a^{\prime}_{\underline{{(2)}}(0)}}b_{\underline{{(2)}}}\right)\\
& = \sigma\!\left(x,a^{\prime}b\right)+\sigma\!\left(a^{\prime},b_{\underline{{(1)}}}\right)\sigma\!\left(x,b_{\underline{{(2)}}}\right)+\sigma\!\left(a^{\prime}_{\underline{{(1)}}},{a^{\prime}_{\underline{{(2)}}({-}1)}}\cdot b\right)\sigma\!\left(x,a^{\prime}_{\underline{{(2)}}(0)}\right)\\
&\quad +\sigma\!\left(a^{\prime}_{\underline{{(1)}}},a^{\prime}_{\underline{{(2)}}({-}1)}\cdot b_{\underline{{(1)}}}\right)\sigma\!\left(x,a^{\prime}_{\underline{{(2)}}(0)}b_{\underline{{(2)}}}\right). \end{align*}
\begin{align*} \sigma\!\left(a^{\prime}_{(1)},b_{(1)}\right)\sigma\!\left(x,a^{\prime}_{(2)}b_{(2)}\right) & = \sigma\!\left(a^{\prime},b\right)\sigma(x,1)+\sigma\!\left(a^{\prime},1\right)\sigma(x,b)+\sigma\!\left(a^{\prime},b_{\underline{{(1)}}}\right)\sigma\!\left(x,b_{\underline{{(2)}}}\right)\\
&\quad +\sigma\!\left(1,a^{\prime}_{({-}1)}\cdot b\right)\sigma\!\left(x,a^{\prime}_{(0)}\right)+\sigma(1,1)\sigma\!\left(x,a^{\prime}b\right)+\sigma\!\left(1,a^{\prime}_{({-}1)}\cdot b_{\underline{{(1)}}}\right)\sigma\!\left(x,a^{\prime}_{(0)}b_{\underline{{(2)}}}\right)\\
&\quad +\sigma\!\left(a^{\prime}_{\underline{{(1)}}},{a^{\prime}_{\underline{{(2)}}({-}1)}}\cdot b\right)\sigma\!\left(x,a^{\prime}_{\underline{{(2)}}(0)}\right)+\sigma\!\left(a^{\prime}_{\underline{{(1)}}},1\right)\sigma\!\left(x,a^{\prime}_{\underline{{(2)}}}b\right)\\
&\quad +\sigma\!\left(a^{\prime}_{\underline{{(1)}}},{a^{\prime}_{\underline{{(2)}}({-}1)}}\cdot b_{\underline{{(1)}}}\right)\sigma\!\left(x,{a^{\prime}_{\underline{{(2)}}(0)}}b_{\underline{{(2)}}}\right)\\
& = \sigma\!\left(x,a^{\prime}b\right)+\sigma\!\left(a^{\prime},b_{\underline{{(1)}}}\right)\sigma\!\left(x,b_{\underline{{(2)}}}\right)+\sigma\!\left(a^{\prime}_{\underline{{(1)}}},{a^{\prime}_{\underline{{(2)}}({-}1)}}\cdot b\right)\sigma\!\left(x,a^{\prime}_{\underline{{(2)}}(0)}\right)\\
&\quad +\sigma\!\left(a^{\prime}_{\underline{{(1)}}},a^{\prime}_{\underline{{(2)}}({-}1)}\cdot b_{\underline{{(1)}}}\right)\sigma\!\left(x,a^{\prime}_{\underline{{(2)}}(0)}b_{\underline{{(2)}}}\right). \end{align*}
If
![]() $a=xa^{\prime}$
, then we obtain (3.2). The conclusion is obtained by applying inductive hypothesis on each summand.
$a=xa^{\prime}$
, then we obtain (3.2). The conclusion is obtained by applying inductive hypothesis on each summand.
Definition 3.3. The expression obtained in (3.3) via the recursive process (3.2) is the Hopf cocycle decomposition of
![]() $\sigma$
in terms of the set
$\sigma$
in terms of the set
![]() $S_{\sigma}$
from (3.1).
$S_{\sigma}$
from (3.1).
Example 3.4. We exhibit explicitly the Hopf cocycle decomposition of a cocycle
![]() $\sigma$
, in low degrees.
$\sigma$
, in low degrees.
Let
![]() $x,y,w,z\in V$
and
$x,y,w,z\in V$
and
![]() $b\in \mathbb{B}^+$
, then
$b\in \mathbb{B}^+$
, then
 \begin{align*} \sigma\!\left(xy,b\right)=\,&\sigma\!\left(x,yb\right)+\sigma\!\left(x,b_{\underline{(2)}}\right)\sigma\!\left(y,b_{\underline{(1)}}\right),\\
\sigma\!\left(xyw,b\right)=\,&\sigma\!\left(x,ywb\right)-\sigma\!\left(x,y\right)\sigma\!\left(w,b\right)+\sigma\!\left(y,w_{({-}1)}\cdot b\right)\sigma\!\left(x,w_{(0)}\right)\\
&+\sigma\!\left(y_{({-}2)}\cdot w,y_{({-}1)}\cdot b\right)\sigma\!\left(x,y_{(0)}\right)+\sigma\!\left(yw,b_{\underline{(1)}}\right)\sigma\!\left(x,b_{\underline{(2)}}\right)\\
&+\sigma\!\left(y,w_{({-}1)}\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,w_{(0)}b_{\underline{(2)}}\right)-\sigma\!\left(x,y_{({-}1)}\cdot w\right)\sigma\!\left(y_{(0)},b\right)\\
&+\sigma\!\left(y_{({-}2)}\cdot w, y_{({-}1)}\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,y_{(0)}b_{\underline{(2)}}\right),\\
\sigma\!\left(xywz,b\right)=\,&\sigma\!\left(x,ywzb\right)-\sigma\!\left(x,y\right)\sigma\!\left(wz,b\right)-\sigma\!\left(x,yw\right)\sigma\!\left(z,b\right)\\
&-\sigma\!\left(x,yw_{({-}1)}\cdot z\right)\sigma\!\left(w_{(0)},b\right)-\sigma\!\left(x,y_{({-}1)}\cdot\left(wz\right)\right)\sigma\!\left(y_{(0)},b\right)&\\
&-\sigma\!\left(x,y_{({-}1)}\cdot w\right)\sigma\!\left(y_{(0)}z,b\right)-\sigma\!\left(x,\left(y_{({-}1)}w_{({-}1)}\right)\cdot z\right)\sigma\!\left(y_{(0)}w_{(0)},b\right) \\
&+\sigma\!\left(yw,z_{({-}1)}\cdot b\right)\sigma\!\left(x,z_{(0)}\right)+\sigma\!\left(y\!\left(w_{({-}2)}\cdot z\right),w_{({-}1)}\cdot b\right)\sigma\!\left(x,w_{(0)}\right)\\
&+\sigma\!\left(y,\left(w_{({-}1)}z_{({-}1)}\right)\cdot b\right)\sigma\!\left(x,w_{(0)}z_{(0)}\right)+\sigma\!\left(ywz,b_{\underline{(1)}}\right)\sigma\!\left(x,b_{\underline{(2)}}\right)\\
&+\sigma\!\left(y_{({-}2)}\cdot\left(wz\right),y_{({-}1)}\cdot b\right)\sigma\!\left(x,y_{(0)}\right)\\
&+\sigma\!\left(y_{({-}2)}\cdot\left(wz\right), y_{({-}1)}\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,y_{(0)}b_{\underline{(2)}}\right)\\
&+\sigma\!\left(y_{({-}2)}\cdot w,\left(y_{({-}1)}z_{({-}1)}\right)\cdot b\right)\sigma\!\left(x,y_{(0)}z_{(0)}\right)\\
&+\sigma\!\left(\left(y_{({-}2)}w_{({-}2)}\right)\cdot z,\left(y_{({-}1)}w_{({-}1)}\right)\cdot b\right)\sigma\!\left(x,y_{(0)}w_{(0)}\right) \\
&+\sigma\!\left(yw,z_{({-}1)}\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,z_{(0)}b_{\underline{(2)}}\right)\\
&+\sigma\!\left(yw_{({-}2)}\cdot z,w_{({-}1)}\cdot b_{\underline{(1)}}\right)\sigma\!\left(x, w_{(0)}b_{\underline{(2)}}\right) \\
&+\sigma\!\left(y,\left(w_{({-}1)}z_{({-}1)}\right)\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,w_{(0)}z_{(0)}b_{\underline{(2)}}\right)\\
&+\sigma\!\left(y_{({-}2)}\cdot w,\left(y_{({-}1)}z_{({-}1)}\right)\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,y_{(0)}z_{(0)}b_{\underline{(2)}}\right) \\
&+\sigma\!\left(\left(y_{({-}2)}w_{({-}2)}\right)\cdot z, \left(y_{({-}1)}w_{({-}1)}\right)\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,y_{(0)}w_{(0)}b_{\underline{(2)}}\right). \end{align*}
\begin{align*} \sigma\!\left(xy,b\right)=\,&\sigma\!\left(x,yb\right)+\sigma\!\left(x,b_{\underline{(2)}}\right)\sigma\!\left(y,b_{\underline{(1)}}\right),\\
\sigma\!\left(xyw,b\right)=\,&\sigma\!\left(x,ywb\right)-\sigma\!\left(x,y\right)\sigma\!\left(w,b\right)+\sigma\!\left(y,w_{({-}1)}\cdot b\right)\sigma\!\left(x,w_{(0)}\right)\\
&+\sigma\!\left(y_{({-}2)}\cdot w,y_{({-}1)}\cdot b\right)\sigma\!\left(x,y_{(0)}\right)+\sigma\!\left(yw,b_{\underline{(1)}}\right)\sigma\!\left(x,b_{\underline{(2)}}\right)\\
&+\sigma\!\left(y,w_{({-}1)}\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,w_{(0)}b_{\underline{(2)}}\right)-\sigma\!\left(x,y_{({-}1)}\cdot w\right)\sigma\!\left(y_{(0)},b\right)\\
&+\sigma\!\left(y_{({-}2)}\cdot w, y_{({-}1)}\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,y_{(0)}b_{\underline{(2)}}\right),\\
\sigma\!\left(xywz,b\right)=\,&\sigma\!\left(x,ywzb\right)-\sigma\!\left(x,y\right)\sigma\!\left(wz,b\right)-\sigma\!\left(x,yw\right)\sigma\!\left(z,b\right)\\
&-\sigma\!\left(x,yw_{({-}1)}\cdot z\right)\sigma\!\left(w_{(0)},b\right)-\sigma\!\left(x,y_{({-}1)}\cdot\left(wz\right)\right)\sigma\!\left(y_{(0)},b\right)&\\
&-\sigma\!\left(x,y_{({-}1)}\cdot w\right)\sigma\!\left(y_{(0)}z,b\right)-\sigma\!\left(x,\left(y_{({-}1)}w_{({-}1)}\right)\cdot z\right)\sigma\!\left(y_{(0)}w_{(0)},b\right) \\
&+\sigma\!\left(yw,z_{({-}1)}\cdot b\right)\sigma\!\left(x,z_{(0)}\right)+\sigma\!\left(y\!\left(w_{({-}2)}\cdot z\right),w_{({-}1)}\cdot b\right)\sigma\!\left(x,w_{(0)}\right)\\
&+\sigma\!\left(y,\left(w_{({-}1)}z_{({-}1)}\right)\cdot b\right)\sigma\!\left(x,w_{(0)}z_{(0)}\right)+\sigma\!\left(ywz,b_{\underline{(1)}}\right)\sigma\!\left(x,b_{\underline{(2)}}\right)\\
&+\sigma\!\left(y_{({-}2)}\cdot\left(wz\right),y_{({-}1)}\cdot b\right)\sigma\!\left(x,y_{(0)}\right)\\
&+\sigma\!\left(y_{({-}2)}\cdot\left(wz\right), y_{({-}1)}\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,y_{(0)}b_{\underline{(2)}}\right)\\
&+\sigma\!\left(y_{({-}2)}\cdot w,\left(y_{({-}1)}z_{({-}1)}\right)\cdot b\right)\sigma\!\left(x,y_{(0)}z_{(0)}\right)\\
&+\sigma\!\left(\left(y_{({-}2)}w_{({-}2)}\right)\cdot z,\left(y_{({-}1)}w_{({-}1)}\right)\cdot b\right)\sigma\!\left(x,y_{(0)}w_{(0)}\right) \\
&+\sigma\!\left(yw,z_{({-}1)}\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,z_{(0)}b_{\underline{(2)}}\right)\\
&+\sigma\!\left(yw_{({-}2)}\cdot z,w_{({-}1)}\cdot b_{\underline{(1)}}\right)\sigma\!\left(x, w_{(0)}b_{\underline{(2)}}\right) \\
&+\sigma\!\left(y,\left(w_{({-}1)}z_{({-}1)}\right)\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,w_{(0)}z_{(0)}b_{\underline{(2)}}\right)\\
&+\sigma\!\left(y_{({-}2)}\cdot w,\left(y_{({-}1)}z_{({-}1)}\right)\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,y_{(0)}z_{(0)}b_{\underline{(2)}}\right) \\
&+\sigma\!\left(\left(y_{({-}2)}w_{({-}2)}\right)\cdot z, \left(y_{({-}1)}w_{({-}1)}\right)\cdot b_{\underline{(1)}}\right)\sigma\!\left(x,y_{(0)}w_{(0)}b_{\underline{(2)}}\right). \end{align*}
We have the following straightforward but useful consequence of the decomposition exhibited in Lemma 3.2.
Corollary 3.5. Let
![]() $\sigma$
and
$\sigma$
and
![]() $\sigma^{\prime}$
be two Hopf cocycles in B.
$\sigma^{\prime}$
be two Hopf cocycles in B.
-
(a) If
 $\sigma(x_i,b)=\sigma^{\prime}(x_i,b)$
for each
$\sigma(x_i,b)=\sigma^{\prime}(x_i,b)$
for each
 $i\in\mathbb{I}_\theta$
and every
$i\in\mathbb{I}_\theta$
and every
 $b\in\mathbb{B}$
, then
$b\in\mathbb{B}$
, then
 $\sigma=\sigma^{\prime}$
.
$\sigma=\sigma^{\prime}$
. -
(b) If
 $\alpha\in B^\ast$
is convolution invertible and
$\alpha\in B^\ast$
is convolution invertible and
 $\alpha\rightharpoonup\sigma(x_i,b)=\sigma^{\prime}(x_i,b)$
, for each
$\alpha\rightharpoonup\sigma(x_i,b)=\sigma^{\prime}(x_i,b)$
, for each
 $i\in\mathbb{I}_\theta$
and every
$i\in\mathbb{I}_\theta$
and every
 $b\in\mathbb{B}$
, then
$b\in\mathbb{B}$
, then
 $\alpha\rightharpoonup\sigma=\sigma^{\prime}$
.
$\alpha\rightharpoonup\sigma=\sigma^{\prime}$
.
3.1. Some remarks on
 $\alpha\rightharpoonup\sigma$
$\alpha\rightharpoonup\sigma$
Let
![]() $\sigma\in Z^2_0(A)$
,
$\sigma\in Z^2_0(A)$
,
![]() $\alpha\in U(A^*)$
, so that
$\alpha\in U(A^*)$
, so that
![]() $\sigma^{\prime}\,:\!=\, \alpha\rightharpoonup\sigma$
as in (2.7) is a Hopf cocycle cohomologous to
$\sigma^{\prime}\,:\!=\, \alpha\rightharpoonup\sigma$
as in (2.7) is a Hopf cocycle cohomologous to
![]() $\sigma$
. Moreover, we assume that
$\sigma$
. Moreover, we assume that
![]() $\sigma^{\prime}\in Z^2_0(A)$
. Recall that we may assume
$\sigma^{\prime}\in Z^2_0(A)$
. Recall that we may assume
![]() $\alpha(1)=1$
.
$\alpha(1)=1$
.
Remark 3.6.
![]() $\gamma_\alpha\,:\!=\, \alpha\ast\gamma\colon A\to E$
is another section, with associated cocycle
$\gamma_\alpha\,:\!=\, \alpha\ast\gamma\colon A\to E$
is another section, with associated cocycle
![]() $\alpha\rightharpoonup\sigma$
.
$\alpha\rightharpoonup\sigma$
.
Lemma 3.7. If
![]() $\alpha\rightharpoonup\sigma=\sigma^{\prime}$
, then
$\alpha\rightharpoonup\sigma=\sigma^{\prime}$
, then
![]() $\alpha_{|H}\in\textrm{Alg}(H,\Bbbk)$
. Hence
$\alpha_{|H}\in\textrm{Alg}(H,\Bbbk)$
. Hence
![]() $\alpha_{|H}^{-1}=(\alpha\circ\mathcal{S})_{|H}$
.
$\alpha_{|H}^{-1}=(\alpha\circ\mathcal{S})_{|H}$
.
Proof. The cocycle
![]() $\sigma_\alpha$
associated to
$\sigma_\alpha$
associated to
![]() $\gamma_\alpha$
is
$\gamma_\alpha$
is
![]() $\sigma^{\prime}$
, which satisfies
$\sigma^{\prime}$
, which satisfies
![]() $\sigma^{\prime}(h,k)=\epsilon(hk)$
. But
$\sigma^{\prime}(h,k)=\epsilon(hk)$
. But
which shows that
![]() $\alpha(hk)=\alpha(h)\alpha(k)$
, by uniqueness of the convolution inverse.
$\alpha(hk)=\alpha(h)\alpha(k)$
, by uniqueness of the convolution inverse.
Lemma 3.8. We have
![]() $\alpha(xh)=\alpha(x)\alpha(h)$
and
$\alpha(xh)=\alpha(x)\alpha(h)$
and
![]() $\alpha(hx)=\alpha(x)\alpha(h)$
.
$\alpha(hx)=\alpha(x)\alpha(h)$
.
In particular,
![]() $\alpha_{|B}\,:\,B\to \Bbbk$
is H-linear. That is,
$\alpha_{|B}\,:\,B\to \Bbbk$
is H-linear. That is,
Proof. Notice that
Thus
![]() $\psi(xh)=\alpha(x)\alpha(h)$
is a left convolution inverse to
$\psi(xh)=\alpha(x)\alpha(h)$
is a left convolution inverse to
![]() $\alpha^{-1}$
; hence
$\alpha^{-1}$
; hence
![]() $\psi=\alpha$
. The other equality is similar, considering
$\psi=\alpha$
. The other equality is similar, considering
![]() $\alpha\rightharpoonup\sigma(h,x)$
.
$\alpha\rightharpoonup\sigma(h,x)$
.
Now,
![]() $\alpha_{|B}(h\cdot x)=\alpha(h_{(1)}x \mathcal{S}(h_{2}))=\alpha\!\left(h_{(1)}\right)\alpha(x)\alpha(\mathcal{S}(h_{2}))=\epsilon(h)\alpha(x)$
.
$\alpha_{|B}(h\cdot x)=\alpha(h_{(1)}x \mathcal{S}(h_{2}))=\alpha\!\left(h_{(1)}\right)\alpha(x)\alpha(\mathcal{S}(h_{2}))=\epsilon(h)\alpha(x)$
.
Lemma 3.9. We can assume, without loss of generality, that
![]() $\alpha_{|H}=\epsilon$
.
$\alpha_{|H}=\epsilon$
.
Proof. Set
![]() $\varphi\,:\!=\,\alpha_{|H}$
; if
$\varphi\,:\!=\,\alpha_{|H}$
; if
![]() $\varphi\neq \epsilon$
, consider
$\varphi\neq \epsilon$
, consider
![]() $\tau=\epsilon\#\varphi^{-1}$
and set
$\tau=\epsilon\#\varphi^{-1}$
and set
![]() $\tilde{\alpha}\,:\!=\,\alpha\ast\tau$
. On the one hand,
$\tilde{\alpha}\,:\!=\,\alpha\ast\tau$
. On the one hand,
![]() $\tilde\alpha_{|H}=\epsilon$
, and
$\tilde\alpha_{|H}=\epsilon$
, and
![]() $\tilde{\alpha}(xh)=\alpha(x)\epsilon(h)$
,
$\tilde{\alpha}(xh)=\alpha(x)\epsilon(h)$
,
![]() $\tilde{\alpha}^{-1}(xh)=\alpha^{-1}(x)\epsilon(h)$
. Now, observe that
$\tilde{\alpha}^{-1}(xh)=\alpha^{-1}(x)\epsilon(h)$
. Now, observe that
 \begin{align*}\tilde\alpha\rightharpoonup\sigma(xh,yk)& =\tilde\alpha\!\left(x_{(1)}h_{(1)}\right)\tilde\alpha\!\left(y_{(1)}k_{(1)}\right)\sigma\!\left(x_{(2)}h_{(2)}, y_{(2)}k_{(2)}\right)\tilde\alpha^{-1}\!\left(x_{(3)}h_{(3)} y_{(3)}k_{(3)}\right)\\
&=\alpha\!\left(x_{(1)}\right)\alpha(y_{(1)})\sigma\!\left(x_{(2)}h_{(1)}, y_{(2)}\right)\tilde\alpha^{-1}\!\left(x_{(3)}h_{(2)}\cdot y_{(3)}\right)\epsilon(k)\\
&=\alpha\!\left(x_{(1)}\right)\alpha(y_{(1)})\sigma\!\left(x_{(2)}h_{(1)}, y_{(2)}\right)\alpha^{-1}\!\left(x_{(3)}h_{(2)}\cdot y_{(3)}\right)\epsilon(k)\\
&=\alpha\!\left(x_{(1)}\right)\alpha\!\left(h_{(1)}\cdot y_{(1)}\right)\sigma\!\left(x_{(2)}, h_{(2)}\cdot y_{(2)}\right)\alpha^{-1}\!\left(x_{(3)}h_{(3)}\cdot y_{(3)}\right)\epsilon(k)\\
&=\sigma^{\prime}(x,h\cdot y)\epsilon(k)=\sigma^{\prime}(xh,yk).\end{align*}
\begin{align*}\tilde\alpha\rightharpoonup\sigma(xh,yk)& =\tilde\alpha\!\left(x_{(1)}h_{(1)}\right)\tilde\alpha\!\left(y_{(1)}k_{(1)}\right)\sigma\!\left(x_{(2)}h_{(2)}, y_{(2)}k_{(2)}\right)\tilde\alpha^{-1}\!\left(x_{(3)}h_{(3)} y_{(3)}k_{(3)}\right)\\
&=\alpha\!\left(x_{(1)}\right)\alpha(y_{(1)})\sigma\!\left(x_{(2)}h_{(1)}, y_{(2)}\right)\tilde\alpha^{-1}\!\left(x_{(3)}h_{(2)}\cdot y_{(3)}\right)\epsilon(k)\\
&=\alpha\!\left(x_{(1)}\right)\alpha(y_{(1)})\sigma\!\left(x_{(2)}h_{(1)}, y_{(2)}\right)\alpha^{-1}\!\left(x_{(3)}h_{(2)}\cdot y_{(3)}\right)\epsilon(k)\\
&=\alpha\!\left(x_{(1)}\right)\alpha\!\left(h_{(1)}\cdot y_{(1)}\right)\sigma\!\left(x_{(2)}, h_{(2)}\cdot y_{(2)}\right)\alpha^{-1}\!\left(x_{(3)}h_{(3)}\cdot y_{(3)}\right)\epsilon(k)\\
&=\sigma^{\prime}(x,h\cdot y)\epsilon(k)=\sigma^{\prime}(xh,yk).\end{align*}
Hence, we can replace
![]() $\alpha$
by
$\alpha$
by
![]() $\tilde{\alpha}$
.
$\tilde{\alpha}$
.
Proposition 3.10. Let
![]() $A=B\#H$
. Fix
$A=B\#H$
. Fix
![]() $\sigma=\sigma_B\#\epsilon, \sigma^{\prime}=\sigma^{\prime}_B\#\epsilon\in Z^2(A)$
.
$\sigma=\sigma_B\#\epsilon, \sigma^{\prime}=\sigma^{\prime}_B\#\epsilon\in Z^2(A)$
.
-
(a) If
 $\alpha^{\prime}\colon B\to\Bbbk$
is convolution invertible, H-linear, and
$\alpha^{\prime}\colon B\to\Bbbk$
is convolution invertible, H-linear, and
 $\alpha^{\prime}\rightharpoonup\sigma_B=\sigma^{\prime}_B$
, then
$\alpha^{\prime}\rightharpoonup\sigma_B=\sigma^{\prime}_B$
, then
 $\alpha \rightharpoonup \sigma=\sigma^{\prime}$
, for
$\alpha \rightharpoonup \sigma=\sigma^{\prime}$
, for
 $\alpha=\alpha^{\prime}\#\epsilon$
.
$\alpha=\alpha^{\prime}\#\epsilon$
. -
(b) If
 $\alpha\colon A\to\Bbbk$
is convolution invertible is such that
$\alpha\colon A\to\Bbbk$
is convolution invertible is such that
 $\alpha\rightharpoonup\sigma=\sigma^{\prime}$
, then we have
$\alpha\rightharpoonup\sigma=\sigma^{\prime}$
, then we have
 $\alpha_{|B}\rightharpoonup \sigma_B=\sigma^{\prime}_B$
.
$\alpha_{|B}\rightharpoonup \sigma_B=\sigma^{\prime}_B$
.
Proof. (a) We have that
![]() $\alpha^{\prime}\rightharpoonup\sigma_B=\sigma^{\prime}_B$
, that is for
$\alpha^{\prime}\rightharpoonup\sigma_B=\sigma^{\prime}_B$
, that is for
![]() $x,y\in B$
,
$x,y\in B$
,
Here
![]() $x_{(1)}\otimes x_{(2)}=\Delta_B(x)$
stands for the coproduct in B. Recall that the coproduct
$x_{(1)}\otimes x_{(2)}=\Delta_B(x)$
stands for the coproduct in B. Recall that the coproduct
![]() $\Delta(xh)=x_{(1)}x_{(2)({-}1)}h_{(1)}\otimes x_{(2)(0)}h_{(2)}$
in A from (2.9) so
$\Delta(xh)=x_{(1)}x_{(2)({-}1)}h_{(1)}\otimes x_{(2)(0)}h_{(2)}$
in A from (2.9) so
Now,
![]() $\alpha\rightharpoonup \sigma(xh,yk)$
gives, using that that
$\alpha\rightharpoonup \sigma(xh,yk)$
gives, using that that
![]() $\alpha^{\prime}$
is H-linear:
$\alpha^{\prime}$
is H-linear:
 \begin{align*}&\alpha\!\left(x_{(1)} x_{(2)({-}1)}x_{(3)({-}2)} h_{(1)}\right)\alpha\!\left(y_{(1)}y_{(2)({-}1)}y_{(3)({-}2)} k_{(1)}\right)\\
& \quad \times\sigma\!\left(x_{(2)(0)}x_{(3)({-}1)}h_{(2)},y_{(2)(0)}y_{(3)({-}1)}k_{(2)}\right)\alpha^{-1}\!\left(x_{(3)(0)}h_{(3)}y_{(3)(0)}k_{(3)}\right)\\
&=\alpha^{\prime}\!\left(x_{(1)}\right)\alpha^{\prime}(y_{(1)})\sigma_B\!\left(x_{(2)},x_{(3)({-}1)}h_{(1)}\cdot y_{(2)}\right) \alpha^{\prime}{}^{-1}\!\left(x_{(3)(0)}h_{(2)}y_{(3)}\right)\epsilon(k)\\
&=\alpha^{\prime}\!\left(x_{(1)}\right)\alpha^{\prime}\!\left(x_{(3)({-}2)}x_{(2)({-}1)}h_{(1)}\cdot y_{(1)}\right)\\
& \quad \times\sigma_B\!\left(x_{(2)(0)},x_{(3)({-}1)}h_{(2)}y_{(2)}\right)\alpha^{\prime}{}^{-1}\!\left(x_{(3)(0)}h_{(3)}y_{(3)}\right)\epsilon(k)\\
&=\sigma^{\prime}_B(x,h\cdot y)\epsilon(k)=\sigma^{\prime}(xh,yk).\end{align*}
\begin{align*}&\alpha\!\left(x_{(1)} x_{(2)({-}1)}x_{(3)({-}2)} h_{(1)}\right)\alpha\!\left(y_{(1)}y_{(2)({-}1)}y_{(3)({-}2)} k_{(1)}\right)\\
& \quad \times\sigma\!\left(x_{(2)(0)}x_{(3)({-}1)}h_{(2)},y_{(2)(0)}y_{(3)({-}1)}k_{(2)}\right)\alpha^{-1}\!\left(x_{(3)(0)}h_{(3)}y_{(3)(0)}k_{(3)}\right)\\
&=\alpha^{\prime}\!\left(x_{(1)}\right)\alpha^{\prime}(y_{(1)})\sigma_B\!\left(x_{(2)},x_{(3)({-}1)}h_{(1)}\cdot y_{(2)}\right) \alpha^{\prime}{}^{-1}\!\left(x_{(3)(0)}h_{(2)}y_{(3)}\right)\epsilon(k)\\
&=\alpha^{\prime}\!\left(x_{(1)}\right)\alpha^{\prime}\!\left(x_{(3)({-}2)}x_{(2)({-}1)}h_{(1)}\cdot y_{(1)}\right)\\
& \quad \times\sigma_B\!\left(x_{(2)(0)},x_{(3)({-}1)}h_{(2)}y_{(2)}\right)\alpha^{\prime}{}^{-1}\!\left(x_{(3)(0)}h_{(3)}y_{(3)}\right)\epsilon(k)\\
&=\sigma^{\prime}_B(x,h\cdot y)\epsilon(k)=\sigma^{\prime}(xh,yk).\end{align*}
(b) Follows as (a), using that
![]() $\alpha^{\prime}$
is H-linear by Lemma 3.8 and the compatibility between
$\alpha^{\prime}$
is H-linear by Lemma 3.8 and the compatibility between
![]() $\Delta_B(x)$
and
$\Delta_B(x)$
and
![]() $\Delta(x\#1)$
, see (2.9).
$\Delta(x\#1)$
, see (2.9).
Next lemma will also allow us to reduce computations when dealing with Hopf cocycles arising as exponentials of Hochschild cocycles.
Lemma 3.11. Let
![]() $\tau,\sigma\in Z^2(B)^H$
and let
$\tau,\sigma\in Z^2(B)^H$
and let
![]() $\alpha\in B^\ast$
be convolution invertible.
$\alpha\in B^\ast$
be convolution invertible.
-
(a) For any
 $x\in V$
,
$x\in V$
,
 $b\in\mathbb{B}$
, we have that
$b\in\mathbb{B}$
, we have that
 \begin{equation*} \alpha\rightharpoonup \tau (x,b)=\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\tau\!\left(x_{(0)}, b_{(2)}\right)\alpha^{-1}\!\left(b_{(3)}\right)+\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\alpha^{-1}\!\left(x_{(0)}b_{(2)}\right). \end{equation*}
\begin{equation*} \alpha\rightharpoonup \tau (x,b)=\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\tau\!\left(x_{(0)}, b_{(2)}\right)\alpha^{-1}\!\left(b_{(3)}\right)+\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\alpha^{-1}\!\left(x_{(0)}b_{(2)}\right). \end{equation*}
-
(b) Assume that
 $\alpha\rightharpoonup \tau=\sigma$
. Then for any
$\alpha\rightharpoonup \tau=\sigma$
. Then for any
 $x,y\in V$
, we have that
(3.5)
$x,y\in V$
, we have that
(3.5) \begin{align}\alpha(x)\alpha(y)-\alpha(xy)=\sigma(x,y)-\tau(x,y).\end{align}
\begin{align}\alpha(x)\alpha(y)-\alpha(xy)=\sigma(x,y)-\tau(x,y).\end{align}
Proof. (1) Let
![]() $x\in V$
and
$x\in V$
and
![]() $b\in \mathbb{B}$
, then
$b\in \mathbb{B}$
, then
 \begin{align*} (\textrm{id}\otimes \Delta)\Delta(x\otimes b)=& \, x\otimes b_{(1)}\otimes 1\otimes b_{(2)}\otimes 1\otimes b_{(3)}\\&+1\otimes x_{({-}1)}\cdot b_{(1)}\otimes x_{(0)}\otimes b_{(2)}\otimes 1\otimes b_{(3)}\\&+1\otimes x_{({-}2)}\cdot b_{(1)}\otimes1\otimes x_{({-}1)}\cdot b_{(2)}\otimes x_{(0)}\otimes b_{(3)}. \end{align*}
\begin{align*} (\textrm{id}\otimes \Delta)\Delta(x\otimes b)=& \, x\otimes b_{(1)}\otimes 1\otimes b_{(2)}\otimes 1\otimes b_{(3)}\\&+1\otimes x_{({-}1)}\cdot b_{(1)}\otimes x_{(0)}\otimes b_{(2)}\otimes 1\otimes b_{(3)}\\&+1\otimes x_{({-}2)}\cdot b_{(1)}\otimes1\otimes x_{({-}1)}\cdot b_{(2)}\otimes x_{(0)}\otimes b_{(3)}. \end{align*}
When we act by
![]() $\alpha$
, we get
$\alpha$
, we get
 \begin{align*} \alpha\rightharpoonup\tau\!\left(x,b\right)=& \,\alpha\!\left(x\right)\alpha\!\left(b_{(1)}\right)\tau\!\left(1,b_{(2)}\right)\alpha^{-1}\!\left(b_{(3)}\right)+\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\tau\!\left(x_{(0)}, b_{(2)}\right)\alpha^{-1}\!\left(b_{(3)}\right)\\
&+\alpha\!\left(x_{\left({-}2\right)}\cdot b_{(1)}\right)\tau\!\left(1, x_{({-}1)}\cdot b_{(2)}\right)\alpha^{-1}\!\left(x_{(0)}b_{(3)}\right)\\
=& \,\alpha\!\left(x\right)\alpha\!\left(b_{(1)}\right)\epsilon\!\left(b_{(2)}\right)\alpha^{-1}\!\left(b_{(2)}\right)+\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\tau\!\left(x_{(0)}, b_{(2)}\right)\alpha^{-1}\!\left(b_{(3)}\right)\\
&+\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\alpha^{-1}\!\left(x_{(0)}b_{(2)}\right)\\
=&\,\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\tau\!\left(x_{(0)}, b_{(2)}\right)\alpha^{-1}\!\left(b_{(3)}\right)+\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\alpha^{-1}\!\left(x_{(0)}b_{(2)}\right). \end{align*}
\begin{align*} \alpha\rightharpoonup\tau\!\left(x,b\right)=& \,\alpha\!\left(x\right)\alpha\!\left(b_{(1)}\right)\tau\!\left(1,b_{(2)}\right)\alpha^{-1}\!\left(b_{(3)}\right)+\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\tau\!\left(x_{(0)}, b_{(2)}\right)\alpha^{-1}\!\left(b_{(3)}\right)\\
&+\alpha\!\left(x_{\left({-}2\right)}\cdot b_{(1)}\right)\tau\!\left(1, x_{({-}1)}\cdot b_{(2)}\right)\alpha^{-1}\!\left(x_{(0)}b_{(3)}\right)\\
=& \,\alpha\!\left(x\right)\alpha\!\left(b_{(1)}\right)\epsilon\!\left(b_{(2)}\right)\alpha^{-1}\!\left(b_{(2)}\right)+\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\tau\!\left(x_{(0)}, b_{(2)}\right)\alpha^{-1}\!\left(b_{(3)}\right)\\
&+\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\alpha^{-1}\!\left(x_{(0)}b_{(2)}\right)\\
=&\,\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\tau\!\left(x_{(0)}, b_{(2)}\right)\alpha^{-1}\!\left(b_{(3)}\right)+\alpha\!\left(x_{({-}1)}\cdot b_{(1)}\right)\alpha^{-1}\!\left(x_{(0)}b_{(2)}\right). \end{align*}
(2) Use the formula in (1) to compute
![]() $\alpha\rightharpoonup \tau(x,y)=\sigma(x,y)$
, then
$\alpha\rightharpoonup \tau(x,y)=\sigma(x,y)$
, then
Now, as
we obtain (3.5).
4. Invariant Hochschild cohomology
We let B, H,
![]() $A=B\# H$
be as in Section 1.1. Recall that
$A=B\# H$
be as in Section 1.1. Recall that
![]() $\{x_1,\dots,x_\theta\}$
denotes a linear basis of
$\{x_1,\dots,x_\theta\}$
denotes a linear basis of
![]() $V\,:\!=\, B_1$
, contained in an homogeneous basis
$V\,:\!=\, B_1$
, contained in an homogeneous basis
![]() $\mathbb{B}$
of B.
$\mathbb{B}$
of B.
Let M be an A-bimodule; hence a B-bimodule by restriction. In this section we focus on the Hochschild cohomology
![]() $\textrm{H}^{\bullet}$
of A with coefficients on M and the relation with
$\textrm{H}^{\bullet}$
of A with coefficients on M and the relation with
![]() $\textrm{H}^{\bullet}(B,M)$
.
$\textrm{H}^{\bullet}(B,M)$
.
In particular, we present a proof of a Theorem of Ştefan in [Reference Ştefan25], which shows that there is an action of H on
![]() $\textrm{H}^{\bullet}(B,M)$
in such a way that
$\textrm{H}^{\bullet}(B,M)$
in such a way that
![]() $\textrm{H}^{\bullet}(A,M)\simeq \textrm{H}^{\bullet}(B,M)^H$
. We give an explicit description of this action in our context.
$\textrm{H}^{\bullet}(A,M)\simeq \textrm{H}^{\bullet}(B,M)^H$
. We give an explicit description of this action in our context.
As well, we will be particularly interested in the case
![]() $M=\Bbbk$
. We write
$M=\Bbbk$
. We write
![]() $\textrm{Z}^{\bullet}(A,M)$
for the space of cocycles and
$\textrm{Z}^{\bullet}(A,M)$
for the space of cocycles and
![]() $\textrm{B}^{\bullet}(A,M)$
for the cobordisms. When
$\textrm{B}^{\bullet}(A,M)$
for the cobordisms. When
![]() $M=\Bbbk$
, we may simply write
$M=\Bbbk$
, we may simply write
![]() $\textrm{H}^{\bullet}(A), \textrm{Z}^{\bullet}(A), \textrm{B}^{\bullet}(A)$
. We denote by
$\textrm{H}^{\bullet}(A), \textrm{Z}^{\bullet}(A), \textrm{B}^{\bullet}(A)$
. We denote by
![]() $\textrm{Z}^{\bullet}(B)^H\subset \textrm{Z}^{\bullet}(B)$
the subset of H-invariant cocycles. The subset
$\textrm{Z}^{\bullet}(B)^H\subset \textrm{Z}^{\bullet}(B)$
the subset of H-invariant cocycles. The subset
![]() $\textrm{Z}^{2}(B)^H$
will be of big relevance in our work.
$\textrm{Z}^{2}(B)^H$
will be of big relevance in our work.
We refer the reader to [Reference Brown8] for details on Hochschild cohomology.
4.1. Hochschild 2-cocycles with coefficients in
 $\Bbbk$
$\Bbbk$
Let
![]() $B^+=\bigoplus_{n > 0} B_n$
. We begin with an alternative description of the set
$B^+=\bigoplus_{n > 0} B_n$
. We begin with an alternative description of the set
![]() $\textrm{Z}^2(B,\Bbbk)$
.
$\textrm{Z}^2(B,\Bbbk)$
.
Lemma 4.1. Let
![]() $\eta\,:\,B\otimes B\to \Bbbk$
be a linear map. The following are equivalent.
$\eta\,:\,B\otimes B\to \Bbbk$
be a linear map. The following are equivalent.
-
(a)
 $\eta\in \textrm{Z}^2(B,\Bbbk)$
.
$\eta\in \textrm{Z}^2(B,\Bbbk)$
. -
(b)
 $\eta\,:\,B\otimes B\to \Bbbk$
satisfies, for
$\eta\,:\,B\otimes B\to \Bbbk$
satisfies, for
 $a,c\in B^+$
,
(4.1)
$a,c\in B^+$
,
(4.1) \begin{equation}\eta(a,1) = \eta(1,c)=0,\end{equation}
(4.2)
\begin{equation}\eta(a,1) = \eta(1,c)=0,\end{equation}
(4.2) \begin{equation}\eta(a,bc) = \eta(ab,c), \quad b\in B.\end{equation}
\begin{equation}\eta(a,bc) = \eta(ab,c), \quad b\in B.\end{equation}
Similarly,
![]() $\eta\in \textrm{B}^2(B,\Bbbk)$
if and only if (4.1) holds and there is a linear map
$\eta\in \textrm{B}^2(B,\Bbbk)$
if and only if (4.1) holds and there is a linear map
![]() $f\colon B\to \Bbbk$
such that
$f\colon B\to \Bbbk$
such that
![]() $\eta(1,1)=f(1)$
and
$\eta(1,1)=f(1)$
and
Proof. Recall that
![]() $\eta\in\textrm{Z}^2(B,\Bbbk)$
if and only if, for
$\eta\in\textrm{Z}^2(B,\Bbbk)$
if and only if, for
![]() $a,b,c\in B$
:
$a,b,c\in B$
:
Now, if
![]() $a,c\in B^+$
, then this becomes (4.2). On the other hand, if
$a,c\in B^+$
, then this becomes (4.2). On the other hand, if
![]() $a=\epsilon(a)\in B_0=\Bbbk$
and
$a=\epsilon(a)\in B_0=\Bbbk$
and
![]() $c\in B^+$
(or viceversa), then this is
$c\in B^+$
(or viceversa), then this is
If
![]() $a,c\in B_0=\Bbbk$
then (4.3) is tautological.
$a,c\in B_0=\Bbbk$
then (4.3) is tautological.
Recall that
![]() $\eta\in\textrm{B}^2(B,\Bbbk)$
if and only if there is
$\eta\in\textrm{B}^2(B,\Bbbk)$
if and only if there is
![]() $f\colon B\to \Bbbk$
in such a way that
$f\colon B\to \Bbbk$
in such a way that
This is in turn equivalent to
![]() $\eta(a,b)=-f(ab)$
,
$\eta(a,b)=-f(ab)$
,
![]() $a,b\in B^+$
.
$a,b\in B^+$
.
We compute an easy example in (4.4) to fix some notation. We will apply Lemma 4.1 to write down in Section 6.2 two more non-trivial examples in (6.8) and (6.9).
Lemma 4.2. For each
![]() $i,j\in I_\theta$
, let
$i,j\in I_\theta$
, let
![]() $\xi_j^i\colon B\otimes B\to \Bbbk$
be the linear map defined by
$\xi_j^i\colon B\otimes B\to \Bbbk$
be the linear map defined by
Then
![]() $\xi_j^i\in \textrm{Z}^2(B,\Bbbk)$
.
$\xi_j^i\in \textrm{Z}^2(B,\Bbbk)$
.
4.2. Ştefan's Theorem revisited
The following result, in general terms is due to Ştefan [Reference Ştefan25], and it is of central importance in our work. It is in fact a compendium of several results in loc.cit., which we have adapted to our setting, and this allows us to find explicit formulas that are implicit in Stefan's work. It is our belief that it is in this shape that might evoke more interest in the scope of this article. In particular, we state it in terms of left actions because of this idea.
Theorem 4.4. Let H be a Hopf algebra with bijective antipode and let
![]() $B\in{}^{H}_{H}\mathcal{YD}$
. Let
$B\in{}^{H}_{H}\mathcal{YD}$
. Let
![]() $A=B\# H$
and let M be an A-bimodule.
$A=B\# H$
and let M be an A-bimodule.
Then there is a left H-action
![]() $\rightharpoonup$
on
$\rightharpoonup$
on
![]() $\textrm{H}^q(B,M)$
,
$\textrm{H}^q(B,M)$
,
![]() $q\geq 0$
.
$q\geq 0$
.
-
For
 $q=0$
, this is
(4.5)for
$q=0$
, this is
(4.5)for \begin{align} h\rightharpoonup m=h_{(1)}\cdot m\cdot \mathcal{S}(h_{(2)}), \end{align}
\begin{align} h\rightharpoonup m=h_{(1)}\cdot m\cdot \mathcal{S}(h_{(2)}), \end{align}
 $h\in H$
and
$h\in H$
and
 $m\in \textrm{H}^0(B,M)=\{m\,:\,b\cdot m=m\cdot b, \forall\,b\in B\}\subseteq M$
.
$m\in \textrm{H}^0(B,M)=\{m\,:\,b\cdot m=m\cdot b, \forall\,b\in B\}\subseteq M$
.
-
For
 $q>0$
, this is
(4.6)for
$q>0$
, this is
(4.6)for \begin{align} (h\rightharpoonup f)({\textbf{x}})=h_{(1)}\cdot f\!\left(\mathcal{S}(h_{(2)})\cdot {\textbf{x}}\right)\cdot \mathcal{S}\!\left(h_{(3)}\right), \end{align}
\begin{align} (h\rightharpoonup f)({\textbf{x}})=h_{(1)}\cdot f\!\left(\mathcal{S}(h_{(2)})\cdot {\textbf{x}}\right)\cdot \mathcal{S}\!\left(h_{(3)}\right), \end{align}
 $h\in H$
and
$h\in H$
and
 $f\in \textrm{Z}^q(B,M)\subset\textrm{Hom}_\Bbbk(B^{\otimes\,q}, M)$
,
$f\in \textrm{Z}^q(B,M)\subset\textrm{Hom}_\Bbbk(B^{\otimes\,q}, M)$
,
 ${\textbf{x}}=(x_1,\cdots, x_q)\in B^{\otimes\,q}$
.
${\textbf{x}}=(x_1,\cdots, x_q)\in B^{\otimes\,q}$
.
If H is semisimple, then
Proof. Following [Reference Ştefan25] we work, equivalently, with a right action. We update our equations and need to show that there is a right H-action
![]() $\leftharpoonup$
on
$\leftharpoonup$
on
![]() $\textrm{H}^q(B,M)$
so that
$\textrm{H}^q(B,M)$
so that
-
For
 $q=0$
, this is
(4.5’)
$q=0$
, this is
(4.5’) \begin{align}m\leftharpoonup h=\mathcal{S}\!\left(h_{(1)}\right)\cdot m \cdot h_{(2)}, \quad m\in \textrm{H}^0(B,M), h\in H; \end{align}
\begin{align}m\leftharpoonup h=\mathcal{S}\!\left(h_{(1)}\right)\cdot m \cdot h_{(2)}, \quad m\in \textrm{H}^0(B,M), h\in H; \end{align}
-
For
 $q>0$
, this is
(4.6’)Observe that the left action
$q>0$
, this is
(4.6’)Observe that the left action \begin{align}(f\leftharpoonup h)({\textbf{x}})=\mathcal{S}\!\left(h_{(1)}\right)\cdot f(h_{(2)}\cdot {\textbf{x}})\cdot h_{(3)}, \quad f\in \textrm{Z}^q(B,M), {\textbf{x}}\in B^{\otimes\,q}. \end{align}
\begin{align}(f\leftharpoonup h)({\textbf{x}})=\mathcal{S}\!\left(h_{(1)}\right)\cdot f(h_{(2)}\cdot {\textbf{x}})\cdot h_{(3)}, \quad f\in \textrm{Z}^q(B,M), {\textbf{x}}\in B^{\otimes\,q}. \end{align}
 $h\cdot b$
can also be interpreted as
$h\cdot b$
can also be interpreted as
 $b\cdot \mathcal{S}^{-1}(h)$
.
$b\cdot \mathcal{S}^{-1}(h)$
.
First, recall that A is a right H-Galois object with coaction
![]() $A\to A\otimes H$
given by
$A\to A\otimes H$
given by
![]() $b\# h\mapsto b\# h_{(1)}\otimes h_{(2)}$
, with
$b\# h\mapsto b\# h_{(1)}\otimes h_{(2)}$
, with
![]() $A^{\textrm{co} H}\simeq B$
by [Reference Schauenburg24, Theorem 2.2.7].
$A^{\textrm{co} H}\simeq B$
by [Reference Schauenburg24, Theorem 2.2.7].
We let
![]() $\textrm{can}\colon A\otimes_B A\to A\otimes H$
be the canonical isomorphism; in particular,
$\textrm{can}\colon A\otimes_B A\to A\otimes H$
be the canonical isomorphism; in particular,
For
![]() $M\in A\textrm{-bimod}$
, we write
$M\in A\textrm{-bimod}$
, we write
![]() $\cdot$
both for the left and right action. By [Reference Ştefan25], the H-action
$\cdot$
both for the left and right action. By [Reference Ştefan25], the H-action
![]() $\leftharpoonup$
on
$\leftharpoonup$
on
![]() $H^0(B,M)=M^{B}$
is given by
$H^0(B,M)=M^{B}$
is given by
![]() $m\leftharpoonup h=\sum \ell_i(h)\cdot m\cdot r_i(h)$
, which in this case translates to (4.5’):
$m\leftharpoonup h=\sum \ell_i(h)\cdot m\cdot r_i(h)$
, which in this case translates to (4.5’):
For left actions, this is (4.5).
Assume this action (4.5’) has been extended to
![]() $\textrm{H}^q(B,M)$
(here we admit
$\textrm{H}^q(B,M)$
(here we admit
![]() $q=0$
).
$q=0$
).
Next paragraph is almost verbatim from the proof of [Reference Ştefan25, Proposition 2.4]. We refer the reader to loc.cit. and references therein for fuller details.
If
![]() $R\colon A\textrm{-bimod}\to B\textrm{-bimod}$
is the functor given by restriction of scalars, then
$R\colon A\textrm{-bimod}\to B\textrm{-bimod}$
is the functor given by restriction of scalars, then
![]() $\textrm{H}^{\bullet}(A,-)\circ R$
is a cohomological and coeffaceable
$\textrm{H}^{\bullet}(A,-)\circ R$
is a cohomological and coeffaceable
![]() $\delta$
-functor. Hence the morphisms
$\delta$
-functor. Hence the morphisms
![]() $\rho^h_0\colon \textrm{H}(A,-)\circ R\to \textrm{H}(A,-)\circ R$
,
$\rho^h_0\colon \textrm{H}(A,-)\circ R\to \textrm{H}(A,-)\circ R$
,
![]() $h\in H$
, given by
$h\in H$
, given by
![]() $\rho^h_0(M)(m)=m\leftharpoonup h$
can be extended univocally to morphisms of
$\rho^h_0(M)(m)=m\leftharpoonup h$
can be extended univocally to morphisms of
![]() $\delta$
-functors
$\delta$
-functors
![]() $\rho^h_{\bullet}\colon \textrm{H}^{\bullet}(A,-)\circ R\to \textrm{H}^{\bullet}(A,-)\circ R$
.
$\rho^h_{\bullet}\colon \textrm{H}^{\bullet}(A,-)\circ R\to \textrm{H}^{\bullet}(A,-)\circ R$
.
We will describe this action explicitly in our context. For the content of this proof, we shall write, for shortness,
![]() $H^\bullet(A,-)\circ R(M)=H^\bullet(M)$
,
$H^\bullet(A,-)\circ R(M)=H^\bullet(M)$
,
![]() $M\in\mathcal{A}\textrm{-bimod}$
. We denote by
$M\in\mathcal{A}\textrm{-bimod}$
. We denote by
![]() $d^q_{M}\colon \textrm{Hom}_\Bbbk(B^{\otimes q},M)\to \textrm{Hom}_\Bbbk(B^{\otimes q+1},M)$
the differential.
$d^q_{M}\colon \textrm{Hom}_\Bbbk(B^{\otimes q},M)\to \textrm{Hom}_\Bbbk(B^{\otimes q+1},M)$
the differential.
Let us fix a short exact sequence
in
![]() $A\textrm{-bimod}$
; we write
$A\textrm{-bimod}$
; we write
![]() $M\ni m\twoheadrightarrow\bar{m}\in M^{\prime\prime}$
for the projection.
$M\ni m\twoheadrightarrow\bar{m}\in M^{\prime\prime}$
for the projection.
First, the fact that
![]() $\rho^h_{\bullet}$
is a morphism of
$\rho^h_{\bullet}$
is a morphism of
![]() $\delta$
-functors establishes that
$\delta$
-functors establishes that
In other words this is the recipe to extend the action, as it gives
We shall write, wlog,
![]() $\delta(f)\colon B^{\otimes q}\to M^{\prime}$
for an element in
$\delta(f)\colon B^{\otimes q}\to M^{\prime}$
for an element in
![]() $\textrm{Z}^{q+1}(M^{\prime})$
such that
$\textrm{Z}^{q+1}(M^{\prime})$
such that
![]() $[\delta(f)]=\delta([f])$
. Now, the morphism
$[\delta(f)]=\delta([f])$
. Now, the morphism
![]() $\delta\colon \textrm{H}^q(M^{\prime\prime})\to \textrm{H}^{q+1}(M^{\prime})$
is the usual connecting homomorphism for the long exact sequence in cohomology:
$\delta\colon \textrm{H}^q(M^{\prime\prime})\to \textrm{H}^{q+1}(M^{\prime})$
is the usual connecting homomorphism for the long exact sequence in cohomology:
Explicitly, for
![]() $f\in\textrm{Z}^q(M^{\prime\prime})=\ker d^q_{M^{\prime\prime}}$
, let
$f\in\textrm{Z}^q(M^{\prime\prime})=\ker d^q_{M^{\prime\prime}}$
, let
![]() $\tilde{f}\colon B^{\otimes q}\to M$
be such that
$\tilde{f}\colon B^{\otimes q}\to M$
be such that
![]() $\pi(\tilde{f})=f$
, in the sense that
$\pi(\tilde{f})=f$
, in the sense that
![]() $f\!\left(b_1,\dots,b_q\right)(\pi(m))=\tilde{f}\!\left(b_1,\dots,b_q\right)(m)$
. Now we consider
$f\!\left(b_1,\dots,b_q\right)(\pi(m))=\tilde{f}\!\left(b_1,\dots,b_q\right)(m)$
. Now we consider
![]() $d^q_M\!\left({\tilde{f}}\right)\in \textrm{Z}^{q+1}(M^{\prime\prime})$
and see that
$d^q_M\!\left({\tilde{f}}\right)\in \textrm{Z}^{q+1}(M^{\prime\prime})$
and see that
![]() $\textrm{H}^{q+1}(\pi)\left(\left[d^q_M\!\left({\tilde{f}}\right)\right]\right)=d^q_{M^{\prime\prime}}(\textrm{H}^{q}(\pi)(\tilde{f}))=d^q_{M^{\prime\prime}}(f)=0$
. That is
$\textrm{H}^{q+1}(\pi)\left(\left[d^q_M\!\left({\tilde{f}}\right)\right]\right)=d^q_{M^{\prime\prime}}(\textrm{H}^{q}(\pi)(\tilde{f}))=d^q_{M^{\prime\prime}}(f)=0$
. That is
![]() $\left[d^q_M\!\left({\tilde{f}}\right)\right]\in\ker \textrm{H}^{q+1}(\pi)=\textrm{img} \textrm{H}^{q+1}(\iota)$
and we can consider
$\left[d^q_M\!\left({\tilde{f}}\right)\right]\in\ker \textrm{H}^{q+1}(\pi)=\textrm{img} \textrm{H}^{q+1}(\iota)$
and we can consider
![]() $\left[d^q_M\!\left({\tilde{f}}\right)\right]$
as an element
$\left[d^q_M\!\left({\tilde{f}}\right)\right]$
as an element
![]() $\delta([f])\in \textrm{H}^{q+1}(M^{\prime})$
. By abuse of notation we shall write
$\delta([f])\in \textrm{H}^{q+1}(M^{\prime})$
. By abuse of notation we shall write
![]() $\delta(f)=df$
.
$\delta(f)=df$
.
In our setting, if
![]() ${\textbf{b}}=\left(b_1,\dots,b_{q+1}\right)$
${\textbf{b}}=\left(b_1,\dots,b_{q+1}\right)$
If
![]() $q=0$
,
$q=0$
,
![]() $m\in M, b\in B$
, then
$m\in M, b\in B$
, then
![]() $dm(b)=b\cdot m-m\cdot b$
. Also, recall the commutations (2.8). The connection reads as
$dm(b)=b\cdot m-m\cdot b$
. Also, recall the commutations (2.8). The connection reads as
 \begin{align*}(\delta(m)\leftharpoonup h)(b)&=d(m \leftharpoonup h)(b)=\left(d\!\left(\mathcal{S}\!\left(h_{(1)}\right)\cdot m \cdot h_{(2)}\right)(b)\right)\\
&=b\cdot \mathcal{S}\!\left(h_{(1)}\right)\cdot m\cdot h_{(2)} -\mathcal{S}\!\left(h_{(1)}\right)\cdot m \cdot h_{(2)}\cdot b\\
&=\left(b\mathcal{S}\left(h_{(1)}\right)\right)\cdot m\cdot h_{(2)} -\mathcal{S}\!\left(h_{(1)}\right)\cdot m \cdot \left(h_{(2)}b\right)\\
&=\mathcal{S}\!\left(h_{(1)}\right)\left(h_{(2)}\cdot b\right)\cdot m \cdot h_{(3)}-\mathcal{S}\!\left(h_{(1)}\right)\cdot m \cdot \left(h_{(2)}\cdot b\right)h_{(3)}\\
&=\mathcal{S}\!\left(h_{(1)}\right)\cdot \left(h_{(2)}\cdot b\cdot m - m\cdot h_{(2)}\cdot b\right)\cdot h_{(3)}\\
&=\mathcal{S}\!\left(h_{(1)}\right)\cdot dm\!\left(h_{(2)}\cdot b\right)\cdot h_{(3)},\end{align*}
\begin{align*}(\delta(m)\leftharpoonup h)(b)&=d(m \leftharpoonup h)(b)=\left(d\!\left(\mathcal{S}\!\left(h_{(1)}\right)\cdot m \cdot h_{(2)}\right)(b)\right)\\
&=b\cdot \mathcal{S}\!\left(h_{(1)}\right)\cdot m\cdot h_{(2)} -\mathcal{S}\!\left(h_{(1)}\right)\cdot m \cdot h_{(2)}\cdot b\\
&=\left(b\mathcal{S}\left(h_{(1)}\right)\right)\cdot m\cdot h_{(2)} -\mathcal{S}\!\left(h_{(1)}\right)\cdot m \cdot \left(h_{(2)}b\right)\\
&=\mathcal{S}\!\left(h_{(1)}\right)\left(h_{(2)}\cdot b\right)\cdot m \cdot h_{(3)}-\mathcal{S}\!\left(h_{(1)}\right)\cdot m \cdot \left(h_{(2)}\cdot b\right)h_{(3)}\\
&=\mathcal{S}\!\left(h_{(1)}\right)\cdot \left(h_{(2)}\cdot b\cdot m - m\cdot h_{(2)}\cdot b\right)\cdot h_{(3)}\\
&=\mathcal{S}\!\left(h_{(1)}\right)\cdot dm\!\left(h_{(2)}\cdot b\right)\cdot h_{(3)},\end{align*}
so
![]() $dm\leftharpoonup h$
is as in (4.5’).
$dm\leftharpoonup h$
is as in (4.5’).
Now, we turn to
![]() $q>0$
. If
$q>0$
. If
![]() ${\textbf{b}}=b_1\otimes \cdots \otimes b_{q+1}\in B^{\otimes\,q+1}$
, then recall that we write
${\textbf{b}}=b_1\otimes \cdots \otimes b_{q+1}\in B^{\otimes\,q+1}$
, then recall that we write
![]() ${\textbf{b}}=b_1\otimes {\textbf{b}}^2={\textbf{b}}^q\otimes b_{q+1}$
and
${\textbf{b}}=b_1\otimes {\textbf{b}}^2={\textbf{b}}^q\otimes b_{q+1}$
and
![]() ${\textbf{b}}_{i\,i+1}=b_1\otimes \cdots \otimes b_ib_{i+1}\otimes \cdots\otimes b_{q+1}\in B^{\otimes\,q}$
,
${\textbf{b}}_{i\,i+1}=b_1\otimes \cdots \otimes b_ib_{i+1}\otimes \cdots\otimes b_{q+1}\in B^{\otimes\,q}$
,
![]() $i\in\mathbb{I}_q$
.
$i\in\mathbb{I}_q$
.
Hence, we obtain, with commutations (2.8) as above:
 \begin{align*}d(f \leftharpoonup h)({\textbf{b}})& = b_1\cdot (f \leftharpoonup h)\left({\textbf{b}}^2\right)-(f \leftharpoonup h)({\textbf{b}}_{12})+(f \leftharpoonup h)({\textbf{b}}_{23})\\
&\quad +\cdots +({-}1)^{n-1}(f \leftharpoonup h)({\textbf{b}}_{q-1q})+({-}1)^n(f \leftharpoonup h)({\textbf{b}}^q)\cdot b_{q+1}\\
&=b_1\cdot \mathcal{S}\!\left(h_{(1)}\right)\cdot f\!\left(h_{(2)}\cdot {\textbf{b}}^2\right) \cdot h_{(3)}-\mathcal{S}\!\left(h_{(1)}\right)\cdot f\!\left(h_{(2)}\cdot {\textbf{b}}_{12}\right)h_{(3)}\\
&\quad +\cdots +({-}1)^n\mathcal{S}\!\left(h_{(1)}\right)\cdot f \!\left(h_{(2)}\cdot {\textbf{b}}^q\right)\cdot h_{(3)}\cdot b_{q+1}\\
&=\mathcal{S}(h_{(1)} ) \cdot h_{(2)}\cdot b_1 \cdot f\!\left(h_{(3)}\cdot {\textbf{b}}^2\right) \cdot h_{(3)}-\mathcal{S}\!\left(h_{(1)}\right)\cdot f\!\left(h_{(2)}\cdot {\textbf{b}}_{12}\right)h_{(3)}\\
&\quad +\cdots +({-}1)^n\mathcal{S}\!\left(h_{(1)}\right)\cdot f \!\left(h_{(2)}\cdot {\textbf{b}}^q\right)\cdot h_{(3)}\cdot b_{q+1}\cdot h_{(4)}\\
&=\mathcal{S}(h_{(1)} ) \cdot \left(h_{(2)}\cdot {\textbf{b}}\right)_1 \cdot f\!\left(\left(h_{(2)}\cdot {\textbf{b}}\right)^2\right) \cdot h_{(3)}-\mathcal{S}\!\left(h_{(1)}\right)\cdot f\!\left(\left(h_{(2)}\cdot {\textbf{b}}\right)_{12}\right)h_{(3)}\\
&\quad +\cdots +({-}1)^n\mathcal{S}\!\left(h_{(1)}\right)\cdot f \!\left(\left(h_{(2)}\cdot {\textbf{b}}\right)^q\right)\cdot \left(h_{(2)}\cdot {\textbf{b}}\right)_{q+1}\cdot h_{(3)}\\
&=\mathcal{S}\!\left(h_{(1)}\right)df\!\left(h_{(2)}\cdot {\textbf{b}}\right)h_{(3)},\end{align*}
\begin{align*}d(f \leftharpoonup h)({\textbf{b}})& = b_1\cdot (f \leftharpoonup h)\left({\textbf{b}}^2\right)-(f \leftharpoonup h)({\textbf{b}}_{12})+(f \leftharpoonup h)({\textbf{b}}_{23})\\
&\quad +\cdots +({-}1)^{n-1}(f \leftharpoonup h)({\textbf{b}}_{q-1q})+({-}1)^n(f \leftharpoonup h)({\textbf{b}}^q)\cdot b_{q+1}\\
&=b_1\cdot \mathcal{S}\!\left(h_{(1)}\right)\cdot f\!\left(h_{(2)}\cdot {\textbf{b}}^2\right) \cdot h_{(3)}-\mathcal{S}\!\left(h_{(1)}\right)\cdot f\!\left(h_{(2)}\cdot {\textbf{b}}_{12}\right)h_{(3)}\\
&\quad +\cdots +({-}1)^n\mathcal{S}\!\left(h_{(1)}\right)\cdot f \!\left(h_{(2)}\cdot {\textbf{b}}^q\right)\cdot h_{(3)}\cdot b_{q+1}\\
&=\mathcal{S}(h_{(1)} ) \cdot h_{(2)}\cdot b_1 \cdot f\!\left(h_{(3)}\cdot {\textbf{b}}^2\right) \cdot h_{(3)}-\mathcal{S}\!\left(h_{(1)}\right)\cdot f\!\left(h_{(2)}\cdot {\textbf{b}}_{12}\right)h_{(3)}\\
&\quad +\cdots +({-}1)^n\mathcal{S}\!\left(h_{(1)}\right)\cdot f \!\left(h_{(2)}\cdot {\textbf{b}}^q\right)\cdot h_{(3)}\cdot b_{q+1}\cdot h_{(4)}\\
&=\mathcal{S}(h_{(1)} ) \cdot \left(h_{(2)}\cdot {\textbf{b}}\right)_1 \cdot f\!\left(\left(h_{(2)}\cdot {\textbf{b}}\right)^2\right) \cdot h_{(3)}-\mathcal{S}\!\left(h_{(1)}\right)\cdot f\!\left(\left(h_{(2)}\cdot {\textbf{b}}\right)_{12}\right)h_{(3)}\\
&\quad +\cdots +({-}1)^n\mathcal{S}\!\left(h_{(1)}\right)\cdot f \!\left(\left(h_{(2)}\cdot {\textbf{b}}\right)^q\right)\cdot \left(h_{(2)}\cdot {\textbf{b}}\right)_{q+1}\cdot h_{(3)}\\
&=\mathcal{S}\!\left(h_{(1)}\right)df\!\left(h_{(2)}\cdot {\textbf{b}}\right)h_{(3)},\end{align*}
which shows (4.6’).
By uniqueness of the extension; this shows that (4.6') is indeed the action announced on [Reference Ştefan25, Proposition 2.4]; which implies (4.6) for the case of left actions.
The identity (4.7) is [Reference Ştefan25, (3.6.1) in p.229].
4.3. Invariant Hochschild 2-cocycles with coefficients in
 $\Bbbk$
$\Bbbk$
In this setting, the action
![]() $\rightharpoonup$
in (4.6) from Theorem 4.4 becomes
$\rightharpoonup$
in (4.6) from Theorem 4.4 becomes
Since the antipode
![]() $\mathcal{S}$
is bijective, a cocycle
$\mathcal{S}$
is bijective, a cocycle
![]() $\eta\in \textrm{Z}^2(B)$
is H-invariant when
$\eta\in \textrm{Z}^2(B)$
is H-invariant when
Similarly, if
![]() $\eta\in Z^2(B)^H$
, then
$\eta\in Z^2(B)^H$
, then
![]() $\eta$
extends to
$\eta$
extends to
![]() $\eta\in \textrm{Z}^2(B\# H)$
via the formula
$\eta\in \textrm{Z}^2(B\# H)$
via the formula
Conversely, if
![]() $\eta\in Z^2(B\# H)$
then the restriction
$\eta\in Z^2(B\# H)$
then the restriction
defines a cocycle
![]() $\eta_{|B}\in Z^2(B)$
; this is not necessarily H-invariant. If
$\eta_{|B}\in Z^2(B)$
; this is not necessarily H-invariant. If
![]() $\int\in H$
is an integral with
$\int\in H$
is an integral with
![]() $\epsilon({\int})=1$
, then we can project
$\epsilon({\int})=1$
, then we can project
![]() $\eta\in Z^2(B)$
onto
$\eta\in Z^2(B)$
onto
![]() $\eta^{\int}\in Z^2(B)^H$
by
$\eta^{\int}\in Z^2(B)^H$
by
5. Hopfschild cohomology
Let
![]() $(A,m,\Delta)$
be a Hopf algebra and let
$(A,m,\Delta)$
be a Hopf algebra and let
![]() $\eta\in \textrm{Z}^2(A,\Bbbk)$
be a Hochschild 2-cocycle with coefficients in
$\eta\in \textrm{Z}^2(A,\Bbbk)$
be a Hochschild 2-cocycle with coefficients in
![]() $\Bbbk$
. Under certain conditions, it is possible to consider the exponential
$\Bbbk$
. Under certain conditions, it is possible to consider the exponential
which becomes a convolution invertible map with inverse
![]() $e^{-\eta}$
. For instance, this holds when
$e^{-\eta}$
. For instance, this holds when
![]() $\eta_{|A\otimes A_0+A_0\otimes A}=0$
.
$\eta_{|A\otimes A_0+A_0\otimes A}=0$
.
We show that this map is always well-defined in our setting in Section 5.1.
Moreover, there are occasions in which this exponential map is a Hopf 2-cocycle. A sufficient condition is given by the
![]() $\ast$
-commutations in
$\ast$
-commutations in
![]() $\textrm{Hom}(A^{\otimes 3},\Bbbk)$
:
$\textrm{Hom}(A^{\otimes 3},\Bbbk)$
:
However, we observe the following:
On the other hand, under some hypothesis, these equations are equivalent to each other, see [Reference García and Mastnak13]. We investigate some of these instances in Section 5.2.
The sufficiency of (5.1) and (5.2) is clear: for
![]() $\sigma=e^\eta$
, (2.3) becomes
$\sigma=e^\eta$
, (2.3) becomes
 \begin{align*}(\sigma\otimes\epsilon)\ast \sigma(m\otimes\textrm{id})&=e^{\eta\otimes\epsilon}\ast e^{\eta(m\otimes\textrm{id})}\stackrel{(5.2)}{=}e^{\eta\otimes\epsilon+\eta(m\otimes\textrm{id})}\stackrel{(4.3)}{=} e^{\epsilon\otimes\eta+\eta(\textrm{id}\otimes\, m)}\\
&\stackrel{(5.1)}{=}e^{\epsilon\otimes\eta}\ast e^{\eta(\textrm{id}\otimes\, m)}=(\epsilon\otimes\sigma)\ast \sigma(\textrm{id}\otimes\, m).\end{align*}
\begin{align*}(\sigma\otimes\epsilon)\ast \sigma(m\otimes\textrm{id})&=e^{\eta\otimes\epsilon}\ast e^{\eta(m\otimes\textrm{id})}\stackrel{(5.2)}{=}e^{\eta\otimes\epsilon+\eta(m\otimes\textrm{id})}\stackrel{(4.3)}{=} e^{\epsilon\otimes\eta+\eta(\textrm{id}\otimes\, m)}\\
&\stackrel{(5.1)}{=}e^{\epsilon\otimes\eta}\ast e^{\eta(\textrm{id}\otimes\, m)}=(\epsilon\otimes\sigma)\ast \sigma(\textrm{id}\otimes\, m).\end{align*}
This is the content of [Reference Grunelfelder and Mastnak18, Lemma 4.1].
Notice that, in terms of elements, (5.1) and (5.2) are, for
![]() $x,y,z\in A$
:
$x,y,z\in A$
:
Based on our examples, we observe that Hopf cocycle deformations are generically determined by cocycles which do not arise as exponentials. Hence we introduce the following concept, to name and study this phenomenon.
Definition 5.2. We say that a Hopf 2-cocycle
![]() $\sigma\in Z^2(A)$
is pure if it is not cohomologous to an exponential
$\sigma\in Z^2(A)$
is pure if it is not cohomologous to an exponential
![]() $e^\eta$
of a Hochschild 2-cocycle
$e^\eta$
of a Hochschild 2-cocycle
![]() $\eta\in \textrm{Z}^2(A,\Bbbk)$
.
$\eta\in \textrm{Z}^2(A,\Bbbk)$
.
We shall speak of pure deformations and exponential deformations, as expected.
5.1. Exponential and invariance
Let
![]() $H,B\in{}^{H}_{H}\mathcal{YD}$
,
$H,B\in{}^{H}_{H}\mathcal{YD}$
,
![]() $A=B\# H$
be as in Section 1.1.
$A=B\# H$
be as in Section 1.1.
We start with some simple though meaningful observations in Lemma 5.3. Let
![]() $\eta\in \textrm{Z}^2(B,\Bbbk)^H$
be an H-invariant Hochschild 2-cocycle; and set
$\eta\in \textrm{Z}^2(B,\Bbbk)^H$
be an H-invariant Hochschild 2-cocycle; and set
![]() $\eta\in \textrm{Z}^2(A,\Bbbk)$
the extension as in (4.9). Notice that
$\eta\in \textrm{Z}^2(A,\Bbbk)$
the extension as in (4.9). Notice that
so
![]() $\eta_{|A^+\otimes A_0+A_0\otimes A^+}=0$
. Hence if
$\eta_{|A^+\otimes A_0+A_0\otimes A^+}=0$
. Hence if
![]() $\eta_{|A_0\otimes A_0}=0$
, then the exponential
$\eta_{|A_0\otimes A_0}=0$
, then the exponential
![]() $\sigma\,:\!=\, e^\eta$
is well-defined. Moreover, as in our case
$\sigma\,:\!=\, e^\eta$
is well-defined. Moreover, as in our case
![]() $\eta(h,k)=\epsilon(hk)\eta(1,1)$
,
$\eta(h,k)=\epsilon(hk)\eta(1,1)$
,
![]() $h,k\in H=A_0$
, it is enough to require
$h,k\in H=A_0$
, it is enough to require
Next lemma shows that we can always assume (5.4), without loss of generality.
Lemma 5.3. Let
![]() $\eta\in \textrm{Z}^2(B,\Bbbk)^H$
and set
$\eta\in \textrm{Z}^2(B,\Bbbk)^H$
and set
![]() $\eta^{\prime}=\eta - \eta(1,1)\epsilon$
. Then
$\eta^{\prime}=\eta - \eta(1,1)\epsilon$
. Then
-
(a)
 $\eta^{\prime}\in \textrm{Z}^2(B,\Bbbk)$
and
$\eta^{\prime}\in \textrm{Z}^2(B,\Bbbk)$
and
 $[\eta]=[\eta^{\prime}]$
in
$[\eta]=[\eta^{\prime}]$
in
 $\textrm{H}^2(B,\Bbbk)$
.
$\textrm{H}^2(B,\Bbbk)$
. -
(b)
 $\eta^{\prime}(1,1)=0$
and
$\eta^{\prime}(1,1)=0$
and
 $\eta^{\prime}=\eta$
in
$\eta^{\prime}=\eta$
in
 $B^+\otimes B+B\otimes B^+$
.
$B^+\otimes B+B\otimes B^+$
. -
(c)
 $e^{\eta^{\prime}}\colon B\otimes B\to \Bbbk$
is a normalized convolution invertible linear map and
In particular,
$e^{\eta^{\prime}}\colon B\otimes B\to \Bbbk$
is a normalized convolution invertible linear map and
In particular, \begin{equation*}e^{\eta}=e^{\eta(1,1)}e^{\eta^{\prime}}.\end{equation*}
\begin{equation*}e^{\eta}=e^{\eta(1,1)}e^{\eta^{\prime}}.\end{equation*}
 $e^\eta\colon B\otimes B\to \Bbbk$
is a convolution invertible linear map.
$e^\eta\colon B\otimes B\to \Bbbk$
is a convolution invertible linear map.
-
(d)
 $e^\eta$
is a Hopf 2-cocycle if and only if
$e^\eta$
is a Hopf 2-cocycle if and only if
 $e^{\eta^{\prime}}$
is a (normalized) Hopf 2-cocycle.
$e^{\eta^{\prime}}$
is a (normalized) Hopf 2-cocycle.
Proof. Let
![]() $\theta=\eta(1,1)\epsilon$
, then
$\theta=\eta(1,1)\epsilon$
, then
![]() $\theta\in \textrm{B}^2(B,\Bbbk)$
and (a) holds. Also,
$\theta\in \textrm{B}^2(B,\Bbbk)$
and (a) holds. Also,
![]() $e^\theta=e^{\eta(1,1)}\epsilon$
. (b) is clear and it implies that
$e^\theta=e^{\eta(1,1)}\epsilon$
. (b) is clear and it implies that
![]() $e^{\eta^{\prime}}\colon B\otimes B\to \Bbbk$
is well-defined normalized convolution invertible linear map. As
$e^{\eta^{\prime}}\colon B\otimes B\to \Bbbk$
is well-defined normalized convolution invertible linear map. As
![]() $\eta^{\prime}\ast\theta=\theta\ast\eta^{\prime}$
, then
$\eta^{\prime}\ast\theta=\theta\ast\eta^{\prime}$
, then
![]() $e^{\theta}\ast e^{\eta^{\prime}}=e^{\eta}$
, which proves (c). (d) is straightforward, cf. (2.2).
$e^{\theta}\ast e^{\eta^{\prime}}=e^{\eta}$
, which proves (c). (d) is straightforward, cf. (2.2).
Remark 5.4. If
![]() $\eta(1,1)=0$
, then
$\eta(1,1)=0$
, then
In particular,
In our setting, we require that
![]() $\sigma=e^\eta$
satisfies (1.2). Next proposition shows that this is to require that
$\sigma=e^\eta$
satisfies (1.2). Next proposition shows that this is to require that
![]() $\eta\in \textrm{Z}^2(B,\Bbbk)^H$
.
$\eta\in \textrm{Z}^2(B,\Bbbk)^H$
.
Proposition 5.5. Let
![]() $\eta\in \textrm{Z}^2(B,\Bbbk)$
be a Hochschild 2-cocycle. Then
$\eta\in \textrm{Z}^2(B,\Bbbk)$
be a Hochschild 2-cocycle. Then
![]() $e^\eta$
is H-linear if and only if
$e^\eta$
is H-linear if and only if
![]() $\eta\in \textrm{Z}^2(B,\Bbbk)^H$
.
$\eta\in \textrm{Z}^2(B,\Bbbk)^H$
.
Proof. We show that
![]() $e^\eta\in Z^2(B)^H\Rightarrow\eta\in \textrm{Z}^2(B,\Bbbk)^H$
, the other implication is clear. We need to show that
$e^\eta\in Z^2(B)^H\Rightarrow\eta\in \textrm{Z}^2(B,\Bbbk)^H$
, the other implication is clear. We need to show that
![]() $\eta\!\left(h_{(1)}\cdot x,h_{(2)}\cdot y\right)=\epsilon(h)\eta(x,y)$
. If
$\eta\!\left(h_{(1)}\cdot x,h_{(2)}\cdot y\right)=\epsilon(h)\eta(x,y)$
. If
![]() $\deg y=0$
, then this is automatic. If
$\deg y=0$
, then this is automatic. If
![]() $\deg y=1$
, say
$\deg y=1$
, say
![]() $y=x_i$
, then by (5.5) we have that
$y=x_i$
, then by (5.5) we have that
Now, for the general case, assume
![]() $\deg y=n>1$
and let us write
$\deg y=n>1$
and let us write
![]() $y=y^{\prime}x_i$
,
$y=y^{\prime}x_i$
,
![]() $\deg y^{\prime}=n-1$
. Then
$\deg y^{\prime}=n-1$
. Then
Hence the result follows.
Remark 5.6. Set
![]() $\tau=e^{\eta}$
in Lemma 3.11 so
$\tau=e^{\eta}$
in Lemma 3.11 so
![]() $\tau(x,y)=e^{\eta}(x,y)=\eta(x,y)$
. In particular, (3.5) becomes
$\tau(x,y)=e^{\eta}(x,y)=\eta(x,y)$
. In particular, (3.5) becomes
If
![]() $x=y$
, then this is
$x=y$
, then this is
Assume that
![]() $c(x\otimes x)=-x\otimes x$
, thus
$c(x\otimes x)=-x\otimes x$
, thus
![]() $x^2$
is primitive and
$x^2$
is primitive and
![]() $\alpha^{-1}\!\left(x^2\right)=-\alpha\!\left(x^2\right)$
.
$\alpha^{-1}\!\left(x^2\right)=-\alpha\!\left(x^2\right)$
.
If, moreover,
![]() $\alpha$
is H-linear, then
$\alpha$
is H-linear, then
 \begin{align*} -\alpha\!\left(x^2\right)&=\alpha^{-1}\!\left(x^2\right)\stackrel{(3.6)}{=}\alpha(x)^2-\alpha\!\left(x_{({-}1)}\cdot x\right)\alpha^{-1}\!\left(x_{(0)}\right)-\alpha\!\left(x^2\right)\\
&=\alpha(x)^2-\epsilon\!\left(x_{({-}1)}\right)\alpha( x)\alpha^{-1}\!\left(x_{(0)}\right)-\alpha\!\left(x^2\right)\\
&=\alpha(x)^2-\alpha( x)\alpha^{-1}(x)-\alpha\!\left(x^2\right)=2\alpha(x)^2-\alpha\!\left(x^2\right). \end{align*}
\begin{align*} -\alpha\!\left(x^2\right)&=\alpha^{-1}\!\left(x^2\right)\stackrel{(3.6)}{=}\alpha(x)^2-\alpha\!\left(x_{({-}1)}\cdot x\right)\alpha^{-1}\!\left(x_{(0)}\right)-\alpha\!\left(x^2\right)\\
&=\alpha(x)^2-\epsilon\!\left(x_{({-}1)}\right)\alpha( x)\alpha^{-1}\!\left(x_{(0)}\right)-\alpha\!\left(x^2\right)\\
&=\alpha(x)^2-\alpha( x)\alpha^{-1}(x)-\alpha\!\left(x^2\right)=2\alpha(x)^2-\alpha\!\left(x^2\right). \end{align*}
That is,
![]() $\alpha(x)=0$
and (5.6) becomes
$\alpha(x)=0$
and (5.6) becomes
In particular, if
![]() $x^2=0$
(v.g. when B is a Nichols algebra) we obtain
$x^2=0$
(v.g. when B is a Nichols algebra) we obtain
In other words,
![]() $\eta(x,x)=\sigma(x,x)$
is a necessary condition to
$\eta(x,x)=\sigma(x,x)$
is a necessary condition to
![]() $e^{\eta}\sim\sigma$
.
$e^{\eta}\sim\sigma$
.
5.2. Equivalence of the commutation conditions
In [Reference García and Mastnak13], for a Hopf algebra
![]() $A=\mathfrak{B}(V)\# H$
, the authors work with cocycles
$A=\mathfrak{B}(V)\# H$
, the authors work with cocycles
![]() $\eta$
concentrated in degree (1,1), that is
$\eta$
concentrated in degree (1,1), that is
![]() $\eta(A^n,A^m)=0$
if
$\eta(A^n,A^m)=0$
if
![]() $(n,m)\neq (1,1)$
and show in [Reference García and Mastnak13, Lemma 2.3] that (5.1) and (5.2) are equivalent to each other and in turn to two other identities in
$(n,m)\neq (1,1)$
and show in [Reference García and Mastnak13, Lemma 2.3] that (5.1) and (5.2) are equivalent to each other and in turn to two other identities in
![]() $V^{\otimes 4}$
:
$V^{\otimes 4}$
:
We are interested in finding more general contexts where this equivalence holds, to reduce the number of identities to check. We obtain some answers in Lemmas 5.7 and 5.8 below.
Lemma 5.7. Let A be a Hopf algebra. If
![]() $\eta(x,y)=\lambda\,\eta(y,x)$
for every
$\eta(x,y)=\lambda\,\eta(y,x)$
for every
![]() $x,y\in A$
and some
$x,y\in A$
and some
![]() $\lambda\in\Bbbk$
, then (5.1) and (5.2) are equivalent.
$\lambda\in\Bbbk$
, then (5.1) and (5.2) are equivalent.
Proof. Interchange a and c in one of the lines from (5.3) to obtain the other.
The following lemma is rather technical, see (6.17) for a concrete and detailed application.
Lemma 5.8. Let A be a Hopf algebra and fix a linear basis
![]() $\mathbb{B}$
of A. Let
$\mathbb{B}$
of A. Let
![]() $\eta\in\textrm{Z}^2(A,\Bbbk)$
be a Hochschild 2-cocycle. Fix
$\eta\in\textrm{Z}^2(A,\Bbbk)$
be a Hochschild 2-cocycle. Fix
![]() $T=\Bbbk[\tau_x\,:\,x\in\mathbb{B}]$
the polynomial algebra on
$T=\Bbbk[\tau_x\,:\,x\in\mathbb{B}]$
the polynomial algebra on
![]() $\dim A$
variables given by the symbols
$\dim A$
variables given by the symbols
![]() $\tau_x\,:\!=\, \eta({-},x)\colon A\to \Bbbk$
.
$\tau_x\,:\!=\, \eta({-},x)\colon A\to \Bbbk$
.
In particular, for every
![]() $y,z\in A$
, there are families of scalars
$y,z\in A$
, there are families of scalars
![]() $\left(u_x=u_x(y,z)\right)_{x\in\mathbb{B}}$
,
$\left(u_x=u_x(y,z)\right)_{x\in\mathbb{B}}$
,
![]() $\left(d_x=d_x(y,z)\right)_{x\in\mathbb{B}}\in\Bbbk$
such that the following identities hold in T:
$\left(d_x=d_x(y,z)\right)_{x\in\mathbb{B}}\in\Bbbk$
such that the following identities hold in T:
 \begin{align*} \eta\!\left({-},y_{(1)}z_{(1)}\right)\eta\!\left(y_{(2)},z_{(2)}\right)&=\sum_{x\in\mathbb{B}} u_x(y,z)\tau_x, \\
\eta\!\left(y_{(1)},z_{(1)}\right)\eta\!\left({-},y_{(2)}z_{(2)}\right)&=\sum_{x\in\mathbb{B}} d_x(y,z)\tau_x. \end{align*}
\begin{align*} \eta\!\left({-},y_{(1)}z_{(1)}\right)\eta\!\left(y_{(2)},z_{(2)}\right)&=\sum_{x\in\mathbb{B}} u_x(y,z)\tau_x, \\
\eta\!\left(y_{(1)},z_{(1)}\right)\eta\!\left({-},y_{(2)}z_{(2)}\right)&=\sum_{x\in\mathbb{B}} d_x(y,z)\tau_x. \end{align*}
Assume that
The converse is also true, mutatis mutandis.
Proof. Assume that (5.1) and (5.10) hold. Let us set
![]() $\omega_z\,:\!=\, \eta({-},z)\colon A\to \Bbbk$
, for each
$\omega_z\,:\!=\, \eta({-},z)\colon A\to \Bbbk$
, for each
![]() $z\in\mathbb{B}$
. Now, if
$z\in\mathbb{B}$
. Now, if
![]() $x,y\in A$
, then
$x,y\in A$
, then
 \begin{align*}\eta\!\left(x_{(1)}y_{(1)}, - \right)\eta\!\left(x_{(2)},y_{(2)}\right)&=\sum_{z\in\mathbb{B}}u_z(x,y)\omega_z\stackrel{(5.10)}{=}\sum_{z\in\mathbb{B}}d_z(x,y)\omega_z\\&=\eta\!\left(x_{(1)},y_{(1)}\right)\eta(x_{(2)}y_{(2)},-).\end{align*}
\begin{align*}\eta\!\left(x_{(1)}y_{(1)}, - \right)\eta\!\left(x_{(2)},y_{(2)}\right)&=\sum_{z\in\mathbb{B}}u_z(x,y)\omega_z\stackrel{(5.10)}{=}\sum_{z\in\mathbb{B}}d_z(x,y)\omega_z\\&=\eta\!\left(x_{(1)},y_{(1)}\right)\eta(x_{(2)}y_{(2)},-).\end{align*}
Which shows that (5.2) also holds.
6. An example of abelian type
In this section, we consider the Nichols algebra
![]() $\mathfrak{B}_{\mathfrak{q}}$
associated to a braided vector space
$\mathfrak{B}_{\mathfrak{q}}$
associated to a braided vector space
![]() $(V,c^{\mathfrak{q}})$
of Cartan type
$(V,c^{\mathfrak{q}})$
of Cartan type
![]() $A_2$
, with parameter
$A_2$
, with parameter
![]() $q=-1$
. The Dynkin diagram is
$q=-1$
. The Dynkin diagram is
and the braiding matrix
![]() $\mathfrak{q}=(q_{ij})$
is such that
$\mathfrak{q}=(q_{ij})$
is such that
![]() $q_{11}=q_{22}=-1$
and
$q_{11}=q_{22}=-1$
and
![]() $q_{12}q_{21}=-1$
.
$q_{12}q_{21}=-1$
.
We fix a basis
![]() $\Bbbk\{x_1,x_2\}$
associated to this matrix; then the relations defining the Nichols algebra are given by
$\Bbbk\{x_1,x_2\}$
associated to this matrix; then the relations defining the Nichols algebra are given by
where
![]() $x_{12}\,:\!=\, x_1x_2 - q_{12}x_2x_1$
. A linear PBW basis for this algebra is given by
$x_{12}\,:\!=\, x_1x_2 - q_{12}x_2x_1$
. A linear PBW basis for this algebra is given by
We assume that there is a principal YD-realization
![]() $(\chi_i,g_i)_{i\in\mathbb{I}_2}$
so that
$(\chi_i,g_i)_{i\in\mathbb{I}_2}$
so that
![]() $\mathfrak{B}_{\mathfrak{q}}\in{}^{H}_{H}\mathcal{YD}$
for some Hopf algebra H, cf. (2.10). We set
$\mathfrak{B}_{\mathfrak{q}}\in{}^{H}_{H}\mathcal{YD}$
for some Hopf algebra H, cf. (2.10). We set
![]() $A=B\# H$
and fix
$A=B\# H$
and fix
6.1. Hopf cocycles
The (braided) cleft objects for the Nichols algebra
![]() $\mathfrak{B}_{\mathfrak{q}}$
are given by the family of algebras
$\mathfrak{B}_{\mathfrak{q}}$
are given by the family of algebras
![]() $\mathcal{E}(\boldsymbol\lambda)$
,
$\mathcal{E}(\boldsymbol\lambda)$
,
![]() $\boldsymbol\lambda=(\lambda_1,\lambda_2,\lambda_{12})\in\Bbbk^3$
, generated by
$\boldsymbol\lambda=(\lambda_1,\lambda_2,\lambda_{12})\in\Bbbk^3$
, generated by
![]() $y_1,y_2$
and relations
$y_1,y_2$
and relations
again,
![]() $y_{12}\,:\!=\, y_1y_2 - q_{12}y_2x_1$
. The scalars
$y_{12}\,:\!=\, y_1y_2 - q_{12}y_2x_1$
. The scalars
![]() $\lambda_1,\lambda_2,\lambda_{12}\in\Bbbk$
are subject to:
$\lambda_1,\lambda_2,\lambda_{12}\in\Bbbk$
are subject to:
This conditions can also be written as
This algebra inherits a basis as in (6.2).
Remark 6.1. Observe that unless
![]() $q_{12}=\pm1$
, and thus
$q_{12}=\pm1$
, and thus
![]() $q_{21}=\mp 1$
, then we have
$q_{21}=\mp 1$
, then we have
![]() $\lambda_1=\lambda_2=\lambda_{12}=0$
.
$\lambda_1=\lambda_2=\lambda_{12}=0$
.
For each triple
![]() $\boldsymbol\lambda=(\lambda_1,\lambda_2,\lambda_{12})$
, the corresponding deformation of
$\boldsymbol\lambda=(\lambda_1,\lambda_2,\lambda_{12})$
, the corresponding deformation of
![]() $A=\mathfrak{B}_{\mathfrak{q}}\# H$
is the quotient
$A=\mathfrak{B}_{\mathfrak{q}}\# H$
is the quotient
![]() $\mathfrak{u}_{\mathfrak{q}}(\boldsymbol\lambda)$
of
$\mathfrak{u}_{\mathfrak{q}}(\boldsymbol\lambda)$
of
![]() $T(V)\# H$
modulo the relations
$T(V)\# H$
modulo the relations
Here
![]() $V=\Bbbk\{a_1,a_2\}$
and
$V=\Bbbk\{a_1,a_2\}$
and
![]() $a_{12}\,:\!=\, a_1a_2 - q_{12}a_2a_1$
.
$a_{12}\,:\!=\, a_1a_2 - q_{12}a_2a_1$
.
Remark 6.2. Notice that when
![]() $g_i^2=0$
,
$g_i^2=0$
,
![]() $i=1,2$
, we can normalize
$i=1,2$
, we can normalize
![]() $\lambda_i=0$
in the deformations (6.6), on top of the restriction (6.5). Idem for
$\lambda_i=0$
in the deformations (6.6), on top of the restriction (6.5). Idem for
![]() $g_1^2g_2^2=1$
and
$g_1^2g_2^2=1$
and
![]() $\lambda_{12}$
. However, the cleft objects are not isomorphic, cf. (6.4).
$\lambda_{12}$
. However, the cleft objects are not isomorphic, cf. (6.4).
Henceforward, we will assume that
as we shall investigate Hopf 2-cocycles
![]() $\sigma_{\boldsymbol\lambda}$
associated to non-trivial deformations
$\sigma_{\boldsymbol\lambda}$
associated to non-trivial deformations
![]() $\mathcal{E}(\boldsymbol\lambda)$
and
$\mathcal{E}(\boldsymbol\lambda)$
and
![]() $\mathfrak{u}_{\mathfrak{q}}(\boldsymbol\lambda)$
.
$\mathfrak{u}_{\mathfrak{q}}(\boldsymbol\lambda)$
.
Lemma 6.3. The section
![]() $\gamma\colon\mathfrak{B}_{\mathfrak{q}}\to\mathcal{E}(\boldsymbol\lambda)$
is given by
$\gamma\colon\mathfrak{B}_{\mathfrak{q}}\to\mathcal{E}(\boldsymbol\lambda)$
is given by
The convolution inverse for
![]() $\gamma$
is determined by
$\gamma$
is determined by
 \begin{align*}\gamma^{-1}(x_i)&=-y_i,\ i\in\mathbb{I}_2, & \gamma^{-1}(x_{12})&=y_{12}+2q_{12}y_2y_1, \\\gamma^{-1}(x_{2}x_1)&=q_{21}y_{12}-y_2y_1, &\gamma^{-1}(x_{12}x_1)&=-y_{12}y_1+2q_{21}\lambda_1y_2, \\ \gamma^{-1}(x_2x_{12})&=-y_2y_{12},& \gamma^{-1}(x_2x_{12}x_1)&=y_2y_{12}y_1-\lambda_{12}.\end{align*}
\begin{align*}\gamma^{-1}(x_i)&=-y_i,\ i\in\mathbb{I}_2, & \gamma^{-1}(x_{12})&=y_{12}+2q_{12}y_2y_1, \\\gamma^{-1}(x_{2}x_1)&=q_{21}y_{12}-y_2y_1, &\gamma^{-1}(x_{12}x_1)&=-y_{12}y_1+2q_{21}\lambda_1y_2, \\ \gamma^{-1}(x_2x_{12})&=-y_2y_{12},& \gamma^{-1}(x_2x_{12}x_1)&=y_2y_{12}y_1-\lambda_{12}.\end{align*}
Proof. The values for
![]() $\gamma(x_i), \gamma(x_{12}), \gamma(x_{2}x_1)$
are straightforward. We see that
$\gamma(x_i), \gamma(x_{12}), \gamma(x_{2}x_1)$
are straightforward. We see that
and thus setting
![]() $\gamma(x_{12}x_1)=(y_{12}y_{1} - 2q_{21}\lambda_1 y_2 )$
gives
$\gamma(x_{12}x_1)=(y_{12}y_{1} - 2q_{21}\lambda_1 y_2 )$
gives
![]() $(\gamma\otimes \textrm{id})\Delta(x_{12}x_1)=\rho\gamma(x_{12}x_1)$
as expected. On the other hand, it is easy to see
$(\gamma\otimes \textrm{id})\Delta(x_{12}x_1)=\rho\gamma(x_{12}x_1)$
as expected. On the other hand, it is easy to see
![]() $\gamma(x_2x_{12})=y_{2}y_{12}$
. Finally,
$\gamma(x_2x_{12})=y_{2}y_{12}$
. Finally,
 \begin{align*}\underline{\Delta}(x_2x_{12}x_1)&=2x_2x_1\otimes x_2x_1 - q_{21}^{2}x_1\otimes x_2x_{12} - q_{21}x_{12}\otimes x_2x_1 \\
&\quad - q_{21}^{2}x_{12}x_1\otimes x_2+ x_2\otimes x_{12}x_1 - q_{21}x_2x_1\otimes x_{12} + x_2x_{12}\otimes x_1,\\
\underline{\rho}(y_2y_{12}y_1)&=2q_{21}\lambda_1 y_2\otimes x_2+2y_2y_1\otimes x_2x_1 - q_{21}^{2}y_1\otimes x_2x_{12} - q_{21}y_{12}\otimes x_2x_1 \\
&\quad - q_{21}^{2}y_{12}y_1\otimes x_2+ y_2\otimes x_{12}x_1 - q_{21}y_2y_1\otimes x_{12} + y_2y_{12}\otimes x_1.\end{align*}
\begin{align*}\underline{\Delta}(x_2x_{12}x_1)&=2x_2x_1\otimes x_2x_1 - q_{21}^{2}x_1\otimes x_2x_{12} - q_{21}x_{12}\otimes x_2x_1 \\
&\quad - q_{21}^{2}x_{12}x_1\otimes x_2+ x_2\otimes x_{12}x_1 - q_{21}x_2x_1\otimes x_{12} + x_2x_{12}\otimes x_1,\\
\underline{\rho}(y_2y_{12}y_1)&=2q_{21}\lambda_1 y_2\otimes x_2+2y_2y_1\otimes x_2x_1 - q_{21}^{2}y_1\otimes x_2x_{12} - q_{21}y_{12}\otimes x_2x_1 \\
&\quad - q_{21}^{2}y_{12}y_1\otimes x_2+ y_2\otimes x_{12}x_1 - q_{21}y_2y_1\otimes x_{12} + y_2y_{12}\otimes x_1.\end{align*}
So
![]() $(\gamma\otimes\textrm{id})\Delta(x_2x_{12}x_1)=\rho(y_2y_{12}y_1)$
as (recall
$(\gamma\otimes\textrm{id})\Delta(x_2x_{12}x_1)=\rho(y_2y_{12}y_1)$
as (recall
![]() $\lambda_1q_{21}^3=\lambda_1 q_{21}$
):
$\lambda_1q_{21}^3=\lambda_1 q_{21}$
):
Now, to see that
![]() $\gamma^{-1}$
is the convolution inverse of
$\gamma^{-1}$
is the convolution inverse of
![]() $\gamma$
, we only need to verify that
$\gamma$
, we only need to verify that
![]() $\gamma\ast\gamma^{-1}(b)=0=\gamma^{-1}\ast\gamma(b)$
, for each
$\gamma\ast\gamma^{-1}(b)=0=\gamma^{-1}\ast\gamma(b)$
, for each
![]() $b\in\mathbb{B}_{\mathfrak{q}}$
. To illustrate this, we expose some calculations below.
$b\in\mathbb{B}_{\mathfrak{q}}$
. To illustrate this, we expose some calculations below.
 \begin{align*}\gamma\ast\gamma^{-1}(x_{12}x_1)&=\gamma(x_{12}x_1)-q_{21}y_1\!\left(y_{12}+2q_{12}y_2y_1\right)-y_{12}y_1+2y_1(q_{21}y_{12}-y_2y_1)+\gamma^{-1}(x_{12}x_1)\\
&=-y_{12}y_1+2y_1y_2y_1-y_{12}y_1+2y_{12}y_1-2y_1y_2y_1=0.\\
\gamma\ast\gamma^{-1}(x_{2}x_{12}x_1) & = y_2y_{12}y_1+2y_2y_1(q_{21}y_{12}-y_2y_1)+q_{21}^2y_1y_2y_{12}-y_2y_{12}y_1\\
&\quad -q_{21}y_{12}(q_{21}y_{12}-y_2y_1)+q_{21}^2(y_{12}y_1-2q_{21}\lambda_1y_2)y_2+y_2y_{12}y_1\\
&\quad -q_{21}^2\lambda_{12}+y_2({-}y_{12}y_1+2q_{21}\lambda_1y_2)-q_{21}y_2y_1\!\left(y_{12}+2q_{12}y_2y_1\right)\\
& =2q_{21}y_2y_1y_{12}+q_{21}^2(y_{12}+q_{12}y_2y_1)y_{12}-q_{21}^2\lambda_{12}+q_{21}y_{12}y_2y_1\\
& \quad +q_{21}^2y_{12}y_1y_2-2q_{21}\lambda_1\lambda_2-q_{21}^2\lambda_{12}+2q_{21}\lambda_1\lambda_2-q_{21}y_2y_1y_{12}\\
& =2y_2y_{12}y_1-q_{21}y_2y_1y_{12}+q_{21}y_{12}y_2y_1+q_{21}^2y_{12}(y_{12}+q_{12}y_2y_1)\\
&\quad -q_{21}^2\lambda_{12}-y_2y_{12}y_1\\
& =y_2y_{12}y_1-y_2y_{12}y_1=0.\end{align*}
\begin{align*}\gamma\ast\gamma^{-1}(x_{12}x_1)&=\gamma(x_{12}x_1)-q_{21}y_1\!\left(y_{12}+2q_{12}y_2y_1\right)-y_{12}y_1+2y_1(q_{21}y_{12}-y_2y_1)+\gamma^{-1}(x_{12}x_1)\\
&=-y_{12}y_1+2y_1y_2y_1-y_{12}y_1+2y_{12}y_1-2y_1y_2y_1=0.\\
\gamma\ast\gamma^{-1}(x_{2}x_{12}x_1) & = y_2y_{12}y_1+2y_2y_1(q_{21}y_{12}-y_2y_1)+q_{21}^2y_1y_2y_{12}-y_2y_{12}y_1\\
&\quad -q_{21}y_{12}(q_{21}y_{12}-y_2y_1)+q_{21}^2(y_{12}y_1-2q_{21}\lambda_1y_2)y_2+y_2y_{12}y_1\\
&\quad -q_{21}^2\lambda_{12}+y_2({-}y_{12}y_1+2q_{21}\lambda_1y_2)-q_{21}y_2y_1\!\left(y_{12}+2q_{12}y_2y_1\right)\\
& =2q_{21}y_2y_1y_{12}+q_{21}^2(y_{12}+q_{12}y_2y_1)y_{12}-q_{21}^2\lambda_{12}+q_{21}y_{12}y_2y_1\\
& \quad +q_{21}^2y_{12}y_1y_2-2q_{21}\lambda_1\lambda_2-q_{21}^2\lambda_{12}+2q_{21}\lambda_1\lambda_2-q_{21}y_2y_1y_{12}\\
& =2y_2y_{12}y_1-q_{21}y_2y_1y_{12}+q_{21}y_{12}y_2y_1+q_{21}^2y_{12}(y_{12}+q_{12}y_2y_1)\\
&\quad -q_{21}^2\lambda_{12}-y_2y_{12}y_1\\
& =y_2y_{12}y_1-y_2y_{12}y_1=0.\end{align*}
The rest of the computations, which are simpler, are left to the reader.
Remark 6.4. Notice that
![]() $\gamma\colon\mathfrak{B}_{\mathfrak{q}}\to\mathcal{E}(\boldsymbol\lambda)$
as in Lemma 6.3 is H-linear. Indeed, it suffices to check this on
$\gamma\colon\mathfrak{B}_{\mathfrak{q}}\to\mathcal{E}(\boldsymbol\lambda)$
as in Lemma 6.3 is H-linear. Indeed, it suffices to check this on
![]() $\gamma(x_{12}x_1)$
and this follows since
$\gamma(x_{12}x_1)$
and this follows since
Theorem 6.5. Let
![]() $\boldsymbol\lambda=(\lambda_1,\lambda_2,\lambda_{12})$
. The Hopf cocycle
$\boldsymbol\lambda=(\lambda_1,\lambda_2,\lambda_{12})$
. The Hopf cocycle
![]() $\sigma_{\boldsymbol\lambda}\,:\!=\,\sigma$
associated to the cleft object
$\sigma_{\boldsymbol\lambda}\,:\!=\,\sigma$
associated to the cleft object
![]() $\mathcal{E}(\boldsymbol\lambda)$
is given by
$\mathcal{E}(\boldsymbol\lambda)$
is given by

Proof. In first place, we use Lemma 3.1 to calculate the elements of
![]() $S_\sigma$
as in (3.1). Indeed, let
$S_\sigma$
as in (3.1). Indeed, let
![]() $i,j\in\mathbb{I}_2$
, then
$i,j\in\mathbb{I}_2$
, then
here we use that
![]() $\gamma^{-1}\!\left(x_ix_j\right)=q_{ij}y_jy_i$
. It is easy to see that
$\gamma^{-1}\!\left(x_ix_j\right)=q_{ij}y_jy_i$
. It is easy to see that
For the other hand, we show
![]() $\sigma(x_1,x_2x_{12})$
and
$\sigma(x_1,x_2x_{12})$
and
![]() $\sigma(x_2,x_{12}x_1)$
.
$\sigma(x_2,x_{12}x_1)$
.
 \begin{align*}\sigma(x_1, x_2x_{12}) & =y_2y_{12}y_2-2q_{12}y_2y_1\gamma^{-1}(x_1x_2)-y_2\gamma^{-1}(x_{12}x_1)-y_{12}\gamma^{-1}(x_1x_2) +\gamma^{-1}(x_1x_2x_{12})\\
&=y_2y_{12}y_2-2y_2y_1y_2y_1+y_2(y_{12}-2q_{21}\lambda_1y_2)-q_{12}y_{12}y_2y_1-y_1y_{12}y_2+\lambda_{12}\\
&=y_2y_{12}y_1-2y_2y_{12}y_1-2q_{12}\lambda_1\lambda_2+y_2y_{12}y_1+2q_{12}\lambda_1\lambda_2+\lambda_{12}=\lambda_{12}.\\
\sigma(x_2, x_{12}x_1) & =q_{21}^2(y_{12}y_1-2q_{21}\lambda_1y_2)y_2+y_1y_2y_{12} -q_{21}y_{12}\gamma^{-1}(x_2x_1)+\gamma^{-1}(x_2x_{12}x_1)\\
& =y_{12}y_1y_2-2q_{21}\lambda_1\lambda_2+\lambda_{12}-y_2y_{12}y_1-y_{12}y_1y_2+y_2y_{12}y_1+\lambda_{12}=2q_{12}\lambda_1\lambda_2.\end{align*}
\begin{align*}\sigma(x_1, x_2x_{12}) & =y_2y_{12}y_2-2q_{12}y_2y_1\gamma^{-1}(x_1x_2)-y_2\gamma^{-1}(x_{12}x_1)-y_{12}\gamma^{-1}(x_1x_2) +\gamma^{-1}(x_1x_2x_{12})\\
&=y_2y_{12}y_2-2y_2y_1y_2y_1+y_2(y_{12}-2q_{21}\lambda_1y_2)-q_{12}y_{12}y_2y_1-y_1y_{12}y_2+\lambda_{12}\\
&=y_2y_{12}y_1-2y_2y_{12}y_1-2q_{12}\lambda_1\lambda_2+y_2y_{12}y_1+2q_{12}\lambda_1\lambda_2+\lambda_{12}=\lambda_{12}.\\
\sigma(x_2, x_{12}x_1) & =q_{21}^2(y_{12}y_1-2q_{21}\lambda_1y_2)y_2+y_1y_2y_{12} -q_{21}y_{12}\gamma^{-1}(x_2x_1)+\gamma^{-1}(x_2x_{12}x_1)\\
& =y_{12}y_1y_2-2q_{21}\lambda_1\lambda_2+\lambda_{12}-y_2y_{12}y_1-y_{12}y_1y_2+y_2y_{12}y_1+\lambda_{12}=2q_{12}\lambda_1\lambda_2.\end{align*}
The reader will have no difficulty to see that
Thus,
![]() $S_\sigma=\{0,\lambda_1,\lambda_2,\lambda_{12},2q_{12}\lambda_1\lambda_2\}$
. From now on, we use the formulas of decomposition in Example 3.4 to get the others values of
$S_\sigma=\{0,\lambda_1,\lambda_2,\lambda_{12},2q_{12}\lambda_1\lambda_2\}$
. From now on, we use the formulas of decomposition in Example 3.4 to get the others values of
![]() $\sigma$
, following Lemma 3.2. In this case, the matrix coefficients of the braiding
$\sigma$
, following Lemma 3.2. In this case, the matrix coefficients of the braiding
![]() $\left(c_{i,j}^{p,q}\right)_{ \begin{smallmatrix} i,j,\\ p,q \end{smallmatrix} \in\mathbb{I}}$
are given by
$\left(c_{i,j}^{p,q}\right)_{ \begin{smallmatrix} i,j,\\ p,q \end{smallmatrix} \in\mathbb{I}}$
are given by
![]() $c_{i,j}^{p,q}=\delta_{i,q}\delta_{j,p}q_{ij}$
so
$c_{i,j}^{p,q}=\delta_{i,q}\delta_{j,p}q_{ij}$
so
![]() $\mathbb{Z}\!\left[c_{i,j}^{p,q}\right]_{\begin{smallmatrix} i,j,\\ p,q \end{smallmatrix} \in\mathbb{I}}=\mathbb{Z}\!\left[q_{12}^{\pm 1}\right]\simeq \mathbb{Z}$
, as
$\mathbb{Z}\!\left[c_{i,j}^{p,q}\right]_{\begin{smallmatrix} i,j,\\ p,q \end{smallmatrix} \in\mathbb{I}}=\mathbb{Z}\!\left[q_{12}^{\pm 1}\right]\simeq \mathbb{Z}$
, as
![]() $q_{11}=q_{22}=-1$
and
$q_{11}=q_{22}=-1$
and
![]() $q_{21}=$
$q_{21}=$
![]() $-q_{12}^{-1}=\mp1$
.
$-q_{12}^{-1}=\mp1$
.
One example of application is shown below.
 \begin{align*} \sigma(x_{12}x_1,x_{12}x_1)&=\sigma(x_1,x_2x_1x_{12}x_1)+\sigma(x_2,g_1\cdot (x_{12}x_1))\sigma(x_1,x_1)\\
&\quad+\sigma(g_2\cdot x_1,g_2\cdot (x_{12}x_1))\sigma(x_1,x_2)-\sigma(x_1,x_2)\sigma(x_1,x_{12}x_1)\\
&\quad-\sigma(x_1,g_2\cdot x_1)\sigma(x_2,x_{12}x_1)+\sigma(x_2x_1,2x_1)\sigma(x_1,x_2x_1)\\
&\quad-\sigma(x_2x_1,q_{21}x_1)\sigma(x_1,x_{12})+\sigma(x_2x_1,x_{12})\sigma(x_1,x_1)\\
&\quad+\sigma(x_2,g_1\cdot(2x_1))\sigma(x_1,x_1x_2x_1)-\sigma(x_2,g_1\cdot(q_{21}x_1))\sigma(x_1,x_1x_{12}x_1)\\
&\quad+\sigma(x_2,g_1\cdot x_{12})\sigma(x_1,x_1^2)+\sigma(g_2\cdot x_1,g_2\cdot (2x_1))\sigma\!\left(x_1,x_2^2x_1\right)\\
&\quad-\sigma(g_2\cdot x_1,g_2\cdot (q_{21}x_1))\sigma(x_1,x_2x_{12})+\sigma(g_2\cdot x_1,g_2\cdot x_{12})\sigma(x_1,x_2x_1)\\
&=q_{12}\sigma(x_2, x_{12}x_1)\sigma(x_1,x_1)-q_{21}\sigma(x_1, x_1)\sigma(x_2,x_{12}x_1) -q_{21}\sigma( x_1,x_1)\sigma(x_1,x_2x_{12})\\
&=2q_{12}\sigma(x_2, x_{12}x_1)\sigma(x_1,x_1)+q_{12}\sigma( x_1,x_1)\sigma(x_1,x_2x_{12})\\
&=4\lambda_1^2\lambda_2+q_{12}\lambda_{12}\lambda_1.\end{align*}
\begin{align*} \sigma(x_{12}x_1,x_{12}x_1)&=\sigma(x_1,x_2x_1x_{12}x_1)+\sigma(x_2,g_1\cdot (x_{12}x_1))\sigma(x_1,x_1)\\
&\quad+\sigma(g_2\cdot x_1,g_2\cdot (x_{12}x_1))\sigma(x_1,x_2)-\sigma(x_1,x_2)\sigma(x_1,x_{12}x_1)\\
&\quad-\sigma(x_1,g_2\cdot x_1)\sigma(x_2,x_{12}x_1)+\sigma(x_2x_1,2x_1)\sigma(x_1,x_2x_1)\\
&\quad-\sigma(x_2x_1,q_{21}x_1)\sigma(x_1,x_{12})+\sigma(x_2x_1,x_{12})\sigma(x_1,x_1)\\
&\quad+\sigma(x_2,g_1\cdot(2x_1))\sigma(x_1,x_1x_2x_1)-\sigma(x_2,g_1\cdot(q_{21}x_1))\sigma(x_1,x_1x_{12}x_1)\\
&\quad+\sigma(x_2,g_1\cdot x_{12})\sigma(x_1,x_1^2)+\sigma(g_2\cdot x_1,g_2\cdot (2x_1))\sigma\!\left(x_1,x_2^2x_1\right)\\
&\quad-\sigma(g_2\cdot x_1,g_2\cdot (q_{21}x_1))\sigma(x_1,x_2x_{12})+\sigma(g_2\cdot x_1,g_2\cdot x_{12})\sigma(x_1,x_2x_1)\\
&=q_{12}\sigma(x_2, x_{12}x_1)\sigma(x_1,x_1)-q_{21}\sigma(x_1, x_1)\sigma(x_2,x_{12}x_1) -q_{21}\sigma( x_1,x_1)\sigma(x_1,x_2x_{12})\\
&=2q_{12}\sigma(x_2, x_{12}x_1)\sigma(x_1,x_1)+q_{12}\sigma( x_1,x_1)\sigma(x_1,x_2x_{12})\\
&=4\lambda_1^2\lambda_2+q_{12}\lambda_{12}\lambda_1.\end{align*}
The other values are computed analogously.
6.2. Hochschild cocycles
Recall the cocycles
![]() $\xi_j^i\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)$
,
$\xi_j^i\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)$
,
![]() $i,j\in\mathbb{I}_2$
, from Example 4.2. Additionally, we denote
$i,j\in\mathbb{I}_2$
, from Example 4.2. Additionally, we denote
![]() $\xi_0=\epsilon\otimes\epsilon\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)$
, the cocycle such that
$\xi_0=\epsilon\otimes\epsilon\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)$
, the cocycle such that
![]() $\xi_0(1,1)=1$
, and zero elsewhere.
$\xi_0(1,1)=1$
, and zero elsewhere.
We shall consider two more Hochschild 2-cocycles
![]() $\xi_{121}^2,\xi_{212}^1$
in
$\xi_{121}^2,\xi_{212}^1$
in
![]() $\mathfrak{B}_{\mathfrak{q}}$
. Namely, let
$\mathfrak{B}_{\mathfrak{q}}$
. Namely, let
![]() $\xi_{121}^2\colon \mathfrak{B}_{\mathfrak{q}}\otimes \mathfrak{B}_{\mathfrak{q}}\to \Bbbk$
be the linear map given by
$\xi_{121}^2\colon \mathfrak{B}_{\mathfrak{q}}\otimes \mathfrak{B}_{\mathfrak{q}}\to \Bbbk$
be the linear map given by
and zero elsewhere in the basis
![]() $\mathbb{B}\otimes \mathbb{B}$
. Following Lemma 4.1, it is an easy computation to check that
$\mathbb{B}\otimes \mathbb{B}$
. Following Lemma 4.1, it is an easy computation to check that
![]() $\xi_{121}^2\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)$
. As well, we define
$\xi_{121}^2\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)$
. As well, we define
![]() $\xi_{212}^1\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)$
via
$\xi_{212}^1\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)$
via
and zero elsewhere in
![]() $\mathbb{B}\otimes \mathbb{B}$
.
$\mathbb{B}\otimes \mathbb{B}$
.
We further note that
![]() $\xi_{121}^2+\xi_{212}^1\in\textrm{B}^2(B,\Bbbk)$
. Indeed, let
$\xi_{121}^2+\xi_{212}^1\in\textrm{B}^2(B,\Bbbk)$
. Indeed, let
![]() $f\colon B\to \Bbbk$
be the linear map defined on the basis
$f\colon B\to \Bbbk$
be the linear map defined on the basis
![]() $\mathbb{B}$
by
$\mathbb{B}$
by
![]() $f(x_2x_{12}x_1)=1$
and zero elsewhere. Then
$f(x_2x_{12}x_1)=1$
and zero elsewhere. Then
Recall the group
![]() $\Gamma\leq G(H)$
from (6.3).
$\Gamma\leq G(H)$
from (6.3).
Lemma 6.6.
![]() $\textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^\Gamma$
is spanned over
$\textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^\Gamma$
is spanned over
![]() $\Bbbk$
by
$\Bbbk$
by
![]() $\xi_0, \xi_1^1,\xi_2^2,\xi_{121}^2, \xi_{212}^1$
.
$\xi_0, \xi_1^1,\xi_2^2,\xi_{121}^2, \xi_{212}^1$
.
Furthermore,
-
(a)
 $\xi_i^i\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^H$
if and only if
$\xi_i^i\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^H$
if and only if
 $\chi_i^2=\epsilon$
,
$\chi_i^2=\epsilon$
, -
(b)
 $\xi_{iji}^j\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^H$
if and only if
$\xi_{iji}^j\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^H$
if and only if
 $\left(\chi_{1}\chi_{2}\right)^2=\epsilon$
;
$\left(\chi_{1}\chi_{2}\right)^2=\epsilon$
;
 $i,j\in\mathbb{I}_2$
.
$i,j\in\mathbb{I}_2$
.
Proof. By Lemma 4.1, see Remark 4.3,
![]() $\eta\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)$
is determined by the values
$\eta\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)$
is determined by the values
 \begin{align*}\eta&(x_1,x_1), & \eta&(x_1,x_2), & \eta&(x_{1},x_{12}), & \eta&(x_1,x_2x_{12}), \\\eta&(x_1,x_2x_1), & \eta&(x_2,x_2), & \eta&(x_{2},x_1), & \eta&(x_2,x_{12}), \\\eta&(x_2,x_{12}x_1) & \eta&(1,1).\end{align*}
\begin{align*}\eta&(x_1,x_1), & \eta&(x_1,x_2), & \eta&(x_{1},x_{12}), & \eta&(x_1,x_2x_{12}), \\\eta&(x_1,x_2x_1), & \eta&(x_2,x_2), & \eta&(x_{2},x_1), & \eta&(x_2,x_{12}), \\\eta&(x_2,x_{12}x_1) & \eta&(1,1).\end{align*}
Furthermore, as
![]() $x_1x_2x_1=x_{12}x_1$
and
$x_1x_2x_1=x_{12}x_1$
and
![]() $x_2x_1x_2=x_2x_{12}$
, we get
$x_2x_1x_2=x_2x_{12}$
, we get
Also, it is easy to see that
Now we let
![]() $\Gamma$
act and obtain
$\Gamma$
act and obtain
which forces
![]() $q_{12}=-1$
but also
$q_{12}=-1$
but also
which also gives
![]() $q_{21}=-1$
, a contradiction to
$q_{21}=-1$
, a contradiction to
![]() $q_{12}q_{21}=-1$
. Thus
$q_{12}q_{21}=-1$
. Thus
![]() $\eta(x_1,x_2)=0$
, similarly
$\eta(x_1,x_2)=0$
, similarly
![]() $\eta(x_2,x_1)=0$
. Similarly, we need to have
$\eta(x_2,x_1)=0$
. Similarly, we need to have
which gives
![]() $\eta(x_{1},x_{12})=0$
; and similarly
$\eta(x_{1},x_{12})=0$
; and similarly
so
![]() $\eta(x_{12},x_2)=0$
. That is, we are left with the values
$\eta(x_{12},x_2)=0$
. That is, we are left with the values
and therefore
![]() $\eta\in\Bbbk\left\{\xi_0, \xi_1^1,\xi_2^2,\xi_{121}^2, \xi_{212}^1\right\}$
.
$\eta\in\Bbbk\left\{\xi_0, \xi_1^1,\xi_2^2,\xi_{121}^2, \xi_{212}^1\right\}$
.
The second statement is straightforward; recall
![]() $h\cdot x_i=\chi_i(h)x_i$
,
$h\cdot x_i=\chi_i(h)x_i$
,
![]() $h\in H, i\in\mathbb{I}_\theta$
.
$h\in H, i\in\mathbb{I}_\theta$
.
6.3. Exponentials
Let
![]() $\eta\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^H$
, we are interested in finding the conditions for
$\eta\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^H$
, we are interested in finding the conditions for
![]() $\eta$
such that
$\eta$
such that
![]() $e^\eta$
is a Hopf cocycle; set
$e^\eta$
is a Hopf cocycle; set
In particular,
![]() $\eta(x_i,x_i)=\eta_i$
,
$\eta(x_i,x_i)=\eta_i$
,
![]() $i\in\mathbb{I}_2$
,
$i\in\mathbb{I}_2$
,
![]() $\eta(x_{2},x_{12}x_1)=\eta_{121}$
and
$\eta(x_{2},x_{12}x_1)=\eta_{121}$
and
![]() $\eta(x_{1},x_2x_{12})=\eta_{212}$
.
$\eta(x_{1},x_2x_{12})=\eta_{212}$
.
Next proposition characterizes the cocycles
![]() $\eta$
that satisfy (5.1) and (5.2); so in particular
$\eta$
that satisfy (5.1) and (5.2); so in particular
![]() $e^{\eta}$
is a Hopf cocycle. It is enough to assume that
$e^{\eta}$
is a Hopf cocycle. It is enough to assume that
![]() $\eta\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^\Gamma$
.
$\eta\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^\Gamma$
.
Proposition 6.7. A cocycle
![]() $\eta\in\textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^\Gamma$
satisfies (5.1) and (5.2) if and only if
$\eta\in\textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^\Gamma$
satisfies (5.1) and (5.2) if and only if
In particular if
![]() $\eta\in \textrm{C}$
, then
$\eta\in \textrm{C}$
, then
![]() $e^\eta$
is a Hopf 2-cocycle.
$e^\eta$
is a Hopf 2-cocycle.
We will show in Lemma 6.11 that conditions (5.1) and (5.2) are not necessary for
![]() $e^\eta$
to be a Hopf 2-cocycle.
$e^\eta$
to be a Hopf 2-cocycle.
Remark 6.8. Let
![]() $\eta=\eta_1\xi_1^1+ \eta_2\xi^2_2+\eta_{121}\xi_{121}^2+\eta_{212}\xi_{212}^1\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^\Gamma$
. We can rephrase Proposition 6.7 as follows:
$\eta=\eta_1\xi_1^1+ \eta_2\xi^2_2+\eta_{121}\xi_{121}^2+\eta_{212}\xi_{212}^1\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^\Gamma$
. We can rephrase Proposition 6.7 as follows:
![]() $\eta\in \textrm{C}$
if and only if
$\eta\in \textrm{C}$
if and only if
Proof. Suppose that
![]() $\eta$
verifies (5.1) and (5.2). That is for any
$\eta$
verifies (5.1) and (5.2). That is for any
![]() $x,y,z\in \mathfrak{B}_{\mathfrak{q}}$
,
$x,y,z\in \mathfrak{B}_{\mathfrak{q}}$
,
Now, we see that if
![]() $y=x_2x_1$
and
$y=x_2x_1$
and
![]() $z=x_2$
, then (6.13) gives
$z=x_2$
, then (6.13) gives
Similarly, if
![]() $y=x_1x_2$
and
$y=x_1x_2$
and
![]() $z=x_1$
, then (6.13) gives
$z=x_1$
, then (6.13) gives
Thus, from (6.15) and (6.16), we obtain
If we suppose that
![]() $\eta(x_1,x_1)\neq 0$
, then
$\eta(x_1,x_1)\neq 0$
, then
![]() $\eta(x_2,x_2)=\eta(x_1,x_2x_{12})=0$
. Furthermore, if
$\eta(x_2,x_2)=\eta(x_1,x_2x_{12})=0$
. Furthermore, if
![]() $y=x_{12}x_1$
and
$y=x_{12}x_1$
and
![]() $z=x_1$
, then we obtain from (6.13) that
$z=x_1$
, then we obtain from (6.13) that
for any
![]() $x\in\mathfrak{B}_{\mathfrak{q}}$
. Hence, we get that
$x\in\mathfrak{B}_{\mathfrak{q}}$
. Hence, we get that
![]() $\eta(x_2,x_{12}x_1)=0$
. Through the same calculations for
$\eta(x_2,x_{12}x_1)=0$
. Through the same calculations for
![]() $\eta(x_2,x_2)\neq 0$
, we get that
$\eta(x_2,x_2)\neq 0$
, we get that
![]() $\eta(x_1,x_1)=\eta(x_2,x_{12}x_1)=\eta(x_1,x_2x_{12})=0$
. Thus,
$\eta(x_1,x_1)=\eta(x_2,x_{12}x_1)=\eta(x_1,x_2x_{12})=0$
. Thus,
![]() $\eta\in \textrm{C}$
.
$\eta\in \textrm{C}$
.
Conversely, suppose that
![]() $\eta\in \textrm{C}$
. On one hand, if
$\eta\in \textrm{C}$
. On one hand, if
![]() $\eta=\eta_1\xi_i^i$
,
$\eta=\eta_1\xi_i^i$
,
![]() $i\in\mathbb{I}_2$
, then by [Reference García and Mastnak13, Lemma 2.3.], we have the conclusion as
$i\in\mathbb{I}_2$
, then by [Reference García and Mastnak13, Lemma 2.3.], we have the conclusion as
![]() $\eta$
clearly satisfies (5.9).
$\eta$
clearly satisfies (5.9).
Now, we show that the hypothesis of Lemma 5.8 hold when
Let
![]() $x,y,z\in\mathbb{B}_\mathfrak{q}$
, such that
$x,y,z\in\mathbb{B}_\mathfrak{q}$
, such that
![]() $\deg(y), \deg(z)$
are positive. In first place, note that if
$\deg(y), \deg(z)$
are positive. In first place, note that if
![]() $\deg(y)+\deg(z)<4$
, then we obtain zero in both sides of (5.1) and thus
$\deg(y)+\deg(z)<4$
, then we obtain zero in both sides of (5.1) and thus
![]() $u_x(y,z)=d_x(y,z)=0$
. Now, if
$u_x(y,z)=d_x(y,z)=0$
. Now, if
![]() $\deg(y)+\deg(z)=4$
, then (5.1) becomes
$\deg(y)+\deg(z)=4$
, then (5.1) becomes
![]() $\eta(x,1)\eta(y,z)$
and so,
$\eta(x,1)\eta(y,z)$
and so,
![]() $u_x(y,z)=0=d_x(y,z)$
when
$u_x(y,z)=0=d_x(y,z)$
when
![]() $x\neq 1$
and
$x\neq 1$
and
![]() $u_1(y,z)=\eta(y,z)=d_1(y,z)$
. On the other hand, we explicitly show the most representative calculations below.
$u_1(y,z)=\eta(y,z)=d_1(y,z)$
. On the other hand, we explicitly show the most representative calculations below.
deg(y) + deg(z) = 5:
-
(i)
 $y=x_{12}$
and
$y=x_{12}$
and
 $z=x_{12}x_1$
:
Here
$z=x_{12}x_1$
:
Here \begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&2\eta({-},x_1)\eta(x_2,x_{12}x_1)-2q_{21}\eta({-},x_1)\eta(x_{12},x_2x_1) +\eta({-},x_1)\eta(x_{12},x_{12}),\\
\eta(y_1,z_1)\eta({-},y_2z_2)=&\eta(x_{12},x_{12})\eta({-},x_1).\end{align*}
\begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&2\eta({-},x_1)\eta(x_2,x_{12}x_1)-2q_{21}\eta({-},x_1)\eta(x_{12},x_2x_1) +\eta({-},x_1)\eta(x_{12},x_{12}),\\
\eta(y_1,z_1)\eta({-},y_2z_2)=&\eta(x_{12},x_{12})\eta({-},x_1).\end{align*}
-
 $u_{x_1}\!\left(x_{12},x_{12}x_1\right)=\eta(x_{12},x_{12})=d_{x_1}\!\left(x_{12},x_{12}x_1\right)$
.
$u_{x_1}\!\left(x_{12},x_{12}x_1\right)=\eta(x_{12},x_{12})=d_{x_1}\!\left(x_{12},x_{12}x_1\right)$
. -
 $u_x\!\left(x_{12},x_{12}x_1\right)=d_x\!\left(x_{12},x_{12}x_1\right)=0$
for
$u_x\!\left(x_{12},x_{12}x_1\right)=d_x\!\left(x_{12},x_{12}x_1\right)=0$
for
 $x\neq x_1$
.
$x\neq x_1$
.
-
(ii)
 $y=x_{12}$
and
$y=x_{12}$
and
 $z=x_2x_{12}$
:
Then
$z=x_2x_{12}$
:
Then \begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&\eta({-},x_2)\eta(x_1,x_2x_{12})-q_{12}\eta({-},x_2)\eta(x_2x_1,x_{12}),\\\eta(y_1,z_1)\eta({-},y_2z_2)=&-q_{21}\eta(x_2x_1,x_{12})\eta({-},x_2)+\eta(x_1,x_2x_{12})\eta({-},x_2)\\&+2\eta(x_2x_1,x_2x_1)\eta({-},x_2).\end{align*}
\begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&\eta({-},x_2)\eta(x_1,x_2x_{12})-q_{12}\eta({-},x_2)\eta(x_2x_1,x_{12}),\\\eta(y_1,z_1)\eta({-},y_2z_2)=&-q_{21}\eta(x_2x_1,x_{12})\eta({-},x_2)+\eta(x_1,x_2x_{12})\eta({-},x_2)\\&+2\eta(x_2x_1,x_2x_1)\eta({-},x_2).\end{align*}
-
 $u_{x_2}(x_{12},x_2x_{12})=\eta(x_{12},x_{12})=d_{x_2}(x_{12},x_2x_{12})$
.
$u_{x_2}(x_{12},x_2x_{12})=\eta(x_{12},x_{12})=d_{x_2}(x_{12},x_2x_{12})$
. -
 $u_x(x_{12},x_2x_{12})=d_x(x_{12},x_2x_{12})=0$
for
$u_x(x_{12},x_2x_{12})=d_x(x_{12},x_2x_{12})=0$
for
 $x\neq x_2$
.
$x\neq x_2$
.
-
(iii)
 $y=x_2x_1$
and
$y=x_2x_1$
and
 $z=x_{12}x_{1}$
:
In this case
$z=x_{12}x_{1}$
:
In this case \begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&q_{21}\eta({-},x_1)\eta(x_2,x_{12}x_1)-2q_{21}\eta({-},x_1)\eta(x_2x_1,x_2x_1)\\&+\eta({-},x_1)\eta(x_2x_1,x_{12}),\\\eta(y_1,z_1)\eta({-},y_2z_2)=&\eta(x_2x_1,x_{12})\eta({-},x_1)+q_{12}\eta(x_2,x_{12}x_1)\eta({-},x_1).\end{align*}
\begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&q_{21}\eta({-},x_1)\eta(x_2,x_{12}x_1)-2q_{21}\eta({-},x_1)\eta(x_2x_1,x_2x_1)\\&+\eta({-},x_1)\eta(x_2x_1,x_{12}),\\\eta(y_1,z_1)\eta({-},y_2z_2)=&\eta(x_2x_1,x_{12})\eta({-},x_1)+q_{12}\eta(x_2,x_{12}x_1)\eta({-},x_1).\end{align*}
 $u_{x}(x_{12},x_2x_{12})=0=d_{x}(x_{12},x_2x_{12})$
for any
$u_{x}(x_{12},x_2x_{12})=0=d_{x}(x_{12},x_2x_{12})$
for any
 $x\in \mathbb{B}_\mathfrak{q}$
.
$x\in \mathbb{B}_\mathfrak{q}$
.
-
(iv)
 $y=x_{2}x_1$
and
$y=x_{2}x_1$
and
 $z=x_{2}x_{12}$
:
Then,
$z=x_{2}x_{12}$
:
Then, \begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&\eta({-},x_2)\eta(x_1,x_2x_{12})-q_{12}\eta({-},x_2)\eta(x_2x_1,x_{12}),\\\eta(y_1,z_1)\eta({-},y_2z_2)=&-q_{21}\eta(x_2x_1,x_{12})\eta({-},x_2)+\eta(x_1,x_2x_{12})\eta({-},x_2)\\&+2\eta(x_2x_1,x_2x_1)\eta({-},x_2).\end{align*}
\begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&\eta({-},x_2)\eta(x_1,x_2x_{12})-q_{12}\eta({-},x_2)\eta(x_2x_1,x_{12}),\\\eta(y_1,z_1)\eta({-},y_2z_2)=&-q_{21}\eta(x_2x_1,x_{12})\eta({-},x_2)+\eta(x_1,x_2x_{12})\eta({-},x_2)\\&+2\eta(x_2x_1,x_2x_1)\eta({-},x_2).\end{align*}
-
 $u_{x_2}(x_{2}x_1,x_2x_{12})=\eta(x_{12},x_{12})=d_{x_2}(x_{2}x_1,x_2x_{12})$
.
$u_{x_2}(x_{2}x_1,x_2x_{12})=\eta(x_{12},x_{12})=d_{x_2}(x_{2}x_1,x_2x_{12})$
. -
 $u_x(x_{2}x_1,x_2x_{12})=d_x(x_{2}x_1,x_2x_{12})=0$
for
$u_x(x_{2}x_1,x_2x_{12})=d_x(x_{2}x_1,x_2x_{12})=0$
for
 $x\neq x_2$
.
$x\neq x_2$
.
-
(v)
 $y=x_{2}$
and
$y=x_{2}$
and
 $z=x_{2}x_{12}x_1$
:
Then,
$z=x_{2}x_{12}x_1$
:
Then, \begin{align*}\eta(x,y_1z_1)\eta(y_2,z_2)=&-\eta(x,x_2)\eta(x_2,x_{12}x_1),\\\eta(y_1,z_1)\eta(x,y_2z_2)=&-\eta(x_2,x_{12}x_1)\eta(x,x_2).\end{align*}
\begin{align*}\eta(x,y_1z_1)\eta(y_2,z_2)=&-\eta(x,x_2)\eta(x_2,x_{12}x_1),\\\eta(y_1,z_1)\eta(x,y_2z_2)=&-\eta(x_2,x_{12}x_1)\eta(x,x_2).\end{align*}
-
 $u_{x_2}(x_{2},x_2x_{12}x_1)=-\eta(x_{2},x_{12}x_1)=d_{x_2}(x_{2},x_2x_{12}x_1)$
.
$u_{x_2}(x_{2},x_2x_{12}x_1)=-\eta(x_{2},x_{12}x_1)=d_{x_2}(x_{2},x_2x_{12}x_1)$
. -
 $u_x(x_{2},x_2x_{12}x_1)=d_x(x_{2},x_2x_{12}x_1)=0$
for
$u_x(x_{2},x_2x_{12}x_1)=d_x(x_{2},x_2x_{12}x_1)=0$
for
 $x\neq x_2$
.
$x\neq x_2$
.
deg(y) + deg(z) = 6:
-
(i)
 $y=x_{12}$
and
$y=x_{12}$
and
 $z=x_2x_{12}x_1$
:
Then,
$z=x_2x_{12}x_1$
:
Then, \begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&q_{21}\eta({-},x_2x_{1})\eta(x_{12},x_{12}),\\\eta(y_1,z_1)\eta({-},y_2z_2)=&\eta(x_{12},x_2x_1)\eta({-},x_2x_1)+q_{21}\eta(x_1,x_2x_{12})\eta({-},x_2x_1).\end{align*}
\begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&q_{21}\eta({-},x_2x_{1})\eta(x_{12},x_{12}),\\\eta(y_1,z_1)\eta({-},y_2z_2)=&\eta(x_{12},x_2x_1)\eta({-},x_2x_1)+q_{21}\eta(x_1,x_2x_{12})\eta({-},x_2x_1).\end{align*}
-
 $u_{x_2x_1}(x_{12},x_2x_{12}x_1)=q_{21}\eta(x_{12},x_{12})=d_{x_2x_1}(x_{12},x_2x_{12}x_1)$
.
$u_{x_2x_1}(x_{12},x_2x_{12}x_1)=q_{21}\eta(x_{12},x_{12})=d_{x_2x_1}(x_{12},x_2x_{12}x_1)$
. -
 $u_x(x_{12},x_2x_{12}x_1)=d_x(x_{12},x_2x_{12}x_1)=0$
for
$u_x(x_{12},x_2x_{12}x_1)=d_x(x_{12},x_2x_{12}x_1)=0$
for
 $x\neq x_2x_1$
.
$x\neq x_2x_1$
.
-
(ii)
 $y=x_{2}x_1$
and
$y=x_{2}x_1$
and
 $z=x_2x_{12}x_1$
:
Thus,
$z=x_2x_{12}x_1$
:
Thus, \begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&\eta({-},x_2x_1)\eta(x_1,x_2x_{12})-q_{21}\eta({-},x_{12})\eta(x_2,x_{12}x_1)\\&+q_{21}\eta({-},x_{12})\eta(x_2x_1,x_2x_1),\\\eta(y_1,z_1)\eta({-},y_2z_2)=&\eta(x_1,x_2x_{12})\eta({-},x_2x_1).\end{align*}
\begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&\eta({-},x_2x_1)\eta(x_1,x_2x_{12})-q_{21}\eta({-},x_{12})\eta(x_2,x_{12}x_1)\\&+q_{21}\eta({-},x_{12})\eta(x_2x_1,x_2x_1),\\\eta(y_1,z_1)\eta({-},y_2z_2)=&\eta(x_1,x_2x_{12})\eta({-},x_2x_1).\end{align*}
-
 $u_{x_2x_1}(x_{2}x_1,x_2x_{12}x_1)=\eta(x_{1},x_2x_{12})=d_{x_2x_1}(x_{2}x_1,x_2x_{12}x_1)$
.
$u_{x_2x_1}(x_{2}x_1,x_2x_{12}x_1)=\eta(x_{1},x_2x_{12})=d_{x_2x_1}(x_{2}x_1,x_2x_{12}x_1)$
. -
 $u_x(x_{2}x_1,x_2x_{12}x_1)=d_x(x_{2}x_1,x_2x_{12}x_1)=0$
for
$u_x(x_{2}x_1,x_2x_{12}x_1)=d_x(x_{2}x_1,x_2x_{12}x_1)=0$
for
 $x\neq x_2x_1$
.
$x\neq x_2x_1$
.
-
(iii)
 $y=x_{12}x_1$
and
$y=x_{12}x_1$
and
 $z=x_2x_{12}$
:
Then,
$z=x_2x_{12}$
:
Then, \begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&-2q_{12}\eta({-},x_1x_2)\eta(x_2x_1,x_{12})-\eta({-},x_1x_2)\eta(x_{12},x_{12})\\&+\eta({-},x_{12})\eta(x_1,x_2x_{12}),\\\eta(y_1,z_1)\eta({-},y_2z_2)=&-2q_{12}\eta(x_{12},x_2x_1)\eta({-},x_1x_2)-\eta(x_{12},x_{12})\eta({-},x_{1}x_2)\\&+\eta(x_1,x_2x_{12})\eta({-},x_{12}).\end{align*}
\begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2)=&-2q_{12}\eta({-},x_1x_2)\eta(x_2x_1,x_{12})-\eta({-},x_1x_2)\eta(x_{12},x_{12})\\&+\eta({-},x_{12})\eta(x_1,x_2x_{12}),\\\eta(y_1,z_1)\eta({-},y_2z_2)=&-2q_{12}\eta(x_{12},x_2x_1)\eta({-},x_1x_2)-\eta(x_{12},x_{12})\eta({-},x_{1}x_2)\\&+\eta(x_1,x_2x_{12})\eta({-},x_{12}).\end{align*}
-
 $u_{x_{12}}(x_{12}x_1,x_2x_{12})=-q_{12}\eta(x_2x_1,x_{12})=d_{x_{12}}(x_{12}x_1,x_2x_{12})$
.
$u_{x_{12}}(x_{12}x_1,x_2x_{12})=-q_{12}\eta(x_2x_1,x_{12})=d_{x_{12}}(x_{12}x_1,x_2x_{12})$
. -
 $u_{x_{2}x_1}(x_{12}x_1,x_2x_{12})=-\eta(x_2x_1,x_{12})=d_{x_{2}x_1}(x_{12}x_1,x_2x_{12})$
.
$u_{x_{2}x_1}(x_{12}x_1,x_2x_{12})=-\eta(x_2x_1,x_{12})=d_{x_{2}x_1}(x_{12}x_1,x_2x_{12})$
. -
 $u_x(x_{12}x_1,x_2x_{12})=d_x(x_{12}x_1,x_2x_{12})=0$
for
$u_x(x_{12}x_1,x_2x_{12})=d_x(x_{12}x_1,x_2x_{12})=0$
for
 $x\neq x_{12},x_2x_1$
.
$x\neq x_{12},x_2x_1$
.
-
(iv)
 $y=x_{12}x_1=z$
or
$y=x_{12}x_1=z$
or
 $y=x_2x_{12}=z$
. In these cases, we obtain zero in both sides of (5.1) and so
$y=x_2x_{12}=z$
. In these cases, we obtain zero in both sides of (5.1) and so
 $u_x(y,z)=0=d_x(y,z)$
.
$u_x(y,z)=0=d_x(y,z)$
.
deg(y) + deg(z) = 7:
-
(i)
 $y=x_{12}x_1$
and
$y=x_{12}x_1$
and
 $z=x_2x_{12}x_1$
:
Here we have
$z=x_2x_{12}x_1$
:
Here we have \begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2) & = -4\eta({-},x_1x_2x_1)\eta(x_2x_1,x_2x_1)+2q_{21}\eta({-},x_1x_{12})\eta(x_2x_1,x_2x_1)\\
& \quad +2q_{21}\eta({-},x_1x_2x_1)\eta(x_2x_1,x_{12})-\eta({-},x_1x_{12})\eta(x_{12},x_2x_1)\\
&\quad +2q_{21}\eta({-},x_1x_2x_1)\eta(x_{12},x_2x_1)-\eta({-},x_1x_2x_1)\eta(x_{12},x_{12})\\
&\quad +\eta({-},x_{12}x_1)\eta(x_1,x_2x_{12})+\eta({-},x_{12}x_1)\eta(x_{12}x_1,x_2),\\
\eta(y_1,z_1)\eta({-},y_2z_2) & =\eta(x_{12}x_1,x_2)\eta({-},x_{12}x_1)+\eta(x_1,x_2x_{12})\eta({-},x_{12}x_1)\\
&\quad -2q_{12}\eta(x_{12},x_2x_1)\eta({-},x_1x_2x_1)-\eta(x_{12},x_{12})\eta({-},x_1x_2x_1)\\
&\quad -\eta(x_{12},x_2x_1)\eta({-},x_1x_{12}).\end{align*}
\begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2) & = -4\eta({-},x_1x_2x_1)\eta(x_2x_1,x_2x_1)+2q_{21}\eta({-},x_1x_{12})\eta(x_2x_1,x_2x_1)\\
& \quad +2q_{21}\eta({-},x_1x_2x_1)\eta(x_2x_1,x_{12})-\eta({-},x_1x_{12})\eta(x_{12},x_2x_1)\\
&\quad +2q_{21}\eta({-},x_1x_2x_1)\eta(x_{12},x_2x_1)-\eta({-},x_1x_2x_1)\eta(x_{12},x_{12})\\
&\quad +\eta({-},x_{12}x_1)\eta(x_1,x_2x_{12})+\eta({-},x_{12}x_1)\eta(x_{12}x_1,x_2),\\
\eta(y_1,z_1)\eta({-},y_2z_2) & =\eta(x_{12}x_1,x_2)\eta({-},x_{12}x_1)+\eta(x_1,x_2x_{12})\eta({-},x_{12}x_1)\\
&\quad -2q_{12}\eta(x_{12},x_2x_1)\eta({-},x_1x_2x_1)-\eta(x_{12},x_{12})\eta({-},x_1x_2x_1)\\
&\quad -\eta(x_{12},x_2x_1)\eta({-},x_1x_{12}).\end{align*}
-
 $u_{x_{12}x_1}(x_{12}x_1,x_2x_{12}x_1)=2\eta(x_1,x_2x_{12})=d_{x_{12}x_1}(x_{12}x_1,x_2x_{12}x_1)$
.
$u_{x_{12}x_1}(x_{12}x_1,x_2x_{12}x_1)=2\eta(x_1,x_2x_{12})=d_{x_{12}x_1}(x_{12}x_1,x_2x_{12}x_1)$
. -
 $u_x(x_{12}x_1,x_2x_{12}x_1)=d_x(x_{12}x_1,x_2x_{12}x_1)=0$
for
$u_x(x_{12}x_1,x_2x_{12}x_1)=d_x(x_{12}x_1,x_2x_{12}x_1)=0$
for
 $x\neq x_{12}x_1$
.
$x\neq x_{12}x_1$
.
-
(ii)
 $y=x_2x_{12}$
and
$y=x_2x_{12}$
and
 $z=x_2x_{12}x_1$
:
Then,
$z=x_2x_{12}x_1$
:
Then, \begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2) & =q_{21}\eta({-},x_{12}x_2)\eta(x_2,x_{12}x_1)-2\eta({-},x_2x_1x_2)\eta(x_2,x_{12}x_1)\\
&\quad +q_{21}\eta({-},x_2x_{12})\eta(x_{12},x_2x_1)-\eta({-},x_2x_{12})\eta(x_2x_{12},x_1),\\
\eta(y_1,z_1)\eta({-},y_2z_2) & =-\eta(x_2x_{12},x_1)\eta({-},x_2x_{12})-q_{21}\eta(x_{12},x_2x_1)\eta({-},x_2x_{12})\\
&\quad +2\eta(x_2x_1,x_2x_1)\eta({-},x_2x_{12})-q_{21}\eta(x_{12},x_{2}x_1)\eta({-},x_2x_{12}).\end{align*}
\begin{align*}\eta({-},y_1z_1)\eta(y_2,z_2) & =q_{21}\eta({-},x_{12}x_2)\eta(x_2,x_{12}x_1)-2\eta({-},x_2x_1x_2)\eta(x_2,x_{12}x_1)\\
&\quad +q_{21}\eta({-},x_2x_{12})\eta(x_{12},x_2x_1)-\eta({-},x_2x_{12})\eta(x_2x_{12},x_1),\\
\eta(y_1,z_1)\eta({-},y_2z_2) & =-\eta(x_2x_{12},x_1)\eta({-},x_2x_{12})-q_{21}\eta(x_{12},x_2x_1)\eta({-},x_2x_{12})\\
&\quad +2\eta(x_2x_1,x_2x_1)\eta({-},x_2x_{12})-q_{21}\eta(x_{12},x_{2}x_1)\eta({-},x_2x_{12}).\end{align*}
-
 $u_{x_2x_{12}}(x_{2}x_{12},x_2x_{12}x_1)=-\eta(x_2,x_{12}x_1)=d_{x_2x_{12}}(x_2x_{12},x_2x_{12}x_1)$
.
$u_{x_2x_{12}}(x_{2}x_{12},x_2x_{12}x_1)=-\eta(x_2,x_{12}x_1)=d_{x_2x_{12}}(x_2x_{12},x_2x_{12}x_1)$
. -
 $u_x(x_{2}x_{12},x_2x_{12}x_1)=d_x(x_{2}x_{12},x_2x_{12}x_1)=0$
for
$u_x(x_{2}x_{12},x_2x_{12}x_1)=d_x(x_{2}x_{12},x_2x_{12}x_1)=0$
for
 $x\neq x_2x_{12}$
.
$x\neq x_2x_{12}$
.
![]() $gr(y)+gr(z)=8$
:
$gr(y)+gr(z)=8$
:
(i) We obtain zero in both sides of (5.1), hence
![]() $u_x(y,z)=d_x(y,z)=0$
.
$u_x(y,z)=d_x(y,z)=0$
.
The other cases are very similar. Now, we have that
![]() $\eta$
verifies (5.1) and the hypothesis of the Lemma 5.8; hence
$\eta$
verifies (5.1) and the hypothesis of the Lemma 5.8; hence
![]() $\eta$
verifies (5.2) and
$\eta$
verifies (5.2) and
![]() $e^{\eta}$
is multiplicative.
$e^{\eta}$
is multiplicative.
Lemma 6.9. Let
![]() $\sigma=\sigma_{\boldsymbol\lambda}$
be as in Theorem 6.5 and
$\sigma=\sigma_{\boldsymbol\lambda}$
be as in Theorem 6.5 and
![]() $\eta\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^H$
as in (6.11).
$\eta\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^H$
as in (6.11).
Assume that
![]() $e^{\eta}$
is a Hopf cocycle, cohomologous to
$e^{\eta}$
is a Hopf cocycle, cohomologous to
![]() $\sigma$
. Then
$\sigma$
. Then
Moreover, if
![]() $\alpha\rightharpoonup\sigma=e^{\eta}$
,
$\alpha\rightharpoonup\sigma=e^{\eta}$
,
![]() $\alpha\in U\!\left(\mathfrak{B}_{\mathfrak{q}}^{\ast}\right)$
, then
$\alpha\in U\!\left(\mathfrak{B}_{\mathfrak{q}}^{\ast}\right)$
, then
![]() $\alpha(1)=1$
and
$\alpha(1)=1$
and
Proof. Suppose that there exist
![]() $\alpha\in U(\mathfrak{B}_{\mathfrak{q}}^\ast)$
such that
$\alpha\in U(\mathfrak{B}_{\mathfrak{q}}^\ast)$
such that
![]() $\alpha\rightharpoonup \sigma=e^\eta$
. In first place, we may define
$\alpha\rightharpoonup \sigma=e^\eta$
. In first place, we may define
![]() $\alpha(1)=1$
and then Remark 5.6 gives us
$\alpha(1)=1$
and then Remark 5.6 gives us
![]() $\lambda_1=\eta_1$
and
$\lambda_1=\eta_1$
and
![]() $\lambda_2=\eta_2$
. In particular, it follows that
$\lambda_2=\eta_2$
. In particular, it follows that
-
 $\alpha(x_1)=\alpha(x_2)=0$
.
$\alpha(x_1)=\alpha(x_2)=0$
. -
 $\alpha\!\left(x_ix_j\right)=0$
, for all
$\alpha\!\left(x_ix_j\right)=0$
, for all
 $i,j\in \mathbb{I}_2$
with
$i,j\in \mathbb{I}_2$
with
 $i\neq j$
.
$i\neq j$
.
On the other hand, from the relations
we obtain that
![]() $\alpha^{-1}(x_ix_jx_i)=0$
, so
$\alpha^{-1}(x_ix_jx_i)=0$
, so
![]() $\alpha(x_ix_jx_i)=0$
. Now we compute
$\alpha(x_ix_jx_i)=0$
. Now we compute
![]() $\alpha(x_2x_{12}x_1)$
, expanding
$\alpha(x_2x_{12}x_1)$
, expanding
![]() $\alpha\rightharpoonup \sigma(x_1,x_2x_{12})=e^\eta(x_1,x_2x_{12})$
and
$\alpha\rightharpoonup \sigma(x_1,x_2x_{12})=e^\eta(x_1,x_2x_{12})$
and
![]() $\alpha\rightharpoonup \sigma(x_2,x_{12}x_1)=e^\eta(x_2,x_{12}x_1)$
. For the first,
$\alpha\rightharpoonup \sigma(x_2,x_{12}x_1)=e^\eta(x_2,x_{12}x_1)$
. For the first,
 \begin{align*}\alpha\rightharpoonup \sigma(x_2,x_{12}x_1)&=\eta_{121}\\\sigma(x_2,x_{12}x_1)+\alpha^{-1}(x_2x_{12}x_1)&=\eta_{121}\\\alpha^{-1}(x_2x_{12}x_1)&=\eta_{121}-2q_{12}\lambda_1\lambda_2.\end{align*}
\begin{align*}\alpha\rightharpoonup \sigma(x_2,x_{12}x_1)&=\eta_{121}\\\sigma(x_2,x_{12}x_1)+\alpha^{-1}(x_2x_{12}x_1)&=\eta_{121}\\\alpha^{-1}(x_2x_{12}x_1)&=\eta_{121}-2q_{12}\lambda_1\lambda_2.\end{align*}
For the second, we obtain
 \begin{align*}\alpha\rightharpoonup \sigma(x_1,x_{2}x_{12})&=\eta_{212}\\\sigma(x_1,x_{2}x_{12})-\alpha^{-1}(x_2x_{12}x_1)&=\eta_{212}\\\alpha^{-1}(x_2x_{12}x_1)&=\lambda_{12}-\eta_{212}.\end{align*}
\begin{align*}\alpha\rightharpoonup \sigma(x_1,x_{2}x_{12})&=\eta_{212}\\\sigma(x_1,x_{2}x_{12})-\alpha^{-1}(x_2x_{12}x_1)&=\eta_{212}\\\alpha^{-1}(x_2x_{12}x_1)&=\lambda_{12}-\eta_{212}.\end{align*}
Hence, as
![]() $\alpha^{-1}(x_2x_{12}x_1)$
exists, then
$\alpha^{-1}(x_2x_{12}x_1)$
exists, then
![]() $\eta_{121}+\eta_{212}=\lambda_{12}+2q_{12}\lambda_1\lambda_2$
.
$\eta_{121}+\eta_{212}=\lambda_{12}+2q_{12}\lambda_1\lambda_2$
.
Let
![]() $\overline{\textrm{C}}\subset\textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^\Gamma$
be the set defined by
$\overline{\textrm{C}}\subset\textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^\Gamma$
be the set defined by
Notice that
![]() $\eta\in \overline{\textrm{C}}$
if and only if
$\eta\in \overline{\textrm{C}}$
if and only if
Remark 6.10. In particular,
![]() $\textrm{C}\subset \overline{\textrm{C}}$
and this inclusion is strict. However, they coincide up to cobordisms, see (6.10):
$\textrm{C}\subset \overline{\textrm{C}}$
and this inclusion is strict. However, they coincide up to cobordisms, see (6.10):
We have the following characterization of Hopf cocycles that are an exponential map of a Hochschild cocycle.
Lemma 6.11.
![]() $e^\eta$
is a Hopf 2-cocycle if and only if
$e^\eta$
is a Hopf 2-cocycle if and only if
![]() $\eta \in \overline{\textrm{C}}$
.
$\eta \in \overline{\textrm{C}}$
.
Proof. Let
![]() $\eta\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^\Gamma$
be a Hochschild cocycle as in (6.11). Assume
$\eta\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^\Gamma$
be a Hochschild cocycle as in (6.11). Assume
![]() $e^\eta$
is a Hopf 2-cocycle. We compute the values of
$e^\eta$
is a Hopf 2-cocycle. We compute the values of
![]() $e^\eta$
in two ways. Namely, via the decomposition formulas in Example 3.4 and via the definition of an exponential map. We obtain a list of equations that imply that
$e^\eta$
in two ways. Namely, via the decomposition formulas in Example 3.4 and via the definition of an exponential map. We obtain a list of equations that imply that
![]() $\eta \in \overline{\textrm{C}}$
. We show below some of these calculations.
$\eta \in \overline{\textrm{C}}$
. We show below some of these calculations.
![]() $e^{\eta}(x_2x_1,x_{12})$
: Using the decomposition formula, we obtain
$e^{\eta}(x_2x_1,x_{12})$
: Using the decomposition formula, we obtain
but the definition of exponential map gives
Thus,
![]() $\eta_1\eta_2=0$
. From now on, we suppose that this relations hold.
$\eta_1\eta_2=0$
. From now on, we suppose that this relations hold.
![]() $e^{\eta}(x_{12}x_1,x_{12}x_1)$
: We obtain
$e^{\eta}(x_{12}x_1,x_{12}x_1)$
: We obtain
So, we get the relation
![]() $\eta_1(\eta_{121}+\eta_{212})=0$
.
$\eta_1(\eta_{121}+\eta_{212})=0$
.
![]() $e^{\eta}(x_2x_{12},x_2x_{12})$
: Here we get
$e^{\eta}(x_2x_{12},x_2x_{12})$
: Here we get
Hence
![]() $\eta_2(\eta_{121}+\eta_{212})=0$
.
$\eta_2(\eta_{121}+\eta_{212})=0$
.
Therefore, we see that
![]() $\eta\in\overline{\textrm{C}}$
.
$\eta\in\overline{\textrm{C}}$
.
Conversely, suppose that
![]() $\eta\in\overline{\textrm{C}}$
. If
$\eta\in\overline{\textrm{C}}$
. If
![]() $\eta=\eta_{121}\xi_{121}^2+\eta_{212}\xi_{212}^1$
, then
$\eta=\eta_{121}\xi_{121}^2+\eta_{212}\xi_{212}^1$
, then
![]() $e^{\eta}$
is a Hopf cocycle by Proposition 6.7. Now, suppose that
$e^{\eta}$
is a Hopf cocycle by Proposition 6.7. Now, suppose that
![]() $\eta=\eta_1\xi_1^1+\eta_{121}\xi_{121}^2-\eta_{121}\xi_{212}^1$
. The case
$\eta=\eta_1\xi_1^1+\eta_{121}\xi_{121}^2-\eta_{121}\xi_{212}^1$
. The case
![]() $\eta=\eta_2\xi_2^2+\eta_{121}\xi_{121}^2-\eta_{121}\xi_{212}^1$
is analogous.
$\eta=\eta_2\xi_2^2+\eta_{121}\xi_{121}^2-\eta_{121}\xi_{212}^1$
is analogous.
We claim that, by definition,
![]() $e^{\eta}$
is given by the table
$e^{\eta}$
is given by the table
Indeed, by Remark 5.4 and a degree argument, plus considering that
![]() $\eta_1\eta_2=0$
, we see that
$\eta_1\eta_2=0$
, we see that
![]() $e^{\eta}(x,y)=\eta(x,y)$
for
$e^{\eta}(x,y)=\eta(x,y)$
for
![]() $\deg x+\deg y\leq4$
.
$\deg x+\deg y\leq4$
.
On the other hand, if
![]() $\deg x+\deg y=5$
, then
$\deg x+\deg y=5$
, then

so
![]() $e^\eta(x,y)=0$
in this case. Now, when
$e^\eta(x,y)=0$
in this case. Now, when
![]() $\deg x+\deg y=6$
and
$\deg x+\deg y=6$
and
![]() $\deg x\neq\deg y$
, it follows that for each of the four possible cases, there are scalars
$\deg x\neq\deg y$
, it follows that for each of the four possible cases, there are scalars
![]() $(a_{ij})_{i,j}$
, depending on x, y, such that the following relation holds:
$(a_{ij})_{i,j}$
, depending on x, y, such that the following relation holds:
Thus
![]() $e^\eta(x,y)=0$
as
$e^\eta(x,y)=0$
as
![]() $\eta(x,y)=0$
and
$\eta(x,y)=0$
and
![]() $\eta\!\left(x_j,x_{ij}x_j\right)=q_{ij}\eta\!\left(x_j,x_jx_{ij}\right)=0$
. If
$\eta\!\left(x_j,x_{ij}x_j\right)=q_{ij}\eta\!\left(x_j,x_jx_{ij}\right)=0$
. If
![]() $\deg x=\deg y=3$
, then it follows that
$\deg x=\deg y=3$
, then it follows that
![]() $e^\eta(x,y)=0$
.
$e^\eta(x,y)=0$
.
If
![]() $\deg x+\deg y=7$
, then we see that
$\deg x+\deg y=7$
, then we see that
![]() $e^\eta(x,y)=0$
. Finally, if
$e^\eta(x,y)=0$
. Finally, if
![]() $x=y=x_2x_{12}x_1$
, then it is easy to see that
$x=y=x_2x_{12}x_1$
, then it is easy to see that
![]() $\eta^{\ast k}(x,y)=0$
for
$\eta^{\ast k}(x,y)=0$
for
![]() $k\neq 2$
and
$k\neq 2$
and
 \begin{align*}\eta^{\ast 2}(x,y)=&\, -4\eta(x_2x_1,x_2x_1)^2 +4q_{21}\eta(x_2x_1,x_{12})\eta(x_2x_1,x_2x_1)\\
&+\eta(x_1,x_2x_{12})\eta(x_2x_{12},x_1)+2q_{21}\eta(x_{12},x_2x_1)\eta(x_2x_1,x_2x_1)\\
&-\eta(x_{12},x_{12})\eta(x_2x_1,x_2x_1)-\eta(x_{12},x_2x_1)\eta(x_2x_1,x_{12})
\end{align*}
\begin{align*}\eta^{\ast 2}(x,y)=&\, -4\eta(x_2x_1,x_2x_1)^2 +4q_{21}\eta(x_2x_1,x_{12})\eta(x_2x_1,x_2x_1)\\
&+\eta(x_1,x_2x_{12})\eta(x_2x_{12},x_1)+2q_{21}\eta(x_{12},x_2x_1)\eta(x_2x_1,x_2x_1)\\
&-\eta(x_{12},x_{12})\eta(x_2x_1,x_2x_1)-\eta(x_{12},x_2x_1)\eta(x_2x_1,x_{12})
\end{align*}
 \begin{align*}
&+2\eta(x_{12}x_1,x_2)\eta(x_2,x_{12}x_1)+2q_{21}\eta(x_2x_1,x_2x_1)\eta(x_{12},x_2x_1)\\
&-\eta(x_2x_1,x_{12})\eta(x_{12},x_2x_1)-\eta(x_2x_1,x_2x_1)\eta(x_{12},x_{12})\\
&+\eta(x_2x_{12},x_1)\eta(x_1,x_2x_{12})\\
=&\, -4\eta_{121}^2+4\eta_{121}^2+\eta_{212}\eta_{121}+2\eta_{121}^2-\eta_{121}^2-\eta_{212}\eta_{121}-\eta_{121}^2\\
&+2\eta_{212}\eta_{121}+2\eta_{121}^2-\eta_{121}^2-\eta_{121}^2-\eta_{212}\eta_{121}+\eta_{121}\eta_{212}\\
=&\, 2\eta_{212}\eta_{121}.\end{align*}
\begin{align*}
&+2\eta(x_{12}x_1,x_2)\eta(x_2,x_{12}x_1)+2q_{21}\eta(x_2x_1,x_2x_1)\eta(x_{12},x_2x_1)\\
&-\eta(x_2x_1,x_{12})\eta(x_{12},x_2x_1)-\eta(x_2x_1,x_2x_1)\eta(x_{12},x_{12})\\
&+\eta(x_2x_{12},x_1)\eta(x_1,x_2x_{12})\\
=&\, -4\eta_{121}^2+4\eta_{121}^2+\eta_{212}\eta_{121}+2\eta_{121}^2-\eta_{121}^2-\eta_{212}\eta_{121}-\eta_{121}^2\\
&+2\eta_{212}\eta_{121}+2\eta_{121}^2-\eta_{121}^2-\eta_{121}^2-\eta_{212}\eta_{121}+\eta_{121}\eta_{212}\\
=&\, 2\eta_{212}\eta_{121}.\end{align*}
Hence, recalling that
![]() $\eta_{212}=-\eta_{121}$
, we obtain that
$\eta_{212}=-\eta_{121}$
, we obtain that
![]() $e^\eta(x,y)=\frac{1}{2}\eta^{\ast 2}(x,y)=-\eta_{121}^2$
.
$e^\eta(x,y)=\frac{1}{2}\eta^{\ast 2}(x,y)=-\eta_{121}^2$
.
Now, let
![]() $\sigma=\sigma_{\eta_1,0,0}$
as in Theorem 6.5 and
$\sigma=\sigma_{\eta_1,0,0}$
as in Theorem 6.5 and
![]() $\alpha\in U\!\left(\mathfrak{B}_{\mathfrak{q}}^{\ast}\right)$
as in (6.19). Then
$\alpha\in U\!\left(\mathfrak{B}_{\mathfrak{q}}^{\ast}\right)$
as in (6.19). Then
![]() $\alpha\rightharpoonup\sigma_{\eta_1,0,0}(x_i,b)=e^\eta(x_i,b)$
, for any
$\alpha\rightharpoonup\sigma_{\eta_1,0,0}(x_i,b)=e^\eta(x_i,b)$
, for any
![]() $i\in\mathbb{I}_2$
,
$i\in\mathbb{I}_2$
,
![]() $b\in \mathbb{B}_\mathfrak{q}$
, see Lemma 6.9. Next, we apply the decomposition formulas to compute all values of the Hopf cocycle
$b\in \mathbb{B}_\mathfrak{q}$
, see Lemma 6.9. Next, we apply the decomposition formulas to compute all values of the Hopf cocycle
![]() $\alpha\rightharpoonup\sigma_{\eta_1,0,0}$
and we obtain that
$\alpha\rightharpoonup\sigma_{\eta_1,0,0}$
and we obtain that
![]() $\alpha\rightharpoonup\sigma=e^{\eta}$
. Therefore,
$\alpha\rightharpoonup\sigma=e^{\eta}$
. Therefore,
![]() $e^{\eta}$
is a Hopf cocycle.
$e^{\eta}$
is a Hopf cocycle.
Let
![]() $\textrm{Exp}(\textrm{C}), \textrm{Exp}(\overline{\textrm{C}})\subset Z^2(\mathfrak{B}_{\mathfrak{q}})$
be the subsets of Hopf cocycles that arise as exponential maps of elements of C and
$\textrm{Exp}(\textrm{C}), \textrm{Exp}(\overline{\textrm{C}})\subset Z^2(\mathfrak{B}_{\mathfrak{q}})$
be the subsets of Hopf cocycles that arise as exponential maps of elements of C and
![]() $\overline{\textrm{C}}$
, respectively. Next, we show that it is enough to consider exponential cocycles in
$\overline{\textrm{C}}$
, respectively. Next, we show that it is enough to consider exponential cocycles in
![]() $\textrm{Exp}(\textrm{C})$
.
$\textrm{Exp}(\textrm{C})$
.
Lemma 6.12. Let
![]() $\sigma_{\boldsymbol\lambda}\in Z^2(\mathfrak{B}_{\mathfrak{q}})$
be as in Theorem 6.5. Then
$\sigma_{\boldsymbol\lambda}\in Z^2(\mathfrak{B}_{\mathfrak{q}})$
be as in Theorem 6.5. Then
![]() $\sigma$
is cohomologous to a cocycle in
$\sigma$
is cohomologous to a cocycle in
![]() $\textrm{Exp}(\textrm{C})$
if and only
$\textrm{Exp}(\textrm{C})$
if and only
![]() $\sigma$
is cohomologous to a cocycle in
$\sigma$
is cohomologous to a cocycle in
![]() $\textrm{Exp}(\overline{\textrm{C}})$
.
$\textrm{Exp}(\overline{\textrm{C}})$
.
Proof. One implication is trivial. Assume
![]() $\sigma\sim_\alpha e^\eta$
,
$\sigma\sim_\alpha e^\eta$
,
![]() $\eta\in \overline{\textrm{C}}$
. That is,
$\eta\in \overline{\textrm{C}}$
. That is,
![]() $\alpha\rightharpoonup\sigma=e^\eta$
.
$\alpha\rightharpoonup\sigma=e^\eta$
.
If
![]() $\eta=\eta_{121}\xi_{121}^2+\eta_{212}\xi_{212}^1$
, then
$\eta=\eta_{121}\xi_{121}^2+\eta_{212}\xi_{212}^1$
, then
![]() $\eta\in \textrm{C}$
and we can take
$\eta\in \textrm{C}$
and we can take
![]() $\alpha=\epsilon$
.
$\alpha=\epsilon$
.
Fix now
![]() $\eta=\eta_1\xi_1^1+\eta_{121}\xi_{121}^2-\eta_{121}\xi_{212}^1$
. By Lemma 6.9, (notice that
$\eta=\eta_1\xi_1^1+\eta_{121}\xi_{121}^2-\eta_{121}\xi_{212}^1$
. By Lemma 6.9, (notice that
![]() $\eta_{212}=-\eta_{121}$
) if we define
$\eta_{212}=-\eta_{121}$
) if we define
![]() $\alpha^{\prime}$
by
$\alpha^{\prime}$
by
then
![]() $\alpha^{\prime}\rightharpoonup e^\eta=\sigma_{\eta_1,0,0}$
. But
$\alpha^{\prime}\rightharpoonup e^\eta=\sigma_{\eta_1,0,0}$
. But
![]() $\sigma_{\eta_1,0,0}=e^{\eta^{\prime}}$
and
$\sigma_{\eta_1,0,0}=e^{\eta^{\prime}}$
and
![]() $\eta^{\prime}=\eta_1\xi_1^1\in \textrm{C}$
. Hence
$\eta^{\prime}=\eta_1\xi_1^1\in \textrm{C}$
. Hence
![]() $\sigma\sim_\beta e^{\eta^{\prime}}$
, for
$\sigma\sim_\beta e^{\eta^{\prime}}$
, for
![]() $\beta=\alpha^{\prime}\ast\alpha$
.
$\beta=\alpha^{\prime}\ast\alpha$
.
The next theorem characterizes the cocycles that are co-homologous to an exponential map of a Hochschild cocycle.
Theorem 6.13. Let
![]() $\sigma=\sigma_{\boldsymbol\lambda}$
be a Hopf 2-cocycle as in Theorem 6.5,
$\sigma=\sigma_{\boldsymbol\lambda}$
be a Hopf 2-cocycle as in Theorem 6.5,
![]() $\sigma\neq\epsilon$
. Then the following are equivalent:
$\sigma\neq\epsilon$
. Then the following are equivalent:
-
(a)
 $\sigma\sim e^\eta$
for some
$\sigma\sim e^\eta$
for some
 $\eta\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^H$
.
$\eta\in \textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^H$
. -
(b) There is a unique no null
 $\lambda\in\{\lambda_1,\lambda_2,\lambda_{12}\}$
.
$\lambda\in\{\lambda_1,\lambda_2,\lambda_{12}\}$
. -
(c)
 $\sigma\in \textrm{Exp}\!\left(\textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^H\right)$
$\sigma\in \textrm{Exp}\!\left(\textrm{Z}^2\!\left(\mathfrak{B}_{\mathfrak{q}},\Bbbk\right)^H\right)$
In particular, any
![]() $\sigma=\sigma_{\lambda_1,\lambda_2,\lambda_{12}}$
with at least two nonzero parameters is pure.
$\sigma=\sigma_{\lambda_1,\lambda_2,\lambda_{12}}$
with at least two nonzero parameters is pure.
Proof. First, notice that we can assume
![]() $\eta\in \textrm{C}$
, by Lemma 6.12.
$\eta\in \textrm{C}$
, by Lemma 6.12.
![]() $(a)\Rightarrow (b)$
. Combining Lemma 6.9 with equations (6.12), we obtain
$(a)\Rightarrow (b)$
. Combining Lemma 6.9 with equations (6.12), we obtain
![]() $(b)\Rightarrow (c)$
. By looking at the tables in Theorem 6.5 and in the proof of Lemma 6.11, we see that this implication is clear as
$(b)\Rightarrow (c)$
. By looking at the tables in Theorem 6.5 and in the proof of Lemma 6.11, we see that this implication is clear as
![]() $\sigma_{(\lambda,0,0)}=e^{\lambda\xi_1^1}$
. Similarly,
$\sigma_{(\lambda,0,0)}=e^{\lambda\xi_1^1}$
. Similarly,
![]() $\sigma_{(0,\lambda,0)}=e^{\lambda\xi_2^2}$
. Finally, if
$\sigma_{(0,\lambda,0)}=e^{\lambda\xi_2^2}$
. Finally, if
![]() $\eta=\lambda\xi_{212}^1$
, it follows from Lemma 6.9 that
$\eta=\lambda\xi_{212}^1$
, it follows from Lemma 6.9 that
![]() $\sigma_{(0,0,\lambda)}=e^\eta$
, as
$\sigma_{(0,0,\lambda)}=e^\eta$
, as
![]() $\alpha=\epsilon$
therein.
$\alpha=\epsilon$
therein.
![]() $(c)\Rightarrow (a)$
. Clear.
$(c)\Rightarrow (a)$
. Clear.
Remark 6.14. In the setting of Lemma 6.9, we see that if
![]() $e^\eta\sim \epsilon$
, then
$e^\eta\sim \epsilon$
, then
![]() $\eta_1=\eta_2=0$
and
$\eta_1=\eta_2=0$
and
![]() $\eta_{121}=-\eta_{212}$
. In other words,
$\eta_{121}=-\eta_{212}$
. In other words,
![]() $\eta\in \textrm{B}^2(B,\Bbbk)$
as it is a scalar multiple of
$\eta\in \textrm{B}^2(B,\Bbbk)$
as it is a scalar multiple of
![]() $\beta\,:\!=\,\xi_{121}^2-\xi_{212}^1$
, see (6.10). Conversely,
$\beta\,:\!=\,\xi_{121}^2-\xi_{212}^1$
, see (6.10). Conversely,
![]() $e^\beta$
is a Hopf cocycle by Proposition 6.7 and Lemma 6.9 shows that
$e^\beta$
is a Hopf cocycle by Proposition 6.7 and Lemma 6.9 shows that
![]() $e^\beta\sim\sigma_{(0,0,0)}=\epsilon$
.
$e^\beta\sim\sigma_{(0,0,0)}=\epsilon$
.
We remark that
![]() $e^\beta\neq \epsilon$
, as shown in the table in the proof of Lemma 6.11.
$e^\beta\neq \epsilon$
, as shown in the table in the proof of Lemma 6.11.
Acknowledgments
We thank Andrea Solotar for conversations in early stages of this work, particularly about the contents of [Reference Ştefan25].