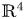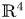Singularities of 3-parameter line congruences in

Débora Lopes; Maria Aparecida Soares Ruas; Igor Chagas Santos

doi:10.1017/prm.2022.41

Singularities of 3-parameter line congruences in $\mathbb {R}^{4}$

Part of: Differential topology Theory of singularities and catastrophe theory Classical differential geometry

Published online by Cambridge University Press: 21 June 2022

Débora Lopes

Maria Aparecida Soares Ruas

and

Igor Chagas Santos

Show author details

Débora Lopes: Affiliation:
Departmento de Matemática, Universidade Federal do Sergipe Av. Marechal Rondon, s/n Jardim Rosa Elze - CEP 49100-000 São Cristóvão, SE, Brazil ([email protected])
Maria Aparecida Soares Ruas: Affiliation:
Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, Av. Trabalhador S ao-carlense 400, São Carlos, SP 13566-590, Brazil ([email protected], [email protected])
Igor Chagas Santos: Affiliation:
Instituto de Ciências Matemáticas e de Computação, Universidade de São Paulo, Av. Trabalhador S ao-carlense 400, São Carlos, SP 13566-590, Brazil ([email protected], [email protected])

Article contents

Abstract
Introduction
Fixing notations, definitions and some basic results
Line congruences
Generic classification of 3-parameter line congruences in $\mathbb {R}^{4}$
Normal congruences
Blaschke normal congruences
References

Rights & Permissions

Abstract

In this paper, we give the generic classification of the singularities of 3-parameter line congruences in $\mathbb {R}^{4}$. We also classify the generic singularities of normal and Blaschke (affine) normal congruences.

Keywords

Line congruences Blaschke normal congruences Lagrangian singularities

MSC classification

Primary: 57R45: Singularities of differentiable mappings

Secondary: 58K25: Stability 53A15: Affine differential geometry

Type: Research Article
Information: Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 153 , Issue 3 , June 2023 , pp. 1045 - 1070

DOI: https://doi.org/10.1017/prm.2022.41 [Opens in a new window]
Copyright: Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of The Royal Society of Edinburgh

1. Introduction

In [Reference Monge20] Monge was one of the first authors to discuss line congruences in $\mathbb {R}^{3}$(see [Reference Ghys7] for historical notes). In recent decades, some papers are dedicated to the study of line congruences from singularity theory and differential affine geometry viewpoints [Reference Barajas, Craizer and Garcia1, Reference Craizer, Domitrz and Rios4, Reference Craizer and Garcia5, Reference Giblin and Zakalyukin8, Reference Izumiya, Saji and Takeuchi14]. There is a particular interest in the Blaschke normal congruences, in the behaviour of affine principal lines near an affine umbilic point [Reference Barajas, Craizer and Garcia1] and the behaviour of affine curvature lines at isolated umbilic points [Reference Craizer and Garcia5]. From singularity theory viewpoint, there is a particular interest in the classification of the singularities related to line congruences [Reference Izumiya, Saji and Takeuchi14].

A 3-parameter line congruence in $\mathbb {R}^{4}$ is nothing but a 3-parameter family of lines over a hypersurface in $\mathbb {R}^{4}$. Locally, we denote a line congruence by $\mathcal {C}$ = $\lbrace \boldsymbol {x}(u),\, \boldsymbol {\xi }(u) \rbrace$, where $\boldsymbol {x}$ is a parametrization of the reference hypersurface $S$ and $\boldsymbol {\xi }$ is a parametrization of a director hypersurface. A classical example appears when we consider the congruence generated by the normal lines to a regular hypersurface $S$ in $\mathbb {R}^{4}$, which is called an exact normal congruence. Here, we look at a line congruence $\mathcal {C}$ = $\lbrace \boldsymbol {x}(u),\, \boldsymbol {\xi }(u) \rbrace$ as a smooth map $F_{(\boldsymbol {x}, \boldsymbol {\xi })}: U \times I \rightarrow \mathbb {R}^{4}$, given by $F_{(\boldsymbol {x}, \boldsymbol {\xi })}(u,\,t) = \boldsymbol {x}(u) + t\boldsymbol {\xi }(u)$, where $I$ is an open interval and $U \subset \mathbb {R}^{3}$ is an open subset.

Taking into account [Reference Izumiya, Saji and Takeuchi14], we seek to provide a classification of the generic singularities of 3-parameter line congruences, 3-parameter normal congruences and Blaschke normal congruences in $\mathbb {R}^{4}$. As we want to use methods of singularity theory to classify congruences, in § 2 we review some results that are useful for the next sections. In § 3, we give some basic definitions and results on 3-parameter line congruences. In § 4 and 5 we use the same approach as in [Reference Izumiya, Saji and Takeuchi14] to classify generically the singularities of 3-parameter line congruences and 3-parameter normal congruences in theorems 4.1 and 5.2, respectively. The comparison of these two theorems shows that the generic singularities of 3-parameter line congruences are different from the generic singularities of 3-parameter normal congruences. Furthermore, we show that generically we also have singularities of corank $2$ in both cases and the proof of theorem 4.1 relies on a refinement of $\mathcal {K}$-orbits by $\mathcal {A}$-orbits of $\mathcal {A}_{e}$-codimension $1$.

In § 6, we look at the Blaschke (affine) normal congruences, i.e. congruences related to the Blaschke vector field of a non-degenerate hypersurface in $\mathbb {R}^{4}$, which is a classical equiaffine transversal vector field. Based on the theory of Lagrangian singularities, we define the family of support functions associated to the Blaschke congruence and prove that this is a Morse family of functions. We then classify the generic singularities of the Blaschke exact normal congruences and Blaschke normal congruences, providing a positive answer to the following conjecture presented in [Reference Izumiya, Saji and Takeuchi14]:

Conjecture Germs of generic Blaschke affine normal congruences at any point are Lagrangian stable.

2. Fixing notations, definitions and some basic results

We denote by $I \subset \mathbb {R}$ an open interval and $U$ an open subset of $\mathbb {R}^{3}$, where $t \in I$ and $u = (u_{1},\, u_{2},\, u_{3}) \in U$. Here, $\boldsymbol {x}: U \rightarrow \mathbb {R}^{4}$ is not necessarily an immersion, i.e. it may have singularities. Given any smooth map $f: U \rightarrow \mathbb {R}$, we denote by $f_{u_{i}}$ the derivative of $f$ with respect to $u_{i}$, $i=1,\,2,\,3$.

We now present some basic results in singularity theory which help us in the next sections. More details can be found in [Reference Gibson9, Reference Mond and Nuño Ballesteros19] and [Reference Wall23]. Given map germs $f,\,g: (\mathbb {R}^{n},\, \textbf {0}) \rightarrow (\mathbb {R}^{p},\, \textbf {0})$, if there is a germ of a diffeomorphism $h: (\mathbb {R}^{n},\, \boldsymbol {0}) \rightarrow (\mathbb {R}^{n},\, \boldsymbol {0})$, such that $h^{*}(f^{*}(\mathcal {M}_{p})) = g^{*}(\mathcal {M}_{p})$, where $h^{*}(f^{*}(\mathcal {M}_{p}))$ is the ideal generated by the coordinate functions of $f \circ h$ and $g^{*}(\mathcal {M}_{p})$ is the ideal generated by the coordinate functions of $g$, we say that $f$ and $g$ are $\mathcal {K}$-equivalent, denoted by, $f \underset {\mathcal {K}}{\sim } g$. Let $J^{k}(n,\,p)$ be the $k$-jet space of map germs from $\mathbb {R}^{n}$ to $\mathbb {R}^{p}$. For any $j^{k}f(0)$, we set

\[ \mathcal{K}^{k}(j^{k}f(0)) = \lbrace j^{k}g(0): f \underset{\mathcal{K}}{\sim} g \rbrace, \]

for the $\mathcal {K}$-orbit of $f$ in the space of $k$-jets $J^{k}(n,\,p)$. For a map germ $f: (\mathbb {R}^{n} \times \mathbb {R}^{r},\, \textbf {0}) \rightarrow (\mathbb {R}^{p},\, \textbf {0})$ we define

\begin{align*} j^{k}_{1}f: (\mathbb{R}^{n} \times \mathbb{R}^{r}, \textbf{0}) & \rightarrow J^{k}(n,p)\\ (x,u) & \mapsto j^{k}_{1}f(x,u), \end{align*}

where $j^{k}_{1}f(x,\,u)$ indicates the $k$-jet with respect to the first variable.

The next definition of unfolding is locally equivalent to the usual parametrized one (see [Reference Gibson, Wirthmüller, du Plessis and Looijenga10], chapter 3).

Definition 2.1 Let $f: (N,\, x_{0}) \rightarrow (P,\, y_{o})$ be a map germ between manifolds. An unfolding of $f$ is a triple $(F,\,i,\,j)$ of map germs, where $i: (N,\, x_0) \rightarrow (N',\, x'_{0})$, $j:(P,\, y_0) \rightarrow (P',\, y'_{0})$ are immersions and $j$ is transverse to $F$, such that $F \circ i = j \circ f$ and $(i,\,f): N \rightarrow \lbrace (x',\, y)\in N' \times P: F(x') = j(y) \rbrace$ is a diffeomorphism germ (see the associated diagram in figure 1). The dimension of the unfolding is $dim(N') - dim(N)$.

Figure 1. Associated diagram.

Lemma 2.1 [Reference Izumiya, Saji and Takeuchi14], lemma 3.1

Let $F: (\mathbb {R}^{n-1} \times \mathbb {R},\, (\boldsymbol {0},\, 0)) \rightarrow (\mathbb {R}^{n},\, \boldsymbol {0})$ be a map germ with components $F_{i}(x,\,t),$ $i=1,\,2,\,\cdots,\, n,$ i.e.

\[ F(x,t) = (F_{1}(x,t), \cdots, F_{n}(x,t)). \]

Suppose that $\dfrac {\partial F_{n}}{\partial t}(0,\,0) \neq 0$. We know by the Implicit Function Theorem that there is a germ of function $g: (\mathbb {R}^{n-1},\, \boldsymbol {0}) \rightarrow (\mathbb {R},\, 0),$ such that

\[ F_{n}^{{-}1}(0) = \lbrace (x, g(x)): x \in (\mathbb{R}^{n-1}, \boldsymbol{0}) \rbrace. \]

Let us consider the immersion germs $i: (\mathbb {R}^{n-1},\, \boldsymbol {0}) \rightarrow (\mathbb {R}^{n},\, (\boldsymbol {0},\,0)),$ given by $i(x) = (x,\,g(x)),$ $j: (\mathbb {R}^{n-1},\, \boldsymbol {0}) \rightarrow (\mathbb {R}^{n},\, (\boldsymbol {0},\, 0)),$ given by $j(y) = (y,\,0)$ and a map germ $f: (\mathbb {R}^{n-1},\, \boldsymbol {0}) \rightarrow (\mathbb {R}^{n-1},\, \boldsymbol {0}),$ given by $f(x) = (F_{1}(x,\,g(x)),\, \cdots,\, F_{n-1}(x,\,g(x)))$. Then the triple $(F,\,i,\,j)$ is a one-dimensional unfolding of $f$.

Lemma 2.2 [Reference Izumiya and Takeuchi13], lemma 3.3

Let $F : (\mathbb {R}^{n} \times \mathbb {R}^{r},\, \boldsymbol {0}) \rightarrow (\mathbb {R}^{p} \times \mathbb {R}^{r},\, \boldsymbol {0})$ be an unfolding of $f_{0}$ of the form $F (x,\, u) = (f(x,\, u),\, u)$. If $j^{k}_{1}f$ is transverse to $\mathcal {K}^{k}(j^{k}f_{0}(0))$ for a sufficiently large $k,$ then $F$ is infinitesimally $\mathcal {A}$-stable.

Definition 2.2 We say that a $r$-parameter family of germs of functions $F : (\mathbb {R}^{n} \times \mathbb {R}^{r},\, \boldsymbol {0}) \rightarrow (\mathbb {R},\, 0)$ is a Morse family of functions if the map germ $\Delta _{F}:(\mathbb {R}^{n} \times \mathbb {R}^{r},\, \boldsymbol {0}) \rightarrow (\mathbb {R}^{n},\, \boldsymbol {0})$, given by

\[ \Delta_{F}(x,u) = \left( \frac{\partial F}{\partial x_{1}}, \cdots, \frac{\partial F}{\partial x_{n}}\right)(x,u) \]

is not singular.

Definition 2.3 Let $\mathcal {G}$ be one of Mather's subgroups of $\mathcal {K}$ and $\mathcal {B}$ a smooth manifold. A family of maps $F: \mathbb {R}^{n} \times \mathcal {B} \rightarrow \mathbb {R}^{k}$, given by $F(x,\,u) = f_{u}(x)$, is said to be locally $\mathcal {G}$-versal if for every $(x,\,u) \in \mathbb {R}^{n} \times \mathcal {B}$, the germ of $F$ at $(x,\,u)$ is a $\mathcal {G}$-versal unfolding of $f_{u}$ at $x$.

Let $g: M \rightarrow \mathbb {R}^{n}$ be an immersion, where $M$ is a smooth manifold, and denote by $\phi _{g}: M \times \mathcal {B} \rightarrow \mathbb {R}^{k}$ the map given by

\[ \phi_{g}(y,u) = F(g(y), u). \]

Denote by $Imm(M,\, \mathbb {R}^{n})$ the subset of $C^{\infty }(M,\, \mathbb {R}^{n})$ whose elements are proper $C^{\infty }$-immersions from $M$ to $\mathbb {R}^{n}$.

Theorem 2.1 [Reference Montaldi21], theorem 1

Suppose $F: \mathbb {R}^{n} \times \mathcal {B} \rightarrow \mathbb {R}^{k}$ as above is locally $\mathcal {G}$-versal. Let $W \subset J^{r}(M,\, \mathbb {R}^{k})$ be a $\mathcal {G}$-invariant submanifold, where $M$ is a manifold and let

\[ R_{W} = \lbrace g \in Imm(M, \mathbb{R}^{n}): j^{r}_{1}\phi_{g} \pitchfork W \rbrace. \]

Then $R_{W}$ is residual in $Imm(M,\, \mathbb {R}^{n})$. Moreover, if $\mathcal {B}$ is compact and $W$ is closed, then $R_{W}$ is open and dense.

3. Line congruences

In this section, we define 3-parameter line congruences and discuss some of their properties.

Definition 3.1 A 3-parameter line congruence in $\mathbb {R}^{4}$ is a 3-parameter family of lines in $\mathbb {R}^{4}$. Locally, we write $\mathcal {C}=\lbrace \boldsymbol {x}(u),\, \boldsymbol {\xi }(u) \rbrace$ and the line congruence is given by a smooth map

\begin{align*} F_{(\boldsymbol{x}, \boldsymbol{\xi})}: U \times I & \rightarrow \mathbb{R}^{4}\\ (u,t) & \mapsto F(u,t) = \boldsymbol{x}(u) + t\boldsymbol{\xi}(u), \end{align*}

where

• $\boldsymbol {x}: U \rightarrow \mathbb {R}^{4}$ is smooth and it is called a reference hypersurface of the congruence;
• $\boldsymbol {\xi }: U \rightarrow \mathbb {R}^{4} \setminus \lbrace \textbf {0} \rbrace$ is smooth and it is called the director hypersurface of the congruence.

When there is no risk of confusion, we denote the line congruence just by $F$ instead of $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$.

Lemma 3.1 The singular points of a line congruence $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$ are the points $(u,\,t)$ such that

\begin{align*} & t^{3} \langle \boldsymbol{\xi}, \boldsymbol{\xi}_{u_1}\wedge \boldsymbol{\xi}_{u_2} \wedge \boldsymbol{\xi}_{u_3} \rangle + t^{2} \langle \boldsymbol{\xi}, \boldsymbol{x}_{u_1}\wedge \boldsymbol{\xi}_{u_2} \wedge \boldsymbol{\xi}_{u_3} + \boldsymbol{\xi}_{u_1}\wedge \boldsymbol{x}_{u_2} \wedge \boldsymbol{\xi}_{u_3} + \boldsymbol{\xi}_{u_1}\wedge \boldsymbol{\xi}_{u_2} \wedge \boldsymbol{x}_{u_3} \rangle\\ & \quad+ t \langle \boldsymbol{\xi}, \boldsymbol{x}_{u_1}\wedge \boldsymbol{x}_{u_2} \wedge \boldsymbol{\xi}_{u_3} + \boldsymbol{x}_{u_1}\wedge \boldsymbol{\xi}_{u_2} \wedge \boldsymbol{x}_{u_3} + \boldsymbol{\xi}_{u_1}\wedge \boldsymbol{x}_{u_2} \wedge \boldsymbol{x}_{u_3} \rangle \\ & \quad+ \langle \boldsymbol{\xi}, \boldsymbol{x}_{u_1}\wedge \boldsymbol{x}_{u_2} \wedge \boldsymbol{x}_{u_3} \rangle = 0. \end{align*}

Proof. The Jacobian matrix of $F$ is

\[ JF = \left[ \boldsymbol{x}_{u_1} + t\boldsymbol{\xi}_{u_1} \ \ \boldsymbol{x}_{u_2} + t\boldsymbol{\xi}_{u_2} \ \ \boldsymbol{x}_{u_3} + t\boldsymbol{\xi}_{u_3} \ \ \boldsymbol{\xi} \right]. \]

As we know, $(u,\,t)$ is a singular point of $F$ if, and only if, $\det JF(u,\,t) = 0$, thus the result follows from

\[ \det JF(u,t) = \langle \boldsymbol{\xi}, (\boldsymbol{x}_{u_1} + t\boldsymbol{\xi}_{u_1}) \wedge (\boldsymbol{x}_{u_2} + t\boldsymbol{\xi}_{u_2}) \wedge (\boldsymbol{x}_{u_3} + t\boldsymbol{\xi}_{u_3}) \rangle = 0. \]

Definition 3.2 We say that $\boldsymbol {y}(u) = \boldsymbol {x}(u) + t(u)\boldsymbol {\xi }(u)$ is a focal hypersurface of the line congruence $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$ if

(3.1)\begin{equation} \langle \boldsymbol{\xi}(u), \boldsymbol{y}_{u_{1}} \wedge \boldsymbol{y}_{u_{2}} \wedge\boldsymbol{y}_{u_{3}} \rangle = 0.\end{equation}

If $\boldsymbol {y}(u) = \boldsymbol {x}(u) + t(u)\boldsymbol {\xi }(u)$ is a focal hypersurface of the line congruence $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$ then

\begin{align*} & t^{3} \langle \boldsymbol{\xi}, \boldsymbol{\xi}_{u_1}\wedge \boldsymbol{\xi}_{u_2} \wedge \boldsymbol{\xi}_{u_3} \rangle + t^{2} \langle \boldsymbol{\xi}, \boldsymbol{x}_{u_1}\wedge \boldsymbol{\xi}_{u_2} \wedge \boldsymbol{\xi}_{u_3} + \boldsymbol{\xi}_{u_1}\wedge \boldsymbol{x}_{u_2} \wedge \boldsymbol{\xi}_{u_3} + \boldsymbol{\xi}_{u_1}\wedge \boldsymbol{\xi}_{u_2} \wedge \boldsymbol{x}_{u_3} \rangle\\ & \quad+ t \langle \boldsymbol{\xi}, \boldsymbol{x}_{u_1}\wedge \boldsymbol{x}_{u_2} \wedge \boldsymbol{\xi}_{u_3} + \boldsymbol{x}_{u_1}\wedge \boldsymbol{\xi}_{u_2} \wedge \boldsymbol{x}_{u_3} + \boldsymbol{\xi}_{u_1}\wedge \boldsymbol{x}_{u_2} \wedge \boldsymbol{x}_{u_3} \rangle\\ & \quad + \langle \boldsymbol{\xi}, \boldsymbol{x}_{u_1}\wedge \boldsymbol{x}_{u_2} \wedge \boldsymbol{x}_{u_3} \rangle = 0. \end{align*}

3.1 Ruled surfaces of the congruence

There is a geometric interpretation related to definition 3.2, when $\boldsymbol {x}$ is an embedding and $\boldsymbol {\xi }$ is an immersion, as follows. Let $\lbrace \boldsymbol {x}(u),\, \boldsymbol {\xi }(u) \rbrace$ be a 3-parameter line congruence and $C$ a regular curve on the reference hypersurface $\boldsymbol {x}$. If we restrict the director hypersurface $\boldsymbol {\xi }$ to this curve, we obtain a ruled surface associated to the 1-parameter family of lines $\lbrace \boldsymbol {x}(s),\, \boldsymbol {\xi }(s) \rbrace$, where $s$ is the parameter of $C$, $\boldsymbol {x}(s) = \boldsymbol {x}(u(s))$ and $\boldsymbol {\xi }(s) = \boldsymbol {\xi }(u(s))$. The line obtained by fixing $s$ is called a generator of the ruled surface. These kind of ruled surfaces are called surfaces of the congruence and since $\boldsymbol {\xi }'(s) \neq 0$, it is possible to define its striction curve (see § 3.5 in [Reference Do Carmo6] for details). In the special case where this ruled surface is developable, the points of contact of a generator with the striction curve are called focal points. Let us write $\alpha (s) = \boldsymbol {x}(u(s)) + \rho (u(s))\boldsymbol {\xi }(u(s))$ as the striction curve, where $\rho (u(s))$ denotes the coordinate of the focal point relative to $\boldsymbol {\xi }(u(s))$. Suppose $\alpha '(s) \neq 0$ for all $s$, then it is possible to show that $\alpha '$ is parallel to $\boldsymbol {\xi }$ and assuming $\lVert \boldsymbol {\xi } \rVert = 1$, $\alpha '$ is perpendicular to $\boldsymbol {\xi }_{u_{i}}$, $i=1,\,2,\,3$, thus

\[ \begin{cases} u_{1}'(h_{11} + \rho g_{11}) + u_{2}'(h_{21} + \rho g_{12}) + u_{3}'(h_{31} + \rho g_{13}) = 0\\ u_{1}'(h_{12} + \rho g_{12}) + u_{2}'(h_{22} + \rho g_{22}) + u_{3}'(h_{32} + \rho g_{23}) =0\\ u_{1}'(h_{13} + \rho g_{13}) + u_{2}'(h_{23} + \rho g_{23}) + u_{3}'(h_{33} + \rho g_{33}) = 0, \end{cases} \]

where $g_{ij} = \langle \boldsymbol {\xi }_{u_{i}},\, \boldsymbol {\xi }_{u_{j}} \rangle$ and $h_{ij} = \langle \boldsymbol {x}_{u_{i}},\, \boldsymbol {\xi }_{u_{j}} \rangle$. As we want to find a non-trivial solution for the above system, we obtain the cubic equation

\[ \left| \begin{array}{@{}ccc@{}} h_{11} + \rho g_{11} & h_{21} + \rho g_{12} & h_{31} + \rho g_{13} \\ h_{12} + \rho g_{12} & h_{22} + \rho g_{22} & h_{32} + \rho g_{23}\\ h_{13} + \rho g_{13} & h_{23} + \rho g_{23} & h_{33} + \rho g_{33} \end{array} \right| = 0, \]

from which we obtain the coordinates $\rho _{i}$ of the focal points, $i=1,\,2,\,3$. Hence, related to each line of the congruence we have (possibly) three focal points. We define a focal set of the congruence as

\[ \boldsymbol{y}_{i}(u) = \boldsymbol{x}(u) + \rho_{i}(u)\boldsymbol{\xi}(u),\quad i=1,2,3. \]

Thus, for every $u_{0}$, $\boldsymbol {y}_{i}(u_{0})$ is a focal point and there is a curve in this focal set (striction curve) $\alpha (s) = \boldsymbol {x}(u(s)) + \rho _{i}(u(s))\boldsymbol {\xi }(u(s))$, such that $\alpha (s_{0}) = \boldsymbol {y}_{i}(u_{0})$ and $\alpha '(s_{0})$ is parallel to $\boldsymbol {\xi }(u_{0})$, then

(3.2)\begin{equation} \langle\boldsymbol{\xi}(u_{0}), \boldsymbol{y}_{iu_{1}} \wedge \boldsymbol{y}_{iu_{2}} \wedge\boldsymbol{y}_{iu_{3}} \rangle = 0. \end{equation}

Therefore, the focal points are located at the focal hypersurfaces defined 3.2.

4. Generic classification of 3-parameter line congruences in $\mathbb {R}^{4}$

In this section we use methods of singularity theory to obtain the generic singularities of 3-parameter line congruences in $\mathbb {R}^{4}$. Our approach is the same as in [Reference Izumiya, Saji and Takeuchi14], but here we are dealing with the case of 3 parameters in $\mathbb {R}^{4}$. Let $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$ be a line congruence and take $x_{i}$ and $\xi _{i}$, $i=1,\,2,\,3,\,4$, as the coordinate functions of $\boldsymbol {x}$ and $\boldsymbol {\xi }$, respectively, thus we have

\[ F_{(\boldsymbol{x}, \boldsymbol{\xi})}(u,t) = \left( x_{1}(u) + t\xi_{1}(u), x_{2}(u) + t\xi_{2}(u), x_{3}(u) + t\xi_{3}(u), x_{4}(u) + t\xi_{4}(u) \right). \]

If $(u_{0},\, t_{0}) \in U \times I$ and $\xi _{4}(u_{0}) \neq 0$ then there exists $U_{4} \subset U$ an open subset given by $\lbrace u \in U: \xi _{4}(u) \neq 0 \rbrace$. Let us define

(4.1)\begin{equation} c_{4}(u) ={-}\dfrac{x_{4}(u) - a_{0}}{\xi_{4}(u)}, \end{equation}

where $u \in U_{4}$ and $a_{0} = x_{4}(u_{0}) + t_{0}\xi _{4}(u_{0})$. Therefore,

\begin{align*} F_{(\boldsymbol{x},\boldsymbol{\xi})}(u,t) & = \boldsymbol{x}(u) + c_{4}(u)\boldsymbol{\xi}(u) + \left( t - c_{4}(u) \right)\boldsymbol{\xi}(u)\\ & = \boldsymbol{x}(u) + c_{4}(u)\boldsymbol{\xi}(u) + \tilde{t}\boldsymbol{\xi}(u),\text{ where } \tilde{t} = t - c_{4}(u). \end{align*}

Then, if we look at $\widetilde {F}_{(\boldsymbol {x}, \boldsymbol {\xi })}(u,\,\tilde {t}) = \boldsymbol {x}(u) + c_{4}(u)\boldsymbol {\xi }(u) + \tilde {t}\boldsymbol {\xi }(u)$ we can see that its fourth coordinate, which is denoted by $\widetilde {F}_{4}$, is $x_{4}(u) + c_{4}(u)\xi _{4}(u) + \tilde {t}\xi _{4}(u) =a_{0} + \tilde {t}\xi _{4}(u)$, by (4.1). Furthermore, $\widetilde {F}_{4}^{-1}(a_{0}) = \lbrace (u,\,0): u \in U_{4} \rbrace$ and via the Implicit Function Theorem and lemma 2.1, the germ of $\widetilde {F}_{(\boldsymbol {x}, \boldsymbol {\xi })}$ at $(u_{0},\,0)$ is an one-dimensional unfolding of

\[ \tilde{f}(u) = \tilde{\pi}_{4} \circ \widetilde{F}_{(\boldsymbol{x}, \boldsymbol{\xi})}(u,0) = \left( x_{1}(u) + c_{4}(u)\xi_{1}(u), x_{2}(u) + c_{4}(u)\xi_{2}(u), x_{3}(u) + c_{4}(u)\xi_{3}(u) \right), \]

where $\tilde {\pi }_{4}(y_{1},\, y_{2},\, y_{3},\, y_{4}) = (y_{1},\, y_{2},\, y_{3})$.

Lemma 4.1 Let $F_{(\boldsymbol {x}, \boldsymbol {\xi })}: U \times I \rightarrow \mathbb {R}^{4}$ be a line congruence. With notation as above, the singularity of $\tilde {f}$ at $u_{0}$ is determined by $\tilde {\pi }_{4} \circ \boldsymbol {x}$.

Proof. Let us suppose $\boldsymbol {\xi }_{4}(u_{0}) \neq 0$ (other cases are analogous), $(u_{0},\, t_{0}) = (0,\,0) \in U \times I$ and $\boldsymbol {\xi }(0) = (0,\,0,\,0,\,1)$. Using the above notation, $c_{4}(0) = 0$, thus the Jacobian matrix of $\tilde {f}$ at $0$ is equal to the Jacobian matrix of $\tilde {\pi }_{4} \circ \boldsymbol {x}$ at $0$.

The above lemma is important because it shows that the singularity of $\tilde {f}$, and therefore the unfolding $\widetilde {F}$, is determined by $\tilde {\pi }_{4} \circ \boldsymbol {x}: U \rightarrow \mathbb {R}^{3}$.

Lemma 4.2 [Reference Golubitsky and Guillemin11], lemma 4.6 (Basic Transversality Lemma)

Let $X,$ $B$ and $Y$ be smooth manifolds with $W$ a submanifold of $Y$. Consider $j: B \rightarrow C^{\infty }(X,\, Y )$ a non-necessarily continuous map and define $\Phi : X \times B \rightarrow Y$ by $\Phi (x,\,b) = j(b)(x)$. Suppose $\Phi$ smooth and transversal to $W,$ then the set

\[ \left\lbrace b \in B: j(b) \pitchfork W \right\rbrace \]

is a dense subset of $B$.

The next lemma is the result for 3-parameter line congruences in $\mathbb {R}^{4}$ which corresponds to the lemma 4.1 in [Reference Izumiya, Saji and Takeuchi14].

Lemma 4.3 Let $W \subset J^{k}(3,\,3)$ be a submanifold. For any fixed map germ $\boldsymbol {\xi }: U \rightarrow \mathbb {R}^{4} \setminus \lbrace 0 \rbrace$ and any fixed point $(u_{0},\, t_{0}) \in U \times I$ with $\xi _{4}(u_{0}) \neq 0,$ the set

\[ T^{\boldsymbol{\xi}}_{4,W, (u_{0}, t_{0})} = \left\lbrace \boldsymbol{x} \in C^{\infty}(U, \mathbb{R}^{4}): j^{k}_{1} \left( \tilde{\pi}_{4} \circ \widetilde{F}_{(\boldsymbol{x},\boldsymbol{\xi})} \right) \pitchfork W \text{ at } (u_{0}, t_{0}) \right\rbrace \]

is a residual subset of $C^{\infty }( U,\, \mathbb {R}^{4} )$.

Proof. See lemma 4.1 in [Reference Izumiya, Saji and Takeuchi14].

If $\xi _{j}(u_{0}) \neq 0$, $j=1,\,2,\,3$, we can define the set

\[ T^{\boldsymbol{\xi}}_{j,W, (u_{0}, t_{0})} = \left\lbrace \boldsymbol{x} \in C^{\infty}(U, \mathbb{R}^{4}): j^{k}_{1} \left( \tilde{\pi}_{j} \circ \widetilde{F}_{(\boldsymbol{x},\boldsymbol{\xi})} \right) \pitchfork W \text{ at } (u_{0}, t_{0}) \right\rbrace,\quad j=1,2,3 \]

where $\tilde {\pi }_{j}$ is the projection in the coordinates different than $j$. Thus, the above lemma holds for the sets $T^{\boldsymbol {\xi }}_{j,W, (u_{0},\, t_{0})}$, $j=1,\,2,\,3,\,4$.

Remark 4.1 Define

\begin{align*} {\mathcal{O}}_{1}& =\left\{ \boldsymbol{\xi} \in C^{\infty}\left(U, \mathbb{R}^{4} \setminus \lbrace \textbf{0} \rbrace \right): \boldsymbol{\xi}_{u_1} \wedge \boldsymbol{\xi}_{u_2} \wedge \boldsymbol{\xi} \neq \textbf{0},\text{ or } \boldsymbol{\xi}_{u_1} \wedge \boldsymbol{\xi}_{u_3} \wedge \boldsymbol{\xi} \neq \textbf{0},\right. \\ & \quad \left. \text{or } \boldsymbol{\xi}_{u_2} \wedge \boldsymbol{\xi}_{u_3} \wedge \boldsymbol{\xi} \neq \textbf{0} , \forall\; u \in U \right\} \end{align*}

Then, ${\mathcal {O}}_{1}$ is residual as follows. Take the matrix $[ \boldsymbol {\xi } \ \ \boldsymbol {\xi }_{u_1} \ \ \boldsymbol {\xi }_{u_2} \ \boldsymbol {\xi }_{u_3} ]$ and suppose that $\boldsymbol {\xi } \notin {\mathcal {O}}_{1}$. Thus, $\boldsymbol {\xi }_{u_i}(u_{0}) \wedge \boldsymbol {\xi }_{u_j}(u_{0}) \wedge \boldsymbol {\xi }(u_{0}) = 0$, for some $u_{0} \in U$ and $i,\,j=1,\,2,\,3$, i.e., the sets $\lbrace \boldsymbol {\xi }(u_{0}),\, \boldsymbol {\xi }_{u_i}(u_{0}),\, \boldsymbol {\xi }_{u_j}(u_{0}) \rbrace$ are linearly dependent. So we have two cases:

(i) $\lbrace \boldsymbol {\xi }_{u_1}(u_{0}),\, \boldsymbol {\xi }_{u_2}(u_{0}),\, \boldsymbol {\xi }_{u_3}(u_{0}) \rbrace$ is a linearly independent set, then we would have $\boldsymbol {\xi }(u_{0})=0$. Contradiction.
(ii) $\lbrace \boldsymbol {\xi }_{u_1}(u_{0}),\, \boldsymbol {\xi }_{u_2}(u_{0}),\, \boldsymbol {\xi }_{u_3}(u_{0}) \rbrace$ is a linearly dependent set, thus $[ \boldsymbol {\xi }(u_{0}) \; \boldsymbol {\xi }_{u_1}(u_{0}) \boldsymbol {\xi }_{u_2}(u_{0})\; \boldsymbol {\xi }_{u_3}(u_{0}) ]$ has rank less than or equal to $2$.

Let $\Sigma$ be a submanifold of the space of $4 \times 4$ matrices formed by the matrices with $rank \leq 2$, i.e., in which the minors of order $3 \times 3$ are zero, so, $\Sigma$ has codimension $4$. Since $\boldsymbol {\xi } \in C^{\infty }(U,\, \mathbb {R}^{4} \setminus \lbrace \textbf {0} \rbrace )$ is such that $j^{1}\boldsymbol {\xi } \pitchfork \Sigma$ and $U$ is an open subset of $\mathbb {R}^{3}$, we have $j^{1}\boldsymbol {\xi }(U) \cap \Sigma = \emptyset$, what happens if, and only if, $\boldsymbol {\xi } \in {\mathcal {O}}_{1}$. Therefore, by Thom's Transversality Theorem, ${\mathcal {O}}_{1}$ is residual. Note above that we are denoting $j^{1}\boldsymbol {\xi }(u) = [\boldsymbol {\xi }(u) \ \ \boldsymbol {\xi }_{u_1}(u) \ \ \boldsymbol {\xi }_{u_2}(u) \ \ \boldsymbol {\xi }_{u_3}(u)]$.

Thus, it follows from lemma 4.3 that

\[ \widetilde{T}_{4,W, (u_{0}, t_{0})} = \left\lbrace (\boldsymbol{x}, \boldsymbol{\xi}): j^{k}_{1} \left( \tilde{\pi}_{4} \circ \widetilde{F}_{(\boldsymbol{x}, \boldsymbol{\xi})} \right) \pitchfork W\text{ at } (u_{0}, t_{0}), \boldsymbol{\xi} \in {\mathcal{O}}_{1} \right\rbrace \]

is residual.

Now, we are able to prove our first main theorem, which provides a classification of the generic singularities of 3-parameter line congruences in $\mathbb {R}^{4}$.

Theorem 4.1 There is an open dense set ${\mathcal {O}} \subset C^{\infty } ( U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace 0 \rbrace ) ),$ such that:

(a) For all $(\boldsymbol {x},\, \boldsymbol {\xi }) \in \mathcal {O},$ the germ of the line congruence $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$ at any point $(u_{0},\, t_{0}) \in U \times I$ is stable;
(b) For all $(\boldsymbol {x},\, \boldsymbol {\xi }) \in \mathcal {O},$ the germ of the line congruence $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$ at any point $(u_{0},\, t_{0}) \in U \times I$ is a 1-parameter versal unfolding of a germ $f: (\mathbb {R}^{3},\, u_{0}) \rightarrow \mathbb {R}^{3}$ at $t = t_{0}$. Then, $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$ is $\mathcal {A}$-equivalent to one of the normal forms below

• $(x,\,y,\,z,\,w) \mapsto (x,\,y,\,w,\, z^{2})$(Fold).
• $(x,\,y,\,z,\,w) \mapsto (x,\,y,\,w,\, z^{3} + xz)$(Cusp).
• $(x,\,y,\,z,\,w) \mapsto (x,\,y,\,z^{3} + (x^{2} \pm y^{2})z + wz,\, w)$(Lips/Beaks).
• $(x,\,y,\,z,\,w) \mapsto (x,\,y,\,w,\,z^{4} + xz + yz^{2})$(Swallowtail).
• $(x,\,y,\,z,\,w) \mapsto (x,\,y,\,w,\,z^{4} + xz \pm y^{2}z^{2} + wz^{2})$.
• $(x,\,y,\,z,\,w) \mapsto (x,\,y,\,w,\,z^{5} + xz + yz^{2} + wz^{3})$(Butterfly).
• $( x,\,y,\,z,\,w ) \mapsto (z,\, x^{2} + y^{2} + zx + wy,\, xy,\, w)$(Hyperbolic Umbilic).
• $( x,\,y,\,z,\,w ) \mapsto (z,\, x^{2} - y^{2} + zx + wy,\, xy,\, w)$(Elliptic Umbilic).

Proof. We first prove item $(a)$. Given $f \in \mathcal {E}_{3,3}$ and $z = j^{k}f(0)$, define

\[ {\mathcal{K}}^{k}(z) = \lbrace j^{k}g(0): g \underset{\mathcal{K}}{\sim} f \rbrace. \]

For a sufficiently large $k$, define

\[ \Pi_{k}(3,3) = \lbrace f \in J^{k}(3,3):\, cod_{e}({\mathcal{K}}, f) \geq 5 \rbrace. \]

Consider

\[ \Sigma^{i} = \lbrace \sigma \in J^{1}(3,3): \text{kernel rank}(\sigma) = i \rbrace \subset J^{1}(3,3), \]

which is a submanifold of codimension $i^{2}$.

(i) We look at the slice of $\Pi _{k}(3,\,3)$ in $\Sigma ^{1}$, i.e., $f \in \Pi _{k}(3,\,3)$ such that $kernel\; rank(df(0)) = 1$. Then, we are dealing with $f \in \Pi _{k}(3,\,3)$ of $corank$ $1$. Therefore, we can write $f(x,\,y,\,z) = (x,\,y,\, g(x,\,y,\,z))$, where $g(0,\,0,\,z)$ has a singularity of $A_{r}$ type, for some $5 \leq r \leq k-1$ and we call them ${\mathcal {K}}$-singularities of $A_{r}$-type. Note that if we regard the ‘good’ set as the complement of $\Pi _{k}(3,\,3)$ in $\Sigma ^{1}$, then its singularities are the ${\mathcal {K}}$-singularities of $A_{1}$, $A_{2}$, $A_{3}$ and $A_{4}$-type. Therefore, the slice $\Pi _{k}(3,\,3) \cap \Sigma ^{1}$ is a semialgebraic set of codimension greater than or equal to $5$, so it has a stratification $\lbrace {\mathcal {S}}_{i}^{1} \rbrace _{i=1}^{m_{1}}$, with $codim({\mathcal {S}}_{i}^{1})\geq 5$.
(ii) As we did in the first case, define $\Pi _{k}(3,\,3) \cap \Sigma ^{2}$, i.e., the set of $f \in \Pi _{k}(3,\,3)$ of $corank$ $2$. We may assume that $f(x,\,y,\,z) = (z,\, g_{1}(x,\,y,\,z),\, g_{2}(x,\,y,\,z))$, where $g_{i}$ has zero $1$-jet and $(g_{1}(x,\,y,\,0),\, g_{2}(x,\,y,\,0))$ has $2$-jet in $H^{2}(2,\,2)$, therefore, $(g_{1}(x,\,y,\,0),\, g_{2}(x,\,y,\,0))$ has $2$-jet given by one of the normal forms below (see [Reference Gibson9] or [Reference Mond and Nuño Ballesteros19]):
\[ (x^{2} + y^{2}, xy);\; (x^{2}-y^{2}, xy);\; (x^{2}, xy);\; (x^{2}, 0);\; (x^{2} \pm y^{2}, 0);\; (0,0). \]
Hence, by looking at the first two normal forms and its local algebras, $f$ is $\mathcal {K}$-equivalent to one of the forms below:
- • $W_{1}: (z,\, x^{2} + y^{2} + xz,\, xy )$
- • $W_{2}: (z,\, x^{2} - y^{2} + xz,\, xy )$
and both of these forms have $cod_{e}({\mathcal {K}}) = 4$. The other ${\mathcal {K}}$-orbits have $cod_{e}({\mathcal {K}})\geq 5$. Note that $\overline {\Sigma ^{2}} \setminus ( W_{1} \cup W_{2} )$ is a semialgebraic set of codimension greater than or equal to $5$. $\Pi _{k}(3,\,3) \cap \Sigma ^{2}$ is a semialgebraic set contained in $\overline {\Sigma ^{2}} \setminus ( W_{1} \cup W_{2} )$, then its codimension is greater than or equal to $5$, thus, there is a stratification $\lbrace {\mathcal {S}}_{i}^{2} \rbrace _{i=1}^{m_{2}}$ of it, with $codim({\mathcal {S}}_{i}^{2})\geq 5$. Furthermore, the ‘good’ set contains only $W_{1}$ and $W_{2}$.
(iii) In a similar way, we define $\Pi _{k}(3,\,3) \cap \Sigma ^{3}$, i.e., the set of the $k$-jets $f \in \Pi _{k}(3,\,3)$ whose $corank$ is $3$. It is well-known that $\Sigma ^{3}$ has codimension $9$, so $\Pi _{k}(3,\,3) \cap \Sigma ^{3}$ is a semialgebraic set of codimension greater than or equal to $9$, hence, there is a stratification $\lbrace {\mathcal {S}}_{i}^{3} \rbrace _{i=1}^{m_{3}}$, with $codim({\mathcal {S}}_{i}^{3})> 5$.

Then, it follows that the ‘good’ set, i.e., the set of the ${\mathcal {K}}$-orbits of codimension less than or equal to $4$, contains the following ${\mathcal {K}}$-orbits
- • type $A_{r}$, for $1 \leq r \leq 4$;
- • type $W_{1}$;
- • type $W_{2}$.

Applying lemma 4.3 and remark 4.1 to each strata of the above stratification, we obtain that

\begin{align*} \mathcal{T}_{j} & = \bigcap\limits_{i=1}^{m_{j}}\widetilde{T}_{4,S_{i}^{j}, (u_{0}, t_{0})},\quad j=1,2,3\\ \mathcal{T}_{3+r}& = \widetilde{T}_{4,A_{r}, (u_{0}, t_{0})}, \, 1\leq r \leq 4 \\ \mathcal{T}_{7+i}& = \widetilde{T}_{4,W_{i}, (u_{0}, t_{0})}, \, i=1,2. \end{align*}

are residual subsets of $C^{\infty }(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace 0 \rbrace ))$. Hence,

\[ {\mathcal{O}}_{4,(u_{0}, t_{0})} = \bigcap\limits_{i=1}^{9}\mathcal{T}_{i} \]

is residual. The same is true for the sets ${\mathcal {O}}_{j,(u_{0},\, t_{0})}$, $j=1,\,2,\,3$, defined in a similar way.

Since $\boldsymbol {\xi }(u) \neq 0$ for all $u \in U$, given a point $(u_{0},\, t_{0}) \in U \times I$, $\xi _{j}(u_{0}) \neq 0$, for some $j$, there is a residual set ${\mathcal {O}}_{(u_{0},\, t_{0})} \subset C^{\infty }(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace 0 \rbrace ))$, such that

\[ (\boldsymbol{x},\boldsymbol{\xi}) \in {\mathcal{O}}_{(u_{0}, t_{0})} \Leftrightarrow j^{k}_{1}\left( \tilde{\pi}_{j} \circ \widetilde{F}_{(\boldsymbol{x},\boldsymbol{\xi})} \right) \pitchfork {\mathcal{A}}_{r},\, W_{1}, \, W_{2}, \, {\mathcal{S}}^{j}_{i},\quad j=1,2,3, \, r=1, \cdots, 4. \]

It follows from what we already have done that the germ of $\widetilde {F}_{(\boldsymbol {x},\boldsymbol {\xi })}$ at $(u_{0},\, 0)$, which is equivalent to the germ of $F_{(\boldsymbol {x},\boldsymbol {\xi })}$ at $(u_{0},\, t_{0})$, is a 1-dimensional unfolding of $\tilde {\pi }_{j} \circ \widetilde {F}(u,\,0)$ and it follows from lemma 2.2 that $F_{(\boldsymbol {x},\boldsymbol {\xi })}$ is ${\mathcal {A}}$-infinitesimally stable for all $(\boldsymbol {x},\,\boldsymbol {\xi }) \in {\mathcal {O}}_{(u_{0},\, t_{0})}$. Since a germ ${\mathcal {A}}$-infinitesimally stable is ${\mathcal {A}}$-stable (see [Reference Mather18]), there is a neighbourhood $U_{u_{0}} \times I_{t_{0}}$ of $(u_{0},\, t_{0})$ in $U \times I$, such that $F_{(\boldsymbol {x},\boldsymbol {\xi })}{\big |}_{U_{u_{0}} \times I_{t_{0}}}$ is ${\mathcal {A}}$-stable. This result holds independently of the fixed point $(u_{0},\, t_{0})$, so we can consider a countable family of points $(u_{i},\, t_{i}) \in U \times I$ and neighbourhoods $U_{u_{i}} \times I_{t_{i}}$, $(i=1,\,2,\, \cdots )$, such that $F_{(\boldsymbol {x},\boldsymbol {\xi })}{\big |}_{U_{u_{i}} \times I_{t_{i}}}$ is ${\mathcal {A}}$-stable and

\[ U \times I = \bigcup\limits_{i=1}^{\infty} U_{u_{i}} \times I_{t_{i}}. \]

Since ${\mathcal {O}}_{(u_{i},\, t_{i})}$ is a residual subset of $C^{\infty }(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace 0 \rbrace ))$, it follows that

\[ {\mathcal{O}}_{2} = \bigcap\limits_{i=1}^{\infty} {\mathcal{O}}_{(u_{i}, t_{i})} \]

is residual. Furthermore, the germ of $F_{(\boldsymbol {x},\boldsymbol {\xi })}$ at any point $(u,\,t) \in U \times I$ is ${\mathcal {A}}$-infinitesimally stable, for all $(\boldsymbol {x},\,\boldsymbol {\xi }) \in {\mathcal {O}}_{2}$.

Since ${\mathcal {F}}: C^{\infty }(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace 0 \rbrace )) \rightarrow C^{\infty }(U \times I,\, \mathbb {R}^{4})$, defined by ${\mathcal {F}}(\boldsymbol {x},\,\boldsymbol {\xi })= F_{(\boldsymbol {x},\boldsymbol {\xi })}$, is continuous and

\[ S=\lbrace f \in C^{\infty}(U \times I, \mathbb{R}^{4}): f \ \ {\mathcal{A}}-infinitesimally \ \ stable \rbrace \]

is open (see [Reference Golubitsky and Guillemin11] p. 111), ${\mathcal {O}} = {\mathcal {F}}^{-1}(S)$ is open. By previous arguments ${\mathcal {O}}_{2}\subset {\mathcal {O}}$ and ${\mathcal {O}}_{2}$ is dense, therefore ${\mathcal {O}}$ is an open dense subset.

To prove $(b)$, we refine the $\mathcal {K}$-orbits of type $A_2$ and $A_3$ of the above stratification, by taking the $\mathcal {A}$-orbits of $\mathcal {A}_e$-codimension $\leq 1$ inside these $\mathcal {K}$-orbits. Then, the relevant strata in this stratification are the $\mathcal {A}$-orbits of stable singularities $A_k$, $k=1,\, 2,\, 3$, and the $\mathcal {A}$-orbits of singularities of $\mathcal {A}_e$-codimension $1$ of type $A_2$, $A_3$, $A_{4}$ and $D_4$. The complement of their union is a semialgebraic set of codimension greater than or equal to $5$.

(i) ${\mathcal {K}}$-orbit of $A_{1}$ type

$f(x,\,y,\,z) = (x,\,y,\,z^{2})$ which is stable, hence, we have just this ${\mathcal {A}}$-orbit. Its suspension in $\mathbb {R}^{4}$ is the stable germ that we are looking for.
(ii) ${\mathcal {K}}$-orbits of $A_{2}$ type

It follows from the classification made by Marar and Tari [Reference Marar and Tari17], that the possible normal forms are
\[ f(x,y,z) = \left( x, y, z^{3} + P(x,y)z \right), \]
where $P(x,\,y)$ is one of the singularities $A_{k}$, $D_{k}$, $E_{6}$, $E_{7}$ or $E_{8}$ and $\text {cod}_{\text {e}}( {\mathcal {A}},\, f ) = \mu (P)$.
As we are looking for $f$ which have a versal unfolding of dimension $1$ that is a stable germ, we must have $P(x,\,y) = x$ or $P(x,\,y) = x^{2} \pm y^{2}$. Therefore, we have the ${\mathcal {A}}$-orbits
\begin{align*} f_{1}(x,y,z) & = (x,y,z^{3} + xz) \ (\text{Cusp});\\ f_{2}(x,y,z) & = (x,y,z^{3} + (x^{2} \pm y^{2})z) \ (\text{Lips} (+) \; / \; \text{Beaks} (-)), \end{align*}
with $\text {cod}_{\text {e}}( {\mathcal {A}},\, f_{1} ) = 0$ and $\text {cod}_{\text {e}}( {\mathcal {A}},\, f_{2} ) = 1$. The stable germs $\mathbb {R}^{4},\,0 \rightarrow \mathbb {R}^{4},\,0$ are, respectively
\begin{align*} F_{1}(x,y,z,w) & = (x,y,z^{3} + xz, w);\\ F_{2}(x,y,z, w) & = (x,y,z^{3} + (x^{2} \pm y^{2})z + wz, w). \end{align*}
These germs are $\mathcal {A}$-equivalent, however they are considered separately, because they are versal unfoldings of $f_{1}$ and $f_{2}$, respectively, which are not $\mathcal {A}$-equivalent.
(iii) ${\mathcal {K}}$-orbits of $A_{3}$ type

In a similar way, the possible normal forms are (see [Reference Marar and Tari17], § 1)
\begin{align*} & (x,y, z^{4} + xz \pm y^{k}z^{2}), k \geq 1. \text{ cod}_{\text{e}}\left( {\mathcal{A}}\right) = k-1; \\ & (x,y, z^{4} + (y^{2} \pm x^{k})z + xz^{2}), k \geq 2. \text{ cod}_{\text{e}}\left( {\mathcal{A}} \right) = k. \end{align*}
Hence,the useful cases are those where $k=1$ or $k=2$ in the first type of orbit, i.e.,
\begin{align*} f_{1}(x,y,z) & = (x,y, z^{4} + xz + yz^{2}) \ \text{(Swallowtail)};\\ f_{2}(x,y,z) & = (x,y, z^{4} + xz \pm y^{2}z^{2}), \end{align*}
with $\text {cod}_{\text {e}}( {\mathcal {A}},\, f_{1} ) = 0$ e $\text {cod}_{\text {e}}( {\mathcal {A}},\, f_{2} ) = 1$. The stable germs $\mathbb {R}^{4},\,0 \rightarrow \mathbb {R}^{4},\,0$ are, respectively
\begin{align*} F_{1}(x,y,z,w)& = (x,y, z^{4} + xz + yz^{2}, w)\\ F_{2}(x,y,z,w) & = (x,y, z^{4} + xz \pm y^{2}z^{2} + wz^{2}, w). \end{align*}
(iv) ${\mathcal {K}}$-orbits of $A_{4}$ type

Via [Reference Marar and Tari17], the possible normal forms are
\begin{align*} & (x,y, z^{5} + xz + yz^{2}), \text{ cod}_{\text{e}}({\mathcal{A}}) = 1;\\ & (x,y, z^{5} + xz + y^{2}z^{2} + yz^{3}), \text{ cod}_{\text{e}}({\mathcal{A}}) = 2;\\ & (x,y, z^{5} + xz + yz^{3}), \text{ cod}_{\text{e}}({\mathcal{A}}) = 3.\\ \end{align*}
Thus, the only case to be considered is
\[ f(x,y,z) = (x,y, z^{5} + xz + yz^{2}), \]
whose associated stable germ is
\[ F(x,y,z,w) = (x,y, z^{5} + xz + yz^{2} + wz^{3}, w). \]
(v) ${\mathcal {K}}$-orbits $W_{1}$ and $W_{2}$

The germs
\begin{align*} F_{1}(x,y,z,w) & = (z, x^{2} + y^{2} + zx + wy, xy, w);\\ F_{2}(x,y,z,w) & = (z, x^{2} - y^{2} + zx + wy, xy, w). \end{align*}
are, respectively, $1$-parameter versal unfoldings of (see [Reference Bruce2], § 3)
\begin{align*} f_{1}(x,y,z) & = (z, x^{2} + y^{2} + zx, xy);\\ f_{2}(x,y,z) & = \left(z, x^{2} - y^{2} + zx, xy \right), \end{align*}
where $f_{1}$ and $f_{2}$ are of the type $W_{1}$ e $W_{2}$, respectively and both have $\text {cod}_{\text {e}}(\mathcal {A})=1$. Then, we conclude the proof.

5. Normal congruences

In this section, our approach is the same as in [Reference Izumiya, Saji and Takeuchi14] and we seek to provide a classification of the generic singularities of 3-parameter normal congruences in $\mathbb {R}^{4}$. For this, it is necessary to characterize normal congruences and consider some aspects of Lagrangian singularities.

Definition 5.1 A 3-parameter line congruence $\mathcal {C}=\lbrace \boldsymbol {x}(u),\, \boldsymbol {\xi }(u) \rbrace$, for $u \in U \subset \mathbb {R}^{3}$, is said to be normal if for each point $u_{0} \in U$ there is a neighbourhood $\tilde {U}$ of $u_{0}$ and a regular hypersurface, given by $\boldsymbol {y}(u) = \boldsymbol {x}(u) + t(u)\boldsymbol {\xi }(u)$, whose normal vectors are parallel to $\boldsymbol {\xi }(u)$, for all $u \in \tilde {U}$. The congruence is an exact normal congruence if $\boldsymbol {\xi }(u)$ is a normal vector at $\boldsymbol {x}(u)$, for all $u \in U$.

The next proposition characterizes 3-parameter normal line congruences in $\mathbb {R}^{4}$ and corresponds to the proposition 5.1 in [Reference Izumiya, Saji and Takeuchi14].

Proposition 5.1 Let $\mathcal {C}$ = $\lbrace \boldsymbol {x}(u),\, \boldsymbol {\xi }(u) \rbrace,$ $u\in U \subset \mathbb {R}^{3},$ be a 3-parameter line congruence in $\mathbb {R}^{4}$. $\mathcal {C}$ is normal if, and only if, $h_{ij}(u) = h_{ji}(u),$ $i,\,j \in \lbrace 1,\,2,\,3 \rbrace,$ for all $u \in U,$ where $h_{ij} = \left \langle \boldsymbol {x}_{u_i},\, (\dfrac {\boldsymbol {\xi }}{\lVert \boldsymbol {\xi } \rVert })_{u_j} \right \rangle$.

Proof. Let $\mathcal {C}$ be a normal congruence and $S'$ a hypersurface parameterized locally by $\boldsymbol {y}(u) = \boldsymbol {x}(u) + t(u)\boldsymbol {\xi }(u)$, whose normal vectors are parallel to $\boldsymbol {\xi }(u)$. Let us suppose that $\lVert \boldsymbol {\xi }(u) \rVert = 1$. Then, $y_{u_i}(u)$, $i=1,\,2,\,3$ are orthogonal to $\boldsymbol {\xi }(u)$, therefore, $\langle \boldsymbol {\xi },\, \boldsymbol {y}_{u_i} \rangle = 0$. From these expressions, we obtain

(5.1)\begin{equation} t_{u_i} ={-}\langle \boldsymbol{x}_{u_i}, \boldsymbol{\xi} \rangle,\quad i=1,2,3. \end{equation}

Since $t$ is smooth, $t_{u_1u_2} = t_{u_2u_1}$, $t_{u_1u_3} = t_{u_3u_1}$ and $t_{u_2u_3} = t_{u_3u_2}$. From $t_{u_1u_2} = t_{u_2u_1}$, we obtain

\[ - \langle \boldsymbol{x}_{u_1u_2}, \boldsymbol{\xi} \rangle - \langle \boldsymbol{x}_{u_1}, \boldsymbol{\xi}_{u_2} \rangle ={-} \langle \boldsymbol{x}_{u_1u_2}, \boldsymbol{\xi} \rangle - \langle \boldsymbol{x}_{u_2}, \boldsymbol{\xi}_{u_1} \rangle \]

Therefore, $h_{12} = \langle \boldsymbol {x}_{u_1},\, \boldsymbol {\xi }_{u_2} \rangle = \langle \boldsymbol {x}_{u_2},\, \boldsymbol {\xi }_{u_1} \rangle = h_{21}$. The other cases are analogous.

Reciprocally, suppose $h_{ij} = h_{ji}$, for $i,\,j=1,\,2,\,3$. Taking into account the differential equations in (5.1), it follows from $h_{ij} = h_{ji}$ that $t_{u_1u_2} = t_{u_2u_1}$, $t_{u_1u_3} = t_{u_3u_1}$ and $t_{u_2u_3} = t_{u_3u_2}$. Therefore, the above system has a solution $t$. Write $\boldsymbol {y}(u) = \boldsymbol {x}(u) + t(u)\boldsymbol {\xi }(u)$. Note that

\begin{align*} \langle \boldsymbol{\xi}, \boldsymbol{y}_{u_i} \rangle & = \langle \boldsymbol{\xi}, \boldsymbol{x}_{u_i} \rangle + t_{u_i}\\ & = \langle \boldsymbol{\xi}, \boldsymbol{x}_{u_i} \rangle - \langle \boldsymbol{\xi}, \boldsymbol{x}_{u_i} \rangle = 0. \end{align*}

If $\boldsymbol {y}$ is not an immersion, there is a positive real number $\lambda$ such that $\tilde {\boldsymbol {y}}(u) = \boldsymbol {x}(u) + (t(u) + \lambda )\boldsymbol {\xi }(u)$ is an immersion. For the last part, it is sufficient to look at the case when $\boldsymbol {y}(u)$ belongs to the focal set of the congruence.

Denote by

\[ Emb(U, \mathbb{R}^{4}) = \lbrace \boldsymbol{x}: U \rightarrow \mathbb{R}^{4}: \boldsymbol{x}\; \text{is an embedding} \rbrace \]

the space of the regular hypersurfaces in $\mathbb {R}^{4}$ with the Whitney $C^{\infty }$-topology, and by

\[ EN\left(U, \mathbb{R}^{4} \times \left(\mathbb{R}^{4} \setminus \lbrace \textbf{0} \rbrace \right)\right) = \left\lbrace (\boldsymbol{x},\boldsymbol{\xi}): \boldsymbol{x} \in Emb(U, \mathbb{R}^{4}),\; \boldsymbol{\xi}(u)\; \text{is normal to}\; \boldsymbol{x}\; \text{at}\; \boldsymbol{x}(u) \right\rbrace \]

the space of the exact normal congruences. So, we have the following well-known theorem.

Theorem 5.1 There is an open dense subset $O \subset Emb(U,\, \mathbb {R}^{4}),$ such that the germ of an exact normal congruence $F_{(\boldsymbol {x},\boldsymbol {\xi })}$ at any point $(u_{0},\, t_{0}) \in U \times I$ is a Lagrangian stable map germ for any $\boldsymbol {x} \in O,$ i.e., $\forall \, \boldsymbol {x} \in O,$ $F_{(\boldsymbol {x},\boldsymbol {\xi })}$ is an immersive germ, or $\mathcal {A}$-equivalent to one of the normal forms in table 1.

TABLE I. Generic singularities of exact normal congruences

Proof. See theorem 5.2 in [Reference Izumiya, Saji and Takeuchi14] or chapters 4 and 5 in [Reference Izumiya, Romero Fuster, Ruas and Tari12].

Now, we define a natural projection $P: EN(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace \textbf {0} \rbrace )) \rightarrow Emb(U,\, \mathbb {R}^{4}),\,$ given by $P(\boldsymbol {x},\,\boldsymbol {\xi }) = \boldsymbol {x}$. Then, we have the following corollary, which provides a classification of the generic singularities of 3-parameter exact normal congruences.

Corollary 5.1 There is an open dense subset $O \subset EN(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace \textbf {0} \rbrace )),$ such that the germ of an exact normal congruence $F_{(\boldsymbol {x},\boldsymbol {\xi })}$ at any point $(u_{0},\, t_{0}) \in U \times I$ is a Lagrangian stable map germ, for all $(\boldsymbol {x},\,\boldsymbol {\xi }) \in O$.

Proof. It follows from the fact that $P: EN(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace \textbf {0} \rbrace )) \rightarrow Emb(U,\, \mathbb {R}^{4})$ is an open continuous map and from theorem 5.1.

Let us consider some aspects of Lagrangian singularities (see chapter 5 in [Reference Izumiya, Romero Fuster, Ruas and Tari12]). Take the cotangent bundle $\pi : T^{*}\mathbb {R}^{4} \rightarrow \mathbb {R}^{4}$, whose symplectic structure is given locally by the 2-form $\omega = -d\lambda$, where $\lambda$ is the Liouville 1-form, given locally by $\lambda = \sum _{i=1}^{4}p_{i}dz_{i}$, where $(z_{1},\, z_{2},\, z_{3},\, z_{4},\, p_{1},\, p_{2},\, p_{3},\, p_{4})$ are the cotangent coordinates. For a given congruence $F_{(\boldsymbol {x},\boldsymbol {\xi })}$, we define a smooth map $L_{(\boldsymbol {x},\boldsymbol {\xi })}: U \times I \rightarrow T^{*}\mathbb {R}^{4} \simeq \mathbb {R}^{4} \times (\mathbb {R}^{4})^{*}$, given by

\[ L_{(\boldsymbol{x},\boldsymbol{\xi})}(u,t) = \left( \boldsymbol{x}(u) + t \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert}(u), \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert}(u) \right). \]

Definition 5.2 We say that $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$ is a Lagrangian Line Congruence if $L_{(\boldsymbol {x},\boldsymbol {\xi })}$ is a Lagrangian immersion.

Proposition 5.2 Suppose that $L_{(\boldsymbol {x}, \boldsymbol {\xi })}$ is an immersion. Then $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$ is a Lagrangian congruence if, and only if, it is a normal congruence

Proof. Locally, the Liouville $1$-form of $T^{*}\mathbb {R}^{4}$ is given by $\lambda = \sum _{i=1}^{4}p_{i}dz_{i}$. So,

\[ L^{*}_{(\boldsymbol{x},\boldsymbol{\xi})}(\lambda) = \sum_{i=1}^{4}\left( \dfrac{\xi_{i}}{\lVert \boldsymbol{\xi} \rVert}(u)dx_{i}(u) + t\dfrac{\xi_{i}}{\lVert \boldsymbol{\xi} \rVert}(u) d\dfrac{\xi_{i}}{\lVert \boldsymbol{\xi} \rVert}(u) \right) + dt, \]

Therefore, being $\omega = -d\lambda$, we have

\begin{align*} -L^{*}_{(\boldsymbol{x},\boldsymbol{\xi})}(\omega) = dL^{*}_{(\boldsymbol{x},\boldsymbol{\xi})}(\lambda) & = \sum_{i=1}^{4}\left( d\dfrac{\xi_{i}}{\lVert \boldsymbol{\xi} \rVert}(u) \wedge dx_{i}(u) + \dfrac{\xi_{i}}{\lVert \boldsymbol{\xi} \rVert}(u)dt \wedge d\dfrac{\xi_{i}}{\lVert \boldsymbol{\xi} \rVert}(u) \right)\\ & = \left( \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_1}, \boldsymbol{x}_{u_2} \right\rangle - \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_2}, \boldsymbol{x}_{u_1} \right\rangle \right)du_1 \wedge du_{2} \\ & \quad+ \left( \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_1}, \boldsymbol{x}_{u_3} \right\rangle - \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_3}, \boldsymbol{x}_{u_1} \right\rangle \right)du_{1} \wedge du_{3}\\ & \quad+ \left( \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_2}, \boldsymbol{x}_{u_3} \right\rangle - \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_3}, \boldsymbol{x}_{u_2} \right\rangle \right)du_{2} \wedge du_{3}\\ & \quad+ \sum_{i=1}^{3}\left\langle \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert}, \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_i} \right\rangle dt \wedge du_{i}, \end{align*}

where $\boldsymbol {x}(u) = (x_{1}(u),\, x_{2}(u),\, x_{3}(u),\, x_{4}(u))$ and $\boldsymbol {\xi }(u) = (\xi _{1}(u),\, \xi _{2}(u),\, \xi _{3}(u),\, \xi _{4}(u))$. Thus

\begin{align*} -L^{*}_{(\boldsymbol{x},\boldsymbol{\xi})}(\omega) & = \left( \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_1}, \boldsymbol{x}_{u_2} \right\rangle - \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_2}, \boldsymbol{x}_{u_1} \right\rangle \right)du_1 \wedge du_{2}\\ & \quad+ \left( \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_1}, \boldsymbol{x}_{u_3} \right\rangle - \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_3}, \boldsymbol{x}_{u_1} \right\rangle \right)du_1 \wedge du_{3}\\ & \quad+ \left( \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_2}, \boldsymbol{x}_{u_3} \right\rangle - \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_3}, \boldsymbol{x}_{u_2} \right\rangle \right)du_2 \wedge du_{3}. \end{align*}

Therefore, $L^{*}_{(x,e)}(\omega ) = 0$ if, and only if,

\begin{align*} h_{21} = \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_1}, \boldsymbol{x}_{u_2} \right\rangle& = \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_2}, \boldsymbol{x}_{u_1} \right\rangle =h_{12}\\ h_{31} = \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_1}, \boldsymbol{x}_{u_3}\right\rangle & = \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert} \right)_{u_3}, \boldsymbol{x}_{u_1}\right\rangle = h_{13}\\ h_{32}=\left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert}\right)_{u_2},\boldsymbol{x}_{u_3} \right\rangle & = \left\langle \left( \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert}\right)_{u_3}, \boldsymbol{x}_{u_2} \right\rangle = h_{23}. \end{align*}

By proposition 5.1, we can regard the space of the Lagrangian congruences as follows. A line congruence $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$ is a Lagrangian congruence if, and only if, there is a smooth function $t: U \rightarrow \mathbb {R}$, such that $\boldsymbol {x}(u) + t(u)\boldsymbol {\xi }(u)$ is an immersion and the following conditions hold

(5.2)\begin{equation} \begin{cases} t_{u_1}(u) + \left \langle \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert}(u), \boldsymbol{x}_{u_1}(u) \right \rangle = 0\\ t_{u_2}(u) + \left \langle \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert}(u), \boldsymbol{x}_{u_2}(u) \right \rangle = 0\\ t_{u_3}(u) + \left \langle \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert}(u), \boldsymbol{x}_{u_3}(u) \right \rangle = 0. \end{cases} \end{equation}

So, we can define the space of the Lagrangian congruences

\[ L(U, \mathbb{R}^{4} \,{\times} \left( \mathbb{R}^{4} {\setminus} \lbrace \textbf{0} \rbrace \right)) \,{=}\, \left\lbrace (\boldsymbol{x},t,\boldsymbol{\xi}): \boldsymbol{x}(u) + t(u)\boldsymbol{\xi}(u)\; \text{is an immersion and}\; (5.2)\; \text{holds} \right\rbrace \]

with the Whitney $C^{\infty }$-topology. Our idea now is to show that the generic singularities of normal congruences are the same as the generic singularities of exact normal congruences, so, let us define the map

\begin{align*} T_{rp}: C^{\infty}(U, \mathbb{R}^{4} \times \mathbb{R} \times \left( \mathbb{R}^{4} \setminus \lbrace \textbf{0} \rbrace\right)) & \rightarrow C^{\infty}(U, \mathbb{R}^{4} \times \left( \mathbb{R}^{4} \setminus \lbrace \textbf{0} \rbrace\right))\\ (\boldsymbol{x}(u), t(u), \boldsymbol{\xi}(u)) & \mapsto (\boldsymbol{x}(u) + t(u)\boldsymbol{\xi}(u), \boldsymbol{\xi}(u)). \end{align*}

By using the method of the proof of proposition 5.6 in [Reference Izumiya, Saji and Takeuchi14] one can get the following result:

Proposition 5.3 $T_{rp}$ is an open continuous map under the Whitney $C^{\infty }$-topology.

Now, take

\[ N(U, \mathbb{R}^{4} \times \left( \mathbb{R}^{4} \setminus \lbrace \textbf{0} \rbrace \right)) = T_{rp}\left( L\left(U, \mathbb{R}^{4} \times \left( \mathbb{R}^{4} \setminus \lbrace \textbf{0} \rbrace \right)\right) \right) \subset C^{\infty}\left(U, \mathbb{R}^{4} \times \left( \mathbb{R}^{4} \setminus \lbrace \textbf{0} \rbrace \right)\right), \]

with the Whitney $C^{\infty }$-topology induced from $C^{\infty }(U,\, \mathbb {R}^{4} \times ( \mathbb {R}^{4} \setminus \lbrace \textbf {0} \rbrace ))$. Note that we can regard $N(U,\, \mathbb {R}^{4} \times ( \mathbb {R}^{4} \setminus \lbrace \textbf {0} \rbrace ))$ as the space of the normal congruences. Then, we have the following theorem.

Theorem 5.2 There is an open dense set $O' \subset N(U,\, \mathbb {R}^{4} \times ( \mathbb {R}^{4} \setminus \lbrace \textbf {0} \rbrace )),$ such that the germ of normal congruence $F_{(\boldsymbol {x},\boldsymbol {\xi } )}$ at any point $(u_0,\, t_0)$ is a Lagrangian stable germ, for any $(\boldsymbol {x},\,\boldsymbol {\xi }) \in O'$.

Proof. From corollary 5.1, there exists an open dense subset $O \subset EN(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace \textbf {0} \rbrace ))$, such that the germ of exact normal congruence $F_{(\boldsymbol {x},\boldsymbol {\xi })}$ is a Lagrangian stable germ for all $(\boldsymbol {x},\,\boldsymbol {\xi }) \in O$ at any point $(u_0,\, t_0) \in U \times I$. As we know, $T_{rp}$ is an open map, so we just need to take $O' = T_{rp}(O)$.

6. Blaschke normal congruences

In this section we deal with one of the most important classes of equiaffine line congruences, which is the class of Blaschke normal congruences. Our goal is to provide a positive answer to the following conjecture, presented in [Reference Izumiya, Saji and Takeuchi14]:

Conjecture Germs of generic Blaschke affine normal congruences at any point are Lagrangian stable.

Taking this into account, let us regard $\mathbb {R}^{4}$ as a four-dimensional affine space with volume element given by $\omega (e_{1},\, e_{2},\, e_{3},\, e_{4}) = \det (e_{1},\, e_{2},\, e_{3},\, e_{4})$, where $\lbrace e_{1},\, e_{2},\, e_{3},\, e_{4} \rbrace$ is the standard basis of $\mathbb {R}^{4}$. Let $D$ be the standard flat connection on $\mathbb {R}^{4}$, thus $\omega$ is a parallel volume element. Let $\boldsymbol {x}: U \rightarrow \mathbb {R}^{4}$ be a regular hypersurface with $\boldsymbol {x}(U) = M$ and $\boldsymbol {\xi }: U \rightarrow \mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace$ a vector field which is transversal to $M$. Thus, decompose the tangent space

\[ T_{p}\mathbb{R}^{4} = T_{p}M \oplus \langle \boldsymbol{\xi}(u) \rangle_{\mathbb{R}}, \]

where $\boldsymbol {x}(u) = p$. So, it follows that given $X$ and $Y$ vector fields on $M$, we have the decomposition

\[ D_{X}Y = \nabla_{X}Y + h(X,Y)\boldsymbol{\xi}, \]

where $\nabla$ is the induced affine connection and $h$ is the affine fundamental form induced by $\boldsymbol {\xi }$, which defines a symmetric bilinear form on each tangent space of $M$. We say that $M$ is non-degenerate if $h$ is non-degenerate which is equivalent to say that the Gaussian curvature of $M$ never vanishes (see chapter 3 in [Reference Nomizu and Sasaki22]). Using the same idea, we decompose

\[ D_{X}\boldsymbol{\xi} ={-}S(X) + \tau(X)\boldsymbol{\xi}, \]

where $S$ is the shape operator and $\tau$ is the transversal connection form. We say that $\boldsymbol {\xi }$ is an equiaffine transversal vector field if $\tau =0$, i.e $D_{X}\boldsymbol {\xi }$ is tangent to $M$.

Using the volume element $\omega$ and the transversal vector field $\boldsymbol {\xi }$, we induce a volume element $\theta$ on $M$ as follows

\[ \theta(X, Y,Z) = \omega(X,Y,Z, \boldsymbol{\xi}), \]

where $X$, $Y$ and $Z$ are tangent to $M$.

Given a non-degenerate hypersurface $\boldsymbol {x}: U \rightarrow \mathbb {R}^{4}$ and a vector field $\boldsymbol {\xi }: U \rightarrow \mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace$ which is transversal to $M = \boldsymbol {x}(U)$, we take the line congruence generated by $(\boldsymbol {x},\, \boldsymbol {\xi })$ and the map

\begin{align*} F_{(\boldsymbol{x}, \boldsymbol{\xi})}: U \times I & \rightarrow \mathbb{R}^{4}\\ (u,t) & \mapsto \boldsymbol{x}(u) + t\boldsymbol{\xi}(u), \end{align*}

where $I$ is an open interval.

Definition 6.1 A point $p = F(u,\,t)$ is called a focal point of multiplicity $m>0$ if the differential $dF$ has nullity $m$ at $(u,\,t)$, where nullity indicates the dimension of the kernel of $dF$.

The next proposition relates the shape operator $S$ and the above definition.

Proposition 6.1 [Reference Cecil3], proposition 1

Let $\boldsymbol {x}: U \rightarrow \mathbb {R}^{4}$ be a non-degenerate hypersurface with transversal equiaffine vector field $\boldsymbol {\xi }$. Let $S$ be the shape operator related to $M$ and $\boldsymbol {\xi }$. A point $p = F(u,\,t)$ is a focal point of $M$ of multiplicity $m>0$ if and only if $1/t$ is an eigenvalue of $S$ with eigenspace of dimension $m$ at $u$.

For each $u \in U$ and $p \in \mathbb {R}^{4}$, we decompose $p-\boldsymbol {x}(u)$ into tangential and transversal components as follows

(6.1)\begin{equation} p - \boldsymbol{x}(u) = v(u) + \rho_{p}(u)\boldsymbol{\xi}(u), \end{equation}

where $v(u) \in T_{\boldsymbol {x}(u)}M$. The real function $\rho _{p}$ is called an affine support function associated to $M$ and $\boldsymbol {\xi }$. If we fix an Euclidean inner product $\langle.\,,\,. \rangle$ in $\mathbb {R}^{4}$, the support function is given by

(6.2)\begin{equation} \rho_{p}(u) = \left \langle p - \boldsymbol{x}(u), \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert^{2}}(u) \right\rangle - \left\langle v(u), \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert^{2}}(u) \right\rangle, \end{equation}

thus

\begin{align*} \dfrac{\partial \rho}{\partial p_{i}}(u) & = \dfrac{\boldsymbol{\xi}_{i}}{\lVert \boldsymbol{\xi} \rVert^{2}}(u). \end{align*}

Proposition 6.2 [Reference Cecil3], proposition 2

Let $\boldsymbol {x}: U \rightarrow \mathbb {R}^{4}$ be a non-degenerate hypersurface and $\boldsymbol {\xi }$ an equiaffine transversal vector field. Then

(a) The affine support function $\rho _{p}$ has a critical point at $u$ if and only if $p-\boldsymbol {x}(u)$ is a multiple of $\boldsymbol {\xi }(u)$.
(b) If $u$ is a critical point of $\rho _{p},$ then the Hessian of $\rho _{p}$ at u has the form
\[ H(X,Y) = h(X, (I - \rho_{p}(u)S)Y), \; X,\, Y \in T_{\boldsymbol{x}(u)}M. \]
(c) A critical point $u$ of the function $\rho _{p}$ is degenerate if and only if $p$ is a focal point of $M$.

Remark 6.1 It follows from item (a) that the catastrophe set of $\rho$, which is also called the Criminant set of $\rho$, is

\[ C_{\rho} = \lbrace (u,p): p = \boldsymbol{x}(u) + t\boldsymbol{\xi}(u),\text{ for some }t \in \mathbb{R} \rbrace. \]

Proposition 6.3 Let $\boldsymbol {x}: U \rightarrow \mathbb {R}^{4}$ be a non-degenerate hypersurface with transversal equiaffine vector field $\boldsymbol {\xi }$. Then the family of germs of functions $\rho : (U \times \mathbb {R}^{4}, (u_{0},\, p_{0})) \rightarrow (\mathbb {R},\,t_{0}),$ where $t_{0} = \rho (u_{0},\, p_{0})$ and $u_{0}$ is a critical point of $\rho _{p_{0}}$ is a Morse family of functions.

Proof. Let us denote $(u,\,p) = (u_{1},\, u_{2},\, u_{3},\, p_{1},\, p_{2},\, p_{3},\, p_{4})$. In order to prove that $\rho$ is a Morse family we need to prove that the map germ $\Delta\rho : (U \times \mathbb {R}^{4},\, (u_{0},\, p_{0})) \rightarrow \mathbb {R}^{3}$, given by

\[ \Delta \rho(u, p) = \left( \dfrac{\partial \rho}{\partial u_{1}}, \dfrac{\partial \rho}{\partial u_{2}}, \dfrac{\partial \rho}{\partial u_{3}} \right)(u,p) \]

is not singular. Its Jacobian matrix is given by

(6.3)\begin{gather} J(\Delta\rho)(u_{0}, p_{0}) = \left[\begin{array}{@{}cccc@{}} \dfrac{\partial^{2}\rho_{p_{0}}}{\partial u_{1}\partial u_{1}} & \dfrac{\partial^{2}\rho_{p_{0}}}{\partial u_{1}\partial u_{2}} & \dfrac{\partial^{2}\rho_{p_{0}}}{\partial u_{1}\partial u_{3}} & \dfrac{1}{\lVert \boldsymbol{\xi} \rVert^{2}} \boldsymbol{\xi}_{u_{1}} - \dfrac{2 \langle \boldsymbol{\xi}, \boldsymbol{\xi}_{u_{1}}\rangle}{\lVert \boldsymbol{\xi} \rVert^{4}}\boldsymbol{\xi} \\ \dfrac{\partial^{2}\rho_{p_{0}}}{\partial u_{1}\partial u_{2}} & \dfrac{\partial^{2}\rho_{p_{0}}}{\partial u_{2}\partial u_{2}} & \dfrac{\partial^{2}\rho_{p_{0}}}{\partial u_{2}\partial u_{3}} & \dfrac{1}{\lVert \boldsymbol{\xi} \rVert^{2}} \boldsymbol{\xi}_{u_{2}} - \dfrac{2 \langle \boldsymbol{\xi}, \boldsymbol{\xi}_{u_{2}}\rangle}{\lVert \boldsymbol{\xi} \rVert^{4}}\boldsymbol{\xi} \\ \dfrac{\partial^{2}\rho_{p_{0}}}{\partial u_{1}\partial u_{3}} & \dfrac{\partial^{2}\rho_{p_{0}}}{\partial u_{2}\partial u_{3}} & \dfrac{\partial^{2}\rho_{p_{0}}}{\partial u_{3}\partial u_{3}} & \dfrac{1}{\lVert \boldsymbol{\xi} \rVert^{2}} \boldsymbol{\xi}_{u_{3}} - \dfrac{2 \langle \boldsymbol{\xi}, \boldsymbol{\xi}_{u_{3}}\rangle}{\lVert \boldsymbol{\xi} \rVert^{4}}\boldsymbol{\xi} \end{array}\right]_{3 \times 7}.\end{gather}

If $u_{0}$ is a non-degenerate critical point of $\rho _{p_{0}}$, then $\operatorname {\mathrm {rank}}(Hess(\rho _{p_{0}})(u_{0})) = 3$ and the map germ $\Delta \rho$ is not singular. Thus, we just need to check the case in which $u_{0}$ is a degenerate critical point.

(i) $\boldsymbol {\operatorname {\mathrm {rank}} Hess(\rho _{p_{0}})(u_{0}) = 0}$

In this case, using proposition 6.2, we obtain that the eigenspace associated to the eigenvalue $\frac {1}{\rho _{p_{0}}}$ has dimension $3$, hence, the matrix of the shape operator has $\operatorname {\mathrm {rank}}$ $3$ and considering that the $\boldsymbol {\xi }$ is equiaffine, $J(\Delta \rho )(u_{0},\, p_{0})$ has $\operatorname {\mathrm {rank}}$ $3$.
(ii) $\boldsymbol {\operatorname {\mathrm {rank}} Hess(\rho _{p_{0}})(u_{0}) = 1}$

In this case, there are two linearly independent vectors $Y,\,Z \in T_{x(u_{0})}M$, such that $H(X,\,Y) = H(X,\,Z)=0$, for all $X \in T_{x(u_{0})}M$. Hence, as seen in proposition 6.2, the vectors $Y$ and $Z$ are eigenvectors of the shape operator $S$, with eigenvalue $\frac {1}{\rho _{p_{0}}(u_{0})}$. Notice that $\lbrace \boldsymbol {x}_{u_{1}}(u_{0}),\, \boldsymbol {x}_{u_{2}}(u_{0}),\, \boldsymbol {x}_{u_{3}}(u_{0}) \rbrace$ is a set of linearly independent vectors and one of these vectors form a basis of $T_{x(u_{0})}M$ together with $Y$ and $Z$. Let us say that $\beta = \lbrace \boldsymbol {x}_{u_{1}}(u_{0}),\, Y,\, Z \rbrace$ is a basis of $T_{\boldsymbol {x}(u_{0})}M$ (the other cases are analogues). Thus, we can write
(6.4)\begin{align} \boldsymbol{x}_{u_{2}}(u_{0}) & = a_{1}\boldsymbol{x}_{u_{1}} + a_{2}Y + a_{3}Z \end{align}

(6.5)\begin{align} \boldsymbol{x}_{u_{3}}(u_{0}) & = b_{1}\boldsymbol{x}_{u_{1}} + b_{2}Y + b_{3}Z \end{align}
which implies that $J(\Delta \rho )$ is given by
(6.6)\begin{align} \left[\begin{array}{@{}cccc@{}} H( \boldsymbol{x}_{u_{1}}, \boldsymbol{x}_{u_{1}}) & a_{1}H(\boldsymbol{x}_{u_{1}}, \boldsymbol{x}_{u_{1}}) & b_{1}H(\boldsymbol{x}_{u_{1}}, \boldsymbol{x}_{u_{1}}) & \dfrac{1}{\lVert \boldsymbol{\xi} \rVert^{2}} \boldsymbol{\xi}_{u_{1}} - \dfrac{2 \langle \boldsymbol{\xi}, \boldsymbol{\xi}_{u_{1}}\rangle}{\lVert \boldsymbol{\xi} \rVert^{4}}\boldsymbol{\xi} \\ a_{1}H( \boldsymbol{x}_{u_{1}}, \boldsymbol{x}_{u_{1}}) & a_{1}^{2}H(\boldsymbol{x}_{u_{1}}, \boldsymbol{x}_{u_{1}}) & a_{1}b_{1}H(\boldsymbol{x}_{u_{1}}, \boldsymbol{x}_{u_{1}}) & \dfrac{1}{\lVert \boldsymbol{\xi} \rVert^{2}} \boldsymbol{\xi}_{u_{2}} - \dfrac{2 \langle \boldsymbol{\xi}, \boldsymbol{\xi}_{u_{2}}\rangle}{\lVert \boldsymbol{\xi} \rVert^{4}}\boldsymbol{\xi}\\ b_{1}H( \boldsymbol{x}_{u_{1}}, \boldsymbol{x}_{u_{1}}) & a_{1}b_{1}H(\boldsymbol{x}_{u_{1}}, \boldsymbol{x}_{u_{1}}) & b_{1}^{2}H(\boldsymbol{x}_{u_{1}}, \boldsymbol{x}_{u_{1}}) & \dfrac{1}{\lVert \boldsymbol{\xi} \rVert^{2}} \boldsymbol{\xi}_{u_{3}} - \dfrac{2 \langle \boldsymbol{\xi}, \boldsymbol{\xi}_{u_{3}}\rangle}{\lVert \boldsymbol{\xi} \rVert^{4}}\boldsymbol{\xi} \end{array}\right], \end{align}
where $H(\boldsymbol {x}_{u_{1}},\, \boldsymbol {x}_{u_{1}}) \neq 0$, since the Hessian matrix has $\operatorname {\mathrm {rank}}$ $1$. It follows from the fact that the shape operator $S$ has two linearly independent eigenvectors with nonzero eigenvalue that its $\operatorname {\mathrm {rank}}$ is at least $2$, so in the set $\lbrace \boldsymbol {\xi }_{u_1},\, \boldsymbol {\xi }_{u_2},\, \boldsymbol {\xi }_{u_3} \rbrace$ two of these vectors need to be linearly independent. It is sufficient to analyse the case when $\boldsymbol {\xi }_{u_{1}}$ and $\boldsymbol {\xi }_{u_{2} }$ are linearly independent, the other subcases are similar.
Subcase: $\lbrace \boldsymbol {\xi }_{u_{1}},\, \boldsymbol {\xi }_{u_{2}}\rbrace$ linearly independent

First of all, if $\boldsymbol {\xi }_{u_{1}}$ and $\boldsymbol {\xi }_{u_{2}}$ are linearly independent and $\boldsymbol {\xi }$ is equiaffine, then $\boldsymbol {\xi }_{u_{1}} - \frac {2 \langle \boldsymbol {\xi },\, \boldsymbol {\xi }_{u_{1}}\rangle }{\lVert \boldsymbol {\xi } \rVert ^{4}}\boldsymbol {\xi }$ and $\boldsymbol {\xi }_{u_{2}} - \frac {2 \langle \boldsymbol {\xi },\, \boldsymbol {\xi }_{u_{2}}\rangle }{\lVert \boldsymbol {\xi } \rVert ^{4}}\boldsymbol {\xi }$ are linearly independent. Thus, the only case when $J(\Delta \rho )(u_{0},\, p_{0})$ has $\operatorname {\mathrm {rank}}$ less than $3$ is when its third row is a linear combination of the first and the second rows. Then the same occurs with the Hessian matrix of $\rho _{p_{0}}$ and if we call $L_{1},\, L_{2}$ and $L_{3}$ the rows of this matrix, we have
\[ L_{3} = \lambda L_{1} + \gamma L_{2}, \text{ where } \lambda,\, \gamma \in \mathbb{R}. \]
But we know that $L_{2} = a_{1}L_{1}$ and $L_{3} = b_{1}L_{1}$ and using the above equation
(6.7)\begin{equation} b_{1} = \lambda + \gamma a_{1}. \end{equation}
By considering the same combination on the block $3\times 4$ on the right, we have
\[ \frac{1}{\lVert \boldsymbol{\xi} \rVert^{2}} \boldsymbol{\xi}_{u_{3}} - \frac{2 \langle \boldsymbol{\xi}, \boldsymbol{\xi}_{u_{3}}\rangle}{\lVert \boldsymbol{\xi} \rVert^{4}}\boldsymbol{\xi} = \lambda \left( \frac{1}{\lVert \boldsymbol{\xi} \rVert^{2}} \boldsymbol{\xi}_{u_{1}} - \frac{2 \langle \boldsymbol{\xi}, \boldsymbol{\xi}_{u_{1}}\rangle}{\lVert \boldsymbol{\xi} \rVert^{4}}\boldsymbol{\xi} \right) + \gamma \left( \frac{1}{\lVert \boldsymbol{\xi} \rVert^{2}} \boldsymbol{\xi}_{u_{2}} - \frac{2 \langle \boldsymbol{\xi}, \boldsymbol{\xi}_{u_{2}}\rangle}{\lVert \boldsymbol{\xi} \rVert^{4}}\boldsymbol{\xi} \right)\!. \]
Using (6.7), $\lambda = b_{1} - a_{1} \gamma$. Consequently
\[ \frac{1}{\lVert \boldsymbol{\xi} \rVert^{2}} \boldsymbol{\xi}_{u_{3}} - \left( b_{1} - a_{1} \gamma \right)\frac{1}{\lVert \boldsymbol{\xi} \rVert^{2}} \boldsymbol{\xi}_{u_{1}} - \gamma \frac{1}{\lVert \boldsymbol{\xi} \rVert^{2}} \boldsymbol{\xi}_{u_{2}} \in TM \cap{<}\boldsymbol{\xi}>{=} \lbrace \boldsymbol{0} \rbrace, \]
thus $\boldsymbol {\xi }_{u_{3}} = (b_{1} - a_{1}\gamma )\boldsymbol {\xi }_{u_{1}} + \gamma \boldsymbol {\xi }_{u_{2}}$. We know that $\boldsymbol {\xi }_{u_{i}} = -S(\boldsymbol {x}_{u_{i}})$ and from (6.5)
\[ b_{1}\boldsymbol{\xi}_{u_{1}} - \frac{b_{2}}{\rho_{p_{0}}}Y - \frac{b_{3}}{\rho_{p_{0}}}Z = (b_{1} - a_{1}\gamma)\boldsymbol{\xi}_{u_{1}} + \gamma \left(a_{1}\boldsymbol{\xi}_{u_1} - \frac{a_{2}}{\rho_{p_{0}}}Y - \frac{a_{3}}{\rho_{p_{0}}}Z\right), \]
therefore,
(6.8)\begin{equation} -\frac{b_{2}}{\rho_{p_{0}}}Y - \frac{b_{3}}{\rho_{p_{0}}}Z ={-}\gamma \frac{a_{2}}{\rho_{p_{0}}}Y - \gamma \frac{a_{3}}{\rho_{p_{0}}}Z. \end{equation}
Then,
\begin{align*} a_{2}\gamma & = b_{2}\\ a_{3}\gamma & = b_{3}. \end{align*}
Finally
\begin{align*} \gamma \boldsymbol{x}_{u_{2}} & = a_{1}\gamma \boldsymbol{x}_{u_{1}} + a_{2}\gamma Y + a_{3} \gamma Z\\ & = \left(-\lambda + b_{1}\right)\boldsymbol{x}_{u_{1}} + b_{2}Y + b_{3}Z \\ & ={-}\lambda \boldsymbol{x}_{u_{1}} + \boldsymbol{x}_{u_{3}}. \end{align*}
But this contradicts the fact that $\lbrace \boldsymbol {x}_{u_{1}},\, \boldsymbol {x}_{u_{2}},\, \boldsymbol {x}_{u_{3}} \rbrace$ are linearly independent.
(iii) $\boldsymbol {\operatorname {\mathrm {rank}} Hess(\rho _{p_{0}})(u_{0}) = 2}$ In this case, there is $Y \in T_{\boldsymbol {x}(u_{0})}M$ eigenvector of the shape operator $S$ with eigenvalue $\frac {1}{\rho _{p_{0}}(u_{0})}$, by proposition 6.2. Since $\operatorname {\mathrm {rank}} Hess(\rho _{p_{0}})(u_{0}) = 2$, it follows that at least two of the vectors $\boldsymbol {x}_{u_{i}}$, $i=1,\,2,\,3$ do not belong to the eigenspace of $\frac {1}{\rho _{p_{0}}(u_{0})}$, otherwise $\operatorname {\mathrm {rank}} Hess(\rho _{p_{0}})(u_{0}) < 2$, by proposition 6.2. If we look at $\lbrace \boldsymbol {x}_{u_{1}}(u_{0}),\, \boldsymbol {x}_{u_{2}}(u_{0}),\, Y \rbrace$ as a basis of $T_{\boldsymbol {x}(u_{0})}M$ (the other cases are analogous) and write (in $u_{0}$)
\[ \boldsymbol{x}_{u_{3}} = a_{1}\boldsymbol{x}_{u_{1}} + a_{2}\boldsymbol{x}_{u_{2}} + a_{3}Y, \]
this case follows in a similar way to the last one.

Remark 6.2 It follows from the above proposition that the 4-parameter family of germs of functions $\rho : (U \times \mathbb {R}^{4},\, (u_{0},\, p_{0})) \rightarrow (\mathbb {R},\,t_0)$, where $u_{0}$ is a critical point of $\rho _{p_{0}}$, is a Morse family. Furthermore, if $p_{0} = \boldsymbol {x}(u_{0}) + t_{0}\boldsymbol {\xi }(u_{0})$ (where $t_{0} = \rho _{p_{0}}(u_{0})$), the Lagrangian immersion associated to this Morse family is $L: ( U \times \mathbb {R},\, (u_{0},\, t_{0}) ) \rightarrow T^{*}\mathbb {R}^{4}$, given by

\[ L(u,t) = \left( \boldsymbol{x}(u) + t\boldsymbol{\xi}(u), \dfrac{\boldsymbol{\xi}}{\lVert \boldsymbol{\xi} \rVert^{2}}(u) \right), \]

whose Lagrangian map associated is $F_{(\boldsymbol {x},\, \boldsymbol {\xi })} = \pi \circ L(u,\,t) = \boldsymbol {x}(u) + t\boldsymbol {\xi }(u)$, where $\pi : T^{*}\mathbb {R}^{4} \rightarrow \mathbb {R}^{4}$.

Definition 6.2 Let $\boldsymbol {x}: U \rightarrow \mathbb {R}^{4}$, with $\boldsymbol {x}(U)=M$, be a non-degenerate hypersurface and take $\boldsymbol {\xi }: U \rightarrow (\mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace )$ an equiaffine transversal vector field. Define $\boldsymbol {\nu }: U \rightarrow (\mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace )$, such that for each $\boldsymbol {x}(u) = p \in M$ and $v \in T_{p}(M)$

(6.9)\begin{equation} \langle \boldsymbol{\nu}(u), \boldsymbol{\xi}(u) \rangle =1\; and \; \langle \boldsymbol{\nu}(u), v \rangle =0. \end{equation}

Each $\boldsymbol {\nu }(u)$ is called the conormal vector of $\boldsymbol {x}$ relative to $\boldsymbol {\xi }$ at $p$. The map $\boldsymbol {\nu }$ is called the conormal map.

Remark 6.3 Using (6.1) and (6.9), we obtain

\[ \rho_{p}(u) = \langle p-\boldsymbol{x}(u), \boldsymbol{\nu}(u) \rangle, \]

where $\rho _{p}$ is the affine support function.

6.1 Blaschke exact normal congruences

Given a non-degenerate hypersurface $\boldsymbol {x}(U) = M$, we know that the affine fundamental form $h$ is non-degenerate, then it can be treated as a non-degenerate metric (not necessarily positive-definite) on $M$.

Definition 6.3 Let $\boldsymbol {x}: U \rightarrow \mathbb {R}^{4}$ be a non-degenerate hypersurface. A transversal vector field $\boldsymbol {\xi }: U \rightarrow \mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace$ satisfying

(i) $\boldsymbol {\xi }$ is equiaffine.
(ii) The induced volume element $\theta$ coincides with the volume element $\omega _{h}$ of the non-degenerate metric $h$.

is called the Blaschke normal vector field of $M$.

Let $Emb_{ng}(U,\, \mathbb {R}^{4}) = \lbrace \boldsymbol {x}: U \rightarrow \mathbb {R}^{4}: \boldsymbol {x}\; \text {is a non-degenerate embedding} \rbrace$ be the space of non-degenerate regular hypersurfaces with the Whitney $C^{\infty }$- topology. Define the space of the Blaschke exact normal congruences as

\begin{align*} BEN(U, \mathbb{R}^{4} \times (\mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace))& = \left\lbrace (\boldsymbol{x}, \boldsymbol{\xi}): \boldsymbol{x} \in Emb_{ng}(U, \mathbb{R}^{4}),\; \boldsymbol{\xi}\; \text{is the} \right.\\ & \quad\left. \text{Blaschke normal vector field of}\; \boldsymbol{x} \right\rbrace. \end{align*}

Remark 6.4 Given a non-degenerate hypersurface $\boldsymbol {x}(U) = M$, its Blaschke vector field is unique up to sign and is given by

(6.10)\begin{equation} \boldsymbol{\xi}(u) = \left|K(u)\right|^{1/5}N(u) + Z(u), \end{equation}

where $K$ is the Gaussian curvature of $M$, $N$ its unit normal and $Z$ is a vector field on $M$, such that

\[ II(Z, X) ={-}X(\left| K \right|^{1/5}), \forall X \in TM \]

where $II$ denotes the second fundamental form of $M$ (for details, see page 45 item (5) in [Reference Nomizu and Sasaki22]). We can write the vector field $Z$ in terms of the coefficients of the second fundamental form and the partial derivatives of $\left | K \right |^{1/5}$. From (6.10) it follows that the conormal vector relative to the Blaschke vector field of a non-degenerate hypersurface in $\mathbb {R}^{4}$ is given by

(6.11)\begin{equation} \boldsymbol{\nu}(u) = \left|K(u)\right|^{{-}1/5}N(u) \end{equation}

Then, we identify (with the Whitney $C^{\infty }$-topology) the spaces $Emb_{ng}(U,\, \mathbb {R}^{4})$ and

\begin{align*} S_{con}(U, \mathbb{R}^{4} \times \mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace)& = \left\lbrace (\boldsymbol{x}, \nu) \in C^{\infty}(U, \mathbb{R}^{4} \times \mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace): \boldsymbol{x} \in Emb_{ng}(U, \mathbb{R}^{4}) \right.\\ & \quad\left. \text{and}\; \boldsymbol{\nu}\; \text{is}\; \text{the conormal of $\boldsymbol{x}$ relative to the Blaschke vector field} \right\rbrace \end{align*}

Definition 6.4 Let $\boldsymbol {x}: U \rightarrow \mathbb {R}^{4}$, with $\boldsymbol {x}(U)=M$, be a non-degenerate hypersurface. We define the conormal bundle of $M$ by

\[ N^{*}_{\boldsymbol{x}} = \lbrace (p,v): p \in M,\; \langle v, w \rangle = 0,\; \forall\; w \in T_{p}M \rbrace \subset T^{*}\mathbb{R}^{4}. \]

Remark 6.5 Note that we can look at $S_{con}(U,\, \mathbb {R}^{4} \times \mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace )$ as a section of the conormal bundle of $M$.

Let us define the following maps

(6.12)\begin{align} H: \left( \mathbb{R}^{4} \times \mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace \right) \times \mathbb{R}^{4} & \rightarrow \mathbb{R}\end{align}

(6.13)\begin{align} (A, B, C) & \mapsto \langle B, C-A \rangle \nonumber\\ g: U & \rightarrow \mathbb{R}^{4} \times \mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace \\ u & \mapsto (\boldsymbol{x}(u), \boldsymbol{\nu}(u)), \nonumber \end{align}

where $g \in S_{con}(U,\, \mathbb {R}^{4} \times \mathbb {R}^{4} {\setminus} \lbrace \boldsymbol {0} \rbrace )$. If we fix a parameter $C$, $H_{C}: \mathbb {R}^{4} \times \mathbb {R}^{4} {\setminus} \lbrace \boldsymbol {0} \rbrace \rightarrow \mathbb {R}$ is a submersion, therefore, $H_{C} \circ g$ is a contact map. Finally, note that

\[ \rho(u,p) = H \circ \left(g, I_{d}\big|_{\mathbb{R}^{4}} \right)(u,p). \]

Proposition 6.4 For a residual subset of $Emb_{ng}(U,\, \mathbb {R}^{4}\times \mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace )$ the family $\rho$ is locally $\mathcal {P}$-$\mathcal {R}^{+}$-versal.

Proof. Following the identification in remark 6.4 and the notation in remark 6.5 we can apply theorem 2.1 in order to show that there is a residual subset of $Emb_{ng}(U,\, \mathbb {R}^{4} \times \mathbb {R}^{4} \setminus \lbrace 0 \rbrace )$ for which $\rho$ is locally $\mathcal {P}$- ${\mathcal {R}}^{+}$-versal.

Theorem 6.1 There is a residual subset $O \subset Emb_{ng}(U,\, \mathbb {R}^{4})$ such that the germ of the Blaschke exact normal congruence $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$ at any point $(u_{0},\, t_{0}) \in U \times I$ is a Lagrangian stable map germ for any $\boldsymbol {x} \in O,$ i.e., $\forall \, \boldsymbol {x} \in O$, $F_{(\boldsymbol {x},\boldsymbol {\xi })}$ is an immersive germ, or $\mathcal {A}$-equivalent to one of the normal forms in table 1.

Proof. Let us take the map germ $F_{(\boldsymbol {x},\, \boldsymbol {\xi })}: (U \times \mathbb {R},\, (u_{0},\, t_{0})) \rightarrow (\mathbb {R}^{4},\, p_{0})$. Thus $u_{0}$ is a critical point of $\rho _{p_{0}}$, by proposition 6.2. Then, $\rho : (U \times \mathbb {R}^{3},\, (u_{0},\, p_{0})) \rightarrow (\mathbb {R},\,t_{0})$ is a Morse family of functions. Furthermore, by remark 6.1, the Lagrangian map related to this family is $F_{(\boldsymbol {x},\, \boldsymbol {\xi })}$. It is known that if $\rho$ is $\mathcal {P}$-${\mathcal {R}}^{+}$-versal, then $F_{(\boldsymbol {x},\, \boldsymbol {\xi })}$ is Lagrangian stable (see theorem 5.4 in [Reference Izumiya, Romero Fuster, Ruas and Tari12]), so the result follows from proposition 6.4.

The map

(6.14)\begin{equation} \Pi: BEN\left(U, \mathbb{R}^{4} \times \left(\mathbb{R}^{4} \setminus \lbrace \textbf{0} \rbrace \right)\right) \rightarrow Emb_{ng}(U, \mathbb{R}^{4}),\end{equation}

given by $\Pi (\boldsymbol {x},\, \boldsymbol {\xi }) = \boldsymbol {x}$, is open and continuous. Using this, we obtain the following corollary.

Corollary 6.1 There is a residual subset $\mathcal {O} \subset BEN(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace )),$ such that the germ of the Blaschke exact normal congruence $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$ at any point $(u_{0},\, t_{0}) \in U \times I$ is a Lagrangian stable map germ for any $(\boldsymbol {x},\, \boldsymbol {\xi }) \in \mathcal {O},$ i.e., $\forall \, (\boldsymbol {x},\, \boldsymbol {\xi }) \in \mathcal {O}$, $F_{(\boldsymbol {x},\boldsymbol {\xi })}$ is an immersive germ, or $\mathcal {A}$-equivalent to one of the normal forms in table 1.

6.2 Blaschke normal congruences

Let

\begin{align*} BN(U, \mathbb{R}^{4} & \times(\mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace))= \left\{ (\boldsymbol{x}, \boldsymbol{\xi}): \exists\, t \in C^{\infty}(U, \mathbb{R}),\, s.t.\, \boldsymbol{\xi}\, \text{is the Blaschke normal} \right. \\ & \left. \text{vector field of}\,\boldsymbol{y}(u) = \boldsymbol{x}(u) + t(u)\boldsymbol{\xi}(u)\, \text{and}\, \boldsymbol{y} \in Emb_{ng}(U, \mathbb{R}^{4}) \right\} \end{align*}

be the space of the Blaschke normal congruences. Alternatively, we look at this space as a subspace of $C^{\infty }(U,\, \mathbb {R}^{4} \times \mathbb {R} \times (\mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace ))$

\begin{align*} BN(U, \mathbb{R}^{4} \times \mathbb{R} & \times(\mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace)) = \left\{ (\boldsymbol{x}(u), t(u), \boldsymbol{\xi}(u)):\boldsymbol{\xi}\, \text{is the Blaschke normal vector} \right. \\ & \left. \text{field of}\,\boldsymbol{y}(u) = \boldsymbol{x}(u) + t(u)\boldsymbol{\xi}(u)\, \text{and}\, \boldsymbol{y} \in Emb_{ng}(U, \mathbb{R}^{4}) \right\} \end{align*}

In both cases, with the Whitney $C^{\infty }$-topology.

The map

\begin{align*} T_{rp}: C^{\infty}(U, \mathbb{R}^{4} \times \mathbb{R} \times \left( \mathbb{R}^{4} \setminus \lbrace \textbf{0} \rbrace \right)) & \rightarrow C^{\infty}(U, \mathbb{R}^{4} \times \left( \mathbb{R}^{4} \setminus \lbrace \textbf{0} \rbrace \right))\\ (\boldsymbol{x}(u), t(u), \boldsymbol{\xi}(u)) & \mapsto (\boldsymbol{x}(u) + t(u)\boldsymbol{\xi}(u), \boldsymbol{\xi}(u)), \end{align*}

is open and continuous (see proposition 5.3) in the Whitney $C^{\infty }$-topology. Notice that

\[ BEN\left(U, \mathbb{R}^{4} \times \left(\mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace \right)\right) \subset C^{\infty}(U, \mathbb{R}^{4} \times \mathbb{R} \times \left( \mathbb{R}^{4} \setminus \lbrace \textbf{0} \rbrace \right)) \]

with the following identification

\[ BEN\left(U, \mathbb{R}^{4} \times \left(\mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace \right)\right) \ni (\boldsymbol{x}, \boldsymbol{\xi}) \sim (\boldsymbol{x}, 0, \boldsymbol{\xi}), \]

where $\boldsymbol {x} \in Emb_{ng}(U,\, \mathbb {R}^{4})$ and $\boldsymbol {\xi }$ is its Blaschke normal vector field. Furthermore, we can look at the space of the Blaschke normal congruences as the space

(6.15)\begin{equation} \widetilde{BN}(U, \mathbb{R}^{4} \times (\mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace)) = T_{rp}\left( BN(U, \mathbb{R}^{4} \times \mathbb{R} \times (\mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace)) \right). \end{equation}

Thus, $T_{rp}(BEN(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace ))) = \widetilde {BN}(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace ))$. Hence, we obtain the following theorem.

Theorem 6.2 There is a residual subset $\mathcal {O}' \subset \widetilde {BN}(U,\, \mathbb {R}^{4} \times ( \mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace )),$ such that the germ of Blaschke normal congruence $F_{(\boldsymbol {x},\,\boldsymbol {e} )}$ at any point $(u_{0},\, t_{0}) \in U \times I$ is a Lagrangian stable map germ for any $(\boldsymbol {x},\, \boldsymbol {\xi }) \in \mathcal {O}',$ i.e., $\forall \, (\boldsymbol {x},\, \boldsymbol {\xi }) \in \mathcal {O}',$ $F_{(\boldsymbol {x},\boldsymbol {\xi })}$ is an immersive germ, or $\mathcal {A}$-equivalent to one of the normal forms in table 1.

Proof. It is known that map $T_{rp}$ is open and continuous and

\[ T_{rp}(BEN\left(U, \mathbb{R}^{4} \times \left(\mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace \right)\right)) = \widetilde{BN}\left(U, \mathbb{R}^{4} \times \left(\mathbb{R}^{4} \setminus \lbrace \boldsymbol{0} \rbrace \right)\right). \]

If $\mathcal {U} \subset BEN(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace ))$ is open and dense, then its image by $T_{rp}$ is an open dense subset of $\widetilde {BN}(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace ))$. Take $\mathcal {O} = \bigcap \limits _{i \in \mathbb {N}}\mathcal {O}_{i}$ the residual subset of $BEN(U,\, \mathbb {R}^{4} \times (\mathbb {R}^{4} \setminus \lbrace \boldsymbol {0} \rbrace ))$ given in corollary 6.1. We can show that $T_{rp}(\mathcal {O}) = \mathcal {O}' = \bigcap \limits _{i \in \mathbb {N}}\mathcal {O}'_{i}$, where $T_{rp}(\mathcal {O}_{i}) = \mathcal {O}'_{i}$, therefore $\mathcal {O}'$ is residual.

Example 6.1 Taking into account [Reference Leichtweiß15](section 2) and [Reference Li, Simon, Zhao and Hu16](section 2.2.4) it is possible to parametrize a non-degenerate hypersurface $M$ around an elliptic point, by considering not only $\mathcal {R}$-equivalence but also affine transformations of $\mathbb {R}^{4}$, as a graph of a function $h: U \rightarrow \mathbb {R}$, such that

(6.16)\begin{align} h(u) & = 1/2(u_{1}^{2}+u_{2}^{2}+u_{3}^{2})+ a_{111}u_{1}u_{2}u_{3}+1/6 \left( - a_{120}-a_{102} \right)u_{1}^{3}+1/2 a_{210}u_{1}^{2}u_{2} \nonumber\\ & \quad+1/2 a_{201}u_{1}^{2}u_{3}+1/6 \left({-}a_{210}-a_{012} \right) u_{2}^{3 }+1/2 a_{120}u_{1}u_{2}^{2}+1/2 a_{021}u_{2}^{2}u_{3} \nonumber\\ & \quad+1/6\left( - a_{201}-a_{021} \right) u_{3}^{3}+1/2 a_{102}u_{1}u_{3}^{2}+1/2 a_{012}u_{2}u_{3}^{2} + O(3). \end{align}

Here $O(3)$ means functions of order higher than 3. Since the group of affine transformations is different from the group of Euclidean motions (translations and rotations) it follows that this is not necessarily a local parametrization of $M$ around an Euclidean umbilic point. Using this parametrization, the Blaschke normal vector of $M$ at the origin is given by $(0,\,0,\,0,\,1)$. If we choose $a_{111}= a_{210} = a_{012} = a_{201} = 0$, $a_{120} = a_{102} = 1$ and $a_{021} = 2$, it follows that

\[ h(u) = 1/2(u_{1}^{2}+u_{2}^{2}+u_{3}^{2})-1/3u_{1}^{3}+1/2u_{1}u_{2}^{2}+1/2 u_{1}u_{3}^{2}+u_{2}^{2}u_{3}-1/3u_{3}^{3}. \]

Using (6.10) we can compute the Blaschke normal vector field of $M$

\begin{align*} \boldsymbol{\xi}(u)& =(6/5u_{1}+ 18/5u_{1}^{2} - 17/5(u_{2}^{2} + u_{3}^{2}) + O(3), 2u_{2} - 6u_{1}u_{2}-52/5u_{2}u_{3} + O(3), \\ & \quad 2u_{3}-6u_{1}u_{3}-26/5(u_{2}^{2} - u_{3}^{2}) + O(3), 1+ 3/5u_{1}^{2} + u_{2}^{2} + u_{3}^{2} + O(3)). \end{align*}

Furthermore, the congruence map $F_{(\boldsymbol {x}, \boldsymbol {\xi })}(u,\,t) = \boldsymbol {x}(u_{1},\, u_{2},\, u_{3}) + t \boldsymbol {\xi }(u_{1},\, u_{2},\, u_{3})$ has a singular point at $(0,\,0,\,0,\,-1/2)$ and its 2-jet at this point is given by

\begin{align*} F_{(\boldsymbol{x}, \boldsymbol{\xi})}(u,t) & = (2/5u_{1}-9/5u_{1}^{2}+17/10(u_{2}^{2}+u_{3}^{2})+6/5 \left( t+1/2 \right)u_{1}, 3u_{1}u_{2}+26/5u_{2}u_{3} \\ & \quad+2 \left( t+1/2 \right) u_{2}, 3u_{1}u_{3}+ 13/5u_{2}^{2}-13/5u_{3}^{2}+2 \left( t+1/2 \right) u_{3}, t+1/5u_{1}^{2}). \end{align*}

If we take $\lambda = s+\frac {1}{2} = t + \frac {1}{5}u_{1}^{2}$, then it is possible to verify that $F_{(\boldsymbol {x}, \boldsymbol {\xi })}(u,\, \lambda )$ is a versal deformation of $f_{0}(u) = (2/5u_{1}-9/5{u_{1}}^{2}+17/10u_{2}^{2}+17/10u_{3}^{2},\,$ $3u_{1}u_{2} + 26/5 u_{2}u_{3},\, 3u_{1}\,u_{3}+13/5u_{2}^{2} - 13/5u_{3}^{2})$, which is an elliptic umbilic singularity.

Example 6.2 Let us take a non-degenerate hypersurface given by the graph of

(6.17)\begin{align} h(u) & ={-}1/2u_{1}^{2}-1/2u_{2}^{2}+1/2u_{3}^{2}+1/6u_{1}^{3}-1 /2u_{1}^{2}u_{2} \nonumber\\ & \quad+1/2u_{1}u_{3}^{2}+1/3u_{2}^{3}+1/2u_{ 2}u_{3}^{2}. \end{align}

Then, in a similar way to the last example, it is possible to verify that the map $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$, where $\boldsymbol {x}(u_{1},\, u_{2},\, u_{3}) = (u_{1},\, u_{2},\, u_{3},\, h(u_{1},\, u_{2},\, u_{3}))$ and $\boldsymbol {\xi }$ is the Blaschke normal vector field of $\boldsymbol {x}$, has a hyperbolic umbilic singularity at $(0,\,0,\,0,\,5/4)$.

Example 6.3 By taking a non-degenerate hypersurface given by the graph of

(6.18)\begin{equation} h(u) = 1/2({-}u_{1}^{2}-u_{2}^{2}+u_{3}^{2})+2u_{1}u_{2}u_{3}+1/2u_{1}u_{2}^{2}+1/2u_{1}u_{3}^{2}+1/4u_{2}^{4} \end{equation}

it follows, in a similar way to the first example, that the map $F_{(\boldsymbol {x}, \boldsymbol {\xi })}$, associated to the Blaschke exact normal congruence, has a parabolic umbilic singularity at $(0,\,0,\,0,\,-5/6)$.

Acknowledgements

The first author was supported by INCTMat/CAPES Proc. 88887.510549/2020-00. The second author was partially supported by FAPESP Proc. 2019/21181-0 and CNPq Proc. 305695/2019-3. The third author was supported by CAPES Proc. PROEX-11365975/D.

References

Barajas, M., Craizer, M. and Garcia, R.. Lines of affine principal curvatures of surfaces in 3-space. Res. Math. 75 (2020), 1422-6383/20/010001-29–CrossRef Google Scholar

Bruce, J. W.. A classification of 1-parameter families of map germs $\mathbb {R}^{3},\, 0 \rightarrow \mathbb {R}^{3},\, 0$

, with applications to condensation problems. J. London Math. Soc. 33 (1986), 375–384.CrossRef Google Scholar

Cecil, T.. Focal points and support functions in affine differential geometry. Geom. Dedicata 50 (1994), 291–300.CrossRef Google Scholar

Craizer, M., Domitrz, W. and Rios, P. D. M.. Singular improper affine spheres from a given Lagrangian submanifold. Adv. Math. 374 (2020), 107326.CrossRef Google Scholar

Craizer, M. and Garcia, R., Curvature lines of an equiaffine vector field transversal to a surface in 3-space, preprint arXiv:2008.04765v3.Google Scholar

Do Carmo, M. P.. Differential Geometry of Curves and Surfaces (Prentice Hall Inc, Upper Saddle River, 1976).Google Scholar

Ghys, E., Gaspar Monge - le mémoire sur les déblais et les remblais. Images des Mathématiques (2012), (www.images.math.cnrs.fr).Google Scholar

Giblin, P. J. and Zakalyukin, V.M.. Singularities of centre symmetry sets. Proc. London Math. Soc. 90 (2005), 132–166.10.1112/S0024611504014923CrossRef Google Scholar

Gibson, C. G., Singular Points of Smooth Mappings, Pitman research notes in Mathematics, Vol. 25 (Pitman, Boston, 1979).Google Scholar

Gibson, C. G., Wirthmüller, K., du Plessis, A. A. and Looijenga, E. J. N.. Topological stability of smooth mappings Lecture Notes in Mathematics, Vol. 552 (Springer, Berlin, 1970).Google Scholar

Golubitsky, M. and Guillemin, V., Stable Mappings and Their Singularities. Graduate Texts in Mathematics Vol. 14 (Springer-Verlag, Berlin, 1973).CrossRef Google Scholar

Izumiya, S., Romero Fuster, M. C., Ruas, M. A. S. and Tari, F.. Differential Geometry from a Singularity theory viewpoint (World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2016).Google Scholar

Izumiya, S. and Takeuchi, N.. Singularities of ruled surfaces in R3. Math. Proc. Camb. Phil. Soc. 130 (2001), 1–11.CrossRef Google Scholar

Izumiya, S., Saji, K. and Takeuchi, N.. Singularities of line congruences. Proc. R. Soc. Edinb. 133A (2003), 1341–1359.CrossRef Google Scholar

Leichtweiß, K.. Über eine geometrische Deutung des Affinnormalenvektors einseitig gekümmter Hyperflächen. Arch. Math. 53 (1989), 613–621.CrossRef Google Scholar

Li, A.-M, Simon, U., Zhao, G. and Hu, Z., Global affine differential geometry of hypersurfaces, extended ed, 11, De Gruyter Expositions in Mathematics (De Gruyter, Berlin, 2015).CrossRef Google Scholar

Marar, W. L. and Tari, F.. On the geometry of simple germs of co-rank 1 maps from $\mathbb {R}^{3}$

to $\mathbb {R}^{3}$

. Math. Proc. Cambridge Philos. Soc. 119 (1996), 469–481.CrossRef Google Scholar

Mather, J. N.. Stability of $C^{\infty }$

mappings, II: Infenitesimal stability implies stability. Ann. Math. 89 (1969), 254–291.CrossRef Google Scholar

Mond, D. and Nuño Ballesteros, J. J.. Singularities of Mappings: The Local Behaviour of Smooth and Complex Analytic Mappings, Grundlehren der mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 357. (Springer Nature Switzerland, Cham, 2020).10.1007/978-3-030-34440-5CrossRef Google Scholar

Monge, G., Mémoire sur la théorie des déblais et des remblais, Histoire de l'Académie royale des sciences avec les mémoires de mathématique et de physique tirés des registres de cette Académie (1781), 666–705.Google Scholar

Montaldi, J. A.. On generic composites of maps. Bull. London Math. Soc. 23 (1991), 81–85.CrossRef Google Scholar

Nomizu, K. and Sasaki, T., Affine differential geometry. Geometry of affine immersions. Cambridge Tracts in Mathematics, Vol. 111 (Cambridge University Press, 1994).Google Scholar

Wall, C. T. C.. Finite determinacy of smooth map-germs. Bull. London Math. Soc. 13 (1981), 481–539.CrossRef Google Scholar