Introduction
A fundamental problem asks for a formula for the cohomology (or Chow) class of a degeneracy locus, as a polynomial in the Chern classes of the vector bundles involved. In its simplest form, the answer is given by the Giambelli–Thom–Porteous formula: the locus is where two subbundles of a given vector bundle meet in at least a given dimension, and the formula is a determinant.
The aim of this article is to prove formulas for certain degeneracy loci in classical types. One has maps of vector bundles, or flags of subbundles of a given bundle; degeneracy loci come from imposing conditions on the ranks of maps, or dimensions of intersections. The particular loci we consider are indexed by triples of
![]() $s$
-tuples of integers,
$s$
-tuples of integers,
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{r},\mathbf{p},\mathbf{q})$
(in type A) or
$\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{r},\mathbf{p},\mathbf{q})$
(in type A) or
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{k},\mathbf{p},\mathbf{q})$
(in types B, C, and D). In type A, each
$\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{k},\mathbf{p},\mathbf{q})$
(in types B, C, and D). In type A, each
![]() $(r_{i},p_{i},q_{i})$
specifies a rank condition on maps of vector bundles
$(r_{i},p_{i},q_{i})$
specifies a rank condition on maps of vector bundles
![]() $\operatorname{rk}(E_{p_{i}}\rightarrow F_{q_{i}})\leqslant r_{i}$
; in other types,
$\operatorname{rk}(E_{p_{i}}\rightarrow F_{q_{i}})\leqslant r_{i}$
; in other types,
![]() $E_{\bullet }$
and
$E_{\bullet }$
and
![]() $F_{\bullet }$
are flags of isotropic or coisotropic bundles inside some vector bundle with bilinear form, and each
$F_{\bullet }$
are flags of isotropic or coisotropic bundles inside some vector bundle with bilinear form, and each
![]() $(k_{i},p_{i},q_{i})$
specifies
$(k_{i},p_{i},q_{i})$
specifies
![]() $\dim (E_{p_{i}}\cap F_{q_{i}})\geqslant k_{i}$
.
$\dim (E_{p_{i}}\cap F_{q_{i}})\geqslant k_{i}$
.
In each case, we will write
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}\subseteq X$
for the degeneracy locus. Its expected codimension depends on the type. In fact, to each triple we associate a partition
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}\subseteq X$
for the degeneracy locus. Its expected codimension depends on the type. In fact, to each triple we associate a partition
![]() $\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
(again depending on type), whose size is equal to the codimension of
$\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
(again depending on type), whose size is equal to the codimension of
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
.
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
.
The resulting degeneracy loci of type A have a determinantal formula which generalizes that of Giambelli–Thom–Porteous. The loci corresponding to triples are exactly those defined by vexillary permutations according to the recipe of [Reference FultonFul92]; building on work of Kempf and Laksov, Lascoux and Schützenberger, and others, it was shown in [Reference FultonFul92] that
Here each
![]() $c(k)$
is a (total) Chern class
$c(k)$
is a (total) Chern class
![]() $c(F_{q_{i}}-E_{p_{i}})=c(F_{q_{i}})/c(E_{p_{i}})$
, and
$c(F_{q_{i}}-E_{p_{i}})=c(F_{q_{i}})/c(E_{p_{i}})$
, and
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}$
is a Schur determinant; more details will be given in §1.
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}$
is a Schur determinant; more details will be given in §1.
In other classical types, work of Pragacz and his collaborators showed that Pfaffians should play a role analogous to determinants in type A, at least for cases where there is a single bundle
![]() $E$
and all
$E$
and all
![]() $F_{\bullet }$
are isotropic [Reference PragaczPra88, Reference PragaczPra91, Reference Pragacz and RatajskiPR97, Reference Lascoux and PragaczLP00]. More recent work of Buch, Kresch, and Tamvakis exploits a crucial insight: both determinants and Pfaffians can be defined via raising operators, and by adopting the raising operator point of view, one can define theta- and eta-polynomials, which interpolate between determinants and Pfaffians. These provide representatives for Schubert classes in nonmaximal isotropic Grassmannians; here one has a single isotropic
$F_{\bullet }$
are isotropic [Reference PragaczPra88, Reference PragaczPra91, Reference Pragacz and RatajskiPR97, Reference Lascoux and PragaczLP00]. More recent work of Buch, Kresch, and Tamvakis exploits a crucial insight: both determinants and Pfaffians can be defined via raising operators, and by adopting the raising operator point of view, one can define theta- and eta-polynomials, which interpolate between determinants and Pfaffians. These provide representatives for Schubert classes in nonmaximal isotropic Grassmannians; here one has a single isotropic
![]() $E$
, and a flag of trivial bundles
$E$
, and a flag of trivial bundles
![]() $F_{\bullet }$
, some of which may be coisotropic [Reference Buch, Kresch and TamvakisBKT17, Reference Buch, Kresch and TamvakisBKT15, Reference TamvakisTam14]. Wilson extended this idea to define double theta-polynomials, and conjectured that they represent equivariant Schubert classes in nonmaximal isotropic Grassmannians [Reference WilsonWil10]. This was proved in [Reference Ikeda and MatsumuraIM15], and, via a different method, in [Reference Tamvakis and WilsonTW16].
$F_{\bullet }$
, some of which may be coisotropic [Reference Buch, Kresch and TamvakisBKT17, Reference Buch, Kresch and TamvakisBKT15, Reference TamvakisTam14]. Wilson extended this idea to define double theta-polynomials, and conjectured that they represent equivariant Schubert classes in nonmaximal isotropic Grassmannians [Reference WilsonWil10]. This was proved in [Reference Ikeda and MatsumuraIM15], and, via a different method, in [Reference Tamvakis and WilsonTW16].
We will introduce triples
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
for each classical type, and study degeneracy loci defined by
$\boldsymbol{\unicode[STIX]{x1D70F}}$
for each classical type, and study degeneracy loci defined by
![]() $\dim (E_{p_{i}}\cap F_{q_{i}})\geqslant k_{i}$
, with all
$\dim (E_{p_{i}}\cap F_{q_{i}})\geqslant k_{i}$
, with all
![]() $E_{\bullet }$
isotropic, and
$E_{\bullet }$
isotropic, and
![]() $F_{\bullet }$
either isotropic or coisotropic. When the
$F_{\bullet }$
either isotropic or coisotropic. When the
![]() $F_{\bullet }$
are all isotropic, the formulas are (multi-)Pfaffians (as in the preprints [Reference KazarianKaz00] and [Reference Anderson and FultonAF12]); allowing coisotropic conditions presents some subtleties, but leads directly to the definitions of multi-theta polynomials
$F_{\bullet }$
are all isotropic, the formulas are (multi-)Pfaffians (as in the preprints [Reference KazarianKaz00] and [Reference Anderson and FultonAF12]); allowing coisotropic conditions presents some subtleties, but leads directly to the definitions of multi-theta polynomials
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}$
and multi-eta-polynomials
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}$
and multi-eta-polynomials
![]() $\text{H}_{\unicode[STIX]{x1D706}}$
. Our main theorem is stated in terms of these polynomials.
$\text{H}_{\unicode[STIX]{x1D706}}$
. Our main theorem is stated in terms of these polynomials.
Theorem. Let
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
be a triple, and let
$\boldsymbol{\unicode[STIX]{x1D70F}}$
be a triple, and let
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
be the corresponding degeneracy locus (of type C, B, or D).
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
be the corresponding degeneracy locus (of type C, B, or D).
- (C)
In type C, we have
 $$\begin{eqnarray}[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}(c(1),\ldots ,c(\ell )).\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}(c(1),\ldots ,c(\ell )).\end{eqnarray}$$
- (B)
In type B, we have
 $$\begin{eqnarray}[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=2^{-k_{a}}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}(c(1),\ldots ,c(\ell )).\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=2^{-k_{a}}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}(c(1),\ldots ,c(\ell )).\end{eqnarray}$$
- (D)
In type D, we have
 $$\begin{eqnarray}[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=2^{-k_{a}}\text{H}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}(c(1),\ldots ,c(\ell )).\end{eqnarray}$$
$$\begin{eqnarray}[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=2^{-k_{a}}\text{H}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}(c(1),\ldots ,c(\ell )).\end{eqnarray}$$
The entries
![]() $c(i)$
vary by type, and along with the definitions of
$c(i)$
vary by type, and along with the definitions of
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}$
and
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}$
and
![]() $\text{H}_{\unicode[STIX]{x1D706}}$
, these are specified in Theorems 2, 3, and 4. For now, let us mention some special cases. When the triple has all
$\text{H}_{\unicode[STIX]{x1D706}}$
, these are specified in Theorems 2, 3, and 4. For now, let us mention some special cases. When the triple has all
![]() $q_{i}\geqslant 0$
, the loci are defined by conditions on isotropic bundles, and each formula is a Pfaffian. If the triple has all
$q_{i}\geqslant 0$
, the loci are defined by conditions on isotropic bundles, and each formula is a Pfaffian. If the triple has all
![]() $p_{i}=p$
, the loci come from Grassmannians; in the type C case, we recover the formulas of [Reference Ikeda and MatsumuraIM15] and [Reference Tamvakis and WilsonTW16], and in case the
$p_{i}=p$
, the loci come from Grassmannians; in the type C case, we recover the formulas of [Reference Ikeda and MatsumuraIM15] and [Reference Tamvakis and WilsonTW16], and in case the
![]() $F$
are trivial, we recover the formulas of [Reference Buch, Kresch and TamvakisBKT17, Reference Buch, Kresch and TamvakisBKT15]. (The general type D formula includes a definition of double eta-polynomial, which is new even in the Grassmannian case.Footnote
1
)
$F$
are trivial, we recover the formulas of [Reference Buch, Kresch and TamvakisBKT17, Reference Buch, Kresch and TamvakisBKT15]. (The general type D formula includes a definition of double eta-polynomial, which is new even in the Grassmannian case.Footnote
1
)
The structure of the argument in each type is essentially the same. First, one has a basic formula for the case where the only condition is
![]() $E_{p_{1}}\subseteq F_{q_{1}}$
, and furthermore
$E_{p_{1}}\subseteq F_{q_{1}}$
, and furthermore
![]() $E_{p_{1}}$
is a line bundle. Next, there is the case where
$E_{p_{1}}$
is a line bundle. Next, there is the case where
![]() $E_{p_{i}}$
has rank
$E_{p_{i}}$
has rank
![]() $i$
, and the conditions are
$i$
, and the conditions are
![]() $E_{p_{i}}\subseteq F_{q_{i}}$
; the formula here is easily seen to be a product, and one uses some elementary algebra to convert the product into a raising operator formula. (In type A, these loci correspond to dominant permutations.) The ‘main case’ is where the conditions are
$E_{p_{i}}\subseteq F_{q_{i}}$
; the formula here is easily seen to be a product, and one uses some elementary algebra to convert the product into a raising operator formula. (In type A, these loci correspond to dominant permutations.) The ‘main case’ is where the conditions are
![]() $\dim (E_{p_{i}}\cap F_{q_{i}})\geqslant i$
; such loci are resolved by a birational map from a dominant locus, and the pushforward can be decomposed into a series of projective bundles. Finally, a little more elementary algebra reduces the general case to the main case.
$\dim (E_{p_{i}}\cap F_{q_{i}})\geqslant i$
; such loci are resolved by a birational map from a dominant locus, and the pushforward can be decomposed into a series of projective bundles. Finally, a little more elementary algebra reduces the general case to the main case.
Proving the theorem requires only a few general facts. Some of these are treated in the appendices, but we collect four basic formulas here for reference. Let
![]() $E$
be a vector bundle of rank
$E$
be a vector bundle of rank
![]() $e$
on a variety
$e$
on a variety
![]() $X$
.
$X$
.
(a) If
 $L$
is a line bundle on
$L$
is a line bundle on
 $X$
, then
$X$
, then  $$\begin{eqnarray}c_{e}(E-L)=c_{e}(E\otimes L^{\ast }).\end{eqnarray}$$
$$\begin{eqnarray}c_{e}(E-L)=c_{e}(E\otimes L^{\ast }).\end{eqnarray}$$
(b) If
 $L$
is a line bundle on
$L$
is a line bundle on
 $X$
, for any
$X$
, for any
 $b\geqslant 0$
and
$b\geqslant 0$
and
 $j\geqslant e$
we have
$j\geqslant e$
we have  $$\begin{eqnarray}(-c_{1}(L))^{b}\,c_{j}(E-L)=c_{b+j}(E-L).\end{eqnarray}$$
$$\begin{eqnarray}(-c_{1}(L))^{b}\,c_{j}(E-L)=c_{b+j}(E-L).\end{eqnarray}$$
(c) If
 $F^{\prime }$
is a subbundle of a vector bundle
$F^{\prime }$
is a subbundle of a vector bundle
 $F$
, then
$F$
, then  $$\begin{eqnarray}c(E-F/F^{\prime })=c(E-F)\,c(F^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}c(E-F/F^{\prime })=c(E-F)\,c(F^{\prime }).\end{eqnarray}$$
(d) Let
 $\unicode[STIX]{x1D70B}:\mathbb{P}(E)\rightarrow X$
be the projective bundle, and
$\unicode[STIX]{x1D70B}:\mathbb{P}(E)\rightarrow X$
be the projective bundle, and
 $Q=\unicode[STIX]{x1D70B}^{\ast }E/{\mathcal{O}}(-1)$
the universal quotient bundle. For any
$Q=\unicode[STIX]{x1D70B}^{\ast }E/{\mathcal{O}}(-1)$
the universal quotient bundle. For any
 $\unicode[STIX]{x1D70E}\in A^{\ast }X$
, we have
$\unicode[STIX]{x1D70E}\in A^{\ast }X$
, we have  $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\ast }(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D70E}\cdot c_{j}(Q))=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D70E}\quad & \text{if }j=e-1,\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{\ast }(\unicode[STIX]{x1D70B}^{\ast }\unicode[STIX]{x1D70E}\cdot c_{j}(Q))=\left\{\begin{array}{@{}ll@{}}\unicode[STIX]{x1D70E}\quad & \text{if }j=e-1,\\ 0\quad & \text{otherwise.}\end{array}\right.\end{eqnarray}$$
(Identities (a)–(c) are easy to deduce from the Whitney sum formula, and (d) follows from the formula for
![]() $A^{\ast }\mathbb{P}(E)$
as an algebra over
$A^{\ast }\mathbb{P}(E)$
as an algebra over
![]() $A^{\ast }X$
.)
$A^{\ast }X$
.)
We conclude this introduction with some remarks on the development and context of our results. The double Schubert polynomials of Lascoux and Schützenberger, which represent type A degeneracy loci, have many wonderful combinatorial properties. A problem that received a great deal of attention in the 1990s was to find similar polynomials representing loci of other classical types. First steps in this direction were taken by Billey and Haiman, who defined (single) Schubert polynomials for types B, C, and D [Reference Billey and HaimanBH95]; double versions were obtained by Ikeda et al. [Reference Ikeda, Mihalcea and NaruseIMN11] and studied further by Tamvakis [Reference TamvakisTam14]. A simplified development of these double Schubert polynomials follows from the degeneracy locus formulas proved here. We should point out that in types B, C, and D, any theory of Schubert polynomials involves working not in a polynomial ring, but in a ring with relations; modulo these relations, however, stable formulas are essentially unique. See [Reference Anderson and FultonAF12], or the survey [Reference TamvakisTam16a], for more perspective on this history.
The Schubert varieties and degeneracy loci in types B, C, and D are indexed by signed permutations, and it is natural to ask whether certain signed permutations correspond to Pfaffians, by analogy with the determinantal formulas for vexillary permutations in type A. In the preprint [Reference Anderson and FultonAF12], we identified such a class of vexillary signed permutations,Footnote
2
defined via triples
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
such that all
$\boldsymbol{\unicode[STIX]{x1D70F}}$
such that all
![]() $q_{i}\geqslant 0$
. Following ideas of Kazarian [Reference KazarianKaz00], we proved Pfaffian formulas for vexillary loci, and also studied the relationship between these Pfaffians and the double Schubert polynomials of [Reference Ikeda, Mihalcea and NaruseIMN11]. We plan to revisit the combinatorics and algebra of Schubert polynomials in separate work.
$q_{i}\geqslant 0$
. Following ideas of Kazarian [Reference KazarianKaz00], we proved Pfaffian formulas for vexillary loci, and also studied the relationship between these Pfaffians and the double Schubert polynomials of [Reference Ikeda, Mihalcea and NaruseIMN11]. We plan to revisit the combinatorics and algebra of Schubert polynomials in separate work.
In the present work, we focus on the Pfaffian formulas and their generalizations. The setup is heavily influenced by Kazarian’s preprint [Reference KazarianKaz00]. We wish to emphasize that our key contribution is the argument itself: by including the more general vexillary loci, we separate algebra (showing a product equals a determinant or Pfaffian, in the ‘dominant’ case of the proof) from geometry (constructing a resolution of singularities and pushing forward the formula, in the ‘main’ case).
In revisiting our earlier approach, we found the situation was clarified by making explicit the role of raising operators. For this, we owe a great debt to the work of Buch, Kresch and Tamvakis, whose remarkable theta- and eta-polynomial formulas have convincingly demonstrated the utility of raising operators in geometry. This inspired us to apply our geometric method to more general loci, simultaneously generalizing their formulas and yielding shorter and more uniform proofs.
Finally, although the recent prominence of raising operators is due to Buch, Kresch and Tamvakis, it was Pragacz who first brought them to geometry. We take both combinatorial and geometric inspiration from his work, and dedicate this article to him on the occasion of his sixtieth birthday.
1 Type A revisited
The determinantal formula describing degeneracy loci in Grassmann bundles, or (more generally) vexillary loci in flag bundles, is, by now, quite well known; see [Reference Kempf and LaksovKL74, Reference FultonFul92] for recent versions. However, our reformulation of its setup and proof will provide a model for the (new) formulas in other types, so we will go through it in detail.
A triple of type A is the data
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{r},\mathbf{p},\mathbf{q})$
, where each of
$\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{r},\mathbf{p},\mathbf{q})$
, where each of
![]() $\mathbf{r}$
,
$\mathbf{r}$
,
![]() $\mathbf{p}$
, and
$\mathbf{p}$
, and
![]() $\mathbf{q}$
is an
$\mathbf{q}$
is an
![]() $s$
-tuple of nonnegative integers, with
$s$
-tuple of nonnegative integers, with
Setting
![]() $k_{i}=p_{i}-r_{i}$
and
$k_{i}=p_{i}-r_{i}$
and
![]() $l_{i}=q_{i}-r_{i}$
, we further require that
$l_{i}=q_{i}-r_{i}$
, we further require that
The last condition is equivalent to requiring
for all
![]() $i$
.
$i$
.
Associated to a triple there is a partition
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
, defined by setting
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
, defined by setting
![]() $\unicode[STIX]{x1D706}_{k_{i}}=l_{i}$
, and filling in the remaining parts minimally so that
$\unicode[STIX]{x1D706}_{k_{i}}=l_{i}$
, and filling in the remaining parts minimally so that
![]() $\unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D706}_{2}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{k_{s}}\geqslant 0$
. (An essential triple specifies only the ‘corners’ of the Young diagram for
$\unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D706}_{2}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{k_{s}}\geqslant 0$
. (An essential triple specifies only the ‘corners’ of the Young diagram for
![]() $\unicode[STIX]{x1D706}$
, so in a sense it is a minimal way of packaging this information.)
$\unicode[STIX]{x1D706}$
, so in a sense it is a minimal way of packaging this information.)
Given a partition
![]() $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{\ell }\geqslant 0)$
and symbols
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{\ell }\geqslant 0)$
and symbols
![]() $c(1),\ldots ,c(\ell )$
, the associated Schur determinant is
$c(1),\ldots ,c(\ell )$
, the associated Schur determinant is
For a positive integer
![]() $\ell$
, let
$\ell$
, let
![]() $R^{(\ell )}$
be the raising operator
$R^{(\ell )}$
be the raising operator
where
![]() $R_{ij}=T_{i}/T_{j}$
is the operator defined in Appendix A.2. A simple application of the Vandermonde identity shows that
$R_{ij}=T_{i}/T_{j}$
is the operator defined in Appendix A.2. A simple application of the Vandermonde identity shows that
and we will use this observation crucially in proving the degeneracy locus formula.
Here is the geometric setup. On a variety
![]() $X$
we have a sequence of vector bundles
$X$
we have a sequence of vector bundles
where subscripts indicate ranks; for each
![]() $i$
, there is an induced map
$i$
, there is an induced map
![]() $E_{p_{i}}\rightarrow F_{q_{i}}$
. The degeneracy locus corresponding to the triple
$E_{p_{i}}\rightarrow F_{q_{i}}$
. The degeneracy locus corresponding to the triple
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
is
$\boldsymbol{\unicode[STIX]{x1D70F}}$
is
This comes equipped with a natural subscheme structure defined locally by the vanishing of certain determinants.
Let
![]() $c(k_{i})=c(F_{q_{i}}-E_{p_{i}})$
, and set
$c(k_{i})=c(F_{q_{i}}-E_{p_{i}})$
, and set
![]() $c(k)=c(k_{i})$
whenever
$c(k)=c(k_{i})$
whenever
![]() $k_{i-1}<k\leqslant k_{i}$
. We also set
$k_{i-1}<k\leqslant k_{i}$
. We also set
![]() $\ell =k_{s}$
, and by convention we always take
$\ell =k_{s}$
, and by convention we always take
![]() $k_{0}=0$
. With this notation, the degeneracy locus formula can be stated as follows.
$k_{0}=0$
. With this notation, the degeneracy locus formula can be stated as follows.
Theorem 1 (Cf. [Reference Kempf and LaksovKL74, Reference FultonFul92]).
We have
![]() $[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}(c(1),\ldots ,c(\ell ))$
.
$[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}(c(1),\ldots ,c(\ell ))$
.
The case where there is only one
![]() $F$
, so
$F$
, so
![]() $q_{1}=\cdots =q_{s}$
, was proved by Kempf and Laksov, starting the modern search for such formulas. The general case was proved in [Reference FultonFul92].
$q_{1}=\cdots =q_{s}$
, was proved by Kempf and Laksov, starting the modern search for such formulas. The general case was proved in [Reference FultonFul92].
These formulas are to be interpreted as usual: when the bundles and the map
![]() $\unicode[STIX]{x1D711}$
are sufficiently generic, then
$\unicode[STIX]{x1D711}$
are sufficiently generic, then
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
has codimension equal to
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
has codimension equal to
![]() $|\unicode[STIX]{x1D706}|$
and the formula is an identity relating the fundamental class of
$|\unicode[STIX]{x1D706}|$
and the formula is an identity relating the fundamental class of
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
with the Chern classes of
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
with the Chern classes of
![]() $E$
and
$E$
and
![]() $F$
. In general, the left-hand side should be regarded as a refined class of codimension
$F$
. In general, the left-hand side should be regarded as a refined class of codimension
![]() $|\unicode[STIX]{x1D706}|$
, supported on
$|\unicode[STIX]{x1D706}|$
, supported on
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
; see [Reference FultonFul98].
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
; see [Reference FultonFul98].
The proof proceeds in four steps.
1.1 Basic case
Assume
![]() $s=1$
,
$s=1$
,
![]() $p_{1}=1$
,
$p_{1}=1$
,
![]() $r_{1}=0$
, so
$r_{1}=0$
, so
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}=(0,1,q_{1})$
. The locus is where
$\boldsymbol{\unicode[STIX]{x1D70F}}=(0,1,q_{1})$
. The locus is where
![]() $E_{1}\rightarrow F_{q_{1}}$
vanishes, so it is the zeroes of a section of
$E_{1}\rightarrow F_{q_{1}}$
vanishes, so it is the zeroes of a section of
![]() $E_{1}^{\ast }\otimes F_{q_{1}}$
, a vector bundle of rank
$E_{1}^{\ast }\otimes F_{q_{1}}$
, a vector bundle of rank
![]() $q_{1}$
. Therefore
$q_{1}$
. Therefore
using identity (a) to obtain the second equality.
1.2 Dominant case
Assume
![]() $p_{i}=i$
and
$p_{i}=i$
and
![]() $r_{i}=0$
for
$r_{i}=0$
for
![]() $1\leqslant i\leqslant s$
, so
$1\leqslant i\leqslant s$
, so
![]() $k_{i}=i$
and
$k_{i}=i$
and
![]() $l_{i}=q_{i}$
. By imposing one condition at a time, we obtain a sequence
$l_{i}=q_{i}$
. By imposing one condition at a time, we obtain a sequence
![]() $Z_{1}$
is the locus where
$Z_{1}$
is the locus where
![]() $E_{1}\rightarrow F_{q_{1}}$
is zero;
$E_{1}\rightarrow F_{q_{1}}$
is zero;
![]() $Z_{2}$
is where also
$Z_{2}$
is where also
![]() $E_{2}/E_{1}\rightarrow F_{q_{2}}$
is zero; and generally
$E_{2}/E_{1}\rightarrow F_{q_{2}}$
is zero; and generally
![]() $Z_{j}$
is defined on
$Z_{j}$
is defined on
![]() $Z_{j-1}$
by the condition that
$Z_{j-1}$
by the condition that
![]() $E_{j}/E_{j-1}\rightarrow F_{q_{j}}$
be zero. This is an instance of the basic case, and using the projection formula, it follows that
$E_{j}/E_{j-1}\rightarrow F_{q_{j}}$
be zero. This is an instance of the basic case, and using the projection formula, it follows that
Writing
![]() $c(j)=c(F_{q_{j}}-E_{j})$
and
$c(j)=c(F_{q_{j}}-E_{j})$
and
![]() $t_{i}=-c_{1}(E_{i}/E_{i-1})$
, an application of identity (c) transforms (3) into
$t_{i}=-c_{1}(E_{i}/E_{i-1})$
, an application of identity (c) transforms (3) into
Using identity (b), this becomes
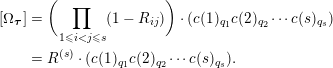 $$\begin{eqnarray}\displaystyle [\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}] & = & \displaystyle \biggl(\mathop{\prod }_{1\leqslant i<j\leqslant s}(1-R_{ij})\biggr)\cdot (c(1)_{q_{1}}c(2)_{q_{2}}\cdots c(s)_{q_{s}})\nonumber\\ \displaystyle & = & \displaystyle R^{(s)}\cdot (c(1)_{q_{1}}c(2)_{q_{2}}\cdots c(s)_{q_{s}}).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}] & = & \displaystyle \biggl(\mathop{\prod }_{1\leqslant i<j\leqslant s}(1-R_{ij})\biggr)\cdot (c(1)_{q_{1}}c(2)_{q_{2}}\cdots c(s)_{q_{s}})\nonumber\\ \displaystyle & = & \displaystyle R^{(s)}\cdot (c(1)_{q_{1}}c(2)_{q_{2}}\cdots c(s)_{q_{s}}).\end{eqnarray}$$
In other words, the product (3) is equal to the determinant
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(c(1),\ldots ,c(s))$
, where
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(c(1),\ldots ,c(s))$
, where
![]() $\unicode[STIX]{x1D706}=(q_{1}\geqslant q_{2}\geqslant \cdots \geqslant q_{s})$
. (To deduce (5) from (4), use identity (b) and descending induction on
$\unicode[STIX]{x1D706}=(q_{1}\geqslant q_{2}\geqslant \cdots \geqslant q_{s})$
. (To deduce (5) from (4), use identity (b) and descending induction on
![]() $k$
to show (4) equals
$k$
to show (4) equals
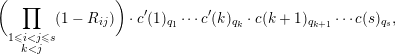 $$\begin{eqnarray}\displaystyle \biggl(\mathop{\prod }_{\substack{ 1\leqslant i<j\leqslant s \\ k<j}}(1-R_{ij})\biggr)\cdot c^{\prime }(1)_{q_{1}}\cdots c^{\prime }(k)_{q_{k}}\cdot c(k+1)_{q_{k+1}}\cdots c(s)_{q_{s}}, & & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \biggl(\mathop{\prod }_{\substack{ 1\leqslant i<j\leqslant s \\ k<j}}(1-R_{ij})\biggr)\cdot c^{\prime }(1)_{q_{1}}\cdots c^{\prime }(k)_{q_{k}}\cdot c(k+1)_{q_{k+1}}\cdots c(s)_{q_{s}}, & & \displaystyle \nonumber\end{eqnarray}$$
where
![]() $c^{\prime }(k)=c(F_{q_{k}}-E_{k}/E_{k-1})=c(k)\cdot \prod _{i=1}^{k-1}(1-t_{i})$
. The case
$c^{\prime }(k)=c(F_{q_{k}}-E_{k}/E_{k-1})=c(k)\cdot \prod _{i=1}^{k-1}(1-t_{i})$
. The case
![]() $k=s$
is (4), and the case
$k=s$
is (4), and the case
![]() $k=1$
is (5).)
$k=1$
is (5).)
1.3 Main case
Assume
![]() $k_{i}=p_{i}-r_{i}=i$
for
$k_{i}=p_{i}-r_{i}=i$
for
![]() $1\leqslant i\leqslant s$
. There is a sequence of projective bundles
$1\leqslant i\leqslant s$
. There is a sequence of projective bundles
where, suppressing notation for pullbacks of bundles,
![]() $D_{j}/D_{j-1}\subseteq E_{p_{j}}/D_{j-1}$
is the tautological line bundle on
$D_{j}/D_{j-1}\subseteq E_{p_{j}}/D_{j-1}$
is the tautological line bundle on
![]() $X_{j}$
. Let us write
$X_{j}$
. Let us write
![]() $\unicode[STIX]{x1D70B}^{(j)}:X_{j}\rightarrow X_{j-1}$
for the projection, and
$\unicode[STIX]{x1D70B}^{(j)}:X_{j}\rightarrow X_{j-1}$
for the projection, and
![]() $\unicode[STIX]{x1D70B}:X_{s}\rightarrow X$
for the composition of all the projections
$\unicode[STIX]{x1D70B}:X_{s}\rightarrow X$
for the composition of all the projections
![]() $\unicode[STIX]{x1D70B}^{(j)}$
.
$\unicode[STIX]{x1D70B}^{(j)}$
.
On
![]() $X_{s}$
, there is the locus
$X_{s}$
, there is the locus
![]() $\widetilde{\unicode[STIX]{x1D6FA}}$
where
$\widetilde{\unicode[STIX]{x1D6FA}}$
where
![]() $D_{i}/D_{i-1}\rightarrow F_{q_{i}}$
is zero for
$D_{i}/D_{i-1}\rightarrow F_{q_{i}}$
is zero for
![]() $1\leqslant i\leqslant s$
. This is an instance of the dominant case, so in
$1\leqslant i\leqslant s$
. This is an instance of the dominant case, so in
![]() $A^{\ast }X_{s}$
we have
$A^{\ast }X_{s}$
we have
where
![]() $\widetilde{\unicode[STIX]{x1D706}}_{j}=q_{j}$
and
$\widetilde{\unicode[STIX]{x1D706}}_{j}=q_{j}$
and
![]() $\widetilde{c}(j)=c(F_{q_{j}}-D_{j})$
. Furthermore,
$\widetilde{c}(j)=c(F_{q_{j}}-D_{j})$
. Furthermore,
![]() $\unicode[STIX]{x1D70B}$
maps
$\unicode[STIX]{x1D70B}$
maps
![]() $\widetilde{\unicode[STIX]{x1D6FA}}$
birationally onto
$\widetilde{\unicode[STIX]{x1D6FA}}$
birationally onto
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
; it is an isomorphism over the dense open set where
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
; it is an isomorphism over the dense open set where
![]() $\operatorname{rk}(E_{p_{i}}\rightarrow F_{q_{i}})=r_{i}$
. (Take
$\operatorname{rk}(E_{p_{i}}\rightarrow F_{q_{i}})=r_{i}$
. (Take
![]() $D_{i}$
to be the kernel.) So
$D_{i}$
to be the kernel.) So
![]() $[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=\unicode[STIX]{x1D70B}_{\ast }[\widetilde{\unicode[STIX]{x1D6FA}}]$
.
$[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=\unicode[STIX]{x1D70B}_{\ast }[\widetilde{\unicode[STIX]{x1D6FA}}]$
.
To compute this pushforward, use identity (c) to write
![]() $\widetilde{c}(j)=c(j)\cdot c(E_{p_{j}}/D_{j})$
, recalling that
$\widetilde{c}(j)=c(j)\cdot c(E_{p_{j}}/D_{j})$
, recalling that
![]() $c(j)=c(F_{q_{j}}-E_{p_{j}})$
. Note that
$c(j)=c(F_{q_{j}}-E_{p_{j}})$
. Note that
![]() $E_{p_{j}}/D_{j}$
is the tautological quotient bundle for
$E_{p_{j}}/D_{j}$
is the tautological quotient bundle for
![]() $\unicode[STIX]{x1D70B}^{(j)}:X_{j}\rightarrow X_{j-1}$
. By identity (d), we have
$\unicode[STIX]{x1D70B}^{(j)}:X_{j}\rightarrow X_{j-1}$
. By identity (d), we have
when
![]() $b=p_{j}-j$
, and this pushforward equals
$b=p_{j}-j$
, and this pushforward equals
![]() $0$
otherwise. Therefore
$0$
otherwise. Therefore
Applying
![]() $\unicode[STIX]{x1D70B}_{\ast }$
to (6) and using linearity of the raising operator yields
$\unicode[STIX]{x1D70B}_{\ast }$
to (6) and using linearity of the raising operator yields
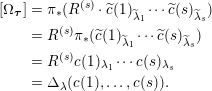 $$\begin{eqnarray}\displaystyle [\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}] & = & \displaystyle \unicode[STIX]{x1D70B}_{\ast }(R^{(s)}\cdot \widetilde{c}(1)_{\widetilde{\unicode[STIX]{x1D706}}_{1}}\cdots \widetilde{c}(s)_{\widetilde{\unicode[STIX]{x1D706}}_{s}})\nonumber\\ \displaystyle & = & \displaystyle R^{(s)}\unicode[STIX]{x1D70B}_{\ast }(\widetilde{c}(1)_{\widetilde{\unicode[STIX]{x1D706}}_{1}}\cdots \widetilde{c}(s)_{\widetilde{\unicode[STIX]{x1D706}}_{s}})\nonumber\\ \displaystyle & = & \displaystyle R^{(s)}c(1)_{\unicode[STIX]{x1D706}_{1}}\cdots c(s)_{\unicode[STIX]{x1D706}_{s}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(c(1),\ldots ,c(s)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}] & = & \displaystyle \unicode[STIX]{x1D70B}_{\ast }(R^{(s)}\cdot \widetilde{c}(1)_{\widetilde{\unicode[STIX]{x1D706}}_{1}}\cdots \widetilde{c}(s)_{\widetilde{\unicode[STIX]{x1D706}}_{s}})\nonumber\\ \displaystyle & = & \displaystyle R^{(s)}\unicode[STIX]{x1D70B}_{\ast }(\widetilde{c}(1)_{\widetilde{\unicode[STIX]{x1D706}}_{1}}\cdots \widetilde{c}(s)_{\widetilde{\unicode[STIX]{x1D706}}_{s}})\nonumber\\ \displaystyle & = & \displaystyle R^{(s)}c(1)_{\unicode[STIX]{x1D706}_{1}}\cdots c(s)_{\unicode[STIX]{x1D706}_{s}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(c(1),\ldots ,c(s)).\nonumber\end{eqnarray}$$
1.4 General case
Any triple
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{r},\mathbf{p},\mathbf{q})$
can be ‘inflated’ to
$\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{r},\mathbf{p},\mathbf{q})$
can be ‘inflated’ to
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }=(\mathbf{r}^{\prime },\mathbf{p}^{\prime },\mathbf{q}^{\prime })$
with
$\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }=(\mathbf{r}^{\prime },\mathbf{p}^{\prime },\mathbf{q}^{\prime })$
with
![]() $k_{i}^{\prime }=p_{i}^{\prime }-r_{i}^{\prime }=i$
, without essentially altering the locus
$k_{i}^{\prime }=p_{i}^{\prime }-r_{i}^{\prime }=i$
, without essentially altering the locus
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
or the polynomial representing it. Suppose
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
or the polynomial representing it. Suppose
![]() $k_{i}-k_{i-1}>1$
, so either
$k_{i}-k_{i-1}>1$
, so either
![]() $q_{i-1}>q_{i}$
or
$q_{i-1}>q_{i}$
or
![]() $p_{i-1}<p_{i}$
(or both). If
$p_{i-1}<p_{i}$
(or both). If
![]() $q_{i-1}>q_{i}$
, then inserting
$q_{i-1}>q_{i}$
, then inserting
![]() $(r_{i}+1,p_{i},q_{i}+1)$
between the
$(r_{i}+1,p_{i},q_{i}+1)$
between the
![]() $(i-1)\text{st}$
and
$(i-1)\text{st}$
and
![]() $i\text{th}$
positions produces a new triple
$i\text{th}$
positions produces a new triple
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }$
with
$\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }$
with
![]() $\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})=\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime })$
. If there is a bundle
$\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})=\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime })$
. If there is a bundle
![]() $F_{q_{i}+1}$
fitting into
$F_{q_{i}+1}$
fitting into
![]() $F_{q_{i-1}}{\twoheadrightarrow}F_{q_{i}+1}{\twoheadrightarrow}F_{q_{i}}$
, then one easily checks
$F_{q_{i-1}}{\twoheadrightarrow}F_{q_{i}+1}{\twoheadrightarrow}F_{q_{i}}$
, then one easily checks
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }}=\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
. In general, it can be arranged for such an
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }}=\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
. In general, it can be arranged for such an
![]() $F_{q_{i}+1}$
to exist by passing to an appropriate projective bundle; then the locus
$F_{q_{i}+1}$
to exist by passing to an appropriate projective bundle; then the locus
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }}$
maps birationally to the original
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }}$
maps birationally to the original
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
. (In the case
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
. (In the case
![]() $q_{i-1}=q_{i}$
, then
$q_{i-1}=q_{i}$
, then
![]() $p_{i-1}<p_{i}-1$
and one proceeds similarly, by inserting a bundle between
$p_{i-1}<p_{i}-1$
and one proceeds similarly, by inserting a bundle between
![]() $E_{p_{i-1}}$
and
$E_{p_{i-1}}$
and
![]() $E_{p_{i}}$
.) The fact that
$E_{p_{i}}$
.) The fact that
![]() $\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(c^{\prime }(1),\ldots ,c^{\prime }(\ell ))=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(c(1),\ldots ,c(\ell ))$
is a special case of §A.3, Lemma A.1.
$\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(c^{\prime }(1),\ldots ,c^{\prime }(\ell ))=\unicode[STIX]{x1D6E5}_{\unicode[STIX]{x1D706}}(c(1),\ldots ,c(\ell ))$
is a special case of §A.3, Lemma A.1.
This concludes the proof. ◻
2 Type C: symplectic bundles
A triple of type C is
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{k},\mathbf{p},\mathbf{q})$
, with
$\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{k},\mathbf{p},\mathbf{q})$
, with
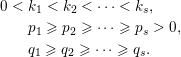 $$\begin{eqnarray}\displaystyle 0 & {<} & \displaystyle k_{1}<k_{2}<\cdots <k_{s},\nonumber\\ \displaystyle & & \displaystyle p_{1}\geqslant p_{2}\geqslant \cdots \geqslant p_{s}>0,\nonumber\\ \displaystyle & & \displaystyle q_{1}\geqslant q_{2}\geqslant \cdots \geqslant q_{s}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0 & {<} & \displaystyle k_{1}<k_{2}<\cdots <k_{s},\nonumber\\ \displaystyle & & \displaystyle p_{1}\geqslant p_{2}\geqslant \cdots \geqslant p_{s}>0,\nonumber\\ \displaystyle & & \displaystyle q_{1}\geqslant q_{2}\geqslant \cdots \geqslant q_{s}.\nonumber\end{eqnarray}$$
The
![]() $q_{i}$
are allowed to be negative, but not zero, and if
$q_{i}$
are allowed to be negative, but not zero, and if
![]() $p_{s}=1$
then all
$p_{s}=1$
then all
![]() $q_{i}$
must be positive. Since the difference between positive and negative
$q_{i}$
must be positive. Since the difference between positive and negative
![]() $q$
plays a major role, let
$q$
plays a major role, let
![]() $a=a(\boldsymbol{\unicode[STIX]{x1D70F}})$
be the index such that
$a=a(\boldsymbol{\unicode[STIX]{x1D70F}})$
be the index such that
![]() $q_{a}>0>q_{a+1}$
(allowing
$q_{a}>0>q_{a+1}$
(allowing
![]() $a=0$
and
$a=0$
and
![]() $a=s$
for the cases where all
$a=s$
for the cases where all
![]() $q_{i}$
are negative or all
$q_{i}$
are negative or all
![]() $q_{i}$
are positive, respectively). We will also require five further conditions, listed as (c1)–(c5) below, which arise naturally from the geometric setup. Consider an even-rank vector bundle
$q_{i}$
are positive, respectively). We will also require five further conditions, listed as (c1)–(c5) below, which arise naturally from the geometric setup. Consider an even-rank vector bundle
![]() $V$
, equipped with a symplectic form and two flags of subbundles
$V$
, equipped with a symplectic form and two flags of subbundles
When
![]() $q>0$
, the subbundles
$q>0$
, the subbundles
![]() $F_{q}$
are isotropic; when
$F_{q}$
are isotropic; when
![]() $q<0$
,
$q<0$
,
![]() $F_{q}$
is coisotropic; and all the bundles
$F_{q}$
is coisotropic; and all the bundles
![]() $E_{p}$
are isotropic. If the rank of
$E_{p}$
are isotropic. If the rank of
![]() $V$
is
$V$
is
![]() $2n$
, the isotropic bundles
$2n$
, the isotropic bundles
![]() $E_{p}$
and
$E_{p}$
and
![]() $F_{q}$
(for
$F_{q}$
(for
![]() $q>0$
) have rank
$q>0$
) have rank
![]() $n+1-p$
and
$n+1-p$
and
![]() $n+1-q$
, respectively; and for
$n+1-q$
, respectively; and for
![]() $q<0$
, the coisotropic bundles
$q<0$
, the coisotropic bundles
![]() $F_{q}$
have rank
$F_{q}$
have rank
![]() $n-q$
. (So the order on the
$n-q$
. (So the order on the
![]() $p_{i}$
and
$p_{i}$
and
![]() $q_{i}$
is compatible with the inclusion of bundles of corresponding ranks.)
$q_{i}$
is compatible with the inclusion of bundles of corresponding ranks.)
The degeneracy locus is
Note that
![]() $E_{1}^{\bot }=E_{1}$
, so a condition on its intersection with a coisotropic space is equivalent to one for the intersection with an isotropic space; we shall prefer the latter, and this explains why negative
$E_{1}^{\bot }=E_{1}$
, so a condition on its intersection with a coisotropic space is equivalent to one for the intersection with an isotropic space; we shall prefer the latter, and this explains why negative
![]() $q_{i}$
are prohibited when
$q_{i}$
are prohibited when
![]() $p=1$
. Demanding that the rank conditions be feasible, and generically attained with equality, leads to the further requirements on the triple
$p=1$
. Demanding that the rank conditions be feasible, and generically attained with equality, leads to the further requirements on the triple
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
.
$\boldsymbol{\unicode[STIX]{x1D70F}}$
.
The conditions on
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
are likely to appear somewhat technical at first. The reader may find it helpful to first assume all
$\boldsymbol{\unicode[STIX]{x1D70F}}$
are likely to appear somewhat technical at first. The reader may find it helpful to first assume all
![]() $q_{i}$
are positive, which is the simplest case. The next easiest case is when
$q_{i}$
are positive, which is the simplest case. The next easiest case is when
![]() $k_{i}=i$
for all
$k_{i}=i$
for all
![]() $i$
, which corresponds to the ‘main case’ in the proof. Linear-algebraic reasons for the conditions, as well as combinatorial explanations and the relationship with [Reference Buch, Kresch and TamvakisBKT17], can be found in the remarks at the end of this section.
$i$
, which corresponds to the ‘main case’ in the proof. Linear-algebraic reasons for the conditions, as well as combinatorial explanations and the relationship with [Reference Buch, Kresch and TamvakisBKT17], can be found in the remarks at the end of this section.
In what follows, when indices fall out of the range
![]() $[1,s]$
, we use conventions so that the inequalities become trivial, e.g.,
$[1,s]$
, we use conventions so that the inequalities become trivial, e.g.,
![]() $k_{0}=0$
,
$k_{0}=0$
,
![]() $q_{0}=+\infty$
, and
$q_{0}=+\infty$
, and
![]() $q_{s+1}=-\infty$
.
$q_{s+1}=-\infty$
.
First, for
![]() $i\leqslant a$
, we require
$i\leqslant a$
, we require
When
![]() $k_{i}=i$
for all
$k_{i}=i$
for all
![]() $i$
, this says that either
$i$
, this says that either
![]() $p_{i-1}>p_{i}$
or
$p_{i-1}>p_{i}$
or
![]() $q_{i-1}>q_{i}$
. When all
$q_{i-1}>q_{i}$
. When all
![]() $q_{i}$
are positive, this is the only condition required of a triple
$q_{i}$
are positive, this is the only condition required of a triple
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
.
$\boldsymbol{\unicode[STIX]{x1D70F}}$
.
The other requirements on
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
concern negative
$\boldsymbol{\unicode[STIX]{x1D70F}}$
concern negative
![]() $q$
, so they describe intersections of an isotropic
$q$
, so they describe intersections of an isotropic
![]() $E_{p}$
with a coisotropic
$E_{p}$
with a coisotropic
![]() $F_{q}$
.
$F_{q}$
.
For each
![]() $j\leqslant a$
, let
$j\leqslant a$
, let
![]() $m(j)=\min \{m\,|\,q_{j}+(k_{j}-k_{j-1}-1)\geqslant q_{m}\}$
. The second condition is as follows.
$m(j)=\min \{m\,|\,q_{j}+(k_{j}-k_{j-1}-1)\geqslant q_{m}\}$
. The second condition is as follows.
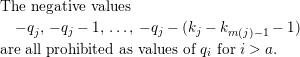 $$\begin{eqnarray}\displaystyle & & \displaystyle \text{The negative values }\nonumber\\ \displaystyle & & \displaystyle \quad -q_{j},\,-q_{j}-1,\,\ldots ,\,-q_{j}-(k_{j}-k_{m(j)-1}-1)\nonumber\\ \displaystyle & & \displaystyle \text{are all prohibited as values of }q_{i}\text{ for }i>a.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \text{The negative values }\nonumber\\ \displaystyle & & \displaystyle \quad -q_{j},\,-q_{j}-1,\,\ldots ,\,-q_{j}-(k_{j}-k_{m(j)-1}-1)\nonumber\\ \displaystyle & & \displaystyle \text{are all prohibited as values of }q_{i}\text{ for }i>a.\end{eqnarray}$$
(Here is an equivalent, algorithmic condition: let
![]() $N_{0}=\{1,2,3,\ldots \}$
; form
$N_{0}=\{1,2,3,\ldots \}$
; form
![]() $N_{1}$
by removing the
$N_{1}$
by removing the
![]() $k_{1}$
consecutive elements of
$k_{1}$
consecutive elements of
![]() $N_{0}$
starting at
$N_{0}$
starting at
![]() $q_{1}$
; then form
$q_{1}$
; then form
![]() $N_{2}$
by removing
$N_{2}$
by removing
![]() $k_{2}-k_{1}$
consecutive elements of
$k_{2}-k_{1}$
consecutive elements of
![]() $N_{1}$
, starting at the
$N_{1}$
, starting at the
![]() $q_{2}$
th element; and so on up to
$q_{2}$
th element; and so on up to
![]() $N_{a}$
. The absolute values of
$N_{a}$
. The absolute values of
![]() $q_{i}$
for
$q_{i}$
for
![]() $i\geqslant a$
are required to lie in
$i\geqslant a$
are required to lie in
![]() $N_{a}$
.) When
$N_{a}$
.) When
![]() $k_{i}=i$
for all
$k_{i}=i$
for all
![]() $i$
, this simply says that a negative value
$i$
, this simply says that a negative value
![]() $q_{i}$
cannot appear if
$q_{i}$
cannot appear if
![]() $|q_{i}|$
has already appeared as some
$|q_{i}|$
has already appeared as some
![]() $q_{j}$
for
$q_{j}$
for
![]() $j<i$
.
$j<i$
.
Next, for each
![]() $i>a$
, so
$i>a$
, so
![]() $q_{i}<0$
, we define
$q_{i}<0$
, we define
where
![]() $j$
is the index such that
$j$
is the index such that
![]() $q_{j}>-q_{i}>q_{j+1}$
, and require that
$q_{j}>-q_{i}>q_{j+1}$
, and require that
When
![]() $k_{i}=i$
for all
$k_{i}=i$
for all
![]() $i$
,
$i$
,
![]() $\unicode[STIX]{x1D70C}$
has an easy characterization as
$\unicode[STIX]{x1D70C}$
has an easy characterization as
![]() $\unicode[STIX]{x1D70C}_{i}=\#\{j<i\,|\,q_{j}>-q_{i}\}$
.
$\unicode[STIX]{x1D70C}_{i}=\#\{j<i\,|\,q_{j}>-q_{i}\}$
.
The fourth condition is that
for
![]() $i>a+1$
. This is a refinement of the first requirement (c1).
$i>a+1$
. This is a refinement of the first requirement (c1).
The fifth and final condition is that
for
![]() $i>a$
. (In conjunction with (c4), it suffices to require (c5) only for
$i>a$
. (In conjunction with (c4), it suffices to require (c5) only for
![]() $i=s$
.)
$i=s$
.)
As in type A, a triple of type C has an associated partition
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
, defined by
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
, defined by
The conditions on
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
imply that
$\boldsymbol{\unicode[STIX]{x1D70F}}$
imply that
The other parts of
![]() $\unicode[STIX]{x1D706}$
are defined by filling in
$\unicode[STIX]{x1D706}$
are defined by filling in
![]() $\unicode[STIX]{x1D706}_{k}$
minimally subject to these inequalities (strict if
$\unicode[STIX]{x1D706}_{k}$
minimally subject to these inequalities (strict if
![]() $k<k_{a}$
, weak if
$k<k_{a}$
, weak if
![]() $k>k_{a}$
).
$k>k_{a}$
).
Generally, given a sequence of nonnegative integers
![]() $\unicode[STIX]{x1D70C}=(\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{\ell })$
, we will say that a partition
$\unicode[STIX]{x1D70C}=(\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{\ell })$
, we will say that a partition
![]() $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{\ell })$
is
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{\ell })$
is
![]() $\boldsymbol{\unicode[STIX]{x1D70C}}$
-strict if the sequence
$\boldsymbol{\unicode[STIX]{x1D70C}}$
-strict if the sequence
![]() $\unicode[STIX]{x1D707}_{j}=\unicode[STIX]{x1D706}_{j}+\unicode[STIX]{x1D70C}_{j}$
is nonincreasing. (See Remark 3 for the relation with the corresponding notion from [Reference Buch, Kresch and TamvakisBKT17].)
$\unicode[STIX]{x1D707}_{j}=\unicode[STIX]{x1D706}_{j}+\unicode[STIX]{x1D70C}_{j}$
is nonincreasing. (See Remark 3 for the relation with the corresponding notion from [Reference Buch, Kresch and TamvakisBKT17].)
From this point of view, it is useful to extend the definition of
![]() $\unicode[STIX]{x1D70C}$
given above to a unimodal sequence of integers
$\unicode[STIX]{x1D70C}$
given above to a unimodal sequence of integers
![]() $\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})=(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2},\ldots ,\unicode[STIX]{x1D70C}_{k_{s}})$
, as follows. As before, for
$\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})=(\unicode[STIX]{x1D70C}_{1},\unicode[STIX]{x1D70C}_{2},\ldots ,\unicode[STIX]{x1D70C}_{k_{s}})$
, as follows. As before, for
![]() $i>a$
, define
$i>a$
, define
![]() $\unicode[STIX]{x1D70C}_{k_{i}}=k_{j}$
, where
$\unicode[STIX]{x1D70C}_{k_{i}}=k_{j}$
, where
![]() $q_{j}>-q_{i}>q_{j+1}$
. For
$q_{j}>-q_{i}>q_{j+1}$
. For
![]() $k\leqslant k_{a}$
, set
$k\leqslant k_{a}$
, set
![]() $\unicode[STIX]{x1D70C}_{k}=k-1$
. Then fill in the remaining entries by setting
$\unicode[STIX]{x1D70C}_{k}=k-1$
. Then fill in the remaining entries by setting
![]() $\unicode[STIX]{x1D70C}_{k}=\unicode[STIX]{x1D70C}_{k_{i}}$
for
$\unicode[STIX]{x1D70C}_{k}=\unicode[STIX]{x1D70C}_{k_{i}}$
for
![]() $i>a$
and
$i>a$
and
![]() $k_{i-1}<k\leqslant k_{i}$
. This means
$k_{i-1}<k\leqslant k_{i}$
. This means
![]() $\unicode[STIX]{x1D70C}_{k_{a}+1}\geqslant \cdots \geqslant \unicode[STIX]{x1D70C}_{k_{s}}$
.
$\unicode[STIX]{x1D70C}_{k_{a}+1}\geqslant \cdots \geqslant \unicode[STIX]{x1D70C}_{k_{s}}$
.
The conditions (c1) and (c3)–(c5) are equivalent to requiring that
![]() $\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is a
$\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is a
![]() $\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})$
-strict partition, with
$\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})$
-strict partition, with
![]() $\unicode[STIX]{x1D706}_{k_{a}}>\unicode[STIX]{x1D706}_{k_{a}+1}$
.
$\unicode[STIX]{x1D706}_{k_{a}}>\unicode[STIX]{x1D706}_{k_{a}+1}$
.
For example, suppose
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}=(\,1\,3\,5\,6\,7\,9\,,\;9\,7\,6\,5\,2\,2\,,\;6\,3\,\overline{2}\,\overline{5}\,\overline{7}\,\overline{9}\,)$
, using a bar to indicate negative integers. Here
$\boldsymbol{\unicode[STIX]{x1D70F}}=(\,1\,3\,5\,6\,7\,9\,,\;9\,7\,6\,5\,2\,2\,,\;6\,3\,\overline{2}\,\overline{5}\,\overline{7}\,\overline{9}\,)$
, using a bar to indicate negative integers. Here
![]() $a=2$
,
$a=2$
,
![]() $\unicode[STIX]{x1D70C}=(0,1,2,3,3,1,0,0,0)$
, and
$\unicode[STIX]{x1D70C}=(0,1,2,3,3,1,0,0,0)$
, and
![]() $\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})=(14,10,9,5,5,4,1,1,1)$
. (See Figure 1.)
$\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})=(14,10,9,5,5,4,1,1,1)$
. (See Figure 1.)
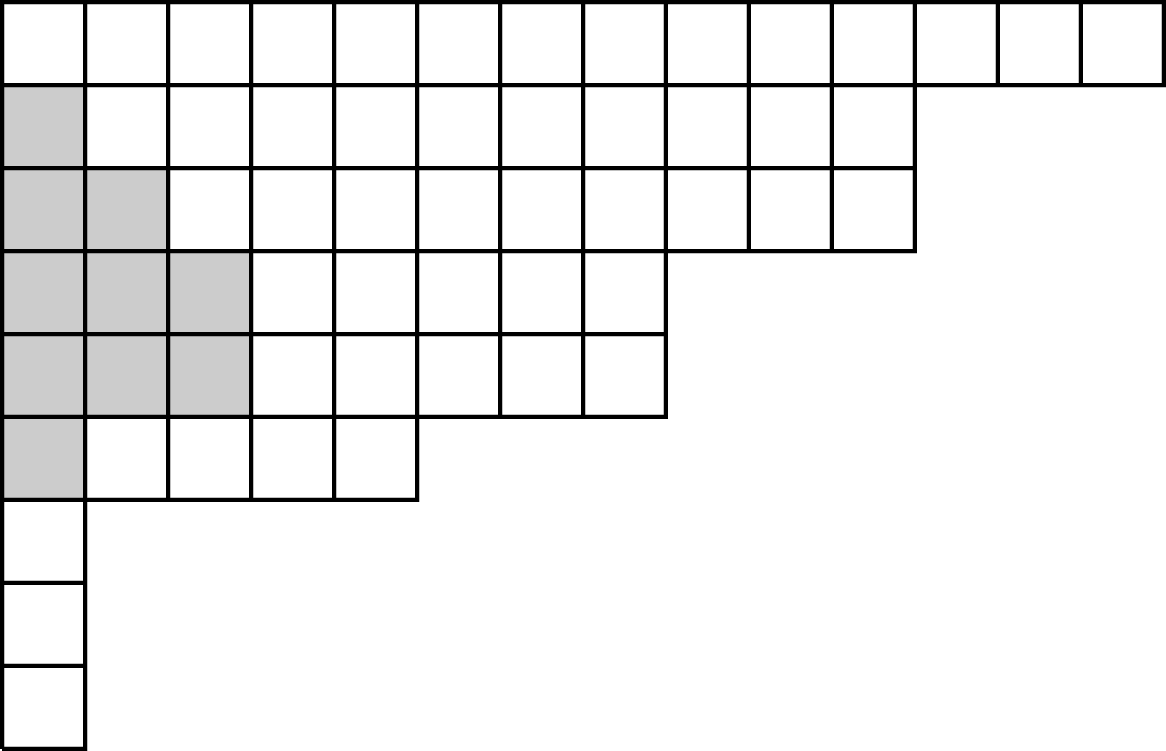
Figure 1. The shape for a
![]() $\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})$
-strict partition
$\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})$
-strict partition
![]() $\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
. The boxes of
$\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
. The boxes of
![]() $\unicode[STIX]{x1D70C}$
are shaded.
$\unicode[STIX]{x1D70C}$
are shaded.
Given an integer
![]() $\ell >0$
, a sequence of nonnegative integers
$\ell >0$
, a sequence of nonnegative integers
![]() $\unicode[STIX]{x1D70C}=(\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{\ell })$
with
$\unicode[STIX]{x1D70C}=(\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{\ell })$
with
![]() $\unicode[STIX]{x1D70C}_{j}<j$
, define the raising operator
$\unicode[STIX]{x1D70C}_{j}<j$
, define the raising operator
Inspired by [Reference Buch, Kresch and TamvakisBKT17], given symbols
![]() $c(1),\ldots ,c(\ell )$
, and a
$c(1),\ldots ,c(\ell )$
, and a
![]() $\unicode[STIX]{x1D70C}$
-strict partition
$\unicode[STIX]{x1D70C}$
-strict partition
![]() $\unicode[STIX]{x1D706}$
, we define the theta-polynomial to be
$\unicode[STIX]{x1D706}$
, we define the theta-polynomial to be
When
![]() $\unicode[STIX]{x1D70C}=\emptyset$
,
$\unicode[STIX]{x1D70C}=\emptyset$
,
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}$
is a Schur determinant, and when
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}$
is a Schur determinant, and when
![]() $\unicode[STIX]{x1D70C}_{j}=j-1$
,
$\unicode[STIX]{x1D70C}_{j}=j-1$
,
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}$
is a Schur Pfaffian.
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}$
is a Schur Pfaffian.
For a triple and the corresponding geometry described above, let
![]() $c(k_{i})=c(V-E_{p_{i}}-F_{q_{i}})$
, and for general
$c(k_{i})=c(V-E_{p_{i}}-F_{q_{i}})$
, and for general
![]() $k$
, take
$k$
, take
![]() $c(k)=c(k_{i})$
where
$c(k)=c(k_{i})$
where
![]() $i$
is minimal such that
$i$
is minimal such that
![]() $k_{i}\geqslant k$
. Set
$k_{i}\geqslant k$
. Set
![]() $\ell =k_{s}$
.
$\ell =k_{s}$
.
Theorem 2. We have
![]() $[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}^{(\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}}))}(c(1),c(2),\ldots ,c(\ell ))$
.
$[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}^{(\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}}))}(c(1),c(2),\ldots ,c(\ell ))$
.
The proof follows the same pattern as the one we saw in type A. As before, there are four cases. The appearance of Pfaffians in the formulas can be traced to a basic fact about isotropic subbundles: if
![]() $D\subset V$
is isotropic, then the symplectic form identifies
$D\subset V$
is isotropic, then the symplectic form identifies
![]() $D^{\bot }$
with
$D^{\bot }$
with
![]() $(V/D)^{\ast }$
. This is used in the second case.
$(V/D)^{\ast }$
. This is used in the second case.
2.1 Basic case
Take
![]() $s=1$
,
$s=1$
,
![]() $k_{1}=\ell =1$
, and
$k_{1}=\ell =1$
, and
![]() $p_{1}=n$
, so
$p_{1}=n$
, so
![]() $E_{n}$
is a line bundle and we are looking at
$E_{n}$
is a line bundle and we are looking at
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}=\{x\,|\,E_{n}\subseteq F_{q_{1}}\}$
. Equivalently,
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}=\{x\,|\,E_{n}\subseteq F_{q_{1}}\}$
. Equivalently,
![]() $E_{n}\rightarrow V/F_{q_{1}}$
is zero, so identity (a) lets us write
$E_{n}\rightarrow V/F_{q_{1}}$
is zero, so identity (a) lets us write
where
2.2 Dominant case
Now take
![]() $k_{i}=i$
and
$k_{i}=i$
and
![]() $p_{i}=n+1-i$
, for
$p_{i}=n+1-i$
, for
![]() $1\leqslant i\leqslant s$
. Write
$1\leqslant i\leqslant s$
. Write
![]() $D_{i}=E_{p_{i}}$
, so this is a vector bundle of rank
$D_{i}=E_{p_{i}}$
, so this is a vector bundle of rank
![]() $i$
, and we have
$i$
, and we have
![]() $D_{1}\subset D_{2}\subset \cdots \subset D_{s}\subset V$
. Letting
$D_{1}\subset D_{2}\subset \cdots \subset D_{s}\subset V$
. Letting
![]() $Z_{j}$
be the locus in
$Z_{j}$
be the locus in
![]() $X$
where
$X$
where
![]() $D_{i}\subseteq F_{q_{i}}$
for all
$D_{i}\subseteq F_{q_{i}}$
for all
![]() $i\leqslant j$
, we have
$i\leqslant j$
, we have
On
![]() $Z_{j-1}$
, we have
$Z_{j-1}$
, we have
![]() $D_{j-1}\subseteq F_{q_{j-1}}\subseteq F_{q_{j}}\subseteq V$
. Since
$D_{j-1}\subseteq F_{q_{j-1}}\subseteq F_{q_{j}}\subseteq V$
. Since
![]() $D_{j}$
is isotropic, we automatically have
$D_{j}$
is isotropic, we automatically have
![]() $D_{j}\subseteq D_{j-1}^{\bot }$
, so
$D_{j}\subseteq D_{j-1}^{\bot }$
, so
![]() $Z_{j}$
is defined by the condition
$Z_{j}$
is defined by the condition
or equivalently,
![]() $D_{j}/D_{j-1}\rightarrow D_{j-1}^{\bot }/(F_{q_{j}}\cap D_{j-1}^{\bot })$
is zero.
$D_{j}/D_{j-1}\rightarrow D_{j-1}^{\bot }/(F_{q_{j}}\cap D_{j-1}^{\bot })$
is zero.
When
![]() $j\leqslant a$
, the bundle
$j\leqslant a$
, the bundle
![]() $F_{q_{j}}$
is isotropic, and this implies
$F_{q_{j}}$
is isotropic, and this implies
![]() $F_{q_{j}}\subseteq D_{j-1}^{\bot }$
. In this case,
$F_{q_{j}}\subseteq D_{j-1}^{\bot }$
. In this case,
![]() $Z_{j}$
is equivalently defined by
$Z_{j}$
is equivalently defined by
![]() $D_{j}/D_{j-1}\subseteq F_{q_{j}}/D_{j-1}\subseteq D_{j-1}^{\bot }/D_{j-1}$
, and the basic case says
$D_{j}/D_{j-1}\subseteq F_{q_{j}}/D_{j-1}\subseteq D_{j-1}^{\bot }/D_{j-1}$
, and the basic case says
with
![]() $\unicode[STIX]{x1D706}_{j}=q_{j}+p_{j}-1=q_{j}+n-j$
. (That is,
$\unicode[STIX]{x1D706}_{j}=q_{j}+p_{j}-1=q_{j}+n-j$
. (That is,
![]() $\unicode[STIX]{x1D706}_{j}=\operatorname{rk}(D_{j-1}^{\bot }/F_{q_{j}})$
.)
$\unicode[STIX]{x1D706}_{j}=\operatorname{rk}(D_{j-1}^{\bot }/F_{q_{j}})$
.)
When
![]() $j>a$
(so
$j>a$
(so
![]() $q_{j}<0$
), we have
$q_{j}<0$
), we have
by property (∗) from Remark 1. (Recall that
![]() $\unicode[STIX]{x1D70C}_{j}=i$
, where
$\unicode[STIX]{x1D70C}_{j}=i$
, where
![]() $q_{i}>-q_{j}>q_{i+1}$
.) The basic case says
$q_{i}>-q_{j}>q_{i+1}$
.) The basic case says
with
![]() $\unicode[STIX]{x1D706}_{j}=n+q_{j}-i=p_{j}+q_{j}+j-1-\unicode[STIX]{x1D70C}_{j}$
. (That is,
$\unicode[STIX]{x1D706}_{j}=n+q_{j}-i=p_{j}+q_{j}+j-1-\unicode[STIX]{x1D70C}_{j}$
. (That is,
![]() $\unicode[STIX]{x1D706}_{j}=\operatorname{rk}(D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/F_{q_{j}})$
.)
$\unicode[STIX]{x1D706}_{j}=\operatorname{rk}(D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/F_{q_{j}})$
.)
With
![]() $\unicode[STIX]{x1D70C}_{j}=j-1$
for
$\unicode[STIX]{x1D70C}_{j}=j-1$
for
![]() $1\leqslant j\leqslant a$
, it follows that
$1\leqslant j\leqslant a$
, it follows that
Using the symplectic form to identify
![]() $D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }$
with
$D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }$
with
![]() $(V/D_{\unicode[STIX]{x1D70C}_{j}})^{\ast }$
, we have
$(V/D_{\unicode[STIX]{x1D70C}_{j}})^{\ast }$
, we have
setting
![]() $t_{j}=-c_{1}(D_{j}/D_{j-1})$
and applying identity (c), this becomes
$t_{j}=-c_{1}(D_{j}/D_{j-1})$
and applying identity (c), this becomes
Setting
![]() $c(j)=c(V-D_{j}-F_{q_{j}})=c(V-E_{p_{j}}-F_{q_{j}})$
and applying identity (b), this is
$c(j)=c(V-D_{j}-F_{q_{j}})=c(V-E_{p_{j}}-F_{q_{j}})$
and applying identity (b), this is
2.3 Main case
Here we only assume
![]() $k_{i}=i$
, for
$k_{i}=i$
, for
![]() $1\leqslant i\leqslant s$
. For
$1\leqslant i\leqslant s$
. For
![]() $j\leqslant a$
, we set
$j\leqslant a$
, we set
![]() $\unicode[STIX]{x1D70C}_{j}=j-1$
, and for
$\unicode[STIX]{x1D70C}_{j}=j-1$
, and for
![]() $j>a$
, we have
$j>a$
, we have
![]() $\unicode[STIX]{x1D70C}_{j}=i$
, where
$\unicode[STIX]{x1D70C}_{j}=i$
, where
![]() $q_{i}>-q_{j}>q_{i+1}$
. We have the same sequence of projective bundles as in type A,
$q_{i}>-q_{j}>q_{i+1}$
. We have the same sequence of projective bundles as in type A,
again,
![]() $D_{j}/D_{j-1}\subseteq E_{p_{j}}/D_{j-1}$
is the tautological subbundle on
$D_{j}/D_{j-1}\subseteq E_{p_{j}}/D_{j-1}$
is the tautological subbundle on
![]() $X_{j}$
. Write
$X_{j}$
. Write
![]() $\unicode[STIX]{x1D70B}^{(j)}:X_{j}\rightarrow X_{j-1}$
for the projection, and
$\unicode[STIX]{x1D70B}^{(j)}:X_{j}\rightarrow X_{j-1}$
for the projection, and
![]() $\unicode[STIX]{x1D70B}:X_{s}\rightarrow X$
for the composition.
$\unicode[STIX]{x1D70B}:X_{s}\rightarrow X$
for the composition.
On
![]() $X_{s}$
, we have the locus
$X_{s}$
, we have the locus
![]() $\widetilde{\unicode[STIX]{x1D6FA}}=\{D_{i}\subseteq F_{q_{i}}\,|\,\text{for }1\leqslant i\leqslant s\}$
. By the previous case, as a class in
$\widetilde{\unicode[STIX]{x1D6FA}}=\{D_{i}\subseteq F_{q_{i}}\,|\,\text{for }1\leqslant i\leqslant s\}$
. By the previous case, as a class in
![]() $A^{\ast }X_{s}$
we have
$A^{\ast }X_{s}$
we have
where
![]() $\widetilde{c}(j)=c(V-D_{j}-F_{q_{j}})$
and
$\widetilde{c}(j)=c(V-D_{j}-F_{q_{j}})$
and
Furthermore,
![]() $\unicode[STIX]{x1D70B}$
maps
$\unicode[STIX]{x1D70B}$
maps
![]() $\widetilde{\unicode[STIX]{x1D6FA}}$
birationally onto
$\widetilde{\unicode[STIX]{x1D6FA}}$
birationally onto
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
.
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
.
For each
![]() $i$
, using identity (d) we have
$i$
, using identity (d) we have
where
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
. (Note that
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
. (Note that
![]() $\unicode[STIX]{x1D706}_{i}=\widetilde{\unicode[STIX]{x1D706}}_{i}-\operatorname{rk}(E_{p_{i}}/D_{i})=\widetilde{\unicode[STIX]{x1D706}}_{i}-n-1+p_{i}+i$
.)
$\unicode[STIX]{x1D706}_{i}=\widetilde{\unicode[STIX]{x1D706}}_{i}-\operatorname{rk}(E_{p_{i}}/D_{i})=\widetilde{\unicode[STIX]{x1D706}}_{i}-n-1+p_{i}+i$
.)
This case follows, since
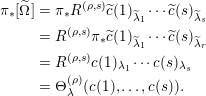 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{\ast }[\widetilde{\unicode[STIX]{x1D6FA}}] & = & \displaystyle \unicode[STIX]{x1D70B}_{\ast }R^{(\unicode[STIX]{x1D70C},s)}\widetilde{c}(1)_{\widetilde{\unicode[STIX]{x1D706}}_{1}}\cdots \widetilde{c}(s)_{\widetilde{\unicode[STIX]{x1D706}}_{s}}\nonumber\\ \displaystyle & = & \displaystyle R^{(\unicode[STIX]{x1D70C},s)}\unicode[STIX]{x1D70B}_{\ast }\widetilde{c}(1)_{\widetilde{\unicode[STIX]{x1D706}}_{1}}\cdots \widetilde{c}(s)_{\widetilde{\unicode[STIX]{x1D706}}_{r}}\nonumber\\ \displaystyle & = & \displaystyle R^{(\unicode[STIX]{x1D70C},s)}c(1)_{\unicode[STIX]{x1D706}_{1}}\cdots c(s)_{\unicode[STIX]{x1D706}_{s}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c(1),\ldots ,c(s)).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{\ast }[\widetilde{\unicode[STIX]{x1D6FA}}] & = & \displaystyle \unicode[STIX]{x1D70B}_{\ast }R^{(\unicode[STIX]{x1D70C},s)}\widetilde{c}(1)_{\widetilde{\unicode[STIX]{x1D706}}_{1}}\cdots \widetilde{c}(s)_{\widetilde{\unicode[STIX]{x1D706}}_{s}}\nonumber\\ \displaystyle & = & \displaystyle R^{(\unicode[STIX]{x1D70C},s)}\unicode[STIX]{x1D70B}_{\ast }\widetilde{c}(1)_{\widetilde{\unicode[STIX]{x1D706}}_{1}}\cdots \widetilde{c}(s)_{\widetilde{\unicode[STIX]{x1D706}}_{r}}\nonumber\\ \displaystyle & = & \displaystyle R^{(\unicode[STIX]{x1D70C},s)}c(1)_{\unicode[STIX]{x1D706}_{1}}\cdots c(s)_{\unicode[STIX]{x1D706}_{s}}\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c(1),\ldots ,c(s)).\nonumber\end{eqnarray}$$
2.4 General case
As in type A, any triple
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{k},\mathbf{p},\mathbf{q})$
can be inflated to a triple
$\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{k},\mathbf{p},\mathbf{q})$
can be inflated to a triple
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }=(\mathbf{k}^{\prime },\mathbf{p}^{\prime },\mathbf{q}^{\prime })$
having
$\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }=(\mathbf{k}^{\prime },\mathbf{p}^{\prime },\mathbf{q}^{\prime })$
having
![]() $k_{i}^{\prime }=i$
, for
$k_{i}^{\prime }=i$
, for
![]() $1\leqslant i\leqslant \ell =k_{s}$
, so that
$1\leqslant i\leqslant \ell =k_{s}$
, so that
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
and
$\boldsymbol{\unicode[STIX]{x1D70F}}$
and
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }$
define equivalent degeneracy loci. To do this, it suffices to insert
$\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }$
define equivalent degeneracy loci. To do this, it suffices to insert
![]() $(k^{\prime },p^{\prime },q^{\prime })$
between
$(k^{\prime },p^{\prime },q^{\prime })$
between
![]() $(k_{i-1},p_{i-1},q_{i-1})$
and
$(k_{i-1},p_{i-1},q_{i-1})$
and
![]() $(k_{i},p_{i},q_{i})$
whenever
$(k_{i},p_{i},q_{i})$
whenever
![]() $k_{i}-k_{i-1}>1$
. If
$k_{i}-k_{i-1}>1$
. If
![]() $p_{i-1}>p_{i}$
, one can always insert
$p_{i-1}>p_{i}$
, one can always insert
![]() $(k_{i}-1,p_{i}+1,q_{i})$
. If
$(k_{i}-1,p_{i}+1,q_{i})$
. If
![]() $q_{i-1}>q_{i}$
, when
$q_{i-1}>q_{i}$
, when
![]() $i\leqslant a$
, one can insert
$i\leqslant a$
, one can insert
![]() $(k_{i}-1,p_{i},q_{i}+1)$
. (Condition (c2) ensures the result is still a triple.) When
$(k_{i}-1,p_{i},q_{i}+1)$
. (Condition (c2) ensures the result is still a triple.) When
![]() $i>a$
, one can insert
$i>a$
, one can insert
![]() $(k_{i}-1,p_{i},q^{\prime })$
, where
$(k_{i}-1,p_{i},q^{\prime })$
, where
![]() $q^{\prime }$
is the smallest negative integer greater than
$q^{\prime }$
is the smallest negative integer greater than
![]() $q_{i}$
which is allowed by condition (c2).
$q_{i}$
which is allowed by condition (c2).
When all the additional bundles
![]() $E_{p_{i}^{\prime }}$
and
$E_{p_{i}^{\prime }}$
and
![]() $F_{q_{i}^{\prime }}$
are present on
$F_{q_{i}^{\prime }}$
are present on
![]() $X$
, one has
$X$
, one has
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }}=\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
; otherwise, they can be found by appropriate projective bundles, producing a birational map
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }}=\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
; otherwise, they can be found by appropriate projective bundles, producing a birational map
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }}\rightarrow \unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
.
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }}\rightarrow \unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
.
The ‘main case’ provides a theta-polynomial formula using the triple
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }$
and classes
$\boldsymbol{\unicode[STIX]{x1D70F}}^{\prime }$
and classes
![]() $c^{\prime }(k_{i}^{\prime })=c^{\prime }(i)=c(V-E_{p_{i}^{\prime }}-F_{q_{i}^{\prime }})$
. For
$c^{\prime }(k_{i}^{\prime })=c^{\prime }(i)=c(V-E_{p_{i}^{\prime }}-F_{q_{i}^{\prime }})$
. For
![]() $k\leqslant k_{a}$
and
$k\leqslant k_{a}$
and
![]() $m\geqslant \unicode[STIX]{x1D706}_{k}$
, we have relations
$m\geqslant \unicode[STIX]{x1D706}_{k}$
, we have relations
Indeed, we may suppose
![]() $k=k_{i}$
for some
$k=k_{i}$
for some
![]() $i$
, so the left-hand side can be written
$i$
, so the left-hand side can be written
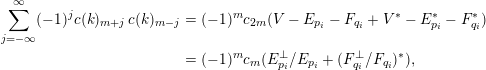 $$\begin{eqnarray}\displaystyle \mathop{\sum }_{j=-\infty }^{\infty }(-1)^{j}c(k)_{m+j}\,c(k)_{m-j} & = & \displaystyle (-1)^{m}c_{2m}(V-E_{p_{i}}-F_{q_{i}}+V^{\ast }-E_{p_{i}}^{\ast }-F_{q_{i}}^{\ast })\nonumber\\ \displaystyle & = & \displaystyle (-1)^{m}c_{m}(E_{p_{i}}^{\bot }/E_{p_{i}}+(F_{q_{i}}^{\bot }/F_{q_{i}})^{\ast }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \mathop{\sum }_{j=-\infty }^{\infty }(-1)^{j}c(k)_{m+j}\,c(k)_{m-j} & = & \displaystyle (-1)^{m}c_{2m}(V-E_{p_{i}}-F_{q_{i}}+V^{\ast }-E_{p_{i}}^{\ast }-F_{q_{i}}^{\ast })\nonumber\\ \displaystyle & = & \displaystyle (-1)^{m}c_{m}(E_{p_{i}}^{\bot }/E_{p_{i}}+(F_{q_{i}}^{\bot }/F_{q_{i}})^{\ast }),\nonumber\end{eqnarray}$$
which vanishes because the bundle in the last line has rank
![]() $2\unicode[STIX]{x1D706}_{k}-2$
. These are the relations required in the hypothesis of §A.3, Lemma A.1, which shows that
$2\unicode[STIX]{x1D706}_{k}-2$
. These are the relations required in the hypothesis of §A.3, Lemma A.1, which shows that
![]() $\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c^{\prime }(1),\ldots ,c^{\prime }(\ell ))=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c(1),\ldots ,c(\ell ))$
. ◻
$\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c^{\prime }(1),\ldots ,c^{\prime }(\ell ))=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c(1),\ldots ,c(\ell ))$
. ◻
As mentioned above, in extreme cases the theta-polynomial is a determinant or Pfaffian. To include the case where
![]() $\ell$
is odd, we recall that Pfaffians can be defined for odd matrices
$\ell$
is odd, we recall that Pfaffians can be defined for odd matrices
![]() $(m_{ij})$
by introducing a zeroth row,
$(m_{ij})$
by introducing a zeroth row,
![]() $m_{0j}$
(see §A.1).
$m_{0j}$
(see §A.1).
Corollary. If all
![]() $q_{i}>0$
, then
$q_{i}>0$
, then
where the right-hand side is defined to be the Pfaffian of the matrix
![]() $(m_{ij})$
, with
$(m_{ij})$
, with
and when
![]() $\ell$
is odd, the matrix is augmented by
$\ell$
is odd, the matrix is augmented by
![]() $m_{0j}=c(j)_{\unicode[STIX]{x1D706}_{j}}$
for
$m_{0j}=c(j)_{\unicode[STIX]{x1D706}_{j}}$
for
![]() $0<j\leqslant \ell$
.
$0<j\leqslant \ell$
.
This follows from the proposition of §A.2. Our conventions for Pfaffians, as in Appendix A, are that one forms a skew-symmetric matrix by defining
![]() $m_{ji}=-m_{ij}$
for
$m_{ji}=-m_{ij}$
for
![]() $i<j$
, and
$i<j$
, and
![]() $m_{ii}=0$
. (In fact, following the proof of [Reference KazarianKaz00, Theorem 1.1], it is equivalent to define the
$m_{ii}=0$
. (In fact, following the proof of [Reference KazarianKaz00, Theorem 1.1], it is equivalent to define the
![]() $m_{ij}$
for all
$m_{ij}$
for all
![]() $i,j$
by the formula of the above corollary, but we do not need this.)
$i,j$
by the formula of the above corollary, but we do not need this.)
Remark 1. Here are geometric reasons for the conditions on a triple. Only elementary linear algebra and basic facts about nondegenerate bilinear forms are needed: an isotropic subspace has dimension at most half that of the ambient space;
![]() $(E\cap F)^{\bot }=E^{\bot }+F^{\bot }$
; and
$(E\cap F)^{\bot }=E^{\bot }+F^{\bot }$
; and
![]() $(V/E)^{\ast }\cong E^{\bot }$
.
$(V/E)^{\ast }\cong E^{\bot }$
.
Condition (c1) has a simple explanation:
Condition (c3) arises from asking that the coisotropic condition imposed by
![]() $F_{q_{i}}$
be independent of any isotropic conditions, in the following sense. With
$F_{q_{i}}$
be independent of any isotropic conditions, in the following sense. With
![]() $i$
and
$i$
and
![]() $j$
as in the definition of
$j$
as in the definition of
![]() $\unicode[STIX]{x1D70C}$
, so
$\unicode[STIX]{x1D70C}$
, so
![]() $i>a$
and
$i>a$
and
![]() $\unicode[STIX]{x1D70C}_{k_{i}}=k_{j}$
, we have
$\unicode[STIX]{x1D70C}_{k_{i}}=k_{j}$
, we have
![]() $F_{q_{j}}\subseteq F_{q_{i}}^{\bot }$
(and this is the largest among the
$F_{q_{j}}\subseteq F_{q_{i}}^{\bot }$
(and this is the largest among the
![]() $F_{q}$
which is contained in
$F_{q}$
which is contained in
![]() $F_{q_{i}}^{\bot }$
). For generic
$F_{q_{i}}^{\bot }$
). For generic
![]() $E_{p}\supseteq E_{p_{j}}$
, we require
$E_{p}\supseteq E_{p_{j}}$
, we require
and in particular this holds for
![]() $p=p_{i}$
and
$p=p_{i}$
and
![]() $p=p_{i-1}$
. Thus
$p=p_{i-1}$
. Thus
for generic spaces, a formulation which is used in proving the main theorem of this section. Now Condition (c3) is a consequence of (∗) and the fact that
(Since
![]() $\dim (F_{q_{i}}/F_{q_{i}}^{\bot })=-2q_{i}$
, an isotropic subspace has dimension at most
$\dim (F_{q_{i}}/F_{q_{i}}^{\bot })=-2q_{i}$
, an isotropic subspace has dimension at most
![]() $-q_{i}$
.)
$-q_{i}$
.)
Condition (c4) is similar to (c1): one has
and one sees
![]() $\dim ((E_{p_{i}}+F_{q_{i}})/(E_{p_{i-1}}+F_{q_{i-1}}))\geqslant \unicode[STIX]{x1D70C}_{k_{i-1}}-\unicode[STIX]{x1D70C}_{k_{i}}$
from the following diagram.
$\dim ((E_{p_{i}}+F_{q_{i}})/(E_{p_{i-1}}+F_{q_{i-1}}))\geqslant \unicode[STIX]{x1D70C}_{k_{i-1}}-\unicode[STIX]{x1D70C}_{k_{i}}$
from the following diagram.
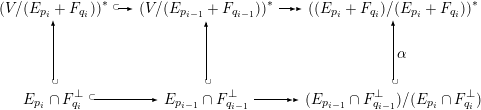
The map
![]() $\unicode[STIX]{x1D6FC}$
is injective because
$\unicode[STIX]{x1D6FC}$
is injective because
![]() $(E_{p_{i}}^{\bot }\cap F_{q_{i}}^{\bot })\cap (E_{p_{i}}\cap F_{q_{i}}^{\bot })=E_{p_{i}}\cap F_{q_{i}}^{\bot }$
.
$(E_{p_{i}}^{\bot }\cap F_{q_{i}}^{\bot })\cap (E_{p_{i}}\cap F_{q_{i}}^{\bot })=E_{p_{i}}\cap F_{q_{i}}^{\bot }$
.
Condition (c5) comes from writing
![]() $E_{p_{i}}\cap F_{q_{i}}$
as the kernel of
$E_{p_{i}}\cap F_{q_{i}}$
as the kernel of
Finally, for (c2), consider the case of a single
![]() $q_{i}=q$
; if
$q_{i}=q$
; if
![]() $E_{p}$
and
$E_{p}$
and
![]() $F_{q}$
are isotropic subspaces such that
$F_{q}$
are isotropic subspaces such that
![]() $\dim (E_{p}\cap F_{q})=k$
, then for generic subspaces
$\dim (E_{p}\cap F_{q})=k$
, then for generic subspaces
![]() $F_{q}\supset F_{q+1}\supset \cdots \supset F_{q+k}$
, one has
$F_{q}\supset F_{q+1}\supset \cdots \supset F_{q+k}$
, one has
For any isotropic
![]() $E_{p^{\prime }}\supseteq E_{p}$
, it follows that
$E_{p^{\prime }}\supseteq E_{p}$
, it follows that
so we should only impose rank conditions on the first of these. Writing
![]() $F_{q}^{\bot }=F_{-q+1}$
,
$F_{q}^{\bot }=F_{-q+1}$
,
![]() $F_{q+1}^{\bot }=F_{-q}$
, etc., this means the values
$F_{q+1}^{\bot }=F_{-q}$
, etc., this means the values
![]() $-q,-q-1,\ldots ,-q-k+1$
should be prohibited. Accounting for intersections previously imposed leads to the above condition (c2).
$-q,-q-1,\ldots ,-q-k+1$
should be prohibited. Accounting for intersections previously imposed leads to the above condition (c2).
Remark 2. A type C triple determines a signed permutation
![]() $w(\boldsymbol{\unicode[STIX]{x1D70F}})$
, as follows. Starting in position
$w(\boldsymbol{\unicode[STIX]{x1D70F}})$
, as follows. Starting in position
![]() $p_{1}$
, first place
$p_{1}$
, first place
![]() $k_{1}$
consecutive integers in increasing order, ending with
$k_{1}$
consecutive integers in increasing order, ending with
![]() $\overline{q}_{1}$
. Then starting in position
$\overline{q}_{1}$
. Then starting in position
![]() $p_{2}$
(or the next available position to the right of
$p_{2}$
(or the next available position to the right of
![]() $p_{2}$
), place
$p_{2}$
), place
![]() $k_{2}-k_{1}$
integers, consecutive among those whose absolute values have not been used, ending in at most
$k_{2}-k_{1}$
integers, consecutive among those whose absolute values have not been used, ending in at most
![]() $\overline{q}_{2}$
. Continue until
$\overline{q}_{2}$
. Continue until
![]() $k_{s}$
numbers have been placed, and finish by filling in the gaps with the smallest available positive integers.
$k_{s}$
numbers have been placed, and finish by filling in the gaps with the smallest available positive integers.
The conditions on
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
can be understood combinatorially: they guarantee that the length of the signed permutation
$\boldsymbol{\unicode[STIX]{x1D70F}}$
can be understood combinatorially: they guarantee that the length of the signed permutation
![]() $w(\boldsymbol{\unicode[STIX]{x1D70F}})$
is equal to the size of the partition
$w(\boldsymbol{\unicode[STIX]{x1D70F}})$
is equal to the size of the partition
![]() $\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
; this can be checked directly from the construction, using the combinatorial characterization of length from [Reference Björner and BrentiBB05, §8.1]. They also ensure that
$\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
; this can be checked directly from the construction, using the combinatorial characterization of length from [Reference Björner and BrentiBB05, §8.1]. They also ensure that
![]() $\unicode[STIX]{x1D70C}_{k_{i}}$
is the number of entries of
$\unicode[STIX]{x1D70C}_{k_{i}}$
is the number of entries of
![]() $w$
which are less than
$w$
which are less than
![]() $-|q_{i}|$
; that the
$-|q_{i}|$
; that the
![]() $k_{a}$
entries of
$k_{a}$
entries of
![]() $w$
placed in the first
$w$
placed in the first
![]() $a$
steps of the above recipe are all negative; and that the entries placed after the first
$a$
steps of the above recipe are all negative; and that the entries placed after the first
![]() $a$
steps are all positive.
$a$
steps are all positive.
For example, consider
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}=(\,1\,3\,5\,6\,7\,9\,,\;9\,7\,6\,5\,2\,2\,,\;6\,3\,\overline{2}\,\overline{5}\,\overline{7}\,\overline{9}\,)$
. The corresponding signed permutation is built in seven steps:
$\boldsymbol{\unicode[STIX]{x1D70F}}=(\,1\,3\,5\,6\,7\,9\,,\;9\,7\,6\,5\,2\,2\,,\;6\,3\,\overline{2}\,\overline{5}\,\overline{7}\,\overline{9}\,)$
. The corresponding signed permutation is built in seven steps:
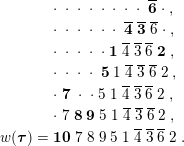 $$\begin{eqnarray}\displaystyle & & \displaystyle \cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\overline{\mathbf{6}}\;\cdot \;,\nonumber\\ \displaystyle & & \displaystyle \cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\overline{\mathbf{4}}\;\overline{\mathbf{3}}\;\overline{6}\;\cdot \;,\nonumber\\ \displaystyle & & \displaystyle \cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\mathbf{1}\;\overline{4}\;\overline{3}\;\overline{6}\;\mathbf{2}\;,\nonumber\\ \displaystyle & & \displaystyle \cdot \;\cdot \;\cdot \;\cdot \;\mathbf{5}\;1\;\overline{4}\;\overline{3}\;\overline{6}\;2\;,\nonumber\\ \displaystyle & & \displaystyle \cdot \;\mathbf{7}\;\cdot \;\cdot \;5\;1\;\overline{4}\;\overline{3}\;\overline{6}\;2\;,\nonumber\\ \displaystyle & & \displaystyle \cdot \;7\;\mathbf{8}\;\mathbf{9}\;5\;1\;\overline{4}\;\overline{3}\;\overline{6}\;2\;,\nonumber\\ \displaystyle w(\boldsymbol{\unicode[STIX]{x1D70F}}) & = & \displaystyle \mathbf{10}\;7\;8\;9\;5\;1\;\overline{4}\;\overline{3}\;\overline{6}\;2\;.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\overline{\mathbf{6}}\;\cdot \;,\nonumber\\ \displaystyle & & \displaystyle \cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\overline{\mathbf{4}}\;\overline{\mathbf{3}}\;\overline{6}\;\cdot \;,\nonumber\\ \displaystyle & & \displaystyle \cdot \;\cdot \;\cdot \;\cdot \;\cdot \;\mathbf{1}\;\overline{4}\;\overline{3}\;\overline{6}\;\mathbf{2}\;,\nonumber\\ \displaystyle & & \displaystyle \cdot \;\cdot \;\cdot \;\cdot \;\mathbf{5}\;1\;\overline{4}\;\overline{3}\;\overline{6}\;2\;,\nonumber\\ \displaystyle & & \displaystyle \cdot \;\mathbf{7}\;\cdot \;\cdot \;5\;1\;\overline{4}\;\overline{3}\;\overline{6}\;2\;,\nonumber\\ \displaystyle & & \displaystyle \cdot \;7\;\mathbf{8}\;\mathbf{9}\;5\;1\;\overline{4}\;\overline{3}\;\overline{6}\;2\;,\nonumber\\ \displaystyle w(\boldsymbol{\unicode[STIX]{x1D70F}}) & = & \displaystyle \mathbf{10}\;7\;8\;9\;5\;1\;\overline{4}\;\overline{3}\;\overline{6}\;2\;.\nonumber\end{eqnarray}$$
Since
![]() $a=2$
, the
$a=2$
, the
![]() $k_{a}=3$
negative entries all appear in the first and second steps. The partition
$k_{a}=3$
negative entries all appear in the first and second steps. The partition
![]() $\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is the one displayed in Figure 1, and a computation shows that
$\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is the one displayed in Figure 1, and a computation shows that
![]() $\ell (w(\boldsymbol{\unicode[STIX]{x1D70F}}))=|\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})|=50$
.
$\ell (w(\boldsymbol{\unicode[STIX]{x1D70F}}))=|\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})|=50$
.
It would be interesting to know more about the combinatorial properties of signed permutations arising this way. For example, are they characterized by pattern avoidance?Footnote 3
Remark 3. When all
![]() $p_{i}=p$
, then a
$p_{i}=p$
, then a
![]() $\unicode[STIX]{x1D70C}$
-strict partition
$\unicode[STIX]{x1D70C}$
-strict partition
![]() $\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is one so that all parts of size greater than
$\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is one so that all parts of size greater than
![]() $p-1$
are distinct; that is, it is a
$p-1$
are distinct; that is, it is a
![]() $(p-1)$
-strict partition as defined in [Reference Buch, Kresch and TamvakisBKT17]. Geometrically, all
$(p-1)$
-strict partition as defined in [Reference Buch, Kresch and TamvakisBKT17]. Geometrically, all
![]() $E_{p_{i}}$
have rank
$E_{p_{i}}$
have rank
![]() $n+1-p$
, so the locus comes from an isotropic Grassmannian. Conversely, given a
$n+1-p$
, so the locus comes from an isotropic Grassmannian. Conversely, given a
![]() $(p-1)$
-strict partition
$(p-1)$
-strict partition
![]() $\unicode[STIX]{x1D706}$
, following [Reference Buch, Kresch and TamvakisBKT17] define
$\unicode[STIX]{x1D706}$
, following [Reference Buch, Kresch and TamvakisBKT17] define
If we define a type C triple by setting
![]() $k_{j}=j$
,
$k_{j}=j$
,
![]() $p_{j}=p$
, and
$p_{j}=p$
, and
one recovers
![]() $\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
. Indeed, one can check that
$\unicode[STIX]{x1D706}=\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
. Indeed, one can check that
![]() $\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is given by
$\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is given by
in this situation.
Similarly, for a triple
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
with all
$\boldsymbol{\unicode[STIX]{x1D70F}}$
with all
![]() $p_{i}=p$
and
$p_{i}=p$
and
![]() $k_{i}=i$
, the characteristic index
$k_{i}=i$
, the characteristic index
![]() $\unicode[STIX]{x1D712}$
used in [Reference Ikeda and MatsumuraIM15] is given by
$\unicode[STIX]{x1D712}$
used in [Reference Ikeda and MatsumuraIM15] is given by
![]() $\unicode[STIX]{x1D712}_{i}=q_{i}-1$
for
$\unicode[STIX]{x1D712}_{i}=q_{i}-1$
for
![]() $i\leqslant a$
, and
$i\leqslant a$
, and
![]() $\unicode[STIX]{x1D712}_{i}=q_{i}$
for
$\unicode[STIX]{x1D712}_{i}=q_{i}$
for
![]() $i>a$
.
$i>a$
.
3 Type B: odd orthogonal bundles
A triple of type B is the same as in type C, as are the definitions of the sequence
![]() $\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})$
, the partition
$\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})$
, the partition
![]() $\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
, the raising operator
$\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
, the raising operator
![]() $R^{(\unicode[STIX]{x1D70C},\ell )}$
, and the theta-polynomial.
$R^{(\unicode[STIX]{x1D70C},\ell )}$
, and the theta-polynomial.
The geometry starts with a vector bundle
![]() $V$
of rank
$V$
of rank
![]() $2n+1$
, equipped with a nondegenerate quadratic form. We have two flags of subbundles,
$2n+1$
, equipped with a nondegenerate quadratic form. We have two flags of subbundles,
the isotropicity and ranks of these are exactly as in type C. The degeneracy locus is
Let
![]() $M$
be the line bundle
$M$
be the line bundle
![]() $\det V$
, and note that
$\det V$
, and note that
for any maximal isotropic
![]() $F\subset V$
. In fact, we have
$F\subset V$
. In fact, we have
![]() $M\cong \det (D^{\bot }/D)$
for any isotropic
$M\cong \det (D^{\bot }/D)$
for any isotropic
![]() $D\subset V$
.
$D\subset V$
.
Given a triple, let
![]() $\ell =k_{s}$
and
$\ell =k_{s}$
and
![]() $r=k_{a}$
, recalling that
$r=k_{a}$
, recalling that
![]() $a$
is the index such that
$a$
is the index such that
![]() $q_{a}>0>q_{a+1}$
. For
$q_{a}>0>q_{a+1}$
. For
![]() $i\leqslant a$
let
$i\leqslant a$
let
![]() $c(k_{i})=c(V-E_{p_{i}}-F_{q_{i}}-M)$
, and for
$c(k_{i})=c(V-E_{p_{i}}-F_{q_{i}}-M)$
, and for
![]() $i>a$
, let
$i>a$
, let
![]() $c(k_{i})=c(V-E_{p_{i}}-F_{q_{i}})$
. As before, when
$c(k_{i})=c(V-E_{p_{i}}-F_{q_{i}})$
. As before, when
![]() $k_{i-1}<k\leqslant k_{i}$
, we set
$k_{i-1}<k\leqslant k_{i}$
, we set
![]() $c(k)=c(k_{i})$
.
$c(k)=c(k_{i})$
.
Theorem 3. We have
![]() $2^{r}\,[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}^{(\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}}))}(c(1),c(2),\ldots ,c(\ell ))$
.
$2^{r}\,[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}^{(\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}}))}(c(1),c(2),\ldots ,c(\ell ))$
.
The four steps of the proof are almost the same as in type C. We will indicate the differences.
3.1 Basic case
Take
![]() $s=1$
,
$s=1$
,
![]() $k_{1}=\ell =1$
, and
$k_{1}=\ell =1$
, and
![]() $p_{1}=n$
, so
$p_{1}=n$
, so
![]() $E_{n}$
is a line bundle and
$E_{n}$
is a line bundle and
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
is the locus where
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
is the locus where
![]() $E_{n}\subseteq F_{q_{1}}$
. When
$E_{n}\subseteq F_{q_{1}}$
. When
![]() $q_{1}>0$
, so
$q_{1}>0$
, so
![]() $F_{q_{1}}$
is isotropic, the proposition of Appendix B gives
$F_{q_{1}}$
is isotropic, the proposition of Appendix B gives
On the other hand, when
![]() $q_{1}<0$
, so
$q_{1}<0$
, so
![]() $F_{q_{1}}$
is coisotropic, the locus is defined (scheme-theoretically) by the vanishing of
$F_{q_{1}}$
is coisotropic, the locus is defined (scheme-theoretically) by the vanishing of
![]() $E_{n}\rightarrow V/F_{q_{1}}$
, and
$E_{n}\rightarrow V/F_{q_{1}}$
, and
in this case.
3.2 Dominant case
Now take
![]() $k_{i}=i$
and
$k_{i}=i$
and
![]() $p_{i}=n+1-i$
, for
$p_{i}=n+1-i$
, for
![]() $1\leqslant i\leqslant s$
, and write
$1\leqslant i\leqslant s$
, and write
![]() $D_{i}=E_{p_{i}}$
. As in type C, we have a filtration by
$D_{i}=E_{p_{i}}$
. As in type C, we have a filtration by
![]() $Z_{j}$
, the locus where
$Z_{j}$
, the locus where
![]() $D_{i}\subseteq F_{q_{i}}$
for all
$D_{i}\subseteq F_{q_{i}}$
for all
![]() $i\leqslant j$
, so that
$i\leqslant j$
, so that
![]() $Z_{0}=X$
and
$Z_{0}=X$
and
![]() $Z_{s}=\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
. When
$Z_{s}=\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
. When
![]() $j\leqslant a$
(so
$j\leqslant a$
(so
![]() $q_{j}>0$
), the basic case says that
$q_{j}>0$
), the basic case says that
and when
![]() $j>a$
(so
$j>a$
(so
![]() $q_{j}<0$
),
$q_{j}<0$
),
where in each case
![]() $\unicode[STIX]{x1D70C}_{j}$
and
$\unicode[STIX]{x1D70C}_{j}$
and
![]() $\unicode[STIX]{x1D706}_{j}$
is defined as in type C. We therefore have
$\unicode[STIX]{x1D706}_{j}$
is defined as in type C. We therefore have
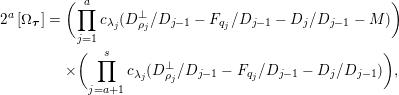 $$\begin{eqnarray}\displaystyle 2^{a}\,[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}] & = & \displaystyle \biggl(\mathop{\prod }_{j=1}^{a}c_{\unicode[STIX]{x1D706}_{j}}(D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/D_{j-1}-F_{q_{j}}/D_{j-1}-D_{j}/D_{j-1}-M)\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \biggl(\mathop{\prod }_{j=a+1}^{s}c_{\unicode[STIX]{x1D706}_{j}}(D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/D_{j-1}-F_{q_{j}}/D_{j-1}-D_{j}/D_{j-1})\biggr),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2^{a}\,[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}] & = & \displaystyle \biggl(\mathop{\prod }_{j=1}^{a}c_{\unicode[STIX]{x1D706}_{j}}(D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/D_{j-1}-F_{q_{j}}/D_{j-1}-D_{j}/D_{j-1}-M)\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \biggl(\mathop{\prod }_{j=a+1}^{s}c_{\unicode[STIX]{x1D706}_{j}}(D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/D_{j-1}-F_{q_{j}}/D_{j-1}-D_{j}/D_{j-1})\biggr),\nonumber\end{eqnarray}$$
as before.
The rest of the proof proceeds exactly as in type C. ◻
As in type C, we recover a Pfaffian formula for vexillary signed permutations.
Corollary. If all
![]() $q_{i}>0$
, then
$q_{i}>0$
, then
4 Type D: even orthogonal bundles
A triple of type D is
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{k},\mathbf{p},\mathbf{q})$
, with
$\boldsymbol{\unicode[STIX]{x1D70F}}=(\mathbf{k},\mathbf{p},\mathbf{q})$
, with
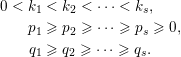 $$\begin{eqnarray}\displaystyle 0<k_{1} & {<} & \displaystyle k_{2}<\cdots <k_{s},\nonumber\\ \displaystyle p_{1} & {\geqslant} & \displaystyle p_{2}\geqslant \cdots \geqslant p_{s}\geqslant 0,\nonumber\\ \displaystyle q_{1} & {\geqslant} & \displaystyle q_{2}\geqslant \cdots \geqslant q_{s}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 0<k_{1} & {<} & \displaystyle k_{2}<\cdots <k_{s},\nonumber\\ \displaystyle p_{1} & {\geqslant} & \displaystyle p_{2}\geqslant \cdots \geqslant p_{s}\geqslant 0,\nonumber\\ \displaystyle q_{1} & {\geqslant} & \displaystyle q_{2}\geqslant \cdots \geqslant q_{s}.\nonumber\end{eqnarray}$$
The value
![]() $q=-1$
is prohibited, and if
$q=-1$
is prohibited, and if
![]() $p_{s}=0$
, then all
$p_{s}=0$
, then all
![]() $q_{i}\geqslant 0$
. Set
$q_{i}\geqslant 0$
. Set
![]() $a=a(\boldsymbol{\unicode[STIX]{x1D70F}})$
to be the integer such that
$a=a(\boldsymbol{\unicode[STIX]{x1D70F}})$
to be the integer such that
![]() $q_{a}>-1>q_{a+1}$
.
$q_{a}>-1>q_{a+1}$
.
A quick way to characterize the further requirements on a type D triple is as follows. Form
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}^{+}$
by replacing each
$\boldsymbol{\unicode[STIX]{x1D70F}}^{+}$
by replacing each
![]() $p_{i}$
in
$p_{i}$
in
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
with
$\boldsymbol{\unicode[STIX]{x1D70F}}$
with
![]() $p_{i}+1$
, and replacing each
$p_{i}+1$
, and replacing each
![]() $q_{i}\geqslant 0$
in
$q_{i}\geqslant 0$
in
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
with
$\boldsymbol{\unicode[STIX]{x1D70F}}$
with
![]() $q_{i}+1$
; then a type D triple is one such that
$q_{i}+1$
; then a type D triple is one such that
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}^{+}$
is a type C triple.
$\boldsymbol{\unicode[STIX]{x1D70F}}^{+}$
is a type C triple.
To be completely clear, we will spell out the conditions. Their geometric explanations are analogous to those for type C. For
![]() $i\leqslant a$
,
$i\leqslant a$
,
and, as before, this is the only condition when all
![]() $q_{i}$
are nonnegative.
$q_{i}$
are nonnegative.
For each
![]() $i\leqslant a$
, let
$i\leqslant a$
, let
![]() $m(i)=\min \{m\,|\,q_{i}+(k_{i}-k_{i-1})\geqslant q_{m}\}$
. The negative values
$m(i)=\min \{m\,|\,q_{i}+(k_{i}-k_{i-1})\geqslant q_{m}\}$
. The negative values
are prohibited as values of
![]() $q_{j}$
for
$q_{j}$
for
![]() $j>a$
.
$j>a$
.
The sequence
![]() $\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is defined similarly as in type C. Set
$\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is defined similarly as in type C. Set
![]() $\unicode[STIX]{x1D70C}_{k}=k-1$
for
$\unicode[STIX]{x1D70C}_{k}=k-1$
for
![]() $k\leqslant k_{a}$
. For
$k\leqslant k_{a}$
. For
![]() $i>a$
, set
$i>a$
, set
![]() $\unicode[STIX]{x1D70C}_{k_{i}}=k_{j}$
, where
$\unicode[STIX]{x1D70C}_{k_{i}}=k_{j}$
, where
![]() $j$
is the index such that
$j$
is the index such that
![]() $q_{j}\geqslant -q_{i}>q_{j+1}+1$
. Then fill in the other parts minimally subject to
$q_{j}\geqslant -q_{i}>q_{j+1}+1$
. Then fill in the other parts minimally subject to
![]() $\unicode[STIX]{x1D70C}_{k_{a}+1}\geqslant \cdots \geqslant \unicode[STIX]{x1D70C}_{k_{s}}\geqslant 0$
. We require
$\unicode[STIX]{x1D70C}_{k_{a}+1}\geqslant \cdots \geqslant \unicode[STIX]{x1D70C}_{k_{s}}\geqslant 0$
. We require
for all
![]() $i>a$
.
$i>a$
.
Finally, for
![]() $i>a+1$
,
$i>a+1$
,
and
The associated partition
![]() $\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is defined by
$\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is defined by
filling in the other parts minimally subject to
where
![]() $\ell =k_{s}$
. That is,
$\ell =k_{s}$
. That is,
![]() $\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is a
$\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
is a
![]() $\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})$
-strict partition.Footnote
4
(In contrast to type C, we allow
$\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}})$
-strict partition.Footnote
4
(In contrast to type C, we allow
![]() $\unicode[STIX]{x1D706}_{k_{a}}=\unicode[STIX]{x1D706}_{k_{a}+1}$
.)
$\unicode[STIX]{x1D706}_{k_{a}}=\unicode[STIX]{x1D706}_{k_{a}+1}$
.)
A key difference in type D is that
![]() $\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
may have a part equal to
$\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})$
may have a part equal to
![]() $0$
, and this is included in the data. (For example, this happens when
$0$
, and this is included in the data. (For example, this happens when
![]() $p_{s}=q_{s}=0$
; in this case, the total number of parts determines the dimension of the intersection of two maximal isotropic subspaces.)
$p_{s}=q_{s}=0$
; in this case, the total number of parts determines the dimension of the intersection of two maximal isotropic subspaces.)
The raising operators and polynomials require some setup; details are explained in Appendix A. We will have elements
![]() $c(i)=d(i)+e(i)$
, so that
$c(i)=d(i)+e(i)$
, so that
![]() $c(i)_{k}=d(i)_{k}+e(i)_{k}$
. We will also have operators
$c(i)_{k}=d(i)_{k}+e(i)_{k}$
. We will also have operators
![]() $\unicode[STIX]{x1D6FF}_{i}$
, which acts on a monomial
$\unicode[STIX]{x1D6FF}_{i}$
, which acts on a monomial
![]() $c(1)_{\unicode[STIX]{x1D6FC}_{1}}\cdots c(\ell )_{\unicode[STIX]{x1D6FC}_{\ell }}$
by replacing
$c(1)_{\unicode[STIX]{x1D6FC}_{1}}\cdots c(\ell )_{\unicode[STIX]{x1D6FC}_{\ell }}$
by replacing
![]() $c(i)_{\unicode[STIX]{x1D6FC}_{i}}$
with
$c(i)_{\unicode[STIX]{x1D6FC}_{i}}$
with
![]() $d(i)_{\unicode[STIX]{x1D6FC}_{i}}$
; that is,
$d(i)_{\unicode[STIX]{x1D6FC}_{i}}$
; that is,
![]() $\unicode[STIX]{x1D6FF}_{i}$
sends
$\unicode[STIX]{x1D6FF}_{i}$
sends
![]() $e(i)$
to zero and leaves everything else unchanged.
$e(i)$
to zero and leaves everything else unchanged.
Given integers
![]() $0\leqslant r\leqslant \ell$
, and a sequence of nonnegative integers
$0\leqslant r\leqslant \ell$
, and a sequence of nonnegative integers
![]() $\unicode[STIX]{x1D70C}=(\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{\ell })$
with
$\unicode[STIX]{x1D70C}=(\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{\ell })$
with
![]() $\unicode[STIX]{x1D70C}_{j}<j$
and
$\unicode[STIX]{x1D70C}_{j}<j$
and
![]() $\unicode[STIX]{x1D70C}_{j}=j-1$
for
$\unicode[STIX]{x1D70C}_{j}=j-1$
for
![]() $1\leqslant j\leqslant k$
, we define the raising operator
$1\leqslant j\leqslant k$
, we define the raising operator
and using these, the eta-polynomial for a
![]() $\unicode[STIX]{x1D70C}$
-strict partition is defined as
$\unicode[STIX]{x1D70C}$
-strict partition is defined as
Here is the geometry. We have a vector bundle
![]() $V$
of rank
$V$
of rank
![]() $2n$
, equipped with a nondegenerate quadratic form taking values in the trivial bundle. There are flags of subbundles,
$2n$
, equipped with a nondegenerate quadratic form taking values in the trivial bundle. There are flags of subbundles,
each
![]() $E_{p}$
has rank
$E_{p}$
has rank
![]() $n-p$
and is isotropic; and each
$n-p$
and is isotropic; and each
![]() $F_{q}$
has rank
$F_{q}$
has rank
![]() $n-q$
, and is isotropic when
$n-q$
, and is isotropic when
![]() $q\geqslant 0$
and coisotropic when
$q\geqslant 0$
and coisotropic when
![]() $q<0$
. Note that
$q<0$
. Note that
![]() $F_{q}^{\bot }=F_{-q}$
.
$F_{q}^{\bot }=F_{-q}$
.
The degeneracy locus is defined as before, by
The usual type D caveat applies: this acquires its scheme structure via pullback from a Schubert bundle in a flag bundle, and even there it must be taken to mean the closure of the locus where equality holds (see, for example, [Reference Fulton and PragaczFP98, §6] or [Reference TamvakisTam16a, §6.3.2]).
Now given a type D triple, set
![]() $\ell =k_{s}$
and
$\ell =k_{s}$
and
![]() $r=k_{a}$
. Let
$r=k_{a}$
. Let
![]() $d(k_{i})=c(V-E_{p_{i}}-F_{q_{i}})$
, and for
$d(k_{i})=c(V-E_{p_{i}}-F_{q_{i}})$
, and for
![]() $i\leqslant a$
(so
$i\leqslant a$
(so
![]() $q_{i}\geqslant 0$
), set
$q_{i}\geqslant 0$
), set
![]() $e(k_{i})=e(E_{p_{i}},F_{q_{i}})$
, where the latter is defined as
$e(k_{i})=e(E_{p_{i}},F_{q_{i}})$
, where the latter is defined as
for some maximal isotropic bundles
![]() $E\supseteq E_{p_{i}}$
and
$E\supseteq E_{p_{i}}$
and
![]() $F\supseteq F_{q_{i}}$
. (Only the Euler class
$F\supseteq F_{q_{i}}$
. (Only the Euler class
![]() $e_{p_{i}+q_{i}}(E_{p_{i}},F_{q_{i}})$
appears in our formulas, and this is independent of the choice of such maximal
$e_{p_{i}+q_{i}}(E_{p_{i}},F_{q_{i}})$
appears in our formulas, and this is independent of the choice of such maximal
![]() $E$
and
$E$
and
![]() $F$
.) When
$F$
.) When
![]() $i>a$
, we set
$i>a$
, we set
![]() $e(k_{i})=0$
; and as usual, when
$e(k_{i})=0$
; and as usual, when
![]() $k_{i-1}<k\leqslant k_{i}$
, we set
$k_{i-1}<k\leqslant k_{i}$
, we set
![]() $d(k)=d(k_{i})$
and
$d(k)=d(k_{i})$
and
![]() $e(k)=e(k_{i})$
. Finally, let
$e(k)=e(k_{i})$
. Finally, let
Theorem 4. We have
![]() $2^{r}\,[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=\text{H}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}^{(\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}}))}(c(1),c(2),\ldots ,c(\ell ))$
.
$2^{r}\,[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}]=\text{H}_{\unicode[STIX]{x1D706}(\boldsymbol{\unicode[STIX]{x1D70F}})}^{(\unicode[STIX]{x1D70C}(\boldsymbol{\unicode[STIX]{x1D70F}}))}(c(1),c(2),\ldots ,c(\ell ))$
.
Most of the proof proceeds exactly as in type B. We will go through the outline briefly, to point out the differences.
4.1 Basic case
Here
![]() $s=1$
,
$s=1$
,
![]() $k_{1}=\ell =1$
, and
$k_{1}=\ell =1$
, and
![]() $p_{1}=n-1$
, so
$p_{1}=n-1$
, so
![]() $E_{n-1}$
is a line bundle and
$E_{n-1}$
is a line bundle and
![]() $\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
is the locus where
$\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
is the locus where
![]() $E_{n-1}\subseteq F_{q_{1}}$
. Just as before, we have
$E_{n-1}\subseteq F_{q_{1}}$
. Just as before, we have
The proof is the same as in type B.
4.2 Dominant case
Now
![]() $k_{i}=i$
for
$k_{i}=i$
for
![]() $1\leqslant i\leqslant s$
, and
$1\leqslant i\leqslant s$
, and
![]() $p_{i}=n-i$
, so
$p_{i}=n-i$
, so
![]() $D_{i}=E_{n-i}$
has rank
$D_{i}=E_{n-i}$
has rank
![]() $i$
. Let
$i$
. Let
![]() $Z_{j}$
be the locus where
$Z_{j}$
be the locus where
![]() $D_{j}\subseteq F_{q_{j}}$
, so
$D_{j}\subseteq F_{q_{j}}$
, so
![]() $Z_{0}=X$
and
$Z_{0}=X$
and
![]() $Z_{s}=\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
. When
$Z_{s}=\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}$
. When
![]() $j\leqslant a$
, applying the basic case with
$j\leqslant a$
, applying the basic case with
![]() $V$
replaced by
$V$
replaced by
![]() $D_{j-1}^{\bot }/D_{j-1}$
, we obtain
$D_{j-1}^{\bot }/D_{j-1}$
, we obtain
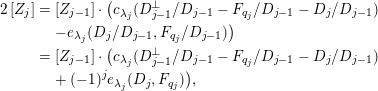 $$\begin{eqnarray}\displaystyle 2\,[Z_{j}] & = & \displaystyle [Z_{j-1}]\cdot \big(c_{\unicode[STIX]{x1D706}_{j}}(D_{j-1}^{\bot }/D_{j-1}-F_{q_{j}}/D_{j-1}-D_{j}/D_{j-1})\nonumber\\ \displaystyle & & \displaystyle -e_{\unicode[STIX]{x1D706}_{j}}(D_{j}/D_{j-1},F_{q_{j}}/D_{j-1})\big)\nonumber\\ \displaystyle & = & \displaystyle [Z_{j-1}]\cdot \big(c_{\unicode[STIX]{x1D706}_{j}}(D_{j-1}^{\bot }/D_{j-1}-F_{q_{j}}/D_{j-1}-D_{j}/D_{j-1})\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{j}e_{\unicode[STIX]{x1D706}_{j}}(D_{j},F_{q_{j}})\big),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\,[Z_{j}] & = & \displaystyle [Z_{j-1}]\cdot \big(c_{\unicode[STIX]{x1D706}_{j}}(D_{j-1}^{\bot }/D_{j-1}-F_{q_{j}}/D_{j-1}-D_{j}/D_{j-1})\nonumber\\ \displaystyle & & \displaystyle -e_{\unicode[STIX]{x1D706}_{j}}(D_{j}/D_{j-1},F_{q_{j}}/D_{j-1})\big)\nonumber\\ \displaystyle & = & \displaystyle [Z_{j-1}]\cdot \big(c_{\unicode[STIX]{x1D706}_{j}}(D_{j-1}^{\bot }/D_{j-1}-F_{q_{j}}/D_{j-1}-D_{j}/D_{j-1})\nonumber\\ \displaystyle & & \displaystyle +\,(-1)^{j}e_{\unicode[STIX]{x1D706}_{j}}(D_{j},F_{q_{j}})\big),\nonumber\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D706}_{j}=n-j+q_{j}$
.
$\unicode[STIX]{x1D706}_{j}=n-j+q_{j}$
.
When
![]() $j>a$
, using
$j>a$
, using
![]() $D_{j-1}^{\bot }/(F_{q_{j}}\cap D_{j-1}^{\bot })=D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/F_{q_{j}}$
(by (∗) as in type C), the locus is given by the vanishing of
$D_{j-1}^{\bot }/(F_{q_{j}}\cap D_{j-1}^{\bot })=D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/F_{q_{j}}$
(by (∗) as in type C), the locus is given by the vanishing of
![]() $D_{j}/D_{j-1}\rightarrow D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/F_{q_{j}}$
, so the basic case says
$D_{j}/D_{j-1}\rightarrow D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/F_{q_{j}}$
, so the basic case says
where
![]() $\unicode[STIX]{x1D70C}_{j}$
and
$\unicode[STIX]{x1D70C}_{j}$
and
![]() $\unicode[STIX]{x1D706}_{j}$
are defined as above.
$\unicode[STIX]{x1D706}_{j}$
are defined as above.
It follows that
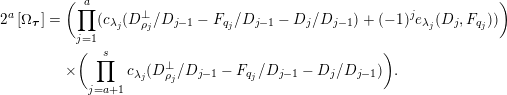 $$\begin{eqnarray}\displaystyle 2^{a}\,[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}] & = & \displaystyle \biggl(\mathop{\prod }_{j=1}^{a}(c_{\unicode[STIX]{x1D706}_{j}}(D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/D_{j-1}-F_{q_{j}}/D_{j-1}-D_{j}/D_{j-1})+(-1)^{j}e_{\unicode[STIX]{x1D706}_{j}}(D_{j},F_{q_{j}}))\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \biggl(\mathop{\prod }_{j=a+1}^{s}c_{\unicode[STIX]{x1D706}_{j}}(D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/D_{j-1}-F_{q_{j}}/D_{j-1}-D_{j}/D_{j-1})\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2^{a}\,[\unicode[STIX]{x1D6FA}_{\boldsymbol{\unicode[STIX]{x1D70F}}}] & = & \displaystyle \biggl(\mathop{\prod }_{j=1}^{a}(c_{\unicode[STIX]{x1D706}_{j}}(D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/D_{j-1}-F_{q_{j}}/D_{j-1}-D_{j}/D_{j-1})+(-1)^{j}e_{\unicode[STIX]{x1D706}_{j}}(D_{j},F_{q_{j}}))\biggr)\nonumber\\ \displaystyle & & \displaystyle \times \biggl(\mathop{\prod }_{j=a+1}^{s}c_{\unicode[STIX]{x1D706}_{j}}(D_{\unicode[STIX]{x1D70C}_{j}}^{\bot }/D_{j-1}-F_{q_{j}}/D_{j-1}-D_{j}/D_{j-1})\biggr).\nonumber\end{eqnarray}$$
This leads to
with
![]() $c(j)=d(j)+(-1)^{j}e(j)$
for
$c(j)=d(j)+(-1)^{j}e(j)$
for
![]() $j\leqslant a$
and
$j\leqslant a$
and
![]() $c(j)=d(j)$
for
$c(j)=d(j)$
for
![]() $j>a$
, as defined above. The deduction of (9) differs slightly from the previous cases (e.g., deducing (8) from (7)): one must verify
$j>a$
, as defined above. The deduction of (9) differs slightly from the previous cases (e.g., deducing (8) from (7)): one must verify
for
![]() $i\leqslant a$
, where
$i\leqslant a$
, where
![]() $t_{i}=-c_{1}(D_{i}/D_{i-1})$
, since this shows that
$t_{i}=-c_{1}(D_{i}/D_{i-1})$
, since this shows that
![]() $t_{i}$
acts as
$t_{i}$
acts as
![]() $\unicode[STIX]{x1D6FF}_{i}T_{i}$
on the factor
$\unicode[STIX]{x1D6FF}_{i}T_{i}$
on the factor
![]() $c(i)_{\unicode[STIX]{x1D706}_{i}}$
. To do this, by replacing
$c(i)_{\unicode[STIX]{x1D706}_{i}}$
. To do this, by replacing
![]() $D_{i-1}^{\bot }/D_{i-1}$
with
$D_{i-1}^{\bot }/D_{i-1}$
with
![]() $V$
one may reduce to the case
$V$
one may reduce to the case
![]() $i=1$
; one also reduces to the case
$i=1$
; one also reduces to the case
![]() $b=1$
by applying identity (b). In this case, we compute
$b=1$
by applying identity (b). In this case, we compute
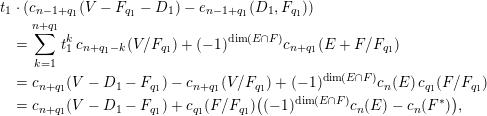 $$\begin{eqnarray}\displaystyle & & \displaystyle t_{1}\cdot (c_{n-1+q_{1}}(V-F_{q_{1}}-D_{1})-e_{n-1+q_{1}}(D_{1},F_{q_{1}}))\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k=1}^{n+q_{1}}t_{1}^{k}\,c_{n+q_{1}-k}(V/F_{q_{1}})+(-1)^{\dim (E\cap F)}c_{n+q_{1}}(E+F/F_{q_{1}})\nonumber\\ \displaystyle & & \displaystyle \quad =c_{n+q_{1}}(V-D_{1}-F_{q_{1}})-c_{n+q_{1}}(V/F_{q_{1}})+(-1)^{\dim (E\cap F)}c_{n}(E)\,c_{q_{1}}(F/F_{q_{1}})\nonumber\\ \displaystyle & & \displaystyle \quad =c_{n+q_{1}}(V-D_{1}-F_{q_{1}})+c_{q_{1}}(F/F_{q_{1}})\big((-1)^{\dim (E\cap F)}c_{n}(E)-c_{n}(F^{\ast })\big),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle t_{1}\cdot (c_{n-1+q_{1}}(V-F_{q_{1}}-D_{1})-e_{n-1+q_{1}}(D_{1},F_{q_{1}}))\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k=1}^{n+q_{1}}t_{1}^{k}\,c_{n+q_{1}-k}(V/F_{q_{1}})+(-1)^{\dim (E\cap F)}c_{n+q_{1}}(E+F/F_{q_{1}})\nonumber\\ \displaystyle & & \displaystyle \quad =c_{n+q_{1}}(V-D_{1}-F_{q_{1}})-c_{n+q_{1}}(V/F_{q_{1}})+(-1)^{\dim (E\cap F)}c_{n}(E)\,c_{q_{1}}(F/F_{q_{1}})\nonumber\\ \displaystyle & & \displaystyle \quad =c_{n+q_{1}}(V-D_{1}-F_{q_{1}})+c_{q_{1}}(F/F_{q_{1}})\big((-1)^{\dim (E\cap F)}c_{n}(E)-c_{n}(F^{\ast })\big),\nonumber\end{eqnarray}$$
and apply the relation
![]() $(-1)^{\dim (E\cap F)}c_{n}(E)=c_{n}(F^{\ast })$
, due to Edidin and Graham [Reference Edidin and GrahamEG95].
$(-1)^{\dim (E\cap F)}c_{n}(E)=c_{n}(F^{\ast })$
, due to Edidin and Graham [Reference Edidin and GrahamEG95].
The remainder of the proof proceeds as in the other types. To deduce the general case, one needs to apply §A.3, Lemma A.2. The relations in the hypothesis of that lemma require that
vanish for all
![]() $m\geqslant \unicode[STIX]{x1D706}_{k}$
. This expression may be re-written as
$m\geqslant \unicode[STIX]{x1D706}_{k}$
. This expression may be re-written as
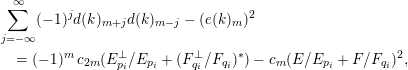 $$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{j=-\infty }^{\infty }(-1)^{j}d(k)_{m+j}d(k)_{m-j}-(e(k)_{m})^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{m}\,c_{2m}(E_{p_{i}}^{\bot }/E_{p_{i}}+(F_{q_{i}}^{\bot }/F_{q_{i}})^{\ast })-c_{m}(E/E_{p_{i}}+F/F_{q_{i}})^{2},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \mathop{\sum }_{j=-\infty }^{\infty }(-1)^{j}d(k)_{m+j}d(k)_{m-j}-(e(k)_{m})^{2}\nonumber\\ \displaystyle & & \displaystyle \quad =(-1)^{m}\,c_{2m}(E_{p_{i}}^{\bot }/E_{p_{i}}+(F_{q_{i}}^{\bot }/F_{q_{i}})^{\ast })-c_{m}(E/E_{p_{i}}+F/F_{q_{i}})^{2},\nonumber\end{eqnarray}$$
which vanishes if
![]() $m>\unicode[STIX]{x1D706}_{k}=p_{i}+q_{i}$
, since this is the rank of
$m>\unicode[STIX]{x1D706}_{k}=p_{i}+q_{i}$
, since this is the rank of
![]() $E/E_{p_{i}}+F/F_{q_{i}}$
. When
$E/E_{p_{i}}+F/F_{q_{i}}$
. When
![]() $m=\unicode[STIX]{x1D706}_{k}$
, we have
$m=\unicode[STIX]{x1D706}_{k}$
, we have
![]() $(-1)^{\unicode[STIX]{x1D706}_{k}}\,c_{2\unicode[STIX]{x1D706}_{k}}(E_{p_{i}}^{\bot }/E_{p_{i}}+(F_{q_{i}}^{\bot }/F_{q_{i}})^{\ast })=c_{\unicode[STIX]{x1D706}_{k}}(E/E_{p_{i}}+F/F_{q_{i}})^{2}$
, so the relation holds in this case as well.◻
$(-1)^{\unicode[STIX]{x1D706}_{k}}\,c_{2\unicode[STIX]{x1D706}_{k}}(E_{p_{i}}^{\bot }/E_{p_{i}}+(F_{q_{i}}^{\bot }/F_{q_{i}})^{\ast })=c_{\unicode[STIX]{x1D706}_{k}}(E/E_{p_{i}}+F/F_{q_{i}})^{2}$
, so the relation holds in this case as well.◻
To extract a Pfaffian from the case where
![]() $a=s$
, so all
$a=s$
, so all
![]() $q_{i}\geqslant 0$
, one needs a little algebra, given by the theorem of §A.2. Applying this proves the following.
$q_{i}\geqslant 0$
, one needs a little algebra, given by the theorem of §A.2. Applying this proves the following.
Corollary. If all
![]() $q_{i}\geqslant 0$
, then
$q_{i}\geqslant 0$
, then
Unpacking the definition of the
![]() $c(i)$
, the right-hand side is the Pfaffian of the matrix
$c(i)$
, the right-hand side is the Pfaffian of the matrix
![]() $(m_{ij})$
, with
$(m_{ij})$
, with
for
![]() $1\leqslant i<j\leqslant \ell$
, and
$1\leqslant i<j\leqslant \ell$
, and
![]() $m_{0j}=d(j)_{\unicode[STIX]{x1D706}_{j}}+e(j)_{\unicode[STIX]{x1D706}_{j}}$
for
$m_{0j}=d(j)_{\unicode[STIX]{x1D706}_{j}}+e(j)_{\unicode[STIX]{x1D706}_{j}}$
for
![]() $0<j\leqslant \ell$
if
$0<j\leqslant \ell$
if
![]() $\ell$
is odd.
$\ell$
is odd.
Remark. A Schubert variety in an orthogonal Grassmannian
![]() $\text{OG}(n-p,2n)$
is defined by a triple
$\text{OG}(n-p,2n)$
is defined by a triple
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}$
with all
$\boldsymbol{\unicode[STIX]{x1D70F}}$
with all
![]() $p_{i}=p$
. To obtain all of these as degeneracy loci according to our setup, one should use two different maximal isotropic spaces in the reference flag
$p_{i}=p$
. To obtain all of these as degeneracy loci according to our setup, one should use two different maximal isotropic spaces in the reference flag
![]() $F_{\bullet }$
. In fact, given a complete isotropic flag, there is a unique maximal isotropic subspace
$F_{\bullet }$
. In fact, given a complete isotropic flag, there is a unique maximal isotropic subspace
![]() $F_{1}\subset F_{0}^{\prime }\subset F_{\overline{1}}$
which is distinct from
$F_{1}\subset F_{0}^{\prime }\subset F_{\overline{1}}$
which is distinct from
![]() $F_{0}$
; both
$F_{0}$
; both
![]() $F_{0}$
and
$F_{0}$
and
![]() $F_{0}^{\prime }$
must be used to define Schubert varieties.
$F_{0}^{\prime }$
must be used to define Schubert varieties.
For example, consider
![]() $\boldsymbol{\unicode[STIX]{x1D70F}}=(1,\,p,\,0)$
, so
$\boldsymbol{\unicode[STIX]{x1D70F}}=(1,\,p,\,0)$
, so
![]() $\unicode[STIX]{x1D706}=(p)$
. In the setup of [Reference Buch, Kresch and TamvakisBKT15], there are two Schubert varieties whose
$\unicode[STIX]{x1D706}=(p)$
. In the setup of [Reference Buch, Kresch and TamvakisBKT15], there are two Schubert varieties whose
![]() $p$
-strict partition is
$p$
-strict partition is
![]() $\unicode[STIX]{x1D706}$
, given by
$\unicode[STIX]{x1D706}$
, given by
![]() $\dim (E_{p}\cap F_{0})\geqslant 1$
and
$\dim (E_{p}\cap F_{0})\geqslant 1$
and
![]() $\dim (E_{p}\cap F_{0}^{\prime })\geqslant 1$
, respectively. (When
$\dim (E_{p}\cap F_{0}^{\prime })\geqslant 1$
, respectively. (When
![]() $p=n-1$
, these are the two maximal linear spaces in the quadric.) The respective formulas are
$p=n-1$
, these are the two maximal linear spaces in the quadric.) The respective formulas are
![]() $c_{p}(V-E_{p}-F_{0})-e_{p}(E_{p},F_{0})$
and
$c_{p}(V-E_{p}-F_{0})-e_{p}(E_{p},F_{0})$
and
![]() $c_{p}(V-E_{p}-F_{0}^{\prime })-e_{p}(E_{p},F_{0}^{\prime })$
. Note that
$c_{p}(V-E_{p}-F_{0}^{\prime })-e_{p}(E_{p},F_{0}^{\prime })$
. Note that
![]() $e_{p}(E_{p},F_{0}^{\prime })=-e_{p}(E_{p},F_{0})$
. (Compare [Reference Buch, Kresch and TamvakisBKT15, Example A.3].)
$e_{p}(E_{p},F_{0}^{\prime })=-e_{p}(E_{p},F_{0})$
. (Compare [Reference Buch, Kresch and TamvakisBKT15, Example A.3].)
Acknowledgements
We must acknowledge the debt we owe to work of Kazarian [Reference KazarianKaz00], whose method guided our approach to these degeneracy locus problems. We thank Harry Tamvakis for comments on an earlier version of the manuscript, and Jordan Lambert Silva for suggesting a clarification in the definition of a type C triple. Finally, we thank the referees for detailed comments and suggestions for improving the paper.
Appendix A Algebra of Pfaffians and raising operators
A.1 A Pfaffian identity
Given
![]() $a_{ij}$
in a commutative ring
$a_{ij}$
in a commutative ring
![]() $A$
, for
$A$
, for
![]() $1\leqslant i<j\leqslant n$
, and
$1\leqslant i<j\leqslant n$
, and
![]() $n$
even, we denote by
$n$
even, we denote by
![]() $\operatorname{Pf}(a_{ij})$
the Pfaffian of the skew-symmetric matrix
$\operatorname{Pf}(a_{ij})$
the Pfaffian of the skew-symmetric matrix
![]() $(a_{ij})$
with entries
$(a_{ij})$
with entries
![]() $a_{ij}$
for
$a_{ij}$
for
![]() $i<j$
, and
$i<j$
, and
![]() $a_{ii}=0$
and
$a_{ii}=0$
and
![]() $a_{ij}=-a_{ji}$
for
$a_{ij}=-a_{ji}$
for
![]() $i>j$
. That is, for
$i>j$
. That is, for
![]() $n=2m$
,
$n=2m$
,
the sum over all permutations
![]() $i_{1}j_{1}i_{2}j_{2}\ldots i_{m}j_{m}$
of
$i_{1}j_{1}i_{2}j_{2}\ldots i_{m}j_{m}$
of
![]() $12\ldots n$
, with
$12\ldots n$
, with
![]() $i_{1}<i_{2}<\cdots <i_{m}$
and
$i_{1}<i_{2}<\cdots <i_{m}$
and
![]() $i_{r}<j_{r}$
for all
$i_{r}<j_{r}$
for all
![]() $r$
, the sign being the sign of the permutation. The same notation is used whenever
$r$
, the sign being the sign of the permutation. The same notation is used whenever
![]() $12\ldots n$
is replaced by any set consisting of an even number of integers in increasing order. For example, the expansion along the first row can be written
$12\ldots n$
is replaced by any set consisting of an even number of integers in increasing order. For example, the expansion along the first row can be written
where the hats denote that the integers are taken from the first
![]() $n-2$
positive integers, omitting
$n-2$
positive integers, omitting
![]() $1$
and
$1$
and
![]() $k$
.
$k$
.
We will often want formulas for odd as well as even
![]() $n$
. For this, when
$n$
. For this, when
![]() $n$
is odd, we will use the integers from
$n$
is odd, we will use the integers from
![]() $0$
to
$0$
to
![]() $n$
. In addition to the
$n$
. In addition to the
![]() $a_{ij}$
for
$a_{ij}$
for
![]() $1\leqslant i<j\leqslant n$
we also need to specify
$1\leqslant i<j\leqslant n$
we also need to specify
![]() $a_{0j}$
for
$a_{0j}$
for
![]() $1\leqslant j\leqslant n$
. Then the Pfaffian is given by the identity
$1\leqslant j\leqslant n$
. Then the Pfaffian is given by the identity
with
![]() $i<j$
taken from positive integers not equal to
$i<j$
taken from positive integers not equal to
![]() $k$
.
$k$
.
Assume now that the ring
![]() $A$
contains elements
$A$
contains elements
![]() $\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{n}$
satisfying
$\unicode[STIX]{x1D6FF}_{1},\ldots ,\unicode[STIX]{x1D6FF}_{n}$
satisfying
![]() $\unicode[STIX]{x1D6FF}_{i}^{2}=\unicode[STIX]{x1D6FF}_{i}$
for all
$\unicode[STIX]{x1D6FF}_{i}^{2}=\unicode[STIX]{x1D6FF}_{i}$
for all
![]() $i$
. Set
$i$
. Set
![]() $\unicode[STIX]{x1D716}_{i}=2\unicode[STIX]{x1D6FF}_{i}-1$
, so
$\unicode[STIX]{x1D716}_{i}=2\unicode[STIX]{x1D6FF}_{i}-1$
, so
![]() $\unicode[STIX]{x1D716}_{i}^{2}=1$
and
$\unicode[STIX]{x1D716}_{i}^{2}=1$
and
![]() $\unicode[STIX]{x1D716}_{i}\unicode[STIX]{x1D6FF}_{i}=\unicode[STIX]{x1D6FF}_{i}$
for all
$\unicode[STIX]{x1D716}_{i}\unicode[STIX]{x1D6FF}_{i}=\unicode[STIX]{x1D6FF}_{i}$
for all
![]() $i$
. (The classical case is when
$i$
. (The classical case is when
![]() $\unicode[STIX]{x1D6FF}_{i}=1$
, so
$\unicode[STIX]{x1D6FF}_{i}=1$
, so
![]() $\unicode[STIX]{x1D716}_{i}=1$
, for all
$\unicode[STIX]{x1D716}_{i}=1$
, for all
![]() $i$
.) Set
$i$
.) Set
![]() $\unicode[STIX]{x1D6FF}_{0}=1$
.
$\unicode[STIX]{x1D6FF}_{0}=1$
.
Let
![]() $T_{1},\ldots ,T_{n}$
be indeterminates, and let
$T_{1},\ldots ,T_{n}$
be indeterminates, and let
![]() $B$
be the localization of
$B$
be the localization of
![]() $A[T_{1},\ldots ,T_{n}]$
at the multiplicative set of non-zero-divisors (which includes all
$A[T_{1},\ldots ,T_{n}]$
at the multiplicative set of non-zero-divisors (which includes all
![]() $T_{j}$
, and all
$T_{j}$
, and all
![]() $T_{j}-\unicode[STIX]{x1D6FF}_{i}\unicode[STIX]{x1D6FF}_{j}T_{i}$
for all
$T_{j}-\unicode[STIX]{x1D6FF}_{i}\unicode[STIX]{x1D6FF}_{j}T_{i}$
for all
![]() $i<j$
). Set, for
$i<j$
). Set, for
![]() $1\leqslant i<j\leqslant n$
,
$1\leqslant i<j\leqslant n$
,
Also set
![]() $T_{0}=0$
, and
$T_{0}=0$
, and
![]() $H_{0j}=1$
for
$H_{0j}=1$
for
![]() $1\leqslant j\leqslant n$
.
$1\leqslant j\leqslant n$
.
Our goal is to write the product
![]() $\prod _{1\leqslant i<j\leqslant n}H_{ij}$
as a Pfaffian. The classical case is due to Schur:
$\prod _{1\leqslant i<j\leqslant n}H_{ij}$
as a Pfaffian. The classical case is due to Schur:
where, if
![]() $n$
is odd, the
$n$
is odd, the
![]() $(0,j)$
entry of the matrix is
$(0,j)$
entry of the matrix is
![]() $1$
, for
$1$
, for
![]() $1\leqslant j\leqslant n$
. Our generalization is as follows.
$1\leqslant j\leqslant n$
. Our generalization is as follows.
Theorem. Set
![]() $a_{ij}=\unicode[STIX]{x1D716}_{i}^{n-i+1}\unicode[STIX]{x1D716}_{j}^{n-j}H_{ij}$
, for
$a_{ij}=\unicode[STIX]{x1D716}_{i}^{n-i+1}\unicode[STIX]{x1D716}_{j}^{n-j}H_{ij}$
, for
![]() $1\leqslant i<j\leqslant n$
, and set
$1\leqslant i<j\leqslant n$
, and set
![]() $a_{0j}=\unicode[STIX]{x1D716}_{j}^{n-j}$
for
$a_{0j}=\unicode[STIX]{x1D716}_{j}^{n-j}$
for
![]() $1\leqslant j\leqslant n$
. Then
$1\leqslant j\leqslant n$
. Then
We will deduce this from a result of Knuth [Reference KnuthKnu96], as simplified by Kazarian [Reference KazarianKaz00]. Following their notation, define, for
![]() $x<y$
nonnegative integers,
$x<y$
nonnegative integers,
Note that
![]() $f[0y]=\unicode[STIX]{x1D716}_{0}H_{0y}=1$
. Set
$f[0y]=\unicode[STIX]{x1D716}_{0}H_{0y}=1$
. Set
![]() $f[xx]=0$
and
$f[xx]=0$
and
![]() $f[xy]=-f[yx]$
for
$f[xy]=-f[yx]$
for
![]() $x>y\geqslant 0$
. For a word
$x>y\geqslant 0$
. For a word
![]() $\unicode[STIX]{x1D6FC}=x_{1}\cdots x_{n}$
, with each
$\unicode[STIX]{x1D6FC}=x_{1}\cdots x_{n}$
, with each
![]() $x_{i}$
a nonnegative integer, define
$x_{i}$
a nonnegative integer, define
![]() $f[\unicode[STIX]{x1D6FC}]$
to be the Pfaffian of the matrix whose
$f[\unicode[STIX]{x1D6FC}]$
to be the Pfaffian of the matrix whose
![]() $(i,j)$
entry is
$(i,j)$
entry is
![]() $f[x_{i}x_{j}]$
, for
$f[x_{i}x_{j}]$
, for
![]() $n$
even; for
$n$
even; for
![]() $n$
odd, define
$n$
odd, define
![]() $f[\unicode[STIX]{x1D6FC}]$
to be
$f[\unicode[STIX]{x1D6FC}]$
to be
![]() $f[0\unicode[STIX]{x1D6FC}]$
. Note that
$f[0\unicode[STIX]{x1D6FC}]$
. Note that
![]() $f[\unicode[STIX]{x1D6FC}]$
vanishes if two letters in
$f[\unicode[STIX]{x1D6FC}]$
vanishes if two letters in
![]() $\unicode[STIX]{x1D6FC}$
coincide, and it changes sign if the positions of two letters are interchanged.
$\unicode[STIX]{x1D6FC}$
coincide, and it changes sign if the positions of two letters are interchanged.
Proposition. For all
![]() $n\geqslant 2$
, and nonnegative integers
$n\geqslant 2$
, and nonnegative integers
![]() $x_{1},\ldots ,x_{n}$
,
$x_{1},\ldots ,x_{n}$
,
Proof. By [Reference KnuthKnu96] and [Reference KazarianKaz00], this identity holds for all
![]() $n$
if it holds for
$n$
if it holds for
![]() $n=3$
.Footnote
5
For
$n=3$
.Footnote
5
For
![]() $n=3$
, it asserts that, for
$n=3$
, it asserts that, for
![]() $x<y<z$
positive integers,
$x<y<z$
positive integers,
or,
![]() $H_{xy}H_{xz}H_{yz}=H_{yz}-\unicode[STIX]{x1D716}_{x}\unicode[STIX]{x1D716}_{y}H_{xz}+\unicode[STIX]{x1D716}_{x}\unicode[STIX]{x1D716}_{y}H_{xy}$
. Clearing denominators, this amounts to a simple identity among cubic polynomials in the three variables
$H_{xy}H_{xz}H_{yz}=H_{yz}-\unicode[STIX]{x1D716}_{x}\unicode[STIX]{x1D716}_{y}H_{xz}+\unicode[STIX]{x1D716}_{x}\unicode[STIX]{x1D716}_{y}H_{xy}$
. Clearing denominators, this amounts to a simple identity among cubic polynomials in the three variables
![]() $T_{x}$
,
$T_{x}$
,
![]() $T_{y}$
, and
$T_{y}$
, and
![]() $T_{z}$
, which is an easy exercise.◻
$T_{z}$
, which is an easy exercise.◻
Corollary. Let
![]() $1\leqslant x_{1}<x_{2}<\cdots <x_{n}$
. Set
$1\leqslant x_{1}<x_{2}<\cdots <x_{n}$
. Set
![]() $a_{ij}=\unicode[STIX]{x1D716}_{x_{i}}H_{x_{i}x_{j}}$
for
$a_{ij}=\unicode[STIX]{x1D716}_{x_{i}}H_{x_{i}x_{j}}$
for
![]() $1\leqslant i<j\leqslant n$
and
$1\leqslant i<j\leqslant n$
and
![]() $a_{0j}=1$
for
$a_{0j}=1$
for
![]() $1\leqslant j\leqslant n$
. Then
$1\leqslant j\leqslant n$
. Then
Equivalently, setting
![]() $b_{ij}=\unicode[STIX]{x1D716}_{x_{i}}^{n-i+1}\unicode[STIX]{x1D716}_{x_{j}}^{n-j}H_{x_{i}x_{j}}$
for
$b_{ij}=\unicode[STIX]{x1D716}_{x_{i}}^{n-i+1}\unicode[STIX]{x1D716}_{x_{j}}^{n-j}H_{x_{i}x_{j}}$
for
![]() $1\leqslant i<j\leqslant n$
and
$1\leqslant i<j\leqslant n$
and
![]() $b_{0j}=\unicode[STIX]{x1D716}_{x_{j}}^{n-j}$
for
$b_{0j}=\unicode[STIX]{x1D716}_{x_{j}}^{n-j}$
for
![]() $1\leqslant j\leqslant n$
,
$1\leqslant j\leqslant n$
,
Proof. The proposition says that
![]() $\prod _{i<j}\unicode[STIX]{x1D716}_{x_{i}}H_{x_{i}x_{j}}=\operatorname{Pf}(\unicode[STIX]{x1D716}_{x_{i}}H_{x_{i}x_{j}})$
, which yields the first statement. The second follows from the first, using the basic identity
$\prod _{i<j}\unicode[STIX]{x1D716}_{x_{i}}H_{x_{i}x_{j}}=\operatorname{Pf}(\unicode[STIX]{x1D716}_{x_{i}}H_{x_{i}x_{j}})$
, which yields the first statement. The second follows from the first, using the basic identity
for any
![]() $a_{ij}$
,
$a_{ij}$
,
![]() $i<j$
and
$i<j$
and
![]() $\unicode[STIX]{x1D716}_{i}$
in the given ring, and nonnegative integers
$\unicode[STIX]{x1D716}_{i}$
in the given ring, and nonnegative integers
![]() $m_{i}$
. (This identity follows immediately from the definition (A.1) of the Pfaffian.)◻
$m_{i}$
. (This identity follows immediately from the definition (A.1) of the Pfaffian.)◻
The theorem of this section is the special case of the corollary when
![]() $x_{i}=i$
for
$x_{i}=i$
for
![]() $1\leqslant i\leqslant n$
.
$1\leqslant i\leqslant n$
.
A.2 Raising operators
Formula (A.2) can be rewritten
With
![]() $T_{i}/T_{j}$
interpreted as a raising operator
$T_{i}/T_{j}$
interpreted as a raising operator
![]() $R_{ij}$
, this formula leads to a classical Pfaffian formula for Schur Q-functions (see [Reference MacdonaldMac95, § III.8]). Our goal here is a small generalization, to be applied to types C and B, and a larger one, using the theorem from §A.1, to be applied to type D.
$R_{ij}$
, this formula leads to a classical Pfaffian formula for Schur Q-functions (see [Reference MacdonaldMac95, § III.8]). Our goal here is a small generalization, to be applied to types C and B, and a larger one, using the theorem from §A.1, to be applied to type D.
We will take raising operators
![]() $R_{ij}$
, for
$R_{ij}$
, for
![]() $1\leqslant i<j\leqslant n$
, to operate on sequences
$1\leqslant i<j\leqslant n$
, to operate on sequences
![]() $s=(s_{1},\ldots ,s_{n})$
in
$s=(s_{1},\ldots ,s_{n})$
in
![]() $\mathbb{Z}^{n}$
, by raising the
$\mathbb{Z}^{n}$
, by raising the
![]() $i$
th index by
$i$
th index by
![]() $1$
, and lowering the
$1$
, and lowering the
![]() $j$
th index by
$j$
th index by
![]() $1$
, keeping the others the same:
$1$
, keeping the others the same:
These operators commute with each other, and satisfy the identities
![]() $R_{ij}R_{jk}=R_{ik}$
for
$R_{ij}R_{jk}=R_{ik}$
for
![]() $i<j<k$
. By a raising operator we mean any monomial
$i<j<k$
. By a raising operator we mean any monomial
![]() $R=\prod _{i<j}R_{ij}^{m_{ij}}$
in these
$R=\prod _{i<j}R_{ij}^{m_{ij}}$
in these
![]() $R_{ij}$
. Any raising operator acts bijectively on the set
$R_{ij}$
. Any raising operator acts bijectively on the set
![]() $\mathbb{Z}^{n}$
of
$\mathbb{Z}^{n}$
of
![]() $s$
values.
$s$
values.
We will follow the tradition of using raising operators to act on expressions
![]() $\sum a_{s}c_{s}$
, for
$\sum a_{s}c_{s}$
, for
![]() $c_{s}$
certain fixed elements of a ring
$c_{s}$
certain fixed elements of a ring
![]() $A$
, and the
$A$
, and the
![]() $a_{s}$
varying elements of
$a_{s}$
varying elements of
![]() $A$
, with
$A$
, with
![]() $R$
taking
$R$
taking
![]() $\sum a_{s}c_{s}$
to
$\sum a_{s}c_{s}$
to
![]() $\sum a_{s}c_{R(s)}$
. Some care needs to be taken here, as the
$\sum a_{s}c_{R(s)}$
. Some care needs to be taken here, as the
![]() $c_{s}$
will evaluate to
$c_{s}$
will evaluate to
![]() $0$
when any entry
$0$
when any entry
![]() $s_{i}$
of
$s_{i}$
of
![]() $s$
is negative, but such
$s$
is negative, but such
![]() $s$
need to appear in the expressions in order for the action of the raising operators to be associative and commutative. (For example,
$s$
need to appear in the expressions in order for the action of the raising operators to be associative and commutative. (For example,
![]() $R_{23}(R_{12}(c_{(1,0,1)}))=R_{23}(c_{(2,-1,1)})=c_{(2,0,0)}$
, which is
$R_{23}(R_{12}(c_{(1,0,1)}))=R_{23}(c_{(2,-1,1)})=c_{(2,0,0)}$
, which is
![]() $R_{12}(R_{23}(c_{(1,0,1)}))=R_{12}(c_{(1,1,0)})$
.) In addition, one wants only finite expressions
$R_{12}(R_{23}(c_{(1,0,1)}))=R_{12}(c_{(1,1,0)})$
.) In addition, one wants only finite expressions
![]() $\sum a_{s}c_{s}$
, but one wants to apply infinitely many raising operators, in expressions like
$\sum a_{s}c_{s}$
, but one wants to apply infinitely many raising operators, in expressions like
![]() $(1-R_{ij})/(1+R_{ij})=1+2\sum _{k>0}(-1)^{k}(R_{ij})^{k}$
. Garsia [Reference GarsiaGar92] described one way to deal with these problems in another setting. We offer here a simple alternative, well suited to our situation.
$(1-R_{ij})/(1+R_{ij})=1+2\sum _{k>0}(-1)^{k}(R_{ij})^{k}$
. Garsia [Reference GarsiaGar92] described one way to deal with these problems in another setting. We offer here a simple alternative, well suited to our situation.
Let
![]() $P\subset \mathbb{Z}^{n}$
be the set of
$P\subset \mathbb{Z}^{n}$
be the set of
![]() $s=(s_{1},\ldots ,s_{n})$
satisfying the inequalities
$s=(s_{1},\ldots ,s_{n})$
satisfying the inequalities
The idea is that any
![]() $c_{s}$
can be set equal to
$c_{s}$
can be set equal to
![]() $0$
if
$0$
if
![]() $s$
is not in
$s$
is not in
![]() $P$
, because any raising operator
$P$
, because any raising operator
![]() $R$
takes such a
$R$
takes such a
![]() $s$
to an
$s$
to an
![]() $R(s)$
that is also not in
$R(s)$
that is also not in
![]() $P$
. We will use the following fact, which is easily proved by induction on
$P$
. We will use the following fact, which is easily proved by induction on
![]() $n$
.
$n$
.
Lemma. For any
![]() $s\in \mathbb{Z}^{n}$
, there are only finitely many raising operators
$s\in \mathbb{Z}^{n}$
, there are only finitely many raising operators
![]() $R$
such that
$R$
such that
![]() $R(s)$
is in
$R(s)$
is in
![]() $P$
.
$P$
.
Now let
![]() $A$
be any commutative ring. Assume we are given elements
$A$
be any commutative ring. Assume we are given elements
![]() $c(i)_{r}$
in
$c(i)_{r}$
in
![]() $A$
, for
$A$
, for
![]() $1\leqslant i\leqslant n$
and
$1\leqslant i\leqslant n$
and
![]() $r\in \mathbb{Z}$
, with
$r\in \mathbb{Z}$
, with
![]() $c(i)_{r}=0$
if
$c(i)_{r}=0$
if
![]() $r<0$
. For
$r<0$
. For
![]() $s\in \mathbb{Z}^{n}$
, we write
$s\in \mathbb{Z}^{n}$
, we write
![]() $c_{s}$
for
$c_{s}$
for
![]() $c(1)_{s_{1}}c(2)_{s_{2}}\cdots c(n)_{s_{n}}$
. By an expression we mean a finite formal sum
$c(1)_{s_{1}}c(2)_{s_{2}}\cdots c(n)_{s_{n}}$
. By an expression we mean a finite formal sum
![]() $\sum _{s\in P}a_{s}c_{s}$
, with
$\sum _{s\in P}a_{s}c_{s}$
, with
![]() $a_{s}$
in
$a_{s}$
in
![]() $A$
. For any raising operator
$A$
. For any raising operator
![]() $R$
, we define
$R$
, we define
![]() $R(\sum a_{s}c_{s})$
to be the sum
$R(\sum a_{s}c_{s})$
to be the sum
![]() $\sum _{R(s)\in P}a_{s}c_{R(s)}$
; that is, one applies
$\sum _{R(s)\in P}a_{s}c_{R(s)}$
; that is, one applies
![]() $R$
to the index
$R$
to the index
![]() $s$
of each
$s$
of each
![]() $c_{s}$
, but discards the term if
$c_{s}$
, but discards the term if
![]() $R(s)$
is not in
$R(s)$
is not in
![]() $P$
.Footnote
6
This gives an action of the polynomial ring
$P$
.Footnote
6
This gives an action of the polynomial ring
![]() $A[R_{ij}]_{1\leqslant i<j\leqslant n}$
on expressions:
$A[R_{ij}]_{1\leqslant i<j\leqslant n}$
on expressions:
By the lemma, this extends to an action of the power series ring
![]() $A[[R_{ij}]]_{1\leqslant i<j\leqslant n}$
on the set of all expressions.Footnote
7
By the evaluation of an expression
$A[[R_{ij}]]_{1\leqslant i<j\leqslant n}$
on the set of all expressions.Footnote
7
By the evaluation of an expression
![]() $\sum a_{s}c_{s}$
we mean the corresponding element
$\sum a_{s}c_{s}$
we mean the corresponding element
![]() $\sum a_{s}c(1)_{s_{1}}\cdots c(n)_{s_{n}}$
in
$\sum a_{s}c(1)_{s_{1}}\cdots c(n)_{s_{n}}$
in
![]() $A$
.
$A$
.
The following is a version of the classical result that suffices for our application to types C and B. It follows from the identity (A.3).
Proposition. Fix
![]() $s=(s_{1},\ldots ,s_{n})$
in
$s=(s_{1},\ldots ,s_{n})$
in
![]() $P$
. The evaluation of
$P$
. The evaluation of
is the Pfaffian of the matrix whose entries are
for
![]() $1\leqslant i<j\leqslant n$
, with
$1\leqslant i<j\leqslant n$
, with
![]() $m_{0j}=c(j)_{s_{j}}$
for
$m_{0j}=c(j)_{s_{j}}$
for
![]() $1\leqslant j\leqslant n$
when
$1\leqslant j\leqslant n$
when
![]() $n$
is odd.
$n$
is odd.
For type D we need a strengthening of this proposition, in which each
![]() $c(i)_{r}$
is written as a sum:
$c(i)_{r}$
is written as a sum:
for elements
![]() $d(i)_{r}$
and
$d(i)_{r}$
and
![]() $e(i)_{r}$
in
$e(i)_{r}$
in
![]() $A$
, with
$A$
, with
![]() $d(i)_{r}=e(i)_{r}=0$
for
$d(i)_{r}=e(i)_{r}=0$
for
![]() $r<0$
.
$r<0$
.
New operators
![]() $\unicode[STIX]{x1D6FF}_{i}$
, for
$\unicode[STIX]{x1D6FF}_{i}$
, for
![]() $1\leqslant i\leqslant n$
act on these expressions, with
$1\leqslant i\leqslant n$
act on these expressions, with
![]() $\unicode[STIX]{x1D6FF}_{i}$
sending
$\unicode[STIX]{x1D6FF}_{i}$
sending
![]() $d(i)_{s_{i}}+e(i)_{s_{i}}$
to
$d(i)_{s_{i}}+e(i)_{s_{i}}$
to
![]() $d(i)_{p_{i}}$
, leaving the other factors alone. That is,
$d(i)_{p_{i}}$
, leaving the other factors alone. That is,
![]() $\unicode[STIX]{x1D6FF}_{i}$
changes
$\unicode[STIX]{x1D6FF}_{i}$
changes
![]() $e(i)$
to
$e(i)$
to
![]() $0$
. Note that the operators
$0$
. Note that the operators
![]() $\unicode[STIX]{x1D6FF}_{i}$
commute with each other and with the raising operators, and
$\unicode[STIX]{x1D6FF}_{i}$
commute with each other and with the raising operators, and
![]() $\unicode[STIX]{x1D6FF}_{i}^{2}=\unicode[STIX]{x1D6FF}_{i}$
for all
$\unicode[STIX]{x1D6FF}_{i}^{2}=\unicode[STIX]{x1D6FF}_{i}$
for all
![]() $i$
. Set
$i$
. Set
![]() $\unicode[STIX]{x1D716}_{i}=2\unicode[STIX]{x1D6FF}_{i}-1$
; this has the effect of changing
$\unicode[STIX]{x1D716}_{i}=2\unicode[STIX]{x1D6FF}_{i}-1$
; this has the effect of changing
![]() $d(i)_{s_{i}}+e(i)_{s_{i}}$
to
$d(i)_{s_{i}}+e(i)_{s_{i}}$
to
![]() $d(i)_{s_{i}}-e(i)_{s_{i}}$
.
$d(i)_{s_{i}}-e(i)_{s_{i}}$
.
Theorem. Fix
![]() $s$
in
$s$
in
![]() $P$
. The evaluation of
$P$
. The evaluation of
is equal to the Pfaffian of the matrix whose entries are
for
![]() $1\leqslant i<j\leqslant n$
, with
$1\leqslant i<j\leqslant n$
, with
![]() $m_{0j}=d(j)_{s_{j}}+(-1)^{n-j}e(j)_{s_{j}}$
for
$m_{0j}=d(j)_{s_{j}}+(-1)^{n-j}e(j)_{s_{j}}$
for
![]() $1\leqslant j\leqslant n$
when
$1\leqslant j\leqslant n$
when
![]() $n$
is odd.
$n$
is odd.
Proof. By the theorem of §A.1,
The conclusion follows, since the evaluation of
![]() $\unicode[STIX]{x1D716}_{i}^{n-i+1}\unicode[STIX]{x1D716}_{j}^{n-j}((1-\unicode[STIX]{x1D6FF}_{i}\unicode[STIX]{x1D6FF}_{j}R_{ij})/(1+\unicode[STIX]{x1D6FF}_{i}\unicode[STIX]{x1D6FF}_{j}R_{ij}))$
on
$\unicode[STIX]{x1D716}_{i}^{n-i+1}\unicode[STIX]{x1D716}_{j}^{n-j}((1-\unicode[STIX]{x1D6FF}_{i}\unicode[STIX]{x1D6FF}_{j}R_{ij})/(1+\unicode[STIX]{x1D6FF}_{i}\unicode[STIX]{x1D6FF}_{j}R_{ij}))$
on
![]() $c_{s}$
is
$c_{s}$
is
![]() $m_{ij}\cdot \prod _{k\neq i,j}c(k)_{s_{k}}$
.◻
$m_{ij}\cdot \prod _{k\neq i,j}c(k)_{s_{k}}$
.◻
Example. The case needed for the type D application is when
![]() $e(i)=(-1)^{i}\widetilde{e}(i)$
for
$e(i)=(-1)^{i}\widetilde{e}(i)$
for
![]() $1\leqslant i\leqslant n$
. In this case
$1\leqslant i\leqslant n$
. In this case
with
![]() $m_{0j}=d(j)_{s_{j}}+\widetilde{e}(j)_{s_{j}}$
.
$m_{0j}=d(j)_{s_{j}}+\widetilde{e}(j)_{s_{j}}$
.
A.3 A theta-polynomial identity
We need a preliminary identity, which holds in any commutative ring
![]() $A$
. For any Laurent series
$A$
. For any Laurent series
![]() $B=B(t)=\sum _{r}b_{r}\,t^{r}$
, with coefficients
$B=B(t)=\sum _{r}b_{r}\,t^{r}$
, with coefficients
![]() $b_{i}$
in
$b_{i}$
in
![]() $A$
, we define
$A$
, we define
![]() $F^{B}=F^{B}(t)=\sum F_{p}^{B}\,t^{p}$
by
$F^{B}=F^{B}(t)=\sum F_{p}^{B}\,t^{p}$
by
with
![]() $u=-t^{2}$
. For any
$u=-t^{2}$
. For any
![]() $C=\sum _{r}c_{r}\,t^{r}$
, with
$C=\sum _{r}c_{r}\,t^{r}$
, with
![]() $(BC)(t)=B(t)\cdot C(t)$
, it follows that
$(BC)(t)=B(t)\cdot C(t)$
, it follows that
![]() $F^{BC}(u)=F^{B}(u)\cdot F^{C}(u)$
, and hence
$F^{BC}(u)=F^{B}(u)\cdot F^{C}(u)$
, and hence
In particular, if for some
![]() $\unicode[STIX]{x1D706}^{\prime }>\unicode[STIX]{x1D706}$
, the relations
$\unicode[STIX]{x1D706}^{\prime }>\unicode[STIX]{x1D706}$
, the relations
![]() $F_{p}^{B}=0$
and
$F_{p}^{B}=0$
and
![]() $F_{q}^{C}=0$
hold in
$F_{q}^{C}=0$
hold in
![]() $A$
for all
$A$
for all
![]() $p>\unicode[STIX]{x1D706}^{\prime }-\unicode[STIX]{x1D706}$
and
$p>\unicode[STIX]{x1D706}^{\prime }-\unicode[STIX]{x1D706}$
and
![]() $q\geqslant \unicode[STIX]{x1D706}$
, then
$q\geqslant \unicode[STIX]{x1D706}$
, then
![]() $F_{r}^{BC}=0$
for all
$F_{r}^{BC}=0$
for all
![]() $r\geqslant \unicode[STIX]{x1D706}^{\prime }$
.
$r\geqslant \unicode[STIX]{x1D706}^{\prime }$
.
We will write
![]() $c(i)$
for a collection of elements
$c(i)$
for a collection of elements
![]() $c(i)_{r}$
, for
$c(i)_{r}$
, for
![]() $1\leqslant i\leqslant \ell$
and
$1\leqslant i\leqslant \ell$
and
![]() $r\in \mathbb{Z}$
, and write
$r\in \mathbb{Z}$
, and write
![]() $c$
for
$c$
for
![]() $(c(1),\ldots ,c(\ell ))$
. If
$(c(1),\ldots ,c(\ell ))$
. If
![]() $c(i)=c(j)$
, then writing
$c(i)=c(j)$
, then writing
![]() $C(t)=\sum _{r}c(i)_{r}\,t^{r}=\sum _{r}c(j)_{r}\,t^{r}$
, we have
$C(t)=\sum _{r}c(i)_{r}\,t^{r}=\sum _{r}c(j)_{r}\,t^{r}$
, we have
Fix an integer
![]() $k$
,
$k$
,
![]() $0\leqslant k\leqslant \ell$
, and a unimodal sequence
$0\leqslant k\leqslant \ell$
, and a unimodal sequence
![]() $\unicode[STIX]{x1D70C}=(\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{\ell })$
such that
$\unicode[STIX]{x1D70C}=(\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D70C}_{\ell })$
such that
![]() $\unicode[STIX]{x1D70C}_{j}=j-1$
when
$\unicode[STIX]{x1D70C}_{j}=j-1$
when
![]() $j\leqslant k$
, and
$j\leqslant k$
, and
![]() $k\geqslant \unicode[STIX]{x1D70C}_{k+1}\geqslant \cdots \geqslant \unicode[STIX]{x1D70C}_{\ell }\geqslant 0$
. A partition
$k\geqslant \unicode[STIX]{x1D70C}_{k+1}\geqslant \cdots \geqslant \unicode[STIX]{x1D70C}_{\ell }\geqslant 0$
. A partition
![]() $\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{\ell }\geqslant 0)$
is called
$\unicode[STIX]{x1D706}=(\unicode[STIX]{x1D706}_{1}\geqslant \cdots \geqslant \unicode[STIX]{x1D706}_{\ell }\geqslant 0)$
is called
![]() $\unicode[STIX]{x1D70C}$
-strict if the sequence
$\unicode[STIX]{x1D70C}$
-strict if the sequence
![]() $\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D706}_{\ell }+\unicode[STIX]{x1D70C}_{\ell }$
is nonincreasing. (As with any partition, such a
$\unicode[STIX]{x1D706}_{1}+\unicode[STIX]{x1D70C}_{1},\ldots ,\unicode[STIX]{x1D706}_{\ell }+\unicode[STIX]{x1D70C}_{\ell }$
is nonincreasing. (As with any partition, such a
![]() $\unicode[STIX]{x1D706}$
belongs to the set
$\unicode[STIX]{x1D706}$
belongs to the set
![]() $P$
.) Given a
$P$
.) Given a
![]() $\unicode[STIX]{x1D70C}$
-strict partition
$\unicode[STIX]{x1D70C}$
-strict partition
![]() $\unicode[STIX]{x1D706}$
, the theta-polynomial is
$\unicode[STIX]{x1D706}$
, the theta-polynomial is
where
![]() $R^{(\unicode[STIX]{x1D70C},\ell )}$
is the raising operator
$R^{(\unicode[STIX]{x1D70C},\ell )}$
is the raising operator
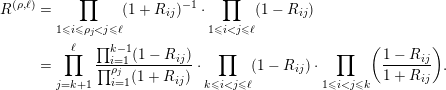 $$\begin{eqnarray}\displaystyle R^{(\unicode[STIX]{x1D70C},\ell )} & = & \displaystyle \mathop{\prod }_{1\leqslant i\leqslant \unicode[STIX]{x1D70C}_{j}<j\leqslant \ell }(1+R_{ij})^{-1}\cdot \mathop{\prod }_{1\leqslant i<j\leqslant \ell }(1-R_{ij})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{j=k+1}^{\ell }\frac{\mathop{\prod }_{i=1}^{k-1}(1-R_{ij})}{\mathop{\prod }_{i=1}^{\unicode[STIX]{x1D70C}_{j}}(1+R_{ij})}\cdot \mathop{\prod }_{k\leqslant i<j\leqslant \ell }(1-R_{ij})\cdot \mathop{\prod }_{1\leqslant i<j\leqslant k}\biggl(\frac{1-R_{ij}}{1+R_{ij}}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle R^{(\unicode[STIX]{x1D70C},\ell )} & = & \displaystyle \mathop{\prod }_{1\leqslant i\leqslant \unicode[STIX]{x1D70C}_{j}<j\leqslant \ell }(1+R_{ij})^{-1}\cdot \mathop{\prod }_{1\leqslant i<j\leqslant \ell }(1-R_{ij})\nonumber\\ \displaystyle & = & \displaystyle \mathop{\prod }_{j=k+1}^{\ell }\frac{\mathop{\prod }_{i=1}^{k-1}(1-R_{ij})}{\mathop{\prod }_{i=1}^{\unicode[STIX]{x1D70C}_{j}}(1+R_{ij})}\cdot \mathop{\prod }_{k\leqslant i<j\leqslant \ell }(1-R_{ij})\cdot \mathop{\prod }_{1\leqslant i<j\leqslant k}\biggl(\frac{1-R_{ij}}{1+R_{ij}}\biggr).\nonumber\end{eqnarray}$$
Let
![]() $R_{\unicode[STIX]{x1D6FC}}$
,
$R_{\unicode[STIX]{x1D6FC}}$
,
![]() $R_{\unicode[STIX]{x1D6FD}}$
, and
$R_{\unicode[STIX]{x1D6FD}}$
, and
![]() $R_{\unicode[STIX]{x1D6FE}}$
be the three indexed products in the second line, so
$R_{\unicode[STIX]{x1D6FE}}$
be the three indexed products in the second line, so
![]() $R^{(\unicode[STIX]{x1D70C},\ell )}=R_{\unicode[STIX]{x1D6FC}}\cdot R_{\unicode[STIX]{x1D6FD}}\cdot R_{\unicode[STIX]{x1D6FE}}$
. Note that
$R^{(\unicode[STIX]{x1D70C},\ell )}=R_{\unicode[STIX]{x1D6FC}}\cdot R_{\unicode[STIX]{x1D6FD}}\cdot R_{\unicode[STIX]{x1D6FE}}$
. Note that
![]() $R_{\unicode[STIX]{x1D6FD}}$
is a determinant and
$R_{\unicode[STIX]{x1D6FD}}$
is a determinant and
![]() $R_{\unicode[STIX]{x1D6FE}}$
is a Pfaffian.
$R_{\unicode[STIX]{x1D6FE}}$
is a Pfaffian.
Lemma A.1. Fix a
![]() $\unicode[STIX]{x1D70C}$
-strict partition
$\unicode[STIX]{x1D70C}$
-strict partition
![]() $\unicode[STIX]{x1D706}$
, integers
$\unicode[STIX]{x1D706}$
, integers
![]() $1\leqslant m<n\leqslant \ell$
, and elements
$1\leqslant m<n\leqslant \ell$
, and elements
![]() $b_{1},\ldots ,b_{n-m}$
in the ring
$b_{1},\ldots ,b_{n-m}$
in the ring
![]() $A$
. Assume
$A$
. Assume
![]() $c(m)=c(m+1)=\cdots =c(n)$
. Let
$c(m)=c(m+1)=\cdots =c(n)$
. Let
![]() $c^{\prime }(m)=c(m)\cdot (1+b_{1}+\cdots +b_{n-m})$
, and
$c^{\prime }(m)=c(m)\cdot (1+b_{1}+\cdots +b_{n-m})$
, and
![]() $c^{\prime }(i)=c(i)$
for
$c^{\prime }(i)=c(i)$
for
![]() $i\neq m$
.
$i\neq m$
.
(i) Suppose
 $k\leqslant m<n\leqslant \ell$
, and
$k\leqslant m<n\leqslant \ell$
, and
 $\unicode[STIX]{x1D706}_{m}=\unicode[STIX]{x1D706}_{m+1}=\cdots =\unicode[STIX]{x1D706}_{n}$
. Then
$\unicode[STIX]{x1D706}_{m}=\unicode[STIX]{x1D706}_{m+1}=\cdots =\unicode[STIX]{x1D706}_{n}$
. Then  $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c^{\prime })=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c^{\prime })=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c).\end{eqnarray}$$
(ii) Suppose
 $1\leqslant m<n\leqslant k$
, and
$1\leqslant m<n\leqslant k$
, and
 $\unicode[STIX]{x1D706}_{m}=\unicode[STIX]{x1D706}_{m+1}+1=\cdots =\unicode[STIX]{x1D706}_{n}+n-m$
. Assume that for each
$\unicode[STIX]{x1D706}_{m}=\unicode[STIX]{x1D706}_{m+1}+1=\cdots =\unicode[STIX]{x1D706}_{n}+n-m$
. Assume that for each
 $1\leqslant i\leqslant k$
, with
$1\leqslant i\leqslant k$
, with
 $C=\sum c(i)_{r}\,t^{r}$
, the relations
$C=\sum c(i)_{r}\,t^{r}$
, the relations
 $F_{p}^{C}=0$
hold for all
$F_{p}^{C}=0$
hold for all
 $p\geqslant \unicode[STIX]{x1D706}_{i}$
. Then and the relations
$p\geqslant \unicode[STIX]{x1D706}_{i}$
. Then and the relations $$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c^{\prime })=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c^{\prime })=\unicode[STIX]{x1D6E9}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c),\end{eqnarray}$$
 $F_{p}^{C^{\prime }}=0$
hold for all
$F_{p}^{C^{\prime }}=0$
hold for all
 $p\geqslant \unicode[STIX]{x1D706}_{i}$
, where
$p\geqslant \unicode[STIX]{x1D706}_{i}$
, where
 $C^{\prime }=\sum c^{\prime }(i)_{r}\,t^{r}$
.
$C^{\prime }=\sum c^{\prime }(i)_{r}\,t^{r}$
.
Proof. When
![]() $k\leqslant m<n\leqslant \ell$
, we claim
$k\leqslant m<n\leqslant \ell$
, we claim
![]() $R_{\unicode[STIX]{x1D6FD}}\cdot c_{\unicode[STIX]{x1D706}}^{\prime }=R_{\unicode[STIX]{x1D6FD}}\cdot c_{\unicode[STIX]{x1D706}}$
. Indeed, when one expands the left-hand side using multi-linearity of the determinant, one finds the right-hand side, plus a linear combination of determinants which have repeated rows, and therefore vanish.
$R_{\unicode[STIX]{x1D6FD}}\cdot c_{\unicode[STIX]{x1D706}}^{\prime }=R_{\unicode[STIX]{x1D6FD}}\cdot c_{\unicode[STIX]{x1D706}}$
. Indeed, when one expands the left-hand side using multi-linearity of the determinant, one finds the right-hand side, plus a linear combination of determinants which have repeated rows, and therefore vanish.
When
![]() $1\leqslant m<n\leqslant k$
, we claim that
$1\leqslant m<n\leqslant k$
, we claim that
![]() $R_{\unicode[STIX]{x1D6FE}}\cdot c_{\unicode[STIX]{x1D706}}^{\prime }=R_{\unicode[STIX]{x1D6FE}}\cdot c_{\unicode[STIX]{x1D706}}$
in the ring
$R_{\unicode[STIX]{x1D6FE}}\cdot c_{\unicode[STIX]{x1D706}}^{\prime }=R_{\unicode[STIX]{x1D6FE}}\cdot c_{\unicode[STIX]{x1D706}}$
in the ring
![]() $A$
. Indeed,
$A$
. Indeed,
and by assumption
![]() $c(m)_{\unicode[STIX]{x1D706}_{m}-i}=c(m+i)_{\unicode[STIX]{x1D706}_{m+i}}$
. We also assumed these satisfy
$c(m)_{\unicode[STIX]{x1D706}_{m}-i}=c(m+i)_{\unicode[STIX]{x1D706}_{m+i}}$
. We also assumed these satisfy
![]() $F_{\unicode[STIX]{x1D706}_{m+i}}^{C}=0$
, so applying
$F_{\unicode[STIX]{x1D706}_{m+i}}^{C}=0$
, so applying
![]() $R_{\unicode[STIX]{x1D6FE}}$
kills all terms except
$R_{\unicode[STIX]{x1D6FE}}$
kills all terms except
![]() $c_{\unicode[STIX]{x1D706}}$
on the right-hand side. (Cf. [Reference KazarianKaz00], proof of Theorem 1.1.) The final statement is a consequence of (A.4).◻
$c_{\unicode[STIX]{x1D706}}$
on the right-hand side. (Cf. [Reference KazarianKaz00], proof of Theorem 1.1.) The final statement is a consequence of (A.4).◻
A similar statement holds for eta-polynomials. These are defined using raising operators
![]() $\widetilde{R}^{(\unicode[STIX]{x1D70C},k,\ell )}=R_{\unicode[STIX]{x1D6FC}}\cdot R_{\unicode[STIX]{x1D6FD}}\cdot \widetilde{R}_{\unicode[STIX]{x1D6FE}}$
, with
$\widetilde{R}^{(\unicode[STIX]{x1D70C},k,\ell )}=R_{\unicode[STIX]{x1D6FC}}\cdot R_{\unicode[STIX]{x1D6FD}}\cdot \widetilde{R}_{\unicode[STIX]{x1D6FE}}$
, with
![]() $R_{\unicode[STIX]{x1D6FC}}$
and
$R_{\unicode[STIX]{x1D6FC}}$
and
![]() $R_{\unicode[STIX]{x1D6FD}}$
as above, and
$R_{\unicode[STIX]{x1D6FD}}$
as above, and
which, like
![]() $R_{\unicode[STIX]{x1D6FE}}$
, is a Pfaffian by the theorem of §A.2. For
$R_{\unicode[STIX]{x1D6FE}}$
, is a Pfaffian by the theorem of §A.2. For
![]() $1\leqslant i\leqslant \ell$
, given elements
$1\leqslant i\leqslant \ell$
, given elements
![]() $c(i)_{r}=d(i)_{r}+e(i)_{r}$
, with
$c(i)_{r}=d(i)_{r}+e(i)_{r}$
, with
![]() $e(i)=0$
for
$e(i)=0$
for
![]() $i>k$
, the eta-polynomial is defined as
$i>k$
, the eta-polynomial is defined as
Given such
![]() $c(i)$
, with
$c(i)$
, with
![]() $C(t)=\sum c(i)_{r}\,t^{r}$
and
$C(t)=\sum c(i)_{r}\,t^{r}$
and
![]() $D(t)=\sum d(i)_{r}\,t^{r}$
, let
$D(t)=\sum d(i)_{r}\,t^{r}$
, let
![]() $\widetilde{F}_{p}^{C}=F_{p}^{D}-e(i)_{p}^{2}$
; if
$\widetilde{F}_{p}^{C}=F_{p}^{D}-e(i)_{p}^{2}$
; if
![]() $d(i)=d(j)$
and
$d(i)=d(j)$
and
![]() $e(i)=e(j)$
, this is
$e(i)=e(j)$
, this is
Lemma A.2. Assume the hypotheses and notation of Lemma A.1.
(i) With the same hypotheses as in Lemma A.1(i), we have
 $$\begin{eqnarray}\text{H}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c^{\prime })=\text{H}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c).\end{eqnarray}$$
$$\begin{eqnarray}\text{H}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c^{\prime })=\text{H}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c).\end{eqnarray}$$
(ii) With the hypotheses of Lemma A.1(i), assume additionally that
 $d(m)=d(m+1)=\cdots =d(n)$
, so also
$d(m)=d(m+1)=\cdots =d(n)$
, so also
 $e(m)=\cdots =e(n)$
. Assume that for each
$e(m)=\cdots =e(n)$
. Assume that for each
 $1\leqslant i\leqslant k$
, the relations
$1\leqslant i\leqslant k$
, the relations
 $\widetilde{F}_{p}^{C}=0$
and
$\widetilde{F}_{p}^{C}=0$
and
 $e(i)_{q}=0$
hold for all
$e(i)_{q}=0$
hold for all
 $p\geqslant \unicode[STIX]{x1D706}_{i}$
and
$p\geqslant \unicode[STIX]{x1D706}_{i}$
and
 $q>\unicode[STIX]{x1D706}_{i}$
. Then and the relations
$q>\unicode[STIX]{x1D706}_{i}$
. Then and the relations $$\begin{eqnarray}\text{H}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c^{\prime })=\text{H}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c),\end{eqnarray}$$
$$\begin{eqnarray}\text{H}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c^{\prime })=\text{H}_{\unicode[STIX]{x1D706}}^{(\unicode[STIX]{x1D70C})}(c),\end{eqnarray}$$
 $\widetilde{F}_{p}^{C^{\prime }}=0$
and
$\widetilde{F}_{p}^{C^{\prime }}=0$
and
 $e^{\prime }(i)_{q}=0$
hold for all
$e^{\prime }(i)_{q}=0$
hold for all
 $p\geqslant \unicode[STIX]{x1D706}_{i}$
and
$p\geqslant \unicode[STIX]{x1D706}_{i}$
and
 $q>\unicode[STIX]{x1D706}_{i}$
, where
$q>\unicode[STIX]{x1D706}_{i}$
, where
 $C^{\prime }=\sum c^{\prime }(i)_{r}\,t^{r}$
and
$C^{\prime }=\sum c^{\prime }(i)_{r}\,t^{r}$
and
 $e^{\prime }(i)=e(i)\cdot b$
.
$e^{\prime }(i)=e(i)\cdot b$
.
The proof is similar to that of Lemma A.1. For the last statement, concerning the relations, when
![]() $i\neq m$
there is nothing to check, since
$i\neq m$
there is nothing to check, since
![]() $\widetilde{F}^{C^{\prime }}=\widetilde{F}^{C}$
by definition. For
$\widetilde{F}^{C^{\prime }}=\widetilde{F}^{C}$
by definition. For
![]() $i=m$
, observe that
$i=m$
, observe that
where
![]() $e^{\prime }(m)_{p}=e(m)_{p}+b_{1}e(m)_{p-1}+\cdots \,$
. Since
$e^{\prime }(m)_{p}=e(m)_{p}+b_{1}e(m)_{p-1}+\cdots \,$
. Since
![]() $e(m)_{q}=e(n)_{q}=0$
for
$e(m)_{q}=e(n)_{q}=0$
for
![]() $q>\unicode[STIX]{x1D706}_{n}$
, and
$q>\unicode[STIX]{x1D706}_{n}$
, and
![]() $b_{q}=0$
for
$b_{q}=0$
for
![]() $q>n-m$
, we have
$q>n-m$
, we have
![]() $e^{\prime }(m)_{p}=0$
for
$e^{\prime }(m)_{p}=0$
for
![]() $p>\unicode[STIX]{x1D706}_{n}+n-m=\unicode[STIX]{x1D706}_{m}$
, and
$p>\unicode[STIX]{x1D706}_{n}+n-m=\unicode[STIX]{x1D706}_{m}$
, and
![]() $e^{\prime }(m)_{\unicode[STIX]{x1D706}_{m}}=b_{n-m}e(m)_{\unicode[STIX]{x1D706}_{m}-n+m}$
. Similarly, the relations
$e^{\prime }(m)_{\unicode[STIX]{x1D706}_{m}}=b_{n-m}e(m)_{\unicode[STIX]{x1D706}_{m}-n+m}$
. Similarly, the relations
![]() $\widetilde{F}_{p}^{C}$
imply
$\widetilde{F}_{p}^{C}$
imply
![]() $F_{p}^{D}=0$
for
$F_{p}^{D}=0$
for
![]() $p>\unicode[STIX]{x1D706}_{n}$
, so using (A.4) we have
$p>\unicode[STIX]{x1D706}_{n}$
, so using (A.4) we have
![]() $F_{p}^{BD}=0$
for
$F_{p}^{BD}=0$
for
![]() $p>\unicode[STIX]{x1D706}_{m}$
and
$p>\unicode[STIX]{x1D706}_{m}$
and
![]() $F_{\unicode[STIX]{x1D706}_{m}}^{BD}=b_{n-m}^{2}F_{\unicode[STIX]{x1D706}_{m}-n+m}^{D}$
. It follows that
$F_{\unicode[STIX]{x1D706}_{m}}^{BD}=b_{n-m}^{2}F_{\unicode[STIX]{x1D706}_{m}-n+m}^{D}$
. It follows that
![]() $\widetilde{F}_{p}^{C^{\prime }}=0$
for
$\widetilde{F}_{p}^{C^{\prime }}=0$
for
![]() $p>\unicode[STIX]{x1D706}_{m}$
, and
$p>\unicode[STIX]{x1D706}_{m}$
, and
![]() $\widetilde{F}_{\unicode[STIX]{x1D706}_{m}}^{C^{\prime }}=b_{n-m}^{2}\widetilde{F}_{\unicode[STIX]{x1D706}_{m}-n+m}^{C}=0$
as well.
$\widetilde{F}_{\unicode[STIX]{x1D706}_{m}}^{C^{\prime }}=b_{n-m}^{2}\widetilde{F}_{\unicode[STIX]{x1D706}_{m}-n+m}^{C}=0$
as well.
Appendix B On quadric bundles
Let
![]() $V$
be a vector bundle on
$V$
be a vector bundle on
![]() $X$
of rank either
$X$
of rank either
![]() $2n+1$
or
$2n+1$
or
![]() $2n$
, to be specified, and equip
$2n$
, to be specified, and equip
![]() $V$
with a nondegenerate quadratic form taking values in the trivial line bundle. We will compute a basic degeneracy class on
$V$
with a nondegenerate quadratic form taking values in the trivial line bundle. We will compute a basic degeneracy class on
![]() $X$
.
$X$
.
Let
![]() $E_{p}\subset V$
be an isotropic subbundle; when the rank of
$E_{p}\subset V$
be an isotropic subbundle; when the rank of
![]() $V$
is odd,
$V$
is odd,
![]() $E_{p}$
has rank
$E_{p}$
has rank
![]() $n+1-p$
, and in the even rank case,
$n+1-p$
, and in the even rank case,
![]() $E_{p}$
has rank
$E_{p}$
has rank
![]() $n-p$
. Let
$n-p$
. Let
![]() $F^{\prime }\subset V$
be an isotropic line bundle. We assume
$F^{\prime }\subset V$
be an isotropic line bundle. We assume
![]() $E_{p}\subseteq E$
and
$E_{p}\subseteq E$
and
![]() $F^{\prime }\subseteq F$
are contained in some fixed maximal isotropic subbundles (of rank
$F^{\prime }\subseteq F$
are contained in some fixed maximal isotropic subbundles (of rank
![]() $n$
).
$n$
).
The quadratic form induces isomorphisms
![]() $V\cong V^{\ast }$
, and more generally
$V\cong V^{\ast }$
, and more generally
![]() $V/E^{\bot }\cong E^{\ast }$
, for isotropic subbundles
$V/E^{\bot }\cong E^{\ast }$
, for isotropic subbundles
![]() $E\subset V$
.
$E\subset V$
.
We assume that the bundles
![]() $E_{p}$
and
$E_{p}$
and
![]() $F^{\prime }$
are in general position, so the locus on
$F^{\prime }$
are in general position, so the locus on
![]() $X$
where
$X$
where
![]() $\dim (E_{p}\cap F^{\prime })\geqslant 1$
has codimension
$\dim (E_{p}\cap F^{\prime })\geqslant 1$
has codimension
![]() $p+n-1$
. This locus,
$p+n-1$
. This locus,
![]() $\unicode[STIX]{x1D6FA}=\{x\in X\,|\,E_{p}\supseteq F^{\prime }\}$
, is the one whose class we will compute.
$\unicode[STIX]{x1D6FA}=\{x\in X\,|\,E_{p}\supseteq F^{\prime }\}$
, is the one whose class we will compute.
Let
![]() ${\mathcal{Q}}(V)\xrightarrow[{}]{\unicode[STIX]{x1D70B}}X$
be the quadric bundle associated to
${\mathcal{Q}}(V)\xrightarrow[{}]{\unicode[STIX]{x1D70B}}X$
be the quadric bundle associated to
![]() $V$
, with tautological bundle
$V$
, with tautological bundle
![]() $S=S_{1}\subset V$
. The line bundle
$S=S_{1}\subset V$
. The line bundle
![]() $F^{\prime }$
defines a section
$F^{\prime }$
defines a section
and the task is to compute
![]() $[\unicode[STIX]{x1D6FA}]=s^{\ast }[\mathbb{P}(E_{p})]$
.
$[\unicode[STIX]{x1D6FA}]=s^{\ast }[\mathbb{P}(E_{p})]$
.
Proposition. When
![]() $V$
has odd rank, we have
$V$
has odd rank, we have
where
![]() $M=F^{\bot }/F$
. When
$M=F^{\bot }/F$
. When
![]() $V$
has even rank, we have
$V$
has even rank, we have
where
![]() $e(E_{p},F^{\prime })=(-1)^{\dim (E\cap F)}c_{p+n-1}(E/E_{p}+F/F^{\prime })$
.
$e(E_{p},F^{\prime })=(-1)^{\dim (E\cap F)}c_{p+n-1}(E/E_{p}+F/F^{\prime })$
.
Recall that the parity of
![]() $\dim (E\cap F)$
is constant in (connected) families, so the sign is well defined.
$\dim (E\cap F)$
is constant in (connected) families, so the sign is well defined.
The proof of the proposition relies on the presentation of the Chow ring of quadric bundles.
Theorem ([Reference Edidin and GrahamEG95, Theorem 7], [Reference AndersonAnd11, Theorem B.1]). With the notation as above, write
![]() $f=[\mathbb{P}(F)]$
in
$f=[\mathbb{P}(F)]$
in
![]() $A^{\ast }{\mathcal{Q}}(V)$
and
$A^{\ast }{\mathcal{Q}}(V)$
and
![]() $h=c_{1}(S^{\ast })$
. Then
$h=c_{1}(S^{\ast })$
. Then
![]() $A^{\ast }{\mathcal{Q}}(V)=(A^{\ast }X)[h,f]/I$
, where
$A^{\ast }{\mathcal{Q}}(V)=(A^{\ast }X)[h,f]/I$
, where
![]() $I$
is generated by
$I$
is generated by
when
![]() $V$
has rank
$V$
has rank
![]() $2n+1$
, and by
$2n+1$
, and by
when
![]() $V$
has rank
$V$
has rank
![]() $2n$
.
$2n$
.
We need a lemma.
Lemma. Let
![]() $k\geqslant 0$
. If the rank of
$k\geqslant 0$
. If the rank of
![]() $V$
is odd, then we have
$V$
is odd, then we have
If the rank of
![]() $V$
is even, we have
$V$
is even, we have
Proof. First suppose
![]() $V$
has rank
$V$
has rank
![]() $2n+1$
. Let
$2n+1$
. Let
![]() $\unicode[STIX]{x1D70C}:\mathbb{P}(E)\rightarrow X$
be the projection. Using the relation (B.1), we get
$\unicode[STIX]{x1D70C}:\mathbb{P}(E)\rightarrow X$
be the projection. Using the relation (B.1), we get
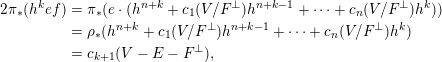 $$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}_{\ast }(h^{k}ef) & = & \displaystyle \unicode[STIX]{x1D70B}_{\ast }(e\cdot (h^{n+k}+c_{1}(V/F^{\bot })h^{n+k-1}+\cdots +c_{n}(V/F^{\bot })h^{k}))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70C}_{\ast }(h^{n+k}+c_{1}(V/F^{\bot })h^{n+k-1}+\cdots +c_{n}(V/F^{\bot })h^{k})\nonumber\\ \displaystyle & = & \displaystyle c_{k+1}(V-E-F^{\bot }),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 2\unicode[STIX]{x1D70B}_{\ast }(h^{k}ef) & = & \displaystyle \unicode[STIX]{x1D70B}_{\ast }(e\cdot (h^{n+k}+c_{1}(V/F^{\bot })h^{n+k-1}+\cdots +c_{n}(V/F^{\bot })h^{k}))\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D70C}_{\ast }(h^{n+k}+c_{1}(V/F^{\bot })h^{n+k-1}+\cdots +c_{n}(V/F^{\bot })h^{k})\nonumber\\ \displaystyle & = & \displaystyle c_{k+1}(V-E-F^{\bot }),\nonumber\end{eqnarray}$$
as claimed.
In the case
![]() $V$
has rank
$V$
has rank
![]() $2n$
, we have
$2n$
, we have
for
![]() $k>0$
. Using the relation (B.3), this yields the desired formula,
$k>0$
. Using the relation (B.3), this yields the desired formula,
![]() $2\unicode[STIX]{x1D70B}_{\ast }(h^{k}ef)=c_{k}(V-E-F)$
. The case
$2\unicode[STIX]{x1D70B}_{\ast }(h^{k}ef)=c_{k}(V-E-F)$
. The case
![]() $k=0$
is proved by taking
$k=0$
is proved by taking
![]() $X$
to be a point and applying, e.g., [Reference Edidin and GrahamEG95, Lemma 2].◻
$X$
to be a point and applying, e.g., [Reference Edidin and GrahamEG95, Lemma 2].◻
Proof of Proposition.
We have
![]() $s(X)=\mathbb{P}(F^{\prime })$
, so that
$s(X)=\mathbb{P}(F^{\prime })$
, so that
![]() $s^{\ast }[\mathbb{P}(E_{p})]=\unicode[STIX]{x1D70B}_{\ast }([\mathbb{P}(E_{p})]\cdot [\mathbb{P}(F^{\prime })])$
.
$s^{\ast }[\mathbb{P}(E_{p})]=\unicode[STIX]{x1D70B}_{\ast }([\mathbb{P}(E_{p})]\cdot [\mathbb{P}(F^{\prime })])$
.
First consider the case when the rank of
![]() $V$
is odd. Then
$V$
is odd. Then
![]() $[\mathbb{P}(E_{p})]=c_{p-1}(E/E_{p}\otimes S^{\ast })\cdot e$
and
$[\mathbb{P}(E_{p})]=c_{p-1}(E/E_{p}\otimes S^{\ast })\cdot e$
and
![]() $[\mathbb{P}(F^{\prime })]=c_{n-1}(F/F^{\prime }\otimes S^{\ast })\cdot f$
, so we must compute
$[\mathbb{P}(F^{\prime })]=c_{n-1}(F/F^{\prime }\otimes S^{\ast })\cdot f$
, so we must compute
Using the above lemma, this is equal to
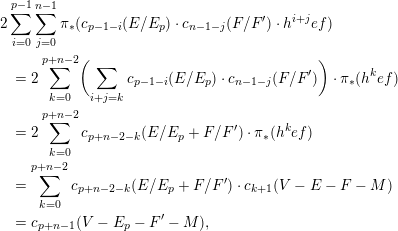 $$\begin{eqnarray}\displaystyle & & \displaystyle 2\mathop{\sum }_{i=0}^{p-1}\mathop{\sum }_{j=0}^{n-1}\unicode[STIX]{x1D70B}_{\ast }(c_{p-1-i}(E/E_{p})\cdot c_{n-1-j}(F/F^{\prime })\cdot h^{i+j}ef)\nonumber\\ \displaystyle & & \displaystyle \quad =2\mathop{\sum }_{k=0}^{p+n-2}\biggl(\mathop{\sum }_{i+j=k}c_{p-1-i}(E/E_{p})\cdot c_{n-1-j}(F/F^{\prime })\biggr)\cdot \unicode[STIX]{x1D70B}_{\ast }(h^{k}ef)\nonumber\\ \displaystyle & & \displaystyle \quad =2\mathop{\sum }_{k=0}^{p+n-2}c_{p+n-2-k}(E/E_{p}+F/F^{\prime })\cdot \unicode[STIX]{x1D70B}_{\ast }(h^{k}ef)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k=0}^{p+n-2}c_{p+n-2-k}(E/E_{p}+F/F^{\prime })\cdot c_{k+1}(V-E-F-M)\nonumber\\ \displaystyle & & \displaystyle \quad =c_{p+n-1}(V-E_{p}-F^{\prime }-M),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 2\mathop{\sum }_{i=0}^{p-1}\mathop{\sum }_{j=0}^{n-1}\unicode[STIX]{x1D70B}_{\ast }(c_{p-1-i}(E/E_{p})\cdot c_{n-1-j}(F/F^{\prime })\cdot h^{i+j}ef)\nonumber\\ \displaystyle & & \displaystyle \quad =2\mathop{\sum }_{k=0}^{p+n-2}\biggl(\mathop{\sum }_{i+j=k}c_{p-1-i}(E/E_{p})\cdot c_{n-1-j}(F/F^{\prime })\biggr)\cdot \unicode[STIX]{x1D70B}_{\ast }(h^{k}ef)\nonumber\\ \displaystyle & & \displaystyle \quad =2\mathop{\sum }_{k=0}^{p+n-2}c_{p+n-2-k}(E/E_{p}+F/F^{\prime })\cdot \unicode[STIX]{x1D70B}_{\ast }(h^{k}ef)\nonumber\\ \displaystyle & & \displaystyle \quad =\mathop{\sum }_{k=0}^{p+n-2}c_{p+n-2-k}(E/E_{p}+F/F^{\prime })\cdot c_{k+1}(V-E-F-M)\nonumber\\ \displaystyle & & \displaystyle \quad =c_{p+n-1}(V-E_{p}-F^{\prime }-M),\nonumber\end{eqnarray}$$
where the last line uses
![]() $c_{p+n-1}(E/E_{p}+F/F^{\prime })=0$
.
$c_{p+n-1}(E/E_{p}+F/F^{\prime })=0$
.
Next consider the case where
![]() $V$
has rank
$V$
has rank
![]() $2n$
. Now
$2n$
. Now
![]() $[\mathbb{P}(E_{p})]=c_{p}(E/E_{p}\otimes S^{\ast })\cdot e$
, and
$[\mathbb{P}(E_{p})]=c_{p}(E/E_{p}\otimes S^{\ast })\cdot e$
, and
![]() $[\mathbb{P}(F^{\prime })]=c_{n-1}(F/F^{\prime }\otimes S^{\ast })\cdot f$
. An analogous computation gives
$[\mathbb{P}(F^{\prime })]=c_{n-1}(F/F^{\prime }\otimes S^{\ast })\cdot f$
. An analogous computation gives
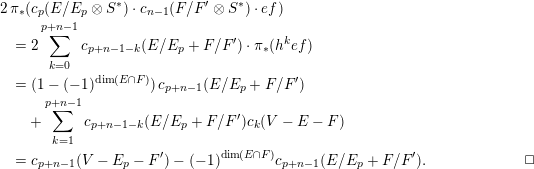 $$\begin{eqnarray}\displaystyle & & \displaystyle 2\,\unicode[STIX]{x1D70B}_{\ast }(c_{p}(E/E_{p}\otimes S^{\ast })\cdot c_{n-1}(F/F^{\prime }\otimes S^{\ast })\cdot ef)\nonumber\\ \displaystyle & & \displaystyle \quad =2\mathop{\sum }_{k=0}^{p+n-1}c_{p+n-1-k}(E/E_{p}+F/F^{\prime })\cdot \unicode[STIX]{x1D70B}_{\ast }(h^{k}ef)\nonumber\\ \displaystyle & & \displaystyle \quad =(1-(-1)^{\dim (E\cap F)})\,c_{p+n-1}(E/E_{p}+F/F^{\prime })\nonumber\\ \displaystyle & & \displaystyle \qquad +\mathop{\sum }_{k=1}^{p+n-1}c_{p+n-1-k}(E/E_{p}+F/F^{\prime })c_{k}(V-E-F)\nonumber\\ \displaystyle & & \displaystyle \quad =c_{p+n-1}(V-E_{p}-F^{\prime })-(-1)^{\dim (E\cap F)}c_{p+n-1}(E/E_{p}+F/F^{\prime }).\square\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 2\,\unicode[STIX]{x1D70B}_{\ast }(c_{p}(E/E_{p}\otimes S^{\ast })\cdot c_{n-1}(F/F^{\prime }\otimes S^{\ast })\cdot ef)\nonumber\\ \displaystyle & & \displaystyle \quad =2\mathop{\sum }_{k=0}^{p+n-1}c_{p+n-1-k}(E/E_{p}+F/F^{\prime })\cdot \unicode[STIX]{x1D70B}_{\ast }(h^{k}ef)\nonumber\\ \displaystyle & & \displaystyle \quad =(1-(-1)^{\dim (E\cap F)})\,c_{p+n-1}(E/E_{p}+F/F^{\prime })\nonumber\\ \displaystyle & & \displaystyle \qquad +\mathop{\sum }_{k=1}^{p+n-1}c_{p+n-1-k}(E/E_{p}+F/F^{\prime })c_{k}(V-E-F)\nonumber\\ \displaystyle & & \displaystyle \quad =c_{p+n-1}(V-E_{p}-F^{\prime })-(-1)^{\dim (E\cap F)}c_{p+n-1}(E/E_{p}+F/F^{\prime }).\square\nonumber\end{eqnarray}$$



