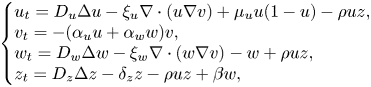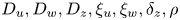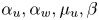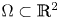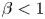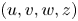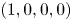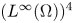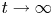1. Introduction
As compared to the traditional treatment like chemotherapy or radiotherapy for cancer diseases, the prominent advantage of virotherapy is that the therapy can reduce the side-effect on the healthy tissue. In clinical treatments, the so-called oncolytic viruses which are either genetically engineered or naturally occurring can selectively attack the cancer cells and eventually destroy them without harming normal cells because virus can replicate inside the infected cells and proceed to infect adjacent cancer cells with the aim to drive the tumour cells to extinction [Reference Fukuhara, Ino and Todo8, Reference Gujar, Pol, Kim, Lee and Kroemer9]. Despite some partial success, implementation of virotherapy is not in sight. In fact, clinical data reveal that the efficacy of virotherapy will be reduced by many factors, such as circulating antibodies, various immune cells or even deposits of extracellular matrix (ECM) may essentially decrease [Reference Ganly and Kirn10, Reference Nemunaitis and Ganly16]. Therefore, to facilitate the understanding of the mechanisms that hinder virus spread, the authors of [Reference Alzahrani, Eftimie and Trucu1] proposed a mathematical model to describe the interaction between both uninfected and infected cancer cells, as well as ECM and oncolytic virus particles, which is given by

in a smoothly bounded domain $\Omega \subset \mathbb {R}^{n}$![]() , with positive parameters $D_u,D_w,D_z,\xi _u, \xi _w,\alpha _u,\alpha _w$
, with positive parameters $D_u,D_w,D_z,\xi _u, \xi _w,\alpha _u,\alpha _w$![]() , $\mu _u, \delta _w,\delta _z,\beta$
, $\mu _u, \delta _w,\delta _z,\beta$![]() and nonnegative constants $\mu _v,\rho _u, \rho _w, \rho _z$
and nonnegative constants $\mu _v,\rho _u, \rho _w, \rho _z$![]() , and with the unknown variables $u, w, z$
, and with the unknown variables $u, w, z$![]() and $v$
and $v$![]() denoting the population densities of uninfected cancer cells, infected cancer cells, virus particles and ECM, respectively. Here, the crucial modelling hypothesis underlying (1.1), which accounts for haptotactic motion of cancer cells and thereby marks a substantial difference between (1.1) and related more classical reaction–diffusion models for virus dynamics [Reference Komarova13, Reference Prüss, Zacher and Schnaubelt19], is that apart from its random diffusion, both uninfected and infected cancer cells bias their motion upward ECM gradients simultaneously due to the attraction by some macromolecules trapped in the ECM. In addition, the oncolytic virus particles infect the uninfected cancer cells upon contact with uninfected tumour cells, and new infectious virus particles are released at rate $\beta >0$
denoting the population densities of uninfected cancer cells, infected cancer cells, virus particles and ECM, respectively. Here, the crucial modelling hypothesis underlying (1.1), which accounts for haptotactic motion of cancer cells and thereby marks a substantial difference between (1.1) and related more classical reaction–diffusion models for virus dynamics [Reference Komarova13, Reference Prüss, Zacher and Schnaubelt19], is that apart from its random diffusion, both uninfected and infected cancer cells bias their motion upward ECM gradients simultaneously due to the attraction by some macromolecules trapped in the ECM. In addition, the oncolytic virus particles infect the uninfected cancer cells upon contact with uninfected tumour cells, and new infectious virus particles are released at rate $\beta >0$![]() when infected cells burst (a process known as lysis); beyond this, (1.1) presupposes that the ECM is degraded upon interacting with both type of cancer cells, and is possibly remodelled by the normal tissue according to logistic laws.
when infected cells burst (a process known as lysis); beyond this, (1.1) presupposes that the ECM is degraded upon interacting with both type of cancer cells, and is possibly remodelled by the normal tissue according to logistic laws.
Due to its relevance in several biological contexts, inter alia the cancer invasion [Reference Anderson, Chaplain, Newman, Steele and Thompson2, Reference Chaplain and Lolas5], haptotaxis mechanism has received considerable attention in the analytical literature [Reference Cao3, Reference Jin11, Reference Jin and Xiang12, Reference Li and Lankeit14, Reference Pang and Wang17, Reference Stinner, Surulescu and Winkler21, Reference Tao and Winkler27–Reference Wang30, Reference Zheng and Ke32, Reference Zhigun, Surulescu and Uatay33]. The most characteristic ingredient of the model (1.1) is the presence of two simultaneous haptotaxis processes of cancer cells, and thereby distinguishes it from most haptotaxis [Reference Jin11, Reference Walker and Webb29, Reference Zhigun, Surulescu and Uatay33] and chemotaxis–haptotaxis systems [Reference Cao3, Reference Pang and Wang17, Reference Tao and Winkler27] studied in the literature, especially the ECM is degraded by both type of cancer cells in (1.1) directly, rather matrix-degrading enzymes secreted by tumour cells (see e.g. [Reference Jin and Xiang12, Reference Pang and Wang17, Reference Pang and Wang18, Reference Tao and Winkler27]). It is observed that the former circumstance seems to widely restrict the accessibility to the approaches well established in the analysis of related reaction–diffusion systems, and accordingly the considerable challenges arise for the rigorous analysis of (1.1), particularly when addressing issues related to qualitative solution behaviour.
To the best of our knowledge, so far the quantitative comprehension available for (1.1) is yet mainly limited in some simple setting [Reference Chen4, Reference Li and Wang15, Reference Ren and Liu20, Reference Tao and Winkler22–Reference Tao and Winkler26]. For instance, based on the construction of certain quasi-Lyapunov functional, Tao and Winkler [Reference Tao and Winkler22] established the global classical solvability of (1.1) in the two-dimensional case. With respect to the boundedness of solutions to (1.1), authors in [Reference Li and Wang15] considered some slightly more comprehensive variants of (1.1), which accounts for the haptotaxis mechanisms of both cancer cells and virions, in the situation when zero-order term has suitably strong degradation. Apart from that, existing analytical works indicate that the virus reproduction rate relative to the lysis rate of infected cancer cells appears to be critical in determining the large time behaviour of the corresponding solutions at least in some simplified version of (1.1), inter alia upon neglecting haptotactic cross-diffusion of infected cancer cells and renew of ECM. Indeed, for the reaction–diffusion–taxis system

it is shown in [Reference Tao and Winkler24] that if $\beta >1$![]() , then for any reasonably regular initial data satisfying $\overline {u_0}>{1}/{(\beta -1)}$
, then for any reasonably regular initial data satisfying $\overline {u_0}>{1}/{(\beta -1)}$![]() the global classical solution of (1.2) with $\rho =0,\mu _u=0$
the global classical solution of (1.2) with $\rho =0,\mu _u=0$![]() must blow up in infinite time, which is also implemented by the result on boundedness in the case when $\overline {u_0}<{1}/{(\beta -1)_{+}}$
must blow up in infinite time, which is also implemented by the result on boundedness in the case when $\overline {u_0}<{1}/{(\beta -1)_{+}}$![]() and $v_0\equiv 0$
and $v_0\equiv 0$![]() for any $\beta >0$
for any $\beta >0$![]() . Beyond the latter, it was proved that when $\rho >0$
. Beyond the latter, it was proved that when $\rho >0$![]() and $\mu _u=0$
and $\mu _u=0$![]() , the first solution component $u$
, the first solution component $u$![]() of (1.2) possesses a positive lower bounds whenever $0<\beta <1$
of (1.2) possesses a positive lower bounds whenever $0<\beta <1$![]() and the initial data $u_0\not \equiv 0$
and the initial data $u_0\not \equiv 0$![]() [Reference Tao and Winkler25]. Furthermore, as an extension of above outcome, the asymptotic behaviour of solution was investigated in [Reference Tao and Winkler26] if $0<\beta <1$
[Reference Tao and Winkler25]. Furthermore, as an extension of above outcome, the asymptotic behaviour of solution was investigated in [Reference Tao and Winkler26] if $0<\beta <1$![]() . It is remarked that for system (1.2) with $\mu _u>0$
. It is remarked that for system (1.2) with $\mu _u>0$![]() and $0<\beta <1$
and $0<\beta <1$![]() , the convergence properties of the corresponding solutions was also discussed in [Reference Chen4]. We would like to mention that as the complementing results of [Reference Tao and Winkler26], the recent paper [Reference Tao and Winkler23] reveals that for any prescribed level $\gamma \in (0,{1}/{(\beta -1)_{+}})$
, the convergence properties of the corresponding solutions was also discussed in [Reference Chen4]. We would like to mention that as the complementing results of [Reference Tao and Winkler26], the recent paper [Reference Tao and Winkler23] reveals that for any prescribed level $\gamma \in (0,{1}/{(\beta -1)_{+}})$![]() , the corresponding solution of (1.2) with $\mu _u=0,\rho \geq 0,\beta >0$
, the corresponding solution of (1.2) with $\mu _u=0,\rho \geq 0,\beta >0$![]() will approach the constant equilibrium $(u_\infty, 0, 0, 0)$
will approach the constant equilibrium $(u_\infty, 0, 0, 0)$![]() asymptotically with some $u_\infty >0$
asymptotically with some $u_\infty >0$![]() whenever the initial deviation from homogeneous distribution $(\gamma, 0, 0, 0)$
whenever the initial deviation from homogeneous distribution $(\gamma, 0, 0, 0)$![]() is suitably small.
is suitably small.
The purpose of this work is to investigate the dynamical features of the models involving the simultaneous haptotactic processes of both uninfected and infected cancer cells when the virus replication rate $\beta <1$![]() . To this end, we are concerned with the comprehensive haptotactic cross-diffusion systems of the form
. To this end, we are concerned with the comprehensive haptotactic cross-diffusion systems of the form

in a smoothly bounded domain $\Omega \subset \mathbb {R}^{2}$![]() . To import the precise framework underlying the basic theory from [Reference Tao and Winkler22] we shall henceforth assume that
. To import the precise framework underlying the basic theory from [Reference Tao and Winkler22] we shall henceforth assume that

Hence the outcome of [Reference Tao and Winkler22] asserts the global existence of a unique classical solution $(u,v,w,z)$![]() to (1.3). Our main results reveal that whenever $\beta <1$
to (1.3). Our main results reveal that whenever $\beta <1$![]() , $(u,v,w,z)$
, $(u,v,w,z)$![]() is uniformly bounded and exponentially converges to the constant equilibrium $(1, 0, 0, 0)$
is uniformly bounded and exponentially converges to the constant equilibrium $(1, 0, 0, 0)$![]() in the topology $(L^{\infty }(\Omega ))^{4}$
in the topology $(L^{\infty }(\Omega ))^{4}$![]() in a large time limit, which can be stated as follows.
in a large time limit, which can be stated as follows.
Theorem 1.1 Let $\Omega \subset \mathbb {R}^{2}$![]() be a bounded domain with smooth boundary, $D_u,D_w,D_z,\xi _u,\xi _w,$
be a bounded domain with smooth boundary, $D_u,D_w,D_z,\xi _u,\xi _w,$![]() $\mu _u,\rho,\alpha _u,\alpha _w,\delta _z$
$\mu _u,\rho,\alpha _u,\alpha _w,\delta _z$![]() are positive parameters, and suppose that $0<\beta <1$
are positive parameters, and suppose that $0<\beta <1$![]() . Then system (1.3) admits a unique global classic positive solution satisfying
. Then system (1.3) admits a unique global classic positive solution satisfying
Moreover there exist positive constants $\eta,\varrho,\gamma _1,$![]() $\gamma _2$
$\gamma _2$![]() and $C>0$
and $C>0$![]() such that
such that
as well as
Since the third equation in (1.3) is merely an ordinary differential equation, no smoothing action on the spatial regularity of $v$![]() can be expected. To overcome the analytical difficulties arising from the latter, inter alia in the derivation of global boundedness of solutions, we accordingly introduce the variable transformation $a={\rm e}^{-\chi _u v}u$
can be expected. To overcome the analytical difficulties arising from the latter, inter alia in the derivation of global boundedness of solutions, we accordingly introduce the variable transformation $a={\rm e}^{-\chi _u v}u$![]() and $b={\rm e}^{-\chi _w v}w$
and $b={\rm e}^{-\chi _w v}w$![]() , and establish a priori estimate for the solution components $a,b$
, and establish a priori estimate for the solution components $a,b$![]() of the corresponding equivalent system (2.2) below in the space $L\log L(\Omega )$
of the corresponding equivalent system (2.2) below in the space $L\log L(\Omega )$![]() rather than the solution components $u,w$
rather than the solution components $u,w$![]() to (1.3). Note that in the evolution of density $v$
to (1.3). Note that in the evolution of density $v$![]() of ECM fibres the quantity $u,w$
of ECM fibres the quantity $u,w$![]() appears via a sink term, whereas it turns to a genuine superlinear production terms of system (2.2) in the style of $\chi _u a(\alpha _u a{\rm e}^{\chi _u v} + \alpha _w b{\rm e}^{\chi _w v})v$
appears via a sink term, whereas it turns to a genuine superlinear production terms of system (2.2) in the style of $\chi _u a(\alpha _u a{\rm e}^{\chi _u v} + \alpha _w b{\rm e}^{\chi _w v})v$![]() and $\chi _w b(\alpha _u a{\rm e}^{\chi _u v} + \alpha _w b{\rm e}^{\chi _w v})v$
and $\chi _w b(\alpha _u a{\rm e}^{\chi _u v} + \alpha _w b{\rm e}^{\chi _w v})v$![]() . Taking advantage of the exponential decay of $w$
. Taking advantage of the exponential decay of $w$![]() in $L^{1}$
in $L^{1}$![]() norm in the case $0<\beta <1$
norm in the case $0<\beta <1$![]() , we shall track the time evolution of
, we shall track the time evolution of
with $a={\rm e}^{-\chi _u v}u$![]() and $b={\rm e}^{-\chi _w v}w$
and $b={\rm e}^{-\chi _w v}w$![]() , which is somewhat different from the quasi-Lyapunov functional (4.11) in [Reference Tao and Winkler22] where a Dirichlet integral of $\sqrt {v}$
, which is somewhat different from the quasi-Lyapunov functional (4.11) in [Reference Tao and Winkler22] where a Dirichlet integral of $\sqrt {v}$![]() is involved. Here, the quadratic degradation term in the first equation of (1.3) seems to be necessary. Thereafter applying a variant of the Gagliardo–Nirenberg inequality involving certain $L\log L$
is involved. Here, the quadratic degradation term in the first equation of (1.3) seems to be necessary. Thereafter applying a variant of the Gagliardo–Nirenberg inequality involving certain $L\log L$![]() -type norms and performing a Moser-type iteration, the $L^{\infty }$
-type norms and performing a Moser-type iteration, the $L^{\infty }$![]() -bounds of solutions is derived.
-bounds of solutions is derived.
In addition, our result indicates that although haptotaxis mechanism may have some important influence on the properties of the related system on short or intermediate time scales, the large time behaviour of solution to (1.3) can essentially be described by the corresponding haptotaxis-free system at least under the biological meaningful restriction $\beta <1$![]() . In order to prove theorem 1.1, a first step is to derive a pointwise lower bound for $a:={\rm e}^{-\chi _u v}u$
. In order to prove theorem 1.1, a first step is to derive a pointwise lower bound for $a:={\rm e}^{-\chi _u v}u$![]() (lemma 4.2), which, in turn, amounts to establishing an exponential decay of $z$
(lemma 4.2), which, in turn, amounts to establishing an exponential decay of $z$![]() with respect to the norm in $L^{\infty }(\Omega )$
with respect to the norm in $L^{\infty }(\Omega )$![]() (lemma 4.2). To achieve the latter, we will make use of $L^{1}(\Omega )$
(lemma 4.2). To achieve the latter, we will make use of $L^{1}(\Omega )$![]() -decay information of $w,z$
-decay information of $w,z$![]() explicitly contained in lemma 2.3. Secondly, as a consequence of the former, the exponential decay of $v$
explicitly contained in lemma 2.3. Secondly, as a consequence of the former, the exponential decay of $v$![]() with respect to $L^{\infty }(\Omega )$
with respect to $L^{\infty }(\Omega )$![]() norm is achieved (lemma 4.3), which along a $a^{-1}$
norm is achieved (lemma 4.3), which along a $a^{-1}$![]() -testing procedure will provide quite weak convergence information of $u$
-testing procedure will provide quite weak convergence information of $u$![]() , inter alia the integrability property of $\nabla \sqrt {a}$
, inter alia the integrability property of $\nabla \sqrt {a}$![]() in $L^{2}((0,\infty ); L^{2}(\Omega ))$
in $L^{2}((0,\infty ); L^{2}(\Omega ))$![]() (lemma 4.4). The next step will consist of verifying the integrability of $\nabla v$
(lemma 4.4). The next step will consist of verifying the integrability of $\nabla v$![]() in $L^{2}((0,\infty ); L^{2}(\Omega ))$
in $L^{2}((0,\infty ); L^{2}(\Omega ))$![]() rather than that of $a_{t}$
rather than that of $a_{t}$![]() (lemma 4.5), which will turn out to be sufficient a condition in the derivation of exponential decay property of $\|u(\cdot,t)-1\|_{L^{p}(\Omega )}$
(lemma 4.5), which will turn out to be sufficient a condition in the derivation of exponential decay property of $\|u(\cdot,t)-1\|_{L^{p}(\Omega )}$![]() . Indeed, this integrability property of $\nabla v$
. Indeed, this integrability property of $\nabla v$![]() enables us to derive an exponential decay of $\int _{\Omega }|\nabla v|^{2}$
enables us to derive an exponential decay of $\int _{\Omega }|\nabla v|^{2}$![]() (lemma 4.6), upon which and through a testing procedure, it is shown that the convergence property of $u$
(lemma 4.6), upon which and through a testing procedure, it is shown that the convergence property of $u$![]() actually takes place in the type of (4.22) (lemma 4.7). Furthermore, upon the above decay properties, we are able to verify that $\int _{\Omega }|\nabla v|^{4}$
actually takes place in the type of (4.22) (lemma 4.7). Furthermore, upon the above decay properties, we are able to verify that $\int _{\Omega }|\nabla v|^{4}$![]() decays exponentially by means of the suitable quasi-Lyapunov functional (lemma 4.9). At this position, thanks to the integrability exponent in $\int _{\Omega }|\nabla v|^{4}$
decays exponentially by means of the suitable quasi-Lyapunov functional (lemma 4.9). At this position, thanks to the integrability exponent in $\int _{\Omega }|\nabla v|^{4}$![]() exceeding the considered spatial dimension $n=2$
exceeding the considered spatial dimension $n=2$![]() , the desired decay property stated in theorem 1.1 can be exactly achieved.
, the desired decay property stated in theorem 1.1 can be exactly achieved.
This paper will be organized as follows: § 2 will introduce an equivalent system of (1.3) and give out some basic priori estimates of classical solutions thereof, inter alia the weak decay properties of $w,z$![]() . Section 3 will focus on the construction of an entropy-type functional, which entails certain $L\log L$
. Section 3 will focus on the construction of an entropy-type functional, which entails certain $L\log L$![]() -type norms and thereby allows us to establish the $L^{\infty }$
-type norms and thereby allows us to establish the $L^{\infty }$![]() -bounds. Finally, starting from the exponential decay of quantities $w,z$
-bounds. Finally, starting from the exponential decay of quantities $w,z$![]() with respect to the norm in $L^{1}(\Omega )$
with respect to the norm in $L^{1}(\Omega )$![]() , we established the exponential convergence properties of the solutions in § 4.
, we established the exponential convergence properties of the solutions in § 4.
2. Preliminaries
Let us firstly recall the result in [Reference Tao and Winkler22] which warrants the global smooth solvability of problem (1.3).
Lemma 2.1 Let $\Omega \subset \mathbb {R}^{2}$![]() be a bounded domain with smooth boundary, $D_u,D_w,D_z,\xi _u,\xi _w,$
be a bounded domain with smooth boundary, $D_u,D_w,D_z,\xi _u,\xi _w,$![]() $\mu _u,\rho,\alpha _u,\alpha _w,\delta _z,\beta$
$\mu _u,\rho,\alpha _u,\alpha _w,\delta _z,\beta$![]() are positive parameters. Then for any choice of $(u_0,v_0,w_0,z_0)$
are positive parameters. Then for any choice of $(u_0,v_0,w_0,z_0)$![]() fulfilling (1.4), the problem (1.3) (1.4) possesses a uniquely determined classical solution $(u,v,w,z)\in (C^{2,1}(\overline {\Omega } \times [0,\infty )))^{4}$
fulfilling (1.4), the problem (1.3) (1.4) possesses a uniquely determined classical solution $(u,v,w,z)\in (C^{2,1}(\overline {\Omega } \times [0,\infty )))^{4}$![]() for which $u>0,w>0,z>0$
for which $u>0,w>0,z>0$![]() and $v\geq 0$
and $v\geq 0$![]() .
.
Following the variable of change used in related literature [Reference Fontelos, Friedman and Hu6, Reference Li and Wang15, Reference Tao and Winkler26, Reference Tao and Winkler28], which can conveniently reformulate the haptotactic interaction in (1.3), we define $\chi _u:={\xi _u}/{D_u}$![]() and $\chi _w:={\xi _w}/{D_w}$
and $\chi _w:={\xi _w}/{D_w}$![]() and set
and set
Then we transform (1.3) into an equivalent system as below

with
as well as
In our subsequent analysis, unless otherwise stated we shall assume that $(a, v, b, z)$![]() is the global classical solution to (2.2) addressed in lemma 2.1.
is the global classical solution to (2.2) addressed in lemma 2.1.
The damping effects of quadratic degradation in the first equation in (1.3) will be important for us to verify the global boundedness of the solutions. Let us first apply straightforward argument to achieve the following basic $L^{1}$![]() -bounds for $u,w$
-bounds for $u,w$![]() and $z$
and $z$![]() , which is also valid for the solution components $a,b$
, which is also valid for the solution components $a,b$![]() of (2.2).
of (2.2).
Lemma 2.2 For all $t>0,$![]() the solution $(u,w,v,z)$
the solution $(u,w,v,z)$![]() satisfies
satisfies
and
and
as well as
Proof. It is easy to see that (2.3) can be derived through an integration of the first equation in (1.3) along with Cauchy–Schwarz's inequality, and (2.4) is a direct consequence of $(\alpha _u u+\alpha _w w)v\geq 0$![]() due to the nonnegativity of $u,w$
due to the nonnegativity of $u,w$![]() and $v$
and $v$![]() .
.
In addition, integrating the $w$![]() -equation as well as $u$
-equation as well as $u$![]() -equation respectively and adding the corresponding results, we then have
-equation respectively and adding the corresponding results, we then have
which readily leads to (2.5) upon an ODE comparison. At last, thanks to (2.5), (2.6) clearly results from the integration of $z$![]() -equation in (1.3).
-equation in (1.3).
Beyond that, making use of the restriction $\beta \in (0,1)$![]() , one can derive the decay properties of the solution components $w$
, one can derive the decay properties of the solution components $w$![]() and $z$
and $z$![]() with respect to $L^{1}(\Omega )$
with respect to $L^{1}(\Omega )$![]() , which will be used later on.
, which will be used later on.
Lemma 2.3 Suppose that $0<\beta <1$![]() then there exists constant $C>0$
then there exists constant $C>0$![]() such that
such that
with $\delta =\min \{1-\beta,\delta _z\}$![]() .
.
Proof. We use the $z$![]() -equation and $w$
-equation and $w$![]() -equation to compute
-equation to compute
Due to $0<\beta <1$![]() , this readily implies that
, this readily implies that
and hence (2.8) is valid with $C=\int _{\Omega } w_0+\int _{\Omega }z_0$![]() .
.
3. Global boundedness
As in [Reference Li and Wang15, Reference Tao and Winkler28], the crucial step in establishing a priori $L^{\infty }$![]() bounds for $a,b$
bounds for $a,b$![]() and $z$
and $z$![]() is to derive estimates for $a$
is to derive estimates for $a$![]() and $b$
and $b$![]() in $L\log L$
in $L\log L$![]() , which turn out to be consequences of a quasi-energy structure associated with the system (2.2) rather than the system (1.3). Indeed, making appropriate use of the logistic degradation in the first equation of (2.2) and inter alia the $L^{1}$
, which turn out to be consequences of a quasi-energy structure associated with the system (2.2) rather than the system (1.3). Indeed, making appropriate use of the logistic degradation in the first equation of (2.2) and inter alia the $L^{1}$![]() -decay property of the solution component $w$
-decay property of the solution component $w$![]() , one can verify that functional
, one can verify that functional
which does not involve the Dirichlet integral of $\sqrt {v}$![]() , actually possesses a certain quasi-dissipative property for all $t>t_0$
, actually possesses a certain quasi-dissipative property for all $t>t_0$![]() with constant $t_0>1$
with constant $t_0>1$![]() suitably chosen.
suitably chosen.
Lemma 3.1 For any $\varepsilon >0$![]() , there exists $C(\varepsilon )>0$
, there exists $C(\varepsilon )>0$![]() such that
such that

for all $t>0$![]() .
.
Proof. From the first equation in (1.3), it follows that
Hence, a testing procedure on the first equation in (2.2) leads to

Thanks to lemma 2.2 and the elementary inequality $a\log a\geq -\frac {1}{e}$![]() valid for all $a>0$
valid for all $a>0$![]() , one can find $c_1>0$
, one can find $c_1>0$![]() such that
such that

which along with Young's inequality implies that for any $\varepsilon >0$![]()

Further invoking the inequality $a^{2}\leq \varepsilon _1 a^{2}\log a+{\rm e}^{{2}/{\varepsilon _1}}$![]() for any $\varepsilon _1>0$
for any $\varepsilon _1>0$![]() , we arrive at
, we arrive at

with some $c_2(\varepsilon )>0$![]() . Accordingly, (3.1) is a consequence of (3.3) and the fact that $a\log a\leq \varepsilon _2 a^{2}\log a- \varepsilon _2^{-1} \ln \varepsilon _2$
. Accordingly, (3.1) is a consequence of (3.3) and the fact that $a\log a\leq \varepsilon _2 a^{2}\log a- \varepsilon _2^{-1} \ln \varepsilon _2$![]() with $\varepsilon _2={\mu _u}/{(4(\mu _u+1))}$
with $\varepsilon _2={\mu _u}/{(4(\mu _u+1))}$![]() .
.
For the solution component $b$![]() of (2.2), we also have
of (2.2), we also have
Lemma 3.2 Let $0<\beta <1$![]() . Then one can find $C>0$
. Then one can find $C>0$![]() and $t_0>0$
and $t_0>0$![]() such that for all $t>t_0$
such that for all $t>t_0$![]()

Proof. From the second equation in (1.3), it follows that
Relying on $0\leq v\leq m_v$![]() in $\overline {\Omega }\times (0,\infty )$
in $\overline {\Omega }\times (0,\infty )$![]() , a straightforward calculation along with the Young's inequality yields
, a straightforward calculation along with the Young's inequality yields

with some $c_1>0$![]() , where we use the fact that there exits $c_2>0$
, where we use the fact that there exits $c_2>0$![]() such that $\log ^{4} s\leq s+c_2$
such that $\log ^{4} s\leq s+c_2$![]() for all $s\geq 1$
for all $s\geq 1$![]() and $w^{2}={\rm e}^{2\chi _w v}b^{2}\leq {\rm e}^{2\chi _w m_v} b^{2}$
and $w^{2}={\rm e}^{2\chi _w v}b^{2}\leq {\rm e}^{2\chi _w m_v} b^{2}$![]() .
.
Furthermore, in order to appropriately estimate the first summand on the right-hand side of (3.5), we apply the two-dimensional Gagliardo–Nirenberg inequalities
to get

Therefore combining (3.6) with (3.5), we arrive at

By lemma 2.3, we can pick $t_0>0$![]() suitably large such that
suitably large such that
and thereby for $t\geq t_0$![]() ,
,

which along with lemma 2.2 and the Young's inequality completes the proof.
While the expressions $\int _{\Omega }a^{2}$![]() appearing in (3.4) turns out to be conveniently digestible through the dissipation rate in (3.1), it remains to estimate $\left (\int _{\Omega } z^{4}\right )^{ 1/2}$
appearing in (3.4) turns out to be conveniently digestible through the dissipation rate in (3.1), it remains to estimate $\left (\int _{\Omega } z^{4}\right )^{ 1/2}$![]() by means of an interpolation argument.
by means of an interpolation argument.
Lemma 3.3 Let $0<\beta <1$![]() and define
and define
Then there exist $t_1>t_0$![]() and constant $C>0$
and constant $C>0$![]() such that for all $t\geq t_1$
such that for all $t\geq t_1$![]()
Proof. Testing the fourth equation in (2.2) by $z$![]() , we can see that
, we can see that

Hence lemmas 3.1 and 3.2 provide positive constants $c_i>0~ (i=1,2)$![]() such that
such that

for all $t\geq t_0$![]() with $t_0$
with $t_0$![]() given by lemma 3.2.
given by lemma 3.2.
Now again since $a^{2}\leq \varepsilon _1 a^{2}\log a+{\rm e}^{{2}/{\varepsilon _1}}$![]() for any $\varepsilon _1>0$
for any $\varepsilon _1>0$![]() ,
,
with $c_3>0$![]() , whereas according to the two-dimensional Gagliardo–Nirenberg inequalities,
, whereas according to the two-dimensional Gagliardo–Nirenberg inequalities,

In summary, (3.11), (3.10) and (3.9) show that for $t\geq t_0$![]()

with some $c_4>0$![]() .
.
Furthermore to estimate $\left (\int _{\Omega }z^{4}\right )^{{1}/{2}}$![]() on the right-hand side of (3.12), we employ (2.8), the Gagliardo–Nirenberg inequalities and Young's inequality once more to conclude that there exists $t_1>t_0$
on the right-hand side of (3.12), we employ (2.8), the Gagliardo–Nirenberg inequalities and Young's inequality once more to conclude that there exists $t_1>t_0$![]() such that for all $t\geq t_1$
such that for all $t\geq t_1$![]()

with $c_5>0$![]() , which together with (3.12) readily establishes (3.8).
, which together with (3.12) readily establishes (3.8).
As a consequence of (3.8), the $L\log L$![]() -estimate of quantities $a$
-estimate of quantities $a$![]() and $b$
and $b$![]() is achieved as follows.
is achieved as follows.
Lemma 3.4 Let $0<\beta <1$![]() . Then there exists $C> 0$
. Then there exists $C> 0$![]() such that for all $t> t_0,$
such that for all $t> t_0,$![]()
as well as
Proof. As in lemma 3.4 of [Reference Li and Wang15], by the inequality $a\log a>-{\rm e}^{-1}$![]() in $\Omega \times (0,\infty )$
in $\Omega \times (0,\infty )$![]() , we have
, we have

Likewise, we can also obtain
According to (3.8), there exits $c_1>0$![]() such that
such that
Therefore by the definition of $\mathcal {F}(t)$![]() , we can see that
, we can see that
with $c_2= ({2|\Omega |}/ e)({\rm e}^{\chi _w m_v} +{\rm e}^{\chi _u m_v} )+ c_1$![]() for all $t>t_0$
for all $t>t_0$![]() , and thus complete the proof.
, and thus complete the proof.
The a priori estimates for $a, b$![]() gained in lemma 3.4 is the cornerstone to establish a $L^{\infty }(\Omega )$
gained in lemma 3.4 is the cornerstone to establish a $L^{\infty }(\Omega )$![]() -bound for solution $(u,v,w,z)$
-bound for solution $(u,v,w,z)$![]() . Indeed, one can proceed to derive obtain $L^{\infty }(\Omega )$
. Indeed, one can proceed to derive obtain $L^{\infty }(\Omega )$![]() -bound by means of some quite straightforward $L^{p}$
-bound by means of some quite straightforward $L^{p}$![]() testing procedures.
testing procedures.
Lemma 3.5 Let $0<\beta <1$![]() . Then there exists $C> 0$
. Then there exists $C> 0$![]() such that for all $t>0$
such that for all $t>0$![]()
Proof. Testing the first equation in (2.2) by ${\rm e}^{\chi _u v}a^{r-1}$![]() with $r\geq 2$
with $r\geq 2$![]() , we obtain $c_1(r)>0$
, we obtain $c_1(r)>0$![]()

which together with the Young's inequality, leads to

with constant $c_2(r)>0$![]() . Likewise, there exist $c_i(r)>0~ (i=3,4)$
. Likewise, there exist $c_i(r)>0~ (i=3,4)$![]() such that
such that

as well as
Collecting (3.18)–(3.20), we then arrive at

with $c_5>0$![]() and $c_6(r)>0$
and $c_6(r)>0$![]() .
.
According to lemma 3.4, there exists $c_7(r)>0$![]() such that
such that
Now we invoke the logarithm-type Gagliardo–Nirenberg inequality (we refer to lemma A.5 in [Reference Tao and Winkler28] for details) to obtain that there exists $c_8(r)>0$![]() such that
such that
and
as well as
Therefore combining (3.22)–(3.25) and by lemma 2.2, we arrive at
and thereby
with $c_{9}(r)> 0, c_{10}(r)>0$![]() by a standard ODE comparison argument. At this position, one can derive a bound for $a,b,z$
by a standard ODE comparison argument. At this position, one can derive a bound for $a,b,z$![]() with respect to the norm in $L^{\infty }(\Omega )$
with respect to the norm in $L^{\infty }(\Omega )$![]() by means of a Moser-type iteration argument in quite a standard manner. We omit the proof thereof, and would like refer to [Reference Li and Wang15, Reference Tao and Winkler26, Reference Tao and Winkler28] for details in a closely related setting.
by means of a Moser-type iteration argument in quite a standard manner. We omit the proof thereof, and would like refer to [Reference Li and Wang15, Reference Tao and Winkler26, Reference Tao and Winkler28] for details in a closely related setting.
4. Asymptotic behaviour
On the basis of the exponential decay of quantities $w,z$![]() with respect to the norm in $L^{1}(\Omega )$
with respect to the norm in $L^{1}(\Omega )$![]() and global boundedness of solutions, we will address the large time asymptotics of the solution $(u,v,w,z)$
and global boundedness of solutions, we will address the large time asymptotics of the solution $(u,v,w,z)$![]() to (1.3). To this end, we first turn the $L^{1}$
to (1.3). To this end, we first turn the $L^{1}$![]() -decay information explicitly contained in lemma 2.3 to the decay property of $z$
-decay information explicitly contained in lemma 2.3 to the decay property of $z$![]() in $L^{\infty }$
in $L^{\infty }$![]() -norm by an appropriate application of the parabolic smoothing estimates in the two-dimensional domain.
-norm by an appropriate application of the parabolic smoothing estimates in the two-dimensional domain.
Lemma 4.1 Let $\beta \in (0,1)$![]() . Then there exists $C>0$
. Then there exists $C>0$![]() such that
such that
with $\gamma _1={\min \{1-\beta,\delta _z\}}/2$![]() .
.
Proof. We invoke lemma 2.3 along with (3.17) to see that there exist $c_1>0$![]() and $c_2>0$
and $c_2>0$![]() such that
such that
with $\delta =\min \{1-\beta,\delta _z\}>0$![]() . According to known smoothing properties of the Neumann heat semigroup $( {\rm e}^{\sigma \Delta } )_{\sigma > 0}$
. According to known smoothing properties of the Neumann heat semigroup $( {\rm e}^{\sigma \Delta } )_{\sigma > 0}$![]() on the domain $\Omega \subset \mathbb {R}^{2}$
on the domain $\Omega \subset \mathbb {R}^{2}$![]() [Reference Winkler31], there exists $c_3 >0$
[Reference Winkler31], there exists $c_3 >0$![]() such that for all $\sigma >0$
such that for all $\sigma >0$![]() and $\varphi \in C^{0}(\Omega )$
and $\varphi \in C^{0}(\Omega )$![]() ,
,
Due to the nonnegativity of $z$![]() and the comparison principle, we may use (4.2) and (4.3) to infer that
and the comparison principle, we may use (4.2) and (4.3) to infer that

with some $c_4>0$![]() , which along with the nonnegativity of $z$
, which along with the nonnegativity of $z$![]() entails that (4.1) holds with $C=\|z_0\|_{L^{\infty }(\Omega )} +\beta c_2 c_3 c_4.$
entails that (4.1) holds with $C=\|z_0\|_{L^{\infty }(\Omega )} +\beta c_2 c_3 c_4.$![]()
Now thanks to the uniform decay property of $z$![]() , a pointwise lower bound for $a=u{\rm e}^{-\chi _u v}$
, a pointwise lower bound for $a=u{\rm e}^{-\chi _u v}$![]() can be achieved by means of an argument based on comparison with spatially flat functions, which is documented as follows.
can be achieved by means of an argument based on comparison with spatially flat functions, which is documented as follows.
Lemma 4.2 Let $\beta <1$![]() . Then there exist $\gamma >0$
. Then there exist $\gamma >0$![]() and $t_1>0$
and $t_1>0$![]() such that
such that
Proof. According to lemma 4.1, one can pick $t_1>0$![]() sufficiently large such that for all $t>t_1$
sufficiently large such that for all $t>t_1$![]()
Hence by means of a straightforward computation based on (2.2), one can see that

for all $t>t_1$![]() .
.
Now let $\underline {a}(t)$![]() be the smooth solution to the initial value problem:
be the smooth solution to the initial value problem:

then through the explicit solution of above Bernoulli-type ODE, we have
for all $t>t_1$![]() . It is observed that
. It is observed that
and $a(x,t_1)\geq \underline {a}(t_1)$![]() . Hence from the comparison principle of the parabolic equation, one can conclude that
. Hence from the comparison principle of the parabolic equation, one can conclude that
and thereby (4.5) is valid with $\gamma = c_1$![]() .
.
In view of the $v$![]() -equation in (2.2), the latter information immediately entails the exponential decay of $v$
-equation in (2.2), the latter information immediately entails the exponential decay of $v$![]() with respect to $L^{\infty }(\Omega )$
with respect to $L^{\infty }(\Omega )$![]() norm.
norm.
Lemma 4.3 Let $\beta <1$![]() . Then there exists $C>0$
. Then there exists $C>0$![]() such that for all $t>0$
such that for all $t>0$![]()
with $\gamma _2=\alpha _u\gamma$![]() .
.
Proof. By recalling the outcomes of lemma 4.2, we have
for all $t>t_1$![]() and hence $v(x,t)\leq v_0(x) {\rm e}^{-\alpha _u\gamma (t-t_1)}\leq \|v_0\|_{L^{\infty }(\Omega )} {\rm e}^{\alpha _u\gamma t_1}{\rm e}^{-\alpha _u\gamma t}$
and hence $v(x,t)\leq v_0(x) {\rm e}^{-\alpha _u\gamma (t-t_1)}\leq \|v_0\|_{L^{\infty }(\Omega )} {\rm e}^{\alpha _u\gamma t_1}{\rm e}^{-\alpha _u\gamma t}$![]() . On the other hand, $v(x,t)\leq \|v_0\|_{L^{\infty }(\Omega )}\leq \|v_0\|_{L^{\infty }(\Omega )} {\rm e}^{\alpha _u\gamma t_1}{\rm e}^{-\alpha _u\gamma t}$
. On the other hand, $v(x,t)\leq \|v_0\|_{L^{\infty }(\Omega )}\leq \|v_0\|_{L^{\infty }(\Omega )} {\rm e}^{\alpha _u\gamma t_1}{\rm e}^{-\alpha _u\gamma t}$![]() for $t\in (0, t_1)$
for $t\in (0, t_1)$![]() . Hence (4.11) is valid with $C=\|v_0\|_{L^{\infty }(\Omega )} {\rm e}^{\alpha _u\gamma t_1}$
. Hence (4.11) is valid with $C=\|v_0\|_{L^{\infty }(\Omega )} {\rm e}^{\alpha _u\gamma t_1}$![]() .
.
Furthermore upon the decay property of $v$![]() with respect to $L^{\infty }(\Omega )$
with respect to $L^{\infty }(\Omega )$![]() , one can derive the following basic stabilization feature of $a(={\rm e}^{-\chi _u v}u)$
, one can derive the following basic stabilization feature of $a(={\rm e}^{-\chi _u v}u)$![]() .
.
Lemma 4.4 Let $\beta <1$![]() . Then we have
. Then we have
as well as
Proof. In view of $s-1-\log s>0$![]() for all $s>0$
for all $s>0$![]() and $v_t<0$
and $v_t<0$![]() , we can conclude that
, we can conclude that

Here by Young's inequality,

Due to the fact that ${\rm e}^{s}\leq 1+2s$![]() for all $s\in [0,\log 2]$
for all $s\in [0,\log 2]$![]() , (4.11) allows us to fix a $t_1>1$
, (4.11) allows us to fix a $t_1>1$![]() suitably large such that for all $t\geq t_1$
suitably large such that for all $t\geq t_1$![]() ,
,
which together with (4.15) entails that for $t\geq t_1$![]()
Therefore we infer from (3.17) and (4.14) that for all $t\geq t_1$![]()

with some $c_1>0$![]() . After a time integration this leads to
. After a time integration this leads to

and thereby implies that both (4.12) and (4.13) is valid thanks to (4.1) and (4.11).
In order to improve yet quite weak decay information of $u$![]() , we turn to consider the exponential decay properties of $\int _{\Omega }|\nabla v(\cdot,t)|^{2}$
, we turn to consider the exponential decay properties of $\int _{\Omega }|\nabla v(\cdot,t)|^{2}$![]() , rather than the integrability of $a_{t}$
, rather than the integrability of $a_{t}$![]() in $L^{2}((0,\infty ); L^{2}(\Omega ))$
in $L^{2}((0,\infty ); L^{2}(\Omega ))$![]() . As the first step towards this, we first show the convergence of integral $\int ^{\infty }_0\int _{\Omega }|\nabla v|^{2}$
. As the first step towards this, we first show the convergence of integral $\int ^{\infty }_0\int _{\Omega }|\nabla v|^{2}$![]() , which is stated below.
, which is stated below.
Lemma 4.5 Assume that $\beta <1,$![]() then we have
then we have
Proof. Multiplying the second equation in (2.2) by ${\rm e}^{\chi _w v}b$![]() and integrating by parts, one can conclude that
and integrating by parts, one can conclude that

which together with the global-in-time boundedness property of $a$![]() and $b$
and $b$![]() , implies that
, implies that
for some $c_1>0$![]() . Hence according to lemmas 4.3 and 2.3, we can get
. Hence according to lemmas 4.3 and 2.3, we can get
Now since
a direct computation shows that

Therefore, recalling the pointwise lower bound in (4.5), (3.17) and by the Young's inequality, we can find a constant $c_2>0$![]() such that
such that
and thus for any $t>0$![]() ,
,
which along with (4.17) and (4.12) makes sure that (4.16) is actually valid.
Beyond the integrability of $\int _{\Omega }|\nabla v|^{2}$![]() over $(0,\infty )$
over $(0,\infty )$![]() , we make use of the explicit expression of $\nabla v$
, we make use of the explicit expression of $\nabla v$![]() together with (4.17) and (4.12) to identify that $\int _{\Omega }|\nabla v|^{2}$
together with (4.17) and (4.12) to identify that $\int _{\Omega }|\nabla v|^{2}$![]() exponentially decays.
exponentially decays.
Lemma 4.6 Let $\beta <1$![]() . Then one can find constant $C>0$
. Then one can find constant $C>0$![]() such that
such that
where $\gamma$![]() is given by lemma 4.2.
is given by lemma 4.2.
Proof. On the basis of the $v$![]() -equation in (1.3), we have
-equation in (1.3), we have
which along with (4.5) and the Young's inequality entails that

Furthermore observing that
as well as
we conclude from (4.20) that there exists $c_1>0$![]() such that
such that

and thus
On the basis of smoothing estimates for the Neumann heat semigroup on $\Omega$![]() , and decay information provided by lemma 4.6, we can make sure that $u-1$
, and decay information provided by lemma 4.6, we can make sure that $u-1$![]() decays exponentially with respect to $L^{p}(\Omega )$
decays exponentially with respect to $L^{p}(\Omega )$![]() -norm.
-norm.
Lemma 4.7 Assume that $\beta <1,$![]() then there exists $\eta _1>0$
then there exists $\eta _1>0$![]() such that for every $p\geq 2,$
such that for every $p\geq 2,$![]()
with some $C(p)>0$![]() for all $t>0$
for all $t>0$![]() .
.
Proof. Testing the first equation in (1.3) by $u-1$![]() and integrating by parts, we have
and integrating by parts, we have

We thereupon make use of lemmas 4.2, 3.5 along with the Young's inequality to get

with some $c_1>0$![]() .
.
According to lemmas 4.6 and 2.3, (4.23) implies that
with $\eta _1:=\min \{2\mu _u\gamma,2\gamma,\delta \}$![]() and $c_2>0$
and $c_2>0$![]() for all $t>0$
for all $t>0$![]() .
.
Recalling known smoothing estimates for the Neumann heat semigroup on $\Omega \subset \mathbb {R}^{2}$![]() [Reference Winkler31], there exist $c_3=c_3(p,q)>0$
[Reference Winkler31], there exist $c_3=c_3(p,q)>0$![]() , $c_4=c_4(p,q)>0$
, $c_4=c_4(p,q)>0$![]() fulfilling
fulfilling
for each $\varphi \in C^{0}(\Omega )$![]() , and for all $\varphi \in ( L^{q}( \Omega ) )^{2}$
, and for all $\varphi \in ( L^{q}( \Omega ) )^{2}$![]() ,
,
with $\lambda _{1}> 0$![]() the first nonzero eigenvalue of $-\Delta$
the first nonzero eigenvalue of $-\Delta$![]() in $\Omega$
in $\Omega$![]() under the Neumann boundary condition.
under the Neumann boundary condition.
Relying on a variation-of-constants representation of $u$![]() related to the first equation in (1.3), we utilize (4.25) and (4.26) to infer that
related to the first equation in (1.3), we utilize (4.25) and (4.26) to infer that

for some $c_5(p)>0$![]() . Therefore by (4.24), (4.19), (2.8) and thanks to the fact that for $\alpha \in (0,1)$
. Therefore by (4.24), (4.19), (2.8) and thanks to the fact that for $\alpha \in (0,1)$![]() $\gamma _1$
$\gamma _1$![]() and $\delta _1$
and $\delta _1$![]() positive constants with $\gamma _1 \neq \delta _1$
positive constants with $\gamma _1 \neq \delta _1$![]() , there exists $c_6> 0$
, there exists $c_6> 0$![]() such that
such that
(4.22) readily results from (4.27) with $\eta _1=\frac 12 \min \{ \gamma, \mu _u \gamma, \frac {1-\beta }2, \frac {\delta _z}2\}$![]() and some $C(p)>0$
and some $C(p)>0$![]() .
.
At this position, due to the fact that the integrability exponent in (4.19) does not exceed the considered spatial dimension $n=2$![]() , the uniform decay of $w$
, the uniform decay of $w$![]() is not achieved herein, however a somewhat optimal decay rate thereof with respect to $L^{p}(\Omega )$
is not achieved herein, however a somewhat optimal decay rate thereof with respect to $L^{p}(\Omega )$![]() may be derived by the argument similar to that in lemma 4.7 instead of the simple interpolation. The desired result can be stated below and the corresponding proof is omitted herein.
may be derived by the argument similar to that in lemma 4.7 instead of the simple interpolation. The desired result can be stated below and the corresponding proof is omitted herein.
Lemma 4.8 Let $\beta <1$![]() . Then there exists $\varrho _1>0$
. Then there exists $\varrho _1>0$![]() such that for every $p\geq 2,$
such that for every $p\geq 2,$![]()
with some $C(p)>0$![]() for all $t>0$
for all $t>0$![]() .
.
Next we proceed to establish the convergence properties in (1.6)–(1.7) stated in theorem 1.1, which are beyond that in lemmas 4.7 and 4.8. To this end, thanks to lemmas 4.7, 4.8, 4.1, 4.2 and 4.3, we turn to make sure that $\int _{\Omega }|\nabla v|^{4}$![]() decays exponentially, which results from a series of testing procedures.
decays exponentially, which results from a series of testing procedures.
Lemma 4.9 Let conditions in theorem 1.1 hold. Then there exist $\eta _2>0$![]() and $C>0$
and $C>0$![]() such that
such that
Proof. Testing the identity
with $f(x,t)=\mu _u a(1-u)-\displaystyle \rho a z+\chi _u a(\alpha _u u + \alpha _w w)v$![]() by $-\triangle a$
by $-\triangle a$![]() , and using Young's inequality, we get
, and using Young's inequality, we get

Note that by the Gagliardo–Nirenberg type interpolation with standard elliptic regularity theory and Poincaré's inequality, one can find constants $c_1> 0$![]() and $c_2> 0$
and $c_2> 0$![]() such that for all $\varphi \in W^{2,2}(\Omega )$
such that for all $\varphi \in W^{2,2}(\Omega )$![]() with ${\partial \varphi }/{\partial \nu }=0$
with ${\partial \varphi }/{\partial \nu }=0$![]() on $\partial \Omega$
on $\partial \Omega$![]() ,
,
and
(see lemmas A.1 and A.3 in [Reference Fuest7]). Hence thanks to lemma 3.5, we can pick $c_3>0$![]() such that
such that
for all $x \in \Omega$![]() and $t > 0$
and $t > 0$![]() , and thereby have
, and thereby have
as well as
Combining (4.31) with (4.30), the Young's inequality shows that

which readily implies that

Likely, we can get

with $g(x,t)=- b+\displaystyle \rho u{\rm e}^{-\chi _w v}z + \chi _w b(\alpha _u u+ \alpha _w w)v$![]() .
.
Now in order to appropriately compensate the first summand on right-hand side of (4.34) and (4.35), we use the third equation in (2.2) to see that

Here, recalling the uniform positivity of $a$![]() stated in lemma 4.2, we can pick $c_4>0$
stated in lemma 4.2, we can pick $c_4>0$![]() fulfilling
fulfilling
and thus infer by the Young's inequality and lemma 2.2 that for all $t>t_0$![]()

with constants $c_5>0$![]() , $c_6>0$
, $c_6>0$![]() .
.
Now if we write $d_1:=({8c_1c_3^{2}( D_u\chi _u^{4}+ D_w\chi _w^{4})})/{c_5}$![]() , combining (4.37), (4.34) with (4.35) yields
, combining (4.37), (4.34) with (4.35) yields

which together with (4.31), (4.32) and lemma 4.3 entails that there exists $t_1>1$![]() suitably large such that for all $t>t_1$
suitably large such that for all $t>t_1$![]() ,
,

Due to lemma 3.5, we see that
with some $c_7>0$![]() , and thus there exist $\eta _3>0$
, and thus there exist $\eta _3>0$![]() and $c_8>0$
and $c_8>0$![]() such that
such that
thanks to lemmas 4.7, 4.8, 4.1 and 4.3. Therefore (4.29) readily results from (4.40) and (4.39).
At this position, as an application of known smoothing estimates for the Neumann heat semigroup, the latter readily turns to the exponential decay property of $u-1$![]() as well as $w$
as well as $w$![]() with respect to $L^{\infty }(\Omega )$
with respect to $L^{\infty }(\Omega )$![]() -norm.
-norm.
Lemma 4.10 Let the conditions in theorem 1.1 hold. Then there exist $\eta,\varrho >0$![]() and $C>0$
and $C>0$![]() fulfilling
fulfilling
as well as
for all $t>0$![]() .
.
Proof. Since the proof is similar to that of lemma 4.7, we only give a short proof of (4.41). In view to known smoothing estimates for the Neumann heat semigroup on $\Omega \subset \mathbb {R}^{2}$![]() [Reference Winkler31], there exist $c_1>0$
[Reference Winkler31], there exist $c_1>0$![]() , $c_2>0$
, $c_2>0$![]() fulfilling
fulfilling
for each $\varphi \in C^{0}(\Omega )$![]() , and for all $\varphi \in ( L^{4}( \Omega ) )^{2}$
, and for all $\varphi \in ( L^{4}( \Omega ) )^{2}$![]() ,
,
with $\lambda _{1}> 0$![]() the first nonzero eigenvalue of $-\Delta$
the first nonzero eigenvalue of $-\Delta$![]() in $\Omega$
in $\Omega$![]() under the Neumann boundary condition.
under the Neumann boundary condition.
According to the variation-of-constants representation of $u$![]() related to the first equation in (1.3), we utilize (4.43) and (4.44) to infer that
related to the first equation in (1.3), we utilize (4.43) and (4.44) to infer that

with some $c_3>0$![]() . This readily establishes (4.41) with appropriate $\eta >0$
. This readily establishes (4.41) with appropriate $\eta >0$![]() in view of (4.29), (4.22) and (4.1).
in view of (4.29), (4.22) and (4.1).
Thereby our main result has essentially been proved already.
Acknowledgments
The authors would like to express their gratitude to the anonymous referee for the careful reading with useful comments to improve the manuscript. This work is supported by the NNSF of China (No. 12071030) and Beijing key laboratory on MCAACI.