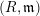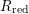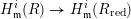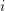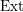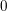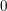1 Introduction
The notion of Du Bois singularities was introduced by Steenbrink based on work of Du Bois [Reference Du BoisDBoi81], which itself was an attempt to localize Deligne’s Hodge theory of singular varieties [Reference DeligneDel74]. Steenbrink studied them initially because families with Du Bois fibers have remarkable base-change properties [Reference SteenbrinkSte81]. On the other hand, Du Bois singularities have recently found new connections across several areas of mathematics [Reference Kollár and KovácsKK10, Reference Kovács and SchwedeKS16a, Reference LeeLee09, Reference Cortiñas, Haesemeyer, Walker and WeibelCHWW11, Reference Huber and JörderHJ14]. In this paper we find numerous applications of Du Bois singularities especially to questions of local cohomology. Our key observation is as follows.
Key Lemma (Lemma 3.3). Suppose that
$(S,\mathfrak{m})$
is a local ring essentially of finite type over
$\mathbb{C}$
and that
$S_{\text{red}}=S/\sqrt{0}$
has Du Bois singularities. Then
$$\begin{eqnarray}H_{\mathfrak{m}}^{i}(S)\rightarrow H_{\mathfrak{ m}}^{i}(S_{\text{red}})\end{eqnarray}$$
is surjective for every
$i$
.
In fact, we obtain this surjectivity for Du Bois pairs, but we leave the statement simple in the introduction. Utilizing this lemma and related methods, we prove several results.
Theorem A (Corollary 3.9).
Let
$X$
be a reduced scheme and let
$H\subseteq X$
be a Cartier divisor. If
$H$
is Du Bois and
$X\backslash H$
is Cohen–Macaulay, then
$X$
is Cohen–Macaulay and hence so is
$H$
.
This first consequence answers a question of Kovács and the second author and should be viewed as a generalization of several results in [Reference Kollár and KovácsKK10, §7]. In particular, we do not need a projective family. This result holds if one replaces Cohen–Macaulay with
$\text{S}_{k}$
and also generalizes to the context of Du Bois pairs as in [Reference Kovács and SchwedeKS16b]. Theorem A should also be viewed as a characteristic-0 analog of [Reference Fedder and WatanabeFW89, Proposition 2.13] and [Reference Horiuchi, Miller and ShimomotoHMS14, Corollary A.4]. Theorem A also implies that if
$X\setminus H$
has rational singularities and
$H$
has Du Bois singularities, then
$X$
has rational singularities (see Corollary 3.10), generalizing [Reference Kovács and SchwedeKS16b, Theorem E].
Our next consequence of the key lemma is the following.
Theorem B (Proposition 4.1).
Let
$(R,\mathfrak{m})$
be a Gorenstein local ring essentially of finite type over
$\mathbb{C}$
, and let
$I\subseteq R$
be an ideal such that
$R/I$
has Du Bois singularities. Then the natural map
$\operatorname{Ext}_{R}^{j}(R/I,R)\rightarrow H_{I}^{j}(R)$
is injective for every
$j$
.
This gives a partial characteristic-
$0$
answer to [Reference Eisenbud, Mustaţă and StillmanEMS00, Question 6.2], asking when such maps are injective. A special case of the analogous characteristic
$p>0$
result was obtained by Singh–Walther [Reference Singh and WaltherSW07]. This result leads to an answer of [Reference De Stefani and Núñez-BetancourtDN16, Question 7.5] on the bounds on the projective dimension of Du Bois and log canonical singularities. In the graded setting, we can prove a much stronger result on the injectivity of Ext.
Theorem C (Theorem 4.5).
Let
$(R,\mathfrak{m})$
be a reduced Noetherian
$\mathbb{N}$
-graded
$(R_{0}=\mathbb{C})$
-algebra with
$\mathfrak{m}$
the unique homogeneous maximal ideal. Suppose that
$R_{P}$
is Du Bois for all
$P\neq \mathfrak{m}$
. Write
$R=A/I$
, where
$A=\mathbb{C}[x_{1},\ldots ,x_{n}]$
is a polynomial ring with
$\deg x_{i}=d_{i}>0$
and
$I$
is a homogeneous ideal. Then the natural degree-preserving map
$\operatorname{Ext}_{A}^{j}(R,A)\rightarrow H_{I}^{j}(A)$
induces an injection
$$\begin{eqnarray}[\operatorname{Ext}_{A}^{j}(R,A)]_{{\geqslant}-d}{\hookrightarrow}[H_{I}^{j}(A)]_{{\geqslant}-d}\end{eqnarray}$$
for every
$j$
, where
$d=\sum d_{i}$
.
Theorem C leads to new vanishing for local cohomology for
$\mathbb{N}$
-graded isolated non-Du Bois singularities (Theorem 4.8), a generalization of the Kodaira vanishing theorem for Cohen–Macaulay Du Bois projective varieties.
Our next consequence of the key lemma answers a longstanding question, but first we give some background. Du Bois singularities are closely related to the notion of
$F$
-injective singularities (rings where the Frobenius acts injectively on local cohomology of maximal ideals). In particular, it is conjectured that
$X$
has Du Bois singularities if and only if its reduction to characteristic
$p>0$
has
$F$
-injective singularities for a Zariski dense set of primes
$p\gg 0$
(this is called dense
$F$
-injective type). This conjecture is expected to be quite difficult, as it is closely related to asking for infinitely many ordinary characteristic
$p>0$
reductions for smooth projective varieties over
$\mathbb{C}$
[Reference Bhatt, Schwede and TakagiBST13]. On the other hand, several recent papers have studied how Du Bois and
$F$
-injective singularities deform [Reference Kovács and SchwedeKS16a, Reference Horiuchi, Miller and ShimomotoHMS14]. We know that if a Cartier divisor
$H\subseteq X$
has Du Bois singularities, then
$X$
also has Du Bois singularities near
$H$
. However, the analogous statement for
$F$
-injective singularities in characteristic
$p>0$
is open and has been since [Reference FedderFed83]. In fact,
$F$
-injective singularities were introduced because it was observed that Cohen–Macaulay
$F$
-injective singularities deform in this way but
$F$
-pure singularitiesFootnote
1
do not. We show that at least the property of having dense
$F$
-injective type satisfies such a deformation result, in other words that
$F$
-injectivity deforms when
$p$
is large.
Theorem D (Theorem 5.3).
Let
$(R,\mathfrak{m})$
be a local ring essentially of finite type over
$\mathbb{C}$
and let
$x$
be a non-zero divisor on
$R$
. Suppose that
$R/xR$
has dense
$F$
-injective type. Then, for infinitely many
$p>0$
, the Frobenius action
$x^{p-1}F$
on
$H_{\mathfrak{m}_{p}}^{i}(R_{p})$
is injective for every
$i$
, where
$(R_{p},\mathfrak{m}_{p})$
is the reduction mod
$p$
of
$R$
. In particular,
$R$
has dense
$F$
-injective type.
Our final result is a characteristic-
$0$
analog of a strengthening of the main result of [Reference Hochster and RobertsHR76], and we can give a characteristic
$p>0$
generalization as well.
Theorem E (Corollary 4.13).
Let
$R$
be a Noetherian
$\mathbb{N}$
-graded
$k$
-algebra, with
$\mathfrak{m}$
the unique homogeneous maximal ideal. Suppose that
$R$
is equidimensional and Cohen–Macaulay on
$\operatorname{Spec}R-\{\mathfrak{m}\}$
. Assume one of the following:
-
(a)
$k$
has characteristic
$p>0$
and
$R$
is
$F$
-injective; -
(b)
$k$
has characteristic
$0$
and
$R$
is Du Bois.
Then
$[H^{r}(\text{}\underline{x},R)]_{0}\cong H_{\mathfrak{m}}^{r}(R)$
for every
$r<n=\dim R$
and every homogeneous system of parameters
$\text{}\underline{x}=x_{1},\ldots ,x_{n}$
, where
$H^{r}(\text{}\underline{x},R)$
denotes the
$r$
th Koszul cohomology of
$\text{}\underline{x}$
. In other words, it is not necessary to take a direct limit when computing the local cohomology.
In fact, we prove a more general result (Theorem 4.12), which does not require any
$F$
-injective or Du Bois conditions, from which Theorem E follows immediately thanks to our injectivity and vanishing results (Theorems 4.5 and 4.8).
2 Preliminaries
Throughout this paper, all rings will be Noetherian and all schemes will be Noetherian and separated. When in equal characteristic 0, we will work with rings and schemes that are essentially of finite type over
$\mathbb{C}$
. Of course, nearly all of our results also hold over all other fields of characteristic
$0$
by base change.
2.1 Du Bois singularities
We give a brief introduction to Du Bois singularities and pairs. For more details, see for instance [Reference Kovács, Schwede, Friedman, Hunsicker, Libgober and MaximKS11] and [Reference KollárKol13]. Frequently we will work in the setting of pairs in the Du Bois sense.
Definition 2.1. Suppose that
$X$
and
$Z$
are schemes of essentially finite type over
$\mathbb{C}$
. By a pair we will mean the combined data of
$(X,Z)$
. We will call the pair reduced if both
$X$
and
$Z$
are reduced.
Suppose that
$X$
is a scheme essentially of finite type over
$\mathbb{C}$
. Associated to
$X$
is an object
$\text{}\underline{\unicode[STIX]{x1D6FA}}_{X}^{0}\in D_{\text{coh}}^{b}(X)$
with a map
${\mathcal{O}}_{X}\rightarrow \text{}\underline{\unicode[STIX]{x1D6FA}}_{X}^{0}$
functorial in the following way. If
$f:Y\rightarrow X$
is a map of schemes, then we have a commutative square
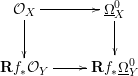
If
$X$
is non-reduced, then
$\text{}\underline{\unicode[STIX]{x1D6FA}}_{X}^{0}=\text{}\underline{\unicode[STIX]{x1D6FA}}_{X_{\text{red}}}^{0}$
by definition. To define
$\text{}\underline{\unicode[STIX]{x1D6FA}}_{X}^{0}$
in general, let
$\unicode[STIX]{x1D70B}:X_{\boldsymbol{\cdot }}\rightarrow X$
be a hyper-resolution and set
$\text{}\underline{\unicode[STIX]{x1D6FA}}_{X}^{0}=\mathbf{R}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{X_{\boldsymbol{\cdot }}}$
(alternatively, see [Reference SchwedeSch07]).
If
$Z\subseteq X$
is a closed subscheme, then we define
$\text{}\underline{\unicode[STIX]{x1D6FA}}_{X,Z}^{0}$
as the object completing the following distinguished triangle:
$$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D6FA}}_{X,Z}^{0}\rightarrow \text{}\underline{\unicode[STIX]{x1D6FA}}_{X}^{0}\rightarrow \text{}\underline{\unicode[STIX]{x1D6FA}}_{Z}^{0}\xrightarrow[{}]{+1}.\end{eqnarray}$$
We observe that there is an induced map
$\mathscr{I}_{Z\subseteq X}\rightarrow \text{}\underline{\unicode[STIX]{x1D6FA}}_{X,Z}^{0}$
. We also note that by this definition and the fact that
$\text{}\underline{\unicode[STIX]{x1D6FA}}_{X}^{0}=\text{}\underline{\unicode[STIX]{x1D6FA}}_{X_{\text{red}}}^{0}$
, we have
$\text{}\underline{\unicode[STIX]{x1D6FA}}_{X,Z}^{0}=\text{}\underline{\unicode[STIX]{x1D6FA}}_{X_{\text{red}},Z_{\text{red}}}^{0}$
.
Definition 2.2 (Du Bois singularities).
We say that
$X$
has Du Bois singularities if the map
${\mathcal{O}}_{X}\rightarrow \text{}\underline{\unicode[STIX]{x1D6FA}}_{X}^{0}$
is a quasi-isomorphism. If
$Z\subseteq X$
is a closed subscheme, we say that
$(X,Z)$
has Du Bois singularities if the map
$\mathscr{I}_{Z\subseteq X}\rightarrow \text{}\underline{\unicode[STIX]{x1D6FA}}_{X,Z}^{0}$
is a quasi-isomorphism.
Remark 2.3. It is clear that Du Bois singularities are reduced. In general, a pair
$(X,Z)$
being Du Bois does not necessarily imply that
$X$
or
$Z$
is reduced. However, if a pair
$(X,Z)$
is Du Bois and
$X$
is reduced, then so is
$Z$
[Reference Kovács and SchwedeKS16b, Lemma 2.9].
2.2 Cyclic covers of non-reduced schemes
In this paper we will need to take cyclic covers of non-reduced schemes. We will work in the following setting. We assume what follows is well known to experts but we do not know a reference in the generality we need (see [Reference Kollár and MoriKM98, §2.4] or [Reference de Fernex, Ein and MustaţădFEM, §2.1.1]). Note also that the reason we are able to work with non-reduced schemes is because our
$\mathscr{L}$
is actually locally free and not just a reflexive rank-1 sheaf.
Setting 2.4. Suppose that
$X$
is a scheme of finite type over
$\mathbb{C}$
(typically projective). Suppose also that
$\mathscr{L}$
is a line bundle (typically semi-ample). Choose a (typically general) global section
$s\in H^{0}(X,\mathscr{L}^{n})$
for some
$n>0$
(typically
$n\gg 0$
) and form the sheaf of rings
$$\begin{eqnarray}\mathscr{R}(X,\mathscr{L},s)={\mathcal{O}}_{X}\oplus \mathscr{L}^{-1}\oplus \cdots \oplus \mathscr{L}^{-n+1},\end{eqnarray}$$
where, for
$i,j<n$
and
$i+j>n$
, the multiplication
$\mathscr{L}^{-i}\otimes \mathscr{L}^{-j}\rightarrow \mathscr{L}^{-i-j+n}$
is performed by the formula
$a\otimes b\mapsto abs$
. We define
$\unicode[STIX]{x1D708}:Y=Y_{\mathscr{L},s}=\mathbf{Spec}\,\mathscr{R}(X,\mathscr{L},s)\rightarrow X$
. Note we did not assume that
$s$
was non-zero or even locally a non-zero divisor.
Now let us work locally on an affine chart
$U$
trivializing
$\mathscr{L}$
, where
$U=\operatorname{Spec}R\subseteq X$
with corresponding
$\unicode[STIX]{x1D708}^{-1}(U)=\operatorname{Spec}S$
. Fix an isomorphism
$\mathscr{L}|_{U}\cong {\mathcal{O}}_{U}$
and write
$$\begin{eqnarray}S=R\oplus Rt\oplus Rt^{2}\oplus \cdots \oplus Rt^{n-1},\end{eqnarray}$$
where
$t$
is a dummy variable used to help keep track of the degree. The choice of the section
$s|_{U}\in H^{0}(X,\mathscr{L}^{n})$
is the same as the choice of map
${\mathcal{O}}_{X}\rightarrow \mathscr{L}^{n}$
(send
$1$
to the section
$s$
). If
$s$
is chosen to be general and
$\mathscr{L}^{n}$
is very ample, then this map is an inclusion, but it is not injective in general. Working locally where we have fixed
$\mathscr{L}|_{U}={\mathcal{O}}_{U}$
, we also have implicitly chosen
$\mathscr{L}^{n}={\mathcal{O}}_{U}$
and hence we have just specified that
$t^{n}=s|_{U}\in \unicode[STIX]{x1D6E4}(U,\mathscr{L}^{n})=\unicode[STIX]{x1D6E4}(U,{\mathcal{O}}_{U})$
. In other words,
$$\begin{eqnarray}S=R[t]/\langle t^{n}-s\rangle .\end{eqnarray}$$
In particular, it follows that
$\unicode[STIX]{x1D708}$
is a finite map.
Lemma 2.5. The map
$\unicode[STIX]{x1D708}$
is functorial with respect to taking closed subschemes of
$X$
. In particular, if
$Z\subseteq X$
is a closed subscheme and
$\mathscr{L}$
and
$s$
are as above, then we have the following commutative diagram.
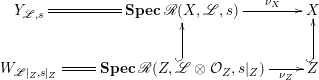
Furthermore,
$W_{\mathscr{L}|_{Z},s|_{Z}}=\unicode[STIX]{x1D70B}^{-1}(Z)$
is the scheme-theoretic preimage of
$Z$
.
Proof. The first statement follows since
$\mathscr{R}(X,\mathscr{L},s)={\mathcal{O}}_{X}\oplus \mathscr{L}^{-1}\oplus \cdots \oplus \mathscr{L}^{-n+1}$
surjects onto
$\mathscr{R}(Z,\mathscr{L}|_{Z},s|_{Z})={\mathcal{O}}_{Z}\oplus \mathscr{L}|_{Z}^{-1}\oplus \cdots \oplus \mathscr{L}|_{Z}^{-n+1}$
in the obvious way. For the second statement, we simply notice that
$$\begin{eqnarray}\mathscr{R}(X,\mathscr{L},s)\otimes _{{\mathcal{O}}_{X}}{\mathcal{O}}_{Z}=\mathscr{R}(Z,\mathscr{L}|_{Z},s|_{Z}).\Box\end{eqnarray}$$
Lemma 2.6. Suppose that we are working in Setting 2.4 and that
$X$
is projective and also reduced (respectively normal),
$\mathscr{L}^{n}$
is globally generated and
$s$
is chosen to be general. Then
$Y=Y_{\mathscr{L},s}$
is also reduced (respectively normal).
Proof. To show that
$Y$
is reduced, we will show that it is
$\text{S}_{1}$
and
$\text{R}_{0}$
. We work locally on an open affine chart
$U=\operatorname{Spec}R\subseteq X$
.
To show that it is
$\text{R}_{0}$
, it suffices to consider the case where
$R=K$
is a field. Because
$s$
was picked generally, we may assume that the image of
$s$
in
$K$
is non-zero (we identify
$s$
with its image). Then we need to show that
$K[t]/\langle t^{n}-s\rangle$
is a product of fields. But this is obvious since we are working in characteristic
$0$
.
Next, we show that it is
$\text{S}_{1}$
. Indeed, if
$(R,\mathfrak{m})$
is a local ring of depth
${\geqslant}1$
, then obviously
$S=R[t]/\langle t^{n}-s\rangle$
has depth
${\geqslant}1$
as well since it is a free
$R$
-module. Finally, the depth condition is preserved after localizing at the maximal ideals of the semilocal ring of
$S$
.
This proves the reduced case. The normal case is well known but we sketch it. The
$\text{R}_{1}$
condition follows from [Reference Kollár and MoriKM98, Lemma 2.51] and the fact that
$s$
is chosen generally, utilizing Bertini’s theorem. The
$\text{S}_{2}$
condition follows in the same way that
$\text{S}_{1}$
followed above.◻
2.3
$F$
-pure and
$F$
-injective singularities
Du Bois singularities are conjectured to be the characteristic-
$0$
analog of
$F$
-injective singularities [Reference SchwedeSch09, Reference Bhatt, Schwede and TakagiBST13]. In this short subsection we collect some definitions about singularities in positive characteristic. Our main focuses are
$F$
-pure and
$F$
-injective singularities.
A local ring
$(R,\mathfrak{m})$
is called
$F$
-pure if the Frobenius endomorphism
$F$
:
$R\rightarrow R$
is pure.Footnote
2
Under mild conditions, for example when
$R$
is
$F$
-finite, which means that the Frobenius map
$R\xrightarrow[{}]{F}R$
is a finite map,
$R$
being
$F$
-pure is equivalent to the condition that the Frobenius endomorphism
$R\xrightarrow[{}]{F}R$
is split [Reference Hochster and RobertsHR76, Corollary 5.3]. The Frobenius endomorphism on
$R$
induces a natural Frobenius action on each local cohomology module
$H_{\mathfrak{m}}^{i}(R)$
and we say that a local ring is
$F$
-injective if this natural Frobenius action on
$H_{\mathfrak{m}}^{i}(R)$
is injective for every
$i$
[Reference FedderFed83]. This holds if
$R$
is
$F$
-pure [Reference Hochster and RobertsHR76, Lemma 2.2]. For some other basic properties of
$F$
-pure and
$F$
-injective singularities, see [Reference Hochster and RobertsHR76, Reference FedderFed83, Reference Enescu and HochsterEH08].
3 The Cohen–Macaulay property for families of Du Bois pairs
We begin with a lemma, which we assume is well known to experts; indeed, it is explicitly stated in [Reference KollárKol13, Corollary 6.9]. However, because many of the standard references also include implicit reducedness hypotheses, we include a careful proof that deduces it from the reduced case. Of course, one could also go back to first principles but we believe the path we take below is quicker.
Lemma 3.1. Let
$X$
be a projective scheme over
$\mathbb{C}$
and let
$Z\subseteq X$
be a closed subscheme (
$X,Z$
are not necessarily reduced). Then the natural map
$$\begin{eqnarray}H^{i}(X,\mathscr{I}_{Z})\rightarrow \mathbb{H}^{i}(X_{\text{red}},\text{}\underline{\unicode[STIX]{x1D6FA}}_{X_{\text{red}},Z_{\text{red}}}^{0})\cong \mathbb{H}^{i}(X,\text{}\underline{\unicode[STIX]{x1D6FA}}_{X,Z}^{0})\end{eqnarray}$$
is surjective for every
$i\in \mathbb{Z}$
.
Proof. Note that if the result holds for
$\mathbb{C}$
, it certainly also holds for other fields of characteristic
$0$
. The isomorphism in the statement of the lemma follows from the definition. For the surjectivity, we consider the following commutative diagram, where we let
$U=X\backslash Z$
. Note that the rows are not exact.
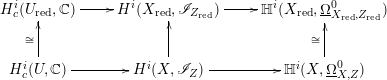
The composite map in the top horizontal line is a surjection by [Reference Kovács and SchwedeKS16b, Lemma 2.17] or [Reference KovácsKov11, Corollary 4.2]. The vertical isomorphism on the left holds because the constant sheaf
$\mathbb{C}$
does not see the non-reduced structure. Likewise for the vertical isomorphism on the right, where
$\text{}\underline{\unicode[STIX]{x1D6FA}}_{X,Z}^{0}$
does not see the non-reduced structure. The diagram then shows that
$H^{i}(X,\mathscr{I}_{Z})\rightarrow \mathbb{H}^{i}(X_{\text{red}},\text{}\underline{\unicode[STIX]{x1D6FA}}_{X_{\text{red}},Z_{\text{red}}}^{0})$
is a surjection.◻
Next, we prove the key injectivity lemma for possibly non-reduced pairs. The proof is essentially the same as in [Reference Kovács and SchwedeKS16b] or [Reference Kovács and SchwedeKS16a]. We reproduce it here carefully because we need it in the non-reduced setting.
Lemma 3.2. Let
$X$
be a scheme of essentially finite type over
$\mathbb{C}$
and
$Z\subseteq X$
a closed subscheme (
$X$
and
$Z$
are not necessarily reduced). Then the natural map
$$\begin{eqnarray}h^{j}(\text{}\underline{\unicode[STIX]{x1D714}}_{X,Z}^{\boldsymbol{\cdot }}){\hookrightarrow}h^{j}(\mathbf{R}\,\mathscr{H}\!\!\operatorname{om}_{{\mathcal{O}}_{X}}(\mathscr{I}_{Z},\unicode[STIX]{x1D714}_{X}^{\boldsymbol{\cdot }}))\end{eqnarray}$$
is injective for every
$j\in \mathbb{Z}$
, where
$\text{}\underline{\unicode[STIX]{x1D714}}_{X,Z}^{\boldsymbol{\cdot }}=\mathbf{R}\,\mathscr{H}\!\!\operatorname{om}_{{\mathcal{O}}_{X}}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{X,Z}^{0},\unicode[STIX]{x1D714}_{X}^{\boldsymbol{\cdot }})$
.
Proof. The question is local and compatible with restricting to an open subset; hence, we may assume that
$X$
is projective with ample line bundle
$\mathscr{L}$
. Let
$s\in H^{0}(X,\mathscr{L}^{n})$
be a general global section for some
$n\gg 0$
and let
$\unicode[STIX]{x1D702}$
:
$Y=\mathbf{Spec}\,\bigoplus _{i=0}^{n-1}\mathscr{L}^{-i}\rightarrow X$
be the
$n$
th cyclic cover corresponding to
$s$
. Set
$W=\unicode[STIX]{x1D702}^{-1}(Z)$
. Then, for
$n\gg 0$
and
$s$
general, the restriction of
$\unicode[STIX]{x1D702}$
to
$W$
is the cyclic cover
$W=\mathbf{Spec}\,\bigoplus _{i=0}^{n-1}\mathscr{L}|_{Z}^{-i}\rightarrow Z$
by Lemma 2.5. Likewise,
$\unicode[STIX]{x1D702}$
also induces the corresponding cyclic covers of the closed subschemes
$Y_{\text{red}}\rightarrow X_{\text{red}}$
and
$W_{\text{red}}\rightarrow Z_{\text{red}}$
by Lemmas 2.5 and 2.6. We have
$\unicode[STIX]{x1D702}_{\ast }\mathscr{I}_{W}=\bigoplus _{i=0}^{n-1}\mathscr{I}_{Z}\otimes \mathscr{L}^{-i}$
and
$$\begin{eqnarray}\unicode[STIX]{x1D702}_{\ast }\text{}\underline{\unicode[STIX]{x1D6FA}}_{Y,W}^{0}\cong \unicode[STIX]{x1D702}_{\ast }\text{}\underline{\unicode[STIX]{x1D6FA}}_{Y_{\text{red}},W_{\text{red}}}^{0}\cong \bigoplus _{i=0}^{n-1}\text{}\underline{\unicode[STIX]{x1D6FA}}_{X_{\text{red}},Z_{\text{red}}}^{0}\otimes \mathscr{L}^{-i}\cong \bigoplus _{i=0}^{n-1}\text{}\underline{\unicode[STIX]{x1D6FA}}_{X,Z}^{0}\otimes \mathscr{L}^{-i},\end{eqnarray}$$
where the second isomorphism is [Reference Kovács and SchwedeKS16b, Lemma 3.1] (see also [Reference Kovács and SchwedeKS16a, Lemma 3.1]). Since Lemma 3.1 implies that
$H^{j}(Y,\mathscr{I}_{W}){\twoheadrightarrow}\mathbb{H}^{j}(Y,\text{}\underline{\unicode[STIX]{x1D6FA}}_{Y,W}^{0})$
is surjective for every
$j\in \mathbb{Z}$
, we know that
$H^{j}(X,\mathscr{I}_{Z}\otimes \mathscr{L}^{-i}){\twoheadrightarrow}\mathbb{H}^{j}(X,\text{}\underline{\unicode[STIX]{x1D6FA}}_{X,Z}^{0}\otimes \mathscr{L}^{-i})$
is surjective for every
$i\geqslant 0$
and
$j\in \mathbb{Z}$
.
Applying Grothendieck–Serre duality, we obtain an injection
$$\begin{eqnarray}\mathbb{H}^{j}(X,\text{}\underline{\unicode[STIX]{x1D714}}_{X,Z}^{\boldsymbol{\cdot }}\otimes \mathscr{L}^{i}){\hookrightarrow}\mathbb{H}^{j}(X,\mathbf{R}\,\mathscr{H}\!\!\operatorname{om}_{{\mathcal{O}}_{X}}(\mathscr{I}_{Z},\unicode[STIX]{x1D714}_{X}^{\boldsymbol{\cdot }})\otimes \mathscr{L}^{i})\end{eqnarray}$$
for all
$i\geqslant 0$
and
$j\in \mathbb{Z}$
. Since
$\mathscr{L}$
is ample, for
$i\gg 0$
the spectral sequence computing the above hypercohomology degenerates. Hence, for
$i\gg 0$
, we get
$$\begin{eqnarray}H^{0}(X,h^{j}(\text{}\underline{\unicode[STIX]{x1D714}}_{X,Z}^{\boldsymbol{\cdot }})\otimes \mathscr{L}^{i}){\hookrightarrow}H^{0}(X,h^{j}(\mathbf{R}\,\mathscr{H}\!\!\operatorname{om}_{{\mathcal{O}}_{X}}(\mathscr{I}_{Z},\unicode[STIX]{x1D714}_{X}^{\boldsymbol{\cdot }}))\otimes \mathscr{L}^{i}).\end{eqnarray}$$
But again since
$\mathscr{L}$
is ample, the above injection for
$i\gg 0$
implies the injection
$h^{j}(\text{}\underline{\unicode[STIX]{x1D714}}_{X,Z}){\hookrightarrow}h^{j}(\mathbf{R}\,\mathscr{H}\!\!\operatorname{om}_{{\mathcal{O}}_{X}}(\mathscr{I}_{Z},\unicode[STIX]{x1D714}_{X}^{\boldsymbol{\cdot }}))$
.◻
Next, we prove the key lemma stated in the introduction (and we do the generalized pair version). It follows immediately from the above injectivity, Lemma 3.2. For simplicity, we will use
$(S,S/J)$
to denote the pair
$(\operatorname{Spec}S,\operatorname{Spec}S/J)$
.
Lemma 3.3. Let
$(S,\mathfrak{m})$
be a local ring essentially of finite type over
$\mathbb{C}$
and let
$J\subseteq S$
be an ideal. Suppose further that
$S^{\prime }=S/N$
, where
$N\subseteq S$
is an ideal contained in the nilradical (for instance,
$N$
could be the nilradical and then
$S^{\prime }=S_{\text{red}}$
). Suppose that
$(S^{\prime },S^{\prime }/JS^{\prime })$
is a Du Bois pair. Then the natural map
$H_{\mathfrak{m}}^{i}(J)\rightarrow H_{\mathfrak{m}}^{i}(JS^{\prime })$
is surjective for every
$i$
. In particular, if
$S_{\text{red}}$
is Du Bois, then
$H_{\mathfrak{m}}^{i}(S)\rightarrow H_{\mathfrak{m}}^{i}(S_{\text{red}})$
is surjective for every
$i$
.
Proof. We consider the following commutative diagram.
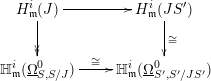
Here the left vertical map is surjective by the Matlis dual of Lemma 3.2 applied to
$X=\operatorname{Spec}S$
and
$Z=\operatorname{Spec}S/J$
, the right vertical map is an isomorphism because
$(S^{\prime },S^{\prime }/JS^{\prime })$
is a Du Bois pair and the bottom map is an isomorphism because
$S_{\text{red}}=S_{\text{red}}^{\prime }$
. Chasing the diagram shows that
$H_{\mathfrak{m}}^{i}(J)\rightarrow H_{\mathfrak{m}}^{i}(JS^{\prime })$
is surjective. The last sentence is the case that
$J$
is the unit ideal (i.e., the non-pair version).◻
Remark 3.4. The characteristic
$p>0$
analog of the above lemma (in the case
$J=S$
, i.e., the non-pair version) holds if
$S_{\text{red}}$
is
$F$
-pure. We give a short argument here. Without loss of generality, we may assume that
$S$
and
$S_{\text{red}}$
are complete, so
$S=A/I$
and
$S_{\text{red}}=A/\sqrt{I}$
, where
$A$
is a complete regular local ring. We may pick
$e\gg 0$
such that
$(\sqrt{I})^{[p^{e}]}\subseteq I$
. We have a composite map
$$\begin{eqnarray}H_{\mathfrak{m}}^{i}(A/(\sqrt{I})^{[p^{e}]})\rightarrow H_{\mathfrak{m}}^{i}(A/I)\cong H_{\mathfrak{ m}}^{i}(S)\xrightarrow[{}]{\unicode[STIX]{x1D719}}H_{\mathfrak{ m}}^{i}(A/\sqrt{I})\cong H_{\mathfrak{ m}}^{i}(S_{\text{red}}).\end{eqnarray}$$
We know from [Reference LyubeznikLyu06, Lemma 2.2] that the image of the composite map is equal to
$\operatorname{span}_{A}\langle f^{e}(H_{\mathfrak{m}}^{i}(S_{\text{red}}))\rangle$
, where
$f^{e}$
denotes the natural
$e$
th Frobenius action on
$H_{\mathfrak{m}}^{i}(S_{\text{red}})$
. In particular, the Frobenius action on
$H_{\mathfrak{m}}^{i}(S_{\text{red}})/\text{im}\,\unicode[STIX]{x1D719}$
is nilpotent. However, since
$\operatorname{im}\unicode[STIX]{x1D719}$
is an
$F$
-stable submodule of
$H_{\mathfrak{m}}^{i}(S_{\text{red}})$
and
$S_{\text{red}}$
is
$F$
-pure, [Reference MaMa14, Theorem 3.7] shows that the Frobenius acts injectively on
$H_{\mathfrak{m}}^{i}(S_{\text{red}})/\text{im}\,\unicode[STIX]{x1D719}$
. Hence, we must have
$H_{\mathfrak{m}}^{i}(S_{\text{red}})=\operatorname{im}\unicode[STIX]{x1D719}$
, that is,
$H_{\mathfrak{m}}^{i}(S)\rightarrow H_{\mathfrak{m}}^{i}(S_{\text{red}})$
is surjective.
We next give an example showing that the analog of Lemma 3.3 for
$F$
-injectivity fails in general. The example is a modification of [Reference Enescu and HochsterEH08, Example 2.16].
Example 3.5. Let
$K=k(u,v)$
, where
$k$
is an algebraically closed field of characteristic
$p>0$
, and let
$L=K[z]/(z^{2p}+uz^{p}+v)$
be as in [Reference Enescu and HochsterEH08, Example 2.16]. Now let
$R=K+(x,y)L[[x,y]]$
with
$\mathfrak{m}=(x,y)L[[x,y]]$
. Then it is easy to see that
$(R,\mathfrak{m})$
is a local ring of dimension
$2$
and we have a short exact sequence:
$$\begin{eqnarray}0\rightarrow R\rightarrow L[[x,y]]\rightarrow L/K\rightarrow 0.\end{eqnarray}$$
The long exact sequence of local cohomology gives
$$\begin{eqnarray}H_{\mathfrak{m}}^{1}(R)\cong L/K,\hspace{10.00002pt}H_{\mathfrak{ m}}^{2}(R)\cong H_{\mathfrak{ m}}^{2}(L[[x,y]]).\end{eqnarray}$$
Moreover, one can check that the Frobenius action on
$H_{\mathfrak{m}}^{1}(R)$
is exactly the Frobenius action on
$L/K$
. The Frobenius action on
$L/K$
is injective since
$L^{p}\cap K=K^{p}$
, and the Frobenius action on
$H_{\mathfrak{m}}^{2}(L[[x,y]])$
is injective because
$L[[x,y]]$
is regular. Hence, the Frobenius actions on both
$H_{\mathfrak{m}}^{1}(R)$
and
$H_{\mathfrak{m}}^{2}(R)$
are injective. This proves that
$R$
is
$F$
-injective.
Write
$R=A/I$
for a regular local ring
$(A,\mathfrak{m})$
. One checks that the Frobenius action
$F:H_{\mathfrak{m}}^{1}(R)\rightarrow H_{\mathfrak{m}}^{1}(R)$
is not surjective up to
$K$
-span (and hence not surjective up to
$R$
-span, since the residue field of
$R$
is
$K$
) because
$L\neq L^{p}[K]$
by our choice of
$K$
and
$L$
(see [Reference Enescu and HochsterEH08, Example 2.16] for a detailed computation on this). But now [Reference LyubeznikLyu06, Lemma 2.2] shows that
$H_{\mathfrak{m}}^{1}(A/I^{[p]})\rightarrow H_{\mathfrak{m}}^{1}(A/I)$
is not surjective. Therefore, we can take
$S=A/I^{[p]}$
with
$S_{\text{red}}=R$
that is
$F$
-injective, but
$H_{\mathfrak{m}}^{1}(S)\rightarrow H_{\mathfrak{m}}^{1}(S_{\text{red}})$
is not surjective.
In view of Remark 3.4 and Example 3.5 and the relation between
$F$
-injective and Du Bois singularities, it is tempting to try to define a more restrictive variant of
$F$
-injective singularities for local rings. In particular, if
$(R,\mathfrak{m})$
is a local ring such that
$R_{\text{red}}$
has these more restrictive
$F$
-injective singularities, then it should follow that
$H_{\mathfrak{m}}^{i}(R)\rightarrow H_{\mathfrak{m}}^{i}(R_{\text{red}})$
surjects for all
$i$
.
Theorem 3.6. Suppose that
$(X,Z)$
is a reduced pair and that
$H\subseteq X$
is a Cartier divisor such that
$H$
does not contain any irreducible components of either
$X$
or
$Z$
. If
$(H,Z\cap H)$
is a Du Bois pair, then for all
$i$
and all points
$\unicode[STIX]{x1D702}\in H\subseteq X$
, the following segment of the long exact sequence:
$$\begin{eqnarray}0\rightarrow H_{\unicode[STIX]{x1D702}}^{i}(\mathscr{I}_{Z,\unicode[STIX]{x1D702}}\cdot {\mathcal{O}}_{H,\unicode[STIX]{x1D702}}){\hookrightarrow}H_{\unicode[STIX]{x1D702}}^{i+1}(\mathscr{I}_{Z,\unicode[STIX]{x1D702}}\cdot {\mathcal{O}}_{X,\unicode[STIX]{x1D702}}(-H)){\twoheadrightarrow}H_{\unicode[STIX]{x1D702}}^{i+1}(\mathscr{I}_{Z,\unicode[STIX]{x1D702}})\rightarrow 0\end{eqnarray}$$
is exact for all
$i$
. Dually, in the special case that
$\mathscr{I}_{Z}={\mathcal{O}}_{X}$
, we can also phrase this as saying that
$$\begin{eqnarray}0\rightarrow h^{-i}(\unicode[STIX]{x1D714}_{X}^{\boldsymbol{\cdot }})\rightarrow h^{-i}(\unicode[STIX]{x1D714}_{X}^{\boldsymbol{\cdot }}(H))\rightarrow h^{-i+1}(\unicode[STIX]{x1D714}_{H}^{\boldsymbol{\cdot }})\rightarrow 0\end{eqnarray}$$
is exact for all
$i$
.
Proof. Localizing at
$\unicode[STIX]{x1D702}$
, we may assume that
$X=\operatorname{Spec}R$
,
$Z=\operatorname{Spec}R/I$
,
$H=\operatorname{div}(x)$
with
$(R,\mathfrak{m})$
a local ring and
$\unicode[STIX]{x1D702}=\{\mathfrak{m}\}$
. Moreover, the hypotheses imply that
$x$
is a non-zero divisor on both
$R$
and
$R/I$
. It is enough to show that the segment of the long exact sequence
$$\begin{eqnarray}0\rightarrow H_{\mathfrak{m}}^{i}(I/xI)\rightarrow H_{\mathfrak{ m}}^{i+1}(I)\xrightarrow[{}]{\cdot x}H_{\mathfrak{ m}}^{i+1}(I)\rightarrow 0\end{eqnarray}$$
induced by
$0\rightarrow I\xrightarrow[{}]{\cdot x}I\rightarrow I/xI\rightarrow 0$
is exact.
Consider
$S=R/x^{n}R$
and
$J=I(R/x^{n}R)$
. The pair
$(S^{\prime }=R/xR,S^{\prime }/IS^{\prime })=(H,Z\cap H)$
is Du Bois by hypothesis (note that we do not assume that
$H$
is reduced). Thus, Lemma 3.3 implies that
$$\begin{eqnarray}H_{\mathfrak{m}}^{i}(I(R/x^{n}R)){\twoheadrightarrow}H_{\mathfrak{ m}}^{i}(I(R/xR))\end{eqnarray}$$
is surjective for every
$i$
,
$n$
. Since
$x$
is a non-zero divisor on
$R/I$
,
$x^{n}I=I\cap x^{n}R$
. Thus,
$$\begin{eqnarray}I(R/x^{n}R)=\frac{I+x^{n}R}{x^{n}R}\cong \frac{I}{I\cap x^{n}R}=I/x^{n}I.\end{eqnarray}$$
Hence, (3.6.2) shows that
$$\begin{eqnarray}H_{\mathfrak{m}}^{i}(I/x^{n}I){\twoheadrightarrow}H_{\mathfrak{ m}}^{i}(I/xI)\end{eqnarray}$$
is surjective for every
$i$
,
$n$
. The long exact sequence of local cohomology induced by
$0\rightarrow I/x^{n-1}I\xrightarrow[{}]{\cdot x}I/x^{n}I\rightarrow I/xI\rightarrow 0$
tells us that
$$\begin{eqnarray}H_{\mathfrak{m}}^{i}(I/x^{n-1}I)\xrightarrow[{}]{\cdot x}H_{\mathfrak{ m}}^{i}(I/x^{n}I)\end{eqnarray}$$
is injective for every
$i$
,
$n$
. Hence, after taking a direct limit, we obtain that
$$\begin{eqnarray}\unicode[STIX]{x1D719}_{i}:H_{\mathfrak{m}}^{i}(I/xI)\rightarrow \underset{n}{\varinjlim }H_{\mathfrak{ m}}^{i}(I/x^{n}I)\cong H_{\mathfrak{ m}}^{i}\biggl(\underset{n}{\varinjlim }(I/x^{n}I)\biggr)\cong H_{\mathfrak{ m}}^{i}(H_{x}^{1}(I))\cong H_{\mathfrak{ m}}^{i+1}(I)\end{eqnarray}$$
is injective for every
$i$
. Here the last two isomorphisms come from the fact that
$x$
is a non-zero divisor on
$I$
(since it is a non-zero divisor on
$R$
) and a simple computation using the local cohomology spectral sequence.
Claim 3.7. The
$\unicode[STIX]{x1D719}_{i}$
are exactly the connection maps in the long exact sequence of local cohomology induced by
$0\rightarrow I\xrightarrow[{}]{\cdot x}I\rightarrow I/xI\rightarrow 0$
:
$$\begin{eqnarray}\cdots \rightarrow H_{\mathfrak{m}}^{i}(I)\rightarrow H_{\mathfrak{ m}}^{i}(I/xI)\xrightarrow[{}]{\unicode[STIX]{x1D719}_{i}}H_{\mathfrak{m}}^{i+1}(I)\xrightarrow[{}]{\cdot x}H_{\mathfrak{ m}}^{i+1}(I)\rightarrow \cdots \,.\end{eqnarray}$$
This claim immediately produces (3.6.1) because we proved that
$\unicode[STIX]{x1D719}_{i}$
is injective for every
$i$
. Thus, it remains to prove the claim.
Proof of claim.
Observe that, by definition,
$\unicode[STIX]{x1D719}_{i}$
is the natural map in the long exact sequence of local cohomology
$$\begin{eqnarray}\cdots \rightarrow H_{\mathfrak{m}}^{i}(I/xI)\xrightarrow[{}]{\unicode[STIX]{x1D719}_{i}}H_{\mathfrak{m}}^{i}(I_{x}/I)\xrightarrow[{}]{\cdot x}H_{\mathfrak{m}}^{i}(I_{x}/I)\rightarrow \cdots \,,\end{eqnarray}$$
which is induced by
$0\rightarrow I/xI\rightarrow I_{x}/I\xrightarrow[{}]{\cdot x}I_{x}/I\rightarrow 0$
(note that
$x$
is a non-zero divisor on
$I$
and
$H_{x}^{1}(I)\cong I_{x}/I$
). However, it is easy to see that the multiplication by
$x$
map
$H_{\mathfrak{m}}^{i}(I_{x}/I)\xrightarrow[{}]{\cdot x}H_{\mathfrak{m}}^{i}(I_{x}/I)$
can be identified with the multiplication by
$x$
map
$H_{\mathfrak{m}}^{i+1}(I)\xrightarrow[{}]{\cdot x}H_{\mathfrak{m}}^{i+1}(I)$
because we have a natural identification
$H_{\mathfrak{m}}^{i}(I_{x}/I)\cong H_{\mathfrak{m}}^{i}(H_{x}^{1}(I))\cong H_{\mathfrak{m}}^{i+1}(I)$
. This finishes the proof of the claim and thus also the local cohomology statement.◻
The global statement can be checked locally, where it is simply a special case of the local dual of the local cohomology statement. ◻
The following is the main theorem of the section; it answers a question of Kovács and the second author [Reference Kovács and SchwedeKS16b, Question 5.7] and is a generalization to pairs of a characteristic-
$0$
analog of [Reference Horiuchi, Miller and ShimomotoHMS14, Corollary A.5].
Theorem 3.8. Suppose that
$(X,Z)$
is a reduced pair and that
$H\subseteq X$
is a Cartier divisor such that
$H$
does not contain any irreducible components of either
$X$
or
$Z$
. If
$(H,Z\cap H)$
is a Du Bois pair and
$\mathscr{I}_{Z}|_{X\backslash H}$
is
$\text{S}_{k}$
, then
$\mathscr{I}_{Z}$
is
$\text{S}_{k}$
.
Proof. Suppose that
$\mathscr{I}_{Z}$
is not
$\text{S}_{k}$
; choose an irreducible component
$Y$
of the non-
$\text{S}_{k}$
locus of
$\mathscr{I}_{Z}$
. Since
$\mathscr{I}_{Z}|_{X\backslash H}$
is
$\text{S}_{k}$
, we know that
$Y\subseteq H$
. Let
$\unicode[STIX]{x1D702}$
be the generic point of
$Y$
. Theorem 3.6 tells us that
$$\begin{eqnarray}H_{\unicode[STIX]{x1D702}}^{i}(\mathscr{I}_{Z}\cdot {\mathcal{O}}_{X}(-H)){\twoheadrightarrow}H_{\unicode[STIX]{x1D702}}^{i}(\mathscr{I}_{Z})\end{eqnarray}$$
is surjective for every
$i$
. Note that if we localize at
$\unicode[STIX]{x1D702}$
and use the same notation as in the proof of Theorem 3.6, this surjection is the multiplication by
$x$
map
$H_{\mathfrak{m}}^{i}(I)\xrightarrow[{}]{\cdot x}H_{\mathfrak{m}}^{i}(I)$
.
However, after we localize at
$\unicode[STIX]{x1D702}$
,
$I$
is
$\text{S}_{k}$
on the punctured spectrum and
$H_{\mathfrak{m}}^{i}(I)$
has finite length for every
$i<k$
. In particular, for
$h\gg 0$
,
$x^{h}$
annihilates
$H_{\mathfrak{m}}^{i}(I)$
for every
$i<k$
. Therefore, for
$i<k$
, the multiplication by
$x$
map
$H_{\mathfrak{m}}^{i}(I)\xrightarrow[{}]{\cdot x}H_{\mathfrak{m}}^{i}(I)$
cannot be surjective unless
$H_{\mathfrak{m}}^{i}(I)=0$
, which means that
$I$
is
$\text{S}_{k}$
as an
$R$
-module. But this contradicts our choice of
$Y$
(because we pick
$Y$
as an irreducible component of the non-
$\text{S}_{k}$
locus of
$\mathscr{I}_{Z}$
). Therefore,
$\mathscr{I}_{Z}$
is
$\text{S}_{k}$
.◻
Corollary 3.9. Let
$X$
be a reduced scheme and let
$H\subseteq X$
be a Cartier divisor. If
$H$
is Du Bois and
$X\backslash H$
is Cohen–Macaulay, then
$X$
is Cohen–Macaulay and hence so is
$H$
.
As mentioned in the Introduction, these results should be viewed as a generalization of [Reference Kollár and KovácsKK10, Corollaries 1.3 and 7.13] and [Reference Kovács and SchwedeKS16b, Theorem 5.5]. In those results, one considered a flat projective family
$X\rightarrow B$
with Du Bois fibers such that the general fiber is
$\text{S}_{k}$
. It was then shown that the special fiber is
$S_{k}$
. Let us explain this result in a simple case. Suppose that
$B$
is a smooth curve,
$Z=0$
, the special fiber is a Cartier divisor
$H$
and
$X\setminus H$
is Cohen–Macaulay. Then we are trying to show that
$H$
is Cohen–Macaulay, which is of course the same as showing that
$X$
is Cohen–Macaulay, which is exactly what our result proves. The point is that we had to make no projectivity hypothesis for our family.
This result also implies [Reference Kovács and SchwedeKS16b, Conjecture 7.9], which we state next. We leave out the definition of a rational pair here (this is a rational pair in the sense of Kollár and Kovács: a generalization of rational singularities analogous to divisorially log terminal singularities; see [Reference KollárKol13]); the interested reader can look it up, or simply assume that
$D=0$
.
Corollary 3.10. Suppose that
$(X,D)$
is a pair with
$D$
a reduced Weil divisor. Further suppose that
$H$
is a Cartier divisor on
$X$
not having any components in common with
$D$
such that
$(H,D\cap H)$
is Du Bois and such that
$(X\setminus H,D\setminus H)$
is a rational pair in the sense of Kollár and Kovács. Then
$(X,D)$
is a rational pair in the sense of Kollár and Kovács.
Proof. We follow [Reference Kovács and SchwedeKS16b, Proof of Theorem 7.1]. It goes through word for word once one observes that
${\mathcal{O}}_{X}(-D)$
is Cohen–Macaulay, which follows immediately from Theorem 3.8.◻
This corollary is also an analog of [Reference Fedder and WatanabeFW89, Proposition 2.13] and [Reference Horiuchi, Miller and ShimomotoHMS14, Corollary A.4].
4 Applications to local cohomology
In this section we give many applications of Lemma 3.3 to local cohomology; several of these applications are quite easy to prove. However, they provide strong and surprising characteristic-
$0$
analogs and generalizations of results in [Reference Hochster and RobertsHR76, Reference Singh and WaltherSW05, Reference Singh and WaltherSW07, Reference VarbaroVar13, Reference De Stefani and Núñez-BetancourtDN16] as well as answer their questions. Moreover, our results can give a generalization of the classical Kodaira vanishing theorem.
4.1 Injectivity of Ext and a generalization of the Kodaira vanishing theorem
Our first application gives a solution to [Reference Eisenbud, Mustaţă and StillmanEMS00, Question 6.2] on the injectivity of
$\operatorname{Ext}$
in characteristic
$0$
, which parallels its characteristic
$p>0$
analog [Reference Singh and WaltherSW07, Theorem 1.3].
Proposition 4.1. Let
$(R,\mathfrak{m})$
be a Gorenstein local ring essentially of finite type over
$\mathbb{C}$
, and let
$I\subseteq R$
be an ideal such that
$R/I$
has Du Bois singularities. Then the natural map
$\operatorname{Ext}_{R}^{j}(R/I,R)\rightarrow H_{I}^{j}(R)$
is injective for every
$j$
.
Proof. By Lemma 3.3 applied to
$S=R/I^{t}$
and applying local duality, we know that
$$\begin{eqnarray}\operatorname{Ext}_{R}^{j}(R/I,R)\rightarrow \operatorname{Ext}_{R}^{j}(R/I^{t},R)\end{eqnarray}$$
is injective for every
$j$
and every
$t>0$
. Now taking a direct limit, we obtain the desired injectivity
$\operatorname{Ext}_{R}^{j}(R/I,R)\rightarrow H_{I}^{j}(R)$
. ◻
Remark 4.2. Theorem 1.3 of [Reference Singh and WaltherSW07] proves the same injectivity result in characteristic
$p>0$
when
$R/I$
is
$F$
-pure (and when
$R$
is regular). Perhaps it is worth pointing out that Proposition 4.1 fails in general if we replace Du Bois by
$F$
-injective: Example 3.5 is a counterexample, because there we have that
$S=A/I$
is
$F$
-injective but
$H_{\mathfrak{m}}^{1}(A/I^{[p]})\rightarrow H_{\mathfrak{m}}^{1}(A/I)$
is not surjective. Hence, applying local duality shows that
$$\begin{eqnarray}\operatorname{Ext}_{A}^{\dim A-1}(A/I,A)\rightarrow \operatorname{Ext}_{A}^{\dim A-1}(A/I^{[p]},A)\end{eqnarray}$$
is not injective, so neither is
$\operatorname{Ext}_{A}^{\dim A-1}(A/I,A)\rightarrow H_{I}^{\dim A-1}(A)$
.
An immediate corollary of Proposition 4.1 is the following, which is a characteristic-
$0$
analog of [Reference De Stefani and Núñez-BetancourtDN16, Theorem 7.3] (this also answers [Reference De Stefani and Núñez-BetancourtDN16, Question 7.5], which is motivated by Stillman’s conjecture).
Corollary 4.3. Let
$R$
be a regular ring of essentially finite type over
$\mathbb{C}$
. Let
$I\subseteq R$
be an ideal such that
$S=R/I$
has Du Bois singularities. Then
$\operatorname{pd}_{R}S\leqslant \unicode[STIX]{x1D708}(I)$
, where
$\unicode[STIX]{x1D708}(I)$
denotes the minimal number of generators of
$I$
.
Proof. For every
$j>\unicode[STIX]{x1D708}(I)$
and every maximal ideal
$\mathfrak{m}$
of
$R$
, we have
$H_{IR_{\mathfrak{m}}}^{j}(R_{\mathfrak{m}})=0$
. Therefore, by Proposition 4.1, we have
$\operatorname{Ext}_{R_{\mathfrak{m}}}^{j}(S_{\mathfrak{m}},R_{\mathfrak{m}})=0$
for every
$j>\unicode[STIX]{x1D708}(I)$
. Since
$\operatorname{pd}_{R_{\mathfrak{m}}}S_{\mathfrak{m}}<\infty$
, we have
$$\begin{eqnarray}\operatorname{pd}_{R_{\mathfrak{m}}}S_{\mathfrak{m}}=\sup \{j\mid \operatorname{Ext}_{R_{\mathfrak{m}}}^{j}(S_{\mathfrak{ m}},R_{\mathfrak{m}})\neq 0\}\leqslant \unicode[STIX]{x1D708}(I)^{3}.\end{eqnarray}$$
Because this is true for every maximal ideal
$\mathfrak{m}$
, we have
$\operatorname{pd}_{R}S\leqslant \unicode[STIX]{x1D708}(I)$
.◻
Next, we want to prove a stronger form of Proposition 4.1 in the graded case. We will first need the following criterion of Du Bois singularities for
$\mathbb{N}$
-graded rings. This result and related results should be well known to experts (or at least well believed by experts): for example [Reference MaMa15, Theorem 4.4], [Reference Bhatt, Schwede and TakagiBST13, Lemma 2.14], [Reference Kovács and SchwedeKS16b, Lemma 2.12] or [Reference Graf and KovácsGK14]. However, all these references only deal with the case that
$R$
is the section ring of a projective variety with respect to a certain ample line bundle, while here we allow arbitrary
$\mathbb{N}$
-graded rings which are not even normal. We could not find a reference that handles the generality that we will need and hence we write down a careful argument.
Proposition 4.4. Let
$(R,\mathfrak{m})$
be a reduced Noetherian
$\mathbb{N}$
-graded
$(R_{0}=k)$
-algebra with
$\mathfrak{m}$
the unique homogeneous maximal ideal. Suppose that
$R_{P}$
is Du Bois for all
$P\neq \mathfrak{m}$
. Then we have
$$\begin{eqnarray}h^{i}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\cong [H_{\mathfrak{ m}}^{i+1}(R)]_{{>}0}\end{eqnarray}$$
for every
$i>0$
and
$$\begin{eqnarray}h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})/R\cong [H_{\mathfrak{ m}}^{1}(R)]_{{>}0}.\end{eqnarray}$$
In particular,
$R$
is Du Bois if and only if
$[H_{\mathfrak{m}}^{i}(R)]_{{>}0}=0$
for every
$i>0$
.
Proof. Let
$R^{\natural }$
denote the Rees algebra of
$R$
with respect to the natural filtration
$R_{{\geqslant}t}$
. That is,
$R^{\natural }=R\oplus R_{{\geqslant}1}\oplus R_{{\geqslant}2}\oplus \cdots \,.$
Let
$Y=\operatorname{Proj}R^{\natural }$
. We first claim that
$Y$
is Du Bois:
$Y$
is covered by
$D_{+}(f)$
for homogeneous elements
$f\in R_{{\geqslant}t}$
and
$t\in \mathbb{N}$
.
If
$\deg f>t$
, then
$[R_{f}^{\natural }]_{0}\cong R_{f}$
is Du Bois. If
$\deg f=t$
, then
$[R_{f}^{\natural }]_{0}\cong [R_{f}]_{{\geqslant}0}$
is also Du BoisFootnote
4
(see [Reference Kurano, Sato, Singh and WatanabeKSSW09, Lemma 5.4] for an analogous analysis on rational singularities).
Since
$R$
and thus
$R^{\natural }$
are Noetherian, there exists
$n$
such that
$R_{{\geqslant}nt}=(R_{{\geqslant}n})^{t}$
for every
$t\geqslant 1$
[Reference BourbakiBou98, ch. III, §3, Proposition 3]. Let
$I=(R_{{\geqslant}n})$
; then we immediately see that
$Y\cong \operatorname{Proj}(R\oplus I\oplus I^{2}\oplus \cdots \,)$
is the blow up of
$\operatorname{Spec}R$
at
$I$
. We define the exceptional divisor to be
$E\cong \operatorname{Proj}(R/I\oplus I/I^{2}\oplus I^{2}/I^{3}\oplus \cdots \,)$
. We next claim that
$$\begin{eqnarray}(R/I\oplus I/I^{2}\oplus I^{2}/I^{3}\oplus \cdots \,)_{\text{red}}\cong R_{0}\oplus R_{n}\oplus R_{2n}\oplus \cdots \,.\end{eqnarray}$$
The point is that, for
$\overline{x}\in I^{t}/I^{t+1}=R_{{\geqslant}nt}/R_{{\geqslant}n(t+1)}$
, if
$x\in R_{nt+a}$
for some
$a>0$
, then we can pick
$b>0$
such that
$ba>n$
; we then have
$$\begin{eqnarray}x^{b}\in R_{bnt+ba}\subseteq R_{{\geqslant}n(bt+1)}.\end{eqnarray}$$
But this means that
$\overline{x}^{b}=0$
in
$I^{bt}/I^{bt+1}$
and thus
$\overline{x}$
is nilpotent in
$R/I\oplus I/I^{2}\oplus I^{2}/I^{3}\oplus \cdots \,$
. This proves (4.4.1).
By (4.4.1), we have
$E_{\text{red}}\cong \operatorname{Proj}R_{0}\oplus R_{n}\oplus R_{2n}\oplus \cdots \cong \operatorname{Proj}R$
is Du Bois (because
$[R_{f}]_{0}$
is Du Bois for every homogeneous
$f\in R$
). We consider the following commutative diagram.
Since
$Y$
,
$E_{\text{red}}$
and
$(\operatorname{Spec}R/I)_{\text{red}}\cong \operatorname{Spec}k$
are all Du Bois by the above discussion, the exact triangle
$\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0}\rightarrow \mathbf{R}\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{\unicode[STIX]{x1D6FA}}_{Y}^{0}\oplus \text{}\underline{\unicode[STIX]{x1D6FA}}_{R/I}^{0}\rightarrow \mathbf{R}\unicode[STIX]{x1D70B}_{\ast }\text{}\underline{\unicode[STIX]{x1D6FA}}_{E}^{0}\xrightarrow[{}]{+1}$
reduces to
$$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0}\rightarrow \mathbf{R}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{Y}\oplus k\rightarrow \mathbf{R}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{E_{\text{red}}}\xrightarrow[{}]{+1}.\end{eqnarray}$$
Next, we study the map
$\mathbf{R}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{Y}\rightarrow \mathbf{R}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{E_{\text{red}}}$
using the Čech complex. We pick
$x_{1},\ldots ,x_{m}\in I=(R_{{\geqslant}n})$
in
$R\oplus I\oplus I^{2}\oplus \cdots \,$
such that:
-
(a) the internal degree
$\deg x_{i}=n$
for each
$x_{i}$
(in other words,
$x_{i}\in R_{n}\subseteq R_{{\geqslant}n}=I$
); -
(b) the images
$\overline{x}_{1},\ldots ,\overline{x}_{m}$
in
$(R/I\oplus I/I^{2}\oplus I^{2}/I^{3}\oplus \cdots \,)_{\text{red}}=R_{0}\oplus R_{n}\oplus R_{2n}\oplus \cdots \,$
are algebra generators of
$R_{0}\oplus R_{n}\oplus R_{2n}\oplus \cdots \,$
over
$R_{0}=k$
.
Note that conditions (a) and (b) together imply that the radical of
$(x_{1},\ldots ,x_{m})$
in
$R\oplus I\oplus I^{2}\oplus \cdots \,$
is the irrelevant ideal
$I\oplus I^{2}\oplus \cdots \,$
. In particular,
$\{D_{+}(x_{i})\}_{1\leqslant i\leqslant m}$
forms an affine open cover of
$Y$
. The point is that for any
$y\in I^{t}=R_{{\geqslant}tn}$
,
$y^{n}\in I^{tn}=R_{{\geqslant}tn^{2}}$
as an element in
$R\oplus I\oplus I^{2}\oplus \cdots \,$
is always contained in the ideal
$(x_{1},\ldots ,x_{m})$
; this is because the internal degree of
$y^{n}$
is divisible by
$n$
, so it can be written as a sum of monomials in
$x_{i}$
by (b).
The natural map
${\mathcal{O}}_{Y}\rightarrow {\mathcal{O}}_{E_{\text{red}}}$
induces a map between the
$s$
th spot of the Čech complexes of
${\mathcal{O}}_{Y}$
and
${\mathcal{O}}_{E_{\text{red}}}$
with respect to the affine cover
$\{D_{+}(x_{i})\}_{1\leqslant i\leqslant m}$
. The induced map on Čech complexes can be explicitly described as follows (all the direct sums in the following diagram are taken over all
$s$
-tuples
$1\leqslant i_{1}<\cdots <i_{s}\leqslant m$
):
The induced map on the second line takes the element
$y/(x_{i_{1}}x_{i_{2}}\cdots x_{i_{s}})^{n}$
to
$\overline{y}/(\overline{x}_{i_{1}}\overline{x}_{i_{2}}\cdots \overline{x}_{i_{s}})^{n}$
, where
$\overline{y}$
denotes the image of
$y$
in
$R_{nsh}$
. Hence, the same map
$\unicode[STIX]{x1D719}$
on the third line is exactly ‘taking the degree-
$0$
part’. Therefore, we have
$$\begin{eqnarray}\mathbf{R}^{i}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{Y}\cong H^{i}(Y,{\mathcal{O}}_{Y})=[H_{\mathfrak{m}}^{i+1}(R)]_{{\geqslant}0},\end{eqnarray}$$
while
$$\begin{eqnarray}\mathbf{R}^{i}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{E_{\text{red}}}\cong H^{i}(E_{\text{red}},{\mathcal{O}}_{E_{\text{red}}})\cong [H_{\mathfrak{m}}^{i+1}(R)]_{0}\end{eqnarray}$$
for every
$i\geqslant 1$
, and the map
$\mathbf{R}^{i}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{Y}\rightarrow \mathbf{R}^{i}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{E_{\text{red}}}$
is taking the degree-
$0$
part. Therefore, taking cohomology of (4.4.2), we have
$$\begin{eqnarray}h^{i}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\cong [H_{\mathfrak{ m}}^{i+1}(R)]_{{>}0}\quad \text{for every }i\geqslant 2.\end{eqnarray}$$
Moreover, for
$i=0,1$
, the cohomology of (4.4.2) gives
$$\begin{eqnarray}0\rightarrow h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\rightarrow H^{0}(Y,{\mathcal{O}}_{Y})\oplus k\xrightarrow[{}]{\unicode[STIX]{x1D719}}H^{0}(E_{\text{red}},{\mathcal{O}}_{E_{\text{red}}})\rightarrow h^{1}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\rightarrow [H_{\mathfrak{ m}}^{2}(R)]_{{>}0}\rightarrow 0.\end{eqnarray}$$
A similar Čech complex computation as above shows that
$$\begin{eqnarray}H^{0}(Y,{\mathcal{O}}_{Y})=\ker (\oplus [R_{x_{i}}]_{{\geqslant}0}\rightarrow \oplus [R_{x_{i}x_{j}}]_{{\geqslant}0}),\end{eqnarray}$$
while
$H^{0}(E_{\text{red}},{\mathcal{O}}_{E_{\text{red}}})=\ker (\oplus [R_{x_{i}}]_{0}\rightarrow \oplus [R_{x_{i}x_{j}}]_{0})$
. Therefore,
$\unicode[STIX]{x1D719}$
is surjective, which implies that
$$\begin{eqnarray}h^{1}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\cong [H_{\mathfrak{ m}}^{2}(R)]_{{>}0}.\end{eqnarray}$$
Taking the degree
${>}0$
part of (4.4.4), we get an exact sequence
$$\begin{eqnarray}0\rightarrow h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})_{{>}0}\rightarrow \oplus [R_{x_{i}}]_{{>}0}\rightarrow \oplus [R_{x_{i}x_{j}}]_{{>}0}.\end{eqnarray}$$
This implies that
$h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})_{{>}0}\cong (\unicode[STIX]{x1D6E4}(\operatorname{Spec}R\setminus \mathfrak{m},{\mathcal{O}}_{\operatorname{Spec}R}))_{{>}0}$
and so
$$\begin{eqnarray}h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})_{{>}0}/R_{{>}0}\cong [H_{\mathfrak{m}}^{1}(R)]_{{>}0}.\end{eqnarray}$$
Finally, we notice that
$h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\cong R^{\text{sn}}$
is the seminormalization of
$R$
[Reference SaitoSai00, 5.2]. We know that
$R_{0}^{\text{sn}}\subseteq R^{\text{sn}}$
is reduced. But we can also view
$R_{0}^{\text{sn}}$
as the quotient
$R^{\text{sn}}/R_{{>}0}^{\text{sn}}$
; in particular, the prime ideals of
$R_{0}^{\text{sn}}$
correspond to prime ideals of
$R^{\text{sn}}$
that contain
$R_{{>}0}^{\text{sn}}$
, so they all contract to
$\mathfrak{m}$
in
$R$
. Since seminormalization induces a bijection on spectrum,
$R_{0}^{\text{sn}}$
has a unique prime ideal. Thus,
$R_{0}^{\text{sn}}$
, being a reduced Artinian local ring, must be a field. Since seminormalization also induces isomorphism on residue fields,
$R_{0}^{\text{sn}}=k$
and thus
$h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})_{0}\cong R_{0}^{\text{sn}}=R_{0}$
. Hence, (4.4.6) tells us that
$$\begin{eqnarray}h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})/R\cong [H_{\mathfrak{ m}}^{1}(R)]_{{>}0}.\end{eqnarray}$$
Now (4.4.3), (4.4.5) and (4.4.7) together finish the proof. ◻
Now we prove our result on injectivity of
$\operatorname{Ext}$
. Later we will see that this theorem can be viewed as a generalization of the Kodaira vanishing theorem.
Theorem 4.5. Let
$(R,\mathfrak{m})$
be a reduced Noetherian
$\mathbb{N}$
-graded
$(R_{0}=\mathbb{C})$
-algebra with
$\mathfrak{m}$
the unique homogeneous maximal ideal. Suppose that
$R_{P}$
is Du Bois for all
$P\neq \mathfrak{m}$
. Write
$R=A/I$
, where
$A=\mathbb{C}[x_{1},\ldots ,x_{n}]$
is a polynomial ring with
$\deg x_{i}=d_{i}>0$
and
$I$
is a homogeneous ideal. Then the natural degree-preserving map
$\operatorname{Ext}_{A}^{j}(R,A)\rightarrow H_{I}^{j}(A)$
induces an injection
$$\begin{eqnarray}[\operatorname{Ext}_{A}^{j}(R,A)]_{{\geqslant}-d}{\hookrightarrow}[H_{I}^{j}(A)]_{{\geqslant}-d}\end{eqnarray}$$
for every
$j$
, where
$d=\sum d_{i}$
.
Proof. We have the hypercohomology spectral sequence
$$\begin{eqnarray}H_{\mathfrak{m}}^{p}(h^{q}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0}))\Rightarrow \mathbb{H}_{\mathfrak{ m}}^{p+q}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0}).\end{eqnarray}$$
Since
$R$
is Du Bois away from
$V(\mathfrak{m})$
,
$h^{q}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})$
has finite length when
$q\geqslant 1$
. Thus, we know that
$H_{\mathfrak{m}}^{p}(h^{q}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0}))=0$
unless
$p=0$
or
$q=0$
. We also have that
$H_{\mathfrak{m}}^{0}(h^{i}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0}))\cong h^{i}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})$
for
$i\geqslant 1$
. Hence, the above spectral sequence carries the data of a long exact sequence
$$\begin{eqnarray}\begin{array}{@{}cccccc@{}}0\ & \rightarrow \ & H_{\mathfrak{m}}^{1}(h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0}))\rightarrow \ & \mathbb{H}_{\mathfrak{m}}^{1}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\rightarrow \ & h^{1}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\rightarrow \ & \\ \ & \rightarrow \ & H_{\mathfrak{m}}^{2}(h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0}))\rightarrow \ & \mathbb{H}_{\mathfrak{m}}^{2}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\rightarrow \ & h^{2}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\rightarrow \ & \\ \ & \ & \cdots \,\ & \cdots \,\ & \cdots \,\ & \\ \ & \rightarrow \ & H_{\mathfrak{m}}^{i}(h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0}))\rightarrow \ & \mathbb{H}_{\mathfrak{m}}^{i}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\rightarrow \ & h^{i}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\rightarrow \ & \cdots \end{array}\end{eqnarray}$$
We also have a short exact sequence
$0\rightarrow R\rightarrow h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})\rightarrow [H_{\mathfrak{m}}^{1}(R)]_{{>}0}\rightarrow 0$
by Proposition 4.4. Therefore, the long exact sequence of local cohomology and the observation that
$[H_{\mathfrak{m}}^{1}(R)]_{{>}0}$
has finite length tell us that
$$\begin{eqnarray}H_{\mathfrak{m}}^{1}(h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0}))\cong H_{\mathfrak{ m}}^{1}(R)/[H_{\mathfrak{ m}}^{1}(R)]_{{>}0}\end{eqnarray}$$
and
$$\begin{eqnarray}H_{\mathfrak{m}}^{i}(h^{0}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0}))\cong H_{\mathfrak{ m}}^{i}(R)\quad \text{for every }i\geqslant 2.\end{eqnarray}$$
Now taking the degree
${\leqslant}0$
part of (4.5.1) and again using Proposition 4.4 yields
$$\begin{eqnarray}[H_{\mathfrak{m}}^{i}(R)]_{{\leqslant}0}\cong [\mathbb{H}_{\mathfrak{m}}^{i}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})]_{{\leqslant}0}\quad \text{for every }i.\end{eqnarray}$$
At this point, note that by the Matlis dual of Lemma 3.2 (see the proof of Lemma 3.3 applied to
$S=A/J$
for
$\sqrt{J}=I$
, and thus
$S_{\text{red}}=A/I=R$
), we always have a surjection
$H_{\mathfrak{m}}^{i}(A/J){\twoheadrightarrow}\mathbb{H}_{\mathfrak{m}}^{i}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})$
for every
$i$
and
$\sqrt{J}=I$
. Taking the degree
${\leqslant}0$
part and applying (4.5.2), we thus get that
$$\begin{eqnarray}[H_{\mathfrak{m}}^{i}(A/J)]_{{\leqslant}0}{\twoheadrightarrow}[H_{\mathfrak{m}}^{i}(R)]_{{\leqslant}0}\end{eqnarray}$$
is surjective for every
$i$
and
$\sqrt{J}=I$
. Now taking
$J=I^{t}$
and applying graded local duality (we refer to [Reference Brodmann and SharpBS98] for definitions and standard properties of graded canonical modules, graded injective hulls and graded local duality, but we emphasize here that the graded canonical module of
$A$
is
$A(-d)$
), we have that
$$\begin{eqnarray}[\operatorname{Ext}_{A}^{j}(R,A(-d))]_{{\geqslant}0}{\hookrightarrow}[\operatorname{Ext}_{A}^{j}(A/I^{t},A(-d))]_{{\geqslant}0}\end{eqnarray}$$
is injective for every
$j$
and
$t$
. So, after taking a direct limit and a degree shift, we have
$$\begin{eqnarray}[\operatorname{Ext}_{A}^{j}(R,A)]_{{\geqslant}-d}{\hookrightarrow}[H_{I}^{j}(A)]_{{\geqslant}-d}\end{eqnarray}$$
is injective for every
$j$
. This finishes the proof.◻
Remark 4.6. The dual form of Theorem 4.5 says that
$[H_{\mathfrak{m}}^{i}(A/J)]_{t}{\twoheadrightarrow}[H_{\mathfrak{m}}^{i}(R)]_{t}$
is surjective for every
$i$
, every
$t\leqslant 0$
and every
$\sqrt{J}=I$
; see (4.5.3). When
$R=A/I$
has an isolated singularity,
$A$
is standard graded and
$t=0$
, this was proved in [Reference VarbaroVar13, Proposition 3.8]. Therefore, our Theorem 4.5 greatly generalizes this result.
In general, we cannot expect that
$[\operatorname{Ext}_{A}^{j}(R,A)]_{{<}-d}{\hookrightarrow}[H_{I}^{j}(A)]_{{<}-d}$
is injective under the hypothesis of Theorem 4.5 (even if
$R$
is an isolated singularity). Consider the following example.
Example 4.7 (Cf. [Reference Singh and WaltherSW07, Example 3.5]).
Let
$R=\mathbb{C}[s^{4},s^{3}t,st^{3},t^{4}]$
. Then we can write
$R=A/I$
, where
$A=\mathbb{C}[x,y.z,w]$
with standard grading (i.e.,
$x,y,z,w$
all have degree one). It is straightforward to check that
$R$
is an isolated singularity with
$$\begin{eqnarray}H_{\mathfrak{m}}^{1}(R)=[H_{\mathfrak{ m}}^{1}(R)]_{{>}0}\neq 0\end{eqnarray}$$
(in particular,
$\operatorname{depth}R=1$
). By graded local duality, we have
$[\operatorname{Ext}_{A}^{3}(R,A)]_{{<}-4}\neq 0$
. On the other hand, using standard vanishing theorems in [Reference Huneke and LyubeznikHL90, Theorem 2.9], we know that
$H_{I}^{3}(A)=0$
. Therefore, the map
$[\operatorname{Ext}_{A}^{3}(R,A)]_{{<}-4}\rightarrow [H_{I}^{3}(A)]_{{<}-4}$
is not injective.
An important consequence of Theorem 4.5 (in fact, we only need the injectivity in degree
${>}-d$
) is the following vanishing result.
Theorem 4.8. Let
$(R,\mathfrak{m})$
be a Noetherian
$\mathbb{N}$
-graded
$(R_{0}=\mathbb{C})$
-algebra with
$\mathfrak{m}$
the unique homogeneous maximal ideal. Suppose that
$R_{P}$
is Du Bois for all
$P\neq \mathfrak{m}$
and
$H_{\mathfrak{m}}^{i}(R)$
has finite length for some
$i$
. Then
$[H_{\mathfrak{m}}^{i}(R)]_{{<}0}=0$
.
In particular, if
$R$
is equidimensional and is Cohen–Macaulay Du Bois on
$\operatorname{Spec}R-\{\mathfrak{m}\}$
, then
$[H_{\mathfrak{m}}^{i}(R)]_{{<}0}=0$
for every
$i<\dim R$
.
Proof. Let
$R=A/I$
, where
$A=\mathbb{C}[x_{1},\ldots ,x_{n}]$
is a (not necessarily standard graded) polynomial ring and
$I$
is a homogeneous ideal. Set
$\deg x_{i}=d_{i}>0$
and
$d=\sum d_{i}$
. The graded canonical module of
$A$
is
$A(-d)$
. By graded local duality,
$$\begin{eqnarray}\operatorname{Ext}_{A}^{n-i}(R,A)(-d)\cong H_{\mathfrak{ m}}^{i}(R)^{\ast }.\end{eqnarray}$$
Therefore, if
$[H_{\mathfrak{m}}^{i}(R)]_{-j}\neq 0$
for some
$j>0$
, then
$[\operatorname{Ext}_{A}^{n-i}(R,A)]_{j-d}\neq 0$
for some
$j>0$
. By Theorem 4.5, we have an injection
$$\begin{eqnarray}[\operatorname{Ext}_{A}^{n-i}(R,A)]_{j-d}{\hookrightarrow}[H_{I}^{n-i}(A)]_{j-d}.\end{eqnarray}$$
Since
$H_{\mathfrak{m}}^{i}(R)$
has finite length,
$\operatorname{Ext}_{A}^{n-i}(R,A)$
also has finite length. Hence, the natural degree-preserving map
$\operatorname{Ext}_{A}^{n-i}(R,A)\rightarrow H_{I}^{n-i}(A)$
factors through
$$\begin{eqnarray}\operatorname{Ext}_{A}^{n-i}(R,A)\rightarrow H_{\mathfrak{ m}}^{0}H_{I}^{n-i}(A)\rightarrow H_{I}^{n-i}(A).\end{eqnarray}$$
Taking the degree-
$(j-d)$
part, we thus get an injection
$$\begin{eqnarray}[\operatorname{Ext}_{A}^{n-i}(R,A)]_{j-d}\rightarrow [H_{\mathfrak{m}}^{0}H_{I}^{n-i}(A)]_{j-d}.\end{eqnarray}$$
It follows that
$[H_{\mathfrak{m}}^{0}H_{I}^{n-i}(A)]_{j-d}\neq 0$
for some
$j>0$
. However,
$H_{\mathfrak{m}}^{0}H_{I}^{n-i}(A)$
is an Eulerian graded
$\mathscr{D}$
-module supported only at
$\mathfrak{m}$
. Thus, by [Reference Ma and ZhangMZ14, Theorem 1.2],Footnote
5
the socle of
$H_{\mathfrak{m}}^{0}H_{I}^{n-i}(A)$
is concentrated in degree
$-d$
, so that
$[H_{\mathfrak{m}}^{0}H_{I}^{n-i}(A)]_{{>}-d}=0$
, which is a contradiction.◻
If
$R$
is the section ring of a normal Cohen–Macaulay and Du Bois projective variety
$X$
with respect to an ample line bundle
$\mathscr{L}$
, then
$[H_{\mathfrak{m}}^{i}(R)]_{{<}0}=0$
is exactly the Kodaira vanishing for
$X$
(which is well known; for example see [Reference MaMa15] or [Reference PatakfalviPat15]). But Theorem 4.8 can handle more general
$R$
, i.e.,
$R$
need not be a section ring of an ample line bundle. If
$R$
is normal, then any graded ring is the section ring of some
$\mathbb{Q}$
-divisor [Reference DemazureDem88] and, in that case, our results yield variants and consequences of Kawamata–Viehweg vanishing (also see [Reference WatanabeWat81, Lemma 2.1 and Proposition 2.2]). But for general graded rings we do not know how to view them as section rings. Thus, our results (Theorems 4.5 and 4.8) should be viewed as generalizations of the Kodaira vanishing theorem for Cohen–Macaulay Du Bois projective varieties. It would also be natural to try to generalize the results of Proposition 4.4 through Theorem 4.8 to the context of Du Bois pairs. One particular obstruction is the use of the Eulerian graded
$\mathscr{D}$
-module at the end of the proof of Theorem 4.8.
4.2 Set-theoretic Cohen–Macaulayness
Our next application is a characteristic-
$0$
analog of [Reference Singh and WaltherSW05, Lemma 3.1] on set-theoretic Cohen–Macaulayness. Recall that an ideal
$I$
in a regular ring
$R$
is set-theoretically Cohen–Macaulay if there exists an ideal
$J$
such that
$\sqrt{I}=\sqrt{J}$
and
$R/J$
is Cohen–Macaulay.
Proposition 4.9. Let
$(R,\mathfrak{m})$
be a regular local ring essentially of finite type over
$\mathbb{C}$
and let
$I\subseteq R$
be an ideal. If
$R/I$
is Du Bois but not Cohen–Macaulay, then the ideal
$I$
is not set-theoretically Cohen–Macaulay.
Proof. Suppose that
$I=\sqrt{J}$
for some
$J$
such that
$R/J$
is Cohen–Macaulay. Applying Lemma 3.3 to
$S=R/J$
, we find that for every
$i<\dim R/I$
,
$$\begin{eqnarray}0=H_{\mathfrak{m}}^{i}(R/J){\twoheadrightarrow}H_{\mathfrak{ m}}^{i}(R/I)\end{eqnarray}$$
is surjective and thus
$R/I$
is Cohen–Macaulay, which is a contradiction.◻
In the graded characteristic-
$0$
case, we have a stronger criterion for set-theoretic Cohen–Macaulayness.
Corollary 4.10. Let
$R=\mathbb{C}[x_{1},\ldots ,x_{n}]$
be a polynomial ring with possibly non-standard grading. Let
$I$
be a homogeneous ideal of
$R$
such that
$R/I$
is Du Bois on
$\operatorname{Spec}R-\{\mathfrak{m}\}$
(e.g.,
$R/I$
has an isolated singularity at
$\{\mathfrak{m}\}$
).
Suppose that
$[H_{\mathfrak{m}}^{i}(R/I)]_{{\leqslant}0}\neq 0$
for some
$i<\dim R/I$
(e.g.,
$R/I$
is not Cohen–Macaulay on
$\operatorname{Spec}R-\{\mathfrak{m}\}$
, or
$H^{i}(X,{\mathcal{O}}_{X})\neq 0$
for
$X=\operatorname{Proj}R/I$
). Then
$I$
is not set-theoretically Cohen–Macaulay.
Proof. Suppose that
$I=\sqrt{J}$
for some
$J$
such that
$R/J$
is Cohen–Macaulay. Applying the dual form of Theorem 4.5 (see Remark 4.6), we get
$$\begin{eqnarray}0=[H_{\mathfrak{m}}^{i}(R/J)]_{{\leqslant}0}{\twoheadrightarrow}[H_{\mathfrak{m}}^{i}(R/I)]_{{\leqslant}0}\end{eqnarray}$$
is surjective for every
$i<\dim R/I$
. This clearly contradicts our hypothesis.◻
We point out the following example as an application.
Example 4.11. Let
$k$
be a field and let
$E_{k}\subseteq \mathbb{P}_{k}^{2}$
be a smooth elliptic curve over
$k$
. We want to study the defining ideal of the Segre embedding
$E_{k}\times \mathbb{P}_{k}^{1}\subseteq \mathbb{P}_{k}^{5}$
. We let
$k[x_{0},\ldots ,x_{5}]/I=A/I$
be this homogeneous coordinate ring. It is well known that
$A/I$
is not Cohen–Macaulay.
-
(a)
$k$
has characteristic
$p>0$
and
$E_{k}$
is an ordinary elliptic curve. In this case it is well known that
$A/I$
is
$F$
-pure, so [Reference Singh and WaltherSW05, Lemma 3.1] shows that
$I$
is not set-theoretically Cohen–Macaulay. -
(b)
$k$
has characteristic
$p>0$
and
$E_{k}$
is supersingular. We want to point out that, at least when
$k$
is
$F$
-finite,
$I$
is still not set-theoretically Cohen–Macaulay. This answers a question in [Reference Singh and WaltherSW05, Remark 3.4]. Suppose that there exists
$J$
such that
$\sqrt{J}=I$
and
$A/J$
is Cohen–Macaulay. Let
$e\gg 0$
be such that
$I^{[p^{e}]}\subseteq J$
. The composite of the Frobenius map on
$A/I$
with the natural surjection
$A/I\xrightarrow[{}]{F}A/I^{[p^{e}]}{\twoheadrightarrow}A/J$
makes
$A/J$
a small Cohen–Macaulay algebra over
$A/I$
(note that
$k$
, and hence
$A$
, is
$F$
-finite). However, by a result of Bhatt [Reference BhattBha14, Example 3.11],
$A/I$
does not have any small Cohen–Macaulay algebra, which is a contradiction. -
(c)
$k$
has characteristic
$0$
. In this case, it is easy to check using Proposition 4.4 that
$A/I$
is Du Bois. Hence, Proposition 4.9 immediately shows that
$I$
is not set-theoretically Cohen–Macaulay. This example was originally obtained in [Reference Singh and WaltherSW05, Theorem 3.3] using reduction to characteristic
$p>0$
. Thus, our Proposition 4.9 can be viewed as a vast generalization of that result.
It is worth pointing out that in Example 4.11, we know that
$H_{\mathfrak{m}}^{i}(A/J){\twoheadrightarrow}H_{\mathfrak{m}}^{i}(A/I)$
for every
$i$
and every
$\sqrt{J}=I$
in characteristic
$0$
, since
$A/I$
is Du Bois. In characteristic
$p>0$
, we have
$H_{\mathfrak{m}}^{i}(A/J){\twoheadrightarrow}H_{\mathfrak{m}}^{i}(A/I)$
for every
$i$
and every
$\sqrt{J}=I$
when
$E_{k}$
is ordinary; however, it is straightforward to check that
$H_{\mathfrak{m}}^{2}(A/I^{[p]})\rightarrow H_{\mathfrak{m}}^{2}(A/I)$
is not surjective (it is the zero map) when
$E_{k}$
is supersingular. Therefore, the surjective property proved in Lemma 3.3 does not pass to reduction mod
$p\gg 0$
.
4.3 Koszul cohomology versus local cohomology
Our last application in this section is a strengthening of the main result of [Reference Hochster and RobertsHR76]. We start by proving a general result, which is characteristic-free. The proof is inspired by [Reference SchenzelSch82].
Theorem 4.12. Let
$R$
be a Noetherian
$\mathbb{N}$
-graded
$k$
-algebra, where
$k=R_{0}$
is an arbitrary field. Let
$\mathfrak{m}$
be the unique homogenous maximal ideal. If
$H_{\mathfrak{m}}^{r}(R)=[H_{\mathfrak{m}}^{r}(R)]_{0}$
for every
$r<n=\dim R$
, then
$[H^{r}(\text{}\underline{x},R)]_{0}\cong H_{\mathfrak{m}}^{r}(R)$
for every
$r<n$
and every homogeneous system of parameters
$\text{}\underline{x}=x_{1},\ldots ,x_{n}$
, where
$H^{r}(\text{}\underline{x},R)$
denotes the
$r$
th Koszul cohomology of
$\text{}\underline{x}$
. In other words, it is not necessary to take a direct limit when computing the local cohomology.
Proof. We fix
$\text{}\underline{x}=x_{1},\ldots ,x_{n}$
, a homogeneous system of parameters. Let
$\deg x_{i}=d_{i}>0$
. Consider the graded Koszul complex
$$\begin{eqnarray}K_{\boldsymbol{\cdot }}:0\rightarrow R(-d_{1}-d_{2}-\cdots -d_{n})\rightarrow \cdots \rightarrow \oplus R(-d_{i})\rightarrow R\rightarrow 0.\end{eqnarray}$$
After we apply
$\operatorname{Hom}_{R}(-,R)$
, we obtain the graded Koszul cocomplex
$$\begin{eqnarray}K^{\boldsymbol{\cdot }}:0\rightarrow R\rightarrow \oplus R(d_{i})\rightarrow \cdots \rightarrow R(d_{1}+d_{2}+\cdots +d_{n})\rightarrow 0.\end{eqnarray}$$
We note that
$K^{\boldsymbol{\cdot }}$
lives in cohomology degree
$0,1,\ldots ,n$
.
Let
$\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }}$
be the graded normalized dualizing complex of
$R$
; thus,
$\unicode[STIX]{x1D714}_{R}=h^{-n}\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }}$
is the graded canonical module of
$R$
. Let
$(-)^{\ast }=\operatorname{Hom}_{R}(-,^{\ast }E)$
, where
$^{\ast }E$
is the graded injective hull of
$k$
. We have a triangle
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{R}[n]\rightarrow \unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }}\rightarrow \unicode[STIX]{x1D70F}_{{>}-n}\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }}\xrightarrow[{}]{+1}.\end{eqnarray}$$
Applying
$\mathbf{R}\operatorname{Hom}_{R}(K^{\boldsymbol{\cdot }},-)$
, we get
$$\begin{eqnarray}\mathbf{R}\operatorname{Hom}_{R}(K^{\boldsymbol{\cdot }},\unicode[STIX]{x1D714}_{R}[n])\rightarrow \mathbf{R}\operatorname{Hom}_{R}(K^{\boldsymbol{\cdot }},\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }})\rightarrow \mathbf{R}\operatorname{Hom}_{R}(K^{\boldsymbol{\cdot }},\unicode[STIX]{x1D70F}_{{>}-n}\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }})\xrightarrow[{}]{+1}.\end{eqnarray}$$
Applying
$\operatorname{Hom}_{R}(-,^{\ast }E)$
and using graded local duality, we obtain
$$\begin{eqnarray}\mathbf{R}\operatorname{Hom}_{R}(K^{\boldsymbol{\cdot }},\unicode[STIX]{x1D70F}_{{>}-n}\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }})^{\ast }\rightarrow K^{\boldsymbol{\cdot }}\rightarrow \mathbf{R}\operatorname{Hom}_{R}(K^{\boldsymbol{\cdot }},\unicode[STIX]{x1D714}_{R}[n])^{\ast }\xrightarrow[{}]{+1}.\end{eqnarray}$$
Note that
$\mathbf{R}\operatorname{Hom}_{R}(K^{\boldsymbol{\cdot }},\unicode[STIX]{x1D714}_{R}[n])^{\ast }$
lives in cohomological degree
$n,n+1,\ldots ,2n$
; hence, we obtain a graded isomorphism in the derived category:
$$\begin{eqnarray}\unicode[STIX]{x1D70F}^{{<}n}K^{\boldsymbol{\cdot }}\cong \unicode[STIX]{x1D70F}^{{<}n}\mathbf{R}\operatorname{Hom}_{R}(K^{\boldsymbol{\cdot }},\unicode[STIX]{x1D70F}_{{>}-n}\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }})^{\ast }.\end{eqnarray}$$
Therefore, for every
$r<n$
, we have
$$\begin{eqnarray}h^{r}(K^{\boldsymbol{\cdot }})\cong h^{r}(\mathbf{R}\operatorname{Hom}_{R}(K^{\boldsymbol{\cdot }},\unicode[STIX]{x1D70F}_{{>}-n}\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }})^{\ast }).\end{eqnarray}$$
At this point, notice that
$H_{\mathfrak{m}}^{r}(R)=[H_{\mathfrak{m}}^{r}(R)]_{0}$
for every
$r<n$
implies that
$R$
is Buchsbaum by [Reference SchenzelSch82, Theorem 3.1]. This means that
$\unicode[STIX]{x1D70F}_{{>}-n}\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }}$
is quasi-isomorphic to a complex of graded
$k$
-vector spaces. Moreover, we know that all these graded vector spaces have degree
$0$
because
$H_{\mathfrak{m}}^{i}(R)=[H_{\mathfrak{m}}^{i}(R)]_{0}$
for every
$i<n$
. In other words, we have
$$\begin{eqnarray}\unicode[STIX]{x1D70F}_{{>}-n}\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }}\cong 0\rightarrow k^{s_{n-1}}\rightarrow k^{s_{n-2}}\rightarrow \cdots \rightarrow k^{s_{1}}\rightarrow k^{s_{0}}\rightarrow 0,\end{eqnarray}$$
where the complex on the right-hand side has zero differentials and
$k^{s_{i}}$
has internal degree
$0$
and sits in cohomology degree
$-i$
, with
$s_{i}=\dim _{k}[H_{\mathfrak{m}}^{i}(R)]_{0}$
.
Recall that
$d_{i}>0$
; hence, by keeping track of the internal degrees, we see that
$$\begin{eqnarray}[\mathbf{R}\operatorname{Hom}_{R}(K^{\boldsymbol{\cdot }},\unicode[STIX]{x1D70F}_{{>}-n}\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }})]_{0}\cong \unicode[STIX]{x1D70F}_{{>}-n}\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }}.\end{eqnarray}$$
Now, by graded local duality, we have
$$\begin{eqnarray}[H^{r}(\text{}\underline{x},R)]_{0}=[h^{r}(K^{\boldsymbol{\cdot }})]_{0}\cong [h^{r}(\mathbf{R}\operatorname{Hom}_{R}(K^{\boldsymbol{\cdot }},\unicode[STIX]{x1D70F}_{{>}-n}\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }})^{\ast })]_{0}\cong h^{r}((\unicode[STIX]{x1D70F}_{{>}n}\unicode[STIX]{x1D714}_{R}^{\boldsymbol{\cdot }})^{\ast })\cong H_{\mathfrak{ m}}^{r}(R)\end{eqnarray}$$
for every
$r<n$
. This finishes the proof.◻
Now we can prove the following extension of the main result of [Reference Hochster and RobertsHR76].
Corollary 4.13. Let
$R$
be a Noetherian
$\mathbb{N}$
-graded
$(R_{0}=k)$
-algebra with
$\mathfrak{m}$
the unique homogeneous maximal ideal. Suppose that
$R$
is equidimensional and Cohen–Macaulay on
$\operatorname{Spec}R-\{\mathfrak{m}\}$
. Assume one of the following:
-
(a)
$k$
has characteristic
$p>0$
and
$R$
is
$F$
-injective; -
(b)
$k$
has characteristic
$0$
and
$R$
is Du Bois.
Then
$[H^{r}(\text{}\underline{x},R)]_{0}\cong H_{\mathfrak{m}}^{r}(R)$
for every
$r<n=\dim R$
and every homogeneous system of parameters
$\text{}\underline{x}=x_{1},\ldots ,x_{n}$
, where
$H^{r}(\text{}\underline{x},R)$
denotes the
$r$
th Koszul cohomology of
$\text{}\underline{x}$
. In other words, it is not necessary to take a direct limit when computing the local cohomology.
Proof. Since
$R$
is equidimensional and Cohen–Macaulay on the punctured spectrum, we know that
$H_{\mathfrak{m}}^{r}(R)$
has finite length for every
$r<n=\dim R$
. We will show that
$H_{\mathfrak{m}}^{r}(R)=[H_{\mathfrak{m}}^{r}(R)]_{0}$
for every
$r<n$
in situation (a) or (b). This will finish the proof by Theorem 4.12.
In situation (a),
$H_{\mathfrak{m}}^{r}(R)=[H_{\mathfrak{m}}^{r}(R)]_{0}$
is obvious because
$H_{\mathfrak{m}}^{r}(R)$
has finite length and the Frobenius acts injectively on it. In situation (b), notice that
$[H_{\mathfrak{m}}^{r}(R)]_{{<}0}=0$
by Theorem 4.8 while
$[H_{\mathfrak{m}}^{r}(R)]_{{>}0}=0$
by Theorem 4.4; hence,
$H_{\mathfrak{m}}^{r}(R)=[H_{\mathfrak{m}}^{r}(R)]_{0}$
.◻
Remark 4.14. In situation (b) above, if
$R$
is normal standard graded, then
$H_{\mathfrak{m}}^{r}(R)=[H_{\mathfrak{m}}^{r}(R)]_{0}$
also follows from [Reference MaMa15, Theorem 4.5]. However, in the above proof we do not need any normal or standard graded hypothesis thanks to Proposition 4.4 and Theorem 4.8.
Remark 4.15. Corollary 4.13 was proved when
$R$
is
$F$
-pure and
$k$
is perfect in [Reference Hochster and RobertsHR76, Theorem 1.1] and, by a technical reduction to a
$p>0$
technique, it was also proved when
$R$
is of
$F$
-pure type [Reference Hochster and RobertsHR76, Theorem 4.8]. Since
$F$
-pure certainly implies
$F$
-injective and
$F$
-injective type implies Du Bois (see [Reference SchwedeSch09]), our theorem gives a generalization of Hochster–Roberts’s result, and our proof is quite different from that of [Reference Hochster and RobertsHR76].
We end this section by pointing out an example showing that in Theorem 4.12 or Corollary 4.13, it is possible that
$H^{r}(\text{}\underline{x},R)\neq H_{\mathfrak{m}}^{r}(R)$
, i.e., we must take the degree-0 piece of the Koszul cohomology. This is a variant of Example 4.11.
Example 4.16. Let
$R=(k[x,y,z]/(x^{3}+y^{3}+z^{3}))\#k[a,b,c]$
be the Segre product of
$k[x,y,z]/(x^{3}+y^{3}+z^{3})$
and
$k[a,b,c]$
, where the characteristic of
$k$
is either 0 or congruent to
$1$
mod
$3$
. Therefore,
$R$
is the homogeneous coordinate ring of the Segre embedding of
$X=E\times \mathbb{P}^{2}$
to
$\mathbb{P}^{8}$
, where
$E=\operatorname{Proj}(k[x,y,z]/(x^{3}+y^{3}+z^{3}))$
is an elliptic curve. Notice that
$\dim X=3$
and
$\dim R=4$
. Since
$R$
has an isolated singularity, it is Cohen–Macaulay on the punctured spectrum. It is easy to check that
$R$
is Du Bois in characteristic
$0$
and
$F$
-pure (and thus
$F$
-injective) in characteristic
$p>0$
, since
$p\equiv 1$
mod
$3$
. So, we know that
$H_{\mathfrak{m}}^{i}(R)=[H_{\mathfrak{m}}^{i}(R)]_{0}$
for every
$i<4$
, where
$\mathfrak{m}$
is the unique homogeneous maximal ideal of
$R$
. Now we compute
$$\begin{eqnarray}\displaystyle H_{\mathfrak{m}}^{2}(R) & = & \displaystyle [H_{\mathfrak{m}}^{2}(R)]_{0}=H^{1}(X,{\mathcal{O}}_{X})=\bigoplus _{i+j=1}H^{i}(E,{\mathcal{O}}_{E})\otimes _{k}H^{j}(\mathbb{P}^{2},{\mathcal{O}}_{\mathbb{P}^{2}})\cong k,\nonumber\\ \displaystyle H_{\mathfrak{m}}^{3}(R) & = & \displaystyle [H_{\mathfrak{m}}^{3}(R)]_{0}=H^{2}(X,{\mathcal{O}}_{X})=\bigoplus _{i+j=2}H^{i}(E,{\mathcal{O}}_{E})\otimes _{k}H^{j}(\mathbb{P}^{2},{\mathcal{O}}_{\mathbb{P}^{2}})=0.\nonumber\end{eqnarray}$$
The first line shows that
$R$
is not Cohen–Macaulay (actually, we have
$\operatorname{depth}R=2$
), so for any homogeneous system of parameters
$\text{}\underline{x}$
of
$R$
, we have
$H^{3}(\text{}\underline{x},R)\cong H_{1}(\text{}\underline{x},R)\neq 0$
. Hence,
$H^{3}(\text{}\underline{x},R)\neq H_{\mathfrak{m}}^{3}(R)$
.
5 Deformation of dense
$F$
-injective type
In this section we use results in §3 to prove that singularities of (dense)
$F$
-injective type in characteristic
$0$
deform. In fact, we prove a slightly stronger result. Our motivation for studying this question is a recent result of Kovács and Schwede [Reference Kovács and SchwedeKS16a] that Du Bois singularities in characteristic
$0$
deform.
By the main result of [Reference SchwedeSch09], singularities of dense
$F$
-injective type are always Du Bois. It is conjectured [Reference Bhatt, Schwede and TakagiBST13, Conjecture 4.1] that Du Bois singularities should be equivalent to singularities of dense
$F$
-injective type. This conjecture is equivalent to the weak ordinarity conjecture of Mustaţă and Srinivas [Reference Mustaţă and SrinivasMS11]. If this conjecture is true, then singularities of dense
$F$
-injective type deform because Du Bois singularities deform [Reference Kovács and SchwedeKS16a]. However, the weak ordinarity conjecture is wide open.
Setup 5.1 (Reduction to characteristic
$p>0$
).
We recall briefly reduction to characteristic
$p>0$
. For more details in our setting, see [Reference Hochster and HunekeHH06, §2.1] and [Reference SchwedeSch09, §6].
Suppose that
$(R,\mathfrak{m})$
is essentially of finite type over
$\mathbb{C}$
(or another field of characteristic
$0$
, which we will also call
$\mathbb{C}$
), so that
$(R,\mathfrak{m})$
is a homomorphic image of
$T_{P}$
, where
$T=\mathbb{C}[x_{1},\ldots ,x_{t}]$
and
$P\subseteq T$
is a prime ideal, so that
$R=(T/J)_{P}$
. Given a finite collection of finitely generated
$R$
-modules
$M_{i}$
(and finitely many maps between them), we may assume that each
$M_{i}=(M_{i}^{\prime })_{P}$
for a finitely generated
$T$
-module
$M_{i}^{\prime }$
annihilated by
$J$
. Suppose that
$E\rightarrow \operatorname{Spec}T/J$
is the reduced preimage of
$T/J$
in a log resolution of
$(\operatorname{Spec}T,\operatorname{Spec}T/J)$
. We also keep track of
$E\rightarrow \operatorname{Spec}T/J$
in the reduction to characteristic
$p>0$
process, as well as the modules
$h^{i}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{T/J}^{0})=\mathbf{R}^{i}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{E}$
. Assume that
$x$
is the image of
$h(x_{1},\ldots ,x_{t})\in T$
(note that if
$x$
has a problematic denominator, we can replace
$x$
by another element that generates the same ideal and does not have a denominator).
We pick a finitely generated regular
$\mathbb{Z}$
-algebra
$A\subseteq \mathbb{C}$
such that the coefficients of the generators of
$P$
, the coefficients of
$h$
, the coefficients of
$J$
and the coefficients of a presentation of the
$M_{i}^{\prime }$
are contained in
$A$
. Form
$T_{A}=A[x_{1},\ldots ,x_{t}]$
and let
$P_{A}=P\cap T_{A},J_{A}=J\cap T_{A}$
and observe that
$P_{A}\otimes _{A}\mathbb{C}=P,J_{A}\otimes _{A}\mathbb{C}=J$
by construction. Note that by generic flatness, we can replace
$A$
by
$A[b^{-1}]$
and so shrink
$\operatorname{Spec}A$
if necessary to assume that
$R_{A}$
is a flat
$A$
-module and
$x$
is a non-zero divisor on
$R_{A}$
. Likewise form
$(M_{i}^{\prime })_{A}$
with the same presentation matrix of
$M_{i}^{\prime }$
(and likewise with maps between the modules) and form
$E_{A}\rightarrow \operatorname{Spec}T_{A}/J_{A}$
, so that
$(M_{i}^{\prime })_{A}\otimes _{A}\mathbb{C}=M_{i}^{\prime }$
and that
$(\mathbf{R}^{i}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{E_{A}})\otimes _{A}\mathbb{C}=(\mathbf{R}^{i}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{E_{A}})$
. Shrinking
$\operatorname{Spec}A$
yet again if necessary, we can assume that all these modules are flat over
$A$
(and that any relevant kernels and cokernels of the finitely many maps between them are also flat).
We now mod out by a maximal ideal
$\mathfrak{n}$
of
$A$
with
$\unicode[STIX]{x1D705}=A/\mathfrak{n}$
. In particular, we use
$R_{A}=(T_{A}/J_{A})_{P_{A}}$
etc. and
$R_{\unicode[STIX]{x1D705}}$
,
$T_{\unicode[STIX]{x1D705}}$
,
$E_{\unicode[STIX]{x1D705}}$
etc. to denote the corresponding rings, schemes and modules over
$A$
and
$\unicode[STIX]{x1D705}$
, where
$\unicode[STIX]{x1D705}=A/\mathfrak{n}$
for
$\mathfrak{n}$
a maximal ideal in
$A$
. Since all relevant kernels and cokernels of the maps are flat by shrinking
$\operatorname{Spec}A$
,
$x$
is a non-zero divisor on
$R_{\unicode[STIX]{x1D705}}$
for every
$\unicode[STIX]{x1D705}$
.
We also need a slightly different version of the main result of [Reference SchwedeSch09]. In that paper, it was assumed that if
$R$
is of finite type over a field of characteristic
$0$
, and of dense
$F$
-injective type, then
$R$
has Du Bois singularities. We need a version of this result in which
$R$
is local. The reason is, that, in the notation of Theorem 5.3, if
$R$
is of finite type, and
$R_{p}/x_{p}R_{p}$
is
$F$
-injective, then for
$p$
sufficiently divisible, we obtain that
$R_{p}$
is
$F$
-injective in a neighborhood of
$V(x_{p})$
. The problem is that we do not know how to control these neighborhoods as
$p$
varies. Thus, we need the following preliminary result. In particular, we do not know whether having dense
$F$
-injective type is an open property in characteristic
$0$
.
Theorem 5.2. Let
$(R,\mathfrak{m})$
be a local ring essentially of finite type over
$\mathbb{C}$
and suppose that
$R$
has dense
$F$
-injective type. Then
$R$
is Du Bois.
The strategy is the same as in [Reference SchwedeSch09]; indeed, the proof only differs in how carefully we keep track of a minimal prime of the non-Du Bois locus.
Sketch of the proof.
It is easy to see that
$R$
is seminormal, so we need to show that
$h^{i}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{R}^{0})=0$
for all
$i>0$
. We use the notation of Setup 5.1. Let
$Q_{\mathbb{C}}\subseteq P\subseteq T/J$
correspond to a minimal prime of the non-Du Bois locus of
$(R,\mathfrak{m})$
, so that
$h^{i}(\text{}\underline{\unicode[STIX]{x1D6FA}}_{(T/J)_{Q_{\mathbb{C}}}}^{0})=h^{i}(\mathbf{R}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{E})_{Q_{\mathbb{C}}}$
has finite length for
$i>0$
. Since
$(R,\mathfrak{m})$
has dense
$F$
-injective type, it is easy to see that so does
$(R_{Q_{\mathbb{C}}},Q_{\mathbb{C}}R_{Q_{\mathbb{C}}})$
, so we may assume that
$\mathfrak{m}=Q_{\mathbb{C}}$
. Now using Setup 5.1, reduce to some model so that
$(R_{\unicode[STIX]{x1D705}},\mathfrak{m}_{\unicode[STIX]{x1D705}})$
is
$F$
-injective. The proof now follows exactly that of [Reference SchwedeSch09, Proof 6.1], where we obtain that
$$\begin{eqnarray}h^{i}(\mathbf{R}(\unicode[STIX]{x1D70B}_{\unicode[STIX]{x1D705}})_{\ast }{\mathcal{O}}_{E_{\unicode[STIX]{x1D705}}})_{Q_{\unicode[STIX]{x1D705}}}{\hookrightarrow}H_{Q_{\unicode[STIX]{x1D705}}}^{i+1}(R_{\unicode[STIX]{x1D705}}).\end{eqnarray}$$
But the left-hand side is annihilated by a power of Frobenius by [Reference SchwedeSch09, Theorem 7.1] and Frobenius acts injectively on the right by hypothesis. The result follows. ◻
Theorem 5.3. Let
$(R,\mathfrak{m})$
be a local ring essentially of finite type over
$\mathbb{C}$
and let
$x$
be a non-zero divisor on
$R$
. Suppose that
$R/xR$
has dense
$F$
-injective type. Then, for infinitely many
$p>0$
, the Frobenius action
$x^{p-1}F$
on
$H_{\mathfrak{m}_{p}}^{i}(R_{p})$
is injective for every
$i$
, where
$(R_{p},\mathfrak{m}_{p})$
is the reduction mod
$p$
of
$R$
. In particular,
$R$
has dense
$F$
-injective type.
Proof. By Theorem 5.2,
$R/xR$
has Du Bois singularities. By Theorem 3.6 (taking
$Z=\emptyset$
),
$H_{\mathfrak{m}}^{i}(R)\xrightarrow[{}]{\cdot x}H_{\mathfrak{m}}^{i}(R)$
surjects for all
$i$
. By Matlis duality,
$\operatorname{Ext}_{T}^{i}(R,T)\xrightarrow[{}]{\cdot x}\operatorname{Ext}^{i}(R,T)$
injects for all
$i$
. Spreading this out to
$A$
, and possibly inverting an element of
$A$
, we see that
$\operatorname{Ext}_{T_{A}}^{i}(R_{A},T_{A})\xrightarrow[{}]{\cdot x}\operatorname{Ext}_{T_{A}}^{i}(R_{A},T_{A})$
injects for all
$i$
(note that there are only finitely many
$\operatorname{Ext}$
to consider). Inverting another element of
$A$
if necessary, we deduce that
$$\begin{eqnarray}\operatorname{Ext}_{T_{\unicode[STIX]{x1D705}}}^{i}(R_{\unicode[STIX]{x1D705}},T_{\unicode[STIX]{x1D705}})\xrightarrow[{}]{\cdot x}\operatorname{Ext}_{T_{\unicode[STIX]{x1D705}}}^{i}(R_{\unicode[STIX]{x1D705}},T_{\unicode[STIX]{x1D705}})\end{eqnarray}$$
injects for every
$i$
and each maximal ideal
$\mathfrak{n}\subseteq A$
, setting
$\unicode[STIX]{x1D705}=A/\mathfrak{n}$
. We abuse notation and let
$x$
denote the image of
$x$
in
$R_{\unicode[STIX]{x1D705}}$
. Applying Matlis duality again and considering the Frobenius on the local cohomology modules, we have the following collection of short exact sequences for each
$i$
:
where
$p$
is the characteristic of
$\unicode[STIX]{x1D705}$
and
$F$
denotes the natural Frobenius action on
$H_{\mathfrak{m}_{\unicode[STIX]{x1D705}}}^{i}(R_{\unicode[STIX]{x1D705}}/xR_{\unicode[STIX]{x1D705}})$
and
$H_{\mathfrak{m}_{\unicode[STIX]{x1D705}}}^{i+1}(R_{\unicode[STIX]{x1D705}})$
.
At this point, recall that
$R/xR$
has dense
$F$
-injective type. It follows that for infinitely many
$p>0$
, if the residue field
$\unicode[STIX]{x1D705}$
of
$A$
has characteristic
$p>0$
, then the natural Frobenius action on
$H_{\mathfrak{m}_{\unicode[STIX]{x1D705}}}^{i}(R_{\unicode[STIX]{x1D705}}/xR_{\unicode[STIX]{x1D705}})$
is injective for every
$i$
. Now chasing the above diagram, if
$x^{p-1}F$
is not injective, then we can pick
$0\neq y\in \operatorname{socle}(H_{\mathfrak{m}_{\unicode[STIX]{x1D705}}}^{i+1}(R_{\unicode[STIX]{x1D705}}))\cap \ker (x^{p-1}F)$
. Since
$y$
is in the socle of
$H_{\mathfrak{m}_{\unicode[STIX]{x1D705}}}^{i+1}(R_{\unicode[STIX]{x1D705}})$
, it maps to zero under multiplication by
$x$
. But then
$0\neq y\in H_{\mathfrak{m}_{\unicode[STIX]{x1D705}}}^{i}(R_{\unicode[STIX]{x1D705}}/xR_{\unicode[STIX]{x1D705}})$
, and chasing the diagram we find that
$x^{p-1}F(y)\neq 0$
, which is a contradiction.
We have established that for infinitely many
$p$
, after we do reduction to
$p$
, the Frobenius action
$x^{p-1}F$
on
$H_{\mathfrak{m}_{\unicode[STIX]{x1D705}}}^{i+1}(R_{\unicode[STIX]{x1D705}})$
is injective for every
$i$
. This certainly implies that the natural Frobenius action
$F$
on
$H_{\mathfrak{m}_{\unicode[STIX]{x1D705}}}^{i+1}(R_{\unicode[STIX]{x1D705}})$
is injective for every
$i$
. Hence,
$R$
has dense
$F$
-injective type.◻
Remark 5.4. It is still unknown whether
$F$
-injective singularities in characteristic
$p>0$
deform (and this has been open since [Reference FedderFed83]). Our theorem is in support of this conjecture: it shows that this is true ‘in characteristic
$p\gg 0$
’. For the most recent progress on deformation of
$F$
-injectivity in characteristic
$p>0$
, we refer to [Reference Horiuchi, Miller and ShimomotoHMS14]. On the other hand, Theorem 5.3 provides evidence for the weak ordinarity conjecture [Reference Mustaţă and SrinivasMS11] because of the relation between the weak ordinarity conjecture and the conjecture that Du Bois singularities have dense
$F$
-injective type [Reference Bhatt, Schwede and TakagiBST13].
Acknowledgements
The authors are thankful to Sándor Kovács, Shunsuke Takagi and the referee for valuable discussions and comments on a previous draft of the paper. We would like to thank Pham Hung Quy for discussions which motivated the proof of Theorem 3.8. We also thank Zsolt Patakfalvi, Anurag K. Singh and Kevin Tucker for valuable discussions.
