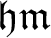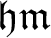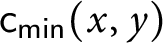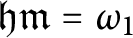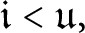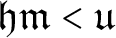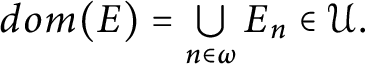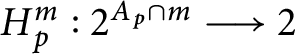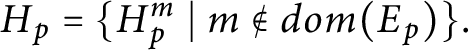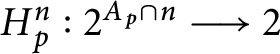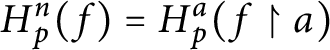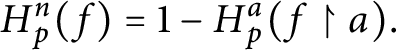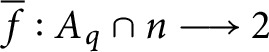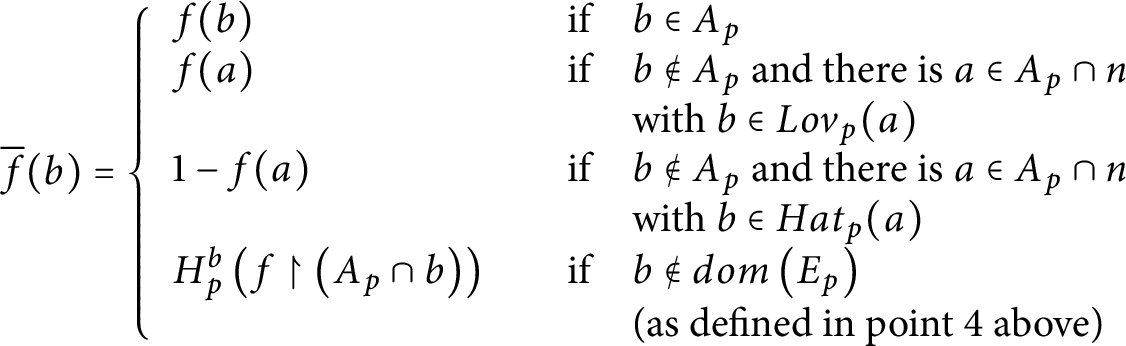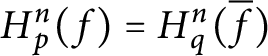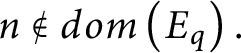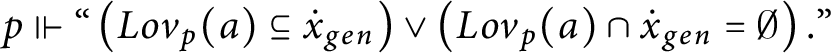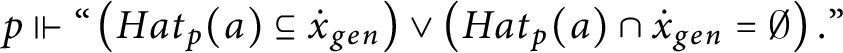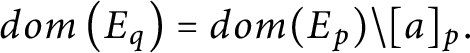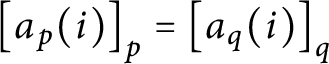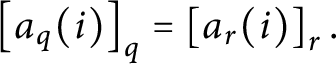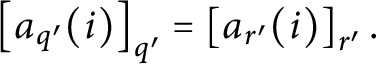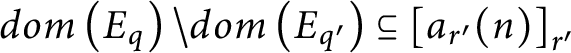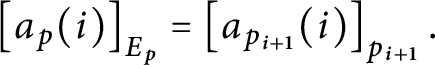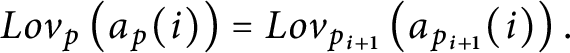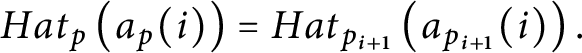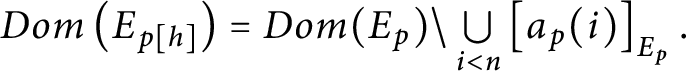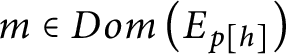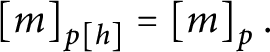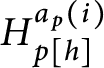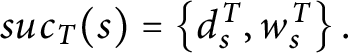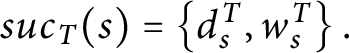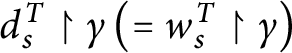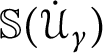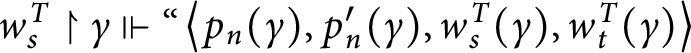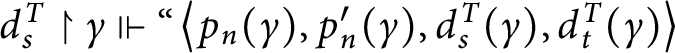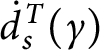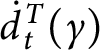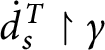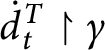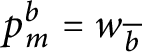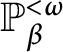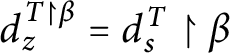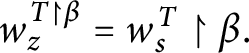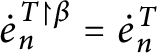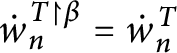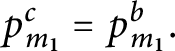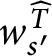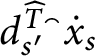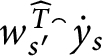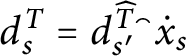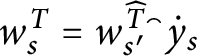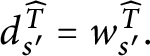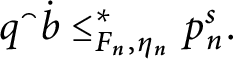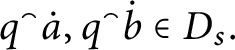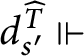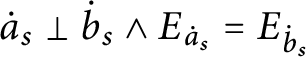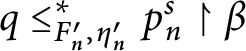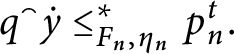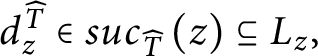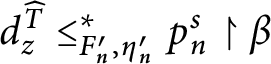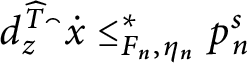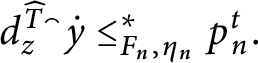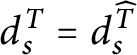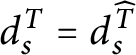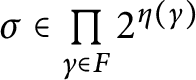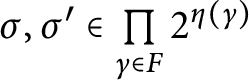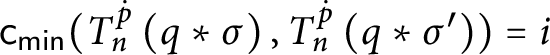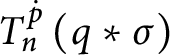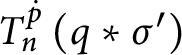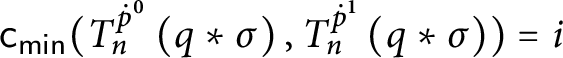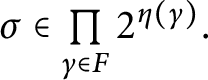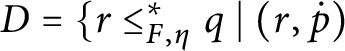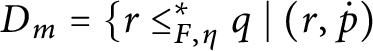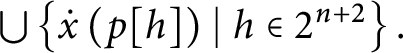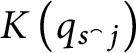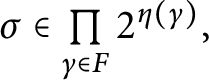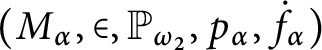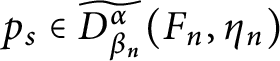1 Introduction
In [Reference Geschke9], Geschke et al. defined the coloring
![]() $\mathsf {c} _{\mathsf {min}}:[ 2^{\omega }] ^{2}\longrightarrow 2$
given by
$\mathsf {c} _{\mathsf {min}}:[ 2^{\omega }] ^{2}\longrightarrow 2$
given by
![]() $\mathsf {c}_{\mathsf {min}}( x,y) =0$
if
$\mathsf {c}_{\mathsf {min}}( x,y) =0$
if
![]() $\triangle ( x,y) $
is even and
$\triangle ( x,y) $
is even and
![]() $\mathsf {c}_{\mathsf {min}}( x,y) =1$
in case
$\mathsf {c}_{\mathsf {min}}( x,y) =1$
in case
![]() $\triangle ( x,y) $
is odd (where
$\triangle ( x,y) $
is odd (where
![]() $\triangle ( x,y) $
is the length of the largest initial segment that x and y have in common). They defined the cardinal invariant
$\triangle ( x,y) $
is the length of the largest initial segment that x and y have in common). They defined the cardinal invariant
![]() $\mathfrak {hm}$
as the smallest size of a family of
$\mathfrak {hm}$
as the smallest size of a family of
![]() $\mathsf {c}_{\mathsf {min}}$
-monochromatic sets that covers
$\mathsf {c}_{\mathsf {min}}$
-monochromatic sets that covers
![]() $2^{\omega }.$
Since every
$2^{\omega }.$
Since every
![]() $\mathsf {c}_{\mathsf {min}} $
-monochromatic set is nowhere dense, it follows that
$\mathsf {c}_{\mathsf {min}} $
-monochromatic set is nowhere dense, it follows that
![]() $\mathsf{cov}( \mathcal {M}) \leq \mathfrak {hm}$
(by
$\mathsf{cov}( \mathcal {M}) \leq \mathfrak {hm}$
(by
![]() $\mathsf{cov}( \mathcal {M}) $
, we denote the smallest family of meager sets that are needed to cover
$\mathsf{cov}( \mathcal {M}) $
, we denote the smallest family of meager sets that are needed to cover
![]() $2^{\omega }$
). However, the cardinal invariant
$2^{\omega }$
). However, the cardinal invariant
![]() $\mathfrak {hm}$
may be much larger than
$\mathfrak {hm}$
may be much larger than
![]() $\mathsf{cov}( \mathcal {M}) :$
$\mathsf{cov}( \mathcal {M}) :$
Proposition 1 [Reference Jorge, Fischer, Guzmán and Jaroslav7, Reference Geschke9]
![]() $\mathsf{cof}( \mathcal {N}) ,\mathfrak {c}^{-}\leq \mathfrak {hm}$
(where
$\mathsf{cof}( \mathcal {N}) ,\mathfrak {c}^{-}\leq \mathfrak {hm}$
(where
![]() $\mathfrak {c} ^{-}=\mathfrak {c}$
if
$\mathfrak {c} ^{-}=\mathfrak {c}$
if
![]() $\mathfrak {c}$
is a limit cardinal and if
$\mathfrak {c}$
is a limit cardinal and if
![]() $\mathfrak {c} =\kappa ^{+}$
then
$\mathfrak {c} =\kappa ^{+}$
then
![]() $\mathfrak {c}^{-}=\kappa $
).
$\mathfrak {c}^{-}=\kappa $
).
Above,
![]() $\mathsf{cof}( \mathcal {N}) $
denotes the cofinality of the ideal of Lebesgue-null subsets of
$\mathsf{cof}( \mathcal {N}) $
denotes the cofinality of the ideal of Lebesgue-null subsets of
![]() $2^{\omega }.$
Therefore,
$2^{\omega }.$
Therefore,
![]() $\mathfrak {hm}$
is bigger than all the cardinal invariants that appear in the Cichoń diagram (see [Reference Bartoszyński and Judah2, Reference Blass3]). On the other hand, it is known that the inequality
$\mathfrak {hm}$
is bigger than all the cardinal invariants that appear in the Cichoń diagram (see [Reference Bartoszyński and Judah2, Reference Blass3]). On the other hand, it is known that the inequality
![]() $\mathfrak {hm<c}$
is consistent; in fact, it holds in the Sacks model [Reference Geschke9] and in the Miller lite model [Reference Jorge, Fischer, Guzmán and Jaroslav7]. It is interesting to compare it with the other cardinal invariants of the continuum. The following is an interesting open problem of Thilo Weinert:
$\mathfrak {hm<c}$
is consistent; in fact, it holds in the Sacks model [Reference Geschke9] and in the Miller lite model [Reference Jorge, Fischer, Guzmán and Jaroslav7]. It is interesting to compare it with the other cardinal invariants of the continuum. The following is an interesting open problem of Thilo Weinert:
Problem 2 (Weinert)
Is the inequality
![]() $\mathfrak {hm<r}$
consistent?
$\mathfrak {hm<r}$
consistent?
Where
![]() $\mathfrak {r}$
denotes the smallest size of a reaping family, i.e., the smallest size of a family
$\mathfrak {r}$
denotes the smallest size of a reaping family, i.e., the smallest size of a family
![]() $\mathcal {R}\subseteq [ \omega ] ^{\omega }$
such that for every
$\mathcal {R}\subseteq [ \omega ] ^{\omega }$
such that for every
![]() $A\in [ \omega ] ^{\omega },$
there is
$A\in [ \omega ] ^{\omega },$
there is
![]() $R\in \mathcal {R}$
such that either
$R\in \mathcal {R}$
such that either
![]() $R\subseteq ^{\ast }A$
or
$R\subseteq ^{\ast }A$
or
![]() $R\subseteq ^{\ast }\omega \setminus A.$
This problem is still open. Weinert made some interesting advances with respect to the question in his thesis (and it was after reading the first chapters of his thesis that the author became interested on the topic). In his thesis, he asked the following:
$R\subseteq ^{\ast }\omega \setminus A.$
This problem is still open. Weinert made some interesting advances with respect to the question in his thesis (and it was after reading the first chapters of his thesis that the author became interested on the topic). In his thesis, he asked the following:
Problem 3 (Weinert)
Is the inequality
![]() $\mathfrak {hm<u}$
consistent?
$\mathfrak {hm<u}$
consistent?
Where
![]() $\mathfrak {u}$
denotes the ultrafilter number, the smallest size of a base of an ultrafilterFootnote
1
in
$\mathfrak {u}$
denotes the ultrafilter number, the smallest size of a base of an ultrafilterFootnote
1
in
![]() $\omega .$
In this note, we will provide a positive answer to the question. Since
$\omega .$
In this note, we will provide a positive answer to the question. Since
![]() $\mathfrak {r\leq u}$
our solution to may be viewed as a partial solution to the first problem.
$\mathfrak {r\leq u}$
our solution to may be viewed as a partial solution to the first problem.
In [Reference Shelah13], Shelah built a model of
![]() $\mathfrak {i<u}$
and we will prove that
$\mathfrak {i<u}$
and we will prove that
![]() $\mathfrak {hm<u}$
holds in that model too. A variant of the forcing of Shelah was recently used in [Reference Chodounský, Fischer and Grebík5] by Chodounský et al. in order to show that the inequality
$\mathfrak {hm<u}$
holds in that model too. A variant of the forcing of Shelah was recently used in [Reference Chodounský, Fischer and Grebík5] by Chodounský et al. in order to show that the inequality
![]() $\mathfrak {f<u}$
is consistent (
$\mathfrak {f<u}$
is consistent (
![]() $\mathfrak {f}$
is the free sequence number introduced by Monk, the reader may consult the interesting paper [Reference Chodounský, Fischer and Grebík5] for the definition of
$\mathfrak {f}$
is the free sequence number introduced by Monk, the reader may consult the interesting paper [Reference Chodounský, Fischer and Grebík5] for the definition of
![]() $\mathfrak {f}$
and will not be used in here).
$\mathfrak {f}$
and will not be used in here).
Recall that an infinite family
![]() $\mathcal {A\subseteq } [ \omega ] ^{\omega }$
is an almost disjoint family (
AD
) if the intersection of any two of its elements is finite and
$\mathcal {A\subseteq } [ \omega ] ^{\omega }$
is an almost disjoint family (
AD
) if the intersection of any two of its elements is finite and
![]() $\mathcal {A}$
is
$\mathcal {A}$
is
![]() $\mathsf {MAD}$
if it is maximal with this property. The almost disjointness number
$\mathsf {MAD}$
if it is maximal with this property. The almost disjointness number
![]() $\mathfrak {a}$
is defined as the smallest size of a
$\mathfrak {a}$
is defined as the smallest size of a
![]() $\mathsf {MAD}$
family. In the last part of the paper, we will prove that
$\mathsf {MAD}$
family. In the last part of the paper, we will prove that
![]() $\mathfrak {a}=\omega _{1}$
holds in the model of Shelah. In order to prove that there is small
$\mathfrak {a}=\omega _{1}$
holds in the model of Shelah. In order to prove that there is small
![]() $\mathsf {MAD}$
family in such model, we prove that Hrušák diamonds
$\mathsf {MAD}$
family in such model, we prove that Hrušák diamonds
![]() $\Diamond _{\mathfrak {d}}$
holds in there. This is enough since Hrušák proved that
$\Diamond _{\mathfrak {d}}$
holds in there. This is enough since Hrušák proved that
![]() $\Diamond _{\mathfrak {d}}$
implies that
$\Diamond _{\mathfrak {d}}$
implies that
![]() $\mathfrak {a}=\omega _{1}.$
$\mathfrak {a}=\omega _{1}.$
We would like to point out that the following problem of Weinert is still open:
Problem 4 (Weinert)
Is the inequality
![]() $\mathfrak {hm<a}$
consistent?
$\mathfrak {hm<a}$
consistent?
This problem seems very hard since the only known method to construct models of
![]() $\mathsf{cof}( \mathcal {N}) \mathfrak {<a}$
is with the aid of templates (see [Reference Brendle4, Reference Shelah15]) but this method does not seem to help with the question.
$\mathsf{cof}( \mathcal {N}) \mathfrak {<a}$
is with the aid of templates (see [Reference Brendle4, Reference Shelah15]) but this method does not seem to help with the question.
In a recent work with Cruz-Chapital et al., we obtained a different prove that
![]() $\mathfrak {a}=\omega _{1}$
holds in the model of Shelah mentioned above. In [Reference Ishiu12], it is proved that the Shelah forcing strongly preserves the tightness of
$\mathfrak {a}=\omega _{1}$
holds in the model of Shelah mentioned above. In [Reference Ishiu12], it is proved that the Shelah forcing strongly preserves the tightness of
![]() $\mathsf {MAD}$
families, which is a property that guarantees us that certain type of
$\mathsf {MAD}$
families, which is a property that guarantees us that certain type of
![]() $\mathsf {MAD}$
families are preserved (even in the iteration). The proof from [Reference Ishiu12] and the one from this paper are complementary. On the one hand, the argument of [Reference Ishiu12] is much simpler and it proves that there are tight
$\mathsf {MAD}$
families are preserved (even in the iteration). The proof from [Reference Ishiu12] and the one from this paper are complementary. On the one hand, the argument of [Reference Ishiu12] is much simpler and it proves that there are tight
![]() $\mathsf {MAD}$
families on the Shelah model. On the other hand, we get that
$\mathsf {MAD}$
families on the Shelah model. On the other hand, we get that
![]() $\Diamond _{\mathfrak {d}}$
holds in that model.
$\Diamond _{\mathfrak {d}}$
holds in that model.
We would like to mention that although the cardinal invariant
![]() $\mathfrak {hm}$
is not very well known, it is very interesting. We would like to mention some of the motivations for studying this invariant. Given a polish space X and a continuous coloring
$\mathfrak {hm}$
is not very well known, it is very interesting. We would like to mention some of the motivations for studying this invariant. Given a polish space X and a continuous coloring
![]() $c:[ X] ^{2}\longrightarrow 2,$
define
$c:[ X] ^{2}\longrightarrow 2,$
define
![]() $\mathfrak {hm}( c) $
as the smallest size of a family of c-monochromatic sets that cover
$\mathfrak {hm}( c) $
as the smallest size of a family of c-monochromatic sets that cover
![]() $X.$
Note that
$X.$
Note that
![]() $\mathfrak {hm=hm}( c_{\min }) .$
It turns out that
$\mathfrak {hm=hm}( c_{\min }) .$
It turns out that
![]() $\mathfrak {hm}$
and
$\mathfrak {hm}$
and
![]() $c_{\min }$
are critical in the study of continuous colorings, if
$c_{\min }$
are critical in the study of continuous colorings, if
![]() $c:[ X] ^{2}\longrightarrow 2$
is a continuous coloring such that
$c:[ X] ^{2}\longrightarrow 2$
is a continuous coloring such that
![]() $\mathfrak {hm}( c) $
is uncountable, then
$\mathfrak {hm}( c) $
is uncountable, then
![]() $\mathfrak {hm\leq hm}( c) $
Footnote
2
. Furthermore, the study of the cardinal invariants for continuous colorings has important implications in the study of the structure of nonconvex closed subsets of the Euclidean plane. This and more very interesting and deep results can be consulted in [Reference Jorge, Fischer, Guzmán and Jaroslav7–Reference Geschke9].
$\mathfrak {hm\leq hm}( c) $
Footnote
2
. Furthermore, the study of the cardinal invariants for continuous colorings has important implications in the study of the structure of nonconvex closed subsets of the Euclidean plane. This and more very interesting and deep results can be consulted in [Reference Jorge, Fischer, Guzmán and Jaroslav7–Reference Geschke9].
Our notation is mostly standard, with one important exemption. A tree
![]() $T\subseteq X^{<\omega }$
is a set closed under taking subsequences and the set of branches of T (denoted by
$T\subseteq X^{<\omega }$
is a set closed under taking subsequences and the set of branches of T (denoted by
![]() $[ T] $
) is the set
$[ T] $
) is the set
![]() $\left \{ f\in X^{\omega }\mid \forall n\in \omega \left ( f\upharpoonright n\in T\right ) \right \} .$
If
$\left \{ f\in X^{\omega }\mid \forall n\in \omega \left ( f\upharpoonright n\in T\right ) \right \} .$
If
![]() $s,t\in X^{<\omega },$
by
$s,t\in X^{<\omega },$
by
![]() $s^{\frown }t$
, we denote the concatenation of s and
$s^{\frown }t$
, we denote the concatenation of s and
![]() $t,$
if
$t,$
if
![]() $x\in X,$
we will often write
$x\in X,$
we will often write
![]() $s^{\frown }x$
instead of
$s^{\frown }x$
instead of
![]() $s^{\frown }\langle x\rangle .$
Given a tree
$s^{\frown }\langle x\rangle .$
Given a tree
![]() $T\subseteq X^{<\omega }$
and
$T\subseteq X^{<\omega }$
and
![]() $s\in T,$
define
$s\in T,$
define
![]() $suc_{T}( s) =\{ x\in X\mid s^{\frown }x\in T \} .$
Given
$suc_{T}( s) =\{ x\in X\mid s^{\frown }x\in T \} .$
Given
![]() $n\in \omega ,$
the n-level of T is defined as
$n\in \omega ,$
the n-level of T is defined as
![]() $T_{n}=\{ s\in T\mid \vert s\vert =n+1 \} $
Footnote
3
and let
$T_{n}=\{ s\in T\mid \vert s\vert =n+1 \} $
Footnote
3
and let
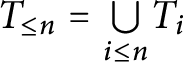 $T_{\leq n}= {\textstyle \bigcup \limits _{i\leq n}} T_{i} $
as well as
$T_{\leq n}= {\textstyle \bigcup \limits _{i\leq n}} T_{i} $
as well as
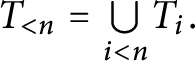 $T_{<n}= {\textstyle \bigcup \limits _{i<n}} T_{i}.$
Note that if
$T_{<n}= {\textstyle \bigcup \limits _{i<n}} T_{i}.$
Note that if
![]() $s=\left \langle x_{0},\ldots ,x_{n}\right \rangle \in T,$
then
$s=\left \langle x_{0},\ldots ,x_{n}\right \rangle \in T,$
then
![]() $s\in T_{n}.$
$s\in T_{n}.$
2 Shelah’s forcing with respect to an ultrafilter
Given a partial order
![]() $\mathbb {P}$
and an ultrafilter
$\mathbb {P}$
and an ultrafilter
![]() $\mathcal {U},$
we say that
$\mathcal {U},$
we say that
![]() $\mathbb {P}$
ultradestroys
$\mathbb {P}$
ultradestroys
![]() $\mathcal {U}$
if
$\mathcal {U}$
if
![]() $\mathbb {P}$
forces that
$\mathbb {P}$
forces that
![]() $\mathcal {U}$
is no longer the base for an ultrafilter. In [Reference Shelah13], Shelah designed a forcing to ultradestroy any given ultrafilter while causing “minimal damage” to the ground model.
$\mathcal {U}$
is no longer the base for an ultrafilter. In [Reference Shelah13], Shelah designed a forcing to ultradestroy any given ultrafilter while causing “minimal damage” to the ground model.
Definition 5 Let
![]() $\mathcal {U}$
be an ultrafilter. A set
$\mathcal {U}$
be an ultrafilter. A set
![]() $E=\left \{ E_{n}\mid n\in \omega \right \} \subseteq \wp ( \omega ) $
is called an
$E=\left \{ E_{n}\mid n\in \omega \right \} \subseteq \wp ( \omega ) $
is called an
![]() $\mathcal {U}$
-partition if E satisfies the following properties:
$\mathcal {U}$
-partition if E satisfies the following properties:
-
1. E is a pairwise disjoint family of elements of
 $\mathcal {U}^{\ast }$
(where
$\mathcal {U}^{\ast }$
(where
 $\mathcal {U}^{\ast }$
denotes the dual ideal of
$\mathcal {U}^{\ast }$
denotes the dual ideal of
 $\mathcal {U}$
, i.e.,
$\mathcal {U}$
, i.e.,
 $\mathcal {U}^{\ast }=\left \{ \omega \setminus A\mid A\in \mathcal {U}\right \} $
).
$\mathcal {U}^{\ast }=\left \{ \omega \setminus A\mid A\in \mathcal {U}\right \} $
). -
2.
 $dom( E ) =\bigcup \limits _{n\in \omega }E_{n}\in \mathcal {U}.$
$dom( E ) =\bigcup \limits _{n\in \omega }E_{n}\in \mathcal {U}.$
-
3. Each
 $E_{n}$
is nonempty.
$E_{n}$
is nonempty.
In other words, E is an
![]() $\mathcal {U}$
-partition if E is a partition of some element in
$\mathcal {U}$
-partition if E is a partition of some element in
![]() $\mathcal {U}$
such that all of its classes are in
$\mathcal {U}$
such that all of its classes are in
![]() $\mathcal {U}^{\ast }.$
Given
$\mathcal {U}^{\ast }.$
Given
![]() $a\in dom( E ) $
we define
$a\in dom( E ) $
we define
![]() $[ a] _{E}$
as the unique
$[ a] _{E}$
as the unique
![]() $E_{n}\in E$
such that
$E_{n}\in E$
such that
![]() $a\in E_{n}.$
Define
$a\in E_{n}.$
Define
![]() $A_{E}=\left \{ a_{E}( n) \mid n\in \omega \right \} $
, where
$A_{E}=\left \{ a_{E}( n) \mid n\in \omega \right \} $
, where
![]() $a_{E}( n) =min( E_{n}) $
and this set will be called the leaders of
$a_{E}( n) =min( E_{n}) $
and this set will be called the leaders of
![]() $E.$
We will always assume that if
$E.$
We will always assume that if
![]() $E=\{ E_{n}\mid n\in \omega \} $
is an
$E=\{ E_{n}\mid n\in \omega \} $
is an
![]() $\mathcal {U}$
-partition and
$\mathcal {U}$
-partition and
![]() $n<m,$
then
$n<m,$
then
![]() $a_{E}( n) <a_{E}( m ) .$
$a_{E}( n) <a_{E}( m ) .$
Definition 6 Let E and
![]() $E^{^{\prime }}$
be two
$E^{^{\prime }}$
be two
![]() $\mathcal {U}$
-partitions, we say that
$\mathcal {U}$
-partitions, we say that
![]() $E^{\prime }<_{part}E$
if every
$E^{\prime }<_{part}E$
if every
![]() $E^{\prime }$
-class is the union of E-classes.
$E^{\prime }$
-class is the union of E-classes.
Equivalently,
![]() $E^{\prime }$
can be constructed by throwing away entire classes of E and merging (i.e., taking unions) some classes of E (obviously, making sure that the new classes are elements of
$E^{\prime }$
can be constructed by throwing away entire classes of E and merging (i.e., taking unions) some classes of E (obviously, making sure that the new classes are elements of
![]() $\mathcal {U}^{\ast }$
). Note that if
$\mathcal {U}^{\ast }$
). Note that if
![]() $E^{\prime }<_{part}E$
then
$E^{\prime }<_{part}E$
then
![]() $dom\left ( E^{\prime }\right ) \subseteq dom( E ) $
and
$dom\left ( E^{\prime }\right ) \subseteq dom( E ) $
and
![]() $A_{E^{\prime }}\subseteq A_{E}.$
$A_{E^{\prime }}\subseteq A_{E}.$
Definition 7 Let
![]() $\mathcal {U}$
be an ultrafilter. The Shelah forcing with respect to
$\mathcal {U}$
be an ultrafilter. The Shelah forcing with respect to
![]() $\mathcal {U}$
(denoted by
$\mathcal {U}$
(denoted by
![]() $\mathbb {S}( \mathcal {U} ) $
) is the set of all
$\mathbb {S}( \mathcal {U} ) $
) is the set of all
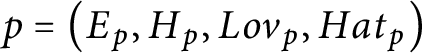 $p=\left ( E_{p},H_{p},Lov_{p},Hat_{p}\right ) $
with the following properties:
$p=\left ( E_{p},H_{p},Lov_{p},Hat_{p}\right ) $
with the following properties:
-
1.
 $E_{p}$
is a
$E_{p}$
is a
 $\mathcal {U}$
-partition (let
$\mathcal {U}$
-partition (let
 $A_{p}=A_{E_{p}}$
,
$A_{p}=A_{E_{p}}$
,
 $a_{p}( n) =a_{E_{p}}( n) $
and
$a_{p}( n) =a_{E_{p}}( n) $
and
 $[ a_{p}( n) ] _{p}= [ a_{p}( n) ] _{E_{p}}$
).
$[ a_{p}( n) ] _{p}= [ a_{p}( n) ] _{E_{p}}$
). -
2. If
 $n\in \omega $
then
$n\in \omega $
then
 $\{ Lov_{p}( a_{p}( n) ) ,Hat_{p}( a_{p}( n) ) \} $
is a partition of
$\{ Lov_{p}( a_{p}( n) ) ,Hat_{p}( a_{p}( n) ) \} $
is a partition of
 $ [ a_{p}( n) ] _{p}$
and
$ [ a_{p}( n) ] _{p}$
and
 $a_{p}( n) \in Lov_{p}( a_{p}( n) ) .$
$a_{p}( n) \in Lov_{p}( a_{p}( n) ) .$
-
3.
 $Lov_{p}=\{ Lov_{p}( a_{p}( n) ) \mid n\in \omega \} $
and
$Lov_{p}=\{ Lov_{p}( a_{p}( n) ) \mid n\in \omega \} $
and
 $Hat_{p}=\{ Hat_{p}( a_{p}( n) ) \mid n\in \omega \} .$
$Hat_{p}=\{ Hat_{p}( a_{p}( n) ) \mid n\in \omega \} .$
-
4. If
 $m\notin dom( E_{p}) $
then
$m\notin dom( E_{p}) $
then
 $H_{p}^{m}:2^{A_{p}\cap m}\longrightarrow 2$
.
$H_{p}^{m}:2^{A_{p}\cap m}\longrightarrow 2$
. -
5.
 $H_{p}=\{ H_{p}^{m}\mid m\notin dom( E_{p}) \} .$
$H_{p}=\{ H_{p}^{m}\mid m\notin dom( E_{p}) \} .$
Given
![]() $p,q\in \mathbb {S}( \mathcal {U}) ,$
define
$p,q\in \mathbb {S}( \mathcal {U}) ,$
define
![]() $p\leq q$
if the following holds:
$p\leq q$
if the following holds:
-
1.
 $E_{p} <_{part} E_{q}$
(so
$E_{p} <_{part} E_{q}$
(so
 $A_{p}\subseteq A_{q}$
).
$A_{p}\subseteq A_{q}$
). -
2. If
 $a\in A_{p}$
(so
$a\in A_{p}$
(so
 $a\in A_{q}$
and its class was not thrown away) then
$a\in A_{q}$
and its class was not thrown away) then
 $Lov_{q}( a) \subseteq Lov_{p}( a) $
and
$Lov_{q}( a) \subseteq Lov_{p}( a) $
and
 $Hat_{q}( a) \subseteq Hat_{p}( a) .$
$Hat_{q}( a) \subseteq Hat_{p}( a) .$
-
3. If
 $a\in A_{q}$
and there is
$a\in A_{q}$
and there is
 $b\in A_{p}$
such that
$b\in A_{p}$
such that
 $b<a$
and
$b<a$
and
 $a\in [ b] _{p}$
(so the class of a was merged with a previous class) then we have the following:
$a\in [ b] _{p}$
(so the class of a was merged with a previous class) then we have the following:-
(a) If
 $a\in Lov_{p}( b) $
then
$a\in Lov_{p}( b) $
then
 $Lov_{q}( a) \subseteq Lov_{p}( b) $
and
$Lov_{q}( a) \subseteq Lov_{p}( b) $
and
 $Hat_{q}( a) \subseteq Hat_{p}( b) .$
$Hat_{q}( a) \subseteq Hat_{p}( b) .$
-
(b) If
 $a\in Hat_{p}( b) $
then
$a\in Hat_{p}( b) $
then
 $Lov_{q}( a) \subseteq Hat_{p}( b) $
and
$Lov_{q}( a) \subseteq Hat_{p}( b) $
and
 $Hat_{q}( a) \subseteq Lov_{p}( b) .$
$Hat_{q}( a) \subseteq Lov_{p}( b) .$
-
-
4. If
 $a\in A_{q} \backslash dom( E_{p}) $
and
$a\in A_{q} \backslash dom( E_{p}) $
and
 $n\in [ a ] _{q}$
then
$n\in [ a ] _{q}$
then
 $H_{p}^{n}:2^{A_{p}\cap n}\longrightarrow 2$
is defined as follows:
$H_{p}^{n}:2^{A_{p}\cap n}\longrightarrow 2$
is defined as follows:-
(a)
 $H_{p}^{a}$
may be any function (with domain
$H_{p}^{a}$
may be any function (with domain
 $2^{A_{p}\cap n}$
and codomain
$2^{A_{p}\cap n}$
and codomain
 $2$
of course).
$2$
of course). -
(b) If
 $f\in 2^{A_{p}\cap n}$
and
$f\in 2^{A_{p}\cap n}$
and
 $n\in Lov_{q}( a) $
then
$n\in Lov_{q}( a) $
then
 $H_{p}^{n}( f) =H_{p}^{a}( f\upharpoonright a ) $
and if
$H_{p}^{n}( f) =H_{p}^{a}( f\upharpoonright a ) $
and if
 $n\in Hat_{q}( a) $
then
$n\in Hat_{q}( a) $
then
 $H_{p}^{n}( f) =1-H_{p}^{a}( f\upharpoonright a ) .$
$H_{p}^{n}( f) =1-H_{p}^{a}( f\upharpoonright a ) .$
Let
 $n\notin dom( E_{q} ) $
and
$n\notin dom( E_{q} ) $
and
 $f:A_{p}\cap n\longrightarrow 2.$
Define
$f:A_{p}\cap n\longrightarrow 2.$
Define
 $\overline {f}:A_{q}\cap n\longrightarrow 2$
as follows:
$\overline {f}:A_{q}\cap n\longrightarrow 2$
as follows:  $$ \begin{align*} \overline{f}( b) =\left\{ \begin{array}{llll} f( b) & & \mbox{if} & b\in A_{p}\\ f( a) & & \mbox{if} & b\notin A_{p}\ \mbox{and there is}\ a\in A_{p}\cap n\\ & & & \mbox{with}\ b\in Lov_{p}( a) \\ 1-f( a) & & \mbox{if} & b\notin A_{p}\ \mbox{and there is}\ a\in A_{p}\cap n\\ & & & \mbox{with}\ b\in Hat_{p}( a) \\ H_{p}^{b}\left( f\upharpoonright\left( A_{p}\cap b\right) \right) & & \mbox{if} & b\notin dom\left( E_{p}\right) \\ & & & \mbox{(as defined in point 4 above)} \end{array} \ \right. \end{align*} $$
$$ \begin{align*} \overline{f}( b) =\left\{ \begin{array}{llll} f( b) & & \mbox{if} & b\in A_{p}\\ f( a) & & \mbox{if} & b\notin A_{p}\ \mbox{and there is}\ a\in A_{p}\cap n\\ & & & \mbox{with}\ b\in Lov_{p}( a) \\ 1-f( a) & & \mbox{if} & b\notin A_{p}\ \mbox{and there is}\ a\in A_{p}\cap n\\ & & & \mbox{with}\ b\in Hat_{p}( a) \\ H_{p}^{b}\left( f\upharpoonright\left( A_{p}\cap b\right) \right) & & \mbox{if} & b\notin dom\left( E_{p}\right) \\ & & & \mbox{(as defined in point 4 above)} \end{array} \ \right. \end{align*} $$
-
-
5.
 $H_{p}^{n}( f) =H_{q}^{n}(\overline {f})$
for every
$H_{p}^{n}( f) =H_{q}^{n}(\overline {f})$
for every
 $n\notin dom\left ( E_{q}\right ) .$
$n\notin dom\left ( E_{q}\right ) .$
Point 5 in the definition of
![]() $p\leq q$
might be the hardest to understand. We can see an example. Assume that
$p\leq q$
might be the hardest to understand. We can see an example. Assume that
![]() $0,1,2,3\in A_{q}$
and
$0,1,2,3\in A_{q}$
and
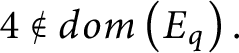 $4\notin dom\left ( E_{q}\right ) .$
Let
$4\notin dom\left ( E_{q}\right ) .$
Let
![]() $p\leq q$
such that
$p\leq q$
such that
![]() $0,2\in A_{p}$
and
$0,2\in A_{p}$
and
![]() $1\in Hat_{p}( 0) $
while
$1\in Hat_{p}( 0) $
while
![]() $3\in Lov_{p}( 2) .$
Let
$3\in Lov_{p}( 2) .$
Let
![]() $g,h\in 2^{A_{p}\cap 4}$
given by
$g,h\in 2^{A_{p}\cap 4}$
given by
![]() $g( 0) =0$
and
$g( 0) =0$
and
![]() $g( 2) =1,$
while
$g( 2) =1,$
while
![]() $h( 0) =1$
and
$h( 0) =1$
and
![]() $h( 2) =1.$
In this case, we have that
$h( 2) =1.$
In this case, we have that
![]() $\overline {g}=\left \{ \left ( 0,0\right ) ,\left ( 1,1\right ) ,\left ( 2,1\right ) ,\left ( 3,1\right ) \right \} $
and
$\overline {g}=\left \{ \left ( 0,0\right ) ,\left ( 1,1\right ) ,\left ( 2,1\right ) ,\left ( 3,1\right ) \right \} $
and
![]() $\overline {h}=\left \{ \left ( 0,1\right ) ,\left ( 1,0\right ) ,\left ( 2,1\right ) ,\left ( 3,1\right ) \right \} .$
$\overline {h}=\left \{ \left ( 0,1\right ) ,\left ( 1,0\right ) ,\left ( 2,1\right ) ,\left ( 3,1\right ) \right \} .$
In general, we need to argue that
![]() $H_{p}^{n}$
is well-defined (i.e., if
$H_{p}^{n}$
is well-defined (i.e., if
![]() $f:A_{p}\cap n\longrightarrow 2,$
then
$f:A_{p}\cap n\longrightarrow 2,$
then
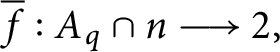 $\overline {f}:A_{q}\cap n\longrightarrow 2,$
so we are allowed to apply
$\overline {f}:A_{q}\cap n\longrightarrow 2,$
so we are allowed to apply
![]() $H_{q}^{n}$
to
$H_{q}^{n}$
to
![]() $\overline {f}$
). We prove this in the following lemma:
$\overline {f}$
). We prove this in the following lemma:
Lemma 8 Let
![]() $\mathcal {U}$
be an ultrafilter and
$\mathcal {U}$
be an ultrafilter and
![]() $p,q\in \mathbb {S(\mathcal {U})}$
that satisfy points 1–4 of the definition of
$p,q\in \mathbb {S(\mathcal {U})}$
that satisfy points 1–4 of the definition of
![]() $p\leq q.$
If n is a natural number such that
$p\leq q.$
If n is a natural number such that
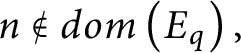 $n\notin dom\left ( E_{q}\right ) ,$
then
$n\notin dom\left ( E_{q}\right ) ,$
then
![]() $H_{p}^{n}$
is well-defined.
$H_{p}^{n}$
is well-defined.
Proof Let
![]() $n\in \omega $
such that
$n\in \omega $
such that
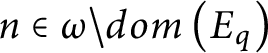 $n\in \omega \setminus dom\left ( E_{q}\right ) $
and
$n\in \omega \setminus dom\left ( E_{q}\right ) $
and
![]() $f:A_{p}\cap n\longrightarrow 2,$
we need to prove that
$f:A_{p}\cap n\longrightarrow 2,$
we need to prove that
![]() $\overline {f}$
is well-defined. Let
$\overline {f}$
is well-defined. Let
![]() $b\in A_{q}\cap n,$
we need to argue that
$b\in A_{q}\cap n,$
we need to argue that
![]() $\overline {f}( b) $
is actually defined. We proceed by cases:
$\overline {f}( b) $
is actually defined. We proceed by cases:
Case 9
![]() $b\in dom( E_{p}) .$
$b\in dom( E_{p}) .$
Here,
![]() $\overline {f}( b) $
is defined by one of the first three clauses in the definition of
$\overline {f}( b) $
is defined by one of the first three clauses in the definition of
![]() $\overline {f}$
(if b is a leader in
$\overline {f}$
(if b is a leader in
![]() $E_{p},$
then the first clause applies, otherwise, either clause 2 or 3 applies).
$E_{p},$
then the first clause applies, otherwise, either clause 2 or 3 applies).
Case 10
![]() $b\notin dom( E_{p}) .$
$b\notin dom( E_{p}) .$
Here, we have that
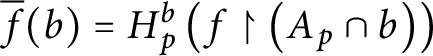 $\overline {f}( b) =H_{p}^{b}\left ( f\upharpoonright \left ( A_{p}\cap b\right ) \right ) $
and this is well-defined by point 4 of the definition of
$\overline {f}( b) =H_{p}^{b}\left ( f\upharpoonright \left ( A_{p}\cap b\right ) \right ) $
and this is well-defined by point 4 of the definition of
![]() $p\leq q.$
▪
$p\leq q.$
▪
Now, we define the following:
Definition 11 Let
![]() $G\subseteq \mathbb {S}( \mathcal {U}) $
be a generic filter. In
$G\subseteq \mathbb {S}( \mathcal {U}) $
be a generic filter. In
![]() $V\left [ G\right ] $
, we define the generic real
$V\left [ G\right ] $
, we define the generic real
![]() $x_{gen}$
as the set of all
$x_{gen}$
as the set of all
![]() $n\in \omega $
such that there is
$n\in \omega $
such that there is
![]() $p\in G$
for which
$p\in G$
for which
![]() $n\notin dom( E_{p}) $
and
$n\notin dom( E_{p}) $
and
![]() $H_{p}^{n}$
is the constant
$H_{p}^{n}$
is the constant
![]() $1$
function.
$1$
function.
We would like to mention that the term generic real may not be completely justified. We do not know if the generic filter G can be reconstructed from
![]() $x_{gen}.$
Footnote
4
$x_{gen}.$
Footnote
4
Recall that if
![]() $p\in \mathbb {S}( \mathcal {U}) $
and
$p\in \mathbb {S}( \mathcal {U}) $
and
![]() $n\notin dom( E_{p}) $
then the domain of
$n\notin dom( E_{p}) $
then the domain of
![]() $H_{p}^{n}$
is
$H_{p}^{n}$
is
![]() $2^{A_{p}\cap n}.$
Since we can always throw away a given class, for every
$2^{A_{p}\cap n}.$
Since we can always throw away a given class, for every
![]() $p\in \mathbb {S}( \mathcal {U}) $
and for every
$p\in \mathbb {S}( \mathcal {U}) $
and for every
![]() $n\in \omega ,$
there is
$n\in \omega ,$
there is
![]() $q\leq p$
such that
$q\leq p$
such that
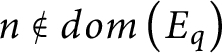 $n\notin dom\left ( E_{q}\right ) $
and
$n\notin dom\left ( E_{q}\right ) $
and
![]() $H_{q}^{n}$
is a constant function (this is the case if
$H_{q}^{n}$
is a constant function (this is the case if
![]() $A_{q}\cap n$
is empty). The following lemma follows from the definitions:
$A_{q}\cap n$
is empty). The following lemma follows from the definitions:
Lemma 12 [Reference Shelah13]
Let
![]() $p\in \mathbb {S}( \mathcal {U}) $
,
$p\in \mathbb {S}( \mathcal {U}) $
,
![]() $a\in A_{p}$
and
$a\in A_{p}$
and
![]() $n\notin dom( E_{p}) .$
$n\notin dom( E_{p}) .$
-
1.
 $p\Vdash \text{``}\left ( Lov_{p}( a) \subseteq \dot {x} _{gen}\right ) \vee \left ( Lov_{p}( a) \cap \dot {x}_{gen} =\emptyset \right ).\text{''}$
$p\Vdash \text{``}\left ( Lov_{p}( a) \subseteq \dot {x} _{gen}\right ) \vee \left ( Lov_{p}( a) \cap \dot {x}_{gen} =\emptyset \right ).\text{''}$
-
2.
 $p\Vdash \text{``}\left ( Hat_{p}( a) \subseteq \dot {x} _{gen}\right ) \vee \left ( Hat_{p}( a) \cap \dot {x}_{gen} =\emptyset \right ).\text{''}$
$p\Vdash \text{``}\left ( Hat_{p}( a) \subseteq \dot {x} _{gen}\right ) \vee \left ( Hat_{p}( a) \cap \dot {x}_{gen} =\emptyset \right ).\text{''}$
-
3. There are
 $q_{0},q_{1}\leq p$
such that the following holds:
$q_{0},q_{1}\leq p$
such that the following holds:
 $q_{0}\Vdash \text{``}Lov_{p}( a) \subseteq \dot {x}_{gen} \text{''}$
and
$q_{0}\Vdash \text{``}Lov_{p}( a) \subseteq \dot {x}_{gen} \text{''}$
and
 $q_{1}\Vdash \text{``}Lov_{p}( a) \cap \dot {x}_{gen}=\emptyset .\text{''}$
$q_{1}\Vdash \text{``}Lov_{p}( a) \cap \dot {x}_{gen}=\emptyset .\text{''}$
-
4. There are
 $q_{0},q_{1}\leq p$
such that the following holds:
$q_{0},q_{1}\leq p$
such that the following holds:
 $q_{0}\Vdash \text{``}Hat_{p}( a) \subseteq \dot {x}_{gen} \text{''}$
and
$q_{0}\Vdash \text{``}Hat_{p}( a) \subseteq \dot {x}_{gen} \text{''}$
and
 $q_{1}\Vdash \text{``}Hat_{p}( a) \cap \dot {x}_{gen}=\emptyset .\text{''}$
$q_{1}\Vdash \text{``}Hat_{p}( a) \cap \dot {x}_{gen}=\emptyset .\text{''}$
-
5.
 $H_{p}^{n}$
is the constant
$H_{p}^{n}$
is the constant
 $1$
function if and only if
$1$
function if and only if
 $p\Vdash \text{``}n\in \dot {x}_{gen}.\text{''}$
$p\Vdash \text{``}n\in \dot {x}_{gen}.\text{''}$
-
6.
 $H_{p}^{n}$
is the constant
$H_{p}^{n}$
is the constant
 $0$
function if and only if
$0$
function if and only if
 $p\Vdash \text{``}n\notin \dot {x}_{gen}.\text{''}$
$p\Vdash \text{``}n\notin \dot {x}_{gen}.\text{''}$
Now it is possible to conclude the following:
Lemma 13 [Reference Shelah13]
![]() $\mathbb {S}( \mathcal {U}) $
ultradestroys
$\mathbb {S}( \mathcal {U}) $
ultradestroys
![]() $\mathcal {U},$
in fact, both
$\mathcal {U},$
in fact, both
![]() $\dot {x}_{gen}$
and
$\dot {x}_{gen}$
and
![]() $\omega \backslash \dot {x}_{gen}$
are forced to have infinite intersection with every element of
$\omega \backslash \dot {x}_{gen}$
are forced to have infinite intersection with every element of
![]() $\ \mathcal {U}.$
$\ \mathcal {U}.$
Proof We will prove that
![]() $\dot {x}_{gen}$
is forced to intersect every element of
$\dot {x}_{gen}$
is forced to intersect every element of
![]() $\mathcal {U},$
the proof for
$\mathcal {U},$
the proof for
![]() $\omega \backslash \dot {x}_{gen}$
is similar. Let
$\omega \backslash \dot {x}_{gen}$
is similar. Let
![]() $B\in \mathcal {U}, p\in \mathbb {S}( \mathcal {U}) $
and
$B\in \mathcal {U}, p\in \mathbb {S}( \mathcal {U}) $
and
![]() $n\in \omega .$
It is enough to prove that there is
$n\in \omega .$
It is enough to prove that there is
![]() $q\leq p$
such that
$q\leq p$
such that
![]() $q\Vdash \text{``}B\cap \dot {x}_{gen}\nsubseteq n.\text{''}$
Since
$q\Vdash \text{``}B\cap \dot {x}_{gen}\nsubseteq n.\text{''}$
Since
![]() $dom( E_{p}) \in \mathcal {U},$
there is
$dom( E_{p}) \in \mathcal {U},$
there is
![]() $m>n$
such that
$m>n$
such that
![]() $m\in B\cap dom( E_{p}) .$
Since
$m\in B\cap dom( E_{p}) .$
Since
![]() $m\in dom( E_{p}) ,$
we know there is a (unique)
$m\in dom( E_{p}) ,$
we know there is a (unique)
![]() $a\in A_{p}$
such that
$a\in A_{p}$
such that
![]() $m\in [ a] _{p}.$
Define a condition q with the following properties:
$m\in [ a] _{p}.$
Define a condition q with the following properties:
-
1.
 $q\leq p.$
$q\leq p.$
-
2.
 $dom\left ( E_{q}\right ) =dom( E_{p}) \setminus [ a] _{p}.$
$dom\left ( E_{q}\right ) =dom( E_{p}) \setminus [ a] _{p}.$
-
3. If
 $b\in dom( E_{p}) \setminus [ a] _{p}$
then
$b\in dom( E_{p}) \setminus [ a] _{p}$
then
 $[ b] _{p}=[ b] _{q}.$
$[ b] _{p}=[ b] _{q}.$
-
4. If
 $m\in Lov_{p}( a) $
then
$m\in Lov_{p}( a) $
then
 $H_{q}^{a}$
is the constant
$H_{q}^{a}$
is the constant
 $1$
function, and if
$1$
function, and if
 $m\in Hat_{p}( a) ,$
then
$m\in Hat_{p}( a) ,$
then
 $H_{q}^{a}$
is the constant
$H_{q}^{a}$
is the constant
 $0$
function.
$0$
function.
It is easy to see that
![]() $q\Vdash \text{``}m\in B\cap \dot {x}_{gen},\text{''}$
so we are done.▪
$q\Vdash \text{``}m\in B\cap \dot {x}_{gen},\text{''}$
so we are done.▪
The following definitions will be frequently used:
Definition 14 Let
![]() $p,q\in \mathbb {S}( \mathcal {U}) $
and
$p,q\in \mathbb {S}( \mathcal {U}) $
and
![]() $n\in \omega .$
We define the following orders on
$n\in \omega .$
We define the following orders on
![]() $\mathbb {S}( \mathcal {U}) : $
$\mathbb {S}( \mathcal {U}) : $
-
1.
 $p\leq _{n}q$
if
$p\leq _{n}q$
if
 $p\leq q$
and
$p\leq q$
and
 $\left [ a_{p}( i) \right ] _{p}=\left [ a_{q}( i) \right ] _{q}$
for every
$\left [ a_{p}( i) \right ] _{p}=\left [ a_{q}( i) \right ] _{q}$
for every
 $i\leq n.$
$i\leq n.$
-
2.
 $p\leq _{n}^{\ast }q$
if
$p\leq _{n}^{\ast }q$
if
 $p\leq _{n-1}q$
and
$p\leq _{n-1}q$
and
 $a_{p}( n) =a_{q}( n) $
.Footnote
5
$a_{p}( n) =a_{q}( n) $
.Footnote
5
-
3.
 $p\leq _{n}^{\ast \ast }q$
if
$p\leq _{n}^{\ast \ast }q$
if
 $p\leq _{n}^{\ast }q$
and
$p\leq _{n}^{\ast }q$
and
 $dom( E_{p}) =dom( E_{q} ) .$
$dom( E_{p}) =dom( E_{q} ) .$
In other words,
![]() $p\leq _{n}q$
, if p extends q and the first n-classes of
$p\leq _{n}q$
, if p extends q and the first n-classes of
![]() $E_{q}$
do not get thrown away nor they merge with other classes. Meanwhile,
$E_{q}$
do not get thrown away nor they merge with other classes. Meanwhile,
![]() $p\leq _{n}^{\ast }q$
if
$p\leq _{n}^{\ast }q$
if
![]() $p\leq _{n-1}q$
and the n-class of
$p\leq _{n-1}q$
and the n-class of
![]() $E_{q}$
was not thrown away (but it could have been merge with other later classes). In a similar fashion,
$E_{q}$
was not thrown away (but it could have been merge with other later classes). In a similar fashion,
![]() $p\leq _{n}^{\ast \ast }q$
means that
$p\leq _{n}^{\ast \ast }q$
means that
![]() $p\leq _{n}^{\ast }q$
and no class was thrown away. Note that
$p\leq _{n}^{\ast }q$
and no class was thrown away. Note that
![]() $p\leq _{0}^{\ast }q$
means that p extends q and the
$p\leq _{0}^{\ast }q$
means that p extends q and the
![]() $0$
-class was not thrown away. It is easy (but not automatic) to see that these relations are transitive and symmetric. Note that if
$0$
-class was not thrown away. It is easy (but not automatic) to see that these relations are transitive and symmetric. Note that if
![]() $n<m$
and
$n<m$
and
![]() $p\leq _{m}q,$
then
$p\leq _{m}q,$
then
![]() $p\leq _{n}q.$
A similar remark apply for the other relations.
$p\leq _{n}q.$
A similar remark apply for the other relations.
Definition 15 Let
![]() $q,r,q^{\prime },r^{\prime }\in \mathbb {S}( \mathcal {U}) $
and
$q,r,q^{\prime },r^{\prime }\in \mathbb {S}( \mathcal {U}) $
and
![]() $n\in \omega .$
We say
$n\in \omega .$
We say
![]() $\,\left \langle q,r,q^{\prime },r^{\prime }\right \rangle $
is an n-nice sequence if the following holds:
$\,\left \langle q,r,q^{\prime },r^{\prime }\right \rangle $
is an n-nice sequence if the following holds:
-
1.
 $q\perp r$
(i.e., q and r are incompatible).
$q\perp r$
(i.e., q and r are incompatible). -
2. If
 $n<i$
then
$n<i$
then
 $\left [ a_{q}( i) \right ] _{q}=\left [ a_{r}( i) \right ] _{r}.$
$\left [ a_{q}( i) \right ] _{q}=\left [ a_{r}( i) \right ] _{r}.$
-
3.
 $q^{\prime }\leq _{n}^{\ast }q$
and
$q^{\prime }\leq _{n}^{\ast }q$
and
 $r^{\prime }\leq _{n}^{\ast }r$
.
$r^{\prime }\leq _{n}^{\ast }r$
. -
4. If
 $n+1<i$
then
$n+1<i$
then
 $\left [ a_{q^{\prime }}( i) \right ] _{q^{\prime }}=\left [ a_{r^{\prime }}( i) \right ] _{r^{\prime }}.$
$\left [ a_{q^{\prime }}( i) \right ] _{q^{\prime }}=\left [ a_{r^{\prime }}( i) \right ] _{r^{\prime }}.$
-
5.
 $dom\left ( E_{q}\right ) \backslash dom\left ( E_{q^{\prime } }\right ) \subseteq \left [ a_{r^{\prime }}( n) \right ] _{r^{\prime }}$
and
$dom\left ( E_{q}\right ) \backslash dom\left ( E_{q^{\prime } }\right ) \subseteq \left [ a_{r^{\prime }}( n) \right ] _{r^{\prime }}$
and
 $dom\left ( E_{r}\right ) \backslash dom\left ( E_{r^{\prime }}\right ) \subseteq \left [ a_{q^{\prime }}( n) \right ] _{q^{\prime }}.$
$dom\left ( E_{r}\right ) \backslash dom\left ( E_{r^{\prime }}\right ) \subseteq \left [ a_{q^{\prime }}( n) \right ] _{q^{\prime }}.$
The incompatibility of q and r is not required for most arguments. However, most of time we want to work using nice sequences, they will already be incompatible from the beginning. Note that
![]() $\left \langle q,r,q,r\right \rangle $
is an n-nice sequence if and only if q and r are incompatible and if
$\left \langle q,r,q,r\right \rangle $
is an n-nice sequence if and only if q and r are incompatible and if
![]() $n<i$
then
$n<i$
then
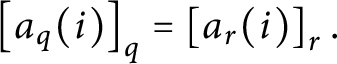 $\left [ a_{q}( i) \right ] _{q}=\left [ a_{r}( i) \right ] _{r}.$
$\left [ a_{q}( i) \right ] _{q}=\left [ a_{r}( i) \right ] _{r}.$
We will also need the following notions:
Definition 16 Let
![]() $p\in \mathbb {S}( \mathcal {U}) , n\in \omega $
and
$p\in \mathbb {S}( \mathcal {U}) , n\in \omega $
and
![]() $D\subseteq \mathbb {S}( \mathcal {U}) .$
$D\subseteq \mathbb {S}( \mathcal {U}) .$
-
1. D is
 $\leq _{n}$
-dense below p if for every
$\leq _{n}$
-dense below p if for every
 $q\leq _{n}p$
there is
$q\leq _{n}p$
there is
 $r\leq _{n}q$
such that
$r\leq _{n}q$
such that
 $r\in D.$
$r\in D.$
-
2. D is
 $\leq _{n}$
-open below p if for every r such that
$\leq _{n}$
-open below p if for every r such that
 $r\leq _{n}p$
and
$r\leq _{n}p$
and
 $r\in D$
then
$r\in D$
then
 $q\in D$
whenever
$q\in D$
whenever
 $q\leq _{n}r.$
$q\leq _{n}r.$
-
3. D is
 $\leq _{n}$
-open dense below p if it is both
$\leq _{n}$
-open dense below p if it is both
 $\leq _{n} $
-open and
$\leq _{n} $
-open and
 $\leq _{n}$
-dense below
$\leq _{n}$
-dense below
 $p.$
$p.$
-
4. The same definitions apply for
 $\leq _{n}^{\ast }.$
$\leq _{n}^{\ast }.$
In the above definitions, if D is
![]() $\leq _{n}$
-dense below
$\leq _{n}$
-dense below
![]() $1_{\mathbb {S} ( \mathcal {U}) } $
(where
$1_{\mathbb {S} ( \mathcal {U}) } $
(where
![]() $1_{\mathbb {S}\left ( \mathcal {U} \right ) } $
is the largest element of
$1_{\mathbb {S}\left ( \mathcal {U} \right ) } $
is the largest element of
![]() $\mathbb {S}( \mathcal {U}) $
), then we will simply write “D is
$\mathbb {S}( \mathcal {U}) $
), then we will simply write “D is
![]() $\leq _{n}$
-dense.” Similar conventions are adopted for the other notions. Expressions like “D is
$\leq _{n}$
-dense.” Similar conventions are adopted for the other notions. Expressions like “D is
![]() $\leq _{n}^{\ast }$
-open and
$\leq _{n}^{\ast }$
-open and
![]() $\leq _{m}^{\ast }$
-dense below p,” actually mean “D is
$\leq _{m}^{\ast }$
-dense below p,” actually mean “D is
![]() $\leq _{n}^{\ast }$
-open below p and
$\leq _{n}^{\ast }$
-open below p and
![]() $\leq _{m}^{\ast } $
-dense below p.”
$\leq _{m}^{\ast } $
-dense below p.”
Note that if
![]() $n<m$
and
$n<m$
and
![]() $D$
is
$D$
is
![]() $\leq _{n}$
-open below
$\leq _{n}$
-open below
![]() $p,$
then
$p,$
then
![]() $D$
is
$D$
is
![]() $\leq _{m}$
-open below
$\leq _{m}$
-open below
![]() $p.$
The following lemma is the base for several constructions in the paper:
$p.$
The following lemma is the base for several constructions in the paper:
Lemma 17 Let
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $q,r$
be two conditions such that
$q,r$
be two conditions such that
![]() $\left \langle q,r,q,r\right \rangle $
is an n-nice sequence. Let
$\left \langle q,r,q,r\right \rangle $
is an n-nice sequence. Let
![]() $D_{q}$
be an
$D_{q}$
be an
![]() $\leq _{n}^{\ast }$
-open dense set below q and
$\leq _{n}^{\ast }$
-open dense set below q and
![]() $D_{r}$
be an
$D_{r}$
be an
![]() $\leq _{n}^{\ast }$
-open dense set below
$\leq _{n}^{\ast }$
-open dense set below
![]() $r.$
There are
$r.$
There are
![]() $q^{\prime }\in D_{q}$
and
$q^{\prime }\in D_{q}$
and
![]() $r^{\prime }\in D_{r}$
such that
$r^{\prime }\in D_{r}$
such that
![]() $\left \langle q,r,q^{\prime },r^{\prime }\right \rangle $
is an n-nice sequence.
$\left \langle q,r,q^{\prime },r^{\prime }\right \rangle $
is an n-nice sequence.
Proof We first find
![]() $q_{1}\leq _{n}^{\ast }q$
such that
$q_{1}\leq _{n}^{\ast }q$
such that
![]() $q_{1}\in D_{q}.$
Let
$q_{1}\in D_{q}.$
Let
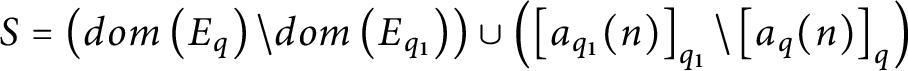 $S=\left(dom\left ( E_{q}\right ) \backslash dom\left ( E_{q_{1}}\right ) \right)\cup \left(\left [ a_{q_{1}}( n) \right ] _{q_{1}}\backslash \left [ a_{q}( n) \right ] _{q}\right)$
and note it is an element of
$S=\left(dom\left ( E_{q}\right ) \backslash dom\left ( E_{q_{1}}\right ) \right)\cup \left(\left [ a_{q_{1}}( n) \right ] _{q_{1}}\backslash \left [ a_{q}( n) \right ] _{q}\right)$
and note it is an element of
![]() $\mathcal {U}^{\ast }.$
Let
$\mathcal {U}^{\ast }.$
Let
![]() $r_{1}$
be any condition such that:
$r_{1}$
be any condition such that:
-
1.
 $r_{1}\leq _{n}^{\ast }r.$
$r_{1}\leq _{n}^{\ast }r.$
-
2.
 $\left [ a_{r_{1}}( n) \right ] _{r_{1}}=\left [ a_{r}( n) \right ] _{r}\cup S.$
$\left [ a_{r_{1}}( n) \right ] _{r_{1}}=\left [ a_{r}( n) \right ] _{r}\cup S.$
-
3.
 $dom\left ( E_{r_{1}}\right ) =dom\left ( E_{r}\right ) .$
$dom\left ( E_{r_{1}}\right ) =dom\left ( E_{r}\right ) .$
-
4.
 $E_{r_{1}}$
and
$E_{r_{1}}$
and
 $E_{q_{1}}$
are equal on
$E_{q_{1}}$
are equal on
 $\bigcup \{[ a_{q_{1} }( i) ] _{q_{1}}\mid n<i\}$
(i.e., for every
$\bigcup \{[ a_{q_{1} }( i) ] _{q_{1}}\mid n<i\}$
(i.e., for every
 $x\in \bigcup \{[ a_{q_{1}}( i) ] _{q_{1}}\mid n<i\},$
we have that
$x\in \bigcup \{[ a_{q_{1}}( i) ] _{q_{1}}\mid n<i\},$
we have that
 $[ x] _{E_{r_{1}}}=[ x] _{E_{r_{2}}}$
, recall that if
$[ x] _{E_{r_{1}}}=[ x] _{E_{r_{2}}}$
, recall that if
 $n<i$
then
$n<i$
then
 $\left [ a_{q}( i) \right ] _{q}=\left [ a_{r}( i) \right ] _{r}$
).
$\left [ a_{q}( i) \right ] _{q}=\left [ a_{r}( i) \right ] _{r}$
).
Now we find
![]() $r_{2}\leq _{n}^{\ast }r_{1}$
(so
$r_{2}\leq _{n}^{\ast }r_{1}$
(so
![]() $r_{2}\leq _{n}^{\ast }r$
) such that
$r_{2}\leq _{n}^{\ast }r$
) such that
![]() $r_{2}\in D_{r}.$
Let
$r_{2}\in D_{r}.$
Let
![]() $Z=(dom\left ( r_{1}\right ) \backslash dom\left ( r_{2}\right ) )\cup (\left [ a_{r_{2}}( n) \right ] _{r_{2} }\backslash \left [ a_{r_{1}}( n) \right ] _{r_{1}})$
which is also an element of
$Z=(dom\left ( r_{1}\right ) \backslash dom\left ( r_{2}\right ) )\cup (\left [ a_{r_{2}}( n) \right ] _{r_{2} }\backslash \left [ a_{r_{1}}( n) \right ] _{r_{1}})$
which is also an element of
![]() $\mathcal {U}^{\ast }.$
Let
$\mathcal {U}^{\ast }.$
Let
![]() $q_{2}$
be any condition such that:
$q_{2}$
be any condition such that:
-
1.
 $q_{2}\leq _{n}^{\ast }q_{1}.$
$q_{2}\leq _{n}^{\ast }q_{1}.$
-
2.
 $\left [ a_{q_{2}}( n) \right ] _{q_{2}}=\left [ a_{q_{1} }( n) \right ] _{q_{1}}\cup Z.$
$\left [ a_{q_{2}}( n) \right ] _{q_{2}}=\left [ a_{q_{1} }( n) \right ] _{q_{1}}\cup Z.$
-
3.
 $dom\left ( E_{q_{2}}\right ) =dom\left ( E_{q_{1}}\right ) .$
$dom\left ( E_{q_{2}}\right ) =dom\left ( E_{q_{1}}\right ) .$
-
4.
 $E_{q_{2}}$
and
$E_{q_{2}}$
and
 $E_{r_{2}}$
are equal on
$E_{r_{2}}$
are equal on
 $\bigcup \{\left [ a_{r_{2} }( i) \right ] _{r_{2}}\mid n+1<i\}$
(in the same sense as above).
$\bigcup \{\left [ a_{r_{2} }( i) \right ] _{r_{2}}\mid n+1<i\}$
(in the same sense as above).
Since
![]() $q_{2}\leq _{n}^{\ast }q_{1}$
and
$q_{2}\leq _{n}^{\ast }q_{1}$
and
![]() $D_{q}$
is
$D_{q}$
is
![]() $\leq _{n}^{\ast }$
-open, it follows that
$\leq _{n}^{\ast }$
-open, it follows that
![]() $q_{2}\in D_{q}.$
It is clear that
$q_{2}\in D_{q}.$
It is clear that
![]() $\left \langle q,r,q_{2} ,r_{2}\right \rangle $
has the desired properties.▪
$\left \langle q,r,q_{2} ,r_{2}\right \rangle $
has the desired properties.▪
The axiom A structure in a forcing is very useful. Unfortunately, it does not seem that
![]() $\mathbb {S}( \mathcal {U}) $
has one (however, in [Reference Shelah13] it was proved that
$\mathbb {S}( \mathcal {U}) $
has one (however, in [Reference Shelah13] it was proved that
![]() $\mathbb {S}( \mathcal {U}) $
is
$\mathbb {S}( \mathcal {U}) $
is
![]() $<\omega _{1}$
-proper, so by a theorem of Tetsuya Ishiu, [Reference Hrušák11]
$<\omega _{1}$
-proper, so by a theorem of Tetsuya Ishiu, [Reference Hrušák11]
![]() $\mathbb {S}( \mathcal {U}) $
is forcing equivalent to a partial order with an axiom A structure. Unfortunately, we were unable to take advantage of this result). The purpose of the following definitions and results are to obtain a similar structure to the one of an axiom A forcing.
$\mathbb {S}( \mathcal {U}) $
is forcing equivalent to a partial order with an axiom A structure. Unfortunately, we were unable to take advantage of this result). The purpose of the following definitions and results are to obtain a similar structure to the one of an axiom A forcing.
Definition 18 We say
![]() $T=\left \langle q_{i},r_{i}\right \rangle _{i<\omega }$
is a
$T=\left \langle q_{i},r_{i}\right \rangle _{i<\omega }$
is a
![]() $1$
-fusion sequence if the following holds:
$1$
-fusion sequence if the following holds:
-
1.
 $q_{0}$
and
$q_{0}$
and
 $r_{0}$
are incompatible but
$r_{0}$
are incompatible but
 $E_{q_{0}}=E_{r_{0}}.$
$E_{q_{0}}=E_{r_{0}}.$
-
2. If
 $i<\omega $
then
$i<\omega $
then
 $\left \langle q_{i},r_{i},q_{i+1},r_{i+1} \right \rangle $
is an i-nice sequence.
$\left \langle q_{i},r_{i},q_{i+1},r_{i+1} \right \rangle $
is an i-nice sequence.
We will say
![]() $T=\left \langle q_{i},r_{i}\right \rangle _{i\leq n+1}$
is a
$T=\left \langle q_{i},r_{i}\right \rangle _{i\leq n+1}$
is a
![]() $1$
-finite fusion sequence if it satisfy the previous points for every
$1$
-finite fusion sequence if it satisfy the previous points for every
![]() $i<n+1.$
$i<n+1.$
Definition 19 Let
![]() $\left \langle p_{i}\right \rangle _{i\in \omega }\subseteq \mathbb {S}( \mathcal {U}) $
such that
$\left \langle p_{i}\right \rangle _{i\in \omega }\subseteq \mathbb {S}( \mathcal {U}) $
such that
![]() $p_{i+1}\leq _{i}^{\ast }p_{i}$
for every
$p_{i+1}\leq _{i}^{\ast }p_{i}$
for every
![]() $i\in \omega .$
We define the limit of
$i\in \omega .$
We define the limit of
![]() $\left \langle p_{i}\right \rangle _{i\in \omega }$
as
$\left \langle p_{i}\right \rangle _{i\in \omega }$
as
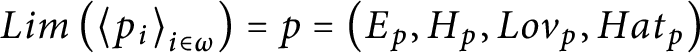 $Lim\left ( \left \langle p_{i}\right \rangle _{i\in \omega }\right ) =p=\left ( E_{p},H_{p},Lov_{p},Hat_{p}\right ) $
as follows:
$Lim\left ( \left \langle p_{i}\right \rangle _{i\in \omega }\right ) =p=\left ( E_{p},H_{p},Lov_{p},Hat_{p}\right ) $
as follows:
-
1.
 $dom( E_{p}) =\bigcup \limits _{i<\omega }\left [ a_{p_{i+1} }( i) \right ] _{p_{i+1}}.$
$dom( E_{p}) =\bigcup \limits _{i<\omega }\left [ a_{p_{i+1} }( i) \right ] _{p_{i+1}}.$
-
2.
 $\left [ a_{p}( i) \right ] _{E_{p}}=\left [ a_{p_{i+1} }( i) \right ] _{p_{i+1}}.$
$\left [ a_{p}( i) \right ] _{E_{p}}=\left [ a_{p_{i+1} }( i) \right ] _{p_{i+1}}.$
-
3.
 $Lov_{p}\left ( a_{p}( i) \right ) =Lov_{p_{i+1}}\left ( a_{p_{i+1}}( i) \right ). $
$Lov_{p}\left ( a_{p}( i) \right ) =Lov_{p_{i+1}}\left ( a_{p_{i+1}}( i) \right ). $
-
4.
 $Hat_{p}\left ( a_{p}( i) \right ) =Hat_{p_{i+1}}\left ( a_{p_{i+1}}( i) \right ) .$
$Hat_{p}\left ( a_{p}( i) \right ) =Hat_{p_{i+1}}\left ( a_{p_{i+1}}( i) \right ) .$
-
5. If
 $m\notin dom( E_{p}) $
then
$m\notin dom( E_{p}) $
then
 $H_{p}^{m}=H_{p_{m}}^{m}.$
$H_{p}^{m}=H_{p_{m}}^{m}.$
Above we are not claiming that the limit is a condition. In fact,
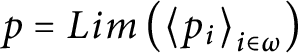 $p=Lim\left ( \left \langle p_{i}\right \rangle _{i\in \omega }\right ) $
may not be in
$p=Lim\left ( \left \langle p_{i}\right \rangle _{i\in \omega }\right ) $
may not be in
![]() $\mathbb {S}( \mathcal {U}) $
since it might be the case that
$\mathbb {S}( \mathcal {U}) $
since it might be the case that
![]() $dom( E_{p}) $
is not an element of
$dom( E_{p}) $
is not an element of
![]() $\mathcal {U}$
. Nevertheless, if p is indeed a condition, then
$\mathcal {U}$
. Nevertheless, if p is indeed a condition, then
![]() $p\leq _{i}^{\ast }p_{i}$
for every
$p\leq _{i}^{\ast }p_{i}$
for every
![]() $i\in \omega .$
The following result plays the role of a fusion sequence in an Axiom A forcing:
$i\in \omega .$
The following result plays the role of a fusion sequence in an Axiom A forcing:
Lemma 20 If
![]() $T=\left \langle q_{i},r_{i}\right \rangle _{i<\omega }$
is a
$T=\left \langle q_{i},r_{i}\right \rangle _{i<\omega }$
is a
![]() $1$
-fusion sequence in
$1$
-fusion sequence in
![]() $\mathbb {S}( \mathcal {U}) $
then there is
$\mathbb {S}( \mathcal {U}) $
then there is
![]() $\overline {p}$
that either is a lower bound of
$\overline {p}$
that either is a lower bound of
![]() $\ \left \langle \,q_{i} \right \rangle _{i<\omega }$
or it is a lower bound of
$\ \left \langle \,q_{i} \right \rangle _{i<\omega }$
or it is a lower bound of
![]() $\left \langle \,r_{i}\right \rangle _{i<\omega }.$
In fact, either
$\left \langle \,r_{i}\right \rangle _{i<\omega }.$
In fact, either
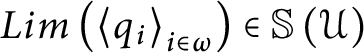 $Lim\left ( \left \langle q_{i}\right \rangle _{i\in \omega }\right ) \in \mathbb {S}\left ( \mathcal {U} \right ) $
or
$Lim\left ( \left \langle q_{i}\right \rangle _{i\in \omega }\right ) \in \mathbb {S}\left ( \mathcal {U} \right ) $
or
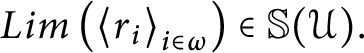 $Lim\left ( \left \langle r_{i}\right \rangle _{i\in \omega }\right ) \in \mathbb {S}( \mathcal {U}) .$
$Lim\left ( \left \langle r_{i}\right \rangle _{i\in \omega }\right ) \in \mathbb {S}( \mathcal {U}) .$
Proof Assume
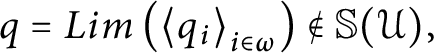 $q=Lim\left ( \left \langle q_{i}\right \rangle _{i\in \omega }\right ) \notin \mathbb {S}( \mathcal {U}) ,$
we will that
$q=Lim\left ( \left \langle q_{i}\right \rangle _{i\in \omega }\right ) \notin \mathbb {S}( \mathcal {U}) ,$
we will that
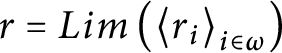 $r=Lim\left ( \left \langle r_{i}\right \rangle _{i\in \omega }\right ) $
is a condition in
$r=Lim\left ( \left \langle r_{i}\right \rangle _{i\in \omega }\right ) $
is a condition in
![]() $\mathbb {S}( \mathcal {U}) .$
In order to show this, we must first argue that
$\mathbb {S}( \mathcal {U}) .$
In order to show this, we must first argue that
![]() $dom( E_{q_{0}}) =dom( E_{q}) \cup dom( E_{r}) .$
If
$dom( E_{q_{0}}) =dom( E_{q}) \cup dom( E_{r}) .$
If
![]() $n\in dom( E_{q_{0}}) \backslash dom( E_{q}) $
, we then may find
$n\in dom( E_{q_{0}}) \backslash dom( E_{q}) $
, we then may find
![]() $i\in \omega $
such that
$i\in \omega $
such that
![]() $n\in dom\left ( q_{i}\right ) \backslash dom\left ( q_{i+1}\right ) $
. Since
$n\in dom\left ( q_{i}\right ) \backslash dom\left ( q_{i+1}\right ) $
. Since
![]() $\left \langle q_{i},q_{i+1},r_{i},r_{i+1}\right \rangle $
is i-nice then
$\left \langle q_{i},q_{i+1},r_{i},r_{i+1}\right \rangle $
is i-nice then
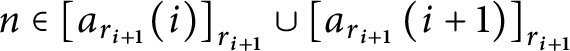 $n\in \left [ a_{r_{i+1}}( i) \right ] _{r_{i+1}}\cup \left [ a_{r_{i+1}}\left ( i+1\right ) \right ] _{r_{i+1}}$
so
$n\in \left [ a_{r_{i+1}}( i) \right ] _{r_{i+1}}\cup \left [ a_{r_{i+1}}\left ( i+1\right ) \right ] _{r_{i+1}}$
so
![]() $n\in dom\left ( E_{r}\right ) .$
Since
$n\in dom\left ( E_{r}\right ) .$
Since
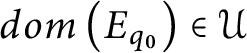 $dom\left ( E_{q_{0}}\right ) \in \mathcal {U}$
and
$dom\left ( E_{q_{0}}\right ) \in \mathcal {U}$
and
![]() $\mathcal {U}$
is an ultrafilter, it must be the case that
$\mathcal {U}$
is an ultrafilter, it must be the case that
![]() $dom\left ( E_{r}\right ) \in \mathcal {U}.$
▪
$dom\left ( E_{r}\right ) \in \mathcal {U}.$
▪
In the above case, we would say that
 $Lim\left ( \left \langle q_{i} \right \rangle _{i\in \omega }\right ) $
(or
$Lim\left ( \left \langle q_{i} \right \rangle _{i\in \omega }\right ) $
(or
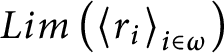 $Lim\left ( \left \langle r_{i}\right \rangle _{i\in \omega }\right ) $
in case
$Lim\left ( \left \langle r_{i}\right \rangle _{i\in \omega }\right ) $
in case
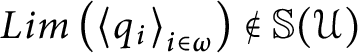 $Lim\left ( \left \langle q_{i}\right \rangle _{i\in \omega }\right ) \notin \mathbb {S}( \mathcal {U}) $
) is a fusion for
$Lim\left ( \left \langle q_{i}\right \rangle _{i\in \omega }\right ) \notin \mathbb {S}( \mathcal {U}) $
) is a fusion for
![]() $T.$
For the case of
$T.$
For the case of
![]() $\leq ^{\ast \ast }$
the situation is simpler:
$\leq ^{\ast \ast }$
the situation is simpler:
Lemma 21 If
![]() $\left \langle p_{i}\right \rangle _{i\in \omega }\subseteq \mathbb {S}( \mathcal {U}) $
is a sequence such that
$\left \langle p_{i}\right \rangle _{i\in \omega }\subseteq \mathbb {S}( \mathcal {U}) $
is a sequence such that
![]() $p_{i+1}\leq _{i}^{\ast \ast } p_{i}$
for every
$p_{i+1}\leq _{i}^{\ast \ast } p_{i}$
for every
![]() $i\in \omega $
then there is
$i\in \omega $
then there is
![]() $q\in \mathbb {S}( \mathcal {U}) $
such that
$q\in \mathbb {S}( \mathcal {U}) $
such that
![]() $q\leq _{i}^{\ast \ast }p_{i}$
for every
$q\leq _{i}^{\ast \ast }p_{i}$
for every
![]() $i\in \omega .$
$i\in \omega .$
Proof We claim that
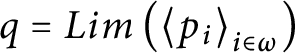 $q=Lim\left ( \left \langle p_{i}\right \rangle _{i\in \omega }\right ) $
is as desired. We only need to prove that q is really a condition. In order to achieve that, it is enough to prove that
$q=Lim\left ( \left \langle p_{i}\right \rangle _{i\in \omega }\right ) $
is as desired. We only need to prove that q is really a condition. In order to achieve that, it is enough to prove that
 $dom\left ( E_{q}\right ) \in \mathcal {U}$
. Since the sequence
$dom\left ( E_{q}\right ) \in \mathcal {U}$
. Since the sequence
![]() $\left \langle p_{i}\right \rangle _{i\in \omega }$
is
$\left \langle p_{i}\right \rangle _{i\in \omega }$
is
![]() $\leq _{i}^{\ast \ast }$
-decreasing, it follows that
$\leq _{i}^{\ast \ast }$
-decreasing, it follows that
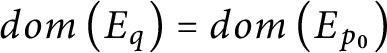 $dom\left ( E_{q}\right ) =dom\left ( E_{p_{0}}\right ) $
and we are done.▪
$dom\left ( E_{q}\right ) =dom\left ( E_{p_{0}}\right ) $
and we are done.▪
We will need the following definition:
Definition 22 Let
![]() $p\in \mathbb {S}( \mathcal {U}) , n>0$
and
$p\in \mathbb {S}( \mathcal {U}) , n>0$
and
![]() $h:n\longrightarrow 2.$
We define
$h:n\longrightarrow 2.$
We define
![]() $p[ h] $
as the condition extending p with the following properties:
$p[ h] $
as the condition extending p with the following properties:
-
1.
 $Dom\left ( E_{p[ h] }\right ) =Dom( E_{p}) \backslash \bigcup \limits _{i<n}\left [ a_{p}( i) \right ] _{E_{p}}.$
$Dom\left ( E_{p[ h] }\right ) =Dom( E_{p}) \backslash \bigcup \limits _{i<n}\left [ a_{p}( i) \right ] _{E_{p}}.$
-
2. If
 $m\in Dom\left ( E_{p[ h] }\right ) $
then
$m\in Dom\left ( E_{p[ h] }\right ) $
then
 $\left [ m\right ] _{p[ h] }=\left [ m\right ] _{p}.$
$\left [ m\right ] _{p[ h] }=\left [ m\right ] _{p}.$
-
3. If
 $a\in A_{p[ h] }$
then
$a\in A_{p[ h] }$
then
 $Lov_{p[ h] }( a) =Lov_{p}( a) $
and
$Lov_{p[ h] }( a) =Lov_{p}( a) $
and
 $Hat_{p[ h] }( a) =Hat_{p}( a) .$
$Hat_{p[ h] }( a) =Hat_{p}( a) .$
-
4. If
 $i<n$
then
$i<n$
then
 $H_{p[ h] }^{a_{p}( i) }$
is the constant function with value
$H_{p[ h] }^{a_{p}( i) }$
is the constant function with value
 $h( i) .$
$h( i) .$
In other words,
![]() $p[ h] $
is obtained by throwing out the first n-classes and tell their leaders to “follow h.”
$p[ h] $
is obtained by throwing out the first n-classes and tell their leaders to “follow h.”
The following lemma (which we leave to the reader) is very easy, yet it will be often used in future arguments:
Lemma 23 Let
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $p,q\in \mathbb {S}\mathcal {(U)}$
such that
$p,q\in \mathbb {S}\mathcal {(U)}$
such that
![]() $q\leq _{n}^{\ast }p.$
If
$q\leq _{n}^{\ast }p.$
If
![]() $h\in 2^{n+1},$
then
$h\in 2^{n+1},$
then
![]() $q[ h] \leq p[ h] .$
$q[ h] \leq p[ h] .$
We have the following:
Lemma 24 Let
![]() $p\in \mathbb {S}( \mathcal {U}) $
and
$p\in \mathbb {S}( \mathcal {U}) $
and
![]() $n>0.$
The set
$n>0.$
The set
![]() $\left \{ p[ h] \mid h\in 2^{n}\right \} $
is a maximal antichain below
$\left \{ p[ h] \mid h\in 2^{n}\right \} $
is a maximal antichain below
![]() $p.$
$p.$
Proof Let
![]() $h,g\in 2^{n}$
with
$h,g\in 2^{n}$
with
![]() $h\neq g$
, we will see that
$h\neq g$
, we will see that
![]() $p[ h] $
and
$p[ h] $
and
![]() $p\left [ g\right ] $
are incompatible. Let
$p\left [ g\right ] $
are incompatible. Let
![]() $i<n$
such that
$i<n$
such that
![]() $h( i) =0$
and
$h( i) =0$
and
![]() $g( i) =1.$
In this way, we have that
$g( i) =1.$
In this way, we have that
![]() $p[ h] \Vdash $
“
$p[ h] \Vdash $
“
![]() $i\notin \dot {x}_{gen}$
” and
$i\notin \dot {x}_{gen}$
” and
![]() $p\left [ g\right ] \Vdash $
“
$p\left [ g\right ] \Vdash $
“
![]() $i\in \dot {x}_{gen} $
,” so this two conditions are incompatible.
$i\in \dot {x}_{gen} $
,” so this two conditions are incompatible.
We now need to prove that the set
![]() $\left \{ p[ h] \mid h\in 2^{n}\right \} $
is predense below
$\left \{ p[ h] \mid h\in 2^{n}\right \} $
is predense below
![]() $p.$
Let
$p.$
Let
![]() $q\leq p,$
take
$q\leq p,$
take
![]() $r\leq q$
such that for every
$r\leq q$
such that for every
![]() $i<n,$
either
$i<n,$
either
![]() $r\Vdash $
“
$r\Vdash $
“
![]() $i\in \dot {x}_{gen} $
” or
$i\in \dot {x}_{gen} $
” or
![]() $r\Vdash $
“
$r\Vdash $
“
![]() $i\notin \dot {x}_{gen} $
.” Define
$i\notin \dot {x}_{gen} $
.” Define
![]() $h:n\longrightarrow 2$
such that
$h:n\longrightarrow 2$
such that
![]() $h( i) =1$
if and only if
$h( i) =1$
if and only if
![]() $r\Vdash $
“
$r\Vdash $
“
![]() $i\in \dot {x}_{gen} $
.” It follows that
$i\in \dot {x}_{gen} $
.” It follows that
![]() $r\leq p[ h] .$
▪
$r\leq p[ h] .$
▪
We now define the following,
Definition 25 Let
![]() $D\subseteq \mathbb {S}( \mathcal {U}) $
be an open dense set below p and
$D\subseteq \mathbb {S}( \mathcal {U}) $
be an open dense set below p and
![]() $n>0.$
We define
$n>0.$
We define
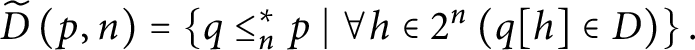 $\widetilde {D}\left ( p,n\right ) =\left \{ q\leq _{n}^{\ast }p\mid \forall h\in 2^{n}\left ( q[ h] \in D\right ) \right \} .$
$\widetilde {D}\left ( p,n\right ) =\left \{ q\leq _{n}^{\ast }p\mid \forall h\in 2^{n}\left ( q[ h] \in D\right ) \right \} .$
We now have the next result,
Lemma 26 If
![]() $D\subseteq \mathbb {S}( \mathcal {U}) $
is an open dense set below p and
$D\subseteq \mathbb {S}( \mathcal {U}) $
is an open dense set below p and
![]() $n>0,$
then
$n>0,$
then
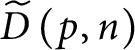 $\widetilde {D}\left ( p,n\right ) $
is
$\widetilde {D}\left ( p,n\right ) $
is
![]() $\leq _{n}^{\ast }$
-open dense below
$\leq _{n}^{\ast }$
-open dense below
![]() $p.$
$p.$
Proof We first show that
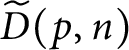 $\widetilde {D}( p,n) $
is
$\widetilde {D}( p,n) $
is
![]() $\leq _{n}^{\ast } $
-dense below
$\leq _{n}^{\ast } $
-dense below
![]() $p.$
Let
$p.$
Let
![]() $q\leq _{n}^{\ast }p$
and enumerate
$q\leq _{n}^{\ast }p$
and enumerate
![]() $2^{n}=\left \{ h_{i}\mid i<k\right \} $
, we can then recursively find a sequence
$2^{n}=\left \{ h_{i}\mid i<k\right \} $
, we can then recursively find a sequence
![]() $\left \langle q_{i}\right \rangle _{i<k+1}$
with the following properties:
$\left \langle q_{i}\right \rangle _{i<k+1}$
with the following properties:
-
1.
 $q_{0}=q.$
$q_{0}=q.$
-
2.
 $\left \langle q_{i}\right \rangle _{i<k+1}$
is
$\left \langle q_{i}\right \rangle _{i<k+1}$
is
 $\leq _{n}^{\ast }$
-decreasing.
$\leq _{n}^{\ast }$
-decreasing. -
3.
 $q_{i+1}\left [ h_{i}\right ] \in D.$
$q_{i+1}\left [ h_{i}\right ] \in D.$
It is then easy to see that
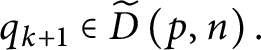 $q_{k+1}\in \widetilde {D}\left ( p,n\right ) .$
Finally,
$q_{k+1}\in \widetilde {D}\left ( p,n\right ) .$
Finally,
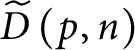 $\widetilde {D}\left ( p,n\right ) $
is
$\widetilde {D}\left ( p,n\right ) $
is
![]() $\leq _{n}^{\ast }$
-open, since whenever
$\leq _{n}^{\ast }$
-open, since whenever
![]() $r\leq _{n}^{\ast }q$
then
$r\leq _{n}^{\ast }q$
then
![]() $r[ h] \leq q[ h] $
for every
$r[ h] \leq q[ h] $
for every
![]() $h\in 2^{n}.$
▪
$h\in 2^{n}.$
▪
With these results, we can finally prove that Shelah’s forcing is proper.
Proposition 27 [Reference Shelah13]
If
![]() $\mathcal {U}$
is an ultrafilter, then
$\mathcal {U}$
is an ultrafilter, then
![]() $\mathbb {S}( \mathcal {U}) $
is a proper forcing.
$\mathbb {S}( \mathcal {U}) $
is a proper forcing.
Proof We will prove that
![]() $\mathbb {S}( \mathcal {U}) $
is proper. Let M be a countable elementary submodel of some
$\mathbb {S}( \mathcal {U}) $
is proper. Let M be a countable elementary submodel of some
![]() $H\left ( \kappa \right ) $
and
$H\left ( \kappa \right ) $
and
![]() $p\in M.$
Let
$p\in M.$
Let
![]() $\left \{ D_{n}\mid n\in \omega \right \} $
enumerate all open dense subsets of
$\left \{ D_{n}\mid n\in \omega \right \} $
enumerate all open dense subsets of
![]() $\mathbb {S}( \mathcal {U}) $
that belong to
$\mathbb {S}( \mathcal {U}) $
that belong to
![]() $M.$
For every
$M.$
For every
![]() $n\in \omega $
let
$n\in \omega $
let
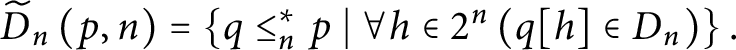 $\widetilde {D}_{n}\left ( p,n\right ) =\left \{ q\leq _{n}^{\ast }p\mid \forall h\in 2^{n}\left ( q[ h] \in D_{n}\right ) \right \} .$
We know that
$\widetilde {D}_{n}\left ( p,n\right ) =\left \{ q\leq _{n}^{\ast }p\mid \forall h\in 2^{n}\left ( q[ h] \in D_{n}\right ) \right \} .$
We know that
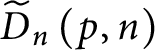 $\widetilde {D}_{n}\left ( p,n\right ) $
is
$\widetilde {D}_{n}\left ( p,n\right ) $
is
![]() $\leq _{n}^{\ast }$
-open dense. It is also clear that each
$\leq _{n}^{\ast }$
-open dense. It is also clear that each
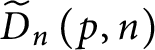 $\widetilde {D}_{n}\left ( p,n\right ) $
is an element of
$\widetilde {D}_{n}\left ( p,n\right ) $
is an element of
![]() $M.$
Using Lemma 17, we can construct
$M.$
Using Lemma 17, we can construct
![]() $T=\left \langle q_{i},r_{i}\right \rangle _{i<\omega }$
a
$T=\left \langle q_{i},r_{i}\right \rangle _{i<\omega }$
a
![]() $1$
-fusion sequence with the following properties:
$1$
-fusion sequence with the following properties:
-
1.
 $T\subseteq M.$
$T\subseteq M.$
-
2.
 $q_{0},r_{0}\leq p.$
$q_{0},r_{0}\leq p.$
-
3.
 $q_{i+1}\in \widetilde {D}_{i}\left ( q_{i},i\right ) $
and
$q_{i+1}\in \widetilde {D}_{i}\left ( q_{i},i\right ) $
and
 $r_{i+1} \in \widetilde {D}_{i}\left ( r_{i},i\right ) $
for every
$r_{i+1} \in \widetilde {D}_{i}\left ( r_{i},i\right ) $
for every
 $i\in \omega .$
$i\in \omega .$
It is easy to see that if
![]() $\overline {p}$
is a fusion of
$\overline {p}$
is a fusion of
![]() $T,$
then
$T,$
then
![]() $\overline {p}$
will be an
$\overline {p}$
will be an
![]() $\left ( M,\mathbb {S}( \mathcal {U}) \right ) $
-generic condition extending
$\left ( M,\mathbb {S}( \mathcal {U}) \right ) $
-generic condition extending
![]() $p.$
▪
$p.$
▪
Recall that a forcing
![]() $\mathbb {P}$
has the Sacks property if for every
$\mathbb {P}$
has the Sacks property if for every
![]() $p\in \mathbb {P}$
and
$p\in \mathbb {P}$
and
![]() $\dot {f}$
such that
$\dot {f}$
such that
![]() $p\Vdash $
“
$p\Vdash $
“
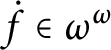 $\dot {f}\in \omega ^{\omega }$
,” there are
$\dot {f}\in \omega ^{\omega }$
,” there are
![]() $q\leq p$
and a sequence
$q\leq p$
and a sequence
![]() $S=\left \langle S_{n}\right \rangle _{n\in \omega }\in V$
such that
$S=\left \langle S_{n}\right \rangle _{n\in \omega }\in V$
such that
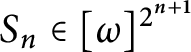 $S_{n}\in [ \omega ] ^{2^{n+1}}$
and
$S_{n}\in [ \omega ] ^{2^{n+1}}$
and
![]() $q\Vdash $
“
$q\Vdash $
“
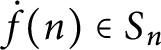 $\dot {f}( n) \in S_{n}$
” for every
$\dot {f}( n) \in S_{n}$
” for every
![]() $n\in \omega .$
We will soon prove that
$n\in \omega .$
We will soon prove that
![]() $\mathbb {S}( \mathcal {U}) $
has the Sacks property.
$\mathbb {S}( \mathcal {U}) $
has the Sacks property.
Definition 28 Let
![]() $\mathbb {P}$
be a partial order,
$\mathbb {P}$
be a partial order,
![]() $p\in \mathbb {P}$
and
$p\in \mathbb {P}$
and
![]() $\dot {x}$
a
$\dot {x}$
a
![]() $\mathbb {P}$
-name for an element of
$\mathbb {P}$
-name for an element of
![]() $\omega ^{\omega }.$
Define
$\omega ^{\omega }.$
Define
![]() $\dot {x}\left [ p\right ] =\bigcup \left \{ t\in \omega ^{<\omega }\mid p\Vdash \text{``}t\subseteq \dot {x}\text{''}\right \} .$
$\dot {x}\left [ p\right ] =\bigcup \left \{ t\in \omega ^{<\omega }\mid p\Vdash \text{``}t\subseteq \dot {x}\text{''}\right \} .$
In case
![]() $\dot {x}$
is forced to be a new element of
$\dot {x}$
is forced to be a new element of
![]() $\omega ^{\omega }$
(which is often the case we are interested in), we will have that
$\omega ^{\omega }$
(which is often the case we are interested in), we will have that
![]() $\dot {x}\left [ p\right ] \in \omega ^{<\omega }.$
$\dot {x}\left [ p\right ] \in \omega ^{<\omega }.$
Definition 29 Let
![]() $p\in \mathbb {S}( \mathcal {U}) $
and
$p\in \mathbb {S}( \mathcal {U}) $
and
![]() $\dot {x}$
such that
$\dot {x}$
such that
![]() $p\Vdash $
“
$p\Vdash $
“
![]() $\dot {x}\in \omega ^{\omega }$
.” We say p is
$\dot {x}\in \omega ^{\omega }$
.” We say p is
![]() $\dot {x}$
-nice if
$\dot {x}$
-nice if
![]() $p[ h] $
determines
$p[ h] $
determines
![]() $\dot {x}\upharpoonright n$
for every
$\dot {x}\upharpoonright n$
for every
![]() $h:n\longrightarrow 2.$
$h:n\longrightarrow 2.$
We now have the following:
Lemma 30 [Reference Shelah13]
Let
![]() $\dot {f}$
be a
$\dot {f}$
be a
![]() $\mathbb {S}( \mathcal {U}) $
-name for a new element of
$\mathbb {S}( \mathcal {U}) $
-name for a new element of
![]() $\omega ^{\omega }.$
The set of all
$\omega ^{\omega }.$
The set of all
![]() $\dot {f}$
-nice conditions is a dense set.
$\dot {f}$
-nice conditions is a dense set.
Proof Let
![]() $p\in \mathbb {S}( \mathcal {U}) $
and
$p\in \mathbb {S}( \mathcal {U}) $
and
![]() $n\in \omega .$
Define
$n\in \omega .$
Define
![]() $D_{n}=\{q\leq p\mid \exists s\in \omega ^{n+1}(q\Vdash $
“
$D_{n}=\{q\leq p\mid \exists s\in \omega ^{n+1}(q\Vdash $
“
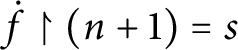 $\dot {f}\upharpoonright ( n+1) = s$
”
$\dot {f}\upharpoonright ( n+1) = s$
”
![]() $)\}.$
Clearly
$)\}.$
Clearly
![]() $D_{n}$
is an open dense set below
$D_{n}$
is an open dense set below
![]() $p,$
so by Lemma 26, we get that
$p,$
so by Lemma 26, we get that
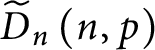 $\widetilde {D}_{n}\left ( n,p\right ) $
is
$\widetilde {D}_{n}\left ( n,p\right ) $
is
![]() $\leq _{n}^{\ast }$
-open dense.
$\leq _{n}^{\ast }$
-open dense.
Let
![]() $q_{0},r_{0}\leq p$
be two incompatible conditions with
$q_{0},r_{0}\leq p$
be two incompatible conditions with
![]() $E_{q_{0} }=E_{r_{0}}.$
Using the previous remark and Lemma 17, we can construct a
$E_{q_{0} }=E_{r_{0}}.$
Using the previous remark and Lemma 17, we can construct a
![]() $1$
-fusion sequence
$1$
-fusion sequence
![]() $T=\left \langle q_{i},r_{i}\right \rangle _{i\in \omega }$
such that
$T=\left \langle q_{i},r_{i}\right \rangle _{i\in \omega }$
such that
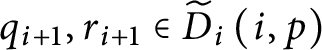 $q_{i+1},r_{i+1}\in \widetilde {D}_{i}\left ( i,p\right ) $
for every
$q_{i+1},r_{i+1}\in \widetilde {D}_{i}\left ( i,p\right ) $
for every
![]() $i\in \omega .$
By Lemma 20, let
$i\in \omega .$
By Lemma 20, let
![]() $\overline {p}$
be a fusion of
$\overline {p}$
be a fusion of
![]() $T.$
It follows that
$T.$
It follows that
![]() $\overline {p}\leq p$
and
$\overline {p}\leq p$
and
![]() $\overline {p}$
is
$\overline {p}$
is
![]() $\dot {f}$
-nice.▪
$\dot {f}$
-nice.▪
With this result, we can conclude the following:
Proposition 31 [Reference Shelah13]
If
![]() $\ \mathcal {U}$
is an ultrafilter, then
$\ \mathcal {U}$
is an ultrafilter, then
![]() $\mathbb {S}( \mathcal {U}) $
has the Sacks property.
$\mathbb {S}( \mathcal {U}) $
has the Sacks property.
Proof Let
![]() $\dot {f}$
be an
$\dot {f}$
be an
![]() $\mathbb {S}( \mathcal {U}) $
-name for a new real and
$\mathbb {S}( \mathcal {U}) $
-name for a new real and
![]() $p\in \mathbb {S}( \mathcal {U}) .$
By the previous result, we can find
$p\in \mathbb {S}( \mathcal {U}) .$
By the previous result, we can find
![]() $q\leq p$
that is
$q\leq p$
that is
![]() $\dot {f}$
-nice. For every
$\dot {f}$
-nice. For every
![]() $n\in \omega ,$
define
$n\in \omega ,$
define
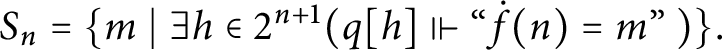 $S_{n}=\{m\mid \exists h\in 2^{n+1}(q[ h] \Vdash \text{``}\dot {f}( n) =m\text {'' })\}.$
It follows that
$S_{n}=\{m\mid \exists h\in 2^{n+1}(q[ h] \Vdash \text{``}\dot {f}( n) =m\text {'' })\}.$
It follows that
![]() $S_{n}$
has size at most
$S_{n}$
has size at most
![]() $2^{n+1}$
and
$2^{n+1}$
and
![]() $q\Vdash $
“
$q\Vdash $
“
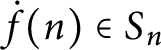 $\dot {f}( n) \in S_{n}$
.” This finishes the proof.▪
$\dot {f}( n) \in S_{n}$
.” This finishes the proof.▪
Most of the arguments in this section were based on the ones of [Reference Shelah13]. Instead of our fusion sequences, Shelah used games to prove the properness and the Sacks property. We decided to use the fusion sequences instead of games because it will be easier to work with sequences rather than with games when dealing with the iteration.
3 Forcing with
 $\mathbb {S}( \mathcal {U}) $
preserves
$\mathbb {S}( \mathcal {U}) $
preserves
 $\mathsf {c}_{\mathsf {min}}$
-covering
$\mathsf {c}_{\mathsf {min}}$
-covering
It is easy to see that if
![]() $X\subseteq 2^{\omega }$
is
$X\subseteq 2^{\omega }$
is
![]() $\mathsf {c}_{\mathsf {min} }$
-monochromatic, then the closure
$\mathsf {c}_{\mathsf {min} }$
-monochromatic, then the closure
![]() $\overline {X}$
is also
$\overline {X}$
is also
![]() $\mathsf {c} _{\mathsf {min}}$
-monochromatic. In this way,
$\mathsf {c} _{\mathsf {min}}$
-monochromatic. In this way,
![]() $\mathfrak {hm}$
is the smallest size of a family of
$\mathfrak {hm}$
is the smallest size of a family of
![]() $\mathsf {c}_{\mathsf {min}}$
-monochromatic closed sets that covers
$\mathsf {c}_{\mathsf {min}}$
-monochromatic closed sets that covers
![]() $2^{\omega }.$
We will say that a tree
$2^{\omega }.$
We will say that a tree
![]() $T\subseteq 2^{<\omega }$
is
$T\subseteq 2^{<\omega }$
is
![]() $\mathsf {c}_{\mathsf {min}}$
-monochromatic if
$\mathsf {c}_{\mathsf {min}}$
-monochromatic if
![]() $\left [ T\right ] $
is
$\left [ T\right ] $
is
![]() $\mathsf {c}_{\mathsf {min}}$
-monochromatic. This means that T either only splits at odd levels or at even levels.
$\mathsf {c}_{\mathsf {min}}$
-monochromatic. This means that T either only splits at odd levels or at even levels.
Definition 32 We say that a forcing notion
![]() $\mathbb {P}$
preserves
$\mathbb {P}$
preserves
![]() $\mathsf {c} _{\mathsf {min}}$
-covering if for every
$\mathsf {c} _{\mathsf {min}}$
-covering if for every
![]() $p\in \mathbb {P}$
and for every
$p\in \mathbb {P}$
and for every
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {x}$
for a real in
$\dot {x}$
for a real in
![]() $2^{\omega },$
there are
$2^{\omega },$
there are
![]() $q\leq p$
and
$q\leq p$
and
![]() $T\in V$
a
$T\in V$
a
![]() $\mathsf {c}_{\mathsf {min}}$
-monochromatic tree such that
$\mathsf {c}_{\mathsf {min}}$
-monochromatic tree such that
![]() $q\Vdash \text{``}\dot {x}\in \left [ T\right ].\text{''}$
$q\Vdash \text{``}\dot {x}\in \left [ T\right ].\text{''}$
Recall that if
![]() $\mathbb {P}$
is a partial order,
$\mathbb {P}$
is a partial order,
![]() $p\in \mathbb {P}$
and
$p\in \mathbb {P}$
and
![]() $\dot {x}$
a
$\dot {x}$
a
![]() $\mathbb {P}$
-name for a new element of
$\mathbb {P}$
-name for a new element of
![]() $2^{\omega },$
we defined
$2^{\omega },$
we defined
![]() $\dot {x}\left [ p\right ] =\bigcup \left \{ t\in 2^{<\omega }\mid p\Vdash \text{``}t\subseteq \dot {x}\text{''}\right \}.$
Since
$\dot {x}\left [ p\right ] =\bigcup \left \{ t\in 2^{<\omega }\mid p\Vdash \text{``}t\subseteq \dot {x}\text{''}\right \}.$
Since
![]() $\dot {x}$
is forced to be a new real, then
$\dot {x}$
is forced to be a new real, then
![]() $\dot {x}\left [ p\right ] \in 2^{<\omega }.$
Note that for every
$\dot {x}\left [ p\right ] \in 2^{<\omega }.$
Note that for every
![]() $p\in \mathbb {P}$
there are
$p\in \mathbb {P}$
there are
![]() $q,r\leq p$
such that
$q,r\leq p$
such that
![]() $\dot {x}\left [ q\right ] $
and
$\dot {x}\left [ q\right ] $
and
![]() $\dot {x}\left [ r\right ] $
are incompatible elements of
$\dot {x}\left [ r\right ] $
are incompatible elements of
![]() $2^{<\omega }.$
In this section, we will prove that Shelah’s forcing
$2^{<\omega }.$
In this section, we will prove that Shelah’s forcing
![]() $\mathbb {S}( \mathcal {U}) $
preserves
$\mathbb {S}( \mathcal {U}) $
preserves
![]() $\mathsf {c}_{\mathsf {min}} $
-covering. We will deal with the iteration in later sections. For the rest of this section, fix
$\mathsf {c}_{\mathsf {min}} $
-covering. We will deal with the iteration in later sections. For the rest of this section, fix
![]() $\dot {x}$
a
$\dot {x}$
a
![]() $\mathbb {S}( \mathcal {U}) $
-name for a new real. Recall that a condition p is
$\mathbb {S}( \mathcal {U}) $
-name for a new real. Recall that a condition p is
![]() $\dot {x}$
-nice if
$\dot {x}$
-nice if
![]() $p[ h] $
determines
$p[ h] $
determines
![]() $\dot {x}\upharpoonright n$
for every
$\dot {x}\upharpoonright n$
for every
![]() $h:n\longrightarrow 2.$
$h:n\longrightarrow 2.$
Definition 33 Let
![]() $p\in \mathbb {S}( \mathcal {U}) $
, define
$p\in \mathbb {S}( \mathcal {U}) $
, define
![]() $S_{p}\left ( \dot {x}\right ) =\bigcup \left \{ \dot {x}\left [ p[ h] \right ] \mid h\in 2^{<\omega }\right \} .$
$S_{p}\left ( \dot {x}\right ) =\bigcup \left \{ \dot {x}\left [ p[ h] \right ] \mid h\in 2^{<\omega }\right \} .$
It is easy to see that if p is
![]() $\dot {x}$
-nice, then
$\dot {x}$
-nice, then
![]() $S_{p}( \dot {x} ) $
is a tree and
$S_{p}( \dot {x} ) $
is a tree and
![]() $p\Vdash \text{``}\dot {x}\in [ S_{p}( \dot {x}) ] .\text{''}$
Recall that a tree
$p\Vdash \text{``}\dot {x}\in [ S_{p}( \dot {x}) ] .\text{''}$
Recall that a tree
![]() $p\subseteq 2^{<\omega }$
is a Sacks tree if for for every
$p\subseteq 2^{<\omega }$
is a Sacks tree if for for every
![]() $s\in p$
there is
$s\in p$
there is
![]() $t\in p$
such that
$t\in p$
such that
![]() $s\subseteq t$
and t is a splitting node of p (i.e.,
$s\subseteq t$
and t is a splitting node of p (i.e.,
![]() $t^{\frown }0, t^{\frown }1\in p$
). Since
$t^{\frown }0, t^{\frown }1\in p$
). Since
![]() $\dot {x}$
is a new real,
$\dot {x}$
is a new real,
![]() $S_{p}\left ( \dot {x}\right ) $
is a Sacks tree. Recall that the set of all
$S_{p}\left ( \dot {x}\right ) $
is a Sacks tree. Recall that the set of all
![]() $\dot {x}$
-nice conditions is a dense set.
$\dot {x}$
-nice conditions is a dense set.
Lemma 34 Let p be
![]() $\dot {x}$
-nice and
$\dot {x}$
-nice and
![]() $n>0.$
$n>0.$
-
1. If
 $h:n\longrightarrow 2$
then there is
$h:n\longrightarrow 2$
then there is
 $q\leq _{n}p$
such that
$q\leq _{n}p$
such that
 $\dot {x}\left [ q\left [ h^{\frown }0\right ] \right ] $
and
$\dot {x}\left [ q\left [ h^{\frown }0\right ] \right ] $
and
 $\dot {x}\left [ q\left [ h^{\frown }1\right ] \right ] $
are incompatible (as nodes in the tree
$\dot {x}\left [ q\left [ h^{\frown }1\right ] \right ] $
are incompatible (as nodes in the tree
 $2^{<\omega }$
).
$2^{<\omega }$
). -
2. There is
 $r\leq _{n}p$
such that
$r\leq _{n}p$
such that
 $\dot {x}\left [ r\left [ h^{\frown }0\right ] \right ] $
and
$\dot {x}\left [ r\left [ h^{\frown }0\right ] \right ] $
and
 $\dot {x}\left [ r\left [ h^{\frown }1\right ] \right ] $
are incompatible for every
$\dot {x}\left [ r\left [ h^{\frown }1\right ] \right ] $
are incompatible for every
 $h:n\longrightarrow 2.$
$h:n\longrightarrow 2.$
Proof Let
![]() $h:n\longrightarrow 2$
and since
$h:n\longrightarrow 2$
and since
![]() $S_{p}\left ( \dot {x}\right ) $
is a Sacks tree, there must be
$S_{p}\left ( \dot {x}\right ) $
is a Sacks tree, there must be
![]() $h ^{\frown }0\subseteq g_{0}^{0}, g_{0}^{1}$
and
$h ^{\frown }0\subseteq g_{0}^{0}, g_{0}^{1}$
and
![]() $h ^{\frown }1\subseteq g_{1}^{0}, g_{1}^{1}$
such that both
$h ^{\frown }1\subseteq g_{1}^{0}, g_{1}^{1}$
such that both
![]() $\dot {x} [p[g_{0}^{0}]]$
and
$\dot {x} [p[g_{0}^{0}]]$
and
![]() $\dot {x}[p[g_{0}^{1}]]$
are incompatible and both
$\dot {x}[p[g_{0}^{1}]]$
are incompatible and both
![]() $\dot {x}[p[g_{1}^{0}]]$
and
$\dot {x}[p[g_{1}^{0}]]$
and
![]() $\dot {x}[p[g_{1}^{1}]]$
are incompatible. We may also assume there is m such that all
$\dot {x}[p[g_{1}^{1}]]$
are incompatible. We may also assume there is m such that all
![]() $g_{0}^{0}, g_{0}^{1}, g_{1}^{0}$
and
$g_{0}^{0}, g_{0}^{1}, g_{1}^{0}$
and
![]() $g_{1}^{1}$
have m as its domain. There must be
$g_{1}^{1}$
have m as its domain. There must be
![]() $i,j$
such that
$i,j$
such that
![]() $\dot {x}[p[g_{0}^{i}]]$
and
$\dot {x}[p[g_{0}^{i}]]$
and
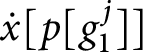 $\dot {x}[p[g_{1}^{j}]]$
are incompatible, with out loosing generality, we may assume
$\dot {x}[p[g_{1}^{j}]]$
are incompatible, with out loosing generality, we may assume
![]() $i=j=0.$
We define the condition
$i=j=0.$
We define the condition
![]() $q\leq p$
with the following properties:
$q\leq p$
with the following properties:
-
1.
 $E_{q}=E_{p}\setminus \{\left [ a_{p}( l) \right ] _{p}\mid l\in (n,m)\}.$
$E_{q}=E_{p}\setminus \{\left [ a_{p}( l) \right ] _{p}\mid l\in (n,m)\}.$
-
2. If
 $l\in (n,m)$
and
$l\in (n,m)$
and
 $f: 2^{A_{p}\cap a_{p}( l) }\longrightarrow 2$
then the following holds:
$f: 2^{A_{p}\cap a_{p}( l) }\longrightarrow 2$
then the following holds:-
(a) If
 $f( a_{p}( n) ) =0$
then
$f( a_{p}( n) ) =0$
then
 $H_{q} ^{a_{p}( l) }( f) =g_{0}^{0}( l) .$
$H_{q} ^{a_{p}( l) }( f) =g_{0}^{0}( l) .$
-
(b) If
 $f( a_{p}( n) ) =1$
then
$f( a_{p}( n) ) =1$
then
 $H_{q} ^{a_{p}( l) }( f) =g_{1}^{0}( l) .$
$H_{q} ^{a_{p}( l) }( f) =g_{1}^{0}( l) .$
-
Note that
![]() $q\left [ h^{\frown }0\right ] =p[g_{0}^{0}]$
and
$q\left [ h^{\frown }0\right ] =p[g_{0}^{0}]$
and
![]() $q\left [ h^{\frown }1\right ] =p[g_{1}^{0}],$
so the result immediately follows.
$q\left [ h^{\frown }1\right ] =p[g_{1}^{0}],$
so the result immediately follows.
The second part of the lemma is proved by applying iteratively the first part.▪
We need the following notion:
Definition 35 Let p be an
![]() $\dot {x}$
-nice condition and
$\dot {x}$
-nice condition and
![]() $n\in \omega .$
We say that p is n-separating if for all
$n\in \omega .$
We say that p is n-separating if for all
![]() $h,g:n+1\longrightarrow 2$
then
$h,g:n+1\longrightarrow 2$
then
![]() $\dot {x}\left [ p[ h] \right ] $
and
$\dot {x}\left [ p[ h] \right ] $
and
![]() $\dot {x}\left [ p\left [ g\right ] \right ] $
are incompatible whenever
$\dot {x}\left [ p\left [ g\right ] \right ] $
are incompatible whenever
![]() $h\neq g.$
We say p is
$h\neq g.$
We say p is
![]() $\omega $
-separating if it is n-separating for every
$\omega $
-separating if it is n-separating for every
![]() $n\in \omega .$
$n\in \omega .$
Note that if p is n-separating and
![]() $q\leq _{n}^{\ast }p$
then q is n-separating too (see Lemma 23). For convenience, we will say that every n-nice condition is
$q\leq _{n}^{\ast }p$
then q is n-separating too (see Lemma 23). For convenience, we will say that every n-nice condition is
![]() $-1$
-separating.
$-1$
-separating.
Lemma 36 If p is
![]() $\left ( n-1\right ) $
-separating then
$\left ( n-1\right ) $
-separating then
![]() $D=\{r\leq _{n}^{\ast }p\mid r$
is n-separating
$D=\{r\leq _{n}^{\ast }p\mid r$
is n-separating
![]() $\}$
is
$\}$
is
![]() $\leq _{n}^{\ast }$
-open dense below
$\leq _{n}^{\ast }$
-open dense below
![]() $p.$
$p.$
Proof Note that D is
![]() $\leq _{n}^{\ast }$
-open by the previous remark, we will see it is also
$\leq _{n}^{\ast }$
-open by the previous remark, we will see it is also
![]() $\leq _{n}^{\ast }$
-dense below
$\leq _{n}^{\ast }$
-dense below
![]() $p.$
Let
$p.$
Let
![]() $q\leq _{n}^{\ast }p$
and by the previous lemma, we can find
$q\leq _{n}^{\ast }p$
and by the previous lemma, we can find
![]() $r\leq _{n}q$
(so
$r\leq _{n}q$
(so
![]() $r\leq _{n}^{\ast }q$
) such that for that
$r\leq _{n}^{\ast }q$
) such that for that
![]() $\dot {x}\left [ r\left [ h^{\frown }0\right ] \right ] $
and
$\dot {x}\left [ r\left [ h^{\frown }0\right ] \right ] $
and
![]() $\dot {x}\left [ r\left [ h^{\frown }1\right ] \right ] $
are incompatible for every
$\dot {x}\left [ r\left [ h^{\frown }1\right ] \right ] $
are incompatible for every
![]() $h:n\longrightarrow 2.$
Since p is
$h:n\longrightarrow 2.$
Since p is
![]() $\left ( n-1\right ) $
-separating, r is n-separating.▪
$\left ( n-1\right ) $
-separating, r is n-separating.▪
We can now conclude the following:
Corollary 37 The set of all
![]() $\omega $
-separating conditions is dense. Furthermore, if p is n-nice, then there is
$\omega $
-separating conditions is dense. Furthermore, if p is n-nice, then there is
![]() $q\leq _{n}^{\ast }p$
such that q is
$q\leq _{n}^{\ast }p$
such that q is
![]() $\omega $
-separating.
$\omega $
-separating.
Proof Let
![]() $p\in \mathbb {S}( \mathcal {U}) $
be an n-nice condition, we will prove p has a
$p\in \mathbb {S}( \mathcal {U}) $
be an n-nice condition, we will prove p has a
![]() $\omega $
-separating extension. We recursively construct a
$\omega $
-separating extension. We recursively construct a
![]() $1$
-fusion sequence
$1$
-fusion sequence
![]() $T=\left \langle q_{i},r_{i}\right \rangle _{i<\omega }$
with the following properties:
$T=\left \langle q_{i},r_{i}\right \rangle _{i<\omega }$
with the following properties:
-
1.
 $q_{0}$
and
$q_{0}$
and
 $r_{0}$
are two incompatible extensions of p with
$r_{0}$
are two incompatible extensions of p with
 $E_{q_{0}}=E_{r_{0}}.$
$E_{q_{0}}=E_{r_{0}}.$
-
2. Both
 $q_{i},r_{i}$
are i-separating.
$q_{i},r_{i}$
are i-separating.
This can be done by Lemmas 17 and 36. It is easy to see that any fusion of T will have the desired properties.▪
If
![]() $s,t\in 2^{<\omega }$
are two incompatible finite sequences, define
$s,t\in 2^{<\omega }$
are two incompatible finite sequences, define
![]() $\mathsf {c}_{\mathsf {min}}\left ( s,t\right ) $
to be the parity of the length of the biggest initial segment shared by both s and
$\mathsf {c}_{\mathsf {min}}\left ( s,t\right ) $
to be the parity of the length of the biggest initial segment shared by both s and
![]() $t.$
Note that this is an abuse of notation since the domain of
$t.$
Note that this is an abuse of notation since the domain of
![]() $\mathsf {c}_{\mathsf {min}}$
is
$\mathsf {c}_{\mathsf {min}}$
is
![]() $[ 2^{\omega }] ^{2}.$
We will now define the following:
$[ 2^{\omega }] ^{2}.$
We will now define the following:
Definition 38 Let
![]() $p\in \mathbb {S}( \mathcal {U}) , n\in \omega $
and
$p\in \mathbb {S}( \mathcal {U}) , n\in \omega $
and
![]() $i<2.$
The condition p is called
$i<2.$
The condition p is called
![]() $\left ( n,i\right ) $
-faithful if p is n-separating and
$\left ( n,i\right ) $
-faithful if p is n-separating and
![]() $\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ p[ h] \right ] ,\dot {x}\left [ p\left [ g\right ] \right ] \right ) =i$
for every
$\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ p[ h] \right ] ,\dot {x}\left [ p\left [ g\right ] \right ] \right ) =i$
for every
![]() $h,g\in 2^{n+1}$
such that
$h,g\in 2^{n+1}$
such that
![]() $h\neq g.$
$h\neq g.$
If p is
![]() $\left ( n,i\right ) $
-faithful and
$\left ( n,i\right ) $
-faithful and
![]() $q\leq _{n}^{\ast }p,$
then q is also
$q\leq _{n}^{\ast }p,$
then q is also
![]() $\left ( n,i\right ) $
-faithful (see Lemma 23). Once again, for convenience, we will say that p is
$\left ( n,i\right ) $
-faithful (see Lemma 23). Once again, for convenience, we will say that p is
![]() $\left ( -1,i\right ) $
-faithful if p is
$\left ( -1,i\right ) $
-faithful if p is
![]() $\dot {x}$
-nice. We can finally prove the main result on this section.
$\dot {x}$
-nice. We can finally prove the main result on this section.
Proposition 39 If
![]() $\ \mathcal {U}$
is an ultrafilter, then
$\ \mathcal {U}$
is an ultrafilter, then
![]() $\mathbb {S}\left ( \mathcal {U} \right ) $
preserves
$\mathbb {S}\left ( \mathcal {U} \right ) $
preserves
![]() $\mathsf {c}_{\mathsf {min}}$
-covering.
$\mathsf {c}_{\mathsf {min}}$
-covering.
Proof Let
![]() $\dot {x}$
be a
$\dot {x}$
be a
![]() $\mathbb {S(\mathcal {U})}$
-name for a new element of
$\mathbb {S(\mathcal {U})}$
-name for a new element of
![]() $2^{\omega }.$
Fix a condition p that is
$2^{\omega }.$
Fix a condition p that is
![]() $\omega $
-separating. Given
$\omega $
-separating. Given
![]() $n\in \omega , q\leq p$
and
$n\in \omega , q\leq p$
and
![]() $h:n\longrightarrow 2,$
let
$h:n\longrightarrow 2,$
let
![]() $I_{q}\left ( h\right ) $
be the union of all the classes
$I_{q}\left ( h\right ) $
be the union of all the classes
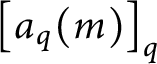 $\left [ a_{q}( m ) \right ] _{q}$
with the following properties:
$\left [ a_{q}( m ) \right ] _{q}$
with the following properties:
-
1.
 $n<m.$
$n<m.$
-
2. For every function
 $g\in 2^{m}$
with the property that
$g\in 2^{m}$
with the property that
 $h\subseteq g$
, we have that
$h\subseteq g$
, we have that
 $\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ q\left [ g^{\frown }0\right ] \right ] ,\dot {x}\left [ q\left [ g^{\frown }1\right ] \right ] \right ) =1.$
$\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ q\left [ g^{\frown }0\right ] \right ] ,\dot {x}\left [ q\left [ g^{\frown }1\right ] \right ] \right ) =1.$
We will now proceed by cases, first assume there are
![]() $q\leq p$
and
$q\leq p$
and
![]() $h\in 2^{<\omega }$
such that
$h\in 2^{<\omega }$
such that
![]() $I_{q}\left ( h\right ) \in \mathcal {U}.$
Let
$I_{q}\left ( h\right ) \in \mathcal {U}.$
Let
![]() $r\leq q[ h] $
such that
$r\leq q[ h] $
such that
![]() $dom\left ( E_{r}\right ) =I_{q}\left ( h\right ) $
and every
$dom\left ( E_{r}\right ) =I_{q}\left ( h\right ) $
and every
![]() $H_{r}^{l}$
is a constant function for
$H_{r}^{l}$
is a constant function for
![]() $l\in A_{q} \backslash A_{r}.$
It is then easy to see that
$l\in A_{q} \backslash A_{r}.$
It is then easy to see that
![]() $S_{r}\left ( \dot {x}\right ) $
is a
$S_{r}\left ( \dot {x}\right ) $
is a
![]() $1$
-monochromatic tree and we are done.
$1$
-monochromatic tree and we are done.
Now, we assume that
![]() $I_{q}\left ( h\right ) \notin \mathcal {U}$
for every
$I_{q}\left ( h\right ) \notin \mathcal {U}$
for every
![]() $q\leq p$
and
$q\leq p$
and
![]() $h\in 2^{<\omega }.$
Given
$h\in 2^{<\omega }.$
Given
![]() $q\leq p$
and
$q\leq p$
and
![]() $n<\omega $
let
$n<\omega $
let
![]() $F_{n}\left ( q\right ) =\{r\leq _{n}^{\ast }q\mid r$
is
$F_{n}\left ( q\right ) =\{r\leq _{n}^{\ast }q\mid r$
is
![]() $\left ( n,0\right ) $
-faithful
$\left ( n,0\right ) $
-faithful
![]() $\}.$
$\}.$
Claim 40 If q is
![]() $\left ( n-1,0\right ) $
-faithful then
$\left ( n-1,0\right ) $
-faithful then
![]() $F_{n}\left ( q\right ) $
is
$F_{n}\left ( q\right ) $
is
![]() $\leq _{n}^{\ast }$
-open dense below q.
$\leq _{n}^{\ast }$
-open dense below q.
It is clear that
![]() $F_{n+1}\left ( q\right ) $
is
$F_{n+1}\left ( q\right ) $
is
![]() $\leq _{n}^{\ast }$
-open below
$\leq _{n}^{\ast }$
-open below
![]() $q,$
we will now prove that it is also
$q,$
we will now prove that it is also
![]() $\leq _{n}^{\ast }$
-dense. Let
$\leq _{n}^{\ast }$
-dense. Let
![]() $r\leq _{n}^{\ast }q,$
we will extend r to a
$r\leq _{n}^{\ast }q,$
we will extend r to a
![]() $\left ( n,0\right ) $
-faithful condition. Every
$\left ( n,0\right ) $
-faithful condition. Every
![]() $\leq _{n}^{\ast }$
-extension of q is n-nice, so by Corollary 37, we may assume that r is
$\leq _{n}^{\ast }$
-extension of q is n-nice, so by Corollary 37, we may assume that r is
![]() $\omega $
-separating. Let
$\omega $
-separating. Let
![]() $2^{n+1}=\left \{ h_{i}\mid i<k\right \} .$
We know
$2^{n+1}=\left \{ h_{i}\mid i<k\right \} .$
We know
![]() $B=I_{r}\left ( h_{1}\right ) \cup \cdots \cup I_{r}\left ( h_{k}\right ) \in \mathcal {U}^{\ast }$
(since each
$B=I_{r}\left ( h_{1}\right ) \cup \cdots \cup I_{r}\left ( h_{k}\right ) \in \mathcal {U}^{\ast }$
(since each
![]() $I_{r}\left ( h_{i}\right ) \in \mathcal {U}^{\ast }$
by hypothesis) and since B is the union of
$I_{r}\left ( h_{i}\right ) \in \mathcal {U}^{\ast }$
by hypothesis) and since B is the union of
![]() $E_{r}$
-classes, then there is
$E_{r}$
-classes, then there is
![]() $m>n+1$
such that
$m>n+1$
such that
![]() $\left [ a_{r}( m ) \right ] _{r}\cap B=\emptyset .$
Since
$\left [ a_{r}( m ) \right ] _{r}\cap B=\emptyset .$
Since
![]() $a_{r}( m ) \notin I_{r}( h_{i}) $
, then for every
$a_{r}( m ) \notin I_{r}( h_{i}) $
, then for every
![]() $i<k$
, there is
$i<k$
, there is
![]() $g_{i}:m\longrightarrow 2$
extending
$g_{i}:m\longrightarrow 2$
extending
![]() $h_{i}$
such that
$h_{i}$
such that
![]() $\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ r\left [ g_{i}^{\frown }0\right ] \right ] ,\dot {x}\left [ r\left [ g_{i}^{\frown }1\right ] \right ] \right ) =0$
(recall that r is
$\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ r\left [ g_{i}^{\frown }0\right ] \right ] ,\dot {x}\left [ r\left [ g_{i}^{\frown }1\right ] \right ] \right ) =0$
(recall that r is
![]() $\omega $
-separating, so in particular it is m-nice for every
$\omega $
-separating, so in particular it is m-nice for every
![]() $m\in \omega $
). We now define a condition
$m\in \omega $
). We now define a condition
![]() $r_{1}$
with the following properties:
$r_{1}$
with the following properties:
-
1.
 $r_{1}\leq _{n}r.$
$r_{1}\leq _{n}r.$
-
2.
 $dom\left ( E_{r_{1}}\right ) =dom\left ( E_{r}\right ) \backslash \bigcup \left \{ [ a_{r}( l) ] _{r}\mid n<l<m\right \} .$
$dom\left ( E_{r_{1}}\right ) =dom\left ( E_{r}\right ) \backslash \bigcup \left \{ [ a_{r}( l) ] _{r}\mid n<l<m\right \} .$
-
3. If
 $m\leq l$
then
$m\leq l$
then
 $ [ a_{r_{1}}( l) ] _{r_{1} }=[ a_{r}( l) ] _{r}.$
$ [ a_{r_{1}}( l) ] _{r_{1} }=[ a_{r}( l) ] _{r}.$
-
4. If
 $n<l<m$
and
$n<l<m$
and
 $f\in 2^{A_{r_{1}}\cap a_{r}( l) }$
then
$f\in 2^{A_{r_{1}}\cap a_{r}( l) }$
then
 $H_{r_{1}}^{a_{r}( l) }( f) =g_{i}( l), $
where
$H_{r_{1}}^{a_{r}( l) }( f) =g_{i}( l), $
where
 $i<k$
is (the unique) such that
$i<k$
is (the unique) such that
 $f\left ( a_{r}( j) \right ) =h_{i}( j) $
for every
$f\left ( a_{r}( j) \right ) =h_{i}( j) $
for every
 $j\leq n.$
$j\leq n.$
It is now easy to see that
![]() $r_{1}$
is
$r_{1}$
is
![]() $\left ( n,0\right ) $
-faithful, this finishes the proof of the claim.
$\left ( n,0\right ) $
-faithful, this finishes the proof of the claim.
We now recursively construct a
![]() $1$
-fusion sequence
$1$
-fusion sequence
![]() $T=\left \langle q_{i} ,r_{i}\right \rangle _{i<\omega }$
with the following properties:
$T=\left \langle q_{i} ,r_{i}\right \rangle _{i<\omega }$
with the following properties:
-
1.
 $q_{0}$
and
$q_{0}$
and
 $r_{0}$
are two incompatible extensions of p with
$r_{0}$
are two incompatible extensions of p with
 $E_{q_{0}}=E_{r_{0}}.$
$E_{q_{0}}=E_{r_{0}}.$
-
2. Both
 $q_{i}$
and
$q_{i}$
and
 $r_{i}$
are
$r_{i}$
are
 $\left ( i,0\right ) $
-faithful.
$\left ( i,0\right ) $
-faithful.
Let
![]() $\overline {p}$
be a fusion of
$\overline {p}$
be a fusion of
![]() $T.$
It follows that
$T.$
It follows that
![]() $\overline {p}$
is an extension of p and
$\overline {p}$
is an extension of p and
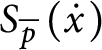 $S_{\overline {p}}\left ( \dot {x}\right ) $
is a
$S_{\overline {p}}\left ( \dot {x}\right ) $
is a
![]() $0$
-monochromatic tree.▪
$0$
-monochromatic tree.▪
4 Iterating the Shelah forcing
Our next task is to prove that if we perform a countable support iteration
![]() $\langle \mathbb {P}_{\alpha },\mathbb {\dot {Q}}_{\alpha }\mid \alpha \leq \omega _{2}\rangle $
such that for
$\langle \mathbb {P}_{\alpha },\mathbb {\dot {Q}}_{\alpha }\mid \alpha \leq \omega _{2}\rangle $
such that for
![]() $\mathbb {P}_{\alpha }\Vdash \text{``}\mathbb {\dot {Q} }_{\alpha }=\mathbb {S(}\mathcal {\dot {U}}_{\alpha }\mathcal {)}\text{''}$
for all
$\mathbb {P}_{\alpha }\Vdash \text{``}\mathbb {\dot {Q} }_{\alpha }=\mathbb {S(}\mathcal {\dot {U}}_{\alpha }\mathcal {)}\text{''}$
for all
![]() $\alpha <\omega _{2}$
(where
$\alpha <\omega _{2}$
(where
![]() $\mathcal {\dot {U}}_{\alpha }$
is a
$\mathcal {\dot {U}}_{\alpha }$
is a
![]() $\mathbb {P}_{\alpha }$
-name for an ultrafilter), then
$\mathbb {P}_{\alpha }$
-name for an ultrafilter), then
![]() $\mathbb {P}_{\omega _{2}}$
preserves
$\mathbb {P}_{\omega _{2}}$
preserves
![]() $\mathsf {c}_{\mathsf {min}}$
-covering. We do not know, in general, if the iteration of forcings that preserve
$\mathsf {c}_{\mathsf {min}}$
-covering. We do not know, in general, if the iteration of forcings that preserve
![]() $\mathsf {c}_{\mathsf {min}}$
-covering preserves
$\mathsf {c}_{\mathsf {min}}$
-covering preserves
![]() $\mathsf {c}_{\mathsf {min}}$
-covering, but we were able to prove it in our case. In this section, we will prove some technical lemmas regarding the iteration that will be useful in the following sections. Right now, our purpose is to extend our work with fusion sequences to every
$\mathsf {c}_{\mathsf {min}}$
-covering, but we were able to prove it in our case. In this section, we will prove some technical lemmas regarding the iteration that will be useful in the following sections. Right now, our purpose is to extend our work with fusion sequences to every
![]() $\mathbb {P} _{\alpha }.$
We hope that the material developed in this section will have more applications in the future, since it provides a very convenient way to work with the iteration of forcings of the form
$\mathbb {P} _{\alpha }.$
We hope that the material developed in this section will have more applications in the future, since it provides a very convenient way to work with the iteration of forcings of the form
![]() $\mathbb {S}\left ( \mathcal {U} \right ) .$
Moreover, it should be possible to perform a similar analysis for other forcings that do not have an axiom A structure, yet its main properties (like properness, not adding unbounded reals
$\mathbb {S}\left ( \mathcal {U} \right ) .$
Moreover, it should be possible to perform a similar analysis for other forcings that do not have an axiom A structure, yet its main properties (like properness, not adding unbounded reals
![]() $\ldots $
) are proved using games or trees (the first example that comes to mind is the Grigorieff forcing of a P-point).
$\ldots $
) are proved using games or trees (the first example that comes to mind is the Grigorieff forcing of a P-point).
For the following sections, fix a countable support iteration
![]() $\langle \mathbb {P}_{\alpha },\mathbb {\dot {Q}}_{\alpha }\mid \alpha \leq \omega _{2}\rangle $
as described in the beginning of the section.
$\langle \mathbb {P}_{\alpha },\mathbb {\dot {Q}}_{\alpha }\mid \alpha \leq \omega _{2}\rangle $
as described in the beginning of the section.
Definition 41 Let
![]() $\alpha \leq \omega _{2}, F\in \left [ \alpha \right ] ^{<\omega }, \eta :F\longrightarrow \omega $
and
$\alpha \leq \omega _{2}, F\in \left [ \alpha \right ] ^{<\omega }, \eta :F\longrightarrow \omega $
and
![]() $p,q\in \mathbb {P}_{\alpha }.$
$p,q\in \mathbb {P}_{\alpha }.$
-
1. Define
 $p\leq _{F,\eta }q$
if
$p\leq _{F,\eta }q$
if
 $p\leq q$
and for every
$p\leq q$
and for every
 $\beta \in F$
it is the case that
$\beta \in F$
it is the case that
 $p\upharpoonright \beta \Vdash \text{``}p\left ( \beta \right ) \leq _{\eta ( \beta ) }q( \beta ).\text{''}$
$p\upharpoonright \beta \Vdash \text{``}p\left ( \beta \right ) \leq _{\eta ( \beta ) }q( \beta ).\text{''}$
-
2.
 $p\leq _{F,\eta }^{\ast }q$
if
$p\leq _{F,\eta }^{\ast }q$
if
 $p\leq q$
and for every
$p\leq q$
and for every
 $\beta \in F$
it is the case that
$\beta \in F$
it is the case that
 $p\upharpoonright \beta \Vdash \text{``}p( \beta ) \leq _{\eta ( \beta ) }^{\ast }q( \beta ).'' $
$p\upharpoonright \beta \Vdash \text{``}p( \beta ) \leq _{\eta ( \beta ) }^{\ast }q( \beta ).'' $
-
3. If
 $\sigma \in \prod \limits _{\beta \in F}2^{\eta ( \beta ) }$
, we define the condition
$\sigma \in \prod \limits _{\beta \in F}2^{\eta ( \beta ) }$
, we define the condition
 $p\ast \sigma \in \mathbb {P}_{\alpha }$
as follows:
$p\ast \sigma \in \mathbb {P}_{\alpha }$
as follows:-
(a) If
 $\delta \notin F$
then
$\delta \notin F$
then
 $\left ( p\ast \sigma \right ) \upharpoonright \delta \Vdash \text{``}\left ( p\ast \sigma \right ) \left ( \delta \right ) =p\left ( \delta \right ).\text{''}$
$\left ( p\ast \sigma \right ) \upharpoonright \delta \Vdash \text{``}\left ( p\ast \sigma \right ) \left ( \delta \right ) =p\left ( \delta \right ).\text{''}$
-
(b) If
 $\delta \in F$
then
$\delta \in F$
then
 $\left ( p\ast \sigma \right ) \upharpoonright \delta \Vdash \text{``}\left ( p\ast \sigma \right ) \left ( \delta \right ) =p\left ( \delta \right ) \left [ \sigma \left ( \delta \right ) \right ] \text{''}$
(recall that
$\left ( p\ast \sigma \right ) \upharpoonright \delta \Vdash \text{``}\left ( p\ast \sigma \right ) \left ( \delta \right ) =p\left ( \delta \right ) \left [ \sigma \left ( \delta \right ) \right ] \text{''}$
(recall that
 $\sigma \left ( \delta \right ) \in 2^{\eta \left ( \delta \right ) }$
).
$\sigma \left ( \delta \right ) \in 2^{\eta \left ( \delta \right ) }$
).
-
In a similar way as before, define the following:
Definition 42 Let
![]() $\alpha \leq \omega _{2}, F\in \left [ \alpha \right ] ^{<\omega }, \eta :F\longrightarrow \omega , p\in \mathbb {P}_{\alpha }$
and
$\alpha \leq \omega _{2}, F\in \left [ \alpha \right ] ^{<\omega }, \eta :F\longrightarrow \omega , p\in \mathbb {P}_{\alpha }$
and
![]() $D\subseteq \mathbb {P}_{\alpha }.$
$D\subseteq \mathbb {P}_{\alpha }.$
-
1. D is
 $( F,\eta ) ^{\ast }$
-dense below p if for every
$( F,\eta ) ^{\ast }$
-dense below p if for every
 $q\leq _{F,\eta }^{\ast }p$
there is
$q\leq _{F,\eta }^{\ast }p$
there is
 $r\leq _{F,\eta }^{\ast }q$
such that
$r\leq _{F,\eta }^{\ast }q$
such that
 $r\in D.$
$r\in D.$
-
2. D is
 $( F,\eta ) ^{\ast }$
-open below p if for every r such that
$( F,\eta ) ^{\ast }$
-open below p if for every r such that
 $r\leq _{F,\eta }^{\ast }p$
and
$r\leq _{F,\eta }^{\ast }p$
and
 $r\in D$
then
$r\in D$
then
 $q\in D$
whenever
$q\in D$
whenever
 $q\leq _{F,\eta }^{\ast }r.$
$q\leq _{F,\eta }^{\ast }r.$
-
3. D is
 $( F,\eta ) ^{\ast }$
-open dense below p if it is both
$( F,\eta ) ^{\ast }$
-open dense below p if it is both
 $( F,\eta ) ^{\ast }$
-open and
$( F,\eta ) ^{\ast }$
-open and
 $( F,\eta ) ^{\ast }$
-dense below
$( F,\eta ) ^{\ast }$
-dense below
 $p.$
$p.$
-
4. D is
 $( F,\eta ) $
-dense below p if for every
$( F,\eta ) $
-dense below p if for every
 $q\leq _{F,\eta }p$
there is
$q\leq _{F,\eta }p$
there is
 $r\leq _{F,\eta }q$
such that
$r\leq _{F,\eta }q$
such that
 $r\in D.$
$r\in D.$
-
5. D is
 $( F,\eta ) $
-open below p if for every r such that
$( F,\eta ) $
-open below p if for every r such that
 $r\leq _{F,\eta }p$
and
$r\leq _{F,\eta }p$
and
 $r\in D$
then
$r\in D$
then
 $q\in D$
whenever
$q\in D$
whenever
 $q\leq _{F,\eta }r.$
$q\leq _{F,\eta }r.$
-
6. D is
 $( F,\eta ) $
-open dense below p if it is both
$( F,\eta ) $
-open dense below p if it is both
 $( F,\eta ) $
-open and
$( F,\eta ) $
-open and
 $( F,\eta ) $
-dense below
$( F,\eta ) $
-dense below
 $p.$
$p.$
We use similar conventions as before. The expression “D is
![]() $( F,\eta ) $
-dense” actually means that D is
$( F,\eta ) $
-dense” actually means that D is
![]() $( F,\eta ) $
-dense below the largest condition (similarly for the other notions). The expression “D is
$( F,\eta ) $
-dense below the largest condition (similarly for the other notions). The expression “D is
![]() $( F,\eta ) $
-open and
$( F,\eta ) $
-open and
![]() $\left ( F_{1},\eta _{1}\right ) $
-dense below p” is a shorthand for “D is
$\left ( F_{1},\eta _{1}\right ) $
-dense below p” is a shorthand for “D is
![]() $( F,\eta ) $
-open below p and
$( F,\eta ) $
-open below p and
![]() $\left ( F_{1},\eta _{1}\right ) $
-dense below p.” Note that if
$\left ( F_{1},\eta _{1}\right ) $
-dense below p.” Note that if
![]() $F\subseteq F_{1}$
,
$F\subseteq F_{1}$
,
![]() $\eta \leq \eta _{1}\upharpoonright F_{1}$
and D is
$\eta \leq \eta _{1}\upharpoonright F_{1}$
and D is
![]() $( F,\eta ) $
-open below
$( F,\eta ) $
-open below
![]() $p,$
then D is
$p,$
then D is
![]() $\left ( F_{1},\eta _{1}\right ) $
-open below
$\left ( F_{1},\eta _{1}\right ) $
-open below
![]() $p.$
$p.$
Let
![]() $\eta :F\longrightarrow \omega ,$
by
$\eta :F\longrightarrow \omega ,$
by
![]() $\eta +1:F\longrightarrow \omega $
we denote the function given by
$\eta +1:F\longrightarrow \omega $
we denote the function given by
![]() $\left ( \eta +1\right ) \left ( \alpha \right ) =\eta \left ( \alpha \right ) +1.$
For
$\left ( \eta +1\right ) \left ( \alpha \right ) =\eta \left ( \alpha \right ) +1.$
For
![]() $\eta _{1},\eta _{2}\in \omega ^{F},$
define
$\eta _{1},\eta _{2}\in \omega ^{F},$
define
![]() $\eta _{1}\leq \eta _{2}$
if
$\eta _{1}\leq \eta _{2}$
if
![]() $\eta _{1}\left ( \alpha \right ) \leq \eta _{2}\left ( \alpha \right ) $
for every
$\eta _{1}\left ( \alpha \right ) \leq \eta _{2}\left ( \alpha \right ) $
for every
![]() $\alpha \in F.$
$\alpha \in F.$
The following is the generalization of Lemma 23:
Lemma 43 Let
![]() $\alpha \leq \omega _{2}, F\in \left [ \alpha \right ] ^{<\omega }, \eta :F\longrightarrow \omega , p,q\in \mathbb {P}_{\alpha }$
such that
$\alpha \leq \omega _{2}, F\in \left [ \alpha \right ] ^{<\omega }, \eta :F\longrightarrow \omega , p,q\in \mathbb {P}_{\alpha }$
such that
![]() $q\leq _{F,\eta }^{\ast }p.$
If
$q\leq _{F,\eta }^{\ast }p.$
If
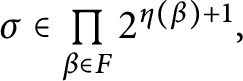 $\sigma \in \prod \limits _{\beta \in F}2^{\eta ( \beta ) +1},$
then
$\sigma \in \prod \limits _{\beta \in F}2^{\eta ( \beta ) +1},$
then
![]() $q\ast \sigma \leq p\ast \sigma .$
$q\ast \sigma \leq p\ast \sigma .$
If
![]() $D\subseteq \mathbb {P}_{\alpha }$
is an open dense set and
$D\subseteq \mathbb {P}_{\alpha }$
is an open dense set and
![]() $F\in \left [ \alpha \right ] ^{<\omega },\eta :F\longrightarrow \alpha ,$
define
$F\in \left [ \alpha \right ] ^{<\omega },\eta :F\longrightarrow \alpha ,$
define
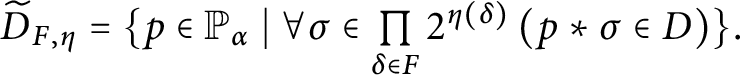 $\widetilde {D}_{F,\eta }=\{p\in \mathbb {P}_{\alpha }\mid \forall \sigma \in \prod \limits _{\delta \in F}2^{\eta \left ( \delta \right ) }\left ( p\ast \sigma \in D\right ) \}.$
$\widetilde {D}_{F,\eta }=\{p\in \mathbb {P}_{\alpha }\mid \forall \sigma \in \prod \limits _{\delta \in F}2^{\eta \left ( \delta \right ) }\left ( p\ast \sigma \in D\right ) \}.$
Lemma 44 Let
![]() $D\subseteq \mathbb {P}_{\alpha }$
be an open dense set,
$D\subseteq \mathbb {P}_{\alpha }$
be an open dense set,
![]() $F\in \left [ \alpha \right ] ^{<\omega }$
and
$F\in \left [ \alpha \right ] ^{<\omega }$
and
![]() $\eta :F\longrightarrow \alpha .$
The set
$\eta :F\longrightarrow \alpha .$
The set
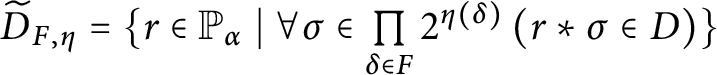 $\widetilde {D}_{F,\eta }=\{r\in \mathbb {P}_{\alpha }\mid \forall \sigma \in \prod \limits _{\delta \in F}2^{\eta \left ( \delta \right ) }\left ( r\ast \sigma \in D\right ) \}$
is
$\widetilde {D}_{F,\eta }=\{r\in \mathbb {P}_{\alpha }\mid \forall \sigma \in \prod \limits _{\delta \in F}2^{\eta \left ( \delta \right ) }\left ( r\ast \sigma \in D\right ) \}$
is
![]() $( F,\eta ) $
-open dense.
$( F,\eta ) $
-open dense.
Proof We will first prove that
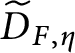 $\widetilde {D}_{F,\eta }$
is
$\widetilde {D}_{F,\eta }$
is
![]() $( F,\eta ) $
-dense. Let p be a condition, enumerate
$( F,\eta ) $
-dense. Let p be a condition, enumerate
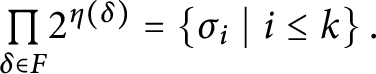 $ {\textstyle \prod \limits _{\delta \in F}} 2^{\eta \left ( \delta \right ) }=\left \{ \sigma _{i}\mid i\leq k\right \} .$
Recursively, we build
$ {\textstyle \prod \limits _{\delta \in F}} 2^{\eta \left ( \delta \right ) }=\left \{ \sigma _{i}\mid i\leq k\right \} .$
Recursively, we build
![]() $\left \{ p_{i}\mid i\leq k\right \} $
such that the following holds:
$\left \{ p_{i}\mid i\leq k\right \} $
such that the following holds:
-
1.
 $p_{0}\leq _{F,\eta }p.$
$p_{0}\leq _{F,\eta }p.$
-
2.
 $p_{i+1}\leq _{F,\eta }p_{i}$
for
$p_{i+1}\leq _{F,\eta }p_{i}$
for
 $i+1\leq k.$
$i+1\leq k.$
-
3.
 $p_{i}\ast \sigma _{i}\in D.$
$p_{i}\ast \sigma _{i}\in D.$
This is easy to do. It follows that
![]() $p_{k}\in D$
and
$p_{k}\in D$
and
![]() $p_{k}\leq _{F,\eta }p.$
It is easy to see that
$p_{k}\leq _{F,\eta }p.$
It is easy to see that
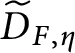 $\widetilde {D}_{F,\eta }$
is
$\widetilde {D}_{F,\eta }$
is
![]() $( F,\eta ) $
-open.▪
$( F,\eta ) $
-open.▪
We will recall a well-known forcing lemma that will be frequently used (for a proof, see Lemma 1.19 in the first chapter of the book [Reference Shelah14]):
Lemma 45 (Definition by cases)
Let
![]() $\mathbb {P}$
be a partial order,
$\mathbb {P}$
be a partial order,
![]() $A=\left \{ p_{\alpha }\mid \alpha \in \kappa \right \} \subseteq \mathbb {P}$
an antichain and
$A=\left \{ p_{\alpha }\mid \alpha \in \kappa \right \} \subseteq \mathbb {P}$
an antichain and
![]() $\{\dot {x}_{\alpha }\mid \alpha \in \kappa \}$
be a set of
$\{\dot {x}_{\alpha }\mid \alpha \in \kappa \}$
be a set of
![]() $\mathbb {P}$
-names. There is a
$\mathbb {P}$
-names. There is a
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {y}$
such that
$\dot {y}$
such that
![]() $p_{\alpha }\Vdash \text{``}\dot {y}=\dot {x}_{\alpha }\text{''}$
for every
$p_{\alpha }\Vdash \text{``}\dot {y}=\dot {x}_{\alpha }\text{''}$
for every
![]() $\alpha \in \kappa .$
$\alpha \in \kappa .$
The following technical notion will be frequently used:
Definition 46 Let M be a countable elementary submodel of
![]() $\mathsf{H}( \kappa ) $
(for some big enough regular
$\mathsf{H}( \kappa ) $
(for some big enough regular
![]() $\kappa $
) and
$\kappa $
) and
![]() $\alpha \in M$
an ordinal. We say that
$\alpha \in M$
an ordinal. We say that
![]() $L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
is suitable for
$L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
is suitable for
![]() $\left ( M,\alpha \right ) $
if the following holds for every
$\left ( M,\alpha \right ) $
if the following holds for every
![]() $n\in \omega $
:
$n\in \omega $
:
-
1.
 $F_{n}$
is a finite subset of
$F_{n}$
is a finite subset of
 $M\cap \alpha .$
$M\cap \alpha .$
-
2.
 $F_{n}\subseteq F_{n+1}.$
$F_{n}\subseteq F_{n+1}.$
-
3.
 $\left \vert F_{n}\right \vert \leq n$
and
$\left \vert F_{n}\right \vert \leq n$
and
 $\left \vert F_{n+1}\right \vert \leq \left \vert F_{n}\right \vert +1.$
$\left \vert F_{n+1}\right \vert \leq \left \vert F_{n}\right \vert +1.$
-
4.
 $\bigcup \limits _{n\in \omega }F_{n}=M\cap \alpha .$
$\bigcup \limits _{n\in \omega }F_{n}=M\cap \alpha .$
-
5.
 $\eta _{n}:F_{n}\longrightarrow \omega .$
$\eta _{n}:F_{n}\longrightarrow \omega .$
-
6.
 $\eta _{n}\leq \eta _{n+1}\upharpoonright F_{n}$
$\eta _{n}\leq \eta _{n+1}\upharpoonright F_{n}$
-
7. If
 $\beta \in M\cap \alpha $
then
$\beta \in M\cap \alpha $
then
 $\left \langle \eta _{n}( \beta ) \right \rangle _{n\in \omega }\longrightarrow \infty .$
$\left \langle \eta _{n}( \beta ) \right \rangle _{n\in \omega }\longrightarrow \infty .$
Note that if
![]() $L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
is suitable for
$L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
is suitable for
![]() $\left ( M,\alpha \right ) ,$
then
$\left ( M,\alpha \right ) ,$
then
![]() $F_{n},\eta _{n}\in M$
for every
$F_{n},\eta _{n}\in M$
for every
![]() $n\in \omega $
(however, it may be the case that
$n\in \omega $
(however, it may be the case that
![]() $L\notin M$
). The following lemma is easy and left to the reader:
$L\notin M$
). The following lemma is easy and left to the reader:
Lemma 47 Let M be a countable elementary submodel of
![]() $\mathsf{H}( \kappa ) $
,
$\mathsf{H}( \kappa ) $
,
![]() $\alpha \in M$
and
$\alpha \in M$
and
![]() $L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
$L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
![]() $\left ( M,\alpha \right ) .$
Let
$\left ( M,\alpha \right ) .$
Let
![]() $\beta \in M\cap \alpha ,$
define
$\beta \in M\cap \alpha ,$
define
![]() $F_{n}^{\prime }=F_{n}\cap \beta , \eta _{n}^{\prime }=\eta _{n}\upharpoonright F_{n}^{\prime }$
and
$F_{n}^{\prime }=F_{n}\cap \beta , \eta _{n}^{\prime }=\eta _{n}\upharpoonright F_{n}^{\prime }$
and
![]() $L^{\prime }=\left \{ \left ( F_{n}^{\prime },\eta _{n}^{\prime }\right ) \mid n\in \omega \right \} .$
Then
$L^{\prime }=\left \{ \left ( F_{n}^{\prime },\eta _{n}^{\prime }\right ) \mid n\in \omega \right \} .$
Then
![]() $L^{\prime }$
is suitable for
$L^{\prime }$
is suitable for
![]() $\left ( M,\beta \right ) .$
$\left ( M,\beta \right ) .$
The following is the generalization of a
![]() $1$
-fusion sequence:
$1$
-fusion sequence:
Definition 48 Let M be a countable elementary submodel of
![]() $\mathsf{H}( \kappa) $
(for some big enough regular
$\mathsf{H}( \kappa) $
(for some big enough regular
![]() $\kappa $
) such that
$\kappa $
) such that
![]() $\mathbb {P}_{\alpha }\in M$
and
$\mathbb {P}_{\alpha }\in M$
and
![]() $L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
be suitable for
$L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
be suitable for
![]() $\left ( M,\alpha \right ) .$
We say that a tree
$\left ( M,\alpha \right ) .$
We say that a tree
![]() $T\subseteq \left ( \mathbb {P}_{\alpha }\cap M\right ) ^{<\omega }$
(ordered by end-extension) is an
$T\subseteq \left ( \mathbb {P}_{\alpha }\cap M\right ) ^{<\omega }$
(ordered by end-extension) is an
![]() $\alpha $
-fusion tree (with respect to M and L) if there are
$\alpha $
-fusion tree (with respect to M and L) if there are
![]() $d_{-}^{T}, w_{-}^{T} :T\longrightarrow \mathbb {P}_{\alpha }$
and
$d_{-}^{T}, w_{-}^{T} :T\longrightarrow \mathbb {P}_{\alpha }$
and
![]() $\langle \dot {e}_{n}^{T},\dot {u} _{n}^{T}\rangle _{n\in \omega }$
a sequence of
$\langle \dot {e}_{n}^{T},\dot {u} _{n}^{T}\rangle _{n\in \omega }$
a sequence of
![]() $\mathbb {P}_{\alpha }$
-names such that the following conditions hold:
$\mathbb {P}_{\alpha }$
-names such that the following conditions hold:
-
1.
 $\left \vert T_{0}\right \vert =1$
and if
$\left \vert T_{0}\right \vert =1$
and if
 $s=\left \langle p_{0} ,\ldots ,p_{n}\right \rangle \in T,$
then
$s=\left \langle p_{0} ,\ldots ,p_{n}\right \rangle \in T,$
then
 $p_{m+1}\leq _{F_{m},\eta _{m}}^{\ast } p_{m}$
for every
$p_{m+1}\leq _{F_{m},\eta _{m}}^{\ast } p_{m}$
for every
 $m<n.$
$m<n.$
-
2. If
 $s\in T,$
then
$s\in T,$
then
 $suc_{T}( s) =\left \{ d_{s}^{T} ,w_{s}^{T}\right \} .$
$suc_{T}( s) =\left \{ d_{s}^{T} ,w_{s}^{T}\right \} .$
-
3. If
 $F_{n+1}=F_{n}$
and
$F_{n+1}=F_{n}$
and
 $s\in T_{n},$
then
$s\in T_{n},$
then
 $d_{s}^{T}=w_{s}^{T}$
(so s has only one immediate successor in T).
$d_{s}^{T}=w_{s}^{T}$
(so s has only one immediate successor in T). -
4. Let
 $n\in \omega $
such that
$n\in \omega $
such that
 $F_{n+1}\setminus F_{n}\neq \emptyset .$
Pick
$F_{n+1}\setminus F_{n}\neq \emptyset .$
Pick
 $\gamma $
the (unique) element of
$\gamma $
the (unique) element of
 $F_{n+1}\setminus F_{n}$
and
$F_{n+1}\setminus F_{n}$
and
 $s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T_{n}.$
The following conditions hold:
$s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T_{n}.$
The following conditions hold:-
(a)
 $suc_{T}( s) =\left \{ d_{s}^{T},w_{s}^{T}\right \} .$
$suc_{T}( s) =\left \{ d_{s}^{T},w_{s}^{T}\right \} .$
-
(b)
 $d_{s}^{T}\upharpoonright \gamma =w_{s}^{T}\upharpoonright \gamma .$
$d_{s}^{T}\upharpoonright \gamma =w_{s}^{T}\upharpoonright \gamma .$
-
(c)
 $d_{s}^{T}\upharpoonright \gamma \Vdash \text{``}d_{s}^{T}( \gamma ) =\dot {e}_{{n}^{T}}\text{''}$
and
$d_{s}^{T}\upharpoonright \gamma \Vdash \text{``}d_{s}^{T}( \gamma ) =\dot {e}_{{n}^{T}}\text{''}$
and
 $w_{s}^{T}\upharpoonright \gamma \Vdash \text{``}w_{s}^{T}( \gamma ) =\dot {u}_{n}^{T}.\text{''}$
$w_{s}^{T}\upharpoonright \gamma \Vdash \text{``}w_{s}^{T}( \gamma ) =\dot {u}_{n}^{T}.\text{''}$
-
(d)
 $d_{s}^{T}\upharpoonright \gamma \left ( =w_{s}^{T}\upharpoonright \gamma \right ) $
forces that
$d_{s}^{T}\upharpoonright \gamma \left ( =w_{s}^{T}\upharpoonright \gamma \right ) $
forces that
 $\dot {e}_{n}^{T},\dot {u}_{n}^{T}$
are incompatible elements of
$\dot {e}_{n}^{T},\dot {u}_{n}^{T}$
are incompatible elements of
 $\mathbb {S(}\mathcal {\dot {U}}_{\gamma })$
but
$\mathbb {S(}\mathcal {\dot {U}}_{\gamma })$
but
 $E_{\dot {e}_{n}^{T}}=E_{\dot {u}_{n}^{T}}.$
$E_{\dot {e}_{n}^{T}}=E_{\dot {u}_{n}^{T}}.$
-
-
5. Assume
 $s=\left \langle p_{0},\ldots ,p_{n}\right \rangle , t=\left \langle p_{0}^{\prime },\ldots ,p_{n}^{\prime }\right \rangle , m=\triangle \left ( s,t\right ) $
and
$s=\left \langle p_{0},\ldots ,p_{n}\right \rangle , t=\left \langle p_{0}^{\prime },\ldots ,p_{n}^{\prime }\right \rangle , m=\triangle \left ( s,t\right ) $
and
 $\gamma \in F_{m+1}\backslash F_{m}.$
If
$\gamma \in F_{m+1}\backslash F_{m}.$
If
 $p_{n} \upharpoonright \gamma =p_{n}^{\prime }\upharpoonright \gamma $
the following holds:
$p_{n} \upharpoonright \gamma =p_{n}^{\prime }\upharpoonright \gamma $
the following holds:-
(a) In case
 $F_{n}\neq F_{n+1}$
the following holds:
$F_{n}\neq F_{n+1}$
the following holds:-
i.
 $d_{s}^{T}\upharpoonright \gamma =d_{t}^{T}\upharpoonright \gamma $
and
$d_{s}^{T}\upharpoonright \gamma =d_{t}^{T}\upharpoonright \gamma $
and
 $w_{s}^{T}\upharpoonright \gamma =w_{t}^{T}\upharpoonright \gamma .$
$w_{s}^{T}\upharpoonright \gamma =w_{t}^{T}\upharpoonright \gamma .$
-
ii.
 $d_{s}^{T}\upharpoonright \gamma \Vdash \text{``}\left \langle p_{n}( \gamma ) ,p_{n}^{\prime }( \gamma ) ,d_{s}^{T}( \gamma ) ,d_{t}^{T}( \gamma ) \right \rangle $
is an
$d_{s}^{T}\upharpoonright \gamma \Vdash \text{``}\left \langle p_{n}( \gamma ) ,p_{n}^{\prime }( \gamma ) ,d_{s}^{T}( \gamma ) ,d_{t}^{T}( \gamma ) \right \rangle $
is an
 $\eta _{n}( \gamma ) $
-nice sequence.
$\eta _{n}( \gamma ) $
-nice sequence.
 $\text{''}$
$\text{''}$
-
iii.
 $w_{s}^{T}\upharpoonright \gamma \Vdash \text{``}\left \langle p_{n}( \gamma ) ,p_{n}^{\prime }( \gamma ) ,w_{s}^{T}( \gamma ) ,w_{t}^{T}( \gamma ) \right \rangle $
is an
$w_{s}^{T}\upharpoonright \gamma \Vdash \text{``}\left \langle p_{n}( \gamma ) ,p_{n}^{\prime }( \gamma ) ,w_{s}^{T}( \gamma ) ,w_{t}^{T}( \gamma ) \right \rangle $
is an
 $\eta _{n}( \gamma ) $
-nice sequence.
$\eta _{n}( \gamma ) $
-nice sequence.
 $\text{''}$
$\text{''}$
-
-
(b) In case
 $F_{n}=F_{n+1},$
we have the following:
$F_{n}=F_{n+1},$
we have the following:-
i.
 $d_{s}^{T}\upharpoonright \gamma =d_{t}^{T}\upharpoonright \gamma .$
$d_{s}^{T}\upharpoonright \gamma =d_{t}^{T}\upharpoonright \gamma .$
-
ii.
 $d_{s}^{T}\upharpoonright \gamma \Vdash \text{``}\left \langle p_{n}( \gamma ) ,p_{n}^{\prime }( \gamma ) ,d_{s}^{T}( \gamma ) ,d_{t}^{T}( \gamma ) \right \rangle $
is an
$d_{s}^{T}\upharpoonright \gamma \Vdash \text{``}\left \langle p_{n}( \gamma ) ,p_{n}^{\prime }( \gamma ) ,d_{s}^{T}( \gamma ) ,d_{t}^{T}( \gamma ) \right \rangle $
is an
 $\eta _{n}( \gamma ) $
-nice sequence.
$\eta _{n}( \gamma ) $
-nice sequence.
 $\text{''}$
$\text{''}$
-
-
Since this definition is crucial for the paper, we find it convenient to make the following clarifications:
-
1. We view
 $d_{-}^{T}, w_{-}^{T}:T\longrightarrow \mathbb {P}_{\alpha }$
as operators that help us define the immediate successors of a node of
$d_{-}^{T}, w_{-}^{T}:T\longrightarrow \mathbb {P}_{\alpha }$
as operators that help us define the immediate successors of a node of
 $T.$
In this way, if
$T.$
In this way, if
 $s\in T_{n},$
then the immediate successors of s are
$s\in T_{n},$
then the immediate successors of s are
 $s^{\frown }d_{s}^{T}$
and
$s^{\frown }d_{s}^{T}$
and
 $s^{\frown }w_{s}^{T}$
. We also have that
$s^{\frown }w_{s}^{T}$
. We also have that
 $s^{\frown }d_{s} ^{T}=s^{\frown }w_{s}^{T}$
(so s has only one immediate successor) if and only if
$s^{\frown }d_{s} ^{T}=s^{\frown }w_{s}^{T}$
(so s has only one immediate successor) if and only if
 $F_{n+1}=F_{n}.$
$F_{n+1}=F_{n}.$
-
2. Let
 $n\in \omega $
and
$n\in \omega $
and
 $\gamma $
are such that
$\gamma $
are such that
 $\gamma \in F_{n+1}\setminus F_{n}.$
If
$\gamma \in F_{n+1}\setminus F_{n}.$
If
 $s\in T_{n},$
then
$s\in T_{n},$
then
 $\dot {d}_{s}^{T}( \gamma ) $
is forced to be
$\dot {d}_{s}^{T}( \gamma ) $
is forced to be
 $\dot {e}_{n}^{T}$
and
$\dot {e}_{n}^{T}$
and
 $\dot {w}_{s}^{T}( \gamma ) $
is forced to be
$\dot {w}_{s}^{T}( \gamma ) $
is forced to be
 $\dot {u}_{n}^{T}.$
Note that
$\dot {u}_{n}^{T}.$
Note that
 $\dot {e}_{n}^{T}$
and
$\dot {e}_{n}^{T}$
and
 $\dot {u} _{n}^{T}$
depend only on n and not in
$\dot {u} _{n}^{T}$
depend only on n and not in
 $s.$
In this way, if t is also in
$s.$
In this way, if t is also in
 $T_{n},$
then
$T_{n},$
then
 $\dot {d}_{t}^{T}( \gamma ) $
is also forced to be
$\dot {d}_{t}^{T}( \gamma ) $
is also forced to be
 $\dot {e}_{n}^{T}$
and
$\dot {e}_{n}^{T}$
and
 $\dot {w}_{t}^{T}( \gamma ) $
is also forced to be
$\dot {w}_{t}^{T}( \gamma ) $
is also forced to be
 $\dot {u}_{n}^{T}.$
However, since
$\dot {u}_{n}^{T}.$
However, since
 $\dot {e}_{n}^{T}$
and
$\dot {e}_{n}^{T}$
and
 $\dot {w}_{s} ^{T}( \gamma ) $
are names and not “real objects,” it might be the case that
$\dot {w}_{s} ^{T}( \gamma ) $
are names and not “real objects,” it might be the case that
 $\dot {d}_{s} ^{T}\upharpoonright \gamma $
and
$\dot {d}_{s} ^{T}\upharpoonright \gamma $
and
 $\dot {d}_{t}^{T}\upharpoonright \gamma $
evaluate
$\dot {d}_{t}^{T}\upharpoonright \gamma $
evaluate
 $\dot {e}_{n}^{T}$
in very different ways (the same for
$\dot {e}_{n}^{T}$
in very different ways (the same for
 $\dot {w}_{s} ^{T}\upharpoonright \gamma $
and
$\dot {w}_{s} ^{T}\upharpoonright \gamma $
and
 $\dot {w}_{t}^{T}\upharpoonright \gamma $
).
$\dot {w}_{t}^{T}\upharpoonright \gamma $
). -
3. By “T is a fusion tree,” we mean that T is an
 $\alpha $
-fusion tree for some
$\alpha $
-fusion tree for some
 $\alpha .$
$\alpha .$
-
4. In case
 $F_{n+1}=F_{n},$
we have no use for
$F_{n+1}=F_{n},$
we have no use for
 $\dot {e}_{n}^{T}$
and
$\dot {e}_{n}^{T}$
and
 $\dot {u}_{n}^{T}.$
In the definition of
$\dot {u}_{n}^{T}.$
In the definition of
 $\alpha $
-fusion tree, we could have asked that
$\alpha $
-fusion tree, we could have asked that
 $\dot {e}_{n}^{T}$
and
$\dot {e}_{n}^{T}$
and
 $\dot {u}_{n}^{T}$
are only defined for the
$\dot {u}_{n}^{T}$
are only defined for the
 $n\in \omega $
such that
$n\in \omega $
such that
 $F_{n+1}\neq F_{n}.$
We did not do it this way because we thought it would only add extra complexity to the (already quite complex) definition. In the paper, when we are building fusion trees, we will simply leave this case undefined.
$F_{n+1}\neq F_{n}.$
We did not do it this way because we thought it would only add extra complexity to the (already quite complex) definition. In the paper, when we are building fusion trees, we will simply leave this case undefined. -
5. In the definition of fusion tree, we demanded that
 $T\subseteq M,$
so the operators
$T\subseteq M,$
so the operators
 $d_{-}^{T}$
and
$d_{-}^{T}$
and
 $w_{-}^{T}$
must always take values in M and the names
$w_{-}^{T}$
must always take values in M and the names
 $\dot {e}_{n}^{T}$
and
$\dot {e}_{n}^{T}$
and
 $\dot {u}_{n}^{T}$
must always be in
$\dot {u}_{n}^{T}$
must always be in
 $M.$
$M.$
-
6. If T is a fusion tree, the operators will always be denoted by
 $d_{-}^{T}$
and
$d_{-}^{T}$
and
 $w_{-}^{T}$
and the sequence of names will always be
$w_{-}^{T}$
and the sequence of names will always be
 $\dot {e}_{n}^{T}$
and
$\dot {e}_{n}^{T}$
and
 $\dot {u}_{n}^{T}$
for
$\dot {u}_{n}^{T}$
for
 $n\in \omega .$
However, if there is no risk of confusion, we will simply write
$n\in \omega .$
However, if there is no risk of confusion, we will simply write
 $d_{s},w_{s},\dot {e}_{n}$
, and
$d_{s},w_{s},\dot {e}_{n}$
, and
 $\dot {u}_{n}$
instead of
$\dot {u}_{n}$
instead of
 $d_{s}^{T},w_{s}^{T},\dot {e}_{n}^{T}$
, and
$d_{s}^{T},w_{s}^{T},\dot {e}_{n}^{T}$
, and
 $\dot {u}_{n} ^{T}.$
$\dot {u}_{n} ^{T}.$
-
7. For the convenience of the reader, whenever there is a fusion tree around, every occurrence of
 $d,w,e$
, and u (with either subindices or superinduces) refer to the operators of a fusion tree.
$d,w,e$
, and u (with either subindices or superinduces) refer to the operators of a fusion tree.
The definition of
![]() $1$
-fusion sequence from the previous section is essentially the same as the one of a
$1$
-fusion sequence from the previous section is essentially the same as the one of a
![]() $1$
-fusion tree, the only difference is the presence for the elementary submodel (in fact, the role of M is simply to help us with bookkeeping arguments, but it really could be avoided if we wanted). If a tree
$1$
-fusion tree, the only difference is the presence for the elementary submodel (in fact, the role of M is simply to help us with bookkeeping arguments, but it really could be avoided if we wanted). If a tree
![]() $T\subseteq \left ( \mathbb {P}_{\alpha }\cap M\right ) ^{<\omega }$
of height k satisfy all the above properties but only for
$T\subseteq \left ( \mathbb {P}_{\alpha }\cap M\right ) ^{<\omega }$
of height k satisfy all the above properties but only for
![]() $n\leq k,$
we will say that T is an
$n\leq k,$
we will say that T is an
![]() $\alpha $
-finite fusion tree of height
$\alpha $
-finite fusion tree of height
![]() $k.$
$k.$
Lemma 49 Let M be a countable elementary submodel of
![]() $\mathsf{H} ( \kappa ) $
,
$\mathsf{H} ( \kappa ) $
,
![]() $\alpha \in M, L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
$\alpha \in M, L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
![]() $\left ( M,\alpha \right ) $
and
$\left ( M,\alpha \right ) $
and
![]() $T\subseteq \left ( \mathbb {P}_{\alpha }\cap M\right ) ^{<\omega }$
an
$T\subseteq \left ( \mathbb {P}_{\alpha }\cap M\right ) ^{<\omega }$
an
![]() $\alpha $
-fusion tree (with respect to M and L). Let
$\alpha $
-fusion tree (with respect to M and L). Let
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $s=\left \langle p_{0},\ldots ,p_{n+1}\right \rangle , t=\left \langle q_{0},\ldots ,q_{n+1}\right \rangle \in T_{n+1}.$
If
$s=\left \langle p_{0},\ldots ,p_{n+1}\right \rangle , t=\left \langle q_{0},\ldots ,q_{n+1}\right \rangle \in T_{n+1}.$
If
![]() $s\neq t,$
then
$s\neq t,$
then
![]() $p_{n+1}$
and
$p_{n+1}$
and
![]() $q_{n+1}$
are incompatible.
$q_{n+1}$
are incompatible.
Proof Let
![]() $m=\triangle \left ( s,t\right ) ,$
by point 4 of definition 48, we get that
$m=\triangle \left ( s,t\right ) ,$
by point 4 of definition 48, we get that
![]() $p_{m}$
and
$p_{m}$
and
![]() $q_{m}$
are incompatible. Since
$q_{m}$
are incompatible. Since
![]() $p_{n+1}\leq p_{m}$
and
$p_{n+1}\leq p_{m}$
and
![]() $q_{n+1}\leq q_{m},$
the result follows.▪
$q_{n+1}\leq q_{m},$
the result follows.▪
By the above lemma, given
![]() $T\subseteq \left ( \mathbb {P}_{\alpha }\cap M\right ) ^{<\omega }$
an
$T\subseteq \left ( \mathbb {P}_{\alpha }\cap M\right ) ^{<\omega }$
an
![]() $\alpha $
-fusion tree, we could identify each
$\alpha $
-fusion tree, we could identify each
![]() $s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T$
with its last element. There is no risk of confusion by the lemma. Using this identification, the order of the tree corresponds with the order of
$s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T$
with its last element. There is no risk of confusion by the lemma. Using this identification, the order of the tree corresponds with the order of
![]() $\mathbb {P}_{\alpha }.$
In this section, we will not use the identification, but it will be convenient in later sections when the notation becomes even more involved (we will warn the reader when we use this abuse of notation).
$\mathbb {P}_{\alpha }.$
In this section, we will not use the identification, but it will be convenient in later sections when the notation becomes even more involved (we will warn the reader when we use this abuse of notation).
In order to use inductive arguments, we need to restrict an
![]() $\alpha $
-fusion tree to a lesser ordinal. The objective of the following definitions and results is to prove that the restriction of a fusion tree is a fusion tree.
$\alpha $
-fusion tree to a lesser ordinal. The objective of the following definitions and results is to prove that the restriction of a fusion tree is a fusion tree.
Definition 50 Let T be an
![]() $\alpha $
-fusion tree and
$\alpha $
-fusion tree and
![]() $\beta <\alpha .$
Define
$\beta <\alpha .$
Define
![]() $\sim _{\beta }$
a relation on T as follows: given
$\sim _{\beta }$
a relation on T as follows: given
![]() $s=\left ( p_{0}^{s},\ldots ,p_{n}^{s}\right ) $
and
$s=\left ( p_{0}^{s},\ldots ,p_{n}^{s}\right ) $
and
![]() $t=\left ( p_{0}^{t},\ldots ,p_{n}^{t}\right ) ,$
define
$t=\left ( p_{0}^{t},\ldots ,p_{n}^{t}\right ) ,$
define
![]() $s\sim _{\beta }t$
if the following conditions hold:
$s\sim _{\beta }t$
if the following conditions hold:
-
1.
 $n=m.$
$n=m.$
-
2.
 $p_{i}^{s}\upharpoonright \beta =p_{i}^{t}\upharpoonright \beta $
for every
$p_{i}^{s}\upharpoonright \beta =p_{i}^{t}\upharpoonright \beta $
for every
 $i\leq n.$
$i\leq n.$
It is easy to see that
![]() $\sim _{\beta }$
is an equivalence relation on
$\sim _{\beta }$
is an equivalence relation on
![]() $T.$
We now have the following:
$T.$
We now have the following:
Lemma 51 Let M be a countable elementary submodel of
![]() $\mathsf{H} ( \kappa ) $
,
$\mathsf{H} ( \kappa ) $
,
![]() $\alpha \in M$
and
$\alpha \in M$
and
![]() $L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
$L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
![]() $\left ( M,\alpha \right ) .$
Let
$\left ( M,\alpha \right ) .$
Let
![]() $\beta \in M\cap \alpha ,$
define
$\beta \in M\cap \alpha ,$
define
![]() $F_{i}^{\prime }=F_{i}\cap \beta $
for every
$F_{i}^{\prime }=F_{i}\cap \beta $
for every
![]() $i\in \omega .$
Let
$i\in \omega .$
Let
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $s,z\in T_{n}$
such that
$s,z\in T_{n}$
such that
![]() $s\sim _{\beta }z.$
The following holds:
$s\sim _{\beta }z.$
The following holds:
-
1.
 $d_{s}\upharpoonright \beta =d_{z}\upharpoonright \beta $
and
$d_{s}\upharpoonright \beta =d_{z}\upharpoonright \beta $
and
 $w_{s} \upharpoonright \beta =w_{z}\upharpoonright \beta $
.
$w_{s} \upharpoonright \beta =w_{z}\upharpoonright \beta $
. -
2.
 $\left ( s^{\frown }d_{s}\right ) \sim _{\beta }\left ( z^{\frown } d_{z}\right ) $
and
$\left ( s^{\frown }d_{s}\right ) \sim _{\beta }\left ( z^{\frown } d_{z}\right ) $
and
 $\left ( s^{\frown }w_{s}\right ) \sim _{\beta }\left ( z^{\frown }w_{z}\right ) .$
$\left ( s^{\frown }w_{s}\right ) \sim _{\beta }\left ( z^{\frown }w_{z}\right ) .$
-
3. If
 $F_{n+1}^{\prime }\setminus F_{n}^{\prime }\neq \emptyset ,$
then
$F_{n+1}^{\prime }\setminus F_{n}^{\prime }\neq \emptyset ,$
then
 $d_{s}\upharpoonright \beta \neq w_{s}\upharpoonright \beta .$
$d_{s}\upharpoonright \beta \neq w_{s}\upharpoonright \beta .$
-
4. If
 $F_{n+1}^{\prime }\setminus F_{n}^{\prime }=\emptyset ,$
then
$F_{n+1}^{\prime }\setminus F_{n}^{\prime }=\emptyset ,$
then
 $d_{s}\upharpoonright \beta =w_{s}\upharpoonright \beta .$
$d_{s}\upharpoonright \beta =w_{s}\upharpoonright \beta .$
Proof We will first prove point 1. Denote by A the
![]() $\sim _{\beta }$
-equivalence class of s (and of z as well, obviously). Let
$\sim _{\beta }$
-equivalence class of s (and of z as well, obviously). Let
![]() $a=\left ( p_{0} ^{a},\ldots ,p_{n}^{a}\right ) $
and
$a=\left ( p_{0} ^{a},\ldots ,p_{n}^{a}\right ) $
and
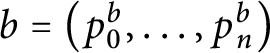 $b=\left ( p_{0}^{b},\ldots ,p_{n}^{b}\right ) $
be two elements of A and
$b=\left ( p_{0}^{b},\ldots ,p_{n}^{b}\right ) $
be two elements of A and
![]() $\xi <\alpha .$
We say that
$\xi <\alpha .$
We say that
![]() $\xi $
is a disagreement point of a and b if the following conditions hold:
$\xi $
is a disagreement point of a and b if the following conditions hold:
-
1. There is
 $m\leq n$
such that
$m\leq n$
such that
 $\xi \in F_{m+1}\setminus F_{m}.$
$\xi \in F_{m+1}\setminus F_{m}.$
-
2. Denote
 $\overline {a}=\left ( p_{0}^{a},\ldots ,p_{m-1}^{a}\right ) $
and
$\overline {a}=\left ( p_{0}^{a},\ldots ,p_{m-1}^{a}\right ) $
and
 $\overline {b}=\left ( p_{0}^{b},\ldots ,p_{m-1}^{b}\right ) .$
Either
$\overline {b}=\left ( p_{0}^{b},\ldots ,p_{m-1}^{b}\right ) .$
Either
 $p_{m} ^{a}=d_{\overline {a}}$
and
$p_{m} ^{a}=d_{\overline {a}}$
and
 $p_{m}^{b}=w_{\overline {b}}$
or
$p_{m}^{b}=w_{\overline {b}}$
or
 $p_{m} ^{a}=w_{\overline {a}}$
and
$p_{m} ^{a}=w_{\overline {a}}$
and
 $p_{m}^{b}=d_{\overline {b}}.$
$p_{m}^{b}=d_{\overline {b}}.$
Note that if
![]() $\xi $
is a disagreement point of a and
$\xi $
is a disagreement point of a and
![]() $b,$
then
$b,$
then
![]() $\beta \leq \xi $
(this is because
$\beta \leq \xi $
(this is because
![]() $a\sim _{\beta }b$
). Denote by
$a\sim _{\beta }b$
). Denote by
![]() $dis\left ( a,b\right ) $
the set of all disagreement points of a and
$dis\left ( a,b\right ) $
the set of all disagreement points of a and
![]() $b.$
The following remarks are easy to see:
$b.$
The following remarks are easy to see:
-
1.
 $dis\left ( a,b\right ) $
is a finite set and
$dis\left ( a,b\right ) $
is a finite set and
 $\beta \cap dis\left ( a,b\right ) =\emptyset .$
$\beta \cap dis\left ( a,b\right ) =\emptyset .$
-
2.
 $dis\left ( a,b\right ) =\emptyset $
if and only if
$dis\left ( a,b\right ) =\emptyset $
if and only if
 $a=b.$
$a=b.$
-
3. If
 $\triangle \left ( a,b\right ) =m$
and
$\triangle \left ( a,b\right ) =m$
and
 $\xi \in F_{m+1}\setminus F_{m},$
then
$\xi \in F_{m+1}\setminus F_{m},$
then
 $\xi \in dis\left ( a,b\right ) .$
$\xi \in dis\left ( a,b\right ) .$
We will say that a and b are near if
![]() $dis\left ( a,b\right ) $
has at most one element. We will now prove the following:
$dis\left ( a,b\right ) $
has at most one element. We will now prove the following:
Claim 52 Let
![]() $a,b\in A.$
If a and b are near, then
$a,b\in A.$
If a and b are near, then
![]() $d_{a}\upharpoonright \beta =d_{b}\upharpoonright \beta $
and
$d_{a}\upharpoonright \beta =d_{b}\upharpoonright \beta $
and
![]() $w_{a}\upharpoonright \beta =w_{b} \upharpoonright \beta .$
$w_{a}\upharpoonright \beta =w_{b} \upharpoonright \beta .$
Let
![]() $a=\left ( p_{0}^{a},\ldots ,p_{n}^{a}\right ) $
and
$a=\left ( p_{0}^{a},\ldots ,p_{n}^{a}\right ) $
and
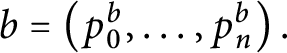 $b=\left ( p_{0} ^{b},\ldots ,p_{n}^{b}\right ) .$
If
$b=\left ( p_{0} ^{b},\ldots ,p_{n}^{b}\right ) .$
If
![]() $a=b$
, the claim is trivially true, so assume that
$a=b$
, the claim is trivially true, so assume that
![]() $a\neq b.$
Let
$a\neq b.$
Let
![]() $\xi \in dis\left ( a,b\right ) $
and
$\xi \in dis\left ( a,b\right ) $
and
![]() $m\in \omega $
such that
$m\in \omega $
such that
![]() $\xi \in F_{m+1}\setminus F_{m}.$
We claim that
$\xi \in F_{m+1}\setminus F_{m}.$
We claim that
![]() $a\sim _{\xi }b$
(in other words,
$a\sim _{\xi }b$
(in other words,
![]() $p_{i}^{a}\upharpoonright \xi =p_{i}^{b}\upharpoonright \xi $
for every
$p_{i}^{a}\upharpoonright \xi =p_{i}^{b}\upharpoonright \xi $
for every
![]() $i\leq n$
).
$i\leq n$
).
-
1. If
 $i<m,$
then
$i<m,$
then
 $p_{i}^{a}=p_{i}^{b}$
(so
$p_{i}^{a}=p_{i}^{b}$
(so
 $p_{i}^{a}\upharpoonright \xi =p_{i}^{b}\upharpoonright \xi $
).
$p_{i}^{a}\upharpoonright \xi =p_{i}^{b}\upharpoonright \xi $
). -
2. If
 $i=m,$
then
$i=m,$
then
 $p_{i}^{a}\upharpoonright \xi =p_{i}^{b}\upharpoonright \xi $
by point 5(a) of Definition 48.
$p_{i}^{a}\upharpoonright \xi =p_{i}^{b}\upharpoonright \xi $
by point 5(a) of Definition 48. -
3. If
 $i>m,$
then
$i>m,$
then
 $p_{i}^{a}\upharpoonright \xi =p_{i}^{b}\upharpoonright \xi $
because T is fusion tree and
$p_{i}^{a}\upharpoonright \xi =p_{i}^{b}\upharpoonright \xi $
because T is fusion tree and
 $\xi $
is the only point of disagreement between a and
$\xi $
is the only point of disagreement between a and
 $b.$
$b.$
We will provide more details for the last point. We proceed by induction over
![]() $i.$
Assume that
$i.$
Assume that
![]() $p_{i}^{a}\upharpoonright \xi =p_{i}^{b}\upharpoonright \xi $
for
$p_{i}^{a}\upharpoonright \xi =p_{i}^{b}\upharpoonright \xi $
for
![]() $m\leq i<n,$
we will prove that
$m\leq i<n,$
we will prove that
![]() $p_{i+1}^{a}\upharpoonright \xi =p_{i+1} ^{b}\upharpoonright \xi .$
In case
$p_{i+1}^{a}\upharpoonright \xi =p_{i+1} ^{b}\upharpoonright \xi .$
In case
![]() $F_{i+1}=F_{i},$
the conclusion follows by point 5(b) of Definition 48. Now assume that
$F_{i+1}=F_{i},$
the conclusion follows by point 5(b) of Definition 48. Now assume that
![]() $F_{i+1}\neq F_{i}$
and let
$F_{i+1}\neq F_{i}$
and let
![]() $\delta \in F_{i+1}\setminus F_{i}.$
Since
$\delta \in F_{i+1}\setminus F_{i}.$
Since
![]() $\delta $
is not a disagreement point, by point 5(a) of Definition 48, we conclude that
$\delta $
is not a disagreement point, by point 5(a) of Definition 48, we conclude that
![]() $p_{i+1}^{a}\upharpoonright \xi =p_{i+1}^{b}\upharpoonright \xi .$
$p_{i+1}^{a}\upharpoonright \xi =p_{i+1}^{b}\upharpoonright \xi .$
In particular, we get that
![]() $p_{n}^{a}\upharpoonright \xi =p_{n}^{b} \upharpoonright \xi .$
By point 5 of Definition 48, we get that
$p_{n}^{a}\upharpoonright \xi =p_{n}^{b} \upharpoonright \xi .$
By point 5 of Definition 48, we get that
![]() $d_{a}\upharpoonright \xi =d_{b}\upharpoonright \xi $
and
$d_{a}\upharpoonright \xi =d_{b}\upharpoonright \xi $
and
![]() $w_{a} \upharpoonright \xi =w_{b}\upharpoonright \xi .$
Since
$w_{a} \upharpoonright \xi =w_{b}\upharpoonright \xi .$
Since
![]() $\beta \leq \xi ,$
we conclude that
$\beta \leq \xi ,$
we conclude that
![]() $d_{a}\upharpoonright \beta =d_{b}\upharpoonright \beta $
and
$d_{a}\upharpoonright \beta =d_{b}\upharpoonright \beta $
and
![]() $w_{a} \upharpoonright \beta =w_{b}\upharpoonright \beta .$
This finishes the proof of the claim.
$w_{a} \upharpoonright \beta =w_{b}\upharpoonright \beta .$
This finishes the proof of the claim.
Claim 53 Let
![]() $a,b\in A$
with
$a,b\in A$
with
![]() $a\neq b.$
There is
$a\neq b.$
There is
![]() $c\in A$
such that the following holds:
$c\in A$
such that the following holds:
-
1. a and c are near.
-
2.
 $\left \vert dis\left ( c,b\right ) \right \vert <\left \vert dis\left ( a,b\right ) \right \vert .$
$\left \vert dis\left ( c,b\right ) \right \vert <\left \vert dis\left ( a,b\right ) \right \vert .$
Let
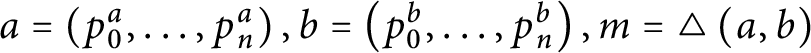 $a=\left ( p_{0}^{a},\ldots ,p_{n}^{a}\right ) , b=\left ( p_{0} ^{b},\ldots ,p_{n}^{b}\right ) , m=\triangle \left ( a,b\right ) $
, and
$a=\left ( p_{0}^{a},\ldots ,p_{n}^{a}\right ) , b=\left ( p_{0} ^{b},\ldots ,p_{n}^{b}\right ) , m=\triangle \left ( a,b\right ) $
, and
![]() $\xi \in F_{m+1}\setminus F_{m}.$
Define
$\xi \in F_{m+1}\setminus F_{m}.$
Define
![]() $c=\left ( p_{0}^{c},\ldots ,p_{n}^{c}\right ) $
as follows:
$c=\left ( p_{0}^{c},\ldots ,p_{n}^{c}\right ) $
as follows:
-
1.
 $p_{i}^{c}=p_{i}^{a}$
for
$p_{i}^{c}=p_{i}^{a}$
for
 $i<m$
(so
$i<m$
(so
 $p_{i}^{c}=p_{i}^{b}$
).
$p_{i}^{c}=p_{i}^{b}$
). -
2.
 $p_{m}^{c}=p_{m}^{b}.$
$p_{m}^{c}=p_{m}^{b}.$
-
3. Let
 $i\geq m,$
denote
$i\geq m,$
denote
 $\overline {a}=\left ( p_{0}^{a},\ldots ,p_{i} ^{a}\right ) $
and
$\overline {a}=\left ( p_{0}^{a},\ldots ,p_{i} ^{a}\right ) $
and
 $\overline {c}=\left ( p_{0}^{c},\ldots ,p_{i}^{c}\right ) .$
Let
$\overline {c}=\left ( p_{0}^{c},\ldots ,p_{i}^{c}\right ) .$
Let
 $p_{i+1}^{c}=d_{\overline {c}}$
if
$p_{i+1}^{c}=d_{\overline {c}}$
if
 $p_{i+1}^{a}=d_{\overline {a}}$
and
$p_{i+1}^{a}=d_{\overline {a}}$
and
 $p_{i+1}^{c}=w_{\overline {c}}$
if
$p_{i+1}^{c}=w_{\overline {c}}$
if
 $p_{i+1}^{a}=w_{\overline {a}}.$
$p_{i+1}^{a}=w_{\overline {a}}.$
Note that c is in the tree T since we are always taking the successor of a node in
![]() $T.$
It follows by the construction that
$T.$
It follows by the construction that
![]() $\triangle \left ( a,c\right ) =m$
and by point 5 of Definition 48, we get that
$\triangle \left ( a,c\right ) =m$
and by point 5 of Definition 48, we get that
![]() $p_{i} ^{c}\upharpoonright \xi =p_{i}^{a}\upharpoonright \xi $
for all
$p_{i} ^{c}\upharpoonright \xi =p_{i}^{a}\upharpoonright \xi $
for all
![]() $i\leq n,$
hence
$i\leq n,$
hence
![]() $c\in A.$
It is clear that a and c are near and
$c\in A.$
It is clear that a and c are near and
![]() $\left \vert dis\left ( c,b\right ) \right \vert =\left \vert dis\left ( a,b\right ) \right \vert -1.$
This finishes the proof of the claim.
$\left \vert dis\left ( c,b\right ) \right \vert =\left \vert dis\left ( a,b\right ) \right \vert -1.$
This finishes the proof of the claim.
We can now finish the proof of the first point of the lemma. Recall that
![]() $s\sim _{\beta }z$
and we wanted to prove that
$s\sim _{\beta }z$
and we wanted to prove that
![]() $d_{s}\upharpoonright \beta =d_{z}\upharpoonright \beta $
and
$d_{s}\upharpoonright \beta =d_{z}\upharpoonright \beta $
and
![]() $w_{s}\upharpoonright \beta =w_{z} \upharpoonright \beta $
. Now, by claim 53, we can find a sequence
$w_{s}\upharpoonright \beta =w_{z} \upharpoonright \beta $
. Now, by claim 53, we can find a sequence
![]() $\left ( a_{0},\ldots ,a_{k}\right ) $
such that for every
$\left ( a_{0},\ldots ,a_{k}\right ) $
such that for every
![]() $i\leq k,$
the following conditions hold:
$i\leq k,$
the following conditions hold:
-
1.
 $a_{i}\in A.$
$a_{i}\in A.$
-
2.
 $a_{0}=s$
and
$a_{0}=s$
and
 $a_{k}=z.$
$a_{k}=z.$
-
3.
 $a_{i+1}$
is near of
$a_{i+1}$
is near of
 $a_{i}.$
$a_{i}.$
By Claim 52, we conclude that
![]() $d_{s}\upharpoonright \beta =d_{z}\upharpoonright \beta $
and
$d_{s}\upharpoonright \beta =d_{z}\upharpoonright \beta $
and
![]() $w_{s}\upharpoonright \beta =w_{z} \upharpoonright \beta $
.
$w_{s}\upharpoonright \beta =w_{z} \upharpoonright \beta $
.
The second point of the lemma follows by the first one, we will now prove the third point. Assume that
![]() $F_{n+1}^{\prime }\setminus F_{n}^{\prime } \neq \emptyset ,$
we want to prove that
$F_{n+1}^{\prime }\setminus F_{n}^{\prime } \neq \emptyset ,$
we want to prove that
![]() $d_{s}\upharpoonright \beta \neq w_{s}\upharpoonright \beta .$
Let
$d_{s}\upharpoonright \beta \neq w_{s}\upharpoonright \beta .$
Let
![]() $\gamma \in F_{n+1}^{\prime }\setminus F_{n}^{\prime }.$
Since
$\gamma \in F_{n+1}^{\prime }\setminus F_{n}^{\prime }.$
Since
![]() $F_{n+1}^{\prime }=F_{n+1}\cap \beta $
and
$F_{n+1}^{\prime }=F_{n+1}\cap \beta $
and
![]() $F_{n}^{\prime }=F_{n}\cap \beta ,$
it follows that
$F_{n}^{\prime }=F_{n}\cap \beta ,$
it follows that
![]() $\gamma <\beta $
. By point 4 of definition 48, we know that
$\gamma <\beta $
. By point 4 of definition 48, we know that
![]() $d_{s}$
and
$d_{s}$
and
![]() $w_{s}$
differ in the
$w_{s}$
differ in the
![]() $\gamma $
component, which entails that
$\gamma $
component, which entails that
![]() $d_{s}\upharpoonright \beta \neq w_{s} \upharpoonright \beta .$
$d_{s}\upharpoonright \beta \neq w_{s} \upharpoonright \beta .$
We now prove point 4 of the lemma. Assume that
![]() $F_{n+1}^{\prime }\setminus F_{n}^{\prime }=\emptyset ,$
we want to prove that
$F_{n+1}^{\prime }\setminus F_{n}^{\prime }=\emptyset ,$
we want to prove that
![]() $d_{s}\upharpoonright \beta =w_{s}\upharpoonright \beta .$
If
$d_{s}\upharpoonright \beta =w_{s}\upharpoonright \beta .$
If
![]() $F_{n+1}\setminus F_{n}=\emptyset ,$
it follows by point 3 of Definition 48 that
$F_{n+1}\setminus F_{n}=\emptyset ,$
it follows by point 3 of Definition 48 that
![]() $d_{s}=w_{s},$
so
$d_{s}=w_{s},$
so
![]() $d_{s}\upharpoonright \beta =w_{s}\upharpoonright \beta .$
Assume now that
$d_{s}\upharpoonright \beta =w_{s}\upharpoonright \beta .$
Assume now that
![]() $F_{n+1}\setminus F_{n}\neq \emptyset .$
Let
$F_{n+1}\setminus F_{n}\neq \emptyset .$
Let
![]() $\gamma \in F_{n+1}\setminus F_{n}.$
Since
$\gamma \in F_{n+1}\setminus F_{n}.$
Since
![]() $F_{n+1}^{\prime }\setminus F_{n}^{\prime }=\emptyset ,$
it must be the case that
$F_{n+1}^{\prime }\setminus F_{n}^{\prime }=\emptyset ,$
it must be the case that
![]() $\beta \leq \gamma .$
By point 5 of Definition 48 we know that
$\beta \leq \gamma .$
By point 5 of Definition 48 we know that
![]() $d_{s}\upharpoonright \gamma =w_{s}\upharpoonright \gamma ,$
which implies that
$d_{s}\upharpoonright \gamma =w_{s}\upharpoonright \gamma ,$
which implies that
![]() $d_{s}\upharpoonright \beta =w_{s}\upharpoonright \beta .$
▪
$d_{s}\upharpoonright \beta =w_{s}\upharpoonright \beta .$
▪
We can now make the following definition:
Definition 54 Let M be a countable elementary submodel of
![]() $\mathsf{H} ( \kappa ) $
(for some big enough regular cardinal
$\mathsf{H} ( \kappa ) $
(for some big enough regular cardinal
![]() $\kappa $
) such that
$\kappa $
) such that
![]() $\mathbb {P}_{\alpha }\in M, L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
$\mathbb {P}_{\alpha }\in M, L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
![]() $\left ( M,\alpha \right ) $
and
$\left ( M,\alpha \right ) $
and
![]() $T\subseteq \left ( \mathbb {P}_{\alpha }\cap M\right ) ^{<\omega }$
an
$T\subseteq \left ( \mathbb {P}_{\alpha }\cap M\right ) ^{<\omega }$
an
![]() $\alpha $
-fusion tree. Let
$\alpha $
-fusion tree. Let
![]() $\beta <\alpha $
with
$\beta <\alpha $
with
![]() $\beta \in M.$
$\beta \in M.$
-
1. Define
 $T\upharpoonright \beta $
as the tree in
$T\upharpoonright \beta $
as the tree in
 $\mathbb {P}_{\beta }^{<\omega }$
obtained by restricting every condition of T to
$\mathbb {P}_{\beta }^{<\omega }$
obtained by restricting every condition of T to
 $\beta .$
In other words, if
$\beta .$
In other words, if
 $s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T,$
then
$s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T,$
then
 $s^{\prime }=\left \langle p_{0}\upharpoonright \beta ,\ldots ,p_{n}\upharpoonright \beta \right \rangle \in T\upharpoonright \beta .$
$s^{\prime }=\left \langle p_{0}\upharpoonright \beta ,\ldots ,p_{n}\upharpoonright \beta \right \rangle \in T\upharpoonright \beta .$
-
2. Let
 $s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T$
and
$s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T$
and
 $z=\left \langle p_{0}\upharpoonright \beta ,\ldots ,p_{n}\upharpoonright \beta \right \rangle .$
Define
$z=\left \langle p_{0}\upharpoonright \beta ,\ldots ,p_{n}\upharpoonright \beta \right \rangle .$
Define
 $d_{z}^{T\upharpoonright \beta }=d_{s} ^{T}\upharpoonright \beta $
and
$d_{z}^{T\upharpoonright \beta }=d_{s} ^{T}\upharpoonright \beta $
and
 $w_{z}^{T\upharpoonright \beta }=w_{s} ^{T}\upharpoonright \beta .$
$w_{z}^{T\upharpoonright \beta }=w_{s} ^{T}\upharpoonright \beta .$
-
3. For every
 $n\in \omega $
such that
$n\in \omega $
such that
 $\left ( F_{n+1}\setminus F_{n}\right ) \cap \beta \neq \emptyset ,$
let
$\left ( F_{n+1}\setminus F_{n}\right ) \cap \beta \neq \emptyset ,$
let
 $\dot {e}_{n}^{T\upharpoonright \beta }=\dot {e} _{n}^{T}$
and
$\dot {e}_{n}^{T\upharpoonright \beta }=\dot {e} _{n}^{T}$
and
 $\dot {w}_{n}^{T\upharpoonright \beta }=\dot {w}_{n}^{T}$
$\dot {w}_{n}^{T\upharpoonright \beta }=\dot {w}_{n}^{T}$
The operators
 $d_{\_}^{T\upharpoonright \beta }$
and
$d_{\_}^{T\upharpoonright \beta }$
and
 $w_{\_}^{T\upharpoonright \beta }$
are well defined by Lemma 51. We need that the restriction of a fusion tree is a fusion tree. This is the content of the following proposition.
$w_{\_}^{T\upharpoonright \beta }$
are well defined by Lemma 51. We need that the restriction of a fusion tree is a fusion tree. This is the content of the following proposition.
Proposition 55 Let M be a countable elementary submodel of
![]() $\mathsf{H} ( \kappa ) $
,
$\mathsf{H} ( \kappa ) $
,
![]() $\alpha \in M$
and
$\alpha \in M$
and
![]() $L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
$L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
![]() $\left ( M,\alpha \right ) .$
Let
$\left ( M,\alpha \right ) .$
Let
![]() $\beta \in M\cap \alpha ,$
define
$\beta \in M\cap \alpha ,$
define
![]() $F_{n}^{\prime }=F_{n}\cap \beta , \eta _{n}^{\prime }=\eta _{n}\upharpoonright F_{n}^{\prime }$
and
$F_{n}^{\prime }=F_{n}\cap \beta , \eta _{n}^{\prime }=\eta _{n}\upharpoonright F_{n}^{\prime }$
and
![]() $L^{\prime }=\left \{ \left ( F_{n}^{\prime },\eta _{n}^{\prime }\right ) \mid n\in \omega \right \} .$
If
$L^{\prime }=\left \{ \left ( F_{n}^{\prime },\eta _{n}^{\prime }\right ) \mid n\in \omega \right \} .$
If
![]() $T\subseteq \left ( \mathbb {P}_{\alpha }\cap M\right ) ^{<\omega }$
is an
$T\subseteq \left ( \mathbb {P}_{\alpha }\cap M\right ) ^{<\omega }$
is an
![]() $\alpha $
-fusion tree (with respect to M and L), then
$\alpha $
-fusion tree (with respect to M and L), then
 $T\upharpoonright \beta \subseteq \left ( \mathbb {P}_{\beta }\cap M\right ) ^{<\omega }$
is a
$T\upharpoonright \beta \subseteq \left ( \mathbb {P}_{\beta }\cap M\right ) ^{<\omega }$
is a
![]() $\beta $
-fusion tree (with respect to M and
$\beta $
-fusion tree (with respect to M and
![]() $L^{\prime }$
).
$L^{\prime }$
).
Proof We already noted that
![]() $L^{\prime }$
is suitable for
$L^{\prime }$
is suitable for
![]() $\left ( M,\beta \right ) .$
Let
$\left ( M,\beta \right ) .$
Let
![]() $S=T\upharpoonright \beta .$
For this proof, we adopt the following convention: if
$S=T\upharpoonright \beta .$
For this proof, we adopt the following convention: if
![]() $s=\left \langle q_{0},\ldots ,q_{n}\right \rangle \in T,$
define
$s=\left \langle q_{0},\ldots ,q_{n}\right \rangle \in T,$
define
![]() $s^{\prime }=\left \langle q_{0}\upharpoonright \beta ,\ldots ,q_{n}\upharpoonright \beta \right \rangle $
(we are not assuming this convention outside this proof, unless when we mention it explicitly). Note that
$s^{\prime }=\left \langle q_{0}\upharpoonright \beta ,\ldots ,q_{n}\upharpoonright \beta \right \rangle $
(we are not assuming this convention outside this proof, unless when we mention it explicitly). Note that
![]() $S_{n}=\left \{ s^{\prime }\mid s\in T_{n}\right \} $
for every
$S_{n}=\left \{ s^{\prime }\mid s\in T_{n}\right \} $
for every
![]() $n\in \omega .$
We will prove that S is a
$n\in \omega .$
We will prove that S is a
![]() $\beta $
-fusion tree. The first point from Definition 48 is clear.
$\beta $
-fusion tree. The first point from Definition 48 is clear.
Note that for every
![]() $s\in S$
there may be many
$s\in S$
there may be many
![]() $t\in T$
such that
$t\in T$
such that
![]() $t^{\prime }=s.$
This is where Lemma 51 comes into play. It is easy to see that
$t^{\prime }=s.$
This is where Lemma 51 comes into play. It is easy to see that
![]() $suc_{S}( s) =\left \{ x\upharpoonright \beta \mid \exists t\in T\left ( t^{\prime }=s\wedge x\in suc_{T}\left ( t\right ) \right ) \right \} .$
Point 2 from Definition 48 follows by point 1 of Lemma 51. Point 3 of the definition of fusion tree follows by point 4 of Lemma 51. Point 4 follows from the definition of
$suc_{S}( s) =\left \{ x\upharpoonright \beta \mid \exists t\in T\left ( t^{\prime }=s\wedge x\in suc_{T}\left ( t\right ) \right ) \right \} .$
Point 2 from Definition 48 follows by point 1 of Lemma 51. Point 3 of the definition of fusion tree follows by point 4 of Lemma 51. Point 4 follows from the definition of
![]() $T\upharpoonright \beta $
and Lemma 51.
$T\upharpoonright \beta $
and Lemma 51.
We will now prove point 5 of the definition of fusion tree. Let
![]() $s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle $
and
$s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle $
and
![]() $t=\left \langle p_{0}^{t},\ldots ,p_{n}^{t}\right \rangle $
two nodes in
$t=\left \langle p_{0}^{t},\ldots ,p_{n}^{t}\right \rangle $
two nodes in
![]() $S, m=\triangle \left ( s,t\right ) , \gamma \in F_{m+1}^{\prime }\setminus F_{m}^{\prime }$
such that
$S, m=\triangle \left ( s,t\right ) , \gamma \in F_{m+1}^{\prime }\setminus F_{m}^{\prime }$
such that
![]() $p_{n}^{s}\upharpoonright \gamma =p_{n}^{t}\upharpoonright \gamma .$
now we need the following:
$p_{n}^{s}\upharpoonright \gamma =p_{n}^{t}\upharpoonright \gamma .$
now we need the following:
Claim 56 There are
![]() $a=\left \langle p_{0}^{a},\ldots ,p_{n}^{a}\right \rangle $
and
$a=\left \langle p_{0}^{a},\ldots ,p_{n}^{a}\right \rangle $
and
 $b=\left \langle p_{0}^{b},\ldots ,p_{n}^{b}\right \rangle $
nodes in T such that:
$b=\left \langle p_{0}^{b},\ldots ,p_{n}^{b}\right \rangle $
nodes in T such that:
-
1.
 $a^{\prime }=s$
and
$a^{\prime }=s$
and
 $b^{\prime }=t.$
$b^{\prime }=t.$
-
2.
 $m=\triangle \left ( a,b\right ) .$
$m=\triangle \left ( a,b\right ) .$
We proceed to prove the claim. First, note that if
![]() $a^{\prime }=s$
and
$a^{\prime }=s$
and
![]() $b^{\prime }=t,$
then
$b^{\prime }=t,$
then
![]() $\triangle \left ( a,b\right ) \leq m.$
We need to prove that we can realize the value
$\triangle \left ( a,b\right ) \leq m.$
We need to prove that we can realize the value
![]() $m.$
In order to do that, it is enough to prove the following: If
$m.$
In order to do that, it is enough to prove the following: If
![]() $a,b$
are such that
$a,b$
are such that
![]() $a^{\prime }=s$
and
$a^{\prime }=s$
and
![]() $b^{\prime }=t$
and
$b^{\prime }=t$
and
![]() $m_{1}=\triangle \left ( a,b\right ) <m,$
then there are
$m_{1}=\triangle \left ( a,b\right ) <m,$
then there are
![]() $a_{1},b_{1}$
with the following properties:
$a_{1},b_{1}$
with the following properties:
-
1.
 $a_{1}^{\prime }=s.$
$a_{1}^{\prime }=s.$
-
2.
 $b_{1}^{\prime }=t.$
$b_{1}^{\prime }=t.$
-
3.
 $m_{1}<\triangle \left ( a_{1},b_{1}\right ) .$
$m_{1}<\triangle \left ( a_{1},b_{1}\right ) .$
Let
![]() $\xi \in F_{m_{1}+1}\setminus F_{m_{1}}.$
Since
$\xi \in F_{m_{1}+1}\setminus F_{m_{1}}.$
Since
![]() $m_{1}<m,$
it must be the case that
$m_{1}<m,$
it must be the case that
![]() $\beta \leq \xi .$
We now define
$\beta \leq \xi .$
We now define
![]() $c=\left \langle p_{0}^{c} ,\ldots ,p_{n}^{c}\right \rangle $
as follows:
$c=\left \langle p_{0}^{c} ,\ldots ,p_{n}^{c}\right \rangle $
as follows:
-
1. If
 $i<m_{1},$
then
$i<m_{1},$
then
 $p_{i}^{c}=p_{i}^{b}$
(so
$p_{i}^{c}=p_{i}^{b}$
(so
 $p_{i}^{c}=p_{i}^{a}$
as well).
$p_{i}^{c}=p_{i}^{a}$
as well). -
2. If
 $i=m_{1},$
then
$i=m_{1},$
then
 $p_{m_{1}}^{c}=p_{m_{1}}^{b}.$
$p_{m_{1}}^{c}=p_{m_{1}}^{b}.$
-
3. If
 $i>m,$
denote
$i>m,$
denote
 $\overline {a}=\left ( p_{0}^{a},\ldots ,p_{i}^{a}\right ) $
and
$\overline {a}=\left ( p_{0}^{a},\ldots ,p_{i}^{a}\right ) $
and
 $\overline {c}=\left ( p_{0}^{c},\ldots ,p_{i}^{c}\right ) .$
Let
$\overline {c}=\left ( p_{0}^{c},\ldots ,p_{i}^{c}\right ) .$
Let
 $p_{i+1} ^{c}=d_{\overline {c}}$
if
$p_{i+1} ^{c}=d_{\overline {c}}$
if
 $p_{i+1}^{a}=d_{\overline {a}}$
and
$p_{i+1}^{a}=d_{\overline {a}}$
and
 $p_{i+1} ^{c}=w_{\overline {c}}$
if
$p_{i+1} ^{c}=w_{\overline {c}}$
if
 $p_{i+1}^{a}=w_{\overline {a}}.$
$p_{i+1}^{a}=w_{\overline {a}}.$
It follows that
![]() $c^{\prime }=a^{\prime }$
(since
$c^{\prime }=a^{\prime }$
(since
![]() $\beta \leq \xi $
and by point 5 of the definition of fusion tree) and
$\beta \leq \xi $
and by point 5 of the definition of fusion tree) and
![]() $m_{1}<\triangle \left ( c,b\right ) ,$
so c and b have the desired properties. This finishes the proof of the claim.
$m_{1}<\triangle \left ( c,b\right ) ,$
so c and b have the desired properties. This finishes the proof of the claim.
We now return to prove that S satisfies point 5 of the definition of fusion tree. Using the claim above, we pick
![]() $a=\left \langle p_{0}^{a},\ldots ,p_{n} ^{a}\right \rangle $
and
$a=\left \langle p_{0}^{a},\ldots ,p_{n} ^{a}\right \rangle $
and
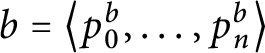 $b=\left \langle p_{0}^{b},\ldots ,p_{n}^{b}\right \rangle $
such that
$b=\left \langle p_{0}^{b},\ldots ,p_{n}^{b}\right \rangle $
such that
![]() $a^{\prime }=s, b^{\prime }=t$
and
$a^{\prime }=s, b^{\prime }=t$
and
![]() $m=\triangle \left ( a,b\right ) .$
Since
$m=\triangle \left ( a,b\right ) .$
Since
![]() $p_{n}^{s}\upharpoonright \gamma =p_{n}^{t}\upharpoonright \gamma ,$
it follows that
$p_{n}^{s}\upharpoonright \gamma =p_{n}^{t}\upharpoonright \gamma ,$
it follows that
![]() $p_{n}^{a}\upharpoonright \gamma =p_{n}^{b}\upharpoonright \gamma .$
Recall that
$p_{n}^{a}\upharpoonright \gamma =p_{n}^{b}\upharpoonright \gamma .$
Recall that
![]() $d_{s}^{S}=d_{a}^{T}\upharpoonright \beta , w_{s}^{S}=w_{a} ^{T}\upharpoonright \beta $
and
$d_{s}^{S}=d_{a}^{T}\upharpoonright \beta , w_{s}^{S}=w_{a} ^{T}\upharpoonright \beta $
and
![]() $d_{t}^{S}=d_{b}^{T}\upharpoonright \beta , w_{t}^{S}=w_{b}^{T}\upharpoonright \beta .$
We need to proceed by cases:
$d_{t}^{S}=d_{b}^{T}\upharpoonright \beta , w_{t}^{S}=w_{b}^{T}\upharpoonright \beta .$
We need to proceed by cases:
Case 57
![]() $F_{n+1}^{\prime }\neq F_{n}^{\prime }.$
$F_{n+1}^{\prime }\neq F_{n}^{\prime }.$
In particular, we get that
![]() $F_{n+1}\neq F_{n}.$
Since T is a fusion tree (in particular, it satisfies point 5(a) of Definition 48), we get the desired conclusion.
$F_{n+1}\neq F_{n}.$
Since T is a fusion tree (in particular, it satisfies point 5(a) of Definition 48), we get the desired conclusion.
Case 58
![]() $F_{n+1}^{\prime }=F_{n}^{\prime }$
and
$F_{n+1}^{\prime }=F_{n}^{\prime }$
and
![]() $F_{n+1}=F_{n}.$
$F_{n+1}=F_{n}.$
In this case, we use that T satisfies point 5(b) of Definition 48 and we are done.
Case 59
![]() $F_{n+1}^{\prime }=F_{n}^{\prime }$
and
$F_{n+1}^{\prime }=F_{n}^{\prime }$
and
![]() $F_{n+1}\neq F_{n}.$
$F_{n+1}\neq F_{n}.$
For this case, we must prove that
![]() $d_{s}^{S}\upharpoonright \gamma =d_{t} ^{S}\upharpoonright \gamma .$
Since T satisfies point 5(a) of Definition 48, we are fine in this case.
$d_{s}^{S}\upharpoonright \gamma =d_{t} ^{S}\upharpoonright \gamma .$
Since T satisfies point 5(a) of Definition 48, we are fine in this case.
This finishes the proof that S is a fusion tree.▪
We will need the following lemma later on.
Lemma 60 Let M be a countable elementary submodel of
![]() $\mathsf{H}( \kappa ) $
,
$\mathsf{H}( \kappa ) $
,
![]() $\beta +1\in M$
and
$\beta +1\in M$
and
![]() $L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
$L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
![]() $\left ( M,\beta +1\right ) .$
Let T be a
$\left ( M,\beta +1\right ) .$
Let T be a
![]() $\left ( \beta +1\right ) $
-fusion tree and
$\left ( \beta +1\right ) $
-fusion tree and
![]() $n\in \omega $
the first such that
$n\in \omega $
the first such that
![]() $\beta \in F_{n+1}.$
Let
$\beta \in F_{n+1}.$
Let
![]() $m>n$
and
$m>n$
and
![]() $s=\left \langle p_{0}^{s},\ldots ,p_{m}^{s}\right \rangle \in T_{m}.$
There is a unique
$s=\left \langle p_{0}^{s},\ldots ,p_{m}^{s}\right \rangle \in T_{m}.$
There is a unique
![]() $t=\left \langle p_{0}^{t},\ldots ,p_{m}^{t}\right \rangle \in T_{m}$
such that
$t=\left \langle p_{0}^{t},\ldots ,p_{m}^{t}\right \rangle \in T_{m}$
such that
![]() $\triangle \left ( s,t\right ) =n$
and
$\triangle \left ( s,t\right ) =n$
and
![]() $s\sim _{\beta }t.$
$s\sim _{\beta }t.$
Proof Define
![]() $t=\left \langle p_{0}^{t},\ldots ,p_{m}^{t}\right \rangle $
as follows:
$t=\left \langle p_{0}^{t},\ldots ,p_{m}^{t}\right \rangle $
as follows:
-
1. If
 $i<n,$
then
$i<n,$
then
 $p_{i}^{t}=p_{i}^{s}.$
$p_{i}^{t}=p_{i}^{s}.$
-
2. If
 $i=n,$
let
$i=n,$
let
 $a=\left \langle p_{0}^{s},\ldots ,p_{n-1}^{s}\right \rangle $
(so
$a=\left \langle p_{0}^{s},\ldots ,p_{n-1}^{s}\right \rangle $
(so
 $a=\left \langle p_{0}^{t},\ldots ,p_{n-1}^{t}\right \rangle $
). Let
$a=\left \langle p_{0}^{t},\ldots ,p_{n-1}^{t}\right \rangle $
). Let
 $p_{n} ^{t}\in suc_{T}( a) $
such that
$p_{n} ^{t}\in suc_{T}( a) $
such that
 $p_{n}^{t}\neq p_{n}^{s}.$
$p_{n}^{t}\neq p_{n}^{s}.$
-
3. For
 $i>n,$
let
$i>n,$
let
 $\overline {s}=\left \langle p_{0}^{s},\ldots ,p_{i-1} ^{s}\right \rangle $
and
$\overline {s}=\left \langle p_{0}^{s},\ldots ,p_{i-1} ^{s}\right \rangle $
and
 $\overline {t}=\left \langle p_{0}^{t},\ldots ,p_{i-1} ^{t}\right \rangle .$
Define
$\overline {t}=\left \langle p_{0}^{t},\ldots ,p_{i-1} ^{t}\right \rangle .$
Define
 $p_{i}^{t}=d_{\overline {t}}$
if
$p_{i}^{t}=d_{\overline {t}}$
if
 $p_{i} ^{s}=d_{\overline {s}}$
and
$p_{i} ^{s}=d_{\overline {s}}$
and
 $p_{i}^{t}=w_{\overline {t}}$
if
$p_{i}^{t}=w_{\overline {t}}$
if
 $p_{i} ^{s}=w_{\overline {s}}.$
$p_{i} ^{s}=w_{\overline {s}}.$
We clearly have that
![]() $\triangle \left ( s,t\right ) =n$
and
$\triangle \left ( s,t\right ) =n$
and
![]() $s\sim _{\beta }t.$
We will now prove that there cannot be more that one. Assume that there is
$s\sim _{\beta }t.$
We will now prove that there cannot be more that one. Assume that there is
![]() $a=\left \langle p_{1}^{a},\ldots ,p_{m}^{a}\right \rangle \in T_{m}$
with the following properties:
$a=\left \langle p_{1}^{a},\ldots ,p_{m}^{a}\right \rangle \in T_{m}$
with the following properties:
-
1.
 $a\neq t$
and
$a\neq t$
and
 $a\neq s.$
$a\neq s.$
-
2.
 $\triangle \left ( a,s\right ) =\triangle \left ( t,s\right ) =n.$
$\triangle \left ( a,s\right ) =\triangle \left ( t,s\right ) =n.$
-
3.
 $p_{i}^{a}\upharpoonright \beta =p_{i}^{s}\upharpoonright \beta =p_{i} ^{t}\upharpoonright \beta $
for every
$p_{i}^{a}\upharpoonright \beta =p_{i}^{s}\upharpoonright \beta =p_{i} ^{t}\upharpoonright \beta $
for every
 $i\leq m.$
$i\leq m.$
By the above properties, we must have that
![]() $n<\triangle \left ( a,t\right ) .$
Let
$n<\triangle \left ( a,t\right ) .$
Let
![]() $k=\triangle \left ( a,t\right ) $
and
$k=\triangle \left ( a,t\right ) $
and
![]() $\xi \in F_{k+1}\setminus F_{k}.$
Since
$\xi \in F_{k+1}\setminus F_{k}.$
Since
![]() $n<k,$
we get that
$n<k,$
we get that
![]() $\xi \neq \beta ,$
so
$\xi \neq \beta ,$
so
![]() $\xi <\beta .$
We will now have that
$\xi <\beta .$
We will now have that
![]() $p_{k+1}^{a}\upharpoonright \left ( \xi +1\right ) \neq p_{k+1}^{s} \upharpoonright \left ( \xi +1\right ) ,$
so
$p_{k+1}^{a}\upharpoonright \left ( \xi +1\right ) \neq p_{k+1}^{s} \upharpoonright \left ( \xi +1\right ) ,$
so
![]() $p_{k+1}^{a}\upharpoonright \beta \neq p_{k+1}^{s}\upharpoonright \beta ,$
which is a contradiction.▪
$p_{k+1}^{a}\upharpoonright \beta \neq p_{k+1}^{s}\upharpoonright \beta ,$
which is a contradiction.▪
The following lemma will play a key role in our work:
Definition 61 Let T be an
![]() $\alpha $
-fusion tree and
$\alpha $
-fusion tree and
![]() $q\in \mathbb {P}_{\alpha }.$
We say q is compatible with T if there is a
$q\in \mathbb {P}_{\alpha }.$
We say q is compatible with T if there is a
![]() $\mathbb {P}_{\alpha }$
-name for a (possibly new) branch
$\mathbb {P}_{\alpha }$
-name for a (possibly new) branch
![]() $\dot {R}$
of
$\dot {R}$
of
![]() $T$
such that
$T$
such that
![]() $q\Vdash $
“
$q\Vdash $
“
![]() $\dot {R}\subseteq \dot {G}$
” (where
$\dot {R}\subseteq \dot {G}$
” (where
![]() $\dot {G}$
is the name for the
$\dot {G}$
is the name for the
![]() $\mathbb {P}_{\alpha }$
-generic filter).
$\mathbb {P}_{\alpha }$
-generic filter).
In the above definition, we are identifying a branch with its image. The following result was inspired by the “properness iteration lemma” used to prove that the iteration of proper forcing is proper (see [Reference Abraham1, Reference Shelah14]).
Lemma 62 Let M be a countable elementary submodel of
![]() $\mathsf{H} ( \kappa ) ,\ \alpha ,\beta \in M$
with
$\mathsf{H} ( \kappa ) ,\ \alpha ,\beta \in M$
with
![]() $\beta <\alpha $
and T an
$\beta <\alpha $
and T an
![]() $\alpha $
-fusion tree. Assume there is
$\alpha $
-fusion tree. Assume there is
![]() $q\in \mathbb {P}_{\beta }$
that is compatible with
$q\in \mathbb {P}_{\beta }$
that is compatible with
![]() $T\upharpoonright \beta .$
There is
$T\upharpoonright \beta .$
There is
![]() $\dot {r}$
such that
$\dot {r}$
such that
![]() $q^{\frown }\dot {r}\in \mathbb {P}_{\alpha }$
and
$q^{\frown }\dot {r}\in \mathbb {P}_{\alpha }$
and
![]() $q^{\frown }\dot {r}$
is compatible with
$q^{\frown }\dot {r}$
is compatible with
![]() $T.$
Moreover, if
$T.$
Moreover, if
![]() $\dot {R}$
is a
$\dot {R}$
is a
![]() $\mathbb {P}_{\beta }$
-name for a branch through
$\mathbb {P}_{\beta }$
-name for a branch through
![]() $T\upharpoonright \beta $
such that
$T\upharpoonright \beta $
such that
![]() $q\Vdash $
“
$q\Vdash $
“
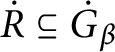 $\dot {R} \subseteq \dot {G}_{\beta }$
,” then there is
$\dot {R} \subseteq \dot {G}_{\beta }$
,” then there is
![]() $\dot {R}^{\prime }$
a
$\dot {R}^{\prime }$
a
![]() $\mathbb {P}_{\alpha }$
-name for a branch through T such that
$\mathbb {P}_{\alpha }$
-name for a branch through T such that
![]() $q^{\frown }\dot {r}\Vdash \text{``}\dot {R}^{\prime }\subseteq \dot {G} _{\alpha }\text {'' and}\ q^{\frown }\dot {r}\Vdash $
“
$q^{\frown }\dot {r}\Vdash \text{``}\dot {R}^{\prime }\subseteq \dot {G} _{\alpha }\text {'' and}\ q^{\frown }\dot {r}\Vdash $
“
![]() $\dot {R}^{\prime }\upharpoonright \beta =\dot {R}$
”(
$\dot {R}^{\prime }\upharpoonright \beta =\dot {R}$
”(
![]() $\dot {G}_{\beta }$
is the
$\dot {G}_{\beta }$
is the
![]() $\mathbb {P}_{\beta }$
-name for the generic filter of
$\mathbb {P}_{\beta }$
-name for the generic filter of
![]() $\mathbb {P}_{\beta }$
and
$\mathbb {P}_{\beta }$
and
![]() $\dot {G}_{\alpha }$
is the
$\dot {G}_{\alpha }$
is the
![]() $\mathbb {P}_{\alpha }$
-name for the generic filter of
$\mathbb {P}_{\alpha }$
-name for the generic filter of
![]() $\mathbb {P}_{\alpha }$
).
$\mathbb {P}_{\alpha }$
).
Proof We prove it by induction on
![]() $\alpha ,$
the case
$\alpha ,$
the case
![]() $\alpha =1$
follows from the argument of Lemma 20. Now assume
$\alpha =1$
follows from the argument of Lemma 20. Now assume
![]() $\alpha =\delta +1$
and the lemma holds for
$\alpha =\delta +1$
and the lemma holds for
![]() $\delta .$
We first tackle the case of
$\delta .$
We first tackle the case of
![]() $\beta =\delta .$
$\beta =\delta .$
Let
![]() $G\subseteq \mathbb {P}_{\beta }$
be a generic filter with
$G\subseteq \mathbb {P}_{\beta }$
be a generic filter with
![]() $q\in G.$
Find n the first natural number such that
$q\in G.$
Find n the first natural number such that
![]() $\beta \in F_{n}.$
For the moment, we work in
$\beta \in F_{n}.$
For the moment, we work in
![]() $V\left [ G\right ] .$
In
$V\left [ G\right ] .$
In
![]() $V\left [ G\right ] $
define the following set:
$V\left [ G\right ] $
define the following set:
In other words, for every
![]() $s=\left \langle p_{0},\ldots ,p_{l}\right \rangle \in T$
we have that
$s=\left \langle p_{0},\ldots ,p_{l}\right \rangle \in T$
we have that
![]() $s\in H$
if and only if
$s\in H$
if and only if
![]() $l\geq n$
and
$l\geq n$
and
![]() $\left \langle p_{0}\upharpoonright \beta ,\ldots ,p_{l}\upharpoonright \beta \right \rangle $
is an initial segment of the branch
$\left \langle p_{0}\upharpoonright \beta ,\ldots ,p_{l}\upharpoonright \beta \right \rangle $
is an initial segment of the branch
![]() $\dot {R}\left [ G\right ] .$
$\dot {R}\left [ G\right ] .$
Claim 63 If
![]() $m>n,$
then
$m>n,$
then
![]() $\left \vert T_{m}\cap H\right \vert =2$
(in
$\left \vert T_{m}\cap H\right \vert =2$
(in
![]() $V\left [ G\right ] $
).
$V\left [ G\right ] $
).
We prove the claim. Since
![]() $\dot {R}\left [ G\right ] $
is a branch, it follows that
$\dot {R}\left [ G\right ] $
is a branch, it follows that
![]() $T_{m}\cap H$
has at least one element. Let
$T_{m}\cap H$
has at least one element. Let
![]() $s=\left \langle p_{0},\ldots ,p_{m}\right \rangle \in T_{m}\cap H$
, by Lemma 60, there is a unique
$s=\left \langle p_{0},\ldots ,p_{m}\right \rangle \in T_{m}\cap H$
, by Lemma 60, there is a unique
![]() $t=\left \langle q_{0},\ldots ,q_{m}\right \rangle \in T_{m}$
such that
$t=\left \langle q_{0},\ldots ,q_{m}\right \rangle \in T_{m}$
such that
![]() $\triangle \left ( s,t\right ) =n$
and
$\triangle \left ( s,t\right ) =n$
and
![]() $q_{i}\upharpoonright \beta =p_{i}\upharpoonright \beta $
for every
$q_{i}\upharpoonright \beta =p_{i}\upharpoonright \beta $
for every
![]() $i\leq m.$
It follows that
$i\leq m.$
It follows that
![]() $t\in T_{m}\cap H,$
so
$t\in T_{m}\cap H,$
so
![]() $T_{m}\cap H$
has at least two elements. Furthermore, if there was
$T_{m}\cap H$
has at least two elements. Furthermore, if there was
![]() $u=\left \langle r_{0},\ldots ,r_{m}\right \rangle \in T_{m}\cap H$
with
$u=\left \langle r_{0},\ldots ,r_{m}\right \rangle \in T_{m}\cap H$
with
![]() $u\neq s,$
we must have that
$u\neq s,$
we must have that
![]() $\triangle \left ( s,u\right ) =n$
(because if
$\triangle \left ( s,u\right ) =n$
(because if
![]() $k=\triangle \left ( s,u\right ) \neq n,$
then
$k=\triangle \left ( s,u\right ) \neq n,$
then
![]() $r_{k}\upharpoonright \beta $
would be incompatible with
$r_{k}\upharpoonright \beta $
would be incompatible with
![]() $p_{k}\upharpoonright \beta $
by point 4 of Definition 48, so
$p_{k}\upharpoonright \beta $
by point 4 of Definition 48, so
![]() $r_{m}\upharpoonright \beta $
and
$r_{m}\upharpoonright \beta $
and
![]() $p_{m}\upharpoonright \beta $
would be incompatible, but this is a contradiction since both are in the generic filter). Since t is unique, it follows that
$p_{m}\upharpoonright \beta $
would be incompatible, but this is a contradiction since both are in the generic filter). Since t is unique, it follows that
![]() $T_{m}\cap H$
has exactly two elements.
$T_{m}\cap H$
has exactly two elements.
It will be convenient to introduce some notation. Given
![]() $K\subseteq T,$
define
$K\subseteq T,$
define
![]() $Last\left ( K\right ) =\left \{ s\left ( \left \vert s\right \vert -1\right ) \mid s\in K\right \} .$
In other words,
$Last\left ( K\right ) =\left \{ s\left ( \left \vert s\right \vert -1\right ) \mid s\in K\right \} .$
In other words,
![]() $Last\left ( K\right ) $
is obtained by collecting all the last component of every sequence in
$Last\left ( K\right ) $
is obtained by collecting all the last component of every sequence in
![]() $K.$
$K.$
As we saw above, if
![]() $s=\left \langle p_{0},\ldots ,p_{m}\right \rangle , t=\left \langle q_{0},\ldots ,q_{m}\right \rangle \in T_{m}\cap H$
and
$s=\left \langle p_{0},\ldots ,p_{m}\right \rangle , t=\left \langle q_{0},\ldots ,q_{m}\right \rangle \in T_{m}\cap H$
and
![]() $s\neq t,$
then
$s\neq t,$
then
![]() $\triangle \left ( s,t\right ) =n.$
Furthermore, by Lemma 49, we get that
$\triangle \left ( s,t\right ) =n.$
Furthermore, by Lemma 49, we get that
![]() $p_{i}\upharpoonright \beta =q_{i} \upharpoonright \beta $
for every
$p_{i}\upharpoonright \beta =q_{i} \upharpoonright \beta $
for every
![]() $i\leq m.$
In this way, for every
$i\leq m.$
In this way, for every
![]() $m>n$
there must be
$m>n$
there must be
![]() $r_{m}\in \mathbb {P}_{\beta }$
and
$r_{m}\in \mathbb {P}_{\beta }$
and
![]() $\dot {x}_{m},\dot {y}_{m}$
two
$\dot {x}_{m},\dot {y}_{m}$
two
![]() $\mathbb {P}_{\beta }$
-names such that
$\mathbb {P}_{\beta }$
-names such that
![]() $Last\left ( T_{m}\cap H\right ) =\left \{ r_{m}{}^{\frown }\dot {x}_{m},r_{m}{}^{\frown }\dot {y}_{m}\right \} $
. Since T is an
$Last\left ( T_{m}\cap H\right ) =\left \{ r_{m}{}^{\frown }\dot {x}_{m},r_{m}{}^{\frown }\dot {y}_{m}\right \} $
. Since T is an
![]() $\alpha $
-fusion tree, then
$\alpha $
-fusion tree, then
![]() $S=\left ( \left \langle \dot {x} _{m}\right \rangle ,\left \langle \dot {y}_{m}\right \rangle \right ) _{m>n}$
is forced to be a
$S=\left ( \left \langle \dot {x} _{m}\right \rangle ,\left \langle \dot {y}_{m}\right \rangle \right ) _{m>n}$
is forced to be a
![]() $1$
-fusion sequence. By Lemma 20 there is
$1$
-fusion sequence. By Lemma 20 there is
![]() $\dot {a}$
a
$\dot {a}$
a
![]() $\mathbb {P}_{\beta }$
-name for a condition in
$\mathbb {P}_{\beta }$
-name for a condition in
![]() $\mathbb {S(}\mathcal {\dot {U} }_{\alpha })$
that is forced to be a lower bound of either
$\mathbb {S(}\mathcal {\dot {U} }_{\alpha })$
that is forced to be a lower bound of either
![]() $\left \langle \dot {x}_{m}\right \rangle _{m>n}$
or
$\left \langle \dot {x}_{m}\right \rangle _{m>n}$
or
![]() $\left \langle \dot {y}_{m}\right \rangle _{m>n}$
(note however, that it could happen that we do not know which possibility occurs without extending q). Clearly
$\left \langle \dot {y}_{m}\right \rangle _{m>n}$
(note however, that it could happen that we do not know which possibility occurs without extending q). Clearly
![]() $q^{\frown }\dot {a}$
is the condition we were looking for.
$q^{\frown }\dot {a}$
is the condition we were looking for.
Now, we consider the case where
![]() $\beta <\delta .$
By the inductive hypothesis, there are
$\beta <\delta .$
By the inductive hypothesis, there are
![]() $\dot {r}$
such that
$\dot {r}$
such that
![]() $q_{1}=q^{\frown }\dot {r}\in \mathbb {P}_{\delta }$
and
$q_{1}=q^{\frown }\dot {r}\in \mathbb {P}_{\delta }$
and
![]() $\dot {R}^{\prime }$
a
$\dot {R}^{\prime }$
a
![]() $\mathbb {P}_{\delta }$
-name for a branch through
$\mathbb {P}_{\delta }$
-name for a branch through
![]() $T\upharpoonright \delta $
such that
$T\upharpoonright \delta $
such that
![]() $q_{1}\Vdash _{\delta } \text{``}\dot {R}^{\prime }\subseteq \dot {G}_{\delta }\text {'' and}\ q_{1}\Vdash _{\delta }$
“
$q_{1}\Vdash _{\delta } \text{``}\dot {R}^{\prime }\subseteq \dot {G}_{\delta }\text {'' and}\ q_{1}\Vdash _{\delta }$
“
![]() $\dot {R}^{\prime }\upharpoonright \beta =\dot {R}$
.” Now, by the previous case, there are
$\dot {R}^{\prime }\upharpoonright \beta =\dot {R}$
.” Now, by the previous case, there are
![]() $\dot {r}_{1}$
such that
$\dot {r}_{1}$
such that
![]() $q_{2}=q_{1} ^{\frown } \dot {r}_{1}\in \mathbb {P}_{\alpha }$
and
$q_{2}=q_{1} ^{\frown } \dot {r}_{1}\in \mathbb {P}_{\alpha }$
and
![]() $\dot {R}^{\prime \prime }$
a
$\dot {R}^{\prime \prime }$
a
![]() $\mathbb {P}_{\alpha }$
-name for a branch through T such that
$\mathbb {P}_{\alpha }$
-name for a branch through T such that
![]() $q_{2} \Vdash _{\alpha }\text{``}\dot {R}^{\prime \prime }\subseteq \dot {G}_{\alpha }\text {'' and}\ q_{2}\Vdash _{\alpha }$
“
$q_{2} \Vdash _{\alpha }\text{``}\dot {R}^{\prime \prime }\subseteq \dot {G}_{\alpha }\text {'' and}\ q_{2}\Vdash _{\alpha }$
“
![]() $\dot {R}^{\prime \prime }\upharpoonright \delta =\dot {R}^{\prime }$
.” This clearly finishes the proof of this case.
$\dot {R}^{\prime \prime }\upharpoonright \delta =\dot {R}^{\prime }$
.” This clearly finishes the proof of this case.
Assume
![]() $\alpha $
is a limit ordinal and let
$\alpha $
is a limit ordinal and let
![]() $\left \langle \delta _{n} \right \rangle _{n\in \omega }\subseteq M$
be an increasing sequence such that
$\left \langle \delta _{n} \right \rangle _{n\in \omega }\subseteq M$
be an increasing sequence such that
 $ {\textstyle \bigcup \limits _{n\in \omega }} \delta _{n}=\bigcup \left ( M\cap \alpha \right ) ,$
we also assume
$ {\textstyle \bigcup \limits _{n\in \omega }} \delta _{n}=\bigcup \left ( M\cap \alpha \right ) ,$
we also assume
![]() $\beta =\delta _{0}$
and
$\beta =\delta _{0}$
and
![]() $F_{n}\subseteq \delta _{n+1}.$
We do the following:
$F_{n}\subseteq \delta _{n+1}.$
We do the following:
-
1. By the inductive hypothesis, we can find
 $q_{1}\in \mathbb {P}_{\delta _{1}}$
and
$q_{1}\in \mathbb {P}_{\delta _{1}}$
and
 $\dot {R}_{1}$
with the following properties:
$\dot {R}_{1}$
with the following properties:-
(a)
 $\dot {R}_{1}$
is a
$\dot {R}_{1}$
is a
 $\mathbb {P}_{\delta _{1}}$
-name for a branch of the tree
$\mathbb {P}_{\delta _{1}}$
-name for a branch of the tree
 $T\upharpoonright \delta _{1}.$
$T\upharpoonright \delta _{1}.$
-
(b)
 $q_{1}\upharpoonright \delta _{0}=q_{0}$
(where
$q_{1}\upharpoonright \delta _{0}=q_{0}$
(where
 $q_{0}=q$
).
$q_{0}=q$
). -
(c)
 $q_{1}\Vdash $
“
$q_{1}\Vdash $
“
 $\dot {R}_{1}\subseteq \dot {G}_{\delta _{1}} $
” and
$\dot {R}_{1}\subseteq \dot {G}_{\delta _{1}} $
” and
 $q_{1}\Vdash $
“
$q_{1}\Vdash $
“
 $\dot {R}_{1} \upharpoonright \delta _{0}=\dot {R}_{0}$
” (where
$\dot {R}_{1} \upharpoonright \delta _{0}=\dot {R}_{0}$
” (where
 $\dot {R} _{0}=\dot {R}$
).
$\dot {R} _{0}=\dot {R}$
).
-
-
2. By the inductive hypothesis, we can find
 $q_{2}\in \mathbb {P}_{\delta _{2}}$
and
$q_{2}\in \mathbb {P}_{\delta _{2}}$
and
 $\dot {R}_{2}$
with the following properties:
$\dot {R}_{2}$
with the following properties:-
(a)
 $\dot {R}_{2}$
is a
$\dot {R}_{2}$
is a
 $\mathbb {P}_{\delta _{2}}$
-name for a branch of the tree
$\mathbb {P}_{\delta _{2}}$
-name for a branch of the tree
 $T\upharpoonright \delta _{2}.$
$T\upharpoonright \delta _{2}.$
-
(b)
 $q_{2}\upharpoonright \delta _{1}=q_{1}.$
$q_{2}\upharpoonright \delta _{1}=q_{1}.$
-
(c)
 $q_{2}\Vdash $
“
$q_{2}\Vdash $
“
 $\dot {R}_{2}\subseteq \dot {G}_{\delta _{2}} $
” and
$\dot {R}_{2}\subseteq \dot {G}_{\delta _{2}} $
” and
 $q_{2}\Vdash $
“
$q_{2}\Vdash $
“
 $\dot {R}_{2} \upharpoonright \delta _{1}=\dot {R}_{1}$
.”
$\dot {R}_{2} \upharpoonright \delta _{1}=\dot {R}_{1}$
.”
-
-
⋮
 $\hspace{132pt}\vdots $
$\hspace{132pt}\vdots $
-
n+1. By the inductive hypothesis, we can find
 $q_{n+1}\in \mathbb {P}_{\delta _{n+1}}$
and
$q_{n+1}\in \mathbb {P}_{\delta _{n+1}}$
and
 $\dot {R}_{n+1}$
with the following properties:
$\dot {R}_{n+1}$
with the following properties:-
(a)
 $\dot {R}_{n+1}$
is a
$\dot {R}_{n+1}$
is a
 $\mathbb {P}_{\delta _{n+1}}$
-name for a branch of the tree
$\mathbb {P}_{\delta _{n+1}}$
-name for a branch of the tree
 $T\upharpoonright \delta _{n+1}.$
$T\upharpoonright \delta _{n+1}.$
-
(b)
 $q_{n+1}\upharpoonright \delta _{n}=q_{n}.$
$q_{n+1}\upharpoonright \delta _{n}=q_{n}.$
-
(c)
 $q_{n+1}\Vdash $
“
$q_{n+1}\Vdash $
“
 $\dot {R}_{n+1}\subseteq \dot {G} _{\delta _{n}}$
” and
$\dot {R}_{n+1}\subseteq \dot {G} _{\delta _{n}}$
” and
 $q_{n+1}\Vdash $
“
$q_{n+1}\Vdash $
“
 $\dot {R}_{n+1}\upharpoonright \delta _{n}=\dot {R}_{n}$
.”
$\dot {R}_{n+1}\upharpoonright \delta _{n}=\dot {R}_{n}$
.”
-
For every
![]() $n\in \omega ,$
let
$n\in \omega ,$
let
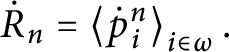 $\dot {R}_{n}=\left \langle \dot {p}_{i} ^{n}\right \rangle _{i\in \omega }.$
By construction, we have that
$\dot {R}_{n}=\left \langle \dot {p}_{i} ^{n}\right \rangle _{i\in \omega }.$
By construction, we have that
![]() $\dot {p} _{i}^{n+1}\upharpoonright \delta _{n}$
and
$\dot {p} _{i}^{n+1}\upharpoonright \delta _{n}$
and
![]() $\dot {p}_{i}^{n}$
are forced to be equal and
$\dot {p}_{i}^{n}$
are forced to be equal and
![]() $q_{n+1}\upharpoonright \delta _{n}=q_{n}.$
Define
$q_{n+1}\upharpoonright \delta _{n}=q_{n}.$
Define
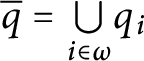 $\overline {q}= {\textstyle \bigcup \limits _{i\in \omega }} q_{i}$
and
$\overline {q}= {\textstyle \bigcup \limits _{i\in \omega }} q_{i}$
and
![]() $\dot {p}_{i}$
be a name for
$\dot {p}_{i}$
be a name for
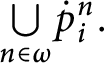 $ {\textstyle \bigcup \limits _{n\in \omega }} \dot {p}_{i}^{n}.$
Let
$ {\textstyle \bigcup \limits _{n\in \omega }} \dot {p}_{i}^{n}.$
Let
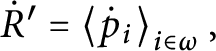 $\dot {R}^{\prime }=\left \langle \dot {p}_{i}\right \rangle _{i\in \omega },$
we claim that
$\dot {R}^{\prime }=\left \langle \dot {p}_{i}\right \rangle _{i\in \omega },$
we claim that
![]() $\overline {q}$
and
$\overline {q}$
and
![]() $\dot {R}^{\prime }$
have the desired properties. It is clear that
$\dot {R}^{\prime }$
have the desired properties. It is clear that
![]() $\overline {q}\upharpoonright \beta =q$
and
$\overline {q}\upharpoonright \beta =q$
and
![]() $\overline {q}\Vdash $
“
$\overline {q}\Vdash $
“
![]() $\dot {R}^{\prime }\upharpoonright \beta =\dot {R}$
.”
$\dot {R}^{\prime }\upharpoonright \beta =\dot {R}$
.”
We will now prove that
![]() $\dot {R}^{\prime }$
is forced by
$\dot {R}^{\prime }$
is forced by
![]() $\overline {q}$
to be a branch through
$\overline {q}$
to be a branch through
![]() $T.$
For every
$T.$
For every
![]() $m\in \omega ,$
let
$m\in \omega ,$
let
![]() $\dot {R}_{m}^{\prime }=\left \langle \dot {p}_{0},\ldots ,\dot {p}_{m}\right \rangle .$
We need to prove that
$\dot {R}_{m}^{\prime }=\left \langle \dot {p}_{0},\ldots ,\dot {p}_{m}\right \rangle .$
We need to prove that
![]() $\overline {q}\Vdash $
“
$\overline {q}\Vdash $
“
![]() $\dot {R}_{m}^{\prime }\in T$
” for every
$\dot {R}_{m}^{\prime }\in T$
” for every
![]() $m\in \omega .$
Assume this is not the case. In this way, we can find
$m\in \omega .$
Assume this is not the case. In this way, we can find
![]() $m\in \omega $
such that
$m\in \omega $
such that
![]() $\overline {q}\Vdash $
“
$\overline {q}\Vdash $
“
![]() $\dot {R}_{m}^{\prime }\in T$
” but
$\dot {R}_{m}^{\prime }\in T$
” but
![]() $\overline {q}\not \Vdash $
“
$\overline {q}\not \Vdash $
“
![]() $\dot {R}_{m+1}^{\prime }\in T$
” (recall point 1 in Definition 48). In this way, we can find
$\dot {R}_{m+1}^{\prime }\in T$
” (recall point 1 in Definition 48). In this way, we can find
![]() $q_{1}\leq \overline {q}$
such that
$q_{1}\leq \overline {q}$
such that
![]() $q_{1}\Vdash $
“
$q_{1}\Vdash $
“
![]() $\dot {p}_{m+1}\notin suc_{T}(\dot {R}_{m}^{\prime } )$
.” Let
$\dot {p}_{m+1}\notin suc_{T}(\dot {R}_{m}^{\prime } )$
.” Let
![]() $r\leq q_{1}$
and
$r\leq q_{1}$
and
![]() $s\in T$
such that
$s\in T$
such that
![]() $r\Vdash $
“
$r\Vdash $
“
![]() $s=\dot {R}_{m}^{\prime }$
.” Since
$s=\dot {R}_{m}^{\prime }$
.” Since
![]() $suc_{T}( s) $
is finite (has at most two elements in fact), we can find
$suc_{T}( s) $
is finite (has at most two elements in fact), we can find
![]() $r_{1}\leq r$
and
$r_{1}\leq r$
and
![]() $\xi \in M\cap \alpha $
such that
$\xi \in M\cap \alpha $
such that
![]() $r_{1}\Vdash $
“
$r_{1}\Vdash $
“
![]() $\dot {p}_{m}\upharpoonright \xi \neq x\upharpoonright \xi $
” for every
$\dot {p}_{m}\upharpoonright \xi \neq x\upharpoonright \xi $
” for every
![]() $x\in suc_{T}( s) .$
Pick
$x\in suc_{T}( s) .$
Pick
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $\xi <\delta _{n}.$
In this way, we get that
$\xi <\delta _{n}.$
In this way, we get that
![]() $r_{1}\upharpoonright \delta _{n}$
forces that
$r_{1}\upharpoonright \delta _{n}$
forces that
![]() $\dot {R}^{\prime }$
is not a branch trough
$\dot {R}^{\prime }$
is not a branch trough
![]() $T\upharpoonright \delta _{n},$
but this is a contradiction.
$T\upharpoonright \delta _{n},$
but this is a contradiction.
It remains to prove that
![]() $\overline {q}\Vdash $
“
$\overline {q}\Vdash $
“
![]() $\dot {R} ^{\prime }\subseteq \dot {G}_{\alpha }$
.” We need to prove that if
$\dot {R} ^{\prime }\subseteq \dot {G}_{\alpha }$
.” We need to prove that if
![]() $i\in \omega ,$
then
$i\in \omega ,$
then
![]() $\overline {q}\Vdash $
“
$\overline {q}\Vdash $
“
![]() $\dot {p}_{i}\in \dot {G}_{\alpha }$
.” Recall that
$\dot {p}_{i}\in \dot {G}_{\alpha }$
.” Recall that
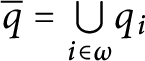 $\overline {q}= {\textstyle \bigcup \limits _{i\in \omega }} q_{i}$
and
$\overline {q}= {\textstyle \bigcup \limits _{i\in \omega }} q_{i}$
and
![]() $\dot {p}_{i}$
be a name for
$\dot {p}_{i}$
be a name for
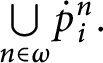 $ {\textstyle \bigcup \limits _{n\in \omega }} \dot {p}_{i}^{n}.$
By construction, we have that
$ {\textstyle \bigcup \limits _{n\in \omega }} \dot {p}_{i}^{n}.$
By construction, we have that
![]() $q_{n}\Vdash $
“
$q_{n}\Vdash $
“
![]() $\dot {p}_{i}^{n}\in \dot {G}_{\delta _{n}}$
” for every
$\dot {p}_{i}^{n}\in \dot {G}_{\delta _{n}}$
” for every
![]() $n\in \omega ,$
so we conclude that
$n\in \omega ,$
so we conclude that
![]() $\overline {q}\Vdash $
“
$\overline {q}\Vdash $
“
![]() $\dot {p}_{i}\in \dot {G}_{\alpha }$
.”▪
$\dot {p}_{i}\in \dot {G}_{\alpha }$
.”▪
The next task is to be able to extend finite fusion trees. We will need a preliminary lemma.
Lemma 64 Let
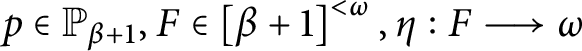 $p\in \mathbb {P}_{\beta +1}, F\in \left [ \beta +1\right ] ^{<\omega }, \eta :F\longrightarrow \omega $
and
$p\in \mathbb {P}_{\beta +1}, F\in \left [ \beta +1\right ] ^{<\omega }, \eta :F\longrightarrow \omega $
and
![]() $D\subseteq \mathbb {P}_{\beta +1}$
be
$D\subseteq \mathbb {P}_{\beta +1}$
be
![]() $( F,\eta ) ^{\ast }$
-open dense below
$( F,\eta ) ^{\ast }$
-open dense below
![]() $p.$
The set
$p.$
The set
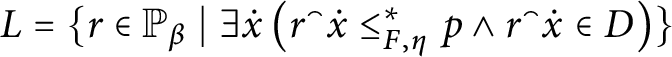 $$ \begin{align*} \begin{array}{l} L=\{r\in\mathbb{P}_{\beta}\mid\exists\dot{x}\left( r^{\frown}\dot{x} \leq_{F,\eta}^{\ast}p\wedge r^{\frown}\dot{x}\in D\right) \} \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} L=\{r\in\mathbb{P}_{\beta}\mid\exists\dot{x}\left( r^{\frown}\dot{x} \leq_{F,\eta}^{\ast}p\wedge r^{\frown}\dot{x}\in D\right) \} \end{array} \end{align*} $$
is
![]() $\left ( F^{\prime },\eta ^{\prime }\right ) ^{\ast }$
-open dense below
$\left ( F^{\prime },\eta ^{\prime }\right ) ^{\ast }$
-open dense below
![]() $p\upharpoonright \beta $
(where
$p\upharpoonright \beta $
(where
![]() $F^{\prime }=F\cap \beta $
and
$F^{\prime }=F\cap \beta $
and
![]() $\eta ^{\prime } =\eta \upharpoonright F$
).
$\eta ^{\prime } =\eta \upharpoonright F$
).
Proof We first show that L is
![]() $\left ( F^{\prime },\eta ^{\prime }\right ) ^{\ast } $
-open below
$\left ( F^{\prime },\eta ^{\prime }\right ) ^{\ast } $
-open below
![]() $p\upharpoonright \beta .$
Let
$p\upharpoonright \beta .$
Let
![]() $q\in L$
and
$q\in L$
and
![]() $r\leq _{F^{\prime } ,\eta ^{\prime }}^{\ast }q.$
Since
$r\leq _{F^{\prime } ,\eta ^{\prime }}^{\ast }q.$
Since
![]() $q\in L,$
there is
$q\in L,$
there is
![]() $\dot {x}$
such that
$\dot {x}$
such that
![]() $q^{\frown }\dot {x}\leq _{F,\eta }^{\ast }p$
and
$q^{\frown }\dot {x}\leq _{F,\eta }^{\ast }p$
and
![]() $q^{\frown }\dot {x}\in D.$
It follows that
$q^{\frown }\dot {x}\in D.$
It follows that
![]() $r^{\frown }\dot {x}\leq _{F,\eta }^{\ast }q^{\frown }\dot {x},$
so
$r^{\frown }\dot {x}\leq _{F,\eta }^{\ast }q^{\frown }\dot {x},$
so
![]() $r^{\frown }\dot {x}\leq _{F,\eta }^{\ast }p.$
Since D is
$r^{\frown }\dot {x}\leq _{F,\eta }^{\ast }p.$
Since D is
![]() $( F,\eta ) ^{\ast }$
-open and
$( F,\eta ) ^{\ast }$
-open and
![]() $q^{\frown }\dot {x}\in D,$
we get that
$q^{\frown }\dot {x}\in D,$
we get that
![]() $r^{\frown }\dot {x}\in D$
which implies that
$r^{\frown }\dot {x}\in D$
which implies that
![]() $r\in L.$
$r\in L.$
We will now prove that L is
![]() $\left ( F^{\prime },\eta ^{\prime }\right ) ^{\ast }$
-dense below
$\left ( F^{\prime },\eta ^{\prime }\right ) ^{\ast }$
-dense below
![]() $p\upharpoonright \beta .$
Let
$p\upharpoonright \beta .$
Let
![]() $q\leq _{F^{\prime } ,\eta ^{\prime }}^{\ast }p\upharpoonright \beta ,$
define
$q\leq _{F^{\prime } ,\eta ^{\prime }}^{\ast }p\upharpoonright \beta ,$
define
![]() $q_{1}=q^{\frown }p( \beta ) $
and note that
$q_{1}=q^{\frown }p( \beta ) $
and note that
![]() $q_{1}\leq _{F,\eta }^{\ast }p.$
Since D is
$q_{1}\leq _{F,\eta }^{\ast }p.$
Since D is
![]() $( F,\eta ) ^{\ast }$
-dense, there is
$( F,\eta ) ^{\ast }$
-dense, there is
![]() $q_{2}\leq _{F,\eta }^{\ast }q_{1}$
such that
$q_{2}\leq _{F,\eta }^{\ast }q_{1}$
such that
![]() $q_{2}\in D.$
Let
$q_{2}\in D.$
Let
![]() $r=q_{2}\upharpoonright \beta .$
It follows that
$r=q_{2}\upharpoonright \beta .$
It follows that
![]() $r\in L$
since
$r\in L$
since
![]() $q_{2}=r^{\frown }q_{2}( \beta ) .$
▪
$q_{2}=r^{\frown }q_{2}( \beta ) .$
▪
We conclude with the following key result, which will allow us to keep extending finite trees.
Lemma 65 Let
![]() $\alpha \in M\preceq $
$\alpha \in M\preceq $
![]() $\mathsf{H}( \kappa ) , L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
$\mathsf{H}( \kappa ) , L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
![]() $\left ( M,\alpha \right ) $
and T an
$\left ( M,\alpha \right ) $
and T an
![]() $\alpha $
-finite fusion tree of height
$\alpha $
-finite fusion tree of height
![]() $n.$
For every
$n.$
For every
![]() $s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T$
let
$s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T$
let
![]() $D_{s}\in M$
be an
$D_{s}\in M$
be an
![]() $\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-open dense set below
$\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-open dense set below
![]() $p_{n}.$
Then there is
$p_{n}.$
Then there is
![]() $\widetilde {T}$
with the following properties:
$\widetilde {T}$
with the following properties:
-
1.
 $\widetilde {T}$
is a
$\widetilde {T}$
is a
 $\alpha $
-finite fusion tree of height
$\alpha $
-finite fusion tree of height
 $n+1.$
$n+1.$
-
2.
 $\widetilde {T}$
is an end-extention of
$\widetilde {T}$
is an end-extention of
 $T.$
$T.$
-
3. If
 $s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T,$
then
$s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T,$
then
 $suc_{\widetilde {T}}( s) \subseteq D_{s}.$
$suc_{\widetilde {T}}( s) \subseteq D_{s}.$
Proof We prove it by induction on
![]() $\alpha .$
The case
$\alpha .$
The case
![]() $\alpha =1$
follows by the argument of Lemma 17. Now assume
$\alpha =1$
follows by the argument of Lemma 17. Now assume
![]() $\alpha =\beta +1$
and the lemma holds for
$\alpha =\beta +1$
and the lemma holds for
![]() $\beta ,$
let
$\beta ,$
let
![]() $S=T\upharpoonright \beta .$
For every
$S=T\upharpoonright \beta .$
For every
![]() $m\in \omega ,$
let
$m\in \omega ,$
let
![]() $F_{m}^{\prime }=F_{m}\cap \beta $
and
$F_{m}^{\prime }=F_{m}\cap \beta $
and
![]() $\eta _{m}^{\prime }=\eta _{m}\upharpoonright F_{m}^{\prime }.$
For the proof in this case, given
$\eta _{m}^{\prime }=\eta _{m}\upharpoonright F_{m}^{\prime }.$
For the proof in this case, given
![]() $s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T,$
we will denote
$s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T,$
we will denote
![]() $s^{\prime }=\left \langle p_{0}\upharpoonright \beta ,\ldots ,p_{n}\upharpoonright \beta \right \rangle .$
There are several cases to consider:
$s^{\prime }=\left \langle p_{0}\upharpoonright \beta ,\ldots ,p_{n}\upharpoonright \beta \right \rangle .$
There are several cases to consider:
Case 66
![]() $\beta \notin F_{n+1}.$
$\beta \notin F_{n+1}.$
In this case, we have that
![]() $F_{n+1}^{\prime }=F_{n+1}$
and
$F_{n+1}^{\prime }=F_{n+1}$
and
![]() $F_{n}^{\prime } =F_{n}.$
This is the easiest case since “
$F_{n}^{\prime } =F_{n}.$
This is the easiest case since “
![]() $\beta $
has not come into play yet.” We provide the details.
$\beta $
has not come into play yet.” We provide the details.
Let
![]() $s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle \in T.$
Define
$s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle \in T.$
Define
 $$ \begin{align*} \begin{array}{l} L_{s}=\left\{ q\in\mathbb{P}_{\beta}\mid\exists\dot{x}\left( q^{\frown} \dot{x}\leq_{F_{n},\eta_{n}}^{\ast}p_{n}^{s}\wedge q^{\frown}\dot{x}\in D_{s}\right) \right\}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} L_{s}=\left\{ q\in\mathbb{P}_{\beta}\mid\exists\dot{x}\left( q^{\frown} \dot{x}\leq_{F_{n},\eta_{n}}^{\ast}p_{n}^{s}\wedge q^{\frown}\dot{x}\in D_{s}\right) \right\}. \end{array} \end{align*} $$
By Lemma 64, we know that
![]() $L_{s}$
is
$L_{s}$
is
![]() $\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-open dense below
$\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-open dense below
![]() $p_{n}^{s}\upharpoonright \beta $
.
$p_{n}^{s}\upharpoonright \beta $
.
We now claim that if
![]() $s=\left \langle p_{0},\ldots ,p_{n}\right \rangle ,t=\left \langle q_{0},\ldots ,q_{n}\right \rangle \in T$
and
$s=\left \langle p_{0},\ldots ,p_{n}\right \rangle ,t=\left \langle q_{0},\ldots ,q_{n}\right \rangle \in T$
and
![]() $s\neq t,$
then
$s\neq t,$
then
![]() $s^{\prime }=\left \langle p_{0}\upharpoonright \beta ,\ldots ,p_{n}\upharpoonright \beta \right \rangle $
and
$s^{\prime }=\left \langle p_{0}\upharpoonright \beta ,\ldots ,p_{n}\upharpoonright \beta \right \rangle $
and
![]() $t^{\prime }=\left \langle q_{0}\upharpoonright \beta ,\ldots ,q_{n}\upharpoonright \beta \right \rangle $
are different. Let
$t^{\prime }=\left \langle q_{0}\upharpoonright \beta ,\ldots ,q_{n}\upharpoonright \beta \right \rangle $
are different. Let
![]() $m=\triangle \left ( s,t\right ) ,$
we know that
$m=\triangle \left ( s,t\right ) ,$
we know that
![]() $p_{m}\perp q_{m}$
and since
$p_{m}\perp q_{m}$
and since
![]() $\beta \notin F_{m+1},$
it follows that
$\beta \notin F_{m+1},$
it follows that
![]() $p_{m}\upharpoonright \beta \perp q_{m}\upharpoonright \beta $
(and in particular, they are different).
$p_{m}\upharpoonright \beta \perp q_{m}\upharpoonright \beta $
(and in particular, they are different).
By the remark above, for every
![]() $z=\left \langle p_{0}^{\prime },\ldots ,p_{n} ^{\prime }\right \rangle \in S,$
there is an unique
$z=\left \langle p_{0}^{\prime },\ldots ,p_{n} ^{\prime }\right \rangle \in S,$
there is an unique
![]() $s=\langle p_{0},\ldots ,p_{n}\rangle \in T$
such that
$s=\langle p_{0},\ldots ,p_{n}\rangle \in T$
such that
![]() $s^{\prime }=z.$
We also know that
$s^{\prime }=z.$
We also know that
![]() $L_{s}$
is
$L_{s}$
is
![]() $\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-open dense below
$\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-open dense below
![]() $p_{n}^{\prime }.$
By the inductive hypothesis, there is a fusion tree
$p_{n}^{\prime }.$
By the inductive hypothesis, there is a fusion tree
![]() $\widehat {T}$
such that the following holds:
$\widehat {T}$
such that the following holds:
-
1.
 $\widehat {T}$
is a
$\widehat {T}$
is a
 $\beta $
-finite fusion tree of height
$\beta $
-finite fusion tree of height
 $n+1.$
$n+1.$
-
2.
 $\widehat {T}$
is an end-extention of
$\widehat {T}$
is an end-extention of
 $S.$
$S.$
-
3. If
 $s\in T_{n},$
then
$s\in T_{n},$
then
 $suc_{\widehat {T}}\left ( s^{\prime }\right ) \subseteq L_{s}.$
$suc_{\widehat {T}}\left ( s^{\prime }\right ) \subseteq L_{s}.$
We now define the tree
![]() $\widetilde {T}$
as follows:
$\widetilde {T}$
as follows:
-
1.
 $\widetilde {T}$
is a tree of height
$\widetilde {T}$
is a tree of height
 $n+1.$
$n+1.$
-
2.
 $\widetilde {T}$
is an end-extention of
$\widetilde {T}$
is an end-extention of
 $T.$
$T.$
Let
 $s=\langle p_{0},\ldots ,p_{n}\rangle \in T$
.
$s=\langle p_{0},\ldots ,p_{n}\rangle \in T$
. -
3. We know that
 $d_{s^{\prime }}^{\widehat {T}}$
and
$d_{s^{\prime }}^{\widehat {T}}$
and
 $w_{s^{\prime } }^{\widehat {T}}$
are elements of
$w_{s^{\prime } }^{\widehat {T}}$
are elements of
 $L_{s}.$
This means that there are
$L_{s}.$
This means that there are
 $\dot {x}_{s}$
and
$\dot {x}_{s}$
and
 $\dot {y}_{s}$
such that
$\dot {y}_{s}$
such that
 $d_{s^{\prime }}^{\widehat {T}\frown } \dot {x}_{s}$
and
$d_{s^{\prime }}^{\widehat {T}\frown } \dot {x}_{s}$
and
 $w_{s^{\prime }}^{\widehat {T}\frown }\dot {y}_{s}$
are
$w_{s^{\prime }}^{\widehat {T}\frown }\dot {y}_{s}$
are
 $\leq _{F_{n},\eta _{n}}^{\ast }$
-extensions of
$\leq _{F_{n},\eta _{n}}^{\ast }$
-extensions of
 $p_{n}$
and are in
$p_{n}$
and are in
 $D_{s}.$
Define
$D_{s}.$
Define
 $d_{s}^{T}= d_{s^{\prime }}^{\widehat {T}\frown }\dot {x}_{s}$
and
$d_{s}^{T}= d_{s^{\prime }}^{\widehat {T}\frown }\dot {x}_{s}$
and
 $w_{s}^{T}=w_{s^{\prime }}^{\widehat {T}\frown }\dot {y}_{s}$
(in case that
$w_{s}^{T}=w_{s^{\prime }}^{\widehat {T}\frown }\dot {y}_{s}$
(in case that
 $F_{n}=F_{n+1}$
we have that
$F_{n}=F_{n+1}$
we have that
 $F_{n}^{\prime }=F_{n+1}^{\prime }.$
The definition of fusion tree demands that
$F_{n}^{\prime }=F_{n+1}^{\prime }.$
The definition of fusion tree demands that
 $d_{s^{\prime }}^{\widehat {T}}=w_{s^{\prime } }^{\widehat {T}}.$
We take
$d_{s^{\prime }}^{\widehat {T}}=w_{s^{\prime } }^{\widehat {T}}.$
We take
 $\dot {x}_{s}=\dot {y}_{s}$
so that we get
$\dot {x}_{s}=\dot {y}_{s}$
so that we get
 $d_{s} ^{T}=w_{s}^{T}$
).
$d_{s} ^{T}=w_{s}^{T}$
).
We need to prove that
![]() $\widetilde {T}$
is an
$\widetilde {T}$
is an
![]() $\alpha $
-finite fusion tree, but this is easy since
$\alpha $
-finite fusion tree, but this is easy since
![]() $\widehat {T}$
is a
$\widehat {T}$
is a
![]() $\beta $
-finite fusion tree and
$\beta $
-finite fusion tree and
![]() $\beta \notin F_{n+1}$
. This finishes the proof for this case.
$\beta \notin F_{n+1}$
. This finishes the proof for this case.
Case 67
![]() $\beta \in F_{n+1} \backslash F_{n}.$
$\beta \in F_{n+1} \backslash F_{n}.$
In this case, we have that
![]() $F_{n+1}^{\prime }=F_{n}$
and
$F_{n+1}^{\prime }=F_{n}$
and
![]() $F_{n}^{\prime }=F_{n}.$
$F_{n}^{\prime }=F_{n}.$
As in the previous case, for every
![]() $s=\left \langle p_{0}^{s},\ldots ,p_{n} ^{s}\right \rangle \in T,$
define
$s=\left \langle p_{0}^{s},\ldots ,p_{n} ^{s}\right \rangle \in T,$
define
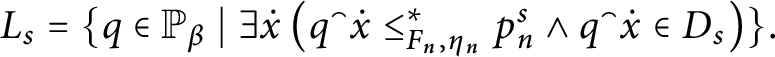 $L_{s}=\{q\in \mathbb {P}_{\beta }\mid \exists \dot {x}\left ( q^{\frown }\dot {x}\leq _{F_{n},\eta _{n}}^{\ast }p_{n} ^{s}\wedge q^{\frown }\dot {x}\in D_{s}\right ) \}.$
Again, by Lemma 64, we already know that this set is
$L_{s}=\{q\in \mathbb {P}_{\beta }\mid \exists \dot {x}\left ( q^{\frown }\dot {x}\leq _{F_{n},\eta _{n}}^{\ast }p_{n} ^{s}\wedge q^{\frown }\dot {x}\in D_{s}\right ) \}.$
Again, by Lemma 64, we already know that this set is
![]() $\left ( F_{n}^{\prime },\eta _{n}^{\prime }\right ) ^{\ast }$
-open dense below
$\left ( F_{n}^{\prime },\eta _{n}^{\prime }\right ) ^{\ast }$
-open dense below
![]() $p_{n}^{s} \upharpoonright \beta .$
Now, note that if
$p_{n}^{s} \upharpoonright \beta .$
Now, note that if
![]() $q\in L_{s}$
and
$q\in L_{s}$
and
![]() $\dot {x}$
is such that
$\dot {x}$
is such that
![]() $q^{\frown }\dot {x}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
$q^{\frown }\dot {x}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
![]() $q^{\frown }\dot {x}\in D_{s}$
, we can now take
$q^{\frown }\dot {x}\in D_{s}$
, we can now take
![]() $\dot {a}$
and
$\dot {a}$
and
![]() $\dot {b}$
be two
$\dot {b}$
be two
![]() $\mathbb {P}_{\beta }$
-names for conditions on
$\mathbb {P}_{\beta }$
-names for conditions on
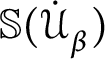 $\mathbb {S(\mathcal {\dot {U}} }_{\beta }\mathbb {)}$
such that q forces that they are incompatible extensions of
$\mathbb {S(\mathcal {\dot {U}} }_{\beta }\mathbb {)}$
such that q forces that they are incompatible extensions of
![]() $\dot {x}$
, yet
$\dot {x}$
, yet
![]() $E_{\dot {a}}$
and
$E_{\dot {a}}$
and
![]() $E_{\dot {b}}.$
$E_{\dot {b}}.$
In this way, if
![]() $q\in L_{s},$
we can find
$q\in L_{s},$
we can find
![]() $\dot {a}$
and
$\dot {a}$
and
![]() $\dot {b}$
with the following properties:
$\dot {b}$
with the following properties:
-
1.
 $q^{\frown }\dot {a}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
$q^{\frown }\dot {a}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
 $q^{\frown }\dot {b}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}.$
$q^{\frown }\dot {b}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}.$
-
2.
 $q^{\frown }\dot {a}, q^{\frown }\dot {b}\in D_{s}.$
$q^{\frown }\dot {a}, q^{\frown }\dot {b}\in D_{s}.$
-
3.
 $q\Vdash $
“
$q\Vdash $
“
 $\dot {a}\perp \dot {b}\wedge E_{\dot {a}} =E_{\dot {b}}$
.”
$\dot {a}\perp \dot {b}\wedge E_{\dot {a}} =E_{\dot {b}}$
.”
The second point follows because
![]() $D_{s}$
is
$D_{s}$
is
![]() $\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-open below
$\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-open below
![]() $p_{n}^{s}$
.
$p_{n}^{s}$
.
In the same way as in the previous case, we have that if
![]() $s=\langle p_{0}^{s},\ldots ,p_{n}^{s}\rangle , t=\langle p_{0}^{t} ,\ldots ,p_{n}^{t}\rangle \in T$
and
$s=\langle p_{0}^{s},\ldots ,p_{n}^{s}\rangle , t=\langle p_{0}^{t} ,\ldots ,p_{n}^{t}\rangle \in T$
and
![]() $s\neq t,$
then
$s\neq t,$
then
![]() $s^{\prime }\neq t^{\prime }$
. Once again, for every
$s^{\prime }\neq t^{\prime }$
. Once again, for every
![]() $z\in S_{n},$
there is a unique
$z\in S_{n},$
there is a unique
![]() $s\in T_{n}$
such that
$s\in T_{n}$
such that
![]() $s^{\prime }=z.$
We also know that
$s^{\prime }=z.$
We also know that
![]() $L_{s}$
is
$L_{s}$
is
![]() $\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-open dense below
$\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-open dense below
![]() $p_{n}^{s}\upharpoonright \beta .$
By the inductive hypothesis, there is a tree
$p_{n}^{s}\upharpoonright \beta .$
By the inductive hypothesis, there is a tree
![]() $\widehat {T}$
such that the following holds:
$\widehat {T}$
such that the following holds:
-
1.
 $\widehat {T}$
is a
$\widehat {T}$
is a
 $\beta $
-finite fusion tree of height
$\beta $
-finite fusion tree of height
 $n+1.$
$n+1.$
-
2.
 $\widehat {T}$
is an end-extention of
$\widehat {T}$
is an end-extention of
 $S.$
$S.$
-
3. If
 $s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle \in T_{n},$
then
$s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle \in T_{n},$
then
 $d_{s^{\prime }}^{\widehat {T}}=w_{s^{\prime }}^{\widehat {T}}$
and it belongs to
$d_{s^{\prime }}^{\widehat {T}}=w_{s^{\prime }}^{\widehat {T}}$
and it belongs to
 $L_{s}$
(recall that
$L_{s}$
(recall that
 $F_{n}^{\prime }=F_{n+1}^{\prime }=F_{n}$
holds in this case).
$F_{n}^{\prime }=F_{n+1}^{\prime }=F_{n}$
holds in this case).
Let
![]() $s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle \in T,$
we know that
$s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle \in T,$
we know that
![]() $s^{\prime }\in \widehat {T}$
and
$s^{\prime }\in \widehat {T}$
and
![]() $suc_{\widehat {T}}\left ( s^{\prime }\right ) $
has only one element. Since
$suc_{\widehat {T}}\left ( s^{\prime }\right ) $
has only one element. Since
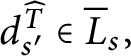 $d_{s^{\prime }}^{\widehat {T}}\in \overline {L}_{s},$
by the above remark, we know that there are
$d_{s^{\prime }}^{\widehat {T}}\in \overline {L}_{s},$
by the above remark, we know that there are
![]() $\dot {a}_{s}$
and
$\dot {a}_{s}$
and
![]() $\dot {b}_{s}$
such that the following holds:
$\dot {b}_{s}$
such that the following holds:
-
1.
 $d_{s^{\prime }}^{\widehat {T}}$
$d_{s^{\prime }}^{\widehat {T}}$
 ${}^{\frown }\dot {a}_{s}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
${}^{\frown }\dot {a}_{s}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
 $d_{s^{\prime }}^{\widehat {T}}$
$d_{s^{\prime }}^{\widehat {T}}$
 ${}^{\frown }\dot {b}_{s}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}.$
${}^{\frown }\dot {b}_{s}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}.$
-
2.
 $d_{s^{\prime }}^{\widehat {T}}$
$d_{s^{\prime }}^{\widehat {T}}$
 ${}^{\frown }\dot {a}_{s}, d_{s^{\prime } }^{\widehat {T}}$
${}^{\frown }\dot {a}_{s}, d_{s^{\prime } }^{\widehat {T}}$
 ${} ^{\frown }\dot {b}_{s}\in D_{s}.$
${} ^{\frown }\dot {b}_{s}\in D_{s}.$
-
3.
 $d_{s^{\prime }}^{\widehat {T}}\Vdash $
“
$d_{s^{\prime }}^{\widehat {T}}\Vdash $
“
 $\dot {a}_{s} \perp \dot {b}_{s}\wedge E_{\dot {a}_{s}}=E_{\dot {b}_{s}}$
.”
$\dot {a}_{s} \perp \dot {b}_{s}\wedge E_{\dot {a}_{s}}=E_{\dot {b}_{s}}$
.”
Recall that
![]() $S_{n}$
is an antichain (see Lemma 49). In this way, using Lemma 45, we can find two
$S_{n}$
is an antichain (see Lemma 49). In this way, using Lemma 45, we can find two
![]() $\mathbb {P}_{\beta } $
-names
$\mathbb {P}_{\beta } $
-names
![]() $\dot {e}_{n}^{T}$
and
$\dot {e}_{n}^{T}$
and
![]() $\dot {u}_{n}^{T}$
such that if
$\dot {u}_{n}^{T}$
such that if
![]() $s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle \in T,$
then
$s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle \in T,$
then
![]() $p_{n}^{s}\upharpoonright \beta \Vdash $
“
$p_{n}^{s}\upharpoonright \beta \Vdash $
“
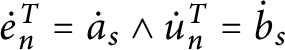 $\dot {e}_{n}^{T}=\dot {a}_{s}\wedge \dot {u}_{n} ^{T}=\dot {b}_{s}$
.” Define
$\dot {e}_{n}^{T}=\dot {a}_{s}\wedge \dot {u}_{n} ^{T}=\dot {b}_{s}$
.” Define
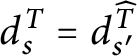 $d_{s}^{T}=d_{s^{\prime } }^{\widehat {T}}$
$d_{s}^{T}=d_{s^{\prime } }^{\widehat {T}}$
![]() ${}^{\frown }\dot {e}_{n}^{T}$
and
${}^{\frown }\dot {e}_{n}^{T}$
and
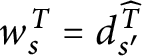 $w_{s}^{T}=d_{s^{\prime } }^{\widehat {T}}$
$w_{s}^{T}=d_{s^{\prime } }^{\widehat {T}}$
![]() ${}^{\frown }\dot {u}_{n}^{T}$
(which is the same as
${}^{\frown }\dot {u}_{n}^{T}$
(which is the same as
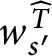 $w_{s^{\prime }}^{\widehat {T}}$
$w_{s^{\prime }}^{\widehat {T}}$
![]() ${}^{\frown }\dot {u}_{n}^{T}$
). Define the tree
${}^{\frown }\dot {u}_{n}^{T}$
). Define the tree
![]() $\widetilde {T}$
as follows:
$\widetilde {T}$
as follows:
-
1.
 $\widetilde {T}$
is a tree of height
$\widetilde {T}$
is a tree of height
 $n+1.$
$n+1.$
-
2.
 $\widetilde {T}$
is an end-extention of
$\widetilde {T}$
is an end-extention of
 $T.$
$T.$
-
3. If
 $s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T,$
then
$s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T,$
then
 $suc_{\widetilde {T}}( s) =\{d_{s}^{T},w_{s}^{T}\}.$
$suc_{\widetilde {T}}( s) =\{d_{s}^{T},w_{s}^{T}\}.$
It is easy to see that
![]() $\widetilde {T}$
has the desired properties. This finishes the proof for this case.
$\widetilde {T}$
has the desired properties. This finishes the proof for this case.
Case 68
![]() $\beta \in F_{n}.$
$\beta \in F_{n}.$
In this case, we have that
![]() $F_{n+1}^{\prime }=F_{n+1}\setminus \left \{ \beta \right \} $
and
$F_{n+1}^{\prime }=F_{n+1}\setminus \left \{ \beta \right \} $
and
![]() $F_{n}^{\prime }=F_{n}\setminus \left \{ \beta \right \} .$
$F_{n}^{\prime }=F_{n}\setminus \left \{ \beta \right \} .$
Let
![]() $s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle \in T$
and note that there is a unique
$s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle \in T$
and note that there is a unique
![]() $t=\left \langle p_{0}^{t},\ldots ,p_{n}^{t}\right \rangle \in T$
such that
$t=\left \langle p_{0}^{t},\ldots ,p_{n}^{t}\right \rangle \in T$
such that
![]() $s^{\prime }=t^{\prime }$
and
$s^{\prime }=t^{\prime }$
and
![]() $s\neq t$
(see Lemma 60). Let
$s\neq t$
(see Lemma 60). Let
![]() $z=s^{\prime }=t^{\prime }$
(which is a node in S). Define
$z=s^{\prime }=t^{\prime }$
(which is a node in S). Define
![]() $L_{z}$
as the set of all
$L_{z}$
as the set of all
![]() $q\in \mathbb {P}_{\beta }$
such that there are
$q\in \mathbb {P}_{\beta }$
such that there are
![]() $\dot {x},\dot {y}$
with the following properties:
$\dot {x},\dot {y}$
with the following properties:
-
1.
 $q\leq _{F_{n}^{\prime },\eta _{n}^{\prime }}^{\ast }p_{n}^{s}\upharpoonright \beta $
(recall that
$q\leq _{F_{n}^{\prime },\eta _{n}^{\prime }}^{\ast }p_{n}^{s}\upharpoonright \beta $
(recall that
 $p_{n}^{s}\upharpoonright \beta =p_{n}^{t}\upharpoonright \beta $
).
$p_{n}^{s}\upharpoonright \beta =p_{n}^{t}\upharpoonright \beta $
). -
2.
 $q^{\frown }\dot {x}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
$q^{\frown }\dot {x}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
 $q^{\frown }\dot {y}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{t}.$
$q^{\frown }\dot {y}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{t}.$
-
3.
 $q^{\frown }\dot {x}\in D_{s}$
and
$q^{\frown }\dot {x}\in D_{s}$
and
 $q^{\frown }\dot {y}\in D_{t}.$
$q^{\frown }\dot {y}\in D_{t}.$
-
4.
 $q\Vdash \text{``}\langle p_{n}^{s}( \beta ) ,p_{n}^{t}( \beta ) ,\dot {x},\dot {y}\rangle $
is an
$q\Vdash \text{``}\langle p_{n}^{s}( \beta ) ,p_{n}^{t}( \beta ) ,\dot {x},\dot {y}\rangle $
is an
 $\eta _{n}( \beta ) $
-nice sequence
$\eta _{n}( \beta ) $
-nice sequence
 $''.$
$''.$
We claim that
![]() $L_{z}$
is
$L_{z}$
is
![]() $\left ( F_{n}^{\prime },\eta _{n}^{\prime }\right ) ^{\ast }$
-open dense below
$\left ( F_{n}^{\prime },\eta _{n}^{\prime }\right ) ^{\ast }$
-open dense below
![]() $p_{n}^{s}\upharpoonright \beta .$
It is easy to see that
$p_{n}^{s}\upharpoonright \beta .$
It is easy to see that
![]() $L_{z}$
is
$L_{z}$
is
![]() $\left ( F_{n}^{\prime },\eta _{n}^{\prime }\right ) ^{\ast } $
-open below
$\left ( F_{n}^{\prime },\eta _{n}^{\prime }\right ) ^{\ast } $
-open below
![]() $p_{n}^{s}\upharpoonright \beta .$
The proof that it is also dense is more elaborate, we basically follow the argument of Lemma 17. It will be convenient for the reader to review the proof of this lemma before continuing.
$p_{n}^{s}\upharpoonright \beta .$
The proof that it is also dense is more elaborate, we basically follow the argument of Lemma 17. It will be convenient for the reader to review the proof of this lemma before continuing.
Let
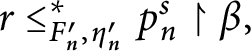 $r\leq _{F_{n}^{\prime },\eta _{n}^{\prime }}^{\ast }p_{n}^{s}\upharpoonright \beta ,$
we need to find an
$r\leq _{F_{n}^{\prime },\eta _{n}^{\prime }}^{\ast }p_{n}^{s}\upharpoonright \beta ,$
we need to find an
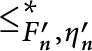 $\leq _{F_{n}^{\prime },\eta _{n}^{\prime }}^{\ast } $
-extension that is in
$\leq _{F_{n}^{\prime },\eta _{n}^{\prime }}^{\ast } $
-extension that is in
![]() $L_{z}.$
Since
$L_{z}.$
Since
![]() $r^{\frown }p_{n}^{s}( \beta ) $
is an
$r^{\frown }p_{n}^{s}( \beta ) $
is an
![]() $\leq _{F_{n},\eta _{n}}^{\ast }$
-extension of
$\leq _{F_{n},\eta _{n}}^{\ast }$
-extension of
![]() $p_{n}^{s}$
and
$p_{n}^{s}$
and
![]() $D_{s}$
is
$D_{s}$
is
![]() $\leq _{F_{n},\eta _{n}}^{\ast }$
-dense below it, we can find
$\leq _{F_{n},\eta _{n}}^{\ast }$
-dense below it, we can find
![]() $r_{1}\in \mathbb {P}_{\beta }$
and
$r_{1}\in \mathbb {P}_{\beta }$
and
![]() $\dot {x}$
a
$\dot {x}$
a
![]() $\mathbb {P}_{\beta }\,$
-name for an element of
$\mathbb {P}_{\beta }\,$
-name for an element of
 $\mathbb {S(\mathcal {\dot {U}}}_{\alpha }\mathbb {)}$
such that
$\mathbb {S(\mathcal {\dot {U}}}_{\alpha }\mathbb {)}$
such that
![]() $r_{1} ^{\frown }\dot {x}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
$r_{1} ^{\frown }\dot {x}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
![]() $r_{1} ^{\frown }\dot {x}\in D_{s}.$
Let
$r_{1} ^{\frown }\dot {x}\in D_{s}.$
Let
![]() $\dot {U}$
be the name for the following set:
$\dot {U}$
be the name for the following set:
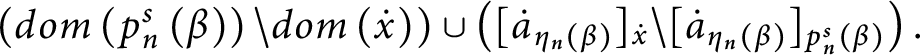 $$ \begin{align*} \begin{array}{l} \left( dom\left( p_{n}^{s}\left( \beta\right) \right) \setminus dom\left( \dot{x}\right) \right) \cup\left( \lbrack\dot{a}_{\eta _{n}\left( \beta\right) }]_{\dot{x}}\setminus\lbrack\dot{a}_{\eta_{n}\left( \beta\right) }]_{p_{n}^{s}\left( \beta\right) }\right). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} \left( dom\left( p_{n}^{s}\left( \beta\right) \right) \setminus dom\left( \dot{x}\right) \right) \cup\left( \lbrack\dot{a}_{\eta _{n}\left( \beta\right) }]_{\dot{x}}\setminus\lbrack\dot{a}_{\eta_{n}\left( \beta\right) }]_{p_{n}^{s}\left( \beta\right) }\right). \end{array} \end{align*} $$
Now, let
![]() $\dot {y}$
be the
$\dot {y}$
be the
![]() $\mathbb {P}_{\beta }$
-name for the extension of
$\mathbb {P}_{\beta }$
-name for the extension of
![]() $p_{n}^{t}( \beta ) $
obtained by adding
$p_{n}^{t}( \beta ) $
obtained by adding
![]() $\dot {U}$
to the
$\dot {U}$
to the
![]() $\eta _{n}( \beta ) $
-class of the partition of
$\eta _{n}( \beta ) $
-class of the partition of
![]() $p_{n}^{t}( \beta ) .$
Note that
$p_{n}^{t}( \beta ) .$
Note that
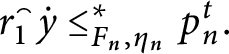 $r_{1} ^{\frown }\dot {y}\leq _{F_{n},\eta _{n} }^{\ast }p_{n}^{t}.$
Using the density of
$r_{1} ^{\frown }\dot {y}\leq _{F_{n},\eta _{n} }^{\ast }p_{n}^{t}.$
Using the density of
![]() $D_{t},$
we can now find
$D_{t},$
we can now find
![]() $\dot {y} _{1}$
and q such that
$\dot {y} _{1}$
and q such that
![]() $q ^{\frown }\dot {y}_{1}\leq _{F_{n},\eta _{n}}^{\ast }r_{1} ^{\frown }\dot {y}$
and
$q ^{\frown }\dot {y}_{1}\leq _{F_{n},\eta _{n}}^{\ast }r_{1} ^{\frown }\dot {y}$
and
![]() $q ^{\frown }\dot {y}_{1}\in D_{t}.$
Let
$q ^{\frown }\dot {y}_{1}\in D_{t}.$
Let
![]() $\dot {U}_{1}$
be the name for the following set:
$\dot {U}_{1}$
be the name for the following set:
 $$ \begin{align*} \begin{array}{l} \left( dom(\dot{y})\setminus dom\left( \dot{y}_{1}\right) \right) \cup\left( \lbrack\dot{a}_{\eta_{n}\left( \beta\right) }]_{\dot{y}_{1} }\setminus\lbrack\dot{a}_{\eta_{n}\left( \beta\right) }]_{\dot{y}}\right). \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} \left( dom(\dot{y})\setminus dom\left( \dot{y}_{1}\right) \right) \cup\left( \lbrack\dot{a}_{\eta_{n}\left( \beta\right) }]_{\dot{y}_{1} }\setminus\lbrack\dot{a}_{\eta_{n}\left( \beta\right) }]_{\dot{y}}\right). \end{array} \end{align*} $$
Now, let
![]() $\dot {x}_{1}$
be the
$\dot {x}_{1}$
be the
![]() $\mathbb {P}_{\beta }$
-name for the extension of
$\mathbb {P}_{\beta }$
-name for the extension of
![]() $\dot {x}$
obtained by adding
$\dot {x}$
obtained by adding
![]() $\dot {U}_{1}$
to the
$\dot {U}_{1}$
to the
![]() $\eta _{n}( \beta ) $
-class of the partition of
$\eta _{n}( \beta ) $
-class of the partition of
![]() $\dot {x}.$
It follows that q has the desired properties (note that
$\dot {x}.$
It follows that q has the desired properties (note that
![]() $q^{\frown }\dot {x}_{2}\in D_{s}$
since
$q^{\frown }\dot {x}_{2}\in D_{s}$
since
![]() $q^{\frown }\dot {x}_{2}\leq _{F_{n},\eta _{n}}^{\ast }r_{1} ^{\frown }\dot {x}$
).
$q^{\frown }\dot {x}_{2}\leq _{F_{n},\eta _{n}}^{\ast }r_{1} ^{\frown }\dot {x}$
).
For every
![]() $z\in S_{n}$
we have the set
$z\in S_{n}$
we have the set
![]() $L_{z}.$
By the inductive hypothesis, there is a tree
$L_{z}.$
By the inductive hypothesis, there is a tree
![]() $\widehat {T}$
such that the following holds:
$\widehat {T}$
such that the following holds:
-
1.
 $\widehat {T}$
is a
$\widehat {T}$
is a
 $\beta $
-finite fusion tree of height
$\beta $
-finite fusion tree of height
 $n+1.$
$n+1.$
-
2.
 $\widehat {T}$
is an end-extention of
$\widehat {T}$
is an end-extention of
 $T^{\prime }.$
$T^{\prime }.$
-
3. If
 $z\in \widehat {T}_{n},$
then
$z\in \widehat {T}_{n},$
then
 $suc_{\widehat {T}}\left ( z\right ) \subseteq L_{z}.$
$suc_{\widehat {T}}\left ( z\right ) \subseteq L_{z}.$
We now define the tree
![]() $\widetilde {T}$
as follows:
$\widetilde {T}$
as follows:
-
1.
 $\widetilde {T}$
is a tree of height
$\widetilde {T}$
is a tree of height
 $n+1.$
$n+1.$
-
2.
 $\widetilde {T}$
is an end-extention of
$\widetilde {T}$
is an end-extention of
 $T.$
$T.$
Let
 $s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle , t=\left \langle p_{0}^{t},\ldots ,p_{n}^{t}\right \rangle \in T$
with
$s=\left \langle p_{0}^{s},\ldots ,p_{n}^{s}\right \rangle , t=\left \langle p_{0}^{t},\ldots ,p_{n}^{t}\right \rangle \in T$
with
 $z=s^{\prime }=t^{\prime }.$
$z=s^{\prime }=t^{\prime }.$
-
3. In case
 $F_{n}=F_{n+1}$
, we have that
$F_{n}=F_{n+1}$
, we have that
 $F_{n}^{\prime }=F_{n+1.}^{\prime }$
Since
$F_{n}^{\prime }=F_{n+1.}^{\prime }$
Since
 $d_{z}^{\widehat {T}}\in suc_{\widehat {T}}\left ( z\right ) \subseteq L_{z},$
we know that there are
$d_{z}^{\widehat {T}}\in suc_{\widehat {T}}\left ( z\right ) \subseteq L_{z},$
we know that there are
 $\dot {x}$
and
$\dot {x}$
and
 $\dot {y}$
with the following properties:
$\dot {y}$
with the following properties:-
(a)
 $d_{z}^{\widehat {T}}\leq _{F_{n}^{\prime },\eta _{n}^{\prime }}^{\ast } p_{n}^{s}\upharpoonright \beta $
.
$d_{z}^{\widehat {T}}\leq _{F_{n}^{\prime },\eta _{n}^{\prime }}^{\ast } p_{n}^{s}\upharpoonright \beta $
. -
(b)
 $d_{z}^{\widehat {T}\frown }\dot {x}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
$d_{z}^{\widehat {T}\frown }\dot {x}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
 $d_{z}^{\widehat {T}\frown }\dot {y}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{t}.$
$d_{z}^{\widehat {T}\frown }\dot {y}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{t}.$
-
(c)
 $d_{z}^{\widehat {T}\frown }\dot {x}\in D_{s}$
and
$d_{z}^{\widehat {T}\frown }\dot {x}\in D_{s}$
and
 $d_{z}^{\widehat {T}\frown }\dot {y}\in D_{t}.$
$d_{z}^{\widehat {T}\frown }\dot {y}\in D_{t}.$
-
(d)
 $d_{z}^{\widehat {T}}\Vdash \text{``}\langle p_{n}^{s}( \beta ) ,p_{n}^{t}( \beta ) ,\dot {x},\dot {y}\rangle $
is an
$d_{z}^{\widehat {T}}\Vdash \text{``}\langle p_{n}^{s}( \beta ) ,p_{n}^{t}( \beta ) ,\dot {x},\dot {y}\rangle $
is an
 $\eta _{n}( \beta ) $
-nice sequence.
$\eta _{n}( \beta ) $
-nice sequence.
 $\text{''}$
$\text{''}$
Define
 $d_{s}^{T}=w_{s}^{T}=d_{z}^{\widehat {T}}$
$d_{s}^{T}=w_{s}^{T}=d_{z}^{\widehat {T}}$
 ${}^{\frown }\dot {x}$
and
${}^{\frown }\dot {x}$
and
 $d_{t}^{T}=w_{t}^{T}=d_{z}^{\widehat {T}}$
$d_{t}^{T}=w_{t}^{T}=d_{z}^{\widehat {T}}$
 ${}^{\frown }\dot {y}.$
${}^{\frown }\dot {y}.$
-
-
4. In case
 $F_{n}\neq F_{n+1},$
first note that
$F_{n}\neq F_{n+1},$
first note that
 $F_{n}^{\prime }\neq F_{n+1}^{\prime }$
as well (if
$F_{n}^{\prime }\neq F_{n+1}^{\prime }$
as well (if
 $\gamma \in F_{n+1}\setminus F_{n},$
then
$\gamma \in F_{n+1}\setminus F_{n},$
then
 $\gamma \neq \beta $
so
$\gamma \neq \beta $
so
 $\gamma \in F_{n+1}^{\prime }\setminus F_{n}^{\prime }$
). Since
$\gamma \in F_{n+1}^{\prime }\setminus F_{n}^{\prime }$
). Since
 $suc_{\widehat {T}}\left ( z\right ) \subseteq L_{z},$
we know there are
$suc_{\widehat {T}}\left ( z\right ) \subseteq L_{z},$
we know there are
 $\dot {x}_{0},\dot {y}_{0},\dot {x}_{1}$
, and
$\dot {x}_{0},\dot {y}_{0},\dot {x}_{1}$
, and
 $\dot {y}_{1}$
such that the following holds:
$\dot {y}_{1}$
such that the following holds:-
(a)
 $d_{z}^{\widehat {T}},w_{z}^{\widehat {T}}\leq _{F_{n}^{\prime },\eta _{n}^{\prime }}^{\ast }p_{n}^{s}\upharpoonright \beta .$
$d_{z}^{\widehat {T}},w_{z}^{\widehat {T}}\leq _{F_{n}^{\prime },\eta _{n}^{\prime }}^{\ast }p_{n}^{s}\upharpoonright \beta .$
-
(b)
 $d_{z}^{\widehat {T}}$
$d_{z}^{\widehat {T}}$
 ${}^{\frown }\dot {x}_{0}, w_{z}^{\widehat {T}}$
${}^{\frown }\dot {x}_{0}, w_{z}^{\widehat {T}}$
 ${}^{\frown }\dot {x}_{1}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
${}^{\frown }\dot {x}_{1}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{s}$
and
 $d_{z} ^{\widehat {T}}$
$d_{z} ^{\widehat {T}}$
 ${}^{\frown }\dot {y}_{0}, w_{z}^{\widehat {T}}$
${}^{\frown }\dot {y}_{0}, w_{z}^{\widehat {T}}$
 ${}^{\frown } \dot {y}_{1}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{t}.$
${}^{\frown } \dot {y}_{1}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}^{t}.$
-
(c)
 $d_{z}^{\widehat {T}}$
$d_{z}^{\widehat {T}}$
 ${}^{\frown }\dot {x}_{0}\in D_{s}, d_{z} ^{\widehat {T}}$
${}^{\frown }\dot {x}_{0}\in D_{s}, d_{z} ^{\widehat {T}}$
 ${}^{\frown }\dot {y}_{0}\in D_{t}$
and
${}^{\frown }\dot {y}_{0}\in D_{t}$
and
 $w_{z}^{\widehat {T}}$
$w_{z}^{\widehat {T}}$
 ${}^{\frown }\dot {x}_{1}\in D_{s}, w_{z}^{\widehat {T}}$
${}^{\frown }\dot {x}_{1}\in D_{s}, w_{z}^{\widehat {T}}$
 ${}^{\frown }\dot {y} _{1}\in D_{t}.$
${}^{\frown }\dot {y} _{1}\in D_{t}.$
-
(d)
 $d_{z}^{\widehat {T}}\Vdash \text{``}\langle p_{n}^{s}( \beta ) ,p_{n}^{t}( \beta ) ,\dot {x}_{0},\dot {y}_{0}\rangle $
is an
$d_{z}^{\widehat {T}}\Vdash \text{``}\langle p_{n}^{s}( \beta ) ,p_{n}^{t}( \beta ) ,\dot {x}_{0},\dot {y}_{0}\rangle $
is an
 $\eta _{n}( \beta ) $
-nice sequence
$\eta _{n}( \beta ) $
-nice sequence
 $\text{''}$
and
$\text{''}$
and
 $w_{z}^{\widehat {T}}\Vdash \text{``}\langle p_{n}^{s}( \beta ) ,p_{n} ^{t}( \beta ) ,\dot {x}_{1},\dot {y}_{1}\rangle $
is an
$w_{z}^{\widehat {T}}\Vdash \text{``}\langle p_{n}^{s}( \beta ) ,p_{n} ^{t}( \beta ) ,\dot {x}_{1},\dot {y}_{1}\rangle $
is an
 $\eta _{n}( \beta ) $
-nice sequence.
$\eta _{n}( \beta ) $
-nice sequence.
 $\text{''}$
$\text{''}$
We now define
 $d_{s}^{T}=d_{z}^{\widehat {T}\frown }\dot {x}_{0}, w_{s}^{T} =w_{z}^{\widehat {T}}$
$d_{s}^{T}=d_{z}^{\widehat {T}\frown }\dot {x}_{0}, w_{s}^{T} =w_{z}^{\widehat {T}}$
 ${}^{\frown }\dot {x}_{1}$
and
${}^{\frown }\dot {x}_{1}$
and
 $d_{t}^{T}=d_{z} ^{\widehat {T}\frown }\dot {y}_{0}, w_{t}^{T} =w_{z}^{\widehat {T}}$
$d_{t}^{T}=d_{z} ^{\widehat {T}\frown }\dot {y}_{0}, w_{t}^{T} =w_{z}^{\widehat {T}}$
 ${}^{\frown }\dot {y}_{1}.$
${}^{\frown }\dot {y}_{1}.$
-
We need to prove that
![]() $\widetilde {T}$
is an
$\widetilde {T}$
is an
![]() $\alpha $
-finite fusion tree. Points 1–3 of Definition 48 hold by construction, while point 4 holds since
$\alpha $
-finite fusion tree. Points 1–3 of Definition 48 hold by construction, while point 4 holds since
![]() $\widehat {T}$
is a
$\widehat {T}$
is a
![]() $\beta $
-fusion tree. We now prove that point 5 also holds. Let
$\beta $
-fusion tree. We now prove that point 5 also holds. Let
![]() $s=\left \langle p_{0}^{s},\ldots ,p_{n} ^{s}\right \rangle , t=\left \langle p_{0}^{t},\ldots ,p_{n}^{t}\right \rangle \in T, m=\triangle \left ( s,t\right ) , \gamma \in F_{m+1}\setminus F_{m}$
and assume that
$s=\left \langle p_{0}^{s},\ldots ,p_{n} ^{s}\right \rangle , t=\left \langle p_{0}^{t},\ldots ,p_{n}^{t}\right \rangle \in T, m=\triangle \left ( s,t\right ) , \gamma \in F_{m+1}\setminus F_{m}$
and assume that
![]() $p_{n}^{s}\upharpoonright \gamma =p_{n}^{t}\upharpoonright \gamma $
holds. In case
$p_{n}^{s}\upharpoonright \gamma =p_{n}^{t}\upharpoonright \gamma $
holds. In case
![]() $\gamma =\beta $
(so
$\gamma =\beta $
(so
![]() $m=n$
), we get the desired conclusion by construction, if
$m=n$
), we get the desired conclusion by construction, if
![]() $\gamma <\beta $
, we get the conclusion because
$\gamma <\beta $
, we get the conclusion because
![]() $\widehat {T}$
is a
$\widehat {T}$
is a
![]() $\beta $
-fusion tree. This finishes the proof for this case.
$\beta $
-fusion tree. This finishes the proof for this case.
We conclude that the result is true for successor ordinals.
Finally, assume
![]() $\alpha $
is a limit ordinal and the conclusion holds for every ordinal less than
$\alpha $
is a limit ordinal and the conclusion holds for every ordinal less than
![]() $\alpha .$
Choose
$\alpha .$
Choose
![]() $\beta \in M\cap \alpha $
such that
$\beta \in M\cap \alpha $
such that
![]() $F_{n+1}\subseteq \beta .$
For the rest of the proof, if
$F_{n+1}\subseteq \beta .$
For the rest of the proof, if
![]() $t=\left \langle q_{0},\ldots ,q_{n}\right \rangle \in T$
, we will denote
$t=\left \langle q_{0},\ldots ,q_{n}\right \rangle \in T$
, we will denote
![]() $t^{\prime }=\left \langle q_{0}\upharpoonright \beta ,\ldots ,q_{n}\upharpoonright \beta \right \rangle .$
By the same arguments as before, it is easy to prove that if
$t^{\prime }=\left \langle q_{0}\upharpoonright \beta ,\ldots ,q_{n}\upharpoonright \beta \right \rangle .$
By the same arguments as before, it is easy to prove that if
![]() $s=\left \langle p_{0},\ldots ,p_{n}\right \rangle , t=\left \langle q_{0},\ldots ,q_{n}\right \rangle \in T$
and
$s=\left \langle p_{0},\ldots ,p_{n}\right \rangle , t=\left \langle q_{0},\ldots ,q_{n}\right \rangle \in T$
and
![]() $s\neq t,$
then
$s\neq t,$
then
![]() $s^{\prime }\neq t^{\prime }.$
$s^{\prime }\neq t^{\prime }.$
For every
![]() $s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T,$
define the set
$s=\left \langle p_{0},\ldots ,p_{n}\right \rangle \in T,$
define the set
 $$ \begin{align*} \begin{array}{l} L_{s}=\left\{ q\in\mathbb{P}_{\beta}\mid\exists\dot{x}\left( q^{\frown} \dot{x}\leq_{F_{n},\eta_{n}}^{\ast}p_{n}\wedge q^{\frown}\dot{x}\in D_{s}\right) \right\}. \end{array} \end{align*} $$
$$ \begin{align*} \begin{array}{l} L_{s}=\left\{ q\in\mathbb{P}_{\beta}\mid\exists\dot{x}\left( q^{\frown} \dot{x}\leq_{F_{n},\eta_{n}}^{\ast}p_{n}\wedge q^{\frown}\dot{x}\in D_{s}\right) \right\}. \end{array} \end{align*} $$
With the same argument as Lemma 64, we can prove that
![]() $L_{s}$
is
$L_{s}$
is
![]() $\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-open and
$\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-open and
![]() $\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-dense below
$\left ( F_{n},\eta _{n}\right ) ^{\ast }$
-dense below
![]() $p_{n}\upharpoonright \beta .$
Let
$p_{n}\upharpoonright \beta .$
Let
![]() $S=T\upharpoonright \beta .$
$S=T\upharpoonright \beta .$
For every
![]() $s^{\prime }\in S_{n},$
we have
$s^{\prime }\in S_{n},$
we have
![]() $L_{s}.$
By the inductive hypothesis, there is a tree
$L_{s}.$
By the inductive hypothesis, there is a tree
![]() $\widehat {T}$
such that the following holds:
$\widehat {T}$
such that the following holds:
-
1.
 $\widehat {T}$
is a
$\widehat {T}$
is a
 $\beta $
-finite fusion tree of height
$\beta $
-finite fusion tree of height
 $n+1.$
$n+1.$
-
2.
 $\widehat {T}$
is an end-extention of
$\widehat {T}$
is an end-extention of
 $S.$
$S.$
-
3. If
 $s^{\prime }\in \widehat {T}_{n},$
then
$s^{\prime }\in \widehat {T}_{n},$
then
 $suc_{\widehat {T}}\left ( s^{\prime }\right ) \subseteq L_{s}.$
$suc_{\widehat {T}}\left ( s^{\prime }\right ) \subseteq L_{s}.$
We now define the tree
![]() $\widetilde {T}$
as follows:
$\widetilde {T}$
as follows:
-
1.
 $\widetilde {T}$
is a tree of height
$\widetilde {T}$
is a tree of height
 $n+1.$
$n+1.$
-
2.
 $\widetilde {T}$
is an end-extention of
$\widetilde {T}$
is an end-extention of
 $T.$
$T.$
Let
 $s=\langle p_{0},\ldots ,p_{n}\rangle \in T$
.
$s=\langle p_{0},\ldots ,p_{n}\rangle \in T$
. -
3. Case
 $F_{n}=F_{n+1}.$
Since
$F_{n}=F_{n+1}.$
Since
 $d_{s}^{\widehat {T}}\in L_{s},$
there is
$d_{s}^{\widehat {T}}\in L_{s},$
there is
 $\dot {x}$
such that
$\dot {x}$
such that
 $d_{s}^{\widehat {T}}$
$d_{s}^{\widehat {T}}$
 ${}^{\frown }\dot {x}\leq _{F_{n} ,\eta _{n}}^{\ast }p_{n}$
and
${}^{\frown }\dot {x}\leq _{F_{n} ,\eta _{n}}^{\ast }p_{n}$
and
 $d_{s}^{\widehat {T}}$
$d_{s}^{\widehat {T}}$
 ${}^{\frown }\dot {x}\in D_{s}.$
Define
${}^{\frown }\dot {x}\in D_{s}.$
Define
 $d_{s}^{T}=d_{s}^{\widehat {T}}$
$d_{s}^{T}=d_{s}^{\widehat {T}}$
 ${}^{\frown }\dot {x}.$
${}^{\frown }\dot {x}.$
-
4. Case
 $F_{n}\neq F_{n+1}.$
We know there are
$F_{n}\neq F_{n+1}.$
We know there are
 $\dot {x}$
and
$\dot {x}$
and
 $\dot {y}$
such that
$\dot {y}$
such that
 $d_{s}^{\widehat {T}}$
$d_{s}^{\widehat {T}}$
 ${}^{\frown }\dot {x}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}$
with
${}^{\frown }\dot {x}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}$
with
 $d_{s}^{\widehat {T}}$
$d_{s}^{\widehat {T}}$
 ${}^{\frown }\dot {x}\in D_{s}$
and also
${}^{\frown }\dot {x}\in D_{s}$
and also
 $w_{s} ^{\widehat {T}}$
$w_{s} ^{\widehat {T}}$
 ${}^{\frown }\dot {y}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}$
with
${}^{\frown }\dot {y}\leq _{F_{n},\eta _{n}}^{\ast }p_{n}$
with
 $w_{s}^{\widehat {T}}$
$w_{s}^{\widehat {T}}$
 ${}^{\frown }\dot {y}\in D_{s}.$
Define
${}^{\frown }\dot {y}\in D_{s}.$
Define
 $d_{s}^{T}= d_{s}^{\widehat {T}}$
$d_{s}^{T}= d_{s}^{\widehat {T}}$
 ${}^{\frown }\dot {x}$
and
${}^{\frown }\dot {x}$
and
 $w_{s}^{T}= w_{s}^{\widehat {T}}$
$w_{s}^{T}= w_{s}^{\widehat {T}}$
 ${}^{\frown }\dot {y}.$
${}^{\frown }\dot {y}.$
We need to prove that
![]() $\widetilde {T}$
is a
$\widetilde {T}$
is a
![]() $\alpha $
-finite fusion tree, but this is easy since
$\alpha $
-finite fusion tree, but this is easy since
![]() $\widehat {T}$
is a
$\widehat {T}$
is a
![]() $\beta $
-finite fusion tree and
$\beta $
-finite fusion tree and
![]() $F_{n+1}\subseteq \beta $
(so everything interesting happens before
$F_{n+1}\subseteq \beta $
(so everything interesting happens before
![]() $\beta $
). This finishes the proof for this case and the proof overall.▪
$\beta $
). This finishes the proof for this case and the proof overall.▪
5 Preserving
 $\mathsf {c}_{\mathsf {min}}$
-covering at successor steps
$\mathsf {c}_{\mathsf {min}}$
-covering at successor steps
With the tools developed in the last section, we can finally start the proof that the iteration of the Shelah’s forcing preserves
![]() $\mathsf {c} _{\mathsf {min}}$
-covering. The proof will be by induction. The base case has already been done, we will do the successor step in this section and the limit step in the next one. This proof takes inspiration in the result by Geschke that the iteration of the Miller lite forcing preserves
$\mathsf {c} _{\mathsf {min}}$
-covering. The proof will be by induction. The base case has already been done, we will do the successor step in this section and the limit step in the next one. This proof takes inspiration in the result by Geschke that the iteration of the Miller lite forcing preserves
![]() $\mathsf {c} _{\mathsf {min}}$
-covering (see [Reference Jorge, Fischer, Guzmán and Jaroslav7]). For this section, assume
$\mathsf {c} _{\mathsf {min}}$
-covering (see [Reference Jorge, Fischer, Guzmán and Jaroslav7]). For this section, assume
![]() $\alpha =\beta +1$
and
$\alpha =\beta +1$
and
![]() $\dot {x}$
is the name of a real that was not added at the
$\dot {x}$
is the name of a real that was not added at the
![]() $\beta $
-step.
$\beta $
-step.
Definition 69 Let T and S be two finite subtrees of
![]() $2^{<\omega }$
and
$2^{<\omega }$
and
![]() $i<2.$
We say that
$i<2.$
We say that
![]() $\mathsf {c}_{\mathsf {min}}\left ( T,S\right ) =i$
if for every maximal node t of T and every maximal node s of S the following holds:
$\mathsf {c}_{\mathsf {min}}\left ( T,S\right ) =i$
if for every maximal node t of T and every maximal node s of S the following holds:
-
1. t and s are incompatible.
-
2.
 $\mathsf {c}_{\mathsf {min}}\left ( t,s\right ) =i.$
$\mathsf {c}_{\mathsf {min}}\left ( t,s\right ) =i.$
Note that if
![]() $\mathsf {c}_{\mathsf {min}}\left ( T,S\right ) =i$
and
$\mathsf {c}_{\mathsf {min}}\left ( T,S\right ) =i$
and
![]() $\overline {T}$
and
$\overline {T}$
and
![]() $\overline {S}$
are end-extentions of T and S respectively, then
$\overline {S}$
are end-extentions of T and S respectively, then
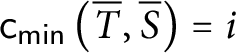 $\mathsf {c}_{\mathsf {min}}\left ( \overline {T},\overline {S}\right ) =i$
holds as well. Recall that
$\mathsf {c}_{\mathsf {min}}\left ( \overline {T},\overline {S}\right ) =i$
holds as well. Recall that
![]() $\mathbb {P}$
is a partial order,
$\mathbb {P}$
is a partial order,
![]() $\dot {y}$
is a
$\dot {y}$
is a
![]() $\mathbb {P}$
-name for an element in
$\mathbb {P}$
-name for an element in
![]() $2^{\omega }$
and
$2^{\omega }$
and
![]() $p\in \mathbb {P},$
we defined
$p\in \mathbb {P},$
we defined
![]() $\dot {y}\left [ p\right ] = {\textstyle \bigcup } \left \{ t\mid p\Vdash \text{``}t\subseteq \dot {y}''\right \} .$
Also remember that if
$\dot {y}\left [ p\right ] = {\textstyle \bigcup } \left \{ t\mid p\Vdash \text{``}t\subseteq \dot {y}''\right \} .$
Also remember that if
![]() $p\in \mathbb {S}( \mathcal {U}) ,$
we defined
$p\in \mathbb {S}( \mathcal {U}) ,$
we defined
![]() $S_{p}\left ( \dot {y}\right ) =\bigcup \left \{ \dot {y}\left [ p[ h] \right ] \mid h\in 2^{<\omega }\right \} .$
$S_{p}\left ( \dot {y}\right ) =\bigcup \left \{ \dot {y}\left [ p[ h] \right ] \mid h\in 2^{<\omega }\right \} .$
Definition 70 Let
![]() $q\in \mathbb {P}_{\beta }$
and
$q\in \mathbb {P}_{\beta }$
and
![]() $\dot {p}$
a
$\dot {p}$
a
![]() $\mathbb {P}_{\beta }$
-name for a condition of
$\mathbb {P}_{\beta }$
-name for a condition of
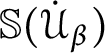 $\mathbb {S}(\mathcal {\dot {U}}_{\beta })$
and
$\mathbb {S}(\mathcal {\dot {U}}_{\beta })$
and
![]() $n\in \omega .$
We say that q determines
$n\in \omega .$
We say that q determines
![]() $\dot {p}$
to the n-level if there is a tree
$\dot {p}$
to the n-level if there is a tree
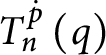 $T_{n}^{\dot {p}}\left ( q\right ) $
such that
$T_{n}^{\dot {p}}\left ( q\right ) $
such that
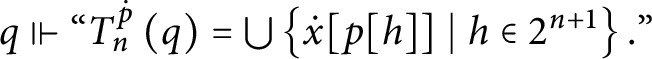 $q\Vdash \text{``}T_{n} ^{\dot {p}}\left ( q\right ) =\bigcup \left \{ \dot {x}[p[ h] ]\mid h\in 2^{n+1}\right \} .\text{''}$
$q\Vdash \text{``}T_{n} ^{\dot {p}}\left ( q\right ) =\bigcup \left \{ \dot {x}[p[ h] ]\mid h\in 2^{n+1}\right \} .\text{''}$
The name above may be a little misleading, since q is not really determining
![]() $p,$
but the tree of possibilities of
$p,$
but the tree of possibilities of
![]() $\dot {x}$
to the n-branching level. However, we prefer this name instead of something more descriptive, yet much more notationally complicated (like “q determines
$\dot {x}$
to the n-branching level. However, we prefer this name instead of something more descriptive, yet much more notationally complicated (like “q determines
 $\dot {S}_{p}( x) \upharpoonright \textit{Split}_{n}$
” or something similar).
$\dot {S}_{p}( x) \upharpoonright \textit{Split}_{n}$
” or something similar).
By the results of the previous sections, we know that if
![]() $q\in \mathbb {P} _{\beta }$
and
$q\in \mathbb {P} _{\beta }$
and
![]() $\dot {p}_{1}$
is a
$\dot {p}_{1}$
is a
![]() $\mathbb {P}_{\beta }$
-name for a condition of
$\mathbb {P}_{\beta }$
-name for a condition of
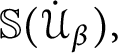 $\mathbb {S(}\mathcal {\dot {U}}_{\beta }),$
then we can find
$\mathbb {S(}\mathcal {\dot {U}}_{\beta }),$
then we can find
![]() $\dot {p}_{2}$
a
$\dot {p}_{2}$
a
![]() $\mathbb {P}_{\beta }$
-name for a condition of
$\mathbb {P}_{\beta }$
-name for a condition of
 $\mathbb {S(}\mathcal {\dot {U} }_{\beta })$
such that q forces that
$\mathbb {S(}\mathcal {\dot {U} }_{\beta })$
such that q forces that
![]() $\dot {p}_{2}$
is an extension of
$\dot {p}_{2}$
is an extension of
![]() $\dot {p}_{1}$
,
$\dot {p}_{1}$
,
![]() $\dot {p}_{2}$
is
$\dot {p}_{2}$
is
![]() $\omega $
-separative and
$\omega $
-separative and
![]() $S_{\dot {p}_{2} }\left ( \dot {x}\right ) $
is forced to be a monochromatic Sacks tree (although we might not know of which color without extending q first).
$S_{\dot {p}_{2} }\left ( \dot {x}\right ) $
is forced to be a monochromatic Sacks tree (although we might not know of which color without extending q first).
Definition 71 Let
![]() $q\in \mathbb {P}_{\beta }$
and
$q\in \mathbb {P}_{\beta }$
and
![]() $\dot {p}$
a
$\dot {p}$
a
![]() $\mathbb {P}_{\beta }$
-name for a condition of
$\mathbb {P}_{\beta }$
-name for a condition of
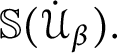 $\mathbb {S(}\mathcal {\dot {U}}_{\beta }).$
Let
$\mathbb {S(}\mathcal {\dot {U}}_{\beta }).$
Let
![]() $F\in \left [ \beta \right ] ^{<\omega }$
and
$F\in \left [ \beta \right ] ^{<\omega }$
and
![]() $\eta :F\longrightarrow \omega .$
We say
$\eta :F\longrightarrow \omega .$
We say
![]() $\left ( q,\dot {p}\right ) $
is
$\left ( q,\dot {p}\right ) $
is
![]() $\left ( F,\eta ,n,i\right ) $
-faithful if the following holds:
$\left ( F,\eta ,n,i\right ) $
-faithful if the following holds:
-
1. q forces that
 $\dot {p}$
is
$\dot {p}$
is
 $\omega $
-separative and
$\omega $
-separative and
 $S_{\dot {p}} (\dot {x})$
is an i-monochromatic Sacks tree.
$S_{\dot {p}} (\dot {x})$
is an i-monochromatic Sacks tree. -
2. If
 $\sigma \in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }$
then
$\sigma \in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }$
then
 $q\ast \sigma $
determines
$q\ast \sigma $
determines
 $\dot {p}$
to the n-level.
$\dot {p}$
to the n-level. -
3. If
 $\sigma ,\sigma ^{\prime }\in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }$
and
$\sigma ,\sigma ^{\prime }\in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }$
and
 $\sigma \neq \sigma ^{\prime }$
then
$\sigma \neq \sigma ^{\prime }$
then
 $\mathsf {c} _{\mathsf {min}}(T_{n}^{\dot {p}}\left ( q\ast \sigma \right ) ,T_{n}^{\dot {p} }\left ( q\ast \sigma ^{\prime }\right ) )=i$
(where
$\mathsf {c} _{\mathsf {min}}(T_{n}^{\dot {p}}\left ( q\ast \sigma \right ) ,T_{n}^{\dot {p} }\left ( q\ast \sigma ^{\prime }\right ) )=i$
(where
 $T_{n}^{\dot {p}}\left ( q\ast \sigma \right ) $
and
$T_{n}^{\dot {p}}\left ( q\ast \sigma \right ) $
and
 $T_{n}^{\dot {p}}\left ( q\ast \sigma ^{\prime }\right ) $
are as in Definition 70).
$T_{n}^{\dot {p}}\left ( q\ast \sigma ^{\prime }\right ) $
are as in Definition 70).
It is important to remark the following:
Lemma 72 Let
![]() $F\in \left [ \beta \right ] ^{<\omega },\eta :F\longrightarrow \omega $
and
$F\in \left [ \beta \right ] ^{<\omega },\eta :F\longrightarrow \omega $
and
![]() $\left ( q,\dot {p}\right ) $
be
$\left ( q,\dot {p}\right ) $
be
![]() $\left ( F,\eta ,n,i\right ) $
-faithful. If
$\left ( F,\eta ,n,i\right ) $
-faithful. If
![]() $r\leq _{F,\eta }^{\ast }q,$
then
$r\leq _{F,\eta }^{\ast }q,$
then
![]() $\left ( r,\dot {p}\right ) $
is
$\left ( r,\dot {p}\right ) $
is
![]() $\left ( F,\eta ,n,i\right ) $
-faithful.
$\left ( F,\eta ,n,i\right ) $
-faithful.
We will now prove the next lemma:
Lemma 73 Let
![]() $\left ( q,\dot {p}\right ) $
be
$\left ( q,\dot {p}\right ) $
be
![]() $(F,\eta ,n+1,i)$
-faithful. There are
$(F,\eta ,n+1,i)$
-faithful. There are
![]() $\dot {p}^{0},\dot {p}^{1}$
with the following properties:
$\dot {p}^{0},\dot {p}^{1}$
with the following properties:
-
1.
 $(q,\dot {p}^{0})$
and
$(q,\dot {p}^{0})$
and
 $(q,\dot {p}^{1})$
are
$(q,\dot {p}^{1})$
are
 $(F,\eta ,n,i)$
-faithful.
$(F,\eta ,n,i)$
-faithful. -
2.
 $q\Vdash $
“
$q\Vdash $
“
 $\dot {p}^{0},\dot {p}^{1}\leq _{n}^{\ast \ast }\dot {p}$
.”
$\dot {p}^{0},\dot {p}^{1}\leq _{n}^{\ast \ast }\dot {p}$
.” -
3.
 $\mathsf {c}_{\mathsf {min}}(T_{n}^{\dot {p}^{0}}\left ( q\ast \sigma \right ) ,T_{n}^{\dot {p}^{1}}\left ( q\ast \sigma \right ) )=i$
whenever
$\mathsf {c}_{\mathsf {min}}(T_{n}^{\dot {p}^{0}}\left ( q\ast \sigma \right ) ,T_{n}^{\dot {p}^{1}}\left ( q\ast \sigma \right ) )=i$
whenever
 $\sigma \in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }.$
$\sigma \in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }.$
Proof Assume
![]() $\left ( q,\dot {p}\right ) $
is
$\left ( q,\dot {p}\right ) $
is
![]() $\left ( F,\eta ,n+1,i\right ) $
-faithful. Let
$\left ( F,\eta ,n+1,i\right ) $
-faithful. Let
![]() $\dot {p}^{0}$
be (the name of) the condition obtained by merging
$\dot {p}^{0}$
be (the name of) the condition obtained by merging
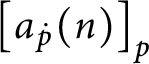 $\left [ a_{\dot {p}}( n) \right ] _{p}$
with
$\left [ a_{\dot {p}}( n) \right ] _{p}$
with
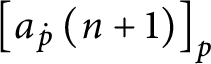 $\left [ a_{\dot {p}}\left ( n+1\right ) \right ] _{p}$
and
$\left [ a_{\dot {p}}\left ( n+1\right ) \right ] _{p}$
and
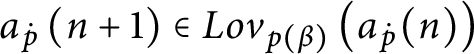 $a_{\dot {p}}\left ( n+1\right ) \in Lov_{p( \beta ) }\left ( a_{\dot {p}}( n) \right ) $
and let
$a_{\dot {p}}\left ( n+1\right ) \in Lov_{p( \beta ) }\left ( a_{\dot {p}}( n) \right ) $
and let
![]() $\dot {p}^{1}$
be (the name of) the condition obtained by merging
$\dot {p}^{1}$
be (the name of) the condition obtained by merging
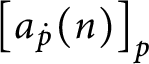 $\left [ a_{\dot {p}}( n) \right ] _{p}$
with
$\left [ a_{\dot {p}}( n) \right ] _{p}$
with
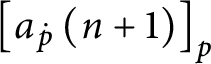 $\left [ a_{\dot {p}}\left ( n+1\right ) \right ] _{p}$
and
$\left [ a_{\dot {p}}\left ( n+1\right ) \right ] _{p}$
and
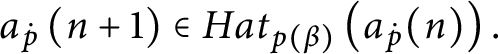 $a_{\dot {p}}\left ( n+1\right ) \in Hat_{p( \beta ) }\left ( a_{\dot {p}}( n) \right ) .$
It follows that
$a_{\dot {p}}\left ( n+1\right ) \in Hat_{p( \beta ) }\left ( a_{\dot {p}}( n) \right ) .$
It follows that
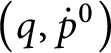 $\left ( q,\dot {p}^{0}\right ) $
and
$\left ( q,\dot {p}^{0}\right ) $
and
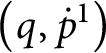 $\left ( q,\dot {p}^{1}\right ) $
are
$\left ( q,\dot {p}^{1}\right ) $
are
![]() $\left ( F,\eta ,n,i\right ) $
-faithful. It is also easy to see that if
$\left ( F,\eta ,n,i\right ) $
-faithful. It is also easy to see that if
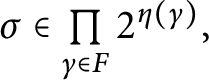 $\sigma \in \prod \limits _{\gamma \in F} 2^{\eta ( \gamma ) },$
then
$\sigma \in \prod \limits _{\gamma \in F} 2^{\eta ( \gamma ) },$
then
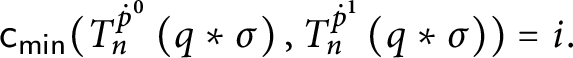 $\mathsf {c}_{\mathsf {min}}(T_{n} ^{\dot {p}^{0}}\left ( q\ast \sigma \right ) ,T_{n}^{\dot {p}^{1}}\left ( q\ast \sigma \right ) )=i.$
▪
$\mathsf {c}_{\mathsf {min}}(T_{n} ^{\dot {p}^{0}}\left ( q\ast \sigma \right ) ,T_{n}^{\dot {p}^{1}}\left ( q\ast \sigma \right ) )=i.$
▪
We will need the following:
Lemma 74 Let
![]() $\left ( q,\dot {p}\right ) $
be
$\left ( q,\dot {p}\right ) $
be
![]() $\left ( F,\eta ,n,i\right ) $
-faithful.
$\left ( F,\eta ,n,i\right ) $
-faithful.
-
1. The set
 $D=\{r\leq _{F,\eta }^{\ast }q\mid (r,\dot {p})$
is
$D=\{r\leq _{F,\eta }^{\ast }q\mid (r,\dot {p})$
is
 $\left ( F,\eta ,n+1,i\right ) $
-faithful
$\left ( F,\eta ,n+1,i\right ) $
-faithful
 $\}$
is
$\}$
is
 $( F,\eta ) ^{\ast }$
-open dense below
$( F,\eta ) ^{\ast }$
-open dense below
 $q.$
$q.$
-
2. For every
 $m\in \omega $
with
$m\in \omega $
with
 $m>n,$
the set
$m>n,$
the set
 $D_{m}=\{r\leq _{F,\eta } ^{\ast }q\mid (r,\dot {p})$
is
$D_{m}=\{r\leq _{F,\eta } ^{\ast }q\mid (r,\dot {p})$
is
 $\left ( F,\eta ,m,i\right ) $
-faithful
$\left ( F,\eta ,m,i\right ) $
-faithful
 $\}$
is
$\}$
is
 $( F,\eta ) ^{\ast }$
-open dense below
$( F,\eta ) ^{\ast }$
-open dense below
 $q.$
$q.$
Proof Obviously the first point implies the second one. It is easy to see that D is
![]() $( F,\eta ) ^{\ast }$
-open. We will now prove that D is
$( F,\eta ) ^{\ast }$
-open. We will now prove that D is
![]() $( F,\eta ) ^{\ast }$
-dense. Let
$( F,\eta ) ^{\ast }$
-dense. Let
![]() $q_{1}\leq _{F,\eta }^{\ast }q$
and fix an enumeration
$q_{1}\leq _{F,\eta }^{\ast }q$
and fix an enumeration
 $\prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }=\left \{ \sigma _{j}\mid j<k\right \} .$
We can recursively build conditions
$\prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }=\left \{ \sigma _{j}\mid j<k\right \} .$
We can recursively build conditions
![]() $q_{1}^{0},\ldots ,q_{1}^{k+1}$
with the following properties:
$q_{1}^{0},\ldots ,q_{1}^{k+1}$
with the following properties:
-
1.
 $\langle q_{1}^{0},\ldots ,q_{1}^{k+1}\rangle $
is an
$\langle q_{1}^{0},\ldots ,q_{1}^{k+1}\rangle $
is an
 $\leq _{( F,\eta ) }$
-decreasing sequence.
$\leq _{( F,\eta ) }$
-decreasing sequence. -
2.
 $q_{1}^{0}=q_{1}.$
$q_{1}^{0}=q_{1}.$
-
3.
 $q_{1}^{i+1}\ast \sigma _{j}$
determines
$q_{1}^{i+1}\ast \sigma _{j}$
determines
 $\bigcup \left \{ \dot {x}\left ( p[ h] \right ) \mid h\in 2^{n+2}\right \} .$
$\bigcup \left \{ \dot {x}\left ( p[ h] \right ) \mid h\in 2^{n+2}\right \} .$
We claim that
![]() $r=q_{1}^{k+1}$
is the condition we are looking for. In order to prove this, note that if
$r=q_{1}^{k+1}$
is the condition we are looking for. In order to prove this, note that if
![]() $j_{1}\neq j_{2},$
then
$j_{1}\neq j_{2},$
then
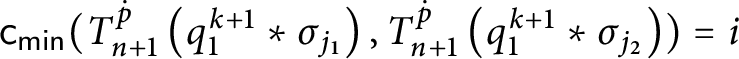 $\mathsf {c}_{\mathsf {min} }(T_{n+1}^{\dot {p}}\left ( q_{1}^{k+1}\ast \sigma _{j_{1}}\right ) ,T_{n+1}^{\dot {p}}\left ( q_{1}^{k+1}\ast \sigma _{j_{2}}\right ) )=i$
because
$\mathsf {c}_{\mathsf {min} }(T_{n+1}^{\dot {p}}\left ( q_{1}^{k+1}\ast \sigma _{j_{1}}\right ) ,T_{n+1}^{\dot {p}}\left ( q_{1}^{k+1}\ast \sigma _{j_{2}}\right ) )=i$
because
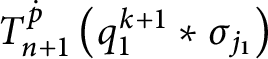 $T_{n+1}^{\dot {p}}\left ( q_{1}^{k+1}\ast \sigma _{j_{1}}\right ) $
and
$T_{n+1}^{\dot {p}}\left ( q_{1}^{k+1}\ast \sigma _{j_{1}}\right ) $
and
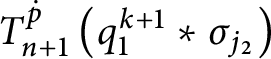 $T_{n+1}^{\dot {p}}\left ( q_{1}^{k+1}\ast \sigma _{j_{2}}\right ) $
are end-extentions of trees that already have that property.▪
$T_{n+1}^{\dot {p}}\left ( q_{1}^{k+1}\ast \sigma _{j_{2}}\right ) $
are end-extentions of trees that already have that property.▪
The following lemma is easy and follows from the definitions:
Lemma 75 Let
![]() $\left ( q,\dot {p}\right ) $
be
$\left ( q,\dot {p}\right ) $
be
![]() $\left ( F,\eta ,n,i\right ) $
-faithful and
$\left ( F,\eta ,n,i\right ) $
-faithful and
![]() $\gamma \notin F.$
Define
$\gamma \notin F.$
Define
![]() $F^{\prime }=F\cup \left \{ \gamma \right \} $
and
$F^{\prime }=F\cup \left \{ \gamma \right \} $
and
![]() $\eta ^{\prime }=\eta \cup \left \{ \left ( \gamma ,0\right ) \right \} .$
The condition
$\eta ^{\prime }=\eta \cup \left \{ \left ( \gamma ,0\right ) \right \} .$
The condition
![]() $\left ( q,\dot {p}\right ) $
is
$\left ( q,\dot {p}\right ) $
is
![]() $\left ( F^{\prime },\eta ^{\prime },n,i\right ) $
-faithful.
$\left ( F^{\prime },\eta ^{\prime },n,i\right ) $
-faithful.
We will need one more lemma:
Lemma 76 Assume
![]() $\left ( q,\dot {p}\right ) $
is
$\left ( q,\dot {p}\right ) $
is
![]() $\left ( F,\eta ,n+1,i\right ) $
-faithful. Let
$\left ( F,\eta ,n+1,i\right ) $
-faithful. Let
![]() $\delta \in F$
and define
$\delta \in F$
and define
![]() $\eta ^{\prime }:F\longrightarrow \omega $
where
$\eta ^{\prime }:F\longrightarrow \omega $
where
![]() $\eta ^{\prime }\left ( \xi \right ) =\eta \left ( \xi \right ) $
if
$\eta ^{\prime }\left ( \xi \right ) =\eta \left ( \xi \right ) $
if
![]() $\xi \neq \delta $
and
$\xi \neq \delta $
and
![]() $\eta ^{\prime }\left ( \delta \right ) =\eta \left ( \delta \right ) +1.$
There is
$\eta ^{\prime }\left ( \delta \right ) =\eta \left ( \delta \right ) +1.$
There is
![]() $\dot {p}_{\#}$
such that
$\dot {p}_{\#}$
such that
![]() $q\Vdash $
“
$q\Vdash $
“
![]() $\dot {p}_{\#}\leq _{n}^{\ast \ast }\dot {p}$
” and
$\dot {p}_{\#}\leq _{n}^{\ast \ast }\dot {p}$
” and
![]() $(q,\dot {p}_{\#})$
is
$(q,\dot {p}_{\#})$
is
![]() $\left ( F,\eta ^{\prime },n,i\right ) $
-faithful.
$\left ( F,\eta ^{\prime },n,i\right ) $
-faithful.
Proof Let
![]() $\dot {p}^{0}$
and
$\dot {p}^{0}$
and
![]() $\dot {p}^{1}$
be as in Lemma 73. Now, define a
$\dot {p}^{1}$
be as in Lemma 73. Now, define a
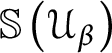 $\mathbb {S}\left ( \mathcal {U}_{\beta }\right ) $
-name
$\mathbb {S}\left ( \mathcal {U}_{\beta }\right ) $
-name
![]() $\dot {p}_{\#}$
such that if
$\dot {p}_{\#}$
such that if
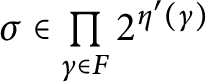 $\sigma \in \prod \limits _{\gamma \in F}2^{\eta ^{\prime }( \gamma ) }$
then
$\sigma \in \prod \limits _{\gamma \in F}2^{\eta ^{\prime }( \gamma ) }$
then
![]() $q\ast \sigma \Vdash \text{``}\dot {p}_{\#}=\dot {p}^{\sigma \left ( \delta \right ) \left ( \eta ( \gamma ) \right )}{}'' $
(In other words, if the last digit of
$q\ast \sigma \Vdash \text{``}\dot {p}_{\#}=\dot {p}^{\sigma \left ( \delta \right ) \left ( \eta ( \gamma ) \right )}{}'' $
(In other words, if the last digit of
![]() $\sigma \left ( \delta \right ) $
is
$\sigma \left ( \delta \right ) $
is
![]() $k,$
then
$k,$
then
![]() $q\ast \sigma \Vdash $
“
$q\ast \sigma \Vdash $
“
![]() $\dot {p}_{\#}=\dot {p}^{k} $
”). It follows that
$\dot {p}_{\#}=\dot {p}^{k} $
”). It follows that
![]() $\left ( q,\dot {p}_{\#}\right ) $
is
$\left ( q,\dot {p}_{\#}\right ) $
is
![]() $\left ( F,\eta ^{\prime },n,i\right ) $
-faithful.▪
$\left ( F,\eta ^{\prime },n,i\right ) $
-faithful.▪
We can now prove the most important result on this section:
Proposition 77 Let
![]() $\alpha =\beta +1$
and assume
$\alpha =\beta +1$
and assume
![]() $\dot {x}$
is a
$\dot {x}$
is a
![]() $\mathbb {P}_{\alpha }$
-name for a real that was not added by
$\mathbb {P}_{\alpha }$
-name for a real that was not added by
![]() $\mathbb {P}_{\beta }.$
If
$\mathbb {P}_{\beta }.$
If
![]() $q^{\prime }\in \mathbb {P}_{\alpha },$
then there are
$q^{\prime }\in \mathbb {P}_{\alpha },$
then there are
![]() $\overline {q}\leq q^{\prime }$
and
$\overline {q}\leq q^{\prime }$
and
![]() $S\in V$
a
$S\in V$
a
![]() $\mathsf {c}_{\mathsf {min}}$
-monochromatic tree such that
$\mathsf {c}_{\mathsf {min}}$
-monochromatic tree such that
![]() $\overline {q}\Vdash \text{``}\dot {x}\in \left [ S\right ].\text{''}$
$\overline {q}\Vdash \text{``}\dot {x}\in \left [ S\right ].\text{''}$
Proof We may assume that there are
![]() $q\in \mathbb {P}_{\beta }$
and
$q\in \mathbb {P}_{\beta }$
and
![]() $\dot {p}$
a
$\dot {p}$
a
![]() $\mathbb {P}_{\beta }$
-name for a condition of
$\mathbb {P}_{\beta }$
-name for a condition of
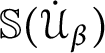 $\mathbb {S(}\mathcal {\dot {U} }_{\beta })$
such that q forces that
$\mathbb {S(}\mathcal {\dot {U} }_{\beta })$
such that q forces that
![]() $\dot {p}$
is
$\dot {p}$
is
![]() $\omega $
-separative,
$\omega $
-separative,
![]() $S_{\dot {p}}\left ( \dot {x}\right ) $
is an i-monochromatic Sacks tree (for some
$S_{\dot {p}}\left ( \dot {x}\right ) $
is an i-monochromatic Sacks tree (for some
![]() $i<2$
) and
$i<2$
) and
![]() $q^{\prime }=q^{\frown }\dot {p}.$
Let M be a countable elementary submodel of
$q^{\prime }=q^{\frown }\dot {p}.$
Let M be a countable elementary submodel of
![]() $\mathsf{H} ( \kappa ) $
(for a big large enough regular cardinal
$\mathsf{H} ( \kappa ) $
(for a big large enough regular cardinal
![]() $\kappa $
) such that
$\kappa $
) such that
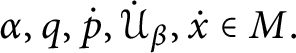 $\alpha ,q,\dot {p},\mathcal {\dot {U}}_{\beta },\dot {x}\in M.$
$\alpha ,q,\dot {p},\mathcal {\dot {U}}_{\beta },\dot {x}\in M.$
For every
![]() $l<3,$
define
$l<3,$
define
![]() $A_{l}=\{n\mid n=_{3}l\}$
(where
$A_{l}=\{n\mid n=_{3}l\}$
(where
![]() $n=_{3}l$
means that n is equal to l mod
$n=_{3}l$
means that n is equal to l mod
![]() $3$
). We now find
$3$
). We now find
![]() $L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
$L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
![]() $\left ( M,\beta \right ) $
with the following extra properties:
$\left ( M,\beta \right ) $
with the following extra properties:
-
1.
 $F_{0}=\emptyset $
and
$F_{0}=\emptyset $
and
 $\eta _{0}=\emptyset .$
$\eta _{0}=\emptyset .$
-
2. Let
 $n\in \omega $
and assume
$n\in \omega $
and assume
 $F_{n},\eta _{n}$
are already defined, we will now define
$F_{n},\eta _{n}$
are already defined, we will now define
 $F_{n+1}$
and
$F_{n+1}$
and
 $\eta _{n+1}.$
$\eta _{n+1}.$
-
(a) Case
 $n\in A_{0}.$
$n\in A_{0}.$
Let
 $F_{n+1}=F_{n}$
and
$F_{n+1}=F_{n}$
and
 $\eta _{n+1}=\eta _{n}.$
$\eta _{n+1}=\eta _{n}.$
-
(b) Case
 $n\in A_{1}.$
$n\in A_{1}.$
Let
 $F_{n+1}=F_{n}$
and there is a unique
$F_{n+1}=F_{n}$
and there is a unique
 $\xi \in F_{n}$
such
$\xi \in F_{n}$
such
 $\eta _{n+1}\left ( \xi \right ) =\eta _{n}\left ( \xi \right ) +1$
and
$\eta _{n+1}\left ( \xi \right ) =\eta _{n}\left ( \xi \right ) +1$
and
 $\eta _{n+1}( \gamma ) =\eta _{n}( \gamma ) $
for every other
$\eta _{n+1}( \gamma ) =\eta _{n}( \gamma ) $
for every other
 $\gamma \in F_{n}.$
$\gamma \in F_{n}.$
-
(c) Case
 $n\in A_{2}.$
$n\in A_{2}.$
 $F_{n+1}\setminus F_{n}$
has size at most
$F_{n+1}\setminus F_{n}$
has size at most
 $1, \eta _{n+1}\upharpoonright F_{n}=\eta _{n}\upharpoonright F_{n}$
and if
$1, \eta _{n+1}\upharpoonright F_{n}=\eta _{n}\upharpoonright F_{n}$
and if
 $\gamma \in F_{n+1}\setminus F_{n},$
then
$\gamma \in F_{n+1}\setminus F_{n},$
then
 $\eta _{n+1}( \gamma ) =0.$
$\eta _{n+1}( \gamma ) =0.$
-
Define a tree
![]() $Y\subseteq 2^{<\omega }$
as follows:
$Y\subseteq 2^{<\omega }$
as follows:
-
1.
 $\emptyset \in Y.$
$\emptyset \in Y.$
-
2. If
 $s\in Y_{n}$
and
$s\in Y_{n}$
and
 $F_{n+1}=F_{n},$
then
$F_{n+1}=F_{n},$
then
 $s^{\frown }0\in Y_{n+1}.$
$s^{\frown }0\in Y_{n+1}.$
-
3. If
 $s\in Y_{n}$
and
$s\in Y_{n}$
and
 $F_{n+1}\neq F_{n},$
then
$F_{n+1}\neq F_{n},$
then
 $s^{\frown }0, s^{\frown }1\in Y_{n+1}.$
$s^{\frown }0, s^{\frown }1\in Y_{n+1}.$
It follows that if
![]() $s\in Y$
is a splitting node, then
$s\in Y$
is a splitting node, then
![]() $\left \vert s\right \vert \in A_{2}$
(but not every node whose height is in
$\left \vert s\right \vert \in A_{2}$
(but not every node whose height is in
![]() $A_{2}$
must be a splitting node).
$A_{2}$
must be a splitting node).
We will now recursively build a
![]() $\beta $
-fusion tree
$\beta $
-fusion tree
![]() $T=\left \{ q_{s}\mid s\in Y\right \} \subseteq M, \left \{ k_{n}\mid n\in \omega \right \} \subseteq \omega $
and
$T=\left \{ q_{s}\mid s\in Y\right \} \subseteq M, \left \{ k_{n}\mid n\in \omega \right \} \subseteq \omega $
and
![]() $\left \{ \dot {p}_{s}\mid s\in Y\right \} \subseteq M$
with the following propertiesFootnote
6
:
$\left \{ \dot {p}_{s}\mid s\in Y\right \} \subseteq M$
with the following propertiesFootnote
6
:
-
1.
 $k_{0}=0$
.
$k_{0}=0$
. -
2.
 $q_{\emptyset }\leq q$
and
$q_{\emptyset }\leq q$
and
 $q_{\emptyset }\Vdash $
“
$q_{\emptyset }\Vdash $
“
 $\dot {p}_{\emptyset }\leq \dot {p}$
.”
$\dot {p}_{\emptyset }\leq \dot {p}$
.” -
3. if
 $s\in Y_{n},$
then
$s\in Y_{n},$
then
 $\left ( q_{s},\dot {p}_{s}\right ) $
is
$\left ( q_{s},\dot {p}_{s}\right ) $
is
 $(F_{n},\eta _{n},k_{n},i)$
-faithful. Define
$(F_{n},\eta _{n},k_{n},i)$
-faithful. Define
 $K\left ( q_{s}\right ) =\bigcup \{T_{n}^{\dot {p}_{s}}\left ( q_{s}\ast \sigma \right ) \mid \sigma \in \prod \limits _{\gamma \in F_{n}}2^{\eta _{n}( \gamma ) }\}.$
$K\left ( q_{s}\right ) =\bigcup \{T_{n}^{\dot {p}_{s}}\left ( q_{s}\ast \sigma \right ) \mid \sigma \in \prod \limits _{\gamma \in F_{n}}2^{\eta _{n}( \gamma ) }\}.$
-
4. If
 $s\in Y_{n}$
and
$s\in Y_{n}$
and
 $j\in suc_{Y}( s) ,$
then
$j\in suc_{Y}( s) ,$
then
 $q_{s^{\frown }j}\leq _{F_{n},\eta _{n}}^{\ast }q_{s}$
and
$q_{s^{\frown }j}\leq _{F_{n},\eta _{n}}^{\ast }q_{s}$
and
 $q_{s^{\frown }j} \Vdash \text{``}\,\dot {p}_{s^{\frown }j}\leq _{k_{n}}^{\ast \ast }\dot {p}_{s} ''.$
$q_{s^{\frown }j} \Vdash \text{``}\,\dot {p}_{s^{\frown }j}\leq _{k_{n}}^{\ast \ast }\dot {p}_{s} ''.$
-
5. If
 $s\in Y$
and
$s\in Y$
and
 $j\in suc_{Y}( s) ,$
then
$j\in suc_{Y}( s) ,$
then
 $K\left ( q_{s^{\frown }j}\right ) $
is an end-extension of
$K\left ( q_{s^{\frown }j}\right ) $
is an end-extension of
 $K\left ( q_{s}\right ) .$
$K\left ( q_{s}\right ) .$
-
6. If
 $s\in Y$
and
$s\in Y$
and
 $s^{\frown }0, s^{\frown }1\in Y,$
then
$s^{\frown }0, s^{\frown }1\in Y,$
then
 $K\left ( q_{s^{\frown }0}\right ) $
and
$K\left ( q_{s^{\frown }0}\right ) $
and
 $K\left ( q_{s^{\frown }1}\right ) $
are two end-extensions of
$K\left ( q_{s^{\frown }1}\right ) $
are two end-extensions of
 $K\left ( q_{s}\right ) $
and
$K\left ( q_{s}\right ) $
and
 $\mathsf {c}_{\mathsf {min} }\left ( K\left ( q_{s^{\frown }0}\right ) ,K\left ( q_{s^{\frown }1}\right ) \right ) =i.$
$\mathsf {c}_{\mathsf {min} }\left ( K\left ( q_{s^{\frown }0}\right ) ,K\left ( q_{s^{\frown }1}\right ) \right ) =i.$
-
7. Let
 $n\in \omega $
and assume
$n\in \omega $
and assume
 $\left \{ q_{t}\mid t\in Y_{n}\right \} , \left \{ k_{l}\mid l\leq n\right \} $
, and
$\left \{ q_{t}\mid t\in Y_{n}\right \} , \left \{ k_{l}\mid l\leq n\right \} $
, and
 $\left \{ \dot {p}_{t}\mid t\in Y_{n}\right \} $
have already been constructed. We will now build the items for the nodes in
$\left \{ \dot {p}_{t}\mid t\in Y_{n}\right \} $
have already been constructed. We will now build the items for the nodes in
 $Y_{n+1}.$
Let
$Y_{n+1}.$
Let
 $s\in Y_{n},$
we will define
$s\in Y_{n},$
we will define
 $q_{s^{\frown } l}, k_{s^{\frown }l}$
and
$q_{s^{\frown } l}, k_{s^{\frown }l}$
and
 $\dot {p}_{s^{\frown }l}$
for
$\dot {p}_{s^{\frown }l}$
for
 $l\in suc_{Y}( s) .$
We are assuming that
$l\in suc_{Y}( s) .$
We are assuming that
 $\left \{ q_{t}\mid t\in Y_{n}\right \} $
is a (finite)
$\left \{ q_{t}\mid t\in Y_{n}\right \} $
is a (finite)
 $\beta $
-fusion tree and
$\beta $
-fusion tree and
 $(q_{s},\dot {p}_{s})$
is
$(q_{s},\dot {p}_{s})$
is
 $(F_{n} ,\eta _{n},k_{n},i)$
-faithful.
$(F_{n} ,\eta _{n},k_{n},i)$
-faithful.-
(a) Case
 $n\in A_{0}$
(recall that
$n\in A_{0}$
(recall that
 $F_{n+1}=F_{n}$
,
$F_{n+1}=F_{n}$
,
 $\eta _{n+1}=\eta _{n}$
and
$\eta _{n+1}=\eta _{n}$
and
 $suc_{Y}( s) =\left \{ 0\right \} $
).
$suc_{Y}( s) =\left \{ 0\right \} $
).Let
 $\dot {p}_{s^{\frown }0}=\dot {p}_{s}$
and
$\dot {p}_{s^{\frown }0}=\dot {p}_{s}$
and
 $k_{n+1}=k_{n}+3.$
We choose
$k_{n+1}=k_{n}+3.$
We choose
 $q_{s^{\frown }0}\leq _{F_{n},\eta _{n}}^{\ast }q_{s}$
such that
$q_{s^{\frown }0}\leq _{F_{n},\eta _{n}}^{\ast }q_{s}$
such that
 $(q_{s^{\frown } 0},\dot {p}_{s^{\frown }0})$
is
$(q_{s^{\frown } 0},\dot {p}_{s^{\frown }0})$
is
 $(F_{n},\eta _{n},k_{n}+3,i)$
-faithful. This is possible by Lemmas 65 and 74.
$(F_{n},\eta _{n},k_{n}+3,i)$
-faithful. This is possible by Lemmas 65 and 74. -
(b) Case
 $n\in A_{1}$
(recall that
$n\in A_{1}$
(recall that
 $F_{n+1}=F_{n}$
,
$F_{n+1}=F_{n}$
,
 $\eta _{n+1}$
increases by one in just one point and
$\eta _{n+1}$
increases by one in just one point and
 $suc_{Y}( s) =\left \{ 0\right \} $
).
$suc_{Y}( s) =\left \{ 0\right \} $
).Let
 $q_{s^{\frown }0}=q_{s},\ k_{n+1}=k_{n}-1$
and we find
$q_{s^{\frown }0}=q_{s},\ k_{n+1}=k_{n}-1$
and we find
 $\dot {p}_{s^{\frown }0}$
such that
$\dot {p}_{s^{\frown }0}$
such that
 $(q_{s},\dot {p}_{s^{\frown }0})$
is
$(q_{s},\dot {p}_{s^{\frown }0})$
is
 $(F_{n} ,\eta _{n+1},k_{n}-1,i)$
-faithful and
$(F_{n} ,\eta _{n+1},k_{n}-1,i)$
-faithful and
 $q_{s}\Vdash $
“
$q_{s}\Vdash $
“
 $\dot {p}_{s^{\frown }0}\leq _{k_{n+1}}^{\ast \ast }\dot {p}_{s}$
.” This is possible by Lemma 76.
$\dot {p}_{s^{\frown }0}\leq _{k_{n+1}}^{\ast \ast }\dot {p}_{s}$
.” This is possible by Lemma 76. -
(c) Case
 $n\in A_{2}$
and
$n\in A_{2}$
and
 $F_{n+1}=F_{n}$
(recall that
$F_{n+1}=F_{n}$
(recall that
 $\eta _{n+1}\upharpoonright F_{n}=\eta _{n}$
and
$\eta _{n+1}\upharpoonright F_{n}=\eta _{n}$
and
 $suc_{Y}( s) = \{ 0\} $
).
$suc_{Y}( s) = \{ 0\} $
).Let
 $q_{s^{\frown }0}=q_{s},\ k_{n+1}=k_{n}$
and
$q_{s^{\frown }0}=q_{s},\ k_{n+1}=k_{n}$
and
 $\dot {p}_{s^{\frown }0} =\dot {p}_{s}.$
$\dot {p}_{s^{\frown }0} =\dot {p}_{s}.$
-
(d) Case
 $n\in A_{2}$
and
$n\in A_{2}$
and
 $F_{n+1}\neq F_{n}$
(recall that
$F_{n+1}\neq F_{n}$
(recall that
 $\left \vert F_{n+1}\right \vert =\left \vert F_{n}\right \vert +1$
,
$\left \vert F_{n+1}\right \vert =\left \vert F_{n}\right \vert +1$
,
 $\eta _{n+1}$
takes value
$\eta _{n+1}$
takes value
 $0$
in the new point and
$0$
in the new point and
 $suc_{Y}( s) =\left \{ 0,1\right \} $
).
$suc_{Y}( s) =\left \{ 0,1\right \} $
).Let
 $k_{n+1}=k_{n}-1.$
We use Lemma 73 to find
$k_{n+1}=k_{n}-1.$
We use Lemma 73 to find
 $\dot {p}_{s}^{0}, \dot {p}_{s}^{1}$
such that the following conditions hold:
$\dot {p}_{s}^{0}, \dot {p}_{s}^{1}$
such that the following conditions hold:-
i.
 $(q_{s},\dot {p}_{s}^{0})$
and
$(q_{s},\dot {p}_{s}^{0})$
and
 $(q_{s},\dot {p}_{s}^{1})$
are
$(q_{s},\dot {p}_{s}^{1})$
are
 $(F_{n} ,\eta _{n},k_{n}-1,i)$
-faithful.
$(F_{n} ,\eta _{n},k_{n}-1,i)$
-faithful. -
ii.
 $q_{s}\Vdash $
“
$q_{s}\Vdash $
“
 $\dot {p}_{s}^{0},\dot {p}_{s}^{1} \leq _{k_{n+1}}^{\ast \ast }\dot {p}$
.”
$\dot {p}_{s}^{0},\dot {p}_{s}^{1} \leq _{k_{n+1}}^{\ast \ast }\dot {p}$
.” -
iii.
 $\mathsf {c}_{\mathsf {min}}(T_{n}^{\dot {p}_{s}^{0}}\left ( q_{s} \ast \sigma \right ) ,T_{n}^{\dot {p}_{s}^{1}}\left ( q_{s}\ast \sigma \right ) )=i$
whenever
$\mathsf {c}_{\mathsf {min}}(T_{n}^{\dot {p}_{s}^{0}}\left ( q_{s} \ast \sigma \right ) ,T_{n}^{\dot {p}_{s}^{1}}\left ( q_{s}\ast \sigma \right ) )=i$
whenever
 $\sigma \in \prod \limits _{\gamma \in F_{n}}2^{\eta _{n}( \gamma ) }.$
$\sigma \in \prod \limits _{\gamma \in F_{n}}2^{\eta _{n}( \gamma ) }.$
We now apply Lemma 65 to find
 $\left \{ q_{t^{\frown } l}\mid t\in Y_{n}\wedge l\in 2\right \} $
a
$\left \{ q_{t^{\frown } l}\mid t\in Y_{n}\wedge l\in 2\right \} $
a
 $\beta $
-fusion tree extending our current tree (in the statement of Lemma 65 we can take
$\beta $
-fusion tree extending our current tree (in the statement of Lemma 65 we can take
 $D_{t}=\mathbb {P}_{\beta }$
for every
$D_{t}=\mathbb {P}_{\beta }$
for every
 $t\in Y_{n}$
). Let
$t\in Y_{n}$
). Let
 $\dot {p}_{s^{\frown } 0}=\dot {p}_{s}^{0}$
and
$\dot {p}_{s^{\frown } 0}=\dot {p}_{s}^{0}$
and
 $\dot {p}_{s^{\frown }1}=\dot {p}_{s}^{1}.$
$\dot {p}_{s^{\frown }1}=\dot {p}_{s}^{1}.$
-
-
Now that we have constructed
![]() $T,$
it follows by faithfulness that
$T,$
it follows by faithfulness that
![]() $K\left ( q_{s}\right ) $
is an i-monochromatic tree for every
$K\left ( q_{s}\right ) $
is an i-monochromatic tree for every
![]() $s\in Y$
. Furthermore, we know that
$s\in Y$
. Furthermore, we know that
![]() $K\left ( q_{s^{\frown }0}\right ) $
and
$K\left ( q_{s^{\frown }0}\right ) $
and
![]() $K\left ( q_{s^{\frown } 1}\right ) $
are two end-extensions of
$K\left ( q_{s^{\frown } 1}\right ) $
are two end-extensions of
![]() $K\left ( p_{s}\right ) $
and
$K\left ( p_{s}\right ) $
and
![]() $\mathsf {c}_{\mathsf {min}}\left ( K\left ( q_{s^{\frown }0}\right ) ,K\left ( q_{s^{\frown }1}\right ) \right ) =i.$
In this way,
$\mathsf {c}_{\mathsf {min}}\left ( K\left ( q_{s^{\frown }0}\right ) ,K\left ( q_{s^{\frown }1}\right ) \right ) =i.$
In this way,
 $K= {\textstyle \bigcup \limits _{s\in Y}} K( q_{s}) $
is an i-monochromatic tree, which is an element of V.
$K= {\textstyle \bigcup \limits _{s\in Y}} K( q_{s}) $
is an i-monochromatic tree, which is an element of V.
By Lemma 62, there is
![]() $\overline {q}\in \mathbb {P}_{\beta }$
compatible with T and
$\overline {q}\in \mathbb {P}_{\beta }$
compatible with T and
![]() $\dot {R}$
a name for a branch through T such that
$\dot {R}$
a name for a branch through T such that
![]() $\overline {q}$
forces
$\overline {q}$
forces
![]() $\dot {R}$
to be contained in the generic filter. In this way
$\dot {R}$
to be contained in the generic filter. In this way
![]() $\overline {p}=Lim\left ( \left \{ \dot {p}_{R\upharpoonright n}\mid n\in \omega \right \} \right ) $
is a name for a condition of
$\overline {p}=Lim\left ( \left \{ \dot {p}_{R\upharpoonright n}\mid n\in \omega \right \} \right ) $
is a name for a condition of
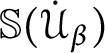 $\mathbb {S(} \mathcal {\dot {U}}_{\beta })$
(since it is forced to be the limit of a
$\mathbb {S(} \mathcal {\dot {U}}_{\beta })$
(since it is forced to be the limit of a
![]() $\leq ^{\ast \ast }$
-decreasing sequence). Finally,
$\leq ^{\ast \ast }$
-decreasing sequence). Finally,
![]() $r=\overline {q}^{\frown }\overline {p}$
is an extension of
$r=\overline {q}^{\frown }\overline {p}$
is an extension of
![]() $q^{\frown }\dot {p}$
and
$q^{\frown }\dot {p}$
and
![]() $r\Vdash \text{``}\dot {x} \in \left [ K\right ],\text{''}$
which is what we desired the most. This finishes the construction and the proof of the successor case.▪
$r\Vdash \text{``}\dot {x} \in \left [ K\right ],\text{''}$
which is what we desired the most. This finishes the construction and the proof of the successor case.▪
6 Preserving
 $\mathsf {c}_{\mathsf {min}}$
-covering at limit steps
$\mathsf {c}_{\mathsf {min}}$
-covering at limit steps
The last task is to prove that the
![]() $\mathsf {c}_{\mathsf {min}}$
-covering is preserved at limit steps of the iteration. For this section, let
$\mathsf {c}_{\mathsf {min}}$
-covering is preserved at limit steps of the iteration. For this section, let
![]() $\alpha $
be a limit ordinal and
$\alpha $
be a limit ordinal and
![]() $\dot {x}$
a
$\dot {x}$
a
![]() $\mathbb {P}_{\alpha }$
-name for an element of
$\mathbb {P}_{\alpha }$
-name for an element of
![]() $2^{\omega }$
that was not added by any
$2^{\omega }$
that was not added by any
![]() $\mathbb {P}_{\beta }$
for
$\mathbb {P}_{\beta }$
for
![]() $\beta <\alpha $
(this entails that
$\beta <\alpha $
(this entails that
![]() $\alpha $
has countable cofinality).
$\alpha $
has countable cofinality).
Given
![]() $i<2$
, define
$i<2$
, define
![]() $W_{i}$
as the set of all
$W_{i}$
as the set of all
![]() $p\in \mathbb {P}_{\alpha }$
such that for every
$p\in \mathbb {P}_{\alpha }$
such that for every
![]() $\beta <\alpha $
and for every
$\beta <\alpha $
and for every
![]() $q\leq p$
there are
$q\leq p$
there are
![]() $q^{\prime }\leq q$
and
$q^{\prime }\leq q$
and
![]() $q_{0},q_{1}$
with the following properties:
$q_{0},q_{1}$
with the following properties:
-
1.
 $q_{0}\upharpoonright \beta =q_{1}\upharpoonright \beta =q^{\prime }\upharpoonright \beta .$
$q_{0}\upharpoonright \beta =q_{1}\upharpoonright \beta =q^{\prime }\upharpoonright \beta .$
-
2.
 $q_{0},q_{1}\leq q^{\prime }.$
$q_{0},q_{1}\leq q^{\prime }.$
-
3.
 $\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ q_{0}\right ] ,\dot {x}\left [ q_{1}\right ] \right ) =i.$
$\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ q_{0}\right ] ,\dot {x}\left [ q_{1}\right ] \right ) =i.$
The following is Lemma 30 of [Reference Geschke9] (in [Reference Geschke9], the lemma is only stated for the iteration of Sacks forcing, but it is mentioned that it is true for any iteration, see also Lemma 6.11 of [Reference Jorge, Fischer, Guzmán and Jaroslav7]).
Lemma 78 [Reference Geschke9]
Both
![]() $W_{0}$
and
$W_{0}$
and
![]() $W_{1}$
are open and
$W_{1}$
are open and
![]() $W_{0}\cup W_{1}$
is an open dense set.
$W_{0}\cup W_{1}$
is an open dense set.
We will need the following concepts:
Definition 79 Let
![]() $F\in \left [ \alpha \right ] ^{<\omega }$
,
$F\in \left [ \alpha \right ] ^{<\omega }$
,
![]() $\eta :F\longrightarrow \omega $
,
$\eta :F\longrightarrow \omega $
,
![]() $i<2, \beta =max( f) +1$
and
$i<2, \beta =max( f) +1$
and
![]() $p\in \mathbb {P}_{\alpha }.$
$p\in \mathbb {P}_{\alpha }.$
-
1. We say p is
 $\left ( F,\eta ,i\right ) $
-faithful if
$\left ( F,\eta ,i\right ) $
-faithful if
 $p\in W_{i}$
and for every
$p\in W_{i}$
and for every
 $\sigma ,\sigma ^{\prime }\in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }$
such that
$\sigma ,\sigma ^{\prime }\in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }$
such that
 $\sigma \neq \sigma ^{\prime }$
then
$\sigma \neq \sigma ^{\prime }$
then
 $\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ p\ast \sigma \right ] ,\dot {x}\left [ p\ast \sigma ^{\prime }\right ] \right ) =i.$
$\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ p\ast \sigma \right ] ,\dot {x}\left [ p\ast \sigma ^{\prime }\right ] \right ) =i.$
-
2. We say p is
 $( F,\eta ,i) $
-splitting at
$( F,\eta ,i) $
-splitting at
 $\beta $
if p is
$\beta $
if p is
 $( F,\eta ,i) $
-faithful and there are
$( F,\eta ,i) $
-faithful and there are
 $p^{0},p^{1}$
such that:
$p^{0},p^{1}$
such that:-
(a)
 $p^{0},p^{1}\leq p.$
$p^{0},p^{1}\leq p.$
-
(b)
 $p^{0}\upharpoonright \beta =p^{1}\upharpoonright \beta =p\upharpoonright \beta .$
$p^{0}\upharpoonright \beta =p^{1}\upharpoonright \beta =p\upharpoonright \beta .$
-
(c) If
 $\sigma \in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) },$
then
$\sigma \in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) },$
then
 $\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ p^{0}\ast \sigma \right ] ,\dot {x}\left [ p^{1}\ast \sigma \right ] \right ) =i.$
$\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ p^{0}\ast \sigma \right ] ,\dot {x}\left [ p^{1}\ast \sigma \right ] \right ) =i.$
-
In the above case, we say that
![]() $p^{0}$
and
$p^{0}$
and
![]() $p^{1}$
witness that p is
$p^{1}$
witness that p is
![]() $\left ( F,\eta ,i\right ) $
-splitting at
$\left ( F,\eta ,i\right ) $
-splitting at
![]() $\beta .$
The following are some simple remarks:
$\beta .$
The following are some simple remarks:
Lemma 80 Let
![]() $F\in \left [ \alpha \right ] ^{<\omega }$
,
$F\in \left [ \alpha \right ] ^{<\omega }$
,
![]() $\eta :F\longrightarrow \omega $
,
$\eta :F\longrightarrow \omega $
,
![]() $i<2$
, and
$i<2$
, and
![]() $p\in \mathbb {P}_{\alpha }.$
$p\in \mathbb {P}_{\alpha }.$
-
1. If
 $p\in W_{i}$
then p is
$p\in W_{i}$
then p is
 $\left ( \emptyset ,\emptyset ,i\right ) $
-faithful.
$\left ( \emptyset ,\emptyset ,i\right ) $
-faithful. -
2. If p is
 $\left ( F,\eta ,i\right ) $
-faithful and
$\left ( F,\eta ,i\right ) $
-faithful and
 $q\leq _{F,\eta } ^{\ast }p,$
then q is
$q\leq _{F,\eta } ^{\ast }p,$
then q is
 $\left ( F,\eta ,i\right ) $
-faithful.
$\left ( F,\eta ,i\right ) $
-faithful. -
3. If
 $\xi \notin F$
and p is
$\xi \notin F$
and p is
 $\left ( F,\eta ,i\right ) $
-faithful then p is
$\left ( F,\eta ,i\right ) $
-faithful then p is
 $\left ( F\cup \left \{ \xi \right \} ,\eta \cup \left \{ \left ( \xi ,0\right ) \right \} ,i\right ) $
-faithful.
$\left ( F\cup \left \{ \xi \right \} ,\eta \cup \left \{ \left ( \xi ,0\right ) \right \} ,i\right ) $
-faithful.
It does not seem that the set of all
![]() $\left ( F,\eta ,i\right ) $
-splitting conditions is
$\left ( F,\eta ,i\right ) $
-splitting conditions is
![]() $( F,\eta ) ^{\ast }$
-open (below an
$( F,\eta ) ^{\ast }$
-open (below an
![]() $\left ( F,\eta ,i\right ) $
-splitting condition). Nevertheless, they are open when we restrict to an ordinal smaller than
$\left ( F,\eta ,i\right ) $
-splitting condition). Nevertheless, they are open when we restrict to an ordinal smaller than
![]() $\alpha .$
$\alpha .$
Lemma 81 Let
![]() $F\in \left [ \alpha \right ] ^{<\omega }$
with
$F\in \left [ \alpha \right ] ^{<\omega }$
with
![]() $\beta =\max ( f) +1, \eta :F\longrightarrow \omega $
,
$\beta =\max ( f) +1, \eta :F\longrightarrow \omega $
,
![]() $i<2$
and
$i<2$
and
![]() $p\in \mathbb {P}_{\alpha }$
be
$p\in \mathbb {P}_{\alpha }$
be
![]() $\left ( F,\eta ,i\right ) $
-faithful. The set
$\left ( F,\eta ,i\right ) $
-faithful. The set
![]() $D\subseteq \mathbb {P}_{\beta }$
of all
$D\subseteq \mathbb {P}_{\beta }$
of all
![]() $r\in \mathbb {P}_{\beta }$
for which there is
$r\in \mathbb {P}_{\beta }$
for which there is
![]() $\overline {r}\in \mathbb {P}_{\alpha }$
with the following properties:
$\overline {r}\in \mathbb {P}_{\alpha }$
with the following properties:
-
1.
 $\overline {r}\upharpoonright \beta =r.$
$\overline {r}\upharpoonright \beta =r.$
-
2.
 $\overline {r}\leq _{F,\eta }^{\ast }p$
(so
$\overline {r}\leq _{F,\eta }^{\ast }p$
(so
 $r\leq _{F,\eta }^{\ast }p\upharpoonright \beta $
).
$r\leq _{F,\eta }^{\ast }p\upharpoonright \beta $
). -
3.
 $\overline {r}$
is
$\overline {r}$
is
 $\left ( F,\eta ,i\right ) $
-splitting at
$\left ( F,\eta ,i\right ) $
-splitting at
 $\beta .$
$\beta .$
Is an
![]() $( F,\eta ) ^{\ast }$
-open dense below
$( F,\eta ) ^{\ast }$
-open dense below
![]() $p\upharpoonright \beta .$
$p\upharpoonright \beta .$
Proof We first prove that D is
![]() $( F,\eta ) ^{\ast }$
-open below
$( F,\eta ) ^{\ast }$
-open below
![]() $p\upharpoonright \beta .$
Let
$p\upharpoonright \beta .$
Let
![]() $r\in D$
and
$r\in D$
and
![]() $q\in \mathbb {P}_{\beta }$
such that
$q\in \mathbb {P}_{\beta }$
such that
![]() $q\leq _{F,\eta }^{\ast }r.$
Let
$q\leq _{F,\eta }^{\ast }r.$
Let
![]() $\overline {r}$
as above and
$\overline {r}$
as above and
![]() $\overline {r} _{0},\overline {r}_{1}$
witness that
$\overline {r} _{0},\overline {r}_{1}$
witness that
![]() $\overline {r}$
is
$\overline {r}$
is
![]() $\left ( F,\eta ,i\right ) $
-splitting at
$\left ( F,\eta ,i\right ) $
-splitting at
![]() $\beta $
. Define
$\beta $
. Define
-
1.
 $\overline {q}=q^{\frown }\overline {r}\upharpoonright \lbrack \beta ,\alpha ).$
$\overline {q}=q^{\frown }\overline {r}\upharpoonright \lbrack \beta ,\alpha ).$
-
2.
 $\overline {q}_{0}=q^{\frown }\overline {r}_{0}\upharpoonright \lbrack \beta ,\alpha ).$
$\overline {q}_{0}=q^{\frown }\overline {r}_{0}\upharpoonright \lbrack \beta ,\alpha ).$
-
3.
 $\overline {q}_{1}=q^{\frown }\overline {r}_{1}\upharpoonright \lbrack \beta ,\alpha ).$
$\overline {q}_{1}=q^{\frown }\overline {r}_{1}\upharpoonright \lbrack \beta ,\alpha ).$
Note that
![]() $\overline {q}\leq _{F,\eta }^{\ast }\overline {r}$
as well as
$\overline {q}\leq _{F,\eta }^{\ast }\overline {r}$
as well as
![]() $\overline {q}_{0}\leq _{F,\eta }^{\ast }\overline {r}_{0}$
and
$\overline {q}_{0}\leq _{F,\eta }^{\ast }\overline {r}_{0}$
and
![]() $\overline {q} _{1}\leq _{F,\eta }^{\ast }\overline {r}_{1}.$
Since
$\overline {q} _{1}\leq _{F,\eta }^{\ast }\overline {r}_{1}.$
Since
![]() $\overline {q}\leq _{F,\eta }^{\ast }\overline {r}$
it follows that
$\overline {q}\leq _{F,\eta }^{\ast }\overline {r}$
it follows that
![]() $\overline {q}$
is
$\overline {q}$
is
![]() $\left ( F,\eta ,i\right ) $
-faithful. It is easy to see that
$\left ( F,\eta ,i\right ) $
-faithful. It is easy to see that
![]() $\overline {q} _{0},\overline {q}_{1}$
witness that
$\overline {q} _{0},\overline {q}_{1}$
witness that
![]() $\overline {q}$
is
$\overline {q}$
is
![]() $\left ( F,\eta ,i\right ) $
-splitting at
$\left ( F,\eta ,i\right ) $
-splitting at
![]() $\beta $
.
$\beta $
.
We will now prove that D is
![]() $( F,\eta ) ^{\ast }$
-dense below
$( F,\eta ) ^{\ast }$
-dense below
![]() $p\upharpoonright \beta .$
Take an enumeration
$p\upharpoonright \beta .$
Take an enumeration
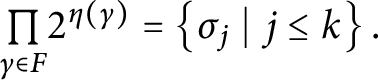 $ {\textstyle \prod \limits _{\gamma \in F}} 2^{\eta ( \gamma ) }=\left \{ \sigma _{j}\mid j\leq k\right \} .$
We will recursively construct
$ {\textstyle \prod \limits _{\gamma \in F}} 2^{\eta ( \gamma ) }=\left \{ \sigma _{j}\mid j\leq k\right \} .$
We will recursively construct
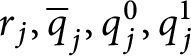 $r_{j},\overline {q}_{j},q_{j}^{0},q_{j}^{1}$
for
$r_{j},\overline {q}_{j},q_{j}^{0},q_{j}^{1}$
for
![]() $j\leq k$
such that the following conditions hold:
$j\leq k$
such that the following conditions hold:
-
1.
 $p=r_{0}.$
$p=r_{0}.$
-
2.
 $r_{j+1}\leq _{F,\eta }r_{j}$
for
$r_{j+1}\leq _{F,\eta }r_{j}$
for
 $j+1\leq k.$
$j+1\leq k.$
-
3.
 $\overline {q}_{j}\leq r_{j}\ast \sigma _{j}.$
$\overline {q}_{j}\leq r_{j}\ast \sigma _{j}.$
-
4.
 $q_{j}^{0},q_{j}^{1}\leq \overline {q}_{j}.$
$q_{j}^{0},q_{j}^{1}\leq \overline {q}_{j}.$
-
5.
 $q_{j}^{0}\upharpoonright \beta =q_{j}^{1}\upharpoonright \beta =\overline {q}_{j}\upharpoonright \beta .$
$q_{j}^{0}\upharpoonright \beta =q_{j}^{1}\upharpoonright \beta =\overline {q}_{j}\upharpoonright \beta .$
-
6.
 $\mathsf {c}_{\mathsf {min}}(\dot {x}[q_{j}^{0}],\dot {x}[q_{j}^{1}])=i.$
$\mathsf {c}_{\mathsf {min}}(\dot {x}[q_{j}^{0}],\dot {x}[q_{j}^{1}])=i.$
-
7.
 $r_{j+1}\ast \sigma _{j}=\overline {q}_{j}$
for
$r_{j+1}\ast \sigma _{j}=\overline {q}_{j}$
for
 $j+1\leq j.$
$j+1\leq j.$
The construction is as follows: we start with
![]() $p=r_{0}.$
Since
$p=r_{0}.$
Since
![]() $r_{0} \ast \sigma _{0}\leq p$
and
$r_{0} \ast \sigma _{0}\leq p$
and
![]() $p\in W_{i},$
there is
$p\in W_{i},$
there is
![]() $\overline {q}_{0}\leq r_{0}\ast \sigma _{0}$
and
$\overline {q}_{0}\leq r_{0}\ast \sigma _{0}$
and
![]() $q_{0}^{0},q_{0}^{1}\leq \overline {q}_{0}$
such that
$q_{0}^{0},q_{0}^{1}\leq \overline {q}_{0}$
such that
![]() $q_{0}^{0}\upharpoonright \beta =q_{0}^{1}\upharpoonright \beta =\overline {q} _{0}\upharpoonright \beta $
and
$q_{0}^{0}\upharpoonright \beta =q_{0}^{1}\upharpoonright \beta =\overline {q} _{0}\upharpoonright \beta $
and
![]() $\mathsf {c}_{\mathsf {min}}(\dot {x}[q_{0} ^{0}],\dot {x}[q_{0}^{1}])=i.$
Now, assume we are at step
$\mathsf {c}_{\mathsf {min}}(\dot {x}[q_{0} ^{0}],\dot {x}[q_{0}^{1}])=i.$
Now, assume we are at step
![]() $j,$
we will define the items at step
$j,$
we will define the items at step
![]() $j+1.$
We first find
$j+1.$
We first find
![]() $r_{j+1}$
such that
$r_{j+1}$
such that
![]() $r_{j+1} \leq _{F,\eta }r_{j}$
and
$r_{j+1} \leq _{F,\eta }r_{j}$
and
![]() $r_{j+1}\ast \sigma _{j}=\overline {q}_{j}.$
Since
$r_{j+1}\ast \sigma _{j}=\overline {q}_{j}.$
Since
![]() $r_{j+1}\ast \sigma _{j+1}\leq r_{j+1}$
and
$r_{j+1}\ast \sigma _{j+1}\leq r_{j+1}$
and
![]() $r_{j+1}\in W_{i},$
we know that there is
$r_{j+1}\in W_{i},$
we know that there is
![]() $\overline {q}_{j+1}\leq r_{j+1}\ast \sigma _{j+1}$
and
$\overline {q}_{j+1}\leq r_{j+1}\ast \sigma _{j+1}$
and
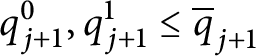 $q_{j+1} ^{0},q_{j+1}^{1}\leq \overline {q}_{j+1}$
such that
$q_{j+1} ^{0},q_{j+1}^{1}\leq \overline {q}_{j+1}$
such that
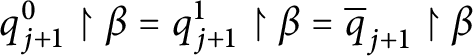 $q_{j+1}^{0}\upharpoonright \beta =q_{j+1}^{1}\upharpoonright \beta =\overline {q}_{j+1}\upharpoonright \beta $
and
$q_{j+1}^{0}\upharpoonright \beta =q_{j+1}^{1}\upharpoonright \beta =\overline {q}_{j+1}\upharpoonright \beta $
and
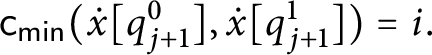 $\mathsf {c}_{\mathsf {min}}(\dot {x}[q_{j+1}^{0}],\dot {x}[q_{j+1}^{1}])=i.$
$\mathsf {c}_{\mathsf {min}}(\dot {x}[q_{j+1}^{0}],\dot {x}[q_{j+1}^{1}])=i.$
Now, let q such that
![]() $q\leq _{F,\eta }r_{k}$
and
$q\leq _{F,\eta }r_{k}$
and
![]() $q\ast \sigma _{k}=\overline {q}_{k}.$
We claim that
$q\ast \sigma _{k}=\overline {q}_{k}.$
We claim that
![]() $q\ast \sigma _{j}\leq \overline {q}_{j}$
for every
$q\ast \sigma _{j}\leq \overline {q}_{j}$
for every
![]() $j\leq k.$
The statement is clear for
$j\leq k.$
The statement is clear for
![]() $j=k.$
Given
$j=k.$
Given
![]() $j<k$
, we have that
$j<k$
, we have that
![]() $q\leq _{F,\eta }r_{j+1},$
so
$q\leq _{F,\eta }r_{j+1},$
so
![]() $q\ast \sigma _{j}\leq r_{j+1}\ast \sigma _{j}=\overline {q}_{j}$
and we are done.
$q\ast \sigma _{j}\leq r_{j+1}\ast \sigma _{j}=\overline {q}_{j}$
and we are done.
By the definition by cases lemma (Lemma 45), we can find
![]() $\dot {a},\dot {b}$
two
$\dot {a},\dot {b}$
two
![]() $\mathbb {P}_{\beta }$
-names such that if
$\mathbb {P}_{\beta }$
-names such that if
![]() $j\leq k,$
then the following holds:
$j\leq k,$
then the following holds:
-
1.
 $q\ast \sigma _{j}\Vdash $
“
$q\ast \sigma _{j}\Vdash $
“
 $\dot {a}=q_{j}^{0} \upharpoonright \lbrack \delta ,\alpha )$
.”
$\dot {a}=q_{j}^{0} \upharpoonright \lbrack \delta ,\alpha )$
.” -
2.
 $q\ast \sigma _{j}\Vdash $
“
$q\ast \sigma _{j}\Vdash $
“
 $\dot {b}=q_{j}^{1} \upharpoonright \lbrack \delta ,\alpha )$
.”
$\dot {b}=q_{j}^{1} \upharpoonright \lbrack \delta ,\alpha )$
.”
We now define
![]() $\overline {p}=\left ( q\upharpoonright \beta \right ) ^{\frown }p\upharpoonright \lbrack \beta ,\alpha ).$
We claim that
$\overline {p}=\left ( q\upharpoonright \beta \right ) ^{\frown }p\upharpoonright \lbrack \beta ,\alpha ).$
We claim that
![]() $\overline {p}$
is
$\overline {p}$
is
![]() $\left ( F,\eta ,i\right ) $
-splitting at
$\left ( F,\eta ,i\right ) $
-splitting at
![]() $\beta $
. Let
$\beta $
. Let
![]() $p_{0}=\left ( q\upharpoonright \beta \right ){} ^{\frown }\dot {a}$
and
$p_{0}=\left ( q\upharpoonright \beta \right ){} ^{\frown }\dot {a}$
and
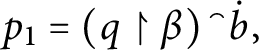 $p_{1}=\left ( q\upharpoonright \beta \right ){} ^{\frown }\dot {b},$
we will show that
$p_{1}=\left ( q\upharpoonright \beta \right ){} ^{\frown }\dot {b},$
we will show that
![]() $p_{0}$
and
$p_{0}$
and
![]() $p_{1}$
have the desired properties.
$p_{1}$
have the desired properties.
It is clear that
![]() $p_{0},p_{1}\leq \overline {p}$
, and
$p_{0},p_{1}\leq \overline {p}$
, and
![]() $p_{0}\upharpoonright \beta =p_{1}\upharpoonright \beta =\overline {p}\upharpoonright \beta .$
Now, let
$p_{0}\upharpoonright \beta =p_{1}\upharpoonright \beta =\overline {p}\upharpoonright \beta .$
Now, let
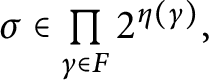 $\sigma \in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) },$
we need to prove that
$\sigma \in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) },$
we need to prove that
![]() $\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ p_{0}\ast \sigma \right ] ,\dot {x}\left [ p_{1}\ast \sigma \right ] \right ) =i.$
Let
$\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ p_{0}\ast \sigma \right ] ,\dot {x}\left [ p_{1}\ast \sigma \right ] \right ) =i.$
Let
![]() $j\leq k$
such that
$j\leq k$
such that
![]() $\sigma =\sigma _{j}.$
Since
$\sigma =\sigma _{j}.$
Since
![]() $q\ast \sigma _{j}\leq \overline {q}_{j},$
we get that
$q\ast \sigma _{j}\leq \overline {q}_{j},$
we get that
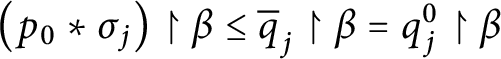 $\left ( p_{0}\ast \sigma _{j}\right ) \upharpoonright \beta \leq \overline {q}_{j}\upharpoonright \beta =q_{j} ^{0}\upharpoonright \beta $
and
$\left ( p_{0}\ast \sigma _{j}\right ) \upharpoonright \beta \leq \overline {q}_{j}\upharpoonright \beta =q_{j} ^{0}\upharpoonright \beta $
and
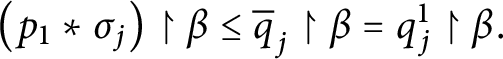 $\left ( p_{1}\ast \sigma _{j}\right ) \upharpoonright \beta \leq \overline {q}_{j}\upharpoonright \beta =q_{j} ^{1}\upharpoonright \beta .$
It follows by the definition of
$\left ( p_{1}\ast \sigma _{j}\right ) \upharpoonright \beta \leq \overline {q}_{j}\upharpoonright \beta =q_{j} ^{1}\upharpoonright \beta .$
It follows by the definition of
![]() $\dot {a}$
and
$\dot {a}$
and
![]() $\dot {b}$
that
$\dot {b}$
that
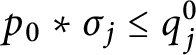 $p_{0}\ast \sigma _{j}\leq q_{j}^{0}$
and
$p_{0}\ast \sigma _{j}\leq q_{j}^{0}$
and
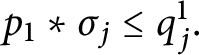 $p_{1}\ast \sigma _{j}\leq q_{j}^{1}.$
Since
$p_{1}\ast \sigma _{j}\leq q_{j}^{1}.$
Since
 $\mathsf {c}_{\mathsf {min}}(\dot {x}[q_{j}^{0} ],\dot {x}[q_{j}^{1}])=i,$
we get that
$\mathsf {c}_{\mathsf {min}}(\dot {x}[q_{j}^{0} ],\dot {x}[q_{j}^{1}])=i,$
we get that
![]() $\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ p_{0}\ast \sigma \right ] ,\dot {x}\left [ p_{1}\ast \sigma \right ] \right ) =i.$
▪
$\mathsf {c}_{\mathsf {min}}\left ( \dot {x}\left [ p_{0}\ast \sigma \right ] ,\dot {x}\left [ p_{1}\ast \sigma \right ] \right ) =i.$
▪
We will now prove the following:
Lemma 82 Let
![]() $F\in \left [ \alpha \right ] ^{<\omega }$
with
$F\in \left [ \alpha \right ] ^{<\omega }$
with
![]() $\beta =\max ( f) +1, \eta :F\longrightarrow \omega $
,
$\beta =\max ( f) +1, \eta :F\longrightarrow \omega $
,
![]() $i<2$
and
$i<2$
and
![]() $p\in \mathbb {P}_{\alpha }$
be
$p\in \mathbb {P}_{\alpha }$
be
![]() $\left ( F,\eta ,i\right ) $
-splitting at
$\left ( F,\eta ,i\right ) $
-splitting at
![]() $\beta .$
Pick
$\beta .$
Pick
![]() $\xi \in F$
and define
$\xi \in F$
and define
![]() $\eta ^{\prime }:F\longrightarrow \omega $
where
$\eta ^{\prime }:F\longrightarrow \omega $
where
![]() $\eta ^{\prime }\left ( \xi \right ) =\eta \left ( \xi \right ) +1$
and
$\eta ^{\prime }\left ( \xi \right ) =\eta \left ( \xi \right ) +1$
and
![]() $\eta ^{\prime }( \gamma ) =\eta ( \gamma ) $
whenever
$\eta ^{\prime }( \gamma ) =\eta ( \gamma ) $
whenever
![]() $\gamma \neq \xi .$
There is
$\gamma \neq \xi .$
There is
![]() $r\in \mathbb {P}_{\alpha }$
with the following properties:
$r\in \mathbb {P}_{\alpha }$
with the following properties:
-
1.
 $r\upharpoonright \beta =p\upharpoonright \beta .$
$r\upharpoonright \beta =p\upharpoonright \beta .$
-
2. r is
 $\left ( F,\eta ^{\prime },i\right ) $
-faithful.
$\left ( F,\eta ^{\prime },i\right ) $
-faithful.
Proof We know that p is
![]() $\left ( F,\eta ,i\right ) $
-splitting at
$\left ( F,\eta ,i\right ) $
-splitting at
![]() $\beta .$
Let
$\beta .$
Let
![]() $p^{0}$
and
$p^{0}$
and
![]() $p^{1}$
witness that p is
$p^{1}$
witness that p is
![]() $\left ( F,\eta ,i\right ) $
-splitting at
$\left ( F,\eta ,i\right ) $
-splitting at
![]() $\beta $
. For every
$\beta $
. For every
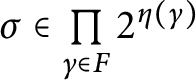 $\sigma \in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }$
and for each
$\sigma \in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }$
and for each
![]() $j<2$
let
$j<2$
let
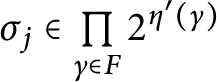 $\sigma _{j}\in \prod \limits _{\gamma \in F}2^{\eta ^{\prime }( \gamma ) }$
such that
$\sigma _{j}\in \prod \limits _{\gamma \in F}2^{\eta ^{\prime }( \gamma ) }$
such that
![]() $\sigma _{j}( \beta ) =\sigma ( \beta ) ^{\frown }j$
and
$\sigma _{j}( \beta ) =\sigma ( \beta ) ^{\frown }j$
and
![]() $\sigma _{j}( \gamma ) =\sigma ( \gamma ) $
for every
$\sigma _{j}( \gamma ) =\sigma ( \gamma ) $
for every
![]() $\gamma \neq \beta .$
Let
$\gamma \neq \beta .$
Let
![]() $\dot {a}$
be a
$\dot {a}$
be a
![]() $\mathbb {P}_{\beta }$
-name such that
$\mathbb {P}_{\beta }$
-name such that
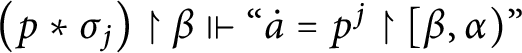 $\left ( p\ast \sigma _{j}\right ) \upharpoonright \beta \Vdash \text{``}\dot {a}=p^{j}\upharpoonright \lbrack \beta ,\alpha )\text{''}$
for every
$\left ( p\ast \sigma _{j}\right ) \upharpoonright \beta \Vdash \text{``}\dot {a}=p^{j}\upharpoonright \lbrack \beta ,\alpha )\text{''}$
for every
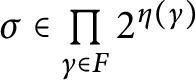 $\sigma \in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }$
and for each
$\sigma \in \prod \limits _{\gamma \in F}2^{\eta ( \gamma ) }$
and for each
![]() $j<2$
(such name exists by the definition by cases lemma (Lemma 45)). The condition
$j<2$
(such name exists by the definition by cases lemma (Lemma 45)). The condition
![]() $r=\left ( p\upharpoonright \beta \right ) ^{\frown }\dot {a}$
has the desired properties.▪
$r=\left ( p\upharpoonright \beta \right ) ^{\frown }\dot {a}$
has the desired properties.▪
We can now prove that the
![]() $\mathsf {c}_{\mathsf {min}}$
-covering is preserved at limit steps:
$\mathsf {c}_{\mathsf {min}}$
-covering is preserved at limit steps:
Proposition 83 Let
![]() $\alpha $
be a limit ordinal and assume
$\alpha $
be a limit ordinal and assume
![]() $\dot {x}$
is a
$\dot {x}$
is a
![]() $\mathbb {P} _{\alpha }$
-name for a real that was not added by
$\mathbb {P} _{\alpha }$
-name for a real that was not added by
![]() $\mathbb {P}_{\beta }$
for every
$\mathbb {P}_{\beta }$
for every
![]() $\beta <\alpha .$
If
$\beta <\alpha .$
If
![]() $p\in \mathbb {P}_{\alpha },$
then there are
$p\in \mathbb {P}_{\alpha },$
then there are
![]() $q\leq p$
and
$q\leq p$
and
![]() $S\in V$
a
$S\in V$
a
![]() $\mathsf {c}_{\mathsf {min}}$
-monochromatic tree such that
$\mathsf {c}_{\mathsf {min}}$
-monochromatic tree such that
![]() $q\Vdash \text{``}\dot {x}\in \left [ S\right ].\text{''}$
$q\Vdash \text{``}\dot {x}\in \left [ S\right ].\text{''}$
Proof By Lemma 78, we may assume that there is
![]() $i<2$
such that
$i<2$
such that
![]() $p\in W_{i}.$
Let M be a countable elementary submodel of
$p\in W_{i}.$
Let M be a countable elementary submodel of
![]() $\mathsf{H}( \kappa) $
(for a big large enough
$\mathsf{H}( \kappa) $
(for a big large enough
![]() $\kappa $
) such that
$\kappa $
) such that
![]() $\alpha ,\mathbb {P}_{\alpha },p,\dot {x}\in M.$
Let
$\alpha ,\mathbb {P}_{\alpha },p,\dot {x}\in M.$
Let
![]() $L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
be suitable for
$L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
be suitable for
![]() $\left ( M,\alpha \right ) $
with the following properties:
$\left ( M,\alpha \right ) $
with the following properties:
For every
![]() $l<4,$
define
$l<4,$
define
![]() $A_{l}=\{n\mid n=_{4}l\}$
(where
$A_{l}=\{n\mid n=_{4}l\}$
(where
![]() $n=_{4}l$
means that n is equal to l mod
$n=_{4}l$
means that n is equal to l mod
![]() $4$
). We now find
$4$
). We now find
![]() $L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
$L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
suitable for
![]() $\left ( M,\alpha \right ) $
with the following extra properties:
$\left ( M,\alpha \right ) $
with the following extra properties:
-
1.
 $F_{0}=\emptyset $
and
$F_{0}=\emptyset $
and
 $\eta _{0}=\emptyset .$
$\eta _{0}=\emptyset .$
-
2. Let
 $n\in \omega $
and assume
$n\in \omega $
and assume
 $F_{n}$
and
$F_{n}$
and
 $\eta _{n}$
are already defined. We wish to define
$\eta _{n}$
are already defined. We wish to define
 $F_{n+1}$
and
$F_{n+1}$
and
 $\eta _{n+1}.$
$\eta _{n+1}.$
-
(a) Case
 $n\in A_{0}.$
$n\in A_{0}.$
Let
 $F_{n+1}=F_{n}$
and
$F_{n+1}=F_{n}$
and
 $\eta _{n+1}=\eta _{n}.$
$\eta _{n+1}=\eta _{n}.$
-
(b) Case
 $n\in A_{1}.$
$n\in A_{1}.$
Let
 $F_{n+1}=F_{n}$
and there is a unique
$F_{n+1}=F_{n}$
and there is a unique
 $\xi \in F_{n}$
such that
$\xi \in F_{n}$
such that
 $\eta _{n+1}\left ( \xi \right ) =\eta _{n}\left ( \xi \right ) +1$
while
$\eta _{n+1}\left ( \xi \right ) =\eta _{n}\left ( \xi \right ) +1$
while
 $\eta _{n+1}( \gamma ) =\eta _{n}( \gamma ) $
in case
$\eta _{n+1}( \gamma ) =\eta _{n}( \gamma ) $
in case
 $\gamma \neq \xi .$
$\gamma \neq \xi .$
-
(c) Case
 $n\in A_{2}.$
$n\in A_{2}.$
Let
 $F_{n+1}=F_{n}$
and
$F_{n+1}=F_{n}$
and
 $\eta _{n+1}=\eta _{n}.$
$\eta _{n+1}=\eta _{n}.$
-
(d) Case
 $n\in A_{3}.$
$n\in A_{3}.$
In here,
 $\left \vert F_{n+1}\right \vert =\left \vert F_{n}\right \vert +1, \eta _{n+1}\upharpoonright F_{n}=\eta _{n}\upharpoonright F_{n}$
and in the new point
$\left \vert F_{n+1}\right \vert =\left \vert F_{n}\right \vert +1, \eta _{n+1}\upharpoonright F_{n}=\eta _{n}\upharpoonright F_{n}$
and in the new point
 $\eta _{n+1}$
takes value
$\eta _{n+1}$
takes value
 $0.$
$0.$
-
We now recursively define a tree
![]() $Y\subseteq 2^{<\omega }$
as follows:
$Y\subseteq 2^{<\omega }$
as follows:
-
1.
 $\emptyset \in Y.$
$\emptyset \in Y.$
-
2. Let
 $s\in Y_{n}.$
$s\in Y_{n}.$
-
(a) If
 $F_{n+1}=F_{n},$
then
$F_{n+1}=F_{n},$
then
 $s^{\frown }0$
is the only immediate successor of s in
$s^{\frown }0$
is the only immediate successor of s in
 $Y.$
$Y.$
-
(b) If
 $F_{n+1}\neq F_{n},$
then
$F_{n+1}\neq F_{n},$
then
 $s^{\frown }0, s^{\frown }1\in Y.$
$s^{\frown }0, s^{\frown }1\in Y.$
-
We now recursively construct an
![]() $\alpha $
-fusion tree
$\alpha $
-fusion tree
![]() $T=\left \{ p_{s}\mid s\in Y\right \} \subseteq \mathbb {P}_{\alpha }\cap M$
with the following propertiesFootnote
7
:
$T=\left \{ p_{s}\mid s\in Y\right \} \subseteq \mathbb {P}_{\alpha }\cap M$
with the following propertiesFootnote
7
:
-
1.
 $p_{\emptyset }\leq p.$
$p_{\emptyset }\leq p.$
-
2. If
 $s\in Y_{n},$
then
$s\in Y_{n},$
then
 $p_{s}$
is
$p_{s}$
is
 $(F_{n},\eta _{n},i)$
-faithful. Define
$(F_{n},\eta _{n},i)$
-faithful. Define
 $K\left ( p_{s}\right ) =\bigcup \{\dot {x}\left [ p_{s}\ast \sigma \right ] \mid \sigma \in \prod \limits _{\gamma \in F_{n}}2^{\eta _{n}( \gamma ) }\}.$
$K\left ( p_{s}\right ) =\bigcup \{\dot {x}\left [ p_{s}\ast \sigma \right ] \mid \sigma \in \prod \limits _{\gamma \in F_{n}}2^{\eta _{n}( \gamma ) }\}.$
-
3. If
 $s\in Y_{n}$
and
$s\in Y_{n}$
and
 $j\in suc_{Y}( s) ,$
then
$j\in suc_{Y}( s) ,$
then
 $p_{s^{\frown }j}\leq _{F_{n},\eta _{n}}^{\ast }p_{s}.$
$p_{s^{\frown }j}\leq _{F_{n},\eta _{n}}^{\ast }p_{s}.$
-
4. If
 $s\in Y$
and
$s\in Y$
and
 $j\in suc_{Y}( s) ,$
then
$j\in suc_{Y}( s) ,$
then
 $K\left ( p_{s^{\frown }j}\right ) $
is an end-extension of
$K\left ( p_{s^{\frown }j}\right ) $
is an end-extension of
 $K\left ( p_{s}\right ) .$
$K\left ( p_{s}\right ) .$
-
5. If
 $s\in Y$
and
$s\in Y$
and
 $s^{\frown }0, s^{\frown }1\in Y,$
then
$s^{\frown }0, s^{\frown }1\in Y,$
then
 $K\left ( p_{s^{\frown }0}\right ) $
and
$K\left ( p_{s^{\frown }0}\right ) $
and
 $K\left ( p_{s^{\frown }1}\right ) $
are two end-extensions of
$K\left ( p_{s^{\frown }1}\right ) $
are two end-extensions of
 $K\left ( p_{s}\right ) $
and
$K\left ( p_{s}\right ) $
and
 $\mathsf {c}_{\mathsf {min} }\left ( K\left ( p_{s^{\frown }0}\right ) ,K\left ( p_{s^{\frown }1}\right ) \right ) =i.$
$\mathsf {c}_{\mathsf {min} }\left ( K\left ( p_{s^{\frown }0}\right ) ,K\left ( p_{s^{\frown }1}\right ) \right ) =i.$
-
6. Let
 $n\in \omega $
and assume
$n\in \omega $
and assume
 $\left \{ p_{t}\mid t\in Y_{n}\right \} $
has already been constructed. We will now build the items for the nodes in
$\left \{ p_{t}\mid t\in Y_{n}\right \} $
has already been constructed. We will now build the items for the nodes in
 $Y_{n+1}.$
Let
$Y_{n+1}.$
Let
 $s\in Y_{n},$
we will define
$s\in Y_{n},$
we will define
 $p_{s^{\frown }l}$
for
$p_{s^{\frown }l}$
for
 $l\in suc_{Y}( s) .$
We are are assuming that
$l\in suc_{Y}( s) .$
We are are assuming that
 $\left \{ p_{t}\mid t\in Y_{n}\right \} $
is a (finite)
$\left \{ p_{t}\mid t\in Y_{n}\right \} $
is a (finite)
 $\alpha $
-fusion tree and
$\alpha $
-fusion tree and
 $p_{s}$
is
$p_{s}$
is
 $(F_{n},\eta _{n},i)$
-faithful. Let
$(F_{n},\eta _{n},i)$
-faithful. Let
 $\beta =\max \left ( F_{n}\right ) +1.$
$\beta =\max \left ( F_{n}\right ) +1.$
-
(a) Case
 $n\in A_{0}$
(recall that
$n\in A_{0}$
(recall that
 $F_{n+1}=F_{n}$
,
$F_{n+1}=F_{n}$
,
 $\eta _{n+1}=\eta _{n}$
and
$\eta _{n+1}=\eta _{n}$
and
 $suc_{Y}( s) =\left \{ 0\right \} $
).
$suc_{Y}( s) =\left \{ 0\right \} $
).We want
 $p_{s^{\frown }0}$
to be
$p_{s^{\frown }0}$
to be
 $\left ( F_{n+1},\eta _{n+1},i\right ) $
-splitting at
$\left ( F_{n+1},\eta _{n+1},i\right ) $
-splitting at
 $\beta .$
This is possible by Lemmas 65 and 81.
$\beta .$
This is possible by Lemmas 65 and 81. -
(b) Case
 $n\in A_{1}$
(recall that
$n\in A_{1}$
(recall that
 $F_{n+1}=F_{n}$
,
$F_{n+1}=F_{n}$
,
 $\eta _{n+1}$
increases by one in just one point and
$\eta _{n+1}$
increases by one in just one point and
 $suc_{Y}( s) = \{ 0 \} $
).
$suc_{Y}( s) = \{ 0 \} $
).In here, we know that
 $n-1\in A_{0},$
so by the previous case we know that
$n-1\in A_{0},$
so by the previous case we know that
 $p_{s}$
is
$p_{s}$
is
 $( F_{n},\eta _{n},i ) $
-splitting at
$( F_{n},\eta _{n},i ) $
-splitting at
 $\beta .$
We want
$\beta .$
We want
 $p_{s^{\frown }0}$
such that
$p_{s^{\frown }0}$
such that
 $p_{s^{\frown }0}\upharpoonright \beta =p_{s}\upharpoonright \beta $
and
$p_{s^{\frown }0}\upharpoonright \beta =p_{s}\upharpoonright \beta $
and
 $p_{s^{\frown }0}$
is
$p_{s^{\frown }0}$
is
 $\left ( F_{n+1} ,\eta _{n+1},i\right ) $
-faithful. This is possible by Lemma 82.
$\left ( F_{n+1} ,\eta _{n+1},i\right ) $
-faithful. This is possible by Lemma 82. -
(c) Case
 $n\in A_{2}$
(recall that
$n\in A_{2}$
(recall that
 $F_{n+1}=F_{n}$
,
$F_{n+1}=F_{n}$
,
 $\eta _{n+1}=\eta _{n}$
and
$\eta _{n+1}=\eta _{n}$
and
 $suc_{Y}( s) =\left \{ 0\right \} $
).
$suc_{Y}( s) =\left \{ 0\right \} $
).We want
 $p_{s^{\frown }0}$
to be
$p_{s^{\frown }0}$
to be
 $\left ( F_{n+1},\eta _{n+1},i\right ) $
-splitting at
$\left ( F_{n+1},\eta _{n+1},i\right ) $
-splitting at
 $\beta .$
This is possible by and Lemmas 65 and 81 (this point is the same as in the case where
$\beta .$
This is possible by and Lemmas 65 and 81 (this point is the same as in the case where
 $n\in A_{0}$
).
$n\in A_{0}$
). -
(d) Case
 $n\in A_{3}$
(recall that
$n\in A_{3}$
(recall that
 $\left \vert F_{n+1}\right \vert =\left \vert F_{n}\right \vert +1$
,
$\left \vert F_{n+1}\right \vert =\left \vert F_{n}\right \vert +1$
,
 $\eta _{n+1}\upharpoonright F_{n}=\eta _{n}\upharpoonright F_{n}$
in the new point
$\eta _{n+1}\upharpoonright F_{n}=\eta _{n}\upharpoonright F_{n}$
in the new point
 $\eta _{n+1}$
takes value
$\eta _{n+1}$
takes value
 $0$
and
$0$
and
 $suc_{Y}( s) =\left \{ 0,1\right \} $
).
$suc_{Y}( s) =\left \{ 0,1\right \} $
).In here, we know that
 $n-1\in A_{2},$
so by the previous case, we know that
$n-1\in A_{2},$
so by the previous case, we know that
 $p_{s}$
is
$p_{s}$
is
 $\left ( F_{n},\eta _{n},i\right ) $
-splitting at
$\left ( F_{n},\eta _{n},i\right ) $
-splitting at
 $\beta .$
For each
$\beta .$
For each
 $s\in Y_{n},$
choose
$s\in Y_{n},$
choose
 $p_{s}^{0}$
and
$p_{s}^{0}$
and
 $p_{s}^{1}$
that witness that
$p_{s}^{1}$
that witness that
 $p_{s}$
is
$p_{s}$
is
 $\left ( F_{n},\eta _{n},i\right ) $
-splitting at
$\left ( F_{n},\eta _{n},i\right ) $
-splitting at
 $\beta .$
$\beta .$
Let
 $\widetilde {T}= \{ p_{t}\upharpoonright \beta \mid t\in Y_{\leq n}\} ,$
which we know is a
$\widetilde {T}= \{ p_{t}\upharpoonright \beta \mid t\in Y_{\leq n}\} ,$
which we know is a
 $\beta $
-fusion tree. Apply Lemma 65 to find
$\beta $
-fusion tree. Apply Lemma 65 to find
 $\{\overline {p}_{t^{\frown }l}\mid t\in Y_{n}\wedge l\in 2\}$
a
$\{\overline {p}_{t^{\frown }l}\mid t\in Y_{n}\wedge l\in 2\}$
a
 $\beta $
-fusion tree extending
$\beta $
-fusion tree extending
 $\widetilde {T}$
(in the statement of Lemma 65, we can take
$\widetilde {T}$
(in the statement of Lemma 65, we can take
 $D_{t}=\mathbb {P} _{\beta }$
for every
$D_{t}=\mathbb {P} _{\beta }$
for every
 $t\in Y_{n}$
). Define
$t\in Y_{n}$
). Define
 $p_{s^{\frown }0}=\overline {p}_{s^{\frown }0} ^{\frown }p_{s}^{0}\upharpoonright \lbrack \beta ,\alpha )$
and
$p_{s^{\frown }0}=\overline {p}_{s^{\frown }0} ^{\frown }p_{s}^{0}\upharpoonright \lbrack \beta ,\alpha )$
and
 $p_{s^{\frown }1}=\overline {p}_{s^{\frown }1} ^{\frown }p_{s}^{1} \upharpoonright \lbrack \beta ,\alpha ).$
$p_{s^{\frown }1}=\overline {p}_{s^{\frown }1} ^{\frown }p_{s}^{1} \upharpoonright \lbrack \beta ,\alpha ).$
-
Using the faithfulness of the conditions, it is easy to see that
![]() $K\left ( p_{s}\right ) $
is an i-monochromatic tree. Furthermore, we know that
$K\left ( p_{s}\right ) $
is an i-monochromatic tree. Furthermore, we know that
![]() $K\left ( p_{s^{\frown }0}\right ) $
and
$K\left ( p_{s^{\frown }0}\right ) $
and
![]() $K\left ( p_{s^{\frown }1}\right ) $
are two end-extensions of
$K\left ( p_{s^{\frown }1}\right ) $
are two end-extensions of
![]() $K\left ( p_{s}\right ) $
and
$K\left ( p_{s}\right ) $
and
![]() $\mathsf {c} _{\mathsf {min}}\left ( K\left ( p_{s^{\frown }0}\right ) ,K\left ( p_{s^{\frown }1}\right ) \right ) =i.$
In this way,
$\mathsf {c} _{\mathsf {min}}\left ( K\left ( p_{s^{\frown }0}\right ) ,K\left ( p_{s^{\frown }1}\right ) \right ) =i.$
In this way,
 $K= {\textstyle \bigcup \limits _{s\in Y}} K\left ( p_{s}\right ) $
is an i-monochromatic tree, which is an element of V. By Lemma 62, there is
$K= {\textstyle \bigcup \limits _{s\in Y}} K\left ( p_{s}\right ) $
is an i-monochromatic tree, which is an element of V. By Lemma 62, there is
![]() $\overline {p}\in \mathbb {P}_{\alpha }$
compatible with T and
$\overline {p}\in \mathbb {P}_{\alpha }$
compatible with T and
![]() $\dot {R}$
a name for a branch through T such that
$\dot {R}$
a name for a branch through T such that
![]() $\overline {p}$
forces
$\overline {p}$
forces
![]() $\dot {R}$
to be contained in the generic filter. It follows that
$\dot {R}$
to be contained in the generic filter. It follows that
![]() $\overline {p}\Vdash \text{``}\dot {x}\in [ K ], \text{''}$
which is what we wanted.▪
$\overline {p}\Vdash \text{``}\dot {x}\in [ K ], \text{''}$
which is what we wanted.▪
After all our hard work, we can finally prove the main result of the paper:
Theorem 84 The inequality
![]() $\mathfrak {hm<u}$
is consistent with the axioms of
$\mathfrak {hm<u}$
is consistent with the axioms of
![]() $\mathsf {ZFC}$
.
$\mathsf {ZFC}$
.
Proof We start with a model V of the Generalized Continuum Hypothesis. We perform a countable support iteration
![]() $\langle \mathbb {P}_{\alpha },\mathbb {\dot {Q} }_{\alpha }\mid \alpha \leq \omega _{2}\rangle $
such that if
$\langle \mathbb {P}_{\alpha },\mathbb {\dot {Q} }_{\alpha }\mid \alpha \leq \omega _{2}\rangle $
such that if
![]() $\alpha <\omega _{2}$
then
$\alpha <\omega _{2}$
then
![]() $\mathbb {P}_{\alpha }\Vdash \text{``}\mathbb {\dot {Q}}_{\alpha }=\mathbb {S(} \mathcal {\dot {U}}_{\alpha }\mathcal {)}\text{''}$
where
$\mathbb {P}_{\alpha }\Vdash \text{``}\mathbb {\dot {Q}}_{\alpha }=\mathbb {S(} \mathcal {\dot {U}}_{\alpha }\mathcal {)}\text{''}$
where
![]() $\mathcal {\dot {U}}_{\alpha }$
is a
$\mathcal {\dot {U}}_{\alpha }$
is a
![]() $\mathbb {P}_{\alpha }$
-name for an ultrafilter. Furthermore, with a carefully chosen book-keeping devise we can make sure that
$\mathbb {P}_{\alpha }$
-name for an ultrafilter. Furthermore, with a carefully chosen book-keeping devise we can make sure that
![]() $\mathbb {P}_{\omega _{2}}\Vdash \text{``}\mathfrak {u}=\omega _{2}.\text{''}$
By the results in the last sections, we know that
$\mathbb {P}_{\omega _{2}}\Vdash \text{``}\mathfrak {u}=\omega _{2}.\text{''}$
By the results in the last sections, we know that
![]() $\mathbb {P}_{\omega _{2}}$
preserves
$\mathbb {P}_{\omega _{2}}$
preserves
![]() $\mathsf {c}_{\mathsf {min}}$
-covering, so
$\mathsf {c}_{\mathsf {min}}$
-covering, so
![]() $\mathbb {P}_{\omega _{2} }\Vdash \text{``}\mathfrak {hm}=\omega _{1}.\text{''}$
▪
$\mathbb {P}_{\omega _{2} }\Vdash \text{``}\mathfrak {hm}=\omega _{1}.\text{''}$
▪
7
 $\mathsf {MAD}$
families in the Shelah model
$\mathsf {MAD}$
families in the Shelah model
By the Shelah model, we mean an iteration as in the last theorem. We already know that
![]() $\mathfrak {hm}=\omega _{1}$
holds in such model, so all the cardinal invariants in the Cichoń diagram are small. Furthermore, in that model
$\mathfrak {hm}=\omega _{1}$
holds in such model, so all the cardinal invariants in the Cichoń diagram are small. Furthermore, in that model
![]() $\mathfrak {u=} \omega _{2}$
and
$\mathfrak {u=} \omega _{2}$
and
![]() $\mathfrak {i}=\omega _{1}$
(see [Reference Shelah13]). The only one of the usual cardinal invariants that is missing to compute
$\mathfrak {i}=\omega _{1}$
(see [Reference Shelah13]). The only one of the usual cardinal invariants that is missing to compute
![]() $\mathfrak {a}.$
In this last section, we will prove that there is a
$\mathfrak {a}.$
In this last section, we will prove that there is a
![]() $\mathsf {MAD}$
family of size
$\mathsf {MAD}$
family of size
![]() $\omega _{1}$
in the Shelah model. As mentioned in the introduction, in recent work with Cruz-Chapital et al., we obtained a different proof of this result (see [Reference Ishiu12]).
$\omega _{1}$
in the Shelah model. As mentioned in the introduction, in recent work with Cruz-Chapital et al., we obtained a different proof of this result (see [Reference Ishiu12]).
Let
![]() $f,g\in \omega ^{\omega }$
, define
$f,g\in \omega ^{\omega }$
, define
![]() $f\leq ^{\ast }g$
if and only if
$f\leq ^{\ast }g$
if and only if
![]() $f( n) \leq g( n) $
for all
$f( n) \leq g( n) $
for all
![]() $n\in \omega $
except finitely many. A family
$n\in \omega $
except finitely many. A family
![]() $\mathcal {D}\subseteq \omega ^{\omega }$
is a dominating family if for every
$\mathcal {D}\subseteq \omega ^{\omega }$
is a dominating family if for every
![]() $f\in \omega ^{\omega }$
, there is
$f\in \omega ^{\omega }$
, there is
![]() $g\in \mathcal {D}$
such that
$g\in \mathcal {D}$
such that
![]() $f\leq ^{\ast }g.$
The dominating number
$f\leq ^{\ast }g.$
The dominating number
![]() $\mathfrak {d}$
is defined as the least size of a dominating family. In [Reference Geschke, Goldstern and Kojman10], Hrušák introduced a diamond principle for the dominating number:
$\mathfrak {d}$
is defined as the least size of a dominating family. In [Reference Geschke, Goldstern and Kojman10], Hrušák introduced a diamond principle for the dominating number:
 $\Diamond _{\mathfrak {d}}$
There is a sequence
$\Diamond _{\mathfrak {d}}$
There is a sequence
 $\left \langle d_{\alpha }\mid \alpha <\omega _{1}\right \rangle $
where
$\left \langle d_{\alpha }\mid \alpha <\omega _{1}\right \rangle $
where
 $d_{\alpha }:\alpha \longrightarrow \omega $
such that for every
$d_{\alpha }:\alpha \longrightarrow \omega $
such that for every
 $f:\omega _{1}\longrightarrow \omega $
the set
$f:\omega _{1}\longrightarrow \omega $
the set
 $\left \{ \alpha>\omega \mid f\upharpoonright \alpha \leq ^{\ast }d_{\alpha }\right \} $
is nonempty. The sequence is called a
$\left \{ \alpha>\omega \mid f\upharpoonright \alpha \leq ^{\ast }d_{\alpha }\right \} $
is nonempty. The sequence is called a
 $\Diamond _{\mathfrak {d}} $
-sequence.
$\Diamond _{\mathfrak {d}} $
-sequence.
Above,
![]() $f\upharpoonright \alpha \leq ^{\ast }d_{\alpha }$
means that the set
$f\upharpoonright \alpha \leq ^{\ast }d_{\alpha }$
means that the set
![]() $\left \{ \xi <\alpha \mid d_{\alpha }\left ( \xi \right ) <f\left ( \xi \right ) \right \} $
is finite. It is easy to see that
$\left \{ \xi <\alpha \mid d_{\alpha }\left ( \xi \right ) <f\left ( \xi \right ) \right \} $
is finite. It is easy to see that
![]() $\Diamond _{\delta }$
implies that
$\Diamond _{\delta }$
implies that
![]() $\mathfrak {d}=\omega _{1}.$
It is an old problem of Roitman if
$\mathfrak {d}=\omega _{1}.$
It is an old problem of Roitman if
![]() $\mathfrak {d} =\omega _{1}$
implies
$\mathfrak {d} =\omega _{1}$
implies
![]() $\mathfrak {a}=\omega _{1},$
however, Hrušák proved the following:
$\mathfrak {a}=\omega _{1},$
however, Hrušák proved the following:
Proposition 85 [Reference Geschke, Goldstern and Kojman10]
![]() $\mathfrak {\Diamond }_{\mathfrak {d}}$
implies
$\mathfrak {\Diamond }_{\mathfrak {d}}$
implies
![]() $\mathfrak {a}=\omega _{1}.$
$\mathfrak {a}=\omega _{1}.$
In order to show that
![]() $\mathfrak {a}=\omega _{1}$
holds in the Shelah model, we will prove that
$\mathfrak {a}=\omega _{1}$
holds in the Shelah model, we will prove that
![]() $\Diamond _{\mathfrak {d}}$
is true in there. Recall that
$\Diamond _{\mathfrak {d}}$
is true in there. Recall that
![]() $\Diamond $
is the following statement:
$\Diamond $
is the following statement:
 $\Diamond $
There is
$\Diamond $
There is
 $\mathcal {D}=\left \{ D_{\alpha }\mid \alpha \in \omega _{1}\right \} $
with
$\mathcal {D}=\left \{ D_{\alpha }\mid \alpha \in \omega _{1}\right \} $
with
 $D_{\alpha }\subseteq \alpha $
such that for every
$D_{\alpha }\subseteq \alpha $
such that for every
 $X\subseteq \omega _{1},$
the set
$X\subseteq \omega _{1},$
the set
 $\left \{ \alpha \mid X\cap \alpha =D_{\alpha }\right \} $
is stationary.
$\left \{ \alpha \mid X\cap \alpha =D_{\alpha }\right \} $
is stationary.
We will use
![]() $\Diamond $
in order to construct a
$\Diamond $
in order to construct a
![]() $\Diamond _{\mathfrak {d}} $
-sequence for the Shelah model. By
$\Diamond _{\mathfrak {d}} $
-sequence for the Shelah model. By
![]() $LIM\left ( \omega _{1}\right ) $
, we denote the set of all countable limit ordinals. We start with the following:
$LIM\left ( \omega _{1}\right ) $
, we denote the set of all countable limit ordinals. We start with the following:
Lemma 86 Let
![]() $V\models \Diamond $
and
$V\models \Diamond $
and
![]() $\kappa $
a large enough regular cardinal. There is a sequence
$\kappa $
a large enough regular cardinal. There is a sequence
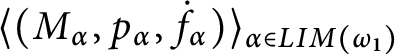 $\langle (M_{\alpha },p_{\alpha },\dot {f}_{\alpha })\rangle _{\alpha \in LIM\left ( \omega _{1}\right ) }$
such that for every
$\langle (M_{\alpha },p_{\alpha },\dot {f}_{\alpha })\rangle _{\alpha \in LIM\left ( \omega _{1}\right ) }$
such that for every
![]() $\alpha <\omega _{1}$
the following holds:
$\alpha <\omega _{1}$
the following holds:
-
1.
 $M_{\alpha }$
is a countable elementary submodel of
$M_{\alpha }$
is a countable elementary submodel of
 $\mathsf{H}( \kappa ) $
such that
$\mathsf{H}( \kappa ) $
such that
 $\mathbb {P}_{\omega _{2}},p_{\alpha },\dot {f} _{\alpha }\in M_{\alpha }$
(where
$\mathbb {P}_{\omega _{2}},p_{\alpha },\dot {f} _{\alpha }\in M_{\alpha }$
(where
 $\mathbb {P}_{\omega _{2}}$
is the iteration of the Shelah forcing).
$\mathbb {P}_{\omega _{2}}$
is the iteration of the Shelah forcing). -
2.
 $p_{\alpha }\in \mathbb {P}_{\omega _{2}}$
and
$p_{\alpha }\in \mathbb {P}_{\omega _{2}}$
and
 $p_{\alpha }\Vdash \text{``}\dot {f}_{\alpha }:\omega _{1}\longrightarrow \omega .\text{''}$
$p_{\alpha }\Vdash \text{``}\dot {f}_{\alpha }:\omega _{1}\longrightarrow \omega .\text{''}$
With the property that for every
![]() $p\in \mathbb {P}_{\omega _{2}}$
and
$p\in \mathbb {P}_{\omega _{2}}$
and
![]() $\dot {f}$
such that
$\dot {f}$
such that
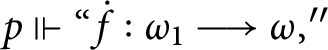 $p\Vdash \text{``}\dot {f}:\omega _{1}\longrightarrow \omega ,'' $
there are countable
$p\Vdash \text{``}\dot {f}:\omega _{1}\longrightarrow \omega ,'' $
there are countable
![]() $N\preceq $
H
$N\preceq $
H
![]() $\left ( \kappa \right ) $
and
$\left ( \kappa \right ) $
and
![]() $\alpha <\omega _{1}$
such that the following conditions hold:
$\alpha <\omega _{1}$
such that the following conditions hold:
-
1.
 $\mathbb {P}_{\omega _{2}},p,\dot {f}\in N.$
$\mathbb {P}_{\omega _{2}},p,\dot {f}\in N.$
-
2.
 $M_{\alpha }\cap \omega _{1}=\alpha .$
$M_{\alpha }\cap \omega _{1}=\alpha .$
-
3. The structures
 $(N,\in ,\mathbb {P}_{\omega _{2}},p,\dot {f})$
and
$(N,\in ,\mathbb {P}_{\omega _{2}},p,\dot {f})$
and
 $(M_{\alpha },\in ,\mathbb {P}_{\omega _{2}},p_{\alpha },\dot {f}_{\alpha })$
are isomorphic.
$(M_{\alpha },\in ,\mathbb {P}_{\omega _{2}},p_{\alpha },\dot {f}_{\alpha })$
are isomorphic.
Proof Using
![]() $\Diamond ,$
we can find a sequence
$\Diamond ,$
we can find a sequence
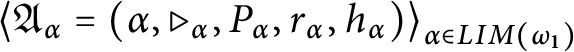 $\left \langle \mathfrak {A}_{\alpha }=\left ( \alpha ,\vartriangleright _{\alpha },P_{\alpha },r_{\alpha },h_{\alpha }\right ) \right \rangle _{\alpha \in LIM\left ( \omega _{1}\right ) }$
such that for every structure
$\left \langle \mathfrak {A}_{\alpha }=\left ( \alpha ,\vartriangleright _{\alpha },P_{\alpha },r_{\alpha },h_{\alpha }\right ) \right \rangle _{\alpha \in LIM\left ( \omega _{1}\right ) }$
such that for every structure
![]() $\mathfrak {A}=\left ( \omega _{1},\vartriangleright ,P,r,h\right ) $
there are stationary many
$\mathfrak {A}=\left ( \omega _{1},\vartriangleright ,P,r,h\right ) $
there are stationary many
![]() $\alpha $
such that
$\alpha $
such that
![]() $\mathfrak {A} _{\alpha }$
is a substructure of
$\mathfrak {A} _{\alpha }$
is a substructure of
![]() $\mathfrak {A.}$
Given
$\mathfrak {A.}$
Given
![]() $\alpha $
a limit ordinal, in case there are a countable
$\alpha $
a limit ordinal, in case there are a countable
![]() $M\preceq $
H
$M\preceq $
H
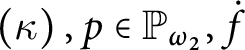 $\left ( \kappa \right ) , p\in \mathbb {P}_{\omega _{2}}, \dot {f}$
such that
$\left ( \kappa \right ) , p\in \mathbb {P}_{\omega _{2}}, \dot {f}$
such that
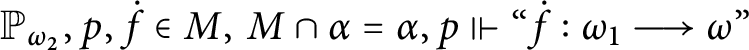 $\mathbb {P}_{\omega _{2}},p,\dot {f}\in M,\,M\cap \alpha =\alpha , p\Vdash \text{``}\dot {f}:\omega _{1}\longrightarrow \omega \text{''}$
and
$\mathbb {P}_{\omega _{2}},p,\dot {f}\in M,\,M\cap \alpha =\alpha , p\Vdash \text{``}\dot {f}:\omega _{1}\longrightarrow \omega \text{''}$
and
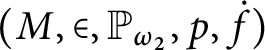 $(M,\in ,\mathbb {P}_{\omega _{2}},p,\dot {f})$
is isomorphic to
$(M,\in ,\mathbb {P}_{\omega _{2}},p,\dot {f})$
is isomorphic to
![]() $\mathfrak {A} _{\alpha }$
then we choose one of them and define
$\mathfrak {A} _{\alpha }$
then we choose one of them and define
![]() $M_{\alpha }=M, p_{\alpha }=p$
and
$M_{\alpha }=M, p_{\alpha }=p$
and
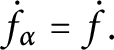 $\dot {f}_{\alpha }=\dot {f}.$
If there is no M satisfying those properties, we just take any
$\dot {f}_{\alpha }=\dot {f}.$
If there is no M satisfying those properties, we just take any
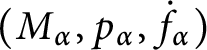 $(M_{\alpha },p_{\alpha },\dot {f}_{\alpha })$
satisfying the properties 1 and 2. We will now prove
$(M_{\alpha },p_{\alpha },\dot {f}_{\alpha })$
satisfying the properties 1 and 2. We will now prove
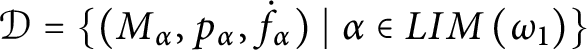 $\mathcal {D} =\{(M_{\alpha },p_{\alpha },\dot {f}_{\alpha })\mid \alpha \in LIM\left ( \omega _{1}\right ) \}$
has the desired properties.
$\mathcal {D} =\{(M_{\alpha },p_{\alpha },\dot {f}_{\alpha })\mid \alpha \in LIM\left ( \omega _{1}\right ) \}$
has the desired properties.
Let
![]() $p\in \mathbb {P}_{\omega _{2}}$
and
$p\in \mathbb {P}_{\omega _{2}}$
and
![]() $\dot {f}$
such that
$\dot {f}$
such that
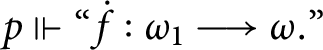 $p\Vdash \text{``}\dot {f}:\omega _{1}\longrightarrow \omega .\text{''}$
Recursively, we build
$p\Vdash \text{``}\dot {f}:\omega _{1}\longrightarrow \omega .\text{''}$
Recursively, we build
![]() $\left \{ N_{\alpha }\mid \alpha <\omega _{1}\right \} $
a continuous
$\left \{ N_{\alpha }\mid \alpha <\omega _{1}\right \} $
a continuous
![]() $\in $
-chain of countable elementary submodels of H
$\in $
-chain of countable elementary submodels of H
![]() $\left ( \kappa \right ) $
such that
$\left ( \kappa \right ) $
such that
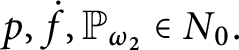 $p,\dot {f},\mathbb {P}_{\omega _{2}}\in N_{0}.$
Let
$p,\dot {f},\mathbb {P}_{\omega _{2}}\in N_{0}.$
Let
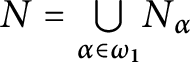 $N= {\textstyle \bigcup \limits _{\alpha \in \omega _{1}}} N_{\alpha }$
, since N has size
$N= {\textstyle \bigcup \limits _{\alpha \in \omega _{1}}} N_{\alpha }$
, since N has size
![]() $\omega _{1}$
then we can define a structure
$\omega _{1}$
then we can define a structure
![]() $\mathfrak {A}=\left ( \omega _{1},\vartriangleright ,P,r,h\right ) $
that is isomorphic to
$\mathfrak {A}=\left ( \omega _{1},\vartriangleright ,P,r,h\right ) $
that is isomorphic to
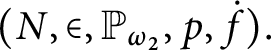 $(N,\in ,\mathbb {P}_{\omega _{2}},p,\dot {f}).$
Let
$(N,\in ,\mathbb {P}_{\omega _{2}},p,\dot {f}).$
Let
![]() $F:\omega _{1}\longrightarrow N$
be an isomorphism.
$F:\omega _{1}\longrightarrow N$
be an isomorphism.
It is easy to see that
![]() $\left \{ \alpha \in LIM\left ( \omega _{1}\right ) \mid N_{\alpha }\cap \omega _{1}=\alpha \wedge F\left [ \alpha \right ] =N_{\alpha }\right \} $
is a club. In this way, we can find
$\left \{ \alpha \in LIM\left ( \omega _{1}\right ) \mid N_{\alpha }\cap \omega _{1}=\alpha \wedge F\left [ \alpha \right ] =N_{\alpha }\right \} $
is a club. In this way, we can find
![]() $\alpha $
such that
$\alpha $
such that
![]() $F\left [ \alpha \right ] =N_{\alpha },N_{\alpha }\cap \omega _{1}=\alpha $
and
$F\left [ \alpha \right ] =N_{\alpha },N_{\alpha }\cap \omega _{1}=\alpha $
and
![]() $\mathfrak {A} _{\alpha }$
is a substructure of
$\mathfrak {A} _{\alpha }$
is a substructure of
![]() $\mathfrak {A}.$
Note that
$\mathfrak {A}.$
Note that
![]() $N_{\alpha },p$
and
$N_{\alpha },p$
and
![]() $\dot {f}$
satisfy the conditions of the definition at step
$\dot {f}$
satisfy the conditions of the definition at step
![]() $\alpha ,$
so
$\alpha ,$
so
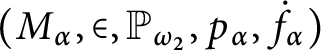 $(M_{\alpha },\in ,\mathbb {P}_{\omega _{2}},p_{\alpha },\dot {f}_{\alpha })$
is isomorphic to
$(M_{\alpha },\in ,\mathbb {P}_{\omega _{2}},p_{\alpha },\dot {f}_{\alpha })$
is isomorphic to
![]() $\mathfrak {A}_{\alpha }$
hence it is also isomorphic to
$\mathfrak {A}_{\alpha }$
hence it is also isomorphic to
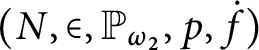 $(N,\in ,\mathbb {P}_{\omega _{2}},p,\dot {f})$
(of course it might be the case
$(N,\in ,\mathbb {P}_{\omega _{2}},p,\dot {f})$
(of course it might be the case
![]() $M_{\alpha }=N_{\alpha }$
but this is highly unlikely).▪
$M_{\alpha }=N_{\alpha }$
but this is highly unlikely).▪
With the lemma, we can now prove the following:
Proposition 87
![]() $\Diamond _{\mathfrak {d}}$
holds in the Shelah model.
$\Diamond _{\mathfrak {d}}$
holds in the Shelah model.
Proof It is well known that we may assume that
![]() $\Diamond $
holds in
$\Diamond $
holds in
![]() $V.$
Fix a sequence
$V.$
Fix a sequence
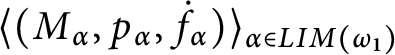 $\langle (M_{\alpha },p_{\alpha },\dot {f}_{\alpha })\rangle _{\alpha \in LIM\left ( \omega _{1}\right ) }$
as in the previous lemma, we will now define
$\langle (M_{\alpha },p_{\alpha },\dot {f}_{\alpha })\rangle _{\alpha \in LIM\left ( \omega _{1}\right ) }$
as in the previous lemma, we will now define
![]() $\mathcal {D}=\left \{ d_{\alpha }:\alpha \longrightarrow \omega \mid \alpha <\omega _{1}\right \} .$
In case
$\mathcal {D}=\left \{ d_{\alpha }:\alpha \longrightarrow \omega \mid \alpha <\omega _{1}\right \} .$
In case
![]() $M_{\alpha }\cap \omega _{1}\neq \alpha ,$
let
$M_{\alpha }\cap \omega _{1}\neq \alpha ,$
let
![]() $d_{\alpha }$
be any constant function. Fix
$d_{\alpha }$
be any constant function. Fix
![]() $\alpha $
such that
$\alpha $
such that
![]() $M_{\alpha } \cap \omega _{1}=\alpha ,$
we will see how to define
$M_{\alpha } \cap \omega _{1}=\alpha ,$
we will see how to define
![]() $d_{\alpha }.$
$d_{\alpha }.$
Let
![]() $L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
that is
$L=\left \{ \left ( F_{n},\eta _{n}\right ) \mid n\in \omega \right \} $
that is
![]() $\left ( M_{\alpha },\omega _{2}\right ) $
-suitable. Fix an enumeration
$\left ( M_{\alpha },\omega _{2}\right ) $
-suitable. Fix an enumeration
![]() $\alpha =\left \{ \alpha _{n}\mid n\in \omega \right \} $
. For every
$\alpha =\left \{ \alpha _{n}\mid n\in \omega \right \} $
. For every
![]() $\beta <\alpha $
define
$\beta <\alpha $
define
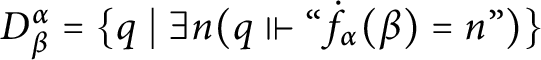 $D_{\beta }^{\alpha }=\{q\mid \exists n(q\Vdash \text{``}\dot {f}_{\alpha } ( \beta ) =n\text{''})\}$
and recall that the set
$D_{\beta }^{\alpha }=\{q\mid \exists n(q\Vdash \text{``}\dot {f}_{\alpha } ( \beta ) =n\text{''})\}$
and recall that the set
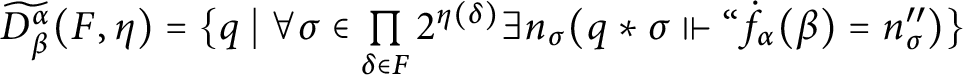 $\widetilde {D_{\beta }^{\alpha }}( F,\eta ) =\{q\mid \forall \sigma \in \prod \limits _{\delta \in F}2^{\eta ( \delta ) }\exists n_{\sigma }(q\ast \sigma \Vdash \text{``}\dot {f}_{\alpha }( \beta ) =n_{\sigma }'')\}$
is
$\widetilde {D_{\beta }^{\alpha }}( F,\eta ) =\{q\mid \forall \sigma \in \prod \limits _{\delta \in F}2^{\eta ( \delta ) }\exists n_{\sigma }(q\ast \sigma \Vdash \text{``}\dot {f}_{\alpha }( \beta ) =n_{\sigma }'')\}$
is
![]() $( F,\eta ) ^{\ast }$
-open dense and it is an element of
$( F,\eta ) ^{\ast }$
-open dense and it is an element of
![]() $M_{\alpha }.$
We can build a fusion tree
$M_{\alpha }.$
We can build a fusion tree
![]() $T=\{ p_{s}\mid s\in 2^{<\omega } \} $
with the following properties:
$T=\{ p_{s}\mid s\in 2^{<\omega } \} $
with the following properties:
-
1.
 $p_{\emptyset }=p_{\alpha }.$
$p_{\emptyset }=p_{\alpha }.$
-
2. If
 $s\in 2^{n+1}$
then
$s\in 2^{n+1}$
then
 $p_{s}\in \widetilde {D_{\beta _{n}}^{\alpha } }( F_{n},\eta _{n} ) $
.
$p_{s}\in \widetilde {D_{\beta _{n}}^{\alpha } }( F_{n},\eta _{n} ) $
.
Define
![]() $d_{\alpha }:\alpha \longrightarrow \omega $
such that if
$d_{\alpha }:\alpha \longrightarrow \omega $
such that if
![]() $n\in \omega $
then
$n\in \omega $
then
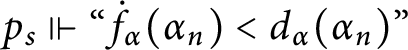 $p_{s}\Vdash \text{``}\dot {f}_{\alpha }( \alpha _{n}) <d_{\alpha }( \alpha _{n})\text{''}$
for every
$p_{s}\Vdash \text{``}\dot {f}_{\alpha }( \alpha _{n}) <d_{\alpha }( \alpha _{n})\text{''}$
for every
![]() $s\in 2^{n+1}.$
We will prove that
$s\in 2^{n+1}.$
We will prove that
![]() $\mathcal {D}=\left \{ d_{\alpha }:\alpha \longrightarrow \omega \mid \alpha <\omega _{1}\right \} $
will be a
$\mathcal {D}=\left \{ d_{\alpha }:\alpha \longrightarrow \omega \mid \alpha <\omega _{1}\right \} $
will be a
![]() $\Diamond _{\mathfrak {d}}$
-sequence after forcing with
$\Diamond _{\mathfrak {d}}$
-sequence after forcing with
![]() $\mathbb {P}_{\omega _{2}}.$
Let
$\mathbb {P}_{\omega _{2}}.$
Let
![]() $p\in \mathbb {P}_{\omega _{2} }$
and
$p\in \mathbb {P}_{\omega _{2} }$
and
![]() $\dot {f}$
such that
$\dot {f}$
such that
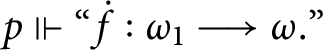 $p\Vdash \text{``}\dot {f}:\omega _{1}\longrightarrow \omega .\text{''}$
Applying the previous lemma, we can find a countable N for which
$p\Vdash \text{``}\dot {f}:\omega _{1}\longrightarrow \omega .\text{''}$
Applying the previous lemma, we can find a countable N for which
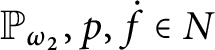 $\mathbb {P}_{\omega _{2}},p,\dot {f}\in N$
and
$\mathbb {P}_{\omega _{2}},p,\dot {f}\in N$
and
![]() $\alpha <\omega _{1}$
such that
$\alpha <\omega _{1}$
such that
![]() $M_{\alpha }\cap \omega _{1}=\alpha $
and the structures
$M_{\alpha }\cap \omega _{1}=\alpha $
and the structures
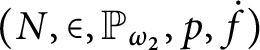 $(N,\in ,\mathbb {P}_{\omega _{2}},p,\dot {f})$
and
$(N,\in ,\mathbb {P}_{\omega _{2}},p,\dot {f})$
and
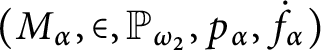 $(M_{\alpha } ,\in ,\mathbb {P}_{\omega _{2}},p_{\alpha },\dot {f}_{\alpha })$
are isomorphic. Let
$(M_{\alpha } ,\in ,\mathbb {P}_{\omega _{2}},p_{\alpha },\dot {f}_{\alpha })$
are isomorphic. Let
![]() $H:M_{\alpha }\longrightarrow N$
be the isomorphism. Let
$H:M_{\alpha }\longrightarrow N$
be the isomorphism. Let
![]() $F_{n}^{\prime }=H ( F_{n} ) $
and
$F_{n}^{\prime }=H ( F_{n} ) $
and
![]() $\eta _{n}^{\prime }=H ( \eta _{n}) .$
Let
$\eta _{n}^{\prime }=H ( \eta _{n}) .$
Let
![]() $L^{\prime }=\{ ( F_{n}^{\prime },\eta _{n}^{\prime }) \mid n\in \omega \} .$
For every
$L^{\prime }=\{ ( F_{n}^{\prime },\eta _{n}^{\prime }) \mid n\in \omega \} .$
For every
![]() $s\in 2^{<\omega }$
define
$s\in 2^{<\omega }$
define
![]() $p_{s}^{\prime }=H( p_{s}) .$
In this way,
$p_{s}^{\prime }=H( p_{s}) .$
In this way,
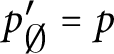 $p_{\emptyset }^{\prime }=p$
and it is easy to see that
$p_{\emptyset }^{\prime }=p$
and it is easy to see that
![]() $T^{\prime }=\{ p_{s}^{\prime }\mid s\in 2^{<\omega }\} $
is a fusion tree.
$T^{\prime }=\{ p_{s}^{\prime }\mid s\in 2^{<\omega }\} $
is a fusion tree.
Let q be compatible with
![]() $T^{\prime }$
(which is obviously an extension of p). We will now prove that
$T^{\prime }$
(which is obviously an extension of p). We will now prove that
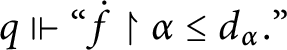 $q\Vdash \text{``}\dot {f}\upharpoonright \alpha \leq d_{\alpha }.\text{''}$
Let
$q\Vdash \text{``}\dot {f}\upharpoonright \alpha \leq d_{\alpha }.\text{''}$
Let
![]() $n\in \omega $
and
$n\in \omega $
and
![]() $s\in 2^{n+1},$
since
$s\in 2^{n+1},$
since
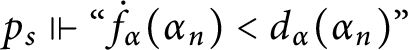 $p_{s}\Vdash \text{``}\dot {f}_{\alpha }( \alpha _{n}) <d_{\alpha }( \alpha _{n})\text{''}$
it follows that
$p_{s}\Vdash \text{``}\dot {f}_{\alpha }( \alpha _{n}) <d_{\alpha }( \alpha _{n})\text{''}$
it follows that
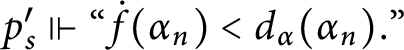 $p_{s}^{\prime } \Vdash \text{``}\dot {f}( \alpha _{n}) <d_{\alpha }( \alpha _{n}).\text{''}$
Finally, since q is compatible with
$p_{s}^{\prime } \Vdash \text{``}\dot {f}( \alpha _{n}) <d_{\alpha }( \alpha _{n}).\text{''}$
Finally, since q is compatible with
![]() $T^{\prime },$
it follows that
$T^{\prime },$
it follows that
![]() $\{ p_{s}^{\prime }\mid s\in 2^{n+1} \} $
is predense below
$\{ p_{s}^{\prime }\mid s\in 2^{n+1} \} $
is predense below
![]() $q,$
so
$q,$
so
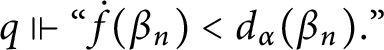 $q\Vdash \text{``}\dot {f}( \beta _{n} ) <d_{\alpha } ( \beta _{n} ).\text{''}$
▪
$q\Vdash \text{``}\dot {f}( \beta _{n} ) <d_{\alpha } ( \beta _{n} ).\text{''}$
▪
8 Open questions
We do not know the answer to the following:
Problem 88 Can a generic filter for
![]() $\mathbb {S}( \mathcal {U}) $
be reconstructed from the generic real?
$\mathbb {S}( \mathcal {U}) $
be reconstructed from the generic real?
Much of the work in this paper would be simplified if
![]() $\mathbb {S}( \mathcal {U}) $
was an Axiom A forcing, so we could ask the following:
$\mathbb {S}( \mathcal {U}) $
was an Axiom A forcing, so we could ask the following:
Problem 89 Let
![]() $\mathcal {U}$
be an ultrafilter. Is it possible to give
$\mathcal {U}$
be an ultrafilter. Is it possible to give
![]() $\mathbb {S}( \mathcal {U}) $
an Axiom A structure?
$\mathbb {S}( \mathcal {U}) $
an Axiom A structure?
Unfortunately, we conjecture that this is not possible. An iteration theorem would greatly simplify the work in this paper, as well as in [Reference Jorge, Fischer, Guzmán and Jaroslav7, Reference Geschke9]. We could ask the following:
Problem 90 If
![]() $\mathbb {P}$
preserves
$\mathbb {P}$
preserves
![]() $\mathsf {c}_{\mathsf {min}}$
-covering and
$\mathsf {c}_{\mathsf {min}}$
-covering and
![]() $\mathbb {P\Vdash }\text{``}\mathbb {\dot {Q}}$
preserves
$\mathbb {P\Vdash }\text{``}\mathbb {\dot {Q}}$
preserves
![]() $\mathsf {c}_{\mathsf {min}} $
-covering
$\mathsf {c}_{\mathsf {min}} $
-covering
![]() $,\text{''}$
is it true that
$,\text{''}$
is it true that
![]() $\mathbb {P\ast \dot {Q}}$
preserves
$\mathbb {P\ast \dot {Q}}$
preserves
![]() $\mathsf {c}_{\mathsf {min}}$
-covering?
$\mathsf {c}_{\mathsf {min}}$
-covering?
Problem 91 If
![]() $\delta $
is a limit ordinal,
$\delta $
is a limit ordinal,
![]() $\langle \mathbb {P}_{\alpha } ,\mathbb {\dot {R}}_{\alpha }\mid \alpha <\delta \rangle $
is a countable support iteration of proper forcings such that each
$\langle \mathbb {P}_{\alpha } ,\mathbb {\dot {R}}_{\alpha }\mid \alpha <\delta \rangle $
is a countable support iteration of proper forcings such that each
![]() $\mathbb {P}_{\alpha }$
preserves
$\mathbb {P}_{\alpha }$
preserves
![]() $\mathsf {c}_{\mathsf {min}}$
-covering, is it true that
$\mathsf {c}_{\mathsf {min}}$
-covering, is it true that
![]() $\mathbb {P} _{\delta }$
preserves
$\mathbb {P} _{\delta }$
preserves
![]() $\mathsf {c}_{\mathsf {min}}$
-covering?
$\mathsf {c}_{\mathsf {min}}$
-covering?
It might be possible to use the results from chapter VI of [Reference Shelah14] to prove an iteration theorem for preserving
![]() $\mathsf {c}_{\mathsf {min}}$
-covering, but we were unable to do so.
$\mathsf {c}_{\mathsf {min}}$
-covering, but we were unable to do so.
We do not know the answer to the following question:
Problem 92 Are there P-points in the Shelah model of
![]() $\mathfrak {i<u}$
?
$\mathfrak {i<u}$
?
We conjecture that the answer is negative. It might be possible that similar ideas to the ones used in [Reference Chodounský and Guzmán6] can be used to prove that there are no P-points in the Shelah model, but we were unable to prove it.
Acknowledgment
I would like to thank Thilo Weinert for several interesting discussions regarding
![]() $\mathfrak {hm},$
to Jonathan Cancino for explaining the forcing
$\mathfrak {hm},$
to Jonathan Cancino for explaining the forcing
![]() $\mathbb {S}( \mathcal {U}) $
to me for the first time, to David Chodounský and Jan Grebík for several interesting conversations regarding the topic of the paper and to Michael Hrušák and Arturo Martínez for their valuable comments and discussions. I would like to thank the referees of the paper, their comments and suggestions greatly improved the paper.
$\mathbb {S}( \mathcal {U}) $
to me for the first time, to David Chodounský and Jan Grebík for several interesting conversations regarding the topic of the paper and to Michael Hrušák and Arturo Martínez for their valuable comments and discussions. I would like to thank the referees of the paper, their comments and suggestions greatly improved the paper.