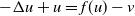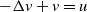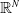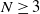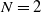1. Introduction
In this paper, we prove the existence of a solution of the following system
where
![]() $f\;:\;\mathbb{R} \to \mathbb{R}$
is a continuous function which is allowed to have critical growth: polynomial in case
$f\;:\;\mathbb{R} \to \mathbb{R}$
is a continuous function which is allowed to have critical growth: polynomial in case
![]() $N\geq 3$
and exponential if
$N\geq 3$
and exponential if
![]() $N=2$
, quoted in (1.2)–(1.6) below.
$N=2$
, quoted in (1.2)–(1.6) below.
System (1.1) fits in the class of activator–inhibitor models, where u is the concentration of the activator and v is the concentration of some inhibitor. The function
![]() $f(u)-v$
is the kinetics and it is responsible for the balance between u and v in the medium given by
$f(u)-v$
is the kinetics and it is responsible for the balance between u and v in the medium given by
![]() $\mathbb{R}^{N}$
. The general theory of such systems can be found in [Reference Yagi37] and at Remark 3 below.
$\mathbb{R}^{N}$
. The general theory of such systems can be found in [Reference Yagi37] and at Remark 3 below.
Let
![]() $H_{rad}^1(\mathbb{R}^N)$
be the space of
$H_{rad}^1(\mathbb{R}^N)$
be the space of
![]() $H^1$
functions defined in
$H^1$
functions defined in
![]() $\mathbb{R}^N$
which are radially symmetric. A weak solution of (1.1) is a pair
$\mathbb{R}^N$
which are radially symmetric. A weak solution of (1.1) is a pair
![]() $(u,v) \in H^{1}_{rad}(\mathbb{R}^{N})\times H^{1}_{rad}(\mathbb{R}^{N})$
with radially symmetric components that satisfies
$(u,v) \in H^{1}_{rad}(\mathbb{R}^{N})\times H^{1}_{rad}(\mathbb{R}^{N})$
with radially symmetric components that satisfies
and
Since we intend to find a nonnegative solution, we will assume that
![]() $f(s) =0$
for every
$f(s) =0$
for every
![]() $s \leq 0$
.
$s \leq 0$
.
The continuous function
![]() $f\;:\;\mathbb{R} \to \mathbb{R}$
is subject to the following conditions:
$f\;:\;\mathbb{R} \to \mathbb{R}$
is subject to the following conditions:
There are
![]() $q \in (2, 2^{*})$
in the case
$q \in (2, 2^{*})$
in the case
![]() $N\geq3$
,
$N\geq3$
,
![]() $q >2$
in the case
$q >2$
in the case
![]() $N=2$
and
$N=2$
and
![]() $\tau > \tau^{*}$
such that
$\tau > \tau^{*}$
such that
As we can see, the critical growth for the function f is allowed by (1.3) and (1.6). The constant
![]() $\beta_0=0$
in (1.6) represents the subcritical behavior of f, and in this case one has to suppress the
$\beta_0=0$
in (1.6) represents the subcritical behavior of f, and in this case one has to suppress the
![]() $+\infty$
limit. This situation is also covered in this paper. Notice that we are imposing a weaker condition, namely (1.4), than the classical Ambrosetti–Rabinowitz hypothesis on f.
$+\infty$
limit. This situation is also covered in this paper. Notice that we are imposing a weaker condition, namely (1.4), than the classical Ambrosetti–Rabinowitz hypothesis on f.
We stress two estimates which will be frequently used henceforth. From (1.2) and (1.3), for every
![]() $\varepsilon > 0$
there exists
$\varepsilon > 0$
there exists
![]() $C_{\varepsilon} > 0$
such that
$C_{\varepsilon} > 0$
such that
and, then by integration,
We intend to use variational methods to get a weak solution of (1.1). We recall that for each
![]() $u \in H^{1}(\mathbb{R}^{N})$
, the linear problem
$u \in H^{1}(\mathbb{R}^{N})$
, the linear problem
has a unique solution
![]() $v\in H^{1}(\mathbb{R}^{N})$
, that is,
$v\in H^{1}(\mathbb{R}^{N})$
, that is,
Notice that B denotes the solution operator associated to (1.9). It is well known that
![]() $B\;:\;H^{1}(\mathbb{R}^{N})\rightarrow L^{2}(\mathbb{R}^{N})$
is linear, continuous, symmetric, and positive, that is,
$B\;:\;H^{1}(\mathbb{R}^{N})\rightarrow L^{2}(\mathbb{R}^{N})$
is linear, continuous, symmetric, and positive, that is,
Notice that (1.1) is equivalent to the nonlocal problem
Using the fact that B is linear, continuous, and positive, we conclude that
![]() $X=(H^{1}(\mathbb{R}^{N}), \langle.,.\rangle)$
is a Hilbert space with scalar product
$X=(H^{1}(\mathbb{R}^{N}), \langle.,.\rangle)$
is a Hilbert space with scalar product
and corresponding norm
Moreover, since B is linear, this norm is bounded from above by the standard norm of
![]() $H^{1}(\mathbb{R}^{N})$
and X is continuously embedded in
$H^{1}(\mathbb{R}^{N})$
and X is continuously embedded in
![]() $L^{p}(\mathbb{R})$
for
$L^{p}(\mathbb{R})$
for
![]() $2\leq p\leq 2^{*}$
.
$2\leq p\leq 2^{*}$
.
Let
and
We define the energy functional
![]() $I\;:\;X \to \mathbb{R}$
corresponding to (1.10) by
$I\;:\;X \to \mathbb{R}$
corresponding to (1.10) by
which is well defined in view of (1.2)–(1.3). From the Sobolev embeddings, we conclude that
![]() $I \in C^1(X ,\mathbb{R})$
and
$I \in C^1(X ,\mathbb{R})$
and
In synthesis, we see that if u is a critical point of I, then the pair (u, v), with
![]() $v=Bu$
, is a weak solution of (1.1).
$v=Bu$
, is a weak solution of (1.1).
We consider the set of nontrivial critical points of I, corresponding to nontrivial solutions of (1.10),
We define the ground state level (or least energy level) associated to (1.10) by
We introduce the constrained minimum
in the set
or
The underlying idea in the proof of our results is to show that D is attained.
We state the main theorems.
Theorem 1.1. Suppose that
![]() $N \geq 3$
and f satisfies (1.2)–(1.5). Then system (1.1) admits a solution (u, v) where each component is nonnegative, radially symmetric, decreasing and such that
$N \geq 3$
and f satisfies (1.2)–(1.5). Then system (1.1) admits a solution (u, v) where each component is nonnegative, radially symmetric, decreasing and such that
![]() $u(x) \to 0$
and
$u(x) \to 0$
and
![]() $v(x) \to 0$
as
$v(x) \to 0$
as
![]() $|x| \to \infty$
.
$|x| \to \infty$
.
Theorem 1.2. Suppose that
![]() $N = 2$
and f satisfies (1.2), (1.4), (1.5) and (1.6). Then system (1.1) admits a solution (u, v) where each component is nonnegative, radially symmetric, decreasing and such that
$N = 2$
and f satisfies (1.2), (1.4), (1.5) and (1.6). Then system (1.1) admits a solution (u, v) where each component is nonnegative, radially symmetric, decreasing and such that
![]() $u(x) \to 0$
and
$u(x) \to 0$
and
![]() $v(x) \to 0$
as
$v(x) \to 0$
as
![]() $|x| \to \infty$
.
$|x| \to \infty$
.
In addition, we define the minimax level associated to the functional I,
where
is nonempty since I satisfies the conditions of the Mountain Pass Theorem.
Remark 1. Focusing only on equation (1.10), the above defined quantities satisfy,
and
The proof follows after accomplishing the arguments of Sections 2–5. The conclusion follows from the ideas of [Reference Berestycki and Lions10, Theorem 3] in dimension
![]() $N \geq 3$
and [Reference Alves, Montenegro and Souto3, Corollary 1.5] joint with [Reference Jeanjean and Tanaka25] in the case
$N \geq 3$
and [Reference Alves, Montenegro and Souto3, Corollary 1.5] joint with [Reference Jeanjean and Tanaka25] in the case
![]() $N=2$
. We will not dwell on this since these equalities are not fundamental in the present paper.
$N=2$
. We will not dwell on this since these equalities are not fundamental in the present paper.
Remark 2. A simple application of the strong maximum principle in the scalar case for a solution pair (u, v) with
![]() $u \geq 0$
and
$u \geq 0$
and
![]() $v \geq 0$
, both nontrivial, gives
$v \geq 0$
, both nontrivial, gives
![]() $u \geq 0$
,
$u \geq 0$
,
![]() $u \not\equiv 0$
and
$u \not\equiv 0$
and
![]() $v>0$
. We do not know if
$v>0$
. We do not know if
![]() $u>0$
, due to the fact that we are not in position to use the maximum principle for systems as in [Reference Chen and Tanaka16, Reference de Figueiredo and Mitidieri19, Reference Reinecke and Sweers33], where they adjust the parameters d and
$u>0$
, due to the fact that we are not in position to use the maximum principle for systems as in [Reference Chen and Tanaka16, Reference de Figueiredo and Mitidieri19, Reference Reinecke and Sweers33], where they adjust the parameters d and
![]() $\gamma$
to do so. The system studied in [Reference Chen and Tanaka16] reads as
$\gamma$
to do so. The system studied in [Reference Chen and Tanaka16] reads as
with
![]() $d>0$
and
$d>0$
and
![]() $\gamma > 0$
. In [Reference Chen and Tanaka16], the authors conclude that
$\gamma > 0$
. In [Reference Chen and Tanaka16], the authors conclude that
![]() $u>0$
and
$u>0$
and
![]() $v>0$
, assuming that there exist
$v>0$
, assuming that there exist
![]() $\zeta_0 > 0$
and
$\zeta_0 > 0$
and
![]() $\gamma_0 >0$
such that
$\gamma_0 >0$
such that
![]() $F(\zeta_0) \geq \zeta_0^2/ 2 \gamma_0$
,
$F(\zeta_0) \geq \zeta_0^2/ 2 \gamma_0$
,
![]() $\gamma > \max\{\gamma_0, 2 \sqrt{d}\}$
and either
$\gamma > \max\{\gamma_0, 2 \sqrt{d}\}$
and either
if
![]() $f(s) > 0 \ \forall s \geq \zeta_0$
, then
$f(s) > 0 \ \forall s \geq \zeta_0$
, then
![]() $f(s) +\displaystyle \frac{1}{d}\left(\gamma_0-2\sqrt{d}\right)s \geq 0, \ \forall s \in [0, \zeta_0]$
$f(s) +\displaystyle \frac{1}{d}\left(\gamma_0-2\sqrt{d}\right)s \geq 0, \ \forall s \in [0, \zeta_0]$
or
if there is
![]() $\zeta_1>\zeta_0$
such that
$\zeta_1>\zeta_0$
such that
![]() $f(\zeta_1) = 0$
, then
$f(\zeta_1) = 0$
, then
![]() $f(s)+\displaystyle \frac{1}{d}\left(\gamma_0-2\sqrt{d}\right)s \geq 0, \ \forall s \in [0, \zeta_1].$
$f(s)+\displaystyle \frac{1}{d}\left(\gamma_0-2\sqrt{d}\right)s \geq 0, \ \forall s \in [0, \zeta_1].$
Our approach in the present paper contrasts with the procedure adopted in [Reference Chen and Tanaka16, Reference Reinecke and Sweers33], and actually Chen–Tanaka leave the question on page 113 if the constrained minimization (1.13) is a good strategy to treat their problem. We answer affirmatively such question. The system (1.1) was studied in [Reference Chen and Tanaka16] with a subcritical nonlinearity f, where the authors showed that the mountain pass level of the energy functional
![]() $\tilde{I}_\gamma$
associated to (1.1) is attained by some pair (u, v), corresponding to a solution for a larger interval of parameters
$\tilde{I}_\gamma$
associated to (1.1) is attained by some pair (u, v), corresponding to a solution for a larger interval of parameters
![]() $\gamma,d$
when compared to [Reference Reinecke and Sweers33]. The assumptions (1.2)–(1.6) are considerable improvements compared to [Reference Chen and Tanaka16], since we are capable of considering a general nonlinearity f not only with subcritical growth, but also with critical polynomial growth in case
$\gamma,d$
when compared to [Reference Reinecke and Sweers33]. The assumptions (1.2)–(1.6) are considerable improvements compared to [Reference Chen and Tanaka16], since we are capable of considering a general nonlinearity f not only with subcritical growth, but also with critical polynomial growth in case
![]() $N\geq 3$
or critical exponential behavior if
$N\geq 3$
or critical exponential behavior if
![]() $N=2$
, and we do not need further assumptions on
$N=2$
, and we do not need further assumptions on
![]() $\gamma$
and d to show existence of solution.
$\gamma$
and d to show existence of solution.
In [Reference Chen and Tanaka16], the authors employ a truncation of f and apply minimax arguments to the corresponding augmented functional
![]() $\tilde{I}_\gamma \;:\; \mathbb{R} \times H_{rad}^1 (\mathbb{R}^N) \times H_{rad}^1 (\mathbb{R}^N) \to \mathbb{R}$
defined by
$\tilde{I}_\gamma \;:\; \mathbb{R} \times H_{rad}^1 (\mathbb{R}^N) \times H_{rad}^1 (\mathbb{R}^N) \to \mathbb{R}$
defined by
instead of working directly with the strongly indefinite functional
![]() $\tilde{I}_\gamma (0, u, v)$
defined on
$\tilde{I}_\gamma (0, u, v)$
defined on
![]() $H_{rad}^1 (\mathbb{R}^N) \times H_{rad}^1 (\mathbb{R}^N)$
, see also [Reference Hirata, Ikoma and Tanaka22]. The functional
$H_{rad}^1 (\mathbb{R}^N) \times H_{rad}^1 (\mathbb{R}^N)$
, see also [Reference Hirata, Ikoma and Tanaka22]. The functional
![]() $\tilde{I}_\gamma (\theta, u, v)$
is more adequate to show the Palais–Smale condition. This strategy is based on the ideas in [Reference Azzollini, d’Avenia and Pomponio4, Reference Bartsch and de la Valeriola6, Reference Benci and Rabinowitz7, Reference Jeanjean24, Reference Moroz and Van Schaftingen30]. The positivity of the solution follows from the maximum principle for systems due to the fact that the parametres d and
$\tilde{I}_\gamma (\theta, u, v)$
is more adequate to show the Palais–Smale condition. This strategy is based on the ideas in [Reference Azzollini, d’Avenia and Pomponio4, Reference Bartsch and de la Valeriola6, Reference Benci and Rabinowitz7, Reference Jeanjean24, Reference Moroz and Van Schaftingen30]. The positivity of the solution follows from the maximum principle for systems due to the fact that the parametres d and
![]() $\gamma$
verify the assumptions of [Reference de Figueiredo and Mitidieri19].
$\gamma$
verify the assumptions of [Reference de Figueiredo and Mitidieri19].
We do not work with
![]() $\tilde{I}_\gamma (\theta, u, v)$
nor with
$\tilde{I}_\gamma (\theta, u, v)$
nor with
![]() $\tilde{I}_\gamma (0, u, v)$
. Instead, we invert the second equation of (1.1) for v and replace the solution in the first one, dealing with the single equation (1.10) with a nonlocal term Bu. The resulting functional I defined in (1.11) on the space X with norm endowed by a scalar product that takes into account the aforesaid nonlocal term, is the one that prevails in our work.
$\tilde{I}_\gamma (0, u, v)$
. Instead, we invert the second equation of (1.1) for v and replace the solution in the first one, dealing with the single equation (1.10) with a nonlocal term Bu. The resulting functional I defined in (1.11) on the space X with norm endowed by a scalar product that takes into account the aforesaid nonlocal term, is the one that prevails in our work.
The critical nonlinearity f brings some difficulties, e.g., choosing the adequate space of functions and dealing with the lack of compactness that spoils the Palais–Smale condition. We show that the solution exists by solving equivalently, say, the action minima problem (1.13), where the corresponding minimizing sequence is weak convergent and the sequence of Lagrange multipliers is also convergent. This strategy has been developed by Coleman–Glaser–Martin [Reference Coleman, Glaser and Martin17] and successfully adopted in [Reference Berestycki, Gallouët and Kavian8, Reference Berestycki and Lions10], and subsequently undertaken in [Reference Alves, Montenegro and Souto3, Reference Cao11, Reference Jeanjean and Tanaka25, Reference Zhang and Zou38], respectively, for subcritical and critical scalar equations. We substantially improve the results of [Reference Chen and Tanaka16, Reference Reinecke and Sweers33] using different techniques to find a solution of (1.1).
Remark 3. We do not study system (1.1) when
![]() $f(u)=u(1-u)(u-\alpha)$
with
$f(u)=u(1-u)(u-\alpha)$
with
![]() $0<\alpha<1/2$
. This is the case of the so-called FitzHugh–Nagumo (FHN) model, which has been introduced by the authors of the papers FitzHugh [Reference FitzHugh21] and Nagumo–Arimoto–Yoshizawa [Reference Nagumo, Arimoto and Yoshizawa31]. They proposed a way of describing an excitable medium with a simplified counterpart of the Hodgkin–Huxley pattern [Reference Hodgkin and Huxley23]. In fact, they studied the activator–inhibitor dynamics of a neuron electric pulse along the axon.
$0<\alpha<1/2$
. This is the case of the so-called FitzHugh–Nagumo (FHN) model, which has been introduced by the authors of the papers FitzHugh [Reference FitzHugh21] and Nagumo–Arimoto–Yoshizawa [Reference Nagumo, Arimoto and Yoshizawa31]. They proposed a way of describing an excitable medium with a simplified counterpart of the Hodgkin–Huxley pattern [Reference Hodgkin and Huxley23]. In fact, they studied the activator–inhibitor dynamics of a neuron electric pulse along the axon.
Let
where
![]() $\tau$
,
$\tau$
,
![]() $d_1 \geq 0$
and
$d_1 \geq 0$
and
![]() $d_2 \geq 0$
are constants. The original FHN model is an ODE system where
$d_2 \geq 0$
are constants. The original FHN model is an ODE system where
![]() $f(u)=u(1-u)(u-\alpha)$
with
$f(u)=u(1-u)(u-\alpha)$
with
![]() $0<\alpha<1/2$
and with
$0<\alpha<1/2$
and with
![]() $d_1=d_2=0$
in (1.18).
$d_1=d_2=0$
in (1.18).
Periodic solutions and stability involving the equilibrium solutions have been studied in [Reference Klaasen and Mitidieri27, Reference Klaasen and Troy28] for
![]() $d_1 > 0$
,
$d_1 > 0$
,
![]() $d_2>0$
and
$d_2>0$
and
![]() $N=1$
, and in [Reference Oshita32] on bounded domains and more dimensions, see also [Reference Sweers and Troy34].
$N=1$
, and in [Reference Oshita32] on bounded domains and more dimensions, see also [Reference Sweers and Troy34].
More recently, other stability issues, pattern formation, standing, and traveling waves were addressed in [Reference Chen and Choi12–Reference Chen and Séré15].
The stationary system on bounded domains
![]() $\Omega \subset \mathbb{R}^{N}$
,
$\Omega \subset \mathbb{R}^{N}$
,
has been treated in [Reference Dancer and Yan18, Reference Wei and Winter35, Reference Wei and Winter36] with suitable boundary conditions.
System (1.19) with
![]() $\Omega = \mathbb{R}^{N}$
,
$\Omega = \mathbb{R}^{N}$
,
![]() $a=0$
,
$a=0$
,
![]() $d_1=d_2=1$
has been considered in [Reference Reinecke and Sweers33] by transforming it into a quasimonotone system. Restricted to a ball, the authors found a subsolution and a supersolution, which are ordered and give rise to a solution by the method of [Reference Amann2]. Such a solution defined on a ball tends to a genuine solution of (1.1) as the radius of the ball tends to infinity, it is an idea already used in [Reference Berestycki and Lions9]. There the positivity of the solution follows from the results of [Reference de Figueiredo and Mitidieri19]. An extension of the result on existence of solution of [Reference Reinecke and Sweers33] by means of variational methods is in [Reference Chen and Tanaka16].
$d_1=d_2=1$
has been considered in [Reference Reinecke and Sweers33] by transforming it into a quasimonotone system. Restricted to a ball, the authors found a subsolution and a supersolution, which are ordered and give rise to a solution by the method of [Reference Amann2]. Such a solution defined on a ball tends to a genuine solution of (1.1) as the radius of the ball tends to infinity, it is an idea already used in [Reference Berestycki and Lions9]. There the positivity of the solution follows from the results of [Reference de Figueiredo and Mitidieri19]. An extension of the result on existence of solution of [Reference Reinecke and Sweers33] by means of variational methods is in [Reference Chen and Tanaka16].
The plan of the paper is as follows. In Section 2, we show that the set
![]() $\mathcal{M}$
is nonempty and we introduce the Pohozaev manifold to show a lower bound for b. Section 3 is devoted to the extensive task of recovering compactness. For that matter we deal with minimizing sequences and Lagrange multipliers sequences. As a consequence, we find a weak limit function which is the candidate to be a solution of the nonlocal equation. Such fact is confirmed in Section 4, thus proving Theorem 1.1. Theorem 1.2 is proved in Section 5. The constant
$\mathcal{M}$
is nonempty and we introduce the Pohozaev manifold to show a lower bound for b. Section 3 is devoted to the extensive task of recovering compactness. For that matter we deal with minimizing sequences and Lagrange multipliers sequences. As a consequence, we find a weak limit function which is the candidate to be a solution of the nonlocal equation. Such fact is confirmed in Section 4, thus proving Theorem 1.1. Theorem 1.2 is proved in Section 5. The constant
![]() $\tau^*$
is determined in Lemmas 3.6 and 5.4.
$\tau^*$
is determined in Lemmas 3.6 and 5.4.
2. The set
 $\mathcal{M}$
and the Pohozaev manifold
$\mathcal{M}$
and the Pohozaev manifold
We will use the set
![]() $\mathcal{M}$
in the minimizing arguments, next we show that it is a nontrivial manifold.
$\mathcal{M}$
in the minimizing arguments, next we show that it is a nontrivial manifold.
Lemma 2.1. The set
![]() $\mathcal{M}$
defined in (1.14) is nonempty and it is a
$\mathcal{M}$
defined in (1.14) is nonempty and it is a
![]() $C^1$
manifold.
$C^1$
manifold.
Proof. Observe that for a fixed
![]() $\varphi\in C^{\infty}_{0}(\mathbb R^{N})$
,
$\varphi\in C^{\infty}_{0}(\mathbb R^{N})$
,
![]() $\varphi\geq0$
,
$\varphi\geq0$
,
![]() $\varphi \not\equiv 0$
, using (1.2), the function
$\varphi \not\equiv 0$
, using (1.2), the function
![]() $h(t)=\int_{\mathbb R^{N}}G(t\varphi)dx $
is strictly negative for small t and by (1.5), we have that
$h(t)=\int_{\mathbb R^{N}}G(t\varphi)dx $
is strictly negative for small t and by (1.5), we have that
![]() $h(t)>0$
for t large; this implies that there exists some
$h(t)>0$
for t large; this implies that there exists some
![]() $\bar t>0$
such that
$\bar t>0$
such that
![]() $\bar t\varphi\in \mathcal M.$
Moreover,
$\bar t\varphi\in \mathcal M.$
Moreover,
![]() $\mathcal M$
is a
$\mathcal M$
is a
![]() $C^{1}$
manifold. In fact, define the
$C^{1}$
manifold. In fact, define the
![]() $C^{1}$
functional
$C^{1}$
functional
![]() $J(u) = \int_{\mathbb R^{N}} G(u)dx -1$
, it holds from (1.4) that
$J(u) = \int_{\mathbb R^{N}} G(u)dx -1$
, it holds from (1.4) that
Lemma 2.2. The set
![]() $\mathcal{M}$
defined in (1.15) is nonempty and it is a
$\mathcal{M}$
defined in (1.15) is nonempty and it is a
![]() $C^1$
manifold.
$C^1$
manifold.
Proof. Consider
![]() $\zeta \in C^{\infty}_{0}(\mathbb R)$
with
$\zeta \in C^{\infty}_{0}(\mathbb R)$
with
![]() $\zeta(x)>0$
and define the function
$\zeta(x)>0$
and define the function
From (1.2) for
![]() $t>0$
small we have
$t>0$
small we have
For
![]() $\varepsilon <1$
, we get
$\varepsilon <1$
, we get
![]() $h(t)<0$
for
$h(t)<0$
for
![]() $t>0$
small.
$t>0$
small.
By virtue of (1.5) we obtain
and
Then,
![]() $h(t)>0$
for
$h(t)>0$
for
![]() $t>0$
large and
$t>0$
large and
![]() $h'(t)>0$
for
$h'(t)>0$
for
![]() $t>0$
large. Then there is a
$t>0$
large. Then there is a
![]() $\overline{t}>0$
such that
$\overline{t}>0$
such that
Now we prove that
![]() $\mathcal{M}$
is a manifold. Indeed, if
$\mathcal{M}$
is a manifold. Indeed, if
![]() $\zeta\in \mathcal{M}$
, then
$\zeta\in \mathcal{M}$
, then
![]() $\zeta \not=0$
. Then, from (1.2) and the fact that
$\zeta \not=0$
. Then, from (1.2) and the fact that
![]() $\lim_{|x|\to \infty}\zeta(x)=0 $
and
$\lim_{|x|\to \infty}\zeta(x)=0 $
and
![]() $B\geq 0$
, there exists
$B\geq 0$
, there exists
![]() $ x_0 \in \mathbb R^{2}$
such that
$ x_0 \in \mathbb R^{2}$
such that
![]() $g(\zeta(x_0))<0$
. Thereby, the continuity implies that there is an open interval
$g(\zeta(x_0))<0$
. Thereby, the continuity implies that there is an open interval
![]() $B_\delta(x_0)$
such that
$B_\delta(x_0)$
such that
As a consequence we can always find
![]() $\phi \in C_0^{\infty}(\mathbb R^{2}) \subset X$
such that
$\phi \in C_0^{\infty}(\mathbb R^{2}) \subset X$
such that
![]() $J'(\zeta)[\phi]=\displaystyle\int_{\mathbb R^{2}}g(\zeta)\phi \,dx < 0$
, where
$J'(\zeta)[\phi]=\displaystyle\int_{\mathbb R^{2}}g(\zeta)\phi \,dx < 0$
, where
![]() $J(u) = \int_{\mathbb R} G(u)dx$
, showing that
$J(u) = \int_{\mathbb R} G(u)dx$
, showing that
![]() $J'(\zeta) \not=0$
.
$J'(\zeta) \not=0$
.
We will need an estimate for the minimax value b defined by (1.16). For that matter we use the Pohozaev manifold associated to the first equation in (1.1) for
![]() $N \geq 3$
, given by
$N \geq 3$
, given by
where
![]() $v= Bu$
. Then we can rewrite it as
$v= Bu$
. Then we can rewrite it as
which, by a direct computation, contains every weak solution of (1.10).
We set the notation
Since B is linear and arguing as in [Reference Jeanjean and Tanaka25, proof of Lemma 3.1], we can see that
where D is as in (1.13).
We prove next some results involving the Pohozaev manifold.
Lemma 2.3. It holds
where b is the minimax level of I defined in (1.16).
Proof. Indeed, since B is linear and arguing as [Reference Jeanjean and Tanaka25, step 3 of Lemma 1.4], for each
![]() $\overline \gamma \in \Gamma$
, it results
$\overline \gamma \in \Gamma$
, it results
![]() $\overline{\gamma}([0, 1]) \cap \mathcal{P} \neq \emptyset$
. Then, there exists
$\overline{\gamma}([0, 1]) \cap \mathcal{P} \neq \emptyset$
. Then, there exists
![]() $t_0 \in [0, 1]$
such that
$t_0 \in [0, 1]$
such that
![]() $\overline{\gamma}(t_0) \in \mathcal{P}$
. The property
$\overline{\gamma}(t_0) \in \mathcal{P}$
. The property
![]() $\int_{\mathbb{R}^{N}}u B(u) dx \geq 0$
, implies
$\int_{\mathbb{R}^{N}}u B(u) dx \geq 0$
, implies
Hence,
![]() $p_0 \leq b$
and the result follows from (2.2).
$p_0 \leq b$
and the result follows from (2.2).
3. Minimizing sequences and Lagrange multipliers
We establish some preliminary results which will be useful in order to prove Theorem 1.1. Along the paper, we will take advantage of the following rephrased form of (1.13)–(1.14), namely
The next steps consist in proving the boundedness of the minimizing sequences in
![]() $H^{1}(\mathbb{R}^N)$
for D.
$H^{1}(\mathbb{R}^N)$
for D.
Lemma 3.1. Any minimizing sequence
![]() $\{ u_n \}\subset \mathcal M$
for T is bounded in X.
$\{ u_n \}\subset \mathcal M$
for T is bounded in X.
Proof. Let
![]() $\{ u_n \}\subset \mathcal M $
be a minimizing sequence for T, then
$\{ u_n \}\subset \mathcal M $
be a minimizing sequence for T, then
and
Then
and
By using (1.7) with
![]() $\varepsilon = 1/2$
, we get
$\varepsilon = 1/2$
, we get
Then, for every
![]() $n \in \mathbb N$
, by using (3.2), it follows
$n \in \mathbb N$
, by using (3.2), it follows
Consequently
![]() $\{ u_n \} $
is bounded also in
$\{ u_n \} $
is bounded also in
![]() $L^2(\mathbb R^N)$
. Moreover,
$L^2(\mathbb R^N)$
. Moreover,
![]() $ \displaystyle\int_{\mathbb R^N} u_n B(u_n) \, dx \leq \|B\|_{X^{-1}} \int_{\mathbb R^N} u_n^2 dx$
and this ensures its boundedness in X (here
$ \displaystyle\int_{\mathbb R^N} u_n B(u_n) \, dx \leq \|B\|_{X^{-1}} \int_{\mathbb R^N} u_n^2 dx$
and this ensures its boundedness in X (here
![]() $X^{-1}$
is the dual space of X).
$X^{-1}$
is the dual space of X).
By the Ekeland Variational Principle (see [Reference Ekeland20]), we can assume that the minimizing sequence
![]() $\{u_{n}\}$
is also a Palais–Smale sequence, that is, using (2.1) there exists a sequence of Lagrange multipliers
$\{u_{n}\}$
is also a Palais–Smale sequence, that is, using (2.1) there exists a sequence of Lagrange multipliers
![]() $\{ \lambda_n \} \subset \mathbb R$
such that
$\{ \lambda_n \} \subset \mathbb R$
such that
and
In the remaining part of this section,
![]() $\{\lambda_{n}\}$
will be the associated sequence of Lagrange multipliers. At this point, it is useful to establish some properties of the levels D and b.
$\{\lambda_{n}\}$
will be the associated sequence of Lagrange multipliers. At this point, it is useful to establish some properties of the levels D and b.
Lemma 3.2. The number D given by (3.1) is positive.
Proof. Clearly by definition
![]() $D \geq 0$
. Suppose, by contradiction, that
$D \geq 0$
. Suppose, by contradiction, that
![]() $D =0$
. If
$D =0$
. If
![]() $\{ u_n \} $
is a minimizing sequence for
$\{ u_n \} $
is a minimizing sequence for
![]() $D =0$
, then
$D =0$
, then
and
Then, for any
![]() $\varepsilon>0$
, see (1.8),
$\varepsilon>0$
, see (1.8),
so that
By choosing
![]() $\varepsilon = 1/2$
, we obtain
$\varepsilon = 1/2$
, we obtain
This contradiction concludes the proof that
![]() $D > 0$
.
$D > 0$
.
Lemma 3.3. The sequence of Lagrange multipliers
![]() $\{ \lambda_n \}$
associated to the minimizing sequence
$\{ \lambda_n \}$
associated to the minimizing sequence
![]() $\{u_{n}\}$
is bounded. More precisely, we have that
$\{u_{n}\}$
is bounded. More precisely, we have that
Hence, for some subsequence, still denoted by
![]() $\{\lambda_n\}$
, we can assume that
$\{\lambda_n\}$
, we can assume that
![]() $\lambda_n \to \lambda^{*}$
, for some
$\lambda_n \to \lambda^{*}$
, for some
![]() $\lambda^{*} \in (0, D]$
.
$\lambda^{*} \in (0, D]$
.
Proof. By (3.4),
Then, from (2.1)
which implies, taking into account (3.3),
Since
![]() $\{u_{n}\}$
is a bounded minimizing sequence, it is easy to see that
$\{u_{n}\}$
is a bounded minimizing sequence, it is easy to see that
![]() $|J'(u_{n})[u_{n}] |= |\int_{\mathbb R^{N}} g(u_{n}) u_{n}| \leq C$
, and then by (3.5) and the fact that
$|J'(u_{n})[u_{n}] |= |\int_{\mathbb R^{N}} g(u_{n}) u_{n}| \leq C$
, and then by (3.5) and the fact that
![]() $2T(u_{n})\to 2D>0$
, we infer that
$2T(u_{n})\to 2D>0$
, we infer that
The proof is thereby completed.
In the sequel, we will show that a minimizing sequence for (3.1) can be chosen to be nonnegative and radially symmetric around the origin. Note that for our proof we do not need to consider the “odd extension” of the nonlinearity, as it is usually done in the literature to show that the minimizing sequence can be replaced by the sequence of the absolute values. In fact we will prove that the minimizing sequence can be replaced, roughly speaking, by the sequence of the positive parts.
Lemma 3.4. Any minimizing sequence
![]() $\{u_n\}$
for (3.1) can be assumed to be radially symmetric around the origin and nonnegative.
$\{u_n\}$
for (3.1) can be assumed to be radially symmetric around the origin and nonnegative.
Proof. To begin with, we recall that
![]() $F(s)=0$
for all
$F(s)=0$
for all
![]() $s \leq 0$
. Thus,
$s \leq 0$
. Thus,
![]() $F(u_n)=F(u_n^{+})$
for all
$F(u_n)=F(u_n^{+})$
for all
![]() $n \in \mathbb{N}$
with
$n \in \mathbb{N}$
with
![]() $u_n^{+}=\max\{0,u_n\}$
. From this, the equality
$u_n^{+}=\max\{0,u_n\}$
. From this, the equality
leads to
Defining the function
![]() $h_n\;:\;[0,1] \to \mathbb R$
by
$h_n\;:\;[0,1] \to \mathbb R$
by
the conditions on f yield that h is continuous with
![]() $h_n(1) \geq 1$
. Once
$h_n(1) \geq 1$
. Once
![]() $u_n^+ \not=0$
for all
$u_n^+ \not=0$
for all
![]() $n \in \mathbb{N}$
, the condition (1.2) ensures that
$n \in \mathbb{N}$
, the condition (1.2) ensures that
![]() $h_n(t)<0$
for t close to 0. Thus, there is
$h_n(t)<0$
for t close to 0. Thus, there is
![]() $t_n \in (0,1]$
such that
$t_n \in (0,1]$
such that
![]() $h_n(t_n)=1$
, that is,
$h_n(t_n)=1$
, that is,
implying that
![]() $t_n u_n^+ \in \mathcal{M}$
. We also know that
$t_n u_n^+ \in \mathcal{M}$
. We also know that
Since
![]() $t_n \in (0,1]$
, the last inequality gives
$t_n \in (0,1]$
, the last inequality gives
that is,
showing that
![]() $\{t_n u_n^+\}$
is a minimizing sequence for T. Hence, without lost of generality, we can assume that
$\{t_n u_n^+\}$
is a minimizing sequence for T. Hence, without lost of generality, we can assume that
![]() $\{u_n\}$
is a nonnegative sequence.
$\{u_n\}$
is a nonnegative sequence.
Moreover,
(see [Reference Baernstein5, Theorem 3]) and
which implies
where
![]() $u_n^{*}$
is the Schwartz symmetrization of
$u_n^{*}$
is the Schwartz symmetrization of
![]() $u_n$
. Then, every minimizing sequence can be assumed radially symmetric, nonnegative and decreasing in
$u_n$
. Then, every minimizing sequence can be assumed radially symmetric, nonnegative and decreasing in
![]() $r=|x|$
.
$r=|x|$
.
Let
![]() $X_{rad}$
be the space of radially symmetric functions of X. In what follows, we will use that the embedding
$X_{rad}$
be the space of radially symmetric functions of X. In what follows, we will use that the embedding
is compact for all
![]() $p \in (2,2^{*})$
, recall the similar embedding of
$p \in (2,2^{*})$
, recall the similar embedding of
![]() $H^1_{rad}(\mathbb R^N)$
and see Lions [Reference Lions29] for more details.
$H^1_{rad}(\mathbb R^N)$
and see Lions [Reference Lions29] for more details.
It turns out that the key point in the proof of Theorem 1.1 is to verify that the weak limit of
![]() $\{u_{n}\}$
in
$\{u_{n}\}$
in
![]() $X_{rad}$
, denoted hereafter by u, is a solution of the minimizing problem (3.1). Before verifying this in Section 4, some preliminary lemmas are required in order to recover compactness.
$X_{rad}$
, denoted hereafter by u, is a solution of the minimizing problem (3.1). Before verifying this in Section 4, some preliminary lemmas are required in order to recover compactness.
Remark 4. Due to the boundedness in
![]() $X_{rad}$
of the nonnegative and radially symmetric minimizing sequence
$X_{rad}$
of the nonnegative and radially symmetric minimizing sequence
![]() $\{u_{n}\}$
, assume for the moment that its weak limit u in
$\{u_{n}\}$
, assume for the moment that its weak limit u in
![]() $X_{rad}$
is a solution of (1.10). Observe also that, by the boundedness in
$X_{rad}$
is a solution of (1.10). Observe also that, by the boundedness in
![]() $L^{2}(\mathbb R^{N})$
we have the uniform decay
$L^{2}(\mathbb R^{N})$
we have the uniform decay
![]() $|u_{n}(x)| \leq C |x|^{-(N-1)/2}$
, see [Reference Kavian26, Lemma 1.1. p. 250]. Therefore, arguing with a subsequence, if necessary, we deduce that the weak limit u is nonnegative, radially symmetric, and decreasing. These properties do also hold for
$|u_{n}(x)| \leq C |x|^{-(N-1)/2}$
, see [Reference Kavian26, Lemma 1.1. p. 250]. Therefore, arguing with a subsequence, if necessary, we deduce that the weak limit u is nonnegative, radially symmetric, and decreasing. These properties do also hold for
![]() $v=B(u)$
. Therefore, one has the decay of
$v=B(u)$
. Therefore, one has the decay of
![]() $u(x) \to 0$
and
$u(x) \to 0$
and
![]() $v(x) \to 0$
as
$v(x) \to 0$
as
![]() $|x| \to \infty$
, where (u, v) is a solution of (1.1). This observation is valid for
$|x| \to \infty$
, where (u, v) is a solution of (1.1). This observation is valid for
![]() $N \geq 2$
.
$N \geq 2$
.
In the next result, we use the following constant
 \begin{equation*}S= \displaystyle\inf_{u\in \mathcal{D}^{1,2}(\mathbb{R}^{N})\setminus \{0\}}\frac{\displaystyle\int_{\mathbb{R}^{N}}|\nabla u|^{2} dx}{\left(\displaystyle\int_{\mathbb{R}^{N}}|u|^{2^{*}} dx\right)^{2/2^{*}}}.\end{equation*}
\begin{equation*}S= \displaystyle\inf_{u\in \mathcal{D}^{1,2}(\mathbb{R}^{N})\setminus \{0\}}\frac{\displaystyle\int_{\mathbb{R}^{N}}|\nabla u|^{2} dx}{\left(\displaystyle\int_{\mathbb{R}^{N}}|u|^{2^{*}} dx\right)^{2/2^{*}}}.\end{equation*}
Lemma 3.5. Assume that
![]() $w_n=u_n-u\rightharpoonup 0$
in
$w_n=u_n-u\rightharpoonup 0$
in
![]() $X_{rad}$
and
$X_{rad}$
and
![]() $\| w_n\|^{2} \to L>0$
. Then
$\| w_n\|^{2} \to L>0$
. Then
Proof. First of all, we recall (2.1) and that the limit
![]() $T'(u_n) - \lambda_n J'(u_n) \rightarrow 0$
as
$T'(u_n) - \lambda_n J'(u_n) \rightarrow 0$
as
![]() $n \rightarrow + \infty$
gives
$n \rightarrow + \infty$
gives
Using standard arguments, it is possible to prove that
and
where
![]() $\lambda^{*}$
is the same which appear in Lemma 3.3. Then
$\lambda^{*}$
is the same which appear in Lemma 3.3. Then
![]() $T'(w_n)[w_n]-\lambda_{n} J'(w_n)[w_n]=o_n(1)$
, or equivalently,
$T'(w_n)[w_n]-\lambda_{n} J'(w_n)[w_n]=o_n(1)$
, or equivalently,
Using the growth conditions on f, fixed
![]() $q \in (2,2^{*})$
and given
$q \in (2,2^{*})$
and given
![]() $\varepsilon >0$
, there exists
$\varepsilon >0$
, there exists
![]() $C=C(\varepsilon, q)>0$
such that
$C=C(\varepsilon, q)>0$
such that
From this,
Now, using the definition of S, we get
 \begin{eqnarray} \int_{\mathbb R^N} |\nabla w_n|^2 \, dx &\leq &\lambda_n \left(\varepsilon \int_{\mathbb R^N} w_n^2 dx + C \int_{\mathbb R^N} |w_n|^q dx +(1+\varepsilon) \left( \frac{1}{S} \int_{\mathbb R^N} |\nabla w_n|^{2} \, dx\right)^{2^{*}/ 2} \right)+ o_n(1)\nonumber\\&\leq & \lambda_n \left(\varepsilon \int_{\mathbb R^N} w_n^2 dx + C \int_{\mathbb R^N} |w_n|^q dx +(1+\varepsilon) \left( \frac{1}{S} \int_{\mathbb R^N} |\nabla w_n|^2 \, dx \right)^{2^{*}/ 2} \right)+ o_n(1).\end{eqnarray}
\begin{eqnarray} \int_{\mathbb R^N} |\nabla w_n|^2 \, dx &\leq &\lambda_n \left(\varepsilon \int_{\mathbb R^N} w_n^2 dx + C \int_{\mathbb R^N} |w_n|^q dx +(1+\varepsilon) \left( \frac{1}{S} \int_{\mathbb R^N} |\nabla w_n|^{2} \, dx\right)^{2^{*}/ 2} \right)+ o_n(1)\nonumber\\&\leq & \lambda_n \left(\varepsilon \int_{\mathbb R^N} w_n^2 dx + C \int_{\mathbb R^N} |w_n|^q dx +(1+\varepsilon) \left( \frac{1}{S} \int_{\mathbb R^N} |\nabla w_n|^2 \, dx \right)^{2^{*}/ 2} \right)+ o_n(1).\end{eqnarray}
Taking to the limit in (3.7), recalling that
![]() $\{w_n\}$
is bounded,
$\{w_n\}$
is bounded,
and that
![]() $w_n \to 0$
in
$w_n \to 0$
in
![]() $L^{q}(\mathbb R^N)$
(see (3.6)), we obtain
$L^{q}(\mathbb R^N)$
(see (3.6)), we obtain
 \begin{equation*}L\leq \lambda^*\left( \varepsilon C_1 + (1+\varepsilon)\left(\frac{L}{S}\right)^{2^{*}/2} \right).\end{equation*}
\begin{equation*}L\leq \lambda^*\left( \varepsilon C_1 + (1+\varepsilon)\left(\frac{L}{S}\right)^{2^{*}/2} \right).\end{equation*}
Since
![]() $\varepsilon$
arbitrary and the fact that
$\varepsilon$
arbitrary and the fact that
![]() $\lambda^{*}\leq D$
(recall Lemma 3.3), we derive
$\lambda^{*}\leq D$
(recall Lemma 3.3), we derive
![]() $L\leq D \left(L/S \right)^{2^{*}/2}$
, or equivalently,
$L\leq D \left(L/S \right)^{2^{*}/2}$
, or equivalently,
On the other, hand (3.8) implies that
![]() $L = 2D -\|u\|^2 \leq 2D$
. Hence (3.9) becomes
$L = 2D -\|u\|^2 \leq 2D$
. Hence (3.9) becomes
and the proof is finished.
Now we consider the equation
where
![]() $\Omega$
is a smooth bounded domain in
$\Omega$
is a smooth bounded domain in
![]() $\mathbb{R}^{N}$
and q is the constant which appears in the hypothesis (1.5). The functional
$\mathbb{R}^{N}$
and q is the constant which appears in the hypothesis (1.5). The functional
![]() $I_q\;:\; H^{1,}_0(\Omega)\rightarrow \mathbb{R}$
associated to (3.10) is given by
$I_q\;:\; H^{1,}_0(\Omega)\rightarrow \mathbb{R}$
associated to (3.10) is given by
Since
![]() $\Omega$
is bounded, the expression
$\Omega$
is bounded, the expression
 \begin{equation*}\| u \|_{\Omega} = \left( \int\limits_{\Omega}\left[|\nabla u|^2+|u|^2 + B(u)u \right]dx \right)^\frac{1}{2}\end{equation*}
\begin{equation*}\| u \|_{\Omega} = \left( \int\limits_{\Omega}\left[|\nabla u|^2+|u|^2 + B(u)u \right]dx \right)^\frac{1}{2}\end{equation*}
is equivalent the usual norm of
![]() $H^{1}_{0}(\Omega)$
, by the Mountain Pass Theorem [Reference Ambrosetti and Rabinowitz1], there exists
$H^{1}_{0}(\Omega)$
, by the Mountain Pass Theorem [Reference Ambrosetti and Rabinowitz1], there exists
![]() $\omega_q\in H^{1}_{0}(\Omega)$
such that
$\omega_q\in H^{1}_{0}(\Omega)$
such that
Moreover,
In the next result, the condition
![]() $\tau>\tau^{*}$
given in (1.5) plays a crucial role. We fix
$\tau>\tau^{*}$
given in (1.5) plays a crucial role. We fix
Lemma 3.6. It holds
Proof. Take
![]() $\omega_q \in H^{1}_{0}(\Omega)$
a solution of problem (3.10). By (1.5) and the definition of b at (1.16), we get
$\omega_q \in H^{1}_{0}(\Omega)$
a solution of problem (3.10). By (1.5) and the definition of b at (1.16), we get
 \begin{eqnarray*}b \leq \max_{ t \geq 0} I(t \omega_q) & \leq &\max_{t \geq 0} \left\{ \frac{t^2}{2}\|\omega_q\|^2_{\Omega} - \tau \frac{t^q}{q} \int_{\mathbb R^N} |\omega_q|^q \, dx \right\} \leq \max_{t \geq 0} \left\{ \frac{t^2}{2} - \tau \frac{t^q}{q} \right\} \int_{\mathbb R^N} |\omega_q|^q \, dx\\& = & \max_{t \geq 0} \left\{ \frac{t^2}{2} - \tau \frac{t^q}{q} \right\} c_q \frac{2q}{q-2} = \frac{c_q}{\tau^{2/(q-2)}}.\end{eqnarray*}
\begin{eqnarray*}b \leq \max_{ t \geq 0} I(t \omega_q) & \leq &\max_{t \geq 0} \left\{ \frac{t^2}{2}\|\omega_q\|^2_{\Omega} - \tau \frac{t^q}{q} \int_{\mathbb R^N} |\omega_q|^q \, dx \right\} \leq \max_{t \geq 0} \left\{ \frac{t^2}{2} - \tau \frac{t^q}{q} \right\} \int_{\mathbb R^N} |\omega_q|^q \, dx\\& = & \max_{t \geq 0} \left\{ \frac{t^2}{2} - \tau \frac{t^q}{q} \right\} c_q \frac{2q}{q-2} = \frac{c_q}{\tau^{2/(q-2)}}.\end{eqnarray*}
The conclusion of the lemma follows.
Lemma 3.7. If
![]() $u_n \rightharpoonup u$
in
$u_n \rightharpoonup u$
in
![]() $X_{rad}$
, then
$X_{rad}$
, then
![]() $u_n \to u$
in
$u_n \to u$
in
![]() $D^{1,2}(\mathbb{R}^N)$
. In particular,
$D^{1,2}(\mathbb{R}^N)$
. In particular,
![]() $u_n \to u$
in
$u_n \to u$
in
![]() $L^{2^{*}}(\mathbb{R}^N)$
.
$L^{2^{*}}(\mathbb{R}^N)$
.
Proof. Suppose by contradiction that
![]() $u_n \not\to u $
in
$u_n \not\to u $
in
![]() $D^{1,2}(\mathbb{R}^N)$
and let
$D^{1,2}(\mathbb{R}^N)$
and let
![]() $w_n = u_n - u$
. Thus
$w_n = u_n - u$
. Thus
![]() $\int_{\mathbb R^N} |\nabla w_n|^{2} \, dx \to L>0$
for some subsequence. Then, by Lemma 3.5,
$\int_{\mathbb R^N} |\nabla w_n|^{2} \, dx \to L>0$
for some subsequence. Then, by Lemma 3.5,
From Lemma 2.3
from which, using (3.12), it follows that
This contradicts Lemma 3.6 and accomplishes the proof.
4. Proof of Theorem 1.1
The results of the last section will be used next.
Proof of Theorem 1.1. We wish to show that D is attained by u, where u is the weak limit of
![]() $\{ u_n \}$
. First of all, we know that
$\{ u_n \}$
. First of all, we know that
so we just need to prove that
![]() $u\in \mathcal M$
.
$u\in \mathcal M$
.
Since
for all
![]() $t\geq 1$
, for
$t\geq 1$
, for
![]() $R>0$
large, we have
$R>0$
large, we have
![]() $B_{R}$
being the ball of radius R centered in
$B_{R}$
being the ball of radius R centered in
![]() $0.$
Since
$0.$
Since
![]() $u_n \to u $
in
$u_n \to u $
in
![]() $L^{2^{*}}(B_R)$
, reasoning with a subsequence if needed, we have
$L^{2^{*}}(B_R)$
, reasoning with a subsequence if needed, we have
![]() $u_{n} \to u $
a.e. in
$u_{n} \to u $
a.e. in
![]() $B_{R}$
and there exists
$B_{R}$
and there exists
![]() $h\in L^{2^{*}}(B_{R})$
such that
$h\in L^{2^{*}}(B_{R})$
such that
![]() $|u_{n}(x)|\leq h(x)$
. Moreover, we have
$|u_{n}(x)|\leq h(x)$
. Moreover, we have
![]() $F(u_{n}(x)) \to F(u(x))$
a.e. and
$F(u_{n}(x)) \to F(u(x))$
a.e. and
![]() $|F(u_{n})|\leq 2^{-1}\varepsilon u_{n}^{2} + C_{\varepsilon} |u_{n}|^{2^{*}}\leq2^{-1}\varepsilon u_{n}^{2} + C_{\varepsilon} |v|^{2^{*}} $
which, joint with the fact that
$|F(u_{n})|\leq 2^{-1}\varepsilon u_{n}^{2} + C_{\varepsilon} |u_{n}|^{2^{*}}\leq2^{-1}\varepsilon u_{n}^{2} + C_{\varepsilon} |v|^{2^{*}} $
which, joint with the fact that
![]() $\varepsilon$
is arbitrary and the Dominated Convergence Theorem, give
$\varepsilon$
is arbitrary and the Dominated Convergence Theorem, give
![]() $\int_{B_{R}} F(u_{n})dx \to \int_{B_{R}} F(u)dx$
. Then by
$\int_{B_{R}} F(u_{n})dx \to \int_{B_{R}} F(u)dx$
. Then by
taking into account the above considerations and the Fatou Lemma we infer
which leads to
Suppose by contradiction that
and define
![]() $h\;:\;[0, 1] \rightarrow \mathbb R$
by
$h\;:\;[0, 1] \rightarrow \mathbb R$
by
![]() $h(t) = \int_{\mathbb R^N} G(tu) \, dx$
. The growth conditions on f ensure that
$h(t) = \int_{\mathbb R^N} G(tu) \, dx$
. The growth conditions on f ensure that
![]() $h(t) < 0$
for t close to 0 and
$h(t) < 0$
for t close to 0 and
![]() $h(1) = \int_{\mathbb R^N} G(u) \, dx > 1$
. Then, by the continuity of h, there exists
$h(1) = \int_{\mathbb R^N} G(u) \, dx > 1$
. Then, by the continuity of h, there exists
![]() $t_0 \in (0, 1)$
such that
$t_0 \in (0, 1)$
such that
![]() $h(t_0)=1$
. Then,
$h(t_0)=1$
. Then,
Consequently, by (4.1)
which is an absurd. Thus
![]() $ \int_{\mathbb R^N} G(u) \, dx =1 $
, i.e.
$ \int_{\mathbb R^N} G(u) \, dx =1 $
, i.e.
![]() $ u\in \mathcal M$
. The fact that the solution u of the minimizing problem gives rise to a solution of (1.10), follows by standard arguments; indeed, since u is a solution of the minimizing problem (3.1), i.e.
$ u\in \mathcal M$
. The fact that the solution u of the minimizing problem gives rise to a solution of (1.10), follows by standard arguments; indeed, since u is a solution of the minimizing problem (3.1), i.e.
![]() $D =T(u)= \inf_{w\in \mathcal M}T(w)$
, then there exists an associated Lagrange multiplier
$D =T(u)= \inf_{w\in \mathcal M}T(w)$
, then there exists an associated Lagrange multiplier
![]() $\lambda$
such that, in the weak sense,
$\lambda$
such that, in the weak sense,
Testing the previous equation on the same minimizer u, we deduce
so that, by Lemma 3.2,
![]() $T(u)\geq\lambda>0$
. Setting
$T(u)\geq\lambda>0$
. Setting
![]() $u_{\sigma}(x)=u(\sigma x)$
for
$u_{\sigma}(x)=u(\sigma x)$
for
![]() $\sigma>0$
, we easily see that
$\sigma>0$
, we easily see that
Choosing
![]() $\sigma=\lambda^{-1/2}$
we obtain a solution of (1.10). Arguing as in [Reference Berestycki and Lions10, Theorem 3],
$\sigma=\lambda^{-1/2}$
we obtain a solution of (1.10). Arguing as in [Reference Berestycki and Lions10, Theorem 3],
![]() $u_\sigma$
is a solution of (1.10). Rewriting
$u_\sigma$
is a solution of (1.10). Rewriting
![]() $u_{\sigma}$
as u, and since
$u_{\sigma}$
as u, and since
![]() $v=B(u)$
, we conclude that (u, v) is a solution of (1.1).
$v=B(u)$
, we conclude that (u, v) is a solution of (1.1).
5. Proof of Theorem 1.2
We establish preliminary results in the entire plan which will be useful in order to prove Theorem 1.2. Here we point out that, we will deal with minimizing sequences
![]() $\{u_{n}\}$
for the minimization problem (1.13)–(1.15), rewritten in the form
$\{u_{n}\}$
for the minimization problem (1.13)–(1.15), rewritten in the form
We suppose that
![]() $u_{n}$
is nonnegative and radially symmetric.
$u_{n}$
is nonnegative and radially symmetric.
It is useful to state the next result which is a consequence of [Reference Alves, Montenegro and Souto3, Lemma 5.1]. The proof is based on Trudinger–Moser inequality and the Compactness Lemma of Strauss [Reference Berestycki and Lions10, Theorem A.I].
Lemma 5.1. Assume that f satisfies (1.2), (1.5), and (1.6). Let
![]() $\{w_n\}\subset X_{rad}$
be a sequence of radially symmetric functions such that
$\{w_n\}\subset X_{rad}$
be a sequence of radially symmetric functions such that
and
Then,
The relation between the minimum D and the minimax level b defined in (1.16) is stated in the following lemma.
Lemma 5.2. The numbers D and b satisfy the inequality
![]() $D\leq b$
.
$D\leq b$
.
Proof. Arguing as in Lemma 2.2, given
![]() $\eta \in X$
with
$\eta \in X$
with
![]() $\eta^{+}=\max\{\eta,0\}\neq 0$
, there is
$\eta^{+}=\max\{\eta,0\}\neq 0$
, there is
![]() $t_{0}>0$
such that
$t_{0}>0$
such that
![]() $t_0 \eta^{+} \in \mathcal{M}$
. Then,
$t_0 \eta^{+} \in \mathcal{M}$
. Then,
Due to the fact that
![]() $f(s)=0$
for
$f(s)=0$
for
![]() $s\leq 0$
, for
$s\leq 0$
, for
![]() $\eta\in X$
,
$\eta\in X$
,
![]() $\eta\neq 0$
with
$\eta\neq 0$
with
![]() $\eta^{+}=0$
, we obtain
$\eta^{+}=0$
, we obtain
![]() $\max_{t\geq 0}I(tv)=\infty$
. Hence in any case
$\max_{t\geq 0}I(tv)=\infty$
. Hence in any case
![]() $D\leq b$
.
$D\leq b$
.
Lemma 5.3. The number D given by (5.1) is positive.
Proof. By definition
![]() $D\geq 0$
. Assume by contradiction that
$D\geq 0$
. Assume by contradiction that
![]() $D=0$
an let
$D=0$
an let
![]() $\{u_n\}$
be a (nonnegative and radially symmetric) minimizing sequence in
$\{u_n\}$
be a (nonnegative and radially symmetric) minimizing sequence in
![]() $X_{rad}$
for T, that is,
$X_{rad}$
for T, that is,
For each
![]() $\mu_n>0$
, the function
$\mu_n>0$
, the function
![]() $\xi_n(x)=u_n( x / \mu_n)$
satisfies
$\xi_n(x)=u_n( x / \mu_n)$
satisfies
Since
we choose
![]() $\mu_{n}^{2}=\biggl[\displaystyle\int_{\mathbb R^{2}} u_n^{2}dx+ \displaystyle\int_{\mathbb R^{2}} u_nB(u_n)dx\biggl]^{-1}$
to obtain
$\mu_{n}^{2}=\biggl[\displaystyle\int_{\mathbb R^{2}} u_n^{2}dx+ \displaystyle\int_{\mathbb R^{2}} u_nB(u_n)dx\biggl]^{-1}$
to obtain
We can assume that there exists
![]() $ v \in X_{rad}$
, radially symmetric, such that
$ v \in X_{rad}$
, radially symmetric, such that
![]() $\xi_n \rightharpoonup \xi$
in
$\xi_n \rightharpoonup \xi$
in
![]() $X_{rad}$
. From Lemma 5.1, we get
$X_{rad}$
. From Lemma 5.1, we get
Notice that
![]() $\int_{\mathbb R^{2}} G(\xi_n) \, dx =0$
implies
$\int_{\mathbb R^{2}} G(\xi_n) \, dx =0$
implies
![]() $\int_{\mathbb R^{2}} F(\xi_n) \, dx =1/2$
and
$\int_{\mathbb R^{2}} F(\xi_n) \, dx =1/2$
and
![]() $\int_{\mathbb R^{2}} F(\xi) \, dx = 1/2$
. Then
$\int_{\mathbb R^{2}} F(\xi) \, dx = 1/2$
. Then
![]() $v \neq 0$
. But
$v \neq 0$
. But
implies
![]() $\xi=0$
, which is an absurd.
$\xi=0$
, which is an absurd.
Lemma 5.4. We have
![]() $ b < 1/2.$
$ b < 1/2.$
Proof. It is enough to repeat the same argument of the proof of Lemma 3.6, recalling now that
![]() $N=2$
and by (1.5) we choose
$N=2$
and by (1.5) we choose
Proof of Theorem 1.2. We will show that D is attained by u, where u is the weak limit of
![]() $\{ u_n \}$
. Indeed, since
$\{ u_n \}$
. Indeed, since
![]() $u_n \rightharpoonup u$
in
$u_n \rightharpoonup u$
in
![]() $X_{rad}$
we have
$X_{rad}$
we have
Moreover, by Lemma 5.1 we have
leading to
As in the previous case
![]() $N\geq3$
, we just need to prove that
$N\geq3$
, we just need to prove that
![]() $u\in \mathcal M$
, i.e.
$u\in \mathcal M$
, i.e.
![]() $\int_{\mathbb R^N} G(u) \, dx = 0$
.
$\int_{\mathbb R^N} G(u) \, dx = 0$
.
We again argue by contradiction. Suppose that
As in the proof of Lemma 2.2, we set
![]() $h\;:\;[0, 1] \rightarrow \mathbb R$
by
$h\;:\;[0, 1] \rightarrow \mathbb R$
by
![]() $h(t) = \int_{\mathbb R} G(tu) \, dx$
. Using the growth condition of f, we have
$h(t) = \int_{\mathbb R} G(tu) \, dx$
. Using the growth condition of f, we have
![]() $h(t) < 0$
for t close to 0 and
$h(t) < 0$
for t close to 0 and
![]() $h(1) = \int_{\mathbb R} G(u) \, dx > 0$
. Hence, by the continuity of h, there exists
$h(1) = \int_{\mathbb R} G(u) \, dx > 0$
. Hence, by the continuity of h, there exists
![]() $t_0 \in (0, 1)$
such that
$t_0 \in (0, 1)$
such that
![]() $h(t_0)=0$
, that is,
$h(t_0)=0$
, that is,
![]() $t_{0}u\in \mathcal M$
. Consequently, by (5.2)
$t_{0}u\in \mathcal M$
. Consequently, by (5.2)
which is an absurd.
As for the case
![]() $N\geq3$
, one shows that the minimizer u of (5.1) gives rise to a solution of (1.10), and then (u, v) with
$N\geq3$
, one shows that the minimizer u of (5.1) gives rise to a solution of (1.10), and then (u, v) with
![]() $v=B(u)$
solves (1.1).
$v=B(u)$
solves (1.1).
Acknowledgement
G. Figueiredo has been partially supported by CNPq and FAPDF and M. Montenegro has been partially supported by CNPq and FAPESP.