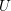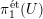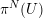1 Introduction
1.1 Nori’s fundamental group scheme
Let
![]() $X$
be an algebraic variety over a field
$X$
be an algebraic variety over a field
![]() $k$
. In [Reference GrothendieckSGA1], Grothendieck defined the étale fundamental group
$k$
. In [Reference GrothendieckSGA1], Grothendieck defined the étale fundamental group
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
as a generalization of the fundamental group of a topological space. It is the smallest profinite group classifying
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
as a generalization of the fundamental group of a topological space. It is the smallest profinite group classifying
![]() $G$
-coverings over
$G$
-coverings over
![]() $X$
, where
$X$
, where
![]() $G$
is a finite group. In the case where
$G$
is a finite group. In the case where
![]() $k$
is an algebraically closed field of characteristic zero with
$k$
is an algebraically closed field of characteristic zero with
![]() $k{\hookrightarrow}\mathbb{C}$
, it is known that
$k{\hookrightarrow}\mathbb{C}$
, it is known that
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
is isomorphic to the profinite completion of the topological one
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
is isomorphic to the profinite completion of the topological one
![]() $\unicode[STIX]{x1D70B}_{1}^{\text{top}}(X(\mathbb{C}))$
. For example, as the complex line
$\unicode[STIX]{x1D70B}_{1}^{\text{top}}(X(\mathbb{C}))$
. For example, as the complex line
![]() $\mathbb{A}^{1}(\mathbb{C})$
is simply connected, we have
$\mathbb{A}^{1}(\mathbb{C})$
is simply connected, we have
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{\mathbb{C}}^{1})=0$
. On the other hand, in the case where
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{\mathbb{C}}^{1})=0$
. On the other hand, in the case where
![]() $k$
is of positive characteristic
$k$
is of positive characteristic
![]() $p>0$
, the situation is quite different. This can be seen even in the case where
$p>0$
, the situation is quite different. This can be seen even in the case where
![]() $X=\mathbb{A}_{k}^{1}$
is the affine line. Indeed, it is known that
$X=\mathbb{A}_{k}^{1}$
is the affine line. Indeed, it is known that
![]() $\operatorname{dim}_{\mathbb{F}_{p}}\operatorname{Hom}(\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{k}^{1}),\mathbb{F}_{p})=\infty$
. On the other hand, if
$\operatorname{dim}_{\mathbb{F}_{p}}\operatorname{Hom}(\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{k}^{1}),\mathbb{F}_{p})=\infty$
. On the other hand, if
![]() $X=U$
is a smooth affine curve, the Abhyankar conjecture [Reference AbhyankarAbh57], proved by Raynaud and Harbater [Reference HarbaterHar94, Reference RaynaudRay94], gives us another estimate of the difference between
$X=U$
is a smooth affine curve, the Abhyankar conjecture [Reference AbhyankarAbh57], proved by Raynaud and Harbater [Reference HarbaterHar94, Reference RaynaudRay94], gives us another estimate of the difference between
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)$
and the topological one of a Riemann surface of the same type. The conjecture describes the set
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)$
and the topological one of a Riemann surface of the same type. The conjecture describes the set
for any smooth affine curve
![]() $U$
. Here, more precisely,
$U$
. Here, more precisely,
![]() $\unicode[STIX]{x1D70B}_{A}^{\acute{\text{e}}\text{t}}(U)$
is the set of isomorphism classes of finite groups which appears as a finite quotient of
$\unicode[STIX]{x1D70B}_{A}^{\acute{\text{e}}\text{t}}(U)$
is the set of isomorphism classes of finite groups which appears as a finite quotient of
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)$
. For example, it says for any integers
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)$
. For example, it says for any integers
![]() $n>0$
and
$n>0$
and
![]() $r>0$
, there exists a surjective homomorphism
$r>0$
, there exists a surjective homomorphism
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\operatorname{SL}_{n}(\mathbb{F}_{p^{r}})$
(cf. [Reference KambayashiKam86, Reference NoriNor94, Reference SerreSer92]).
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\operatorname{SL}_{n}(\mathbb{F}_{p^{r}})$
(cf. [Reference KambayashiKam86, Reference NoriNor94, Reference SerreSer92]).
In [Reference NoriNor76], [Reference NoriNor82, ch. II], Nori defined the fundamental group scheme
![]() $\unicode[STIX]{x1D70B}^{N}(X)$
as a generalization of Grothendieck’s étale geometric fundamental group of an algebraic variety
$\unicode[STIX]{x1D70B}^{N}(X)$
as a generalization of Grothendieck’s étale geometric fundamental group of an algebraic variety
![]() $X$
over a field
$X$
over a field
![]() $k$
(cf. [Reference GrothendieckSGA1]). It is a profinite
$k$
(cf. [Reference GrothendieckSGA1]). It is a profinite
![]() $k$
-group scheme classifying
$k$
-group scheme classifying
![]() $G$
-torsors over
$G$
-torsors over
![]() $X$
with
$X$
with
![]() $G$
a finite
$G$
a finite
![]() $k$
-group scheme. In [Reference NoriNor76], he first constructed it under the assumption that
$k$
-group scheme. In [Reference NoriNor76], he first constructed it under the assumption that
![]() $X$
is proper over
$X$
is proper over
![]() $k$
by using the theory of Tannakian categories. On the other hand, in [Reference NoriNor82], he also proved that such a profinite one
$k$
by using the theory of Tannakian categories. On the other hand, in [Reference NoriNor82], he also proved that such a profinite one
![]() $\unicode[STIX]{x1D70B}^{N}(X)$
exists also for arbitrary (not necessarily proper)
$\unicode[STIX]{x1D70B}^{N}(X)$
exists also for arbitrary (not necessarily proper)
![]() $X$
without relying on a Tannakian construction (cf. § 2.1). Note that, if
$X$
without relying on a Tannakian construction (cf. § 2.1). Note that, if
![]() $k$
is an algebraically closed field, then Grothendieck’s étale fundamental group
$k$
is an algebraically closed field, then Grothendieck’s étale fundamental group
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
classifies all finite étale torsors over
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
classifies all finite étale torsors over
![]() $X$
and is universal for this property. Hence, there exists a homomorphism of
$X$
and is universal for this property. Hence, there exists a homomorphism of
![]() $\unicode[STIX]{x1D70B}^{N}(X)$
into the pro-constant
$\unicode[STIX]{x1D70B}^{N}(X)$
into the pro-constant
![]() $k$
-group scheme, denoted by
$k$
-group scheme, denoted by
![]() $\unicode[STIX]{x1D70B}^{\acute{\text{e}}\text{t}}(X)$
, associated with
$\unicode[STIX]{x1D70B}^{\acute{\text{e}}\text{t}}(X)$
, associated with
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
. In fact
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
. In fact
![]() $\unicode[STIX]{x1D70B}^{\acute{\text{e}}\text{t}}(X)$
gives the maximal pro-étale quotient of
$\unicode[STIX]{x1D70B}^{\acute{\text{e}}\text{t}}(X)$
gives the maximal pro-étale quotient of
![]() $\unicode[STIX]{x1D70B}^{N}(X)$
, called the étale fundamental group scheme. In the case where
$\unicode[STIX]{x1D70B}^{N}(X)$
, called the étale fundamental group scheme. In the case where
![]() $k$
is of characteristic zero, then the surjective homomorphism
$k$
is of characteristic zero, then the surjective homomorphism
![]() $\unicode[STIX]{x1D70B}^{N}(X){\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\acute{\text{e}}\text{t}}(X)$
is in fact an isomorphism. This is valid because under the assumption that
$\unicode[STIX]{x1D70B}^{N}(X){\twoheadrightarrow}\unicode[STIX]{x1D70B}^{\acute{\text{e}}\text{t}}(X)$
is in fact an isomorphism. This is valid because under the assumption that
![]() $k$
is an algebraically closed field of characteristic zero, any finite
$k$
is an algebraically closed field of characteristic zero, any finite
![]() $G$
-torsor
$G$
-torsor
![]() $P\rightarrow X$
with
$P\rightarrow X$
with
![]() $G$
a finite
$G$
a finite
![]() $k$
-group scheme is nothing but a
$k$
-group scheme is nothing but a
![]() $G(k)$
-covering over
$G(k)$
-covering over
![]() $X$
. On the other hand, in the case where
$X$
. On the other hand, in the case where
![]() $k$
is of positive characteristic
$k$
is of positive characteristic
![]() $p>0$
, then
$p>0$
, then
![]() $\unicode[STIX]{x1D70B}^{N}(X)$
is strictly larger than
$\unicode[STIX]{x1D70B}^{N}(X)$
is strictly larger than
![]() $\unicode[STIX]{x1D70B}^{\acute{\text{e}}\text{t}}(X)$
, in general. Indeed, finite local (‘purely inseparable’) torsors make a contribution to occur the difference between these fundamental group schemes. Here a finite
$\unicode[STIX]{x1D70B}^{\acute{\text{e}}\text{t}}(X)$
, in general. Indeed, finite local (‘purely inseparable’) torsors make a contribution to occur the difference between these fundamental group schemes. Here a finite
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
is said to be local if it is connected, i.e., if
$G$
is said to be local if it is connected, i.e., if
![]() $G^{0}$
denotes the connected component of the identity
$G^{0}$
denotes the connected component of the identity
![]() $1\in G$
, then
$1\in G$
, then
![]() $G^{0}=G$
. For example,
$G^{0}=G$
. For example,
![]() $G=\unicode[STIX]{x1D6FC}_{p}$
, or
$G=\unicode[STIX]{x1D6FC}_{p}$
, or
![]() $\unicode[STIX]{x1D707}_{p}$
.
$\unicode[STIX]{x1D707}_{p}$
.
1.2 Main results
In the present paper, we will attempt to estimate the difference between
![]() $\unicode[STIX]{x1D70B}^{N}(U)$
and
$\unicode[STIX]{x1D70B}^{N}(U)$
and
![]() $\unicode[STIX]{x1D70B}^{\acute{\text{e}}\text{t}}(U)$
for a smooth affine curve
$\unicode[STIX]{x1D70B}^{\acute{\text{e}}\text{t}}(U)$
for a smooth affine curve
![]() $U$
defined over an algebraically closed field
$U$
defined over an algebraically closed field
![]() $k$
of positive characteristic
$k$
of positive characteristic
![]() $p>0$
from the viewpoint of the inverse Galois problem. We will study a purely inseparable analogue of the Abhyankar conjecture for affine curves
$p>0$
from the viewpoint of the inverse Galois problem. We will study a purely inseparable analogue of the Abhyankar conjecture for affine curves
![]() $U$
(cf. [Reference AbhyankarAbh57, Reference AbhyankarAbh92]; see also § 1.3), i.e., we will try to describe the set
$U$
(cf. [Reference AbhyankarAbh57, Reference AbhyankarAbh92]; see also § 1.3), i.e., we will try to describe the set
More precisely,
![]() $\unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
is the set of isomorphism classes of finite local
$\unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
is the set of isomorphism classes of finite local
![]() $k$
-group schemes which appears as a finite quotient of
$k$
-group schemes which appears as a finite quotient of
![]() $\unicode[STIX]{x1D70B}^{N}(U)$
.
$\unicode[STIX]{x1D70B}^{N}(U)$
.
Now let us explain the contents of the present paper. In § 2, we will briefly review the definition of Nori’s profinite fundamental group scheme and the maximal linearly reductive quotient of it. In § 3, we will see the maximal local linearly reductive quotient of
![]() $\unicode[STIX]{x1D70B}^{N}(U)$
provides a necessary condition for a finite local
$\unicode[STIX]{x1D70B}^{N}(U)$
provides a necessary condition for a finite local
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
to belong to the set
$G$
to belong to the set
![]() $\unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
(cf. Proposition 3.1). Now let us explain this. Let
$\unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
(cf. Proposition 3.1). Now let us explain this. Let
![]() $X$
be a smooth compactification of
$X$
be a smooth compactification of
![]() $U$
. Let
$U$
. Let
![]() $n\overset{\operatorname{def}}{=}\#(X\setminus U)$
. Note that the affineness assumption of
$n\overset{\operatorname{def}}{=}\#(X\setminus U)$
. Note that the affineness assumption of
![]() $U$
implies
$U$
implies
![]() $n>0$
. Let
$n>0$
. Let
![]() $\unicode[STIX]{x1D6FE}$
be the
$\unicode[STIX]{x1D6FE}$
be the
![]() $p$
-rank of the Jacobian variety of
$p$
-rank of the Jacobian variety of
![]() $X$
, i.e.,
$X$
, i.e.,
![]() $\unicode[STIX]{x1D6FE}=\operatorname{dim}_{\mathbb{F}_{p}}\text{Pic}_{X}^{0}[p](k)$
. We will see that for any finite local
$\unicode[STIX]{x1D6FE}=\operatorname{dim}_{\mathbb{F}_{p}}\text{Pic}_{X}^{0}[p](k)$
. We will see that for any finite local
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
, if
$G$
, if
![]() $G\in \unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
, then the character group
$G\in \unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
, then the character group
![]() $\mathbb{X}(G)\overset{\operatorname{def}}{=}\operatorname{Hom}(G,\mathbb{G}_{m})$
must be embeddable as a subgroup into
$\mathbb{X}(G)\overset{\operatorname{def}}{=}\operatorname{Hom}(G,\mathbb{G}_{m})$
must be embeddable as a subgroup into
![]() $(\mathbb{Q}_{p}/\mathbb{Z}_{p})^{\oplus \unicode[STIX]{x1D6FE}+n-1}$
. Then we can ask whether or not the converse is true (cf. Question 3.3).
$(\mathbb{Q}_{p}/\mathbb{Z}_{p})^{\oplus \unicode[STIX]{x1D6FE}+n-1}$
. Then we can ask whether or not the converse is true (cf. Question 3.3).
Question 1.1. Let
![]() $U$
be a smooth affine curve and
$U$
be a smooth affine curve and
![]() $G$
a finite local
$G$
a finite local
![]() $k$
-group scheme. If there exists an injective homomorphism
$k$
-group scheme. If there exists an injective homomorphism
![]() $\mathbb{X}(G){\hookrightarrow}(\mathbb{Q}_{p}/\mathbb{Z}_{p})^{\oplus \unicode[STIX]{x1D6FE}+n-1}$
, then does
$\mathbb{X}(G){\hookrightarrow}(\mathbb{Q}_{p}/\mathbb{Z}_{p})^{\oplus \unicode[STIX]{x1D6FE}+n-1}$
, then does
![]() $G$
belong to the set
$G$
belong to the set
![]() $\unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
?
$\unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
?
The main purpose of the present paper is to give a partial affirmative answer to Question 1.1. The main result is the following theorem (cf. Proposition 3.4; Corollaries 4.19; 4.15).
Theorem 1.2.
(1) For any smooth affine curve
 $U$
over
$U$
over
 $k$
and any finite local nilpotent
$k$
and any finite local nilpotent
 $k$
-group scheme
$k$
-group scheme
 $G$
, if there exists an injective homomorphism
$G$
, if there exists an injective homomorphism
 $\mathbb{X}(G){\hookrightarrow}(\mathbb{Q}_{p}/\mathbb{Z}_{p})^{\oplus \unicode[STIX]{x1D6FE}+n-1}$
, then there exists a surjective homomorphism
$\mathbb{X}(G){\hookrightarrow}(\mathbb{Q}_{p}/\mathbb{Z}_{p})^{\oplus \unicode[STIX]{x1D6FE}+n-1}$
, then there exists a surjective homomorphism
 $\unicode[STIX]{x1D70B}^{N}(U){\twoheadrightarrow}G$
.
$\unicode[STIX]{x1D70B}^{N}(U){\twoheadrightarrow}G$
.(2) Let
 $\unicode[STIX]{x1D6F4}$
be a semi-simple simply connected algebraic group over
$\unicode[STIX]{x1D6F4}$
be a semi-simple simply connected algebraic group over
 $k$
. Then for any integer
$k$
. Then for any integer
 $r>0$
, there exists a surjective homomorphism of
$r>0$
, there exists a surjective homomorphism of $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{N}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\unicode[STIX]{x1D6F4}_{(r)}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{N}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\unicode[STIX]{x1D6F4}_{(r)}\end{eqnarray}$$
 $\unicode[STIX]{x1D70B}^{N}(\mathbb{A}_{k}^{1})$
onto the
$\unicode[STIX]{x1D70B}^{N}(\mathbb{A}_{k}^{1})$
onto the
 $r$
th Frobenius kernel
$r$
th Frobenius kernel
 $\unicode[STIX]{x1D6F4}_{(r)}\overset{\operatorname{def}}{=}\operatorname{Ker}(F^{(r)}:\unicode[STIX]{x1D6F4}^{(-r)}\rightarrow \unicode[STIX]{x1D6F4})$
.
$\unicode[STIX]{x1D6F4}_{(r)}\overset{\operatorname{def}}{=}\operatorname{Ker}(F^{(r)}:\unicode[STIX]{x1D6F4}^{(-r)}\rightarrow \unicode[STIX]{x1D6F4})$
.(3) Assume
 $p=2$
. Then for any integer
$p=2$
. Then for any integer
 $r>0$
, there exists a surjective homomorphism of
$r>0$
, there exists a surjective homomorphism of $$\begin{eqnarray}\unicode[STIX]{x1D70B}^{N}(\mathbb{G}_{m}){\twoheadrightarrow}\operatorname{GL}_{2(r)}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}^{N}(\mathbb{G}_{m}){\twoheadrightarrow}\operatorname{GL}_{2(r)}\end{eqnarray}$$
 $\unicode[STIX]{x1D70B}^{N}(\mathbb{G}_{m})$
onto the
$\unicode[STIX]{x1D70B}^{N}(\mathbb{G}_{m})$
onto the
 $r$
th Frobenius kernel
$r$
th Frobenius kernel
 $\operatorname{GL}_{2(r)}$
of
$\operatorname{GL}_{2(r)}$
of
 $\operatorname{GL}_{2}$
.
$\operatorname{GL}_{2}$
.
Here, for each integer
![]() $r>0$
,
$r>0$
,
![]() $\unicode[STIX]{x1D6F4}^{(-r)}$
denotes the
$\unicode[STIX]{x1D6F4}^{(-r)}$
denotes the
![]() $(-r)$
th Frobenius twist of
$(-r)$
th Frobenius twist of
![]() $\unicode[STIX]{x1D6F4}$
and
$\unicode[STIX]{x1D6F4}$
and
![]() $F^{(r)}:\unicode[STIX]{x1D6F4}^{(-r)}\rightarrow \unicode[STIX]{x1D6F4}$
is the
$F^{(r)}:\unicode[STIX]{x1D6F4}^{(-r)}\rightarrow \unicode[STIX]{x1D6F4}$
is the
![]() $r$
th relative Frobenius morphism, which is a homomorphism of algebraic groups. Furthermore, its kernel
$r$
th relative Frobenius morphism, which is a homomorphism of algebraic groups. Furthermore, its kernel
![]() $\unicode[STIX]{x1D6F4}_{(r)}=\operatorname{Ker}(F^{(r)})$
is a finite local
$\unicode[STIX]{x1D6F4}_{(r)}=\operatorname{Ker}(F^{(r)})$
is a finite local
![]() $k$
-group scheme.
$k$
-group scheme.
Remark 1.3. (1) If
![]() $\unicode[STIX]{x1D6F4}$
is a semi-simple simply connected algebraic group over
$\unicode[STIX]{x1D6F4}$
is a semi-simple simply connected algebraic group over
![]() $k$
, it turns out that
$k$
, it turns out that
![]() $\mathbb{X}(\unicode[STIX]{x1D6F4}_{(r)})=1$
(cf. Remark 3.7(3)). Therefore, Theorem 1.2(2) gives an affirmative answer to Question 1.1 for the affine line
$\mathbb{X}(\unicode[STIX]{x1D6F4}_{(r)})=1$
(cf. Remark 3.7(3)). Therefore, Theorem 1.2(2) gives an affirmative answer to Question 1.1 for the affine line
![]() $\mathbb{A}_{k}^{1}$
and for the Frobenius kernels
$\mathbb{A}_{k}^{1}$
and for the Frobenius kernels
![]() $\unicode[STIX]{x1D6F4}_{(r)}~(r>0)$
of a semi-simple simply connected algebraic group
$\unicode[STIX]{x1D6F4}_{(r)}~(r>0)$
of a semi-simple simply connected algebraic group
![]() $\unicode[STIX]{x1D6F4}$
.
$\unicode[STIX]{x1D6F4}$
.
(2) Since
![]() $\mathbb{X}(\operatorname{GL}_{2(r)})=\mathbb{Z}/2^{r}\mathbb{Z}\subset \mathbb{Q}_{2}/\mathbb{Z}_{2}$
if
$\mathbb{X}(\operatorname{GL}_{2(r)})=\mathbb{Z}/2^{r}\mathbb{Z}\subset \mathbb{Q}_{2}/\mathbb{Z}_{2}$
if
![]() $p=2$
, Theorem 1.2(3) gives an affirmative answer to Question 1.1 for the multiplicative group
$p=2$
, Theorem 1.2(3) gives an affirmative answer to Question 1.1 for the multiplicative group
![]() $U=\mathbb{G}_{m}$
and for the Frobenius kernels
$U=\mathbb{G}_{m}$
and for the Frobenius kernels
![]() $\operatorname{GL}_{2(r)}~(r>0)$
of
$\operatorname{GL}_{2(r)}~(r>0)$
of
![]() $\operatorname{GL}_{2}$
in the case where
$\operatorname{GL}_{2}$
in the case where
![]() $k$
is of characteristic
$k$
is of characteristic
![]() $p=2$
.
$p=2$
.
(3) Note that each homomorphism
![]() $\unicode[STIX]{x1D70B}^{N}(U)\rightarrow G$
of
$\unicode[STIX]{x1D70B}^{N}(U)\rightarrow G$
of
![]() $\unicode[STIX]{x1D70B}^{N}(U)$
into a finite
$\unicode[STIX]{x1D70B}^{N}(U)$
into a finite
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
corresponds bijectively to a (fpqc)
$G$
corresponds bijectively to a (fpqc)
![]() $G$
-torsor
$G$
-torsor
![]() $P\rightarrow U$
(cf. Proposition 2.2). To prove Theorem 1.2(2), we will show there exists a
$P\rightarrow U$
(cf. Proposition 2.2). To prove Theorem 1.2(2), we will show there exists a
![]() $k$
-morphism
$k$
-morphism
![]() $f:\mathbb{A}_{k}^{1}\rightarrow \unicode[STIX]{x1D6F4}$
such that the resulting
$f:\mathbb{A}_{k}^{1}\rightarrow \unicode[STIX]{x1D6F4}$
such that the resulting
![]() $\unicode[STIX]{x1D6F4}_{(r)}$
-torsor
$\unicode[STIX]{x1D6F4}_{(r)}$
-torsor
![]() $f^{\ast }\unicode[STIX]{x1D6F4}^{(-r)}\rightarrow \mathbb{A}_{k}^{1}$
realizes a surjective homomorphism
$f^{\ast }\unicode[STIX]{x1D6F4}^{(-r)}\rightarrow \mathbb{A}_{k}^{1}$
realizes a surjective homomorphism
![]() $\unicode[STIX]{x1D70B}^{N}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\unicode[STIX]{x1D6F4}_{(r)}$
. To prove the existence of such a morphism
$\unicode[STIX]{x1D70B}^{N}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\unicode[STIX]{x1D6F4}_{(r)}$
. To prove the existence of such a morphism
![]() $f$
, we will first reduce the problem to the case where
$f$
, we will first reduce the problem to the case where
![]() $r=1$
(cf. Lemma 4.2). Next we will deduce the existence of such an
$r=1$
(cf. Lemma 4.2). Next we will deduce the existence of such an
![]() $f$
from a Bertini type theorem for height one torsors (cf. Theorem 4.17).
$f$
from a Bertini type theorem for height one torsors (cf. Theorem 4.17).
(4) In particular, Theorem 1.2(1) (or Theorem 1.2(2)) implies that if
![]() $p=2$
, then
$p=2$
, then
![]() $\operatorname{SL}_{2(1)}$
appears as a finite quotient of
$\operatorname{SL}_{2(1)}$
appears as a finite quotient of
![]() $\unicode[STIX]{x1D70B}^{N}(\mathbb{A}_{k}^{1})$
(cf. Example 3.6). On the other hand, it turns out that any
$\unicode[STIX]{x1D70B}^{N}(\mathbb{A}_{k}^{1})$
(cf. Example 3.6). On the other hand, it turns out that any
![]() $\operatorname{SL}_{2(1)}$
-torsor must be of the form
$\operatorname{SL}_{2(1)}$
-torsor must be of the form
![]() $f^{\ast }\operatorname{SL}_{2}^{(-1)}\rightarrow \mathbb{A}_{k}^{1}$
for some
$f^{\ast }\operatorname{SL}_{2}^{(-1)}\rightarrow \mathbb{A}_{k}^{1}$
for some
![]() $k$
-morphism
$k$
-morphism
![]() $f:\mathbb{A}_{k}^{1}\rightarrow \operatorname{SL}_{2}$
. In this case, we can explicitly describe the subset of
$f:\mathbb{A}_{k}^{1}\rightarrow \operatorname{SL}_{2}$
. In this case, we can explicitly describe the subset of
![]() $\text{Mor}_{k}(\mathbb{A}_{k}^{1},\operatorname{SL}_{2})$
consisting of
$\text{Mor}_{k}(\mathbb{A}_{k}^{1},\operatorname{SL}_{2})$
consisting of
![]() $k$
-morphisms
$k$
-morphisms
![]() $f$
such that the torsor
$f$
such that the torsor
![]() $f^{\ast }\operatorname{SL}_{2}^{(-1)}$
realizes a surjective homomorphism
$f^{\ast }\operatorname{SL}_{2}^{(-1)}$
realizes a surjective homomorphism
![]() $\unicode[STIX]{x1D70B}^{N}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\operatorname{SL}_{2(1)}$
(cf. Corollary 4.13).
$\unicode[STIX]{x1D70B}^{N}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\operatorname{SL}_{2(1)}$
(cf. Corollary 4.13).
Remark 1.4. Considering recent developments of the theory of ‘tame stacks’ (cf. [Reference Abramovich, Olsson and VistoliAOV08, Reference MarquesMar12, Reference GillibertGil12]), the author expects that the notion of linearly reductiveness might provide us with a good analogy between the answer of Question 1.1 and the Abhyankar conjecture (cf. Theorem 1.5) and that Question 1.1 might be affirmative for any smooth affine curve
![]() $U$
and for any finite local
$U$
and for any finite local
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
. See also Remark 1.8.
$G$
. See also Remark 1.8.
1.3 The Abhyankar conjecture
All the ideas of our arguments in the present paper come from Serre’s work [Reference SerreSer90] (the method of embedding problems) or Nori’s one [Reference KambayashiKam86, Reference NoriNor94] in the pursuit of the Abhyankar conjecture for the affine line. Hence, we would like to briefly review the conjecture.
First we will recall the precise statement of it (in a weak form). Let
![]() $k$
be an algebraically closed field of positive characteristic
$k$
be an algebraically closed field of positive characteristic
![]() $p>0$
and
$p>0$
and
![]() $X$
a smooth projective curve over
$X$
a smooth projective curve over
![]() $k$
of genus
$k$
of genus
![]() $g\geqslant 0$
. Let
$g\geqslant 0$
. Let
![]() $\emptyset \neq U\subset X$
be a nonempty open subset with
$\emptyset \neq U\subset X$
be a nonempty open subset with
![]() $n\overset{\operatorname{def}}{=}\#(X\setminus U)\geqslant 0$
. Let
$n\overset{\operatorname{def}}{=}\#(X\setminus U)\geqslant 0$
. Let
![]() $\unicode[STIX]{x1D6E4}_{g,n}$
be the group defined by
$\unicode[STIX]{x1D6E4}_{g,n}$
be the group defined by
and
![]() $\widehat{\unicode[STIX]{x1D6E4}}_{g,n}$
by its profinite completion. Note that if
$\widehat{\unicode[STIX]{x1D6E4}}_{g,n}$
by its profinite completion. Note that if
![]() $n>0$
, then
$n>0$
, then
![]() $\unicode[STIX]{x1D6E4}_{g,n}$
is a free group
$\unicode[STIX]{x1D6E4}_{g,n}$
is a free group
![]() $F_{2g+n-1}$
of rank
$F_{2g+n-1}$
of rank
![]() $2g+n-1$
. A classical result due to Grothendieck [Reference GrothendieckSGA1] implies:
$2g+n-1$
. A classical result due to Grothendieck [Reference GrothendieckSGA1] implies:
Here
![]() $(-)^{(p^{\prime })}$
means the maximal pro-prime to
$(-)^{(p^{\prime })}$
means the maximal pro-prime to
![]() $p$
quotient. In particular, if
$p$
quotient. In particular, if
![]() $n>0$
, i.e.,
$n>0$
, i.e.,
![]() $U$
is affine, then
$U$
is affine, then
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)^{(p^{\prime })}\simeq \widehat{F}_{2g+n-1}^{(p^{\prime })}$
. Hence, in this case, if a finite group
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)^{(p^{\prime })}\simeq \widehat{F}_{2g+n-1}^{(p^{\prime })}$
. Hence, in this case, if a finite group
![]() $G$
appears as a finite quotient of
$G$
appears as a finite quotient of
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)$
, then
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)$
, then
![]() $G^{(p^{\prime })}$
must be generated by at most
$G^{(p^{\prime })}$
must be generated by at most
![]() $2g+n-1$
elements. Here, the group
$2g+n-1$
elements. Here, the group
![]() $G^{(p^{\prime })}$
is the quotient of
$G^{(p^{\prime })}$
is the quotient of
![]() $G$
by the subgroup
$G$
by the subgroup
![]() $p(G)$
generated by all the
$p(G)$
generated by all the
![]() $p$
-Sylow subgroups of
$p$
-Sylow subgroups of
![]() $G$
. The Abhyankar conjecture claims that the converse is also true.
$G$
. The Abhyankar conjecture claims that the converse is also true.
Theorem 1.5 (The Abhyankar conjecture in a weak form [Reference RaynaudRay94, Reference HarbaterHar94]).
Assume that
![]() $U$
is affine. Let
$U$
is affine. Let
![]() $G$
be an arbitrary finite group. Then
$G$
be an arbitrary finite group. Then
![]() $G\in \unicode[STIX]{x1D70B}_{A}^{\acute{\text{e}}\text{t}}(U)$
(cf. (1.1)) if and only if
$G\in \unicode[STIX]{x1D70B}_{A}^{\acute{\text{e}}\text{t}}(U)$
(cf. (1.1)) if and only if
![]() $G^{(p^{\prime })}$
can be generated by at most
$G^{(p^{\prime })}$
can be generated by at most
![]() $2g+n-1$
elements.
$2g+n-1$
elements.
Raynaud proved the theorem for the case where
![]() $U=\mathbb{A}_{k}^{1}$
[Reference RaynaudRay94]. Soon after, Harbater obtained the theorem for the general case [Reference HarbaterHar94].
$U=\mathbb{A}_{k}^{1}$
[Reference RaynaudRay94]. Soon after, Harbater obtained the theorem for the general case [Reference HarbaterHar94].
Remark 1.6. (1) Theorem 1.5 implies that
![]() $\unicode[STIX]{x1D70B}_{A}^{\acute{\text{e}}\text{t}}(U)$
is determined by the topological one
$\unicode[STIX]{x1D70B}_{A}^{\acute{\text{e}}\text{t}}(U)$
is determined by the topological one
![]() $\unicode[STIX]{x1D70B}_{1}^{\text{top}}(U_{0})$
of a Riemann surface
$\unicode[STIX]{x1D70B}_{1}^{\text{top}}(U_{0})$
of a Riemann surface
![]() $U_{0}$
of the same type
$U_{0}$
of the same type
![]() $(g,n)$
as
$(g,n)$
as
![]() $U$
. An affirmative answer to our question (Question 1.1) says that the set of finite local quotients of
$U$
. An affirmative answer to our question (Question 1.1) says that the set of finite local quotients of
![]() $\unicode[STIX]{x1D70B}^{N}(U)$
might be determined by the étale one
$\unicode[STIX]{x1D70B}^{N}(U)$
might be determined by the étale one
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)$
. Note that the number
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)$
. Note that the number
![]() $\unicode[STIX]{x1D6FE}+n-1$
can be reconstructed from
$\unicode[STIX]{x1D6FE}+n-1$
can be reconstructed from
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)$
group-theoretically (cf. [Reference TamagawaTam99]).
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(U)$
group-theoretically (cf. [Reference TamagawaTam99]).
(2) The assumption that
![]() $U$
is affine is essential. This is because if
$U$
is affine is essential. This is because if
![]() $U=X$
is projective, then
$U=X$
is projective, then
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
is topologically finitely generated and the isomorphism class of
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
is topologically finitely generated and the isomorphism class of
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
can be completely determined by the set
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
can be completely determined by the set
![]() $\unicode[STIX]{x1D70B}_{A}^{\acute{\text{e}}\text{t}}(X)$
of finite quotients of it (cf. [Reference Fried and JardenFJ08, Proposition 5.4]). On the other hand, it is known that
$\unicode[STIX]{x1D70B}_{A}^{\acute{\text{e}}\text{t}}(X)$
of finite quotients of it (cf. [Reference Fried and JardenFJ08, Proposition 5.4]). On the other hand, it is known that
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
itself has much information about the moduli of
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)$
itself has much information about the moduli of
![]() $X$
(cf. [Reference TamagawaTam99, Reference TamagawaTam04]) if the genus of
$X$
(cf. [Reference TamagawaTam99, Reference TamagawaTam04]) if the genus of
![]() $X$
is
$X$
is
![]() $g\geqslant 2$
. Therefore, such a simple answer as above (Theorem 1.5) cannot be expected and the corresponding problem is much more challenging (cf. [Reference Pacheco and StevensonPS00]).
$g\geqslant 2$
. Therefore, such a simple answer as above (Theorem 1.5) cannot be expected and the corresponding problem is much more challenging (cf. [Reference Pacheco and StevensonPS00]).
In the particular case
![]() $U=\mathbb{A}_{k}^{1}$
is the affine line, the Abhyankar conjecture states that a finite group
$U=\mathbb{A}_{k}^{1}$
is the affine line, the Abhyankar conjecture states that a finite group
![]() $G$
belongs to the set
$G$
belongs to the set
![]() $\unicode[STIX]{x1D70B}_{A}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{k}^{1})$
if and only if
$\unicode[STIX]{x1D70B}_{A}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{k}^{1})$
if and only if
![]() $G^{(p^{\prime })}=1$
. The latter condition is equivalent to the one that
$G^{(p^{\prime })}=1$
. The latter condition is equivalent to the one that
![]() $G$
can be generated by
$G$
can be generated by
![]() $p$
-Sylow subgroups of it, and such a group is called a quasi-
$p$
-Sylow subgroups of it, and such a group is called a quasi-
![]() $p$
-group. Obviously, any
$p$
-group. Obviously, any
![]() $p$
-group is a quasi-
$p$
-group is a quasi-
![]() $p$
-group. In [Reference AbhyankarAbh57, Reference AbhyankarAbh92], Abhyankar found an explicit equation defining a finite étale Galois covering over
$p$
-group. In [Reference AbhyankarAbh57, Reference AbhyankarAbh92], Abhyankar found an explicit equation defining a finite étale Galois covering over
![]() $\mathbb{A}_{k}^{1}$
whose corresponding homomorphism
$\mathbb{A}_{k}^{1}$
whose corresponding homomorphism
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{k}^{1})\rightarrow G$
is surjective for various nontrivial quasi-
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{k}^{1})\rightarrow G$
is surjective for various nontrivial quasi-
![]() $p$
-groups
$p$
-groups
![]() $G$
. In [Reference SerreSer90], Serre approached the conjecture for the affine line
$G$
. In [Reference SerreSer90], Serre approached the conjecture for the affine line
![]() $\mathbb{A}_{k}^{1}$
by the method of embedding problems. As a result, he proved that the conjecture is ture for any solvable quasi-
$\mathbb{A}_{k}^{1}$
by the method of embedding problems. As a result, he proved that the conjecture is ture for any solvable quasi-
![]() $p$
-group. This result gives a first reduction step in the proof due to Raynaud [Reference RaynaudRay94]. On the other hand, although his result was not used in Raynaud’s proof, Nori provided many examples of quasi-
$p$
-group. This result gives a first reduction step in the proof due to Raynaud [Reference RaynaudRay94]. On the other hand, although his result was not used in Raynaud’s proof, Nori provided many examples of quasi-
![]() $p$
-groups appearing as a finite quotient of
$p$
-groups appearing as a finite quotient of
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{k}^{1})$
, which gave another evidence of the Abhyankar conjetcure for
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{k}^{1})$
, which gave another evidence of the Abhyankar conjetcure for
![]() $\mathbb{A}_{k}^{1}$
(cf. [Reference KambayashiKam86, Reference NoriNor94]). Let
$\mathbb{A}_{k}^{1}$
(cf. [Reference KambayashiKam86, Reference NoriNor94]). Let
![]() $\unicode[STIX]{x1D6F4}$
be a semi-simple simply connected algebraic group (for example,
$\unicode[STIX]{x1D6F4}$
be a semi-simple simply connected algebraic group (for example,
![]() $\unicode[STIX]{x1D6F4}=\operatorname{SL}_{n}$
) over
$\unicode[STIX]{x1D6F4}=\operatorname{SL}_{n}$
) over
![]() $\mathbb{F}_{p^{r}}$
. Let
$\mathbb{F}_{p^{r}}$
. Let
![]() $L:\unicode[STIX]{x1D6F4}\rightarrow \unicode[STIX]{x1D6F4};~g\mapsto g^{-1}F^{r}(g)$
be the Lang map, where
$L:\unicode[STIX]{x1D6F4}\rightarrow \unicode[STIX]{x1D6F4};~g\mapsto g^{-1}F^{r}(g)$
be the Lang map, where
![]() $F$
is the absolute Frobenius morphism of
$F$
is the absolute Frobenius morphism of
![]() $\unicode[STIX]{x1D6F4}$
. Note that
$\unicode[STIX]{x1D6F4}$
. Note that
![]() $L$
gives a Galois covering with group
$L$
gives a Galois covering with group
![]() $\unicode[STIX]{x1D6F4}(\mathbb{F}_{p^{r}})$
. Nori showed the existence of a closed immersion
$\unicode[STIX]{x1D6F4}(\mathbb{F}_{p^{r}})$
. Nori showed the existence of a closed immersion
![]() $\unicode[STIX]{x1D704}:\mathbb{A}_{\mathbb{F}_{p^{r}}}^{1}{\hookrightarrow}\unicode[STIX]{x1D6F4}$
such that
$\unicode[STIX]{x1D704}:\mathbb{A}_{\mathbb{F}_{p^{r}}}^{1}{\hookrightarrow}\unicode[STIX]{x1D6F4}$
such that
![]() $\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6F4}$
is geometrically connected, whence the Galois covering
$\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6F4}$
is geometrically connected, whence the Galois covering
![]() $(\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6F4})_{k}\rightarrow \mathbb{A}_{k}^{1}$
corresponds to a surjective homomorphism
$(\unicode[STIX]{x1D704}^{\ast }\unicode[STIX]{x1D6F4})_{k}\rightarrow \mathbb{A}_{k}^{1}$
corresponds to a surjective homomorphism
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\unicode[STIX]{x1D6F4}(\mathbb{F}_{p^{r}})$
. For a brief survey of all the above results, see, for example, [Reference Harbater, Obus, Pries and StevensonHOPS14, § 3].
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\unicode[STIX]{x1D6F4}(\mathbb{F}_{p^{r}})$
. For a brief survey of all the above results, see, for example, [Reference Harbater, Obus, Pries and StevensonHOPS14, § 3].
Remark 1.7. (1) Our result for finite local nilpotent group schemes (Theorem 1.2(1) (cf. Proposition 3.4)) is motivated by Serre’s result on solvable quasi-
![]() $p$
-groups [Reference SerreSer90]. However, we can extend his method only in the nilpotent case.
$p$
-groups [Reference SerreSer90]. However, we can extend his method only in the nilpotent case.
(2) Theorem 1.2(2) can be considered as a purely inseparable analogue of Nori’s result [Reference KambayashiKam86, Reference NoriNor94]. To prove this, we will rely on a Bertini type theorem (Theorem 4.17). Hence, we cannot give an explicit equation defining a saturated
![]() $\unicode[STIX]{x1D6F4}_{(1)}$
-torsor over
$\unicode[STIX]{x1D6F4}_{(1)}$
-torsor over
![]() $\mathbb{A}_{k}^{1}$
for general
$\mathbb{A}_{k}^{1}$
for general
![]() $\unicode[STIX]{x1D6F4}$
. In the case where
$\unicode[STIX]{x1D6F4}$
. In the case where
![]() $p=2$
and
$p=2$
and
![]() $\unicode[STIX]{x1D6F4}=\operatorname{SL}_{2}$
, we can clarify this situation in not a conceptual but an explicit way.
$\unicode[STIX]{x1D6F4}=\operatorname{SL}_{2}$
, we can clarify this situation in not a conceptual but an explicit way.
(3) In the classical conjecture, in particular, in the proof due to Raynaud or Harbater, the rigid analytic or formal patching method and the theory of stable curves provide us with strong tools to solve the problem. The author is not sure if these methods can be applicable in our situation.
Remark 1.8. The full statement of the classical Abhyankar conjecture (proved by Harbater) states that as a covering realizing a finite quotient
![]() $G\in \unicode[STIX]{x1D70B}_{A}^{\acute{\text{e}}\text{t}}(U)$
, one can take a
$G\in \unicode[STIX]{x1D70B}_{A}^{\acute{\text{e}}\text{t}}(U)$
, one can take a
![]() $G$
-covering tamely ramified except for one point
$G$
-covering tamely ramified except for one point
![]() $x_{0}\in X\setminus U$
(cf. [Reference HarbaterHar94, Conjecture 1.2]). So, it might be natural to ask for an analogous problem. To formulate it, we need the notion of tamely ramified torsors, a similar notion to tamely remified coverings.
$x_{0}\in X\setminus U$
(cf. [Reference HarbaterHar94, Conjecture 1.2]). So, it might be natural to ask for an analogous problem. To formulate it, we need the notion of tamely ramified torsors, a similar notion to tamely remified coverings.
The notion of tameness of an action of a group scheme
![]() $G$
on a scheme
$G$
on a scheme
![]() $X$
was introduced by Chinburg et al. [Reference Chinburg, Erez, Pappas and TaylorCEPT96]. On the other hand, Abramovich et al. gave another formulation in terms of tame stacks (cf. [Reference Abramovich, Olsson and VistoliAOV08]). A relation between these two works has been studied by Marques [Reference MarquesMar12]. Moreover, in [Reference BorneBor09], Borne defined the fundamental group scheme which classifies tamely ramified torsors by using the Tannakian category of parabolic bundles. To obtain a good analogue of the notion of tame coverings, one needs to consider an extension of a
$X$
was introduced by Chinburg et al. [Reference Chinburg, Erez, Pappas and TaylorCEPT96]. On the other hand, Abramovich et al. gave another formulation in terms of tame stacks (cf. [Reference Abramovich, Olsson and VistoliAOV08]). A relation between these two works has been studied by Marques [Reference MarquesMar12]. Moreover, in [Reference BorneBor09], Borne defined the fundamental group scheme which classifies tamely ramified torsors by using the Tannakian category of parabolic bundles. To obtain a good analogue of the notion of tame coverings, one needs to consider an extension of a
![]() $G$
-torsor
$G$
-torsor
![]() $P$
over an open subset
$P$
over an open subset
![]() $U$
of
$U$
of
![]() $X$
with
$X$
with
![]() $D=X\setminus U$
a normal crossing divisor to an
$D=X\setminus U$
a normal crossing divisor to an
![]() $X$
-scheme
$X$
-scheme
![]() $Q$
together with an action of
$Q$
together with an action of
![]() $G$
. In [Reference GillibertGil12], Gillibert discussed this point. Recently, in [Reference ZalamanskyZal16], Zalamansky formulated a ramification theory in a purely inseparable setting in terms of ramification divisors. The author is not sure if there exist any relations between Zalamansky’s formulation and the previous ones.
$G$
. In [Reference GillibertGil12], Gillibert discussed this point. Recently, in [Reference ZalamanskyZal16], Zalamansky formulated a ramification theory in a purely inseparable setting in terms of ramification divisors. The author is not sure if there exist any relations between Zalamansky’s formulation and the previous ones.
In view of the above recent developments of the theory of tamely ramified torsors, one can formulate a naive analogue of the strong Abhyankar conjecture [Reference HarbaterHar94, Conjecture 1.2] in an obvious way. However, the author has no evidence of it. So, in the present paper, we will concentrate on an analogue of the weak Abhyankar conjecture.
Notation
In this paper,
![]() $k$
always means a perfect field; an algebraic variety over
$k$
always means a perfect field; an algebraic variety over
![]() $k$
means a geometrically connected and reduced scheme separated of finite type over
$k$
means a geometrically connected and reduced scheme separated of finite type over
![]() $k$
; a curve over
$k$
; a curve over
![]() $k$
is an algebraic variety over
$k$
is an algebraic variety over
![]() $k$
of dimension one; an algebraic group over
$k$
of dimension one; an algebraic group over
![]() $k$
means a group object of the category of algebraic varieties over
$k$
means a group object of the category of algebraic varieties over
![]() $k$
. Note that, automatically, any algebraic group over
$k$
. Note that, automatically, any algebraic group over
![]() $k$
is smooth.
$k$
is smooth.
Let
![]() $k$
be a perfect field of positive characteristic
$k$
be a perfect field of positive characteristic
![]() $p>0$
and
$p>0$
and
![]() $X$
an algebraic variety over
$X$
an algebraic variety over
![]() $k$
. We denote by
$k$
. We denote by
![]() $F_{X}$
, or simply
$F_{X}$
, or simply
![]() $F$
, the absolute Frobenius morphism
$F$
, the absolute Frobenius morphism
![]() $F=F_{X}:X\rightarrow X$
. For each integer
$F=F_{X}:X\rightarrow X$
. For each integer
![]() $n\in \mathbb{Z}$
, we denote by
$n\in \mathbb{Z}$
, we denote by
![]() $X^{(n)}$
the
$X^{(n)}$
the
![]() $n$
th Frobenius twist of
$n$
th Frobenius twist of
![]() $X$
.
$X$
.

If
![]() $n>0$
, the morphism
$n>0$
, the morphism
![]() $F^{n}:X\rightarrow X$
then factors uniquely through
$F^{n}:X\rightarrow X$
then factors uniquely through
![]() $X^{(n)}$
. The resulting morphism, denoted by
$X^{(n)}$
. The resulting morphism, denoted by
![]() $F^{(n)}:X\rightarrow X^{(n)}$
, is the
$F^{(n)}:X\rightarrow X^{(n)}$
, is the
![]() $n$
th relative Frobenius morphism.
$n$
th relative Frobenius morphism.
We denote by
![]() $\operatorname{Vec}_{k}$
the category of finite dimensional vector spaces over
$\operatorname{Vec}_{k}$
the category of finite dimensional vector spaces over
![]() $k$
. For an affine
$k$
. For an affine
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
, we denote by
$G$
, we denote by
![]() $\operatorname{Rep}_{k}(G)$
the category of finite dimensional left
$\operatorname{Rep}_{k}(G)$
the category of finite dimensional left
![]() $k$
-linear representations of
$k$
-linear representations of
![]() $G$
. For each
$G$
. For each
![]() $(V,\unicode[STIX]{x1D70C})\in \operatorname{Rep}_{k}(G)$
, we denote by
$(V,\unicode[STIX]{x1D70C})\in \operatorname{Rep}_{k}(G)$
, we denote by
![]() $V^{G}$
the
$V^{G}$
the
![]() $G$
-invariant subspace of
$G$
-invariant subspace of
![]() $V$
, i.e.,
$V$
, i.e.,
![]() $V^{G}=\{v\in V\,|\,\unicode[STIX]{x1D70C}(v)=v\otimes 1\}$
.
$V^{G}=\{v\in V\,|\,\unicode[STIX]{x1D70C}(v)=v\otimes 1\}$
.
2 Fundamental group scheme
2.1 Profinite fundamental group scheme
In this subsection, we will briefly recall the definition of Nori’s profinite fundamental group scheme [Reference NoriNor76, Reference NoriNor82].
Let
![]() $X$
be an algebraic variety over
$X$
be an algebraic variety over
![]() $k$
together with a rational point
$k$
together with a rational point
![]() $x\in X(k)$
. We define the category
$x\in X(k)$
. We define the category
![]() $N(X,x)$
as follows. The objects of
$N(X,x)$
as follows. The objects of
![]() $N(X,x)$
are all the triples
$N(X,x)$
are all the triples
![]() $(P,G,p)$
where:
$(P,G,p)$
where:
∙
 $G$
: a finite
$G$
: a finite
 $k$
-group scheme;
$k$
-group scheme;∙ an (fpqc)
 $G$
-torsor
$G$
-torsor
 $\unicode[STIX]{x1D70B}:P\rightarrow X$
;
$\unicode[STIX]{x1D70B}:P\rightarrow X$
;∙
 $p\in P(k)$
: a rational point with
$p\in P(k)$
: a rational point with
 $\unicode[STIX]{x1D70B}(p)=x$
.
$\unicode[STIX]{x1D70B}(p)=x$
.
Let
![]() $(P,G,p),(Q,H,q)\in N(X,x)$
be arbitrary two objects. Then a morphism
$(P,G,p),(Q,H,q)\in N(X,x)$
be arbitrary two objects. Then a morphism
![]() $(P,G,p)\rightarrow \,(Q,H,q)$
is a pair
$(P,G,p)\rightarrow \,(Q,H,q)$
is a pair
![]() $(f,\unicode[STIX]{x1D719})$
of an
$(f,\unicode[STIX]{x1D719})$
of an
![]() $X$
-morphism
$X$
-morphism
![]() $f:P\rightarrow Q$
and a
$f:P\rightarrow Q$
and a
![]() $k$
-homomorphism
$k$
-homomorphism
![]() $\unicode[STIX]{x1D719}:G\rightarrow H$
making the following diagram commute.
$\unicode[STIX]{x1D719}:G\rightarrow H$
making the following diagram commute.

Here, the above two horizontal morphisms are the ones defining the actions of torsors. By these objects and morphisms,
![]() $N(X,x)$
becomes a category. In [Reference NoriNor82], Nori proved that the category
$N(X,x)$
becomes a category. In [Reference NoriNor82], Nori proved that the category
![]() $N(X,x)$
is a cofiltered category and, in particular that the projective limit
$N(X,x)$
is a cofiltered category and, in particular that the projective limit
exists.
Definition 2.1. The projective limit of underlying group schemes
is called the profinite fundamental group scheme, or shortly the fundamental group scheme, of
![]() $(X,x)$
.
$(X,x)$
.
From the definition, the following is immediate.
Proposition 2.2. The fundamental group scheme
![]() $\unicode[STIX]{x1D70B}^{N}(X,x)$
is a profinite
$\unicode[STIX]{x1D70B}^{N}(X,x)$
is a profinite
![]() $k$
-group scheme such that for any finite
$k$
-group scheme such that for any finite
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
, the map
$G$
, the map
is bijective. Here
and
![]() $\text{Tors}(G,(X,x))$
is the set of isomorphism classes of pointed
$\text{Tors}(G,(X,x))$
is the set of isomorphism classes of pointed
![]() $G$
-torsors over
$G$
-torsors over
![]() $(X,x)$
. Moreover, the torsor
$(X,x)$
. Moreover, the torsor
![]() $(X_{x}^{N},x^{N}){\times ^{\unicode[STIX]{x1D70B}^{N}(X,x)}}^{\unicode[STIX]{x1D719}}G$
associated with a homomorphism
$(X_{x}^{N},x^{N}){\times ^{\unicode[STIX]{x1D70B}^{N}(X,x)}}^{\unicode[STIX]{x1D719}}G$
associated with a homomorphism
![]() $\unicode[STIX]{x1D719}$
is defined as the quotient of the product
$\unicode[STIX]{x1D719}$
is defined as the quotient of the product
![]() $(X_{x}^{N},x^{N})\times G$
by the diagonal action of
$(X_{x}^{N},x^{N})\times G$
by the diagonal action of
![]() $\unicode[STIX]{x1D70B}^{N}(X,x)$
:
$\unicode[STIX]{x1D70B}^{N}(X,x)$
:
for
![]() $(x,g)\in X_{x}^{N}\times G$
and
$(x,g)\in X_{x}^{N}\times G$
and
![]() $\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D70B}^{N}(X,x)$
.
$\unicode[STIX]{x1D6FE}\in \unicode[STIX]{x1D70B}^{N}(X,x)$
.
Definition 2.3. A
![]() $G$
-torsor
$G$
-torsor
![]() $(P,p)\rightarrow (X,x)$
is said to be saturated if the corresponding homomorphism
$(P,p)\rightarrow (X,x)$
is said to be saturated if the corresponding homomorphism
![]() $\unicode[STIX]{x1D70B}^{N}(X,x)\rightarrow G$
is surjective.
$\unicode[STIX]{x1D70B}^{N}(X,x)\rightarrow G$
is surjective.
Remark 2.4. If
![]() $k$
is algebraically closed, then for any finite étale
$k$
is algebraically closed, then for any finite étale
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
is the constant group scheme associated with the finite group
$G$
is the constant group scheme associated with the finite group
![]() $G(k)$
and a
$G(k)$
and a
![]() $G$
-torsor over
$G$
-torsor over
![]() $X$
is nothing but a
$X$
is nothing but a
![]() $G(k)$
-covering over
$G(k)$
-covering over
![]() $X$
. Therefore, from the universality of Grothendieck’s étale fundamental group
$X$
. Therefore, from the universality of Grothendieck’s étale fundamental group
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X,\overline{x})$
, there exists a
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X,\overline{x})$
, there exists a
![]() $k$
-homomorphism of
$k$
-homomorphism of
![]() $\unicode[STIX]{x1D70B}^{N}(X,x)$
to the pro-constant group scheme associated with
$\unicode[STIX]{x1D70B}^{N}(X,x)$
to the pro-constant group scheme associated with
![]() $\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X,\overline{x})$
. In fact, this homomorphism is surjective. Furthermore, if
$\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X,\overline{x})$
. In fact, this homomorphism is surjective. Furthermore, if
![]() $k$
is of characteristic zero, then it is an isomorphism. For details, see [Reference Esnault, Hai and SunEHS08, Remark 2.10].
$k$
is of characteristic zero, then it is an isomorphism. For details, see [Reference Esnault, Hai and SunEHS08, Remark 2.10].
2.2 The maximal linearly reductive quotient of
 $\unicode[STIX]{x1D70B}^{N}$
$\unicode[STIX]{x1D70B}^{N}$
Now let us recall the maximal linearly reductive quotient
![]() $\unicode[STIX]{x1D70B}^{\operatorname{lin.red}}(X,x)$
of
$\unicode[STIX]{x1D70B}^{\operatorname{lin.red}}(X,x)$
of
![]() $\unicode[STIX]{x1D70B}^{N}(X,x)$
(cf. [Reference Borne and VistoliBV15]).
$\unicode[STIX]{x1D70B}^{N}(X,x)$
(cf. [Reference Borne and VistoliBV15]).
Definition 2.5 (Cf. [Reference Abramovich, Olsson and VistoliAOV08, § 2]).
A finite
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
is said to be linearly reductive if one of the following equivalent conditions is satisfied:
$G$
is said to be linearly reductive if one of the following equivalent conditions is satisfied:
(a) the functor
 $\operatorname{Rep}_{k}(G)\rightarrow \operatorname{Vec}_{k};~V\mapsto V^{G}$
is exact;
$\operatorname{Rep}_{k}(G)\rightarrow \operatorname{Vec}_{k};~V\mapsto V^{G}$
is exact;(b) the category
 $\operatorname{Rep}_{k}(G)$
is semi-simple.
$\operatorname{Rep}_{k}(G)$
is semi-simple.
Proposition 2.6 (Abramovich et al. [Reference Abramovich, Olsson and VistoliAOV08, Proposition 2.13]).
A finite
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
is linearly reductive if and only if for an algebraic closure
$G$
is linearly reductive if and only if for an algebraic closure
![]() $\overline{k}$
of
$\overline{k}$
of
![]() $k$
, then
$k$
, then
![]() $G_{\overline{k}}:=G\times _{k}\overline{k}$
is isomorphic to a semi-direct product
$G_{\overline{k}}:=G\times _{k}\overline{k}$
is isomorphic to a semi-direct product
![]() $H\ltimes \unicode[STIX]{x1D6E5}$
where
$H\ltimes \unicode[STIX]{x1D6E5}$
where
![]() $H$
is a finite constant
$H$
is a finite constant
![]() $\overline{k}$
-group scheme of order prime to the characteristic of
$\overline{k}$
-group scheme of order prime to the characteristic of
![]() $k$
and
$k$
and
![]() $\unicode[STIX]{x1D6E5}$
is a finite diagonalizable
$\unicode[STIX]{x1D6E5}$
is a finite diagonalizable
![]() $\overline{k}$
-group scheme.
$\overline{k}$
-group scheme.
Here a finite group scheme
![]() $G$
is said to be diagonalizable if it is abelian and its Cartier dual is constant (cf. [Reference WaterhouseWat79, § 2.2]). Proposition 2.6 does not require the assumption that
$G$
is said to be diagonalizable if it is abelian and its Cartier dual is constant (cf. [Reference WaterhouseWat79, § 2.2]). Proposition 2.6 does not require the assumption that
![]() $k$
is perfect.
$k$
is perfect.
Remark 2.7. Assume that
![]() $k$
is an algebraically closed field of characteristic
$k$
is an algebraically closed field of characteristic
![]() $p>0$
. From Proposition 2.6, we can deduce that if a finite étale group scheme
$p>0$
. From Proposition 2.6, we can deduce that if a finite étale group scheme
![]() $G$
is linearly reductive if and only if
$G$
is linearly reductive if and only if
![]() $p\nmid \#G(k)$
and that a finite local
$p\nmid \#G(k)$
and that a finite local
![]() $k$
-group scheme is linearly reductive if and only if
$k$
-group scheme is linearly reductive if and only if
![]() $G\overset{\simeq }{\rightarrow }\operatorname{Diag}(\mathbb{X}(G))$
with
$G\overset{\simeq }{\rightarrow }\operatorname{Diag}(\mathbb{X}(G))$
with
![]() $\mathbb{X}(G)=\operatorname{Hom}(G,\mathbb{G}_{m})$
a
$\mathbb{X}(G)=\operatorname{Hom}(G,\mathbb{G}_{m})$
a
![]() $p$
-group.
$p$
-group.
Definition 2.8 (Cf. [Reference Borne and VistoliBV15, § 10]).
We denote by
![]() $\unicode[STIX]{x1D70B}^{\operatorname{lin.red}}(X,x)$
the maximal linearly reductive quotient of
$\unicode[STIX]{x1D70B}^{\operatorname{lin.red}}(X,x)$
the maximal linearly reductive quotient of
![]() $\unicode[STIX]{x1D70B}^{N}(X,x)$
.
$\unicode[STIX]{x1D70B}^{N}(X,x)$
.
Remark 2.9. (1) In [Reference Borne and VistoliBV15], Borne–Vistoli studied the linearly reductive quotient in terms of fundamental gerbes. They called it the tame fundamental gerbe. Here, the word ‘tame’ stems from the notion of tame stacks (cf. [Reference Abramovich, Olsson and VistoliAOV08]).
(2) If
![]() $k$
is of characteristic zero, then any finite
$k$
is of characteristic zero, then any finite
![]() $k$
-group scheme is linearly reductive and
$k$
-group scheme is linearly reductive and
![]() $\unicode[STIX]{x1D70B}^{N}(X,x)=\unicode[STIX]{x1D70B}^{\operatorname{lin.red}}(X,x)$
.
$\unicode[STIX]{x1D70B}^{N}(X,x)=\unicode[STIX]{x1D70B}^{\operatorname{lin.red}}(X,x)$
.
From now on assume that
![]() $k$
is of positive characteristic
$k$
is of positive characteristic
![]() $p>0$
. Then a finite
$p>0$
. Then a finite
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
is said to be local if it is connected. We denote by
$G$
is said to be local if it is connected. We denote by
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X,x)$
the maximal local quotient of
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X,x)$
the maximal local quotient of
![]() $\unicode[STIX]{x1D70B}^{N}(X,x)$
. The arguments in [Reference ÜnverÜnv10] then imply that
$\unicode[STIX]{x1D70B}^{N}(X,x)$
. The arguments in [Reference ÜnverÜnv10] then imply that
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X,x)$
does not depend on the choice of a rational point
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X,x)$
does not depend on the choice of a rational point
![]() $x\in X(k)$
. More precisely, let
$x\in X(k)$
. More precisely, let
![]() $L(X)$
be the category of pairs
$L(X)$
be the category of pairs
![]() $(P,G)$
where
$(P,G)$
where
![]() $G$
is a finite local
$G$
is a finite local
![]() $k$
-group scheme and
$k$
-group scheme and
![]() $P\rightarrow X$
is a
$P\rightarrow X$
is a
![]() $G$
-torsor. Then the projective limit
$G$
-torsor. Then the projective limit
exists and for any
![]() $x\in X(k)$
, there exists a canonical isomorphism
$x\in X(k)$
, there exists a canonical isomorphism
In particular, for any finite local
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
, the map in Proposition 2.2 induces a bijection:
$G$
, the map in Proposition 2.2 induces a bijection:
Hence, we write simply
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)$
instead of
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)$
instead of
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X,x)$
.
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X,x)$
.
If
![]() $k$
is algebraically closed, then the maximal linearly reductive quotient
$k$
is algebraically closed, then the maximal linearly reductive quotient
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)^{\operatorname{lin.red}}$
is diagonalizable and we have the following:
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)^{\operatorname{lin.red}}$
is diagonalizable and we have the following:
Here
![]() $\mathbb{X}(\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X))=\operatorname{Hom}(\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X),\mathbb{G}_{m})$
, the group of characters of
$\mathbb{X}(\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X))=\operatorname{Hom}(\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X),\mathbb{G}_{m})$
, the group of characters of
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)$
and for any abelian group
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)$
and for any abelian group
![]() $A$
, we denote by
$A$
, we denote by
![]() $\operatorname{Diag}(A)$
the diagonalizable
$\operatorname{Diag}(A)$
the diagonalizable
![]() $k$
-group scheme associated with
$k$
-group scheme associated with
![]() $A$
[Reference WaterhouseWat79, § 2.2]. On the other hand, any homomorphism
$A$
[Reference WaterhouseWat79, § 2.2]. On the other hand, any homomorphism
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)\rightarrow \mathbb{G}_{m}$
factors through
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)\rightarrow \mathbb{G}_{m}$
factors through
![]() $\unicode[STIX]{x1D707}_{p^{n}}=\operatorname{Diag}(\mathbb{Z}/p^{n}\mathbb{Z})$
for some integer
$\unicode[STIX]{x1D707}_{p^{n}}=\operatorname{Diag}(\mathbb{Z}/p^{n}\mathbb{Z})$
for some integer
![]() $n>0$
. Hence,
$n>0$
. Hence,
Here, since all the
![]() $\unicode[STIX]{x1D707}_{p^{n}}$
are abelian, the map in Proposition 2.2 induces the last isomorphism. Hence, we have seen that the following holds.
$\unicode[STIX]{x1D707}_{p^{n}}$
are abelian, the map in Proposition 2.2 induces the last isomorphism. Hence, we have seen that the following holds.
Proposition 2.10. If
![]() $k$
is an algebraically closed field of characteristic
$k$
is an algebraically closed field of characteristic
![]() $p>0$
, then there exists a canonical isomorphism:
$p>0$
, then there exists a canonical isomorphism:
Note that
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)^{\operatorname{lin.red}}$
is nothing but the maximal local linearly reductive quotient of
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)^{\operatorname{lin.red}}$
is nothing but the maximal local linearly reductive quotient of
![]() $\unicode[STIX]{x1D70B}^{N}(X,x)$
.
$\unicode[STIX]{x1D70B}^{N}(X,x)$
.
3 A purely inseparable analogue of the Abhyankar conjecture
Let
![]() $k$
be an algebraically closed field of positive characteristic
$k$
be an algebraically closed field of positive characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $X$
be a projective smooth curve over
$X$
be a projective smooth curve over
![]() $k$
of genus
$k$
of genus
![]() $g\geqslant 0$
. Let
$g\geqslant 0$
. Let
![]() $U$
be a nonempty open subset of
$U$
be a nonempty open subset of
![]() $X$
with
$X$
with
![]() $n\overset{\operatorname{def}}{=}\#(X\setminus U)>0$
. The scheme
$n\overset{\operatorname{def}}{=}\#(X\setminus U)>0$
. The scheme
![]() $U$
is then an affine smooth curve over
$U$
is then an affine smooth curve over
![]() $k$
. We denote by
$k$
. We denote by
![]() $\unicode[STIX]{x1D6FE}$
the
$\unicode[STIX]{x1D6FE}$
the
![]() $p$
-rank of the Jacobian variety
$p$
-rank of the Jacobian variety
![]() $\text{Pic}_{X}^{0}$
of
$\text{Pic}_{X}^{0}$
of
![]() $X$
, i.e.,
$X$
, i.e.,
Since
![]() $X$
is smooth and projective, the invariant
$X$
is smooth and projective, the invariant
![]() $\unicode[STIX]{x1D6FE}$
coincides with the dimension of the
$\unicode[STIX]{x1D6FE}$
coincides with the dimension of the
![]() $\mathbb{F}_{p}$
-vector space
$\mathbb{F}_{p}$
-vector space
![]() $\operatorname{Hom}_{\mathbb{Z}}(\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)^{\operatorname{ab}},\mathbb{F}_{p})$
(cf. [Reference BouwBou00]). Moreover, in this case, for any integer
$\operatorname{Hom}_{\mathbb{Z}}(\unicode[STIX]{x1D70B}_{1}^{\acute{\text{e}}\text{t}}(X)^{\operatorname{ab}},\mathbb{F}_{p})$
(cf. [Reference BouwBou00]). Moreover, in this case, for any integer
![]() $m>0$
, we have
$m>0$
, we have
Here, for the first equality, see, for example, [Reference AnteiAnt11, Proposition 3.2]; for the second equality, see, for example, [Reference MumfordMum08, ch. IV].
Let
![]() $\unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
be the set of isomorphism classes of finite local
$\unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
be the set of isomorphism classes of finite local
![]() $k$
-group schemes
$k$
-group schemes
![]() $G$
such that there exists a surjective homomorphism
$G$
such that there exists a surjective homomorphism
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U){\twoheadrightarrow}G$
.
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U){\twoheadrightarrow}G$
.
3.1 Question
We first give a necessary condition for a finite local
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
to belong to the set
$G$
to belong to the set
![]() $\unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
.
$\unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
.
Proposition 3.1. For any finite local
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
, if
$G$
, if
![]() $G\in \unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
, then there exists an injective homomorphism
$G\in \unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
, then there exists an injective homomorphism
![]() $\mathbb{X}(G){\hookrightarrow}(\mathbb{Q}_{p}/\mathbb{Z}_{p})^{\oplus \unicode[STIX]{x1D6FE}+n-1}$
.
$\mathbb{X}(G){\hookrightarrow}(\mathbb{Q}_{p}/\mathbb{Z}_{p})^{\oplus \unicode[STIX]{x1D6FE}+n-1}$
.
By virtue of Proposition 2.10, Proposition 3.1 is an immediate consequence of the following.
Proposition 3.2. For any integer
![]() $m>0$
, we have
$m>0$
, we have
Proof [Cf. [Sta, Tag 03RN, Lemma 53.68.3]]. Let
![]() $X\setminus U=\{x_{1},\ldots ,x_{n}\}$
. Then there exists an isomorphism
$X\setminus U=\{x_{1},\ldots ,x_{n}\}$
. Then there exists an isomorphism
![]() $\text{Pic}(U)\simeq \text{Pic}(X)/R$
with
$\text{Pic}(U)\simeq \text{Pic}(X)/R$
with
![]() $R\overset{\operatorname{def}}{=}\langle {\mathcal{O}}_{X}(x_{i})\,|\,1\leqslant i\leqslant n\,\rangle _{\mathbb{Z}}\subset \text{Pic}(X)$
. Therefore,
$R\overset{\operatorname{def}}{=}\langle {\mathcal{O}}_{X}(x_{i})\,|\,1\leqslant i\leqslant n\,\rangle _{\mathbb{Z}}\subset \text{Pic}(X)$
. Therefore,
 $$\begin{eqnarray}\displaystyle H_{\operatorname{fpqc}}^{1}(U,\unicode[STIX]{x1D707}_{p^{m}}) & \simeq & \displaystyle \{(L,\unicode[STIX]{x1D6FC})\,|\,L\in \text{Pic}(U),\unicode[STIX]{x1D6FC}:L^{\otimes p^{m}}\xrightarrow[{}]{\simeq }{\mathcal{O}}_{U}\}/\simeq \nonumber\\ \displaystyle & \simeq & \displaystyle \biggl\{(\overline{L},D,\overline{\unicode[STIX]{x1D6FC}})\,\bigg|\,\begin{array}{@{}c@{}}\overline{L}\in \text{Pic}(X),D\in \mathbb{Z}x_{1}+\cdots +\mathbb{Z}x_{n},\\ \overline{\unicode[STIX]{x1D6FC}}:\overline{L}^{\otimes p^{m}}\xrightarrow[{}]{\simeq }{\mathcal{O}}_{X}(D)\end{array}\biggr\}/\overline{R},\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\operatorname{fpqc}}^{1}(U,\unicode[STIX]{x1D707}_{p^{m}}) & \simeq & \displaystyle \{(L,\unicode[STIX]{x1D6FC})\,|\,L\in \text{Pic}(U),\unicode[STIX]{x1D6FC}:L^{\otimes p^{m}}\xrightarrow[{}]{\simeq }{\mathcal{O}}_{U}\}/\simeq \nonumber\\ \displaystyle & \simeq & \displaystyle \biggl\{(\overline{L},D,\overline{\unicode[STIX]{x1D6FC}})\,\bigg|\,\begin{array}{@{}c@{}}\overline{L}\in \text{Pic}(X),D\in \mathbb{Z}x_{1}+\cdots +\mathbb{Z}x_{n},\\ \overline{\unicode[STIX]{x1D6FC}}:\overline{L}^{\otimes p^{m}}\xrightarrow[{}]{\simeq }{\mathcal{O}}_{X}(D)\end{array}\biggr\}/\overline{R},\nonumber\end{eqnarray}$$
where
![]() $\overline{R}$
is the group defined by
$\overline{R}$
is the group defined by
We identify the group
![]() $H_{\operatorname{fpqc}}^{1}(U,\unicode[STIX]{x1D707}_{p^{m}})$
with the second one in the right-hand side of the above equation. We then obtain the following exact sequence:
$H_{\operatorname{fpqc}}^{1}(U,\unicode[STIX]{x1D707}_{p^{m}})$
with the second one in the right-hand side of the above equation. We then obtain the following exact sequence:
Here the second map is given by
![]() $(\overline{L},\unicode[STIX]{x1D6FC})\mapsto (\overline{L},0,\unicode[STIX]{x1D6FC})$
and the third one by
$(\overline{L},\unicode[STIX]{x1D6FC})\mapsto (\overline{L},0,\unicode[STIX]{x1D6FC})$
and the third one by
![]() $(\overline{L},D,\unicode[STIX]{x1D6FC})\mapsto (\overline{a_{i}})_{i=1}^{n}$
with
$(\overline{L},D,\unicode[STIX]{x1D6FC})\mapsto (\overline{a_{i}})_{i=1}^{n}$
with
![]() $D=\sum _{i=1}^{n}a_{i}x_{i}$
. This completes the proof (cf. (3.1)).◻
$D=\sum _{i=1}^{n}a_{i}x_{i}$
. This completes the proof (cf. (3.1)).◻
Considering the Abhyankar conjecture (cf. Theorem 1.5), the following question naturally arises.
Question 3.3. Let
![]() $G$
be a finite local
$G$
be a finite local
![]() $k$
-group scheme. If there exists an injective homomorphism
$k$
-group scheme. If there exists an injective homomorphism
![]() $\mathbb{X}(G){\hookrightarrow}(\mathbb{Q}_{p}/\mathbb{Z}_{p})^{\oplus \unicode[STIX]{x1D6FE}+n-1}$
, then does the group scheme
$\mathbb{X}(G){\hookrightarrow}(\mathbb{Q}_{p}/\mathbb{Z}_{p})^{\oplus \unicode[STIX]{x1D6FE}+n-1}$
, then does the group scheme
![]() $G$
belong to the set
$G$
belong to the set
![]() $\unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
?
$\unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
?
3.2 Nilpotent case
Now we will show that, for any finite local nilpotent
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
, Question 3.3 has an affirmative answer.
$G$
, Question 3.3 has an affirmative answer.
Proposition 3.4. Let
![]() $G$
be a finite local nilpotent
$G$
be a finite local nilpotent
![]() $k$
-group scheme. Then
$k$
-group scheme. Then
![]() $G\in \unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
if and only if there exists an injective homomorphism
$G\in \unicode[STIX]{x1D70B}_{A}^{\operatorname{loc}}(U)$
if and only if there exists an injective homomorphism
![]() $\mathbb{X}(G){\hookrightarrow}(\mathbb{Q}_{p}/\mathbb{Z}_{p})^{\oplus \unicode[STIX]{x1D6FE}+n-1}$
.
$\mathbb{X}(G){\hookrightarrow}(\mathbb{Q}_{p}/\mathbb{Z}_{p})^{\oplus \unicode[STIX]{x1D6FE}+n-1}$
.
Proof. First we remark on
![]() $\unicode[STIX]{x1D6FC}_{p}$
-torsors over
$\unicode[STIX]{x1D6FC}_{p}$
-torsors over
![]() $U$
. Since
$U$
. Since
![]() $U$
is affine,
$U$
is affine,
we have
On the other hand, since
![]() $U$
is an affine smooth integral scheme, there exists a dominant morphism
$U$
is an affine smooth integral scheme, there exists a dominant morphism
![]() $U\rightarrow \mathbb{A}_{k}^{1}$
, whence
$U\rightarrow \mathbb{A}_{k}^{1}$
, whence
where
![]() $t$
is the coordinate of
$t$
is the coordinate of
![]() $\mathbb{A}^{1}$
. Furthermore, since
$\mathbb{A}^{1}$
. Furthermore, since
![]() $\unicode[STIX]{x1D6FC}_{p}$
is simple, any nonzero element of
$\unicode[STIX]{x1D6FC}_{p}$
is simple, any nonzero element of
![]() $H_{\operatorname{fpqc}}^{1}(U,\unicode[STIX]{x1D6FC}_{p})$
corresponds to a surjective homomorphism
$H_{\operatorname{fpqc}}^{1}(U,\unicode[STIX]{x1D6FC}_{p})$
corresponds to a surjective homomorphism
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U){\twoheadrightarrow}\unicode[STIX]{x1D6FC}_{p}$
(cf. (2.1)).
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U){\twoheadrightarrow}\unicode[STIX]{x1D6FC}_{p}$
(cf. (2.1)).
Now let us prove the proposition. It suffices to show the ‘if’ part. We prove this by induction on the order
![]() $\operatorname{dim}_{k}k[G]=p^{r}~(r>0)$
. From the assumption,
$\operatorname{dim}_{k}k[G]=p^{r}~(r>0)$
. From the assumption,
![]() $G$
is obtained by central extensions of
$G$
is obtained by central extensions of
![]() $\unicode[STIX]{x1D6FC}_{p}$
or
$\unicode[STIX]{x1D6FC}_{p}$
or
![]() $\unicode[STIX]{x1D707}_{p}$
. If
$\unicode[STIX]{x1D707}_{p}$
. If
![]() $\operatorname{dim}_{k}k[G]=p$
, then
$\operatorname{dim}_{k}k[G]=p$
, then
![]() $G=\unicode[STIX]{x1D6FC}_{p}$
, or
$G=\unicode[STIX]{x1D6FC}_{p}$
, or
![]() $=\unicode[STIX]{x1D707}_{p}$
and the statement is immediate from (3.2), or from the assumption. Since
$=\unicode[STIX]{x1D707}_{p}$
and the statement is immediate from (3.2), or from the assumption. Since
![]() $G$
is a nontrivial nilpotent group scheme, the center
$G$
is a nontrivial nilpotent group scheme, the center
![]() $Z(G)$
is nontrivial. Let
$Z(G)$
is nontrivial. Let
![]() $H\subset Z(G)$
be a subgroup scheme of order
$H\subset Z(G)$
be a subgroup scheme of order
![]() $p$
. Then we get a central extension of finite
$p$
. Then we get a central extension of finite
![]() $k$
-group schemes:
$k$
-group schemes:
Since
![]() $\operatorname{dim}_{k}k[G/H]<\operatorname{dim}_{k}k[G]$
and
$\operatorname{dim}_{k}k[G/H]<\operatorname{dim}_{k}k[G]$
and
![]() $\mathbb{X}(G/H)\subseteq \mathbb{X}(G)$
, by induction hypothesis, there exists a surjective homomorphism
$\mathbb{X}(G/H)\subseteq \mathbb{X}(G)$
, by induction hypothesis, there exists a surjective homomorphism
![]() $\overline{\unicode[STIX]{x1D719}}:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U)\rightarrow G/H$
. Since
$\overline{\unicode[STIX]{x1D719}}:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U)\rightarrow G/H$
. Since
![]() $U$
is affine,
$U$
is affine,
![]() $H_{\operatorname{fpqc}}^{q}(U,\mathbb{G}_{a})=0$
if
$H_{\operatorname{fpqc}}^{q}(U,\mathbb{G}_{a})=0$
if
![]() $q\neq 0$
, we have
$q\neq 0$
, we have
![]() $H_{\operatorname{fpqc}}^{2}(U,\unicode[STIX]{x1D6FC}_{p})=0$
. On the other hand,
$H_{\operatorname{fpqc}}^{2}(U,\unicode[STIX]{x1D6FC}_{p})=0$
. On the other hand,
![]() $H_{\operatorname{fpqc}}^{1}(U,\mathbb{G}_{m})=\text{Pic}(U)$
is divisible (cf. [Sta, Tag 03RN, Proof of Lemma 53.68.3]) and
$H_{\operatorname{fpqc}}^{1}(U,\mathbb{G}_{m})=\text{Pic}(U)$
is divisible (cf. [Sta, Tag 03RN, Proof of Lemma 53.68.3]) and
![]() $H_{\operatorname{fpqc}}^{2}(U,\mathbb{G}_{m})=\text{Br}(U)=0$
, we then also have
$H_{\operatorname{fpqc}}^{2}(U,\mathbb{G}_{m})=\text{Br}(U)=0$
, we then also have
![]() $H_{\operatorname{fpqc}}^{2}(U,\unicode[STIX]{x1D707}_{p})=0$
. Therefore, we find that
$H_{\operatorname{fpqc}}^{2}(U,\unicode[STIX]{x1D707}_{p})=0$
. Therefore, we find that
![]() $H_{\operatorname{fpqc}}^{2}(U,H)=0$
and the exactness of (3.3), noticing that
$H_{\operatorname{fpqc}}^{2}(U,H)=0$
and the exactness of (3.3), noticing that
![]() $H_{\operatorname{fpqc}}^{0}(U,G/H)=0$
, implies that the resulting sequence
$H_{\operatorname{fpqc}}^{0}(U,G/H)=0$
, implies that the resulting sequence
is an exact sequence of pointed sets (cf. [Reference GiraudGir71, p. 284, Remarque 4.2.10]). Therefore, the isomorphism (2.1) implies that there exists a lift
![]() $\unicode[STIX]{x1D719}:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U)\rightarrow G$
of
$\unicode[STIX]{x1D719}:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U)\rightarrow G$
of
![]() $\overline{\unicode[STIX]{x1D719}}$
and we obtain the following commutative diagram:
$\overline{\unicode[STIX]{x1D719}}$
and we obtain the following commutative diagram:

where
![]() $K\overset{\operatorname{def}}{=}\operatorname{Ker}(\overline{\unicode[STIX]{x1D719}})$
. If
$K\overset{\operatorname{def}}{=}\operatorname{Ker}(\overline{\unicode[STIX]{x1D719}})$
. If
![]() $f$
is nontrivial, then it is surjective, whence so is
$f$
is nontrivial, then it is surjective, whence so is
![]() $\unicode[STIX]{x1D719}$
. Thus, from now on assume
$\unicode[STIX]{x1D719}$
. Thus, from now on assume
![]() $f=0$
. In this case, the homomorphism
$f=0$
. In this case, the homomorphism
![]() $\unicode[STIX]{x1D719}$
factors through
$\unicode[STIX]{x1D719}$
factors through
![]() $G/H$
. Thus, the central extension (3.3) is trivial, i.e.,
$G/H$
. Thus, the central extension (3.3) is trivial, i.e.,
![]() $G=H\times (G/H)$
. We claim that
$G=H\times (G/H)$
. We claim that
If the claim (3.4) is true, then one takes a
![]() $k$
-homomorphism
$k$
-homomorphism
![]() $g:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U)\rightarrow H$
so that
$g:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U)\rightarrow H$
so that
![]() $g|_{K}\neq 0$
and the one
$g|_{K}\neq 0$
and the one
![]() $(g,\overline{\unicode[STIX]{x1D719}}):\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U)\rightarrow G=H\times (G/H)$
is surjective. Thus, it remains to show the claim (3.4). Notice that
$(g,\overline{\unicode[STIX]{x1D719}}):\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U)\rightarrow G=H\times (G/H)$
is surjective. Thus, it remains to show the claim (3.4). Notice that
Thus, if
![]() $H\simeq \unicode[STIX]{x1D6FC}_{p}$
, then the claim (3.4) follows from
$H\simeq \unicode[STIX]{x1D6FC}_{p}$
, then the claim (3.4) follows from
![]() $\operatorname{dim}_{k}H_{\operatorname{fpqc}}^{1}(U,\unicode[STIX]{x1D6FC}_{p})=\infty$
. If
$\operatorname{dim}_{k}H_{\operatorname{fpqc}}^{1}(U,\unicode[STIX]{x1D6FC}_{p})=\infty$
. If
![]() $H\simeq \unicode[STIX]{x1D707}_{p}$
, then the claim (3.4) follows from the following inequality:
$H\simeq \unicode[STIX]{x1D707}_{p}$
, then the claim (3.4) follows from the following inequality:
Here for the first inequality, we use
![]() $G\simeq \unicode[STIX]{x1D707}_{p}\times (G/H)$
. This completes the proof.◻
$G\simeq \unicode[STIX]{x1D707}_{p}\times (G/H)$
. This completes the proof.◻
Corollary 3.5. Every finite local unipotent
![]() $k$
-group scheme appears as a finite quotient of
$k$
-group scheme appears as a finite quotient of
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U)$
.
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U)$
.
Example 3.6. Assume
![]() $k$
is of characteristic
$k$
is of characteristic
![]() $p=2$
. In this case, the first Frobenius kernel
$p=2$
. In this case, the first Frobenius kernel
of the algebraic group
![]() $\operatorname{SL}_{2}$
is nilpotent. Indeed, noticing that
$\operatorname{SL}_{2}$
is nilpotent. Indeed, noticing that
for any
![]() $k$
-algebra
$k$
-algebra
![]() $A$
, the maps
$A$
, the maps
then form a
![]() $k$
-homomorphism
$k$
-homomorphism
![]() $\operatorname{SL}_{2(1)}\rightarrow \unicode[STIX]{x1D6FC}_{2}\times \unicode[STIX]{x1D6FC}_{2}$
, which makes the following sequence
$\operatorname{SL}_{2(1)}\rightarrow \unicode[STIX]{x1D6FC}_{2}\times \unicode[STIX]{x1D6FC}_{2}$
, which makes the following sequence
a nonsplit central extension (cf. [Reference WaterhouseWat79, ch. 0, Exercise 3]). In particular,
![]() $\operatorname{SL}_{2(1)}$
is nilpotent. From the facts that
$\operatorname{SL}_{2(1)}$
is nilpotent. From the facts that
![]() $\mathbb{X}(\unicode[STIX]{x1D707}_{2})=\mathbb{Z}/2\mathbb{Z}$
and that any homomorphism
$\mathbb{X}(\unicode[STIX]{x1D707}_{2})=\mathbb{Z}/2\mathbb{Z}$
and that any homomorphism
![]() $\operatorname{SL}_{2(1)}\rightarrow \mathbb{G}_{m}$
factors through
$\operatorname{SL}_{2(1)}\rightarrow \mathbb{G}_{m}$
factors through
![]() $\unicode[STIX]{x1D707}_{2}$
, the nonsplitness of (3.5) deduces the condition that
$\unicode[STIX]{x1D707}_{2}$
, the nonsplitness of (3.5) deduces the condition that
![]() $\mathbb{X}(\operatorname{SL}_{2(1)})=\mathbb{X}(\unicode[STIX]{x1D6FC}_{2}\times \unicode[STIX]{x1D6FC}_{2})=1$
. Therefore, by applying Proposition 3.4, we can conclude that there exists a surjective homomorphism
$\mathbb{X}(\operatorname{SL}_{2(1)})=\mathbb{X}(\unicode[STIX]{x1D6FC}_{2}\times \unicode[STIX]{x1D6FC}_{2})=1$
. Therefore, by applying Proposition 3.4, we can conclude that there exists a surjective homomorphism
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\operatorname{SL}_{2(1)}$
.
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\operatorname{SL}_{2(1)}$
.
Remark 3.7. (1) In the particular case where
![]() $U=\mathbb{A}_{k}^{1}$
, that Question 3.3 is affirmative is equivalent to the assertion that any finite local
$U=\mathbb{A}_{k}^{1}$
, that Question 3.3 is affirmative is equivalent to the assertion that any finite local
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
with
$G$
with
![]() $\mathbb{X}(G)=1$
appears as a quotient of
$\mathbb{X}(G)=1$
appears as a quotient of
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1})$
. For example, for any integers
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1})$
. For example, for any integers
![]() $n,r>0$
, the
$n,r>0$
, the
![]() $r$
th Frobenius kernel
$r$
th Frobenius kernel
![]() $\operatorname{SL}_{n(r)}\overset{\operatorname{def}}{=}\operatorname{Ker}(F^{(r)}:\operatorname{SL}_{n}^{(-r)}\rightarrow \operatorname{SL}_{n})$
of
$\operatorname{SL}_{n(r)}\overset{\operatorname{def}}{=}\operatorname{Ker}(F^{(r)}:\operatorname{SL}_{n}^{(-r)}\rightarrow \operatorname{SL}_{n})$
of
![]() $\operatorname{SL}_{n}$
gives such a one, i.e.,
$\operatorname{SL}_{n}$
gives such a one, i.e.,
![]() $\mathbb{X}(\operatorname{SL}_{n(r)})=1$
(cf. (3) below).
$\mathbb{X}(\operatorname{SL}_{n(r)})=1$
(cf. (3) below).
(2) In general, if a finite
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
is generated by all the unipotent subgroup schemes, then
$G$
is generated by all the unipotent subgroup schemes, then
![]() $G$
has no characters, i.e.,
$G$
has no characters, i.e.,
![]() $\mathbb{X}(G)=1$
. The author expects that the converse might be true, namely, that
$\mathbb{X}(G)=1$
. The author expects that the converse might be true, namely, that
![]() $\mathbb{X}(G)=1$
if and only if
$\mathbb{X}(G)=1$
if and only if
![]() $G$
is generated by all the unipotent subgroup schemes.
$G$
is generated by all the unipotent subgroup schemes.
(3) Let us see another example of finite local
![]() $k$
-group scheme
$k$
-group scheme
![]() $G$
with
$G$
with
![]() $\mathbb{X}(G)=1$
. Let
$\mathbb{X}(G)=1$
. Let
![]() $\unicode[STIX]{x1D6F4}$
be a semi-simple simply connected algebraic group over
$\unicode[STIX]{x1D6F4}$
be a semi-simple simply connected algebraic group over
![]() $k$
. Then for any integer
$k$
. Then for any integer
![]() $r>0$
, the
$r>0$
, the
![]() $r$
th Frobenius kernel
$r$
th Frobenius kernel
has no nontrivial characters, i.e.,
![]() $\mathbb{X}(\unicode[STIX]{x1D6F4}_{(r)})=1$
(indeed, since
$\mathbb{X}(\unicode[STIX]{x1D6F4}_{(r)})=1$
(indeed, since
![]() $\unicode[STIX]{x1D6F4}$
is semi-simple simply connected, any character
$\unicode[STIX]{x1D6F4}$
is semi-simple simply connected, any character
![]() $\unicode[STIX]{x1D6F4}_{(r)}\rightarrow \mathbb{G}_{m}$
comes from some character of
$\unicode[STIX]{x1D6F4}_{(r)}\rightarrow \mathbb{G}_{m}$
comes from some character of
![]() $\unicode[STIX]{x1D6F4}$
[Reference JantzenJan03, Part II, chs 3, 3.15, Proposition and Remarks 2)]. However, since
$\unicode[STIX]{x1D6F4}$
[Reference JantzenJan03, Part II, chs 3, 3.15, Proposition and Remarks 2)]. However, since
![]() $\unicode[STIX]{x1D6F4}$
is semi-simple, there exist no nontrivial characters of
$\unicode[STIX]{x1D6F4}$
is semi-simple, there exist no nontrivial characters of
![]() $\unicode[STIX]{x1D6F4}$
[Reference JantzenJan03, Part II, chs 1, 1.18(3)]). Therefore, if Question 3.3 is affirmative for the affine line
$\unicode[STIX]{x1D6F4}$
[Reference JantzenJan03, Part II, chs 1, 1.18(3)]). Therefore, if Question 3.3 is affirmative for the affine line
![]() $\mathbb{A}_{k}^{1}$
, then the group scheme
$\mathbb{A}_{k}^{1}$
, then the group scheme
![]() $\unicode[STIX]{x1D6F4}_{(r)}$
must appear as a finite quotient of
$\unicode[STIX]{x1D6F4}_{(r)}$
must appear as a finite quotient of
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1})$
. We will prove this fact is actually true (cf. Corollary 4.19).
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1})$
. We will prove this fact is actually true (cf. Corollary 4.19).
(4) Moreover, if
![]() $\unicode[STIX]{x1D6F4}$
is a semi-simple simply connected algebraic group over
$\unicode[STIX]{x1D6F4}$
is a semi-simple simply connected algebraic group over
![]() $k$
, then one can prove that the first Frobenius kernel
$k$
, then one can prove that the first Frobenius kernel
![]() $\unicode[STIX]{x1D6F4}_{(1)}$
is generated by all the unipotent subgroup schemes of it. Indeed, fix a maximal torus
$\unicode[STIX]{x1D6F4}_{(1)}$
is generated by all the unipotent subgroup schemes of it. Indeed, fix a maximal torus
![]() $T<\unicode[STIX]{x1D6F4}$
. Let
$T<\unicode[STIX]{x1D6F4}$
. Let
![]() $R$
be the root system. Choose a positive system
$R$
be the root system. Choose a positive system
![]() $R^{+}\subset R$
and denote by
$R^{+}\subset R$
and denote by
![]() $S$
the corresponding set of simple roots ([Reference JantzenJan03, Part II, chs 1, 1.5]). We denote by
$S$
the corresponding set of simple roots ([Reference JantzenJan03, Part II, chs 1, 1.5]). We denote by
![]() $U^{+}$
(respectively
$U^{+}$
(respectively
![]() $U^{-}$
) the unipotent radical corresponding to the positive roots (respectively the negative roots). By [Reference JantzenJan03, Part II, chs 3, 3.2 Lemma], it suffices to show that
$U^{-}$
) the unipotent radical corresponding to the positive roots (respectively the negative roots). By [Reference JantzenJan03, Part II, chs 3, 3.2 Lemma], it suffices to show that
![]() $T_{(1)}\subset \langle U_{(1)}^{\pm }\rangle$
. Since
$T_{(1)}\subset \langle U_{(1)}^{\pm }\rangle$
. Since
![]() $\unicode[STIX]{x1D6F4}$
is simply connected, we have
$\unicode[STIX]{x1D6F4}$
is simply connected, we have
(cf. [Reference JantzenJan03, Part II, chs 1, 1.6(4)]), where the
![]() $\unicode[STIX]{x1D6FC}^{\vee }$
are dual roots. Hence, we are reduced to showing that
$\unicode[STIX]{x1D6FC}^{\vee }$
are dual roots. Hence, we are reduced to showing that
![]() $\unicode[STIX]{x1D6FC}^{\vee }(\unicode[STIX]{x1D707}_{p})\subset \langle U_{(1)}^{\pm }\rangle$
for any
$\unicode[STIX]{x1D6FC}^{\vee }(\unicode[STIX]{x1D707}_{p})\subset \langle U_{(1)}^{\pm }\rangle$
for any
![]() $\unicode[STIX]{x1D6FC}\in S$
. For this, we may assume that
$\unicode[STIX]{x1D6FC}\in S$
. For this, we may assume that
![]() $\unicode[STIX]{x1D6F4}=\operatorname{SL}_{2}$
. In this case, we have
$\unicode[STIX]{x1D6F4}=\operatorname{SL}_{2}$
. In this case, we have
![]() $\operatorname{dim}k[\operatorname{SL}_{2(1)}]=p^{3}$
and
$\operatorname{dim}k[\operatorname{SL}_{2(1)}]=p^{3}$
and
![]() $\operatorname{dim}k[U_{(1)}^{\pm }]=p$
, whence
$\operatorname{dim}k[U_{(1)}^{\pm }]=p$
, whence
![]() $p^{2}\leqslant \operatorname{dim}k[\langle U_{(1)}^{\pm }\rangle ]\leqslant p^{3}$
. For the equality
$p^{2}\leqslant \operatorname{dim}k[\langle U_{(1)}^{\pm }\rangle ]\leqslant p^{3}$
. For the equality
![]() $\operatorname{SL}_{2(1)}=\langle U_{(1)}^{\pm }\rangle$
, it suffices to show
$\operatorname{SL}_{2(1)}=\langle U_{(1)}^{\pm }\rangle$
, it suffices to show
![]() $\operatorname{dim}k[\langle U_{(1)}^{\pm }\rangle ]=p^{3}$
. However, again by [Reference JantzenJan03, Part II, chs 3, 3.2, Lemma], there exists a surjective
$\operatorname{dim}k[\langle U_{(1)}^{\pm }\rangle ]=p^{3}$
. However, again by [Reference JantzenJan03, Part II, chs 3, 3.2, Lemma], there exists a surjective
![]() $k$
-algebra homomorphism
$k$
-algebra homomorphism
![]() $k[\operatorname{SL}_{2(1)}]{\twoheadrightarrow}k[U_{(1)}^{+}\times U_{(1)}^{-}]$
. This factors through
$k[\operatorname{SL}_{2(1)}]{\twoheadrightarrow}k[U_{(1)}^{+}\times U_{(1)}^{-}]$
. This factors through
![]() $k[\langle U_{(1)}^{\pm }\rangle ]$
and the resulting algebra map
$k[\langle U_{(1)}^{\pm }\rangle ]$
and the resulting algebra map
![]() $\unicode[STIX]{x1D719}:k[\langle U_{(1)}^{\pm }\rangle ]\rightarrow k[U_{(1)}^{+}\times U_{(1)}^{-}]$
is then surjective. The map
$\unicode[STIX]{x1D719}:k[\langle U_{(1)}^{\pm }\rangle ]\rightarrow k[U_{(1)}^{+}\times U_{(1)}^{-}]$
is then surjective. The map
![]() $\unicode[STIX]{x1D719}$
is not isomorphism because
$\unicode[STIX]{x1D719}$
is not isomorphism because
![]() $U_{(1)}^{+}\times U_{(1)}^{-}$
is not a subgroup scheme of
$U_{(1)}^{+}\times U_{(1)}^{-}$
is not a subgroup scheme of
![]() $\operatorname{SL}_{2(1)}$
but
$\operatorname{SL}_{2(1)}$
but
![]() $\langle U_{(1)}^{\pm }\rangle$
is. Therefore, we have
$\langle U_{(1)}^{\pm }\rangle$
is. Therefore, we have
![]() $\operatorname{dim}k[\langle U_{(1)}^{\pm }\rangle ]>\operatorname{dim}k[U_{(1)}^{+}\times U_{(1)}^{-}]=p^{2}$
. Then we must have
$\operatorname{dim}k[\langle U_{(1)}^{\pm }\rangle ]>\operatorname{dim}k[U_{(1)}^{+}\times U_{(1)}^{-}]=p^{2}$
. Then we must have
![]() $\operatorname{dim}k[\langle U_{(1)}^{\pm }\rangle ]=p^{3}$
, which implies that
$\operatorname{dim}k[\langle U_{(1)}^{\pm }\rangle ]=p^{3}$
, which implies that
![]() $\operatorname{SL}_{2(1)}=\langle U_{(1)}^{\pm }\rangle$
. This completes the proof.
$\operatorname{SL}_{2(1)}=\langle U_{(1)}^{\pm }\rangle$
. This completes the proof.
4 Main results
4.1 Torsors coming from Frobenius endmorphisms of an affine algebraic group
Let
![]() $k$
be an algebraically closed field of characteristic
$k$
be an algebraically closed field of characteristic
![]() $p>0$
and
$p>0$
and
![]() $U$
a smooth affine curve over
$U$
a smooth affine curve over
![]() $k$
. Let
$k$
. Let
![]() $\unicode[STIX]{x1D6F4}$
be an affine algebraic group over
$\unicode[STIX]{x1D6F4}$
be an affine algebraic group over
![]() $k$
. Note that for each integer
$k$
. Note that for each integer
![]() $r>0$
, the
$r>0$
, the
![]() $r$
th relative Frobenius morphism
$r$
th relative Frobenius morphism
![]() $F^{(r)}:\unicode[STIX]{x1D6F4}^{(-r)}\rightarrow \unicode[STIX]{x1D6F4}$
gives a saturated
$F^{(r)}:\unicode[STIX]{x1D6F4}^{(-r)}\rightarrow \unicode[STIX]{x1D6F4}$
gives a saturated
![]() $\unicode[STIX]{x1D6F4}_{(r)}\overset{\operatorname{def}}{=}\operatorname{Ker}(F^{(r)})$
-torsor over
$\unicode[STIX]{x1D6F4}_{(r)}\overset{\operatorname{def}}{=}\operatorname{Ker}(F^{(r)})$
-torsor over
![]() $\unicode[STIX]{x1D6F4}$
. Here, recall that the saturatedness means the corresponding homomorphism
$\unicode[STIX]{x1D6F4}$
. Here, recall that the saturatedness means the corresponding homomorphism
![]() $\unicode[STIX]{x1D70B}^{N}(\unicode[STIX]{x1D6F4})\rightarrow \unicode[STIX]{x1D6F4}_{(r)}$
is surjective (cf. Definition 2.3). In § 4, motivated by Question 3.3, we will consider the following question.
$\unicode[STIX]{x1D70B}^{N}(\unicode[STIX]{x1D6F4})\rightarrow \unicode[STIX]{x1D6F4}_{(r)}$
is surjective (cf. Definition 2.3). In § 4, motivated by Question 3.3, we will consider the following question.
Question 4.1. Fix an integer
![]() $r>0$
.
$r>0$
.
(1) Does there exist any
 $k$
-morphism
$k$
-morphism
 $f:U\rightarrow \unicode[STIX]{x1D6F4}$
so that the
$f:U\rightarrow \unicode[STIX]{x1D6F4}$
so that the
 $\unicode[STIX]{x1D6F4}_{(r)}$
-torsor
$\unicode[STIX]{x1D6F4}_{(r)}$
-torsor
 $f^{\ast }\unicode[STIX]{x1D6F4}^{(-r)}\rightarrow U$
defined by the following cartesian diagram is saturated?
$f^{\ast }\unicode[STIX]{x1D6F4}^{(-r)}\rightarrow U$
defined by the following cartesian diagram is saturated? 
(2) Furthermore, if it exists, for which
 $k$
-morphism
$k$
-morphism
 $f:U\rightarrow \unicode[STIX]{x1D6F4}$
, is the resulting
$f:U\rightarrow \unicode[STIX]{x1D6F4}$
, is the resulting
 $\unicode[STIX]{x1D6F4}_{(r)}$
-torsor
$\unicode[STIX]{x1D6F4}_{(r)}$
-torsor
 $f^{\ast }\unicode[STIX]{x1D6F4}^{(-r)}\rightarrow U$
saturated?
$f^{\ast }\unicode[STIX]{x1D6F4}^{(-r)}\rightarrow U$
saturated?
Let us begin with showing that one can reduce the problem to the case
![]() $r=1$
.
$r=1$
.
Lemma 4.2. Let
![]() $\unicode[STIX]{x1D6F4}$
be an affine algebraic group over
$\unicode[STIX]{x1D6F4}$
be an affine algebraic group over
![]() $k$
and
$k$
and
![]() $f:U\rightarrow \unicode[STIX]{x1D6F4}$
a
$f:U\rightarrow \unicode[STIX]{x1D6F4}$
a
![]() $k$
-morphism. If
$k$
-morphism. If
![]() $f^{\ast }\unicode[STIX]{x1D6F4}^{(-1)}$
is saturated, then for any integer
$f^{\ast }\unicode[STIX]{x1D6F4}^{(-1)}$
is saturated, then for any integer
![]() $r>1$
,
$r>1$
,
![]() $f^{\ast }\unicode[STIX]{x1D6F4}^{(-r)}$
is also saturated.
$f^{\ast }\unicode[STIX]{x1D6F4}^{(-r)}$
is also saturated.
Proof. We will show this by induction on
![]() $r\geqslant 1$
. We will denote by
$r\geqslant 1$
. We will denote by
![]() $\unicode[STIX]{x1D719}^{(-r)}:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U)\rightarrow \unicode[STIX]{x1D6F4}_{(r)}$
the homomorphism corresponding to the torsor
$\unicode[STIX]{x1D719}^{(-r)}:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U)\rightarrow \unicode[STIX]{x1D6F4}_{(r)}$
the homomorphism corresponding to the torsor
![]() $f^{\ast }\unicode[STIX]{x1D6F4}^{(-r)}$
. Assume
$f^{\ast }\unicode[STIX]{x1D6F4}^{(-r)}$
. Assume
![]() $\unicode[STIX]{x1D719}^{(-r)}$
is surjective. Let us show that
$\unicode[STIX]{x1D719}^{(-r)}$
is surjective. Let us show that
![]() $\unicode[STIX]{x1D719}^{(-r-1)}$
is also surjective. Since
$\unicode[STIX]{x1D719}^{(-r-1)}$
is also surjective. Since
![]() $F^{(r)\ast }f^{\ast }\unicode[STIX]{x1D6F4}^{(-r)}$
is a trivial torsor, the composition
$F^{(r)\ast }f^{\ast }\unicode[STIX]{x1D6F4}^{(-r)}$
is a trivial torsor, the composition
is trivial. We then obtain the following commutative diagram:

and the map
![]() $\unicode[STIX]{x1D719}^{(-r-1)}\circ F_{\ast }^{(r)}$
factors through
$\unicode[STIX]{x1D719}^{(-r-1)}\circ F_{\ast }^{(r)}$
factors through
![]() $\unicode[STIX]{x1D6F4}_{(1)}^{(-r)}$
. We denote by
$\unicode[STIX]{x1D6F4}_{(1)}^{(-r)}$
. We denote by
![]() $\unicode[STIX]{x1D713}$
the resulting homomorphism
$\unicode[STIX]{x1D713}$
the resulting homomorphism
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U^{(-r)})\rightarrow \unicode[STIX]{x1D6F4}_{(1)}^{(-r)}$
. We are then reduced to showing the surjectivity of
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U^{(-r)})\rightarrow \unicode[STIX]{x1D6F4}_{(1)}^{(-r)}$
. We are then reduced to showing the surjectivity of
![]() $\unicode[STIX]{x1D713}$
. The commutativity of the diagram (4.1) implies that
$\unicode[STIX]{x1D713}$
. The commutativity of the diagram (4.1) implies that
![]() $\text{Ind}_{\unicode[STIX]{x1D6F4}_{(1)}^{(-r)}}^{\unicode[STIX]{x1D6F4}_{(r+1)}}(Q)\simeq F^{(r)\ast }f^{\ast }\unicode[STIX]{x1D6F4}^{(-r-1)}$
, where
$\text{Ind}_{\unicode[STIX]{x1D6F4}_{(1)}^{(-r)}}^{\unicode[STIX]{x1D6F4}_{(r+1)}}(Q)\simeq F^{(r)\ast }f^{\ast }\unicode[STIX]{x1D6F4}^{(-r-1)}$
, where
![]() $Q$
is the torsor over
$Q$
is the torsor over
![]() $U^{(-r)}$
corresponding to the morphism
$U^{(-r)}$
corresponding to the morphism
![]() $\unicode[STIX]{x1D713}$
. On the other hand, by considering the tautological commutative diagram
$\unicode[STIX]{x1D713}$
. On the other hand, by considering the tautological commutative diagram

we can find that
Therefore, by the construction,
![]() $Q$
is nothing but the torsor defined by the cartesian diagram
$Q$
is nothing but the torsor defined by the cartesian diagram

where
![]() $f^{(-r)}$
is just the
$f^{(-r)}$
is just the
![]() $r$
th Frobenius twist of
$r$
th Frobenius twist of
![]() $f$
.
$f$
.

Then, the saturatedness of the torsor
![]() $f^{\ast }\unicode[STIX]{x1D6F4}^{(1)}\rightarrow U$
indicates the saturatedness of the torsor
$f^{\ast }\unicode[STIX]{x1D6F4}^{(1)}\rightarrow U$
indicates the saturatedness of the torsor
![]() $Q\rightarrow U^{(-r)}$
, or equivalently, the surjectivity of
$Q\rightarrow U^{(-r)}$
, or equivalently, the surjectivity of
![]() $\unicode[STIX]{x1D713}$
. This completes the proof.◻
$\unicode[STIX]{x1D713}$
. This completes the proof.◻
Next let us see a basic example. The following proposition gives a complete answer to Question 4.1 for the pairs
![]() $(U,\unicode[STIX]{x1D6F4})=(\mathbb{A}_{k}^{1},\mathbb{G}_{a}^{\oplus n})~(n\geqslant 1)$
.
$(U,\unicode[STIX]{x1D6F4})=(\mathbb{A}_{k}^{1},\mathbb{G}_{a}^{\oplus n})~(n\geqslant 1)$
.
Proposition 4.3. Assume that
![]() $k$
is of characteristic
$k$
is of characteristic
![]() $p>0$
and
$p>0$
and
![]() $n>0$
an integer. Let
$n>0$
an integer. Let
be a
![]() $k$
-morphism
$k$
-morphism
![]() $\mathbb{A}_{k}^{1}\rightarrow \mathbb{G}_{a}^{\oplus n}$
. We define the
$\mathbb{A}_{k}^{1}\rightarrow \mathbb{G}_{a}^{\oplus n}$
. We define the
![]() $\unicode[STIX]{x1D6FC}_{p}^{\oplus n}$
-torsor
$\unicode[STIX]{x1D6FC}_{p}^{\oplus n}$
-torsor
![]() $P_{\text{}\underline{f}}$
over
$P_{\text{}\underline{f}}$
over
![]() $\mathbb{A}_{k}^{1}$
by the pulling back of the relative Frobenius morphism
$\mathbb{A}_{k}^{1}$
by the pulling back of the relative Frobenius morphism
![]() $F^{(1)}:{\mathbb{G}_{a}^{(-1)}}^{\oplus n}\rightarrow \mathbb{G}_{a}^{\oplus n}$
, i.e.,
$F^{(1)}:{\mathbb{G}_{a}^{(-1)}}^{\oplus n}\rightarrow \mathbb{G}_{a}^{\oplus n}$
, i.e.,
![]() $P_{\text{}\underline{f}}\overset{\operatorname{def}}{=}\text{}\underline{f}^{\ast }{\mathbb{G}_{a}^{(-1)}}^{\oplus n}$
. Then
$P_{\text{}\underline{f}}\overset{\operatorname{def}}{=}\text{}\underline{f}^{\ast }{\mathbb{G}_{a}^{(-1)}}^{\oplus n}$
. Then
![]() $P_{\text{}\underline{f}}$
is saturated if and only if the images
$P_{\text{}\underline{f}}$
is saturated if and only if the images
![]() $\overline{f_{i}(t)}\,(\,1\leqslant i\leqslant n)$
in
$\overline{f_{i}(t)}\,(\,1\leqslant i\leqslant n)$
in
![]() $H_{\operatorname{fpqc}}^{1}(\mathbb{A}_{k}^{1},\unicode[STIX]{x1D6FC}_{p})=k[t]/k[t^{p}]$
are linearly independent over
$H_{\operatorname{fpqc}}^{1}(\mathbb{A}_{k}^{1},\unicode[STIX]{x1D6FC}_{p})=k[t]/k[t^{p}]$
are linearly independent over
![]() $k$
.
$k$
.
Proof. We will show this by induction on
![]() $n>0$
. In the case where
$n>0$
. In the case where
![]() $n=1$
, then since
$n=1$
, then since
![]() $\unicode[STIX]{x1D6FC}_{p}$
is simple, the assertion is obvious. From now on assume that
$\unicode[STIX]{x1D6FC}_{p}$
is simple, the assertion is obvious. From now on assume that
![]() $n>1$
and that
$n>1$
and that
![]() $\operatorname{dim}_{k}\langle \overline{f_{i}(t)}\,|\,1\leqslant i\leqslant n-1\rangle _{k}=n-1$
. Put
$\operatorname{dim}_{k}\langle \overline{f_{i}(t)}\,|\,1\leqslant i\leqslant n-1\rangle _{k}=n-1$
. Put
![]() $\text{}\underline{f^{\prime }}:=(f_{1}(t),\ldots ,f_{n-1}(t))$
. Then
$\text{}\underline{f^{\prime }}:=(f_{1}(t),\ldots ,f_{n-1}(t))$
. Then
![]() $P_{\text{}\underline{f^{\prime }}}$
is an
$P_{\text{}\underline{f^{\prime }}}$
is an
![]() $\unicode[STIX]{x1D6FC}_{p}^{\oplus n-1}$
-torsor over
$\unicode[STIX]{x1D6FC}_{p}^{\oplus n-1}$
-torsor over
![]() $\mathbb{A}_{k}^{1}$
. We denote by
$\mathbb{A}_{k}^{1}$
. We denote by
![]() $\unicode[STIX]{x1D719}$
and
$\unicode[STIX]{x1D719}$
and
![]() $\unicode[STIX]{x1D719}^{\prime }$
the homomorphism
$\unicode[STIX]{x1D719}^{\prime }$
the homomorphism
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1})\rightarrow \unicode[STIX]{x1D6FC}_{p}^{\oplus n}$
corresponding to
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1})\rightarrow \unicode[STIX]{x1D6FC}_{p}^{\oplus n}$
corresponding to
![]() $P_{\text{}\underline{f}}$
and the one
$P_{\text{}\underline{f}}$
and the one
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1})\rightarrow \unicode[STIX]{x1D6FC}_{p}^{\oplus n-1}$
to
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1})\rightarrow \unicode[STIX]{x1D6FC}_{p}^{\oplus n-1}$
to
![]() $P_{\text{}\underline{f^{\prime }}}$
, respectively. From the assumption,
$P_{\text{}\underline{f^{\prime }}}$
, respectively. From the assumption,
![]() $\unicode[STIX]{x1D719}^{\prime }$
is surjection. Let
$\unicode[STIX]{x1D719}^{\prime }$
is surjection. Let
![]() $K\overset{\operatorname{def}}{=}\operatorname{Ker}(\unicode[STIX]{x1D719}^{\prime })$
. We then obtain the following commutative diagram.
$K\overset{\operatorname{def}}{=}\operatorname{Ker}(\unicode[STIX]{x1D719}^{\prime })$
. We then obtain the following commutative diagram.

Then we have
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}:\text{surjective} & \Longleftrightarrow & \displaystyle \unicode[STIX]{x1D713}~\neq ~1\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle \text{pr}_{\text{n}}\circ \unicode[STIX]{x1D719}\in \operatorname{Hom}(\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1}),\unicode[STIX]{x1D6FC}_{p})\setminus {\unicode[STIX]{x1D719}^{\prime }}^{\ast }\operatorname{Hom}(\unicode[STIX]{x1D6FC}_{p}^{\oplus n-1},\unicode[STIX]{x1D6FC}_{p})\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle \overline{f_{n}(t)}\in (k[t]/k[t^{p}])\setminus \langle \overline{f_{1}(t)},\ldots ,\overline{f_{n-1}(t)}\rangle _{k}\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle \operatorname{dim}_{k}\langle \overline{f_{i}(t)}\,|\,1\leqslant i\leqslant n\rangle _{k}=n.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}:\text{surjective} & \Longleftrightarrow & \displaystyle \unicode[STIX]{x1D713}~\neq ~1\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle \text{pr}_{\text{n}}\circ \unicode[STIX]{x1D719}\in \operatorname{Hom}(\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1}),\unicode[STIX]{x1D6FC}_{p})\setminus {\unicode[STIX]{x1D719}^{\prime }}^{\ast }\operatorname{Hom}(\unicode[STIX]{x1D6FC}_{p}^{\oplus n-1},\unicode[STIX]{x1D6FC}_{p})\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle \overline{f_{n}(t)}\in (k[t]/k[t^{p}])\setminus \langle \overline{f_{1}(t)},\ldots ,\overline{f_{n-1}(t)}\rangle _{k}\nonumber\\ \displaystyle & \Longleftrightarrow & \displaystyle \operatorname{dim}_{k}\langle \overline{f_{i}(t)}\,|\,1\leqslant i\leqslant n\rangle _{k}=n.\nonumber\end{eqnarray}$$
This completes the proof. ◻
4.2 Explicit equations defining saturated
 $\operatorname{SL}_{2(1)}$
-torsors in the characteristic
$\operatorname{SL}_{2(1)}$
-torsors in the characteristic
 $p=2$
case
$p=2$
case
We will continue to use the same notation as in § 4.1. As we have seen in Example 3.6, in the case where
![]() $k$
is of characteristic
$k$
is of characteristic
![]() $p=2$
, there exists a saturated
$p=2$
, there exists a saturated
![]() $\operatorname{SL}_{2(1)}$
-torsor
$\operatorname{SL}_{2(1)}$
-torsor
![]() $P\rightarrow \mathbb{A}_{k}^{1}$
(cf. Definition 2.3). On the other hand, since
$P\rightarrow \mathbb{A}_{k}^{1}$
(cf. Definition 2.3). On the other hand, since
![]() $H_{\operatorname{fpqc}}^{1}(\mathbb{A}_{k}^{1},\operatorname{GL}_{2})=0$
and
$H_{\operatorname{fpqc}}^{1}(\mathbb{A}_{k}^{1},\operatorname{GL}_{2})=0$
and
![]() $H_{\operatorname{fpqc}}^{0}(\mathbb{A}_{k}^{1},\operatorname{GL}_{2})\rightarrow H_{\operatorname{fpqc}}^{0}(\mathbb{A}_{k}^{1},\mathbb{G}_{m})=k^{\ast }$
is surjective, we have
$H_{\operatorname{fpqc}}^{0}(\mathbb{A}_{k}^{1},\operatorname{GL}_{2})\rightarrow H_{\operatorname{fpqc}}^{0}(\mathbb{A}_{k}^{1},\mathbb{G}_{m})=k^{\ast }$
is surjective, we have
![]() $H_{\operatorname{fpqc}}^{1}(\mathbb{A}_{k}^{1},\operatorname{SL}_{2})=0$
, whence
$H_{\operatorname{fpqc}}^{1}(\mathbb{A}_{k}^{1},\operatorname{SL}_{2})=0$
, whence
Therefore, such a torsor
![]() $P\rightarrow \mathbb{A}_{k}^{1}$
must be obtained by the pulling back of the relative Frobenius morphism
$P\rightarrow \mathbb{A}_{k}^{1}$
must be obtained by the pulling back of the relative Frobenius morphism
![]() $F^{(1)}:\operatorname{SL}_{2}^{(-1)}\rightarrow \operatorname{SL}_{2}$
along some
$F^{(1)}:\operatorname{SL}_{2}^{(-1)}\rightarrow \operatorname{SL}_{2}$
along some
![]() $k$
-morphism
$k$
-morphism
![]() $f:\mathbb{A}_{k}^{1}\rightarrow \operatorname{SL}_{2}$
.
$f:\mathbb{A}_{k}^{1}\rightarrow \operatorname{SL}_{2}$
.

Hence, by Proposition 3.4 and Example 3.6, combining with Lemma 4.2, we can obtain an affirmative answer to Question 4.1(1) for the pair
![]() $(U,\unicode[STIX]{x1D6F4})=(\mathbb{A}_{k}^{1},\operatorname{SL}_{2})$
in the case where
$(U,\unicode[STIX]{x1D6F4})=(\mathbb{A}_{k}^{1},\operatorname{SL}_{2})$
in the case where
![]() $p=2$
. As a consequence of it, we have the following.
$p=2$
. As a consequence of it, we have the following.
Corollary 4.4. Assume
![]() $p=2$
. Then there exists a surjective homomorphism
$p=2$
. Then there exists a surjective homomorphism
In particular, for any integer
![]() $r>0$
, there exists a surjective homomorphism
$r>0$
, there exists a surjective homomorphism
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\operatorname{SL}_{2(r)}$
.
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1}){\twoheadrightarrow}\operatorname{SL}_{2(r)}$
.
Next, we will consider Question 4.1(2) to the pair
![]() $(U,\unicode[STIX]{x1D6F4})=(\mathbb{A}_{k}^{1},\operatorname{SL}_{2})$
in the case where
$(U,\unicode[STIX]{x1D6F4})=(\mathbb{A}_{k}^{1},\operatorname{SL}_{2})$
in the case where
![]() $k$
is of characteristic
$k$
is of characteristic
![]() $p=2$
and will give an answer (cf. Corollary 4.13).
$p=2$
and will give an answer (cf. Corollary 4.13).
Recall that the saturatedness of a finite étale torsor
![]() $P\rightarrow U$
depends only on the underlying scheme of it. In fact, it is saturated if and only if it is (geometrically) connected (cf. [Reference ZhangZha13, Lemma 2.3]). One of the difficulties of our problem is that the saturatedness of a local torsor, in contrast to the étale case, depends also on the multiplicative structure of the underlying group scheme. The following simple example indicates such a situation.
$P\rightarrow U$
depends only on the underlying scheme of it. In fact, it is saturated if and only if it is (geometrically) connected (cf. [Reference ZhangZha13, Lemma 2.3]). One of the difficulties of our problem is that the saturatedness of a local torsor, in contrast to the étale case, depends also on the multiplicative structure of the underlying group scheme. The following simple example indicates such a situation.
Example 4.5. Let
![]() $l$
be a prime number with
$l$
be a prime number with
![]() $l\neq p$
. We define the
$l\neq p$
. We define the
![]() $k$
-morphism
$k$
-morphism
![]() $f:\mathbb{G}_{m}\rightarrow \mathbb{G}_{m}\times \mathbb{G}_{m}$
by
$f:\mathbb{G}_{m}\rightarrow \mathbb{G}_{m}\times \mathbb{G}_{m}$
by
![]() $a\mapsto (a,a^{l})$
. We define the one
$a\mapsto (a,a^{l})$
. We define the one
![]() $g:\mathbb{G}_{m}\rightarrow \mathbb{G}_{a}\times \mathbb{G}_{m}$
as the composition
$g:\mathbb{G}_{m}\rightarrow \mathbb{G}_{a}\times \mathbb{G}_{m}$
as the composition
![]() $\mathbb{G}_{m}\xrightarrow[{}]{f}\mathbb{G}_{m}\times \mathbb{G}_{m}\subset \mathbb{G}_{a}\times \mathbb{G}_{m}$
. Then the underlying schemes of the torsors
$\mathbb{G}_{m}\xrightarrow[{}]{f}\mathbb{G}_{m}\times \mathbb{G}_{m}\subset \mathbb{G}_{a}\times \mathbb{G}_{m}$
. Then the underlying schemes of the torsors
![]() $f^{\ast }(\mathbb{G}_{m}^{(-1)}\times \mathbb{G}_{m}^{(-1)})$
and
$f^{\ast }(\mathbb{G}_{m}^{(-1)}\times \mathbb{G}_{m}^{(-1)})$
and
![]() $g^{\ast }(\mathbb{G}_{a}^{(-1)}\times \mathbb{G}_{m}^{(-1)})$
are isomorphic to each other. However, the former is not saturated, but the latter is.
$g^{\ast }(\mathbb{G}_{a}^{(-1)}\times \mathbb{G}_{m}^{(-1)})$
are isomorphic to each other. However, the former is not saturated, but the latter is.
Hence, it seems to be difficult to obtain a concise characterization of the saturatedness of finite local torsors purely in terms of the category
![]() $N(X,x)$
(cf. § 2). To avoid this problem, we will rely on a Tannakian interpretation of
$N(X,x)$
(cf. § 2). To avoid this problem, we will rely on a Tannakian interpretation of
![]() $\unicode[STIX]{x1D70B}^{N}(U)$
. For definitions and basic notions of Tannakian categories, see [Reference Deligne and MilneDM82, Reference DeligneDel90]. We will use the category of generalized stratified bundles, introduced by Esnault and Hogadi [Reference Esnault and HogadiEH12]. For the full definition of it, see [Reference Esnault and HogadiEH12] (for the definition of stratified bundles in the usual sense, see, for example, [Reference GiesekerGie75, Reference dos SantosdoS07]). By virtue of Lemma 4.2, the category
$\unicode[STIX]{x1D70B}^{N}(U)$
. For definitions and basic notions of Tannakian categories, see [Reference Deligne and MilneDM82, Reference DeligneDel90]. We will use the category of generalized stratified bundles, introduced by Esnault and Hogadi [Reference Esnault and HogadiEH12]. For the full definition of it, see [Reference Esnault and HogadiEH12] (for the definition of stratified bundles in the usual sense, see, for example, [Reference GiesekerGie75, Reference dos SantosdoS07]). By virtue of Lemma 4.2, the category
![]() $\operatorname{Strat}(U,1)$
of
$\operatorname{Strat}(U,1)$
of
![]() $1$
-stratified bundles is large enough for our purpose.
$1$
-stratified bundles is large enough for our purpose.
Definition 4.6. Let
![]() $X$
be a smooth algebraic variety over a perfect field
$X$
be a smooth algebraic variety over a perfect field
![]() $k$
of characteristic
$k$
of characteristic
![]() $p>0$
. A
$p>0$
. A
![]() $1$
-stratified bundle on
$1$
-stratified bundle on
![]() $X$
is a sequence
$X$
is a sequence
![]() $\{E^{(i)}\}_{i=0}^{\infty }$
of coherent sheaves
$\{E^{(i)}\}_{i=0}^{\infty }$
of coherent sheaves
![]() $E^{(i)}$
over
$E^{(i)}$
over
![]() $X^{(i)}$
together with isomorphisms
$X^{(i)}$
together with isomorphisms
![]() $\unicode[STIX]{x1D70E}^{(i)}:E^{(i)}\xrightarrow[{}]{\simeq }F^{(1)\ast }E^{(i+1)}$
for
$\unicode[STIX]{x1D70E}^{(i)}:E^{(i)}\xrightarrow[{}]{\simeq }F^{(1)\ast }E^{(i+1)}$
for
![]() $i\geqslant 1$
and
$i\geqslant 1$
and
Let
![]() $E=\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\},E^{\prime }=\{{E^{\prime }}^{(i)},{\unicode[STIX]{x1D70E}^{\prime }}^{(i)}\}$
be arbitrary two
$E=\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\},E^{\prime }=\{{E^{\prime }}^{(i)},{\unicode[STIX]{x1D70E}^{\prime }}^{(i)}\}$
be arbitrary two
![]() $1$
-stratified bundles. A homomorphism of
$1$
-stratified bundles. A homomorphism of
![]() $E$
into
$E$
into
![]() $E^{\prime }$
is a sequence of
$E^{\prime }$
is a sequence of
![]() ${\mathcal{O}}_{X^{(i)}}$
-linear homomorphisms
${\mathcal{O}}_{X^{(i)}}$
-linear homomorphisms
![]() $\unicode[STIX]{x1D719}^{(i)}:E^{(i)}\rightarrow {E^{\prime }}^{(i)}~(i\geqslant 0)$
satisfying
$\unicode[STIX]{x1D719}^{(i)}:E^{(i)}\rightarrow {E^{\prime }}^{(i)}~(i\geqslant 0)$
satisfying
The homomorphisms of
![]() $1$
-stratified bundles satisfy the composition rule and one obtains the category
$1$
-stratified bundles satisfy the composition rule and one obtains the category
![]() $\operatorname{Strat}(X,1)$
of
$\operatorname{Strat}(X,1)$
of
![]() $1$
-stratified bundles on
$1$
-stratified bundles on
![]() $X$
.
$X$
.
Theorem 4.7 (Esnault–Hogadi [Reference Esnault and HogadiEH12]).
The category
![]() $\operatorname{Strat}(X,1)$
of
$\operatorname{Strat}(X,1)$
of
![]() $1$
-stratified bundles is a
$1$
-stratified bundles is a
![]() $k$
-linear abelian rigid tensor category, and if one takes a
$k$
-linear abelian rigid tensor category, and if one takes a
![]() $k$
-rational point
$k$
-rational point
![]() $x\in X(k)$
, then the functor
$x\in X(k)$
, then the functor
![]() $\unicode[STIX]{x1D714}_{x}:\operatorname{Strat}(X,1)\rightarrow \operatorname{Vec}_{k};\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\}\mapsto x^{\ast }E^{(0)}$
defines a neutral fiber functor. Furthermore, the maximal profinite quotient of its Tannakian fundamental group
$\unicode[STIX]{x1D714}_{x}:\operatorname{Strat}(X,1)\rightarrow \operatorname{Vec}_{k};\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\}\mapsto x^{\ast }E^{(0)}$
defines a neutral fiber functor. Furthermore, the maximal profinite quotient of its Tannakian fundamental group
![]() $\unicode[STIX]{x1D70B}_{1}(\operatorname{Strat}(X,1),\unicode[STIX]{x1D714}_{x})$
coincides with the image of
$\unicode[STIX]{x1D70B}_{1}(\operatorname{Strat}(X,1),\unicode[STIX]{x1D714}_{x})$
coincides with the image of
![]() $F^{(1)}:\unicode[STIX]{x1D70B}^{N}(X,x)\rightarrow \unicode[STIX]{x1D70B}^{N}(X,x)^{(1)}$
.
$F^{(1)}:\unicode[STIX]{x1D70B}^{N}(X,x)\rightarrow \unicode[STIX]{x1D70B}^{N}(X,x)^{(1)}$
.
In particular, if
![]() $G$
is a finite local
$G$
is a finite local
![]() $k$
-group scheme of height one, i.e.,
$k$
-group scheme of height one, i.e.,
![]() $G_{(1)}=G$
, then any homomorphism
$G_{(1)}=G$
, then any homomorphism
![]() $\unicode[STIX]{x1D719}:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)\rightarrow G$
factors through the maximal pro-finite local quotient
$\unicode[STIX]{x1D719}:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)\rightarrow G$
factors through the maximal pro-finite local quotient
![]() $\unicode[STIX]{x1D70B}_{1}(\operatorname{Strat}(X,1),\unicode[STIX]{x1D714}_{x})^{\text{prof.}\operatorname{loc}}$
. Denote by
$\unicode[STIX]{x1D70B}_{1}(\operatorname{Strat}(X,1),\unicode[STIX]{x1D714}_{x})^{\text{prof.}\operatorname{loc}}$
. Denote by
![]() $\unicode[STIX]{x1D713}$
the resulting homomorphism
$\unicode[STIX]{x1D713}$
the resulting homomorphism
Let us consider the composition
Then, from the standard Tannakian argument (cf. [Reference NoriNor82, ch. II, Proposition 3]), we have the following.
Lemma 4.8. The homomorphism
![]() $\unicode[STIX]{x1D719}$
is surjective if and only if
$\unicode[STIX]{x1D719}$
is surjective if and only if
Here
![]() $\mathbb{I}\overset{\operatorname{def}}{=}\{{\mathcal{O}}_{X^{(i)}},\text{id}\}$
is a unit object of
$\mathbb{I}\overset{\operatorname{def}}{=}\{{\mathcal{O}}_{X^{(i)}},\text{id}\}$
is a unit object of
![]() $\operatorname{Strat}(X,1)$
.
$\operatorname{Strat}(X,1)$
.
Remark 4.9. Since
![]() $h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
is an algebra object in
$h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
is an algebra object in
![]() $\operatorname{Strat}(X,1)$
, the
$\operatorname{Strat}(X,1)$
, the
![]() $1$
-stratified bundle
$1$
-stratified bundle
![]() $h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
admits a morphism from the unit object
$h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
admits a morphism from the unit object
![]() $\mathbb{I}\rightarrow h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
corresponding to the unit element of the algebra. Thus, the dimension
$\mathbb{I}\rightarrow h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
corresponding to the unit element of the algebra. Thus, the dimension
![]() $\operatorname{dim}_{k}\operatorname{Hom}_{\operatorname{Strat}(X,1)}(\mathbb{I},h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}}))$
is always greater than or equal to 1.
$\operatorname{dim}_{k}\operatorname{Hom}_{\operatorname{Strat}(X,1)}(\mathbb{I},h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}}))$
is always greater than or equal to 1.
If
![]() $\unicode[STIX]{x1D70B}:P\rightarrow X$
is the
$\unicode[STIX]{x1D70B}:P\rightarrow X$
is the
![]() $G$
-torsor corresponding to the homomorphism
$G$
-torsor corresponding to the homomorphism
![]() $\unicode[STIX]{x1D719}:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)\rightarrow G$
. Then one can describe the
$\unicode[STIX]{x1D719}:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(X)\rightarrow G$
. Then one can describe the
![]() $1$
-stratified bundle
$1$
-stratified bundle
![]() $h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
as follows (cf. [Reference Esnault and HogadiEH12, Construction 4.1]). We define
$h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
as follows (cf. [Reference Esnault and HogadiEH12, Construction 4.1]). We define
![]() $\{E^{(i)}\}_{i=1}^{\infty }$
by
$\{E^{(i)}\}_{i=1}^{\infty }$
by
Here
![]() $G$
acts on
$G$
acts on
![]() $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\otimes k[G]$
by
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\otimes k[G]$
by
We define
![]() $\{\unicode[STIX]{x1D70E}^{(i)}\}_{i=0}^{\infty }$
by
$\{\unicode[STIX]{x1D70E}^{(i)}\}_{i=0}^{\infty }$
by
![]() $\unicode[STIX]{x1D70E}^{(i)}\overset{\operatorname{def}}{=}\text{id}$
for
$\unicode[STIX]{x1D70E}^{(i)}\overset{\operatorname{def}}{=}\text{id}$
for
![]() $i\geqslant 1$
and
$i\geqslant 1$
and
![]() $\unicode[STIX]{x1D70E}^{(0)}$
the canonical trivialization morphism:
$\unicode[STIX]{x1D70E}^{(0)}$
the canonical trivialization morphism:
Here, since
![]() $G$
is of height one, the torsor
$G$
is of height one, the torsor
![]() $F^{(1)\ast }P$
is trivial and admits a canonical section
$F^{(1)\ast }P$
is trivial and admits a canonical section
![]() $F^{(1)\ast }P\supset (F^{(1)\ast }P)_{\text{red}}=X^{(-1)}$
. The isomorphism
$F^{(1)\ast }P\supset (F^{(1)\ast }P)_{\text{red}}=X^{(-1)}$
. The isomorphism
![]() $\unicode[STIX]{x1D70E}^{(0)}$
is the one corresponding to this section. We then have
$\unicode[STIX]{x1D70E}^{(0)}$
is the one corresponding to this section. We then have
![]() $h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})=\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\}$
. Note that
$h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})=\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\}$
. Note that
![]() $(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
is a
$(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
is a
![]() $G$
-torsor object in
$G$
-torsor object in
![]() $\operatorname{Rep}_{k}(G)$
and the functor
$\operatorname{Rep}_{k}(G)$
and the functor
![]() $h_{\unicode[STIX]{x1D719}}$
is a tensor functor, hence
$h_{\unicode[STIX]{x1D719}}$
is a tensor functor, hence
![]() $h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
gives a
$h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
gives a
![]() $G$
-torsor object in
$G$
-torsor object in
![]() $\operatorname{Strat}(X,1)$
. We also denote
$\operatorname{Strat}(X,1)$
. We also denote
![]() $P^{1\text{-strat}}\overset{\operatorname{def}}{=}h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
. Lemma 4.8 implies that
$P^{1\text{-strat}}\overset{\operatorname{def}}{=}h_{\unicode[STIX]{x1D719}}(k[G],\unicode[STIX]{x1D70C}_{\text{reg}})$
. Lemma 4.8 implies that
![]() $P$
is saturated if and only if
$P$
is saturated if and only if
![]() $P^{1\text{-strat}}$
is connected as an algebra object in
$P^{1\text{-strat}}$
is connected as an algebra object in
![]() $\operatorname{Strat}(X,1)$
.
$\operatorname{Strat}(X,1)$
.
Example 4.10. Let
![]() $m>0$
be an integer and
$m>0$
be an integer and
![]() $f:\mathbb{G}_{m}\rightarrow \mathbb{G}_{m}$
a
$f:\mathbb{G}_{m}\rightarrow \mathbb{G}_{m}$
a
![]() $k$
-morphism defined by
$k$
-morphism defined by
![]() $a\mapsto a^{m}$
. Let
$a\mapsto a^{m}$
. Let
![]() $P^{1\text{-strat}}=\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\}$
with
$P^{1\text{-strat}}=\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\}$
with
![]() $P\overset{\operatorname{def}}{=}f^{\ast }\mathbb{G}_{m}^{(-1)}$
a
$P\overset{\operatorname{def}}{=}f^{\ast }\mathbb{G}_{m}^{(-1)}$
a
![]() $\unicode[STIX]{x1D707}_{p}=\operatorname{Spec}k[z]/(z^{p}-1)$
-torsor. Then
$\unicode[STIX]{x1D707}_{p}=\operatorname{Spec}k[z]/(z^{p}-1)$
-torsor. Then
Therefore, the representation matrix
![]() $A\in \operatorname{GL}_{p}(k[x^{(-1)\pm 1}])$
of
$A\in \operatorname{GL}_{p}(k[x^{(-1)\pm 1}])$
of
![]() $\unicode[STIX]{x1D70E}^{(0)}$
with respect to the basis
$\unicode[STIX]{x1D70E}^{(0)}$
with respect to the basis
![]() $\{\overline{yz}^{j}\,|\,0\leqslant j\leqslant p-1\}$
and
$\{\overline{yz}^{j}\,|\,0\leqslant j\leqslant p-1\}$
and
![]() $\{\overline{z}^{j}\,|\,0\leqslant j\leqslant p-1\}$
is given by the diagonal matrix:
$\{\overline{z}^{j}\,|\,0\leqslant j\leqslant p-1\}$
is given by the diagonal matrix:
 $$\begin{eqnarray}A=\left(\begin{array}{@{}cccc@{}}1 & 0 & \cdots \, & 0\\ 0 & {x^{(-1)}}^{m} & \cdots \, & 0\\ & \cdots \, & \cdots \, & \\ 0 & 0 & \cdots \, & {x^{(-1)}}^{m(p-1)}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}cccc@{}}1 & 0 & \cdots \, & 0\\ 0 & {x^{(-1)}}^{m} & \cdots \, & 0\\ & \cdots \, & \cdots \, & \\ 0 & 0 & \cdots \, & {x^{(-1)}}^{m(p-1)}\end{array}\right).\end{eqnarray}$$
A direct computation then recovers the following well-understood result:
Example 4.11. Let
![]() $n>0$
be an integer and
$n>0$
be an integer and
![]() $\text{}\underline{f}=(f_{i}(x))\in k[x]^{\oplus n}=\text{Mor}_{k}(\mathbb{A}_{k}^{1},\mathbb{G}_{a}^{\oplus n})$
a
$\text{}\underline{f}=(f_{i}(x))\in k[x]^{\oplus n}=\text{Mor}_{k}(\mathbb{A}_{k}^{1},\mathbb{G}_{a}^{\oplus n})$
a
![]() $k$
-morphism (cf. Proposition 4.3). Let
$k$
-morphism (cf. Proposition 4.3). Let
![]() $P^{1\text{-}\text{strat}}=\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\}$
with
$P^{1\text{-}\text{strat}}=\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\}$
with
an
![]() $\unicode[STIX]{x1D6FC}_{p}^{\oplus n}=\operatorname{Spec}k[z_{i}(1\leqslant i\leqslant n)]/(z_{i}^{p}(1\leqslant i\leqslant n))$
-torsor. Then
$\unicode[STIX]{x1D6FC}_{p}^{\oplus n}=\operatorname{Spec}k[z_{i}(1\leqslant i\leqslant n)]/(z_{i}^{p}(1\leqslant i\leqslant n))$
-torsor. Then
The representation matrix
![]() $A\in \operatorname{GL}_{p^{n}}(k[x^{(-1)}])$
of
$A\in \operatorname{GL}_{p^{n}}(k[x^{(-1)}])$
of
![]() $\unicode[STIX]{x1D70E}^{(0)}$
with respect to the basis
$\unicode[STIX]{x1D70E}^{(0)}$
with respect to the basis
is unipotent and, by a direct computation, one can verify that the condition that
![]() $\{\overline{f_{i}(x)}\}_{i=1}^{n}\subset k[x]/k[x^{p}]$
is linearly independent over
$\{\overline{f_{i}(x)}\}_{i=1}^{n}\subset k[x]/k[x^{p}]$
is linearly independent over
![]() $k$
is equivalent to the condition that
$k$
is equivalent to the condition that
This then gives another proof of Proposition 4.3.
Now let us prove the main result of this subsection.
Theorem 4.12. Assume
![]() $p=2$
. Let
$p=2$
. Let
be a
![]() $k$
-morphism with
$k$
-morphism with
![]() $f_{ij}(x)\in k[x]~(1\leqslant i,j\leqslant 2)$
and
$f_{ij}(x)\in k[x]~(1\leqslant i,j\leqslant 2)$
and
for some
![]() $m\in \mathbb{Z}_{{\geqslant}0}$
. Let
$m\in \mathbb{Z}_{{\geqslant}0}$
. Let
![]() $P\overset{\operatorname{def}}{=}\text{}\underline{f}^{\ast }\operatorname{GL}_{2}^{(-1)}$
be the resulting torsor over
$P\overset{\operatorname{def}}{=}\text{}\underline{f}^{\ast }\operatorname{GL}_{2}^{(-1)}$
be the resulting torsor over
![]() $\mathbb{G}_{m}$
.
$\mathbb{G}_{m}$
.
(1) In the case
 $2\mid m$
, assume that one of the following conditions is satisfied:
$2\mid m$
, assume that one of the following conditions is satisfied:∙
 $\operatorname{dim}_{k}\langle \overline{f_{11}},\,\overline{f_{21}}\rangle =\operatorname{dim}_{k}\langle \overline{f_{11}f_{21}},\,\overline{f_{12}f_{22}}\rangle =2$
;
$\operatorname{dim}_{k}\langle \overline{f_{11}},\,\overline{f_{21}}\rangle =\operatorname{dim}_{k}\langle \overline{f_{11}f_{21}},\,\overline{f_{12}f_{22}}\rangle =2$
;∙
 $\operatorname{dim}_{k}\langle \overline{f_{12}},\,\overline{f_{22}}\rangle =\operatorname{dim}_{k}\langle \overline{f_{11}f_{21}},\,\overline{f_{12}f_{22}}\rangle =2$
.
$\operatorname{dim}_{k}\langle \overline{f_{12}},\,\overline{f_{22}}\rangle =\operatorname{dim}_{k}\langle \overline{f_{11}f_{21}},\,\overline{f_{12}f_{22}}\rangle =2$
.
Then we have
 $$\begin{eqnarray}\operatorname{Hom}_{\operatorname{Strat}(\mathbb{G}_{m},1)}(\mathbb{I},P^{1\text{-}\text{strat}})\simeq k[\unicode[STIX]{x1D707}_{2}].\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{\operatorname{Strat}(\mathbb{G}_{m},1)}(\mathbb{I},P^{1\text{-}\text{strat}})\simeq k[\unicode[STIX]{x1D707}_{2}].\end{eqnarray}$$
(2) In the case
 $2\nmid m$
, assume that one of the following conditions is satisfied:
$2\nmid m$
, assume that one of the following conditions is satisfied:∙
 $\operatorname{dim}_{k}\langle \overline{f_{11}},\,\overline{f_{21}}\rangle =2$
,
$\operatorname{dim}_{k}\langle \overline{f_{11}},\,\overline{f_{21}}\rangle =2$
,
 $\operatorname{dim}_{k}\langle \overline{f_{11}f_{21}},\,\overline{f_{12}f_{22}}\rangle =\operatorname{dim}_{k}\langle \overline{f_{11}f_{12}},\,\overline{f_{21}f_{22}},\,\overline{x^{m}}\rangle =3$
;
$\operatorname{dim}_{k}\langle \overline{f_{11}f_{21}},\,\overline{f_{12}f_{22}}\rangle =\operatorname{dim}_{k}\langle \overline{f_{11}f_{12}},\,\overline{f_{21}f_{22}},\,\overline{x^{m}}\rangle =3$
;∙
 $\operatorname{dim}_{k}\langle \overline{f_{12}},\,\overline{f_{22}}\rangle =2$
,
$\operatorname{dim}_{k}\langle \overline{f_{12}},\,\overline{f_{22}}\rangle =2$
,
 $\operatorname{dim}_{k}\langle \overline{f_{11}f_{21}},\,\overline{f_{12}f_{22}}\rangle =\operatorname{dim}_{k}\langle \overline{f_{11}f_{12}},\,\overline{f_{21}f_{22}},\,\overline{x^{m}}\rangle =3$
$\operatorname{dim}_{k}\langle \overline{f_{11}f_{21}},\,\overline{f_{12}f_{22}}\rangle =\operatorname{dim}_{k}\langle \overline{f_{11}f_{12}},\,\overline{f_{21}f_{22}},\,\overline{x^{m}}\rangle =3$
Then we have
Here, for each
![]() $f\in k[x]$
,
$f\in k[x]$
,
![]() $\overline{f}$
denotes the image of
$\overline{f}$
denotes the image of
![]() $f$
in
$f$
in
![]() $k[x]/k[x^{p}]$
.
$k[x]/k[x^{p}]$
.
Proof. Let
![]() $P^{1\text{-}\text{strat}}=\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\}$
. Let
$P^{1\text{-}\text{strat}}=\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\}$
. Let
![]() $\unicode[STIX]{x1D70B}:P\rightarrow \mathbb{G}_{m}$
be the structure morphism. We then have
$\unicode[STIX]{x1D70B}:P\rightarrow \mathbb{G}_{m}$
be the structure morphism. We then have
Let
![]() $\unicode[STIX]{x1D70C}_{P}$
(respectively
$\unicode[STIX]{x1D70C}_{P}$
(respectively
![]() $\unicode[STIX]{x1D70C}_{0}$
) be the coaction
$\unicode[STIX]{x1D70C}_{0}$
) be the coaction
![]() $\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\rightarrow \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\otimes k[\operatorname{GL}_{2(1)}]$
induced by the action
$\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\rightarrow \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\otimes k[\operatorname{GL}_{2(1)}]$
induced by the action
![]() $P\times \operatorname{GL}_{2(1)}\rightarrow P$
(respectively the one by the trivial action). Let
$P\times \operatorname{GL}_{2(1)}\rightarrow P$
(respectively the one by the trivial action). Let
![]() $\unicode[STIX]{x1D704}$
be the antipode of
$\unicode[STIX]{x1D704}$
be the antipode of
![]() $k[\operatorname{GL}_{2(1)}]$
. Then the composition
$k[\operatorname{GL}_{2(1)}]$
. Then the composition
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\otimes k[\operatorname{GL}_{2(1)}] & & \displaystyle \xrightarrow[{}]{\unicode[STIX]{x1D70C}\otimes \text{id}}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\otimes k[\operatorname{GL}_{2(1)}]\otimes k[\operatorname{GL}_{2(1)}]\nonumber\\ \displaystyle & & \displaystyle \xrightarrow[{}]{\text{id}\otimes \unicode[STIX]{x1D704}\otimes \text{id}}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\otimes k[\operatorname{GL}_{2(1)}]\otimes k[\operatorname{GL}_{2(1)}]\xrightarrow[{}]{\text{id}\otimes m}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\otimes k[\operatorname{GL}_{2(1)}]\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\otimes k[\operatorname{GL}_{2(1)}] & & \displaystyle \xrightarrow[{}]{\unicode[STIX]{x1D70C}\otimes \text{id}}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\otimes k[\operatorname{GL}_{2(1)}]\otimes k[\operatorname{GL}_{2(1)}]\nonumber\\ \displaystyle & & \displaystyle \xrightarrow[{}]{\text{id}\otimes \unicode[STIX]{x1D704}\otimes \text{id}}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\otimes k[\operatorname{GL}_{2(1)}]\otimes k[\operatorname{GL}_{2(1)}]\xrightarrow[{}]{\text{id}\otimes m}\unicode[STIX]{x1D70B}_{\ast }{\mathcal{O}}_{P}\otimes k[\operatorname{GL}_{2(1)}]\end{eqnarray}$$
gives a
![]() $k[\operatorname{GL}_{2(1)}]$
-comodule isomorphism
$k[\operatorname{GL}_{2(1)}]$
-comodule isomorphism
If one writes
![]() $k[\operatorname{GL}_{2(1)}]=k[z_{ij}]/(z_{ij}^{2}-\unicode[STIX]{x1D6FF}_{ij})$
, then
$k[\operatorname{GL}_{2(1)}]=k[z_{ij}]/(z_{ij}^{2}-\unicode[STIX]{x1D6FF}_{ij})$
, then
Therefore, via the map (4.5), the element
is mapped to
![]() $y_{ij}\otimes 1$
, which belongs to
$y_{ij}\otimes 1$
, which belongs to
Hence, by (4.6), we find that
Notice that
![]() $E^{(i)}\simeq k[x^{\pm 1}]^{\oplus 2^{4}}$
with free basis
$E^{(i)}\simeq k[x^{\pm 1}]^{\oplus 2^{4}}$
with free basis
![]() $\{e_{11}^{m_{11}}e_{12}^{m_{12}}e_{21}^{m_{21}}e_{22}^{m_{22}}\,|\,m_{ij}=0,1\}$
.
$\{e_{11}^{m_{11}}e_{12}^{m_{12}}e_{21}^{m_{21}}e_{22}^{m_{22}}\,|\,m_{ij}=0,1\}$
.
Let
![]() $A\in \operatorname{GL}_{2^{4}}(k[x^{(-1)\pm 1}])$
be the representation matrix of the inverse isomorphism
$A\in \operatorname{GL}_{2^{4}}(k[x^{(-1)\pm 1}])$
be the representation matrix of the inverse isomorphism
![]() $\unicode[STIX]{x1D70E}^{(0)-1}$
with respect to the basis
$\unicode[STIX]{x1D70E}^{(0)-1}$
with respect to the basis
 $$\begin{eqnarray}\displaystyle & & \displaystyle 1,\,\unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{21},\,\unicode[STIX]{x1D708}_{12}\unicode[STIX]{x1D708}_{22},\,\unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{12}\unicode[STIX]{x1D708}_{21}\unicode[STIX]{x1D708}_{22},;\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}_{11},\,\unicode[STIX]{x1D708}_{12},\,\unicode[STIX]{x1D708}_{21},\,\unicode[STIX]{x1D708}_{22},\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{12},\,\unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{22},\,\unicode[STIX]{x1D708}_{12}\unicode[STIX]{x1D708}_{21},\unicode[STIX]{x1D708}_{21}\unicode[STIX]{x1D708}_{22};\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{12}\unicode[STIX]{x1D708}_{21},\,\unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{12}\unicode[STIX]{x1D708}_{22},\,\unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{21}\unicode[STIX]{x1D708}_{22},\,\unicode[STIX]{x1D708}_{12}\unicode[STIX]{x1D708}_{21}\unicode[STIX]{x1D708}_{22}\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle 1,\,\unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{21},\,\unicode[STIX]{x1D708}_{12}\unicode[STIX]{x1D708}_{22},\,\unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{12}\unicode[STIX]{x1D708}_{21}\unicode[STIX]{x1D708}_{22},;\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}_{11},\,\unicode[STIX]{x1D708}_{12},\,\unicode[STIX]{x1D708}_{21},\,\unicode[STIX]{x1D708}_{22},\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{12},\,\unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{22},\,\unicode[STIX]{x1D708}_{12}\unicode[STIX]{x1D708}_{21},\unicode[STIX]{x1D708}_{21}\unicode[STIX]{x1D708}_{22};\nonumber\\ \displaystyle & & \displaystyle \unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{12}\unicode[STIX]{x1D708}_{21},\,\unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{12}\unicode[STIX]{x1D708}_{22},\,\unicode[STIX]{x1D708}_{11}\unicode[STIX]{x1D708}_{21}\unicode[STIX]{x1D708}_{22},\,\unicode[STIX]{x1D708}_{12}\unicode[STIX]{x1D708}_{21}\unicode[STIX]{x1D708}_{22}\nonumber\end{eqnarray}$$
for
![]() $\unicode[STIX]{x1D708}\in \{e,z\}$
. One then obtains
$\unicode[STIX]{x1D708}\in \{e,z\}$
. One then obtains
 $$\begin{eqnarray}A=\left(\begin{array}{@{}ccccc@{}}C & O & O & O & \\ & B\otimes E & O & B\otimes D & \\ & & B\otimes B & O & \!\\ & O & & B\otimes x^{(-1)m}E\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}ccccc@{}}C & O & O & O & \\ & B\otimes E & O & B\otimes D & \\ & & B\otimes B & O & \!\\ & O & & B\otimes x^{(-1)m}E\end{array}\right),\end{eqnarray}$$
with
 $$\begin{eqnarray}\displaystyle & \displaystyle B=\left(\begin{array}{@{}cc@{}}f_{11}^{\prime }(x^{(-1)}) & f_{21}^{\prime }(x^{(-1)})\\ f_{12}^{\prime }(x^{(-1)}) & f_{22}^{\prime }(x^{(-1)})\end{array}\right);\quad E=\left(\begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right); & \displaystyle \\ \displaystyle & \displaystyle C=\left(\begin{array}{@{}cccc@{}}1 & f_{11}^{\prime }(x^{(-1)})f_{21}^{\prime }(x^{(-1)}) & f_{12}^{\prime }(x^{(-1)})f_{22}^{\prime }(x^{(-1)}) & \ast \\ 0 & x^{(-1)m} & 0 & f_{12}^{\prime }(x^{(-1)})f_{22}^{\prime }(x^{(-1)})x^{(-1)m}\\ 0 & 0 & x^{(-1)m} & f_{11}^{\prime }(x^{(-1)})f_{21}^{\prime }(x^{(-1)})x^{(-1)m}\\ 0 & 0 & 0 & x^{m}\end{array}\right);\\ \displaystyle & \displaystyle D=\left(\begin{array}{@{}cc@{}}0 & f_{12}^{\prime }(x^{(-1)})f_{22}^{\prime }(x^{(-1)})\\ f_{11}^{\prime }(x^{(-1)})f_{21}^{\prime }(x^{(-1)}) & 0\end{array}\right),\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle B=\left(\begin{array}{@{}cc@{}}f_{11}^{\prime }(x^{(-1)}) & f_{21}^{\prime }(x^{(-1)})\\ f_{12}^{\prime }(x^{(-1)}) & f_{22}^{\prime }(x^{(-1)})\end{array}\right);\quad E=\left(\begin{array}{@{}cc@{}}1 & 0\\ 0 & 1\end{array}\right); & \displaystyle \\ \displaystyle & \displaystyle C=\left(\begin{array}{@{}cccc@{}}1 & f_{11}^{\prime }(x^{(-1)})f_{21}^{\prime }(x^{(-1)}) & f_{12}^{\prime }(x^{(-1)})f_{22}^{\prime }(x^{(-1)}) & \ast \\ 0 & x^{(-1)m} & 0 & f_{12}^{\prime }(x^{(-1)})f_{22}^{\prime }(x^{(-1)})x^{(-1)m}\\ 0 & 0 & x^{(-1)m} & f_{11}^{\prime }(x^{(-1)})f_{21}^{\prime }(x^{(-1)})x^{(-1)m}\\ 0 & 0 & 0 & x^{m}\end{array}\right);\\ \displaystyle & \displaystyle D=\left(\begin{array}{@{}cc@{}}0 & f_{12}^{\prime }(x^{(-1)})f_{22}^{\prime }(x^{(-1)})\\ f_{11}^{\prime }(x^{(-1)})f_{21}^{\prime }(x^{(-1)}) & 0\end{array}\right),\end{eqnarray}$$
where
![]() $\{f_{ij}^{\prime }(x^{(-1)})\}$
is defined by
$\{f_{ij}^{\prime }(x^{(-1)})\}$
is defined by
Here, notice that
![]() $x^{(-1)2}=x$
and that
$x^{(-1)2}=x$
and that
![]() $\det B=x^{(-1)m}$
. Furthermore, the assumption on
$\det B=x^{(-1)m}$
. Furthermore, the assumption on
![]() $\{f_{ij}(x)\}$
implies the same condition on
$\{f_{ij}(x)\}$
implies the same condition on
![]() $\{f_{ij}^{\prime }(x^{(-1)})\}$
.
$\{f_{ij}^{\prime }(x^{(-1)})\}$
.
Now one can reduce the problem to calculating the right-hand side of the following equation:
First we consider the case where
![]() $2\mid m$
. In this case, without loss of generality, we may assume that
$2\mid m$
. In this case, without loss of generality, we may assume that
![]() $m=0$
. Note that the condition that
$m=0$
. Note that the condition that
![]() $\det (f_{ij}(x))=1$
implies that the set
$\det (f_{ij}(x))=1$
implies that the set
is also linearly independent over
![]() $k$
. Indeed, this follows from the equation:
$k$
. Indeed, this follows from the equation:
We will solve the simultaneous equations
![]() $A\cdot \text{}\underline{a}=\text{}\underline{b}$
from the bottom. Then the condition that the set
$A\cdot \text{}\underline{a}=\text{}\underline{b}$
from the bottom. Then the condition that the set
![]() $\{\overline{f_{11}^{\prime }},\,\overline{f_{21}^{\prime }}\}$
, or
$\{\overline{f_{11}^{\prime }},\,\overline{f_{21}^{\prime }}\}$
, or
![]() $\{\overline{f_{12}^{\prime }},\,\overline{f_{22}^{\prime }}\}$
is linearly independent implies that
$\{\overline{f_{12}^{\prime }},\,\overline{f_{22}^{\prime }}\}$
is linearly independent implies that
Moreover, the conditions that
![]() $\{\overline{f_{11}^{\prime }f_{12}^{\prime }},\,\overline{f_{21}^{\prime }f_{22}^{\prime }}\}$
is linearly independent and that
$\{\overline{f_{11}^{\prime }f_{12}^{\prime }},\,\overline{f_{21}^{\prime }f_{22}^{\prime }}\}$
is linearly independent and that
![]() $\det B=f_{11}^{\prime }f_{22}^{\prime }-f_{12}^{\prime }f_{21}^{\prime }=1$
imply that
$\det B=f_{11}^{\prime }f_{22}^{\prime }-f_{12}^{\prime }f_{21}^{\prime }=1$
imply that
By solving the equations
again combined with the assumption on
![]() $\overline{f_{ij}^{\prime }}$
, we have
$\overline{f_{ij}^{\prime }}$
, we have
All the above computations then imply
Finally, let us consider the case where
![]() $2\nmid m$
. In this case, the equations in the part
$2\nmid m$
. In this case, the equations in the part
![]() $B\otimes x^{(-1)m}E$
cannot imply
$B\otimes x^{(-1)m}E$
cannot imply
![]() $a_{i}=0~(13\leqslant i\leqslant 16)$
. However, by solving the simultaneous equations
$a_{i}=0~(13\leqslant i\leqslant 16)$
. However, by solving the simultaneous equations
we can conclude that
Next let us solve the part
![]() $C$
. Notice that
$C$
. Notice that
![]() $\{\overline{x^{(-1)m}},\,\overline{f_{11}^{\prime }f_{21}^{\prime }x^{(-1)m}}\}$
is linearly independent over
$\{\overline{x^{(-1)m}},\,\overline{f_{11}^{\prime }f_{21}^{\prime }x^{(-1)m}}\}$
is linearly independent over
![]() $k$
. Thus, we find that
$k$
. Thus, we find that
![]() $a_{4}=0$
. On the other hand, by the assumption that
$a_{4}=0$
. On the other hand, by the assumption that
![]() $\{\overline{f_{11}^{\prime }f_{21}^{\prime }},\,\overline{f_{12}^{\prime }f_{22}^{\prime }}\}$
is linearly independent, we also have
$\{\overline{f_{11}^{\prime }f_{21}^{\prime }},\,\overline{f_{12}^{\prime }f_{22}^{\prime }}\}$
is linearly independent, we also have
![]() $a_{2}=a_{3}=0$
. Finally let us solve the part
$a_{2}=a_{3}=0$
. Finally let us solve the part
![]() $B\otimes B$
. Then the condition that
$B\otimes B$
. Then the condition that
![]() $\overline{f_{11}^{\prime }f_{21}^{\prime }}\neq 0$
in
$\overline{f_{11}^{\prime }f_{21}^{\prime }}\neq 0$
in
![]() $k[x^{(-1)\pm 1}]/k[x^{(-1)\pm 2}]$
implies that
$k[x^{(-1)\pm 1}]/k[x^{(-1)\pm 2}]$
implies that
![]() $a_{10}=a_{11}$
. Then the condition that
$a_{10}=a_{11}$
. Then the condition that
![]() $\{\overline{f_{11}f_{12}},\,\overline{f_{21}f_{22}},\,\overline{x^{m}}\}$
is linearly independent over
$\{\overline{f_{11}f_{12}},\,\overline{f_{21}f_{22}},\,\overline{x^{m}}\}$
is linearly independent over
![]() $k$
implies that
$k$
implies that
![]() $a_{9}=a_{10}=a_{11}=a_{12}=0$
. Therefore, we can conclude that
$a_{9}=a_{10}=a_{11}=a_{12}=0$
. Therefore, we can conclude that
As an immediate consequence of Theorem 4.12 (or its proof), we have the following.
Corollary 4.13. Assume
![]() $p=2$
. Let
$p=2$
. Let
be a
![]() $k$
-morphism. Then the resulting
$k$
-morphism. Then the resulting
![]() $\operatorname{SL}_{2(1)}$
-torsor
$\operatorname{SL}_{2(1)}$
-torsor
![]() $\text{}\underline{f}^{\ast }\operatorname{SL}_{2}^{(-1)}\rightarrow \mathbb{A}_{k}^{1}$
is saturated if and only if one of the following conditions is satisfied:
$\text{}\underline{f}^{\ast }\operatorname{SL}_{2}^{(-1)}\rightarrow \mathbb{A}_{k}^{1}$
is saturated if and only if one of the following conditions is satisfied:
∙
 $\operatorname{dim}_{k}\langle \overline{f_{11}},\,\overline{f_{21}}\rangle =\operatorname{dim}_{k}\langle \overline{f_{11}f_{21}},\,\overline{f_{12}f_{22}}\rangle =2$
;
$\operatorname{dim}_{k}\langle \overline{f_{11}},\,\overline{f_{21}}\rangle =\operatorname{dim}_{k}\langle \overline{f_{11}f_{21}},\,\overline{f_{12}f_{22}}\rangle =2$
;∙
 $\operatorname{dim}_{k}\langle \overline{f_{12}},\,\overline{f_{22}}\rangle =\operatorname{dim}_{k}\langle \overline{f_{11}f_{21}},\,\overline{f_{12}f_{22}}\rangle =2$
.
$\operatorname{dim}_{k}\langle \overline{f_{12}},\,\overline{f_{22}}\rangle =\operatorname{dim}_{k}\langle \overline{f_{11}f_{21}},\,\overline{f_{12}f_{22}}\rangle =2$
.
Proof. By considering the composition
we are reduced to the case where
![]() $\text{}\underline{f}:\mathbb{G}_{m}\rightarrow \operatorname{GL}_{2}$
with
$\text{}\underline{f}:\mathbb{G}_{m}\rightarrow \operatorname{GL}_{2}$
with
![]() $\det (\text{}\underline{f})=1$
. Thus, the statement follows from the argument in the proof of Theorem 4.12, noticing that the condition
$\det (\text{}\underline{f})=1$
. Thus, the statement follows from the argument in the proof of Theorem 4.12, noticing that the condition
implies the image of the homomorphism
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{G}_{m})\rightarrow \operatorname{GL}_{2(1)}$
corresponding to the torsor
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{G}_{m})\rightarrow \operatorname{GL}_{2(1)}$
corresponding to the torsor
![]() $P=\text{}\underline{f}^{\ast }\operatorname{GL}_{2}^{(-1)}\rightarrow \mathbb{G}_{m}$
coincides with
$P=\text{}\underline{f}^{\ast }\operatorname{GL}_{2}^{(-1)}\rightarrow \mathbb{G}_{m}$
coincides with
![]() $\operatorname{SL}_{2(1)}$
.◻
$\operatorname{SL}_{2(1)}$
.◻
Remark 4.14. For example, the embedding
satisfies the condition in Corollary 4.13.
Combined with Lemma 4.2, Theorem 4.12 also implies the following.
Corollary 4.15. Assume
![]() $p=2$
. Then, there exists a surjective homomorphism
$p=2$
. Then, there exists a surjective homomorphism
In particular, for any
![]() $r>0$
, the
$r>0$
, the
![]() $r$
th Frobenius kernel
$r$
th Frobenius kernel
![]() $\operatorname{GL}_{2(r)}$
appears as a finite quotient of
$\operatorname{GL}_{2(r)}$
appears as a finite quotient of
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{G}_{m})$
.
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{G}_{m})$
.
Proof. It suffices to find a
![]() $k$
-morphism
$k$
-morphism
![]() $\text{}\underline{f}\in \operatorname{GL}_{2}(k[x^{\pm 1}])=\text{Mor}_{k}(\mathbb{G}_{m},\operatorname{GL}_{2})$
satisfying the condition of Theorem 4.12. The morphism
$\text{}\underline{f}\in \operatorname{GL}_{2}(k[x^{\pm 1}])=\text{Mor}_{k}(\mathbb{G}_{m},\operatorname{GL}_{2})$
satisfying the condition of Theorem 4.12. The morphism
 $$\begin{eqnarray}\mathbb{G}_{m}\ni a\mapsto \left(\begin{array}{@{}cc@{}}{\displaystyle \frac{1}{a}}+{\displaystyle \frac{1}{a^{4}}} & {\displaystyle \frac{1}{a^{2}}}\\ 1 & {\displaystyle \frac{1}{a}}\end{array}\right)\in \operatorname{GL}_{2}\end{eqnarray}$$
$$\begin{eqnarray}\mathbb{G}_{m}\ni a\mapsto \left(\begin{array}{@{}cc@{}}{\displaystyle \frac{1}{a}}+{\displaystyle \frac{1}{a^{4}}} & {\displaystyle \frac{1}{a^{2}}}\\ 1 & {\displaystyle \frac{1}{a}}\end{array}\right)\in \operatorname{GL}_{2}\end{eqnarray}$$
gives such a one. ◻
Remark 4.16. (1) Corollary 4.13, combined with Lemma 4.2, gives an answer to Question 4.1(2) for the pair
![]() $(U,\unicode[STIX]{x1D6F4})=(\mathbb{A}_{k}^{1},\operatorname{SL}_{2})$
.
$(U,\unicode[STIX]{x1D6F4})=(\mathbb{A}_{k}^{1},\operatorname{SL}_{2})$
.
(2) Theorem 4.12 and the proof of Corollary 4.15, combined with Lemma 4.2, gives an affirmative answer to Question 4.1(1) for the pair
![]() $(U,\unicode[STIX]{x1D6F4})=(\mathbb{G}_{m},\operatorname{GL}_{2})$
in the case where
$(U,\unicode[STIX]{x1D6F4})=(\mathbb{G}_{m},\operatorname{GL}_{2})$
in the case where
![]() $k$
is of characteristic
$k$
is of characteristic
![]() $p=2$
. Furthermore, since
$p=2$
. Furthermore, since
![]() $\mathbb{X}(\operatorname{GL}_{2(r)})=\mathbb{Z}/2^{r}\mathbb{Z}\subset \mathbb{Q}_{2}/\mathbb{Z}_{2}$
(note that the first equality follows from the exactness of
$\mathbb{X}(\operatorname{GL}_{2(r)})=\mathbb{Z}/2^{r}\mathbb{Z}\subset \mathbb{Q}_{2}/\mathbb{Z}_{2}$
(note that the first equality follows from the exactness of
![]() $1\rightarrow \operatorname{SL}_{2(r)}\rightarrow \operatorname{GL}_{2(r)}\rightarrow \unicode[STIX]{x1D707}_{p^{r}}\rightarrow 1$
and
$1\rightarrow \operatorname{SL}_{2(r)}\rightarrow \operatorname{GL}_{2(r)}\rightarrow \unicode[STIX]{x1D707}_{p^{r}}\rightarrow 1$
and
![]() $\mathbb{X}(\operatorname{SL}_{2(r)})=1$
), Corollary 4.15 gives an affirmative answer to Question 3.3 for
$\mathbb{X}(\operatorname{SL}_{2(r)})=1$
), Corollary 4.15 gives an affirmative answer to Question 3.3 for
![]() $\mathbb{G}_{m}$
and for
$\mathbb{G}_{m}$
and for
![]() $\operatorname{GL}_{2(r)}~(r>0)$
in the case where
$\operatorname{GL}_{2(r)}~(r>0)$
in the case where
![]() $k$
is of characteristic
$k$
is of characteristic
![]() $p=2$
. However, we have restricted our attention to a special class of
$p=2$
. However, we have restricted our attention to a special class of
![]() $k$
-morphisms
$k$
-morphisms
![]() $\mathbb{G}_{m}\rightarrow \operatorname{GL}_{2}$
, so it is not enough to give a complete answer to Question 4.1(2).
$\mathbb{G}_{m}\rightarrow \operatorname{GL}_{2}$
, so it is not enough to give a complete answer to Question 4.1(2).
4.3 Bertini type theorem for finite local torsors and its application
Finally let us prove a purely inseparable analogue of a Bertini type theorem (cf. [Reference JouanolouJou83]). As an application, we will give an affirmative answer to Question 4.1(1) for the pair
![]() $(\mathbb{A}_{k}^{1},\unicode[STIX]{x1D6F4})$
with
$(\mathbb{A}_{k}^{1},\unicode[STIX]{x1D6F4})$
with
![]() $\unicode[STIX]{x1D6F4}$
a semi-simple simply connected algebraic group over
$\unicode[STIX]{x1D6F4}$
a semi-simple simply connected algebraic group over
![]() $k$
, whence, to Question 3.3 for
$k$
, whence, to Question 3.3 for
![]() $\mathbb{A}_{k}^{1}$
and for
$\mathbb{A}_{k}^{1}$
and for
![]() $\unicode[STIX]{x1D6F4}_{(r)}~(r>0)$
.
$\unicode[STIX]{x1D6F4}_{(r)}~(r>0)$
.
Theorem 4.17. Let
![]() $n\geqslant 2$
be an integer. Let
$n\geqslant 2$
be an integer. Let
![]() $k$
be a perfect field of positive characteristic
$k$
be a perfect field of positive characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $G$
be a finite local
$G$
be a finite local
![]() $k$
-group scheme of height one and
$k$
-group scheme of height one and
![]() $\unicode[STIX]{x1D70B}:P\rightarrow \mathbb{A}_{k}^{n}$
be a saturated
$\unicode[STIX]{x1D70B}:P\rightarrow \mathbb{A}_{k}^{n}$
be a saturated
![]() $G$
-torsor. Then there exists a closed immersion
$G$
-torsor. Then there exists a closed immersion
![]() $\unicode[STIX]{x1D704}:\mathbb{A}_{k}^{n-1}{\hookrightarrow}\mathbb{A}_{k}^{n}$
such that the
$\unicode[STIX]{x1D704}:\mathbb{A}_{k}^{n-1}{\hookrightarrow}\mathbb{A}_{k}^{n}$
such that the
![]() $G$
-torsor
$G$
-torsor
![]() $\unicode[STIX]{x1D704}^{\ast }P\rightarrow \mathbb{A}_{k}^{n-1}$
obtained by pulling back
$\unicode[STIX]{x1D704}^{\ast }P\rightarrow \mathbb{A}_{k}^{n-1}$
obtained by pulling back
![]() $P$
along
$P$
along
![]() $\unicode[STIX]{x1D704}$
is saturated as well.
$\unicode[STIX]{x1D704}$
is saturated as well.
To prove this theorem, we will rely on the Tannakian interpretation (cf. Theorem 4.7) again. Then we are reduced to showing the following lemma of linear algebras.
Lemma 4.18. Let
![]() $n\geqslant 2$
be an integer. Let
$n\geqslant 2$
be an integer. Let
![]() $k$
be a perfect field of positive characteristic
$k$
be a perfect field of positive characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $V_{1},\ldots ,V_{m}\subset k[x_{1},\ldots ,x_{n}]/k[x_{1}^{p},\ldots ,x_{n}^{p}]$
be finite dimensional subspaces. Then there exists a polynomial
$V_{1},\ldots ,V_{m}\subset k[x_{1},\ldots ,x_{n}]/k[x_{1}^{p},\ldots ,x_{n}^{p}]$
be finite dimensional subspaces. Then there exists a polynomial
![]() $g=g(x_{1},\ldots ,x_{n-1})$
so that the
$g=g(x_{1},\ldots ,x_{n-1})$
so that the
![]() $k$
-linear map
$k$
-linear map
 $$\begin{eqnarray}\displaystyle k[x_{1},\ldots ,x_{n}]/k[x_{1}^{p},\ldots ,x_{n}^{p}] & \rightarrow & \displaystyle k[x_{1},\ldots ,x_{n-1}]/k[x_{1}^{p},\ldots ,x_{n-1}^{p}];\nonumber\\ \displaystyle x_{i} & \mapsto & \displaystyle \left\{\begin{array}{@{}ll@{}}x_{i},\quad & 1\leqslant i\leqslant n-1,\\ g(x_{1},\ldots ,x_{n-1}),\quad & i=n,\end{array}\right.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle k[x_{1},\ldots ,x_{n}]/k[x_{1}^{p},\ldots ,x_{n}^{p}] & \rightarrow & \displaystyle k[x_{1},\ldots ,x_{n-1}]/k[x_{1}^{p},\ldots ,x_{n-1}^{p}];\nonumber\\ \displaystyle x_{i} & \mapsto & \displaystyle \left\{\begin{array}{@{}ll@{}}x_{i},\quad & 1\leqslant i\leqslant n-1,\\ g(x_{1},\ldots ,x_{n-1}),\quad & i=n,\end{array}\right.\nonumber\end{eqnarray}$$
maps all the subspaces
![]() $V_{i}$
injectively into
$V_{i}$
injectively into
![]() $k[x_{1},\ldots ,x_{n-1}]/k[x_{1}^{p},\ldots ,x_{n-1}^{p}]$
.
$k[x_{1},\ldots ,x_{n-1}]/k[x_{1}^{p},\ldots ,x_{n-1}^{p}]$
.
Proof. By considering
![]() $V:=V_{1}+\cdots +V_{m}$
, we are reduced to the case where
$V:=V_{1}+\cdots +V_{m}$
, we are reduced to the case where
![]() $m=1$
. Let
$m=1$
. Let
![]() $V$
be a finite dimensional subspace of
$V$
be a finite dimensional subspace of
![]() $k[x_{1},\ldots ,x_{n}]/k[x_{1}^{p},\ldots ,x_{n}^{p}]$
. Without loss of generality, we may assume that
$k[x_{1},\ldots ,x_{n}]/k[x_{1}^{p},\ldots ,x_{n}^{p}]$
. Without loss of generality, we may assume that
![]() $V$
is of the form
$V$
is of the form
for a sufficiently large integer
![]() $d>0$
. Take an integer
$d>0$
. Take an integer
![]() $M>d$
with
$M>d$
with
![]() $p\nmid M$
and an integer
$p\nmid M$
and an integer
![]() $N>0$
with
$N>0$
with
![]() $p^{N}>d(M+1)$
. Let us define
$p^{N}>d(M+1)$
. Let us define
Note that the following subset of
![]() $k[x_{1},\ldots ,x_{n-1}]/k[x_{1}^{p},\ldots ,x_{n-1}^{p}]$
is linearly independent over
$k[x_{1},\ldots ,x_{n-1}]/k[x_{1}^{p},\ldots ,x_{n-1}^{p}]$
is linearly independent over
![]() $k$
:
$k$
:
 $$\begin{eqnarray}\displaystyle x_{1}^{m_{1}}\cdots x_{n-1}^{m_{n-1}} & & \displaystyle \quad (0\leqslant m_{i}\leqslant d,m_{n}=0;~p\nmid m_{i}~\text{for some }1\leqslant i\leqslant n-1),\nonumber\\ \displaystyle \mathop{\prod }_{i=1}^{n-1}x_{i}^{m_{i}+m_{n}M} & & \displaystyle \quad (p\mid m_{i}~\text{for any }1\leqslant i\leqslant n-1,\text{whence }p\nmid m_{n}),\nonumber\\ \displaystyle \mathop{\prod }_{i=1}^{n-1}x_{i}^{m_{i}+m_{n}p^{N}} & & \displaystyle \quad (0\leqslant m_{i}\leqslant d;~m_{n}\neq 0;~p\nmid m_{i}~\text{for some }1\leqslant i\leqslant n-1).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle x_{1}^{m_{1}}\cdots x_{n-1}^{m_{n-1}} & & \displaystyle \quad (0\leqslant m_{i}\leqslant d,m_{n}=0;~p\nmid m_{i}~\text{for some }1\leqslant i\leqslant n-1),\nonumber\\ \displaystyle \mathop{\prod }_{i=1}^{n-1}x_{i}^{m_{i}+m_{n}M} & & \displaystyle \quad (p\mid m_{i}~\text{for any }1\leqslant i\leqslant n-1,\text{whence }p\nmid m_{n}),\nonumber\\ \displaystyle \mathop{\prod }_{i=1}^{n-1}x_{i}^{m_{i}+m_{n}p^{N}} & & \displaystyle \quad (0\leqslant m_{i}\leqslant d;~m_{n}\neq 0;~p\nmid m_{i}~\text{for some }1\leqslant i\leqslant n-1).\nonumber\end{eqnarray}$$
One can then conclude that the polynomial
![]() $g$
gives a desired polynomial.◻
$g$
gives a desired polynomial.◻
Proof of Theorem 4.17.
We will show that there exists a closed immersion
![]() $\unicode[STIX]{x1D704}:\mathbb{A}_{k}^{n-1}{\hookrightarrow}\mathbb{A}_{k}^{n}$
such that
$\unicode[STIX]{x1D704}:\mathbb{A}_{k}^{n-1}{\hookrightarrow}\mathbb{A}_{k}^{n}$
such that
Note that
![]() $(\unicode[STIX]{x1D704}^{\ast }P)^{1\text{-}\text{strat}}=\unicode[STIX]{x1D704}^{\ast }(P^{1\text{-}\text{strat}})$
and that, from the assumption, we have
$(\unicode[STIX]{x1D704}^{\ast }P)^{1\text{-}\text{strat}}=\unicode[STIX]{x1D704}^{\ast }(P^{1\text{-}\text{strat}})$
and that, from the assumption, we have
Let
![]() $P^{1\text{-}\text{strat}}=\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\}$
. By Serre’s conjecture on vector bundles on an affine space (cf. [Reference LamLam78]), the vector bundle
$P^{1\text{-}\text{strat}}=\{E^{(i)},\unicode[STIX]{x1D70E}^{(i)}\}$
. By Serre’s conjecture on vector bundles on an affine space (cf. [Reference LamLam78]), the vector bundle
![]() $E^{(0)}$
is a free
$E^{(0)}$
is a free
![]() ${\mathcal{O}}_{\mathbb{A}_{k}^{n}}$
-module. Let
${\mathcal{O}}_{\mathbb{A}_{k}^{n}}$
-module. Let
with
![]() $q=\operatorname{dim}_{k}k[G]$
, which is some power of
$q=\operatorname{dim}_{k}k[G]$
, which is some power of
![]() $p$
, be the representation matrix of
$p$
, be the representation matrix of
![]() $\unicode[STIX]{x1D70E}^{(0)-1}$
with respect to some basis. The assumption (4.7) then amounts to saying that the vector space
$\unicode[STIX]{x1D70E}^{(0)-1}$
with respect to some basis. The assumption (4.7) then amounts to saying that the vector space
is of dimension one. Then, by permuting basis if necessary, we may assume that
 $$\begin{eqnarray}\{\text{}\underline{a}\in k^{\oplus q}\,|\,A\cdot \text{}\underline{a}\in k[x_{1},\ldots ,x_{n}]^{\oplus q}\}=\left\{\left.\left(\begin{array}{@{}c@{}}a\\ 0\\ \vdots \\ 0\end{array}\right)\right|a\in k\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\{\text{}\underline{a}\in k^{\oplus q}\,|\,A\cdot \text{}\underline{a}\in k[x_{1},\ldots ,x_{n}]^{\oplus q}\}=\left\{\left.\left(\begin{array}{@{}c@{}}a\\ 0\\ \vdots \\ 0\end{array}\right)\right|a\in k\right\}.\end{eqnarray}$$
Then, the matrix
![]() $A$
has the following form:
$A$
has the following form:
 $$\begin{eqnarray}A=\left(\begin{array}{@{}cccc@{}}a_{11} & \ast & \cdots \, & \ast \\ a_{21} & \ast & \cdots \, & \ast \\ \vdots & & \ddots & \\ a_{q1} & \ast & \cdots \, & \ast \end{array}\right)\quad \text{with }a_{i1}\in k[x_{1},\ldots ,x_{n}]~(1\leqslant i\leqslant q).\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}cccc@{}}a_{11} & \ast & \cdots \, & \ast \\ a_{21} & \ast & \cdots \, & \ast \\ \vdots & & \ddots & \\ a_{q1} & \ast & \cdots \, & \ast \end{array}\right)\quad \text{with }a_{i1}\in k[x_{1},\ldots ,x_{n}]~(1\leqslant i\leqslant q).\end{eqnarray}$$
Let us write
 $$\begin{eqnarray}B\overset{\operatorname{def}}{=}\left(\begin{array}{@{}ccc@{}}a_{12} & \cdots \, & a_{1q}\\ & \cdots \, & \\ a_{q2} & \cdots \, & a_{qq}\end{array}\right).\end{eqnarray}$$
$$\begin{eqnarray}B\overset{\operatorname{def}}{=}\left(\begin{array}{@{}ccc@{}}a_{12} & \cdots \, & a_{1q}\\ & \cdots \, & \\ a_{q2} & \cdots \, & a_{qq}\end{array}\right).\end{eqnarray}$$
Then the condition that
![]() $\operatorname{dim}_{k}\operatorname{Hom}_{\operatorname{Strat}(\mathbb{A}_{k}^{1},1)}(\mathbb{I},P^{1\text{-}\text{strat}})=1$
is equivalent to the condition that
$\operatorname{dim}_{k}\operatorname{Hom}_{\operatorname{Strat}(\mathbb{A}_{k}^{1},1)}(\mathbb{I},P^{1\text{-}\text{strat}})=1$
is equivalent to the condition that
Therefore, we are reduced to showing the following statement: if a matrix
satisfies the condition
then there exists a polynomial
![]() $g=g(x_{1}^{(-1)},\ldots ,x_{n-1}^{(-1)})$
such that the condition
$g=g(x_{1}^{(-1)},\ldots ,x_{n-1}^{(-1)})$
such that the condition
is fulfilled. Here
![]() $B^{\prime }=(b_{ij}^{\prime })$
is a matrix with
$B^{\prime }=(b_{ij}^{\prime })$
is a matrix with
![]() $b_{ij}^{\prime }=b_{ij}(x_{1}^{(-1)},\ldots ,x_{n-1}^{(-1)},g)$
. Indeed, by applying Lemma 4.18 to the subspaces
$b_{ij}^{\prime }=b_{ij}(x_{1}^{(-1)},\ldots ,x_{n-1}^{(-1)},g)$
. Indeed, by applying Lemma 4.18 to the subspaces
we can find a polynomial
![]() $g=g(x_{1}^{(-1)},\ldots ,x_{n-1}^{(-1)})$
so that the homomorphism
$g=g(x_{1}^{(-1)},\ldots ,x_{n-1}^{(-1)})$
so that the homomorphism
induced by
![]() $x_{n}^{(-1)}\mapsto g(x_{1}^{(-1)},\ldots ,x_{n-1}^{(-1)})$
maps all the subspaces
$x_{n}^{(-1)}\mapsto g(x_{1}^{(-1)},\ldots ,x_{n-1}^{(-1)})$
maps all the subspaces
![]() $V_{i}$
injectively into
$V_{i}$
injectively into
Then for any
![]() $\text{}\underline{b}\in k^{\oplus s}$
, the condition that
$\text{}\underline{b}\in k^{\oplus s}$
, the condition that
![]() $B^{\prime }\cdot \text{}\underline{b}\in k[x_{1},\ldots ,x_{n-1}]^{\oplus t}$
implies the condition that
$B^{\prime }\cdot \text{}\underline{b}\in k[x_{1},\ldots ,x_{n-1}]^{\oplus t}$
implies the condition that
![]() $B\cdot \text{}\underline{b}\in k[x_{1},\ldots ,x_{n}]^{\oplus t}$
. This completes the proof.◻
$B\cdot \text{}\underline{b}\in k[x_{1},\ldots ,x_{n}]^{\oplus t}$
. This completes the proof.◻
Corollary 4.19. Let
![]() $k$
be a perfect field of positive characteristic
$k$
be a perfect field of positive characteristic
![]() $p>0$
. Let
$p>0$
. Let
![]() $\unicode[STIX]{x1D6F4}$
be a semi-simple simply connected algebraic group over
$\unicode[STIX]{x1D6F4}$
be a semi-simple simply connected algebraic group over
![]() $k$
. Then there exists a surjective homomorphism
$k$
. Then there exists a surjective homomorphism
In particular, for any
![]() $r>0$
, the
$r>0$
, the
![]() $r$
th Frobenius kernel
$r$
th Frobenius kernel
![]() $\unicode[STIX]{x1D6F4}_{(r)}$
of
$\unicode[STIX]{x1D6F4}_{(r)}$
of
![]() $\unicode[STIX]{x1D6F4}$
appears as a finite quotient of
$\unicode[STIX]{x1D6F4}$
appears as a finite quotient of
![]() $\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1})$
.
$\unicode[STIX]{x1D70B}^{\operatorname{loc}}(\mathbb{A}_{k}^{1})$
.
Proof. We will adopt the argument of [Reference SerreSer92, § 3.2]. Let us find a
![]() $k$
-morphism
$k$
-morphism
![]() $\mathbb{A}_{k}^{1}\rightarrow \unicode[STIX]{x1D6F4}$
so that the resulting tower of torsors
$\mathbb{A}_{k}^{1}\rightarrow \unicode[STIX]{x1D6F4}$
so that the resulting tower of torsors
is saturated. By virtue of Lemma 4.2, it suffices to find a
![]() $k$
-morphism
$k$
-morphism
![]() $\mathbb{A}_{k}^{1}\rightarrow \unicode[STIX]{x1D6F4}$
so that
$\mathbb{A}_{k}^{1}\rightarrow \unicode[STIX]{x1D6F4}$
so that
![]() $\unicode[STIX]{x1D6F4}^{(-1)}|_{\mathbb{A}_{k}^{1}}$
is saturated. Fix a maximal torus
$\unicode[STIX]{x1D6F4}^{(-1)}|_{\mathbb{A}_{k}^{1}}$
is saturated. Fix a maximal torus
![]() $T<\unicode[STIX]{x1D6F4}$
and a set of positive roots. Let
$T<\unicode[STIX]{x1D6F4}$
and a set of positive roots. Let
![]() $U^{+}<\unicode[STIX]{x1D6F4}$
(respectively
$U^{+}<\unicode[STIX]{x1D6F4}$
(respectively
![]() $U^{-}<\unicode[STIX]{x1D6F4}$
) be the unipotent radical corresponding to the positive roots (respectively the negative roots). Let us define a
$U^{-}<\unicode[STIX]{x1D6F4}$
) be the unipotent radical corresponding to the positive roots (respectively the negative roots). Let us define a
![]() $k$
-morphism
$k$
-morphism
![]() $f:U^{+}\times U^{-}\rightarrow \unicode[STIX]{x1D6F4}$
by the composition
$f:U^{+}\times U^{-}\rightarrow \unicode[STIX]{x1D6F4}$
by the composition
Here the first map is the natural inclusion and the second one the multiplication of
![]() $\unicode[STIX]{x1D6F4}$
. Then the pulling-back
$\unicode[STIX]{x1D6F4}$
. Then the pulling-back
![]() $P\overset{\operatorname{def}}{=}f^{\ast }\unicode[STIX]{x1D6F4}$
defines a saturated
$P\overset{\operatorname{def}}{=}f^{\ast }\unicode[STIX]{x1D6F4}$
defines a saturated
![]() $\unicode[STIX]{x1D6F4}_{(1)}$
-torsor over
$\unicode[STIX]{x1D6F4}_{(1)}$
-torsor over
![]() $U^{+}\times U^{-}$
. Indeed, notice that the diagram
$U^{+}\times U^{-}$
. Indeed, notice that the diagram

commutes. Then the
![]() $\unicode[STIX]{x1D6F4}_{(1)}$
-torsor
$\unicode[STIX]{x1D6F4}_{(1)}$
-torsor
![]() $i_{\pm }^{\ast }P\rightarrow U^{\pm }$
is reduced to the saturated
$i_{\pm }^{\ast }P\rightarrow U^{\pm }$
is reduced to the saturated
![]() $U_{(1)}^{\pm }$
-torsor
$U_{(1)}^{\pm }$
-torsor
![]() $U^{\pm (-1)}\rightarrow U^{\pm }$
, i.e.,
$U^{\pm (-1)}\rightarrow U^{\pm }$
, i.e.,
If we denote by
![]() $\unicode[STIX]{x1D719}:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U^{+}\times U^{-})\rightarrow \unicode[STIX]{x1D6F4}_{(1)}$
(respectively
$\unicode[STIX]{x1D719}:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U^{+}\times U^{-})\rightarrow \unicode[STIX]{x1D6F4}_{(1)}$
(respectively
![]() $\unicode[STIX]{x1D713}^{\pm }:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U^{\pm })\rightarrow U_{(1)}^{\pm }$
) the homomorphism corresponding to the torsor
$\unicode[STIX]{x1D713}^{\pm }:\unicode[STIX]{x1D70B}^{\operatorname{loc}}(U^{\pm })\rightarrow U_{(1)}^{\pm }$
) the homomorphism corresponding to the torsor
![]() $P$
(respectively
$P$
(respectively
![]() $i_{\pm }^{\ast }P$
), this amounts to saying that the diagram homomorphism
$i_{\pm }^{\ast }P$
), this amounts to saying that the diagram homomorphism

commutes. Therefore,
![]() $\text{Im}(\unicode[STIX]{x1D719})\supset U_{(1)}^{\pm }$
, whence
$\text{Im}(\unicode[STIX]{x1D719})\supset U_{(1)}^{\pm }$
, whence
![]() $\text{Im}(\unicode[STIX]{x1D719})=\langle U_{(1)}^{\pm }\rangle =\unicode[STIX]{x1D6F4}_{(1)}$
, where, for the last equality, see Remark 3.7(4). Therefore,
$\text{Im}(\unicode[STIX]{x1D719})=\langle U_{(1)}^{\pm }\rangle =\unicode[STIX]{x1D6F4}_{(1)}$
, where, for the last equality, see Remark 3.7(4). Therefore,
![]() $P$
is a saturated
$P$
is a saturated
![]() $\unicode[STIX]{x1D6F4}_{(1)}$
-torsor over
$\unicode[STIX]{x1D6F4}_{(1)}$
-torsor over
![]() $U^{+}\times U^{-}\simeq \mathbb{A}_{k}^{N}$
for some
$U^{+}\times U^{-}\simeq \mathbb{A}_{k}^{N}$
for some
![]() $N>1$
. Then by applying Theorem 4.17, we can conclude that there exists a closed immersion
$N>1$
. Then by applying Theorem 4.17, we can conclude that there exists a closed immersion
![]() $\unicode[STIX]{x1D704}:\mathbb{A}_{k}^{1}{\hookrightarrow}U^{+}\times U^{-}$
so that
$\unicode[STIX]{x1D704}:\mathbb{A}_{k}^{1}{\hookrightarrow}U^{+}\times U^{-}$
so that
![]() $\unicode[STIX]{x1D704}^{\ast }P\rightarrow \mathbb{A}_{k}^{1}$
is saturated as well. Therefore, the
$\unicode[STIX]{x1D704}^{\ast }P\rightarrow \mathbb{A}_{k}^{1}$
is saturated as well. Therefore, the
![]() $k$
-morphism
$k$
-morphism
![]() $f\circ \unicode[STIX]{x1D704}:\mathbb{A}_{k}^{1}\rightarrow \unicode[STIX]{x1D6F4}$
gives a desired one. This completes the proof.◻
$f\circ \unicode[STIX]{x1D704}:\mathbb{A}_{k}^{1}\rightarrow \unicode[STIX]{x1D6F4}$
gives a desired one. This completes the proof.◻
Acknowledgements
The author thanks Professor Takao Yamazaki for his encouragement, fruitful discussions and helpful advice. The author thanks Professor Takuya Yamauchi for conversations about this problem and for the encouragement. The author thanks Doctor Fuetaro Yobuko for answering several questions. The author thanks Professor Seidai Yasuda for pointing out a mistake to him at the conference ‘Regulators in Niseko 2017’. The author thanks the reviewer for giving him detailed and valuable comments on the first version of the present paper.