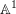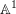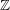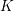Introduction
According to Kontsevich’s proposal [Reference KontsevichKon09], Fukaya categories of Stein manifolds can be described as global sections of a constructible cosheaf of dg categories on a possibly singular Lagrangian spine onto which the manifold retracts. Various approaches to this proposal have been developed, see for example [Reference NadlerNad14, Reference BocklandtBoc11, Reference Sibilla, Treumann and ZaslowSTZ14, Reference Haiden, Katzarkov and KontsevichHKK14, Reference NadlerNad15, Reference Dyckerhoff and KapranovDK13, Reference NadlerNad13].
The specific case we focus on in this work is the following. Let
![]() $S$
be a compact connected Riemann surface, possibly with boundary, and let
$S$
be a compact connected Riemann surface, possibly with boundary, and let
![]() $M\subset S$
be a finite non-empty subset of marked points, so that the complement
$M\subset S$
be a finite non-empty subset of marked points, so that the complement
![]() $S\setminus M$
is a Stein manifold. Any spanning graph
$S\setminus M$
is a Stein manifold. Any spanning graph
![]() $\unicode[STIX]{x1D6E4}$
in
$\unicode[STIX]{x1D6E4}$
in
![]() $S\setminus M$
provides a Lagrangian spine. In [Reference Dyckerhoff and KapranovDK13], the language of cyclic 2-Segal spaces was used to realize Kontsevich’s proposal in this situation. For every commutative ring
$S\setminus M$
provides a Lagrangian spine. In [Reference Dyckerhoff and KapranovDK13], the language of cyclic 2-Segal spaces was used to realize Kontsevich’s proposal in this situation. For every commutative ring
![]() $k$
, this theory produces a constructible cosheaf of
$k$
, this theory produces a constructible cosheaf of
![]() $k$
-linear differential
$k$
-linear differential
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded categories on any spanning graph
$\mathbb{Z}/2\mathbb{Z}$
-graded categories on any spanning graph
![]() $\unicode[STIX]{x1D6E4}$
, shows that the dg category
$\unicode[STIX]{x1D6E4}$
, shows that the dg category
 $F(S,M;k)$
of global sections is independent of the chosen graph, and implies a coherent action of the mapping class group of the surface on
$F(S,M;k)$
of global sections is independent of the chosen graph, and implies a coherent action of the mapping class group of the surface on
 $F(S,M;k)$
. It is expected that the resulting dg category is Morita equivalent to a variant of the wrapped Fukaya category of the surface. We refer to
$F(S,M;k)$
. It is expected that the resulting dg category is Morita equivalent to a variant of the wrapped Fukaya category of the surface. We refer to
 $F(S,M;k)$
as the
$F(S,M;k)$
as the
![]() $k$
-linear topological Fukaya category of the surface
$k$
-linear topological Fukaya category of the surface
![]() $(S,M)$
. If the surface
$(S,M)$
. If the surface
![]() $S\setminus M$
is equipped with a framing then a paracyclic version of the above construction can be used to define a differential
$S\setminus M$
is equipped with a framing then a paracyclic version of the above construction can be used to define a differential
![]() $\mathbb{Z}$
-graded lift of
$\mathbb{Z}$
-graded lift of
 $F(S,M;k)$
(cf. [Reference LurieLur14, Reference Dyckerhoff and KapranovDK15]). The first part of this paper implements these constructions in the framework of
$F(S,M;k)$
(cf. [Reference LurieLur14, Reference Dyckerhoff and KapranovDK15]). The first part of this paper implements these constructions in the framework of
![]() $\infty$
-categories, which provides the flexibility necessary for our purposes.
$\infty$
-categories, which provides the flexibility necessary for our purposes.
A functor
![]() $H$
defined on the category of small
$H$
defined on the category of small
![]() $k$
-linear dg categories with values in a stable
$k$
-linear dg categories with values in a stable
![]() $\infty$
-category
$\infty$
-category
![]() $C$
is called:
$C$
is called:
-
(1) localizing if
 $H$
inverts Morita equivalences and sends exact sequences of dg categories to exact sequences in
$H$
inverts Morita equivalences and sends exact sequences of dg categories to exact sequences in
 $C$
;
$C$
; -
(2)
 $\mathbb{A}^{1}$
-homotopy invariant if, for every dg category
$\mathbb{A}^{1}$
-homotopy invariant if, for every dg category
 $A$
, the functor
$A$
, the functor
 $H$
maps
$H$
maps
 $A\rightarrow A[t]$
to an equivalence in
$A\rightarrow A[t]$
to an equivalence in
 $C$
.
$C$
.
Examples of localizing
![]() $\mathbb{A}^{1}$
-homotopy invariants are provided by periodic cyclic homology over a field of characteristic
$\mathbb{A}^{1}$
-homotopy invariants are provided by periodic cyclic homology over a field of characteristic
![]() $0$
, homotopy
$0$
, homotopy
![]() $K$
-theory,
$K$
-theory,
![]() $K$
-theory with finite coefficients, and topological
$K$
-theory with finite coefficients, and topological
![]() $K$
-theory over
$K$
-theory over
![]() $\mathbb{C}$
(cf. [Reference KellerKel98, Reference Tabuada and Van den BerghTVdB15, Reference BlancBla16]). The main result of this work is the following theorem.
$\mathbb{C}$
(cf. [Reference KellerKel98, Reference Tabuada and Van den BerghTVdB15, Reference BlancBla16]). The main result of this work is the following theorem.
Theorem 0.1. Let
![]() $H$
be a localizing
$H$
be a localizing
![]() $\mathbb{A}^{1}$
-homotopy invariant with values in a stable
$\mathbb{A}^{1}$
-homotopy invariant with values in a stable
![]() $\infty$
-category
$\infty$
-category
![]() $C$
, and let
$C$
, and let
![]() $(S,M)$
be a stable marked surface where
$(S,M)$
be a stable marked surface where
![]() $S\setminus M$
is equipped with a framing. Define
$S\setminus M$
is equipped with a framing. Define
 $E=H(k)$
to be the object of
$E=H(k)$
to be the object of
![]() $C$
obtained by applying
$C$
obtained by applying
![]() $H$
to the dg category with one object and endomorphism ring
$H$
to the dg category with one object and endomorphism ring
![]() $k$
. Then there is an equivalence
$k$
. Then there is an equivalence
 $$\begin{eqnarray}H(F(S,M;k))\simeq E(S,M)[-1],\end{eqnarray}$$
$$\begin{eqnarray}H(F(S,M;k))\simeq E(S,M)[-1],\end{eqnarray}$$
where the right-hand side denotes the relative homology of the pair
![]() $(S,M)$
with coefficients in
$(S,M)$
with coefficients in
![]() $E[-1]$
.
$E[-1]$
.
As a concrete example, we have the following corollary.
Corollary 0.2. Let
![]() $k$
be a field of characteristic
$k$
be a field of characteristic
![]() $0$
. We have the formulas
$0$
. We have the formulas
 $$\begin{eqnarray}\displaystyle \operatorname{HP}_{0}(F(S,M;k)) & \cong & \displaystyle H_{1}(S,M;k),\nonumber\\ \displaystyle \operatorname{HP}_{1}(F(S,M;k)) & \cong & \displaystyle H_{2}(S,M;k)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{HP}_{0}(F(S,M;k)) & \cong & \displaystyle H_{1}(S,M;k),\nonumber\\ \displaystyle \operatorname{HP}_{1}(F(S,M;k)) & \cong & \displaystyle H_{2}(S,M;k)\nonumber\end{eqnarray}$$
for periodic cyclic homology over
![]() $k$
.
$k$
.
Our proof strategy is as follows: we prove a Mayer–Vietoris type statement for localizing
![]() $\mathbb{A}^{1}$
-homotopy invariants of topological Fukaya categories. Roughly speaking, using the local nature of the topological Fukaya category, the result allows us to reduce the calculation of such an invariant to the case when the surface is a boundary-marked disk. The arguments we use are inspired by methods in Thomason–Trobaugh’s algebraic
$\mathbb{A}^{1}$
-homotopy invariants of topological Fukaya categories. Roughly speaking, using the local nature of the topological Fukaya category, the result allows us to reduce the calculation of such an invariant to the case when the surface is a boundary-marked disk. The arguments we use are inspired by methods in Thomason–Trobaugh’s algebraic
![]() $K$
-theory of schemes and may be of independent interest: we establish localization sequences for topological Fukaya categories which are analogous to the ones for derived categories of schemes appearing in [Reference Thomason and TrobaughTT90]. Similar localization techniques for Fukaya categories play a role in [Reference Haiden, Katzarkov and KontsevichHKK14], where the Grothendieck group is computed, and the forthcoming work [Reference Pascaleff and SibillaPS16]. The Mayer–Vietoris theorem expresses
$K$
-theory of schemes and may be of independent interest: we establish localization sequences for topological Fukaya categories which are analogous to the ones for derived categories of schemes appearing in [Reference Thomason and TrobaughTT90]. Similar localization techniques for Fukaya categories play a role in [Reference Haiden, Katzarkov and KontsevichHKK14], where the Grothendieck group is computed, and the forthcoming work [Reference Pascaleff and SibillaPS16]. The Mayer–Vietoris theorem expresses
 $H(F(S,M))$
as a state sum of a coparacyclic
$H(F(S,M))$
as a state sum of a coparacyclic
![]() $1$
-Segal object in a stable
$1$
-Segal object in a stable
![]() $\infty$
-category. We conclude by proving a delooping statement for such objects, which allows us to compute the state sum explicitly. Finally, I would like to point out that Jacob Lurie has communicated to me a version of Theorem 0.1 that does not assume
$\infty$
-category. We conclude by proving a delooping statement for such objects, which allows us to compute the state sum explicitly. Finally, I would like to point out that Jacob Lurie has communicated to me a version of Theorem 0.1 that does not assume
![]() $\mathbb{A}^{1}$
-homotopy invariance but assumes that the surface has no internal marked points.
$\mathbb{A}^{1}$
-homotopy invariance but assumes that the surface has no internal marked points.
We will use the language of
![]() $\infty$
-categories and refer to [Reference LurieLur09] as a general reference.
$\infty$
-categories and refer to [Reference LurieLur09] as a general reference.
1 Cyclic and paracyclic 2-Segal objects
We begin with a translation of some constructions in [Reference Dyckerhoff and KapranovDK13] into the context of
![]() $\infty$
-categories.
$\infty$
-categories.
1.1 The Segal conditions
We start by formulating the Segal conditions (cf. [Reference SegalSeg74, Reference RezkRez01, Reference Dyckerhoff and KapranovDK12]).
Remark 1.1. Let
![]() $\boldsymbol{\unicode[STIX]{x1D6E5}}$
denote the category of finite non-empty linearly ordered sets. This category contains the simplex category
$\boldsymbol{\unicode[STIX]{x1D6E5}}$
denote the category of finite non-empty linearly ordered sets. This category contains the simplex category
![]() $\unicode[STIX]{x1D6E5}$
as the full subcategory spanned by the collection of standard ordinals
$\unicode[STIX]{x1D6E5}$
as the full subcategory spanned by the collection of standard ordinals
 $\{[n],n\geqslant 0\}$
. For every object of
$\{[n],n\geqslant 0\}$
. For every object of
![]() $\boldsymbol{\unicode[STIX]{x1D6E5}}$
, there exists a unique isomorphism with an object of
$\boldsymbol{\unicode[STIX]{x1D6E5}}$
, there exists a unique isomorphism with an object of
![]() $\unicode[STIX]{x1D6E5}$
so that we can identify any diagram in
$\unicode[STIX]{x1D6E5}$
so that we can identify any diagram in
![]() $\boldsymbol{\unicode[STIX]{x1D6E5}}$
with a unique diagram in
$\boldsymbol{\unicode[STIX]{x1D6E5}}$
with a unique diagram in
![]() $\unicode[STIX]{x1D6E5}$
. With this in mind, we may use arbitrary finite non-empty linearly ordered sets to describe diagrams in
$\unicode[STIX]{x1D6E5}$
. With this in mind, we may use arbitrary finite non-empty linearly ordered sets to describe diagrams in
![]() $\unicode[STIX]{x1D6E5}$
without ambiguity.
$\unicode[STIX]{x1D6E5}$
without ambiguity.
Definition 1.2. Let
![]() $C$
be an
$C$
be an
![]() $\infty$
-category, and let
$\infty$
-category, and let
 $X^{\bullet }:\operatorname{N}(\unicode[STIX]{x1D6E5})\rightarrow C$
be a cosimplicial object in
$X^{\bullet }:\operatorname{N}(\unicode[STIX]{x1D6E5})\rightarrow C$
be a cosimplicial object in
![]() $C$
.
$C$
.
-
(1) The cosimplicial object
 $X^{\bullet }$
is called 1-Segal if, for every
$X^{\bullet }$
is called 1-Segal if, for every
 $0<k<n$
, the resulting diagramin
$0<k<n$
, the resulting diagramin
 $C$
is a pushout diagram.
$C$
is a pushout diagram.
-
(2) Let
 $P$
be a planar convex polygon with vertices labelled cyclically by the set
$P$
be a planar convex polygon with vertices labelled cyclically by the set
 $\{0,1,\ldots ,n\}$
,
$\{0,1,\ldots ,n\}$
,
 $n\geqslant 3$
. Consider a diagonal of
$n\geqslant 3$
. Consider a diagonal of
 $P$
with vertices labelled by
$P$
with vertices labelled by
 $i<j$
so that we obtain a subdivision of
$i<j$
so that we obtain a subdivision of
 $P$
into two subpolygons with vertex sets
$P$
into two subpolygons with vertex sets
 $\{0,1,\ldots ,i,j,\ldots ,n\}$
and
$\{0,1,\ldots ,i,j,\ldots ,n\}$
and
 $\{i,i+1,\ldots ,j\}$
, respectively. The resulting triple of numbers
$\{i,i+1,\ldots ,j\}$
, respectively. The resulting triple of numbers
 $0\leqslant i<j\leqslant n$
is called a polygonal subdivision.
$0\leqslant i<j\leqslant n$
is called a polygonal subdivision.
-
(i) The cosimplicial object
 $X^{\bullet }$
is called 2-Segal if, for every polygonal subdivision
$X^{\bullet }$
is called 2-Segal if, for every polygonal subdivision
 $0\leqslant i<j\leqslant n$
, the resulting diagram(1.3)in
$0\leqslant i<j\leqslant n$
, the resulting diagram(1.3)in
 $C$
is a pushout diagram.
$C$
is a pushout diagram.
-
(ii) We say
 $X^{\bullet }$
is a unital
$X^{\bullet }$
is a unital
 $2$
-Segal object if, in addition to (i), for every
$2$
-Segal object if, in addition to (i), for every
 $0\leqslant k<n$
, the diagram(1.4)in
$0\leqslant k<n$
, the diagram(1.4)in
 $C$
is a pushout diagram.
$C$
is a pushout diagram.
Proposition 1.5. Every
![]() $1$
-Segal cosimplicial object
$1$
-Segal cosimplicial object
 $X^{\bullet }:\operatorname{N}(\unicode[STIX]{x1D6E5})\rightarrow C$
is unital
$X^{\bullet }:\operatorname{N}(\unicode[STIX]{x1D6E5})\rightarrow C$
is unital
![]() $2$
-Segal.
$2$
-Segal.
Proof. Given a polygonal subdivision
 $0\leqslant i\leqslant j\leqslant n$
, we augment the corresponding square (1.3) to the following diagram.
$0\leqslant i\leqslant j\leqslant n$
, we augment the corresponding square (1.3) to the following diagram.

The
![]() $1$
-Segal condition on
$1$
-Segal condition on
![]() $X^{\bullet }$
implies that the left-hand square and outer square are pushouts. Hence, by [Reference LurieLur09, 4.4.2.1], the right-hand square is a pushout. Similarly, to obtain unitality, we augment the square (1.4) to the following diagram.
$X^{\bullet }$
implies that the left-hand square and outer square are pushouts. Hence, by [Reference LurieLur09, 4.4.2.1], the right-hand square is a pushout. Similarly, to obtain unitality, we augment the square (1.4) to the following diagram.

The 1-Segal condition on
![]() $X^{\bullet }$
implies that the top and outer squares are pushouts so that, again by [Reference LurieLur09, 4.4.2.1], the bottom square is a pushout.◻
$X^{\bullet }$
implies that the top and outer squares are pushouts so that, again by [Reference LurieLur09, 4.4.2.1], the bottom square is a pushout.◻
1.2 Cyclically ordered sets and ribbon graphs
Let
![]() $S$
be a compact oriented surface, possibly with boundary
$S$
be a compact oriented surface, possibly with boundary
![]() $\unicode[STIX]{x2202}S$
, together with a chosen finite subset
$\unicode[STIX]{x2202}S$
, together with a chosen finite subset
![]() $M\subset S$
of marked points. We call
$M\subset S$
of marked points. We call
![]() $(S,M)$
stable if:
$(S,M)$
stable if:
-
(1) every connected component of
 $S$
has at least one marked point;
$S$
has at least one marked point; -
(2) every connected component of
 $\unicode[STIX]{x2202}S$
has at least one marked point;
$\unicode[STIX]{x2202}S$
has at least one marked point; -
(3) every connected component of
 $S$
that is homeomorphic to the
$S$
that is homeomorphic to the
 $2$
-sphere has at least two marked points.
$2$
-sphere has at least two marked points.
In this section, we develop a categorified state sum formalism based on a version of the well-known combinatorial description of stable oriented marked surfaces
![]() $(S,M)$
in terms of ribbon graphs.
$(S,M)$
in terms of ribbon graphs.
1.2.1 Cyclically ordered sets
In § 1.1, we enlarged the simplex category
![]() $\unicode[STIX]{x1D6E5}$
to the equivalent category
$\unicode[STIX]{x1D6E5}$
to the equivalent category
![]() $\boldsymbol{\unicode[STIX]{x1D6E5}}$
of finite non-empty linearly ordered sets. In analogy, we introduce the category of non-empty finite cyclically ordered sets
$\boldsymbol{\unicode[STIX]{x1D6E5}}$
of finite non-empty linearly ordered sets. In analogy, we introduce the category of non-empty finite cyclically ordered sets
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
following [Reference Dyckerhoff and KapranovDK15], which plays the same role for the cyclic category
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
following [Reference Dyckerhoff and KapranovDK15], which plays the same role for the cyclic category
![]() $\unicode[STIX]{x1D6EC}$
.
$\unicode[STIX]{x1D6EC}$
.
Let
![]() $J$
be a finite non-empty set. We define a cyclic order on
$J$
be a finite non-empty set. We define a cyclic order on
![]() $J$
to be a transitive action of the group
$J$
to be a transitive action of the group
![]() $\mathbb{Z}$
. Note that any such action induces a simply transitive action of the group
$\mathbb{Z}$
. Note that any such action induces a simply transitive action of the group
![]() $\mathbb{Z}/N\mathbb{Z}$
on
$\mathbb{Z}/N\mathbb{Z}$
on
![]() $J$
where
$J$
where
![]() $N$
denotes the cardinality of the set
$N$
denotes the cardinality of the set
![]() $J$
.
$J$
.
Example 1.6. Let
![]() $I$
be a finite non-empty linearly ordered set. We obtain a cyclic order on
$I$
be a finite non-empty linearly ordered set. We obtain a cyclic order on
![]() $I$
as follows: let
$I$
as follows: let
 $i_{0}<i_{1}<\cdots <i_{n}$
denote the elements of
$i_{0}<i_{1}<\cdots <i_{n}$
denote the elements of
![]() $I$
. We set, for
$I$
. We set, for
 $0\leqslant k<n$
,
$0\leqslant k<n$
,
 $i_{k}+1=i_{k+1}$
, and
$i_{k}+1=i_{k+1}$
, and
 $i_{n}+1=i_{0}$
. We call the resulting cyclic order on
$i_{n}+1=i_{0}$
. We call the resulting cyclic order on
![]() $I$
the cyclic closure of the given linear order. We denote the cyclic closure of the standard ordinal
$I$
the cyclic closure of the given linear order. We denote the cyclic closure of the standard ordinal
![]() $[n]$
by
$[n]$
by
![]() $\langle n\rangle$
.
$\langle n\rangle$
.
Example 1.7. More generally, let
 $f:J\rightarrow J^{\prime }$
be a map of finite non-empty sets. Assume that
$f:J\rightarrow J^{\prime }$
be a map of finite non-empty sets. Assume that
![]() $J^{\prime }$
carries a cyclic order and that every fiber of
$J^{\prime }$
carries a cyclic order and that every fiber of
![]() $f$
is equipped with a linear order. We define the lexicographic cyclic order on
$f$
is equipped with a linear order. We define the lexicographic cyclic order on
![]() $J$
as follows: let
$J$
as follows: let
![]() $j\in J$
. If
$j\in J$
. If
![]() $j$
is not maximal in its fiber then we define
$j$
is not maximal in its fiber then we define
![]() $j+1$
to be the successor to
$j+1$
to be the successor to
![]() $j$
in its fiber. If
$j$
in its fiber. If
![]() $j$
is maximal in its fiber, then we define
$j$
is maximal in its fiber, then we define
![]() $j+1$
to be the minimal element of the successor fiber. (The cyclic order on
$j+1$
to be the minimal element of the successor fiber. (The cyclic order on
![]() $J^{\prime }$
induces a cyclic order on the fibers of
$J^{\prime }$
induces a cyclic order on the fibers of
![]() $f$
where we simply skip empty fibers.)
$f$
where we simply skip empty fibers.)
A morphism
![]() $J\rightarrow J^{\prime }$
of cyclically ordered sets consists of
$J\rightarrow J^{\prime }$
of cyclically ordered sets consists of
-
(1) a map
 $f:J\rightarrow J^{\prime }$
of underlying sets,
$f:J\rightarrow J^{\prime }$
of underlying sets, -
(2) the choice of a linear order on every fiber of
 $J^{\prime }$
$J^{\prime }$
such that the cyclic order on
![]() $J$
is the lexicographic order from Example 1.7. We denote the resulting category of cyclically ordered sets by
$J$
is the lexicographic order from Example 1.7. We denote the resulting category of cyclically ordered sets by
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
. Given a cyclically ordered set
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
. Given a cyclically ordered set
![]() $J$
, we define the set of interstices
$J$
, we define the set of interstices
 $$\begin{eqnarray}J^{\vee }=\operatorname{Hom}_{\boldsymbol{\unicode[STIX]{x1D6EC}}}(J,\langle 0\rangle ),\end{eqnarray}$$
$$\begin{eqnarray}J^{\vee }=\operatorname{Hom}_{\boldsymbol{\unicode[STIX]{x1D6EC}}}(J,\langle 0\rangle ),\end{eqnarray}$$
which, by definition, is the set of linear orders on
![]() $J$
whose cyclic closure agrees with the given cyclic order on
$J$
whose cyclic closure agrees with the given cyclic order on
![]() $J$
. If the set
$J$
. If the set
![]() $J$
has cardinality
$J$
has cardinality
![]() $n+1$
, then we may identify
$n+1$
, then we may identify
![]() $J^{\vee }$
with the set of isomorphisms
$J^{\vee }$
with the set of isomorphisms
 $J\rightarrow \langle n\rangle$
in
$J\rightarrow \langle n\rangle$
in
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
. The
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
. The
![]() $\mathbb{Z}$
-action on
$\mathbb{Z}$
-action on
![]() $\langle n\rangle$
induces a
$\langle n\rangle$
induces a
![]() $\mathbb{Z}$
-action on
$\mathbb{Z}$
-action on
![]() $J^{\vee }$
that defines a cyclic order.
$J^{\vee }$
that defines a cyclic order.
Proposition 1.8. The association
 $J\mapsto J^{\vee }$
extends to an equivalence of categories
$J\mapsto J^{\vee }$
extends to an equivalence of categories
 $\boldsymbol{\unicode[STIX]{x1D6EC}}^{\operatorname{op}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}$
.
$\boldsymbol{\unicode[STIX]{x1D6EC}}^{\operatorname{op}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}$
.
Proof. Given a morphism
 $f:J\rightarrow J^{\prime }$
in
$f:J\rightarrow J^{\prime }$
in
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
, we have to define a dual
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
, we have to define a dual
 $f^{\vee }:(J^{\prime })^{\vee }\rightarrow J^{\vee }$
. The datum of
$f^{\vee }:(J^{\prime })^{\vee }\rightarrow J^{\vee }$
. The datum of
![]() $f$
includes a choice of linear order on each fiber of
$f$
includes a choice of linear order on each fiber of
![]() $f$
. Given a linear order on
$f$
. Given a linear order on
![]() $J^{\prime }$
, we can form the lexicographic linear order on
$J^{\prime }$
, we can form the lexicographic linear order on
![]() $J$
by a linear analog of the construction in Example 1.7. This defines the map
$J$
by a linear analog of the construction in Example 1.7. This defines the map
![]() $f^{\vee }$
on underlying sets. We further have to define a linear order on the fibers of
$f^{\vee }$
on underlying sets. We further have to define a linear order on the fibers of
![]() $f^{\vee }$
. Given linear orders
$f^{\vee }$
. Given linear orders
 $h:J^{\prime }\cong [n]$
and
$h:J^{\prime }\cong [n]$
and
 $h^{\prime }:J^{\prime }\cong [n]$
such that
$h^{\prime }:J^{\prime }\cong [n]$
such that
 $f^{\vee }(h)=f^{\vee }(h^{\prime })$
, we fix any
$f^{\vee }(h)=f^{\vee }(h^{\prime })$
, we fix any
![]() $j\in J$
and declare
$j\in J$
and declare
![]() $h\leqslant h^{\prime }$
if
$h\leqslant h^{\prime }$
if
 $h(j)\leqslant h^{\prime }(j)$
. This defines a linear order on each fiber of
$h(j)\leqslant h^{\prime }(j)$
. This defines a linear order on each fiber of
![]() $f^{\vee }$
which does in fact not depend on the chosen element
$f^{\vee }$
which does in fact not depend on the chosen element
![]() $j\in J$
. To verify that
$j\in J$
. To verify that
 $J\mapsto J^{\vee }$
is an equivalence, we observe that the double dual is naturally equivalent to the identity functor: an element
$J\mapsto J^{\vee }$
is an equivalence, we observe that the double dual is naturally equivalent to the identity functor: an element
![]() $j\in J$
determines a linear order on
$j\in J$
determines a linear order on
![]() $J^{\vee }$
by declaring, for
$J^{\vee }$
by declaring, for
 $h:J\cong [n]$
and
$h:J\cong [n]$
and
 $h^{\prime }:J\cong [n]$
,
$h^{\prime }:J\cong [n]$
,
![]() $h\leqslant h^{\prime }$
if
$h\leqslant h^{\prime }$
if
 $h(j)\leqslant h^{\prime }(j)$
. We leave to the reader the verification that this association defines an isomorphism
$h(j)\leqslant h^{\prime }(j)$
. We leave to the reader the verification that this association defines an isomorphism
 $$\begin{eqnarray}J\rightarrow (J^{\vee })^{\vee }\end{eqnarray}$$
$$\begin{eqnarray}J\rightarrow (J^{\vee })^{\vee }\end{eqnarray}$$
in
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
that extends to a natural isomorphism between the identity functor and the double dual.◻
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
that extends to a natural isomorphism between the identity functor and the double dual.◻
We refer to the equivalence
 $\boldsymbol{\unicode[STIX]{x1D6EC}}^{\operatorname{op}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}$
as interstice duality. The following lemma will be important for the interplay between cyclic
$\boldsymbol{\unicode[STIX]{x1D6EC}}^{\operatorname{op}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}$
as interstice duality. The following lemma will be important for the interplay between cyclic
![]() $2$
-Segal objects and ribbon graphs.
$2$
-Segal objects and ribbon graphs.
Lemma 1.9. Let
![]() $I,J$
be finite sets with elements
$I,J$
be finite sets with elements
![]() $i\in I$
,
$i\in I$
,
![]() $j\in J$
, and consider the pullback square
$j\in J$
, and consider the pullback square

where the maps
![]() $p$
and
$p$
and
![]() $q$
are determined by
$q$
are determined by
 $p^{-1}(i)=\{i\}$
and
$p^{-1}(i)=\{i\}$
and
 $q^{-1}(j)=\{j\}$
. Assume that
$q^{-1}(j)=\{j\}$
. Assume that
![]() $K$
is non-empty and that the sets
$K$
is non-empty and that the sets
![]() $I$
and
$I$
and
![]() $J$
are equipped with cyclic orders. Then the following hold.
$J$
are equipped with cyclic orders. Then the following hold.
-
(1) The above diagram lifts uniquely to a diagram in
 $\boldsymbol{\unicode[STIX]{x1D6EC}}$
such that the induced cyclic orders in
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
such that the induced cyclic orders in
 $I$
and
$I$
and
 $J$
are the given ones.
$J$
are the given ones. -
(2) The resulting square in
 $\boldsymbol{\unicode[STIX]{x1D6EC}}$
is a pullback square.
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
is a pullback square.
Proof. Follows by direct inspection.◻
Example 1.11. Consider the diagram of linearly ordered sets

corresponding to a polygonal subdivision
 $0\leqslant i<j\leqslant n$
of a planar convex polygon as in § 1.1. Passing to cyclic closures we obtain a diagram in
$0\leqslant i<j\leqslant n$
of a planar convex polygon as in § 1.1. Passing to cyclic closures we obtain a diagram in
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
. By applying interstice duality we obtain a diagram in
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
. By applying interstice duality we obtain a diagram in
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
of the form (1.10) which is hence a pullback diagram. We deduce that the original diagram (1.12) is a pushout diagram in
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
of the form (1.10) which is hence a pullback diagram. We deduce that the original diagram (1.12) is a pushout diagram in
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
. Further, the same argument implies that, for every
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
. Further, the same argument implies that, for every
 $0\leqslant k<n$
, the diagram
$0\leqslant k<n$
, the diagram

is a pushout diagram in
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
.
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
.
Definition 1.14. Let
![]() $C$
be an
$C$
be an
![]() $\infty$
-category. A cocyclic object
$\infty$
-category. A cocyclic object
 $X:\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}})\rightarrow C$
is called (unital)
$X:\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}})\rightarrow C$
is called (unital)
![]() $2$
-Segal (respectively
$2$
-Segal (respectively
![]() $1$
-Segal) if the underlying cosimplicial object is (unital)
$1$
-Segal) if the underlying cosimplicial object is (unital)
![]() $2$
-Segal (respectively
$2$
-Segal (respectively
![]() $1$
-Segal).
$1$
-Segal).
Remark 1.15. Note, that the diagram

is a pushout diagram in
![]() $\boldsymbol{\unicode[STIX]{x1D6E5}}$
and the
$\boldsymbol{\unicode[STIX]{x1D6E5}}$
and the
![]() $1$
-Segal condition requires a cosimplicial object
$1$
-Segal condition requires a cosimplicial object
 $X:\unicode[STIX]{x1D6E5}\rightarrow C$
to preserve this pushout. In light of this observation, the
$X:\unicode[STIX]{x1D6E5}\rightarrow C$
to preserve this pushout. In light of this observation, the
![]() $2$
-Segal condition becomes very natural for cocyclic objects: while the cyclic closure of (1.16) is not a pushout square in
$2$
-Segal condition becomes very natural for cocyclic objects: while the cyclic closure of (1.16) is not a pushout square in
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
, the squares (1.12) and (1.13) are pushout squares. The
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
, the squares (1.12) and (1.13) are pushout squares. The
![]() $2$
-Segal condition requires that these pushouts are preserved.
$2$
-Segal condition requires that these pushouts are preserved.
1.2.2 Ribbon graphs
A graph
![]() $\unicode[STIX]{x1D6E4}$
is a pair of finite sets
$\unicode[STIX]{x1D6E4}$
is a pair of finite sets
![]() $(H,V)$
equipped with an involution
$(H,V)$
equipped with an involution
 $\unicode[STIX]{x1D70F}:H\rightarrow H$
and a map
$\unicode[STIX]{x1D70F}:H\rightarrow H$
and a map
 $s:H\rightarrow V$
. The elements of the set
$s:H\rightarrow V$
. The elements of the set
![]() $H$
are called half-edges. We call a half-edge external if it is fixed by
$H$
are called half-edges. We call a half-edge external if it is fixed by
![]() $\unicode[STIX]{x1D70F}$
, and internal otherwise. A pair of
$\unicode[STIX]{x1D70F}$
, and internal otherwise. A pair of
![]() $\unicode[STIX]{x1D70F}$
-conjugate internal half-edges is called an edge and we denote the set of edges by
$\unicode[STIX]{x1D70F}$
-conjugate internal half-edges is called an edge and we denote the set of edges by
![]() $E$
. The elements of
$E$
. The elements of
![]() $V$
are called vertices. Given a vertex
$V$
are called vertices. Given a vertex
![]() $v$
, the half-edges in the set
$v$
, the half-edges in the set
 $H(v)=s^{-1}(v)$
are said to be incident to
$H(v)=s^{-1}(v)$
are said to be incident to
![]() $v$
. A graph with one vertex and
$v$
. A graph with one vertex and
![]() $n$
half-edges equipped with the trivial involution is called an
$n$
half-edges equipped with the trivial involution is called an
![]() $n$
-corolla.
$n$
-corolla.
A ribbon graph is a graph
![]() $\unicode[STIX]{x1D6E4}$
where, for every vertex
$\unicode[STIX]{x1D6E4}$
where, for every vertex
![]() $v$
of
$v$
of
![]() $\unicode[STIX]{x1D6E4}$
, the set
$\unicode[STIX]{x1D6E4}$
, the set
![]() $H(v)$
of half-edges incident to
$H(v)$
of half-edges incident to
![]() $v$
is equipped with a cyclic order. We give an interpretation of this datum in terms of the category of cyclically ordered sets: let
$v$
is equipped with a cyclic order. We give an interpretation of this datum in terms of the category of cyclically ordered sets: let
![]() $\unicode[STIX]{x1D6E4}$
be a graph. We define the incidence category
$\unicode[STIX]{x1D6E4}$
be a graph. We define the incidence category
![]() $I(\unicode[STIX]{x1D6E4})$
to have set of objects given by
$I(\unicode[STIX]{x1D6E4})$
to have set of objects given by
![]() $V\cup E$
and, for every internal half-edge
$V\cup E$
and, for every internal half-edge
![]() $h$
, a unique morphism from the vertex
$h$
, a unique morphism from the vertex
![]() $s(h)$
to the edge
$s(h)$
to the edge
 $\{h,\unicode[STIX]{x1D70F}(h)\}$
. We define a functor
$\{h,\unicode[STIX]{x1D70F}(h)\}$
. We define a functor
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}:I(\unicode[STIX]{x1D6E4})\longrightarrow {\mathcal{S}}et\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}:I(\unicode[STIX]{x1D6E4})\longrightarrow {\mathcal{S}}et\end{eqnarray}$$
that, on objects, associates to a vertex
![]() $v$
the set
$v$
the set
![]() $H(v)$
and to an edge
$H(v)$
and to an edge
![]() $e$
the set of half-edges underlying
$e$
the set of half-edges underlying
![]() $e$
. To a morphism
$e$
. To a morphism
![]() $v\rightarrow e$
, given by a half-edge
$v\rightarrow e$
, given by a half-edge
 $h\in H(v)$
with
$h\in H(v)$
with
![]() $h\in e$
, we associate the map
$h\in e$
, we associate the map
 $\unicode[STIX]{x1D70B}:H(v)\rightarrow e$
which is determined by
$\unicode[STIX]{x1D70B}:H(v)\rightarrow e$
which is determined by
 $\unicode[STIX]{x1D70B}^{-1}(h)=\{h\}$
so that
$\unicode[STIX]{x1D70B}^{-1}(h)=\{h\}$
so that
![]() $\unicode[STIX]{x1D70B}$
maps
$\unicode[STIX]{x1D70B}$
maps
 $H(v)\setminus h$
to
$H(v)\setminus h$
to
![]() $\unicode[STIX]{x1D70F}(h)$
. We call the functor
$\unicode[STIX]{x1D70F}(h)$
. We call the functor
![]() $\unicode[STIX]{x1D6FE}$
the incidence diagram of the graph
$\unicode[STIX]{x1D6FE}$
the incidence diagram of the graph
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Proposition 1.17. Let
![]() $\unicode[STIX]{x1D6E4}$
be a graph. A ribbon structure on
$\unicode[STIX]{x1D6E4}$
be a graph. A ribbon structure on
![]() $\unicode[STIX]{x1D6E4}$
is equivalent to a lift
$\unicode[STIX]{x1D6E4}$
is equivalent to a lift

of the incidence diagram of
![]() $\unicode[STIX]{x1D6E4}$
where
$\unicode[STIX]{x1D6E4}$
where
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
denotes the category of cyclically ordered sets.
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
denotes the category of cyclically ordered sets.
The advantage of the interpretation of a ribbon structure given in Proposition 1.17 is that it facilitates the passage to interstices: given a ribbon graph
![]() $\unicode[STIX]{x1D6E4}$
with corresponding incidence diagram
$\unicode[STIX]{x1D6E4}$
with corresponding incidence diagram
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}:I(\unicode[STIX]{x1D6E4})\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}:I(\unicode[STIX]{x1D6E4})\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}},\end{eqnarray}$$
we introduce the coincidence diagram
 $$\begin{eqnarray}\unicode[STIX]{x1D6FF}:I(\unicode[STIX]{x1D6E4})^{\operatorname{op}}\longrightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FF}:I(\unicode[STIX]{x1D6E4})^{\operatorname{op}}\longrightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}\end{eqnarray}$$
obtained by postcomposing
![]() $\unicode[STIX]{x1D6FE}^{\operatorname{op}}$
with the interstice duality functor
$\unicode[STIX]{x1D6FE}^{\operatorname{op}}$
with the interstice duality functor
 $\boldsymbol{\unicode[STIX]{x1D6EC}}^{\operatorname{op}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}$
.
$\boldsymbol{\unicode[STIX]{x1D6EC}}^{\operatorname{op}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}$
.
A morphism
 $(f,\unicode[STIX]{x1D702}):\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
of ribbon graphs consists of:
$(f,\unicode[STIX]{x1D702}):\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
of ribbon graphs consists of:
-
(1) a functor
 $f:I(\unicode[STIX]{x1D6E4})\rightarrow I(\unicode[STIX]{x1D6E4}^{\prime })$
of incidence categories;
$f:I(\unicode[STIX]{x1D6E4})\rightarrow I(\unicode[STIX]{x1D6E4}^{\prime })$
of incidence categories; -
(2) a natural transformation
 $\unicode[STIX]{x1D702}:f^{\ast }\unicode[STIX]{x1D6FE}^{\prime }\rightarrow \unicode[STIX]{x1D6FE}$
of incidence diagrams.
$\unicode[STIX]{x1D702}:f^{\ast }\unicode[STIX]{x1D6FE}^{\prime }\rightarrow \unicode[STIX]{x1D6FE}$
of incidence diagrams.
We denote the resulting category of ribbon graphs by
![]() ${\mathcal{R}}ib$
.
${\mathcal{R}}ib$
.
Example 1.18. Let
![]() $\unicode[STIX]{x1D6E4}$
be a graph and let
$\unicode[STIX]{x1D6E4}$
be a graph and let
![]() $e$
be an edge incident to two distinct vertices
$e$
be an edge incident to two distinct vertices
![]() $v$
and
$v$
and
![]() $w$
. We define a new graph
$w$
. We define a new graph
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
obtained from
$\unicode[STIX]{x1D6E4}^{\prime }$
obtained from
![]() $\unicode[STIX]{x1D6E4}$
by contracting
$\unicode[STIX]{x1D6E4}$
by contracting
![]() $e$
as follows: the set of half-edges
$e$
as follows: the set of half-edges
![]() $H^{\prime }$
is given by
$H^{\prime }$
is given by
![]() $H\setminus e$
and the set of vertices
$H\setminus e$
and the set of vertices
![]() $V^{\prime }$
is obtained from
$V^{\prime }$
is obtained from
![]() $V$
by identifying
$V$
by identifying
![]() $v$
and
$v$
and
![]() $w$
. The involution
$w$
. The involution
![]() $\unicode[STIX]{x1D70F}$
on
$\unicode[STIX]{x1D70F}$
on
![]() $H$
restricts to an involution
$H$
restricts to an involution
![]() $\unicode[STIX]{x1D70F}^{\prime }$
on
$\unicode[STIX]{x1D70F}^{\prime }$
on
![]() $H^{\prime }$
. We define
$H^{\prime }$
. We define
 $s:H^{\prime }\rightarrow V^{\prime }$
as the composite of the restriction of
$s:H^{\prime }\rightarrow V^{\prime }$
as the composite of the restriction of
 $s:H\rightarrow V$
to
$s:H\rightarrow V$
to
![]() $H^{\prime }$
and the quotient map
$H^{\prime }$
and the quotient map
 $V\rightarrow V^{\prime }$
.
$V\rightarrow V^{\prime }$
.
We obtain a natural functor
 $f:I(\unicode[STIX]{x1D6E4})\rightarrow I(\unicode[STIX]{x1D6E4}^{\prime })$
of incidence categories which collapses the objects
$f:I(\unicode[STIX]{x1D6E4})\rightarrow I(\unicode[STIX]{x1D6E4}^{\prime })$
of incidence categories which collapses the objects
![]() $v$
,
$v$
,
![]() $w$
, and
$w$
, and
![]() $e$
to
$e$
to
![]() $\overline{v}$
. Denoting by
$\overline{v}$
. Denoting by
![]() $\unicode[STIX]{x1D6FE}$
and
$\unicode[STIX]{x1D6FE}$
and
![]() $\unicode[STIX]{x1D6FE}^{\prime }$
the set-valued incidence diagrams, we construct a natural transformation
$\unicode[STIX]{x1D6FE}^{\prime }$
the set-valued incidence diagrams, we construct a natural transformation
 $\unicode[STIX]{x1D702}:f^{\ast }\unicode[STIX]{x1D6FE}^{\prime }\rightarrow \unicode[STIX]{x1D6FE}$
as follows. On objects of
$\unicode[STIX]{x1D702}:f^{\ast }\unicode[STIX]{x1D6FE}^{\prime }\rightarrow \unicode[STIX]{x1D6FE}$
as follows. On objects of
![]() $I(\unicode[STIX]{x1D6E4})$
different from
$I(\unicode[STIX]{x1D6E4})$
different from
![]() $v$
,
$v$
,
![]() $w$
, and
$w$
, and
![]() $e$
, we define
$e$
, we define
![]() $\unicode[STIX]{x1D702}$
to be the identity map. To obtain the values of
$\unicode[STIX]{x1D702}$
to be the identity map. To obtain the values of
![]() $\unicode[STIX]{x1D702}$
at
$\unicode[STIX]{x1D702}$
at
![]() $v$
,
$v$
,
![]() $w$
, and
$w$
, and
![]() $e$
, note that we have a natural commutative diagram
$e$
, note that we have a natural commutative diagram

as in Lemma 1.9. The maps in the diagram determine the values of
![]() $\unicode[STIX]{x1D702}$
as indicated.
$\unicode[STIX]{x1D702}$
as indicated.
Finally, assume that
![]() $\unicode[STIX]{x1D6E4}$
carries a ribbon structure. Then Lemma 1.9(1) implies that
$\unicode[STIX]{x1D6E4}$
carries a ribbon structure. Then Lemma 1.9(1) implies that
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
carries a unique ribbon structure such that the natural transformation
$\unicode[STIX]{x1D6E4}^{\prime }$
carries a unique ribbon structure such that the natural transformation
![]() $\unicode[STIX]{x1D702}$
lifts to
$\unicode[STIX]{x1D702}$
lifts to
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
-valued incidence diagrams.
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
-valued incidence diagrams.
A morphism of ribbon graphs
![]() $\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
as constructed in Example 1.18 is called an edge contraction. Note that the category
$\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
as constructed in Example 1.18 is called an edge contraction. Note that the category
![]() ${\mathcal{R}}ib$
contains morphisms that cannot be obtained as compositions of edge contractions: for example, it contains a copy of the cyclic category
${\mathcal{R}}ib$
contains morphisms that cannot be obtained as compositions of edge contractions: for example, it contains a copy of the cyclic category
![]() $\unicode[STIX]{x1D6EC}$
, given by the full subcategory spanned by the corollas. The following proposition indicates the relevance of Lemma 1.9(2).
$\unicode[STIX]{x1D6EC}$
, given by the full subcategory spanned by the corollas. The following proposition indicates the relevance of Lemma 1.9(2).
Proposition 1.19. Let
![]() $\unicode[STIX]{x1D6E4}$
be a ribbon graph and let
$\unicode[STIX]{x1D6E4}$
be a ribbon graph and let
 $(f,\unicode[STIX]{x1D702}):\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
be an edge contraction. Then the natural transformation
$(f,\unicode[STIX]{x1D702}):\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
be an edge contraction. Then the natural transformation
 $$\begin{eqnarray}\unicode[STIX]{x1D702}:f^{\ast }\unicode[STIX]{x1D6FE}^{\prime }\longrightarrow \unicode[STIX]{x1D6FE}\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D702}:f^{\ast }\unicode[STIX]{x1D6FE}^{\prime }\longrightarrow \unicode[STIX]{x1D6FE}\end{eqnarray}$$
exhibits
![]() $\unicode[STIX]{x1D6FE}^{\prime }$
as a right Kan extension of
$\unicode[STIX]{x1D6FE}^{\prime }$
as a right Kan extension of
![]() $\unicode[STIX]{x1D6FE}$
along
$\unicode[STIX]{x1D6FE}$
along
![]() $f$
.
$f$
.
Proof. By the pointwise formula for right Kan extensions, it suffices to verify that, for every object
 $y\in I(\unicode[STIX]{x1D6E4}^{\prime })$
, the natural transformation
$y\in I(\unicode[STIX]{x1D6E4}^{\prime })$
, the natural transformation
![]() $\unicode[STIX]{x1D702}$
exhibits
$\unicode[STIX]{x1D702}$
exhibits
![]() $\unicode[STIX]{x1D6FE}^{\prime }(y)$
as the limit of the diagram
$\unicode[STIX]{x1D6FE}^{\prime }(y)$
as the limit of the diagram
 $$\begin{eqnarray}y/f\longrightarrow \unicode[STIX]{x1D6EC},\quad (x,y\rightarrow f(x))\mapsto \unicode[STIX]{x1D6FE}(x).\end{eqnarray}$$
$$\begin{eqnarray}y/f\longrightarrow \unicode[STIX]{x1D6EC},\quad (x,y\rightarrow f(x))\mapsto \unicode[STIX]{x1D6FE}(x).\end{eqnarray}$$
Unravelling the definitions, this is a trivial condition unless
![]() $y$
is the object corresponding to the vertex
$y$
is the object corresponding to the vertex
![]() $\overline{v}$
under the contracted edge. For
$\overline{v}$
under the contracted edge. For
![]() $y=\overline{v}$
the condition reduces to Lemma 1.9(2).◻
$y=\overline{v}$
the condition reduces to Lemma 1.9(2).◻
1.2.3 State sums on ribbon graphs
We introduce a category
![]() ${\mathcal{R}}ib^{\ast }$
with objects given by pairs
${\mathcal{R}}ib^{\ast }$
with objects given by pairs
![]() $(\unicode[STIX]{x1D6E4},x)$
where
$(\unicode[STIX]{x1D6E4},x)$
where
![]() $\unicode[STIX]{x1D6E4}$
is a ribbon graph and
$\unicode[STIX]{x1D6E4}$
is a ribbon graph and
![]() $x$
is an object of the incidence category
$x$
is an object of the incidence category
![]() $I(\unicode[STIX]{x1D6E4})$
. A morphism
$I(\unicode[STIX]{x1D6E4})$
. A morphism
 $(\unicode[STIX]{x1D6E4},x)\rightarrow (\unicode[STIX]{x1D6E4}^{\prime },y)$
consists of a morphism
$(\unicode[STIX]{x1D6E4},x)\rightarrow (\unicode[STIX]{x1D6E4}^{\prime },y)$
consists of a morphism
 $(f,\unicode[STIX]{x1D702}):\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
of ribbon graphs together with a morphism
$(f,\unicode[STIX]{x1D702}):\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
of ribbon graphs together with a morphism
 $y\rightarrow f(x)$
in
$y\rightarrow f(x)$
in
![]() $I(\unicode[STIX]{x1D6E4}^{\prime })$
. The category
$I(\unicode[STIX]{x1D6E4}^{\prime })$
. The category
![]() ${\mathcal{R}}ib^{\ast }$
comes equipped with a forgetful functor
${\mathcal{R}}ib^{\ast }$
comes equipped with a forgetful functor
 $\unicode[STIX]{x1D70B}:{\mathcal{R}}ib^{\ast }\rightarrow {\mathcal{R}}ib$
and an evaluation functor
$\unicode[STIX]{x1D70B}:{\mathcal{R}}ib^{\ast }\rightarrow {\mathcal{R}}ib$
and an evaluation functor
 $$\begin{eqnarray}\operatorname{ev}:{\mathcal{R}}ib^{\ast }\longrightarrow \boldsymbol{\unicode[STIX]{x1D6EC}},\quad (\unicode[STIX]{x1D6E4},x)\mapsto \unicode[STIX]{x1D6FF}(x),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{ev}:{\mathcal{R}}ib^{\ast }\longrightarrow \boldsymbol{\unicode[STIX]{x1D6EC}},\quad (\unicode[STIX]{x1D6E4},x)\mapsto \unicode[STIX]{x1D6FF}(x),\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FF}$
denotes the coincidence diagram of
$\unicode[STIX]{x1D6FF}$
denotes the coincidence diagram of
![]() $\unicode[STIX]{x1D6E4}$
. Let
$\unicode[STIX]{x1D6E4}$
. Let
![]() $C$
be an
$C$
be an
![]() $\infty$
-category with colimits, and let
$\infty$
-category with colimits, and let
 $X:\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}})\rightarrow C$
be a cocyclic object in
$X:\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}})\rightarrow C$
be a cocyclic object in
![]() $C$
. The functor
$C$
. The functor
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{X}=\operatorname{N}(\unicode[STIX]{x1D70B})_{!}(X\circ \operatorname{N}(\operatorname{ev})):\operatorname{N}({\mathcal{R}}ib)\longrightarrow C\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{X}=\operatorname{N}(\unicode[STIX]{x1D70B})_{!}(X\circ \operatorname{N}(\operatorname{ev})):\operatorname{N}({\mathcal{R}}ib)\longrightarrow C\end{eqnarray}$$
is called the state sum functor of
![]() $X$
. Here,
$X$
. Here,
![]() $\operatorname{N}(\unicode[STIX]{x1D70B})_{!}$
denotes the
$\operatorname{N}(\unicode[STIX]{x1D70B})_{!}$
denotes the
![]() $\infty$
-categorical left Kan extension defined in [Reference LurieLur09, 4.3.3.2]. For a ribbon graph
$\infty$
-categorical left Kan extension defined in [Reference LurieLur09, 4.3.3.2]. For a ribbon graph
![]() $\unicode[STIX]{x1D6E4}$
, the object
$\unicode[STIX]{x1D6E4}$
, the object
 $X(\unicode[STIX]{x1D6E4}):=\unicode[STIX]{x1D70C}_{X}(\unicode[STIX]{x1D6E4})$
is called the state sum of
$X(\unicode[STIX]{x1D6E4}):=\unicode[STIX]{x1D70C}_{X}(\unicode[STIX]{x1D6E4})$
is called the state sum of
![]() $X$
on
$X$
on
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Proposition 1.20. The state sum of
![]() $X$
on
$X$
on
![]() $\unicode[STIX]{x1D6E4}$
admits the formula
$\unicode[STIX]{x1D6E4}$
admits the formula
 $$\begin{eqnarray}X(\unicode[STIX]{x1D6E4})\simeq \operatorname{colim}X\circ \operatorname{N}(\unicode[STIX]{x1D6FF}),\end{eqnarray}$$
$$\begin{eqnarray}X(\unicode[STIX]{x1D6E4})\simeq \operatorname{colim}X\circ \operatorname{N}(\unicode[STIX]{x1D6FF}),\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6FF}:I(\unicode[STIX]{x1D6E4})^{\operatorname{op}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}$
denotes the coincidence diagram of
$\unicode[STIX]{x1D6FF}:I(\unicode[STIX]{x1D6E4})^{\operatorname{op}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}$
denotes the coincidence diagram of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Proof. By the pointwise formula for left Kan extensions, we have
 $$\begin{eqnarray}X(\unicode[STIX]{x1D6E4})=\operatorname{colim}X\circ \operatorname{N}(\operatorname{ev})_{|\operatorname{N}(\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D6E4})}.\end{eqnarray}$$
$$\begin{eqnarray}X(\unicode[STIX]{x1D6E4})=\operatorname{colim}X\circ \operatorname{N}(\operatorname{ev})_{|\operatorname{N}(\unicode[STIX]{x1D70B}/\unicode[STIX]{x1D6E4})}.\end{eqnarray}$$
The nerve of the functor
 $$\begin{eqnarray}I(\unicode[STIX]{x1D6E4})^{\operatorname{op}}\longrightarrow \unicode[STIX]{x1D70B}/\unicode[STIX]{x1D6E4},\quad x\mapsto ((\unicode[STIX]{x1D6E4},x),\unicode[STIX]{x1D6E4}\overset{\operatorname{id}}{\rightarrow }\unicode[STIX]{x1D6E4})\end{eqnarray}$$
$$\begin{eqnarray}I(\unicode[STIX]{x1D6E4})^{\operatorname{op}}\longrightarrow \unicode[STIX]{x1D70B}/\unicode[STIX]{x1D6E4},\quad x\mapsto ((\unicode[STIX]{x1D6E4},x),\unicode[STIX]{x1D6E4}\overset{\operatorname{id}}{\rightarrow }\unicode[STIX]{x1D6E4})\end{eqnarray}$$
is cofinal, which implies the claim.◻
Example 1.21. The universal example of a cocyclic object with values in an
![]() $\infty$
-category with colimits is the Yoneda embedding
$\infty$
-category with colimits is the Yoneda embedding
 $j:\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}})\rightarrow P(\boldsymbol{\unicode[STIX]{x1D6EC}})$
where
$j:\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}})\rightarrow P(\boldsymbol{\unicode[STIX]{x1D6EC}})$
where
![]() $P(\boldsymbol{\unicode[STIX]{x1D6EC}})$
denotes the
$P(\boldsymbol{\unicode[STIX]{x1D6EC}})$
denotes the
![]() $\infty$
-category
$\infty$
-category
 $\operatorname{Fun}(\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}})^{\operatorname{op}},S)$
of cyclic spaces. We obtain a functor
$\operatorname{Fun}(\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}})^{\operatorname{op}},S)$
of cyclic spaces. We obtain a functor
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{j}:\operatorname{N}({\mathcal{R}}ib)\longrightarrow P(\boldsymbol{\unicode[STIX]{x1D6EC}})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{j}:\operatorname{N}({\mathcal{R}}ib)\longrightarrow P(\boldsymbol{\unicode[STIX]{x1D6EC}})\end{eqnarray}$$
that realizes a ribbon graph as a cyclic space. This functor is the universal state sum: given any cocyclic object
 $X:\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}})\rightarrow C$
where
$X:\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}})\rightarrow C$
where
![]() $C$
has colimits, we have
$C$
has colimits, we have
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{X}\simeq j_{!}X\circ \unicode[STIX]{x1D70C}_{j},\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{X}\simeq j_{!}X\circ \unicode[STIX]{x1D70C}_{j},\end{eqnarray}$$
where we use Proposition 1.20 and the fact [Reference LurieLur09, 5.1.5.5] that
![]() $j_{!}X$
commutes with colimits. We will use the notation
$j_{!}X$
commutes with colimits. We will use the notation
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6E4}):=\unicode[STIX]{x1D70C}_{j}(\unicode[STIX]{x1D6E4})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}(\unicode[STIX]{x1D6E4}):=\unicode[STIX]{x1D70C}_{j}(\unicode[STIX]{x1D6E4})\end{eqnarray}$$
for the state sum of
![]() $j$
on
$j$
on
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
The following proposition explains the relevance of the
![]() $2$
-Segal condition for state sums.
$2$
-Segal condition for state sums.
Proposition 1.23. Let
![]() $C$
be an
$C$
be an
![]() $\infty$
-category with colimits and let
$\infty$
-category with colimits and let
 $X:\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}})\rightarrow C$
be a cocyclic object. Then
$X:\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}})\rightarrow C$
be a cocyclic object. Then
![]() $X$
is unital
$X$
is unital
![]() $2$
-Segal if and only if the state sum functor
$2$
-Segal if and only if the state sum functor
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{X}:\operatorname{N}({\mathcal{R}}ib)\longrightarrow C,\quad \unicode[STIX]{x1D6E4}\mapsto X(\unicode[STIX]{x1D6E4})\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{X}:\operatorname{N}({\mathcal{R}}ib)\longrightarrow C,\quad \unicode[STIX]{x1D6E4}\mapsto X(\unicode[STIX]{x1D6E4})\end{eqnarray}$$
maps edge contractions in
![]() ${\mathcal{R}}ib$
to equivalences in
${\mathcal{R}}ib$
to equivalences in
![]() $C$
.
$C$
.
Proof. Let
 $(f,\unicode[STIX]{x1D702}):\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
be a morphism of ribbon graphs. The associated morphism
$(f,\unicode[STIX]{x1D702}):\unicode[STIX]{x1D6E4}\rightarrow \unicode[STIX]{x1D6E4}^{\prime }$
be a morphism of ribbon graphs. The associated morphism
 $\unicode[STIX]{x1D70C}_{X}(f,\unicode[STIX]{x1D702}):X(\unicode[STIX]{x1D6E4})\rightarrow X(\unicode[STIX]{x1D6E4}^{\prime })$
is given by the composite
$\unicode[STIX]{x1D70C}_{X}(f,\unicode[STIX]{x1D702}):X(\unicode[STIX]{x1D6E4})\rightarrow X(\unicode[STIX]{x1D6E4}^{\prime })$
is given by the composite
 $$\begin{eqnarray}\operatorname{colim}(X\circ \unicode[STIX]{x1D6FF})\overset{X\circ \unicode[STIX]{x1D702}^{\vee }}{\longrightarrow }\operatorname{colim}(X\circ \unicode[STIX]{x1D6FF}^{\prime }\circ f^{\operatorname{op}})\longrightarrow \operatorname{colim}(X\circ \unicode[STIX]{x1D6FF}^{\prime }).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{colim}(X\circ \unicode[STIX]{x1D6FF})\overset{X\circ \unicode[STIX]{x1D702}^{\vee }}{\longrightarrow }\operatorname{colim}(X\circ \unicode[STIX]{x1D6FF}^{\prime }\circ f^{\operatorname{op}})\longrightarrow \operatorname{colim}(X\circ \unicode[STIX]{x1D6FF}^{\prime }).\end{eqnarray}$$
We claim that, if
![]() $(f,\unicode[STIX]{x1D702})$
is an edge contraction, then
$(f,\unicode[STIX]{x1D702})$
is an edge contraction, then
![]() $X\circ \unicode[STIX]{x1D702}^{\vee }$
exhibits
$X\circ \unicode[STIX]{x1D702}^{\vee }$
exhibits
![]() $X\circ \unicode[STIX]{x1D6FF}^{\prime }$
as a left Kan extension of
$X\circ \unicode[STIX]{x1D6FF}^{\prime }$
as a left Kan extension of
![]() $X\circ \unicode[STIX]{x1D6FF}$
. This implies the result since a colimit is given by the left Kan extension to the final category and left Kan extension functors are functorial in the sense
$X\circ \unicode[STIX]{x1D6FF}$
. This implies the result since a colimit is given by the left Kan extension to the final category and left Kan extension functors are functorial in the sense
 $f_{!}\circ g_{!}\simeq (f\circ g)_{!}$
. The claim follows immediately from the argument of Proposition 1.19, Lemma 1.9, and Remark 1.15.◻
$f_{!}\circ g_{!}\simeq (f\circ g)_{!}$
. The claim follows immediately from the argument of Proposition 1.19, Lemma 1.9, and Remark 1.15.◻
Remark 1.24. In the situation of Proposition 1.23, we may restrict ourselves to the subcategory
 ${\mathcal{R}}ib^{\prime }\subset {\mathcal{R}}ib$
generated by edge contractions and isomorphisms. Then by the statement of the theorem, we obtain a functor
${\mathcal{R}}ib^{\prime }\subset {\mathcal{R}}ib$
generated by edge contractions and isomorphisms. Then by the statement of the theorem, we obtain a functor
 $$\begin{eqnarray}\operatorname{N}({\mathcal{R}}ib^{\prime })_{\simeq }\rightarrow C,\quad \unicode[STIX]{x1D6E4}\mapsto X(\unicode[STIX]{x1D6E4}),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{N}({\mathcal{R}}ib^{\prime })_{\simeq }\rightarrow C,\quad \unicode[STIX]{x1D6E4}\mapsto X(\unicode[STIX]{x1D6E4}),\end{eqnarray}$$
where
 $\operatorname{N}({\mathcal{R}}ib^{\prime })_{\simeq }=\operatorname{Sing}|\operatorname{N}({\mathcal{R}}ib^{\prime })|$
denotes the
$\operatorname{N}({\mathcal{R}}ib^{\prime })_{\simeq }=\operatorname{Sing}|\operatorname{N}({\mathcal{R}}ib^{\prime })|$
denotes the
![]() $\infty$
-groupoid completion of the
$\infty$
-groupoid completion of the
![]() $\infty$
-category
$\infty$
-category
 $\operatorname{N}({\mathcal{R}}ib^{\prime })$
. The automorphism group in
$\operatorname{N}({\mathcal{R}}ib^{\prime })$
. The automorphism group in
 $\operatorname{N}({\mathcal{R}}ib^{\prime })_{\simeq }$
of a ribbon graph
$\operatorname{N}({\mathcal{R}}ib^{\prime })_{\simeq }$
of a ribbon graph
![]() $\unicode[STIX]{x1D6E4}$
that represents a stable oriented marked surface
$\unicode[STIX]{x1D6E4}$
that represents a stable oriented marked surface
![]() $(S,M)$
can be identified with the mapping class group
$(S,M)$
can be identified with the mapping class group
 $\operatorname{Mod}(S,M)$
. The above functor implies the existence of an
$\operatorname{Mod}(S,M)$
. The above functor implies the existence of an
![]() $\infty$
-categorical action of
$\infty$
-categorical action of
 $\operatorname{Mod}(S,M)$
on
$\operatorname{Mod}(S,M)$
on
![]() $X(\unicode[STIX]{x1D6E4})$
, which is a main result of [Reference Dyckerhoff and KapranovDK13].
$X(\unicode[STIX]{x1D6E4})$
, which is a main result of [Reference Dyckerhoff and KapranovDK13].
1.3 Paracyclically ordered sets and framed graphs
Let
![]() $(S,M)$
be a stable oriented marked surface. We may interpret the orientation as a reduction of the structure group of the tangent bundle of
$(S,M)$
be a stable oriented marked surface. We may interpret the orientation as a reduction of the structure group of the tangent bundle of
![]() $S\setminus M$
along
$S\setminus M$
along
 $\operatorname{GL}_{2}^{+}(\mathbb{R})\subset \operatorname{GL}_{2}(\mathbb{R})$
. We define a framing of
$\operatorname{GL}_{2}^{+}(\mathbb{R})\subset \operatorname{GL}_{2}(\mathbb{R})$
. We define a framing of
![]() $(S,M)$
as a further lift of the structure group along the universal cover
$(S,M)$
as a further lift of the structure group along the universal cover
 $$\begin{eqnarray}\widetilde{\operatorname{GL}_{2}^{+}(\mathbb{R})}\longrightarrow \operatorname{GL}_{2}^{+}(\mathbb{R}).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{\operatorname{GL}_{2}^{+}(\mathbb{R})}\longrightarrow \operatorname{GL}_{2}^{+}(\mathbb{R}).\end{eqnarray}$$
Up to contractible choice, this datum is equivalent to a trivialization of the tangent bundle of
![]() $S\setminus M$
. In this section, we describe a state sum formalism based on a combinatorial model for stable framed marked surfaces as developed in [Reference Dyckerhoff and KapranovDK15]. This amounts to a variation of the constructions in the previous section, obtained by replacing the cyclic category by the paracyclic category.
$S\setminus M$
. In this section, we describe a state sum formalism based on a combinatorial model for stable framed marked surfaces as developed in [Reference Dyckerhoff and KapranovDK15]. This amounts to a variation of the constructions in the previous section, obtained by replacing the cyclic category by the paracyclic category.
1.3.1 Paracyclically ordered sets
Let
![]() $J$
be a finite non-empty set. We define a paracyclic order on
$J$
be a finite non-empty set. We define a paracyclic order on
![]() $J$
to be a cyclic order on
$J$
to be a cyclic order on
![]() $J$
together with the choice of a
$J$
together with the choice of a
![]() $\mathbb{Z}$
-torsor
$\mathbb{Z}$
-torsor
![]() $\widetilde{J}$
and a
$\widetilde{J}$
and a
![]() $\mathbb{Z}$
-equivariant map
$\mathbb{Z}$
-equivariant map
![]() $\widetilde{J}\rightarrow J$
. A morphism of paracyclically ordered sets
$\widetilde{J}\rightarrow J$
. A morphism of paracyclically ordered sets
 $(J,\widetilde{J})\rightarrow (J^{\prime },\widetilde{J^{\prime }})$
consists of a commutative diagram of sets
$(J,\widetilde{J})\rightarrow (J^{\prime },\widetilde{J^{\prime }})$
consists of a commutative diagram of sets

such that
![]() $\widetilde{f}$
is monotone with respect to the
$\widetilde{f}$
is monotone with respect to the
![]() $\mathbb{Z}$
-torsor linear orders. The lift
$\mathbb{Z}$
-torsor linear orders. The lift
![]() $\widetilde{f}$
equips
$\widetilde{f}$
equips
![]() $f$
naturally with the structure of a morphism of cyclically ordered sets so that we obtain a forgetful functor
$f$
naturally with the structure of a morphism of cyclically ordered sets so that we obtain a forgetful functor
 $$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }\longrightarrow \boldsymbol{\unicode[STIX]{x1D6EC}},\end{eqnarray}$$
$$\begin{eqnarray}\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }\longrightarrow \boldsymbol{\unicode[STIX]{x1D6EC}},\end{eqnarray}$$
where
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }$
denotes the category of paracyclically ordered sets. As for cyclically ordered sets, there is a skeleton
$\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }$
denotes the category of paracyclically ordered sets. As for cyclically ordered sets, there is a skeleton
 $\unicode[STIX]{x1D6EC}_{\infty }\subset \boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }$
consisting of standard paracyclically ordered sets
$\unicode[STIX]{x1D6EC}_{\infty }\subset \boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }$
consisting of standard paracyclically ordered sets
 $(\langle n\rangle ,\widetilde{\langle n\rangle })$
where we define
$(\langle n\rangle ,\widetilde{\langle n\rangle })$
where we define
 $\widetilde{\langle n\rangle }=\mathbb{Z}$
and
$\widetilde{\langle n\rangle }=\mathbb{Z}$
and
 $\widetilde{\langle n\rangle }\rightarrow \langle n\rangle$
is given by the natural quotient map.
$\widetilde{\langle n\rangle }\rightarrow \langle n\rangle$
is given by the natural quotient map.
Given a paracyclically ordered set
![]() $(J,\widetilde{J})$
, then the cyclic order on the interstice dual
$(J,\widetilde{J})$
, then the cyclic order on the interstice dual
![]() $J^{\vee }$
lifts to a natural paracyclic order given by
$J^{\vee }$
lifts to a natural paracyclic order given by
 $$\begin{eqnarray}\widetilde{J^{\vee }}=\operatorname{Hom}_{\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }}((J,\widetilde{J}),(\langle 0\rangle ,\widetilde{\langle 0\rangle })).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{J^{\vee }}=\operatorname{Hom}_{\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }}((J,\widetilde{J}),(\langle 0\rangle ,\widetilde{\langle 0\rangle })).\end{eqnarray}$$
This construction extends the self duality of
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}$
to one for
$\boldsymbol{\unicode[STIX]{x1D6EC}}$
to one for
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }$
. All statements of § 1.2.1 hold mutatis mutandis for
$\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }$
. All statements of § 1.2.1 hold mutatis mutandis for
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }$
.
$\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }$
.
1.3.2 Framed graphs and state sums
We define a framed graph
![]() $\unicode[STIX]{x1D6E4}$
to be a graph
$\unicode[STIX]{x1D6E4}$
to be a graph
![]() $\unicode[STIX]{x1D6E4}$
equipped with a lift
$\unicode[STIX]{x1D6E4}$
equipped with a lift

of the incidence diagram of
![]() $\unicode[STIX]{x1D6E4}$
where
$\unicode[STIX]{x1D6E4}$
where
![]() $\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }$
denotes the category of paracyclically ordered sets. Framed graphs form a category
$\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }$
denotes the category of paracyclically ordered sets. Framed graphs form a category
![]() ${\mathcal{R}}ib_{\infty }$
which is defined in complete analogy with
${\mathcal{R}}ib_{\infty }$
which is defined in complete analogy with
![]() ${\mathcal{R}}ib$
.
${\mathcal{R}}ib$
.
Let
![]() $\unicode[STIX]{x1D6E4}$
be a framed graph with incidence diagram
$\unicode[STIX]{x1D6E4}$
be a framed graph with incidence diagram
 $$\begin{eqnarray}\unicode[STIX]{x1D6FE}:I(\unicode[STIX]{x1D6E4})\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FE}:I(\unicode[STIX]{x1D6E4})\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }.\end{eqnarray}$$
Let
 $e=\{h,\unicode[STIX]{x1D70F}(h)\}$
be an edge in
$e=\{h,\unicode[STIX]{x1D70F}(h)\}$
be an edge in
![]() $\unicode[STIX]{x1D6E4}$
incident to the vertices
$\unicode[STIX]{x1D6E4}$
incident to the vertices
 $v=s(h)$
and
$v=s(h)$
and
 $w=s(\unicode[STIX]{x1D70F}(h))$
, and let
$w=s(\unicode[STIX]{x1D70F}(h))$
, and let
![]() $h^{\prime }$
be a half-edge incident to
$h^{\prime }$
be a half-edge incident to
![]() $w$
. Let
$w$
. Let
![]() $\widetilde{h}$
be a lift of
$\widetilde{h}$
be a lift of
![]() $h$
to an element of the
$h$
to an element of the
![]() $\mathbb{Z}$
-torsor
$\mathbb{Z}$
-torsor
![]() $\widetilde{H(v)}$
that is part of the paracyclic structure on
$\widetilde{H(v)}$
that is part of the paracyclic structure on
![]() $H(v)$
. Then we may transport this lift along the edge
$H(v)$
. Then we may transport this lift along the edge
![]() $e$
to obtain a lift of
$e$
to obtain a lift of
![]() $h^{\prime }$
to an element
$h^{\prime }$
to an element
![]() $\widetilde{h^{\prime }}$
of
$\widetilde{h^{\prime }}$
of
![]() $\widetilde{H(w^{\prime })}$
as follows: there is a unique lift of
$\widetilde{H(w^{\prime })}$
as follows: there is a unique lift of
 $\widetilde{\unicode[STIX]{x1D70F}(h)}\in \widetilde{H(w^{\prime })}$
of
$\widetilde{\unicode[STIX]{x1D70F}(h)}\in \widetilde{H(w^{\prime })}$
of
![]() $\unicode[STIX]{x1D70F}(h)$
which maps to
$\unicode[STIX]{x1D70F}(h)$
which maps to
![]() $\widetilde{h}-1$
under
$\widetilde{h}-1$
under
![]() $\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D70F}(h))$
. We then set
$\unicode[STIX]{x1D6FE}(\unicode[STIX]{x1D70F}(h))$
. We then set
 $\widetilde{h^{\prime }}=\widetilde{\unicode[STIX]{x1D70F}(h)}+i$
where
$\widetilde{h^{\prime }}=\widetilde{\unicode[STIX]{x1D70F}(h)}+i$
where
![]() $i\geqslant 0$
is minimal such that
$i\geqslant 0$
is minimal such that
![]() $\widetilde{h^{\prime }}$
lifts
$\widetilde{h^{\prime }}$
lifts
![]() $h^{\prime }$
. Iterating this transport along a loop
$h^{\prime }$
. Iterating this transport along a loop
![]() $l$
returning to the half-edge
$l$
returning to the half-edge
![]() $h$
, we obtain another lift
$h$
, we obtain another lift
![]() $\overline{h}$
of
$\overline{h}$
of
![]() $h$
. The integer
$h$
. The integer
![]() $\overline{h}-\widetilde{h}$
only depends on
$\overline{h}-\widetilde{h}$
only depends on
![]() $l$
and we refer to it as the winding number of l.
$l$
and we refer to it as the winding number of l.
Remark 1.25. As explained in [Reference Dyckerhoff and KapranovDK15], framed graphs provide a combinatorial model for stable marked surfaces
![]() $(S,M)$
equipped with a trivialization of the tangent bundle of
$(S,M)$
equipped with a trivialization of the tangent bundle of
![]() $S\setminus M$
. The above combinatorial construction then coincides with the geometric concept of winding number computed with respect to the framing.
$S\setminus M$
. The above combinatorial construction then coincides with the geometric concept of winding number computed with respect to the framing.
Let
![]() $C$
be an
$C$
be an
![]() $\infty$
-category with colimits, and let
$\infty$
-category with colimits, and let
 $X^{\bullet }:\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty })\rightarrow C$
be a coparacyclic object in
$X^{\bullet }:\operatorname{N}(\boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty })\rightarrow C$
be a coparacyclic object in
![]() $C$
. Then, given a framed graph
$C$
. Then, given a framed graph
![]() $\unicode[STIX]{x1D6E4}$
, we have a state sum
$\unicode[STIX]{x1D6E4}$
, we have a state sum
 $$\begin{eqnarray}X(\unicode[STIX]{x1D6E4})=\operatorname{colim}X\circ \unicode[STIX]{x1D6FF},\end{eqnarray}$$
$$\begin{eqnarray}X(\unicode[STIX]{x1D6E4})=\operatorname{colim}X\circ \unicode[STIX]{x1D6FF},\end{eqnarray}$$
where
 $\unicode[STIX]{x1D6FF}:I(\unicode[STIX]{x1D6E4})^{\operatorname{op}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }$
denotes the coincidence diagram of
$\unicode[STIX]{x1D6FF}:I(\unicode[STIX]{x1D6E4})^{\operatorname{op}}\rightarrow \boldsymbol{\unicode[STIX]{x1D6EC}}_{\infty }$
denotes the coincidence diagram of
![]() $\unicode[STIX]{x1D6E4}$
. The various state sums naturally organize into a functor
$\unicode[STIX]{x1D6E4}$
. The various state sums naturally organize into a functor
 $$\begin{eqnarray}\operatorname{N}({\mathcal{R}}ib_{\infty })\longrightarrow C,\quad \unicode[STIX]{x1D6E4}\mapsto X(\unicode[STIX]{x1D6E4}).\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{N}({\mathcal{R}}ib_{\infty })\longrightarrow C,\quad \unicode[STIX]{x1D6E4}\mapsto X(\unicode[STIX]{x1D6E4}).\end{eqnarray}$$
Remark 1.26. As shown in [Reference Dyckerhoff and KapranovDK15], the state sum
![]() $X(\unicode[STIX]{x1D6E4})$
of a framed graph with values in a coparacyclic unital
$X(\unicode[STIX]{x1D6E4})$
of a framed graph with values in a coparacyclic unital
![]() $2$
-Segal object
$2$
-Segal object
![]() $X$
admits an action of the framed mapping class group of the surface.
$X$
admits an action of the framed mapping class group of the surface.
1.4 The universal loop space
We give a first example of a state sum that will play an important role later on. Consider the functor
 $$\begin{eqnarray}\unicode[STIX]{x1D6EC}\longrightarrow \operatorname{Grp},\quad \langle n\rangle \mapsto \unicode[STIX]{x1D70B}_{1}(D/\{0,1,\ldots ,n\}),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6EC}\longrightarrow \operatorname{Grp},\quad \langle n\rangle \mapsto \unicode[STIX]{x1D70B}_{1}(D/\{0,1,\ldots ,n\}),\end{eqnarray}$$
where
 $D/\{0,1,\ldots ,n\}$
denotes the quotient of the unit disk by
$D/\{0,1,\ldots ,n\}$
denotes the quotient of the unit disk by
![]() $n+1$
marked points on the boundary. Replacing the fundamental groups by their nerves, we obtain a functor
$n+1$
marked points on the boundary. Replacing the fundamental groups by their nerves, we obtain a functor
 $$\begin{eqnarray}L^{\bullet }:\operatorname{N}(\unicode[STIX]{x1D6EC})\longrightarrow S_{\ast },\end{eqnarray}$$
$$\begin{eqnarray}L^{\bullet }:\operatorname{N}(\unicode[STIX]{x1D6EC})\longrightarrow S_{\ast },\end{eqnarray}$$
where
![]() $S_{\ast }$
denotes the
$S_{\ast }$
denotes the
![]() $\infty$
-category of pointed spaces. The cosimplicial pointed space underlying
$\infty$
-category of pointed spaces. The cosimplicial pointed space underlying
![]() $L^{\bullet }$
is
$L^{\bullet }$
is
![]() $1$
-Segal and hence, by Proposition 1.5, unital
$1$
-Segal and hence, by Proposition 1.5, unital
![]() $2$
-Segal.
$2$
-Segal.
Remark 1.28. Note that the group
 $\unicode[STIX]{x1D70B}_{1}(D/\{0,1,\ldots ,n\})$
is a free group on
$\unicode[STIX]{x1D70B}_{1}(D/\{0,1,\ldots ,n\})$
is a free group on
![]() $n$
generators so that
$n$
generators so that
![]() $L^{n}$
is equivalent to a bouquet of
$L^{n}$
is equivalent to a bouquet of
![]() $n$
one-dimensional spheres. Given any pointed space
$n$
one-dimensional spheres. Given any pointed space
![]() $X$
, the cyclic pointed
$X$
, the cyclic pointed
![]() $1$
-Segal space
$1$
-Segal space
 $\operatorname{Map}(L^{\bullet },X)$
describes the loop space
$\operatorname{Map}(L^{\bullet },X)$
describes the loop space
![]() $\unicode[STIX]{x1D6FA}X$
together with its natural group structure. Similarly, the cocyclic pointed
$\unicode[STIX]{x1D6FA}X$
together with its natural group structure. Similarly, the cocyclic pointed
![]() $1$
-Segal space
$1$
-Segal space
![]() $L^{\bullet }\otimes X$
describes the suspension of
$L^{\bullet }\otimes X$
describes the suspension of
![]() $X$
together with its natural cogroup structure.
$X$
together with its natural cogroup structure.
Proposition 1.29. Let
![]() $(S,M)$
be a stable marked oriented surface represented by a ribbon graph
$(S,M)$
be a stable marked oriented surface represented by a ribbon graph
![]() $\unicode[STIX]{x1D6E4}$
. Then we have
$\unicode[STIX]{x1D6E4}$
. Then we have
 $$\begin{eqnarray}L(\unicode[STIX]{x1D6E4})\simeq S/M.\end{eqnarray}$$
$$\begin{eqnarray}L(\unicode[STIX]{x1D6E4})\simeq S/M.\end{eqnarray}$$
Proof. We can compute the state sum defining
![]() $L(\unicode[STIX]{x1D6E4})$
explicitly as a homotopy colimit in the category of pointed spaces. We may replace the diagram by a homotopy equivalent one which assigns to each
$L(\unicode[STIX]{x1D6E4})$
explicitly as a homotopy colimit in the category of pointed spaces. We may replace the diagram by a homotopy equivalent one which assigns to each
![]() $(n+1)$
-corolla of the graph
$(n+1)$
-corolla of the graph
![]() $\unicode[STIX]{x1D6E4}$
the space
$\unicode[STIX]{x1D6E4}$
the space
 $D/\{0,1,\ldots ,n\}$
. The homotopy colimit is then obtained by identifying the boundary cycles of the various spaces
$D/\{0,1,\ldots ,n\}$
. The homotopy colimit is then obtained by identifying the boundary cycles of the various spaces
 $D/\{0,1,\ldots ,n\}$
according to the incidence relations given by the edges of the ribbon graphs. It is apparent that the resulting space is equivalent to the quotient space
$D/\{0,1,\ldots ,n\}$
according to the incidence relations given by the edges of the ribbon graphs. It is apparent that the resulting space is equivalent to the quotient space
![]() $S/M$
.◻
$S/M$
.◻
Example 1.30. As an illustration of the gluing procedure described in the proof of Proposition 1.29, consider the ribbon graph with one vertex and two half-edges forming a loop at the vertex. This graph models a sphere
![]() $S^{2}$
with two marked points
$S^{2}$
with two marked points
![]() $M$
. The colimit in the proof describes the space
$M$
. The colimit in the proof describes the space
![]() $S^{2}/M$
as obtained from
$S^{2}/M$
as obtained from
 $D/\{0,1\}$
by identifying the two boundary circles given by the images of the two boundary arcs connecting the points
$D/\{0,1\}$
by identifying the two boundary circles given by the images of the two boundary arcs connecting the points
![]() $0$
and
$0$
and
![]() $1$
on
$1$
on
![]() $\unicode[STIX]{x2202}D$
.
$\unicode[STIX]{x2202}D$
.
For a slight elaboration on Proposition 1.29, let
![]() $C$
be a stable
$C$
be a stable
![]() $\infty$
-category with colimits and let
$\infty$
-category with colimits and let
![]() $E$
be an object of
$E$
be an object of
![]() $C$
. By [Reference LurieLur11, 1.4.2.21], the functor
$C$
. By [Reference LurieLur11, 1.4.2.21], the functor
 $$\begin{eqnarray}\operatorname{Sp}(C)=\operatorname{Fun}^{c}(S_{\ast }^{\operatorname{fin}},C)\rightarrow C,\quad f\mapsto f(S^{0})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Sp}(C)=\operatorname{Fun}^{c}(S_{\ast }^{\operatorname{fin}},C)\rightarrow C,\quad f\mapsto f(S^{0})\end{eqnarray}$$
from the
![]() $\infty$
-category of spectrum objects in
$\infty$
-category of spectrum objects in
![]() $C$
to
$C$
to
![]() $C$
is an equivalence. Therefore, the object
$C$
is an equivalence. Therefore, the object
![]() $E$
defines an essentially unique functor
$E$
defines an essentially unique functor
 $$\begin{eqnarray}E:S_{\ast }^{\operatorname{fin}}\rightarrow C,\end{eqnarray}$$
$$\begin{eqnarray}E:S_{\ast }^{\operatorname{fin}}\rightarrow C,\end{eqnarray}$$
which we still denote by
![]() $E$
.
$E$
.
Definition 1.32. Let
![]() $(X,Y)$
be a pair of finite spaces. We introduce the pointed quotient space
$(X,Y)$
be a pair of finite spaces. We introduce the pointed quotient space
![]() $X/Y$
as the pushout
$X/Y$
as the pushout

in
![]() $S$
. The object
$S$
. The object
 $E(X/Y)$
of
$E(X/Y)$
of
![]() $C$
is called the relative homology of the pair
$C$
is called the relative homology of the pair
![]() $(X,Y)$
with coefficients in
$(X,Y)$
with coefficients in
![]() $E$
. In the case when
$E$
. In the case when
![]() $C$
is the category of spectra, this terminology agrees with the customary one.
$C$
is the category of spectra, this terminology agrees with the customary one.
We introduce the cocyclic object
 $$\begin{eqnarray}L_{E}=E(L^{\bullet }):\operatorname{N}(\unicode[STIX]{x1D6EC})\longrightarrow C\end{eqnarray}$$
$$\begin{eqnarray}L_{E}=E(L^{\bullet }):\operatorname{N}(\unicode[STIX]{x1D6EC})\longrightarrow C\end{eqnarray}$$
obtained from (1.27) by postcomposing with
 $E:S_{\ast }^{\operatorname{fin}}\rightarrow C$
.
$E:S_{\ast }^{\operatorname{fin}}\rightarrow C$
.
Proposition 1.34. Let
![]() $(S,M)$
be a stable marked oriented surface represented by a ribbon graph
$(S,M)$
be a stable marked oriented surface represented by a ribbon graph
![]() $\unicode[STIX]{x1D6E4}$
. Then we have an equivalence
$\unicode[STIX]{x1D6E4}$
. Then we have an equivalence
 $$\begin{eqnarray}L_{E}(\unicode[STIX]{x1D6E4})\simeq E(S/M)\end{eqnarray}$$
$$\begin{eqnarray}L_{E}(\unicode[STIX]{x1D6E4})\simeq E(S/M)\end{eqnarray}$$
in
![]() $C$
.
$C$
.
Proof. The functor
![]() $E(-)$
commutes with finite colimits so that the statement follows immediately from Proposition 1.29.◻
$E(-)$
commutes with finite colimits so that the statement follows immediately from Proposition 1.29.◻
Remark 1.35. We may pullback a cocyclic
![]() $2$
-Segal object
$2$
-Segal object
![]() $X^{\bullet }$
along the functor
$X^{\bullet }$
along the functor
 $\unicode[STIX]{x1D6EC}_{\infty }\rightarrow \unicode[STIX]{x1D6EC}$
to obtain a coparacyclic
$\unicode[STIX]{x1D6EC}_{\infty }\rightarrow \unicode[STIX]{x1D6EC}$
to obtain a coparacyclic
![]() $2$
-Segal object
$2$
-Segal object
![]() $\widetilde{X^{\bullet }}$
. Given a framed graph
$\widetilde{X^{\bullet }}$
. Given a framed graph
![]() $\unicode[STIX]{x1D6E4}$
, we have
$\unicode[STIX]{x1D6E4}$
, we have
 $$\begin{eqnarray}\widetilde{X}(\unicode[STIX]{x1D6E4})\simeq X(\overline{\unicode[STIX]{x1D6E4}}),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{X}(\unicode[STIX]{x1D6E4})\simeq X(\overline{\unicode[STIX]{x1D6E4}}),\end{eqnarray}$$
where
![]() $\overline{\unicode[STIX]{x1D6E4}}$
is the ribbon graph underlying
$\overline{\unicode[STIX]{x1D6E4}}$
is the ribbon graph underlying
![]() $\unicode[STIX]{x1D6E4}$
. In particular, in the context of Proposition 1.34, we obtain
$\unicode[STIX]{x1D6E4}$
. In particular, in the context of Proposition 1.34, we obtain
 $$\begin{eqnarray}\widetilde{L_{E}}(\unicode[STIX]{x1D6E4})\simeq E(S/M).\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{L_{E}}(\unicode[STIX]{x1D6E4})\simeq E(S/M).\end{eqnarray}$$
2 Differential graded categories
2.1 Morita equivalences
We introduce some terminology for the derived Morita theory of differential graded categories and refer the reader to [Reference TabuadaTab05, Reference ToënToë07] for more detailed treatments. Let
![]() $k$
be a commutative ring, and let
$k$
be a commutative ring, and let
![]() $Cat_{\operatorname{dg}}$
be the category of small
$Cat_{\operatorname{dg}}$
be the category of small
![]() $k$
-linear differential
$k$
-linear differential
![]() $\mathbb{Z}$
-graded categories. Recall that a functor
$\mathbb{Z}$
-graded categories. Recall that a functor
 $f:A\rightarrow B$
is called a quasi-equivalence if:
$f:A\rightarrow B$
is called a quasi-equivalence if:
-
(1) the functor
 $H^{0}(f):H^{0}(A)\rightarrow H^{0}(B)$
of homotopy categories is an equivalence of categories;
$H^{0}(f):H^{0}(A)\rightarrow H^{0}(B)$
of homotopy categories is an equivalence of categories; -
(2) for every pair of objects
 $(x,y)$
in
$(x,y)$
in
 $A$
, the morphism
$A$
, the morphism
 $f:\operatorname{Hom}_{A}(x,y)\rightarrow \operatorname{Hom}_{B}(f(x),f(y))$
of complexes is a quasi-isomorphism.
$f:\operatorname{Hom}_{A}(x,y)\rightarrow \operatorname{Hom}_{B}(f(x),f(y))$
of complexes is a quasi-isomorphism.
We denote by
 $\operatorname{L}_{\operatorname{qe}}(Cat_{\operatorname{dg}})$
the
$\operatorname{L}_{\operatorname{qe}}(Cat_{\operatorname{dg}})$
the
![]() $\infty$
-category obtained by localizing
$\infty$
-category obtained by localizing
![]() $Cat_{\operatorname{dg}}$
along quasi-equivalences [Reference LurieLur11, 1.3.4.1]. The collection of quasi-equivalences can be supplemented to a combinatorial model structure on
$Cat_{\operatorname{dg}}$
along quasi-equivalences [Reference LurieLur11, 1.3.4.1]. The collection of quasi-equivalences can be supplemented to a combinatorial model structure on
![]() $Cat_{\operatorname{dg}}$
which facilitates calculations in
$Cat_{\operatorname{dg}}$
which facilitates calculations in
 $\operatorname{L}_{\operatorname{qe}}(Cat_{\operatorname{dg}})$
.
$\operatorname{L}_{\operatorname{qe}}(Cat_{\operatorname{dg}})$
.
Given dg categories
![]() $A$
,
$A$
,
![]() $B$
, we denote the dg category of enriched functors from
$B$
, we denote the dg category of enriched functors from
![]() $A$
to
$A$
to
![]() $B$
by
$B$
by
 $\text{}\underline{\operatorname{Hom}}(A,B)$
. We denote by
$\text{}\underline{\operatorname{Hom}}(A,B)$
. We denote by
![]() $\operatorname{Mod}_{k}$
the dg category of unbounded complexes of
$\operatorname{Mod}_{k}$
the dg category of unbounded complexes of
![]() $k$
-modules, and further, by
$k$
-modules, and further, by
![]() $\operatorname{Mod}_{A}$
the dg category
$\operatorname{Mod}_{A}$
the dg category
 $\text{}\underline{\operatorname{Hom}}(A^{\operatorname{op}},\operatorname{Mod}_{k})$
. We equip
$\text{}\underline{\operatorname{Hom}}(A^{\operatorname{op}},\operatorname{Mod}_{k})$
. We equip
![]() $\operatorname{Mod}_{A}$
with the projective model structure and denote by
$\operatorname{Mod}_{A}$
with the projective model structure and denote by
 $\operatorname{Perf}_{A}\subset \operatorname{Mod}_{A}$
the full dg category spanned by those objects
$\operatorname{Perf}_{A}\subset \operatorname{Mod}_{A}$
the full dg category spanned by those objects
![]() $x$
such that:
$x$
such that:
-
(1)
 $x$
is cofibrant;
$x$
is cofibrant; -
(2) the image of
 $x$
in
$x$
in
 $H^{0}(\operatorname{Mod}_{A})$
is compact, i.e.
$H^{0}(\operatorname{Mod}_{A})$
is compact, i.e.
 $\operatorname{Hom}(x,-)$
commutes with coproducts.
$\operatorname{Hom}(x,-)$
commutes with coproducts.
Given a dg functor
 $f:A\rightarrow B$
, we have a Quillen adjunction
$f:A\rightarrow B$
, we have a Quillen adjunction
 $$\begin{eqnarray}f_{!}:\operatorname{Mod}_{A}\longrightarrow \operatorname{Mod}_{B}:f^{\ast }\end{eqnarray}$$
$$\begin{eqnarray}f_{!}:\operatorname{Mod}_{A}\longrightarrow \operatorname{Mod}_{B}:f^{\ast }\end{eqnarray}$$
and obtain an induced functor
 $$\begin{eqnarray}f_{!}:\operatorname{Perf}_{A}\longrightarrow \operatorname{Perf}_{B}\!.\end{eqnarray}$$
$$\begin{eqnarray}f_{!}:\operatorname{Perf}_{A}\longrightarrow \operatorname{Perf}_{B}\!.\end{eqnarray}$$
The functor
 $f:A\rightarrow B$
is called a Morita equivalence if the induced functor (2.1) is a quasi-equivalence. We denote by
$f:A\rightarrow B$
is called a Morita equivalence if the induced functor (2.1) is a quasi-equivalence. We denote by
 $\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
the
$\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
the
![]() $\infty$
-category obtained by localizing
$\infty$
-category obtained by localizing
![]() $Cat_{\operatorname{dg}}$
along Morita equivalences. We have an adjunction
$Cat_{\operatorname{dg}}$
along Morita equivalences. We have an adjunction
 $$\begin{eqnarray}l:\operatorname{L}_{\operatorname{qe}}(Cat_{\operatorname{dg}})\longleftrightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}}):i,\end{eqnarray}$$
$$\begin{eqnarray}l:\operatorname{L}_{\operatorname{qe}}(Cat_{\operatorname{dg}})\longleftrightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}}):i,\end{eqnarray}$$
where
![]() $i$
is fully faithful so that
$i$
is fully faithful so that
![]() $l$
is a localization functor.
$l$
is a localization functor.
Let
![]() $Cat_{\operatorname{dg}}^{(2)}$
denote the category of small
$Cat_{\operatorname{dg}}^{(2)}$
denote the category of small
![]() $\mathbf{k}$
-linear differential
$\mathbf{k}$
-linear differential
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded categories. All of the above theory can be translated mutatis mutandis via the adjunction
$\mathbb{Z}/2\mathbb{Z}$
-graded categories. All of the above theory can be translated mutatis mutandis via the adjunction
 $$\begin{eqnarray}P:Cat_{\operatorname{dg}}\longleftrightarrow Cat_{\operatorname{dg}}^{(2)}:Q,\end{eqnarray}$$
$$\begin{eqnarray}P:Cat_{\operatorname{dg}}\longleftrightarrow Cat_{\operatorname{dg}}^{(2)}:Q,\end{eqnarray}$$
which is a Quillen adjunction with respect to an adaptation of the quasi-equivalence model structure on
![]() $Cat_{\operatorname{dg}}^{(2)}$
. The periodization functor
$Cat_{\operatorname{dg}}^{(2)}$
. The periodization functor
![]() $P$
associates to a differential
$P$
associates to a differential
![]() $\mathbb{Z}$
-graded category the differential
$\mathbb{Z}$
-graded category the differential
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded category with the same objects and
$\mathbb{Z}/2\mathbb{Z}$
-graded category with the same objects and
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded mapping complexes obtained by summing over all even (respectively odd) terms of the
$\mathbb{Z}/2\mathbb{Z}$
-graded mapping complexes obtained by summing over all even (respectively odd) terms of the
![]() $\mathbb{Z}$
-graded mapping complexes. We will refer to the
$\mathbb{Z}$
-graded mapping complexes. We will refer to the
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded analogs of the above constructions via the superscript
$\mathbb{Z}/2\mathbb{Z}$
-graded analogs of the above constructions via the superscript
![]() $(2)$
.
$(2)$
.
Remark 2.3. Note that, due to the adjunction (2.2), the functor
![]() $l$
commutes with colimits so that we may compute colimits in the category
$l$
commutes with colimits so that we may compute colimits in the category
 $\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
as colimits in
$\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
as colimits in
 $\operatorname{L}_{\operatorname{qe}}(Cat_{\operatorname{dg}})$
. The latter category is equipped with the quasi-equivalence model structure so that, by [Reference LurieLur09], we can compute colimits as homotopy colimits with respect to this model structure. The analogous statement holds for the
$\operatorname{L}_{\operatorname{qe}}(Cat_{\operatorname{dg}})$
. The latter category is equipped with the quasi-equivalence model structure so that, by [Reference LurieLur09], we can compute colimits as homotopy colimits with respect to this model structure. The analogous statement holds for the
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded variants.
$\mathbb{Z}/2\mathbb{Z}$
-graded variants.
2.2 Exact sequences of dg categories
A morphism in
 $\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
is called quasi-fully faithful if it is equivalent to the image of a quasi-fully faithful morphism under the localization functor
$\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
is called quasi-fully faithful if it is equivalent to the image of a quasi-fully faithful morphism under the localization functor
 $\operatorname{N}(Cat_{\operatorname{dg}})\rightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
. A pushout square
$\operatorname{N}(Cat_{\operatorname{dg}})\rightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
. A pushout square

in
 $\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
with
$\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
with
![]() $g$
quasi-fully faithful is called an exact sequence. The following technical statement will be used below.
$g$
quasi-fully faithful is called an exact sequence. The following technical statement will be used below.
Lemma 2.4. Quasi-fully faithful morphisms are stable under pushouts in
 $\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
.
$\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
.
Proof. The adjunction (2.2) implies that the left adjoint
 $l:\operatorname{L}_{\operatorname{qe}}(Cat_{\operatorname{dg}})\rightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
preserves colimits so that it suffices to prove the corresponding statement for
$l:\operatorname{L}_{\operatorname{qe}}(Cat_{\operatorname{dg}})\rightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
preserves colimits so that it suffices to prove the corresponding statement for
 $\operatorname{L}_{\operatorname{qe}}(Cat_{\operatorname{dg}})$
. To this end it suffices to show that quasi-fully faithful functors in the category
$\operatorname{L}_{\operatorname{qe}}(Cat_{\operatorname{dg}})$
. To this end it suffices to show that quasi-fully faithful functors in the category
![]() $Cat_{\operatorname{dg}}$
are stable under homotopy pushouts with respect to the quasi-equivalence model structure defined in [Reference TabuadaTab05]. Given a diagram
$Cat_{\operatorname{dg}}$
are stable under homotopy pushouts with respect to the quasi-equivalence model structure defined in [Reference TabuadaTab05]. Given a diagram

with
![]() $g$
quasi-fully faithful, we may assume that all objects are cofibrant, and
$g$
quasi-fully faithful, we may assume that all objects are cofibrant, and
![]() $f$
,
$f$
,
![]() $g$
are cofibrations so that the homotopy pushout is given by an ordinary pushout. Denoting by
$g$
are cofibrations so that the homotopy pushout is given by an ordinary pushout. Denoting by
![]() $I$
the set of generating cofibrations of
$I$
the set of generating cofibrations of
![]() $Cat_{\operatorname{dg}}$
, we may, by Quillen’s small object argument, factor the morphism
$Cat_{\operatorname{dg}}$
, we may, by Quillen’s small object argument, factor the morphism
![]() $f$
as
$f$
as
 $$\begin{eqnarray}S\overset{f_{1}}{\rightarrow }\widetilde{S^{\prime }}\overset{f_{2}}{\rightarrow }S^{\prime },\end{eqnarray}$$
$$\begin{eqnarray}S\overset{f_{1}}{\rightarrow }\widetilde{S^{\prime }}\overset{f_{2}}{\rightarrow }S^{\prime },\end{eqnarray}$$
where
![]() $f_{1}$
is a relative
$f_{1}$
is a relative
![]() $I$
-cell complex and
$I$
-cell complex and
![]() $f_{2}$
is a trivial fibration. Forming pushouts we obtain a diagram
$f_{2}$
is a trivial fibration. Forming pushouts we obtain a diagram

Since
![]() $\widetilde{g}$
is a cofibration, the bottom square is a homotopy pushout square and thus
$\widetilde{g}$
is a cofibration, the bottom square is a homotopy pushout square and thus
![]() $r$
is a quasi-equivalence. It hence suffices to show that
$r$
is a quasi-equivalence. It hence suffices to show that
![]() $\widetilde{g}$
is quasi-fully faithful so that we may assume that
$\widetilde{g}$
is quasi-fully faithful so that we may assume that
![]() $f$
is a relative
$f$
is a relative
![]() $I$
-cell complex. Using that filtered colimits of complexes are homotopy colimits [Reference Toën and VaquiéTV07], and hence preserve quasi-isomorphisms, we reduce to the case that
$I$
-cell complex. Using that filtered colimits of complexes are homotopy colimits [Reference Toën and VaquiéTV07], and hence preserve quasi-isomorphisms, we reduce to the case that
![]() $f$
is the pushout of a single generating cofibration from
$f$
is the pushout of a single generating cofibration from
![]() $I$
. This leaves us with the following two cases.
$I$
. This leaves us with the following two cases.
-
(1)
 $S^{\prime }$
is obtained from
$S^{\prime }$
is obtained from
 $S$
by adjoining one object, and the pushout
$S$
by adjoining one object, and the pushout
 $T^{\prime }$
of (2.5) is obtained from
$T^{\prime }$
of (2.5) is obtained from
 $T$
by adjoining one object. Clearly, the functor
$T$
by adjoining one object. Clearly, the functor
 $S^{\prime }\rightarrow T^{\prime }$
is quasi-fully faithful.
$S^{\prime }\rightarrow T^{\prime }$
is quasi-fully faithful. -
(2)
 $S^{\prime }$
is obtained from
$S^{\prime }$
is obtained from
 $S$
by freely adjoining a morphism
$S$
by freely adjoining a morphism
 $p:a\rightarrow b$
of some degree
$p:a\rightarrow b$
of some degree
 $n$
between objects
$n$
between objects
 $a,b$
of
$a,b$
of
 $S$
where
$S$
where
 $d(p)$
is a prescribed morphism
$d(p)$
is a prescribed morphism
 $q$
of
$q$
of
 $S$
. The morphism complex between objects
$S$
. The morphism complex between objects
 $x,y$
in
$x,y$
in
 $S^{\prime }$
can be described explicitly as where
$S^{\prime }$
can be described explicitly as where $$\begin{eqnarray}S^{\prime }(x,y)=\bigoplus _{n\geqslant 0}S(x,a)\otimes kp\otimes S(b,a)\otimes kp\otimes \cdots \otimes S(b,y),\end{eqnarray}$$
$$\begin{eqnarray}S^{\prime }(x,y)=\bigoplus _{n\geqslant 0}S(x,a)\otimes kp\otimes S(b,a)\otimes kp\otimes \cdots \otimes S(b,y),\end{eqnarray}$$
 $n$
copies of
$n$
copies of
 $kp$
appear in the
$kp$
appear in the
 $n$
th summand. The differential is given by the Leibniz rule where, upon replacing
$n$
th summand. The differential is given by the Leibniz rule where, upon replacing
 $p$
by
$p$
by
 $d(p)=q$
, we also compose with the neighboring morphisms so that the level is decreased from
$d(p)=q$
, we also compose with the neighboring morphisms so that the level is decreased from
 $n$
to
$n$
to
 $n-1$
. The morphism complexes of the pushout
$n-1$
. The morphism complexes of the pushout
 $T^{\prime }$
admit an analogous expression with
$T^{\prime }$
admit an analogous expression with
 $p$
replaced by
$p$
replaced by
 $g(p)$
. We have to show that, for every pair of objects, the morphism of complexes is a quasi-isomorphism. To this end, we filter both complexes by the level
$g(p)$
. We have to show that, for every pair of objects, the morphism of complexes is a quasi-isomorphism. To this end, we filter both complexes by the level $$\begin{eqnarray}S^{\prime }(x,y)\rightarrow T^{\prime }(g(x),g(y))\end{eqnarray}$$
$$\begin{eqnarray}S^{\prime }(x,y)\rightarrow T^{\prime }(g(x),g(y))\end{eqnarray}$$
 $n$
. On the associated graded complexes we have a quasi-isomorphism, since
$n$
. On the associated graded complexes we have a quasi-isomorphism, since
 $g$
is quasi-fully faithful. The corresponding spectral sequence converges, which yields the desired quasi-isomorphism.
$g$
is quasi-fully faithful. The corresponding spectral sequence converges, which yields the desired quasi-isomorphism.
◻
Remark 2.7. The proof of the lemma works verbatim for
![]() $Cat_{\operatorname{dg}}^{(2)}$
instead of
$Cat_{\operatorname{dg}}^{(2)}$
instead of
![]() $Cat_{\operatorname{dg}}$
.
$Cat_{\operatorname{dg}}$
.
3 Topological Fukaya categories
3.1
 $\mathbb{Z}/2\mathbb{Z}$
-graded
$\mathbb{Z}/2\mathbb{Z}$
-graded
Let
![]() $k$
be a commutative ring, and let
$k$
be a commutative ring, and let
 $R=k[z]$
denote the polynomial ring with coefficients in
$R=k[z]$
denote the polynomial ring with coefficients in
![]() $k$
, considered as a
$k$
, considered as a
 $\mathbb{Z}/(n+1)$
-graded
$\mathbb{Z}/(n+1)$
-graded
![]() $k$
-algebra with
$k$
-algebra with
![]() $|z|=1$
. A matrix factorization
$|z|=1$
. A matrix factorization
![]() $(X,d_{X})$
of
$(X,d_{X})$
of
 $w=z^{n+1}$
consists of:
$w=z^{n+1}$
consists of:
-
– a pair
 $X^{0}$
,
$X^{0}$
,
 $X^{1}$
of
$X^{1}$
of
 $\mathbb{Z}/(n+1)$
-graded
$\mathbb{Z}/(n+1)$
-graded
 $R$
-modules;
$R$
-modules; -
– a pair of homogeneous
 $R$
-linear homomorphismsof degree
$R$
-linear homomorphismsof degree
 $0$
;
$0$
;
such that
-
–
 $d^{1}\circ d^{0}=w\operatorname{id}_{X^{0}}$
and
$d^{1}\circ d^{0}=w\operatorname{id}_{X^{0}}$
and
 $d^{0}\circ d^{1}=w\operatorname{id}_{X^{1}}$
.
$d^{0}\circ d^{1}=w\operatorname{id}_{X^{1}}$
.
Example 3.1. For
 $i,j\in \mathbb{Z}/(n+1)$
,
$i,j\in \mathbb{Z}/(n+1)$
,
![]() $i\neq j$
, we have a corresponding scalar matrix factorization
$i\neq j$
, we have a corresponding scalar matrix factorization
![]() $[i,j]$
defined as
$[i,j]$
defined as

where the exponents of
![]() $z$
are to be interpreted via their representatives in
$z$
are to be interpreted via their representatives in
 $\{1,2,\ldots ,n\}$
. For
$\{1,2,\ldots ,n\}$
. For
![]() $i=j$
, we have two scalar matrix factorizations
$i=j$
, we have two scalar matrix factorizations

and

which we denote by
![]() $[i,i]_{r}$
and
$[i,i]_{r}$
and
![]() $[i,i]_{l}$
, respectively.
$[i,i]_{l}$
, respectively.
Given matrix factorizations
![]() $X$
,
$X$
,
![]() $Y$
of
$Y$
of
![]() $w$
, we form the
$w$
, we form the
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded
$\mathbb{Z}/2\mathbb{Z}$
-graded
![]() $k$
-module
$k$
-module
 $\operatorname{Hom}^{\bullet }(X,Y)$
with
$\operatorname{Hom}^{\bullet }(X,Y)$
with
 $$\begin{eqnarray}\displaystyle \operatorname{Hom}^{0}(X,Y) & = & \displaystyle \operatorname{Hom}_{R}(X^{0},Y^{0})\oplus \operatorname{Hom}_{R}(X^{1},Y^{1}),\nonumber\\ \displaystyle \operatorname{Hom}^{1}(X,Y) & = & \displaystyle \operatorname{Hom}_{R}(X^{0},Y^{1})\oplus \operatorname{Hom}_{R}(X^{1},Y^{0}),\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{Hom}^{0}(X,Y) & = & \displaystyle \operatorname{Hom}_{R}(X^{0},Y^{0})\oplus \operatorname{Hom}_{R}(X^{1},Y^{1}),\nonumber\\ \displaystyle \operatorname{Hom}^{1}(X,Y) & = & \displaystyle \operatorname{Hom}_{R}(X^{0},Y^{1})\oplus \operatorname{Hom}_{R}(X^{1},Y^{0}),\nonumber\end{eqnarray}$$
where
![]() $\operatorname{Hom}_{R}$
denotes homogeneous
$\operatorname{Hom}_{R}$
denotes homogeneous
![]() $R$
-linear homomorphisms of degree
$R$
-linear homomorphisms of degree
![]() $0$
. It is readily verified that the formula
$0$
. It is readily verified that the formula
 $$\begin{eqnarray}d(f)=d_{Y}\circ f-(-1)^{|f|}f\circ d_{X}\end{eqnarray}$$
$$\begin{eqnarray}d(f)=d_{Y}\circ f-(-1)^{|f|}f\circ d_{X}\end{eqnarray}$$
defines a differential on
 $\operatorname{Hom}^{\bullet }(X,Y)$
, i.e.
$\operatorname{Hom}^{\bullet }(X,Y)$
, i.e.
![]() $d^{2}=0$
. Therefore, the collection of all matrix factorizations of
$d^{2}=0$
. Therefore, the collection of all matrix factorizations of
![]() $w$
organizes into a differential
$w$
organizes into a differential
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded
$\mathbb{Z}/2\mathbb{Z}$
-graded
![]() $k$
-linear category which we denote by
$k$
-linear category which we denote by
 $\operatorname{MF}^{\mathbb{Z}/(n+1)}(k[z],z^{n+1})$
. We further define
$\operatorname{MF}^{\mathbb{Z}/(n+1)}(k[z],z^{n+1})$
. We further define
 $$\begin{eqnarray}\bar{\operatorname{F}}^{n}\subset \operatorname{MF}^{\mathbb{Z}/(n+1)}(k[z],z^{n+1})\end{eqnarray}$$
$$\begin{eqnarray}\bar{\operatorname{F}}^{n}\subset \operatorname{MF}^{\mathbb{Z}/(n+1)}(k[z],z^{n+1})\end{eqnarray}$$
to be the full dg subcategory spanned by the scalar matrix factorizations from Example 3.1.
Theorem 3.2. The association
 $n\mapsto \bar{\operatorname{F}}^{n}$
extends to a cocyclic object
$n\mapsto \bar{\operatorname{F}}^{n}$
extends to a cocyclic object
 $$\begin{eqnarray}\bar{\operatorname{F}}:\operatorname{N}(\unicode[STIX]{x1D6EC})\rightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}}^{(2)})\end{eqnarray}$$
$$\begin{eqnarray}\bar{\operatorname{F}}:\operatorname{N}(\unicode[STIX]{x1D6EC})\rightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}}^{(2)})\end{eqnarray}$$
which is unital 2-Segal.
Proof. This is the content of [Reference Dyckerhoff and KapranovDK13, 2.4.1] where the dg category
![]() $\bar{\operatorname{F}}^{n}$
is denoted by
$\bar{\operatorname{F}}^{n}$
is denoted by
![]() ${\mathcal{E}}^{n}$
.◻
${\mathcal{E}}^{n}$
.◻
Remark 3.3. Let
![]() $A^{n}$
denote the
$A^{n}$
denote the
![]() $k$
-linear envelope of the category associated to the linearly ordered set
$k$
-linear envelope of the category associated to the linearly ordered set
 $\{1,2,\ldots ,n\}$
, considered as a differential
$\{1,2,\ldots ,n\}$
, considered as a differential
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded category concentrated in degree
$\mathbb{Z}/2\mathbb{Z}$
-graded category concentrated in degree
![]() $0$
. There is a dg functor
$0$
. There is a dg functor
 $$\begin{eqnarray}g:A^{n}\rightarrow \bar{\operatorname{F}}^{n},\quad i\mapsto [0,i]\end{eqnarray}$$
$$\begin{eqnarray}g:A^{n}\rightarrow \bar{\operatorname{F}}^{n},\quad i\mapsto [0,i]\end{eqnarray}$$
that maps the generating morphism
![]() $i\rightarrow j$
to the closed morphism of matrix factorizations
$i\rightarrow j$
to the closed morphism of matrix factorizations

An explicit calculation enables the following observations to be made.
-
– The functor
 $g$
is quasi-fully faithful.
$g$
is quasi-fully faithful. -
– The object
 $[i,j]$
is a cone over the above morphism
$[i,j]$
is a cone over the above morphism
 $[0,i]\rightarrow [0,j]$
.
$[0,i]\rightarrow [0,j]$
. -
– The objects
 $[i,i]_{l}$
and
$[i,i]_{l}$
and
 $[i,i]_{r}$
are zero objects.
$[i,i]_{r}$
are zero objects.
These observations imply that the functor
![]() $g$
is a Morita equivalence (cf. [Reference Dyckerhoff and KapranovDK13, 2.3.6]). The reason for using
$g$
is a Morita equivalence (cf. [Reference Dyckerhoff and KapranovDK13, 2.3.6]). The reason for using
![]() $\bar{\operatorname{F}}^{n}$
instead of the much simpler dg category
$\bar{\operatorname{F}}^{n}$
instead of the much simpler dg category
![]() $A^{n}$
is the following: the cocyclic object in Theorem 3.2 is difficult to describe in terms of
$A^{n}$
is the following: the cocyclic object in Theorem 3.2 is difficult to describe in terms of
![]() $A^{n}$
while the association
$A^{n}$
while the association
 $n\mapsto \bar{\operatorname{F}}^{n}$
defines a strict functor
$n\mapsto \bar{\operatorname{F}}^{n}$
defines a strict functor
 $\unicode[STIX]{x1D6EC}\rightarrow Cat_{\operatorname{dg}}^{(2)}$
which induces
$\unicode[STIX]{x1D6EC}\rightarrow Cat_{\operatorname{dg}}^{(2)}$
which induces
![]() $\bar{\operatorname{F}}^{\bullet }$
by passing to the Morita localization.
$\bar{\operatorname{F}}^{\bullet }$
by passing to the Morita localization.
The state sum formalism of § 1.2.3 yields a functor
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\bar{\operatorname{F}}}:\operatorname{N}({\mathcal{R}}ib)\longrightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}}^{(2)}),\quad \unicode[STIX]{x1D6E4}\mapsto \bar{\operatorname{F}}(\unicode[STIX]{x1D6E4}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\bar{\operatorname{F}}}:\operatorname{N}({\mathcal{R}}ib)\longrightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}}^{(2)}),\quad \unicode[STIX]{x1D6E4}\mapsto \bar{\operatorname{F}}(\unicode[STIX]{x1D6E4}).\end{eqnarray}$$
The state sum
![]() $\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4})$
of
$\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4})$
of
![]() $\bar{\operatorname{F}}$
on a ribbon graph
$\bar{\operatorname{F}}$
on a ribbon graph
![]() $\unicode[STIX]{x1D6E4}$
is called the (
$\unicode[STIX]{x1D6E4}$
is called the (
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded) topological Fukaya category of
$\mathbb{Z}/2\mathbb{Z}$
-graded) topological Fukaya category of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Example 3.4. Consider the ribbon graph
![]() $\unicode[STIX]{x1D6E4}$
given by
$\unicode[STIX]{x1D6E4}$
given by
The corresponding topological Fukaya category
![]() $\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4})$
can, by Proposition 4.4(i), Remarks 2.3, and 3.3, be computed as the homotopy pushout of the diagram
$\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4})$
can, by Proposition 4.4(i), Remarks 2.3, and 3.3, be computed as the homotopy pushout of the diagram

with respect to the quasi-equivalence model structure on
![]() $Cat_{\operatorname{dg}}^{(2)}$
. All objects are cofibrant and the vertical functor is a cofibration so that the homotopy pushout can be computed as an ordinary pushout. Therefore, we obtain
$Cat_{\operatorname{dg}}^{(2)}$
. All objects are cofibrant and the vertical functor is a cofibration so that the homotopy pushout can be computed as an ordinary pushout. Therefore, we obtain
 $$\begin{eqnarray}\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4})\simeq k[t]\end{eqnarray}$$
$$\begin{eqnarray}\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4})\simeq k[t]\end{eqnarray}$$
the
![]() $k$
-linear category with one object and endomorphism ring
$k$
-linear category with one object and endomorphism ring
![]() $k[t]$
, considered as a differential
$k[t]$
, considered as a differential
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded category with zero differential. We can therefore interpret
$\mathbb{Z}/2\mathbb{Z}$
-graded category with zero differential. We can therefore interpret
![]() $\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4})$
as the
$\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4})$
as the
![]() $\mathbb{Z}/2\mathbb{Z}$
-folding of the bounded derived dg category of coherent sheaves on the affine line
$\mathbb{Z}/2\mathbb{Z}$
-folding of the bounded derived dg category of coherent sheaves on the affine line
![]() $\mathbb{A}_{k}^{1}$
over
$\mathbb{A}_{k}^{1}$
over
![]() $k$
.
$k$
.
Example 3.5. Consider the ribbon graph
![]() $\unicode[STIX]{x1D6E4}$
given by
$\unicode[STIX]{x1D6E4}$
given by
We replace
![]() $\unicode[STIX]{x1D6E4}$
by the ribbon graph
$\unicode[STIX]{x1D6E4}$
by the ribbon graph
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
$\unicode[STIX]{x1D6E4}^{\prime }$
which, by Proposition 1.23, has an equivalent topological Fukaya category. Using [Reference LurieLur09, Proposition 4.2.3.8], Remarks 2.3, and 3.3, we can obtain
![]() $\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4}^{\prime })$
as the homotopy pushout of
$\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4}^{\prime })$
as the homotopy pushout of

with respect to the quasi-equivalence model structure on
![]() $Cat_{\operatorname{dg}}^{(2)}$
. Since all objects in this diagram are cofibrant and all functors cofibrations, we can form the ordinary pushout to obtain a description of
$Cat_{\operatorname{dg}}^{(2)}$
. Since all objects in this diagram are cofibrant and all functors cofibrations, we can form the ordinary pushout to obtain a description of
![]() $\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4})$
as the
$\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4})$
as the
![]() $k$
-linear category generated by the Kronecker quiver with two vertices
$k$
-linear category generated by the Kronecker quiver with two vertices
![]() $0$
and
$0$
and
![]() $1$
and two edges from
$1$
and two edges from
![]() $0$
to
$0$
to
![]() $1$
. In virtue of Beilinson’s famous result [Reference BeilinsonBei78], we can therefore interpret
$1$
. In virtue of Beilinson’s famous result [Reference BeilinsonBei78], we can therefore interpret
![]() $\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4})$
as the
$\bar{\operatorname{F}}(\unicode[STIX]{x1D6E4})$
as the
![]() $\mathbb{Z}/2\mathbb{Z}$
-folding of the bounded derived dg category of coherent sheaves on the projective line
$\mathbb{Z}/2\mathbb{Z}$
-folding of the bounded derived dg category of coherent sheaves on the projective line
![]() $\mathbb{P}_{k}^{1}$
over
$\mathbb{P}_{k}^{1}$
over
![]() $k$
.
$k$
.
3.2
 $\mathbb{Z}$
-graded
$\mathbb{Z}$
-graded
We discuss a
![]() $\mathbb{Z}$
-graded variant of the topological Fukaya category which can be associated to any framed stable marked surface and provides a lift of the
$\mathbb{Z}$
-graded variant of the topological Fukaya category which can be associated to any framed stable marked surface and provides a lift of the
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded category associated to the underlying oriented surface. It can be obtained via a minor modification of the constructions in § 3.1: we introduce a differential
$\mathbb{Z}/2\mathbb{Z}$
-graded category associated to the underlying oriented surface. It can be obtained via a minor modification of the constructions in § 3.1: we introduce a differential
![]() $\mathbb{Z}$
-graded category
$\mathbb{Z}$
-graded category
 $\operatorname{MF}^{\mathbb{Z}}(k[z],z^{n+1})$
of
$\operatorname{MF}^{\mathbb{Z}}(k[z],z^{n+1})$
of
![]() $\mathbb{Z}$
-graded matrix factorizations.
$\mathbb{Z}$
-graded matrix factorizations.
Let
![]() $k$
be a commutative ring, and let
$k$
be a commutative ring, and let
 $R=k[z]$
denote the polynomial ring, considered as a
$R=k[z]$
denote the polynomial ring, considered as a
![]() $\mathbb{Z}$
-graded ring with
$\mathbb{Z}$
-graded ring with
![]() $|z|=1$
. A
$|z|=1$
. A
![]() $\mathbb{Z}$
-graded matrix factorization
$\mathbb{Z}$
-graded matrix factorization
![]() $(X,d)$
of
$(X,d)$
of
 $w=z^{n+1}$
consists of:
$w=z^{n+1}$
consists of:
-
– a pair
 $X^{0}$
,
$X^{0}$
,
 $X^{1}$
of
$X^{1}$
of
 $\mathbb{Z}$
-graded
$\mathbb{Z}$
-graded
 $R$
-modules;
$R$
-modules; -
– a pair of homogeneous
 $R$
-linear homomorphismswhere
$R$
-linear homomorphismswhere
 $|d^{0}|=0$
and
$|d^{0}|=0$
and
 $|d^{1}|=n+1$
;
$|d^{1}|=n+1$
;
such that
-
–
 $d^{1}\circ d^{0}=w\operatorname{id}_{X^{0}}$
and
$d^{1}\circ d^{0}=w\operatorname{id}_{X^{0}}$
and
 $d^{0}\circ d^{1}=w\operatorname{id}_{X^{1}}$
.
$d^{0}\circ d^{1}=w\operatorname{id}_{X^{1}}$
.
Example 3.6. For
![]() $i,j\in \mathbb{Z}$
,
$i,j\in \mathbb{Z}$
,
 $0\leqslant j-i\leqslant n+1$
, we have a corresponding scalar matrix factorization
$0\leqslant j-i\leqslant n+1$
, we have a corresponding scalar matrix factorization
![]() $[i,j]$
defined as
$[i,j]$
defined as

Given matrix factorizations
![]() $X,Y$
, we define a
$X,Y$
, we define a
![]() $\mathbb{Z}$
-graded mapping complex
$\mathbb{Z}$
-graded mapping complex
 $\operatorname{Hom}^{\bullet }(X,Y)$
as follows. We extend
$\operatorname{Hom}^{\bullet }(X,Y)$
as follows. We extend
![]() $X$
to a
$X$
to a
![]() $\mathbb{Z}$
-sequence
$\mathbb{Z}$
-sequence
 $$\begin{eqnarray}\cdots \overset{d}{\longrightarrow }\widetilde{X}^{i-1}\overset{d}{\longrightarrow }\widetilde{X}^{i}\overset{d}{\longrightarrow }\widetilde{X}^{i+1}\longrightarrow \cdots\end{eqnarray}$$
$$\begin{eqnarray}\cdots \overset{d}{\longrightarrow }\widetilde{X}^{i-1}\overset{d}{\longrightarrow }\widetilde{X}^{i}\overset{d}{\longrightarrow }\widetilde{X}^{i+1}\longrightarrow \cdots\end{eqnarray}$$
setting
 $$\begin{eqnarray}\widetilde{X}^{i}:=X^{\overline{i}}\biggl((n+1)\left\lfloor \frac{i}{2}\right\rfloor \biggr),\end{eqnarray}$$
$$\begin{eqnarray}\widetilde{X}^{i}:=X^{\overline{i}}\biggl((n+1)\left\lfloor \frac{i}{2}\right\rfloor \biggr),\end{eqnarray}$$
where
![]() $\overline{i}$
denotes the residue of
$\overline{i}$
denotes the residue of
![]() $i$
modulo
$i$
modulo
![]() $2$
. In particular, we have
$2$
. In particular, we have
 $\widetilde{X}^{i+2}=\widetilde{X}^{i}(n+1)$
. The morphisms
$\widetilde{X}^{i+2}=\widetilde{X}^{i}(n+1)$
. The morphisms
![]() $d$
in the sequence
$d$
in the sequence
![]() $\widetilde{X}$
are homogeneous of degree
$\widetilde{X}$
are homogeneous of degree
![]() $0$
and satisfy
$0$
and satisfy
![]() $d^{2}=w$
. Given matrix factorizations
$d^{2}=w$
. Given matrix factorizations
![]() $X,Y$
, we define the
$X,Y$
, we define the
![]() $\mathbb{Z}$
-graded complex
$\mathbb{Z}$
-graded complex
 $\operatorname{Hom}^{\bullet }(X,Y)$
by setting
$\operatorname{Hom}^{\bullet }(X,Y)$
by setting
 $$\begin{eqnarray}\operatorname{Hom}^{j}(X,Y)=\{(f_{i})_{i\in \mathbb{Z}}\;|\;f_{i+2}=f_{i}(n+1)\}\subset \mathop{\prod }_{i\in \mathbb{Z}}\operatorname{Hom}_{R}(\widetilde{X}^{i},\widetilde{X}^{i+j})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}^{j}(X,Y)=\{(f_{i})_{i\in \mathbb{Z}}\;|\;f_{i+2}=f_{i}(n+1)\}\subset \mathop{\prod }_{i\in \mathbb{Z}}\operatorname{Hom}_{R}(\widetilde{X}^{i},\widetilde{X}^{i+j})\end{eqnarray}$$
equipped with the differential given by the formula
 $$\begin{eqnarray}d(f)=d_{\widetilde{Y}}f-(-1)^{|f|}f\circ d_{\widetilde{X}}.\end{eqnarray}$$
$$\begin{eqnarray}d(f)=d_{\widetilde{Y}}f-(-1)^{|f|}f\circ d_{\widetilde{X}}.\end{eqnarray}$$
Therefore, the collection of all
![]() $\mathbb{Z}$
-graded matrix factorizations of
$\mathbb{Z}$
-graded matrix factorizations of
![]() $w$
organizes into a differential
$w$
organizes into a differential
![]() $\mathbb{Z}$
-graded
$\mathbb{Z}$
-graded
![]() $k$
-linear category which we denote by
$k$
-linear category which we denote by
 $\operatorname{MF}^{\mathbb{Z}}(k[z],z^{n+1})$
. In analogy with the
$\operatorname{MF}^{\mathbb{Z}}(k[z],z^{n+1})$
. In analogy with the
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded case, we further define
$\mathbb{Z}/2\mathbb{Z}$
-graded case, we further define
 $$\begin{eqnarray}\operatorname{F}^{n}\subset \operatorname{MF}^{\mathbb{Z}}(k[z],z^{n+1})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{F}^{n}\subset \operatorname{MF}^{\mathbb{Z}}(k[z],z^{n+1})\end{eqnarray}$$
to be the full dg subcategory spanned by the scalar matrix factorizations from Example 3.6.
Theorem 3.7. The association
 $n\mapsto \operatorname{F}^{n}$
extends to a coparacyclic object
$n\mapsto \operatorname{F}^{n}$
extends to a coparacyclic object
 $$\begin{eqnarray}\operatorname{F}:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{F}:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\end{eqnarray}$$
which is unital
![]() $2$
-Segal.
$2$
-Segal.
Proof. See [Reference LurieLur14, Reference Dyckerhoff and KapranovDK15]. ◻
Remark 3.8. The statement of Remark 3.3 has a
![]() $\mathbb{Z}$
-graded analog: for every
$\mathbb{Z}$
-graded analog: for every
![]() $n\geqslant 0$
, the association
$n\geqslant 0$
, the association
 $i\mapsto [0,i]$
defines a Morita equivalence of
$i\mapsto [0,i]$
defines a Morita equivalence of
![]() $\mathbb{Z}$
-graded categories
$\mathbb{Z}$
-graded categories
 $$\begin{eqnarray}A_{\mathbb{Z}}^{n}\longrightarrow \operatorname{F}^{n},\end{eqnarray}$$
$$\begin{eqnarray}A_{\mathbb{Z}}^{n}\longrightarrow \operatorname{F}^{n},\end{eqnarray}$$
where
![]() $A_{\mathbb{Z}}^{n}$
denotes the
$A_{\mathbb{Z}}^{n}$
denotes the
![]() $\mathbb{Z}$
-graded variant of
$\mathbb{Z}$
-graded variant of
![]() $A^{n}$
.
$A^{n}$
.
We obtain a state sum functor
 $$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\operatorname{F}}:\operatorname{N}({\mathcal{R}}ib_{\infty })\longrightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}}),\quad \unicode[STIX]{x1D6E4}\mapsto \operatorname{F}(\unicode[STIX]{x1D6E4}).\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70C}_{\operatorname{F}}:\operatorname{N}({\mathcal{R}}ib_{\infty })\longrightarrow \operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}}),\quad \unicode[STIX]{x1D6E4}\mapsto \operatorname{F}(\unicode[STIX]{x1D6E4}).\end{eqnarray}$$
The state sum
![]() $\operatorname{F}(\unicode[STIX]{x1D6E4})$
of
$\operatorname{F}(\unicode[STIX]{x1D6E4})$
of
![]() $\operatorname{F}$
on a framed graph
$\operatorname{F}$
on a framed graph
![]() $\unicode[STIX]{x1D6E4}$
is called the (
$\unicode[STIX]{x1D6E4}$
is called the (
![]() $\mathbb{Z}$
-graded) topological Fukaya category of
$\mathbb{Z}$
-graded) topological Fukaya category of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Remark 3.9. It is immediate from the definitions that we have a commutative square

in
![]() $Cat_{\infty }$
where the left vertical arrow is the natural forgetful functor. Since the periodization functor
$Cat_{\infty }$
where the left vertical arrow is the natural forgetful functor. Since the periodization functor
![]() $P$
commutes with colimits it follows that, for a framed graph
$P$
commutes with colimits it follows that, for a framed graph
![]() $\unicode[STIX]{x1D6E4}$
, we have
$\unicode[STIX]{x1D6E4}$
, we have
 $$\begin{eqnarray}P(\operatorname{F}(\unicode[STIX]{x1D6E4}))\simeq \bar{\operatorname{F}}(\bar{\unicode[STIX]{x1D6E4}}),\end{eqnarray}$$
$$\begin{eqnarray}P(\operatorname{F}(\unicode[STIX]{x1D6E4}))\simeq \bar{\operatorname{F}}(\bar{\unicode[STIX]{x1D6E4}}),\end{eqnarray}$$
where
![]() $\bar{\unicode[STIX]{x1D6E4}}$
denotes the ribbon graph underlying
$\bar{\unicode[STIX]{x1D6E4}}$
denotes the ribbon graph underlying
![]() $\unicode[STIX]{x1D6E4}$
. In other words,
$\unicode[STIX]{x1D6E4}$
. In other words,
![]() $\operatorname{F}(\unicode[STIX]{x1D6E4})$
provides a lift of the differential
$\operatorname{F}(\unicode[STIX]{x1D6E4})$
provides a lift of the differential
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded category
$\mathbb{Z}/2\mathbb{Z}$
-graded category
![]() $\bar{\operatorname{F}}(\bar{\unicode[STIX]{x1D6E4}})$
to a differential
$\bar{\operatorname{F}}(\bar{\unicode[STIX]{x1D6E4}})$
to a differential
![]() $\mathbb{Z}$
-graded category.
$\mathbb{Z}$
-graded category.
Example 3.10. Consider the ribbon graph
![]() $\unicode[STIX]{x1D6E4}$
given by
$\unicode[STIX]{x1D6E4}$
given by
equipped with framing corresponding to the winding number
![]() $r$
around the loop. A calculation analogous to that in Example 3.4 yields
$r$
around the loop. A calculation analogous to that in Example 3.4 yields
 $$\begin{eqnarray}\operatorname{F}(\unicode[STIX]{x1D6E4})\simeq k[t],\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{F}(\unicode[STIX]{x1D6E4})\simeq k[t],\end{eqnarray}$$
the
![]() $k$
-linear category with one object and endomorphism ring
$k$
-linear category with one object and endomorphism ring
![]() $k[t]$
,
$k[t]$
,
![]() $|t|=2r$
, considered as a differential
$|t|=2r$
, considered as a differential
![]() $\mathbb{Z}$
-graded category with zero differential. The endomorphism dga of the
$\mathbb{Z}$
-graded category with zero differential. The endomorphism dga of the
![]() $k[t]$
-module
$k[t]$
-module
 $k\cong k[t]/(t)$
is given by the graded ring
$k\cong k[t]/(t)$
is given by the graded ring
![]() $k[\unicode[STIX]{x1D6FF}]$
,
$k[\unicode[STIX]{x1D6FF}]$
,
![]() $\unicode[STIX]{x1D6FF}^{2}=0$
,
$\unicode[STIX]{x1D6FF}^{2}=0$
,
 $|\unicode[STIX]{x1D6FF}|=1-2r$
.
$|\unicode[STIX]{x1D6FF}|=1-2r$
.
Example 3.11. Consider the ribbon graph
![]() $\unicode[STIX]{x1D6E4}$
$\unicode[STIX]{x1D6E4}$
with framing corresponding to the winding number
![]() $r$
. An analogous calculation to Example 3.5 gives a description of
$r$
. An analogous calculation to Example 3.5 gives a description of
![]() $\operatorname{F}(\unicode[STIX]{x1D6E4})$
as the
$\operatorname{F}(\unicode[STIX]{x1D6E4})$
as the
![]() $k$
-linear category generated by the graded Kronecker quiver with two vertices
$k$
-linear category generated by the graded Kronecker quiver with two vertices
![]() $0$
and
$0$
and
![]() $1$
and two edges from
$1$
and two edges from
![]() $0$
to
$0$
to
![]() $1$
where the edges have degree
$1$
where the edges have degree
![]() $0$
and
$0$
and
![]() $2r$
, respectively. Therefore,
$2r$
, respectively. Therefore,
![]() $\operatorname{F}(\unicode[STIX]{x1D6E4})$
can be interpreted as a twisted version of the derived dg category of
$\operatorname{F}(\unicode[STIX]{x1D6E4})$
can be interpreted as a twisted version of the derived dg category of
![]() $\mathbb{P}_{k}^{1}$
(cf. [Reference SeidelSei04] for an appearance of this quiver in another Fukaya-categorical context). The objects of
$\mathbb{P}_{k}^{1}$
(cf. [Reference SeidelSei04] for an appearance of this quiver in another Fukaya-categorical context). The objects of
 $\operatorname{Perf}_{\operatorname{F}(\unicode[STIX]{x1D6E4})}$
given by the cones of the two edges of the quiver have endomorphism algebras given by
$\operatorname{Perf}_{\operatorname{F}(\unicode[STIX]{x1D6E4})}$
given by the cones of the two edges of the quiver have endomorphism algebras given by
![]() $k[\unicode[STIX]{x1D6FF}]$
,
$k[\unicode[STIX]{x1D6FF}]$
,
![]() $\unicode[STIX]{x1D6FF}^{2}=0$
, where
$\unicode[STIX]{x1D6FF}^{2}=0$
, where
![]() $\unicode[STIX]{x1D6FF}$
has degree
$\unicode[STIX]{x1D6FF}$
has degree
![]() $1-2r$
and
$1-2r$
and
![]() $1+2r$
, respectively.
$1+2r$
, respectively.
4 Localization and Mayer–Vietoris
4.1 Localization for topological Fukaya categories
We construct localization sequences for topological Fukaya categories which are analogous to the proto-localization sequences of Thomason–Trobaugh for derived categories of schemes. A refined analysis of certain such sequences will feature in our proof of the Mayer–Vietoris theorem in § 4.2. We focus on the
![]() $\mathbb{Z}$
-graded case, the
$\mathbb{Z}$
-graded case, the
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded case can be treated mutatis mutandis.
$\mathbb{Z}/2\mathbb{Z}$
-graded case can be treated mutatis mutandis.
Let
![]() $\unicode[STIX]{x1D6E4}$
be a graph. A subgraph
$\unicode[STIX]{x1D6E4}$
be a graph. A subgraph
![]() $\unicode[STIX]{x1D6E4}^{\prime }\subset \unicode[STIX]{x1D6E4}$
is called open if, for every vertex
$\unicode[STIX]{x1D6E4}^{\prime }\subset \unicode[STIX]{x1D6E4}$
is called open if, for every vertex
![]() $v\in \unicode[STIX]{x1D6E4}^{\prime }$
, the graph
$v\in \unicode[STIX]{x1D6E4}^{\prime }$
, the graph
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
contains all half-edges incident to
$\unicode[STIX]{x1D6E4}^{\prime }$
contains all half-edges incident to
![]() $v$
in
$v$
in
![]() $\unicode[STIX]{x1D6E4}$
. The complement
$\unicode[STIX]{x1D6E4}$
. The complement
 $\unicode[STIX]{x1D6E4}^{\prime \prime }=\unicode[STIX]{x1D6E4}\setminus \unicode[STIX]{x1D6E4}^{\prime }$
of an open graph
$\unicode[STIX]{x1D6E4}^{\prime \prime }=\unicode[STIX]{x1D6E4}\setminus \unicode[STIX]{x1D6E4}^{\prime }$
of an open graph
![]() $\unicode[STIX]{x1D6E4}^{\prime }\subset \unicode[STIX]{x1D6E4}$
is the subgraph of
$\unicode[STIX]{x1D6E4}^{\prime }\subset \unicode[STIX]{x1D6E4}$
is the subgraph of
![]() $\unicode[STIX]{x1D6E4}$
with set of vertices
$\unicode[STIX]{x1D6E4}$
with set of vertices
![]() $V\setminus V^{\prime }$
and set of half-edges
$V\setminus V^{\prime }$
and set of half-edges
![]() $H\setminus H^{\prime }$
. Note that the complement of an open graph is open. Given an open subgraph
$H\setminus H^{\prime }$
. Note that the complement of an open graph is open. Given an open subgraph
![]() $\unicode[STIX]{x1D6E4}^{\prime }\subset \unicode[STIX]{x1D6E4}$
, we define the closure
$\unicode[STIX]{x1D6E4}^{\prime }\subset \unicode[STIX]{x1D6E4}$
, we define the closure
![]() $\overline{\unicode[STIX]{x1D6E4}^{\prime }}$
to be the graph which is obtained from
$\overline{\unicode[STIX]{x1D6E4}^{\prime }}$
to be the graph which is obtained from
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
by adding, for every external half-edge
$\unicode[STIX]{x1D6E4}^{\prime }$
by adding, for every external half-edge
![]() $h$
of
$h$
of
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
which becomes internal in
$\unicode[STIX]{x1D6E4}^{\prime }$
which becomes internal in
![]() $\unicode[STIX]{x1D6E4}$
, a new half-edge
$\unicode[STIX]{x1D6E4}$
, a new half-edge
![]() $\unicode[STIX]{x1D70F}(h)$
and vertex
$\unicode[STIX]{x1D70F}(h)$
and vertex
![]() $v$
which is declared incident to
$v$
which is declared incident to
![]() $\unicode[STIX]{x1D70F}(h)$
. We further define the retract
$\unicode[STIX]{x1D70F}(h)$
. We further define the retract
![]() $\text{}\underline{\unicode[STIX]{x1D6E4}^{\prime }}$
of
$\text{}\underline{\unicode[STIX]{x1D6E4}^{\prime }}$
of
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
to be the graph obtained from
$\unicode[STIX]{x1D6E4}^{\prime }$
to be the graph obtained from
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
by removing all half-edges which become internal in
$\unicode[STIX]{x1D6E4}^{\prime }$
by removing all half-edges which become internal in
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Example 4.1. Consider the graph
![]() $\unicode[STIX]{x1D6E4}$
depicted by
$\unicode[STIX]{x1D6E4}$
depicted by
It contains the open subgraph
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
given by
$\unicode[STIX]{x1D6E4}^{\prime }$
given by
with closure
![]() $\overline{\unicode[STIX]{x1D6E4}^{\prime }}$
$\overline{\unicode[STIX]{x1D6E4}^{\prime }}$
retract
![]() $\text{}\underline{\unicode[STIX]{x1D6E4}^{\prime }}$
$\text{}\underline{\unicode[STIX]{x1D6E4}^{\prime }}$
and complement
![]() $\unicode[STIX]{x1D6E4}\setminus \unicode[STIX]{x1D6E4}^{\prime }$
$\unicode[STIX]{x1D6E4}\setminus \unicode[STIX]{x1D6E4}^{\prime }$
Note that if
![]() $\unicode[STIX]{x1D6E4}$
is a framed (respectively ribbon) graph then any open subgraph inherits a canonical framing (respectively ribbon structure). We will need the following special case of a general descent statement which can be proved with the same technique.
$\unicode[STIX]{x1D6E4}$
is a framed (respectively ribbon) graph then any open subgraph inherits a canonical framing (respectively ribbon structure). We will need the following special case of a general descent statement which can be proved with the same technique.
Proposition 4.2. Let
![]() $C$
be an
$C$
be an
![]() $\infty$
-category with finite colimits. Let
$\infty$
-category with finite colimits. Let
![]() $\unicode[STIX]{x1D6E4}$
be a graph, and let
$\unicode[STIX]{x1D6E4}$
be a graph, and let
![]() $\unicode[STIX]{x1D6E4}^{\prime }\subset \unicode[STIX]{x1D6E4}$
be an open subgraph of
$\unicode[STIX]{x1D6E4}^{\prime }\subset \unicode[STIX]{x1D6E4}$
be an open subgraph of
![]() $\unicode[STIX]{x1D6E4}$
with complement
$\unicode[STIX]{x1D6E4}$
with complement
![]() $\unicode[STIX]{x1D6E4}^{\prime \prime }$
. Assume that
$\unicode[STIX]{x1D6E4}^{\prime \prime }$
. Assume that
![]() $\unicode[STIX]{x1D6E4}$
carries a ribbon (respectively framed) structure and
$\unicode[STIX]{x1D6E4}$
carries a ribbon (respectively framed) structure and
![]() $X$
is a co(para)cyclic object in
$X$
is a co(para)cyclic object in
![]() $C$
. Then there is a canonical pushout square
$C$
. Then there is a canonical pushout square

in
![]() $C$
, where
$C$
, where
![]() $\unicode[STIX]{x1D6EF}$
denotes the graph given by the disjoint union of copies of the corolla
$\unicode[STIX]{x1D6EF}$
denotes the graph given by the disjoint union of copies of the corolla
indexed by those half-edges in
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
which become internal in
$\unicode[STIX]{x1D6E4}^{\prime }$
which become internal in
![]() $\unicode[STIX]{x1D6E4}$
, equipped with the (para)cyclic order induced from the corresponding edges of
$\unicode[STIX]{x1D6E4}$
, equipped with the (para)cyclic order induced from the corresponding edges of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Proof. This is an immediate consequence of [Reference LurieLur09, 4.2.3.8], which allows us to compute the state sum colimit
![]() $X(\unicode[STIX]{x1D6E4})$
by covering the state sum diagram with two subdiagrams whose corresponding colimits yield
$X(\unicode[STIX]{x1D6E4})$
by covering the state sum diagram with two subdiagrams whose corresponding colimits yield
![]() $X(\unicode[STIX]{x1D6E4}^{\prime \prime })$
and
$X(\unicode[STIX]{x1D6E4}^{\prime \prime })$
and
![]() $X(\unicode[STIX]{x1D6E4}^{\prime })$
, respectively.◻
$X(\unicode[STIX]{x1D6E4}^{\prime })$
, respectively.◻
Example 4.4. The following examples of pushout squares as given by Proposition 4.2 will be used below:
-
(1)
(4.5)
-
(2)
(4.6)
-
(3) Let
 $\unicode[STIX]{x1D6E4}$
be a ribbon (framed) graph which contains the graphas a subgraph and so that the central vertex has valency
$\unicode[STIX]{x1D6E4}$
be a ribbon (framed) graph which contains the graphas a subgraph and so that the central vertex has valency
 $4$
in
$4$
in
 $\unicode[STIX]{x1D6E4}$
. Let
$\unicode[STIX]{x1D6E4}$
. Let
 $\unicode[STIX]{x1D6E4}^{\prime }$
denote the ribbon (framed) graph obtained by removing the graphThen we have a pushout square
$\unicode[STIX]{x1D6E4}^{\prime }$
denote the ribbon (framed) graph obtained by removing the graphThen we have a pushout square (4.7)
(4.7)
-
(4) The pushout square
(4.8)is a special case of (4.7).
We use Proposition 4.2 to obtain localization sequences for topological Fukaya categories.
Proposition 4.9 (Localization).
Let
![]() $\unicode[STIX]{x1D6E4}$
be a ribbon graph and
$\unicode[STIX]{x1D6E4}$
be a ribbon graph and
![]() $\unicode[STIX]{x1D6E4}^{\prime }\subset \unicode[STIX]{x1D6E4}$
an open subgraph with complement
$\unicode[STIX]{x1D6E4}^{\prime }\subset \unicode[STIX]{x1D6E4}$
an open subgraph with complement
![]() $\unicode[STIX]{x1D6E4}^{\prime \prime }$
.
$\unicode[STIX]{x1D6E4}^{\prime \prime }$
.
-
(1) There is a canonical pushout square
(4.10)in
 $\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}}^{(2)})$
.
$\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}}^{(2)})$
.
-
(2) Assume that
 $\unicode[STIX]{x1D6E4}$
carries the structure of a framed graph. Then there is a lift of (4.10) to a pushout diagram of
$\unicode[STIX]{x1D6E4}$
carries the structure of a framed graph. Then there is a lift of (4.10) to a pushout diagram of
 $\mathbb{Z}$
-graded Fukaya categoriesin
$\mathbb{Z}$
-graded Fukaya categoriesin
 $\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
.
$\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
.
Proof. We treat the framed case; the ribbon case is analogous. By Proposition 4.2, we have a pushout square

Another application of Proposition 4.2 yields a pushout square

where
![]() $\unicode[STIX]{x1D6F9}$
denotes a disjoint union of copies of the corolla
$\unicode[STIX]{x1D6F9}$
denotes a disjoint union of copies of the corolla
again indexed by those half-edges in
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
which become internal in
$\unicode[STIX]{x1D6E4}^{\prime }$
which become internal in
![]() $\unicode[STIX]{x1D6E4}$
. We have
$\unicode[STIX]{x1D6E4}$
. We have
 $\operatorname{F}(\unicode[STIX]{x1D6F9})\simeq 0$
so that, using the universal property of the pushout (4.11), we may combine (4.11) and (4.12) to obtain a canonical diagram
$\operatorname{F}(\unicode[STIX]{x1D6F9})\simeq 0$
so that, using the universal property of the pushout (4.11), we may combine (4.11) and (4.12) to obtain a canonical diagram

The top and exterior square are pushouts so that, by [Reference LurieLur09, 4.4.2.1], the bottom square is a pushout square as well. To obtain the final statement, we note that, by the
![]() $2$
-Segal property of
$2$
-Segal property of
![]() $\operatorname{F}$
, we have an equivalence
$\operatorname{F}$
, we have an equivalence
 $\operatorname{F}(\overline{\unicode[STIX]{x1D6E4}^{\prime \prime }})\simeq \operatorname{F}(\text{}\underline{\unicode[STIX]{x1D6E4}^{\prime \prime }})$
.◻
$\operatorname{F}(\overline{\unicode[STIX]{x1D6E4}^{\prime \prime }})\simeq \operatorname{F}(\text{}\underline{\unicode[STIX]{x1D6E4}^{\prime \prime }})$
.◻
Remark 4.13. Note that the argument of Proposition 4.9 generalizes to any co(para)cyclic
![]() $2$
-Segal object
$2$
-Segal object
![]() $X$
with values in a pointed
$X$
with values in a pointed
![]() $\infty$
-category satisfying
$\infty$
-category satisfying
![]() $X^{0}\simeq 0$
.
$X^{0}\simeq 0$
.
Remark 4.14. Define
 $\operatorname{F}(\unicode[STIX]{x1D6E4}\;\text{on}\;\unicode[STIX]{x1D6E4}^{\prime })$
to be the full dg subcategory of
$\operatorname{F}(\unicode[STIX]{x1D6E4}\;\text{on}\;\unicode[STIX]{x1D6E4}^{\prime })$
to be the full dg subcategory of
![]() $\operatorname{F}(\unicode[STIX]{x1D6E4})$
spanned by the image of
$\operatorname{F}(\unicode[STIX]{x1D6E4})$
spanned by the image of
![]() $\operatorname{F}(\unicode[STIX]{x1D6E4}^{\prime })$
. We call
$\operatorname{F}(\unicode[STIX]{x1D6E4}^{\prime })$
. We call
 $\operatorname{F}(\unicode[STIX]{x1D6E4}\;\text{on}\;\unicode[STIX]{x1D6E4}^{\prime })$
the topological Fukaya category of
$\operatorname{F}(\unicode[STIX]{x1D6E4}\;\text{on}\;\unicode[STIX]{x1D6E4}^{\prime })$
the topological Fukaya category of
![]() $\unicode[STIX]{x1D6E4}$
with support in
$\unicode[STIX]{x1D6E4}$
with support in
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
. Then, in the terminology of § 2.2, we have an exact sequence
$\unicode[STIX]{x1D6E4}^{\prime }$
. Then, in the terminology of § 2.2, we have an exact sequence

which should be regarded as an analog of Thomason–Trobaugh’s proto-localization sequence for derived categories of perfect complexes in the context of algebraic
![]() $K$
-theory of schemes. It is an interesting question whether there is a general dévissage statement saying that
$K$
-theory of schemes. It is an interesting question whether there is a general dévissage statement saying that
 $H(\unicode[STIX]{x1D6E4}^{\prime })\rightarrow H(\operatorname{F}(\unicode[STIX]{x1D6E4}\;\text{on}\;\unicode[STIX]{x1D6E4}^{\prime }))$
is an equivalence for a suitable class of additive invariants
$H(\unicode[STIX]{x1D6E4}^{\prime })\rightarrow H(\operatorname{F}(\unicode[STIX]{x1D6E4}\;\text{on}\;\unicode[STIX]{x1D6E4}^{\prime }))$
is an equivalence for a suitable class of additive invariants
![]() $H$
. Lemma 4.21 can be regarded as the simplest instance of such a result.
$H$
. Lemma 4.21 can be regarded as the simplest instance of such a result.
4.2 A Mayer–Vietoris theorem
In this section, we use localization sequences for topological Fukaya categories to prove a Mayer–Vietoris theorem. The argument is inspired by similar techniques in the context of algebraic
![]() $K$
-theory for schemes [Reference Thomason and TrobaughTT90]. We focus on the
$K$
-theory for schemes [Reference Thomason and TrobaughTT90]. We focus on the
![]() $\mathbb{Z}$
-graded version but all results have obvious
$\mathbb{Z}$
-graded version but all results have obvious
![]() $\mathbb{Z}/2\mathbb{Z}$
-graded analogs that admit similar proofs.
$\mathbb{Z}/2\mathbb{Z}$
-graded analogs that admit similar proofs.
Definition 4.15. Let
 $H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a functor with values in a stable
$H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a functor with values in a stable
![]() $\infty$
-category
$\infty$
-category
![]() $C$
.
$C$
.
-
(1) We say
 $H$
is localizing if it preserves finite sums and exact sequences.
$H$
is localizing if it preserves finite sums and exact sequences. -
(2) The functor
 $H$
is called
$H$
is called
 $\mathbb{A}^{1}$
-homotopy invariant if, for every dg category
$\mathbb{A}^{1}$
-homotopy invariant if, for every dg category
 $A$
, the morphism is an
$A$
, the morphism is an $$\begin{eqnarray}A\longrightarrow A[t]\end{eqnarray}$$
$$\begin{eqnarray}A\longrightarrow A[t]\end{eqnarray}$$
 $H$
-equivalence (i.e. is mapped to an equivalence under
$H$
-equivalence (i.e. is mapped to an equivalence under
 $H$
). Here, the morphism
$H$
). Here, the morphism
 $A\rightarrow A[t]$
is defined as the tensor product of
$A\rightarrow A[t]$
is defined as the tensor product of
 $A$
with the morphism
$A$
with the morphism
 $k\rightarrow k[t]$
of
$k\rightarrow k[t]$
of
 $k$
-algebras, interpreted as a dg functor of dg categories with one object.
$k$
-algebras, interpreted as a dg functor of dg categories with one object.
Let
![]() $C$
be an
$C$
be an
![]() $\infty$
-category with finite colimits and let
$\infty$
-category with finite colimits and let
 $H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a functor, we have a canonical morphism
$H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a functor, we have a canonical morphism
 $$\begin{eqnarray}(HF)(\unicode[STIX]{x1D6E4})\longrightarrow H(F(\unicode[STIX]{x1D6E4}))\end{eqnarray}$$
$$\begin{eqnarray}(HF)(\unicode[STIX]{x1D6E4})\longrightarrow H(F(\unicode[STIX]{x1D6E4}))\end{eqnarray}$$
in
![]() $C$
which is obtained by applying
$C$
which is obtained by applying
![]() $H$
to the colimit cone over the diagram
$H$
to the colimit cone over the diagram
![]() $F\circ \unicode[STIX]{x1D6FF}$
.
$F\circ \unicode[STIX]{x1D6FF}$
.
Definition 4.17. We say a framed graph
![]() $\unicode[STIX]{x1D6E4}$
satisfies Mayer–Vietoris with respect to
$\unicode[STIX]{x1D6E4}$
satisfies Mayer–Vietoris with respect to
![]() $H$
if the morphism (4.16) is an equivalence. In other words, a framed graph
$H$
if the morphism (4.16) is an equivalence. In other words, a framed graph
![]() $\unicode[STIX]{x1D6E4}$
satisfies Mayer–Vietoris with respect to
$\unicode[STIX]{x1D6E4}$
satisfies Mayer–Vietoris with respect to
![]() $H$
, if
$H$
, if
![]() $H$
commutes with the state sum colimit parametrized by the incidence category of
$H$
commutes with the state sum colimit parametrized by the incidence category of
![]() $\unicode[STIX]{x1D6E4}$
.
$\unicode[STIX]{x1D6E4}$
.
Theorem 4.18 (Mayer–Vietoris).
Let
![]() $C$
be a stable
$C$
be a stable
![]() $\infty$
-category and let
$\infty$
-category and let
 $H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a localizing
$H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a localizing
![]() $\mathbb{A}^{1}$
-homotopy invariant functor. Then every framed graph satisfies Mayer–Vietoris with respect to
$\mathbb{A}^{1}$
-homotopy invariant functor. Then every framed graph satisfies Mayer–Vietoris with respect to
![]() $H$
.
$H$
.
Proof. The proof will use the results from § 4.3 below. Note that, by definition, every framed corolla satisfies Mayer–Vietoris. By Lemma 4.27, with respect to (4.5), and Lemma 4.25(2), we deduce that the graph
provided with any framing, satisfies Mayer–Vietoris. By Proposition 1.23, we may contract an internal edge to obtain that
satisfies Mayer–Vietoris. Similarly, by Lemma 4.27, with respect to (4.6), and Lemma 4.25(2), we obtain that the graph
with any framing, satisfies Mayer–Vietoris. Here, we again use Proposition 1.23 to contract the internal edge of the graph in the bottom right corner of (4.6).
Let
![]() $\unicode[STIX]{x1D6E4}$
be any framed graph. Since
$\unicode[STIX]{x1D6E4}$
be any framed graph. Since
![]() $H$
commutes with finite sums, we may assume that
$H$
commutes with finite sums, we may assume that
![]() $\unicode[STIX]{x1D6E4}$
is connected. By Proposition 1.23,
$\unicode[STIX]{x1D6E4}$
is connected. By Proposition 1.23,
![]() $\unicode[STIX]{x1D6E4}$
satisfies Mayer–Vietoris if and only if the graph
$\unicode[STIX]{x1D6E4}$
satisfies Mayer–Vietoris if and only if the graph
![]() $\unicode[STIX]{x1D6E4}^{\prime }$
with one vertex obtained by collapsing a maximal forest in
$\unicode[STIX]{x1D6E4}^{\prime }$
with one vertex obtained by collapsing a maximal forest in
![]() $\unicode[STIX]{x1D6E4}$
satisfies Mayer–Vietoris. Therefore, we may assume that
$\unicode[STIX]{x1D6E4}$
satisfies Mayer–Vietoris. Therefore, we may assume that
![]() $\unicode[STIX]{x1D6E4}$
has one vertex
$\unicode[STIX]{x1D6E4}$
has one vertex
![]() $v$
. We now proceed inductively on the number of loops in
$v$
. We now proceed inductively on the number of loops in
![]() $\unicode[STIX]{x1D6E4}$
. If
$\unicode[STIX]{x1D6E4}$
. If
![]() $\unicode[STIX]{x1D6E4}$
does not have any loops then
$\unicode[STIX]{x1D6E4}$
does not have any loops then
![]() $\unicode[STIX]{x1D6E4}$
is a corolla and satisfies Mayer–Vietoris. Assume
$\unicode[STIX]{x1D6E4}$
is a corolla and satisfies Mayer–Vietoris. Assume
![]() $\unicode[STIX]{x1D6E4}$
has a loop
$\unicode[STIX]{x1D6E4}$
has a loop
![]() $l$
. We isolate the loop
$l$
. We isolate the loop
![]() $l$
by blowing up two edges so that we obtain a graph
$l$
by blowing up two edges so that we obtain a graph
![]() $\widetilde{\unicode[STIX]{x1D6E4}}$
with three vertices that contains the subgraph
$\widetilde{\unicode[STIX]{x1D6E4}}$
with three vertices that contains the subgraph
with loop
![]() $l$
, satisfies the conditions of Example 4.4(3), and
$l$
, satisfies the conditions of Example 4.4(3), and
![]() $\unicode[STIX]{x1D6E4}$
is obtained from
$\unicode[STIX]{x1D6E4}$
is obtained from
![]() $\widetilde{\unicode[STIX]{x1D6E4}}$
by contracting the two internal edges. We now apply the induction hypothesis, Lemma 4.27 with respect to (4.7), and Lemma 4.25(1) to deduce that
$\widetilde{\unicode[STIX]{x1D6E4}}$
by contracting the two internal edges. We now apply the induction hypothesis, Lemma 4.27 with respect to (4.7), and Lemma 4.25(1) to deduce that
![]() $\widetilde{\unicode[STIX]{x1D6E4}}$
and hence, by Proposition 1.23,
$\widetilde{\unicode[STIX]{x1D6E4}}$
and hence, by Proposition 1.23,
![]() $\unicode[STIX]{x1D6E4}$
satisfy Mayer–Vietoris, concluding the argument.◻
$\unicode[STIX]{x1D6E4}$
satisfy Mayer–Vietoris, concluding the argument.◻
Remark 4.19. Let
![]() $k$
be a field of characteristic
$k$
be a field of characteristic
![]() $0$
. An example of a localizing functor for which Mayer–Vietoris fails (since
$0$
. An example of a localizing functor for which Mayer–Vietoris fails (since
![]() $\mathbb{A}^{1}$
-homotopy invariance does not hold) is given by Hochschild homology. Applying
$\mathbb{A}^{1}$
-homotopy invariance does not hold) is given by Hochschild homology. Applying
 $HH_{\ast }\circ j_{!}F$
to the square (4.5), we obtain
$HH_{\ast }\circ j_{!}F$
to the square (4.5), we obtain

where the left vertical morphism becomes an equivalence by Proposition 4.20. However, the right vertical morphism is not an equivalence: by the Hochschild–Kostant–Rosenberg theorem, we have
 $HH_{1}(k[t])\cong k[t]$
while
$HH_{1}(k[t])\cong k[t]$
while
 $HH_{1}(k)\cong 0$
. In this situation, replacing Hochschild homology by periodic cyclic homology leads to an
$HH_{1}(k)\cong 0$
. In this situation, replacing Hochschild homology by periodic cyclic homology leads to an
![]() $\mathbb{A}^{1}$
-homotopy invariant functor that therefore satisfies Mayer–Vietoris.
$\mathbb{A}^{1}$
-homotopy invariant functor that therefore satisfies Mayer–Vietoris.
4.3 Lemmas
We collect technical results for the proof of the Mayer–Vietoris theorem.
Proposition 4.20. Let
![]() $C$
be a stable
$C$
be a stable
![]() $\infty$
-category and let
$\infty$
-category and let
 $H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a localizing functor. Then the coparacyclic object
$H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a localizing functor. Then the coparacyclic object
 $$\begin{eqnarray}HF:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\longrightarrow C\end{eqnarray}$$
$$\begin{eqnarray}HF:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\longrightarrow C\end{eqnarray}$$
is
![]() $1$
-Segal.
$1$
-Segal.
Proof. We have to show that, for every
![]() $n\geqslant 1$
, the natural map
$n\geqslant 1$
, the natural map
 $$\begin{eqnarray}H(\operatorname{F}^{\{0,1\}})\amalg H(\operatorname{F}^{\{1,2\}})\amalg \ldots \amalg H(\operatorname{F}^{\{n-1,n\}})\rightarrow H(\operatorname{F}^{\{0,1,\ldots ,n\}})\end{eqnarray}$$
$$\begin{eqnarray}H(\operatorname{F}^{\{0,1\}})\amalg H(\operatorname{F}^{\{1,2\}})\amalg \ldots \amalg H(\operatorname{F}^{\{n-1,n\}})\rightarrow H(\operatorname{F}^{\{0,1,\ldots ,n\}})\end{eqnarray}$$
is an equivalence in
![]() $C$
. We have a diagram in
$C$
. We have a diagram in
 $\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
$\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$

with exact rows. After applying
![]() $H$
, the rows stay exact, and
$H$
, the rows stay exact, and
![]() $H(f)$
must be an equivalence, since its cofiber is
$H(f)$
must be an equivalence, since its cofiber is
![]() $0$
. We now proceed by induction on
$0$
. We now proceed by induction on
![]() $n$
.◻
$n$
.◻
Lemma 4.21. Let
![]() $k[\unicode[STIX]{x1D6FF}]$
denote the differential
$k[\unicode[STIX]{x1D6FF}]$
denote the differential
![]() $\mathbb{Z}$
-graded
$\mathbb{Z}$
-graded
![]() $k$
-algebra generated by
$k$
-algebra generated by
![]() $\unicode[STIX]{x1D6FF}$
in some degree with relation
$\unicode[STIX]{x1D6FF}$
in some degree with relation
![]() $\unicode[STIX]{x1D6FF}^{2}=0$
and zero differential. Let
$\unicode[STIX]{x1D6FF}^{2}=0$
and zero differential. Let
![]() $A$
be a dg category and consider a pushout diagram
$A$
be a dg category and consider a pushout diagram

so that
![]() $A^{\unicode[STIX]{x1D6FF}}$
is obtained from
$A^{\unicode[STIX]{x1D6FF}}$
is obtained from
![]() $A$
by adjoining the endomorphism
$A$
by adjoining the endomorphism
![]() $\unicode[STIX]{x1D6FF}$
to a fixed object in
$\unicode[STIX]{x1D6FF}$
to a fixed object in
![]() $A$
. Then, for any localizing
$A$
. Then, for any localizing
![]() $\mathbb{A}^{1}$
-homotopy invariant
$\mathbb{A}^{1}$
-homotopy invariant
 $H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
, the morphism
$H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
, the morphism
![]() $H(i)$
is an equivalence.
$H(i)$
is an equivalence.
Proof. We may extend (4.22) to the diagram

in which both squares are pushout squares so that
 $pi\simeq \operatorname{id}_{A}$
. We will construct a commutative diagram
$pi\simeq \operatorname{id}_{A}$
. We will construct a commutative diagram

in
 $\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
, where
$\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
, where
![]() $\operatorname{ev}_{0}$
and
$\operatorname{ev}_{0}$
and
![]() $\operatorname{ev}_{1}$
are
$\operatorname{ev}_{1}$
are
![]() $H$
-equivalences. This will imply that
$H$
-equivalences. This will imply that
![]() $i\,\circ \,p$
is an
$i\,\circ \,p$
is an
![]() $H$
-equivalence so that the diagram exhibits
$H$
-equivalence so that the diagram exhibits
 $p:A^{\unicode[STIX]{x1D6FF}}\rightarrow A$
as an
$p:A^{\unicode[STIX]{x1D6FF}}\rightarrow A$
as an
![]() $\mathbb{A}^{1}$
-homotopy inverse of
$\mathbb{A}^{1}$
-homotopy inverse of
 $i:A\rightarrow A^{\unicode[STIX]{x1D6FF}}$
. In particular, we have that
$i:A\rightarrow A^{\unicode[STIX]{x1D6FF}}$
. In particular, we have that
![]() $i$
is an
$i$
is an
![]() $H$
-equivalence.
$H$
-equivalence.
To construct (4.24), consider the morphism
 $\unicode[STIX]{x1D706}:k[\unicode[STIX]{x1D6FF}]\rightarrow k[\unicode[STIX]{x1D6FF},t]$
determined by
$\unicode[STIX]{x1D706}:k[\unicode[STIX]{x1D6FF}]\rightarrow k[\unicode[STIX]{x1D6FF},t]$
determined by
 $\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}t$
. Further, let
$\unicode[STIX]{x1D706}(\unicode[STIX]{x1D6FF})=\unicode[STIX]{x1D6FF}t$
. Further, let
 $g:k[\unicode[STIX]{x1D6FF},t]\rightarrow A^{\unicode[STIX]{x1D6FF}}[t]$
be the morphism obtained by tensoring
$g:k[\unicode[STIX]{x1D6FF},t]\rightarrow A^{\unicode[STIX]{x1D6FF}}[t]$
be the morphism obtained by tensoring
 $k[\unicode[STIX]{x1D6FF}]\rightarrow A^{\unicode[STIX]{x1D6FF}}$
with
$k[\unicode[STIX]{x1D6FF}]\rightarrow A^{\unicode[STIX]{x1D6FF}}$
with
![]() $k[t]$
. Further, let
$k[t]$
. Further, let
 $f:A\rightarrow A^{\unicode[STIX]{x1D6FF}}[t]$
be the composite of the bottom horizontal morphisms in the diagram
$f:A\rightarrow A^{\unicode[STIX]{x1D6FF}}[t]$
be the composite of the bottom horizontal morphisms in the diagram

where all morphisms are the apparent ones. By construction, the above morphisms fit into a cone diagram

that determines the dashed morphism
![]() $h$
(up to contractible choice). It is now immediate to verify that the morphism
$h$
(up to contractible choice). It is now immediate to verify that the morphism
![]() $h$
fits into a diagram of the form (4.24), where
$h$
fits into a diagram of the form (4.24), where
![]() $\operatorname{ev}_{0}$
and
$\operatorname{ev}_{0}$
and
![]() $\operatorname{ev}_{1}$
are the morphisms obtained by applying
$\operatorname{ev}_{1}$
are the morphisms obtained by applying
![]() $A^{\unicode[STIX]{x1D6FF}}\otimes -$
to the morphisms
$A^{\unicode[STIX]{x1D6FF}}\otimes -$
to the morphisms
 $k[t]\rightarrow k,t\mapsto 0$
, and
$k[t]\rightarrow k,t\mapsto 0$
, and
 $k[t]\rightarrow k,t\mapsto 1$
, respectively.◻
$k[t]\rightarrow k,t\mapsto 1$
, respectively.◻
Lemma 4.25. Let
![]() $C$
be a stable
$C$
be a stable
![]() $\infty$
-category, and let
$\infty$
-category, and let
 $H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a localizing functor. Suppose
$H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a localizing functor. Suppose

is a pushout diagram in
![]() $P(\unicode[STIX]{x1D6EC}_{\infty })$
that stays a pushout diagram after application of
$P(\unicode[STIX]{x1D6EC}_{\infty })$
that stays a pushout diagram after application of
 $H\circ j_{!}\operatorname{F}$
.
$H\circ j_{!}\operatorname{F}$
.
-
(1) Assume that
 $\unicode[STIX]{x1D6E4}_{1}$
,
$\unicode[STIX]{x1D6E4}_{1}$
,
 $\unicode[STIX]{x1D6E4}_{2}$
, and
$\unicode[STIX]{x1D6E4}_{2}$
, and
 $\unicode[STIX]{x1D6E4}_{3}$
satisfy Mayer–Vietoris. Then
$\unicode[STIX]{x1D6E4}_{3}$
satisfy Mayer–Vietoris. Then
 $\unicode[STIX]{x1D6E4}_{4}$
satisfies Mayer–Vietoris.
$\unicode[STIX]{x1D6E4}_{4}$
satisfies Mayer–Vietoris. -
(2) Suppose
 $F(\unicode[STIX]{x1D6E4}_{3})\simeq 0$
and assume that any two among the ribbon graphs
$F(\unicode[STIX]{x1D6E4}_{3})\simeq 0$
and assume that any two among the ribbon graphs
 $\unicode[STIX]{x1D6E4}_{1}$
,
$\unicode[STIX]{x1D6E4}_{1}$
,
 $\unicode[STIX]{x1D6E4}_{2}$
,
$\unicode[STIX]{x1D6E4}_{2}$
,
 $\unicode[STIX]{x1D6E4}_{4}$
satisfy Mayer–Vietoris. Then all ribbon graphs in (4.26) satisfy Mayer–Vietoris.
$\unicode[STIX]{x1D6E4}_{4}$
satisfy Mayer–Vietoris. Then all ribbon graphs in (4.26) satisfy Mayer–Vietoris.
Proof. Since
 $H\circ j_{!}\operatorname{F}$
is a left extension of
$H\circ j_{!}\operatorname{F}$
is a left extension of
 $H\operatorname{F}:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow C$
along
$H\operatorname{F}:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow C$
along
 $j:\unicode[STIX]{x1D6EC}_{\infty }\rightarrow P(\unicode[STIX]{x1D6EC}_{\infty })$
, we have a canonical morphism
$j:\unicode[STIX]{x1D6EC}_{\infty }\rightarrow P(\unicode[STIX]{x1D6EC}_{\infty })$
, we have a canonical morphism
 $\unicode[STIX]{x1D709}:j_{!}(H\operatorname{F})\rightarrow H\circ j_{!}\operatorname{F}$
in
$\unicode[STIX]{x1D709}:j_{!}(H\operatorname{F})\rightarrow H\circ j_{!}\operatorname{F}$
in
 $\operatorname{Fun}(P(\unicode[STIX]{x1D6EC}_{\infty }),C)$
which, evaluated at an object of the form
$\operatorname{Fun}(P(\unicode[STIX]{x1D6EC}_{\infty }),C)$
which, evaluated at an object of the form
![]() $\unicode[STIX]{x1D6EC}_{\infty }(\unicode[STIX]{x1D6E4})$
, yields the canonical morphism
$\unicode[STIX]{x1D6EC}_{\infty }(\unicode[STIX]{x1D6E4})$
, yields the canonical morphism
 $$\begin{eqnarray}(H\operatorname{F})(\unicode[STIX]{x1D6E4})\rightarrow H(\operatorname{F}(\unicode[STIX]{x1D6E4}))\end{eqnarray}$$
$$\begin{eqnarray}(H\operatorname{F})(\unicode[STIX]{x1D6E4})\rightarrow H(\operatorname{F}(\unicode[STIX]{x1D6E4}))\end{eqnarray}$$
in
![]() $C$
of (4.16). We give the argument for (1). Applying
$C$
of (4.16). We give the argument for (1). Applying
![]() $\unicode[STIX]{x1D709}$
to the square (4.26), we obtain a morphism of pushout squares in
$\unicode[STIX]{x1D709}$
to the square (4.26), we obtain a morphism of pushout squares in
![]() $C$
that is an equivalence on all vertices except for the bottom right vertex
$C$
that is an equivalence on all vertices except for the bottom right vertex
 $$\begin{eqnarray}(H\operatorname{F})(\unicode[STIX]{x1D6E4}_{4})\rightarrow H(\operatorname{F}(\unicode[STIX]{x1D6E4}_{4})).\end{eqnarray}$$
$$\begin{eqnarray}(H\operatorname{F})(\unicode[STIX]{x1D6E4}_{4})\rightarrow H(\operatorname{F}(\unicode[STIX]{x1D6E4}_{4})).\end{eqnarray}$$
But pushouts of equivalences are equivalences, so that this morphism must be an equivalence as well. The statement of (2) follows similarly.◻
Lemma 4.27. Let
 $H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a localizing
$H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a localizing
![]() $\mathbb{A}^{1}$
-homotopy invariant. The pushout diagrams (4.5), (4.6), and (4.7) (cf. Proposition 4.4), with
$\mathbb{A}^{1}$
-homotopy invariant. The pushout diagrams (4.5), (4.6), and (4.7) (cf. Proposition 4.4), with
 $X=j:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow P(\unicode[STIX]{x1D6EC}_{\infty })$
, stay pushout diagrams after application of
$X=j:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow P(\unicode[STIX]{x1D6EC}_{\infty })$
, stay pushout diagrams after application of
 $H\circ j_{!}\operatorname{F}$
.
$H\circ j_{!}\operatorname{F}$
.
Proof. (1) Applying
![]() $j_{!}\operatorname{F}$
to (4.5), with
$j_{!}\operatorname{F}$
to (4.5), with
![]() $X=j$
, we obtain, by Example 3.4, the pushout diagram
$X=j$
, we obtain, by Example 3.4, the pushout diagram

where
![]() $f$
is a
$f$
is a
![]() $1$
-Segal map so that, by Proposition 4.20,
$1$
-Segal map so that, by Proposition 4.20,
![]() $H(f)$
is an equivalence. The morphism
$H(f)$
is an equivalence. The morphism
![]() $H(f^{\prime })$
is an equivalence, by the argument of [Reference TabuadaTab12, Lemma 4.1], since
$H(f^{\prime })$
is an equivalence, by the argument of [Reference TabuadaTab12, Lemma 4.1], since
![]() $H$
is
$H$
is
![]() $\mathbb{A}^{1}$
-homotopy invariant. Therefore, the square remains a pushout square upon applying
$\mathbb{A}^{1}$
-homotopy invariant. Therefore, the square remains a pushout square upon applying
![]() $H$
. The statement for (4.6) follows from an argument similar to (2) below, but easier.
$H$
. The statement for (4.6) follows from an argument similar to (2) below, but easier.
(2) Applying
![]() $j_{!}\operatorname{F}$
to (4.7), with
$j_{!}\operatorname{F}$
to (4.7), with
![]() $X=j$
, we obtain the pushout square
$X=j$
, we obtain the pushout square

which is the top rectangle of the diagram

in which all squares are pushout squares, the exterior square is given by (4.8) with
![]() $X=\operatorname{F}$
. We use the notation from Lemma 4.21 with
$X=\operatorname{F}$
. We use the notation from Lemma 4.21 with
 $|\unicode[STIX]{x1D6FF}_{1}|=1-2r$
,
$|\unicode[STIX]{x1D6FF}_{1}|=1-2r$
,
 $|\unicode[STIX]{x1D6FF}_{2}|=1+2r$
, where
$|\unicode[STIX]{x1D6FF}_{2}|=1+2r$
, where
![]() $r$
is the winding number of the loop in the top right framed graph. The morphisms
$r$
is the winding number of the loop in the top right framed graph. The morphisms
![]() $H(f)$
and
$H(f)$
and
![]() $H(f^{\prime })$
are equivalences by Lemma 4.21. The morphism
$H(f^{\prime })$
are equivalences by Lemma 4.21. The morphism
![]() $g$
is quasi-fully faithful by explicit verification (cf. Example 3.11), and hence
$g$
is quasi-fully faithful by explicit verification (cf. Example 3.11), and hence
![]() $g^{\prime }$
is quasi-fully faithful by Lemma 2.4. Therefore, the bottom right square and the right rectangle are exact sequences in
$g^{\prime }$
is quasi-fully faithful by Lemma 2.4. Therefore, the bottom right square and the right rectangle are exact sequences in
 $\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
and thus stay exact after applying
$\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})$
and thus stay exact after applying
![]() $H$
. But this implies that the top right square stays a pushout square after applying
$H$
. But this implies that the top right square stays a pushout square after applying
![]() $H$
. Hence the top rectangle stays a pushout diagram after applying
$H$
. Hence the top rectangle stays a pushout diagram after applying
![]() $H$
as claimed.◻
$H$
as claimed.◻
5 Delooping of paracyclic 1-Segal objects
The methods used in this section are inspired by similar techniques used in [Reference LurieLur09, ch. 6], specifically § 6.1, which develops an
![]() $\infty$
-categorical theory of effective groupoid objects. Let
$\infty$
-categorical theory of effective groupoid objects. Let
![]() $C$
be a stable
$C$
be a stable
![]() $\infty$
-category and let
$\infty$
-category and let
 $H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a localizing
$H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\rightarrow C$
be a localizing
![]() $\mathbb{A}^{1}$
-homotopy invariant functor. Given a framed graph
$\mathbb{A}^{1}$
-homotopy invariant functor. Given a framed graph
![]() $\unicode[STIX]{x1D6E4}$
, Theorem 4.18 reduces the calculation of
$\unicode[STIX]{x1D6E4}$
, Theorem 4.18 reduces the calculation of
 $H(F(\unicode[STIX]{x1D6E4}))$
to a state sum of the coparacyclic object
$H(F(\unicode[STIX]{x1D6E4}))$
to a state sum of the coparacyclic object
 $$\begin{eqnarray}HF:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\longrightarrow C,\end{eqnarray}$$
$$\begin{eqnarray}HF:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\longrightarrow C,\end{eqnarray}$$
which, by Proposition 4.20, is
![]() $1$
-Segal. We establish a general result in order to evaluate this state sum explicitly.
$1$
-Segal. We establish a general result in order to evaluate this state sum explicitly.
Theorem 5.1. Let
![]() $C$
be a stable
$C$
be a stable
![]() $\infty$
-category with colimits and let
$\infty$
-category with colimits and let
 $X:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow C$
be a coparacyclic
$X:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow C$
be a coparacyclic
![]() $1$
-Segal object with
$1$
-Segal object with
![]() $X^{0}\simeq 0$
. Let
$X^{0}\simeq 0$
. Let
![]() $\unicode[STIX]{x1D6E4}$
be a framed graph modelling a stable framed marked surface
$\unicode[STIX]{x1D6E4}$
be a framed graph modelling a stable framed marked surface
![]() $(S,M)$
. Then we have an equivalence in
$(S,M)$
. Then we have an equivalence in
![]() $C$
$C$
 $$\begin{eqnarray}X(\unicode[STIX]{x1D6E4})\simeq \unicode[STIX]{x1D6FA}(X^{1})(S/M),\end{eqnarray}$$
$$\begin{eqnarray}X(\unicode[STIX]{x1D6E4})\simeq \unicode[STIX]{x1D6FA}(X^{1})(S/M),\end{eqnarray}$$
where the right-hand side is defined using (1.31), and
 $\unicode[STIX]{x1D6FA}=[-1]$
denotes the loop functor on
$\unicode[STIX]{x1D6FA}=[-1]$
denotes the loop functor on
![]() $C$
.
$C$
.
The results of § 1.4 reduce the proof of Theorem 5.1 to the following statement.
Proposition 5.2 (Delooping).
Let
![]() $C$
be a stable
$C$
be a stable
![]() $\infty$
-category. Let
$\infty$
-category. Let
![]() $C$
be a stable
$C$
be a stable
![]() $\infty$
-category with colimits. Let
$\infty$
-category with colimits. Let
 $X:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow C$
be a coparacyclic
$X:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow C$
be a coparacyclic
![]() $1$
-Segal object with
$1$
-Segal object with
![]() $X^{0}\simeq 0$
. Then there is an equivalence
$X^{0}\simeq 0$
. Then there is an equivalence
 $$\begin{eqnarray}X\simeq L_{\unicode[STIX]{x1D6FA}(X^{1})},\end{eqnarray}$$
$$\begin{eqnarray}X\simeq L_{\unicode[STIX]{x1D6FA}(X^{1})},\end{eqnarray}$$
where the right-hand side denotes the coparacyclic object of (1.33).
Remark 5.3. Let
![]() $M$
be a monoid object in an abelian category
$M$
be a monoid object in an abelian category
![]() $A$
(equipped with the Cartesian monoidal structure so that the tensor product is given by the direct sum). Then it is easy to see that the monoid structure must be given by the unit
$A$
(equipped with the Cartesian monoidal structure so that the tensor product is given by the direct sum). Then it is easy to see that the monoid structure must be given by the unit
 $0\longrightarrow M$
and multiplication
$0\longrightarrow M$
and multiplication
 $M\otimes M\rightarrow M$
given by the sum. In particular,
$M\otimes M\rightarrow M$
given by the sum. In particular,
![]() $M$
is automatically a group object with inverse given by
$M$
is automatically a group object with inverse given by
 $-\operatorname{id}:M\rightarrow M$
. Proposition 5.2 is an
$-\operatorname{id}:M\rightarrow M$
. Proposition 5.2 is an
![]() $\infty$
-categorical analog of this statement, where the abelian category
$\infty$
-categorical analog of this statement, where the abelian category
![]() $A$
gets replaced by the stable
$A$
gets replaced by the stable
![]() $\infty$
-category
$\infty$
-category
![]() $C^{\operatorname{op}}$
. In this context, the statement becomes even nicer since we can describe the group object in terms of the delooping
$C^{\operatorname{op}}$
. In this context, the statement becomes even nicer since we can describe the group object in terms of the delooping
![]() $\unicode[STIX]{x1D6FA}X^{1}$
. We also note that the statement of Proposition 5.2 becomes false if we replace the paracyclic category by the cyclic category: there may be various inequivalent cocyclic structures on a cosimplicial
$\unicode[STIX]{x1D6FA}X^{1}$
. We also note that the statement of Proposition 5.2 becomes false if we replace the paracyclic category by the cyclic category: there may be various inequivalent cocyclic structures on a cosimplicial
![]() $1$
-Segal object.
$1$
-Segal object.
We establish some preparatory results for the proof of Proposition 5.2.
Proposition 5.4. Let
![]() $C$
be a stable
$C$
be a stable
![]() $\infty$
-category and let
$\infty$
-category and let
 $X:\operatorname{N}(\unicode[STIX]{x1D6E5})\rightarrow C$
be a cosimplicial
$X:\operatorname{N}(\unicode[STIX]{x1D6E5})\rightarrow C$
be a cosimplicial
![]() $1$
-Segal object. Then
$1$
-Segal object. Then
 $\lim _{\operatorname{N}(\unicode[STIX]{x1D6E5})}X\simeq \unicode[STIX]{x1D6FA}X_{1}$
.
$\lim _{\operatorname{N}(\unicode[STIX]{x1D6E5})}X\simeq \unicode[STIX]{x1D6FA}X_{1}$
.
Proof. Let
![]() ${\mathcal{I}}$
be the full subcategory of
${\mathcal{I}}$
be the full subcategory of
![]() $\unicode[STIX]{x1D6E5}$
spanned by the objects
$\unicode[STIX]{x1D6E5}$
spanned by the objects
![]() $[0]$
and
$[0]$
and
![]() $[1]$
. Let
$[1]$
. Let
![]() ${\mathcal{I}}_{+}$
denote the category obtained from
${\mathcal{I}}_{+}$
denote the category obtained from
![]() ${\mathcal{I}}$
by adjoining an initial object. We have a diagram of right Kan extension functors
${\mathcal{I}}$
by adjoining an initial object. We have a diagram of right Kan extension functors

which commutes up to equivalence. We show that
![]() $X$
is a right Kan extension of
$X$
is a right Kan extension of
![]() $X_{|\operatorname{N}({\mathcal{I}})}$
. The statement of the proposition then follows immediately from (5.5).
$X_{|\operatorname{N}({\mathcal{I}})}$
. The statement of the proposition then follows immediately from (5.5).
Since
![]() $X^{0}\simeq 0$
, the cosimplicial object
$X^{0}\simeq 0$
, the cosimplicial object
![]() $X$
is a right Kan extension of
$X$
is a right Kan extension of
![]() $X_{|\operatorname{N}({\mathcal{I}})}$
if and only if, for every
$X_{|\operatorname{N}({\mathcal{I}})}$
if and only if, for every
![]() $n\geqslant 2$
, the maps
$n\geqslant 2$
, the maps
 $X_{n}\rightarrow X_{1}$
induced by the
$X_{n}\rightarrow X_{1}$
induced by the
![]() $n$
surjective maps
$n$
surjective maps
 $p_{i}:[n]\mapsto [1]$
exhibit
$p_{i}:[n]\mapsto [1]$
exhibit
![]() $X^{n}$
as a product
$X^{n}$
as a product
 $$\begin{eqnarray}X^{n}\simeq X^{1}\times X^{1}\times \cdots \times X^{1},\end{eqnarray}$$
$$\begin{eqnarray}X^{n}\simeq X^{1}\times X^{1}\times \cdots \times X^{1},\end{eqnarray}$$
with
![]() $n$
factors. This can be verified in the homotopy category
$n$
factors. This can be verified in the homotopy category
![]() $\operatorname{h}\!C$
which is additive. Since
$\operatorname{h}\!C$
which is additive. Since
![]() $X$
is
$X$
is
![]() $1$
-Segal, the maps
$1$
-Segal, the maps
 $[1]\rightarrow [n]$
given by the inclusions
$[1]\rightarrow [n]$
given by the inclusions
 $q_{j}:\{j,j+1\}\subset [n]$
exhibit
$q_{j}:\{j,j+1\}\subset [n]$
exhibit
![]() $X^{n}$
as a coproduct of
$X^{n}$
as a coproduct of
![]() $n$
copies of
$n$
copies of
![]() $X^{1}$
. The morphisms
$X^{1}$
. The morphisms
 $X^{1}\rightarrow X^{1}$
induced by
$X^{1}\rightarrow X^{1}$
induced by
![]() $p_{i}\circ q_{j}$
are homotopic to the identity on
$p_{i}\circ q_{j}$
are homotopic to the identity on
![]() $X_{1}$
if
$X_{1}$
if
![]() $i=j$
and zero if
$i=j$
and zero if
![]() $i\neq j$
. This implies the equivalence (5.6).◻
$i\neq j$
. This implies the equivalence (5.6).◻
Let
 $i:\unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D6EC}_{\infty }$
denote the natural inclusion functor.
$i:\unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D6EC}_{\infty }$
denote the natural inclusion functor.
Lemma 5.7. The opposite inclusion functor
 $$\begin{eqnarray}\operatorname{N}(i)^{\operatorname{op}}:\operatorname{N}(\unicode[STIX]{x1D6E5})^{\operatorname{op}}\longrightarrow \operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })^{\operatorname{op}}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{N}(i)^{\operatorname{op}}:\operatorname{N}(\unicode[STIX]{x1D6E5})^{\operatorname{op}}\longrightarrow \operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })^{\operatorname{op}}\end{eqnarray}$$
is cofinal.
Proof. By [Reference LurieLur09, 4.1.3.1], it suffices to show that, for every object
![]() $\langle m\rangle$
of
$\langle m\rangle$
of
![]() $\unicode[STIX]{x1D6EC}_{\infty }$
, the nerve of the category
$\unicode[STIX]{x1D6EC}_{\infty }$
, the nerve of the category
![]() $\unicode[STIX]{x1D6E5}/\langle m\rangle$
has a contractible geometric realization. The nerve of the category
$\unicode[STIX]{x1D6E5}/\langle m\rangle$
has a contractible geometric realization. The nerve of the category
![]() $\unicode[STIX]{x1D6E5}/\langle m\rangle$
can be identified with the simplicial set
$\unicode[STIX]{x1D6E5}/\langle m\rangle$
can be identified with the simplicial set
 $$\begin{eqnarray}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{\infty }}(-,\langle m\rangle )_{|\unicode[STIX]{x1D6E5}^{\operatorname{op}}}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Hom}_{\unicode[STIX]{x1D6EC}_{\infty }}(-,\langle m\rangle )_{|\unicode[STIX]{x1D6E5}^{\operatorname{op}}}\end{eqnarray}$$
whose geometric realization is homeomorphic to
 $|\unicode[STIX]{x1D6E5}^{m}|\times \mathbb{R}$
(cf. [Reference Fiedorowicz and LodayFL91]).◻
$|\unicode[STIX]{x1D6E5}^{m}|\times \mathbb{R}$
(cf. [Reference Fiedorowicz and LodayFL91]).◻
Corollary 5.8. Let
![]() $C$
be a stable
$C$
be a stable
![]() $\infty$
-category and let
$\infty$
-category and let
 $X:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow C$
be a coparacyclic
$X:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow C$
be a coparacyclic
![]() $1$
-Segal object. Then
$1$
-Segal object. Then
 $\lim _{\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })}X\simeq \unicode[STIX]{x1D6FA}X_{1}$
.
$\lim _{\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })}X\simeq \unicode[STIX]{x1D6FA}X_{1}$
.
We denote by
![]() $\unicode[STIX]{x1D6EC}_{\infty }^{+}$
the augmented paracyclic category obtained from
$\unicode[STIX]{x1D6EC}_{\infty }^{+}$
the augmented paracyclic category obtained from
![]() $\unicode[STIX]{x1D6EC}_{\infty }$
by adjoining an initial object
$\unicode[STIX]{x1D6EC}_{\infty }$
by adjoining an initial object
![]() $\emptyset$
. Consider the full subcategory
$\emptyset$
. Consider the full subcategory
 $j:\operatorname{N}(J)\subset \operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty }^{+})$
spanned by the objects
$j:\operatorname{N}(J)\subset \operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty }^{+})$
spanned by the objects
![]() $\emptyset$
and
$\emptyset$
and
![]() $\langle 0\rangle$
and the map
$\langle 0\rangle$
and the map
 $p:\operatorname{N}(J)\rightarrow \unicode[STIX]{x1D6E5}^{1}$
which maps the unique edge
$p:\operatorname{N}(J)\rightarrow \unicode[STIX]{x1D6E5}^{1}$
which maps the unique edge
 $\emptyset \rightarrow \langle 0\rangle$
to
$\emptyset \rightarrow \langle 0\rangle$
to
![]() $\{0,1\}$
.
$\{0,1\}$
.
Proposition 5.9. Let
![]() $C$
be a stable
$C$
be a stable
![]() $\infty$
-category and let
$\infty$
-category and let
 $X:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow C$
be a coparacyclic
$X:\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow C$
be a coparacyclic
![]() $1$
-Segal object with
$1$
-Segal object with
![]() $X^{0}\simeq 0$
. Let
$X^{0}\simeq 0$
. Let
![]() $X^{+}$
denote the limit cone of
$X^{+}$
denote the limit cone of
![]() $X$
, i.e. the right Kan extension of
$X$
, i.e. the right Kan extension of
![]() $X$
along
$X$
along
 $\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow \operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty }^{+})$
. Then there is an equivalence
$\operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })\rightarrow \operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty }^{+})$
. Then there is an equivalence
 $$\begin{eqnarray}X\simeq j_{!}(p^{\ast }(\unicode[STIX]{x1D6FA}(X^{1})\longrightarrow 0))\end{eqnarray}$$
$$\begin{eqnarray}X\simeq j_{!}(p^{\ast }(\unicode[STIX]{x1D6FA}(X^{1})\longrightarrow 0))\end{eqnarray}$$
of coparacyclic objects.
Proof. By Proposition 5.8, we have
 $$\begin{eqnarray}X^{+}(\emptyset )\simeq \unicode[STIX]{x1D6FA}(X^{1})\end{eqnarray}$$
$$\begin{eqnarray}X^{+}(\emptyset )\simeq \unicode[STIX]{x1D6FA}(X^{1})\end{eqnarray}$$
and by assumption
 $X^{+}(\langle 0\rangle )\simeq 0$
so that we may exhibit
$X^{+}(\langle 0\rangle )\simeq 0$
so that we may exhibit
![]() $X^{+}$
is a left extension of
$X^{+}$
is a left extension of
 $p^{\ast }(\unicode[STIX]{x1D6FA}(X^{1})\longrightarrow 0)$
along
$p^{\ast }(\unicode[STIX]{x1D6FA}(X^{1})\longrightarrow 0)$
along
 $\operatorname{N}(J)\rightarrow \operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })$
. We use the pointwise formula to show that it is a left Kan extension. For the object
$\operatorname{N}(J)\rightarrow \operatorname{N}(\unicode[STIX]{x1D6EC}_{\infty })$
. We use the pointwise formula to show that it is a left Kan extension. For the object
![]() $\langle 1\rangle$
, this amounts to the statement that the square
$\langle 1\rangle$
, this amounts to the statement that the square

is a pushout square, which holds since
![]() $C$
is stable. For the object
$C$
is stable. For the object
![]() $\langle n\rangle$
, the pointwise formula reduces to the requirement that the
$\langle n\rangle$
, the pointwise formula reduces to the requirement that the
![]() $n$
coface maps
$n$
coface maps
 $X^{1}\rightarrow X^{n}$
exhibit
$X^{1}\rightarrow X^{n}$
exhibit
![]() $X^{n}$
as an
$X^{n}$
as an
![]() $n$
-fold coproduct of copies of
$n$
-fold coproduct of copies of
![]() $X^{1}$
. This holds since
$X^{1}$
. This holds since
![]() $X$
is assumed
$X$
is assumed
![]() $1$
-Segal.◻
$1$
-Segal.◻
Proof of Proposition 5.2.
Let
 $\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D6EC}_{\infty }\rightarrow \unicode[STIX]{x1D6EC}$
be the covering functor. Consider
$\unicode[STIX]{x1D70B}:\unicode[STIX]{x1D6EC}_{\infty }\rightarrow \unicode[STIX]{x1D6EC}$
be the covering functor. Consider
![]() $L^{\bullet }$
from (1.27) as a coparacyclic
$L^{\bullet }$
from (1.27) as a coparacyclic
![]() $1$
-Segal pointed space via pullback along
$1$
-Segal pointed space via pullback along
![]() $\unicode[STIX]{x1D70B}$
(cf. Remark 1.35). Given an object
$\unicode[STIX]{x1D70B}$
(cf. Remark 1.35). Given an object
![]() $E\in C$
, the functor
$E\in C$
, the functor
![]() $E(-)$
from (1.31) commutes with finite colimits so that the coparacyclic object
$E(-)$
from (1.31) commutes with finite colimits so that the coparacyclic object
![]() $E(L^{\bullet })$
in
$E(L^{\bullet })$
in
![]() $C$
is
$C$
is
![]() $1$
-Segal. We have
$1$
-Segal. We have
 $E(L^{1})\simeq E(S^{1})\simeq E[1]$
so that, by Proposition 5.9, we have
$E(L^{1})\simeq E(S^{1})\simeq E[1]$
so that, by Proposition 5.9, we have
 $$\begin{eqnarray}L_{E}\simeq E(L^{\bullet })\simeq j_{!}(p^{\ast }(E\longrightarrow 0)).\end{eqnarray}$$
$$\begin{eqnarray}L_{E}\simeq E(L^{\bullet })\simeq j_{!}(p^{\ast }(E\longrightarrow 0)).\end{eqnarray}$$
Combining this with another application of Proposition 5.9 to the given coparacyclic
![]() $1$
-Segal object
$1$
-Segal object
![]() $X$
yields the desired equivalence
$X$
yields the desired equivalence
 $$\begin{eqnarray}\hspace{130.0002pt}X\simeq j_{!}(p^{\ast }(\unicode[STIX]{x1D6FA}(X^{1})\longrightarrow 0))\simeq L_{\unicode[STIX]{x1D6FA}(X^{1})}.\hspace{115.00017pt}\square\end{eqnarray}$$
$$\begin{eqnarray}\hspace{130.0002pt}X\simeq j_{!}(p^{\ast }(\unicode[STIX]{x1D6FA}(X^{1})\longrightarrow 0))\simeq L_{\unicode[STIX]{x1D6FA}(X^{1})}.\hspace{115.00017pt}\square\end{eqnarray}$$
6 Main result and examples
Combining Theorems 4.18 and 5.1, we obtain the following main result of this work.
Theorem 6.1. Let
![]() $C$
be a stable
$C$
be a stable
![]() $\infty$
-category with colimits and let
$\infty$
-category with colimits and let
 $$\begin{eqnarray}H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\longrightarrow C\end{eqnarray}$$
$$\begin{eqnarray}H:\operatorname{L}_{\operatorname{mo}}(Cat_{\operatorname{dg}})\longrightarrow C\end{eqnarray}$$
be a localizing
![]() $\mathbb{A}^{1}$
-homotopy invariant. Let
$\mathbb{A}^{1}$
-homotopy invariant. Let
![]() $\unicode[STIX]{x1D6E4}$
be a framed graph which models a stable framed marked surface
$\unicode[STIX]{x1D6E4}$
be a framed graph which models a stable framed marked surface
![]() $(S,M)$
and let
$(S,M)$
and let
 $\operatorname{F}(S,M)$
denote its
$\operatorname{F}(S,M)$
denote its
![]() $\mathbb{Z}$
-graded topological Fukaya category. Then there is an equivalence
$\mathbb{Z}$
-graded topological Fukaya category. Then there is an equivalence
 $$\begin{eqnarray}H(\operatorname{F}(S,M))\simeq \unicode[STIX]{x1D6F4}^{\infty }(S/M)\otimes H(k)[-1].\end{eqnarray}$$
$$\begin{eqnarray}H(\operatorname{F}(S,M))\simeq \unicode[STIX]{x1D6F4}^{\infty }(S/M)\otimes H(k)[-1].\end{eqnarray}$$
As a specific application, we obtain the following corollary.
Corollary 6.2. Let
![]() $k$
be a field of characteristic
$k$
be a field of characteristic
![]() $0$
. We have the formulas
$0$
. We have the formulas
 $$\begin{eqnarray}\displaystyle \operatorname{HP}_{0}(\operatorname{F}(S,M)) & \cong & \displaystyle H_{1}(S,M;k),\nonumber\\ \displaystyle \operatorname{HP}_{1}(\operatorname{F}(S,M)) & \cong & \displaystyle H_{2}(S,M;k)\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{HP}_{0}(\operatorname{F}(S,M)) & \cong & \displaystyle H_{1}(S,M;k),\nonumber\\ \displaystyle \operatorname{HP}_{1}(\operatorname{F}(S,M)) & \cong & \displaystyle H_{2}(S,M;k)\nonumber\end{eqnarray}$$
for periodic cyclic homology over
![]() $k$
.
$k$
.
Example 6.3. We compute some explicit examples.
-
(1) Let
 $(S,M)=(S^{2},\{0,\infty \})$
be a
$(S,M)=(S^{2},\{0,\infty \})$
be a
 $2$
-sphere with two marked points. Then, equipping the punctured sphere with the standard framing with winding number
$2$
-sphere with two marked points. Then, equipping the punctured sphere with the standard framing with winding number
 $0$
, we have
$0$
, we have
 $\operatorname{F}(S,M)\simeq \operatorname{Perf}(\mathbb{A}^{1}\setminus \{0\})$
. In agreement with Hochschild–Kostant–Rosenberg, we obtain
$\operatorname{F}(S,M)\simeq \operatorname{Perf}(\mathbb{A}^{1}\setminus \{0\})$
. In agreement with Hochschild–Kostant–Rosenberg, we obtain  $$\begin{eqnarray}\displaystyle \operatorname{HP}_{0}(\operatorname{F}(S,M)) & \cong & \displaystyle H_{1}(S,M;k)\cong k,\nonumber\\ \displaystyle \operatorname{HP}_{1}(\operatorname{F}(S,M)) & \cong & \displaystyle H_{2}(S,M;k)\cong k.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{HP}_{0}(\operatorname{F}(S,M)) & \cong & \displaystyle H_{1}(S,M;k)\cong k,\nonumber\\ \displaystyle \operatorname{HP}_{1}(\operatorname{F}(S,M)) & \cong & \displaystyle H_{2}(S,M;k)\cong k.\nonumber\end{eqnarray}$$
-
(2) Let
 $(S,M)=(T,\{0\})$
be a once marked torus equipped with standard framing. We have a Morita equivalence where
$(S,M)=(T,\{0\})$
be a once marked torus equipped with standard framing. We have a Morita equivalence where $$\begin{eqnarray}\operatorname{F}(S,M)\simeq D^{b}(\operatorname{coh}(C)),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{F}(S,M)\simeq D^{b}(\operatorname{coh}(C)),\end{eqnarray}$$
 $C$
denotes a nodal plane cubic. We obtain
$C$
denotes a nodal plane cubic. We obtain  $$\begin{eqnarray}\displaystyle \operatorname{HP}_{0}(\operatorname{F}(S,M)) & \cong & \displaystyle H_{1}(S,M;k)\cong k^{2},\nonumber\\ \displaystyle \operatorname{HP}_{1}(\operatorname{F}(S,M)) & \cong & \displaystyle H_{2}(S,M;k)\cong k.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \operatorname{HP}_{0}(\operatorname{F}(S,M)) & \cong & \displaystyle H_{1}(S,M;k)\cong k^{2},\nonumber\\ \displaystyle \operatorname{HP}_{1}(\operatorname{F}(S,M)) & \cong & \displaystyle H_{2}(S,M;k)\cong k.\nonumber\end{eqnarray}$$
Acknowledgements
I would like to thank Chris Brav, Mikhail Kapranov, Jacob Lurie, Pranav Pandit, Paul Seidel, and Nicolo Sibilla for inspiring conversations on the subject of this paper. Further, I am very grateful to an anonymous referee for carefully reading this work and providing useful suggestions.