Introduction

There is currently great concern about the possible effects of global climatic change, much of which is believed to be caused by human activities (IPCC,2001). Globally averaged surface temperature is predicted to increase by 1.4–5.8˚C from 1990 to 2100; precipitation will likely increase globally and especially over northern mid- to high latitudes, and the Greenland ice sheet (GIS) is likely to shrink as a result of global warming (IPCC, 2001). This is because increased surface melt/runoff around the climatically sensitive margin of the GIS is expected to outweigh increased precipitation and snow accumulation (Reference Ohmura, Wild and BengtssonOhmura and others, 1996). However, two more recent modelling studies suggest that greater run-off may be largely compensated by increased accumulation (Reference BugnionBugnion, 2000; Reference Van de Wal, Wild and WoldeVan de Wal and others, 2001). Were the GIS to melt in its entirety (which would probably take millennia of global warming at current levels), it would contribute ~6–7m to global sea-level rise (Reference HvidbergHvidberg, 2000).

Various attempts have recently been made to assess the current state of surface mass balance (SMB) of either large parts or the whole of the GIS. These have been from aircraft laser altimeter surveys (Reference KrabillKrabill and others, 2000), satellite radar altimeter measurements (Reference Davis, Kluever, Haines, Perez and YoonDavis and others, 2000) and total snow-accumulation and ice-discharge estimates (Reference ThomasThomas and others, 2000). the consensus is that while the higher-elevation interior parts of the GIS are on average approximately in balance or growing slightly (albeit with large regional discrepancies), the lower-elevation marginal zones have thinned substantially during the 1990s. However, it is uncertain how much of this pattern is due to (i) short-term mass-balance-only variations and (ii) longer-term processes (e.g. changes in ice dynamics). Temporal variations in snow accumulation are thought to be the main factor driving interannual elevation (and SMB) changes over interior southern Greenland (Reference McConnellMcConnell and others, 2000), whereas fluctuations in runoff are likely to be an important influence on the SMB of the ice margins.

Here accumulation refers to net snow accumulation, i.e. solid precipitation (snowfall) minus evaporation/sublimation. Net runoff is runoff of surface meltwater minus that part which refreezes (or is retained) on or in the ice before it is lost. Runoff is sometimes rather confusingly referred to as ablation, of which it is a key component, but strictly ablation also includes other processes (most importantly iceberg calving). to good approximation, SMB equals (net) accumulation minus (net) runoff.

Recently available climate-centre (re-)analyses and accumulation/runoff models, if suitably validated, can be used to provide first-order estimates of the SMB of the GIS and its interannual variations, to help interpret patterns and trends in the laser, radar and ice-core (observational) results. Such analyses have the advantage over atmospheric general circulation model (GCM) simulations of ice-sheet climate, that they are based partly on observed meteorological data, so in principle they depict actual year-to-year changes in surface temperature, precipitation, accumulation, runoff and SMB.

In previous studies, E. Hanna:

1. (1) validated European Centre for Medium-RangeWeather Forecasts (ECMWF) analysis surface climate fields for Greenland and assessed their suitability for use in modelling the GIS SMB (Reference Hanna and ValdesHanna and Valdes, 2001), and

2. (2) used the ECMWFre-analyses (1979–94) and operational analysis (1994–98) with a simple meteorological model to produce maps of GIS snow accumulation, which were verified using contemporaneous Program for Arctic Regional Climate Assessment (PARCA) ice-core data (Reference Hanna, Valdes and McConnellHanna and others, 2001).

The limited spatial resolution (~1.12561.125˚) of the above-mentioned analyses is problematic when they are used to model steep accumulation and especially runoff gradients over relatively small distances (less than a few hundred km) near the ice-sheet margin. Consequently, here we use higher-resolution (N160 ≌ 0.5660.56˚) ECMWF operational analyses from 1992–98 in conjunction with the Reference Hanna, Valdes and McConnellHanna and others (2001) meteorological model of snow accumulation and a meltwater runoff/retention model (Reference Janssens and HuybrechtsJanssens and Huybrechts, 2000), to produce preliminary/ exploratory annual maps of the GIS runoff and SMB over this period. ECMWF operational analyses were produced by a data-assimilation system based on a numerical weather-prediction model (ECMWF, 2000).

The original model grid on which the physics were computed was reduced in longitude as latitude increased, so that the grid remained approximately isotropic everywhere on the globe. Thismeans that the original ECMWF grid had a resolution ranging from ~1.1˚ in longitude over southern Greenland to ~2.8˚ in longitude over North Greenland. ECMWF used bilinear interpolation to calculate its N160 analyses’ values for intermediate gridpoints in longitude. This interpolation could cause problems where there is a strong east–west contrast/small-scale variations in surface meteorology: specifically near the (eastern or western) edge of the GIS. In our modelling based on the ECMWF analyses, we effectively downscaled the resolution to ~0.56˚ in longitude by using S. Ekholm’s digital elevation model (DEM) (Reference EkholmEkholm,1996), the latter upscaled to ~0.5660.56˚, to``correct’’ECMWF surface air temperature for (ECMWF) errors in elevation. the underlying assumption is that sub-grid-scale variations in surface air temperature (and hence accumulation and runoff) are primarily controlled by sub-grid-scale changes in surface altitude (Reference GloverGlover,1999). This approach substantially improved ECMWF temperatures around the edge of the GIS (Reference Hanna, Valdes and McConnellHanna and Valdes, 2001).

We discuss interannual variations in modelled snow accumulation, runoff and SMB. We compare our net runoff maps with maps of net runoff derived from Special Sensor Microwave/Imager (SSM/I) passive-microwave satellite data (Reference MoteMote, 2000). Finally, we comment on how useful our accumulation/runoff modelling might be when applied to Greenland surface climate fields from the forthcoming ``second-generation’’ ECMWFre-analysis (ERA-40) (Reference Simmons and GibsonSimmons and Gibson, 2000).

Accumulation

Snowfall, surface air temperature and surface latent-heat flux from the ECMWFanalyses were used to calculate snow accumulation (snowfall minus evaporation/sublimation). This was as in Reference Hanna, Valdes and McConnellHanna and others (2001), except that forecast snowfall (with a lead-time of 12 hours to avoid problems with spin-up in the ECMWF model) was used instead of ECMWF total precipitation being split into rain and snow according to surface air temperature. Analyses-based accumulation has already been validated against ice-core and other data (Reference Hanna, Valdes and McConnellHanna and others, 2001; McConnell and others, in press). It was found to give a good depiction of temporal and spatial accumulation variations across the GIS, although actual amounts of accumulation are ~20–30% too low in central Greenland and possibly somewhat too high near the outer ice edge.

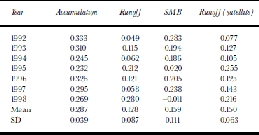
Modelled accumulation ranges from <0.1m in parts of the ``precipitation desert’’ of central North Greenland, to >1m in the southeast mountains, with a secondary peak in northwest Greenland; values are generally higher in coastal areas (Fig. 1a). Mean (1992–98) annual accumulation averaged across W. Abdalati’s GIS mask (Reference Abdalati and SteffenAbdalati and Steffen, 1997) was 0.287 ma^–1.This compares very well with the 0.297 ma^–1mean annual specific accumulation for the GIS calculated by Reference Ohmura, Calanca, Wild and AnklinOhmura and others, (1999) and the 0.300ma^–1 average accumulation for the GIS for 1971–90 reported by Reference Bales, McConnell, Mosley-Thompson and LamoreyBales and others (2001). There was considerable interannual variability, with a standard deviation (SD) of 0.039ma^–1: annual accumulation ranged from 0.232 ma^–1 in 1995 to 0.333 ma^–1 in 1992 (Table 1). This is undoubtedly partly due to changes in atmospheric circulation patterns and precipitation across Greenland during these years, as seen by validation of the spatially coarser modelled accumulation against ice-core accumulation data (McConnell and others, in press). However, changes to the model and data-assimilation scheme used for producing the ECMWF analyses for that period may also have contributed.

Fig. 1 Mean annual (1992–98) accumulation (a), runoff (b) and surface mass balance (c) over GIS.

Table 1. GIS accumulation, runoff and SMB, 1992–98, with mean and SD values, based on ECMWF analyses. Satellite-derived runoff is given for comparison with ECMWF runoff. All values are in m a^–1w.e. and are for W. Abdalati’s GIS mask area

Runoff

A meltwater runoff/retention model (Reference Janssens and HuybrechtsJanssens and Huybrechts, 2000) was used with ECMWF analyses’annual precipitation and annual and July 2 m surface air temperatures to produce maps of GIS surface meltwater net runoff (some meltwater percolates and/or refreezes within the ice and is therefore retained) (Fig. 1b). As in Reference Hanna, Valdes and McConnellHanna and others (2001), the Ekholm DEM (Reference EkholmEkholm,1996) was used to correct ECMWF temperatures for errors in the ECMWF orography schemes, using an assumed lapse rate derived from comparison of model temperatures with those from in situ stations (Reference Hanna, Valdes and McConnellHanna and Valdes, 2001). the melt model is a degree-day model that uses the corrected annual and July temperatures, at ~0.5660.56˚ resolution, to produce a yearly march given by a sine. Use of a degree-day model, in preference to a more physically based energy-balance model, is justified because longwave radiation typically comprises 60–80% of total energy sources and sinks for glaciers worldwide (Reference OhmuraOhmura, 2001). the sum of degree-days is produced in a look-up table, and melt, refreezing, percolation and retention then calculated. the runoff model adds rain and meltwater together in the calculations, so implicitly takes account of rain warming up the snowpack. the retention part of the model accounts for refreezing and capillary suction of the snowpack (Reference Janssens and HuybrechtsJanssens and Huybrechts, 2000).

Using this technique, runoff averaged 0.128ma^–1 (1992– 98) across Abdalati’s ice-mask area, or ~45% of mean accumulation. There was a very considerable SD of 0.087ma^–1, and annual runoff ranged from 0.049 ma^–1 in 1992 to 0.280ma^–1 in 1998 (this was the only year in which runoff exceeded accumulation) (Table 1). Runoff was very probably quite sensitive to interannual temperature variability (as depicted in the analyses, at least some of which was likely to have been real). Greatest surface melt runoff was in the warmer, lower-elevation areas of the southwest, and there was a larger area of lesser runoff in the north in most years. Although the area of significant runoff was much smaller than the accumulation area, this was partly compensated by locally very large runoff values of up to 7 or 8 ma^–1 in odd pixels (e.g. around 66˚N, 50˚W in 1995 and 69˚N, 50˚Win 1998).

The ECMWF-based runoff values were compared with runoff (melt minus refreezing) estimated from passive-microwave satellite brightness temperature (T _B) data (Reference MoteMote, 2000). Mote’s method is quite similar, but the data on which it was based were completely independent. T _B data were used to calculate daily melt occurrence and, from the latter, sea sonalmelt frequency. Melt frequency closely corresponded to local measurements of the frequency of days with temperature above freezing (Reference MoteMote, 2000). Melt frequency was used to compute the number of positive degree-days (PDDs) and runoff. Annual snow accumulation, fixed by year, was melted and made to refreeze until melt for the year in question exceeded 0.6 times accumulation, at which point runoff occurred. Snow accumulation was based on an updated version of the Reference Ohmura and ReehOhmura and Reeh (1991) data.

Satellite-based runoff (for Abdalati’s GIS mask) averaged 0.150ma^–1 for 1992–98, or slightly (~17%) higher than ECMWF-based runoff, but the SD was somewhat lower (Table 1). There is good agreement between the ECMWF-and satellite-based estimates of low- and high-runoff years; the least annual runoff, as estimated by both methods, was in 1992, and the two years of greatest runoff were1995 and 1998. Gross spatial patterns of runoff also agreed well between the two techniques (Fig. 2). Both methods show strong runoff in western marginal areas, with maxima around 69^o N, 50^oW (just inland from Illulissat/Jakobshavn). They also both show a second significant area of runoff in the extreme north of the GIS, which is relatively low-lying. There are some regional disparities between the two methods (e.g. ECMWF/Janssens and Huybrechts tends to show a smaller area of melt in West Greenland and a broader zone in the north), but overall the results of the comparison are encouraging.

Fig. 2 GIS annual runoff from ECMWF data/Janssens and Huybrechts model, 1992 (a), 1995 (b) and 1998 (c), and from T. Mote’s satellite method, 1992 (d), 1995 (e) and 1998 (f).

Runoff is likely underestimated, primarily because Abdalati’s ice mask omits ~6% of the GIS (Reference Abdalati and SteffenAbdalati and Steffen, 1997), whereas progressively greater melting and runoff occurs near the ice-sheet margin. the difference is substantial. Thus, including all cells in the U.S. National Snow and Ice Data Center (NSIDC) polar grid with 450% ice as determined from a Geological Survey of Greenland map (T. Mote’s GIS mask) and remapped onto the N160 grid, we obtained a mean satellite-based runoff of 0.214 ma^–1, or ~43% higher than for Abdalati’s mask. Corresponding ECMWF-based runoff for the same area was 0.151 ma^–1, or only ~18% higher than for Abdalati’s mask. the satellite/ECMWF runoff ratio was therefore greater (1.42:1) when considering the larger (Mote) mask.

The relatively crude resolution of the grid near the ice-sheet margin might also cause marginal areas of high runoff to be missed. An over-cold boundary layer in the earlier ECMWF analyses until 1996 may be causing over-low surface air temperatures (Reference Hanna, Valdes and McConnellHanna and others, 2001), which would suppress melt relative to reality. Melting surfaces tend to force surface inversions since the surface must remain at freezing temperature, whatever the atmospheric temperature. Therefore, a wrong parameterization of strongly stable boundary layers in the ECMWF model may well affect the energy balance of melting regions. However, this problem is thought mainly to have been in the interior of the GIS, where little melting occurs. Saturation of the microwave signal may lower satellite estimates of runoff, especially south of~65˚N, and additional localized errors are likely to be caused by inaccurate accumulation rates going into the microwave algorithm. Uncertainties in calculated runoff arise from the value of the PDD factors and the temperature standard deviation, none of which are better known than ~ ±30%, and uncertainties in PDD factors scale almost directly into the total runoff. Additional but lesser uncertainties arise from differences in the treatment of the runoff retention process (which is being updated in Mote’s method so that it is equivalent to that for theJanssens and Huybrechts model).

We plan to use a high-resolution, detailed map of the ice-sheet margin to extrapolate runoff values out to the margin, and eventually downscale our method further, which should make our runoff estimates more accurate and meaningful.

Surface Mass Balance

SMB is simply net accumulation minus net runoff. for the Abdalati mask area, it averaged 0.159 ma^–1 for 1992–98, and was lowest at –0.011ma^–1 in 1998 (the only year when it was negative) and highest at 0.283 ma^–1 in 1992 (Table 1). SMB was only slightly lower for Mote’s mask (for which runoff is 0.023 ma^–1, and accumulation 0.020 ma^–1, greater). This would give a very slightly revised SMB of 0.156 ma^–1. Mean annual SMB is substantially greater than two other recent estimates: 0.099 ma^–1 (Reference Zwally and GiovinettoZwally and Giovinetto, 2001) and 0.097 ma^–1 (Reference Ohmura, Calanca, Wild and AnklinOhmura and others, 1999). This difference may perhaps be explained by an underestimation of our modelled runoff (which is considerably lower than satellite-derived runoff). However, interannual variability is large and our SMB value lies well within the range of other estimates reported in Reference Zwally and GiovinettoZwally and Giovinetto (2001).

Our greatest positive SMB, ≥2ma^–1, was near the south-east margin of the GIS; the most negative SMB, ≤–2ma^–1, was in the southwest (Fig.1c), especially in 1995 and 1998.

Overall, our SMB values suggest that the GIS is currently (based on 1990s data) overall in a state of decidedly positive SMB, although there are considerable interannual variations. Once we allow for iceberg calving, which is estimated to be ~0.14ma^–1 (Reference Reeh, Mayer, Miller, Thomsen and WeidickReeh and others, 1999) or 0.098– 0.156ma^–1 (Reference BiggBigg, 1999), and probably somewhat underestimated runoff, it seems that the recent mass budget of the GIS is either near equilibrium or, more probably, some what negative. the latter agrees tentatively with the negative mass balance of the GIS inferred from repeat laser surveys (Reference KrabillKrabill and others, 2000). However, further work is required to differentiate between the effects of changes in SMB and (maybe longer-term) ice dynamics/isostatic adjustment on surface elevation changes.

Conclusions

These results show that climate analyses’ surface fields can be successfully combined with simple meteorological and glaciological models to produce realistic first-order maps of accumulation and runoff, and therefore SMB, of the GIS. the advantage of climate analyses over conventional GCMs is that, as they are based partly on observations, they attempt to simulate actual conditions and interannual variability over the ice sheet. We have presented the first such published runoff and SMB data/maps, and validated them against independent satellite data.

This is very much a pilot study using ECMWF operational analyses for a limited period, and, as such, the results are bound to be exploratory and preliminary. We plan to produce more accurate/longer-term versions of our maps based on the shortly forthcoming ``second-generation’’ ECMWF re-analyses, ERA-40. ERA-40 will cover the period 1957–2001 and is expected to incorporate improved parameterizations of the boundary layer and ice physics (compared with the original ECMWF re-analysis and existing operational analyses). the new re-analysis (like its predecessor) will use a fixed assimilation scheme, reducing the risk of biases over time due to changes in the model. the ERA 40-based model results will be validated, as far as possible, using meteorological synoptic station, ice-core and other field data. Increasing model resolution and/or incorporating a more detailed ice margin at the sub-pixel level will be paramount for more accurately modelling runoff near the GIS edge (where it is greatest and most variable) and hence SMB. Comparison of ERA 40-based SMB maps with laser and radar survey results should help answer a key question: how important are short-term (interannual) fluctuations in SMB in influencing surface elevation changes across the ice sheet?