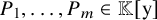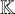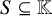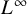1 Introduction
Szemerédi’s famous theorem [Reference Szemerédi43] states that any set S of integers with positive (upper) density must necessarily contain arbitrarily long arithmetic progressions. Quantitative versions have been obtained by several authors, first by Roth [Reference Roth40] for three-term arithmetic progressions and by Gowers [Reference Gowers18] in general, with the current best bounds due to Bloom and Sisask [Reference Bloom and Sisask7], Kelley and Meke [Reference Kelley and Meka21] in the three-term case and Leng, Sah and Sawhney [Reference Leng, Sah and Sawhney26] for longer progressions (see also Green and Tao [Reference Green and Tao17] and Gowers [Reference Gowers18]). More generally, one can consider polynomial progressions
![]() $x, x+P_1(y), \ldots , x + P_m(y)$
for
$x, x+P_1(y), \ldots , x + P_m(y)$
for
![]() $x,y \in {\mathbb Z}$
with
$x,y \in {\mathbb Z}$
with
![]() $y\not = 0$
, where
$y\not = 0$
, where
![]() $P_j \in {\mathbb Z}[\mathrm {y}]$
is a sequence of polynomials with integer coefficients and no constant terms (the case of arithmetic progressions corresponding to linear polynomials). Bergelson and Leibman [Reference Bergelson and Leibman6], extending earlier work of Bergelson, Furstenberg and Weiss [Reference Bergelson, Furstenberg and Weiss5], generalised Szemerédi’s theorem to polynomial progressions. Obtaining quantitative versions of Bergelson and Leibman’s result has been a challenging problem and no progress (outside a few results on two-term progressions) has been made until very recently.
$P_j \in {\mathbb Z}[\mathrm {y}]$
is a sequence of polynomials with integer coefficients and no constant terms (the case of arithmetic progressions corresponding to linear polynomials). Bergelson and Leibman [Reference Bergelson and Leibman6], extending earlier work of Bergelson, Furstenberg and Weiss [Reference Bergelson, Furstenberg and Weiss5], generalised Szemerédi’s theorem to polynomial progressions. Obtaining quantitative versions of Bergelson and Leibman’s result has been a challenging problem and no progress (outside a few results on two-term progressions) has been made until very recently.
Inspired by the earlier work of Bergelson, Furstenberg and Weiss, Bourgain obtained a quantitative lower bound on the count of three-term polynomial progressions in the setting of the real field
![]() ${\mathbb R}$
. He accomplished this by coupling a technique he developed in his work on arithmetic progressions [Reference Bourgain2], together with Fourier-analytic methods.
${\mathbb R}$
. He accomplished this by coupling a technique he developed in his work on arithmetic progressions [Reference Bourgain2], together with Fourier-analytic methods.
Theorem 1.1 (Bourgain [Reference Bourgain3]).
Given
![]() $\varepsilon>0$
, there exists a
$\varepsilon>0$
, there exists a
![]() $\delta (\varepsilon )>0$
such that for any
$\delta (\varepsilon )>0$
such that for any
![]() $N\ge 1$
and measurable set
$N\ge 1$
and measurable set
![]() $S \subseteq [0,N]$
satisfying
$S \subseteq [0,N]$
satisfying
![]() $|S\cap [0,N]|\ge \varepsilon N$
, we have
$|S\cap [0,N]|\ge \varepsilon N$
, we have
In particular, we have the existence of a triple
![]() $x, x+y$
and
$x, x+y$
and
![]() $x+y^d$
belonging to S with y satisfying the gap condition
$x+y^d$
belonging to S with y satisfying the gap condition
![]() $y \ge \delta N^{1/d}$
.
$y \ge \delta N^{1/d}$
.
The bound (1.2) implies a quantitative multiple recurrence result. Only recently have there been extensions to more general three-term progressions
![]() $x, x +P_1(y), x + P_2(y)$
; see the work of Durcik, Guo and Roos [Reference Durcik, Guo and Roos11] when
$x, x +P_1(y), x + P_2(y)$
; see the work of Durcik, Guo and Roos [Reference Durcik, Guo and Roos11] when
![]() $P_1(y) = y$
and general
$P_1(y) = y$
and general
![]() $P_2$
and of Chen, Guo and Li [Reference Chen, Guo and Li8] for general
$P_2$
and of Chen, Guo and Li [Reference Chen, Guo and Li8] for general
![]() $P_1, P_2 \in {\mathbb R}[\mathrm {y}]$
with distinct degrees. The methods in these papers, using delicate oscillatory integral operator bounds, seem limited to three-term progressions.
$P_1, P_2 \in {\mathbb R}[\mathrm {y}]$
with distinct degrees. The methods in these papers, using delicate oscillatory integral operator bounds, seem limited to three-term progressions.
In another direction, Bourgain and Chang [Reference Bourgain and Chang4] gave quantitative bounds for three-term progressions of the form
![]() $x, x+y, x+y^2$
in the setting of finite fields
$x, x+y, x+y^2$
in the setting of finite fields
![]() ${\mathbb F}_q$
. This result was extended to more general three-term polynomial progressions by Peluse [Reference Peluse36] and Dong, Li and Sawin [Reference Dong, Li and Sawin10]. The techinques in these papers, using a Fourier-analytic approach which relies on sophisticated exponential sum bounds over finite fields, also seem limited to three-term progressions.
${\mathbb F}_q$
. This result was extended to more general three-term polynomial progressions by Peluse [Reference Peluse36] and Dong, Li and Sawin [Reference Dong, Li and Sawin10]. The techinques in these papers, using a Fourier-analytic approach which relies on sophisticated exponential sum bounds over finite fields, also seem limited to three-term progressions.
By using new ideas in additive combinatorics, by-passing the need of inverse theorems for Gowers’ uniformity norms of degree greater than 2, Peluse [Reference Peluse37] recently made a significant advance, giving quantitative bounds for general polynomial progressions
![]() $x, x+P_1(y), \ldots , x+P_m(y)$
in
$x, x+P_1(y), \ldots , x+P_m(y)$
in
![]() ${\mathbb F}_q$
, where
${\mathbb F}_q$
, where
![]() $\{P_1,\ldots , P_m\} \subseteq {\mathbb Z}[\mathrm {y}]$
are linearly independent over
$\{P_1,\ldots , P_m\} \subseteq {\mathbb Z}[\mathrm {y}]$
are linearly independent over
![]() ${\mathbb Q}$
.
${\mathbb Q}$
.
Inspired by this work, Peluse and Prendiville [Reference Peluse and Prendiville39] obtained the first quantitative bounds for three-term polynomal progressions in the setting of the integers
![]() ${\mathbb Z}$
. This has been extended recently to general polynomial progressions
${\mathbb Z}$
. This has been extended recently to general polynomial progressions
![]() $x, x+P_1(y), \ldots , x + P_m(y)$
with
$x, x+P_1(y), \ldots , x + P_m(y)$
with
![]() $P_j \in {\mathbb Z}[\mathrm {y}] $
having distinct degrees by Peluse [Reference Peluse38]. So although the first quantitative bounds for polynomial progressions were made in the setting of the real field
$P_j \in {\mathbb Z}[\mathrm {y}] $
having distinct degrees by Peluse [Reference Peluse38]. So although the first quantitative bounds for polynomial progressions were made in the setting of the real field
![]() ${\mathbb R}$
, we have seen major advances in both the finite field
${\mathbb R}$
, we have seen major advances in both the finite field
![]() ${\mathbb F}_q$
and integer
${\mathbb F}_q$
and integer
![]() ${\mathbb Z}$
settings by employing new ideas in additive combinatorics.
${\mathbb Z}$
settings by employing new ideas in additive combinatorics.
One purpose of this paper is to rectify this situation for the continuous setting by establishing quantitative bounds for general polynomial progressions in the real field
![]() ${\mathbb R}$
, bringing it in line with the recent advances in the finite field and integer settings. Another purpose is to illustrate how one can marry these new ideas in additive combinatorics with other ideas, notably from the work of Krause, Mirek and Tao [Reference Krause, Mirek and Tao23] to obtain compactness results for general multilinear polynomial averaging operators which have implications for problems in euclidean harmonic analysis. These ideas and arguments are robust enough to allow us to obtain quantitative bounds for polynomial progressions in a general local field.
${\mathbb R}$
, bringing it in line with the recent advances in the finite field and integer settings. Another purpose is to illustrate how one can marry these new ideas in additive combinatorics with other ideas, notably from the work of Krause, Mirek and Tao [Reference Krause, Mirek and Tao23] to obtain compactness results for general multilinear polynomial averaging operators which have implications for problems in euclidean harmonic analysis. These ideas and arguments are robust enough to allow us to obtain quantitative bounds for polynomial progressions in a general local field.
Theorem 1.3. Let
![]() $\mathbb {K}$
be a local field with Haar measure
$\mathbb {K}$
be a local field with Haar measure
![]() $\mu $
. Let
$\mu $
. Let
![]() ${\mathcal P} = \{P_1, \ldots , P_m\}$
be a sequence of polynomials in
${\mathcal P} = \{P_1, \ldots , P_m\}$
be a sequence of polynomials in
![]() $\mathbb {K}[\mathrm {y}]$
with distinct degrees and no constant terms, and let d denote the largest degree among the polynomials in
$\mathbb {K}[\mathrm {y}]$
with distinct degrees and no constant terms, and let d denote the largest degree among the polynomials in
![]() ${\mathcal P}$
. When
${\mathcal P}$
. When
![]() $\mathbb {K}$
has positive characteristic, we assume the characteristic is larger than d.
$\mathbb {K}$
has positive characteristic, we assume the characteristic is larger than d.
For any
![]() $\varepsilon>0$
, there exists a
$\varepsilon>0$
, there exists a
![]() $\delta (\varepsilon , {\mathcal P})> 0$
and
$\delta (\varepsilon , {\mathcal P})> 0$
and
![]() $N(\varepsilon , {\mathcal P}) \ge 1$
such that for any
$N(\varepsilon , {\mathcal P}) \ge 1$
such that for any
![]() $N \ge N(\varepsilon , {\mathcal P})$
and measurable set
$N \ge N(\varepsilon , {\mathcal P})$
and measurable set
![]() $S \subseteq \mathbb {K}$
satisfying
$S \subseteq \mathbb {K}$
satisfying
![]() $\mu (S \cap B_N) \ge \varepsilon N$
, we have
$\mu (S \cap B_N) \ge \varepsilon N$
, we have
In particular, we have the existence of a progression
![]() $x, x+P_1(y), \ldots , x+ P_m(y)$
belonging to S with y satisfying the gap condition
$x, x+P_1(y), \ldots , x+ P_m(y)$
belonging to S with y satisfying the gap condition
![]() $|y| \ge \delta N^{1/d}$
. The proof will show that we can take
$|y| \ge \delta N^{1/d}$
. The proof will show that we can take
![]() $\delta = \varepsilon ^{C\varepsilon ^{-2m-2}}$
for some
$\delta = \varepsilon ^{C\varepsilon ^{-2m-2}}$
for some
![]() $C = C_{\mathcal P}> 0$
and
$C = C_{\mathcal P}> 0$
and
![]() $N(\varepsilon , {\mathcal P}) = \varepsilon ^{-C' \varepsilon ^{-2m-2}}$
for a slightly larger
$N(\varepsilon , {\mathcal P}) = \varepsilon ^{-C' \varepsilon ^{-2m-2}}$
for a slightly larger
![]() $C'> C_{\mathcal P}$
.
$C'> C_{\mathcal P}$
.
When
![]() $\mathbb {K} = {\mathbb R}$
is the real field, Theorem 1.3 extends the work in [Reference Bourgain3], [Reference Durcik, Guo and Roos11] and [Reference Chen, Guo and Li8] from three-term polynomial progressions to general polynomial progressions albeit for large N, depending on
$\mathbb {K} = {\mathbb R}$
is the real field, Theorem 1.3 extends the work in [Reference Bourgain3], [Reference Durcik, Guo and Roos11] and [Reference Chen, Guo and Li8] from three-term polynomial progressions to general polynomial progressions albeit for large N, depending on
![]() $\varepsilon $
.
$\varepsilon $
.
When
![]() $\mathbb {K}={\mathbb C}$
, Theorem 1.3 represents the first known results for complex polynomial progressions. The absolute value
$\mathbb {K}={\mathbb C}$
, Theorem 1.3 represents the first known results for complex polynomial progressions. The absolute value
![]() $|\cdot |$
used in the statement of Theorem 1.3 is normalised so that we can express the result in this generality (see Section 3). For any sequence of complex polynomials
$|\cdot |$
used in the statement of Theorem 1.3 is normalised so that we can express the result in this generality (see Section 3). For any sequence of complex polynomials
![]() $\{P_1,\ldots , P_m\} \subseteq {\mathbb C}[\mathrm {z}]$
with distinct degrees and
$\{P_1,\ldots , P_m\} \subseteq {\mathbb C}[\mathrm {z}]$
with distinct degrees and
![]() $P_j(0) = 0$
, Theorem 1.3 has the following consequence: Given
$P_j(0) = 0$
, Theorem 1.3 has the following consequence: Given
![]() $\varepsilon>0$
, there is a
$\varepsilon>0$
, there is a
![]() $\delta>0$
such that for sufficiently large N and any set S in the complex plane satisfying
$\delta>0$
such that for sufficiently large N and any set S in the complex plane satisfying
![]() $|S\cap {\mathbb D}_N| \ge \varepsilon N^2$
, we can find a progression of the form
$|S\cap {\mathbb D}_N| \ge \varepsilon N^2$
, we can find a progression of the form
![]() $w, w+ P_1(z), \ldots , w + P_m(z)$
lying in S such that
$w, w+ P_1(z), \ldots , w + P_m(z)$
lying in S such that
![]() $|z| \ge \delta N^{2/d}$
.
$|z| \ge \delta N^{2/d}$
.
Important in our analysis are certain properties for
![]() $m+1$
linear forms formed from our collection
$m+1$
linear forms formed from our collection
![]() ${\mathcal P} = \{P_1, \ldots , P_m\} \subseteq \mathbb {K}[\mathrm {y}]$
of m polynomials with distinct degrees, say
${\mathcal P} = \{P_1, \ldots , P_m\} \subseteq \mathbb {K}[\mathrm {y}]$
of m polynomials with distinct degrees, say
![]() $1\le \deg (P_1) < \ldots < \deg (P_m) =: d$
. Let
$1\le \deg (P_1) < \ldots < \deg (P_m) =: d$
. Let
![]() $N \ge 1$
and consider the form
$N \ge 1$
and consider the form
 $$ \begin{align*}\Lambda_{{\mathcal P}; N}(f_0,\ldots, f_m):= \frac{1}{N^d} \int_{\mathbb{K}^2}f_0(x)\prod_{i=1}^mf_{i}(x-P_i(y))d\mu_{[N]}(y)d\mu(x). \end{align*} $$
$$ \begin{align*}\Lambda_{{\mathcal P}; N}(f_0,\ldots, f_m):= \frac{1}{N^d} \int_{\mathbb{K}^2}f_0(x)\prod_{i=1}^mf_{i}(x-P_i(y))d\mu_{[N]}(y)d\mu(x). \end{align*} $$
Here, ![]() is normalised measure on the ball
is normalised measure on the ball
![]() $B_N(0)$
(we will describe notation used in the paper in Section 4). The key result in the proof of Theorem 1.3 is the following
$B_N(0)$
(we will describe notation used in the paper in Section 4). The key result in the proof of Theorem 1.3 is the following
![]() $L^{\infty }$
inverse theorem for
$L^{\infty }$
inverse theorem for
![]() $\Lambda _{{\mathcal P}; N}$
which is of independent interest.
$\Lambda _{{\mathcal P}; N}$
which is of independent interest.
Theorem 1.5 (Inverse theorem for
 $(m+1)$
-linear forms).
$(m+1)$
-linear forms).
With the setup above, let
![]() $f_0, f_1,\ldots , f_m$
be
$f_0, f_1,\ldots , f_m$
be
![]() $1$
-bounded functions supported on a ball
$1$
-bounded functions supported on a ball
![]() $B\subset \mathbb {K}$
of measure
$B\subset \mathbb {K}$
of measure
![]() $N^d$
. Suppose that
$N^d$
. Suppose that
Then there exists
![]() $N_1\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_1)}$
such that
$N_1\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_1)}$
such that
The main application of Theorem 1.5 for us will be to prove a precise structural result for multilinear polynomial operators of the form
We will use ideas in the recent work of Krause, Mirek and Tao [Reference Krause, Mirek and Tao23] to accomplish this, and consequently, we will be able to establish the following important Sobolev estimate.
Theorem 1.6 (A Sobolev inequality for
 $A_N^{\mathcal P}$
).
$A_N^{\mathcal P}$
).
Let
![]() $1<p_1,\ldots , p_m<\infty $
satisfying
$1<p_1,\ldots , p_m<\infty $
satisfying
![]() $\frac {1}{p_1}+\ldots +\frac {1}{p_m}=1$
be given. Then for
$\frac {1}{p_1}+\ldots +\frac {1}{p_m}=1$
be given. Then for
![]() $N_j\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_j)}$
, we have
$N_j\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_j)}$
, we have
 $$ \begin{align*} \|A_N^{\mathcal P}(f_1,\ldots,f_{j-1}, (\delta_0-\varphi_{N_j})*f_j,f_{j+1}\ldots, f_m)\|_{L^1(\mathbb{K})} \lesssim \delta^{1/8} \prod_{i=1}^{m} \|f_i\|_{L^{p_i}(\mathbb{K})}, \end{align*} $$
$$ \begin{align*} \|A_N^{\mathcal P}(f_1,\ldots,f_{j-1}, (\delta_0-\varphi_{N_j})*f_j,f_{j+1}\ldots, f_m)\|_{L^1(\mathbb{K})} \lesssim \delta^{1/8} \prod_{i=1}^{m} \|f_i\|_{L^{p_i}(\mathbb{K})}, \end{align*} $$
provided
![]() $N\gtrsim \delta ^{-O_{\mathcal P}(1)}$
. Here,
$N\gtrsim \delta ^{-O_{\mathcal P}(1)}$
. Here,
![]() $\varphi _{N_j}$
is a smooth cut-off function such that
$\varphi _{N_j}$
is a smooth cut-off function such that
![]() ${\widehat {\varphi _{N_j}}}(\xi ) \equiv 1$
for
${\widehat {\varphi _{N_j}}}(\xi ) \equiv 1$
for
![]() $\xi \in B_{{N_j}^{-1}}(0)$
.
$\xi \in B_{{N_j}^{-1}}(0)$
.
Following an argument of Bourgain in [Reference Bourgain3], we will show how Theorem 1.6 implies Theorem 1.3. Versions of Theorem 1.6 for two real polynomials
![]() $\{P_1, P_2\} \subseteq {\mathbb R}[\mathrm {y}]$
were established in [Reference Bourgain3], [Reference Durcik, Guo and Roos11] and [Reference Chen, Guo and Li8] using delicate oscillatory integral operator bounds. Our arguments are much more elementary in nature and do not require deep oscillatory integral/exponential sum/character sum bounds outside a standard application of van der Corput bounds (see [Reference Stein41]) when
$\{P_1, P_2\} \subseteq {\mathbb R}[\mathrm {y}]$
were established in [Reference Bourgain3], [Reference Durcik, Guo and Roos11] and [Reference Chen, Guo and Li8] using delicate oscillatory integral operator bounds. Our arguments are much more elementary in nature and do not require deep oscillatory integral/exponential sum/character sum bounds outside a standard application of van der Corput bounds (see [Reference Stein41]) when
![]() $\mathbb {K} = {\mathbb R}$
or Hua’s exponential sum bound [Reference Hua13] when
$\mathbb {K} = {\mathbb R}$
or Hua’s exponential sum bound [Reference Hua13] when
![]() $\mathbb {K} = {\mathbb Q}_p$
(which extends Mordell’s classical bound from the finite field setting to complete exponenial sums over
$\mathbb {K} = {\mathbb Q}_p$
(which extends Mordell’s classical bound from the finite field setting to complete exponenial sums over
![]() ${\mathbb Z}/p^m{\mathbb Z}$
) – these bounds extend readily to any local field
${\mathbb Z}/p^m{\mathbb Z}$
) – these bounds extend readily to any local field
![]() ${\mathbb K}$
; see Section 3. Furthermore, the Sobolev inequalities in [Reference Durcik, Guo and Roos11] and [Reference Chen, Guo and Li8] were only established for certain sparse sequences of scales N. The bound in Theorem 1.6 holds for all sufficiently large scales N.
${\mathbb K}$
; see Section 3. Furthermore, the Sobolev inequalities in [Reference Durcik, Guo and Roos11] and [Reference Chen, Guo and Li8] were only established for certain sparse sequences of scales N. The bound in Theorem 1.6 holds for all sufficiently large scales N.
The Sobolev bound in Theorem 1.6 potentially has many other applications. See [Reference Bourgain3] for a discussion on the implications of Theorem 1.6 to compactness properties of the multilinear operator
![]() $A_N^{\mathcal P}$
. Pointwise convergence results for multilinear polynomial averages are common applications of such Sobolev bounds. See [Reference Chen, Guo and Li8] where the Sobolev inequality is used to prove the existence of polynomial progressions in sets of sufficiently large Hausdorff dimension. See also [Reference Krause22], [Reference Laba and Pramanik24], [Reference Keleti19], [Reference Keleti20] and [Reference Chang and Laba9].
$A_N^{\mathcal P}$
. Pointwise convergence results for multilinear polynomial averages are common applications of such Sobolev bounds. See [Reference Chen, Guo and Li8] where the Sobolev inequality is used to prove the existence of polynomial progressions in sets of sufficiently large Hausdorff dimension. See also [Reference Krause22], [Reference Laba and Pramanik24], [Reference Keleti19], [Reference Keleti20] and [Reference Chang and Laba9].
Our results require the scales N to be large. It would be interesting, for various applications, to establish these results for small scales as well.
2 Structure of the paper
After a review of analysis in the setting of local fields, including some essential but basic oscillatory integral bounds, we set up some notation and detail some tools involving the Gowers uniformity norms. In Section 5, we give some preliminary results necessary to carry out the core arguments. In Section 6, we give the proof of Theorem 1.5 which is based on a polynomial ergodic theorem (PET) induction scheme and a degree lowering argument developed by the third author in earlier work. In Section 7, we will prove Theorem 1.6. Finally, in Section 8, we show how Theorem 1.3 follows as a consequence of Theorem 1.6.
3 Review of basic analysis on local fields
A basic reference for the material reviewed in this section is [Reference Neukirch35].
Let
![]() $\mathbb {K}$
be a locally compact topological field with a nondiscrete topology. Such fields are called local fields and have a unique (up to a positive multiple) Haar measure
$\mathbb {K}$
be a locally compact topological field with a nondiscrete topology. Such fields are called local fields and have a unique (up to a positive multiple) Haar measure
![]() $\mu $
. They also carry a nontrivial absolute value
$\mu $
. They also carry a nontrivial absolute value
![]() $|\cdot |$
such that the corresponding balls
$|\cdot |$
such that the corresponding balls
![]() $B_r(x) = \{y \in \mathbb {K}: |y-x|\le r\}$
generate the topology.
$B_r(x) = \{y \in \mathbb {K}: |y-x|\le r\}$
generate the topology.
Recall that an absolute value on a field
![]() $\mathbb {K}$
is a map
$\mathbb {K}$
is a map
![]() $|\cdot | : \mathbb {K} \to {\mathbb R}^{+}$
satisfying
$|\cdot | : \mathbb {K} \to {\mathbb R}^{+}$
satisfying
for some
![]() $C\ge 1$
. It is nontrivial if there is an
$C\ge 1$
. It is nontrivial if there is an
![]() $x\not = 0$
such that
$x\not = 0$
such that
![]() $|x| \not = 1$
. Two absolute values
$|x| \not = 1$
. Two absolute values
![]() $|\cdot |_1$
and
$|\cdot |_1$
and
![]() $|\cdot |_2$
are said to be equivalent if there is a
$|\cdot |_2$
are said to be equivalent if there is a
![]() $\theta> 0$
such that
$\theta> 0$
such that
![]() $|x|_2 = |x|_1^{\theta }$
for all
$|x|_2 = |x|_1^{\theta }$
for all
![]() $x\in \mathbb {K}$
. Equivalent absolute values give the same topology. There is always an equivalent absolute value such that the triangle inequality
$x\in \mathbb {K}$
. Equivalent absolute values give the same topology. There is always an equivalent absolute value such that the triangle inequality
![]() $(c)$
holds with
$(c)$
holds with
![]() $C = 1$
. If
$C = 1$
. If
![]() $|\cdot |$
satisfies the stronger triangle inequality
$|\cdot |$
satisfies the stronger triangle inequality
![]() $(c') \, |x+y| \le \max (|x|,|y|)$
, we say that
$(c') \, |x+y| \le \max (|x|,|y|)$
, we say that
![]() $|\cdot |$
is non-Archimedean. Note that if
$|\cdot |$
is non-Archimedean. Note that if
![]() $|\cdot |$
is non-Archimedean, then all equivalent absolute values are non-Archimedean. The field
$|\cdot |$
is non-Archimedean, then all equivalent absolute values are non-Archimedean. The field
![]() $\mathbb {K}$
is said to be non-Archimedean if the underlying absolute value (and hence all equivalent ones) is non-Archimedean. Otherwise, we say
$\mathbb {K}$
is said to be non-Archimedean if the underlying absolute value (and hence all equivalent ones) is non-Archimedean. Otherwise, we say
![]() $\mathbb {K}$
is Archimedean.
$\mathbb {K}$
is Archimedean.
When
![]() $\mathbb {K}$
is Archimedean, then it is isomorphic to the real
$\mathbb {K}$
is Archimedean, then it is isomorphic to the real
![]() ${\mathbb R}$
or complex
${\mathbb R}$
or complex
![]() ${\mathbb C}$
field with the usual topology. In this case, Haar measure is a multiple of Lebesgue measure. When
${\mathbb C}$
field with the usual topology. In this case, Haar measure is a multiple of Lebesgue measure. When
![]() $\mathbb {K}$
is non-Archimedean, then it is a finite extension of a p-adic field
$\mathbb {K}$
is non-Archimedean, then it is a finite extension of a p-adic field
![]() ${\mathbb Q}_p$
in the characteristic zero case and a function field of Laurent series over a finite field in the positive characteristic case. Furthermore, the ring of integers
${\mathbb Q}_p$
in the characteristic zero case and a function field of Laurent series over a finite field in the positive characteristic case. Furthermore, the ring of integers
![]() $o_{\mathbb {K}} := \{x \in \mathbb {K}: |x|\le 1\}$
and the unique maximal ideal
$o_{\mathbb {K}} := \{x \in \mathbb {K}: |x|\le 1\}$
and the unique maximal ideal
![]() $m_{\mathbb {K}} := \{x \in \mathbb {K} : |x| < 1\}$
do not depend on the choice of absolute value (it is invariant when we pass to an equivalent absolute value). For any
$m_{\mathbb {K}} := \{x \in \mathbb {K} : |x| < 1\}$
do not depend on the choice of absolute value (it is invariant when we pass to an equivalent absolute value). For any
![]() $\mathbb {K}$
, we normalise Haar measure so that
$\mathbb {K}$
, we normalise Haar measure so that
![]() $\mu (B_1(0)) = 1$
.
$\mu (B_1(0)) = 1$
.
When
![]() $\mathbb {K}$
is non-Archimedean, the unique maximal ideal
$\mathbb {K}$
is non-Archimedean, the unique maximal ideal
![]() $m_{\mathbb {K}} = (\pi )$
is principal and we call any generating element
$m_{\mathbb {K}} = (\pi )$
is principal and we call any generating element
![]() $\pi $
a uniformizer. Furthermore, the residue field
$\pi $
a uniformizer. Furthermore, the residue field
![]() $k := o_{\mathbb {K}}/m_{\mathbb {K}}$
is finite, say with q elements. For
$k := o_{\mathbb {K}}/m_{\mathbb {K}}$
is finite, say with q elements. For
![]() $x\in \mathbb {K}$
, there is a unique
$x\in \mathbb {K}$
, there is a unique
![]() $n\in {\mathbb Z}$
such that
$n\in {\mathbb Z}$
such that
![]() $x = \pi ^n u$
where u is a unit. We can go further and expand any
$x = \pi ^n u$
where u is a unit. We can go further and expand any
![]() $x\in \mathbb {K}$
as a Laurent series in
$x\in \mathbb {K}$
as a Laurent series in
![]() $\pi $
;
$\pi $
;
![]() $x = \sum _{j\ge -L} x_j \pi ^j$
, where each
$x = \sum _{j\ge -L} x_j \pi ^j$
, where each
![]() $x_j$
belongs to the residue field k. If
$x_j$
belongs to the residue field k. If
![]() $x_{-L} \not =0$
, then
$x_{-L} \not =0$
, then
![]() $x = \pi ^{-L} u$
, where
$x = \pi ^{-L} u$
, where
![]() $u = \sum _{j\ge -L} x_j \pi ^{j+L}$
is a unit.
$u = \sum _{j\ge -L} x_j \pi ^{j+L}$
is a unit.
There is a choice of (equivalent) absolute value
![]() $|\cdot |$
such that
$|\cdot |$
such that
![]() $\mu (B_r(x)) \simeq r$
for all
$\mu (B_r(x)) \simeq r$
for all
![]() $r>0$
and
$r>0$
and
![]() $x\in \mathbb {K}$
. When
$x\in \mathbb {K}$
. When
![]() $\mathbb {K}= {\mathbb R}$
, we have
$\mathbb {K}= {\mathbb R}$
, we have
![]() $|x| = x \, \mathrm {sgn}(x)$
and when
$|x| = x \, \mathrm {sgn}(x)$
and when
![]() $\mathbb {K} = {\mathbb C}$
, we have
$\mathbb {K} = {\mathbb C}$
, we have
![]() $|z| = z{\overline {z}}$
. When
$|z| = z{\overline {z}}$
. When
![]() $\mathbb {K}$
is non-Archimedean, then the absolute value
$\mathbb {K}$
is non-Archimedean, then the absolute value
![]() $|x| := q^{-m}$
, where
$|x| := q^{-m}$
, where
![]() $x = \pi ^m u$
and u a unit has the property that its balls satisfy
$x = \pi ^m u$
and u a unit has the property that its balls satisfy
![]() $\mu (B_r(x)) = q^n$
, where
$\mu (B_r(x)) = q^n$
, where
![]() $q^n \le r < q^{n+1}$
and so
$q^n \le r < q^{n+1}$
and so
![]() $\mu (B_r(x)) \simeq r$
. We choose the absolute value with this normalisation.
$\mu (B_r(x)) \simeq r$
. We choose the absolute value with this normalisation.
We will need a couple simple change of variable formulae which we will use again and again:
The first follows from the translation invariance of the Haar measure
![]() $\mu $
. For the second formula, the measure
$\mu $
. For the second formula, the measure
![]() $E \to \mu (yE)$
defined by an element
$E \to \mu (yE)$
defined by an element
![]() $y\in \mathbb {K}$
is translation-invariant and so by the uniqueness of Haar measure, we have
$y\in \mathbb {K}$
is translation-invariant and so by the uniqueness of Haar measure, we have
![]() $\mu (yE) = \mathrm {mod}_{\mu }(y) \mu (E)$
for some nonnegative number
$\mu (yE) = \mathrm {mod}_{\mu }(y) \mu (E)$
for some nonnegative number
![]() $\mathrm {mod}_{\mu }(y)$
, the so-called modulus of the measure
$\mathrm {mod}_{\mu }(y)$
, the so-called modulus of the measure
![]() $\mu $
. In fact
$\mu $
. In fact
![]() $|y| := \mathrm {mod}_{\mu }(y)$
defines the absolute value with the desired normalisation whose balls
$|y| := \mathrm {mod}_{\mu }(y)$
defines the absolute value with the desired normalisation whose balls
![]() $B_r(x)$
satisfy
$B_r(x)$
satisfy
![]() $\mu (B_r(x)) \simeq r$
. This proves the second change of variables formula. There is one additional, more sophisticated, nonlinear change of variable formula which we will need at one point, but we will justify this change of variables at the time.
$\mu (B_r(x)) \simeq r$
. This proves the second change of variables formula. There is one additional, more sophisticated, nonlinear change of variable formula which we will need at one point, but we will justify this change of variables at the time.
The (additive) character group of
![]() $\mathbb {K}$
is isomorphic to itself. Starting with any nonprincipal character
$\mathbb {K}$
is isomorphic to itself. Starting with any nonprincipal character
![]() $\mathrm {e}$
on
$\mathrm {e}$
on
![]() $\mathbb {K}$
, all other characters
$\mathbb {K}$
, all other characters
![]() $\chi $
can be identified with an element
$\chi $
can be identified with an element
![]() $y\in \mathbb {K}$
via
$y\in \mathbb {K}$
via
![]() $\chi (x) = \mathrm {e}(yx)$
. We fix a convenient choice for
$\chi (x) = \mathrm {e}(yx)$
. We fix a convenient choice for
![]() $\mathrm {e}$
; when
$\mathrm {e}$
; when
![]() $\mathbb {K}={\mathbb R}$
, we take
$\mathbb {K}={\mathbb R}$
, we take
![]() $\mathrm {e}(x) = e^{2\pi i x}$
. When
$\mathrm {e}(x) = e^{2\pi i x}$
. When
![]() $\mathbb {K}$
is non-Archimedean, we choose
$\mathbb {K}$
is non-Archimedean, we choose
![]() $\mathrm {e}$
so that
$\mathrm {e}$
so that
![]() $\mathrm {e} \equiv 1$
on
$\mathrm {e} \equiv 1$
on
![]() $o_{\mathbb {K}}$
and nontrivial on
$o_{\mathbb {K}}$
and nontrivial on
![]() $B_q(0)$
; that is, there is a
$B_q(0)$
; that is, there is a
![]() $x_0$
with
$x_0$
with
![]() $|x_0| = q$
such that
$|x_0| = q$
such that
![]() $\mathrm {e}(x_0) \not = 1$
. The choice of
$\mathrm {e}(x_0) \not = 1$
. The choice of
![]() $\mathrm {e}$
on
$\mathrm {e}$
on
![]() ${\mathbb C}$
does not really matter but a convenient choice is
${\mathbb C}$
does not really matter but a convenient choice is
![]() $\mathrm {e}(z) = e^{2\pi i \operatorname {\mathrm {Re}}{z}}$
. We define the Fourier transform
$\mathrm {e}(z) = e^{2\pi i \operatorname {\mathrm {Re}}{z}}$
. We define the Fourier transform
Plancherel’s theorem and the Fourier inversion formula hold as in the real setting.
3.1 An oscillatory integral estimate
For
![]() $P(x) = a_d x^d + \cdots + a_1 x \in \mathbb {K}[\mathrm {x}]$
, we will use the following oscillatory integral bound:
$P(x) = a_d x^d + \cdots + a_1 x \in \mathbb {K}[\mathrm {x}]$
, we will use the following oscillatory integral bound:
When
![]() $\mathbb {K} = {\mathbb R}$
, it is a simple matter to deduce the bound (3.1) from general oscillatory bounds due to van der Corput (see [Reference Stein41]). When
$\mathbb {K} = {\mathbb R}$
, it is a simple matter to deduce the bound (3.1) from general oscillatory bounds due to van der Corput (see [Reference Stein41]). When
![]() $\mathbb {K} = {\mathbb Q}_p$
is the p-adic field, then
$\mathbb {K} = {\mathbb Q}_p$
is the p-adic field, then
 $$ \begin{align*}I(P) \ = \ p^{-s} \sum_{x=0}^{p^s -1} e^{2\pi i Q(x)/p^s} \ \ \ \mathrm{where} \ \ \ p^s = \max_j |a_j| \ \ \mathrm{and} \ \ Q(x) = b_d x^d + \cdots + b_1 x \in {\mathbb Z}[\mathrm{x}] \end{align*} $$
$$ \begin{align*}I(P) \ = \ p^{-s} \sum_{x=0}^{p^s -1} e^{2\pi i Q(x)/p^s} \ \ \ \mathrm{where} \ \ \ p^s = \max_j |a_j| \ \ \mathrm{and} \ \ Q(x) = b_d x^d + \cdots + b_1 x \in {\mathbb Z}[\mathrm{x}] \end{align*} $$
satisfies
![]() $\mathrm {gcd}(b_d, \ldots , b_1, p) = 1$
; hence, a classical result of Hua [Reference Hua13] implies
$\mathrm {gcd}(b_d, \ldots , b_1, p) = 1$
; hence, a classical result of Hua [Reference Hua13] implies
![]() $|I(P)| \le C_d p^{-s/d}$
which is Equation (3.1) in this case. It is natural to extend Hua’s bound to other non-Archimedean fields; see, for example, [Reference Wright45] where character sums are treated over general Dedekind domains which in particular establishes Equation (3.1) for any non-Archimedean field
$|I(P)| \le C_d p^{-s/d}$
which is Equation (3.1) in this case. It is natural to extend Hua’s bound to other non-Archimedean fields; see, for example, [Reference Wright45] where character sums are treated over general Dedekind domains which in particular establishes Equation (3.1) for any non-Archimedean field
![]() $\mathbb {K}$
when the characteristic of
$\mathbb {K}$
when the characteristic of
![]() $\mathbb {K}$
(if positive) is larger than d, a basic assumption appearing in our main result Theorem 1.3.
$\mathbb {K}$
(if positive) is larger than d, a basic assumption appearing in our main result Theorem 1.3.
It is not straightforward to apply van der Corput bounds when
![]() $\mathbb {K} = {\mathbb C}$
. However, we can see the bound (3.1) for both
$\mathbb {K} = {\mathbb C}$
. However, we can see the bound (3.1) for both
![]() $\mathbb {K} = {\mathbb R}$
and
$\mathbb {K} = {\mathbb R}$
and
![]() $\mathbb {K} = {\mathbb C}$
as a consequence of the following general bound due to Arkhipov, Chubarikov and Karatsuba [Reference Arkhipov, Chubarikov and Karatsuba1]: Let
$\mathbb {K} = {\mathbb C}$
as a consequence of the following general bound due to Arkhipov, Chubarikov and Karatsuba [Reference Arkhipov, Chubarikov and Karatsuba1]: Let
![]() $P \in {\mathbb R}[X_1, \ldots , X_n]$
be a real polynomial of degree d in n variables. If
$P \in {\mathbb R}[X_1, \ldots , X_n]$
be a real polynomial of degree d in n variables. If
![]() ${\mathbb B}^n$
denotes the unit ball in
${\mathbb B}^n$
denotes the unit ball in
![]() ${\mathbb R}^n$
, then
${\mathbb R}^n$
, then
A simple equivalence of norms argument shows that
![]() $H(P) \ge c_d [\max _{\alpha } |a_{\alpha }|]^{1/d}$
, where
$H(P) \ge c_d [\max _{\alpha } |a_{\alpha }|]^{1/d}$
, where
![]() $P({\underline {x}}) = \sum _{\alpha } a_{\alpha } {\underline {x}}^{\alpha }$
and d is the degree of P. Hence, Equation (3.2) implies Equation (3.1) when
$P({\underline {x}}) = \sum _{\alpha } a_{\alpha } {\underline {x}}^{\alpha }$
and d is the degree of P. Hence, Equation (3.2) implies Equation (3.1) when
![]() $\mathbb {K} = {\mathbb R}$
. When
$\mathbb {K} = {\mathbb R}$
. When
![]() $\mathbb {K} = {\mathbb C}$
and
$\mathbb {K} = {\mathbb C}$
and
![]() $f(z) = a_d z^d + \cdots + a_1 z \in {\mathbb C}[\mathrm {z}]$
, write
$f(z) = a_d z^d + \cdots + a_1 z \in {\mathbb C}[\mathrm {z}]$
, write
![]() $f(x+iy) = P(x,y) + i Q(x,y)$
and note that
$f(x+iy) = P(x,y) + i Q(x,y)$
and note that
for the choice of character
![]() $\mathrm {e}(z) = e^{2\pi i \operatorname {\mathrm {Re}}{z}}$
. From the Cauchy–Riemann equations, we have
$\mathrm {e}(z) = e^{2\pi i \operatorname {\mathrm {Re}}{z}}$
. From the Cauchy–Riemann equations, we have
![]() $H(P) \simeq _d \min _{|z|\le 1} \max _k |f^{(k)}(z)|^{1/2k} \ge c_d [\max _j |a_j|]^{1/2d}$
(recall we are using the absolute value
$H(P) \simeq _d \min _{|z|\le 1} \max _k |f^{(k)}(z)|^{1/2k} \ge c_d [\max _j |a_j|]^{1/2d}$
(recall we are using the absolute value
![]() $|z| = z{\overline {z}}$
on
$|z| = z{\overline {z}}$
on
![]() ${\mathbb C}$
), and so Equation (3.2) implies Equation (3.1) with exponent
${\mathbb C}$
), and so Equation (3.2) implies Equation (3.1) with exponent
![]() $1/2d$
in this case. There is an alternative argument which establishes Equation (3.1) with the exponent
$1/2d$
in this case. There is an alternative argument which establishes Equation (3.1) with the exponent
![]() $1/d$
when
$1/d$
when
![]() $\mathbb {K} = {\mathbb C}$
but this is unimportant for our purposes.
$\mathbb {K} = {\mathbb C}$
but this is unimportant for our purposes.
4 Some notation and basic tools
By a scale N, we mean a positive number when
![]() $\mathbb {K}$
is Archimedean and when
$\mathbb {K}$
is Archimedean and when
![]() $\mathbb {K}$
is non-Archimedean, it denotes a discrete value
$\mathbb {K}$
is non-Archimedean, it denotes a discrete value
![]() $N = q^k, \, k\in {\mathbb Z}$
, a power of the cardinality of the residue field k. When N is a scale, we denote by
$N = q^k, \, k\in {\mathbb Z}$
, a power of the cardinality of the residue field k. When N is a scale, we denote by
![]() $[N] := B_N(0)$
the ball with centre
$[N] := B_N(0)$
the ball with centre
![]() $0$
and radius N. In this case, we have
$0$
and radius N. In this case, we have
![]() $\mu ([N]) \simeq N$
(equality in the non-Archimedean case) by our normalisations of the absolute value
$\mu ([N]) \simeq N$
(equality in the non-Archimedean case) by our normalisations of the absolute value
![]() $|\cdot |$
and Haar measure
$|\cdot |$
and Haar measure
![]() $\mu $
. An interval I is a ball
$\mu $
. An interval I is a ball
![]() $I = B_{r_I}(x_I)$
with some centre
$I = B_{r_I}(x_I)$
with some centre
![]() $x_I \in \mathbb {K}$
and radius
$x_I \in \mathbb {K}$
and radius
![]() $r_I>0$
. For an interval I, we associate the measure
$r_I>0$
. For an interval I, we associate the measure
For an interval I, we define the Fejér kernel ![]() and the corresponding measure
and the corresponding measure
![]() $d\nu _I(x) = \kappa _I(x) d\mu (x)$
. When
$d\nu _I(x) = \kappa _I(x) d\mu (x)$
. When
![]() $I = [N]$
for some scale N, we have
$I = [N]$
for some scale N, we have
![]() $-I = I$
and so
$-I = I$
and so ![]() . Furthermore, when
. Furthermore, when
![]() $\mathbb {K}$
is non-Archimedean, we have
$\mathbb {K}$
is non-Archimedean, we have ![]() and so
and so
![]() $d\nu _I = d\mu _I$
in this case. When
$d\nu _I = d\mu _I$
in this case. When
![]() $\mathbb {K} = {\mathbb R}$
and
$\mathbb {K} = {\mathbb R}$
and
![]() $I = [0,N]$
, we have
$I = [0,N]$
, we have
![]() $\kappa _I(x) = N^{-1}(1 - |x|/N)$
when
$\kappa _I(x) = N^{-1}(1 - |x|/N)$
when
![]() $|x|\le N$
and zero otherwise.
$|x|\le N$
and zero otherwise.
We now give precise notation which we will use throughout the paper.
4.1 Basic notation
As usual,
![]() $\mathbb Z$
will denote the ring of rational integers.
$\mathbb Z$
will denote the ring of rational integers.
-
1. We use
 $\mathbb Z_+:=\{1, 2,\ldots \}$
and
$\mathbb Z_+:=\{1, 2,\ldots \}$
and
 $\mathbb {N} := \mathbb Z_+\cup \{0\}$
to denote the sets of positive integers and nonnegative integers, respectively.
$\mathbb {N} := \mathbb Z_+\cup \{0\}$
to denote the sets of positive integers and nonnegative integers, respectively. -
2. For any
 $L\in \mathbb R_+$
, we will use the notation
$L\in \mathbb R_+$
, we will use the notation 
-
3. We use
 to denote the indicator function of a set A. If S is a statement, we write
to denote the indicator function of a set A. If S is a statement, we write  to denote its indicator, equal to
to denote its indicator, equal to
 $1$
if S is true and
$1$
if S is true and
 $0$
if S is false. For instance,
$0$
if S is false. For instance,  .
.
4.2 Asymptotic notation and magnitudes
The letters
![]() $C,c, C_0, C_1, \ldots>0$
will always denote absolute constants; however, their values may vary from occurrence to occurrence.
$C,c, C_0, C_1, \ldots>0$
will always denote absolute constants; however, their values may vary from occurrence to occurrence.
-
1. For two nonnegative quantities
 $A, B$
, we write
$A, B$
, we write
 $A \lesssim _{\delta } B$
(
$A \lesssim _{\delta } B$
(
 $A \gtrsim _{\delta } B$
) if there is an absolute constant
$A \gtrsim _{\delta } B$
) if there is an absolute constant
 $C_{\delta }>0$
(which possibly depends on
$C_{\delta }>0$
(which possibly depends on
 $\delta>0$
) such that
$\delta>0$
) such that
 $A\le C_{\delta }B$
(
$A\le C_{\delta }B$
(
 $A\ge C_{\delta }B$
). We will write
$A\ge C_{\delta }B$
). We will write
 $A \simeq _{\delta } B$
when
$A \simeq _{\delta } B$
when
 $A \lesssim _{\delta } B$
and
$A \lesssim _{\delta } B$
and
 $A\gtrsim _{\delta } B$
hold simultaneously. We will omit the subscript
$A\gtrsim _{\delta } B$
hold simultaneously. We will omit the subscript
 $\delta $
if irrelevant.
$\delta $
if irrelevant. -
2. For a function
 $f:X\to \mathbb C$
and positive-valued function
$f:X\to \mathbb C$
and positive-valued function
 $g:X\to (0, \infty )$
, write
$g:X\to (0, \infty )$
, write
 $f = O(g)$
if there exists a constant
$f = O(g)$
if there exists a constant
 $C>0$
such that
$C>0$
such that
 $|f(x)| \le C g(x)$
for all
$|f(x)| \le C g(x)$
for all
 $x\in X$
. We will also write
$x\in X$
. We will also write
 $f = O_{\delta }(g)$
if the implicit constant depends on
$f = O_{\delta }(g)$
if the implicit constant depends on
 $\delta $
. For two functions
$\delta $
. For two functions
 $f, g:X\to \mathbb C$
such that
$f, g:X\to \mathbb C$
such that
 $g(x)\neq 0$
for all
$g(x)\neq 0$
for all
 $x\in X$
we write
$x\in X$
we write
 $f = o(g)$
if
$f = o(g)$
if
 $\lim _{x\to \infty }f(x)/g(x)=0$
.
$\lim _{x\to \infty }f(x)/g(x)=0$
.
4.3 Polynomials
Let
![]() $\mathbb {K}[\mathrm {t}]$
denote the space of all polynomials in one indeterminate
$\mathbb {K}[\mathrm {t}]$
denote the space of all polynomials in one indeterminate
![]() $\mathrm {t}$
with coefficients in
$\mathrm {t}$
with coefficients in
![]() $\mathbb {K}$
. Every polynomial
$\mathbb {K}$
. Every polynomial
![]() $P\in \mathbb {K}[\mathrm {t}]$
can be written as a formal power series
$P\in \mathbb {K}[\mathrm {t}]$
can be written as a formal power series
 $$ \begin{align} P(t)=\sum_{j=0}^{\infty}c_jt^j, \end{align} $$
$$ \begin{align} P(t)=\sum_{j=0}^{\infty}c_jt^j, \end{align} $$
where all but finitely many coefficients
![]() $c_j\in \mathbb {K}$
vanish.
$c_j\in \mathbb {K}$
vanish.
-
1. We define the degree of
 $P\in \mathbb {K}[\mathrm {t}]$
by
$P\in \mathbb {K}[\mathrm {t}]$
by  $$ \begin{align*} \deg(P):=&\max\{j\in {\mathbb Z}_+: c_j\neq0\}. \end{align*} $$
$$ \begin{align*} \deg(P):=&\max\{j\in {\mathbb Z}_+: c_j\neq0\}. \end{align*} $$
-
2. A finite collection
 ${\mathcal P}\subset \mathbb {K}[\mathrm {t}]$
has degree
${\mathcal P}\subset \mathbb {K}[\mathrm {t}]$
has degree
 $d\in \mathbb {N}$
, if
$d\in \mathbb {N}$
, if
 $d=\max \{\deg (P): P\in {\mathcal P}\}$
.
$d=\max \{\deg (P): P\in {\mathcal P}\}$
. -
3. For a polynomial
 $P\in \mathbb {K}[\mathrm {t}]$
and
$P\in \mathbb {K}[\mathrm {t}]$
and
 $j\in \mathbb {N}$
, let
$j\in \mathbb {N}$
, let
 $\operatorname {\mathrm {c}}_j(P)$
denote j-th coefficient of P. We also let
$\operatorname {\mathrm {c}}_j(P)$
denote j-th coefficient of P. We also let
 $\ell (P)$
denote the leading coefficient of P; that is, for P as in Equation (4.1) we have
$\ell (P)$
denote the leading coefficient of P; that is, for P as in Equation (4.1) we have
 $\operatorname {\mathrm {c}}_j(P)=c_j$
for
$\operatorname {\mathrm {c}}_j(P)=c_j$
for
 $j\in \mathbb {N}$
and
$j\in \mathbb {N}$
and
 $\ell (P)=c_{d}$
where
$\ell (P)=c_{d}$
where
 $d = \deg {P}$
.
$d = \deg {P}$
.
4.4
 $L^p$
spaces
$L^p$
spaces
![]() $(X, {\mathcal B}(X), \lambda )$
denotes a measure space X with
$(X, {\mathcal B}(X), \lambda )$
denotes a measure space X with
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() ${\mathcal B}(X)$
and
${\mathcal B}(X)$
and
![]() $\sigma $
-finite measure
$\sigma $
-finite measure
![]() $\lambda $
.
$\lambda $
.
-
1. The set of
 $\lambda $
-measurable complex-valued functions defined on X will be denoted by
$\lambda $
-measurable complex-valued functions defined on X will be denoted by
 $L^0(X)$
.
$L^0(X)$
. -
2. The set of functions in
 $L^0(X)$
whose modulus is integrable with p-th power is denoted by
$L^0(X)$
whose modulus is integrable with p-th power is denoted by
 $L^p(X)$
for
$L^p(X)$
for
 $p\in (0, \infty )$
, whereas
$p\in (0, \infty )$
, whereas
 $L^{\infty }(X)$
denotes the space of all essentially bounded functions in
$L^{\infty }(X)$
denotes the space of all essentially bounded functions in
 $L^0(X)$
.
$L^0(X)$
. -
3. We will say that a function
 $f\in L^0(X)$
is
$f\in L^0(X)$
is
 $1$
-bounded if
$1$
-bounded if
 $f\in L^{\infty }(X)$
and
$f\in L^{\infty }(X)$
and
 $\|f\|_{L^{\infty }(X)}\le 1$
.
$\|f\|_{L^{\infty }(X)}\le 1$
. -
4. For any
 $n\in \mathbb Z_+$
the measure
$n\in \mathbb Z_+$
the measure
 $\lambda ^{\otimes n}$
will denote the product measure
$\lambda ^{\otimes n}$
will denote the product measure
 $\lambda \otimes \ldots \otimes \lambda $
on the product space
$\lambda \otimes \ldots \otimes \lambda $
on the product space
 $X^n$
with the product
$X^n$
with the product
 $\sigma $
-algebra
$\sigma $
-algebra
 ${\mathcal B}(X)\otimes \ldots \otimes {\mathcal B}(X)$
.
${\mathcal B}(X)\otimes \ldots \otimes {\mathcal B}(X)$
.
4.5 Gowers box and uniformity norms
We will use the Gowers norm and Gowers box norm of a function f which is defined in terms of the multiplicative discrete derivatives
![]() $\Delta _{h_1.\ldots , h_s} f(x)$
: for
$\Delta _{h_1.\ldots , h_s} f(x)$
: for
![]() $x, h \in \mathbb {K}$
, we set
$x, h \in \mathbb {K}$
, we set
![]() $\Delta _h f(x) = f(x){\overline {f(x+h)}}$
, and iteratively, we define
$\Delta _h f(x) = f(x){\overline {f(x+h)}}$
, and iteratively, we define
When
![]() $h = (h_1, \ldots , h_s) \in \mathbb {K}^s$
, we often write
$h = (h_1, \ldots , h_s) \in \mathbb {K}^s$
, we often write
![]() $\Delta _{h_1, \ldots , h_s}f(x)$
as
$\Delta _{h_1, \ldots , h_s}f(x)$
as
![]() $\Delta _h f(x)$
or
$\Delta _h f(x)$
or
![]() $\Delta _h^s f(x)$
. For
$\Delta _h^s f(x)$
. For
![]() $\omega = (\omega _1, \ldots , \omega _s) \in \{0,1\}^s$
, we write
$\omega = (\omega _1, \ldots , \omega _s) \in \{0,1\}^s$
, we write
![]() $\omega \cdot h := \sum _{i=1}^s \omega _i h_i$
and
$\omega \cdot h := \sum _{i=1}^s \omega _i h_i$
and
![]() $|\omega |:= \omega _1 + \cdots + \omega _s$
. If
$|\omega |:= \omega _1 + \cdots + \omega _s$
. If
![]() ${\mathcal C} z = {\overline {z}}$
denotes the conjugation operator, we observe that
${\mathcal C} z = {\overline {z}}$
denotes the conjugation operator, we observe that
For any integer
![]() $s\ge 1$
, we define the Gowers
$s\ge 1$
, we define the Gowers
![]() $U^s$
norm of f by
$U^s$
norm of f by
We note that
![]() $\|f\|_{U^2} = \|{\widehat {f}}\|_{L^4}$
.
$\|f\|_{U^2} = \|{\widehat {f}}\|_{L^4}$
.
For intervals
![]() $I, I_1, \ldots , I_s$
, we define the Gowers box norm as
$I, I_1, \ldots , I_s$
, we define the Gowers box norm as
From Equation (4.2), we see that
A similar formula relates the Gowers
![]() $U^{s+1}$
norm to the Gowers
$U^{s+1}$
norm to the Gowers
![]() $U^s$
norm.
$U^s$
norm.
4.6 The Gowers–Cauchy–Schwarz inequality
When
![]() $s\ge 2$
, both the Gowers uniformity norm and the Gowers box norm are in fact norms. In particular, the triangle inequality holds. The triangle inequality also holds when
$s\ge 2$
, both the Gowers uniformity norm and the Gowers box norm are in fact norms. In particular, the triangle inequality holds. The triangle inequality also holds when
![]() $s=1$
and so we have that
$s=1$
and so we have that
holds for every
![]() $s\ge 1$
. These inequalities follow from a more general inequality which we will find useful.
$s\ge 1$
. These inequalities follow from a more general inequality which we will find useful.
Let A be a finite set and for each
![]() $\alpha \in A$
; let
$\alpha \in A$
; let
![]() $(X_{\alpha }, du_{\alpha })$
be a probability space. Set
$(X_{\alpha }, du_{\alpha })$
be a probability space. Set
![]() $X = \prod _{\alpha \in A} X_{\alpha }$
, and let
$X = \prod _{\alpha \in A} X_{\alpha }$
, and let
![]() $f : X \to {\mathbb C}$
be a complex-valued function. For any
$f : X \to {\mathbb C}$
be a complex-valued function. For any
![]() $x^{(0)} = (x_{\alpha }^{(0)})_{\alpha \in A}$
and
$x^{(0)} = (x_{\alpha }^{(0)})_{\alpha \in A}$
and
![]() $x^{(1)} = (x_{\alpha }^{(1)})_{\alpha \in A}$
in X and
$x^{(1)} = (x_{\alpha }^{(1)})_{\alpha \in A}$
in X and
![]() $\omega = (\omega _{\alpha })_{\alpha \in A} \in \{0,1\}^A$
, we write
$\omega = (\omega _{\alpha })_{\alpha \in A} \in \{0,1\}^A$
, we write
![]() $x^{(\omega )} = (x_{\alpha }^{(\omega _{\alpha })})_{\alpha \in A}$
. We define the generalised Gowers box norm of f on X as
$x^{(\omega )} = (x_{\alpha }^{(\omega _{\alpha })})_{\alpha \in A}$
. We define the generalised Gowers box norm of f on X as
 $$ \begin{align*} \|f\|_{\square (X)}^{2^{|A|}} \ = \ \iint_{X^2} \prod_{\omega \in \{0,1\}^A} {\mathcal C}^{|\omega|} f(x^{(\omega)}) \ du(x^{(0)}) \, du(x^{(1)}), \end{align*} $$
$$ \begin{align*} \|f\|_{\square (X)}^{2^{|A|}} \ = \ \iint_{X^2} \prod_{\omega \in \{0,1\}^A} {\mathcal C}^{|\omega|} f(x^{(\omega)}) \ du(x^{(0)}) \, du(x^{(1)}), \end{align*} $$
where
![]() $du$
denotes the product measure
$du$
denotes the product measure
![]() $\otimes _{\alpha \in A} du_{\alpha }$
. The following lemma is established in [Reference Green and Tao16].
$\otimes _{\alpha \in A} du_{\alpha }$
. The following lemma is established in [Reference Green and Tao16].
Lemma 4.5 (Gowers–Cauchy–Schwarz inequality).
With the setup above, let
![]() $f_{\omega } : X \to {\mathbb C}$
for every
$f_{\omega } : X \to {\mathbb C}$
for every
![]() $\omega \in \{0,1\}^A$
. We have
$\omega \in \{0,1\}^A$
. We have
 $$ \begin{align} \Big| \iint_{X^2} \prod_{\omega \in \{0,1\}^A} {\mathcal C}^{|\omega|} f_{\omega} (x^{(\omega)}) \ du(x^{(0)}) \, du(x^{(1)}) \Big| \ \le \ \prod_{\omega \in \{0,1\}^A} \|f_{\omega}\|_{{\square (X)}}. \end{align} $$
$$ \begin{align} \Big| \iint_{X^2} \prod_{\omega \in \{0,1\}^A} {\mathcal C}^{|\omega|} f_{\omega} (x^{(\omega)}) \ du(x^{(0)}) \, du(x^{(1)}) \Big| \ \le \ \prod_{\omega \in \{0,1\}^A} \|f_{\omega}\|_{{\square (X)}}. \end{align} $$
We will need the following consequence.
Corollary 4.7. Let
![]() $f : X \to {\mathbb C}$
and for each
$f : X \to {\mathbb C}$
and for each
![]() $\alpha \in A$
, suppose
$\alpha \in A$
, suppose
![]() $g_{\alpha }: X \to {\mathbb C}$
is a 1-bounded function that is independent of the
$g_{\alpha }: X \to {\mathbb C}$
is a 1-bounded function that is independent of the
![]() $x_{\alpha }$
variable. Then
$x_{\alpha }$
variable. Then
 $$ \begin{align} \Big| \int_X f(x) \prod_{\alpha \in A} g_{\alpha}(x) du(x) \Big|^{2^{|A|}} \ \le \ \int_{X^2} \prod_{\omega\in \{0,1\}^A} {\mathcal C}^{|\omega|} f(x^{(\omega)}) \, du(x^{(0)}) du(x^{(1)}). \end{align} $$
$$ \begin{align} \Big| \int_X f(x) \prod_{\alpha \in A} g_{\alpha}(x) du(x) \Big|^{2^{|A|}} \ \le \ \int_{X^2} \prod_{\omega\in \{0,1\}^A} {\mathcal C}^{|\omega|} f(x^{(\omega)}) \, du(x^{(0)}) du(x^{(1)}). \end{align} $$
Proof. For
![]() $\omega ^0 = (0, \ldots , 0)$
, set
$\omega ^0 = (0, \ldots , 0)$
, set
![]() $f_{\omega ^0} = f$
and for
$f_{\omega ^0} = f$
and for
![]() $\omega ^{\beta } = (\omega _{\alpha })_{\alpha \in A}$
with
$\omega ^{\beta } = (\omega _{\alpha })_{\alpha \in A}$
with
![]() $\omega _{\alpha } = 0$
when
$\omega _{\alpha } = 0$
when
![]() $\alpha \not = \beta $
and
$\alpha \not = \beta $
and
![]() $\omega _{\beta } = 1$
, set
$\omega _{\beta } = 1$
, set
![]() $f_{\omega ^{\beta }} = {\overline {g_{\beta }}}$
. For all other choices of
$f_{\omega ^{\beta }} = {\overline {g_{\beta }}}$
. For all other choices of
![]() $\omega \in \{0,1\}^A$
, set
$\omega \in \{0,1\}^A$
, set
![]() $f_{\omega } = 1$
. Hence,
$f_{\omega } = 1$
. Hence,
 $$ \begin{align*}\prod_{\omega\in \{0,1\}^A}{\mathcal C}^{|\omega|} f_{\omega}(x^{(\omega)}) = f(x^{(0)}) \prod_{\alpha \in A} g_{\alpha}(x^{(0)}) \end{align*} $$
$$ \begin{align*}\prod_{\omega\in \{0,1\}^A}{\mathcal C}^{|\omega|} f_{\omega}(x^{(\omega)}) = f(x^{(0)}) \prod_{\alpha \in A} g_{\alpha}(x^{(0)}) \end{align*} $$
since
![]() $g_{\alpha }$
is independent of the
$g_{\alpha }$
is independent of the
![]() $\alpha $
variable. Therefore, the inequality (4.6) implies
$\alpha $
variable. Therefore, the inequality (4.6) implies
 $$ \begin{align*}\Big| \int_X f(x) \prod_{\alpha \in A} g_{\alpha}(x) du(x) \Big| \le \prod_{\omega\in \{0,1\}^A} \|f_{\omega}\|_{{\square (X)}} \le \|f\|_{{\square (X)}} \end{align*} $$
$$ \begin{align*}\Big| \int_X f(x) \prod_{\alpha \in A} g_{\alpha}(x) du(x) \Big| \le \prod_{\omega\in \{0,1\}^A} \|f_{\omega}\|_{{\square (X)}} \le \|f\|_{{\square (X)}} \end{align*} $$
by the 1-boundedness of each
![]() $g_{\alpha }$
. This proves Equation (4.8).
$g_{\alpha }$
. This proves Equation (4.8).
5 Some preliminaries
In this section, we establish a few useful results which we will need in our arguments.
5.1
 $U^2$
-inverse theorem
$U^2$
-inverse theorem
We will use the following inverse theorem for the Gowers box norms.
Lemma 5.1 (
 $U^2$
-inverse theorem).
$U^2$
-inverse theorem).
Let
![]() $H_1$
and
$H_1$
and
![]() $H_2$
be two scales, and let f be a 1-bounded function supported in an interval I. Then
$H_2$
be two scales, and let f be a 1-bounded function supported in an interval I. Then
Proof. We have
 $$ \begin{align*} \|f\|_{\square^2_{[H_1],[H_2]}(I)}^4 \ = \ \frac{1}{\mu(I)} {\mathop{\iiint}_{\mathbb{K}^3}} \Delta_{h_1, h_2} f(x) d\nu_{[H_1]}(h_1) d\nu_{[H_2]}(h_2) d\mu(x) \end{align*} $$
$$ \begin{align*} \|f\|_{\square^2_{[H_1],[H_2]}(I)}^4 \ = \ \frac{1}{\mu(I)} {\mathop{\iiint}_{\mathbb{K}^3}} \Delta_{h_1, h_2} f(x) d\nu_{[H_1]}(h_1) d\nu_{[H_2]}(h_2) d\mu(x) \end{align*} $$
 $$ \begin{align*}= \ {\mathop{\iint}_{\mathbb{K}^2}} g(h_1, h_2) \, d\nu_{[H_1]}(h_1) d\nu_{[H_2]}(h_2) \ = \ {\mathop{\iint}_{\mathbb{K}^2}} {\widehat{g}}(\xi_1, \xi_2) \, {\overline{{\widehat{\nu_{[H_1]}}}(\xi_1) {\widehat{\nu_{[H_2]}}}(\xi_2)}} \, d\mu(\xi_1) d\mu(\xi_2), \end{align*} $$
$$ \begin{align*}= \ {\mathop{\iint}_{\mathbb{K}^2}} g(h_1, h_2) \, d\nu_{[H_1]}(h_1) d\nu_{[H_2]}(h_2) \ = \ {\mathop{\iint}_{\mathbb{K}^2}} {\widehat{g}}(\xi_1, \xi_2) \, {\overline{{\widehat{\nu_{[H_1]}}}(\xi_1) {\widehat{\nu_{[H_2]}}}(\xi_2)}} \, d\mu(\xi_1) d\mu(\xi_2), \end{align*} $$
where
Hence,
 $$ \begin{align*}= \ \frac{H_1^{-1}H_2^{-1}}{\mu(I)} \ \sup_{{\underline{\xi}}\in \mathbb{K}^2} \Big| {\mathop{\iiint}_{\mathbb{K}^3}} f_{00}(x) {\overline{f_{10}(x+h_1)}} {\overline{f_{01}(x+h_2)}} f_{11}(x+h_1+h_2) \, d\mu(x) d\mu(h_1) d\mu(h_2), \Big| \end{align*} $$
$$ \begin{align*}= \ \frac{H_1^{-1}H_2^{-1}}{\mu(I)} \ \sup_{{\underline{\xi}}\in \mathbb{K}^2} \Big| {\mathop{\iiint}_{\mathbb{K}^3}} f_{00}(x) {\overline{f_{10}(x+h_1)}} {\overline{f_{01}(x+h_2)}} f_{11}(x+h_1+h_2) \, d\mu(x) d\mu(h_1) d\mu(h_2), \Big| \end{align*} $$
where
![]() $f_{00}(x) = f(x) \mathrm {e}(-\xi _1 x - \xi _2 x),$
$f_{00}(x) = f(x) \mathrm {e}(-\xi _1 x - \xi _2 x),$
The final equality follows since
![]() $|\widehat {\nu }_{[H_j]}(\xi )| = |\widehat {\mu }_{[H_j]}(\xi )|^2$
, and so
$|\widehat {\nu }_{[H_j]}(\xi )| = |\widehat {\mu }_{[H_j]}(\xi )|^2$
, and so
by Plancherel’s theorem. Furthermore,
 $$ \begin{align*}{\widehat{g}}(\xi_1, \xi_2) \ = \ \frac{1}{\mu(I)} {\mathop{\iiint}_{\mathbb{K}^3}} \Delta_{h_1, h_2} f(x) \, \mathrm{e}(\xi_1 h_1 + \xi_2 h_2) \, d\mu(h_1) d\mu(h_2) d\mu(x). \end{align*} $$
$$ \begin{align*}{\widehat{g}}(\xi_1, \xi_2) \ = \ \frac{1}{\mu(I)} {\mathop{\iiint}_{\mathbb{K}^3}} \Delta_{h_1, h_2} f(x) \, \mathrm{e}(\xi_1 h_1 + \xi_2 h_2) \, d\mu(h_1) d\mu(h_2) d\mu(x). \end{align*} $$
Appealing to the Gowers–Cauchy–Schwarz inequality (4.6), we see that
as desired. The last inequality follows from Plancherel’s theorem, the 1-boundedness of f and
![]() $\mathrm {supp}(f) \subset I$
which implies
$\mathrm {supp}(f) \subset I$
which implies
5.2 van der Corput’s inequality
We will need the following useful inequality.
Lemma 5.3 (van der Corput’s inequality).
Let
![]() $\mathfrak g \in L^1(\mathbb {K})$
, and let
$\mathfrak g \in L^1(\mathbb {K})$
, and let
![]() $J = B_{r_J}(x_J)$
be an interval. Then for any scale H,
$J = B_{r_J}(x_J)$
be an interval. Then for any scale H,
![]() $0<H\le \mu (J)$
, we have
$0<H\le \mu (J)$
, we have
 $$ \begin{align} \bigg|\int_{\mathbb{K}} \mathfrak g(y)d\mu_J(y)\bigg|^2\leq \frac{C}{\mu(J)}\int_{\mathbb{K}}\int_{J\cap(J-h)}\Delta_h\mathfrak g(y) d\mu(y) d\nu_{[H]}(h). \end{align} $$
$$ \begin{align} \bigg|\int_{\mathbb{K}} \mathfrak g(y)d\mu_J(y)\bigg|^2\leq \frac{C}{\mu(J)}\int_{\mathbb{K}}\int_{J\cap(J-h)}\Delta_h\mathfrak g(y) d\mu(y) d\nu_{[H]}(h). \end{align} $$
We can take
![]() $C = 4$
when
$C = 4$
when
![]() $\mathbb {K}$
is Archimedean. When
$\mathbb {K}$
is Archimedean. When
![]() $\mathbb {K}$
is non-Archimedean, we can take
$\mathbb {K}$
is non-Archimedean, we can take
![]() $C = 1$
and furthermore,
$C = 1$
and furthermore, ![]() for any
for any
![]() $h \in [H]$
so that the above inequality can be expressed as
$h \in [H]$
so that the above inequality can be expressed as
 $$ \begin{align} \bigg|\int_{\mathbb{K}} \mathfrak g(y)d\mu_J(y)\bigg|^2\leq \iint_{\mathbb{K}^2}\Delta_h\mathfrak g(y) d\mu_{[H]}(h) d\mu_J(y) \end{align} $$
$$ \begin{align} \bigg|\int_{\mathbb{K}} \mathfrak g(y)d\mu_J(y)\bigg|^2\leq \iint_{\mathbb{K}^2}\Delta_h\mathfrak g(y) d\mu_{[H]}(h) d\mu_J(y) \end{align} $$
since
![]() $d\nu _{[H]} = d\mu _{[H]}$
in this case.
$d\nu _{[H]} = d\mu _{[H]}$
in this case.
Proof. We define ![]() . By a change of variables and Fubini’s theorem, we note
. By a change of variables and Fubini’s theorem, we note
The function
![]() $y\mapsto \int _{\mathbb {K}}\mathfrak {g}_J(y+h) d\mu _{[H]}(h)$
is supported on the set
$y\mapsto \int _{\mathbb {K}}\mathfrak {g}_J(y+h) d\mu _{[H]}(h)$
is supported on the set
![]() $J - [H]$
which in turn lies in
$J - [H]$
which in turn lies in
![]() $B_{2(r_J + H)}(x_J)$
(in the non-Archimedean case,
$B_{2(r_J + H)}(x_J)$
(in the non-Archimedean case,
![]() $J-[H] = J$
). Hence, by the Cauchy–Schwarz inequality and a change of variables, we conclude that
$J-[H] = J$
). Hence, by the Cauchy–Schwarz inequality and a change of variables, we conclude that
 $$ \begin{align*} \bigg|\int_{\mathbb{K}}\mathfrak{g}(y) d\mu_J(y)\bigg|^2 &= \frac{1}{\mu(J)^2}\bigg|\iint_{\mathbb{K}^2} \mathfrak g_J(y+h) d\mu_{[H]}(h) d\mu(y)\bigg|^2\\ &\le 2 \frac{\mu(J)+H}{\mu(J)^2}\iiint_{\mathbb{K}^3} \mathfrak g_J(y+h_1)\overline{\mathfrak g_J(y+h_2)} d\mu_{[H]}(h_1) d\mu_{[H]}(h_2) d\mu(y)\\ &= 2 \frac{\mu(J)+H}{\mu(J)^2}\iint_{\mathbb{K}^2}\kappa_{[H]}(h)\mathfrak g_J(y)\overline{\mathfrak g_J(y+h)} d\mu(h)d\mu(y)\\ &\le 4 \mu(J)^{-1} \int_{\mathbb{K}}\int_{J\cap(J-h)}\mathfrak{g}(y)\overline{\mathfrak{g}(y+h)} d\mu(y) d\nu_{[H]}(h), \end{align*} $$
$$ \begin{align*} \bigg|\int_{\mathbb{K}}\mathfrak{g}(y) d\mu_J(y)\bigg|^2 &= \frac{1}{\mu(J)^2}\bigg|\iint_{\mathbb{K}^2} \mathfrak g_J(y+h) d\mu_{[H]}(h) d\mu(y)\bigg|^2\\ &\le 2 \frac{\mu(J)+H}{\mu(J)^2}\iiint_{\mathbb{K}^3} \mathfrak g_J(y+h_1)\overline{\mathfrak g_J(y+h_2)} d\mu_{[H]}(h_1) d\mu_{[H]}(h_2) d\mu(y)\\ &= 2 \frac{\mu(J)+H}{\mu(J)^2}\iint_{\mathbb{K}^2}\kappa_{[H]}(h)\mathfrak g_J(y)\overline{\mathfrak g_J(y+h)} d\mu(h)d\mu(y)\\ &\le 4 \mu(J)^{-1} \int_{\mathbb{K}}\int_{J\cap(J-h)}\mathfrak{g}(y)\overline{\mathfrak{g}(y+h)} d\mu(y) d\nu_{[H]}(h), \end{align*} $$
since ![]() . This gives the desired conclusion.
. This gives the desired conclusion.
5.3 Preparation for the PET induction scheme
We now give a simple application of van der Corput’s inequality which will be repeatedly applied in the PET induction scheme.
Lemma 5.6. Let
![]() $c\ge 1$
, and let
$c\ge 1$
, and let
![]() $I, J\subset \mathbb {K}$
be two intervals with
$I, J\subset \mathbb {K}$
be two intervals with
![]() $\mu (I) = N_0$
. Assume that
$\mu (I) = N_0$
. Assume that
![]() $\mathfrak g_1\in L^\infty (\mathbb {K})$
and
$\mathfrak g_1\in L^\infty (\mathbb {K})$
and
![]() $\mathfrak g_2\in L^\infty (\mathbb {K}^2)$
are
$\mathfrak g_2\in L^\infty (\mathbb {K}^2)$
are
![]() $1$
-bounded functions such that
$1$
-bounded functions such that
Suppose H is a scale such that
![]() $0<H\le \mu (J)$
. When
$0<H\le \mu (J)$
. When
![]() $\mathbb {K}$
is Archimedean, we have
$\mathbb {K}$
is Archimedean, we have
 $$ \begin{align*} &\bigg|\frac{1}{N_0}\iint_{\mathbb{K}^2} \mathfrak g_1(x)\mathfrak g_2(x, y)d\mu_J(y)d\mu(x)\bigg|^2\\ \le 4 \bigg|\frac{1}{N_0}\iiint_{\mathbb{K}^3}&\mathfrak g_2(x, y)\overline{\mathfrak g_2(x, y+h)}d\mu_J(y)d\nu_{[H]}(h)d\mu(x)\bigg| + 8 c \bigg[\frac{\mu([H])}{\mu(J)}\bigg]^{\theta}, \end{align*} $$
$$ \begin{align*} &\bigg|\frac{1}{N_0}\iint_{\mathbb{K}^2} \mathfrak g_1(x)\mathfrak g_2(x, y)d\mu_J(y)d\mu(x)\bigg|^2\\ \le 4 \bigg|\frac{1}{N_0}\iiint_{\mathbb{K}^3}&\mathfrak g_2(x, y)\overline{\mathfrak g_2(x, y+h)}d\mu_J(y)d\nu_{[H]}(h)d\mu(x)\bigg| + 8 c \bigg[\frac{\mu([H])}{\mu(J)}\bigg]^{\theta}, \end{align*} $$
where
![]() $\theta = 1$
when
$\theta = 1$
when
![]() $\mathbb {K} = {\mathbb R}$
and
$\mathbb {K} = {\mathbb R}$
and
![]() $\theta = 1/2$
when
$\theta = 1/2$
when
![]() $\mathbb {K} = {\mathbb C}$
. When
$\mathbb {K} = {\mathbb C}$
. When
![]() $\mathbb {K}$
is non-Archimedean, this improves to
$\mathbb {K}$
is non-Archimedean, this improves to
 $$ \begin{align*} &\bigg|\frac{1}{N_0}\iint_{\mathbb{K}^2} \mathfrak g_1(x)\mathfrak g_2(x, y)d\mu_J(y)d\mu(x)\bigg|^2\\ \le \frac{1}{N_0} &\iiint_{\mathbb{K}^3}\mathfrak g_2(x, y)\overline{\mathfrak g_2(x, y+h)}d\mu_J(y)d\mu_{[H]}(h)d\mu(x). \end{align*} $$
$$ \begin{align*} &\bigg|\frac{1}{N_0}\iint_{\mathbb{K}^2} \mathfrak g_1(x)\mathfrak g_2(x, y)d\mu_J(y)d\mu(x)\bigg|^2\\ \le \frac{1}{N_0} &\iiint_{\mathbb{K}^3}\mathfrak g_2(x, y)\overline{\mathfrak g_2(x, y+h)}d\mu_J(y)d\mu_{[H]}(h)d\mu(x). \end{align*} $$
Proof. Applying the Cauchy–Schwarz inequality in the x variable, it follows that
 $$ \begin{align*}\bigg|\frac{1}{N_0} \iint_{\mathbb{K}^2}\mathfrak g_1(x)\mathfrak g_2(x, y)d\mu_J(y)d\mu(x)\bigg|^2\leq \frac{1}{N_0} \int_{\mathbb{K}} \bigg|\int_{\mathbb{K}} \mathfrak g_2(x, y)d\mu_J(y)\bigg|^2 d\mu(x) \end{align*} $$
$$ \begin{align*}\bigg|\frac{1}{N_0} \iint_{\mathbb{K}^2}\mathfrak g_1(x)\mathfrak g_2(x, y)d\mu_J(y)d\mu(x)\bigg|^2\leq \frac{1}{N_0} \int_{\mathbb{K}} \bigg|\int_{\mathbb{K}} \mathfrak g_2(x, y)d\mu_J(y)\bigg|^2 d\mu(x) \end{align*} $$
since by Equation (5.7) and the
![]() $1$
-boundedness of
$1$
-boundedness of
![]() $\mathfrak g_1$
, we have
$\mathfrak g_1$
, we have
![]() $\|\mathfrak g_1 \|_{L^2(\mathbb {K})}^2 \le N_0$
. By van der Corput’s inequality in Lemma 5.3, we obtain
$\|\mathfrak g_1 \|_{L^2(\mathbb {K})}^2 \le N_0$
. By van der Corput’s inequality in Lemma 5.3, we obtain
 $$ \begin{align*} \int_{\mathbb{K}} &\bigg|\int_{\mathbb{K}} \mathfrak g_2(x, y)d\mu_J(y)\bigg|^2d\mu(x)\\ \leq 4 \int_{\mathbb{K}}\int_{\mathbb{K}}\kappa_{[H]}(h)&\frac{1}{\mu(J)}\int_{J\cap(J-h)} \mathfrak g_2(x, y)\overline{\mathfrak g_2(x, y+h)}d\mu(y)d\mu(h)d\mu(x) \end{align*} $$
$$ \begin{align*} \int_{\mathbb{K}} &\bigg|\int_{\mathbb{K}} \mathfrak g_2(x, y)d\mu_J(y)\bigg|^2d\mu(x)\\ \leq 4 \int_{\mathbb{K}}\int_{\mathbb{K}}\kappa_{[H]}(h)&\frac{1}{\mu(J)}\int_{J\cap(J-h)} \mathfrak g_2(x, y)\overline{\mathfrak g_2(x, y+h)}d\mu(y)d\mu(h)d\mu(x) \end{align*} $$
when
![]() $\mathbb {K}$
is Archimedean. In this case, we have
$\mathbb {K}$
is Archimedean. In this case, we have
![]() $\mu (J\setminus {[J\cap (J-h)]}) \le 2 \mu ([H])$
when
$\mu (J\setminus {[J\cap (J-h)]}) \le 2 \mu ([H])$
when
![]() $\mathbb {K} = {\mathbb R}$
and
$\mathbb {K} = {\mathbb R}$
and
![]() $\mu (J\setminus {[J\cap (J-h)]}) \le 2 \sqrt {\mu ([H]) \mu (J)}$
when
$\mu (J\setminus {[J\cap (J-h)]}) \le 2 \sqrt {\mu ([H]) \mu (J)}$
when
![]() $\mathbb {K} = {\mathbb C}$
. Hence,
$\mathbb {K} = {\mathbb C}$
. Hence,
 $$ \begin{align*} \frac{4}{N_0} \int_{\mathbb{K}}\kappa_{[H]}(h)\frac{1}{\mu(J)}\int_{J\setminus (J\cap(J-h))}\int_{\mathbb{K}}|\mathfrak g_2(x, y)| d\mu(x)d\mu(y)d\mu(h)\le 8 c \bigg[\frac{\mu([H])}{\mu(J)}\bigg]^{\theta}. \end{align*} $$
$$ \begin{align*} \frac{4}{N_0} \int_{\mathbb{K}}\kappa_{[H]}(h)\frac{1}{\mu(J)}\int_{J\setminus (J\cap(J-h))}\int_{\mathbb{K}}|\mathfrak g_2(x, y)| d\mu(x)d\mu(y)d\mu(h)\le 8 c \bigg[\frac{\mu([H])}{\mu(J)}\bigg]^{\theta}. \end{align*} $$
In the last line, we used Fubini’s theorem and Equation (5.7) for
![]() $\mathfrak g_2$
. This gives the desired bound when
$\mathfrak g_2$
. This gives the desired bound when
![]() $\mathbb {K}$
is Archimedean.
$\mathbb {K}$
is Archimedean.
When
![]() $\mathbb {K}$
is non-Archimedean, the bound (5.5) in Lemma 5.3 gives
$\mathbb {K}$
is non-Archimedean, the bound (5.5) in Lemma 5.3 gives
 $$ \begin{align*} &\frac{1}{N_0} \int_{\mathbb{K}} \bigg|\int_{\mathbb{K}} \mathfrak g_2(x, y)d\mu_J(y)\bigg|^2d\mu(x)\\ \leq \frac{1}{N_0} &\iiint_{\mathbb{K}^3}\mathfrak g_2(x, y)\overline{\mathfrak g_2(x, y+h)}d\mu_J(y)d\mu_{[H]}(h)d\mu(x) \end{align*} $$
$$ \begin{align*} &\frac{1}{N_0} \int_{\mathbb{K}} \bigg|\int_{\mathbb{K}} \mathfrak g_2(x, y)d\mu_J(y)\bigg|^2d\mu(x)\\ \leq \frac{1}{N_0} &\iiint_{\mathbb{K}^3}\mathfrak g_2(x, y)\overline{\mathfrak g_2(x, y+h)}d\mu_J(y)d\mu_{[H]}(h)d\mu(x) \end{align*} $$
which is the desired bound in this case.
The next result is an essential building block of the PET induction scheme, which will be employed in Section 6.
Proposition 5.8. Let
![]() $N, N_0>0$
be two scales, I an interval such that
$N, N_0>0$
be two scales, I an interval such that
![]() $\mu (I) = N_0$
,
$\mu (I) = N_0$
,
![]() $m\in \mathbb N$
,
$m\in \mathbb N$
, ![]() , and let
, and let
![]() ${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of polynomials. Suppose that
${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of polynomials. Suppose that
![]() $\mathfrak f_0, \mathfrak f_1,\ldots , \mathfrak f_m\in L^0(\mathbb {K})$
are
$\mathfrak f_0, \mathfrak f_1,\ldots , \mathfrak f_m\in L^0(\mathbb {K})$
are
![]() $1$
-bounded functions such that
$1$
-bounded functions such that
![]() $\|\mathfrak f_i\|_{L^1(\mathbb {K})}\le N_0$
for every
$\|\mathfrak f_i\|_{L^1(\mathbb {K})}\le N_0$
for every ![]() .
.
Let
![]() $0<\delta \le 1$
, and suppose that
$0<\delta \le 1$
, and suppose that
 $$ \begin{align} \bigg|\frac{1}{N_0} \iint_{\mathbb{K}^2}\mathfrak f_0(x)\prod_{i=1}^m\mathfrak f_{i}(x-P_i(y))d\mu_{[N]}(y)d\mu(x)\bigg|\ge\delta. \end{align} $$
$$ \begin{align} \bigg|\frac{1}{N_0} \iint_{\mathbb{K}^2}\mathfrak f_0(x)\prod_{i=1}^m\mathfrak f_{i}(x-P_i(y))d\mu_{[N]}(y)d\mu(x)\bigg|\ge\delta. \end{align} $$
Then there exists an absolute constant
![]() $C\gtrsim _{\mathcal P}1$
such that for all
$C\gtrsim _{\mathcal P}1$
such that for all
![]() $\delta '\le \delta ^4/C$
we have
$\delta '\le \delta ^4/C$
we have
 $$ \begin{align} \bigg|\frac{1}{N_0} \iint_{\mathbb{K}^2}\mathfrak f^{\prime}_0(x)\prod_{i=1}^{m'}\mathfrak f^{\prime}_{i}(x-P^{\prime}_i(y))d\mu_{[N]}(y)d\mu(x)\bigg|\gtrsim_C\delta^2, \end{align} $$
$$ \begin{align} \bigg|\frac{1}{N_0} \iint_{\mathbb{K}^2}\mathfrak f^{\prime}_0(x)\prod_{i=1}^{m'}\mathfrak f^{\prime}_{i}(x-P^{\prime}_i(y))d\mu_{[N]}(y)d\mu(x)\bigg|\gtrsim_C\delta^2, \end{align} $$
where
![]() $m'< 2m$
and
$m'< 2m$
and
![]() ${\mathcal P}':=\{P_1^{\prime },\ldots , P_{m'}^{\prime }\}$
is a new collection of polynomials such that
${\mathcal P}':=\{P_1^{\prime },\ldots , P_{m'}^{\prime }\}$
is a new collection of polynomials such that
for some
![]() $\delta '\delta ^2N/C^2\le |h|\le \delta 'N\le \delta ^4N/C$
, where
$\delta '\delta ^2N/C^2\le |h|\le \delta 'N\le \delta ^4N/C$
, where
![]() $P_{m'}^{\prime }(y):=P_m(y)-P_{i_0}(y)$
, and
$P_{m'}^{\prime }(y):=P_m(y)-P_{i_0}(y)$
, and
![]() $\{\mathfrak f_0^{\prime },\ldots , \mathfrak f_{m'}^{\prime }\}:=\{\mathfrak f_1, \overline {\mathfrak f_1},\ldots , \mathfrak f_m, \overline {\mathfrak f_m}\}$
with
$\{\mathfrak f_0^{\prime },\ldots , \mathfrak f_{m'}^{\prime }\}:=\{\mathfrak f_1, \overline {\mathfrak f_1},\ldots , \mathfrak f_m, \overline {\mathfrak f_m}\}$
with
![]() $\mathfrak f_{m'}^{\prime }:=\mathfrak f_{m}$
.
$\mathfrak f_{m'}^{\prime }:=\mathfrak f_{m}$
.
Proof. Let ![]() and
and
![]() $C\ge 1$
be a large constant to be determined later. We shall apply Lemma 5.6 with
$C\ge 1$
be a large constant to be determined later. We shall apply Lemma 5.6 with
![]() $J=[N]$
, the functions
$J=[N]$
, the functions
![]() $\mathfrak g_1(x)=\mathfrak f_0(x)$
and
$\mathfrak g_1(x)=\mathfrak f_0(x)$
and
![]() $\mathfrak g_2(x, y)=\prod _{i\in \mathbb I}\mathfrak f_{i}(x-P_i(y))$
, and the parameter
$\mathfrak g_2(x, y)=\prod _{i\in \mathbb I}\mathfrak f_{i}(x-P_i(y))$
, and the parameter
![]() $H=\delta 'N$
. Note that
$H=\delta 'N$
. Note that
![]() $\|\mathfrak g_1\|_{L^{\infty }(\mathbb {K})}\le 1$
and
$\|\mathfrak g_1\|_{L^{\infty }(\mathbb {K})}\le 1$
and
![]() $\|\mathfrak g_2\|_{L^{\infty }(\mathbb {K}^2)}\le 1$
since
$\|\mathfrak g_2\|_{L^{\infty }(\mathbb {K}^2)}\le 1$
since
![]() $\|\mathfrak f_i\|_{L^{\infty }(\mathbb {K})}\le 1$
for all
$\|\mathfrak f_i\|_{L^{\infty }(\mathbb {K})}\le 1$
for all
![]() $i\in \mathbb I$
. Moreover,
$i\in \mathbb I$
. Moreover,
![]() $\mathfrak g_1$
and
$\mathfrak g_1$
and
![]() $\mathfrak g_2$
satisfy Equation (5.7). If
$\mathfrak g_2$
satisfy Equation (5.7). If
![]() $\delta '\le \delta ^4/C$
and
$\delta '\le \delta ^4/C$
and
![]() $C\ge 1$
is sufficiently large, using Lemma 5.6, we conclude
$C\ge 1$
is sufficiently large, using Lemma 5.6, we conclude
 $$ \begin{align*} \bigg|\frac{1}{N_0}\iiint_{\mathbb{K}^3}\mathfrak g_2(x, y)\overline{\mathfrak g_2(x, y+h)}d\mu_{[N]}(y)d\nu_{[H]}(h) d\mu(x)\bigg| \gtrsim \delta^2. \end{align*} $$
$$ \begin{align*} \bigg|\frac{1}{N_0}\iiint_{\mathbb{K}^3}\mathfrak g_2(x, y)\overline{\mathfrak g_2(x, y+h)}d\mu_{[N]}(y)d\nu_{[H]}(h) d\mu(x)\bigg| \gtrsim \delta^2. \end{align*} $$
By the pigeonhole principle, there exists
![]() $|h|\ge \delta ^2 H/C^2$
so that
$|h|\ge \delta ^2 H/C^2$
so that
 $$ \begin{align*} \bigg|\frac{1}{N_0} \iint_{\mathbb{K}^2}\mathfrak g_2(x, y)\overline{\mathfrak g_2(x, y+h)}d\mu_{[N]}(y)d\mu(x)\bigg| \gtrsim \delta^2. \end{align*} $$
$$ \begin{align*} \bigg|\frac{1}{N_0} \iint_{\mathbb{K}^2}\mathfrak g_2(x, y)\overline{\mathfrak g_2(x, y+h)}d\mu_{[N]}(y)d\mu(x)\bigg| \gtrsim \delta^2. \end{align*} $$
We make the change of variables
![]() $x\mapsto x+P_{i_0}(y)$
to conclude
$x\mapsto x+P_{i_0}(y)$
to conclude
 $$ \begin{align*} \bigg|\frac{1}{N_0}\iint_{\mathbb{K}^2} \prod_{i\in\mathbb I}\mathfrak f_{i}(x-P_i(y)+P_{i_0}(y))\overline{\mathfrak f_{i}(x-P_i(y+h)+P_{i_0}(y))} d\mu_{[N]}(y)d\mu(x)\bigg|\gtrsim\delta^2. \end{align*} $$
$$ \begin{align*} \bigg|\frac{1}{N_0}\iint_{\mathbb{K}^2} \prod_{i\in\mathbb I}\mathfrak f_{i}(x-P_i(y)+P_{i_0}(y))\overline{\mathfrak f_{i}(x-P_i(y+h)+P_{i_0}(y))} d\mu_{[N]}(y)d\mu(x)\bigg|\gtrsim\delta^2. \end{align*} $$
This completes the proof.
6 The
 $L^\infty $
-inverse theorem
$L^\infty $
-inverse theorem
The goal of this section is to present the proof of Theorem 1.5, the key
![]() $L^\infty $
-inverse theorem for general polynomials with distinct degrees, which we now restate in a more formal, precise way.
$L^\infty $
-inverse theorem for general polynomials with distinct degrees, which we now restate in a more formal, precise way.
Theorem 6.1 (Inverse theorem for
 $(m+1)$
-linear forms).
$(m+1)$
-linear forms).
Let
![]() $N \ge 1$
be a scale,
$N \ge 1$
be a scale,
![]() $m\in \mathbb Z_+$
and
$m\in \mathbb Z_+$
and
![]() $0<\delta \le 1$
be given. Let
$0<\delta \le 1$
be given. Let
![]() ${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of polynomials such that
${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of polynomials such that
![]() $1\le \deg {P_1}<\ldots <\deg {P_m}$
. Set
$1\le \deg {P_1}<\ldots <\deg {P_m}$
. Set
![]() $N_0 = N^{\deg (P_m)}$
, and let
$N_0 = N^{\deg (P_m)}$
, and let
![]() $f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
$f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
![]() $1$
-bounded functions supported on an interval
$1$
-bounded functions supported on an interval
![]() $I\subset \mathbb {K}$
of measure
$I\subset \mathbb {K}$
of measure
![]() $N_0$
. Define an
$N_0$
. Define an
![]() $(m+1)$
-linear form corresponding to the pair
$(m+1)$
-linear form corresponding to the pair
![]() $({\mathcal P}; N)$
by
$({\mathcal P}; N)$
by
 $$ \begin{align} \Lambda_{{\mathcal P}; N}(f_0,\ldots, f_m):= \frac{1}{N_0} \int_{\mathbb{K}^2}f_0(x)\prod_{i=1}^mf_{i}(x-P_i(y))d\mu_{[N]}(y)d\mu(x). \end{align} $$
$$ \begin{align} \Lambda_{{\mathcal P}; N}(f_0,\ldots, f_m):= \frac{1}{N_0} \int_{\mathbb{K}^2}f_0(x)\prod_{i=1}^mf_{i}(x-P_i(y))d\mu_{[N]}(y)d\mu(x). \end{align} $$
Suppose that
Then there exists
![]() $N_1\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_1)}$
so that
$N_1\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_1)}$
so that
If necessary, we will also write
![]() $\Lambda _{{\mathcal P}; N}(f_0,\ldots , f_m)=\Lambda _{{\mathcal P}; N, I}(f_0,\ldots , f_m)$
in order to emphasize that the functions
$\Lambda _{{\mathcal P}; N}(f_0,\ldots , f_m)=\Lambda _{{\mathcal P}; N, I}(f_0,\ldots , f_m)$
in order to emphasize that the functions
![]() $f_0, f_1,\ldots , f_m$
are supported on I.
$f_0, f_1,\ldots , f_m$
are supported on I.
Remark
When
![]() $\mathbb {K} = {\mathbb C}$
is the complex field, the proof of Theorem 6.1 will also hold if the form
$\mathbb {K} = {\mathbb C}$
is the complex field, the proof of Theorem 6.1 will also hold if the form
![]() $\Lambda _{{\mathcal P}; N}$
is defined with the disc
$\Lambda _{{\mathcal P}; N}$
is defined with the disc
![]() $[N] = {\mathbb D}_{\sqrt {N}}$
replaced by the square
$[N] = {\mathbb D}_{\sqrt {N}}$
replaced by the square
In this case, the conlusion is
![]() $N_0^{-1} \| \mu _{[N_1]_{sq}} * f_1\|_{L^1({\mathbb C})} \gtrsim \delta ^{O_{\mathcal P}(1)}$
. This observation will be needed at one point in the proof of Theorem 1.6.
$N_0^{-1} \| \mu _{[N_1]_{sq}} * f_1\|_{L^1({\mathbb C})} \gtrsim \delta ^{O_{\mathcal P}(1)}$
. This observation will be needed at one point in the proof of Theorem 1.6.
The proof of Theorem 6.1 breaks into two main steps: First, an application of PET induction to show that whenever
is large, then necessarily
![]() $f_m$
has a fairly large
$f_m$
has a fairly large
![]() $U^s$
norm for an appropriately large
$U^s$
norm for an appropriately large
![]() $s = s_{\mathcal {P}}$
. Second, an inductive ‘degree-lowering’ step to reduce
$s = s_{\mathcal {P}}$
. Second, an inductive ‘degree-lowering’ step to reduce
![]() $U^s$
control to
$U^s$
control to
![]() $U^2$
control. We accordingly subdivide the argument into two subsections.
$U^2$
control. We accordingly subdivide the argument into two subsections.
6.1 PET induction
Our first goal is to show that whenever the multilinear form
![]() $\Lambda _{{\mathcal P};I}$
is large, necessarily
$\Lambda _{{\mathcal P};I}$
is large, necessarily
![]() $f_m$
has some fairly large (sufficiently high degree) Gowers box norm. We begin with the definition of
$f_m$
has some fairly large (sufficiently high degree) Gowers box norm. We begin with the definition of
![]() $(d,j)$
-admissible polynomials. Recall that for a polynomial
$(d,j)$
-admissible polynomials. Recall that for a polynomial
![]() $P \in \mathbb {K}[\mathrm {y}]$
, the leading coefficient is denoted by
$P \in \mathbb {K}[\mathrm {y}]$
, the leading coefficient is denoted by
![]() $\ell (P)$
.
$\ell (P)$
.
Definition 6.5 (The class of
 $(d,j)$
-admissible polynomials).
$(d,j)$
-admissible polynomials).
Let
![]() $N\ge 1$
be a scale,
$N\ge 1$
be a scale,
![]() $0<\delta \le 1$
,
$0<\delta \le 1$
,
![]() $d\in \mathbb Z_+$
,
$d\in \mathbb Z_+$
, ![]() and parameters
and parameters
![]() $A_0\ge 1$
and
$A_0\ge 1$
and
![]() $A\ge 0$
be given. Assume that a finite collection of polynomials
$A\ge 0$
be given. Assume that a finite collection of polynomials
![]() ${\mathcal P}$
has degree j, and define
${\mathcal P}$
has degree j, and define
![]() $\mathcal {P}_j := \{ P\in {\mathcal P} : \deg (P) = j\}$
. We will say that
$\mathcal {P}_j := \{ P\in {\mathcal P} : \deg (P) = j\}$
. We will say that
![]() ${\mathcal P}$
is
${\mathcal P}$
is
![]() $(d, j)$
-admissible with tolerance
$(d, j)$
-admissible with tolerance
![]() $(A_0, A)$
if the following properties are satisfied:
$(A_0, A)$
if the following properties are satisfied:
-
1. For every
 $P\in {\mathcal P}_j$
, we have (6.6)
$P\in {\mathcal P}_j$
, we have (6.6) $$ \begin{align} A_0^{-1}\delta^{A} N^{d-j} \leq |\ell(P)| \leq A_0\delta^{-A}N^{d-j}. \end{align} $$
$$ \begin{align} A_0^{-1}\delta^{A} N^{d-j} \leq |\ell(P)| \leq A_0\delta^{-A}N^{d-j}. \end{align} $$
-
2. Whenever
 $P, Q\in {\mathcal P}_j$
and
$P, Q\in {\mathcal P}_j$
and
 $\ell (P) \neq \ell (Q)$
, we have (6.7)
$\ell (P) \neq \ell (Q)$
, we have (6.7) $$ \begin{align} A_0^{-1}\delta^{A} N^{d-j} \leq |\ell(P) - \ell(Q)| \leq A_0\delta^{-A} N^{d-j}. \end{align} $$
$$ \begin{align} A_0^{-1}\delta^{A} N^{d-j} \leq |\ell(P) - \ell(Q)| \leq A_0\delta^{-A} N^{d-j}. \end{align} $$
-
3. Whenever
 $P, Q\in {\mathcal P}_j$
and
$P, Q\in {\mathcal P}_j$
and
 $P\neq Q$
and
$P\neq Q$
and
 $\ell (P) = \ell (Q)$
, we have (6.8)and
$\ell (P) = \ell (Q)$
, we have (6.8)and $$ \begin{align} A_0^{-1}\delta^{A} N^{d-j+1} \leq |\ell(P - Q)| \leq A_0\delta^{-A} N^{d-j+1}, \end{align} $$
$$ \begin{align} A_0^{-1}\delta^{A} N^{d-j+1} \leq |\ell(P - Q)| \leq A_0\delta^{-A} N^{d-j+1}, \end{align} $$
 $\deg (P-Q) = j-1$
.
$\deg (P-Q) = j-1$
.
In the special case where the polynomials in
![]() $\mathcal {P}$
are linear, we require that
$\mathcal {P}$
are linear, we require that
![]() $\ell (P) \neq \ell (Q)$
for each
$\ell (P) \neq \ell (Q)$
for each
![]() $P, Q\in {\mathcal P}$
. The constants
$P, Q\in {\mathcal P}$
. The constants
![]() $A_0, A$
will be always independent of
$A_0, A$
will be always independent of
![]() $\delta $
and N but may depend on
$\delta $
and N but may depend on
![]() ${\mathcal P}$
. In our applications, the exact values of
${\mathcal P}$
. In our applications, the exact values of
![]() $A_0, A$
will be unimportant, and then we will simply say that the collection
$A_0, A$
will be unimportant, and then we will simply say that the collection
![]() $\mathcal {P}$
is
$\mathcal {P}$
is
![]() $(d, j)$
-admissible.
$(d, j)$
-admissible.
Remark 6.9. Under the hypotheses of Theorem 6.1, it is not difficult to see that the collection of polynomials
![]() ${\mathcal P}=\{P_1,\ldots , P_m\}$
such that
${\mathcal P}=\{P_1,\ldots , P_m\}$
such that
![]() $1\le \deg {P_1}<\ldots <\deg {P_m}=d$
is
$1\le \deg {P_1}<\ldots <\deg {P_m}=d$
is
![]() $(d,d)$
-admissible with the tolerance
$(d,d)$
-admissible with the tolerance
![]() $(\max \{|\ell (P_m)|^{-1}, |\ell (P_m)|\}, 0)$
. Indeed, condition (6.6) can be easily verified and conditions (6.7) and (6.8) are vacuous as
$(\max \{|\ell (P_m)|^{-1}, |\ell (P_m)|\}, 0)$
. Indeed, condition (6.6) can be easily verified and conditions (6.7) and (6.8) are vacuous as
![]() ${\mathcal P}_d=\{P_m\}$
.
${\mathcal P}_d=\{P_m\}$
.
The main result of this subsection is the following theorem.
Theorem 6.10 (Gowers box norms control
 $(m+1)$
-linear forms).
$(m+1)$
-linear forms).
Let
![]() ${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of
${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of
![]() $(d, d)$
-admissible polynomials such that
$(d, d)$
-admissible polynomials such that
![]() $1\le \deg {P_1}\le \ldots \le \deg {P_m}=d$
. Let
$1\le \deg {P_1}\le \ldots \le \deg {P_m}=d$
. Let
![]() $N, N_0\ge 1$
be two scales, I an interval with measure
$N, N_0\ge 1$
be two scales, I an interval with measure
![]() $N_0$
and
$N_0$
and
![]() $0<\delta \le 1$
be given, and let
$0<\delta \le 1$
be given, and let
![]() $f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
$f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
![]() $1$
-bounded functions such that
$1$
-bounded functions such that
![]() $\|f_i\|_{L^1(\mathbb {K})}\le N_0$
for all
$\|f_i\|_{L^1(\mathbb {K})}\le N_0$
for all ![]() . If Equation (6.3) is satisfied, then there exists
. If Equation (6.3) is satisfied, then there exists
![]() $s:=s_{\mathcal P}\in \mathbb Z_+$
such that
$s:=s_{\mathcal P}\in \mathbb Z_+$
such that
where
![]() $H_i\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_m)}$
for
$H_i\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_m)}$
for ![]() .
.
The proof of Theorem 6.10 requires a subtle downwards induction based on a repetitive application of Proposition 5.8 on the class of
![]() $(d, j)$
-admissible polynomials. To make our induction rigorous, we will assign a weight vector to each collection
$(d, j)$
-admissible polynomials. To make our induction rigorous, we will assign a weight vector to each collection
![]() $\mathcal {P}\subset \mathbb {K}[\mathrm {t}]$
of polynomials.
$\mathcal {P}\subset \mathbb {K}[\mathrm {t}]$
of polynomials.
Definition 6.12 (Weight vector).
For any finite
![]() $\mathcal {P}\subset \mathbb {K}[\mathrm {t}]$
, define the weight vector
$\mathcal {P}\subset \mathbb {K}[\mathrm {t}]$
, define the weight vector
where
is the number of distinct leading coefficients of
![]() $\mathcal {P}$
of degree
$\mathcal {P}$
of degree
![]() $j\in \mathbb Z_+$
.
$j\in \mathbb Z_+$
.
For example, the weight vector for the family
![]() ${\mathcal P}=\{x, 5x, x^2, x^2+x, x^4\}$
is
${\mathcal P}=\{x, 5x, x^2, x^2+x, x^4\}$
is
![]() $v({\mathcal P})=(2, 1, 0, 1, 0, 0, \ldots )$
. There is a natural ordering on the set of weight vectors.
$v({\mathcal P})=(2, 1, 0, 1, 0, 0, \ldots )$
. There is a natural ordering on the set of weight vectors.
Definition 6.13 (Well-ordering on the set of weight vectors).
For any two weight vectors
![]() $v({\mathcal P})=(v_1({\mathcal P}),v_2({\mathcal P}),\dots )$
and
$v({\mathcal P})=(v_1({\mathcal P}),v_2({\mathcal P}),\dots )$
and
![]() $ v(\mathcal Q)=(v_j(\mathcal Q),v_j(\mathcal Q),\dots )$
corresponding to finite collections
$ v(\mathcal Q)=(v_j(\mathcal Q),v_j(\mathcal Q),\dots )$
corresponding to finite collections
![]() $\mathcal {P}, \mathcal Q\subset \mathbb {K}[\mathrm {t}]$
we define an ordering
$\mathcal {P}, \mathcal Q\subset \mathbb {K}[\mathrm {t}]$
we define an ordering
![]() $\prec $
on the set of weight vectors by declaring that
$\prec $
on the set of weight vectors by declaring that
if there is a degree
![]() $j\in \mathbb Z_+$
such that
$j\in \mathbb Z_+$
such that
![]() $v_j({\mathcal P})<v_j(\mathcal Q)$
and
$v_j({\mathcal P})<v_j(\mathcal Q)$
and
![]() $v_k({\mathcal P})=v_k(\mathcal Q)$
for all
$v_k({\mathcal P})=v_k(\mathcal Q)$
for all
![]() $k>j$
.
$k>j$
.
It is a standard fact that
![]() $\prec $
is a well ordering, we omit the details.
$\prec $
is a well ordering, we omit the details.
Proof of Theorem 6.10.
We begin by stating the following claim:
Claim 6.14. Let
![]() $N, N_0\ge 1$
be two scales,
$N, N_0\ge 1$
be two scales,
![]() $0<\delta \le 1$
,
$0<\delta \le 1$
,
![]() $d, m\in \mathbb Z_+$
and
$d, m\in \mathbb Z_+$
and ![]() be given, and let
be given, and let
![]() ${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of
${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of
![]() $(d, j)$
-admissible polynomials with tolerance
$(d, j)$
-admissible polynomials with tolerance
![]() $(A_0, A)$
such that
$(A_0, A)$
such that
![]() $\deg {P_1}\le \ldots \le \deg {P_m} =j$
. Let I be an interval with
$\deg {P_1}\le \ldots \le \deg {P_m} =j$
. Let I be an interval with
![]() $\mu (I) = N_0$
, and let
$\mu (I) = N_0$
, and let
![]() $f_0, f_1,\ldots , f_m \in L^0(\mathbb {K})$
be
$f_0, f_1,\ldots , f_m \in L^0(\mathbb {K})$
be
![]() $1$
-bounded functions such that
$1$
-bounded functions such that
![]() $\|f_i\|_{L^1(\mathbb {K})}\le N_0$
for all
$\|f_i\|_{L^1(\mathbb {K})}\le N_0$
for all ![]() . Suppose that
. Suppose that
Then there exists a collection
![]() ${\mathcal P}':=\{P_1^{\prime },\ldots , P_{m'}^{\prime }\}$
of
${\mathcal P}':=\{P_1^{\prime },\ldots , P_{m'}^{\prime }\}$
of
![]() $(d, j-1)$
-admissible polynomials with tolerance
$(d, j-1)$
-admissible polynomials with tolerance
![]() $(A_0^{\prime }, A')$
and
$(A_0^{\prime }, A')$
and
![]() $m':=\#{\mathcal P}'$
so that
$m':=\#{\mathcal P}'$
so that
![]() $\deg (P_1^{\prime })\le \ldots \le \deg (P_{m'}^{\prime })=j-1$
, and
$\deg (P_1^{\prime })\le \ldots \le \deg (P_{m'}^{\prime })=j-1$
, and
![]() $1$
-bounded functions
$1$
-bounded functions
![]() $f_0^{\prime }, f_1^{\prime },\ldots , f_{m'}^{\prime }\in L^0(\mathbb {K})$
such that
$f_0^{\prime }, f_1^{\prime },\ldots , f_{m'}^{\prime }\in L^0(\mathbb {K})$
such that
![]() $\|f_i^{\prime }\|_{L^1(\mathbb {K})}\le N_0$
for all
$\|f_i^{\prime }\|_{L^1(\mathbb {K})}\le N_0$
for all ![]() with
with
![]() $f_{m'}^{\prime }:=f_m$
and satisfying
$f_{m'}^{\prime }:=f_m$
and satisfying
The proof of Claim 6.14 will use the polynomial exhaustion technique based on an iterative application of the PET induction scheme from Proposition 5.8. The key steps of this method are gathered in Proposition 6.20. Assuming momentarily that Claim 6.14 is true, we can easily close the argument to prove Theorem 6.10. We begin with a collection of
![]() $(d, d)$
-admissible polynomials such that
$(d, d)$
-admissible polynomials such that
![]() $\deg {P_1}\le \ldots \le \deg {P_m}=d$
and apply our claim
$\deg {P_1}\le \ldots \le \deg {P_m}=d$
and apply our claim
![]() $d-1$
times until we reach a collection of
$d-1$
times until we reach a collection of
![]() $(d,1)$
-admissible linear polynomials
$(d,1)$
-admissible linear polynomials
![]() $\mathcal L$
with distinct leading terms, which satisfies Equation (6.16) with
$\mathcal L$
with distinct leading terms, which satisfies Equation (6.16) with
![]() ${\mathcal P}'={\mathcal L}$
. In the special case where all polynomials are linear matters simplify and can be handled using the next result, Proposition 6.17, which in turn implies Equation (6.11) from Theorem 6.10 as desired.
${\mathcal P}'={\mathcal L}$
. In the special case where all polynomials are linear matters simplify and can be handled using the next result, Proposition 6.17, which in turn implies Equation (6.11) from Theorem 6.10 as desired.
Proposition 6.17. Let
![]() $N, N_0 \ge 1$
be two scales, I an interval with
$N, N_0 \ge 1$
be two scales, I an interval with
![]() $\mu (I) = N_0$
,
$\mu (I) = N_0$
,
![]() $0<\delta \le 1$
,
$0<\delta \le 1$
,
![]() $d, m\in \mathbb Z_+$
be given and let
$d, m\in \mathbb Z_+$
be given and let
![]() $\mathcal L:=\{L_1,\ldots , L_m\}$
be a collection of
$\mathcal L:=\{L_1,\ldots , L_m\}$
be a collection of
![]() $(d,1)$
-admissible linear polynomials. Let
$(d,1)$
-admissible linear polynomials. Let
![]() $f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
$f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
![]() $1$
-bounded functions such that
$1$
-bounded functions such that
![]() $\|f_i\|_{L^1(\mathbb {K})}\le N_0$
for all
$\|f_i\|_{L^1(\mathbb {K})}\le N_0$
for all ![]() . Suppose that
. Suppose that
Then we have
where
![]() $H_i\simeq \delta ^{O_{\mathcal L}(1)}N^{d}$
for
$H_i\simeq \delta ^{O_{\mathcal L}(1)}N^{d}$
for ![]() .
.
In fact Proposition 6.17 is a special case of Theorem 6.10 with the collection of linear polynomials
![]() $\mathcal L$
in place of
$\mathcal L$
in place of
![]() ${\mathcal P}$
.
${\mathcal P}$
.
Proof of Proposition 6.17.
Defining ![]() we see that each
we see that each
![]() $L'\in {\mathcal L}'$
is linear with vanishing constant term and
$L'\in {\mathcal L}'$
is linear with vanishing constant term and
where
![]() $g_i(x)=\mathrm {T}_{{-L_i(0)}}f_i(x)=f_i(x+L_i(0))$
for each
$g_i(x)=\mathrm {T}_{{-L_i(0)}}f_i(x)=f_i(x+L_i(0))$
for each ![]() . We now apply Lemma 5.6 with functions
. We now apply Lemma 5.6 with functions
![]() $\mathfrak g_1(x)=g_0(x)$
and
$\mathfrak g_1(x)=g_0(x)$
and
![]() $\mathfrak g_2(x, y)=\prod _{i=1}^mg_i(x-L_i^{\prime }(y))$
and intervals
$\mathfrak g_2(x, y)=\prod _{i=1}^mg_i(x-L_i^{\prime }(y))$
and intervals
![]() $J=[N]$
, and a parameter
$J=[N]$
, and a parameter
![]() $H=\delta ^{M}N/M$
for some large absolute constant
$H=\delta ^{M}N/M$
for some large absolute constant
![]() $M\ge 1$
, which will be specified later. Using Lemma 5.6 and changing the variables
$M\ge 1$
, which will be specified later. Using Lemma 5.6 and changing the variables
![]() $x\mapsto x-L_1(y)$
we obtain
$x\mapsto x-L_1(y)$
we obtain
 $$ \begin{align*} \bigg|\frac{1}{N_0} \iiint_{\mathbb{K}^3}\Delta_{\ell(L_1)h} g_1(x)\prod_{i=2}^m\Delta_{\ell(L_i)h}g_{i}(x-(L_i-L_1)(y))d\mu_{[N]}(y)d\mu(x)d\nu_{[H]}(h)\bigg|\gtrsim_M \delta^2. \end{align*} $$
$$ \begin{align*} \bigg|\frac{1}{N_0} \iiint_{\mathbb{K}^3}\Delta_{\ell(L_1)h} g_1(x)\prod_{i=2}^m\Delta_{\ell(L_i)h}g_{i}(x-(L_i-L_1)(y))d\mu_{[N]}(y)d\mu(x)d\nu_{[H]}(h)\bigg|\gtrsim_M \delta^2. \end{align*} $$
Applying Lemma 5.6
![]() $m-2$
more times and changing the variables
$m-2$
more times and changing the variables
![]() $x\mapsto x-L_m(0)$
, we obtain
$x\mapsto x-L_m(0)$
, we obtain
 $$ \begin{align*} \bigg|\frac{1}{N_0} \int_{\mathbb{K}^{m+1}}\Delta_{u_1h_1}\cdots\Delta_{u_{m-1}h_{m-1}}\Delta_{\ell(L_m)h_m}f_{m}(x) d\nu_{[H]}^{\otimes m}(h_1,\ldots, h_m)d\mu(x)\bigg|\gtrsim_M \delta^{2^{m-1}}, \end{align*} $$
$$ \begin{align*} \bigg|\frac{1}{N_0} \int_{\mathbb{K}^{m+1}}\Delta_{u_1h_1}\cdots\Delta_{u_{m-1}h_{m-1}}\Delta_{\ell(L_m)h_m}f_{m}(x) d\nu_{[H]}^{\otimes m}(h_1,\ldots, h_m)d\mu(x)\bigg|\gtrsim_M \delta^{2^{m-1}}, \end{align*} $$
where
![]() $u_i:=\ell (L_m)-\ell (L_{i})$
for
$u_i:=\ell (L_m)-\ell (L_{i})$
for ![]() . By another change of variables we obtain Equation (6.19) with
. By another change of variables we obtain Equation (6.19) with
for ![]() . Using Equation (6.6) with
. Using Equation (6.6) with
![]() $P=L_m$
, and Equation (6.7) with
$P=L_m$
, and Equation (6.7) with
![]() $P=L_m$
and
$P=L_m$
and
![]() $Q=L_i$
we obtain that
$Q=L_i$
we obtain that
![]() $H_i\simeq \delta ^{O_{\mathcal L}(1)}N^{d}$
for
$H_i\simeq \delta ^{O_{\mathcal L}(1)}N^{d}$
for ![]() provided that
provided that
![]() $M\ge 1$
is sufficiently large. This completes the proof of Proposition 6.17.
$M\ge 1$
is sufficiently large. This completes the proof of Proposition 6.17.
Proposition 6.20. Let
![]() $N, N_0>0$
be two scales,
$N, N_0>0$
be two scales,
![]() $0<\delta \le 1$
,
$0<\delta \le 1$
,
![]() $d, m\in \mathbb Z_+$
and
$d, m\in \mathbb Z_+$
and ![]() be given, and let
be given, and let
![]() ${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of
${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of
![]() $(d, j)$
-admissible polynomials with tolerance
$(d, j)$
-admissible polynomials with tolerance
![]() $(A_0, A)$
such that
$(A_0, A)$
such that
![]() $i =\deg {P_1}\le \ldots \le \deg {P_m} =j$
. Let I be an interval with
$i =\deg {P_1}\le \ldots \le \deg {P_m} =j$
. Let I be an interval with
![]() $\mu (I) = N_0$
, and let
$\mu (I) = N_0$
, and let
![]() $f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
$f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
![]() $1$
-bounded functions such that
$1$
-bounded functions such that
![]() $\|f_i\|_{L^1(\mathbb {K})}\le N_0$
for all
$\|f_i\|_{L^1(\mathbb {K})}\le N_0$
for all ![]() . Suppose that
. Suppose that
Then there exists a collection of polynomials
![]() ${\mathcal P}':=\{P_1^{\prime },\ldots , P_{m'}^{\prime }\}$
with
${\mathcal P}':=\{P_1^{\prime },\ldots , P_{m'}^{\prime }\}$
with
![]() $m':=\#{\mathcal P}'<2\#{\mathcal P}$
satisfying
$m':=\#{\mathcal P}'<2\#{\mathcal P}$
satisfying
![]() $P_{m'}^{\prime }:=P_m-P_1$
and
$P_{m'}^{\prime }:=P_m-P_1$
and
![]() $\deg (P_1^{\prime })\le \ldots \le \deg (P_{m'}^{\prime })$
, and
$\deg (P_1^{\prime })\le \ldots \le \deg (P_{m'}^{\prime })$
, and
![]() $1$
-bounded functions
$1$
-bounded functions
![]() $f_0^{\prime }, f_1^{\prime },\ldots , f_{m'}^{\prime }\in L^0(\mathbb {K})$
such that
$f_0^{\prime }, f_1^{\prime },\ldots , f_{m'}^{\prime }\in L^0(\mathbb {K})$
such that
![]() $\|f_i^{\prime }\|_{L^1(\mathbb {K})}\le N_0$
for all
$\|f_i^{\prime }\|_{L^1(\mathbb {K})}\le N_0$
for all ![]() and satisfying
and satisfying
We also know that
![]() $\{f_0^{\prime }, f_1^{\prime },\ldots , f_{m'}^{\prime }\}=\{f_1,\overline {f_1},\ldots , f_m,\overline {f_m}\}$
with
$\{f_0^{\prime }, f_1^{\prime },\ldots , f_{m'}^{\prime }\}=\{f_1,\overline {f_1},\ldots , f_m,\overline {f_m}\}$
with
![]() $f_{m'}^{\prime } =f_m$
.
$f_{m'}^{\prime } =f_m$
.
Moreover,
![]() $v({\mathcal P}')\prec v({\mathcal P})$
, and one of the following three scenarios occurs.
$v({\mathcal P}')\prec v({\mathcal P})$
, and one of the following three scenarios occurs.
-
(i) The collection
 ${\mathcal P}$
is of type I; that is,
${\mathcal P}$
is of type I; that is,
 ${\mathcal P}\neq {\mathcal P}_j$
. In this case,
${\mathcal P}\neq {\mathcal P}_j$
. In this case,
 ${\mathcal P}'$
is a
${\mathcal P}'$
is a
 $(d, j)$
-admissible collection of polynomials with tolerance
$(d, j)$
-admissible collection of polynomials with tolerance
 $(A_0^{\prime }, A')$
and for some
$(A_0^{\prime }, A')$
and for some
 $1\le i \le j-1$
, (6.23)
$1\le i \le j-1$
, (6.23) $$ \begin{align} \qquad v({\mathcal P}')=(v_1({\mathcal P}'),\ldots, v_{i-1}({\mathcal P}'), v_i({\mathcal P})-1, v_{i+1}({\mathcal P}), \ldots, v_{j}({\mathcal P}),0, 0, \ldots). \end{align} $$
$$ \begin{align} \qquad v({\mathcal P}')=(v_1({\mathcal P}'),\ldots, v_{i-1}({\mathcal P}'), v_i({\mathcal P})-1, v_{i+1}({\mathcal P}), \ldots, v_{j}({\mathcal P}),0, 0, \ldots). \end{align} $$
-
(ii) The collection
 ${\mathcal P}$
is of type II; that is,
${\mathcal P}$
is of type II; that is,
 ${\mathcal P}={\mathcal P}_j$
and
${\mathcal P}={\mathcal P}_j$
and
 $v_j({\mathcal P})>1$
. In this case,
$v_j({\mathcal P})>1$
. In this case,
 ${\mathcal P}'$
is a
${\mathcal P}'$
is a
 $(d, j)$
-admissible collection of polynomials with tolerance
$(d, j)$
-admissible collection of polynomials with tolerance
 $(A_0^{\prime }, A')$
and (6.24)
$(A_0^{\prime }, A')$
and (6.24) $$ \begin{align} v({\mathcal P}')=(v_1({\mathcal P}'),\ldots, v_{j-1}({\mathcal P}'), v_j({\mathcal P})-1, 0,0, \ldots). \end{align} $$
$$ \begin{align} v({\mathcal P}')=(v_1({\mathcal P}'),\ldots, v_{j-1}({\mathcal P}'), v_j({\mathcal P})-1, 0,0, \ldots). \end{align} $$
-
(iii) The collection
 ${\mathcal P}$
is of type III; that is,
${\mathcal P}$
is of type III; that is,
 ${\mathcal P}={\mathcal P}_j$
and
${\mathcal P}={\mathcal P}_j$
and
 $v_j({\mathcal P})=1$
. In this case,
$v_j({\mathcal P})=1$
. In this case,
 ${\mathcal P}'$
is a
${\mathcal P}'$
is a
 $(d, j-1)$
-admissible collection of polynomials with tolerance
$(d, j-1)$
-admissible collection of polynomials with tolerance
 $(A_0^{\prime }, A')$
and (6.25)Moreover, the leading coefficients of the polynomials in
$(A_0^{\prime }, A')$
and (6.25)Moreover, the leading coefficients of the polynomials in $$ \begin{align} v({\mathcal P}')=(0,\ldots,0, v_{j-1}({\mathcal P}'), 0,0, \ldots). \end{align} $$
$$ \begin{align} v({\mathcal P}')=(0,\ldots,0, v_{j-1}({\mathcal P}'), 0,0, \ldots). \end{align} $$
 ${\mathcal P}'$
are pairwise distinct.
${\mathcal P}'$
are pairwise distinct.
The tolerance
![]() $(A_0^{\prime }, A')$
of the collection
$(A_0^{\prime }, A')$
of the collection
![]() ${\mathcal P}'$
only depends on the tolerance
${\mathcal P}'$
only depends on the tolerance
![]() $(A_0, A)$
of the collection
$(A_0, A)$
of the collection
![]() ${\mathcal P}$
and is independent of
${\mathcal P}$
and is independent of
![]() $\delta $
and N.
$\delta $
and N.
Using Proposition 6.20, we now prove Claim 6.14.
Proof of Claim 6.14.
We may assume, without loss of generality, that the collection
![]() ${\mathcal P}$
from Claim 6.14 is of type I or type II. Then we apply Proposition 6.20 until we reach a collection of polynomials of type III with weight vector
${\mathcal P}$
from Claim 6.14 is of type I or type II. Then we apply Proposition 6.20 until we reach a collection of polynomials of type III with weight vector
![]() $v({\mathcal P})=(0,\ldots ,0, v_{j}({\mathcal P}), 0,0, \ldots )$
, where
$v({\mathcal P})=(0,\ldots ,0, v_{j}({\mathcal P}), 0,0, \ldots )$
, where
![]() $v_j({\mathcal P}) = 1$
and such that Equation (6.16) holds. We apply Proposition 6.20 once more to reach a collection of
$v_j({\mathcal P}) = 1$
and such that Equation (6.16) holds. We apply Proposition 6.20 once more to reach a collection of
![]() $(d, j-1)$
-admissible polynomials satisfying Equation (6.16). This completes the proof of the claim.
$(d, j-1)$
-admissible polynomials satisfying Equation (6.16). This completes the proof of the claim.
Proof of Proposition 6.20.
Appealing to Proposition 5.8 with
![]() $i_0=1$
, we may conclude that there exists a collection of polynomials
$i_0=1$
, we may conclude that there exists a collection of polynomials
![]() ${\mathcal P}':=\{P_1^{\prime },\ldots , P_{m'}^{\prime }\}$
with
${\mathcal P}':=\{P_1^{\prime },\ldots , P_{m'}^{\prime }\}$
with
![]() $m'=\#{\mathcal P}'<2\#{\mathcal P}$
and
$m'=\#{\mathcal P}'<2\#{\mathcal P}$
and
![]() $P_{m'}^{\prime }=P_m-P_1$
such that
$P_{m'}^{\prime }=P_m-P_1$
such that
for some
![]() $\delta '\delta ^2N/C^2\le |h| \le \delta 'N\le \delta ^4N/C$
. Proposition 5.8 also ensures that bound (6.22) holds for certain
$\delta '\delta ^2N/C^2\le |h| \le \delta 'N\le \delta ^4N/C$
. Proposition 5.8 also ensures that bound (6.22) holds for certain
![]() $1$
-bounded functions
$1$
-bounded functions
![]() $f_0^{\prime }, f_1^{\prime },\ldots , f_{m'}^{\prime }\in L^0(\mathbb {K})$
such that
$f_0^{\prime }, f_1^{\prime },\ldots , f_{m'}^{\prime }\in L^0(\mathbb {K})$
such that
![]() $\|f_i^{\prime }\|_{L^1(\mathbb {K})}\le N_0$
for all
$\|f_i^{\prime }\|_{L^1(\mathbb {K})}\le N_0$
for all ![]() and satisfying
and satisfying
![]() $\{f_0^{\prime }, f_1^{\prime },\ldots , f_{m'}^{\prime }\}=\{f_1,\overline {f_1},\ldots , f_m,\overline {f_m}\}$
with
$\{f_0^{\prime }, f_1^{\prime },\ldots , f_{m'}^{\prime }\}=\{f_1,\overline {f_1},\ldots , f_m,\overline {f_m}\}$
with
![]() $f_{m'}^{\prime }=f_m$
. Now, it remains to verify conclusions from (i), (ii) and (iii). For this purpose, we will have to adjust
$f_{m'}^{\prime }=f_m$
. Now, it remains to verify conclusions from (i), (ii) and (iii). For this purpose, we will have to adjust
![]() $\delta '\le \delta ^4/C$
, which can be made as small as necessary.
$\delta '\le \delta ^4/C$
, which can be made as small as necessary.
Proof of the conclusion from (i)
Suppose that the collection
![]() ${\mathcal P}$
is of type I. Then
${\mathcal P}$
is of type I. Then
![]() $i=\deg (P_1)<\deg (P_m)=j$
and
$i=\deg (P_1)<\deg (P_m)=j$
and
![]() $v({\mathcal P})=(0,\ldots , 0, v_i({\mathcal P}),\ldots , v_j({\mathcal P}), 0, 0, \ldots )$
. To establish Equation (6.23), we consider three cases. Let
$v({\mathcal P})=(0,\ldots , 0, v_i({\mathcal P}),\ldots , v_j({\mathcal P}), 0, 0, \ldots )$
. To establish Equation (6.23), we consider three cases. Let
![]() $P\in {\mathcal P}$
. If
$P\in {\mathcal P}$
. If
![]() $\deg (P)>i$
, then
$\deg (P)>i$
, then
 $$ \begin{align} \begin{aligned} \deg(P-P_1)=\deg(P(\cdot+h)-P_1)=\deg(P), \\ \ell(P-P_1)=\ell(P(\cdot+h)-P_1)=\ell(P), \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \deg(P-P_1)=\deg(P(\cdot+h)-P_1)=\deg(P), \\ \ell(P-P_1)=\ell(P(\cdot+h)-P_1)=\ell(P), \end{aligned} \end{align} $$
which yields that
![]() $v_k({\mathcal P}')=v_k({\mathcal P})$
for all
$v_k({\mathcal P}')=v_k({\mathcal P})$
for all
![]() $k>i$
. If
$k>i$
. If
![]() $\deg (P)=i$
and
$\deg (P)=i$
and
![]() $\ell (P)\neq \ell (P_1)$
, then
$\ell (P)\neq \ell (P_1)$
, then
 $$ \begin{align} \begin{aligned} \deg(P-P_1)=\deg(P(\cdot+h)-P_1)=i, \\ \ell(P-P_1)=\ell(P(\cdot+h)-P_1)=\ell(P)- \ell(P_1). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \deg(P-P_1)=\deg(P(\cdot+h)-P_1)=i, \\ \ell(P-P_1)=\ell(P(\cdot+h)-P_1)=\ell(P)- \ell(P_1). \end{aligned} \end{align} $$
If
![]() $\deg (P)=i$
and
$\deg (P)=i$
and
![]() $\ell (P)=\ell (P_1)$
, then
$\ell (P)=\ell (P_1)$
, then
The latter two cases show that
![]() $v_{k}({\mathcal P}')\ge 0$
for all
$v_{k}({\mathcal P}')\ge 0$
for all ![]() and
and
![]() $v_i({\mathcal P}')=v_i({\mathcal P})-1$
. Hence, Equation (6.23) holds. We now show that
$v_i({\mathcal P}')=v_i({\mathcal P})-1$
. Hence, Equation (6.23) holds. We now show that
![]() ${\mathcal P}'$
is
${\mathcal P}'$
is
![]() $(d, j)$
-admissible.
$(d, j)$
-admissible.
We begin with verifying Equation (6.6) for
![]() $P'\in {\mathcal P}_j^{\prime }$
. We may write
$P'\in {\mathcal P}_j^{\prime }$
. We may write
![]() $P'=P(\cdot +\varepsilon h)-P_1$
for some
$P'=P(\cdot +\varepsilon h)-P_1$
for some
![]() $P\in {\mathcal P}_j$
and
$P\in {\mathcal P}_j$
and
![]() $\varepsilon \in \{0, 1\}$
. By Equations (6.26) and (6.6) for
$\varepsilon \in \{0, 1\}$
. By Equations (6.26) and (6.6) for
![]() $P\in {\mathcal P}_j$
, we obtain
$P\in {\mathcal P}_j$
, we obtain
We now verify Equation (6.7) for
![]() $Q_1^{\prime }, Q_2^{\prime }\in {\mathcal P}^{\prime }_j$
with
$Q_1^{\prime }, Q_2^{\prime }\in {\mathcal P}^{\prime }_j$
with
![]() $\ell (Q_1^{\prime })\neq \ell (Q_2^{\prime })$
. We may write
$\ell (Q_1^{\prime })\neq \ell (Q_2^{\prime })$
. We may write
for some
![]() $Q_1, Q_2\in {\mathcal P}_j$
and
$Q_1, Q_2\in {\mathcal P}_j$
and
![]() $\varepsilon _1, \varepsilon _2\in \{0, 1\}$
. By Equation (6.26), we have
$\varepsilon _1, \varepsilon _2\in \{0, 1\}$
. By Equation (6.26), we have
![]() $\ell (Q_1^{\prime })=\ell (Q_1)$
and
$\ell (Q_1^{\prime })=\ell (Q_1)$
and
![]() $\ell (Q_2^{\prime })=\ell (Q_2)$
. Then
$\ell (Q_2^{\prime })=\ell (Q_2)$
. Then
![]() $\ell (Q_1)\neq \ell (Q_2)$
and by Equation (6.7) for
$\ell (Q_1)\neq \ell (Q_2)$
and by Equation (6.7) for
![]() $Q_1, Q_2\in {\mathcal P}_j$
, we deduce
$Q_1, Q_2\in {\mathcal P}_j$
, we deduce
We finally verify Equation (6.8) for
![]() $Q_1^{\prime }, Q_2^{\prime }\in {\mathcal P}^{\prime }_j$
as in Equation (6.29) such that
$Q_1^{\prime }, Q_2^{\prime }\in {\mathcal P}^{\prime }_j$
as in Equation (6.29) such that
![]() $Q_1^{\prime }\neq Q_2^{\prime }$
and
$Q_1^{\prime }\neq Q_2^{\prime }$
and
![]() $\ell (Q_1^{\prime })=\ell (Q_2^{\prime })=\ell $
. By Equation (6.26), we see that
$\ell (Q_1^{\prime })=\ell (Q_2^{\prime })=\ell $
. By Equation (6.26), we see that
![]() $\ell (Q_1)=\ell (Q_2)=\ell $
. Since
$\ell (Q_1)=\ell (Q_2)=\ell $
. Since
![]() ${\mathcal P}$
is
${\mathcal P}$
is
![]() $(d, j)$
-admissible, using Equation (6.6), we also have
$(d, j)$
-admissible, using Equation (6.6), we also have
Recall that
![]() $\delta '\delta ^2N/C^2\le |h| \le \delta 'N$
, where
$\delta '\delta ^2N/C^2\le |h| \le \delta 'N$
, where
![]() $\delta '>0$
is an arbitrarily small number such that
$\delta '>0$
is an arbitrarily small number such that
![]() $\delta '\le \delta ^4/C$
. Set
$\delta '\le \delta ^4/C$
. Set
![]() $\delta ':=\delta ^{M}(CM)^{-1}$
for a large number
$\delta ':=\delta ^{M}(CM)^{-1}$
for a large number
![]() $M\ge 1$
, which will be chosen later.
$M\ge 1$
, which will be chosen later.
First, suppose
![]() $Q_1 = Q_2$
. Then
$Q_1 = Q_2$
. Then
![]() $\varepsilon _1 \not = \varepsilon _2$
and
$\varepsilon _1 \not = \varepsilon _2$
and
![]() $\deg (Q_1^{\prime }-Q_2^{\prime })=j-1$
. Furthermore,
$\deg (Q_1^{\prime }-Q_2^{\prime })=j-1$
. Furthermore,
![]() $\ell (Q_1^{\prime }-Q_2^{\prime })= j\ell h(\varepsilon _1-\varepsilon _2)$
implying
$\ell (Q_1^{\prime }-Q_2^{\prime })= j\ell h(\varepsilon _1-\varepsilon _2)$
implying
![]() $|\ell (Q_1^{\prime } - Q_2^{\prime })| = |j \ell h|$
, and so by Equation (6.31),
$|\ell (Q_1^{\prime } - Q_2^{\prime })| = |j \ell h|$
, and so by Equation (6.31),
and this verifies Equations (6.8) in the case
![]() $Q_1 = Q_2$
.
$Q_1 = Q_2$
.
Now, suppose
![]() $Q_1 \not = Q_2$
so that
$Q_1 \not = Q_2$
so that
![]() $\deg (Q_1 - Q_2) = j-1$
and Equation (6.8) holds for
$\deg (Q_1 - Q_2) = j-1$
and Equation (6.8) holds for
![]() $\ell (Q_1 - Q_2)$
; that is,
$\ell (Q_1 - Q_2)$
; that is,
Taking
![]() $M:=\max \{2A, 2|j|A_0^2\}$
in Equation (6.32), we see that
$M:=\max \{2A, 2|j|A_0^2\}$
in Equation (6.32), we see that
![]() $|j\ell h| \le \frac 12 A_0^{-1}\delta ^{A} N^{d-j+1}$
if
$|j\ell h| \le \frac 12 A_0^{-1}\delta ^{A} N^{d-j+1}$
if
![]() $C> 1$
is large enough.
$C> 1$
is large enough.
In this case,
![]() $\ell (Q_1^{\prime } - Q_2^{\prime }) = \ell (Q_1 - Q_2) + j h\ell (\varepsilon _1-\varepsilon _2)$
and so
$\ell (Q_1^{\prime } - Q_2^{\prime }) = \ell (Q_1 - Q_2) + j h\ell (\varepsilon _1-\varepsilon _2)$
and so
From Equation (6.33) and
![]() $|j\ell h| \le \frac 12 A_0^{-1} \delta ^A N^{d-j+1}$
, we conclude
$|j\ell h| \le \frac 12 A_0^{-1} \delta ^A N^{d-j+1}$
, we conclude
This verifies Equation (6.8) in the case
![]() $Q_1 \not = Q_2$
.
$Q_1 \not = Q_2$
.
In either case, we see that
![]() $\deg (Q_1^{\prime } - Q_2^{\prime }) = j-1$
and (see Equations (6.32) and (6.34)) we can find a tolerance pair
$\deg (Q_1^{\prime } - Q_2^{\prime }) = j-1$
and (see Equations (6.32) and (6.34)) we can find a tolerance pair
![]() $(A_0^{\prime }, A')$
for
$(A_0^{\prime }, A')$
for
![]() ${\mathcal P}'$
depending on the tolerance
${\mathcal P}'$
depending on the tolerance
![]() $(A_0, A)$
of
$(A_0, A)$
of
![]() ${\mathcal P}$
and the constants C and M such that
${\mathcal P}$
and the constants C and M such that
holds, establishing Equation (6.8).
Proof of the conclusion from (ii)
Suppose that the collection
![]() ${\mathcal P}$
is of type II. Then
${\mathcal P}$
is of type II. Then
![]() $\deg (P_1)=\ldots =\deg (P_m)=j$
and
$\deg (P_1)=\ldots =\deg (P_m)=j$
and
![]() $v({\mathcal P})=(0,\ldots , 0, v_j({\mathcal P}), 0, 0, \ldots )$
with
$v({\mathcal P})=(0,\ldots , 0, v_j({\mathcal P}), 0, 0, \ldots )$
with
![]() $v_j({\mathcal P})>1$
. To establish Equation (6.24), we will proceed in a similar way as in (i). If
$v_j({\mathcal P})>1$
. To establish Equation (6.24), we will proceed in a similar way as in (i). If
![]() $P\in {\mathcal P}={\mathcal P}_j$
and
$P\in {\mathcal P}={\mathcal P}_j$
and
![]() $\ell (P)\neq \ell (P_1)$
, then
$\ell (P)\neq \ell (P_1)$
, then
 $$ \begin{align} \begin{aligned} \deg(P-P_1)=\deg(P(\cdot+h)-P_1)=j, \\ \ell(P-P_1)=\ell(P(\cdot+h)-P_1)=\ell(P)- \ell(P_1). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \deg(P-P_1)=\deg(P(\cdot+h)-P_1)=j, \\ \ell(P-P_1)=\ell(P(\cdot+h)-P_1)=\ell(P)- \ell(P_1). \end{aligned} \end{align} $$
If
![]() $P\in {\mathcal P}={\mathcal P}_j$
and
$P\in {\mathcal P}={\mathcal P}_j$
and
![]() $\ell (P)=\ell (P_1)$
, then by the fact that
$\ell (P)=\ell (P_1)$
, then by the fact that
![]() ${\mathcal P}$
is
${\mathcal P}$
is
![]() $(d, j)$
-admissible, and by Equation (6.8), we see that
$(d, j)$
-admissible, and by Equation (6.8), we see that
This shows that
![]() $v_{k}({\mathcal P}')\ge 0$
for all
$v_{k}({\mathcal P}')\ge 0$
for all ![]() and
and
![]() $v_j({\mathcal P}')=v_j({\mathcal P})-1$
. Hence, Equation (6.24) holds. We now show that
$v_j({\mathcal P}')=v_j({\mathcal P})-1$
. Hence, Equation (6.24) holds. We now show that
![]() ${\mathcal P}'$
is
${\mathcal P}'$
is
![]() $(d, j)$
-admissible.
$(d, j)$
-admissible.
We begin with verifying Equation (6.6) for
![]() $P'\in {\mathcal P}_j^{\prime }$
. We may write
$P'\in {\mathcal P}_j^{\prime }$
. We may write
![]() $P'=P(\cdot +\varepsilon h)-P_1$
for some
$P'=P(\cdot +\varepsilon h)-P_1$
for some
![]() $P\in {\mathcal P}_j$
such that
$P\in {\mathcal P}_j$
such that
![]() $\ell (P)\neq \ell (P_1)$
and
$\ell (P)\neq \ell (P_1)$
and
![]() $\varepsilon \in \{0, 1\}$
. Since
$\varepsilon \in \{0, 1\}$
. Since
![]() ${\mathcal P}$
is
${\mathcal P}$
is
![]() $(d, j)$
-admissible, using Equations (6.36) and (6.7) (with
$(d, j)$
-admissible, using Equations (6.36) and (6.7) (with
![]() $\ell (P)- \ell (P_1)$
in place of
$\ell (P)- \ell (P_1)$
in place of
![]() $\ell (P)- \ell (Q)$
), we obtain Equation (6.28) which is Equation (6.6) for
$\ell (P)- \ell (Q)$
), we obtain Equation (6.28) which is Equation (6.6) for
![]() $P' \in \mathcal P_j^{\prime }$
.
$P' \in \mathcal P_j^{\prime }$
.
We now verify Equation (6.7) for
![]() $Q_1^{\prime }, Q_2^{\prime }\in {\mathcal P}^{\prime }_j$
with
$Q_1^{\prime }, Q_2^{\prime }\in {\mathcal P}^{\prime }_j$
with
![]() $\ell (Q_1^{\prime })\neq \ell (Q_2^{\prime })$
. As in Equation (6.29), we may write
$\ell (Q_1^{\prime })\neq \ell (Q_2^{\prime })$
. As in Equation (6.29), we may write
![]() $Q_1^{\prime }=Q_1(\cdot +\varepsilon _1 h)-P_1$
, and
$Q_1^{\prime }=Q_1(\cdot +\varepsilon _1 h)-P_1$
, and
![]() $Q_2^{\prime }=Q_2(\cdot +\varepsilon _2 h)-P_1$
for some
$Q_2^{\prime }=Q_2(\cdot +\varepsilon _2 h)-P_1$
for some
![]() $Q_1, Q_2\in {\mathcal P}_j$
and
$Q_1, Q_2\in {\mathcal P}_j$
and
![]() $\varepsilon _1, \varepsilon _2\in \{0, 1\}$
such that
$\varepsilon _1, \varepsilon _2\in \{0, 1\}$
such that
![]() $\ell (Q_1)\neq \ell (P_1)$
and
$\ell (Q_1)\neq \ell (P_1)$
and
![]() $\ell (Q_2)\neq \ell (P_1)$
. By Equation (6.36), we have
$\ell (Q_2)\neq \ell (P_1)$
. By Equation (6.36), we have
![]() $\ell (Q_1^{\prime })=\ell (Q_1)-\ell (P_1)$
and
$\ell (Q_1^{\prime })=\ell (Q_1)-\ell (P_1)$
and
![]() $\ell (Q_2^{\prime })=\ell (Q_2)-\ell (P_1)$
. Then
$\ell (Q_2^{\prime })=\ell (Q_2)-\ell (P_1)$
. Then
![]() $\ell (Q_1)\neq \ell (Q_2)$
and Equation (6.30) is verified by appealing to Equation (6.7) (with
$\ell (Q_1)\neq \ell (Q_2)$
and Equation (6.30) is verified by appealing to Equation (6.7) (with
![]() $\ell (Q_1) - \ell (Q_2)$
in place of
$\ell (Q_1) - \ell (Q_2)$
in place of
![]() $\ell (P) - \ell (Q)$
).
$\ell (P) - \ell (Q)$
).
We finally verify Equation (6.8) for
![]() $Q_1^{\prime }, Q_2^{\prime }\in {\mathcal P}^{\prime }_j$
as in Equation (6.29) such that
$Q_1^{\prime }, Q_2^{\prime }\in {\mathcal P}^{\prime }_j$
as in Equation (6.29) such that
![]() $Q_1^{\prime }\neq Q_2^{\prime }$
and
$Q_1^{\prime }\neq Q_2^{\prime }$
and
![]() $\ell (Q_1^{\prime })=\ell (Q_2^{\prime })=\ell $
. By Equation (6.36),
$\ell (Q_1^{\prime })=\ell (Q_2^{\prime })=\ell $
. By Equation (6.36),
![]() $\ell (Q_1)-\ell (P_1)=\ell (Q_2)-\ell (P_1)=\ell $
and since
$\ell (Q_1)-\ell (P_1)=\ell (Q_2)-\ell (P_1)=\ell $
and since
![]() ${\mathcal P}$
is
${\mathcal P}$
is
![]() $(d,j)$
-admissible, we see that
$(d,j)$
-admissible, we see that
![]() $\ell $
satisfies Equation (6.31). Now, by following the last part of the proof from (i), we conclude that Equation (6.35) holds.
$\ell $
satisfies Equation (6.31). Now, by following the last part of the proof from (i), we conclude that Equation (6.35) holds.
Proof of the conclusion from (iii)
Suppose that the collection
![]() ${\mathcal P}$
is of type III. Then
${\mathcal P}$
is of type III. Then
![]() $\deg (P_1)=\ldots =\deg (P_m)=j$
and
$\deg (P_1)=\ldots =\deg (P_m)=j$
and
![]() $v({\mathcal P})=(0,\ldots , 0, v_j({\mathcal P}), 0, 0, \ldots )$
with
$v({\mathcal P})=(0,\ldots , 0, v_j({\mathcal P}), 0, 0, \ldots )$
with
![]() $v_j({\mathcal P})=1$
, thus
$v_j({\mathcal P})=1$
, thus
![]() $\ell (P_1)=\ldots =\ell (P_m):=\ell $
. To establish Equation (6.25), we will proceed in a similar way as in (i) and (ii). If
$\ell (P_1)=\ldots =\ell (P_m):=\ell $
. To establish Equation (6.25), we will proceed in a similar way as in (i) and (ii). If
![]() $P\in {\mathcal P}_j$
and
$P\in {\mathcal P}_j$
and
![]() $\ell (P)=\ell $
, then Equation (6.31) holds for
$\ell (P)=\ell $
, then Equation (6.31) holds for
![]() $\ell $
and once again Equation (6.37) holds. This in turn implies that
$\ell $
and once again Equation (6.37) holds. This in turn implies that
![]() $v_{j-1}({\mathcal P}')>0$
and
$v_{j-1}({\mathcal P}')>0$
and
![]() $v_{k}({\mathcal P}')=0$
for all
$v_{k}({\mathcal P}')=0$
for all
![]() $k\neq j-1$
. Hence, Equation (6.25) holds. We now show that
$k\neq j-1$
. Hence, Equation (6.25) holds. We now show that
![]() ${\mathcal P}'$
is
${\mathcal P}'$
is
![]() $(d, j-1)$
-admissible.
$(d, j-1)$
-admissible.
We begin with verifying Equation (6.6) (or equivalently Equation (6.28) with j replaced by
![]() $j-1$
) for
$j-1$
) for
![]() $P'\in {\mathcal P}_{j-1}'$
. We may write
$P'\in {\mathcal P}_{j-1}'$
. We may write
![]() $P'=P(\cdot +\varepsilon h)-P_1$
for some
$P'=P(\cdot +\varepsilon h)-P_1$
for some
![]() $P\in {\mathcal P}_j$
such that
$P\in {\mathcal P}_j$
such that
![]() $\ell (P)=\ell (P_1)$
and
$\ell (P)=\ell (P_1)$
and
![]() $\varepsilon \in \{0, 1\}$
. Then
$\varepsilon \in \{0, 1\}$
. Then
As in (i) we have
![]() $\delta '\delta ^2N/C^2\le |h| \le \delta 'N$
, where
$\delta '\delta ^2N/C^2\le |h| \le \delta 'N$
, where
![]() $\delta ':=\delta ^{M}(CM)^{-1}$
for a large number
$\delta ':=\delta ^{M}(CM)^{-1}$
for a large number
![]() $M\ge 1$
, which will be chosen later. Furthermore if
$M\ge 1$
, which will be chosen later. Furthermore if
![]() $P \not = P_1$
, then
$P \not = P_1$
, then
![]() $A_0^{-1} \delta ^A N^{d-j+1} \le |\ell (P-P_1)| \le A_0 \delta ^{-A} N^{d-j+1}$
since
$A_0^{-1} \delta ^A N^{d-j+1} \le |\ell (P-P_1)| \le A_0 \delta ^{-A} N^{d-j+1}$
since
![]() ${\mathcal P}$
is
${\mathcal P}$
is
![]() $(d,j)$
-admissible and so Equation (6.8) holds with
$(d,j)$
-admissible and so Equation (6.8) holds with
![]() $Q = P_1$
. This takes care of the case
$Q = P_1$
. This takes care of the case
![]() $\varepsilon = 0$
.
$\varepsilon = 0$
.
If
![]() $\varepsilon =1$
and
$\varepsilon =1$
and
![]() $P = P_1$
, then Equation (6.32) gives the desired bound for
$P = P_1$
, then Equation (6.32) gives the desired bound for
![]() $|\ell (P')|$
. When
$|\ell (P')|$
. When
![]() $P \not = P_1$
, we use the upper bound from Equation (6.32)
$P \not = P_1$
, we use the upper bound from Equation (6.32)
when
![]() $M = \max (2A, 2|j|A_0^2)$
and
$M = \max (2A, 2|j|A_0^2)$
and
![]() $C>1$
chosen large enough. Thus, as before, condition (6.6) holds for
$C>1$
chosen large enough. Thus, as before, condition (6.6) holds for
![]() $P'$
with some tolerance pair
$P'$
with some tolerance pair
![]() $(A_0^{\prime }, A')$
as desired.
$(A_0^{\prime }, A')$
as desired.
For
![]() $Q_1^{\prime } \not = Q_2^{\prime }\in {\mathcal P}^{\prime }_{j-1}$
, we may write
$Q_1^{\prime } \not = Q_2^{\prime }\in {\mathcal P}^{\prime }_{j-1}$
, we may write
![]() $Q_1^{\prime }=Q_1(\cdot +\varepsilon _1 h)-P_1$
, and
$Q_1^{\prime }=Q_1(\cdot +\varepsilon _1 h)-P_1$
, and
![]() $Q_2^{\prime }=Q_2(\cdot +\varepsilon _2 h)-P_1$
for some
$Q_2^{\prime }=Q_2(\cdot +\varepsilon _2 h)-P_1$
for some
![]() $Q_1, Q_2\in {\mathcal P}_j$
and
$Q_1, Q_2\in {\mathcal P}_j$
and
![]() $\varepsilon _1, \varepsilon _2\in \{0, 1\}$
such that
$\varepsilon _1, \varepsilon _2\in \{0, 1\}$
such that
![]() $\ell (Q_1)=\ell (Q_2) = \ell (P_1) = \ell $
. We have
$\ell (Q_1)=\ell (Q_2) = \ell (P_1) = \ell $
. We have
![]() $\ell (Q_1 - P_1) - \ell (Q_2 - P_1) = \ell (Q_1 - Q_2)$
and so by Equation (6.38),
$\ell (Q_1 - P_1) - \ell (Q_2 - P_1) = \ell (Q_1 - Q_2)$
and so by Equation (6.38),
We consider two cases.
If
![]() $Q_1 = Q_2$
, then necessarily
$Q_1 = Q_2$
, then necessarily
![]() $|\varepsilon _1 - \varepsilon _2| = 1$
and so
$|\varepsilon _1 - \varepsilon _2| = 1$
and so
![]() $\ell (Q_1^{\prime }) \not = \ell (Q_2^{\prime })$
,
$\ell (Q_1^{\prime }) \not = \ell (Q_2^{\prime })$
,
![]() $\deg (Q_1^{\prime } - Q_2^{\prime }) = j-1$
, and Equation (6.32) shows that Equation (6.7) holds for
$\deg (Q_1^{\prime } - Q_2^{\prime }) = j-1$
, and Equation (6.32) shows that Equation (6.7) holds for
![]() $Q_1^{\prime }, Q_2^{\prime } \in {\mathcal P}^{\prime }_{j-1}$
.
$Q_1^{\prime }, Q_2^{\prime } \in {\mathcal P}^{\prime }_{j-1}$
.
If
![]() $Q_1 \not = Q_2$
, then
$Q_1 \not = Q_2$
, then
![]() $A_0^{-1} \delta ^A N^{d-j+1} \le |\ell (Q_1-Q_2)| \le A_0 \delta ^{-A} N^{d-j+1}$
since
$A_0^{-1} \delta ^A N^{d-j+1} \le |\ell (Q_1-Q_2)| \le A_0 \delta ^{-A} N^{d-j+1}$
since
![]() ${\mathcal P}$
is
${\mathcal P}$
is
![]() $(d,j)$
-admissible, and so Equation (6.8) holds with
$(d,j)$
-admissible, and so Equation (6.8) holds with
![]() $P=Q_1 $
and
$P=Q_1 $
and
![]() $Q=Q_2$
. From Equation (6.39), we see that
$Q=Q_2$
. From Equation (6.39), we see that
![]() $\ell (Q_1^{\prime }) \not = \ell (Q_2^{\prime })$
and Equation (6.40) implies that Equation (6.7) holds for
$\ell (Q_1^{\prime }) \not = \ell (Q_2^{\prime })$
and Equation (6.40) implies that Equation (6.7) holds for
![]() $Q_1^{\prime }, Q_2^{\prime }\in {\mathcal P}^{\prime }_{j-1}$
.
$Q_1^{\prime }, Q_2^{\prime }\in {\mathcal P}^{\prime }_{j-1}$
.
In either case, we see that Equation (6.8) is vacuously satisfied by
![]() ${\mathcal P}'$
and Equation (6.7) holds for
${\mathcal P}'$
and Equation (6.7) holds for
![]() $Q_1^{\prime }, Q_2^{\prime } \in {\mathcal P}^{\prime }_{j-1}$
with (necessarily)
$Q_1^{\prime }, Q_2^{\prime } \in {\mathcal P}^{\prime }_{j-1}$
with (necessarily)
![]() $\ell (Q_1^{\prime })\neq \ell (Q_2^{\prime })$
.
$\ell (Q_1^{\prime })\neq \ell (Q_2^{\prime })$
.
Concluding, we are able to find a tolerance pair
![]() $(A_0^{\prime }, A')$
for
$(A_0^{\prime }, A')$
for
![]() ${\mathcal P}'$
depending on the tolerance
${\mathcal P}'$
depending on the tolerance
![]() $(A_0, A)$
of
$(A_0, A)$
of
![]() ${\mathcal P}$
and the constants C and M such that the required estimates for Equations (6.38) and (6.40) hold. This completes the proof of Proposition 6.20.
${\mathcal P}$
and the constants C and M such that the required estimates for Equations (6.38) and (6.40) hold. This completes the proof of Proposition 6.20.
6.2 Degree-lowering
Here, we establish a modulated version of the inverse theorem, which will imply Theorem 6.1.
Theorem 6.41 (Inverse theorem for modulated
 $(m+1)$
-linear forms).
$(m+1)$
-linear forms).
Let
![]() $N\ge 1$
be a scale, and let
$N\ge 1$
be a scale, and let
![]() $0<\delta \le 1$
,
$0<\delta \le 1$
,
![]() $m\in \mathbb Z_+$
and
$m\in \mathbb Z_+$
and
![]() $n\in \mathbb {N}$
be given. Let
$n\in \mathbb {N}$
be given. Let
![]() ${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
![]() $\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials such that
$\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials such that
Let
![]() $f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
$f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
![]() $1$
-bounded functions supported on an interval
$1$
-bounded functions supported on an interval
![]() $I\subset \mathbb {K}$
of measure
$I\subset \mathbb {K}$
of measure
![]() $N_0 := N^{\deg {P_m}}$
. For
$N_0 := N^{\deg {P_m}}$
. For
![]() $n\in \mathbb Z_+$
, we define an
$n\in \mathbb Z_+$
, we define an
![]() $(m+1)$
-linear form corresponding to the triple
$(m+1)$
-linear form corresponding to the triple
![]() $({\mathcal P}, \mathcal Q; N)$
and a frequency vector
$({\mathcal P}, \mathcal Q; N)$
and a frequency vector
![]() $\xi =(\xi _1,\ldots , \xi _n)\in \mathbb {K}^n$
by
$\xi =(\xi _1,\ldots , \xi _n)\in \mathbb {K}^n$
by
 $$ \begin{align} \Lambda_{{\mathcal P}; N}^{\mathcal Q; \xi}(f_0,\ldots, f_m):=\frac{1}{N_0} \int_{\mathbb{K}^2}f_0(x)\prod_{i=1}^mf_{i}(x-P_i(y))\mathrm{e}\Big(\sum_{j=1}^n\xi_jQ_j(y)\Big)d\mu_{[N]}(y)d\mu(x). \end{align} $$
$$ \begin{align} \Lambda_{{\mathcal P}; N}^{\mathcal Q; \xi}(f_0,\ldots, f_m):=\frac{1}{N_0} \int_{\mathbb{K}^2}f_0(x)\prod_{i=1}^mf_{i}(x-P_i(y))\mathrm{e}\Big(\sum_{j=1}^n\xi_jQ_j(y)\Big)d\mu_{[N]}(y)d\mu(x). \end{align} $$
For
![]() $n=0$
, we set
$n=0$
, we set
![]() $\mathcal Q=\emptyset $
and we simply write
$\mathcal Q=\emptyset $
and we simply write
![]() $\Lambda _{{\mathcal P}; N}^{\mathcal Q; \xi }(f_0,\ldots , f_m):=\Lambda _{{\mathcal P}; N}(f_0,\ldots , f_m)$
as in Equation (6.2). Suppose that
$\Lambda _{{\mathcal P}; N}^{\mathcal Q; \xi }(f_0,\ldots , f_m):=\Lambda _{{\mathcal P}; N}(f_0,\ldots , f_m)$
as in Equation (6.2). Suppose that
Then there exists a
![]() $C_1 = C_1({\mathcal P}) \gg 1$
such that
$C_1 = C_1({\mathcal P}) \gg 1$
such that
for any
![]() $N_1 = \delta ^C N^{\deg {P_1}}$
with
$N_1 = \delta ^C N^{\deg {P_1}}$
with
![]() $C\ge C_1$
.
$C\ge C_1$
.
If necessary we will also write
![]() $\Lambda _{{\mathcal P}; N}^{\mathcal Q; \xi }(f_0,\ldots , f_m)=\Lambda _{{\mathcal P}; N, I}^{\mathcal Q; \xi }(f_0,\ldots , f_m)$
in order to emphasise that the functions
$\Lambda _{{\mathcal P}; N}^{\mathcal Q; \xi }(f_0,\ldots , f_m)=\Lambda _{{\mathcal P}; N, I}^{\mathcal Q; \xi }(f_0,\ldots , f_m)$
in order to emphasise that the functions
![]() $f_0, f_1,\ldots , f_m$
are supported on I.
$f_0, f_1,\ldots , f_m$
are supported on I.
We first show how the Gowers box norms control the dual functions. The dual function, or more precisely the m-th dual function, corresponding to Equation (6.42) is defined as
where
 $$ \begin{align} F_{m; y}^{\xi}(x):=f_0(x+P_m(y))\prod_{i=1}^{m-1}f_{i}(x-P_i(y)+P_m(y))\mathrm{e}\Big(\sum_{j=1}^n\xi_jQ_j(y)\Big). \end{align} $$
$$ \begin{align} F_{m; y}^{\xi}(x):=f_0(x+P_m(y))\prod_{i=1}^{m-1}f_{i}(x-P_i(y)+P_m(y))\mathrm{e}\Big(\sum_{j=1}^n\xi_jQ_j(y)\Big). \end{align} $$
Proposition 6.47 (Gowers box norms control the dual functions).
Let
![]() $N\ge 1$
be a scale, and let
$N\ge 1$
be a scale, and let
![]() $0<\delta \le 1$
,
$0<\delta \le 1$
,
![]() $d, m\in \mathbb Z_+$
with
$d, m\in \mathbb Z_+$
with
![]() $m\ge 2$
and
$m\ge 2$
and
![]() $n\in \mathbb {N}$
be given. Let
$n\in \mathbb {N}$
be given. Let
![]() ${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
![]() $\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials such that
$\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials such that
![]() ${\mathcal P}$
is
${\mathcal P}$
is
![]() $(d, d)$
-admissible and
$(d, d)$
-admissible and
Let
![]() $f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
$f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
![]() $1$
-bounded functions supported on an interval
$1$
-bounded functions supported on an interval
![]() $I\subset \mathbb {K}$
of measure
$I\subset \mathbb {K}$
of measure
![]() $N_0 := N^{\deg {P_m}}$
. For
$N_0 := N^{\deg {P_m}}$
. For
![]() $\xi \in \mathbb {K}^n$
, let
$\xi \in \mathbb {K}^n$
, let
![]() $F_m^{\xi }$
be the dual function defined in Equation (6.45). Suppose that Equation (6.43) is satisfied. Then for the exponent
$F_m^{\xi }$
be the dual function defined in Equation (6.45). Suppose that Equation (6.43) is satisfied. Then for the exponent
![]() $s\in \mathbb Z_+$
which appears in the conclusion of Theorem 6.10, we have
$s\in \mathbb Z_+$
which appears in the conclusion of Theorem 6.10, we have
where
![]() $H_i\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_m)}$
for
$H_i\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_m)}$
for ![]() .
.
Proof. By changing the variables
![]() $x\mapsto x+P_m(y)$
in Equation (6.42), we may write
$x\mapsto x+P_m(y)$
in Equation (6.42), we may write
By the Cauchy–Schwarz inequality (observing once again that
![]() $\|f_m\|_{L^2(\mathbb {K})}^2 \le N_0$
), we have
$\|f_m\|_{L^2(\mathbb {K})}^2 \le N_0$
), we have
 $$ \begin{align*} \delta^2 &\le \frac{1}{N_0} \int_{\mathbb{K}} \Big|\int_{\mathbb{K}} F_{m; y}^{\xi}(x)d\mu_{[N]}(y)\Big|^2 d\mu(x) \\ & = \frac{1}{N_0}\bigg|\int_{\mathbb{K}^3}F_{m; y_1}^{\xi}(x)\overline{F_{m; y_2}^{\xi}(x)}d\mu_{[N]}^{\otimes2}(y_1, y_2)d\mu(x)\bigg| \\ &= |\Lambda_{{\mathcal P}; N}^{\mathcal Q; \xi}(f_0, f_1,\ldots, f_{m-1}, \overline{F_m^{\xi}})|, \end{align*} $$
$$ \begin{align*} \delta^2 &\le \frac{1}{N_0} \int_{\mathbb{K}} \Big|\int_{\mathbb{K}} F_{m; y}^{\xi}(x)d\mu_{[N]}(y)\Big|^2 d\mu(x) \\ & = \frac{1}{N_0}\bigg|\int_{\mathbb{K}^3}F_{m; y_1}^{\xi}(x)\overline{F_{m; y_2}^{\xi}(x)}d\mu_{[N]}^{\otimes2}(y_1, y_2)d\mu(x)\bigg| \\ &= |\Lambda_{{\mathcal P}; N}^{\mathcal Q; \xi}(f_0, f_1,\ldots, f_{m-1}, \overline{F_m^{\xi}})|, \end{align*} $$
where in the last step we changed variables
![]() $x\mapsto x-P_m(y_1)$
. Denote
$x\mapsto x-P_m(y_1)$
. Denote
![]() $g_m:=\overline {F_m^{\xi }}$
, and
$g_m:=\overline {F_m^{\xi }}$
, and
![]() $g_j:=f_j$
for
$g_j:=f_j$
for ![]() . Our strategy will be to reduce the matter to Theorem 6.10 with the family
. Our strategy will be to reduce the matter to Theorem 6.10 with the family
![]() ${\mathcal P}$
. Observe that
${\mathcal P}$
. Observe that
![]() $g_j$
is a
$g_j$
is a
![]() $1$
-bounded function and
$1$
-bounded function and
![]() $\|g_j\|_{L^1(\mathbb {K})}\lesssim N_0$
for all
$\|g_j\|_{L^1(\mathbb {K})}\lesssim N_0$
for all ![]() . Changing the variables
. Changing the variables
![]() $x \mapsto x+h$
in the definition of
$x \mapsto x+h$
in the definition of
![]() $\Lambda _{{\mathcal P}; N}^{\mathcal Q; \xi }$
and averaging over
$\Lambda _{{\mathcal P}; N}^{\mathcal Q; \xi }$
and averaging over
![]() $h\in [H_{s+1}]$
where
$h\in [H_{s+1}]$
where
![]() $H_{s+1} =\delta ^{O(1)}N^{\mathrm {deg} P_m}$
, we have
$H_{s+1} =\delta ^{O(1)}N^{\mathrm {deg} P_m}$
, we have
 $$ \begin{align*} \delta^4&\le |\Lambda_{{\mathcal P}; N}^{\mathcal Q; \xi}(g_0,\ldots, g_m)|^2\\ &\lesssim \frac{1}{N_0}\int_{\mathbb{K}^2}\Big|\int_{\mathbb{K}}g_0(x+h)\prod_{i=1}^mg_{i}(x+h-P_i(y)) d\mu_{[H_{s+1}]}(h)\Big|^2 d\mu_{[N]}(y)d\mu(x), \end{align*} $$
$$ \begin{align*} \delta^4&\le |\Lambda_{{\mathcal P}; N}^{\mathcal Q; \xi}(g_0,\ldots, g_m)|^2\\ &\lesssim \frac{1}{N_0}\int_{\mathbb{K}^2}\Big|\int_{\mathbb{K}}g_0(x+h)\prod_{i=1}^mg_{i}(x+h-P_i(y)) d\mu_{[H_{s+1}]}(h)\Big|^2 d\mu_{[N]}(y)d\mu(x), \end{align*} $$
where in the last line we have used the Cauchy–Schwarz inequality in the x and y variables, noting that
![]() $x \to g_0(x+h)$
is supported a fixed dilate of I for every
$x \to g_0(x+h)$
is supported a fixed dilate of I for every
![]() $h\in [H_{s+1}]$
. By another change of variables, we obtain
$h\in [H_{s+1}]$
. By another change of variables, we obtain
Now, we may find a measurable set
![]() $X \subseteq [H_{s+1}]$
such that
$X \subseteq [H_{s+1}]$
such that
for all
![]() $h\in X$
and
$h\in X$
and
![]() $\nu _{[H_{s+1}]}(X)\gtrsim \delta ^4$
. Since
$\nu _{[H_{s+1}]}(X)\gtrsim \delta ^4$
. Since
![]() $\Delta _hg_j$
is a
$\Delta _hg_j$
is a
![]() $1$
-bounded function and
$1$
-bounded function and
![]() $\|\Delta _hg_j\|_{L^1(\mathbb {K})}\lesssim N_0$
for all
$\|\Delta _hg_j\|_{L^1(\mathbb {K})}\lesssim N_0$
for all ![]() , we may invoke Theorem 6.10 and conclude that
, we may invoke Theorem 6.10 and conclude that
for all
![]() $h\in X$
, where
$h\in X$
, where
![]() $H_i\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_m)}$
for
$H_i\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_m)}$
for ![]() . Averaging over
. Averaging over
![]() $h\in X$
and using
$h\in X$
and using
![]() $\nu _{[H_{s+1}]}(X)\gtrsim \delta ^4$
, we obtain
$\nu _{[H_{s+1}]}(X)\gtrsim \delta ^4$
, we obtain
which is Equation (6.48) as desired.
We first establish a simple consequence of the oscillatory integral bound (3.1) which will be important later.
Lemma 6.49. Let
![]() $N>1$
be a scale,
$N>1$
be a scale,
![]() $m\in \mathbb Z_+$
and
$m\in \mathbb Z_+$
and
![]() $n\in \mathbb {N}$
be given. Let
$n\in \mathbb {N}$
be given. Let
![]() ${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
![]() $\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials such that
$\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials such that
Define the multiplier corresponding to the families
![]() ${\mathcal P}$
and
${\mathcal P}$
and
![]() $\mathcal Q$
as follows:
$\mathcal Q$
as follows:
 $$ \begin{align*} m_N^{{\mathcal P}, \mathcal Q}(\zeta, \xi):=\int_{\mathbb{K}} e\Big(\sum_{i=1}^m\zeta_iP_i(y)+\sum_{j=1}^n\xi_jQ_j(y)\Big)d\mu_{[N]}(y), \end{align*} $$
$$ \begin{align*} m_N^{{\mathcal P}, \mathcal Q}(\zeta, \xi):=\int_{\mathbb{K}} e\Big(\sum_{i=1}^m\zeta_iP_i(y)+\sum_{j=1}^n\xi_jQ_j(y)\Big)d\mu_{[N]}(y), \end{align*} $$
where
![]() $\zeta =(\zeta _1,\ldots , \zeta _m)\in \mathbb {K}^m$
and
$\zeta =(\zeta _1,\ldots , \zeta _m)\in \mathbb {K}^m$
and
![]() $\xi =(\xi _1,\ldots , \xi _n)\in \mathbb {K}^n$
. Let
$\xi =(\xi _1,\ldots , \xi _n)\in \mathbb {K}^n$
. Let
![]() $0<\delta \le 1$
and suppose that
$0<\delta \le 1$
and suppose that
Then there exists a large constant
![]() $A\gtrsim _{{\mathcal P}, \mathcal Q} 1$
such that
$A\gtrsim _{{\mathcal P}, \mathcal Q} 1$
such that

Proof. Fix an element
![]() $\alpha \in \mathbb {K}$
such that
$\alpha \in \mathbb {K}$
such that
![]() $|\alpha | = N$
, and make the change of variables
$|\alpha | = N$
, and make the change of variables
![]() $y \to \alpha y$
to write
$y \to \alpha y$
to write
 $$ \begin{align*}m_N^{{\mathcal P}, \mathcal Q}(\zeta, \xi) \ = \ \int_{B_1(0)} \mathrm{e} \Big(\sum_{i=1}^m\zeta_iP_i(\alpha y)+\sum_{j=1}^n\xi_jQ_j(\alpha y)\Big) d\mu(y). \end{align*} $$
$$ \begin{align*}m_N^{{\mathcal P}, \mathcal Q}(\zeta, \xi) \ = \ \int_{B_1(0)} \mathrm{e} \Big(\sum_{i=1}^m\zeta_iP_i(\alpha y)+\sum_{j=1}^n\xi_jQ_j(\alpha y)\Big) d\mu(y). \end{align*} $$
Define
![]() $R(y):=\sum _{i=1}^m\zeta _iP_i(y)+\sum _{j=1}^n\xi _jQ_j(y)$
. Then
$R(y):=\sum _{i=1}^m\zeta _iP_i(y)+\sum _{j=1}^n\xi _jQ_j(y)$
. Then
![]() $R(y)$
may be rewritten as
$R(y)$
may be rewritten as
 $$ \begin{align*} R(y)=\sum_{l=1}^{\deg{Q_n}}\operatorname{\mathrm{c}}_l(R)y^l \end{align*} $$
$$ \begin{align*} R(y)=\sum_{l=1}^{\deg{Q_n}}\operatorname{\mathrm{c}}_l(R)y^l \end{align*} $$
The oscillatory integral bound (3.1) implies
 $$ \begin{align} |m_N^{{\mathcal P}, \mathcal Q}(\zeta, \xi)|\lesssim \bigg(1+\sum_{l=1}^{\deg{Q_n}}|\operatorname{\mathrm{c}}_l(R)|N^l\bigg)^{-1/\deg{Q_n}}. \end{align} $$
$$ \begin{align} |m_N^{{\mathcal P}, \mathcal Q}(\zeta, \xi)|\lesssim \bigg(1+\sum_{l=1}^{\deg{Q_n}}|\operatorname{\mathrm{c}}_l(R)|N^l\bigg)^{-1/\deg{Q_n}}. \end{align} $$
Hence, Equation (6.51) implies
![]() $\max _l |\operatorname {\mathrm {c}}_l(R)| N^{l} \lesssim \delta ^{-d_{*}}$
, where
$\max _l |\operatorname {\mathrm {c}}_l(R)| N^{l} \lesssim \delta ^{-d_{*}}$
, where
![]() $d_{*} = \deg {Q_n}$
and the maximum is taken over all
$d_{*} = \deg {Q_n}$
and the maximum is taken over all ![]() . From this, we see that for any sufficiently large
. From this, we see that for any sufficiently large
![]() $A\ge d_{*}$
,
$A\ge d_{*}$
,
for all ![]() .
.
Using Equation (6.50), we observe that


Using Equation (6.55) for
![]() $j=n$
, we see that Equation (6.54) implies Equation (6.52) for
$j=n$
, we see that Equation (6.54) implies Equation (6.52) for
![]() $N^{\deg {Q_n}} |\xi _n|$
. Inductively, we now deduce, using Equation (6.55), that Equation (6.54) implies that Equation (6.52) holds for all
$N^{\deg {Q_n}} |\xi _n|$
. Inductively, we now deduce, using Equation (6.55), that Equation (6.54) implies that Equation (6.52) holds for all
![]() $N^{\deg {Q_j}} |\xi _j|$
,
$N^{\deg {Q_j}} |\xi _j|$
, ![]() . Similarly, using Equations (6.56) and (6.54), we see that that the second displayed equation in Equation (6.52) holds.
. Similarly, using Equations (6.56) and (6.54), we see that that the second displayed equation in Equation (6.52) holds.
The key ingredient in the proof of Theorem 6.41 will be a degree-lowering argument, which reads as follows.
Theorem 6.57 (Degree-lowering argument).
Let
![]() $N\ge 1$
be a scale, and let
$N\ge 1$
be a scale, and let
![]() $0<\delta \le 1$
,
$0<\delta \le 1$
,
![]() $m\in \mathbb Z_+$
and
$m\in \mathbb Z_+$
and
![]() $n\in \mathbb {N}$
be given. Let
$n\in \mathbb {N}$
be given. Let
![]() ${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
![]() $\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials such that
$\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials such that
For
![]() $\xi \in \mathbb {K}^n$
, let
$\xi \in \mathbb {K}^n$
, let
![]() $F_m^{\xi }$
be the dual function from Equation (6.45) corresponding to the form (6.42) and
$F_m^{\xi }$
be the dual function from Equation (6.45) corresponding to the form (6.42) and
![]() $1$
-bounded functions
$1$
-bounded functions
![]() $f_0, f_1,\ldots , f_{m-1}\in L^0(\mathbb {K})$
supported on an interval
$f_0, f_1,\ldots , f_{m-1}\in L^0(\mathbb {K})$
supported on an interval
![]() $I\subset \mathbb {K}$
of measure
$I\subset \mathbb {K}$
of measure
![]() $N_0 := N^{\deg {P_m}}$
. Suppose that for some integer
$N_0 := N^{\deg {P_m}}$
. Suppose that for some integer
![]() $s\in \mathbb Z_+$
one has
$s\in \mathbb Z_+$
one has
where
![]() $H_i\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_m)}$
for
$H_i\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg (P_m)}$
for ![]() . Then
. Then
Assuming momentarily Theorem 6.57, we prove Theorem 6.41.
Proof of Theorem 6.41.
Our goal is to prove Equation (6.44) when
The proof is by induction on
![]() $m\in \mathbb Z_+$
. We divide the proof into two steps. In the first step, we establish the base case for
$m\in \mathbb Z_+$
. We divide the proof into two steps. In the first step, we establish the base case for
![]() $m=1$
. In the second step, we will use Theorem 6.57 to establish the inductive step.
$m=1$
. In the second step, we will use Theorem 6.57 to establish the inductive step.
Step 1.
Assume that
![]() $m=1$
so that
$m=1$
so that
![]() $N_0 = N^{\deg {P_1}}$
. For
$N_0 = N^{\deg {P_1}}$
. For
![]() $\zeta \in \mathbb {K}$
and
$\zeta \in \mathbb {K}$
and
![]() $\xi =(\xi _1,\ldots , \xi _n)\in \mathbb {K}^n$
, we define the multiplier
$\xi =(\xi _1,\ldots , \xi _n)\in \mathbb {K}^n$
, we define the multiplier
 $$ \begin{align*} m_N(\zeta, \xi):=\int_{\mathbb{K}} e\Big(-\zeta P_1(y) + \sum_{j=1}^n \xi_j Q_j(y)\Big)d\mu_{[N]}(y). \end{align*} $$
$$ \begin{align*} m_N(\zeta, \xi):=\int_{\mathbb{K}} e\Big(-\zeta P_1(y) + \sum_{j=1}^n \xi_j Q_j(y)\Big)d\mu_{[N]}(y). \end{align*} $$
We now express
Using the Cauchy–Schwarz inequality and Plancherel’s theorem, we see
When
![]() $\mathbb {K}$
is non-Archimedean, let
$\mathbb {K}$
is non-Archimedean, let ![]() so that
so that ![]() . When
. When
![]() $\mathbb {K}$
is Archimedean, choose a Schwartz function
$\mathbb {K}$
is Archimedean, choose a Schwartz function
![]() $\varphi : \mathbb {K} \to \mathbb {K}$
such that
$\varphi : \mathbb {K} \to \mathbb {K}$
such that
For a scale M, we set
![]() $\varphi _M(x) = M^{-1} \varphi (M^{-1} x)$
when
$\varphi _M(x) = M^{-1} \varphi (M^{-1} x)$
when
![]() $\mathbb {K} = {\mathbb R}$
and when
$\mathbb {K} = {\mathbb R}$
and when
![]() $\mathbb {K} = {\mathbb C}$
, we set
$\mathbb {K} = {\mathbb C}$
, we set
![]() $\varphi _{M}(z) = M^{-1} \varphi (M^{-1/2} z)$
. When
$\varphi _{M}(z) = M^{-1} \varphi (M^{-1/2} z)$
. When
![]() $\mathbb {K}$
is non-Archimedean, we set
$\mathbb {K}$
is non-Archimedean, we set ![]() .
.
Consider two scales
![]() $M_1\simeq \delta ^{C}N^{\deg {P_1}}$
and
$M_1\simeq \delta ^{C}N^{\deg {P_1}}$
and
![]() $N_1\simeq \delta ^{2C}N^{\deg {P_1}}/C$
. Then we obtain
$N_1\simeq \delta ^{2C}N^{\deg {P_1}}/C$
. Then we obtain
Note that
and
 $$ \begin{align*} \|\varphi_{M_1}*f_1\|_{L^1(\mathbb{K})}&\le \|\varphi_{M_1}*\mu_{[N_1]}*f_1\|_{L^1(\mathbb{K})}+ \|(\varphi_{M_1}-\varphi_{M_1}*\mu_{[N_1]})*f_1\|_{L^1(\mathbb{K})}\\ &\lesssim \|\mu_{[N_1]}*f_1\|_{L^1(\mathbb{K})} +C^{-1}\delta^C N_0 \end{align*} $$
$$ \begin{align*} \|\varphi_{M_1}*f_1\|_{L^1(\mathbb{K})}&\le \|\varphi_{M_1}*\mu_{[N_1]}*f_1\|_{L^1(\mathbb{K})}+ \|(\varphi_{M_1}-\varphi_{M_1}*\mu_{[N_1]})*f_1\|_{L^1(\mathbb{K})}\\ &\lesssim \|\mu_{[N_1]}*f_1\|_{L^1(\mathbb{K})} +C^{-1}\delta^C N_0 \end{align*} $$
since
![]() $\varphi _{M_1}-\varphi _{M_1}*\mu _{[N_1]} = 0$
when
$\varphi _{M_1}-\varphi _{M_1}*\mu _{[N_1]} = 0$
when
![]() $\mathbb {K}$
is non-Archimedean and when
$\mathbb {K}$
is non-Archimedean and when
![]() $\mathbb {K}$
is Archimedean, we have the pointwise bound
$\mathbb {K}$
is Archimedean, we have the pointwise bound
If
![]() $C\ge 1$
is sufficiently large, then we may write
$C\ge 1$
is sufficiently large, then we may write
By Equation (6.60), we have that
since
![]() $\| f_0 \|_{L^2(\mathbb {K})}\le N_0^{1/2}$
and
$\| f_0 \|_{L^2(\mathbb {K})}\le N_0^{1/2}$
and
![]() $\|f_1\|_{L^2(\mathbb {K})}\le N_0^{1/2}$
. We now prove that
$\|f_1\|_{L^2(\mathbb {K})}\le N_0^{1/2}$
. We now prove that
Suppose that inequality (6.63) does not hold, then one has
for some
![]() $\zeta \in \mathbb {K}$
so that
$\zeta \in \mathbb {K}$
so that
![]() $|\zeta |\ge M_1^{-1}$
. Then Lemma 6.49 implies
$|\zeta |\ge M_1^{-1}$
. Then Lemma 6.49 implies
![]() $N^{\deg {P_1}} |\zeta | \lesssim \delta ^{-A}$
for some large, fixed
$N^{\deg {P_1}} |\zeta | \lesssim \delta ^{-A}$
for some large, fixed
![]() $A\gtrsim 1$
by Equation (6.52). Since
$A\gtrsim 1$
by Equation (6.52). Since
![]() $M_1 = \delta ^C N^{\deg {P_1}}$
, we have
$M_1 = \delta ^C N^{\deg {P_1}}$
, we have
![]() $\delta ^{-C} \lesssim \delta ^{-A}$
which is a contradiction if
$\delta ^{-C} \lesssim \delta ^{-A}$
which is a contradiction if
![]() $C \gg A$
. Thus, Equation (6.63) holds.
$C \gg A$
. Thus, Equation (6.63) holds.
Hence, by Equations (6.63), (6.62) and (6.61), we see that
which establishes Theorem 6.41 when
![]() $m=1$
.
$m=1$
.
Step 2.
We now assume that Theorem 6.41 is true for
![]() $m-1$
in place of m for some integer
$m-1$
in place of m for some integer
![]() $m\ge 2$
. Using Theorem 6.57, we show that this implies Theorem 6.41 for
$m\ge 2$
. Using Theorem 6.57, we show that this implies Theorem 6.41 for
![]() $m\ge 2$
. Note that bound (6.43) implies inequality (6.48) from Proposition 6.47. Now, by Theorem 6.57 applied
$m\ge 2$
. Note that bound (6.43) implies inequality (6.48) from Proposition 6.47. Now, by Theorem 6.57 applied
![]() $s-2$
times we may conclude that
$s-2$
times we may conclude that
where
![]() $H_1, H_2\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg {P_m}}$
. By Lemma 5.1, we can find a
$H_1, H_2\simeq \delta ^{O_{\mathcal P}(1)}N^{\deg {P_m}}$
. By Lemma 5.1, we can find a
![]() $\xi _0\in \mathbb {K}$
such that
$\xi _0\in \mathbb {K}$
such that
since
![]() $N_0 = N^{\deg {P_m}}$
. By definitions (6.45) and (6.46) and making the change of variables
$N_0 = N^{\deg {P_m}}$
. By definitions (6.45) and (6.46) and making the change of variables
![]() $x\mapsto x-P_m(y)$
, we may write
$x\mapsto x-P_m(y)$
, we may write
 $$ \begin{align*} N_0^{-1}\widehat{F_m^{\xi}}(\xi_0)&=N_0^{-1}\iint_{\mathbb{K}^2}F_{m;y}^{\xi}(x)e(-\xi_0 x)d\mu_{[N]}(y)d\mu(x)\\&=N_0^{-1}\iint_{\mathbb{K}^2}\mathrm{M}_{\xi_0}f_0(x)\prod_{i=1}^{m-1}f_{i}(x-P_i(y))e\Big(\xi_0 P_m(y)+\sum_{j=1}^n\xi_jQ_j(y)\Big)d\mu_{[N]}(y)d\mu(x)\\&=M^{-1} \Lambda_{{\mathcal P}'; N}^{\mathcal Q', \xi'}(\mathrm{M}_{\xi_0}f_0, f_1,\ldots, f_{m-1}), \end{align*} $$
$$ \begin{align*} N_0^{-1}\widehat{F_m^{\xi}}(\xi_0)&=N_0^{-1}\iint_{\mathbb{K}^2}F_{m;y}^{\xi}(x)e(-\xi_0 x)d\mu_{[N]}(y)d\mu(x)\\&=N_0^{-1}\iint_{\mathbb{K}^2}\mathrm{M}_{\xi_0}f_0(x)\prod_{i=1}^{m-1}f_{i}(x-P_i(y))e\Big(\xi_0 P_m(y)+\sum_{j=1}^n\xi_jQ_j(y)\Big)d\mu_{[N]}(y)d\mu(x)\\&=M^{-1} \Lambda_{{\mathcal P}'; N}^{\mathcal Q', \xi'}(\mathrm{M}_{\xi_0}f_0, f_1,\ldots, f_{m-1}), \end{align*} $$
where
![]() $\mathrm {M}_{\xi _0}f_0(x):=\mathrm {e}(-\xi _0 x)f_0(x), \, {\mathcal P}':={\mathcal P}\setminus \{P_m\}, \, \mathcal Q':=\mathcal Q\cup \{P_m\}, \, \xi ':=(\xi _0, \xi _1,\ldots , \xi _n)\in \mathbb {K}^{n+1}$
and
$\mathrm {M}_{\xi _0}f_0(x):=\mathrm {e}(-\xi _0 x)f_0(x), \, {\mathcal P}':={\mathcal P}\setminus \{P_m\}, \, \mathcal Q':=\mathcal Q\cup \{P_m\}, \, \xi ':=(\xi _0, \xi _1,\ldots , \xi _n)\in \mathbb {K}^{n+1}$
and
![]() $M:=N^{\deg (P_m)-\deg (P_{m-1})}$
. The parameter
$M:=N^{\deg (P_m)-\deg (P_{m-1})}$
. The parameter
![]() $N_0^{\prime } := N_0 M^{-1}$
is what appears in the m-linear form
$N_0^{\prime } := N_0 M^{-1}$
is what appears in the m-linear form
![]() $\Lambda _{{\mathcal P}';N}^{\mathcal Q', \xi '}$
. We note that
$\Lambda _{{\mathcal P}';N}^{\mathcal Q', \xi '}$
. We note that
![]() $N_0^{\prime } = N^{\deg {P_{m-1}}}$
.
$N_0^{\prime } = N^{\deg {P_{m-1}}}$
.
Thus, Equation (6.64) implies
By translation invariance, we may assume that all functions
![]() $f_0, f_1,\ldots , f_{m-1}$
are supported in
$f_0, f_1,\ldots , f_{m-1}$
are supported in
![]() $[N_0]$
. We can partition
$[N_0]$
. We can partition ![]() into
into
![]() $L \simeq M$
sets, each with measure
$L \simeq M$
sets, each with measure
![]() $\simeq N_0^{\prime }$
contained in an interval
$\simeq N_0^{\prime }$
contained in an interval
![]() $I_k$
lying in an
$I_k$
lying in an
![]() $O(N_0^{\prime })$
neighbourhood of
$O(N_0^{\prime })$
neighbourhood of
![]() $E_k$
. Furthermore,
$E_k$
. Furthermore,
![]() $E_k$
is an
$E_k$
is an
![]() $O(N_1)$
neighbourhood of a set
$O(N_1)$
neighbourhood of a set
![]() $F_k$
such that
$F_k$
such that
![]() $\mu (E_k\setminus F_k) \lesssim N_1$
and
$\mu (E_k\setminus F_k) \lesssim N_1$
and ![]() . Here,
. Here,
![]() $N_1 \simeq \delta ^{O_{\mathcal P}(1)} N^{\deg (P_1)}$
. In the non-Archimedean setting, this decomposition is straightforward; in this case, we can take
$N_1 \simeq \delta ^{O_{\mathcal P}(1)} N^{\deg (P_1)}$
. In the non-Archimedean setting, this decomposition is straightforward; in this case, we can take
![]() $F_k = E_k = I_k$
. If fact if
$F_k = E_k = I_k$
. If fact if
![]() $N_0 = q^{n_0}$
and
$N_0 = q^{n_0}$
and
![]() $N_0^{\prime } = q^{n_0 - \ell }$
so that
$N_0^{\prime } = q^{n_0 - \ell }$
so that
![]() $M = q^{\ell }$
, then
$M = q^{\ell }$
, then
gives our partition of
![]() $[N_0]$
, where
$[N_0]$
, where
![]() ${\mathcal F} = \{ x = \sum _{j=0}^{\ell -1} x_j \pi ^{-n_0 + j} : x_j \in o_{\mathbb {K}}/m_{\mathbb {K}} \}$
. Note
${\mathcal F} = \{ x = \sum _{j=0}^{\ell -1} x_j \pi ^{-n_0 + j} : x_j \in o_{\mathbb {K}}/m_{\mathbb {K}} \}$
. Note
![]() $\# {\mathcal F} = q^{\ell } = M$
. When
$\# {\mathcal F} = q^{\ell } = M$
. When
![]() $\mathbb {K} = {\mathbb R}$
, one simply decomposes the interval
$\mathbb {K} = {\mathbb R}$
, one simply decomposes the interval
![]() $[N_0] = [-N_0, N_0]$
into M subintervals
$[N_0] = [-N_0, N_0]$
into M subintervals ![]() of equal length and then extend and shrink to obtain intervals
of equal length and then extend and shrink to obtain intervals
![]() $I_k$
and
$I_k$
and
![]() $F_k$
with the desired properties.
$F_k$
with the desired properties.
When
![]() $\mathbb {K} = {\mathbb C}$
, the set
$\mathbb {K} = {\mathbb C}$
, the set
![]() $[N_0]$
is a disc and the decomposition is not as straightforward but not difficult to construct by starting with a mesh of squares of side length
$[N_0]$
is a disc and the decomposition is not as straightforward but not difficult to construct by starting with a mesh of squares of side length
![]() $\sqrt {N_0^{\prime }}$
which cover
$\sqrt {N_0^{\prime }}$
which cover
![]() $[N_0]$
. It is important that for this case (when
$[N_0]$
. It is important that for this case (when
![]() $\mathbb {K} = {\mathbb C}$
) that we allow the sets
$\mathbb {K} = {\mathbb C}$
) that we allow the sets
![]() $E_k$
and
$E_k$
and
![]() $F_k$
to be general sets (not necessarily intervals) with the above properties. The picture should be clear.
$F_k$
to be general sets (not necessarily intervals) with the above properties. The picture should be clear.
Hence, by changing variables
![]() $x \to x+P_1(y)$
and then back again,
$x \to x+P_1(y)$
and then back again,

where ![]() and
and ![]() .
.
By the pigeonhole principle, there exists ![]() such that
such that
![]() $\# L_0\gtrsim \delta ^{O_{{\mathcal P}'}(1)}M$
, and for every
$\# L_0\gtrsim \delta ^{O_{{\mathcal P}'}(1)}M$
, and for every
![]() $k\in L_0$
, we have
$k\in L_0$
, we have
By the inductive hypothesis, we have
for every
![]() $k\in L_0$
and for every
$k\in L_0$
and for every
![]() $N_1 = \delta ^C N^{\deg {P_1}}$
with
$N_1 = \delta ^C N^{\deg {P_1}}$
with
![]() $C \ge C_1({\mathcal P}')$
. Note that
$C \ge C_1({\mathcal P}')$
. Note that
and hence for
![]() $C\gg 1$
large enough,
$C\gg 1$
large enough,
Now, we can sum over
![]() $k\in L_0$
, using the bound
$k\in L_0$
, using the bound
![]() $\# L_0\gtrsim \delta ^{O(1)}M$
and the pairwise disjoint supports of
$\# L_0\gtrsim \delta ^{O(1)}M$
and the pairwise disjoint supports of ![]() , we obtain
, we obtain

which by (6.65) yields
as desired.
We now state two auxiliary technical lemmas which will be needed in the proof of Theorem 6.57. For
![]() $\omega = (\omega _1, \ldots , \omega _n) \in \{0,1\}^n$
and
$\omega = (\omega _1, \ldots , \omega _n) \in \{0,1\}^n$
and
![]() $h = (h_1, \ldots , h_n) \in \mathbb {K}^n$
, we write
$h = (h_1, \ldots , h_n) \in \mathbb {K}^n$
, we write
![]() $\omega \cdot h = \sum _{i=1}^n \omega _i h_i$
and
$\omega \cdot h = \sum _{i=1}^n \omega _i h_i$
and
![]() $1-\omega = (1-\omega _1, \ldots , 1-\omega _n)$
.
$1-\omega = (1-\omega _1, \ldots , 1-\omega _n)$
.
Lemma 6.66. Let
![]() $N\ge 1$
be a scale, and let
$N\ge 1$
be a scale, and let
![]() $0<\delta \le 1$
,
$0<\delta \le 1$
,
![]() $m\in \mathbb Z_+$
with
$m\in \mathbb Z_+$
with
![]() $m\ge 2$
,
$m\ge 2$
,
![]() $n\in \mathbb {N}$
and scales
$n\in \mathbb {N}$
and scales
![]() $H_1,\ldots , H_n$
with each
$H_1,\ldots , H_n$
with each
![]() $H_i\le N$
be given. Assume that
$H_i\le N$
be given. Assume that
![]() $\phi :X\to \mathbb R$
is a measurable function defined on a measurable set
$\phi :X\to \mathbb R$
is a measurable function defined on a measurable set
![]() $X\subseteq H:=\prod _{i=1}^n [H_i]$
. Let
$X\subseteq H:=\prod _{i=1}^n [H_i]$
. Let
![]() ${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
![]() $\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials. For
$\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials. For
![]() $\xi \in \mathbb {K}^n$
, let
$\xi \in \mathbb {K}^n$
, let
![]() $F_m^{\xi }$
be the dual function defined in Equation (6.45) that corresponds to the form (6.42) and
$F_m^{\xi }$
be the dual function defined in Equation (6.45) that corresponds to the form (6.42) and
![]() $1$
-bounded functions
$1$
-bounded functions
![]() $f_0, f_1,\ldots , f_{m-1}\in L^0(\mathbb {K})$
supported on an interval
$f_0, f_1,\ldots , f_{m-1}\in L^0(\mathbb {K})$
supported on an interval
![]() $I\subset \mathbb {K}$
of measure
$I\subset \mathbb {K}$
of measure
![]() $N_0 := N^{\deg {P_m}}$
. Suppose that
$N_0 := N^{\deg {P_m}}$
. Suppose that

Then
 $$ \begin{align} \int_{\square_n(X)}\bigg|N_0^{-1}\int_{\mathbb{K}} F_m(x; h, h')e(-\psi(h, h')x)d\mu(x)\bigg|^2 d\Big(\bigotimes_{i=1}^{n}\nu_{[H_i]}\Big)^{\otimes2}(h, h') \gtrsim \delta^{O(1)}, \end{align} $$
$$ \begin{align} \int_{\square_n(X)}\bigg|N_0^{-1}\int_{\mathbb{K}} F_m(x; h, h')e(-\psi(h, h')x)d\mu(x)\bigg|^2 d\Big(\bigotimes_{i=1}^{n}\nu_{[H_i]}\Big)^{\otimes2}(h, h') \gtrsim \delta^{O(1)}, \end{align} $$
where
and
 $$ \begin{align*} F_m(x; h, h'):=\int_{\mathbb{K}}{\Delta}_{h'-h}^nf_0(x+P_m(y))\prod_{i=1}^{m-1} {\Delta}_{h'-h}^nf_{i}(x-P_i(y)+P_m(y))d\mu_{[N]}(y),\\ \psi(h, h'):=\sum_{\omega\in\{0, 1\}^n}(-1)^{|\omega|}\phi\Big(\omega \cdot h + (1-\omega)\cdot h'\Big). \end{align*} $$
$$ \begin{align*} F_m(x; h, h'):=\int_{\mathbb{K}}{\Delta}_{h'-h}^nf_0(x+P_m(y))\prod_{i=1}^{m-1} {\Delta}_{h'-h}^nf_{i}(x-P_i(y)+P_m(y))d\mu_{[N]}(y),\\ \psi(h, h'):=\sum_{\omega\in\{0, 1\}^n}(-1)^{|\omega|}\phi\Big(\omega \cdot h + (1-\omega)\cdot h'\Big). \end{align*} $$
Proof. We shall write
![]() ${\boldsymbol{\nu }}_n:=\bigotimes _{i=1}^{n}\nu _{[H_i]}$
. Using Equations (4.2), (6.45) and (6.46), we see that the left-hand side of Equation (6.67) can be written as
${\boldsymbol{\nu }}_n:=\bigotimes _{i=1}^{n}\nu _{[H_i]}$
. Using Equations (4.2), (6.45) and (6.46), we see that the left-hand side of Equation (6.67) can be written as
 $$ \begin{align*} \frac{1}{N_0^2} \int_{\mathbb{K}^{2^{n+1}}}\int_{\mathbb{K}^2}\int_{\mathbb{K}^n}G_0(x, z, h;\boldsymbol{y}) d{\boldsymbol{\nu }}_n(h)d\mu(x)d\mu(z)d\mu^{\otimes 2^{n+1}}_{[N]}(\boldsymbol{y}), \end{align*} $$
$$ \begin{align*} \frac{1}{N_0^2} \int_{\mathbb{K}^{2^{n+1}}}\int_{\mathbb{K}^2}\int_{\mathbb{K}^n}G_0(x, z, h;\boldsymbol{y}) d{\boldsymbol{\nu }}_n(h)d\mu(x)d\mu(z)d\mu^{\otimes 2^{n+1}}_{[N]}(\boldsymbol{y}), \end{align*} $$
where for
![]() $\boldsymbol{y}=(y_{(\omega , 0)}, y_{(\omega , 1)})_{\omega \in \{0, 1\}^n}\in \mathbb {K}^{2^{n+1}}$
,
$\boldsymbol{y}=(y_{(\omega , 0)}, y_{(\omega , 1)})_{\omega \in \{0, 1\}^n}\in \mathbb {K}^{2^{n+1}}$
,
![]() $x, z\in \mathbb {K}$
and
$x, z\in \mathbb {K}$
and
![]() $h\in \mathbb {K}^n$
. We have set
$h\in \mathbb {K}^n$
. We have set

Write elements in X as
![]() $(h_1, h)$
with
$(h_1, h)$
with
![]() $h_1 \in \mathbb {K}$
, and apply the Cauchy–Schwarz inequality in all but the
$h_1 \in \mathbb {K}$
, and apply the Cauchy–Schwarz inequality in all but the
![]() $h_1$
variable (noting that
$h_1$
variable (noting that
![]() $(x,z) \to G_0(x, z, h;\boldsymbol{y})$
is supported in a product of intervals of measure
$(x,z) \to G_0(x, z, h;\boldsymbol{y})$
is supported in a product of intervals of measure
![]() $\simeq N_0^2$
) to conclude
$\simeq N_0^2$
) to conclude
 $$ \begin{align} \frac{1}{N_0^2} \int_{\mathbb{K}^{2^{n}}}\int_{\mathbb{K}^2}\int_{\mathbb{K}^{n-1}} H_0(x, z, h;\boldsymbol{y}) d{\boldsymbol{\nu }}_{n-1}(h)d\mu(x)d\mu(z)d\mu^{\otimes 2^{n}}_{[N]}(\boldsymbol{y})\gtrsim \delta^{O(1)}, \end{align} $$
$$ \begin{align} \frac{1}{N_0^2} \int_{\mathbb{K}^{2^{n}}}\int_{\mathbb{K}^2}\int_{\mathbb{K}^{n-1}} H_0(x, z, h;\boldsymbol{y}) d{\boldsymbol{\nu }}_{n-1}(h)d\mu(x)d\mu(z)d\mu^{\otimes 2^{n}}_{[N]}(\boldsymbol{y})\gtrsim \delta^{O(1)}, \end{align} $$
where
 $$ \begin{align*} H_0(x, z, h;\boldsymbol{y}):=\bigg|\int_{\mathbb{K}}G_0^1(x, z, (h_1, h);\boldsymbol{y})d\nu_{[H_1]}(h_1)\bigg|^2, \end{align*} $$
$$ \begin{align*} H_0(x, z, h;\boldsymbol{y}):=\bigg|\int_{\mathbb{K}}G_0^1(x, z, (h_1, h);\boldsymbol{y})d\nu_{[H_1]}(h_1)\bigg|^2, \end{align*} $$
and

for
![]() $\boldsymbol{y}=(y_{(1, \omega , 0)}, y_{(1, \omega , 1)})_{(j,\omega )\in \{0, 1\}^{n}}\in \mathbb {K}^{2^{n}}$
and
$\boldsymbol{y}=(y_{(1, \omega , 0)}, y_{(1, \omega , 1)})_{(j,\omega )\in \{0, 1\}^{n}}\in \mathbb {K}^{2^{n}}$
and
![]() $x, z, h_1\in \mathbb {K}$
,
$x, z, h_1\in \mathbb {K}$
,
![]() $h\in \mathbb {K}^{n-1}$
. Expanding the square and changing variables
$h\in \mathbb {K}^{n-1}$
. Expanding the square and changing variables
![]() $x\mapsto x-h_1$
and
$x\mapsto x-h_1$
and
![]() $z\mapsto z-h_1$
, we may rewrite Equation (6.69) as
$z\mapsto z-h_1$
, we may rewrite Equation (6.69) as
 $$ \begin{align} \nonumber \frac{1}{N_0^2} \int_{\mathbb{K}^{2^{n}}}\int_{\mathbb{K}^2}\int_{\mathbb{K}^{n+1}} G_1(x, z, h_1, h_1^{\prime}, h;\boldsymbol{y})d\nu_{[H_1]}^{\otimes2}&(h_1, h_1^{\prime}) d{\boldsymbol{\nu }}_{n-1}(h)d\mu(x)d\mu(z)d\mu^{\otimes 2^{n}}_{[N]}(\boldsymbol{y})\\&\gtrsim \delta^{O(1)}, \end{align} $$
$$ \begin{align} \nonumber \frac{1}{N_0^2} \int_{\mathbb{K}^{2^{n}}}\int_{\mathbb{K}^2}\int_{\mathbb{K}^{n+1}} G_1(x, z, h_1, h_1^{\prime}, h;\boldsymbol{y})d\nu_{[H_1]}^{\otimes2}&(h_1, h_1^{\prime}) d{\boldsymbol{\nu }}_{n-1}(h)d\mu(x)d\mu(z)d\mu^{\otimes 2^{n}}_{[N]}(\boldsymbol{y})\\&\gtrsim \delta^{O(1)}, \end{align} $$
where

Iteratively, for each
![]() $i\in \{2,\ldots , n\}$
, we apply the Cauchy–Schwarz inequality in all but the
$i\in \{2,\ldots , n\}$
, we apply the Cauchy–Schwarz inequality in all but the
![]() $h_i$
variable to conclude that
$h_i$
variable to conclude that
 $$ \begin{align*} \frac{1}{N_0^2}\int_{\mathbb{K}^2}\int_{\mathbb{K}^2}\int_{\square_n(X)} G_n(x, z, h, h';y, y') d{\boldsymbol{\nu }}_n^{\otimes2}(h, h')d\mu(x)d\mu(z)d\mu^{\otimes 2}_{[N]}(y, y') \gtrsim \delta^{O(1)}, \end{align*} $$
$$ \begin{align*} \frac{1}{N_0^2}\int_{\mathbb{K}^2}\int_{\mathbb{K}^2}\int_{\square_n(X)} G_n(x, z, h, h';y, y') d{\boldsymbol{\nu }}_n^{\otimes2}(h, h')d\mu(x)d\mu(z)d\mu^{\otimes 2}_{[N]}(y, y') \gtrsim \delta^{O(1)}, \end{align*} $$
where
We have arrived at Equation (6.68), completing the proof of the lemma
The following lemma is a slight variant of a result found in [Reference Peluse38].
Lemma 6.71. Given a scale
![]() $N\ge 1$
,
$N\ge 1$
,
![]() $0<\delta \le 1$
,
$0<\delta \le 1$
,
![]() $m\in \mathbb Z_+$
with
$m\in \mathbb Z_+$
with
![]() $m\ge 2$
,
$m\ge 2$
,
![]() $n\in \mathbb {N}$
and scales
$n\in \mathbb {N}$
and scales
![]() $H_1,\ldots , H_{n+1}$
with each
$H_1,\ldots , H_{n+1}$
with each
![]() $H_i \le N$
. We assume for every
$H_i \le N$
. We assume for every ![]() that
that
![]() $\varphi _i:\mathbb {K}^n\to \mathbb {K}$
is a measurable function independent of the variable
$\varphi _i:\mathbb {K}^n\to \mathbb {K}$
is a measurable function independent of the variable
![]() $h_i$
in a vector
$h_i$
in a vector
![]() $h=(h_1, \ldots , h_n)\in \mathbb {K}^n$
. Let
$h=(h_1, \ldots , h_n)\in \mathbb {K}^n$
. Let
![]() ${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
![]() $\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials. For
$\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials. For
![]() $\xi \in \mathbb {K}^n$
, let
$\xi \in \mathbb {K}^n$
, let
![]() $F_m^{\xi }$
be the dual function defined in Equation (6.45) that corresponds to the form (6.42) and
$F_m^{\xi }$
be the dual function defined in Equation (6.45) that corresponds to the form (6.42) and
![]() $1$
-bounded functions
$1$
-bounded functions
![]() $f_0, f_1,\ldots , f_{m-1}\in L^0(\mathbb {K})$
supported on an interval
$f_0, f_1,\ldots , f_{m-1}\in L^0(\mathbb {K})$
supported on an interval
![]() $I\subset \mathbb {K}$
of measure
$I\subset \mathbb {K}$
of measure
![]() $N_0 = N^{\deg {P_m}}$
. Suppose that
$N_0 = N^{\deg {P_m}}$
. Suppose that

Then
Proof. We shall write as before
![]() ${\boldsymbol{\nu }}_n:=\bigotimes _{i=1}^{n}\nu _{[H_i]}$
and also let
${\boldsymbol{\nu }}_n:=\bigotimes _{i=1}^{n}\nu _{[H_i]}$
and also let
![]() ${\boldsymbol{\mu}}_n:=\bigotimes _{i=1}^n\mu _{[H_i]}$
. Expanding the Fejér kernel, we may write the left-hand side of Equation (6.72) as
${\boldsymbol{\mu}}_n:=\bigotimes _{i=1}^n\mu _{[H_i]}$
. Expanding the Fejér kernel, we may write the left-hand side of Equation (6.72) as

We apply the Cauchy–Schwarz inequality in the
![]() $x, z$
and
$x, z$
and
![]() $h'$
variables and Corollary 4.7 to deduce that
$h'$
variables and Corollary 4.7 to deduce that
 $$ \begin{align*} {\mathcal I}^{2^n}&\le \frac{1}{N_0^{2}}\int_{\mathbb{K}^{3n+2}} \prod_{\omega\in\{0, 1\}^n}\mathcal C^{|\omega|}\big({\Delta}_{h^{(\omega)}-h}^nF_m^{\xi}(x) \overline{{\Delta}_{h^{(\omega)}-h}^nF_m^{\xi}(z)}\big)d{\boldsymbol{\mu}}_n^{\otimes3}(h^{(0)}, h^{(1)}, h)d\mu(x)d\mu(z)\\ =& \frac{1}{N_0^2} \int_{\mathbb{K}^{3n}} {\mathcal A}(x,z, h_n^{\prime}, h^{(0)}, h^{(1)}, h'){{\mathcal B}}(x,z,h^{(0)}, h^{(1)}, h') d\mu(x) d\mu(z) d{\boldsymbol{\mu}}_{n-1}^{\otimes3}(h^{(0)}, h^{(1)}, h')d\mu_{[H_n]}(h_n^{\prime}), \end{align*} $$
$$ \begin{align*} {\mathcal I}^{2^n}&\le \frac{1}{N_0^{2}}\int_{\mathbb{K}^{3n+2}} \prod_{\omega\in\{0, 1\}^n}\mathcal C^{|\omega|}\big({\Delta}_{h^{(\omega)}-h}^nF_m^{\xi}(x) \overline{{\Delta}_{h^{(\omega)}-h}^nF_m^{\xi}(z)}\big)d{\boldsymbol{\mu}}_n^{\otimes3}(h^{(0)}, h^{(1)}, h)d\mu(x)d\mu(z)\\ =& \frac{1}{N_0^2} \int_{\mathbb{K}^{3n}} {\mathcal A}(x,z, h_n^{\prime}, h^{(0)}, h^{(1)}, h'){{\mathcal B}}(x,z,h^{(0)}, h^{(1)}, h') d\mu(x) d\mu(z) d{\boldsymbol{\mu}}_{n-1}^{\otimes3}(h^{(0)}, h^{(1)}, h')d\mu_{[H_n]}(h_n^{\prime}), \end{align*} $$
where
 $$ \begin{align*} {\mathcal A}(x,z,h_n^{\prime}, h^{(0)}, h^{(1)}, h') :=& \int_{\mathbb{K}^2} \prod_{\omega'\in\{0, 1\}^{n-1}}{\mathcal C}^{|\omega'|} \Big[{\Delta}_{h^{(\omega')}-h'}^{n-1} \Big( F_m^{\xi}(x + h_n^0 - h_n^{\prime})\\ &\times{\overline{F_m^{\xi}(x+h_n^1 - h_n^{\prime}) F_m^{\xi}(z+ h_n^0 - h_n^{\prime})}} F_m^{\xi}(z + h_n^1 - h_n^{\prime}) \Big)\Big] d\mu_{[H_n]}^{\otimes2}(h_n^0, h_n^1), \end{align*} $$
$$ \begin{align*} {\mathcal A}(x,z,h_n^{\prime}, h^{(0)}, h^{(1)}, h') :=& \int_{\mathbb{K}^2} \prod_{\omega'\in\{0, 1\}^{n-1}}{\mathcal C}^{|\omega'|} \Big[{\Delta}_{h^{(\omega')}-h'}^{n-1} \Big( F_m^{\xi}(x + h_n^0 - h_n^{\prime})\\ &\times{\overline{F_m^{\xi}(x+h_n^1 - h_n^{\prime}) F_m^{\xi}(z+ h_n^0 - h_n^{\prime})}} F_m^{\xi}(z + h_n^1 - h_n^{\prime}) \Big)\Big] d\mu_{[H_n]}^{\otimes2}(h_n^0, h_n^1), \end{align*} $$
 $$ \begin{align*} {\mathcal B}(x,z,h^{(0)}, h^{(1)}, h'):=\prod_{\omega'\in\{0, 1\}^{n-1}} {\mathcal C}^{|\omega'|} \Big[{\Delta}_{h^{(\omega')}-h'}^{n-1} \Big( |F_m^{\xi}(x)|^2 |F_m^{\xi}(z)|^2 \Big)\Big]. \end{align*} $$
$$ \begin{align*} {\mathcal B}(x,z,h^{(0)}, h^{(1)}, h'):=\prod_{\omega'\in\{0, 1\}^{n-1}} {\mathcal C}^{|\omega'|} \Big[{\Delta}_{h^{(\omega')}-h'}^{n-1} \Big( |F_m^{\xi}(x)|^2 |F_m^{\xi}(z)|^2 \Big)\Big]. \end{align*} $$
Since
![]() ${\mathcal A}\ge 0$
, we see that
${\mathcal A}\ge 0$
, we see that
 $$ \begin{align*} {\mathcal I}^{2^n} \le &N_0^{-2} \int_{\mathbb{K}^{3n}} {\mathcal A}(x,z, h_n^{\prime}, h^{(0)}, h^{(1)}, h') d\mu(x) d\mu(z) d{\boldsymbol{\mu}}_{n-1}^{\otimes3}(h^{(0)}, h^{(1)}, h')d\mu_{[H_n]}(h_n^{\prime})\\ &= \frac{1}{N_0^2} \int_{\mathbb{K}^{3n+1}} \prod_{\omega'\in\{0, 1\}^{n-1}}{\mathcal C}^{|\omega'|} \Big[{\Delta}_{h^{(\omega')}-h'}^{n-1} \Big( F_m^{\xi}(x + h_n^0)\overline{F_m^{\xi}(x+h_n^1)}\\ &\hspace{3cm} \times \overline{F_m^{\xi}(z+ h_n^0)} F_m^{\xi}(z + h_n^1) \Big)\Big] d\mu(x) d\mu(z) d{\boldsymbol{\mu}}_{n}^{\otimes2}(h^{(0)}, h^{(1)}) d{\boldsymbol{\mu}}_{n-1}(h')\\ &= \frac{1}{N_0^2} \int_{\mathbb{K}^{3n+1}} \mathcal C(x,z,h^{(0)}, h^{(1)}, h') d\mu(x) d\mu(z) d{\boldsymbol{\mu}}_{n}^{\otimes2}(h^{(0)}, h^{(1)}) d{\boldsymbol{\mu}}_{n-1}(h'), \end{align*} $$
$$ \begin{align*} {\mathcal I}^{2^n} \le &N_0^{-2} \int_{\mathbb{K}^{3n}} {\mathcal A}(x,z, h_n^{\prime}, h^{(0)}, h^{(1)}, h') d\mu(x) d\mu(z) d{\boldsymbol{\mu}}_{n-1}^{\otimes3}(h^{(0)}, h^{(1)}, h')d\mu_{[H_n]}(h_n^{\prime})\\ &= \frac{1}{N_0^2} \int_{\mathbb{K}^{3n+1}} \prod_{\omega'\in\{0, 1\}^{n-1}}{\mathcal C}^{|\omega'|} \Big[{\Delta}_{h^{(\omega')}-h'}^{n-1} \Big( F_m^{\xi}(x + h_n^0)\overline{F_m^{\xi}(x+h_n^1)}\\ &\hspace{3cm} \times \overline{F_m^{\xi}(z+ h_n^0)} F_m^{\xi}(z + h_n^1) \Big)\Big] d\mu(x) d\mu(z) d{\boldsymbol{\mu}}_{n}^{\otimes2}(h^{(0)}, h^{(1)}) d{\boldsymbol{\mu}}_{n-1}(h')\\ &= \frac{1}{N_0^2} \int_{\mathbb{K}^{3n+1}} \mathcal C(x,z,h^{(0)}, h^{(1)}, h') d\mu(x) d\mu(z) d{\boldsymbol{\mu}}_{n}^{\otimes2}(h^{(0)}, h^{(1)}) d{\boldsymbol{\mu}}_{n-1}(h'), \end{align*} $$
where
 $$\begin{align*}\mathcal C(x,z,h^{(0)}, h^{(1)}, h'):=\prod_{\omega'\in\{0, 1\}^{n-1}}{\mathcal C}^{|\omega'|} \Big[{\Delta}_{h^{(\omega')}-h'}^{n-1} {\Delta}_{h_n^1 - h_n^0}\Big( F_m^{\xi}(x) {\overline{F_m^{\xi}(z)}}\Big)\Big]. \end{align*}$$
$$\begin{align*}\mathcal C(x,z,h^{(0)}, h^{(1)}, h'):=\prod_{\omega'\in\{0, 1\}^{n-1}}{\mathcal C}^{|\omega'|} \Big[{\Delta}_{h^{(\omega')}-h'}^{n-1} {\Delta}_{h_n^1 - h_n^0}\Big( F_m^{\xi}(x) {\overline{F_m^{\xi}(z)}}\Big)\Big]. \end{align*}$$
In the penultimate equality, we made the change of variables
![]() $x \to x -h_n^0+h_n^{\prime }$
and
$x \to x -h_n^0+h_n^{\prime }$
and
![]() $z \to z - h_n^0+ h_n^{\prime }$
. Now, proceeding inductively we see that
$z \to z - h_n^0+ h_n^{\prime }$
. Now, proceeding inductively we see that
 $$ \begin{align*}{\mathcal I}^{2^n} \le \frac{1}{N_0^2}\int_{\mathbb{K}^{2n+2}} {\Delta}_{h-h'}^n F_m^{\xi}(x) {\overline{{\Delta}^n_{h-h'} F_m^{\xi}(z)}} d\mu(x) d\mu(z) d{\boldsymbol{\mu}}_{n}^{\otimes2}(h, h'). \end{align*} $$
$$ \begin{align*}{\mathcal I}^{2^n} \le \frac{1}{N_0^2}\int_{\mathbb{K}^{2n+2}} {\Delta}_{h-h'}^n F_m^{\xi}(x) {\overline{{\Delta}^n_{h-h'} F_m^{\xi}(z)}} d\mu(x) d\mu(z) d{\boldsymbol{\mu}}_{n}^{\otimes2}(h, h'). \end{align*} $$
Inserting an extra average in the x variable and using the pigeonhole principle to fix z, it follows that
To conclude, we apply the Cauchy–Schwarz inequality to double the w variable and so
This completes the proof of the lemma.
Proof of Theorem 6.57.
The proof is by induction on
![]() $m\in \mathbb Z_+$
. The proof will consist of several steps. We begin by establishing the following claim.
$m\in \mathbb Z_+$
. The proof will consist of several steps. We begin by establishing the following claim.
Claim 6.73. Let
![]() $N\ge 1$
be a scale,
$N\ge 1$
be a scale,
![]() $0<\delta \le 1$
,
$0<\delta \le 1$
,
![]() $m\in \mathbb Z_+$
with
$m\in \mathbb Z_+$
with
![]() $m\ge 2$
and
$m\ge 2$
and
![]() $n\in \mathbb {N}$
be given. Let
$n\in \mathbb {N}$
be given. Let
![]() ${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
${\mathcal P}:=\{P_1,\ldots , P_{m}\}$
and
![]() $\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials such that
$\mathcal Q:=\{Q_1,\ldots , Q_n\}$
be collections of polynomials such that
For
![]() $\xi \in \mathbb {K}^n$
, let
$\xi \in \mathbb {K}^n$
, let
![]() $F_m^{\xi }$
be the dual function defined in Equation (6.45) that corresponds to the form (6.42) and
$F_m^{\xi }$
be the dual function defined in Equation (6.45) that corresponds to the form (6.42) and
![]() $1$
-bounded functions
$1$
-bounded functions
![]() $f_0, f_1,\ldots , f_{m-1}\in L^0(\mathbb {K})$
supported on an interval
$f_0, f_1,\ldots , f_{m-1}\in L^0(\mathbb {K})$
supported on an interval
![]() $I\subset \mathbb {K}$
of measure
$I\subset \mathbb {K}$
of measure
![]() $N_0 := N^{\deg {P_m}}$
. Suppose that
$N_0 := N^{\deg {P_m}}$
. Suppose that
Then for any sufficiently large constant
![]() $C\gtrsim _{{\mathcal P}, \mathcal Q}1$
one has
$C\gtrsim _{{\mathcal P}, \mathcal Q}1$
one has
The proof of Claim 6.73 for each integer
![]() $m\ge 2$
is itself part of the inductive proof of Theorem 6.57. In the first step, we prove Claim 6.73 for
$m\ge 2$
is itself part of the inductive proof of Theorem 6.57. In the first step, we prove Claim 6.73 for
![]() $m=2$
. In the second step, we show that Claim 6.73 for all integers
$m=2$
. In the second step, we show that Claim 6.73 for all integers
![]() $m\ge 2$
implies Theorem 6.57, this in particular will establish Theorem 6.57 for
$m\ge 2$
implies Theorem 6.57, this in particular will establish Theorem 6.57 for
![]() $m=2$
. In the third step, we finally show that Claim 6.73 for all integers
$m=2$
. In the third step, we finally show that Claim 6.73 for all integers
![]() $m\ge 3$
follows from Claim 6.73 and Theorem 6.57 for
$m\ge 3$
follows from Claim 6.73 and Theorem 6.57 for
![]() $m-1$
. Taken together, this shows that Claim 6.73 and Theorem 6.57 hold for each integer
$m-1$
. Taken together, this shows that Claim 6.73 and Theorem 6.57 hold for each integer
![]() $m\ge 2$
, completing the proof of Theorem 6.57.
$m\ge 2$
, completing the proof of Theorem 6.57.
Step 1.
We now prove Claim 6.73 for
![]() $m=2$
. Here,
$m=2$
. Here,
![]() $N_0 = N^{\deg {P_2}}$
. For
$N_0 = N^{\deg {P_2}}$
. For
![]() $\zeta _1, \zeta _2\in \mathbb {K}$
and
$\zeta _1, \zeta _2\in \mathbb {K}$
and
![]() $\xi \in \mathbb {K}^n$
, we define the multiplier
$\xi \in \mathbb {K}^n$
, we define the multiplier
 $$ \begin{align*} m_N(\zeta_1, \zeta_2, \xi):=\int_{B_1(0)} \mathrm{e}\Big(-\zeta_1P_1(\alpha y)+\zeta_2 P_2(\alpha y)+\sum_{j=1}^n\xi_jQ_j(\alpha y)\Big) d\mu(y), \end{align*} $$
$$ \begin{align*} m_N(\zeta_1, \zeta_2, \xi):=\int_{B_1(0)} \mathrm{e}\Big(-\zeta_1P_1(\alpha y)+\zeta_2 P_2(\alpha y)+\sum_{j=1}^n\xi_jQ_j(\alpha y)\Big) d\mu(y), \end{align*} $$
where
![]() $\alpha \in \mathbb {K}$
satisfies
$\alpha \in \mathbb {K}$
satisfies
![]() $|\alpha | = N$
. By definitions (6.45) and (6.46) and making the change of variables
$|\alpha | = N$
. By definitions (6.45) and (6.46) and making the change of variables
![]() $x\mapsto x-P_2(y)$
, we may write
$x\mapsto x-P_2(y)$
, we may write
 $$ \begin{align*} N_0^{-1}\widehat{F_2^{\xi}}(\zeta_2)&=N_0^{-1}\int_{\mathbb{K}}\int_{\mathbb{K}}F_{2;y}^{\xi}(x)\mathrm{e}(-\zeta_2 x)d\mu_{[N]}(y)d\mu(x)\\ &=N_0^{-1}\int_{\mathbb{K}}\widehat{f}_0(\zeta_2-\zeta_1)\widehat{f}_1(\zeta_1)m_N(\zeta_1, \zeta_2, \xi)d\zeta_1. \end{align*} $$
$$ \begin{align*} N_0^{-1}\widehat{F_2^{\xi}}(\zeta_2)&=N_0^{-1}\int_{\mathbb{K}}\int_{\mathbb{K}}F_{2;y}^{\xi}(x)\mathrm{e}(-\zeta_2 x)d\mu_{[N]}(y)d\mu(x)\\ &=N_0^{-1}\int_{\mathbb{K}}\widehat{f}_0(\zeta_2-\zeta_1)\widehat{f}_1(\zeta_1)m_N(\zeta_1, \zeta_2, \xi)d\zeta_1. \end{align*} $$
By the Cauchy–Schwarz inequality and Plancherel’s theorem, we obtain
 $$ \begin{align*} \delta\le N_0^{-1}|\widehat{F_2^{\xi}}(\zeta_2)|\lesssim N_0^{-1}\|f_0\|_{L^2(\mathbb{K})} \|f_1\|_{L^2(\mathbb{K})}\sup_{\zeta_1\in \mathbb{K}}|m_N(\zeta_1, \zeta_2, \xi)|, \end{align*} $$
$$ \begin{align*} \delta\le N_0^{-1}|\widehat{F_2^{\xi}}(\zeta_2)|\lesssim N_0^{-1}\|f_0\|_{L^2(\mathbb{K})} \|f_1\|_{L^2(\mathbb{K})}\sup_{\zeta_1\in \mathbb{K}}|m_N(\zeta_1, \zeta_2, \xi)|, \end{align*} $$
which gives for some
![]() $\zeta _1\in \mathbb {K}$
that
$\zeta _1\in \mathbb {K}$
that
since
![]() $\|f_0\|_{L^2(\mathbb {K})}, \|f_1\|_{L^2(\mathbb {K})}\lesssim N_0^{1/2}$
. Applying Lemma 6.49 with
$\|f_0\|_{L^2(\mathbb {K})}, \|f_1\|_{L^2(\mathbb {K})}\lesssim N_0^{1/2}$
. Applying Lemma 6.49 with
![]() ${\mathcal P}=\{-P_1, P_2\}$
and
${\mathcal P}=\{-P_1, P_2\}$
and
![]() $\mathcal Q=\{Q_1,\ldots , Q_n\}$
, we deduce that for every sufficiently large
$\mathcal Q=\{Q_1,\ldots , Q_n\}$
, we deduce that for every sufficiently large
![]() $C\gtrsim 1$
one has
$C\gtrsim 1$
one has
This completes the proof of Claim 6.73 for
![]() $m=2$
.
$m=2$
.
Step 2.
In this step, we show that Claim 6.73 for all integers
![]() $m\ge 2$
implies Theorem 6.57. In view of Step 1, this will in particular establish Theorem 6.57 for
$m\ge 2$
implies Theorem 6.57. In view of Step 1, this will in particular establish Theorem 6.57 for
![]() $m=2$
, which is the base case of our double induction. As before, we shall write
$m=2$
, which is the base case of our double induction. As before, we shall write
![]() ${\boldsymbol{\nu }}_{j}:=\bigotimes _{i=1}^{j}\nu _{[H_i]}$
for any
${\boldsymbol{\nu }}_{j}:=\bigotimes _{i=1}^{j}\nu _{[H_i]}$
for any
![]() $j\in \mathbb Z_+$
. Recall that
$j\in \mathbb Z_+$
. Recall that
![]() $N_0 = N^{\deg (P_m)}$
and note
$N_0 = N^{\deg (P_m)}$
and note
By Equation (6.58) and the pigeonhole principle, there exists a measurable set
![]() $X\subseteq \prod _{i=1}^{s-2}[H_i]$
so that
$X\subseteq \prod _{i=1}^{s-2}[H_i]$
so that
![]() ${\boldsymbol{\nu }}_{s-2}(X)\gtrsim \delta ^{O(1)}$
, and for all
${\boldsymbol{\nu }}_{s-2}(X)\gtrsim \delta ^{O(1)}$
, and for all
![]() $h \in X$
one has
$h \in X$
one has
Here, we used that
![]() $\operatorname {\mathrm {supp}} F_m^{\xi }$
is a subset of an interval whose measure is at most
$\operatorname {\mathrm {supp}} F_m^{\xi }$
is a subset of an interval whose measure is at most
![]() $O(N_0)$
. By Lemma 5.1, we have
$O(N_0)$
. By Lemma 5.1, we have
Next, we claim that there is a countable set
![]() ${\mathcal F} \subset \mathbb {K}$
, depending on N and
${\mathcal F} \subset \mathbb {K}$
, depending on N and
![]() $\delta $
such that
$\delta $
such that

for some absolute constant
![]() $C_0\in \mathbb Z_+$
and for all
$C_0\in \mathbb Z_+$
and for all
![]() $h\in X$
. When
$h\in X$
. When
![]() $\mathbb {K}$
is non-Archimedean, we take
$\mathbb {K}$
is non-Archimedean, we take
 $$ \begin{align*}{\mathcal F} \ = \ \bigcup_{M\ge 1} \, \Big\{ z = \sum_{j= -M}^{L-1} z_j \pi^j \in \mathbb{K} : z_j \in o_{\mathbb{K}}/m_{\mathbb{K}}\Big\}, \end{align*} $$
$$ \begin{align*}{\mathcal F} \ = \ \bigcup_{M\ge 1} \, \Big\{ z = \sum_{j= -M}^{L-1} z_j \pi^j \in \mathbb{K} : z_j \in o_{\mathbb{K}}/m_{\mathbb{K}}\Big\}, \end{align*} $$
where
![]() $N_0 = q^L$
. Let
$N_0 = q^L$
. Let
![]() $x \in I = B_{N_0}(x_0)$
. For any
$x \in I = B_{N_0}(x_0)$
. For any
![]() $\zeta \in \mathbb {K}$
, we have
$\zeta \in \mathbb {K}$
, we have
![]() $\zeta \in B_{N_0^{-1}}(\zeta _0)$
for some
$\zeta \in B_{N_0^{-1}}(\zeta _0)$
for some
![]() $\zeta _0 \in {\mathcal F}$
. Note that
$\zeta _0 \in {\mathcal F}$
. Note that
since
![]() $|(x-x_0)(\zeta - \zeta _0)| \le N_0 N_0^{-1} = 1$
and
$|(x-x_0)(\zeta - \zeta _0)| \le N_0 N_0^{-1} = 1$
and
![]() $\mathrm {e} = 1$
on
$\mathrm {e} = 1$
on
![]() $o_{\mathbb {K}}$
. Therefore,
$o_{\mathbb {K}}$
. Therefore, ![]() since
since
![]() ${\Delta }_h^{s-2}F_m$
is supported in I whenever
${\Delta }_h^{s-2}F_m$
is supported in I whenever
![]() $h \in X$
. This shows that Equation (6.76) holds for non-Archimedean fields.
$h \in X$
. This shows that Equation (6.76) holds for non-Archimedean fields.
When
![]() $\mathbb {K}= {\mathbb R}$
, we take
$\mathbb {K}= {\mathbb R}$
, we take
![]() ${\mathcal F} := T_0 {\mathbb Z}$
, where
${\mathcal F} := T_0 {\mathbb Z}$
, where
for a sufficiently large constant
![]() $C\gtrsim 1$
. When
$C\gtrsim 1$
. When
![]() $\mathbb {K} = {\mathbb C}$
, we take
$\mathbb {K} = {\mathbb C}$
, we take
![]() ${\mathcal F} := T_1 {\mathbb Z}^2$
, where
${\mathcal F} := T_1 {\mathbb Z}^2$
, where
![]() $T_1 := \delta ^{C_0} (C \sqrt {N_0})^{-1}$
. By the Lipschitz nature of characters on
$T_1 := \delta ^{C_0} (C \sqrt {N_0})^{-1}$
. By the Lipschitz nature of characters on
![]() ${\mathbb R}$
or
${\mathbb R}$
or
![]() ${\mathbb C}$
, we again see that Equation (6.76) holds in the Archimedean cases. In particular, there exists a measurable function
${\mathbb C}$
, we again see that Equation (6.76) holds in the Archimedean cases. In particular, there exists a measurable function
![]() $\phi : X \to {\mathcal F}$
so that
$\phi : X \to {\mathcal F}$
so that
for all
![]() $h\in X$
. If necessary, we may additionally assume that the range of
$h\in X$
. If necessary, we may additionally assume that the range of
![]() $\phi $
is finite.
$\phi $
is finite.
By Lemma 6.66, it follows that
 $$ \begin{align*} \int_{\square_{s-2}(X)}\bigg|N^{-1}_0\int_{\mathbb{K}} F_m(x; h, h')e(-\psi((h, h'))x)d\mu(x)\bigg|^2 d{\boldsymbol{\nu }}_{s-2}^{\otimes2}(h, h') \gtrsim \delta^{O(1)}, \end{align*} $$
$$ \begin{align*} \int_{\square_{s-2}(X)}\bigg|N^{-1}_0\int_{\mathbb{K}} F_m(x; h, h')e(-\psi((h, h'))x)d\mu(x)\bigg|^2 d{\boldsymbol{\nu }}_{s-2}^{\otimes2}(h, h') \gtrsim \delta^{O(1)}, \end{align*} $$
where
 $$ \begin{align*} F_m(x; h, h')&:=\int_{\mathbb{K}}{\Delta}_{h'-h}^{s-2}f_0(x+P_m(y))\prod_{i=1}^{m-1}{\Delta}_{h'-h}^{s-2}f_{i}(x-P_i(y)+P_m(y))d\mu_{[N]}(y),\\\psi(h, h')&:=\sum_{\omega\in\{0, 1\}^{s-2}}(-1)^{|\omega|}\phi\Big(\omega\cdot h+(1-\omega)\cdot h')\Big). \end{align*} $$
$$ \begin{align*} F_m(x; h, h')&:=\int_{\mathbb{K}}{\Delta}_{h'-h}^{s-2}f_0(x+P_m(y))\prod_{i=1}^{m-1}{\Delta}_{h'-h}^{s-2}f_{i}(x-P_i(y)+P_m(y))d\mu_{[N]}(y),\\\psi(h, h')&:=\sum_{\omega\in\{0, 1\}^{s-2}}(-1)^{|\omega|}\phi\Big(\omega\cdot h+(1-\omega)\cdot h')\Big). \end{align*} $$
Thus, by the pigeonhole principle, there exists a measurable set
![]() $X_0\subseteq \square _{s-2}(X)$
with
$X_0\subseteq \square _{s-2}(X)$
with
![]() ${\boldsymbol{\nu }}_{s-2}^{\otimes 2}(X_0)\gtrsim \delta ^{O(1)}$
such that for every
${\boldsymbol{\nu }}_{s-2}^{\otimes 2}(X_0)\gtrsim \delta ^{O(1)}$
such that for every
![]() $(h, h')\in X_0$
one has
$(h, h')\in X_0$
one has
 $$ \begin{align*} \bigg|N^{-\deg(P_m)}\int_{\mathbb{K}} F_m(x; h, h')e(-\psi((h, h'))x)d\mu(x)\bigg| \gtrsim \delta^{O(1)}. \end{align*} $$
$$ \begin{align*} \bigg|N^{-\deg(P_m)}\int_{\mathbb{K}} F_m(x; h, h')e(-\psi((h, h'))x)d\mu(x)\bigg| \gtrsim \delta^{O(1)}. \end{align*} $$
By Claim 6.73, there is a
![]() $c:=c_{m, s}\ge 1$
such that for each
$c:=c_{m, s}\ge 1$
such that for each
![]() $(h, h')\in X_0$
, one has
$(h, h')\in X_0$
, one has
By the pigeonhole principle, there exists
![]() $h'\in \prod _{i=1}^{s-2}[H_i]$
and a measurable set
$h'\in \prod _{i=1}^{s-2}[H_i]$
and a measurable set
satisfying
![]() ${\boldsymbol{\nu }}_{s-2}(X_0(h'))\gtrsim \delta ^{O(1)}$
. Since
${\boldsymbol{\nu }}_{s-2}(X_0(h'))\gtrsim \delta ^{O(1)}$
. Since
![]() $\psi ((h, h'))\in {\mathcal F}$
, we see that
$\psi ((h, h'))\in {\mathcal F}$
, we see that
where
![]() ${\mathbb {K}} = [{O(\delta ^{-O(1)})}]\cap {\mathbb Z}$
when
${\mathbb {K}} = [{O(\delta ^{-O(1)})}]\cap {\mathbb Z}$
when
![]() $\mathbb {K} = {\mathbb R}$
. In this case,
$\mathbb {K} = {\mathbb R}$
. In this case,
![]() $X_{0}^k(h'):=\{h\in X: \psi ((h, h'))=T_0k\}$
. When
$X_{0}^k(h'):=\{h\in X: \psi ((h, h'))=T_0k\}$
. When
![]() $\mathbb {K} = {\mathbb C}$
, we have
$\mathbb {K} = {\mathbb C}$
, we have
![]() ${\mathbb {K}} = [{O(\delta ^{-O(1)})}]\cap {\mathbb Z}^2$
and
${\mathbb {K}} = [{O(\delta ^{-O(1)})}]\cap {\mathbb Z}^2$
and
![]() $X_{0}^k(h'):=\{h\in X: \psi ((h, h'))=T_1 k\}$
. Finally when
$X_{0}^k(h'):=\{h\in X: \psi ((h, h'))=T_1 k\}$
. Finally when
![]() $\mathbb {K}$
is non-Archimedean,
$\mathbb {K}$
is non-Archimedean,
 $$ \begin{align*}{\mathbb{K}} = \bigl[{O(\delta^{-O(1)})}\bigr] \cap \bigl\{ k = \sum_{j= -M}^{-1} k_j \pi^j \in \mathbb{K} : k_j \in o_{\mathbb{K}}/m_{\mathbb{K}}\bigr\} \end{align*} $$
$$ \begin{align*}{\mathbb{K}} = \bigl[{O(\delta^{-O(1)})}\bigr] \cap \bigl\{ k = \sum_{j= -M}^{-1} k_j \pi^j \in \mathbb{K} : k_j \in o_{\mathbb{K}}/m_{\mathbb{K}}\bigr\} \end{align*} $$
and
![]() $X_{0}^k(h') := \{h\in X: \psi ((h,h')) = \pi ^L k \}$
.
$X_{0}^k(h') := \{h\in X: \psi ((h,h')) = \pi ^L k \}$
.
Thus, by the pigeonhole principle there is
![]() $k_0\in {\mathbb {K}}$
such that
$k_0\in {\mathbb {K}}$
such that
![]() ${\boldsymbol{\nu }}_{s-2}(X_0^{k_0}(h'))\big )\gtrsim \delta ^{O(1)}$
. When
${\boldsymbol{\nu }}_{s-2}(X_0^{k_0}(h'))\big )\gtrsim \delta ^{O(1)}$
. When
![]() $\mathbb {K} = {\mathbb R}$
, this shows that
$\mathbb {K} = {\mathbb R}$
, this shows that
![]() $\psi (h, h')=T_0 k_0 =: \phi _m$
for all
$\psi (h, h')=T_0 k_0 =: \phi _m$
for all
![]() $h\in X_0^{k_0}(h')$
. When
$h\in X_0^{k_0}(h')$
. When
![]() $\mathbb {K} = {\mathbb C}$
, we have
$\mathbb {K} = {\mathbb C}$
, we have
![]() $\phi (h,h') = T_1 k_0$
for all
$\phi (h,h') = T_1 k_0$
for all
![]() $h \in X_0^{k_0}(h')$
and when
$h \in X_0^{k_0}(h')$
and when
![]() $\mathbb {K}$
is non-Archimedean,
$\mathbb {K}$
is non-Archimedean,
![]() $\phi (h,h') = \pi ^L k_0$
for all
$\phi (h,h') = \pi ^L k_0$
for all
![]() $h \in X_0^{k_0}(h')$
. We will denote these values by
$h \in X_0^{k_0}(h')$
. We will denote these values by
![]() $\phi _m$
in all cases.
$\phi _m$
in all cases.
Set
 $$ \begin{align*} \psi_1(h, h'):=(-1)^{s+1}\sum_{\substack{\omega\in\{0,1\}^{s-2} \\ \omega_1=0}}(-1)^{|\omega|}\phi\Big((\omega\cdot h+(1-\omega)\cdot h')\Big) + (-1)^s \phi_m \end{align*} $$
$$ \begin{align*} \psi_1(h, h'):=(-1)^{s+1}\sum_{\substack{\omega\in\{0,1\}^{s-2} \\ \omega_1=0}}(-1)^{|\omega|}\phi\Big((\omega\cdot h+(1-\omega)\cdot h')\Big) + (-1)^s \phi_m \end{align*} $$
and, for ![]() , set
, set
 $$ \begin{align*} \psi_i(h, h'):=(-1)^{s+1}\sum_{\substack{\omega\in\{0,1\}^{s-2}\setminus\{0\} \\ \omega_1=\ldots=\omega_{i-1}=1 \\ \omega_{i}=0}}(-1)^{|\omega|}\phi\Big((\omega\cdot h+(1-\omega)\cdot h')\Big). \end{align*} $$
$$ \begin{align*} \psi_i(h, h'):=(-1)^{s+1}\sum_{\substack{\omega\in\{0,1\}^{s-2}\setminus\{0\} \\ \omega_1=\ldots=\omega_{i-1}=1 \\ \omega_{i}=0}}(-1)^{|\omega|}\phi\Big((\omega\cdot h+(1-\omega)\cdot h')\Big). \end{align*} $$
Note that
![]() $\psi _i$
does not depend on
$\psi _i$
does not depend on
![]() $h_{i}$
and we can write
$h_{i}$
and we can write
 $$ \begin{align*} \phi(h)=\sum_{i=1}^{s-2}\psi_i(h, h'). \end{align*} $$
$$ \begin{align*} \phi(h)=\sum_{i=1}^{s-2}\psi_i(h, h'). \end{align*} $$
Averaging Equation (6.77) over
![]() $\mathbb {X}:=X_0^{k_0}(h')$
and using positivity, we obtain
$\mathbb {X}:=X_0^{k_0}(h')$
and using positivity, we obtain

Invoking Lemma 6.71, we conclude that
Step 3.
Gathering together the conclusions of Step 1 and Step 2 (for
![]() $m=2$
), we see that the base step of a double induction has been established. In this step, we shall illustrate how to establish the inductive step. We assume that Claim 6.73 and Theorem 6.57 hold for
$m=2$
), we see that the base step of a double induction has been established. In this step, we shall illustrate how to establish the inductive step. We assume that Claim 6.73 and Theorem 6.57 hold for
![]() $m-1$
in place m for some integer
$m-1$
in place m for some integer
![]() $m\ge 3$
. Then we will prove that Claim 6.73 holds for
$m\ge 3$
. Then we will prove that Claim 6.73 holds for
![]() $m\ge 3$
, which in view of Step 2 will allow us to deduce that Theorem 6.57 also holds for
$m\ge 3$
, which in view of Step 2 will allow us to deduce that Theorem 6.57 also holds for
![]() $m\ge 3$
. This will complete the proof of Theorem 6.57.
$m\ge 3$
. This will complete the proof of Theorem 6.57.
Recall that
![]() $N_0 = N^{\deg (P_m)}$
. By definitions (6.45) and (6.46) and making the change of variables
$N_0 = N^{\deg (P_m)}$
. By definitions (6.45) and (6.46) and making the change of variables
![]() $x\mapsto x-P_m(y)$
, we may write
$x\mapsto x-P_m(y)$
, we may write
 $$ \begin{align*} N_0^{-1}\widehat{F_m^{\xi}}(\zeta_m)&=N_0^{-1}\int_{\mathbb{K}^2}F_{m;y}^{\xi}(x)\mathrm{e}(-\zeta_m x)d\mu(x)d\mu_{[N]}(y)\\&=N_0^{-1}\int_{\mathbb{K}^2}\mathrm{M}_{\zeta_m}f_0(x)\prod_{i=1}^{m-1}f_{i}(x-P_i(y))\mathrm{e}\Big(\zeta_m P_m(y)+\sum_{j=1}^n\xi_jQ_j(y)\Big)d\mu_{[N]}(y)d\mu(x)\\&=: M^{-1} \Lambda_{{\mathcal P}'; N}^{\mathcal Q', \xi'}(\mathrm{M}_{\zeta_m}f_0, f_1,\ldots f_{m-1}), \end{align*} $$
$$ \begin{align*} N_0^{-1}\widehat{F_m^{\xi}}(\zeta_m)&=N_0^{-1}\int_{\mathbb{K}^2}F_{m;y}^{\xi}(x)\mathrm{e}(-\zeta_m x)d\mu(x)d\mu_{[N]}(y)\\&=N_0^{-1}\int_{\mathbb{K}^2}\mathrm{M}_{\zeta_m}f_0(x)\prod_{i=1}^{m-1}f_{i}(x-P_i(y))\mathrm{e}\Big(\zeta_m P_m(y)+\sum_{j=1}^n\xi_jQ_j(y)\Big)d\mu_{[N]}(y)d\mu(x)\\&=: M^{-1} \Lambda_{{\mathcal P}'; N}^{\mathcal Q', \xi'}(\mathrm{M}_{\zeta_m}f_0, f_1,\ldots f_{m-1}), \end{align*} $$
where
![]() $\mathrm {M}_{\zeta _m}f_0(x):=\mathrm {e}(-\zeta _m x)f_0(z)$
,
$\mathrm {M}_{\zeta _m}f_0(x):=\mathrm {e}(-\zeta _m x)f_0(z)$
,
![]() ${\mathcal P}':={\mathcal P}\setminus \{P_m\}$
,
${\mathcal P}':={\mathcal P}\setminus \{P_m\}$
,
![]() $\mathcal Q':=\mathcal Q\cup \{P_m\}$
,
$\mathcal Q':=\mathcal Q\cup \{P_m\}$
,
![]() $\xi ':=(\zeta _m, \xi _1,\ldots , \xi _n)\in \mathbb {K}^{n+1}$
and
$\xi ':=(\zeta _m, \xi _1,\ldots , \xi _n)\in \mathbb {K}^{n+1}$
and
![]() $M = N_0 {N_0^{\prime }}^{-1}$
, where
$M = N_0 {N_0^{\prime }}^{-1}$
, where
![]() $N_0^{\prime }$
is the scale
$N_0^{\prime }$
is the scale
![]() $N^{\deg (P_{m-1})}$
.
$N^{\deg (P_{m-1})}$
.
Thus, Equation (6.74) implies
As in the proof of Theorem 6.1, by the pigeonhole principle, we can find an interval
![]() $I'\subset \mathbb {K}$
of measure about
$I'\subset \mathbb {K}$
of measure about
![]() $ N_0^{\prime }$
such that
$ N_0^{\prime }$
such that
where ![]() .
.
Consequently, by Proposition 6.47, there exists an
![]() $s\in \mathbb Z_+$
such that
$s\in \mathbb Z_+$
such that
where
![]() $F_{m-1}^{\xi '}$
is the dual function respect the form
$F_{m-1}^{\xi '}$
is the dual function respect the form
![]() $\Lambda _{{\mathcal P}'; N, I'}^{\mathcal Q', \xi '}(f_0^{\prime }, f_1^{\prime },\ldots , f_{m-1}')$
and
$\Lambda _{{\mathcal P}'; N, I'}^{\mathcal Q', \xi '}(f_0^{\prime }, f_1^{\prime },\ldots , f_{m-1}')$
and
![]() $H_i\simeq \delta ^{O_{{\mathcal P}'}(1)}N^{\deg (P_{m-1})}$
for
$H_i\simeq \delta ^{O_{{\mathcal P}'}(1)}N^{\deg (P_{m-1})}$
for ![]() . By the induction hypothesis (for Theorem 6.57), we deduce that
. By the induction hypothesis (for Theorem 6.57), we deduce that
which in turn by Lemma 5.1 implies
for some
![]() $\zeta _{m-1}\in \mathbb {K}$
. By the induction hypothesis (for Claim 6.73), we deduce that
$\zeta _{m-1}\in \mathbb {K}$
. By the induction hypothesis (for Claim 6.73), we deduce that

which in particular implies Equation (6.75), and we are done.
7 Sobolev estimates
As a consequence of the
![]() $L^\infty $
-inverse theorem from the previous section, we establish some Sobolev estimates, which will be critical in the proof of Theorem 1.3.
$L^\infty $
-inverse theorem from the previous section, we establish some Sobolev estimates, which will be critical in the proof of Theorem 1.3.
We begin with a smooth variant of Theorem 6.1. When
![]() $\mathbb {K}$
is Archimedean, we fix a Schwartz function
$\mathbb {K}$
is Archimedean, we fix a Schwartz function
![]() $\varphi $
on
$\varphi $
on
![]() $\mathbb {K}$
so that
$\mathbb {K}$
so that
When
![]() $\mathbb {K}={\mathbb R}$
, we set
$\mathbb {K}={\mathbb R}$
, we set
![]() $\varphi _N(x) = N^{-1} \varphi (N^{-1} x)$
for any
$\varphi _N(x) = N^{-1} \varphi (N^{-1} x)$
for any
![]() $N>0$
and when
$N>0$
and when
![]() $\mathbb {K} = {\mathbb C}$
, we set
$\mathbb {K} = {\mathbb C}$
, we set
![]() $\varphi _{N}(z) = N^{-1} \varphi (N^{-1/2} z)$
for any
$\varphi _{N}(z) = N^{-1} \varphi (N^{-1/2} z)$
for any
![]() $N> 0$
. When
$N> 0$
. When
![]() $\mathbb {K}$
is non-Archimedean, we set
$\mathbb {K}$
is non-Archimedean, we set ![]() so that
so that ![]() and we set
and we set ![]() for any scale N.
for any scale N.
Theorem 7.1 (A smooth variant of the inverse theorem).
Let
![]() $N\ge 1$
be a scale,
$N\ge 1$
be a scale,
![]() $0<\delta \le 1$
,
$0<\delta \le 1$
,
![]() $m\in \mathbb Z_+$
be given. Let
$m\in \mathbb Z_+$
be given. Let
![]() ${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of polynomials such that
${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of polynomials such that
![]() $1\le \deg {P_1}<\ldots <\deg {P_m}$
. Let
$1\le \deg {P_1}<\ldots <\deg {P_m}$
. Let
![]() $f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
$f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
![]() $1$
-bounded functions supported on an interval
$1$
-bounded functions supported on an interval
![]() $I\subset \mathbb {K}$
of measure
$I\subset \mathbb {K}$
of measure
![]() $N_0 = N^{\deg {P_m}}$
. Suppose that the
$N_0 = N^{\deg {P_m}}$
. Suppose that the
![]() $(m+1)$
-linear form defined in Equation (6.2) satisfies
$(m+1)$
-linear form defined in Equation (6.2) satisfies
Then for any ![]() there exists an absolute constant
there exists an absolute constant
![]() $C_j\gtrsim _{\mathcal P}1$
so that
$C_j\gtrsim _{\mathcal P}1$
so that
where
![]() $N_j\simeq \delta ^{C_j}N^{\deg (P_j)}$
, provided
$N_j\simeq \delta ^{C_j}N^{\deg (P_j)}$
, provided
![]() $N \gtrsim \delta ^{-O_{\mathcal P}(1)}$
.
$N \gtrsim \delta ^{-O_{\mathcal P}(1)}$
.
Proof. By translation invariance, we can assume that
![]() $f_j$
is supported on
$f_j$
is supported on
![]() $[N_0]$
for every
$[N_0]$
for every ![]() . The proof will consist of two steps. In the first step, we will invoke Theorem 6.1 to prove Equation (7.3) for
. The proof will consist of two steps. In the first step, we will invoke Theorem 6.1 to prove Equation (7.3) for
![]() $j=1$
. In the second step, we will use Equation (7.3) for
$j=1$
. In the second step, we will use Equation (7.3) for
![]() $j=1$
to establish Equation (7.3) for
$j=1$
to establish Equation (7.3) for
![]() $j=2$
, and continuing inductively we will obtain Equation (7.3) for all
$j=2$
, and continuing inductively we will obtain Equation (7.3) for all ![]() .
.
Step 1.
We first establish Equation (7.3) for
![]() $j=1$
. When
$j=1$
. When
![]() $\mathbb {K}$
is non-Archimedean, this is an immediate consequence of Theorem 6.1 since
$\mathbb {K}$
is non-Archimedean, this is an immediate consequence of Theorem 6.1 since
![]() $\varphi _{N_1} = \mu _{[N_1]}$
in this case. Nevertheless, we make the observation that
$\varphi _{N_1} = \mu _{[N_1]}$
in this case. Nevertheless, we make the observation that
holds. In fact, we will see that Equation (7.4) holds for any
![]() $\mathbb {K}$
, non-Archimedean or Archimedean. First, let us see Equation (7.4) when
$\mathbb {K}$
, non-Archimedean or Archimedean. First, let us see Equation (7.4) when
![]() $\mathbb {K}$
is non-Archimedean. Suppose that
$\mathbb {K}$
is non-Archimedean. Suppose that
![]() $|\Lambda _{{\mathcal P}; N}(f_0,\varphi _{N_1}*f_1, \ldots , f_m)| \le c \, \delta $
for some small
$|\Lambda _{{\mathcal P}; N}(f_0,\varphi _{N_1}*f_1, \ldots , f_m)| \le c \, \delta $
for some small
![]() $c>0$
. Then, since
$c>0$
. Then, since
we conclude that
![]() $|\Lambda _{{\mathcal P}; N}(f_0,f_1 - \varphi _{N_1}*f_1, \ldots , f_m)|\gtrsim \delta $
. Therefore, Theorem 6.1 implies that
$|\Lambda _{{\mathcal P}; N}(f_0,f_1 - \varphi _{N_1}*f_1, \ldots , f_m)|\gtrsim \delta $
. Therefore, Theorem 6.1 implies that
![]() $N_0^{-1} \|\varphi _{N_1} *(f_1 - \varphi _{N_1} * f_1)\|_{L^1(\mathbb {K})}| \gtrsim \delta ^{O(1)}$
, but this is a contradiction since
$N_0^{-1} \|\varphi _{N_1} *(f_1 - \varphi _{N_1} * f_1)\|_{L^1(\mathbb {K})}| \gtrsim \delta ^{O(1)}$
, but this is a contradiction since
![]() $\varphi _{N_1} * \varphi _{N_1} = \varphi _{N_1}$
when
$\varphi _{N_1} * \varphi _{N_1} = \varphi _{N_1}$
when
![]() $\mathbb {K}$
is non-Archimedean (in which case
$\mathbb {K}$
is non-Archimedean (in which case ![]() ) and so
) and so
![]() $\varphi _{N_1} * (f_1 - \varphi _{N_1}* f_1) \equiv 0$
.
$\varphi _{N_1} * (f_1 - \varphi _{N_1}* f_1) \equiv 0$
.
We now turn to establish (7.3) for
![]() $j=1$
when
$j=1$
when
![]() $\mathbb {K}$
is Archimedean (when
$\mathbb {K}$
is Archimedean (when
![]() $\mathbb {K} = {\mathbb R}$
or
$\mathbb {K} = {\mathbb R}$
or
![]() $\mathbb {K} = {\mathbb C}$
). Let
$\mathbb {K} = {\mathbb C}$
). Let
![]() $\eta :\mathbb {K} \to [0, \infty )$
be a Schwartz function so that
$\eta :\mathbb {K} \to [0, \infty )$
be a Schwartz function so that
![]() $\int _{\mathbb {K}}\eta =1$
,
$\int _{\mathbb {K}}\eta =1$
,
![]() ${\widehat {\eta }}\equiv 1$
near 0 and
${\widehat {\eta }}\equiv 1$
near 0 and
![]() $\mathrm {supp}\:\widehat {\eta }\subseteq [2]$
. For
$\mathrm {supp}\:\widehat {\eta }\subseteq [2]$
. For
![]() $t>0$
, we write
$t>0$
, we write
![]() $\eta _{t}(x):=t^{-1}\eta (t^{-1}x)$
when
$\eta _{t}(x):=t^{-1}\eta (t^{-1}x)$
when
![]() $\mathbb {K}={\mathbb R}$
and
$\mathbb {K}={\mathbb R}$
and
![]() $\eta _t(x):= t^{-2}\eta (t^{-1}x)$
when
$\eta _t(x):= t^{-2}\eta (t^{-1}x)$
when
![]() $\mathbb {K} = {\mathbb C}$
. We will also need a Schwartz function
$\mathbb {K} = {\mathbb C}$
. We will also need a Schwartz function
![]() $\rho :\mathbb {K}\to [0, \infty )$
such that
$\rho :\mathbb {K}\to [0, \infty )$
such that
for some large absolute constant
![]() $M\ge 1$
, which will be specified later. We shall also write
$M\ge 1$
, which will be specified later. We shall also write
![]() $\rho _{(t)}(x):=\rho (t^{-1}x)$
for
$\rho _{(t)}(x):=\rho (t^{-1}x)$
for
![]() $t>0$
and
$t>0$
and
![]() $x\in \mathbb {K}$
.
$x\in \mathbb {K}$
.
Let
![]() $N_0^{\prime }\simeq N_0$
when
$N_0^{\prime }\simeq N_0$
when
![]() $\mathbb {K} = {\mathbb R}$
and
$\mathbb {K} = {\mathbb R}$
and
![]() $N_0^{\prime } \simeq \sqrt {N_0}$
when
$N_0^{\prime } \simeq \sqrt {N_0}$
when
![]() $\mathbb {K} = {\mathbb C}$
. Observe that Equation (7.2) implies that at least one of the following lower bounds holds:
$\mathbb {K} = {\mathbb C}$
. Observe that Equation (7.2) implies that at least one of the following lower bounds holds:
By Theorem 6.1, it is easy to see that Equation (7.5) yields that
which in turn will imply Equation (7.3) for
![]() $j=1$
provided that the remaining two alternatives (7.6) and (7.7) do not hold. If this is the case, then Equation (7.4) also holds when
$j=1$
provided that the remaining two alternatives (7.6) and (7.7) do not hold. If this is the case, then Equation (7.4) also holds when
![]() $\mathbb {K}={\mathbb R}, {\mathbb C}$
is Archimedean.
$\mathbb {K}={\mathbb R}, {\mathbb C}$
is Archimedean.
If the second alternative holds we, let
![]() $f_1^{\prime }:= \rho _{(N_0^{\prime })}(f_1-\varphi _{N_1}*f_1)$
and then Theorem 6.1 implies that
$f_1^{\prime }:= \rho _{(N_0^{\prime })}(f_1-\varphi _{N_1}*f_1)$
and then Theorem 6.1 implies that
with
![]() $N_1^{\prime }\simeq \delta ^{C_1^{\prime }}N^{\deg (P_1)}$
. By the Cauchy–Schwarz inequality (the support of
$N_1^{\prime }\simeq \delta ^{C_1^{\prime }}N^{\deg (P_1)}$
. By the Cauchy–Schwarz inequality (the support of
![]() $\mu _{[N_1^{\prime }]}, *f_1^{\prime }$
is contained in a fixed dilate of
$\mu _{[N_1^{\prime }]}, *f_1^{\prime }$
is contained in a fixed dilate of
![]() $[N_0]$
), we have
$[N_0]$
), we have
Let
![]() $N_1^{\prime \prime }:= \delta ^{A+C_1^{\prime }}N^{\deg (P_1)}/A$
for some
$N_1^{\prime \prime }:= \delta ^{A+C_1^{\prime }}N^{\deg (P_1)}/A$
for some
![]() $A\ge 1$
to be determined later. We now show that
$A\ge 1$
to be determined later. We now show that
We note that for
![]() $|x| \ge C N_1^{\prime }$
,
$|x| \ge C N_1^{\prime }$
,
and so

When
![]() $|x| \le C N_1^{\prime }$
is small, we use the Cauchy–Schwarz inequality
$|x| \le C N_1^{\prime }$
is small, we use the Cauchy–Schwarz inequality

and then Plancherel’s theorem,
Here, we use the facts that
![]() $\widehat {\eta } \equiv 1$
near
$\widehat {\eta } \equiv 1$
near
![]() $0$
and the Fourier decay bound for Euclidean balls,
$0$
and the Fourier decay bound for Euclidean balls,
This establishes Equation (7.8) and so
 $$ \begin{align*} N_0^{-1}\big\| (\mu_{[N_1^{\prime}]}-\mu_{[N_1^{\prime}]}*\eta_{N_1^{\prime\prime}})*f_1^{\prime}\big\|_{L^2(\mathbb{K})}^2&\lesssim \big\| \mu_{[N_1^{\prime}]}-\mu_{[N_1^{\prime}]}*\eta_{N_1^{\prime\prime}}\big\|_{L^1(\mathbb{K})}^2\\ &\lesssim \sqrt{N_1^{\prime\prime} /N_1^{\prime}} \lesssim \sqrt{\delta^{A}/A}. \end{align*} $$
$$ \begin{align*} N_0^{-1}\big\| (\mu_{[N_1^{\prime}]}-\mu_{[N_1^{\prime}]}*\eta_{N_1^{\prime\prime}})*f_1^{\prime}\big\|_{L^2(\mathbb{K})}^2&\lesssim \big\| \mu_{[N_1^{\prime}]}-\mu_{[N_1^{\prime}]}*\eta_{N_1^{\prime\prime}}\big\|_{L^1(\mathbb{K})}^2\\ &\lesssim \sqrt{N_1^{\prime\prime} /N_1^{\prime}} \lesssim \sqrt{\delta^{A}/A}. \end{align*} $$
Consequently,
which for sufficiently large
![]() $A\ge C_0^{\prime }$
yields
$A\ge C_0^{\prime }$
yields
Taking
![]() $N_1:=\frac {1}{2}N_1^{\prime \prime }$
and using support properties of
$N_1:=\frac {1}{2}N_1^{\prime \prime }$
and using support properties of
![]() $\widehat {\varphi }$
and
$\widehat {\varphi }$
and
![]() $\widehat {\eta }$
, by the Plancherel theorem we may write (when
$\widehat {\eta }$
, by the Plancherel theorem we may write (when
![]() $\mathbb {K} = {\mathbb R}$
)
$\mathbb {K} = {\mathbb R}$
)
 $$ \begin{align*} N_0^{-1}\big\| \eta_{N_1^{\prime\prime}}*f_1^{\prime}\big\|_{L^2({\mathbb R})}^2 =N_0^{-1}\big\| \widehat{\eta}_{N_1^{\prime\prime}}\big(\widehat{\rho_{(N_0^{\prime})}}*((1-\widehat{\varphi}_{N_1})\widehat{f}_1)\big)\big\|_{L^2(\mathbb R)}^2\\ \lesssim N_0^{-1}\int_{\mathbb R}\bigg(\int_{\mathbb R}\frac{N_0^{\prime}}{(1+N_0^{\prime}|\xi-\zeta|)^{200}}|\widehat{f}_1(\zeta)(1-\widehat{\varphi}(N_1\zeta))||\widehat{\eta}(N_1^{\prime\prime}\xi)|\bigg)^2d\mu(\xi)\\ &\kern-200pt\lesssim N_0^{-1}\delta^{100(A+C_1^{\prime})}\|f_1\|_{L^2(\mathbb R)}^2. \end{align*} $$
$$ \begin{align*} N_0^{-1}\big\| \eta_{N_1^{\prime\prime}}*f_1^{\prime}\big\|_{L^2({\mathbb R})}^2 =N_0^{-1}\big\| \widehat{\eta}_{N_1^{\prime\prime}}\big(\widehat{\rho_{(N_0^{\prime})}}*((1-\widehat{\varphi}_{N_1})\widehat{f}_1)\big)\big\|_{L^2(\mathbb R)}^2\\ \lesssim N_0^{-1}\int_{\mathbb R}\bigg(\int_{\mathbb R}\frac{N_0^{\prime}}{(1+N_0^{\prime}|\xi-\zeta|)^{200}}|\widehat{f}_1(\zeta)(1-\widehat{\varphi}(N_1\zeta))||\widehat{\eta}(N_1^{\prime\prime}\xi)|\bigg)^2d\mu(\xi)\\ &\kern-200pt\lesssim N_0^{-1}\delta^{100(A+C_1^{\prime})}\|f_1\|_{L^2(\mathbb R)}^2. \end{align*} $$
A similar bound holds when
![]() $\mathbb {K} = {\mathbb C}$
. Therefore,
$\mathbb {K} = {\mathbb C}$
. Therefore,
which is impossible if
![]() $A\ge 1$
is large enough. Thus, the second alternative (7.6) is impossible. To see that the third alternative (7.7) is also impossible observe that
$A\ge 1$
is large enough. Thus, the second alternative (7.6) is impossible. To see that the third alternative (7.7) is also impossible observe that
 $$ \begin{align*} \delta\lesssim |\Lambda_{{\mathcal P}; N}(f_0,(1-\rho_{(N_0^{\prime})})(f_1-\varphi_{N_1}*f_1), \ldots, f_m)|\lesssim N_0^{-1}\int_{[N_0^{\prime}]}(1-\rho_{(N_0^{\prime})})(x)d\mu(x)\lesssim \delta^M, \end{align*} $$
$$ \begin{align*} \delta\lesssim |\Lambda_{{\mathcal P}; N}(f_0,(1-\rho_{(N_0^{\prime})})(f_1-\varphi_{N_1}*f_1), \ldots, f_m)|\lesssim N_0^{-1}\int_{[N_0^{\prime}]}(1-\rho_{(N_0^{\prime})})(x)d\mu(x)\lesssim \delta^M, \end{align*} $$
which is also impossible if
![]() $M\ge 1$
is sufficiently large. Hence, Equation (7.5) must necessarily hold, and we are done.
$M\ge 1$
is sufficiently large. Hence, Equation (7.5) must necessarily hold, and we are done.
Step 2.
Let
![]() $M\ge 1$
be a large constant to be determined later, and define
$M\ge 1$
be a large constant to be determined later, and define
![]() $N'\simeq \delta ^MN$
and
$N'\simeq \delta ^MN$
and
![]() $N_0^{\prime } \simeq \delta ^M N_0$
. The main idea is to partition the intervals
$N_0^{\prime } \simeq \delta ^M N_0$
. The main idea is to partition the intervals
![]() $[N]$
and
$[N]$
and
![]() $[N_0]$
into
$[N_0]$
into
![]() $\mathbb {K}\simeq \delta ^{-M}$
disjoint intervals of measure
$\mathbb {K}\simeq \delta ^{-M}$
disjoint intervals of measure
![]() $\simeq N'$
and
$\simeq N'$
and
![]() $\simeq N_0^{\prime }$
, respectively. Such partitions are straightforward when
$\simeq N_0^{\prime }$
, respectively. Such partitions are straightforward when
![]() $\mathbb {K} = {\mathbb R}$
. When
$\mathbb {K} = {\mathbb R}$
. When
![]() $\mathbb {K}$
is non-Archimedean, we only need to partition
$\mathbb {K}$
is non-Archimedean, we only need to partition
![]() $[N]$
and not
$[N]$
and not
![]() $[N_0]$
. Finally, when
$[N_0]$
. Finally, when
![]() $\mathbb {K} = {\mathbb C}$
, intervals are discs and it is not possible to partition a disc into subdiscs and so we will need to be careful with this technical issue.
$\mathbb {K} = {\mathbb C}$
, intervals are discs and it is not possible to partition a disc into subdiscs and so we will need to be careful with this technical issue.
We first concentrate on the case when
![]() $\mathbb {K}$
is non-Archimedean. In this case, we only need to partition
$\mathbb {K}$
is non-Archimedean. In this case, we only need to partition
![]() $[N]$
and not
$[N]$
and not
![]() $[N_0]$
. Such a partition was given in the proof of Theorem 6.41. In fact, choosing
$[N_0]$
. Such a partition was given in the proof of Theorem 6.41. In fact, choosing
![]() $\ell \gg 1$
such that
$\ell \gg 1$
such that
![]() $q^{-\ell } \simeq \delta ^M$
and setting
$q^{-\ell } \simeq \delta ^M$
and setting
![]() $N = q^n$
so that
$N = q^n$
so that
![]() $N' = q^{n-\ell }$
, we have
$N' = q^{n-\ell }$
, we have
 $$ \begin{align*} [N] \ = \ B_{q^{n}}(0) \ = \ \bigcup_{y \in {\mathcal F}} B_{q^{n -\ell}}(y), \end{align*} $$
$$ \begin{align*} [N] \ = \ B_{q^{n}}(0) \ = \ \bigcup_{y \in {\mathcal F}} B_{q^{n -\ell}}(y), \end{align*} $$
which gives a partition of
![]() $[N]$
where
$[N]$
where
![]() ${\mathcal F} = \{ y = \sum _{j=0}^{\ell -1} y_j \pi ^{-n + j} : y_j \in o_{\mathbb {K}}/m_{\mathbb {K}} \}$
. Note
${\mathcal F} = \{ y = \sum _{j=0}^{\ell -1} y_j \pi ^{-n + j} : y_j \in o_{\mathbb {K}}/m_{\mathbb {K}} \}$
. Note
![]() $\# {\mathcal F} = q^{\ell }$
so that
$\# {\mathcal F} = q^{\ell }$
so that
![]() $\# {\mathcal F} \simeq \delta ^{-M}$
. Hence,
$\# {\mathcal F} \simeq \delta ^{-M}$
. Hence,
![]() $\Lambda _{{\mathcal P}; N}(f_0,\varphi _{N_1}*f_1, \ldots , f_m) =$
$\Lambda _{{\mathcal P}; N}(f_0,\varphi _{N_1}*f_1, \ldots , f_m) =$
 $$ \begin{align*}\frac{1}{N_0 N} \sum_{y_0 \in {\mathcal F}} \int_{\mathbb{K}} \int_{B_{q^{n-\ell}}(y_0)} f_0(x) \varphi_{N_1} * f_1 (x - P_1(y)) \prod_{i=2}^m f_i(x - P_i(y)) d\mu(y) d\mu(x). \end{align*} $$
$$ \begin{align*}\frac{1}{N_0 N} \sum_{y_0 \in {\mathcal F}} \int_{\mathbb{K}} \int_{B_{q^{n-\ell}}(y_0)} f_0(x) \varphi_{N_1} * f_1 (x - P_1(y)) \prod_{i=2}^m f_i(x - P_i(y)) d\mu(y) d\mu(x). \end{align*} $$
We observe that
![]() $\varphi _{N_1} * f_1 (x - P_1(y)) = \varphi _{N_1}* f_1(x - P_1(y_0))$
for any
$\varphi _{N_1} * f_1 (x - P_1(y)) = \varphi _{N_1}* f_1(x - P_1(y_0))$
for any
![]() $y \in B_{q^{n-\ell }}(y_0)$
by the non-Archimedean nature of
$y \in B_{q^{n-\ell }}(y_0)$
by the non-Archimedean nature of
![]() $\mathbb {K}$
, if M is chosen large enough depending on
$\mathbb {K}$
, if M is chosen large enough depending on
![]() $P_1$
. Hence, by the pigeonhole principle, we can find a
$P_1$
. Hence, by the pigeonhole principle, we can find a
![]() $y_0 \in {\mathcal F}$
such that
$y_0 \in {\mathcal F}$
such that
 $$ \begin{align*}\Big| \frac{1}{N_0 N'} \int_{\mathbb{K}} \int_{B_{q^{n-\ell}}(y_0)} f_0(x) \varphi_{N_1} * f_1 (x - P_1(y_0)) \prod_{i=2}^m f_i(x - P_i(y)) d\mu(y) d\mu(x) \Big| \gtrsim \delta. \end{align*} $$
$$ \begin{align*}\Big| \frac{1}{N_0 N'} \int_{\mathbb{K}} \int_{B_{q^{n-\ell}}(y_0)} f_0(x) \varphi_{N_1} * f_1 (x - P_1(y_0)) \prod_{i=2}^m f_i(x - P_i(y)) d\mu(y) d\mu(x) \Big| \gtrsim \delta. \end{align*} $$
Changing variables
![]() $y \to y_0 + y$
allows us to write the above as
$y \to y_0 + y$
allows us to write the above as
 $$ \begin{align*}\Lambda_{{\mathcal P}', N'}(f_0^{\prime}, f_2^{\prime},\ldots, f_m^{\prime}) \ = \frac{1}{N_0} \int_{\mathbb{K}^2} f_0^{\prime}(x) \prod_{j=2}^m f_j^{\prime}(x - P_j^{\prime}(y)) d\mu_{[N']}(y) d\mu(x), \end{align*} $$
$$ \begin{align*}\Lambda_{{\mathcal P}', N'}(f_0^{\prime}, f_2^{\prime},\ldots, f_m^{\prime}) \ = \frac{1}{N_0} \int_{\mathbb{K}^2} f_0^{\prime}(x) \prod_{j=2}^m f_j^{\prime}(x - P_j^{\prime}(y)) d\mu_{[N']}(y) d\mu(x), \end{align*} $$
with
![]() $P_j^{\prime }(y) = \ P_j(y_0 + y) - P_j(y_0)$
,
$P_j^{\prime }(y) = \ P_j(y_0 + y) - P_j(y_0)$
,
![]() $f_0^{\prime }(x) \ = \ f_0(x) \varphi _{N_1}*f_1(x - P_1(y_0))$
and
$f_0^{\prime }(x) \ = \ f_0(x) \varphi _{N_1}*f_1(x - P_1(y_0))$
and
![]() $f_j^{\prime }(x) = f_j (x + P_j(y_0))$
. Note that each
$f_j^{\prime }(x) = f_j (x + P_j(y_0))$
. Note that each
![]() $f_j^{\prime }$
is supported in a fix dilate of I. In order to apply Theorem 6.1, we require
$f_j^{\prime }$
is supported in a fix dilate of I. In order to apply Theorem 6.1, we require
![]() $N' \simeq \delta ^M N \ge 1$
and here is where the condition
$N' \simeq \delta ^M N \ge 1$
and here is where the condition
![]() $N \gtrsim \delta ^{-O_{\mathcal P}(1)}$
is needed. Therefore, Theorem 6.1 implies that
$N \gtrsim \delta ^{-O_{\mathcal P}(1)}$
is needed. Therefore, Theorem 6.1 implies that
The equality of
![]() $L^1$
norms follows from the change of variables
$L^1$
norms follows from the change of variables
![]() $x \to x + P_2(y_0)$
. This completes the proof of Equation (6.4) for
$x \to x + P_2(y_0)$
. This completes the proof of Equation (6.4) for
![]() $j=2$
when
$j=2$
when
![]() $\mathbb {K}$
is non-Archimedean since
$\mathbb {K}$
is non-Archimedean since
![]() $\mu _{[N_2]} = \varphi _{N_2}$
.
$\mu _{[N_2]} = \varphi _{N_2}$
.
We now turn to the Archimedian case, when
![]() $\mathbb {K} = {\mathbb R}$
or when
$\mathbb {K} = {\mathbb R}$
or when
![]() $\mathbb {K}={\mathbb C}$
. Here, we argue as in Step 1 and establish the version of Equation (7.4) for the function
$\mathbb {K}={\mathbb C}$
. Here, we argue as in Step 1 and establish the version of Equation (7.4) for the function
![]() $f_2$
. More precisely, writing
$f_2$
. More precisely, writing
the argument in Step 1 shows that Equation (7.2) implies
This inequality allows us to reduce matters to showing that Equation (7.2) implies
![]() $N_0^{-1}\|\mu _{[N_2]}*f_2\|_{L^1(\mathbb {K})} \gtrsim \delta ^{O(1)}$
since then (7.9) would imply
$N_0^{-1}\|\mu _{[N_2]}*f_2\|_{L^1(\mathbb {K})} \gtrsim \delta ^{O(1)}$
since then (7.9) would imply
establishing (7.3) for
![]() $j=2$
.
$j=2$
.
We give the details when
![]() $\mathbb {K} = {\mathbb C}$
since there are additional technical difficulties alluded to above. The case
$\mathbb {K} = {\mathbb C}$
since there are additional technical difficulties alluded to above. The case
![]() ${\mathbb R}$
is easier. Given a large, general interval
${\mathbb R}$
is easier. Given a large, general interval
![]() ${\mathcal I}$
in
${\mathcal I}$
in
![]() ${\mathbb C}$
(that is,
${\mathbb C}$
(that is,
![]() ${\mathcal I}$
is a disc with large radius R), we can clearly find a mesh of
${\mathcal I}$
is a disc with large radius R), we can clearly find a mesh of
![]() $K\simeq \delta ^{-M}$
disjoint squares
$K\simeq \delta ^{-M}$
disjoint squares ![]() of side length
of side length
![]() $\delta ^{M/2} R$
which sit inside
$\delta ^{M/2} R$
which sit inside
![]() ${\mathcal I}$
such that
${\mathcal I}$
such that ![]() . We fix such a mesh of squares
. We fix such a mesh of squares ![]() for
for
![]() $[N]$
and a mesh of squares
$[N]$
and a mesh of squares ![]() for
for
![]() $[N_0]$
so that
$[N_0]$
so that

Since
![]() $|\Lambda _{{\mathcal P}; N}(f_0, \varphi _{N_1}*f_1, \ldots , f_m)| \gtrsim \delta $
by Equation (7.4) and since the number of terms in each sum above is about
$|\Lambda _{{\mathcal P}; N}(f_0, \varphi _{N_1}*f_1, \ldots , f_m)| \gtrsim \delta $
by Equation (7.4) and since the number of terms in each sum above is about
![]() $\delta ^{-M}$
, the pigeonhole principle gives us a square
$\delta ^{-M}$
, the pigeonhole principle gives us a square
![]() $T_0$
in
$T_0$
in
![]() $[N_0]$
and a square
$[N_0]$
and a square
![]() $S_0$
in
$S_0$
in
![]() $[N]$
such that
$[N]$
such that
 $$ \begin{align*}\Big| \frac{1}{N_0^{\prime} N'} \int_{T_0} \int_{S_0} f_0(x) f_0(x) \varphi_{N_1}*f_1(x - P_1(y)) \prod_{i=2}^m f_i(x - P_i(y)) d\mu(x) d\mu(y) \Big| \gtrsim \delta. \end{align*} $$
$$ \begin{align*}\Big| \frac{1}{N_0^{\prime} N'} \int_{T_0} \int_{S_0} f_0(x) f_0(x) \varphi_{N_1}*f_1(x - P_1(y)) \prod_{i=2}^m f_i(x - P_i(y)) d\mu(x) d\mu(y) \Big| \gtrsim \delta. \end{align*} $$
Write
![]() $[N']_{sq} = \{ z \in {\mathbb C}: |z |_{\infty } \le \sqrt {N'}\}$
, where
$[N']_{sq} = \{ z \in {\mathbb C}: |z |_{\infty } \le \sqrt {N'}\}$
, where
![]() $|z|_{\infty } = \max (|x|, |y|)$
for
$|z|_{\infty } = \max (|x|, |y|)$
for
![]() $z = x+iy$
. Hence,
$z = x+iy$
. Hence,
![]() $S_0 = y_0 + [N']_{sq}$
for some
$S_0 = y_0 + [N']_{sq}$
for some
![]() $y_0 \in [N]$
. For
$y_0 \in [N]$
. For
![]() $z \in S_0$
, we have
$z \in S_0$
, we have
![]() $z = y_0 + y$
for some
$z = y_0 + y$
for some
![]() $y\in [N']_{sq}$
and so by the mean value theorem and the 1-boundedness of
$y\in [N']_{sq}$
and so by the mean value theorem and the 1-boundedness of
![]() $f_1$
,
$f_1$
,
 $$ \begin{align*} &|\varphi_{N_1}* f_1 (x - P_1(y_0 + y)) - \varphi_{N_1}*f_1(x - P_1(y_0))| \\ &\le \ \sqrt{\frac{(N')^{\mathrm{Deg}P_1}}{N_1}} \int_{{\mathbb C}} \|(\nabla \varphi)_{N_1}(z)\| d\mu(z) \ \lesssim_{\varphi} \ \delta^{(M\mathrm{Deg}P_1 - C_1)/2}, \end{align*} $$
$$ \begin{align*} &|\varphi_{N_1}* f_1 (x - P_1(y_0 + y)) - \varphi_{N_1}*f_1(x - P_1(y_0))| \\ &\le \ \sqrt{\frac{(N')^{\mathrm{Deg}P_1}}{N_1}} \int_{{\mathbb C}} \|(\nabla \varphi)_{N_1}(z)\| d\mu(z) \ \lesssim_{\varphi} \ \delta^{(M\mathrm{Deg}P_1 - C_1)/2}, \end{align*} $$
where
![]() $N_1 = \delta ^{C_1} N^{\mathrm {Deg}P_1}$
. Ensuring that
$N_1 = \delta ^{C_1} N^{\mathrm {Deg}P_1}$
. Ensuring that
![]() $M \deg {P_1} - C_1 \ge 4$
, we see that
$M \deg {P_1} - C_1 \ge 4$
, we see that
 $$ \begin{align*}\Big| \frac{1}{N_0^{\prime} N'} \int_{T_0} \int_{[N']_{sq}} f_0(x) \varphi_{N_1}*f_1(x - P_1(y_0)) \prod_{i=2}^m f_i^t(x - P_i^{\prime}(y)) d\mu(x) d\mu(y) \Big| \gtrsim \delta, \end{align*} $$
$$ \begin{align*}\Big| \frac{1}{N_0^{\prime} N'} \int_{T_0} \int_{[N']_{sq}} f_0(x) \varphi_{N_1}*f_1(x - P_1(y_0)) \prod_{i=2}^m f_i^t(x - P_i^{\prime}(y)) d\mu(x) d\mu(y) \Big| \gtrsim \delta, \end{align*} $$
where
![]() $P_i^{\prime }(y) = P_i(y_0 + y) - P_i(y_0)$
and
$P_i^{\prime }(y) = P_i(y_0 + y) - P_i(y_0)$
and
![]() $f_i^t(x) = f_i(x + P_i(y_0))$
. For an appropriate interval
$f_i^t(x) = f_i(x + P_i(y_0))$
. For an appropriate interval
![]() $I'$
containing
$I'$
containing
![]() $T_0$
with measure
$T_0$
with measure
![]() $\simeq N_0^{\prime }$
, we can write the above inequality as
$\simeq N_0^{\prime }$
, we can write the above inequality as
![]() $|\Lambda _{{\mathcal P}'; N'}(f_0^{\prime }, f_2^{\prime }, \ldots , f_m^{\prime })| \gtrsim \delta $
, where
$|\Lambda _{{\mathcal P}'; N'}(f_0^{\prime }, f_2^{\prime }, \ldots , f_m^{\prime })| \gtrsim \delta $
, where
![]() ${\mathcal P}' = \{P_2^{\prime },\ldots , P_m^{\prime }\}$
,
${\mathcal P}' = \{P_2^{\prime },\ldots , P_m^{\prime }\}$
, ![]() and
and ![]() for
for ![]() . Here,
. Here,
 $$ \begin{align*}\Lambda_{{\mathcal P}'; N'}(f_0^{\prime},\ldots, f_m^{\prime}) = \frac{1}{N_0^{\prime}} \iint_{{\mathbb C}^2} f_0^{\prime}(x) \prod_{i=2}^m f_i^{\prime}(x-P_i^{\prime}(y)) d\mu_{[N']_{sq}}(y) d\mu(x). \end{align*} $$
$$ \begin{align*}\Lambda_{{\mathcal P}'; N'}(f_0^{\prime},\ldots, f_m^{\prime}) = \frac{1}{N_0^{\prime}} \iint_{{\mathbb C}^2} f_0^{\prime}(x) \prod_{i=2}^m f_i^{\prime}(x-P_i^{\prime}(y)) d\mu_{[N']_{sq}}(y) d\mu(x). \end{align*} $$
Again, in order to apply Theorem 6.1, we need
![]() $N' = \delta ^M N \ge 1$
which holds provided
$N' = \delta ^M N \ge 1$
which holds provided
![]() $N \gtrsim \delta ^{-O_{\mathcal P}(1)}$
. Therefore, by Theorem 6.1 (see the remark following the statement of Theorem 6.1), we conclude that
$N \gtrsim \delta ^{-O_{\mathcal P}(1)}$
. Therefore, by Theorem 6.1 (see the remark following the statement of Theorem 6.1), we conclude that
for some
![]() $N_2\simeq \delta ^{C_2+M\deg (P_2)}N^{\deg (P_2)}$
. The function
$N_2\simeq \delta ^{C_2+M\deg (P_2)}N^{\deg (P_2)}$
. The function
![]() $\mu _{[N_2]}*f_2^{\prime }$
is supported on an interval
$\mu _{[N_2]}*f_2^{\prime }$
is supported on an interval
![]() $I"\supseteq I'$
such that
$I"\supseteq I'$
such that
![]() $\mu (I"\setminus I') \lesssim N_2$
. Furthermore, we can find an interval
$\mu (I"\setminus I') \lesssim N_2$
. Furthermore, we can find an interval
![]() $I"'\subseteq I'$
so that
$I"'\subseteq I'$
so that
![]() $\mu (I'\setminus I"') \lesssim N_2$
and for
$\mu (I'\setminus I"') \lesssim N_2$
and for
![]() $x\in I"'$
, we have
$x\in I"'$
, we have ![]() for all
for all
![]() $u \in [N_2]_{sq}$
. Hence,
$u \in [N_2]_{sq}$
. Hence,
 $$ \begin{align*}\delta^{O(1)} \lesssim \frac{1}{N_0^{\prime}} \int_{I"'} \Big| \int_{\mathbb C} f_2(x+P_2(y_0) - u) d\mu_{[N_2]_{sq}}(u) \Big| d\mu(x) \ + \ O(N_2 (N_0^{\prime})^{-1}), \end{align*} $$
$$ \begin{align*}\delta^{O(1)} \lesssim \frac{1}{N_0^{\prime}} \int_{I"'} \Big| \int_{\mathbb C} f_2(x+P_2(y_0) - u) d\mu_{[N_2]_{sq}}(u) \Big| d\mu(x) \ + \ O(N_2 (N_0^{\prime})^{-1}), \end{align*} $$
where
![]() $N_2/N_0^{\prime } \lesssim \delta ^{M(\deg {P_2} - 1)}$
and
$N_2/N_0^{\prime } \lesssim \delta ^{M(\deg {P_2} - 1)}$
and
![]() $\deg {P_2} -1 \ge 1$
. Hence, for
$\deg {P_2} -1 \ge 1$
. Hence, for
![]() $M\gg 1$
sufficiently large, we conclude that
$M\gg 1$
sufficiently large, we conclude that
 $$ \begin{align} \delta^{O(1)} \lesssim \frac{1}{N_0^{\prime}} \int_{I"'} \Big| \int_{\mathbb C} f_2(x+P_2(y_0) - u) d\mu_{[N_2]_{sq}}(u) \Big| d\mu(x) \lesssim N_0^{-1} \|\mu_{[N_2]_{sq}} * f_2 \|_{L^1({\mathbb C})}. \end{align} $$
$$ \begin{align} \delta^{O(1)} \lesssim \frac{1}{N_0^{\prime}} \int_{I"'} \Big| \int_{\mathbb C} f_2(x+P_2(y_0) - u) d\mu_{[N_2]_{sq}}(u) \Big| d\mu(x) \lesssim N_0^{-1} \|\mu_{[N_2]_{sq}} * f_2 \|_{L^1({\mathbb C})}. \end{align} $$
In the final inequality, we promoted the integration in x to all of
![]() ${\mathbb C}$
and changed variables
${\mathbb C}$
and changed variables
![]() $x \to x + P_2(y_0)$
. Hence, we have shown that Equation (7.2) implies
$x \to x + P_2(y_0)$
. Hence, we have shown that Equation (7.2) implies
![]() $N_0^{-1}\|\mu _{[N_2]_{sq}}*f_2\|_{L^1({\mathbb C})} \gtrsim \delta ^{O(1)}$
. Since Equation (7.2) holds with
$N_0^{-1}\|\mu _{[N_2]_{sq}}*f_2\|_{L^1({\mathbb C})} \gtrsim \delta ^{O(1)}$
. Since Equation (7.2) holds with
![]() $f_2$
replaced by
$f_2$
replaced by
![]() $\varphi _{N_2}*f_2$
(this is Equation (7.9)), we see that
$\varphi _{N_2}*f_2$
(this is Equation (7.9)), we see that
establishing Equation (7.3) for
![]() $j=2$
. Now, we can proceed inductively and obtain Equation (7.3) for all
$j=2$
. Now, we can proceed inductively and obtain Equation (7.3) for all ![]() .
.
7.1 Multilinear functions and their duals
Recall the multilinear form
 $$ \begin{align*}\Lambda_{{\mathcal P}; N}(f_0, f_1, \ldots, f_m) = \frac{1}{N_0} \iint_{\mathbb{K}^2} f_0(x) \prod_{i=1}^m f_i(x - P_i(y)) d\mu_{[N]}(y) d\mu(x). \end{align*} $$
$$ \begin{align*}\Lambda_{{\mathcal P}; N}(f_0, f_1, \ldots, f_m) = \frac{1}{N_0} \iint_{\mathbb{K}^2} f_0(x) \prod_{i=1}^m f_i(x - P_i(y)) d\mu_{[N]}(y) d\mu(x). \end{align*} $$
We define the multilinear function
 $$ \begin{align*} A_N^{\mathcal P}(f_1,\ldots, f_m)(x):=\int_{\mathbb{K}}\prod_{i=1}^mf_{i}(x-P_i(y))d\mu_{[N]}(y) \end{align*} $$
$$ \begin{align*} A_N^{\mathcal P}(f_1,\ldots, f_m)(x):=\int_{\mathbb{K}}\prod_{i=1}^mf_{i}(x-P_i(y))d\mu_{[N]}(y) \end{align*} $$
so that
![]() $\Lambda _{{\mathcal P}; N}$
can be written as a pairing of
$\Lambda _{{\mathcal P}; N}$
can be written as a pairing of
![]() $A_N^{\mathcal P}$
with
$A_N^{\mathcal P}$
with
![]() $f_0$
,
$f_0$
,
where
![]() $\langle f, g\rangle = \int _{\mathbb {K}} f(x) g(x) d\mu (x)$
. By duality, we have
$\langle f, g\rangle = \int _{\mathbb {K}} f(x) g(x) d\mu (x)$
. By duality, we have
where
 $$ \begin{align*} (A_N^{\mathcal P})^{*j}(f_1,\ldots, f_0, \ldots, f_m) (x) := \int_{\mathbb{K}}\prod_{\substack{i=1\\i\neq j}}^mf_{i}(x-P_i(y)+P_j(y))f_0(x+P_j(y))d\mu_{[N]}(y). \end{align*} $$
$$ \begin{align*} (A_N^{\mathcal P})^{*j}(f_1,\ldots, f_0, \ldots, f_m) (x) := \int_{\mathbb{K}}\prod_{\substack{i=1\\i\neq j}}^mf_{i}(x-P_i(y)+P_j(y))f_0(x+P_j(y))d\mu_{[N]}(y). \end{align*} $$
Lemma 7.11 (Application of Hahn–Banach).
Let
![]() $A,B> 0$
, let
$A,B> 0$
, let
![]() $I\subset \mathbb {K}$
be an interval, and let G be an element of
$I\subset \mathbb {K}$
be an interval, and let G be an element of
![]() $L^2(I)$
. Let
$L^2(I)$
. Let
![]() $\Phi $
be a family of vectors in
$\Phi $
be a family of vectors in
![]() $L^2(I)$
, and assume the following inverse theorem: Whenever
$L^2(I)$
, and assume the following inverse theorem: Whenever
![]() $f \in L^2(I)$
is such that
$f \in L^2(I)$
is such that
![]() $\|f\|_{L^\infty (I)} \leq 1$
and
$\|f\|_{L^\infty (I)} \leq 1$
and
![]() $|\langle f, G \rangle |> A$
, then
$|\langle f, G \rangle |> A$
, then
![]() $|\langle f, \phi \rangle |> B$
for some
$|\langle f, \phi \rangle |> B$
for some
![]() $\phi \in \Phi $
. Then G lies in the closed convex hull of
$\phi \in \Phi $
. Then G lies in the closed convex hull of
Proof. By way of contradiction, suppose that G does not lie in
![]() $W = \overline {\mathrm {conv} V}^{\|\cdot \|_{L^2(I)}}$
. From the Hahn–Banach theorem, we can find a continuous linear functional
$W = \overline {\mathrm {conv} V}^{\|\cdot \|_{L^2(I)}}$
. From the Hahn–Banach theorem, we can find a continuous linear functional
![]() $\Lambda $
of
$\Lambda $
of
![]() $L^2(I)$
which separates G from W; that is, there is a
$L^2(I)$
which separates G from W; that is, there is a
![]() $C \in {\mathbb R}$
such that
$C \in {\mathbb R}$
such that
![]() $\operatorname {\mathrm {Re}}\Lambda (h) \le C < \operatorname {\mathrm {Re}} \Lambda (G)$
for all
$\operatorname {\mathrm {Re}}\Lambda (h) \le C < \operatorname {\mathrm {Re}} \Lambda (G)$
for all
![]() $h \in W$
. Scaling
$h \in W$
. Scaling
![]() $\Lambda $
allows us to change the constant C, so we can choose
$\Lambda $
allows us to change the constant C, so we can choose
![]() $\Lambda $
such that
$\Lambda $
such that
![]() $C=A$
is in the statement of the lemma. Since W is balanced, we see that
$C=A$
is in the statement of the lemma. Since W is balanced, we see that
![]() $|\Lambda (h)| \le A < \operatorname {\mathrm {Re}} \Lambda (G)$
for all
$|\Lambda (h)| \le A < \operatorname {\mathrm {Re}} \Lambda (G)$
for all
![]() $h \in W$
. By the Riesz representation theorem, there is an
$h \in W$
. By the Riesz representation theorem, there is an
![]() $f \in L^2(I)$
which represents
$f \in L^2(I)$
which represents
![]() $\Lambda $
so that
$\Lambda $
so that
![]() $|\langle f, h\rangle |\le A < \mathrm {Re} \langle f, G \rangle $
for all
$|\langle f, h\rangle |\le A < \mathrm {Re} \langle f, G \rangle $
for all
![]() $h\in V$
. This implies that
$h\in V$
. This implies that
for all
![]() $\phi \in \Phi $
and that
$\phi \in \Phi $
and that
contradicting the hypothesis of the lemma. This completes the proof of the lemma.
Corollary 7.13 (Structure of dual functions).
Let
![]() $N\ge 1$
be a scale,
$N\ge 1$
be a scale,
![]() $m\in \mathbb Z_+$
and
$m\in \mathbb Z_+$
and
![]() $0<\delta \le 1$
be given. Let
$0<\delta \le 1$
be given. Let
![]() ${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of polynomials such that
${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of polynomials such that
![]() $1\le \deg {P_1}<\ldots <\deg {P_m}$
. Let
$1\le \deg {P_1}<\ldots <\deg {P_m}$
. Let
![]() $f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
$f_0, f_1,\ldots , f_m\in L^0(\mathbb {K})$
be
![]() $1$
-bounded functions supported on an interval of measure
$1$
-bounded functions supported on an interval of measure
![]() $N_0 = N^{\deg (P_m)}$
. Then for every
$N_0 = N^{\deg (P_m)}$
. Then for every ![]() , provided
, provided
![]() $N\gtrsim \delta ^{-O_{\mathcal P}(1)}$
, there exist a decomposition
$N\gtrsim \delta ^{-O_{\mathcal P}(1)}$
, there exist a decomposition
where
![]() $H_j \in L^2(\mathbb {K})$
has Fourier transform supported in
$H_j \in L^2(\mathbb {K})$
has Fourier transform supported in
![]() $[(N_j)^{-1}]$
, where
$[(N_j)^{-1}]$
, where
![]() $N_j \simeq \delta ^{C_j} N^{\deg {P_j}}$
and
$N_j \simeq \delta ^{C_j} N^{\deg {P_j}}$
and
![]() $C_j$
is as in Theorem 7.1, and obeys the bounds
$C_j$
is as in Theorem 7.1, and obeys the bounds
The error term
![]() $E_j\in L^1(\mathbb {K})$
obeys the bound
$E_j\in L^1(\mathbb {K})$
obeys the bound
Proof. Fix ![]() , let
, let
![]() $I_0:=\operatorname {\mathrm {supp}}{(A_N^{\mathcal P})^{*j}(f_1,\ldots , f_0, \ldots , f_m)}$
and recall that
$I_0:=\operatorname {\mathrm {supp}}{(A_N^{\mathcal P})^{*j}(f_1,\ldots , f_0, \ldots , f_m)}$
and recall that
![]() $N_0= N^{\deg (P_m)}$
. By translation invariance we may assume
$N_0= N^{\deg (P_m)}$
. By translation invariance we may assume
![]() $\operatorname {\mathrm {supp}}{f_j}\subseteq [N_0]$
for all
$\operatorname {\mathrm {supp}}{f_j}\subseteq [N_0]$
for all ![]() , and that
, and that
![]() $I_0:=[O(N_0)]$
. If there exists
$I_0:=[O(N_0)]$
. If there exists
![]() $f\in L^{\infty }(I_0)$
with
$f\in L^{\infty }(I_0)$
with
![]() $\|f\|_{L^{\infty }(I_0)}\le 1$
such that
$\|f\|_{L^{\infty }(I_0)}\le 1$
such that
then proceeding as in the proof of Theorem 7.1 we may conclude that
where
![]() $N_i\simeq \delta ^{C_i} N^{\deg (P_i)}$
for
$N_i\simeq \delta ^{C_i} N^{\deg (P_i)}$
for ![]() . This implies that there exists a 1-bounded
. This implies that there exists a 1-bounded
![]() $F\in L^2(\mathbb {K})$
with
$F\in L^2(\mathbb {K})$
with
![]() $\|F\|_{L^1(\mathbb {K})} \le N_0$
such that
$\|F\|_{L^1(\mathbb {K})} \le N_0$
such that
![]() $\operatorname {\mathrm {supp}}{\widehat {F}}\subseteq [N_j^{-1}]$
and
$\operatorname {\mathrm {supp}}{\widehat {F}}\subseteq [N_j^{-1}]$
and
If fact, we can take
where
![]() ${\tilde {\varphi }}(x) = \varphi (-x)$
. Let
${\tilde {\varphi }}(x) = \varphi (-x)$
. Let
![]() $\Psi $
denote the collection of all 1-bounded
$\Psi $
denote the collection of all 1-bounded
![]() $F\in L^2(\mathbb {K})$
with
$F\in L^2(\mathbb {K})$
with
![]() $\operatorname {\mathrm {supp}}{\widehat {F}}\subseteq [N_j^{-1}]$
and
$\operatorname {\mathrm {supp}}{\widehat {F}}\subseteq [N_j^{-1}]$
and
![]() $\|F\|_{L^1(\mathbb {K})}\le N_0$
. Invoking Lemma 7.11 with
$\|F\|_{L^1(\mathbb {K})}\le N_0$
. Invoking Lemma 7.11 with
![]() $A=\delta N_0/4$
and
$A=\delta N_0/4$
and
![]() $B = c_m \delta N_0$
and the set
$B = c_m \delta N_0$
and the set ![]() , we obtain a decomposition
, we obtain a decomposition
 $$ \begin{align} (A_N^{\mathcal P})^{*j}(f_1,\ldots, f_{j-1}, f_0, f_{j+1}, \ldots, f_m) = \sum_{l=1}^{\infty}c_l\phi_l+E(1)+E(2), \end{align} $$
$$ \begin{align} (A_N^{\mathcal P})^{*j}(f_1,\ldots, f_{j-1}, f_0, f_{j+1}, \ldots, f_m) = \sum_{l=1}^{\infty}c_l\phi_l+E(1)+E(2), \end{align} $$
with the following properties:
-
(i) for each
 $l\in \mathbb Z_+$
, we have that
$l\in \mathbb Z_+$
, we have that  ,
,
 $F_l \in \Psi $
and
$F_l \in \Psi $
and
 $\lambda _l\in \mathbb C$
such that
$\lambda _l\in \mathbb C$
such that
 $|\lambda _l|\lesssim _m 1$
;
$|\lambda _l|\lesssim _m 1$
; -
(ii) the coefficients
 $c_l$
are nonnegative with
$c_l$
are nonnegative with
 $\sum _{l=1}^{\infty }c_l\le 1$
, and all but finitely
$\sum _{l=1}^{\infty }c_l\le 1$
, and all but finitely
 $c_l$
vanish;
$c_l$
vanish; -
(iii) the error term
 $E(1)\in L^1(I_0)$
satisfies
$E(1)\in L^1(I_0)$
satisfies
 $\|E(1)\|_{L^1(I_0)} \leq \delta N_0/2$
;
$\|E(1)\|_{L^1(I_0)} \leq \delta N_0/2$
; -
(iv) the error term
 $E(2)\in L^2(I_0)$
satisfies
$E(2)\in L^2(I_0)$
satisfies
 $\|E(2)\|_{L^2(I_0)} \leq \delta $
.
$\|E(2)\|_{L^2(I_0)} \leq \delta $
.
The latter error term arises as a consequence of the fact that one is working with the closed convex hull instead of the convex hull. In fact, its
![]() $L^2(I_0)$
norm can be made arbitrarily small, but
$L^2(I_0)$
norm can be made arbitrarily small, but
![]() $\delta $
will suffice for our purposes.
$\delta $
will suffice for our purposes.
Grouping together terms in the decomposition (7.19), we have
where

 $$ \begin{align*} \|H_j^{\prime}\|_{L^{\infty}(\mathbb{K})} \le \sup_{l\in\mathbb N} \|F_l\|_{L^{\infty}(\mathbb{K})} \sum_{l=1}^{\infty} c_l |\lambda_l| \lesssim_m 1. \end{align*} $$
$$ \begin{align*} \|H_j^{\prime}\|_{L^{\infty}(\mathbb{K})} \le \sup_{l\in\mathbb N} \|F_l\|_{L^{\infty}(\mathbb{K})} \sum_{l=1}^{\infty} c_l |\lambda_l| \lesssim_m 1. \end{align*} $$
Also,
![]() $E_j^{\prime } = E(1) + E(2)$
satisfies
$E_j^{\prime } = E(1) + E(2)$
satisfies
![]() $\|E_j^{\prime }\|_{L^1(I_0)} \le \delta N_0$
by (iii) and (iv) above since by the Cauchy–Schwarz inequality, we have
$\|E_j^{\prime }\|_{L^1(I_0)} \le \delta N_0$
by (iii) and (iv) above since by the Cauchy–Schwarz inequality, we have
![]() $\|E(2)\|_{L^1(I_0)} \leq \delta N_0^{1/2}$
.
$\|E(2)\|_{L^1(I_0)} \leq \delta N_0^{1/2}$
.
We note that the function
![]() $F(x) = \sum _{i=1}^{\infty } c_i \lambda _i F_i (x)$
is Fourier supported in the interval
$F(x) = \sum _{i=1}^{\infty } c_i \lambda _i F_i (x)$
is Fourier supported in the interval
![]() $[N_j^{-1}]$
.
$[N_j^{-1}]$
.
When
![]() $\mathbb {K}$
is non-Archimedean,
$\mathbb {K}$
is non-Archimedean, ![]() and so the Fourier transform of
and so the Fourier transform of
![]() $H_j^{\prime }$
is supported in
$H_j^{\prime }$
is supported in
![]() $[N_j^{-1}]$
. This verifies Equation (7.15) in this case and completes the proof when
$[N_j^{-1}]$
. This verifies Equation (7.15) in this case and completes the proof when
![]() $\mathbb {K}$
is non-Archimedean since the decomposition
$\mathbb {K}$
is non-Archimedean since the decomposition
![]() $H_j^{\prime } + E_j^{\prime }$
of
$H_j^{\prime } + E_j^{\prime }$
of
![]() $(A_N^{\mathcal P})^{*j}$
satisfies Equations (7.15) and (7.16).
$(A_N^{\mathcal P})^{*j}$
satisfies Equations (7.15) and (7.16).
Now, suppose
![]() $\mathbb {K}$
is Archimedean. Let
$\mathbb {K}$
is Archimedean. Let
![]() $\psi $
be a Schwartz function such that
$\psi $
be a Schwartz function such that
![]() $\int _{\mathbb {K}}\psi (x)d\mu (x)=1$
and
$\int _{\mathbb {K}}\psi (x)d\mu (x)=1$
and
![]() $\operatorname {\mathrm {supp}}{\widehat {\psi }}\subseteq [2]$
. Let
$\operatorname {\mathrm {supp}}{\widehat {\psi }}\subseteq [2]$
. Let
![]() $M\simeq \delta ^{O(1)} N_0$
and as usual, set
$M\simeq \delta ^{O(1)} N_0$
and as usual, set
![]() $\psi _M(x) = M^{-1} \psi (M^{-1}x)$
when
$\psi _M(x) = M^{-1} \psi (M^{-1}x)$
when
![]() $\mathbb {K} = {\mathbb R}$
and
$\mathbb {K} = {\mathbb R}$
and
![]() $\psi _M(x) = M^{-1}\psi (M^{-1/2} x)$
when
$\psi _M(x) = M^{-1}\psi (M^{-1/2} x)$
when
![]() $\mathbb {K} = {\mathbb C}$
. From the proof of Equation (7.8), we have
$\mathbb {K} = {\mathbb C}$
. From the proof of Equation (7.8), we have
We set ![]() and
and ![]() so that
so that
From Equation (7.20), we see that
![]() $E_j$
satisfies Equation (7.16). The properties
$E_j$
satisfies Equation (7.16). The properties
![]() $\|H_j\|_{L^\infty (\mathbb {K})} \lesssim _m 1$
and
$\|H_j\|_{L^\infty (\mathbb {K})} \lesssim _m 1$
and
![]() $\|H_j\|_{L^1(\mathbb {K})} \lesssim _m N_0$
are still preserved. Moreover,
$\|H_j\|_{L^1(\mathbb {K})} \lesssim _m N_0$
are still preserved. Moreover,
![]() $\operatorname {\mathrm {supp}}{\widehat {H}_j}\subseteq [O(N_j^{-1})]$
since
$\operatorname {\mathrm {supp}}{\widehat {H}_j}\subseteq [O(N_j^{-1})]$
since
The shows that Equation (7.15) holds for
![]() $H_j$
and this completes the proof of the corollary.
$H_j$
and this completes the proof of the corollary.
We will combine Corollary 7.13 and the following
![]() $L^p$
improving bound for polynomial averages to establish the key Sobolev inequality.
$L^p$
improving bound for polynomial averages to establish the key Sobolev inequality.
Lemma 7.21 (
 $L^p$
-improving for polynomial averages).
$L^p$
-improving for polynomial averages).
Let
![]() $Q \in \mathbb {K}[\mathrm {y}]$
with
$Q \in \mathbb {K}[\mathrm {y}]$
with
![]() $\deg (Q) = d$
, and let
$\deg (Q) = d$
, and let
![]() $N\gg _Q 1$
be a large scale. Consider the averaging operator
$N\gg _Q 1$
be a large scale. Consider the averaging operator
For any parameters
![]() $1 < r < s< \infty $
satisfying
$1 < r < s< \infty $
satisfying
![]() $1/s = 1/r - 1/d$
, the following inequality holds:
$1/s = 1/r - 1/d$
, the following inequality holds:
Proof. As our bounds are allowed to depend on Q, we may assume that Q is monic. Let
![]() $\alpha \in \mathbb {K}$
be such that
$\alpha \in \mathbb {K}$
be such that
![]() $|\alpha | = N$
, and change variables
$|\alpha | = N$
, and change variables
![]() $y \to \alpha y$
to write
$y \to \alpha y$
to write
where
![]() $g_{\alpha }(x) = g(\alpha ^d x)$
and
$g_{\alpha }(x) = g(\alpha ^d x)$
and
![]() $Q_{\alpha }(y) = \alpha ^{-d} Q(\alpha y) = y^d + \alpha ^{-1} a_{d-1} y^{d-1} + \ldots +\alpha ^{-d}a_0$
. Hence, the right-hand side above can be written as
$Q_{\alpha }(y) = \alpha ^{-d} Q(\alpha y) = y^d + \alpha ^{-1} a_{d-1} y^{d-1} + \ldots +\alpha ^{-d}a_0$
. Hence, the right-hand side above can be written as
![]() $M^1_{Q_{\alpha }} g_{\alpha }( \alpha ^{-d} x)$
. Since
$M^1_{Q_{\alpha }} g_{\alpha }( \alpha ^{-d} x)$
. Since
![]() $\|g_{\alpha }\|_{L^r(\mathbb {K})} = N^{-d/r} \|g\|_{L^r(\mathbb {K})}$
, we see that matters are reduced to proving Equation (7.22) for
$\|g_{\alpha }\|_{L^r(\mathbb {K})} = N^{-d/r} \|g\|_{L^r(\mathbb {K})}$
, we see that matters are reduced to proving Equation (7.22) for
![]() $N=1$
and
$N=1$
and
![]() $Q = Q_{\alpha }$
with uniform bounds in
$Q = Q_{\alpha }$
with uniform bounds in
![]() $\alpha $
.
$\alpha $
.
The mapping
![]() $y \to Q_{\alpha }(y)$
is d-to-
$y \to Q_{\alpha }(y)$
is d-to-
![]() $1$
, and we can use a generalised change of variables formula to see that
$1$
, and we can use a generalised change of variables formula to see that
when
![]() $N\gg _{Q} 1$
. Hence
$N\gg _{Q} 1$
. Hence
![]() $M^1_{\alpha }$
is controlled by fractional integration, uniformly in
$M^1_{\alpha }$
is controlled by fractional integration, uniformly in
![]() $\alpha $
. When
$\alpha $
. When
![]() $\mathbb {K}$
is Archimedean, such a change of variables formula is well known. Recall that when
$\mathbb {K}$
is Archimedean, such a change of variables formula is well known. Recall that when
![]() $\mathbb {K} = {\mathbb C}$
,
$\mathbb {K} = {\mathbb C}$
,
![]() $|s| = s {\overline {s}}$
is the square of the usual absolute value.
$|s| = s {\overline {s}}$
is the square of the usual absolute value.
When
![]() $\mathbb {K} = {\mathbb Q}_p$
is the p-adic field, such a formula is given in [Reference Evans12]. The argument in [Reference Evans12] generalises to general non-Archimedean fields (when the characteristic, if positive, is larger than d). Alternatively, one can use a construction in [Reference Wright46], valid in any local field and valid for any polynomial Q where
$\mathbb {K} = {\mathbb Q}_p$
is the p-adic field, such a formula is given in [Reference Evans12]. The argument in [Reference Evans12] generalises to general non-Archimedean fields (when the characteristic, if positive, is larger than d). Alternatively, one can use a construction in [Reference Wright46], valid in any local field and valid for any polynomial Q where
![]() $Q'(x)$
does not equal to zero mod
$Q'(x)$
does not equal to zero mod
![]() $m_{\mathbb {K}}$
for any nonzero x (we need the condition on the characteristic of the field for this), in which the unit group
$m_{\mathbb {K}}$
for any nonzero x (we need the condition on the characteristic of the field for this), in which the unit group ![]() is partitioned into
is partitioned into
![]() $J=\mathrm {gcd}(d, q-1)$
open sets and analytic isomorphisms
$J=\mathrm {gcd}(d, q-1)$
open sets and analytic isomorphisms
![]() $\phi _j :D_j \to \phi _j(D_j)$
are constructed such that
$\phi _j :D_j \to \phi _j(D_j)$
are constructed such that
![]() $y = \phi _j(x)$
precisely when
$y = \phi _j(x)$
precisely when
![]() $Q(y) = x$
. For us,
$Q(y) = x$
. For us,
![]() $Q_{\alpha }'(x) \not = 0$
mod
$Q_{\alpha }'(x) \not = 0$
mod
![]() $m_{\mathbb {K}}$
for any nonzero x if
$m_{\mathbb {K}}$
for any nonzero x if
![]() $|\alpha | = N \gg _Q 1$
is sufficiently large.
$|\alpha | = N \gg _Q 1$
is sufficiently large.
By the Hardy–Littlewood–Sobolev inequality (easily seen to be valid over general locally compact topological fields), we have
uniformly in
![]() $\alpha $
whenever
$\alpha $
whenever
![]() $1/s = 1/r - 1/d$
, completing the proof of the lemma.
$1/s = 1/r - 1/d$
, completing the proof of the lemma.
We now come to the proof of Theorem 1.6.
As in the set up for Theorem 7.1, we fix a smooth function
![]() $\varphi $
with compact Fourier support. When
$\varphi $
with compact Fourier support. When
![]() $\mathbb {K}$
is Archimedean, let
$\mathbb {K}$
is Archimedean, let
![]() $\varphi $
be a Schwartz function on
$\varphi $
be a Schwartz function on
![]() $\mathbb {K}$
so that
$\mathbb {K}$
so that
When
![]() $\mathbb {K}={\mathbb R}$
, we set
$\mathbb {K}={\mathbb R}$
, we set
![]() $\varphi _N(x) = N^{-1} \varphi (N^{-1} x)$
for any
$\varphi _N(x) = N^{-1} \varphi (N^{-1} x)$
for any
![]() $N>0$
and when
$N>0$
and when
![]() $\mathbb {K} = {\mathbb C}$
, we set
$\mathbb {K} = {\mathbb C}$
, we set
![]() $\varphi _{N}(z) = N^{-1} \varphi (N^{-1/2} z)$
for any
$\varphi _{N}(z) = N^{-1} \varphi (N^{-1/2} z)$
for any
![]() $N> 0$
. When
$N> 0$
. When
![]() $\mathbb {K}$
is non-Archimedean, we set
$\mathbb {K}$
is non-Archimedean, we set ![]() so that
so that ![]() and we set
and we set ![]() for any scale N. We restate Theorem 1.6 in a more formal, precise way.
for any scale N. We restate Theorem 1.6 in a more formal, precise way.
Theorem 7.23 (A Sobolev inequality for
 $A_N^{\mathcal P}$
).
$A_N^{\mathcal P}$
).
Let
![]() ${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of polynomials such that
${\mathcal P}:=\{P_1,\ldots , P_m\}$
be a collection of polynomials such that
![]() $1\le \deg {P_1}<\ldots <\deg {P_m}$
. Let
$1\le \deg {P_1}<\ldots <\deg {P_m}$
. Let
![]() $N \gg _{\mathcal P} 1$
be a scale,
$N \gg _{\mathcal P} 1$
be a scale,
![]() $m\in \mathbb Z_+$
and
$m\in \mathbb Z_+$
and
![]() $0<\delta \le 1$
be given. Let
$0<\delta \le 1$
be given. Let
![]() $1<p_1,\ldots , p_m<\infty $
satisfying
$1<p_1,\ldots , p_m<\infty $
satisfying
![]() $\frac {1}{p_1}+\ldots +\frac {1}{p_m}=1$
be given. Suppose
$\frac {1}{p_1}+\ldots +\frac {1}{p_m}=1$
be given. Suppose
![]() $N\gtrsim \delta ^{-O_{\mathcal P}(1)}$
. Then for all
$N\gtrsim \delta ^{-O_{\mathcal P}(1)}$
. Then for all
![]() $f_1\in L^{p_1}(\mathbb {K}),\ldots , f_m\in L^{p_m}(\mathbb {K})$
we have
$f_1\in L^{p_1}(\mathbb {K}),\ldots , f_m\in L^{p_m}(\mathbb {K})$
we have
 $$ \begin{align} \|A_N^{\mathcal P}(f_1,\ldots,f_{j-1}, (\delta_0-\varphi_{N_j})*f_j,f_{j+1}\ldots, f_m)\|_{L^1(\mathbb{K})} \lesssim \delta^{1/8} \prod_{i=1}^{m} \|f_i\|_{L^{p_i}(\mathbb{K})}, \end{align} $$
$$ \begin{align} \|A_N^{\mathcal P}(f_1,\ldots,f_{j-1}, (\delta_0-\varphi_{N_j})*f_j,f_{j+1}\ldots, f_m)\|_{L^1(\mathbb{K})} \lesssim \delta^{1/8} \prod_{i=1}^{m} \|f_i\|_{L^{p_i}(\mathbb{K})}, \end{align} $$
where
![]() $N_j \simeq \delta ^{C_j} N^{\deg {P_j}}$
and
$N_j \simeq \delta ^{C_j} N^{\deg {P_j}}$
and
![]() $C_j$
is the parameter from Theorem 7.1. Here,
$C_j$
is the parameter from Theorem 7.1. Here,
![]() $\widehat {\delta _0} \equiv 1$
.
$\widehat {\delta _0} \equiv 1$
.
Remark. The proof of Theorem 7.23 (and its statement) implicitly assumes that
![]() $m\ge 2$
, but there is a version when
$m\ge 2$
, but there is a version when
![]() $m=1$
, which will be given in Section 8 where it is needed.
$m=1$
, which will be given in Section 8 where it is needed.
Proof. We fix ![]() and recall
and recall
![]() $N_j\simeq \delta ^{O(1)}N^{\deg (P_j)}$
. We first prove that for every functions
$N_j\simeq \delta ^{O(1)}N^{\deg (P_j)}$
. We first prove that for every functions
![]() $f_1,\ldots , f_{j-1}, f_{j+1},\ldots , f_{m-1}\in L^{\infty }(\mathbb {K})$
and
$f_1,\ldots , f_{j-1}, f_{j+1},\ldots , f_{m-1}\in L^{\infty }(\mathbb {K})$
and
![]() $f_j, f_m\in L^2(\mathbb {K})$
, we have
$f_j, f_m\in L^2(\mathbb {K})$
, we have
 $$ \begin{align} \begin{split} \|A_N^{\mathcal P}(f_1,\ldots,f_{j-1}, (\delta_0-\varphi_{N_j})*f_j,f_{j+1}\ldots, f_m)\|_{L^1(\mathbb{K})}\\ \lesssim \delta^{1/8} \bigg(\prod_{\substack{i=1\\i\neq j}}^{m-1} \|f_i\|_{L^\infty(\mathbb{K})}\bigg)\|f_j\|_{L^2(\mathbb{K})}\|f_m\|_{L^2(\mathbb{K})}.\qquad \end{split} \end{align} $$
$$ \begin{align} \begin{split} \|A_N^{\mathcal P}(f_1,\ldots,f_{j-1}, (\delta_0-\varphi_{N_j})*f_j,f_{j+1}\ldots, f_m)\|_{L^1(\mathbb{K})}\\ \lesssim \delta^{1/8} \bigg(\prod_{\substack{i=1\\i\neq j}}^{m-1} \|f_i\|_{L^\infty(\mathbb{K})}\bigg)\|f_j\|_{L^2(\mathbb{K})}\|f_m\|_{L^2(\mathbb{K})}.\qquad \end{split} \end{align} $$
Choose
![]() $f_0\in L^{\infty }(\mathbb {K})$
so that
$f_0\in L^{\infty }(\mathbb {K})$
so that
![]() $\|f_0\|_{L^{\infty }(\mathbb {K})}=1$
and
$\|f_0\|_{L^{\infty }(\mathbb {K})}=1$
and
 $$ \begin{align*} \|A_N^{\mathcal P}(f_1,&\ldots,f_{j-1}, (\delta_0-\varphi_{N_j})*f_j,f_{j+1}\ldots, f_m)\|_{L^1(\mathbb{K})}\\ &\simeq |\langle A_N^{\mathcal P}(f_1,\ldots,f_{j-1}, (\delta_0-\varphi_{N_j})*f_j,f_{j+1}\ldots, f_m), f_0\rangle|\\ &=|\langle (\delta_0-\varphi_{N_j})*(A_N^{\mathcal P})^{*j}(f_1,\ldots, f_0, \ldots, f_m), f_j\rangle|. \end{align*} $$
$$ \begin{align*} \|A_N^{\mathcal P}(f_1,&\ldots,f_{j-1}, (\delta_0-\varphi_{N_j})*f_j,f_{j+1}\ldots, f_m)\|_{L^1(\mathbb{K})}\\ &\simeq |\langle A_N^{\mathcal P}(f_1,\ldots,f_{j-1}, (\delta_0-\varphi_{N_j})*f_j,f_{j+1}\ldots, f_m), f_0\rangle|\\ &=|\langle (\delta_0-\varphi_{N_j})*(A_N^{\mathcal P})^{*j}(f_1,\ldots, f_0, \ldots, f_m), f_j\rangle|. \end{align*} $$
By the Cauchy–Schwarz inequality, it will suffice to prove
 $$ \begin{align} \begin{split} \|(\delta_0-\varphi_{N_j})*(A_N^{\mathcal P})^{*j}(f_1,\ldots, f_0, \ldots, f_m)\|_{L^2(\mathbb{K})}\\ \lesssim \delta^{1/8} \|f_0\|_{L^\infty(\mathbb{K})}\bigg(\prod_{\substack{i=1\\i\neq j}}^{m-1} \|f_i\|_{L^\infty(\mathbb{K})}\bigg)\|f_m\|_{L^2(\mathbb{K})}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \|(\delta_0-\varphi_{N_j})*(A_N^{\mathcal P})^{*j}(f_1,\ldots, f_0, \ldots, f_m)\|_{L^2(\mathbb{K})}\\ \lesssim \delta^{1/8} \|f_0\|_{L^\infty(\mathbb{K})}\bigg(\prod_{\substack{i=1\\i\neq j}}^{m-1} \|f_i\|_{L^\infty(\mathbb{K})}\bigg)\|f_m\|_{L^2(\mathbb{K})}. \end{split} \end{align} $$
By multilinear interpolation, the bounds (7.25) imply Equation (7.24) and so the proof of Theorem 7.23 is reduced to establishing Equation (7.26) which will be divided into three steps. In the first two steps, we will assume that
![]() $f_m$
is supported in some interval of measure
$f_m$
is supported in some interval of measure
![]() $N_0$
where
$N_0$
where
![]() $N_0 \simeq N^{\deg (P_m)}$
.
$N_0 \simeq N^{\deg (P_m)}$
.
Step 1
In this step, we will establish the bound
 $$ \begin{align} \begin{split} \|(\delta_0-\varphi_{N_j})*(A_N^{\mathcal P})^{*j}(f_1,\ldots, f_0, \ldots, f_m)\|_{L^2(\mathbb{K})}\quad \\ \lesssim \delta^{1/2}N_0^{1/2} \|f_0\|_{L^\infty(\mathbb{K})}\bigg(\prod_{\substack{i=1\\ i\neq j}}^{m-1} \|f_i\|_{L^\infty(\mathbb{K})}\bigg)\|f_m\|_{L^\infty(\mathbb{K})} \end{split} \end{align} $$
$$ \begin{align} \begin{split} \|(\delta_0-\varphi_{N_j})*(A_N^{\mathcal P})^{*j}(f_1,\ldots, f_0, \ldots, f_m)\|_{L^2(\mathbb{K})}\quad \\ \lesssim \delta^{1/2}N_0^{1/2} \|f_0\|_{L^\infty(\mathbb{K})}\bigg(\prod_{\substack{i=1\\ i\neq j}}^{m-1} \|f_i\|_{L^\infty(\mathbb{K})}\bigg)\|f_m\|_{L^\infty(\mathbb{K})} \end{split} \end{align} $$
under the assumption that
![]() $f_m$
is supported in an interval of measure
$f_m$
is supported in an interval of measure
![]() $N_0$
(when
$N_0$
(when
![]() $\mathbb {K} = {\mathbb C}$
, this implies in particular that
$\mathbb {K} = {\mathbb C}$
, this implies in particular that
![]() $f_m$
is supported in a square with measure about
$f_m$
is supported in a square with measure about
![]() $N_0$
, which in Step 3 will be a helpful observation). When
$N_0$
, which in Step 3 will be a helpful observation). When
![]() $f_m$
has this support condition,
$f_m$
has this support condition,
where ![]() for some interval
for some interval
![]() $I_0$
of measure
$I_0$
of measure
![]() $O(N_0)$
. To prove Equation (7.27), it suffices to assume
$O(N_0)$
. To prove Equation (7.27), it suffices to assume
![]() $\|f_i\|_{L^{\infty }(\mathbb {K})} = 1$
for
$\|f_i\|_{L^{\infty }(\mathbb {K})} = 1$
for
![]() $i=0,1,\ldots , j-1, j+1,\ldots , m$
and so Equation (7.27) takes the form
$i=0,1,\ldots , j-1, j+1,\ldots , m$
and so Equation (7.27) takes the form
We apply the decomposition (7.14) to
![]() $(A_N^{\mathcal P})^{*j}(f_1^{\prime },\ldots , f_0^{\prime }, \ldots , f_m^{\prime })$
to write
$(A_N^{\mathcal P})^{*j}(f_1^{\prime },\ldots , f_0^{\prime }, \ldots , f_m^{\prime })$
to write
where
![]() $H_j$
satisfies Equation (7.15) and
$H_j$
satisfies Equation (7.15) and
![]() $E_j$
satisfies Equation (7.16). Using the fact that
$E_j$
satisfies Equation (7.16). Using the fact that
![]() $\widehat {H}_j\subseteq [(N_j)^{-1}]$
, we conclude that
$\widehat {H}_j\subseteq [(N_j)^{-1}]$
, we conclude that
![]() $(\delta _0-\varphi _{N_j})*H_j=0$
. Thus,
$(\delta _0-\varphi _{N_j})*H_j=0$
. Thus,
From Equation (7.16) and the 1-boundedness of
![]() $(A_N^{\mathcal P})^{*j}(f_1,\ldots , f_0, \ldots , f_m)$
, we have
$(A_N^{\mathcal P})^{*j}(f_1,\ldots , f_0, \ldots , f_m)$
, we have
respectively. Therefore,
establishing (7.28) and hence Equation (7.27). This completes Step 1.
Step 2.
We continue with our assumption that
![]() $f_m$
is supported in an interval of measure
$f_m$
is supported in an interval of measure
![]() $N_0$
, but now we relax the
$N_0$
, but now we relax the
![]() $L^\infty (\mathbb {K})$
control on
$L^\infty (\mathbb {K})$
control on
![]() $f_m$
to
$f_m$
to
![]() $L^2(\mathbb {K})$
control and show that
$L^2(\mathbb {K})$
control and show that
 $$ \begin{align} \begin{split} \|(\delta_0-\varphi_{N_j})*(A_N^{\mathcal P})^{*j}(f_1,\ldots, f_0, \ldots, f_m)\|_{L^2(\mathbb{K})}\\ \lesssim \delta^{1/4}\|f_0\|_{L^\infty(\mathbb{K})}\bigg(\prod_{\substack{i=1\\i\neq j}}^{m-1} \|f_i\|_{L^\infty(\mathbb{K})}\bigg)\|f_m\|_{L^2(\mathbb{K})}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \|(\delta_0-\varphi_{N_j})*(A_N^{\mathcal P})^{*j}(f_1,\ldots, f_0, \ldots, f_m)\|_{L^2(\mathbb{K})}\\ \lesssim \delta^{1/4}\|f_0\|_{L^\infty(\mathbb{K})}\bigg(\prod_{\substack{i=1\\i\neq j}}^{m-1} \|f_i\|_{L^\infty(\mathbb{K})}\bigg)\|f_m\|_{L^2(\mathbb{K})}. \end{split} \end{align} $$
The main tool for this will be the
![]() $L^p$
-improving estimate (7.22) for the polynomial average
$L^p$
-improving estimate (7.22) for the polynomial average
![]() $M_N^Q$
. We have a pointwise bound
$M_N^Q$
. We have a pointwise bound
which combined with Equation (7.22) (for
![]() $Q=P_m-P_j$
,
$Q=P_m-P_j$
,
![]() $d = \deg (P_m)$
,
$d = \deg (P_m)$
,
![]() $s=2$
and
$s=2$
and
![]() $r=(d+2)/2d$
) yields
$r=(d+2)/2d$
) yields
 $$ \begin{align} \begin{split} \|(\delta_0-\varphi_{N_j})*(A_N^{\mathcal P})^{*j}(f_1,\ldots, f_0, \ldots, f_m)\|_{L^2(\mathbb{K})}\quad\\ \lesssim N_0^{- 1/d}\|f_0\|_{L^\infty(\mathbb{K})}\bigg(\prod_{\substack{i=1\\i\neq j}}^{m-1} \|f_i\|_{L^\infty(\mathbb{K})}\bigg)\|f_m\|_{L^r(\mathbb{K})}. \end{split} \end{align} $$
$$ \begin{align} \begin{split} \|(\delta_0-\varphi_{N_j})*(A_N^{\mathcal P})^{*j}(f_1,\ldots, f_0, \ldots, f_m)\|_{L^2(\mathbb{K})}\quad\\ \lesssim N_0^{- 1/d}\|f_0\|_{L^\infty(\mathbb{K})}\bigg(\prod_{\substack{i=1\\i\neq j}}^{m-1} \|f_i\|_{L^\infty(\mathbb{K})}\bigg)\|f_m\|_{L^r(\mathbb{K})}. \end{split} \end{align} $$
Interpolating Equations (7.27) and (7.30), we obtain Equation (7.29) as desired.
Step 3.
In this final step, we remove the support condition on
![]() $f_m$
and establish (7.26). To prove Equation (7.26), we may assume that
$f_m$
and establish (7.26). To prove Equation (7.26), we may assume that
![]() $\|f_i\|_{L^{\infty }(\mathbb {K})} = 1$
for
$\|f_i\|_{L^{\infty }(\mathbb {K})} = 1$
for
![]() $i=0, 1, \ldots , j-1, j+1, \ldots , m-1$
. We split
$i=0, 1, \ldots , j-1, j+1, \ldots , m-1$
. We split ![]() , where I ranges over a partition
, where I ranges over a partition
![]() $\mathcal I$
of
$\mathcal I$
of
![]() $\mathbb {K}$
into intervals I of measure
$\mathbb {K}$
into intervals I of measure
![]() $N_0$
. We have seen this is possible when
$N_0$
. We have seen this is possible when
![]() $\mathbb {K}$
is non-Archimedean or when
$\mathbb {K}$
is non-Archimedean or when
![]() $\mathbb {K}={\mathbb R}$
. This is not possible when
$\mathbb {K}={\mathbb R}$
. This is not possible when
![]() $\mathbb {K} = {\mathbb C}$
, but in this case, we can find a partition
$\mathbb {K} = {\mathbb C}$
, but in this case, we can find a partition
![]() $\mathcal I$
of squares. By Step 1 and Step 2, the local dual function
$\mathcal I$
of squares. By Step 1 and Step 2, the local dual function ![]() obeys the bound
obeys the bound
for each interval I, and we wish to establish
We will square out the sum. To handle the off-diagonal terms, we observe that for finite intervals
![]() $I, J\subset \mathbb {K}$
(squares when
$I, J\subset \mathbb {K}$
(squares when
![]() $\mathbb {K} = {\mathbb C}$
) of measure
$\mathbb {K} = {\mathbb C}$
) of measure
![]() $N_0$
and
$N_0$
and
![]() $M>0$
and
$M>0$
and
![]() $1\le p<\infty $
, we have
$1\le p<\infty $
, we have
By squaring and applying Schur’s test, it suffices to obtain the decay bound
for all intervals
![]() $I,J$
of measure
$I,J$
of measure
![]() $N_0$
. By Cauchy–Schwarz and Equation (7.31), we know
$N_0$
. By Cauchy–Schwarz and Equation (7.31), we know
On the other hand,
![]() $D_I$
is supported in a
$D_I$
is supported in a
![]() $O(N_0)$
-neighborhood of I, and similarly for
$O(N_0)$
-neighborhood of I, and similarly for
![]() $D_J$
. From Equation (7.32) and Cauchy–Schwarz, we thus have
$D_J$
. From Equation (7.32) and Cauchy–Schwarz, we thus have
 $$ \begin{align*} \langle (\delta_0 - \varphi_{N_j})* D_I, (1 - \varphi_{N_j})* D_J \rangle &\lesssim \big(1+N_0^{-1}\mathrm{dist}(I,J) \big)^{-10} \| D_I \|_{L^2(\mathbb{K})} \| D_J \|_{L^2(\mathbb{K})}\\ &\lesssim \big(1+N_0^{-1}\mathrm{dist}(I,J) \big)^{-10} \| f_m \|_{L^2(I)} \| f_m \|_{L^2(J)}. \end{align*} $$
$$ \begin{align*} \langle (\delta_0 - \varphi_{N_j})* D_I, (1 - \varphi_{N_j})* D_J \rangle &\lesssim \big(1+N_0^{-1}\mathrm{dist}(I,J) \big)^{-10} \| D_I \|_{L^2(\mathbb{K})} \| D_J \|_{L^2(\mathbb{K})}\\ &\lesssim \big(1+N_0^{-1}\mathrm{dist}(I,J) \big)^{-10} \| f_m \|_{L^2(I)} \| f_m \|_{L^2(J)}. \end{align*} $$
Taking the geometric mean of the two estimates, we obtain the claim in Equation (7.26). This completes the proof of Theorem 7.23.
8 The implication Theorem 1.6
 $\Longrightarrow $
Theorem 1.3
$\Longrightarrow $
Theorem 1.3
Here, we give the details of Bourgain’s argument in [Reference Bourgain3] which allow us to pass from Theorem 1.6 to Theorem 1.3 on polynomial progressions. Let
![]() ${\mathcal P} = \{P_1, \ldots , P_m\}$
be a sequence of polynomials in
${\mathcal P} = \{P_1, \ldots , P_m\}$
be a sequence of polynomials in
![]() $\mathbb {K}[\mathrm {y}]$
with distinct degrees and no constant terms. Without loss of generality, we may assume
$\mathbb {K}[\mathrm {y}]$
with distinct degrees and no constant terms. Without loss of generality, we may assume
and we set
![]() $d_{m-j} := \deg {P_j}$
and
$d_{m-j} := \deg {P_j}$
and
![]() $d := d_0 = \deg {P_m}$
so that
$d := d_0 = \deg {P_m}$
so that
![]() $d_{m-1} < \cdots < d_1 < d$
.
$d_{m-1} < \cdots < d_1 < d$
.
Since the argument showing how Theorem 1.6 implies Theorem 1.3 has been given in [Reference Bourgain3], [Reference Durcik, Guo and Roos11] and [Reference Chen, Guo and Li8] in the Euclidean setting (albeit for shorter polynomial progressions), we will only give the details for non-Archimedean fields
![]() $\mathbb {K}$
where uniform notation can be employed.
$\mathbb {K}$
where uniform notation can be employed.
We will proceed in several steps.
Step 1
When
![]() $\mathbb {K}$
is non-Archimedean, the family
$\mathbb {K}$
is non-Archimedean, the family
![]() $(Q_t)_{t>0}$
of convolution operators defined by
$(Q_t)_{t>0}$
of convolution operators defined by
 $$\begin{align*}Q_t f (x) \ = \ f * \mu_{[t]}(x) = \ \frac{1}{t} \int_{|y|\le t} f(x - u) d\mu(u) \quad \text{for scales} \quad t>0 \end{align*}$$
$$\begin{align*}Q_t f (x) \ = \ f * \mu_{[t]}(x) = \ \frac{1}{t} \int_{|y|\le t} f(x - u) d\mu(u) \quad \text{for scales} \quad t>0 \end{align*}$$
gives us a natural approximation of the identity and form the analogue of the Poisson semigroup in the non-Archimedean setting. They also give us Fourier localization since
We will need the following bound for
![]() $(Q_t)_{t>0}$
(see Lemma 6 in [Reference Bourgain3] or Lemma 2.1 in [Reference Durcik, Guo and Roos11]): For
$(Q_t)_{t>0}$
(see Lemma 6 in [Reference Bourgain3] or Lemma 2.1 in [Reference Durcik, Guo and Roos11]): For
![]() $f \ge 0$
and scales
$f \ge 0$
and scales
![]() $0 < t_1, \ldots , t_m \le 1$
,
$0 < t_1, \ldots , t_m \le 1$
,
 $$ \begin{align} \int_{B_1(0)} f(x) Q_{t_1} f(x) \cdots Q_{t_m} f(x) d\mu(x) \ \ge \ \Big( \int_{B_1(0)} f(x) d\mu(x) \Big)^{m+1}. \end{align} $$
$$ \begin{align} \int_{B_1(0)} f(x) Q_{t_1} f(x) \cdots Q_{t_m} f(x) d\mu(x) \ \ge \ \Big( \int_{B_1(0)} f(x) d\mu(x) \Big)^{m+1}. \end{align} $$
The proof in the euclidean setting given in [Reference Durcik, Guo and Roos11] established Equation (8.2) for general approximations of the identity, but the first step is to show Equation (8.2) for martingales
![]() $(E_k)_{k\in \mathbb {N}}$
defined with respect to dyadic intervals. However, a small scale t in a non-Archimedean field
$(E_k)_{k\in \mathbb {N}}$
defined with respect to dyadic intervals. However, a small scale t in a non-Archimedean field
![]() $\mathbb {K}$
is the form
$\mathbb {K}$
is the form
![]() $t = q^{-k}$
and
$t = q^{-k}$
and

 $$\begin{align*}{\mathcal C}_k \ = \ \{ {\underline{x}}=x_0 + x_1 \pi + \cdots + x_{k-1}\pi^{k-1} : x_j \in o_{\mathbb{K}}/m_{\mathbb{K}} \} \quad \text{ and } \quad A_{k,\underline{x}}f = q^{k} \int_{B_{q^{-k}({\underline{x}})}} f(u) d\mu(u). \end{align*}$$
$$\begin{align*}{\mathcal C}_k \ = \ \{ {\underline{x}}=x_0 + x_1 \pi + \cdots + x_{k-1}\pi^{k-1} : x_j \in o_{\mathbb{K}}/m_{\mathbb{K}} \} \quad \text{ and } \quad A_{k,\underline{x}}f = q^{k} \int_{B_{q^{-k}({\underline{x}})}} f(u) d\mu(u). \end{align*}$$
Hence,
![]() $(Q_t)_{t>0}$
is a martingale with respect to the dyadic structure of non-Archimedean fields and so the argument in [Reference Durcik, Guo and Roos11] extends without change to establish Equation(8.2).
$(Q_t)_{t>0}$
is a martingale with respect to the dyadic structure of non-Archimedean fields and so the argument in [Reference Durcik, Guo and Roos11] extends without change to establish Equation(8.2).
Step 2
Fix
![]() $\varepsilon>0$
. Our goal is to find a
$\varepsilon>0$
. Our goal is to find a
![]() $\delta (\varepsilon , {\mathcal P})> 0$
and
$\delta (\varepsilon , {\mathcal P})> 0$
and
![]() $N(\varepsilon , {\mathcal P}) \ge 1$
such that for any scale
$N(\varepsilon , {\mathcal P}) \ge 1$
such that for any scale
![]() $N \ge N(\varepsilon , {\mathcal P})$
and
$N \ge N(\varepsilon , {\mathcal P})$
and
![]() $f \in L^0(\mathbb {K})$
with
$f \in L^0(\mathbb {K})$
with
![]() $0\le f \le 1$
satisfying
$0\le f \le 1$
satisfying
![]() $\int _{\mathbb {K}} f d\mu \ge \varepsilon N^d$
, we have
$\int _{\mathbb {K}} f d\mu \ge \varepsilon N^d$
, we have
Taking ![]() with
with
![]() $S\subseteq \mathbb {K}$
in Theorem 1.3 implies Equation (1.4), the desired conclusion. We may assume the f is supported in the interval
$S\subseteq \mathbb {K}$
in Theorem 1.3 implies Equation (1.4), the desired conclusion. We may assume the f is supported in the interval
![]() $[N^d]$
.
$[N^d]$
.
Let
![]() $\alpha , \beta \in \mathbb {K}$
satisfy
$\alpha , \beta \in \mathbb {K}$
satisfy
![]() $|\alpha | = N^d$
and
$|\alpha | = N^d$
and
![]() $|\beta | = N$
, and write
$|\beta | = N$
, and write
where
![]() $g(x) = f(\alpha x)$
and
$g(x) = f(\alpha x)$
and
![]() $R_j(y) = \alpha ^{-1} P_j(\beta y)$
. In particular, we have
$R_j(y) = \alpha ^{-1} P_j(\beta y)$
. In particular, we have
![]() $\int _{\mathbb {K}} g \ge \varepsilon $
. We note that g is supported in
$\int _{\mathbb {K}} g \ge \varepsilon $
. We note that g is supported in
![]() $[1] = B_1(0)$
. Fix three small scales
$[1] = B_1(0)$
. Fix three small scales
![]() $0<t_0 \ll t_1 \ll t \ll 1$
and decompose
$0<t_0 \ll t_1 \ll t \ll 1$
and decompose
where
 $$ \begin{align*}I_1 &= \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-1} g(x + R_j(y))\ Q_t g(x +R_m(y)) d\mu_{[t_1]}(y) d\mu(x),\\I_2 &= \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-1} g(x + R_j(y))\ [Q_{t_0} - Q_t ] g(x +R_m(y)) d\mu_{[t_1]}(y) d\mu(x) \ \ \mathrm{and}\\I_3 &= \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-1} g(x + R_j(y))\ [ \mathrm{Id} - Q_{t_0}] g(x +R_m(y)) d\mu_{[t_1]}(y) d\mu(x). \end{align*} $$
$$ \begin{align*}I_1 &= \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-1} g(x + R_j(y))\ Q_t g(x +R_m(y)) d\mu_{[t_1]}(y) d\mu(x),\\I_2 &= \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-1} g(x + R_j(y))\ [Q_{t_0} - Q_t ] g(x +R_m(y)) d\mu_{[t_1]}(y) d\mu(x) \ \ \mathrm{and}\\I_3 &= \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-1} g(x + R_j(y))\ [ \mathrm{Id} - Q_{t_0}] g(x +R_m(y)) d\mu_{[t_1]}(y) d\mu(x). \end{align*} $$
For
![]() $I_1$
, we note that for
$I_1$
, we note that for
![]() $t_1 \ll _{P_m} t$
,
$t_1 \ll _{P_m} t$
,
whenever
![]() $|y| \le t_1$
. For the final equality, we made the change of variables
$|y| \le t_1$
. For the final equality, we made the change of variables
![]() $u \to u - R_m(y)$
, noting that when
$u \to u - R_m(y)$
, noting that when
![]() $|y| \le t_1$
, then
$|y| \le t_1$
, then
![]() $|R_m(y)| \le C_{P_m} t_1 \le t$
. Hence,
$|R_m(y)| \le C_{P_m} t_1 \le t$
. Hence,
 $$ \begin{align*} I_1 = \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-1} g(x + R_j(y))\ Q_t g(x)\, d\mu_{[t_1]}(y) d\mu(x). \end{align*} $$
$$ \begin{align*} I_1 = \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-1} g(x + R_j(y))\ Q_t g(x)\, d\mu_{[t_1]}(y) d\mu(x). \end{align*} $$
For
![]() $I_2$
, we use the Cauchy–Schwarz inequality to see that
$I_2$
, we use the Cauchy–Schwarz inequality to see that
For
![]() $I_3$
, we will use the more precise formulation of Theorem 1.6 given in Theorem 7.23. We rescale
$I_3$
, we will use the more precise formulation of Theorem 1.6 given in Theorem 7.23. We rescale
![]() $I_3$
, moving from
$I_3$
, moving from
![]() $g, R_j$
back to
$g, R_j$
back to
![]() $f, P_j$
and write
$f, P_j$
and write
 $$\begin{align*}I_3 = \frac{1}{N^d} \iint_{\mathbb{K}^2} f(x) \prod_{j=1}^{m-1} f(x + P_j(y))\ [\mathrm{Id} - Q_{t_0 N^d}] f (x + P_m(y)) d\mu_{[t_1N]}(y) d\mu(x), \end{align*}$$
$$\begin{align*}I_3 = \frac{1}{N^d} \iint_{\mathbb{K}^2} f(x) \prod_{j=1}^{m-1} f(x + P_j(y))\ [\mathrm{Id} - Q_{t_0 N^d}] f (x + P_m(y)) d\mu_{[t_1N]}(y) d\mu(x), \end{align*}$$
where the function
![]() $h(x) = [\mathrm {Id} - Q_{t_0N^d}] f(x)$
has the property that
$h(x) = [\mathrm {Id} - Q_{t_0N^d}] f(x)$
has the property that
![]() ${\widehat {h}}(\xi ) = 0$
whenever
${\widehat {h}}(\xi ) = 0$
whenever
![]() $|\xi | \le (t_0 N^d)^{-1}$
; See (8.1). Hence,
$|\xi | \le (t_0 N^d)^{-1}$
; See (8.1). Hence,
and we will want to apply Theorem 7.23 to the expression on the right with N replaced by
![]() $t_1N$
and
$t_1N$
and
![]() $0 < \delta \le 1$
defined by
$0 < \delta \le 1$
defined by
![]() $\delta ^{C_m} (N t_1)^d = N^d t_0$
or
$\delta ^{C_m} (N t_1)^d = N^d t_0$
or
![]() $\delta = (t_0/ t_1^d)^{1/C_m}$
. In order to apply Theorem 7.23, we will need to ensure
$\delta = (t_0/ t_1^d)^{1/C_m}$
. In order to apply Theorem 7.23, we will need to ensure
for some appropriate large
![]() $C' = C^{\prime }_{\mathcal P}$
. If Equation (8.6) holds, then Theorem 7.23 implies there exists a constant
$C' = C^{\prime }_{\mathcal P}$
. If Equation (8.6) holds, then Theorem 7.23 implies there exists a constant
![]() $b = b_{\mathcal P}> 0$
such that
$b = b_{\mathcal P}> 0$
such that
 $$ \begin{align*}\|A^{\mathcal P}_{t_1N}(f,f, \ldots, f, h)\|_{L^1(\mathbb{K})} \lesssim_{\mathcal P} \bigl(t_0/t_1^d\bigr)^b \prod_{j=1}^m \|f\|_{L^{p_i}(\mathbb{K})} \le \bigl(t_0/t_1^d\bigr)^b N^d \end{align*} $$
$$ \begin{align*}\|A^{\mathcal P}_{t_1N}(f,f, \ldots, f, h)\|_{L^1(\mathbb{K})} \lesssim_{\mathcal P} \bigl(t_0/t_1^d\bigr)^b \prod_{j=1}^m \|f\|_{L^{p_i}(\mathbb{K})} \le \bigl(t_0/t_1^d\bigr)^b N^d \end{align*} $$
since
![]() $1/p_1 + \cdots + 1/p_m = 1$
and
$1/p_1 + \cdots + 1/p_m = 1$
and
![]() $\|f\|_{L^{p_i}(\mathbb {K})} \le N^{d/p_i}$
for
$\|f\|_{L^{p_i}(\mathbb {K})} \le N^{d/p_i}$
for ![]() (which follows since f is 1-bounded and supported in
(which follows since f is 1-bounded and supported in
![]() $[N^d]$
). Hence,
$[N^d]$
). Hence,
Step 3
Next we decompose
![]() $I_1 = I_1^1 + I_{2}^1 + I_3^1$
, where
$I_1 = I_1^1 + I_{2}^1 + I_3^1$
, where
 $$ \begin{align*}I_1^1 \ = \ \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-2} g(x + R_j(y))\ Q_{t/N^{d-d_1}} g(x + R_{m-1}(y)) Q_t g(x) \, d\mu_{[t_1]}(y) d\mu(x), \end{align*} $$
$$ \begin{align*}I_1^1 \ = \ \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-2} g(x + R_j(y))\ Q_{t/N^{d-d_1}} g(x + R_{m-1}(y)) Q_t g(x) \, d\mu_{[t_1]}(y) d\mu(x), \end{align*} $$
 $$ \begin{align*}I_{2}^1 = \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-2} g(x + R_j(y))\ [Q_{t_0/N^{d-d_1}} - Q_{t/N^{d-d_1}} ] g(x +R_{m-1}(y)) Q_t g(x) d\mu_{[t_1]}(y) d\mu(x) \ \ \mathrm{and} \end{align*} $$
$$ \begin{align*}I_{2}^1 = \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-2} g(x + R_j(y))\ [Q_{t_0/N^{d-d_1}} - Q_{t/N^{d-d_1}} ] g(x +R_{m-1}(y)) Q_t g(x) d\mu_{[t_1]}(y) d\mu(x) \ \ \mathrm{and} \end{align*} $$
 $$ \begin{align*}I_{3}^1 = \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-2} g(x + R_j(y))\ [ \mathrm{Id} - Q_{t_0/N^{d-d_1}}] g(x +R_{m-1}(y)) Q_t g(x) d\mu_{[t_1]}(y) d\mu(x). \end{align*} $$
$$ \begin{align*}I_{3}^1 = \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-2} g(x + R_j(y))\ [ \mathrm{Id} - Q_{t_0/N^{d-d_1}}] g(x +R_{m-1}(y)) Q_t g(x) d\mu_{[t_1]}(y) d\mu(x). \end{align*} $$
For
![]() $I_1^1$
, we set
$I_1^1$
, we set
![]() $s = t/N^{d-d_1}$
and note that for
$s = t/N^{d-d_1}$
and note that for
![]() $t_1 \ll _{\mathcal P} t$
,
$t_1 \ll _{\mathcal P} t$
,
whenever
![]() $|y| \le t_1$
. For the final equality we made the change of variables
$|y| \le t_1$
. For the final equality we made the change of variables
![]() $u \to u - R_{m-1}(y)$
, noting that when
$u \to u - R_{m-1}(y)$
, noting that when
![]() $|y| \le t_1$
, then
$|y| \le t_1$
, then
![]() $|R_{m-1}(y)| \le C_{P_{m-1}} N^{-(d-d_1)}t_1 \le s$
since
$|R_{m-1}(y)| \le C_{P_{m-1}} N^{-(d-d_1)}t_1 \le s$
since
![]() $ t_1 \ll _{\mathcal P} t$
. Hence,
$ t_1 \ll _{\mathcal P} t$
. Hence,
 $$ \begin{align*} I_1^1 = \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-2} g(x + R_j(y))\ Q_{t/N^{d-d_1}} g(x) Q_t g(x) \, d\mu_{[t_1]}(y) d\mu(x). \end{align*} $$
$$ \begin{align*} I_1^1 = \iint_{\mathbb{K}^2} g(x) \prod_{j=1}^{m-2} g(x + R_j(y))\ Q_{t/N^{d-d_1}} g(x) Q_t g(x) \, d\mu_{[t_1]}(y) d\mu(x). \end{align*} $$
As in Equation (8.5), we have
For
![]() $I_{3}^1$
, we will use Theorem 7.23. We rescale
$I_{3}^1$
, we will use Theorem 7.23. We rescale
![]() $I_{3}^1$
, moving from
$I_{3}^1$
, moving from
![]() $g, R_j$
back to
$g, R_j$
back to
![]() $f, P_j$
and write
$f, P_j$
and write
 $$ \begin{align*}I_{3}^1 = \frac{1}{N^d} \iint_{\mathbb{K}^2} f(x) \prod_{j=1}^{m-2} f(x + P_j(y))\ [\mathrm{Id} - Q_{t_0 N^{d_1}}] f (x + P_{m-1}(y)) Q_{t N^d} f(x) d\mu_{[t_1N]}(y) d\mu(x), \end{align*} $$
$$ \begin{align*}I_{3}^1 = \frac{1}{N^d} \iint_{\mathbb{K}^2} f(x) \prod_{j=1}^{m-2} f(x + P_j(y))\ [\mathrm{Id} - Q_{t_0 N^{d_1}}] f (x + P_{m-1}(y)) Q_{t N^d} f(x) d\mu_{[t_1N]}(y) d\mu(x), \end{align*} $$
where the function
![]() $h'(x) = [\mathrm {Id} - Q_{t_0 N^{d_1}}] f(x)$
has the property that
$h'(x) = [\mathrm {Id} - Q_{t_0 N^{d_1}}] f(x)$
has the property that
![]() ${\widehat {h'}}(\xi ) = 0$
whenever
${\widehat {h'}}(\xi ) = 0$
whenever
![]() $|\xi | \le (t_0 N^{d_1})^{-1}$
. Hence, for
$|\xi | \le (t_0 N^{d_1})^{-1}$
. Hence, for
![]() ${{\mathcal P}'} = \{P_1, \ldots , P_{m-1}\}$
,
${{\mathcal P}'} = \{P_1, \ldots , P_{m-1}\}$
,
and so, as long as Equation (8.6) holds, Theorem 7.23 implies there exists a constant
![]() $b' = b_{{\mathcal P}'}> 0$
such that
$b' = b_{{\mathcal P}'}> 0$
such that
 $$ \begin{align*}\|A^{{\mathcal P}'}_{t_1N}(fQ_{t N^d} f,f, \ldots, f, h')\|_{L^1(\mathbb{K})} \lesssim_{{\mathcal P}'} \bigl(t_0/t_1^d\bigr)^{b'} \prod_{j=1}^m \|f\|_{L^{p_i}(\mathbb{K})} \le \bigl(t_0/t_1^d\bigr)^{b'} N^d \end{align*} $$
$$ \begin{align*}\|A^{{\mathcal P}'}_{t_1N}(fQ_{t N^d} f,f, \ldots, f, h')\|_{L^1(\mathbb{K})} \lesssim_{{\mathcal P}'} \bigl(t_0/t_1^d\bigr)^{b'} \prod_{j=1}^m \|f\|_{L^{p_i}(\mathbb{K})} \le \bigl(t_0/t_1^d\bigr)^{b'} N^d \end{align*} $$
since
![]() $1/p_1 + \cdots + 1/p_{m-1} = 1$
and
$1/p_1 + \cdots + 1/p_{m-1} = 1$
and
![]() $\|f\|_{L^{p_i}(\mathbb {K})} \le N^{d/p_i}$
for
$\|f\|_{L^{p_i}(\mathbb {K})} \le N^{d/p_i}$
for ![]() (which follows since f is 1-bounded and supported in
(which follows since f is 1-bounded and supported in
![]() $[N^d]$
). Hence,
$[N^d]$
). Hence,
Step 4
We iterate, decomposing
![]() $I_1^1 = I_{1}^2 + I_{2}^2 + I_{3}^2$
, followed by decomposing
$I_1^1 = I_{1}^2 + I_{2}^2 + I_{3}^2$
, followed by decomposing
![]() $I_1^2 = I_1^3 + I_2^3 + I_3^3$
and so on. For each
$I_1^2 = I_1^3 + I_2^3 + I_3^3$
and so on. For each
![]() $0\le j \le m-1$
, we have
$0\le j \le m-1$
, we have
 $$ \begin{align} &I_1^j = \iint_{\mathbb{K}^2} g(x) \Big(\prod_{i=1}^{m-j-1} g(x+ R_i(y))\Big) \, \Big(\prod_{i=0}^jQ_{t/N^{d-d_i}} g(x)\Big)\, d\mu_{[t_1]}(y) d\mu(x), \end{align} $$
$$ \begin{align} &I_1^j = \iint_{\mathbb{K}^2} g(x) \Big(\prod_{i=1}^{m-j-1} g(x+ R_i(y))\Big) \, \Big(\prod_{i=0}^jQ_{t/N^{d-d_i}} g(x)\Big)\, d\mu_{[t_1]}(y) d\mu(x), \end{align} $$
again if Equation (8.6) holds. Strictly speaking, the estimate (8.8) for
![]() $I_3^j$
does not follow from Theorem 7.23 when
$I_3^j$
does not follow from Theorem 7.23 when
![]() $j=m-1$
since the proof of Theorem 7.23 assumed that the collection
$j=m-1$
since the proof of Theorem 7.23 assumed that the collection
![]() ${\mathcal P}$
of polynomials consisted of at least two polynomials. Nevertheless, the bound (8.8) holds when
${\mathcal P}$
of polynomials consisted of at least two polynomials. Nevertheless, the bound (8.8) holds when
![]() $j=m-1$
. To see this, we apply the Cauchy–Schwarz inequality and Plancherel’s theorem to see that
$j=m-1$
. To see this, we apply the Cauchy–Schwarz inequality and Plancherel’s theorem to see that
 $$ \begin{align*} | I_3^{m-1} |^2 \ \le \ \frac{1}{N^{d}} \int_{\mathbb{K}} \bigl| \int_{\mathbb{K}} [\mathrm{Id} - Q_{t_0N^{d_{m-1}}}] f (x + P_1(y)) \, d\mu_{[t_1N ]}(y)\bigr|^2\, d\mu(x) \qquad\qquad\qquad\\= \frac{1}{N^{d}} \int_{|\xi|\ge (N^{d_{m-1}} t_0)^{-1}} |{\widehat{f}}(\xi)|^2 |m_{N,t_1}(\xi)|^2\, d\mu(\xi), \quad \text{ where } \quad m_{N, t_1}(\xi) := \int_{B_1(0)} \mathrm{e}(P_1(t_1N y)\xi)\, d\mu(y). \end{align*} $$
$$ \begin{align*} | I_3^{m-1} |^2 \ \le \ \frac{1}{N^{d}} \int_{\mathbb{K}} \bigl| \int_{\mathbb{K}} [\mathrm{Id} - Q_{t_0N^{d_{m-1}}}] f (x + P_1(y)) \, d\mu_{[t_1N ]}(y)\bigr|^2\, d\mu(x) \qquad\qquad\qquad\\= \frac{1}{N^{d}} \int_{|\xi|\ge (N^{d_{m-1}} t_0)^{-1}} |{\widehat{f}}(\xi)|^2 |m_{N,t_1}(\xi)|^2\, d\mu(\xi), \quad \text{ where } \quad m_{N, t_1}(\xi) := \int_{B_1(0)} \mathrm{e}(P_1(t_1N y)\xi)\, d\mu(y). \end{align*} $$
The oscillatory integral bound (3.1) implies that
![]() $|m_{N,t_1}(\xi )| \lesssim _{\mathcal P} (t_0/t_1)^b$
whenever
$|m_{N,t_1}(\xi )| \lesssim _{\mathcal P} (t_0/t_1)^b$
whenever
![]() $|\xi | \ge (N^{d_{m-1}} t_0)^{-1}$
, and so Equation (8.8) for
$|\xi | \ge (N^{d_{m-1}} t_0)^{-1}$
, and so Equation (8.8) for
![]() $I_3^j$
follows when
$I_3^j$
follows when
![]() $j=m-1$
since
$j=m-1$
since
![]() $\|f\|_{L^2(\mathbb {K})}^2 \le N^d$
.
$\|f\|_{L^2(\mathbb {K})}^2 \le N^d$
.
Step 5
From Equation (8.4) and the iterated decomposition of
![]() $I_1$
, we see that
$I_1$
, we see that
![]() $t_1^{-1} I \ge A + B + C$
, where
$t_1^{-1} I \ge A + B + C$
, where
 $$ \begin{align*}A = \int_{\mathbb{K}} g(x) \prod_{j=0}^{m-1}Q_{t/N^{d-d_j}} g(x) \, d\mu(x) \ \ge \ \varepsilon^{m+1} \end{align*} $$
$$ \begin{align*}A = \int_{\mathbb{K}} g(x) \prod_{j=0}^{m-1}Q_{t/N^{d-d_j}} g(x) \, d\mu(x) \ \ge \ \varepsilon^{m+1} \end{align*} $$
by Equation (8.2), and for some
![]() $C_{\mathcal P}>0$
, we have
$C_{\mathcal P}>0$
, we have
 $$\begin{align*}|B| \le C_{\mathcal P} \sum_{j=0}^{m-1} \|Q_{t_0/N^{d-d_j}} g - Q_{t/N^{d-d_j}} g \|_{L^2(\mathbb{K})} \quad \text{and} \quad |C| \ \le C_{\mathcal P} \ \bigl(t_0/t_1^d\bigr)^{b} \le \varepsilon^{m+1}/4 \end{align*}$$
$$\begin{align*}|B| \le C_{\mathcal P} \sum_{j=0}^{m-1} \|Q_{t_0/N^{d-d_j}} g - Q_{t/N^{d-d_j}} g \|_{L^2(\mathbb{K})} \quad \text{and} \quad |C| \ \le C_{\mathcal P} \ \bigl(t_0/t_1^d\bigr)^{b} \le \varepsilon^{m+1}/4 \end{align*}$$
if
![]() $t_0 \le c_0 \, \varepsilon ^{(m+1)/b} \, t_1^d$
and
$t_0 \le c_0 \, \varepsilon ^{(m+1)/b} \, t_1^d$
and
![]() $c_0^b C_{\mathcal P}<1/4$
and Equation (8.6) holds.
$c_0^b C_{\mathcal P}<1/4$
and Equation (8.6) holds.
Finally, we claim that we can find a triple
![]() $t_0 \ll t_1 \ll t$
of small scales such that
$t_0 \ll t_1 \ll t$
of small scales such that
![]() $|B| \le \varepsilon ^{m+1}/4$
. If we are able to do this, then
$|B| \le \varepsilon ^{m+1}/4$
. If we are able to do this, then
![]() $I \ge \varepsilon ^{m+1} t_1/2$
and the proof is complete.
$I \ge \varepsilon ^{m+1} t_1/2$
and the proof is complete.
Define
![]() $v:=-C_0\log _q( c_0 \varepsilon ^{(m+1)/b})$
for some large constant
$v:=-C_0\log _q( c_0 \varepsilon ^{(m+1)/b})$
for some large constant
![]() $C_0\gg d$
. Choose a sequence of small scales
$C_0\gg d$
. Choose a sequence of small scales
![]() $t_0 = q^{-\ell _j}$
and
$t_0 = q^{-\ell _j}$
and
![]() $t_1 = q^{-k_j}$
and
$t_1 = q^{-k_j}$
and
![]() $t=q^{-u_j}$
satisfying
$t=q^{-u_j}$
satisfying
 $$ \begin{align} \begin{aligned} 0\le u_1< dk_1+v < \ell_1 <u_2< dk_2+v < \ell_2 < \ldots < u_n<dk_n+v<\ell_n<\ldots \\ \text{ and } \qquad\ell_{n+1}\le \ell_n-C_0\log_q( c_0 \varepsilon^{(m+1)/b}). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} 0\le u_1< dk_1+v < \ell_1 <u_2< dk_2+v < \ell_2 < \ldots < u_n<dk_n+v<\ell_n<\ldots \\ \text{ and } \qquad\ell_{n+1}\le \ell_n-C_0\log_q( c_0 \varepsilon^{(m+1)/b}). \end{aligned} \end{align} $$
Taking
![]() $L\in \mathbb N$
such that
$L\in \mathbb N$
such that
![]() $L=\lfloor 16C_{\mathcal P}m^2\varepsilon ^{-2(m+1)}\rfloor +1$
we claim that there exists
$L=\lfloor 16C_{\mathcal P}m^2\varepsilon ^{-2(m+1)}\rfloor +1$
we claim that there exists ![]() such that
such that
 $$ \begin{align} C_{\mathcal P}\sum_{n=0}^{m-1} \|Q_{q^{-\ell_j} N^{-(d-d_n)}} g - Q_{q^{-u_j }N^{-(d-d_n)}} g \|_{L^2(\mathbb{K})} <\varepsilon^{m+1}/4. \end{align} $$
$$ \begin{align} C_{\mathcal P}\sum_{n=0}^{m-1} \|Q_{q^{-\ell_j} N^{-(d-d_n)}} g - Q_{q^{-u_j }N^{-(d-d_n)}} g \|_{L^2(\mathbb{K})} <\varepsilon^{m+1}/4. \end{align} $$
Indeed, suppose for a contradiction that Equation (8.10) does not hold. Then for all ![]() by the Cauchy–Schwarz inequality, we have
by the Cauchy–Schwarz inequality, we have
 $$ \begin{align*}\varepsilon^{2(m+1)} \le 16C_{\mathcal P}^2m \sum_{n=0}^{m-1} \|Q_{q^{-\ell_j} N^{-(d-d_n)}} g - Q_{q^{-u_j }N^{-(d-d_n)}} g \|_{L^2(\mathbb{K})}^2. \end{align*} $$
$$ \begin{align*}\varepsilon^{2(m+1)} \le 16C_{\mathcal P}^2m \sum_{n=0}^{m-1} \|Q_{q^{-\ell_j} N^{-(d-d_n)}} g - Q_{q^{-u_j }N^{-(d-d_n)}} g \|_{L^2(\mathbb{K})}^2. \end{align*} $$
Then

and this implies
![]() $L \le 16C_{\mathcal P}^2m^2\varepsilon ^{-2(m+1)}$
since
$L \le 16C_{\mathcal P}^2m^2\varepsilon ^{-2(m+1)}$
since
![]() $\|g\|_{L^2(\mathbb {K})} \le 1$
, which is impossible by our choice of L.
$\|g\|_{L^2(\mathbb {K})} \le 1$
, which is impossible by our choice of L.
Therefore, there exists ![]() and a corresponding triple of scales
and a corresponding triple of scales
![]() $t_0 = q^{-\ell _j}\ll t_1 = q^{-k_j}\ll t=q^{-u_j}$
satisfying the desired properties for which Equation (8.10) is true. In particular,
$t_0 = q^{-\ell _j}\ll t_1 = q^{-k_j}\ll t=q^{-u_j}$
satisfying the desired properties for which Equation (8.10) is true. In particular,
![]() $|B| \le \varepsilon ^{m+1}/4$
holds.
$|B| \le \varepsilon ^{m+1}/4$
holds.
Step 6
Furthermore, with these scales by Equation (8.9), we have
![]() $t_0= q^{-\ell _j} \gtrsim (c_0 \varepsilon ^{m+1})^{O_{\mathcal P}(m^2 \varepsilon ^{-2(m+1)})}$
. In order to ensure that Equation (8.6) holds for every iteration in the decomposition, we set
$t_0= q^{-\ell _j} \gtrsim (c_0 \varepsilon ^{m+1})^{O_{\mathcal P}(m^2 \varepsilon ^{-2(m+1)})}$
. In order to ensure that Equation (8.6) holds for every iteration in the decomposition, we set
so that for every
![]() $N\ge N(\varepsilon , {\mathcal P})$
condition (8.6) holds. Hence,
$N\ge N(\varepsilon , {\mathcal P})$
condition (8.6) holds. Hence,
establishing the desired bound (8.3) with
![]() $\delta = \varepsilon ^{C_1 \varepsilon ^{-2m-2}}$
for some
$\delta = \varepsilon ^{C_1 \varepsilon ^{-2m-2}}$
for some
![]() $C_1>0$
depending only on
$C_1>0$
depending only on
![]() ${\mathcal P}$
.
${\mathcal P}$
.
This completes the proof of Theorem 1.3.
Acknowledgements
We thank the referees for careful reading of the manuscript and useful remarks that led to the improvement of the presentation.
Competing interest
The authors have no competing interest to declare.
Financial support
Mariusz Mirek is supported by the NSF grant DMS-2154712 and by the NSF CAREER grant DMS-2236493. Sarah Peluse is supported by the NSF grant DMS-2401117 and was supported by the NSF Mathematical Sciences Postdoctoral Research Fellowship Program under grant DMS-1903038. James Wright is supported by a Leverhulme Research Fellowship RF-2023-709
![]() $\backslash $
9
$\backslash $
9