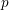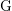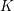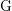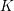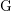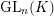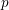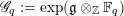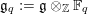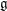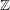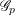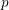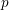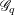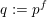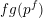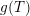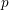1 Introduction
Let
![]() $\text{G}$
be a finite group and let
$\text{G}$
be a finite group and let
![]() $K$
be a field. The faithful dimension of
$K$
be a field. The faithful dimension of
![]() $\text{G}$
over
$\text{G}$
over
![]() $K$
, denoted by
$K$
, denoted by
![]() $m_{\text{faithful},K}(\text{G})$
, is defined to be the smallest possible dimension of a faithful
$m_{\text{faithful},K}(\text{G})$
, is defined to be the smallest possible dimension of a faithful
![]() $K$
-representation of
$K$
-representation of
![]() $\text{G}$
. The question of computing or estimating
$\text{G}$
. The question of computing or estimating
![]() $m_{\text{faithful},K}(\text{G})$
has found many applications. For instance, it is intimately connected to computing the essential dimension
$m_{\text{faithful},K}(\text{G})$
has found many applications. For instance, it is intimately connected to computing the essential dimension
![]() $\text{ed}_{K}(\text{G})$
of
$\text{ed}_{K}(\text{G})$
of
![]() $\text{G}$
, defined by Buhler and Reichstein [Reference Buhler and ReichsteinBR97], which is the smallest dimension of a linearizable
$\text{G}$
, defined by Buhler and Reichstein [Reference Buhler and ReichsteinBR97], which is the smallest dimension of a linearizable
![]() $\text{G}$
-variety with a faithful
$\text{G}$
-variety with a faithful
![]() $\text{G}$
-action. It is known [Reference Berhuy and FaviBF13, Proposition 4.15] that
$\text{G}$
-action. It is known [Reference Berhuy and FaviBF13, Proposition 4.15] that
![]() $\text{ed}_{K}(\text{G})\leqslant m_{\text{faithful},K}(\text{G})$
for every finite group
$\text{ed}_{K}(\text{G})\leqslant m_{\text{faithful},K}(\text{G})$
for every finite group
![]() $\text{G}$
. Karpenko and Merkurjev [Reference Karpenko and MerkurjevKM08] proved that if
$\text{G}$
. Karpenko and Merkurjev [Reference Karpenko and MerkurjevKM08] proved that if
![]() $\text{G}$
is a
$\text{G}$
is a
![]() $p$
-group and
$p$
-group and
![]() $K$
contains a primitive
$K$
contains a primitive
![]() $p$
th root of unity, then
$p$
th root of unity, then
![]() $\text{ed}_{K}(\text{G})=m_{\text{faithful},K}(\text{G})$
. For further details the reader may wish to consult [Reference MerkurjevMer17].
$\text{ed}_{K}(\text{G})=m_{\text{faithful},K}(\text{G})$
. For further details the reader may wish to consult [Reference MerkurjevMer17].
Note that by a result of Brauer, every complex representation of a
![]() $p$
-group
$p$
-group
![]() $\text{G}$
is defined over
$\text{G}$
is defined over
![]() $\mathbb{Q}(\unicode[STIX]{x1D701})$
, where
$\mathbb{Q}(\unicode[STIX]{x1D701})$
, where
![]() $\unicode[STIX]{x1D701}$
is a primitive
$\unicode[STIX]{x1D701}$
is a primitive
![]() $|\text{G}|$
th root of unity. This implies that
$|\text{G}|$
th root of unity. This implies that
![]() $m_{\text{faithful},K}(\text{G})=m_{\text{faithful},\mathbb{C}}(\text{G})$
whenever
$m_{\text{faithful},K}(\text{G})=m_{\text{faithful},\mathbb{C}}(\text{G})$
whenever
![]() $K\supseteq \mathbb{Q}(\unicode[STIX]{x1D701})$
. Therefore we will only consider complex representations and use the shorthand
$K\supseteq \mathbb{Q}(\unicode[STIX]{x1D701})$
. Therefore we will only consider complex representations and use the shorthand
![]() $m_{\text{faithful}}(\text{G})$
instead of
$m_{\text{faithful}}(\text{G})$
instead of
![]() $m_{\text{faithful},\mathbb{C}}(\text{G})$
.
$m_{\text{faithful},\mathbb{C}}(\text{G})$
.
This work is a continuation of [Reference Bardestani, Mallahi-Karai and SalmasianBMS16] in which the faithful dimension of a large class of
![]() $p$
-groups was studied. Let us start by recalling some of the results from [Reference Bardestani, Mallahi-Karai and SalmasianBMS16]. Let
$p$
-groups was studied. Let us start by recalling some of the results from [Reference Bardestani, Mallahi-Karai and SalmasianBMS16]. Let
![]() $F$
be a non-Archimedean local field with a discrete valuation
$F$
be a non-Archimedean local field with a discrete valuation
![]() $\unicode[STIX]{x1D708}$
. We will denote the ring of integers of
$\unicode[STIX]{x1D708}$
. We will denote the ring of integers of
![]() $F$
by
$F$
by
![]() ${\mathcal{O}}$
, the unique maximal ideal of
${\mathcal{O}}$
, the unique maximal ideal of
![]() ${\mathcal{O}}$
by
${\mathcal{O}}$
by
![]() $\mathfrak{p}$
, and the residue field
$\mathfrak{p}$
, and the residue field
![]() ${\mathcal{O}}/\mathfrak{p}$
by
${\mathcal{O}}/\mathfrak{p}$
by
![]() $\mathbb{F}_{q}$
, the finite field of order
$\mathbb{F}_{q}$
, the finite field of order
![]() $q:=p^{f}$
, where
$q:=p^{f}$
, where
![]() $f$
is the absolute inertia degree of
$f$
is the absolute inertia degree of
![]() $F$
. The number
$F$
. The number
![]() $e=\unicode[STIX]{x1D708}(p)$
is called the absolute ramification index of
$e=\unicode[STIX]{x1D708}(p)$
is called the absolute ramification index of
![]() $F$
.
$F$
.
For a (commutative and unital) ring
![]() $\text{R}$
and an integer
$\text{R}$
and an integer
![]() $k\geqslant 1$
, the
$k\geqslant 1$
, the
![]() $k$
th Heisenberg group with entries in
$k$
th Heisenberg group with entries in
![]() $\text{R}$
, denoted by
$\text{R}$
, denoted by
![]() $\operatorname{Heis}_{2k+1}(\text{R})$
, consists of
$\operatorname{Heis}_{2k+1}(\text{R})$
, consists of
![]() $(k+2)\times (k+2)$
matrices of the form
$(k+2)\times (k+2)$
matrices of the form
![]() $I_{k+2}+A$
, where
$I_{k+2}+A$
, where
![]() $A$
is strictly upper triangular and all of its entries other than those on the first row and the last column are zero. Similarly,
$A$
is strictly upper triangular and all of its entries other than those on the first row and the last column are zero. Similarly,
![]() $\text{U}_{k}(\text{R})$
denotes the subgroup of unitriangular matrices in
$\text{U}_{k}(\text{R})$
denotes the subgroup of unitriangular matrices in
![]() $\operatorname{GL}_{k}(\text{R})$
, so that
$\operatorname{GL}_{k}(\text{R})$
, so that
![]() $H_{2k+1}(\text{R})\subseteq U_{k+2}(\text{R})$
. In [Reference Bardestani, Mallahi-Karai and SalmasianBMS16, Theorem 1.1] we proved that
$H_{2k+1}(\text{R})\subseteq U_{k+2}(\text{R})$
. In [Reference Bardestani, Mallahi-Karai and SalmasianBMS16, Theorem 1.1] we proved that
where
![]() $\unicode[STIX]{x1D709}=\min \{e,n\}$
. Also, when
$\unicode[STIX]{x1D709}=\min \{e,n\}$
. Also, when
![]() $\text{char}({\mathcal{O}}/\mathfrak{p})\neq 2$
, in [Reference Bardestani, Mallahi-Karai and SalmasianBMS16, Theorem 1.2] we showed that
$\text{char}({\mathcal{O}}/\mathfrak{p})\neq 2$
, in [Reference Bardestani, Mallahi-Karai and SalmasianBMS16, Theorem 1.2] we showed that
for any subgroup
![]() $\text{G}$
of
$\text{G}$
of
![]() $\text{U}_{k+2}({\mathcal{O}}/\mathfrak{p}^{n})$
that contains
$\text{U}_{k+2}({\mathcal{O}}/\mathfrak{p}^{n})$
that contains
![]() $\operatorname{Heis}_{2k+1}({\mathcal{O}}/\mathfrak{p}^{n})$
. In particular for
$\operatorname{Heis}_{2k+1}({\mathcal{O}}/\mathfrak{p}^{n})$
. In particular for
![]() $F=\mathbb{F}_{p}((T))$
, where
$F=\mathbb{F}_{p}((T))$
, where
![]() $p\geqslant 3$
, we obtained
$p\geqslant 3$
, we obtained
The latter statement implies that if
![]() $p\geqslant 3$
then
$p\geqslant 3$
then
The right-hand side of (2) is a polynomial in
![]() $p$
. Note that
$p$
. Note that
![]() $\text{U}_{k}(\mathbb{F}_{p})=\exp (\mathfrak{u}_{k}\otimes \mathbb{F}_{p})$
, where
$\text{U}_{k}(\mathbb{F}_{p})=\exp (\mathfrak{u}_{k}\otimes \mathbb{F}_{p})$
, where
![]() $\mathfrak{u}_{k}$
is the Lie algebra of strictly upper triangular matrices with entries in
$\mathfrak{u}_{k}$
is the Lie algebra of strictly upper triangular matrices with entries in
![]() $\mathbb{Z}$
(for the definition of the exponential map in this context, see § 2). Equation (2) suggests the following problem.
$\mathbb{Z}$
(for the definition of the exponential map in this context, see § 2). Equation (2) suggests the following problem.
Problem 1.1 (Polynomiality problem).
Among all nilpotent
![]() $\mathbb{Z}$
-Lie algebras
$\mathbb{Z}$
-Lie algebras
![]() $\mathfrak{g}$
which are finitely generated as abelian groups, characterize those for which there exists a polynomial
$\mathfrak{g}$
which are finitely generated as abelian groups, characterize those for which there exists a polynomial
![]() $g(T)$
, only depending on
$g(T)$
, only depending on
![]() $\mathfrak{g}$
, such that
$\mathfrak{g}$
, such that
for all sufficiently large primes
![]() $p$
.
$p$
.
This problem is the central guiding principle of this work. Before stating our results, let us mention that the methods applied in [Reference Bardestani, Mallahi-Karai and SalmasianBMS16] were based on a suitably adapted version of the Stone–von Neumann theory, whose application is mostly limited to groups of nilpotency class
![]() $2$
. In this paper, we will replace the Stone–von Neumann theory by Kirillov’s orbit method for finite
$2$
. In this paper, we will replace the Stone–von Neumann theory by Kirillov’s orbit method for finite
![]() $p$
-groups. The orbit method was initially introduced by Kirillov [Reference KirillovKir62] to study unitary representations of nilpotent Lie groups. This machinery was later adapted to other classes of groups, such as
$p$
-groups. The orbit method was initially introduced by Kirillov [Reference KirillovKir62] to study unitary representations of nilpotent Lie groups. This machinery was later adapted to other classes of groups, such as
![]() $p$
-adic analytic groups, finitely generated nilpotent groups, and finite
$p$
-adic analytic groups, finitely generated nilpotent groups, and finite
![]() $p$
-groups (see [Reference HoweHow77b, Reference HoweHow77a] and [Reference KazhdanKaz77, Proposition 1]). Jaikin-Zapirain [Reference Jaikin-ZapirainJai06] used this machinery to study the representation zeta functions of compact
$p$
-groups (see [Reference HoweHow77b, Reference HoweHow77a] and [Reference KazhdanKaz77, Proposition 1]). Jaikin-Zapirain [Reference Jaikin-ZapirainJai06] used this machinery to study the representation zeta functions of compact
![]() $p$
-adic analytic groups. These zeta functions have also been studied by Avni et al. [Reference Avni, Klopsch, Onn and VollAKOV13]. We refer the reader to these papers and references therein for more details.
$p$
-adic analytic groups. These zeta functions have also been studied by Avni et al. [Reference Avni, Klopsch, Onn and VollAKOV13]. We refer the reader to these papers and references therein for more details.
Our approach to Problem 1.1 relies heavily on the notion of the commutator matrix associated to a nilpotent
![]() $\mathbb{Z}$
-Lie algebra. Since its introduction in the work of Grunewald and Segal [Reference Grunewald and SegalGS84] as a tool for classification of torsion-free finitely generated nilpotent groups, the notion of the commutator matrix has been used in studying a large variety of problems related to finite and infinite groups. Voll [Reference VollVol05, Reference VollVol04] has used commutator matrices in his works on normal subgroup lattices of nilpotent groups. Stasinski and Voll [Reference Stasinski and VollSV14] also employed them to study the representation growth of infinite groups. In addition, O’Brien and Voll [Reference O’Brien and VollO’BV15] used commutator matrices for counting conjugacy classes and characters of certain finite
$\mathbb{Z}$
-Lie algebra. Since its introduction in the work of Grunewald and Segal [Reference Grunewald and SegalGS84] as a tool for classification of torsion-free finitely generated nilpotent groups, the notion of the commutator matrix has been used in studying a large variety of problems related to finite and infinite groups. Voll [Reference VollVol05, Reference VollVol04] has used commutator matrices in his works on normal subgroup lattices of nilpotent groups. Stasinski and Voll [Reference Stasinski and VollSV14] also employed them to study the representation growth of infinite groups. In addition, O’Brien and Voll [Reference O’Brien and VollO’BV15] used commutator matrices for counting conjugacy classes and characters of certain finite
![]() $p$
-groups. In our work, we relate the faithful dimension of finite
$p$
-groups. In our work, we relate the faithful dimension of finite
![]() $p$
-groups to the question of existence of sufficiently many points in general position on rank varieties associated with the commutator matrices that were considered by O’Brien and Voll.
$p$
-groups to the question of existence of sufficiently many points in general position on rank varieties associated with the commutator matrices that were considered by O’Brien and Voll.
2 Main results
Before we state our results we will need to set some notation. Let
![]() $\mathfrak{g}$
be a Lie algebra over a commutative ring
$\mathfrak{g}$
be a Lie algebra over a commutative ring
![]() $\text{R}$
. For
$\text{R}$
. For
![]() $x\in \mathfrak{g}$
, the map defined by
$x\in \mathfrak{g}$
, the map defined by
![]() $y\mapsto [x,y]$
is denoted by
$y\mapsto [x,y]$
is denoted by
![]() $\operatorname{ad}_{x}$
. Let
$\operatorname{ad}_{x}$
. Let
![]() $(\mathfrak{g}^{l})_{l\geqslant 1}$
denote the descending central series of
$(\mathfrak{g}^{l})_{l\geqslant 1}$
denote the descending central series of
![]() $\mathfrak{g}$
. In other words we set
$\mathfrak{g}$
. In other words we set
![]() $\mathfrak{g}^{1}:=\mathfrak{g}$
, and we define
$\mathfrak{g}^{1}:=\mathfrak{g}$
, and we define
![]() $\mathfrak{g}^{l+1}$
for
$\mathfrak{g}^{l+1}$
for
![]() $l\geqslant 1$
inductively, as the
$l\geqslant 1$
inductively, as the
![]() $\text{R}$
-submodule of
$\text{R}$
-submodule of
![]() $\mathfrak{g}$
generated by commutators of the form
$\mathfrak{g}$
generated by commutators of the form
![]() $[x,y]$
, where
$[x,y]$
, where
![]() $x\in \mathfrak{g}$
and
$x\in \mathfrak{g}$
and
![]() $y\in \mathfrak{g}^{l}$
. The commutator subalgebra of
$y\in \mathfrak{g}^{l}$
. The commutator subalgebra of
![]() $\mathfrak{g}$
will be denoted by
$\mathfrak{g}$
will be denoted by
![]() $\mathfrak{g}^{\prime }$
. Note that
$\mathfrak{g}^{\prime }$
. Note that
![]() $\mathfrak{g}^{\prime }=\mathfrak{g}^{2}$
. The Lie algebra
$\mathfrak{g}^{\prime }=\mathfrak{g}^{2}$
. The Lie algebra
![]() $\mathfrak{g}$
is said to be nilpotent if
$\mathfrak{g}$
is said to be nilpotent if
![]() $\mathfrak{g}^{c+1}=0$
for some
$\mathfrak{g}^{c+1}=0$
for some
![]() $c\in \mathbb{N}$
. If
$c\in \mathbb{N}$
. If
![]() $c$
is the smallest integer with this property, then
$c$
is the smallest integer with this property, then
![]() $\mathfrak{g}$
is said to be
$\mathfrak{g}$
is said to be
![]() $c$
-step nilpotent or nilpotent of class
$c$
-step nilpotent or nilpotent of class
![]() $c$
.
$c$
.
Suppose now that
![]() $\mathfrak{g}$
is a finite
$\mathfrak{g}$
is a finite
![]() $\mathbb{Z}$
-Lie algebra whose cardinality is a power of
$\mathbb{Z}$
-Lie algebra whose cardinality is a power of
![]() $p$
, and assume that
$p$
, and assume that
![]() $\mathfrak{g}$
is nilpotent of class
$\mathfrak{g}$
is nilpotent of class
![]() $c<p$
. One may define a group operation on
$c<p$
. One may define a group operation on
![]() $\mathfrak{g}$
by the Campbell–Baker–Hausdorff formula: for all
$\mathfrak{g}$
by the Campbell–Baker–Hausdorff formula: for all
![]() $x,y\in \mathfrak{g}$
we define the group multiplication by
$x,y\in \mathfrak{g}$
we define the group multiplication by
 $$\begin{eqnarray}x\ast y:=\mathop{\sum }_{n>0}\frac{(-1)^{n+1}}{n}\mathop{\sum }_{\substack{ (a_{1},b_{1}),\ldots ,(a_{n},b_{n}) \\ a_{j}+b_{j}\geqslant 1}}\frac{(\mathop{\sum }_{1\leqslant i\leqslant n}a_{i}+b_{i})^{-1}}{a_{1}!b_{1}!\cdots a_{n}!b_{n}!}(\operatorname{ad}_{x})^{a_{1}}(\operatorname{ad}_{y})^{b_{1}}\cdots (\operatorname{ad}_{x})^{a_{n}}(\operatorname{ad}_{y})^{b_{n}-1}(y),\end{eqnarray}$$
$$\begin{eqnarray}x\ast y:=\mathop{\sum }_{n>0}\frac{(-1)^{n+1}}{n}\mathop{\sum }_{\substack{ (a_{1},b_{1}),\ldots ,(a_{n},b_{n}) \\ a_{j}+b_{j}\geqslant 1}}\frac{(\mathop{\sum }_{1\leqslant i\leqslant n}a_{i}+b_{i})^{-1}}{a_{1}!b_{1}!\cdots a_{n}!b_{n}!}(\operatorname{ad}_{x})^{a_{1}}(\operatorname{ad}_{y})^{b_{1}}\cdots (\operatorname{ad}_{x})^{a_{n}}(\operatorname{ad}_{y})^{b_{n}-1}(y),\end{eqnarray}$$
where if
![]() $b_{n}=0$
then the last term
$b_{n}=0$
then the last term
![]() $(\operatorname{ad}_{y})^{b_{n}-1}(y)$
is dropped. Plainly, if
$(\operatorname{ad}_{y})^{b_{n}-1}(y)$
is dropped. Plainly, if
![]() $b_{n}>1$
, or if
$b_{n}>1$
, or if
![]() $b_{n}=0$
and
$b_{n}=0$
and
![]() $a_{n}>1$
, then the corresponding summand vanishes. Note that the above sum is finite, because
$a_{n}>1$
, then the corresponding summand vanishes. Note that the above sum is finite, because
![]() $\mathfrak{g}$
is nilpotent. The group defined in this way is denoted by
$\mathfrak{g}$
is nilpotent. The group defined in this way is denoted by
![]() $\exp (\mathfrak{g})$
. For instance, when
$\exp (\mathfrak{g})$
. For instance, when
![]() $\mathfrak{g}$
is 2-step nilpotent and
$\mathfrak{g}$
is 2-step nilpotent and
![]() $p\geqslant 3$
, the group multiplication of
$p\geqslant 3$
, the group multiplication of
![]() $\exp (\mathfrak{g})$
takes the simple form
$\exp (\mathfrak{g})$
takes the simple form
and when
![]() $\mathfrak{g}$
is 3-step nilpotent and
$\mathfrak{g}$
is 3-step nilpotent and
![]() $p\geqslant 5$
we obtain
$p\geqslant 5$
we obtain
Similar formulas can be written for any given nilpotency class when
![]() $p$
is large enough. The group
$p$
is large enough. The group
![]() $\exp (\mathfrak{g})$
defined above is a
$\exp (\mathfrak{g})$
defined above is a
![]() $p$
-group of nilpotency class
$p$
-group of nilpotency class
![]() $c$
. In fact Lazard proved [Reference KhukhroKhu88, ch. 9] that every
$c$
. In fact Lazard proved [Reference KhukhroKhu88, ch. 9] that every
![]() $p$
-group
$p$
-group
![]() $\text{G}$
of nilpotency class
$\text{G}$
of nilpotency class
![]() $c<p$
arises in this way from a unique Lie algebra
$c<p$
arises in this way from a unique Lie algebra
![]() $\mathfrak{g}:=\text{Lie}(\text{G})$
.
$\mathfrak{g}:=\text{Lie}(\text{G})$
.
From now on, for a
![]() $c$
-step nilpotent
$c$
-step nilpotent
![]() $\mathbb{Z}$
-Lie algebra
$\mathbb{Z}$
-Lie algebra
![]() $\mathfrak{g}$
which is finitely generated as an abelian group, and for
$\mathfrak{g}$
which is finitely generated as an abelian group, and for
![]() $q:=p^{f}$
with
$q:=p^{f}$
with
![]() $p>c$
, we set
$p>c$
, we set
where
![]() $\mathbb{F}_{q}$
is the finite field with
$\mathbb{F}_{q}$
is the finite field with
![]() $q$
elements.
$q$
elements.
2.1 A palette of possibilities
To illustrate the range of possibilities that can arise, we will start this section with three examples, and then state our main results. We will elaborate on these examples in § 5.
Example 2.1 (Elliptic curve).
Let
![]() $a$
be a non-zero integer. Consider the
$a$
be a non-zero integer. Consider the
![]() $\mathbb{Z}$
-Lie algebra
$\mathbb{Z}$
-Lie algebra
![]() $\mathfrak{g}_{a}$
, introduced by Boston and Isaacs [Reference Boston and IsaacsBI04, § 3], which is spanned as a free
$\mathfrak{g}_{a}$
, introduced by Boston and Isaacs [Reference Boston and IsaacsBI04, § 3], which is spanned as a free
![]() $\mathbb{Z}$
-module by
$\mathbb{Z}$
-module by
![]() $\{v_{1},\ldots ,v_{9}\}$
, subject to the relations
$\{v_{1},\ldots ,v_{9}\}$
, subject to the relations
All other brackets
![]() $[v_{i},v_{j}]$
with
$[v_{i},v_{j}]$
with
![]() $i<j$
vanish. It will be shown in § 5.2 that if
$i<j$
vanish. It will be shown in § 5.2 that if
![]() $p$
is a sufficiently large prime (
$p$
is a sufficiently large prime (
![]() $p>1800$
will suffice) and
$p>1800$
will suffice) and
![]() $p$
does not divide
$p$
does not divide
![]() $a$
, then
$a$
, then
As we will see in the proof, the uniformity in
![]() $p$
is related to the fact that for such values of
$p$
is related to the fact that for such values of
![]() $p$
the cubic curve
$p$
the cubic curve
![]() $Y^{2}=4aX^{3}+X^{2}-4X$
has a non-zero rational point over
$Y^{2}=4aX^{3}+X^{2}-4X$
has a non-zero rational point over
![]() $\mathbb{F}_{p}$
. Note that in this example, aside from a finite set of primes, the value of
$\mathbb{F}_{p}$
. Note that in this example, aside from a finite set of primes, the value of
![]() $m_{\text{faithful}}(\exp (\mathfrak{g}_{a}\otimes _{\mathbb{Z}}\mathbb{F}_{p}))$
is given by one polynomial in
$m_{\text{faithful}}(\exp (\mathfrak{g}_{a}\otimes _{\mathbb{Z}}\mathbb{F}_{p}))$
is given by one polynomial in
![]() $p$
.
$p$
.
Example 2.2 (Binary quadratic form).
Consider the
![]() $\mathbb{Z}$
-Lie algebra
$\mathbb{Z}$
-Lie algebra
![]() $\mathfrak{g}$
spanned as a free
$\mathfrak{g}$
spanned as a free
![]() $\mathbb{Z}$
-module by
$\mathbb{Z}$
-module by
![]() $\{v_{1},\ldots ,v_{6}\}$
subject to the relations
$\{v_{1},\ldots ,v_{6}\}$
subject to the relations
where all other commutators
![]() $[v_{i},v_{j}]$
with
$[v_{i},v_{j}]$
with
![]() $i<j$
are defined to be
$i<j$
are defined to be
![]() $0$
. Then in § 5.3 we will show that for odd primes
$0$
. Then in § 5.3 we will show that for odd primes
![]() $p$
, the value of
$p$
, the value of
![]() $m_{\text{faithful}}(\mathscr{G}_{p})$
is given by two different polynomials along two arithmetic progressions, namely,
$m_{\text{faithful}}(\mathscr{G}_{p})$
is given by two different polynomials along two arithmetic progressions, namely,
Put more formally, set
Also, set
![]() $g_{1}(T):=2T$
and
$g_{1}(T):=2T$
and
![]() $g_{2}(T):=2T^{2}$
. Then
$g_{2}(T):=2T^{2}$
. Then
![]() $m_{\text{faithful}}(\mathscr{G}_{p})=g_{i}(p)$
for all
$m_{\text{faithful}}(\mathscr{G}_{p})=g_{i}(p)$
for all
![]() $p\in \mathscr{P}_{i}$
,
$p\in \mathscr{P}_{i}$
,
![]() $i=1,2$
.
$i=1,2$
.
As the next example shows, even this is not the end of the story.
Example 2.3 (Binary cubic form).
Consider the
![]() $\mathbb{Z}$
-Lie algebra
$\mathbb{Z}$
-Lie algebra
![]() $\mathfrak{g}$
spanned as a free
$\mathfrak{g}$
spanned as a free
![]() $\mathbb{Z}$
-module by
$\mathbb{Z}$
-module by
![]() $\{v_{1},\ldots ,v_{8}\}$
with the following relations:
$\{v_{1},\ldots ,v_{8}\}$
with the following relations:
All other commutators
![]() $[v_{i},v_{j}]$
with
$[v_{i},v_{j}]$
with
![]() $i<j$
vanish. Let
$i<j$
vanish. Let
![]() $p$
be an odd prime. In § 5.4 we will show that
$p$
be an odd prime. In § 5.4 we will show that
 $$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{p})=\left\{\begin{array}{@{}ll@{}}p^{2}+p^{3}\quad & \displaystyle \text{if }\biggl(\frac{p}{23}\biggr)=-1,\\ 2p^{3}\quad & \text{if }p\text{ is represented by the form }2x^{2}+xy+3y^{2},\\ 2p^{2}\quad & \text{if }p\text{ is represented by the form }x^{2}+xy+6y^{2}\quad \text{or}\quad p=23,\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{p})=\left\{\begin{array}{@{}ll@{}}p^{2}+p^{3}\quad & \displaystyle \text{if }\biggl(\frac{p}{23}\biggr)=-1,\\ 2p^{3}\quad & \text{if }p\text{ is represented by the form }2x^{2}+xy+3y^{2},\\ 2p^{2}\quad & \text{if }p\text{ is represented by the form }x^{2}+xy+6y^{2}\quad \text{or}\quad p=23,\end{array}\right.\end{eqnarray}$$
where
![]() $(\frac{\cdot }{p})$
is the Legendre symbol. The conditions defining this function split the set of prime numbers
$(\frac{\cdot }{p})$
is the Legendre symbol. The conditions defining this function split the set of prime numbers
![]() $p\geqslant 3$
into disjoint sets
$p\geqslant 3$
into disjoint sets
![]() $\mathscr{P}_{1},\mathscr{P}_{2}$
and
$\mathscr{P}_{1},\mathscr{P}_{2}$
and
![]() $\mathscr{P}_{3}$
. On each one of these sets, one of the polynomials
$\mathscr{P}_{3}$
. On each one of these sets, one of the polynomials
![]() $g_{1}(T)=T^{2}+T^{3}$
,
$g_{1}(T)=T^{2}+T^{3}$
,
![]() $g_{2}(T)=2T^{3}$
and
$g_{2}(T)=2T^{3}$
and
![]() $g_{3}(T)=2T^{2}$
is applicable. It is worth mentioning that by Gauss genus theory, the sets
$g_{3}(T)=2T^{2}$
is applicable. It is worth mentioning that by Gauss genus theory, the sets
![]() $\mathscr{P}_{2}$
and
$\mathscr{P}_{2}$
and
![]() $\mathscr{P}_{3}$
are not unions of arithmetic progressions (for example see [Reference KusabaKus67]).
$\mathscr{P}_{3}$
are not unions of arithmetic progressions (for example see [Reference KusabaKus67]).
Example 2.4 (Lee’s Lie algebra).
Consider the
![]() $\mathbb{Z}$
-Lie algebra
$\mathbb{Z}$
-Lie algebra
![]() $\mathfrak{g}$
spanned as a free
$\mathfrak{g}$
spanned as a free
![]() $\mathbb{Z}$
-module by
$\mathbb{Z}$
-module by
![]() $\{v_{1},\ldots ,v_{8}\}$
with the following relations:
$\{v_{1},\ldots ,v_{8}\}$
with the following relations:
All other commutators
![]() $[v_{i},v_{j}]$
with
$[v_{i},v_{j}]$
with
![]() $i<j$
vanish. This Lie algebra was defined in [Reference LeeLee16]. Let
$i<j$
vanish. This Lie algebra was defined in [Reference LeeLee16]. Let
![]() $p$
be an odd prime. In § 5.5 we will show that
$p$
be an odd prime. In § 5.5 we will show that
 $$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{p})=\left\{\begin{array}{@{}ll@{}}p+2p^{2}\quad & \displaystyle \text{if }p\equiv 2\;(\text{mod}\;3)\text{ or }p=3,\\ 3p\quad & \text{if }p\equiv 1\;(\text{mod}\;3)\text{ and }p\text{ is represented by the form }x^{2}+27y^{2},\\ 3p^{2}\quad & \text{if }p\equiv 1\;(\text{mod}\;3)\text{ and }p\text{ is not represented by the form }x^{2}+27y^{2}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{p})=\left\{\begin{array}{@{}ll@{}}p+2p^{2}\quad & \displaystyle \text{if }p\equiv 2\;(\text{mod}\;3)\text{ or }p=3,\\ 3p\quad & \text{if }p\equiv 1\;(\text{mod}\;3)\text{ and }p\text{ is represented by the form }x^{2}+27y^{2},\\ 3p^{2}\quad & \text{if }p\equiv 1\;(\text{mod}\;3)\text{ and }p\text{ is not represented by the form }x^{2}+27y^{2}.\end{array}\right.\end{eqnarray}$$
We remark that in [Reference LeeLee16], the author computes the order of the automorphism group of the Lie algebra
![]() $\mathfrak{g}_{p}$
. The formula obtained in [Reference LeeLee16] is given by different polynomials depending on the splitting of
$\mathfrak{g}_{p}$
. The formula obtained in [Reference LeeLee16] is given by different polynomials depending on the splitting of
![]() $\unicode[STIX]{x1D706}^{3}-2$
in
$\unicode[STIX]{x1D706}^{3}-2$
in
![]() $\mathbb{F}_{p}$
, and therefore its cases are parallel to the ones that appear above.
$\mathbb{F}_{p}$
, and therefore its cases are parallel to the ones that appear above.
The important point to note here is that in each one of the above examples, the set of primes can be decomposed into finitely many arithmetically defined sets, such that the value of
![]() $m_{\text{faithful}}(\mathscr{G}_{p})$
on each one of these sets is given by a polynomial. Let us explain this in more detail. For a polynomial
$m_{\text{faithful}}(\mathscr{G}_{p})$
on each one of these sets is given by a polynomial. Let us explain this in more detail. For a polynomial
![]() $g(T)\in \mathbb{Z}[T]$
, denote by
$g(T)\in \mathbb{Z}[T]$
, denote by
![]() ${\mathcal{V}}_{g}$
the set of primes
${\mathcal{V}}_{g}$
the set of primes
![]() $p$
for which the congruence
$p$
for which the congruence
![]() $g(T)\equiv 0\;(\text{mod}\;p)$
has a solution. We will call
$g(T)\equiv 0\;(\text{mod}\;p)$
has a solution. We will call
![]() ${\mathcal{V}}_{g}$
an elementary Frobenius set. Let
${\mathcal{V}}_{g}$
an elementary Frobenius set. Let
![]() $\mathbb{P}$
denote the set of prime numbers. By a Frobenius set we mean an element of the Boolean algebra inside the power set of
$\mathbb{P}$
denote the set of prime numbers. By a Frobenius set we mean an element of the Boolean algebra inside the power set of
![]() $\mathbb{P}$
that is generated by elementary Frobenius sets. In other words, a Frobenius set is a finite union of sets of the form
$\mathbb{P}$
that is generated by elementary Frobenius sets. In other words, a Frobenius set is a finite union of sets of the form
We remark that every Frobenius set is a Frobenian set, as defined by Serre [Reference SerreSer12, § 3.3.1], but the converse does not hold. For more details about the connection between Frobenius and Frobenian sets, see [Reference LagariasLag83].
For
![]() $p>2$
the equation
$p>2$
the equation
![]() $x^{2}+1=0$
has a solution in
$x^{2}+1=0$
has a solution in
![]() $\mathbb{F}_{p}$
if and only if
$\mathbb{F}_{p}$
if and only if
![]() $p\equiv 1\;(\text{mod}\;4)$
. This shows that the sets appearing in Example 2.2 are Frobenius sets. One can see that the sets
$p\equiv 1\;(\text{mod}\;4)$
. This shows that the sets appearing in Example 2.2 are Frobenius sets. One can see that the sets
![]() $\mathscr{P}_{i}$
in Example 2.3 are Frobenius sets as follows. First, using the quadratic reciprocity law one can easily verify that the set
$\mathscr{P}_{i}$
in Example 2.3 are Frobenius sets as follows. First, using the quadratic reciprocity law one can easily verify that the set
![]() $\mathscr{P}_{1}$
consists of those primes
$\mathscr{P}_{1}$
consists of those primes
![]() $p\geqslant 3$
for which the equation
$p\geqslant 3$
for which the equation
![]() $x^{2}+23$
has no solution in
$x^{2}+23$
has no solution in
![]() $\mathbb{F}_{p}$
. The other two parts are based on the less trivial fact that
$\mathbb{F}_{p}$
. The other two parts are based on the less trivial fact that
![]() $p\geqslant 3$
can be represented by the quadratic form
$p\geqslant 3$
can be represented by the quadratic form
![]() $a^{2}+ab+6b^{2}$
(respectively,
$a^{2}+ab+6b^{2}$
(respectively,
![]() $2a^{2}+ab+3b^{2}$
) if and only if
$2a^{2}+ab+3b^{2}$
) if and only if
![]() $p\not \in \mathscr{P}_{1}$
and
$p\not \in \mathscr{P}_{1}$
and
![]() $x^{3}-x-1$
has a solution (respectively, no solution) in
$x^{3}-x-1$
has a solution (respectively, no solution) in
![]() $\mathbb{F}_{p}$
. Consequently, each
$\mathbb{F}_{p}$
. Consequently, each
![]() $\mathscr{P}_{i}$
is a Frobenius set.
$\mathscr{P}_{i}$
is a Frobenius set.
Let
![]() $\mathscr{P}$
be any set of primes. The Dirichlet density of
$\mathscr{P}$
be any set of primes. The Dirichlet density of
![]() $\mathscr{P}$
is defined by
$\mathscr{P}$
is defined by
if the limit exists. The Chebotarev density theorem implies that any infinite Frobenius set has a positive Dirichlet density. It follows from Dirichlet’s theorem on primes in arithmetic progressions that the Dirichlet density of the sets
![]() $\mathscr{P}_{i}$
in Example 2.2 is positive. For the sets
$\mathscr{P}_{i}$
in Example 2.2 is positive. For the sets
![]() $\mathscr{P}_{i}$
in Example 2.3, positivity of the Dirichlet density can be proved by class field theory. For more details we refer the reader to [Reference CoxCox13, Theorem 9.12].
$\mathscr{P}_{i}$
in Example 2.3, positivity of the Dirichlet density can be proved by class field theory. For more details we refer the reader to [Reference CoxCox13, Theorem 9.12].
With this preparation, we are now ready to state our first result.
Theorem 2.5. Let
![]() $\mathfrak{g}$
be a nilpotent
$\mathfrak{g}$
be a nilpotent
![]() $\mathbb{Z}$
-Lie algebra of nilpotency class
$\mathbb{Z}$
-Lie algebra of nilpotency class
![]() $c$
which is finitely generated as an abelian group. Then there exist a partition
$c$
which is finitely generated as an abelian group. Then there exist a partition
![]() $\mathscr{P}_{1},\ldots ,\mathscr{P}_{r}$
of the set of prime numbers larger than
$\mathscr{P}_{1},\ldots ,\mathscr{P}_{r}$
of the set of prime numbers larger than
![]() $c$
into Frobenius sets, and polynomials
$c$
into Frobenius sets, and polynomials
![]() $g_{1}(T),\ldots ,g_{r}(T)$
with non-negative integer coefficients, depending only on
$g_{1}(T),\ldots ,g_{r}(T)$
with non-negative integer coefficients, depending only on
![]() $\mathfrak{g}$
, such that
$\mathfrak{g}$
, such that
where
![]() $1\leqslant i\leqslant r$
.
$1\leqslant i\leqslant r$
.
The proof of this theorem relies on a theorem of Ax [Reference AxAx67] from model theory (see also van den Dries [Reference van den DriesVdDri91]), coupled with a parameterization of irreducible representations provided by the Kirillov machinery. As we shall see, studying
![]() $m_{\text{faithful}}(\mathscr{G}_{p})$
leads to questions related to the existence of rational points over finite fields of certain determinantal varieties associated with the commutator matrix. We remark that our proof is effective and we can use its method to describe the associated Frobenius sets and polynomials. We will demonstrate this by a detailed analysis of the above examples after we give the proof of Theorem 2.5.
$m_{\text{faithful}}(\mathscr{G}_{p})$
leads to questions related to the existence of rational points over finite fields of certain determinantal varieties associated with the commutator matrix. We remark that our proof is effective and we can use its method to describe the associated Frobenius sets and polynomials. We will demonstrate this by a detailed analysis of the above examples after we give the proof of Theorem 2.5.
One can also consider
![]() $m_{\text{faithful}}(\mathscr{G}_{q})$
for
$m_{\text{faithful}}(\mathscr{G}_{q})$
for
![]() $q:=p^{f}$
when the prime
$q:=p^{f}$
when the prime
![]() $p$
is fixed and
$p$
is fixed and
![]() $f$
varies. Let
$f$
varies. Let
![]() $\mathscr{P}$
be one of the Frobenius sets in Theorem 2.5 with the associated polynomial
$\mathscr{P}$
be one of the Frobenius sets in Theorem 2.5 with the associated polynomial
![]() $g(T)\in \mathbb{Z}[T]$
. The following example shows that it is not necessarily true that
$g(T)\in \mathbb{Z}[T]$
. The following example shows that it is not necessarily true that
Example 2.6. Take
![]() $\mathfrak{g}$
as in Example 2.2 and set
$\mathfrak{g}$
as in Example 2.2 and set
![]() $\mathscr{P}:=\mathscr{P}_{2}$
, where
$\mathscr{P}:=\mathscr{P}_{2}$
, where
![]() $\mathscr{P}_{2}$
is as in the same example. Recall that
$\mathscr{P}_{2}$
is as in the same example. Recall that
However, in § 5.3 we shall demonstrate that
Nevertheless, we prove the following theorem which shows that in general, the behaviour of
![]() $m_{\text{faithful}}(\mathscr{G}_{q})$
for
$m_{\text{faithful}}(\mathscr{G}_{q})$
for
![]() $q:=p^{f}$
with
$q:=p^{f}$
with
![]() $p$
fixed is very similar to the above example.
$p$
fixed is very similar to the above example.
Theorem 2.7. Let
![]() $\mathfrak{g}$
be a nilpotent
$\mathfrak{g}$
be a nilpotent
![]() $\mathbb{Z}$
-Lie algebra of nilpotency class
$\mathbb{Z}$
-Lie algebra of nilpotency class
![]() $c$
which is finitely generated as an abelian group. Fix a prime
$c$
which is finitely generated as an abelian group. Fix a prime
![]() $p>C$
, where
$p>C$
, where
![]() $C$
is the constant given in (31). Then there exist a partition
$C$
is the constant given in (31). Then there exist a partition
![]() $\mathscr{A}_{1},\ldots ,\mathscr{A}_{r}$
of the set of natural numbers, and polynomials
$\mathscr{A}_{1},\ldots ,\mathscr{A}_{r}$
of the set of natural numbers, and polynomials
![]() $g_{1}(T),\ldots ,g_{r}(T)$
with non-negative integer coefficients, depending on
$g_{1}(T),\ldots ,g_{r}(T)$
with non-negative integer coefficients, depending on
![]() $p$
and
$p$
and
![]() $\mathfrak{g}$
, such that:
$\mathfrak{g}$
, such that:
(1) each
 $\mathscr{A}_{i}$
,
$\mathscr{A}_{i}$
,
 $1\leqslant i\leqslant r$
, is a union of a finite set and finitely many arithmetic progressions;
$1\leqslant i\leqslant r$
, is a union of a finite set and finitely many arithmetic progressions;(2) for all
 $1\leqslant i\leqslant r$
, if
$1\leqslant i\leqslant r$
, if
 $q=p^{f}$
where
$q=p^{f}$
where
 $f\in \mathscr{A}_{i}$
, then
$f\in \mathscr{A}_{i}$
, then
 $m_{\text{faithful}}(\mathscr{G}_{q})=fg_{i}(q)$
.
$m_{\text{faithful}}(\mathscr{G}_{q})=fg_{i}(q)$
.
The proof of Theorem 2.7 uses Dwork’s theorem on rationality of zeta functions of varieties and the Skolem–Mahler–Lech theorem.
At this point two remarks are in order. On the one hand, Theorems 2.5 and 2.7 set an upper limit on how complicated the value of
![]() $m_{\text{faithful}}(\mathscr{G}_{q})$
as a function of
$m_{\text{faithful}}(\mathscr{G}_{q})$
as a function of
![]() $p$
and
$p$
and
![]() $f$
can be. It would be desirable to know to what extent the collection of functions appearing in Theorem 2.5 can be realized as
$f$
can be. It would be desirable to know to what extent the collection of functions appearing in Theorem 2.5 can be realized as
![]() $m_{\text{faithful}}(\mathscr{G}_{q})$
for some Lie algebra
$m_{\text{faithful}}(\mathscr{G}_{q})$
for some Lie algebra
![]() $\mathfrak{g}$
. On the other hand, one may still hope that at least for a large class of naturally arising Lie algebras
$\mathfrak{g}$
. On the other hand, one may still hope that at least for a large class of naturally arising Lie algebras
![]() $\mathfrak{g}$
, the function
$\mathfrak{g}$
, the function
![]() $m_{\text{faithful}}(\mathscr{G}_{q})$
is given by a single polynomial. In the next section we address these two problems.
$m_{\text{faithful}}(\mathscr{G}_{q})$
is given by a single polynomial. In the next section we address these two problems.
2.2 Pattern groups
Let us begin this section by introducing a large class of nilpotent groups which can be viewed as a generalization of the
![]() $n$
th Heisenberg group
$n$
th Heisenberg group
![]() $\operatorname{Heis}_{2n+1}(\mathbb{F}_{q})$
defined in the introduction.
$\operatorname{Heis}_{2n+1}(\mathbb{F}_{q})$
defined in the introduction.
Set
![]() $[n]:=\{1,2,\ldots ,n\}$
, and let
$[n]:=\{1,2,\ldots ,n\}$
, and let
![]() $([n],\prec )$
be a partially ordered set. Without loss of generality, we can assume that if
$([n],\prec )$
be a partially ordered set. Without loss of generality, we can assume that if
![]() $i\prec j$
then
$i\prec j$
then
![]() $i<j$
. To this partial order we assign the pattern Lie algebra
$i<j$
. To this partial order we assign the pattern Lie algebra
where
![]() $\mathbf{e}_{ij}$
denotes the
$\mathbf{e}_{ij}$
denotes the
![]() $n\times n$
matrix whose unique non-zero entry is a
$n\times n$
matrix whose unique non-zero entry is a
![]() $1$
in the
$1$
in the
![]() $(i,j)$
position.
$(i,j)$
position.
Note that
![]() $\mathfrak{g}_{\prec }$
is nilpotent since the commutator relation
$\mathfrak{g}_{\prec }$
is nilpotent since the commutator relation
ensures that
![]() $\mathfrak{g}_{\prec }$
is a subalgebra of the Lie algebra
$\mathfrak{g}_{\prec }$
is a subalgebra of the Lie algebra
![]() $\mathfrak{u}_{n}$
of strictly upper-triangular
$\mathfrak{u}_{n}$
of strictly upper-triangular
![]() $n$
by
$n$
by
![]() $n$
matrices. For instance, the
$n$
matrices. For instance, the
![]() $(2n+1)$
-dimensional Heisenberg Lie algebra corresponds to the partial order
$(2n+1)$
-dimensional Heisenberg Lie algebra corresponds to the partial order
For all
![]() $i\prec j$
define
$i\prec j$
define
Moreover, the length of
![]() $([n],\prec )$
, denoted by
$([n],\prec )$
, denoted by
![]() $\unicode[STIX]{x1D706}_{\prec }$
, is defined to be the maximum value of
$\unicode[STIX]{x1D706}_{\prec }$
, is defined to be the maximum value of
![]() $r$
such that there exists a chain
$r$
such that there exists a chain
![]() $i_{0}\prec \cdots \prec i_{r}$
in
$i_{0}\prec \cdots \prec i_{r}$
in
![]() $([n],\prec )$
. For instance the length of the partial order given in (3) is equal to
$([n],\prec )$
. For instance the length of the partial order given in (3) is equal to
![]() $2$
. We remark that
$2$
. We remark that
![]() $\unicode[STIX]{x1D706}_{\prec }$
is equal to the nilpotency class of
$\unicode[STIX]{x1D706}_{\prec }$
is equal to the nilpotency class of
![]() $\mathfrak{g}_{\prec }$
(see Lemma 4.1).
$\mathfrak{g}_{\prec }$
(see Lemma 4.1).
Definition 2.9. An ordered pair
![]() $(i,j)$
is called an extreme pair if
$(i,j)$
is called an extreme pair if
![]() $i$
is a minimal element in
$i$
is a minimal element in
![]() $([n],\prec )$
,
$([n],\prec )$
,
![]() $j$
is a maximal element in
$j$
is a maximal element in
![]() $([n],\prec )$
, and
$([n],\prec )$
, and
![]() $i\prec j$
. The set of extreme pairs will be denoted by
$i\prec j$
. The set of extreme pairs will be denoted by
![]() $I_{\text{ex}}$
.
$I_{\text{ex}}$
.
We can now state our theorem on the faithful dimension of pattern groups.
Theorem 2.10. Let
![]() $\prec$
be a partial order of length
$\prec$
be a partial order of length
![]() $\unicode[STIX]{x1D706}_{\prec }$
on the set
$\unicode[STIX]{x1D706}_{\prec }$
on the set
![]() $[n]$
, and let
$[n]$
, and let
![]() $q:=p^{f}$
where
$q:=p^{f}$
where
![]() $p>\unicode[STIX]{x1D706}_{\prec }$
. Then
$p>\unicode[STIX]{x1D706}_{\prec }$
. Then
Theorem 2.10 generalizes (2), and its proof relies on Kirillov theory and more specifically on an explicit description of the size of coadjoint orbits in terms of combinatorial data of the partial order. Note that by Theorems 2.5 and 2.7, a priori there is no reason to expect the faithful dimension to be given by a single formula of the form
![]() $fg(p^{f})$
for a polynomial
$fg(p^{f})$
for a polynomial
![]() $g(T)$
. Theorem 2.10 is proved by a detailed analysis of the size of coadjoint orbits and a combinatorial lemma due to Rado and Horn.
$g(T)$
. Theorem 2.10 is proved by a detailed analysis of the size of coadjoint orbits and a combinatorial lemma due to Rado and Horn.
Question 2.11. Let
![]() $F$
be a non-Archimedean local field with the ring of integers
$F$
be a non-Archimedean local field with the ring of integers
![]() ${\mathcal{O}}$
, the unique maximal ideal
${\mathcal{O}}$
, the unique maximal ideal
![]() $\mathfrak{p}$
and the associated residue field
$\mathfrak{p}$
and the associated residue field
![]() $\mathbb{F}_{q}$
. Is it true that
$\mathbb{F}_{q}$
. Is it true that
![]() $m_{\text{faithful}}(\exp (\mathfrak{g}_{\prec }\otimes _{\mathbb{Z}}{\mathcal{O}}/\mathfrak{p}^{n}))$
is given by the formula
$m_{\text{faithful}}(\exp (\mathfrak{g}_{\prec }\otimes _{\mathbb{Z}}{\mathcal{O}}/\mathfrak{p}^{n}))$
is given by the formula
where
![]() $f$
is the absolute inertia degree and
$f$
is the absolute inertia degree and
![]() $e$
is the absolute ramification index of
$e$
is the absolute ramification index of
![]() $F$
? Formula (4) is suggested by (1) and Theorem 2.10.
$F$
? Formula (4) is suggested by (1) and Theorem 2.10.
An immediate consequence of Theorem 2.10 is the following corollary.
Corollary 2.12. For any non-zero polynomial
![]() $g(T)\in \mathbb{Z}[T]$
with non-negative coefficients, there exists a nilpotent
$g(T)\in \mathbb{Z}[T]$
with non-negative coefficients, there exists a nilpotent
![]() $\mathbb{Z}$
-Lie algebra
$\mathbb{Z}$
-Lie algebra
![]() $\mathfrak{g}$
which is finitely generated as an abelian group such that
$\mathfrak{g}$
which is finitely generated as an abelian group such that
when
![]() $p\geqslant \deg g(T)+2$
and
$p\geqslant \deg g(T)+2$
and
![]() $f\geqslant 1$
.
$f\geqslant 1$
.
2.3 Relatively free nilpotent groups
In this section we will turn to free objects in certain categories of nilpotent Lie algebras. Let
![]() $\mathfrak{f}_{n,c}:=\mathfrak{f}_{n,c}(\mathbb{Z})$
be the free nilpotent
$\mathfrak{f}_{n,c}:=\mathfrak{f}_{n,c}(\mathbb{Z})$
be the free nilpotent
![]() $\mathbb{Z}$
-Lie algebra on
$\mathbb{Z}$
-Lie algebra on
![]() $n$
generators and of class
$n$
generators and of class
![]() $c$
; it is defined to be the quotient algebra
$c$
; it is defined to be the quotient algebra
![]() $\mathfrak{f}_{n}/\mathfrak{f}_{n}^{c+1}$
, where
$\mathfrak{f}_{n}/\mathfrak{f}_{n}^{c+1}$
, where
![]() $\mathfrak{f}_{n}$
is the free
$\mathfrak{f}_{n}$
is the free
![]() $\mathbb{Z}$
-Lie algebra on
$\mathbb{Z}$
-Lie algebra on
![]() $n$
generators, and
$n$
generators, and
![]() $\mathfrak{f}_{n}^{c+1}$
denotes the
$\mathfrak{f}_{n}^{c+1}$
denotes the
![]() $(c+1)$
th term in the lower central series of
$(c+1)$
th term in the lower central series of
![]() $\mathfrak{f}_{n}$
starting with
$\mathfrak{f}_{n}$
starting with
![]() $\mathfrak{f}_{n}^{1}=\mathfrak{f}_{n}$
. It is well known that the rank of the quotient
$\mathfrak{f}_{n}^{1}=\mathfrak{f}_{n}$
. It is well known that the rank of the quotient
![]() $\mathfrak{f}_{n}^{c}/\mathfrak{f}_{n}^{c+1}$
(as a
$\mathfrak{f}_{n}^{c}/\mathfrak{f}_{n}^{c+1}$
(as a
![]() $\mathbb{Z}$
-module) is given by Witt’s formula
$\mathbb{Z}$
-module) is given by Witt’s formula
where
![]() $\unicode[STIX]{x1D707}$
is the Möbius function. Using the orbit method one can prove that
$\unicode[STIX]{x1D707}$
is the Möbius function. Using the orbit method one can prove that
This lower bound is sharp for
![]() $\mathfrak{f}_{n,2}$
and
$\mathfrak{f}_{n,2}$
and
![]() $\mathfrak{f}_{n,3}$
.
$\mathfrak{f}_{n,3}$
.
Theorem 2.13. Let
![]() $n\geqslant 2$
and let
$n\geqslant 2$
and let
![]() $\mathbb{F}_{q}$
be the finite field with
$\mathbb{F}_{q}$
be the finite field with
![]() $q=p^{f}$
elements. Then, we have:
$q=p^{f}$
elements. Then, we have:
(1)
 $m_{\text{faithful}}(\exp (\mathfrak{f}_{n,2}\otimes _{\mathbb{Z}}\mathbb{F}_{q}))=((n^{2}-n)/2)fq$
for
$m_{\text{faithful}}(\exp (\mathfrak{f}_{n,2}\otimes _{\mathbb{Z}}\mathbb{F}_{q}))=((n^{2}-n)/2)fq$
for
 $p\geqslant 3$
;
$p\geqslant 3$
;(2)
 $m_{\text{faithful}}(\exp (\mathfrak{f}_{n,3}\otimes _{\mathbb{Z}}\mathbb{F}_{q}))=((n^{3}-n)/3)fq$
for
$m_{\text{faithful}}(\exp (\mathfrak{f}_{n,3}\otimes _{\mathbb{Z}}\mathbb{F}_{q}))=((n^{3}-n)/3)fq$
for
 $p\geqslant 5$
.
$p\geqslant 5$
.
The proofs of these results involve explicit computations with Hall bases and rely on a subtle combinatorial optimization.
Remark 2.14. For
![]() $2\leqslant c\leqslant 6$
, the value of
$2\leqslant c\leqslant 6$
, the value of
![]() $m_{\text{faithful}}(\exp (\mathfrak{f}_{2,c}\otimes _{\mathbb{Z}}\mathbb{F}_{p}))$
is given by Table 1.
$m_{\text{faithful}}(\exp (\mathfrak{f}_{2,c}\otimes _{\mathbb{Z}}\mathbb{F}_{p}))$
is given by Table 1.
Table 1. The faithful dimension for 2-generated relatively free nilpotent groups of small nilpotency.

In § 7.4, we outline the computations that yield the values of
![]() $m_{\text{faithful}}(\exp (\mathfrak{f}_{2,c}\otimes _{\mathbb{Z}}\mathbb{F}_{p}))$
in Table 1. However, we are not able to obtain any general formula for
$m_{\text{faithful}}(\exp (\mathfrak{f}_{2,c}\otimes _{\mathbb{Z}}\mathbb{F}_{p}))$
in Table 1. However, we are not able to obtain any general formula for
![]() $m_{\text{faithful}}(\exp (\mathfrak{f}_{2,c}\otimes _{\mathbb{Z}}\mathbb{F}_{p}))$
in terms of
$m_{\text{faithful}}(\exp (\mathfrak{f}_{2,c}\otimes _{\mathbb{Z}}\mathbb{F}_{p}))$
in terms of
![]() $c$
.
$c$
.
For a Lie algebra
![]() $\mathfrak{g}$
, let
$\mathfrak{g}$
, let
![]() $(D^{k}\mathfrak{g})_{k\geqslant 0}$
be the derived series of
$(D^{k}\mathfrak{g})_{k\geqslant 0}$
be the derived series of
![]() $\mathfrak{g}$
. Thus
$\mathfrak{g}$
. Thus
![]() $D^{0}\mathfrak{g}=\mathfrak{g}$
,
$D^{0}\mathfrak{g}=\mathfrak{g}$
,
![]() $D\mathfrak{g}=[\mathfrak{g},\mathfrak{g}]$
, and
$D\mathfrak{g}=[\mathfrak{g},\mathfrak{g}]$
, and
![]() $D^{k+1}\mathfrak{g}=[D^{k}\mathfrak{g},D^{k}\mathfrak{g}]$
for
$D^{k+1}\mathfrak{g}=[D^{k}\mathfrak{g},D^{k}\mathfrak{g}]$
for
![]() $k\geqslant 1$
. Note that
$k\geqslant 1$
. Note that
![]() $\mathfrak{g}/D^{2}\mathfrak{g}$
is the largest metabelian quotient of
$\mathfrak{g}/D^{2}\mathfrak{g}$
is the largest metabelian quotient of
![]() $\mathfrak{g}$
. When
$\mathfrak{g}$
. When
![]() $\mathfrak{g}=\mathfrak{f}_{n,c}$
, this quotient is called the free metabelian Lie algebra of class
$\mathfrak{g}=\mathfrak{f}_{n,c}$
, this quotient is called the free metabelian Lie algebra of class
![]() $c$
on
$c$
on
![]() $n$
generators and will be denoted by
$n$
generators and will be denoted by
![]() $\mathfrak{m}_{n,c}$
.
$\mathfrak{m}_{n,c}$
.
Theorem 2.15. Let
![]() $c\geqslant 2$
. Then
$c\geqslant 2$
. Then
![]() $m_{\text{faithful}}(\exp (\mathfrak{m}_{2,c}\otimes _{\mathbb{Z}}\mathbb{F}_{q}))=(c-1)fq$
for
$m_{\text{faithful}}(\exp (\mathfrak{m}_{2,c}\otimes _{\mathbb{Z}}\mathbb{F}_{q}))=(c-1)fq$
for
![]() $q:=p^{f}$
with
$q:=p^{f}$
with
![]() $p>c$
.
$p>c$
.
In the course of the proof of Theorem 2.15 we will see that computing the faithful dimension of
![]() $\exp (\mathfrak{m}_{2,c}\otimes _{\mathbb{Z}}\mathbb{F}_{q})$
is linked to rational normal curves, that is, the image of the Veronese map given by
$\exp (\mathfrak{m}_{2,c}\otimes _{\mathbb{Z}}\mathbb{F}_{q})$
is linked to rational normal curves, that is, the image of the Veronese map given by
This suggests that other tools (e.g. from the theory of determinantal varieties) might be relevant in the more general situation.
3 Preliminaries
In this section we introduce some notation and prove a number of basic facts which will be used throughout this paper. In particular, we will explain the connection between faithful representations and the central characters of their irreducible components. We will also briefly recall the orbit method.
Notation. Let
![]() $\text{G}$
be a group with the identity element
$\text{G}$
be a group with the identity element
![]() $\mathbf{1}$
. The centre and the commutator subgroup of
$\mathbf{1}$
. The centre and the commutator subgroup of
![]() $\text{G}$
will be denoted, respectively, by
$\text{G}$
will be denoted, respectively, by
![]() $\text{Z}(\text{G})$
and
$\text{Z}(\text{G})$
and
![]() $\text{G}^{\prime }=[\text{G},\text{G}]$
. For an abelian
$\text{G}^{\prime }=[\text{G},\text{G}]$
. For an abelian
![]() $p$
-group
$p$
-group
![]() $\text{G}$
, we write
$\text{G}$
, we write
which is a
![]() $\mathbb{Z}/p\mathbb{Z}$
-vector space. The Pontryagin dual of an abelian group
$\mathbb{Z}/p\mathbb{Z}$
-vector space. The Pontryagin dual of an abelian group
![]() $A$
, i.e.
$A$
, i.e.
![]() $\operatorname{Hom}(A,\mathbb{C}^{\ast })$
, will be denoted by
$\operatorname{Hom}(A,\mathbb{C}^{\ast })$
, will be denoted by
![]() $\widehat{A}$
. Evidently, when
$\widehat{A}$
. Evidently, when
![]() $A$
is an elementary abelian
$A$
is an elementary abelian
![]() $p$
-group,
$p$
-group,
![]() $\widehat{A}$
has a canonical
$\widehat{A}$
has a canonical
![]() $\mathbb{Z}/p\mathbb{Z}$
-vector space structure. We denote the cardinality of a set
$\mathbb{Z}/p\mathbb{Z}$
-vector space structure. We denote the cardinality of a set
![]() $S$
by
$S$
by
![]() $\#S$
.
$\#S$
.
3.1 Central characters of faithful representations of
 $p$
-groups
$p$
-groups
Let
![]() $A$
be a finite abelian group. We denote the minimal number of generators of
$A$
be a finite abelian group. We denote the minimal number of generators of
![]() $A$
by
$A$
by
![]() $d(A)$
. For an exact sequence of finite abelian groups
$d(A)$
. For an exact sequence of finite abelian groups
![]() $0\rightarrow A_{1}\rightarrow A\rightarrow A_{2}\rightarrow 0$
, the numbers
$0\rightarrow A_{1}\rightarrow A\rightarrow A_{2}\rightarrow 0$
, the numbers
![]() $d(A)$
,
$d(A)$
,
![]() $d(A_{1})$
and
$d(A_{1})$
and
![]() $d(A_{2})$
satisfy the inequalities
$d(A_{2})$
satisfy the inequalities
The number of invariant factors of
![]() $A$
will be denoted by
$A$
will be denoted by
![]() $d^{\prime }(A)$
. It can be easily seen from elementary divisor theory that
$d^{\prime }(A)$
. It can be easily seen from elementary divisor theory that
![]() $d^{\prime }(A)=d(A)$
. Evidently
$d^{\prime }(A)=d(A)$
. Evidently
![]() $m_{\text{faithful}}(A)\leqslant d^{\prime }(A)$
. Now for a given faithful representation
$m_{\text{faithful}}(A)\leqslant d^{\prime }(A)$
. Now for a given faithful representation
![]() $\unicode[STIX]{x1D70C}:A\rightarrow \operatorname{GL}_{m}(\mathbb{C})$
, by decomposing
$\unicode[STIX]{x1D70C}:A\rightarrow \operatorname{GL}_{m}(\mathbb{C})$
, by decomposing
![]() $\unicode[STIX]{x1D70C}$
into irreducible components and applying (5) we obtain
$\unicode[STIX]{x1D70C}$
into irreducible components and applying (5) we obtain
![]() $d(A)=d^{\prime }(A)\leqslant m_{\text{faithful}}(A)$
. This implies that
$d(A)=d^{\prime }(A)\leqslant m_{\text{faithful}}(A)$
. This implies that
In particular, we obtain the following lemma.
Lemma 3.1. For a finite abelian
![]() $p$
-group
$p$
-group
![]() $A$
,
$A$
,
Let
![]() $E$
be a finite elementary abelian
$E$
be a finite elementary abelian
![]() $p$
-group equipped with the canonical
$p$
-group equipped with the canonical
![]() $\mathbb{Z}/p\mathbb{Z}$
-vector space structure. Every one-dimensional representation
$\mathbb{Z}/p\mathbb{Z}$
-vector space structure. Every one-dimensional representation
![]() $\unicode[STIX]{x1D712}:E\rightarrow \mathbb{C}^{\ast }$
factors uniquely as
$\unicode[STIX]{x1D712}:E\rightarrow \mathbb{C}^{\ast }$
factors uniquely as
![]() $\unicode[STIX]{x1D712}=\unicode[STIX]{x1D716}\circ \unicode[STIX]{x1D712}_{\circ }$
, where
$\unicode[STIX]{x1D712}=\unicode[STIX]{x1D716}\circ \unicode[STIX]{x1D712}_{\circ }$
, where
![]() $\unicode[STIX]{x1D712}_{\circ }\in \operatorname{Hom}(E,\mathbb{Z}/p\mathbb{Z})$
and the embedding
$\unicode[STIX]{x1D712}_{\circ }\in \operatorname{Hom}(E,\mathbb{Z}/p\mathbb{Z})$
and the embedding
![]() $\unicode[STIX]{x1D716}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}^{\ast }$
is defined by
$\unicode[STIX]{x1D716}:\mathbb{Z}/p\mathbb{Z}\rightarrow \mathbb{C}^{\ast }$
is defined by
Hence the
![]() $\mathbb{Z}/p\mathbb{Z}$
-linear map
$\mathbb{Z}/p\mathbb{Z}$
-linear map
provides an isomorphism of
![]() $\mathbb{Z}/p\mathbb{Z}$
-vector spaces between
$\mathbb{Z}/p\mathbb{Z}$
-vector spaces between
![]() $\widehat{E}$
and
$\widehat{E}$
and
![]() $\operatorname{Hom}(E,\mathbb{Z}/p\mathbb{Z})$
. Now, let
$\operatorname{Hom}(E,\mathbb{Z}/p\mathbb{Z})$
. Now, let
![]() $\text{G}$
be a finite
$\text{G}$
be a finite
![]() $p$
-group. Applying (6) to
$p$
-group. Applying (6) to
![]() $\unicode[STIX]{x1D6FA}_{1}(\text{Z}(G))$
, we obtain the
$\unicode[STIX]{x1D6FA}_{1}(\text{Z}(G))$
, we obtain the
![]() $\mathbb{Z}/p\mathbb{Z}$
-isomorphism
$\mathbb{Z}/p\mathbb{Z}$
-isomorphism
Hereafter the
![]() $\mathbb{Z}/p\mathbb{Z}$
-vector space
$\mathbb{Z}/p\mathbb{Z}$
-vector space
![]() $\text{Hom}(\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\text{G})),\mathbb{C}^{\ast })$
will be denoted by
$\text{Hom}(\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\text{G})),\mathbb{C}^{\ast })$
will be denoted by
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\text{G}))$
.
$\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\text{G}))$
.
Remark 3.2. Recall the standard fact that for a finite
![]() $p$
-group
$p$
-group
![]() $\text{G}$
, every non-trivial normal subgroup of
$\text{G}$
, every non-trivial normal subgroup of
![]() $\text{G}$
intersects
$\text{G}$
intersects
![]() $\text{Z}(\text{G})$
and hence
$\text{Z}(\text{G})$
and hence
![]() $\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\text{G}))$
non-trivially. Consequently, a representation of
$\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\text{G}))$
non-trivially. Consequently, a representation of
![]() $\text{G}$
is faithful if and only if its restriction to
$\text{G}$
is faithful if and only if its restriction to
![]() $\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\text{G}))$
is faithful.
$\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\text{G}))$
is faithful.
We recall the following simple lemma.
Lemma 3.3. Let
![]() $L,L_{1},\ldots ,L_{n}$
be linear functionals on a vector space
$L,L_{1},\ldots ,L_{n}$
be linear functionals on a vector space
![]() $V$
with respective null spaces
$V$
with respective null spaces
![]() $N$
,
$N$
,
![]() $N_{1},\ldots ,N_{n}$
. Then
$N_{1},\ldots ,N_{n}$
. Then
![]() $L$
is a linear combination of
$L$
is a linear combination of
![]() $L_{1},\ldots ,L_{n}$
if and only if
$L_{1},\ldots ,L_{n}$
if and only if
![]() $N$
contains the intersection
$N$
contains the intersection
![]() $N_{1}\cap \cdots \cap N_{n}$
.
$N_{1}\cap \cdots \cap N_{n}$
.
The following observation, due to Meyer and Reichstein [Reference Meyer and ReichsteinMR10], will play a crucial role in computing the faithful dimension of
![]() $p$
-groups.
$p$
-groups.
Lemma 3.4. Let
![]() $\text{G}$
be a finite
$\text{G}$
be a finite
![]() $p$
-group and let
$p$
-group and let
![]() $(\unicode[STIX]{x1D70C}_{i},V_{i})_{1\leqslant i\leqslant n}$
be a family of irreducible representations of
$(\unicode[STIX]{x1D70C}_{i},V_{i})_{1\leqslant i\leqslant n}$
be a family of irreducible representations of
![]() $\text{G}$
with central characters
$\text{G}$
with central characters
![]() $\unicode[STIX]{x1D712}_{i}$
. Assume that the set of characters
$\unicode[STIX]{x1D712}_{i}$
. Assume that the set of characters
spans
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\text{G}))$
. Then
$\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\text{G}))$
. Then
![]() $\bigoplus _{1\leqslant i\leqslant n}\unicode[STIX]{x1D70C}_{i}$
is a faithful representation of
$\bigoplus _{1\leqslant i\leqslant n}\unicode[STIX]{x1D70C}_{i}$
is a faithful representation of
![]() $\text{G}$
.
$\text{G}$
.
Proof. Since the set
![]() $\{{\unicode[STIX]{x1D712}_{i}}_{|_{\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\text{G}))}}:1\leqslant i\leqslant n\}$
spans
$\{{\unicode[STIX]{x1D712}_{i}}_{|_{\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\text{G}))}}:1\leqslant i\leqslant n\}$
spans
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\text{G}))$
, from the
$\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\text{G}))$
, from the
![]() $\mathbb{Z}/p\mathbb{Z}$
-isomorphism (7) and Lemma 3.3 we obtain
$\mathbb{Z}/p\mathbb{Z}$
-isomorphism (7) and Lemma 3.3 we obtain
Hence
![]() $\bigoplus _{1\leqslant i\leqslant n}\unicode[STIX]{x1D70C}_{i}$
is a faithful representation of
$\bigoplus _{1\leqslant i\leqslant n}\unicode[STIX]{x1D70C}_{i}$
is a faithful representation of
![]() $\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\text{G}))$
. Remark 3.2 implies that
$\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\text{G}))$
. Remark 3.2 implies that
![]() $\bigoplus _{1\leqslant i\leqslant n}\unicode[STIX]{x1D70C}_{i}$
is a faithful representation of
$\bigoplus _{1\leqslant i\leqslant n}\unicode[STIX]{x1D70C}_{i}$
is a faithful representation of
![]() $\text{G}$
.◻
$\text{G}$
.◻
Lemma 3.5. Let
![]() $\text{G}$
be a finite
$\text{G}$
be a finite
![]() $p$
-group and let
$p$
-group and let
![]() $\unicode[STIX]{x1D70C}$
be a faithful representation of
$\unicode[STIX]{x1D70C}$
be a faithful representation of
![]() $\text{G}$
with the smallest possible dimension. Then
$\text{G}$
with the smallest possible dimension. Then
![]() $\unicode[STIX]{x1D70C}$
decomposes as a direct sum of exactly
$\unicode[STIX]{x1D70C}$
decomposes as a direct sum of exactly
![]() $r:=d(\text{Z}(\text{G}))$
irreducible representations
$r:=d(\text{Z}(\text{G}))$
irreducible representations
Therefore the set of central characters
![]() $\{{\unicode[STIX]{x1D712}_{i}}_{|_{\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\text{G}))}}:1\leqslant i\leqslant r\}$
is a basis of
$\{{\unicode[STIX]{x1D712}_{i}}_{|_{\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\text{G}))}}:1\leqslant i\leqslant r\}$
is a basis of
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\text{G}))$
.
$\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\text{G}))$
.
Proof. Let
![]() $\unicode[STIX]{x1D70C}=\bigoplus _{1\leqslant i\leqslant n}\unicode[STIX]{x1D70C}_{i}$
be the decomposition of
$\unicode[STIX]{x1D70C}=\bigoplus _{1\leqslant i\leqslant n}\unicode[STIX]{x1D70C}_{i}$
be the decomposition of
![]() $\unicode[STIX]{x1D70C}$
, and let
$\unicode[STIX]{x1D70C}$
, and let
![]() $\unicode[STIX]{x1D712}_{i}$
,
$\unicode[STIX]{x1D712}_{i}$
,
![]() $1\leqslant i\leqslant n$
, denote the central character of
$1\leqslant i\leqslant n$
, denote the central character of
![]() $\unicode[STIX]{x1D70C}_{i}$
. Since
$\unicode[STIX]{x1D70C}_{i}$
. Since
![]() $\unicode[STIX]{x1D70C}$
is faithful and
$\unicode[STIX]{x1D70C}$
is faithful and
![]() $r=d(\text{Z}(\text{G}))$
, it follows that
$r=d(\text{Z}(\text{G}))$
, it follows that
![]() $n\geqslant r$
. Furthermore, faithfulness of
$n\geqslant r$
. Furthermore, faithfulness of
![]() $\unicode[STIX]{x1D70C}$
also implies
$\unicode[STIX]{x1D70C}$
also implies
![]() $\bigcap _{i=1}^{n}\ker \unicode[STIX]{x1D712}_{i}=\{\mathbf{1}\}$
. Hence, from Lemma 3.3, Lemma 3.4, and the minimality of
$\bigcap _{i=1}^{n}\ker \unicode[STIX]{x1D712}_{i}=\{\mathbf{1}\}$
. Hence, from Lemma 3.3, Lemma 3.4, and the minimality of
![]() $\dim (\unicode[STIX]{x1D70C})$
it follows that
$\dim (\unicode[STIX]{x1D70C})$
it follows that
![]() $n=r$
and also that the set
$n=r$
and also that the set
is a basis of
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\text{G}))$
.◻
$\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\text{G}))$
.◻
3.2 Kirillov’s orbit method
The orbit method was introduced by Kirillov [Reference KirillovKir62] to study unitary representations of simply connected nilpotent Lie groups. For such a group
![]() $\text{G}$
with Lie algebra
$\text{G}$
with Lie algebra
![]() $\mathfrak{g}$
, this method provides an explicit bijection between the unitary dual
$\mathfrak{g}$
, this method provides an explicit bijection between the unitary dual
![]() $\widehat{\text{G}}$
of
$\widehat{\text{G}}$
of
![]() $\text{G}$
, and the set
$\text{G}$
, and the set
![]() $\operatorname{Hom}^{\text{cont}}(\mathfrak{g},\mathbb{C}^{\ast })/\text{G}$
of orbits of the induced action of
$\operatorname{Hom}^{\text{cont}}(\mathfrak{g},\mathbb{C}^{\ast })/\text{G}$
of orbits of the induced action of
![]() $\text{G}$
on
$\text{G}$
on
![]() $\operatorname{Hom}^{\text{cont}}(\mathfrak{g},\mathbb{C}^{\ast })$
, called the coadjoint orbits. Since Kirillov’s work, this method has been extended to study representations of nilpotent groups in other contexts. Relevant to this work is the version applicable to finite
$\operatorname{Hom}^{\text{cont}}(\mathfrak{g},\mathbb{C}^{\ast })$
, called the coadjoint orbits. Since Kirillov’s work, this method has been extended to study representations of nilpotent groups in other contexts. Relevant to this work is the version applicable to finite
![]() $p$
-groups, which we now briefly explain. For more details we refer the reader to [Reference Boyarchenko and SabitovaBS08]. Let
$p$
-groups, which we now briefly explain. For more details we refer the reader to [Reference Boyarchenko and SabitovaBS08]. Let
![]() $\text{G}$
be a
$\text{G}$
be a
![]() $p$
-group of nilpotency class
$p$
-group of nilpotency class
![]() $c<p$
. By the Lazard correspondence, there exists a unique finite
$c<p$
. By the Lazard correspondence, there exists a unique finite
![]() $\mathbb{Z}$
-Lie algebra
$\mathbb{Z}$
-Lie algebra
![]() $\mathfrak{g}:=\text{Lie}(\text{G})$
of cardinality
$\mathfrak{g}:=\text{Lie}(\text{G})$
of cardinality
![]() $|\text{G}|$
and nilpotency class
$|\text{G}|$
and nilpotency class
![]() $c$
such that
$c$
such that
![]() $\text{G}\cong \exp (\mathfrak{g})$
. Note that in the definition of
$\text{G}\cong \exp (\mathfrak{g})$
. Note that in the definition of
![]() $\exp (\mathfrak{g})$
the underlying set of the group is
$\exp (\mathfrak{g})$
the underlying set of the group is
![]() $\mathfrak{g}$
and the multiplication law is defined by the Campbell–Baker–Hausdorff formula. Usually we identify the underlying sets of the group
$\mathfrak{g}$
and the multiplication law is defined by the Campbell–Baker–Hausdorff formula. Usually we identify the underlying sets of the group
![]() $\text{G}$
and the Lie algebra
$\text{G}$
and the Lie algebra
![]() $\mathfrak{g}$
. A simple application of the Campbell–Baker–Hausdorff formula shows that in this identification the centre of
$\mathfrak{g}$
. A simple application of the Campbell–Baker–Hausdorff formula shows that in this identification the centre of
![]() $\mathfrak{g}$
(as a Lie algebra) will be mapped onto the centre of
$\mathfrak{g}$
(as a Lie algebra) will be mapped onto the centre of
![]() $\text{G}$
as a group.
$\text{G}$
as a group.
Consider now the coadjoint action of
![]() $\text{G}$
on
$\text{G}$
on
![]() $\widehat{\mathfrak{g}}:=\operatorname{Hom}_{\mathbb{Z}}(\mathfrak{g},\mathbb{C}^{\ast })$
, defined by
$\widehat{\mathfrak{g}}:=\operatorname{Hom}_{\mathbb{Z}}(\mathfrak{g},\mathbb{C}^{\ast })$
, defined by
where
![]() $x,y\in \mathfrak{g}$
and
$x,y\in \mathfrak{g}$
and
![]() $\unicode[STIX]{x1D703}\in \widehat{\mathfrak{g}}$
. Note that since
$\unicode[STIX]{x1D703}\in \widehat{\mathfrak{g}}$
. Note that since
![]() $p>c$
, the sum is well defined.
$p>c$
, the sum is well defined.
Theorem 3.6. Assume that
![]() $p\geqslant 3$
and let
$p\geqslant 3$
and let
![]() $\text{G}$
be a
$\text{G}$
be a
![]() $p$
-group of nilpotency class
$p$
-group of nilpotency class
![]() $c<p$
. Furthermore, assume that
$c<p$
. Furthermore, assume that
![]() $\mathfrak{g}=\text{Lie}(\text{G})$
. Then there exists a bijection between
$\mathfrak{g}=\text{Lie}(\text{G})$
. Then there exists a bijection between
![]() $\text{G}$
-orbits
$\text{G}$
-orbits
![]() $\unicode[STIX]{x1D6E9}\subseteq \widehat{\mathfrak{g}}$
and irreducible representations
$\unicode[STIX]{x1D6E9}\subseteq \widehat{\mathfrak{g}}$
and irreducible representations
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6E9}}\in \widehat{\text{G}}$
such that Kirillov’s character formula holds:
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6E9}}\in \widehat{\text{G}}$
such that Kirillov’s character formula holds:
Proof. See [Reference Boyarchenko and SabitovaBS08, Theorem 2.6]. ◻
Remark 3.7. For an extension of Kirillov’s orbit method to the case
![]() $p=2$
, see [Reference Stasinski and VollSV14, Theorem 2.6].
$p=2$
, see [Reference Stasinski and VollSV14, Theorem 2.6].
Let
![]() $\unicode[STIX]{x1D6E9}\subset \widehat{\mathfrak{g}}$
be the orbit of
$\unicode[STIX]{x1D6E9}\subset \widehat{\mathfrak{g}}$
be the orbit of
![]() $\unicode[STIX]{x1D703}_{0}\in \widehat{\mathfrak{g}}$
. Then from Kirillov’s character formula we see that the central character of
$\unicode[STIX]{x1D703}_{0}\in \widehat{\mathfrak{g}}$
. Then from Kirillov’s character formula we see that the central character of
![]() $\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6E9}}$
is
$\unicode[STIX]{x1D70C}_{\unicode[STIX]{x1D6E9}}$
is
![]() ${\unicode[STIX]{x1D703}_{0}}_{|_{\text{Z}(\mathfrak{g})}}$
and
${\unicode[STIX]{x1D703}_{0}}_{|_{\text{Z}(\mathfrak{g})}}$
and
Proposition 3.8. The stabilizer of
![]() $\unicode[STIX]{x1D703}_{0}$
is given by
$\unicode[STIX]{x1D703}_{0}$
is given by
Proof. One inclusion is obvious. For the inclusion
![]() $\subseteq$
note that
$\subseteq$
note that
Fix
![]() $x\in \text{Stab}_{\text{G}}(\unicode[STIX]{x1D703}_{0})$
. Then
$x\in \text{Stab}_{\text{G}}(\unicode[STIX]{x1D703}_{0})$
. Then
Choose an arbitrary element
![]() $y\in \mathfrak{g}^{c-1}$
. Since
$y\in \mathfrak{g}^{c-1}$
. Since
![]() $\mathfrak{g}^{c+1}=0$
, it follows from (10) that
$\mathfrak{g}^{c+1}=0$
, it follows from (10) that
![]() $\unicode[STIX]{x1D703}_{0}(\operatorname{ad}_{x}(y))=0$
. Next choose an arbitrary
$\unicode[STIX]{x1D703}_{0}(\operatorname{ad}_{x}(y))=0$
. Next choose an arbitrary
![]() $y\in \mathfrak{g}^{c-2}$
, and note that
$y\in \mathfrak{g}^{c-2}$
, and note that
In light of the previous step,
![]() $\unicode[STIX]{x1D703}_{0}(\operatorname{ad}_{x}(y))=0$
. Continuing this process, the claim follows for all
$\unicode[STIX]{x1D703}_{0}(\operatorname{ad}_{x}(y))=0$
. Continuing this process, the claim follows for all
![]() $y\in \mathfrak{g}$
.◻
$y\in \mathfrak{g}$
.◻
Let us now illustrate the power of the orbit method by showing how it can be used to compute the faithful dimension of certain 2-step nilpotent groups.
Proposition 3.9. Let
![]() $\text{G}$
be a 2-step nilpotent
$\text{G}$
be a 2-step nilpotent
![]() $p$
-group, where
$p$
-group, where
![]() $p\geqslant 3$
. Assume that
$p\geqslant 3$
. Assume that
![]() $\text{Z}(G)$
is cyclic. Then
$\text{Z}(G)$
is cyclic. Then
![]() $m_{\text{faithful}}(\text{G})=\sqrt{[\text{G}:\text{Z}(\text{G})]}$
.
$m_{\text{faithful}}(\text{G})=\sqrt{[\text{G}:\text{Z}(\text{G})]}$
.
Proof. Let
![]() $\unicode[STIX]{x1D70C}$
be a faithful representation of
$\unicode[STIX]{x1D70C}$
be a faithful representation of
![]() $\text{G}$
of minimal dimension. Since the centre of
$\text{G}$
of minimal dimension. Since the centre of
![]() $\text{G}$
is cyclic, it follows from Lemma 3.5 that
$\text{G}$
is cyclic, it follows from Lemma 3.5 that
![]() $\unicode[STIX]{x1D70C}$
is irreducible. By the Lazard correspondence
$\unicode[STIX]{x1D70C}$
is irreducible. By the Lazard correspondence
![]() $\text{G}=\exp (\mathfrak{g})$
, where
$\text{G}=\exp (\mathfrak{g})$
, where
![]() $\mathfrak{g}$
is a finite Lie algebra of class
$\mathfrak{g}$
is a finite Lie algebra of class
![]() $2$
. It suffices to show that
$2$
. It suffices to show that
![]() $\dim \unicode[STIX]{x1D70C}=\sqrt{[\mathfrak{g}:\text{Z}(\mathfrak{g})]}$
. Thanks to the orbit method, there exists
$\dim \unicode[STIX]{x1D70C}=\sqrt{[\mathfrak{g}:\text{Z}(\mathfrak{g})]}$
. Thanks to the orbit method, there exists
![]() $\unicode[STIX]{x1D703}_{0}\in \widehat{\mathfrak{g}}$
such that
$\unicode[STIX]{x1D703}_{0}\in \widehat{\mathfrak{g}}$
such that
where
![]() $\unicode[STIX]{x1D6E9}$
is the
$\unicode[STIX]{x1D6E9}$
is the
![]() $\text{G}$
-orbit of
$\text{G}$
-orbit of
![]() $\unicode[STIX]{x1D703}_{0}$
. Therefore
$\unicode[STIX]{x1D703}_{0}$
. Therefore
Recall that we identify
![]() $\text{Z}(\text{G})$
with
$\text{Z}(\text{G})$
with
![]() $\text{Z}(\mathfrak{g})$
. The restriction to
$\text{Z}(\mathfrak{g})$
. The restriction to
![]() $\text{Z}(\mathfrak{g})$
of the central character of
$\text{Z}(\mathfrak{g})$
of the central character of
![]() $\unicode[STIX]{x1D70C}$
is
$\unicode[STIX]{x1D70C}$
is
![]() $\unicode[STIX]{x1D703}_{0}$
, and so
$\unicode[STIX]{x1D703}_{0}$
, and so
![]() $\unicode[STIX]{x1D703}_{0}:\text{Z}(\mathfrak{g})\rightarrow \mathbb{C}^{\ast }$
is faithful. Now let
$\unicode[STIX]{x1D703}_{0}:\text{Z}(\mathfrak{g})\rightarrow \mathbb{C}^{\ast }$
is faithful. Now let
![]() $x\in \text{Stab}_{\text{G}}(\unicode[STIX]{x1D703}_{0})$
. Then
$x\in \text{Stab}_{\text{G}}(\unicode[STIX]{x1D703}_{0})$
. Then
![]() $\unicode[STIX]{x1D703}_{0}([x,y])=1$
for all
$\unicode[STIX]{x1D703}_{0}([x,y])=1$
for all
![]() $y\in \mathfrak{g}$
, so that
$y\in \mathfrak{g}$
, so that
![]() $[x,y]=0$
. Consequently,
$[x,y]=0$
. Consequently,
![]() $\text{Stab}_{\text{G}}(\unicode[STIX]{x1D703}_{0})=\text{Z}(\mathfrak{g})$
. This completes the proof.◻
$\text{Stab}_{\text{G}}(\unicode[STIX]{x1D703}_{0})=\text{Z}(\mathfrak{g})$
. This completes the proof.◻
The class of
![]() $p$
-groups covered by Proposition 3.9 includes all the extra special
$p$
-groups covered by Proposition 3.9 includes all the extra special
![]() $p$
-groups for
$p$
-groups for
![]() $p\geqslant 3$
; a
$p\geqslant 3$
; a
![]() $p$
-group
$p$
-group
![]() $\text{G}$
is called extra special when its centre
$\text{G}$
is called extra special when its centre
![]() $\text{Z}(\text{G})$
has
$\text{Z}(\text{G})$
has
![]() $p$
elements and
$p$
elements and
![]() $\text{G}/\text{Z}(\text{G})$
is an elementary abelian
$\text{G}/\text{Z}(\text{G})$
is an elementary abelian
![]() $p$
-group. It is well known that an extra special
$p$
-group. It is well known that an extra special
![]() $p$
-group has order
$p$
-group has order
![]() $p^{2n+1}$
for some positive integer
$p^{2n+1}$
for some positive integer
![]() $n$
. Thus the faithful dimension of
$n$
. Thus the faithful dimension of
![]() $\text{G}$
is
$\text{G}$
is
![]() $p^{n}$
.
$p^{n}$
.
4 Faithful dimension of pattern groups
This section is devoted to the proof of Theorem 2.10. We start by recalling some notation that was defined in § 2.2. Let
![]() $\prec$
be a partial order on the set
$\prec$
be a partial order on the set
![]() $[n]:=\{1,\ldots ,n\}$
. We can associate to
$[n]:=\{1,\ldots ,n\}$
. We can associate to
![]() $\prec$
the Lie algebra defined by
$\prec$
the Lie algebra defined by
Recall that the length of
![]() $([n],\prec )$
, denoted by
$([n],\prec )$
, denoted by
![]() $\unicode[STIX]{x1D706}_{\prec }$
, is defined to be the maximum value of
$\unicode[STIX]{x1D706}_{\prec }$
, is defined to be the maximum value of
![]() $r$
such that there exists a chain
$r$
such that there exists a chain
![]() $i_{0}\prec \cdots \prec i_{r}$
in
$i_{0}\prec \cdots \prec i_{r}$
in
![]() $([n],\prec )$
.
$([n],\prec )$
.
Lemma 4.1. The nilpotency class of
![]() $\mathfrak{g}$
is equal to the length of
$\mathfrak{g}$
is equal to the length of
![]() $([n],\prec )$
.
$([n],\prec )$
.
Proof of Lemma 4.1.
First note that
From (11) it follows that
![]() $[\mathbf{e}_{ij},\mathbf{e}_{kl}]=\mathbf{e}_{il}$
when
$[\mathbf{e}_{ij},\mathbf{e}_{kl}]=\mathbf{e}_{il}$
when
![]() $i\prec j=k\prec l$
and
$i\prec j=k\prec l$
and
![]() $[\mathbf{e}_{ij},\mathbf{e}_{kl}]=-\mathbf{e}_{kj}$
when
$[\mathbf{e}_{ij},\mathbf{e}_{kl}]=-\mathbf{e}_{kj}$
when
![]() $k\prec l=i\prec j$
. In other cases
$k\prec l=i\prec j$
. In other cases
![]() $[\mathbf{e}_{ij},\mathbf{e}_{kl}]=0$
. Given a chain
$[\mathbf{e}_{ij},\mathbf{e}_{kl}]=0$
. Given a chain
![]() $i_{0}\prec \cdots \prec i_{r}$
in
$i_{0}\prec \cdots \prec i_{r}$
in
![]() $([n],\prec )$
, one can see that
$([n],\prec )$
, one can see that
and hence the nilpotency class of
![]() $\mathfrak{g}$
is at least
$\mathfrak{g}$
is at least
![]() $r$
. Similarly, one can see that a non-zero commutator of length
$r$
. Similarly, one can see that a non-zero commutator of length
![]() $r+1$
leads to a chain of length
$r+1$
leads to a chain of length
![]() $r+1$
, proving the claim.◻
$r+1$
, proving the claim.◻
Recall that
![]() $I_{\text{ex}}$
is the set of extreme pairs (see Definition 2.9).
$I_{\text{ex}}$
is the set of extreme pairs (see Definition 2.9).
Lemma 4.2. The centre
![]() $\text{Z}(\mathfrak{g})$
of
$\text{Z}(\mathfrak{g})$
of
![]() $\mathfrak{g}$
is spanned by
$\mathfrak{g}$
is spanned by
![]() $\{\mathbf{e}_{ij}:(i,j)\in I_{\text{ex}}\}$
.
$\{\mathbf{e}_{ij}:(i,j)\in I_{\text{ex}}\}$
.
Proof. We first show that
![]() $\mathbf{e}_{ij}$
with
$\mathbf{e}_{ij}$
with
![]() $(i,j)\in I_{\text{ex}}$
is in the centre of
$(i,j)\in I_{\text{ex}}$
is in the centre of
![]() $\mathfrak{g}$
. From (11) it follows that
$\mathfrak{g}$
. From (11) it follows that
since
![]() $i$
is minimal and
$i$
is minimal and
![]() $j$
is maximal. Conversely, suppose
$j$
is maximal. Conversely, suppose
![]() $z=\sum _{i\prec j}x_{ij}\mathbf{e}_{ij}\in \text{Z}(\mathfrak{g})$
. We show that for each
$z=\sum _{i\prec j}x_{ij}\mathbf{e}_{ij}\in \text{Z}(\mathfrak{g})$
. We show that for each
![]() $i_{1}\prec j_{1}$
, if
$i_{1}\prec j_{1}$
, if
![]() $x_{i_{1}j_{1}}\neq 0$
then
$x_{i_{1}j_{1}}\neq 0$
then
![]() $(i_{1},j_{1})\in I_{\text{ex}}$
. Assume
$(i_{1},j_{1})\in I_{\text{ex}}$
. Assume
![]() $i_{1}$
is not minimal, and pick a minimal element
$i_{1}$
is not minimal, and pick a minimal element
![]() $k\prec i_{1}$
. Then (11) implies that
$k\prec i_{1}$
. Then (11) implies that
and thus
![]() $x_{i_{1}j_{1}}=0$
, which is a contradiction. A similar argument shows that
$x_{i_{1}j_{1}}=0$
, which is a contradiction. A similar argument shows that
![]() $j_{1}$
is maximal.◻
$j_{1}$
is maximal.◻
An additive character
![]() $\unicode[STIX]{x1D713}:\mathbb{F}_{q}\rightarrow \mathbb{C}^{\ast }$
is called primitive if the pairing
$\unicode[STIX]{x1D713}:\mathbb{F}_{q}\rightarrow \mathbb{C}^{\ast }$
is called primitive if the pairing
is non-degenerate. We fix a primitive character
![]() $\unicode[STIX]{x1D713}$
by choosing
$\unicode[STIX]{x1D713}$
by choosing
![]() $\unicode[STIX]{x1D704}:\mathbb{F}_{p}\rightarrow \mathbb{C}^{\ast }$
to be a faithful character and defining
$\unicode[STIX]{x1D704}:\mathbb{F}_{p}\rightarrow \mathbb{C}^{\ast }$
to be a faithful character and defining
![]() $\unicode[STIX]{x1D713}(x):=\unicode[STIX]{x1D704}(\mathbf{Tr}(x))$
, where
$\unicode[STIX]{x1D713}(x):=\unicode[STIX]{x1D704}(\mathbf{Tr}(x))$
, where
![]() $\mathbf{Tr}:=\text{Tr}_{\mathbb{F}_{q}/\mathbb{F}_{p}}:\mathbb{F}_{q}\rightarrow \mathbb{F}_{p}$
is the trace map. Using
$\mathbf{Tr}:=\text{Tr}_{\mathbb{F}_{q}/\mathbb{F}_{p}}:\mathbb{F}_{q}\rightarrow \mathbb{F}_{p}$
is the trace map. Using
![]() $\unicode[STIX]{x1D713}$
we can identify the Pontryagin dual of the additive group of
$\unicode[STIX]{x1D713}$
we can identify the Pontryagin dual of the additive group of
![]() $\mathbb{F}_{q}$
with
$\mathbb{F}_{q}$
with
![]() $\mathbb{F}_{q}$
. It follows that all characters of
$\mathbb{F}_{q}$
. It follows that all characters of
![]() $\mathfrak{g}_{q}$
are obtained by vectors
$\mathfrak{g}_{q}$
are obtained by vectors
![]() $\mathbf{b}=(b_{ij})\in \bigoplus _{i\prec j}\mathbb{F}_{q}$
, via
$\mathbf{b}=(b_{ij})\in \bigoplus _{i\prec j}\mathbb{F}_{q}$
, via
By Lemma 4.1, the Lie algebra
![]() $\mathfrak{g}_{q}$
has nilpotency class
$\mathfrak{g}_{q}$
has nilpotency class
![]() $\unicode[STIX]{x1D706}_{\prec }$
. In the rest of this section we assume that
$\unicode[STIX]{x1D706}_{\prec }$
. In the rest of this section we assume that
![]() $p>\unicode[STIX]{x1D706}_{\prec }$
. By the orbit method every irreducible representation of
$p>\unicode[STIX]{x1D706}_{\prec }$
. By the orbit method every irreducible representation of
![]() $\mathscr{G}_{q}$
is constructed from the orbit of a character
$\mathscr{G}_{q}$
is constructed from the orbit of a character
![]() $\unicode[STIX]{x1D713}_{\mathbf{b}}\in \widehat{\mathfrak{g}}_{q}$
in the coadjoint action. We denote the irreducible representation obtained from
$\unicode[STIX]{x1D713}_{\mathbf{b}}\in \widehat{\mathfrak{g}}_{q}$
in the coadjoint action. We denote the irreducible representation obtained from
![]() $\unicode[STIX]{x1D713}_{\mathbf{b}}$
by
$\unicode[STIX]{x1D713}_{\mathbf{b}}$
by
![]() $\unicode[STIX]{x1D70C}_{\mathbf{b}}$
.
$\unicode[STIX]{x1D70C}_{\mathbf{b}}$
.
Proposition 4.3. Let
![]() $\mathbf{b}=(b_{ij})$
be an element of
$\mathbf{b}=(b_{ij})$
be an element of
![]() $\bigoplus _{i\prec j}\mathbb{F}_{q}$
and let
$\bigoplus _{i\prec j}\mathbb{F}_{q}$
and let
![]() $\unicode[STIX]{x1D70C}_{\mathbf{b}}$
be the irreducible representation of
$\unicode[STIX]{x1D70C}_{\mathbf{b}}$
be the irreducible representation of
![]() $\mathscr{G}_{q}$
associated to the orbit of
$\mathscr{G}_{q}$
associated to the orbit of
![]() $\unicode[STIX]{x1D713}_{\mathbf{b}}$
. For all
$\unicode[STIX]{x1D713}_{\mathbf{b}}$
. For all
![]() $(i_{1},j_{1})\in I_{\text{ex}}$
, if
$(i_{1},j_{1})\in I_{\text{ex}}$
, if
![]() $b_{i_{1}j_{1}}\neq 0$
then
$b_{i_{1}j_{1}}\neq 0$
then
Proof. Set
![]() $I:=\{(i,j):i\prec j\}$
. For
$I:=\{(i,j):i\prec j\}$
. For
![]() $x=\sum _{i\prec j}x_{ij}\mathbf{e}_{ij}\in \text{Stab}_{\mathscr{G}_{q}}(\unicode[STIX]{x1D713}_{\mathbf{b}})$
and
$x=\sum _{i\prec j}x_{ij}\mathbf{e}_{ij}\in \text{Stab}_{\mathscr{G}_{q}}(\unicode[STIX]{x1D713}_{\mathbf{b}})$
and
![]() $y=\sum _{i\prec j}y_{ij}\mathbf{e}_{ij}\in \mathfrak{g}_{q}$
, it follows from (11) that
$y=\sum _{i\prec j}y_{ij}\mathbf{e}_{ij}\in \mathfrak{g}_{q}$
, it follows from (11) that
 $$\begin{eqnarray}\displaystyle 1=\unicode[STIX]{x1D713}_{\mathbf{b}}([x,y]) & = & \displaystyle \unicode[STIX]{x1D713}_{\mathbf{b}}\biggl(\mathop{\sum }_{i\prec j,k\prec l}x_{ij}y_{kl}[\mathbf{e}_{ij},\mathbf{e}_{kl}]\biggr)=\unicode[STIX]{x1D713}\biggl(\mathop{\sum }_{i\prec j}\mathop{\sum }_{i\prec k\prec j}b_{ij}(x_{ik}y_{kj}-x_{kj}y_{ik})\biggr)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D713}\biggl(\mathop{\sum }_{i\prec j}\biggl(\mathop{\sum }_{k\prec i}b_{kj}x_{ki}-\mathop{\sum }_{j\prec l}b_{il}x_{jl}\biggr)y_{ij}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle 1=\unicode[STIX]{x1D713}_{\mathbf{b}}([x,y]) & = & \displaystyle \unicode[STIX]{x1D713}_{\mathbf{b}}\biggl(\mathop{\sum }_{i\prec j,k\prec l}x_{ij}y_{kl}[\mathbf{e}_{ij},\mathbf{e}_{kl}]\biggr)=\unicode[STIX]{x1D713}\biggl(\mathop{\sum }_{i\prec j}\mathop{\sum }_{i\prec k\prec j}b_{ij}(x_{ik}y_{kj}-x_{kj}y_{ik})\biggr)\nonumber\\ \displaystyle & = & \displaystyle \unicode[STIX]{x1D713}\biggl(\mathop{\sum }_{i\prec j}\biggl(\mathop{\sum }_{k\prec i}b_{kj}x_{ki}-\mathop{\sum }_{j\prec l}b_{il}x_{jl}\biggr)y_{ij}\biggr).\nonumber\end{eqnarray}$$
Since
![]() $y_{ij}\in \mathbb{F}_{q}$
is arbitrary and
$y_{ij}\in \mathbb{F}_{q}$
is arbitrary and
![]() $\unicode[STIX]{x1D713}$
is a primitive character, we obtain a system of linear equations
$\unicode[STIX]{x1D713}$
is a primitive character, we obtain a system of linear equations
which describes the stabilizer of
![]() $\unicode[STIX]{x1D713}_{\mathbf{b}}$
. The equations in (12) have coefficients in
$\unicode[STIX]{x1D713}_{\mathbf{b}}$
. The equations in (12) have coefficients in
![]() $\mathbb{F}_{q}$
and are indexed by pairs
$\mathbb{F}_{q}$
and are indexed by pairs
![]() $i,j$
such that
$i,j$
such that
![]() $i\prec j$
. We now consider only the linear forms
$i\prec j$
. We now consider only the linear forms
![]() $L_{i_{1}i}(x_{st})$
and
$L_{i_{1}i}(x_{st})$
and
![]() $L_{jj_{1}}(x_{st})$
, for
$L_{jj_{1}}(x_{st})$
, for
![]() $i_{1}\prec i\prec j_{1}$
and
$i_{1}\prec i\prec j_{1}$
and
![]() $i_{1}\prec j\prec j_{1}$
. From these
$i_{1}\prec j\prec j_{1}$
. From these
![]() $i$
and
$i$
and
![]() $j$
, we obtain
$j$
, we obtain
![]() $2\unicode[STIX]{x1D6FC}(i_{1},j_{1})$
linear equations with coefficients in
$2\unicode[STIX]{x1D6FC}(i_{1},j_{1})$
linear equations with coefficients in
![]() $\mathbb{F}_{q}$
, as follows:
$\mathbb{F}_{q}$
, as follows:
 $$\begin{eqnarray}\displaystyle & \displaystyle b_{i_{1}j_{1}}x_{ij_{1}}=-\mathop{\sum }_{i\prec k\neq j_{1}}b_{i_{1}k}x_{ik},\quad i_{1}\prec i\prec j_{1}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{i_{1}j_{1}}x_{i_{1}j}=-\mathop{\sum }_{i_{1}\neq l\prec j}b_{lj_{1}}x_{lj},\quad i_{1}\prec j\prec j_{1}. & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle b_{i_{1}j_{1}}x_{ij_{1}}=-\mathop{\sum }_{i\prec k\neq j_{1}}b_{i_{1}k}x_{ik},\quad i_{1}\prec i\prec j_{1}, & \displaystyle \nonumber\\ \displaystyle & \displaystyle b_{i_{1}j_{1}}x_{i_{1}j}=-\mathop{\sum }_{i_{1}\neq l\prec j}b_{lj_{1}}x_{lj},\quad i_{1}\prec j\prec j_{1}. & \displaystyle\end{eqnarray}$$
From
![]() $b_{i_{1}j_{1}}\neq 0$
it follows that
$b_{i_{1}j_{1}}\neq 0$
it follows that
![]() $x_{ij_{1}}$
(
$x_{ij_{1}}$
(
![]() $i_{1}\prec i\prec j_{1}$
) and
$i_{1}\prec i\prec j_{1}$
) and
![]() $x_{i_{1}j}$
(
$x_{i_{1}j}$
(
![]() $i_{1}\prec j\prec j_{1}$
) are dependent variables and thus, by noticing that each linear form has
$i_{1}\prec j\prec j_{1}$
) are dependent variables and thus, by noticing that each linear form has
![]() $\#I$
variables, the number of solutions of (13) is at most
$\#I$
variables, the number of solutions of (13) is at most
Thus the size of the stabilizer (12) is at most (14) and this gives the lower bound by (8). ◻
Lemma 4.4. Let
![]() $b$
be a non-zero element of
$b$
be a non-zero element of
![]() $\mathbb{F}_{q}$
. Fix
$\mathbb{F}_{q}$
. Fix
![]() $(i,j)\in I_{\text{ex}}$
and define
$(i,j)\in I_{\text{ex}}$
and define
![]() $\mathbf{b}=(b_{kl})_{k\prec l}$
, where
$\mathbf{b}=(b_{kl})_{k\prec l}$
, where
![]() $b_{ij}=b$
and the other components are zero. Then the dimension of the irreducible representation
$b_{ij}=b$
and the other components are zero. Then the dimension of the irreducible representation
![]() $\unicode[STIX]{x1D70C}_{\mathbf{b}}$
is
$\unicode[STIX]{x1D70C}_{\mathbf{b}}$
is
![]() $q^{\unicode[STIX]{x1D6FC}(i,j)}$
.
$q^{\unicode[STIX]{x1D6FC}(i,j)}$
.
Proof. Set
![]() $I:=\{(i,j):i\prec j\}$
. The proof of Proposition 4.3, namely (12), shows that the stabilizer of
$I:=\{(i,j):i\prec j\}$
. The proof of Proposition 4.3, namely (12), shows that the stabilizer of
![]() $\unicode[STIX]{x1D70C}_{\mathbf{b}}$
is defined by the equations
$\unicode[STIX]{x1D70C}_{\mathbf{b}}$
is defined by the equations
![]() $bx_{ik}=0$
and
$bx_{ik}=0$
and
![]() $bx_{kj}=0$
, where
$bx_{kj}=0$
, where
![]() $i\prec k\prec j$
. These show that the stabilizer has cardinality
$i\prec k\prec j$
. These show that the stabilizer has cardinality
![]() $q^{\#I-2\unicode[STIX]{x1D6FC}(i,j)}$
, and therefore the dimension of
$q^{\#I-2\unicode[STIX]{x1D6FC}(i,j)}$
, and therefore the dimension of
![]() $\unicode[STIX]{x1D70C}_{\mathbf{b}}$
is
$\unicode[STIX]{x1D70C}_{\mathbf{b}}$
is
![]() $q^{\unicode[STIX]{x1D6FC}(i,j)}$
by (8).◻
$q^{\unicode[STIX]{x1D6FC}(i,j)}$
by (8).◻
Using this we now construct a faithful representation of
![]() $\mathscr{G}_{q}$
.
$\mathscr{G}_{q}$
.
Lemma 4.5. The group
![]() $\mathscr{G}_{q}$
has a faithful representation of dimension
$\mathscr{G}_{q}$
has a faithful representation of dimension
Proof. First note that
![]() $\text{Z}(\mathscr{G}_{q})\cong \text{Z}(\mathfrak{g}_{q})$
and so
$\text{Z}(\mathscr{G}_{q})\cong \text{Z}(\mathfrak{g}_{q})$
and so
Let
![]() $\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{f}$
be a basis of
$\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{f}$
be a basis of
![]() $\mathbb{F}_{q}$
over
$\mathbb{F}_{q}$
over
![]() $\mathbb{F}_{p}$
. For
$\mathbb{F}_{p}$
. For
![]() $(i,j)\in I_{\text{ex}}$
and
$(i,j)\in I_{\text{ex}}$
and
![]() $1\leqslant l\leqslant f$
, define the vectors
$1\leqslant l\leqslant f$
, define the vectors
![]() $\mathbf{b}_{l}(i,j)\in \bigoplus _{s\prec t}\mathbb{F}_{q}$
, with the
$\mathbf{b}_{l}(i,j)\in \bigoplus _{s\prec t}\mathbb{F}_{q}$
, with the
![]() $(i,j)$
coordinate equal to
$(i,j)$
coordinate equal to
![]() $\unicode[STIX]{x1D714}_{l}$
and the other coordinates equal to
$\unicode[STIX]{x1D714}_{l}$
and the other coordinates equal to
![]() $0$
. Then the set
$0$
. Then the set
is a basis of
![]() $\text{Z}(\mathfrak{g}_{q})$
as an
$\text{Z}(\mathfrak{g}_{q})$
as an
![]() $\mathbb{F}_{p}$
-vector space. It follows that the set
$\mathbb{F}_{p}$
-vector space. It follows that the set
is a basis of
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\mathfrak{g}_{q}))$
and thus of
$\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\mathfrak{g}_{q}))$
and thus of
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\mathscr{G}_{q}))$
by (15). Since
$\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\mathscr{G}_{q}))$
by (15). Since
![]() $\unicode[STIX]{x1D713}_{\mathbf{b}_{l}(i,j)}$
is the central character of
$\unicode[STIX]{x1D713}_{\mathbf{b}_{l}(i,j)}$
is the central character of
![]() $\unicode[STIX]{x1D70C}_{\mathbf{b}_{l}(i,j)}$
, it follows from Lemma 3.4 that the representation
$\unicode[STIX]{x1D70C}_{\mathbf{b}_{l}(i,j)}$
, it follows from Lemma 3.4 that the representation
is faithful. By Lemma 4.4 the dimension of
![]() $\unicode[STIX]{x1D70C}_{\mathbf{b}_{l}(i,j)}$
is equal to
$\unicode[STIX]{x1D70C}_{\mathbf{b}_{l}(i,j)}$
is equal to
![]() $q^{\unicode[STIX]{x1D6FC}(i,j)}$
and hence
$q^{\unicode[STIX]{x1D6FC}(i,j)}$
and hence
This finishes the proof. ◻
We are now ready to prove Theorem 2.10.
4.1 Proof of Theorem 2.10
Write
![]() $m:=\#I_{\text{ex}}$
and
$m:=\#I_{\text{ex}}$
and
![]() $n:=fm$
. As before, we identify
$n:=fm$
. As before, we identify
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\mathfrak{g}_{q}))$
with
$\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\mathfrak{g}_{q}))$
with
![]() $\bigoplus _{(i,j)\in I_{\text{ex}}}\mathbb{F}_{q}$
which has dimension
$\bigoplus _{(i,j)\in I_{\text{ex}}}\mathbb{F}_{q}$
which has dimension
![]() $n$
as an
$n$
as an
![]() $\mathbb{F}_{p}$
-vector space. Let
$\mathbb{F}_{p}$
-vector space. Let
![]() $\unicode[STIX]{x1D70C}$
be a faithful representation of
$\unicode[STIX]{x1D70C}$
be a faithful representation of
![]() $\mathscr{G}_{q}$
with the smallest possible dimension. We will show that the dimension of
$\mathscr{G}_{q}$
with the smallest possible dimension. We will show that the dimension of
![]() $\unicode[STIX]{x1D70C}$
is bounded from below by the right-hand side of (16). Using Lemma 3.5 we can decompose
$\unicode[STIX]{x1D70C}$
is bounded from below by the right-hand side of (16). Using Lemma 3.5 we can decompose
![]() $\unicode[STIX]{x1D70C}$
as a direct sum of
$\unicode[STIX]{x1D70C}$
as a direct sum of
![]() $n$
irreducible representations, each of which obtained via the orbit method as described above. Hence, we can write
$n$
irreducible representations, each of which obtained via the orbit method as described above. Hence, we can write
with vectors
![]() $\mathbf{a}_{k}$
given by
$\mathbf{a}_{k}$
given by
Since the central character of
![]() $\unicode[STIX]{x1D70C}_{\mathbf{a}_{k}}$
is the restriction of
$\unicode[STIX]{x1D70C}_{\mathbf{a}_{k}}$
is the restriction of
![]() $\unicode[STIX]{x1D713}_{\mathbf{a}_{k}}$
, Lemma 3.5 implies that the set
$\unicode[STIX]{x1D713}_{\mathbf{a}_{k}}$
, Lemma 3.5 implies that the set
![]() $\{\unicode[STIX]{x1D713}_{\mathbf{a}_{k}}:1\leqslant k\leqslant n\}$
is a basis of
$\{\unicode[STIX]{x1D713}_{\mathbf{a}_{k}}:1\leqslant k\leqslant n\}$
is a basis of
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\mathscr{G}_{q}))$
and therefore the set
$\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\mathscr{G}_{q}))$
and therefore the set
is a basis of the
![]() $\mathbb{F}_{p}$
-vector space
$\mathbb{F}_{p}$
-vector space
![]() $\bigoplus _{(i,j)\in I_{\text{ex}}}\mathbb{F}_{q}$
. At this point we need a combinatorial lemma whose proof relies on a theorem of Rado and Horn.
$\bigoplus _{(i,j)\in I_{\text{ex}}}\mathbb{F}_{q}$
. At this point we need a combinatorial lemma whose proof relies on a theorem of Rado and Horn.
Lemma 4.6. Let
![]() $V$
be an
$V$
be an
![]() $m$
-dimensional
$m$
-dimensional
![]() $\mathbb{F}_{q}$
-vector space. Suppose that
$\mathbb{F}_{q}$
-vector space. Suppose that
![]() $S=\{v_{1},\ldots ,v_{fm}\}$
is a basis of
$S=\{v_{1},\ldots ,v_{fm}\}$
is a basis of
![]() $V$
viewed as a vector space over the subfield
$V$
viewed as a vector space over the subfield
![]() $\mathbb{F}_{p}$
. Then there exists a partition
$\mathbb{F}_{p}$
. Then there exists a partition
![]() $S_{1},\ldots ,S_{f}$
of
$S_{1},\ldots ,S_{f}$
of
![]() $S$
into
$S$
into
![]() $f$
sets of size
$f$
sets of size
![]() $m$
such that each
$m$
such that each
![]() $S_{i}$
is a basis of
$S_{i}$
is a basis of
![]() $V$
as an
$V$
as an
![]() $\mathbb{F}_{q}$
-vector space.
$\mathbb{F}_{q}$
-vector space.
We will use the following theorem of Rado and Horn [Reference HornHor55]. The proof of this theorem itself is based on Hall’s marriage theorem and ideas from matroid theory. We refer the reader to [Reference BollobásBol86, § 18] for more details.
Theorem 4.7 (Rado–Horn).
Let
![]() $V$
be a vector space over a field
$V$
be a vector space over a field
![]() $E$
and let
$E$
and let
![]() $\{v_{i}:1\leqslant i\leqslant M\}$
be a set of non-zero vectors in
$\{v_{i}:1\leqslant i\leqslant M\}$
be a set of non-zero vectors in
![]() $V$
. Then the following statements are equivalent.
$V$
. Then the following statements are equivalent.
(i) The set
 $\{1,\ldots ,M\}$
can be partitioned into sets
$\{1,\ldots ,M\}$
can be partitioned into sets
 $\{{\mathcal{A}}_{j}\}_{j=1}^{k}$
such that
$\{{\mathcal{A}}_{j}\}_{j=1}^{k}$
such that
 $\{v_{i}:i\in {\mathcal{A}}_{j}\}$
is a linearly independent set for all
$\{v_{i}:i\in {\mathcal{A}}_{j}\}$
is a linearly independent set for all
 $j=1,2,\ldots ,k$
.
$j=1,2,\ldots ,k$
.(ii) For all non-empty subsets
 $J\subseteq \{1,\ldots ,M\}$
,
$J\subseteq \{1,\ldots ,M\}$
,  $$\begin{eqnarray}\#J\leqslant k\dim _{E}\text{Span}_{E}\{v_{j}:j\in J\}.\end{eqnarray}$$
$$\begin{eqnarray}\#J\leqslant k\dim _{E}\text{Span}_{E}\{v_{j}:j\in J\}.\end{eqnarray}$$
Proof of Lemma 4.6.
We apply Theorem 4.7 with
![]() $k=f$
to the set of vectors
$k=f$
to the set of vectors
![]() $S$
. Consider an arbitrary set
$S$
. Consider an arbitrary set
![]() $J\subseteq \{1,\ldots ,mf\}$
and let
$J\subseteq \{1,\ldots ,mf\}$
and let
![]() $d=\dim _{\mathbb{F}_{q}}\text{Span}_{\mathbb{F}_{q}}\{v_{j}:j\in J\}$
. Then
$d=\dim _{\mathbb{F}_{q}}\text{Span}_{\mathbb{F}_{q}}\{v_{j}:j\in J\}$
. Then
Clearly
![]() $\text{Span}_{\mathbb{F}_{p}}\{v_{j}:j\in J\}\subseteq \text{Span}_{\mathbb{F}_{q}}\{v_{j}:j\in J\}$
, and since
$\text{Span}_{\mathbb{F}_{p}}\{v_{j}:j\in J\}\subseteq \text{Span}_{\mathbb{F}_{q}}\{v_{j}:j\in J\}$
, and since
![]() $\{v_{j}:j\in J\}$
is linearly independent over
$\{v_{j}:j\in J\}$
is linearly independent over
![]() $\mathbb{F}_{p}$
we obtain
$\mathbb{F}_{p}$
we obtain
It follows from the above inequality that
Thus by the Rado–Horn theorem, the set
![]() $\{1,\ldots ,fm\}$
can be partitioned into
$\{1,\ldots ,fm\}$
can be partitioned into
![]() ${\mathcal{A}}_{1},\ldots ,{\mathcal{A}}_{f}$
such that each of the sets
${\mathcal{A}}_{1},\ldots ,{\mathcal{A}}_{f}$
such that each of the sets
![]() $\{v_{\ell }:\ell \in {\mathcal{A}}_{i}\}$
is linearly independent over
$\{v_{\ell }:\ell \in {\mathcal{A}}_{i}\}$
is linearly independent over
![]() $\mathbb{F}_{q}$
. Note that
$\mathbb{F}_{q}$
. Note that
![]() $\#{\mathcal{A}}_{i}\leqslant m$
since
$\#{\mathcal{A}}_{i}\leqslant m$
since
![]() $\dim _{\mathbb{F}_{q}}V=m$
. But the
$\dim _{\mathbb{F}_{q}}V=m$
. But the
![]() ${\mathcal{A}}_{i}$
partition
${\mathcal{A}}_{i}$
partition
![]() $\{1,\ldots ,mf\}$
and so
$\{1,\ldots ,mf\}$
and so
![]() ${\mathcal{A}}_{i}$
has the size
${\mathcal{A}}_{i}$
has the size
![]() $m$
which implies that
$m$
which implies that
![]() $\{v_{\ell }:\ell \in {\mathcal{A}}_{i}\}$
is a basis of
$\{v_{\ell }:\ell \in {\mathcal{A}}_{i}\}$
is a basis of
![]() $V$
over
$V$
over
![]() $\mathbb{F}_{q}$
.◻
$\mathbb{F}_{q}$
.◻
We return to the proof of Theorem 2.10. Set
![]() $V=\bigoplus _{(i,j)\in I_{\text{ex}}}\mathbb{F}_{q}$
, which is an
$V=\bigoplus _{(i,j)\in I_{\text{ex}}}\mathbb{F}_{q}$
, which is an
![]() $\mathbb{F}_{p}$
-vector space of dimension
$\mathbb{F}_{p}$
-vector space of dimension
![]() $n=mf$
. Also set
$n=mf$
. Also set
![]() $v_{k}=(a_{ij}(k))_{(i,j)\in I_{\text{ex}}}\in V$
. Recall that
$v_{k}=(a_{ij}(k))_{(i,j)\in I_{\text{ex}}}\in V$
. Recall that
![]() $S=\{v_{k}:1\leqslant k\leqslant n\}$
is a basis of
$S=\{v_{k}:1\leqslant k\leqslant n\}$
is a basis of
![]() $V$
as an
$V$
as an
![]() $\mathbb{F}_{p}$
-vector space and so by Lemma 4.6 there exist
$\mathbb{F}_{p}$
-vector space and so by Lemma 4.6 there exist
![]() $f$
disjoint sets
$f$
disjoint sets
![]() $S_{1},\ldots ,S_{f}$
, each of size
$S_{1},\ldots ,S_{f}$
, each of size
![]() $m$
, such that each
$m$
, such that each
![]() $S_{\ell }$
is a basis of
$S_{\ell }$
is a basis of
![]() $V$
as an
$V$
as an
![]() $\mathbb{F}_{q}$
-vector space. For
$\mathbb{F}_{q}$
-vector space. For
![]() $1\leqslant \ell \leqslant f$
, let
$1\leqslant \ell \leqslant f$
, let
![]() $A_{\ell }$
denote an
$A_{\ell }$
denote an
![]() $m\times m$
matrix whose rows are elements of
$m\times m$
matrix whose rows are elements of
![]() $S_{\ell }$
. Note that
$S_{\ell }$
. Note that
![]() $A_{\ell }$
is invertible, since
$A_{\ell }$
is invertible, since
![]() $S_{\ell }$
is a basis of
$S_{\ell }$
is a basis of
![]() $V$
as an
$V$
as an
![]() $\mathbb{F}_{q}$
-vector space. Using the Leibniz expansion of the determinant of
$\mathbb{F}_{q}$
-vector space. Using the Leibniz expansion of the determinant of
![]() $A$
, we can assume that up to a permutation of the rows, all of the diagonal entries of
$A$
, we can assume that up to a permutation of the rows, all of the diagonal entries of
![]() $A_{\ell }$
are non-zero. Thus Proposition 4.3 implies that
$A_{\ell }$
are non-zero. Thus Proposition 4.3 implies that
Summing over all
![]() $\ell$
, we obtain
$\ell$
, we obtain
which finishes the proof.
5 The commutator matrix of nilpotent Lie algebras
We now consider general nilpotent Lie algebras by rebuilding the argument presented in § 4. Let
![]() $\mathfrak{g}$
be a nilpotent
$\mathfrak{g}$
be a nilpotent
![]() $\mathbb{Z}$
-Lie algebra of nilpotency class
$\mathbb{Z}$
-Lie algebra of nilpotency class
![]() $c$
which is finitely generated as an abelian group, and let
$c$
which is finitely generated as an abelian group, and let
![]() $\mathbb{F}_{q}$
be a finite field with
$\mathbb{F}_{q}$
be a finite field with
![]() $q=p^{f}$
elements. We set
$q=p^{f}$
elements. We set
![]() $\mathfrak{g}_{q}:=\mathfrak{g}\otimes _{\mathbb{Z}}\mathbb{F}_{q}$
throughout this section. In order to apply the orbit method, we will also assume that
$\mathfrak{g}_{q}:=\mathfrak{g}\otimes _{\mathbb{Z}}\mathbb{F}_{q}$
throughout this section. In order to apply the orbit method, we will also assume that
![]() $p>c$
. Existence of torsion elements in
$p>c$
. Existence of torsion elements in
![]() $\mathfrak{g}$
and some of its quotients results in some technical difficulties which are addressed in what follows.
$\mathfrak{g}$
and some of its quotients results in some technical difficulties which are addressed in what follows.
We call a subset
![]() $S$
of a finitely generated abelian group
$S$
of a finitely generated abelian group
![]() $\unicode[STIX]{x1D6E4}$
a semibasis if it represents a basis over
$\unicode[STIX]{x1D6E4}$
a semibasis if it represents a basis over
![]() $\mathbb{Z}$
of the free abelian group
$\mathbb{Z}$
of the free abelian group
![]() $\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{\text{tor}}$
, where
$\unicode[STIX]{x1D6E4}/\unicode[STIX]{x1D6E4}_{\text{tor}}$
, where
![]() $\unicode[STIX]{x1D6E4}_{\text{tor}}$
denotes the subgroup of torsion elements of
$\unicode[STIX]{x1D6E4}_{\text{tor}}$
denotes the subgroup of torsion elements of
![]() $\unicode[STIX]{x1D6E4}$
. Clearly
$\unicode[STIX]{x1D6E4}$
. Clearly
![]() $\#S=\text{rk}_{\mathbb{Z}}\unicode[STIX]{x1D6E4}$
. We define
$\#S=\text{rk}_{\mathbb{Z}}\unicode[STIX]{x1D6E4}$
. We define
![]() $\mathsf{e}(\unicode[STIX]{x1D6E4})$
to be the largest prime divisor of the exponent of
$\mathsf{e}(\unicode[STIX]{x1D6E4})$
to be the largest prime divisor of the exponent of
![]() $\unicode[STIX]{x1D6E4}_{\text{tor}}$
.
$\unicode[STIX]{x1D6E4}_{\text{tor}}$
.
Remark 5.1. Let
![]() $v_{1},\ldots ,v_{d}$
be
$v_{1},\ldots ,v_{d}$
be
![]() $\mathbb{Z}$
-linearly independent vectors in a finitely generated abelian group
$\mathbb{Z}$
-linearly independent vectors in a finitely generated abelian group
![]() $\unicode[STIX]{x1D6E4}$
such that
$\unicode[STIX]{x1D6E4}$
such that
![]() $\text{rk}_{\mathbb{Z}}(\unicode[STIX]{x1D6E4})=d$
, and let
$\text{rk}_{\mathbb{Z}}(\unicode[STIX]{x1D6E4})=d$
, and let
![]() $M$
be the subgroup of
$M$
be the subgroup of
![]() $\unicode[STIX]{x1D6E4}$
generated by the
$\unicode[STIX]{x1D6E4}$
generated by the
![]() $v_{i}$
. Set
$v_{i}$
. Set
![]() $q:=p^{f}$
, where
$q:=p^{f}$
, where
![]() $f$
is a positive integer and
$f$
is a positive integer and
![]() $p$
is a prime such that
$p$
is a prime such that
![]() $p>\mathsf{e}(\unicode[STIX]{x1D6E4}/M)$
. Then the elements
$p>\mathsf{e}(\unicode[STIX]{x1D6E4}/M)$
. Then the elements
![]() $v_{1}\otimes _{\mathbb{Z}}1,\ldots ,v_{d}\otimes _{\mathbb{Z}}1$
form a basis of the
$v_{1}\otimes _{\mathbb{Z}}1,\ldots ,v_{d}\otimes _{\mathbb{Z}}1$
form a basis of the
![]() $\mathbb{F}_{q}$
-vector space
$\mathbb{F}_{q}$
-vector space
![]() $\unicode[STIX]{x1D6E4}_{q}:=\unicode[STIX]{x1D6E4}\otimes _{\mathbb{Z}}\mathbb{F}_{q}$
.
$\unicode[STIX]{x1D6E4}_{q}:=\unicode[STIX]{x1D6E4}\otimes _{\mathbb{Z}}\mathbb{F}_{q}$
.
Remark 5.2. For every prime
![]() $p$
we have
$p$
we have
![]() $[\mathfrak{g},\mathfrak{g}]_{q}=[\mathfrak{g}_{q},\mathfrak{g}_{q}]$
. The equality
$[\mathfrak{g},\mathfrak{g}]_{q}=[\mathfrak{g}_{q},\mathfrak{g}_{q}]$
. The equality
![]() $\text{Z}(\mathfrak{g}_{q})=\text{Z}(\mathfrak{g})_{q}$
also holds for
$\text{Z}(\mathfrak{g}_{q})=\text{Z}(\mathfrak{g})_{q}$
also holds for
![]() $p$
sufficiently large. An explicit lower bound for
$p$
sufficiently large. An explicit lower bound for
![]() $p$
can be obtained as follows. Let
$p$
can be obtained as follows. Let
![]() $\mathbf{v}_{1},\ldots ,\mathbf{v}_{n}$
be a semibasis of
$\mathbf{v}_{1},\ldots ,\mathbf{v}_{n}$
be a semibasis of
![]() $\mathfrak{g}/\text{Z}(\mathfrak{g})$
, and let
$\mathfrak{g}/\text{Z}(\mathfrak{g})$
, and let
![]() $\mathbf{w}_{1},\ldots ,\mathbf{w}_{m}$
be a semibasis of
$\mathbf{w}_{1},\ldots ,\mathbf{w}_{m}$
be a semibasis of
![]() $[\mathfrak{g},\mathfrak{g}]$
. Then for
$[\mathfrak{g},\mathfrak{g}]$
. Then for
![]() $1\leqslant i<j\leqslant n$
we can write
$1\leqslant i<j\leqslant n$
we can write
![]() $[\mathbf{v}_{i},\mathbf{v}_{j}]=\sum _{k=1}^{m}\unicode[STIX]{x1D706}_{ij}^{k}\mathbf{w}_{k}+\mathbf{y}_{ij}$
, where
$[\mathbf{v}_{i},\mathbf{v}_{j}]=\sum _{k=1}^{m}\unicode[STIX]{x1D706}_{ij}^{k}\mathbf{w}_{k}+\mathbf{y}_{ij}$
, where
![]() $\unicode[STIX]{x1D706}_{ij}^{k}\in \mathbb{Z}$
and
$\unicode[STIX]{x1D706}_{ij}^{k}\in \mathbb{Z}$
and
![]() $\mathbf{y}_{ij}\in [\mathfrak{g},\mathfrak{g}]_{\text{tor}}$
. Setting
$\mathbf{y}_{ij}\in [\mathfrak{g},\mathfrak{g}]_{\text{tor}}$
. Setting
![]() $x_{j+n(k-1),i}:=\unicode[STIX]{x1D706}_{ij}^{k}$
, we obtain an
$x_{j+n(k-1),i}:=\unicode[STIX]{x1D706}_{ij}^{k}$
, we obtain an
![]() $mn\times n$
matrix
$mn\times n$
matrix
![]() $X:=[x_{a,b}]$
. Now for every
$X:=[x_{a,b}]$
. Now for every
![]() $n\times n$
submatrix
$n\times n$
submatrix
![]() $X^{\prime }$
of
$X^{\prime }$
of
![]() $X$
we define
$X$
we define
![]() $\mathsf{m}(X^{\prime }):=\max \{p:p\mid \text{det}(X^{\prime })\}$
, where
$\mathsf{m}(X^{\prime }):=\max \{p:p\mid \text{det}(X^{\prime })\}$
, where
![]() $\mathsf{m}(X^{\prime }):=1$
whenever
$\mathsf{m}(X^{\prime }):=1$
whenever
![]() $\det (X^{\prime })=\pm 1$
. Further, set
$\det (X^{\prime })=\pm 1$
. Further, set
![]() $\mathsf{m}(X):=\min _{X^{\prime }}\{\mathsf{m}(X^{\prime })\}$
, where the minimum is taken over
$\mathsf{m}(X):=\min _{X^{\prime }}\{\mathsf{m}(X^{\prime })\}$
, where the minimum is taken over
![]() $n\times n$
submatrices of
$n\times n$
submatrices of
![]() $X$
. For the equality
$X$
. For the equality
![]() $\text{Z}(\mathfrak{g}_{q})=\text{Z}(\mathfrak{g})_{q}$
it is enough to assume that
$\text{Z}(\mathfrak{g}_{q})=\text{Z}(\mathfrak{g})_{q}$
it is enough to assume that
![]() $p>C_{1}$
, where
$p>C_{1}$
, where
Now let
![]() $\mathbf{w}_{1},\ldots ,\mathbf{w}_{l_{1}}$
be a semibasis of
$\mathbf{w}_{1},\ldots ,\mathbf{w}_{l_{1}}$
be a semibasis of
![]() $\text{Z}(\mathfrak{g})\cap [\mathfrak{g},\mathfrak{g}]$
. Let
$\text{Z}(\mathfrak{g})\cap [\mathfrak{g},\mathfrak{g}]$
. Let
![]() $\mathbf{w}_{l_{1}+1},\ldots ,\mathbf{w}_{m}$
be elements of
$\mathbf{w}_{l_{1}+1},\ldots ,\mathbf{w}_{m}$
be elements of
![]() $\mathfrak{g}$
which represent a semibasis of
$\mathfrak{g}$
which represent a semibasis of
![]() $[\mathfrak{g},\mathfrak{g}]/(\text{Z}(\mathfrak{g})\cap [\mathfrak{g},\mathfrak{g}])$
. Finally, let
$[\mathfrak{g},\mathfrak{g}]/(\text{Z}(\mathfrak{g})\cap [\mathfrak{g},\mathfrak{g}])$
. Finally, let
![]() $\mathbf{z}_{1},\ldots ,\mathbf{z}_{l_{2}}$
be elements of
$\mathbf{z}_{1},\ldots ,\mathbf{z}_{l_{2}}$
be elements of
![]() $\mathfrak{g}$
which represent a semibasis of
$\mathfrak{g}$
which represent a semibasis of
![]() $\text{Z}(\mathfrak{g})/(\text{Z}(\mathfrak{g})\cap [\mathfrak{g},\mathfrak{g}])$
. It is straightforward to verify that the vectors
$\text{Z}(\mathfrak{g})/(\text{Z}(\mathfrak{g})\cap [\mathfrak{g},\mathfrak{g}])$
. It is straightforward to verify that the vectors
![]() $\{\mathbf{w}_{1},\ldots ,\mathbf{w}_{m},\mathbf{z}_{1},\ldots ,\mathbf{z}_{l_{2}}\}$
are
$\{\mathbf{w}_{1},\ldots ,\mathbf{w}_{m},\mathbf{z}_{1},\ldots ,\mathbf{z}_{l_{2}}\}$
are
![]() $\mathbb{Z}$
-linearly independent. Clearly the choice of these vectors implies that
$\mathbb{Z}$
-linearly independent. Clearly the choice of these vectors implies that
![]() $\text{rk}_{\mathbb{Z}}(\text{Z}(\mathfrak{g})+[\mathfrak{g},\mathfrak{g}])=l_{2}+m$
. Let
$\text{rk}_{\mathbb{Z}}(\text{Z}(\mathfrak{g})+[\mathfrak{g},\mathfrak{g}])=l_{2}+m$
. Let
![]() $M$
be the
$M$
be the
![]() $\mathbb{Z}$
-submodule of
$\mathbb{Z}$
-submodule of
![]() $\mathfrak{g}$
generated by the
$\mathfrak{g}$
generated by the
![]() $\mathbf{w}_{i}$
,
$\mathbf{w}_{i}$
,
![]() $1\leqslant i\leqslant m$
, and the
$1\leqslant i\leqslant m$
, and the
![]() $\mathbf{z}_{j}$
,
$\mathbf{z}_{j}$
,
![]() $1\leqslant j\leqslant l_{2}$
, and set
$1\leqslant j\leqslant l_{2}$
, and set
From Remark 5.1 it follows that if
![]() $p>\max \{C_{1},C_{2}\}$
, where
$p>\max \{C_{1},C_{2}\}$
, where
![]() $C_{1}$
is defined in Remark 5.2, then after tensoring with
$C_{1}$
is defined in Remark 5.2, then after tensoring with
![]() $\mathbb{F}_{q}$
, these vectors form a basis of the
$\mathbb{F}_{q}$
, these vectors form a basis of the
![]() $\mathbb{F}_{q}$
-vector space
$\mathbb{F}_{q}$
-vector space
![]() $[\mathfrak{g}_{q},\mathfrak{g}_{q}]+\text{Z}(\mathfrak{g}_{q})$
.
$[\mathfrak{g}_{q},\mathfrak{g}_{q}]+\text{Z}(\mathfrak{g}_{q})$
.
Now let
![]() $\mathbf{v}_{1}^{\prime },\ldots ,\mathbf{v}_{n}^{\prime }$
be elements of
$\mathbf{v}_{1}^{\prime },\ldots ,\mathbf{v}_{n}^{\prime }$
be elements of
![]() $\mathfrak{g}$
which represent a semibasis of
$\mathfrak{g}$
which represent a semibasis of
![]() $\mathfrak{g}/\text{Z}(\mathfrak{g})$
. For
$\mathfrak{g}/\text{Z}(\mathfrak{g})$
. For
![]() $1\leqslant i<j\leqslant n$
, there exist integers
$1\leqslant i<j\leqslant n$
, there exist integers
![]() $\unicode[STIX]{x1D702}_{ij}^{k}$
,
$\unicode[STIX]{x1D702}_{ij}^{k}$
,
![]() $1\leqslant k\leqslant m$
, such that the elements
$1\leqslant k\leqslant m$
, such that the elements
are torsion modulo
![]() $[\mathfrak{g},\mathfrak{g}]\cap \text{Z}(\mathfrak{g})$
. Set
$[\mathfrak{g},\mathfrak{g}]\cap \text{Z}(\mathfrak{g})$
. Set
![]() $K$
equal to the exponent of
$K$
equal to the exponent of
![]() $([\mathfrak{g},\mathfrak{g}]/[\mathfrak{g},\mathfrak{g}]\cap \text{Z}(\mathfrak{g}))_{\text{tor}}$
. It follows that
$([\mathfrak{g},\mathfrak{g}]/[\mathfrak{g},\mathfrak{g}]\cap \text{Z}(\mathfrak{g}))_{\text{tor}}$
. It follows that
![]() $K\mathbf{v}_{i,j}^{\prime }\in [\mathfrak{g},\mathfrak{g}]\cap \text{Z}(\mathfrak{g})$
for every
$K\mathbf{v}_{i,j}^{\prime }\in [\mathfrak{g},\mathfrak{g}]\cap \text{Z}(\mathfrak{g})$
for every
![]() $1\leqslant i<j\leqslant n$
. Now set
$1\leqslant i<j\leqslant n$
. Now set
![]() $\mathbf{v}_{i}:=K\mathbf{v}_{i}^{\prime }$
for
$\mathbf{v}_{i}:=K\mathbf{v}_{i}^{\prime }$
for
![]() $1\leqslant i\leqslant n$
. Then there exist integers
$1\leqslant i\leqslant n$
. Then there exist integers
![]() $\unicode[STIX]{x1D706}_{ij}^{k}$
such that
$\unicode[STIX]{x1D706}_{ij}^{k}$
such that
where
![]() $\mathbf{x}_{ij}\in ([\mathfrak{g},\mathfrak{g}]\cap \text{Z}(\mathfrak{g}))_{\text{tor}}$
. We remark that
$\mathbf{x}_{ij}\in ([\mathfrak{g},\mathfrak{g}]\cap \text{Z}(\mathfrak{g}))_{\text{tor}}$
. We remark that
![]() $\unicode[STIX]{x1D706}_{ij}^{k}=K^{2}\unicode[STIX]{x1D702}_{ij}^{k}$
for
$\unicode[STIX]{x1D706}_{ij}^{k}=K^{2}\unicode[STIX]{x1D702}_{ij}^{k}$
for
![]() $l_{1}+1\leqslant k\leqslant m$
.
$l_{1}+1\leqslant k\leqslant m$
.
For each
![]() $1\leqslant i,j\leqslant n$
, we define the linear forms
$1\leqslant i,j\leqslant n$
, we define the linear forms
It is clear that
![]() $\unicode[STIX]{x1D6EC}_{ii}=0$
and
$\unicode[STIX]{x1D6EC}_{ii}=0$
and
![]() $\unicode[STIX]{x1D6EC}_{ij}=-\unicode[STIX]{x1D6EC}_{ji}$
for
$\unicode[STIX]{x1D6EC}_{ij}=-\unicode[STIX]{x1D6EC}_{ji}$
for
![]() $1\leqslant i,j\leqslant n$
. The commutator matrix of
$1\leqslant i,j\leqslant n$
. The commutator matrix of
![]() $\mathfrak{g}$
(relative to the chosen ordered basis) is the skew-symmetric matrix of linear forms defined by
$\mathfrak{g}$
(relative to the chosen ordered basis) is the skew-symmetric matrix of linear forms defined by
This matrix has previously been used in several papers, such as those by Grunewald and Segal [Reference Grunewald and SegalGS84], Voll [Reference VollVol05, Reference VollVol04], O’Brien and Voll [Reference O’Brien and VollO’BV15], Avni, Klopsch, Onn and Voll [Reference Avni, Klopsch, Onn and VollAKOV13], and Stasinski and Voll [Reference Stasinski and VollSV14].
The following theorem expresses the faithful dimension of
![]() $\mathscr{G}_{q}$
as the solution to a rank minimization problem. For the next theorem, we set
$\mathscr{G}_{q}$
as the solution to a rank minimization problem. For the next theorem, we set
Theorem 5.3. Let
![]() $\mathfrak{g}$
be a nilpotent
$\mathfrak{g}$
be a nilpotent
![]() $\mathbb{Z}$
-Lie algebra of nilpotency class
$\mathbb{Z}$
-Lie algebra of nilpotency class
![]() $c$
which is finitely generated as an abelian group. If
$c$
which is finitely generated as an abelian group. If
![]() $p>\max \{c,C_{1},C_{2},C_{3}\}$
, then
$p>\max \{c,C_{1},C_{2},C_{3}\}$
, then
 $$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{q})=\min \left\{\mathop{\sum }_{\ell =1}^{l_{1}}fq^{\text{rk}_{\mathbb{F}_{q}}(F_{\mathfrak{g}}(x_{\ell 1},\ldots ,x_{\ell m}))/2}:\left(\begin{array}{@{}ccc@{}}x_{11} & \cdots \, & x_{1l_{1}}\\ \vdots & \ddots & \vdots \\ x_{l_{1}1} & \cdots \, & x_{l_{1}l_{1}}\end{array}\right)\in \text{GL}_{l_{1}}(\mathbb{F}_{q})\right\}+fl_{2},\end{eqnarray}$$
$$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{q})=\min \left\{\mathop{\sum }_{\ell =1}^{l_{1}}fq^{\text{rk}_{\mathbb{F}_{q}}(F_{\mathfrak{g}}(x_{\ell 1},\ldots ,x_{\ell m}))/2}:\left(\begin{array}{@{}ccc@{}}x_{11} & \cdots \, & x_{1l_{1}}\\ \vdots & \ddots & \vdots \\ x_{l_{1}1} & \cdots \, & x_{l_{1}l_{1}}\end{array}\right)\in \text{GL}_{l_{1}}(\mathbb{F}_{q})\right\}+fl_{2},\end{eqnarray}$$
where
![]() $m:=\text{rk}_{\mathbb{Z}}([\mathfrak{g},\mathfrak{g}])$
,
$m:=\text{rk}_{\mathbb{Z}}([\mathfrak{g},\mathfrak{g}])$
,
![]() $l_{1}:=\text{rk}_{\mathbb{Z}}([\mathfrak{g},\mathfrak{g}]\cap \text{Z}(\mathfrak{g}))$
and
$l_{1}:=\text{rk}_{\mathbb{Z}}([\mathfrak{g},\mathfrak{g}]\cap \text{Z}(\mathfrak{g}))$
and
![]() $l_{2}:=\text{rk}_{\mathbb{Z}}(\text{Z}(\mathfrak{g})/\text{Z}(\mathfrak{g})\cap [\mathfrak{g},\mathfrak{g}])$
.
$l_{2}:=\text{rk}_{\mathbb{Z}}(\text{Z}(\mathfrak{g})/\text{Z}(\mathfrak{g})\cap [\mathfrak{g},\mathfrak{g}])$
.
Remark 5.4. We note that when
![]() $n=0$
, the commutator matrix is the zero matrix and thus from Theorem 5.3 we obtain
$n=0$
, the commutator matrix is the zero matrix and thus from Theorem 5.3 we obtain
![]() $m_{\text{faithful}}(\mathscr{G}_{q})=(l_{1}+l_{2})f$
. This formula can also be obtained from Lemma 3.1 since in this case for
$m_{\text{faithful}}(\mathscr{G}_{q})=(l_{1}+l_{2})f$
. This formula can also be obtained from Lemma 3.1 since in this case for
![]() $p$
as in Theorem 5.3 the group
$p$
as in Theorem 5.3 the group
![]() $\mathscr{G}_{q}$
is abelian.
$\mathscr{G}_{q}$
is abelian.
5.1 Proof of Theorem 5.3
In this section we assume that
![]() $p$
is chosen as in Theorem 5.3. By abuse of notation, we denote the images in
$p$
is chosen as in Theorem 5.3. By abuse of notation, we denote the images in
![]() $\mathfrak{g}_{q}$
of the
$\mathfrak{g}_{q}$
of the
![]() $\mathbf{v}_{i}$
, the
$\mathbf{v}_{i}$
, the
![]() $\mathbf{w}_{i}$
and the
$\mathbf{w}_{i}$
and the
![]() $\mathbf{z}_{i}$
that are chosen above by the same letters. Let
$\mathbf{z}_{i}$
that are chosen above by the same letters. Let
![]() $\unicode[STIX]{x1D713}:\mathbb{F}_{q}\rightarrow \mathbb{C}^{\ast }$
be the primitive additive character defined in § 4. Choose a basis
$\unicode[STIX]{x1D713}:\mathbb{F}_{q}\rightarrow \mathbb{C}^{\ast }$
be the primitive additive character defined in § 4. Choose a basis
of
![]() $\mathfrak{g}_{q}/(\text{Z}(\mathfrak{g}_{q})+\mathfrak{g}_{q}^{\prime })$
. Since
$\mathfrak{g}_{q}/(\text{Z}(\mathfrak{g}_{q})+\mathfrak{g}_{q}^{\prime })$
. Since
![]() $p>C_{2}$
, the set
$p>C_{2}$
, the set
is a basis of
![]() $\mathfrak{g}_{q}$
. For
$\mathfrak{g}_{q}$
. For
let
![]() $\unicode[STIX]{x1D713}_{\mathbf{a}}\in \widehat{\mathfrak{g}}_{q}$
be defined by
$\unicode[STIX]{x1D713}_{\mathbf{a}}\in \widehat{\mathfrak{g}}_{q}$
be defined by
 $$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D713}_{\mathbf{a}}\biggl(\mathop{\sum }_{i=1}^{l_{1}}w_{i}\mathbf{w}_{i}+\mathop{\sum }_{i=l_{1}+1}^{m}w_{i}\mathbf{w}_{i}+\mathop{\sum }_{i=1}^{l_{2}}z_{i}\mathbf{z}_{i}+\mathop{\sum }_{i=1}^{l_{3}}u_{i}\mathbf{u}_{i}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad :=\unicode[STIX]{x1D713}\biggl(\mathop{\sum }_{i=1}^{l_{1}}a_{i}w_{i}+\mathop{\sum }_{i=l_{1}+1}^{m}a_{i}w_{i}+\mathop{\sum }_{i=1}^{l_{2}}b_{i}z_{i}+\mathop{\sum }_{i=1}^{l_{3}}c_{i}u_{i}\biggr).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle \unicode[STIX]{x1D713}_{\mathbf{a}}\biggl(\mathop{\sum }_{i=1}^{l_{1}}w_{i}\mathbf{w}_{i}+\mathop{\sum }_{i=l_{1}+1}^{m}w_{i}\mathbf{w}_{i}+\mathop{\sum }_{i=1}^{l_{2}}z_{i}\mathbf{z}_{i}+\mathop{\sum }_{i=1}^{l_{3}}u_{i}\mathbf{u}_{i}\biggr)\nonumber\\ \displaystyle & & \displaystyle \quad :=\unicode[STIX]{x1D713}\biggl(\mathop{\sum }_{i=1}^{l_{1}}a_{i}w_{i}+\mathop{\sum }_{i=l_{1}+1}^{m}a_{i}w_{i}+\mathop{\sum }_{i=1}^{l_{2}}b_{i}z_{i}+\mathop{\sum }_{i=1}^{l_{3}}c_{i}u_{i}\biggr).\nonumber\end{eqnarray}$$
The assignment
![]() $\mathbf{a}\mapsto \unicode[STIX]{x1D713}_{\mathbf{a}}$
identifies
$\mathbf{a}\mapsto \unicode[STIX]{x1D713}_{\mathbf{a}}$
identifies
![]() $\widehat{\mathfrak{g}}_{q}$
with
$\widehat{\mathfrak{g}}_{q}$
with
![]() $\mathbb{F}_{q}^{m+l_{2}+l_{3}}$
. For
$\mathbb{F}_{q}^{m+l_{2}+l_{3}}$
. For
![]() $\mathbf{a}$
as in (19), we write
$\mathbf{a}$
as in (19), we write
![]() $\mathbf{a}=(\mathbf{a}^{\prime },\mathbf{a}^{\prime \prime },\mathbf{b},\mathbf{c})$
, where
$\mathbf{a}=(\mathbf{a}^{\prime },\mathbf{a}^{\prime \prime },\mathbf{b},\mathbf{c})$
, where
![]() $\mathbf{a}^{\prime }\in \mathbb{F}_{q}^{l_{1}}$
,
$\mathbf{a}^{\prime }\in \mathbb{F}_{q}^{l_{1}}$
,
![]() $\mathbf{a}^{\prime \prime }\in \mathbb{F}_{q}^{m-\ell _{1}}$
,
$\mathbf{a}^{\prime \prime }\in \mathbb{F}_{q}^{m-\ell _{1}}$
,
![]() $\mathbf{b}\in \mathbb{F}_{q}^{l_{2}}$
and
$\mathbf{b}\in \mathbb{F}_{q}^{l_{2}}$
and
![]() $\mathbf{c}\in \mathbb{F}_{q}^{l_{3}}$
, and define the projection maps
$\mathbf{c}\in \mathbb{F}_{q}^{l_{3}}$
, and define the projection maps
by
![]() $\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{1}(\mathbf{a})=(\mathbf{a}^{\prime },\mathbf{a}^{\prime \prime },\mathbf{b})$
,
$\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{1}(\mathbf{a})=(\mathbf{a}^{\prime },\mathbf{a}^{\prime \prime },\mathbf{b})$
,
![]() $\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{2}(\mathbf{a})=(\mathbf{a}^{\prime },\mathbf{b})$
, and
$\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{2}(\mathbf{a})=(\mathbf{a}^{\prime },\mathbf{b})$
, and
![]() $\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{3}(\mathbf{a})=(\mathbf{a}^{\prime },\mathbf{a}^{\prime \prime })$
.
$\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{3}(\mathbf{a})=(\mathbf{a}^{\prime },\mathbf{a}^{\prime \prime })$
.
In the rest of this section, we identify
![]() $\text{Z}(\mathscr{G}_{q})$
with
$\text{Z}(\mathscr{G}_{q})$
with
![]() $\text{Z}(\mathfrak{g}_{q})$
. Let
$\text{Z}(\mathfrak{g}_{q})$
. Let
![]() $\unicode[STIX]{x1D70C}$
be an irreducible representation of
$\unicode[STIX]{x1D70C}$
be an irreducible representation of
![]() $\mathscr{G}_{q}$
. By the orbit method,
$\mathscr{G}_{q}$
. By the orbit method,
![]() $\unicode[STIX]{x1D70C}$
is obtained from a character
$\unicode[STIX]{x1D70C}$
is obtained from a character
![]() $\unicode[STIX]{x1D703}\in \widehat{\mathfrak{g}}_{q}$
, whose restriction to
$\unicode[STIX]{x1D703}\in \widehat{\mathfrak{g}}_{q}$
, whose restriction to
![]() $\text{Z}(\mathfrak{g}_{q})$
coincides with the central character of
$\text{Z}(\mathfrak{g}_{q})$
coincides with the central character of
![]() $\unicode[STIX]{x1D70C}$
. Assume that
$\unicode[STIX]{x1D70C}$
. Assume that
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x1D713}_{\mathbf{a}}$
for some
$\unicode[STIX]{x1D703}=\unicode[STIX]{x1D713}_{\mathbf{a}}$
for some
![]() $\mathbf{a}\in \mathbb{F}_{q}^{m+l_{2}+l_{3}}$
, whose entries are indexed as in (19). Our next goal is to prove that
$\mathbf{a}\in \mathbb{F}_{q}^{m+l_{2}+l_{3}}$
, whose entries are indexed as in (19). Our next goal is to prove that
The proof is similar to the argument of [Reference O’Brien and VollO’BV15, Lemma 3.3], but for the reader’s convenience we provide some details. Proposition 3.8 implies that
![]() $\text{Z}(\mathfrak{g}_{q})\subseteq \text{Stab}_{\mathscr{G}_{q}}(\unicode[STIX]{x1D703})$
. Since
$\text{Z}(\mathfrak{g}_{q})\subseteq \text{Stab}_{\mathscr{G}_{q}}(\unicode[STIX]{x1D703})$
. Since
![]() $p>C_{3}$
, it follows that
$p>C_{3}$
, it follows that
![]() $K$
is invertible in
$K$
is invertible in
![]() $\mathbb{F}_{q}$
, so that after tensoring by
$\mathbb{F}_{q}$
, so that after tensoring by
![]() $\mathbb{F}_{q}$
the
$\mathbb{F}_{q}$
the
![]() $\mathbf{v}_{i}$
form a basis of
$\mathbf{v}_{i}$
form a basis of
![]() $\mathfrak{g}_{q}/\text{Z}(\mathfrak{g}_{q})$
. For
$\mathfrak{g}_{q}/\text{Z}(\mathfrak{g}_{q})$
. For
![]() $x=\sum _{i=1}^{n}x_{i}\mathbf{v}_{i}\in \text{Stab}_{\mathscr{G}_{q}}(\unicode[STIX]{x1D703})$
and
$x=\sum _{i=1}^{n}x_{i}\mathbf{v}_{i}\in \text{Stab}_{\mathscr{G}_{q}}(\unicode[STIX]{x1D703})$
and
![]() $y=\sum _{i=1}^{n}y_{i}\mathbf{v}_{i}\in \mathfrak{g}_{q}/\text{Z}(\mathfrak{g}_{q})$
we have
$y=\sum _{i=1}^{n}y_{i}\mathbf{v}_{i}\in \mathfrak{g}_{q}/\text{Z}(\mathfrak{g}_{q})$
we have
![]() $\unicode[STIX]{x1D703}([x,y])=1$
. From (17) and the fact that
$\unicode[STIX]{x1D703}([x,y])=1$
. From (17) and the fact that
![]() $p>C_{1}$
it follows that
$p>C_{1}$
it follows that
Since
![]() $\unicode[STIX]{x1D713}$
is a primitive character, it follows that
$\unicode[STIX]{x1D713}$
is a primitive character, it follows that
![]() $\text{Stab}_{\mathscr{G}_{q}}(\unicode[STIX]{x1D703})/\text{Z}(\mathfrak{g}_{q})$
is defined by the linear equations
$\text{Stab}_{\mathscr{G}_{q}}(\unicode[STIX]{x1D703})/\text{Z}(\mathfrak{g}_{q})$
is defined by the linear equations
Consequently,
![]() $x=\sum _{i=1}^{n}x_{i}\mathbf{v}_{i}\in \text{Stab}_{\mathscr{G}_{q}}(\unicode[STIX]{x1D703})/\text{Z}(\mathfrak{g}_{q})$
if and only if
$x=\sum _{i=1}^{n}x_{i}\mathbf{v}_{i}\in \text{Stab}_{\mathscr{G}_{q}}(\unicode[STIX]{x1D703})/\text{Z}(\mathfrak{g}_{q})$
if and only if
![]() $(x_{1},\ldots ,x_{n})\in \ker F_{\mathfrak{g}}(a_{1},\ldots ,a_{m})$
. The last statement implies that
$(x_{1},\ldots ,x_{n})\in \ker F_{\mathfrak{g}}(a_{1},\ldots ,a_{m})$
. The last statement implies that
![]() $\#\text{Stab}_{\mathscr{G}_{q}}(\unicode[STIX]{x1D703})=q^{\dim _{\mathbb{F}_{q}}(\mathfrak{g}_{q})-\text{rk}_{\mathbb{F}_{q}}(F_{\mathfrak{g}}(a_{1},\ldots ,a_{m}))}$
. Equality (20) now follows from (8).
$\#\text{Stab}_{\mathscr{G}_{q}}(\unicode[STIX]{x1D703})=q^{\dim _{\mathbb{F}_{q}}(\mathfrak{g}_{q})-\text{rk}_{\mathbb{F}_{q}}(F_{\mathfrak{g}}(a_{1},\ldots ,a_{m}))}$
. Equality (20) now follows from (8).
Definition 5.5 (Admissible sets of vectors).
A set of vectors
is called an admissible set of vectors if
![]() $\{\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{2}(\mathbf{a}_{\ell }):1\leqslant \ell \leqslant (l_{1}+l_{2})f\}$
is a basis of the
$\{\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{2}(\mathbf{a}_{\ell }):1\leqslant \ell \leqslant (l_{1}+l_{2})f\}$
is a basis of the
![]() $\mathbb{F}_{p}$
-vector space
$\mathbb{F}_{p}$
-vector space
![]() $\mathbb{F}_{q}^{l_{1}+l_{2}}$
.
$\mathbb{F}_{q}^{l_{1}+l_{2}}$
.
Now let
![]() $\tilde{\unicode[STIX]{x1D70C}}$
be a faithful representation of
$\tilde{\unicode[STIX]{x1D70C}}$
be a faithful representation of
![]() $\mathscr{G}_{q}$
with the smallest possible dimension. Note that the dimension of
$\mathscr{G}_{q}$
with the smallest possible dimension. Note that the dimension of
![]() $\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\mathfrak{g}_{q}))=\text{Z}(\mathfrak{g}_{q})$
over
$\unicode[STIX]{x1D6FA}_{1}(\text{Z}(\mathfrak{g}_{q}))=\text{Z}(\mathfrak{g}_{q})$
over
![]() $\mathbb{F}_{p}$
is
$\mathbb{F}_{p}$
is
![]() $(l_{1}+l_{2})f$
and
$(l_{1}+l_{2})f$
and
![]() $\text{Z}(\mathscr{G}_{q})\cong \text{Z}(\mathfrak{g}_{q})$
. Therefore
$\text{Z}(\mathscr{G}_{q})\cong \text{Z}(\mathfrak{g}_{q})$
. Therefore
Thus by Lemma 3.5 the representation
![]() $\tilde{\unicode[STIX]{x1D70C}}$
decomposes into
$\tilde{\unicode[STIX]{x1D70C}}$
decomposes into
![]() $(l_{1}+l_{2})f$
irreducible representations
$(l_{1}+l_{2})f$
irreducible representations
where the representation
![]() $\unicode[STIX]{x1D70C}_{\mathbf{a}_{\ell }}$
is obtained by
$\unicode[STIX]{x1D70C}_{\mathbf{a}_{\ell }}$
is obtained by
![]() $\unicode[STIX]{x1D713}_{\mathbf{a}_{\ell }}\in \widehat{\mathfrak{g}}_{q}$
. Since the restriction of
$\unicode[STIX]{x1D713}_{\mathbf{a}_{\ell }}\in \widehat{\mathfrak{g}}_{q}$
. Since the restriction of
![]() $\unicode[STIX]{x1D713}_{\mathbf{a}_{\ell }}$
is the central character of
$\unicode[STIX]{x1D713}_{\mathbf{a}_{\ell }}$
is the central character of
![]() $\unicode[STIX]{x1D70C}_{\mathbf{a}_{\ell }}$
, it follows from Lemma 3.5 that the set
$\unicode[STIX]{x1D70C}_{\mathbf{a}_{\ell }}$
, it follows from Lemma 3.5 that the set
is a basis of
![]() $\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\mathfrak{g}_{q}))$
and therefore the set
$\widehat{\unicode[STIX]{x1D6FA}}_{1}(\text{Z}(\mathfrak{g}_{q}))$
and therefore the set
is a basis of the
![]() $\mathbb{F}_{p}$
-vector space
$\mathbb{F}_{p}$
-vector space
![]() $\mathbb{F}_{q}^{l_{1}+l_{2}}$
. To summarize, we have proven that for each faithful representation
$\mathbb{F}_{q}^{l_{1}+l_{2}}$
. To summarize, we have proven that for each faithful representation
![]() $\tilde{\unicode[STIX]{x1D70C}}$
with the smallest possible dimension we can find an admissible set of vectors
$\tilde{\unicode[STIX]{x1D70C}}$
with the smallest possible dimension we can find an admissible set of vectors
such that
Conversely, let
![]() $\{\mathbf{a}_{\ell }\in \mathbb{F}_{q}^{m+l_{2}+l_{3}}:1\leqslant \ell \leqslant (l_{1}+l_{2})f\}$
be an admissible set of vectors. Then by Lemma 3.4, we can construct a faithful representation
$\{\mathbf{a}_{\ell }\in \mathbb{F}_{q}^{m+l_{2}+l_{3}}:1\leqslant \ell \leqslant (l_{1}+l_{2})f\}$
be an admissible set of vectors. Then by Lemma 3.4, we can construct a faithful representation
![]() $\tilde{\unicode[STIX]{x1D70C}}$
, not necessarily of minimal dimension, such that its dimension is equal to (21). In the definition of admissible vectors we considered
$\tilde{\unicode[STIX]{x1D70C}}$
, not necessarily of minimal dimension, such that its dimension is equal to (21). In the definition of admissible vectors we considered
![]() $\mathbb{F}_{q}^{l_{1}+l_{2}}$
as an
$\mathbb{F}_{q}^{l_{1}+l_{2}}$
as an
![]() $\mathbb{F}_{p}$
-vector space. We now consider
$\mathbb{F}_{p}$
-vector space. We now consider
![]() $\mathbb{F}_{q}^{l_{1}+l_{2}}$
as an
$\mathbb{F}_{q}^{l_{1}+l_{2}}$
as an
![]() $\mathbb{F}_{q}$
-vector space and define the following notion.
$\mathbb{F}_{q}$
-vector space and define the following notion.
Definition 5.6 (Regular sets of vectors).
A set of vectors
is called a regular set of vectors if the set
![]() $\{\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{2}(\mathbf{a}_{\ell }):1\leqslant \ell \leqslant (l_{1}+l_{2})\}$
is a basis of the
$\{\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{2}(\mathbf{a}_{\ell }):1\leqslant \ell \leqslant (l_{1}+l_{2})\}$
is a basis of the
![]() $\mathbb{F}_{q}$
-vector space
$\mathbb{F}_{q}$
-vector space
![]() $\mathbb{F}_{q}^{l_{1}+l_{2}}$
.
$\mathbb{F}_{q}^{l_{1}+l_{2}}$
.
We now claim that
Let
![]() $\{\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{f}\}$
be a basis of
$\{\unicode[STIX]{x1D714}_{1},\ldots ,\unicode[STIX]{x1D714}_{f}\}$
be a basis of
![]() $\mathbb{F}_{q}$
over
$\mathbb{F}_{q}$
over
![]() $\mathbb{F}_{p}$
and let
$\mathbb{F}_{p}$
and let
be a regular set of vectors that minimizes (22). Clearly
![]() $\{\unicode[STIX]{x1D714}_{i}\mathbf{a}_{\ell }:1\leqslant i\leqslant f,1\leqslant \ell \leqslant l_{1}+l_{2}\}$
is an admissible set of vectors and
$\{\unicode[STIX]{x1D714}_{i}\mathbf{a}_{\ell }:1\leqslant i\leqslant f,1\leqslant \ell \leqslant l_{1}+l_{2}\}$
is an admissible set of vectors and
Conversely, let
![]() $\tilde{\unicode[STIX]{x1D70C}}$
be a faithful representation with the smallest possible dimension. From the above discussion we obtain an admissible set of vectors
$\tilde{\unicode[STIX]{x1D70C}}$
be a faithful representation with the smallest possible dimension. From the above discussion we obtain an admissible set of vectors
From Lemma 4.6 this set can be partitioned into
![]() $f$
sets
$f$
sets
![]() ${\mathcal{B}}_{i}$
in which each
${\mathcal{B}}_{i}$
in which each
![]() ${\mathcal{B}}_{i}$
is a regular set of vectors. Without loss of generality assume that
${\mathcal{B}}_{i}$
is a regular set of vectors. Without loss of generality assume that
Thus
which proves the claim.
We are now ready to finish the proof of Theorem 5.3. Let
![]() $\{\mathbf{a}_{\ell }\in \mathbb{F}_{q}^{m+l_{2}+l_{3}}:1\leqslant \ell \leqslant l_{1}+l_{2}\}$
be a regular set of vectors. Let
$\{\mathbf{a}_{\ell }\in \mathbb{F}_{q}^{m+l_{2}+l_{3}}:1\leqslant \ell \leqslant l_{1}+l_{2}\}$
be a regular set of vectors. Let
![]() $A\in \text{GL}_{l_{1}+l_{2}}(\mathbb{F}_{q})$
be the matrix whose rows are
$A\in \text{GL}_{l_{1}+l_{2}}(\mathbb{F}_{q})$
be the matrix whose rows are
Therefore
 $$\begin{eqnarray}A=\left(\begin{array}{@{}cccccc@{}}a_{11} & \cdots \, & a_{1l_{1}} & b_{11} & \cdots \, & b_{1l_{2}}\\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ a_{l_{1}1} & \cdots \, & a_{l_{1}l_{1}} & b_{l_{1}1} & \cdots \, & b_{l_{1}l_{2}}\\ a_{(l_{1}+1)1} & \cdots \, & a_{(l_{1}+1)l_{1}} & b_{(l_{1}+1)1} & \cdots \, & b_{(l_{1}+1)l_{2}}\\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ a_{(l_{1}+l_{2})1} & \cdots \, & a_{(l_{1}+l_{2})l_{1}} & b_{(l_{1}+l_{2})1} & \cdots \, & b_{(l_{1}+l_{2})l_{2}}\end{array}\right)\!,\end{eqnarray}$$
$$\begin{eqnarray}A=\left(\begin{array}{@{}cccccc@{}}a_{11} & \cdots \, & a_{1l_{1}} & b_{11} & \cdots \, & b_{1l_{2}}\\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ a_{l_{1}1} & \cdots \, & a_{l_{1}l_{1}} & b_{l_{1}1} & \cdots \, & b_{l_{1}l_{2}}\\ a_{(l_{1}+1)1} & \cdots \, & a_{(l_{1}+1)l_{1}} & b_{(l_{1}+1)1} & \cdots \, & b_{(l_{1}+1)l_{2}}\\ \vdots & \ddots & \vdots & \vdots & \ddots & \vdots \\ a_{(l_{1}+l_{2})1} & \cdots \, & a_{(l_{1}+l_{2})l_{1}} & b_{(l_{1}+l_{2})1} & \cdots \, & b_{(l_{1}+l_{2})l_{2}}\end{array}\right)\!,\end{eqnarray}$$
where
![]() $\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{2}(\mathbf{a}_{i})=(a_{i1},\ldots ,a_{il_{1}},b_{i1},\ldots ,b_{il_{2}})$
. The first
$\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{2}(\mathbf{a}_{i})=(a_{i1},\ldots ,a_{il_{1}},b_{i1},\ldots ,b_{il_{2}})$
. The first
![]() $l_{1}$
columns of
$l_{1}$
columns of
![]() $A$
are linearly independent over
$A$
are linearly independent over
![]() $\mathbb{F}_{q}$
, and therefore we can find an invertible
$\mathbb{F}_{q}$
, and therefore we can find an invertible
![]() $l_{1}\times l_{1}$
submatrix of the first
$l_{1}\times l_{1}$
submatrix of the first
![]() $l_{1}$
columns. By possibly permuting the rows of
$l_{1}$
columns. By possibly permuting the rows of
![]() $A$
we can assume that this submatrix lies at the intersection of the first
$A$
we can assume that this submatrix lies at the intersection of the first
![]() $l_{1}$
rows and
$l_{1}$
rows and
![]() $l_{1}$
columns of
$l_{1}$
columns of
![]() $A$
. It is clear that
$A$
. It is clear that
From this and (22) we conclude that
 $$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{q})\geqslant \min \left\{\mathop{\sum }_{\ell =1}^{l_{1}}fq^{\text{rk}_{\mathbb{F}_{q}}(F_{\mathfrak{g}}(a_{\ell 1},\ldots ,a_{\ell m}))/2}:\left(\begin{array}{@{}ccc@{}}a_{11} & \cdots \, & a_{1l_{1}}\\ \vdots & \ddots & \vdots \\ a_{l_{1}1} & \cdots \, & a_{l_{1}l_{1}}\end{array}\right)\in \operatorname{GL}_{l_{1}}(\mathbb{F}_{q})\right\}+fl_{2}.\end{eqnarray}$$
$$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{q})\geqslant \min \left\{\mathop{\sum }_{\ell =1}^{l_{1}}fq^{\text{rk}_{\mathbb{F}_{q}}(F_{\mathfrak{g}}(a_{\ell 1},\ldots ,a_{\ell m}))/2}:\left(\begin{array}{@{}ccc@{}}a_{11} & \cdots \, & a_{1l_{1}}\\ \vdots & \ddots & \vdots \\ a_{l_{1}1} & \cdots \, & a_{l_{1}l_{1}}\end{array}\right)\in \operatorname{GL}_{l_{1}}(\mathbb{F}_{q})\right\}+fl_{2}.\end{eqnarray}$$
Conversely, let
be an arbitrary set of elements of
![]() $\mathbb{F}_{q}$
and let
$\mathbb{F}_{q}$
and let
 $$\begin{eqnarray}B:=\left(\begin{array}{@{}ccc@{}}a_{11} & \cdots \, & a_{1l_{1}}\\ \vdots & \ddots & \vdots \\ a_{l_{1}1} & \cdots \, & a_{l_{1}l_{1}}\end{array}\right)\in \operatorname{GL}_{l_{1}}(\mathbb{F}_{q})\end{eqnarray}$$
$$\begin{eqnarray}B:=\left(\begin{array}{@{}ccc@{}}a_{11} & \cdots \, & a_{1l_{1}}\\ \vdots & \ddots & \vdots \\ a_{l_{1}1} & \cdots \, & a_{l_{1}l_{1}}\end{array}\right)\in \operatorname{GL}_{l_{1}}(\mathbb{F}_{q})\end{eqnarray}$$
be an arbitrary invertible matrix. Then the rows of the matrix
are projections (under
![]() $\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{2}$
) of a regular set of vectors in
$\mathsf{p}\mathsf{r}\mathsf{o}\mathsf{j}_{2}$
) of a regular set of vectors in
![]() $\mathbb{F}_{q}^{m+l_{2}+l_{3}}$
. Similar to the proof of (22), using this regular set of vectors we can construct a faithful representation of
$\mathbb{F}_{q}^{m+l_{2}+l_{3}}$
. Similar to the proof of (22), using this regular set of vectors we can construct a faithful representation of
![]() $\mathscr{G}_{q}$
of dimension
$\mathscr{G}_{q}$
of dimension
From this we conclude that
 $$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{q})\leqslant \min \left\{\mathop{\sum }_{\ell =1}^{l_{1}}fq^{\text{rk}_{\mathbb{F}_{q}}(F_{\mathfrak{g}}(a_{\ell 1},\ldots ,a_{\ell m}))/2}:\left(\begin{array}{@{}ccc@{}}a_{11} & \cdots \, & a_{1l_{1}}\\ \vdots & \ddots & \vdots \\ a_{l_{1}1} & \cdots \, & a_{l_{1}l_{1}}\end{array}\right)\in \operatorname{GL}_{l_{1}}(\mathbb{F}_{q})\right\}+fl_{2}.\end{eqnarray}$$
$$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{q})\leqslant \min \left\{\mathop{\sum }_{\ell =1}^{l_{1}}fq^{\text{rk}_{\mathbb{F}_{q}}(F_{\mathfrak{g}}(a_{\ell 1},\ldots ,a_{\ell m}))/2}:\left(\begin{array}{@{}ccc@{}}a_{11} & \cdots \, & a_{1l_{1}}\\ \vdots & \ddots & \vdots \\ a_{l_{1}1} & \cdots \, & a_{l_{1}l_{1}}\end{array}\right)\in \operatorname{GL}_{l_{1}}(\mathbb{F}_{q})\right\}+fl_{2}.\end{eqnarray}$$
Therefore, by combining (23) and (24) we obtain Theorem 5.3.
We now address Examples 2.1, 2.2, 2.3, and 2.6 in detail. By a straightforward calculation, one can verify that in all of these examples
![]() $C_{1}=C_{2}=C_{3}=1$
, and hence Theorem 5.3 is applicable for
$C_{1}=C_{2}=C_{3}=1$
, and hence Theorem 5.3 is applicable for
![]() $p>2$
.
$p>2$
.
5.2 Details for Example 2.1
From the defining bracket relations we deduce that
![]() $\mathfrak{g}_{a}^{\prime }=\text{Z}(\mathfrak{g}_{a})=\operatorname{Span}_{\mathbb{Z}}\{v_{7},v_{8},v_{9}\}$
and so
$\mathfrak{g}_{a}^{\prime }=\text{Z}(\mathfrak{g}_{a})=\operatorname{Span}_{\mathbb{Z}}\{v_{7},v_{8},v_{9}\}$
and so
![]() $\mathfrak{g}_{a}$
is a 2-step nilpotent Lie algebra. From the relations we also obtain the following commutator matrix:
$\mathfrak{g}_{a}$
is a 2-step nilpotent Lie algebra. From the relations we also obtain the following commutator matrix:
 $$\begin{eqnarray}F_{\mathfrak{g}}(T_{1},T_{2},T_{3})=\left(\begin{array}{@{}cc@{}}0 & M\\ -M^{\text{tr}} & 0\end{array}\right)\!,\quad M:=M(T_{1},T_{2},T_{3})=\left(\begin{array}{@{}ccc@{}}T_{1} & T_{2} & aT_{3}\\ T_{3} & T_{1} & T_{2}\\ T_{3} & 0 & T_{1}\end{array}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}F_{\mathfrak{g}}(T_{1},T_{2},T_{3})=\left(\begin{array}{@{}cc@{}}0 & M\\ -M^{\text{tr}} & 0\end{array}\right)\!,\quad M:=M(T_{1},T_{2},T_{3})=\left(\begin{array}{@{}ccc@{}}T_{1} & T_{2} & aT_{3}\\ T_{3} & T_{1} & T_{2}\\ T_{3} & 0 & T_{1}\end{array}\right)\!.\end{eqnarray}$$
Observe that the determinant of
![]() $M$
is
$M$
is
By Theorem 5.3 the faithful dimension of
![]() $\mathscr{G}_{a,p}=\exp (\mathfrak{g}_{a}\otimes _{\mathbb{Z}}\mathbb{F}_{p})$
, for
$\mathscr{G}_{a,p}=\exp (\mathfrak{g}_{a}\otimes _{\mathbb{Z}}\mathbb{F}_{p})$
, for
![]() $p\geqslant 3$
, is the minimum value of
$p\geqslant 3$
, is the minimum value of
subject to the condition
 $$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}x_{11} & x_{12} & x_{13}\\ x_{21} & x_{22} & x_{23}\\ x_{31} & x_{32} & x_{33}\end{array}\right)\in \operatorname{GL}_{3}(\mathbb{F}_{p}).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccc@{}}x_{11} & x_{12} & x_{13}\\ x_{21} & x_{22} & x_{23}\\ x_{31} & x_{32} & x_{33}\end{array}\right)\in \operatorname{GL}_{3}(\mathbb{F}_{p}).\end{eqnarray}$$
Let
![]() $p$
be a prime not dividing
$p$
be a prime not dividing
![]() $a$
. Computing all
$a$
. Computing all
![]() $2\times 2$
minors of
$2\times 2$
minors of
![]() $M$
shows that
$M$
shows that
unless
![]() $x=y=z=0$
. Let us consider the question of existence of a vector
$x=y=z=0$
. Let us consider the question of existence of a vector
![]() $(x,y,z)\in \mathbb{F}_{p}^{3}$
such that
$(x,y,z)\in \mathbb{F}_{p}^{3}$
such that
![]() $x\neq 0$
and
$x\neq 0$
and
Obviously we should take
![]() $z\neq 0$
Picking
$z\neq 0$
Picking
![]() $x=1$
, we obtain the equation
$x=1$
, we obtain the equation
![]() $zy^{2}-zy+(1-az^{2})=0$
, whose discriminant with respect to
$zy^{2}-zy+(1-az^{2})=0$
, whose discriminant with respect to
![]() $y$
is equal to
$y$
is equal to
![]() $4az^{3}+z^{2}-4z$
. Thus to solve (27) it suffices to show that for any non-zero
$4az^{3}+z^{2}-4z$
. Thus to solve (27) it suffices to show that for any non-zero
![]() $a\in \mathbb{Z}$
the curve
$a\in \mathbb{Z}$
the curve
![]() $Y^{2}=4aX^{3}+X^{2}-4X$
has a rational point in
$Y^{2}=4aX^{3}+X^{2}-4X$
has a rational point in
![]() $\mathbb{F}_{p}$
with
$\mathbb{F}_{p}$
with
![]() $X\neq 0$
. This can be done by noticing that
$X\neq 0$
. This can be done by noticing that
![]() $Y^{2}-4aX^{3}-X^{2}+4X$
is absolutely irreducible [Reference SchmidtSch76, Corollary, p. 13] and thus by Hasse’s bound on the number of
$Y^{2}-4aX^{3}-X^{2}+4X$
is absolutely irreducible [Reference SchmidtSch76, Corollary, p. 13] and thus by Hasse’s bound on the number of
![]() $\mathbb{F}_{p}$
-points of elliptic curves [Reference SchmidtSch76, Theorem 2A, p. 10] one can verify that such a point exists for
$\mathbb{F}_{p}$
-points of elliptic curves [Reference SchmidtSch76, Theorem 2A, p. 10] one can verify that such a point exists for
![]() $p>1800$
. Let
$p>1800$
. Let
![]() $(1,y,z)$
be a solution of (27). Then the vectors
$(1,y,z)$
be a solution of (27). Then the vectors
![]() $(0,1,0)$
and
$(0,1,0)$
and
![]() $(0,0,1)$
and
$(0,0,1)$
and
![]() $(1,y,z)$
satisfy (26), and minimize (25). Thus the faithful dimension of
$(1,y,z)$
satisfy (26), and minimize (25). Thus the faithful dimension of
![]() $\mathscr{G}_{a,p}$
is equal to
$\mathscr{G}_{a,p}$
is equal to
![]() $3p^{2}$
.
$3p^{2}$
.
5.3 Details for Examples 2.2 and 2.6
We discuss these examples together by proving the following formula:
 $$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{q})=\left\{\begin{array}{@{}ll@{}}2fq\quad & \text{if }p\equiv 1\;(\text{mod}\;4),\\ 2fq\quad & \text{if }p\equiv 3\;(\text{mod}\;4)\text{ and }f\text{ is even},\\ 2fq^{2}\quad & \text{if }p\equiv 3\;(\text{mod}\;4)\text{ and }f\text{ is odd}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{q})=\left\{\begin{array}{@{}ll@{}}2fq\quad & \text{if }p\equiv 1\;(\text{mod}\;4),\\ 2fq\quad & \text{if }p\equiv 3\;(\text{mod}\;4)\text{ and }f\text{ is even},\\ 2fq^{2}\quad & \text{if }p\equiv 3\;(\text{mod}\;4)\text{ and }f\text{ is odd}.\end{array}\right.\end{eqnarray}$$
The commutator relations imply that
![]() $\mathfrak{g}^{\prime }=\text{Z}(\mathfrak{g})=\operatorname{Span}_{\mathbb{Z}}\{v_{5},v_{6}\}$
, and that
$\mathfrak{g}^{\prime }=\text{Z}(\mathfrak{g})=\operatorname{Span}_{\mathbb{Z}}\{v_{5},v_{6}\}$
, and that
![]() $\mathfrak{g}$
is a 2-step nilpotent Lie algebra. The commutator matrix of
$\mathfrak{g}$
is a 2-step nilpotent Lie algebra. The commutator matrix of
![]() $\mathfrak{g}$
can be easily seen to be
$\mathfrak{g}$
can be easily seen to be
 $$\begin{eqnarray}F_{\mathfrak{g}}(T_{1},T_{2})=\left(\begin{array}{@{}cccc@{}}0 & T_{1} & 0 & T_{2}\\ -T_{1} & 0 & T_{2} & 0\\ 0 & -T_{2} & 0 & T_{1}\\ -T_{2} & 0 & -T_{1} & 0\end{array}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}F_{\mathfrak{g}}(T_{1},T_{2})=\left(\begin{array}{@{}cccc@{}}0 & T_{1} & 0 & T_{2}\\ -T_{1} & 0 & T_{2} & 0\\ 0 & -T_{2} & 0 & T_{1}\\ -T_{2} & 0 & -T_{1} & 0\end{array}\right)\!.\end{eqnarray}$$
Note that
![]() $\det F_{\mathfrak{g}}(T_{1},T_{2})=(T_{1}^{2}+T_{2}^{2})^{2}$
. By Theorem 5.3 the faithful dimension of
$\det F_{\mathfrak{g}}(T_{1},T_{2})=(T_{1}^{2}+T_{2}^{2})^{2}$
. By Theorem 5.3 the faithful dimension of
![]() $\mathscr{G}_{q}$
is given by
$\mathscr{G}_{q}$
is given by
For
![]() $p\equiv 1\;(\text{mod}\;4)$
, let
$p\equiv 1\;(\text{mod}\;4)$
, let
![]() $\unicode[STIX]{x1D6FC}$
denote a square root of
$\unicode[STIX]{x1D6FC}$
denote a square root of
![]() $-1$
in
$-1$
in
![]() $\mathbb{F}_{q}$
. Then the trivial lower bound
$\mathbb{F}_{q}$
. Then the trivial lower bound
![]() $2fq$
can be realized by the choice of vectors
$2fq$
can be realized by the choice of vectors
![]() $(\unicode[STIX]{x1D6FC},1)$
and
$(\unicode[STIX]{x1D6FC},1)$
and
![]() $(-\unicode[STIX]{x1D6FC},1)$
. We now consider the case
$(-\unicode[STIX]{x1D6FC},1)$
. We now consider the case
![]() $p\equiv 3\;(\text{mod}\;4)$
. For these primes, observe that
$p\equiv 3\;(\text{mod}\;4)$
. For these primes, observe that
![]() $-1$
is a square in
$-1$
is a square in
![]() $\mathbb{F}_{q}$
if and only if
$\mathbb{F}_{q}$
if and only if
![]() $f$
is even. By the above argument the faithful dimension of
$f$
is even. By the above argument the faithful dimension of
![]() $\mathscr{G}_{q}$
is
$\mathscr{G}_{q}$
is
![]() $2fq$
when
$2fq$
when
![]() $f$
is even. Now suppose that
$f$
is even. Now suppose that
![]() $f$
is odd. Then
$f$
is odd. Then
![]() $-1$
is not a square in
$-1$
is not a square in
![]() $\mathbb{F}_{q}$
, and therefore
$\mathbb{F}_{q}$
, and therefore
![]() $\det F_{\mathfrak{g}}(a_{1},a_{2})\neq 0$
for all non-zero vectors
$\det F_{\mathfrak{g}}(a_{1},a_{2})\neq 0$
for all non-zero vectors
![]() $(a_{1},a_{2})\in \mathbb{F}_{q}^{2}$
. This implies that
$(a_{1},a_{2})\in \mathbb{F}_{q}^{2}$
. This implies that
Therefore the faithful dimension of
![]() $\mathscr{G}_{q}$
is at least
$\mathscr{G}_{q}$
is at least
![]() $2fq^{2}$
, which can be realized by the standard basis.
$2fq^{2}$
, which can be realized by the standard basis.
5.4 Details for Example 2.3
The commutator relations imply that
![]() $\mathfrak{g}^{\prime }=\text{Z}(\mathfrak{g})=\operatorname{Span}_{\mathbb{Z}}\{v_{7},v_{8}\}$
, implying that
$\mathfrak{g}^{\prime }=\text{Z}(\mathfrak{g})=\operatorname{Span}_{\mathbb{Z}}\{v_{7},v_{8}\}$
, implying that
![]() $\mathfrak{g}$
is a 2-step nilpotent Lie algebra with the commutator matrix given by
$\mathfrak{g}$
is a 2-step nilpotent Lie algebra with the commutator matrix given by
 $$\begin{eqnarray}F_{\mathfrak{g}}(T_{1},T_{2})=\left(\begin{array}{@{}cc@{}}0 & M\\ -M^{\text{tr}} & 0\end{array}\right)\quad \text{where }M:=M(T_{1},T_{2})=\left(\begin{array}{@{}ccc@{}}T_{1} & T_{2} & 0\\ 0 & T_{1} & T_{2}\\ -T_{2} & T_{2} & T_{1}\end{array}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}F_{\mathfrak{g}}(T_{1},T_{2})=\left(\begin{array}{@{}cc@{}}0 & M\\ -M^{\text{tr}} & 0\end{array}\right)\quad \text{where }M:=M(T_{1},T_{2})=\left(\begin{array}{@{}ccc@{}}T_{1} & T_{2} & 0\\ 0 & T_{1} & T_{2}\\ -T_{2} & T_{2} & T_{1}\end{array}\right)\!.\end{eqnarray}$$
By Theorem 5.3 the faithful dimension of
![]() $\mathscr{G}_{p}$
is given by
$\mathscr{G}_{p}$
is given by
A simple inspection of
![]() $2\times 2$
minors of
$2\times 2$
minors of
![]() $M$
shows that for a non-zero vector
$M$
shows that for a non-zero vector
![]() $(T_{1},T_{2})$
, the matrix
$(T_{1},T_{2})$
, the matrix
![]() $M(T_{1},T_{2})$
has rank at least
$M(T_{1},T_{2})$
has rank at least
![]() $2$
, implying
$2$
, implying
![]() $m_{\text{faithful}}(\mathscr{G}_{p})\geqslant 2p^{2}$
. Note that
$m_{\text{faithful}}(\mathscr{G}_{p})\geqslant 2p^{2}$
. Note that
![]() $\det M=T_{1}^{3}-T_{1}T_{2}^{2}-T_{2}^{3}$
is the homogenization of the polynomial
$\det M=T_{1}^{3}-T_{1}T_{2}^{2}-T_{2}^{3}$
is the homogenization of the polynomial
![]() $T_{1}^{3}-T_{1}-1$
. This leads us to consider the number of roots of
$T_{1}^{3}-T_{1}-1$
. This leads us to consider the number of roots of
![]() $f(T)=T^{3}-T-1$
over
$f(T)=T^{3}-T-1$
over
![]() $\mathbb{F}_{p}$
.
$\mathbb{F}_{p}$
.
At this point we will make a digression and consider the more general question of determining the number of roots of a given integer polynomial over finite fields. Let
![]() $C_{f}$
be the companion matrix of a given polynomial
$C_{f}$
be the companion matrix of a given polynomial
![]() $f(T)\in \text{Z}[T]$
, and set
$f(T)\in \text{Z}[T]$
, and set
![]() $M(T_{1},T_{2})=T_{1}I_{d\times d}-T_{2}C_{f}$
, where
$M(T_{1},T_{2})=T_{1}I_{d\times d}-T_{2}C_{f}$
, where
![]() $d:=\deg f(T)$
. The determinant of
$d:=\deg f(T)$
. The determinant of
![]() $M(T_{1},T_{2})$
is the homogenization of
$M(T_{1},T_{2})$
is the homogenization of
![]() $f(T)$
. This construction leads to a general collection of interesting examples of 2-step nilpotent Lie algebras with commutator matrix as in (28). We refer the reader to Serre’s book [Reference SerreSer12, § 2.1.2] or his beautiful paper [Reference SerreSer03] for more details on what follows.
$f(T)$
. This construction leads to a general collection of interesting examples of 2-step nilpotent Lie algebras with commutator matrix as in (28). We refer the reader to Serre’s book [Reference SerreSer12, § 2.1.2] or his beautiful paper [Reference SerreSer03] for more details on what follows.
Let
![]() $f(T)\in \mathbb{Z}[T]$
be a monic integer polynomial. The discriminant of
$f(T)\in \mathbb{Z}[T]$
be a monic integer polynomial. The discriminant of
![]() $f(T)$
is defined to be
$f(T)$
is defined to be
where
![]() $\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}$
are the roots of
$\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}$
are the roots of
![]() $f(T)$
in an algebraic closure of
$f(T)$
in an algebraic closure of
![]() $\mathbb{Q}$
. Note that since
$\mathbb{Q}$
. Note that since
![]() $f(T)$
is a monic polynomial, the discriminant
$f(T)$
is a monic polynomial, the discriminant
![]() $\text{Disc}_{f}$
is in
$\text{Disc}_{f}$
is in
![]() $\mathbb{Z}$
. Henceforth,
$\mathbb{Z}$
. Henceforth,
![]() $p$
will denote an odd prime which does not divide
$p$
will denote an odd prime which does not divide
![]() $\text{Disc}_{f}$
. Denote the reduction of
$\text{Disc}_{f}$
. Denote the reduction of
![]() $f(T)$
modulo
$f(T)$
modulo
![]() $p$
by
$p$
by
![]() $\bar{f}$
. Then the roots of
$\bar{f}$
. Then the roots of
![]() $\bar{f}(T)$
are also simple. Define
$\bar{f}(T)$
are also simple. Define
![]() ${\mathcal{O}}_{f}=\mathbb{Z}[\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}]$
and let
${\mathcal{O}}_{f}=\mathbb{Z}[\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n}]$
and let
![]() $\mathfrak{p}$
be a prime ideal of
$\mathfrak{p}$
be a prime ideal of
![]() ${\mathcal{O}}_{f}$
such that
${\mathcal{O}}_{f}$
such that
![]() $\mathfrak{p}\cap \mathbb{Z}=p\mathbb{Z}$
. Such an ideal exists since
$\mathfrak{p}\cap \mathbb{Z}=p\mathbb{Z}$
. Such an ideal exists since
![]() ${\mathcal{O}}_{f}$
is integral over
${\mathcal{O}}_{f}$
is integral over
![]() $\mathbb{Z}$
. For such a prime we can define a unique element in the Galois group of
$\mathbb{Z}$
. For such a prime we can define a unique element in the Galois group of
![]() $f$
, which is called the Frobenius automorphism.
$f$
, which is called the Frobenius automorphism.
Theorem 5.7 (Dedekind).
Let
![]() $E=\mathbb{Q}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})$
be the splitting field of
$E=\mathbb{Q}(\unicode[STIX]{x1D6FC}_{1},\ldots ,\unicode[STIX]{x1D6FC}_{n})$
be the splitting field of
![]() $f(T)$
. There exists a unique element
$f(T)$
. There exists a unique element
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{p}}\in \text{Gal}(E/\mathbb{Q})$
such that
$\unicode[STIX]{x1D70E}_{\mathfrak{p}}\in \text{Gal}(E/\mathbb{Q})$
such that
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{p}}(\unicode[STIX]{x1D6FC})\equiv \unicode[STIX]{x1D6FC}^{p}\;\text{mod}\;\mathfrak{p}$
, for all
$\unicode[STIX]{x1D70E}_{\mathfrak{p}}(\unicode[STIX]{x1D6FC})\equiv \unicode[STIX]{x1D6FC}^{p}\;\text{mod}\;\mathfrak{p}$
, for all
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{f}$
. Moreover, if
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{f}$
. Moreover, if
![]() $\bar{f}(T)=f_{1}(T)\cdots f_{g}(T)$
with
$\bar{f}(T)=f_{1}(T)\cdots f_{g}(T)$
with
![]() $f_{i}$
irreducible over
$f_{i}$
irreducible over
![]() $\mathbb{F}_{p}$
of degree
$\mathbb{F}_{p}$
of degree
![]() $n_{i}$
, then
$n_{i}$
, then
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
, when viewed as a permutation of the roots of
$\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
, when viewed as a permutation of the roots of
![]() $f$
, has the cyclic decomposition
$f$
, has the cyclic decomposition
![]() $\unicode[STIX]{x1D70E}_{1}\cdots \unicode[STIX]{x1D70E}_{g}$
with
$\unicode[STIX]{x1D70E}_{1}\cdots \unicode[STIX]{x1D70E}_{g}$
with
![]() $\unicode[STIX]{x1D70E}_{i}$
a cycle of length
$\unicode[STIX]{x1D70E}_{i}$
a cycle of length
![]() $n_{i}$
.
$n_{i}$
.
Proof. See [Reference JacobsonJac85, Theorems 4.37 and 4.38]. ◻
For a monic integer polynomial
![]() $f(T)\in \mathbb{Z}[T]$
define
$f(T)\in \mathbb{Z}[T]$
define
Theorem 5.7 shows that
![]() $N_{f}(p)$
also counts the number of fixed points of
$N_{f}(p)$
also counts the number of fixed points of
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
permuting the roots of
$\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
permuting the roots of
![]() $f$
.
$f$
.
Let
![]() ${\mathcal{O}}_{E}$
be the ring of integers of
${\mathcal{O}}_{E}$
be the ring of integers of
![]() $E$
and
$E$
and
![]() $\mathfrak{P}$
be a prime ideal of
$\mathfrak{P}$
be a prime ideal of
![]() ${\mathcal{O}}_{E}$
such that
${\mathcal{O}}_{E}$
such that
![]() $\mathfrak{P}\cap \mathbb{Z}=p\mathbb{Z}$
, where
$\mathfrak{P}\cap \mathbb{Z}=p\mathbb{Z}$
, where
![]() $p$
does not divide the discriminant of
$p$
does not divide the discriminant of
![]() $E$
. Then, as above, one can prove the existence of a unique automorphism
$E$
. Then, as above, one can prove the existence of a unique automorphism
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{P}}\in \text{Gal}(E/\mathbb{Q})$
such that
$\unicode[STIX]{x1D70E}_{\mathfrak{P}}\in \text{Gal}(E/\mathbb{Q})$
such that
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{P}}(\unicode[STIX]{x1D6FC})\equiv \unicode[STIX]{x1D6FC}^{p}\;(\text{mod}\;\mathfrak{P})$
for all
$\unicode[STIX]{x1D70E}_{\mathfrak{P}}(\unicode[STIX]{x1D6FC})\equiv \unicode[STIX]{x1D6FC}^{p}\;(\text{mod}\;\mathfrak{P})$
for all
![]() $\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{E}$
. Let
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{E}$
. Let
![]() $\mathfrak{P}\cap {\mathcal{O}}_{f}=\mathfrak{p}$
. Since the elements of
$\mathfrak{P}\cap {\mathcal{O}}_{f}=\mathfrak{p}$
. Since the elements of
![]() $\text{Gal}(E/\mathbb{Q})$
are uniquely determined by their restrictions to
$\text{Gal}(E/\mathbb{Q})$
are uniquely determined by their restrictions to
![]() ${\mathcal{O}}_{f}$
, we have
${\mathcal{O}}_{f}$
, we have
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{P}}=\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
. The automorphism
$\unicode[STIX]{x1D70E}_{\mathfrak{P}}=\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
. The automorphism
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
is called the Frobenius automorphism and it describes the splitting behaviour of the prime
$\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
is called the Frobenius automorphism and it describes the splitting behaviour of the prime
![]() $p$
. It is well known that
$p$
. It is well known that
![]() $p$
splits completely in
$p$
splits completely in
![]() $E$
if and only if
$E$
if and only if
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
is the identity element. Now let
$\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
is the identity element. Now let
![]() $\mathfrak{P}$
and
$\mathfrak{P}$
and
![]() $\mathfrak{P}^{\prime }$
be two primes in
$\mathfrak{P}^{\prime }$
be two primes in
![]() ${\mathcal{O}}_{E}$
lying above the rational prime
${\mathcal{O}}_{E}$
lying above the rational prime
![]() $p$
. One can show (see [Reference NeukirchNeu99, § 9] for more details) that there exists
$p$
. One can show (see [Reference NeukirchNeu99, § 9] for more details) that there exists
![]() $\unicode[STIX]{x1D70F}\in \text{Gal}(E/\mathbb{Q})$
such that
$\unicode[STIX]{x1D70F}\in \text{Gal}(E/\mathbb{Q})$
such that
![]() $\unicode[STIX]{x1D70F}\unicode[STIX]{x1D70E}_{\mathfrak{P}}\unicode[STIX]{x1D70F}^{-1}=\unicode[STIX]{x1D70E}_{\mathfrak{P}^{\prime }}$
. This implies that the conjugacy class of
$\unicode[STIX]{x1D70F}\unicode[STIX]{x1D70E}_{\mathfrak{P}}\unicode[STIX]{x1D70F}^{-1}=\unicode[STIX]{x1D70E}_{\mathfrak{P}^{\prime }}$
. This implies that the conjugacy class of
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{P}}$
is independent of the choice of
$\unicode[STIX]{x1D70E}_{\mathfrak{P}}$
is independent of the choice of
![]() $\mathfrak{P}$
. Let us now turn to the question of computing
$\mathfrak{P}$
. Let us now turn to the question of computing
![]() $N_{f}(p)$
when
$N_{f}(p)$
when
![]() $f(T)$
is a cubic polynomial. The following proposition relates the Legendre symbol of the discriminant of
$f(T)$
is a cubic polynomial. The following proposition relates the Legendre symbol of the discriminant of
![]() $f$
to the number of the irreducible factors of
$f$
to the number of the irreducible factors of
![]() $\bar{f}$
.
$\bar{f}$
.
Proposition 5.8. Let
![]() $f(T)\in \mathbb{Z}[T]$
be a monic irreducible polynomial of degree
$f(T)\in \mathbb{Z}[T]$
be a monic irreducible polynomial of degree
![]() $n$
with the discriminant
$n$
with the discriminant
![]() $D$
, and suppose
$D$
, and suppose
![]() $p$
is an odd prime which does not divide the discriminant of
$p$
is an odd prime which does not divide the discriminant of
![]() $f$
. If
$f$
. If
![]() $\bar{f}=f_{1}\cdots f_{g}$
with
$\bar{f}=f_{1}\cdots f_{g}$
with
![]() $f_{i}$
irreducible over
$f_{i}$
irreducible over
![]() $\mathbb{F}_{p}$
then
$\mathbb{F}_{p}$
then
![]() $(\frac{D}{p})=(-1)^{n-g}$
, where
$(\frac{D}{p})=(-1)^{n-g}$
, where
![]() $(\frac{\cdot }{p})$
is the Legendre symbol.
$(\frac{\cdot }{p})$
is the Legendre symbol.
Proof. Continuing to use the same notation as before, we denote the splitting field of
![]() $f$
by
$f$
by
![]() $E$
and its ring of integers by
$E$
and its ring of integers by
![]() ${\mathcal{O}}_{E}$
. Set
${\mathcal{O}}_{E}$
. Set
![]() $D=\text{Disc}_{f}$
and set
$D=\text{Disc}_{f}$
and set
![]() $K=\mathbb{Q}(\sqrt{D})$
which is a subfield of
$K=\mathbb{Q}(\sqrt{D})$
which is a subfield of
![]() $E$
. Let
$E$
. Let
![]() $\mathfrak{p}$
be a prime in
$\mathfrak{p}$
be a prime in
![]() ${\mathcal{O}}_{E}$
lying over
${\mathcal{O}}_{E}$
lying over
![]() $p$
and write
$p$
and write
![]() ${\wp}=\mathfrak{p}\cap K$
. Then
${\wp}=\mathfrak{p}\cap K$
. Then
![]() $\unicode[STIX]{x1D70E}_{{\wp}}:=\unicode[STIX]{x1D70E}_{\mathfrak{p}|_{K}}$
is the Frobenius automorphism assigned to
$\unicode[STIX]{x1D70E}_{{\wp}}:=\unicode[STIX]{x1D70E}_{\mathfrak{p}|_{K}}$
is the Frobenius automorphism assigned to
![]() ${\wp}$
in
${\wp}$
in
![]() $K/\mathbb{Q}$
. Suppose
$K/\mathbb{Q}$
. Suppose
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
is an even permutation. Then
$\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
is an even permutation. Then
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{p}}(\unicode[STIX]{x1D6E5}_{f})=\unicode[STIX]{x1D6E5}_{f}$
and so
$\unicode[STIX]{x1D70E}_{\mathfrak{p}}(\unicode[STIX]{x1D6E5}_{f})=\unicode[STIX]{x1D6E5}_{f}$
and so
![]() $\unicode[STIX]{x1D70E}_{{\wp}}$
is trivial over
$\unicode[STIX]{x1D70E}_{{\wp}}$
is trivial over
![]() $K$
, which implies that
$K$
, which implies that
![]() $(\frac{D}{p})=1$
. If, on the other hand,
$(\frac{D}{p})=1$
. If, on the other hand,
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
is an odd permutation, then
$\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
is an odd permutation, then
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{p}}(\unicode[STIX]{x1D6E5}_{f})=-\unicode[STIX]{x1D6E5}_{f}$
, and
$\unicode[STIX]{x1D70E}_{\mathfrak{p}}(\unicode[STIX]{x1D6E5}_{f})=-\unicode[STIX]{x1D6E5}_{f}$
, and
![]() $\unicode[STIX]{x1D70E}_{{\wp}}$
is not-trivial, implying that
$\unicode[STIX]{x1D70E}_{{\wp}}$
is not-trivial, implying that
![]() $(\frac{D}{p})=-1$
. We have thus shown that
$(\frac{D}{p})=-1$
. We have thus shown that
![]() $\text{sgn}(\unicode[STIX]{x1D70E}_{\mathfrak{p}})=(\frac{D}{p})$
. Let
$\text{sgn}(\unicode[STIX]{x1D70E}_{\mathfrak{p}})=(\frac{D}{p})$
. Let
![]() $n_{i}=\deg f_{i}$
. Viewing
$n_{i}=\deg f_{i}$
. Viewing
![]() $\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
as a permutation of the roots of
$\unicode[STIX]{x1D70E}_{\mathfrak{p}}$
as a permutation of the roots of
![]() $f$
, from Theorem 5.7, we obtain
$f$
, from Theorem 5.7, we obtain
since
![]() $\sum _{i=1}^{g}n_{i}=n$
. This finishes the proof.◻
$\sum _{i=1}^{g}n_{i}=n$
. This finishes the proof.◻
As an application we obtain the following result.
Corollary 5.9. Let
![]() $f(T)\in \mathbb{Z}[T]$
be an irreducible monic cubic polynomial with discriminant
$f(T)\in \mathbb{Z}[T]$
be an irreducible monic cubic polynomial with discriminant
![]() $D$
, and suppose
$D$
, and suppose
![]() $p$
is an odd prime which does not divide
$p$
is an odd prime which does not divide
![]() $D$
. Then
$D$
. Then
 $$\begin{eqnarray}N_{f}(p)=\left\{\begin{array}{@{}ll@{}}0\text{ or }3\quad & \displaystyle \text{if }\biggl(\frac{D}{p}\biggr)=1,\\ 1\quad & \displaystyle \text{if }\biggl(\frac{D}{p}\biggr)=-1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}N_{f}(p)=\left\{\begin{array}{@{}ll@{}}0\text{ or }3\quad & \displaystyle \text{if }\biggl(\frac{D}{p}\biggr)=1,\\ 1\quad & \displaystyle \text{if }\biggl(\frac{D}{p}\biggr)=-1.\end{array}\right.\end{eqnarray}$$
We now turn to the special case
![]() $f(T)=T^{3}-T-1$
. The discriminant of
$f(T)=T^{3}-T-1$
. The discriminant of
![]() $f$
is
$f$
is
![]() $-23$
and then by the quadratic reciprocity we deduce that for
$-23$
and then by the quadratic reciprocity we deduce that for
![]() $p\neq 23$
$p\neq 23$
 $$\begin{eqnarray}N_{f}(p)=\left\{\begin{array}{@{}ll@{}}0\text{ or }3\quad & \displaystyle \text{if }\biggl(\frac{p}{23}\biggr)=1,\\ 1\quad & \displaystyle \text{if }\biggl(\frac{p}{23}\biggr)=-1.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}N_{f}(p)=\left\{\begin{array}{@{}ll@{}}0\text{ or }3\quad & \displaystyle \text{if }\biggl(\frac{p}{23}\biggr)=1,\\ 1\quad & \displaystyle \text{if }\biggl(\frac{p}{23}\biggr)=-1.\end{array}\right.\end{eqnarray}$$
When
![]() $(\frac{p}{23})=1$
, we will need the reduction theory of binary quadratic forms to determine
$(\frac{p}{23})=1$
, we will need the reduction theory of binary quadratic forms to determine
![]() $N_{f}(p)$
. We refer the reader to [Reference FlathFla89, ch. 2, § 8] for more details. Let
$N_{f}(p)$
. We refer the reader to [Reference FlathFla89, ch. 2, § 8] for more details. Let
![]() $\unicode[STIX]{x1D6E5}<0$
be an integer and assume that
$\unicode[STIX]{x1D6E5}<0$
be an integer and assume that
![]() $\unicode[STIX]{x1D6E5}\equiv 0,1\;(\text{mod}\;4)$
. The modular group
$\unicode[STIX]{x1D6E5}\equiv 0,1\;(\text{mod}\;4)$
. The modular group
![]() $\text{SL}_{2}(\mathbb{Z})$
acts on
$\text{SL}_{2}(\mathbb{Z})$
acts on
by linear change of variables. By the reduction theory of positive definite integral binary quadratic forms (for example see [Reference CoxCox13, Theorem 3.9]), the number
![]() $h(\unicode[STIX]{x1D6E5})$
of
$h(\unicode[STIX]{x1D6E5})$
of
![]() $\text{SL}_{2}(\mathbb{Z})$
-orbits is finite. This number is called the class number of
$\text{SL}_{2}(\mathbb{Z})$
-orbits is finite. This number is called the class number of
![]() $\unicode[STIX]{x1D6E5}$
. In the case at hand, we have
$\unicode[STIX]{x1D6E5}$
. In the case at hand, we have
![]() $h(-23)=3$
, and
$h(-23)=3$
, and
![]() $\text{SL}_{2}(\mathbb{Z})$
-orbits of
$\text{SL}_{2}(\mathbb{Z})$
-orbits of
![]() $\unicode[STIX]{x1D6F4}_{-23}$
are represented by the forms
$\unicode[STIX]{x1D6F4}_{-23}$
are represented by the forms
![]() $x^{2}+xy+6y^{2}$
and
$x^{2}+xy+6y^{2}$
and
![]() $2x^{2}\pm xy+3y^{2}$
. Note that
$2x^{2}\pm xy+3y^{2}$
. Note that
![]() $2x^{2}+xy+3y^{2}$
and
$2x^{2}+xy+3y^{2}$
and
![]() $2x^{2}-xy+3y^{2}$
are
$2x^{2}-xy+3y^{2}$
are
![]() $\text{GL}_{2}(\mathbb{Z})$
-equivalent and thus represent the same set of integers. It is easy to show that
$\text{GL}_{2}(\mathbb{Z})$
-equivalent and thus represent the same set of integers. It is easy to show that
![]() $(\frac{p}{23})=1$
, if and only if
$(\frac{p}{23})=1$
, if and only if
![]() $p$
is represented by exactly one of the form
$p$
is represented by exactly one of the form
![]() $x^{2}+xy+6y^{2}$
or
$x^{2}+xy+6y^{2}$
or
![]() $2x^{2}+xy+3y^{2}$
(see [Reference FlathFla89, Proposition 10.2]). Let
$2x^{2}+xy+3y^{2}$
(see [Reference FlathFla89, Proposition 10.2]). Let
![]() $L$
be the cubic extension of
$L$
be the cubic extension of
![]() $\mathbb{Q}$
obtained by adding a root of
$\mathbb{Q}$
obtained by adding a root of
![]() $f(T)$
and set
$f(T)$
and set
![]() $K=\mathbb{Q}(\sqrt{-23})$
.
$K=\mathbb{Q}(\sqrt{-23})$
.

Note that
![]() $\text{Gal}(E/\mathbb{Q})=S_{3}$
. For
$\text{Gal}(E/\mathbb{Q})=S_{3}$
. For
![]() $p\neq 23$
, set
$p\neq 23$
, set
![]() $p{\mathcal{O}}_{K}=\mathfrak{p}\overline{\mathfrak{p}}$
. Since the class number of
$p{\mathcal{O}}_{K}=\mathfrak{p}\overline{\mathfrak{p}}$
. Since the class number of
![]() $K$
is
$K$
is
![]() $3$
and
$3$
and
![]() $E$
is unramified over
$E$
is unramified over
![]() $K$
,
$K$
,
![]() $E$
is the Hilbert class field of
$E$
is the Hilbert class field of
![]() $K$
, i.e. the maximal unramified abelian extension of
$K$
, i.e. the maximal unramified abelian extension of
![]() $K$
. From this we can conclude that
$K$
. From this we can conclude that
![]() $\mathfrak{p}$
splits completely in
$\mathfrak{p}$
splits completely in
![]() $E$
if and only if
$E$
if and only if
![]() $\mathfrak{p}$
is a principal ideal [Reference CoxCox13, Corollary 5.25]. Moreover, note that the ring of integers of the quadratic extension
$\mathfrak{p}$
is a principal ideal [Reference CoxCox13, Corollary 5.25]. Moreover, note that the ring of integers of the quadratic extension
![]() $K$
is
$K$
is
![]() $\mathbb{Z}[(1+\sqrt{-23})/2]$
and so
$\mathbb{Z}[(1+\sqrt{-23})/2]$
and so
![]() $\mathfrak{p}$
is a principal ideal if and only if
$\mathfrak{p}$
is a principal ideal if and only if
![]() $p=x^{2}+xy+6y^{2}$
. Putting all these together, we conclude that
$p=x^{2}+xy+6y^{2}$
. Putting all these together, we conclude that
![]() $p=x^{2}+xy+6y^{2}$
if and only if
$p=x^{2}+xy+6y^{2}$
if and only if
![]() $p$
splits completely in
$p$
splits completely in
![]() $E$
. This means that
$E$
. This means that
![]() $T^{3}-T-1$
has three roots in
$T^{3}-T-1$
has three roots in
![]() $\mathbb{F}_{p}$
if and only if
$\mathbb{F}_{p}$
if and only if
![]() $p=x^{2}+xy+6y^{2}$
. This also shows that
$p=x^{2}+xy+6y^{2}$
. This also shows that
![]() $p=2x^{2}+xy+3y^{2}$
if and only if
$p=2x^{2}+xy+3y^{2}$
if and only if
![]() $T^{3}-T-1$
has no root in
$T^{3}-T-1$
has no root in
![]() $\mathbb{F}_{p}$
. Consequently,
$\mathbb{F}_{p}$
. Consequently,
 $$\begin{eqnarray}N_{f}(p)=\left\{\begin{array}{@{}ll@{}}1\quad & \displaystyle \text{if }\biggl(\frac{p}{23}\biggr)=-1,\\ 0\quad & \text{if }p\text{ is of the form }2x^{2}+xy+3y^{2},\\ 3\quad & \text{if }p\text{ is of the form }x^{2}+xy+6y^{2}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}N_{f}(p)=\left\{\begin{array}{@{}ll@{}}1\quad & \displaystyle \text{if }\biggl(\frac{p}{23}\biggr)=-1,\\ 0\quad & \text{if }p\text{ is of the form }2x^{2}+xy+3y^{2},\\ 3\quad & \text{if }p\text{ is of the form }x^{2}+xy+6y^{2}.\end{array}\right.\end{eqnarray}$$
Let
![]() $N_{\mathbf{X}}(p)$
denote the number of rational points of the projective variety
$N_{\mathbf{X}}(p)$
denote the number of rational points of the projective variety
![]() $\mathbf{X}:=T_{1}^{3}-T_{1}T_{2}^{2}-T_{2}^{3}=0$
in
$\mathbf{X}:=T_{1}^{3}-T_{1}T_{2}^{2}-T_{2}^{3}=0$
in
![]() $\mathbf{P}^{1}(\mathbb{F}_{p})$
. Then from (29), for all
$\mathbf{P}^{1}(\mathbb{F}_{p})$
. Then from (29), for all
![]() $p\neq 23$
we obtain
$p\neq 23$
we obtain
 $$\begin{eqnarray}N_{\mathbf{X}}(p)=\left\{\begin{array}{@{}ll@{}}1\quad & \displaystyle \text{if }\biggl(\frac{p}{23}\biggr)=-1,\\ 0\quad & \text{if }p\text{ is of the form }2x^{2}+xy+3y^{2},\\ 3\quad & \text{if }p\text{ is of the form }x^{2}+xy+6y^{2}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}N_{\mathbf{X}}(p)=\left\{\begin{array}{@{}ll@{}}1\quad & \displaystyle \text{if }\biggl(\frac{p}{23}\biggr)=-1,\\ 0\quad & \text{if }p\text{ is of the form }2x^{2}+xy+3y^{2},\\ 3\quad & \text{if }p\text{ is of the form }x^{2}+xy+6y^{2}.\end{array}\right.\end{eqnarray}$$
When
![]() $(\frac{p}{23})=-1$
, we have
$(\frac{p}{23})=-1$
, we have
![]() $N_{\mathbf{X}}(p)=1$
and hence the faithful dimension of
$N_{\mathbf{X}}(p)=1$
and hence the faithful dimension of
![]() $\mathscr{G}_{p}$
equals
$\mathscr{G}_{p}$
equals
![]() $p^{2}+p^{3}$
. When
$p^{2}+p^{3}$
. When
![]() $p$
is of the form
$p$
is of the form
![]() $2x^{2}+xy+3y^{2}$
then
$2x^{2}+xy+3y^{2}$
then
![]() $N_{\mathbf{X}}(p)=0$
and so the minimum is exactly
$N_{\mathbf{X}}(p)=0$
and so the minimum is exactly
![]() $2p^{3}$
. This implies that the faithful dimension is
$2p^{3}$
. This implies that the faithful dimension is
![]() $2p^{3}$
. In the remaining case, we can find distinct points
$2p^{3}$
. In the remaining case, we can find distinct points
![]() $(x_{11},x_{12})$
and
$(x_{11},x_{12})$
and
![]() $(x_{21},x_{22})$
in
$(x_{21},x_{22})$
in
![]() $\mathbf{X}$
. Since
$\mathbf{X}$
. Since
![]() $M(x_{11},x_{12})$
and
$M(x_{11},x_{12})$
and
![]() $M(x_{21},x_{22})$
have both rank
$M(x_{21},x_{22})$
have both rank
![]() $2$
, it follows that in this case the faithful dimension is
$2$
, it follows that in this case the faithful dimension is
![]() $2p^{2}$
. Moreover,
$2p^{2}$
. Moreover,
![]() $T_{1}^{3}-T_{1}-1$
has a double root and a simple root in
$T_{1}^{3}-T_{1}-1$
has a double root and a simple root in
![]() $\mathbb{F}_{23}$
. Thus the same argument shows that in this case the faithful dimension is
$\mathbb{F}_{23}$
. Thus the same argument shows that in this case the faithful dimension is
![]() $2(23)^{2}$
.
$2(23)^{2}$
.
5.5 Details for Example 2.4
The commutator relations imply that
![]() $\mathfrak{g}^{\prime }=\text{Z}(\mathfrak{g})=\operatorname{Span}_{\mathbb{Z}}\{v_{6},v_{7},v_{8}\}$
, implying that
$\mathfrak{g}^{\prime }=\text{Z}(\mathfrak{g})=\operatorname{Span}_{\mathbb{Z}}\{v_{6},v_{7},v_{8}\}$
, implying that
![]() $\mathfrak{g}$
is a 2-step nilpotent Lie algebra with the commutator matrix given by
$\mathfrak{g}$
is a 2-step nilpotent Lie algebra with the commutator matrix given by
 $$\begin{eqnarray}F_{\mathfrak{g}}(T_{1},T_{2},T_{3})=\left(\begin{array}{@{}cc@{}}0 & M\\ -M^{\text{tr}} & 0\end{array}\right)\!,\quad M:=M(T_{1},T_{2},T_{3})=\left(\begin{array}{@{}cc@{}}T_{1} & T_{2}\\ T_{3} & T_{1}\\ 2T_{2} & T_{3}\end{array}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}F_{\mathfrak{g}}(T_{1},T_{2},T_{3})=\left(\begin{array}{@{}cc@{}}0 & M\\ -M^{\text{tr}} & 0\end{array}\right)\!,\quad M:=M(T_{1},T_{2},T_{3})=\left(\begin{array}{@{}cc@{}}T_{1} & T_{2}\\ T_{3} & T_{1}\\ 2T_{2} & T_{3}\end{array}\right)\!.\end{eqnarray}$$
For a given odd prime
![]() $p$
, and a non-zero vector
$p$
, and a non-zero vector
![]() $(T_{1},T_{2},T_{3})\in \mathbb{F}_{p}^{3}$
, the rank over
$(T_{1},T_{2},T_{3})\in \mathbb{F}_{p}^{3}$
, the rank over
![]() $\mathbb{F}_{p}$
of
$\mathbb{F}_{p}$
of
![]() $M$
is equal to
$M$
is equal to
![]() $1$
if and only if
$1$
if and only if
![]() $(T_{1},T_{2},T_{3})$
is proportional to
$(T_{1},T_{2},T_{3})$
is proportional to
![]() $(\unicode[STIX]{x1D706}^{2}/2,\unicode[STIX]{x1D706}/2,1)$
such that
$(\unicode[STIX]{x1D706}^{2}/2,\unicode[STIX]{x1D706}/2,1)$
such that
![]() $\unicode[STIX]{x1D706}^{3}-2=0$
, and is equal to
$\unicode[STIX]{x1D706}^{3}-2=0$
, and is equal to
![]() $2$
otherwise. Set
$2$
otherwise. Set
![]() $f(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D706}^{3}-2$
. As noted in [Reference LeeLee16, Corollary 2.3],
$f(\unicode[STIX]{x1D706})=\unicode[STIX]{x1D706}^{3}-2$
. As noted in [Reference LeeLee16, Corollary 2.3],
 $$\begin{eqnarray}N_{f}(p)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }p\equiv 2\;(\text{mod}\;3)\text{ or }p=3,\\ 3\quad & \text{if }p\equiv 1\;(\text{mod}\;3)\text{ and }p\text{ is represented by the form }x^{2}+27y^{2},\\ 0\quad & \text{if }p\equiv 1\;(\text{mod}\;3)\text{ and }p\text{ is not represented by the form }x^{2}+27y^{2}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}N_{f}(p)=\left\{\begin{array}{@{}ll@{}}1\quad & \text{if }p\equiv 2\;(\text{mod}\;3)\text{ or }p=3,\\ 3\quad & \text{if }p\equiv 1\;(\text{mod}\;3)\text{ and }p\text{ is represented by the form }x^{2}+27y^{2},\\ 0\quad & \text{if }p\equiv 1\;(\text{mod}\;3)\text{ and }p\text{ is not represented by the form }x^{2}+27y^{2}.\end{array}\right.\end{eqnarray}$$
The rest of the argument is similar to Example 2.3.
6 Proofs of Theorems 2.5 and 2.7
Before we begin the proofs of Theorems 2.5 and 2.7, let us recall the setting. As before, let
![]() $\mathfrak{g}$
be a nilpotent
$\mathfrak{g}$
be a nilpotent
![]() $\mathbb{Z}$
-Lie algebra of nilpotency class
$\mathbb{Z}$
-Lie algebra of nilpotency class
![]() $c$
which is finitely generated as an abelian group, and set
$c$
which is finitely generated as an abelian group, and set
![]() $q:=p^{f}$
for some
$q:=p^{f}$
for some
![]() $f\geqslant 1$
. Let
$f\geqslant 1$
. Let
![]() $F_{\mathfrak{g}}(T_{1},\ldots ,T_{m})$
denote the matrix of linear forms that is defined in (18). Since
$F_{\mathfrak{g}}(T_{1},\ldots ,T_{m})$
denote the matrix of linear forms that is defined in (18). Since
![]() $F_{\mathfrak{g}}(T_{1},\ldots ,T_{m})$
is a skew-symmetric
$F_{\mathfrak{g}}(T_{1},\ldots ,T_{m})$
is a skew-symmetric
![]() $n\times n$
matrix it follows that for all
$n\times n$
matrix it follows that for all
![]() $x_{1},\ldots ,x_{m}\in \mathbb{F}_{q}$
, the rank of
$x_{1},\ldots ,x_{m}\in \mathbb{F}_{q}$
, the rank of
![]() $F_{\mathfrak{g}}(x_{1},\ldots ,x_{m})$
is an even number no larger than
$F_{\mathfrak{g}}(x_{1},\ldots ,x_{m})$
is an even number no larger than
![]() $n$
. Let
$n$
. Let
![]() $M$
be the set of all integer vectors
$M$
be the set of all integer vectors
![]() $\unicode[STIX]{x1D707}=(a_{1},\ldots ,a_{l_{1}})\in \mathbb{Z}^{l_{1}}$
, with
$\unicode[STIX]{x1D707}=(a_{1},\ldots ,a_{l_{1}})\in \mathbb{Z}^{l_{1}}$
, with
![]() $0\leqslant a_{i}\leqslant n/2$
, and assign to each
$0\leqslant a_{i}\leqslant n/2$
, and assign to each
![]() $\unicode[STIX]{x1D707}\in M$
the polynomial of degree at most
$\unicode[STIX]{x1D707}\in M$
the polynomial of degree at most
![]() $n/2$
given by
$n/2$
given by
Since
![]() $g_{\unicode[STIX]{x1D707}}$
is symmetric in
$g_{\unicode[STIX]{x1D707}}$
is symmetric in
![]() $a_{1},\ldots ,a_{l_{1}}$
, we will only consider those integer vectors
$a_{1},\ldots ,a_{l_{1}}$
, we will only consider those integer vectors
![]() $\unicode[STIX]{x1D707}$
with
$\unicode[STIX]{x1D707}$
with
and order them with the reverse lexicographical order, i.e.
![]() $\unicode[STIX]{x1D707}{\vartriangleleft}\unicode[STIX]{x1D707}^{\prime }$
if the rightmost non-zero component of the vector
$\unicode[STIX]{x1D707}{\vartriangleleft}\unicode[STIX]{x1D707}^{\prime }$
if the rightmost non-zero component of the vector
![]() $\unicode[STIX]{x1D707}^{\prime }-\unicode[STIX]{x1D707}$
is positive. If
$\unicode[STIX]{x1D707}^{\prime }-\unicode[STIX]{x1D707}$
is positive. If
![]() $\unicode[STIX]{x1D707}{\vartriangleleft}\unicode[STIX]{x1D707}^{\prime }$
and
$\unicode[STIX]{x1D707}{\vartriangleleft}\unicode[STIX]{x1D707}^{\prime }$
and
![]() $q>l_{1}$
, then we can easily see that
$q>l_{1}$
, then we can easily see that
Since
![]() $r=\#M<\infty$
, we can sort its elements as
$r=\#M<\infty$
, we can sort its elements as
![]() $\unicode[STIX]{x1D707}_{1}{\vartriangleleft}\cdots {\vartriangleleft}\unicode[STIX]{x1D707}_{r}$
. For a given vector
$\unicode[STIX]{x1D707}_{1}{\vartriangleleft}\cdots {\vartriangleleft}\unicode[STIX]{x1D707}_{r}$
. For a given vector
![]() $\unicode[STIX]{x1D707}$
, define the following affine variety associated to
$\unicode[STIX]{x1D707}$
, define the following affine variety associated to
![]() $\unicode[STIX]{x1D707}=(a_{1},\ldots ,a_{l_{1}})$
:
$\unicode[STIX]{x1D707}=(a_{1},\ldots ,a_{l_{1}})$
:
 $$\begin{eqnarray}\mathbf{X}_{\unicode[STIX]{x1D707}}:=\left\{(x_{ij})\in \text{M}_{l_{1},m}(\mathbb{C}):\text{rk}_{\mathbb{C}}(F_{\mathfrak{g}}(x_{i1},\ldots ,x_{im}))=2a_{i},\det \left(\begin{array}{@{}ccc@{}}x_{11} & \cdots \, & x_{1l_{1}}\\ \vdots & \ddots & \vdots \\ x_{l_{1}1} & \cdots \, & x_{l_{1}l_{1}}\end{array}\right)\neq 0\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{X}_{\unicode[STIX]{x1D707}}:=\left\{(x_{ij})\in \text{M}_{l_{1},m}(\mathbb{C}):\text{rk}_{\mathbb{C}}(F_{\mathfrak{g}}(x_{i1},\ldots ,x_{im}))=2a_{i},\det \left(\begin{array}{@{}ccc@{}}x_{11} & \cdots \, & x_{1l_{1}}\\ \vdots & \ddots & \vdots \\ x_{l_{1}1} & \cdots \, & x_{l_{1}l_{1}}\end{array}\right)\neq 0\right\}.\end{eqnarray}$$
Note that the non-vanishing condition on the determinant can be turned into an equation by introducing a new variable, standing for the inverse of the determinant. We also remark that
![]() $\mathbf{X}_{\unicode[STIX]{x1D707}}$
is defined over
$\mathbf{X}_{\unicode[STIX]{x1D707}}$
is defined over
![]() $\mathbb{Z}$
because
$\mathbb{Z}$
because
![]() $F_{\mathfrak{g}}(T_{1},\ldots ,T_{m})$
is an integer matrix.
$F_{\mathfrak{g}}(T_{1},\ldots ,T_{m})$
is an integer matrix.
6.1 Proof of Theorem 2.5
For
![]() $\unicode[STIX]{x1D707}\in M$
set
$\unicode[STIX]{x1D707}\in M$
set
where the
![]() $C_{i}$
are as in Theorem 5.3. For every integer
$C_{i}$
are as in Theorem 5.3. For every integer
![]() $k$
such that
$k$
such that
![]() $1\leqslant k\leqslant r$
, Theorem 5.3 and (30) imply that
$1\leqslant k\leqslant r$
, Theorem 5.3 and (30) imply that
![]() $m_{\text{faithful}}(\mathscr{G}_{p})=g_{\unicode[STIX]{x1D707}_{k}}(p)$
whenever
$m_{\text{faithful}}(\mathscr{G}_{p})=g_{\unicode[STIX]{x1D707}_{k}}(p)$
whenever
Since finite sets are Frobenius, the assertion of Theorem 2.5 now follows from the following theorem due to Ax [Reference AxAx67, Theorem 1].
Theorem 6.1 (Ax).
With the above notation,
![]() $\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D707}}$
is a Frobenius set.
$\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D707}}$
is a Frobenius set.
Remark 6.2. An analogue of Theorem 2.5 holds for
![]() $m_{\text{faithful}}(\mathscr{G}_{p^{f}})$
when
$m_{\text{faithful}}(\mathscr{G}_{p^{f}})$
when
![]() $f$
is fixed and
$f$
is fixed and
![]() $p$
varies. This statement can be established by a modification of the proof given above and applying [Reference SerreSer12, § 7.2.4, Example 2].
$p$
varies. This statement can be established by a modification of the proof given above and applying [Reference SerreSer12, § 7.2.4, Example 2].
6.2 Proof of Theorem 2.7
The proof of this theorem is similar to that of Theorem 2.5. Hence we will maintain the notation for the matrix
![]() $F_{\mathfrak{g}}(T_{1},\ldots ,T_{m})$
, the ordered set
$F_{\mathfrak{g}}(T_{1},\ldots ,T_{m})$
, the ordered set
![]() $M$
, the polynomial
$M$
, the polynomial
![]() $g_{\unicode[STIX]{x1D707}}$
, and the variety
$g_{\unicode[STIX]{x1D707}}$
, and the variety
![]() $\mathbf{X}_{\unicode[STIX]{x1D707}}$
as above. Now assume that
$\mathbf{X}_{\unicode[STIX]{x1D707}}$
as above. Now assume that
![]() $p>C$
, where
$p>C$
, where
Consider the sets
It follows from a theorem of Dwork [Reference SerreSer12, p. 6 and § 4.3] that there exists a function
![]() $\unicode[STIX]{x1D708}:\mathbb{C}\rightarrow \mathbb{Z}$
with finite support such that
$\unicode[STIX]{x1D708}:\mathbb{C}\rightarrow \mathbb{Z}$
with finite support such that
It is easy to see that the sequence
![]() $c_{f}=N_{\mathbf{X}_{\unicode[STIX]{x1D707}}}(p^{f})$
satisfies a linear recurrence relation of the form
$c_{f}=N_{\mathbf{X}_{\unicode[STIX]{x1D707}}}(p^{f})$
satisfies a linear recurrence relation of the form
![]() $c_{n}=\sum _{k=1}^{r}a_{k}c_{n-k}$
. We will now invoke the following theorem of Skolem, Mahler and Lech.
$c_{n}=\sum _{k=1}^{r}a_{k}c_{n-k}$
. We will now invoke the following theorem of Skolem, Mahler and Lech.
Theorem 6.3 (Skolem–Mahler–Lech [Reference Myerson and van der PoortenMVdP95]).
Let
![]() $\{u_{n}\}_{n\geqslant 1}$
be a sequence of complex numbers satisfying a linear recurrence equation. Then its zero set
$\{u_{n}\}_{n\geqslant 1}$
be a sequence of complex numbers satisfying a linear recurrence equation. Then its zero set
![]() $\{n:u_{n}=0\}$
is a union of a finite set and a finite number of sets of the form
$\{n:u_{n}=0\}$
is a union of a finite set and a finite number of sets of the form
![]() $n\equiv a\;(\text{mod}\;b)$
for integers
$n\equiv a\;(\text{mod}\;b)$
for integers
![]() $a,b$
.
$a,b$
.
One can easily verify that the sets of the form
![]() $F\cup A$
, where
$F\cup A$
, where
![]() $F$
is finite and
$F$
is finite and
![]() $A$
is a finite union of arithmetic progressions form a Boolean algebra. To complete the proof of Theorem 2.7, note that from (30) and Theorem 5.3 it follows that if
$A$
is a finite union of arithmetic progressions form a Boolean algebra. To complete the proof of Theorem 2.7, note that from (30) and Theorem 5.3 it follows that if
![]() $p>C$
and
$p>C$
and
![]() $f\in \mathscr{A}_{k}:=\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D707}_{k}}^{\prime }\setminus \bigcup _{1\leqslant i<k}\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D707}_{i}}^{\prime }$
then
$f\in \mathscr{A}_{k}:=\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D707}_{k}}^{\prime }\setminus \bigcup _{1\leqslant i<k}\unicode[STIX]{x1D6F4}_{\unicode[STIX]{x1D707}_{i}}^{\prime }$
then
![]() $m_{\text{faithful}}(\exp (\mathscr{G}_{q}))=fg_{k}(q)$
.
$m_{\text{faithful}}(\exp (\mathscr{G}_{q}))=fg_{k}(q)$
.
7 Free nilpotent Lie algebras
In this section we will consider faithful representations of groups related to free nilpotent and free metabelian Lie algebras. Let us recall some definitions. The free nilpotent Lie algebra of class
![]() $c$
on
$c$
on
![]() $n$
generators, denoted by
$n$
generators, denoted by
![]() $\mathfrak{f}_{n,c}$
, is the free object in the category of
$\mathfrak{f}_{n,c}$
, is the free object in the category of
![]() $n$
-generated nilpotent Lie algebras (over
$n$
-generated nilpotent Lie algebras (over
![]() $\mathbb{Z}$
) of class
$\mathbb{Z}$
) of class
![]() $c$
. More concretely,
$c$
. More concretely,
![]() $\mathfrak{f}_{n,c}$
can be constructed from the free Lie algebra on
$\mathfrak{f}_{n,c}$
can be constructed from the free Lie algebra on
![]() $n$
generators after quotienting out the ideal generated by commutators of length
$n$
generators after quotienting out the ideal generated by commutators of length
![]() $c+1$
.
$c+1$
.
Recall that a Lie algebra
![]() $\mathfrak{l}$
is called metabelian if
$\mathfrak{l}$
is called metabelian if
![]() $[[\mathfrak{l},\mathfrak{l}],[\mathfrak{l},\mathfrak{l}]]=0$
. Similarly, one can define the free metabelian Lie algebra of class
$[[\mathfrak{l},\mathfrak{l}],[\mathfrak{l},\mathfrak{l}]]=0$
. Similarly, one can define the free metabelian Lie algebra of class
![]() $c$
on
$c$
on
![]() $n$
generators as the free object in the category of
$n$
generators as the free object in the category of
![]() $n$
-generated metabelian Lie algebras of class
$n$
-generated metabelian Lie algebras of class
![]() $c$
.
$c$
.
For computational purposes, it will be convenient to work with Hall bases of free nilpotent Lie algebras. We will briefly review their constructions, and refer the reader to [Reference BourbakiBou98, ch. II] or [Reference SerreSer06, ch. IV] for more details.
7.1 Hall bases of free nilpotent Lie algebras
Our exposition of the notion of a Hall basis follows [Reference BourbakiBou98, ch. II] or [Reference SerreSer06, ch. IV]. We will first need some basic definitions. A set
![]() $M$
with a map
$M$
with a map
![]() $M\times M\rightarrow M$
sending
$M\times M\rightarrow M$
sending
![]() $(x,y)\mapsto [x,y]$
is called a magma. Let
$(x,y)\mapsto [x,y]$
is called a magma. Let
![]() $X$
be a set and define inductively a family of sets
$X$
be a set and define inductively a family of sets
![]() $X_{n}$
$X_{n}$
![]() $(n\geqslant 1)$
as follows:
$(n\geqslant 1)$
as follows:
![]() $X_{1}=X$
and
$X_{1}=X$
and
![]() $X_{n}=\amalg _{p+q=n}(X_{p}\times X_{q})$
. Let
$X_{n}=\amalg _{p+q=n}(X_{p}\times X_{q})$
. Let
![]() $M(X)$
denote the disjoint union
$M(X)$
denote the disjoint union
![]() $\amalg _{n=1}^{\infty }X_{n}$
and define
$\amalg _{n=1}^{\infty }X_{n}$
and define
![]() $M(X)\times M(X)\rightarrow M(X)$
via
$M(X)\times M(X)\rightarrow M(X)$
via
![]() $X_{p}\times X_{q}\rightarrow X_{p+q}\subseteq M(X).$
The magma
$X_{p}\times X_{q}\rightarrow X_{p+q}\subseteq M(X).$
The magma
![]() $M(X)$
is called the free magma on
$M(X)$
is called the free magma on
![]() $X$
. An element
$X$
. An element
![]() $w$
of
$w$
of
![]() $M(X)$
is called a non-associative word on
$M(X)$
is called a non-associative word on
![]() $X$
. Its length,
$X$
. Its length,
![]() $\ell (w)$
, is the unique
$\ell (w)$
, is the unique
![]() $n$
such that
$n$
such that
![]() $w\in X_{n}$
.
$w\in X_{n}$
.
Definition 7.1. A Hall set relative to
![]() $X$
is a totally ordered subset
$X$
is a totally ordered subset
![]() ${\mathcal{H}}$
of
${\mathcal{H}}$
of
![]() $M(X)$
satisfying the following conditions:
$M(X)$
satisfying the following conditions:
(A) if
 $u\in {\mathcal{H}}$
,
$u\in {\mathcal{H}}$
,
 $v\in {\mathcal{H}}$
and
$v\in {\mathcal{H}}$
and
 $\ell (u)<\ell (v)$
, then
$\ell (u)<\ell (v)$
, then
 $u<v$
in the total order;
$u<v$
in the total order;(B)
 $X\subseteq {\mathcal{H}}$
and
$X\subseteq {\mathcal{H}}$
and
 ${\mathcal{H}}\cap X_{2}$
consists of the products
${\mathcal{H}}\cap X_{2}$
consists of the products
 $[x,y]$
with
$[x,y]$
with
 $x,y$
in
$x,y$
in
 $X$
and
$X$
and
 $x<y$
;
$x<y$
;(C) an element
 $w$
of
$w$
of
 $M(X)$
of length
$M(X)$
of length
 ${\geqslant}3$
belongs to
${\geqslant}3$
belongs to
 ${\mathcal{H}}$
if and only if it is of the form
${\mathcal{H}}$
if and only if it is of the form
 $[a,[b,c]]$
with
$[a,[b,c]]$
with
 $a,b,c$
in
$a,b,c$
in
 ${\mathcal{H}}$
,
${\mathcal{H}}$
,
 $[b,c]\in {\mathcal{H}}$
,
$[b,c]\in {\mathcal{H}}$
,
 $b\leqslant a<[b,c]$
and
$b\leqslant a<[b,c]$
and
 $b<c$
.
$b<c$
.
In the rest of this section,
![]() $[x,y]$
denotes the Lie bracket of a free Lie algebra. Set
$[x,y]$
denotes the Lie bracket of a free Lie algebra. Set
![]() ${\mathcal{H}}^{i}={\mathcal{H}}\cap X_{i}$
and let
${\mathcal{H}}^{i}={\mathcal{H}}\cap X_{i}$
and let
![]() $\#X=n$
. The rank of
$\#X=n$
. The rank of
![]() $\mathfrak{f}_{n}^{k}/\mathfrak{f}_{n}^{k+1}$
is given by Witt’s formula:
$\mathfrak{f}_{n}^{k}/\mathfrak{f}_{n}^{k+1}$
is given by Witt’s formula:
where
![]() $\unicode[STIX]{x1D707}$
is the Möbius function. Under the natural projection
$\unicode[STIX]{x1D707}$
is the Möbius function. Under the natural projection
![]() $\mathfrak{f}_{n}^{k}\rightarrow \mathfrak{f}_{n}^{k}/\mathfrak{f}_{n}^{k+1}$
, the images of elements of
$\mathfrak{f}_{n}^{k}\rightarrow \mathfrak{f}_{n}^{k}/\mathfrak{f}_{n}^{k+1}$
, the images of elements of
![]() ${\mathcal{H}}^{k}$
form a
${\mathcal{H}}^{k}$
form a
![]() $\mathbb{Z}$
-basis of
$\mathbb{Z}$
-basis of
![]() $\mathfrak{f}_{n}^{k}/\mathfrak{f}_{n}^{k+1}$
. For a proof see [Reference BourbakiBou98, ch. II] or [Reference SerreSer06, Theorem 4.2]. Let
$\mathfrak{f}_{n}^{k}/\mathfrak{f}_{n}^{k+1}$
. For a proof see [Reference BourbakiBou98, ch. II] or [Reference SerreSer06, Theorem 4.2]. Let
![]() $\mathfrak{f}_{n,c}:=\mathfrak{f}_{n,c}(\mathbb{Z})$
be the free nilpotent
$\mathfrak{f}_{n,c}:=\mathfrak{f}_{n,c}(\mathbb{Z})$
be the free nilpotent
![]() $\mathbb{Z}$
-Lie algebra on
$\mathbb{Z}$
-Lie algebra on
![]() $n$
generators and of class
$n$
generators and of class
![]() $c$
; it is defined to be the quotient algebra
$c$
; it is defined to be the quotient algebra
![]() $\mathfrak{f}_{n}/\mathfrak{f}_{n}^{c+1}$
. The following facts are well known. Since we do not know a reference and their proofs are easy, we outline the arguments.
$\mathfrak{f}_{n}/\mathfrak{f}_{n}^{c+1}$
. The following facts are well known. Since we do not know a reference and their proofs are easy, we outline the arguments.
Proposition 7.2. For
![]() $n\geqslant 2$
and
$n\geqslant 2$
and
![]() $c\geqslant 2$
, we have the following.
$c\geqslant 2$
, we have the following.
(1) The image of
 $\bigcup _{i=1}^{c}{\mathcal{H}}^{i}$
under the natural projection
$\bigcup _{i=1}^{c}{\mathcal{H}}^{i}$
under the natural projection
 $\mathfrak{f}_{n}\rightarrow \mathfrak{f}_{n,c}$
is a basis of
$\mathfrak{f}_{n}\rightarrow \mathfrak{f}_{n,c}$
is a basis of
 $\mathfrak{f}_{n,c}$
.
$\mathfrak{f}_{n,c}$
.(2) The image of
 $\bigcup _{i=2}^{c}{\mathcal{H}}^{i}$
under the natural projection
$\bigcup _{i=2}^{c}{\mathcal{H}}^{i}$
under the natural projection
 $\mathfrak{f}_{n}\rightarrow \mathfrak{f}_{n,c}$
is a basis of
$\mathfrak{f}_{n}\rightarrow \mathfrak{f}_{n,c}$
is a basis of
 $\mathfrak{f}_{n,c}^{\prime }$
.
$\mathfrak{f}_{n,c}^{\prime }$
.(3) The image of
 ${\mathcal{H}}^{c}$
under the natural projection
${\mathcal{H}}^{c}$
under the natural projection
 $\mathfrak{f}_{n}\rightarrow \mathfrak{f}_{n,c}$
is a basis of
$\mathfrak{f}_{n}\rightarrow \mathfrak{f}_{n,c}$
is a basis of
 $\text{Z}(\mathfrak{f}_{n,c})$
.
$\text{Z}(\mathfrak{f}_{n,c})$
.
Proof. The first statement follows from the fact that
![]() $\bigcup _{i=1}^{\infty }{\mathcal{H}}^{i}$
is a basis of
$\bigcup _{i=1}^{\infty }{\mathcal{H}}^{i}$
is a basis of
![]() $\mathfrak{f}_{n}$
, and the
$\mathfrak{f}_{n}$
, and the
![]() $\mathbb{Z}$
-submodule
$\mathbb{Z}$
-submodule
![]() $\mathfrak{f}_{n}^{c+1}$
of
$\mathfrak{f}_{n}^{c+1}$
of
![]() $\mathfrak{f}_{n}$
is generated by
$\mathfrak{f}_{n}$
is generated by
![]() $\bigcup _{i=c+1}^{\infty }{\mathcal{H}}^{i}$
. For the second statement, it is now enough to note that
$\bigcup _{i=c+1}^{\infty }{\mathcal{H}}^{i}$
. For the second statement, it is now enough to note that
![]() $\bigcup _{i=2}^{c}{\mathcal{H}}^{i}$
generates the
$\bigcup _{i=2}^{c}{\mathcal{H}}^{i}$
generates the
![]() $\mathbb{Z}$
-module
$\mathbb{Z}$
-module
![]() $\mathfrak{f}_{n,c}^{\prime }$
. The proof of the third statement is similar.◻
$\mathfrak{f}_{n,c}^{\prime }$
. The proof of the third statement is similar.◻
Example 7.3. The image of
![]() $\bigcup _{i=1}^{3}{\mathcal{H}}^{i}$
under the natural projection
$\bigcup _{i=1}^{3}{\mathcal{H}}^{i}$
under the natural projection
![]() $\mathfrak{f}_{3}\rightarrow \mathfrak{f}_{3,3}$
is a basis of
$\mathfrak{f}_{3}\rightarrow \mathfrak{f}_{3,3}$
is a basis of
![]() $\mathfrak{f}_{3,3}$
. The elements of this union are explicitly given as follows:
$\mathfrak{f}_{3,3}$
. The elements of this union are explicitly given as follows:

Note that
![]() $\text{Z}(\mathfrak{f}_{3,3})\subseteq \mathfrak{f}_{3,3}^{\prime }$
and furthermore one can check that the image of
$\text{Z}(\mathfrak{f}_{3,3})\subseteq \mathfrak{f}_{3,3}^{\prime }$
and furthermore one can check that the image of
![]() $\{\mathbf{w}_{1},\ldots ,\mathbf{w}_{8}\}$
is a basis of
$\{\mathbf{w}_{1},\ldots ,\mathbf{w}_{8}\}$
is a basis of
![]() $\text{Z}(\mathfrak{f}_{3,3})$
, while the image of
$\text{Z}(\mathfrak{f}_{3,3})$
, while the image of
![]() $\{\mathbf{w}_{1},\ldots ,\mathbf{w}_{11}\}$
is a basis of
$\{\mathbf{w}_{1},\ldots ,\mathbf{w}_{11}\}$
is a basis of
![]() $\mathfrak{f}_{3,3}^{\prime }$
. By an explicit calculation and using the Jacobi identity, we obtain the following commutator matrix
$\mathfrak{f}_{3,3}^{\prime }$
. By an explicit calculation and using the Jacobi identity, we obtain the following commutator matrix

Now we consider the general case. Set
By Proposition 7.2, the natural projection maps
![]() $\bigcup _{i=1}^{c-1}{\mathcal{H}}^{i}$
to a basis of
$\bigcup _{i=1}^{c-1}{\mathcal{H}}^{i}$
to a basis of
![]() $\mathfrak{f}_{n,c}/(\text{Z}(\mathfrak{f}_{n,c}))$
. Note that the commutator matrix
$\mathfrak{f}_{n,c}/(\text{Z}(\mathfrak{f}_{n,c}))$
. Note that the commutator matrix
![]() $F_{\mathfrak{f}_{n,c}}(\mathbf{T})\in M_{m_{1}}(\mathbb{Z}[\mathbf{T}])$
is a skew-symmetric matrix whose entries are
$F_{\mathfrak{f}_{n,c}}(\mathbf{T})\in M_{m_{1}}(\mathbb{Z}[\mathbf{T}])$
is a skew-symmetric matrix whose entries are
![]() $\mathbb{Z}$
-linear forms in
$\mathbb{Z}$
-linear forms in
![]() $m$
variables. We label the variables as follows. For each
$m$
variables. We label the variables as follows. For each
![]() $2\leqslant k\leqslant c$
we write
$2\leqslant k\leqslant c$
we write
![]() $\mathbf{T}^{(k)}=(T_{1}^{(k)},\ldots ,T_{r_{n}(k)}^{(k)})$
, so that
$\mathbf{T}^{(k)}=(T_{1}^{(k)},\ldots ,T_{r_{n}(k)}^{(k)})$
, so that
![]() $\mathbf{T}=(\mathbf{T}^{(k)})_{2\leqslant k\leqslant c}$
and
$\mathbf{T}=(\mathbf{T}^{(k)})_{2\leqslant k\leqslant c}$
and
 $$\begin{eqnarray}F_{\mathfrak{f}_{n,c}}(\mathbf{T})=\left(\begin{array}{@{}cccc@{}}F_{11}(\mathbf{T}^{(2)}) & F_{12}(\mathbf{T}^{(3)}) & \cdots \, & F_{1(c-1)}(\mathbf{T}^{(c)})\\ F_{21}(\mathbf{T}^{(3)}) & F_{22}(\mathbf{T}^{(4)}) & \cdots \, & 0\\ \vdots & \vdots & \vdots & \vdots \\ F_{(c-1)1}(\mathbf{T}^{(c)}) & 0 & 0 & 0\\ \end{array}\right)\!,\end{eqnarray}$$
$$\begin{eqnarray}F_{\mathfrak{f}_{n,c}}(\mathbf{T})=\left(\begin{array}{@{}cccc@{}}F_{11}(\mathbf{T}^{(2)}) & F_{12}(\mathbf{T}^{(3)}) & \cdots \, & F_{1(c-1)}(\mathbf{T}^{(c)})\\ F_{21}(\mathbf{T}^{(3)}) & F_{22}(\mathbf{T}^{(4)}) & \cdots \, & 0\\ \vdots & \vdots & \vdots & \vdots \\ F_{(c-1)1}(\mathbf{T}^{(c)}) & 0 & 0 & 0\\ \end{array}\right)\!,\end{eqnarray}$$
where
![]() $F_{ij}(\mathbf{T}^{(i+j)})$
is the zero matrix if
$F_{ij}(\mathbf{T}^{(i+j)})$
is the zero matrix if
![]() $i+j>c$
, and
$i+j>c$
, and
![]() $F_{ij}(\mathbf{T}^{(i+j)})=-F_{ji}^{\text{tr}}(\mathbf{T}^{(i+j)})$
.
$F_{ij}(\mathbf{T}^{(i+j)})=-F_{ji}^{\text{tr}}(\mathbf{T}^{(i+j)})$
.
In order to use Theorem 5.3 to compute the faithful dimension of
![]() $\exp (\mathfrak{f}_{n,c}\otimes _{\mathbb{Z}}\mathbb{F}_{q})$
we need to find
$\exp (\mathfrak{f}_{n,c}\otimes _{\mathbb{Z}}\mathbb{F}_{q})$
we need to find
![]() $r_{n}(c)$
vectors
$r_{n}(c)$
vectors
![]() $\mathbf{a}_{\ell }=(\mathbf{a}_{\ell }^{(k)})$
,
$\mathbf{a}_{\ell }=(\mathbf{a}_{\ell }^{(k)})$
,
![]() $2\leqslant k\leqslant c$
, with
$2\leqslant k\leqslant c$
, with
![]() $\mathbf{a}_{\ell }^{(k)}=(a_{\ell 1}^{(k)},\ldots ,a_{\ell r_{n}(k)}^{(k)})$
such that the vectors
$\mathbf{a}_{\ell }^{(k)}=(a_{\ell 1}^{(k)},\ldots ,a_{\ell r_{n}(k)}^{(k)})$
such that the vectors
![]() $\mathbf{a}_{\ell }$
minimize
$\mathbf{a}_{\ell }$
minimize
subject to the condition
 $$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}a_{11}^{(c)} & a_{12}^{(c)} & \cdots \, & a_{1r_{n}(c)}^{(c)}\\ \vdots & & & \vdots \\ a_{r_{n}(c)1}^{(c)} & a_{r_{n}(c)2}^{(c)} & \cdots \, & a_{r_{n}(c)r_{n}(c)}^{(c)}\end{array}\right)\in \operatorname{GL}_{r_{n}(c)}(\mathbb{F}_{q}).\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}cccc@{}}a_{11}^{(c)} & a_{12}^{(c)} & \cdots \, & a_{1r_{n}(c)}^{(c)}\\ \vdots & & & \vdots \\ a_{r_{n}(c)1}^{(c)} & a_{r_{n}(c)2}^{(c)} & \cdots \, & a_{r_{n}(c)r_{n}(c)}^{(c)}\end{array}\right)\in \operatorname{GL}_{r_{n}(c)}(\mathbb{F}_{q}).\end{eqnarray}$$
Let us define the reduced commutator matrix of
![]() $\mathfrak{f}_{n,c}$
to be
$\mathfrak{f}_{n,c}$
to be
 $$\begin{eqnarray}F_{\mathfrak{f}_{n,c}}^{\text{red}}(\mathbf{T}_{\boldsymbol{ c}})=\left(\begin{array}{@{}ccccc@{}}0 & 0 & \cdots \, & 0 & F_{1(c-1)}(\mathbf{T}^{(c)})\\ 0 & 0 & \cdots \, & F_{2(c-2)}(\mathbf{T}^{(c)}) & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & F_{(c-2)2}(\mathbf{T}^{(c)}) & 0 & \cdots \, & 0\\ F_{(c-1)1}(\mathbf{T}^{(c)}) & 0 & 0 & \cdots \, & 0\\ \end{array}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}F_{\mathfrak{f}_{n,c}}^{\text{red}}(\mathbf{T}_{\boldsymbol{ c}})=\left(\begin{array}{@{}ccccc@{}}0 & 0 & \cdots \, & 0 & F_{1(c-1)}(\mathbf{T}^{(c)})\\ 0 & 0 & \cdots \, & F_{2(c-2)}(\mathbf{T}^{(c)}) & 0\\ \vdots & \vdots & \vdots & \vdots & \vdots \\ 0 & F_{(c-2)2}(\mathbf{T}^{(c)}) & 0 & \cdots \, & 0\\ F_{(c-1)1}(\mathbf{T}^{(c)}) & 0 & 0 & \cdots \, & 0\\ \end{array}\right)\!.\end{eqnarray}$$
In other words,
![]() $F_{\mathfrak{f}_{n,c}}^{\text{red}}$
is the matrix obtained from
$F_{\mathfrak{f}_{n,c}}^{\text{red}}$
is the matrix obtained from
![]() $F_{\mathfrak{f}_{n,c}}$
by setting the variables
$F_{\mathfrak{f}_{n,c}}$
by setting the variables
![]() $\mathbf{T}^{(k)}$
equal to zero when
$\mathbf{T}^{(k)}$
equal to zero when
![]() $k\neq c$
, so that the
$k\neq c$
, so that the
![]() $(i,c-i)$
-block of
$(i,c-i)$
-block of
![]() $F_{\mathfrak{f}_{n,c}}^{\text{red}}$
is equal to
$F_{\mathfrak{f}_{n,c}}^{\text{red}}$
is equal to
![]() $F_{i(c-i)}(\mathbf{T}^{(c)})$
for
$F_{i(c-i)}(\mathbf{T}^{(c)})$
for
![]() $1\leqslant i\leqslant c-1$
, and all other blocks in
$1\leqslant i\leqslant c-1$
, and all other blocks in
![]() $F_{\mathfrak{f}_{n,c}}^{\text{red}}$
are equal to zero. For instance in Example 7.3, the reduced commutator matrix is
$F_{\mathfrak{f}_{n,c}}^{\text{red}}$
are equal to zero. For instance in Example 7.3, the reduced commutator matrix is
Note that for each
![]() $2\leqslant k\leqslant c$
, the variables
$2\leqslant k\leqslant c$
, the variables
![]() $\mathbf{T}^{(k)}$
only occur in the matrices
$\mathbf{T}^{(k)}$
only occur in the matrices
![]() $F_{ij}$
with
$F_{ij}$
with
![]() $i+j=k$
. Clearly,
$i+j=k$
. Clearly,
Note that the only entries of
![]() $\mathbf{a}_{\ell }$
that appear in the invertibility condition (33) are those of
$\mathbf{a}_{\ell }$
that appear in the invertibility condition (33) are those of
![]() $\mathbf{a}_{\ell }^{(c)}$
. Further, by setting all of the components of
$\mathbf{a}_{\ell }^{(c)}$
. Further, by setting all of the components of
![]() $\mathbf{a}_{\ell }^{k}$
to zero for
$\mathbf{a}_{\ell }^{k}$
to zero for
![]() $2\leqslant k<c$
, we do not increase the rank of the matrix
$2\leqslant k<c$
, we do not increase the rank of the matrix
![]() $F_{\mathfrak{f}_{n,c}}(\mathbf{a}_{\ell })$
. Therefore the minima of the two sides of (34) are equal. Thus from Theorem 5.3 we can conclude the following proposition.
$F_{\mathfrak{f}_{n,c}}(\mathbf{a}_{\ell })$
. Therefore the minima of the two sides of (34) are equal. Thus from Theorem 5.3 we can conclude the following proposition.
Proposition 7.4. Let
![]() $F:=F_{\mathfrak{f}_{n,c}}^{\text{red}}$
be the reduced commutator matrix of
$F:=F_{\mathfrak{f}_{n,c}}^{\text{red}}$
be the reduced commutator matrix of
![]() $\mathfrak{f}_{n,c}$
. Then the faithful dimension of
$\mathfrak{f}_{n,c}$
. Then the faithful dimension of
![]() $\exp (\mathfrak{f}_{n,c}\otimes _{\mathbb{Z}}\mathbb{F}_{q})$
is
$\exp (\mathfrak{f}_{n,c}\otimes _{\mathbb{Z}}\mathbb{F}_{q})$
is
 $$\begin{eqnarray}\min \left\{\mathop{\sum }_{\ell =1}^{r_{n}(c)}fq^{\text{rk}_{\mathbb{F}_{q}}(F(a_{\ell 1},\ldots ,a_{\ell r_{n}(c)}))/2}:\left(\begin{array}{@{}ccc@{}}a_{11} & \cdots \, & a_{1r_{n}(c)}\\ \vdots & \ddots & \vdots \\ a_{r_{n}(c)1} & \cdots \, & a_{r_{n}(c)r_{n}(c)}\end{array}\right)\in \text{GL}_{r_{n}(c)}(\mathbb{F}_{q})\right\}.\end{eqnarray}$$
$$\begin{eqnarray}\min \left\{\mathop{\sum }_{\ell =1}^{r_{n}(c)}fq^{\text{rk}_{\mathbb{F}_{q}}(F(a_{\ell 1},\ldots ,a_{\ell r_{n}(c)}))/2}:\left(\begin{array}{@{}ccc@{}}a_{11} & \cdots \, & a_{1r_{n}(c)}\\ \vdots & \ddots & \vdots \\ a_{r_{n}(c)1} & \cdots \, & a_{r_{n}(c)r_{n}(c)}\end{array}\right)\in \text{GL}_{r_{n}(c)}(\mathbb{F}_{q})\right\}.\end{eqnarray}$$
7.2 Proof of Theorem 2.13
We now prove Theorem 2.13. The proof relies upon an explicit description of the commutator matrix and so it is combinatorial in nature. First we consider the statement for
![]() $\mathfrak{f}_{n,2}$
. The image of the set
$\mathfrak{f}_{n,2}$
. The image of the set
where
![]() $x_{ij}:=[x_{i},x_{j}]$
for
$x_{ij}:=[x_{i},x_{j}]$
for
![]() $1\leqslant i<j\leqslant n$
, is a basis of
$1\leqslant i<j\leqslant n$
, is a basis of
![]() $\mathfrak{f}_{n,2}$
. Thus the commutator matrix of
$\mathfrak{f}_{n,2}$
. Thus the commutator matrix of
![]() $\mathfrak{f}_{n,2}$
is
$\mathfrak{f}_{n,2}$
is
 $$\begin{eqnarray}F_{\mathfrak{f}_{n,2}}(\mathbf{T})=\left(\begin{array}{@{}ccccc@{}}0 & T_{12} & T_{13} & \cdots \, & T_{1n}\\ -T_{12} & 0 & T_{23} & \cdots \, & T_{2n}\\ -T_{13} & -T_{23} & 0 & \cdots \, & T_{3n}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -T_{1n} & -T_{2n} & -T_{3n} & \cdots \, & 0\end{array}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}F_{\mathfrak{f}_{n,2}}(\mathbf{T})=\left(\begin{array}{@{}ccccc@{}}0 & T_{12} & T_{13} & \cdots \, & T_{1n}\\ -T_{12} & 0 & T_{23} & \cdots \, & T_{2n}\\ -T_{13} & -T_{23} & 0 & \cdots \, & T_{3n}\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ -T_{1n} & -T_{2n} & -T_{3n} & \cdots \, & 0\end{array}\right)\!.\end{eqnarray}$$
Observe that each variable
![]() $T_{ij}$
,
$T_{ij}$
,
![]() $1\leqslant i<j\leqslant n$
, appears exactly twice. Therefore if exactly one of the
$1\leqslant i<j\leqslant n$
, appears exactly twice. Therefore if exactly one of the
![]() $T_{ij}$
is non-zero, then the rank of the above matrix will be equal to 2. Now by applying Proposition 7.4, we obtain the statement of the theorem for
$T_{ij}$
is non-zero, then the rank of the above matrix will be equal to 2. Now by applying Proposition 7.4, we obtain the statement of the theorem for
![]() $\mathfrak{f}_{n,2}$
.
$\mathfrak{f}_{n,2}$
.
Let us now turn to the case of
![]() $\mathfrak{f}_{n,3}$
. First note that the reduced commutator matrix of
$\mathfrak{f}_{n,3}$
. First note that the reduced commutator matrix of
![]() $\mathfrak{f}_{n,3}$
is equal to
$\mathfrak{f}_{n,3}$
is equal to
In particular,
![]() $\text{rk}_{\mathbb{F}_{q}}(F(\mathbf{T}^{(3)}))=2\text{rk}_{\mathbb{F}_{q}}(F_{12}(\mathbf{T}^{(3)}))$
. Our goal is to find
$\text{rk}_{\mathbb{F}_{q}}(F(\mathbf{T}^{(3)}))=2\text{rk}_{\mathbb{F}_{q}}(F_{12}(\mathbf{T}^{(3)}))$
. Our goal is to find
![]() $F_{12}(\mathbf{T}^{(3)})$
explicitly with respect to the basis obtained by the image of
$F_{12}(\mathbf{T}^{(3)})$
explicitly with respect to the basis obtained by the image of
![]() ${\mathcal{H}}^{1}\cup {\mathcal{H}}^{2}\cup {\mathcal{H}}^{3}$
. The latter set consists of
${\mathcal{H}}^{1}\cup {\mathcal{H}}^{2}\cup {\mathcal{H}}^{3}$
. The latter set consists of

Consider the sets
![]() $R_{1}:=\{1,2,\ldots ,n\},$
$R_{1}:=\{1,2,\ldots ,n\},$
![]() $R_{2}:=\{(i,j):1\leqslant i<j\leqslant n\},$
and
$R_{2}:=\{(i,j):1\leqslant i<j\leqslant n\},$
and
The elements of the
![]() $R_{i}$
parameterize the sets
$R_{i}$
parameterize the sets
![]() ${\mathcal{H}}^{1},{\mathcal{H}}^{2}$
and
${\mathcal{H}}^{1},{\mathcal{H}}^{2}$
and
![]() ${\mathcal{H}}^{3}$
. Set
${\mathcal{H}}^{3}$
. Set
and define

It is clear that
![]() $R_{3}=R_{3}^{0}\cup R_{3}^{+}\cup R_{3}^{-}$
is a partition of
$R_{3}=R_{3}^{0}\cup R_{3}^{+}\cup R_{3}^{-}$
is a partition of
![]() $R_{3}$
. We will now give an explicit description of
$R_{3}$
. We will now give an explicit description of
![]() $F_{12}(\mathbf{T}^{(3)})$
in terms of these sets. It will be more convenient to use the variables
$F_{12}(\mathbf{T}^{(3)})$
in terms of these sets. It will be more convenient to use the variables
![]() $T_{\unicode[STIX]{x1D6FC}}$
with
$T_{\unicode[STIX]{x1D6FC}}$
with
![]() $\unicode[STIX]{x1D6FC}\in R_{3}$
instead of
$\unicode[STIX]{x1D6FC}\in R_{3}$
instead of
![]() $\mathbf{T}^{(3)}=(T_{1}^{(3)},\ldots ,T_{r_{n}(3)}^{(3)})$
. We will also use
$\mathbf{T}^{(3)}=(T_{1}^{(3)},\ldots ,T_{r_{n}(3)}^{(3)})$
. We will also use
![]() $\mathbf{T}$
to denote the vector with entries
$\mathbf{T}$
to denote the vector with entries
![]() $T_{\unicode[STIX]{x1D6FC}}$
with
$T_{\unicode[STIX]{x1D6FC}}$
with
![]() $\unicode[STIX]{x1D6FC}\in R_{3}$
. For instance
$\unicode[STIX]{x1D6FC}\in R_{3}$
. For instance
![]() $T_{213}$
and
$T_{213}$
and
![]() $T_{312}$
correspond, respectively, to
$T_{312}$
correspond, respectively, to
![]() $T_{4}$
and
$T_{4}$
and
![]() $T_{6}$
in Example 7.3. For
$T_{6}$
in Example 7.3. For
![]() $i\in R_{1}$
and
$i\in R_{1}$
and
![]() $(j,k)\in R_{2}$
, a simple computation shows that
$(j,k)\in R_{2}$
, a simple computation shows that
Therefore the entry of the matrix
![]() $F_{12}$
in the row associated to
$F_{12}$
in the row associated to
![]() $i\in R_{1}$
and column associated to
$i\in R_{1}$
and column associated to
![]() $(j,k)\in R_{2}$
is given by
$(j,k)\in R_{2}$
is given by
![]() $T_{ijk}$
if
$T_{ijk}$
if
![]() $(i,j,k)\in R_{3}$
and by
$(i,j,k)\in R_{3}$
and by
![]() $T_{jik}-T_{kij}$
otherwise.
$T_{jik}-T_{kij}$
otherwise.
Lemma 7.5. For
![]() $1\leqslant i,j,k\leqslant n$
the following hold.
$1\leqslant i,j,k\leqslant n$
the following hold.
(a) For
 $i<k$
, the variable
$i<k$
, the variable
 $T_{iik}$
appears exactly once in
$T_{iik}$
appears exactly once in
 $F_{12}(\mathbf{T})$
, namely, in row
$F_{12}(\mathbf{T})$
, namely, in row
 $i$
and column
$i$
and column
 $(i,k)$
.
$(i,k)$
.(b) For
 $j<i$
, the variable
$j<i$
, the variable
 $T_{iji}$
appears exactly once in
$T_{iji}$
appears exactly once in
 $F_{12}(\mathbf{T})$
, namely, in row
$F_{12}(\mathbf{T})$
, namely, in row
 $i$
and column
$i$
and column
 $(j,i)$
.
$(j,i)$
.(c) For
 $(i,j,k)\in R_{3}^{+}$
, the variable
$(i,j,k)\in R_{3}^{+}$
, the variable
 $T_{ijk}$
appears exactly twice in the entries of
$T_{ijk}$
appears exactly twice in the entries of
 $F_{12}(\mathbf{T})$
. Namely, the entry in row
$F_{12}(\mathbf{T})$
. Namely, the entry in row
 $i$
and column
$i$
and column
 $(j,k)$
is equal to
$(j,k)$
is equal to
 $T_{ijk}$
, and the entry in row
$T_{ijk}$
, and the entry in row
 $j$
and column
$j$
and column
 $(i,k)$
is equal to
$(i,k)$
is equal to
 $T_{ijk}-T_{kji}$
.
$T_{ijk}-T_{kji}$
.(d) For
 $(i,j,k)\in R_{3}^{-}$
, the variable
$(i,j,k)\in R_{3}^{-}$
, the variable
 $T_{ijk}$
appears exactly twice in
$T_{ijk}$
appears exactly twice in
 $F_{12}(\mathbf{T})$
. Namely, the entry in row
$F_{12}(\mathbf{T})$
. Namely, the entry in row
 $i$
and column
$i$
and column
 $(j,k)$
is equal to
$(j,k)$
is equal to
 $T_{ijk}$
, and the entry in row
$T_{ijk}$
, and the entry in row
 $j$
and column
$j$
and column
 $(k,i)$
is equal to
$(k,i)$
is equal to
 $T_{kji}-T_{ijk}$
.
$T_{kji}-T_{ijk}$
.
Proof of the Lemma 7.5.
Parts (a) and (b) of the lemma are clear, since if
![]() $T_{ijk}$
appears twice then
$T_{ijk}$
appears twice then
![]() $i,j,k$
must be pairwise distinct. We will now prove part (c). Suppose
$i,j,k$
must be pairwise distinct. We will now prove part (c). Suppose
![]() $j<i<k$
. It is clear from (35) that
$j<i<k$
. It is clear from (35) that
![]() $T_{ijk}$
can only potentially appear in a bracket of the form
$T_{ijk}$
can only potentially appear in a bracket of the form
![]() $[x_{\unicode[STIX]{x1D6FC}},[x_{\unicode[STIX]{x1D6FD}},x_{\unicode[STIX]{x1D6FE}}]]$
, where the indices are permutations of
$[x_{\unicode[STIX]{x1D6FC}},[x_{\unicode[STIX]{x1D6FD}},x_{\unicode[STIX]{x1D6FE}}]]$
, where the indices are permutations of
![]() $i,j,k$
and
$i,j,k$
and
![]() $\unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D6FE}$
. This leaves three possibilities
$\unicode[STIX]{x1D6FD}<\unicode[STIX]{x1D6FE}$
. This leaves three possibilities
![]() $(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})=(i,j,k),(j,i,k),(k,j,i)$
. However, since
$(\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD},\unicode[STIX]{x1D6FE})=(i,j,k),(j,i,k),(k,j,i)$
. However, since
![]() $[x_{k},[x_{j},x_{i}]]=x_{kji}\in {\mathcal{H}}^{3}$
, the third possibility does not occur. Moreover,
$[x_{k},[x_{j},x_{i}]]=x_{kji}\in {\mathcal{H}}^{3}$
, the third possibility does not occur. Moreover,
which proves the statement. Part (d) can be proven in a similar way. ◻
From this it follows that
![]() $\text{rk}_{\mathbb{F}_{q}}(F_{12}(\mathbf{a}))\geqslant 1$
for every non-zero vector
$\text{rk}_{\mathbb{F}_{q}}(F_{12}(\mathbf{a}))\geqslant 1$
for every non-zero vector
![]() $\mathbf{a}\in \mathbb{F}_{q}^{d}$
, where
$\mathbf{a}\in \mathbb{F}_{q}^{d}$
, where
![]() $d:=r_{n}(3)$
. In the rest of this section, for each
$d:=r_{n}(3)$
. In the rest of this section, for each
![]() $\unicode[STIX]{x1D6FC}\in R_{3}$
, we will find a vector
$\unicode[STIX]{x1D6FC}\in R_{3}$
, we will find a vector
![]() $\mathbf{a}_{\unicode[STIX]{x1D6FC}}=(a_{1,\unicode[STIX]{x1D6FC}},\ldots ,a_{d,\unicode[STIX]{x1D6FC}})\in \mathbb{F}_{q}^{d}$
such that the rank of
$\mathbf{a}_{\unicode[STIX]{x1D6FC}}=(a_{1,\unicode[STIX]{x1D6FC}},\ldots ,a_{d,\unicode[STIX]{x1D6FC}})\in \mathbb{F}_{q}^{d}$
such that the rank of
![]() $M_{\unicode[STIX]{x1D6FC}}:=F_{12}(\mathbf{a}_{\unicode[STIX]{x1D6FC}})$
is equal to
$M_{\unicode[STIX]{x1D6FC}}:=F_{12}(\mathbf{a}_{\unicode[STIX]{x1D6FC}})$
is equal to
![]() $1$
and the
$1$
and the
![]() $M_{\unicode[STIX]{x1D6FC}}$
are linearly independent matrices over
$M_{\unicode[STIX]{x1D6FC}}$
are linearly independent matrices over
![]() $\mathbb{F}_{q}$
. It follows that the
$\mathbb{F}_{q}$
. It follows that the
![]() $\mathbf{a}_{\unicode[STIX]{x1D6FC}}$
are linearly independent over
$\mathbf{a}_{\unicode[STIX]{x1D6FC}}$
are linearly independent over
![]() $\mathbb{F}_{q}$
and thus the matrix
$\mathbb{F}_{q}$
and thus the matrix
![]() $(\mathbf{a}_{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}\in R_{3}}$
is invertible. Then from Proposition 7.4 we conclude that the faithful dimension of
$(\mathbf{a}_{\unicode[STIX]{x1D6FC}})_{\unicode[STIX]{x1D6FC}\in R_{3}}$
is invertible. Then from Proposition 7.4 we conclude that the faithful dimension of
![]() $\exp (\mathfrak{f}_{n,3}\otimes _{\mathbb{Z}}\mathbb{F}_{q})$
is equal to
$\exp (\mathfrak{f}_{n,3}\otimes _{\mathbb{Z}}\mathbb{F}_{q})$
is equal to
![]() $r_{n}(3)fq$
when
$r_{n}(3)fq$
when
![]() $p\geqslant 5$
.
$p\geqslant 5$
.
We now construct
![]() $M_{\unicode[STIX]{x1D6FC}}$
for
$M_{\unicode[STIX]{x1D6FC}}$
for
![]() $\unicode[STIX]{x1D6FC}\in R_{3}$
. For every
$\unicode[STIX]{x1D6FC}\in R_{3}$
. For every
![]() $\unicode[STIX]{x1D6FF}=(i,j,k)$
with
$\unicode[STIX]{x1D6FF}=(i,j,k)$
with
![]() $1\leqslant i,j,k\leqslant n$
, define
$1\leqslant i,j,k\leqslant n$
, define
(I): Suppose
![]() $\unicode[STIX]{x1D6FC}=(i,j,k)\in R_{3}^{0}$
, that is
$\unicode[STIX]{x1D6FC}=(i,j,k)\in R_{3}^{0}$
, that is
![]() $i=k$
or
$i=k$
or
![]() $i=j$
. In either case,
$i=j$
. In either case,
![]() $T_{ijk}$
appears only once in
$T_{ijk}$
appears only once in
![]() $F_{12}(\mathbf{T})$
by parts (a) and (b) of Lemma 7.5. Let
$F_{12}(\mathbf{T})$
by parts (a) and (b) of Lemma 7.5. Let
![]() $M_{\unicode[STIX]{x1D6FC}}$
be the matrix obtained from
$M_{\unicode[STIX]{x1D6FC}}$
be the matrix obtained from
![]() $F_{12}(\mathbf{T})$
by setting
$F_{12}(\mathbf{T})$
by setting
![]() $T_{ijk}=1$
and letting the rest of variables to be zero. Then the rank of
$T_{ijk}=1$
and letting the rest of variables to be zero. Then the rank of
![]() $M_{\unicode[STIX]{x1D6FC}}$
is
$M_{\unicode[STIX]{x1D6FC}}$
is
![]() $1$
.
$1$
.
(II): Let
![]() $\unicode[STIX]{x1D6FC}=(i,j,k)\in R_{3}^{+}$
, that is
$\unicode[STIX]{x1D6FC}=(i,j,k)\in R_{3}^{+}$
, that is
![]() $j<i<k$
. Let
$j<i<k$
. Let
![]() $M_{\unicode[STIX]{x1D6FC}}$
be the matrix obtained from
$M_{\unicode[STIX]{x1D6FC}}$
be the matrix obtained from
![]() $F_{12}(\mathbf{T})$
by setting
$F_{12}(\mathbf{T})$
by setting
![]() $T_{ijk}=T_{iik}=T_{jjk}=1$
, and zero for the rest of variables. From part (c) of Lemma 7.5 we can see that in this case
$T_{ijk}=T_{iik}=T_{jjk}=1$
, and zero for the rest of variables. From part (c) of Lemma 7.5 we can see that in this case

Note that this matrix has rank
![]() $1$
and the rows in which non-zero entries are located correspond to the
$1$
and the rows in which non-zero entries are located correspond to the
![]() $\unicode[STIX]{x1D6FC}^{-}$
and
$\unicode[STIX]{x1D6FC}^{-}$
and
![]() $\unicode[STIX]{x1D6FC}^{0}$
.
$\unicode[STIX]{x1D6FC}^{0}$
.
(III): Let
![]() $\unicode[STIX]{x1D6FC}=(i,j,k)\in R_{3}^{-}$
, that is
$\unicode[STIX]{x1D6FC}=(i,j,k)\in R_{3}^{-}$
, that is
![]() $j<k<i$
. Let
$j<k<i$
. Let
![]() $M_{\unicode[STIX]{x1D6FC}}$
be the matrix obtained from
$M_{\unicode[STIX]{x1D6FC}}$
be the matrix obtained from
![]() $F_{12}(\mathbf{T})$
by setting
$F_{12}(\mathbf{T})$
by setting
![]() $T_{jjk}=T_{ijk}=1$
and
$T_{jjk}=T_{ijk}=1$
and
![]() $T_{iki}=-1$
and zero elsewhere. One can verify that in this case
$T_{iki}=-1$
and zero elsewhere. One can verify that in this case

Note that this matrix has rank
![]() $1$
and the rows in which non-zero entries are located correspond to the
$1$
and the rows in which non-zero entries are located correspond to the
![]() $\unicode[STIX]{x1D6FC}^{-}$
and
$\unicode[STIX]{x1D6FC}^{-}$
and
![]() $\unicode[STIX]{x1D6FC}^{+}$
.
$\unicode[STIX]{x1D6FC}^{+}$
.
Let us show that the matrices constructed above are linearly independent. Suppose that
We will show that
![]() $c_{\unicode[STIX]{x1D6FC}}=0$
for all
$c_{\unicode[STIX]{x1D6FC}}=0$
for all
![]() $\unicode[STIX]{x1D6FC}\in R_{3}$
. Let
$\unicode[STIX]{x1D6FC}\in R_{3}$
. Let
![]() $\unicode[STIX]{x1D6FD}=(s,r,t)\in R_{3}^{+}$
be an arbitrary element. The definition of
$\unicode[STIX]{x1D6FD}=(s,r,t)\in R_{3}^{+}$
be an arbitrary element. The definition of
![]() $R_{3}^{+}$
implies that
$R_{3}^{+}$
implies that
![]() $r<s<t$
. Consider the entry of
$r<s<t$
. Consider the entry of
![]() $M$
associated to row
$M$
associated to row
![]() $s$
and column
$s$
and column
![]() $(r,t)$
. Note that since
$(r,t)$
. Note that since
![]() $s=\unicode[STIX]{x1D6FD}^{0}$
, a case by case verification shows that the
$s=\unicode[STIX]{x1D6FD}^{0}$
, a case by case verification shows that the
![]() $(s,(r,t))$
entry of every matrix
$(s,(r,t))$
entry of every matrix
![]() $M_{\unicode[STIX]{x1D6FC}}$
with
$M_{\unicode[STIX]{x1D6FC}}$
with
![]() $\unicode[STIX]{x1D6FC}\in R_{3}^{0}\cup R_{3}^{-}$
is equal to zero. Furthermore, the only
$\unicode[STIX]{x1D6FC}\in R_{3}^{0}\cup R_{3}^{-}$
is equal to zero. Furthermore, the only
![]() $\unicode[STIX]{x1D6FC}\in R_{3}^{+}$
for which
$\unicode[STIX]{x1D6FC}\in R_{3}^{+}$
for which
![]() $M_{\unicode[STIX]{x1D6FC}}$
has a non-zero entry in row
$M_{\unicode[STIX]{x1D6FC}}$
has a non-zero entry in row
![]() $s$
and column
$s$
and column
![]() $(r,t)$
is
$(r,t)$
is
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}$
. This gives
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}$
. This gives
![]() $c_{\unicode[STIX]{x1D6FD}}=0$
, which, in turn, shows that
$c_{\unicode[STIX]{x1D6FD}}=0$
, which, in turn, shows that
![]() $c_{\unicode[STIX]{x1D6FD}}=0$
for all
$c_{\unicode[STIX]{x1D6FD}}=0$
for all
![]() $\unicode[STIX]{x1D6FD}\in R_{3}^{+}$
.
$\unicode[STIX]{x1D6FD}\in R_{3}^{+}$
.
Now let
![]() $\unicode[STIX]{x1D6FE}=(t^{\prime },r^{\prime },s^{\prime })\in R_{3}^{-}$
be an arbitrary element. Then from the definition of
$\unicode[STIX]{x1D6FE}=(t^{\prime },r^{\prime },s^{\prime })\in R_{3}^{-}$
be an arbitrary element. Then from the definition of
![]() $R_{3}^{-}$
we have
$R_{3}^{-}$
we have
![]() $r^{\prime }<s^{\prime }<t^{\prime }$
. Consider the entry of
$r^{\prime }<s^{\prime }<t^{\prime }$
. Consider the entry of
![]() $M$
associated to row
$M$
associated to row
![]() $t^{\prime }$
and column
$t^{\prime }$
and column
![]() $(r^{\prime },s^{\prime })$
. The
$(r^{\prime },s^{\prime })$
. The
![]() $(t^{\prime },(r^{\prime },s^{\prime }))$
entry of every matrix
$(t^{\prime },(r^{\prime },s^{\prime }))$
entry of every matrix
![]() $M_{\unicode[STIX]{x1D6FC}}$
with
$M_{\unicode[STIX]{x1D6FC}}$
with
![]() $\unicode[STIX]{x1D6FC}\in R_{3}^{0}$
is equal to zero. Furthermore, the only
$\unicode[STIX]{x1D6FC}\in R_{3}^{0}$
is equal to zero. Furthermore, the only
![]() $\unicode[STIX]{x1D6FC}\in R_{3}^{-}$
for which
$\unicode[STIX]{x1D6FC}\in R_{3}^{-}$
for which
![]() $M_{\unicode[STIX]{x1D6FC}}$
has a non-zero entry in row
$M_{\unicode[STIX]{x1D6FC}}$
has a non-zero entry in row
![]() $t^{\prime }$
and column
$t^{\prime }$
and column
![]() $(r^{\prime },s^{\prime })$
is
$(r^{\prime },s^{\prime })$
is
![]() $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FE}$
. Comparing coefficients yields
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FE}$
. Comparing coefficients yields
![]() $c_{\unicode[STIX]{x1D6FE}}=0$
. This shows that
$c_{\unicode[STIX]{x1D6FE}}=0$
. This shows that
![]() $c_{\unicode[STIX]{x1D6FE}}=0$
for all
$c_{\unicode[STIX]{x1D6FE}}=0$
for all
![]() $\unicode[STIX]{x1D6FE}\in R_{3}^{-}$
. Hence
$\unicode[STIX]{x1D6FE}\in R_{3}^{-}$
. Hence
It is however clear that for distinct
![]() $\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\in R_{3}^{0}$
non-zero entries of
$\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{2}\in R_{3}^{0}$
non-zero entries of
![]() $M_{\unicode[STIX]{x1D6FC}}$
do not overlap. This implies that
$M_{\unicode[STIX]{x1D6FC}}$
do not overlap. This implies that
![]() $c_{\unicode[STIX]{x1D6FC}}=0$
for all
$c_{\unicode[STIX]{x1D6FC}}=0$
for all
![]() $\unicode[STIX]{x1D6FC}\in R_{3}^{0}$
, and the proof is complete.
$\unicode[STIX]{x1D6FC}\in R_{3}^{0}$
, and the proof is complete.
7.3 Proof of Theorem 2.15
We first note that, similar to the case of
![]() $\mathfrak{f}_{n,c}$
, one can define the reduced commutator matrix of
$\mathfrak{f}_{n,c}$
, one can define the reduced commutator matrix of
![]() $\mathfrak{m}_{n,c}$
and prove the same result as Proposition 7.4. Let us now turn to the Lie algebra
$\mathfrak{m}_{n,c}$
and prove the same result as Proposition 7.4. Let us now turn to the Lie algebra
![]() $\mathfrak{m}_{2,c}$
generated by
$\mathfrak{m}_{2,c}$
generated by
![]() $x_{1}$
and
$x_{1}$
and
![]() $x_{2}$
. Note that since
$x_{2}$
. Note that since
![]() $\mathfrak{m}_{2,c}$
is metabelian, the only elements of the Hall basis whose images in
$\mathfrak{m}_{2,c}$
is metabelian, the only elements of the Hall basis whose images in
![]() $\mathfrak{m}_{2,c}$
are non-zero are of the form
$\mathfrak{m}_{2,c}$
are non-zero are of the form
where
![]() $k\leqslant c-1$
and
$k\leqslant c-1$
and
![]() $1=i_{1}\leqslant i_{2}\leqslant \cdots \leqslant i_{k}\leqslant 2$
. Moreover, the images in
$1=i_{1}\leqslant i_{2}\leqslant \cdots \leqslant i_{k}\leqslant 2$
. Moreover, the images in
![]() $\mathfrak{m}_{2,c}$
of the words in (36) with
$\mathfrak{m}_{2,c}$
of the words in (36) with
![]() $k=c-1$
form a basis of the centre of
$k=c-1$
form a basis of the centre of
![]() $\mathfrak{m}_{2,c}$
. Write
$\mathfrak{m}_{2,c}$
. Write
![]() $y_{\ell }^{k}$
for the image in
$y_{\ell }^{k}$
for the image in
![]() $\mathfrak{m}_{2,c}$
of the unique element of the Hall basis of the form (36) of length
$\mathfrak{m}_{2,c}$
of the unique element of the Hall basis of the form (36) of length
![]() $k$
in which the generator
$k$
in which the generator
![]() $x_{2}$
occurs
$x_{2}$
occurs
![]() $\ell$
times. For instance,
$\ell$
times. For instance,
![]() $y_{1}^{3}=[x_{1},[x_{1},x_{2}]]$
and
$y_{1}^{3}=[x_{1},[x_{1},x_{2}]]$
and
![]() $y_{2}^{3}=[x_{2},[x_{1},x_{2}]]$
. Then the image of
$y_{2}^{3}=[x_{2},[x_{1},x_{2}]]$
. Then the image of
![]() $\{y_{1}^{c},\ldots ,y_{c-1}^{c}\}$
is a basis of
$\{y_{1}^{c},\ldots ,y_{c-1}^{c}\}$
is a basis of
![]() $\mathfrak{m}_{2,c}^{c}=\text{Z}(\mathfrak{m}_{2,c})$
and the image of
$\mathfrak{m}_{2,c}^{c}=\text{Z}(\mathfrak{m}_{2,c})$
and the image of
![]() $\{y_{1}^{c-1},\ldots ,y_{c-2}^{c-1},y_{1}^{c},\ldots ,y_{c-1}^{c}\}$
is a basis of
$\{y_{1}^{c-1},\ldots ,y_{c-2}^{c-1},y_{1}^{c},\ldots ,y_{c-1}^{c}\}$
is a basis of
![]() $\mathfrak{m}_{2,c}^{c-1}$
. The fact that
$\mathfrak{m}_{2,c}^{c-1}$
. The fact that
![]() $\mathfrak{m}_{2,c}$
is metabelian implies that
$\mathfrak{m}_{2,c}$
is metabelian implies that
Thus the reduced commutator matrix of
![]() $\mathfrak{m}_{2,c}$
is of the form
$\mathfrak{m}_{2,c}$
is of the form
where
![]() $F$
is a
$F$
is a
![]() $2\times (c-2)$
matrix of the form
$2\times (c-2)$
matrix of the form
Note that
![]() $\text{rk}_{\mathbb{F}_{q}}(F(\mathbf{a}))\geqslant 1$
for every non-zero vector
$\text{rk}_{\mathbb{F}_{q}}(F(\mathbf{a}))\geqslant 1$
for every non-zero vector
![]() $\mathbf{a}\in \mathbb{F}_{q}^{c-1}$
, and the matrix
$\mathbf{a}\in \mathbb{F}_{q}^{c-1}$
, and the matrix
![]() $F(T_{1},\ldots ,T_{c-1})$
has rank
$F(T_{1},\ldots ,T_{c-1})$
has rank
![]() $1$
if we set
$1$
if we set
![]() $T_{i}=\unicode[STIX]{x1D706}^{i-1}$
, where
$T_{i}=\unicode[STIX]{x1D706}^{i-1}$
, where
![]() $\unicode[STIX]{x1D706}\in \mathbb{F}_{q}$
. Since
$\unicode[STIX]{x1D706}\in \mathbb{F}_{q}$
. Since
![]() $q\geqslant p>c$
, we can find at least
$q\geqslant p>c$
, we can find at least
![]() $c-1$
distinct elements
$c-1$
distinct elements
![]() $\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{c-1}$
in
$\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{c-1}$
in
![]() $\mathbb{F}_{q}$
. Consider the
$\mathbb{F}_{q}$
. Consider the
![]() $(c-1)\times (c-1)$
matrix with the
$(c-1)\times (c-1)$
matrix with the
![]() $i$
th row given by
$i$
th row given by
This is the well-known Vandermonde matrix, whose determinant is non-zero. Similar to the proof of Proposition 7.4, the claim follows from Theorem 5.3.
Remark 7.6. In the above proof, the issue of finding
![]() $c-1$
matrices of rank equal to
$c-1$
matrices of rank equal to
![]() $1$
is intimately related to finding points in general position on the rational normal curve obtained as the image of the Veronese map given by
$1$
is intimately related to finding points in general position on the rational normal curve obtained as the image of the Veronese map given by
It is likely that in the cases corresponding to
![]() $\mathfrak{m}_{n,c}$
(for
$\mathfrak{m}_{n,c}$
(for
![]() $n>2$
) and
$n>2$
) and
![]() $\mathfrak{f}_{n,c}$
(for
$\mathfrak{f}_{n,c}$
(for
![]() $n\geqslant 2$
and
$n\geqslant 2$
and
![]() $c>3$
), the faithful dimension can be computed using tools from algebraic geometry.
$c>3$
), the faithful dimension can be computed using tools from algebraic geometry.
7.4 Outline of the argument for Remark 2.14
We will only consider the case
![]() $c=6$
, since the other cases are similar (and the calculations are a bit simpler). For
$c=6$
, since the other cases are similar (and the calculations are a bit simpler). For
![]() $\mathfrak{f}:=\mathfrak{f}_{2,6}$
, the reduced commutator matrix is a block matrix of the form
$\mathfrak{f}:=\mathfrak{f}_{2,6}$
, the reduced commutator matrix is a block matrix of the form
 $$\begin{eqnarray}F(x_{1},\ldots ,x_{9})=\left(\begin{array}{@{}ccccc@{}}0 & 0 & 0 & 0 & F_{1,5}\\ 0 & 0 & 0 & F_{2,4} & 0\\ 0 & 0 & F_{3,3} & 0 & 0\\ 0 & -F_{2,4}^{\text{tr}} & 0 & 0 & 0\\ -F_{1,5}^{\text{tr}} & 0 & 0 & 0 & 0\end{array}\right)\!,\end{eqnarray}$$
$$\begin{eqnarray}F(x_{1},\ldots ,x_{9})=\left(\begin{array}{@{}ccccc@{}}0 & 0 & 0 & 0 & F_{1,5}\\ 0 & 0 & 0 & F_{2,4} & 0\\ 0 & 0 & F_{3,3} & 0 & 0\\ 0 & -F_{2,4}^{\text{tr}} & 0 & 0 & 0\\ -F_{1,5}^{\text{tr}} & 0 & 0 & 0 & 0\end{array}\right)\!,\end{eqnarray}$$
where
 $$\begin{eqnarray}\displaystyle & & \displaystyle F_{1,5}(x_{1},\ldots ,x_{9})=\left(\begin{array}{@{}cccccc@{}}x_{1} & x_{2}+x_{6} & x_{3}+2x_{7}-x_{9} & x_{4}+2x_{8} & x_{6} & x_{7}+x_{9}\\ x_{2} & x_{3} & x_{4} & x_{5} & x_{7}-x_{9} & x_{8}\end{array}\right)\!,\nonumber\\ \displaystyle & & \displaystyle F_{2,4}(x_{1},\ldots ,x_{9})=\left(\begin{array}{@{}ccc@{}}x_{6} & x_{7} & x_{8}\end{array}\right)\!,\nonumber\\ \displaystyle & & \displaystyle F_{3,3}(x_{1},\ldots ,x_{9})=\left(\begin{array}{@{}cc@{}}0 & x_{9}\\ -x_{9} & 0\end{array}\right)\!.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & & \displaystyle F_{1,5}(x_{1},\ldots ,x_{9})=\left(\begin{array}{@{}cccccc@{}}x_{1} & x_{2}+x_{6} & x_{3}+2x_{7}-x_{9} & x_{4}+2x_{8} & x_{6} & x_{7}+x_{9}\\ x_{2} & x_{3} & x_{4} & x_{5} & x_{7}-x_{9} & x_{8}\end{array}\right)\!,\nonumber\\ \displaystyle & & \displaystyle F_{2,4}(x_{1},\ldots ,x_{9})=\left(\begin{array}{@{}ccc@{}}x_{6} & x_{7} & x_{8}\end{array}\right)\!,\nonumber\\ \displaystyle & & \displaystyle F_{3,3}(x_{1},\ldots ,x_{9})=\left(\begin{array}{@{}cc@{}}0 & x_{9}\\ -x_{9} & 0\end{array}\right)\!.\end{eqnarray}$$
For
![]() $p\geqslant 7$
, Proposition 7.4 implies that
$p\geqslant 7$
, Proposition 7.4 implies that
 $$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{p})=\min \left\{\mathop{\sum }_{\ell =1}^{9}p^{\text{rk}_{\mathbb{F}_{p}}(F(a_{\ell 1},\ldots ,a_{\ell 9}))/2}:\left(\begin{array}{@{}ccc@{}}a_{11} & \cdots \, & a_{19}\\ \vdots & \ddots & \vdots \\ a_{91} & \cdots \, & a_{99}\end{array}\right)\in \text{GL}_{9}(\mathbb{F}_{p})\right\}.\end{eqnarray}$$
$$\begin{eqnarray}m_{\text{faithful}}(\mathscr{G}_{p})=\min \left\{\mathop{\sum }_{\ell =1}^{9}p^{\text{rk}_{\mathbb{F}_{p}}(F(a_{\ell 1},\ldots ,a_{\ell 9}))/2}:\left(\begin{array}{@{}ccc@{}}a_{11} & \cdots \, & a_{19}\\ \vdots & \ddots & \vdots \\ a_{91} & \cdots \, & a_{99}\end{array}\right)\in \text{GL}_{9}(\mathbb{F}_{p})\right\}.\end{eqnarray}$$
We can easily verify that
![]() $\text{rk}_{\mathbb{F}_{p}}(F_{1,5}(\mathbf{x}))\geqslant 1$
when
$\text{rk}_{\mathbb{F}_{p}}(F_{1,5}(\mathbf{x}))\geqslant 1$
when
![]() $0\neq \mathbf{x}:=(x_{1},\ldots ,x_{9})\in \mathbb{F}_{p}^{9}$
. Also,
$0\neq \mathbf{x}:=(x_{1},\ldots ,x_{9})\in \mathbb{F}_{p}^{9}$
. Also,
whenever at least one of
![]() $x_{6}$
,
$x_{6}$
,
![]() $x_{7}$
or
$x_{7}$
or
![]() $x_{8}$
is not zero. Similarly,
$x_{8}$
is not zero. Similarly,
![]() $\text{rk}_{\mathbb{F}_{p}}(F(x_{1},\ldots ,x_{9}))\geqslant 6$
whenever
$\text{rk}_{\mathbb{F}_{p}}(F(x_{1},\ldots ,x_{9}))\geqslant 6$
whenever
![]() $x_{9}\neq 0$
.
$x_{9}\neq 0$
.
Now let
![]() $\mathbf{x}_{i}:=(x_{i1},\ldots ,x_{i9})\in \mathbb{F}_{p}^{9}$
,
$\mathbf{x}_{i}:=(x_{i1},\ldots ,x_{i9})\in \mathbb{F}_{p}^{9}$
,
![]() $1\leqslant i\leqslant 9$
, be
$1\leqslant i\leqslant 9$
, be
![]() $9$
vectors with
$9$
vectors with
![]() $\det (x_{ij})\neq 0$
. Thus after permuting the indices of the
$\det (x_{ij})\neq 0$
. Thus after permuting the indices of the
![]() $\mathbf{x}_{i}$
, we can assume that all of the diagonal entries
$\mathbf{x}_{i}$
, we can assume that all of the diagonal entries
![]() $x_{ii}$
,
$x_{ii}$
,
![]() $1\leqslant i\leqslant 9$
, are non-zero. Hence, from (39) and the above discussion we deduce that the faithful dimension of
$1\leqslant i\leqslant 9$
, are non-zero. Hence, from (39) and the above discussion we deduce that the faithful dimension of
![]() $\mathscr{G}_{p}$
is at least
$\mathscr{G}_{p}$
is at least
![]() $p^{3}+3p^{2}+5p$
. This dimension can be realized by the rows of following matrix:
$p^{3}+3p^{2}+5p$
. This dimension can be realized by the rows of following matrix:
 $$\begin{eqnarray}\left(\begin{array}{@{}ccccccccc@{}}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 1 & \unicode[STIX]{x1D706}_{1} & \unicode[STIX]{x1D706}_{1}^{2} & \unicode[STIX]{x1D706}_{1}^{3} & \unicode[STIX]{x1D706}_{1}^{4} & 0 & 0 & 0 & 0\\ 1 & \unicode[STIX]{x1D706}_{2} & \unicode[STIX]{x1D706}_{2}^{2} & \unicode[STIX]{x1D706}_{2}^{3} & \unicode[STIX]{x1D706}_{2}^{4} & 0 & 0 & 0 & 0\\ 1 & \unicode[STIX]{x1D706}_{3} & \unicode[STIX]{x1D706}_{3}^{2} & \unicode[STIX]{x1D706}_{3}^{3} & \unicode[STIX]{x1D706}_{3}^{4} & 0 & 0 & 0 & 0\\ 1 & \unicode[STIX]{x1D706}_{4} & \unicode[STIX]{x1D706}_{4}^{2} & \unicode[STIX]{x1D706}_{4}^{3} & \unicode[STIX]{x1D706}_{4}^{4} & 0 & 0 & 0 & 0\\ 0 & 0 & \unicode[STIX]{x1D707}_{1} & 3\unicode[STIX]{x1D707}_{1}^{2} & 5\unicode[STIX]{x1D707}_{1}^{3} & 1 & \unicode[STIX]{x1D707}_{1} & \unicode[STIX]{x1D707}_{1}^{2} & 0\\ 0 & 0 & \unicode[STIX]{x1D707}_{2} & 3\unicode[STIX]{x1D707}_{2}^{2} & 5\unicode[STIX]{x1D707}_{2}^{3} & 1 & \unicode[STIX]{x1D707}_{2} & \unicode[STIX]{x1D707}_{2}^{2} & 0\\ 0 & 0 & \unicode[STIX]{x1D707}_{3} & 3\unicode[STIX]{x1D707}_{3}^{2} & 5\unicode[STIX]{x1D707}_{3}^{3} & 1 & \unicode[STIX]{x1D707}_{3} & \unicode[STIX]{x1D707}_{3}^{2} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D702} & 5\unicode[STIX]{x1D702}^{2} & 0 & 1 & 2\unicode[STIX]{x1D702} & 1\end{array}\right)\in \operatorname{GL}_{9}(\mathbb{F}_{p}),\end{eqnarray}$$
$$\begin{eqnarray}\left(\begin{array}{@{}ccccccccc@{}}1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 1 & \unicode[STIX]{x1D706}_{1} & \unicode[STIX]{x1D706}_{1}^{2} & \unicode[STIX]{x1D706}_{1}^{3} & \unicode[STIX]{x1D706}_{1}^{4} & 0 & 0 & 0 & 0\\ 1 & \unicode[STIX]{x1D706}_{2} & \unicode[STIX]{x1D706}_{2}^{2} & \unicode[STIX]{x1D706}_{2}^{3} & \unicode[STIX]{x1D706}_{2}^{4} & 0 & 0 & 0 & 0\\ 1 & \unicode[STIX]{x1D706}_{3} & \unicode[STIX]{x1D706}_{3}^{2} & \unicode[STIX]{x1D706}_{3}^{3} & \unicode[STIX]{x1D706}_{3}^{4} & 0 & 0 & 0 & 0\\ 1 & \unicode[STIX]{x1D706}_{4} & \unicode[STIX]{x1D706}_{4}^{2} & \unicode[STIX]{x1D706}_{4}^{3} & \unicode[STIX]{x1D706}_{4}^{4} & 0 & 0 & 0 & 0\\ 0 & 0 & \unicode[STIX]{x1D707}_{1} & 3\unicode[STIX]{x1D707}_{1}^{2} & 5\unicode[STIX]{x1D707}_{1}^{3} & 1 & \unicode[STIX]{x1D707}_{1} & \unicode[STIX]{x1D707}_{1}^{2} & 0\\ 0 & 0 & \unicode[STIX]{x1D707}_{2} & 3\unicode[STIX]{x1D707}_{2}^{2} & 5\unicode[STIX]{x1D707}_{2}^{3} & 1 & \unicode[STIX]{x1D707}_{2} & \unicode[STIX]{x1D707}_{2}^{2} & 0\\ 0 & 0 & \unicode[STIX]{x1D707}_{3} & 3\unicode[STIX]{x1D707}_{3}^{2} & 5\unicode[STIX]{x1D707}_{3}^{3} & 1 & \unicode[STIX]{x1D707}_{3} & \unicode[STIX]{x1D707}_{3}^{2} & 0\\ 0 & 0 & 0 & \unicode[STIX]{x1D702} & 5\unicode[STIX]{x1D702}^{2} & 0 & 1 & 2\unicode[STIX]{x1D702} & 1\end{array}\right)\in \operatorname{GL}_{9}(\mathbb{F}_{p}),\end{eqnarray}$$
where the
![]() $\unicode[STIX]{x1D706}_{i}$
and the
$\unicode[STIX]{x1D706}_{i}$
and the
![]() $\unicode[STIX]{x1D707}_{i}$
are distinct elements of
$\unicode[STIX]{x1D707}_{i}$
are distinct elements of
![]() $\mathbb{F}_{p}$
.
$\mathbb{F}_{p}$
.
Acknowledgements
We would like to thank Martin Bays, Emmanuel Breuillard, Tim Clausen, Jamshid Derakhshan, Martin Hils, Alan Huckleberry, Franziska Jahnke, Aleksandra Kwiatkowska, Gunter Malle, Katrin Tent and Pierre Touchard for several useful discussions. Eamonn O’Brien and Christopher Voll brought a mistaken entry in Table 1 to our attention. We thank Christopher Voll for many useful comments. The authors would like to thank the referee for carefully reading the manuscript and for providing numerous suggestions that substantially improved both the content and the exposition of the paper.