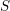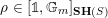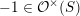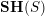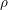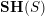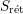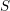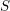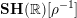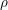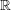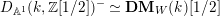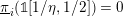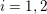1 Introduction
For a scheme
![]() $S$
we denote by
$S$
we denote by
![]() $\mathbf{SH}(S)$
the motivic stable homotopy category [Reference Morel and VoevodskyMV99, Reference AyoubAyo07]. We recall that this is a triangulated category which is the homotopy category of a stable model category that (roughly) is obtained from the homotopy theory of (smooth, pointed) schemes by making the ‘Riemann sphere’
$\mathbf{SH}(S)$
the motivic stable homotopy category [Reference Morel and VoevodskyMV99, Reference AyoubAyo07]. We recall that this is a triangulated category which is the homotopy category of a stable model category that (roughly) is obtained from the homotopy theory of (smooth, pointed) schemes by making the ‘Riemann sphere’
![]() $\mathbb{P}_{S}^{1}$
into an invertible object.
$\mathbb{P}_{S}^{1}$
into an invertible object.
If
 $\unicode[STIX]{x1D6FC}:k{\hookrightarrow}\mathbb{C}$
is an embedding of a field
$\unicode[STIX]{x1D6FC}:k{\hookrightarrow}\mathbb{C}$
is an embedding of a field
![]() $k$
into the complex numbers, then we obtain a complex realisation functor
$k$
into the complex numbers, then we obtain a complex realisation functor
 $R_{\unicode[STIX]{x1D6FC},\mathbb{C}}:\mathbf{SH}(k)\rightarrow \mathbf{SH}$
(where now
$R_{\unicode[STIX]{x1D6FC},\mathbb{C}}:\mathbf{SH}(k)\rightarrow \mathbf{SH}$
(where now
![]() $\mathbf{SH}$
denotes the classical stable homotopy category) connecting the world of motivic stable homotopy theory to classical stable homotopy theory [Reference Morel and VoevodskyMV99, § 3.3.2]. This functor is induced from the functor which sends a smooth scheme
$\mathbf{SH}$
denotes the classical stable homotopy category) connecting the world of motivic stable homotopy theory to classical stable homotopy theory [Reference Morel and VoevodskyMV99, § 3.3.2]. This functor is induced from the functor which sends a smooth scheme
![]() $S$
over
$S$
over
![]() $k$
to its topological space of complex points
$k$
to its topological space of complex points
![]() $S(\mathbb{C})$
(this depends on
$S(\mathbb{C})$
(this depends on
![]() $\unicode[STIX]{x1D6FC}$
). Similarly if
$\unicode[STIX]{x1D6FC}$
). Similarly if
 $\unicode[STIX]{x1D6FD}:k{\hookrightarrow}\mathbb{R}$
is an embedding into the real numbers, then there is a real realisation functor
$\unicode[STIX]{x1D6FD}:k{\hookrightarrow}\mathbb{R}$
is an embedding into the real numbers, then there is a real realisation functor
 $R_{\unicode[STIX]{x1D6FD},\mathbb{R}}:\mathbf{SH}(k)\rightarrow \mathbf{SH}$
induced from
$R_{\unicode[STIX]{x1D6FD},\mathbb{R}}:\mathbf{SH}(k)\rightarrow \mathbf{SH}$
induced from
 $S\mapsto S(\mathbb{R})$
[Reference Morel and VoevodskyMV99, § 3.3.3] [Reference Heller and OrmsbyHO16, Proposition 4.8].
$S\mapsto S(\mathbb{R})$
[Reference Morel and VoevodskyMV99, § 3.3.3] [Reference Heller and OrmsbyHO16, Proposition 4.8].
These functors serve as a good source of inspiration and a convenient test of conjectures in stable motivic homotopy theory. For example, in order for a morphism
 $f:E\rightarrow F$
to be an equivalence it is necessary that
$f:E\rightarrow F$
to be an equivalence it is necessary that
 $R_{\unicode[STIX]{x1D6FC},\mathbb{C}}(f)$
and
$R_{\unicode[STIX]{x1D6FC},\mathbb{C}}(f)$
and
 $R_{\unicode[STIX]{x1D6FD},\mathbb{R}}(f)$
are equivalences, for all such embeddings
$R_{\unicode[STIX]{x1D6FD},\mathbb{R}}(f)$
are equivalences, for all such embeddings
![]() $\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
. On the other hand, this criterion is clearly not sufficient; there are fields without any real or complex embeddings!
$\unicode[STIX]{x1D6FC},\unicode[STIX]{x1D6FD}$
. On the other hand, this criterion is clearly not sufficient; there are fields without any real or complex embeddings!
It is thus a very natural question to ask how far these functors are from being an equivalence, or what their ‘kernel’ is. The aim of this article is to give some kind of complete answer to this question in the case of real realisation. We begin with the simplest formulation of our result. Write
![]() $R_{\mathbb{R}}$
for the (unique) real realisation functor for the field
$R_{\mathbb{R}}$
for the (unique) real realisation functor for the field
![]() $k=\mathbb{R}$
. The first clue comes from the observation that
$k=\mathbb{R}$
. The first clue comes from the observation that
 $R_{\mathbb{R}}(\mathbb{G}_{m})=\mathbb{R}\setminus 0\simeq \{\pm 1\}=S^{0}$
. That is to say
$R_{\mathbb{R}}(\mathbb{G}_{m})=\mathbb{R}\setminus 0\simeq \{\pm 1\}=S^{0}$
. That is to say
![]() $R_{\mathbb{R}}$
identifies
$R_{\mathbb{R}}$
identifies
![]() $\mathbb{G}_{m}$
and
$\mathbb{G}_{m}$
and
![]() $S^{0}$
. We can even do better. Write
$S^{0}$
. We can even do better. Write
 $\unicode[STIX]{x1D70C}^{\prime }:S^{0}\rightarrow \mathbb{G}_{m}$
for the map of pointed motivic spaces corresponding to
$\unicode[STIX]{x1D70C}^{\prime }:S^{0}\rightarrow \mathbb{G}_{m}$
for the map of pointed motivic spaces corresponding to
 $-1\in \mathbb{R}^{\times }$
. Then one may check easily that
$-1\in \mathbb{R}^{\times }$
. Then one may check easily that
![]() $R_{\mathbb{R}}(\unicode[STIX]{x1D70C}^{\prime })$
is an equivalence between
$R_{\mathbb{R}}(\unicode[STIX]{x1D70C}^{\prime })$
is an equivalence between
 $S^{0}\simeq R_{\mathbb{R}}(S^{0})$
and
$S^{0}\simeq R_{\mathbb{R}}(S^{0})$
and
 $R_{\mathbb{R}}(\mathbb{G}_{m})$
.
$R_{\mathbb{R}}(\mathbb{G}_{m})$
.
We prove that
 $\mathbf{SH}(\mathbb{R})[{\unicode[STIX]{x1D70C}^{\prime }}^{-1}]\simeq \mathbf{SH}$
via real realisation. That is to say
$\mathbf{SH}(\mathbb{R})[{\unicode[STIX]{x1D70C}^{\prime }}^{-1}]\simeq \mathbf{SH}$
via real realisation. That is to say
![]() $R_{\mathbb{R}}$
is in some sense the universal functor turning
$R_{\mathbb{R}}$
is in some sense the universal functor turning
![]() $\unicode[STIX]{x1D70C}^{\prime }$
into an equivalence. More precisely, the functor
$\unicode[STIX]{x1D70C}^{\prime }$
into an equivalence. More precisely, the functor
 $R_{\mathbb{R}}:\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}$
has a right adjoint
$R_{\mathbb{R}}:\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}$
has a right adjoint
![]() $R^{\ast }$
(e.g. by Neeman’s version of Brown representability) and we show that
$R^{\ast }$
(e.g. by Neeman’s version of Brown representability) and we show that
![]() $R^{\ast }$
is fully faithful with image consisting of the
$R^{\ast }$
is fully faithful with image consisting of the
![]() $\unicode[STIX]{x1D70C}^{\prime }$
-stable motivic spectra, i.e. those
$\unicode[STIX]{x1D70C}^{\prime }$
-stable motivic spectra, i.e. those
 $E\in \mathbf{SH}(\mathbb{R})$
such that
$E\in \mathbf{SH}(\mathbb{R})$
such that
 $E(X\wedge \mathbb{G}_{m})\xrightarrow[{}]{\unicode[STIX]{x1D70C}^{\ast }}E(X)$
is an equivalence for all
$E(X\wedge \mathbb{G}_{m})\xrightarrow[{}]{\unicode[STIX]{x1D70C}^{\ast }}E(X)$
is an equivalence for all
 $X\in Sm(\mathbb{R})$
.
$X\in Sm(\mathbb{R})$
.
Of course, our description of
 $\mathbf{SH}(\mathbb{R})[{\unicode[STIX]{x1D70C}^{\prime }}^{-1}]$
is just an explicit description of a certain Bousfield localisation of
$\mathbf{SH}(\mathbb{R})[{\unicode[STIX]{x1D70C}^{\prime }}^{-1}]$
is just an explicit description of a certain Bousfield localisation of
![]() $\mathbf{SH}(\mathbb{R})$
. Moreover the element
$\mathbf{SH}(\mathbb{R})$
. Moreover the element
![]() $\unicode[STIX]{x1D70C}^{\prime }$
exists not only over
$\unicode[STIX]{x1D70C}^{\prime }$
exists not only over
![]() $\mathbb{R}$
but already over
$\mathbb{R}$
but already over
![]() $\mathbb{Z}$
, so we are lead to study more generally the category
$\mathbb{Z}$
, so we are lead to study more generally the category
 $\mathbf{SH}(S)[{\unicode[STIX]{x1D70C}^{\prime }}^{-1}]$
, for more or less arbitrary base schemes
$\mathbf{SH}(S)[{\unicode[STIX]{x1D70C}^{\prime }}^{-1}]$
, for more or less arbitrary base schemes
![]() $S$
. Actually, for some formulas it is nicer to consider
$S$
. Actually, for some formulas it is nicer to consider
 $\unicode[STIX]{x1D70C}:=-\unicode[STIX]{x1D70C}^{\prime }\in [S,\unicode[STIX]{x1D6F4}^{\infty }\mathbb{G}_{m}]$
and we shall write this from now on. Of course
$\unicode[STIX]{x1D70C}:=-\unicode[STIX]{x1D70C}^{\prime }\in [S,\unicode[STIX]{x1D6F4}^{\infty }\mathbb{G}_{m}]$
and we shall write this from now on. Of course
 $\mathbf{SH}(S)[{\unicode[STIX]{x1D70C}^{\prime }}^{-1}]=\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
. In this generality we can no longer expect that
$\mathbf{SH}(S)[{\unicode[STIX]{x1D70C}^{\prime }}^{-1}]=\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
. In this generality we can no longer expect that
 $\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}$
. Indeed as we have said before in general there is no real realisation! As a first attempt, one might guess that if
$\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}$
. Indeed as we have said before in general there is no real realisation! As a first attempt, one might guess that if
![]() $X$
is a scheme over
$X$
is a scheme over
![]() $\mathbb{R}$
, then
$\mathbb{R}$
, then
 $\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}(S(\mathbb{R}))$
, where the right-hand side denotes some form of parametrised homotopy theory [Reference May and SigurdssonMS06]. This cannot be quite true unless
$\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}(S(\mathbb{R}))$
, where the right-hand side denotes some form of parametrised homotopy theory [Reference May and SigurdssonMS06]. This cannot be quite true unless
![]() $S$
is proper, because the category
$S$
is proper, because the category
 $\mathbf{SH}(S(\mathbb{R}))$
will then not be compactly generated. The way out is to use semi-algebraic topology. For this we have to recall that if
$\mathbf{SH}(S(\mathbb{R}))$
will then not be compactly generated. The way out is to use semi-algebraic topology. For this we have to recall that if
![]() $S$
is a scheme, then there exists a topological space
$S$
is a scheme, then there exists a topological space
![]() $R(S)$
[Reference ScheidererSch94, (0.4.2)]. Its points are pairs
$R(S)$
[Reference ScheidererSch94, (0.4.2)]. Its points are pairs
![]() $(x,\unicode[STIX]{x1D6FC})$
with
$(x,\unicode[STIX]{x1D6FC})$
with
![]() $x\in S$
and
$x\in S$
and
![]() $\unicode[STIX]{x1D6FC}$
an ordering of the residue field
$\unicode[STIX]{x1D6FC}$
an ordering of the residue field
![]() $k(x)$
. This is given a topology incorporating all of these orderings. Write
$k(x)$
. This is given a topology incorporating all of these orderings. Write
 $\operatorname{Shv}(RS)$
for the category of sheaves on this topological space.
$\operatorname{Shv}(RS)$
for the category of sheaves on this topological space.
Now, given any topos
![]() ${\mathcal{X}}$
, there is a naturally associated stable homotopy category
${\mathcal{X}}$
, there is a naturally associated stable homotopy category
![]() $\text{SH}({\mathcal{X}})$
. If
$\text{SH}({\mathcal{X}})$
. If
 ${\mathcal{X}}\simeq \operatorname{Set}$
then
${\mathcal{X}}\simeq \operatorname{Set}$
then
![]() $\text{SH}({\mathcal{X}})$
is just the ordinary stable homotopy category. In general, if
$\text{SH}({\mathcal{X}})$
is just the ordinary stable homotopy category. In general, if
 ${\mathcal{X}}\simeq \operatorname{Shv}({\mathcal{C}})$
where
${\mathcal{X}}\simeq \operatorname{Shv}({\mathcal{C}})$
where
![]() ${\mathcal{C}}$
is a Grothendieck site, then
${\mathcal{C}}$
is a Grothendieck site, then
![]() $\text{SH}(X)$
is the local homotopy category of presheaves of spectra on
$\text{SH}(X)$
is the local homotopy category of presheaves of spectra on
![]() ${\mathcal{C}}$
.
${\mathcal{C}}$
.
With this preparation out of the way, we can state our main result as follows.
Theorem (See Theorem 35). Let
![]() $S$
be a Noetherian scheme of finite dimension. Then there is a canonical equivalence of categories
$S$
be a Noetherian scheme of finite dimension. Then there is a canonical equivalence of categories
 $$\begin{eqnarray}\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]\simeq \text{SH}(\operatorname{Shv}(RS)).\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]\simeq \text{SH}(\operatorname{Shv}(RS)).\end{eqnarray}$$
A more detailed formulation is given later in this introduction. For now let us mention one application. We go back to
 $S=\operatorname{Spec}(\mathbb{R})$
. In this case Proposition 36 in § 10 assures us that the equivalence from the above theorem does indeed come from real realisation. But given
$S=\operatorname{Spec}(\mathbb{R})$
. In this case Proposition 36 in § 10 assures us that the equivalence from the above theorem does indeed come from real realisation. But given
 $E\in \mathbf{SH}(\mathbb{R})$
, its
$E\in \mathbf{SH}(\mathbb{R})$
, its
![]() $\unicode[STIX]{x1D70C}$
-localisation can be calculated quite explicitly (see Lemma 15). From this one concludes that
$\unicode[STIX]{x1D70C}$
-localisation can be calculated quite explicitly (see Lemma 15). From this one concludes that
 $\unicode[STIX]{x1D70B}_{i}(R_{\mathbb{R}}E)=\operatorname{colim}_{n}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{n}(\mathbb{R})$
, where the colimit is along multiplication by
$\unicode[STIX]{x1D70B}_{i}(R_{\mathbb{R}}E)=\operatorname{colim}_{n}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{n}(\mathbb{R})$
, where the colimit is along multiplication by
![]() $\unicode[STIX]{x1D70C}$
in the second grading of the bigraded homotopy sheaves of
$\unicode[STIX]{x1D70C}$
in the second grading of the bigraded homotopy sheaves of
![]() $E$
. (Recall that
$E$
. (Recall that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{n}(\mathbb{R})=[\unicode[STIX]{x1D7D9}[i],E\wedge \mathbb{G}_{m}^{\wedge n}]$
so
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{n}(\mathbb{R})=[\unicode[STIX]{x1D7D9}[i],E\wedge \mathbb{G}_{m}^{\wedge n}]$
so
![]() $\unicode[STIX]{x1D70C}$
indeed induces
$\unicode[STIX]{x1D70C}$
indeed induces
 $\unicode[STIX]{x1D70C}:\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{n}(\mathbb{R})\rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{n+1}(\mathbb{R})$
.)
$\unicode[STIX]{x1D70C}:\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{n}(\mathbb{R})\rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{n+1}(\mathbb{R})$
.)
This may seem slightly esoteric, but actually
 $\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1},2^{-1}]=\mathbf{SH}(S)[\unicode[STIX]{x1D702}^{-1},2^{-1}]$
and so our computations apply, after inverting two, to the more conventional
$\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1},2^{-1}]=\mathbf{SH}(S)[\unicode[STIX]{x1D702}^{-1},2^{-1}]$
and so our computations apply, after inverting two, to the more conventional
![]() $\unicode[STIX]{x1D702}$
-localisation as well. As a corollary, we obtain the following.
$\unicode[STIX]{x1D702}$
-localisation as well. As a corollary, we obtain the following.
Theorem. The motivic stable 2-local,
![]() $\unicode[STIX]{x1D702}$
-local stems over
$\unicode[STIX]{x1D702}$
-local stems over
![]() $\mathbb{R}$
agree with the classical stable 2-local stems:
$\mathbb{R}$
agree with the classical stable 2-local stems:
 $$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D702},2})_{j}(\mathbb{R})=\unicode[STIX]{x1D70B}_{i}^{s}\otimes _{\mathbb{ Z}}\mathbb{Z}[1/2].\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D702},2})_{j}(\mathbb{R})=\unicode[STIX]{x1D70B}_{i}^{s}\otimes _{\mathbb{ Z}}\mathbb{Z}[1/2].\end{eqnarray}$$
Some more applications will be described later in this introduction.
Overview of the proof. The proof uses a different description of the category
 $\operatorname{Shv}(RS)$
. Namely, there is a topology on all schemes called the real étale topology and abbreviated rét-topology [Reference ScheidererSch94, (1.2)]. (The covers are families of étale morphisms which induce a jointly surjective family on the associated real spaces
$\operatorname{Shv}(RS)$
. Namely, there is a topology on all schemes called the real étale topology and abbreviated rét-topology [Reference ScheidererSch94, (1.2)]. (The covers are families of étale morphisms which induce a jointly surjective family on the associated real spaces
![]() $R(\bullet )$
.) We write
$R(\bullet )$
.) We write
 $Sm(S)_{\text{r}\acute{\text{e}}\text{t}}$
for the site of all smooth schemes over
$Sm(S)_{\text{r}\acute{\text{e}}\text{t}}$
for the site of all smooth schemes over
![]() $S$
with this topology, and
$S$
with this topology, and
![]() $S_{\text{r}\acute{\text{e}}\text{t}}$
for the site of all étale schemes over
$S_{\text{r}\acute{\text{e}}\text{t}}$
for the site of all étale schemes over
![]() $S$
with this topology. Then
$S$
with this topology. Then
 $\operatorname{Shv}(S_{\text{r}\acute{\text{e}}\text{t}})\simeq \operatorname{Shv}(RS)$
[Reference ScheidererSch94, Theorem (1.3)].
$\operatorname{Shv}(S_{\text{r}\acute{\text{e}}\text{t}})\simeq \operatorname{Shv}(RS)$
[Reference ScheidererSch94, Theorem (1.3)].
Write
![]() $\mathbf{SH}(S)$
for the motivic stable homotopy category,
$\mathbf{SH}(S)$
for the motivic stable homotopy category,
 $\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
for the
$\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
for the
![]() $\unicode[STIX]{x1D70C}$
-local motivic stable homotopy category,
$\unicode[STIX]{x1D70C}$
-local motivic stable homotopy category,
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}$
for the rét-local motivic stable homotopy category (i.e. the category obtained from the site
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}$
for the rét-local motivic stable homotopy category (i.e. the category obtained from the site
 $Sm(S)_{\text{r}\acute{\text{e}}\text{t}}$
by precisely the same construction as is used to build
$Sm(S)_{\text{r}\acute{\text{e}}\text{t}}$
by precisely the same construction as is used to build
![]() $\mathbf{SH}(S)$
from
$\mathbf{SH}(S)$
from
 $Sm(S)_{\operatorname{Nis}}$
), and
$Sm(S)_{\operatorname{Nis}}$
), and
 $\mathbf{SH}^{S^{1}}(S)$
for the motivic
$\mathbf{SH}^{S^{1}}(S)$
for the motivic
![]() $S^{1}$
-stable homotopy category. We trust that
$S^{1}$
-stable homotopy category. We trust that
 $\mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}$
,
$\mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}$
,
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
and so on have evident meanings. Write
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
and so on have evident meanings. Write
 $\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
for the rét-local stable homotopy category on the small real étale site. This is just the homotopy category of the category of presheaves of spectra on
$\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
for the rét-local stable homotopy category on the small real étale site. This is just the homotopy category of the category of presheaves of spectra on
![]() $S_{\text{r}\acute{\text{e}}\text{t}}$
with the local model structure. Similarly
$S_{\text{r}\acute{\text{e}}\text{t}}$
with the local model structure. Similarly
 $\text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
means the rét-local presheaves of spectra on
$\text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
means the rét-local presheaves of spectra on
![]() $Sm(S)$
. Then for example
$Sm(S)$
. Then for example
 $\mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}$
is the
$\mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}$
is the
![]() $\mathbb{A}^{1}$
-localisation of
$\mathbb{A}^{1}$
-localisation of
 $\text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
.
$\text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
.
The canonical functor
 $e:\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
(extending a (pre)sheaf on the small site to the large site) is fully faithful by general results (see Corollary 6). It is moreover
$e:\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
(extending a (pre)sheaf on the small site to the large site) is fully faithful by general results (see Corollary 6). It is moreover
![]() $t$
-exact: for
$t$
-exact: for
 $E\in \text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
we have
$E\in \text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
we have
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(eE)=e\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)$
. Here
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(eE)=e\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)$
. Here
![]() $\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }$
denotes the homotopy sheaves.
$\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }$
denotes the homotopy sheaves.
If
![]() $F$
is a sheaf on the small real étale site of a scheme
$F$
is a sheaf on the small real étale site of a scheme
![]() $Y$
, then
$Y$
, then
 $H^{p}(Y\times \mathbb{A}^{1},F)=H^{p}(Y,F)$
and
$H^{p}(Y\times \mathbb{A}^{1},F)=H^{p}(Y,F)$
and
 $H^{p}(Y_{+}\wedge \mathbb{G}_{m},F)=H^{p}(Y,F)$
. If
$H^{p}(Y_{+}\wedge \mathbb{G}_{m},F)=H^{p}(Y,F)$
. If
![]() $Y$
is of finite type over
$Y$
is of finite type over
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
![]() $F$
is locally constant, then this follows by comparison of real étale cohomology with Betti cohomology of the real points [Reference DelfsDel91, Theorem II.5.7]. For the general case, see Theorem 8.
$F$
is locally constant, then this follows by comparison of real étale cohomology with Betti cohomology of the real points [Reference DelfsDel91, Theorem II.5.7]. For the general case, see Theorem 8.
Now the category
 $\mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is obtained from
$\mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is obtained from
 $\text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
by
$\text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
by
![]() $(\mathbb{A}^{1},\unicode[STIX]{x1D70C})$
-localisation. It follows from
$(\mathbb{A}^{1},\unicode[STIX]{x1D70C})$
-localisation. It follows from
![]() $t$
-exactness of
$t$
-exactness of
![]() $e$
, the descent spectral sequence, and the above result about rét-cohomology that the composite
$e$
, the descent spectral sequence, and the above result about rét-cohomology that the composite
 $\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is still fully faithful.
$\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is still fully faithful.
The category
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is obtained from
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is obtained from
 $\mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
by
$\mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
by
![]() $\otimes$
-inverting
$\otimes$
-inverting
![]() $\mathbb{G}_{m}$
. However in the latter category we have
$\mathbb{G}_{m}$
. However in the latter category we have
 $\mathbb{G}_{m}\simeq \unicode[STIX]{x1D7D9}$
(via
$\mathbb{G}_{m}\simeq \unicode[STIX]{x1D7D9}$
(via
![]() $\unicode[STIX]{x1D70C}$
!), so
$\unicode[STIX]{x1D70C}$
!), so
![]() $\mathbb{G}_{m}$
is already invertible, and inverting it has no effect:
$\mathbb{G}_{m}$
is already invertible, and inverting it has no effect:
 $\mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
. We have thus shown that
$\mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
. We have thus shown that
 $$\begin{eqnarray}\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\end{eqnarray}$$
$$\begin{eqnarray}\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\end{eqnarray}$$
is fully faithful.
The next step is to show that it is essentially surjective. This follows from the proper base change theorem by a clever argument of Cisinski–Déglise. Of course this first requires that we know that
 $\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
and
$\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
and
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
satisfy proper base change. For
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
satisfy proper base change. For
 $\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
this is a consequence of the proper base change theorem in real étale cohomology established by Scheiderer, see Theorem 9. For
$\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
this is a consequence of the proper base change theorem in real étale cohomology established by Scheiderer, see Theorem 9. For
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
this would follow from the axiomatic six functors formalism of Voevodsky/Ayoub/Cisinski–Déglise, see § 5. It is in fact not very hard to show directly that
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
this would follow from the axiomatic six functors formalism of Voevodsky/Ayoub/Cisinski–Déglise, see § 5. It is in fact not very hard to show directly that
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
satisfies the six functors formalism. Instead we shall show (without assuming the six functors formalism) that
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
satisfies the six functors formalism. Instead we shall show (without assuming the six functors formalism) that
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
, and that this latter category satisfies the six functors formalism.
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
, and that this latter category satisfies the six functors formalism.
The next step is thus to show that the localisation functor
 $\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence. It clearly has dense image, so it suffices to show that it is fully faithful. Using the fact that
$\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence. It clearly has dense image, so it suffices to show that it is fully faithful. Using the fact that
 $\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
satisfies continuity and gluing (which follows quite easily from the same statement for
$\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
satisfies continuity and gluing (which follows quite easily from the same statement for
![]() $\mathbf{SH}(S)$
), we may reduce to the case where
$\mathbf{SH}(S)$
), we may reduce to the case where
![]() $S$
is the spectrum of a field
$S$
is the spectrum of a field
![]() $k$
. The case where
$k$
. The case where
 $\text{char}(k)>0$
is easily dealt with (note that such fields are never orderable), so we may assume that
$\text{char}(k)>0$
is easily dealt with (note that such fields are never orderable), so we may assume that
![]() $k$
has characteristic zero and so in particular is perfect.
$k$
has characteristic zero and so in particular is perfect.
The
![]() $\unicode[STIX]{x1D70C}$
-localisation can be described rather explicitly. For
$\unicode[STIX]{x1D70C}$
-localisation can be described rather explicitly. For
 $E\in \mathbf{SH}(k)$
, consider the directed system
$E\in \mathbf{SH}(k)$
, consider the directed system
 $$\begin{eqnarray}E\xrightarrow[{}]{\unicode[STIX]{x1D70C}}E\wedge \mathbb{G}_{m}\xrightarrow[{}]{\unicode[STIX]{x1D70C}}E\wedge \mathbb{G}_{m}\wedge \mathbb{G}_{m}\xrightarrow[{}]{\unicode[STIX]{x1D70C}}\cdots \,.\end{eqnarray}$$
$$\begin{eqnarray}E\xrightarrow[{}]{\unicode[STIX]{x1D70C}}E\wedge \mathbb{G}_{m}\xrightarrow[{}]{\unicode[STIX]{x1D70C}}E\wedge \mathbb{G}_{m}\wedge \mathbb{G}_{m}\xrightarrow[{}]{\unicode[STIX]{x1D70C}}\cdots \,.\end{eqnarray}$$
Then
 $\operatorname{hocolim}_{n}E\wedge \mathbb{G}_{m}^{\wedge n}$
is a model for the
$\operatorname{hocolim}_{n}E\wedge \mathbb{G}_{m}^{\wedge n}$
is a model for the
![]() $\unicode[STIX]{x1D70C}$
-localisation
$\unicode[STIX]{x1D70C}$
-localisation
![]() $E[\unicode[STIX]{x1D70C}^{-1}]$
of
$E[\unicode[STIX]{x1D70C}^{-1}]$
of
![]() $E$
(see Lemma 15). It follows that its homotopy sheaves are given by
$E$
(see Lemma 15). It follows that its homotopy sheaves are given by
 $$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E[\unicode[STIX]{x1D70C}^{-1}])=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{\ast }[\unicode[STIX]{x1D70C}^{-1}]=:\operatorname{colim}_{n}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{n}.\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E[\unicode[STIX]{x1D70C}^{-1}])=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{\ast }[\unicode[STIX]{x1D70C}^{-1}]=:\operatorname{colim}_{n}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{n}.\end{eqnarray}$$
Here the colimit is along multiplication by
![]() $\unicode[STIX]{x1D70C}$
. (Let us remark here that the homotopy sheaves in
$\unicode[STIX]{x1D70C}$
. (Let us remark here that the homotopy sheaves in
![]() $\mathbf{SH}(k)$
are bigraded, and so, technically, are those in
$\mathbf{SH}(k)$
are bigraded, and so, technically, are those in
 $\mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
. However inverting
$\mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
. However inverting
![]() $\unicode[STIX]{x1D70C}$
means that up to canonical isomorphism, the homotopy sheaf is independent of the second index, so we suppress it.) It then follows from the descent spectral sequence that in order to prove that the functor
$\unicode[STIX]{x1D70C}$
means that up to canonical isomorphism, the homotopy sheaf is independent of the second index, so we suppress it.) It then follows from the descent spectral sequence that in order to prove that the functor
 $\mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]\rightarrow \mathbf{SH}(k)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence, it is enough to prove that if
$\mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]\rightarrow \mathbf{SH}(k)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence, it is enough to prove that if
![]() $F_{\ast }$
is a homotopy module (element in the heart of
$F_{\ast }$
is a homotopy module (element in the heart of
![]() $\mathbf{SH}(k)$
) such that
$\mathbf{SH}(k)$
) such that
 $\unicode[STIX]{x1D70C}:F_{n}\rightarrow F_{n+1}$
is an isomorphism for all
$\unicode[STIX]{x1D70C}:F_{n}\rightarrow F_{n+1}$
is an isomorphism for all
![]() $n$
(we call such a homotopy module
$n$
(we call such a homotopy module
![]() $\unicode[STIX]{x1D70C}$
-stable), then
$\unicode[STIX]{x1D70C}$
-stable), then
 $H_{\text{r}\acute{\text{e}}\text{t}}^{n}(X,F_{\ast })=H_{\operatorname{Nis}}^{n}(X,F_{\ast })$
for all
$H_{\text{r}\acute{\text{e}}\text{t}}^{n}(X,F_{\ast })=H_{\operatorname{Nis}}^{n}(X,F_{\ast })$
for all
![]() $X$
smooth over
$X$
smooth over
![]() $k$
. In particular, we need to show that
$k$
. In particular, we need to show that
![]() $F_{\ast }$
is a sheaf in the real étale topology. This is actually sufficient, because Nisnevich, Zariski and real étale cohomology of real étale sheaves all agree [Reference ScheidererSch94, Proposition 19.2.1].
$F_{\ast }$
is a sheaf in the real étale topology. This is actually sufficient, because Nisnevich, Zariski and real étale cohomology of real étale sheaves all agree [Reference ScheidererSch94, Proposition 19.2.1].
This ties in with work of Jacobson and Scheiderer. Recall that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9})_{\ast }=\text{}\underline{K}_{\ast }^{MW}$
, i.e. the zeroth stable motivic homotopy sheaf is unramified Milnor–Witt
$\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9})_{\ast }=\text{}\underline{K}_{\ast }^{MW}$
, i.e. the zeroth stable motivic homotopy sheaf is unramified Milnor–Witt
![]() $K$
-theory. A theorem of Jacobson [Reference JacobsonJac17] together with work of Morel implies that
$K$
-theory. A theorem of Jacobson [Reference JacobsonJac17] together with work of Morel implies that
 $\text{}\underline{K}_{\ast }^{MW}[\unicode[STIX]{x1D70C}^{-1}]=\operatorname{colim}_{n}\text{}\underline{I}^{n}=a_{\text{r}\acute{\text{e}}\text{t}}\text{}\underline{\mathbb{Z}}$
; here
$\text{}\underline{K}_{\ast }^{MW}[\unicode[STIX]{x1D70C}^{-1}]=\operatorname{colim}_{n}\text{}\underline{I}^{n}=a_{\text{r}\acute{\text{e}}\text{t}}\text{}\underline{\mathbb{Z}}$
; here
![]() $\text{}\underline{I}$
is the sheaf of fundamental ideals. Finally if
$\text{}\underline{I}$
is the sheaf of fundamental ideals. Finally if
![]() $F_{\ast }$
is a general
$F_{\ast }$
is a general
![]() $\unicode[STIX]{x1D70C}$
-stable homotopy module, we use properties of transfers for homotopy modules together with the structure of
$\unicode[STIX]{x1D70C}$
-stable homotopy module, we use properties of transfers for homotopy modules together with the structure of
![]() $F_{\ast }$
as a module over
$F_{\ast }$
as a module over
 $\text{}\underline{K}_{\ast }^{MW}[\unicode[STIX]{x1D70C}^{-1}]=a_{\text{r}\acute{\text{e}}\text{t}}\text{}\underline{\mathbb{Z}}$
to show that
$\text{}\underline{K}_{\ast }^{MW}[\unicode[STIX]{x1D70C}^{-1}]=a_{\text{r}\acute{\text{e}}\text{t}}\text{}\underline{\mathbb{Z}}$
to show that
![]() $F_{\ast }$
is a sheaf in the real étale topology. This concludes the overview of the proof.
$F_{\ast }$
is a sheaf in the real étale topology. This concludes the overview of the proof.
Throughout the article we actually establish all our results for both the stable motivic homotopy category
![]() $\mathbf{SH}(S)$
and the stable
$\mathbf{SH}(S)$
and the stable
![]() $\mathbb{A}^{1}$
-derived category
$\mathbb{A}^{1}$
-derived category
![]() $D_{\mathbb{A}^{1}}(S)$
. The proofs in the latter case are essentially always the same as in the former, so we do not tend to give them. (In fact in some cases proofs just for the latter category would be simpler.)
$D_{\mathbb{A}^{1}}(S)$
. The proofs in the latter case are essentially always the same as in the former, so we do not tend to give them. (In fact in some cases proofs just for the latter category would be simpler.)
Overview of the article. In § 2 we recall some results from local homotopy theory, including the existence and basic properties of the homotopy
![]() $t$
-structure, a general compact generation criterion and a fully faithfulness result.
$t$
-structure, a general compact generation criterion and a fully faithfulness result.
In § 3 we recall the real étale topology and establish some supplements.
In § 4 we recall some results about motivic stable homotopy categories and transfers for finite étale morphisms. In particular we establish the base change and projection formulas for these.
In § 5 we recall the formalism of pre-motivic and motivic categories and how it can be used to establish that a category satisfies the six functors formalism.
In § 6 we carefully prove some basic facts about monoidal Bousfield localisation.
We judge these five sections as preliminary and the results as not very original. The ‘real work’ is contained in the next three sections. In § 7 we review Jacobson’s theorem on the colimit of the powers of the sheaf of fundamental ideals and use it together with our results on transfers to prove that
![]() $\unicode[STIX]{x1D70C}$
-stable homotopy modules are sheaves in the real étale topology.
$\unicode[STIX]{x1D70C}$
-stable homotopy modules are sheaves in the real étale topology.
Section 8 contains various preliminary observations and reductions.
Finally in § 9 we carry out the proof as outlined above.
The remaining three sections contain some applications. In § 10 we show that our functor
 $\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]\simeq \text{SH}(\operatorname{Spec}(\mathbb{R})_{\text{r}\acute{\text{e}}\text{t}})\simeq \mathbf{SH}$
coincides with the real realisation functor. It follows that the
$\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]\simeq \text{SH}(\operatorname{Spec}(\mathbb{R})_{\text{r}\acute{\text{e}}\text{t}})\simeq \mathbf{SH}$
coincides with the real realisation functor. It follows that the
![]() $\unicode[STIX]{x1D70C}$
-inverted stable homotopy sheaves of
$\unicode[STIX]{x1D70C}$
-inverted stable homotopy sheaves of
 $E\in \mathbf{SH}(\mathbb{R})$
are just the stable homotopy groups of its real realisation.
$E\in \mathbf{SH}(\mathbb{R})$
are just the stable homotopy groups of its real realisation.
In § 11 we collect some consequences for the
![]() $\unicode[STIX]{x1D702}$
-inverted sphere. We use that
$\unicode[STIX]{x1D702}$
-inverted sphere. We use that
 $\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D70C}]\simeq \unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D702}]$
. Since the classical stable stems
$\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D70C}]\simeq \unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D702}]$
. Since the classical stable stems
 $\unicode[STIX]{x1D70B}_{i}^{s}=\mathbb{Z}/2$
for
$\unicode[STIX]{x1D70B}_{i}^{s}=\mathbb{Z}/2$
for
![]() $i=1,2$
are
$i=1,2$
are
![]() $2$
-torsion, it follows that
$2$
-torsion, it follows that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D702}])(\mathbb{R})=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D702}])(\mathbb{R})=0$
for
![]() $i=1,2$
. Since the
$i=1,2$
. Since the
![]() $\unicode[STIX]{x1D70C}$
-local homotopy sheaves are unramified sheaves in the real étale topology, this (more or less) implies that
$\unicode[STIX]{x1D70C}$
-local homotopy sheaves are unramified sheaves in the real étale topology, this (more or less) implies that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D702}])=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D702}])=0$
for
![]() $i=1,2$
. This reproves a result of Röndigs [Reference RöndigsRön16].
$i=1,2$
. This reproves a result of Röndigs [Reference RöndigsRön16].
A different but related question is to determine rational motivic stable homotopy theory. By a recent result of Ananyevskiy et al. [Reference Ananyevskiy, Levine and PaninALP17] we have
 $\mathbf{SH}(k)_{\mathbb{Q}}^{-}\simeq \mathbf{DM}_{W}(k,\mathbb{Q})$
, where the right-hand side denotes a category of rational Witt-motives. Our results show easily that
$\mathbf{SH}(k)_{\mathbb{Q}}^{-}\simeq \mathbf{DM}_{W}(k,\mathbb{Q})$
, where the right-hand side denotes a category of rational Witt-motives. Our results show easily that
 $\mathbf{DM}_{W}(k,\mathbb{Z}[1/2])\simeq D_{\mathbb{A}^{1}}(k,\mathbb{Z}[1/2])^{-}\simeq D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}},\mathbb{Z}[1/2])$
and more generally that
$\mathbf{DM}_{W}(k,\mathbb{Z}[1/2])\simeq D_{\mathbb{A}^{1}}(k,\mathbb{Z}[1/2])^{-}\simeq D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}},\mathbb{Z}[1/2])$
and more generally that
 $D_{\mathbb{A}^{1}}(k,\mathbb{Z})[1/\unicode[STIX]{x1D70C}]\simeq D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})$
. By the same proof as in classical rational stable homotopy theory we have
$D_{\mathbb{A}^{1}}(k,\mathbb{Z})[1/\unicode[STIX]{x1D70C}]\simeq D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})$
. By the same proof as in classical rational stable homotopy theory we have
 $\mathbf{SH}(k)_{\mathbb{Q}}^{-}\simeq D_{\mathbb{A}^{1}}(k,\mathbb{Q})^{-}$
, and so we consider our results as one version of an integral strengthening of the result of Ananyevskiy–Levine–Panin.
$\mathbf{SH}(k)_{\mathbb{Q}}^{-}\simeq D_{\mathbb{A}^{1}}(k,\mathbb{Q})^{-}$
, and so we consider our results as one version of an integral strengthening of the result of Ananyevskiy–Levine–Panin.
In § 12 we collect some applications to the rigidity problem. A sheaf
![]() $F$
on
$F$
on
![]() $Sm(k)$
is called rigid if for every essentially smooth, Henselian local scheme
$Sm(k)$
is called rigid if for every essentially smooth, Henselian local scheme
![]() $X$
with closed point
$X$
with closed point
![]() $x$
we have
$x$
we have
 $F(X)=F(x)$
. For example, sheaves with transfers in the sense of Voevodsky which are of torsion prime to the characteristic of the perfect base field are rigid (see [Reference Suslin and VoevodskySV96, Theorem 4.4]). Our results imply that the homotopy sheaves of any
$F(X)=F(x)$
. For example, sheaves with transfers in the sense of Voevodsky which are of torsion prime to the characteristic of the perfect base field are rigid (see [Reference Suslin and VoevodskySV96, Theorem 4.4]). Our results imply that the homotopy sheaves of any
 $E\in \mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
are real étale sheaves extended from the small real étale site of
$E\in \mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
are real étale sheaves extended from the small real étale site of
![]() $k$
. One might already call this a rigidity result, but it is also not hard to see (and we show) that all such sheaves are rigid in the above sense. As an application, we show that the motivic stable homotopy sheaves
$k$
. One might already call this a rigidity result, but it is also not hard to see (and we show) that all such sheaves are rigid in the above sense. As an application, we show that the motivic stable homotopy sheaves
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9})_{0}[1/e]$
are all rigid, where
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9})_{0}[1/e]$
are all rigid, where
![]() $e$
is the exponential characteristic. This ties up a loose end of the author’s PhD thesis.
$e$
is the exponential characteristic. This ties up a loose end of the author’s PhD thesis.
Notation. If
![]() $S$
is a scheme, we denote the motivic stable homotopy category by
$S$
is a scheme, we denote the motivic stable homotopy category by
![]() $\mathbf{SH}(S)$
. We denote the
$\mathbf{SH}(S)$
. We denote the
![]() $S^{1}$
-stable motivic homotopy category (i.e. where
$S^{1}$
-stable motivic homotopy category (i.e. where
![]() $\mathbb{G}_{m}$
has not been inverted yet) by
$\mathbb{G}_{m}$
has not been inverted yet) by
 $\mathbf{SH}^{S^{1}}(S)$
. If
$\mathbf{SH}^{S^{1}}(S)$
. If
![]() ${\mathcal{X}}$
is a topos or site, we denote by
${\mathcal{X}}$
is a topos or site, we denote by
![]() $\text{SH}({\mathcal{X}})$
the associated stable homotopy category, see § 2. In particular
$\text{SH}({\mathcal{X}})$
the associated stable homotopy category, see § 2. In particular
 $\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}}),\text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
and
$\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}}),\text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
and
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}$
should be carefully distinguished: the first is the stable homotopy category of the small rét-site on
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}$
should be carefully distinguished: the first is the stable homotopy category of the small rét-site on
![]() $S$
, the second is the stable homotopy category of the site of all smooth schemes, with the rét-topology, and the latter is the rét-localisation of the motivic stable homotopy category. This last category is
$S$
, the second is the stable homotopy category of the site of all smooth schemes, with the rét-topology, and the latter is the rét-localisation of the motivic stable homotopy category. This last category is
![]() $\mathbb{A}^{1}$
-local and
$\mathbb{A}^{1}$
-local and
![]() $\mathbb{G}_{m}$
-stable, whereas the second category is neither, and these notions do not even make sense for the first category.
$\mathbb{G}_{m}$
-stable, whereas the second category is neither, and these notions do not even make sense for the first category.
The classical stable homotopy category will still be denoted by
![]() $\mathbf{SH}$
.
$\mathbf{SH}$
.
We denote the unit of a monoidal category
![]() ${\mathcal{C}}$
by
${\mathcal{C}}$
by
![]() $\unicode[STIX]{x1D7D9}_{{\mathcal{C}}}$
or just by
$\unicode[STIX]{x1D7D9}_{{\mathcal{C}}}$
or just by
![]() $\unicode[STIX]{x1D7D9}$
, if
$\unicode[STIX]{x1D7D9}$
, if
![]() ${\mathcal{C}}$
is clear from the context. Thus if
${\mathcal{C}}$
is clear from the context. Thus if
![]() ${\mathcal{C}}$
is a stable homotopy category of some sort, then
${\mathcal{C}}$
is a stable homotopy category of some sort, then
![]() $\unicode[STIX]{x1D7D9}$
is the sphere spectrum.
$\unicode[STIX]{x1D7D9}$
is the sphere spectrum.
2 Recollections on local homotopy theory
If
![]() $({\mathcal{C}},\unicode[STIX]{x1D70F})$
is a Grothendieck site, we can consider the associated category
$({\mathcal{C}},\unicode[STIX]{x1D70F})$
is a Grothendieck site, we can consider the associated category
 $\operatorname{Shv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
of sheaves (a topos), the category
$\operatorname{Shv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
of sheaves (a topos), the category
![]() $\operatorname{sPre}({\mathcal{C}})$
of simplicial presheaves on
$\operatorname{sPre}({\mathcal{C}})$
of simplicial presheaves on
![]() ${\mathcal{C}}$
, as well as the categories
${\mathcal{C}}$
, as well as the categories
![]() ${\mathcal{S}}{\mathcal{H}}({\mathcal{C}})$
of presheaves of spectra and
${\mathcal{S}}{\mathcal{H}}({\mathcal{C}})$
of presheaves of spectra and
![]() $C({\mathcal{C}})$
of presheaves of complexes of abelian groups on
$C({\mathcal{C}})$
of presheaves of complexes of abelian groups on
![]() ${\mathcal{C}}$
. The latter three categories carry various local model structures, in particular the injective and the projective one [Reference JardineJar15]. We denote the homotopy category of
${\mathcal{C}}$
. The latter three categories carry various local model structures, in particular the injective and the projective one [Reference JardineJar15]. We denote the homotopy category of
![]() ${\mathcal{S}}{\mathcal{H}}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
by
${\mathcal{S}}{\mathcal{H}}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
by
![]() $\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
and the homotopy category of
$\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
and the homotopy category of
![]() $C({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
by
$C({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
by
![]() $D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
.
$D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
.
It is also possible to model
![]() $\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
and so on by sheaves. For this, let
$\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
and so on by sheaves. For this, let
 $\operatorname{sShv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
denote the category of sheaves of simplicial sets, and similarly let
$\operatorname{sShv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
denote the category of sheaves of simplicial sets, and similarly let
 ${\mathcal{S}}{\mathcal{H}}^{\text{s}}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
be the category of sheaves of spectra, and let
${\mathcal{S}}{\mathcal{H}}^{\text{s}}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
be the category of sheaves of spectra, and let
![]() $C^{\text{s}}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
be the category of sheaves of chain complexes. (Here we mean sheaves in the 1-categorical sense, so this category is equivalent to the category of chain complexes of sheaves of abelian groups, and similarly for the spectra.) These also afford local model structures, and
$C^{\text{s}}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
be the category of sheaves of chain complexes. (Here we mean sheaves in the 1-categorical sense, so this category is equivalent to the category of chain complexes of sheaves of abelian groups, and similarly for the spectra.) These also afford local model structures, and
 $\operatorname{Ho}(\operatorname{sShv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}}))\simeq \operatorname{Ho}(\operatorname{sPre}({\mathcal{C}}_{\unicode[STIX]{x1D70F}}))$
, and so on.
$\operatorname{Ho}(\operatorname{sShv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}}))\simeq \operatorname{Ho}(\operatorname{sPre}({\mathcal{C}}_{\unicode[STIX]{x1D70F}}))$
, and so on.
Given a functor
 $f^{\ast }:{\mathcal{C}}\rightarrow {\mathcal{D}}$
, there is an induced restriction functor
$f^{\ast }:{\mathcal{C}}\rightarrow {\mathcal{D}}$
, there is an induced restriction functor
 $f_{\ast }:\operatorname{Pre}({\mathcal{D}})\rightarrow \operatorname{Pre}({\mathcal{C}})$
, where
$f_{\ast }:\operatorname{Pre}({\mathcal{D}})\rightarrow \operatorname{Pre}({\mathcal{C}})$
, where
![]() $\operatorname{Pre}({\mathcal{C}})$
denotes the category of presheaves (of sets) on
$\operatorname{Pre}({\mathcal{C}})$
denotes the category of presheaves (of sets) on
![]() ${\mathcal{C}}$
(and similarly for
${\mathcal{C}}$
(and similarly for
![]() ${\mathcal{D}}$
). The functor
${\mathcal{D}}$
). The functor
![]() $f_{\ast }$
has a left adjoint
$f_{\ast }$
has a left adjoint
 $f^{\ast }:\operatorname{Pre}({\mathcal{C}})\rightarrow \operatorname{Pre}({\mathcal{D}})$
. It is in fact the left Kan extension of
$f^{\ast }:\operatorname{Pre}({\mathcal{C}})\rightarrow \operatorname{Pre}({\mathcal{D}})$
. It is in fact the left Kan extension of
 $f^{\ast }:{\mathcal{C}}\rightarrow {\mathcal{D}}$
.
$f^{\ast }:{\mathcal{C}}\rightarrow {\mathcal{D}}$
.
If
![]() ${\mathcal{C}},{\mathcal{D}}$
are sites the functor
${\mathcal{C}},{\mathcal{D}}$
are sites the functor
![]() $f^{\ast }$
is called continuous if
$f^{\ast }$
is called continuous if
 $f_{\ast }:\operatorname{Pre}({\mathcal{D}})\rightarrow \operatorname{Pre}({\mathcal{C}})$
preserves sheaves. In this case the induced functor
$f_{\ast }:\operatorname{Pre}({\mathcal{D}})\rightarrow \operatorname{Pre}({\mathcal{C}})$
preserves sheaves. In this case the induced functor
 $f_{\ast }:\operatorname{Shv}({\mathcal{D}})\rightarrow \operatorname{Shv}({\mathcal{C}})$
has a left adjoint still denoted
$f_{\ast }:\operatorname{Shv}({\mathcal{D}})\rightarrow \operatorname{Shv}({\mathcal{C}})$
has a left adjoint still denoted
 $f^{\ast }:\operatorname{Shv}({\mathcal{C}})\rightarrow \operatorname{Shv}({\mathcal{D}})$
. If this induced functor is left exact (commutes with finite limits) then
$f^{\ast }:\operatorname{Shv}({\mathcal{C}})\rightarrow \operatorname{Shv}({\mathcal{D}})$
. If this induced functor is left exact (commutes with finite limits) then
![]() $f$
is called a geometric morphism.
$f$
is called a geometric morphism.
More generally, an adjunction
 $f^{\ast }:\operatorname{Shv}({\mathcal{C}})\leftrightarrows \operatorname{Shv}({\mathcal{D}}):f_{\ast }$
(where
$f^{\ast }:\operatorname{Shv}({\mathcal{C}})\leftrightarrows \operatorname{Shv}({\mathcal{D}}):f_{\ast }$
(where
![]() $f^{\ast }\vdash f_{\ast }$
does not necessarily come from a functor
$f^{\ast }\vdash f_{\ast }$
does not necessarily come from a functor
 $f^{\ast }:{\mathcal{C}}\rightarrow {\mathcal{D}}$
) is called a geometric morphism if
$f^{\ast }:{\mathcal{C}}\rightarrow {\mathcal{D}}$
) is called a geometric morphism if
![]() $f^{\ast }$
preserves finite limits.
$f^{\ast }$
preserves finite limits.
If
 $f:{\mathcal{C}}\rightarrow {\mathcal{D}}$
is any functor, then there are induced adjunctions
$f:{\mathcal{C}}\rightarrow {\mathcal{D}}$
is any functor, then there are induced adjunctions
 $f^{\ast }:\operatorname{sPre}({\mathcal{C}})\leftrightarrows \operatorname{sPre}({\mathcal{D}}):f_{\ast }$
, and similarly for spectra and chain complexes. Similarly if
$f^{\ast }:\operatorname{sPre}({\mathcal{C}})\leftrightarrows \operatorname{sPre}({\mathcal{D}}):f_{\ast }$
, and similarly for spectra and chain complexes. Similarly if
 $f^{\ast }:\operatorname{Shv}({\mathcal{C}})\leftrightarrows \operatorname{Shv}({\mathcal{D}}):f_{\ast }$
is any adjunction, then there are induced adjunctions
$f^{\ast }:\operatorname{Shv}({\mathcal{C}})\leftrightarrows \operatorname{Shv}({\mathcal{D}}):f_{\ast }$
is any adjunction, then there are induced adjunctions
 $f^{\ast }:\operatorname{sShv}({\mathcal{C}})\leftrightarrows \operatorname{sShv}({\mathcal{D}}):f_{\ast }$
, and so on. If
$f^{\ast }:\operatorname{sShv}({\mathcal{C}})\leftrightarrows \operatorname{sShv}({\mathcal{D}}):f_{\ast }$
, and so on. If
![]() $f^{\ast }\vdash f_{\ast }$
is a geometric morphism in either of the above senses, then the induced adjunctions on presheaves (sheaves) of simplicial sets, spectra, and chain complexes are Quillen adjunctions in the local model structure [Reference JardineJar15, § 5.3] [Reference Cisinski and DégliseCD09, Theorem 1.18].
$f^{\ast }\vdash f_{\ast }$
is a geometric morphism in either of the above senses, then the induced adjunctions on presheaves (sheaves) of simplicial sets, spectra, and chain complexes are Quillen adjunctions in the local model structure [Reference JardineJar15, § 5.3] [Reference Cisinski and DégliseCD09, Theorem 1.18].
The above discussion allows us to prove the following useful result.
Lemma 1. Let
 $f^{\ast }:\operatorname{Shv}({\mathcal{C}})\leftrightarrows \operatorname{Shv}({\mathcal{D}}):f_{\ast }$
be a geometric morphism such that
$f^{\ast }:\operatorname{Shv}({\mathcal{C}})\leftrightarrows \operatorname{Shv}({\mathcal{D}}):f_{\ast }$
be a geometric morphism such that
![]() $f^{\ast }$
is fully faithful and
$f^{\ast }$
is fully faithful and
![]() $f_{\ast }$
preserves colimits. Then the induced functors
$f_{\ast }$
preserves colimits. Then the induced functors
 $$\begin{eqnarray}Lf^{\ast }:\text{SH}({\mathcal{C}})\rightarrow \text{SH}({\mathcal{D}})\end{eqnarray}$$
$$\begin{eqnarray}Lf^{\ast }:\text{SH}({\mathcal{C}})\rightarrow \text{SH}({\mathcal{D}})\end{eqnarray}$$
and
 $$\begin{eqnarray}Lf^{\ast }:D({\mathcal{C}})\rightarrow D({\mathcal{D}})\end{eqnarray}$$
$$\begin{eqnarray}Lf^{\ast }:D({\mathcal{C}})\rightarrow D({\mathcal{D}})\end{eqnarray}$$
are fully faithful.
The same result also holds for
 $Lf^{\ast }:\operatorname{Ho}(\operatorname{sPre}({\mathcal{C}}))\rightarrow \operatorname{Ho}(\operatorname{sPre}({\mathcal{D}}))$
, with the same proof.
$Lf^{\ast }:\operatorname{Ho}(\operatorname{sPre}({\mathcal{C}}))\rightarrow \operatorname{Ho}(\operatorname{sPre}({\mathcal{D}}))$
, with the same proof.
Proof. We give the proof for the derived categories, it is the same for spectra.
Since
![]() $f_{\ast }$
preserves colimits it affords a right adjoint
$f_{\ast }$
preserves colimits it affords a right adjoint
![]() $f^{!}$
. Then
$f^{!}$
. Then
![]() $f_{\ast }\vdash f^{!}$
is a geometric morphism in the opposite direction (note that
$f_{\ast }\vdash f^{!}$
is a geometric morphism in the opposite direction (note that
![]() $f_{\ast }$
preserves finite limits, and in fact all limits, since it is a right adjoint) and consequently
$f_{\ast }$
preserves finite limits, and in fact all limits, since it is a right adjoint) and consequently
![]() $f_{\ast }$
is bi-Quillen. It follows that
$f_{\ast }$
is bi-Quillen. It follows that
 $f_{\ast }:C^{\text{s}}({\mathcal{D}})\rightarrow C^{\text{s}}({\mathcal{C}})$
preserves weak equivalences, and consequently coincides (up to weak equivalence) with its derived functor.
$f_{\ast }:C^{\text{s}}({\mathcal{D}})\rightarrow C^{\text{s}}({\mathcal{C}})$
preserves weak equivalences, and consequently coincides (up to weak equivalence) with its derived functor.
Now to show that
![]() $Lf^{\ast }$
is fully faithful we need to show that
$Lf^{\ast }$
is fully faithful we need to show that
 $Rf_{\ast }Lf^{\ast }\simeq \operatorname{id}$
. But
$Rf_{\ast }Lf^{\ast }\simeq \operatorname{id}$
. But
 $Rf_{\ast }\simeq f_{\ast }$
since
$Rf_{\ast }\simeq f_{\ast }$
since
![]() $f_{\ast }$
is bi-Quillen. Let
$f_{\ast }$
is bi-Quillen. Let
 $E\in C^{\text{s}}({\mathcal{C}})$
be cofibrant. Then
$E\in C^{\text{s}}({\mathcal{C}})$
be cofibrant. Then
 $Lf^{\ast }E\simeq f^{\ast }E$
and consequently
$Lf^{\ast }E\simeq f^{\ast }E$
and consequently
 $Rf_{\ast }Lf^{\ast }E\simeq f_{\ast }f^{\ast }E$
. Since
$Rf_{\ast }Lf^{\ast }E\simeq f_{\ast }f^{\ast }E$
. Since
![]() $f^{\ast }$
is fully faithful we have
$f^{\ast }$
is fully faithful we have
 $f_{\ast }f^{\ast }E\cong E$
. This concludes the proof.◻
$f_{\ast }f^{\ast }E\cong E$
. This concludes the proof.◻
We will also make use of
![]() $t$
-structures. We shall use homological notation for
$t$
-structures. We shall use homological notation for
![]() $t$
-structures [Reference LurieLur16, Definition 1.2.1.1]. Briefly, a
$t$
-structures [Reference LurieLur16, Definition 1.2.1.1]. Briefly, a
![]() $t$
-structure on a triangulated category
$t$
-structure on a triangulated category
![]() ${\mathcal{C}}$
consists of two (strictly full) subcategories
${\mathcal{C}}$
consists of two (strictly full) subcategories
![]() ${\mathcal{C}}_{{\geqslant}0}$
and
${\mathcal{C}}_{{\geqslant}0}$
and
![]() ${\mathcal{C}}_{{\leqslant}0}$
, satisfying various axioms. We put
${\mathcal{C}}_{{\leqslant}0}$
, satisfying various axioms. We put
 ${\mathcal{C}}_{{\geqslant}n}={\mathcal{C}}_{{\geqslant}0}[n]$
and
${\mathcal{C}}_{{\geqslant}n}={\mathcal{C}}_{{\geqslant}0}[n]$
and
 ${\mathcal{C}}_{{\leqslant}n}={\mathcal{C}}_{{\leqslant}0}[n]$
. One then has
${\mathcal{C}}_{{\leqslant}n}={\mathcal{C}}_{{\leqslant}0}[n]$
. One then has
 ${\mathcal{C}}_{{\geqslant}n+1}\subset {\mathcal{C}}_{{\geqslant}n}$
and
${\mathcal{C}}_{{\geqslant}n+1}\subset {\mathcal{C}}_{{\geqslant}n}$
and
 ${\mathcal{C}}_{{\leqslant}n}\subset {\mathcal{C}}_{{\leqslant}n+1}$
and
${\mathcal{C}}_{{\leqslant}n}\subset {\mathcal{C}}_{{\leqslant}n+1}$
and
 $[{\mathcal{C}}_{{\geqslant}n+1},{\mathcal{C}}_{{\leqslant}n}]=0$
. In fact
$[{\mathcal{C}}_{{\geqslant}n+1},{\mathcal{C}}_{{\leqslant}n}]=0$
. In fact
 $E\in {\mathcal{C}}_{{\geqslant}n+1}$
if and only if for all
$E\in {\mathcal{C}}_{{\geqslant}n+1}$
if and only if for all
 $F\in {\mathcal{C}}_{{\leqslant}n}$
we have
$F\in {\mathcal{C}}_{{\leqslant}n}$
we have
 $[E,F]=0$
, and vice versa. The inclusion
$[E,F]=0$
, and vice versa. The inclusion
 ${\mathcal{C}}_{{\geqslant}n}{\hookrightarrow}{\mathcal{C}}$
has a right adjoint which we denote
${\mathcal{C}}_{{\geqslant}n}{\hookrightarrow}{\mathcal{C}}$
has a right adjoint which we denote
 $E\mapsto E_{{\geqslant}n}$
, and the inclusion
$E\mapsto E_{{\geqslant}n}$
, and the inclusion
 ${\mathcal{C}}_{{\leqslant}n}{\hookrightarrow}{\mathcal{C}}$
has a left adjoint which we denote
${\mathcal{C}}_{{\leqslant}n}{\hookrightarrow}{\mathcal{C}}$
has a left adjoint which we denote
 $E\mapsto E_{{\leqslant}n}$
. The adjunctions furnish map
$E\mapsto E_{{\leqslant}n}$
. The adjunctions furnish map
 $E_{{\geqslant}n+1}\rightarrow E\rightarrow E_{{\leqslant}n}$
and this extends to a distinguished triangle in a unique and functorial way. The intersection
$E_{{\geqslant}n+1}\rightarrow E\rightarrow E_{{\leqslant}n}$
and this extends to a distinguished triangle in a unique and functorial way. The intersection
 ${\mathcal{C}}^{\heartsuit }:={\mathcal{C}}_{{\geqslant}0}\cap {\mathcal{C}}_{{\leqslant}0}$
called the heart. It is an abelian category. We put
${\mathcal{C}}^{\heartsuit }:={\mathcal{C}}_{{\geqslant}0}\cap {\mathcal{C}}_{{\leqslant}0}$
called the heart. It is an abelian category. We put
 $\unicode[STIX]{x1D70B}_{0}^{{\mathcal{C}}}(E)=(E_{{\leqslant}0})_{{\geqslant}0}\simeq (E_{{\geqslant}0})_{{\leqslant}0}\in {\mathcal{C}}^{\heartsuit }$
and
$\unicode[STIX]{x1D70B}_{0}^{{\mathcal{C}}}(E)=(E_{{\leqslant}0})_{{\geqslant}0}\simeq (E_{{\geqslant}0})_{{\leqslant}0}\in {\mathcal{C}}^{\heartsuit }$
and
 $\unicode[STIX]{x1D70B}_{i}^{{\mathcal{C}}}(E)=\unicode[STIX]{x1D70B}_{0}^{{\mathcal{C}}}(E[i])$
. Then
$\unicode[STIX]{x1D70B}_{i}^{{\mathcal{C}}}(E)=\unicode[STIX]{x1D70B}_{0}^{{\mathcal{C}}}(E[i])$
. Then
![]() $\unicode[STIX]{x1D70B}_{\ast }^{{\mathcal{C}}}$
is a homological functor on
$\unicode[STIX]{x1D70B}_{\ast }^{{\mathcal{C}}}$
is a homological functor on
![]() ${\mathcal{C}}$
. The
${\mathcal{C}}$
. The
![]() $t$
-structure is called non-degenerate if
$t$
-structure is called non-degenerate if
 $\unicode[STIX]{x1D70B}_{i}^{{\mathcal{C}}}(E)=0$
implies that
$\unicode[STIX]{x1D70B}_{i}^{{\mathcal{C}}}(E)=0$
implies that
![]() $E\simeq 0$
.
$E\simeq 0$
.
By a
![]() $t$
-category we mean a triangulated category with a fixed
$t$
-category we mean a triangulated category with a fixed
![]() $t$
-structure.
$t$
-structure.
Suppose that
![]() $({\mathcal{C}},\unicode[STIX]{x1D70F})$
is a site. Let for
$({\mathcal{C}},\unicode[STIX]{x1D70F})$
is a site. Let for
 $E\in {\mathcal{S}}{\mathcal{H}}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
and
$E\in {\mathcal{S}}{\mathcal{H}}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
and
![]() $i\in \mathbb{Z}$
the sheaf
$i\in \mathbb{Z}$
the sheaf
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)\in \operatorname{Shv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
be defined as the sheaf associated with the presheaf
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)\in \operatorname{Shv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
be defined as the sheaf associated with the presheaf
 ${\mathcal{C}}\ni X\mapsto \unicode[STIX]{x1D70B}_{i}(E(X))$
. Here we view
${\mathcal{C}}\ni X\mapsto \unicode[STIX]{x1D70B}_{i}(E(X))$
. Here we view
![]() $E$
as a presheaf of spectra. By definition, local weak equivalences of spectra induce isomorphisms on
$E$
as a presheaf of spectra. By definition, local weak equivalences of spectra induce isomorphisms on
![]() $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}$
, so
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}$
, so
![]() $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)$
is well defined for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)$
is well defined for
 $E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
. This is a sheaf of abelian groups. Put
$E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
. This is a sheaf of abelian groups. Put
 $$\begin{eqnarray}\displaystyle \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\geqslant}0} & = & \displaystyle \{E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}}):\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)=0\text{ for }i<0\},\nonumber\\ \displaystyle \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\leqslant}0} & = & \displaystyle \{E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}}):\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)=0\text{ for }i>0\}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\geqslant}0} & = & \displaystyle \{E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}}):\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)=0\text{ for }i<0\},\nonumber\\ \displaystyle \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\leqslant}0} & = & \displaystyle \{E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}}):\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)=0\text{ for }i>0\}.\nonumber\end{eqnarray}$$
We define similarly for
 $E\in D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
the sheaf
$E\in D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
the sheaf
![]() $\text{}\underline{h}_{i}(E)$
, and then the subcategories
$\text{}\underline{h}_{i}(E)$
, and then the subcategories
 $D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\geqslant}0},D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\leqslant}0}.$
$D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\geqslant}0},D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\leqslant}0}.$
Lemma 2. If
![]() $({\mathcal{C}},\unicode[STIX]{x1D70F})$
is a Grothendieck site, then the above construction provides
$({\mathcal{C}},\unicode[STIX]{x1D70F})$
is a Grothendieck site, then the above construction provides
![]() $\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
with a non-degenerate
$\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
with a non-degenerate
![]() $t$
-structure. The functor
$t$
-structure. The functor
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{0}:\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})^{\heartsuit }\rightarrow \operatorname{Shv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
is an equivalence of categories. Moreover let
$\text{}\underline{\unicode[STIX]{x1D70B}}_{0}:\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})^{\heartsuit }\rightarrow \operatorname{Shv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
is an equivalence of categories. Moreover let
 $F\in \operatorname{Shv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})\simeq \text{SH}({\mathcal{C}})^{\heartsuit }$
. Then for
$F\in \operatorname{Shv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})\simeq \text{SH}({\mathcal{C}})^{\heartsuit }$
. Then for
![]() $X\in {\mathcal{C}}$
there is a natural isomorphism
$X\in {\mathcal{C}}$
there is a natural isomorphism
 $[\unicode[STIX]{x1D6F4}^{\infty }X_{+},F[n]]=H_{\unicode[STIX]{x1D70F}}^{n}(X,F)$
.
$[\unicode[STIX]{x1D6F4}^{\infty }X_{+},F[n]]=H_{\unicode[STIX]{x1D70F}}^{n}(X,F)$
.
Similar statements hold for
![]() $D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
in place of
$D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
in place of
![]() $\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
.
$\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
.
Proof. For derived categories, this result is classical. For
![]() $\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
, the result is also fairly well known, but the author does not know an explicit reference, so we sketch a proof.
$\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
, the result is also fairly well known, but the author does not know an explicit reference, so we sketch a proof.
Note that there is a Quillen adjunction (in the local model structures)
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{\infty }:\operatorname{sPre}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{\ast }\leftrightarrows {\mathcal{S}}{\mathcal{H}}({\mathcal{C}}_{\unicode[STIX]{x1D70F}}):\unicode[STIX]{x1D6FA}^{\infty }.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}^{\infty }:\operatorname{sPre}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{\ast }\leftrightarrows {\mathcal{S}}{\mathcal{H}}({\mathcal{C}}_{\unicode[STIX]{x1D70F}}):\unicode[STIX]{x1D6FA}^{\infty }.\end{eqnarray}$$
By direct computation using the above adjunction, we find that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D6FA}^{\infty }E)=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)$
, for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D6FA}^{\infty }E)=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)$
, for
 $E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
and
$E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
and
![]() $i\geqslant 0$
.
$i\geqslant 0$
.
By [Reference LurieLur16, Proposition 1.4.3.4 and Remark 1.4.3.5] the category
![]() $\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
admits a
$\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
admits a
![]() $t$
-structure,Footnote
1
where
$t$
-structure,Footnote
1
where
 $E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\leqslant}0}$
if and only if
$E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\leqslant}0}$
if and only if
 $\unicode[STIX]{x1D6FA}^{\infty }(E)\simeq \ast$
, and the subcategory
$\unicode[STIX]{x1D6FA}^{\infty }(E)\simeq \ast$
, and the subcategory
 $\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\geqslant}0}$
is generated under homotopy colimits and extensions by
$\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\geqslant}0}$
is generated under homotopy colimits and extensions by
![]() $\unicode[STIX]{x1D6F4}^{\infty }{\mathcal{C}}_{+}$
. We first need to show that this is the
$\unicode[STIX]{x1D6F4}^{\infty }{\mathcal{C}}_{+}$
. We first need to show that this is the
![]() $t$
-structure we want, i.e. that the positive and negative parts are determined by vanishing of homotopy sheaves. Since
$t$
-structure we want, i.e. that the positive and negative parts are determined by vanishing of homotopy sheaves. Since
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D6FA}^{\infty }E)=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)$
, this is correct for the negative part. I claim that if
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D6FA}^{\infty }E)=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)$
, this is correct for the negative part. I claim that if
 $E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\geqslant}0}$
, then
$E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\geqslant}0}$
, then
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)=0$
for
![]() $i<0$
. If
$i<0$
. If
 $X\in \operatorname{sPre}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{\ast }$
, then
$X\in \operatorname{sPre}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{\ast }$
, then
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D6F4}^{\infty }X)=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D6F4}^{\infty }X)=0$
for
![]() $i<0$
by direct computation. It thus remains to show that the subcategory of
$i<0$
by direct computation. It thus remains to show that the subcategory of
 $E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
with
$E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
with
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)=0$
for
![]() $i<0$
is closed under homotopy colimits and extensions. For extensions this is clear. Homotopy colimits are generated by pushouts and filtered colimits [Reference LurieLur09, Propositions 4.4.2.6 and 4.4.2.7], so we need only deal with cones and filtered colimits. For cones this is again clear, and for filtered colimits it holds because homotopy groups of spectra commute with filtered colimits, and hence the same is true for homotopy sheaves (see the proof of Corollary 3 for more details on this). This proves the claim. Conversely, let
$i<0$
is closed under homotopy colimits and extensions. For extensions this is clear. Homotopy colimits are generated by pushouts and filtered colimits [Reference LurieLur09, Propositions 4.4.2.6 and 4.4.2.7], so we need only deal with cones and filtered colimits. For cones this is again clear, and for filtered colimits it holds because homotopy groups of spectra commute with filtered colimits, and hence the same is true for homotopy sheaves (see the proof of Corollary 3 for more details on this). This proves the claim. Conversely, let
 $E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
with
$E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
with
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)=0$
for
![]() $i<0$
. Consider the decomposition
$i<0$
. Consider the decomposition
 $E_{{\geqslant}0}\rightarrow E\rightarrow E_{{<}0}$
. Then
$E_{{\geqslant}0}\rightarrow E\rightarrow E_{{<}0}$
. Then
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E_{{\geqslant}0})=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E_{{\geqslant}0})=0$
for
![]() $i<0$
, so
$i<0$
, so
 $0=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E_{{<}0})$
for
$0=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E_{{<}0})$
for
![]() $i<0$
. It follows that
$i<0$
. It follows that
 $E_{{<}0}\simeq 0$
and so
$E_{{<}0}\simeq 0$
and so
 $E\simeq E_{{\geqslant}0}\in \text{SH}(E)_{{\geqslant}0}$
.
$E\simeq E_{{\geqslant}0}\in \text{SH}(E)_{{\geqslant}0}$
.
The
![]() $t$
-structure is non-degenerate because it is defined in terms of homotopy sheaves, and homotopy sheaves detect weak equivalences by definition.
$t$
-structure is non-degenerate because it is defined in terms of homotopy sheaves, and homotopy sheaves detect weak equivalences by definition.
We have an adjunction
 $$\begin{eqnarray}M:\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})\leftrightarrows D({\mathcal{C}}_{\unicode[STIX]{x1D70F}}):U.\end{eqnarray}$$
$$\begin{eqnarray}M:\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})\leftrightarrows D({\mathcal{C}}_{\unicode[STIX]{x1D70F}}):U.\end{eqnarray}$$
By construction
![]() $U$
is
$U$
is
![]() $t$
-exact and thus
$t$
-exact and thus
![]() $M$
is right
$M$
is right
![]() $t$
-exact. Consider the induced adjunction
$t$
-exact. Consider the induced adjunction
 $$\begin{eqnarray}M^{\heartsuit }:\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})^{\heartsuit }\leftrightarrows D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})^{\heartsuit }:U.\end{eqnarray}$$
$$\begin{eqnarray}M^{\heartsuit }:\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})^{\heartsuit }\leftrightarrows D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})^{\heartsuit }:U.\end{eqnarray}$$
By direct computation using the classical Hurewicz isomorphism (and the above adjunction),
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(UME)=\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(E)$
if
$\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(UME)=\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(E)$
if
 $E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\geqslant}0}$
. It follows that
$E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})_{{\geqslant}0}$
. It follows that
 $UM^{\heartsuit }\simeq \operatorname{id}$
. Since
$UM^{\heartsuit }\simeq \operatorname{id}$
. Since
![]() $U$
is faithful by definition, from this we deduce that
$U$
is faithful by definition, from this we deduce that
 $M^{\heartsuit }U\simeq \operatorname{id}$
as well. Thus
$M^{\heartsuit }U\simeq \operatorname{id}$
as well. Thus
 $\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})^{\heartsuit }\simeq D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})^{\heartsuit }\simeq \operatorname{Shv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
, the latter equivalence being classical. Finally if
$\text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})^{\heartsuit }\simeq D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})^{\heartsuit }\simeq \operatorname{Shv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
, the latter equivalence being classical. Finally if
![]() $X\in {\mathcal{C}}$
and
$X\in {\mathcal{C}}$
and
 $F\in \operatorname{Shv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
then
$F\in \operatorname{Shv}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
then
 $[\unicode[STIX]{x1D6F4}^{\infty }X_{+},F[n]]=[\unicode[STIX]{x1D6F4}^{\infty }X_{+},UF[n]]=H_{\unicode[STIX]{x1D70F}}^{n}(X,F)$
, the first equality by definition and the second by adjunction and the same result in
$[\unicode[STIX]{x1D6F4}^{\infty }X_{+},F[n]]=[\unicode[STIX]{x1D6F4}^{\infty }X_{+},UF[n]]=H_{\unicode[STIX]{x1D70F}}^{n}(X,F)$
, the first equality by definition and the second by adjunction and the same result in
![]() $D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
.◻
$D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
.◻
Corollary 3. Let
![]() $({\mathcal{C}},\unicode[STIX]{x1D70F})$
be a Grothendieck site.
$({\mathcal{C}},\unicode[STIX]{x1D70F})$
be a Grothendieck site.
(1) Let
 $X\in {\mathcal{C}}$
. If
$X\in {\mathcal{C}}$
. If
 $\unicode[STIX]{x1D70F}$
-cohomology on
$\unicode[STIX]{x1D70F}$
-cohomology on
 $X$
commutes with filtered colimits of sheaves and the
$X$
commutes with filtered colimits of sheaves and the
 $\unicode[STIX]{x1D70F}$
-cohomological dimension of
$\unicode[STIX]{x1D70F}$
-cohomological dimension of
 $X$
is finite, then
$X$
is finite, then
 $\unicode[STIX]{x1D6F4}^{\infty }X_{+}\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
is a compact object.
$\unicode[STIX]{x1D6F4}^{\infty }X_{+}\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
is a compact object.(2) For any collection
 $E_{i}\in \text{SH}({\mathcal{C}})$
and
$E_{i}\in \text{SH}({\mathcal{C}})$
and
 $j\in \mathbb{Z}$
we have
$j\in \mathbb{Z}$
we have
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{j}(\bigoplus _{i}E_{i})=\bigoplus _{i}\text{}\underline{\unicode[STIX]{x1D70B}}_{j}(E_{i})$
.
$\text{}\underline{\unicode[STIX]{x1D70B}}_{j}(\bigoplus _{i}E_{i})=\bigoplus _{i}\text{}\underline{\unicode[STIX]{x1D70B}}_{j}(E_{i})$
.
Similarly for
![]() $D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
.
$D({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
.
Proof. Let us show that (1) reduces to (2). For
 $E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
there is a conditionally convergent spectral sequence
$E\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
there is a conditionally convergent spectral sequence
 $$\begin{eqnarray}H_{\unicode[STIX]{x1D70F}}^{p}(X,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}E)\Rightarrow [X,E[p+q]].\end{eqnarray}$$
$$\begin{eqnarray}H_{\unicode[STIX]{x1D70F}}^{p}(X,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}E)\Rightarrow [X,E[p+q]].\end{eqnarray}$$
Under our assumptions on the cohomological dimension of
![]() $X$
, it converges strongly to the right-hand side. Under the assumption of commutation of cohomology with filtered colimits, by spectral sequence comparison, it thus suffices to show that for
$X$
, it converges strongly to the right-hand side. Under the assumption of commutation of cohomology with filtered colimits, by spectral sequence comparison, it thus suffices to show that for
 $E_{i}\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
we have
$E_{i}\in \text{SH}({\mathcal{C}}_{\unicode[STIX]{x1D70F}})$
we have
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{n}(\bigoplus _{i}E_{i})=\bigoplus _{i}\text{}\underline{\unicode[STIX]{x1D70B}}_{n}E_{i}$
.
$\text{}\underline{\unicode[STIX]{x1D70B}}_{n}(\bigoplus _{i}E_{i})=\bigoplus _{i}\text{}\underline{\unicode[STIX]{x1D70B}}_{n}E_{i}$
.
Now we prove (2). For
 $E\in {\mathcal{S}}{\mathcal{H}}({\mathcal{C}})$
write
$E\in {\mathcal{S}}{\mathcal{H}}({\mathcal{C}})$
write
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{j}^{p}(E)(X)=\unicode[STIX]{x1D70B}_{j}(E(X))$
; this defines a presheaf of abelian groups on
$\text{}\underline{\unicode[STIX]{x1D70B}}_{j}^{p}(E)(X)=\unicode[STIX]{x1D70B}_{j}(E(X))$
; this defines a presheaf of abelian groups on
![]() ${\mathcal{C}}$
. By definition
${\mathcal{C}}$
. By definition
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{j}(E)=a_{\unicode[STIX]{x1D70F}}\text{}\underline{\unicode[STIX]{x1D70B}}_{j}^{p}(E)$
. Let
$\text{}\underline{\unicode[STIX]{x1D70B}}_{j}(E)=a_{\unicode[STIX]{x1D70F}}\text{}\underline{\unicode[STIX]{x1D70B}}_{j}^{p}(E)$
. Let
 $\{E_{i}\}_{i}\in {\mathcal{S}}{\mathcal{H}}({\mathcal{C}})$
. Then
$\{E_{i}\}_{i}\in {\mathcal{S}}{\mathcal{H}}({\mathcal{C}})$
. Then
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{j}^{p}(\bigoplus _{i}E_{i})=\bigoplus _{i}\text{}\underline{\unicode[STIX]{x1D70B}}_{j}^{p}(E_{i})$
, since homotopy groups of spectra commute with filtered colimits. We may assume that all the
$\text{}\underline{\unicode[STIX]{x1D70B}}_{j}^{p}(\bigoplus _{i}E_{i})=\bigoplus _{i}\text{}\underline{\unicode[STIX]{x1D70B}}_{j}^{p}(E_{i})$
, since homotopy groups of spectra commute with filtered colimits. We may assume that all the
![]() $E_{i}$
are cofibrant, so their presheaf direct sum coincides with the derived direct sum. In this case it remains to show that
$E_{i}$
are cofibrant, so their presheaf direct sum coincides with the derived direct sum. In this case it remains to show that
 $$\begin{eqnarray}{a_{\unicode[STIX]{x1D70F}}\bigoplus }_{i}\text{}\underline{\unicode[STIX]{x1D70B}}_{j}^{p}(E_{i})\cong \bigoplus _{i}a_{\unicode[STIX]{x1D70F}}\text{}\underline{\unicode[STIX]{x1D70B}}_{j}^{p}(E_{i}).\end{eqnarray}$$
$$\begin{eqnarray}{a_{\unicode[STIX]{x1D70F}}\bigoplus }_{i}\text{}\underline{\unicode[STIX]{x1D70B}}_{j}^{p}(E_{i})\cong \bigoplus _{i}a_{\unicode[STIX]{x1D70F}}\text{}\underline{\unicode[STIX]{x1D70B}}_{j}^{p}(E_{i}).\end{eqnarray}$$
(Note that here we write
![]() $\bigoplus _{i}$
for both direct sums of presheaves and direct sums of sheaves, depending on whether the terms on the right are presheaves or sheaves.) But this holds for any collection of presheaves on any site (both sides satisfy the same universal property).
$\bigoplus _{i}$
for both direct sums of presheaves and direct sums of sheaves, depending on whether the terms on the right are presheaves or sheaves.) But this holds for any collection of presheaves on any site (both sides satisfy the same universal property).
The proof for
![]() $D$
is the same.◻
$D$
is the same.◻
We can enhance the functoriality of the
![]() $\text{SH}$
construction as follows. Recall that a triangulated functor
$\text{SH}$
construction as follows. Recall that a triangulated functor
 $F:{\mathcal{C}}\rightarrow {\mathcal{D}}$
between
$F:{\mathcal{C}}\rightarrow {\mathcal{D}}$
between
![]() $t$
-categories is called right (respectively left)
$t$
-categories is called right (respectively left)
![]() $t$
-exact if
$t$
-exact if
 $F({\mathcal{C}}_{{\geqslant}0})\subset {\mathcal{D}}_{{\geqslant}0}$
(respectively
$F({\mathcal{C}}_{{\geqslant}0})\subset {\mathcal{D}}_{{\geqslant}0}$
(respectively
 $F({\mathcal{C}}_{{\leqslant}0})\subset {\mathcal{D}}_{{\leqslant}0}$
). The functor is called
$F({\mathcal{C}}_{{\leqslant}0})\subset {\mathcal{D}}_{{\leqslant}0}$
). The functor is called
![]() $t$
-exact if it is both left and right
$t$
-exact if it is both left and right
![]() $t$
-exact.
$t$
-exact.
Lemma 4. Let
 $f^{\ast }:\operatorname{Shv}({\mathcal{C}})\leftrightarrows \operatorname{Shv}({\mathcal{D}}):f_{\ast }$
be a geometric morphism, where
$f^{\ast }:\operatorname{Shv}({\mathcal{C}})\leftrightarrows \operatorname{Shv}({\mathcal{D}}):f_{\ast }$
be a geometric morphism, where
![]() $\operatorname{Shv}({\mathcal{D}})$
has enough points. Then in the adjunction
$\operatorname{Shv}({\mathcal{D}})$
has enough points. Then in the adjunction
 $$\begin{eqnarray}Lf^{\ast }:\text{SH}({\mathcal{C}})\leftrightarrows \text{SH}({\mathcal{D}}):Rf_{\ast }\end{eqnarray}$$
$$\begin{eqnarray}Lf^{\ast }:\text{SH}({\mathcal{C}})\leftrightarrows \text{SH}({\mathcal{D}}):Rf_{\ast }\end{eqnarray}$$
the left adjoint
![]() $Lf^{\ast }$
is
$Lf^{\ast }$
is
![]() $t$
-exact, the right adjoint
$t$
-exact, the right adjoint
![]() $Rf_{\ast }$
is left
$Rf_{\ast }$
is left
![]() $t$
-exact, and the induced functors
$t$
-exact, and the induced functors
 $$\begin{eqnarray}(Lf^{\ast })^{\heartsuit }:\text{SH}({\mathcal{C}})^{\heartsuit }\leftrightarrows \text{SH}({\mathcal{D}})^{\heartsuit }:(Rf_{\ast })^{\heartsuit }\end{eqnarray}$$
$$\begin{eqnarray}(Lf^{\ast })^{\heartsuit }:\text{SH}({\mathcal{C}})^{\heartsuit }\leftrightarrows \text{SH}({\mathcal{D}})^{\heartsuit }:(Rf_{\ast })^{\heartsuit }\end{eqnarray}$$
coincide (under the identification from Lemma 2) with
![]() $f^{\ast }\vdash f_{\ast }$
.
$f^{\ast }\vdash f_{\ast }$
.
Similar statements hold for
![]() $D$
in place of
$D$
in place of
![]() $\text{SH}$
.
$\text{SH}$
.
The author contends that the assumption that
![]() ${\mathcal{D}}$
has enough points is not really necessary. See also [Reference LurieLur09, Remark 6.5.1.4].
${\mathcal{D}}$
has enough points is not really necessary. See also [Reference LurieLur09, Remark 6.5.1.4].
Proof. Certainly
![]() $Rf_{\ast }$
is left
$Rf_{\ast }$
is left
![]() $t$
-exact if
$t$
-exact if
![]() $Lf^{\ast }$
is
$Lf^{\ast }$
is
![]() $t$
-exact by adjunction, and
$t$
-exact by adjunction, and
![]() $(Rf_{\ast })^{\heartsuit }$
is right adjoint to
$(Rf_{\ast })^{\heartsuit }$
is right adjoint to
![]() $(Lf^{\ast })^{\heartsuit }$
, so it suffices to prove the claims for
$(Lf^{\ast })^{\heartsuit }$
, so it suffices to prove the claims for
![]() $Lf^{\ast }$
.
$Lf^{\ast }$
.
Since
![]() ${\mathcal{D}}$
has enough points, it is then enough to assume that
${\mathcal{D}}$
has enough points, it is then enough to assume that
 $\operatorname{Shv}({\mathcal{D}})=\operatorname{Set}$
. (Indeed let
$\operatorname{Shv}({\mathcal{D}})=\operatorname{Set}$
. (Indeed let
 $p:\operatorname{Set}\rightarrow \operatorname{Shv}({\mathcal{D}})$
be a point; we will have
$p:\operatorname{Set}\rightarrow \operatorname{Shv}({\mathcal{D}})$
be a point; we will have
 $$\begin{eqnarray}p^{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(Lf^{\ast }E)=\unicode[STIX]{x1D70B}_{i}(Lp^{\ast }Lf^{\ast }E)=p^{\ast }f^{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{i}E\end{eqnarray}$$
$$\begin{eqnarray}p^{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(Lf^{\ast }E)=\unicode[STIX]{x1D70B}_{i}(Lp^{\ast }Lf^{\ast }E)=p^{\ast }f^{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{i}E\end{eqnarray}$$
for all
 $E\in \text{SH}({\mathcal{C}})$
by applying the reduced case to
$E\in \text{SH}({\mathcal{C}})$
by applying the reduced case to
![]() $p$
and
$p$
and
![]() $fp$
which are points of
$fp$
which are points of
![]() ${\mathcal{D}}$
and
${\mathcal{D}}$
and
![]() ${\mathcal{C}}$
, respectively. Since
${\mathcal{C}}$
, respectively. Since
![]() ${\mathcal{D}}$
has enough points it follows that
${\mathcal{D}}$
has enough points it follows that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(Lf^{\ast }E)=f^{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)$
, as was to be shown.)
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(Lf^{\ast }E)=f^{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)$
, as was to be shown.)
Let
 $p^{\ast }:\operatorname{Shv}({\mathcal{C}})\leftrightarrows \operatorname{Set}:p_{\ast }$
be a point of
$p^{\ast }:\operatorname{Shv}({\mathcal{C}})\leftrightarrows \operatorname{Set}:p_{\ast }$
be a point of
![]() ${\mathcal{C}}$
. Then
${\mathcal{C}}$
. Then
![]() $p^{\ast }$
corresponds to a pro-object in
$p^{\ast }$
corresponds to a pro-object in
![]() ${\mathcal{C}}$
, which is to say that there is a filtered family
${\mathcal{C}}$
, which is to say that there is a filtered family
![]() $X_{\unicode[STIX]{x1D6FC}}\in {\mathcal{C}}$
such that for
$X_{\unicode[STIX]{x1D6FC}}\in {\mathcal{C}}$
such that for
 $F\in \operatorname{Shv}({\mathcal{C}})$
we have
$F\in \operatorname{Shv}({\mathcal{C}})$
we have
 $p^{\ast }(F)=\operatorname{colim}_{\unicode[STIX]{x1D6FC}}F(X_{\unicode[STIX]{x1D6FC}})$
[Reference Gabber and KellyGK15, Proposition 1.4 and Remark 1.5].
$p^{\ast }(F)=\operatorname{colim}_{\unicode[STIX]{x1D6FC}}F(X_{\unicode[STIX]{x1D6FC}})$
[Reference Gabber and KellyGK15, Proposition 1.4 and Remark 1.5].
It follows that for
 $E\in {\mathcal{S}}{\mathcal{H}}^{\text{s}}({\mathcal{C}})$
we have
$E\in {\mathcal{S}}{\mathcal{H}}^{\text{s}}({\mathcal{C}})$
we have
 $$\begin{eqnarray}\unicode[STIX]{x1D70B}_{i}(p^{\ast }E)=\unicode[STIX]{x1D70B}_{i}(\operatorname{colim}_{\unicode[STIX]{x1D6FC}}E(X_{\unicode[STIX]{x1D6FC}}))\cong \operatorname{colim}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D70B}_{i}(E(X_{\unicode[STIX]{x1D6FC}}))=p^{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E),\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D70B}_{i}(p^{\ast }E)=\unicode[STIX]{x1D70B}_{i}(\operatorname{colim}_{\unicode[STIX]{x1D6FC}}E(X_{\unicode[STIX]{x1D6FC}}))\cong \operatorname{colim}_{\unicode[STIX]{x1D6FC}}\unicode[STIX]{x1D70B}_{i}(E(X_{\unicode[STIX]{x1D6FC}}))=p^{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E),\end{eqnarray}$$
where the isomorphism in the middle holds because homotopy groups commute with filtered colimits of spectra. In particular
![]() $p^{\ast }$
preserves weak equivalences and so
$p^{\ast }$
preserves weak equivalences and so
 $p^{\ast }\simeq Lp^{\ast }$
. Thus the previous equation is precisely what we intended to prove.◻
$p^{\ast }\simeq Lp^{\ast }$
. Thus the previous equation is precisely what we intended to prove.◻
3 Recollections on real étale cohomology
If
![]() $X$
is a scheme, let
$X$
is a scheme, let
![]() $R(X)$
be the set of pairs
$R(X)$
be the set of pairs
![]() $(x,p)$
where
$(x,p)$
where
![]() $x\in X$
and
$x\in X$
and
![]() $p$
is an ordering of the residue field
$p$
is an ordering of the residue field
![]() $k(x)$
. For a ring
$k(x)$
. For a ring
![]() $A$
we put
$A$
we put
 $\operatorname{Sper}(A)=R(\operatorname{Spec}(A))$
. A family of morphisms
$\operatorname{Sper}(A)=R(\operatorname{Spec}(A))$
. A family of morphisms
 $\{\unicode[STIX]{x1D6FC}_{i}:X_{i}\rightarrow X\}_{i\in I}$
is called a real étale covering if each
$\{\unicode[STIX]{x1D6FC}_{i}:X_{i}\rightarrow X\}_{i\in I}$
is called a real étale covering if each
![]() $\unicode[STIX]{x1D6FC}$
is étale and
$\unicode[STIX]{x1D6FC}$
is étale and
 $R(X)=\bigcup _{i}\unicode[STIX]{x1D6FC}(R(X_{i}))$
. (Note that for
$R(X)=\bigcup _{i}\unicode[STIX]{x1D6FC}(R(X_{i}))$
. (Note that for
 $(x,p)\in X_{i}$
the extension
$(x,p)\in X_{i}$
the extension
 $k(x)/k(\unicode[STIX]{x1D6FC}(x))$
defines by restriction an ordering of
$k(x)/k(\unicode[STIX]{x1D6FC}(x))$
defines by restriction an ordering of
 $k(\unicode[STIX]{x1D6FC}(x))$
.) The real étale coverings define a topology on all schemes [Reference ScheidererSch94, (1.1)] called the real étale topology. We often abbreviate this name to ‘rét-topology’.
$k(\unicode[STIX]{x1D6FC}(x))$
.) The real étale coverings define a topology on all schemes [Reference ScheidererSch94, (1.1)] called the real étale topology. We often abbreviate this name to ‘rét-topology’.
For a scheme
![]() $X$
, we let
$X$
, we let
![]() $X_{\text{r}\acute{\text{e}}\text{t}}$
denote the small real étale site on
$X_{\text{r}\acute{\text{e}}\text{t}}$
denote the small real étale site on
![]() $X$
and
$X$
and
 $Sm(X)_{\text{r}\acute{\text{e}}\text{t}}$
the site of smooth (separated, finite type) schemes over
$Sm(X)_{\text{r}\acute{\text{e}}\text{t}}$
the site of smooth (separated, finite type) schemes over
![]() $X$
with the real étale topology. If
$X$
with the real étale topology. If
 $f:X\rightarrow Y$
is any morphism of schemes, we get the usual base change functors
$f:X\rightarrow Y$
is any morphism of schemes, we get the usual base change functors
 $f^{\ast }:Y_{\text{r}\acute{\text{e}}\text{t}}\rightarrow X_{\text{r}\acute{\text{e}}\text{t}}$
and
$f^{\ast }:Y_{\text{r}\acute{\text{e}}\text{t}}\rightarrow X_{\text{r}\acute{\text{e}}\text{t}}$
and
 $f^{\ast }:Sm(Y)\rightarrow Sm(X)$
. Also the natural inclusion
$f^{\ast }:Sm(Y)\rightarrow Sm(X)$
. Also the natural inclusion
 $e:X_{\text{r}\acute{\text{e}}\text{t}}\rightarrow Sm(X)$
induces an adjunction
$e:X_{\text{r}\acute{\text{e}}\text{t}}\rightarrow Sm(X)$
induces an adjunction
 $e^{p}:\operatorname{Pre}(X_{\text{r}\acute{\text{e}}\text{t}})\leftrightarrows \operatorname{Pre}(Sm(X)):r=e_{\ast }$
.
$e^{p}:\operatorname{Pre}(X_{\text{r}\acute{\text{e}}\text{t}})\leftrightarrows \operatorname{Pre}(Sm(X)):r=e_{\ast }$
.
Lemma 5. If
![]() $X$
is a scheme, the above adjunction induces a geometric morphism
$X$
is a scheme, the above adjunction induces a geometric morphism
 $e:\operatorname{Shv}(X_{\text{r}\acute{\text{e}}\text{t}})\leftrightarrows \operatorname{Shv}(Sm(X)_{\text{r}\acute{\text{e}}\text{t}}):r$
where
$e:\operatorname{Shv}(X_{\text{r}\acute{\text{e}}\text{t}})\leftrightarrows \operatorname{Shv}(Sm(X)_{\text{r}\acute{\text{e}}\text{t}}):r$
where
![]() $e$
is fully faithful and
$e$
is fully faithful and
![]() $r$
preserves colimits.
$r$
preserves colimits.
Proof. The functor
![]() $r$
is restriction and
$r$
is restriction and
![]() $e$
is left Kan extension. Since
$e$
is left Kan extension. Since
![]() $e$
preserves covers,
$e$
preserves covers,
![]() $r$
preserves sheaves. Moreover
$r$
preserves sheaves. Moreover
![]() $r$
commutes with taking the associated sheaf, because every cover of
$r$
commutes with taking the associated sheaf, because every cover of
 $Y\in X_{\text{r}\acute{\text{e}}\text{t}}$
in
$Y\in X_{\text{r}\acute{\text{e}}\text{t}}$
in
![]() $Sm(X)$
comes from a cover in
$Sm(X)$
comes from a cover in
![]() $X_{\text{r}\acute{\text{e}}\text{t}}$
(because étale morphisms are stable under composition). It follows that
$X_{\text{r}\acute{\text{e}}\text{t}}$
(because étale morphisms are stable under composition). It follows that
![]() $r$
commutes with colimits. Since
$r$
commutes with colimits. Since
 $e:X_{\text{r}\acute{\text{e}}\text{t}}\rightarrow Sm(X)_{\text{r}\acute{\text{e}}\text{t}}$
preserves pullbacks (and
$e:X_{\text{r}\acute{\text{e}}\text{t}}\rightarrow Sm(X)_{\text{r}\acute{\text{e}}\text{t}}$
preserves pullbacks (and
![]() $X_{\text{r}\acute{\text{e}}\text{t}}$
has pullbacks!), the adjunction is a geometric morphism [Sta17, Tag 00X6]. In order to see that
$X_{\text{r}\acute{\text{e}}\text{t}}$
has pullbacks!), the adjunction is a geometric morphism [Sta17, Tag 00X6]. In order to see that
![]() $e$
is fully faithful, i.e.
$e$
is fully faithful, i.e.
 $F\rightarrow reF$
an isomorphism for every
$F\rightarrow reF$
an isomorphism for every
 $F\in \operatorname{Shv}(X_{\text{r}\acute{\text{e}}\text{t}})$
, we note that for the presheaf adjunction
$F\in \operatorname{Shv}(X_{\text{r}\acute{\text{e}}\text{t}})$
, we note that for the presheaf adjunction
 $e^{p}:\operatorname{Pre}(X_{\text{r}\acute{\text{e}}\text{t}})\leftrightarrows \operatorname{Pre}(Sm(k)):r$
we have
$e^{p}:\operatorname{Pre}(X_{\text{r}\acute{\text{e}}\text{t}})\leftrightarrows \operatorname{Pre}(Sm(k)):r$
we have
 $re^{p}F=F$
. Indeed this holds for
$re^{p}F=F$
. Indeed this holds for
![]() $F$
representable by definition, every sheaf is a colimit of representables, and
$F$
representable by definition, every sheaf is a colimit of representables, and
![]() $e^{p}$
and
$e^{p}$
and
![]() $f$
both commute with taking colimits. Finally note that for a sheaf
$f$
both commute with taking colimits. Finally note that for a sheaf
![]() $F$
we have
$F$
we have
 $eF=a_{\text{r}\acute{\text{e}}\text{t}}e^{p}F$
and thus
$eF=a_{\text{r}\acute{\text{e}}\text{t}}e^{p}F$
and thus
 $reF=ra_{\text{r}\acute{\text{e}}\text{t}}e^{p}F=a_{\text{r}\acute{\text{e}}\text{t}}re^{p}F=a_{\text{r}\acute{\text{e}}\text{t}}F=F$
, where we have used again that
$reF=ra_{\text{r}\acute{\text{e}}\text{t}}e^{p}F=a_{\text{r}\acute{\text{e}}\text{t}}re^{p}F=a_{\text{r}\acute{\text{e}}\text{t}}F=F$
, where we have used again that
![]() $r$
commutes with taking the associated sheaf.◻
$r$
commutes with taking the associated sheaf.◻
Corollary 6. If
![]() $X$
is a scheme, the induced derived functor
$X$
is a scheme, the induced derived functor
 $Le:\text{SH}(X_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \text{SH}(Sm(X)_{\text{r}\acute{\text{e}}\text{t}})$
is
$Le:\text{SH}(X_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \text{SH}(Sm(X)_{\text{r}\acute{\text{e}}\text{t}})$
is
![]() $t$
-exact and fully faithful. Similarly for
$t$
-exact and fully faithful. Similarly for
![]() $D$
in place of
$D$
in place of
![]() $\text{SH}$
.
$\text{SH}$
.
Lemma 7. If
 $f:X\rightarrow Y$
is a morphism of schemes, then the induced functor
$f:X\rightarrow Y$
is a morphism of schemes, then the induced functor
 $f^{\ast }:Y_{\text{r}\acute{\text{e}}\text{t}}\rightarrow X_{\text{r}\acute{\text{e}}\text{t}}$
is the left adjoint of a geometric morphism of sites. Moreover the derived functor
$f^{\ast }:Y_{\text{r}\acute{\text{e}}\text{t}}\rightarrow X_{\text{r}\acute{\text{e}}\text{t}}$
is the left adjoint of a geometric morphism of sites. Moreover the derived functor
 $$\begin{eqnarray}Lf^{\ast }:\text{SH}(Y_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \text{SH}(X_{\text{r}\acute{\text{e}}\text{t}})\end{eqnarray}$$
$$\begin{eqnarray}Lf^{\ast }:\text{SH}(Y_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \text{SH}(X_{\text{r}\acute{\text{e}}\text{t}})\end{eqnarray}$$
is
![]() $t$
-exact, and similarly for
$t$
-exact, and similarly for
 $Lf^{\ast }:D(Y_{\text{r}\acute{\text{e}}\text{t}})\rightarrow D(X_{\text{r}\acute{\text{e}}\text{t}})$
.
$Lf^{\ast }:D(Y_{\text{r}\acute{\text{e}}\text{t}})\rightarrow D(X_{\text{r}\acute{\text{e}}\text{t}})$
.
Proof. The ‘moreover’ part follows from Lemma 4.
Since
 $f^{\ast }:Y_{\text{r}\acute{\text{e}}\text{t}}\rightarrow X_{\text{r}\acute{\text{e}}\text{t}}$
preserves covers
$f^{\ast }:Y_{\text{r}\acute{\text{e}}\text{t}}\rightarrow X_{\text{r}\acute{\text{e}}\text{t}}$
preserves covers
 $f_{\ast }:\operatorname{Pre}(X_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \operatorname{Pre}(Y_{\text{r}\acute{\text{e}}\text{t}})$
preserves sheaves and the morphism is continuous. It is a geometric morphism of sites because
$f_{\ast }:\operatorname{Pre}(X_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \operatorname{Pre}(Y_{\text{r}\acute{\text{e}}\text{t}})$
preserves sheaves and the morphism is continuous. It is a geometric morphism of sites because
![]() $f^{\ast }$
preserves pullbacks [Sta17, Tag 00X6].◻
$f^{\ast }$
preserves pullbacks [Sta17, Tag 00X6].◻
If
![]() $X$
is a scheme, there is the natural map
$X$
is a scheme, there is the natural map
 $X\rightarrow X\times \mathbb{A}^{1}$
corresponding to the point
$X\rightarrow X\times \mathbb{A}^{1}$
corresponding to the point
![]() $0\in \mathbb{A}^{1}$
. Similarly there is the natural map
$0\in \mathbb{A}^{1}$
. Similarly there is the natural map
 $X\coprod X\rightarrow X\times (\mathbb{A}^{1}\setminus 0)$
corresponding to the points
$X\coprod X\rightarrow X\times (\mathbb{A}^{1}\setminus 0)$
corresponding to the points
 $\pm 1\in \mathbb{A}^{1}\setminus 0$
.
$\pm 1\in \mathbb{A}^{1}\setminus 0$
.
Theorem 8. Let
![]() $X$
be a scheme and
$X$
be a scheme and
 $F\in \operatorname{Shv}(X_{\text{r}\acute{\text{e}}\text{t}})$
. Then for any
$F\in \operatorname{Shv}(X_{\text{r}\acute{\text{e}}\text{t}})$
. Then for any
![]() $p\geqslant 0$
the natural maps
$p\geqslant 0$
the natural maps
 $X\rightarrow X\times \mathbb{A}^{1}$
and
$X\rightarrow X\times \mathbb{A}^{1}$
and
 $X\coprod X\rightarrow X\times (\mathbb{A}^{1}\setminus 0)$
induce isomorphisms
$X\coprod X\rightarrow X\times (\mathbb{A}^{1}\setminus 0)$
induce isomorphisms
 $$\begin{eqnarray}\displaystyle & H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X\times \mathbb{A}^{1},F)\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X,F) & \displaystyle \nonumber\\ \displaystyle & H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X\times (\mathbb{A}^{1}\setminus 0),F)\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X,F)\oplus H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X,F). & \displaystyle \nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X\times \mathbb{A}^{1},F)\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X,F) & \displaystyle \nonumber\\ \displaystyle & H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X\times (\mathbb{A}^{1}\setminus 0),F)\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X,F)\oplus H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X,F). & \displaystyle \nonumber\end{eqnarray}$$
Proof. The first statement is homotopy invariance, see [Reference ScheidererSch94, Example 16.7.2].
For the second statement, we follow closely that proof. Let
 $f:X\coprod X\rightarrow X\times (\mathbb{A}^{1}\setminus 0)$
be the canonical map. It suffices to show that
$f:X\coprod X\rightarrow X\times (\mathbb{A}^{1}\setminus 0)$
be the canonical map. It suffices to show that
 $R^{n}f_{\ast }F=0$
for
$R^{n}f_{\ast }F=0$
for
![]() $n>0$
and
$n>0$
and
 $R^{0}f_{\ast }F=F$
, where we identify
$R^{0}f_{\ast }F=F$
, where we identify
![]() $F$
with its pullback to
$F$
with its pullback to
![]() $X\coprod X$
and
$X\coprod X$
and
 $X\times (\mathbb{A}^{1}\setminus 0)$
for notational convenience. All of these statements are local on
$X\times (\mathbb{A}^{1}\setminus 0)$
for notational convenience. All of these statements are local on
![]() $X$
, so we may assume that
$X$
, so we may assume that
![]() $X$
is affine.
$X$
is affine.
Then one may assume that
![]() $F$
is constructible (since
$F$
is constructible (since
![]() $\text{r}\acute{\text{e}}\text{t}$
-cohomology commutes with filtered colimits of sheaves, and all sheaves on a spectral space are filtered colimits of constructible sheaves; see again [Reference ScheidererSch94, Example 16.7.2]). Next, writing
$\text{r}\acute{\text{e}}\text{t}$
-cohomology commutes with filtered colimits of sheaves, and all sheaves on a spectral space are filtered colimits of constructible sheaves; see again [Reference ScheidererSch94, Example 16.7.2]). Next, writing
 $X=\operatorname{Spec}(A)$
as the inverse limit of the filtering system
$X=\operatorname{Spec}(A)$
as the inverse limit of the filtering system
 $\operatorname{Spec}(A^{\prime })$
, with
$\operatorname{Spec}(A^{\prime })$
, with
![]() $A^{\prime }\subset A$
finitely generated over
$A^{\prime }\subset A$
finitely generated over
![]() $\mathbb{Z}$
, and using Proposition (A.9) of [Reference ScheidererSch94, Example 16.7.2], we may assume that
$\mathbb{Z}$
, and using Proposition (A.9) of [Reference ScheidererSch94, Example 16.7.2], we may assume that
![]() $X$
is of finite type over
$X$
is of finite type over
![]() $\mathbb{Z}$
.
$\mathbb{Z}$
.
But
 $\operatorname{Sper}(\mathbb{Z})=\operatorname{Sper}(\mathbb{Q})=\operatorname{Sper}(\mathbb{R})$
, whence
$\operatorname{Sper}(\mathbb{Z})=\operatorname{Sper}(\mathbb{Q})=\operatorname{Sper}(\mathbb{R})$
, whence
 $H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X,F)=H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X\times _{\mathbb{Z}}\mathbb{R},F)$
, so we may assume that
$H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X,F)=H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X\times _{\mathbb{Z}}\mathbb{R},F)$
, so we may assume that
![]() $X$
is of finite type over
$X$
is of finite type over
![]() $\mathbb{R}$
.
$\mathbb{R}$
.
We may further assume that
 $F=M_{Z}$
is the constant sheaf on a closed, constructible subset of
$F=M_{Z}$
is the constant sheaf on a closed, constructible subset of
![]() $X$
(Proposition (A.6) of [Reference ScheidererSch94, Example 16.7.2]).
$X$
(Proposition (A.6) of [Reference ScheidererSch94, Example 16.7.2]).
It is thus enough to prove the analog of our result for an affine semi-algebraic space
![]() $X$
over
$X$
over
![]() $\mathbb{R}$
and
$\mathbb{R}$
and
![]() $F=M$
a constant sheaf. But then
$F=M$
a constant sheaf. But then
 $H_{\text{r}\acute{\text{e}}\text{t}}^{\ast }(X,M)=H_{\text{sing}}^{\ast }(X(\mathbb{R}),M)$
[Reference DelfsDel91, Theorem II.5.7] and so on, so this is obvious.◻
$H_{\text{r}\acute{\text{e}}\text{t}}^{\ast }(X,M)=H_{\text{sing}}^{\ast }(X(\mathbb{R}),M)$
[Reference DelfsDel91, Theorem II.5.7] and so on, so this is obvious.◻
Theorem 9 (Proper base change).
Consider a cartesian square of schemes

with
![]() $f$
proper and
$f$
proper and
![]() $Y$
finite-dimensional Noetherian. Then for any
$Y$
finite-dimensional Noetherian. Then for any
 $E\in \text{SH}(X_{\text{r}\acute{\text{e}}\text{t}})$
(respectively
$E\in \text{SH}(X_{\text{r}\acute{\text{e}}\text{t}})$
(respectively
 $E\in D(X_{\text{r}\acute{\text{e}}\text{t}})$
) the canonical map
$E\in D(X_{\text{r}\acute{\text{e}}\text{t}})$
) the canonical map
 $$\begin{eqnarray}g^{\ast }Rf_{\ast }(E)\rightarrow Rf_{\ast }^{\prime }{g^{\prime }}^{\ast }(E)\end{eqnarray}$$
$$\begin{eqnarray}g^{\ast }Rf_{\ast }(E)\rightarrow Rf_{\ast }^{\prime }{g^{\prime }}^{\ast }(E)\end{eqnarray}$$
is a weak equivalence.
Proof. We prove the claim for
![]() $\text{SH}$
, the proof we give will work just as well for
$\text{SH}$
, the proof we give will work just as well for
![]() $D$
. We proceed in several steps.
$D$
. We proceed in several steps.
Step 0. If
![]() $g$
is étale, then the claim follows from the observation that
$g$
is étale, then the claim follows from the observation that
 $f^{\ast }g_{\#}=g_{\#}^{\prime }{f^{\prime }}^{\ast }$
.
$f^{\ast }g_{\#}=g_{\#}^{\prime }{f^{\prime }}^{\ast }$
.
Step 1. If
 $f:X\rightarrow Y$
is any morphism and
$f:X\rightarrow Y$
is any morphism and
 $E\in \text{SH}(X_{\text{r}\acute{\text{e}}\text{t}})$
, then there is a conditionally convergent spectral sequence
$E\in \text{SH}(X_{\text{r}\acute{\text{e}}\text{t}})$
, then there is a conditionally convergent spectral sequence
 $$\begin{eqnarray}E_{2}^{pq}=R^{p}f_{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}E\Rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{-p-q}(Rf_{\ast }E).\end{eqnarray}$$
$$\begin{eqnarray}E_{2}^{pq}=R^{p}f_{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}E\Rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{-p-q}(Rf_{\ast }E).\end{eqnarray}$$
For this, let
 $E\in \operatorname{Spt}(X_{\text{r}\acute{\text{e}}\text{t}})$
also denote a fibrant model. Then
$E\in \operatorname{Spt}(X_{\text{r}\acute{\text{e}}\text{t}})$
also denote a fibrant model. Then
 $Rf_{\ast }E\simeq f_{\ast }E$
and for
$Rf_{\ast }E\simeq f_{\ast }E$
and for
 $U\in Y_{\text{r}\acute{\text{e}}\text{t}}$
we have
$U\in Y_{\text{r}\acute{\text{e}}\text{t}}$
we have
 $f_{\ast }(E)(U)=E(f^{\ast }U)$
. Since
$f_{\ast }(E)(U)=E(f^{\ast }U)$
. Since
![]() $E$
is fibrant there is a conditionally convergent descent spectral sequence
$E$
is fibrant there is a conditionally convergent descent spectral sequence
 $$\begin{eqnarray}H^{p}(f^{\ast }U,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E))\Rightarrow \unicode[STIX]{x1D70B}_{-p-q}(E(f^{\ast }U)).\end{eqnarray}$$
$$\begin{eqnarray}H^{p}(f^{\ast }U,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E))\Rightarrow \unicode[STIX]{x1D70B}_{-p-q}(E(f^{\ast }U)).\end{eqnarray}$$
By varying
![]() $U$
, this yields a presheaf of spectral sequences on
$U$
, this yields a presheaf of spectral sequences on
![]() $Y_{\text{r}\acute{\text{e}}\text{t}}$
. Equivalently, this is a spectral sequence of presheaves. Taking the associated sheaf on both sides we obtain a conditionally convergent spectral sequence
$Y_{\text{r}\acute{\text{e}}\text{t}}$
. Equivalently, this is a spectral sequence of presheaves. Taking the associated sheaf on both sides we obtain a conditionally convergent spectral sequence
 $$\begin{eqnarray}a_{\text{r}\acute{\text{e}}\text{t}}H_{\text{r}\acute{\text{e}}\text{t}}^{p}(f^{\ast }\bullet ,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E))\Rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{-p-q}(f_{\ast }E).\end{eqnarray}$$
$$\begin{eqnarray}a_{\text{r}\acute{\text{e}}\text{t}}H_{\text{r}\acute{\text{e}}\text{t}}^{p}(f^{\ast }\bullet ,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E))\Rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{-p-q}(f_{\ast }E).\end{eqnarray}$$
It remains to see that
 $a_{\text{r}\acute{\text{e}}\text{t}}H_{\text{r}\acute{\text{e}}\text{t}}^{p}(f^{\ast }\bullet ,F)=R^{p}f_{\ast }F$
, for any sheaf
$a_{\text{r}\acute{\text{e}}\text{t}}H_{\text{r}\acute{\text{e}}\text{t}}^{p}(f^{\ast }\bullet ,F)=R^{p}f_{\ast }F$
, for any sheaf
![]() $F$
on
$F$
on
![]() $X_{\text{r}\acute{\text{e}}\text{t}}$
. For this we view
$X_{\text{r}\acute{\text{e}}\text{t}}$
. For this we view
 $F\in D(X_{\text{r}\acute{\text{e}}\text{t}})^{\heartsuit }$
. Then by definition
$F\in D(X_{\text{r}\acute{\text{e}}\text{t}})^{\heartsuit }$
. Then by definition
 $R^{p}f_{\ast }F=\text{}\underline{\unicode[STIX]{x1D70B}}_{-p}Rf_{\ast }F$
. Repeating the above argument with
$R^{p}f_{\ast }F=\text{}\underline{\unicode[STIX]{x1D70B}}_{-p}Rf_{\ast }F$
. Repeating the above argument with
 $D(X_{\text{r}\acute{\text{e}}\text{t}})$
in place of
$D(X_{\text{r}\acute{\text{e}}\text{t}})$
in place of
 $\text{SH}(X_{\text{r}\acute{\text{e}}\text{t}})$
, we obtain a conditionally convergent spectral sequence
$\text{SH}(X_{\text{r}\acute{\text{e}}\text{t}})$
, we obtain a conditionally convergent spectral sequence
 $$\begin{eqnarray}a_{\text{r}\acute{\text{e}}\text{t}}H_{\text{r}\acute{\text{e}}\text{t}}^{p}(f^{\ast }\bullet ,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}F)\Rightarrow R^{p+q}f_{\ast }F.\end{eqnarray}$$
$$\begin{eqnarray}a_{\text{r}\acute{\text{e}}\text{t}}H_{\text{r}\acute{\text{e}}\text{t}}^{p}(f^{\ast }\bullet ,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}F)\Rightarrow R^{p+q}f_{\ast }F.\end{eqnarray}$$
Since
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}F=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}F=0$
for
![]() $q\neq 0$
this spectral sequence converges strongly, yielding the desired identification.
$q\neq 0$
this spectral sequence converges strongly, yielding the desired identification.
Step 2. If
![]() $f$
is proper and of relative dimension at most
$f$
is proper and of relative dimension at most
![]() $n$
, then for
$n$
, then for
 $F\in \operatorname{Shv}(X_{\text{r}\acute{\text{e}}\text{t}})$
and
$F\in \operatorname{Shv}(X_{\text{r}\acute{\text{e}}\text{t}})$
and
![]() $p>n$
we have
$p>n$
we have
 $R^{p}f_{\ast }F=0$
.
$R^{p}f_{\ast }F=0$
.
Indeed in this situation, by the proper base change theorem in real étale cohomology [Reference ScheidererSch94, Theorem 16.2], for any real closed point
![]() $y\rightarrow Y$
we get
$y\rightarrow Y$
we get
 $(R^{p}f_{\ast }F)_{y}=H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X_{y},F|_{X_{y}})$
. Since real closed fields are the stalks of the rét-topology, in order for a sheaf
$(R^{p}f_{\ast }F)_{y}=H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X_{y},F|_{X_{y}})$
. Since real closed fields are the stalks of the rét-topology, in order for a sheaf
 $G\in \operatorname{Shv}(Y_{\text{r}\acute{\text{e}}\text{t}})$
to be zero it is necessary and sufficient that
$G\in \operatorname{Shv}(Y_{\text{r}\acute{\text{e}}\text{t}})$
to be zero it is necessary and sufficient that
![]() $G_{y}=0$
for all such
$G_{y}=0$
for all such
![]() $y$
. But real étale cohomological dimension is bounded by Krull dimension [Reference ScheidererSch94, Theorem 7.6], so we find that
$y$
. But real étale cohomological dimension is bounded by Krull dimension [Reference ScheidererSch94, Theorem 7.6], so we find that
 $R^{p}f_{\ast }F=0$
for
$R^{p}f_{\ast }F=0$
for
![]() $p>n$
, as claimed.
$p>n$
, as claimed.
Conclusion of proof. Since isomorphism in
 $\text{SH}(Y_{\text{r}\acute{\text{e}}\text{t}}^{\prime })$
is local on
$\text{SH}(Y_{\text{r}\acute{\text{e}}\text{t}}^{\prime })$
is local on
![]() $Y^{\prime }$
, it is an easy consequence of step 0 that we may assume that
$Y^{\prime }$
, it is an easy consequence of step 0 that we may assume that
![]() $Y^{\prime }$
is quasi-compact (e.g. affine). Then
$Y^{\prime }$
is quasi-compact (e.g. affine). Then
![]() $f^{\prime }$
is of bounded relative dimension (being of finite type).
$f^{\prime }$
is of bounded relative dimension (being of finite type).
Now let
 $E\in \text{SH}(X_{\text{r}\acute{\text{e}}\text{t}})$
. By
$E\in \text{SH}(X_{\text{r}\acute{\text{e}}\text{t}})$
. By
![]() $t$
-exactness of
$t$
-exactness of
![]() $g^{\ast }$
and
$g^{\ast }$
and
![]() ${g^{\prime }}^{\ast }$
we get from step 1 conditionally convergent spectral sequences
${g^{\prime }}^{\ast }$
we get from step 1 conditionally convergent spectral sequences
 $$\begin{eqnarray}g^{\ast }R^{p}f_{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}E\Rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{-p-q}(g^{\ast }Rf_{\ast }E)\end{eqnarray}$$
$$\begin{eqnarray}g^{\ast }R^{p}f_{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}E\Rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{-p-q}(g^{\ast }Rf_{\ast }E)\end{eqnarray}$$
and
 $$\begin{eqnarray}R^{p}f_{\ast }^{\prime }{g^{\prime }}^{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}E\Rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{-p-q}(Rf_{\ast }^{\prime }{g^{\prime }}^{\ast }E).\end{eqnarray}$$
$$\begin{eqnarray}R^{p}f_{\ast }^{\prime }{g^{\prime }}^{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}E\Rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{-p-q}(Rf_{\ast }^{\prime }{g^{\prime }}^{\ast }E).\end{eqnarray}$$
The exchange transformation
 $g^{\ast }Rf_{\ast }(E)\rightarrow Rf_{\ast }^{\prime }{g^{\prime }}^{\ast }(E)$
induces a morphism of spectral sequences (i.e. respecting the differentials and filtrations). By proper base change for sheaves, we have
$g^{\ast }Rf_{\ast }(E)\rightarrow Rf_{\ast }^{\prime }{g^{\prime }}^{\ast }(E)$
induces a morphism of spectral sequences (i.e. respecting the differentials and filtrations). By proper base change for sheaves, we have
 $g^{\ast }R^{p}f_{\ast }\cong R^{p}f_{\ast }^{\prime }{g^{\prime }}^{\ast }$
. Thus the two spectral sequences are isomorphic. By step 2 the second one converges strongly, and hence so does the first. Thus the result follows from spectral sequence comparison.◻
$g^{\ast }R^{p}f_{\ast }\cong R^{p}f_{\ast }^{\prime }{g^{\prime }}^{\ast }$
. Thus the two spectral sequences are isomorphic. By step 2 the second one converges strongly, and hence so does the first. Thus the result follows from spectral sequence comparison.◻
Remark.
The only place in the above proof where we have used the assumption on
![]() $Y$
is in step 1, namely in the construction of the conditionally convergent spectral sequence
$Y$
is in step 1, namely in the construction of the conditionally convergent spectral sequence
 $$\begin{eqnarray}R^{p}f_{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}E\Rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{-p-q}(Rf_{\ast }E).\end{eqnarray}$$
$$\begin{eqnarray}R^{p}f_{\ast }\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}E\Rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{-p-q}(Rf_{\ast }E).\end{eqnarray}$$
The author does not know how to construct such a spectral sequence in general. He nonetheless contends that the proper base change theorem should be true without assumptions on
![]() $Y$
, but perhaps a different proof is needed.
$Y$
, but perhaps a different proof is needed.
Remark.
In the above proof we deduce proper base change for spectra and unbounded complexes from proper base change for bounded complexes. Since we are dealing with hypercomplete toposes, this is not tautological; see for example [Reference LurieLur09, Counterexample 6.5.4.2 and Remark 6.5.4.3]. The crucial property which seems to make the proof work is encapsulated in step 2 and might be phrased as ‘a proper morphism is locally of finite relative rét-cohomological dimension’. The same is true in étale (instead of real étale) cohomology and this seems to be what the proof of proper base change for unbounded étale complexes [Reference Cisinski and DégliseCD13, Theorem 1.2.1] ultimately rests on, in the guise of [Reference Cisinski and DégliseCD13, Lemma 1.1.7]. This fails for a general proper morphism of topological spaces (consider for example an infinite product of compact positive dimensional spaces mapping to the point).
4 Recollections on motivic homotopy theory
We denote the stable motivic homotopy category over a base scheme
![]() $X$
[Reference AyoubAyo07] by
$X$
[Reference AyoubAyo07] by
![]() $\mathbf{SH}(X)$
, and the stable
$\mathbf{SH}(X)$
, and the stable
![]() $\mathbb{A}^{1}$
-derived category over
$\mathbb{A}^{1}$
-derived category over
![]() $X$
[Reference Cisinski and DégliseCD12, § 5.3] by
$X$
[Reference Cisinski and DégliseCD12, § 5.3] by
 $D_{\mathbb{A}^{1}}(X)$
. We write
$D_{\mathbb{A}^{1}}(X)$
. We write
 $\unicode[STIX]{x1D7D9}_{X}\in \mathbf{SH}(X)$
for the monoidal unit. If the context is clear we may just write
$\unicode[STIX]{x1D7D9}_{X}\in \mathbf{SH}(X)$
for the monoidal unit. If the context is clear we may just write
![]() $\unicode[STIX]{x1D7D9}$
.
$\unicode[STIX]{x1D7D9}$
.
Let
 $f:Y\rightarrow X$
be a finite étale morphism of schemes. Then in the category
$f:Y\rightarrow X$
be a finite étale morphism of schemes. Then in the category
![]() $\mathbf{SH}(X)$
we have an induced morphism
$\mathbf{SH}(X)$
we have an induced morphism
 $f:f_{\#}\unicode[STIX]{x1D7D9}_{Y}\rightarrow \unicode[STIX]{x1D7D9}_{X}$
and consequently
$f:f_{\#}\unicode[STIX]{x1D7D9}_{Y}\rightarrow \unicode[STIX]{x1D7D9}_{X}$
and consequently
 $D(f):D(\unicode[STIX]{x1D7D9}_{X})\rightarrow D(f_{\#}\unicode[STIX]{x1D7D9}_{Y})$
. Here
$D(f):D(\unicode[STIX]{x1D7D9}_{X})\rightarrow D(f_{\#}\unicode[STIX]{x1D7D9}_{Y})$
. Here
 $DE:=\text{}\underline{\operatorname{Hom}}(E,\unicode[STIX]{x1D7D9})$
. Now in fact whenever
$DE:=\text{}\underline{\operatorname{Hom}}(E,\unicode[STIX]{x1D7D9})$
. Now in fact whenever
 $f:Y\rightarrow X$
is smooth proper then
$f:Y\rightarrow X$
is smooth proper then
 $D(f_{\#}\unicode[STIX]{x1D7D9}_{Y})\simeq f_{\ast }\unicode[STIX]{x1D7D9}_{Y}$
[Reference Cisinski and DégliseCD12, Proposition 2.4.31] and if
$D(f_{\#}\unicode[STIX]{x1D7D9}_{Y})\simeq f_{\ast }\unicode[STIX]{x1D7D9}_{Y}$
[Reference Cisinski and DégliseCD12, Proposition 2.4.31] and if
![]() $f$
is étale then
$f$
is étale then
 $f_{\ast }(\unicode[STIX]{x1D7D9}_{Y})\simeq f_{\#}(\unicode[STIX]{x1D7D9}_{Y})$
[Reference Cisinski and DégliseCD12, Example 2.4.3(2), Definition 2.4.24 and Proposition 2.4.31]. Let us write
$f_{\ast }(\unicode[STIX]{x1D7D9}_{Y})\simeq f_{\#}(\unicode[STIX]{x1D7D9}_{Y})$
[Reference Cisinski and DégliseCD12, Example 2.4.3(2), Definition 2.4.24 and Proposition 2.4.31]. Let us write
 $\unicode[STIX]{x1D6FC}_{X,Y}:f_{\#}\unicode[STIX]{x1D7D9}_{Y}\rightarrow D(f_{\#}\unicode[STIX]{x1D7D9}_{Y})$
for this canonical isomorphism. We can then form the commutative diagram
$\unicode[STIX]{x1D6FC}_{X,Y}:f_{\#}\unicode[STIX]{x1D7D9}_{Y}\rightarrow D(f_{\#}\unicode[STIX]{x1D7D9}_{Y})$
for this canonical isomorphism. We can then form the commutative diagram

where
![]() $\text{tr}_{f}$
is defined so that the diagram commutes. This is the duality transfer of
$\text{tr}_{f}$
is defined so that the diagram commutes. This is the duality transfer of
![]() $f$
as defined in [Reference Röndigs and ØstværRØ08, § 2.3].
$f$
as defined in [Reference Röndigs and ØstværRØ08, § 2.3].
Now suppose that
![]() $k$
is a perfect field. Recall that then
$k$
is a perfect field. Recall that then
![]() $\mathbf{SH}(k)$
has a
$\mathbf{SH}(k)$
has a
![]() $t$
-structure. To define it, for
$t$
-structure. To define it, for
 $E\in \mathbf{SH}(k)$
denote by
$E\in \mathbf{SH}(k)$
denote by
![]() $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{j}$
the Nisnevich sheaf associated with the presheaf
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{j}$
the Nisnevich sheaf associated with the presheaf
 $X\mapsto [\unicode[STIX]{x1D6F4}^{\infty }X_{+}[i],E\wedge \mathbb{G}_{m}^{\wedge j}]$
. Then
$X\mapsto [\unicode[STIX]{x1D6F4}^{\infty }X_{+}[i],E\wedge \mathbb{G}_{m}^{\wedge j}]$
. Then
 $E\in \mathbf{SH}(k)_{{\geqslant}0}$
if and only if
$E\in \mathbf{SH}(k)_{{\geqslant}0}$
if and only if
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{j}=0$
for all
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)_{j}=0$
for all
![]() $i<0$
and all
$i<0$
and all
![]() $j\in \mathbb{Z}$
. This indeed defines a
$j\in \mathbb{Z}$
. This indeed defines a
![]() $t$
-structure [Reference MorelMor03, § 5.2], and then its heart can be described explicitly: it is equivalent to the category of homotopy modules [Reference MorelMor03, Theorem 5.2.6].
$t$
-structure [Reference MorelMor03, § 5.2], and then its heart can be described explicitly: it is equivalent to the category of homotopy modules [Reference MorelMor03, Theorem 5.2.6].
Let
 $F_{\ast }\in \mathbf{SH}(k)$
is a homotopy module, which we identify with an element in the heart of the homotopy
$F_{\ast }\in \mathbf{SH}(k)$
is a homotopy module, which we identify with an element in the heart of the homotopy
![]() $t$
-structure. Given a finite étale morphism
$t$
-structure. Given a finite étale morphism
 $f:Y\rightarrow X$
of essentially
$f:Y\rightarrow X$
of essentially
![]() $k$
-smooth schemes, write
$k$
-smooth schemes, write
 $s:X\rightarrow \operatorname{Spec}(k)$
for the structure map. We then define
$s:X\rightarrow \operatorname{Spec}(k)$
for the structure map. We then define
 $\text{tr}_{f}:F_{n}(Y)\rightarrow F_{n}(X)$
as
$\text{tr}_{f}:F_{n}(Y)\rightarrow F_{n}(X)$
as
 $$\begin{eqnarray}\text{tr}_{f}(F):=\text{tr}_{f}^{\ast }:[f_{\#}\unicode[STIX]{x1D7D9}_{Y},s^{\ast }F\wedge \mathbb{G}_{m}^{\wedge n}]\rightarrow [\unicode[STIX]{x1D7D9}_{X},s^{\ast }F\wedge \mathbb{G}_{m}^{\wedge n}].\end{eqnarray}$$
$$\begin{eqnarray}\text{tr}_{f}(F):=\text{tr}_{f}^{\ast }:[f_{\#}\unicode[STIX]{x1D7D9}_{Y},s^{\ast }F\wedge \mathbb{G}_{m}^{\wedge n}]\rightarrow [\unicode[STIX]{x1D7D9}_{X},s^{\ast }F\wedge \mathbb{G}_{m}^{\wedge n}].\end{eqnarray}$$
This transfer has the usual properties, of which we recall two.
Proposition 10 (Base change).
Let
![]() $k$
be a perfect field,
$k$
be a perfect field,
 $g:V\rightarrow X$
be a morphism of essentially
$g:V\rightarrow X$
be a morphism of essentially
![]() $k$
-smooth schemes and
$k$
-smooth schemes and
 $f:Y\rightarrow X$
finite étale. Consider the following cartesian square.
$f:Y\rightarrow X$
finite étale. Consider the following cartesian square.

Then for any homotopy module
![]() $F_{\ast }$
, we have
$F_{\ast }$
, we have
 $g^{\ast }\text{tr}_{f}=\text{tr}_{p}q^{\ast }:F_{\ast }(Y)\rightarrow F_{\ast }(V)$
.
$g^{\ast }\text{tr}_{f}=\text{tr}_{p}q^{\ast }:F_{\ast }(Y)\rightarrow F_{\ast }(V)$
.
Proof. Note that
 $p:W\rightarrow V$
is finite étale, so this makes sense. By continuity (of
$p:W\rightarrow V$
is finite étale, so this makes sense. By continuity (of
![]() $F$
), we may assume that
$F$
), we may assume that
![]() $X$
and
$X$
and
![]() $V$
are smooth (and hence so are
$V$
are smooth (and hence so are
![]() $Y$
and
$Y$
and
![]() $W$
). Write
$W$
). Write
 $s:X\rightarrow \operatorname{Spec}(k)$
for the structure map.
$s:X\rightarrow \operatorname{Spec}(k)$
for the structure map.
If
 $t:A\rightarrow B$
is any map in
$t:A\rightarrow B$
is any map in
![]() $\mathbf{SH}(X)$
, then the canonical diagram
$\mathbf{SH}(X)$
, then the canonical diagram

commutes, since
![]() $g^{\ast }$
is a functor. Applying this to
$g^{\ast }$
is a functor. Applying this to
 $\text{tr}_{f}:\unicode[STIX]{x1D7D9}_{X}\rightarrow f_{\#}\unicode[STIX]{x1D7D9}_{Y}$
it is enough to prove that
$\text{tr}_{f}:\unicode[STIX]{x1D7D9}_{X}\rightarrow f_{\#}\unicode[STIX]{x1D7D9}_{Y}$
it is enough to prove that
 $g^{\ast }(\text{tr}_{f})=\text{tr}_{p}$
under the canonical identifications.
$g^{\ast }(\text{tr}_{f})=\text{tr}_{p}$
under the canonical identifications.
Let
 $f_{+}:f_{\#}\unicode[STIX]{x1D7D9}_{Y}\simeq \unicode[STIX]{x1D6F4}_{X}^{\infty }Y_{+}\rightarrow \unicode[STIX]{x1D6F4}_{X}^{\infty }X_{+}=\unicode[STIX]{x1D7D9}_{X}$
be the canonical map (so that
$f_{+}:f_{\#}\unicode[STIX]{x1D7D9}_{Y}\simeq \unicode[STIX]{x1D6F4}_{X}^{\infty }Y_{+}\rightarrow \unicode[STIX]{x1D6F4}_{X}^{\infty }X_{+}=\unicode[STIX]{x1D7D9}_{X}$
be the canonical map (so that
 $\text{tr}_{f}=D(f_{+})$
via
$\text{tr}_{f}=D(f_{+})$
via
![]() $\unicode[STIX]{x1D6FC}_{X,Y}$
), and similarly for
$\unicode[STIX]{x1D6FC}_{X,Y}$
), and similarly for
![]() $p_{+}$
. Then
$p_{+}$
. Then
 $g^{\ast }(f_{+})\simeq p_{+}$
and consequently
$g^{\ast }(f_{+})\simeq p_{+}$
and consequently
 $g^{\ast }(D(f_{+}))\simeq D(p_{+})$
. It thus remains to show that
$g^{\ast }(D(f_{+}))\simeq D(p_{+})$
. It thus remains to show that
![]() $\unicode[STIX]{x1D6FC}_{\bullet ,\bullet }$
is natural, i.e. that
$\unicode[STIX]{x1D6FC}_{\bullet ,\bullet }$
is natural, i.e. that
 $g^{\ast }\unicode[STIX]{x1D6FC}_{X,Y}=\unicode[STIX]{x1D6FC}_{V,W}:\unicode[STIX]{x1D6F4}_{V}^{\infty }W_{+}\rightarrow D(\unicode[STIX]{x1D6F4}_{V}^{\infty }W_{+})$
.
$g^{\ast }\unicode[STIX]{x1D6FC}_{X,Y}=\unicode[STIX]{x1D6FC}_{V,W}:\unicode[STIX]{x1D6F4}_{V}^{\infty }W_{+}\rightarrow D(\unicode[STIX]{x1D6F4}_{V}^{\infty }W_{+})$
.
For this we use the notation of [Reference Cisinski and DégliseCD12, Example 2.4.3(2), Definition 2.4.24 and Proposition 2.4.31]. The isomorphism
 $\unicode[STIX]{x1D6FC}_{X,Y}:f_{\#}\unicode[STIX]{x1D7D9}\rightarrow D(f_{\#}\unicode[STIX]{x1D7D9})$
is factored into the isomorphisms
$\unicode[STIX]{x1D6FC}_{X,Y}:f_{\#}\unicode[STIX]{x1D7D9}\rightarrow D(f_{\#}\unicode[STIX]{x1D7D9})$
is factored into the isomorphisms
 $D(f_{\#}\unicode[STIX]{x1D7D9})\rightarrow f_{\ast }\unicode[STIX]{x1D7D9}$
, the Thom transformation
$D(f_{\#}\unicode[STIX]{x1D7D9})\rightarrow f_{\ast }\unicode[STIX]{x1D7D9}$
, the Thom transformation
 $f_{\#}\unicode[STIX]{x1D6FA}_{f}\unicode[STIX]{x1D7D9}\rightarrow f_{\ast }\unicode[STIX]{x1D7D9}$
[Reference Cisinski and DégliseCD12, Definition 2.4.21] and
$f_{\#}\unicode[STIX]{x1D6FA}_{f}\unicode[STIX]{x1D7D9}\rightarrow f_{\ast }\unicode[STIX]{x1D7D9}$
[Reference Cisinski and DégliseCD12, Definition 2.4.21] and
 $\unicode[STIX]{x1D6FA}_{f}\unicode[STIX]{x1D7D9}\rightarrow \unicode[STIX]{x1D7D9}$
. All of these are natural in the required sense.◻
$\unicode[STIX]{x1D6FA}_{f}\unicode[STIX]{x1D7D9}\rightarrow \unicode[STIX]{x1D7D9}$
. All of these are natural in the required sense.◻
Lemma 11 (Commutation of transfer with external product).
Let
 $f:X^{\prime }\rightarrow X$
and
$f:X^{\prime }\rightarrow X$
and
 $g:Y^{\prime }\rightarrow Y$
be finite étale. Then
$g:Y^{\prime }\rightarrow Y$
be finite étale. Then
 $$\begin{eqnarray}\displaystyle s_{X\times Y\#}(\text{tr}_{f\times g}) & = & \displaystyle s_{X\#}(\text{tr}_{f})\wedge s_{Y\#}(\text{tr}_{g}):\unicode[STIX]{x1D6F4}^{\infty }(X^{\prime }\times Y^{\prime })_{+}\simeq \unicode[STIX]{x1D6F4}^{\infty }X_{+}^{\prime }\wedge \unicode[STIX]{x1D6F4}^{\infty }Y_{+}^{\prime }\nonumber\\ \displaystyle & \rightarrow & \displaystyle \unicode[STIX]{x1D6F4}^{\infty }(X\times Y)_{+}\simeq \unicode[STIX]{x1D6F4}^{\infty }X_{+}\wedge \unicode[STIX]{x1D6F4}^{\infty }Y_{+}.\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle s_{X\times Y\#}(\text{tr}_{f\times g}) & = & \displaystyle s_{X\#}(\text{tr}_{f})\wedge s_{Y\#}(\text{tr}_{g}):\unicode[STIX]{x1D6F4}^{\infty }(X^{\prime }\times Y^{\prime })_{+}\simeq \unicode[STIX]{x1D6F4}^{\infty }X_{+}^{\prime }\wedge \unicode[STIX]{x1D6F4}^{\infty }Y_{+}^{\prime }\nonumber\\ \displaystyle & \rightarrow & \displaystyle \unicode[STIX]{x1D6F4}^{\infty }(X\times Y)_{+}\simeq \unicode[STIX]{x1D6F4}^{\infty }X_{+}\wedge \unicode[STIX]{x1D6F4}^{\infty }Y_{+}.\nonumber\end{eqnarray}$$
Here we write
 $s_{X}:X\rightarrow \operatorname{Spec}(k)$
for the canonical map, and similarly for
$s_{X}:X\rightarrow \operatorname{Spec}(k)$
for the canonical map, and similarly for
 $Y,X\times Y$
.
$Y,X\times Y$
.
Proof. Write
 $p_{X}:X\times Y\rightarrow X$
and
$p_{X}:X\times Y\rightarrow X$
and
 $p_{Y}:X\times Y\rightarrow Y$
for the projections. I claim that the following diagram commutes up to natural isomorphism.
$p_{Y}:X\times Y\rightarrow Y$
for the projections. I claim that the following diagram commutes up to natural isomorphism.

To prove the claim, first note that there is, for
 $T\in \mathbf{SH}(X),U\in \mathbf{SH}(Y)$
, a natural map
$T\in \mathbf{SH}(X),U\in \mathbf{SH}(Y)$
, a natural map
 $s_{X\times Y\#}(p_{X}^{\ast }T\wedge p_{Y}^{\ast }U)\rightarrow s_{X\#}T\wedge s_{y\#}U$
, which can be obtained by adjunctions, using that the pullback functors are monoidal, and that
$s_{X\times Y\#}(p_{X}^{\ast }T\wedge p_{Y}^{\ast }U)\rightarrow s_{X\#}T\wedge s_{y\#}U$
, which can be obtained by adjunctions, using that the pullback functors are monoidal, and that
 $s_{X\times Y}=s_{X}\circ p_{X}$
(and similarly for
$s_{X\times Y}=s_{X}\circ p_{X}$
(and similarly for
![]() $Y$
). Then to prove that the comparison map is an isomorphism it suffices to consider
$Y$
). Then to prove that the comparison map is an isomorphism it suffices to consider
 $T=\unicode[STIX]{x1D6F4}^{\infty }X^{\prime },U=\unicode[STIX]{x1D6F4}^{\infty }Y^{\prime }$
for
$T=\unicode[STIX]{x1D6F4}^{\infty }X^{\prime },U=\unicode[STIX]{x1D6F4}^{\infty }Y^{\prime }$
for
 $X^{\prime }\rightarrow X$
smooth any
$X^{\prime }\rightarrow X$
smooth any
 $Y^{\prime }\rightarrow Y$
smooth (note that all our functors are left adjoints and so commute with arbitrary sums, and objects of the forms
$Y^{\prime }\rightarrow Y$
smooth (note that all our functors are left adjoints and so commute with arbitrary sums, and objects of the forms
![]() $T,U$
are generators). But then the claim boils down to
$T,U$
are generators). But then the claim boils down to
 $$\begin{eqnarray}X^{\prime }\times _{k}Y^{\prime }\cong (X^{\prime }\times Y)\times _{X\times Y}(X\times Y^{\prime })\end{eqnarray}$$
$$\begin{eqnarray}X^{\prime }\times _{k}Y^{\prime }\cong (X^{\prime }\times Y)\times _{X\times Y}(X\times Y^{\prime })\end{eqnarray}$$
which is clear.
To prove the lemma, we now specialise to
 $f:X^{\prime }\rightarrow X$
and
$f:X^{\prime }\rightarrow X$
and
 $g:Y^{\prime }\rightarrow Y$
finite étale. Then
$g:Y^{\prime }\rightarrow Y$
finite étale. Then
 $$\begin{eqnarray}\text{tr}_{f\times g}=s_{X\times Y\#}(D\unicode[STIX]{x1D6F4}_{X\times Y}^{\infty }(f\times g)_{+}).\end{eqnarray}$$
$$\begin{eqnarray}\text{tr}_{f\times g}=s_{X\times Y\#}(D\unicode[STIX]{x1D6F4}_{X\times Y}^{\infty }(f\times g)_{+}).\end{eqnarray}$$
Note that
 $$\begin{eqnarray}\unicode[STIX]{x1D6F4}_{X\times Y}^{\infty }(f\times g)_{+}=p_{X}^{\ast }\unicode[STIX]{x1D6F4}_{X}^{\infty }f_{+}\wedge p_{Y}^{\ast }\unicode[STIX]{x1D6F4}_{Y}^{\infty }g_{+}.\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6F4}_{X\times Y}^{\infty }(f\times g)_{+}=p_{X}^{\ast }\unicode[STIX]{x1D6F4}_{X}^{\infty }f_{+}\wedge p_{Y}^{\ast }\unicode[STIX]{x1D6F4}_{Y}^{\infty }g_{+}.\end{eqnarray}$$
Since
![]() $p_{X}^{\ast },p_{Y}^{\ast }$
are monoidal we compute
$p_{X}^{\ast },p_{Y}^{\ast }$
are monoidal we compute
 $$\begin{eqnarray}\text{tr}_{f\times g}=s_{X\times Y\#}p_{X}^{\ast }D\unicode[STIX]{x1D6F4}_{X}^{\infty }f_{+}\wedge p_{Y}^{\ast }D\unicode[STIX]{x1D6F4}_{Y}^{\infty }g_{+}=s_{X\#}D\unicode[STIX]{x1D6F4}_{X}^{\infty }f_{+}\wedge s_{Y\#}D\unicode[STIX]{x1D6F4}_{Y}^{\infty }g_{+},\end{eqnarray}$$
$$\begin{eqnarray}\text{tr}_{f\times g}=s_{X\times Y\#}p_{X}^{\ast }D\unicode[STIX]{x1D6F4}_{X}^{\infty }f_{+}\wedge p_{Y}^{\ast }D\unicode[STIX]{x1D6F4}_{Y}^{\infty }g_{+}=s_{X\#}D\unicode[STIX]{x1D6F4}_{X}^{\infty }f_{+}\wedge s_{Y\#}D\unicode[STIX]{x1D6F4}_{Y}^{\infty }g_{+},\end{eqnarray}$$
where in the last equality we have used the claim. Since
 $s_{X\#}D\unicode[STIX]{x1D6F4}_{X}^{\infty }f_{+}=\text{tr}_{f}$
by definition (and similarly for
$s_{X\#}D\unicode[STIX]{x1D6F4}_{X}^{\infty }f_{+}=\text{tr}_{f}$
by definition (and similarly for
![]() $Y$
), this is what we wanted to prove.◻
$Y$
), this is what we wanted to prove.◻
Recall also the homotopy module
 $\text{}\underline{K}_{\ast }^{MW}=\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9})_{\ast }$
of Milnor–Witt K-theory [Reference MorelMor12, ch. 3]. Every homotopy module
$\text{}\underline{K}_{\ast }^{MW}=\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9})_{\ast }$
of Milnor–Witt K-theory [Reference MorelMor12, ch. 3]. Every homotopy module
![]() $F_{\ast }$
is a module over
$F_{\ast }$
is a module over
![]() $\text{}\underline{K}_{\ast }^{MW}$
in the sense that there are natural pairings
$\text{}\underline{K}_{\ast }^{MW}$
in the sense that there are natural pairings
 $\text{}\underline{K}_{\ast }^{MW}(X)\otimes F_{\ast }(X)\rightarrow F_{\ast +\ast }(X)$
.
$\text{}\underline{K}_{\ast }^{MW}(X)\otimes F_{\ast }(X)\rightarrow F_{\ast +\ast }(X)$
.
Corollary 12 (Projection formula).
Let
![]() $k$
be a perfect field,
$k$
be a perfect field,
 $f:Y\rightarrow X$
a finite étale morphism of essentially
$f:Y\rightarrow X$
a finite étale morphism of essentially
![]() $k$
-smooth schemes, and
$k$
-smooth schemes, and
![]() $F_{\ast }$
a homotopy module. Then for
$F_{\ast }$
a homotopy module. Then for
 $a\in \text{}\underline{K}_{\ast }^{MW}(Y)$
and
$a\in \text{}\underline{K}_{\ast }^{MW}(Y)$
and
 $b\in F_{\ast }(X)$
we have
$b\in F_{\ast }(X)$
we have
 $\text{tr}_{f}(af^{\ast }b)=\text{tr}_{f}(a)b$
. Similarly for
$\text{tr}_{f}(af^{\ast }b)=\text{tr}_{f}(a)b$
. Similarly for
 $a\in \text{}\underline{K}_{\ast }^{MW}(X)$
and
$a\in \text{}\underline{K}_{\ast }^{MW}(X)$
and
 $b\in F_{\ast }(Y)$
we have
$b\in F_{\ast }(Y)$
we have
 $\text{tr}_{f}(f^{\ast }(a)b)=a\text{tr}_{f}(b)$
.
$\text{tr}_{f}(f^{\ast }(a)b)=a\text{tr}_{f}(b)$
.
Proof. The usual proof works, see for example [Reference Calmès and FaselCF17, Proof of Corollary 3.5]. We review it. We only show the first statement, the second is similar. Consider the cartesian square

where
 $\unicode[STIX]{x1D6FF}_{X}:X\rightarrow X\times X$
is the diagonal and similarly for
$\unicode[STIX]{x1D6FF}_{X}:X\rightarrow X\times X$
is the diagonal and similarly for
![]() $Y$
. We have the map
$Y$
. We have the map
 $\unicode[STIX]{x1D6FD}:\unicode[STIX]{x1D6F4}^{\infty }Y_{+}\wedge \unicode[STIX]{x1D6F4}^{\infty }X_{+}\rightarrow \text{}\underline{K}_{\ast }^{MW}\wedge F\rightarrow F$
, where
$\unicode[STIX]{x1D6FD}:\unicode[STIX]{x1D6F4}^{\infty }Y_{+}\wedge \unicode[STIX]{x1D6F4}^{\infty }X_{+}\rightarrow \text{}\underline{K}_{\ast }^{MW}\wedge F\rightarrow F$
, where
 $\text{}\underline{K}_{\ast }^{MW}\wedge F\rightarrow F$
is the module structure and the first map is the tensor product of
$\text{}\underline{K}_{\ast }^{MW}\wedge F\rightarrow F$
is the module structure and the first map is the tensor product of
 $\unicode[STIX]{x1D6F4}^{\infty }Y_{+}\rightarrow \text{}\underline{K}_{\ast }^{MW}$
(corresponding to
$\unicode[STIX]{x1D6F4}^{\infty }Y_{+}\rightarrow \text{}\underline{K}_{\ast }^{MW}$
(corresponding to
![]() $a$
) and
$a$
) and
 $\unicode[STIX]{x1D6F4}^{\infty }X_{+}\rightarrow F$
(corresponding to
$\unicode[STIX]{x1D6F4}^{\infty }X_{+}\rightarrow F$
(corresponding to
![]() $b$
). This defines an element
$b$
). This defines an element
 $\unicode[STIX]{x1D6FD}\in F(Y\times X)$
. We have
$\unicode[STIX]{x1D6FD}\in F(Y\times X)$
. We have
 $\text{tr}_{f}((\operatorname{id}\times f)\unicode[STIX]{x1D6FF}_{Y})^{\ast }\unicode[STIX]{x1D6FD}=\text{tr}_{f}(af^{\ast }b)$
and
$\text{tr}_{f}((\operatorname{id}\times f)\unicode[STIX]{x1D6FF}_{Y})^{\ast }\unicode[STIX]{x1D6FD}=\text{tr}_{f}(af^{\ast }b)$
and
 $\unicode[STIX]{x1D6FF}_{X}^{\ast }\text{tr}_{f\times \operatorname{id}_{Y}}\unicode[STIX]{x1D6FD}=\text{tr}_{f}(a)b$
(the latter since
$\unicode[STIX]{x1D6FF}_{X}^{\ast }\text{tr}_{f\times \operatorname{id}_{Y}}\unicode[STIX]{x1D6FD}=\text{tr}_{f}(a)b$
(the latter since
 $\text{tr}_{\operatorname{id}}=\operatorname{id}$
and
$\text{tr}_{\operatorname{id}}=\operatorname{id}$
and
 $\text{tr}_{f\times g}(x\otimes y)=\text{tr}_{f}(x)\otimes \text{tr}_{g}(y)$
by Lemma 11). These two elements are equal by the base change formula, i.e. Proposition 10.◻
$\text{tr}_{f\times g}(x\otimes y)=\text{tr}_{f}(x)\otimes \text{tr}_{g}(y)$
by Lemma 11). These two elements are equal by the base change formula, i.e. Proposition 10.◻
5 Recollections on pre-motivic categories
The six functors formalism [Reference Cisinski and DégliseCD12, § A.5] is a very strong, and very general, duality theory. As such it is no surprise that proving that any theory satisfies it requires some work. Fortunately it is now possible to reduce this to establishing a few axioms.
Let
![]() ${\mathcal{S}}$
be a base category of schemes. Recall that a pre-motivic category
${\mathcal{S}}$
be a base category of schemes. Recall that a pre-motivic category
![]() ${\mathcal{M}}$
over
${\mathcal{M}}$
over
![]() ${\mathcal{S}}$
consists of [Reference Cisinski and DégliseCD13, Definition A.1.1] a pseudofunctor
${\mathcal{S}}$
consists of [Reference Cisinski and DégliseCD13, Definition A.1.1] a pseudofunctor
![]() ${\mathcal{M}}$
on
${\mathcal{M}}$
on
![]() ${\mathcal{S}}$
, taking values in triangulated, closed symmetric monoidal categories. Often these categories will be obtained as the homotopy categories of a pseudofunctor taking values in suitable Quillen model categories and left Quillen functors. For
${\mathcal{S}}$
, taking values in triangulated, closed symmetric monoidal categories. Often these categories will be obtained as the homotopy categories of a pseudofunctor taking values in suitable Quillen model categories and left Quillen functors. For
 $f:X\rightarrow Y\in {\mathcal{S}}$
, the functor
$f:X\rightarrow Y\in {\mathcal{S}}$
, the functor
 ${\mathcal{M}}(f):{\mathcal{M}}(Y)\rightarrow {\mathcal{M}}(X)$
is denoted
${\mathcal{M}}(f):{\mathcal{M}}(Y)\rightarrow {\mathcal{M}}(X)$
is denoted
![]() $f^{\ast }$
. For any
$f^{\ast }$
. For any
![]() $f$
, the functor
$f$
, the functor
![]() $f^{\ast }$
has a triangulated right adjoint
$f^{\ast }$
has a triangulated right adjoint
![]() $f_{\ast }$
(which is not required to be monoidal). If
$f_{\ast }$
(which is not required to be monoidal). If
![]() $f$
is smooth, then
$f$
is smooth, then
![]() $f^{\ast }$
has a triangulated left adjoint
$f^{\ast }$
has a triangulated left adjoint
![]() $f_{\#}$
(also not required to be monoidal). Moreover,
$f_{\#}$
(also not required to be monoidal). Moreover,
![]() ${\mathcal{M}}$
needs to satisfy smooth base change and the smooth projection formula, in the following sense.
${\mathcal{M}}$
needs to satisfy smooth base change and the smooth projection formula, in the following sense.
Let

be a cartesian square in
![]() ${\mathcal{S}}$
, with
${\mathcal{S}}$
, with
![]() $p$
smooth. Then smooth base change means that the natural transformation
$p$
smooth. Then smooth base change means that the natural transformation
 $q_{\#}g^{\ast }\rightarrow f^{\ast }p_{\#}$
is required to be a natural isomorphism.
$q_{\#}g^{\ast }\rightarrow f^{\ast }p_{\#}$
is required to be a natural isomorphism.
Finally, let
 $f:Y\rightarrow X$
be a smooth morphism in
$f:Y\rightarrow X$
be a smooth morphism in
![]() ${\mathcal{S}}$
. Then the smooth projection formula means that, for
${\mathcal{S}}$
. Then the smooth projection formula means that, for
 $E\in {\mathcal{M}}(X)$
and
$E\in {\mathcal{M}}(X)$
and
 $F\in {\mathcal{M}}(Y)$
we have
$F\in {\mathcal{M}}(Y)$
we have
 $f_{\#}(F\otimes f^{\ast }E)\simeq f_{\#}(F)\otimes E$
, via the canonical map.
$f_{\#}(F\otimes f^{\ast }E)\simeq f_{\#}(F)\otimes E$
, via the canonical map.
Here are some further properties a pre-motivic category can satisfy. We say
![]() ${\mathcal{M}}$
satisfies the homotopy property if for every
${\mathcal{M}}$
satisfies the homotopy property if for every
![]() $X\in {\mathcal{S}}$
the natural map
$X\in {\mathcal{S}}$
the natural map
 $p_{\#}\unicode[STIX]{x1D7D9}\rightarrow \unicode[STIX]{x1D7D9}\in {\mathcal{M}}(X)$
is an isomorphism, where
$p_{\#}\unicode[STIX]{x1D7D9}\rightarrow \unicode[STIX]{x1D7D9}\in {\mathcal{M}}(X)$
is an isomorphism, where
 $p:\mathbb{A}^{1}\times X\rightarrow X$
is the canonical map.
$p:\mathbb{A}^{1}\times X\rightarrow X$
is the canonical map.
Let now
 $q:\mathbb{P}^{1}\times X\rightarrow X$
be the canonical map. We say that
$q:\mathbb{P}^{1}\times X\rightarrow X$
be the canonical map. We say that
![]() ${\mathcal{M}}$
satisfies the stability property if the cone of the canonical map
${\mathcal{M}}$
satisfies the stability property if the cone of the canonical map
 $q_{\#}\unicode[STIX]{x1D7D9}\rightarrow \unicode[STIX]{x1D7D9}\in {\mathcal{M}}(X)$
is a
$q_{\#}\unicode[STIX]{x1D7D9}\rightarrow \unicode[STIX]{x1D7D9}\in {\mathcal{M}}(X)$
is a
![]() $\otimes$
-invertible object. In this case we write
$\otimes$
-invertible object. In this case we write
 $\unicode[STIX]{x1D7D9}(1)=fib(q_{\#}\unicode[STIX]{x1D7D9}\rightarrow \unicode[STIX]{x1D7D9})[-2]$
and then as usual
$\unicode[STIX]{x1D7D9}(1)=fib(q_{\#}\unicode[STIX]{x1D7D9}\rightarrow \unicode[STIX]{x1D7D9})[-2]$
and then as usual
 $E(n)=E\otimes \unicode[STIX]{x1D7D9}(1)^{\otimes n}$
for
$E(n)=E\otimes \unicode[STIX]{x1D7D9}(1)^{\otimes n}$
for
 $n\in \mathbb{Z},E\in {\mathcal{M}}(X)$
.
$n\in \mathbb{Z},E\in {\mathcal{M}}(X)$
.
Finally, let
![]() $X\in {\mathcal{S}}$
,
$X\in {\mathcal{S}}$
,
 $j:U\rightarrow X\in {\mathcal{S}}$
an open immersion, and
$j:U\rightarrow X\in {\mathcal{S}}$
an open immersion, and
 $i:Z\rightarrow {\mathcal{S}}$
a complementary closed immersion. Then for
$i:Z\rightarrow {\mathcal{S}}$
a complementary closed immersion. Then for
 $E\in {\mathcal{M}}(U)$
there are the adjunction maps
$E\in {\mathcal{M}}(U)$
there are the adjunction maps
 $$\begin{eqnarray}j_{\#}j^{\ast }E\rightarrow E\rightarrow i_{\ast }i^{\ast }E.\end{eqnarray}$$
$$\begin{eqnarray}j_{\#}j^{\ast }E\rightarrow E\rightarrow i_{\ast }i^{\ast }E.\end{eqnarray}$$
We say that
![]() ${\mathcal{M}}$
satisfies the localisation property if these maps are always part of a distinguished triangle.
${\mathcal{M}}$
satisfies the localisation property if these maps are always part of a distinguished triangle.
One then has the following fundamental result. It was discovered by Voevodsky, first worked out in detail by Ayoub, and then formalised by Cisinski–Déglise.
Theorem 13 (Ayoub, Cisinski–Déglise).
Let
![]() ${\mathcal{S}}$
be the category of Noetherian schemes of finite dimension and
${\mathcal{S}}$
be the category of Noetherian schemes of finite dimension and
![]() ${\mathcal{M}}$
a pre-motivic category which satisfies the homotopy property, the stability property, and the localisation property. Then if
${\mathcal{M}}$
a pre-motivic category which satisfies the homotopy property, the stability property, and the localisation property. Then if
![]() ${\mathcal{M}}(X)$
is a well-generated triangulated category for every
${\mathcal{M}}(X)$
is a well-generated triangulated category for every
![]() $X$
,
$X$
,
![]() ${\mathcal{M}}$
satisfies the full six functors formalism.
${\mathcal{M}}$
satisfies the full six functors formalism.
Proof. This is proved for ‘adequate categories of schemes’ in [Reference Cisinski and DégliseCD12, Theorem 2.4.50], of which Noetherian finite dimensional schemes are an example. ◻
One further property we will make use of is continuity. This can be formulated as follows. Let
 $\{S_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}\in A}$
be an inverse system in
$\{S_{\unicode[STIX]{x1D6FC}}\}_{\unicode[STIX]{x1D6FC}\in A}$
be an inverse system in
![]() ${\mathcal{S}}$
, where all the transition morphisms are affine and the limit
${\mathcal{S}}$
, where all the transition morphisms are affine and the limit
 $S:=\lim _{\unicode[STIX]{x1D6FC}}S_{\unicode[STIX]{x1D6FC}}$
exists in
$S:=\lim _{\unicode[STIX]{x1D6FC}}S_{\unicode[STIX]{x1D6FC}}$
exists in
![]() ${\mathcal{S}}$
. Write
${\mathcal{S}}$
. Write
 $p_{\unicode[STIX]{x1D6FC}}:S\rightarrow S_{\unicode[STIX]{x1D6FC}}$
for the canonical projection. Let
$p_{\unicode[STIX]{x1D6FC}}:S\rightarrow S_{\unicode[STIX]{x1D6FC}}$
for the canonical projection. Let
 $E\in {\mathcal{M}}(S_{\unicode[STIX]{x1D6FC}_{0}})$
for some
$E\in {\mathcal{M}}(S_{\unicode[STIX]{x1D6FC}_{0}})$
for some
![]() $\unicode[STIX]{x1D6FC}_{0}\in A$
and write for
$\unicode[STIX]{x1D6FC}_{0}\in A$
and write for
 $\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{0},$
$\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{0},$
 $E_{\unicode[STIX]{x1D6FC}}=(S_{\unicode[STIX]{x1D6FC}}\rightarrow S_{\unicode[STIX]{x1D6FC}_{0}})^{\ast }E$
. We say that
$E_{\unicode[STIX]{x1D6FC}}=(S_{\unicode[STIX]{x1D6FC}}\rightarrow S_{\unicode[STIX]{x1D6FC}_{0}})^{\ast }E$
. We say that
![]() ${\mathcal{M}}$
satisfies the continuity property if for every affine inverse system
${\mathcal{M}}$
satisfies the continuity property if for every affine inverse system
![]() $S_{\unicode[STIX]{x1D6FC}}$
as above, every
$S_{\unicode[STIX]{x1D6FC}}$
as above, every
![]() $E$
and every
$E$
and every
![]() $i\in \mathbb{Z}$
the canonical map
$i\in \mathbb{Z}$
the canonical map
 $$\begin{eqnarray}\operatorname{colim}_{\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{0}}[\unicode[STIX]{x1D7D9}(i),E_{\unicode[STIX]{x1D6FC}}]_{{\mathcal{M}}(S_{\unicode[STIX]{x1D6FC}})}\rightarrow [\unicode[STIX]{x1D7D9}(i),p_{\unicode[STIX]{x1D6FC}_{0}}^{\ast }E]_{{\mathcal{M}}(S)}\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{colim}_{\unicode[STIX]{x1D6FC}>\unicode[STIX]{x1D6FC}_{0}}[\unicode[STIX]{x1D7D9}(i),E_{\unicode[STIX]{x1D6FC}}]_{{\mathcal{M}}(S_{\unicode[STIX]{x1D6FC}})}\rightarrow [\unicode[STIX]{x1D7D9}(i),p_{\unicode[STIX]{x1D6FC}_{0}}^{\ast }E]_{{\mathcal{M}}(S)}\end{eqnarray}$$
is an isomorphism.
We in particular use the following consequence of continuity and localisation.
Corollary 14. Suppose that
![]() ${\mathcal{M}}$
be a pre-motivic category over
${\mathcal{M}}$
be a pre-motivic category over
![]() ${\mathcal{S}}$
(where
${\mathcal{S}}$
(where
![]() ${\mathcal{S}}$
contains all Henselizations of its schemes), coming from a pseudofunctor valued in model categories. Assume that
${\mathcal{S}}$
contains all Henselizations of its schemes), coming from a pseudofunctor valued in model categories. Assume that
![]() ${\mathcal{M}}$
satisfies continuity and localisation.
${\mathcal{M}}$
satisfies continuity and localisation.
Let
 $E\in {\mathcal{M}}(X)$
, where
$E\in {\mathcal{M}}(X)$
, where
![]() $X$
is Noetherian of finite dimension. Then
$X$
is Noetherian of finite dimension. Then
![]() $E\simeq 0$
if and only if for every morphism
$E\simeq 0$
if and only if for every morphism
 $f:\operatorname{Spec}(k)\rightarrow X$
with
$f:\operatorname{Spec}(k)\rightarrow X$
with
![]() $k$
a field we have
$k$
a field we have
 $f^{\ast }E\simeq 0$
.
$f^{\ast }E\simeq 0$
.
Proof. By localisation, we may assume that
![]() $X$
is reduced (see for example [Reference Cisinski and DégliseCD12, Proposition 2.3.6(1)]). By [Reference Cisinski and DégliseCD12, Proposition 4.3.9] (this result requires
$X$
is reduced (see for example [Reference Cisinski and DégliseCD12, Proposition 2.3.6(1)]). By [Reference Cisinski and DégliseCD12, Proposition 4.3.9] (this result requires
![]() ${\mathcal{M}}$
to come from a model category) we may assume that
${\mathcal{M}}$
to come from a model category) we may assume that
![]() $X$
is (Henselian) local with closed point
$X$
is (Henselian) local with closed point
![]() $x$
and open complement
$x$
and open complement
![]() $U$
. By localisation, it suffices to show that
$U$
. By localisation, it suffices to show that
 $E|_{x}\simeq 0$
and
$E|_{x}\simeq 0$
and
 $E|_{U}\simeq 0$
. The former holds by assumption, and the latter by induction on the dimension. This concludes the proof.◻
$E|_{U}\simeq 0$
. The former holds by assumption, and the latter by induction on the dimension. This concludes the proof.◻
Example.
The pseudofunctors
 $X\mapsto \mathbf{SH}(X)$
and
$X\mapsto \mathbf{SH}(X)$
and
 $X\mapsto D_{\mathbb{A}^{1}}(X)$
satisfy the six functors formalism and continuity (for the base category of Noetherian finite dimensional schemes) [Reference AyoubAyo07, Reference Cisinski and DégliseCD12].
$X\mapsto D_{\mathbb{A}^{1}}(X)$
satisfy the six functors formalism and continuity (for the base category of Noetherian finite dimensional schemes) [Reference AyoubAyo07, Reference Cisinski and DégliseCD12].
6 Recollections on monoidal bousfield localisation
Let
![]() ${\mathcal{M}}$
be a monoidal model category and
${\mathcal{M}}$
be a monoidal model category and
 $\unicode[STIX]{x1D6FC}:Y^{\prime }\rightarrow Y\in {\mathcal{M}}$
a morphism. We wish to ‘monoidally invert
$\unicode[STIX]{x1D6FC}:Y^{\prime }\rightarrow Y\in {\mathcal{M}}$
a morphism. We wish to ‘monoidally invert
![]() $\unicode[STIX]{x1D6FC}$
’, by which we mean passing to a model category
$\unicode[STIX]{x1D6FC}$
’, by which we mean passing to a model category
![]() $L_{\unicode[STIX]{x1D6FC}}^{\otimes }{\mathcal{M}}$
obtained by localising
$L_{\unicode[STIX]{x1D6FC}}^{\otimes }{\mathcal{M}}$
obtained by localising
![]() ${\mathcal{M}}$
and such that for every
${\mathcal{M}}$
and such that for every
 $T\in L_{\unicode[STIX]{x1D6FC}}^{\otimes }{\mathcal{M}}$
the induced map
$T\in L_{\unicode[STIX]{x1D6FC}}^{\otimes }{\mathcal{M}}$
the induced map
 $\unicode[STIX]{x1D6FC}_{T}:T\otimes ^{L}Y^{\prime }\rightarrow T\otimes ^{L}Y$
is a weak equivalence. We will also write
$\unicode[STIX]{x1D6FC}_{T}:T\otimes ^{L}Y^{\prime }\rightarrow T\otimes ^{L}Y$
is a weak equivalence. We will also write
 $L_{\unicode[STIX]{x1D6FC}}^{\otimes }{\mathcal{M}}=:{\mathcal{M}}[\unicode[STIX]{x1D6FC}^{-1}]$
and even
$L_{\unicode[STIX]{x1D6FC}}^{\otimes }{\mathcal{M}}=:{\mathcal{M}}[\unicode[STIX]{x1D6FC}^{-1}]$
and even
 $\operatorname{Ho}({\mathcal{M}}[\unicode[STIX]{x1D6FC}^{-1}])=:\operatorname{Ho}({\mathcal{M}})[\unicode[STIX]{x1D6FC}^{-1}]$
.
$\operatorname{Ho}({\mathcal{M}}[\unicode[STIX]{x1D6FC}^{-1}])=:\operatorname{Ho}({\mathcal{M}})[\unicode[STIX]{x1D6FC}^{-1}]$
.
The monoidal
![]() $\unicode[STIX]{x1D6FC}$
-localisation exists very generally. Suppose that
$\unicode[STIX]{x1D6FC}$
-localisation exists very generally. Suppose that
![]() $Y^{\prime }$
and
$Y^{\prime }$
and
![]() $Y$
are cofibrant, and that
$Y$
are cofibrant, and that
![]() ${\mathcal{M}}$
admits a set of cofibrant homotopy generators
${\mathcal{M}}$
admits a set of cofibrant homotopy generators
![]() $G$
(for example
$G$
(for example
![]() ${\mathcal{M}}$
combinatorial [Reference BarwickBar10, Corollary 4.33]). Let
${\mathcal{M}}$
combinatorial [Reference BarwickBar10, Corollary 4.33]). Let
 $H_{\unicode[STIX]{x1D6FC}}=\{Y^{\prime }\otimes T\xrightarrow[{}]{\unicode[STIX]{x1D6FC}\otimes \operatorname{id}}Y\otimes T\mid T\in G\}$
. When no confusion can arise, we will denote
$H_{\unicode[STIX]{x1D6FC}}=\{Y^{\prime }\otimes T\xrightarrow[{}]{\unicode[STIX]{x1D6FC}\otimes \operatorname{id}}Y\otimes T\mid T\in G\}$
. When no confusion can arise, we will denote
![]() $H_{\unicode[STIX]{x1D6FC}}$
just by
$H_{\unicode[STIX]{x1D6FC}}$
just by
![]() $H$
. Then the Bousfield localisation
$H$
. Then the Bousfield localisation
![]() $L_{H}{\mathcal{M}}$
, if it exists (for example if
$L_{H}{\mathcal{M}}$
, if it exists (for example if
![]() ${\mathcal{M}}$
is left proper and combinatorial) is
${\mathcal{M}}$
is left proper and combinatorial) is
 ${\mathcal{M}}[\unicode[STIX]{x1D6FC}^{-1}]$
. We will call
${\mathcal{M}}[\unicode[STIX]{x1D6FC}^{-1}]$
. We will call
![]() $H_{\unicode[STIX]{x1D6FC}}$
-local objects
$H_{\unicode[STIX]{x1D6FC}}$
-local objects
![]() $\unicode[STIX]{x1D6FC}$
-local. As a further sanity check, the model category
$\unicode[STIX]{x1D6FC}$
-local. As a further sanity check, the model category
![]() $L_{H}{\mathcal{M}}$
is still monoidal as follows from [Reference BarwickBar10, Proposition 4.47].
$L_{H}{\mathcal{M}}$
is still monoidal as follows from [Reference BarwickBar10, Proposition 4.47].
The situation simplifies somewhat if
![]() $Y^{\prime }$
and
$Y^{\prime }$
and
![]() $Y$
are invertible and
$Y$
are invertible and
![]() ${\mathcal{M}}$
is stable. Then we may as well assume that
${\mathcal{M}}$
is stable. Then we may as well assume that
![]() $Y^{\prime }=\unicode[STIX]{x1D7D9}$
. Given
$Y^{\prime }=\unicode[STIX]{x1D7D9}$
. Given
![]() $T\in {\mathcal{M}}$
cofibrant we can consider the directed system
$T\in {\mathcal{M}}$
cofibrant we can consider the directed system
 $$\begin{eqnarray}T\cong T\otimes \unicode[STIX]{x1D7D9}\xrightarrow[{}]{\operatorname{id}\otimes \unicode[STIX]{x1D6FC}}T\otimes Y\cong T\otimes Y\otimes \unicode[STIX]{x1D7D9}\rightarrow T\otimes Y^{\otimes 2}\rightarrow \cdots\end{eqnarray}$$
$$\begin{eqnarray}T\cong T\otimes \unicode[STIX]{x1D7D9}\xrightarrow[{}]{\operatorname{id}\otimes \unicode[STIX]{x1D6FC}}T\otimes Y\cong T\otimes Y\otimes \unicode[STIX]{x1D7D9}\rightarrow T\otimes Y^{\otimes 2}\rightarrow \cdots\end{eqnarray}$$
and its homotopy colimit
 $T[\unicode[STIX]{x1D6FC}^{-1}]:=\operatorname{hocolim}_{n}T\otimes X^{\otimes n}$
. More generally, if
$T[\unicode[STIX]{x1D6FC}^{-1}]:=\operatorname{hocolim}_{n}T\otimes X^{\otimes n}$
. More generally, if
![]() $T$
is not cofibrant, we can either first cofibrantly replace it, or use the derived tensor product. Either way, we denote the result still by
$T$
is not cofibrant, we can either first cofibrantly replace it, or use the derived tensor product. Either way, we denote the result still by
![]() $T[\unicode[STIX]{x1D6FC}^{-1}]$
. The main point of this section is to show that under suitable conditions,
$T[\unicode[STIX]{x1D6FC}^{-1}]$
. The main point of this section is to show that under suitable conditions,
![]() $T[\unicode[STIX]{x1D6FC}^{-1}]$
is the
$T[\unicode[STIX]{x1D6FC}^{-1}]$
is the
![]() $\unicode[STIX]{x1D6FC}$
-localisation of
$\unicode[STIX]{x1D6FC}$
-localisation of
![]() $T$
.
$T$
.
Clearly this is only a reasonable expectation under some compact generation assumption. More generally, one would expect a transfinite iteration of
![]() $\unicode[STIX]{x1D6FC}$
. Since all our applications will be in compactly generated situations, we refrain from giving the more general argument.
$\unicode[STIX]{x1D6FC}$
. Since all our applications will be in compactly generated situations, we refrain from giving the more general argument.
Recall that by a set of compact homotopy generators
![]() $G$
for
$G$
for
![]() ${\mathcal{M}}$
we mean a set of (usually cofibrant) objects
${\mathcal{M}}$
we mean a set of (usually cofibrant) objects
 $G\subset Ob({\mathcal{M}})$
such that
$G\subset Ob({\mathcal{M}})$
such that
![]() ${\mathcal{M}}$
is generated by the objects in
${\mathcal{M}}$
is generated by the objects in
![]() $G$
under homotopy colimits, and such that for any directed system
$G$
under homotopy colimits, and such that for any directed system
 $X_{1}\rightarrow X_{2}\rightarrow \cdots \in {\mathcal{M}}$
and
$X_{1}\rightarrow X_{2}\rightarrow \cdots \in {\mathcal{M}}$
and
![]() $T\in G$
, the canonical map
$T\in G$
, the canonical map
 $\operatorname{hocolim}_{i}\text{Map}^{d}(T,X_{i})\rightarrow \text{Map}^{d}(T,\operatorname{hocolim}_{i}X_{i})$
is an equivalence.
$\operatorname{hocolim}_{i}\text{Map}^{d}(T,X_{i})\rightarrow \text{Map}^{d}(T,\operatorname{hocolim}_{i}X_{i})$
is an equivalence.
Lemma 15. Let
 $\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D7D9}\rightarrow Y$
be a map between objects in a symmetric monoidal, stable model category such that
$\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D7D9}\rightarrow Y$
be a map between objects in a symmetric monoidal, stable model category such that
![]() $Y$
is invertible (in the homotopy category). Assume that
$Y$
is invertible (in the homotopy category). Assume that
![]() ${\mathcal{M}}$
has a set of compact homotopy generators
${\mathcal{M}}$
has a set of compact homotopy generators
![]() $G$
, and that
$G$
, and that
 ${\mathcal{M}}[\unicode[STIX]{x1D6FC}^{-1}]$
exists.
${\mathcal{M}}[\unicode[STIX]{x1D6FC}^{-1}]$
exists.
Then for each
![]() $U\in {\mathcal{M}}$
the object
$U\in {\mathcal{M}}$
the object
![]() $U[\unicode[STIX]{x1D6FC}^{-1}]$
is
$U[\unicode[STIX]{x1D6FC}^{-1}]$
is
![]() $\unicode[STIX]{x1D6FC}$
-local and
$\unicode[STIX]{x1D6FC}$
-local and
![]() $\unicode[STIX]{x1D6FC}$
-locally weakly equivalent to
$\unicode[STIX]{x1D6FC}$
-locally weakly equivalent to
![]() $U$
. In other words,
$U$
. In other words,
 $U\mapsto U[\unicode[STIX]{x1D6FC}^{-1}]$
is an
$U\mapsto U[\unicode[STIX]{x1D6FC}^{-1}]$
is an
![]() $\unicode[STIX]{x1D6FC}$
-localisation functor.
$\unicode[STIX]{x1D6FC}$
-localisation functor.
Also
![]() $G$
defines a set of compact homotopy generators for
$G$
defines a set of compact homotopy generators for
 ${\mathcal{M}}[\unicode[STIX]{x1D6FC}^{-1}]$
.
${\mathcal{M}}[\unicode[STIX]{x1D6FC}^{-1}]$
.
Proof. We first show that the images of
![]() $G$
in
$G$
in
 $\operatorname{Ho}({\mathcal{M}}[\unicode[STIX]{x1D6FC}^{-1}])$
are compact homotopy generators. Generation is clear, and for homotopy compactness it is enough to show that a filtered homotopy colimit of
$\operatorname{Ho}({\mathcal{M}}[\unicode[STIX]{x1D6FC}^{-1}])$
are compact homotopy generators. Generation is clear, and for homotopy compactness it is enough to show that a filtered homotopy colimit of
![]() $\unicode[STIX]{x1D6FC}$
-local objects is
$\unicode[STIX]{x1D6FC}$
-local objects is
![]() $\unicode[STIX]{x1D6FC}$
-local. But this follows from homotopy compactness of
$\unicode[STIX]{x1D6FC}$
-local. But this follows from homotopy compactness of
 $T\otimes Y^{\otimes n}$
(for
$T\otimes Y^{\otimes n}$
(for
![]() $T\in G$
and
$T\in G$
and
 $n\in \{0,1\}$
) and definition of
$n\in \{0,1\}$
) and definition of
![]() $\unicode[STIX]{x1D6FC}$
-locality.
$\unicode[STIX]{x1D6FC}$
-locality.
In a model category
![]() ${\mathcal{N}}$
with compact homotopy generators, if
${\mathcal{N}}$
with compact homotopy generators, if
 $T_{1}\rightarrow T_{2}\rightarrow \cdots \,$
is a directed system of weak equivalences then
$T_{1}\rightarrow T_{2}\rightarrow \cdots \,$
is a directed system of weak equivalences then
 $\operatorname{hocolim}_{i}T_{i}$
is weakly equivalent to
$\operatorname{hocolim}_{i}T_{i}$
is weakly equivalent to
![]() $T_{1}$
. (This follows from the same result in the category of simplicial sets.) Thus
$T_{1}$
. (This follows from the same result in the category of simplicial sets.) Thus
![]() $U[\unicode[STIX]{x1D6FC}^{-1}]$
is
$U[\unicode[STIX]{x1D6FC}^{-1}]$
is
![]() $\unicode[STIX]{x1D6FC}$
-locally weakly equivalent to
$\unicode[STIX]{x1D6FC}$
-locally weakly equivalent to
![]() $U$
.
$U$
.
It remains to see that
![]() $U[\unicode[STIX]{x1D6FC}^{-1}]$
is
$U[\unicode[STIX]{x1D6FC}^{-1}]$
is
![]() $\unicode[STIX]{x1D6FC}$
-local. This follows from the next two lemmas.◻
$\unicode[STIX]{x1D6FC}$
-local. This follows from the next two lemmas.◻
In the above lemma, we have defined an object
![]() $X$
to be
$X$
to be
![]() $\unicode[STIX]{x1D6FC}$
-local if for all
$\unicode[STIX]{x1D6FC}$
-local if for all
![]() $T\in {\mathcal{M}}$
the induced map
$T\in {\mathcal{M}}$
the induced map
 $\unicode[STIX]{x1D6FC}^{\ast }:\text{Map}^{d}(T\otimes ^{L}Y,X)\rightarrow \text{Map}^{d}(T,X)$
is an equivalence, because this is the way Bousfield localisation works. Another intuitively appealing property would be for the canonical map
$\unicode[STIX]{x1D6FC}^{\ast }:\text{Map}^{d}(T\otimes ^{L}Y,X)\rightarrow \text{Map}^{d}(T,X)$
is an equivalence, because this is the way Bousfield localisation works. Another intuitively appealing property would be for the canonical map
 $X\rightarrow X\otimes Y$
to be an equivalence. As the next lemma shows, these two notions agree in our case.
$X\rightarrow X\otimes Y$
to be an equivalence. As the next lemma shows, these two notions agree in our case.
Lemma 16. Let
![]() ${\mathcal{M}}$
be a symmetric monoidal model category and
${\mathcal{M}}$
be a symmetric monoidal model category and
 $\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D7D9}\rightarrow Y$
a morphism with
$\unicode[STIX]{x1D6FC}:\unicode[STIX]{x1D7D9}\rightarrow Y$
a morphism with
![]() $Y$
invertible.
$Y$
invertible.
Call an object
![]() $X\in {\mathcal{M}}$
$X\in {\mathcal{M}}$
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
-local if
$\unicode[STIX]{x1D6FC}^{\prime }$
-local if
 $X\rightarrow X\otimes ^{L}Y$
is a weak equivalence. Then
$X\rightarrow X\otimes ^{L}Y$
is a weak equivalence. Then
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}$
-local if and only if
$\unicode[STIX]{x1D6FC}$
-local if and only if
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
-local, if and only if
$\unicode[STIX]{x1D6FC}^{\prime }$
-local, if and only if
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC}$
-local.
$\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC}$
-local.
Proof. We shall show that (1)
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}$
-local if and only if it is
$\unicode[STIX]{x1D6FC}$
-local if and only if it is
![]() $\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC}$
-local, (2)
$\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC}$
-local, (2)
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
-local if and only if it is
$\unicode[STIX]{x1D6FC}^{\prime }$
-local if and only if it is
 $(\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC})^{\prime }$
-local, (3)
$(\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC})^{\prime }$
-local, (3)
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
-local if it is
$\unicode[STIX]{x1D6FC}^{\prime }$
-local if it is
![]() $\unicode[STIX]{x1D6FC}$
-local and (4)
$\unicode[STIX]{x1D6FC}$
-local and (4)
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC}$
-local if it is
$\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC}$
-local if it is
 $(\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC})^{\prime }$
-local.
$(\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC})^{\prime }$
-local.
All tensor products and mapping spaces will be derived in this proof.
(1) Consider the string of maps
 $$\begin{eqnarray}\text{Map}(T\otimes Y^{\otimes 3},X)\rightarrow \text{Map}(T\otimes Y^{\otimes 2},X)\rightarrow \text{Map}(T\otimes Y,X)\rightarrow \text{Map}(T,X).\end{eqnarray}$$
$$\begin{eqnarray}\text{Map}(T\otimes Y^{\otimes 3},X)\rightarrow \text{Map}(T\otimes Y^{\otimes 2},X)\rightarrow \text{Map}(T\otimes Y,X)\rightarrow \text{Map}(T,X).\end{eqnarray}$$
If
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC}$
-local, then the composite of any two consecutive maps is an equivalence, and hence all maps are equivalences by 2-out-of-6. Consequently
$\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC}$
-local, then the composite of any two consecutive maps is an equivalence, and hence all maps are equivalences by 2-out-of-6. Consequently
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}$
-local. The converse is clear.
$\unicode[STIX]{x1D6FC}$
-local. The converse is clear.
(2) Consider the string of maps
 $$\begin{eqnarray}X\rightarrow X\otimes Y\rightarrow X\otimes Y^{\otimes 2}\rightarrow X\otimes Y^{\otimes 3}.\end{eqnarray}$$
$$\begin{eqnarray}X\rightarrow X\otimes Y\rightarrow X\otimes Y^{\otimes 2}\rightarrow X\otimes Y^{\otimes 3}.\end{eqnarray}$$
If
![]() $X$
is
$X$
is
 $(\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC})^{\prime }$
-local then so is
$(\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC})^{\prime }$
-local then so is
![]() $Z\otimes X$
for any
$Z\otimes X$
for any
![]() $Z$
, since (derived) tensor product preserves weak equivalences. It follows that
$Z$
, since (derived) tensor product preserves weak equivalences. It follows that
![]() $X\otimes Y$
is
$X\otimes Y$
is
 $(\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC})^{\prime }$
-local, and hence the composite of any two consecutive maps is an equivalence. Again by 2-out-of-6 this implies that
$(\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC})^{\prime }$
-local, and hence the composite of any two consecutive maps is an equivalence. Again by 2-out-of-6 this implies that
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
-local. The converse is clear.
$\unicode[STIX]{x1D6FC}^{\prime }$
-local. The converse is clear.
(3) An object
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}$
-local if (and only if) for all
$\unicode[STIX]{x1D6FC}$
-local if (and only if) for all
![]() $T\in {\mathcal{M}}$
the map
$T\in {\mathcal{M}}$
the map
 $\text{Map}(T\otimes Y,X)\rightarrow \text{Map}(T,X)$
is a weak equivalence (of simplicial sets). In particular
$\text{Map}(T\otimes Y,X)\rightarrow \text{Map}(T,X)$
is a weak equivalence (of simplicial sets). In particular
 $T\rightarrow T\otimes Y$
is an
$T\rightarrow T\otimes Y$
is an
![]() $\unicode[STIX]{x1D6FC}$
-local weak equivalence for all
$\unicode[STIX]{x1D6FC}$
-local weak equivalence for all
![]() $T$
. It also follows that
$T$
. It also follows that
![]() $X\otimes Y$
is
$X\otimes Y$
is
![]() $\unicode[STIX]{x1D6FC}$
-local if
$\unicode[STIX]{x1D6FC}$
-local if
![]() $X$
is (here we use invertibility of
$X$
is (here we use invertibility of
![]() $Y$
). Since
$Y$
). Since
 $X\rightarrow X\otimes Y$
is an
$X\rightarrow X\otimes Y$
is an
![]() $\unicode[STIX]{x1D6FC}$
-local weak equivalence, it is a weak equivalence if
$\unicode[STIX]{x1D6FC}$
-local weak equivalence, it is a weak equivalence if
![]() $X$
(and hence
$X$
(and hence
![]() $X\otimes Y$
) is
$X\otimes Y$
) is
![]() $\unicode[STIX]{x1D6FC}$
-local. Thus
$\unicode[STIX]{x1D6FC}$
-local. Thus
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
-local if it is
$\unicode[STIX]{x1D6FC}^{\prime }$
-local if it is
![]() $\unicode[STIX]{x1D6FC}$
-local.
$\unicode[STIX]{x1D6FC}$
-local.
(4) For any simplicial set
![]() $K$
we have
$K$
we have
 $[K,\text{Map}(T,X)]=[K\otimes T,X]$
(using a framing if the model category is not simplicial). It follows that
$[K,\text{Map}(T,X)]=[K\otimes T,X]$
(using a framing if the model category is not simplicial). It follows that
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}$
-local if and only if for all
$\unicode[STIX]{x1D6FC}$
-local if and only if for all
![]() $T\in {\mathcal{M}}$
the map
$T\in {\mathcal{M}}$
the map
 $\unicode[STIX]{x1D6FC}^{\ast }:[T\otimes Y,X]\rightarrow [T,X]$
is an isomorphism. In particular, this property can be checked entirely in the homotopy category of
$\unicode[STIX]{x1D6FC}^{\ast }:[T\otimes Y,X]\rightarrow [T,X]$
is an isomorphism. In particular, this property can be checked entirely in the homotopy category of
![]() ${\mathcal{M}}$
, in which we will work from now on.
${\mathcal{M}}$
, in which we will work from now on.
Suppose, for now, that
![]() $X$
is
$X$
is
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
-local. (We will find that our strategy does not work, but it will work for
$\unicode[STIX]{x1D6FC}^{\prime }$
-local. (We will find that our strategy does not work, but it will work for
![]() $\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC}$
, and this is all that is left to prove.) We can choose an inverse equivalence
$\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC}$
, and this is all that is left to prove.) We can choose an inverse equivalence
 $\unicode[STIX]{x1D6FD}:X\otimes Y\rightarrow X$
. We consider the map
$\unicode[STIX]{x1D6FD}:X\otimes Y\rightarrow X$
. We consider the map
 $\overline{\unicode[STIX]{x1D6FD}}:[T,X]\rightarrow [T\otimes Y,X]$
sending
$\overline{\unicode[STIX]{x1D6FD}}:[T,X]\rightarrow [T\otimes Y,X]$
sending
 $f:T\rightarrow X$
to
$f:T\rightarrow X$
to
 $T\otimes Y\xrightarrow[{}]{f\otimes \operatorname{id}}X\otimes Y\xrightarrow[{}]{\unicode[STIX]{x1D6FD}}X$
. We would like to say that
$T\otimes Y\xrightarrow[{}]{f\otimes \operatorname{id}}X\otimes Y\xrightarrow[{}]{\unicode[STIX]{x1D6FD}}X$
. We would like to say that
![]() $\overline{\unicode[STIX]{x1D6FD}}$
is inverse to
$\overline{\unicode[STIX]{x1D6FD}}$
is inverse to
![]() $\unicode[STIX]{x1D6FC}^{\ast }$
. Given
$\unicode[STIX]{x1D6FC}^{\ast }$
. Given
 $f:T\rightarrow X$
we get the following commutative diagram.
$f:T\rightarrow X$
we get the following commutative diagram.

Consequently
 $\unicode[STIX]{x1D6FC}_{\ast }\unicode[STIX]{x1D6FC}^{\ast }\overline{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FC}_{\ast }:[T,X]\rightarrow [T,X\otimes Y]$
and thus
$\unicode[STIX]{x1D6FC}_{\ast }\unicode[STIX]{x1D6FC}^{\ast }\overline{\unicode[STIX]{x1D6FD}}=\unicode[STIX]{x1D6FC}_{\ast }:[T,X]\rightarrow [T,X\otimes Y]$
and thus
 $\unicode[STIX]{x1D6FC}^{\ast }\overline{\unicode[STIX]{x1D6FD}}=\operatorname{id}$
(note that
$\unicode[STIX]{x1D6FC}^{\ast }\overline{\unicode[STIX]{x1D6FD}}=\operatorname{id}$
(note that
![]() $\unicode[STIX]{x1D6FC}_{\ast }$
means composition with
$\unicode[STIX]{x1D6FC}_{\ast }$
means composition with
 $X\rightarrow X\otimes Y$
, which is an isomorphism).
$X\rightarrow X\otimes Y$
, which is an isomorphism).
The problem is with showing that
 $\overline{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}^{\ast }=\operatorname{id}$
. For this we fix
$\overline{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}^{\ast }=\operatorname{id}$
. For this we fix
 $f:T\otimes Y\rightarrow X$
and consider the following diagram.
$f:T\otimes Y\rightarrow X$
and consider the following diagram.

If it commutes for all such
![]() $f$
, then
$f$
, then
 $\overline{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}^{\ast }=\operatorname{id}$
. But this is not clear; the two paths differ by a switch of
$\overline{\unicode[STIX]{x1D6FD}}\unicode[STIX]{x1D6FC}^{\ast }=\operatorname{id}$
. But this is not clear; the two paths differ by a switch of
![]() $Y$
.
$Y$
.
However, in any symmetric monoidal category, the switch isomorphism on the square of an invertible object is the identity [Reference DuggerDug14, Propositions 4.20 and 4.21]. Consequently our argument works for
![]() $\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC}$
, and this is what we set out to prove.◻
$\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC}$
, and this is what we set out to prove.◻
Remark.
The assumption that
![]() $Y$
is invertible is necessary in general for the above result. For example, if
$Y$
is invertible is necessary in general for the above result. For example, if
![]() ${\mathcal{M}}$
is a cartesian symmetric monoidal model category, then there cannot be any
${\mathcal{M}}$
is a cartesian symmetric monoidal model category, then there cannot be any
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
-local objects unless
$\unicode[STIX]{x1D6FC}^{\prime }$
-local objects unless
 $\ast =\unicode[STIX]{x1D7D9}\rightarrow Y$
is already an equivalence.
$\ast =\unicode[STIX]{x1D7D9}\rightarrow Y$
is already an equivalence.
Lemma 17. Notations and assumptions as in Lemma 15.
For any (cofibrant)
 $X\in {\mathcal{M}}$
, the object
$X\in {\mathcal{M}}$
, the object
![]() $X[\unicode[STIX]{x1D6FC}^{-1}]$
is
$X[\unicode[STIX]{x1D6FC}^{-1}]$
is
![]() $\unicode[STIX]{x1D6FC}$
-local.
$\unicode[STIX]{x1D6FC}$
-local.
Proof. By the previous lemma, it suffices to show that
![]() $X[\unicode[STIX]{x1D6FC}^{-1}]$
is
$X[\unicode[STIX]{x1D6FC}^{-1}]$
is
 $(\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC})^{\prime }$
-local. Clearly
$(\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC})^{\prime }$
-local. Clearly
 $X[\unicode[STIX]{x1D6FC}^{-1}]\simeq X[(\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC})^{-1}]$
, i.e. we may assume without loss of generality that
$X[\unicode[STIX]{x1D6FC}^{-1}]\simeq X[(\unicode[STIX]{x1D6FC}\otimes \unicode[STIX]{x1D6FC})^{-1}]$
, i.e. we may assume without loss of generality that
![]() $Y$
is a square, and so its switch isomorphism (in the homotopy category) is the identity.
$Y$
is a square, and so its switch isomorphism (in the homotopy category) is the identity.
Since tensor product commutes with colimits (in each variable) we have
 $X[1/f]\simeq X\otimes ^{L}\unicode[STIX]{x1D7D9}[1/f]$
, and we can simplify notation by assuming without loss of generality that
$X[1/f]\simeq X\otimes ^{L}\unicode[STIX]{x1D7D9}[1/f]$
, and we can simplify notation by assuming without loss of generality that
![]() $X=\unicode[STIX]{x1D7D9}$
.
$X=\unicode[STIX]{x1D7D9}$
.
What we need to prove is that the following diagram induces an equivalence on homotopy colimits.

Because of the domains and codomains, it is tempting to guess that
 $f_{i}\simeq h_{i}\simeq f_{i}^{\prime }$
. Here we write
$f_{i}\simeq h_{i}\simeq f_{i}^{\prime }$
. Here we write
![]() $f\simeq g$
to mean that the maps become equal in the homotopy category. We claim that this guess is correct. Then if
$f\simeq g$
to mean that the maps become equal in the homotopy category. We claim that this guess is correct. Then if
![]() $T$
is any homotopy compact object, applying
$T$
is any homotopy compact object, applying
![]() $[T,\bullet ]$
to our diagram we get a diagram of abelian groups which we need to show induces an isomorphism on colimits. Homotopic maps become equal when applying
$[T,\bullet ]$
to our diagram we get a diagram of abelian groups which we need to show induces an isomorphism on colimits. Homotopic maps become equal when applying
![]() $[T,\bullet ]$
, and then the desired result follows from an easy diagram chase. By compact generation and stability, this will conclude the proof.
$[T,\bullet ]$
, and then the desired result follows from an easy diagram chase. By compact generation and stability, this will conclude the proof.
It remains to prove the claim. For this we may work entirely in the homotopy category, which we will do from now on. It is easy to see that indeed
![]() $f_{i}=h_{i}$
. For general
$f_{i}=h_{i}$
. For general
![]() $Y$
, it would not be true that
$Y$
, it would not be true that
![]() $f_{i}^{\prime }=f_{i}$
; one may check that the maps differ by appropriate switches of
$f_{i}^{\prime }=f_{i}$
; one may check that the maps differ by appropriate switches of
![]() $Y$
. However, we have assumed that the switch on
$Y$
. However, we have assumed that the switch on
![]() $Y$
is the identity, so indeed
$Y$
is the identity, so indeed
![]() $f_{i}=f_{i}^{\prime }$
as well.◻
$f_{i}=f_{i}^{\prime }$
as well.◻
Remark.
The stability assumption was used in the above proof in the following form: if
![]() $A\rightarrow B$
is any morphism in
$A\rightarrow B$
is any morphism in
![]() ${\mathcal{M}}$
and
${\mathcal{M}}$
and
 $[T,A]\rightarrow [T,B]$
is an isomorphism for all homotopy compact
$[T,A]\rightarrow [T,B]$
is an isomorphism for all homotopy compact
![]() $T$
, then
$T$
, then
![]() $A\rightarrow B$
is a weak equivalence. This fails for example in the homotopy category of spaces.
$A\rightarrow B$
is a weak equivalence. This fails for example in the homotopy category of spaces.
The stability assumption is in fact necessary for the above result. The author learned the following counterexample from Marc Hoyois: let
![]() ${\mathcal{M}}$
be the model category of small, stable
${\mathcal{M}}$
be the model category of small, stable
![]() $\infty$
-categories,
$\infty$
-categories,
![]() $Y=\unicode[STIX]{x1D7D9}$
the category of finite spectra and
$Y=\unicode[STIX]{x1D7D9}$
the category of finite spectra and
![]() $\unicode[STIX]{x1D6FC}=2$
, i.e. the functor which sends a finite spectrum
$\unicode[STIX]{x1D6FC}=2$
, i.e. the functor which sends a finite spectrum
![]() $s$
to
$s$
to
![]() $s\oplus s$
. Then
$s\oplus s$
. Then
![]() ${\mathcal{C}}\in {\mathcal{M}}$
is
${\mathcal{C}}\in {\mathcal{M}}$
is
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
-local only if it is trivial. Indeed for
$\unicode[STIX]{x1D6FC}^{\prime }$
-local only if it is trivial. Indeed for
![]() $c\in {\mathcal{C}}$
the map
$c\in {\mathcal{C}}$
the map
 $[c,c]\rightarrow [c\oplus c,c\oplus c]$
needs to be an isomorphism, which forces
$[c,c]\rightarrow [c\oplus c,c\oplus c]$
needs to be an isomorphism, which forces
![]() $c\simeq 0$
. But one may show that
$c\simeq 0$
. But one may show that
![]() $\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D6FC}]$
is not the zero category, and so is not
$\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D6FC}]$
is not the zero category, and so is not
![]() $\unicode[STIX]{x1D6FC}^{\prime }$
-local (let alone
$\unicode[STIX]{x1D6FC}^{\prime }$
-local (let alone
![]() $\unicode[STIX]{x1D6FC}$
-local).
$\unicode[STIX]{x1D6FC}$
-local).
See [Reference HoyoisHoy17, Theorem 3.8] for a criterion that can be applied in unstable situations.
7 The theorem of Jacobson and
 $\unicode[STIX]{x1D70C}$
-stable homotopy modules
$\unicode[STIX]{x1D70C}$
-stable homotopy modules
Throughout this section,
![]() $k$
is a field of characteristic zero. Recall that the real étale topology is finer than the Nisnevich topology; in particular every real étale sheaf is a Nisnevich sheaf.
$k$
is a field of characteristic zero. Recall that the real étale topology is finer than the Nisnevich topology; in particular every real étale sheaf is a Nisnevich sheaf.
Theorem 18 (Jacobson [Reference JacobsonJac17, Theorem 8.5]).
There is a canonical isomorphism (in
 $\operatorname{Shv}_{\operatorname{Nis}}(Sm(k))$
)
$\operatorname{Shv}_{\operatorname{Nis}}(Sm(k))$
)
 $$\begin{eqnarray}\operatorname{colim}_{n}\text{}\underline{I}^{n}\rightarrow a_{\text{r}\acute{\text{e}}\text{t}}\text{}\underline{\mathbb{Z}},\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{colim}_{n}\text{}\underline{I}^{n}\rightarrow a_{\text{r}\acute{\text{e}}\text{t}}\text{}\underline{\mathbb{Z}},\end{eqnarray}$$
where the transition maps
 $\text{}\underline{I}^{n}\rightarrow \text{}\underline{I}^{n+1}$
are given by multiplication with
$\text{}\underline{I}^{n}\rightarrow \text{}\underline{I}^{n+1}$
are given by multiplication with
 $2=\langle 1,1\rangle \in \text{}\underline{I}$
.
$2=\langle 1,1\rangle \in \text{}\underline{I}$
.
Here
![]() $\text{}\underline{I}$
denotes the sheaf of fundamental ideals on
$\text{}\underline{I}$
denotes the sheaf of fundamental ideals on
 $Sm(k)_{\operatorname{Nis}}$
, i.e. the sheaf associated with the presheaf
$Sm(k)_{\operatorname{Nis}}$
, i.e. the sheaf associated with the presheaf
 $X\mapsto I(X)$
, where
$X\mapsto I(X)$
, where
![]() $I(X)$
is the fundamental ideal of the Witt ring of
$I(X)$
is the fundamental ideal of the Witt ring of
![]() $X$
[Reference Knebusch and OrzechKne77]. We similarly write
$X$
[Reference Knebusch and OrzechKne77]. We similarly write
![]() $\text{}\underline{W}$
for the sheaf of Witt rings, etc.
$\text{}\underline{W}$
for the sheaf of Witt rings, etc.
Let us recall the construction of the isomorphism in Jacobson’s theorem. If
 $\unicode[STIX]{x1D719}\in W(K)$
, where
$\unicode[STIX]{x1D719}\in W(K)$
, where
![]() $K$
is a field, and
$K$
is a field, and
![]() $p$
is an ordering of
$p$
is an ordering of
![]() $K$
, then there is the signature
$K$
, then there is the signature
 $\unicode[STIX]{x1D70E}_{p}(\unicode[STIX]{x1D719})\in \mathbb{Z}$
. If
$\unicode[STIX]{x1D70E}_{p}(\unicode[STIX]{x1D719})\in \mathbb{Z}$
. If
 $\unicode[STIX]{x1D719}\in W(X)$
, define
$\unicode[STIX]{x1D719}\in W(X)$
, define
 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}):R(X)\rightarrow \mathbb{Z}$
as follows. For
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719}):R(X)\rightarrow \mathbb{Z}$
as follows. For
 $(x,p)\in R(X)$
put
$(x,p)\in R(X)$
put
 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719})(x,p)=\unicode[STIX]{x1D70E}_{p}(\unicode[STIX]{x1D719}|_{x})$
. Then one shows that
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719})(x,p)=\unicode[STIX]{x1D70E}_{p}(\unicode[STIX]{x1D719}|_{x})$
. Then one shows that
![]() $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719})$
is a continuous function from
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719})$
is a continuous function from
![]() $R(X)$
to
$R(X)$
to
![]() $\mathbb{Z}$
, i.e. an element of
$\mathbb{Z}$
, i.e. an element of
 $H_{\text{r}\acute{\text{e}}\text{t}}^{0}(X,\mathbb{Z})$
.
$H_{\text{r}\acute{\text{e}}\text{t}}^{0}(X,\mathbb{Z})$
.
Next if
 $\unicode[STIX]{x1D719}\in I(k)$
then
$\unicode[STIX]{x1D719}\in I(k)$
then
 $\unicode[STIX]{x1D70E}_{p}(\unicode[STIX]{x1D719})\in 2\mathbb{Z}$
. Consequently if
$\unicode[STIX]{x1D70E}_{p}(\unicode[STIX]{x1D719})\in 2\mathbb{Z}$
. Consequently if
 $\unicode[STIX]{x1D719}\in I(X)$
also
$\unicode[STIX]{x1D719}\in I(X)$
also
 $\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719})\in 2H_{\text{r}\acute{\text{e}}\text{t}}^{0}(X,\mathbb{Z})$
. We may thus define
$\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719})\in 2H_{\text{r}\acute{\text{e}}\text{t}}^{0}(X,\mathbb{Z})$
. We may thus define
 $\tilde{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719})/2$
and in this way we obtain
$\tilde{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719})/2$
and in this way we obtain
 $\tilde{\unicode[STIX]{x1D70E}}:I(X)\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{0}(X,\mathbb{Z})$
. Similarly we get
$\tilde{\unicode[STIX]{x1D70E}}:I(X)\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{0}(X,\mathbb{Z})$
. Similarly we get
 $\tilde{\unicode[STIX]{x1D70E}}:I^{n}(X)\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{0}(X,\mathbb{Z})$
with
$\tilde{\unicode[STIX]{x1D70E}}:I^{n}(X)\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{0}(X,\mathbb{Z})$
with
 $\tilde{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719})/2^{n}$
for
$\tilde{\unicode[STIX]{x1D70E}}(\unicode[STIX]{x1D719})=\unicode[STIX]{x1D70E}(\unicode[STIX]{x1D719})/2^{n}$
for
 $\unicode[STIX]{x1D719}\in I^{n}(X)$
. For each
$\unicode[STIX]{x1D719}\in I^{n}(X)$
. For each
![]() $n$
there is a commutative diagram as follows.
$n$
there is a commutative diagram as follows.

Consequently there is an induced map
 $\tilde{\unicode[STIX]{x1D70E}}:\operatorname{colim}_{n}I^{n}(X)\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{0}(X,\mathbb{Z})$
. The claim is that this is an isomorphism after sheafifying, i.e. for
$\tilde{\unicode[STIX]{x1D70E}}:\operatorname{colim}_{n}I^{n}(X)\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{0}(X,\mathbb{Z})$
. The claim is that this is an isomorphism after sheafifying, i.e. for
![]() $X$
local.
$X$
local.
Corollary 19. Let
![]() $\text{}\underline{K}_{n}^{MW}$
denote the
$\text{}\underline{K}_{n}^{MW}$
denote the
![]() $n$
th unramified Milnor–Witt K-theory sheaf. Then there is a canonical isomorphism
$n$
th unramified Milnor–Witt K-theory sheaf. Then there is a canonical isomorphism
 $\operatorname{colim}_{n}\text{}\underline{K}_{n}^{MW}\rightarrow a_{\text{r}\acute{\text{e}}\text{t}}\mathbb{Z}$
. Here the colimit is along multiplication with
$\operatorname{colim}_{n}\text{}\underline{K}_{n}^{MW}\rightarrow a_{\text{r}\acute{\text{e}}\text{t}}\mathbb{Z}$
. Here the colimit is along multiplication with
 $\unicode[STIX]{x1D70C}:=-[-1]\in K_{1}^{MW}(k)$
.
$\unicode[STIX]{x1D70C}:=-[-1]\in K_{1}^{MW}(k)$
.
Proof. Recall the element
 $h\in K_{0}^{MW}(k)$
with the following properties:
$h\in K_{0}^{MW}(k)$
with the following properties:
 $\text{}\underline{K}_{n}^{MW}/h=\text{}\underline{I}^{n}$
[Reference MorelMor04, Théorème 2.1] and for
$\text{}\underline{K}_{n}^{MW}/h=\text{}\underline{I}^{n}$
[Reference MorelMor04, Théorème 2.1] and for
 $a\in K_{1}^{MW}(k)$
we have
$a\in K_{1}^{MW}(k)$
we have
 $a^{2}h=0$
[Reference MorelMor12, Corollary 3.8] (this relation is the analogue of the fact that in a graded commutative ring
$a^{2}h=0$
[Reference MorelMor12, Corollary 3.8] (this relation is the analogue of the fact that in a graded commutative ring
![]() $R_{\ast }$
with
$R_{\ast }$
with
![]() $a\in R_{1}$
we have
$a\in R_{1}$
we have
 $a^{2}=-a^{2}$
by graded commutativity, so
$a^{2}=-a^{2}$
by graded commutativity, so
 $2a^{2}=0$
). Consequently
$2a^{2}=0$
). Consequently
 $\unicode[STIX]{x1D70C}^{2}h=0$
and so
$\unicode[STIX]{x1D70C}^{2}h=0$
and so
 $\operatorname{colim}_{n}\text{}\underline{K}_{n}^{MW}\rightarrow \operatorname{colim}_{n}\text{}\underline{I}^{n}$
is an isomorphism. It remains to note that the image of
$\operatorname{colim}_{n}\text{}\underline{K}_{n}^{MW}\rightarrow \operatorname{colim}_{n}\text{}\underline{I}^{n}$
is an isomorphism. It remains to note that the image of
![]() $\unicode[STIX]{x1D70C}$
in
$\unicode[STIX]{x1D70C}$
in
 $K_{1}^{MW}/h(k)\cong I(k)$
is given by
$K_{1}^{MW}/h(k)\cong I(k)$
is given by
 $-(\langle -1\rangle -1)=2\in I(k)\subset W(k)$
, so the induced transition maps in the colimit are precisely those used in Jacobson’s theorem.◻
$-(\langle -1\rangle -1)=2\in I(k)\subset W(k)$
, so the induced transition maps in the colimit are precisely those used in Jacobson’s theorem.◻
Note that the sheaves
![]() $\text{}\underline{I}^{n}$
form a homotopy module, namely the homotopy module of Witt
$\text{}\underline{I}^{n}$
form a homotopy module, namely the homotopy module of Witt
![]() $K$
-theory [Reference MorelMor12, Examples 3.33 and 3.33] [Reference MorelMor04, Theoreme 2.1]; see also [Reference Gille, Scully and ZhongGSZ16]. Consequently they have transfers for finite separable field extensions. The sheaf
$K$
-theory [Reference MorelMor12, Examples 3.33 and 3.33] [Reference MorelMor04, Theoreme 2.1]; see also [Reference Gille, Scully and ZhongGSZ16]. Consequently they have transfers for finite separable field extensions. The sheaf
![]() $a_{\text{r}\acute{\text{e}}\text{t}}\text{}\underline{\mathbb{Z}}$
also has transfers for finite (separable) field extensions. Indeed if
$a_{\text{r}\acute{\text{e}}\text{t}}\text{}\underline{\mathbb{Z}}$
also has transfers for finite (separable) field extensions. Indeed if
![]() $l/k$
is finite then
$l/k$
is finite then
 $\operatorname{Sper}(l)\rightarrow \operatorname{Sper}(k)$
is a finite-sheeted local homeomorphism [Reference ScharlauSch85, 3.5.6 Remark(ii)] and hence we transfer by ‘taking sums over the values at the preimages’.
$\operatorname{Sper}(l)\rightarrow \operatorname{Sper}(k)$
is a finite-sheeted local homeomorphism [Reference ScharlauSch85, 3.5.6 Remark(ii)] and hence we transfer by ‘taking sums over the values at the preimages’.
Lemma 20. The isomorphism
 $\operatorname{colim}_{n}\text{}\underline{I}^{n}\rightarrow a_{\text{r}\acute{\text{e}}\text{t}}\text{}\underline{\mathbb{Z}}$
is compatible with transfers on fields.
$\operatorname{colim}_{n}\text{}\underline{I}^{n}\rightarrow a_{\text{r}\acute{\text{e}}\text{t}}\text{}\underline{\mathbb{Z}}$
is compatible with transfers on fields.
Proof. It suffices to prove that for a field
![]() $k$
, the total signature
$k$
, the total signature
 $W(k)\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{0}(k,\mathbb{Z})$
is compatible with transfer. Let
$W(k)\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{0}(k,\mathbb{Z})$
is compatible with transfer. Let
![]() $l/k$
be a finite extension and
$l/k$
be a finite extension and
![]() $R/k$
a real closure. There is a commutative diagram
$R/k$
a real closure. There is a commutative diagram

by the base change formula, i.e. Proposition 10. Note that
 $\operatorname{Sper}(R\otimes _{k}l)$
is the fibre of
$\operatorname{Sper}(R\otimes _{k}l)$
is the fibre of
 $\operatorname{Sper}(l)\rightarrow \operatorname{Sper}(k)$
over the ordering corresponding to the inclusion
$\operatorname{Sper}(l)\rightarrow \operatorname{Sper}(k)$
over the ordering corresponding to the inclusion
![]() $k\subset R$
. Consequently we also have the following commutative diagram.
$k\subset R$
. Consequently we also have the following commutative diagram.

Since the signature maps are determined by pulling back to a real closure, this means that we may assume that
![]() $k$
is real closed. (Since both sides we are trying to prove equal are additive, we may still assume that
$k$
is real closed. (Since both sides we are trying to prove equal are additive, we may still assume that
![]() $l$
is a field.) But then either
$l$
is a field.) But then either
![]() $l=k$
or
$l=k$
or
 $l=k[\sqrt{-1}]$
. In the former case the transfer on both sides is the identity, and in the latter it is zero.◻
$l=k[\sqrt{-1}]$
. In the former case the transfer on both sides is the identity, and in the latter it is zero.◻
We will make good use of the following observation.
Corollary 21. Let
 $l_{1},\ldots ,l_{r}/k$
be finite extensions such that
$l_{1},\ldots ,l_{r}/k$
be finite extensions such that
 $\coprod _{i}\operatorname{Spec}(l_{i})\rightarrow \operatorname{Spec}(k)$
is a rét-cover. Then
$\coprod _{i}\operatorname{Spec}(l_{i})\rightarrow \operatorname{Spec}(k)$
is a rét-cover. Then
 $\text{tr}:\bigoplus _{i}H_{\text{r}\acute{\text{e}}\text{t}}^{0}(l_{i},\mathbb{Z})\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{0}(k,\mathbb{Z})$
is surjective.
$\text{tr}:\bigoplus _{i}H_{\text{r}\acute{\text{e}}\text{t}}^{0}(l_{i},\mathbb{Z})\rightarrow H_{\text{r}\acute{\text{e}}\text{t}}^{0}(k,\mathbb{Z})$
is surjective.
Proof. The map
 $\coprod _{i}\operatorname{Sper}(l_{i})\rightarrow \operatorname{Sper}(k)$
is a surjective local homeomorphism of compact, Hausdorff, totally disconnected spaces [Reference ScharlauSch85, Theorem 3.5.1 and Remarks 3.5.6]. The result thus follows from the next lemma.◻
$\coprod _{i}\operatorname{Sper}(l_{i})\rightarrow \operatorname{Sper}(k)$
is a surjective local homeomorphism of compact, Hausdorff, totally disconnected spaces [Reference ScharlauSch85, Theorem 3.5.1 and Remarks 3.5.6]. The result thus follows from the next lemma.◻
Lemma 22. Let
 $\unicode[STIX]{x1D719}:X\rightarrow Y$
be a surjective local homeomorphism of compact, Hausdorff, totally disconnected spaces. Then
$\unicode[STIX]{x1D719}:X\rightarrow Y$
be a surjective local homeomorphism of compact, Hausdorff, totally disconnected spaces. Then
![]() $\unicode[STIX]{x1D719}$
has finite fibers, and the ‘summing over preimages’ transfer
$\unicode[STIX]{x1D719}$
has finite fibers, and the ‘summing over preimages’ transfer
 $H^{0}(X,\mathbb{Z})\rightarrow H^{0}(Y,\mathbb{Z})$
is surjective.
$H^{0}(X,\mathbb{Z})\rightarrow H^{0}(Y,\mathbb{Z})$
is surjective.
Proof. The claim that
![]() $\unicode[STIX]{x1D719}$
has finite fibers is well known. We include a proof for convenience of the reader: since
$\unicode[STIX]{x1D719}$
has finite fibers is well known. We include a proof for convenience of the reader: since
![]() $\unicode[STIX]{x1D719}$
is a local homeomorphism the fibers are discrete, since
$\unicode[STIX]{x1D719}$
is a local homeomorphism the fibers are discrete, since
![]() $Y$
is Hausdorff they are closed, and since
$Y$
is Hausdorff they are closed, and since
![]() $X$
is compact they are compact. Now observe that a compact discrete space is finite.
$X$
is compact they are compact. Now observe that a compact discrete space is finite.
We now prove the surjectivity of the transfer. First we make the following claim: if
![]() $X$
is a compact, Hausdorff, totally disconnected space, then given
$X$
is a compact, Hausdorff, totally disconnected space, then given
 $x\in U\subset X$
with
$x\in U\subset X$
with
![]() $U$
open, there exists
$U$
open, there exists
 $x\in V\subset U$
such that
$x\in V\subset U$
such that
![]() $V$
is clopen in
$V$
is clopen in
![]() $X$
. Indeed for
$X$
. Indeed for
![]() $y\neq x$
let
$y\neq x$
let
![]() $U_{y}$
be a clopen neighbourhood of
$U_{y}$
be a clopen neighbourhood of
![]() $y$
disjoint from
$y$
disjoint from
![]() $x$
. Then
$x$
. Then
 $\bigcup _{y\in X\setminus U}U_{y}$
is an open cover of the compact (since closed) complement
$\bigcup _{y\in X\setminus U}U_{y}$
is an open cover of the compact (since closed) complement
![]() $X\setminus U$
. Let
$X\setminus U$
. Let
 $U_{1},\ldots ,U_{n}$
be a finite subcover. Then
$U_{1},\ldots ,U_{n}$
be a finite subcover. Then
 $V=X\setminus \bigcup _{i}U_{i}$
works.
$V=X\setminus \bigcup _{i}U_{i}$
works.
Now consider the morphism
 $\unicode[STIX]{x1D719}:X\rightarrow Y$
. For
$\unicode[STIX]{x1D719}:X\rightarrow Y$
. For
![]() $y\in Y$
choose a clopen neighbourhood
$y\in Y$
choose a clopen neighbourhood
![]() $U_{y}$
of
$U_{y}$
of
![]() $y\in Y$
such that there exists a clopen set
$y\in Y$
such that there exists a clopen set
![]() $V_{y}\subset X$
with
$V_{y}\subset X$
with
 $\unicode[STIX]{x1D719}(V_{y})=U_{y}$
and
$\unicode[STIX]{x1D719}(V_{y})=U_{y}$
and
 $\unicode[STIX]{x1D719}:V_{y}\rightarrow U_{y}$
a homeomorphism. We will say in this situation that
$\unicode[STIX]{x1D719}:V_{y}\rightarrow U_{y}$
a homeomorphism. We will say in this situation that
![]() $\unicode[STIX]{x1D719}$
splits strongly over
$\unicode[STIX]{x1D719}$
splits strongly over
![]() $U_{y}$
. We note that such
$U_{y}$
. We note that such
![]() $V_{y},U_{y}$
exist: since
$V_{y},U_{y}$
exist: since
![]() $\unicode[STIX]{x1D719}$
is a local homeomorphism, there exists
$\unicode[STIX]{x1D719}$
is a local homeomorphism, there exists
![]() $V_{y}^{\prime }\subset X$
such that
$V_{y}^{\prime }\subset X$
such that
 $U_{y}^{\prime }:=\unicode[STIX]{x1D719}(V_{y})$
is an open neighbourhood of
$U_{y}^{\prime }:=\unicode[STIX]{x1D719}(V_{y})$
is an open neighbourhood of
![]() $y$
and
$y$
and
 $\unicode[STIX]{x1D719}:V_{y}^{\prime }\rightarrow U_{y}^{\prime }$
is a homeomorphism. By the claim, we may assume that
$\unicode[STIX]{x1D719}:V_{y}^{\prime }\rightarrow U_{y}^{\prime }$
is a homeomorphism. By the claim, we may assume that
![]() $V_{y}^{\prime }$
is clopen. Now choose a clopen neighbourhood
$V_{y}^{\prime }$
is clopen. Now choose a clopen neighbourhood
 $U_{y}\subset U_{y}^{\prime }$
, using the claim again. Then
$U_{y}\subset U_{y}^{\prime }$
, using the claim again. Then
 $V_{y}:=\unicode[STIX]{x1D719}^{-1}(U_{y})\cap V_{y}^{\prime }$
is clopen in
$V_{y}:=\unicode[STIX]{x1D719}^{-1}(U_{y})\cap V_{y}^{\prime }$
is clopen in
![]() $X$
and maps homeomorphically to
$X$
and maps homeomorphically to
![]() $U_{y}$
.
$U_{y}$
.
We obtain in this way an open cover
 $\{U_{y}\}_{y\in Y}$
of
$\{U_{y}\}_{y\in Y}$
of
![]() $Y$
. Since
$Y$
. Since
![]() $Y$
is compact, we can choose a finite subcover
$Y$
is compact, we can choose a finite subcover
 $U_{1},\ldots ,U_{n}$
. Using that all the
$U_{1},\ldots ,U_{n}$
. Using that all the
![]() $U_{i}$
are clopen we can refine further until we have found a disjoint clopen cover (replace
$U_{i}$
are clopen we can refine further until we have found a disjoint clopen cover (replace
![]() $U_{i}$
by
$U_{i}$
by
 $U_{i}\setminus (U_{1}\cup U_{2}\cup \cdots \cup U_{i-1})$
) over which
$U_{i}\setminus (U_{1}\cup U_{2}\cup \cdots \cup U_{i-1})$
) over which
![]() $\unicode[STIX]{x1D719}$
splits strongly. (Note that if
$\unicode[STIX]{x1D719}$
splits strongly. (Note that if
![]() $\unicode[STIX]{x1D719}$
splits strongly over a clopen
$\unicode[STIX]{x1D719}$
splits strongly over a clopen
![]() $U\subset Y$
, then it also splits strongly over any clopen
$U\subset Y$
, then it also splits strongly over any clopen
![]() $U^{\prime }\subset U$
.)
$U^{\prime }\subset U$
.)
Since
 $H^{0}(Y,\mathbb{Z})$
is the set of continuous functions from
$H^{0}(Y,\mathbb{Z})$
is the set of continuous functions from
![]() $Y$
to
$Y$
to
![]() $\mathbb{Z}$
, it suffices to prove that the indicator function
$\mathbb{Z}$
, it suffices to prove that the indicator function
 $\unicode[STIX]{x1D712}_{U_{i}}:Y\rightarrow \mathbb{Z}$
of the clopen subset
$\unicode[STIX]{x1D712}_{U_{i}}:Y\rightarrow \mathbb{Z}$
of the clopen subset
![]() $U_{i}$
is in the image of transfer (because
$U_{i}$
is in the image of transfer (because
 $1=\sum _{i}\unicode[STIX]{x1D712}_{U_{i}}$
, and the transfer is additive). But
$1=\sum _{i}\unicode[STIX]{x1D712}_{U_{i}}$
, and the transfer is additive). But
![]() $\unicode[STIX]{x1D719}$
is strongly split over
$\unicode[STIX]{x1D719}$
is strongly split over
![]() $U_{i}$
by construction, so there exists some clopen subset
$U_{i}$
by construction, so there exists some clopen subset
![]() $U\subset X$
such that
$U\subset X$
such that
 $\unicode[STIX]{x1D719}:U\rightarrow U_{i}$
is a homeomorphism. Then
$\unicode[STIX]{x1D719}:U\rightarrow U_{i}$
is a homeomorphism. Then
 $\unicode[STIX]{x1D712}_{U}\in H^{0}(X,\mathbb{Z})$
and this is taken by transfer to
$\unicode[STIX]{x1D712}_{U}\in H^{0}(X,\mathbb{Z})$
and this is taken by transfer to
![]() $\unicode[STIX]{x1D712}_{U_{i}}$
, as follows from the explicit description of transfer in terms of ‘summing over preimages’.◻
$\unicode[STIX]{x1D712}_{U_{i}}$
, as follows from the explicit description of transfer in terms of ‘summing over preimages’.◻
We will want to show that certain presheaves are sheaves in the rét-topology. We find it easiest to first develop a criterion for this. We start with the following result, which is surely well known.
Lemma 23. Let
![]() $\unicode[STIX]{x1D70F}$
be a topology on a category
$\unicode[STIX]{x1D70F}$
be a topology on a category
![]() ${\mathcal{C}}$
and
${\mathcal{C}}$
and
![]() $F$
a presheaf on
$F$
a presheaf on
![]() ${\mathcal{C}}$
which is
${\mathcal{C}}$
which is
![]() $\unicode[STIX]{x1D70F}$
-separated. Let
$\unicode[STIX]{x1D70F}$
-separated. Let
![]() $X\in {\mathcal{C}}$
and
$X\in {\mathcal{C}}$
and
 $U_{\bullet },V_{\bullet }\rightarrow X$
be
$U_{\bullet },V_{\bullet }\rightarrow X$
be
![]() $\unicode[STIX]{x1D70F}$
-coverings. Suppose that
$\unicode[STIX]{x1D70F}$
-coverings. Suppose that
![]() $V_{\bullet }$
refines
$V_{\bullet }$
refines
![]() $U_{\bullet }$
, i.e. we are given a morphism
$U_{\bullet }$
, i.e. we are given a morphism
 $f:V_{\bullet }\rightarrow U_{\bullet }$
over
$f:V_{\bullet }\rightarrow U_{\bullet }$
over
![]() $X$
. Then if
$X$
. Then if
![]() $F$
satisfies the sheaf condition with respect to
$F$
satisfies the sheaf condition with respect to
![]() $V_{\bullet }$
, it also satisfies the sheaf condition with respect to
$V_{\bullet }$
, it also satisfies the sheaf condition with respect to
![]() $U_{\bullet }$
.
$U_{\bullet }$
.
Proof. The proof can be extracted from the proof of [Sta17, Tag 00VX]. We repeat the argument for convenience. For simplicity, suppose that
![]() $U_{\bullet }$
and
$U_{\bullet }$
and
![]() $V_{\bullet }$
use the same indexing set
$V_{\bullet }$
use the same indexing set
![]() $I$
, and that the refinement is of the form
$I$
, and that the refinement is of the form
 $V_{i}\rightarrow U_{i}$
. We are given
$V_{i}\rightarrow U_{i}$
. We are given
 $s_{i}\in F(U_{i})$
for each
$s_{i}\in F(U_{i})$
for each
![]() $i$
, such that
$i$
, such that
 $s_{i}|_{U_{i}\times _{X}U_{j}}=s_{j}|_{U_{i}\times _{X}U_{j}}$
, and we need to show that there is a (necessarily unique)
$s_{i}|_{U_{i}\times _{X}U_{j}}=s_{j}|_{U_{i}\times _{X}U_{j}}$
, and we need to show that there is a (necessarily unique)
 $s\in F(X)$
with
$s\in F(X)$
with
 $s|_{U_{i}}=s_{i}$
.
$s|_{U_{i}}=s_{i}$
.
Let
 $t_{i}=f^{\ast }s_{i}$
. Then
$t_{i}=f^{\ast }s_{i}$
. Then
![]() $t_{\bullet }$
is a compatible family for the covering
$t_{\bullet }$
is a compatible family for the covering
![]() $V_{\bullet }$
, and hence there is
$V_{\bullet }$
, and hence there is
 $s\in F(X)$
with
$s\in F(X)$
with
 $s|_{V_{i}}=t_{i}$
for all
$s|_{V_{i}}=t_{i}$
for all
![]() $i$
. We need to show that also
$i$
. We need to show that also
 $s|_{U_{i}}=s_{i}$
. For this, fix
$s|_{U_{i}}=s_{i}$
. For this, fix
![]() $i_{0}\in I$
and consider the coverings
$i_{0}\in I$
and consider the coverings
 $U_{\bullet }^{\prime },V_{\bullet }^{\prime }\rightarrow U_{i_{0}}$
obtained by base change. Then
$U_{\bullet }^{\prime },V_{\bullet }^{\prime }\rightarrow U_{i_{0}}$
obtained by base change. Then
![]() $V_{\bullet }^{\prime }$
refines
$V_{\bullet }^{\prime }$
refines
![]() $U_{\bullet }^{\prime }$
. We find that
$U_{\bullet }^{\prime }$
. We find that
 $s_{i_{0}}|_{U_{i_{0}}\times _{X}U_{i}}=s_{i}|_{U_{i_{0}}\times _{X}U_{i}}$
by assumption, and hence
$s_{i_{0}}|_{U_{i_{0}}\times _{X}U_{i}}=s_{i}|_{U_{i_{0}}\times _{X}U_{i}}$
by assumption, and hence
 $f^{\ast }(s_{i_{0}}|_{U_{i_{0}}\times _{X}U_{i}})=f^{\ast }(s_{i}|_{U_{i_{0}}\times _{X}U_{i}})=t_{i}|_{U_{i_{0}}\times _{X}V_{i}}=s|_{U_{i_{0}}\times _{X}V_{i}}$
by construction. But now because
$f^{\ast }(s_{i_{0}}|_{U_{i_{0}}\times _{X}U_{i}})=f^{\ast }(s_{i}|_{U_{i_{0}}\times _{X}U_{i}})=t_{i}|_{U_{i_{0}}\times _{X}V_{i}}=s|_{U_{i_{0}}\times _{X}V_{i}}$
by construction. But now because
![]() $F$
is separated in the
$F$
is separated in the
![]() $\unicode[STIX]{x1D70F}$
-topology and
$\unicode[STIX]{x1D70F}$
-topology and
 $V_{\bullet }^{\prime }\rightarrow U_{i_{0}}$
is a cover we conclude that
$V_{\bullet }^{\prime }\rightarrow U_{i_{0}}$
is a cover we conclude that
 $s_{i_{0}}=s|_{U_{i_{0}}}$
, as needed.◻
$s_{i_{0}}=s|_{U_{i_{0}}}$
, as needed.◻
Corollary 24. Let
![]() $F$
be a sheaf on
$F$
be a sheaf on
 $Sm(k)_{\operatorname{Nis}}$
. Then
$Sm(k)_{\operatorname{Nis}}$
. Then
![]() $F$
is a sheaf in the rét-topology if and only if
$F$
is a sheaf in the rét-topology if and only if
![]() $F$
satisfies the sheaf condition for every rét-cover
$F$
satisfies the sheaf condition for every rét-cover
 $f:U\rightarrow X$
, where
$f:U\rightarrow X$
, where
![]() $X$
is (essentially) smooth, Henselian local and
$X$
is (essentially) smooth, Henselian local and
![]() $f$
is finite étale.
$f$
is finite étale.
Proof. For this proof, we call a morphism with the properties of
![]() $f$
a frét-cover.
$f$
a frét-cover.
The condition is clearly necessary; we show the converse.
![]() $(\ast )$
We first claim that every rét-cover
$(\ast )$
We first claim that every rét-cover
 $U_{\bullet }\rightarrow X$
with
$U_{\bullet }\rightarrow X$
with
![]() $X$
smooth Henselian local can be refined by a frét-cover. We can certainly refine
$X$
smooth Henselian local can be refined by a frét-cover. We can certainly refine
![]() $U_{\bullet }$
by an affine cover, so assume that each
$U_{\bullet }$
by an affine cover, so assume that each
![]() $U_{i}$
is affine. Then by [Sta17, Tag 04GJ] each
$U_{i}$
is affine. Then by [Sta17, Tag 04GJ] each
![]() $U_{i}$
splits as
$U_{i}$
splits as
 $U_{i}^{\prime }\coprod U_{i}^{\prime \prime }$
with
$U_{i}^{\prime }\coprod U_{i}^{\prime \prime }$
with
 $U_{i}^{\prime }\rightarrow X$
finite étale and
$U_{i}^{\prime }\rightarrow X$
finite étale and
 $U_{i}^{\prime \prime }\rightarrow X$
not hitting the closed point
$U_{i}^{\prime \prime }\rightarrow X$
not hitting the closed point
![]() $m$
of
$m$
of
![]() $X$
(note that
$X$
(note that
 $U_{i}\rightarrow X$
is everywhere quasi-finite). I claim that
$U_{i}\rightarrow X$
is everywhere quasi-finite). I claim that
![]() $U_{\bullet }^{\prime }$
is also a rét-cover. Indeed étale morphisms induce open maps on real spectra [Reference ScheidererSch94, Proposition 1.8] and
$U_{\bullet }^{\prime }$
is also a rét-cover. Indeed étale morphisms induce open maps on real spectra [Reference ScheidererSch94, Proposition 1.8] and
![]() $U_{\bullet }^{\prime }$
covers
$U_{\bullet }^{\prime }$
covers
 $R(m)\subset R(X)$
by construction. But the only open subset of
$R(m)\subset R(X)$
by construction. But the only open subset of
![]() $R(X)$
containing
$R(X)$
containing
![]() $R(m)$
is all of
$R(m)$
is all of
![]() $R(X)$
, by [Reference Andradas, Bröcker and RuizABR12, Propositions II.2.1 and II.2.4]. Finally the real spectrum of any ring is quasi-compact [Reference Andradas, Bröcker and RuizABR12, II.1.5] whence we can always refine by a finite subcover, and then taking the disjoint union we refine by a singleton cover.
$R(X)$
, by [Reference Andradas, Bröcker and RuizABR12, Propositions II.2.1 and II.2.4]. Finally the real spectrum of any ring is quasi-compact [Reference Andradas, Bröcker and RuizABR12, II.1.5] whence we can always refine by a finite subcover, and then taking the disjoint union we refine by a singleton cover.
If
 $X\in Sm(k)$
, we write
$X\in Sm(k)$
, we write
 $F_{X}:=F|_{X_{\operatorname{Nis}}}$
for the restriction to the small site. Write
$F_{X}:=F|_{X_{\operatorname{Nis}}}$
for the restriction to the small site. Write
![]() $\text{}\underline{\operatorname{Hom}}$
for the internal mapping presheaf functor in this category. Recall that
$\text{}\underline{\operatorname{Hom}}$
for the internal mapping presheaf functor in this category. Recall that
 $\text{}\underline{\operatorname{Hom}}(V,F_{X})(V^{\prime })=F(V\times _{X}V^{\prime })$
; in particular this functor preserves sheaves.
$\text{}\underline{\operatorname{Hom}}(V,F_{X})(V^{\prime })=F(V\times _{X}V^{\prime })$
; in particular this functor preserves sheaves.
Let
 $U_{\bullet }\rightarrow X$
be a rét-cover. To show that
$U_{\bullet }\rightarrow X$
be a rét-cover. To show that
 $F(X)\rightarrow F(U_{\bullet })\rightrightarrows F(U_{\bullet }\times _{X}U_{\bullet })$
is an equaliser diagram (respectively the first map is injective), it is sufficient to show that
$F(X)\rightarrow F(U_{\bullet })\rightrightarrows F(U_{\bullet }\times _{X}U_{\bullet })$
is an equaliser diagram (respectively the first map is injective), it is sufficient to show that
 $F_{X}\rightarrow \text{}\underline{\operatorname{Hom}}(U_{\bullet },F_{X})\rightrightarrows \text{}\underline{\operatorname{Hom}}(U_{\bullet }\times _{X}U_{\bullet },F_{X})$
is an equaliser diagram of sheaves (respectively the first map is an injection of sheaves), since limits of sheaves are computed in presheaves. But finite limits (respectively injectivity) are detected on stalks, whence in both situations we may assume that
$F_{X}\rightarrow \text{}\underline{\operatorname{Hom}}(U_{\bullet },F_{X})\rightrightarrows \text{}\underline{\operatorname{Hom}}(U_{\bullet }\times _{X}U_{\bullet },F_{X})$
is an equaliser diagram of sheaves (respectively the first map is an injection of sheaves), since limits of sheaves are computed in presheaves. But finite limits (respectively injectivity) are detected on stalks, whence in both situations we may assume that
![]() $X$
is Henselian local.
$X$
is Henselian local.
![]() $(\ast \ast )$
$(\ast \ast )$
Now we show that
![]() $F$
is rét-separated. Let
$F$
is rét-separated. Let
 $U_{\bullet }\rightarrow X$
be a rét-cover. By the above, to show that
$U_{\bullet }\rightarrow X$
be a rét-cover. By the above, to show that
 $F(X)\rightarrow F(U_{\bullet })$
is injective we may assume that
$F(X)\rightarrow F(U_{\bullet })$
is injective we may assume that
![]() $X$
is Henselian local. Then
$X$
is Henselian local. Then
 $U_{\bullet }\rightarrow X$
is refined by a frét-cover
$U_{\bullet }\rightarrow X$
is refined by a frét-cover
 $V\rightarrow X$
, by
$V\rightarrow X$
, by
![]() $(\ast )$
. But then
$(\ast )$
. But then
 $F(X)\rightarrow F(U_{\bullet })\rightarrow F(V)$
is injective since
$F(X)\rightarrow F(U_{\bullet })\rightarrow F(V)$
is injective since
![]() $F$
satisfies the sheaf condition for
$F$
satisfies the sheaf condition for
 $V\rightarrow X$
by assumption, so
$V\rightarrow X$
by assumption, so
 $F(X)\rightarrow F(U_{\bullet })$
is injective and
$F(X)\rightarrow F(U_{\bullet })$
is injective and
![]() $F$
is rét-separated.
$F$
is rét-separated.
Finally let
 $U_{\bullet }\rightarrow X$
be any rét-cover. We wish to show that
$U_{\bullet }\rightarrow X$
be any rét-cover. We wish to show that
![]() $F$
satisfies the sheaf condition for this cover. By
$F$
satisfies the sheaf condition for this cover. By
![]() $(\ast \ast )$
, we may assume that
$(\ast \ast )$
, we may assume that
![]() $X$
is Henselian local. Then
$X$
is Henselian local. Then
 $U_{\bullet }\rightarrow X$
is refined by a frét-cover
$U_{\bullet }\rightarrow X$
is refined by a frét-cover
 $V\rightarrow X$
and
$V\rightarrow X$
and
![]() $F$
satisfies the sheaf condition with respect to
$F$
satisfies the sheaf condition with respect to
 $V\rightarrow X$
by assumption, so it satisfies the sheaf condition with respect to
$V\rightarrow X$
by assumption, so it satisfies the sheaf condition with respect to
 $U_{\bullet }\rightarrow X$
by Lemma 23.◻
$U_{\bullet }\rightarrow X$
by Lemma 23.◻
Remark.
Using [Reference Andradas, Bröcker and RuizABR12, Corollary II.1.15], the claim
![]() $(\ast )$
can be extended as follows: Every rét-cover
$(\ast )$
can be extended as follows: Every rét-cover
 $U_{\bullet }\rightarrow X$
with
$U_{\bullet }\rightarrow X$
with
![]() $X$
arbitrary is refined by a cover
$X$
arbitrary is refined by a cover
 $V_{\bullet }^{\prime }\rightarrow V_{\bullet }\rightarrow X$
, where
$V_{\bullet }^{\prime }\rightarrow V_{\bullet }\rightarrow X$
, where
 $V_{\bullet }\rightarrow X$
is a Nisnevich cover and each
$V_{\bullet }\rightarrow X$
is a Nisnevich cover and each
 $V_{i}^{\prime }\rightarrow V_{i}$
is a frét-cover.
$V_{i}^{\prime }\rightarrow V_{i}$
is a frét-cover.
Theorem 25. Let
![]() $F_{\ast }$
be a homotopy module such that
$F_{\ast }$
be a homotopy module such that
 $\unicode[STIX]{x1D70C}:F_{n}\rightarrow F_{n+1}$
is an isomorphism for all
$\unicode[STIX]{x1D70C}:F_{n}\rightarrow F_{n+1}$
is an isomorphism for all
![]() $n$
. Then
$n$
. Then
![]() $F_{\ast }$
consists of rét-sheaves.
$F_{\ast }$
consists of rét-sheaves.
Proof. We apply Corollary 24. Hence let
 $\unicode[STIX]{x1D719}:U\rightarrow X$
be a rét-cover with
$\unicode[STIX]{x1D719}:U\rightarrow X$
be a rét-cover with
![]() $\unicode[STIX]{x1D719}$
finite étale and
$\unicode[STIX]{x1D719}$
finite étale and
![]() $X$
essentially smooth, Henselian local. We need to show that
$X$
essentially smooth, Henselian local. We need to show that
![]() $F$
satisfies the sheaf condition with respect to this cover. Note that
$F$
satisfies the sheaf condition with respect to this cover. Note that
![]() $U$
is then a finite disjoint union of essentially smooth, Henselian local schemes, by [Sta17, Tag 04GH (1)].
$U$
is then a finite disjoint union of essentially smooth, Henselian local schemes, by [Sta17, Tag 04GH (1)].
We now use the transfer
 $\text{tr}:F_{\ast }(U)\rightarrow F_{\ast }(X)$
from § 4. Any homotopy module is a module over
$\text{tr}:F_{\ast }(U)\rightarrow F_{\ast }(X)$
from § 4. Any homotopy module is a module over
![]() $K_{\ast }^{MW}$
and satisfies the projection formula with respect to this module structure. It follows from Corollary 19 and our assumption that
$K_{\ast }^{MW}$
and satisfies the projection formula with respect to this module structure. It follows from Corollary 19 and our assumption that
![]() $\unicode[STIX]{x1D70C}$
acts invertibly on
$\unicode[STIX]{x1D70C}$
acts invertibly on
![]() $F_{\ast }$
that
$F_{\ast }$
that
![]() $F_{\ast }$
is a module over
$F_{\ast }$
is a module over
![]() $a_{\text{r}\acute{\text{e}}\text{t}}\mathbb{Z}$
, and satisfies the projection formula with respect to that module structure.
$a_{\text{r}\acute{\text{e}}\text{t}}\mathbb{Z}$
, and satisfies the projection formula with respect to that module structure.
We know that for a Henselian local ring
![]() $A$
with residue field
$A$
with residue field
![]() $\unicode[STIX]{x1D705}$
, we have
$\unicode[STIX]{x1D705}$
, we have
 $H_{\text{r}\acute{\text{e}}\text{t}}^{0}(A,\mathbb{Z})=H_{\text{r}\acute{\text{e}}\text{t}}^{0}(\unicode[STIX]{x1D705},\mathbb{Z})$
. This follows from [Reference Andradas, Bröcker and RuizABR12, Propositions II.2.2 and II.2.4] (the author learned this argument from [Reference Karoubi, Schlichting and WeibelKSW16, proof of Lemma 6.4]). Consequently by Corollary 21, Proposition 10 and stability of rét-covers under base change, there exists
$H_{\text{r}\acute{\text{e}}\text{t}}^{0}(A,\mathbb{Z})=H_{\text{r}\acute{\text{e}}\text{t}}^{0}(\unicode[STIX]{x1D705},\mathbb{Z})$
. This follows from [Reference Andradas, Bröcker and RuizABR12, Propositions II.2.2 and II.2.4] (the author learned this argument from [Reference Karoubi, Schlichting and WeibelKSW16, proof of Lemma 6.4]). Consequently by Corollary 21, Proposition 10 and stability of rét-covers under base change, there exists
 $a\in H_{\text{r}\acute{\text{e}}\text{t}}^{0}(U,\mathbb{Z})$
such that
$a\in H_{\text{r}\acute{\text{e}}\text{t}}^{0}(U,\mathbb{Z})$
such that
 $\text{tr}(a)=1$
.
$\text{tr}(a)=1$
.
Now suppose given
 $b\in F_{\ast }(X)$
such that
$b\in F_{\ast }(X)$
such that
![]() $b|_{U}=0$
. Then
$b|_{U}=0$
. Then
 $b=1b=\text{tr}(a)b=\text{tr}(a\cdot b|_{U})=0$
by the projection formula (i.e. Corollary 12). Consequently
$b=1b=\text{tr}(a)b=\text{tr}(a\cdot b|_{U})=0$
by the projection formula (i.e. Corollary 12). Consequently
 $F_{\ast }(X)\rightarrow F_{\ast }(U)$
is injective.
$F_{\ast }(X)\rightarrow F_{\ast }(U)$
is injective.
Write
 $p_{1},p_{2}:U\times _{X}U\rightarrow U$
for the two projections and suppose given
$p_{1},p_{2}:U\times _{X}U\rightarrow U$
for the two projections and suppose given
 $b\in F_{\ast }(U)$
such that
$b\in F_{\ast }(U)$
such that
 $p_{1}^{\ast }b=p_{2}^{\ast }b$
. We have to show that there is
$p_{1}^{\ast }b=p_{2}^{\ast }b$
. We have to show that there is
 $c\in F_{\ast }(X)$
such that
$c\in F_{\ast }(X)$
such that
![]() $b=c|_{U}$
. I claim that
$b=c|_{U}$
. I claim that
 $c:=\text{tr}(ab)$
works. Indeed we have
$c:=\text{tr}(ab)$
works. Indeed we have
 $\text{tr}(ab)|_{U}=\unicode[STIX]{x1D719}^{\ast }(\text{tr}_{\unicode[STIX]{x1D719}}(ab))=\text{tr}_{p_{2}}(p_{1}^{\ast }(ab))$
by Proposition 10. Now
$\text{tr}(ab)|_{U}=\unicode[STIX]{x1D719}^{\ast }(\text{tr}_{\unicode[STIX]{x1D719}}(ab))=\text{tr}_{p_{2}}(p_{1}^{\ast }(ab))$
by Proposition 10. Now
 $p_{1}^{\ast }b=p_{2}^{\ast }b$
by assumption, and so
$p_{1}^{\ast }b=p_{2}^{\ast }b$
by assumption, and so
 $\text{tr}_{p_{2}}(p_{1}^{\ast }(a)p_{1}^{\ast }(b))=\text{tr}_{p_{2}}(p_{1}^{\ast }(a)p_{2}^{\ast }(b))=\text{tr}_{p_{2}}(p_{1}^{\ast }a)b$
by the projection formula again. Finally
$\text{tr}_{p_{2}}(p_{1}^{\ast }(a)p_{1}^{\ast }(b))=\text{tr}_{p_{2}}(p_{1}^{\ast }(a)p_{2}^{\ast }(b))=\text{tr}_{p_{2}}(p_{1}^{\ast }a)b$
by the projection formula again. Finally
 $\text{tr}_{p_{2}}(p_{1}^{\ast }a)=\unicode[STIX]{x1D719}^{\ast }\text{tr}_{\unicode[STIX]{x1D719}}(a)=\unicode[STIX]{x1D719}^{\ast }1=1$
by base change again, so we are done.◻
$\text{tr}_{p_{2}}(p_{1}^{\ast }a)=\unicode[STIX]{x1D719}^{\ast }\text{tr}_{\unicode[STIX]{x1D719}}(a)=\unicode[STIX]{x1D719}^{\ast }1=1$
by base change again, so we are done.◻
8 Preliminary observations
We are now almost ready to prove our main theorems. This section collects some preliminary observations and reductions.
Lemma 15 from § 6 applies in particular to
![]() $\mathbf{SH}(S)$
and
$\mathbf{SH}(S)$
and
![]() $D_{\mathbb{A}^{1}}(S)$
for a Noetherian base scheme
$D_{\mathbb{A}^{1}}(S)$
for a Noetherian base scheme
![]() $S$
. We will be particularly interested in the case
$S$
. We will be particularly interested in the case
 $Y=\mathbb{G}_{m}$
and
$Y=\mathbb{G}_{m}$
and
 $\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70C}:S\rightarrow \mathbb{G}_{m}$
the additive inverse of the morphism corresponding to
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D70C}:S\rightarrow \mathbb{G}_{m}$
the additive inverse of the morphism corresponding to
![]() $-$
1. What the lemma says is that the
$-$
1. What the lemma says is that the
![]() $\unicode[STIX]{x1D70C}$
-localisation can be computed as the obvious colimit.
$\unicode[STIX]{x1D70C}$
-localisation can be computed as the obvious colimit.
We write
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}$
for the real étale localisation of
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}$
for the real étale localisation of
![]() $\mathbf{SH}(S)$
and
$\mathbf{SH}(S)$
and
 $D_{\mathbb{A}^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}$
for the real étale localisation of
$D_{\mathbb{A}^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}$
for the real étale localisation of
![]() $D_{\mathbb{A}^{1}}(S)$
. There is possibly a slight confusion as to what this means, since it could mean the localisation at desuspensions of real étale (hyper-) covers, or the category obtained by the same procedure as
$D_{\mathbb{A}^{1}}(S)$
. There is possibly a slight confusion as to what this means, since it could mean the localisation at desuspensions of real étale (hyper-) covers, or the category obtained by the same procedure as
![]() $\mathbf{SH}(S)$
but replacing the Nisnevich topology by the real étale one from the start. This does not actually make a difference:
$\mathbf{SH}(S)$
but replacing the Nisnevich topology by the real étale one from the start. This does not actually make a difference:
Lemma 26. Let
![]() ${\mathcal{M}}$
be a monoidal model category,
${\mathcal{M}}$
be a monoidal model category,
![]() $T\in {\mathcal{M}}$
cofibrant and
$T\in {\mathcal{M}}$
cofibrant and
![]() $H$
a set of maps. There is an isomorphism of Quillen model categories
$H$
a set of maps. There is an isomorphism of Quillen model categories
 $$\begin{eqnarray}\operatorname{Spt}(L_{H}{\mathcal{M}},T)=L_{H^{\prime }}\operatorname{Spt}({\mathcal{M}},T),\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Spt}(L_{H}{\mathcal{M}},T)=L_{H^{\prime }}\operatorname{Spt}({\mathcal{M}},T),\end{eqnarray}$$
provided that all the localisations exist (e.g.
![]() ${\mathcal{M}}$
left proper and combinatorial). Here
${\mathcal{M}}$
left proper and combinatorial). Here
 $H^{\prime }=\bigcup _{i\in \mathbb{Z}}\unicode[STIX]{x1D6F4}^{\infty +i}H$
and
$H^{\prime }=\bigcup _{i\in \mathbb{Z}}\unicode[STIX]{x1D6F4}^{\infty +i}H$
and
 $\operatorname{Spt}({\mathcal{N}},U)$
denotes the model category of (non-symmetric)
$\operatorname{Spt}({\mathcal{N}},U)$
denotes the model category of (non-symmetric)
![]() $U$
-spectra in
$U$
-spectra in
![]() ${\mathcal{N}}$
with the local model structure.
${\mathcal{N}}$
with the local model structure.
Proof. We follow [Reference HoveyHov01]. Recall that
 $\operatorname{Spt}({\mathcal{N}},U)$
denotes the category of sequences
$\operatorname{Spt}({\mathcal{N}},U)$
denotes the category of sequences
 $(X_{1},X_{2},X_{3},\ldots \,)$
together with bonding maps
$(X_{1},X_{2},X_{3},\ldots \,)$
together with bonding maps
 $X_{i}\otimes U\rightarrow X_{i+1}$
, and morphisms the compatible sequences of morphisms. This is firstly provided with a global model structure
$X_{i}\otimes U\rightarrow X_{i+1}$
, and morphisms the compatible sequences of morphisms. This is firstly provided with a global model structure
 $\operatorname{Spt}({\mathcal{N}},U)_{\text{gl}}$
in which a map
$\operatorname{Spt}({\mathcal{N}},U)_{\text{gl}}$
in which a map
 $(X_{\bullet })\rightarrow (Y_{\bullet })$
is a fibration or weak equivalence if and only if
$(X_{\bullet })\rightarrow (Y_{\bullet })$
is a fibration or weak equivalence if and only if
 $X_{i}\rightarrow Y_{i}$
is for all
$X_{i}\rightarrow Y_{i}$
is for all
![]() $i$
. This is also called a levelwise fibration or weak equivalence. The local model structure is then obtained by localisation at a set of maps which is not important to us, because it only depends on a choice of set of generators of
$i$
. This is also called a levelwise fibration or weak equivalence. The local model structure is then obtained by localisation at a set of maps which is not important to us, because it only depends on a choice of set of generators of
![]() ${\mathcal{M}}$
, and for
${\mathcal{M}}$
, and for
![]() $L_{H}{\mathcal{M}}$
we can just choose the same generators.
$L_{H}{\mathcal{M}}$
we can just choose the same generators.
Since in any model category
 $L_{H_{1}}L_{H_{2}}{\mathcal{N}}=L_{H_{1}\cup H_{2}}{\mathcal{N}}$
, it is enough to show that
$L_{H_{1}}L_{H_{2}}{\mathcal{N}}=L_{H_{1}\cup H_{2}}{\mathcal{N}}$
, it is enough to show that
 $L_{H^{\prime }}\operatorname{Spt}({\mathcal{M}},T)_{\text{gl}}=\operatorname{Spt}(L_{H}{\mathcal{M}},T)_{\text{gl}}$
. Note that an acyclic fibration in
$L_{H^{\prime }}\operatorname{Spt}({\mathcal{M}},T)_{\text{gl}}=\operatorname{Spt}(L_{H}{\mathcal{M}},T)_{\text{gl}}$
. Note that an acyclic fibration in
 $\operatorname{Spt}(L_{H}{\mathcal{M}},T)_{\text{gl}}$
is the same as a levelwise acyclic
$\operatorname{Spt}(L_{H}{\mathcal{M}},T)_{\text{gl}}$
is the same as a levelwise acyclic
![]() $H$
-local fibration in
$H$
-local fibration in
![]() ${\mathcal{M}}$
, i.e. a levelwise acyclic fibration. Consequently the cofibrations in
${\mathcal{M}}$
, i.e. a levelwise acyclic fibration. Consequently the cofibrations in
 $\operatorname{Spt}(L_{H}{\mathcal{M}},T)_{\text{gl}}$
are the same as in
$\operatorname{Spt}(L_{H}{\mathcal{M}},T)_{\text{gl}}$
are the same as in
 $\operatorname{Spt}({\mathcal{M}},T)_{\text{gl}}$
, whereas the former has more weak equivalences. Thus the former is a Bousfield localisation of the latter and hence it is enough to show that
$\operatorname{Spt}({\mathcal{M}},T)_{\text{gl}}$
, whereas the former has more weak equivalences. Thus the former is a Bousfield localisation of the latter and hence it is enough to show that
 $L_{H^{\prime }}\operatorname{Spt}({\mathcal{M}},T)_{\text{gl}}$
and
$L_{H^{\prime }}\operatorname{Spt}({\mathcal{M}},T)_{\text{gl}}$
and
 $\operatorname{Spt}(L_{H}{\mathcal{M}},T)_{\text{gl}}$
have the same fibrant objects. An object of
$\operatorname{Spt}(L_{H}{\mathcal{M}},T)_{\text{gl}}$
have the same fibrant objects. An object of
 $\operatorname{Spt}(L_{H}{\mathcal{M}},T)_{\text{gl}}$
is fibrant if and only if it is levelwise
$\operatorname{Spt}(L_{H}{\mathcal{M}},T)_{\text{gl}}$
is fibrant if and only if it is levelwise
![]() $H$
-locally fibrant. An object
$H$
-locally fibrant. An object
![]() $E$
of
$E$
of
 $L_{H^{\prime }}\operatorname{Spt}({\mathcal{M}},T)_{\text{gl}}$
is fibrant if and only if it is levelwise fibrant and
$L_{H^{\prime }}\operatorname{Spt}({\mathcal{M}},T)_{\text{gl}}$
is fibrant if and only if it is levelwise fibrant and
![]() $H^{\prime }$
-local, which means that for each
$H^{\prime }$
-local, which means that for each
 $\unicode[STIX]{x1D6FC}:X\rightarrow Y\in H$
and every
$\unicode[STIX]{x1D6FC}:X\rightarrow Y\in H$
and every
![]() $n\in \mathbb{Z}$
the map
$n\in \mathbb{Z}$
the map
 $$\begin{eqnarray}\text{Map}^{d}(\unicode[STIX]{x1D6F4}^{\infty +n}\unicode[STIX]{x1D6FC},E):\text{Map}^{d}(\unicode[STIX]{x1D6F4}^{\infty +n}Y,E)\rightarrow \text{Map}^{d}(\unicode[STIX]{x1D6F4}^{\infty +n}Y,E)\end{eqnarray}$$
$$\begin{eqnarray}\text{Map}^{d}(\unicode[STIX]{x1D6F4}^{\infty +n}\unicode[STIX]{x1D6FC},E):\text{Map}^{d}(\unicode[STIX]{x1D6F4}^{\infty +n}Y,E)\rightarrow \text{Map}^{d}(\unicode[STIX]{x1D6F4}^{\infty +n}Y,E)\end{eqnarray}$$
is a weak equivalence. By adjunction, this is the same as
 $\text{Map}^{d}(\unicode[STIX]{x1D6FC},E_{n})$
being an equivalence, i.e. all
$\text{Map}^{d}(\unicode[STIX]{x1D6FC},E_{n})$
being an equivalence, i.e. all
![]() $E_{n}$
being
$E_{n}$
being
![]() $H$
-local. This concludes the proof.◻
$H$
-local. This concludes the proof.◻
Write
 $\mathbf{SH}^{S^{1}}(S)$
for the
$\mathbf{SH}^{S^{1}}(S)$
for the
![]() $S^{1}$
-stable homotopy category (i.e. obtained from motivic spaces by just inverting
$S^{1}$
-stable homotopy category (i.e. obtained from motivic spaces by just inverting
![]() $S^{1}$
, but not
$S^{1}$
, but not
![]() $\mathbb{G}_{m}$
).
$\mathbb{G}_{m}$
).
Lemma 27. There are canonical Quillen equivalences
 $\mathbf{SH}^{S^{1}}(S)[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
and similarly for the real étale topology.
$\mathbf{SH}^{S^{1}}(S)[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
and similarly for the real étale topology.
Proof. By Lemma 26 we know that
 $\operatorname{Spt}({\mathcal{S}}{\mathcal{H}}^{S^{1}}(S)[\unicode[STIX]{x1D70C}^{-1}],\mathbb{G}_{m})=\operatorname{Spt}({\mathcal{S}}{\mathcal{H}}^{S^{1}}(S),\mathbb{G}_{m})[\unicode[STIX]{x1D70C}^{-1}]\simeq {\mathcal{S}}{\mathcal{H}}(S)[\unicode[STIX]{x1D70C}^{-1}]$
. But the map
$\operatorname{Spt}({\mathcal{S}}{\mathcal{H}}^{S^{1}}(S)[\unicode[STIX]{x1D70C}^{-1}],\mathbb{G}_{m})=\operatorname{Spt}({\mathcal{S}}{\mathcal{H}}^{S^{1}}(S),\mathbb{G}_{m})[\unicode[STIX]{x1D70C}^{-1}]\simeq {\mathcal{S}}{\mathcal{H}}(S)[\unicode[STIX]{x1D70C}^{-1}]$
. But the map
 $\unicode[STIX]{x1D70C}:S\rightarrow \mathbb{G}_{m}$
is invertible in
$\unicode[STIX]{x1D70C}:S\rightarrow \mathbb{G}_{m}$
is invertible in
 $\mathbf{SH}^{S^{1}}(S)[\unicode[STIX]{x1D70C}^{-1}]$
and thus
$\mathbf{SH}^{S^{1}}(S)[\unicode[STIX]{x1D70C}^{-1}]$
and thus
 $\operatorname{Spt}({\mathcal{S}}{\mathcal{H}}^{S^{1}}(S)[\unicode[STIX]{x1D70C}^{-1}],\mathbb{G}_{m})\simeq {\mathcal{S}}{\mathcal{H}}^{S^{1}}(S)[\unicode[STIX]{x1D70C}^{-1}]$
, i.e. inverting an invertible object has no effect [Reference HoveyHov01, Theorem 5.1].◻
$\operatorname{Spt}({\mathcal{S}}{\mathcal{H}}^{S^{1}}(S)[\unicode[STIX]{x1D70C}^{-1}],\mathbb{G}_{m})\simeq {\mathcal{S}}{\mathcal{H}}^{S^{1}}(S)[\unicode[STIX]{x1D70C}^{-1}]$
, i.e. inverting an invertible object has no effect [Reference HoveyHov01, Theorem 5.1].◻
We also observe the following.
Proposition 28. The pseudofunctor
 $X\mapsto \mathbf{SH}(X)[\unicode[STIX]{x1D70C}^{-1}]$
satisfies the full six functors formalism (on Noetherian schemes of finite dimension), compact generation, and continuity.
$X\mapsto \mathbf{SH}(X)[\unicode[STIX]{x1D70C}^{-1}]$
satisfies the full six functors formalism (on Noetherian schemes of finite dimension), compact generation, and continuity.
Proof. If
 $i:Z\rightarrow X$
is a closed immersion then the functor
$i:Z\rightarrow X$
is a closed immersion then the functor
 $i_{\ast }:\mathbf{SH}(Z)\rightarrow \mathbf{SH}(X)$
commutes with filtered homotopy colimits (being right adjoint to a functor preserving compact objects) and satisfies
$i_{\ast }:\mathbf{SH}(Z)\rightarrow \mathbf{SH}(X)$
commutes with filtered homotopy colimits (being right adjoint to a functor preserving compact objects) and satisfies
 $i_{\ast }(X\otimes \mathbb{G}_{m})\simeq i_{\ast }(X)\otimes \mathbb{G}_{m}$
[Reference Cisinski and DégliseCD12, A.5.1(6) and (3)]. It follows from the explicit description of
$i_{\ast }(X\otimes \mathbb{G}_{m})\simeq i_{\ast }(X)\otimes \mathbb{G}_{m}$
[Reference Cisinski and DégliseCD12, A.5.1(6) and (3)]. It follows from the explicit description of
![]() $\unicode[STIX]{x1D70C}$
-localisation in Lemma 15 that
$\unicode[STIX]{x1D70C}$
-localisation in Lemma 15 that
![]() $i_{\ast }$
commutes with
$i_{\ast }$
commutes with
 $L:\mathbf{SH}(X)\rightarrow \mathbf{SH}(X)[\unicode[STIX]{x1D70C}^{-1}]$
. Thus
$L:\mathbf{SH}(X)\rightarrow \mathbf{SH}(X)[\unicode[STIX]{x1D70C}^{-1}]$
. Thus
 $\mathbf{SH}(X)[\unicode[STIX]{x1D70C}^{-1}]$
satisfies localisation, by [Reference Cisinski and DégliseCD12, Proposition 2.3.19]. Since
$\mathbf{SH}(X)[\unicode[STIX]{x1D70C}^{-1}]$
satisfies localisation, by [Reference Cisinski and DégliseCD12, Proposition 2.3.19]. Since
 $\mathbf{SH}(X)[\unicode[STIX]{x1D70C}^{-1}]$
clearly satisfies the homotopy and stability properties, it satisfies the six functors formalism by Theorem 13.
$\mathbf{SH}(X)[\unicode[STIX]{x1D70C}^{-1}]$
clearly satisfies the homotopy and stability properties, it satisfies the six functors formalism by Theorem 13.
Since
![]() $\mathbf{SH}(X)$
is compactly generated so is
$\mathbf{SH}(X)$
is compactly generated so is
 $\mathbf{SH}(X)[\unicode[STIX]{x1D70C}^{-1}]$
, by the last sentence of Lemma 15.
$\mathbf{SH}(X)[\unicode[STIX]{x1D70C}^{-1}]$
, by the last sentence of Lemma 15.
For any morphism
 $f:X\rightarrow Y$
the functor
$f:X\rightarrow Y$
the functor
 $f^{\ast }:\mathbf{SH}(Y)\rightarrow \mathbf{SH}(X)$
commutes with (filtered) homotopy colimits (being a left adjoint), and consequently it commutes with
$f^{\ast }:\mathbf{SH}(Y)\rightarrow \mathbf{SH}(X)$
commutes with (filtered) homotopy colimits (being a left adjoint), and consequently it commutes with
![]() $\unicode[STIX]{x1D70C}$
-localisation, as above. Thus continuity for
$\unicode[STIX]{x1D70C}$
-localisation, as above. Thus continuity for
 $\mathbf{SH}(X)[\unicode[STIX]{x1D70C}^{-1}]$
follows from continuity for
$\mathbf{SH}(X)[\unicode[STIX]{x1D70C}^{-1}]$
follows from continuity for
![]() $\mathbf{SH}(X)$
.◻
$\mathbf{SH}(X)$
.◻
For completeness, we include the following rather formal observation. It is not used in the remainder of this text (except that it is restated as part of Theorem 35).
Proposition 29. The canonical functor
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence. In other words,
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence. In other words,
![]() $\unicode[STIX]{x1D70C}$
is a weak equivalence in
$\unicode[STIX]{x1D70C}$
is a weak equivalence in
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}$
.
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}$
.
Proof. I claim that in
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}$
there is a splitting
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}$
there is a splitting
 $\mathbb{G}_{m}\simeq \unicode[STIX]{x1D7D9}\vee \unicode[STIX]{x1D6E5}$
such that the composite
$\mathbb{G}_{m}\simeq \unicode[STIX]{x1D7D9}\vee \unicode[STIX]{x1D6E5}$
such that the composite
 $\unicode[STIX]{x1D7D9}\xrightarrow[{}]{\unicode[STIX]{x1D70C}}\mathbb{G}_{m}\simeq \unicode[STIX]{x1D7D9}\vee \unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D7D9}$
is the identity. It will follow from Lemma 30 below that
$\unicode[STIX]{x1D7D9}\xrightarrow[{}]{\unicode[STIX]{x1D70C}}\mathbb{G}_{m}\simeq \unicode[STIX]{x1D7D9}\vee \unicode[STIX]{x1D6E5}\rightarrow \unicode[STIX]{x1D7D9}$
is the identity. It will follow from Lemma 30 below that
![]() $\unicode[STIX]{x1D6E5}\simeq 0$
, proving this lemma.
$\unicode[STIX]{x1D6E5}\simeq 0$
, proving this lemma.
Call
 $a\in {\mathcal{O}}^{\times }(X)$
totally positive if for every real closed field
$a\in {\mathcal{O}}^{\times }(X)$
totally positive if for every real closed field
![]() $r$
and morphism
$r$
and morphism
 $\unicode[STIX]{x1D6FC}:\operatorname{Spec}(r)\rightarrow X$
we have
$\unicode[STIX]{x1D6FC}:\operatorname{Spec}(r)\rightarrow X$
we have
 $\unicode[STIX]{x1D6FC}^{\ast }(a)>0$
. Note that in particular any square of a unit is totally positive.
$\unicode[STIX]{x1D6FC}^{\ast }(a)>0$
. Note that in particular any square of a unit is totally positive.
This defines a sub-presheaf
 $G_{+}\subset R_{\mathbb{A}^{1}\setminus 0}$
of the presheaf represented by
$G_{+}\subset R_{\mathbb{A}^{1}\setminus 0}$
of the presheaf represented by
![]() $\mathbb{A}^{1}\setminus 0$
. Define
$\mathbb{A}^{1}\setminus 0$
. Define
![]() $G_{-}$
analogously using totally negative units. I claim that
$G_{-}$
analogously using totally negative units. I claim that
 $a_{\text{r}\acute{\text{e}}\text{t}}R_{\mathbb{A}^{1}\setminus 0}=a_{\text{r}\acute{\text{e}}\text{t}}G_{+}\coprod a_{\text{r}\acute{\text{e}}\text{t}}G_{-1}$
. We may prove this on stalks, which are Henselian rings with real closed residue fields [Reference ScheidererSch94, (3.7.3)]. If
$a_{\text{r}\acute{\text{e}}\text{t}}R_{\mathbb{A}^{1}\setminus 0}=a_{\text{r}\acute{\text{e}}\text{t}}G_{+}\coprod a_{\text{r}\acute{\text{e}}\text{t}}G_{-1}$
. We may prove this on stalks, which are Henselian rings with real closed residue fields [Reference ScheidererSch94, (3.7.3)]. If
![]() $A$
is such a ring and
$A$
is such a ring and
![]() $a\in A^{\times }$
, then the reduction
$a\in A^{\times }$
, then the reduction
 $\bar{a}\in A/m$
is a unit and so either positive or negative. It follows that either
$\bar{a}\in A/m$
is a unit and so either positive or negative. It follows that either
![]() $\bar{a}$
or
$\bar{a}$
or
![]() $-\bar{a}$
is a square, whence either
$-\bar{a}$
is a square, whence either
![]() $a$
or
$a$
or
![]() $-a$
is a square (
$-a$
is a square (
![]() $A$
being Henselian of characteristic zero). Consequently
$A$
being Henselian of characteristic zero). Consequently
![]() $a$
is either totally positive or totally negative, proving the claim.
$a$
is either totally positive or totally negative, proving the claim.
We may thus define a map
 $a_{\text{r}\acute{\text{e}}\text{t}}\mathbb{G}_{m}\rightarrow a_{\text{r}\acute{\text{e}}\text{t}}S^{0}=a_{\text{r}\acute{\text{e}}\text{t}}(\ast \coprod \ast )$
by mapping
$a_{\text{r}\acute{\text{e}}\text{t}}\mathbb{G}_{m}\rightarrow a_{\text{r}\acute{\text{e}}\text{t}}S^{0}=a_{\text{r}\acute{\text{e}}\text{t}}(\ast \coprod \ast )$
by mapping
![]() $a_{\text{r}\acute{\text{e}}\text{t}}G_{+}$
to the base point and
$a_{\text{r}\acute{\text{e}}\text{t}}G_{+}$
to the base point and
![]() $a_{\text{r}\acute{\text{e}}\text{t}}G_{-}$
to the other point. Since
$a_{\text{r}\acute{\text{e}}\text{t}}G_{-}$
to the other point. Since
![]() $-1$
is totally negative this yields an unstable splitting
$-1$
is totally negative this yields an unstable splitting
 $a_{\text{r}\acute{\text{e}}\text{t}}S^{0}\rightarrow a_{\text{r}\acute{\text{e}}\text{t}}\mathbb{G}_{m}\rightarrow a_{\text{r}\acute{\text{e}}\text{t}}S^{0}$
of the required form. The stable splitting follows.◻
$a_{\text{r}\acute{\text{e}}\text{t}}S^{0}\rightarrow a_{\text{r}\acute{\text{e}}\text{t}}\mathbb{G}_{m}\rightarrow a_{\text{r}\acute{\text{e}}\text{t}}S^{0}$
of the required form. The stable splitting follows.◻
Lemma 30. Let
![]() ${\mathcal{C}}$
be an additive symmetric monoidal category in which
${\mathcal{C}}$
be an additive symmetric monoidal category in which
![]() $\otimes$
distributes over
$\otimes$
distributes over
![]() $\oplus$
.
$\oplus$
.
If
![]() $G\in {\mathcal{C}}$
is an invertible object, such that
$G\in {\mathcal{C}}$
is an invertible object, such that
 $G\cong \unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5}$
, then
$G\cong \unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5}$
, then
![]() $\unicode[STIX]{x1D6E5}\cong 0$
.
$\unicode[STIX]{x1D6E5}\cong 0$
.
Proof. The object
![]() $G$
is rigid (being invertible) and hence
$G$
is rigid (being invertible) and hence
![]() $\unicode[STIX]{x1D6E5}$
is rigid (being a summand of
$\unicode[STIX]{x1D6E5}$
is rigid (being a summand of
![]() $G$
). We have
$G$
). We have
 $\unicode[STIX]{x1D7D9}\cong D(G)\otimes G\cong (D\unicode[STIX]{x1D7D9}\oplus D\unicode[STIX]{x1D6E5})\otimes (\unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5})\cong \unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5}\oplus D(\unicode[STIX]{x1D6E5})\oplus D(\unicode[STIX]{x1D6E5})\otimes \unicode[STIX]{x1D6E5}$
. Thus in order to prove the claim we may assume that
$\unicode[STIX]{x1D7D9}\cong D(G)\otimes G\cong (D\unicode[STIX]{x1D7D9}\oplus D\unicode[STIX]{x1D6E5})\otimes (\unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5})\cong \unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5}\oplus D(\unicode[STIX]{x1D6E5})\oplus D(\unicode[STIX]{x1D6E5})\otimes \unicode[STIX]{x1D6E5}$
. Thus in order to prove the claim we may assume that
![]() $G=\unicode[STIX]{x1D7D9}$
. Now the splitting
$G=\unicode[STIX]{x1D7D9}$
. Now the splitting
 $\unicode[STIX]{x1D7D9}\cong \unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5}$
corresponds to morphisms
$\unicode[STIX]{x1D7D9}\cong \unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5}$
corresponds to morphisms
 $\unicode[STIX]{x1D7D9}\xrightarrow[{}]{e}\unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5}\xrightarrow[{}]{f}\unicode[STIX]{x1D7D9}$
with
$\unicode[STIX]{x1D7D9}\xrightarrow[{}]{e}\unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5}\xrightarrow[{}]{f}\unicode[STIX]{x1D7D9}$
with
![]() $fe=\operatorname{id}$
and
$fe=\operatorname{id}$
and
 $ef\in \text{End}(\unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5})$
the projection. Fixing an isomorphism
$ef\in \text{End}(\unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5})$
the projection. Fixing an isomorphism
 $\unicode[STIX]{x1D7D9}\xrightarrow[{}]{z}\unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5}$
we get corresponding elements
$\unicode[STIX]{x1D7D9}\xrightarrow[{}]{z}\unicode[STIX]{x1D7D9}\oplus \unicode[STIX]{x1D6E5}$
we get corresponding elements
 $z^{-1}e,fz\in [\unicode[STIX]{x1D7D9},\unicode[STIX]{x1D7D9}]$
. We have
$z^{-1}e,fz\in [\unicode[STIX]{x1D7D9},\unicode[STIX]{x1D7D9}]$
. We have
 $\operatorname{id}=fe=f(zz^{-1})e=(fz)(z^{-1}e)$
. But
$\operatorname{id}=fe=f(zz^{-1})e=(fz)(z^{-1}e)$
. But
![]() $\text{End}(\unicode[STIX]{x1D7D9})$
is commutative [Reference BalmerBal10, sentence before Proposition 2.2] so
$\text{End}(\unicode[STIX]{x1D7D9})$
is commutative [Reference BalmerBal10, sentence before Proposition 2.2] so
 $\operatorname{id}=(z^{-1}e)(fz)$
and consequently
$\operatorname{id}=(z^{-1}e)(fz)$
and consequently
 $ef=zz^{-1}=\operatorname{id}$
and
$ef=zz^{-1}=\operatorname{id}$
and
![]() $\unicode[STIX]{x1D6E5}=0$
.◻
$\unicode[STIX]{x1D6E5}=0$
.◻
9 Main theorems
Proposition 31. Let
![]() $k$
be a field of characteristic zero. The functor
$k$
be a field of characteristic zero. The functor
 $L:\mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]\rightarrow \mathbf{SH}(k)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence.
$L:\mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]\rightarrow \mathbf{SH}(k)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence.
Proof. It is enough to show that all objects in
 $\mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
are rét-local. Let
$\mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
are rét-local. Let
 $U_{\bullet }\rightarrow X$
be a rét-hypercover, and let
$U_{\bullet }\rightarrow X$
be a rét-hypercover, and let
![]() $\hat{X}$
be its homotopy colimit (in
$\hat{X}$
be its homotopy colimit (in
![]() $\mathbf{SH}(k)$
). We need to show that if
$\mathbf{SH}(k)$
). We need to show that if
 $E\in \mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
, then
$E\in \mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
, then
 $[\hat{X},E]=[X,E]$
. We have conditionally convergent descent spectral sequences
$[\hat{X},E]=[X,E]$
. We have conditionally convergent descent spectral sequences
 $$\begin{eqnarray}\displaystyle H_{\operatorname{Nis}}^{p}(X,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}) & \Rightarrow & \displaystyle [\unicode[STIX]{x1D6F4}^{\infty }X_{+}\wedge \mathbb{G}_{m}^{\wedge i},E[p+q]]\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle H_{\operatorname{Nis}}^{p}(X,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}) & \Rightarrow & \displaystyle [\unicode[STIX]{x1D6F4}^{\infty }X_{+}\wedge \mathbb{G}_{m}^{\wedge i},E[p+q]]\end{eqnarray}$$
 $$\begin{eqnarray}\displaystyle [\hat{X},\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}[p]] & \Rightarrow & \displaystyle [\hat{X}\wedge \mathbb{G}_{m}^{\wedge i},E[p+q]].\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle [\hat{X},\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}[p]] & \Rightarrow & \displaystyle [\hat{X}\wedge \mathbb{G}_{m}^{\wedge i},E[p+q]].\end{eqnarray}$$
Here we display the
![]() $E_{2}$
-pages on the left-hand side. We moreover have the conditionally convergent homotopy colimit spectral sequence
$E_{2}$
-pages on the left-hand side. We moreover have the conditionally convergent homotopy colimit spectral sequence
 $$\begin{eqnarray}[U_{\ast },\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}[p]]\Rightarrow [\hat{X},\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}[p+\ast ]].\end{eqnarray}$$
$$\begin{eqnarray}[U_{\ast },\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}[p]]\Rightarrow [\hat{X},\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}[p+\ast ]].\end{eqnarray}$$
Here the left-hand side is the
![]() $E_{1}$
-page. We have
$E_{1}$
-page. We have
 $[U_{n},\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}[p]]=H_{\operatorname{Nis}}^{p}(U_{n},\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i})=H_{\text{r}\acute{\text{e}}\text{t}}^{p}(U_{n},\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i})$
; indeed since
$[U_{n},\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}[p]]=H_{\operatorname{Nis}}^{p}(U_{n},\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i})=H_{\text{r}\acute{\text{e}}\text{t}}^{p}(U_{n},\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i})$
; indeed since
![]() $E$
is
$E$
is
![]() $\unicode[STIX]{x1D70C}$
-local each
$\unicode[STIX]{x1D70C}$
-local each
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}$
is a rét-sheaf, by Theorem 25, and for any rét-sheaf
$\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}$
is a rét-sheaf, by Theorem 25, and for any rét-sheaf
![]() $F$
we have
$F$
we have
 $H_{\text{r}\acute{\text{e}}\text{t}}^{p}(U_{n},F)=H_{\operatorname{Nis}}^{p}(U_{n},F)$
[Reference ScheidererSch94, Proposition 19.2.1]. It follows that spectral sequence (3) converges strongly (because the dimension of
$H_{\text{r}\acute{\text{e}}\text{t}}^{p}(U_{n},F)=H_{\operatorname{Nis}}^{p}(U_{n},F)$
[Reference ScheidererSch94, Proposition 19.2.1]. It follows that spectral sequence (3) converges strongly (because the dimension of
![]() $X$
is finite) and identifies with the descent spectral sequence in rét-cohomology for the cover
$X$
is finite) and identifies with the descent spectral sequence in rét-cohomology for the cover
![]() $U_{\bullet }$
. In particular, it converges to
$U_{\bullet }$
. In particular, it converges to
 $H_{\text{r}\acute{\text{e}}\text{t}}^{p+\ast }(X,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i})$
. Thus we find that
$H_{\text{r}\acute{\text{e}}\text{t}}^{p+\ast }(X,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i})$
. Thus we find that
 $[\hat{X},\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}[p]]=H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i})$
. Using [Reference ScheidererSch94, Proposition 19.2.1] again, we conclude that the evident map from spectral sequence (1) to spectral sequence (2) induces an isomorphism on the
$[\hat{X},\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i}[p]]=H_{\text{r}\acute{\text{e}}\text{t}}^{p}(X,\text{}\underline{\unicode[STIX]{x1D70B}}_{-q}(E)_{-i})$
. Using [Reference ScheidererSch94, Proposition 19.2.1] again, we conclude that the evident map from spectral sequence (1) to spectral sequence (2) induces an isomorphism on the
![]() $E_{2}$
-pages, and moreover both converge strongly (again for cohomological dimension reasons). Thus the induced map on targets is an isomorphism, which is what we wanted to show.◻
$E_{2}$
-pages, and moreover both converge strongly (again for cohomological dimension reasons). Thus the induced map on targets is an isomorphism, which is what we wanted to show.◻
Corollary 32. The proposition holds for all fields.
Proof. We claim that if
![]() $k$
has positive characteristic, then
$k$
has positive characteristic, then
![]() $\unicode[STIX]{x1D70C}$
is nilpotent in
$\unicode[STIX]{x1D70C}$
is nilpotent in
![]() $\mathbf{SH}(k)$
. By base change, it suffices to prove this when
$\mathbf{SH}(k)$
. By base change, it suffices to prove this when
![]() $k=\mathbb{F}_{p}$
. That is to say, we wish to show that
$k=\mathbb{F}_{p}$
. That is to say, we wish to show that
![]() $\unicode[STIX]{x1D70C}$
is nilpotent in
$\unicode[STIX]{x1D70C}$
is nilpotent in
 $K_{\ast }^{MW}(\mathbb{F}_{p})$
, or equivalently that
$K_{\ast }^{MW}(\mathbb{F}_{p})$
, or equivalently that
 $\operatorname{colim}_{n}K_{n}^{MW}(\mathbb{F}_{p})=0$
. By the same argument as in the proof of Corollary 19 we know that
$\operatorname{colim}_{n}K_{n}^{MW}(\mathbb{F}_{p})=0$
. By the same argument as in the proof of Corollary 19 we know that
 $\operatorname{colim}_{n}K_{n}^{MW}(\mathbb{F}_{p})=\operatorname{colim}_{n}I^{n}(\mathbb{F}_{p})$
. Thus our claim follows from nilpotence of the fundamental ideal of
$\operatorname{colim}_{n}K_{n}^{MW}(\mathbb{F}_{p})=\operatorname{colim}_{n}I^{n}(\mathbb{F}_{p})$
. Thus our claim follows from nilpotence of the fundamental ideal of
![]() $\mathbb{F}_{p}$
, which is well known [Reference Milnor and HusemollerMH73, III(5.9)].◻
$\mathbb{F}_{p}$
, which is well known [Reference Milnor and HusemollerMH73, III(5.9)].◻
Corollary 33. Let
![]() $S$
be a Noetherian scheme of finite dimension. The functor
$S$
be a Noetherian scheme of finite dimension. The functor
 $L:\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence.
$L:\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence.
In particular
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
satisfies the full six functors formalism.
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
satisfies the full six functors formalism.
Our initial proof of this statement contained a mistake; a correction and vast simplification has kindly been communicated by Denis-Charles Cisinski.
Proof. It suffices to prove that all objects of
 $\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
are rét-local. Thus let
$\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
are rét-local. Thus let
 $X\in Sm(S)$
and
$X\in Sm(S)$
and
 $U_{\bullet }\rightarrow X$
a rét-hypercover. We need to show that
$U_{\bullet }\rightarrow X$
a rét-hypercover. We need to show that
 $$\begin{eqnarray}\unicode[STIX]{x1D6FC}:\operatorname{hocolim}_{\unicode[STIX]{x1D6E5}}\unicode[STIX]{x1D6F4}^{\infty }U_{\bullet }\rightarrow \unicode[STIX]{x1D6F4}^{\infty }X\end{eqnarray}$$
$$\begin{eqnarray}\unicode[STIX]{x1D6FC}:\operatorname{hocolim}_{\unicode[STIX]{x1D6E5}}\unicode[STIX]{x1D6F4}^{\infty }U_{\bullet }\rightarrow \unicode[STIX]{x1D6F4}^{\infty }X\end{eqnarray}$$
is an equivalence in
 $\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
. (See also Lemma 26.) Since
$\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
. (See also Lemma 26.) Since
 $\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
satisfies the six functors formalism by Proposition 28, it follows from Corollary 14 that suffices to show that if
$\mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
satisfies the six functors formalism by Proposition 28, it follows from Corollary 14 that suffices to show that if
 $f:\operatorname{Spec}(k)\rightarrow S$
is a morphism (with
$f:\operatorname{Spec}(k)\rightarrow S$
is a morphism (with
![]() $k$
a field), then
$k$
a field), then
![]() $f^{\ast }\unicode[STIX]{x1D6FC}$
is an equivalence. But
$f^{\ast }\unicode[STIX]{x1D6FC}$
is an equivalence. But
![]() $f^{\ast }$
is a left adjoint so commutes with homotopy colimits (and
$f^{\ast }$
is a left adjoint so commutes with homotopy colimits (and
![]() $\unicode[STIX]{x1D6F4}^{\infty }$
), so
$\unicode[STIX]{x1D6F4}^{\infty }$
), so
![]() $f^{\ast }\unicode[STIX]{x1D6FC}$
is isomorphic to the map
$f^{\ast }\unicode[STIX]{x1D6FC}$
is isomorphic to the map
 $$\begin{eqnarray}\operatorname{hocolim}_{\unicode[STIX]{x1D6E5}}\unicode[STIX]{x1D6F4}^{\infty }f^{\ast }U_{\bullet }\rightarrow \unicode[STIX]{x1D6F4}^{\infty }f^{\ast }X\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{hocolim}_{\unicode[STIX]{x1D6E5}}\unicode[STIX]{x1D6F4}^{\infty }f^{\ast }U_{\bullet }\rightarrow \unicode[STIX]{x1D6F4}^{\infty }f^{\ast }X\end{eqnarray}$$
in
 $\mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
. Since rét-covers are stable by pullback, this is an equivalence by Corollary 32.◻
$\mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
. Since rét-covers are stable by pullback, this is an equivalence by Corollary 32.◻
Proposition 34. Let
![]() $S$
be a Noetherian scheme of finite dimension. Then the canonical functor
$S$
be a Noetherian scheme of finite dimension. Then the canonical functor
 $\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence.
$\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence.
Proof. The functor
 $\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
is fully faithful and
$\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
is fully faithful and
![]() $t$
-exact by Corollary 6. The image of
$t$
-exact by Corollary 6. The image of
 $\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
in
$\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
in
 $\text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
consists of
$\text{SH}(Sm(S)_{\text{r}\acute{\text{e}}\text{t}})$
consists of
![]() $\mathbb{A}^{1}$
-local and
$\mathbb{A}^{1}$
-local and
![]() $\unicode[STIX]{x1D70C}$
-local objects, by the descent spectral sequence and Theorem 8 (and Corollary 6, which implies that the homotopy sheaves of
$\unicode[STIX]{x1D70C}$
-local objects, by the descent spectral sequence and Theorem 8 (and Corollary 6, which implies that the homotopy sheaves of
![]() $LeE$
are the extensions of the homotopy sheaves of
$LeE$
are the extensions of the homotopy sheaves of
![]() $E$
). Consequently
$E$
). Consequently
 $\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is fully faithful. But
$\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is fully faithful. But
 $\mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence by Lemma 27. We have thus established that the functor is fully faithful. We need to show it is essentially surjective.
$\mathbf{SH}^{S^{1}}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is an equivalence by Lemma 27. We have thus established that the functor is fully faithful. We need to show it is essentially surjective.
The category
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is generated by objects of the form
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
is generated by objects of the form
![]() $p_{\ast }(\unicode[STIX]{x1D7D9})$
where
$p_{\ast }(\unicode[STIX]{x1D7D9})$
where
 $p:T\rightarrow S$
is projective [Reference Cisinski and DégliseCD12, Proposition 4.2.13]. Since the functor
$p:T\rightarrow S$
is projective [Reference Cisinski and DégliseCD12, Proposition 4.2.13]. Since the functor
 $e:\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
has a right adjoint it commutes with arbitrary sums, and hence it identifies
$e:\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
has a right adjoint it commutes with arbitrary sums, and hence it identifies
 $\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
with a localising subcategory of
$\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
with a localising subcategory of
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
. It thus suffices to show that
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
. It thus suffices to show that
![]() $e$
commutes with
$e$
commutes with
![]() $p_{\ast }$
, where
$p_{\ast }$
, where
 $p:T\rightarrow S$
is a projective morphism. This is exactly the same as the proof of [Reference Cisinski and DégliseCD13, Proposition 4.4.3]. It boils down to the proper base change theorem holding both in
$p:T\rightarrow S$
is a projective morphism. This is exactly the same as the proof of [Reference Cisinski and DégliseCD13, Proposition 4.4.3]. It boils down to the proper base change theorem holding both in
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
(where it follows from the six functors formalism which we have already established by showing that
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
(where it follows from the six functors formalism which we have already established by showing that
 $\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
) and in
$\mathbf{SH}(S)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}(S)[\unicode[STIX]{x1D70C}^{-1}]$
) and in
 $\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
; the latter is Theorem 9.◻
$\text{SH}(S_{\text{r}\acute{\text{e}}\text{t}})$
; the latter is Theorem 9.◻
Remark.
If
![]() $S$
is the spectrum of a field, the above proof can be simplified greatly, by arguing as in [Reference BachmannBac16, § 5]. See in particular Lemma 21, Corollary 26 and Proposition 28 of [Reference BachmannBac16, § 5]. This way we no longer need to use the proper base change theorems, and thus also do not need to know that
$S$
is the spectrum of a field, the above proof can be simplified greatly, by arguing as in [Reference BachmannBac16, § 5]. See in particular Lemma 21, Corollary 26 and Proposition 28 of [Reference BachmannBac16, § 5]. This way we no longer need to use the proper base change theorems, and thus also do not need to know that
 $\mathbf{SH}(X)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
satisfies the six functors formalism.
$\mathbf{SH}(X)^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
satisfies the six functors formalism.
One may also extract from [Reference BachmannBac16, § 5] a proof of Proposition 31 not relying on Theorem 25. Thus if the base is a field, §§ 3, 5, and 7 can be dispensed with.
In summary, we have thus established the following result.
Theorem 35. Let
![]() $S$
be a Noetherian scheme of finite dimension. In the following two diagrams, all functors are the canonical ones, and are equivalences of categories.
$S$
be a Noetherian scheme of finite dimension. In the following two diagrams, all functors are the canonical ones, and are equivalences of categories.


In particular all these categories satisfy the full six functors formalism, and continuity.
Proof. The functor
![]() $d$
is an equivalence by Corollary 33,
$d$
is an equivalence by Corollary 33,
![]() $b$
and
$b$
and
![]() $b^{\prime }$
are equivalences by Corollary 27,
$b^{\prime }$
are equivalences by Corollary 27,
![]() $c$
is an equivalence by Proposition 29 and
$c$
is an equivalence by Proposition 29 and
![]() $ba$
is an equivalence by Proposition 34. It follows that
$ba$
is an equivalence by Proposition 34. It follows that
![]() $a$
is an equivalence, and so are the two unlabelled functors.
$a$
is an equivalence, and so are the two unlabelled functors.
By Proposition 28,
 $\mathbf{SH}(\bullet )[\unicode[STIX]{x1D70C}^{-1}]$
satisfies the full six functors formalism, and hence so do all the other pseudofunctors, being equivalent.
$\mathbf{SH}(\bullet )[\unicode[STIX]{x1D70C}^{-1}]$
satisfies the full six functors formalism, and hence so do all the other pseudofunctors, being equivalent.
We have provided the proofs for
![]() $\mathbf{SH}$
, the ones for
$\mathbf{SH}$
, the ones for
![]() $D_{\mathbb{A}^{1}}$
are exactly the same.◻
$D_{\mathbb{A}^{1}}$
are exactly the same.◻
10 Real realisation
In this section we work over the field
![]() $\mathbb{R}$
of real numbers. We then have a composite
$\mathbb{R}$
of real numbers. We then have a composite
 $$\begin{eqnarray}R_{1}:\mathbf{SH}(\mathbb{R})\xrightarrow[{}]{L_{\unicode[STIX]{x1D70C}}}\mathbf{SH}(\mathbb{R})^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}^{S^{1}}(\mathbb{R})^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\xrightarrow[{}]{r}\mathbf{SH}^{\text{s}}.\end{eqnarray}$$
$$\begin{eqnarray}R_{1}:\mathbf{SH}(\mathbb{R})\xrightarrow[{}]{L_{\unicode[STIX]{x1D70C}}}\mathbf{SH}(\mathbb{R})^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}^{S^{1}}(\mathbb{R})^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]\xrightarrow[{}]{r}\mathbf{SH}^{\text{s}}.\end{eqnarray}$$
Here by
![]() $\mathbf{SH}^{\text{s}}$
we mean the model of the stable homotopy category
$\mathbf{SH}^{\text{s}}$
we mean the model of the stable homotopy category
![]() $\mathbf{SH}$
built from simplicial sets. Of course
$\mathbf{SH}$
built from simplicial sets. Of course
 $\mathbf{SH}^{\text{s}}\simeq \mathbf{SH}$
canonically (and this may be an equality depending, on our favourite model of
$\mathbf{SH}^{\text{s}}\simeq \mathbf{SH}$
canonically (and this may be an equality depending, on our favourite model of
![]() $\mathbf{SH}$
). Also
$\mathbf{SH}$
). Also
![]() $r$
denotes the functor induced by the right adjoint of
$r$
denotes the functor induced by the right adjoint of
 $e:\operatorname{Pre}(\mathbb{R}_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \operatorname{Pre}(Sm(\mathbb{R}))$
from § 3.
$e:\operatorname{Pre}(\mathbb{R}_{\text{r}\acute{\text{e}}\text{t}})\rightarrow \operatorname{Pre}(Sm(\mathbb{R}))$
from § 3.
Following Heller and Ormsby [Reference Heller and OrmsbyHO16, § 4.4], there is also the real realisation functor
 $LR_{2}:\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}^{\text{t}}$
. Here
$LR_{2}:\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}^{\text{t}}$
. Here
![]() $\mathbf{SH}^{\text{t}}$
is the model of
$\mathbf{SH}^{\text{t}}$
is the model of
![]() $\mathbf{SH}$
built from topological spaces. The functor
$\mathbf{SH}$
built from topological spaces. The functor
![]() $LR_{2}$
is defined by starting with the functor
$LR_{2}$
is defined by starting with the functor
 $R_{2}:Sm(\mathbb{R})\rightarrow \operatorname{Top},X\mapsto X(\mathbb{R})$
assigning a smooth scheme over
$R_{2}:Sm(\mathbb{R})\rightarrow \operatorname{Top},X\mapsto X(\mathbb{R})$
assigning a smooth scheme over
![]() $\mathbb{R}$
its set of real points with the strong topology. We then get a functor
$\mathbb{R}$
its set of real points with the strong topology. We then get a functor
 $R_{2}:\operatorname{sPre}(Sm(\mathbb{R}))_{\ast }\rightarrow \operatorname{Top}$
by left Kan extension, i.e. demanding that
$R_{2}:\operatorname{sPre}(Sm(\mathbb{R}))_{\ast }\rightarrow \operatorname{Top}$
by left Kan extension, i.e. demanding that
 $R_{2}(\unicode[STIX]{x1D6E5}_{+}^{n}\wedge X_{+})=\unicode[STIX]{x1D6E5}_{+}^{n}\wedge X(\mathbb{R})_{+}$
and that
$R_{2}(\unicode[STIX]{x1D6E5}_{+}^{n}\wedge X_{+})=\unicode[STIX]{x1D6E5}_{+}^{n}\wedge X(\mathbb{R})_{+}$
and that
![]() $R_{2}$
preserves colimits. Using the projective model structure on
$R_{2}$
preserves colimits. Using the projective model structure on
 $\operatorname{sPre}(Sm(\mathbb{R}))_{\ast }$
this functor is left Quillen and then one promotes it to
$\operatorname{sPre}(Sm(\mathbb{R}))_{\ast }$
this functor is left Quillen and then one promotes it to
 $LR_{2}:\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}^{\text{t}}$
in the usual way.
$LR_{2}:\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}^{\text{t}}$
in the usual way.
Fortunately the two potential real realisation functors are the same. To state this result, recall that there is an adjunction
 $$\begin{eqnarray}|\bullet |:\text{sSet}\leftrightarrows \operatorname{Top}:\operatorname{Sing}^{\text{t}},\end{eqnarray}$$
$$\begin{eqnarray}|\bullet |:\text{sSet}\leftrightarrows \operatorname{Top}:\operatorname{Sing}^{\text{t}},\end{eqnarray}$$
and then by passing to homotopy categories of spectra one obtains the adjoint equivalence
 $$\begin{eqnarray}L|\bullet |:\mathbf{SH}^{\text{s}}\leftrightarrows \mathbf{SH}^{\text{t}}:R\operatorname{Sing}^{\text{t}}.\end{eqnarray}$$
$$\begin{eqnarray}L|\bullet |:\mathbf{SH}^{\text{s}}\leftrightarrows \mathbf{SH}^{\text{t}}:R\operatorname{Sing}^{\text{t}}.\end{eqnarray}$$
Proposition 36. The two functors
 $L|R_{1}(\bullet )|,LR_{2}(\bullet ):\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}^{\text{t}}$
are canonically isomorphic.
$L|R_{1}(\bullet )|,LR_{2}(\bullet ):\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}^{\text{t}}$
are canonically isomorphic.
Proof. The functor
![]() $R_{2}$
takes multiplication by
$R_{2}$
takes multiplication by
![]() $\unicode[STIX]{x1D70C}$
into a weak equivalence. Consequently it remains left Quillen in the
$\unicode[STIX]{x1D70C}$
into a weak equivalence. Consequently it remains left Quillen in the
![]() $\unicode[STIX]{x1D70C}$
-local model structure and hence
$\unicode[STIX]{x1D70C}$
-local model structure and hence
![]() $LR_{2}$
canonically factors through the localisation
$LR_{2}$
canonically factors through the localisation
 $\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}].$
Since
$\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}].$
Since
 $\mathbf{SH}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}^{S^{1}}(\mathbb{R})^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
the obvious functor
$\mathbf{SH}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]\simeq \mathbf{SH}^{S^{1}}(\mathbb{R})^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
the obvious functor
 $R_{2}^{\prime }:\operatorname{Spt}(Sm(\mathbb{R}))\rightarrow \operatorname{Spt}^{t}$
is left Quillen in the
$R_{2}^{\prime }:\operatorname{Spt}(Sm(\mathbb{R}))\rightarrow \operatorname{Spt}^{t}$
is left Quillen in the
 $(\unicode[STIX]{x1D70C},\text{r}\acute{\text{e}}\text{t},\mathbb{A}^{1})$
-local model structure. (Here we have used twice the following well-known observation: if
$(\unicode[STIX]{x1D70C},\text{r}\acute{\text{e}}\text{t},\mathbb{A}^{1})$
-local model structure. (Here we have used twice the following well-known observation: if
 $L:{\mathcal{M}}\leftrightarrows {\mathcal{N}}:R$
is a Quillen adjunction and
$L:{\mathcal{M}}\leftrightarrows {\mathcal{N}}:R$
is a Quillen adjunction and
![]() $H$
is a set of maps between cofibrant objects in
$H$
is a set of maps between cofibrant objects in
![]() ${\mathcal{M}}$
which is taken by
${\mathcal{M}}$
which is taken by
![]() $L$
into weak equivalences, then
$L$
into weak equivalences, then
 $L:L_{H}{\mathcal{M}}\leftrightarrows {\mathcal{N}}:R$
is also a Quillen adjunction. This follows from [Reference HirschhornHir09, Propositions 8.5.4 and 3.3.16].)
$L:L_{H}{\mathcal{M}}\leftrightarrows {\mathcal{N}}:R$
is also a Quillen adjunction. This follows from [Reference HirschhornHir09, Propositions 8.5.4 and 3.3.16].)
We now have the following diagram (which we do not know to be commutative so far).

Here all the functors are derived; we omit the ‘L’ and ‘R’. The functor
![]() $r$
is an equivalence with inverse
$r$
is an equivalence with inverse
![]() $e$
by Theorem 35. Thus for
$e$
by Theorem 35. Thus for
 $E\in \mathbf{SH}^{S^{1}}(\mathbb{R})^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
we have a canonical isomorphism
$E\in \mathbf{SH}^{S^{1}}(\mathbb{R})^{\text{r}\acute{\text{e}}\text{t}}[\unicode[STIX]{x1D70C}^{-1}]$
we have a canonical isomorphism
 $R_{2}^{\prime }E\simeq R_{2}^{\prime }erE$
and so to prove the proposition it suffices to exhibit a canonical isomorphism of functors
$R_{2}^{\prime }E\simeq R_{2}^{\prime }erE$
and so to prove the proposition it suffices to exhibit a canonical isomorphism of functors
 $R_{2}^{\prime }e\simeq |\bullet |$
.
$R_{2}^{\prime }e\simeq |\bullet |$
.
But this isomorphism exists on the level of underived functors, and then passes to the homotopy categories. Indeed if
 $E\in \operatorname{Spt}^{s}$
then
$E\in \operatorname{Spt}^{s}$
then
![]() $R_{2}^{\prime }eE$
and
$R_{2}^{\prime }eE$
and
![]() $|E|$
are both computed by applying functors (of the same names) levelwise to
$|E|$
are both computed by applying functors (of the same names) levelwise to
![]() $E$
, so we may just as well show that for
$E$
, so we may just as well show that for
 $E\in \text{sSet}_{\ast }$
we have
$E\in \text{sSet}_{\ast }$
we have
 $R_{2}^{\prime }eE\cong |E|$
. But now
$R_{2}^{\prime }eE\cong |E|$
. But now
![]() $R_{2}^{\prime }$
,
$R_{2}^{\prime }$
,
![]() $e$
and
$e$
and
![]() $|\bullet |$
all preserve colimits, so we may just deal with
$|\bullet |$
all preserve colimits, so we may just deal with
 $E=\unicode[STIX]{x1D6E5}_{+}^{n}$
. But then
$E=\unicode[STIX]{x1D6E5}_{+}^{n}$
. But then
 $R_{2}^{\prime }eE\unicode[STIX]{x1D6E5}_{+}^{n}=|\unicode[STIX]{x1D6E5}_{+}^{n}|$
holds basically by definition.◻
$R_{2}^{\prime }eE\unicode[STIX]{x1D6E5}_{+}^{n}=|\unicode[STIX]{x1D6E5}_{+}^{n}|$
holds basically by definition.◻
A similar result can be obtained for the
![]() $\mathbb{A}^{1}$
-derived category. We have
$\mathbb{A}^{1}$
-derived category. We have
 $r:D_{\mathbb{A}^{1}}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]\rightarrow D(\operatorname{Spec}(\mathbb{R})_{\text{r}\acute{\text{e}}\text{t}})\simeq D(Ab).$
There is also
$r:D_{\mathbb{A}^{1}}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]\rightarrow D(\operatorname{Spec}(\mathbb{R})_{\text{r}\acute{\text{e}}\text{t}})\simeq D(Ab).$
There is also
 $R_{2}:D_{\mathbb{A}^{1}}(\mathbb{R})\rightarrow D(Ab)$
which is obtained by (derived) left Kan extension from the functor
$R_{2}:D_{\mathbb{A}^{1}}(\mathbb{R})\rightarrow D(Ab)$
which is obtained by (derived) left Kan extension from the functor
 $Sm(\mathbb{R})\rightarrow C(Ab)$
which sends a smooth scheme
$Sm(\mathbb{R})\rightarrow C(Ab)$
which sends a smooth scheme
![]() $X$
the singular complex of its real points
$X$
the singular complex of its real points
 $C_{\ast }(X(\mathbb{R}))$
. Then there is the following commutative diagram.
$C_{\ast }(X(\mathbb{R}))$
. Then there is the following commutative diagram.

Proposition 37. The functors
 $rL_{\unicode[STIX]{x1D70C}},R_{2}:D_{\mathbb{A}^{1}}(\mathbb{R})\rightarrow D(Ab)$
are canonically isomorphic.
$rL_{\unicode[STIX]{x1D70C}},R_{2}:D_{\mathbb{A}^{1}}(\mathbb{R})\rightarrow D(Ab)$
are canonically isomorphic.
Proof. As before
![]() $R_{2}$
factors through
$R_{2}$
factors through
![]() $L_{\unicode[STIX]{x1D70C}}$
as
$L_{\unicode[STIX]{x1D70C}}$
as
![]() $R_{2}^{\prime }$
and we may show that
$R_{2}^{\prime }$
and we may show that
 $r,R_{2}^{\prime }:D_{\mathbb{A}^{1}}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]\rightarrow D(Ab)$
are canonically isomorphic. The functor
$r,R_{2}^{\prime }:D_{\mathbb{A}^{1}}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]\rightarrow D(Ab)$
are canonically isomorphic. The functor
![]() $r$
is an equivalence with inverse
$r$
is an equivalence with inverse
![]() $e$
, so it is enough to show that
$e$
, so it is enough to show that
 $R_{2}^{\prime }e:D(Ab)\rightarrow D_{\mathbb{A}^{1}}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]\simeq D_{\mathbb{A}^{1}}^{S^{1}}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]\rightarrow D(Ab)$
is canonically isomorphic to the identity. This is the same argument as before.◻
$R_{2}^{\prime }e:D(Ab)\rightarrow D_{\mathbb{A}^{1}}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]\simeq D_{\mathbb{A}^{1}}^{S^{1}}(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]\rightarrow D(Ab)$
is canonically isomorphic to the identity. This is the same argument as before.◻
Let us make explicit the following consequence.
Corollary 38. Let
 $E\in \mathbf{SH}(\mathbb{R})$
. Then
$E\in \mathbf{SH}(\mathbb{R})$
. Then
 $$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]=\unicode[STIX]{x1D70B}_{i}(RE)\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]=\unicode[STIX]{x1D70B}_{i}(RE)\end{eqnarray}$$
and
 $$\begin{eqnarray}\text{}\underline{h}_{i}^{\mathbb{A}^{1}}(E)(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]=H_{i}(RE).\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{h}_{i}^{\mathbb{A}^{1}}(E)(\mathbb{R})[\unicode[STIX]{x1D70C}^{-1}]=H_{i}(RE).\end{eqnarray}$$
Here
 $R:\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}$
denotes any one of the (canonically isomorphic) real realisation functors we have considered and
$R:\mathbf{SH}(\mathbb{R})\rightarrow \mathbf{SH}$
denotes any one of the (canonically isomorphic) real realisation functors we have considered and
 $\text{}\underline{h}_{i}^{\mathbb{A}^{1}}(E):=\text{}\underline{h}_{i}(FE)$
where
$\text{}\underline{h}_{i}^{\mathbb{A}^{1}}(E):=\text{}\underline{h}_{i}(FE)$
where
 $F:\mathbf{SH}(\mathbb{R})\rightarrow D_{\mathbb{A}^{1}}(\mathbb{R})$
is the canonical functor.
$F:\mathbf{SH}(\mathbb{R})\rightarrow D_{\mathbb{A}^{1}}(\mathbb{R})$
is the canonical functor.
Proof. Combine Lemma 15 (saying that
 $L_{\unicode[STIX]{x1D70C}}E=E[\unicode[STIX]{x1D70C}^{-1}]=\operatorname{hocolim}_{n}E\wedge \mathbb{G}_{m}^{\wedge n}$
) with compactness of the units of
$L_{\unicode[STIX]{x1D70C}}E=E[\unicode[STIX]{x1D70C}^{-1}]=\operatorname{hocolim}_{n}E\wedge \mathbb{G}_{m}^{\wedge n}$
) with compactness of the units of
 $\mathbf{SH},D_{\mathbb{A}^{1}}$
and the above two propositions.◻
$\mathbf{SH},D_{\mathbb{A}^{1}}$
and the above two propositions.◻
11 Application 1: the
 $\unicode[STIX]{x1D702}$
-inverted sphere
$\unicode[STIX]{x1D702}$
-inverted sphere
From now on,
![]() $k$
will denote a perfect field. Since essentially all our results concern the
$k$
will denote a perfect field. Since essentially all our results concern the
![]() $\unicode[STIX]{x1D70C}$
-inverted situation, they are really only interesting if
$\unicode[STIX]{x1D70C}$
-inverted situation, they are really only interesting if
![]() $k$
has characteristic zero, so this is not a big restriction.
$k$
has characteristic zero, so this is not a big restriction.
Recall that the motivic Hopf map
 $\unicode[STIX]{x1D702}:\mathbb{A}^{2}\setminus 0\rightarrow \mathbb{P}^{1}$
defines an element of the same name in motivic stable homotopy theory
$\unicode[STIX]{x1D702}:\mathbb{A}^{2}\setminus 0\rightarrow \mathbb{P}^{1}$
defines an element of the same name in motivic stable homotopy theory
 $\unicode[STIX]{x1D702}:\unicode[STIX]{x1D6F4}^{\infty }\mathbb{G}_{m}\rightarrow \unicode[STIX]{x1D7D9}$
. Here we use that
$\unicode[STIX]{x1D702}:\unicode[STIX]{x1D6F4}^{\infty }\mathbb{G}_{m}\rightarrow \unicode[STIX]{x1D7D9}$
. Here we use that
 $\unicode[STIX]{x1D6F4}^{\infty }(\mathbb{A}^{2}\setminus 0)\simeq \unicode[STIX]{x1D6F4}^{\infty }\mathbb{G}_{m}\wedge \unicode[STIX]{x1D6F4}^{\infty }\mathbb{P}^{1}$
. The element
$\unicode[STIX]{x1D6F4}^{\infty }(\mathbb{A}^{2}\setminus 0)\simeq \unicode[STIX]{x1D6F4}^{\infty }\mathbb{G}_{m}\wedge \unicode[STIX]{x1D6F4}^{\infty }\mathbb{P}^{1}$
. The element
 $\unicode[STIX]{x1D702}\in \text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9})_{-1}$
is non-nilpotent, and so inverting it is very natural. The category
$\unicode[STIX]{x1D702}\in \text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9})_{-1}$
is non-nilpotent, and so inverting it is very natural. The category
 $\mathbf{SH}(k)[\unicode[STIX]{x1D702}^{-1}]$
can be constructed very similarly to
$\mathbf{SH}(k)[\unicode[STIX]{x1D702}^{-1}]$
can be constructed very similarly to
 $\mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
. In particular the localisation functor
$\mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
. In particular the localisation functor
 $L:\mathbf{SH}(k)\rightarrow \mathbf{SH}(k)[\unicode[STIX]{x1D702}^{-1}]$
is just the evident colimit, see Lemma 15. It is typically denoted
$L:\mathbf{SH}(k)\rightarrow \mathbf{SH}(k)[\unicode[STIX]{x1D702}^{-1}]$
is just the evident colimit, see Lemma 15. It is typically denoted
 $E\mapsto E_{\unicode[STIX]{x1D702}}$
or
$E\mapsto E_{\unicode[STIX]{x1D702}}$
or
 $E\mapsto E[1/\unicode[STIX]{x1D702}]$
. One may similarly invert other endomorphisms of the sphere spectrum. If
$E\mapsto E[1/\unicode[STIX]{x1D702}]$
. One may similarly invert other endomorphisms of the sphere spectrum. If
 $0\neq n\in \mathbb{Z}$
then there is a corresponding automorphism of
$0\neq n\in \mathbb{Z}$
then there is a corresponding automorphism of
![]() $\unicode[STIX]{x1D7D9}$
, and we denote the localisation by
$\unicode[STIX]{x1D7D9}$
, and we denote the localisation by
 $E\mapsto E[1/n]$
.
$E\mapsto E[1/n]$
.
At least after inverting
![]() $2$
, inverting
$2$
, inverting
![]() $\unicode[STIX]{x1D702}$
is essentially the same as inverting
$\unicode[STIX]{x1D702}$
is essentially the same as inverting
![]() $\unicode[STIX]{x1D70C}$
.
$\unicode[STIX]{x1D70C}$
.
Lemma 39. The endomorphism ring
 $K_{\ast }^{MW}(k)[1/2]=[\unicode[STIX]{x1D7D9}[1/2],\unicode[STIX]{x1D7D9}[1/2]\wedge \mathbb{G}_{m}^{\wedge \ast }]$
splits canonically into two summands
$K_{\ast }^{MW}(k)[1/2]=[\unicode[STIX]{x1D7D9}[1/2],\unicode[STIX]{x1D7D9}[1/2]\wedge \mathbb{G}_{m}^{\wedge \ast }]$
splits canonically into two summands
 $K_{\ast }^{MW}(k)[1/2]=K^{+}\oplus K^{-}$
. In fact
$K_{\ast }^{MW}(k)[1/2]=K^{+}\oplus K^{-}$
. In fact
 $K^{-}=K_{\ast }^{MW}(k)[1/2,1/\unicode[STIX]{x1D702}]$
and
$K^{-}=K_{\ast }^{MW}(k)[1/2,1/\unicode[STIX]{x1D702}]$
and
![]() $K^{+}$
is characterised by the fact that
$K^{+}$
is characterised by the fact that
 $\unicode[STIX]{x1D702}K^{+}=0$
.
$\unicode[STIX]{x1D702}K^{+}=0$
.
In
![]() $K^{-}$
we have the equality
$K^{-}$
we have the equality
![]() $\unicode[STIX]{x1D702}\unicode[STIX]{x1D70C}=2$
, whereas in
$\unicode[STIX]{x1D702}\unicode[STIX]{x1D70C}=2$
, whereas in
![]() $K^{+}$
we have
$K^{+}$
we have
![]() $\unicode[STIX]{x1D70C}^{2}=0$
. In particular
$\unicode[STIX]{x1D70C}^{2}=0$
. In particular
 $$\begin{eqnarray}K_{\ast }^{MW}(k)[1/2,1/\unicode[STIX]{x1D702}]=K^{-}=K_{\ast }^{MW}(k)[1/2,1/\unicode[STIX]{x1D70C}].\end{eqnarray}$$
$$\begin{eqnarray}K_{\ast }^{MW}(k)[1/2,1/\unicode[STIX]{x1D702}]=K^{-}=K_{\ast }^{MW}(k)[1/2,1/\unicode[STIX]{x1D70C}].\end{eqnarray}$$
Proof. This is well known, see for example [Reference MorelMor12, § 3.1]. We summarise: for
![]() $a\in k^{\times }$
let
$a\in k^{\times }$
let
 $\langle a\rangle =1+\unicode[STIX]{x1D702}[a]\in K_{0}^{MW}(k)$
. Put
$\langle a\rangle =1+\unicode[STIX]{x1D702}[a]\in K_{0}^{MW}(k)$
. Put
 $\unicode[STIX]{x1D716}=-\langle -1\rangle$
. Then
$\unicode[STIX]{x1D716}=-\langle -1\rangle$
. Then
![]() $\unicode[STIX]{x1D716}^{2}=1$
and so after inverting
$\unicode[STIX]{x1D716}^{2}=1$
and so after inverting
![]() $2$
,
$2$
,
 $K_{\ast }^{MW}(k)$
splits into the eigenspaces for
$K_{\ast }^{MW}(k)$
splits into the eigenspaces for
![]() $\unicode[STIX]{x1D716}$
. One puts
$\unicode[STIX]{x1D716}$
. One puts
 $h=1-\unicode[STIX]{x1D716}$
and then has
$h=1-\unicode[STIX]{x1D716}$
and then has
![]() $\unicode[STIX]{x1D702}h=0$
. On
$\unicode[STIX]{x1D702}h=0$
. On
![]() $K^{+}$
we have
$K^{+}$
we have
![]() $\unicode[STIX]{x1D716}=-1$
, so
$\unicode[STIX]{x1D716}=-1$
, so
![]() $h=2$
and consequently
$h=2$
and consequently
![]() $\unicode[STIX]{x1D702}=0$
(since
$\unicode[STIX]{x1D702}=0$
(since
![]() $2$
is invertible).
$2$
is invertible).
By definition
 $\unicode[STIX]{x1D70C}=-[-1]$
and consequently
$\unicode[STIX]{x1D70C}=-[-1]$
and consequently
 $\unicode[STIX]{x1D702}\unicode[STIX]{x1D70C}=1+\unicode[STIX]{x1D716}$
. Thus on
$\unicode[STIX]{x1D702}\unicode[STIX]{x1D70C}=1+\unicode[STIX]{x1D716}$
. Thus on
![]() $K^{-}$
where
$K^{-}$
where
![]() $\unicode[STIX]{x1D716}=1$
we find
$\unicode[STIX]{x1D716}=1$
we find
![]() $\unicode[STIX]{x1D702}\unicode[STIX]{x1D70C}=2$
as claimed, and in particular
$\unicode[STIX]{x1D702}\unicode[STIX]{x1D70C}=2$
as claimed, and in particular
![]() $\unicode[STIX]{x1D702}$
is invertible on
$\unicode[STIX]{x1D702}$
is invertible on
![]() $K^{-}$
.
$K^{-}$
.
Finally
 $\unicode[STIX]{x1D70C}^{2}h=0$
in
$\unicode[STIX]{x1D70C}^{2}h=0$
in
 $K_{\ast }^{MW}(k)$
and thus
$K_{\ast }^{MW}(k)$
and thus
 $2\unicode[STIX]{x1D70C}^{2}=0$
in
$2\unicode[STIX]{x1D70C}^{2}=0$
in
![]() $K^{+}$
. (This is just another expression of the fact that
$K^{+}$
. (This is just another expression of the fact that
 $K^{+}\cong K^{M}(k)[1/2]$
is graded-commutative and
$K^{+}\cong K^{M}(k)[1/2]$
is graded-commutative and
![]() $\unicode[STIX]{x1D70C}$
has degree 1, so
$\unicode[STIX]{x1D70C}$
has degree 1, so
 $\unicode[STIX]{x1D70C}^{2}=-\unicode[STIX]{x1D70C}^{2}$
.) But since
$\unicode[STIX]{x1D70C}^{2}=-\unicode[STIX]{x1D70C}^{2}$
.) But since
![]() $2$
is invertible in
$2$
is invertible in
![]() $K^{+}$
we find
$K^{+}$
we find
![]() $\unicode[STIX]{x1D70C}^{2}=0$
(in
$\unicode[STIX]{x1D70C}^{2}=0$
(in
![]() $K^{+}$
). This concludes the proof.◻
$K^{+}$
). This concludes the proof.◻
Röndigs has studied the homotopy sheaves
![]() $\text{}\underline{\unicode[STIX]{x1D70B}}_{1}(\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D702}})$
and
$\text{}\underline{\unicode[STIX]{x1D70B}}_{1}(\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D702}})$
and
![]() $\text{}\underline{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D702}})$
and proved that they vanish [Reference RöndigsRön16]. (Note that
$\text{}\underline{\unicode[STIX]{x1D70B}_{2}}(\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D702}})$
and proved that they vanish [Reference RöndigsRön16]. (Note that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E_{\unicode[STIX]{x1D702}})_{\ast }$
is independent of
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E_{\unicode[STIX]{x1D702}})_{\ast }$
is independent of
![]() $\ast$
, because multiplication by
$\ast$
, because multiplication by
![]() $\unicode[STIX]{x1D702}$
is an isomorphism, so we shall suppress the second index.) He argues that
$\unicode[STIX]{x1D702}$
is an isomorphism, so we shall suppress the second index.) He argues that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9})_{\ast }\rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2])_{\ast }$
is injective for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9})_{\ast }\rightarrow \text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2])_{\ast }$
is injective for
![]() $i=1,2$
(see his Lemma 8.2) and consequently an important part of his work is in showing that
$i=1,2$
(see his Lemma 8.2) and consequently an important part of his work is in showing that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D702},1/2])=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D702},1/2])=0$
for
![]() $i=1,2$
. We can deduce this as an easy corollary from our work.
$i=1,2$
. We can deduce this as an easy corollary from our work.
Proposition 40. Let
![]() $k$
be a perfect field. Then
$k$
be a perfect field. Then
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D702},1/2])=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D702},1/2])=0$
for
![]() $i=1,2$
.
$i=1,2$
.
Proof. By Lemma 39 we know that
 $\mathbf{SH}(k)[1/2,1/\unicode[STIX]{x1D702}]=\mathbf{SH}(k)[1/2,1/\unicode[STIX]{x1D70C}]$
. By Theorem 35, we have
$\mathbf{SH}(k)[1/2,1/\unicode[STIX]{x1D702}]=\mathbf{SH}(k)[1/2,1/\unicode[STIX]{x1D70C}]$
. By Theorem 35, we have
 $\mathbf{SH}(k)[1/2,1/\unicode[STIX]{x1D70C}]=\text{SH}(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})[1/2]$
. In particular this category is trivial unless
$\mathbf{SH}(k)[1/2,1/\unicode[STIX]{x1D70C}]=\text{SH}(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})[1/2]$
. In particular this category is trivial unless
![]() $k$
has characteristic zero, which we shall assume from now on.
$k$
has characteristic zero, which we shall assume from now on.
The sheaves
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D70C}])$
are unramified [Reference MorelMor05, Lemma 6.4.4], so it suffices to show that
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D70C}])$
are unramified [Reference MorelMor05, Lemma 6.4.4], so it suffices to show that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D70C}])(K)=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D70C}])(K)=0$
for
![]() $i=1,2$
and every
$i=1,2$
and every
![]() $K$
(of characteristic zero). Since
$K$
(of characteristic zero). Since
![]() $k$
was also arbitrary, we may just as well show the result for
$k$
was also arbitrary, we may just as well show the result for
![]() $k=K$
, simplifying notation. We are dealing with rét-sheaves by Theorem 25, and so if
$k=K$
, simplifying notation. We are dealing with rét-sheaves by Theorem 25, and so if
 $$\begin{eqnarray}\operatorname{Spec}(l_{1})\coprod \operatorname{Spec}(l_{2})\coprod \ldots \coprod \operatorname{Spec}(l_{n})\rightarrow \operatorname{Spec}(k)\end{eqnarray}$$
$$\begin{eqnarray}\operatorname{Spec}(l_{1})\coprod \operatorname{Spec}(l_{2})\coprod \ldots \coprod \operatorname{Spec}(l_{n})\rightarrow \operatorname{Spec}(k)\end{eqnarray}$$
is a rét-cover, the canonical map
 $$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D70C}])(k)\rightarrow \mathop{\prod }_{m}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D70C}])(l_{m})\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D70C}])(k)\rightarrow \mathop{\prod }_{m}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D70C}])(l_{m})\end{eqnarray}$$
is injective. Consequently we may assume that
![]() $k$
is real closed. But then
$k$
is real closed. But then
 $\text{SH}(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})=\mathbf{SH}$
is just the ordinary stable homotopy category, so it suffices to show:
$\text{SH}(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})=\mathbf{SH}$
is just the ordinary stable homotopy category, so it suffices to show:
 $\unicode[STIX]{x1D70B}_{i}^{s}[1/2]=0$
for
$\unicode[STIX]{x1D70B}_{i}^{s}[1/2]=0$
for
![]() $i=1,2$
, where
$i=1,2$
, where
![]() $\unicode[STIX]{x1D70B}_{i}^{s}$
are the classical stable homotopy groups. But
$\unicode[STIX]{x1D70B}_{i}^{s}$
are the classical stable homotopy groups. But
 $\unicode[STIX]{x1D70B}_{1}^{s}=\mathbb{Z}/2=\unicode[STIX]{x1D70B}_{2}^{s}$
is well known, so we are done.◻
$\unicode[STIX]{x1D70B}_{1}^{s}=\mathbb{Z}/2=\unicode[STIX]{x1D70B}_{2}^{s}$
is well known, so we are done.◻
In classical algebraic topology, it is well known that rational stable homotopy theory is the same as rational homology theory:
 $\mathbf{SH}_{\mathbb{Q}}\simeq D(\mathbb{Q})$
. In motivic stable homotopy theory, the situation is not so simple. As is well known (and follows for example from Lemma 39) there is a splitting
$\mathbf{SH}_{\mathbb{Q}}\simeq D(\mathbb{Q})$
. In motivic stable homotopy theory, the situation is not so simple. As is well known (and follows for example from Lemma 39) there is a splitting
 $\mathbf{SH}(k)_{\mathbb{Q}}=\mathbf{SH}(k)_{\mathbb{Q}}^{+}\times \mathbf{SH}(k)_{\mathbb{Q}}^{-}$
. The + part has been identified with rational motivic homology theory by Cisinski–Déglise [Reference Cisinski and DégliseCD12, § 16]:
$\mathbf{SH}(k)_{\mathbb{Q}}=\mathbf{SH}(k)_{\mathbb{Q}}^{+}\times \mathbf{SH}(k)_{\mathbb{Q}}^{-}$
. The + part has been identified with rational motivic homology theory by Cisinski–Déglise [Reference Cisinski and DégliseCD12, § 16]:
 $\mathbf{SH}(k)_{\mathbb{Q}}^{+}\simeq \mathbf{DM}(k,\mathbb{Q})$
.
$\mathbf{SH}(k)_{\mathbb{Q}}^{+}\simeq \mathbf{DM}(k,\mathbb{Q})$
.
The
![]() $-$
part has been only identified recently with an appropriate category of rational Witt motives by Ananyevskiy et al. [Reference Ananyevskiy, Levine and PaninALP17]:
$-$
part has been only identified recently with an appropriate category of rational Witt motives by Ananyevskiy et al. [Reference Ananyevskiy, Levine and PaninALP17]:
 $\mathbf{SH}(k)_{\mathbb{Q}}^{-}=\mathbf{DM}_{W}(k,\mathbb{Q})$
. Here the category
$\mathbf{SH}(k)_{\mathbb{Q}}^{-}=\mathbf{DM}_{W}(k,\mathbb{Q})$
. Here the category
 $\mathbf{DM}_{W}(k,\mathbb{Q})$
may be conveniently defined as the homotopy category of modules over the (strict ring spectrum model of the) homotopy module of rational Witt theory. That is to say there is the homotopy module
$\mathbf{DM}_{W}(k,\mathbb{Q})$
may be conveniently defined as the homotopy category of modules over the (strict ring spectrum model of the) homotopy module of rational Witt theory. That is to say there is the homotopy module
![]() $\text{}\underline{W}_{\mathbb{Q}}$
with
$\text{}\underline{W}_{\mathbb{Q}}$
with
 $(\text{}\underline{W}_{\mathbb{Q}})_{i}=\text{}\underline{W}\otimes _{\mathbb{Z}}\mathbb{Q}$
for all
$(\text{}\underline{W}_{\mathbb{Q}})_{i}=\text{}\underline{W}\otimes _{\mathbb{Z}}\mathbb{Q}$
for all
![]() $i$
. This is the same as
$i$
. This is the same as
 $K^{-}\otimes _{\mathbb{Z}[1/2]}\mathbb{Q}$
, or equivalently
$K^{-}\otimes _{\mathbb{Z}[1/2]}\mathbb{Q}$
, or equivalently
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D702},\mathbb{Q}})$
. Then corresponding to this homotopy module there is a strict ring spectrum, the Eilenberg–MacLane spectrum
$\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D702},\mathbb{Q}})$
. Then corresponding to this homotopy module there is a strict ring spectrum, the Eilenberg–MacLane spectrum
 $EM\text{}\underline{W}_{\mathbb{Q}}$
. Finally we may form the model category
$EM\text{}\underline{W}_{\mathbb{Q}}$
. Finally we may form the model category
 $EM\text{}\underline{W}_{\mathbb{Q}}\text{}\text{-Mod}$
and its homotopy category
$EM\text{}\underline{W}_{\mathbb{Q}}\text{}\text{-Mod}$
and its homotopy category
 $\operatorname{Ho}(EM\text{}\underline{W}_{\mathbb{Q}}\text{}\text{-Mod})=:\mathbf{DM}_{W}(k,\mathbb{Q})$
.
$\operatorname{Ho}(EM\text{}\underline{W}_{\mathbb{Q}}\text{}\text{-Mod})=:\mathbf{DM}_{W}(k,\mathbb{Q})$
.
More generally, one may define
 $\mathbf{DM}_{W}(k,\mathbb{Z}[1/2])$
by replacing
$\mathbf{DM}_{W}(k,\mathbb{Z}[1/2])$
by replacing
 $\text{}\underline{W}_{\mathbb{Q}}=\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9}_{\mathbb{Q}}[1/\unicode[STIX]{x1D702}])$
in the above construction with
$\text{}\underline{W}_{\mathbb{Q}}=\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9}_{\mathbb{Q}}[1/\unicode[STIX]{x1D702}])$
in the above construction with
 $\text{}\underline{W}[1/2]=\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D702},1/2])$
.
$\text{}\underline{W}[1/2]=\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D702},1/2])$
.
The theorem of Ananyevskiy–Levine–Panin essentially boils down to the computation that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D702},\mathbb{Q}})=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}_{\unicode[STIX]{x1D702},\mathbb{Q}})=0$
for
![]() $i>0$
. We can deduce this and more from our general theory. We write
$i>0$
. We can deduce this and more from our general theory. We write
![]() $H_{\mathbb{A}^{1}}\mathbb{Z}$
for the image of the tensor unit in
$H_{\mathbb{A}^{1}}\mathbb{Z}$
for the image of the tensor unit in
![]() $D_{\mathbb{A}^{1}}(k)$
under the ‘forgetful’ functor
$D_{\mathbb{A}^{1}}(k)$
under the ‘forgetful’ functor
 $D_{\mathbb{A}^{1}}(k)\rightarrow \mathbf{SH}(k)$
.
$D_{\mathbb{A}^{1}}(k)\rightarrow \mathbf{SH}(k)$
.
Proposition 41. We have
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(H_{\mathbb{A}^{1}}\mathbb{Z}[1/\unicode[STIX]{x1D70C}])=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(H_{\mathbb{A}^{1}}\mathbb{Z}[1/\unicode[STIX]{x1D70C}])=0$
for
![]() $i>0$
, and consequently
$i>0$
, and consequently
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(H_{\mathbb{A}^{1}}\mathbb{Z}[1/2,1/\unicode[STIX]{x1D702}])=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(H_{\mathbb{A}^{1}}\mathbb{Z}[1/2,1/\unicode[STIX]{x1D702}])=0$
for
![]() $i>0$
. Similarly
$i>0$
. Similarly
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}_{\mathbb{Q}}[1/\unicode[STIX]{x1D70C}])=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}_{\mathbb{Q}}[1/\unicode[STIX]{x1D702}])=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}_{\mathbb{Q}}[1/\unicode[STIX]{x1D70C}])=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}_{\mathbb{Q}}[1/\unicode[STIX]{x1D702}])=0$
for
![]() $i>0$
.
$i>0$
.
Thus we have the equivalences
 $$\begin{eqnarray}\displaystyle D_{\mathbb{A}^{1}}(k,\mathbb{Z}[1/2])^{-} & \simeq & \displaystyle \mathbf{DM}_{W}(k,\mathbb{Z}[1/2])\simeq D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}},\mathbb{Z}[1/2])\nonumber\\ \displaystyle \mathbf{SH}(k)_{\mathbb{Q}}^{-} & \simeq & \displaystyle \mathbf{DM}_{W}(k,\mathbb{Q})\simeq D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}},\mathbb{Q}).\nonumber\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle D_{\mathbb{A}^{1}}(k,\mathbb{Z}[1/2])^{-} & \simeq & \displaystyle \mathbf{DM}_{W}(k,\mathbb{Z}[1/2])\simeq D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}},\mathbb{Z}[1/2])\nonumber\\ \displaystyle \mathbf{SH}(k)_{\mathbb{Q}}^{-} & \simeq & \displaystyle \mathbf{DM}_{W}(k,\mathbb{Q})\simeq D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}},\mathbb{Q}).\nonumber\end{eqnarray}$$
Proof. As in the proof of Proposition 40 we have
 $$\begin{eqnarray}D_{\mathbb{A}^{1}}(k)[1/2]^{-}:=D_{\mathbb{ A}^{1}}(k)[1/2,1/\unicode[STIX]{x1D702}]=D_{\mathbb{A}^{1}}(k)[1/2,1/\unicode[STIX]{x1D70C}].\end{eqnarray}$$
$$\begin{eqnarray}D_{\mathbb{A}^{1}}(k)[1/2]^{-}:=D_{\mathbb{ A}^{1}}(k)[1/2,1/\unicode[STIX]{x1D702}]=D_{\mathbb{A}^{1}}(k)[1/2,1/\unicode[STIX]{x1D70C}].\end{eqnarray}$$
By Theorem 35, this is the same as
 $D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})[1/2]=D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}},\mathbb{Z}[1/2])$
.
$D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})[1/2]=D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}},\mathbb{Z}[1/2])$
.
Similarly
 $$\begin{eqnarray}\mathbf{SH}(k)_{\mathbb{Q}}^{-}:=\mathbf{SH}(k)_{\mathbb{ Q}}[1/\unicode[STIX]{x1D702}]=\mathbf{SH}(k)_{\mathbb{Q}}[1/\unicode[STIX]{x1D70C}]=\text{SH}(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})_{\mathbb{Q}},\end{eqnarray}$$
$$\begin{eqnarray}\mathbf{SH}(k)_{\mathbb{Q}}^{-}:=\mathbf{SH}(k)_{\mathbb{ Q}}[1/\unicode[STIX]{x1D702}]=\mathbf{SH}(k)_{\mathbb{Q}}[1/\unicode[STIX]{x1D70C}]=\text{SH}(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})_{\mathbb{Q}},\end{eqnarray}$$
and the latter category is equivalent to
 $D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})_{\mathbb{Q}}$
by classical stable rational homotopy theory.
$D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})_{\mathbb{Q}}$
by classical stable rational homotopy theory.
From this we can read off
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }(H_{\mathbb{A}^{1}}\mathbb{Z}[1/2,1/\unicode[STIX]{x1D702}])$
and so on. The main point is that
$\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }(H_{\mathbb{A}^{1}}\mathbb{Z}[1/2,1/\unicode[STIX]{x1D702}])$
and so on. The main point is that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{n}(H_{\mathbb{A}^{1}}\mathbb{Z}[1/2,1/\unicode[STIX]{x1D702}])=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{n}(H_{\mathbb{A}^{1}}\mathbb{Z}[1/2,1/\unicode[STIX]{x1D702}])=0$
for
![]() $n>0$
. It suffices to check this on fields, so we may as well check it for
$n>0$
. It suffices to check this on fields, so we may as well check it for
![]() $k$
(
$k$
(
![]() $k$
being arbitrary), and we have
$k$
being arbitrary), and we have
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{n}(H_{\mathbb{A}^{1}}\mathbb{Z}[1/2,1/\unicode[STIX]{x1D702}])(k)=[\unicode[STIX]{x1D7D9}[n],\unicode[STIX]{x1D7D9}]_{D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}},\mathbb{Z}[1/2])}=H_{\text{r}\acute{\text{e}}\text{t}}^{-n}(k,\mathbb{Z}[1/2])=0$
.
$\text{}\underline{\unicode[STIX]{x1D70B}}_{n}(H_{\mathbb{A}^{1}}\mathbb{Z}[1/2,1/\unicode[STIX]{x1D702}])(k)=[\unicode[STIX]{x1D7D9}[n],\unicode[STIX]{x1D7D9}]_{D(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}},\mathbb{Z}[1/2])}=H_{\text{r}\acute{\text{e}}\text{t}}^{-n}(k,\mathbb{Z}[1/2])=0$
.
It remains to show that
 $D_{\mathbb{A}^{1}}(k,\mathbb{Z}[1/2])^{-}\simeq \mathbf{DM}_{W}(k,\mathbb{Z}[1/2])$
. Our computation of homotopy sheaves implies that
$D_{\mathbb{A}^{1}}(k,\mathbb{Z}[1/2])^{-}\simeq \mathbf{DM}_{W}(k,\mathbb{Z}[1/2])$
. Our computation of homotopy sheaves implies that
 $H_{\mathbb{A}^{1}}\mathbb{Z}[1/\unicode[STIX]{x1D70C},1/2]\rightarrow EM\text{}\underline{W}[1/2]$
is a weak equivalence. The result follows.◻
$H_{\mathbb{A}^{1}}\mathbb{Z}[1/\unicode[STIX]{x1D70C},1/2]\rightarrow EM\text{}\underline{W}[1/2]$
is a weak equivalence. The result follows.◻
Let us also make explicit the following observation.
Corollary 42. Let
![]() $k$
be a real closed field or
$k$
be a real closed field or
![]() $\mathbb{Q}$
. Then
$\mathbb{Q}$
. Then
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D70C}])(k)=\unicode[STIX]{x1D70B}_{\ast }^{s}$
and in particular
$\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D70C}])(k)=\unicode[STIX]{x1D70B}_{\ast }^{s}$
and in particular
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D702},1/2])(k)=\unicode[STIX]{x1D70B}_{\ast }^{s}\otimes _{\mathbb{Z}}\mathbb{Z}[1/2]$
. Here
$\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }(\unicode[STIX]{x1D7D9}[1/\unicode[STIX]{x1D702},1/2])(k)=\unicode[STIX]{x1D70B}_{\ast }^{s}\otimes _{\mathbb{Z}}\mathbb{Z}[1/2]$
. Here
![]() $\unicode[STIX]{x1D70B}_{\ast }^{s}$
denotes the classical stable homotopy groups.
$\unicode[STIX]{x1D70B}_{\ast }^{s}$
denotes the classical stable homotopy groups.
12 Application 2: some rigidity results
In this section we establish some rigidity results. We work with
![]() $\unicode[STIX]{x1D70C}$
-stable sheaves. These sheaves are
$\unicode[STIX]{x1D70C}$
-stable sheaves. These sheaves are
![]() $h$
-torsion (because
$h$
-torsion (because
 $\unicode[STIX]{x1D70C}^{2}h=0$
), explaining to some extent why we do not need the usual torsion assumptions.
$\unicode[STIX]{x1D70C}^{2}h=0$
), explaining to some extent why we do not need the usual torsion assumptions.
There are various notions of rigidity for sheaves. We shall call a presheaf
![]() $F$
on
$F$
on
![]() $Sm(k)$
rigid if for every essentially smooth, Henselian local scheme
$Sm(k)$
rigid if for every essentially smooth, Henselian local scheme
![]() $X$
with residue field
$X$
with residue field
![]() $x$
, the natural map
$x$
, the natural map
 $F(X)\rightarrow F(x)$
is an isomorphism. This notion goes back to perhaps Gillet and Thomason [Reference Gillet and ThomasonGT84] and Gabber [Reference GabberGab92].
$F(X)\rightarrow F(x)$
is an isomorphism. This notion goes back to perhaps Gillet and Thomason [Reference Gillet and ThomasonGT84] and Gabber [Reference GabberGab92].
Lemma 43. Let
 $F\in \operatorname{Shv}(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})$
. Then
$F\in \operatorname{Shv}(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})$
. Then
 $eF\in \operatorname{Shv}(Sm(k)_{\text{r}\acute{\text{e}}\text{t}})$
is rigid.
$eF\in \operatorname{Shv}(Sm(k)_{\text{r}\acute{\text{e}}\text{t}})$
is rigid.
Proof. Extension
![]() $e$
and pullback are both left Kan extensions. From this it is easy to show that they commute, and so we find that
$e$
and pullback are both left Kan extensions. From this it is easy to show that they commute, and so we find that
 $(eF)|_{X_{\text{r}\acute{\text{e}}\text{t}}}=f^{\ast }F\in \operatorname{Shv}(X_{\text{r}\acute{\text{e}}\text{t}})$
, where
$(eF)|_{X_{\text{r}\acute{\text{e}}\text{t}}}=f^{\ast }F\in \operatorname{Shv}(X_{\text{r}\acute{\text{e}}\text{t}})$
, where
![]() $X$
is (essentially) smooth over
$X$
is (essentially) smooth over
![]() $k$
with structural morphism
$k$
with structural morphism
![]() $f$
.
$f$
.
If
 $\text{char}(k)>0$
then
$\text{char}(k)>0$
then
 $\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}}$
and
$\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}}$
and
 $Sm(k)_{\text{r}\acute{\text{e}}\text{t}}$
are both the trivial site, so we may assume that
$Sm(k)_{\text{r}\acute{\text{e}}\text{t}}$
are both the trivial site, so we may assume that
![]() $k$
is of characteristic zero and consequently perfect. In this case, for an essentially
$k$
is of characteristic zero and consequently perfect. In this case, for an essentially
![]() $k$
-smooth Henselian local scheme
$k$
-smooth Henselian local scheme
![]() $X$
with closed point
$X$
with closed point
 $i:x\rightarrow X$
, there exists a retraction
$i:x\rightarrow X$
, there exists a retraction
 $s:X\rightarrow x$
. (Write
$s:X\rightarrow x$
. (Write
![]() $k(x)/k$
as
$k(x)/k$
as
 $k(T_{1},\ldots ,T_{n})[U]/P$
with
$k(T_{1},\ldots ,T_{n})[U]/P$
with
 $P\in k(T_{1},\ldots ,T_{n})[U]$
separable; this is possible because
$P\in k(T_{1},\ldots ,T_{n})[U]$
separable; this is possible because
![]() $k(x)/k$
is separable,
$k(x)/k$
is separable,
![]() $k$
being perfect. Lift the elements
$k$
being perfect. Lift the elements
![]() $T_{i}$
to
$T_{i}$
to
![]() ${\mathcal{O}}_{X}$
arbitrarily and then use Hensel’s lemma to produce a root of
${\mathcal{O}}_{X}$
arbitrarily and then use Hensel’s lemma to produce a root of
![]() $P$
in
$P$
in
![]() ${\mathcal{O}}_{X}$
.)
${\mathcal{O}}_{X}$
.)
It is thus enough to prove: if
 $F\in \operatorname{Shv}(x_{\text{r}\acute{\text{e}}\text{t}})$
then
$F\in \operatorname{Shv}(x_{\text{r}\acute{\text{e}}\text{t}})$
then
 $H^{0}(x,F)=H^{0}(X,s^{\ast }F)$
. It follows from [Reference ScheidererSch94, Discussion after Proposition 19.2.1] and [Reference Andradas, Bröcker and RuizABR12, Propositions II.2.2 and II.2.4] that for any
$H^{0}(x,F)=H^{0}(X,s^{\ast }F)$
. It follows from [Reference ScheidererSch94, Discussion after Proposition 19.2.1] and [Reference Andradas, Bröcker and RuizABR12, Propositions II.2.2 and II.2.4] that for any
 $G\in \operatorname{Shv}(X_{\text{r}\acute{\text{e}}\text{t}})$
we have
$G\in \operatorname{Shv}(X_{\text{r}\acute{\text{e}}\text{t}})$
we have
 $H^{0}(X,G)=H^{0}(x,i^{\ast }G)$
. Consequently
$H^{0}(X,G)=H^{0}(x,i^{\ast }G)$
. Consequently
 $H^{0}(X,s^{\ast }F)=H^{0}(x,i^{\ast }s^{\ast }F)=H^{0}(x,F)$
, because
$H^{0}(X,s^{\ast }F)=H^{0}(x,i^{\ast }s^{\ast }F)=H^{0}(x,F)$
, because
![]() $si=\operatorname{id}$
by construction.◻
$si=\operatorname{id}$
by construction.◻
Corollary 44. If
 $E\in \mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
then all the homotopy sheaves
$E\in \mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
then all the homotopy sheaves
![]() $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)$
are rigid.
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)$
are rigid.
Proof. By Theorem 35 and Corollary 6 we know that all the homotopy sheaves of
![]() $E$
are of the form
$E$
are of the form
![]() $eF$
, with
$eF$
, with
 $F\in \operatorname{Shv}(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})$
. Thus the claim follows immediately from Lemma 43.◻
$F\in \operatorname{Shv}(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})$
. Thus the claim follows immediately from Lemma 43.◻
Corollary 45. Let
![]() $k$
be a perfect field of finite virtual 2-étale cohomological dimension and exponential characteristic
$k$
be a perfect field of finite virtual 2-étale cohomological dimension and exponential characteristic
![]() $e\neq 2$
. Then the homotopy sheaves
$e\neq 2$
. Then the homotopy sheaves
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9})_{0}[1/e]$
are rigid.
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9})_{0}[1/e]$
are rigid.
Proof. We will first assume that
![]() $e=1$
, and explain the necessary changes in positive characteristic at the end.
$e=1$
, and explain the necessary changes in positive characteristic at the end.
For
![]() $i=0$
we have
$i=0$
we have
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9})_{0}=\text{}\underline{GW}$
and this sheaf is known to be rigid [Reference GilleGil17, Theorem 2.4]. We consider the arithmetic square [Reference Röndigs, Spitzweck and ØstværRSØ16, Lemma 3.9] as follows.
$\text{}\underline{\unicode[STIX]{x1D70B}}_{0}(\unicode[STIX]{x1D7D9})_{0}=\text{}\underline{GW}$
and this sheaf is known to be rigid [Reference GilleGil17, Theorem 2.4]. We consider the arithmetic square [Reference Röndigs, Spitzweck and ØstværRSØ16, Lemma 3.9] as follows.

Since rigid sheaves are stable under extension, kernel and cokernel, the five lemma implies that it is enough to show that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }(\unicode[STIX]{x1D7D9}[1/2])_{0},\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }(\unicode[STIX]{x1D7D9}_{2}^{\wedge })_{0}$
and
$\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }(\unicode[STIX]{x1D7D9}[1/2])_{0},\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }(\unicode[STIX]{x1D7D9}_{2}^{\wedge })_{0}$
and
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }(\unicode[STIX]{x1D7D9}_{2}^{\wedge }[1/2])_{0}$
are rigid. Since rigid sheaves are stable by colimit, the case of
$\text{}\underline{\unicode[STIX]{x1D70B}}_{\ast }(\unicode[STIX]{x1D7D9}_{2}^{\wedge }[1/2])_{0}$
are rigid. Since rigid sheaves are stable by colimit, the case of
![]() $\unicode[STIX]{x1D7D9}_{2}^{\wedge }[1/2]$
follows from
$\unicode[STIX]{x1D7D9}_{2}^{\wedge }[1/2]$
follows from
![]() $\unicode[STIX]{x1D7D9}_{2}^{\wedge }$
.
$\unicode[STIX]{x1D7D9}_{2}^{\wedge }$
.
By [Reference Hu, Kriz and OrmsbyHKO11, Theorem 1] and [Reference RöndigsRön16, proof of Theorem 8.1], we know that
![]() $\unicode[STIX]{x1D7D9}_{2}^{\wedge }$
is the target of the convergent motivic Adams spectra sequence. The homotopy sheaves at the
$\unicode[STIX]{x1D7D9}_{2}^{\wedge }$
is the target of the convergent motivic Adams spectra sequence. The homotopy sheaves at the
![]() $E_{1}$
page are all sheaves with transfers in the sense of Voevodsky and torsion prime to the characteristic, and hence rigid, for example by [Reference Hornbostel and YagunovHY07, paragraph after Lemma 1.6]. Since rigid sheaves are stable by extension etc., it follows that the
$E_{1}$
page are all sheaves with transfers in the sense of Voevodsky and torsion prime to the characteristic, and hence rigid, for example by [Reference Hornbostel and YagunovHY07, paragraph after Lemma 1.6]. Since rigid sheaves are stable by extension etc., it follows that the
![]() $E_{\infty }$
page is rigid, and finally so are the homotopy sheaves of
$E_{\infty }$
page is rigid, and finally so are the homotopy sheaves of
![]() $\unicode[STIX]{x1D7D9}_{2}^{\wedge }$
.
$\unicode[STIX]{x1D7D9}_{2}^{\wedge }$
.
By motivic Serre finiteness [Reference Ananyevskiy, Levine and PaninALP17, Theorem 6] (beware that their indexing convention for motivic homotopy groups differs from ours!),
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2])_{0}$
is torsion for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2])_{0}$
is torsion for
![]() $i>0$
. By design, it is of odd torsion prime to the exponential characteristic. Consequently all of the
$i>0$
. By design, it is of odd torsion prime to the exponential characteristic. Consequently all of the
![]() $l$
-torsion subsheaves of
$l$
-torsion subsheaves of
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2]^{+})_{0}$
are rigid by the same argument as before, and so is the colimit
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2]^{+})_{0}$
are rigid by the same argument as before, and so is the colimit
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2]^{+})_{0}$
.
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2]^{+})_{0}$
.
It remains to deal with
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2]^{-})_{0}$
. But this is just the same as
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2]^{-})_{0}$
. But this is just the same as
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D70C}])_{0}$
and so is rigid by Corollary 44.
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9}[1/2,1/\unicode[STIX]{x1D70C}])_{0}$
and so is rigid by Corollary 44.
This concludes the proof if
![]() $e=1$
. If
$e=1$
. If
![]() $e>2$
the same proof works. The only problem might be that we have torsion prime to the characteristic, but we excluded this possibility by inverting
$e>2$
the same proof works. The only problem might be that we have torsion prime to the characteristic, but we excluded this possibility by inverting
![]() $e$
.◻
$e$
.◻
Remark.
We appeal to [Reference Ananyevskiy, Levine and PaninALP17] in order to know that
 $\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9})_{0}\otimes \mathbb{Q}=0$
for
$\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(\unicode[STIX]{x1D7D9})_{0}\otimes \mathbb{Q}=0$
for
![]() $i>0$
. This can also be deduced from Proposition 41, using that
$i>0$
. This can also be deduced from Proposition 41, using that
 $\mathbf{SH}(k)_{\mathbb{Q}}^{+}=\mathbf{DM}(k,\mathbb{Q})$
.
$\mathbf{SH}(k)_{\mathbb{Q}}^{+}=\mathbf{DM}(k,\mathbb{Q})$
.
There is another (older) notion of rigidity first considered by Suslin [Reference SuslinSus83]. This corresponds to (1) in the next result. It is a slightly silly property in our situation, but (2) is a replacement in spirit. It is related to important results in semialgebraic topology due to Coste-Roy, Delfs [Reference DelfsDel91, see in particular Corollary II.6.2] and Scheiderer [Reference ScheidererSch94].
Proposition 46. Let
 $E\in \mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
and
$E\in \mathbf{SH}(k)[\unicode[STIX]{x1D70C}^{-1}]$
and
![]() $i\in \mathbb{Z}$
.
$i\in \mathbb{Z}$
.
(1) If
 $\bar{L}/\bar{K}$
is an extension of algebraically closed fields over
$\bar{L}/\bar{K}$
is an extension of algebraically closed fields over
 $k$
, then
$k$
, then  $$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)(\bar{K})=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)(\bar{L})=0.\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)(\bar{K})=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)(\bar{L})=0.\end{eqnarray}$$
(2) If
 $L^{\text{r}}/K^{\text{r}}$
is an extension of real closed fields over
$L^{\text{r}}/K^{\text{r}}$
is an extension of real closed fields over
 $k$
, then also
$k$
, then also  $$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)(K^{\text{r}})=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)(L^{\text{r}}).\end{eqnarray}$$
$$\begin{eqnarray}\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)(K^{\text{r}})=\text{}\underline{\unicode[STIX]{x1D70B}}_{i}(E)(L^{\text{r}}).\end{eqnarray}$$
Proof. As before, by Theorem 35 and Corollary 6 we know that all the homotopy sheaves of
![]() $E$
are of the form
$E$
are of the form
![]() $eF$
, with
$eF$
, with
 $F\in \operatorname{Shv}(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})$
. For such sheaves we have
$F\in \operatorname{Shv}(\operatorname{Spec}(k)_{\text{r}\acute{\text{e}}\text{t}})$
. For such sheaves we have
 $eF(\bar{K})=0=eF(\bar{L})$
, so (1) holds. Since pullback
$eF(\bar{K})=0=eF(\bar{L})$
, so (1) holds. Since pullback
 $\operatorname{Spec}(K^{\text{r}})_{\text{r}\acute{\text{e}}\text{t}}\rightarrow \operatorname{Spec}(L^{\text{r}})_{\text{r}\acute{\text{e}}\text{t}}$
induces an isomorphism of sites, (2) also follows immediately. (See also the first paragraph of the proof of Lemma 43.)◻
$\operatorname{Spec}(K^{\text{r}})_{\text{r}\acute{\text{e}}\text{t}}\rightarrow \operatorname{Spec}(L^{\text{r}})_{\text{r}\acute{\text{e}}\text{t}}$
induces an isomorphism of sites, (2) also follows immediately. (See also the first paragraph of the proof of Lemma 43.)◻
Acknowledgements
This paper owes a huge debt to a number of people. In May 2016 Denis-Charles Cisinski taught a mini-course on motives in Essen. As a result the author realised that he could extend his theorem from perfect base fields to fairly general base schemes. In particular he learned the pattern of the proof that
 $D(S_{\acute{\text{e}}\text{t}},\mathbb{Z}/p)$
is equivalent to
$D(S_{\acute{\text{e}}\text{t}},\mathbb{Z}/p)$
is equivalent to
 $\mathbf{DM}_{h}(S,\mathbb{Z}/p)$
. In a lot of ways our proof is a variant of that one. A similar strategy is followed in the Cisinski–Déglise article [Reference Cisinski and DégliseCD13] on which we also rely heavily both in spirit and in practice. Just like in that article, many of our results are relatively straightforward consequences of difficult theorems in real étale cohomology established by Scheiderer and other semi-algebraic topologists. The importance of the Voevodsky/Ayoub/Cisinski–Déglise approach to the six functors formalism for our article also cannot be overstated. Discussions with Fabien Morel, Oliver Röndigs, Marc Hoyois, Marco Schlichting, and Markus Spitzweck about early versions of this work were also influential to its current form. The author would further like to thank Denis-Charles Cisinski for carefully reading a draft of this work and pointing out several mistakes, and Elden Elmanto, Daniel Harrer, Marc Levine and Maria Yakerson for providing comments.
$\mathbf{DM}_{h}(S,\mathbb{Z}/p)$
. In a lot of ways our proof is a variant of that one. A similar strategy is followed in the Cisinski–Déglise article [Reference Cisinski and DégliseCD13] on which we also rely heavily both in spirit and in practice. Just like in that article, many of our results are relatively straightforward consequences of difficult theorems in real étale cohomology established by Scheiderer and other semi-algebraic topologists. The importance of the Voevodsky/Ayoub/Cisinski–Déglise approach to the six functors formalism for our article also cannot be overstated. Discussions with Fabien Morel, Oliver Röndigs, Marc Hoyois, Marco Schlichting, and Markus Spitzweck about early versions of this work were also influential to its current form. The author would further like to thank Denis-Charles Cisinski for carefully reading a draft of this work and pointing out several mistakes, and Elden Elmanto, Daniel Harrer, Marc Levine and Maria Yakerson for providing comments.