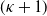1. Introduction
Let
$X=(X_t)_{t\geq 0}$
be a spectrally negative Lévy process, i.e. a Lévy process that does not exhibit positive jumps, starting at zero. In this article we study moments of the first (downward) passage time of
$-x$
,
$x\geq 0$
, of the process X, i.e. moments of
\begin{equation}\tau_x^- \;:\!=\; \inf \{ t>0\colon X_t<-x\},\end{equation}
conditioned on finiteness of this stopping time.
The first passage time
$\tau_x^-$
, sometimes also referred to as the exit time, of (spectrally negative) Lévy processes is a well-known object that has been studied by many authors; see [Reference Doney5, Section 9.5] for a general overview. However, most results are limited on giving a representation of the Laplace transform of the first passage time.
In the case of a Brownian motion with drift
$p\in\mathbb{R}$
, due to the continuity of the paths, the first passage time
$\tau_x^-$
coincides with the first hitting time of
$-x$
, that is, with
$\tau_x^{-,\ast} = \inf\{t> 0\colon X_t=-x\}$
. In this special case,
$\tau_x^-$
is known to have the Laplace transform (cf. [Reference Rogers and Williams12, Eq. I.(9.1)])
\begin{equation}\mathbb{E}[\textrm{e}^{-q \tau_x^-}]= \exp\!\big[{-}\big(\sqrt{p^2+2q}+p\big) x\big], \qquad x\geq 0, q>0,\end{equation}
and its distribution is given explicitly (cf. [Reference Rogers and Williams12, Eq. I.(9.2)]) as
\begin{equation*}\mathbb{P}(\tau_x^- \in \textrm{d} z)= \frac{x}{\sqrt{2\pi z^3}\,}\exp\!\bigg[{-} \frac{(x+pz)^2}{2z}\bigg] \textrm{d} z,\qquad x,z\geq 0, \end{equation*}
where in both formulas we assumed the process to be standardized, i.e. such that
$\sigma^2=1$
.
For general spectrally negative Lévy processes, the first hitting time and the first passage time can be related via the undershoot
$X_{\tau_x^-}+x\leq 0$
, as shown in [Reference Doney4]. In particular, for spectrally negative
$\alpha$
-stable processes (
$1<\alpha<2$
) this relation reads (cf. [Reference Simon17])
\begin{equation}\tau_x^{-,\ast} = \tau_x^- + \big|X_{\tau_x^-}+x\big|^\alpha \cdot \hat{\tau}_x^{+,\ast} ,\end{equation}
where
$\hat{\tau}_x^{+,\ast}$
is an independent copy of the first upwards hitting time
$\tau_x^{+,\ast}= \inf\{t>0\colon X_t=x\}$
. Note that (1.3) is a direct consequence of the self-similarity (of index
$1/\alpha$
) of
$\alpha$
-stable processes, which implies further that
$\big(X_{\tau_x^-}+x\big) \overset{\textrm{d}}{=} x \cdot \big(X_{\tau_1^-}+1\big)$
.
The hitting time
$\tau_x^{-,\ast}$
of a spectrally one-sided stable process has been studied, e.g. in [Reference Kuznetsov, Kyprianou, Pardo and Watson7, Reference Peskir11, Reference Simon17]. In particular, in [Reference Simon17] fractional moments and a series representation of the density
$\tau_x^{-,\ast}$
are provided.
The first downward passage time
$\tau_x^-$
has also been extensively studied in the field of actuarial mathematics, where the spectrally negative Lévy process X is interpreted as a risk process and shifted to start at
$x\geq 0$
. Then, due to the space homogeneity of the Lévy process,
$\tau_x^-$
coincides with the time of ruin, i.e. the first time the process passes the value zero. The most prominent example for such a risk process is the classical Cramér–Lundberg model, where X is chosen to be a spectrally negative compound Poisson process, i.e.
\begin{equation}X_t=x+pt - \sum_{i=1}^{N_t} S_i, \qquad t\geq 0.\end{equation}
Here,
$x\geq 0$
is interpreted as the initial capital,
$p>0$
denotes a constant premium rate, the Poisson process
$(N_t)_{t\geq 0}$
represents the claim counting process, and the independent and identically distributed (i.i.d.) positive random variables
$\{S_i, i\in\mathbb{N}\}$
are the claim size variables which are independent of
$(N_t)_{t\geq 0}$
.
For this model, under the profitability assumption
$\mathbb{E}[X_1]>0$
, it is shown in [Reference Delbaen3], for all
$\kappa>0$
, that the
$\kappa$
th moment of the ruin time exists if and only if the
$(\kappa+1)$
th moment of the claim size distribution exists. In this paper we generalize this result to arbitrary spectrally negative Lévy processes. Note that, while the proof given in [Reference Delbaen3] relies on results on the speed of convergence of random walks, we use a completely different approach here via fractional differentiation of Laplace transforms. In particular, our approach allows us to relate the existence of
$\mathbb{E}[(\tau_x^-)^\kappa\mid\tau_x^-<\infty]$
with the existence of the
$\kappa$
th moment of the subordinator
$(\tau_x^+\!)_{x\geq 0}$
of upwards passage times
$\tau_x^+=\inf\{t>0\colon X_t>x\}$
at a specific random time. As a by-product, we show that
$(\tau_x^+\!)_{x\geq 0}$
is a special subordinator and identify its conjugate subordinator.
Before presenting and proving our main theorem on the existence of moments of the first passage time in Section 3, we collect various preliminary results on (spectrally negative) Lévy processes and fractional derivatives in Section 2.
2. Preliminaries
Throughout this article let
$X=(X_t)_{t\geq 0}$
be a Lévy process, i.e. a càdlàg stochastic process with independent and stationary increments, defined on a filtered probability space
$(\Omega,\mathcal{F}, \mathbb{F}, \mathbb{P})$
. It is well known that the Lévy process X is fully characterized by its characteristic exponent
$\Psi$
, which is defined via
$\textrm{e}^{-t\Psi(\theta)} = \mathbb{E}[\textrm{e}^{\textrm{i}\theta X(t)}]$
and takes the form
\begin{equation*}\Psi(\theta) =\textrm{i} a\theta + \frac{1}{2}\sigma^2 \theta^2 + \int_{\mathbb{R}}\big(1-\textrm{e}^{\textrm{i}\theta y} + \textrm{i}\theta y\textbf{1}_{\{\left\vert{y}\right\vert<1\}}\big)\Pi^*(\textrm{d} y),\qquad \theta \in \mathbb{R},\end{equation*}
for constants
$a\in\mathbb{R}$
,
$\sigma^2\geq 0$
, and a measure
$\Pi^*$
on
$\mathbb{R}\backslash\{0\}$
satisfying
$\int_{\mathbb{R}}(1 \wedge y^2) \Pi^*(\textrm{d} y)<\infty$
. The measure
$\Pi^*$
is called the Lévy measure or jump distribution of X, while
$(\sigma^2,a,\Pi^*)$
is the characteristic triplet of X.
If X has no upwards jumps, i.e. if
$\Pi^*((0,\infty))=0$
, then X is called spectrally negative. In this case, it is handy to use the Laplace exponent
$\psi(\theta) \;:\!=\; ({1}/{t})\log\mathbb{E}\!\left[\textrm{e}^{\theta X_t}\right]$
,
$\theta \geq 0$
, of
$-X$
instead of the characteristic exponent, which can then be written in the form
\begin{equation}\psi(\theta) =c \theta + \frac{1}{2}\sigma^2 \theta ^2 + \int_{(0,\infty)} \big(\textrm{e}^{-\theta y}-1+\theta y \textbf{1}_{\{y<1\}} \big)\Pi(\textrm{d} y),\end{equation}
where
$c=-a\in\mathbb{R}$
,
$\sigma^2 \geq 0$
, and
$\Pi(\textrm{d} y) = \Pi^*(\!-\!\textrm{d} y)$
is the mirrored version of the jump measure, which is therefore defined on
$(0,\infty)$
.
The Laplace exponent
$\psi$
admits some useful properties. Clearly,
$\psi(0)=0$
, and
$\lim_{\theta\to\infty}\psi(\theta) =\infty$
. On
$(0,\infty)$
the function
$\psi$
is infinitely often differentiable and strictly convex. Lastly, as
$\psi$
is nothing more than the cumulant-generating function of
$X_1$
, it carries information on the moments of X. In particular, it is well known (cf. [Reference Sato15, Corollary 25.8]) that, for any
$\kappa>0$
,
\begin{equation*}\mathbb{E}[|X_1|^\kappa]< \infty \; \text{if and only if } \int_{|y|\geq 1} |y|^\kappa \Pi(\textrm{d} y)<\infty ,\end{equation*}
and for
$\kappa=k\in \mathbb{N}_0$
this in turn implies
\begin{equation}|\partial^k \psi(0+\!)|\;:\!=\; |\psi^{(k)}(0+\!)|<\infty.\end{equation}
Note that throughout this article
$\partial_q^k f(q,z)$
denotes the kth derivative of a function f with respect to q, while
$\partial_q\;:\!=\; \partial_q^1$
. In the case of only one parameter, we will usually omit the subscript.
We will also use the Laplace exponent’s right inverse, which we always denote by
\begin{equation*}\Phi(q) \;:\!=\; \sup\{\theta\geq 0 \colon \psi(\theta) = q\},\qquad q\geq 0.\end{equation*}
From the mentioned properties of
$\psi$
, it follows immediately that
$\Phi(0)=0$
if and only if
$\psi'(0+\!)\geq 0$
, while
$\Phi(0) >0$
if and only if
$\psi'(0+\!)<0$
. The function
$q\mapsto \Phi(q)$
is strictly monotone increasing on
$[0,\infty)$
, infinitely often differentiable on
$(0,\infty)$
, and it is the well-defined inverse of
$\psi(\theta)$
on the interval
$[\Phi(0),\infty)$
, i.e.
$\Phi(\psi(\theta)) = \theta$
and
$\psi(\Phi(q)) = q$
for all
$\theta \in [\Phi(0),\infty)$
,
$q\geq 0$
. Thus, applying the chain rule on
$q\mapsto q=\psi(\Phi(q))$
immediately yields
\begin{equation}\Phi'(q)=\partial_q \Phi(q) = \frac{1}{\psi'(\Phi(q))}, \qquad q\geq 0,\end{equation}
where the case
$q=0$
is interpreted in the limiting sense
$q\downarrow 0$
.
Finally, note that, by definition,
\begin{equation*} \lim_{q\downarrow 0} \frac{q}{\Phi(q)} = \begin{cases} \psi'(0+\!) & \text{if }\psi'(0+\!)\geq 0 , \\[5pt] 0 &\text{otherwise.} \end{cases}\end{equation*}
For proofs of the stated properties and a more thorough discussion of Lévy processes in general we refer the reader to [Reference Kyprianou9, Reference Sato15].
As announced in the introduction, we are interested in the first downward passage time
$\tau_x^-$
of
$-x$
,
$x\geq 0$
, as defined in (1.1), or, more precisely, in the first passage time given that the process passes through
$-x$
, i.e.
\begin{equation}(\tau_x^-\mid\tau_x^-<\infty).\end{equation}
Note that in the case that
$ \psi'(0+\!) = \mathbb{E}[X_1]\in [\!-\!\infty, 0]$
we have
$\tau_x^-=(\tau_x^-\mid\tau_x^-<\infty)$
as X enters the negative half-line almost surely. In the case that
$\psi'(0+\!)>0$
the term passage time will typically be used for the conditioned quantity (2.4).
To avoid trivialities we exclude the case that X is a pure drift, which implies a deterministic first passage time. Hence, we always have
$\mathbb{P}(\tau_x^-<\infty)>0$
. Moreover, we exclude the hitting level
$x=0$
whenever
$X_t$
is of unbounded variation, as in this case
$\tau_0^- =0$
almost surely.
To study
$\tau_x^-$
(or
$(\tau_x^-\mid\tau_x^-<\infty)$
) we will use the concept of scale functions. Recall that for any
$q\geq 0$
the q-scale function
$W^{(q)}\colon\mathbb{R}\to[0,\infty)$
of the spectrally negative Lévy process X is the unique function such that, for
$x\geq 0$
, its Laplace transform satisfies
\begin{equation*}\int_0^\infty \textrm{e}^{-\beta x}W^{(q)}(x) \textrm{d} x = \frac{1}{\psi(\beta)-q} \end{equation*}
for all
$\beta >\Phi(q)$
. For
$x<0$
we set
$W^{(q)}(x)=0$
. Furthermore, the integrated q-scale function
$Z^{(q)}\colon\mathbb{R}\to[0,\infty)$
is given by
$Z^{(q)}(x) \;:\!=\; 1+q\int_0^x W^{(q)}(y)\textrm{d} y$
, and it fulfils, cf. [Reference Kyprianou9, Theorem 8.1],
\begin{equation}\mathbb{E}\big[\textrm{e}^{-q\tau_x^-} \textbf{1}_{\{\tau_x^- <\infty\}} \big] = Z^{(q)}(x) - \frac{q}{\Phi(q)} \cdot W^{(q)}(x), \qquad x\in\mathbb{R},\ q\geq 0.\end{equation}
Taking the limit
$q\downarrow 0$
, this immediately implies
$\mathbb{P}(\tau_x^-<\infty)=1- (0 \vee \psi'(0+\!)) \cdot W^{(0)}(x)$
,
$x\in \mathbb{R}$
, where we use the standard notation
$\vee$
to denote the maximum.
Observe that the functions
$q\mapsto W^{(q)}(x)$
and
$q\mapsto Z^{(q)}(x)$
may be extended analytically to
$\mathbb{C}$
, which means especially that they are infinitely often differentiable with bounded derivatives on every compact set
$K\subset\mathbb{C}$
. This implies in particular that limits of type
$q\downarrow 0$
exist. Again, we refer to [Reference Kyprianou9] for missing proofs and further details. For detailed accounts of scale functions and their numerous applications, we also refer to [Reference Avram, Grahovac and Vardar-Acar2, Reference Kuznetsov, Kyprianou and Rivero8].
Lastly, let us recall that fractional moments of non-negative random variables can be computed via fractional differentiation of the corresponding Laplace transform. More precisely, define, for any
$\kappa \in(0,1)$
, the Marchaud fractional derivative of a function f(z),
$z\geq 0$
,
\begin{equation}\textbf{D}^\kappa_z f(z) = \frac{\kappa}{\Gamma (1-\kappa)} \int_{z}^\infty \frac{f(z)-f(u)}{(u-z)^{\kappa+1}} \textrm{d} u,\end{equation}
cf. [Reference Samko, Kilbas and Marichev14, (5.58)], while, for
$\kappa\geq 1$
with
$n\;:\!=\;\lfloor \kappa \rfloor$
denoting the largest integer less than or equal to
$\kappa$
,
$\textbf{D}^\kappa_z f(z) = \partial_z^n \textbf{D}^{\kappa-n}_z f(z)$
. Then, cf. [Reference Wolfe19, Theorem 1], for any non-negative random variable T with Laplace transform
$g(z)=\mathbb{E}[\textrm{e}^{-zT}]$
,
$z\geq 0$
, the
$\kappa$
th absolute moment of T exists if and only if
$\textbf{D}_z^\kappa g(0)$
exists, in which case
\begin{equation}\mathbb{E}[T^\kappa] = \textbf{D}_z^\kappa g(0).\end{equation}
This allows us to derive the following lemma.
Lemma 2.1. For any
$\kappa>0$
and
$x\geq 0$
, the
$\kappa$
th moment of the first downward passage time
$\tau_x^-\mid\tau_x^-<\infty$
of a spectrally negative Lévy process is given by
\begin{equation*} \mathbb{E}[(\tau_x^-)^\kappa\mid\tau_x^- <\infty] = \frac{1}{ \mathbb{P}(\tau_x^- <\infty)} \cdot\bigg[\textbf{D}^\kappa_q \bigg(Z^{(q)}(x) - \frac{q}{\Phi(q)} \cdot W^{(q)}(x)\bigg)\bigg]_{q=0},\end{equation*}
and it exists if and only if the right-hand side exists and is finite.
3. Existence of moments
In [Reference Delbaen3], Delbaen showed in a classical Cramér–Lundberg model (1.4) that is profitable, i.e. with
$\psi'(0+\!)>0$
, that for any
$\kappa>0$
the
$\kappa$
th moment of the ruin time exists if and only if the
$(\kappa+1)$
th moment of the claim sizes exists. Delbaen’s proof relies on results on the speed of convergence of random walks. In this paper we use an alternative approach via fractional derivatives of Laplace transforms to prove an extension of the result in [Reference Delbaen3] to any spectrally negative Lévy process. Moreover, we additionally consider the non-profitable settings of
$\psi'(0+\!)\leq 0$
.
Our main result in this section thus reads as follows. Note that although part (i) of Theorem 3.1 can be derived from [Reference Aurzada, Iksanov and Meiners1, Proposition 1.1 and Theorem 1.1], we give a short proof below for the reader’s convenience.
Theorem 3.1. Let
$(X_t)_{t\geq 0}$
be a spectrally negative Lévy process with Laplace exponent
$\psi$
as in (2.1), and let
$\tau_x^-$
denote its first passage time of
$-x$
for
$x\geq 0$
.
-
(i) If
$\psi'(0+\!)<0$
, then, for any
$x\geq 0$
, there exists
$q^\ast>0$
such that
$\mathbb{E}\big[\textrm{e}^{q^\ast \cdot \tau_x^-} \big] <\infty$
, which implies that, for any
$x\geq 0$
and
$\kappa\geq 0$
,
$\mathbb{E}[(\tau_x^-)^\kappa ] <\infty$
. -
(ii) If
$\psi'(0+\!) >0$
, then, for any
$x \geq 0$
and
$\kappa>0$
,
$\mathbb{E}[(\tau_x^-)^\kappa\mid\tau_x^-<\infty]<\infty$
if and only if
$\int_{[1,\infty)} y^{\kappa+1} \Pi(\textrm{d} y)<\infty$
. -
(iii) Assume
$\psi'(0+\!)=0$
.-
(a) If there exists
$\kappa^*\in (0,1]$
such that
$\int_{[1,\infty)} y^{\kappa^*+1}\Pi(\textrm{d} y) =\infty$
, then, for any
$x\geq 0$
and
$\kappa\geq\kappa^*$
, (3.1)
\begin{equation}\mathbb{E}[(\tau_x^-)^\kappa] =\infty.\end{equation}
-
(b) If
$\psi''(0+\!)<\infty$
, then (3.1) holds for any
$x\geq0$
and
$\kappa>\tfrac{1}{2}$
.
-
In particular, (3.1) holds for any
$x \geq 0$
and
$\kappa\geq 1$
.
Remark 3.1. Note that, a priori, the above theorem needs no restrictions concerning possible choices of the location parameter
$c\in\mathbb{R}$
of
$(X_t)_{t\geq 0}$
. However, since, by [Reference Sato15, Example 25.12],
$c - \int_{[1,\infty)} y \Pi(\textrm{d} y)= \mathbb{E}[X_1]= \psi'(0+\!)$
, in cases (ii) and (iii) the assumption
$\psi'(0+\!)\geq 0$
implies that
$c\geq\int_{[1,\infty)} y \Pi(\textrm{d} y)\geq 0$
. In particular,
$c<0$
is a valid choice only in case (i).
Remark 3.2. At first glance, Theorem 3.1(iii) suggests that, for an oscillating process
$(X_t)_{t\geq 0}$
, no fractional moments of the first passage time of zero exist. This, however, is not true in general and we provide two counterexamples:
-
(a) Consider a (standardized) Brownian motion without drift for which, by (1.2),
$\mathbb{E}\big[\textrm{e}^{-q\cdot \tau_x^-}\big] = \exp\!\big[{-}\sqrt{2q}\cdot x\big]$
,
$x\geq 0$
. Then,
$\mathbb{P}(\tau_x^-<\infty)=1$
and, from (2.6) and (2.7), we obtain, for any
$\kappa\in(0,1)$
, which is finite if and only if
\begin{align*}\mathbb{E}[(\tau_x^-)^\kappa] = \big[ \textbf{D}^\kappa_q \textrm{e}^{-\sqrt{2q}\cdot x}\big]_{q=0}= \frac{\kappa}{\Gamma(1-\kappa)} \int_0^\infty \frac{1 - \textrm{e}^{-\sqrt{2u}\cdot x} }{u^{\kappa +1}} \textrm{d} u,\end{align*}
$\kappa \in\big(0,\tfrac{1}{2}\big)$
. In particular, in this case (3.1) holds for any
$\kappa\geq \tfrac{1}{2}$
, which shows that Theorem 3.1(iii)(b) is near to being sharp.
-
(b) Consider a spectrally negative,
$\alpha$
-stable Lévy process
$(X_t)_{t\geq 0}$
with index
$\alpha\in(1,2)$
such that the Laplace exponent of
$-X$
is given by
$\psi(\theta) = \theta^\alpha$
and, in particular,
$\psi'(0)=0$
. For such a process it has been shown in [Reference Simon17, Proposition 4 and the subsequent remark] that the first passage time
$\tau_x^{-}$
admits finite fractional moments, namely
$\mathbb{E}[(\tau_x^{-})^\kappa]<\infty$
if and only if
$\kappa \in (\!-\!1,1-(1/\alpha))$
.
The identification of the threshold
$\kappa^*\leq 1$
such that
$\mathbb{E}[(\tau_x^-)^\kappa]<\infty$
,
$\kappa<\kappa^*$
, and
$\mathbb{E}[(\tau_x^-)^\kappa] = \infty $
for
$\kappa\geq \kappa^*$
for a general oscillating and spectrally negative Lévy process seems difficult; the chosen approach for our proof of Theorem 3.1 only yields the sufficient condition for (3.1) as stated in Theorem 3.1(iii)(a). Moreover, the above example of a Brownian motion clearly shows that the threshold
$\kappa^\ast$
cannot solely depend on the Lévy measure. We therefore leave this question open for future research.
Proof of Theorem
3.1(i). Recall that if
$\psi'(0+\!)<0$
, then
$\Phi(0)>0$
and, by the convexity of
$\psi$
, we obtain
$\psi'(\Phi(0))>0$
. Furthermore, the Laplace exponent
$\psi$
extended to
$\mathbb{C}$
is analytic on
$\{x\in\mathbb{C}\colon\operatorname{Re}\!(z)>0\}$
, and hence it is analytic in a neighborhood of
$\Phi(0)$
. Consequently, the inverse function theorem of complex analysis, cf. [Reference Rudin13, Theorem 10.30], implies that the inverse of
$\psi(\theta)$
, i.e.
$\Phi(q)$
, is also analytic in a neighborhood of zero. By (2.5), this yields that
$\mathbb{E}[\textrm{e}^{-q\tau_x^-}]$
is analytic in a neighborhood of zero as well, and thus
$\mathbb{E}\!\left[\textrm{e}^{q^*\tau_x^-}\right]<\infty$
for some
$q^*>0$
as claimed.
To prove the second and third parts of Theorem 3.1 we start with a simple lemma that reduces the problem of existence of moments of the first passage time to finiteness of (fractional) derivatives of a certain function in zero.
Lemma 3.1. Set
$\eta(q)\;:\!=\;{q}/{\Phi(q)}$
,
$q>0$
. Then, for any
$x\geq0$
and
$\kappa>0$
,
$\mathbb{E}[(\tau_x^-)^\kappa\mid\tau_x^-<\infty] <\infty$
if and only if
$\lim_{q\downarrow 0} \left\vert{\textbf{D}_q^\kappa \eta(q)}\right\vert <\infty$
.
Proof. It follows immediately from Lemma 2.1 that
$\mathbb{E}[(\tau_x^-)^\kappa\mid\tau_x^-<\infty] <\infty$
if and only if
$\lim_{q\downarrow 0}\textbf{D}^\kappa_q \big(Z^{(q)}(x) - \eta(q) \cdot W^{(q)}(x)\big)<\infty$
. However,
$q\mapsto W^{(q)}(x)$
and
$q\mapsto Z^{(q)}(x)$
are infinitely often differentiable with bounded derivatives on
$[0,\infty)$
. Hence, linearity of the (fractional) derivative reduces the problem to characterization of the finiteness of the derivative
$\lim_{q\downarrow 0}\textbf{D}^\kappa_q \big( \eta(q) \cdot W^{(q)}(x)\big)$
.
Observe that the definition of the Marchaud derivative is equivalent to the Liouville derivative for sufficiently good functions; see [Reference Samko, Kilbas and Marichev14, Remark 5.3] for details. We may therefore apply the product rule for fractional Liouville derivatives (cf. [Reference Uchaikin18, p. 206]) to
$\eta(q) \cdot W^{(q)}(x)$
. Recalling again that
$q\mapsto W^{(q)}(x)$
is infinitely often differentiable with bounded derivatives on every compact
$K\subset \mathbb{C}$
, and that
$W^{(q)}(x)>0$
for any
$x>0$
, we conclude that
$\lim_{q\downarrow 0}\textbf{D}^\kappa_q \big(\eta(q) \cdot W^{(q)}(x)\big)<\infty$
if and only if
$\lim_{q\downarrow 0}\textbf{D}^\kappa_q \eta(q) <\infty$
, as claimed.
If
$x=0$
note that
$W^{(q)}(0)>0$
if and only if
$(X_t)_{t\geq 0}$
is of bounded variation (cf. [Reference Avram, Grahovac and Vardar-Acar2, (25)]), and in this case the above argumentation yields the result.
The remainder of the proof of Theorem 3.1 relies on the interpretation of
$\eta(q)$
as the Laplace exponent of a certain killed subordinator, as shown in the next proposition. Recall that a subordinator
$(Y_t)_{t \geq 0}$
is a Lévy process with non-decreasing paths whose Laplace exponent
$\varphi(\theta) = - ({1}/{t}) \log \mathbb{E}[\textrm{e}^{-\theta Y_t} ]$
is of the form
$\varphi(\theta)= \widetilde{c}\cdot\theta+\int_0^\infty (1-\textrm{e}^{-\theta y}) \widetilde{\Pi}(\textrm{d} y)$
for
$\theta\geq 0$
, a drift
$\widetilde{c}\geq 0$
, and a measure
$\widetilde{\Pi}$
such that
$\int_{(0,\infty)} (1\wedge y) \widetilde{\Pi}(\textrm{d} y)<\infty$
. A killed subordinator
$(Y_t)_{t\geq 0}$
is defined via
\begin{equation*}Y_t = \begin{cases}\widetilde{Y}_t & \text{if } t<\textbf{e}_{\beta}, \\[5pt]\zeta & \text{if } t\geq \textbf{e}_{\beta},\end{cases}\end{equation*}
where
$(\widetilde{Y}_t)_{t\geq 0}$
is a subordinator,
$\textbf{e}_{\beta}$
is an independent
$\operatorname{Exp}\!(\beta)$
-distributed time,
$\beta > 0$
, and
$\zeta$
denotes some cemetery state. As usual, we interpret
$\beta=0$
as
$\textbf{e}_\beta = \infty$
corresponding to no killing. The Laplace exponent
$\varphi_Y$
of a killed subordinator is given by
$\varphi_Y(\theta) = - \!\log \mathbb{E}\big[\textrm{e}^{-\theta Y_1}\big] = - \log \mathbb{E}\big[\textrm{e}^{-\theta \widetilde{Y}_1}\cdot \textbf{1}_{\{1<\textbf{e}_{\beta}\}}\big] = \beta + \varphi_{\widetilde{Y}}(\theta)$
for the Laplace exponent
$\varphi_{\widetilde{Y}}(\theta)$
of
$(\widetilde{Y}_t)_{t\geq 0}$
.
Further, for any
$x\geq 0$
, let
$\tau_x^+ \;:\!=\; \inf\{ t>0\colon X_t >x\}$
be the first upwards passage time of x, i.e. the first time that
$X_t$
is above x. It is well known (cf. [Reference Kyprianou9, Theorem 3.12]) that, for all
$q\geq 0$
,
\begin{equation}\mathbb{E}\big[\textrm{e}^{-q\cdot \tau_x^+}\cdot\textbf{1}_{\{\tau_x^+<\infty\}}\big] = \textrm{e}^{-\Phi(q)x}, \qquad x\geq 0.\end{equation}
If, furthermore,
$\mathbb{E}[X_1]=\psi'(0+\!)\geq 0$
, then
$(\tau_x^+\!)_{x\ge0 }$
is a subordinator with Laplace exponent
$\Phi(q)$
, cf. [Reference Kyprianou9, Corollary 3.14].
Proposition 3.1. Assume
$\psi'(0+\!)\geq 0$
, and define a killed subordinator
$(Y_t)_{t\geq 0}$
, independent of
$(\tau_x^+\!)_{x\geq 0}$
, through its Laplace exponent
$\varphi(\theta)= -t^{-1} \log \mathbb{E}[\textrm{e}^{-\theta Y_t}]$
by setting
\begin{equation*}\varphi(\theta) \;:\!=\; \psi'(0+\!) + \frac{\sigma^2}{2} \theta + \int_0^\infty (1 - \textrm{e}^{-\theta y}) \Pi((y,\infty)) \textrm{d} y, \qquad \theta > 0.\end{equation*}
Then,
$(\tau_{Y_t}^+\!)_{t\geq 0}$
is a killed subordinator with Laplace exponent
\begin{equation}-\frac{1}{t}\log \mathbb{E}\big[\textrm{e}^{-q\cdot \tau_{Y_t}^+} \big]= \eta(q), \qquad q\geq 0.\end{equation}
Proof. An application of [Reference Kyprianou and Rivero10, Theorem 1] on the subordinator
$(Y_t)_{t\geq 0}$
implies that there exists a spectrally negative Lévy process, the so-called parent process, with Laplace exponent
$\theta \!\cdot \varphi(\theta)$
and whose characteristic triplet coincides with that of
$(X_t)_{t\geq 0}$
. Thus,
$\varphi(\theta) = {\psi(\theta)}/{\theta}$
. Equation (3.3) is now a direct consequence of [Reference Sato15, Theorem 30.1] and the fact that
\begin{equation*}\varphi(\Phi(q))= \frac{\psi(\Phi(q))}{\Phi(q)} = \frac{q}{\Phi(q)}=\eta(q).\end{equation*}
Remark 3.3. Note that the above proposition implies that, as long as
$\psi'(0+\!)\geq 0$
, the subordinator
$(\tau^+_x)_{x\geq 0}$
is a special subordinator since its conjugate Laplace exponent
${q}/{\Phi(q)}=\eta(q)$
is shown to be the Laplace exponent of a (killed) subordinator. See, e.g., [Reference Kyprianou9, Section 5.6] or [Reference Schilling, Song and Vondracek16, Chapter 11] for general information on special subordinators and their Laplace exponents, which are also known as special Bernstein functions.
Combining Lemma 3.1, Proposition 3.1, and (2.7), it is an immediate consequence that, assuming
$\psi'(0+\!)\geq 0$
, for all
$\kappa>0$
and
$x\geq 0$
,
\begin{equation}\mathbb{E}[(\tau_x^-)^\kappa\mid\tau_x^-<\infty] <\infty \quad \text{if and only if} \quad\mathbb{E}\big[(\tau_{Y_1}^+\!)^\kappa\big] <\infty.\end{equation}
In order to find suitable conditions for the right-hand side of (3.4), we next prove a general statement concerning the existence of moments of a subordinated subordinator.
Proposition 3.2. Let
$(Z_t)_{t\geq 0}$
be a non-zero subordinator, and let
$(Y_t)_{t\geq 0}$
be a (possibly killed) non-zero subordinator, independent of
$(Z_t)_{t\geq 0}$
. If
$\mathbb{E}[Z_1]<\infty$
, then, for all
$\kappa>0$
,
$\mathbb{E}\big[Z_{Y_1}^\kappa\big] < \infty$
if and only if
$\mathbb{E}[Z_1^\kappa] <\infty$
and
$\mathbb{E}[Y_1^{\kappa}] <\infty$
. If
$\mathbb{E}[Z_1]=\infty$
and
$\kappa\in (0,1)$
, then
$\mathbb{E}\big[Z_{Y_1}^\kappa\big] <\infty$
implies
$\mathbb{E}[Z_1^\kappa] <\infty$
and
$\mathbb{E}[Y_1^{\kappa}] <\infty$
.
To prove this proposition, we need the following lemma.
Lemma 3.2. Let
$(Z_t)_{t\geq 0}$
be a non-zero subordinator with
$\mathbb{E}[Z_1]<\infty$
. If
$\mathbb{E}[Z_1^\kappa] < \infty$
for some
$\kappa>0$
, then
$\mathbb{E}[Z_t^\kappa]<\infty$
for all
$t\geq 0$
and the mapping
$t\mapsto \mathbb{E}[Z_t^\kappa]$
,
$t\geq 1$
, is of polynomial order
$\kappa$
.
Proof. First note that, by Hölder’s inequality, for all
$n\in \mathbb{N}$
,
$a_1,\ldots,a_n\geq 0$
, and
$r\geq 1$
,
\begin{equation}(a_1+ \cdots +a_n)^r \leq n^{r-1}\cdot ( a_1^r + \cdots + a_n^r ),\end{equation}
while for
$r\leq 1$
the inequality in (3.5) holds with
$\geq$
instead of
$\leq$
.
Let
$\varphi$
be the Laplace exponent of the subordinator
$(Z_t)_{t\geq 0}$
. By [Reference Sato15, Corollary 25.8], finiteness of
$\mathbb{E}[Z_1^\kappa]$
for some
$\kappa>0$
implies finiteness of
$\mathbb{E}[Z_t^\kappa]$
for all
$t\geq 0$
.
By our assumptions,
$\mathbb{E}[Z_1] = \varphi'(0+\!)\in(0,\infty)$
and it follows that, cf. [Reference Sato15, Example 25.12],
$\mathbb{E}[Z_t] = t \cdot \varphi'(0+\!) =t\cdot \mathbb{E}[Z_1]$
. Now let
$\kappa \geq 1$
. Then, by Jensen’s inequality we conclude that
$\mathbb{E}[Z_t^\kappa] \geq\mathbb{E}[Z_t]^\kappa= t^\kappa \cdot \mathbb{E}[Z_1]^\kappa$
, which yields a lower bound of degree
$\kappa$
. In order to show an upper bound, set
$n\;:\!=\;\lceil t\rceil$
such that
$t/n \;=\!:\;c_n\in \big[\tfrac12 ,1\big]$
, and let
$\xi_i$
be i.i.d. copies of
$Z_1$
. Then, due to the infinite divisibility and monotonicity of Z, we have
\begin{align}\mathbb{E}[Z_t^\kappa] \leq \mathbb{E}[Z_n^\kappa]& = \mathbb{E}\Bigg[\Bigg(\sum_{i=1}^{n} \xi_i \Bigg)^\kappa\Bigg] \nonumber \\[5pt]& \leq \mathbb{E}\Bigg[ n^{\kappa-1} \cdot \sum_{i=1}^{n} \xi_i^\kappa \Bigg]= n^\kappa \cdot \mathbb{E}[\xi_1^\kappa] = t^\kappa \cdot c_n^{-\kappa} \cdot \mathbb{E}[Z_1^\kappa] \leq t^\kappa \cdot 2^{\kappa} \cdot \mathbb{E}[Z_1^\kappa],\end{align}
where we used (3.5) for the second inequality.
To prove the statement for
$\kappa\in(0,1)$
, note that
$(\!\cdot\!)^\kappa$
is concave. Hence, Jensen’s inequality yields an upper bound in this case. The lower bound follows analogously to (3.6), setting
$n\;:\!=\;\lfloor t\rfloor$
, and applying the variant of (3.5) for
$r\leq 1$
.
Proof of Proposition
3.2. We write
$\nu_Z$
,
$b_Z$
for the Lévy measure and drift of Z, respectively, and likewise
$\nu_Y$
,
$b_Y$
for the Lévy measure and drift of Y. Then, as
$(Z_{Y_t})_{t\geq 0}$
is a (killed) subordinator with Lévy measure
$\nu$
, say,
$\mathbb{E}\big[Z_{Y_1}^\kappa\big] <\infty$
is equivalent (cf. [Reference Sato15, Corollary 25.8]) to
$\int_{[1,\infty)} z^\kappa \nu(\textrm{d} z)<\infty$
, where the Lévy measure
$\nu$
of the subordinated process is given (cf. [Reference Sato15, Theorem 30.1]) by
$\nu(B)= b_Y \nu_Z(B) + \int_{(0,\infty)} \mu^s(B) \nu_Y (\textrm{d} s)$
for any Borel set B in
$(0,\infty)$
, where
$\mu=\mathcal{L}(Z_1)$
denotes the distribution of
$Z_1$
. Thus,
\begin{align}\int_{[1,\infty)} z^\kappa \nu(\textrm{d} z)& = b_Y \int_{[1,\infty)} z^\kappa \nu_Z(\textrm{d} z) + \int_{[1,\infty)} z^\kappa \textrm{d} \bigg(\int_{(0,\infty)}\mu^s (z) \nu_Y (\textrm{d} s)\bigg) \nonumber \\[5pt]& = b_Y \int_{[1,\infty)} z^\kappa \nu_Z(\textrm{d} z) + \int_{(0,\infty)}\int_{[1,\infty)} z^{\kappa} \mu^s (\textrm{d} z) \nu_Y (\textrm{d} s) ,\end{align}
where all the terms are non-negative and hence the sum that appears is finite if and only if both summands are finite. From [Reference Sato15, Corollary 25.8] we know that
$\int_{[1,\infty)} z^\kappa \nu_Z(\textrm{d} z)<\infty$
if and only if
$\mathbb{E}[Z_1^\kappa]<\infty$
if and only if
$\mathbb{E}[Z_s^\kappa]<\infty$
for all
$s\geq 0$
. Thus, assume
$\int_{[1,\infty)} z^\kappa \nu_Z(\textrm{d} z)<\infty$
from now on, which implies
$\int_{[1,\infty)} z^{\kappa} \mu^s(\textrm{d} z) = \mathbb{E}\big[\textbf{1}_{\{Z_s \geq 1\}} Z_s^\kappa\big] <\infty$
. Furthermore,
\begin{align}\int_{(0,\infty)}\int_{[1,\infty)} z^{\kappa} \mu^s & (\textrm{d} z) \nu_Y (\textrm{d} s) \nonumber \\[5pt]& = \int_{(0,\infty)} \mathbb{E}\big[\textbf{1}_{\{Z_s\geq 1\}} Z_s^\kappa \big] \nu_Y (\textrm{d} s) \nonumber \\[5pt]& = \int_{(0,1)} \mathbb{E}\big[\textbf{1}_{\{Z_s\geq 1\}} Z_s^\kappa \big] \nu_Y (\textrm{d} s) \nonumber \\[5pt]& \quad + \int_{[1,\infty)} \mathbb{E}[ Z_s^\kappa ] \nu_Y (\textrm{d} s) -\int_{[1,\infty)} \underbrace{\mathbb{E}\big[\textbf{1}_{\{Z_s<1 \}} Z_s^\kappa \big]}_{\in [0,1)} \nu_Y (\textrm{d} s),\end{align}
where the left-hand side of the equation is finite if and only if the right-hand side is finite. Here, the last integral, as well as the sum of all three, is non-negative.
Consider the first integral. We have that
$\mathbb{E}\big[\textbf{1}_{\{Z_s\geq 1\}} Z_s^\kappa\big]= \mathbb{P}(Z_s\geq 1) \cdot \mathbb{E}[Z_s^\kappa \mid Z_s\geq 1]$
, where
$\mathbb{E}[Z_s^\kappa \mid Z_s\geq 1]\;=\!:\;C_1(s)<\infty$
,
$s\in[0,\infty)$
, since we assumed
$\mathbb{E}[Z_s^\kappa]<\infty$
. From [Reference Sato15, Lemma 30.3], it follows that
$\mathbb{P}(Z_s\geq 1)\leq C_2 s$
for some
$C_2\in (0,\infty)$
. Thus, setting
$C_1\;:\!=\;\sup_{s\in(0,1)}C_1(s)<\infty$
,
\begin{align*}\int_{(0,1)} \mathbb{E}\big[\textbf{1}_{\{Z_s\geq 1\}} Z_s^\kappa \big] \nu_Y (\textrm{d} s)\leq C_1C_2 \int_{(0,1)} s \nu_Y (\textrm{d} s)\end{align*}
is finite because Y is a subordinator, which implies
$\int_{(0,\infty)} (1\wedge y)\nu_Y(\textrm{d} y)<\infty$
.
For the second integral, note that, by Lemma 3.2, the mapping
$s\mapsto \mathbb{E}[Z_s^\kappa]$
is of polynomial order
$\kappa$
for all
$s\geq 1$
. Thus, it follows that the second summand in (3.8), and hence also the second summand in (3.7), is finite if and only if
$\int_{[1,\infty)}s^\kappa \nu_Y(\textrm{d} s)<\infty$
and
$\int_{[1,\infty)} z^\kappa \nu_Z(\textrm{d} z)<\infty$
. This finishes the proof of the claimed equivalence.
In the case
$\mathbb{E}[Z_1]=\infty$
and
$\kappa \in(0,1)$
, we cannot apply Lemma 3.2 to find a necessary and sufficient condition for the finiteness of the second summand in (3.8). However, an inspection of the proof of Lemma 3.2 shows that even in this case the mapping
$s\mapsto \mathbb{E}[Z_s^\kappa]$
can be bounded from below by a function of polynomial order
$\kappa$
for all
$s\geq 1$
. Thus, finiteness of the second summand in (3.8) still implies
$\int_{[1,\infty)} z^\kappa \nu_Z(\textrm{d} z)<\infty$
, and the finiteness of all the summands in (3.7) implies
$\int_{[1,\infty)}s^\kappa \nu_Y(\textrm{d} s)<\infty$
and
$\int_{[1,\infty)} z^\kappa \nu_Z(\textrm{d} z)< \infty$
, as claimed.
Let us now concentrate on the case
$\psi'(0+\!)>0$
treated in Theorem 3.1(ii), where in the light of (3.4) it remains to be proved that
$\mathbb{E}\big[(\tau_{Y_1}^+\!)^\kappa\big]<\infty$
is equivalent to
$\int_{[1,\infty)} y^{\kappa+1} \Pi (\textrm{d} y)<\infty$
. To show this, we need the following useful connection between the existence of integer moments of
$\tau^+_1$
and
$X_1$
.
Lemma 3.3. Assume that
$\psi'(0+\!)> 0$
. Then, for all
$k\in\mathbb{N}_0$
,
\begin{equation}\lim_{q\downarrow 0 }\big| \Phi^{(k)}(q)\big| < \infty \quad \textit{if and only if}\quad \lim_{q\downarrow 0}\big|\psi^{(k)}(q)\big|<\infty.\end{equation}
Proof. We prove the statement by induction. Clearly, for
$k=0$
there is nothing to show. For
$k=1$
it follows from the assumption
$\psi'(0+\!)> 0$
and the fact that
$(X_t)_{t\geq 0}$
is spectrally negative, that
$\psi'(0+\!)\in(0,\infty)$
. By (2.3) we thus conclude that
$\Phi'(0+\!)=1/\psi'(0+\!)\in(0,\infty)$
, and the equivalence is trivially fulfilled. Further, for
$k=2$
we compute, via (2.3),
\begin{align*}\Phi''(q) = \partial_q\bigg( \frac{1}{\psi'(\Phi(q))}\bigg)= - \frac{\psi''(\Phi(q))}{\psi'(\Phi(q))^3}, \qquad q>0,\end{align*}
such that
\begin{equation*}\Phi''(0+\!) = - \frac{\psi''(0+\!)}{\psi'(0+\!)^3},\end{equation*}
which proves the claim for
$k=2$
.
Assume now that (3.9) holds for all
$\ell=1,\ldots,n-1$
. If there exists
$\ell'\in\{1,\ldots,n-1\}$
such that both sides of (3.9) are infinite, then, for all
$\ell\in\{\ell',\ldots,n-1\}$
, both terms are infinite as well. Therefore we assume that both sides are finite for all
$\ell=1,\ldots,n-1$
.
By the definition of
$\Phi$
we have
$\psi(\Phi(q))=q$
for all
$q\geq 0$
, and hence
$\partial_q^n \psi(\Phi(q))=0$
for all
$n\geq 2$
. Using Faà di Bruno’s formula (cf. [Reference Johnson6, (2.2)]) for
$n\geq 2$
, we therefore conclude that
$0 = \sum_{k=1}^n \psi^{(k)}(\Phi(q)) \cdot B_{n,k}(\Phi'(q),\ldots,\Phi^{(n-k+1)}(q))$
, where the functions
$B_{n,k}$
denote the partial Bell polynomials. Thus, we get
\begin{align*}\Phi^{(n)}(q) & = B_{n,1}(\Phi^{(n)}(q)) = \frac{-1}{\psi'(\Phi(q)}\cdot \sum_{k=2}^n \psi^{(k)}(\Phi(q)) \cdot B_{n,k}\big(\Phi'(q),\ldots,\Phi^{(n-k+1)}(q)\big) \\[5pt]& = \frac{-1}{\psi'(\Phi(q))}\cdot \sum_{j=1}^{n-1} \psi^{(n+1-j)}(\Phi(q)) \cdot B_{n,n+1-j}\big(\Phi'(q),\ldots,\Phi^{(j)}(q)\big),\end{align*}
where the left-hand side is finite if and only if the right-hand side is finite. However, the right-hand side is finite in the limit
$q\downarrow 0$
if and only if
\begin{align*}\lim_{q\downarrow 0} \left\vert{\frac{1}{\psi(\Phi(q))} \cdot \psi^{(n)}(\Phi(q)) \cdot B_{n,n}(\Phi'(q))}\right\vert & =\lim_{q\downarrow 0} \left\vert{\frac{1}{\psi(\Phi(q))} \cdot \psi^{(n)}(\Phi(q)) \cdot \Phi'(q)^n}\right\vert \\[5pt] & = \left\vert{\frac{\psi^{(n)}(0+\!)}{\psi'(0+\!)^{n+1}}}\right\vert<\infty,\end{align*}
since all the other summands are finite in the limit
$q\downarrow 0$
by assumption.
We are now in a position to present the proof of Theorem 3.1(ii).
Proof of Theorem
3.1(ii). Assume
$\psi'(0+\!)> 0$
. By Lemma 3.1, Proposition 3.1, and (2.7), we see immediately that, for all
$\kappa>0$
,
$\mathbb{E}[(\tau_x^-)^\kappa\mid\tau_x^-<\infty] <\infty$
if and only if
$\mathbb{E}\big[(\tau_{Y_1}^+)^\kappa\big] <\infty$
. Further applying Proposition 3.2, it follows that
\begin{equation}\mathbb{E}\big[(\tau_{Y_1}^+\!)^\kappa\big] <\infty \quad \text{if and only if} \quad \mathbb{E}[(\tau_1^+\!)^\kappa] <\infty \text{ and } \mathbb{E}[Y_1^\kappa ]<\infty,\end{equation}
since
$\mathbb{E}[\tau_1^+]= \Phi'(0+\!)=1/\psi'(0+\!)<\infty$
as noted in the proof of Lemma 3.3. Furthermore,
$\mathbb{E}[Y_1^\kappa ]<\infty $
is equivalent to finiteness of
\begin{align}\int_{[1,\infty)} y^{\kappa} \Pi((y,\infty)) \textrm{d} y &= \frac{1}{\kappa+1} \int_{[1,\infty)} y^{\kappa+1} \Pi(\textrm{d} x) -\frac{1}{\kappa+1}\Pi((1,\infty))\end{align}
by partial integration. Thus,
$\mathbb{E}[Y_1^\kappa ]<\infty$
if and only if
$\mathbb{E}[|X_1|^{\kappa+1} ]<\infty$
, and
$\mathbb{E}[|X_1|^{\kappa+1} ]<\infty$
is shown to be a necessary condition for
$\mathbb{E}[(\tau_x^-)^\kappa\mid\tau_x^-<\infty] < \infty$
. However,
$\mathbb{E}[|X_1|^{\kappa+1}]< \infty$
is a sufficient condition as well, since it implies
$\mathbb{E}[|X_1|^{k}]<\infty$
for
$k=\lfloor \kappa +1 \rfloor\geq 1$
. This in turn implies
$\mathbb{E}[(\tau^+_1)^{k}]<\infty$
by (2.2) and Lemma 3.3, which then yields
$\mathbb{E}[(\tau^+_1)^{\kappa}]<\infty$
, since
$\kappa<k$
. Thus, both conditions on the right-hand side of (3.10) hold if and only if
$\mathbb{E}[|X_1|^{\kappa+1} ]<\infty$
, which finishes the proof.
Finally, we consider the oscillating case of
$\psi'(0+\!)=0$
. Again, in the light of (3.4) we need to investigate the existence of
$\mathbb{E}\big[(\tau_{Y_1}^+\!)^\kappa\big]$
, where this time we restrict ourselves to finding conditions for
$\mathbb{E}\big[(\tau_{Y_1}^+\!)^\kappa\big]=\infty$
.
Proof of Theorem
3.1(iii). Assume that
$\psi'(0+\!)= 0$
. Consider case (a),
$\kappa\in(0,1]$
. From (3.4) we have
$\mathbb{E}[(\tau_x^-)^\kappa] =\infty$
if and only if
$\mathbb{E}\big[(\tau_{Y_1}^+\!)^\kappa\big] =\infty$
, and, by Proposition 3.2, for
$\kappa \in (0,1)$
the latter follows in particular if
$\mathbb{E}[Y_{1}^\kappa]=\infty$
. This, however, is equivalent to
$\int_{[1,\infty)} y^{\kappa} \Pi((y,\infty)) \textrm{d} y=\infty$
and, via (3.11), it is furthermore equivalent to
$\int_{[1,\infty)} y^{\kappa+1} \Pi(\textrm{d} y)= \infty$
.
Consider now the case
$\kappa = 1$
, i.e.
$\mathbb{E}[Y_{1}]=\infty$
. From (2.3) it follows that
$\Phi'(0+\!)=\mathbb{E}[\tau_1^+]=\infty$
, and an inspection of the proof of Proposition 3.2 reveals that in this setting also
$\mathbb{E}[\tau_{Y_1}^+] =\infty$
. This again implies the statement.
For case (b), we consider a fixed
$\kappa\in \big(\frac12,1\big)$
and prove (3.1) for the chosen
$\kappa$
. This will immediately also imply the statement for any
$\kappa\geq 1$
.
As before, from (3.4) we have
$\mathbb{E}[(\tau_x^-)^\kappa] = \infty$
if and only if
$\mathbb{E}\big[(\tau_{Y_1}^+\!)^\kappa\big] =\infty$
, where, by Proposition 3.2, the latter follows if
$\mathbb{E}[(\tau_{1}^+\!)^\kappa]=\infty$
. Here, by (3.2), (2.7), and (2.6),
\begin{align}\mathbb{E}[(\tau_1^+\!)^\kappa] = \big[ \textbf{D}_q^\kappa \textrm{e}^{-\Phi(q)}\big]_{q=0}& = \bigg[\frac{\kappa}{\Gamma(1-\kappa)} \int_q^\infty \frac{\textrm{e}^{-\Phi(q)}- \textrm{e}^{-\Phi(u)}}{u^{\kappa+1}} \textrm{d} u\bigg]_{q=0} \nonumber \\[5pt]& = \frac{\kappa}{\Gamma(1-\kappa)} \int_0^\infty \frac{1- \textrm{e}^{-\Phi(u)}}{u^{\kappa+1}} \textrm{d} u,\end{align}
where the left-hand side is finite if and only if the right-hand side is finite.
As
$\Phi$
is monotonically increasing with
$\Phi(0)=0$
and
$\Phi(u)\overset{u\to\infty}{\longrightarrow}\infty$
, we clearly have, for all
$\varepsilon>0$
,
\begin{equation*}\int_\varepsilon^\infty \frac{1-\textrm{e}^{-\Phi(u)}}{u^{\kappa+1}} \textrm{d} u \leq \int_\varepsilon^\infty \frac{1}{u^{\kappa+1}}\textrm{d} u <\infty.\end{equation*}
Thus, by (3.12), we have
\begin{equation}\mathbb{E}[(\tau_1^+\!)^\kappa]<\infty\quad \text{ if and only if } \quad\int_0^\varepsilon \frac{1-\textrm{e}^{-\Phi(u)}}{u^{\kappa+1}}<\infty \text{ for some }\varepsilon>0.\end{equation}
By Taylor’s expansion, the term
$1-\textrm{e}^{-\Phi(u)}$
is of the same order as
$u \Phi'(u)\textrm{e}^{-\Phi(u)}$
as
$u\downarrow 0$
. Moreover, by (2.3),
\begin{equation*}\lim_{u\downarrow 0} \frac{u \Phi'(u)}{u^{\kappa}} = \lim_{u\downarrow 0} \frac{\Phi'(u)}{u^{\kappa-1}}= \lim_{u\downarrow 0} \frac{u^{1-\kappa}}{\psi'(\Phi(u))}.\end{equation*}
Recall that
$\kappa\in\big(\frac12 ,1\big)$
and
$\psi''(0+\!)<\infty$
. By a twofold application of l’Hospital’s rule, we get
\begin{align*}\lim_{u\downarrow 0} \frac{u^{1-\kappa}}{\psi'(\Phi(u))}& = \lim_{u\downarrow 0} \frac{(1-\kappa)\cdot u^{-\kappa}}{\psi''(\Phi(u))\cdot\Phi'(u)}=\frac{(1-\kappa)}{\psi''(0+\!)} \cdot \lim_{u\downarrow 0} \frac{\psi'(\Phi(u))}{u^\kappa} \\[5pt]& = \frac{(1-\kappa)}{\psi''(0+\!)} \cdot\lim_{u\downarrow 0} \frac{\psi''(\Phi(u))\cdot\Phi'(u)}{\kappa \cdot u^{\kappa-1}}=\frac{(1-\kappa)}{\kappa} \cdot\lim_{u\downarrow 0} \frac{u^{1-\kappa}}{\psi'(\Phi(u))}.\end{align*}
As
$\kappa\neq \frac12$
this can only be true if
\begin{equation*} \lim_{u\downarrow 0} \frac{u^{1-\kappa}}{\psi'(\Phi(u))} =\lim_{u\downarrow 0} \frac{\psi'(\Phi(u))}{u^\kappa}= \text{ either }0 \text{ or }\infty,\end{equation*}
which in turn implies
\begin{equation*}\lim_{u\downarrow 0} \frac{u\Phi'(u)}{u^\kappa} = \lim_{u\downarrow 0} \frac{u^{1-\kappa}}{\psi'(\Phi(u))} \cdot \frac{\psi'(\Phi(u))}{u^\kappa} = \lim_{u\downarrow 0} u^{1-2\kappa} = \infty.\end{equation*}
Thus also
\begin{equation*}\lim_{u\downarrow 0} \frac{1-\textrm{e}^{-\Phi(u)}}{u^{\kappa}} = \lim_{u\downarrow 0} \frac{u\Phi'(u)\textrm{e}^{-\Phi(u)}}{u^{\kappa}} =\infty,\end{equation*}
and in particular for any
$C>0$
there exists
$u_0>0$
such that
$\frac{1-\textrm{e}^{-\Phi(u)}}{u^{\kappa}}>C$
for all
$u<u_0$
. Hence,
\begin{equation*}\int_0^\varepsilon \frac{1-\textrm{e}^{-\Phi(u)}}{u^{\kappa+1}} \textrm{d} u \geq \int_0^{u_0\wedge \varepsilon} \frac{1-\textrm{e}^{-\Phi(u)}}{u^{\kappa+1}} \textrm{d} u \geq \int_0^{u_0\wedge \varepsilon} \frac{C\cdot u^\kappa}{u^{\kappa+1}} = C\cdot\int_0^{u_0\wedge \varepsilon} \frac{1}{u} \textrm{d} u = \infty.\end{equation*}
By (3.13) this implies
$\mathbb{E}[(\tau_1^+\!)^\kappa]=\infty$
, and thus the statement.
Lastly, note that (3.1) for all
$x>0$
,
$\kappa \geq 1$
is a direct consequence of (a) and (b), as either
$\psi''(0+\!)<\infty$
, in which case we can apply (b), or
$\psi''(0+\!)=\infty$
, which is equivalent to
$\int_{[1,\infty)} y^2 \Pi(\textrm{d} y) = \infty$
and hence
$\kappa^*=1$
is a possible choice in (a).
Acknowledgements
We would like to thank the reviewers for their helpful and constructive comments when preparing the revision of this paper.
Funding information
There are no funding bodies to thank relating to this creation of this article.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.
