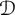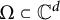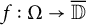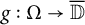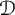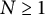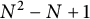1 Introduction
1.1 Motivation
For a domain
$\Omega $
in
${\mathbb C}^d$
(
$d\geq 1$
), let
${\mathbb S}(\Omega )$
denote the set of analytic functions
$f:\Omega \to \overline {{\mathbb D}}$
, where
${\mathbb D}$
denotes the open unit disk in
${\mathbb C}$
. Given a function
$f\in {\mathbb S}(\Omega )$
, this paper revolves around the question when a given subset
${\mathcal D}$
of
$\Omega $
has the property that whenever
$g\in {\mathbb S}(\Omega )$
coincides with f on
${\mathcal D}$
, equals to f on whole
$\Omega $
. When a subset has this property, we call it a determining set for
$(f,\Omega )$
, or just f when the domain is clear from the context. For example,
$\{0,1/2\}$
is a determining set for the identity map (by the Schwarz Lemma); any open subset of
$\Omega $
is determining for any analytic function on
$\Omega $
(by the Identity Theorem). See Rudin [Reference Rudin32, Chapter 5] for some interesting results related to a similar concept for
$\Omega ={\mathbb D}^d$
.
The motivation behind the study of determining sets comes from the Pick interpolation problem. It corresponds to the case when
${\mathcal D}$
is a finite set. Given a finite subset
${\mathcal D}=\{\lambda _1,\lambda _2,\dots ,\lambda _N\}$
of
$\Omega $
and points
$w_1,w_2,\dots ,w_N$
in the open unit disk
${\mathbb D}$
, the Pick interpolation problem asks if there is an analytic function
$f:\Omega \to {\mathbb D}$
such that
$f(\lambda _j)=w_j$
for
$j=1,2,\dots ,N$
. Therefore in this case,
${\mathcal D}$
being a determining set for
$(f,\Omega )$
means that the (solvable) Pick problem
$\lambda _j\mapsto f(\lambda _j)$
has a unique solution. In view of Pick’s pioneering work [Reference Pick31], it is therefore clear that when
$\Omega ={\mathbb D}$
, then
${\mathcal D}$
is determining for f if and only if the Pick matrix
$$ \begin{align*}\begin{bmatrix} \frac{1-f(\lambda_i)\overline{f(\lambda_j)}}{1-\lambda_i\overline{\lambda_j}} \end{bmatrix}_{i,j=1}^N \end{align*} $$
has rank less than N, which is further equivalent to the existence of a Blaschke function of degree less than N solving the data. The classical Pick interpolation problem has seen a wide range of generalizations. To mention a few, a necessary and sufficient condition for the solvability of a given Pick data is known when
$\Omega $
is the polydisk
${\mathbb D}^d$
[Reference Agler2], the Euclidian ball
${\mathbb B}_d$
[Reference Kosiński and Zwonek24], the symmetrized bidisk [Reference Agler and Young10, Reference Bhattacharyya and Sau14], an affine variety [Reference Jury, Knese and McCullough20] and in more general setting of test functions [Reference Dritschel and McCullough18, Reference Dritschel, Marcantognini and McCullough17]. However, unlike the classical case, it is rather obscure in higher dimension when it comes to understanding when a given solvable Pick problem has a unique solution, and usually one has to settle with either necessary or sufficient conditions (see, for example, [Reference Agler and McCarthy4, Reference Scheinker33–Reference Scheinker35]).
1.2 The main results
The purpose of this article is to explore this direction where the domain under consideration is the symmetrized bidisk
$$ \begin{align} \mathbb{G}:=\{(z_1+z_2, z_1 z_2): (z_1, z_2)\in\mathbb{D}^2\}. \end{align} $$
Following the work [Reference Agler and Young7] of Agler and Young, this domain has remained a field of extensive research in operator theory and complex geometry constituting examples and counter-examples to celebrated problems in these areas such as the rational dilation problem [Reference Agler and Young8, Reference Bhattacharyya, Pal and Shyam Roy13] and the Lempert theorem [Reference Costara16]. In quest of understanding the determining sets, we shall actually consider the following more general situation.
Definition 1.1 Let
$\Omega \subset {\mathbb C}^d$
be a domain,
$E\subset \Omega $
and
$f\in {\mathbb S}(\Omega )$
. We say that a subset
${\mathcal D}$
of E is determining for
$(f, E)$
if for every
$g\in {\mathbb S}(\Omega )$
,
$g=f$
on
${\mathcal D}$
implies
$g=f$
on E. If
${\mathcal D}$
is determining for
$(f,E)$
for all
$f\in {\mathbb S}(\Omega )$
, then we say that
${\mathcal D}$
is determining for E. Moreover, when E is the largest set in
$\Omega $
such that
${\mathcal D}$
is determining for
$(f,E)$
, we say that E is the uniqueness set for
$(f,{\mathcal D})$
, i.e., in this case,
$$ \begin{align*}E=\bigcap\{Z(g-f): g\in{\mathbb S}(\Omega)\mbox{ and } g=f \mbox{ on }{\mathcal D}\}. \end{align*} $$
Here, for a function f, we use the standard notation
$Z(f)$
for the zero set of f.
Note that if E is the uniqueness set for
$(f,{\mathcal D})$
, then for every
$z\in \Omega \setminus E$
, there exists a function
$g\in {\mathbb S}(\Omega )$
such that
$g=f$
on
${\mathcal D}$
but
$f(z)\neq g(z)$
. Remarkably, when
${\mathcal D}$
is a finite subset of
${\mathbb G}$
, then for any function
$f\in {\mathbb S}({\mathbb G})$
, the uniqueness set for
$(f,{\mathcal D})$
is an affine variety (see [Reference Agler and McCarthy6, Reference Krishna Das, Kumar and Sau25]). This is owing to the fact that every solvable Pick data in
${\mathbb G}$
always has a rational inner solution (see [Reference Agler and McCarthy3, Reference Krishna Das, Kumar and Sau25]). Also note that if f and g agree on
${\mathcal D}$
, then
${\mathcal D}$
is determining for
$(f,E)$
if and only if
${\mathcal D}$
is determining for
$(g,E)$
also. In view of these facts, we shall mostly be concerned with the case when the function f in Definition 1.1 is rational and inner. Here, a function f in
${\mathbb S}({\mathbb G})$
is called inner, if
$\lim _{r\to 1-}|f(r\zeta _1+r\zeta _2,r^2\zeta _1\zeta _2)|=1$
for almost all
$\zeta _1,\zeta _2$
in
${\mathbb {T}}$
.
Note that
${\mathbb G}$
is the image of
${\mathbb D}^2$
under the (proper) holomorphic map
$\pi :(z_1,z_2)\mapsto (z_1+z_2,z_1z_2)$
. The topological boundary of
${\mathbb G}$
is
$\partial {\mathbb G}:=\pi (\overline {{\mathbb D}}\times {\mathbb {T}})\cup \pi ({\mathbb {T}}\ \times {\mathbb D})$
and the distinguished boundary of
${\mathbb G}$
is
$b{\mathbb G}:=\pi ({\mathbb {T}}\times {\mathbb {T}})$
(see [Reference Agler and Young9]). Here, the distinguished boundary of a bounded domain
$\Omega \subset {\mathbb C}^d$
is the
$\check {\mbox S}$
ilov boundary with respect to the algebra of complex-valued functions continuous on
$\overline {\Omega }$
and holomorphic in
$\Omega $
. A special type of algebraic varieties has been prevalent in the study of uniqueness of the solutions of a Pick interpolation problem (see [Reference Agler and McCarthy6, Reference Kosiński22–Reference Krishna Das, Kumar and Sau25, Reference Maciaszek27]). We define it below. Throughout the paper, the notation
$\xi $
stands for a polynomial in two variables.
Definition 1.2 An algebraic variety
$Z(\xi )$
in
${\mathbb C}^2$
is said to be distinguished with respect to a bounded domain
$\Omega $
, if
$$ \begin{align*}Z(\xi)\cap\Omega\neq \emptyset \quad\text{ and }\quad Z(\xi)\cap\partial \Omega=Z(\xi)\cap b\Omega.\end{align*} $$
An example of a distinguished variety with respect to
${\mathbb G}$
is
$\{(2z,z^2):z\in {\mathbb C}\}$
. We refer the readers to the papers [Reference Agler and McCarthy6, Reference Bhattacharyya, Kumar and Sau12, Reference Krishna Das, Kumar and Sau25, Reference Krishna Das and Sarkar26, Reference Pal and Shalit29] for results concerning these varieties and their connection to interpolation problems.
We now state the main results of this paper in the order they are proved.
-
(1) In Section 2.1, we reformulate the notion of determining set in the more general setting of reproducing kernel Hilbert spaces and find a sufficient condition for a finite subset of a general domain to be determining. This is Theorem 2.1. We also show by an example that the sufficient condition need not be necessary, in general.
-
(2) Starting with a natural number N, Section 2.2 constructs a finite subset of
${\mathbb G}$
consisting exactly of
$N^2-N+1$
many points which is determining for any rational inner function with a natural degree constraint on it. This is Theorem 2.5. Proposition 2.4 is an intermediate step of the construction and is interesting on its own right. -
(3) Given a distinguished variety
${\mathcal W}=Z(\xi )$
, we investigate in Section 2.3, when the intersection
${\mathcal W}\cap \mathbb {G}$
can be the uniqueness set for
$(f,{\mathcal D})$
, where f is a rational inner function and
${\mathcal D}$
a finite subset of
${\mathbb G}$
(see Theorem 2.10). The preparatory results Propositions 2.7 and 2.8 are interesting in their own rights. Proposition 2.7 states that if f is a rational inner function with some regularity assumption, then there is a natural number N depending on f large enough so that any subset of
${\mathcal W}\cap {\mathbb G}$
consisting of N points is determining for
$(f,{\mathcal W}\cap {\mathbb G})$
. This section then goes on to find (in Theorem 2.12) a sufficient condition for
${\mathcal W}\cap {\mathbb G}$
to be determining for a rational inner function f with a regularity assumption on it. The condition is just that the inequality
$$ \begin{align*} \quad 2\operatorname{Re}\langle f, \xi h\rangle_{H^2}< \|\xi h\|^2_2 \end{align*} $$
holds, whenever h is a nonzero analytic function on
${\mathbb G}$
and
$\xi h$
is bounded on
${\mathbb G}$
. Here, the inner product is the Hardy space inner product, briefly discussed in Section 2.3. -
(4) Section 3 proves a bounded extension theorem for distinguished varieties with no singularities on
$b{\mathbb G}$
. More precisely, given a distinguished variety
${\mathcal W}$
, we show that corresponding to every two-variable polynomial f, there is a rational function F on
${\mathbb G}$
such that
$F|_{{\mathcal W}\cap {\mathbb G}}=f$
and that
$\sup _{\mathbb G}|F(s,p)|\leq \alpha \sup _{{\mathcal W}\cap {\mathbb G}}|f|$
, for some constant
$\alpha $
depending only on the distinguished variety
${\mathcal W}$
.
2 Determining and the uniqueness sets
2.1 A result for a general domain
We begin by proving a sufficient condition for a finite subset of a general domain to be determining. The concept of determining set can be formulated in a general setup of reproducing kernel Hilbert spaces. Here, a kernel on a domain
$\Omega $
in
${\mathbb C}^d$
(
$d\geq 1$
) is a function
$k:\Omega \times \Omega \to {\mathbb C}$
such that for every choice of points
$\lambda _1,\lambda _2,\dots ,\lambda _N$
in
$\Omega $
, the
$N\times N$
matrix
$[k(\lambda _i,\lambda _j)]$
is positive-definite. Given a kernel k, there is a unique Hilbert space
$H(k)$
associated with it, called the reproducing kernel Hilbert space; we refer the uninitiated reader to the book [Reference Paulsen and Raghupathi30]. For the purpose of this paper, all that is needed to know is that elements of the form
$\{\sum _{j=1}^nc_jk(\cdot ,\lambda _j):c_j\in {\mathbb C}\mbox { and }\lambda _j\in \Omega \}$
constitute a dense set of
$H(k)$
. A kernel k is said to be a holomorphic kernel, if it is holomorphic in the first and conjugate holomorphic in the second variable. Note that when k is holomorphic, then so are the elements of
$H(k)$
. Let us denote by
$\operatorname {Mult}H(k)$
the algebra of all bounded holomorphic functions
$\varphi $
on
$\Omega $
such that
$\varphi \cdot f \in H(k)$
whenever
$f\in H(k)$
. Such a holomorphic function is generally referred to as a multiplier for
$H(k)$
. Let
$\operatorname {Mult}_1H(k)$
denote the set of all multipliers
$\varphi $
such that the operator norm of
$M_\varphi : f\mapsto \varphi \cdot f$
for all f in
$H(k)$
is no greater than one. A subset
${\mathcal D}\subset \Omega $
is said to be determining for a function
$\varphi $
in
$\operatorname {Mult}_1H(k)$
if whenever
$\psi \in \operatorname {Mult}_1H(k)$
such that
$\varphi =\psi $
on
${\mathcal D}$
, then
$\varphi =\psi $
on
$\Omega $
.
Theorem 2.1 Let k be a holomorphic kernel on a domain
$\Omega $
in
${\mathbb C}^d$
,
$\varphi \in \operatorname {Mult}_1H(k),$
and
${\mathcal D}=\{\lambda _1,\lambda _2,\dots ,\lambda _N\}\subset \Omega $
. If the matrix
$$ \begin{align} [(1-\varphi(\lambda_i)\overline{\varphi(\lambda_j)})k(\lambda_i,\lambda_j)]_{i,j=1}^N \end{align} $$
is singular, then
${\mathcal D}$
is determining for
$\varphi $
.
Proof Since the matrix (2.1) is singular, there is a nonzero vector in its kernel; let us denote it by
$\gamma $
. Let
$\lambda _{N+1}$
be any point in
$\Omega \setminus {\mathcal D}$
, and let
$\psi \in \operatorname {Mult}_1H(k)$
be any function such that
$\varphi =\psi $
on
${\mathcal D}$
. Since
$\psi \in \operatorname {Mult}_1H(k)$
, the operator
$M_\psi :f\mapsto \psi \cdot f$
is a contractive operator on
$H(k)$
and therefore for every
$z\in {\mathbb C}$
,
$$ \begin{align*}\left\langle[(1-\psi(\lambda_i)\overline{\psi(\lambda_j)})k(\lambda_i,\lambda_j)]_{i,j=1}^{N+1}\begin{bmatrix} \gamma \\ z \end{bmatrix}, \begin{bmatrix} \gamma \\ z \end{bmatrix}\right\rangle\geq{0}.\end{align*} $$
Since
$\gamma \in \operatorname {Ker}[(1-\varphi (\lambda _i)\overline {\varphi (\lambda _j)})k(\lambda _i,\lambda _j)]$
and
$\varphi =\psi $
on
${\mathcal D}$
, the above inequality collapses to
$$ \begin{align*}2\operatorname{Re}\left[\overline{z}\sum_{j=1}^N(1-\overline{\psi(\lambda_j)}\psi(\lambda_{N+1}))\gamma_jk(\lambda_{N+1},\lambda_j)\right]+ |z|^2(1-|\psi(\lambda_{N+1})|^2)||k_{\lambda_{N+1}}||^2\geq{0}.\end{align*} $$
Since the above inequality is true for all
$z\in \mathbb {C}$
, we have
$$ \begin{align*}\sum_{j=1}^N(1-\overline{\psi(\lambda_j)}\psi(\lambda_{N+1}))\gamma_jk_{N+1,j}=0,\end{align*} $$
which, after a rearrangement of terms, gives
$$ \begin{align} \psi(\lambda_{N+1})\left(\sum_{j=1}^N\overline{\psi(\lambda_j)}\gamma_jk(\lambda_{N+1}, \lambda_j)\right)=\sum_{j=1}^N\gamma_jk(\lambda_{N+1},\lambda_j). \end{align} $$
Define for z in
$\Omega $
,
$$ \begin{align*}L(z)=\sum_{j=1}^N\gamma_jk_{\lambda_j}(z)=\sum_{j=1}^N\gamma_jk(z,\lambda_j).\end{align*} $$
By definition, it is clear that
$L\in H(k)$
. Consider the open set
${\mathcal O}=\Omega \setminus Z(L)$
. Note that if
$\lambda _{N+1}\in {\mathcal O}$
, then the right-hand side of (2.2) does not vanish, and therefore
$\psi (\lambda _{N+1})$
is uniquely determined.
Now suppose
$\phi =\psi $
on
${\mathcal O}$
. By the assumption that
${\mathcal O}$
is a set of uniqueness for
$\operatorname {Mult}_1(H(k))$
, it follows that
$\phi =\psi $
.
The converse of the above result is not true as the simple example below demonstrates.
Example 2.2 Let k be the Bergman kernel on
$\Omega =\mathbb {D}$
, i.e.,
$k(z, w)= (1-z\overline {w})^{-2}$
. Then it is well known that
$\operatorname {Mult}_1H(k)={\mathbb S}({\mathbb D})$
(see, for example, [Reference Agler and McCarthy5, Section 2.3]. By the Schwarz lemma,
${\mathcal D}=\{0,1/2\}$
is determining for the identity function. However, the matrix
$\left [\begin {smallmatrix} 1 & 1 \\ 1 & 4/3 \end {smallmatrix}\right ]$
is nonsingular.
The rest of the paper specializes to the symmetrized bidisk.
2.2 Finite sets as a determining set
Given a natural number N, this subsection constructs a finite subset
${\mathcal D}$
of
${\mathbb G}$
consisting exactly of
$N^2-N+1$
many points, which is determining for any rational inner function on
${\mathbb G}$
with a degree constraint on it. This is inspired by the work of Scheinker [Reference Scheinker34], which extends the following classical result for the unit disk to the polydisks.
Lemma 2.3 (Pick [Reference Pick31])
Let
${\mathcal D}=\{\lambda _1, \lambda _2,\dots ,\lambda _N\}\subset {\mathbb D}$
, and let f be a rational inner function on
$\mathbb {D}$
with degree strictly less than N. Then if
$g\in {\mathbb S}(\mathbb {D})$
is such that
$f=g$
on
${\mathcal D}$
, then
$f=g$
on
${\mathbb D}$
.
For
$\epsilon>0$
and
$z\in {\mathbb C}$
, let
$D(z;\epsilon ):=\{w\in {\mathbb {D}}: |z-w|<{\epsilon }\}$
. For
$\zeta \in {\mathbb {T}}$
and
$a\in {\mathbb D}$
, let
$m_{\zeta ,a}$
be the Möbius map
$$ \begin{align*}m_{\zeta,a}(z)=\zeta\frac{z-a}{1-\overline{a}z}.\end{align*} $$
We shall have use of two notions of degree for a polynomial in two variables. The one used in this subsection is the following. For a polynomial
$\xi (z,w)=\sum _{i,j}a_{i,j}z^iw^j$
, we define
$\deg \xi :=\max (i+j)$
such that
$a_{i,j}\neq 0$
. The degree of a rational function in its reduced fractional representation is defined to be the degree of the numerator polynomial. The following is an intermediate step to proving Theorem 2.5.
Proposition 2.4 Let N be a positive integer and for each
$j=1,2,\dots ,N$
, let
$\beta _j$
be distinct points in
${\mathbb {T}}$
, and let
$D_j$
be the analytic disks
$D_j=\{(z+\beta _jz, \beta _j z^2):z\in {\mathbb D}\}$
. Then:
-
(a) There exist
$\beta \in {\mathbb {T}}$
and
$\epsilon>0$
such that for every fixed
$\zeta \in D(\beta ;\epsilon )\cap \mathbb {T}$
and
$a\in {D(0;\epsilon )}$
, the analytic disk
$$ \begin{align*}{\mathcal D}_{\zeta,a}=\{(z+m_{\zeta,a}(z), zm_{\zeta, a}(z)):z\in{\mathbb D}\} \end{align*} $$
intersects each of the analytic disks
$D_j$
at a nonzero point. -
(b) For each
$\zeta \in {\mathbb {T}}$
and
$\epsilon>0$
, the set
$$ \begin{align*}{\mathcal D}_\zeta=\{(z+m_{\zeta,a}(z), zm_{\zeta, a}(z)):z\in{\mathbb D} \text{ and } a\in{D(0;\epsilon)}\} \end{align*} $$
is a determining set for any function in
${\mathbb S}(\mathbb {G})$
. -
(c) The set
$$ \begin{align*}E=\{(z+\beta_jz, \beta_j z^2): z\in{\mathbb D} \text{ and } j=1,2,\dots,N\}=\cup_{j=1}^ND_j\end{align*} $$
is a determining set for any rational inner function of degree less than N.
Proof For part (a), note that given a
$\zeta \in {\mathbb {T}}$
and
$a\in {\mathbb D}$
, the analytic disk
${\mathcal D}_{\zeta ,a}$
intersects each
$D_j$
at a nonzero point if and only if there exist
$0\neq z\in {\mathbb D}$
such that for each j,
$\beta _jz=m_{\zeta ,a}(z)$
, which is equivalent to having
$\overline {a}\beta _jz^2+(\beta _j-\zeta )z-a\zeta =0$
. Therefore,
$\zeta $
must belong to
${\mathbb {T}}\setminus \{\beta _j: j=1,2,\dots ,N\}$
. Now fix one such
$\zeta $
and j. Let
$\lambda _1(a),\lambda _2(a)$
be the roots of the polynomial above. Then clearly
$\lambda _1(0)=0=\lambda _2(0)$
. Therefore by continuity of the roots, there exists
$\epsilon>0$
such that whenever
$a\in D(0;\epsilon )$
,
$\lambda _1(a)$
and
$\lambda _2(a)$
belong to
${\mathbb D}$
. This
$\epsilon $
will of course depend on j but since there are only finitely many j, we can find an
$\epsilon>0$
so that (a) holds.
For part (b), we have to show that if
$f:\mathbb {G}\to \overline {\mathbb D}$
is any analytic function such that
$f|_{{\mathcal D}_\zeta }=0$
, then
$f=0$
on
${\mathbb G}$
. Fix
$z\in \mathbb {D}$
and consider
$f_z:\mathbb D\to \overline {\mathbb D}$
defined by
$f_z:w\mapsto f(z+w,zw)$
. Since f vanishes on
$\mathcal D_\zeta $
,
$f_z$
vanishes on
$\{m_{\zeta ,a}(z):a\in D(0;\epsilon )\}$
which shows that
$f_z=0$
on
${\mathbb D}$
. Since
$z\in {\mathbb D}$
is arbitrary,
$f=0$
on
${\mathbb G}$
.
For part (c), let f be a rational inner function of degree less than N and
$g\in {{\mathbb S}(\mathbb {G})}$
be such that
$g=f$
on each
$D_j$
. For each
$\zeta $
and a as in part (a),
${\mathcal D}_{\zeta ,a}$
intersects each
$D_j$
at say
$(s_j,p_j)=(\lambda _j+m_{\zeta ,a}(\lambda _j),\lambda _jm_{\zeta ,a}(\lambda _j))$
. Restrict f and g to
${\mathcal D}_{\zeta ,a}$
to get
$f_{\zeta ,a}(z)=f(z+m_{\zeta ,a}(z), zm_{\zeta , a}(z))$
and
$g_{\zeta ,a}(z)=g(z+m_{\zeta ,a}(z), zm_{\zeta , a}(z))$
. Then clearly
$f_{\zeta ,a}$
is a rational inner function on
${\mathbb D}$
of degree less than N and
$g_{\zeta ,a}\in {\mathbb S}({\mathbb D})$
. Then for each
$j=1,2,\dots , N$
,
$g_{\zeta ,a}(\lambda _j)=f_{\zeta ,a}(\lambda _j)$
. Therefore by Lemma (2.3), we have
$g_{\zeta ,a}=f_{\zeta ,a}$
on
$\mathbb {D}$
for each
$\zeta $
and a as in part (a). Hence
$g=f$
on
${\mathcal D}$
, which by part (b) gives
$g=f$
on
${\mathbb G}$
. This completes the proof.
Theorem 2.5 For any
$N\geq 1$
, there exists a set D consisting of
$(N^2-N+1)$
points in
$\mathbb {G}$
such that
${\mathcal D}$
is a determining set for any rational inner function of degree less than N.
Proof For
$N=1$
, it is trivial because then a rational inner function of degree less than
$1$
is identically constant. So suppose
$N>1$
. Let
$\lambda _1:=0, \lambda _2,\ldots ,\lambda _N$
be distinct points in
$\mathbb {D}$
,
$\beta _1,\ldots , \beta _{N}$
be distinct points in
$\mathbb {T}$
and
$D_1,\ldots ,D_{N}$
be the analytic disks as in Proposition 2.4. Consider the set
$$ \begin{align*}{\mathcal D}=\{(\lambda_j+\beta_k\lambda_j, \beta_k\lambda_j^2): k,j=1,2,\ldots,N\}.\end{align*} $$
Since
$\beta _j$
and
$\lambda _j$
are distinct,
${\mathcal D}$
consists of precisely
$N^2-N+1$
many points. Let f be a rational inner function on
${\mathbb G}$
and
$g\in {\mathbb S}({\mathbb G})$
be such that g agrees with f on
${\mathcal D}$
. As before, restrict f and g to each
$D_k$
to obtain rational inner functions
$f_{k}(z)=f(z+\beta _kz,z^2\beta _k)$
and
$g_k(z)=g(z+\beta _kz,z^2\beta _k)$
on the unit disk
${\mathbb D}$
. We then have
$f_k(\lambda _j)=g_k(\lambda _j)$
for each
$j=1,2,\dots ,N$
. Thus by Lemma 2.3,
$f_k(z)=g_k(z)$
on
${\mathbb D}$
for each
$k=1,2,\dots ,N$
, which is same as saying that
$f=g$
on
$\cup _{k=1}^ND_k$
. Consequently, by part (c) of Proposition 2.4,
$f=g$
on
${\mathbb G}$
.
2.3 Distinguished varieties as a determining and the uniqueness set
A rational function
$f=g/h$
with relatively prime polynomials g and h, is called regular if
$h\neq {0}$
on
$\overline {\mathbb {G}}$
. For example, note that while the rational function
$(3p-s)/(3-s)$
is regular,
$(2p-s)/(2-s)$
is not.
We first recall the known results that will be used later. Let
${\mathcal W}=Z(\xi )$
be a distinguished variety with respect to
$\mathbb {G}$
. Then it follows easily that
${\mathcal V}=Z(\xi \circ \pi )$
defines a distinguished variety with respect to
${\mathbb D}^2$
. Lemma 1.2 of [Reference Agler and McCarthy6] produces a regular Borel measure
$\nu $
on
$\partial {\mathcal V}:={\mathcal V}\cap {\mathbb {T}}^2$
such that
$\nu $
gives rise to a Hardy-type Hilbert function space on
${\mathcal V}\cap {\mathbb D}^2$
, denoted by
$H^2(\nu )$
, i.e.,
$H^2(\nu )$
is the closure in
$L^2(\nu )$
of polynomials such that evaluation at every point in
${\mathcal V}\cap {\mathbb D}^2$
is a bounded linear functional on
$H^2(\nu )$
. It was then shown in [Reference Pal and Shalit29, Lemma 3.2] that the push-forward measure
$\mu (E)=\nu (\pi ^{-1}(E))$
for every Borel subset E of
$\partial {\mathcal W}:={\mathcal W}\cap b\Gamma $
has all the properties that
$\nu $
has. Furthermore, the spaces
$H^2(\mu )$
and
$H^2(\nu )$
are unitary equivalent via the isomorphism given by
$$ \begin{align} U:H^2(\mu)\rightarrow{H^2{(\nu)}}\quad \text{ by } \quad U:f\mapsto f\circ\pi. \end{align} $$
Note that if
$k^\mu $
and
$k^\nu $
are the Szegö-type reproducing kernels for
$H^2(\mu )$
and
$H^2(\nu )$
, respectively, then for every
$(z,w)\in {\mathcal V}\cap {\mathbb D}^2$
and
$f\in H^2(\mu ),$
$$ \begin{align*}\langle U^*k^\nu_{(z,w)}, f\rangle_{H^2(\mu)}=\langle k^\nu_{(z,w)}, Uf\rangle_{H^2(\nu)}=f\circ\pi(z,w)=\langle k^\mu_{\pi(z,w)}, f\rangle_{H^2(\mu)}.\end{align*} $$
We observe the following.
Lemma 2.6 Let
${\mathcal W}$
be a distinguished variety with respect to
$\mathbb G$
, and let
$\mu $
be the regular Borel measure on
$\partial {\mathcal W}$
as in the preceding discussion. Then for every regular rational inner function f on
$\mathbb {G}$
, the multiplication operator
$M_f$
on
$H^2(\mu )$
has a finite dimensional kernel.
Proof We note that for every
$(z,w)\in {\mathcal V}\cap {\mathbb D}^2$
,
$$ \begin{align*} U^*M_{f\circ\pi}^*k^\nu_{(z,w)}=\overline{f\circ\pi(z,w)}U^*k^\nu_{(z,w)}=\overline{f\circ\pi(z,w)}k^\mu_{\pi(z,w)}=M_f^*k^\mu_{\pi(z,w)}=M_{f}^*U^*k^\nu_{(z,w)}. \end{align*} $$
Thus,
$M_f$
on
$H^2(\mu )$
and
$M_{f\circ \pi }$
on
$H^2(\nu )$
are unitarily equivalent via the unitary U as in 2.3. Now the lemma follows from [Reference Scheinker33, Theorem 3.6], which states that
$\operatorname {Ker}M_{f\circ \pi }$
is finite-dimensional.
Proposition 2.7 Let
$\mathcal W=Z(\xi )$
be a distinguished variety with respect to
$\mathbb G$
, and let f be a regular rational inner function on
$\mathbb G$
. If
$\dim \operatorname { Ker} M_{f}^* < N$
, then any N distinct points in
${\mathcal W}\cap {\mathbb G}$
is a determining set for
$(f, {\mathcal W}\cap \mathbb {G})$
.
Proof Let
$\{w_1,w_2,\dots ,w_N\}$
be distinct points in
${\mathcal W}\cap {\mathbb G}$
, and let
$g\in {\mathbb S}({\mathbb G})$
be such that
$g(w_j)=f(w_j)$
for each
$j=1,2,\dots ,N$
. Let
${\mathcal V}=Z(\xi \circ \pi )$
and
$\{v_1,v_2,\dots ,v_N\}$
be in
${\mathcal V}\cap {\mathbb D}^2$
such that
$\pi (v_j)=w_j$
for all
$j=1,2,\ldots ,N$
. Thus,
$g\circ \pi (v_j)=f\circ \pi (v_j)$
for each
$j=1,2,\dots ,N$
. Theorem 1.7 of [Reference Scheinker33] yields
$g\circ \pi =f\circ \pi $
on
${\mathcal V}\cap {\mathbb D}^2$
which is same as
$g=f$
on
${\mathcal W}\cap {\mathbb G}$
. This completes the proof.
The
$2$
-degree of a two-variable polynomial
$\xi \in \mathbb {C}[z,w]$
is defined as
$(d_1, d_2)=:\operatorname {2-deg}\xi $
, where
$d_1$
and
$d_2$
are the largest power of z and w, respectively, in the expansion of
$\xi (z,w)$
. The reflection of a two-variable polynomial
$\xi \in \mathbb {C}[z,w]$
is defined as
$$ \begin{align*}\widetilde{\xi}(z,w)=z^{d_1}w^{d_2}\overline{\xi\big(\frac{1}{\overline{z}},\frac{1}{\overline{w}}\big)}. \end{align*} $$
For a rational function
$f(z,w)=\xi (z,w)/\eta (z,w)$
with
$\xi $
and
$\eta $
having no common factor, the
$2$
-degree of f is defined to be the
$2$
-degree of the numerator. For two pairs of nonnegative integers
$(p,q)$
and
$(m,n)$
, we write
$(p,q)\leq (m,n)$
to indicate that
$p\leq m$
and
$q\leq n$
.
Proposition 2.8 Let
${\mathcal W}=Z(\xi )$
be an irreducible distinguished variety, and let f be a regular rational inner function on
$\mathbb {G}$
of the form
$$ \begin{align} f\circ\pi(z,w)=(zw)^m\frac{\widetilde{\eta\circ\pi}(z,w)}{\eta\circ\pi(z,w)}. \end{align} $$
If
$\operatorname {2-deg}\xi \circ \pi \leq \operatorname {2-deg}f\circ \pi $
, then for each
$(s,p)\in \mathbb {G}\setminus (\mathbb {G}\cap {\mathcal W})$
, there exists a regular rational inner function g on
${\mathbb G}$
such that g coincides with f on
${\mathcal W}\cap {\mathbb G}$
but
$g(s,p)\neq f(s,p)$
.
Proof Let
$\operatorname {2-deg}\eta \circ \pi =(l,l)$
and
$\operatorname {2-deg}\xi \circ \pi =(n,n)$
. The hypothesis then is that
$m+l-n$
is nonnegative. For
$\epsilon>0$
, define a symmetric function
$g_\epsilon $
on
${\mathbb D}^2$
as
$$ \begin{align} g_{\epsilon}(z,w)= \frac{(zw)^m\widetilde{\eta\circ\pi}(z,w)+\epsilon \widetilde{\xi\circ\pi}(z,w)}{\eta\circ\pi(z,w)+\epsilon(zw)^{m+l-n}\xi\circ\pi(z,w)}. \end{align} $$
Simple computation shows that the reflection of the denominator of
$g_\epsilon $
is equal to the numerator of
$g_\epsilon $
, which implies that each each
$g_\epsilon $
is a rational inner function on
${\mathbb D}^2$
provided that the denominator does not vanish on
${\mathbb D}^2$
. Since
$\eta \circ \pi $
does not vanish on
$\overline {{\mathbb D}}^2$
, we can always find a sufficiently small
$\epsilon $
so that the denominator of each
$g_\epsilon $
does not vanish in
$\overline {{\mathbb D}}^2$
, thus making
$g_\epsilon $
regular.
By Proposition 4.3 of [Reference Knese21],
$\xi \circ \pi =c \widetilde {\xi \circ \pi }$
for some
$c\in {\mathbb {T}}$
. This ensures that each
$g_\epsilon $
coincides with f on
${\mathcal W}\cap {\mathbb G}$
. Now, let
$(z_0,w_0)\in {\mathbb D}^2$
be such that
$\pi (z_0,w_0)\in {\mathbb G}\setminus {\mathcal W}$
. Then
$g_\epsilon (z_0,w_0)=f\circ \pi (z_0,w_0)$
if and only if
which, after cross-multiplication and using the fact that
$\xi \circ \pi (z_0,w_0)\neq 0$
, leads to
$$ \begin{align} \overline{c}\eta\circ\pi(z_0,w_0)=(z_0w_0)^{2m+l-n}\widetilde{\eta\circ\pi}(z_0,w_0). \end{align} $$
Since
$\eta \circ \pi $
does not vanish on
$\overline {{\mathbb D}}^2$
, we have
$z_0w_0\neq 0$
. Therefore, the above equation holds if and only if
$$ \begin{align} f\circ\pi(z_0,w_0)=(z_0w_0)^m\frac{\widetilde{\eta\circ\pi}(z_0,w_0)}{\eta\circ\pi(z_0,w_0)}=\frac{\overline{c}}{(z_0w_0)^{m+l-n}}. \end{align} $$
If
$m+l-n=0$
, then f is a constant function. The hypothesis on the 2-degrees of
$\xi $
and f then implies that
$\xi $
must be constant. This is not possible because
$\xi $
defines a distinguished variety. Therefore,
$m+l-n\geq 1$
, in which case, equation (2.7) implies that
$|f\circ \pi (z_0,w_0)|>1$
. This again is a contradiction because f is a rational inner function and so by the Maximum Modulus Principle,
$|f\circ \pi (z)|\leq 1$
for every
$(z,w)\in {\mathbb D}^2$
. Consequently,
$g_\epsilon (s,p)\neq f(s,p)$
for every
$(s,p)\in {\mathbb G}\setminus ({\mathcal W}\cap {\mathbb G})$
.
Remark 2.9 In a forthcoming paper [Reference Bhowmik and Kumar15], it is shown that any rational inner function on
${\mathbb G}$
is of the form (2.4) possibly multiplied by a unimodular constant.
Theorem 2.10 Let
${\mathcal W}=Z(\xi )$
be an irreducible distinguished variety with respect to
$\mathbb {G}$
, let f be a regular rational inner function on
${\mathbb G}$
of the form (2.4) such that
$\operatorname {2-deg}\xi \circ \pi \leq \operatorname {2-deg}f\circ \pi $
, and let
${\mathcal D}$
be any subset of
${\mathcal W}\cap \mathbb {G}$
consisting of at least
$1+\dim \operatorname {Ker}M_f^*$
many points. Then
${\mathcal W}\cap \mathbb {G}$
is the uniqueness set for
$(f,{\mathcal D})$
.
Proof Consider the multiplication operator
$M_{f}$
on
$H^2(\mu )$
, where
$H^2(\mu )$
is the Hilbert space corresponding to
${\mathcal W}$
as mentioned in Lemma 2.6. By this lemma,
$\dim \operatorname {Ker}(M_{f}^*)$
is finite. So let N be such that
$\dim \operatorname {Ker}(M_{f}^*)<N$
and
${\mathcal D}=\{\lambda _1, \lambda _2,\ldots , \lambda _N\}\subset {\mathcal W}\cap \mathbb {G}$
. By Proposition 2.7,
${\mathcal D}$
is determining for
$(f,{\mathcal W}\cap \mathbb {G})$
. We use Proposition 2.8 to show that
${\mathcal W}\cap \mathbb {G}$
is the uniqueness set. Toward that end, pick
$(s,p)\in {\mathbb G}\setminus {\mathcal W}\cap {\mathbb G}$
. Proposition 2.8 guarantees the existence of a (regular) rational inner function g that coincides with f on
${\mathcal W}\cap {\mathbb G}$
but
$g(s,p)\neq f(s,p)$
. This proves that
${\mathcal W}\cap \mathbb {G}$
is the uniqueness set for the interpolation problem. This completes the proof of the theorem.
Remark 2.11 An extremal interpolation problem in
${\mathbb G}$
is a solvable problem with no solution of supremum norm less than
$1$
. Let
${\mathcal D}=\{\lambda _1,\lambda _2,\dots ,\lambda _N\}$
be a subset of
${\mathbb G}$
, and letf be a rational inner function on
${\mathbb G}$
such that the N-point Pick problem
$\lambda _j\mapsto f(\lambda _j)$
is extremal and that none of the
$(N-1)$
-point subproblems is extremel. Then it is shown in [Reference Krishna Das, Kumar and Sau25] that the uniqueness set for
$(f,{\mathcal D})$
contains a distinguished variety. Theorem 2.10 can be seen as a converse to this result. Indeed, Theorem 2.10 starts with a distinguished variety
${\mathcal W}=Z(\xi )$
and produces a regular rational inner function f and a finite set
${\mathcal D}$
depending on
${\mathcal W}$
such that
${\mathcal W}\cap {\mathbb G}$
is the uniqueness set for
$(f,{\mathcal D})$
. In addition, we note that the problem
$\lambda _j\mapsto f(\lambda _j)$
is an extremal problem. This is because if g is any solution of the problem, then by Proposition 2.7,
$g=f$
on
${\mathcal W}\cap {\mathbb G}$
. Thus,
$$ \begin{align*}\|g\|_{\infty,{\mathbb G}}\geq \|g\|_{\infty,{\mathcal W}\cap{\mathbb G}}=\|f\|_{\infty,{\mathcal W}\cap{\mathbb G}}=1.\end{align*} $$
The last equality follows because f is a regular rational inner function.
There is a sufficient condition for a distinguished variety to be determining. In the theorem below and in its proof, the inner product
$\langle ,\rangle _{H^2}$
for analytic functions
$f,g:{\mathbb G}\to {\mathbb C}$
is defined to be
$$ \begin{align}\hspace{18pt} \langle f,g\rangle_{H^2}= \sup_{0<r<1}\int_{{\mathbb{T}}\times{\mathbb{T}}} f\circ\pi(r\zeta_1,r\zeta_2)\overline{g\circ\pi(r\zeta_1,r\zeta_2)}|J(r\zeta_1,r\zeta_2)|^2dm(\zeta_1,\zeta_2), \end{align} $$
where m is the standard normalized Lebesgue measure on
${\mathbb {T}}\times {\mathbb {T}}$
, and
$J(z,w)=z-w$
is the Jacobian of the map
$\pi :(z,w)\mapsto (z+w,zw)$
. See the papers [Reference Bhattacharyya, Das and Sau11, Reference Bhattacharyya and Sau14, Reference Misra, Shyam Roy and Zhang28] for some motivation for and operator theory on the spaces of analytic functions for which
$\|f\|_2:=\sqrt {\langle f,f\rangle }_{H^2}<\infty $
. Note here that if f is an inner function on
${\mathbb G}$
, then
$\|f\|_2=1.$
Theorem 2.12 Let
$\mathcal {W}=Z(\xi )$
be a distinguished variety such that
$\xi =\xi _1.\xi _2\dots \xi _l$
, where
$\xi _i$
are irreducible polynomials with
$\xi _i$
and
$\xi _j$
are co-prime for each
$i\neq j$
, and let f be a regular rational inner function on
$\mathbb {G}$
. If for each analytic function
$h(\not \equiv 0)$
on
$\mathbb {G}$
,
$$ \begin{align*} \quad 2\operatorname{Re}\langle f, \xi h\rangle_{H^2}< \|\xi h\|^2_2 \end{align*} $$
holds, whenever
$\xi h$
is bounded on
${\mathbb G}$
, then
${\mathcal W}\cap {\mathbb G}$
is a determining set for f.
Proof We shall use contrapositive argument. So suppose that there exists
$g\in {{\mathbb S}(\mathbb {G})}$
such that g coincides with f on
${\mathcal W}\cap {\mathbb G}$
but
$g\neq f$
. Choose an integer N so that
$\dim \operatorname {Ker}M_f^*<N$
and pick N distinct points
$\lambda _1,\ldots .,\lambda _N\in {\mathcal W}$
. Consider the N-point (solvable) Nevanlinna–Pick problem
$\lambda _j\mapsto f(\lambda _j)$
. By Proposition 2.7, all the solutions to this problem agree on
${\mathcal W}\cap {\mathbb G}$
. Since
$g\neq f$
, there exists a
$\lambda _{N+1}\in \mathbb {G}\setminus {\mathcal W}$
such that
$g(\lambda _{N+1})\neq f(\lambda _{N+1})$
. Now consider the
$(N+1)$
-point Nevanlinna–Pick problem
$\lambda _j\mapsto g(\lambda _j)$
on
$\mathbb {G}$
. By [Reference Krishna Das, Kumar and Sau25, Theorem 5.3], every solvable Nevanlinna–Pick problem in
${\mathbb G}$
has a rational inner solution. Let
$\psi $
be a rational inner solution to the
$(N+1)$
-point problem
$\lambda _j\mapsto g(\lambda _j)$
. Since
$\psi $
, in particular, solves the problem
$\lambda _j\mapsto f(\lambda _j)$
for each
$j=1,2,\dots ,N$
,
$\psi =f$
on
${\mathcal W}\cap {\mathbb G}$
. But since
$\psi (\lambda _{N+1})=g(\lambda _{N+1})\neq f(\lambda _{N+1})$
,
$\psi $
is distinct from f. Since
$\psi =f$
on
${\mathcal W}\cap {\mathbb G}$
, by the Study Lemma, there exists a rational function h such that
$f-\psi =\xi h$
(see [Reference Fischer19, Chapter 1]. Since
$\psi $
is inner,
$$ \begin{align*}1=\|\psi\|_2^2=\|f-\xi h\|_2^2=\|f\|_2^2-2\operatorname{Re}\langle f, \xi h\rangle_{H^2} +\|\xi h\|_2^2.\end{align*} $$
Since f is an inner function,
$\|f\|_{2}=1$
, and therefore, the above computation leads to
$2\operatorname {Re}\langle f, \xi h\rangle = \|\xi h\|^2_2$
. This contradicts the hypothesis because
$\xi h=f-\psi $
is bounded. Consequently, g must coincide with f on
${\mathbb G}$
.
One can easily find examples of distinguished varieties and regular rational inner functions such that the stringent hypothesis of the above result is satisfied.
Example 2.13 Let
$f\circ \pi (z,w)=(zw)^d$
and
${\mathcal W}=Z(\xi )$
be such that
$$ \begin{align*}\xi\circ\pi(z,w)=(z^m-w^n)(z^n-w^m),\end{align*} $$
where
$m,n$
are mutually prime integers bigger than d. Then it follows that
${\mathcal W}$
is a distinguished variety with respect to
${\mathbb G}$
because
$Z(z^m-w^n)$
is a distinguished variety with respect to
${\mathbb D}^2$
. For concrete example, one can take
$d=1$
and
$(m,n)=(2,3)$
– the corresponding distinguished variety then is the Neil parabole. Note that the inner product
$\langle ,\rangle $
as defined in (2.8) can be expressed in terms of the inner product on the Hardy space of the bidisk
$H^2({\mathbb D}^2)$
as
$$ \begin{align} \langle f, \xi h\rangle_{H^2(\mathbb{G})}=\frac{1}{\|J\|^2} \langle J(f\circ\pi), J\big((\xi\circ\pi)( h\circ\pi)\big) \rangle_{H^2(\mathbb{D}^2)}. \end{align} $$
Let
$h:{\mathbb G}\to {\mathbb C}$
be an analytic function such that
$\|\xi h\|_2<\infty $
. Since
$\{z^iw^j: i,j\geq 0\}$
forms an orthonormal basis for
$H^2({\mathbb D}^2)$
, it is easy to read off from (2.9) that
$\langle f,\xi h\rangle =0$
. Therefore, by Theorem 2.12,
${\mathcal W}\cap {\mathbb G}$
is a determining set for f as chosen above.
3 A bounded extension theorem
We end with a bounded extension theorem for distinguished varieties with no singularities on the distinguished boundary of
$\Gamma $
. Here, singularity of an algebraic variety
$Z(\xi )$
at a point means that both the partial derivatives of
$\xi $
vanish at that point. Note that the substance of the following theorem is not that there is a rational extension of every polynomial, it is that the supremum of the rational extension over
${\mathbb G}$
does not exceed the supremum of the polynomial over the variety intersected with
${\mathbb G}$
multiplied by a constant that only depends on the variety. See the papers [Reference Adachi, Andersson and Cho1, Reference Knese21, Reference Stout36] for similar results in other contexts.
Theorem 3.1 Let
${\mathcal W}$
be a distinguished variety with respect to
$\mathbb {G}$
such that it has no singularities on
$b{\Gamma }$
. Then, for every polynomial
$f\in \mathbb {C}[s,p]$
, there exists a rational extension F of f such that
$$ \begin{align*}|F(s,p)|\leq \alpha\sup_{{{\mathcal W}\cap\mathbb{G}}}|f|\end{align*} $$
for all
$(s,p)\in \mathbb {G}$
, where
$\alpha $
is a constant depends only on
${\mathcal W}$
.
Proof Let
${\mathcal V}$
be a distinguished variety with respect to
$\mathbb {D}^2$
such that
${\mathcal W}=\pi ({\mathcal V})$
. Since
${\mathcal W}$
has no singularities on
$b\Gamma $
, it follows that
${\mathcal V}$
has no singularities on
$\mathbb {T}^2$
. Invoke Theorem 2.20 of [Reference Knese21] to obtain a rational extension G of the polynomial
$f\circ \pi \in \mathbb {C}[z,w]$
such that
$$ \begin{align} |G(z, w)|\leq \alpha\sup_{{\mathcal V}\cap\mathbb{D}^2}|f\circ\pi| \end{align} $$
for all
$(z,w)\in \mathbb {D}^2$
, where
$\alpha $
is a constant depends only on
${\mathcal V}$
. Now, define a rational function H on
$\mathbb {D}^2$
as follows:
$$ \begin{align} H(z,w)= \frac{G(z,w)+G(w, z)}{2}. \end{align} $$
Clearly, H is also a rational extension of
$f\circ \pi $
with
$$ \begin{align*}|H(z, w)|\leq \alpha\sup_{{\mathcal V}\cap\mathbb{D}^2}|f\circ\pi| \quad \text {for all } (z,w)\in\mathbb{D}^2.\end{align*} $$
Note that H is a symmetric rational function on
$\mathbb {D}^2$
. So, there is a rational function F on
$\mathbb {G}$
such that
$$ \begin{align*}H(z,w)=(F\circ\pi)(z,w)=F(z+w,zw) \quad \text {for all } (z,w)\in\mathbb{D}^2.\end{align*} $$
Now, we will show that this F will do our job. It is easy to see that F is a rational extension of f. Let
$(s, p)\in \mathbb {G}$
. Then there exists a point
$(z,w)\in \mathbb {D}^2$
such that
$(s, p)=(z+w, zw)$
. Now,
$$ \begin{align*} |F(s,p)|&=|(F\circ\pi)(z, w)|=|H(z,w)| \leq \alpha\sup_{{\mathcal V}\cap\mathbb{D}^2}|f\circ\pi| =\alpha\sup_{{\mathcal W}\cap\mathbb{G}}|f|. \end{align*} $$
This complete the proof.
Acknowledgment
P.K. thanks his supervisor Professor Tirthankar Bhattacharyya for some fruitful discussions. The authors thank the anonymous referee for some valuable suggestions.
