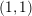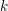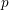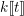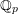Introduction
Many of the deepest conjectures in arithmetic and algebraic geometry concern the existence of algebraic cycles on varieties with certain properties. For example, the Hodge and Tate conjectures state, roughly speaking, that on smooth and projective varieties over
$\mathbb{C}$
(Hodge) or finitely generated fields (Tate) every cohomology class which ‘looks like’ the class of a cycle is indeed so. One can also pose variational forms of these conjectures, giving conditions for extending algebraic classes from one fibre of a smooth, projective morphism
$f:X\rightarrow S$
to the whole space. For divisors, the Hodge forms of both these conjectures (otherwise known as the Lefschetz
$(1,1)$
theorem) are relatively straightforward to prove, using the exponential map, but even for divisors the Tate conjecture remains wide open in general.
Applying the principle that deformation problems in characteristic
$p$
should be studied using
$p$
-adic cohomology, Morrow in [Reference MorrowMor14] formulated a crystalline variational Tate conjecture for smooth and proper families
$f:X\rightarrow S$
of varieties in characteristic
$p$
, and proved the conjecture for divisors, at least when
$f$
is projective. The key step of the proof is a version of this result over
$S=\operatorname{Spec}(k\unicode[STIX]{x27E6}t_{1},\ldots ,t_{n}\unicode[STIX]{x27E7})$
, with
$k$
a perfect field of characteristic
$p$
. When
$n=1$
this is a direct equicharacteristic analogue of Berthelot and Ogus’s theorem [Reference Berthelot and OgusBO83, Theorem 3.8] on lifting line bundles from characteristic
$p$
to characteristic
$0$
.
Morrow’s proof of the local statement uses some fairly heavy machinery from motivic homotopy theory, in particular a ‘continuity’ result for topological cyclic homology. In this paper we provide a new proof of the local crystalline variational Tate conjecture for divisors, at least over the base
$S=\operatorname{Spec}(k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7})$
, which only uses some fairly basic properties of the de Rham–Witt complex, and is close in spirit to the approach taken in [Reference MorrowMor15]. The point of giving this proof is that it adapts essentially verbatim to the case of semistable reduction, once the corresponding basic properties of the logarithmic de Rham–Witt complex are in place.
So let
${\mathcal{X}}$
be a semistable, projective scheme over
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
, with special fibre
$X_{0}$
and generic fibre
$X$
. Write
$K=W(k)[1/p]$
and let
${\mathcal{R}}$
denote the Robba ring over
$K$
. Then there is an isomorphism
$$\begin{eqnarray}H_{\text{rig}}^{2}(X/{\mathcal{R}})^{\unicode[STIX]{x1D6FB}=0}\cong H_{\text{log}\text{\text{-}}\text{crys}}^{2}(X_{0}^{\times }/K^{\times })^{N=0}\end{eqnarray}$$
between the horizontal sections of the Robba ring-valued rigid cohomology of
$X$
and the part of the log-crystalline cohomology of
$X_{0}$
killed by the monodromy operator. The former is defined to be the base change
$H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })\otimes _{{\mathcal{E}}^{\dagger }}{\mathcal{R}}$
to the Robba ring of the
${\mathcal{E}}^{\dagger }$
-valued rigid cohomology
$H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })$
constructed in [Reference Lazda and PálLP16]. These groups are
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$
-modules over
${\mathcal{R}}$
and
${\mathcal{E}}^{\dagger }$
, respectively. In particular, if
${\mathcal{L}}$
is a line bundle on
$X_{0}$
, we can view its first Chern class
$c_{1}({\mathcal{L}})$
as an element of
$H_{\text{rig}}^{2}(X/{\mathcal{R}})$
. Our main result is then the following semistable version of the local crystalline variational Tate conjecture for divisors.
Theorem 4.5
. The line bundle
${\mathcal{L}}$
lifts to
$\operatorname{Pic}({\mathcal{X}})_{\mathbb{Q}}$
if and only if
$c_{1}({\mathcal{L}})$
lies in
$H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })\subset H_{\text{rig}}^{2}(X/{\mathcal{R}})$
.
There is also a version for logarithmic line bundles on
$X_{0}$
. The general philosophy of
$p$
-adic cohomology over
$k(\!(t)\!)$
is that the
${\mathcal{E}}^{\dagger }$
-structure
$H_{\text{rig}}^{i}(X/{\mathcal{E}}^{\dagger })\subset H_{\text{rig}}^{i}(X/{\mathcal{R}})$
is the equicharacteristic analogue of the Hodge filtration on the
$p$
-adic cohomology of varieties over mixed characteristic local fields. With this in mind, this is the direct analogue of Yamashita’s semistable Lefschetz
$(1,1)$
theorem [Reference YamashitaYam11]. As a corollary, we can deduce a global result on the algebraicity of cohomology classes as follows. Let
$F$
be a function field of transcendence degree 1 over
$k$
, and
$X/F$
a smooth projective variety. Let
$v$
be a place of semistable reduction for
$X$
, with reduction
$X_{v}$
. In this situation we can consider the rigid cohomology of
$X/K$
(see §5), and there is a map
$$\begin{eqnarray}\text{sp}_{v}:{\mathcal{H}}_{\text{rig}}^{2}(X/K)^{\unicode[STIX]{x1D6FB}=0}\rightarrow H_{\text{log}\text{\text{-}}\text{crys}}^{2}(X_{v}^{\times }/K_{v}^{\times })\end{eqnarray}$$
from the second cohomology of
$X$
to the log-crystalline cohomology of
$X_{v}$
.
Theorem 5.2
. A class
$\unicode[STIX]{x1D6FC}\in {\mathcal{H}}_{\text{rig}}^{2}(X/K)^{\unicode[STIX]{x1D6FB}=0}$
is in the image of
$\operatorname{Pic}(X)_{\mathbb{Q}}$
under the Chern class map if and only if
$\text{sp}_{v}(\unicode[STIX]{x1D6FC})$
is in the image of
$\operatorname{Pic}(X_{v})_{\mathbb{Q}}$
.
One might wonder whether the analogue of the crystalline variational Tate conjecture holds for line bundles with
$\mathbb{Q}_{p}$
-coefficients (in either the smooth or semistable case). Unfortunately, the answer is no. Indeed, if it were true, then it follows relatively easily that the analogue of Tate’s isogeny theorem would hold over
$k(\!(t)\!)$
; in other words, for any two abelian varieties
$A,B$
over
$k(\!(t)\!)$
, the map
$$\begin{eqnarray}\operatorname{Hom}(A,B)\otimes \mathbb{Q}_{p}\rightarrow \operatorname{Hom}(A[p^{\infty }],B[p^{\infty }])\otimes _{\mathbb{ Z}_{p}}\mathbb{Q}_{p}\end{eqnarray}$$
would be an isomorphism. That this cannot be true is well known, and examples can be easily provided with both
$A$
and
$B$
elliptic curves.
Let us now summarise the contents of this paper. In § 1 we show that the cycle class map in rigid cohomology over
$k(\!(t)\!)$
descends to the bounded Robba ring. In § 2 we recall the relative logarithmic de Rham–Witt complex, and prove certain basic properties of it that we will need later on. In § 3 we reprove a special case of the key step in Morrow’s paper [Reference MorrowMor14], showing the crystalline variational Tate conjecture for smooth and projective schemes over
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
. The argument we give is elementary. In § 4 we prove the semistable version of the crystalline variational Tate conjecture over
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
, more or less copying word for word the argument in § 3. In § 5 we translate these results into algebraicity lifting results for varieties over global function fields. Finally, in § 6 we give a counter-example to the analogue of the of crystalline variational Tate conjecture for line bundles with
$\mathbb{Q}_{p}$
-coefficients.
Notation and conventions
Throughout we will let
$k$
be a perfect field of characteristic
$p>0$
,
$W$
its ring of Witt vectors and
$K=W[1/p]$
. In general we will let
$F=k(\!(t)\!)$
be the field of Laurent series over
$k$
, and
$R=k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
its ring of integers (although this will not be the case in § 5). We will denote by
${\mathcal{E}}^{\dagger },{\mathcal{R}},{\mathcal{E}}$
respectively the bounded Robba ring, the Robba ring, and the Amice ring over
$K$
, and we will also write
${\mathcal{E}}^{+}=W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}\otimes _{W}K$
. For any of the rings
${\mathcal{E}}^{+}$
,
${\mathcal{E}}^{\dagger }$
,
${\mathcal{R}}$
,
${\mathcal{E}}$
we will denote by
$\text{}\underline{\mathbf{M}\unicode[STIX]{x1D6F7}}_{(-)}^{\unicode[STIX]{x1D6FB}}$
the corresponding category of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$
-modules, that is, finite free modules with connection and horizontal Frobenius. A variety over a given Noetherian base scheme will always mean a separated scheme of finite type. For any abelian group
$A$
and any ring
$S$
we will let
$A_{S}$
denote
$A\otimes _{\mathbb{Z}}S$
.
1 Cycle class maps in overconvergent rigid cohomology
Recall that for varieties
$X/F$
over the field of Laurent series
$F=k(\!(t)\!)$
the rigid cohomology groups
$H_{\text{rig}}^{i}(X/{\mathcal{E}})$
are naturally
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$
-modules over the Amice ring
${\mathcal{E}}$
. In the book [Reference Lazda and PálLP16] we showed how to canonically descend these cohomology groups to obtain ‘overconvergent’
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$
-modules
$H_{\text{rig}}^{i}(X/{\mathcal{E}}^{\dagger })$
over the bounded Robba ring
${\mathcal{E}}^{\dagger }$
; these groups satisfy all the expected properties of an ‘extended’ Weil cohomology theory. In particular, there exist versions
$H_{c,\text{rig}}^{i}(X/{\mathcal{E}})$
,
$H_{c,\text{rig}}^{i}(X/{\mathcal{E}}^{\dagger })$
with compact support.
Definition 1.1. Define the (overconvergent) rigid homology of a variety
$X/F$
by
$$\begin{eqnarray}H_{i}^{\text{rig}}(X/{\mathcal{E}}):=H_{\text{rig}}^{i}(X/{\mathcal{E}})^{\vee },\quad H_{i}^{\text{rig}}(X/{\mathcal{E}}^{\dagger }):=H_{\text{rig}}^{i}(X/{\mathcal{E}}^{\dagger })^{\vee },\end{eqnarray}$$
and the (overconvergent) Borel–Moore homology by
$$\begin{eqnarray}H_{i}^{\text{BM},\text{rig}}(X/{\mathcal{E}}):=H_{c,\text{rig}}^{i}(X/{\mathcal{E}})^{\vee },\quad H_{i}^{\text{BM},\text{rig}}(X/{\mathcal{E}}^{\dagger }):=H_{c,\text{rig}}^{i}(X/{\mathcal{E}}^{\dagger })^{\vee }.\end{eqnarray}$$
In [Reference PetrequinPet03] the author constructs cycle class maps in rigid cohomology, which can be viewed as homomorphisms
$$\begin{eqnarray}A_{d}(X)\rightarrow H_{2d}^{\text{BM},\text{rig}}(X/{\mathcal{E}})\end{eqnarray}$$
from the group of
$d$
-dimensional cycles modulo rational equivalence. Our goal in this section is the following entirely straightforward result.
Proposition 1.2. The cycle class map descends to a homomorphism
$$\begin{eqnarray}A_{d}(X)\rightarrow H_{2d}^{\text{BM},\text{rig}}(X/{\mathcal{E}}^{\dagger })^{\unicode[STIX]{x1D6FB}=0,\unicode[STIX]{x1D711}=p^{d}}.\end{eqnarray}$$
Proof. Note that since
$H_{2d}^{\text{BM},\text{rig}}(X/{\mathcal{E}}^{\dagger })^{\unicode[STIX]{x1D6FB}=0,\unicode[STIX]{x1D711}=p^{d}}\subset H_{2d}^{\text{BM},\text{rig}}(X/{\mathcal{E}})$
it suffices to show that for every integral closed subscheme
$Z\subset X$
of dimension
$d$
, the cycle class
$\unicode[STIX]{x1D702}(Z)\in H_{2d}^{\text{BM},\text{rig}}(X/{\mathcal{E}})$
actually lies in the subspace
$H_{2d}^{\text{BM},\text{rig}}(X/{\mathcal{E}}^{\dagger })^{\unicode[STIX]{x1D6FB}=0,\unicode[STIX]{x1D711}=p^{d}}$
.
By construction,
$\unicode[STIX]{x1D702}(Z)$
is the image of the fundamental class of
$Z$
(i.e. the trace map
$\text{Tr}_{Z}:H_{c,\text{rig}}^{2d}(Z/{\mathcal{E}})\rightarrow {\mathcal{E}}(-d)$
) under the map
$$\begin{eqnarray}H_{2d}^{\text{BM},\text{rig}}(Z/{\mathcal{E}})\rightarrow H_{2d}^{\text{BM},\text{rig}}(X/{\mathcal{E}})\end{eqnarray}$$
induced by the natural map
$H_{c,\text{rig}}^{2d}(X/{\mathcal{E}})\rightarrow H_{c,\text{rig}}^{2d}(Z/{\mathcal{E}})$
in compactly supported cohomology. Hence it suffices to simply observe that both this map and the trace map descend to horizontal, Frobenius equivariant maps on the level of
${\mathcal{E}}^{\dagger }$
-valued cohomology. Alternatively, we could observe that both
$H_{c,\text{rig}}^{2d}(X/{\mathcal{E}})\rightarrow H_{c,\text{rig}}^{2d}(Z/{\mathcal{E}})$
and
$\text{Tr}_{Z}$
are horizontal and Frobenius equivariant at the level of
${\mathcal{E}}$
-valued cohomology, which gives
$$\begin{eqnarray}A_{d}(X)\rightarrow H_{2d}^{\text{BM},\text{rig}}(X/{\mathcal{E}})^{\unicode[STIX]{x1D6FB}=0,\unicode[STIX]{x1D711}=p^{d}},\end{eqnarray}$$
then applying Kedlaya’s full faithfulness theorem [Reference KedlayaKed04, Theorem 5.1] gives an isomorphism
$$\begin{eqnarray}H_{2d}^{\text{BM},\text{rig}}(X/{\mathcal{E}})^{\unicode[STIX]{x1D6FB}=0,\unicode[STIX]{x1D711}=p^{d}}\cong H_{2d}^{\text{BM},\text{rig}}(X/{\mathcal{E}}^{\dagger })^{\unicode[STIX]{x1D6FB}=0,\unicode[STIX]{x1D711}=p^{d}}.\Box\end{eqnarray}$$
2 Preliminaries on the de Rham–Witt complex
The purpose of this section is to gather together some results we will need on the various de Rham–Witt complexes that will be used throughout the paper. These are all generalisations to the logarithmic case of well-known results from [Reference IllusieIll79], and should therefore present no surprises. The reader will not lose too much by skimming this section on first reading and referring back to the results as needed.
We will, as throughout, fix a perfect ground field
$k$
of characteristic
$p>0$
; all (log) schemes will be considered over
$k$
. Given a morphism
$(Y,N)\rightarrow (S,L)$
of fine log schemes over
$k$
, Matsuue in [Reference MatsuueMat17] constructed a relative logarithmic de Rham–Witt complex
$W_{\bullet }\unicode[STIX]{x1D714}_{(Y,N)/(S,L)}^{\ast }$
, denoted
$W_{\bullet }\unicode[STIX]{x1D6EC}_{(Y,N)/(S,L)}^{\ast }$
in [Reference MatsuueMat17]. This is an étale sheaf on
$Y$
equipped with operators
$F,V$
satisfying all the usual relations (see, for example, [Reference MatsuueMat17, Definition 3.4(v)]) and which specialises to various previous constructions in particular cases.
(i) When
$S=\operatorname{Spec}(k)$
and the log structures
$L$
and
$N$
are trivial, then this gives the (canonical extension of the) classical de Rham–Witt complex
$W_{\bullet }\unicode[STIX]{x1D6FA}_{Y}^{\ast }$
(to an étale sheaf on
$Y$
).(ii) More generally, when the morphism
$(Y,N)\rightarrow (S,L)$
is strict, it recovers the relative de Rham–Witt complex
$W_{\bullet }\unicode[STIX]{x1D6FA}_{Y/S}^{\ast }$
of Langer and Zink [Reference Langer and ZinkLZ04].(iii) When the base
$(S,L)$
is the scheme
$\operatorname{Spec}(k)$
with the log structure of the punctured point, and
$(Y,N)$
is of semistable type (i.e. étale locally étale over
$k[x_{1},\ldots ,x_{d+1}]/(x_{1}\cdots x_{c})$
with the canonical log structure) then Matsuue’s complex is isomorphic to the logarithmic de Rham–Witt complex
$W\unicode[STIX]{x1D714}_{Y}^{\ast }$
studied in [Reference Hyodo and KatoHK94].(iv) If we take
$(Y,N)$
semistable but instead equip
$\operatorname{Spec}(k)$
with the trivial log structure, the resulting complex is isomorphic to the one denoted
$W\tilde{\unicode[STIX]{x1D714}}_{Y}^{\ast }$
in [Reference Hyodo and KatoHK94].
If we are given a morphism of log schemes
$(Y,N)\rightarrow (S,L)$
over
$k$
, then as in [Reference MatsuueMat17, §2.2] we can lift the log structure
$N\rightarrow {\mathcal{O}}_{Y}$
to a log structure
$W_{r}N\rightarrow W_{r}{\mathcal{O}}_{Y}$
, where by definition
$W_{r}N=N\oplus \ker ((W_{r}{\mathcal{O}}_{Y})^{\ast }\rightarrow {\mathcal{O}}_{Y}^{\ast })$
and the map
$N\rightarrow W_{r}{\mathcal{O}}_{Y}$
is the Teichmüller lift of
$N\rightarrow {\mathcal{O}}_{Y}$
. Since
$W_{r}\unicode[STIX]{x1D714}_{(Y,N)/(S,L)}^{1}$
is a quotient of the pd-log de Rham complex
$\breve{\unicode[STIX]{x1D714}}_{(W_{r}Y,W_{r}N)/(W_{r}S,W_{r}L)}^{\ast }$
(see [Reference MatsuueMat17, §3.4]) there is a natural map
$d\log :W_{r}N\rightarrow W_{r}\unicode[STIX]{x1D714}_{(Y,N)/(S,L)}^{1}$
and hence we obtain maps
$$\begin{eqnarray}d\log :N^{\text{gp}}\rightarrow W_{r}\unicode[STIX]{x1D714}_{(Y,N)/(S,L)}^{1}\end{eqnarray}$$
which are compatible as
$r$
varies. We let
$W_{r}\unicode[STIX]{x1D714}_{(Y,N)/(S,L),\log }^{1}$
denote the image.
When both log structures are trivial, and
$Y\rightarrow \operatorname{Spec}(k)$
is smooth, [Reference IllusieIll79, Proposition I.3.23.2] says that
$d\log$
induces an exact sequence
$$\begin{eqnarray}1\rightarrow ({\mathcal{O}}_{Y}^{\ast })^{p^{r}}\rightarrow {\mathcal{O}}_{Y}^{\ast }\rightarrow W_{r}\unicode[STIX]{x1D6FA}_{Y,\log }^{1}\rightarrow 0,\end{eqnarray}$$
and our first task in this section to obtain an analogue of this result for semistable log schemes over
$k$
. In fact, since we will really only be interested in the case when
$Y$
arises as the special fibre of a semistable scheme over
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
, we will only treat this special case.
We will therefore let
${\mathcal{X}}$
denote a semistable scheme over
$R=k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
(not necessarily proper). We will let
$L$
denote the log structure given by the closed point of
$\operatorname{Spec}(R)$
, and write
$R^{\times }=(R,L)$
. We will denote by
$L_{n}$
the inverse image log structure on
$R_{n}=k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}/(t^{n+1})$
, and write
$R_{n}^{\times }=(R_{n},L_{n})$
. We will also write
$k^{\times }=(k,L_{0})$
. We will denote by
$M$
the log structure on
${\mathcal{X}}$
given by the special fibre, and write
${\mathcal{X}}^{\times }=({\mathcal{X}},M)$
. Similarly, we have log structures
$M_{n}$
on
$X_{n}={\mathcal{X}}\otimes _{R}R_{n}$
, and we will write
$X_{n}^{\times }=(X_{n},M_{n})$
. Finally, when considering the logarithmic de Rham–Witt complex relative to
$k$
(with the trivial log structure) we will drop
$k$
from the notation; for example, we will write
$W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }}^{\ast }$
instead of
$W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k}^{\ast }$
.
Proposition 2.1. The sequence
$$\begin{eqnarray}0\rightarrow p^{r}M_{0}^{\text{gp}}\rightarrow M_{0}^{\text{gp}}\overset{d\log }{\longrightarrow }W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times },\log }^{1}\rightarrow 0\end{eqnarray}$$
is exact.
Proof. The surjectivity of the right-hand map and the injectivity of the left-hand map are by definition, and since
$p^{r}W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times },\log }^{1}=0$
, the sequence is clearly a complex. The key point is then to show exactness in the middle. So suppose that we are given
$m\in M_{0}^{\text{gp}}$
such that
$d\log m=0$
. We will show that
$m\in p^{r}M_{0}^{\text{gp}}$
by induction on
$r$
.
When
$r=1$
we note that the claim is étale local; we may therefore assume
$X_{0}^{\times }$
to be affine, étale and strict over
$\operatorname{Spec}(k[x_{1},\ldots ,x_{d}]/(x_{1}\cdots x_{c}))$
, say
$X_{0}=\operatorname{Spec}(A)$
. We have
$$\begin{eqnarray}\unicode[STIX]{x1D714}_{(A,\mathbb{N}^{c})}^{1}\cong \bigoplus _{i=1}^{c}A\cdot d\log x_{i}\oplus \bigoplus _{i=c+1}^{d}A\cdot dx_{i}.\end{eqnarray}$$
Now suppose that we are given a local section
$m=u\prod _{i=1}^{c}x_{i}^{n_{i}}$
of
$M_{0}^{\text{gp}}$
for
$u\in A^{\ast }$
and
$n_{i}\in \mathbb{Z}$
. Write
$$\begin{eqnarray}d\log u=\mathop{\sum }_{i=1}^{c}a_{i}d\log x_{i}+\mathop{\sum }_{i=c+1}^{d}a_{i}dx_{i}\end{eqnarray}$$
with
$a_{i}\in A$
; note that since
$d\log u$
actually comes from an element of
$\unicode[STIX]{x1D6FA}_{A}^{1}$
it follows that
$a_{i}\in x_{i}A$
for
$1\leqslant i\leqslant c$
. In particular, we have
$n_{i}=-x_{i}b_{i}$
for
$1\leqslant i\leqslant c$
and some
$b_{i}\in A$
; passing to
$A/x_{i}A$
, it therefore follows that
$n_{i}=0$
in
$k$
. Hence each
$n_{i}$
is divisible by
$p$
. It follows that
$\prod _{i=1}^{c}x_{i}^{n_{i}}$
is in
$pM_{0}^{\text{gp}}$
, and its
$d\log$
vanishes. By dividing by this element we may therefore assume that
$m=u\in A^{\ast }$
. Since semistable schemes are of Cartier type, we may apply [Reference KatoKat89, Theorem 4.12], which tells us that (étale locally)
$u\in A^{(p)\ast }$
(since
$d\log u=0\Rightarrow du=0$
). Since
$k$
is perfect,
$A^{(p)\ast }=(A^{\ast })^{p}$
and we may conclude.
When
$r>1$
and
$d\log m=0\in W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times },\log }^{1}$
, we have in particular that
$d\log m=0\in W_{r-1}\unicode[STIX]{x1D714}_{X_{0}^{\times }}^{1}$
; hence by applying the induction hypothesis we obtain
$m=p^{r-1}m_{1}$
. But now this implies that
$p^{r-1}d\log m_{1}=0\in W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }}^{1}$
; we claim that in fact it follows that
$d\log m_{1}=0\in \unicode[STIX]{x1D714}_{X_{0}^{\times }}^{1}$
. Indeed, since
$\unicode[STIX]{x1D714}_{X_{0}^{\times }}^{1}$
is a locally free
${\mathcal{O}}_{X_{0}}$
-module, to prove that a section vanishes it suffices to show that it does so on a dense open subscheme. In particular, by restricting to the smooth locus of
$X_{0}$
we can assume that
$X_{0}$
is smooth and the log structure is given by
${\mathcal{O}}_{X_{0}}^{\ast }\oplus \mathbb{N}$
,
$(u,n)\mapsto u.0^{n}$
. We now apply [Reference IllusieIll79, Proposition I.3.4] and [Reference MatsuueMat17, Lemma 7.4] to conclude that
$d\log m_{1}=0$
as required. Thus applying the case
$r=1$
finishes the proof.◻
The following is analogous to [Reference IllusieIll79, Corollaire I.3.27].
Proposition 2.2. The sequences of pro-sheaves
$$\begin{eqnarray}\displaystyle 0\rightarrow {\{W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times },\log }^{1}\}}_{r} & \rightarrow & \displaystyle {\{W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{1}\}}_{r}\overset{1-F}{\rightarrow }{\{W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{1}\}}_{r}\rightarrow 0,\nonumber\\ \displaystyle 0\rightarrow {\{W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times },\log }^{1}\}}_{r} & \rightarrow & \displaystyle {\{W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times }}^{1}\}}_{r}\overset{1-F}{\rightarrow }{\{W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times }}^{1}\}}_{r}\rightarrow 0\nonumber\end{eqnarray}$$
are exact.
Proof. Let us consider the first sequence. We will apply Néron–Popescu desingularisation [Reference PopescuPop86, Theorem 1.8] to write
${\mathcal{X}}$
as a cofiltered limit
${\mathcal{X}}=\mathop{\varprojlim }\nolimits_{\unicode[STIX]{x1D6FC}\in A}X^{\unicode[STIX]{x1D6FC}}$
of schemes
$X^{\unicode[STIX]{x1D6FC}}$
which are smooth over
$k$
. Moreover, after possibly changing the indexing category
$A$
we may assume that there exist closed subschemes
$D^{\unicode[STIX]{x1D6FC}}\subset X^{\unicode[STIX]{x1D6FC}}$
such that:
–
$D^{\unicode[STIX]{x1D6FD}}=D^{\unicode[STIX]{x1D6FC}}\times _{X^{\unicode[STIX]{x1D6FC}}}X^{\unicode[STIX]{x1D6FD}}$
for all
$\unicode[STIX]{x1D6FD}\rightarrow \unicode[STIX]{x1D6FC}$
;–
$X_{0}=D^{\unicode[STIX]{x1D6FC}}\times _{X^{\unicode[STIX]{x1D6FC}}}{\mathcal{X}}$
for all
$\unicode[STIX]{x1D6FC}$
.
Again, after possibly changing the index category
$A$
we may assume that each
$D^{\unicode[STIX]{x1D6FC}}\subset X^{\unicode[STIX]{x1D6FC}}$
is a normal crossings divisor. Thus, using the fact that the logarithmic de Rham–Witt complex commutes with filtered colimits, we may reduce to considering the analogous question for
$Y$
smooth over
$k$
with log structure
$N$
coming from a normal crossings divisor
$D\subset Y$
. The claim is étale local; we may therefore assume that
$Y$
is étale over
$k[x_{1},\ldots ,x_{n}]$
with
$D$
the inverse image of
$\{x_{1}\cdots x_{c}=0\}$
. Locally,
$N$
is generated by
${\mathcal{O}}_{Y}^{\ast }$
and
$x_{i}$
for
$1\leqslant i\leqslant c$
, so in order to see that the sequence is a complex, or in other words that
$(1-F)(d\log n)=0$
, it suffices to check that
$(1-F)(d\log x_{i})=0$
. This is a straightforward calculation. For the surjectivity of
$1-F$
we claim in fact that
$$\begin{eqnarray}1-F:W_{r+1}\unicode[STIX]{x1D714}_{(Y,N)}^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{(Y,N)}^{1}\end{eqnarray}$$
is surjective. For this we note that by [Reference MatsuueMat17, §9] there exists an exact sequence
$$\begin{eqnarray}0\rightarrow W_{r}\unicode[STIX]{x1D6FA}_{Y}^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{(Y,N)}^{1_{}^{}\rightarrow \bigoplus }W_{r}{\mathcal{O}}_{D_{i}}\cdot d\log x_{i}\rightarrow 0\end{eqnarray}$$
for all
$r$
, where
$D_{i}$
are the irreducible components of
$D$
. Denote the induced map
$W_{r}\unicode[STIX]{x1D714}_{(Y,N)}^{1}\rightarrow W_{r}{\mathcal{O}}_{D_{i}}$
by
$\text{Res}_{i}$
. (In fact, it is assumed in [Reference MatsuueMat17, §9] that
$Y$
is proper over
$k$
; however, the proof of the exactness in [Reference MatsuueMat17, §8.2] is local, and therefore works equally well in the non-proper case.) Since
$(1-F)(d\log x_{i})=0$
it follows that we have the commutative diagram
where
$W_{r}\unicode[STIX]{x1D6FA}_{Y}^{1}$
is the usual (non-logarithmic) de Rham–Witt complex of
$Y$
. It therefore suffices to apply [Reference IllusieIll79, Propositions I.3.26, I.3.28], stating that the left and right vertical maps are surjective. Finally, to show exactness in the middle, suppose that we are given
$\unicode[STIX]{x1D714}\in W_{r+1}\unicode[STIX]{x1D714}_{(Y,N)}^{1}$
such that
$(1-F)(\unicode[STIX]{x1D714})=0$
. Then, applying [Reference IllusieIll79, Proposition I.3.28], we can see that
$$\begin{eqnarray}\text{Res}_{i}(\unicode[STIX]{x1D714})\in \mathbb{Z}/p^{r+1}\mathbb{Z}+\ker (W_{r+1}{\mathcal{O}}_{D_{i}}\rightarrow W_{r}{\mathcal{O}}_{D_{i}})\end{eqnarray}$$
for all
$i$
. Hence after subtracting off an element of
$d\log (N^{\text{gp}})$
we may assume that in fact
$$\begin{eqnarray}\unicode[STIX]{x1D714}\in W_{r+1}\unicode[STIX]{x1D6FA}_{Y}^{1}+\ker (W_{r+1}\unicode[STIX]{x1D714}_{(Y,N)}^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{(Y,N)}^{1}).\end{eqnarray}$$
Now applying [Reference IllusieIll79, Corollaire I.3.27] tells us that
$$\begin{eqnarray}\unicode[STIX]{x1D714}\in d\log (N^{\text{gp}})+\ker (W_{r+1}\unicode[STIX]{x1D714}_{(Y,N)}^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{(Y,N)}^{1})\end{eqnarray}$$
and hence the given sequence of pro-sheaves is exact in the middle.
For the second sequence, the surjectivity of
$1-F$
follows from the corresponding claim for the first sequence, since sections of
$W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times }}^{1}$
can be lifted locally to
$W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{1}$
. We may also argue étale locally; assuming that
$X_{0}^{\times }$
is étale and strict over
$\operatorname{Spec}(\mathbb{N}^{c}\rightarrow k[x_{1},\ldots ,x_{d}]/(x_{1}\cdots x_{c}))$
. The fact that the claimed sequence is a complex follows again from observing that
$(1-F)(d\log x_{i})=0$
for
$1\leqslant i\leqslant c$
. To see exactness in the middle we use the fact that (again working étale locally) we have an exact sequence
$$\begin{eqnarray}0\rightarrow \bigoplus _{i}W_{r}\unicode[STIX]{x1D6FA}_{D_{i}}^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times }}^{1}\rightarrow \bigoplus _{ij}W_{r}{\mathcal{O}}_{D_{ij}}\rightarrow 0\end{eqnarray}$$
by [Reference MatsuueMat17, Lemma 8.4], where
$D_{i}$
are the irreducible components of
$X_{0}^{\times }$
and
$D_{ij}$
their intersections. Moreover, this fits into a diagram
with exact rows. Exactness of the middle vertical sequence at
$W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times }}^{1}$
now follows from the classical result [Reference IllusieIll79, Corollaire I.3.27, Proposition I.3.28] and a simple diagram chase.◻
Next, we will need to understand the kernel of
$W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times },\log }^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times },\log }^{1}$
.
Lemma 2.3. For all
$r\geqslant 1$
the sequence
$$\begin{eqnarray}0\rightarrow \frac{\mathbb{Z}}{p^{r}\mathbb{Z}}\wedge d\log t\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times },\log }^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times },\log }^{1}\rightarrow 0\end{eqnarray}$$
is exact.
Proof. Note that by [Reference MatsuueMat17, Lemma 7.4] it suffices to show that
$$\begin{eqnarray}d\log (M_{0})\cap W_{r}{\mathcal{O}}_{X_{0}}\wedge d\log t=\frac{\mathbb{Z}}{p^{r}\mathbb{Z}}\wedge d\log t\end{eqnarray}$$
inside
$W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }}^{1}$
; the inclusion
$\supset$
is clear. For the other inclusion, suppose that we are given an element of the form
$g\wedge d\log t\in W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }}^{1}$
which is in the image of
$d\log$
. Then we know that
$\tilde{g}\wedge d\log t=d\log n+c$
in
$W_{r+1}\unicode[STIX]{x1D714}_{X_{0}^{\times }}^{1}$
, for some
$c\in \ker (W_{r+1}\unicode[STIX]{x1D714}_{X_{0}^{\times }}^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }}^{1})$
and
$\tilde{g}\in W_{r+1}{\mathcal{O}}_{X_{0}}$
lifting
$g$
. Arguing as in Proposition 2.2 above, we can see that
$(1-F)(d\log n)=0$
, and again applying [Reference MatsuueMat17, Lemma 7.4], we can deduce that in fact
$g=F(g)$
in
$W_{r}{\mathcal{O}}_{X_{0}}$
. Hence
$g\in \mathbb{Z}/p^{r}\mathbb{Z}$
as claimed.◻
Finally, we will need to know that the logarithmic de Rham–Witt complex computes the log-crystalline cohomology of the semistable scheme
${\mathcal{X}}$
. To do so, we need to construct a suitable comparison morphism
$$\begin{eqnarray}\mathbf{R}u_{{\mathcal{X}}^{\times }/W\ast }{\mathcal{O}}_{{\mathcal{X}}^{\times }/W}^{\text{crys}}\overset{{\sim}}{\rightarrow }W\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{\ast },\end{eqnarray}$$
where
$u_{{\mathcal{X}}^{\times }/W}:({\mathcal{X}}^{\times }/W)_{\text{crys}}\rightarrow {\mathcal{X}}_{\acute{\text{e}}\text{t}}$
is the natural projection from the log-crystalline site of
${\mathcal{X}}^{\times }/W$
to the étale site of
${\mathcal{X}}$
. Unfortunately, we cannot directly appeal to the construction of [Reference MatsuueMat17, §6], since
${\mathcal{X}}$
is not of finite type over
$W$
. However, we can easily get round this by exploiting the fact that the log scheme
$\operatorname{Spec}(R^{\times })$
has an obvious log-
$p$
-smooth lift over
$W$
, namely the scheme
$\operatorname{Spec}(W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7})$
together with the log structure
$L_{W}$
defined by the divisor
$t=0$
. We therefore take an embedding system
for the finite-type morphism of log schemes
${\mathcal{X}}^{\times }\rightarrow (\operatorname{Spec}(W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}),L_{W})$
in the sense of [Reference MatsuueMat17, Definition 6.3], and then simply consider
${\mathcal{X}}^{\times },{\mathcal{X}}_{\bullet }^{\times }$
and
$({\mathcal{Y}}_{\bullet },N_{\bullet })$
instead as (simplicial) log schemes over
$\operatorname{Spec}(W)$
, the latter being endowed with the trivial log structure. We now proceed exactly as in [Reference MatsuueMat17, §6] or [Reference IllusieIll79, § II.1] to produce the required comparison morphism
$$\begin{eqnarray}\mathbf{R}u_{{\mathcal{X}}^{\times }/W\ast }{\mathcal{O}}_{{\mathcal{X}}^{\times }/W}^{\text{crys}}\overset{{\sim}}{\rightarrow }W\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{\ast }.\end{eqnarray}$$
Proposition 2.4. The induced map
$$\begin{eqnarray}H_{\text{log}\text{\text{-}}\text{crys}}^{i}({\mathcal{X}}^{\times }/W)\rightarrow H_{\text{cont}}^{i}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{\ast })\end{eqnarray}$$
on cohomology is an isomorphism, for all
$i\geqslant 0$
.
Proof. It suffices to show that
$H_{\text{log}\text{\text{-}}\text{crys}}^{i}({\mathcal{X}}^{\times }/W_{r})\overset{{\sim}}{\rightarrow }H^{i}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{\ast })$
for all
$r$
, where
$W_{r}=W_{r}(k)$
. Arguing locally on
${\mathcal{X}}$
, we may assume in fact that
${\mathcal{X}}$
is affine, and in particular admits a closed embedding
${\mathcal{X}}{\hookrightarrow}{\mathcal{P}}$
into some affine space over
$W_{r}\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
. Thus if we equip
${\mathcal{P}}$
with the log structure coming from the (smooth) divisor defined by
$t=0$
, the closed immersion
${\mathcal{X}}{\hookrightarrow}{\mathcal{P}}$
can be promoted to an exact closed immersion of log schemes.
Now applying Néron–Popescu desingularisation [Reference PopescuPop86, Theorem 1.8] to
$W_{r}[t]\rightarrow W_{r}\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
, we may write
${\mathcal{P}}=\lim _{\unicode[STIX]{x1D6FC}}P^{\unicode[STIX]{x1D6FC}}$
as a limit of smooth
$W_{r}[t]$
-schemes, such that:
– there exist compatible closed subschemes
$X^{\unicode[STIX]{x1D6FC}}\subset P^{\unicode[STIX]{x1D6FC}}$
, each of whose inverse image in
${\mathcal{P}}$
is precisely
${\mathcal{X}}$
, and each of which is smooth over
$k$
;– the divisors
$D^{\unicode[STIX]{x1D6FC}}:=X^{\unicode[STIX]{x1D6FC}}\cap \{t=0\}$
, each of whose inverse image in
${\mathcal{X}}$
is precisely the special fibre
$X_{0}$
, have normal crossings.
Both the log de Rham–Witt complex and étale cohomology commute with cofiltered limits of schemes, thus by using [Reference MatsuueMat17, Theorem 7.2] it suffices to show that the same is true of log-crystalline cohomology, or in other words that we have
$$\begin{eqnarray}H_{\text{log}\text{\text{-}}\text{crys}}^{i}({\mathcal{X}}^{\times }/W_{r})=\text{colim}_{\unicode[STIX]{x1D6FC}}H_{\text{log}\text{\text{-}}\text{crys}}^{i}(X_{\unicode[STIX]{x1D6FC}}^{\times }/W_{r}),\end{eqnarray}$$
where
$X_{\unicode[STIX]{x1D6FC}}^{\times }$
denotes the scheme
$X_{\unicode[STIX]{x1D6FC}}$
endowed with the log structure given by
$D_{\unicode[STIX]{x1D6FC}}$
. By [Reference KatoKat89, Theorem 6.4],
$H_{\text{log}\text{\text{-}}\text{crys}}^{i}(X_{\unicode[STIX]{x1D6FC}}^{\times }/W_{r})$
is computed as the de Rham cohomology of the log-PD envelope of
$X_{\unicode[STIX]{x1D6FC}}^{\times }$
inside
$P_{\unicode[STIX]{x1D6FC}}$
. Since log-PD envelopes commute with cofiltered limits of schemes (i.e. filtered colimits of rings), it suffices to show that
$H_{\text{log}\text{\text{-}}\text{crys}}^{i}({\mathcal{X}}^{\times }/W_{r})$
can be computed as the de Rham cohomology of the log-PD envelope of
${\mathcal{X}}^{\times }$
inside
${\mathcal{P}}$
.
In other words, what we require is a logarithmic analogue of [Reference KatoKat91, Theorem 1.7], or equivalently a log-
$p$
-basis analogue of [Reference KatoKat89, Theorem 6.4]. But this follows from [Reference Caro and VauclairCV15, Proposition 1.6.6].◻
3 Morrow’s variational Tate conjecture for divisors
The goal of this section is to offer a simpler proof of a special case of [Reference MorrowMor14, Theorem 3.5] for smooth and proper schemes
${\mathcal{X}}$
over the power series ring
$R=k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
. This result essentially states that a line bundle on the special fibre of
${\mathcal{X}}$
lifts if and only if its first Chern class in
$H_{\text{crys}}^{2}$
does, and should be viewed as an equicharacteristic analogue of Berthelot and Ogus’s theorem [Reference Berthelot and OgusBO83, Theorem 3.8] stating that a line bundle on the special fibre of a smooth proper scheme over a DVR in mixed characteristic lifts if and only if its Chern class lies in the first piece of the Hodge filtration. We will also give a slightly different interpretation of this result that emphasises the philosophy that in equicharacteristic the ‘correct’ analogue of a Hodge filtration is an
${\mathcal{E}}^{\dagger }$
-structure. Our proof is simpler in that it does not depend on any results from topological cyclic homology, but only on fairly standard properties of the de Rham–Witt complex. As such, it is more readily adaptable to the semistable case, and we shall adapt it in § 4 below.
Throughout this section,
${\mathcal{X}}$
will be a smooth and proper
$R=k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
-scheme. Let
$R_{n}$
denote
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}/(t^{n+1})$
and set
$X_{n}={\mathcal{X}}\otimes _{R}R_{n}$
. Write
$X$
for the generic fibre of
${\mathcal{X}}$
and
$\mathfrak{X}$
for its formal (
$t$
-adic) completion. Since all schemes in this section will have trivial log structure, we will use the notation
$W_{\bullet }\unicode[STIX]{x1D6FA}^{\ast }$
for the de Rham–Witt complex instead of
$W_{\bullet }\unicode[STIX]{x1D714}^{\ast }$
. The key technical calculation we will make is contained in the following lemma.
Lemma 3.1. Fix
$n\geqslant 0$
, write
$n=p^{m}n_{0}$
with
$(n_{0},p)=1$
, and let
$r=m+1$
. Then the map
$$\begin{eqnarray}d\log :1+t^{n}{\mathcal{O}}_{X_{n}}\rightarrow W_{r}\unicode[STIX]{x1D6FA}_{X_{n},\log }^{1}\end{eqnarray}$$
is injective.
Proof. It suffices to prove the corresponding statement for sections on some sufficiently small open affine
$\operatorname{Spec}(A_{n})\subset X_{n}$
, which we may therefore assume to be étale over
$R_{n}[x_{1},\ldots ,x_{d}]$
. In this case, since deformations of smooth affine schemes are trivial, we have
$A_{n}\cong A_{0}\,\otimes _{k}\,R_{n}$
. Hence
$1+t^{n}A_{n}=1+t^{n}A_{0}$
, and our problem therefore reduces to showing that if
$a\in A_{0}$
is such that
$d\log [1+at^{n}]=0$
, then in fact
$a=0$
. But vanishing of
$a$
may be checked over all closed points of
$\operatorname{Spec}(A_{0})$
, so by functoriality of the
$d\log$
map we may in fact assume that
$A_{0}$
is a finite extension of
$k$
; enlarging
$k$
, we may moreover assume that
$A_{0}=k$
. In other words, we need to show that the map
$$\begin{eqnarray}d\log :1+t^{n}k\rightarrow W_{r}\unicode[STIX]{x1D6FA}_{R_{n}}^{1}\end{eqnarray}$$
is injective. Since
$k$
is perfect, any
$1+at^{n}\in 1+t^{n}k$
can be written uniquely as
$(1+t^{n_{0}}b)^{p^{m}}$
for some
$b\in k$
, hence
$d\log [1+at^{n}]=p^{m}d\log (1+t^{n_{0}}b)$
. It follows that if
$d\log [1+at^{n}]=0$
, then
$n_{0}p^{m}bt^{n_{0}-1}dt=0$
in
$W_{r}\unicode[STIX]{x1D6FA}_{R_{n}}^{1}$
; note that although
$b\in k$
, nonetheless
$p^{m}b$
still makes sense as an element of
$W_{m+1}(k)=W_{r}(k)$
. Since any non-zero such
$b$
is invertible, the lemma will follow if we can show that
$p^{m}t^{n_{0}-1}dt$
is non-zero in
$W_{r}\unicode[STIX]{x1D6FA}_{R_{n}}^{1}$
. This can be checked easily using the exact sequence
$$\begin{eqnarray}\frac{W_{r}((t^{n+1}))}{W_{r}((t^{n+1})^{2})}\overset{d}{\rightarrow }W_{r}\unicode[STIX]{x1D6FA}_{k[t]}^{1}\otimes _{W_{r}(k[t])}W_{r}R_{n}\rightarrow W_{r}\unicode[STIX]{x1D6FA}_{R_{n}}^{1}\rightarrow 0\end{eqnarray}$$
from [Reference Langer and ZinkLZ05]. ◻
From this we deduce the following proposition.
Proposition 3.2. For
$r\gg 0$
(depending on
$n$
) there is a commutative diagram
with exact rows.
Proof. It is well known that the top row is exact, and the diagram is clearly commutative; it therefore suffices to show that for all
$n$
the sequence
$$\begin{eqnarray}1\rightarrow 1+t{\mathcal{O}}_{X_{n}}\rightarrow W_{r}\unicode[STIX]{x1D6FA}_{X_{n},\log }^{1}\rightarrow W_{r}\unicode[STIX]{x1D6FA}_{X_{0},\log }^{1}\rightarrow 0\end{eqnarray}$$
is exact for
$r\gg 0$
. From the definition of
$W_{r}\unicode[STIX]{x1D6FA}_{X_{n},\log }^{1}$
and the exactness of the sequence
$$\begin{eqnarray}1\rightarrow 1+t{\mathcal{O}}_{X_{n}}\rightarrow {\mathcal{O}}_{X_{n}}^{\ast }\rightarrow {\mathcal{O}}_{X_{0}}^{\ast }\rightarrow 1\end{eqnarray}$$
it is immediate that
$W_{r}\unicode[STIX]{x1D6FA}_{X_{n},\log }^{1}\rightarrow W_{r}\unicode[STIX]{x1D6FA}_{X_{0},\log }^{1}$
is surjective and the composite
$1+t{\mathcal{O}}_{X_{n}}\rightarrow W_{r}\unicode[STIX]{x1D6FA}_{X_{0},\log }^{1}$
is zero. Given
$\unicode[STIX]{x1D6FC}\in {\mathcal{O}}_{X_{n}}^{\ast }$
mapping to
$0$
in
$W_{r}\unicode[STIX]{x1D6FA}_{X_{0},\log }^{1}$
, it follows from [Reference IllusieIll79, Proposition I.3.23.2] that there exists
$\unicode[STIX]{x1D6FD}\in {\mathcal{O}}_{X_{n}}^{\ast }$
and
$\unicode[STIX]{x1D6FE}\in 1+t{\mathcal{O}}_{X_{n}}$
such that
$\unicode[STIX]{x1D6FC}=\unicode[STIX]{x1D6FD}^{p^{r}}+\unicode[STIX]{x1D6FE}$
, and hence
$d\log \unicode[STIX]{x1D6FC}=d\log \unicode[STIX]{x1D6FE}$
in
$W_{r}\unicode[STIX]{x1D6FA}_{X_{n},\log }^{1}$
. The sequence
$$\begin{eqnarray}1+t{\mathcal{O}}_{X_{n}}\rightarrow W_{r}\unicode[STIX]{x1D6FA}_{X_{n},\log }^{1}\rightarrow W_{r}\unicode[STIX]{x1D6FA}_{X_{0},\log }^{1}\rightarrow 0\end{eqnarray}$$
is therefore exact, and it remains to show that
$$\begin{eqnarray}d\log :1+t{\mathcal{O}}_{X_{n}}\rightarrow W_{r}\unicode[STIX]{x1D6FA}_{X_{n},\log }^{1}\end{eqnarray}$$
is injective for
$r\gg 0$
. By induction on
$n$
this follows from Lemma 3.1 above.◻
We now set
$$\begin{eqnarray}W_{r}\unicode[STIX]{x1D6FA}_{\mathfrak{X},\log }^{i}:=\lim _{n}W_{r}\unicode[STIX]{x1D6FA}_{X_{n},\log }^{i}\end{eqnarray}$$
as sheaves on
$\mathfrak{X}_{\acute{\text{e}}\text{t}}$
and define
$$\begin{eqnarray}H_{\text{cont}}^{j}(\mathfrak{X}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D6FA}_{\mathfrak{X},\log }^{i}):=H^{j}(\mathbf{R}\lim _{r}\mathbf{R}\unicode[STIX]{x1D6E4}(\mathfrak{X}_{\acute{\text{e}}\text{t}},W_{r}\unicode[STIX]{x1D6FA}_{\mathfrak{X},\log }^{i})).\end{eqnarray}$$
As an essentially immediate corollary of Proposition 3.2, we deduce the key step of Morrow’s proof of the variational Tate conjecture in this case.
Corollary 3.3. Let
${\mathcal{L}}\in \operatorname{Pic}(X_{0})$
, with first Chern class
$c_{1}({\mathcal{L}})\in H_{\text{cont}}^{1}(X_{0,\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D6FA}_{X_{0},\log }^{1})$
. Then
${\mathcal{L}}$
lifts to
$\operatorname{Pic}({\mathcal{X}})$
if and only if
$c_{1}({\mathcal{L}})$
lifts to
$H_{\text{cont}}^{1}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D6FA}_{{\mathcal{X}},\log }^{1})$
.
Proof. One direction is obvious. For the other direction, assume that the first Chern class
$c_{1}({\mathcal{L}})$
lifts to
$H_{\text{cont}}^{1}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D6FA}_{{\mathcal{X}},\log }^{1})$
; in particular, it therefore lifts to
$H_{\text{cont}}^{1}(\mathfrak{X}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D6FA}_{\mathfrak{X},\log }^{1})$
. Hence by Proposition 3.2 it follows that
${\mathcal{L}}$
lifts to
$\operatorname{Pic}(\mathfrak{X})$
, and we may conclude using Grothendieck’s algebrisation theorem that it lifts to
$\operatorname{Pic}({\mathcal{X}})$
.◻
From this the
$(\mathit{crys}\text{\text{-}}\unicode[STIX]{x1D719})$
form of the variational Tate conjecture follows as in [Reference MorrowMor14].
Corollary 3.4. Let
${\mathcal{L}}\in \operatorname{Pic}(X_{0})_{\mathbb{Q}}$
, with first Chern class
$c_{1}({\mathcal{L}})\in H_{\text{crys}}^{2}(X_{0}/K)^{\unicode[STIX]{x1D711}=p}$
. Then
${\mathcal{L}}$
lifts to
$\operatorname{Pic}({\mathcal{X}})_{\mathbb{Q}}$
if and only if
$c_{1}({\mathcal{L}})$
lifts to
$H_{\text{crys}}^{2}({\mathcal{X}}/K)^{\unicode[STIX]{x1D711}=p}$
.
Proof. Let us first assume that
$k$
is algebraically closed. By [Reference MorrowMor14, Proposition 3.2] the inclusions
$W\unicode[STIX]{x1D6FA}_{{\mathcal{X}},\log }^{1}[-1]\rightarrow W\unicode[STIX]{x1D6FA}_{{\mathcal{X}},\log }^{\ast }$
and
$W\unicode[STIX]{x1D6FA}_{X_{0},\log }^{1}[-1]\rightarrow W\unicode[STIX]{x1D6FA}_{X_{0},\log }^{\ast }$
induce an isomorphism
$$\begin{eqnarray}H_{\text{cont}}^{1}(X_{0,\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D6FA}_{X_{0},\log }^{1})_{\mathbb{ Q}}\overset{{\sim}}{\rightarrow }H_{\text{crys}}^{2}(X_{0}/K)^{\unicode[STIX]{x1D711}=p}\end{eqnarray}$$
and a surjection
$$\begin{eqnarray}H_{\text{cont}}^{1}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D6FA}_{{\mathcal{X}},\log }^{1})_{\mathbb{ Q}}{\twoheadrightarrow}H_{\text{crys}}^{2}({\mathcal{X}}/K)^{\unicode[STIX]{x1D711}=p}.\end{eqnarray}$$
The claim follows. In general, we argue as in [Reference MorrowMor14, Theorem 1.4]: the claim for
$k$
algebraically closed shows that
${\mathcal{L}}$
lifts to
$\operatorname{Pic}({\mathcal{X}})_{\mathbb{Q}}$
after making the base change
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}\rightarrow \overline{k}\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
. Let
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}^{\text{sh}}$
denote the strict Henselisation of
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
inside
$\overline{k}\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
; by Néron–Popescu desingularisation there exists some smooth local
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}^{\text{sh}}$
-algebra
$A$
such that
${\mathcal{L}}$
lifts to
$\operatorname{Pic}({\mathcal{X}})_{\mathbb{Q}}$
after making the base change
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}\rightarrow A$
. But the map
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}^{\text{sh}}\rightarrow A$
has a section, from which it follows that in fact
${\mathcal{L}}$
lifts to
$\operatorname{Pic}({\mathcal{X}})_{\mathbb{Q}}$
after making some finite field extension
$k\rightarrow k^{\prime }$
. But now simply taking the pushforward via
${\mathcal{X}}\,\otimes _{k}\,k^{\prime }\rightarrow {\mathcal{X}}$
and dividing by
$[k^{\prime }:k]$
gives the result.◻
To finish off this section, we wish to give a slightly different formulation of Corollary 3.4. After [Reference Lazda and PálLP16] we can consider the ‘overconvergent’ rigid cohomology
$H_{\text{rig}}^{i}(X/{\mathcal{E}}^{\dagger })$
of the generic fibre
$X$
, which is a
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$
-module over the bounded Robba ring
${\mathcal{E}}^{\dagger }$
. Set
$H_{\text{rig}}^{i}(X/{\mathcal{R}}):=H_{\text{rig}}^{i}(X/{\mathcal{E}}^{\dagger })\otimes _{{\mathcal{E}}^{\dagger }}{\mathcal{R}}$
. By combining Dwork’s trick with smooth and proper base change in crystalline cohomology we have an isomorphism
$$\begin{eqnarray}H_{\text{rig}}^{i}(X/{\mathcal{R}})^{\unicode[STIX]{x1D6FB}=0}\cong H_{\text{rig}}^{i}(X_{0}/K)\end{eqnarray}$$
for all
$i$
. Thus, for any
${\mathcal{L}}\in \operatorname{Pic}(X_{0})_{\mathbb{Q}}$
we can view
$c_{1}({\mathcal{L}})$
as an element of
$H_{\text{rig}}^{i}(X/{\mathcal{R}})^{\unicode[STIX]{x1D6FB}=0}\subset H_{\text{rig}}^{i}(X/{\mathcal{R}})$
. One of the general philosophies of
$p$
-adic cohomology in equicharacteristic is that while the cohomology groups
$H_{\text{rig}}^{i}(X/{\mathcal{R}})$
in some sense only depend on the special fibre
$X_{0}$
, the ‘lift’
$X$
of
$X_{0}$
is seen in the
${\mathcal{E}}^{\dagger }$
-lattice
$H_{\text{rig}}^{i}(X/{\mathcal{E}}^{\dagger })\subset H_{\text{rig}}^{i}(X/{\mathcal{R}})$
. The correct equicharacteristic analogue of a Hodge filtration, therefore, is an
${\mathcal{E}}^{\dagger }$
-structure. With this in mind, then, the following theorem is a statement of the variational Tate conjecture for divisors which is perhaps slightly more transparently analogous to that in mixed characteristic.
Theorem 3.5. Assume that
${\mathcal{X}}$
is projective over
$R$
. Then a line bundle
${\mathcal{L}}\in \operatorname{Pic}(X_{0})_{\mathbb{Q}}$
lifts to
$\operatorname{Pic}({\mathcal{X}})_{\mathbb{Q}}$
if and only if
$c_{1}({\mathcal{L}})\in H_{\text{rig}}^{2}(X/{\mathcal{R}})$
lies in
$H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })$
.
Proof. This is simply another way of stating the condition (flat) in [Reference MorrowMor14, Theorem 3.5]. ◻
Remark 3.6. It seems entirely plausible that the methods of this section can be easily adapted to give a proof of [Reference MorrowMor14, Theorem 3.5] in general, that is, over
$k\unicode[STIX]{x27E6}t_{1},\ldots ,t_{n}\unicode[STIX]{x27E7}$
rather than just
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
.
4 A semistable variational Tate conjecture for divisors
In this section we will prove a semistable version of Theorem 3.5, or equivalently an equicharacteristic analogue of [Reference YamashitaYam11, Theorem 0.1]. The basic set-up will be to take a proper, semistable scheme
${\mathcal{X}}/R$
; as before, we will consider the semistable schemes
$X_{n}/R_{n}$
as well as the smooth generic fibre
$X/F$
. We will also let
$\mathfrak{X}$
denote the formal completion of
${\mathcal{X}}$
.
The special fibre of
${\mathcal{X}}$
defines a log structure
$M$
, and pulling back via the immersion
$X_{n}\rightarrow {\mathcal{X}}$
defines a log structure
$M_{n}$
on each
$X_{n}$
. For each
$n$
we will put a log structure
$L_{n}$
on
$R_{n}$
via
$\mathbb{N}\rightarrow R_{n}$
,
$1\mapsto t$
; note that for
$n=0$
this is the log structure of the punctured point on
$k$
. We will let
$L$
denote the log structure on
$R$
defined by the same formula. As before, we will write
$R^{\times }=(R,L)$
,
$R_{n}^{\times }=(R_{n},L_{n})$
,
${\mathcal{X}}^{\times }=({\mathcal{X}},M)$
,
$X_{n}^{\times }=(X_{n},M_{n})$
and
$k^{\times }=(k,L_{0})$
. The logarithmic version of Proposition 3.2 is then given by the following proposition.
Proposition 4.1. For
$r\gg 0$
(depending on
$n$
) there is a commutative diagram
with exact rows. Moreover, each
${\mathcal{K}}_{n,r}$
fits into an exact sequence of pro-sheaves on
$X_{n,\acute{\text{e}}\text{t}}$
,
$$\begin{eqnarray}1\rightarrow 1+t{\mathcal{O}}_{X_{n}}\rightarrow \{{\mathcal{K}}_{n,r}\}\text{}_{r}\rightarrow \{\mathbb{Z}/p^{r}\mathbb{Z}\}\text{}_{r}\rightarrow 0,\end{eqnarray}$$
which is split compatibly with varying
$n$
.
Proof. We first claim that if we replace
$W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times },\log }^{1}$
by
$W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times },\log }^{1}$
then we obtain an exact sequence
$$\begin{eqnarray}1\rightarrow 1+t{\mathcal{O}}_{X_{n}}\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{n}^{\times },\log }^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times },\log }^{1}\rightarrow 0\end{eqnarray}$$
for
$r\gg 0$
. Using Proposition 2.1, the proof of the exactness of
$$\begin{eqnarray}1+t{\mathcal{O}}_{X_{n}}\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{n}^{\times },\log }^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times },\log }^{1}\rightarrow 0\end{eqnarray}$$
is exactly as in Proposition 3.2. In fact, to check exactness on the left we can even apply Proposition 3.2: to check that a section of
$1+t{\mathcal{O}}_{X_{n}}$
vanishes it suffices to do so on a dense open subscheme of
$X_{n}$
; we may therefore étale locally replace
$X_{n}$
by the canonical thickening of the smooth locus of the special fibre. But now we are in the smooth case, so we apply Proposition 3.2 (which holds locally).
Applying Lemma 2.3, we know that the kernel of
$$\begin{eqnarray}W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times },\log }^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times },\log }^{1}\end{eqnarray}$$
is isomorphic to
$\mathbb{Z}/p^{r}\mathbb{Z}$
, generated by
$d\log t$
. The snake lemma then shows that, defining
${\mathcal{K}}_{n,r}$
to be the kernel of
$W_{r}\unicode[STIX]{x1D714}_{X_{n}^{\times },\log }^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times },\log }^{1}$
, we have the exact sequence
$$\begin{eqnarray}1\rightarrow 1+t{\mathcal{O}}_{X_{n}}\rightarrow {\mathcal{K}}_{n,r}\rightarrow \mathbb{Z}/p^{r}\mathbb{Z}\rightarrow 0\end{eqnarray}$$
for
$r\gg 0$
. To see that it splits compatibly with varying
$r$
and
$n$
it therefore suffices to show that there exist compatible classes
$\unicode[STIX]{x1D714}_{r}\in W_{r}\unicode[STIX]{x1D714}_{X_{n}^{\times }}^{1}$
whose image in
$W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times },\log }^{1}$
generates the kernel of
$W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times },\log }^{1}\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times },\log }^{1}$
; as we have already observed, the classes of
$d\log t$
will suffice.◻
Let
$\operatorname{Pic}(X_{0}^{\times })=H^{1}(X_{0,\acute{\text{e}}\text{t}},M_{0}^{\text{gp}})$
and
$\operatorname{Pic}({\mathcal{X}}^{\times })=H^{1}({\mathcal{X}}_{\acute{\text{e}}\text{t}},M^{\text{gp}})$
. As before, we therefore obtain the following corollary.
Corollary 4.2. Let
${\mathcal{L}}\in \operatorname{Pic}(X_{0}^{\times })$
(respectively,
$\operatorname{Pic}(X_{0})$
). Then
${\mathcal{L}}$
lifts to
$\operatorname{Pic}({\mathcal{X}}^{\times })$
(respectively,
$\operatorname{Pic}({\mathcal{X}})$
) if and only if
$c_{1}({\mathcal{L}})\in H_{\text{cont}}^{1}(X_{0,\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times },\log }^{1})$
lifts to
$H_{\text{cont}}^{1}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times },\log }^{1})$
.
Proof. This is similar to the proof of Corollary 3.3, although a little more care is needed in taking the limits in
$n$
and
$r$
. Again, one direction is clear, so we assume that we are given a (logarithmic) line bundle whose Chern class lifts. First we note that we have isomorphisms
$$\begin{eqnarray}\operatorname{Pic}(\mathfrak{X})\cong H_{\text{cont}}^{1}(X_{0,\acute{\text{e}}\text{t}},\{{\mathcal{O}}_{X_{n}}^{\ast }\}\text{}_{n}),\quad \operatorname{Pic}(\mathfrak{X}^{\times })\cong H_{\text{cont}}^{1}(X_{0,\acute{\text{e}}\text{t}},\{M_{n}^{\text{gp}}\}\text{}_{n}).\end{eqnarray}$$
This enable us to view the obstruction to lifting (in either case) as an element of
$H_{\text{cont}}^{2}(X_{0,\acute{\text{e}}\text{t}},\{1+t{\mathcal{O}}_{X_{n}}\}\text{}_{n})$
. The fact that the Chern class lifts implies that this obstruction vanishes in
$$\begin{eqnarray}H_{\text{cont}}^{2}(X_{0,\acute{\text{e}}\text{t}},\{{\mathcal{K}}_{n,r}\}\text{}_{n,r}):=H^{2}\Bigl(\mathbf{R}\lim _{n}\mathbf{R}\lim _{r}\mathbf{R}\unicode[STIX]{x1D6E4}(X_{0,\acute{\text{e}}\text{t}},{\mathcal{K}}_{n,r})\Bigr)\end{eqnarray}$$
and hence the fact that the exact sequence of pro-sheaves
$$\begin{eqnarray}1\rightarrow 1+t{\mathcal{O}}_{X_{n}}\rightarrow \{{\mathcal{K}}_{n,r}\}\text{}_{r}\rightarrow \{\mathbb{Z}/p^{r}\mathbb{Z}\}\text{}_{r}\rightarrow 0\end{eqnarray}$$
splits, compatibly with varying
$n$
, shows that the obstruction must itself vanish in
$$\begin{eqnarray}H_{\text{cont}}^{2}(X_{0,\acute{\text{e}}\text{t}},\{1+t{\mathcal{O}}_{X_{n}}\}\text{}_{n}).\end{eqnarray}$$
Finally, we need to see that we have isomorphisms
$\operatorname{Pic}(\mathfrak{X})\cong \operatorname{Pic}({\mathcal{X}})$
and
$\operatorname{Pic}(\mathfrak{X}^{\times })\cong \operatorname{Pic}({\mathcal{X}}^{\times })$
. The first is Grothendieck’s algebrisation theorem; to see the second we note that
$\operatorname{Pic}({\mathcal{X}}^{\times })\cong \operatorname{Pic}(X)$
, the Picard group of the generic fibre of
${\mathcal{X}}$
, and similarly
$\operatorname{Pic}(\mathfrak{X}^{\times })\cong \operatorname{Pic}(X^{\text{an}})$
, the Picard group of its analytification. The two are isomorphic by rigid analytic GAGA.◻
To relate this to log-crystalline cohomology, we use the following lemma.
Lemma 4.3. The inclusions
$W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times },\log }^{1}[-1]\rightarrow W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{\ast }$
and
$W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times },\log }^{1}[-1]\rightarrow W_{r}\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times }}^{\ast }$
induce surjections
$$\begin{eqnarray}\displaystyle H_{\text{cont}}^{1}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times },\log }^{1})_{\mathbb{Q}} & {\twoheadrightarrow} & \displaystyle H_{\text{log}\text{\text{-}}\text{crys}}^{2}({\mathcal{X}}^{\times }/K)^{\unicode[STIX]{x1D711}=p},\nonumber\\ \displaystyle H_{\text{cont}}^{1}({X_{0}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times },\log }^{1})_{\mathbb{Q}} & {\twoheadrightarrow} & \displaystyle H_{\text{log}\text{\text{-}}\text{crys}}^{2}(X_{0}^{\times }/K^{\times })^{\unicode[STIX]{x1D711}=p},\nonumber\end{eqnarray}$$
where
$\unicode[STIX]{x1D711}$
is the semilinear Frobenius operator. If
$k$
is algebraically closed, then the latter is in fact an isomorphism.
Proof. Let us first consider
${\mathcal{X}}^{\times }$
. Define the map
${\mathcal{F}}:\{W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{{\geqslant}1}\}\text{}_{r}\rightarrow \{W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{{\geqslant}1}\}\text{}_{r}$
to be
$p^{i-1}F$
in degree
$i$
; note that in degrees greater than
$1$
it is a contracting operator, and hence
$1-{\mathcal{F}}$
is invertible on
$W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{{>}1}$
. Similarly, the map
$1-V:\{W_{r}{\mathcal{O}}_{{\mathcal{X}}}\}\text{}_{r}\rightarrow \{W_{r}{\mathcal{O}}_{{\mathcal{X}}}\}\text{}_{r}$
is an isomorphism. From this and Proposition 2.2 it follows that the triangle
$$\begin{eqnarray}0\rightarrow \{W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times },\log }^{1}\}\text{}_{r}\rightarrow \{W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{{\geqslant}1}\}\text{}_{r}\overset{1-{\mathcal{F}}}{\rightarrow }\{W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{{\geqslant}1}\}\text{}_{r}\rightarrow 0\end{eqnarray}$$
of complexes of pro-sheaves is exact. Since
$p{\mathcal{F}}=\unicode[STIX]{x1D711}$
on
$W_{r}\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{{\geqslant}1}$
, we deduce an exact sequence
$$\begin{eqnarray}0\rightarrow \frac{H_{\text{cont}}^{1}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{{\geqslant}1})_{\mathbb{ Q}}}{\operatorname{im}(\unicode[STIX]{x1D711}-p)}\rightarrow H_{\text{cont}}^{1}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times },\log }^{1})_{\mathbb{ Q}}\rightarrow H_{\text{cont}}^{2}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{{\geqslant}1})_{\mathbb{ Q}}^{\unicode[STIX]{x1D711}=p}\rightarrow 0.\end{eqnarray}$$
For a complex of
$K$
-modules
$C^{\ast }$
with semilinear Frobenius, let us write
$\mathbf{R}_{\unicode[STIX]{x1D711}=p}(C^{\ast })$
for the mapping cone
$\text{Cone}(C^{\ast }\overset{\unicode[STIX]{x1D711}-p}{\rightarrow }C^{\ast })$
, and
$H_{\unicode[STIX]{x1D711}=p}^{n}(C^{\ast })$
for its cohomology groups. Then since
$1-V=\text{`}1-p\unicode[STIX]{x1D711}^{-1}\text{'}$
is invertible on
$\{W_{r}{\mathcal{O}}_{{\mathcal{X}}}\}\text{}_{r}$
we deduce that
$$\begin{eqnarray}\mathbf{R}_{\unicode[STIX]{x1D711}=p}(\mathbf{R}\unicode[STIX]{x1D6E4}_{\text{cont}}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{{\geqslant}1})_{\mathbb{ Q}})\cong \mathbf{R}_{\unicode[STIX]{x1D711}=p}(\mathbf{R}\unicode[STIX]{x1D6E4}_{\text{cont}}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times }}^{\ast })_{\mathbb{ Q}}).\end{eqnarray}$$
From this we extract the diagram
with exact rows, such that the middle vertical arrow is an isomorphism. In particular, the right vertical arrow is a surjection and, applying Proposition 2.4, we see that the map
$$\begin{eqnarray}H_{\text{cont}}^{1}({\mathcal{X}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D714}_{{\mathcal{X}}^{\times },\log }^{1})_{\mathbb{ Q}}{\twoheadrightarrow}H_{\text{log}\text{\text{-}}\text{crys}}^{2}({\mathcal{X}}^{\times }/K)^{\unicode[STIX]{x1D711}=p}\end{eqnarray}$$
is surjective as claimed. An entirely similar argument works for
$X_{0}^{\times }$
, replacing Proposition 2.4 with [Reference MatsuueMat17, Theorem 7.9], and in fact shows that
$$\begin{eqnarray}H_{\text{cont}}^{1}({X_{0}}_{\acute{\text{e}}\text{t}},W\unicode[STIX]{x1D714}_{X_{0}^{\times }/k^{\times },\log }^{1})_{\mathbb{ Q}}{\twoheadrightarrow}H_{\text{log}\text{\text{-}}\text{crys}}^{2}(X_{0}^{\times }/K^{\times })^{\unicode[STIX]{x1D711}=p}\end{eqnarray}$$
is an isomorphism if and only if
$(\unicode[STIX]{x1D711}-p)$
is surjective on
$H_{\text{log}\text{\text{-}}\text{crys}}^{1}(X_{0}^{\times }/K^{\times })$
. If
$k$
is algebraically closed, this follows from semisimplicity of the category of
$\unicode[STIX]{x1D711}$
-modules over
$K$
.◻
This enables us to deduce the following corollary.
Corollary 4.4. Let
${\mathcal{L}}\in \operatorname{Pic}(X_{0}^{\times })_{\mathbb{Q}}$
(respectively,
$\operatorname{Pic}(X_{0})_{\mathbb{Q}}$
). Then
${\mathcal{L}}$
lifts to
$\operatorname{Pic}({\mathcal{X}}^{\times })_{\mathbb{Q}}$
(respectively,
$\operatorname{Pic}({\mathcal{X}})_{\mathbb{Q}}$
) if and only if
$c_{1}({\mathcal{L}})\in H_{\text{log}\text{\text{-}}\text{crys}}^{2}(X_{0}^{\times }/K^{\times })^{\unicode[STIX]{x1D711}=p}$
lifts to
$H_{\text{log}\text{\text{-}}\text{crys}}^{2}({\mathcal{X}}^{\times }/K)^{\unicode[STIX]{x1D711}=p}$
.
Proof. Exactly as in the proof of Corollary 3.4. ◻
Let us now rephrase this criterion, which is more closely analogous to Yamashita’s criterion in [Reference YamashitaYam11]. Note that, thanks to [Reference Lazda and PálLP16, Corollary 5.8], we have an isomorphism
$$\begin{eqnarray}H_{\text{rig}}^{i}(X/{\mathcal{R}})\cong H_{\text{log}\text{\text{-}}\text{crys}}^{i}(X_{0}^{\times }/K^{\times })\otimes {\mathcal{R}}\end{eqnarray}$$
of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$
-modules over
${\mathcal{R}}$
, which induces an isomorphism
$$\begin{eqnarray}H_{\text{rig}}^{i}(X/{\mathcal{R}})^{\unicode[STIX]{x1D6FB}=0}\cong H_{\text{log}\text{\text{-}}\text{crys}}^{i}(X_{0}^{\times }/K^{\times })^{N=0}.\end{eqnarray}$$
By [Reference YamashitaYam11, Proposition 2.2] (the proof of which does not use the existence of a lift to characteristic
$0$
), the first Chern class
$c_{1}({\mathcal{L}})$
of any
${\mathcal{L}}$
in
$\operatorname{Pic}(X_{0}^{\times })_{\mathbb{Q}}$
or
$\operatorname{Pic}(X_{0})_{\mathbb{Q}}$
satisfies
$N(c_{1}({\mathcal{L}}))=0$
. Hence we may view
$c_{1}({\mathcal{L}})$
as an element of
$H_{\text{rig}}^{2}(X/{\mathcal{R}})$
.
Theorem 4.5. Assume that
${\mathcal{X}}$
is projective over
$R$
. Then
${\mathcal{L}}$
lifts to
$\operatorname{Pic}({\mathcal{X}}^{\times })_{\mathbb{Q}}$
(respectively,
$\operatorname{Pic}({\mathcal{X}})_{\mathbb{Q}}$
) if and only if
$c_{1}({\mathcal{L}})\in H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })\subset H_{\text{rig}}^{2}(X/{\mathcal{R}})$
.
Proof. Note that if
$c_{1}({\mathcal{L}})\in H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })$
, it is automatically in the subspace
$H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })^{\unicode[STIX]{x1D6FB}=0,\unicode[STIX]{x1D711}=p}$
. Now consider the Leray spectral sequence for log-crystalline cohomology
$$\begin{eqnarray}E_{2}^{p,q}=H_{\text{log}\text{\text{-}}\text{crys}}^{q}(\operatorname{Spec}(R^{\times }),\mathbf{R}^{p}f_{\ast }{\mathcal{O}}_{{\mathcal{X}}^{\times }/K}^{\text{crys}})\Rightarrow H_{\text{log}\text{\text{-}}\text{crys}}^{p+q}({\mathcal{X}}^{\times }/K),\end{eqnarray}$$
where
$f:{\mathcal{X}}^{\times }\rightarrow \operatorname{Spec}(R^{\times })$
denotes the structure map. Since
${\mathcal{X}}$
is projective we obtain maps
$$\begin{eqnarray}u^{i}:\mathbf{R}^{d-i}f_{\ast }{\mathcal{O}}_{{\mathcal{X}}^{\times }/K}^{\text{crys}}\rightarrow \mathbf{R}^{d+i}f_{\ast }{\mathcal{O}}_{{\mathcal{X}}^{\times }/K}^{\text{crys}}\end{eqnarray}$$
of log-
$F$
-isocrystals over
$R^{\times }$
by cupping with the class of a hyperplane section; we claim that
$u^{i}$
is an isomorphism. To check this, we note that we can identify the category of log-
$F$
-isocrystals over
$R^{\times }$
with the category
$\text{}\underline{\mathbf{M}\unicode[STIX]{x1D6F7}}_{{\mathcal{E}}^{+}}^{\unicode[STIX]{x1D6FB},\log }$
of log-
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$
-modules over the ring
${\mathcal{E}}^{+}:=W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}\otimes _{W}K$
as considered in [Reference Lazda and PálLP16, §5.3]. We now note that the functor of ‘passing to the generic fibre’ (i.e. tensoring with
${\mathcal{E}}:={\mathcal{E}}^{+}\langle t^{-1}\rangle$
) is fully faithful, by [Reference KedlayaKed04, Theorem 5.1] (together with a simple application of the 5 lemma), and hence by the hard Lefschetz theorem in rigid cohomology [Reference CaroCar16] (together with standard comparison theorems in crystalline cohomology) the isomorphy of
$u^{i}$
follows. Hence applying the formalism of [Reference MorrowMor14, §2] we obtain surjective maps
$$\begin{eqnarray}\displaystyle H_{\text{log}\text{\text{-}}\text{crys}}^{2}({\mathcal{X}}^{\times }/K) & \rightarrow & \displaystyle H_{\text{log}\text{\text{-}}\text{crys}}^{0}(\operatorname{Spec}(R^{\times }),\mathbf{R}^{2}f_{\ast }{\mathcal{O}}_{{\mathcal{X}}^{\times }/K}^{\text{crys}}),\nonumber\\ \displaystyle H_{\text{log}\text{\text{-}}\text{crys}}^{2}({\mathcal{X}}^{\times }/K)^{\unicode[STIX]{x1D711}=p} & \rightarrow & \displaystyle H_{\text{log}\text{\text{-}}\text{crys}}^{0}(\operatorname{Spec}(R^{\times }),\mathbf{R}^{2}f_{\ast }{\mathcal{O}}_{{\mathcal{X}}^{\times }/K}^{\text{crys}})^{\unicode[STIX]{x1D711}=p}\nonumber\end{eqnarray}$$
as the edge maps of degenerate Leray spectral sequences (see, in particular, [Reference MorrowMor14, Lemma 2.4, Theorem 2.5]). Finally, we note that again applying Kedlaya’s full faithfulness theorem, together with the proof of [Reference Lazda and PálLP16, Proposition 5.45], we can see that
$$\begin{eqnarray}H_{\text{log}\text{\text{-}}\text{crys}}^{0}(\operatorname{Spec}(R^{\times }),\mathbf{R}^{2}f_{\ast }{\mathcal{O}}_{{\mathcal{X}}^{\times }/K}^{\text{crys}})^{\unicode[STIX]{x1D711}=p}\cong H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })^{\unicode[STIX]{x1D6FB}=0,\unicode[STIX]{x1D711}=p},\end{eqnarray}$$
and the claim follows. ◻
We will now give one final reformulation of this result.
Definition 4.6.
(i) We say that a cohomology class in
$H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })$
is algebraic if it is in the image of
$\operatorname{Pic}(X)_{\mathbb{Q}}$
under the Chern class map.(ii) We say that a cohomology class in
$H_{\text{log}\text{\text{-}}\text{crys}}^{2}(X_{0}^{\times }/K)$
is log-algebraic if it is in the image of
$\operatorname{Pic}(X_{0}^{\times })_{\mathbb{Q}}$
under the Chern class map.(iii) We say that a cohomology class in
$H_{\text{log}\text{\text{-}}\text{crys}}^{2}(X_{0}^{\times }/K)$
is algebraic if it is in the image of
$\operatorname{Pic}(X_{0})_{\mathbb{Q}}$
under the Chern class map.
Let
$$\begin{eqnarray}\text{sp}:H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })^{\unicode[STIX]{x1D6FB}=0}{\hookrightarrow}H_{\text{rig}}^{2}(X/{\mathcal{R}})^{\unicode[STIX]{x1D6FB}=0}\overset{{\sim}}{\rightarrow }H_{\text{log}\text{\text{-}}\text{crys}}^{2}(X_{0}^{\times }/K)^{N=0}{\hookrightarrow}H_{\text{log}\text{\text{-}}\text{crys}}^{2}(X_{0}^{\times }/K)\end{eqnarray}$$
denote the composite homomorphism.
Theorem 4.7. Assume that
${\mathcal{X}}$
is projective, and let
$\unicode[STIX]{x1D6FC}\in H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })$
. The following statements are equivalent:
(i)
$\unicode[STIX]{x1D6FC}$
is algebraic;(ii)
$\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D6FC})=0$
and
$\text{sp}(\unicode[STIX]{x1D6FC})$
is log-algebraic;(iii)
$\unicode[STIX]{x1D6FB}(\unicode[STIX]{x1D6FC})=0$
and
$\text{sp}(\unicode[STIX]{x1D6FC})$
is algebraic.
Proof. Note that since
$\text{sp}$
is injective, the hypotheses in both (ii) and (iii) imply that
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})=p\unicode[STIX]{x1D6FC}$
. Since
${\mathcal{X}}$
is flat, its special fibre is a principal Cartier divisor, therefore the restriction map
$\operatorname{Pic}({\mathcal{X}})_{\mathbb{Q}}\rightarrow \operatorname{Pic}(X)_{\mathbb{Q}}$
is an isomorphism. The claim then follows from Theorem 4.5.◻
5 Global results
In this section we will deduce some global algebraicity results more closely analogous to the main results of [Reference MorrowMor14]. We will therefore change notation and let
$F$
denote a function field of transcendence degree
$1$
over our perfect field
$k$
of characteristic
$p$
. We will let
$v$
denote a place of
$F$
with completion
$F_{v}$
and residue field
$k_{v}$
. Let
${\mathcal{C}}$
denote the unique smooth, proper, geometrically connected curve over
$k$
with function field
$F$
. Let
$F^{\text{sep}}$
denote a fixed separable closure of
$F$
with Galois group
$G_{F}$
.
Definition 5.1. Define
$F\text{\text{-}}\text{Isoc}(F/K):=2\text{\text{-}}\text{colim}_{U}F\text{\text{-}}\text{Isoc}(U/K)$
, the colimit being taken over all non-empty open subschemes
$U\subset {\mathcal{C}}$
.
Note that, by [Reference KedlayaKed07, Theorem 5.2.1], for any
$E\in F\text{\text{-}}\text{Isoc}(F/K)$
, defined on some
$U\subset {\mathcal{C}}$
, the zeroth cohomology group
$$\begin{eqnarray}E^{\unicode[STIX]{x1D6FB}=0}=H_{\text{rig}}^{0}(U/K,E)\end{eqnarray}$$
is a well-defined (i.e. independent of
$U$
)
$F$
-isocrystal over
$K$
. For any smooth and projective variety
$X/F$
we have cohomology groups
${\mathcal{H}}_{\text{rig}}^{i}(X/K)\in F\text{\text{-}}\text{Isoc}(F/K)$
obtained by choosing a smooth projective model over some
$U\subset {\mathcal{C}}$
, taking the higher direct images and applying [Reference Matsuda and TrihanMT04, Corollaire 3]. As constructed in [Reference PálPál15, §6] (see, in particular Propositions, 6.17 and 7.2) there is a
$p$
-adic Chern class map
$$\begin{eqnarray}c_{1}:\operatorname{Pic}(X)_{\mathbb{Q}}\rightarrow {\mathcal{H}}_{\text{rig}}^{2}(X/K)^{\unicode[STIX]{x1D6FB}=0}\end{eqnarray}$$
and we will call elements in the image algebraic.
Assume now that
$X$
has semistable reduction at
$v$
, and denote the associated log smooth scheme over
$k_{v}^{\times }$
by
$X_{v}^{\times }$
. Let
${\mathcal{E}}_{v}^{\dagger }$
denote a copy of the bounded Robba ring ‘at
$v$
’, so that by [Reference TsuzukiTsu98, §6.1] there is a functor
$$\begin{eqnarray}\mathbf{i}_{v}^{\ast }:F\text{\text{-}}\text{Isoc}(F/K)\rightarrow \text{}\underline{\mathbf{M}\unicode[STIX]{x1D6F7}}_{{\mathcal{E}}_{v}^{\dagger }}^{\unicode[STIX]{x1D6FB}}.\end{eqnarray}$$
Thanks to the proof of [Reference Lazda and PálLP16, Proposition 5.52] this functor sends
${\mathcal{H}}_{\text{rig}}^{2}(X/K)$
to
$H_{\text{rig}}^{2}(X_{F_{v}}/{\mathcal{E}}_{v}^{\dagger })$
. In particular, we obtain a map
$$\begin{eqnarray}r_{v}:{\mathcal{H}}_{\text{rig}}^{2}(X/K)^{\unicode[STIX]{x1D6FB}=0}\rightarrow H_{\text{rig}}^{2}(X_{F_{v}}/{\mathcal{E}}_{v}^{\dagger })^{\unicode[STIX]{x1D6FB}=0}\end{eqnarray}$$
and, composing with the specialisation map considered at the end of § 4, we obtain a homomorphism
$$\begin{eqnarray}\text{sp}_{v}:{\mathcal{H}}_{\text{rig}}^{2}(X/K)^{\unicode[STIX]{x1D6FB}=0}\rightarrow H_{\text{log}\text{\text{-}}\text{crys}}^{2}(X_{v}^{\times }/K_{v}^{\times })\end{eqnarray}$$
where
$K_{v}=W(k_{v})[1/p]$
.
Theorem 5.2. Assume that
$X$
is projective, and let
$\unicode[STIX]{x1D6FC}\in {\mathcal{H}}_{\text{rig}}^{2}(X/K)^{\unicode[STIX]{x1D6FB}=0}$
. The following statements are equivalent:
(i)
$\unicode[STIX]{x1D6FC}$
is algebraic;(ii)
$\text{sp}_{v}(\unicode[STIX]{x1D6FC})$
is algebraic;(iii)
$\text{sp}_{v}(\unicode[STIX]{x1D6FC})$
is log-algebraic.
Proof. As before the hypotheses in (ii) and (iii) imply that
$\unicode[STIX]{x1D711}(\unicode[STIX]{x1D6FC})=p\unicode[STIX]{x1D6FC}$
. By Theorem 4.7 we clearly have
$(\text{i})\Rightarrow (\text{ii})\Leftrightarrow (\text{iii})$
, and if (ii) or (iii) hold then there exists a line bundle
${\mathcal{L}}\in \operatorname{Pic}(X_{F_{v}})_{\mathbb{Q}}$
such that
$r_{v}(\unicode[STIX]{x1D6FC})=c_{1}({\mathcal{L}})$
in
$H_{\text{rig}}^{2}(X_{F_{v}}/{\mathcal{E}}_{v}^{\dagger })^{\unicode[STIX]{x1D6FB}=0}$
. To descend
${\mathcal{L}}$
to
$\operatorname{Pic}(X)_{\mathbb{Q}}$
we follow the proof of Corollary 3.4. Specifically, applying Néron–Popescu desingularisation to the extension
$F_{v}^{h}\rightarrow F_{v}$
from the Henselisation to the completion at
$v$
and arguing exactly as before, we can in fact assume that
${\mathcal{L}}$
descends to
$X_{F_{v}^{h}}$
, and hence to
$X_{F^{\prime }}$
for some finite, separable extension
$F^{\prime }/F$
. Again taking the pushforward and dividing by the degree gives the result.◻
6 A counter-example
A natural question to ask is whether or not the analogue of Corollary 3.4 or Corollary 4.4 holds with
$\operatorname{Pic}(-)_{\mathbb{Q}}$
replaced by
$\operatorname{Pic}(-)_{\mathbb{Q}_{p}}$
. We will show in the section that when
$k$
is a finite field this cannot be the case, since it would imply Tate’s isogeny theorem for elliptic curves over
$k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
. Let us return to the previous notation, writing
$F=k(\!(t)\!)$
and
$R=k\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
for its ring of integers.
We first need to quickly recall some material on Dieudonné modules of abelian varieties over
$k,R$
and
$F$
. As before, we will let
$W$
denote the ring of Witt vectors of
$k$
, set
$\unicode[STIX]{x1D6FA}=W\unicode[STIX]{x27E6}t\unicode[STIX]{x27E7}$
and let
$\unicode[STIX]{x1D6E4}$
be the
$p$
-adic completion of
$\unicode[STIX]{x1D6FA}[t^{-1}]$
, so that we have
${\mathcal{E}}^{+}=\unicode[STIX]{x1D6FA}[1/p]$
and
${\mathcal{E}}=\unicode[STIX]{x1D6E4}[1/p]$
. Fix compatible lifts
$\unicode[STIX]{x1D70E}$
of absolute Frobenius to
$W\subset \unicode[STIX]{x1D6FA}\subset \unicode[STIX]{x1D6E4}$
. By [Reference de JongdeJ95, Main Theorem 1] there are covariant equivalences of categories
$$\begin{eqnarray}\mathbf{D}:\mathbf{BT}_{k}\overset{{\sim}}{\rightarrow }\mathbf{DM}_{W},\quad \mathbf{D}:\mathbf{BT}_{R}\overset{{\sim}}{\rightarrow }\mathbf{DM}_{\unicode[STIX]{x1D6FA}},\quad \mathbf{D}:\mathbf{BT}_{F}\overset{{\sim}}{\rightarrow }\mathbf{DM}_{\unicode[STIX]{x1D6E4}}\end{eqnarray}$$
between
$p$
-divisible groups over
$k$
(respectively,
$R$
,
$F$
) and finite free Dieudonné modules over
$W$
(respectively,
$\unicode[STIX]{x1D6FA}$
,
$\unicode[STIX]{x1D6E4}$
). In particular, if
${\mathcal{A}}$
is an abelian variety over any of these rings, we will let
$\mathbf{D}({\mathcal{A}})$
denote the (covariant) Dieudonné module of its
$p$
-divisible group
${\mathcal{A}}[p^{\infty }]$
. It follows essentially from the construction (see [Reference Berthelot, Breen and MessingBBM82]) together with the comparison between crystalline and rigid cohomology that when
$A/F$
is an abelian variety we have
$\mathbf{D}(A)\otimes _{\unicode[STIX]{x1D6E4}}{\mathcal{E}}\cong H_{\text{rig}}^{1}(A/{\mathcal{E}})^{\vee }(-1)$
as
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$
-modules over
${\mathcal{E}}$
, and from [Reference KedlayaKed00, Theorem 7.0.1] that
$\mathbf{D}(A)\otimes _{\unicode[STIX]{x1D6E4}}{\mathcal{E}}$
canonically descends to a
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$
-module
$\mathbf{D}^{\dagger }(A)\cong H_{\text{rig}}^{1}(A/{\mathcal{E}}^{\dagger })^{\vee }(-1)$
over
${\mathcal{E}}^{\dagger }$
. The results of [Reference Berthelot, Breen and MessingBBM82, §5.1] give a canonical isomorphism
$\mathbf{D}^{\dagger }(A^{\vee })\cong \mathbf{D}^{\dagger }(A)^{\vee }(-1)$
of
$(\unicode[STIX]{x1D711},\unicode[STIX]{x1D6FB})$
-modules over
${\mathcal{E}}^{\dagger }$
. In particular, if
$E$
is an elliptic curve then we have a canonical isomorphism
$E\cong E^{\vee }$
and hence an isomorphism
$\mathbf{D}^{\dagger }(E)\cong \mathbf{D}^{\dagger }(E)^{\vee }(-1)$
.
We can now proceed to the construction of our counter-example. It will be a smooth projective relative surface
${\mathcal{X}}$
over
$R$
, obtained as a product
${\mathcal{E}}_{1}\times _{R}{\mathcal{E}}_{2}^{\vee }$
(
$={\mathcal{E}}_{1}\times _{R}{\mathcal{E}}_{2}$
) where
${\mathcal{E}}_{i}$
are elliptic curves over
$R$
(to be specified later on). Let
$X$
denote the generic fibre of
${\mathcal{X}}$
and
$X_{0}$
the special fibre. As a product of elliptic curves, we know that the Tate conjecture for divisors holds for
$X_{0}$
, that is, the map
$$\begin{eqnarray}c_{1}:\operatorname{Pic}(X_{0})_{\mathbb{Q}_{p}}\rightarrow H_{\text{rig}}^{2}(X_{0}/K)^{\unicode[STIX]{x1D711}=p}\end{eqnarray}$$
is surjective. Functoriality of Dieudonné modules induces a homomorphism
$$\begin{eqnarray}\mathbf{D}_{E_{1},E_{2}}^{\dagger }:\operatorname{Hom}(E_{1},E_{2})\otimes _{\mathbb{Z}}\mathbb{Q}_{p}\rightarrow \operatorname{Hom}_{\text{}\underline{\mathbf{M}\unicode[STIX]{x1D6F7}}_{{\mathcal{E}}^{\dagger }}^{\unicode[STIX]{x1D6FB}}}(\mathbf{D}^{\dagger }(E_{1}),\mathbf{D}^{\dagger }(E_{2}))\end{eqnarray}$$
which is injective by standard results.
Theorem 6.1. Assume that any
${\mathcal{L}}\in \operatorname{Pic}(X_{0})_{\mathbb{Q}_{p}}$
whose first Chern class
$c_{1}({\mathcal{L}})\in H_{\text{rig}}^{2}(X/{\mathcal{R}})$
lies in the subspace
$H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })\subset H_{\text{rig}}^{2}(X/{\mathcal{R}})$
lifts to
$\operatorname{Pic}({\mathcal{X}})_{\mathbb{Q}_{p}}$
; in other words, assume that the
$\mathbb{Q}_{p}$
-analogue of Corollary 3.4 holds. Then the map
$\mathbf{D}_{E_{1},E_{2}}^{\dagger }$
is an isomorphism.
Proof. This is essentially well known. To start with, we note that we have a commutative diagram
with bottom horizontal map surjective. Under the given assumptions the top horizontal map is also surjective, and induces an isomorphism
$\text{NS}(X)_{\mathbb{Q}_{p}}\overset{{\sim}}{\rightarrow }H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })^{\unicode[STIX]{x1D6FB}=0,\unicode[STIX]{x1D711}=p}$
. It follows from the Künneth formula [Reference Lazda and PálLP16, Corollary 3.78] that
$$\begin{eqnarray}H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })\cong {\mathcal{E}}^{\dagger }(-1)\oplus H_{\text{rig}}^{1}(E_{1}/{\mathcal{E}}^{\dagger })\otimes H_{\text{rig}}^{1}(E_{2}^{\vee }/{\mathcal{E}}^{\dagger })\oplus {\mathcal{E}}^{\dagger }(-1),\end{eqnarray}$$
where the terms at either end are
$H^{0}\,\otimes \,H^{2}$
and
$H^{2}\,\otimes \,H^{0}$
, respectively. Since
$H_{\text{rig}}^{1}(E_{1}/{\mathcal{E}}^{\dagger })\cong \mathbf{D}^{\dagger }(E_{1})$
and
$H_{\text{rig}}^{1}(E_{2}^{\vee }/{\mathcal{E}}^{\dagger })\cong \mathbf{D}^{\dagger }(E_{2})^{\vee }(-1)$
we have that
$$\begin{eqnarray}\displaystyle H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })^{\unicode[STIX]{x1D6FB}=0,\unicode[STIX]{x1D711}=p} & = & \displaystyle \mathbb{Q}_{p}\oplus (\mathbf{D}^{\dagger }(E_{1})\otimes _{{\mathcal{E}}^{\dagger }}\mathbf{D}^{\dagger }(E_{2})^{\vee })^{\unicode[STIX]{x1D6FB}=0,\unicode[STIX]{x1D711}=\text{id}}\oplus \mathbb{Q}_{p}\nonumber\\ \displaystyle & = & \displaystyle \mathbb{Q}_{p}\oplus \operatorname{Hom}_{\text{}\underline{\mathbf{M}\unicode[STIX]{x1D6F7}}_{{\mathcal{E}}^{\dagger }}^{\unicode[STIX]{x1D6FB}}}(\mathbf{D}^{\dagger }(E_{1}),\mathbf{D}^{\dagger }(E_{2}))\oplus \mathbb{Q}_{p}.\nonumber\end{eqnarray}$$
Next, let
$\text{DC}_{\text{alg}}(E_{1},E_{2}^{\vee })$
denote the group of divisorial correspondences from
$E_{1}$
to
$E_{2}^{\vee }$
modulo algebraic equivalence; in other words, line bundles on
$E_{1}\times E_{2}^{\vee }$
whose restriction to both
$E_{1}\times \{0\}$
and
$\{0\}\times E_{2}^{\vee }$
is trivial. Then we have shown that the map
$$\begin{eqnarray}\text{DC}_{\text{alg}}(E_{1},E_{2}^{\vee })_{\mathbb{ Q}_{p}}\rightarrow \operatorname{Hom}_{\text{}\underline{\mathbf{M}\unicode[STIX]{x1D6F7}}_{{\mathcal{E}}^{\dagger }}^{\unicode[STIX]{x1D6FB}}}(\mathbf{D}^{\dagger }(E_{1}),\mathbf{D}^{\dagger }(E_{2}))\end{eqnarray}$$
is an isomorphism, and since
$\text{DC}_{\text{alg}}(E_{1},E_{2}^{\vee })_{\mathbb{Q}}\cong \operatorname{Hom}(E_{1},E_{2})_{\mathbb{Q}}$
, it follows that the map
$$\begin{eqnarray}\operatorname{Hom}(E_{1},E_{2})_{\mathbb{Q}_{p}}\rightarrow \operatorname{Hom}_{\text{}\underline{\mathbf{M}\unicode[STIX]{x1D6F7}}_{{\mathcal{E}}^{\dagger }}^{\unicode[STIX]{x1D6FB}}}(\mathbf{D}^{\dagger }(E_{1}),\mathbf{D}^{\dagger }(E_{2}))\end{eqnarray}$$
is also an isomorphism. This completes the proof. ◻
In other words, to produce our required counter-example
${\mathcal{X}}$
we need to produce elliptic curves
${\mathcal{E}}_{1}$
and
${\mathcal{E}}_{2}$
as above such that
$\mathbf{D}_{E_{1},E_{2}}^{\dagger }$
is not surjective. So let
$k=\mathbb{F}_{p^{2}}$
and let
$E_{0}/k$
be a supersingular elliptic curve such that
$\text{Frob}_{p^{2}}=[p]\in \text{End}(E_{0})$
(such elliptic curves exist by Honda–Tate theory). It easily follows that any
$\bar{k}$
-endomorphism of
$E_{0}$
has to commute with
$\text{Frob}_{p^{2}}$
, and is hence defined over
$k$
. By the
$p$
-adic version of Tate’s isogeny theorem the
$p$
-divisible group functor induces an isomorphism:
$$\begin{eqnarray}\operatorname{End}(E_{0})\otimes \mathbb{Z}_{p}\longrightarrow \operatorname{End}(E_{0}[p^{\infty }]).\end{eqnarray}$$
Lemma 6.2. There exists an isomorphism
$\unicode[STIX]{x1D719}:E_{0}[p^{\infty }]\rightarrow E_{0}[p^{\infty }]$
whose
$\mathbb{Q}_{p}$
-linear span in
$\operatorname{End}(E_{0}[p^{\infty }])\otimes _{\mathbb{Z}_{p}}\mathbb{Q}_{p}$
cannot be spanned by an element in
$$\begin{eqnarray}\operatorname{End}(E_{0})\otimes \mathbb{Q}\subset \operatorname{End}(E_{0})\otimes \mathbb{Q}_{p}=\operatorname{End}(E_{0}[p^{\infty }])\otimes _{\mathbb{ Z}_{p}}\mathbb{Q}_{p}.\end{eqnarray}$$
Proof. Since
$\operatorname{End}(E_{0}[p^{\infty }])$
is an order in a quaternion algebra over
$\mathbb{Q}_{p}$
by [Reference SilvermanSil86, ch. V, Theorem 3.1], its group of invertible elements is a
$p$
-adic Lie group of dimension at least
$3$
. Therefore the
$\mathbb{Q}_{p}$
-linear spans of elements of
$\operatorname{End}(E_{0}[p^{\infty }])^{\ast }$
are uncountable. As
$\operatorname{End}(E_{0})\otimes \mathbb{Q}$
is countable, there is a
$\unicode[STIX]{x1D719}\in \operatorname{End}(E_{0}[p^{\infty }])^{\ast }$
whose
$\mathbb{Q}_{p}$
-linear span cannot be spanned by the left-hand side of the inclusion above.◻
Let
${\mathcal{E}}_{1}$
be an elliptic curve over
$R$
whose special fibre is
$E_{0}$
and whose generic fibre
$E_{1}$
over
$F=k(\!(t)\!)$
is ordinary. Via the isomorphism
$\unicode[STIX]{x1D719}$
in the lemma above we can consider
${\mathcal{E}}_{1}[p^{\infty }]$
as a deformation of
$E_{0}[p^{\infty }]$
. By the Serre–Tate theorem [Reference MessingMes72, V. Theorem 2.3] there is a deformation
${\mathcal{E}}_{2}$
of
$E_{0}$
over
$R$
corresponding to this deformation of
$p$
-divisible groups. Let
$E_{2}$
denote the generic fibre of
${\mathcal{E}}_{2}$
over
$F$
.
Proposition 6.3. The map
$$\begin{eqnarray}\mathbf{D}_{E_{1},E_{2}}^{\dagger }:\operatorname{Hom}(E_{1},E_{2})\otimes \mathbb{Q}_{p}\longrightarrow \operatorname{Hom}_{\text{}\underline{\mathbf{M}\unicode[STIX]{x1D6F7}}_{{\mathcal{E}}^{\dagger }}^{\unicode[STIX]{x1D6FB}}}(\mathbf{D}^{\dagger }(E_{1}),\mathbf{D}^{\dagger }(E_{2}))\end{eqnarray}$$
is not surjective.
Proof. Assume for contradiction that in fact
$\mathbf{D}_{E_{1},E_{2}}^{\dagger }$
is an isomorphism. By construction
${\mathcal{E}}_{1}[p^{\infty }]\cong {\mathcal{E}}_{2}[p^{\infty }]$
, so by the functoriality of Dieudonné modules
$\operatorname{Hom}(\mathbf{D}({\mathcal{E}}_{1}),\mathbf{D}({\mathcal{E}}_{2}))$
is non-zero. Hence
$\operatorname{Hom}(\mathbf{D}(E_{1}),\mathbf{D}(E_{2}))$
is also non-zero. As
$$\begin{eqnarray}\mathbf{D}^{\dagger }(E_{i})\otimes _{{\mathcal{E}}^{\dagger }}{\mathcal{E}}=\mathbf{D}(E_{i})\otimes _{\unicode[STIX]{x1D6E4}}{\mathcal{E}},\end{eqnarray}$$
we get that
$\operatorname{Hom}(\mathbf{D}^{\dagger }(E_{1}),\mathbf{D}^{\dagger }(E_{2}))$
is also non-zero, by Kedlaya’s full faithfulness theorem [Reference KedlayaKed04, Theorem 5.1]. So by our assumptions
$\operatorname{Hom}(E_{1},E_{2})$
is also non-zero, and the elliptic curves
$E_{1}$
and
$E_{2}$
are isogeneous.
As
${\mathcal{E}}_{1}$
is generically ordinary but has a supersingular special fibre, it is not constant, that is, the
$j$
-invariant of its generic fibre
$j(E_{1})\not \in \overline{\mathbb{F}}_{p}$
. Therefore End
$(E_{1})=\mathbb{Z}$
, so by the above
$\operatorname{Hom}(E_{1},E_{2})\otimes \mathbb{Q}_{p}$
is one-dimensional. Therefore the same holds for
$\operatorname{Hom}(\mathbf{D}^{\dagger }(E_{1}),\mathbf{D}^{\dagger }(E_{2}))$
, too. We have a commutative diagram
The lower horizontal map is an isomorphism by de Jong’s full faithfulness theorem [Reference de JongdeJ98], the upper horizontal map is an isomorphism since any abelian scheme is the Néron model of its generic fibre, and the right vertical map is an isomorphism by assumption. So the left vertical map is an isomorphism, too. Specialisation furnishes us with another commutative diagram:
By construction the image of the lower horizontal map in
$$\begin{eqnarray}\operatorname{End}(\mathbf{D}(E_{0}))\otimes _{\mathbb{Z}_{p}}\mathbb{Q}_{p}=\operatorname{End}(E_{0}[p^{\infty }])\otimes _{\mathbb{ Z}_{p}}\mathbb{Q}_{p}\end{eqnarray}$$
contains the span of
$\unicode[STIX]{x1D719}$
. Since the domain of this map is one-dimensional, we get that its image is the span of
$\unicode[STIX]{x1D719}$
. Since the left vertical map is an isomorphism by the above, we get that the span of
$\unicode[STIX]{x1D719}$
is spanned by the specialisation of any non-zero isogeny
${\mathcal{E}}_{1}\rightarrow {\mathcal{E}}_{2}$
. This is a contradiction.◻
We therefore arrive at the following result.
Corollary 6.4. There exist a smooth, projective relative surface
${\mathcal{X}}/R$
with generic fibre
$X$
and special fibre
$X_{0}$
, and a class
${\mathcal{L}}\in \operatorname{Pic}(X_{0})_{\mathbb{Q}_{p}}$
whose Chern class
$c_{1}({\mathcal{L}})\in H_{\text{rig}}^{2}(X/{\mathcal{R}})$
lies inside
$H_{\text{rig}}^{2}(X/{\mathcal{E}}^{\dagger })$
but which does not lift to
$\operatorname{Pic}({\mathcal{X}})_{\mathbb{Q}_{p}}$
.
Acknowledgements
A. Pál was partially supported by EPSRC grant P36794. C. Lazda was supported by a Marie Curie fellowship of the Istituto Nazionale di Alta Matematica ‘F. Severi’. Both authors would like to thank Imperial College London and the Università Degli Studi di Padova for hospitality during the writing of this paper.
