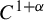1 Introduction
In his 1998 ICM address, Viana proposed the following conjecture.
Conjecture. If a smooth map f has only non-zero Lyapunov exponents at Lebesgue almost every (a.e.) point, then f preserves an SRB measure.
SRB measures were first constructed in the 1970s by Sinai, Ruelle, and Bowen in the context of Axiom A attractors [Reference Bowen and Chazottes6, Reference Ruelle14, Reference Sinai16], that is, topological attractors which are uniformly hyperbolic and contain a dense set of periodic points. SRB measures are hyperbolic measures, meaning that all of their Lyapunov exponents are non-zero, whose conditional measures along almost every unstable manifold are absolutely continuous with respect to leaf volume on those unstables. Later, a somewhat similar notion of u-measures was introduced by Pesin and Sinai in [Reference Pesin and Sinai11], in the context of partially hyperbolic attractors. These measures are characterized by the fact that the conditional measures they generate on unstable manifolds are absolutely continuous with respect to the leaf volume, but these measures may lack some good ergodic properties due to presence of zero Lyapunov exponents in the central direction of the partially hyperbolic system.
Let us mention some recent results on the existence of SRB measures in the partially hyperbolic case. Burns et al [Reference Burns, Dolgopyat, Pesin and Pollicott7] proved that under the assumptions that the Lyapunov exponents in the central direction are negative on a set of positive measure and global unstable leaves are dense, the u-measure turns out to be the unique SRB measure. Bonatti and Viana [Reference Bonatti and Viana5] proved the existence of an SRB measure assuming a splitting
![]() $TM=E^{s} \oplus E^{uu}$
, with uniform expansion in the
$TM=E^{s} \oplus E^{uu}$
, with uniform expansion in the
![]() $E^{uu}$
-direction and non-uniform contraction in the
$E^{uu}$
-direction and non-uniform contraction in the
![]() $E^{s}$
-direction. Alves, Bonatti, and Viana [Reference Alves, Bonatti and Viana1] proved the existence of SRB measures under the assumption that the splitting is of the form
$E^{s}$
-direction. Alves, Bonatti, and Viana [Reference Alves, Bonatti and Viana1] proved the existence of SRB measures under the assumption that the splitting is of the form
![]() $E^{ss}\oplus E^{u}$
. This last result was generalized by Climenhaga, Dolgopyat, and Pesin [Reference Climenhaga, Dolgopyat and Pesin8], who only assumed the splitting to be measurable and the expansion and contractions are both non-uniform. They established the existence of SRB measures under the assumption of effective hyperbolicity. Ben Ovadia [Reference Ben Ovadia4] constructed SRB measures under a certain leaf condition, which we will introduce and discuss later in more detail. His construction uses the theory of Markov partitions and the thermodynamical formalism developed by Sarig in [Reference Sarig15] for countable topological Markov shifts.
$E^{ss}\oplus E^{u}$
. This last result was generalized by Climenhaga, Dolgopyat, and Pesin [Reference Climenhaga, Dolgopyat and Pesin8], who only assumed the splitting to be measurable and the expansion and contractions are both non-uniform. They established the existence of SRB measures under the assumption of effective hyperbolicity. Ben Ovadia [Reference Ben Ovadia4] constructed SRB measures under a certain leaf condition, which we will introduce and discuss later in more detail. His construction uses the theory of Markov partitions and the thermodynamical formalism developed by Sarig in [Reference Sarig15] for countable topological Markov shifts.
One observation about all the papers mentioned above is that they deal only with the forward dynamics of the system, and so they look at the forward Lyapunov exponents, and ask, given that we have a positive volume of points with non-zero forward Lyapunov exponents, what can we say about the existence of the SRB measure. In this paper, we consider the forward and backward behavior of Lyapunov exponents, and ask what can we say about the natural measures for the system? So the central assumption in this paper is the positivity of the Riemannian volume of the set of hyperbolic Lyapunov–Perron regular points, which we define next.
Definition 1.1. A point
![]() $x \in M$
is Lyapunov–Perron regular for a diffeomorphism
$x \in M$
is Lyapunov–Perron regular for a diffeomorphism
![]() $f:M\to M$
if there exist numbers
$f:M\to M$
if there exist numbers
![]() $\unicode{x3bb} _{1}(x) \leq \unicode{x3bb} _{2}(x) \leq \cdots \leq \unicode{x3bb} _{k(x)}(x)$
and an invariant decomposition
$\unicode{x3bb} _{1}(x) \leq \unicode{x3bb} _{2}(x) \leq \cdots \leq \unicode{x3bb} _{k(x)}(x)$
and an invariant decomposition
 $$ \begin{align*} T_{x}M = \bigoplus_{i=1}^{k(x)}E_{i}(x) \end{align*} $$
$$ \begin{align*} T_{x}M = \bigoplus_{i=1}^{k(x)}E_{i}(x) \end{align*} $$
such that for all
![]() $v\in E_{i}(x)$
, we have
$v\in E_{i}(x)$
, we have
 $$ \begin{align*} \lim_{n\to\pm\infty}\frac1n\log\|\det(D_{x}f^{n})\| = \sum_{i=1}^{k(x)}\unicode{x3bb}_{i}(x), \end{align*} $$
$$ \begin{align*} \lim_{n\to\pm\infty}\frac1n\log\|\det(D_{x}f^{n})\| = \sum_{i=1}^{k(x)}\unicode{x3bb}_{i}(x), \end{align*} $$
and that
![]() $\unicode{x3bb} _{i}(x)$
,
$\unicode{x3bb} _{i}(x)$
,
![]() $E_{i}(x)$
, and
$E_{i}(x)$
, and
![]() $k(x)$
depend measurably on x. We denote the set of all Lyapunov–Perron regular points by
$k(x)$
depend measurably on x. We denote the set of all Lyapunov–Perron regular points by
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
Definition 1.2. (Hyperbolic Lyapunov–Perron regular points)
We say that x is a hyperbolic Lyapunov–Perron regular point if it was a Lyapunov–Perron regular point, and if there exists an integer
![]() $1 \leq s < k(x)$
for which we have
$1 \leq s < k(x)$
for which we have
![]() $ \unicode{x3bb} _{s}(x) < 0 < \unicode{x3bb} _{s+1}(x)$
. We denote the set of all hyperbolic Lyapunov–Perron regular points by
$ \unicode{x3bb} _{s}(x) < 0 < \unicode{x3bb} _{s+1}(x)$
. We denote the set of all hyperbolic Lyapunov–Perron regular points by
![]() $\mathcal {R}_{\mathrm {hyp}}$
.
$\mathcal {R}_{\mathrm {hyp}}$
.
The celebrated Oseledets’ multiplicative ergodic theorem states that any invariant probability measure
![]() $\mu $
for a diffeomorphism
$\mu $
for a diffeomorphism
![]() $f : M\to M$
gives full measure to the set of Lyapunov–Perron regular points. That is,
$f : M\to M$
gives full measure to the set of Lyapunov–Perron regular points. That is,
![]() $\mu (\mathcal {R})=1$
. In particular, an SRB measure
$\mu (\mathcal {R})=1$
. In particular, an SRB measure
![]() $\mu ^{+}$
for f gives full measure to the subset
$\mu ^{+}$
for f gives full measure to the subset
![]() $\mathcal {R}_{\mathrm {hyp}}\subset \mathcal {R}$
of hyperbolic Lyapunov–Perron regular points. Notice that this does not necessarily imply that the the set
$\mathcal {R}_{\mathrm {hyp}}\subset \mathcal {R}$
of hyperbolic Lyapunov–Perron regular points. Notice that this does not necessarily imply that the the set
![]() $\mathcal {R}_{\mathrm {hyp}}$
has positive volume. Indeed, for a point x in the basin of attraction of the SRB measure
$\mathcal {R}_{\mathrm {hyp}}$
has positive volume. Indeed, for a point x in the basin of attraction of the SRB measure
![]() $\mu ^{+}$
,
$\mu ^{+}$
,
 $$ \begin{align*}B(\mu^{+}) = \bigg\{x \in M \mid \frac{1}{n} \sum_{k=0}^{n-1} \varphi(f^{k}x) \longrightarrow \int_{M} \varphi \,d\mu^{+} \mbox{ for all } \varphi \in C^{0}(M, \mathbb{R}) \bigg\}, \end{align*} $$
$$ \begin{align*}B(\mu^{+}) = \bigg\{x \in M \mid \frac{1}{n} \sum_{k=0}^{n-1} \varphi(f^{k}x) \longrightarrow \int_{M} \varphi \,d\mu^{+} \mbox{ for all } \varphi \in C^{0}(M, \mathbb{R}) \bigg\}, \end{align*} $$
one has that the limit
exists, but nothing can be said about this limit as
![]() $n\to -\infty $
.
$n\to -\infty $
.
The conjecture of Viana mentioned above is difficult to tackle as is. On the one hand, simply assuming that points with non-zero Lyapunov exponents exist does not seem to be enough to show that SRB measures exist. On the other hand, it is hard to construct a counter example. We instead add the assumption that the set of points with non-zero Lyapunov exponents which are also Perron–Regular and satisfy a recurrence condition have positive volume. The main question with which this paper deals is:
What can we say about the dynamics of f if the set of Lyapunov–Perron regular points which are hyperbolic, has positive volume?
In this paper, we give an answer to the above question, under the assumption that the set
![]() $\mathcal {R}^{\mathrm{PR}} \subset \mathcal {R}_{\mathrm {hyp}}$
of positively recurrent Lyapunov–Perron regular points (see Definition 4.6) has a positive volume. This set consists of points that return infinitely often to a Pesin block along the orbit. The reason for considering such a set is that, under the condition of positivity of volume, one can show that the maps f and
$\mathcal {R}^{\mathrm{PR}} \subset \mathcal {R}_{\mathrm {hyp}}$
of positively recurrent Lyapunov–Perron regular points (see Definition 4.6) has a positive volume. This set consists of points that return infinitely often to a Pesin block along the orbit. The reason for considering such a set is that, under the condition of positivity of volume, one can show that the maps f and
![]() $f^{-1}$
preserve SRB measures, see for example Theorem 5.1. The answer to the above question turns out to be that asking for the set of positively recurrent hyperbolic Lyapunov–Perron regular points to have positive volume is too much; the system not only preserves SRB measures, but these measures are actually absolutely continuous with respect to volume.
$f^{-1}$
preserve SRB measures, see for example Theorem 5.1. The answer to the above question turns out to be that asking for the set of positively recurrent hyperbolic Lyapunov–Perron regular points to have positive volume is too much; the system not only preserves SRB measures, but these measures are actually absolutely continuous with respect to volume.
1.1 Structure of the paper
The rest of the paper is divided as follows. In §2, we will discuss a toy model and prove our main theorem in this special case. The proof here illustrates the main components of the proof of the general theorem. In §3, we introduce ergodic homoclinic components and prove the main result of this paper: we give conditions under which an SRB measure is absolutely continuous with respect to volume. In §4, we introduce the main object of this paper, the set
![]() $\mathcal {R}^{\mathrm{PR}}_{\mathrm{hyp}}$
. We also introduce the set of non-uniformly hyperbolic points and discuss Markov partitions of this set. We end the section by proving another central proposition to our argument (Theorem 4.18). In §5, we complete the proof of our main theorem.
$\mathcal {R}^{\mathrm{PR}}_{\mathrm{hyp}}$
. We also introduce the set of non-uniformly hyperbolic points and discuss Markov partitions of this set. We end the section by proving another central proposition to our argument (Theorem 4.18). In §5, we complete the proof of our main theorem.
2 Informal discussion of the results
2.1 A toy model
Let
![]() $f:M \to M$
be a diffeomorphism of a compact smooth Riemannian manifold preserving a hyperbolic smooth measure
$f:M \to M$
be a diffeomorphism of a compact smooth Riemannian manifold preserving a hyperbolic smooth measure
![]() $\mu $
. By Oseledets’ multiplicative ergodic theorem, the set
$\mu $
. By Oseledets’ multiplicative ergodic theorem, the set
![]() $\mathcal {R}_{\mathrm {hyp}}$
of all hyperbolic Lyapunov–Perron regular points has positive Riemannian volume. In this paper, we consider the following problem:
$\mathcal {R}_{\mathrm {hyp}}$
of all hyperbolic Lyapunov–Perron regular points has positive Riemannian volume. In this paper, we consider the following problem:
Does the opposite hold, namely if
![]() $\mathcal {R}_{\mathrm {hyp}}$
has positive volume, can we conclude that f preserves a hyperbolic smooth measure?
$\mathcal {R}_{\mathrm {hyp}}$
has positive volume, can we conclude that f preserves a hyperbolic smooth measure?
To illustrate our approach, we consider the following toy problem (the case of Anosov diffeomorphisms):
Let
![]() $f:M\to M$
be a transitive Anosov diffeomorphism, and assume that the set of Lyapunov–Perron regular points
$f:M\to M$
be a transitive Anosov diffeomorphism, and assume that the set of Lyapunov–Perron regular points
![]() $\mathcal {R}$
has positive volume, can we conclude that f preserves a smooth measure?
$\mathcal {R}$
has positive volume, can we conclude that f preserves a smooth measure?
The following theorem give an affirmative solution to this problem.
Theorem 2.1. Let
![]() $f: M \longrightarrow M$
be a transitive
$f: M \longrightarrow M$
be a transitive
![]() $C^{1+\alpha }$
Anosov diffeomorphism of compact Riemannian manifold M, and assume that
$C^{1+\alpha }$
Anosov diffeomorphism of compact Riemannian manifold M, and assume that
![]() $\mathrm{Vol}(\mathcal {R}_{\mathrm{hyp}})> 0$
, then the system preserves a unique smooth measure
$\mathrm{Vol}(\mathcal {R}_{\mathrm{hyp}})> 0$
, then the system preserves a unique smooth measure
![]() $\mu $
which is equivalent to volume.
$\mu $
which is equivalent to volume.
According to Bowen [Reference Bowen and Chazottes6], a transitive Anosov diffeomorphism has exactly one SRB measure, which is ergodic, and if a smooth measure is preserved, then it is the unique SRB measure. Therefore, the natural approach is to work with the unique SRB measure for f,
![]() $\mu ^{+}$
, and try to prove that it is actually a smooth measure. Now if
$\mu ^{+}$
, and try to prove that it is actually a smooth measure. Now if
![]() $\mu ^{+}$
is a smooth measure, then it is straight forward to show that the sum of Lyapunov exponents is zero. The good news is that the opposite also holds.
$\mu ^{+}$
is a smooth measure, then it is straight forward to show that the sum of Lyapunov exponents is zero. The good news is that the opposite also holds.
Lemma 2.2. Let
![]() $\mu ^{+}$
be an SRB measure for a diffeomorphism
$\mu ^{+}$
be an SRB measure for a diffeomorphism
![]() $f :M\to M$
of a compact smooth Riemannian manifold M. Assume that the sum of all Lyapunov exponents is zero at
$f :M\to M$
of a compact smooth Riemannian manifold M. Assume that the sum of all Lyapunov exponents is zero at
![]() $\mu ^{+}$
-a.e. point. Then
$\mu ^{+}$
-a.e. point. Then
![]() $\mu ^{+}$
is a smooth measure.
$\mu ^{+}$
is a smooth measure.
This lemma holds for general
![]() $C^{1+\alpha }$
diffeomorphisms preserving an SRB measure, we prove this lemma in §3.
$C^{1+\alpha }$
diffeomorphisms preserving an SRB measure, we prove this lemma in §3.
Using this, a natural strategy would be to prove that the sum of Lyapunov exponents of
![]() $\mu ^{+}$
is zero. Let us denote the Lyapunov exponents of
$\mu ^{+}$
is zero. Let us denote the Lyapunov exponents of
![]() $\mu ^{+}$
by
$\mu ^{+}$
by
![]() $\chi _{1}(\mu ^{+}) \leq \cdots \leq \chi _{n}(\mu ^{+})$
, then by Ruelle’s inequality and the entropy formula for
$\chi _{1}(\mu ^{+}) \leq \cdots \leq \chi _{n}(\mu ^{+})$
, then by Ruelle’s inequality and the entropy formula for
![]() $\mu ^{+}$
, we have that
$\mu ^{+}$
, we have that
 $$ \begin{align*} \sum_{i=1}^{n} \chi_{i}(\mu^{+}) \leq 0. \end{align*} $$
$$ \begin{align*} \sum_{i=1}^{n} \chi_{i}(\mu^{+}) \leq 0. \end{align*} $$
Since
![]() $f^{-1}$
is also an Anosov diffeomorphism, it has an SRB measure
$f^{-1}$
is also an Anosov diffeomorphism, it has an SRB measure
![]() $\mu ^{-}$
, which is characterized by absolutely continuous conditional measures along local stable manifolds. As is the case of the measure
$\mu ^{-}$
, which is characterized by absolutely continuous conditional measures along local stable manifolds. As is the case of the measure
![]() $\mu ^{+}$
, if f preserves a smooth measure, then it is in fact
$\mu ^{+}$
, if f preserves a smooth measure, then it is in fact
![]() $\mu ^{-}$
, and hence
$\mu ^{-}$
, and hence
![]() $\mu ^{+} = \mu ^{-}$
. Note that in general,
$\mu ^{+} = \mu ^{-}$
. Note that in general,
![]() $\mu ^{-}$
is not equal to
$\mu ^{-}$
is not equal to
![]() $\mu ^{+}$
; in fact, this happens only in a very specific situation.
$\mu ^{+}$
; in fact, this happens only in a very specific situation.
Lemma 2.3. Let
![]() $f:M \to M$
be a
$f:M \to M$
be a
![]() $C^{1+\alpha }$
diffeomorphism, and let
$C^{1+\alpha }$
diffeomorphism, and let
![]() $\mu $
be an SRB measure for both f and
$\mu $
be an SRB measure for both f and
![]() $f^{-1}$
, then
$f^{-1}$
, then
![]() $\mu $
is a smooth measure.
$\mu $
is a smooth measure.
The lemma is an immediate consequence of Lemma 2.1 above and the entropy formula, and holds for general
![]() $C^{1+\alpha }$
, not only Anosov diffeomorphisms, again we will prove it in §3 of this paper.
$C^{1+\alpha }$
, not only Anosov diffeomorphisms, again we will prove it in §3 of this paper.
This naturally leads us to trying to show that
![]() $\mu ^{+} = \mu ^{-}$
. To do this, assume that there exists a point
$\mu ^{+} = \mu ^{-}$
. To do this, assume that there exists a point
![]() $x \in M$
whose forward Lyapunov exponents are controlled by
$x \in M$
whose forward Lyapunov exponents are controlled by
![]() $\mu ^{+}$
, that is,
$\mu ^{+}$
, that is,
and whose backward Lyapunov exponents are controlled by
![]() $\mu ^{-}$
, that is,
$\mu ^{-}$
, that is,
This by itself does not give anything, but if in addition we know that
![]() $x\in \mathcal {R}$
, we can immediately conclude that
$x\in \mathcal {R}$
, we can immediately conclude that
for all
![]() $i = 1,\ldots ,n$
. So in particular, we see that
$i = 1,\ldots ,n$
. So in particular, we see that
Using now Ruelle’s inequality applied to both f and
![]() $f^{-1}$
, we obtain that
$f^{-1}$
, we obtain that
Combing this with equation (2.1), yields
Using Lemma 1, we see that both
![]() $\mu ^{+}$
and
$\mu ^{+}$
and
![]() $\mu ^{-}$
are smooth measures, and hence, by uniqueness, we conclude that
$\mu ^{-}$
are smooth measures, and hence, by uniqueness, we conclude that
![]() $\mu ^{+} = \mu ^{-}$
is the unique smooth measure preserved by f.
$\mu ^{+} = \mu ^{-}$
is the unique smooth measure preserved by f.
It is therefore enough to prove the existence of such a point x, the proof of which is not difficult in this case and we sketch it here. First, since
![]() $\mathrm{Vol}(\mathcal {R})>0$
, we can prove, using the absolute continuity properties of the stable and unstable manifolds, that there exists a point (actually a positive volume of points) such that:
$\mathrm{Vol}(\mathcal {R})>0$
, we can prove, using the absolute continuity properties of the stable and unstable manifolds, that there exists a point (actually a positive volume of points) such that:
-
(1) x is a Lyapunov–Perron regular point;
-
(2) the local unstable manifold
 $V^{u}_{\mathrm {loc}}(x)$
at x contains a positive leaf volume of Lyapunov–Perron regular points;
$V^{u}_{\mathrm {loc}}(x)$
at x contains a positive leaf volume of Lyapunov–Perron regular points; -
(3) the local stable manifold
 $V^{s}_{\mathrm {loc}}(x)$
at x contains a positive leaf volume of Lyapunov–Perron regular points.
$V^{s}_{\mathrm {loc}}(x)$
at x contains a positive leaf volume of Lyapunov–Perron regular points.
Now, since
![]() $\mu ^{+}$
and
$\mu ^{+}$
and
![]() $\mu ^{-}$
are SRB measures for f and
$\mu ^{-}$
are SRB measures for f and
![]() $f^{-1}$
respectively, we know that for
$f^{-1}$
respectively, we know that for
![]() $\mu ^{+}$
/
$\mu ^{+}$
/
![]() $\mu ^{-}$
-almost all points
$\mu ^{-}$
-almost all points
![]() $x^{+}/x^{-}$
, almost all points on the local unstable manifold
$x^{+}/x^{-}$
, almost all points on the local unstable manifold
![]() $V^{u}_{\mathrm {loc}}(x^{+})$
with respect to leaf volume are Lyapunov–Perron regular. Furthermore, almost every such point has Lyapunov exponents controlled by
$V^{u}_{\mathrm {loc}}(x^{+})$
with respect to leaf volume are Lyapunov–Perron regular. Furthermore, almost every such point has Lyapunov exponents controlled by
![]() $\mu ^{+}$
. That is, setting
$\mu ^{+}$
. That is, setting
we have that
Now, we note that when f is Anosov, then
is dense in M and hence, there is an
![]() $n\geq 0$
such that
$n\geq 0$
such that
![]() $f^{n}(V^{u}_{\mathrm {loc}}(x^{+}))$
contains an embedded disk
$f^{n}(V^{u}_{\mathrm {loc}}(x^{+}))$
contains an embedded disk
![]() $D^{u}$
which is really close to the local unstable
$D^{u}$
which is really close to the local unstable
![]() $V^{u}_{\mathrm {loc}}(x)$
in the
$V^{u}_{\mathrm {loc}}(x)$
in the
![]() $C^{1}$
topology as in Figure 1 below.
$C^{1}$
topology as in Figure 1 below.

Figure 1 The images of the unstable manifold
![]() $W^u_{\mathrm{loc}}(x^+)$
become more and more dense in the space under the map
$W^u_{\mathrm{loc}}(x^+)$
become more and more dense in the space under the map
![]() $f$
. Therefore, for some
$f$
. Therefore, for some
![]() $n^+ > 0$
, one can find
$n^+ > 0$
, one can find
![]() $\mathbf{D}^u \subset f^{n^+} W^u_{\mathrm{loc}}(x^+)$
which is very close to the unstable manifold
$\mathbf{D}^u \subset f^{n^+} W^u_{\mathrm{loc}}(x^+)$
which is very close to the unstable manifold
![]() $W^u_{\mathrm{loc}}(x)$
, so that
$W^u_{\mathrm{loc}}(x)$
, so that
![]() $\mathcal{D}^u$
intersects all the local stable manifolds of points in
$\mathcal{D}^u$
intersects all the local stable manifolds of points in
![]() $W^u_{\mathrm{loc}}(x)$
.
$W^u_{\mathrm{loc}}(x)$
.
Therefore, the holonomy map
given by
is well defined. One can show that (using Lemma 3.11, which we prove in §3)
![]() $D^{u}$
satisfies
$D^{u}$
satisfies
Now, the holonomy map
![]() $\Gamma ^{s}$
has the absolute continuity property. Therefore, we can see that
$\Gamma ^{s}$
has the absolute continuity property. Therefore, we can see that
![]() $(\Gamma ^{s})^{-1}(D^{u}\cap \mathcal {R}(\mu ^{+}))$
has full leaf volume in
$(\Gamma ^{s})^{-1}(D^{u}\cap \mathcal {R}(\mu ^{+}))$
has full leaf volume in
![]() $V^{u}_{\mathrm {loc}}(x)$
.
$V^{u}_{\mathrm {loc}}(x)$
.
Although the forward Lyapunov exponents of two points on the same stable manifolds coincide, it is not, in general, true that points on the stable manifold of a Lyapunov–Perron regular point are also Lyapunov–Perron regular. This is because a priori we can not compare their backward behavior. So, in general, the pre-image of
![]() $D^{u}\cap \mathcal {R}(\mu ^{+})$
under the holonomy map does not necessarily lie in
$D^{u}\cap \mathcal {R}(\mu ^{+})$
under the holonomy map does not necessarily lie in
![]() $\mathcal {R}(\mu ^{+})$
. However, in our situation, we have chosen x so that its unstable local manifold contains a positive leaf volume of Lyapunov–Perron regular points and hence,
$\mathcal {R}(\mu ^{+})$
. However, in our situation, we have chosen x so that its unstable local manifold contains a positive leaf volume of Lyapunov–Perron regular points and hence,
Now the set
![]() $V^{u}_{\mathrm {loc}}(x)\cap \mathcal {R} \cap (\Gamma ^{s})^{-1}(D^{u}\cap \mathcal {R}(\mu ^{+}))$
consists of Lyapunov–Perron regular points, which lie on the stable manifold of some point in
$V^{u}_{\mathrm {loc}}(x)\cap \mathcal {R} \cap (\Gamma ^{s})^{-1}(D^{u}\cap \mathcal {R}(\mu ^{+}))$
consists of Lyapunov–Perron regular points, which lie on the stable manifold of some point in
![]() $\mathcal {R}(\mu ^{+})$
, using Lemma 3.13 (which we prove in §3); therefore, we see that we have in fact
$\mathcal {R}(\mu ^{+})$
, using Lemma 3.13 (which we prove in §3); therefore, we see that we have in fact
![]() $m_{V^{u}_{\mathrm {loc}}(x)}(V^{u}_{\mathrm {loc}}(x)\cap \mathcal {R}(\mu ^{+}))> 0$
. Since
$m_{V^{u}_{\mathrm {loc}}(x)}(V^{u}_{\mathrm {loc}}(x)\cap \mathcal {R}(\mu ^{+}))> 0$
. Since
![]() $x \in \mathcal {R}$
, we see that this implies, using Lemma 3.13, that the Lyapunov exponents of x with respect to f coincide with the Lyapunov exponents of
$x \in \mathcal {R}$
, we see that this implies, using Lemma 3.13, that the Lyapunov exponents of x with respect to f coincide with the Lyapunov exponents of
![]() $\mu ^{+}$
.
$\mu ^{+}$
.
Similarly, we see that
and that this again implies that that the Lyapunov exponents of x with respect to
![]() $f^{-1}$
coincide with the Lyapunov exponents of
$f^{-1}$
coincide with the Lyapunov exponents of
![]() $\mu ^{-}$
, and that is exactly what we needed to show.
$\mu ^{-}$
, and that is exactly what we needed to show.
So, at least in this toy model, we see that the positivity of volume of the set of hyperbolic Lyapunov–Perron regular points can only be explained by the fact that the system preserves a smooth measure. This paper addresses the problem in the more general case of non-uniformly hyperbolic systems.
2.2 The main result
The approach we have outlined for the toy model cannot be immediately generalized to the case of non-uniformly hyperbolic systems for a few reasons. First, we need to start with SRB measures for f and
![]() $f^{-1}$
, whose existence is not trivial for general systems. Second, even if we know that the system admits two SRB measures
$f^{-1}$
, whose existence is not trivial for general systems. Second, even if we know that the system admits two SRB measures
![]() $\mu ^{+}$
and
$\mu ^{+}$
and
![]() $\mu ^{-}$
for f and
$\mu ^{-}$
for f and
![]() $f^{-1}$
respectively, the images under f of a
$f^{-1}$
respectively, the images under f of a
![]() $\mu ^{+}$
-typical local unstable manifold,
$\mu ^{+}$
-typical local unstable manifold,
![]() $V^{u}_{\mathrm {loc}}(x^{+})$
, do not necessarily fill in the space M, and in particular, we may not be able to bring
$V^{u}_{\mathrm {loc}}(x^{+})$
, do not necessarily fill in the space M, and in particular, we may not be able to bring
![]() $f^{n}(V^{u}_{\mathrm {loc}}(x^{+}))$
close to
$f^{n}(V^{u}_{\mathrm {loc}}(x^{+}))$
close to
![]() $V^{u}_{\mathrm {loc}}(x)$
for any
$V^{u}_{\mathrm {loc}}(x)$
for any
![]() $n\geq 0$
. Third, even if we overcome the first two obstacles, we still need to relate the unstable
$n\geq 0$
. Third, even if we overcome the first two obstacles, we still need to relate the unstable
![]() $f^{n}(V^{u}_{\mathrm {loc}}(x^{+}))$
and
$f^{n}(V^{u}_{\mathrm {loc}}(x^{+}))$
and
![]() $V^{u}_{\mathrm {loc}}(x)$
using local stable manifolds, since the holonomy maps, used in the proof of the model case, may not be well defined. This last problem arises from the non-uniformity of the sizes of unstable and stable manifolds for general non-uniformly hyperbolic systems.
$V^{u}_{\mathrm {loc}}(x)$
using local stable manifolds, since the holonomy maps, used in the proof of the model case, may not be well defined. This last problem arises from the non-uniformity of the sizes of unstable and stable manifolds for general non-uniformly hyperbolic systems.
We will tackle these issues in order, the first of which is the existence of SRB measures for both f and
![]() $f^{-1}$
. The main difference between the toy model and the general non-uniformly hyperbolic case is that now, it is not obvious if SRB measures exist, even when
$f^{-1}$
. The main difference between the toy model and the general non-uniformly hyperbolic case is that now, it is not obvious if SRB measures exist, even when
![]() $\text {Vol}(\mathcal {R}_{\mathrm {hyp}})>0$
. Recently Ben Ovadia [Reference Ben Ovadia4] proved the existence of SRB measures for f under a leaf condition. We will expand on this later, but roughly speaking, the idea is that if there exists an unstable manifold with positive leaf volume of points on it which are hyperbolic and positively recurrent (meaning that the unstable and stable manifolds return to a uniform size frequently along the forward orbit), then the system admits an SRB measure
$\text {Vol}(\mathcal {R}_{\mathrm {hyp}})>0$
. Recently Ben Ovadia [Reference Ben Ovadia4] proved the existence of SRB measures for f under a leaf condition. We will expand on this later, but roughly speaking, the idea is that if there exists an unstable manifold with positive leaf volume of points on it which are hyperbolic and positively recurrent (meaning that the unstable and stable manifolds return to a uniform size frequently along the forward orbit), then the system admits an SRB measure
![]() $\mu ^{+}$
. We will use this to prove the existence of SRB measures
$\mu ^{+}$
. We will use this to prove the existence of SRB measures
![]() $\mu ^{+}$
and
$\mu ^{+}$
and
![]() $\mu ^{-}$
for f and
$\mu ^{-}$
for f and
![]() $f^{-1}$
. Assuming that the set
$f^{-1}$
. Assuming that the set
![]() $\mathcal {R}^{\mathrm{PR}}\subset \mathcal {R}_{\mathrm {hyp}}$
of positively recurrent points has positive volume, we will describe
$\mathcal {R}^{\mathrm{PR}}\subset \mathcal {R}_{\mathrm {hyp}}$
of positively recurrent points has positive volume, we will describe
![]() $\mathcal {R}^{\mathrm{PR}}$
more precisely, but for now, we can say that it consists of hyperbolic Lyapunov–Perron regular points whose stable and unstable manifolds return to uniform sizes frequently along the forward and backward orbits.
$\mathcal {R}^{\mathrm{PR}}$
more precisely, but for now, we can say that it consists of hyperbolic Lyapunov–Perron regular points whose stable and unstable manifolds return to uniform sizes frequently along the forward and backward orbits.
To deal with the second problem, we divide the set
![]() $\mathcal {R}^{\mathrm{PR}}$
into possibly countably many subsets, such that each of these subsets have forward and backward images that lie very close to two hyperbolic points, and then make sure that the SRB measures we constructed lie in the ergodic homocolinic classes (introduced in [Reference Rodriguez Hertz, Rodriguez Hertz, Tahzibi and Ures12]) of these two hyperbolic points. This will allow us to conclude that each of these subsets, which we obtained by dividing
$\mathcal {R}^{\mathrm{PR}}$
into possibly countably many subsets, such that each of these subsets have forward and backward images that lie very close to two hyperbolic points, and then make sure that the SRB measures we constructed lie in the ergodic homocolinic classes (introduced in [Reference Rodriguez Hertz, Rodriguez Hertz, Tahzibi and Ures12]) of these two hyperbolic points. This will allow us to conclude that each of these subsets, which we obtained by dividing
![]() $\mathcal {R}^{\mathrm{PR}}$
, lie in the basin of attraction of the two SRB measures, and with a little bit more work, we will also be able to overcome the third obstacle.
$\mathcal {R}^{\mathrm{PR}}$
, lie in the basin of attraction of the two SRB measures, and with a little bit more work, we will also be able to overcome the third obstacle.
Thus we get our the main theorem of this paper.
Theorem 2.4. (Main Theorem)
Let
![]() $f: M\longrightarrow M$
be a
$f: M\longrightarrow M$
be a
![]() $C^{1+\alpha }$
diffeomorphism of a compact Riemannian manifold M, and assume that the set of hyperbolic positively recurrent Lyapunov–Perron regular points
$C^{1+\alpha }$
diffeomorphism of a compact Riemannian manifold M, and assume that the set of hyperbolic positively recurrent Lyapunov–Perron regular points
![]() $\mathcal {R}^{\mathrm{PR}}_{\mathrm {hyp}}$
has positive volume, then f preserves a smooth measure.
$\mathcal {R}^{\mathrm{PR}}_{\mathrm {hyp}}$
has positive volume, then f preserves a smooth measure.
Our main theorem is an immediate consequence of the following more technical theorem, which we will prove in §5 of this paper.
Theorem 2.5. Let
![]() $f : M \to M$
be a
$f : M \to M$
be a
![]() $C^{1+}$
diffeomorphism, and assume that
$C^{1+}$
diffeomorphism, and assume that
![]() ${\mathrm{Vol}(\mathcal {R}^{\mathrm{PR}}_{\mathrm {hyp}})>0}$
. Then there exists at most countably many ergodic absolutely continuous measures
${\mathrm{Vol}(\mathcal {R}^{\mathrm{PR}}_{\mathrm {hyp}})>0}$
. Then there exists at most countably many ergodic absolutely continuous measures
![]() $\mu _{1},\mu _{2},\ldots $
such that
$\mu _{1},\mu _{2},\ldots $
such that
![]() $\mathrm{Vol}$
-a.e. point in
$\mathrm{Vol}$
-a.e. point in
![]() $\mathcal {R}^{\mathrm{PR}}_{\mathrm {hyp}}$
is Tsuji regular for
$\mathcal {R}^{\mathrm{PR}}_{\mathrm {hyp}}$
is Tsuji regular for
![]() $\mu _{n}$
, for some
$\mu _{n}$
, for some
![]() $n \geq 1$
.
$n \geq 1$
.
Tsuji regularity was first defined in [Reference Tsujii17]. We include the definition here for completeness.
Definition 2.6. [Reference Tsujii17]
Let
![]() $f: M\longrightarrow M $
be a
$f: M\longrightarrow M $
be a
![]() $C^{1+\alpha }$
diffeomorphism on a smooth Riemannian manifold, and let
$C^{1+\alpha }$
diffeomorphism on a smooth Riemannian manifold, and let
![]() $\mu $
be an ergodic invariant measure. We say that a point
$\mu $
be an ergodic invariant measure. We say that a point
![]() $x \in M$
is forward Tsuji regular for
$x \in M$
is forward Tsuji regular for
![]() $\mu $
if the following hold.
$\mu $
if the following hold.
-
(1)
 $({1}/{n})\sum ^{n-1}_{k=0} \delta _{f^{k}x} \longrightarrow \mu $
in the sense of the weak topology.
$({1}/{n})\sum ^{n-1}_{k=0} \delta _{f^{k}x} \longrightarrow \mu $
in the sense of the weak topology. -
(2) The Lyapunov exponents of x with respect to f coincide with the Lyapunov exponents of
 $\mu $
.
$\mu $
.
We say that
![]() $x \in M$
is forward Tsuji regular for
$x \in M$
is forward Tsuji regular for
![]() $\mu $
if it is forward Tsuji regular for
$\mu $
if it is forward Tsuji regular for
![]() $\mu $
with respect to
$\mu $
with respect to
![]() $f^{-1}$
. We say that
$f^{-1}$
. We say that
![]() $x \in M$
is Tsuji regular for
$x \in M$
is Tsuji regular for
![]() $\mu $
if it is both forward and backward Tsuji regular.
$\mu $
if it is both forward and backward Tsuji regular.
The condition
![]() $\text {Vol}(\mathcal {R}^{\mathrm{PR}})> 0$
, as we will see, guarantees the existence of the SRB measures. The next step is to relate the SRB measures to each other, but here we encounter another problem. It is possible that the system admits countably many ergodic SRB measures for f and countably many ergodic SRB measures for
$\text {Vol}(\mathcal {R}^{\mathrm{PR}})> 0$
, as we will see, guarantees the existence of the SRB measures. The next step is to relate the SRB measures to each other, but here we encounter another problem. It is possible that the system admits countably many ergodic SRB measures for f and countably many ergodic SRB measures for
![]() $f^{-1}$
and the question then is:
$f^{-1}$
and the question then is:
Which ones are related to which ones?
We approach this issue by examining the construction of the SRB measures more closely, and then construct two specific SRB measures
![]() $\mu ^{+}$
and
$\mu ^{+}$
and
![]() $\mu ^{-}$
so that they are related almost by construction. To do that, we will have to deal with the symbolic representation of the dynamics on the set
$\mu ^{-}$
so that they are related almost by construction. To do that, we will have to deal with the symbolic representation of the dynamics on the set
![]() $\mathcal {R}^{\mathrm{PR}}$
, and we will have to consider the more general set
$\mathcal {R}^{\mathrm{PR}}$
, and we will have to consider the more general set
![]() $RWT_{\chi }$
which was introduced in [Reference Ben Ovadia4].
$RWT_{\chi }$
which was introduced in [Reference Ben Ovadia4].
The next issue we will deal with is:
Why should there be an
![]() $n\geq 0$
such that
$n\geq 0$
such that
![]() $f^{n}(V^{u}_{\mathrm {loc}}(x^{+}))$
and the local unstable manifold of another chosen point x,
$f^{n}(V^{u}_{\mathrm {loc}}(x^{+}))$
and the local unstable manifold of another chosen point x,
![]() $V^{u}_{\mathrm {loc}}(x)$
, are close to each other so that the stable holonomy map as in the toy model could be defined?
$V^{u}_{\mathrm {loc}}(x)$
, are close to each other so that the stable holonomy map as in the toy model could be defined?
We will resolve this by considering homoclinic ergodic classes as introduced in [Reference Rodriguez Hertz, Rodriguez Hertz, Tahzibi and Ures12]. We will choose
![]() $x\in \mathcal {R}^{\mathrm{PR}}$
so that it is in both of the homoclinic ergodic classes supporting
$x\in \mathcal {R}^{\mathrm{PR}}$
so that it is in both of the homoclinic ergodic classes supporting
![]() $\mu ^{+}$
and
$\mu ^{+}$
and
![]() $\mu ^{-}$
, and then using arguments inspired by those in [Reference Ben Ovadia4], we will replicate the proof of the toy model case.
$\mu ^{-}$
, and then using arguments inspired by those in [Reference Ben Ovadia4], we will replicate the proof of the toy model case.
The last issue we will tackle is to show that the resulting absolutely continuous measures
![]() $\mu ^{+}$
and
$\mu ^{+}$
and
![]() $\mu ^{-}$
are actually equal to each other. Along the way, we will prove an analog of Lemmas 1 and 2 for general non-uniformly hyperbolic systems.
$\mu ^{-}$
are actually equal to each other. Along the way, we will prove an analog of Lemmas 1 and 2 for general non-uniformly hyperbolic systems.
3 The entropy argument
The main goal of this section is to prove the following proposition.
Proposition 3.1. Let
![]() $P^{+}$
and
$P^{+}$
and
![]() $P^{-}$
be two hyperbolic periodic points. Let
$P^{-}$
be two hyperbolic periodic points. Let
![]() $R^{+}$
and
$R^{+}$
and
![]() $R^{-}$
be two rectangles at
$R^{-}$
be two rectangles at
![]() $P^{+}$
and
$P^{+}$
and
![]() $P^{-}$
respectively. Let
$P^{-}$
respectively. Let
![]() $x_{0} \in \mathcal {R}_{\mathrm {hyp}}$
be a hyperbolic Lyapunov–Perron regular point. Let us assume the following items.
$x_{0} \in \mathcal {R}_{\mathrm {hyp}}$
be a hyperbolic Lyapunov–Perron regular point. Let us assume the following items.
-
(1) Each of the homoclinic ergodic classes
 $H(P^{+})$
and
$H(P^{+})$
and
 $H(P^{-})$
supports a unique SRB measure
$H(P^{-})$
supports a unique SRB measure
 $\mu ^{+}$
for f and
$\mu ^{+}$
for f and
 $\mu ^{-}$
for
$\mu ^{-}$
for
 $f^{-1}$
respectively.
$f^{-1}$
respectively. -
(2) There is an unstable
 $W^{+}$
in the rectangle
$W^{+}$
in the rectangle
 $R^{+}$
for which we have:
$R^{+}$
for which we have:-
(a)
 $m_{W^{+}}(W^{+} \cap R^{+} \cap \mathcal {R}_{\mathrm {hyp}} )> 0$
;
$m_{W^{+}}(W^{+} \cap R^{+} \cap \mathcal {R}_{\mathrm {hyp}} )> 0$
; -
(b)
 $f^{-n^{+}}(W^{+} ) \subset V^{u}_{\mathrm {loc}}(x_{0})$
, for some
$f^{-n^{+}}(W^{+} ) \subset V^{u}_{\mathrm {loc}}(x_{0})$
, for some
 $n^{+}> 0$
.
$n^{+}> 0$
.
-
-
(3) There is a stable
 $W^{-}$
in the rectangle
$W^{-}$
in the rectangle
 $R^{-}$
for which we have:
$R^{-}$
for which we have:-
(a)
 $m_{W^{-}}(W^{-} \cap R^{-} \cap \mathcal {R}_{\mathrm {hyp}} ) \geq 0$
;
$m_{W^{-}}(W^{-} \cap R^{-} \cap \mathcal {R}_{\mathrm {hyp}} ) \geq 0$
; -
(b)
 $f^{n^{-}}(W^{-} ) \subset V^{s}_{\mathrm {loc}}(x_{0})$
, for some
$f^{n^{-}}(W^{-} ) \subset V^{s}_{\mathrm {loc}}(x_{0})$
, for some
 $n^{-} \geq 0$
.
$n^{-} \geq 0$
.
-
Then both
![]() $\mu ^{+}$
and
$\mu ^{+}$
and
![]() $\mu ^{-}$
are absolutely continuous with respect to volume.
$\mu ^{-}$
are absolutely continuous with respect to volume.
This proposition is one of the key component of the proof of the main theorem. We will use it to prove that the SRB measures we construct later are absolutely continuous with respect to volume.
3.1 u-measures and s-measures
Definition 3.2. (Global unstable manifolds)
Let
![]() $x \in \mathcal {R}_{\mathrm {hyp}}$
, then the global unstable manifold at x, which we denote by
$x \in \mathcal {R}_{\mathrm {hyp}}$
, then the global unstable manifold at x, which we denote by
![]() $W^{u}(x)$
, is defined to be
$W^{u}(x)$
, is defined to be
This set is an immersed submanifold of M (see [Reference Barreira and Pesin2]).
Definition 3.3. (Partition subordinate to unstable manifolds)
Let
![]() $f:M \longrightarrow M$
be a
$f:M \longrightarrow M$
be a
![]() $C^{1+\alpha }$
, and let
$C^{1+\alpha }$
, and let
![]() $\mu $
be an invariant measure with at least one non-zero Lyapunov exponent, then we say that a measurable partition
$\mu $
be an invariant measure with at least one non-zero Lyapunov exponent, then we say that a measurable partition
![]() $\xi ^{u}$
is subordinate to unstable manifolds if it satisfies the following properties:
$\xi ^{u}$
is subordinate to unstable manifolds if it satisfies the following properties:
-
(1)
 $\xi ^{u}(x)$
is an open subset of
$\xi ^{u}(x)$
is an open subset of
 $W^{u}(x)$
, for
$W^{u}(x)$
, for
 $\mu $
-a.e.
$\mu $
-a.e.
 $x \in M$
;
$x \in M$
; -
(2)
 $\bigvee _{n \geq 0} f^{-n} \xi ^{u} = \epsilon $
, the partition by points;
$\bigvee _{n \geq 0} f^{-n} \xi ^{u} = \epsilon $
, the partition by points; -
(3)
 $f^{-1} \xi ^{u} \geq \xi ^{u}$
;
$f^{-1} \xi ^{u} \geq \xi ^{u}$
; -
(4)
 $\bigwedge _{n \geq 0} f^{n} \xi ^{u} = W^{u}$
, where
$\bigwedge _{n \geq 0} f^{n} \xi ^{u} = W^{u}$
, where
 $W^{u}$
is the partition by global unstable manifolds.
$W^{u}$
is the partition by global unstable manifolds.
Definition 3.4. (u/s-measure)
An invariant measure
![]() $\mu $
is a u-measure if, given any measurable partition
$\mu $
is a u-measure if, given any measurable partition
![]() $\xi $
subordinate to unstable manifolds, the conditional measures
$\xi $
subordinate to unstable manifolds, the conditional measures
![]() $\mu _{x}^{u}$
along
$\mu _{x}^{u}$
along
![]() $\xi (x)$
are absolutely continuous with respect to leaf volume for
$\xi (x)$
are absolutely continuous with respect to leaf volume for
![]() $\mu $
-a.e. x. A measure
$\mu $
-a.e. x. A measure
![]() $\mu $
is an s-measure if it is a u-measure for
$\mu $
is an s-measure if it is a u-measure for
![]() $f^{-1}$
. A u-measure which is also hyperbolic is called an SRB measure for f. Similarly, an s-measure which is also hyperbolic is called an SRB measure for
$f^{-1}$
. A u-measure which is also hyperbolic is called an SRB measure for f. Similarly, an s-measure which is also hyperbolic is called an SRB measure for
![]() $f^{-1}$
.
$f^{-1}$
.
There are many ways to characterize SRB measures, but one of the most remarkable characterizations is the following theorem of Ledrappier and Young [Reference Ledrappier and Young9].
Proposition 3.5. (The entropy formula)
Let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^{1+\alpha }$
diffeomorphism. Then a measure
$C^{1+\alpha }$
diffeomorphism. Then a measure
![]() $\mu $
is an SRB measure for f if and only if the Pesin entropy formula holds
$\mu $
is an SRB measure for f if and only if the Pesin entropy formula holds
 $$ \begin{align*} h_{\mu}(f) = \int_{M} \sum\limits_{i}\unicode{x3bb}_{i}^{+}(x)\,d\mu(x), \end{align*} $$
$$ \begin{align*} h_{\mu}(f) = \int_{M} \sum\limits_{i}\unicode{x3bb}_{i}^{+}(x)\,d\mu(x), \end{align*} $$
where
![]() $\unicode{x3bb} ^{+}_{i}(x) = \max \{\unicode{x3bb} _{i}(x),0\}$
. Similarly,
$\unicode{x3bb} ^{+}_{i}(x) = \max \{\unicode{x3bb} _{i}(x),0\}$
. Similarly,
![]() $\mu $
is an SRB measure for
$\mu $
is an SRB measure for
![]() $f^{-1}$
if and only if
$f^{-1}$
if and only if
 $$ \begin{align*} h_{\mu}(f) = \int_{M}\sum\limits_{i}-\unicode{x3bb}^{-}_{i}(x) \,d\mu(x), \end{align*} $$
$$ \begin{align*} h_{\mu}(f) = \int_{M}\sum\limits_{i}-\unicode{x3bb}^{-}_{i}(x) \,d\mu(x), \end{align*} $$
where
![]() $\unicode{x3bb} ^{-}_{i}(x) = \min \{\unicode{x3bb} _{i}(x),0\}$
.
$\unicode{x3bb} ^{-}_{i}(x) = \min \{\unicode{x3bb} _{i}(x),0\}$
.
Lemma 3.6. Let
![]() $f:M\to M$
be a
$f:M\to M$
be a
![]() $C^{1+\alpha }$
diffeomorphism and let
$C^{1+\alpha }$
diffeomorphism and let
![]() $\mu $
be an SRB measure for f. Let
$\mu $
be an SRB measure for f. Let
![]() $\xi ^{u}$
be a measurable partition subordinate to unstable manifolds. Then for
$\xi ^{u}$
be a measurable partition subordinate to unstable manifolds. Then for
![]() $\mu $
-a.e
$\mu $
-a.e
![]() $x \in M$
, the conditional measure
$x \in M$
, the conditional measure
![]() $\mu _{\xi ^{u}(x)}$
and normalized leaf Riemannian volume
$\mu _{\xi ^{u}(x)}$
and normalized leaf Riemannian volume
![]() $m_{\xi ^{u}(x)}$
are equivalent.
$m_{\xi ^{u}(x)}$
are equivalent.
Proof. In [Reference Ledrappier and Young9, Corollary 6.14], the authors show that for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in M$
, one has that the conditional measure
$x \in M$
, one has that the conditional measure
![]() $\mu_{\xi^u (x) }$
is absolutely continuous with respect to the Riemmanian volume along the global unstable manifold
$\mu_{\xi^u (x) }$
is absolutely continuous with respect to the Riemmanian volume along the global unstable manifold
![]() $V^{u}(X)$
,
$V^{u}(X)$
,
![]() $m_{\xi^u (x)}$
, with a density
$m_{\xi^u (x)}$
, with a density
![]() $\rho $
which is strictly positive on
$\rho $
which is strictly positive on
![]() $\xi ^{u}(x)$
. By straightforward measure theory, one can show that this implies that the two measures
$\xi ^{u}(x)$
. By straightforward measure theory, one can show that this implies that the two measures
![]() $\mu _{\xi ^{u}(x)}$
and
$\mu _{\xi ^{u}(x)}$
and
![]() $m_{\xi^u (x)}$
are equivalent.
$m_{\xi^u (x)}$
are equivalent.
The main goal of this paper is to establish that a diffeomorphism preserves a measure absolutely continuous with respect to volume under some conditions. The strategy we are following is to to establish the existence of a measure
![]() $\mu $
which is an SRB measure for both f and
$\mu $
which is an SRB measure for both f and
![]() $f^{-1}$
at the same time. The goal for the remainder of this section is to establish some conditions under which an SRB measure for f is also an SRB measure for
$f^{-1}$
at the same time. The goal for the remainder of this section is to establish some conditions under which an SRB measure for f is also an SRB measure for
![]() $f^{-1}$
, which implies that it is actually absolutely continuous with respect to volume.
$f^{-1}$
, which implies that it is actually absolutely continuous with respect to volume.
Lemma 3.7. A hyperbolic measure
![]() $\mu $
is absolutely continuous with respect to volume if
$\mu $
is absolutely continuous with respect to volume if
![]() $\mu $
is both an SRB measure for f and for
$\mu $
is both an SRB measure for f and for
![]() $f^{-1}$
.
$f^{-1}$
.
To the best of our knowledge, this statement appears in the paper [Reference Pesin and Sinai11] and in the book [Reference Barreira and Pesin2], but an explicit proof has not been given, so for completeness, we provide a proof of the statement.
Proof of the lemma
Let
![]() $E \subset M$
be such that
$E \subset M$
be such that
![]() $\mu (E)>0$
, and let
$\mu (E)>0$
, and let
![]() $x \in E$
be a density point for x such that
$x \in E$
be a density point for x such that
![]() $m^{u}_{x}(E)>0$
and
$m^{u}_{x}(E)>0$
and
![]() $m^{s}_{x}(E)>0$
, where
$m^{s}_{x}(E)>0$
, where
![]() $m^{u}_{x}$
and
$m^{u}_{x}$
and
![]() $m^{s}_{x}$
are leaf volumes along the unstable and stable manifold of x respectively; such a point exists since the conditional measures
$m^{s}_{x}$
are leaf volumes along the unstable and stable manifold of x respectively; such a point exists since the conditional measures
![]() $\mu ^{u}_{x}$
and
$\mu ^{u}_{x}$
and
![]() $\mu ^{s}_{x}$
of
$\mu ^{s}_{x}$
of
![]() $\mu $
along the unstable and stable manifolds are equivalent to leaf volumes for
$\mu $
along the unstable and stable manifolds are equivalent to leaf volumes for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x\in M$
.
$x\in M$
.
Now locally, volume can be written as the product of the two leaf volumes
![]() $m^{u}_{x}$
and
$m^{u}_{x}$
and
![]() $m^{s}_{x}$
, that is,
$m^{s}_{x}$
, that is,
![]() $\text {Vol} \sim m^{u}_{x}\times m^{s}_{x}$
. Hence, we see that
$\text {Vol} \sim m^{u}_{x}\times m^{s}_{x}$
. Hence, we see that
![]() $\text {Vol}(E)>0$
, which implies that
$\text {Vol}(E)>0$
, which implies that
![]() $\mu <<\text {Vol}$
.
$\mu <<\text {Vol}$
.
The following observation is a simple corollary of the above lemma, the entropy formula, and Ruelle’s inequality.
Lemma 3.8. An ergodic SRB measure
![]() $\mu $
for f satisfies
$\mu $
for f satisfies
and equality holds if and only if it is absolutely continuous with respect to volume.
Proof. The inequality is an immediate consequence of the Pesin entropy formula and the Ruelle inequality, following the argument used in the proof of Lemma 2.3. Since
![]() $\mu $
is an SRB measure, we have
$\mu $
is an SRB measure, we have
Now, since the average of the sum of the Lyapunov exponents is zero, we see that
and since
![]() $h_{\mu }(f) = h_{\mu }(f^{-1})$
,
$h_{\mu }(f) = h_{\mu }(f^{-1})$
,
Hence,
![]() $\mu $
is also an SRB measure for
$\mu $
is also an SRB measure for
![]() $f^{-1}$
, and therefore, absolutely continuous with respect to volume.
$f^{-1}$
, and therefore, absolutely continuous with respect to volume.
3.2 Global manifolds and rectangles
We will need the following definition of hyperbolic rectangles.
Definition 3.9. Let f be a
![]() $C^{1+\alpha }$
diffeomorphism of a smooth compact Riemannian manifold M. Let
$C^{1+\alpha }$
diffeomorphism of a smooth compact Riemannian manifold M. Let
![]() $0<\unicode{x3bb} <1<\nu $
,
$0<\unicode{x3bb} <1<\nu $
,
![]() $\epsilon>0$
, j be an integer between
$\epsilon>0$
, j be an integer between
![]() $1$
and
$1$
and
![]() $dim(M)-1$
, and
$dim(M)-1$
, and
![]() $\ell>0$
. Consider the Pesin block
$\ell>0$
. Consider the Pesin block
![]() $\Lambda ^{\ell }:= \Lambda ^{\ell }_{\unicode{x3bb} , \nu , \epsilon , j}$
. We say that
$\Lambda ^{\ell }:= \Lambda ^{\ell }_{\unicode{x3bb} , \nu , \epsilon , j}$
. We say that
![]() $R \subset M$
is a
$R \subset M$
is a
![]() $\delta $
-rectangle at a point
$\delta $
-rectangle at a point
![]() $w \in \Lambda ^{\ell }$
if
$w \in \Lambda ^{\ell }$
if
![]() $w \in R \subset B(w, \delta ) \cap \Lambda ^{\psi (\ell )}$
, and for any
$w \in R \subset B(w, \delta ) \cap \Lambda ^{\psi (\ell )}$
, and for any
![]() $x, y \in R$
, we have
$x, y \in R$
, we have
where
![]() $V^{s}(z)$
and
$V^{s}(z)$
and
![]() $V^{u}(z)$
are the local stable land unstable manifolds for
$V^{u}(z)$
are the local stable land unstable manifolds for
![]() $z \in \Lambda ^{\ell }$
, and
$z \in \Lambda ^{\ell }$
, and
![]() $\psi (\ell )$
is defined so that for any
$\psi (\ell )$
is defined so that for any
![]() $x \in \Lambda ^{\ell }$
and
$x \in \Lambda ^{\ell }$
and
![]() $y \in \Lambda ^{\ell } \cap B(x, \delta _{\ell })$
, one has
$y \in \Lambda ^{\ell } \cap B(x, \delta _{\ell })$
, one has
![]() $V^{s}(x) \cap V^{u}(u) \in \Lambda ^{\psi (\ell )}$
, where
$V^{s}(x) \cap V^{u}(u) \in \Lambda ^{\psi (\ell )}$
, where
![]() $\delta _{\ell }$
is the scale at which we see local products in
$\delta _{\ell }$
is the scale at which we see local products in
![]() $\Lambda ^{\ell }$
.
$\Lambda ^{\ell }$
.
We say that an unstable manifold
![]() $W^{+}$
is in R if it is the local unstable manifold of a point in R. We say that a stable manifold
$W^{+}$
is in R if it is the local unstable manifold of a point in R. We say that a stable manifold
![]() $W^{-}$
is in R if it is the local stable manifold of a point in R.
$W^{-}$
is in R if it is the local stable manifold of a point in R.
Definition 3.10. Let
![]() $\mu $
be an ergodic invariant measure. We define the set
$\mu $
be an ergodic invariant measure. We define the set
![]() $\mathcal {R}(\mu )$
by
$\mathcal {R}(\mu )$
by
This is an invariant set, and one has by Oseledets’ multiplicative ergodic theorem that
![]() $\mu (\mathcal {R}(\mu )) =1$
.
$\mu (\mathcal {R}(\mu )) =1$
.
We will need the following lemma to show that global unstable manifolds intersect the set
![]() $\mathcal {R}(\mu )$
in a set of full leaf volume when
$\mathcal {R}(\mu )$
in a set of full leaf volume when
![]() $\mu $
is an SRB measure.
$\mu $
is an SRB measure.
Lemma 3.11. Let
![]() $\mu $
be an ergodic SRB measure for f. Let E be an invariant set of non-zero
$\mu $
be an ergodic SRB measure for f. Let E be an invariant set of non-zero
![]() $\mu $
measure. Then for
$\mu $
measure. Then for
![]() $\mu $
-a.e. point
$\mu $
-a.e. point
![]() $x \in M$
, the following is satisfied: any compact subset D of the global unstable manifold
$x \in M$
, the following is satisfied: any compact subset D of the global unstable manifold
![]() $W^{u}(x)$
intersects E in a set of full measure inside D, with respect to the Riemannian volume
$W^{u}(x)$
intersects E in a set of full measure inside D, with respect to the Riemannian volume
![]() $m_{W^{u}(x)}$
on
$m_{W^{u}(x)}$
on
![]() $W^{u}(x)$
.
$W^{u}(x)$
.
Proof.
Step 1. First, since
![]() $\mu $
is ergodic and E is invariant of positive
$\mu $
is ergodic and E is invariant of positive
![]() $\mu $
measure, we know that
$\mu $
measure, we know that
![]() $\mu (E) = 1$
. Now, let
$\mu (E) = 1$
. Now, let
![]() $\xi ^{u}$
be a measurable partition subordinate to unstable manifolds. Then, since
$\xi ^{u}$
be a measurable partition subordinate to unstable manifolds. Then, since
![]() $\mu $
is an SRB measure, we know from Lemma 3.6 that for
$\mu $
is an SRB measure, we know from Lemma 3.6 that for
![]() $\mu $
-a.e. point
$\mu $
-a.e. point
![]() $x \in M$
, one has that
$x \in M$
, one has that
![]() $\mu _{\xi ^{u}(x)}$
is equivalent to
$\mu _{\xi ^{u}(x)}$
is equivalent to
![]() $m_{\xi ^{u}(x)}, $
the leaf volume restricted to
$m_{\xi ^{u}(x)}, $
the leaf volume restricted to
![]() $\xi ^{u}(X)$
. Now, since
$\xi ^{u}(X)$
. Now, since
![]() $\mu (E) = 1$
, we know that for
$\mu (E) = 1$
, we know that for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in M$
, we have that
$x \in M$
, we have that
![]() $\mu _{\xi ^{u}(x)}(\xi ^{u}(x) \cap E) = 1$
, and since
$\mu _{\xi ^{u}(x)}(\xi ^{u}(x) \cap E) = 1$
, and since
![]() $\mu _{\xi ^{u}(x)}$
and
$\mu _{\xi ^{u}(x)}$
and
![]() $mu_{\xi ^{u}(x)}$
are equivalent for
$mu_{\xi ^{u}(x)}$
are equivalent for
![]() $\mu $
-a.e. point x, we see that this implies that we have
$\mu $
-a.e. point x, we see that this implies that we have
![]() $m_{\xi ^{u}(x)}(\xi ^{u}(x) \cap E) = 1$
for
$m_{\xi ^{u}(x)}(\xi ^{u}(x) \cap E) = 1$
for
![]() $\mu $
-a.e
$\mu $
-a.e
![]() $x \in M$
.
$x \in M$
.
Step 2. From [Reference Barreira and Pesin2, Proposition 9.4.1], we know that there is a measurable function
![]() $\beta : M \longrightarrow (0,r_{0})$
, such that for
$\beta : M \longrightarrow (0,r_{0})$
, such that for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in M$
,
$x \in M$
,
![]() $\xi ^{u}(x)$
contains the neighborhood of x defined by
$\xi ^{u}(x)$
contains the neighborhood of x defined by
![]() $\{y \in W^{u}(x) \mid d_{W^{u}(x)}(x, y) < \beta (x) \}$
. Let us fix
$\{y \in W^{u}(x) \mid d_{W^{u}(x)}(x, y) < \beta (x) \}$
. Let us fix
![]() $r_{1}>0$
to be small enough so that the measurable set
$r_{1}>0$
to be small enough so that the measurable set
has positive
![]() $\mu $
-measure. Then by ergodicity of
$\mu $
-measure. Then by ergodicity of
![]() $\mu $
, we see that for
$\mu $
, we see that for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in M$
, one can find infinitely many times
$x \in M$
, one can find infinitely many times
![]() $n \geq 0$
for which we have the following.
$n \geq 0$
for which we have the following.
-
(1)
 $m_{\xi ^{u}(f^{-n}x)}(\xi ^{u}(f^{-n}x) \cap E) = 1$
.
$m_{\xi ^{u}(f^{-n}x)}(\xi ^{u}(f^{-n}x) \cap E) = 1$
. -
(2)
 $\beta (f^{-n}x) \geq r_{1}$
.
$\beta (f^{-n}x) \geq r_{1}$
.
However, we know that for all large enough times
![]() $n> 0$
, we have
$n> 0$
, we have
Therefore, for a time n large enough, which also satisfies (1) and (2), we see that we actually have
and from condition (1) above, we see that we have
![]() $m_{f^{-n}(V^{u}_{\mathrm {loc}}(x))}(f^{-n}(V^{u}_{\mathrm {loc}}(x)) \cap E) = 1$
, and since the pushforward of the measure
$m_{f^{-n}(V^{u}_{\mathrm {loc}}(x))}(f^{-n}(V^{u}_{\mathrm {loc}}(x)) \cap E) = 1$
, and since the pushforward of the measure
![]() $m_{f^{-n}(V^{u}_{\mathrm {loc}}(x))}$
under the map
$m_{f^{-n}(V^{u}_{\mathrm {loc}}(x))}$
under the map
![]() $f^{n}$
is equivalent to the leaf volume
$f^{n}$
is equivalent to the leaf volume
![]() $m_{V^{u}_{\mathrm {loc}}(x)}$
, and since E is invariant, we see that this implies that
$m_{V^{u}_{\mathrm {loc}}(x)}$
, and since E is invariant, we see that this implies that
![]() $m_{V^{u}_{\mathrm {loc}}(x)}(V^{u}_{\mathrm {loc}}(x) \cap E) = 1$
.
$m_{V^{u}_{\mathrm {loc}}(x)}(V^{u}_{\mathrm {loc}}(x) \cap E) = 1$
.
Step 3. Now, since D is a compact subset of
![]() $W^{u}(x)$
, we can find a time n, for which we have
$W^{u}(x)$
, we can find a time n, for which we have
![]() $f^{-n}(D) \subset V^{u}_{\mathrm {loc}}(f^{-n}x)$
. From steps 1 and 2 above, we see that this implies that
$f^{-n}(D) \subset V^{u}_{\mathrm {loc}}(f^{-n}x)$
. From steps 1 and 2 above, we see that this implies that
![]() $E \cap f^{-n}(D)$
has full measure inside
$E \cap f^{-n}(D)$
has full measure inside
![]() $f^{-n}(D)$
with respect to the leaf measure
$f^{-n}(D)$
with respect to the leaf measure
![]() $m_{f^{-n}(V^{u}_{\mathrm {loc}}(x))}$
, for
$m_{f^{-n}(V^{u}_{\mathrm {loc}}(x))}$
, for
![]() $\mu $
-a.e.
$\mu $
-a.e.
![]() $x \in M$
, which in turn implies the lemma.
$x \in M$
, which in turn implies the lemma.
The main lemma in this subsection is the following.
Lemma 3.12. Let
![]() $\mu $
be an SRB measure for f, let R be a hyperbolic rectangle, and let
$\mu $
be an SRB measure for f, let R be a hyperbolic rectangle, and let
![]() $D^{u}$
be a local transversal to all stable manifolds in the rectangle R. Assume furthermore that
$D^{u}$
be a local transversal to all stable manifolds in the rectangle R. Assume furthermore that
![]() $m_{D^{u}}$
-a.e. point in
$m_{D^{u}}$
-a.e. point in
![]() $D^{u}$
is in
$D^{u}$
is in
![]() $\mathcal {R}(\mu )$
. Then for any unstable
$\mathcal {R}(\mu )$
. Then for any unstable
![]() $W^{+}$
in R, we have that
$W^{+}$
in R, we have that
![]() $m_{W^{+}}$
-a.e. point in
$m_{W^{+}}$
-a.e. point in
![]() $W^{+} \cap R \cap \mathcal {R}_{\mathrm {hyp}}$
is in
$W^{+} \cap R \cap \mathcal {R}_{\mathrm {hyp}}$
is in
![]() $\mathcal {R}(\mu )$
.
$\mathcal {R}(\mu )$
.
This lemma allows us to control the Lyapunov exponents of Lyapunov–Perron regular points lying in a hyperbolic rectangle through the Lyapunov exponents of an SRB measure, and is central to the proof of the main proposition of this section. To prove this lemma, we will the following two lemmas.
Lemma 3.13. [Reference Tsujii17, Proposition 16(3)]
Let
![]() $x_{0} \in \mathcal {R}_{\mathrm {hyp}}$
be a hyperbolic Lyapunov–Perron regular point. Assume that x is a point such that we have one of the following satisfied:
$x_{0} \in \mathcal {R}_{\mathrm {hyp}}$
be a hyperbolic Lyapunov–Perron regular point. Assume that x is a point such that we have one of the following satisfied:
-
(1)
 $x \in V^{u}_{\mathrm {loc}}(x_{0}) \cap \mathcal {R}_{\mathrm {hyp}}$
;
$x \in V^{u}_{\mathrm {loc}}(x_{0}) \cap \mathcal {R}_{\mathrm {hyp}}$
; -
(2)
 $x \in V^{s}_{\mathrm {loc}}(x_{0}) \cap \mathcal {R}_{\mathrm {hyp}}$
.
$x \in V^{s}_{\mathrm {loc}}(x_{0}) \cap \mathcal {R}_{\mathrm {hyp}}$
.
Then the points
![]() $x_{0}$
and x have the same Lyapunov exponents with respect to f.
$x_{0}$
and x have the same Lyapunov exponents with respect to f.
Remark 3.14. For more details on Lemma 3.13, see [Reference Tsujii17, Proposition 16(3)], and in particular the proof where the author uses this lemma to prove item (3) in proposition 16.
We also need the following well-known inclination lemma.
Lemma 3.15. (Inclination lemma)
Let
![]() $f : M \longrightarrow M$
be a
$f : M \longrightarrow M$
be a
![]() $C^{1}$
diffeomorphism on a Riemannian manifold M. Let p be a fixed hyperbolic point. Let
$C^{1}$
diffeomorphism on a Riemannian manifold M. Let p be a fixed hyperbolic point. Let
![]() $B \subset W^{u}(p)$
be an embedded
$B \subset W^{u}(p)$
be an embedded
![]() $C^{1}$
disk of the same dimension as
$C^{1}$
disk of the same dimension as
![]() $W^{u}(p)$
. Let D be a
$W^{u}(p)$
. Let D be a
![]() $C^{1}$
embedded disk transversal to the
$C^{1}$
embedded disk transversal to the
![]() $W^{s}(p)$
of the same dimension as
$W^{s}(p)$
of the same dimension as
![]() $W^{u}(p)$
. Then for any
$W^{u}(p)$
. Then for any
![]() $\epsilon>0$
, there is an
$\epsilon>0$
, there is an
![]() $n_{0} \geq 0$
, such that for an
$n_{0} \geq 0$
, such that for an
![]() $n \geq n_{0}$
,
$n \geq n_{0}$
,
![]() $f^{n}(D)$
contains a
$f^{n}(D)$
contains a
![]() $C^{1}$
embedded disk which is
$C^{1}$
embedded disk which is
![]() $\epsilon $
close to B in the
$\epsilon $
close to B in the
![]() $C^{1}$
-topology.
$C^{1}$
-topology.
Now we are ready to prove Lemma 3.12.
Proof of Lemma 3.12
Let us fix an unstable
![]() $W^{+}$
in R. Then we can define the stable holonomy map
$W^{+}$
in R. Then we can define the stable holonomy map
defined by
![]() $\Gamma ^{s}(x) := V^{s}_{\mathrm {loc}}(x) \cap D^{u}$
. We can see that this is a well-defined map since
$\Gamma ^{s}(x) := V^{s}_{\mathrm {loc}}(x) \cap D^{u}$
. We can see that this is a well-defined map since
![]() $D^{u}$
is a transversal to stable manifolds in R. This map is absolutely continuous with respect to the Riemmanian volume on
$D^{u}$
is a transversal to stable manifolds in R. This map is absolutely continuous with respect to the Riemmanian volume on
![]() $W^{+}$
and
$W^{+}$
and
![]() $D^{u}$
, that is,
$D^{u}$
, that is,
![]() $(\Gamma ^{s})^{*}(m_{D^{u}|_{D^{u} \cap R}})$
is equivalent to
$(\Gamma ^{s})^{*}(m_{D^{u}|_{D^{u} \cap R}})$
is equivalent to
![]() $m_{W^{+}}|_{W^{+} \cap R}$
. Now, let us consider the
$m_{W^{+}}|_{W^{+} \cap R}$
. Now, let us consider the
![]() $(\Gamma ^{s})^{-1}(D^{u} \cap R \cap \mathcal {R}(\mu )) \subset W^{+} \cap R$
. We see that since
$(\Gamma ^{s})^{-1}(D^{u} \cap R \cap \mathcal {R}(\mu )) \subset W^{+} \cap R$
. We see that since
![]() $D^{u} \cap \mathcal {R}(\mu )$
has full measure with respect to the measure
$D^{u} \cap \mathcal {R}(\mu )$
has full measure with respect to the measure
![]() $m_{D^{u}}$
, it has full measure with respect to the restriction
$m_{D^{u}}$
, it has full measure with respect to the restriction
![]() $m_{D^{u}}|_{D^{u}\cap R}$
, and by absolute continuity of the stable holonomy map
$m_{D^{u}}|_{D^{u}\cap R}$
, and by absolute continuity of the stable holonomy map
![]() $\Gamma ^{s}$
, this implies that
$\Gamma ^{s}$
, this implies that
![]() $(\Gamma ^{s})^{-1}(D^{u} \cap R \cap \mathcal {R}(\mu )) )$
has full measure with respect to the restriction
$(\Gamma ^{s})^{-1}(D^{u} \cap R \cap \mathcal {R}(\mu )) )$
has full measure with respect to the restriction
![]() $m_{W^{+}}|_{W^{+} \cap R}$
. This implies that
$m_{W^{+}}|_{W^{+} \cap R}$
. This implies that
![]() $(\Gamma ^{s})^{-1}(D^{u} \cap R \cap \mathcal {R}(\mu )) \cap \mathcal {R}_{\mathrm {hyp}}$
has full measure inside
$(\Gamma ^{s})^{-1}(D^{u} \cap R \cap \mathcal {R}(\mu )) \cap \mathcal {R}_{\mathrm {hyp}}$
has full measure inside
![]() $W^{+} \cap R \cap \mathcal {R}_{\mathrm {hyp}}$
with respect to
$W^{+} \cap R \cap \mathcal {R}_{\mathrm {hyp}}$
with respect to
![]() $m_{W^{+}}|_{W^{+} \cap R}$
. Now, the set
$m_{W^{+}}|_{W^{+} \cap R}$
. Now, the set
![]() $(\Gamma ^{s})^{-1}(D^{u} \cap R \cap \mathcal {R}(\mu )) \cap \mathcal {R}_{\mathrm {hyp}}$
consists of all those points in
$(\Gamma ^{s})^{-1}(D^{u} \cap R \cap \mathcal {R}(\mu )) \cap \mathcal {R}_{\mathrm {hyp}}$
consists of all those points in
![]() $W^{+} \cap R$
which are in
$W^{+} \cap R$
which are in
![]() $\mathcal {R}_{\mathrm {hyp}}$
, and at the same time are on the stable manifold of a point in
$\mathcal {R}_{\mathrm {hyp}}$
, and at the same time are on the stable manifold of a point in
![]() $\mathcal {R}(\mu )$
. Using Lemma 3.13, we see that this implies that these points are in
$\mathcal {R}(\mu )$
. Using Lemma 3.13, we see that this implies that these points are in
![]() $\mathcal {R}(\mu )$
, which implies the lemma.
$\mathcal {R}(\mu )$
, which implies the lemma.
3.3 Ergodic homoclinic classes
In [Reference Rodriguez Hertz, Rodriguez Hertz, Tahzibi and Ures12], the authors introduce ergodic homoclinic classes.
Definition 3.16. [Reference Rodriguez Hertz, Rodriguez Hertz, Tahzibi and Ures12]
Let
![]() $P \in M$
be a hyperbolic periodic point and let
$P \in M$
be a hyperbolic periodic point and let
We define the ergodic homoclinic class of P by
![]() $H(P) = H^{u}(P) \cap H^{s}(P)$
.
$H(P) = H^{u}(P) \cap H^{s}(P)$
.
The reason why these homoclinic classes were introduced is to better understand the ergodic components of SRB and smooth measures, precisely, the authors of [Reference Sarig15] and [Reference Sinai16] prove the following result.
Proposition 3.17. Let
![]() $\mu $
be an SRB measure for a
$\mu $
be an SRB measure for a
![]() $C^{1+\alpha }$
diffeomorphism
$C^{1+\alpha }$
diffeomorphism
![]() $f :M\to M$
. Then the following statements hold:
$f :M\to M$
. Then the following statements hold:
-
(1) if
 $\mu (H(P))> 0$
, then the restriction
$\mu (H(P))> 0$
, then the restriction
 $\mu |_{H(P)}$
is an ergodic SRB measure;
$\mu |_{H(P)}$
is an ergodic SRB measure; -
(2) given any ergodic SRB measures
 $\mu _{1}$
and
$\mu _{1}$
and
 $\mu _{2}$
such that
$\mu _{2}$
such that
 $\mu _{1}(H(P))>0$
and
$\mu _{1}(H(P))>0$
and
 $\mu _{2}(H(P))>0$
, one has
$\mu _{2}(H(P))>0$
, one has
 $\mu _{1} = \mu _{2}$
.
$\mu _{1} = \mu _{2}$
.
There are two main reasons we wish to work with ergodic homoclinic classes in our case. First, they allow us to extend the transitivity argument in the proof of the toy model. The following proposition captures this precisely.
Remark 3.18. For a given point x inside a Pesin block
![]() $\Lambda _{\ell }$
, we denote by
$\Lambda _{\ell }$
, we denote by
![]() $W^{u}_{\ell }(x)$
and
$W^{u}_{\ell }(x)$
and
![]() $W^{s}_{\ell }(x)$
the maximal dimensional local unstable and stable manifolds at x, with size bounded below by
$W^{s}_{\ell }(x)$
the maximal dimensional local unstable and stable manifolds at x, with size bounded below by
![]() $e^{-\ell }$
.
$e^{-\ell }$
.
Lemma 3.19. Let P be a hyperbolic periodic point. Let R be rectangle containing P. Let
![]() $\mu $
be an ergoidic SRB measure supported on the ergodic homoclinic class
$\mu $
be an ergoidic SRB measure supported on the ergodic homoclinic class
![]() $H(P)$
. Then there is a local transversal
$H(P)$
. Then there is a local transversal
![]() $D^{u}$
for all stable manifolds in R, such that
$D^{u}$
for all stable manifolds in R, such that
![]() $m_{D^{u}}$
-a.e. point in
$m_{D^{u}}$
-a.e. point in
![]() $D^{u}$
is in
$D^{u}$
is in
![]() $\mathcal {R}(\mu )$
.
$\mathcal {R}(\mu )$
.
Proof. Since the set
![]() $\mathcal {R}(\mu )$
is invariant for f, and has full measure with respect to R, we see that
$\mathcal {R}(\mu )$
is invariant for f, and has full measure with respect to R, we see that
![]() $\mu $
-a.e. point
$\mu $
-a.e. point
![]() $x \in M$
satisfies the conclusion of Lemma 3.11. Let us fix such a point and denote it by
$x \in M$
satisfies the conclusion of Lemma 3.11. Let us fix such a point and denote it by
![]() $x^{u}$
. Since
$x^{u}$
. Since
![]() $\mu $
is supported on
$\mu $
is supported on
![]() $\mu (H(P)) = 1$
, we can assume without loss of generality that
$\mu (H(P)) = 1$
, we can assume without loss of generality that
![]() $x^{u} \in H(P)$
. Let
$x^{u} \in H(P)$
. Let
![]() $x^{u}_{0}$
be a point in
$x^{u}_{0}$
be a point in
![]() $W^{u}(x^{u}) \pitchfork W^{s}(P)$
, where this point exists by the assumption that
$W^{u}(x^{u}) \pitchfork W^{s}(P)$
, where this point exists by the assumption that
![]() $x^{u} \in H(P)$
. Let
$x^{u} \in H(P)$
. Let
![]() $D \subset W^{u}(x^{u})$
be an embedded disk containing the intersection point
$D \subset W^{u}(x^{u})$
be an embedded disk containing the intersection point
![]() $x^{u}_{0}$
, and let
$x^{u}_{0}$
, and let
![]() $p \geq 0$
be the period of the hyperbolic periodic point P. Then for any
$p \geq 0$
be the period of the hyperbolic periodic point P. Then for any
![]() $\epsilon> 0$
, the inclination lemma allows us to find
$\epsilon> 0$
, the inclination lemma allows us to find
![]() $N> 0$
such that
$N> 0$
such that
![]() $f^{Np}(D) $
contains an embedded disk
$f^{Np}(D) $
contains an embedded disk
![]() $D^{u}$
, such that
$D^{u}$
, such that
![]() $d_{C^{1}}(D^{u}, V^{u}_{\mathrm {loc}}(P)) < \epsilon $
(see Figure 2). By taking
$d_{C^{1}}(D^{u}, V^{u}_{\mathrm {loc}}(P)) < \epsilon $
(see Figure 2). By taking
![]() $\epsilon> 0$
small enough, we can ensure that
$\epsilon> 0$
small enough, we can ensure that
![]() $D^{u}$
is transversal for all stable manifolds in R, since
$D^{u}$
is transversal for all stable manifolds in R, since
![]() $V^{u}_{\mathrm {loc}}(P)$
is a transversal to all stable manifolds in R.
$V^{u}_{\mathrm {loc}}(P)$
is a transversal to all stable manifolds in R.

Figure 2 The inclination lemma implies that, for a large
![]() $N$
,
$N$
,
![]() $f^N(\mathcal{D}^u)$
is very close to the unstable manifold of the periodic point
$f^N(\mathcal{D}^u)$
is very close to the unstable manifold of the periodic point
![]() $P$
. Since the unstable manifold of the point
$P$
. Since the unstable manifold of the point
![]() $P$
intersects all the stable manifolds of points in the rectangle
$P$
intersects all the stable manifolds of points in the rectangle
![]() $R$
, we see that
$R$
, we see that
![]() $f^N(\mathcal{D}^u)$
does too.
$f^N(\mathcal{D}^u)$
does too.
Now, we are ready to prove the min proposition of this section, Proposition 3.1.
Proof of Proposition 3.1
Using Lemma 3.19, we see that we can find a local tranversal
![]() $D^{u}$
to all stable manifolds in
$D^{u}$
to all stable manifolds in
![]() $R^{+}$
, and such that
$R^{+}$
, and such that
![]() $m_{D^{u}}$
-a.e. point in
$m_{D^{u}}$
-a.e. point in
![]() $D^{u}$
is in
$D^{u}$
is in
![]() $\mathcal {R}(\mu ^{+})$
. Using Lemma 3.12, we see that this implies that
$\mathcal {R}(\mu ^{+})$
. Using Lemma 3.12, we see that this implies that
![]() $m_{W^{+}}$
-a.e. point in
$m_{W^{+}}$
-a.e. point in
![]() $W^{+} \cap R^{+} \cap \mathcal {R}_{\mathrm {hyp}}$
is in
$W^{+} \cap R^{+} \cap \mathcal {R}_{\mathrm {hyp}}$
is in
![]() $\mathcal {R}(\mu ^{+})$
, and by condition (2) in the proposition, we see that we have
$\mathcal {R}(\mu ^{+})$
, and by condition (2) in the proposition, we see that we have
![]() $m_{W^{+}}(W^{+} \cap \mathcal {R}(\mu ^{+}) )> 0$
. By replacing f by
$m_{W^{+}}(W^{+} \cap \mathcal {R}(\mu ^{+}) )> 0$
. By replacing f by
![]() $f^{-1}$
, we see that the same exact argument implies that we also have
$f^{-1}$
, we see that the same exact argument implies that we also have
![]() $m_{W^{-}}(W^{-} \cap \mathcal {R}(\mu ^{-}) )> 0$
. Now, using the fact that
$m_{W^{-}}(W^{-} \cap \mathcal {R}(\mu ^{-}) )> 0$
. Now, using the fact that
![]() $\mathcal {R}(\mu ^{+})$
and
$\mathcal {R}(\mu ^{+})$
and
![]() $\mathcal {R}(\mu ^{-})$
are invariant sets for f, and conditions (2) and (3) in the proposition, we see that
$\mathcal {R}(\mu ^{-})$
are invariant sets for f, and conditions (2) and (3) in the proposition, we see that
![]() ${m_{V^{u}_{\mathrm {loc}}(x_{0})}(V^{u}_{\mathrm {loc}}(x_{0}) \cap \mathcal {R}(\mu ^{+}))> 0}$
and
${m_{V^{u}_{\mathrm {loc}}(x_{0})}(V^{u}_{\mathrm {loc}}(x_{0}) \cap \mathcal {R}(\mu ^{+}))> 0}$
and
![]() $m_{V^{s}_{\mathrm {loc}}(x_{0})}(V^{s}_{\mathrm {loc}}(x_{0}) \cap \mathcal {R}(\mu ^{-}))> 0$
. Using Lemma 3.13, we see that the Lyapunov exponents of
$m_{V^{s}_{\mathrm {loc}}(x_{0})}(V^{s}_{\mathrm {loc}}(x_{0}) \cap \mathcal {R}(\mu ^{-}))> 0$
. Using Lemma 3.13, we see that the Lyapunov exponents of
![]() $x_{0}$
with respect to f coincide with the Lyapunov exponents of f with respect to the SRB measure
$x_{0}$
with respect to f coincide with the Lyapunov exponents of f with respect to the SRB measure
![]() $\mu ^{+}$
, and that the Lyapunov exponents of
$\mu ^{+}$
, and that the Lyapunov exponents of
![]() $x_{0}$
with respect to
$x_{0}$
with respect to
![]() $f^{-1}$
coincide with the Lyapunov exponents of
$f^{-1}$
coincide with the Lyapunov exponents of
![]() $f^{-1}$
with respect to the measure
$f^{-1}$
with respect to the measure
![]() $\mu ^{-}$
. By the regularity of the point
$\mu ^{-}$
. By the regularity of the point
![]() $x_{0}$
, we know that the Lyapunov exponents of
$x_{0}$
, we know that the Lyapunov exponents of
![]() $x_{0}$
with respect to
$x_{0}$
with respect to
![]() $f^{-1}$
are the negative of the Lyapunov exponents of
$f^{-1}$
are the negative of the Lyapunov exponents of
![]() $x_{0}$
with respect to f. In particular, this means that we have
$x_{0}$
with respect to f. In particular, this means that we have
however, using Lemma 3.8, we see that we have
and that we also have
Therefore, we see that we end up with
Using Lemma 3.8 again, we see that this implies that both
![]() $\mu ^{+}$
and
$\mu ^{+}$
and
![]() $\mu ^{-}$
are absolutely continuous with respect to volume.
$\mu ^{-}$
are absolutely continuous with respect to volume.
4 Non-uniform hyperbolicity
The second reason for considering ergodic homoclinic classes is that they have a convenient symbolic description which we will describe in this section.
4.1 Lyapunov–Perron regularity
Our main object in this paper is the set of hyperbolic Lyapunov–Perron regular points
![]() $\mathcal {R}_{\mathrm {hyp}}$
, which we define next.
$\mathcal {R}_{\mathrm {hyp}}$
, which we define next.
Definition 4.1. A point
![]() $x \in M$
is Lyapunov–Perron regular for a diffeomorphism
$x \in M$
is Lyapunov–Perron regular for a diffeomorphism
![]() $f:M\to M$
if there exist numbers
$f:M\to M$
if there exist numbers
![]() $\unicode{x3bb} _{1}(x) < \unicode{x3bb} _{2}(x) <\cdots <\unicode{x3bb} _{k(x)}(x)$
and an invariant decomposition
$\unicode{x3bb} _{1}(x) < \unicode{x3bb} _{2}(x) <\cdots <\unicode{x3bb} _{k(x)}(x)$
and an invariant decomposition
 $$ \begin{align*} T_{x}M = \bigoplus_{i=1}^{k(x)}E_{i}(x) \end{align*} $$
$$ \begin{align*} T_{x}M = \bigoplus_{i=1}^{k(x)}E_{i}(x) \end{align*} $$
such that for all
![]() $ v \in E_{i}(x)$
, we have
$ v \in E_{i}(x)$
, we have
 $$ \begin{align*} \lim_{n\to\pm \infty}\frac1n \log\|\det(D_{x}f^{n}) \| = \sum_{i=1}^{k(x)}\unicode{x3bb}_{i}(x), \end{align*} $$
$$ \begin{align*} \lim_{n\to\pm \infty}\frac1n \log\|\det(D_{x}f^{n}) \| = \sum_{i=1}^{k(x)}\unicode{x3bb}_{i}(x), \end{align*} $$
and so that
![]() $\unicode{x3bb} _{i}(x)$
,
$\unicode{x3bb} _{i}(x)$
,
![]() $E_{i}(x)$
, and
$E_{i}(x)$
, and
![]() $k(x)$
depend measurably on x. We denote the set of all such Lyapunov–Perron regular points by
$k(x)$
depend measurably on x. We denote the set of all such Lyapunov–Perron regular points by
![]() $\mathcal {R}$
.
$\mathcal {R}$
.
Definition 4.2. A point
![]() $x \in \mathcal {R}$
is hyperbolic if
$x \in \mathcal {R}$
is hyperbolic if
![]() $\unicode{x3bb} _{i}(x) \neq 0$
for all
$\unicode{x3bb} _{i}(x) \neq 0$
for all
![]() $i = 1,\ldots ,k(x)$
and
$i = 1,\ldots ,k(x)$
and
![]() $\unicode{x3bb} _{1}(x)<0 < \unicode{x3bb} _{k(x)}(x)$
. We denote the set of all hyperbolic Lyapunov–Perron regular points by
$\unicode{x3bb} _{1}(x)<0 < \unicode{x3bb} _{k(x)}(x)$
. We denote the set of all hyperbolic Lyapunov–Perron regular points by
![]() $\mathcal {R}_{\mathrm {hyp}}$
. Given
$\mathcal {R}_{\mathrm {hyp}}$
. Given
![]() $\chi>0$
, we define
$\chi>0$
, we define
![]() $\mathcal {R}_{\chi } \subset \mathcal {R}_{\mathrm {hyp}}$
by
$\mathcal {R}_{\chi } \subset \mathcal {R}_{\mathrm {hyp}}$
by
We call it the set of
![]() $\chi $
-hyperbolic Lyapunov–Perron regular points.
$\chi $
-hyperbolic Lyapunov–Perron regular points.
Remark 4.3. We stress that, while by Oseledets theorem, for a given hyperbolic invariant measure
![]() $\mu $
, almost all points with respect to
$\mu $
, almost all points with respect to
![]() $\mu $
are in
$\mu $
are in
![]() $\mathcal {R}_{\mathrm {hyp}}$
, we can easily find that
$\mathcal {R}_{\mathrm {hyp}}$
, we can easily find that
![]() $\mathcal {R}_{\mathrm{hyp}}$
has zero measure with respect to volume, even in the case of Anosov systems. In fact, as we pointed out in the informal discussion above, in the case of an Anosov map,
$\mathcal {R}_{\mathrm{hyp}}$
has zero measure with respect to volume, even in the case of Anosov systems. In fact, as we pointed out in the informal discussion above, in the case of an Anosov map,
![]() $\text {Vol}(\mathcal {R}_{\mathrm {hyp}})>0$
implies that the system preserves a smooth measure, so in general, one can expect that the volume of
$\text {Vol}(\mathcal {R}_{\mathrm {hyp}})>0$
implies that the system preserves a smooth measure, so in general, one can expect that the volume of
![]() $\mathcal {R}_{\mathrm {hyp}} $
is zero.
$\mathcal {R}_{\mathrm {hyp}} $
is zero.
Remark 4.4. A simple observation is that
![]() $\chi $
-hyperbolic regular points exhaust
$\chi $
-hyperbolic regular points exhaust
![]() $\mathcal {R}_{\mathrm{hyp}}$
, that is,
$\mathcal {R}_{\mathrm{hyp}}$
, that is,
We also note that each
![]() $\mathcal {R}_{\chi }$
is invariant under the action of f. In this paper, we will fix a small
$\mathcal {R}_{\chi }$
is invariant under the action of f. In this paper, we will fix a small
![]() $\chi>0$
and work with
$\chi>0$
and work with
![]() $\mathcal {R}_{\chi }$
, then using the fact that they exhaust
$\mathcal {R}_{\chi }$
, then using the fact that they exhaust
![]() $\mathcal {R}_{\mathrm {hyp}}$
, we will be able to obtain our main theorem.
$\mathcal {R}_{\mathrm {hyp}}$
, we will be able to obtain our main theorem.
Definition 4.5. We define the set
![]() $\mathcal {R}^{\mathrm{PR}}_{\mathrm {hyp}}$
of positively recurrent hyperbolic Lyapunov–Perron regular points to be the set of points
$\mathcal {R}^{\mathrm{PR}}_{\mathrm {hyp}}$
of positively recurrent hyperbolic Lyapunov–Perron regular points to be the set of points
![]() $x \in \mathcal {R}_{\mathrm {hyp}}$
, for which there is a Pesin level set
$x \in \mathcal {R}_{\mathrm {hyp}}$
, for which there is a Pesin level set
![]() $\Lambda ^{r_{x}}$
for which we have the following two recurrence conditions satisfied:
$\Lambda ^{r_{x}}$
for which we have the following two recurrence conditions satisfied:
-
(1)
 $\limsup \nolimits _{n \rightarrow \infty } ({1}/{n}) \sum \nolimits _{k=0}^{n-1}1_{\Lambda ^{r_{x}}} \circ f^{k}(x)> 0 $
;
$\limsup \nolimits _{n \rightarrow \infty } ({1}/{n}) \sum \nolimits _{k=0}^{n-1}1_{\Lambda ^{r_{x}}} \circ f^{k}(x)> 0 $
; -
(2)
 $\limsup \nolimits _{n \rightarrow \infty } ({1}/{n}) \sum \nolimits _{k=0}^{n-1}1_{\Lambda ^{r_{x}}} \circ f^{-k}(x)> 0 $
.
$\limsup \nolimits _{n \rightarrow \infty } ({1}/{n}) \sum \nolimits _{k=0}^{n-1}1_{\Lambda ^{r_{x}}} \circ f^{-k}(x)> 0 $
.
Remark 4.6. The definition of positively recurrent hyperbolic Lyapunov–Perron regular points is directly by the definition of
![]() $RWT^{\mathrm{PR}}_{\chi }$
in [Reference Ben Ovadia4]. In fact, we have that
$RWT^{\mathrm{PR}}_{\chi }$
in [Reference Ben Ovadia4]. In fact, we have that
![]() $\mathcal {R}^{\mathrm{PR}}_{\chi } \subset RWT^{\mathrm{PR}}_{\chi }$
. The main difference here is that our definition concerns Lyapunov–Perron regular points, and is also symmetric in time, while the definition of
$\mathcal {R}^{\mathrm{PR}}_{\chi } \subset RWT^{\mathrm{PR}}_{\chi }$
. The main difference here is that our definition concerns Lyapunov–Perron regular points, and is also symmetric in time, while the definition of
![]() $RWT^{\mathrm{PR}}_{\chi }$
is concerned mainly with the forward dynamics of the system.
$RWT^{\mathrm{PR}}_{\chi }$
is concerned mainly with the forward dynamics of the system.
In the course of the proof of the the main theorem, we will have to use stable and unstable holonomy maps, and one problem is that
![]() $\mathcal {R}_{\chi }^{\mathrm{PR}}$
is not invariant under these holonomy maps, so we will find ourselves forced to consider the larger sets of points
$\mathcal {R}_{\chi }^{\mathrm{PR}}$
is not invariant under these holonomy maps, so we will find ourselves forced to consider the larger sets of points
![]() $RWT^{\mathrm{PR}}_{\chi }$
, which we introduce next.
$RWT^{\mathrm{PR}}_{\chi }$
, which we introduce next.
4.2 Non-uniform hyperbolicity
In [Reference Ben Ovadia4], the author introduces the set
![]() $RWT_{\chi }$
. This set is larger than the set
$RWT_{\chi }$
. This set is larger than the set
![]() $\mathcal {R}_{\chi }$
of
$\mathcal {R}_{\chi }$
of
![]() $\chi $
-Lyapunov–Perron regular points. The author observed that the whole theory of invariant manifolds does not require Lyapunov–Perron regularity, instead we only need some notion of hyperbolicity. For many purposes, this set is much more flexible to work with than
$\chi $
-Lyapunov–Perron regular points. The author observed that the whole theory of invariant manifolds does not require Lyapunov–Perron regularity, instead we only need some notion of hyperbolicity. For many purposes, this set is much more flexible to work with than
![]() $\mathcal {R}_{\chi }$
, for the simple reason that we can work with holonomy maps on theses sets while we cannot do that with
$\mathcal {R}_{\chi }$
, for the simple reason that we can work with holonomy maps on theses sets while we cannot do that with
![]() $\mathcal {R}_{\chi }$
.
$\mathcal {R}_{\chi }$
.
Definition 4.7. [Reference Ben Ovadia4, Definition 2.1]
A point
![]() $x \in M $
is
$x \in M $
is
![]() $\chi $
-summable if it satisfies the following condition: There is a unique splitting
$\chi $
-summable if it satisfies the following condition: There is a unique splitting
![]() $T_{x}M = H^{s}(x) \oplus H^{u}(x)$
such that
$T_{x}M = H^{s}(x) \oplus H^{u}(x)$
such that
This set is denoted by
![]() $\chi -summ$
.
$\chi -summ$
.
A point
![]() $x \in M $
is
$x \in M $
is
![]() $\chi $
-hyperbolic if it satisfies the following condition: There is a unique splitting
$\chi $
-hyperbolic if it satisfies the following condition: There is a unique splitting
![]() $T_{x}M = H^{s}(x) \oplus H^{u}(x)$
such that
$T_{x}M = H^{s}(x) \oplus H^{u}(x)$
such that
A measure carried by
![]() $\chi -hyp$
is called a
$\chi -hyp$
is called a
![]() $\chi $
-hyperbolic measure.
$\chi $
-hyperbolic measure.
Theorem 4.8. [Reference Ben Ovadia4, Theorem 2.2]
For all
![]() $x \in \chi -summ$
, there exists an invertible linear map
$x \in \chi -summ$
, there exists an invertible linear map
![]() $C_{\chi }(x):\mathbb {R}^{d} \to T_{x}M$
such that
$C_{\chi }(x):\mathbb {R}^{d} \to T_{x}M$
such that
![]() $D_{\chi }(x) = C_{\chi }(f(x))^{-1}\circ D_{x}f\circ C_{\chi }(x)$
has the block decomposition
$D_{\chi }(x) = C_{\chi }(f(x))^{-1}\circ D_{x}f\circ C_{\chi }(x)$
has the block decomposition
 $$ \begin{align*} D_{\chi}(x)\ = \begin{pmatrix} D_{\chi} {}^{s}(x )& 0 \\ 0 & D_{\chi}^{u}(x) \\ \end{pmatrix} \end{align*} $$
$$ \begin{align*} D_{\chi}(x)\ = \begin{pmatrix} D_{\chi} {}^{s}(x )& 0 \\ 0 & D_{\chi}^{u}(x) \\ \end{pmatrix} \end{align*} $$
with respect to the decomposition
![]() $T_{x}M = H^{s}(x) \oplus H^{u}(x)$
, where
$T_{x}M = H^{s}(x) \oplus H^{u}(x)$
, where
![]() $\|D_{\chi }^{s}(x) v\| \leq e^{-\chi }\|v\|$
and
$\|D_{\chi }^{s}(x) v\| \leq e^{-\chi }\|v\|$
and
![]() $\|D_{\chi }^{u}(x)w\| \geq e^{\chi } \|v\|$
.
$\|D_{\chi }^{u}(x)w\| \geq e^{\chi } \|v\|$
.
Definition 4.9. [Reference Ben Ovadia4, Definition 2.3]
Let
![]() $\epsilon> 0$
, and let
$\epsilon> 0$
, and let
![]() $x \in \chi -summ$
, then
$x \in \chi -summ$
, then
Definition 4.10. [Reference Ben Ovadia4, Definition 2.4]
Let
![]() $\epsilon> 0$
. A point
$\epsilon> 0$
. A point
![]() $x \in \chi -summ$
is called
$x \in \chi -summ$
is called
![]() $\epsilon $
-weakly temperable if there is a function
$\epsilon $
-weakly temperable if there is a function
![]() $q: \{f^{n}(x)\}_{n \in \mathbb {Z}} \longrightarrow (0, \epsilon _{\chi }] \cap \{ e^{({-\ell \epsilon _{\chi }})/{3}}\}_{\ell \geq 0} $
such that
$q: \{f^{n}(x)\}_{n \in \mathbb {Z}} \longrightarrow (0, \epsilon _{\chi }] \cap \{ e^{({-\ell \epsilon _{\chi }})/{3}}\}_{\ell \geq 0} $
such that
-
(1)
 $ e^{-\epsilon _{\chi }} \leq {q\circ f}/{q}\leq e^{\epsilon _{\chi }}$
;
$ e^{-\epsilon _{\chi }} \leq {q\circ f}/{q}\leq e^{\epsilon _{\chi }}$
; -
(2)
 $q \circ f^{n} (x) \leq Q_{\epsilon _{\chi }} \circ f^{n}(x)$
, for all
$q \circ f^{n} (x) \leq Q_{\epsilon _{\chi }} \circ f^{n}(x)$
, for all
 $n \in \mathbb {Z}$
.
$n \in \mathbb {Z}$
.
We call an
![]() $\epsilon $
-weakly temperable point x recurrently
$\epsilon $
-weakly temperable point x recurrently
![]() $\epsilon $
-weakly temperable if we also have
$\epsilon $
-weakly temperable if we also have
![]() $\limsup _{n \rightarrow \infty } q(f^{\pm }(x))> 0$
.
$\limsup _{n \rightarrow \infty } q(f^{\pm }(x))> 0$
.
Definition 4.11. [Reference Ben Ovadia4, Definition 2.4] and [Reference Ben Ovadia4, Definition 7.7]
The set
![]() $RWT_{\chi }$
is defined to be the set of all
$RWT_{\chi }$
is defined to be the set of all
![]() $\chi $
-summable and recurrently
$\chi $
-summable and recurrently
![]() $\epsilon _{\chi }$
-weakly temperable, where
$\epsilon _{\chi }$
-weakly temperable, where
![]() $\epsilon _{\chi }> 0$
is a fixed small constant. The set of positively recurrent points in
$\epsilon _{\chi }> 0$
is a fixed small constant. The set of positively recurrent points in
![]() $RWT_{\chi }$
is defined by
$RWT_{\chi }$
is defined by
 $$ \begin{align*} & RWT^{\mathrm{PR}}_{\chi} \\ &\quad =\bigg\{ x \in RWT_{\chi} \mid \text{there exists } r_{x}> 0 \mbox{ such that } \limsup_{n \rightarrow \infty} \frac{1}{n} \sum\limits_{k=0}^{n-1}1_{\Lambda^{r_{x}}} \circ f^{k}(x) > 0 \bigg\}. \end{align*} $$
$$ \begin{align*} & RWT^{\mathrm{PR}}_{\chi} \\ &\quad =\bigg\{ x \in RWT_{\chi} \mid \text{there exists } r_{x}> 0 \mbox{ such that } \limsup_{n \rightarrow \infty} \frac{1}{n} \sum\limits_{k=0}^{n-1}1_{\Lambda^{r_{x}}} \circ f^{k}(x) > 0 \bigg\}. \end{align*} $$
We emphasize the dependence of
![]() $RWT_{\chi }$
and
$RWT_{\chi }$
and
![]() $RWT^{\mathrm{PR}}_{\chi }$
on the map f by writing
$RWT^{\mathrm{PR}}_{\chi }$
on the map f by writing
![]() $RWT_{\chi }(f)$
and
$RWT_{\chi }(f)$
and
![]() $RWT^{\mathrm{PR}}_{\chi }(f)$
.
$RWT^{\mathrm{PR}}_{\chi }(f)$
.
Remark 4.12. An easy example that illustrates the difference between
![]() $\mathcal {R}_{\chi }$
and
$\mathcal {R}_{\chi }$
and
![]() $RWT_{\chi }$
is the case of Anosov diffeomorphisms. Typically, it has two distinct SRB measures
$RWT_{\chi }$
is the case of Anosov diffeomorphisms. Typically, it has two distinct SRB measures
![]() $\mu ^{+}$
and
$\mu ^{+}$
and
![]() $\mu ^{-}$
for f and
$\mu ^{-}$
for f and
![]() $f^{-1}$
respectively. The basins of attraction of these two SRB measures as
$f^{-1}$
respectively. The basins of attraction of these two SRB measures as
![]() $n\rightarrow \infty $
and as
$n\rightarrow \infty $
and as
![]() $n \rightarrow -\infty $
have full Lebesgue volume respectively, so we see that for almost all points, the forward and backward Lyapunov exponents are different, and therefore we see that
$n \rightarrow -\infty $
have full Lebesgue volume respectively, so we see that for almost all points, the forward and backward Lyapunov exponents are different, and therefore we see that
![]() $\mathcal {R}_{\mathrm {hyp}}$
has zero Lebesgue volume. However, we can see that for
$\mathcal {R}_{\mathrm {hyp}}$
has zero Lebesgue volume. However, we can see that for
![]() $\chi>0$
small enough, one has
$\chi>0$
small enough, one has
![]() $RWT_{\chi } = M$
.
$RWT_{\chi } = M$
.
4.3 The coding of the dynamics on
 $RWT_{\chi }$
$RWT_{\chi }$
The following theorem, proved in [Reference Sarig15] for the surface diffeomorphism case, and in [Reference Ben Ovadia3] for the general case, is going to be a corner stone in the proof of our main result.
Proposition 4.13. [Reference Ben Ovadia3, Theorem 1.1]
Let
![]() $f:M \to M$
be a
$f:M \to M$
be a
![]() $C^{1+\alpha }$
diffeomorphism. Then there exists a locally compact graph
$C^{1+\alpha }$
diffeomorphism. Then there exists a locally compact graph
![]() $(\mathcal {P}, \mathcal {E})$
that induces a topological Markov shift
$(\mathcal {P}, \mathcal {E})$
that induces a topological Markov shift
![]() $ \hat \Sigma ^\#$
and a map
$ \hat \Sigma ^\#$
and a map
![]() $\hat \pi : \Sigma ^\# \to RWT\chi $
satisfying:
$\hat \pi : \Sigma ^\# \to RWT\chi $
satisfying:
-
(1)
 $\hat \pi $
is Holder continuous with respect to the word metric;
$\hat \pi $
is Holder continuous with respect to the word metric; -
(2)
 $ \hat \pi \circ \sigma = f \circ \hat \pi $
;
$ \hat \pi \circ \sigma = f \circ \hat \pi $
; -
(3)
 $\hat \pi $
is a finite-to-one map;
$\hat \pi $
is a finite-to-one map; -
(4)
 $\hat \pi (\Sigma ^\#)$
has full measure with respect to any
$\hat \pi (\Sigma ^\#)$
has full measure with respect to any
 $\chi $
-hyperbolic measure.
$\chi $
-hyperbolic measure.
This result is a far reaching generalization of Bowen’s result for Axiom A systems [Reference Bowen and Chazottes6]. While the approach follows the lines of the argument by Bowen, the technical details are much more intricate than in the Axiom A case. To be able to use this result, we will need a more precise understanding of the topological Markov shift and how it should be interpreted, so for the rest of this subsection, we will give a more detailed description of this coding and some of its properties that we are going to use.
4.3.1 The first coding
Let
![]() $\rho>0 $
and
$\rho>0 $
and
![]() $r>0$
be such that the exponential map
$r>0$
be such that the exponential map
![]() $\exp _{x}:B_{r}(0)\to B_{\rho }(x)$
is a diffeomorphism. Let
$\exp _{x}:B_{r}(0)\to B_{\rho }(x)$
is a diffeomorphism. Let
![]() $Q_{\epsilon }(x)$
be the constant defined in [Reference Ben Ovadia3, Definition 2.12], then we make the following definition.
$Q_{\epsilon }(x)$
be the constant defined in [Reference Ben Ovadia3, Definition 2.12], then we make the following definition.
Definition 4.14. (Pesin Charts)
The Pesin chart at x,
is defined by
![]() $\psi ^{\eta }_{x} := \exp _{x} \circ C_{\chi }(x)$
. A pair
$\psi ^{\eta }_{x} := \exp _{x} \circ C_{\chi }(x)$
. A pair
![]() $\psi _{x}^{p^{s},p^{u}}:=(\psi _{x}^{p^{s}},\psi _{x}^{p^{u}})$
of Pesin charts is called a double-Pesin chart.
$\psi _{x}^{p^{s},p^{u}}:=(\psi _{x}^{p^{s}},\psi _{x}^{p^{u}})$
of Pesin charts is called a double-Pesin chart.
Proposition 4.15. [Reference Ben Ovadia3, Theorem 3.2]
There exists a countable and locally finite graph
![]() $\mathcal {G} = (\mathcal {V},\mathcal {E})$
that induces a topological Markov shift
$\mathcal {G} = (\mathcal {V},\mathcal {E})$
that induces a topological Markov shift
![]() $\Sigma = \{\underline {u}\in \mathcal {V}^{\mathbb {Z}}\mid (u_{i},u_{i+1)}\in \mathcal {E}, \text{for all }\ i\in \mathbb {Z}\}$
such that there is a map
$\Sigma = \{\underline {u}\in \mathcal {V}^{\mathbb {Z}}\mid (u_{i},u_{i+1)}\in \mathcal {E}, \text{for all }\ i\in \mathbb {Z}\}$
such that there is a map
![]() $\pi :\Sigma \to M $
satisfying:
$\pi :\Sigma \to M $
satisfying:
-
(1)
 $f \circ \pi = \pi \circ \sigma $
, where
$f \circ \pi = \pi \circ \sigma $
, where
 $\sigma :\Sigma \to \Sigma $
is the shift map;
$\sigma :\Sigma \to \Sigma $
is the shift map; -
(2)
 $\pi $
is Holder continuous with respect to the word metric on
$\pi $
is Holder continuous with respect to the word metric on
 $\Sigma $
;
$\Sigma $
; -
(3)
 $\pi (\Sigma ^\#)$
carries all invariant
$\pi (\Sigma ^\#)$
carries all invariant
 $\chi $
-hyperbolic measures of f, where
$\chi $
-hyperbolic measures of f, where  $$ \begin{align*} \Sigma^\# & = \big\{\underline{u} \in \Sigma\mid\text{there exists }\ a,b \in \mathcal{V}\ \mbox{such that } u_{n} = a,\ u_{-m}\\&\!\!\qquad=b\ \mbox{for infinitely many } n,m\geq0\big \}. \end{align*} $$
$$ \begin{align*} \Sigma^\# & = \big\{\underline{u} \in \Sigma\mid\text{there exists }\ a,b \in \mathcal{V}\ \mbox{such that } u_{n} = a,\ u_{-m}\\&\!\!\qquad=b\ \mbox{for infinitely many } n,m\geq0\big \}. \end{align*} $$
The edges of the graph are a countable subset of double charts, and an edge corresponds to the overlapping relation
![]() $\psi ^{\eta }_{x} \rightarrow \psi ^{\eta ^{\prime }}_{y}$
. This map is typically infinite-to-one, but we can use a Bowen–Sinai refinement procedure to get a Markov partition, as done in [Reference Ben Ovadia3, Reference Sarig15].
$\psi ^{\eta }_{x} \rightarrow \psi ^{\eta ^{\prime }}_{y}$
. This map is typically infinite-to-one, but we can use a Bowen–Sinai refinement procedure to get a Markov partition, as done in [Reference Ben Ovadia3, Reference Sarig15].
4.3.2 The Markov partition
For any
![]() $v \in \mathcal {V}$
, we define
$v \in \mathcal {V}$
, we define
![]() $Z[v] := \pi ([v]\cap \Sigma ^\#)$
and let
$Z[v] := \pi ([v]\cap \Sigma ^\#)$
and let
![]() $\mathcal {Z} :=\{Z[v]\mid v \in \mathcal {V}\}$
. An essential property of
$\mathcal {Z} :=\{Z[v]\mid v \in \mathcal {V}\}$
. An essential property of
![]() $\mathcal {Z}$
is that it is locally finite, that is,
$\mathcal {Z}$
is that it is locally finite, that is,
![]() $\#\{Z^{\prime } \in \mathcal {Z} \mid Z^{\prime } \cap Z \neq \emptyset \} < \infty $
for all
$\#\{Z^{\prime } \in \mathcal {Z} \mid Z^{\prime } \cap Z \neq \emptyset \} < \infty $
for all
![]() $Z \in \mathcal Z$
. This allows us to perform a Bowen–Sinai refinement on
$Z \in \mathcal Z$
. This allows us to perform a Bowen–Sinai refinement on
![]() $\mathcal {Z}$
to obtain a partition
$\mathcal {Z}$
to obtain a partition
![]() $\mathcal {P}$
, which induces a TMS
$\mathcal {P}$
, which induces a TMS
![]() $(\hat \Sigma , \sigma )$
and a factor map
$(\hat \Sigma , \sigma )$
and a factor map
![]() $\hat \pi :\hat \Sigma \to M$
satisfying:
$\hat \pi :\hat \Sigma \to M$
satisfying:
-
(1)
 $\hat \pi $
is holder continuous with respect to the word metric;
$\hat \pi $
is holder continuous with respect to the word metric; -
(2)
 $\hat \pi |_{\hat \Sigma ^\#}$
is finite-to-one;
$\hat \pi |_{\hat \Sigma ^\#}$
is finite-to-one; -
(3) for all
 $\underline R \in \hat \Sigma ^\#$
, we have
$\underline R \in \hat \Sigma ^\#$
, we have
 $\hat \pi (\underline R) \in \overline R_{0}$
;
$\hat \pi (\underline R) \in \overline R_{0}$
; -
(4) the image of
 $\hat \Sigma ^\#$
carry all
$\hat \Sigma ^\#$
carry all
 $\chi $
-hyperbolic measures.
$\chi $
-hyperbolic measures.
Again, from the fact that
![]() $\mathcal G = (\mathcal {V},\mathcal {E})$
is locally compact, one can prove that the new graph is also locally compact, and from local finiteness of
$\mathcal G = (\mathcal {V},\mathcal {E})$
is locally compact, one can prove that the new graph is also locally compact, and from local finiteness of
![]() $\mathcal {Z}$
, we can see that
$\mathcal {Z}$
, we can see that
![]() $\#\{Z \in \mathcal Z \mid R \in Z \} <~\infty $
.
$\#\{Z \in \mathcal Z \mid R \in Z \} <~\infty $
.
The map
![]() $\hat \pi :\hat \Sigma ^\# \to RWT_{\chi }$
is define by
$\hat \pi :\hat \Sigma ^\# \to RWT_{\chi }$
is define by
One also has the following proposition.
Proposition 4.16. [Reference Ben Ovadia4, Proposition 3.8]
![]() $\hat \pi (\hat \Sigma ^{\#}) = \pi ( \Sigma ^{\#}) = RWT_{\chi } $
.
$\hat \pi (\hat \Sigma ^{\#}) = \pi ( \Sigma ^{\#}) = RWT_{\chi } $
.
Definition 4.17. [Reference Ben Ovadia4, Definitions 4.3 and 4.23]
For a chain
![]() $\underline {R} \in \hat \Sigma _{L}$
, the unstable of
$\underline {R} \in \hat \Sigma _{L}$
, the unstable of
![]() $\underline {R}$
is defined to be
$\underline {R}$
is defined to be
![]() $V^{u}(\underline {R}) := W(R_{0}) \cap V^{u}(\underline {u})$
for some
$V^{u}(\underline {R}) := W(R_{0}) \cap V^{u}(\underline {u})$
for some
![]() $\underline {u}$
covering
$\underline {u}$
covering
![]() $\underline {R}$
(see [Reference Ben Ovadia4, Definition 4.2] for more details).
$\underline {R}$
(see [Reference Ben Ovadia4, Definition 4.2] for more details).
Similarly, for a chain
![]() $\underline {R} \in \hat \Sigma _{R}$
, the stable of
$\underline {R} \in \hat \Sigma _{R}$
, the stable of
![]() $\underline {R}$
is defined to be
$\underline {R}$
is defined to be
![]() $V^{s}(\underline {R}) := W(R_{0}) \cap V^{s}(\underline {u})$
for some
$V^{s}(\underline {R}) := W(R_{0}) \cap V^{s}(\underline {u})$
for some
![]() $\underline {u}$
covering
$\underline {u}$
covering
![]() $\underline {R}$
(see [Reference Ben Ovadia4, Definition 4.23] for more details).
$\underline {R}$
(see [Reference Ben Ovadia4, Definition 4.23] for more details).
Here,
![]() $\hat \Sigma _{L} := \{(R_{i})_{i \leq 0} \mid (R_{i})_{i \in \mathbb {Z}} \in \hat \Sigma \}$
and
$\hat \Sigma _{L} := \{(R_{i})_{i \leq 0} \mid (R_{i})_{i \in \mathbb {Z}} \in \hat \Sigma \}$
and
![]() $\hat \Sigma _{R} := \{(R_{i})_{i \geq 0} \mid (R_{i})_{i \in \mathbb {Z}} \in \hat \Sigma \}$
.
$\hat \Sigma _{R} := \{(R_{i})_{i \geq 0} \mid (R_{i})_{i \in \mathbb {Z}} \in \hat \Sigma \}$
.
In [Reference Ben Ovadia4, Corollary 4.6], the author shows that
![]() $V^{u}(\underline {R})$
and
$V^{u}(\underline {R})$
and
![]() $V^{s}(\underline {R})$
are actually open submanifolds of M.
$V^{s}(\underline {R})$
are actually open submanifolds of M.
The following definition and lemma can be found in [Reference Ben Ovadia4].
Definition 4.18. [Reference Ben Ovadia4, Definition 3.15]
We say that
![]() $R \sim S$
if there exists a path
$R \sim S$
if there exists a path
![]() ${R \rightarrow \cdots \rightarrow S}$
from R to S and a path
${R \rightarrow \cdots \rightarrow S}$
from R to S and a path
![]() $S \to \cdots \rightarrow R$
from S to R. On the sub alphabet of letters satisfying
$S \to \cdots \rightarrow R$
from S to R. On the sub alphabet of letters satisfying
![]() $R \sim R$
, the relation
$R \sim R$
, the relation
![]() $\sim $
is an equivalence relation, and we denote the equivalence class of R by
$\sim $
is an equivalence relation, and we denote the equivalence class of R by
![]() $\langle R \rangle $
. We define the maximal irreducible component corresponding to R to be
$\langle R \rangle $
. We define the maximal irreducible component corresponding to R to be
![]() $\langle R \rangle ^{\mathbb {Z}} \subset \hat \Sigma $
.
$\langle R \rangle ^{\mathbb {Z}} \subset \hat \Sigma $
.
The importance of maximal irreducible components to us is that they correspond to subsets of ergodic homoclinic components as stated in the following lemma.
Lemma 4.19. Given
![]() $R\ \in \mathcal {P}$
for which
$R\ \in \mathcal {P}$
for which
![]() $R \sim R$
, there exists a hyperbolic periodic point P such that
$R \sim R$
, there exists a hyperbolic periodic point P such that
![]() $\hat \pi (\langle R \rangle ^{\mathbb {Z}}) \subset H(P)$
.
$\hat \pi (\langle R \rangle ^{\mathbb {Z}}) \subset H(P)$
.
Remark 4.20. In fact, as shown in [Reference Ben Ovadia4], one can prove that given any hyperbolic measure
![]() $\mu $
, we have
$\mu $
, we have
![]() $H(P)\ = \hat \pi (\langle R \rangle ^{\mathbb {Z}})$
mod
$H(P)\ = \hat \pi (\langle R \rangle ^{\mathbb {Z}})$
mod
![]() $\mu $
.
$\mu $
.
The following theorem is central to the proof of the main theorem. We will use it to show that the SRB measures we are going to construct are related in exactly the same way as in the assumptions of the main theorem in §3.
Proposition 4.21. Assume that
![]() $\mathrm{Vol}(\mathcal {R}^{\mathrm{PR}}_{\chi })>0$
. Then there exists at most countably many hyperbolic periodic points
$\mathrm{Vol}(\mathcal {R}^{\mathrm{PR}}_{\chi })>0$
. Then there exists at most countably many hyperbolic periodic points
![]() $P^{+}_{1},P_{2}^{+},\ldots $
and
$P^{+}_{1},P_{2}^{+},\ldots $
and
![]() $P^{-}_{1}, P^{-}_{2},\ldots $
such that the following hold.
$P^{-}_{1}, P^{-}_{2},\ldots $
such that the following hold.
-
(1) The local unstable manifold of each
 $P^{+}_{n}$
contains a positive volume of points in
$P^{+}_{n}$
contains a positive volume of points in
 $RWT^{\mathrm{PR}}_{\chi }(f)$
for all
$RWT^{\mathrm{PR}}_{\chi }(f)$
for all
 $n\geq 1$
.
$n\geq 1$
. -
(2) The local stable manifold of each
 $P^{-}_{n}$
contains a positive volume of points in
$P^{-}_{n}$
contains a positive volume of points in
 $RWT^{\mathrm{PR}}_{\chi }(f^{-1})$
for all
$RWT^{\mathrm{PR}}_{\chi }(f^{-1})$
for all
 $n \geq 1$
.
$n \geq 1$
. -
(3)
 $\mathrm{Vol}$
-a.e.
$\mathrm{Vol}$
-a.e.
 $x \in \mathcal {R}^{\mathrm{PR}}y_{\chi }$
satisfy conditions (2) and (3) of Proposition 3.1 with respect to
$x \in \mathcal {R}^{\mathrm{PR}}y_{\chi }$
satisfy conditions (2) and (3) of Proposition 3.1 with respect to
 $P^{+}_{n}$
and
$P^{+}_{n}$
and
 $P^{-}_{n}$
, for some
$P^{-}_{n}$
, for some
 $n \geq 1$
.
$n \geq 1$
.
Proof.
Step 1. Let
![]() $x \in \mathcal {R}^{\mathrm{PR}}_{\chi }$
. Then by definition, we know that there is
$x \in \mathcal {R}^{\mathrm{PR}}_{\chi }$
. Then by definition, we know that there is
![]() $r_{x}>0$
and a Pesin level set
$r_{x}>0$
and a Pesin level set
![]() $\Lambda ^{r_{x}}$
for which the following two conditions are satisfied:
$\Lambda ^{r_{x}}$
for which the following two conditions are satisfied:
 $$ \begin{align*} \limsup \limits_{n \rightarrow \infty} \frac{\# \{0 \leq k < n \mid f^{k}(x) \in \Lambda^{r_{x}} \}}{n}> 0; \end{align*} $$
$$ \begin{align*} \limsup \limits_{n \rightarrow \infty} \frac{\# \{0 \leq k < n \mid f^{k}(x) \in \Lambda^{r_{x}} \}}{n}> 0; \end{align*} $$
 $$ \begin{align*} \limsup \limits_{n \rightarrow \infty} \frac{\# \{0 \leq k < n \mid f^{-k}(x) \in \Lambda^{r_{x}} \}}{n}> 0. \end{align*} $$
$$ \begin{align*} \limsup \limits_{n \rightarrow \infty} \frac{\# \{0 \leq k < n \mid f^{-k}(x) \in \Lambda^{r_{x}} \}}{n}> 0. \end{align*} $$
Now, by [Reference Ben Ovadia4, Claim 7.6], we know that
![]() $\mathcal {R}^{\mathrm{PR}}_{\chi } \cap \Lambda ^{r_{x} }$
is contained in at most finitely many partition elements R in the Markov partition
$\mathcal {R}^{\mathrm{PR}}_{\chi } \cap \Lambda ^{r_{x} }$
is contained in at most finitely many partition elements R in the Markov partition
![]() $\mathcal {P}$
. Therefore, we can find two partition elements
$\mathcal {P}$
. Therefore, we can find two partition elements
![]() $R^{+}$
and
$R^{+}$
and
![]() $R^{-}$
in the Markov partition
$R^{-}$
in the Markov partition
![]() $\mathcal {P}$
, for which we have:
$\mathcal {P}$
, for which we have:
 $$ \begin{align*} \limsup \limits_{n \rightarrow \infty} \frac{\# \{0 \leq k < n \mid f^{k}(x) \in R^{+} \}}{n}> 0; \end{align*} $$
$$ \begin{align*} \limsup \limits_{n \rightarrow \infty} \frac{\# \{0 \leq k < n \mid f^{k}(x) \in R^{+} \}}{n}> 0; \end{align*} $$
 $$ \begin{align*} \limsup \limits_{n \rightarrow \infty} \frac{\# \{0 \leq k < n \mid f^{-k}(x) \in R^{-} \}}{n}> 0. \end{align*} $$
$$ \begin{align*} \limsup \limits_{n \rightarrow \infty} \frac{\# \{0 \leq k < n \mid f^{-k}(x) \in R^{-} \}}{n}> 0. \end{align*} $$
Let us define
![]() $\mathcal {R}_{R^{-},R^{+}}^{\mathrm{PR}}$
to be the subset of
$\mathcal {R}_{R^{-},R^{+}}^{\mathrm{PR}}$
to be the subset of
![]() $\mathcal {R}_{\chi }^{\mathrm{PR}}$
that satisfies the two upper density conditions above. Since
$\mathcal {R}_{\chi }^{\mathrm{PR}}$
that satisfies the two upper density conditions above. Since
![]() $\mathcal {P}$
is countable, there are at most countably many partition elements
$\mathcal {P}$
is countable, there are at most countably many partition elements
![]() $R^{+}_{1},R^{+}_{2},\ldots $
and
$R^{+}_{1},R^{+}_{2},\ldots $
and
![]() $R^{-}_{1},R^{-}_{2},\ldots $
so that Lebesgue almost every point in
$R^{-}_{1},R^{-}_{2},\ldots $
so that Lebesgue almost every point in
![]() $\mathcal {R}^{\mathrm{PR}}_{\chi }$
lies in the union
$\mathcal {R}^{\mathrm{PR}}_{\chi }$
lies in the union
![]() $\bigcup \nolimits _{n}\mathcal {R}_{R^{-}_{n},R^{+}_{n}}$
. Since we assume that
$\bigcup \nolimits _{n}\mathcal {R}_{R^{-}_{n},R^{+}_{n}}$
. Since we assume that
![]() $\mathrm{Vol}(\mathcal {R}^{\mathrm{PR}}_{\chi })> 0$
, we can assume without loss of generalization that the volume of each one of the sets
$\mathrm{Vol}(\mathcal {R}^{\mathrm{PR}}_{\chi })> 0$
, we can assume without loss of generalization that the volume of each one of the sets
![]() $ \mathcal {R}_{R^{-}_{n},R^{+}_{n}}$
is positive. We now fix one of the sets constructed above and call it
$ \mathcal {R}_{R^{-}_{n},R^{+}_{n}}$
is positive. We now fix one of the sets constructed above and call it
![]() $\mathcal {R}^{\pm }$
.
$\mathcal {R}^{\pm }$
.
Step 2. Next, let
![]() $R_0$
be an element of the Markov partition
$R_0$
be an element of the Markov partition
![]() $\mathcal{P}$
, such that
$\mathcal{P}$
, such that
![]() $\mathcal{R}^\pm \cap R_0$
has positive volume. We can see that
$\mathcal{R}^\pm \cap R_0$
has positive volume. We can see that
![]() $\mathcal {R}^{\pm } \cap R_{0}$
is exhausted by images of cylinders in
$\mathcal {R}^{\pm } \cap R_{0}$
is exhausted by images of cylinders in
![]() $\hat \Sigma ^{\#}$
of the form
$\hat \Sigma ^{\#}$
of the form
The number of such cylinders is countable; therefore,
![]() $\mathcal {R}^{\pm }_{\chi } \cap R_{0}$
is contained in the image of at most countably many such cylinders, each of which has positive volume. Let us fix one of these rectangles, and denote its image by
$\mathcal {R}^{\pm }_{\chi } \cap R_{0}$
is contained in the image of at most countably many such cylinders, each of which has positive volume. Let us fix one of these rectangles, and denote its image by
![]() $\hat C$
. Then by absolute continuity of local stable and unstable manifolds, we can show that for Vol-a.e point
$\hat C$
. Then by absolute continuity of local stable and unstable manifolds, we can show that for Vol-a.e point
![]() $x\in \hat C \cap \mathcal {R}^{\pm }$
, we have
$x\in \hat C \cap \mathcal {R}^{\pm }$
, we have
Fix such a point
![]() $x_{0} \in \hat C \cap \mathcal {R}^{\pm }_{\chi }$
. Since for all
$x_{0} \in \hat C \cap \mathcal {R}^{\pm }_{\chi }$
. Since for all
![]() $y \in V^{u}_{\mathrm {loc}}(x_{0})\cap \hat C \cap \mathcal {R}^{\pm }$
, we have
$y \in V^{u}_{\mathrm {loc}}(x_{0})\cap \hat C \cap \mathcal {R}^{\pm }$
, we have
![]() $\dim (V^{u}_{\mathrm {loc}}(x_{0})) = \dim (V^{u}(\underline {R}(y)))$
, we see that we can choose
$\dim (V^{u}_{\mathrm {loc}}(x_{0})) = \dim (V^{u}(\underline {R}(y)))$
, we see that we can choose
![]() $\underline {R} \in \hat \Sigma ^{\circ } \cap [R_{0}]$
, such that
$\underline {R} \in \hat \Sigma ^{\circ } \cap [R_{0}]$
, such that
and such that the partition
![]() $R^{+}$
appears infinitely many times in the future of
$R^{+}$
appears infinitely many times in the future of
![]() $\underline {R}$
. Let us define
$\underline {R}$
. Let us define
![]() $\underline {R}^{\prime } \in \hat \Sigma _{L}$
to be the concatenation
$\underline {R}^{\prime } \in \hat \Sigma _{L}$
to be the concatenation
![]() $\underline {R} \cdot (S_{1}, \ldots , R^{+})$
. Then we know that
$\underline {R} \cdot (S_{1}, \ldots , R^{+})$
. Then we know that
![]() $f^{-n^{+}}(V^{u}(\underline {R}^{\prime }) ) \supset V^{u}(\underline {R}) \cap \hat C \cap \mathcal {R}^{\pm }$
. Hence by the invariance of the set
$f^{-n^{+}}(V^{u}(\underline {R}^{\prime }) ) \supset V^{u}(\underline {R}) \cap \hat C \cap \mathcal {R}^{\pm }$
. Hence by the invariance of the set
![]() $\mathcal {R}^{\pm }$
, we see that this means that we have
$\mathcal {R}^{\pm }$
, we see that this means that we have
Step 3. Now, since
![]() $R^{+}$
is a recurring symbol for all the points in
$R^{+}$
is a recurring symbol for all the points in
![]() $R^{+} \cap \mathcal {R}^{\pm }$
, and since
$R^{+} \cap \mathcal {R}^{\pm }$
, and since
![]() $V^{u}(\underline {R}^{\prime })$
gives a positive leaf measure to this set, we can see that we can construct a periodic chain
$V^{u}(\underline {R}^{\prime })$
gives a positive leaf measure to this set, we can see that we can construct a periodic chain
![]() $\underline {P}_{L}^{+} \in \hat \Sigma _{L} \cap [R^{+}]$
. We also have that the stable holonomy map
$\underline {P}_{L}^{+} \in \hat \Sigma _{L} \cap [R^{+}]$
. We also have that the stable holonomy map
is well defined. By the absolute continuity property of stable holonomies, we see that
![]() $V^{u}(\underline {P}^{+}_{L})$
gives
$V^{u}(\underline {P}^{+}_{L})$
gives
![]() $\Gamma ^{s}(V^{u}(\underline {R}^{\prime }) \cap \mathcal {R}^{\pm })$
a positive leaf measure. Now, for any point
$\Gamma ^{s}(V^{u}(\underline {R}^{\prime }) \cap \mathcal {R}^{\pm })$
a positive leaf measure. Now, for any point
![]() $y \in \Gamma ^{s}(V^{u}(\underline {R}^{\prime }) \cap \mathcal {R}^{\pm })$
, we know that
$y \in \Gamma ^{s}(V^{u}(\underline {R}^{\prime }) \cap \mathcal {R}^{\pm })$
, we know that
![]() $y \in V^{s}(\underline {S})$
, where
$y \in V^{s}(\underline {S})$
, where
![]() $\underline {S} \in \hat \Sigma _{R}^{\circ } \cap [R^{+}]$
, and such that
$\underline {S} \in \hat \Sigma _{R}^{\circ } \cap [R^{+}]$
, and such that
![]() $\limsup \nolimits _{n \rightarrow \infty } {\# \{ 0 \leq k < n \mid S_{k} = R^{+} \}}/{n}> 0$
. Hence, by [Reference Ben Ovadia4, Claim 7.6], we see that this implies that
$\limsup \nolimits _{n \rightarrow \infty } {\# \{ 0 \leq k < n \mid S_{k} = R^{+} \}}/{n}> 0$
. Hence, by [Reference Ben Ovadia4, Claim 7.6], we see that this implies that
![]() $y \in RWT^{\mathrm{PR}}_{\chi }(f)$
. Therefore, we see that
$y \in RWT^{\mathrm{PR}}_{\chi }(f)$
. Therefore, we see that
![]() $V^{u}(\underline {P}^{+}_{L})$
gives
$V^{u}(\underline {P}^{+}_{L})$
gives
![]() $RWT^{\mathrm{PR}}_{\chi }$
positive leaf volume. Now, we can continue the chain
$RWT^{\mathrm{PR}}_{\chi }$
positive leaf volume. Now, we can continue the chain
![]() $\underline {P}^{+}_{L}$
to the right periodically to get a periodic chain
$\underline {P}^{+}_{L}$
to the right periodically to get a periodic chain
![]() $\underline {P}^{+} \in \hat \Sigma \cap {R^{+}}$
, and we define the periodic point
$\underline {P}^{+} \in \hat \Sigma \cap {R^{+}}$
, and we define the periodic point
![]() $P^{+}$
to be the image of
$P^{+}$
to be the image of
![]() $\underline {P}^{+}$
under the coding map.
$\underline {P}^{+}$
under the coding map.
Step 4. Now, we can repeat steps 2 and 3 above for the map
![]() $f^{-1}$
to get the periodic point
$f^{-1}$
to get the periodic point
![]() $P^{-}$
. We see that all the conditions in the proposition above are satisfied.
$P^{-}$
. We see that all the conditions in the proposition above are satisfied.
5 Proof of the main theorem
Now we are ready to prove the main theorem by replicating the argument in the proof of the toy model. The first step is the following theorem proved in [Reference Ben Ovadia4], asserting the existence of an ergodic SRB measure supported on the image of a maximal connected component of
![]() $\Sigma ^\#$
under the assumption of a leaf condition: that unstable leafs of points in the image give positive leaf volume to
$\Sigma ^\#$
under the assumption of a leaf condition: that unstable leafs of points in the image give positive leaf volume to
![]() $RWT_{\chi }^{\mathrm{PR}}$
. The following theorem is a reformulation of [Reference Ben Ovadia4, Theorem 7.9].
$RWT_{\chi }^{\mathrm{PR}}$
. The following theorem is a reformulation of [Reference Ben Ovadia4, Theorem 7.9].
Theorem 5.1. [Reference Ben Ovadia4, Theorem 7.9]
Let
![]() $\tilde \Sigma \subset \hat \Sigma ^\#$
be a maximal connected component, and let P be a hyperbolic periodic point in the image
$\tilde \Sigma \subset \hat \Sigma ^\#$
be a maximal connected component, and let P be a hyperbolic periodic point in the image
![]() $\hat \pi (\tilde \Sigma )$
, such that the set
$\hat \pi (\tilde \Sigma )$
, such that the set
![]() $V^{u}_{\mathrm {loc}}(P)\cap RWT_{\chi }^{\mathrm{PR}}$
has positive leaf volume. Then f preserves an ergodic SRB measure
$V^{u}_{\mathrm {loc}}(P)\cap RWT_{\chi }^{\mathrm{PR}}$
has positive leaf volume. Then f preserves an ergodic SRB measure
![]() $\mu ^{+}$
supported on
$\mu ^{+}$
supported on
![]() $\hat \pi (\tilde \Sigma )\subset H(P)$
.
$\hat \pi (\tilde \Sigma )\subset H(P)$
.
Proof of the main theorem
Step 1. Let us fix a pair of periodic hyperbolic points
![]() $P_{n}^{+}$
and
$P_{n}^{+}$
and
![]() $P^{-}_{n}$
constructed in Proposition 4.21. Then properties (1) and (2) of Proposition 4.21 allow us to use Theorem 5.1 to construct two SRB measures
$P^{-}_{n}$
constructed in Proposition 4.21. Then properties (1) and (2) of Proposition 4.21 allow us to use Theorem 5.1 to construct two SRB measures
![]() $\mu ^{+}$
and
$\mu ^{+}$
and
![]() $\mu ^{-}$
for f and
$\mu ^{-}$
for f and
![]() $f^{-1}$
respectively, supported on the ergodic homoclinic components
$f^{-1}$
respectively, supported on the ergodic homoclinic components
![]() $H(P^{+}_{n})$
and
$H(P^{+}_{n})$
and
![]() $H(P^{-}_{n})$
respectively. Now, let us take a point
$H(P^{-}_{n})$
respectively. Now, let us take a point
![]() $x \in \mathcal {R}^{\mathrm{PR}}_{\chi }$
satisfying condition (3) of Proposition 4.21 for
$x \in \mathcal {R}^{\mathrm{PR}}_{\chi }$
satisfying condition (3) of Proposition 4.21 for
![]() $P^{+}_{n}$
and
$P^{+}_{n}$
and
![]() $P^{-}_{n}$
. We see now that all the conditions of Proposition 3.1 are satisfied, and therefore, each of the SRB measures
$P^{-}_{n}$
. We see now that all the conditions of Proposition 3.1 are satisfied, and therefore, each of the SRB measures
![]() $\mu _{n}^{+}$
and
$\mu _{n}^{+}$
and
![]() $\mu _{n}^{-}$
are in fact absolutely continuous with respect to volume.
$\mu _{n}^{-}$
are in fact absolutely continuous with respect to volume.
Step 2. A consequence of the proof of Proposition 4.21 and the construction therein is that there is a hyperbolic rectangle
![]() $R_{0}$
, such that
$R_{0}$
, such that
![]() $R_{0} \cap \mathcal {R}^{\mathrm{PR}}_{\chi }$
has positive volume, and that there are two hyperbolic rectangles
$R_{0} \cap \mathcal {R}^{\mathrm{PR}}_{\chi }$
has positive volume, and that there are two hyperbolic rectangles
![]() $R^{+}$
and R at
$R^{+}$
and R at
![]() $P^{+}_{n}$
and
$P^{+}_{n}$
and
![]() $P^{-}_{n}$
, and two times
$P^{-}_{n}$
, and two times
![]() $n^{+}>0$
and
$n^{+}>0$
and
![]() $n^{-}>0$
for which we have
$n^{-}>0$
for which we have
![]() $f^{n^{+}}(R_{0}) \subset R^{+}$
and
$f^{n^{+}}(R_{0}) \subset R^{+}$
and
![]() $f^{-n^{-}}(R_{0}) \subset R^{-}$
. Now, since
$f^{-n^{-}}(R_{0}) \subset R^{-}$
. Now, since
![]() $\mu ^{+}_n$
is an SRB for both f and
$\mu ^{+}_n$
is an SRB for both f and
![]() $f^{-1}$
(as we saw from step 1), we can show that for
$f^{-1}$
(as we saw from step 1), we can show that for
![]() $\mu ^{+}$
-a.e. point
$\mu ^{+}$
-a.e. point
![]() $x^{+} \in H(P^{+})$
, one can find
$x^{+} \in H(P^{+})$
, one can find
![]() $N>0$
and
$N>0$
and
![]() $N^{\prime }> 0$
such that
$N^{\prime }> 0$
such that
![]() $f^{N}(V^{u}(x^{+}))$
contains an embedded
$f^{N}(V^{u}(x^{+}))$
contains an embedded
![]() $C^{1}$
disk which is transversal to every stable in
$C^{1}$
disk which is transversal to every stable in
![]() $R^{+}$
, and such that
$R^{+}$
, and such that
![]() $f^{-N^{\prime }}(V^{s}(x^{+}))$
contains an embedded
$f^{-N^{\prime }}(V^{s}(x^{+}))$
contains an embedded
![]() $C^{1}$
disk which is transversal to every unstable in
$C^{1}$
disk which is transversal to every unstable in
![]() $R^{+}$
, and such that each of the transversals have a full measure of Tsuji regular points. This follows from an argument similar to the proof of Lemma 3.19, and from Lemma 3.12. By using the fact the holonomy maps are absolutely continuous, we immediately see that this implies that
$R^{+}$
, and such that each of the transversals have a full measure of Tsuji regular points. This follows from an argument similar to the proof of Lemma 3.19, and from Lemma 3.12. By using the fact the holonomy maps are absolutely continuous, we immediately see that this implies that
![]() $\mathrm{Vol}$
-a.e. point in
$\mathrm{Vol}$
-a.e. point in
![]() $f^{n^{+}}(R_{0}) \cap R^{+}$
is forward and backward Tsuji regular with respect to the measure
$f^{n^{+}}(R_{0}) \cap R^{+}$
is forward and backward Tsuji regular with respect to the measure
![]() $\mu ^{+}_n$
. A similar argument can be made for
$\mu ^{+}_n$
. A similar argument can be made for
![]() $\mu ^{-}_n$
by replacing f by
$\mu ^{-}_n$
by replacing f by
![]() $f^{-1}$
in the argument above. This implies two things: first, that
$f^{-1}$
in the argument above. This implies two things: first, that
![]() $\mathrm{Vol}$
-a.e. point in
$\mathrm{Vol}$
-a.e. point in
![]() $\mathcal {R}^{\mathrm{PR}}_{\chi }$
is Tsuji regular for both
$\mathcal {R}^{\mathrm{PR}}_{\chi }$
is Tsuji regular for both
![]() $\mu ^{+}_{n}$
and
$\mu ^{+}_{n}$
and
![]() $\mu ^{-}_{n}$
for some
$\mu ^{-}_{n}$
for some
![]() $n \geq 1$
. Second, that we in fact have
$n \geq 1$
. Second, that we in fact have
![]() $\mu ^{+}_{n} = \mu ^{-}_{n}$
, since all the points in
$\mu ^{+}_{n} = \mu ^{-}_{n}$
, since all the points in
![]() $R_{0}$
are Tsuji regular for both measures
$R_{0}$
are Tsuji regular for both measures
![]() $\mu ^{+}_{n}$
and
$\mu ^{+}_{n}$
and
![]() $\mu ^{-}_n$
.
$\mu ^{-}_n$
.