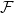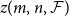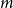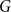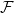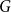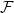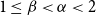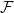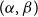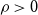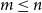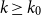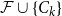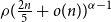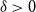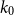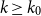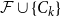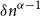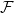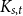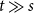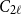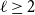1. Introduction
Given a family
![]() $\mathcal{F}$
of graphs, a graph
$\mathcal{F}$
of graphs, a graph
![]() $G$
is called
$G$
is called
![]() $\mathcal{F}$
-free if
$\mathcal{F}$
-free if
![]() $G$
does not contain any member of
$G$
does not contain any member of
![]() $\mathcal{F}$
as a subgraph. If
$\mathcal{F}$
as a subgraph. If
![]() $\mathcal{F}$
consists of a single graph
$\mathcal{F}$
consists of a single graph
![]() $F$
then we simply say that
$F$
then we simply say that
![]() $G$
is
$G$
is
![]() $F$
-free. The Turán number of
$F$
-free. The Turán number of
![]() $\mathcal{F}$
, denoted by
$\mathcal{F}$
, denoted by
![]() $\textrm{ex}(n, \mathcal{F})$
, is the maximum possible number of edges in an
$\textrm{ex}(n, \mathcal{F})$
, is the maximum possible number of edges in an
![]() $n$
-vertex
$n$
-vertex
![]() $\mathcal{F}$
-free graph. As is well known, this function is well understood when
$\mathcal{F}$
-free graph. As is well known, this function is well understood when
![]() $\mathcal{F}$
consists only of non-bipartite graphs due to the celebrated Erdős–Stone–Simonovits theorem [Reference Erdős and Simonovits10,Reference Erdős and Stone12] but is generally open when
$\mathcal{F}$
consists only of non-bipartite graphs due to the celebrated Erdős–Stone–Simonovits theorem [Reference Erdős and Simonovits10,Reference Erdős and Stone12] but is generally open when
![]() $\mathcal{F}$
contains bipartite graphs. For a family of graphs
$\mathcal{F}$
contains bipartite graphs. For a family of graphs
![]() $\mathcal{F}$
, a closely related notion is the so-called Zarankiewicz number
$\mathcal{F}$
, a closely related notion is the so-called Zarankiewicz number
![]() $z(n,\mathcal{F})$
, which is defined to be the maximum number of edges in an
$z(n,\mathcal{F})$
, which is defined to be the maximum number of edges in an
![]() $n$
-vertex
$n$
-vertex
![]() $\mathcal{F}$
-free bipartite graph. More generally, we denote by
$\mathcal{F}$
-free bipartite graph. More generally, we denote by
![]() $z(m,n,\mathcal{F})$
the maximum number of edges in an
$z(m,n,\mathcal{F})$
the maximum number of edges in an
![]() $m$
by
$m$
by
![]() $n$
bipartite graph, that is,
$n$
bipartite graph, that is,
![]() $\mathcal{F}$
-free. In a seminal paper [Reference Erdős and Simonovits11], Erdős and Simonovits raised a number of intriguing conjectures on Turán numbers for bipartite graphs. One of them is the following (Conjecture 3 in [Reference Erdős and Simonovits11]). Given a positive odd integer
$\mathcal{F}$
-free. In a seminal paper [Reference Erdős and Simonovits11], Erdős and Simonovits raised a number of intriguing conjectures on Turán numbers for bipartite graphs. One of them is the following (Conjecture 3 in [Reference Erdős and Simonovits11]). Given a positive odd integer
![]() $k$
, let
$k$
, let
![]() $\mathcal{C}_k$
denote the family of all odd cycles of length at most
$\mathcal{C}_k$
denote the family of all odd cycles of length at most
![]() $k$
. Throughout this paper, we write
$k$
. Throughout this paper, we write
![]() $f(n)\sim g(n)$
for two functions
$f(n)\sim g(n)$
for two functions
![]() $f, g\,{:}\, \mathbb{N}\to \mathbb{R}$
if
$f, g\,{:}\, \mathbb{N}\to \mathbb{R}$
if
![]() $\lim _{n\to \infty } f(n)/g(n)=1$
.
$\lim _{n\to \infty } f(n)/g(n)=1$
.
Conjecture 1.1. (Erdős-Simonovits [Reference Erdős and Simonovits11]). Given any finite family
![]() $\mathcal{F}$
of graphs, there exists an odd integer
$\mathcal{F}$
of graphs, there exists an odd integer
![]() $k$
such that as
$k$
such that as
![]() $n\to \infty$
$n\to \infty$
Erdős and Simonovits [Reference Erdős and Simonovits11] verified the conjecture for
![]() $\mathcal{F}=\{C_4\}$
by showing that
$\mathcal{F}=\{C_4\}$
by showing that
![]() $\textrm{ex}(n, \{C_4,C_5\})\sim z(n, C_4)\sim (\frac{n}{2})^{\frac{3}{2}}$
. Keevash, Sudakov and Verstraëte [Reference Keevash, Sudakov and Verstraëte20] further confirmed this conjecture for
$\textrm{ex}(n, \{C_4,C_5\})\sim z(n, C_4)\sim (\frac{n}{2})^{\frac{3}{2}}$
. Keevash, Sudakov and Verstraëte [Reference Keevash, Sudakov and Verstraëte20] further confirmed this conjecture for
![]() $\mathcal{F}_\ell \,{:\!=}\,\{C_4,C_6,\dots, C_{2\ell }\}$
where
$\mathcal{F}_\ell \,{:\!=}\,\{C_4,C_6,\dots, C_{2\ell }\}$
where
![]() $\ell \in \{2,3,5\}$
in stronger forms and proved a related result for the chromatic number of
$\ell \in \{2,3,5\}$
in stronger forms and proved a related result for the chromatic number of
![]() $\mathcal{F}_\ell \cup \{C_k\}$
-free graphs of minimum degree
$\mathcal{F}_\ell \cup \{C_k\}$
-free graphs of minimum degree
![]() $\Omega (n^{1/\ell })$
. In a subsequent paper [Reference Allen, Keevash, Sudakov and Verstraëte1], Allen, Keevash, Sudakov and Verstraëte provided a general approach to Conjecture 1.1 (using Scott’s sparse regularity lemma [Reference Scott26]), which works for the following families of bipartite graphs.
$\Omega (n^{1/\ell })$
. In a subsequent paper [Reference Allen, Keevash, Sudakov and Verstraëte1], Allen, Keevash, Sudakov and Verstraëte provided a general approach to Conjecture 1.1 (using Scott’s sparse regularity lemma [Reference Scott26]), which works for the following families of bipartite graphs.
Definition 1.2.
Let
![]() $\alpha, \beta$
be reals with
$\alpha, \beta$
be reals with
![]() $2\gt \alpha \gt \beta \geq 1$
. Let
$2\gt \alpha \gt \beta \geq 1$
. Let
![]() $\mathcal{F}$
be a family of bipartite graphs. If there exists some
$\mathcal{F}$
be a family of bipartite graphs. If there exists some
![]() $\rho \gt 0$
such that for every
$\rho \gt 0$
such that for every
![]() $m\leq n$
,
$m\leq n$
,
holds, then we say that
![]() $\mathcal{F}$
is
$\mathcal{F}$
is
![]() $(\alpha,\beta )$
-smooth with relative density
$(\alpha,\beta )$
-smooth with relative density
![]() $\rho$
. We call a bipartite family
$\rho$
. We call a bipartite family
![]() $\mathcal{F}$
smooth if it is
$\mathcal{F}$
smooth if it is
![]() $(\alpha,\beta )$
-smooth for some
$(\alpha,\beta )$
-smooth for some
![]() $\alpha$
and
$\alpha$
and
![]() $\beta$
.
$\beta$
.
It is easy to see that for any
![]() $(\alpha,\beta )$
-smooth family
$(\alpha,\beta )$
-smooth family
![]() $\mathcal{F}$
, we have
$\mathcal{F}$
, we have
![]() $z(n,\mathcal{F})=\rho (n/2)^\alpha +O(n^\beta ).$
$z(n,\mathcal{F})=\rho (n/2)^\alpha +O(n^\beta ).$
Before we mention the results of [Reference Allen, Keevash, Sudakov and Verstraëte1], let us discuss some known examples of smooth families. Improving results of Kövári-Sós-Turán [Reference Kövári, Sós and Turán23], Füredi [Reference Füredi14] showed that if
![]() $m\leq n$
and
$m\leq n$
and
![]() $s,t\in \mathbb{N}$
then
$s,t\in \mathbb{N}$
then
This together with the constructions of Brown [Reference Brown6] and Füredi [Reference Füredi15] shows that
![]() $K_{2,t}$
and
$K_{2,t}$
and
![]() $K_{3,3}$
are smooth families (see [Reference Allen, Keevash, Sudakov and Verstraëte1]). Allen, Keevash, Sudakov and Verstraëte [Reference Allen, Keevash, Sudakov and Verstraëte1] also showed that
$K_{3,3}$
are smooth families (see [Reference Allen, Keevash, Sudakov and Verstraëte1]). Allen, Keevash, Sudakov and Verstraëte [Reference Allen, Keevash, Sudakov and Verstraëte1] also showed that
![]() $\{K_{2,t}, B_t\}$
is smooth, where
$\{K_{2,t}, B_t\}$
is smooth, where
![]() $B_t$
consists of
$B_t$
consists of
![]() $t$
copies of
$t$
copies of
![]() $C_4$
sharing an edge (and no other vertices). However, it is not known if
$C_4$
sharing an edge (and no other vertices). However, it is not known if
![]() $K_{s,t}$
is smooth for any
$K_{s,t}$
is smooth for any
![]() $s\geq 3$
and
$s\geq 3$
and
![]() $t\geq 4$
and if
$t\geq 4$
and if
![]() $C_{2\ell }$
is smooth for any
$C_{2\ell }$
is smooth for any
![]() $\ell \geq 3$
, due to a lack of constructions that asymptotically match upper bounds on Zarankiewicz numbers. We would like to point out that not all families of bipartite graphs are smooth – in the concluding remarks we provide an example of bipartite graphs which are not smooth.
$\ell \geq 3$
, due to a lack of constructions that asymptotically match upper bounds on Zarankiewicz numbers. We would like to point out that not all families of bipartite graphs are smooth – in the concluding remarks we provide an example of bipartite graphs which are not smooth.
The main result of Allen, Keevash, Sudakov and Verstraëte [Reference Allen, Keevash, Sudakov and Verstraëte1] is as follows. A family
![]() $\mathcal{G}$
of graphs is near-bipartite if every graph
$\mathcal{G}$
of graphs is near-bipartite if every graph
![]() $G\in \mathcal{G}$
has a bipartite subgraph
$G\in \mathcal{G}$
has a bipartite subgraph
![]() $H$
such that
$H$
such that
![]() $e(G)\sim e(H)$
as
$e(G)\sim e(H)$
as
![]() $|V(G)|\to \infty$
.
$|V(G)|\to \infty$
.
Theorem 1.3. (Allen-Keevash-Sudakov-Verstraëte [Reference Allen, Keevash, Sudakov and Verstraëte1]). Let
![]() $\mathcal{F}$
be an
$\mathcal{F}$
be an
![]() $(\alpha,\beta )$
-smooth family with
$(\alpha,\beta )$
-smooth family with
![]() $2\gt \alpha \gt \beta \geq 1$
. There exists
$2\gt \alpha \gt \beta \geq 1$
. There exists
![]() $k_0$
such that if
$k_0$
such that if
![]() $k\geq k_0 \in \mathbb{N}$
is odd, then the family of all extremal
$k\geq k_0 \in \mathbb{N}$
is odd, then the family of all extremal
![]() $\mathcal{F}\cup \{C_k\}$
-free graphs is near-bipartite and, in particular,
$\mathcal{F}\cup \{C_k\}$
-free graphs is near-bipartite and, in particular,
![]() $\textrm{ex}(n,\mathcal{F}\cup \{C_k\})\sim z(n,\mathcal{F})$
.
$\textrm{ex}(n,\mathcal{F}\cup \{C_k\})\sim z(n,\mathcal{F})$
.
The authors [Reference Allen, Keevash, Sudakov and Verstraëte1] also raised a question whether the extremal
![]() $n$
-vertex
$n$
-vertex
![]() $\mathcal{F}\cup \{C_k\}$
-free graph in Theorem 1.3 is exactly bipartite when
$\mathcal{F}\cup \{C_k\}$
-free graph in Theorem 1.3 is exactly bipartite when
![]() $n$
is sufficiently large. Motivated by the classic result of Andrásfai, Erdős and Sós [Reference Andrásfai, Erdős and Sós4] stating that any
$n$
is sufficiently large. Motivated by the classic result of Andrásfai, Erdős and Sós [Reference Andrásfai, Erdős and Sós4] stating that any
![]() $n$
-vertex triangle-free graph with minimum degree more than
$n$
-vertex triangle-free graph with minimum degree more than
![]() $2n/5$
must be bipartite, Allen, Keevash, Sudakov and Verstraëte [Reference Allen, Keevash, Sudakov and Verstraëte1] proved the following theorem, which answers their own question for extremal graphs satisfying appropriate minimum degree condition.
$2n/5$
must be bipartite, Allen, Keevash, Sudakov and Verstraëte [Reference Allen, Keevash, Sudakov and Verstraëte1] proved the following theorem, which answers their own question for extremal graphs satisfying appropriate minimum degree condition.
Theorem 1.4. (Allen-Keevash-Sudakov-Verstraëte [Reference Allen, Keevash, Sudakov and Verstraëte1]). Let
![]() $\mathcal{F}$
be an
$\mathcal{F}$
be an
![]() $(\alpha, \beta )$
-smooth family with relative density
$(\alpha, \beta )$
-smooth family with relative density
![]() $\rho$
and
$\rho$
and
![]() $2\gt \alpha \gt \beta \geq 1$
. Then there exists
$2\gt \alpha \gt \beta \geq 1$
. Then there exists
![]() $k_0$
such that for any odd
$k_0$
such that for any odd
![]() $k\geq k_0$
and sufficiently large
$k\geq k_0$
and sufficiently large
![]() $n$
, any
$n$
, any
![]() $n$
-vertex
$n$
-vertex
![]() $\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
$\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
![]() $\rho (\frac{2n}{5}+o(n))^{\alpha -1}$
is bipartite.
$\rho (\frac{2n}{5}+o(n))^{\alpha -1}$
is bipartite.
In this paper, we strengthen Theorem 1.4 by showing that the minimum degree condition can be lowered to
![]() $\delta n^{\alpha -1}$
for any given real
$\delta n^{\alpha -1}$
for any given real
![]() $\delta \gt 0$
and furthermore, the condition on smoothness can be relaxed to the following notion.
$\delta \gt 0$
and furthermore, the condition on smoothness can be relaxed to the following notion.
Definition 1.5.
Let
![]() $\alpha, \beta$
be reals with
$\alpha, \beta$
be reals with
![]() $2\gt \alpha \gt \beta \geq 1$
. Let
$2\gt \alpha \gt \beta \geq 1$
. Let
![]() $\mathcal{F}$
be a family of bipartite graphs. We say that
$\mathcal{F}$
be a family of bipartite graphs. We say that
![]() $\mathcal{F}$
is
$\mathcal{F}$
is
![]() $(\alpha,\beta )$
-quasi-smooth with upper density
$(\alpha,\beta )$
-quasi-smooth with upper density
![]() $\rho$
and lower density
$\rho$
and lower density
![]() $\rho _0$
, if there exist constants
$\rho _0$
, if there exist constants
![]() $\rho,\rho _0\gt 0$
and
$\rho,\rho _0\gt 0$
and
![]() $C$
such that for all positive integers
$C$
such that for all positive integers
![]() $m\leq n$
,
$m\leq n$
,
Note that the
![]() $n^\beta$
term becomes relevant when
$n^\beta$
term becomes relevant when
![]() $m=o(n^{1+\beta -\alpha })$
. If
$m=o(n^{1+\beta -\alpha })$
. If
![]() $\mathcal{F}$
consists of a single graph
$\mathcal{F}$
consists of a single graph
![]() $F$
, then we just say that
$F$
, then we just say that
![]() $F$
is
$F$
is
![]() $(\alpha,\beta )$
-quasi-smooth.
$(\alpha,\beta )$
-quasi-smooth.
Clearly every
![]() $(\alpha,\beta )$
-smooth graph is
$(\alpha,\beta )$
-smooth graph is
![]() $(\alpha,\beta )$
-quasi-smooth. However, it is not known if every
$(\alpha,\beta )$
-quasi-smooth. However, it is not known if every
![]() $(\alpha,\beta )$
-quasi-smooth graph is
$(\alpha,\beta )$
-quasi-smooth graph is
![]() $(\alpha,\beta )$
-smooth. For instance, it is proved that
$(\alpha,\beta )$
-smooth. For instance, it is proved that
![]() $\textrm{ex}(n,K_{s,t})=\Omega (n^{2-1/s})$
for
$\textrm{ex}(n,K_{s,t})=\Omega (n^{2-1/s})$
for
![]() $t\geq (s-1)!+1$
in [Reference Alon, Rónyai and Szabó2,Reference Kollár, Rónyai and Szabó21] and for
$t\geq (s-1)!+1$
in [Reference Alon, Rónyai and Szabó2,Reference Kollár, Rónyai and Szabó21] and for
![]() $t\geq C^s$
in a very recent paper of Bukh [Reference Bukh7] (where
$t\geq C^s$
in a very recent paper of Bukh [Reference Bukh7] (where
![]() $C$
is a constant). Hence
$C$
is a constant). Hence
![]() $K_{s,t}$
is quasi-smooth under these conditions, but it is unknown whether
$K_{s,t}$
is quasi-smooth under these conditions, but it is unknown whether
![]() $K_{s,t}$
is always smooth. The following is our main result in this paper.
$K_{s,t}$
is always smooth. The following is our main result in this paper.
Theorem 1.6.
Let
![]() $\mathcal{F}$
be an
$\mathcal{F}$
be an
![]() $(\alpha,\beta )$
-quasi-smooth family with
$(\alpha,\beta )$
-quasi-smooth family with
![]() $2\gt \alpha \gt \beta \geq 1$
. For any real
$2\gt \alpha \gt \beta \geq 1$
. For any real
![]() $\delta \gt 0$
, there exists a positive integer
$\delta \gt 0$
, there exists a positive integer
![]() $k_0$
such that for any odd integer
$k_0$
such that for any odd integer
![]() $k\geq k_0$
and sufficiently large
$k\geq k_0$
and sufficiently large
![]() $n$
, any
$n$
, any
![]() $n$
-vertex
$n$
-vertex
![]() $\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
$\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
![]() $\delta n^{\alpha -1}$
is bipartite.
$\delta n^{\alpha -1}$
is bipartite.
The proof of Theorem 1.6 uses expansion properties and a robust reachability lemma that is in part inspired by a lemma in a recent paper by Letzter [Reference Letzter24] on the Turán number of tight cycles.
As a direct application of Theorem 1.6, we also obtain the following strengthening of Theorem 1.3.
Theorem 1.7.
Let
![]() $\mathcal{F}$
be an
$\mathcal{F}$
be an
![]() $(\alpha,\beta )$
-smooth family with
$(\alpha,\beta )$
-smooth family with
![]() $2\gt \alpha \gt \beta \geq 1$
. Then there exists
$2\gt \alpha \gt \beta \geq 1$
. Then there exists
![]() $k_0$
such that for any odd
$k_0$
such that for any odd
![]() $k\geq k_0$
and sufficiently large
$k\geq k_0$
and sufficiently large
![]() $n$
, any
$n$
, any
![]() $n$
-vertex
$n$
-vertex
![]() $\mathcal{F}\cup \{C_k\}$
-free extremal graph can be made bipartite by deleting a set of
$\mathcal{F}\cup \{C_k\}$
-free extremal graph can be made bipartite by deleting a set of
![]() $O(n^{1+\beta -\alpha })$
vertices, which together are incident to
$O(n^{1+\beta -\alpha })$
vertices, which together are incident to
![]() $O(n^\beta )$
edges. Therefore,
$O(n^\beta )$
edges. Therefore,
![]() $\text{ex}(n,\mathcal{F}\cup \{C_k\})=z(n,\mathcal{F})+O(n^\beta )$
.
$\text{ex}(n,\mathcal{F}\cup \{C_k\})=z(n,\mathcal{F})+O(n^\beta )$
.
Theorem 1.7 improves Theorem 1.3 in two ways. First, the error term is better. Second, the proof is more concise and avoids the use of the sparse regularity lemma. The theorem gives further evidence to an affirmative answer to the question of [Reference Allen, Keevash, Sudakov and Verstraëte1] that whether the extremal
![]() $n$
-vertex
$n$
-vertex
![]() $\mathcal{F}\cup \{C_k\}$
-free graph
$\mathcal{F}\cup \{C_k\}$
-free graph
![]() $G$
in Theorem 1.3 is bipartite (for sufficiently large
$G$
in Theorem 1.3 is bipartite (for sufficiently large
![]() $n$
).
$n$
).
We also prove an analogous theorem as Theorem 1.6 for
![]() $C_{2\ell }$
-free graphs, which complements the following result in Keevash-Sudakov-Verstraëte [Reference Keevash, Sudakov and Verstraëte20]: For any integer
$C_{2\ell }$
-free graphs, which complements the following result in Keevash-Sudakov-Verstraëte [Reference Keevash, Sudakov and Verstraëte20]: For any integer
![]() $\ell \geq 2$
, odd integer
$\ell \geq 2$
, odd integer
![]() $k\geq 4\ell +1$
and any real
$k\geq 4\ell +1$
and any real
![]() $\delta \gt 0$
, the chromatic number of any
$\delta \gt 0$
, the chromatic number of any
![]() $n$
-vertex
$n$
-vertex
![]() $\{C_4, C_6,\ldots,C_{2\ell }, C_k\}$
-free graph with minimum degree at least
$\{C_4, C_6,\ldots,C_{2\ell }, C_k\}$
-free graph with minimum degree at least
![]() $\delta n^{1/\ell }$
is less than
$\delta n^{1/\ell }$
is less than
![]() $(4k)^{\ell +1}/\delta ^\ell$
.
$(4k)^{\ell +1}/\delta ^\ell$
.
Theorem 1.8.
Let
![]() $\ell \geq 2$
be an integer. For any real
$\ell \geq 2$
be an integer. For any real
![]() $\delta \gt 0$
, let
$\delta \gt 0$
, let
![]() $k_0=3\ell (8\ell/\delta )^\ell +2\ell +2$
. Then for any odd integer
$k_0=3\ell (8\ell/\delta )^\ell +2\ell +2$
. Then for any odd integer
![]() $k\geq k_0$
and sufficiently large
$k\geq k_0$
and sufficiently large
![]() $n$
, any
$n$
, any
![]() $n$
-vertex
$n$
-vertex
![]() $\{C_{2\ell },C_k\}$
-free graph with minimum degree at least
$\{C_{2\ell },C_k\}$
-free graph with minimum degree at least
![]() $\delta n^{1/\ell }$
is bipartite.
$\delta n^{1/\ell }$
is bipartite.
This proof follows the same line as that of Theorem 1.6, except that we will use a more efficient robust reachability lemma for
![]() $C_{2\ell }$
-free graphs and as a result get better control on
$C_{2\ell }$
-free graphs and as a result get better control on
![]() $k_0$
.
$k_0$
.
We should point out that the existence of such graphs in Theorem 1.8 is known only for
![]() $\ell \in \{2,3,5\}$
(see [Reference Füredi and Simonovits16]). Also note that this result is not covered by Theorem 1.6, since
$\ell \in \{2,3,5\}$
(see [Reference Füredi and Simonovits16]). Also note that this result is not covered by Theorem 1.6, since
![]() $C_{2\ell }$
is not known to be
$C_{2\ell }$
is not known to be
![]() $(\alpha,\beta )$
-quasi-smooth for any
$(\alpha,\beta )$
-quasi-smooth for any
![]() $\ell \geq 3$
. In the concluding remarks, we will mention that Theorems 1.6 and 1.8 can be extended to a slightly broader family of bipartite graphs that include both
$\ell \geq 3$
. In the concluding remarks, we will mention that Theorems 1.6 and 1.8 can be extended to a slightly broader family of bipartite graphs that include both
![]() $(\alpha,\beta )$
-quasi-smooth graphs and
$(\alpha,\beta )$
-quasi-smooth graphs and
![]() $C_{2\ell }$
’s.
$C_{2\ell }$
’s.
The rest of the paper is organised as follows. In Section 2, we develop some useful lemmas. In Section 3, we develop a lemma for
![]() $C_{2\ell }$
-free graphs. In Section 4, we prove Theorem 1.6 and Theorem 1.8, respectively. In Section 5, we prove Theorem 1.7. In Section 6, we give some concluding remarks. Throughout this paper, we denote
$C_{2\ell }$
-free graphs. In Section 4, we prove Theorem 1.6 and Theorem 1.8, respectively. In Section 5, we prove Theorem 1.7. In Section 6, we give some concluding remarks. Throughout this paper, we denote
![]() $[k]$
by the set
$[k]$
by the set
![]() $\{1,2,\ldots,k\}$
for positive integers
$\{1,2,\ldots,k\}$
for positive integers
![]() $k$
.
$k$
.
2. Some general lemmas
The main content of this section is to present key lemmas for our main result Theorem 1.6.
Definition 2.1.
Let
![]() $\alpha,\beta$
be reals with
$\alpha,\beta$
be reals with
![]() $2\gt \alpha \gt \beta \geq 1$
. Let
$2\gt \alpha \gt \beta \geq 1$
. Let
![]() $\ell _0(\alpha,\beta )$
be defined as follows:
$\ell _0(\alpha,\beta )$
be defined as follows:
Lemma 2.2.
Let
![]() $\alpha,\beta$
be reals with
$\alpha,\beta$
be reals with
![]() $2\gt \alpha \gt \beta \geq 1$
and
$2\gt \alpha \gt \beta \geq 1$
and
![]() $\ell _0=\ell _0(\alpha,\beta )$
be defined as in Definition 2.1
. Let
$\ell _0=\ell _0(\alpha,\beta )$
be defined as in Definition 2.1
. Let
![]() $\mathcal{F}$
be an
$\mathcal{F}$
be an
![]() $(\alpha,\beta )$
-quasi-smooth family of bipartite graphs that satisfies
$(\alpha,\beta )$
-quasi-smooth family of bipartite graphs that satisfies
![]() $z(m,n,\mathcal{F})\leq \rho mn^{\alpha -1}+Cn^\beta$
for all
$z(m,n,\mathcal{F})\leq \rho mn^{\alpha -1}+Cn^\beta$
for all
![]() $m\leq n$
. For any
$m\leq n$
. For any
![]() $\delta \gt 0$
, there exists a positive real
$\delta \gt 0$
, there exists a positive real
![]() $\mu =\mu (\alpha,\beta,\rho,\delta )$
such that for all sufficiently large
$\mu =\mu (\alpha,\beta,\rho,\delta )$
such that for all sufficiently large
![]() $n$
the following is true. Let
$n$
the following is true. Let
![]() $G$
be an
$G$
be an
![]() $\mathcal{F}$
-free bipartite graph with at most
$\mathcal{F}$
-free bipartite graph with at most
![]() $n$
vertices and minimum degree at least
$n$
vertices and minimum degree at least
![]() $\delta n^{\alpha -1}$
. Let
$\delta n^{\alpha -1}$
. Let
![]() $u\in V(G)$
. For each
$u\in V(G)$
. For each
![]() $i\in \mathbb{N}$
, let
$i\in \mathbb{N}$
, let
![]() $N_i(u)$
denote the set of vertices at distance
$N_i(u)$
denote the set of vertices at distance
![]() $i$
from
$i$
from
![]() $u$
. Then for some
$u$
. Then for some
![]() $j_0\leq \ell _0$
we have
$j_0\leq \ell _0$
we have
![]() $\min \{|N_{j_0}(u)|,|N_{j_0+1}(u)|\}\geq \mu n$
.
$\min \{|N_{j_0}(u)|,|N_{j_0+1}(u)|\}\geq \mu n$
.
Proof. For each
![]() $i\in \mathbb{N}$
, let
$i\in \mathbb{N}$
, let
![]() $B_i$
denote the set of vertices at distance at most
$B_i$
denote the set of vertices at distance at most
![]() $i$
from
$i$
from
![]() $u$
. Let
$u$
. Let
First, we show that
![]() $|B_{\ell _0}|\geq \gamma n$
. Suppose for a contradiction that
$|B_{\ell _0}|\geq \gamma n$
. Suppose for a contradiction that
![]() $|B_{\ell _0}|\lt \gamma n$
. Let
$|B_{\ell _0}|\lt \gamma n$
. Let
![]() $i\in [\ell _0-1]$
. Then clearly
$i\in [\ell _0-1]$
. Then clearly
![]() $|B_i|\lt \gamma n$
, and since
$|B_i|\lt \gamma n$
, and since
![]() $G$
has minimum degree at least
$G$
has minimum degree at least
![]() $\delta n^{\alpha -1}$
, we have
$\delta n^{\alpha -1}$
, we have
On the other hand,
![]() $\sum _{v\in B_i}d(v)=2e(B_i)+e(B_i,B_{i+1}\setminus B_i)$
. Since
$\sum _{v\in B_i}d(v)=2e(B_i)+e(B_i,B_{i+1}\setminus B_i)$
. Since
![]() $G$
is bipartite and
$G$
is bipartite and
![]() $\mathcal{F}$
-free,
$\mathcal{F}$
-free,
![]() $e(B_i)\leq \max _{(a,b)} \{\rho ab^{\alpha -1}+Cb^\beta \}$
over all pairs of positive integers
$e(B_i)\leq \max _{(a,b)} \{\rho ab^{\alpha -1}+Cb^\beta \}$
over all pairs of positive integers
![]() $a\leq b$
with
$a\leq b$
with
![]() $a+b=|B_i|$
. Hence,
$a+b=|B_i|$
. Hence,
![]() $e(B_i)\leq \rho |B_i|^\alpha + C |B_i|^\beta \leq 2\rho |B_i|^\alpha$
, when
$e(B_i)\leq \rho |B_i|^\alpha + C |B_i|^\beta \leq 2\rho |B_i|^\alpha$
, when
![]() $n$
is sufficiently large. With some generosity, we can upper bound
$n$
is sufficiently large. With some generosity, we can upper bound
![]() $e(B_i, B_{i+1}\setminus B_i)$
by
$e(B_i, B_{i+1}\setminus B_i)$
by
![]() $z(|B_i|, |B_{i+1}|,\mathcal{F})$
to get
$z(|B_i|, |B_{i+1}|,\mathcal{F})$
to get
![]() $e(B_i, B_{i+1}\setminus B_i)\leq \rho |B_i||B_{i+1}|^{\alpha -1}+C |B_{i+1}|^\beta$
. Putting the above estimations all together, we get
$e(B_i, B_{i+1}\setminus B_i)\leq \rho |B_i||B_{i+1}|^{\alpha -1}+C |B_{i+1}|^\beta$
. Putting the above estimations all together, we get
If the first term on the right-hand side of (5) is the largest term, then we get
![]() $\delta n^{\alpha -1}|B_i|\leq 12\rho |B_i|^\alpha$
, from which we get
$\delta n^{\alpha -1}|B_i|\leq 12\rho |B_i|^\alpha$
, from which we get
![]() $|B_i|\geq (\delta/12\rho )^{1/(\alpha -1)} n\geq \gamma n$
, contradicting our assumption. If the second term on the right-hand side of (5) is the largest term, then we get
$|B_i|\geq (\delta/12\rho )^{1/(\alpha -1)} n\geq \gamma n$
, contradicting our assumption. If the second term on the right-hand side of (5) is the largest term, then we get
![]() $\delta n^{\alpha -1}|B_i|\leq 3\rho |B_i||B_{i+1}|^{\alpha -1}$
, from which we get
$\delta n^{\alpha -1}|B_i|\leq 3\rho |B_i||B_{i+1}|^{\alpha -1}$
, from which we get
![]() $|B_{i+1}|\geq (\delta/3\rho )^{1/(\alpha -1)} n\geq \gamma n$
and hence
$|B_{i+1}|\geq (\delta/3\rho )^{1/(\alpha -1)} n\geq \gamma n$
and hence
![]() $|B_{\ell _0}|\geq |B_{i+1}|\geq \gamma n$
, contradicting our assumption. Hence we may assume that for each
$|B_{\ell _0}|\geq |B_{i+1}|\geq \gamma n$
, contradicting our assumption. Hence we may assume that for each
![]() $i\in [\ell _0-1]$
, we have
$i\in [\ell _0-1]$
, we have
which yields that for each
![]() $i\in [\ell _0-1]$
,
$i\in [\ell _0-1]$
,
Let
![]() $\{b_i\}$
be a sequence recursively defined by letting
$\{b_i\}$
be a sequence recursively defined by letting
![]() $b_1=\alpha -1$
and
$b_1=\alpha -1$
and
![]() $b_{i+1}=(1/\beta ) b_i+ (\alpha -1)/\beta$
for each
$b_{i+1}=(1/\beta ) b_i+ (\alpha -1)/\beta$
for each
![]() $i\geq 1$
. If
$i\geq 1$
. If
![]() $\beta =1$
then a closed form formula for
$\beta =1$
then a closed form formula for
![]() $b_i$
is
$b_i$
is
![]() $b_i=(\alpha -1)i$
. If
$b_i=(\alpha -1)i$
. If
![]() $\beta \gt 1$
then a closed form formula for
$\beta \gt 1$
then a closed form formula for
![]() $b_i$
is
$b_i$
is
![]() $b_i= \frac{\alpha -1}{\beta -1} + (\frac{1}{\beta })^{i-1}(\alpha -1-\frac{\alpha -1}{\beta -1})$
. Note that we may assume
$b_i= \frac{\alpha -1}{\beta -1} + (\frac{1}{\beta })^{i-1}(\alpha -1-\frac{\alpha -1}{\beta -1})$
. Note that we may assume
![]() $C\geq 1$
, so
$C\geq 1$
, so
![]() $|B_1|\geq \delta n^{\alpha -1}\geq (\delta/3C)n^{b_1}$
. Then it follows by (6) and induction that
$|B_1|\geq \delta n^{\alpha -1}\geq (\delta/3C)n^{b_1}$
. Then it follows by (6) and induction that
![]() $|B_i|\geq (\delta/3C)^i n^{b_i}$
for each
$|B_i|\geq (\delta/3C)^i n^{b_i}$
for each
![]() $i\in [\ell _0]$
. However, using the definition of
$i\in [\ell _0]$
. However, using the definition of
![]() $\ell _0$
we get
$\ell _0$
we get
![]() $b_{\ell _0}\gt 1$
, which yield
$b_{\ell _0}\gt 1$
, which yield
![]() $|B_{\ell _0}|\gt n$
as
$|B_{\ell _0}|\gt n$
as
![]() $n$
is sufficiently large. This is a contradiction and thus proves that
$n$
is sufficiently large. This is a contradiction and thus proves that
![]() $|B_{\ell _0}|\geq \gamma n$
.
$|B_{\ell _0}|\geq \gamma n$
.
Let
![]() $j\in [\ell _0]$
be the smallest index such that
$j\in [\ell _0]$
be the smallest index such that
![]() $|N_j|\geq (\gamma/\ell _0) n$
. By the pigeonhole principle, such
$|N_j|\geq (\gamma/\ell _0) n$
. By the pigeonhole principle, such
![]() $j$
exists. By (2),
$j$
exists. By (2),
![]() $|N_j|\geq \mu n$
. Let
$|N_j|\geq \mu n$
. Let
![]() $U=N_j$
and
$U=N_j$
and
![]() $V=N_{j-1}\cup N_{j+1}$
. We show that
$V=N_{j-1}\cup N_{j+1}$
. We show that
![]() $|V|\geq 2\mu n$
, from which it follows that either
$|V|\geq 2\mu n$
, from which it follows that either
![]() $|N_{j-1}|\geq \mu n$
or
$|N_{j-1}|\geq \mu n$
or
![]() $|N_{j+1}|\geq \mu n$
and thus the lemma holds with
$|N_{j+1}|\geq \mu n$
and thus the lemma holds with
![]() $j_0=j$
or
$j_0=j$
or
![]() $j_0=j-1$
. Since all the edges of
$j_0=j-1$
. Since all the edges of
![]() $G$
that are incident to
$G$
that are incident to
![]() $U$
are between
$U$
are between
![]() $U$
and
$U$
and
![]() $V$
, we have
$V$
, we have
![]() $e(G[U,V])\geq \delta n^{\alpha -1} |U|$
. On the other hand,
$e(G[U,V])\geq \delta n^{\alpha -1} |U|$
. On the other hand,
![]() $G[U,V]$
is
$G[U,V]$
is
![]() $\mathcal{F}$
-free. If
$\mathcal{F}$
-free. If
![]() $|V|\geq |U|$
, then we have
$|V|\geq |U|$
, then we have
![]() $e(G[U,V])\leq \rho |U||V|^{\alpha -1}+ C|V|^\beta \leq 2\rho |U||V|^{\alpha -1}$
, where the last inequality holds as
$e(G[U,V])\leq \rho |U||V|^{\alpha -1}+ C|V|^\beta \leq 2\rho |U||V|^{\alpha -1}$
, where the last inequality holds as
![]() $|U|=|N_j|\geq \mu n$
and
$|U|=|N_j|\geq \mu n$
and
![]() $n$
is sufficiently large. Combining the two inequalities and solving for
$n$
is sufficiently large. Combining the two inequalities and solving for
![]() $|V|$
, we get
$|V|$
, we get
![]() $|V|\geq (\delta/2\rho )^{1/(\alpha -1)} n\geq 2\mu n$
, as desired. Otherwise, we have
$|V|\geq (\delta/2\rho )^{1/(\alpha -1)} n\geq 2\mu n$
, as desired. Otherwise, we have
![]() $|V|\leq |U|$
. Then
$|V|\leq |U|$
. Then
![]() $\delta n^{\alpha -1}|U|\leq e(G[U,V])\leq \rho |V||U|^{\alpha -1}+C|U|^\beta$
. Since
$\delta n^{\alpha -1}|U|\leq e(G[U,V])\leq \rho |V||U|^{\alpha -1}+C|U|^\beta$
. Since
![]() $C|U|^\beta \ll \delta n^{\alpha -1}|U|$
for sufficiently large
$C|U|^\beta \ll \delta n^{\alpha -1}|U|$
for sufficiently large
![]() $n$
, we can derive from the above that
$n$
, we can derive from the above that
![]() $\delta n^{\alpha -1}|U|\leq 2\rho |V||U|^{\alpha -1}$
. Solving for
$\delta n^{\alpha -1}|U|\leq 2\rho |V||U|^{\alpha -1}$
. Solving for
![]() $|V|$
, we have
$|V|$
, we have
![]() $|V|\geq (\delta/2\rho )n^{\alpha -1} |U|^{2-\alpha }\geq (\delta/2\rho ) n^{\alpha -1} (\gamma n)^{2-\alpha }=(\delta/2\rho )\gamma ^{2-\alpha } n\geq 2\mu n,$
where the last inequality holds by (2), as desired.
$|V|\geq (\delta/2\rho )n^{\alpha -1} |U|^{2-\alpha }\geq (\delta/2\rho ) n^{\alpha -1} (\gamma n)^{2-\alpha }=(\delta/2\rho )\gamma ^{2-\alpha } n\geq 2\mu n,$
where the last inequality holds by (2), as desired.
The following lemma, which we call robust reachability lemma is key to our proof of the main results. It is inspired by a lemma used in a recent paper of Letzter [Reference Letzter24] on the Turán number of tight cycles in hypergraphs.
Lemma 2.3.
Let
![]() $\alpha,\beta$
be reals with
$\alpha,\beta$
be reals with
![]() $2\gt \alpha \gt \beta \geq 1$
and
$2\gt \alpha \gt \beta \geq 1$
and
![]() $\ell _0=\ell _0(\alpha,\beta )$
be defined as in Definition 2.1
. Let
$\ell _0=\ell _0(\alpha,\beta )$
be defined as in Definition 2.1
. Let
![]() $\mathcal{F}$
be an
$\mathcal{F}$
be an
![]() $(\alpha,\beta )$
-quasi-smooth family of bipartite graphs that satisfies
$(\alpha,\beta )$
-quasi-smooth family of bipartite graphs that satisfies
![]() $z(m,n,\mathcal{F})\leq \rho mn^{\alpha -1}+Cn^\beta$
for all
$z(m,n,\mathcal{F})\leq \rho mn^{\alpha -1}+Cn^\beta$
for all
![]() $m\leq n$
. Let
$m\leq n$
. Let
![]() $\mu = \mu (\alpha, \beta, \rho, \delta )$
be defined as in Lemma 2.2
. For any real
$\mu = \mu (\alpha, \beta, \rho, \delta )$
be defined as in Lemma 2.2
. For any real
![]() $\delta \gt 0$
, the following holds for all sufficiently large
$\delta \gt 0$
, the following holds for all sufficiently large
![]() $n$
. Let
$n$
. Let
![]() $G$
be an
$G$
be an
![]() $\mathcal{F}$
-free bipartite graph with at most
$\mathcal{F}$
-free bipartite graph with at most
![]() $n$
verticers and minimum degree at least
$n$
verticers and minimum degree at least
![]() $\delta n^{\alpha -1}$
. Let
$\delta n^{\alpha -1}$
. Let
![]() $u\in V(G)$
. Then there exists a set
$u\in V(G)$
. Then there exists a set
![]() $S$
of at least
$S$
of at least
![]() $\mu (\alpha, \beta, \rho, \delta/2) n$
vertices, and a family
$\mu (\alpha, \beta, \rho, \delta/2) n$
vertices, and a family
![]() $\mathcal{P}=\{P_v\,{:}\, v\in S\}$
, where for each
$\mathcal{P}=\{P_v\,{:}\, v\in S\}$
, where for each
![]() $v\in S$
,
$v\in S$
,
![]() $P_v$
is a
$P_v$
is a
![]() $u,v$
-path of length at most
$u,v$
-path of length at most
![]() $\ell _0$
, such that no vertex except
$\ell _0$
, such that no vertex except
![]() $u$
is used on more than
$u$
is used on more than
![]() $\frac{n}{\log n}$
of the paths in
$\frac{n}{\log n}$
of the paths in
![]() $\mathcal{P}$
.
$\mathcal{P}$
.
Proof. Let
![]() $S$
be a maximum set of vertices such that there is an associated family
$S$
be a maximum set of vertices such that there is an associated family
![]() $\mathcal{P}=\{P_v\,{:}\,v\in S\}$
, where for each
$\mathcal{P}=\{P_v\,{:}\,v\in S\}$
, where for each
![]() $v\in S$
,
$v\in S$
,
![]() $P_v$
is a path of length at most
$P_v$
is a path of length at most
![]() $\ell _0$
such that no vertex is on more than
$\ell _0$
such that no vertex is on more than
![]() $\frac{n}{\log n}$
of the paths. Let
$\frac{n}{\log n}$
of the paths. Let
![]() $W$
denote the set of vertices in
$W$
denote the set of vertices in
![]() $G$
(other than
$G$
(other than
![]() $u$
) that lie on exactly
$u$
) that lie on exactly
![]() $\frac{n}{\log n}$
of the paths
$\frac{n}{\log n}$
of the paths
![]() $P_v$
in
$P_v$
in
![]() $\mathcal{P}$
. Then
$\mathcal{P}$
. Then
![]() $|W|\frac{n}{\log n}\leq |S|\ell _0\leq n\ell _0$
and thus
$|W|\frac{n}{\log n}\leq |S|\ell _0\leq n\ell _0$
and thus
![]() $|W|\leq \ell _0\log n\lt (\delta/2)n^{\alpha -1}$
for sufficiently large
$|W|\leq \ell _0\log n\lt (\delta/2)n^{\alpha -1}$
for sufficiently large
![]() $n$
. Hence,
$n$
. Hence,
![]() $G-W$
has minimum degree at least
$G-W$
has minimum degree at least
![]() $(\delta/2)n^{\alpha -1}$
. If
$(\delta/2)n^{\alpha -1}$
. If
![]() $|S|\lt \mu (\alpha, \beta, \rho,\delta/2) n$
, then by Lemma 2.2, there exists a vertex
$|S|\lt \mu (\alpha, \beta, \rho,\delta/2) n$
, then by Lemma 2.2, there exists a vertex
![]() $z\notin S$
and a
$z\notin S$
and a
![]() $u,z$
-path
$u,z$
-path
![]() $P_z$
of length at most
$P_z$
of length at most
![]() $\ell _0$
in
$\ell _0$
in
![]() $G-W$
that we can add to
$G-W$
that we can add to
![]() $S$
to contradict our choice of
$S$
to contradict our choice of
![]() $S$
. Hence
$S$
. Hence
![]() $|S|\geq \mu (\alpha, \beta, \rho,\delta/2) n$
.
$|S|\geq \mu (\alpha, \beta, \rho,\delta/2) n$
.
It is worth noting that the
![]() $\frac{n}{\log{n}}$
threshold could be improved to
$\frac{n}{\log{n}}$
threshold could be improved to
![]() $O(n^{2-\alpha +\varepsilon })$
for any real
$O(n^{2-\alpha +\varepsilon })$
for any real
![]() $\varepsilon \gt 0$
, but for simplicity of presentation, we choose to use
$\varepsilon \gt 0$
, but for simplicity of presentation, we choose to use
![]() $\frac{n}{\log{n}}$
and such a choice suffices for the purpose of our main arguments.
$\frac{n}{\log{n}}$
and such a choice suffices for the purpose of our main arguments.
The next folklore lemma will be used a few times and we include a proof for completeness. We would like to mention that it might be easy for one to overlook the connectedness of
![]() $H$
statement in the conclusion. But this condition will play important role in the main proofs.
$H$
statement in the conclusion. But this condition will play important role in the main proofs.
Lemma 2.4.
Let
![]() $G$
be a connected graph. Let
$G$
be a connected graph. Let
![]() $H$
be a maximum spanning bipartite subgraph of
$H$
be a maximum spanning bipartite subgraph of
![]() $G$
. Then
$G$
. Then
![]() $H$
is connected and for each
$H$
is connected and for each
![]() $v\in V(G), d_H(v)\geq (1/2) d_G(v)$
.
$v\in V(G), d_H(v)\geq (1/2) d_G(v)$
.
Proof. Let
![]() $(X,Y)$
denote a bipartition of
$(X,Y)$
denote a bipartition of
![]() $H$
. Suppose for contradiction that
$H$
. Suppose for contradiction that
![]() $H$
is disconnected and
$H$
is disconnected and
![]() $F$
is a component of
$F$
is a component of
![]() $H$
. Since
$H$
. Since
![]() $G$
is connected, it contains an edge
$G$
is connected, it contains an edge
![]() $e$
joining
$e$
joining
![]() $V(F)$
to
$V(F)$
to
![]() $V(G)\setminus V(F)$
. But then
$V(G)\setminus V(F)$
. But then
![]() $H\cup e$
is still bipartite, since adding
$H\cup e$
is still bipartite, since adding
![]() $e$
does not create a new cycle. Furthermore,
$e$
does not create a new cycle. Furthermore,
![]() $H\cup e$
has more edges than
$H\cup e$
has more edges than
![]() $H$
, contradicting our choice of
$H$
, contradicting our choice of
![]() $H$
.
$H$
.
Next, let
![]() $v$
be any vertex in
$v$
be any vertex in
![]() $H$
. Without loss of generality, suppose
$H$
. Without loss of generality, suppose
![]() $v\in X$
. Suppose
$v\in X$
. Suppose
![]() $d_H(v)\lt (1/2)d_G(v)$
. Then from
$d_H(v)\lt (1/2)d_G(v)$
. Then from
![]() $H$
by deleting the edges incident to
$H$
by deleting the edges incident to
![]() $x$
and adding the edges in
$x$
and adding the edges in
![]() $G$
from
$G$
from
![]() $v$
to
$v$
to
![]() $X$
, we obtained a bipartite subgraph of
$X$
, we obtained a bipartite subgraph of
![]() $G$
that has more edges than
$G$
that has more edges than
![]() $H$
, a contradiction. Hence
$H$
, a contradiction. Hence
![]() $\forall v\in V(G), d_H(v)\geq (1/2)d_G(v)$
.
$\forall v\in V(G), d_H(v)\geq (1/2)d_G(v)$
.
We conclude this section with the following lemma about the diameter. The diameter of a graph
![]() $G$
is the least integer
$G$
is the least integer
![]() $k$
such that there exists a path of length at most
$k$
such that there exists a path of length at most
![]() $k$
between any two vertices in
$k$
between any two vertices in
![]() $G$
.
$G$
.
Lemma 2.5.
Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex connected graph with minimum degree at least
$n$
-vertex connected graph with minimum degree at least
![]() $D$
. Then
$D$
. Then
![]() $G$
has diameter at most
$G$
has diameter at most
![]() $3n/D$
.
$3n/D$
.
Proof. Let
![]() $x,y$
be two vertices at maximum distance in
$x,y$
be two vertices at maximum distance in
![]() $G$
. Let
$G$
. Let
![]() $v_0v_1\cdots v_\ell$
be a shortest
$v_0v_1\cdots v_\ell$
be a shortest
![]() $x,y$
-path in
$x,y$
-path in
![]() $G$
where
$G$
where
![]() $v_0=x$
and
$v_0=x$
and
![]() $v_\ell =y$
. Let
$v_\ell =y$
. Let
![]() $q=\lfloor \ell/3\rfloor$
. Note that
$q=\lfloor \ell/3\rfloor$
. Note that
![]() $N(v_0), N(v_3), N(v_6),\cdots, N(v_{3q})$
are pairwise disjoint (or else we can find a shorter
$N(v_0), N(v_3), N(v_6),\cdots, N(v_{3q})$
are pairwise disjoint (or else we can find a shorter
![]() $x,y$
-path, a contradiction). Hence
$x,y$
-path, a contradiction). Hence
![]() $n\geq \sum _{i=0}^q |N(v_{3i})| \geq$
$n\geq \sum _{i=0}^q |N(v_{3i})| \geq$
![]() $(q+1)D$
. This implies that
$(q+1)D$
. This implies that
![]() $(q+1)\leq n/D$
and hence
$(q+1)\leq n/D$
and hence
![]() $\ell \leq 3(q+1)\leq 3n/D$
.
$\ell \leq 3(q+1)\leq 3n/D$
.
3. An efficient robust reachability lemma for
 $C_{2\boldsymbol\ell }$
-free graphs
$C_{2\boldsymbol\ell }$
-free graphs
In this section, we develop a more efficient robust reachability lemma than Lemma 2.3 for
![]() $C_{2\ell }$
-free graphs, which may be of independent interest. We need the following lemma from [Reference Verstraëte27].
$C_{2\ell }$
-free graphs, which may be of independent interest. We need the following lemma from [Reference Verstraëte27].
Lemma 3.1. (Verstraëte [Reference Verstraëte27]). Let
![]() $\ell \geq 2$
be an integer and
$\ell \geq 2$
be an integer and
![]() $H$
a bipartite graph of average degree at least
$H$
a bipartite graph of average degree at least
![]() $4\ell$
and girth
$4\ell$
and girth
![]() $g$
. Then there exist cycles of at least
$g$
. Then there exist cycles of at least
![]() $(g/2-1)\ell \geq \ell$
consecutive even lengths in
$(g/2-1)\ell \geq \ell$
consecutive even lengths in
![]() $H$
. Moreover, the shortest of these cycles has length at most twice the radius of
$H$
. Moreover, the shortest of these cycles has length at most twice the radius of
![]() $H$
.
$H$
.
Our lemma is as follows.
Lemma 3.2.
Let
![]() $\ell \geq 2$
and
$\ell \geq 2$
and
![]() $d$
be positive integers. Let
$d$
be positive integers. Let
![]() $H$
be a bipartite
$H$
be a bipartite
![]() $C_{2\ell }$
-free graph with minimum degree at least
$C_{2\ell }$
-free graph with minimum degree at least
![]() $d$
. Let
$d$
. Let
![]() $u$
be any vertex in
$u$
be any vertex in
![]() $H$
. Then the following items hold.
$H$
. Then the following items hold.
-
(1) The number of vertices that are at distance at most
 $\ell$
from
$\ell$
from
 $u$
is at least
$u$
is at least
 $(d/4\ell )^\ell$
.
$(d/4\ell )^\ell$
. -
(2) Suppose
 $H$
has at most
$H$
has at most
 $n$
vertices and
$n$
vertices and
 $d\geq 15\ell \log n$
, where
$d\geq 15\ell \log n$
, where
 $n$
is sufficiently large. Then there is a set
$n$
is sufficiently large. Then there is a set
 $S$
of at least
$S$
of at least
 $(1/2)(d/8\ell ^2)^\ell$
vertices together with a family
$(1/2)(d/8\ell ^2)^\ell$
vertices together with a family
 $\mathcal{P}=\{P_v\,{:}\, v\in S\}$
, where for each
$\mathcal{P}=\{P_v\,{:}\, v\in S\}$
, where for each
 $v\in S$
,
$v\in S$
,
 $P_v$
is a
$P_v$
is a
 $u,v$
-path of exactly length
$u,v$
-path of exactly length
 $\ell$
, such that no vertex of
$\ell$
, such that no vertex of
 $H$
except
$H$
except
 $u$
lies on more than
$u$
lies on more than
 $d^{\ell -1}$
of these paths and each vertex
$d^{\ell -1}$
of these paths and each vertex
 $v$
in
$v$
in
 $S$
lies only on
$S$
lies only on
 $P_v$
.
$P_v$
.
Proof. First we prove the first part (1) of the theorem. Let
![]() $B_0=\{u\}$
. Consider any
$B_0=\{u\}$
. Consider any
![]() $i\in [\ell ]$
. Let
$i\in [\ell ]$
. Let
![]() $B_i$
denote the set of vertices at distance at most
$B_i$
denote the set of vertices at distance at most
![]() $i$
from
$i$
from
![]() $u$
in
$u$
in
![]() $H$
and
$H$
and
![]() $H_i$
the subgraph of
$H_i$
the subgraph of
![]() $H$
induced by
$H$
induced by
![]() $B_i$
. If
$B_i$
. If
![]() $H[B_i]$
has average degree at least
$H[B_i]$
has average degree at least
![]() $4\ell$
, then by Lemma 3.1,
$4\ell$
, then by Lemma 3.1,
![]() $G_i$
contains cycles of
$G_i$
contains cycles of
![]() $\ell$
consecutive even lengths the shortest of which has length at most
$\ell$
consecutive even lengths the shortest of which has length at most
![]() $2i\leq 2\ell$
and hence it contains
$2i\leq 2\ell$
and hence it contains
![]() $C_{2\ell }$
, contradicting
$C_{2\ell }$
, contradicting
![]() $G$
being
$G$
being
![]() $C_{2\ell }$
-free. So for each
$C_{2\ell }$
-free. So for each
![]() $i\in [\ell ]$
, we have
$i\in [\ell ]$
, we have
![]() $d(H_i)\lt 4\ell$
, which implies that
$d(H_i)\lt 4\ell$
, which implies that
![]() $e(H_i)\lt 2\ell |B_i|$
. On the other hand,
$e(H_i)\lt 2\ell |B_i|$
. On the other hand,
![]() $H_i$
contains all the edges of
$H_i$
contains all the edges of
![]() $G$
that are incident to
$G$
that are incident to
![]() $B_{i-1}$
. So
$B_{i-1}$
. So
![]() $e(H_i)\geq d|B_{i-1}|/2$
. Combining these two inequalities, we get
$e(H_i)\geq d|B_{i-1}|/2$
. Combining these two inequalities, we get
![]() $ 2\ell |B_i|\gt d|B_{i-1}|/2$
. Hence,
$ 2\ell |B_i|\gt d|B_{i-1}|/2$
. Hence,
![]() $|B_i|\gt (d/4\ell ) |B_{i-1}|$
for each
$|B_i|\gt (d/4\ell ) |B_{i-1}|$
for each
![]() $i\in [\ell ]$
. Thus,
$i\in [\ell ]$
. Thus,
![]() $|B_\ell |\geq (d/4\ell )^\ell$
, as desired.
$|B_\ell |\geq (d/4\ell )^\ell$
, as desired.
Next, we prove the second part (2). Let us randomly split the vertices of
![]() $G$
into
$G$
into
![]() $\ell$
parts
$\ell$
parts
![]() $V_1,\dots, V_\ell$
. For each vertex
$V_1,\dots, V_\ell$
. For each vertex
![]() $x$
, and each
$x$
, and each
![]() $i\in [\ell ]$
, the degree
$i\in [\ell ]$
, the degree
![]() $d_i(x)$
of
$d_i(x)$
of
![]() $x$
in
$x$
in
![]() $V_i$
has a binomial distribution
$V_i$
has a binomial distribution
![]() $\text{Bin}(d(x), 1/\ell )$
. Hence, using Chernoff’s inequality (see [Reference Alon and Spencer3] or [Reference Janson, Luczak and Rucinski17] Corollary 2.3), we have
$\text{Bin}(d(x), 1/\ell )$
. Hence, using Chernoff’s inequality (see [Reference Alon and Spencer3] or [Reference Janson, Luczak and Rucinski17] Corollary 2.3), we have
since
![]() $d(x)\geq 15\ell \log n$
. Hence, for sufficiently large
$d(x)\geq 15\ell \log n$
. Hence, for sufficiently large
![]() $n$
, there exists a splitting of
$n$
, there exists a splitting of
![]() $V(H)$
such that for each
$V(H)$
such that for each
![]() $x\in V(H)$
and for each
$x\in V(H)$
and for each
![]() $i\in [\ell ]$
,
$i\in [\ell ]$
,
![]() $d_i(x)\geq (1/2\ell ) d(x)\geq d/2\ell$
. Now, we form a subgraph
$d_i(x)\geq (1/2\ell ) d(x)\geq d/2\ell$
. Now, we form a subgraph
![]() $H'$
of
$H'$
of
![]() $H$
as follows. First, we include exactly
$H$
as follows. First, we include exactly
![]() $d/2\ell$
of the edges from
$d/2\ell$
of the edges from
![]() $u$
to
$u$
to
![]() $V_1$
. Denote the set of reached vertices in
$V_1$
. Denote the set of reached vertices in
![]() $V_1$
by
$V_1$
by
![]() $S_1$
. Then for each vertex in
$S_1$
. Then for each vertex in
![]() $S_1$
including exactly
$S_1$
including exactly
![]() $d/2\ell$
edges from it to
$d/2\ell$
edges from it to
![]() $V_2$
. Denote the set of reached vertices in
$V_2$
. Denote the set of reached vertices in
![]() $V_2$
by
$V_2$
by
![]() $S_2$
. We continue like this till we define
$S_2$
. We continue like this till we define
![]() $S_\ell$
. Let
$S_\ell$
. Let
![]() $B_0=S_0=\{u\}$
. For each
$B_0=S_0=\{u\}$
. For each
![]() $i\in [\ell ]$
, let
$i\in [\ell ]$
, let
![]() $B_i=\bigcup _{j=0}^i S_i$
. and
$B_i=\bigcup _{j=0}^i S_i$
. and
![]() $H_i$
the subgraph of
$H_i$
the subgraph of
![]() $H'$
induced by
$H'$
induced by
![]() $B_i$
. Note that
$B_i$
. Note that
![]() $H_i$
has radius
$H_i$
has radius
![]() $i$
. As in the proof of the first part of the lemma, since
$i$
. As in the proof of the first part of the lemma, since
![]() $H_i$
is
$H_i$
is
![]() $C_{2\ell }$
-free,
$C_{2\ell }$
-free,
![]() $e(H_i)\lt 2\ell |B_i|$
. On the other hand,
$e(H_i)\lt 2\ell |B_i|$
. On the other hand,
![]() $H_i$
contains all the edges of
$H_i$
contains all the edges of
![]() $H'$
that are incident to
$H'$
that are incident to
![]() $B_{i-1}$
. So
$B_{i-1}$
. So
![]() $e(H_i)\geq (1/2)(d/2\ell )|B_{i-1}|$
. Combining these two inequalities, we get
$e(H_i)\geq (1/2)(d/2\ell )|B_{i-1}|$
. Combining these two inequalities, we get
![]() $ 2\ell |B_i|\gt (d/4\ell )|B_{i-1}|$
. Hence,
$ 2\ell |B_i|\gt (d/4\ell )|B_{i-1}|$
. Hence,
![]() $|B_i|\gt (d/8\ell ^2) |B_{i-1}|$
for each
$|B_i|\gt (d/8\ell ^2) |B_{i-1}|$
for each
![]() $i\in [\ell ]$
. Thus,
$i\in [\ell ]$
. Thus,
![]() $|B_\ell |\geq (d/8\ell ^2)^\ell$
.
$|B_\ell |\geq (d/8\ell ^2)^\ell$
.
It is easy to see that
![]() $\sum _{i=0}^{\ell -1} |S_i|\leq \sum _{i=0}^{\ell -1} (d/2\ell )^i\leq 2(d/2\ell )^{\ell -1}$
, when
$\sum _{i=0}^{\ell -1} |S_i|\leq \sum _{i=0}^{\ell -1} (d/2\ell )^i\leq 2(d/2\ell )^{\ell -1}$
, when
![]() $n$
is sufficiently large. Hence
$n$
is sufficiently large. Hence
where
![]() $n$
(and thus
$n$
(and thus
![]() $d$
) is sufficiently large. By the definition of
$d$
) is sufficiently large. By the definition of
![]() $H'$
, for each
$H'$
, for each
![]() $v\in S_\ell$
, there is a path of length
$v\in S_\ell$
, there is a path of length
![]() $\ell$
from
$\ell$
from
![]() $u$
to
$u$
to
![]() $v$
that intersects each of
$v$
that intersects each of
![]() $V_1,V_2,\dots, V_\ell$
. From the union of these paths one can find a tree
$V_1,V_2,\dots, V_\ell$
. From the union of these paths one can find a tree
![]() $T$
of height
$T$
of height
![]() $\ell$
rooted at
$\ell$
rooted at
![]() $u$
, in which all the vertices in
$u$
, in which all the vertices in
![]() $S_\ell$
are at distance
$S_\ell$
are at distance
![]() $\ell$
from
$\ell$
from
![]() $u$
. Furthermore, by the definition of
$u$
. Furthermore, by the definition of
![]() $H'$
,
$H'$
,
![]() $T$
has maximum degree at most
$T$
has maximum degree at most
![]() $(d/2\ell )+1$
. For each
$(d/2\ell )+1$
. For each
![]() $v\in S_\ell$
, let
$v\in S_\ell$
, let
![]() $P_v$
be the unique
$P_v$
be the unique
![]() $u,v$
-path in
$u,v$
-path in
![]() $T$
. If
$T$
. If
![]() $x$
is any vertex in
$x$
is any vertex in
![]() $T$
other than
$T$
other than
![]() $u$
, then clearly
$u$
, then clearly
![]() $x$
lies on at most
$x$
lies on at most
![]() $(d/2\ell )^{\ell -1}$
of the paths
$(d/2\ell )^{\ell -1}$
of the paths
![]() $P_v$
. Furthermore, each
$P_v$
. Furthermore, each
![]() $v\in S_\ell$
doesn’t lie on any
$v\in S_\ell$
doesn’t lie on any
![]() $P_{w}$
for
$P_{w}$
for
![]() $w\in S_\ell \setminus \{v\}$
.
$w\in S_\ell \setminus \{v\}$
.
4. Proofs of Theorem 1.6 and Theorem 1.8
Even though the proofs of Theorem 1.6 and Theorem 1.8 are essentially the same, there are sufficiently different choices of parameters that we will prove them separately. Before giving the formal proof of Theorem 1.6, we give an overview. Let
![]() $\alpha,\beta$
be reals with
$\alpha,\beta$
be reals with
![]() $2\gt \alpha \gt \beta \geq 1$
. Let
$2\gt \alpha \gt \beta \geq 1$
. Let
![]() $\mathcal{F}$
be an
$\mathcal{F}$
be an
![]() $(\alpha,\beta )$
-quasi-smooth family of bipartite graphs that satisfies
$(\alpha,\beta )$
-quasi-smooth family of bipartite graphs that satisfies
![]() $z(m,n,\mathcal{F})\leq \rho mn^{\alpha -1}+Cn^\beta$
for all
$z(m,n,\mathcal{F})\leq \rho mn^{\alpha -1}+Cn^\beta$
for all
![]() $m\leq n$
. Let
$m\leq n$
. Let
![]() $\delta \gt 0$
be given. We wish to show that there exists a positive integer
$\delta \gt 0$
be given. We wish to show that there exists a positive integer
![]() $k_0$
such that for any odd integer
$k_0$
such that for any odd integer
![]() $k\geq k_0$
and sufficiently large
$k\geq k_0$
and sufficiently large
![]() $n$
, any
$n$
, any
![]() $n$
-vertex
$n$
-vertex
![]() $\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
$\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
![]() $\delta n^{\alpha -1}$
is bipartite.
$\delta n^{\alpha -1}$
is bipartite.
Let
![]() $k_0$
be sufficiently large as a function of
$k_0$
be sufficiently large as a function of
![]() $\alpha,\beta,\rho$
and
$\alpha,\beta,\rho$
and
![]() $\delta$
. Let
$\delta$
. Let
![]() $k\geq k_0$
be an odd integer. Let
$k\geq k_0$
be an odd integer. Let
![]() $G$
be a
$G$
be a
![]() $n$
-vertex
$n$
-vertex
![]() $\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
$\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
![]() $\delta n^{\alpha -1}$
. We take a maximum spanning bipartite subgraph
$\delta n^{\alpha -1}$
. We take a maximum spanning bipartite subgraph
![]() $H$
of
$H$
of
![]() $G$
. Let
$G$
. Let
![]() $(X,Y)$
be a bipartition of
$(X,Y)$
be a bipartition of
![]() $H$
. We show that
$H$
. We show that
![]() $G$
is itself bipartite by showing that
$G$
is itself bipartite by showing that
![]() $X,Y$
must be independent sets in
$X,Y$
must be independent sets in
![]() $G$
. Suppose contradiction there exist two vertices
$G$
. Suppose contradiction there exist two vertices
![]() $u,v$
, say in
$u,v$
, say in
![]() $X$
, such that
$X$
, such that
![]() $uv\in E(G)$
. We derive a contradiction by finding a
$uv\in E(G)$
. We derive a contradiction by finding a
![]() $C_k$
in
$C_k$
in
![]() $G$
that contains
$G$
that contains
![]() $uv$
. To build such a
$uv$
. To build such a
![]() $C_k$
, we utilise expansion properties (as described in Lemma 2.2) and robust reachability properties (as described in Lemma 2.3) of various carefully defined subgraphs of
$C_k$
, we utilise expansion properties (as described in Lemma 2.2) and robust reachability properties (as described in Lemma 2.3) of various carefully defined subgraphs of
![]() $G$
. First, via a random partitioning argument, we can find a partition of
$G$
. First, via a random partitioning argument, we can find a partition of
![]() $V(H)=V(G)$
into two subsets
$V(H)=V(G)$
into two subsets
![]() $A,B$
such that
$A,B$
such that
![]() $H[A]$
has high minimum degree and each vertex in
$H[A]$
has high minimum degree and each vertex in
![]() $A$
has high degree in
$A$
has high degree in
![]() $B$
(inside
$B$
(inside
![]() $H$
). Assume
$H$
). Assume
![]() $u\in A$
. We then apply Lemma 2.3 and some additional cleaning to find a balanced family
$u\in A$
. We then apply Lemma 2.3 and some additional cleaning to find a balanced family
![]() $\mathcal{P}'$
of paths of bounded equal length inside
$\mathcal{P}'$
of paths of bounded equal length inside
![]() $H[A]$
that start at
$H[A]$
that start at
![]() $u$
and reach a linear-sized subset
$u$
and reach a linear-sized subset
![]() $S''$
of
$S''$
of
![]() $A$
with the additional property that vertices in
$A$
with the additional property that vertices in
![]() $S''$
serve only as endpoints of these paths and never as interior points. Since vertices in
$S''$
serve only as endpoints of these paths and never as interior points. Since vertices in
![]() $S''$
have high degree in
$S''$
have high degree in
![]() $H$
into
$H$
into
![]() $B$
and
$B$
and
![]() $S''$
is linear-sized, the subgraph of
$S''$
is linear-sized, the subgraph of
![]() $H$
consisting of edges from
$H$
consisting of edges from
![]() $S''$
to
$S''$
to
![]() $B$
is dense and contains a subgraph
$B$
is dense and contains a subgraph
![]() $H''$
of high minimum degree. We then take a shortest path
$H''$
of high minimum degree. We then take a shortest path
![]() $Q$
in
$Q$
in
![]() $G$
from
$G$
from
![]() $v$
to
$v$
to
![]() $V(H'')$
and denote its unique vertex in
$V(H'')$
and denote its unique vertex in
![]() $V(H'')$
by
$V(H'')$
by
![]() $y$
. The balanced-ness of
$y$
. The balanced-ness of
![]() $\mathcal{P}'$
ensures that most of the paths in
$\mathcal{P}'$
ensures that most of the paths in
![]() $\mathcal{P}'$
reaching
$\mathcal{P}'$
reaching
![]() $S''$
are vertex disjoint from
$S''$
are vertex disjoint from
![]() $Q$
. We then apply Lemma 2.2 inside
$Q$
. We then apply Lemma 2.2 inside
![]() $H''$
along with some additional cleaning to find a path in
$H''$
along with some additional cleaning to find a path in
![]() $H''$
of suitable length from
$H''$
of suitable length from
![]() $y$
to an appropriate vertex
$y$
to an appropriate vertex
![]() $w^*$
in
$w^*$
in
![]() $S''$
. We build a
$S''$
. We build a
![]() $C_k$
by taking the union of this path with
$C_k$
by taking the union of this path with
![]() $Q$
, the edge
$Q$
, the edge
![]() $uv$
and the member of
$uv$
and the member of
![]() $\mathcal{P}'$
from
$\mathcal{P}'$
from
![]() $u$
to
$u$
to
![]() $w^*$
.
$w^*$
.
Proof of Theorem 1.6. Let
![]() $\alpha,\beta$
be reals with
$\alpha,\beta$
be reals with
![]() $2\gt \alpha \gt \beta \geq 1$
. Let
$2\gt \alpha \gt \beta \geq 1$
. Let
![]() $\mathcal{F}$
be an
$\mathcal{F}$
be an
![]() $(\alpha,\beta )$
-quasi-smooth family of bipartite graphs that satisfies
$(\alpha,\beta )$
-quasi-smooth family of bipartite graphs that satisfies
![]() $z(m,n,\mathcal{F})\leq \rho mn^{\alpha -1}+Cn^\beta$
for all
$z(m,n,\mathcal{F})\leq \rho mn^{\alpha -1}+Cn^\beta$
for all
![]() $m\leq n$
.
$m\leq n$
.
Given any real
![]() $\delta \gt 0$
, we first define
$\delta \gt 0$
, we first define
![]() $k_0$
as following. Let
$k_0$
as following. Let
![]() $\ell _0=\ell _0(\alpha,\beta )$
as in Definition 2.1. Let
$\ell _0=\ell _0(\alpha,\beta )$
as in Definition 2.1. Let
![]() $\mu (\delta ) = \mu (\alpha, \beta, \rho, \delta )$
as in the proof of Lemma 2.2. Define
$\mu (\delta ) = \mu (\alpha, \beta, \rho, \delta )$
as in the proof of Lemma 2.2. Define
Let
![]() $k\geq k_0$
be odd. Let
$k\geq k_0$
be odd. Let
![]() $n$
be sufficiently large so that all subsequent inequalities involving
$n$
be sufficiently large so that all subsequent inequalities involving
![]() $n$
hold. Let
$n$
hold. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
$\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
![]() $\delta n^{\alpha -1}$
. We may assume that
$\delta n^{\alpha -1}$
. We may assume that
![]() $G$
is connected. Let
$G$
is connected. Let
![]() $H$
be a maximum bipartite spanning subgraph of
$H$
be a maximum bipartite spanning subgraph of
![]() $G$
. By Lemma 2.4,
$G$
. By Lemma 2.4,
![]() $H$
is connected and has minimum degree at least
$H$
is connected and has minimum degree at least
![]() $(\delta/2) n^{\alpha -1}$
.
$(\delta/2) n^{\alpha -1}$
.
Since
![]() $H$
is
$H$
is
![]() $\mathcal{F}$
-free, by Lemma 2.2, for each vertex
$\mathcal{F}$
-free, by Lemma 2.2, for each vertex
![]() $x$
, the set of vertices that are at distance at most
$x$
, the set of vertices that are at distance at most
![]() $\ell _0$
from
$\ell _0$
from
![]() $x$
is at least
$x$
is at least
![]() $\mu (\delta/2) n$
. Hence by Lemma 2.5 (applied to the
$\mu (\delta/2) n$
. Hence by Lemma 2.5 (applied to the
![]() $\ell _0$
-th power
$\ell _0$
-th power
![]() $H^{\ell _0}$
of
$H^{\ell _0}$
of
![]() $H$
),
$H$
),
![]() $H^{\ell _0}$
has diameter at most
$H^{\ell _0}$
has diameter at most
![]() $\lfloor \frac{3n}{\mu (\delta/2) n}\rfloor =\lfloor \frac{3}{\mu (\delta/2)}\rfloor$
and hence
$\lfloor \frac{3n}{\mu (\delta/2) n}\rfloor =\lfloor \frac{3}{\mu (\delta/2)}\rfloor$
and hence
![]() $H$
has diameter at most
$H$
has diameter at most
![]() $\lfloor \frac{3}{\mu (\delta/2)}\rfloor \cdot \ell _0=L$
, as defined in (7).
$\lfloor \frac{3}{\mu (\delta/2)}\rfloor \cdot \ell _0=L$
, as defined in (7).
Let
![]() $(X,Y)$
be the unique bipartition of
$(X,Y)$
be the unique bipartition of
![]() $H$
. We show that
$H$
. We show that
![]() $G$
is also bipartite with
$G$
is also bipartite with
![]() $(X,Y)$
being a bipartition of it. Suppose otherwise. We may assume, without loss of generality, that there exist two vertices
$(X,Y)$
being a bipartition of it. Suppose otherwise. We may assume, without loss of generality, that there exist two vertices
![]() $u,v\in X$
such that
$u,v\in X$
such that
![]() $uv\in E(G)$
. We will derive a contradiction by finding a copy of
$uv\in E(G)$
. We will derive a contradiction by finding a copy of
![]() $C_k$
in
$C_k$
in
![]() $G$
that contains
$G$
that contains
![]() $uv$
.
$uv$
.
Let us randomly split
![]() $V(H)$
into two subsets
$V(H)$
into two subsets
![]() $A,B$
. For each vertex
$A,B$
. For each vertex
![]() $x$
of degree
$x$
of degree
![]() $d(x)$
in
$d(x)$
in
![]() $H$
, let
$H$
, let
![]() $d_A(x)$
and
$d_A(x)$
and
![]() $d_B(x)$
denote the degree of
$d_B(x)$
denote the degree of
![]() $x$
in
$x$
in
![]() $A$
and
$A$
and
![]() $B$
, respectively. Then both
$B$
, respectively. Then both
![]() $d_A(x)$
and
$d_A(x)$
and
![]() $d_B(x)$
satisfy the binomial distribution
$d_B(x)$
satisfy the binomial distribution
![]() $\text{Bin}(d(x), 1/2)$
. Hence, by Chernoff’s inequality, we have
$\text{Bin}(d(x), 1/2)$
. Hence, by Chernoff’s inequality, we have
since
![]() $d(x)\geq (\delta/2)n^{\alpha -1}$
and
$d(x)\geq (\delta/2)n^{\alpha -1}$
and
![]() $n$
is sufficiently large. Hence with positive probability we can ensure that for any
$n$
is sufficiently large. Hence with positive probability we can ensure that for any
![]() $x\in V(H)$
,
$x\in V(H)$
,
![]() $\min \{d_A(x), d_B(x)\}\geq (1/4)d(x)\geq (\delta/8) n^{\alpha -1}$
. Let us fix such a partition
$\min \{d_A(x), d_B(x)\}\geq (1/4)d(x)\geq (\delta/8) n^{\alpha -1}$
. Let us fix such a partition
![]() $A,B$
of
$A,B$
of
![]() $V(H)$
.
$V(H)$
.
Without loss of generality, suppose that the vertex
![]() $u$
is in
$u$
is in
![]() $A$
. Let
$A$
. Let
![]() $H[A]$
denote the subgraph of
$H[A]$
denote the subgraph of
![]() $H$
induced by
$H$
induced by
![]() $A$
. By our discussion above,
$A$
. By our discussion above,
![]() $H[A]$
has minimum degree at least
$H[A]$
has minimum degree at least
![]() $(\delta/8) n^{\alpha -1}$
. By Lemma 2.3, there exists a set
$(\delta/8) n^{\alpha -1}$
. By Lemma 2.3, there exists a set
![]() $U$
of at least
$U$
of at least
![]() $\mu (\delta/16) n$
vertices and a family
$\mu (\delta/16) n$
vertices and a family
![]() $\mathcal{P}=\{P_z\,{:}\, z\in U\}$
, where for each
$\mathcal{P}=\{P_z\,{:}\, z\in U\}$
, where for each
![]() $z\in U$
,
$z\in U$
,
![]() $P_z$
is a
$P_z$
is a
![]() $u,z$
-path in
$u,z$
-path in
![]() $H[A]$
of length at most
$H[A]$
of length at most
![]() $\ell _0$
and no vertex in
$\ell _0$
and no vertex in
![]() $H$
lies on more than
$H$
lies on more than
![]() $n/\log n$
of these paths
$n/\log n$
of these paths
![]() $P_z$
. By the pigeonhole principle, there exists a value
$P_z$
. By the pigeonhole principle, there exists a value
![]() $p\in [\ell _0]$
and a subset
$p\in [\ell _0]$
and a subset
![]() $S\subseteq U$
of size
$S\subseteq U$
of size
such that for each
![]() $z\in S$
,
$z\in S$
,
![]() $P_z \in \mathcal{P}$
has length
$P_z \in \mathcal{P}$
has length
![]() $p$
. Now, let us randomly colour the vertices in
$p$
. Now, let us randomly colour the vertices in
![]() $H[A]$
with colours
$H[A]$
with colours
![]() $1$
and
$1$
and
![]() $2$
. For each
$2$
. For each
![]() $z\in S$
, the path
$z\in S$
, the path
![]() $P_z$
is good if
$P_z$
is good if
![]() $z$
is coloured
$z$
is coloured
![]() $2$
and the other
$2$
and the other
![]() $p$
vertices on
$p$
vertices on
![]() $P_z$
are coloured
$P_z$
are coloured
![]() $1$
. The probability that
$1$
. The probability that
![]() $P_z$
is good is
$P_z$
is good is
![]() $1/2^{p+1}$
. Hence, for some colouring, there are at least
$1/2^{p+1}$
. Hence, for some colouring, there are at least
![]() $|S|/2^{p+1}$
good paths. Let
$|S|/2^{p+1}$
good paths. Let
![]() $S'$
denote the subset of vertices
$S'$
denote the subset of vertices
![]() $z\in S$
such that
$z\in S$
such that
![]() $P_z$
is good and let
$P_z$
is good and let
![]() $\mathcal{P}'=\{P_z\,{:}\,z\in S'\}$
. By our discussion,
$\mathcal{P}'=\{P_z\,{:}\,z\in S'\}$
. By our discussion,
Note that by our definition of
![]() $\mathcal{P}'$
, no vertex in
$\mathcal{P}'$
, no vertex in
![]() $S'$
is used as an internal vertex of any path in
$S'$
is used as an internal vertex of any path in
![]() $\mathcal{P}'$
. By our earlier discussion, each vertex in
$\mathcal{P}'$
. By our earlier discussion, each vertex in
![]() $S'$
has at least
$S'$
has at least
![]() $(\delta/8)n^{\alpha -1}$
neighbours in
$(\delta/8)n^{\alpha -1}$
neighbours in
![]() $B$
. Let
$B$
. Let
![]() $H'$
be the subgraph of
$H'$
be the subgraph of
![]() $H$
whose edge set contains all the edges in
$H$
whose edge set contains all the edges in
![]() $H$
from
$H$
from
![]() $S'$
to
$S'$
to
![]() $B$
. Therefore,
$B$
. Therefore,
![]() $H'$
is bipartite with partition
$H'$
is bipartite with partition
![]() $S'$
and
$S'$
and
![]() $B$
. Furthermore,
$B$
. Furthermore,
where
![]() $\gamma \,{:\!=}\,\gamma (\delta )=\mu (\delta/16) \delta/(2^{\ell _0+4}\ell _0)$
. So
$\gamma \,{:\!=}\,\gamma (\delta )=\mu (\delta/16) \delta/(2^{\ell _0+4}\ell _0)$
. So
![]() $H'$
has average degree at least
$H'$
has average degree at least
![]() $2\gamma n^{\alpha -1}$
. By a well-known fact,
$2\gamma n^{\alpha -1}$
. By a well-known fact,
![]() $H'$
contains a subgraph
$H'$
contains a subgraph
![]() $H''$
of minimum degree at least
$H''$
of minimum degree at least
![]() $\gamma n^{\alpha -1}$
. Let
$\gamma n^{\alpha -1}$
. Let
![]() $S''=V(H'')\cap S'$
.
$S''=V(H'')\cap S'$
.
Let
![]() $Q$
be a shortest path in
$Q$
be a shortest path in
![]() $H$
from the vertex
$H$
from the vertex
![]() $v$
to
$v$
to
![]() $V(H'')$
. Let
$V(H'')$
. Let
![]() $y$
be the endpoint of
$y$
be the endpoint of
![]() $Q$
in
$Q$
in
![]() $V(H'')$
. By our choice of
$V(H'')$
. By our choice of
![]() $Q$
,
$Q$
,
![]() $y$
is the only vertex in
$y$
is the only vertex in
![]() $V(Q)\cap V(H'')$
(note that it is possible that
$V(Q)\cap V(H'')$
(note that it is possible that
![]() $y=v$
). Let
$y=v$
). Let
![]() $q$
denote the length of
$q$
denote the length of
![]() $Q$
. Since
$Q$
. Since
![]() $H$
has diameter at most
$H$
has diameter at most
![]() $L$
, we have
$L$
, we have
![]() $q\leq L$
.
$q\leq L$
.
By Lemma 2.2, for some
![]() $j_0\leq \ell _0$
, inside the graph
$j_0\leq \ell _0$
, inside the graph
![]() $H''$
we have
$H''$
we have
![]() $\min \{|N_{j_0}(y)|,|N_{j_0+1}(y)|\}\geq \mu ( \gamma ) n$
. Note that one of
$\min \{|N_{j_0}(y)|,|N_{j_0+1}(y)|\}\geq \mu ( \gamma ) n$
. Note that one of
![]() $N_{j_0}(y)$
and
$N_{j_0}(y)$
and
![]() $N_{j_0+1}(y)$
lies completely inside
$N_{j_0+1}(y)$
lies completely inside
![]() $V(H'')\cap A$
. Denote this set by
$V(H'')\cap A$
. Denote this set by
![]() $W$
. Let
$W$
. Let
Since
![]() $Q$
contains at most
$Q$
contains at most
![]() $L+1$
vertices, each of which lies on at most
$L+1$
vertices, each of which lies on at most
![]() $n/\log n$
of the members of
$n/\log n$
of the members of
![]() $\mathcal{P}$
, we see
$\mathcal{P}$
, we see
![]() $|W_0|\leq (L+1)(n/\log n)$
. Since
$|W_0|\leq (L+1)(n/\log n)$
. Since
![]() $n$
is sufficiently large, we have
$n$
is sufficiently large, we have
Let
![]() $H[W\setminus W_0,B]$
denote the subgraph of
$H[W\setminus W_0,B]$
denote the subgraph of
![]() $H$
consisting of edges that have one endpoint in
$H$
consisting of edges that have one endpoint in
![]() $W\setminus W_0$
and the other endpoint in
$W\setminus W_0$
and the other endpoint in
![]() $B$
. Since each vertex in
$B$
. Since each vertex in
![]() $W\setminus W_0$
has at least
$W\setminus W_0$
has at least
![]() $(\delta/8) n^{\alpha -1}$
neighbours in
$(\delta/8) n^{\alpha -1}$
neighbours in
![]() $B$
,
$B$
,
Hence
![]() $H[W\setminus W_0,B]$
contains a subgraph
$H[W\setminus W_0,B]$
contains a subgraph
![]() $H^*$
with minimum degree at least
$H^*$
with minimum degree at least
![]() $(1/16)\mu (\gamma )\delta n^{\alpha -1} \geq k$
, for sufficiently large
$(1/16)\mu (\gamma )\delta n^{\alpha -1} \geq k$
, for sufficiently large
![]() $n$
. Let
$n$
. Let
![]() $w$
be any vertex in
$w$
be any vertex in
![]() $V(H^*)\cap (W\setminus W_0)$
. By our definition of
$V(H^*)\cap (W\setminus W_0)$
. By our definition of
![]() $W$
, there is a path
$W$
, there is a path
![]() $R_w$
in
$R_w$
in
![]() $H''$
of length
$H''$
of length
![]() $r\leq j_0+1\leq \ell _0+1$
from
$r\leq j_0+1\leq \ell _0+1$
from
![]() $y$
to
$y$
to
![]() $w$
. Let
$w$
. Let
![]() $t=k-1-q-r-p$
. Since
$t=k-1-q-r-p$
. Since
![]() $q\leq L, p\leq \ell _0, r\leq \ell _0+1$
and
$q\leq L, p\leq \ell _0, r\leq \ell _0+1$
and
![]() $k\geq k_0= 2\ell _0+L+2$
, we get
$k\geq k_0= 2\ell _0+L+2$
, we get
![]() $t\geq 0$
. Since there is a path in
$t\geq 0$
. Since there is a path in
![]() $H$
of length
$H$
of length
![]() $p$
from
$p$
from
![]() $w$
to
$w$
to
![]() $u$
(by the definition of
$u$
(by the definition of
![]() $S''\subseteq W$
). Since
$S''\subseteq W$
). Since
![]() $V(Q)\cap V(H'')=\{y\}$
,
$V(Q)\cap V(H'')=\{y\}$
,
![]() $R_w\cup Q$
is a path in
$R_w\cup Q$
is a path in
![]() $H$
of length
$H$
of length
![]() $q+r$
from
$q+r$
from
![]() $w$
to
$w$
to
![]() $v$
and
$v$
and
![]() $u,v\in X$
,
$u,v\in X$
,
![]() $p$
and
$p$
and
![]() $q+r$
have the same parity. Since
$q+r$
have the same parity. Since
![]() $k$
is odd, we see that
$k$
is odd, we see that
![]() $t$
is even. Since
$t$
is even. Since
![]() $H^*$
has minimum (much) larger than
$H^*$
has minimum (much) larger than
![]() $k$
, greedily we can build a path
$k$
, greedily we can build a path
![]() $T$
of length
$T$
of length
![]() $t$
in
$t$
in
![]() $H^*$
from
$H^*$
from
![]() $w$
to some vertex
$w$
to some vertex
![]() $w^*$
in
$w^*$
in
![]() $V(H^*)\cap (W\setminus W_0)$
such that
$V(H^*)\cap (W\setminus W_0)$
such that
![]() $T$
intersects
$T$
intersects
![]() $Q\cup R_w$
only in
$Q\cup R_w$
only in
![]() $w$
. Now, let
$w$
. Now, let
By our definitions,
![]() $Q\cup R_w\cup T$
is a path. Also, since
$Q\cup R_w\cup T$
is a path. Also, since
![]() $w^*\in W\setminus W_0$
,
$w^*\in W\setminus W_0$
,
![]() $P_{w^*}$
is vertex disjoint from
$P_{w^*}$
is vertex disjoint from
![]() $Q$
. Finally, by our definition of
$Q$
. Finally, by our definition of
![]() $\mathcal{P}'$
,
$\mathcal{P}'$
,
![]() $V(P_{w^*})\setminus \{w^*\}$
is disjoint from
$V(P_{w^*})\setminus \{w^*\}$
is disjoint from
![]() $S'$
and hence from
$S'$
and hence from
![]() $S''$
. It is certainly also disjoint from
$S''$
. It is certainly also disjoint from
![]() $B$
and hence is vertex disjoint from
$B$
and hence is vertex disjoint from
![]() $R_w\cup T$
. So,
$R_w\cup T$
. So,
![]() $C$
is a cycle in
$C$
is a cycle in
![]() $G$
of length
$G$
of length
![]() $1+q+r+t+p=k$
, a contradiction. This proves Theorem 1.6.
$1+q+r+t+p=k$
, a contradiction. This proves Theorem 1.6.
Proof of Theorem 1.8. Let
![]() $\ell \geq 2$
be an integer. Let
$\ell \geq 2$
be an integer. Let
![]() $\delta \gt 0$
be a real. Define
$\delta \gt 0$
be a real. Define
Let
![]() $k\geq k_0$
be an odd integer. Let
$k\geq k_0$
be an odd integer. Let
![]() $n$
be sufficiently large so that all subsequent inequalities involving
$n$
be sufficiently large so that all subsequent inequalities involving
![]() $n$
hold. Let
$n$
hold. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex
$n$
-vertex
![]() $C_{2\ell }$
-free graph with minimum degree at least
$C_{2\ell }$
-free graph with minimum degree at least
![]() $\delta n^{1/\ell }$
. We may assume that
$\delta n^{1/\ell }$
. We may assume that
![]() $G$
is connected. Let
$G$
is connected. Let
![]() $H$
be a maximum spanning subgraph of
$H$
be a maximum spanning subgraph of
![]() $G$
. By Lemma 2.4,
$G$
. By Lemma 2.4,
![]() $H$
is connected with minimum degree at least
$H$
is connected with minimum degree at least
![]() $(\delta/2) n^{1/\ell }$
. Since
$(\delta/2) n^{1/\ell }$
. Since
![]() $H$
is
$H$
is
![]() $C_{2\ell }$
-free, by Lemma 3.2, the
$C_{2\ell }$
-free, by Lemma 3.2, the
![]() $\ell$
-th power
$\ell$
-th power
![]() $H^{\ell }$
of
$H^{\ell }$
of
![]() $H$
has minimum degree at least
$H$
has minimum degree at least
![]() $(\delta n^{1/\ell }/8\ell )^{\ell } =(\delta/8\ell )^{\ell } n$
. Hence, by Lemma 2.5,
$(\delta n^{1/\ell }/8\ell )^{\ell } =(\delta/8\ell )^{\ell } n$
. Hence, by Lemma 2.5,
![]() $H^\ell$
has diameter at most
$H^\ell$
has diameter at most
![]() $3n/[(\delta/8\ell )^{\ell } n]=3 (8\ell/\delta )^{\ell }$
. Therefore,
$3n/[(\delta/8\ell )^{\ell } n]=3 (8\ell/\delta )^{\ell }$
. Therefore,
![]() $H$
has diameter at most
$H$
has diameter at most
![]() $3\ell (8\ell/\delta )^{\ell }= L$
, as defined in (8).
$3\ell (8\ell/\delta )^{\ell }= L$
, as defined in (8).
Let
![]() $(X,Y)$
the unique bipartition of
$(X,Y)$
the unique bipartition of
![]() $H$
. We show that
$H$
. We show that
![]() $G$
is also bipartite with
$G$
is also bipartite with
![]() $(X,Y)$
being a bipartition of it. Suppose otherwise. Then without loss of generality, we may assume that there exist two vertices
$(X,Y)$
being a bipartition of it. Suppose otherwise. Then without loss of generality, we may assume that there exist two vertices
![]() $u,v\in X$
such that
$u,v\in X$
such that
![]() $uv\in E(G)$
. We will derive a contradiction by finding a copy of
$uv\in E(G)$
. We will derive a contradiction by finding a copy of
![]() $C_k$
in
$C_k$
in
![]() $G$
that contains
$G$
that contains
![]() $uv$
. As in the proof of Theorem 1.6, we can split
$uv$
. As in the proof of Theorem 1.6, we can split
![]() $V(H)$
into two subsets
$V(H)$
into two subsets
![]() $A,B$
such that for each vertex
$A,B$
such that for each vertex
![]() $x\in V(H)$
, we have
$x\in V(H)$
, we have
![]() $d_A(x), d_B(x)\geq (1/4)d(x)\geq (\delta/8) n^{1/\ell }$
.
$d_A(x), d_B(x)\geq (1/4)d(x)\geq (\delta/8) n^{1/\ell }$
.
Without loss of generality, suppose
![]() $u\in A$
. Let
$u\in A$
. Let
![]() $H[A]$
denote the subgraph of
$H[A]$
denote the subgraph of
![]() $H$
induced by
$H$
induced by
![]() $A$
. By our discussion above,
$A$
. By our discussion above,
![]() $H[A]$
has minimum degree at least
$H[A]$
has minimum degree at least
![]() $(\delta/8) n^{1/\ell }$
. By Lemma 3.2 (with
$(\delta/8) n^{1/\ell }$
. By Lemma 3.2 (with
![]() $d=(\delta/8) n^{1/\ell }$
), there exists a set
$d=(\delta/8) n^{1/\ell }$
), there exists a set
![]() $S$
of size at least
$S$
of size at least
![]() $(\delta/64\ell ^2)^\ell (n/2)$
and a family
$(\delta/64\ell ^2)^\ell (n/2)$
and a family
![]() $\mathcal{P}=\{P_z\,{:}\, z\in S\}$
, where for each
$\mathcal{P}=\{P_z\,{:}\, z\in S\}$
, where for each
![]() $z\in S$
,
$z\in S$
,
![]() $P_z$
is a
$P_z$
is a
![]() $u,z$
-path in
$u,z$
-path in
![]() $H[A]$
of length
$H[A]$
of length
![]() $\ell$
, such that no vertex other than
$\ell$
, such that no vertex other than
![]() $u$
in
$u$
in
![]() $H$
lies on more than
$H$
lies on more than
![]() $(\delta n^{1/\ell }/8)^{\ell -1}=(\delta/8)^{\ell -1} n^{1-1/\ell }$
of these paths. Furthermore, for each
$(\delta n^{1/\ell }/8)^{\ell -1}=(\delta/8)^{\ell -1} n^{1-1/\ell }$
of these paths. Furthermore, for each
![]() $z\in S$
,
$z\in S$
,
![]() $z$
lies only on
$z$
lies only on
![]() $P_z$
.
$P_z$
.
Let
![]() $H[S,B]$
denote the bipartite subgraph of
$H[S,B]$
denote the bipartite subgraph of
![]() $H$
induced by the two parts
$H$
induced by the two parts
![]() $S$
and
$S$
and
![]() $B$
. By our earlier discussion, each vertex in
$B$
. By our earlier discussion, each vertex in
![]() $S$
has at least
$S$
has at least
![]() $(\delta/8)n^{1/\ell }$
neighbours in
$(\delta/8)n^{1/\ell }$
neighbours in
![]() $B$
. Hence,
$B$
. Hence,
where
![]() $\gamma \,{:\!=}\,\delta ^{\ell +1}/2^{6\ell +4}\ell ^{2\ell }$
. Then
$\gamma \,{:\!=}\,\delta ^{\ell +1}/2^{6\ell +4}\ell ^{2\ell }$
. Then
![]() $H[S,B]$
has average degree at least
$H[S,B]$
has average degree at least
![]() $2\gamma n^{1/\ell }$
and thus contains a subgraph
$2\gamma n^{1/\ell }$
and thus contains a subgraph
![]() $H'$
of minimum degree at least
$H'$
of minimum degree at least
![]() $\gamma n^{1/\ell }$
. Let
$\gamma n^{1/\ell }$
. Let
![]() $S'=V(H')\cap S$
and
$S'=V(H')\cap S$
and
![]() $B'=V(H')\cap B$
.
$B'=V(H')\cap B$
.
If
![]() $\ell$
is even, then
$\ell$
is even, then
![]() $S'\subseteq X$
and let
$S'\subseteq X$
and let
![]() $Q$
be a shortest path in
$Q$
be a shortest path in
![]() $H$
from
$H$
from
![]() $v$
to
$v$
to
![]() $S'$
. If
$S'$
. If
![]() $\ell$
is odd, then
$\ell$
is odd, then
![]() $B'\subseteq X$
and let
$B'\subseteq X$
and let
![]() $Q$
be a shortest path in
$Q$
be a shortest path in
![]() $H$
from
$H$
from
![]() $v$
to
$v$
to
![]() $B'$
. Let
$B'$
. Let
![]() $y$
denote the endpoint of
$y$
denote the endpoint of
![]() $Q$
opposing
$Q$
opposing
![]() $v$
(it is possible that
$v$
(it is possible that
![]() $y=v$
). Let
$y=v$
). Let
![]() $q$
denote the length of
$q$
denote the length of
![]() $Q$
. So
$Q$
. So
![]() $q$
is even and
$q$
is even and
![]() $y\in X$
. In either case, it is easy to see that
$y\in X$
. In either case, it is easy to see that
![]() $q\leq L+1$
and that
$q\leq L+1$
and that
![]() $V(H')$
contains
$V(H')$
contains
![]() $y$
and at most one other vertex of
$y$
and at most one other vertex of
![]() $Q$
. Hence
$Q$
. Hence
![]() $H'-(V(Q)\setminus \{y\})$
has minimum degree at least
$H'-(V(Q)\setminus \{y\})$
has minimum degree at least
![]() $\gamma n^{1/\ell }-1\geq (\gamma/2)n^{1/\ell }$
. By Lemma 3.2 (with
$\gamma n^{1/\ell }-1\geq (\gamma/2)n^{1/\ell }$
. By Lemma 3.2 (with
![]() $d=(\gamma/2)n^{1/\ell }$
), inside the graph
$d=(\gamma/2)n^{1/\ell }$
), inside the graph
![]() $H'-(V(Q)\setminus \{y\})$
there is a set
$H'-(V(Q)\setminus \{y\})$
there is a set
![]() $W$
of size at least
$W$
of size at least
![]() $(1/2)(\gamma/16\ell ^2)^\ell n$
such that for each
$(1/2)(\gamma/16\ell ^2)^\ell n$
such that for each
![]() $w\in W$
there is a path
$w\in W$
there is a path
![]() $R_w$
of length
$R_w$
of length
![]() $\ell$
from
$\ell$
from
![]() $y$
to
$y$
to
![]() $w$
in
$w$
in
![]() $H'-(V(Q)\setminus \{y\})$
. Furthermore, by our definition of
$H'-(V(Q)\setminus \{y\})$
. Furthermore, by our definition of
![]() $Q$
, we can get
$Q$
, we can get
![]() $W\subseteq S'$
. Recall the paths
$W\subseteq S'$
. Recall the paths
![]() $P_w$
in
$P_w$
in
![]() $\mathcal{P}$
. Let
$\mathcal{P}$
. Let
Since
![]() $Q$
contains at most
$Q$
contains at most
![]() $L+1$
vertices each of which lies on at most
$L+1$
vertices each of which lies on at most
![]() $(\delta/8)^{\ell -1} n^{1-1/\ell }$
of the members of
$(\delta/8)^{\ell -1} n^{1-1/\ell }$
of the members of
![]() $\mathcal{P}$
, we see
$\mathcal{P}$
, we see
![]() $|W_0|\leq (L+1)(\delta/8)^{\ell -1} n^{1-1/\ell }$
. Since
$|W_0|\leq (L+1)(\delta/8)^{\ell -1} n^{1-1/\ell }$
. Since
![]() $n$
is sufficiently large, we have
$n$
is sufficiently large, we have
Since each vertex in
![]() $W\setminus W_0$
has at least
$W\setminus W_0$
has at least
![]() $(\delta/8) n^\ell$
neighbours in
$(\delta/8) n^\ell$
neighbours in
![]() $B$
,
$B$
,
Hence
![]() $H[W\setminus W_0,B]$
contains a subgraph
$H[W\setminus W_0,B]$
contains a subgraph
![]() $H^*$
with minimum degree at least
$H^*$
with minimum degree at least
![]() $(\delta \cdot \gamma ^\ell )/(2^{4\ell +5}\cdot \ell ^{2\ell }) n^{1/\ell }\geq k$
, for sufficiently large
$(\delta \cdot \gamma ^\ell )/(2^{4\ell +5}\cdot \ell ^{2\ell }) n^{1/\ell }\geq k$
, for sufficiently large
![]() $n$
. Let
$n$
. Let
![]() $w$
be any vertex in
$w$
be any vertex in
![]() $V(H^*)\cap (W\setminus W_0)$
. By our definition of
$V(H^*)\cap (W\setminus W_0)$
. By our definition of
![]() $W$
, there is a path
$W$
, there is a path
![]() $R_w$
in
$R_w$
in
![]() $H'-(V(Q)\setminus \{y\})$
of length
$H'-(V(Q)\setminus \{y\})$
of length
![]() $\ell$
from
$\ell$
from
![]() $y$
to
$y$
to
![]() $w$
. Let
$w$
. Let
![]() $t=k-1-q-2\ell$
. Since
$t=k-1-q-2\ell$
. Since
![]() $q\leq L+1$
and
$q\leq L+1$
and
![]() $k\geq k_0= 2\ell +L+2$
, we see
$k\geq k_0= 2\ell +L+2$
, we see
![]() $t\geq 0$
. Since
$t\geq 0$
. Since
![]() $k$
is odd and
$k$
is odd and
![]() $q$
is even, we also see that
$q$
is even, we also see that
![]() $t$
is even. Since
$t$
is even. Since
![]() $H^*$
has minimum degree (much) larger than
$H^*$
has minimum degree (much) larger than
![]() $k$
, greedily we can build a path
$k$
, greedily we can build a path
![]() $T$
of length
$T$
of length
![]() $t$
in
$t$
in
![]() $H^*$
from
$H^*$
from
![]() $w$
to some vertex
$w$
to some vertex
![]() $w^*$
in
$w^*$
in
![]() $V(H^*)\cap (W\setminus W_0)$
such that
$V(H^*)\cap (W\setminus W_0)$
such that
![]() $T$
intersects
$T$
intersects
![]() $Q\cup R_w$
only in
$Q\cup R_w$
only in
![]() $w$
. Now, let
$w$
. Now, let
By our definition of
![]() $T$
,
$T$
,
![]() $Q\cup R_w\cup T$
is path. Also, since
$Q\cup R_w\cup T$
is path. Also, since
![]() $w^*\in W\setminus W_0$
,
$w^*\in W\setminus W_0$
,
![]() $P_{w^*}$
is vertex disjoint from
$P_{w^*}$
is vertex disjoint from
![]() $Q$
. Finally
$Q$
. Finally
![]() $P_{w^*}\setminus \{w^*\}$
does not contain any vertex of
$P_{w^*}\setminus \{w^*\}$
does not contain any vertex of
![]() $S'\cup B$
and hence is vertex disjoint from
$S'\cup B$
and hence is vertex disjoint from
![]() $R_w\cup T$
. Hence,
$R_w\cup T$
. Hence,
![]() $C$
is a cycle in
$C$
is a cycle in
![]() $G$
of length
$G$
of length
![]() $1+q+2\ell +t=k$
, a contradiction.
$1+q+2\ell +t=k$
, a contradiction.
5. Proof of Theorem 1.7
Proof of Theorem 1.7. Let
![]() $2\gt \alpha \gt \beta \geq 1$
and
$2\gt \alpha \gt \beta \geq 1$
and
![]() $\mathcal{F}$
be an
$\mathcal{F}$
be an
![]() $(\alpha,\beta )$
-smooth family with relative density
$(\alpha,\beta )$
-smooth family with relative density
![]() $\rho$
. Then by the remark after Definition 1.2, there exist constants
$\rho$
. Then by the remark after Definition 1.2, there exist constants
![]() $C_1\lt C_2$
such that for sufficiently large
$C_1\lt C_2$
such that for sufficiently large
![]() $n$
,
$n$
,
Fix
![]() $\delta \,{:\!=}\,\rho/2^{\alpha +3}$
. Let
$\delta \,{:\!=}\,\rho/2^{\alpha +3}$
. Let
![]() $k_0$
be from Theorem 1.6 such that for any odd
$k_0$
be from Theorem 1.6 such that for any odd
![]() $k\geq k_0$
and sufficiently large
$k\geq k_0$
and sufficiently large
![]() $m$
, any
$m$
, any
![]() $m$
-vertex
$m$
-vertex
![]() $\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
$\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
![]() $\delta m^{\alpha -1}$
is bipartite.
$\delta m^{\alpha -1}$
is bipartite.
Now consider any odd
![]() $k\geq k_0$
and sufficiently large
$k\geq k_0$
and sufficiently large
![]() $n$
. Let
$n$
. Let
![]() $G$
be an
$G$
be an
![]() $n$
-vertex extremal
$n$
-vertex extremal
![]() $\mathcal{F}\cup \{C_k\}$
-free graph. Then
$\mathcal{F}\cup \{C_k\}$
-free graph. Then
Let
![]() $G_0=G$
. If there exists some vertex
$G_0=G$
. If there exists some vertex
![]() $x$
of degree less than
$x$
of degree less than
![]() $\delta n^{\alpha -1}$
in
$\delta n^{\alpha -1}$
in
![]() $G_0$
, then we delete the vertex
$G_0$
, then we delete the vertex
![]() $x$
and rename the remaining subgraph as
$x$
and rename the remaining subgraph as
![]() $G_0$
. We repeat the above process until there is no such vertex in
$G_0$
. We repeat the above process until there is no such vertex in
![]() $G_0$
. Let
$G_0$
. Let
![]() $H$
denote the remaining induced subgraph of
$H$
denote the remaining induced subgraph of
![]() $G$
and let
$G$
and let
![]() $t=n-|V(H)|$
. We note that as
$t=n-|V(H)|$
. We note that as
![]() $\alpha \lt 2$
and
$\alpha \lt 2$
and
![]() $n$
is sufficiently large, using (9) and
$n$
is sufficiently large, using (9) and
![]() $\delta =\frac{\rho }{2^{\alpha +3}}$
,
$\delta =\frac{\rho }{2^{\alpha +3}}$
,
Let
![]() $m=|V(H)|$
. By definition,
$m=|V(H)|$
. By definition,
![]() $H$
is an
$H$
is an
![]() $m$
-vertex
$m$
-vertex
![]() $\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
$\mathcal{F}\cup \{C_k\}$
-free graph with minimum degree at least
![]() $\delta n^{\alpha -1}\geq \delta m^{\alpha -1}$
. By taking
$\delta n^{\alpha -1}\geq \delta m^{\alpha -1}$
. By taking
![]() $n$
sufficiently large, we can make
$n$
sufficiently large, we can make
![]() $m$
large enough to apply Theorem 1.6 to conclude that
$m$
large enough to apply Theorem 1.6 to conclude that
![]() $H$
is bipartite. Since
$H$
is bipartite. Since
![]() $H$
is also,
$H$
is also,
![]() $\mathcal{F}$
-free, we have
$\mathcal{F}$
-free, we have
Comparing (10) and (11), we see that
![]() $n-t\geq \frac{3}{4}n$
. By (9), (10) and (11), we have
$n-t\geq \frac{3}{4}n$
. By (9), (10) and (11), we have
Recall that
![]() $\delta =\rho/2^{\alpha +3}$
. Rearranging the above inequality, we get
$\delta =\rho/2^{\alpha +3}$
. Rearranging the above inequality, we get
By the Mean Value Theorem, for some
![]() $n - t \leq n' \leq n$
, this is equivalent to
$n - t \leq n' \leq n$
, this is equivalent to
Since
![]() $n-t\geq \frac{3}{4}n$
and
$n-t\geq \frac{3}{4}n$
and
![]() $\frac{\rho \alpha }{2^{\alpha }}(\frac{3}{4})^{\alpha -1} \gt 2\cdot \frac{\rho }{2^{\alpha +3}}$
, the above inequality yields
$\frac{\rho \alpha }{2^{\alpha }}(\frac{3}{4})^{\alpha -1} \gt 2\cdot \frac{\rho }{2^{\alpha +3}}$
, the above inequality yields
So,
![]() $t=O(n^{1+\beta -\alpha })$
and in obtaining
$t=O(n^{1+\beta -\alpha })$
and in obtaining
![]() $H$
from
$H$
from
![]() $G$
at most
$G$
at most
![]() $t\cdot \delta n^{\alpha -1}=O(n^\beta )$
edges are removed.
$t\cdot \delta n^{\alpha -1}=O(n^\beta )$
edges are removed.
6. Concluding remarks
1. As mentioned in the introduction, there are bipartite graphs that are not smooth. We give such an example here. Given integers
![]() $t,\ell \geq 2$
, the theta graph
$t,\ell \geq 2$
, the theta graph
![]() $\theta _{t,\ell }$
is the graph consisting of
$\theta _{t,\ell }$
is the graph consisting of
![]() $t$
internally disjoint paths of length
$t$
internally disjoint paths of length
![]() $\ell$
between two vertices. In particular, we have
$\ell$
between two vertices. In particular, we have
![]() $\theta _{2,\ell }=C_{2\ell }$
. Faudree and Simonovits [Reference Faudree and Simonovits13] showed that for all
$\theta _{2,\ell }=C_{2\ell }$
. Faudree and Simonovits [Reference Faudree and Simonovits13] showed that for all
![]() $t,\ell \geq 2$
,
$t,\ell \geq 2$
,
![]() $\textrm{ex}(n,\theta _{t,\ell })=O(n^{1+1/\ell })$
(the case
$\textrm{ex}(n,\theta _{t,\ell })=O(n^{1+1/\ell })$
(the case
![]() $t=2$
was first proved by Bondy-Simonovits [Reference Bondy and Simonovits5]). Conlon [Reference Conlon9] showed that for each
$t=2$
was first proved by Bondy-Simonovits [Reference Bondy and Simonovits5]). Conlon [Reference Conlon9] showed that for each
![]() $\ell \geq 2$
, there exists a
$\ell \geq 2$
, there exists a
![]() $t_0$
such that for all
$t_0$
such that for all
![]() $t\geq t_0$
,
$t\geq t_0$
,
![]() $\textrm{ex}(n,\theta _{t,\ell })=\Omega (n^{1+1/\ell })$
, the leading coefficients of which were further improved by Bukh-Tait [Reference Bukh and Tait8]. Jiang, Ma and Yepremyan [Reference Jiang, Ma and Yepremyan19] showed that for all
$\textrm{ex}(n,\theta _{t,\ell })=\Omega (n^{1+1/\ell })$
, the leading coefficients of which were further improved by Bukh-Tait [Reference Bukh and Tait8]. Jiang, Ma and Yepremyan [Reference Jiang, Ma and Yepremyan19] showed that for all
![]() $t,\ell$
, there exists a constant
$t,\ell$
, there exists a constant
![]() $c=c(t,\ell )$
such that for all
$c=c(t,\ell )$
such that for all
![]() $m\leq n$
$m\leq n$
 \begin{equation*} z(m,n,\theta _{t,\ell })\le \left \{\begin {array}{ll} c\cdot [(mn)^{\frac {\ell +1}{2\ell }}+m+n] & \text {if } \ell \text { is odd}, \\ c\cdot [m^{\frac {1}{2}+\frac {1}{\ell }}n^{\frac {1}{2}}+m+n] & \text {if } \ell \text { is even}. \end {array}\right . \end{equation*}
\begin{equation*} z(m,n,\theta _{t,\ell })\le \left \{\begin {array}{ll} c\cdot [(mn)^{\frac {\ell +1}{2\ell }}+m+n] & \text {if } \ell \text { is odd}, \\ c\cdot [m^{\frac {1}{2}+\frac {1}{\ell }}n^{\frac {1}{2}}+m+n] & \text {if } \ell \text { is even}. \end {array}\right . \end{equation*}
For the case
![]() $t=2$
, the above bound was first proved by Naor-Verstraëte [Reference Naor and Verstraëte25], and a different form of the upper bound on
$t=2$
, the above bound was first proved by Naor-Verstraëte [Reference Naor and Verstraëte25], and a different form of the upper bound on
![]() $z(m,n,\theta _{2,\ell })$
was obtained by Jiang-Ma [Reference Jiang and Ma18]. On the other hand, using first moment deletion method it is not hard to show that
$z(m,n,\theta _{2,\ell })$
was obtained by Jiang-Ma [Reference Jiang and Ma18]. On the other hand, using first moment deletion method it is not hard to show that
Proposition 6.1.
Let
![]() $\varepsilon \gt 0$
be any real. Let
$\varepsilon \gt 0$
be any real. Let
![]() $\ell \geq 2$
. There exists a
$\ell \geq 2$
. There exists a
![]() $t_0$
such that for all
$t_0$
such that for all
![]() $t\geq t_0$
, if
$t\geq t_0$
, if
![]() $\ell$
is odd then
$\ell$
is odd then
and if
![]() $\ell$
is even then
$\ell$
is even then
Proof. Consider the bipartite random graph
![]() $G\in G(m,n,p)$
with
$G\in G(m,n,p)$
with
![]() $p$
to be chosen later. Let
$p$
to be chosen later. Let
![]() $q=\lfloor \ell/2\rfloor$
. Let
$q=\lfloor \ell/2\rfloor$
. Let
![]() $X=e(G)$
and
$X=e(G)$
and
![]() $Y$
denote the number of copies of
$Y$
denote the number of copies of
![]() $\theta _{t,k}$
in
$\theta _{t,k}$
in
![]() $G$
. We have
$G$
. We have
![]() $\mathbb{E}(X)=mnp$
. If
$\mathbb{E}(X)=mnp$
. If
![]() $\ell$
is odd, then
$\ell$
is odd, then
![]() $\ell =2q+1$
and
$\ell =2q+1$
and
![]() $\mathbb{E}[Y]\leq [m]_{tq+1}[n]_{tq+1} p^{t(2q+1)}\lt (1/2)m^{tq+1}n^{tq+1}p^{t(2q+1)}$
. We now choose
$\mathbb{E}[Y]\leq [m]_{tq+1}[n]_{tq+1} p^{t(2q+1)}\lt (1/2)m^{tq+1}n^{tq+1}p^{t(2q+1)}$
. We now choose
![]() $p$
so that
$p$
so that
![]() $\mathbb{E}[X]\geq 2\mathbb{E}[Y]$
. It suffices to set
$\mathbb{E}[X]\geq 2\mathbb{E}[Y]$
. It suffices to set
![]() $p=m^{\frac{-tq}{2tq+t-1}}n^{\frac{-tq}{2tq+t-1}}$
. Since
$p=m^{\frac{-tq}{2tq+t-1}}n^{\frac{-tq}{2tq+t-1}}$
. Since
![]() $\mathbb{E}(X-Y)\geq (1/2)\mathbb{E}[X]$
, there exists a
$\mathbb{E}(X-Y)\geq (1/2)\mathbb{E}[X]$
, there exists a
![]() $(m,n)$
-bipartite graph
$(m,n)$
-bipartite graph
![]() $G$
for which
$G$
for which
![]() $X-Y\geq (1/2) mnp =(1/2)(mn)^{\frac{tq+t-1}{2tq+t-1}}$
. By deleting one edge from copy of
$X-Y\geq (1/2) mnp =(1/2)(mn)^{\frac{tq+t-1}{2tq+t-1}}$
. By deleting one edge from copy of
![]() $\theta _{t,\ell }$
in
$\theta _{t,\ell }$
in
![]() $G$
, we obtained a
$G$
, we obtained a
![]() $(m,n)$
-bipartite graph
$(m,n)$
-bipartite graph
![]() $G'$
that is
$G'$
that is
![]() $\theta _{t,\ell }$
-free and satisfies
$\theta _{t,\ell }$
-free and satisfies
For sufficiently large
![]() $t$
, we have
$t$
, we have
![]() $e(G')\geq (1/2) (mn)^{\frac{\ell +1}{2\ell }-\varepsilon }$
, as desired.
$e(G')\geq (1/2) (mn)^{\frac{\ell +1}{2\ell }-\varepsilon }$
, as desired.
For even integers
![]() $\ell =2q$
, the analysis is similar, except that we use the bound
$\ell =2q$
, the analysis is similar, except that we use the bound
![]() $\mathbb{E}[Y]\leq [m]_{tq+1}[n]_{t(q-1)+1}+[m]_{t(q-1)+1}[n]_{tq+1}) p^{2tq}\lt (1/2)m^{t(q-1)+1}n^{tq+1}p^{2tq}$
. We omit the details.
$\mathbb{E}[Y]\leq [m]_{tq+1}[n]_{t(q-1)+1}+[m]_{t(q-1)+1}[n]_{tq+1}) p^{2tq}\lt (1/2)m^{t(q-1)+1}n^{tq+1}p^{2tq}$
. We omit the details.
It is quite likely using the random algebraic method used in [Reference Conlon9], one could show that for each
![]() $\ell \geq 2$
, there exist a
$\ell \geq 2$
, there exist a
![]() $t_0$
such that for all
$t_0$
such that for all
![]() $t\geq t_0$
if
$t\geq t_0$
if
![]() $\ell$
is odd then
$\ell$
is odd then
![]() $z(m,n,\theta _{t,\ell })\geq \Omega (m^{\frac{\ell +1}{2\ell }} n^{\frac{\ell +1}{2\ell }})$
and if
$z(m,n,\theta _{t,\ell })\geq \Omega (m^{\frac{\ell +1}{2\ell }} n^{\frac{\ell +1}{2\ell }})$
and if
![]() $\ell$
is even then
$\ell$
is even then
![]() $z(m,n,\theta _{t,\ell })\geq \Omega (m^{\frac{1}{2}+\frac{1}{\ell }} n^{\frac{1}{2}})$
. In any case, Proposition 6.1 already shows that
$z(m,n,\theta _{t,\ell })\geq \Omega (m^{\frac{1}{2}+\frac{1}{\ell }} n^{\frac{1}{2}})$
. In any case, Proposition 6.1 already shows that
![]() $\theta _{t,\ell }$
is not
$\theta _{t,\ell }$
is not
![]() $(\alpha,\beta )$
-quasi-smooth and hence is also not
$(\alpha,\beta )$
-quasi-smooth and hence is also not
![]() $(\alpha,\beta )$
-smooth. (As far as we know, this is the first example of a family of bipartite graphs which are not
$(\alpha,\beta )$
-smooth. (As far as we know, this is the first example of a family of bipartite graphs which are not
![]() $(\alpha,\beta )$
-smooth.) However,
$(\alpha,\beta )$
-smooth.) However,
![]() $\theta _{t,\ell }$
-free graphs have similar expansion properties as
$\theta _{t,\ell }$
-free graphs have similar expansion properties as
![]() $C_{2\ell }$
-free graphs (see [Reference Jiang, Ma and Yepremyan19], Lemma 4.1). By using Lemma 4.1 in [Reference Jiang, Ma and Yepremyan19] instead of Lemma 3.1 in this paper, one can develop an analogous lemma as Lemma 3.2. Then using essentially the same proof as that of Theorem 1.8, one can show the following.
$C_{2\ell }$
-free graphs (see [Reference Jiang, Ma and Yepremyan19], Lemma 4.1). By using Lemma 4.1 in [Reference Jiang, Ma and Yepremyan19] instead of Lemma 3.1 in this paper, one can develop an analogous lemma as Lemma 3.2. Then using essentially the same proof as that of Theorem 1.8, one can show the following.
Theorem 6.2.
Let
![]() $t,\ell \geq 2$
. Let
$t,\ell \geq 2$
. Let
![]() $\delta \gt 0$
be any real. Let
$\delta \gt 0$
be any real. Let
![]() $k_0=3\ell (8\ell/\delta )^\ell +2\ell +2$
. For all odd integers
$k_0=3\ell (8\ell/\delta )^\ell +2\ell +2$
. For all odd integers
![]() $k\geq k_0$
and
$k\geq k_0$
and
![]() $n$
sufficiently large the following is true. If
$n$
sufficiently large the following is true. If
![]() $G$
is an
$G$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $\{\theta _{t,\ell },C_k\}$
-free graph with minimum degree at least
$\{\theta _{t,\ell },C_k\}$
-free graph with minimum degree at least
![]() $\delta n^{1/\ell }$
, then
$\delta n^{1/\ell }$
, then
![]() $G$
is bipartite.
$G$
is bipartite.
2. Our proof method works any family
![]() $\mathcal{F}$
of bipartite graphs satisfying the following property.
$\mathcal{F}$
of bipartite graphs satisfying the following property.
-
(P1) For any
 $\delta \gt 0$
, there are constants
$\delta \gt 0$
, there are constants
 $K$
and
$K$
and
 $\mu$
such that for every
$\mu$
such that for every
 $n$
-vertex
$n$
-vertex
 $\mathcal{F}$
-free graph
$\mathcal{F}$
-free graph
 $G$
with minimum degree
$G$
with minimum degree
 $\delta \textrm{ex}(n,\mathcal{F})/n$
and for each vertex
$\delta \textrm{ex}(n,\mathcal{F})/n$
and for each vertex
 $u$
in
$u$
in
 $G$
, there are at least
$G$
, there are at least
 $\mu n$
vertices within distance
$\mu n$
vertices within distance
 $K$
from
$K$
from
 $u$
.
$u$
.
Analogous theorems as Theorems 1.6 and 1.8 hold for
![]() $\mathcal{F}$
-free graphs. Note that
$\mathcal{F}$
-free graphs. Note that
![]() $(\alpha, \beta )$
-quasi-smooth families and theta graphs (which are not always quasi-smooth) both satisfy (P1).
$(\alpha, \beta )$
-quasi-smooth families and theta graphs (which are not always quasi-smooth) both satisfy (P1).
3. The proof of Theorem 1.7 can be generalised a bit further to yield the following. Suppose
![]() $\mathcal{F}$
is a family of bipartite graphs satisfying the property (P1) and the following property (P2).
$\mathcal{F}$
is a family of bipartite graphs satisfying the property (P1) and the following property (P2).
-
(P2) There exists some constants
 $\lambda \gt 0$
and
$\lambda \gt 0$
and
 $2\gt \alpha \gt \beta \geq 1$
such that
$2\gt \alpha \gt \beta \geq 1$
such that
 $z(n,\mathcal{F})=\lambda n^\alpha +O(n^\beta )$
.
$z(n,\mathcal{F})=\lambda n^\alpha +O(n^\beta )$
.
Then Conjecture 1.1 holds for
![]() $\mathcal{F}$
in the following form: for any odd
$\mathcal{F}$
in the following form: for any odd
![]() $k\geq k_0$
and sufficiently large
$k\geq k_0$
and sufficiently large
![]() $n$
, any
$n$
, any
![]() $n$
-vertex
$n$
-vertex
![]() $\mathcal{F}\cup \{C_k\}$
-free extremal graph can be made bipartite by deleting a set of
$\mathcal{F}\cup \{C_k\}$
-free extremal graph can be made bipartite by deleting a set of
![]() $O(n^{1+\beta -\alpha })$
vertices, which together are incident to
$O(n^{1+\beta -\alpha })$
vertices, which together are incident to
![]() $O(n^\beta )$
edges.
$O(n^\beta )$
edges.
In particular, this also applies to
![]() $\mathcal{F}=\{C_4, C_6,\ldots,C_{2\ell }\}$
for
$\mathcal{F}=\{C_4, C_6,\ldots,C_{2\ell }\}$
for
![]() $\ell \in \{2,3,5\}$
.
$\ell \in \{2,3,5\}$
.
4. One could also prove our main theorems using the sparse regularity lemma ([Reference Kohayakawa22], [Reference Scott26]). However, the proofs would be more technical and would involve longer build-ups. We chose to present a proof that avoids the use of sparse regularity. It seems, however, in order to make more progress on the original conjecture of Erdős and Simonovits (Conjecture 1.1), for instance to verify the conjecture for
![]() $(\alpha,\beta )$
-quasi-smooth families, sparse regularity lemma may still be an effective tool. This is because for
$(\alpha,\beta )$
-quasi-smooth families, sparse regularity lemma may still be an effective tool. This is because for
![]() $(\alpha,\beta )$
-quasi-smooth families
$(\alpha,\beta )$
-quasi-smooth families
![]() $\mathcal{F}$
, like for
$\mathcal{F}$
, like for
![]() $(\alpha,\beta )$
-smooth families (see [Reference Allen, Keevash, Sudakov and Verstraëte1]), there is a transference of density from an
$(\alpha,\beta )$
-smooth families (see [Reference Allen, Keevash, Sudakov and Verstraëte1]), there is a transference of density from an
![]() $\mathcal{F}$
-free host graph to the corresponding cluster graph.
$\mathcal{F}$
-free host graph to the corresponding cluster graph.
Acknowledgement
The authors would like to thank the referrers for many helpful comments.