Introduction
A number of theoretical attempts have been made to estimate or model the rate of possible expansion within the Galaxy of a hypothetical extra-terrestrial civilization (ETC) that has achieved interstellar spaceflight. Among pioneering studies are the calculations of Jones (Reference Jones1976, Reference Jones1981) and Tipler (Reference Tipler1980), who estimated quite rapid expansion times, with the former calculating a timescale of 5 × 106 years for a hypothetical ETC to extend throughout the Galaxy. Such short timescales can lead to strong implications for the incidence and/or behaviour of ETCs if combined with the Fermi Paradox (Tipler Reference Tipler1980). Newman and Sagan (Reference Newman and Sagan1981) modelled expansion of an ETC via a numerical diffusion-based approach, and found notably longer timescales. Børk (Reference Børk2007) simulated the use of a small number of probes to explore regions within ±300 pc of the Galactic midplane, and concluded that “with eight probes, each with eight subprobes, 4% of the Galaxy can be explored in 2.92 × 108 years,” which is on a timescale comparable to a Galactic rotation period. Computational simulations of the dynamics of ETC exploration were also reported by Cotta and Morales (Reference Cotta and Morales2009), and combined with a probabilistic analysis to obtain bounds on the number of ETCs that may have established interstellar spaceflight programs without having come into contact with Earth. Hair and Hedman (Reference Hair and Hedman2013) studied a percolation model for the dispersion of “interstellar civilizations.” The Fermi Paradox has often provided motivation for such numerical studies. Barlow (Reference Barlow2013) considered potential Galactic-wide exploration by use of “directed self-replicating probes.” Carroll-Nellenback et al. (Reference Carroll-Nellenback, Frank, Wright and Scharf2019) and Wright et al. (Reference Wright, Carroll-Nellenback, Frank and Scharf2021) discussed scenarios in which an increasing population of probes traverse and settle a large fraction of the Galactic disc, taking into account the relative space motions of stars. While the above list is not complete, such scenarios often, but not in all cases, assume spacecraft speeds that are not insignificant with respect to 0.01 or 0.1 times the speed of light. At lower velocities, Forgan et al. (Reference Forgan, Papadogiannakis and Kitching2013) considered the potential exploration of stars with a small number of probes on trajectories that are subject to gravitational-assist encounters.
In this paper we focus upon a hypothetical earlier phase of such an ETC in which it first embarks upon sending probes of increasing sophistication into interstellar space. During this first stage the probes which are dispatched are limited to exploring the local stellar neighbourhood around the planetary system of the ETC. Although such an early stage precedes the expansion of probes throughout a large fraction of the Galaxy, nonetheless during this initial phase the possibility first exists for a spacecraft to enter the planetary system of a second less-advanced ETC, and initiate one possible form of first contact, namely the collection of an artefact from one ETC by another.
Kennedy (Reference Kennedy2006) considered a scenario in which a technological society commences upon an evolving interstellar space program during which the travel speeds of the launched probes are increased as the program continues. This leads to a circumstance in which the earliest probes launched into interstellar space may be overtaken by more advanced higher-speed vehicles launched at later dates. This has lead to discussion of whether there is an incentive to postpone the first launches of an interstellar space program until some optimal degree of progress has first been made in launcher and probe technology (Kennedy Reference Kennedy2006 and Heller Reference Heller2017). In the present paper we consider the assumption of an evolving interstellar program with respect to another question, namely: what probes will be the first to arrive at a disparate planetary system within which there is a civilization capable of retrieving the vehicle? In other words, which probes have the potential for instigating a first-contact event?
This subject, hypothetical and controversial though it may seem, is not of uncommon popular interest, particularly when it comes to Earth being the recipient of such a probe. Versions of a first-encounter event which take the form of a spacecraft from an ETC arriving within the Solar System have been conceived of not only in science-fiction novels (e.g. Clarke Reference Clarke1973), but also in theoretical discussions of the possibility of undiscovered artefacts from ETCs already residing at locations within the Solar System (Haqq-Misraab and Kopparapuc Reference Haqq-Misraab and Kopparapuc2012; Lacki Reference Lacki2019; Benford Reference Benford2021).
A hypothetical scenario
We hypothesize two extra-terrestrial civilizations (ETCs) within planetary systems around separate stars. One “active” ETC is taken to have acquired the technology for sending artificial probes over interstellar distances. A second ETC is in a “passive” state throughout the timescale of our scenario, possibly achieving the technology to dispatch probes to bodies within its host planetary system, but not acquiring a practical interstellar capability. We consider a type of first-encounter event in which the passive ETC chances upon the arrival of a vehicle that has originated from the active ETC.
Once the active ETC embarks upon an interstellar program we assume that it seeks the capability of launching probes with increasingly greater speeds, in order to produce transit times between stars that are brief enough for the ETC to garner more benefit from the endeavour. The first artificial vehicle of this interstellar program is taken to leave the planetary system of the active ETC with speed v 0. We refer to this as the initial-generation probe and the time at which it is launched denotes the start of a system t of time keeping. The active ETC thereafter launches increasingly advanced generations of vehicles. A probe in the advanced series is launched at a time t = t l and leaves the planetary system from which it originates with a speed v. Other stars are considered to be at rest with respect to the parent star of the active ETC, and v is the speed with which a probe moves radially away from that parent star. All probes travel a distance D before encountering the planetary system of a passive ETC. The initial-generation probe arrives at this passive-ETC system at a time T 0 = D/v 0 after it was launched, where T 0 is the transit time for this initial probe between the two systems. A more-advanced probe launched at time t l has an arrival time at distance D = v 0 T 0 of
after the launch of the initial probe.
In want of compelling models we consider below three different cases describing the speed at which a probe leaves the planetary system of the active ETC.
Case A: Probe speed scales linearly with launch date
In this first case it is supposed that the technology of the probe-launching civilization advances in such a way that
where v < c and τ LV is a timescale that characterizes the rate of development of launch-vehicle technology. An advanced probe is defined to be of generation n if it is launched at a time t l, n = nτ LV after the launch of an initial (n = 0 zero-generation) probe. This advanced probe leaves the parent planetary system with speed v n = (n + 1)v 0. Here n is not necessarily implied to be an integer, although we round off to integer values in some examples which are discussed below. The advanced probe is taken to arrive at the passive-ETC system at time
after launch of the zero-generation probe.
Eqn (3) is analogous to
Figure 1 shows (t a/τ LV) as a function of (t l/τ LV) for three different values of the ratio (T 0/τ LV). Each curve passes through a minimum (t a/τ LV) that varies according to the parameter (T 0/τ LV). The launch time corresponding to such a minimum indicates the generation n of the probe that arrives first at the stellar system of a passive ETC.
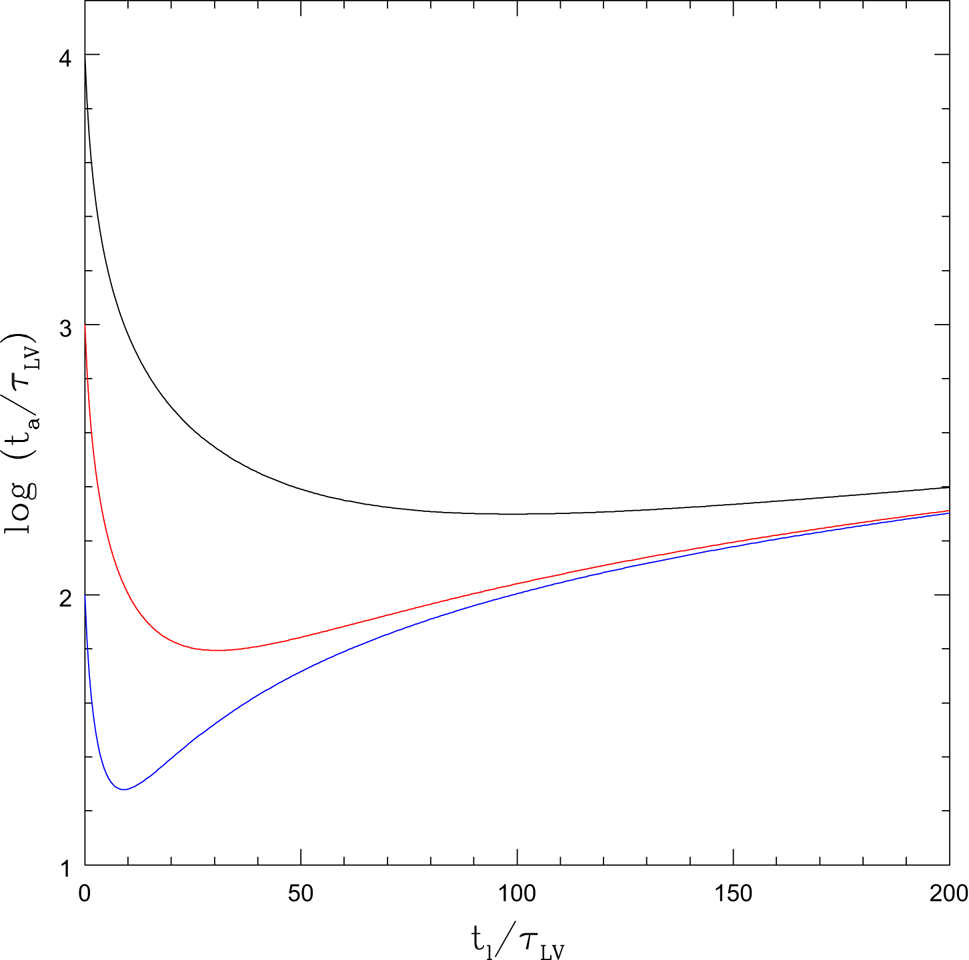
Fig. 1. Arrival time at destination (t a/τ LV) as a function of launch time (t l/τ LV) for a probe speed given by Eqn (2) for Case A, and three examples of the parameter (T 0/τ LV): 102 (blue curve), 103 (red), 104 (black). Both launch and arrival times are normalized by the timescale τ LV that appears in Eqn (2). The greater is (T 0/τ LV), the greater the distance between two stellar systems, or the shorter the time between the launch of probes of successive generations.
Which generation probe would first be capable of reaching the planetary system of the assumed passive ETC?
Case A: The first-arrival probe
Eqn (3) when differentiated gives
Early in a space program (dt a/dt l) is negative, as in Figure 1. However, as t l increases, (dt a/dt l) eventually becomes positive. Solving the criterion dt a/dt l = 0 gives the launch date t l,1p of the first probe to arrive at the planetary system of the recipient civilization
This probe of first-arrival is of generation
If τ LV ≪ T 0 then the first probe to arrive is of generation n 1p ≫ 1, i.e., a relatively advanced probe. The more rapid the rate of active-ETC development, i.e., the shorter the timescale τ LV, the more advanced is the first probe to arrive at the passive ETC. Similarly, the more distant the active ETC from the passive, i.e., the greater the value of T 0, the more advanced is the first probe to reach the later ETC.
The travel speed of the first probe to arrive at the passive ETC is from Eqn (2) and (6)
The transit time taken for this first-encounter probe between planetary systems is
Arrival of the first probe at the passive ETC occurs at time
Suppose that all of the probes launched by the active ETC follow radial trajectories away from their point of origin, and that the motions of stars due to Galactic rotation are ignored. In the absence of any probe acceleration, Eqn (10) can then be re-interpreted as
where D LV = v 0τ LV, i.e., the distance that a zero-generation probe will travel before the launch of a first-generation n = 1 probe, and D max is the maximum distance that any extant probe can feasibly have achieved from an active-ETC system after a time t e has elapsed in the history of that system's interstellar program. In effect, D max approximates the radius of a spherical volume within which any possible “first-encounter” event between the probe and a passive ETC is restricted. This might be envisioned as a first-encounter horizon to any passive ETC that is capable of receiving a probe from the active ETC system. The distance D max expands with time, and it depends on the rate of advance of launch vehicle capabilities as quantified by the parameter τ LV.
Examples of Case A
From Earth to an ETC system
An example might be considered in light of the terrestrial space program although with enormous caution. The first spacecraft have begun to leave the Solar System within 100 yr of the launch of the first liquid-fuel rocket by Robert Goddard. This is a loose basis for considering τ LV = 100 yr in the following example.Footnote 1 The time for a zero-generation probe to reach one of the very nearest stars is taken to be T 0 = 8.0 × 104 yr, which for a speed of v 0 = 15 km s−1, such as for Voyager 2 (Bailor-Jones and Farnocchia Reference Bailor-Jones and Farnocchia2019), corresponds to a traversed distance of 1.2 pc. Therefore, in this example (T 0/τ LV) = 800, and the minimum in (t a/τ LV) occurs for a probe launched at time t l = 27.3τ LV. This 27th-generation probe starts en route some 2730 yr after launch of an initial zero-generation probe, and reaches the nearby star at t a ≈ 5560 yr, i.e., some 74,440 yr before the zero-generation probe arrives, after a time in transit of 2830 yr. The speed of the probe is 420 km s−1.
The above example pertains to a terrestrial probe arriving in the vicinity of one of the nearest stars. However, the situation changes markedly upon considering stellar systems within the Galaxy that are at the limit of the Solar neighbourhood. In this case we take T 0 = 2.0 × 106 yr, which for v 0 = 15 km s−1 by analogy with Voyager 2, corresponds to a travel distance of 31 pc. Travel over such distances might be required to enhance the chance of encountering a stellar system which is potentially an abode to a passive ETC. Nonetheless, a star at a distance of 31 pc from the Sun is still within the Solar vicinity, and as such is still relatively close on a Galactic scale. The first probe to encounter such a system will be of generation n 1p = 140, which is much more advanced than probes of Case A capable of first encounter with one of the nearest stars. A 140th generation probe is launched 14,000 yr into the supposed terrestrial interstellar program. Arrival at the more distant first-encounter point occurs at time t a = 28,200 yr into the program. The similarity of t a to 2t l follows from Eqn (6) and (10), and such a relation will hold for all distant first-encounters for which T 0 ≫ τ LV. The first-encounter spacecraft precedes the zero-generation probe to the destination by almost 1,972,000 yr.
It might be surmised from the above examples, that if the Pioneer 11 or Voyager 2 spacecraft ever do arrive within the home system of an ETC (as opposed to being intercepted en route), particularly within one beyond the Solar neighbourhood, they may have been preceded by terrestrial spacecraft of a much more advanced nature. This is an example of a wait incentive as discussed by Kennedy (Reference Kennedy2006). In this case, study of either the plaque, or phonograph disc (the Voyager Golden Record), onboard these two spacecraft respectively (e.g., Sagan et al. Reference Sagan, Drake, Druyan, Ferris, Lomberg and Sagan1979), may not tell an inquisitive ETC much that it does not already know about Earth and its inhabitants.
From an ETC to Earth
If an active ETC is evolving rapidly in technology, or is exceedingly distant, then a vehicle of relatively advanced state may be more likely to first reach a passive collecting civilization. In this case, there could be a considerable mismatch in the technology level of the first-arrival probe and that of the passive ETC that it encounters. This would presumably have ramifications for what might eventuate if an artefact from an ETC were to arrive within the Solar System and enable first-contact with terrestrials. Hypothetical reverse engineering, for example, might be difficult given the technology gap.
The flight characteristics of objects described in the UAP Task Force report on Unidentified Aerial Phenomena (ODNI 2021), submitted by the Office of the Director of National Intelligence to the United States Congress, might be considered in this context. Are the UAP characteristics so far beyond what terrestrial innovation can currently accomplish, as to be consistent with the first arrival of vehicles from a distant ETC with an interstellar space program? Knuth et al. (Reference Knuth, Powell and Reali2019) have argued for an affirmative answer to this question. Such a circumstance would erase the Fermi Paradox. However, UAPs or UFOs have rarely been given credence in this context by the astronomical community, even though the possibility of, and searches for, ETC artefacts have both been broached in the literature (e.g., Haqq-Misraab and Kopparapuc Reference Haqq-Misraab and Kopparapuc2012; Wright Reference Wright2018; Lacki Reference Lacki2019; Shostak Reference Shostak2020; Benford Reference Benford2021). In this sense the controversial subject of UAPs evinces its own sociological paradox.
Approaching high speeds
In the preceding examples a spacecraft like Voyager 2 was taken to be an archetype for a probe of the n = 0 generation. Voyager 2 has a speed of 15 km s−1 on leaving the Solar System (Bailor-Jones and Farnocchia Reference Bailor-Jones and Farnocchia2019), which corresponds to 5.00 × 10−5c. Thus, even a 27th-generation first-contact probe to a nearby star, such as in the example above, would have a speed that is much less than the speed of light. With the rate of technological advance assumed in the preceding subsection, the generation n for which a probe will be dispatched with a speed of v n = 0.1c can be calculated. If v 0 = 15 km s−1 this corresponds to a generation for which (n + 1) = 0.1c/v 0, i.e., n ≈ 2000. With τ LV = 100 yr, as in the preceding examples, such a probe is launched at a time t l ≈ 200, 000 yr after the commencement of the interstellar program of the active civilization. Therefore, a substantial time elapses with a Case A advance in technology before a probe speed of 0.1c (as assumed, for example, in expansion scenarios such as those of Tipler (Reference Tipler1980), Børk (Reference Børk2007), and Cotta and Morales (Reference Cotta and Morales2009)) is reached.
The value of D max some 200,000 yr into the above Case A interstellar program with τ LV = 100 yr and v 0 = 15 km s−1 is 1.5 kpc. At this time the active civilization can be considered to have established an interstellar program of truly Galactic dimensions. This is still shorter by a factor of 1000 than the mean rotation time of the Galactic disc near the Solar neighbourhood.
Case B: Probe speed scaling exponentially with launch date
By contrast with Case A, it might be instead supposed that the rate of advance in launch vehicle technology by an active ETC scales with the level of sophistication having already been reached in that technology. To explore this type of scenario we consider a case B in which the speed of a probe as it leaves the planetary system of the active ETC varies with time according to an exponential law. This is the scenario discussed by Kennedy (Reference Kennedy2006). Below it is re-expressed in a form analogous to that of Case A.
The equation used here to model the speed of an interstellar probe relative to deep space for Case B is
where v < c. The parameter τ LV is again a timescale that characterizes the rate of development of launch vehicle technology by an active ETC. The generation ratio n = t l/τ LV is again a measure of how advanced a probe is. As before, an nth-generation probe is launched at a time t l, n = nτ LV after launch of the initial (n = 0) generation probe. The speed with which the nth-generation probe leaves the stellar system of the active ETC is related to the speed of the zero-generation probe as v n = v 0 e n.
The analogs to Eqn (3) and (4) for Case B are
and
Once the ratio (T 0/τ LV) is specified, a locus of (t a/τ LV) as a function of (t l/τ LV) follows. Three examples are shown in Figure 2 for the same combination of (T 0/τ LV) upon which Figure 1 is based, namely 100, 103 and 104. Each curve in Figure 2 again shows that an absolute minimum exists for (t a/τ LV), so that first arrival occurs not for a zero-generation probe but for one of an advanced generation. Conceptually the situation is analogous to Case A, however, the contrast between the curves in Figure 2 is much less than in Figure 1, and they essentially overlap for t l/τ LV > 10.

Fig. 2. Probe arrival time at destination (t a/τ LV) as a function of launch time (t l/τ LV) for Case B, in which probe speed follows the exponential law of Eqn (12). Curves are shown for (T 0/τ LV) = 102 (blue line), 103 (red) and 104 (black). Both launch and arrival times are normalized by the timescale τ LV that appears in Eqn (12).
Figure 2 illustrates how the two branches of each curve relate to the two terms on the right-hand side (RHS) of Eqn (1), (13) and (14). In the early stages of the interstellar era of an active ETC the arrival time of a first-encounter probe is determined mainly by the transit time, such that the left-hand side of the curves in both Figures 1 and 2 corresponds to the second term on the RHS of Eqn (1), (4) and (14). By contrast, when t l ≫ τ LV, such that many generations of advanced probes have been dispatched, the first term on the RHS of Eqn (1), (4) and (14) becomes dominant and maps into the right-hand branch of the curves in Figures 1 and 2. In this limit t a ≈ t l and the curves in Figure 2 overlap despite being parameterized by different (T 0/τ LV). This branch of the curves, in a sense, corresponds to an epoch in which an ETC has acquired a capability to visit planetary systems over extended distances. The left-branch of the curves in Figures 1 and 2, by contrast, pertain to an epoch in which first encounters with other planetary systems are coming within range.
The criterion dt a/dt l = 0 again gives the launch date t l,1p of the first probe to potentially encounter a collecting civilization at a distance v 0T 0 from the active ETC. For Case B this is
This probe is of generation n 1p = ln(T 0/τ LV). If τ LV ≪ T 0 then the first probe to arrive is of an advanced n 1p. The travel speed of the first probe to encounter the collecting civilization is v 1p = v 0exp (n 1p) = v 0 (T 0/τ LV). Interestingly, the transit time taken for this probe between planetary systems is T 1p = τ LV. This gives some appreciation of the rate of technology advance needed to produce a Case B situation, the time-scale for advancing by Δn = 1 in the generation number needs to be comparable to the desired transit time between stellar systems.
If T 0 = 8.0 × 104 yr is taken to correspond to the nearest stars to an active ETC, as was done for Case A, and if a longer timescale of τ LV = 200 yr is assumed to accomplish an exponential increase in probe speed according to Case B, then (T 0/τ LV) = 400, and the first encounter with such a nearby star could be attained by a probe of generation n ≈ 6. Such a probe is launched within ≈1200 yr of the commencement of the Case B interstellar program, and the transit time to destination is a mere 200 yr. If v 0 = 15 km s−1, then the speed of such a probe is 6050 km s−1, which is much higher than the analogous Case A probe discussed above. In Case B, therefore, the probe of first-encounter with a nearby star would be of much higher speed than the analogous probe in Case A. Thus, the greater would presumably be the other technological capabilities of the Case B first-encounter probe. Quantitative illustrations of Case B for a terrestrial space program were discussed in much more detail by Kennedy (Reference Kennedy2006). The point to be conveyed here is that a Case B scenario heightens the possibility for a first-encounter disparity in technology between an active and a passive ETC as compared to Case A.
If probe technology continued to progress according to Case B, then with v 0 = 15 km s−1, a vehicle of generation n = 8 would leave the planetary system of an active-ETC with a speed in excess of v = 0.1c. As noted above, such a speed has been adopted in some calculations and models for the propagation of probes from an ETC through the Galaxy, and this can lead to strong implications for the Fermi Paradox, as argued by Tipler (Reference Tipler1980). Eventually the rate of increase in probe speed as a function of launch time in Case B breaks down due to relativistic effects. Modifications to the scenario of Kennedy (Reference Kennedy2006) for special relativity have been considered by Heller (Reference Heller2017).
In the case of a stellar destination at a distance corresponding to T 0 = 2.0 × 106 yr, then with τ LV = 200 yr, it is probes of the 9th generation that are first to arrive in Case B. The speed of such probes exceeds 0.1c. As noted above, a value of T 0 = 2.0 × 106 yr corresponds to a distance between the active-ETC parent star and the destination star of 31 pc for v 0 = 15 km s−1, which is still much smaller than the scale of the Galactic disc. This example emphasises the point that if a first-encounter vehicle were to arrive at Earth in the not-distant future from an ETC stationed kiloparsecs away, the disparity in the technology level of that probe and terrestrial technology could be vast indeed.
Case A with stellar space motions
In the above sections no account has been taken of stellar motions relative to the parent star of the active ETC. However, the speeds with which Pioneer 10–11 and Voyager 1–2 are moving relative to the Sun as they depart from the Solar System (11–17 km s−1; Bailor-Jones and Farnocchia Reference Bailor-Jones and Farnocchia2019), are comparable in magnitude to each of the three components of velocity dispersion among stars in the Solar neighbourhood. As such, the value of the speed v 0 that appears in Eqn (2) may be comparable to the dispersion in space velocities among stars in the neighbourhood of the active ETC. As a first-order attempt to modify Case A to approximate the effect of relative stellar motions, that case is revisited here with a somewhat modified version of Eqn (1), namely
where $v_{\star }$![]() is the velocity of another star relative to the ETC parent-star along the radial trajectory of the outbound probe. Once again v is the speed with which a probe is departing relative to the home star of the active ETC. A positive value of $v_{\star }$
is the velocity of another star relative to the ETC parent-star along the radial trajectory of the outbound probe. Once again v is the speed with which a probe is departing relative to the home star of the active ETC. A positive value of $v_{\star }$![]() corresponds to a star that is approaching the home system of the active ETC, while a negative value corresponds to a recession away from that system. Upon introducing a free parameter q, defined by $q = v_{\star }/v_0$
corresponds to a star that is approaching the home system of the active ETC, while a negative value corresponds to a recession away from that system. Upon introducing a free parameter q, defined by $q = v_{\star }/v_0$![]() , Eqn (2) for the probe speed in Case A becomes
, Eqn (2) for the probe speed in Case A becomes
and
A set of three curves of (t a/τ LV) versus (t l/τ LV) are shown in Figure 3 for (T 0/τ LV) = 102 and three different q. The curve for q = 0 is identical to one of the curves in Figure 1. A non-zero q shifts the location of the minimum in a curve to a different (t l/τ LV), i.e., to a different probe generation. The criterion dt a/dt l = 0 gives the location of the minimum as
so that the first probe to attain a distance of v 0T 0 from the parent star of the active ETC has a generation number of
In the example of Figure 3 with (T 0/τ LV) = 100, for q = 0 a first-arrival probe is of generation n ≈ 9, whereas n 1p ≈ 10 for q = −1 and n 1p ≈ 7 for q = 2. Stellar motions could be of significance in producing a shift Δn = q in the generation of a probe of first encounter, which may typically be Δn = ±1–2 for v 0 = 15 km s−1. This effect could be of most significance for encounters with the nearest stars to an active ETC, where probes of earlier generations have potential for a first encounter.Footnote 2

Fig. 3. Time of probe arrival (t a/τ LV) at a distance D = v 0 T 0 from an active ETC system is shown as a function of launch time (t l/τ LV) for a probe speed given by Eqn (2), but now including a first-order term for relative stellar motions according to Eqn (16). Both launch and arrival times are normalized by the timescale τ LV that appears in Eqn (2). All three curves are plotted for (T 0/τ LV) = 102, but have different values for the parameter q appearing in Eqn (16): black curve for q = 0, blue curve (q = 2.0) and red curve for q = −1.0.
Models of the expansion of a network of probes throughout the Galaxy which take account of the relative space motions of stars have been constructed in detail, for example, by Cartin (Reference Cartin2013) and Carroll-Nellenback et al. (Reference Carroll-Nellenback, Frank, Wright and Scharf2019).
Summary discussion
The approach used in this paper is admittedly very rudimentary compared to the numerical models of ETC propagation within the Galaxy that have been referenced in the Introduction. Notwithstanding the imperfections of their formulation, there is one common conclusion that comes across in the Cases A and B presented above.
The key implication of this paper can be summarized as followed: if an actively space-faring ETC embarks on a program to send probes to interstellar destinations, and if the technology of this ETC advances with time, then the first probe to arrive at the destination of a less-advanced ETC is less likely to be one of the earliest probes launched, but one of more advanced capability. There may thus be a substantial disparity between the level of technology comprising the first-arrival probe and that developed by the receiving ETC, if it has no interstellar capability itself. The greater the initial separation of the two ETCs, or the greater the rate of probe development by the active ETC, the greater is the potential for a technological mismatch at first encounter.
Throughout the discussion above it has been arbitrarily assumed that a civilization which receives a probe from an active ETC is itself, by contrast, passive in having no interstellar capability. A technology mismatch at first encounter is admittedly built into such an assumption. However, the main conclusion from the above cases continues to hold, namely, that the first probe from an active ETC (having a developing technology as concerns probe speed) to arrive at another star system will likely be of more advanced characteristics than the earliest probes sent into interstellar space by that ETC. The nature of a first-encounter event may change, however, if the civilization which collects one of these probes is also an active ETC. In this case the relative mismatch between the two technologies at first encounter could be much more difficult to contemplate. It may then be that a first-encounter event does not occur in the parent stellar system of either ETC, but at some third location. By assuming a passive ETC as the destination for the interstellar program of an active ETC, a situation will pertain in which the mismatch of technologies is most marked. Nonetheless, the scenario of a passive ETC receiving a first-encounter probe is of considerable relevance, since it would pertain to a hypothetical first-encounter event within the Solar System should such occur within the near future.
Taking a very different approach, Kipping et al. (Reference Kipping, Frank and Scharf2020) argued from a proposed model for the temporal distribution of ETCs, that any first-contact event is more likely to be initiated as a consequence of the activity of a relatively older, more-advanced intelligence. The concept of what Kipping et al. (Reference Kipping, Frank and Scharf2020) refer to as a “contact inequality” can arise within a number of contexts for first contact, whether it be via a remote-sensing SETI search, or by encounter with a physical artefact from an ETC, as in the above discussion. These authors also argue that contact inequality is an intuitive concept, and it certainly has motivated the plots of many science-fiction novels and movies.
Development of a model for the propagation of probes through the local stellar vicinity of an active ETC during the earliest stages of an interstellar program would require taking account of factors that have not been considered in this paper. Presumably the probability of any one probe encountering an exoplanetary system that contains within it an ETC would increase with an increase in the distance travelled by a probe. As discussed above, increasing the distance D max of the first-contact horizon increases the likely generation number of a probe of first encounter, thereby enhancing a contact inequality with a passive ETC. Furthermore, if the number of probes launched per unit time increases as an active ETC continues to progress through an interstellar exploration campaign, the probability would be increased that a probe of first contact would be among those more recently launched, again with the consequence of a first-contact discontinuity.
Kipping et al. (Reference Kipping, Frank and Scharf2020) discussed ramifications of a first-contact inequality for the methodology of terrestrial SETI. There would, however, as alluded to above, likely be broad ramifications that extend beyond the realms of scientific progress. If an object sent by an interstellar ETC were to enter the Solar System, chances are it would not be a relic artefact that is perhaps analogous to a time-worn Voyager-like probe, but rather one might expect a vehicle of much greater sophistication, even if it were no longer functioning. This suggests a question: might a hypothetical first-encounter vehicle from an ETC be so sophisticated as to still be functioning upon arrival at the Solar System? As Hawking (Reference Hawking2010) and others have drawn attention to, some potential consequences of such a first-contact event might be of serious concern for humanity. This is a topic that has again found fruitful soil within the realms of science fiction, but is beyond the context within which the present paper has been framed.
Conflict of interest
The author has no conflicts of interest to declare concerning this manuscript.






