We have studied mergers between disk galaxies and smaller companion galaxies by using a 60 000 particle self-gravitating disk in interaction with a point-like perturber. The disk is a stable Mestel disk with an adjustable inert halo, combining to make a flat rotation curve. The hyperbolic, parabolic and circular initial orbits of the perturber have been studied separately (Byrd et al. 1986, Valtaoja 1990, Valtonen et al. 1990). In hyperbolic encounters, the friction may be evaluated by the impulsive approximation by Spitzer (1958). The agreement with experiments is good except for the dependence on the encounter velocity which may deviate somewhat from the analytic theory. In case of circular orbits, we made comparisons with earlier work by Quinn and Goodman (1986) and others by turning off the self-interaction in some of the simulations. In addition, the analytical calculation of dynamical friction by Chandrasekhar (1942) was extended to disk galaxies, and the results were compared with the numerical work. Our results without self-interaction agree well with Quinn and Goodman when we use the same halo/disk mass ratio (Q0 ≅ 1.5) as they did. However, we show that the results are very sensitive to the assumed halo mass. Moreover, the inclusion of self-interaction can change the results considerably in the case of a retrograde satellite. Our analytic theory explains well the merger rate in those situations where self-interaction is not very important, i.e. in case of satellites in direct orbits. The orbital decay time Δt = r (dr/dt)−1 may then be expressed in term of the crossing time in the disk, Tcr = R/v0, where R is the radius of the disk and v0 the constant rotation velocity: 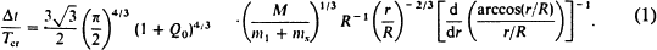Here m1, ms and M are the masses of a star, the satellite and the disk, respectively, and r is the orbital radius of the satellite in its (nearly) circular orbit.