We study reconnection and chromospheric evaporation in flares using a numerical code including nonlinear, anisotropic heat conduction (Yokoyama & Shibata 1998). The two-dimensional, nonlinear, time-dependent, resistive, compressible MHD equations are solved. The evolution from the rise phase to (the early part of) the decay phase of a solar flare is qualitatively reproduced in this simulation. Based on the results, we obtained a relationship between the flare temperature and the coronal magnetic field strength. We assume that the energy input to a loop balances with the conductive cooling rate, that the temperature at the loop apex is TA ≍ (2QL2/κ0)2/7, where Q is the volumetric heating rate, that L is the half-length of the loop, and that the Spitzer thermal conductivity constant is κ0 = 10−6 CGS. In our simulations, the heating mechanism is magnetic reconnection, so the heating rate is described as Q = B2/(4π) · Vin/L · l/sin Θ, where B is the coronal magnetic field strength, Vin is the inflow velocity (≍ 0.1 VA from our result and also from Petschek's theory), and Θ is the angle between the slow-mode MHD shock and the loop and is approximately given by sin Θ ≍ Vin/VA. By manipulating the equations, we find 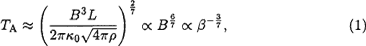where ρ is the mass density of the corona. The simulation results show very good agreement with this scaling law.