In the RTFD(Gusev (1986)) the conception of a Sakharov - Wheeler Metric Elasticity(SWME)(Sakharov (1967), Wheeler (1970)) had been worked out. On the basis of the exact solutions of Einstein equations and qualitative analysis RTFD the global evolution have been studied and the phase portraits of the early Universe is being constructed. An analysis of phase portraits show on the possibility description of spontaneous creation of Universe from an initial Minkowskian's vacuum to an inflationary de Sitter space-time in the frame of phenomenological non-quantum theory (Guth (1991)). During the past decade, a radically new picture of cosmology has emerged. The present homogeneous expanding Universe would have stated out with a de Sitter phase. The purpose of this paper is to shown that the geometry-dynamical approach to the Einstein's gravitation theory in the frame RTFD also is leaded to the nonsingular cosmological models (Brandenberger (1993)). Let us to propose that before the some moment of time the Universe is at the vacuum state and is described the geometry of Minkowskian's space. Deformations of vacuum state, identifying with empty Mikowskian's space are described by the deformations tensor 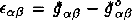, An arising of deformation ∊αβ is leaded to appearance of the stress tensor ∊αβ and the energy-momentum Tαβ(∊γδ) which is connected with “creating” particles in the Universe. Here we are considered the deformations of Minkowskian's space (the initial vacuum state with ∞ αβ = 0) at the linear theory (~ ∊) of finite deformations. The final deformation state gαβ are searched in the metric class of Friedmann's cosmological spaces. In the comoving reference system Uα(0, 0, 0, 1) the Friedmann's equations have form (Narlikar & Padmanabhan (1983), and Gusev (1989)): 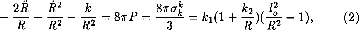where R(t) is so called the expansion factor at the Robertson - Walker line element, k is the curvature parameter with the possible values −1, 0, + 1, P is pressure, k1, k2 are the some combination from a Lame coefficients, l02 is a “initial radius” Universe, a free parameter model. The phase space of this model is the two-dimensional (R, Ṙ) plane. We note that there is only two singular points (Ṙ = 0, Ṙ = 0) in the phase plane. The one of those points is R = l0, Ṙ = 0 and corresponds to Minkowski space - time. There are two classes trajectories which are asymptotically de Sitter. Those starting at large positive values of Ṙ go off to Ṙ = + ∞, reaching their asymptotic value of H from above. Those starting with large negative values of Ṙ tend to R = + ∞ with Ṙ > 0. For small values of Ṙ and R we can see that there are periodic solutions about Minkowski space. The corresponding solutions oscillate with frequency given by H0 (which is possible equal planck scale) about Minkowski space. Based on the preceding discussion of asymptotic solutions we see that there is a separatrix (Gusev, (1989)) in phase space dividing solutions which tend to R = + ∞ from those which oscillate or tend to R = l0. The above analyses of the phase portraits is an indication that in our theory Minkowski space may be unstable toward homogeneous deformations. We stress that all the general features of the phase portrait analyses are true for quadratic deformations of gravitational vacuum. Our model incorporates a very important feature: in the asymptotic de Sitter region, the quadratic deformations and temperature effects does not have an important effect on the geometry. The effective gravitational constant of coupling goes to zero as space - time approaches de Sitter space. In this sense the model is asymptotically free (gravitational confinement Linde, (1990)). At the late times the solutions are described a evolution of the de Sitter Universe R~expHt (Hoyle et al. (1993)).