Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-16T15:16:21.809Z Has data issue: false hasContentIssue false
  • English
  • Français

A MATHEMATICAL COMMITMENT WITHOUT COMPUTATIONAL STRENGTH

Part of: Philosophical aspects of logic and foundations Discrete mathematics in relation to computer science Proof theory and constructive mathematics

Published online by Cambridge University Press:  02 July 2021

ANTON FREUND
ANTON FREUND*
Affiliation:
FACHBEREICH MATHEMATIK TECHNICAL UNIVERSITY OF DARMSTADT SCHLOSSGARTENSTR. 7 64289 DARMSTADT, GERMANY E-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We present a new manifestation of Gödel’s second incompleteness theorem and discuss its foundational significance, in particular with respect to Hilbert’s program. Specifically, we consider a proper extension of Peano arithmetic ($\mathbf {PA}$) by a mathematically meaningful axiom scheme that consists of 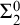$\Sigma ^0_2$-sentences. These sentences assert that each computably enumerable ($\Sigma ^0_1$-definable without parameters) property of finite binary trees has a finite basis. Since this fact entails the existence of polynomial time algorithms, it is relevant for computer science. On a technical level, our axiom scheme is a variant of an independence result due to Harvey Friedman. At the same time, the meta-mathematical properties of our axiom scheme distinguish it from most known independence results: Due to its logical complexity, our axiom scheme does not add computational strength. The only known method to establish its independence relies on Gödel’s second incompleteness theorem. In contrast, Gödel’s theorem is not needed for typical examples of $\Pi ^0_2$-independence (such as the Paris–Harrington principle), since computational strength provides an extensional invariant on the level of 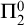$\Pi ^0_2$-sentences.

Keywords

independencecomputational strengthGödel’s second incompleteness theoremHilbert’s programKruskal’s theorempolynomial-time algorithm

MSC classification

Primary: 03F30: First-order arithmetic and fragments
Secondary: 03F40: Gödel numberings and issues of incompleteness 03A05: Philosophical and critical 68R10: Graph theory (including graph drawing)
Type
Research Article
Information
The Review of Symbolic Logic , Volume 15 , Issue 4 , December 2022 , pp. 880 - 906
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of The Association for Symbolic Logic

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

BIBLIOGRAPHY

Beklemishev, L. (1997). Notes on local reflection principles. Theoria, 63, 139–146.CrossRefGoogle Scholar
Beklemishev, L. (2004). Provability algebras and proof-theoretic ordinals, I. Annals of Pure and Applied Logic, 128(1–3), 103–123.CrossRefGoogle Scholar
Beklemishev, L. (2005). Reflection principles and provability algebras in formal arithmetic. Russian Mathematical Surveys, 60(2), 197–268.CrossRefGoogle Scholar
Beklemishev, L., & Visser, A. (2005). On the limit existence principles in elementary arithmetic and ${\Sigma}_{\mathrm{n}}^0$ -consequences of theories. Annals of Pure and Applied Logic, 136, 56–74.CrossRefGoogle Scholar
Buchholz, W. (1991). Notation systems for infinitary derivations. Archive for Mathematical Logic, 30, 277–296.CrossRefGoogle Scholar
Buchholz, W., & Wainer, S. (1987). Provably computable functions and the fast growing hierarchy. In Simpson, S. G., editor. Logic and Combinatorics. Proceedings of the AMS-IMS-SIAM Joint Summer Research Conference 1985. Contemporary Mathematics, Vol. 65. Providence, RI: American Mathematical Society, pp. 179–198.Google Scholar
Cichon, E. A. (1983). A short proof of two recently discovered independence results using recursion theoretic methods. Proceedings of the American Mathematical Society, 87, 704–706.CrossRefGoogle Scholar
de Jongh, D., & Parikh, R. (1977). Well-partial orderings and hierarchies. Indagationes Mathematicae, 80(3), 195–207.CrossRefGoogle Scholar
Ewald, W., & Sieg, W. (eds.). (2013). David Hilbert’s Lectures on the Foundations of Arithmetic and Logic 1917–1933. Berlin: Springer.CrossRefGoogle Scholar
Feferman, S. (1992). Why a little bit goes a long way: Logical foundations of scientifically applicable mathematics, PSA: Proceedings of the 1992 Biennial Meeting of the Philosophy of Science Association. Chicago: University of Chicago, pp. 442–455.Google Scholar
Fellows, M. R., & Langston, M. A. (1988). Nonconstructive tools for proving polynomial-time decidability. Journal of the Association for Computing Machinery, 35(3), 727–735.CrossRefGoogle Scholar
Fellows, M. R., & Langston, M. A. (1992). On well-partial-order theory and its application to combinatorial problems of VLSI design. SIAM Journal on Discrete Mathematics, 5(1), 117–126.CrossRefGoogle Scholar
Freund, A., & Pakhomov, F. (2020). Short proofs for slow consistency. Notre Dame Journal of Formal Logic, 61(1), 31–49.CrossRefGoogle Scholar
Freund, A., Rathjen, M., & Weiermann, A. (2020). Minimal bad sequences are necessary for a uniform Kruskal theorem. Preprint, arXiv:2001.06380.Google Scholar
Friedman, H. (2018). Explicitly ${\varPi}_1^0$ Status 4/20/18. Manuscript. Available from: https://cpb-us-w2.wpmucdn.com/u.osu.edu/dist/1/1952/files/2014/01/CMI_ExplicPi01042018-2ilxsqy.pdf (Accessed 31 March 2020).Google Scholar
Friedman, H., Robertson, N., & Seymour, P. (1987). Metamathematics of the graph minor theorem. In Simpson, S. G., editor. Logic and Combinatorics. Proceedings of the AMS-IMS-SIAM Joint Summer Research Conference 1985. Contemporary Mathematics, Vol. 65. Providence, RI: American Mathematical Society, pp. 229–261.Google Scholar
Friedman, H., & Sheard, M. (1995). Elementary descent recursion and proof theory. Annals of Pure and Applied Logic, 71, 1–45.CrossRefGoogle Scholar
Gentzen, G. (1936). Die Widerspruchsfreiheit der reinen Zahlentheorie. Mathematische Annalen, 112, 493–565.CrossRefGoogle Scholar
Gentzen, G. (1943). Beweisbarkeit und Unbeweisbarkeit von Anfangsfällen der transfiniten Induktion in der reinen Zahlentheorie. Mathematische Annalen, 119, 149–161.CrossRefGoogle Scholar
Hájek, P., & Pudlák, P. (1993). Metamathematics of First-Order Arithmetic. Perspectives in Mathematical Logic, vol. 3. Berlin: Springer.CrossRefGoogle Scholar
Hasegawa, R. (1994). Well-ordering of algebras and Kruskal’s theorem. In Jones, N. D., Hagiya, M., and Sato, M., editors. Logic, Language and Computation. Lecture Notes in Computer Science, Vol. 792. Berlin: Springer, pp. 133–172.CrossRefGoogle Scholar
Hilbert, D. (1926). Über das Unendliche. Mathematische Annalen, 95, 161–190, English translation in [48].CrossRefGoogle Scholar
Hilbert, D. (1928). Die Grundlagen der Mathematik. Abhandlungen aus dem Seminar der Hamburgischen Universität, 6, 65–85, reprinted in [9], English translation in [48].CrossRefGoogle Scholar
Kohlenbach, U. (2008). Applied Proof Theory. Proof Interpretations and their Use in Mathematics. Springer Monographs in Mathematics. Berlin: Springer.Google Scholar
Kreisel, G. (1960). Ordinal logics and the characterization of informal notions of proof. In Todd, J. A., editor. Proceedings of the International Congress of Mathematicians 1958. Cambridge: Cambridge University Press, pp. 289–299.Google Scholar
Kreisel, G. (1982). Finiteness theorems in arithmetic: An application of Herbrand’s theorem for ${\varSigma}_2$ -formulas. In Stern, J., editor. Proceedings of the Herbrand Symposium. Logic Colloquium ’81. Studies in Logic and the Foundations of Mathematics, Vol. 107. Amsterdam: North-Holland, pp. 39–55.CrossRefGoogle Scholar
Kreisel, G., & Lévy, A. (1968). Reflection principles and their use for establishing the complexity of axiomatic systems. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, 14, 97–142.CrossRefGoogle Scholar
Kruskal, J. (1960). Well-quasi-ordering, the tree theorem, and Vazsonyi’s conjecture. Transactions of the American Mathematical Society, 95(2), 210–225.Google Scholar
Lindström, P. (1984). On partially conservative sentences and interpretability. Proceedings of the American Mathematical Society, 91(3), 436–443.CrossRefGoogle Scholar
Lindström, P. (1997). Aspects of Incompleteness. Lecture Notes in Logic, Vol. 10. Berlin: Springer.CrossRefGoogle Scholar
Paris, J., & Harrington, L. (1977). A mathematical incompleteness in Peano arithmetic. In Barwise, J., editor. Handbook of Mathematical Logic. Amsterdam: North-Holland, pp. 1133–1142.CrossRefGoogle Scholar
Pohlers, W. (2009). Proof Theory. The First Step into Impredicativity. Berlin: Springer.Google Scholar
Rathjen, M., & Weiermann, A. (1993). Proof-theoretic investigations on Kruskal’s theorem. Annals of Pure and Applied Logic, 60, 49–88.CrossRefGoogle Scholar
Robertson, N., & Seymour, P. (2004). Graph minors. XX. Wagner’s conjecture. Journal of Combinatorial Theory, Series B, 92(2), 325–357.CrossRefGoogle Scholar
Schmidt, D. (1975). Bounds for the closure ordinals of replete monotonic increasing functions. The Journal of Symbolic Logic, 40(3), 305–316.CrossRefGoogle Scholar
Schmidt, D. (1979). Well-Partial Orderings and Their Maximal Order Types. Habilitationsschrift, Universität Heidelberg.Google Scholar
Shelah, S. (1984). On logical sentences in PA. In Lolli, G., Longo, G., and Marcja, A., editors. Logic Colloquium ’82. Studies in Logic and the Foundations of Mathematics, Vol. 122. Amsterdam: Elsevier, pp. 145–160.CrossRefGoogle Scholar
Simpson, S. G. (1985). Nonprovability of certain combinatorial properties of finite trees. In Harrington, L. A., Morley, M. D., Sčědrov, A., and Simpson, S. G., editors. Harvey Friedman’s Research on the Foundations of Mathematics. Studies in Logic and the Foundations of Mathematics, Vol. 117. Amsterdam: North-Holland, pp. 87–117.CrossRefGoogle Scholar
Simpson, S. G. (1988). Ordinal numbers and the Hilbert basis theorem. The Journal of Symbolic Logic, 53(3), 961–974.CrossRefGoogle Scholar
Simpson, S. G. (2009). Subsystems of Second Order Arithmetic (second edition). Perspectives in Logic. Cambridge: Cambridge University Press.CrossRefGoogle Scholar
Smith, R. L. (1985). The consistency strengths of some finite forms of the Higman and Kruskal theorems. In Harrington, L. A., Morley, M. D., Sčědrov, A., and Simpson, S. G., editors. Harvey Friedman’s Research on the Foundations of Mathematics. Studies in Logic and the Foundations of Mathematics, Vol. 117. Amsterdam: North-Holland, pp. 119–136.CrossRefGoogle Scholar
Smoryński, C. (1977). The incompleteness theorems. In Barwise, J., editor. Handbook of Mathematical Logic. Studies in Logic and the Foundations of Mathematics, Vol. 90. Amsterdam: North-Holland, pp. 821–865.CrossRefGoogle Scholar
Sommer, R. (1995). Transfinite induction within Peano arithmetic. Annals of Pure and Applied Logic 76, 231–289.CrossRefGoogle Scholar
Tait, W. (1981). Finitism. Journal of Philosophy, 78, 524–546.CrossRefGoogle Scholar
Tait, W. (2002). Remarks on finitism. In Sieg, W., Sommer, R., and Talcott, C., editors. Reflections on the Foundations of Mathematics. Essays in Honor of Solomon Feferman. Lecture Notes in Logic, Vol. 15. New York: A.K. Peters, pp. 410–419.Google Scholar
Takeuti, G. (1987). Proof Theory (second edition). Studies in Logic and the Foundations of Mathematics, Vol. 81. Amsterdam: North-Holland.Google Scholar
Tarski, A. (1936). Der Wahrheitsbegriff in den formalisierten Sprachen. Studia Philosophica, 1, 261–405.Google Scholar
van Heijenoort, J. (ed.). (1967). From Frege to Gödel. A Source Book in Mathematical Logic, 1879–1931. Cambridge, MA: Harvard University Press.Google Scholar
Zach, R. Hilbert’s program. In Zalta, E. N., editor. The Stanford Encyclopedia of Philosophy (fall 2019 edition). Available from: https://plato.stanford.edu/archives/fall2019/entries/hilbert-program.Google Scholar