Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-24T02:48:06.454Z Has data issue: false hasContentIssue false
  • English
  • Français

Different time solutions for the firing squad synchronizationproblem on basic grid networks

Published online by Cambridge University Press:  20 July 2006

Jozef Gruska ,
Salvatore La Torre ,
Margherita Napoli  and
Mimmo Parente
Jozef Gruska
Affiliation:
Faculty of Informatics, Masaryk University, Brno, Czech Republic.
Salvatore La Torre
Affiliation:
Facoltà di Scienze Matematiche, Fisiche e Naturali, Università degli Studi di Salerno, Italia.
Margherita Napoli
Affiliation:
Facoltà di Scienze Matematiche, Fisiche e Naturali, Università degli Studi di Salerno, Italia.
Mimmo Parente
Affiliation:
Facoltà di Scienze Matematiche, Fisiche e Naturali, Università degli Studi di Salerno, Italia.
Get access

Abstract

We present several solutions to the Firing Squad Synchronization Problem on grid networks of different shapes. The nodes are finite state processors that work in unison with other processors and in synchronized discrete steps. The networks we deal with are: the line, the ring and the square. For all of these models we consider one- and two-way communication modes and we also constrain the quantity of information that adjacent processors can exchange at each step. We first present synchronization algorithms that work in time n2, nlogn, $n\sqrt n$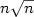, 2n, where n is a total number of processors. Synchronization methods are described through so called signals that are then used as building blocks to compose synchronization solutions for the cases that synchronization times are expressed by polynomials with nonnegative coefficients.

Keywords

Type
Research Article
Information
RAIRO - Theoretical Informatics and Applications , Volume 40 , Issue 2: Alberto Bertoni: Climbing summits , April 2006 , pp. 177 - 206
Copyright
© EDP Sciences, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balzer, R., An 8-states minimal time solution to the firing squad synchronization problem. Inform. Control 10 (1967) 22–42. CrossRef
Coan, B.A., Dolev, D., Dwork, C. and Stockmeyer, L., The Distributed Firing Squad Problem. SIAM J. Comput. 18 (1989) 990–1012. CrossRef
Choffrut, C. and Culik II, K., Real Time Cellular Automata, On and Trellis Automata. Acta Inform 21 (1984) 393–407. CrossRef
Culik, K., Variations of the firing squad problem and applications. Inform. Process. Lett. 30 (1989) 153–157. CrossRef
E. Goto, A Minimal Time Solution of the Firing Squad Problem. Lect. Notes Appl. Math. Harvard University 298 (1962) 52–59.
Imai, K. and Morita, K., Firing squad synchronization problem in reversible cellular automata. Theoret. Comput. Sci. 165 (1996) 475–482. CrossRef
K. Imai, K. Morita and K. Sako, Firing squad synchronization problem in number-conserving cellular automata, in Proc. of the IFIP Workshop on Cellular Automata, Santiago (Chile) (1998).
Kobayashi, K., The Firing Squad Synchronization Problem for Two Dimensional Arrays. Inform. Control 34 (1977) 153–157. CrossRef
Kobayashi, K., Time Optimal Solutions, On of the Firing Squad Synchronization Problem for Two-Dimensional Paths. Theoret. Comput. Sci. 259 (2001) 129–143. CrossRef
S. La Torre, J. Gruska and D. Parente, Optimal Time & Communication Solutions of Firing Squad Synchronization Problems on Square Arrays, Toruses and Rings, in Proc. of DLT'04. Lect. Notes Comput. Sci 3340 (2004) 200–211. Extended version at URL: http://www.dia.unisa.it/~parente/pub/dltExt.ps
S. La Torre, M. Napoli and D. Parente, Synchronization of 1-Way Connected Processors, in Proc. of the 11th International Symposium on Fundamentals of Computation Theory, FCT 1997, Krakow, Poland, September 1–3, 1997, edited by B. Chlebus and L. Czaja, Lect. Notes Comput. Sci. 1279 (1997) 293–304.
La Torre, S., Napoli, M. and Parente, D., Synchronization of a Line of Identical Processors at a Given Time. Fundamenta Informaticae 34 (1998) 103–128.
La Torre, S., Napoli, M. and Parente, D., Compositional Approach, A to Synchronize Two Dimensional Networks of Processors. Theoret. Inform. Appl. 34 (2000) 549–564. CrossRef
Mazoyer, J., A six states minimal time solution to the firing squad synchronization problem. Theoret. Comput. Sci. 50 (1987) 183–238. CrossRef
Mazoyer, J., On optimal solutions to the firing squad synchronization problem. Theoret. Comput. Sci. 168 (1996) 367-404. CrossRef
Mazoyer, J. and Reimen, N., A linear speed up theorem for cellular automata. Theoret. Comput. Sci. 101 (1992) 58–98. CrossRef
J. Mazoyer and V. Terrier, Signals in one dimensional cellular automata. Research Report N. 94–50, École Normale Supérieure de Lyon, France (1994).
F. Minsky, Computation: Finite and Infinite Machines. Prentice-Hall (1967).
E.F. Moore, Sequential Machines, Selected Papers. Addison-Wesley, Reading, Mass, (1964).
Nishitani, Y. and Honda, N., The Firing Squad Synchronization Problem for Graphs. Theoret. Comput. Sci. 14 (1981) 39–61. CrossRef
Roka, Z., The Firing Squad Synchronization Problem on Cayley Graphs, in Proc. of the 20-th International Symposium on Mathematical Foundations of Computer Science MFCS'95, Prague, Czech Republic, 1995. Lect. Notes Comput. Sci. 969 (1995) 402–411. CrossRef
Shinahr, I., Two and Three-Dimensional Firing Squad Synchronization Problems. Inform. Control 24 (1974) 163–180. CrossRef
Waksman, A., An optimum solution to the firing squad synchronization problem. Inform. Control 9 (1966) 66–78. CrossRef