1 INTRODUCTION
The pulsation of a star, as well as it being a component of an eclipsing binary itself, is very important in understanding its evolution. There are several pulsating stars such as Cepheid-type pulsating stars, γ Doradus-type pulsating stars, and δ Scuti-type pulsating stars. All these stars are in the Instability Strip on the main sequence in the Hertzsprung–Russell diagram. An investigation of the frequencies of oscillations, asteroseismology known as stellar seismology, enables us to identify the physical processes behind the pulsating nature and stellar interiors. Pulsating stars play an important role in understanding stellar evolution (Cunha et al. Reference Cunha2007; Aerts, Christensen-Dalsgaard, & Kurtz Reference Aerts, Christensen-Dalsgaard, Kurtz, Burton and Trimble2010). However, in some cases, pulsation features are not enough to solve the entire stellar interior and its nature. In this respect, being a component of a binary can play an important role in solving the problem at hand. In particular, an analysis of the light curve together with radial velocity gives us a large number of physical parameters such as mass, radius, and log g for components of eclipsing binaries (Wilson & Devinney Reference Wilson and Devinney1971; Wilson Reference Wilson1990). Considering both pulsating and eclipsing behaviour, physical natures of stars can be easily identifiable (Lampens Reference Lampens2006; Pigulski Reference Pigulski2006). Although there are many pulsating single stars, a few of them are a component in a binary system, especially an eclipsing system. As seen from the literature, the number of pulsating stars is more than 635, while the incidence of the eclipsing binary component among them is ~5.5% (Kim et al. Reference Kim, Lee, Lee and Youn2010).
In this study, we introduce V1464 Aql as a new candidate for a binary with a pulsating component. In the SIMBAD database, V1464 Aql was classified as a spectroscopic binary system from the spectral type of A2V. In the ASAS database (Pojmánski Reference Pojmánski1997), V1464 Aql’s variability type was suggested to be possibly RR Lyr (RRc), or an eclipsing binary, possibly contact (EC), or a semi-detached system (ESD). The system was listed as a contact binary by Duerbeck (Reference Duerbeck1997) and Pribulla & Rucinski (Reference Pribulla and Rucinski2006) and a spectroscopic binary by Pourbaix et al. (Reference Pourbaix2004). Duerbeck (Reference Duerbeck1997) listed the period of V1464 Aql as 0d.6978, while Rucinski & Duerbeck (Reference Rucinski and Duerbeck2006) listed it as 0d.697822. Detailed spectroscopic observations were made by Rucinski & Duerbeck (Reference Rucinski and Duerbeck2006). They obtained a single-lined radial velocity with an amplitude of 30.62 ± 2.35 s−1. They noted that the lines coming from the visible component are largely broadened. The value of vsin i was found to be 94 ± 4 s−1. They also claim that the spectral type of the system should be F1-2 rather than early A.
In this study, we investigate the nature of this interesting system. For this purpose, we observed the system photometrically and obtained the multi-band light curves, in which short-term intrinsic light variations are seen for the first time. We analysed the light curves and tested the results with the method based on the Fourier transform described by Morris (Reference Morris1985) and Morris & Naftilan (Reference Morris and Naftilan1993). Apart from light-curve analyses, we also detected some large-amplitude pulsation with short period. We analysed the pulsating behaviour.
2 OBSERVATIONS
Observations were acquired with a thermoelectrically cooled ALTA U+42 2048×2048 pixel CCD camera attached to a 40-cm Schmidt–Cassegrains-type MEADE telescope at the Ege University Observatory. Observations were made in BVRI bands during 11 nights on 2011 August 3, 6, 7, 9, 16, and 17, and on 2011 September 4, 8, 15, 19, and 30. V1464 Aql was observed during all the nights in each observation. Some basic parameters of the program stars are listed in Table 1. The names of the stars are listed in the first column, while J2000 coordinates are listed in the second column. The V magnitudes are in the third column and B−V colours are listed in the last column.
Table 1. Basic parameters for the observed stars.

Notes.The coordinates were taken from the SIMBAD database, the brightness and colours were taken from the All-Sky Compiled Catalogue of 2.5 million stars (Kharchenko et al. Reference Kharchenko, Piskunov, Röser, Schilbach, Scholz and Zinnecker2009).
Although program and comparison stars are very close on the sky, using the calibration described by Hardie (Reference Hardie and Hiltner1962), the differential atmospheric extinction corrections were applied. Atmospheric extinction coefficients were obtained from observations of the comparison stars on each night. Heliocentric corrections were also applied to the times of the observations.
The mean averages of the standard deviations are 0.023, 0.011, 0.010, and 0.013 mag for observations acquired in the BVRI bands, respectively. To compute the standard deviations of observations, we used the standard deviations of the reduced differential magnitudes in the sense of comparison minus check stars for each night. No variation was observed in the brightness of comparison stars.
The obtained BVRI data indicated that the system exhibits two main variations in each band. One of them has large amplitude with a longer period, while another has a relatively smaller amplitude with a shorter period. We first investigated the larger variation. For this purpose, we determine the most symmetric and deeper minimum. The light curve obtained in the observations on 2011 September 4 has such a minimum. Using two different methods described by Kwee & van Woerden (Reference Kwee and van Woerden1956) and Winkler (Reference Winkler1967), we computed a minimum time. Both methods gave the same minimum time with almost the same error. Then, using the method of the discrete Fourier transform (DFT; Scargle Reference Scargle1982), we analysed its period by the PERIOD04 software (Lenz & Breger Reference Lenz and Breger2005). The results obtained from DFT were tested by two other methods: first, by CLEANest, which is another Fourier method (Foster Reference Foster1995), and then by the phase dispersion minimization (PDM), which is a statistical method (Stellingwerf Reference Stellingwerf1978). These methods confirmed the results obtained by DFT
All the ephemerides of the system are given by Equation (1). The analyses reveal that the period of the larger variation is close to those given by Duerbeck (Reference Duerbeck1997) and Rucinski & Duerbeck (Reference Rucinski and Duerbeck2006). All the observations were phased with using the ephemeris to prepare the light-curve analyses.
3 LIGHT-CURVE ANALYSES
3.1 Eclipsing binary model
In the literature, V1464 Aql was classified as a contact binary (Duerbeck Reference Duerbeck1997; Pribulla & Rucinski Reference Pribulla and Rucinski2006). In addition, it was noted in the ASAS database (Pojmánski Reference Pojmánski1997) that the system could also be an eclipsing binary, especially a contact binary. Considering this knowledge, we tried to model the light curves with the Wilson–Devinney code (Wilson & Devinney Reference Wilson and Devinney1971; Wilson Reference Wilson1990). For this purpose, we analysed the light curves obtained in the BVRI bands together with the available single-lined radial velocity curve simultaneously, using the PHOEBE V.0.31a software (Prša & Zwitter Reference Prša and Zwitter2005), which is used in the version 2003 of the Wilson–Devinney code (Wilson & Devinney Reference Wilson and Devinney1971; Wilson Reference Wilson1990). We tried to analyse the light curves with several different modes, such as the ‘overcontact binary not in thermal contact’ and ‘double contact binary’ modes. Initial analyses demonstrated that an astrophysically acceptable result can be obtained if the analysis is carried out in the ‘double contact binary’ mode, while no acceptable results could be obtained in the other modes.
In the literature, temperature is given in a range from 6843 K (Ammons et al. Reference Ammons, Robinson, Strader, Laughlin, Fischer and Wolf2006) to 8970 K (Wright et al. Reference Wright, Egan, Kraemer and Price2003) for V1464 Aql. We took JHK brightness of the system (J = 7.963 ± 0.027 mag, H = 7.830 ± 0.027 mag, K = 7.788 ± 0.020 mag) from the NOMAD catalogue (Zacharias et al. Reference Zacharias, Monet, Levine, Urban, Gaume and Wycoff2005). Using these brightnesses, we derived de-reddened colours as (J−H)0 = 0.110 ± 0.038 mag and (H−K)0 = 0.030 ± 0.034 mag for the system. Using the calibrations given by Tokunaga (Reference Tokunaga and Cox2000), we derived the temperature of the primary component as 7420 ± 192 K depending on these de-reddened colours. Taking into account the standard deviation of the brightness in JHK bands, we computed the standard deviation of the temperature as 192 K. Thus, the temperature was found to be 7420 ± 192 K. Thus, the temperature of the primary component was fixed to 7420 ± 192 K in the analyses, and that of the secondary was taken as a free parameter. Considering the spectral type corresponding to this temperature, the albedos (A 1 and A 2) and the gravity-darkening coefficients (g 1 and g 2) of the components were adopted for the stars with the convective envelopes (Lucy Reference Lucy1967; Rucinski Reference Rucinski1969). The nonlinear limb-darkening coefficients (x 1 and x 2) of the components were taken from van Hamme (Reference van Hamme1993). In the analyses, their dimensionless potentials (Ω1 and Ω2), the fractional luminosity (L 1) of the primary component, the inclination (i) of the system, the mass ratio of the system (q), and the semi-major axis (a) were taken as the adjustable free parameters.
Because it is single lined, the available radial velocity curve does not give any mass ratio for the system. Therefore, considering general weighted sum of squared residuals (Σ res2), we tried to find the mass ratio of the system. In analyses, Σ res2 values indicated that the photometric mass ratio of the components is q = 0.71 ± 0.02. According to this result, we assume that the mass ratio of the system is q = 0.71 ± 0.02. The temperature of the secondary component was found to be 6232 K and its error as 27 K. However, the error seems to be unreal in the statistical sense. Taking into account the standard deviation of the brightness in JHK bands, we have computed the standard deviation of the temperature as 161 K. Finally, the temperature was found to be 6232 ± 161 K for the secondary component. All the parameters derived from the analyses are listed in Table 2, while the synthetic light curves are shown in Figure 1. In addition, the radial velocity obtained by Rucinski & Duerbeck (Reference Rucinski and Duerbeck2006) and the synthetic curve are shown in Figure 2. Finally, we also derived the 3D model of Roche geometry and the geometric configurations at four special phases 0.00, 0.25, 0.50, and 0.75 for the system, using the parameters obtained from the light-curve analysis. This 3D model and geometric configurations are shown in Figure 3.
Table 2. Parameters of the components obtained from the light-curve analysis.

a The error is computed depending on the standard deviations of de-reddened colours.

Figure 1. Observed BVRI light curves and synthetic curves obtained from the light-curve analysis and Fourier models. The filled circles represent the observations, while the dashed (blue) lines represent the synthetic curves obtained from the light-curve analysis and the (red) line represents the derived Fourier fits.

Figure 2. Radial velocity (filled circles) obtained by Rucinski & Duerbeck (Reference Rucinski and Duerbeck2006) and the synthetic curve (blue line) derived by using parameters found from the light-curve analysis. The dotted line represents the center-of-mass velocity.

Figure 3. 3D model of Roche geometry and geometric configurations at four special phases 0.00, 0.25, 0.50, and 0.75, illustrated for V1464 Aql, using parameters obtained from the light-curve analysis.
Although no double-lined radial velocity curve is available, we tried to estimate absolute parameters of the components. According to Tokunaga (Reference Tokunaga and Cox2000), the mass of the primary component must be 1.74 ± 0.05 M⊙, corresponding to its surface temperature. Considering possible mass ratio of the system, the mass of the secondary component was found to be 1.23 ± 0.01 M⊙.
Using Kepler’s third law, we calculated the semi-major axis as 4.76 ± 0.03 R⊙. Considering this estimated semi-major axis, the radius of the primary component was computed as 2.10 ± 0.05 R⊙, while that for the secondary component it was 1.80 ± 0.01 R⊙. Using the estimated radii and the obtained temperatures of the components, the luminosity of the primary component was estimated to be 11.97 ± 0.31 L⊙ and that of the secondary component it was 4.41 ± 0.02 L⊙. We have plotted the distribution of radii versus masses and luminosity versus temperature for some stars in Figure 4. The lines represent the ZAMS: Zero-age main sequence theoretical model developed for the stars with Z = 0.02 by Girardi et al. (Reference Girardi, Bressan, Bertelli and Chiosi2000), while dashed lines represent the TAMS: Terminal-age main sequence theoretical model. According to the results, the absolute parameters are generally acceptable in the astrophysical sense.

Figure 4. Locations of the components of V1464 Aql in the mass–radius (upper panel) and temperature–luminosity (bottom panel) distributions. The lines represent the ZAMS theoretical model developed by Girardi et al. (Reference Girardi, Bressan, Bertelli and Chiosi2000), while the dashed lines represent the theoretical TAMS model. The grey lines represent the theoretical evolutional tracks. The filled circles represent the primary component, while the open circles represent the secondary component.
3.2 Elipsoidal binary model
As seen from the Roche geometry shown in Figure 3 and results of the light curve analysis, the system does not exhibit any eclipses. However, the shape of the components should cause some light variation, known as the ellipsoidal variation. Ellipsoidal variable stars are non-eclipsing binary stars and especially close binaries (Morris Reference Morris1985; Beech Reference Beech1985). In the case of the ellipsoidal variables, the inclination angle (i) of the binary is so small that the system does not exhibit any eclipses. The main variation is due to non-spherical shapes of the components. According to Morris (Reference Morris1985), Beech (Reference Beech1985), and Morris & Naftilan (Reference Morris and Naftilan1993), if the main variation occurs due to the ellipsoidal effect, the light curves of the ellipsoidal variables can be modelled by the Fourier analysis given by Equation (2), and one will also expect that the cos (2θ) term must be dominant among all other terms in the results of the Fourier analysis. This is the base of the modern methods used in recent studies, such as Faigler & Mazeh (Reference Faigler and Mazeh2011) and Faigler et al. (Reference Faigler, Mazeh, Quinn, Latham and Tal-Or2012):
All the BVRI light curves were modelled with Fourier series. The derived Fourier models are shown in Figure 1 and Fourier coefficients are listed in Table 3. The Ai coefficients listed in the table are the coefficients of the cos (iθ) terms, while Bi parameters are the coefficients of the sin (iθ) terms given in Equation (2). In fact, the most dominant one is the cos (2θ) term for each of the BVRI bands. Thus, it is obvious that the main effect seen in the light variations is the ellipticity effect. However, if the most dominant one were the cos (θ) term, we would consider the other effects such as magnetic activity occurring on the surface of cool stars. There are many systems that are similar to V1464 Aql, such as 75 Pegasi and 42 Persei (Martin, Hube, & Lyder Reference Martin, Hube and Lyder1990; Martin, Hube, & Brown Reference Martin, Hube and Brown1991), including several others (Faigler & Mazeh Reference Faigler and Mazeh2011; Faigler et al. Reference Faigler, Mazeh, Quinn, Latham and Tal-Or2012).
Table 3. Coefficients derived from the Fourier model.

4 THE PULSATION
Apart from the main variation, there is a shorter period oscillation. To understand the shorter period oscillation, first we obtained all the pre-whitened light curves. To obtain the pre-whitened data, we extracted synthetic light curves from all the observations in each band. In the second step, all the pre-whitened data were analysed with both the DFT (Scargle Reference Scargle1982) and PDM methods (Stellingwerf Reference Stellingwerf1978).
The periods found from the pre-whitened data are listed in Table 4. The normalised power spectra, which exhibit the quality of the period analysis, are shown in Figure 5. Using the light elements given in Equation (1) and the parameters found from the pre-whitened data, all the nightly light variations were modelled for each band. The modelled light variations are shown in Figure 6.
Table 4. Pulsation period found from period analyses in each filter.
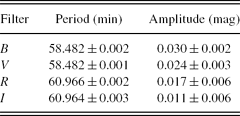

Figure 5. V1464 Aql’s normalised power spectra obtained from period analyses of the pre-whitened data with the DFT method in each band. The power spectra obtained from BVRI bands are given in panels (a–d) respectively.

Figure 6. All the models of nightly light variations.
Soydugan et al. (Reference Soydugan, Soydugan, Demircan and Ibanoǧlu2006) listed some eclipsing binaries whose primary and/or secondary components are pulsating. Using the physical parameters found in this study, the location of V1464 Aql’s primary component is shown in Figure 7. In this figure, following Soydugan et al. (Reference Soydugan, Soydugan, Demircan and Ibanoǧlu2006), the ZAMS (broad line) and TAMS (dashed line) were taken from Girardi et al. (Reference Girardi, Bressan, Bertelli and Chiosi2000). The borders of the Instability Strip on the main sequence were computed from Rolland et al. (Reference Rolland, Costa, Rodriguez, Amado, Garcia-Pelayo, de Coca and Olivares2002). We show that V1464 Aql’s primary component is located among the eclipsing binaries, whose one or two components are in the Instability Strip on the main sequence. The primary component of V1464 Aql is at least a pulsating variable for the case. In the literature, there are also four ellipsoidal variables with a δ Scuti component. As listed in Table 5, these are XX Pyx (Aerts et al. Reference Aerts, Handler, Arentoft, Vandenbussche, Medupe and Sterken2002), HD 173977 (Chapellier et al. Reference Chapellier2004), HD 207651 (Henry, Fekel, & Henry Reference Henry, Fekel and Henry2004), and HD 149420 (Fekel & Henry Reference Fekel and Henry2006). In this case, V1464 Aql is the fifth ellipsoidal variable binary with a δ Scuti component.

Figure 7. Location of V1464 Aql’s primary component in the Instability Strip on the main sequence. The asterisk represents the primary component of V1464 Aql, while the dim circles represent some semi- and undetached binaries taken from Soydugan et al. (Reference Soydugan, Soydugan, Demircan and Ibanoǧlu2006) and references therein. ZAMS and TAMS were taken from Girardi et al. (Reference Girardi, Bressan, Bertelli and Chiosi2000), while the borders of the Instability Strip were computed from Rolland et al. (Reference Rolland, Costa, Rodriguez, Amado, Garcia-Pelayo, de Coca and Olivares2002).
Table 5. Known ellipsoidal binaries having a pulsating component in the literature.

a Taken from the SIMBAD database.
c Henry et al. (Reference Henry, Fekel and Henry2004).
d Chapellier et al. (Reference Chapellier2004).
e Fekel & Henry (Reference Fekel and Henry2006).
As shown by Turner (Reference Turner2011) and Liakos et al. (Reference Liakos, Niarchos, Soydugan and Zasche2012), close binaries with a pulsating component exhibit some calibrations in the log (P orb)–log (P pulse) plane. For this purpose, we took the data of all listed close binaries, with A or F spectral type components, from Turner (Reference Turner2011) and Liakos et al. (Reference Liakos, Niarchos, Soydugan and Zasche2012). We also took the data of listed binaries, with components generally from O or B spectral types, from Aerts & Harmanec (Reference Aerts and Harmanec2004). In addition, we plotted all the long secondary period variables (LSPVs) listed by Kiss et al. (Reference Kiss, Szatmáry, Cadmus and Mattei1999) and Olivier & Wood (Reference Olivier and Wood2003) in the same plane. In the case of binaries with A and F spectral type components, the pulsating components are δ Scuti stars, while the other components are pulsating stars except δ Scuti star for binaries, with spectral type component O or B. Although LSPVs have been a subject of debate in the literature, a relation exists between their periods (Kiss et al. Reference Kiss, Szatmáry, Cadmus and Mattei1999; Olivier & Wood Reference Olivier and Wood2003). In Figure 8, we plotted all the binaries in the log (P orb)–log (P pulse) plane. All the components plotted in this figure are pulsating stars. Moreover, we plotted the pulsating components of all known ellipsoidal variables, whose one component is a δ Scuti star:

Figure 8. Location of V1464 Aql in the log (P orb)–log (P pulse) plane among different types of binary stars. Filled circles represent the observed values, while the lines represent the theoretical linear fit of each group.
Using the GraphPad Prism V5.02 software (Motulsky Reference Motulsky2007), we re-modelled the distribution of each group with the linear fit. Here, the standard deviations of each coefficient and each constant are given in parentheses. The derived linear fits are also plotted in Figure 8. To test whether the derived linear fits are statistically acceptable, we computed the probability value (hereafter p value). The threshold level of significance (α value) was taken to be 0.005 for the p value, which allowed us to test whether the p values are statistically acceptable or not (Wall & Jenkins Reference Wall and Jenkins2003). The derived linear fit is given in Equation (3) for the binaries with spectral type components O and B. The p value was found to be <0.0027. The linear fit of the A–F binaries is given in Equation (4), while that for the ellipsoidal variables is given in Equation (5). The computed p values are <0.0001 for both groups. Considering the α value, the derived linear fits are statistically acceptable.
As Figure 8 shows in the plane of the log (P orb)–log (P pulse) distribution, V1464 Aql is located near the close binaries and ellipsoidal variables with spectral types A and F.
5 RESULTS AND DISCUSSION
In the literature, there are several stars or systems which exhibit combinations of a few different variations. Some of them are eclipsing binaries with a pulsating component, and some semi-regular variables with unknown short-term variations or some pulsating ellipsoidal variables (Derekas et al. Reference Derekas, Kiss, Bedding, Kjeldsen, Lah and Szabó2006; Nie, Zhang, & Jiang Reference Nie, Zhang and Jiang2010; Faigler & Mazeh Reference Faigler and Mazeh2011; Faigler et al. Reference Faigler, Mazeh, Quinn, Latham and Tal-Or2012).
In several studies, V1464 Aql was classified as a spectroscopic binary system, RR Lyr (RRc), an eclipsing binary, possibly contact (EC) or semi-detached system (ESD) (Duerbeck Reference Duerbeck1997; Pourbaix et al. Reference Pourbaix2004; Pribulla & Rucinski Reference Pribulla and Rucinski2006; Rucinski & Duerbeck Reference Rucinski and Duerbeck2006). We analysed the BVRI light curves. As shown in Table 2, the inclination of the system (i) is found to be 38°.45 ± 0°.22. In the case of this (i) value, the system does not exhibit any eclipses. As shown in Figure 3, the 3D geometric configurations derived at four special phases for the system also demonstrated the non-eclipsing cases. However, these configurations indicate that the system is on the edge of eclipsing. Although the system may exhibit grazing eclipses, these eclipses are not seen in other small variability. As estimated in the literature, the 3D model of Roche geometry reveals that the components of the system are close to filling their Roche lobes. According to these results, V1464 Aql should be a candidate of the contact binary system, but non-eclipsing due to the inclination of the system (i). The Fourier analysis also supported this result. The coefficients of the cos (2θ) term (A 2) were found to be 0.0492 ± 0.0008, 0.0372 ± 0.0007, 0.0355 ± 0.0006, and 0.0327 ± 0.0005 for the BVRI bands, respectively. According to these values, the main effect, known as the ellipsoidal effect, in the light variation of the system comes from the shape of the components.
According to the calibration described by Tokunaga (Reference Tokunaga and Cox2000), the mass of the primary component should be 1.74 ± 0.05 M⊙ corresponding to its surface temperature. Under this assumption, the light-curve analysis reveals that the temperature of the secondary component was found to be 6232 ± 161 K. The light-curve analysis indicates that the mass ratio of the system should be q = 0.71 ± 0.02. Note that the standard deviation of the primary component temperature and absolute parameters were computed depending on the standard deviations given for the colours in the NOMAD catalogue (Zacharias et al. Reference Zacharias, Monet, Levine, Urban, Gaume and Wycoff2005). However, the error in temperature was found from the light-curve analysis for the secondary component. Considering the standard deviations of other parameters, it seems slightly lower than expected. The locations of the components plotted in Figure 4 demonstrated that the results of the analysis are acceptable in the astrophysical sense. On the contrary, the secondary component is seen closer to the TAMS than the primary in Figure 4. The stars seem not to be coeval to each other. However, it is well known that there are several binaries such as YY CrB (Essam et al. Reference Essam, Saad, Nouh, Dumitrescu, El-Khateeb and Haroon2010), BS Cas (Yang, Wei, & He Reference Yang, Wei and He2008), VZ Tri (Yang Reference Yang2010). All these samples exhibit the same behaviour. Their common properties are that all of them are contact binaries with a large period variation due to the large mass transfer. Indeed, if V1464 Aql is an analogue of these systems, this makes V1464 Aql very important for future studies.
The fractional radii were found to be r 1 = 0.441 ± 0.002 for the primary component and r 2 = 0.378 ± 0.002 for the secondary component. In this case, the sum of fractional radii was computed as r 1+r 2≃0.80. Thus, V1464 Aql seems to be in agreement with Kopal (Reference Kopal1956)’s criteria for overcontact systems. The period analysis indicates the orbital period as 0.697822 d. In addition, the temperature of the primary component is 7420 ± 192 K and that of the secondary component is 6232 ± 161 K. Although some contact binaries have components with some different surface temperature, they generally have the same surface temperature. Here, the primary component of V1464 Aql is hotter than the secondary component. Considering some characteristics of the system such as the short orbital period, small mass ratio, and hotter primary component, V1464 Aql seems to be in agreement with those of A-type W UMa binaries (Berdyugina Reference Berdyugina2005; Rucinski Reference Rucinski, Pringle and Wade1985). The period analyses reveal that the period of the short-term variation was found to be 58.482 ± 0.002, 58.482 ± 0.001, 60.966 ± 0.002, and 60.964 ± 0.003 min in BVRI bands, respectively. However, we did not find any secondary frequency for the short-term variation. The period differences between each band may be due to the different sensitivity of each band. The sensitivity decreases from the B to I bands, because the amplitude of the pulsation is decreasing from the B to I bands. One can see from the standard deviations given in Table 4 and light curves in Figure 6, the scattering in the light curves increases from the B to I bands. Our period analysis methods depend on the statistical method. The analyses gave the best period statistically for the pulsation in each band. In this case, the most reliable periods are found from the B and V bands.
Figure 5 indicates that the short-term variation is dominant in shorter wavelengths rather than longer wavelengths. In fact, this is also seen clearly in Figure 6. The amplitude of the short-term variation gets larger from the I band to the B band. Moreover, the primary component is located in the Instability Strip on the main sequence, as seen in Figure 7. Considering the mass of the primary component and also the period of this short-term variation, this second variation should be caused due to the pulsation of the primary component. According to Aerts et al. (Reference Aerts, Christensen-Dalsgaard, Kurtz, Burton and Trimble2010), the periods of δ Scuti stars are in the range of 18 min to 8 h. Moreover, their mass is in the range of 1.50–2.50 M⊙. The mass value of the component and the period of the short-term variation are in agreement with these values. In this case, this variation should be caused by the pulsation of a δ Scuti star.
As shown in Figure 1, the light curves seem to be scattered. There are also a few light curves in the ASAS database (Pojmánski Reference Pojmánski1997), which are also very scattered. However, the models of pulsation shown in Figure 6 demonstrate that the scattering in the light curves is caused due to the pulsation.
In the literature, there are four systems whose light curves have the same properties. In addition, these are ellipsoidal variables, which have a δ Scuti component. Aerts et al. (Reference Aerts, Handler, Arentoft, Vandenbussche, Medupe and Sterken2002) found more than 10 frequencies due to the δ Scuti component in XX Pyx, whose orbital period is 1.15 d. HD 207651 is a triple system. Henry et al. (Reference Henry, Fekel and Henry2004) demonstrated that its component A is an ellipsoidal binary with a δ Scuti component. They found a few pulsation frequencies and the more possible one is 0.7354 d. Chapellier et al. (Reference Chapellier2004) found ~0.1169 d for the pulsation in the case of HD 173977. According to the light-curve analysis of Fekel & Henry (Reference Fekel and Henry2006), HD 149420 should be an eclipsing binary. However, it is likely to be an ellipsoidal variable. They found the pulsating periods of δ Scuti component as 0.076082 d and 0.059256 d. In the case of V1464 Aql, we found the pulsating period as ~0.040641 d.
On the contrary, in the literature, the classification of V1464 Aql is a subject of debate (Pojmánski Reference Pojmánski1997; Duerbeck Reference Duerbeck1997; Pribulla & Rucinski Reference Pribulla and Rucinski2006; Pourbaix et al. Reference Pourbaix2004). Because of this, we plotted V1464 Aql among different binary types and variables in the log (P orb)–log (P pulse) plane shown in Figure 8. As shown in the figure, V1464 Aql is indeed located near the close and ellipsoidal binaries with spectral type components A and F. This also supports the observation that the effective temperature found for the primary component of V1464 Aql is generally acceptable in the astrophysical sense. In addition, we also derived some new calibrations for different types of binaries. Both Turner (Reference Turner2011) and Liakos et al. (Reference Liakos, Niarchos, Soydugan and Zasche2012) have already derived the calibration for close binaries. In particular, Liakos et al. (Reference Liakos, Niarchos, Soydugan and Zasche2012) derived the calibrations separately for detached and semi-detached binaries. As given in Equation (3), combining all the close binaries listed by both Turner (Reference Turner2011) and Liakos et al. (Reference Liakos, Niarchos, Soydugan and Zasche2012), we derived the calibration together for close binaries from the spectral types A and F. Thus, we obtained more reliable calibrations, using a larger data set. In addition, the calibration has not been derived previously for binaries from the spectral types O and B. Although one of their components is pulsating in these binaries, they are generally different from δ Scuti stars. As given in Equation (4), we tried, for the first time, to derive a similar calibration for these stars. A similar calibration was derived for ellipsoidal binaries, as given in Equation (5).
Rucinski & Duerbeck (Reference Rucinski and Duerbeck2006) noted that there are largely broadened lines that come from the visible component. They also found that the vsin i value of the component is 94 ± 4 s−1. Although this rapid rotation can cause the broadening in the lines, it can also be caused by pulsation. Moreover, the surface temperature of the primary component is 7420 ± 192 K, while it is 6232 ± 161 K for the secondary component. In this case, it is expected that we see double lines in the spectrum, though the inclination of the system (i) is 38°.45. However, Rucinski & Duerbeck (Reference Rucinski and Duerbeck2006) stated that V1464 Aql is a single-lined system, and the amplitude of the radial velocity is 30.62 ± 2.35 s−1. The amplitude of the radial velocity is large enough that it can easily confuse one’s mind. In this case, we also expected to see the lines of the secondary component and thus its radial velocity. On the contrary, considering both the spectral and photometrical results together, rapid rotation and pulsation nature of the primary component can have some effects on its spectrum in the case of a lower inclination (i) at 38°.45. The broadening of the lines should make the lines coming from the secondary component disappear.
Consequently, V1464 Aql is a new candidate for the ellipsoidal system with a pulsating component. Future work will study its pulsating nature in more detail, thus revealing the absolute nature of the system.
ACKNOWLEDGMENTS
The author acknowledges the generous observing time awarded to the Ege University Observatory. The author also thanks the referee for useful comments that significantly improved the paper.
















