Article contents
XXII.—Tables of the Elliptic-cylinder Functions
Published online by Cambridge University Press: 15 September 2014
Extract
Although the physical problem which originally led to the Mathieu equation
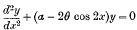
is now well over sixty years old, and although other problems studied in more recent years, such as the scattering of electric waves by an elliptic cylinder, depend essentially on the same equation, no thorough investigation of detail has hitherto been possible owing to the lack of tables of the functions defined by the equation. In fact, until 1924 all attempts to reduce the functions to a form suitable for calculation had failed. In that year a successful method of attack was discovered by the present writer, who then undertook the computation of the tables which are here published.
- Type
- Proceedings
- Information
- Copyright
- Copyright © Royal Society of Edinburgh 1933
References
page 355 note * Mathieu, Émile, “Mémoire sur le mouvement vibratoire d'une membrane de forme elliptique,” Journal de Mathématiques (Liouville) (2), xiii, 1868, 137–203.Google Scholar See also Whittaker and Watson, Modern Analysis, chap, xix, and the Monograph by Humbert, P., “Fonctions de Lamé et Fonctions de Mathieu” (Mémorial des Sciences mathématiques, x, Paris, 1926)Google Scholar, in which will be found a bibliography, practically complete up to 1924.
page 355 note † Ince, , “Researches into the Characteristic Numbers of the Mathieu Equation,” Proceedings of the Royal Society of Edinburgh, xlvi, 1925-1926, 20–29, 316-322; xlvii, 1926-27, 294-301.Google Scholar
page 356 note * An old problem in which u(ξ) is not involved with u(iη) is that of a stretched string one of whose ends is subjected to a periodic vibration (Rayleigh, Lord, “On Maintained Vibrations,” Philosophical Magazine, xv, 1883, 229–235CrossRefGoogle Scholar; Scientific Papers, ii, 188-193).
page 356 note † Except when θ = 0 the Mathieu equation cannot have more than one solution of period π or 2π (cf. Ince, , Proceedings of the Cambridge Philosophical Society, xxi, 1922, 117–120).Google Scholar
page 356 note ‡ The number of zeros of any particular elliptic-cylinder function is independent of θ (cf. Ince, , Journal of the London Mathematical Society, 2, 1925, 47).Google Scholar
page 357 note * This definition was suggested by Goldstein, (Transactions of the Cambridge Philosophical Society, xxiii, 1927, 303)Google Scholar, who, however, defined ce 0(x, θ) exceptionally, so that it should reduce to unity when θ = 0. Unfortunately this destroys the asymptotic equality between ce 0(x, θ) and se 1(x, θ) as θ→ + ∞. According to the present definition, ce 0(x, 0) has the irrational value 1 / √2, but that is a very slight disadvantage.
page 358 note * Note that A0 cannot vanish, except for θ = 0, unless the function vanishes identically. On the other hand, any other coefficient may vanish. Thus A2 vanishes when a = 0, A4 vanishes when a 2 - 4a - 2θ2 = 0, and so on. It is therefore impracticable to define ce 2n(x, θ) by stipulating (as Mathieu did) that the coefficient of cos 2nx in the expansion shall be unity.
page 358 note † The analogy with Σ and Π for series and products will be evident. Note the convention that the leading numerator is unity.
page 361 note * The first of these machines was purchased with a grant given by the Government Grant Committee of the Royal Society; the remainder are machines belonging to the Department of Pure Mathematics of the Egyptian University. The capacity is indicated by (i) the number of setting levers; (ii) the number of figures in the multiplier register; and (iii) the number of figures in the product register. A Miniature Brunsviga (9 : 8 :13) was sometimes used for incidental work.
page 361 note † This work occupied the greater part of the period November 1926 to April 1930. The tables calculated in accordance with this original definition are deposited with the Royal Society of Edinburgh. They are of the same range as the tables now published, but show the functions to eight places of decimals, with second and fourth differences.
page 362 note * Five-figure tables of the Fourier coefficients of the five functions of lowest order, including some very high values of the parameter, were given by Goldstein, , loc. cit., after p. 336.Google Scholar
- 31
- Cited by


