^{page 640 note *} In Euclid's Geometry the functions of definition and axiom are not always clearly separated; at all events, some of his definitions serve purposes for which others are unfit, and this must be kept in view in what follows. With postulates I have at present nothing to do, as I am concerned solely with geometrical theorems. The mixture of problems with theorems is a peculiarity of Euclid's method for which there is no absolute necessity, and which is certainly inconvenient in an elementary text-book. Geometrical constructions are in a sense the applications of geometrical theory, and ought to be kept by themselves. The Society for the Improvement of Geometrical Knowledge have acted wisely, I think, in following this arrangement in their syllabus.

^{page 642 note *} Two figures are said to be congruent when one can be placed on the other, so that every point of one shall coincide with a point of the other, and vice versa. The phrase equal in every respect is used in the same sense in most English editions of Euclid.

^{page 643 note *} It is interesting to notice that any curve already conditioned a number of times less by two than the whole number of conditions that completely determine it, fulfils in many respects the definition of a straight line, for any two points completely determine the curve. A very interesting particular case is that of a series of circles which always pass through a given fixed point. Such a series of circles may take the place of straight lines in many of Euclid's propositions. Most of the propositions as to congruency hold for them. The sum of the three angles of a triangle formed by three such circles is two right angles; the perpendiculars from the vertices of such a triangle on the opposite sides are concurrent; and so on, as is otherwise evident by the theory of inversion.

^{page 644 note *} I have not been able to find a definite settlement of this question by any of the great authorities on hyper space. Frischauf takes double elliptic space as the representative of elliptic space, and seems to hold that this is the only possible kind. Klein (“Mathematische Annalen,” vi. 125) takes single elliptic space, and criticises Frischauf's view (“Fortschritte der Mathematik,” viii. 313, 1876). Newcomb (Borchardt's Journ., lxxxiii. p. 293) professes himself unable to settle the question. If the notion of double elliptic space cannot be shown to be self-contradictory, then it would appear that the question becomes simply one of the choice of axioms. See note below, p. 661.

^{page 645 note *} An ellipse and a circle are unbounded but finite lines; a hyperbola is both unbounded and infinite.

^{page 645 note †} I adopt the sign ≃ used by continental writers for congruent to, or equal in every respect to.

^{page 650 note *} I leave the reader to consider and settle for himself whether a simpler proposition than the above could be established. In particular he should consider the following problem in hyperbolic geometry:—“To construct an isosceles triangle of given area on a given base.”

^{page 651 note *} Before leaving this part of the subject, I may mention the curious solution of the problem of dividing a plane in hyperbolic space into a network of regular polygons.

If n be the number of sides of each polygon, p the number of polygons round a point of the network, A the area of each of the n-gons, then

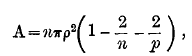
with thecondition

Suppose, for instance, we wish to divide a plane into squares, i.e., regular four-sided figures. Then n = 4. If p = 4, i.c., if the angles of the square be right angles, A = 0, which does not, strictly speaking, give a solution. The next case is p = 5, so that A= is the area of the smallest finite square with which we could pave a plane floor. Of course there are an infinite number of solutions, the angles of the squares becoming less and their area greater as p increases. The area of the greatest possible square tile that we could use would be , but the lengths of the sides would be infinite.

^{page 657 note *} In the language of modern geometry the points at infinity on a straight line in elliptic space are imaginary.

^{page 661 note *} The differential equations (2) and (2) contain all the metrical properties of elliptic and hyperbolic space. (2) suggests that a pair of straight lines diverging at a small angle from a point might intersect again in distinct points any number of times. The proposition proved above for elliptic space generally, that all the lines radiating from any point intersect in the same second point, seems, however, to compel us to conclude that at the point where any line intersects another for the second time, it must return into itself; for a line can be brought by continuous rotation into coincidence with its prolongation, hence we must reach the same second point of intersection in whichever direction we proceed from the first point. I can see no way out of this at present; and if there is none, it would appear that we cannot get beyond double elliptic space, even if we can consistently get so far.

^{page 661 note †} I may refer the reader to Frischauf, “Elemente der Absolute Geometrie,” Leipzig, 1876; Lobatschewsky, Crellc, xvii. p. 295; Klein, Annalen der Mathematik, iv. p. 573. vi. p. 112, &c.; Cayley, Annalen der Mathematik, v. p. 630.