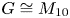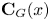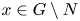1. Introduction
All groups are supposed to be finite. Recall that $G$![]() is called a minimal non-abelian group if $G$
is called a minimal non-abelian group if $G$![]() is non-abelian but every proper subgroup of $G$
is non-abelian but every proper subgroup of $G$![]() is abelian. We denote by ${F}(G)$
is abelian. We denote by ${F}(G)$![]() the Fitting subgroup of $G$
the Fitting subgroup of $G$![]() . The upper nilpotent series $\{F_i(G)\}_{i\geq 0}$
. The upper nilpotent series $\{F_i(G)\}_{i\geq 0}$![]() of a group $G$
of a group $G$![]() is defined recursively by $F_0(G)=1$
is defined recursively by $F_0(G)=1$![]() and $F_i(G)/F_{i-1}(G)=F(G/F_{i-1}(G))$
and $F_i(G)/F_{i-1}(G)=F(G/F_{i-1}(G))$![]() for $i\geq 1$
for $i\geq 1$![]() . If $G$
. If $G$![]() is a solvable group, then the smallest integer $h$
is a solvable group, then the smallest integer $h$![]() such that $F_h(G)=G$
such that $F_h(G)=G$![]() is called the Fitting length (or nilpotent length) of $G$
is called the Fitting length (or nilpotent length) of $G$![]() and is denoted by $h(G)$
and is denoted by $h(G)$![]() . All unexplained notation and terminology are standard (see [Reference Kurzweil and Stellmacher19]).
. All unexplained notation and terminology are standard (see [Reference Kurzweil and Stellmacher19]).
A group $G$![]() is called a CP-group if every element of $G$
is called a CP-group if every element of $G$![]() has prime power order. The question about CP-groups was first addressed by Higman in [Reference Higman16], who determined all solvable CP-groups. In [Reference Heineken15], Heineken gave the general structure of non-solvable CP-groups and listed all simple CP-groups.
has prime power order. The question about CP-groups was first addressed by Higman in [Reference Higman16], who determined all solvable CP-groups. In [Reference Heineken15], Heineken gave the general structure of non-solvable CP-groups and listed all simple CP-groups.
Denote $H_{p^n}(G):=\langle x\in G|x^{p^n}\neq 1 \rangle$![]() for some prime $p\mid |G|$
for some prime $p\mid |G|$![]() . In [Reference Hughes and Thompson14], Hughes and Thompson determined the structure of group $G$
. In [Reference Hughes and Thompson14], Hughes and Thompson determined the structure of group $G$![]() if $H_p(G)$
if $H_p(G)$![]() is a proper subgroup of $G$
is a proper subgroup of $G$![]() and $G$
and $G$![]() is not a $p$
is not a $p$![]() -group. Some authors studied those groups $G$
-group. Some authors studied those groups $G$![]() having a proper subgroup $H_{p^n}(G)$
having a proper subgroup $H_{p^n}(G)$![]() where $n>1$
where $n>1$![]() , for instance, [Reference Bryce3, Reference Espuelas5]. Clearly, each element of $G\setminus H_{p^n}(G)$
, for instance, [Reference Bryce3, Reference Espuelas5]. Clearly, each element of $G\setminus H_{p^n}(G)$![]() is a $p$
is a $p$![]() -element. Motivated by the ideas above, we study the structure of a group $G$
-element. Motivated by the ideas above, we study the structure of a group $G$![]() that satisfies the following:
that satisfies the following:
Property ($\ast$![]() ): Let $G$
): Let $G$![]() be a group and $N$
be a group and $N$![]() be a proper normal subgroup of $G$
be a proper normal subgroup of $G$![]() . Assume that every element of $G\setminus N$
. Assume that every element of $G\setminus N$![]() has prime power order.
has prime power order.
Clearly, every CP-group $G$![]() trivially satisfies property ($\ast$
trivially satisfies property ($\ast$![]() ). Our main theorem is:
). Our main theorem is:
Theorem A Let $G$![]() be a group and $N$
be a group and $N$![]() be a non-trivial normal subgroup of $G$
be a non-trivial normal subgroup of $G$![]() . Suppose that $G$
. Suppose that $G$![]() and $N$
and $N$![]() satisfy property $(\ast )$
satisfy property $(\ast )$![]() . If $N$
. If $N$![]() is non-solvable, then every non-solvable chief factor $H/K$
is non-solvable, then every non-solvable chief factor $H/K$![]() of $G$
of $G$![]() satisfying $H\leq N$
satisfying $H\leq N$![]() is isomorphic to $PSL_2(3^f)$
is isomorphic to $PSL_2(3^f)$![]() , where $f>1$
, where $f>1$![]() is a 2-power. In particular, $G/N$
is a 2-power. In particular, $G/N$![]() is solvable.
is solvable.
Remark 1 In [Reference Zhurtov, Lytkina and Mazurov28, Theorem 1], it is asserted that ‘Let $\Delta (q)$![]() be a subgroup of the automorphism group of a finite simple group $L_2(q)$
be a subgroup of the automorphism group of a finite simple group $L_2(q)$![]() generated by its inner automorphism group and by an automorphism $\varphi \delta$
generated by its inner automorphism group and by an automorphism $\varphi \delta$![]() , where $\varphi$
, where $\varphi$![]() and $\delta$
and $\delta$![]() are the generators for the groups of field and diagonal automorphisms of $L_2(q)$
are the generators for the groups of field and diagonal automorphisms of $L_2(q)$![]() , respectively. If $G$
, respectively. If $G$![]() is a finite generalized Frobenius group with an insoluble kernel $F$
is a finite generalized Frobenius group with an insoluble kernel $F$![]() , then $|G:F| = 2$
, then $|G:F| = 2$![]() and $G/{\rm Sol}(F)$
and $G/{\rm Sol}(F)$![]() is isomorphic to $\Delta (q)$
is isomorphic to $\Delta (q)$![]() , where $q=3^{2^{l}}$
, where $q=3^{2^{l}}$![]() for some natural number $l$
for some natural number $l$![]() . Here, ${\rm Sol}(F)$
. Here, ${\rm Sol}(F)$![]() denotes the largest solvable normal subgroup of $F$
denotes the largest solvable normal subgroup of $F$![]() ’.
’.
In fact, the chief factor in theorem A is not necessarily a simple group. Let $F:= S_1\times S_2$![]() , where $S_1\cong S_2\cong PSL_2(9)$
, where $S_1\cong S_2\cong PSL_2(9)$![]() and let further $\varphi _i,\, \delta _i \in {\rm Aut}(S_i)$
and let further $\varphi _i,\, \delta _i \in {\rm Aut}(S_i)$![]() be field and diagonal automorphisms of $S_i$
be field and diagonal automorphisms of $S_i$![]() , for $i = 1,\, 2$
, for $i = 1,\, 2$![]() , respectively, and $u_i = \varphi _i \delta _i$
, respectively, and $u_i = \varphi _i \delta _i$![]() . It is easy to see that every element in $S_iu_i$
. It is easy to see that every element in $S_iu_i$![]() is a 2-element by [Reference Conway, Curtis, Norton, Parker and Wilson4]. Suppose that $G = F\langle u\rangle$
is a 2-element by [Reference Conway, Curtis, Norton, Parker and Wilson4]. Suppose that $G = F\langle u\rangle$![]() , where $u = u_1u_2$
, where $u = u_1u_2$![]() . Obviously, ${\rm Sol}(F) = 1$
. Obviously, ${\rm Sol}(F) = 1$![]() and $G \setminus F = Fu = (S_1u_1)\times (S_2u_2)$
and $G \setminus F = Fu = (S_1u_1)\times (S_2u_2)$![]() . Hence, every element in $G \setminus F$
. Hence, every element in $G \setminus F$![]() is also a 2-element. But in this case, $F$
is also a 2-element. But in this case, $F$![]() is not a non-abelian simple group. Hence, there must be a mistake in [Reference Zhurtov, Lytkina and Mazurov28, Theorem 1].
is not a non-abelian simple group. Hence, there must be a mistake in [Reference Zhurtov, Lytkina and Mazurov28, Theorem 1].
The key ingredient for proving theorem A is theorem B, which has interest on its own.
Theorem B Let $N$![]() be a non-abelian simple group and Aut$(N)$
be a non-abelian simple group and Aut$(N)$![]() be its automorphism group. If $u\in {\rm Aut}(N)\setminus N$
be its automorphism group. If $u\in {\rm Aut}(N)\setminus N$![]() is an $r$
is an $r$![]() -element for some prime $r$
-element for some prime $r$![]() such that every element of $Nu$
such that every element of $Nu$![]() has prime power order, then $N\cong PSL_2(3^f)$
has prime power order, then $N\cong PSL_2(3^f)$![]() with integer $f$
with integer $f$![]() , $u=\delta \varphi$
, $u=\delta \varphi$![]() is a product of a diagonal automorphism $\delta$
is a product of a diagonal automorphism $\delta$![]() and a field automorphism $\varphi$
and a field automorphism $\varphi$![]() of $N$
of $N$![]() . In particular, $o(\varphi )=f$
. In particular, $o(\varphi )=f$![]() is a power of 2.
is a power of 2.
Remark 2 Although this theorem is proved in [Reference Li and Wang21], our method is quite different since we consider the element orders of the coset of $Soc(G)$![]() , where $G$
, where $G$![]() is an almost simple group, while the proof of [Reference Li and Wang21] is relying on theory of classical groups. Of course, both of the proofs depend on the classification of finite simple groups.
is an almost simple group, while the proof of [Reference Li and Wang21] is relying on theory of classical groups. Of course, both of the proofs depend on the classification of finite simple groups.
It is well-known that maximal subgroups play an important role in researching the structure of groups. For instance, a straightforward result asserts that $G$![]() is solvable when all its maximal subgroups have prime indices. On the contrary, the influence of the centralizers of elements on the structure of groups is also studied extensively. For instance, the authors of [Reference Feit, Hall and Thompson6, Reference Suzuki25] investigated groups in which the centralizer of any non-trivial element is nilpotent, while the authors of [Reference Ashrafi2, Reference Jararian Amiri, Amiri and Rostami18] studied groups with conditions on centralizers. As an application of Theorem A, we get the following result:
is solvable when all its maximal subgroups have prime indices. On the contrary, the influence of the centralizers of elements on the structure of groups is also studied extensively. For instance, the authors of [Reference Feit, Hall and Thompson6, Reference Suzuki25] investigated groups in which the centralizer of any non-trivial element is nilpotent, while the authors of [Reference Ashrafi2, Reference Jararian Amiri, Amiri and Rostami18] studied groups with conditions on centralizers. As an application of Theorem A, we get the following result:
Corollary 1 Let $G$![]() be a group and $N\unlhd G$
be a group and $N\unlhd G$![]() . If every element $x\in G\setminus N$
. If every element $x\in G\setminus N$![]() has prime power order, and ${\bf C}_G(x)$
has prime power order, and ${\bf C}_G(x)$![]() is maximal in $G$
is maximal in $G$![]() , then $N$
, then $N$![]() is solvable.
is solvable.
Furthermore, we investigate the structure of group $G$![]() if the centralizer of each element in $G\setminus N$
if the centralizer of each element in $G\setminus N$![]() is maximal in $G$
is maximal in $G$![]() , where $N$
, where $N$![]() is a normal subgroup of $G$
is a normal subgroup of $G$![]() . Zhao, Chen, and Guo gave the structure of group $G$
. Zhao, Chen, and Guo gave the structure of group $G$![]() when $N=G$
when $N=G$![]() , and proved that:
, and proved that:
Theorem 3 ([Reference Zhao, Chen and Guo26, Theorems A and B])
Let $G$![]() be a non-abelian group. Write $\overline {G}:=G/{\bf Z}(G)$
be a non-abelian group. Write $\overline {G}:=G/{\bf Z}(G)$![]() . If for any $x\in G\setminus {\bf Z}(G)$
. If for any $x\in G\setminus {\bf Z}(G)$![]() , ${\bf C}_G(x)$
, ${\bf C}_G(x)$![]() is maximal in $G$
is maximal in $G$![]() , then $\overline {G}$
, then $\overline {G}$![]() is either an elementary abelian $p$
is either an elementary abelian $p$![]() -group, or $\overline {G}=\overline {P}\rtimes \overline {Q}$
-group, or $\overline {G}=\overline {P}\rtimes \overline {Q}$![]() is an inner abelian group with $|\overline {P}|=p^a$
is an inner abelian group with $|\overline {P}|=p^a$![]() and $|\overline {Q}|=q$
and $|\overline {Q}|=q$![]() , where $p$
, where $p$![]() and $q$
and $q$![]() are two different primes, and $a$
are two different primes, and $a$![]() is a positive integer.
is a positive integer.
In this paper, we consider the case ${\bf Z}(G)< N$![]() , and obtain that:
, and obtain that:
Theorem D Let $G$![]() be a group and $N$
be a group and $N$![]() be a proper normal subgroup of $G$
be a proper normal subgroup of $G$![]() such that ${\bf Z}(G)< N$
such that ${\bf Z}(G)< N$![]() . If ${\bf C}_G(x)$
. If ${\bf C}_G(x)$![]() is maximal in $G$
is maximal in $G$![]() for every element $x\in G\setminus N$
for every element $x\in G\setminus N$![]() , then $G$
, then $G$![]() is solvable with $G/N$
is solvable with $G/N$![]() abelian. Furthermore,
abelian. Furthermore,
(I) If $G$
 is nilpotent, then $G/N$
is nilpotent, then $G/N$ is a $p$
is a $p$ -group for some prime $p$
-group for some prime $p$ . Moreover, $G=P\times {\bf Z}(G)_{p'}$
. Moreover, $G=P\times {\bf Z}(G)_{p'}$ and ${\bf C}_G(x)\unlhd G$
and ${\bf C}_G(x)\unlhd G$ for every $x\in P\setminus N$
for every $x\in P\setminus N$ ;
;(II) $G$
 is non-nilpotent, then $|G:{\bf C}_G(x)|=r^a$
is non-nilpotent, then $|G:{\bf C}_G(x)|=r^a$ with prime $r$
with prime $r$ and positive integer $a$
and positive integer $a$ . Suppose that $R$
. Suppose that $R$ is a Sylow $r$
is a Sylow $r$ -subgroup of $G$
-subgroup of $G$ and $K$
and $K$ is a Hall $r'$
is a Hall $r'$ -subgroup of $G$
-subgroup of $G$ , then one of the statements holds:
, then one of the statements holds:
(1) If $G/N$
 is a $p$
is a $p$ -group for some prime $p$
-group for some prime $p$ , we have
, we have
(1.1) If $r=p$
 , write $\overline {G}:=G/{\bf O}_p(G){\bf Z}(G)$
, write $\overline {G}:=G/{\bf O}_p(G){\bf Z}(G)$ . Then $\overline {G}=\overline {K}\rtimes \overline {P}$
. Then $\overline {G}=\overline {K}\rtimes \overline {P}$ is a Frobenius group with abelian kernel $\overline {K}$
is a Frobenius group with abelian kernel $\overline {K}$ and complement $\overline {P}$
and complement $\overline {P}$ of order $p$
of order $p$ .
.(1.2) If $r\neq p$
 , write $\widetilde {G}:=G/{\bf Z}(G)_r$
, write $\widetilde {G}:=G/{\bf Z}(G)_r$ . Then
. Then
(1.2.1) If ${\bf O}_r(\widetilde {G})=\widetilde {1}$
 , then the Fitting length $h(\widetilde {G})=3$
, then the Fitting length $h(\widetilde {G})=3$ and $\widetilde {G}$
and $\widetilde {G}$ has the following normal series:
\[ \widetilde{1}\unlhd {\bf O}_{r'}(\widetilde{G})\unlhd {\bf O}_{r',r}(\widetilde{G})\unlhd \widetilde{G}={\bf O}_{r',r,r'}(\widetilde{G}), \]where ${\bf O}_{r',r}(\widetilde {G})/{\bf O}_{r'}(\widetilde {G})\cong \widetilde {R}$
has the following normal series:
\[ \widetilde{1}\unlhd {\bf O}_{r'}(\widetilde{G})\unlhd {\bf O}_{r',r}(\widetilde{G})\unlhd \widetilde{G}={\bf O}_{r',r,r'}(\widetilde{G}), \]where ${\bf O}_{r',r}(\widetilde {G})/{\bf O}_{r'}(\widetilde {G})\cong \widetilde {R}$
 is elementary abelian and $\widetilde {G}/{\bf O}_{r',r}(\widetilde {G})$
is elementary abelian and $\widetilde {G}/{\bf O}_{r',r}(\widetilde {G})$ is a $p$
is a $p$ -group;
-group;(1.2.2) Assume that ${\bf O}_r(\widetilde {G})=\widetilde {R}$
 . If ${\bf C}_G(x)_{p'}\nleq {\bf Z}(G)$
. If ${\bf C}_G(x)_{p'}\nleq {\bf Z}(G)$ , then the Fitting length $h(\widetilde {G})=2$
, then the Fitting length $h(\widetilde {G})=2$ and $\widetilde {G}$
and $\widetilde {G}$ has the following normal series:
\[ \widetilde{1}\unlhd \widetilde{R}\unlhd \widetilde{N}\unlhd \widetilde{G}, \]where $\widetilde {R}$
has the following normal series:
\[ \widetilde{1}\unlhd \widetilde{R}\unlhd \widetilde{N}\unlhd \widetilde{G}, \]where $\widetilde {R}$
 is an elementary abelian $r$
is an elementary abelian $r$ -group and $G/R$
-group and $G/R$ is nilpotent.
is nilpotent.(1.2.3) Write $\widehat {G}:=G/{\bf Z}(G)$
 . Assume that ${\bf O}_r(\widetilde {G})=\widetilde {R}$
. Assume that ${\bf O}_r(\widetilde {G})=\widetilde {R}$ . If ${\bf C}_G(x)_{p'}\leq {\bf Z}(G)$
. If ${\bf C}_G(x)_{p'}\leq {\bf Z}(G)$ , then $\widehat {G}=\widehat {R}\rtimes \widehat {P}$
, then $\widehat {G}=\widehat {R}\rtimes \widehat {P}$ , where $P$
, where $P$ is a Sylow $p$
is a Sylow $p$ -subgroup of $G$
-subgroup of $G$ and $R$
and $R$ is a Sylow $r$
is a Sylow $r$ -subgroup of $G$
-subgroup of $G$ with $\widehat {R}$
with $\widehat {R}$ elementary abelian. Let $N_p=N\cap P$
elementary abelian. Let $N_p=N\cap P$ . If $\widehat {N_p}\unlhd \widehat {G}$
. If $\widehat {N_p}\unlhd \widehat {G}$ , then $\widehat {G}/\widehat {N_p}$
, then $\widehat {G}/\widehat {N_p}$ is a Frobenius group; if $\widehat {N_p}\ntrianglelefteq \widehat {G}$
is a Frobenius group; if $\widehat {N_p}\ntrianglelefteq \widehat {G}$ , then ${\bf N}_{\widehat {G}}(\widehat {N_p})=\widehat {P}$
, then ${\bf N}_{\widehat {G}}(\widehat {N_p})=\widehat {P}$ .
.
(2) If $|\pi (G/N)|\geq 2$
 , then one of the following statements holds:
, then one of the following statements holds:
(2.1) Let $\overline {G}:=G/{\bf O}_r(G){\bf Z}(G)$
 . Then $\overline {G}=\overline {K}\rtimes \overline {R}$
. Then $\overline {G}=\overline {K}\rtimes \overline {R}$ is a Frobenius group with abelian kernel $\overline {K}$
is a Frobenius group with abelian kernel $\overline {K}$ and complement $\overline {R}$
and complement $\overline {R}$ of order $r$
of order $r$ ;
;(2.2) Let $\overline {G}:=G/{\bf Z}(G)$
 . Then $\overline {G}=\overline {R}\rtimes \overline {K}$
. Then $\overline {G}=\overline {R}\rtimes \overline {K}$ is a Frobenius group with $\overline {R}$
is a Frobenius group with $\overline {R}$ a minimal normal subgroup of $\overline {G}$
a minimal normal subgroup of $\overline {G}$ and $\overline {K}$
and $\overline {K}$ cyclic. In particular, $R\leq N$
cyclic. In particular, $R\leq N$ .
.
On the contrary, in a very recent paper, Zhao et al. [Reference Zhao, Zhou, Chen, Zuo and Huang27] investigated the structure of a normal subgroup $N$![]() of $G$
of $G$![]() , when ${\bf C}_G(x)$
, when ${\bf C}_G(x)$![]() is maximal for every element $x\in N\setminus {\bf Z}(G)$
is maximal for every element $x\in N\setminus {\bf Z}(G)$![]() . Being inspired by the idea above, in this paper, by using less elements, we study the structure of group $G$
. Being inspired by the idea above, in this paper, by using less elements, we study the structure of group $G$![]() if ${\bf C}_G(x)$
if ${\bf C}_G(x)$![]() is maximal for every element $x\in N\setminus {\bf Z}(N)$
is maximal for every element $x\in N\setminus {\bf Z}(N)$![]() . We obtain:
. We obtain:
Theorem 5 Let $G$![]() be a group and $N\unlhd G$
be a group and $N\unlhd G$![]() . Let $\overline {G}:=G/{\bf Z}(N)$
. Let $\overline {G}:=G/{\bf Z}(N)$![]() . If ${\bf C}_G(x)$
. If ${\bf C}_G(x)$![]() is maximal in $G$
is maximal in $G$![]() for every element $x\in N\setminus {\bf Z}(N)$
for every element $x\in N\setminus {\bf Z}(N)$![]() , then one of the following statements holds:
, then one of the following statements holds:
(1) If $\overline {N}$
 is nilpotent, then $\overline {N}$
is nilpotent, then $\overline {N}$ is an elementary abelian $p$
is an elementary abelian $p$ -group for some prime $p$
-group for some prime $p$ ;
;(2) If $\overline {N}$
 is non-nilpotent, then $\overline {N}= \overline {P}\rtimes \overline {Q}$
is non-nilpotent, then $\overline {N}= \overline {P}\rtimes \overline {Q}$ is a Frobenius group with an elementary abelian kernel $\overline {P}$
is a Frobenius group with an elementary abelian kernel $\overline {P}$ and complement $\overline {Q}$
and complement $\overline {Q}$ with prime order. In particular, $\overline {P}$
with prime order. In particular, $\overline {P}$ is the minimal normal subgroup of $\overline {G}$
is the minimal normal subgroup of $\overline {G}$ .
.
Remark 3 In [Reference Lewis20], Lewis raised an interesting question asserting that: $G$![]() is a group, $N$
is a group, $N$![]() is a normal subgroup, $p$
is a normal subgroup, $p$![]() is a prime, $P$
is a prime, $P$![]() is a Sylow subgroup so that $(G,\, P,\, P\cap N)$
is a Sylow subgroup so that $(G,\, P,\, P\cap N)$![]() is a Frobenius–Wielandt triple, $G=NP$
is a Frobenius–Wielandt triple, $G=NP$![]() , ${\bf O}_p(G)=1$
, ${\bf O}_p(G)=1$![]() , and $G$
, and $G$![]() is non-solvable. Is this enough to imply that $G\cong M_{10}$
is non-solvable. Is this enough to imply that $G\cong M_{10}$![]() ? Theorems A and B partially answered the question above.
? Theorems A and B partially answered the question above.
Remark 4 Corollary 1 can also be obtained by [Reference Lewis20, Theorem 1.1]. It is worth to mention that our method and result are different from Lewis’ since he determined the structure of group $G$![]() while we are concerning on the information of the normal subgroup $N$
while we are concerning on the information of the normal subgroup $N$![]() of $G$
of $G$![]() .
.
Remark 5 Both [Reference Zhao, Zhou, Chen, Zuo and Huang27, Theorems A and B] and theorem C can be considered as corollaries of theorem 5.
2. Proof of theorem B
To show theorem A, we first prove theorem B. Here, we list some notation and lemmas, which will be used below.
We denote by $\omega (G)$![]() the set of the element orders of $G$
the set of the element orders of $G$![]() . If $A\subseteq G$
. If $A\subseteq G$![]() is a subset of $G$
is a subset of $G$![]() , then $\omega (A)$
, then $\omega (A)$![]() denotes the set of element orders of $A$
denotes the set of element orders of $A$![]() , and $k\cdot \omega (A)=\{ka| a\in \omega (A)\}$
, and $k\cdot \omega (A)=\{ka| a\in \omega (A)\}$![]() .
.
If $\varepsilon \in \{+,\,-\}$![]() , we may write $\varepsilon$
, we may write $\varepsilon$![]() instead of $\pm$
instead of $\pm$![]() in arithmetic expressions. The notation used in this section is mainly borrowed from [Reference Conway, Curtis, Norton, Parker and Wilson4, Reference Grechkoseeva10, Reference Grechkoseeva12].
in arithmetic expressions. The notation used in this section is mainly borrowed from [Reference Conway, Curtis, Norton, Parker and Wilson4, Reference Grechkoseeva10, Reference Grechkoseeva12].
Lemma 2.1 ([Reference Moghaddamfar and Shi22, Lemma 2])
Let $p$![]() and $q$
and $q$![]() be two primes and $m,\, n$
be two primes and $m,\, n$![]() be natural numbers such that $p^m = q^n +1$
be natural numbers such that $p^m = q^n +1$![]() . Then one of the following statements holds:
. Then one of the following statements holds:
(1) $n = 1$
 , $m$
, $m$ is a prime number, $p = 2$
is a prime number, $p = 2$ and $q = 2^m-1$
and $q = 2^m-1$ is a Mersenne prime;
is a Mersenne prime;(2) $m = 1$
 , $n$
, $n$ is a power of 2, $q = 2$
is a power of 2, $q = 2$ and $p = 2^n + 1$
and $p = 2^n + 1$ is a Fermat prime;
is a Fermat prime;(3) $p = n = 3$
 and $q = m = 2$
and $q = m = 2$ .
.
Lemma 2.2 ([Reference Zsigmondy29])
Let $a$![]() and $n$
and $n$![]() be integers greater than 1. Then there exists a primitive prime divisor of $a^n- 1$
be integers greater than 1. Then there exists a primitive prime divisor of $a^n- 1$![]() , that is a prime $s$
, that is a prime $s$![]() dividing $a^n-1$
dividing $a^n-1$![]() and not dividing $a^i-1$
and not dividing $a^i-1$![]() for $1 \leq i\leq n-1$
for $1 \leq i\leq n-1$![]() , except if
, except if
(1) $a = 2$
 and $n = 6$
and $n = 6$ , or
, or(2) $a$
 is a Mersenne prime and $n = 2$
is a Mersenne prime and $n = 2$ .
.
Proof of theorem B Since every element of $Nu$![]() has prime power order, we take $nu\in Nu$
has prime power order, we take $nu\in Nu$![]() an $r_1$
an $r_1$![]() -element for some element $n\in N$
-element for some element $n\in N$![]() and prime $r_1$
and prime $r_1$![]() . Note that $N\langle u\rangle =N\langle nu\rangle$
. Note that $N\langle u\rangle =N\langle nu\rangle$![]() . Then $N\langle u\rangle /N=N\langle nu\rangle /N$
. Then $N\langle u\rangle /N=N\langle nu\rangle /N$![]() . Moreover, $N\langle u\rangle /N\cong \langle u\rangle /\langle u\rangle \cap N$
. Moreover, $N\langle u\rangle /N\cong \langle u\rangle /\langle u\rangle \cap N$![]() is an $r$
is an $r$![]() -group and $\langle nu\rangle N/N\cong \langle nu\rangle /\langle nu\rangle \cap N$
-group and $\langle nu\rangle N/N\cong \langle nu\rangle /\langle nu\rangle \cap N$![]() is an $r_1$
is an $r_1$![]() -group. This forces $r=r_1$
-group. This forces $r=r_1$![]() . Consequently, we conclude that every element in $Nu$
. Consequently, we conclude that every element in $Nu$![]() is an $r$
is an $r$![]() -element.
-element.
If $N$![]() is a sporadic simple group, we may take $N=M_{12}$
is a sporadic simple group, we may take $N=M_{12}$![]() as an example. In this case, select $u\in {\rm Aut}(N)\setminus N$
as an example. In this case, select $u\in {\rm Aut}(N)\setminus N$![]() a 2-element. By [Reference Conway, Curtis, Norton, Parker and Wilson4], there exists an element of order 10, against our assumption. By a similar reasoning, we rule out the case that $N$
a 2-element. By [Reference Conway, Curtis, Norton, Parker and Wilson4], there exists an element of order 10, against our assumption. By a similar reasoning, we rule out the case that $N$![]() is a sporadic simple group.
is a sporadic simple group.
Assume then that $N=A_n$![]() is an alternating group of degree $n$
is an alternating group of degree $n$![]() with $n\geq 5$
with $n\geq 5$![]() but $n\neq 6$
but $n\neq 6$![]() . As Out$(N)\cong C_2$
. As Out$(N)\cong C_2$![]() , we select $u=(12)$
, we select $u=(12)$![]() . Take $x=(345)\in N$
. Take $x=(345)\in N$![]() . Then $ux=xu\in Nu$
. Then $ux=xu\in Nu$![]() does not have prime power, also a contradiction.
does not have prime power, also a contradiction.
Now, we consider $N=N(q)$![]() is a simple group of Lie type defined over a field of $q$
is a simple group of Lie type defined over a field of $q$![]() -elements, where $q=p^f$
-elements, where $q=p^f$![]() with $p$
with $p$![]() a prime. As $u\in$
a prime. As $u\in$![]() Aut$(N)$
Aut$(N)$![]() , by [Reference Gorenstein, Lyons and Solomon9, Theorem 2.5.1], we may write $u=\delta \varphi \tau$
, by [Reference Gorenstein, Lyons and Solomon9, Theorem 2.5.1], we may write $u=\delta \varphi \tau$![]() , where $\delta$
, where $\delta$![]() is a diagonal automorphism, $\varphi$
is a diagonal automorphism, $\varphi$![]() is a field automorphism, and $\tau$
is a field automorphism, and $\tau$![]() is a graph automorphism of $N$
is a graph automorphism of $N$![]() , respectively.
, respectively.
If $u$![]() is a field or a graph-field automorphism of $N$
is a field or a graph-field automorphism of $N$![]() , then by [Reference Gorenstein and Lyons8], ${\bf C}_N(u)=N(p^{f/t})$
, then by [Reference Gorenstein and Lyons8], ${\bf C}_N(u)=N(p^{f/t})$![]() is a group of the same type as $N$
is a group of the same type as $N$![]() . Clearly, ${\bf C}_N(u)=N(p^{f/t})$
. Clearly, ${\bf C}_N(u)=N(p^{f/t})$![]() is not a prime power group by [Reference Conway, Curtis, Norton, Parker and Wilson4, Table 6]. Let $1\neq u'\in {\bf C}_N(u)$
is not a prime power group by [Reference Conway, Curtis, Norton, Parker and Wilson4, Table 6]. Let $1\neq u'\in {\bf C}_N(u)$![]() be an $r'$
be an $r'$![]() -element. Then $u'u=uu'\in Nu$
-element. Then $u'u=uu'\in Nu$![]() is not an $r$
is not an $r$![]() -element, contrary to our assumption. If $u$
-element, contrary to our assumption. If $u$![]() is a graph automorphism of $N$
is a graph automorphism of $N$![]() , according to [Reference Conway, Curtis, Norton, Parker and Wilson4], we see that $N\cong PSL^+_n(q)$
, according to [Reference Conway, Curtis, Norton, Parker and Wilson4], we see that $N\cong PSL^+_n(q)$![]() with $n\geq 3$
with $n\geq 3$![]() ; $P\Omega _5(q)$
; $P\Omega _5(q)$![]() with $q$
with $q$![]() even; $P\Omega _{2n}^+(q)$
even; $P\Omega _{2n}^+(q)$![]() with $n\geq 4$
with $n\geq 4$![]() ; $G_2(q)$
; $G_2(q)$![]() with $p=3$
with $p=3$![]() ; $F_4(q)$
; $F_4(q)$![]() with $p=2$
with $p=2$![]() ; or $E_6(q)$
; or $E_6(q)$![]() with $3\mid (q-1)$
with $3\mid (q-1)$![]() . However, there will be a contradiction according to [Reference Aschbacher and Seitz1, Reference Harris13].
. However, there will be a contradiction according to [Reference Aschbacher and Seitz1, Reference Harris13].
Consequently, $u=\delta \varphi \tau$![]() with $\delta \neq 1$
with $\delta \neq 1$![]() . In the following, we will analyse it case by case.
. In the following, we will analyse it case by case.
Case 1. $u=\delta$![]() .
.
As $\delta \neq 1$![]() , according to [Reference Conway, Curtis, Norton, Parker and Wilson4, Table 5], we see that $N\cong PSL_n^+(q)$
, according to [Reference Conway, Curtis, Norton, Parker and Wilson4, Table 5], we see that $N\cong PSL_n^+(q)$![]() with $n\geq 2$
with $n\geq 2$![]() ; $PSL_n^{-}(q)$
; $PSL_n^{-}(q)$![]() with $n\geq 3$
with $n\geq 3$![]() ; $PSp_{2n}(q)$
; $PSp_{2n}(q)$![]() with $n\geq 2$
with $n\geq 2$![]() and $q$
and $q$![]() odd; $P\Omega _{2n+1}(q)$
odd; $P\Omega _{2n+1}(q)$![]() with $n\geq 3$
with $n\geq 3$![]() and $q$
and $q$![]() odd; $P\Omega _{2n}^\varepsilon (q)$
odd; $P\Omega _{2n}^\varepsilon (q)$![]() with $n\geq 4$
with $n\geq 4$![]() ; $E_6^\varepsilon (q)$
; $E_6^\varepsilon (q)$![]() with $3\mid (q-\varepsilon 1)$
with $3\mid (q-\varepsilon 1)$![]() or $E_7(q)$
or $E_7(q)$![]() with $q$
with $q$![]() odd.
odd.
Assume first $N\cong PSL_n^+(q)$![]() . Write $d:=o(u)$
. Write $d:=o(u)$![]() . Easily, $r\mid d$
. Easily, $r\mid d$![]() . If $n=2$
. If $n=2$![]() , then $Nu=PGL_2(q)\setminus PSL_2(q)$
, then $Nu=PGL_2(q)\setminus PSL_2(q)$![]() and $2\mid (2,\, q-1)$
and $2\mid (2,\, q-1)$![]() . As we see that $q$
. As we see that $q$![]() is odd and $r=2$
is odd and $r=2$![]() . It follows by [Reference Grechkoseeva11, Lemma 2.1] that both $(q+(\varepsilon 1))$
. It follows by [Reference Grechkoseeva11, Lemma 2.1] that both $(q+(\varepsilon 1))$![]() and $(q-(\varepsilon 1))$
and $(q-(\varepsilon 1))$![]() are powers of $r$
are powers of $r$![]() . Lemma 2.1 indicates that $q=p=3$
. Lemma 2.1 indicates that $q=p=3$![]() . However, in this case, $N\cong PSL_2(3)$
. However, in this case, $N\cong PSL_2(3)$![]() is not a simple group, a contradiction. Hence, $n\geq 3$
is not a simple group, a contradiction. Hence, $n\geq 3$![]() . Then $G=N\rtimes \langle u\rangle \leq PGL_n^{\varepsilon }(q)$
. Then $G=N\rtimes \langle u\rangle \leq PGL_n^{\varepsilon }(q)$![]() . Let $T:=\langle x_0\rangle$
. Let $T:=\langle x_0\rangle$![]() be a Singer subgroup of $PGL_n^{\varepsilon }(q)$
be a Singer subgroup of $PGL_n^{\varepsilon }(q)$![]() such that $S_0:=T\cap N$
such that $S_0:=T\cap N$![]() is a Singer subgroup of $N$
is a Singer subgroup of $N$![]() . By [Reference Huppert17, Theorem 2.7.3], $|T|={(q^n-(\varepsilon 1)^n)}/{(q-\varepsilon 1)}$
. By [Reference Huppert17, Theorem 2.7.3], $|T|={(q^n-(\varepsilon 1)^n)}/{(q-\varepsilon 1)}$![]() and $|T\cap N|={(q^n-(\varepsilon 1)^n)}/{(d(q-(\varepsilon 1)))}$
and $|T\cap N|={(q^n-(\varepsilon 1)^n)}/{(d(q-(\varepsilon 1)))}$![]() . Note that $PGL_n^{\varepsilon }(q)=PSL_n^{\varepsilon }(q)\langle x_0 \rangle$
. Note that $PGL_n^{\varepsilon }(q)=PSL_n^{\varepsilon }(q)\langle x_0 \rangle$![]() and $x_0^d\in PSL_n^{\varepsilon }(q)$
and $x_0^d\in PSL_n^{\varepsilon }(q)$![]() , without loss of generality, we may assume that $u\in T$
, without loss of generality, we may assume that $u\in T$![]() . Then $u$
. Then $u$![]() centralizes $T\cap N$
centralizes $T\cap N$![]() . It follows that ${(q^n-(\varepsilon 1)^n)}/{(d(q-(\varepsilon 1)))}$
. It follows that ${(q^n-(\varepsilon 1)^n)}/{(d(q-(\varepsilon 1)))}$![]() is an $r$
is an $r$![]() -power. If $n=3$
-power. If $n=3$![]() and $q=2$
and $q=2$![]() , we have $N\cong PSL_3(2)\cong PSL_2(7)$
, we have $N\cong PSL_3(2)\cong PSL_2(7)$![]() , which is a contradiction. Hence, $(n,\,q)\neq (3,\,2)$
, which is a contradiction. Hence, $(n,\,q)\neq (3,\,2)$![]() . If $\varepsilon =+$
. If $\varepsilon =+$![]() , according to lemma 2.1, $q^n-1$
, according to lemma 2.1, $q^n-1$![]() has a prime divisor $p_1$
has a prime divisor $p_1$![]() such that $p_1\neq r$
such that $p_1\neq r$![]() and $p_1\nmid q-1$
and $p_1\nmid q-1$![]() . Hence, $p_1\mid {(q^n-1)}/{(d(q-1))}$
. Hence, $p_1\mid {(q^n-1)}/{(d(q-1))}$![]() , a contradiction. If $\varepsilon =-$
, a contradiction. If $\varepsilon =-$![]() , we can also rule out this case by a similar argument as above.
, we can also rule out this case by a similar argument as above.
Now, consider $N\cong P\Omega _{2n}^\varepsilon (q)$![]() . In this case, $r\mid d=(4,\,q^n-\varepsilon )$
. In this case, $r\mid d=(4,\,q^n-\varepsilon )$![]() , indicating $r=2$
, indicating $r=2$![]() , and thus $q$
, and thus $q$![]() is odd. By [Reference Gorenstein, Lyons and Solomon9, Theorem 2.5.12], we see that all diagonal automorphisms of the same order are conjugate in ${\rm Out}(N)$
is odd. By [Reference Gorenstein, Lyons and Solomon9, Theorem 2.5.12], we see that all diagonal automorphisms of the same order are conjugate in ${\rm Out}(N)$![]() . By [Reference Grechkoseeva12, Figs. 1, 2, 3], $\omega (Nu)=\omega (PCSO_{2n}^\varepsilon (q)\setminus PSO_{2n}^\varepsilon (q))$
. By [Reference Grechkoseeva12, Figs. 1, 2, 3], $\omega (Nu)=\omega (PCSO_{2n}^\varepsilon (q)\setminus PSO_{2n}^\varepsilon (q))$![]() or $\omega (Nu)=\omega (PSO_{2n}^\varepsilon (q)\setminus P\Omega _{2n}^\varepsilon (q))$
or $\omega (Nu)=\omega (PSO_{2n}^\varepsilon (q)\setminus P\Omega _{2n}^\varepsilon (q))$![]() . By [Reference Grechkoseeva12, Lemma 2.9], each element in $\omega (PCSO_{2n}^\varepsilon (q)\setminus PSO_{2n}^\varepsilon (q))$
. By [Reference Grechkoseeva12, Lemma 2.9], each element in $\omega (PCSO_{2n}^\varepsilon (q)\setminus PSO_{2n}^\varepsilon (q))$![]() is not an $r$
is not an $r$![]() -number for $n\geq 4$
-number for $n\geq 4$![]() , contrary to our assumption. By [Reference Grechkoseeva12, Lemmas 2.6 and 2.4], there exists an element in $\omega (Nu)=\omega (PSO_{2n}^\varepsilon (q)\setminus P\Omega _{2n}^\varepsilon (q))$
, contrary to our assumption. By [Reference Grechkoseeva12, Lemmas 2.6 and 2.4], there exists an element in $\omega (Nu)=\omega (PSO_{2n}^\varepsilon (q)\setminus P\Omega _{2n}^\varepsilon (q))$![]() , whose order is not an $r$
, whose order is not an $r$![]() -number, also contradiction.
-number, also contradiction.
Furthermore, according to [Reference Grechkoseeva10], we can rule out the cases $N\cong P\Omega _{2n+1}(q)$![]() and $PSp_{2n}(q)$
and $PSp_{2n}(q)$![]() . The remaining cases can be ruled out by [Reference Zvezdina30].
. The remaining cases can be ruled out by [Reference Zvezdina30].
Case 2. $u=\delta \varphi$![]() with $\delta \neq 1$
with $\delta \neq 1$![]() and $\varphi \neq 1$
and $\varphi \neq 1$![]() .
.
Let $S:={\rm Inndiag}(N)$![]() . Then $S$
. Then $S$![]() is a simple group of Lie type, which is defined over a field of $q$
is a simple group of Lie type, which is defined over a field of $q$![]() -elements, where $q=p^f$
-elements, where $q=p^f$![]() with prime $p$
with prime $p$![]() . Let $\delta _0:=\delta _0(q)$
. Let $\delta _0:=\delta _0(q)$![]() be a generator of $S/N$
be a generator of $S/N$![]() (other than $N\cong P\Omega _{2n}^+(q)$
(other than $N\cong P\Omega _{2n}^+(q)$![]() with $n$
with $n$![]() even) such that $\delta =\delta _0^i$
even) such that $\delta =\delta _0^i$![]() for some positive integer $i$
for some positive integer $i$![]() , and $\varphi _0$
, and $\varphi _0$![]() be a generator of the field automorphism group of $N$
be a generator of the field automorphism group of $N$![]() .
.
Since $\delta \neq 1$![]() , by [Reference Conway, Curtis, Norton, Parker and Wilson4, Table 5], we see that $N\cong PSL_n^{\varepsilon }(q)$
, by [Reference Conway, Curtis, Norton, Parker and Wilson4, Table 5], we see that $N\cong PSL_n^{\varepsilon }(q)$![]() with $n\geq 2$
with $n\geq 2$![]() and $\varepsilon \in \{+,\,-\}$
and $\varepsilon \in \{+,\,-\}$![]() ; $P\Omega _{2n}^\varepsilon (q)$
; $P\Omega _{2n}^\varepsilon (q)$![]() with $n\geq 4$
with $n\geq 4$![]() , or $P\Omega _{2n+1}(q)$
, or $P\Omega _{2n+1}(q)$![]() with $n\geq 3$
with $n\geq 3$![]() and $q$
and $q$![]() odd, $PSp_{2n}(q)$
odd, $PSp_{2n}(q)$![]() , with $n\geq 3$
, with $n\geq 3$![]() and $q$
and $q$![]() odd, $E_6^\varepsilon (q)$
odd, $E_6^\varepsilon (q)$![]() with $3\mid (q-\varepsilon 1)$
with $3\mid (q-\varepsilon 1)$![]() or $E_7(q)$
or $E_7(q)$![]() with $q$
with $q$![]() odd.
odd.
First consider $N\cong PSL_n^{\varepsilon }(q)$![]() . If $n\geq 3$
. If $n\geq 3$![]() , by [Reference Grechkoseeva11, Lemma 3.3], we have $\omega (uN)=k\cdot \omega (\tau ^\alpha \delta (q_0)PSL_n^{\varepsilon }(q_0))$
, by [Reference Grechkoseeva11, Lemma 3.3], we have $\omega (uN)=k\cdot \omega (\tau ^\alpha \delta (q_0)PSL_n^{\varepsilon }(q_0))$![]() , where $\tau$
, where $\tau$![]() is a graph automorphism of $N$
is a graph automorphism of $N$![]() , and $\alpha =0$
, and $\alpha =0$![]() if $\varepsilon =+$
if $\varepsilon =+$![]() and $\alpha =1$
and $\alpha =1$![]() if $\varepsilon =-$
if $\varepsilon =-$![]() . Suppose $o(\varphi )=k$
. Suppose $o(\varphi )=k$![]() . Then $k$
. Then $k$![]() is an $r$
is an $r$![]() -power. Assume first that $\varepsilon =+$
-power. Assume first that $\varepsilon =+$![]() . Then $\omega (uN)=k\cdot \omega (\delta (q_0)PSL_n(q_0))$
. Then $\omega (uN)=k\cdot \omega (\delta (q_0)PSL_n(q_0))$![]() . Furthermore, ${((q_0^n-1)i)}/{(d(q_0-1))}\in \omega (\delta (q_0)PSL_n(q_0))$
. Furthermore, ${((q_0^n-1)i)}/{(d(q_0-1))}\in \omega (\delta (q_0)PSL_n(q_0))$![]() , forcing that ${((q_0^n-1)i)}/{(d(q_0-1))}$
, forcing that ${((q_0^n-1)i)}/{(d(q_0-1))}$![]() is an $r$
is an $r$![]() -power. By applying a similar argument as in case 1, we get a contradiction. Assume now that $\varepsilon =-$
-power. By applying a similar argument as in case 1, we get a contradiction. Assume now that $\varepsilon =-$![]() . Then $\omega (uN)=k\cdot \omega (\tau \delta (q_0)PSL_n(q_0))$
. Then $\omega (uN)=k\cdot \omega (\tau \delta (q_0)PSL_n(q_0))$![]() . Since ${\rm Out}(N)\cong \langle \delta _0 \rangle \rtimes (\langle \varphi _0\rangle \times \langle \tau \rangle )$
. Since ${\rm Out}(N)\cong \langle \delta _0 \rangle \rtimes (\langle \varphi _0\rangle \times \langle \tau \rangle )$![]() , we obtain that $\tau$
, we obtain that $\tau$![]() is conjugate to $\tau \delta$
is conjugate to $\tau \delta$![]() . Hence, $\omega (\tau \delta (q_0)PSL_n(q_0))=\omega (\tau PSL_n(q_0))$
. Hence, $\omega (\tau \delta (q_0)PSL_n(q_0))=\omega (\tau PSL_n(q_0))$![]() . By [Reference Grechkoseeva11, Lemma 4.7], we see that $\omega (\tau PSL_n(q_0))=2\cdot \omega (PSp_n(q_0))$
. By [Reference Grechkoseeva11, Lemma 4.7], we see that $\omega (\tau PSL_n(q_0))=2\cdot \omega (PSp_n(q_0))$![]() if $p\neq 2$
if $p\neq 2$![]() , against [Reference Grechkoseeva11, Lemma 2.2]. Hence, $p=2$
, against [Reference Grechkoseeva11, Lemma 2.2]. Hence, $p=2$![]() . Since $r\mid k$
. Since $r\mid k$![]() and $k\mid (n,\,q+1)$
and $k\mid (n,\,q+1)$![]() , we get that $r$
, we get that $r$![]() is odd. Note that $\langle \delta _0 \rangle \rtimes \langle \tau \rangle$
is odd. Note that $\langle \delta _0 \rangle \rtimes \langle \tau \rangle$![]() is a dihedral group of $2d$
is a dihedral group of $2d$![]() with $d$
with $d$![]() odd. Hence, $u\in \langle \delta _0 \rangle$
odd. Hence, $u\in \langle \delta _0 \rangle$![]() . That is to say, $u$
. That is to say, $u$![]() is a diagonal automorphism of $N$
is a diagonal automorphism of $N$![]() , contrary to our assumption.
, contrary to our assumption.
As a result, $n=2$![]() . That is, $N\cong PSL_2(q)$
. That is, $N\cong PSL_2(q)$![]() with $q$
with $q$![]() odd. Easily, $r=2$
odd. Easily, $r=2$![]() . Let $M:=PGL_2(q)$
. Let $M:=PGL_2(q)$![]() . Then ${\bf C}_M(\varphi )=PGL_2(q_0)$
. Then ${\bf C}_M(\varphi )=PGL_2(q_0)$![]() , where $q_0=p^{f/k}$
, where $q_0=p^{f/k}$![]() . Clearly, $\delta \in {\bf C}_M(\varphi )$
. Clearly, $\delta \in {\bf C}_M(\varphi )$![]() . It follows that $PGL_2(q_0)\setminus PSL_2(q_0)\subseteq Nu$
. It follows that $PGL_2(q_0)\setminus PSL_2(q_0)\subseteq Nu$![]() . Hence, every element in $PGL_2(q_0)\setminus PSL_2(q_0)$
. Hence, every element in $PGL_2(q_0)\setminus PSL_2(q_0)$![]() is a 2-element. By [Reference Grechkoseeva11, Lemma 2.1], both $q_0-1$
is a 2-element. By [Reference Grechkoseeva11, Lemma 2.1], both $q_0-1$![]() and $q_0+1$
and $q_0+1$![]() are 2-power. By lemma 2.1, we get $q_0=p=3$
are 2-power. By lemma 2.1, we get $q_0=p=3$![]() and $f=k$
and $f=k$![]() . Therefore, $N\cong PSL_2(3^f)$
. Therefore, $N\cong PSL_2(3^f)$![]() , where $f$
, where $f$![]() is a 2-power, as required.
is a 2-power, as required.
If $N\cong P\Omega _{2n}^\varepsilon (q)$![]() , then either $(2,\, q-1)=2$
, then either $(2,\, q-1)=2$![]() or $(4,\,q^n-\varepsilon 1)=2,\,$
or $(4,\,q^n-\varepsilon 1)=2,\,$![]() 4, forcing that $q$
4, forcing that $q$![]() is odd. Assume first that $o(\delta )=4$
is odd. Assume first that $o(\delta )=4$![]() . By [Reference Grechkoseeva10, Theorem 2.5.12], we see that $\delta \varphi$
. By [Reference Grechkoseeva10, Theorem 2.5.12], we see that $\delta \varphi$![]() is conjugate to $\delta ^3\varphi$
is conjugate to $\delta ^3\varphi$![]() in ${\rm Out}(N)$
in ${\rm Out}(N)$![]() . It follows that $\omega (uN)=\omega (N\langle \delta \rangle \varphi \setminus (N\langle \delta ^2\rangle \varphi ))$
. It follows that $\omega (uN)=\omega (N\langle \delta \rangle \varphi \setminus (N\langle \delta ^2\rangle \varphi ))$![]() . Assume first that $\varepsilon =+$
. Assume first that $\varepsilon =+$![]() . By [Reference Grechkoseeva12, Lemma 1.2 and Fig. 2], we have that $\omega (uN)= k\cdot \omega (PCSO_{2n}^+(q_0)\setminus PSO_{2n}^+(q_0))$
. By [Reference Grechkoseeva12, Lemma 1.2 and Fig. 2], we have that $\omega (uN)= k\cdot \omega (PCSO_{2n}^+(q_0)\setminus PSO_{2n}^+(q_0))$![]() . Therefore, both $q_0^{n-1}-1$
. Therefore, both $q_0^{n-1}-1$![]() and $(q_0^{n-2}+1)(q_0-1)$
and $(q_0^{n-2}+1)(q_0-1)$![]() are in $\omega (PCSO_{2n}^\varepsilon (q_0)\setminus PSO_{2n}^\varepsilon (q_0))$
are in $\omega (PCSO_{2n}^\varepsilon (q_0)\setminus PSO_{2n}^\varepsilon (q_0))$![]() by [Reference Grechkoseeva12, Lemma 2.9]. Hence, both $q_0^{n-1}-1$
by [Reference Grechkoseeva12, Lemma 2.9]. Hence, both $q_0^{n-1}-1$![]() and $(q_0^{n-2}+1)(q_0-1)$
and $(q_0^{n-2}+1)(q_0-1)$![]() are $r$
are $r$![]() -power, which is a contradiction. Assume now that $\varepsilon =-$
-power, which is a contradiction. Assume now that $\varepsilon =-$![]() . Then $\delta ^\varphi =\delta$
. Then $\delta ^\varphi =\delta$![]() and $n$
and $n$![]() is odd. It follows that $u$
is odd. It follows that $u$![]() is a 2-element. Let $W:=PCSO_{2n}^-(q)$
is a 2-element. Let $W:=PCSO_{2n}^-(q)$![]() . Then ${\bf C}_W(\varphi )=PCSO_{2n}^-(q_0)$
. Then ${\bf C}_W(\varphi )=PCSO_{2n}^-(q_0)$![]() , where $q_0=p^{f/k}$
, where $q_0=p^{f/k}$![]() . Clearly, $\delta \in {\bf C}_W(\varphi )$
. Clearly, $\delta \in {\bf C}_W(\varphi )$![]() . Therefore, we obtain that ${\bf C}_W(\varphi )\varphi \setminus {\bf C}_{N}(\varphi )\langle \delta ^2\rangle \varphi \subseteq Nu$
. Therefore, we obtain that ${\bf C}_W(\varphi )\varphi \setminus {\bf C}_{N}(\varphi )\langle \delta ^2\rangle \varphi \subseteq Nu$![]() . This shows that ${\bf C}_W(\varphi ) \setminus {\bf C}_{N}(\varphi )\langle \delta ^2\rangle =PCSO_{2n}^-(q_0)\setminus PSO_{2n}^-(q_0)$
. This shows that ${\bf C}_W(\varphi ) \setminus {\bf C}_{N}(\varphi )\langle \delta ^2\rangle =PCSO_{2n}^-(q_0)\setminus PSO_{2n}^-(q_0)$![]() is a 2-element, contrary to [Reference Grechkoseeva12, Lemma 2.9].
is a 2-element, contrary to [Reference Grechkoseeva12, Lemma 2.9].
Assume now that $o(\delta )=2$![]() . By [Reference Grechkoseeva12, Lemma 1.2 and Figs. 1, 2, 3], we have that $\omega (uN)= k\cdot \omega (PCSO_{2n}^+(q_0)\setminus PSO_{2n}^+(q_0))$
. By [Reference Grechkoseeva12, Lemma 1.2 and Figs. 1, 2, 3], we have that $\omega (uN)= k\cdot \omega (PCSO_{2n}^+(q_0)\setminus PSO_{2n}^+(q_0))$![]() if $(4,\,q^n-1)=2$
if $(4,\,q^n-1)=2$![]() ; $\omega (\varphi (PSO_{2n}^+(q)\setminus P\Omega _{2n}^+(q)))$
; $\omega (\varphi (PSO_{2n}^+(q)\setminus P\Omega _{2n}^+(q)))$![]() if $n$
if $n$![]() is odd and $(q^n-1,\,4)=4$
is odd and $(q^n-1,\,4)=4$![]() ; $\omega (\varphi (PCSO_{2n}^+(q)\setminus PSO_{2n}^+(q)))$
; $\omega (\varphi (PCSO_{2n}^+(q)\setminus PSO_{2n}^+(q)))$![]() , or $\omega (\varphi (PSO_{2n}^+(q)\setminus P\Omega _{2n}^+(q)))$
, or $\omega (\varphi (PSO_{2n}^+(q)\setminus P\Omega _{2n}^+(q)))$![]() if $n>4$
if $n>4$![]() is even. If $(4,\,q^n-1)=2$
is even. If $(4,\,q^n-1)=2$![]() , by [Reference Grechkoseeva12, Lemma 2.9], we have that $q_0^{n-1}-1\in \omega (PCSO_{2n}^+(q_0)\setminus PSO_{2n}^+(q_0))$
, by [Reference Grechkoseeva12, Lemma 2.9], we have that $q_0^{n-1}-1\in \omega (PCSO_{2n}^+(q_0)\setminus PSO_{2n}^+(q_0))$![]() . It is easy to get a contradiction by lemma 2.2. If $n$
. It is easy to get a contradiction by lemma 2.2. If $n$![]() is odd and $(q^n-1,\,4)=4$
is odd and $(q^n-1,\,4)=4$![]() , then $\omega (\varphi (PSO_{2n}^+(q)\setminus P\Omega _{2n}^+(q)))\supseteq \omega (\varphi PSO_{2n}^+(q))\setminus \omega (\varphi P\Omega _{2n}^+(q))$
, then $\omega (\varphi (PSO_{2n}^+(q)\setminus P\Omega _{2n}^+(q)))\supseteq \omega (\varphi PSO_{2n}^+(q))\setminus \omega (\varphi P\Omega _{2n}^+(q))$![]() . By [Reference Grechkoseeva12, Lemma 1.2], we have $\omega (\varphi (PSO_{2n}^+(q)\setminus P\Omega _{2n}^+(q)))\supseteq k\cdot (\omega (PSO_{2n}^+(q_0))\setminus \omega (P\Omega _{2n}^+(q_0)))$
. By [Reference Grechkoseeva12, Lemma 1.2], we have $\omega (\varphi (PSO_{2n}^+(q)\setminus P\Omega _{2n}^+(q)))\supseteq k\cdot (\omega (PSO_{2n}^+(q_0))\setminus \omega (P\Omega _{2n}^+(q_0)))$![]() . By [Reference Grechkoseeva12, Lemmas 2.4 and 2.6], ${(q_0^n-1)}/{2}\in \omega (PSO_{2n}^+(q_0))\setminus \omega (P\Omega _{2n}^+(q_0))$
. By [Reference Grechkoseeva12, Lemmas 2.4 and 2.6], ${(q_0^n-1)}/{2}\in \omega (PSO_{2n}^+(q_0))\setminus \omega (P\Omega _{2n}^+(q_0))$![]() . It follows that ${(q_0^n-1)}/{2}$
. It follows that ${(q_0^n-1)}/{2}$![]() is an $r$
is an $r$![]() -power. Since $n\geq 3$
-power. Since $n\geq 3$![]() and $q_0$
and $q_0$![]() is odd, there exists some odd prime $p_1\mid (q_0^n-1)$
is odd, there exists some odd prime $p_1\mid (q_0^n-1)$![]() with $p_1\neq r$
with $p_1\neq r$![]() by lemma 2.2, a contradiction. By the same reason, we can also rule out the case $n\geq 4$
by lemma 2.2, a contradiction. By the same reason, we can also rule out the case $n\geq 4$![]() is even.
is even.
If $N\cong P\Omega _{2n+1}(q)$![]() with $n\geq 3$
with $n\geq 3$![]() and $q$
and $q$![]() odd, then $Nu=N\langle \delta \rangle \varphi \setminus N\varphi$
odd, then $Nu=N\langle \delta \rangle \varphi \setminus N\varphi$![]() . By [Reference Grechkoseeva10, Lemma 2.8], we have that $\omega (Nu)\supseteq \omega (N\langle \delta \rangle \varphi )\setminus \omega (N \varphi )=k\cdot (\omega ({\rm Inndiag}(P\Omega _{2n+1}(q_0))\setminus \omega (P\Omega _{2n+1}(q_0)))$
. By [Reference Grechkoseeva10, Lemma 2.8], we have that $\omega (Nu)\supseteq \omega (N\langle \delta \rangle \varphi )\setminus \omega (N \varphi )=k\cdot (\omega ({\rm Inndiag}(P\Omega _{2n+1}(q_0))\setminus \omega (P\Omega _{2n+1}(q_0)))$![]() . By [Reference Grechkoseeva10, Lemma 2.1], we get that $p(q_0^{n-1}\pm 1)\!\in\! \omega ({\rm Inndiag}(P\Omega _{2n+1}(q_0))\setminus \omega (P\Omega _{2n+1}(q_0))$
. By [Reference Grechkoseeva10, Lemma 2.1], we get that $p(q_0^{n-1}\pm 1)\!\in\! \omega ({\rm Inndiag}(P\Omega _{2n+1}(q_0))\setminus \omega (P\Omega _{2n+1}(q_0))$![]() . By hypothesis, $p(q_0^{n-1}\pm 1)$
. By hypothesis, $p(q_0^{n-1}\pm 1)$![]() is an $r$
is an $r$![]() -power, a contradiction. By the same reason, we can also rule out the case $N\cong PSp_{2n}(q)$
-power, a contradiction. By the same reason, we can also rule out the case $N\cong PSp_{2n}(q)$![]() with $n\geq 3$
with $n\geq 3$![]() and $q$
and $q$![]() odd.
odd.
If $N\cong E_6^\varepsilon (q)$![]() , then $u^\tau =\delta ^2\varphi$
, then $u^\tau =\delta ^2\varphi$![]() . It follows that $\omega ({\rm Inndiag}(N)\varphi )=\omega (M\varphi )\cup \omega (N\delta \varphi )$
. It follows that $\omega ({\rm Inndiag}(N)\varphi )=\omega (M\varphi )\cup \omega (N\delta \varphi )$![]() . Hence, $\omega (N\delta \varphi )=\omega ({\rm Inndiag}(N)\varphi )\setminus \omega (N\varphi )$
. Hence, $\omega (N\delta \varphi )=\omega ({\rm Inndiag}(N)\varphi )\setminus \omega (N\varphi )$![]() . By [Reference Zvezdina30, (3) and (5)], we have that $\omega (N\delta \varphi )=\omega ({\rm Inndiag}(N)\varphi )\setminus \omega (N\varphi )=k\cdot (\omega ({\rm Inndiag}(E_6^\varepsilon (q_0))\setminus \omega (E_6^\varepsilon (q_0)))$
. By [Reference Zvezdina30, (3) and (5)], we have that $\omega (N\delta \varphi )=\omega ({\rm Inndiag}(N)\varphi )\setminus \omega (N\varphi )=k\cdot (\omega ({\rm Inndiag}(E_6^\varepsilon (q_0))\setminus \omega (E_6^\varepsilon (q_0)))$![]() . By [Reference Zvezdina30, Lemmas 1 and 3], we see that $q^6+\varepsilon q^3+1,\, (q^2-1)(q^4+1)\in \omega ({\rm Inndiag}(E_6^\varepsilon (q_0))\setminus \omega (E_6^\varepsilon (q_0))$
. By [Reference Zvezdina30, Lemmas 1 and 3], we see that $q^6+\varepsilon q^3+1,\, (q^2-1)(q^4+1)\in \omega ({\rm Inndiag}(E_6^\varepsilon (q_0))\setminus \omega (E_6^\varepsilon (q_0))$![]() . By hypothesis, we obtain that both $q^6+\varepsilon q^3+1$
. By hypothesis, we obtain that both $q^6+\varepsilon q^3+1$![]() and $(q^2-1)(q^4+1)$
and $(q^2-1)(q^4+1)$![]() are $r$
are $r$![]() -power. Since $3\mid (q^6+\varepsilon q^3+1)$
-power. Since $3\mid (q^6+\varepsilon q^3+1)$![]() , we get that $r=3$
, we get that $r=3$![]() . As $(q^2-1)(q^4+1)$
. As $(q^2-1)(q^4+1)$![]() is a 3-power, then both $q^2-1$
is a 3-power, then both $q^2-1$![]() and $q^4+1$
and $q^4+1$![]() are 3-power, a contradiction. Similarly, we may rule out the case $N\cong E_7(q)$
are 3-power, a contradiction. Similarly, we may rule out the case $N\cong E_7(q)$![]() .
.
Case 3. $u=\delta \tau$![]() with $\delta \neq 1,\, \tau \neq 1$
with $\delta \neq 1,\, \tau \neq 1$![]() .
.
By [Reference Conway, Curtis, Norton, Parker and Wilson4, Table 5], we obtain that $N\cong PSL_n(q)$![]() with $n\geq 3$
with $n\geq 3$![]() , $P\Omega _{2n}^+(q)$
, $P\Omega _{2n}^+(q)$![]() with $n\geq 4$
with $n\geq 4$![]() , or $E_6(q)$
, or $E_6(q)$![]() . If $N\cong PSL_n(q)$
. If $N\cong PSL_n(q)$![]() , then $\delta ^\tau =\delta ^{-1}$
, then $\delta ^\tau =\delta ^{-1}$![]() and thus $o(u)=o(\delta \tau )=2$
and thus $o(u)=o(\delta \tau )=2$![]() , yielding $r=2$
, yielding $r=2$![]() . Assume first that $q$
. Assume first that $q$![]() is even. Then $(n,\,q-1)$
is even. Then $(n,\,q-1)$![]() is odd. In this case, $\tau$
is odd. In this case, $\tau$![]() is conjugate to $\tau \delta _0^i$
is conjugate to $\tau \delta _0^i$![]() for every $i$
for every $i$![]() in ${\rm Out}(N)$
in ${\rm Out}(N)$![]() , where $\delta _0$
, where $\delta _0$![]() is the generator of the diagonal automorphism group of $N$
is the generator of the diagonal automorphism group of $N$![]() in ${\rm Out}(N)$
in ${\rm Out}(N)$![]() . Therefore, $\omega (Nu)=\omega (N\tau )=\omega (PGL_n(q)\tau )$
. Therefore, $\omega (Nu)=\omega (N\tau )=\omega (PGL_n(q)\tau )$![]() . By [Reference Aschbacher and Seitz1, 19.9], we have that ${\bf C}_N(\tau )$
. By [Reference Aschbacher and Seitz1, 19.9], we have that ${\bf C}_N(\tau )$![]() is isomorphic to $PSp_n(q)$
is isomorphic to $PSp_n(q)$![]() if $n$
if $n$![]() is even, and to $P\Omega _n(q)$
is even, and to $P\Omega _n(q)$![]() if $n$
if $n$![]() is odd. Hence, there exists an element in $Nu$
is odd. Hence, there exists an element in $Nu$![]() whose order is not a prime power, a contradiction. By the same reason, by applying [Reference Harris13], there is also a contradiction for the case $q$
whose order is not a prime power, a contradiction. By the same reason, by applying [Reference Harris13], there is also a contradiction for the case $q$![]() is odd.
is odd.
If $N\cong P\Omega _{2n}^+(q)$![]() , we have that $(2,\,q-1)=2$
, we have that $(2,\,q-1)=2$![]() or $(4,\,q^n-1)>1$
or $(4,\,q^n-1)>1$![]() , which follows that $q$
, which follows that $q$![]() is odd. If ${\rm Inndiag}(N)/N$
is odd. If ${\rm Inndiag}(N)/N$![]() is cyclic, then $\delta ^\tau =\delta ^{-1}$
is cyclic, then $\delta ^\tau =\delta ^{-1}$![]() . Therefore, $o(u)=o(\delta \tau )=2$
. Therefore, $o(u)=o(\delta \tau )=2$![]() , by the same reason as above, we can also get a contradiction. If ${\rm Inndiag}(N)/N\cong C_2\times C_2$
, by the same reason as above, we can also get a contradiction. If ${\rm Inndiag}(N)/N\cong C_2\times C_2$![]() , first we may consider the case $n>4$
, first we may consider the case $n>4$![]() . By [Reference Gorenstein, Lyons and Solomon9, Theorem 2.5.12] and [Reference Grechkoseeva12, Fig. 3], we have $\omega (Nu)=\omega (PTO_{2n}^+(q_0)\setminus PSO_{2n}^+(q_0))$
. By [Reference Gorenstein, Lyons and Solomon9, Theorem 2.5.12] and [Reference Grechkoseeva12, Fig. 3], we have $\omega (Nu)=\omega (PTO_{2n}^+(q_0)\setminus PSO_{2n}^+(q_0))$![]() , against [Reference Grechkoseeva12, Lemma 2.8]. Now, we consider the case $n=4$
, against [Reference Grechkoseeva12, Lemma 2.8]. Now, we consider the case $n=4$![]() . According to [Reference Gorenstein, Lyons and Solomon9, Theorem 2.5.12], we see that $o(\tau )=2$
. According to [Reference Gorenstein, Lyons and Solomon9, Theorem 2.5.12], we see that $o(\tau )=2$![]() since $o(Nu)\geq 4$
since $o(Nu)\geq 4$![]() is a 2-power. By the same reason above, there is also a contradiction.
is a 2-power. By the same reason above, there is also a contradiction.
If $N\cong E_6(q)$![]() , then $\delta ^\tau =\delta ^{-1}$
, then $\delta ^\tau =\delta ^{-1}$![]() . It follows that $o(u)=2$
. It follows that $o(u)=2$![]() and $u$
and $u$![]() is conjugate to $\tau$
is conjugate to $\tau$![]() in ${\rm Out}(N)$
in ${\rm Out}(N)$![]() . Hence, $\omega (Nu)=\omega (N\tau )$
. Hence, $\omega (Nu)=\omega (N\tau )$![]() . Since ${\bf C}_N(\tau )=F_4(q)$
. Since ${\bf C}_N(\tau )=F_4(q)$![]() , we get that $Nu$
, we get that $Nu$![]() contains a non-$r$
contains a non-$r$![]() -element, a contradiction.
-element, a contradiction.
Case 4. $u=\delta \varphi \tau$![]() with $\delta \neq 1,\, \varphi \neq 1$
with $\delta \neq 1,\, \varphi \neq 1$![]() , and $\tau \neq 1$
, and $\tau \neq 1$![]() .
.
Let $\varphi _0$![]() be a generator of the field automorphism group of $N$
be a generator of the field automorphism group of $N$![]() such that $\varphi =\varphi _0^{f/k}$
such that $\varphi =\varphi _0^{f/k}$![]() and $\delta _0$
and $\delta _0$![]() a generator of the diagonal automorphism group of $N$
a generator of the diagonal automorphism group of $N$![]() such that $\delta =\delta _0^i$
such that $\delta =\delta _0^i$![]() for some positive integer $i$
for some positive integer $i$![]() . Let $q=q_0^k$
. Let $q=q_0^k$![]() . By [Reference Conway, Curtis, Norton, Parker and Wilson4, Table 5], we have $N\cong PSL_n(q)$
. By [Reference Conway, Curtis, Norton, Parker and Wilson4, Table 5], we have $N\cong PSL_n(q)$![]() with $n\geq 3$
with $n\geq 3$![]() , $P\Omega _{2n}^+(q)$
, $P\Omega _{2n}^+(q)$![]() with $n\geq 4$
with $n\geq 4$![]() , or $E_6(q)$
, or $E_6(q)$![]() with $3\mid (q-1)$
with $3\mid (q-1)$![]() .
.
If $N\cong PSL_n(q)$![]() , then, by [Reference Grechkoseeva11, Lemma 3.3] and hypothesis, we see that $k$
, then, by [Reference Grechkoseeva11, Lemma 3.3] and hypothesis, we see that $k$![]() is an $r$
is an $r$![]() -power and every element of $\omega (\delta (-q_0)PSU_n(q_0))$
-power and every element of $\omega (\delta (-q_0)PSU_n(q_0))$![]() is also an $r$
is also an $r$![]() -element. By [Reference Grechkoseeva11, Lemma 2.1], we see that $\delta (-q_0)PSU_n(q_0)$
-element. By [Reference Grechkoseeva11, Lemma 2.1], we see that $\delta (-q_0)PSU_n(q_0)$![]() if $r=2$
if $r=2$![]() or $\delta (q_0)PSL_n(q_0)$
or $\delta (q_0)PSL_n(q_0)$![]() if $r>2$
if $r>2$![]() , has an element of order ${((q_0^n-{(\varepsilon 1)^n})i)}/{((n,\,q_0+\varepsilon 1)(q_0-\varepsilon 1))}$
, has an element of order ${((q_0^n-{(\varepsilon 1)^n})i)}/{((n,\,q_0+\varepsilon 1)(q_0-\varepsilon 1))}$![]() . By hypothesis, this order is an $r$
. By hypothesis, this order is an $r$![]() -power. By a similar argument as in case 1, there is a contradiction.
-power. By a similar argument as in case 1, there is a contradiction.
If $P\Omega _{2n}^+(q)$![]() with $n\geq 4$
with $n\geq 4$![]() , then $q$
, then $q$![]() is odd. By [Reference Grechkoseeva12], there is also a contradiction.
is odd. By [Reference Grechkoseeva12], there is also a contradiction.
The remaining case is $N\cong E_6(q)$![]() . In this case, $3\mid (q-1)$
. In this case, $3\mid (q-1)$![]() . Since $N\langle u\rangle /N$
. Since $N\langle u\rangle /N$![]() is an $r$
is an $r$![]() -group, we see that $u$
-group, we see that $u$![]() is a field or graph, or a graph-field automorphism of $N$
is a field or graph, or a graph-field automorphism of $N$![]() up to conjugation, the final contradiction.
up to conjugation, the final contradiction.
3. Proofs of theorem A and corollary 1
Theorem A Let $G$![]() be a group and $N$
be a group and $N$![]() be a non-trivial normal subgroup of $G$
be a non-trivial normal subgroup of $G$![]() . Suppose that $G$
. Suppose that $G$![]() and $N$
and $N$![]() satisfy property $(\ast )$
satisfy property $(\ast )$![]() . If $N$
. If $N$![]() is non-solvable, then chief factor $H/K$
is non-solvable, then chief factor $H/K$![]() of $G$
of $G$![]() satisfying $H\leq N$
satisfying $H\leq N$![]() is isomorphic to $PSL_2(3^f)$
is isomorphic to $PSL_2(3^f)$![]() , where $f>1$
, where $f>1$![]() is a 2-power. In particular, $G/N$
is a 2-power. In particular, $G/N$![]() is solvable.
is solvable.
Proof. Suppose on the contrary that $G$![]() is a counter-example of minimal order. We first assert that chief factor $H/K$
is a counter-example of minimal order. We first assert that chief factor $H/K$![]() of $G$
of $G$![]() satisfying $H\leq N$
satisfying $H\leq N$![]() is also a non-solvable chief factor of $N\langle u\rangle$
is also a non-solvable chief factor of $N\langle u\rangle$![]() . Let $M_1/N_1$
. Let $M_1/N_1$![]() be a non-solvable chief factor of $G$
be a non-solvable chief factor of $G$![]() satisfying $M_1\leq N$
satisfying $M_1\leq N$![]() . Write $M_1/N_1=F_1\times \cdots \times F_t$
. Write $M_1/N_1=F_1\times \cdots \times F_t$![]() , where $F_i$
, where $F_i$![]() are isomorphic non-abelian simple groups with integer $t\geq 1$
are isomorphic non-abelian simple groups with integer $t\geq 1$![]() . Assume that $N/N_1$
. Assume that $N/N_1$![]() acts transitively on $\Omega =\{F_1,\ldots,F_t\}$
acts transitively on $\Omega =\{F_1,\ldots,F_t\}$![]() . Then $M_1/N_1$
. Then $M_1/N_1$![]() is also a chief factor of $N$
is also a chief factor of $N$![]() and thus is a chief factor of $N\langle u\rangle$
and thus is a chief factor of $N\langle u\rangle$![]() , we are done. Assume that $N/N_1$
, we are done. Assume that $N/N_1$![]() does not act transitively on $\Omega$
does not act transitively on $\Omega$![]() . Therefore, $t>1$
. Therefore, $t>1$![]() . Then there is an element $N_1 w\in G/N_1\setminus N/N_1$
. Then there is an element $N_1 w\in G/N_1\setminus N/N_1$![]() such that $N_1 \langle w\rangle$
such that $N_1 \langle w\rangle$![]() acts non-trivially on $\Omega$
acts non-trivially on $\Omega$![]() . Otherwise, every element in $G/N_1\setminus N/N_1$
. Otherwise, every element in $G/N_1\setminus N/N_1$![]() acts trivially on $\Omega$
acts trivially on $\Omega$![]() , which indicates that $N/N_1$
, which indicates that $N/N_1$![]() acts transitively on $\Omega$
acts transitively on $\Omega$![]() , a contradiction. Hence, there is an orbit $\Omega _1$
, a contradiction. Hence, there is an orbit $\Omega _1$![]() of $N_1 \langle w\rangle$
of $N_1 \langle w\rangle$![]() on $\Omega$
on $\Omega$![]() having size greater than 1. Without loss of generality, we may assume that $\Omega _1=\{F_1,\ldots, F_s\}$
having size greater than 1. Without loss of generality, we may assume that $\Omega _1=\{F_1,\ldots, F_s\}$![]() with $s>1$
with $s>1$![]() . By hypothesis, we get that $N_1 w$
. By hypothesis, we get that $N_1 w$![]() is an $r_1$
is an $r_1$![]() -element for some prime $r_1$
-element for some prime $r_1$![]() . Let $1\neq f_1\in F_1$
. Let $1\neq f_1\in F_1$![]() be an $r_1'$
be an $r_1'$![]() -element. Then there is an element $N_1 w^{j_i}$
-element. Then there is an element $N_1 w^{j_i}$![]() such that $f_1^{N_1 w^{j_i}}\in F_i$
such that $f_1^{N_1 w^{j_i}}\in F_i$![]() where $j_i$
where $j_i$![]() is a positive integer. Now, we get that $N_1 w_0:=\prod _{i=1}^s f_1^{(N_1 w)^{j_i}}$
is a positive integer. Now, we get that $N_1 w_0:=\prod _{i=1}^s f_1^{(N_1 w)^{j_i}}$![]() is centralized by $N_1 w$
is centralized by $N_1 w$![]() . In this case, $N_1 w_0w$
. In this case, $N_1 w_0w$![]() does not have prime power order and thus $w_0w$
does not have prime power order and thus $w_0w$![]() is not a prime power order element, contrary to the assumption of the theorem as $w_0w\in G\setminus N$
is not a prime power order element, contrary to the assumption of the theorem as $w_0w\in G\setminus N$![]() . Consequently, we conclude that $M_1/N_1$
. Consequently, we conclude that $M_1/N_1$![]() is a chief factor of $N$
is a chief factor of $N$![]() . So is of $N\langle u\rangle$
. So is of $N\langle u\rangle$![]() , as required.
, as required.
Take $1\neq u\in G\setminus N$![]() . If $N\langle u\rangle < G$
. If $N\langle u\rangle < G$![]() , by assumption, every non-solvable chief factor $H/K$
, by assumption, every non-solvable chief factor $H/K$![]() of $N\langle u\rangle$
of $N\langle u\rangle$![]() satisfying $H\leq N$
satisfying $H\leq N$![]() is isomorphic to $PSL_2(3^f)$
is isomorphic to $PSL_2(3^f)$![]() , where $f>1$
, where $f>1$![]() is a 2-power. As chief factor $H/K$
is a 2-power. As chief factor $H/K$![]() of $G$
of $G$![]() satisfying $H\leq N$
satisfying $H\leq N$![]() is also a chief factor of $N\langle u\rangle$
is also a chief factor of $N\langle u\rangle$![]() , the theorem holds, against our assumption. As a result, $G=N\langle u\rangle$
, the theorem holds, against our assumption. As a result, $G=N\langle u\rangle$![]() .
.
Let $M>1$![]() be a minimal normal subgroup of $G$
be a minimal normal subgroup of $G$![]() , which is contained in $N$
, which is contained in $N$![]() . Clearly, each element in $G/M\setminus N/M$
. Clearly, each element in $G/M\setminus N/M$![]() has prime power order. This shows that $G/M$
has prime power order. This shows that $G/M$![]() and $N/M$
and $N/M$![]() satisfy property $(\ast )$
satisfy property $(\ast )$![]() . Let $(M_1/M)/(M_2/M)$
. Let $(M_1/M)/(M_2/M)$![]() be a chief factor of $G/M$
be a chief factor of $G/M$![]() such that $M_1/M\leq N/M$
such that $M_1/M\leq N/M$![]() . Then $M_1/M_2$
. Then $M_1/M_2$![]() is also a chief factor of $G$
is also a chief factor of $G$![]() satisfying in $M_1\leq N$
satisfying in $M_1\leq N$![]() . By induction, $(M_1/M)/(M_2/M)$
. By induction, $(M_1/M)/(M_2/M)$![]() isomorphic to $PSL_2(3^f)$
isomorphic to $PSL_2(3^f)$![]() , where some $f>1$
, where some $f>1$![]() is a 2-power, so is $M_1/M_2$
is a 2-power, so is $M_1/M_2$![]() . In the following, we focus on the chief factors which are contained in $M$
. In the following, we focus on the chief factors which are contained in $M$![]() . We only need to consider the case that $M$
. We only need to consider the case that $M$![]() is non-solvable.
is non-solvable.
In this case, $M$![]() is a non-solvable minimal normal subgroup of $G$
is a non-solvable minimal normal subgroup of $G$![]() . Therefore, we may write $M=S_1\times \cdots \times S_t$
. Therefore, we may write $M=S_1\times \cdots \times S_t$![]() , where $t$
, where $t$![]() is a positive integer and $S_i$
is a positive integer and $S_i$![]() are isomorphic non-abelian simple groups for all $i\in \{1,\, \dots,\, t\}$
are isomorphic non-abelian simple groups for all $i\in \{1,\, \dots,\, t\}$![]() . Assume that $t>1$
. Assume that $t>1$![]() . Easily, $\langle u\rangle$
. Easily, $\langle u\rangle$![]() acts transitively on $\{S_1,\ldots, S_t\}$
acts transitively on $\{S_1,\ldots, S_t\}$![]() . Let $o(u)=m$
. Let $o(u)=m$![]() and $1\neq x\in S_1$
and $1\neq x\in S_1$![]() be a $q$
be a $q$![]() -element for some odd prime $q$
-element for some odd prime $q$![]() distinct from $p$
distinct from $p$![]() , where $p$
, where $p$![]() is a prime divisor of $m$
is a prime divisor of $m$![]() . Then $y=\prod _{i=1}^{m} x^{u^i}$
. Then $y=\prod _{i=1}^{m} x^{u^i}$![]() is centralized by $u$
is centralized by $u$![]() . That is, the order of $uy\in G\backslash N$
. That is, the order of $uy\in G\backslash N$![]() is divisible by $pq$
is divisible by $pq$![]() . This contradiction deduces that $t=1$
. This contradiction deduces that $t=1$![]() . Consequently, $M$
. Consequently, $M$![]() is a non-abelian simple group, and $u\in {\rm Aut}(M)$
is a non-abelian simple group, and $u\in {\rm Aut}(M)$![]() , where ${\rm Aut}(M)$
, where ${\rm Aut}(M)$![]() is the automorphism group of $M$
is the automorphism group of $M$![]() .
.
Since $Mu\subseteq Nu\subseteq G\setminus N$![]() , we see that the order of every element in $Mu$
, we see that the order of every element in $Mu$![]() has prime power order. By theorem B, we get that $M\cong PSL_2(3^f)$
has prime power order. By theorem B, we get that $M\cong PSL_2(3^f)$![]() , where $f$
, where $f$![]() is a 2-power and $u$
is a 2-power and $u$![]() is the product of a field and a diagonal automorphism of $PSL_2(3^f)$
is the product of a field and a diagonal automorphism of $PSL_2(3^f)$![]() . Therefore, chief factor $H/K$
. Therefore, chief factor $H/K$![]() of $G$
of $G$![]() satisfying $H\leq N$
satisfying $H\leq N$![]() is isomorphic to $PSL_2(3^f)$
is isomorphic to $PSL_2(3^f)$![]() , with $f>1$
, with $f>1$![]() a 2-power, as required.
a 2-power, as required.
Let $W$![]() be a maximal solvable normal subgroup of $G$
be a maximal solvable normal subgroup of $G$![]() contained in $N$
contained in $N$![]() and $N_0/M$
and $N_0/M$![]() be a chief factor of $G$
be a chief factor of $G$![]() with $N_0\leq N$
with $N_0\leq N$![]() . Then $N_0/W\cong PSL_2(3^{f_1})$
. Then $N_0/W\cong PSL_2(3^{f_1})$![]() , where $f_1$
, where $f_1$![]() is a 2-power. Let $\widetilde {G}:=G/W$
is a 2-power. Let $\widetilde {G}:=G/W$![]() . Take any prime power element $e\in G\setminus N$
. Take any prime power element $e\in G\setminus N$![]() . Then $\widetilde {N_0}\widetilde {e}\subseteq \widetilde {N}\widetilde {e}\subseteq G\setminus N$
. Then $\widetilde {N_0}\widetilde {e}\subseteq \widetilde {N}\widetilde {e}\subseteq G\setminus N$![]() . It follows that every element in $\widetilde {N_0}\widetilde {e}$
. It follows that every element in $\widetilde {N_0}\widetilde {e}$![]() has prime power order. By theorem B, we get that the order of $e$
has prime power order. By theorem B, we get that the order of $e$![]() is a 2-power. By the arbitrariness of $e$
is a 2-power. By the arbitrariness of $e$![]() , we get that $G/N$
, we get that $G/N$![]() is a 2-group, contrary our assumption that $G/N$
is a 2-group, contrary our assumption that $G/N$![]() is non-solvable. Consequently, $G/N$
is non-solvable. Consequently, $G/N$![]() is solvable.
is solvable.
Corollary 1 Let $G$![]() be a group and $N\unlhd G$
be a group and $N\unlhd G$![]() . If every element $x\in G\setminus N$
. If every element $x\in G\setminus N$![]() has prime power order, and ${\bf C}_G(x)$
has prime power order, and ${\bf C}_G(x)$![]() is maximal in $G$
is maximal in $G$![]() , then $N$
, then $N$![]() is solvable.
is solvable.
Proof. Suppose on the contrary that $N$![]() is non-solvable. By theorem A, $G$
is non-solvable. By theorem A, $G$![]() has a non-solvable chief factor $M_2/M_1\cong PSL_2(3^f)$
has a non-solvable chief factor $M_2/M_1\cong PSL_2(3^f)$![]() , where $f$
, where $f$![]() is a 2-power such that $M_2\leq N$
is a 2-power such that $M_2\leq N$![]() and $M_1$
and $M_1$![]() is solvable. Write $\overline {G}:=G/M_1$
is solvable. Write $\overline {G}:=G/M_1$![]() . Since $\overline {M_2}\overline {u}\subseteq \overline {N}\overline {u}\subseteq \overline {G}\setminus \overline {N}$
. Since $\overline {M_2}\overline {u}\subseteq \overline {N}\overline {u}\subseteq \overline {G}\setminus \overline {N}$![]() , we see that each element in $\overline {M_2}\overline {u}$
, we see that each element in $\overline {M_2}\overline {u}$![]() has prime power order. By theorem B, $\overline {u}$
has prime power order. By theorem B, $\overline {u}$![]() is a product of a field automorphism and a diagonal automorphism of $\overline {M_2}$
is a product of a field automorphism and a diagonal automorphism of $\overline {M_2}$![]() , and $\overline {M_2}\cong$
, and $\overline {M_2}\cong$![]() $PSL_2(3^f)$
$PSL_2(3^f)$![]() with $f>1$
with $f>1$![]() a 2-power. Easily, $\overline {u}$
a 2-power. Easily, $\overline {u}$![]() is a 2-element. Without loss of generality, we may consider $u$
is a 2-element. Without loss of generality, we may consider $u$![]() is a 2-element satisfying $G=M_2\langle u\rangle$
is a 2-element satisfying $G=M_2\langle u\rangle$![]() and thus $\overline {G}=\overline {M_2}\langle \overline {u}\rangle$
and thus $\overline {G}=\overline {M_2}\langle \overline {u}\rangle$![]() .
.
Now, consider $P:={\bf C}_G(u)$![]() . Since every element of $G\setminus N$
. Since every element of $G\setminus N$![]() is a 2-element, we see that $P$
is a 2-element, we see that $P$![]() must be a 2-group. The maximality of $P$
must be a 2-group. The maximality of $P$![]() indicates that $P$
indicates that $P$![]() is a Sylow 2-subgroup of $G$
is a Sylow 2-subgroup of $G$![]() . If $M_1 \nleq P$
. If $M_1 \nleq P$![]() , we have that $G=PM_1$
, we have that $G=PM_1$![]() , indicating that $G$
, indicating that $G$![]() is solvable, a contradiction. Hence, $M_1\leq P$
is solvable, a contradiction. Hence, $M_1\leq P$![]() . Then $\overline {P}$
. Then $\overline {P}$![]() is a maximal subgroup of $\overline {G}$
is a maximal subgroup of $\overline {G}$![]() . Let $P_0:=P\cap M_2$
. Let $P_0:=P\cap M_2$![]() . Then $P_0\in$
. Then $P_0\in$![]() Syl$_2(M_2)$
Syl$_2(M_2)$![]() , forcing $\overline {P_0}\in$
, forcing $\overline {P_0}\in$![]() Syl$_2(\overline {M_2})$
Syl$_2(\overline {M_2})$![]() . Let $|\overline {P_0}|=2^a$
. Let $|\overline {P_0}|=2^a$![]() . If $\overline {P_0}$
. If $\overline {P_0}$![]() is maximal in $\overline {M_2}$
is maximal in $\overline {M_2}$![]() , then by [Reference Huppert17, Theorem 2.8.27], $2^a=3^f\pm 1$
, then by [Reference Huppert17, Theorem 2.8.27], $2^a=3^f\pm 1$![]() . By Lemma 2.1, it follows that $a=3$
. By Lemma 2.1, it follows that $a=3$![]() and $f=2$
and $f=2$![]() . Therefore, $\overline {M_2}\cong PSL_2(3^2)$
. Therefore, $\overline {M_2}\cong PSL_2(3^2)$![]() . However, according to [Reference Conway, Curtis, Norton, Parker and Wilson4], we see that $\overline {P_0}$
. However, according to [Reference Conway, Curtis, Norton, Parker and Wilson4], we see that $\overline {P_0}$![]() is not maximal in $\overline {M_2}$
is not maximal in $\overline {M_2}$![]() . This contradiction forces that $\overline {P_0}$
. This contradiction forces that $\overline {P_0}$![]() is not maximal in $\overline {M_2}$
is not maximal in $\overline {M_2}$![]() . Furthermore, as $\overline {M_2} \leq \overline {G}\leq {\rm Aut}(\overline {M_2})$
. Furthermore, as $\overline {M_2} \leq \overline {G}\leq {\rm Aut}(\overline {M_2})$![]() and $\overline {M_2}\cong PSL_2(3^f)$
and $\overline {M_2}\cong PSL_2(3^f)$![]() , we obtain that $\overline {G}\cong M_{10}\cong PSL_2(9) \cdot \langle \overline {u}\rangle$
, we obtain that $\overline {G}\cong M_{10}\cong PSL_2(9) \cdot \langle \overline {u}\rangle$![]() and $\overline {P}\cong C_8\rtimes C_2$
and $\overline {P}\cong C_8\rtimes C_2$![]() or $D_{16}$
or $D_{16}$![]() by [Reference Giudici7, Theorem 1.1]. In this case, $\overline {u}\not \in {\bf Z}(\overline {P})$
by [Reference Giudici7, Theorem 1.1]. In this case, $\overline {u}\not \in {\bf Z}(\overline {P})$![]() , the final contradiction completes the proof.
, the final contradiction completes the proof.
4. Theorem D and its proof
For the reader's convenience, we restate theorem D.
Theorem D Let $G$![]() be a group and $N$
be a group and $N$![]() be a proper normal subgroup of $G$
be a proper normal subgroup of $G$![]() such that ${\bf Z}(G)< N$
such that ${\bf Z}(G)< N$![]() . If ${\bf C}_G(x)$
. If ${\bf C}_G(x)$![]() is maximal in $G$
is maximal in $G$![]() for every element $x\in G\setminus N$
for every element $x\in G\setminus N$![]() , then $G$
, then $G$![]() is solvable with $G/N$
is solvable with $G/N$![]() abelian. Furthermore,
abelian. Furthermore,
(I) If $G$
 is nilpotent, then $G/N$
is nilpotent, then $G/N$ is a $p$
is a $p$ -group for some prime $p$
-group for some prime $p$ . Moreover, $G=P\times {\bf Z}(G)_{p'}$
. Moreover, $G=P\times {\bf Z}(G)_{p'}$ and ${\bf C}_G(x)\unlhd G$
and ${\bf C}_G(x)\unlhd G$ for every $x\in P\setminus N$
for every $x\in P\setminus N$ ;
;(II) $G$
 is non-nilpotent, then $|G:{\bf C}_G(x)|=r^a$
is non-nilpotent, then $|G:{\bf C}_G(x)|=r^a$ with prime $r$
with prime $r$ and positive integer $a$
and positive integer $a$ . Suppose that $R$
. Suppose that $R$ is a Sylow $r$
is a Sylow $r$ -subgroup of $G$
-subgroup of $G$ and $K$
and $K$ is a Hall $r'$
is a Hall $r'$ -subgroup of $G$
-subgroup of $G$ , then one of the statements holds:
, then one of the statements holds:
(1) If $G/N$
 is a $p$
is a $p$ -group for some prime $p$
-group for some prime $p$ , we have
, we have
(1.1) If $r=p$
 , write $\overline {G}:=G/{\bf O}_p(G){\bf Z}(G)$
, write $\overline {G}:=G/{\bf O}_p(G){\bf Z}(G)$ . Then $\overline {G}=\overline {K}\rtimes \overline {P}$
. Then $\overline {G}=\overline {K}\rtimes \overline {P}$ is a Frobenius group with abelian kernel $\overline {K}$
is a Frobenius group with abelian kernel $\overline {K}$ and complement $\overline {P}$
and complement $\overline {P}$ of order $p$
of order $p$ .
.(1.2) If $r\neq p$
 , write $\widetilde {G}:=G/{\bf Z}(G)_r$
, write $\widetilde {G}:=G/{\bf Z}(G)_r$ . Then
. Then
(1.2.1) If ${\bf O}_r(\widetilde {G})=\widetilde {1}$
 , then the Fitting length $h(\widetilde {G})=3$
, then the Fitting length $h(\widetilde {G})=3$ and $\widetilde {G}$
and $\widetilde {G}$ has the following normal series:
\[ \widetilde{1}\unlhd {\bf O}_{r'}(\widetilde{G})\unlhd {\bf O}_{r',r}(\widetilde{G})\unlhd \widetilde{G}={\bf O}_{r',r,r'}(\widetilde{G}), \]where ${\bf O}_{r',r}(\widetilde {G})/{\bf O}_{r'}(\widetilde {G})\cong \widetilde {R}$
has the following normal series:
\[ \widetilde{1}\unlhd {\bf O}_{r'}(\widetilde{G})\unlhd {\bf O}_{r',r}(\widetilde{G})\unlhd \widetilde{G}={\bf O}_{r',r,r'}(\widetilde{G}), \]where ${\bf O}_{r',r}(\widetilde {G})/{\bf O}_{r'}(\widetilde {G})\cong \widetilde {R}$
 is elementary abelian and $\widetilde {G}/{\bf O}_{r',r}(\widetilde {G})$
is elementary abelian and $\widetilde {G}/{\bf O}_{r',r}(\widetilde {G})$ is a $p$
is a $p$ -group;
-group;(1.2.2) Assume that ${\bf O}_r(\widetilde {G})=\widetilde {R}$
 . If ${\bf C}_G(x)_{p'}\nleq {\bf Z}(G)$
. If ${\bf C}_G(x)_{p'}\nleq {\bf Z}(G)$ , then the Fitting length $h(\widetilde {G})=2$
, then the Fitting length $h(\widetilde {G})=2$ and $\widetilde {G}$
and $\widetilde {G}$ has the following normal series:
\[ \widetilde{1}\unlhd \widetilde{R}\unlhd \widetilde{N}\unlhd \widetilde{G}, \]where $\widetilde {R}$
has the following normal series:
\[ \widetilde{1}\unlhd \widetilde{R}\unlhd \widetilde{N}\unlhd \widetilde{G}, \]where $\widetilde {R}$
 is an elementary abelian $r$
is an elementary abelian $r$ -group and $G/R$
-group and $G/R$ is nilpotent.
is nilpotent.(1.2.3) Write $\widehat {G}:=G/{\bf Z}(G)$
 . Assume that ${\bf O}_r(\widetilde {G})=\widetilde {R}$
. Assume that ${\bf O}_r(\widetilde {G})=\widetilde {R}$ . If ${\bf C}_G(x)_{p'}\leq {\bf Z}(G)$
. If ${\bf C}_G(x)_{p'}\leq {\bf Z}(G)$ , then $\widehat {G}=\widehat {R}\rtimes \widehat {P}$
, then $\widehat {G}=\widehat {R}\rtimes \widehat {P}$ , where $P$
, where $P$ is a Sylow $p$
is a Sylow $p$ -subgroup of $G$
-subgroup of $G$ and $R$
and $R$ is a Sylow $r$
is a Sylow $r$ -subgroup of $G$
-subgroup of $G$ with $\widehat {R}$
with $\widehat {R}$ elementary abelian. Let $N_p=N\cap P$
elementary abelian. Let $N_p=N\cap P$ . If $\widehat {N_p}\unlhd \widehat {G}$
. If $\widehat {N_p}\unlhd \widehat {G}$ , then $\widehat {G}/\widehat {N_p}$
, then $\widehat {G}/\widehat {N_p}$ is a Frobenius group; if $\widehat {N_p}\ntrianglelefteq \widehat {G}$
is a Frobenius group; if $\widehat {N_p}\ntrianglelefteq \widehat {G}$ , then ${\bf N}_{\widehat {G}}(\widehat {N_p})=\widehat {P}$
, then ${\bf N}_{\widehat {G}}(\widehat {N_p})=\widehat {P}$ .
.
(2) If $|\pi (G/N)|\geq 2$
 , then one of the following statements holds:
, then one of the following statements holds:
(2.1) Let $\overline {G}:=G/{\bf O}_r(G){\bf Z}(G)$
 . Then $\overline {G}=\overline {K}\rtimes \overline {R}$
. Then $\overline {G}=\overline {K}\rtimes \overline {R}$ is a Frobenius group with abelian kernel $\overline {K}$
is a Frobenius group with abelian kernel $\overline {K}$ and complement $\overline {R}$
and complement $\overline {R}$ of order $r$
of order $r$ ;
;(2.2) Let $\overline {G}:=G/{\bf Z}(G)$
 . Then $\overline {G}=\overline {R}\rtimes \overline {K}$
. Then $\overline {G}=\overline {R}\rtimes \overline {K}$ is a Frobenius group with $\overline {R}$
is a Frobenius group with $\overline {R}$ a minimal normal subgroup of $\overline {G}$
a minimal normal subgroup of $\overline {G}$ and $\overline {K}$
and $\overline {K}$ cyclic. In particular, $R\leq N$
cyclic. In particular, $R\leq N$ .
.
Proof. Let $x\in G\setminus N$![]() be an arbitrary element. Then there exists a component of $x$
be an arbitrary element. Then there exists a component of $x$![]() , say $x_1$
, say $x_1$![]() , such that $x_1\in G\setminus N$
, such that $x_1\in G\setminus N$![]() . Note that ${\bf C}_G(x)\leq {\bf C}_G(x_1)$
. Note that ${\bf C}_G(x)\leq {\bf C}_G(x_1)$![]() and both ${\bf C}_G(x)$
and both ${\bf C}_G(x)$![]() and ${\bf C}_G(x_1)$
and ${\bf C}_G(x_1)$![]() are maximal in $G$
are maximal in $G$![]() . Then ${\bf C}_G(x)={\bf C}_G(x_1)$
. Then ${\bf C}_G(x)={\bf C}_G(x_1)$![]() . Without loss of generality, we may consider $x$
. Without loss of generality, we may consider $x$![]() as a $p$
as a $p$![]() -element for some prime $p$
-element for some prime $p$![]() . Furthermore,
. Furthermore,
Step 1. ${\bf C}_G(x)={\bf C}_G(x)_p\times {\bf C}_G(x)_{p'}$![]() , where ${\bf C}_G(x)_p$
, where ${\bf C}_G(x)_p$![]() is the Sylow $p$
is the Sylow $p$![]() -subgroup of ${\bf C}_G(x)$
-subgroup of ${\bf C}_G(x)$![]() and ${\bf C}_G(x)_{p'}$
and ${\bf C}_G(x)_{p'}$![]() is the Hall $p'$
is the Hall $p'$![]() -subgroup of ${\bf C}_G(x)$
-subgroup of ${\bf C}_G(x)$![]() with ${\bf C}_G(x)_{p'}\leq {\bf Z}({\bf C}_G(x))$
with ${\bf C}_G(x)_{p'}\leq {\bf Z}({\bf C}_G(x))$![]() . In particular, ${\bf C}_G(x)$
. In particular, ${\bf C}_G(x)$![]() is nilpotent.
is nilpotent.
For every $p'$![]() -element $v\in {\bf C}_G(x)$
-element $v\in {\bf C}_G(x)$![]() , we always have $xv\in G\setminus N$
, we always have $xv\in G\setminus N$![]() . By lemma 5.1, it follows that ${\bf C}_G(vx)={\bf C}_G(x)\cap {\bf C}_G(v)$
. By lemma 5.1, it follows that ${\bf C}_G(vx)={\bf C}_G(x)\cap {\bf C}_G(v)$![]() . Note that ${\bf C}_G(x)$
. Note that ${\bf C}_G(x)$![]() and ${\bf C}_G(xv)$
and ${\bf C}_G(xv)$![]() are maximal subgroups of $G$
are maximal subgroups of $G$![]() . Then ${\bf C}_G(vx)={\bf C}_G(x)\leq {\bf C}_G(v)$
. Then ${\bf C}_G(vx)={\bf C}_G(x)\leq {\bf C}_G(v)$![]() , yielding $v\in {\bf Z}({\bf C}_G(x))$
, yielding $v\in {\bf Z}({\bf C}_G(x))$![]() . As a result, ${\bf C}_G(x)={\bf C}_G(x)_p\times {\bf C}_G(x)_{p'}$
. As a result, ${\bf C}_G(x)={\bf C}_G(x)_p\times {\bf C}_G(x)_{p'}$![]() , where ${\bf C}_G(x)_p$
, where ${\bf C}_G(x)_p$![]() is the Sylow $p$
is the Sylow $p$![]() -subgroup of ${\bf C}_G(x)$
-subgroup of ${\bf C}_G(x)$![]() and ${\bf C}_G(x)_{p'}\leq {\bf Z}({\bf C}_G(x))$
and ${\bf C}_G(x)_{p'}\leq {\bf Z}({\bf C}_G(x))$![]() . Clearly, ${\bf C}_G(x)$
. Clearly, ${\bf C}_G(x)$![]() is nilpotent.
is nilpotent.
Step 2. $G/N$![]() is abelian.
is abelian.
For every $y\in G\setminus N$![]() , we see that ${\bf C}_G(y)$
, we see that ${\bf C}_G(y)$![]() is maximal in $G$
is maximal in $G$![]() and ${\bf C}_G(y)N/N\leq {\bf C}_{{G/N}}({yN})$
and ${\bf C}_G(y)N/N\leq {\bf C}_{{G/N}}({yN})$![]() . If $N\leq {\bf C}_G(y)$
. If $N\leq {\bf C}_G(y)$![]() , then $y\in {\bf C}_G(N)$
, then $y\in {\bf C}_G(N)$![]() ; if $N\nleq {\bf C}_G(y)$
; if $N\nleq {\bf C}_G(y)$![]() , then $G={\bf C}_G(y)N$
, then $G={\bf C}_G(y)N$![]() , forcing ${\bf C}_{G/N}({yN})={G/N}$
, forcing ${\bf C}_{G/N}({yN})={G/N}$![]() . Therefore, ${yN}\in {\bf Z}(G/N):=Z/N$
. Therefore, ${yN}\in {\bf Z}(G/N):=Z/N$![]() , yielding to $y\in Z$
, yielding to $y\in Z$![]() . As a result, $G=Z\cup {\bf C}_G(N)$
. As a result, $G=Z\cup {\bf C}_G(N)$![]() , which implies that $G=Z$
, which implies that $G=Z$![]() or $G={\bf C}_G(N)$
or $G={\bf C}_G(N)$![]() . Since ${\bf Z}(G)< N$
. Since ${\bf Z}(G)< N$![]() , we obtain that $G=Z$
, we obtain that $G=Z$![]() . Hence, $G/N=Z/N={\bf Z}(G/N)$
. Hence, $G/N=Z/N={\bf Z}(G/N)$![]() . Consequently, $G/N$
. Consequently, $G/N$![]() is abelian, as required.
is abelian, as required.
Step 3. $G$![]() is solvable.
is solvable.
Assume false. If there exists a $2'$![]() -element $x_0\in G\setminus N$
-element $x_0\in G\setminus N$![]() having prime power order, then by step 1, we see that ${\bf C}_G(x_0)$
having prime power order, then by step 1, we see that ${\bf C}_G(x_0)$![]() is nilpotent. Write ${\bf C}_G(x_0)=T_0\times U_0$
is nilpotent. Write ${\bf C}_G(x_0)=T_0\times U_0$![]() , where $T_0$
, where $T_0$![]() is the Sylow 2-subgroup of ${\bf C}_G(x_0)$
is the Sylow 2-subgroup of ${\bf C}_G(x_0)$![]() and $U_0$
and $U_0$![]() is the Hall $2'$
is the Hall $2'$![]() -subgroup of ${\bf C}_G(x_0)$
-subgroup of ${\bf C}_G(x_0)$![]() . By [Reference Rose23, Theorem 1], we obtain that $U_0\unlhd G$
. By [Reference Rose23, Theorem 1], we obtain that $U_0\unlhd G$![]() , ${\bf Z}(U_0)\leq {\bf Z}(G)$
, ${\bf Z}(U_0)\leq {\bf Z}(G)$![]() , and $G/{\bf Z}(U_0)\cong G/U_0\times U_0/{\bf Z}(U_0)$
, and $G/{\bf Z}(U_0)\cong G/U_0\times U_0/{\bf Z}(U_0)$![]() .
.
Note that $G$![]() is non-solvable. So is $G/U_0$
is non-solvable. So is $G/U_0$![]() . As $T_0U_0/U_0={\bf C}_G(x_0)/U_0$
. As $T_0U_0/U_0={\bf C}_G(x_0)/U_0$![]() is a maximal 2-subgroup of $G/U_0$
is a maximal 2-subgroup of $G/U_0$![]() , we assert that $T_0U_0/U_0$
, we assert that $T_0U_0/U_0$![]() must be a Sylow 2-subgroup of $G/U_0$
must be a Sylow 2-subgroup of $G/U_0$![]() , which indicates that $T_0U_0/U_0$
, which indicates that $T_0U_0/U_0$![]() is not normal in $G/U_0$
is not normal in $G/U_0$![]() as $G/U_0$
as $G/U_0$![]() is non-solvable. On the contrary, by step 1, $T_0$
is non-solvable. On the contrary, by step 1, $T_0$![]() is abelian, so is $T_0U_0/U_0$
is abelian, so is $T_0U_0/U_0$![]() . Hence, ${\bf N}_{G/U_0}(T_0U_0/U_0)\geq {\bf C}_{G/U_0}(T_0U_0/U_0)\geq T_0U_0/U_0$
. Hence, ${\bf N}_{G/U_0}(T_0U_0/U_0)\geq {\bf C}_{G/U_0}(T_0U_0/U_0)\geq T_0U_0/U_0$![]() , which yields to ${\bf N}_{G/U_0}(T_0U_0/U_0)={\bf C}_{G/U_0}(T_0U_0/U_0)$
, which yields to ${\bf N}_{G/U_0}(T_0U_0/U_0)={\bf C}_{G/U_0}(T_0U_0/U_0)$![]() . By [Reference Kurzweil and Stellmacher19, Theorem 7.2.1], we see that $G/U_0$
. By [Reference Kurzweil and Stellmacher19, Theorem 7.2.1], we see that $G/U_0$![]() has a normal 2-complement, against the fact that $G/U_0$
has a normal 2-complement, against the fact that $G/U_0$![]() is non-solvable. Consequently, each element in $G\setminus N$
is non-solvable. Consequently, each element in $G\setminus N$![]() is a 2-element. By corollary 1, $N$
is a 2-element. By corollary 1, $N$![]() is solvable, so is $G$
is solvable, so is $G$![]() by step 2, which is a contradiction.
by step 2, which is a contradiction.
Step 4. If $G$![]() is nilpotent, then $G/N$
is nilpotent, then $G/N$![]() is a $p$
is a $p$![]() -group and $G=P\times {\bf Z}(G)_{p'}$
-group and $G=P\times {\bf Z}(G)_{p'}$![]() with $P\in$
with $P\in$![]() Syl$_p(G)$
Syl$_p(G)$![]() . Furthermore, ${\bf C}_G(x)$
. Furthermore, ${\bf C}_G(x)$![]() is a normal maximal subgroup of $G$
is a normal maximal subgroup of $G$![]() for any $x\in P\setminus N$
for any $x\in P\setminus N$![]() satisfying $|G/{\bf C}_G(x)|=p$
satisfying $|G/{\bf C}_G(x)|=p$![]() .
.
Assume that $G$![]() is nilpotent. If $|\pi (G/N)|\geq 2$
is nilpotent. If $|\pi (G/N)|\geq 2$![]() , then there exist two distinct primes $p,\, q\in \pi (G/N)$
, then there exist two distinct primes $p,\, q\in \pi (G/N)$![]() . Select $w\in P\setminus N$
. Select $w\in P\setminus N$![]() a $p$
a $p$![]() -element and $v\in Q\setminus N$
-element and $v\in Q\setminus N$![]() a $q$
a $q$![]() -element, where $P$
-element, where $P$![]() and $Q$
and $Q$![]() are Sylow $p$
are Sylow $p$![]() -subgroup and Sylow $q$
-subgroup and Sylow $q$![]() -subgroup of $G$
-subgroup of $G$![]() , respectively. In this case, $wv=vw\in G\setminus N$
, respectively. In this case, $wv=vw\in G\setminus N$![]() , showing that ${\bf C}_G(v), {\bf C}_G(w)$
, showing that ${\bf C}_G(v), {\bf C}_G(w)$![]() , and ${\bf C}_G(vw)$
, and ${\bf C}_G(vw)$![]() are all maximal subgroups of $G$
are all maximal subgroups of $G$![]() . On the contrary, lemma 5.1 indicates that ${\bf C}_G(wv)={\bf C}_G(w)\cap {\bf C}_G(v)$
. On the contrary, lemma 5.1 indicates that ${\bf C}_G(wv)={\bf C}_G(w)\cap {\bf C}_G(v)$![]() , which forces that ${\bf C}_G(wv)={\bf C}_G(w)={\bf C}_G(v)$
, which forces that ${\bf C}_G(wv)={\bf C}_G(w)={\bf C}_G(v)$![]() . Write $G=P\times Q\times W$
. Write $G=P\times Q\times W$![]() , where $W$
, where $W$![]() is the Hall $\{p,\, q\}'$
is the Hall $\{p,\, q\}'$![]() -subgroup of $G$
-subgroup of $G$![]() . Clearly, $P\times W\leq {\bf C}_G(v)$
. Clearly, $P\times W\leq {\bf C}_G(v)$![]() and $P\times Q\leq {\bf C}_G(w)$
and $P\times Q\leq {\bf C}_G(w)$![]() , forcing $v\in {\bf Z}(G)< N$
, forcing $v\in {\bf Z}(G)< N$![]() . This contradiction deduces $|\pi (G/N)|=1$
. This contradiction deduces $|\pi (G/N)|=1$![]() . Moreover, $G/N$
. Moreover, $G/N$![]() is a $p$
is a $p$![]() -group. Let $N_{p'}$
-group. Let $N_{p'}$![]() be the Hall $p'$
be the Hall $p'$![]() -subgroup of $N$
-subgroup of $N$![]() . As $N_{p'}$
. As $N_{p'}$![]() char $N\unlhd G$
char $N\unlhd G$![]() , we obtain that $N_{p'}$
, we obtain that $N_{p'}$![]() is a normal Hall $p'$
is a normal Hall $p'$![]() -subgroup of $G$
-subgroup of $G$![]() . Therefore, $G=P\times N_{p'}$
. Therefore, $G=P\times N_{p'}$![]() , where $P$
, where $P$![]() is the Sylow $p$
is the Sylow $p$![]() -subgroup of $G$
-subgroup of $G$![]() .
.
We claim that $N_{p'}\leq {\bf Z}(G)$![]() . If not, select $y\in N_{p'}\setminus {\bf Z}(G)$
. If not, select $y\in N_{p'}\setminus {\bf Z}(G)$![]() . Suppose that $x\in P\setminus N$
. Suppose that $x\in P\setminus N$![]() . By lemma 5.1, we see that ${\bf C}_G(xy)={\bf C}_G(x)\cap {\bf C}_G(y)$
. By lemma 5.1, we see that ${\bf C}_G(xy)={\bf C}_G(x)\cap {\bf C}_G(y)$![]() . Since ${\bf C}_G(x)$
. Since ${\bf C}_G(x)$![]() and ${\bf C}_G(xy)$
and ${\bf C}_G(xy)$![]() are maximal subgroups of $G$
are maximal subgroups of $G$![]() , we get that ${\bf C}_G(xy)={\bf C}_G(x)\leq {\bf C}_G(y)$
, we get that ${\bf C}_G(xy)={\bf C}_G(x)\leq {\bf C}_G(y)$![]() . Moreover, ${\bf C}_G(x)={\bf C}_G(y)$
. Moreover, ${\bf C}_G(x)={\bf C}_G(y)$![]() as $y\not \in {\bf Z}(G)$
as $y\not \in {\bf Z}(G)$![]() . Clearly, $N_{p'}\leq {\bf C}_G(x)$
. Clearly, $N_{p'}\leq {\bf C}_G(x)$![]() and $P\leq {\bf C}_G(y)$
and $P\leq {\bf C}_G(y)$![]() , we get $y\in {\bf Z}(G)$
, we get $y\in {\bf Z}(G)$![]() , a contradiction. Consequently, $N_{p'}\leq {\bf Z}(G)$
, a contradiction. Consequently, $N_{p'}\leq {\bf Z}(G)$![]() , leading that $G/{\bf Z}(G)$
, leading that $G/{\bf Z}(G)$![]() is a $p$
is a $p$![]() -group. Notice that ${\bf C}_G(x)/{\bf Z}(G)$
-group. Notice that ${\bf C}_G(x)/{\bf Z}(G)$![]() is a maximal subgroup of $G/ {\bf Z}(G)$
is a maximal subgroup of $G/ {\bf Z}(G)$![]() . Then ${\bf C}_G(x)$
. Then ${\bf C}_G(x)$![]() is a maximal normal subgroup of $G$
is a maximal normal subgroup of $G$![]() . Moreover, $|G/{\bf C}_G(x)|=|(G/{\bf Z}(G))/({\bf C}_G(x)/{\bf Z}(G))|=p$
. Moreover, $|G/{\bf C}_G(x)|=|(G/{\bf Z}(G))/({\bf C}_G(x)/{\bf Z}(G))|=p$![]() , as required.
, as required.
Step 5. The conclusion when $G$![]() is non-nilpotent.
is non-nilpotent.
In the following, we consider the case that $G$![]() is non-nilpotent. We will divide the proof into two cases depending on $|\pi (G/N)|=1$
is non-nilpotent. We will divide the proof into two cases depending on $|\pi (G/N)|=1$![]() or not.
or not.
Case 1. $|\pi (G/N)|=1$![]() .
.
In this case, $G/N$![]() is a $p$
is a $p$![]() -group. Let $w\in G\setminus N$
-group. Let $w\in G\setminus N$![]() be an arbitrary $p$
be an arbitrary $p$![]() -element. By assumption, ${\bf C}_G(w)$
-element. By assumption, ${\bf C}_G(w)$![]() is a maximal subgroup of $G$
is a maximal subgroup of $G$![]() , implying $|G:{\bf C}_G(w)|=r^a$
, implying $|G:{\bf C}_G(w)|=r^a$![]() as $G$
as $G$![]() is solvable, where $r$
is solvable, where $r$![]() is a prime and $a$
is a prime and $a$![]() is a positive integer.
is a positive integer.
Subcase 1.1. $r=p$![]() .
.
Then $|G:{\bf C}_G(w)|=p^a$![]() . By step 1, ${\bf C}_G(w)=P_w\times K_w$
. By step 1, ${\bf C}_G(w)=P_w\times K_w$![]() is nilpotent with Sylow $p$
is nilpotent with Sylow $p$![]() -subgroup $P_w$
-subgroup $P_w$![]() and abelian Hall $p'$
and abelian Hall $p'$![]() -subgroup $K_w$
-subgroup $K_w$![]() . Clearly, $K:=K_w$
. Clearly, $K:=K_w$![]() is a Hall $p'$
is a Hall $p'$![]() -subgroup of $G$
-subgroup of $G$![]() . Let $P$
. Let $P$![]() be a Sylow $p$
be a Sylow $p$![]() -subgroup of $G$
-subgroup of $G$![]() containing $P_w$
containing $P_w$![]() . Then $P_w\lneq P$
. Then $P_w\lneq P$![]() , leading ${\bf N}_G(P_w)>{\bf C}_G(w)$
, leading ${\bf N}_G(P_w)>{\bf C}_G(w)$![]() . Since ${\bf C}_G(w)$
. Since ${\bf C}_G(w)$![]() is maximal in $G$
is maximal in $G$![]() , we have $P_w\unlhd G$
, we have $P_w\unlhd G$![]() , and thus ${\bf C}_G(P_w)\unlhd G$
, and thus ${\bf C}_G(P_w)\unlhd G$![]() . Note that $K\leq {\bf C}_G(P_w)\leq {\bf C}_G(w)$
. Note that $K\leq {\bf C}_G(P_w)\leq {\bf C}_G(w)$![]() . As ${\bf C}_G(w)$
. As ${\bf C}_G(w)$![]() is nilpotent, so is ${\bf C}_G(P_w)$
is nilpotent, so is ${\bf C}_G(P_w)$![]() . Hence, $K\unlhd G$
. Hence, $K\unlhd G$![]() because $K$
because $K$![]() char ${\bf C}_G(P_w)\unlhd G$
char ${\bf C}_G(P_w)\unlhd G$![]() . As a result, $K={\bf O}_{p'}(G)$
. As a result, $K={\bf O}_{p'}(G)$![]() and $G=K\rtimes P$
and $G=K\rtimes P$![]() .
.
Clearly, $P\ntrianglelefteq G$![]() , since otherwise, $G=P\times K$
, since otherwise, $G=P\times K$![]() with $K\leq {\bf Z}(G)$
with $K\leq {\bf Z}(G)$![]() , implying that $G$
, implying that $G$![]() is nilpotent, against our assumption. Hence, ${\bf O}_p(G)\lneq P$
is nilpotent, against our assumption. Hence, ${\bf O}_p(G)\lneq P$![]() . Along with the fact that ${\bf C}_G(w)=P_w\times K\leq {\bf O}_p(G)\times {\bf O}_{p'}(G)\lneq G$
. Along with the fact that ${\bf C}_G(w)=P_w\times K\leq {\bf O}_p(G)\times {\bf O}_{p'}(G)\lneq G$![]() . The maximality of ${\bf C}_G(w)$
. The maximality of ${\bf C}_G(w)$![]() indicates that ${\bf C}_G(w)={\bf O}_p(G)\times {\bf O}_{p'}(G)\unlhd G$
indicates that ${\bf C}_G(w)={\bf O}_p(G)\times {\bf O}_{p'}(G)\unlhd G$![]() . In particular, $|G:{\bf C}_G(w)|=p$
. In particular, $|G:{\bf C}_G(w)|=p$![]() and $|P:{\bf O}_p(G)|=p$
and $|P:{\bf O}_p(G)|=p$![]() .
.
Let $N_0:={\bf O}_p(G){\bf Z}(G)$![]() . Then $N_0\unlhd G$
. Then $N_0\unlhd G$![]() . Let further $\overline {G}:=G/N_0$
. Let further $\overline {G}:=G/N_0$![]() . Easily, $|\overline {P}|=p$
. Easily, $|\overline {P}|=p$![]() . We show that $\overline {G}=\overline {K}\rtimes \overline {P}$
. We show that $\overline {G}=\overline {K}\rtimes \overline {P}$![]() is a Frobenius group with abelian kernel $\overline {K}$
is a Frobenius group with abelian kernel $\overline {K}$![]() and complement $\overline {P}$
and complement $\overline {P}$![]() . Otherwise, there must exist $k\in K\setminus N_0$
. Otherwise, there must exist $k\in K\setminus N_0$![]() and $y\in P\setminus N_0$
and $y\in P\setminus N_0$![]() such that $[k,\,y]\in N_0$
such that $[k,\,y]\in N_0$![]() . Since $K\unlhd G$
. Since $K\unlhd G$![]() , we see that $[k,\,y]$
, we see that $[k,\,y]$![]() is a $p'$
is a $p'$![]() -element, forcing $[k,\,y]\in {\bf Z}(G)$
-element, forcing $[k,\,y]\in {\bf Z}(G)$![]() . Then $1=[k^{o(k)},\,y]=[k,\,y]^{o(k)}$
. Then $1=[k^{o(k)},\,y]=[k,\,y]^{o(k)}$![]() and $1=[k,\,y^{o(y)}]=[k,\,y]^{o(y)}$
and $1=[k,\,y^{o(y)}]=[k,\,y]^{o(y)}$![]() , forcing $[k,\,y]=1$
, forcing $[k,\,y]=1$![]() . Recall that $K={\bf O}_{p'}(G)$
. Recall that $K={\bf O}_{p'}(G)$![]() is abelian and $y\not \in {\bf O}_p(G)$
is abelian and $y\not \in {\bf O}_p(G)$![]() , we have ${\bf C}_G(k)\geq \langle {\bf C}_G(w),\, y\rangle > {\bf C}_G(w)$
, we have ${\bf C}_G(k)\geq \langle {\bf C}_G(w),\, y\rangle > {\bf C}_G(w)$![]() . The maximality of ${\bf C}_G(w)$
. The maximality of ${\bf C}_G(w)$![]() forces $k\in {\bf Z}(G)\leq N_0$
forces $k\in {\bf Z}(G)\leq N_0$![]() , against the choice of $k$
, against the choice of $k$![]() . Hence, statement (1.1) of the theorem holds.
. Hence, statement (1.1) of the theorem holds.
Subcase 1.2. $r\neq p$![]() .
.
In this case, $w\in G\backslash N$![]() is a $p$
is a $p$![]() -element such that $|G:{\bf C}_G(w)|=r^a$
-element such that $|G:{\bf C}_G(w)|=r^a$![]() is a $p'$
is a $p'$![]() -number. By step 1, ${\bf C}_G(w)=P_w\times K_w$
-number. By step 1, ${\bf C}_G(w)=P_w\times K_w$![]() is nilpotent with Sylow $p$
is nilpotent with Sylow $p$![]() -subgroup $P_w$
-subgroup $P_w$![]() and abelian Hall $p'$
and abelian Hall $p'$![]() -subgroup $K_w$
-subgroup $K_w$![]() , showing that $P:=P_w$
, showing that $P:=P_w$![]() is a Sylow $p$
is a Sylow $p$![]() -subgroup of $G$
-subgroup of $G$![]() .
.
Assume first $P\unlhd G$![]() . Then ${\bf C}_G(P)\unlhd G$
. Then ${\bf C}_G(P)\unlhd G$![]() . As $K_w\leq {\bf C}_G(P)\leq {\bf C}_G(w)$
. As $K_w\leq {\bf C}_G(P)\leq {\bf C}_G(w)$![]() and ${\bf C}_G(w)$
and ${\bf C}_G(w)$![]() is nilpotent, we see that $K_w$
is nilpotent, we see that $K_w$![]() char ${\bf C}_G(P)\unlhd G$
char ${\bf C}_G(P)\unlhd G$![]() , yielding $K_w\unlhd G$
, yielding $K_w\unlhd G$![]() . Hence, ${\bf C}_G(w)=P\times K_w\leq P\times {\bf O}_{p'}(G)$
. Hence, ${\bf C}_G(w)=P\times K_w\leq P\times {\bf O}_{p'}(G)$![]() . Let $K$
. Let $K$![]() be a Hall $p'$
be a Hall $p'$![]() -subgroup of $G$
-subgroup of $G$![]() containing $K_w$
containing $K_w$![]() . If $K\unlhd G$
. If $K\unlhd G$![]() , then $G=P\times K$
, then $G=P\times K$![]() . Under this situation, $K\leq {\bf C}_G(w)$
. Under this situation, $K\leq {\bf C}_G(w)$![]() , forcing $G={\bf C}_G(w)$
, forcing $G={\bf C}_G(w)$![]() . This contradiction indicates that ${\bf C}_G(w)=P\times {\bf O}_{p'}(G)\unlhd G$
. This contradiction indicates that ${\bf C}_G(w)=P\times {\bf O}_{p'}(G)\unlhd G$![]() with $|K/{\bf O}_{p'}(G)|=r$
with $|K/{\bf O}_{p'}(G)|=r$![]() .
.
Let $N_0:={\bf O}_{p'}(G)(P\cap N)$![]() . Then $N_0\unlhd G$
. Then $N_0\unlhd G$![]() . Write $\overline {G}:=G/N_0$
. Write $\overline {G}:=G/N_0$![]() . Then $\overline {N}=\overline {K}\unlhd \overline {G}$
. Then $\overline {N}=\overline {K}\unlhd \overline {G}$![]() as $G/N$
as $G/N$![]() is a $p$
is a $p$![]() -group. Moreover, $\overline {G}=\overline {P}\times \overline {K}$
-group. Moreover, $\overline {G}=\overline {P}\times \overline {K}$![]() is a $\{p,\, r\}$
is a $\{p,\, r\}$![]() -group. Take $z\in G\setminus N_0$
-group. Take $z\in G\setminus N_0$![]() a $\{p,\,r\}$
a $\{p,\,r\}$![]() -element. Write $z=ab$
-element. Write $z=ab$![]() , where $a\in P\setminus N_0$
, where $a\in P\setminus N_0$![]() is the $p$
is the $p$![]() -part and $b\in K\setminus N_0$
-part and $b\in K\setminus N_0$![]() is the $r$
is the $r$![]() -part of $z$
-part of $z$![]() , respectively. By step 1, we see that ${\bf C}_G(a)=P_a\times K_a$
, respectively. By step 1, we see that ${\bf C}_G(a)=P_a\times K_a$![]() , where $P_a$
, where $P_a$![]() is the Sylow $p$
is the Sylow $p$![]() -subgroup of ${\bf C}_G(a)$
-subgroup of ${\bf C}_G(a)$![]() and $K_a$
and $K_a$![]() is the Hall $p'$
is the Hall $p'$![]() -subgroup of ${\bf C}_G(a)$
-subgroup of ${\bf C}_G(a)$![]() . Note that $a\in {\bf C}_G(w)$
. Note that $a\in {\bf C}_G(w)$![]() . Then $K_w\leq K_a$
. Then $K_w\leq K_a$![]() . Analogously, $K_a\leq K_w$
. Analogously, $K_a\leq K_w$![]() since $w\in {\bf C}_G(a)$
since $w\in {\bf C}_G(a)$![]() . This deduces that $b\in K_a=K_w={\bf O}_{p'}(G)\leq N_0$
. This deduces that $b\in K_a=K_w={\bf O}_{p'}(G)\leq N_0$![]() , against our assumption. As a consequence, $P \ntrianglelefteq G$
, against our assumption. As a consequence, $P \ntrianglelefteq G$![]() .
.
Recall that ${\bf C}_G(w)=P\times K_w$![]() with $K_w$
with $K_w$![]() abelian. Then ${\bf C}_G(w)\leq {\bf C}_G(K_w)$
abelian. Then ${\bf C}_G(w)\leq {\bf C}_G(K_w)$![]() , leading to ${\bf C}_G(K_w)={\bf C}_G(w)$
, leading to ${\bf C}_G(K_w)={\bf C}_G(w)$![]() or $K_w\leq {\bf Z}(G)$
or $K_w\leq {\bf Z}(G)$![]() by the maximality of ${\bf C}_G(w)$
by the maximality of ${\bf C}_G(w)$![]() . Assume first the former holds. Let $R_0$
. Assume first the former holds. Let $R_0$![]() be the Sylow $r$
be the Sylow $r$![]() -subgroup of $K_w$
-subgroup of $K_w$![]() and $R$
and $R$![]() be a Sylow $r$
be a Sylow $r$![]() -subgroup of $G$
-subgroup of $G$![]() such that $R_0\lneq R$
such that $R_0\lneq R$![]() . This indicates that ${\bf C}_G(w)<{\bf N}_G(R_0)$
. This indicates that ${\bf C}_G(w)<{\bf N}_G(R_0)$![]() . Furthermore, the maximality of ${\bf C}_G(w)$
. Furthermore, the maximality of ${\bf C}_G(w)$![]() forces $R_0\unlhd G$
forces $R_0\unlhd G$![]() , and thus ${\bf C}_G(R_0)\unlhd G$
, and thus ${\bf C}_G(R_0)\unlhd G$![]() .
.
On the contrary, $K_w$![]() is abelian, implying ${\bf C}_G(w)\leq {\bf C}_G(R_0)$
is abelian, implying ${\bf C}_G(w)\leq {\bf C}_G(R_0)$![]() . Again by the maximality of ${\bf C}_G(w)$
. Again by the maximality of ${\bf C}_G(w)$![]() , we see that either $R_0\leq {\bf Z}(G)$
, we see that either $R_0\leq {\bf Z}(G)$![]() or ${\bf C}_G(w)={\bf C}_G(R_0)$
or ${\bf C}_G(w)={\bf C}_G(R_0)$![]() . If the latter holds, then ${\bf C}_G(R_0)= {\bf C}_G(w)\unlhd G$
. If the latter holds, then ${\bf C}_G(R_0)= {\bf C}_G(w)\unlhd G$![]() . Since ${\bf C}_G(w)$
. Since ${\bf C}_G(w)$![]() is nilpotent, we obtain that $P\unlhd G$
is nilpotent, we obtain that $P\unlhd G$![]() , against our assumption.
, against our assumption.
As a result, $R_0\leq {\bf Z}(G)$![]() . Write $\widetilde {G}:=G/R_0$
. Write $\widetilde {G}:=G/R_0$![]() . Then $\widetilde {G}=\widetilde {R}{\bf C}_{\widetilde {G}}(\widetilde {w})$
. Then $\widetilde {G}=\widetilde {R}{\bf C}_{\widetilde {G}}(\widetilde {w})$![]() . Since ${\bf C}_{\widetilde {G}}(\widetilde {w})={\bf C}_G(w)/R_0$
. Since ${\bf C}_{\widetilde {G}}(\widetilde {w})={\bf C}_G(w)/R_0$![]() is maximal in $\widetilde {G}$
is maximal in $\widetilde {G}$![]() , we have that ${\bf O}_r(\widetilde {G})=\widetilde {1}$
, we have that ${\bf O}_r(\widetilde {G})=\widetilde {1}$![]() or ${\bf O}_r(\widetilde {G})=\widetilde {R}$
or ${\bf O}_r(\widetilde {G})=\widetilde {R}$![]() . Assume first that ${\bf O}_r(\widetilde {G})=\widetilde {1}$
. Assume first that ${\bf O}_r(\widetilde {G})=\widetilde {1}$![]() . Since $G$
. Since $G$![]() is solvable, we have ${\bf O}_{r'}(\widetilde {G})>\widetilde {1}$
is solvable, we have ${\bf O}_{r'}(\widetilde {G})>\widetilde {1}$![]() . We assert that $\widetilde {P}\ntrianglelefteq \widetilde {G}$
. We assert that $\widetilde {P}\ntrianglelefteq \widetilde {G}$![]() . Since otherwise, $P\times R_0\unlhd G$
. Since otherwise, $P\times R_0\unlhd G$![]() , leading $P\unlhd G$
, leading $P\unlhd G$![]() , contrary to our assumption.
, contrary to our assumption.
Consequently, $\widetilde {P}\nleq {\bf O}_{r'}(\widetilde {G})$![]() . Note that $\widetilde {P}{\bf O}_{r'}(\widetilde {G})\leq {\bf C}_{\widetilde {G}}(\widetilde {w})$
. Note that $\widetilde {P}{\bf O}_{r'}(\widetilde {G})\leq {\bf C}_{\widetilde {G}}(\widetilde {w})$![]() and ${\bf C}_{\widetilde {G}}(\widetilde {w})$
and ${\bf C}_{\widetilde {G}}(\widetilde {w})$![]() is nilpotent. Then $\widetilde {J}=\widetilde {P}\times \widetilde {L}$
is nilpotent. Then $\widetilde {J}=\widetilde {P}\times \widetilde {L}$![]() with $\widetilde {L}$
with $\widetilde {L}$![]() abelian, where $L$
abelian, where $L$![]() is a Hall $\{p,\, r\}'$
is a Hall $\{p,\, r\}'$![]() -subgroup of ${\bf O}_{r'}(\widetilde {G})$
-subgroup of ${\bf O}_{r'}(\widetilde {G})$![]() . Easily, $\widetilde {L}\unlhd \widetilde {G}$
. Easily, $\widetilde {L}\unlhd \widetilde {G}$![]() and ${\bf C}_{\widetilde {G}}(\widetilde {L})\geq {\bf C}_{\widetilde {G}}(\widetilde {w})$
and ${\bf C}_{\widetilde {G}}(\widetilde {L})\geq {\bf C}_{\widetilde {G}}(\widetilde {w})$![]() . By the maximality of ${\bf C}_{\widetilde {G}}(\widetilde {w})$
. By the maximality of ${\bf C}_{\widetilde {G}}(\widetilde {w})$![]() , we have ${\bf C}_{\widetilde {G}}(\widetilde {L})= {\bf C}_{\widetilde {G}}(\widetilde {w})$
, we have ${\bf C}_{\widetilde {G}}(\widetilde {L})= {\bf C}_{\widetilde {G}}(\widetilde {w})$![]() or $\widetilde {L}\leq {\bf Z}(\widetilde {G})$
or $\widetilde {L}\leq {\bf Z}(\widetilde {G})$![]() . Assume first that ${\bf C}_{\widetilde {G}}(\widetilde {L})= {\bf C}_{\widetilde {G}}(\widetilde {w})$
. Assume first that ${\bf C}_{\widetilde {G}}(\widetilde {L})= {\bf C}_{\widetilde {G}}(\widetilde {w})$![]() holds. In this situation, ${\bf C}_{\widetilde {G}}(\widetilde {L})\unlhd \widetilde {G}$
holds. In this situation, ${\bf C}_{\widetilde {G}}(\widetilde {L})\unlhd \widetilde {G}$![]() , we get $\widetilde {P}\unlhd \widetilde {G}$
, we get $\widetilde {P}\unlhd \widetilde {G}$![]() , against the argument in the previous paragraph. Hence, $\widetilde {L}\leq {\bf Z}(\widetilde {G})$
, against the argument in the previous paragraph. Hence, $\widetilde {L}\leq {\bf Z}(\widetilde {G})$![]() . Therefore, ${\bf O}_{r'}(\widetilde {G})={\bf O}_p(\widetilde {G})\times {\bf Z}(\widetilde {G})_{p'}$
. Therefore, ${\bf O}_{r'}(\widetilde {G})={\bf O}_p(\widetilde {G})\times {\bf Z}(\widetilde {G})_{p'}$![]() . Furthermore, ${\bf C}_{\widetilde {G}}({\bf O}_{r'}(\widetilde {G}))\leq {\bf O}_{r'}(\widetilde {G})$
. Furthermore, ${\bf C}_{\widetilde {G}}({\bf O}_{r'}(\widetilde {G}))\leq {\bf O}_{r'}(\widetilde {G})$![]() , which indicates that the Hall $\{p,\, r\}'$
, which indicates that the Hall $\{p,\, r\}'$![]() -subgroup of ${\bf O}_{r'}(\widetilde {G})$
-subgroup of ${\bf O}_{r'}(\widetilde {G})$![]() is also a Hall $\{p,\, r\}'$
is also a Hall $\{p,\, r\}'$![]() -subgroup of $\widetilde {G}$
-subgroup of $\widetilde {G}$![]() . Hence, ${\bf C}_{\widetilde {G}}(\widetilde {w})=\widetilde {P}\times {\bf Z}(\widetilde {G})_{p'}$
. Hence, ${\bf C}_{\widetilde {G}}(\widetilde {w})=\widetilde {P}\times {\bf Z}(\widetilde {G})_{p'}$![]() . Without loss of generality, we may assume that ${\bf Z}(\widetilde {G})_{p'}=\widetilde {1}$
. Without loss of generality, we may assume that ${\bf Z}(\widetilde {G})_{p'}=\widetilde {1}$![]() .
.
In this case, ${\bf C}_{\widetilde {G}}(\widetilde {w})=\widetilde {P}$![]() , and thus $\widetilde {G}=\widetilde {R}\widetilde {P}$
, and thus $\widetilde {G}=\widetilde {R}\widetilde {P}$![]() , leading that $\widetilde {G}$
, leading that $\widetilde {G}$![]() is a $\{p,\, r\}$
is a $\{p,\, r\}$![]() -group. Recall that ${\bf O}_{r}(\widetilde {G})=1$
-group. Recall that ${\bf O}_{r}(\widetilde {G})=1$![]() , we have ${\bf O}_{p}(\widetilde {G})\neq 1$
, we have ${\bf O}_{p}(\widetilde {G})\neq 1$![]() . As a result, ${\bf O}_{p}(\widetilde {G})< \widetilde {P}$
. As a result, ${\bf O}_{p}(\widetilde {G})< \widetilde {P}$![]() since $\widetilde {P}\ntrianglelefteq G$
since $\widetilde {P}\ntrianglelefteq G$![]() . Note that ${\bf O}_p(\widetilde {G}/{\bf O}_{p}(\widetilde {G}))=1$
. Note that ${\bf O}_p(\widetilde {G}/{\bf O}_{p}(\widetilde {G}))=1$![]() . We see that ${\bf O}_r(\widetilde {G}/{\bf O}_{p}(\widetilde {G}))\neq 1$
. We see that ${\bf O}_r(\widetilde {G}/{\bf O}_{p}(\widetilde {G}))\neq 1$![]() as $\widetilde {G}$
as $\widetilde {G}$![]() is solvable. Therefore, $\widetilde {G}/{\bf O}_{p}(\widetilde {G})={\bf O}_{p,r}(\widetilde {G})/{\bf O}_{p}(\widetilde {G})\rtimes {\bf C}_{\widetilde {G}}(\widetilde {w})/{\bf O}_{p}(\widetilde {G})$
is solvable. Therefore, $\widetilde {G}/{\bf O}_{p}(\widetilde {G})={\bf O}_{p,r}(\widetilde {G})/{\bf O}_{p}(\widetilde {G})\rtimes {\bf C}_{\widetilde {G}}(\widetilde {w})/{\bf O}_{p}(\widetilde {G})$![]() by the maximality of ${\bf C}_{\widetilde {G}}(\widetilde {w})/{\bf O}_{p}(\widetilde {G})$
by the maximality of ${\bf C}_{\widetilde {G}}(\widetilde {w})/{\bf O}_{p}(\widetilde {G})$![]() . Furthermore, ${\bf C}_{\widetilde {G}}(\widetilde {w})/{\bf O}_{p}(\widetilde {G})$
. Furthermore, ${\bf C}_{\widetilde {G}}(\widetilde {w})/{\bf O}_{p}(\widetilde {G})$![]() acts irreducibly on ${\bf O}_{p,r}(\widetilde {G})/{\bf O}_{p}(\widetilde {G})$
acts irreducibly on ${\bf O}_{p,r}(\widetilde {G})/{\bf O}_{p}(\widetilde {G})$![]() and ${\bf O}_{p,r}(\widetilde {G})/{\bf O}_{p}(\widetilde {G})$
and ${\bf O}_{p,r}(\widetilde {G})/{\bf O}_{p}(\widetilde {G})$![]() is an elementary abelian $r$
is an elementary abelian $r$![]() -group. Since ${\bf O}_{p,r}(\widetilde {G})/{\bf O}_{p}(\widetilde {G})\cong \widetilde {R}$
-group. Since ${\bf O}_{p,r}(\widetilde {G})/{\bf O}_{p}(\widetilde {G})\cong \widetilde {R}$![]() , we get that $\widetilde {R}$
, we get that $\widetilde {R}$![]() is elementary abelian. Clearly, $\widetilde {G}/ {\bf O}_{p}(\widetilde {G})$
is elementary abelian. Clearly, $\widetilde {G}/ {\bf O}_{p}(\widetilde {G})$![]() is not nilpotent. Hence, the Fitting length $h(\widetilde {G})=3$
is not nilpotent. Hence, the Fitting length $h(\widetilde {G})=3$![]() . In this case, $\widetilde {G}$
. In this case, $\widetilde {G}$![]() has the following normal series:
has the following normal series:
where ${\bf O}_{p,r}(\widetilde {G})/{\bf O}_{p}(\widetilde {G})$![]() is an elementary abelian Sylow $r$
is an elementary abelian Sylow $r$![]() -group and $\widetilde {G}/{\bf O}_{p,r}(\widetilde {G})$
-group and $\widetilde {G}/{\bf O}_{p,r}(\widetilde {G})$![]() is a $p$
is a $p$![]() -group, as required in Statement (1.2.1).
-group, as required in Statement (1.2.1).
Assume now that ${\bf O}_r(\widetilde {G})=\widetilde {R}$![]() . Then $\widetilde {G}={\bf O}_r(\widetilde {G})\rtimes {\bf C}_{\widetilde {G}}(\widetilde {w})$
. Then $\widetilde {G}={\bf O}_r(\widetilde {G})\rtimes {\bf C}_{\widetilde {G}}(\widetilde {w})$![]() . By the same reason as above, ${\bf C}_{\widetilde {G}}(\widetilde {w})$
. By the same reason as above, ${\bf C}_{\widetilde {G}}(\widetilde {w})$![]() acts irreducibly on ${\bf O}_{r}(\widetilde {G})$
acts irreducibly on ${\bf O}_{r}(\widetilde {G})$![]() and ${\bf O}_{r}(\widetilde {G})$
and ${\bf O}_{r}(\widetilde {G})$![]() is an elementary abelian $r$
is an elementary abelian $r$![]() -group. In this case, $\widetilde {G}$
-group. In this case, $\widetilde {G}$![]() has the following normal series:
has the following normal series:
where $\widetilde {R}$![]() is an elementary abelian $r$
is an elementary abelian $r$![]() -group and $G/R$
-group and $G/R$![]() is nilpotent, statement (1.2.2) holds.
is nilpotent, statement (1.2.2) holds.
Now, we consider the case that $K_w\leq {\bf Z}(G)$![]() . Let $l\in G\setminus N$
. Let $l\in G\setminus N$![]() be an arbitrary primary element. As ${\bf Z}(G)< N$
be an arbitrary primary element. As ${\bf Z}(G)< N$![]() , then $l\not \in {\bf Z}(G)$
, then $l\not \in {\bf Z}(G)$![]() . By assumption, ${\bf C}_G(l)$
. By assumption, ${\bf C}_G(l)$![]() is maximal in $G$
is maximal in $G$![]() . Recall that $G$
. Recall that $G$![]() is solvable. Therefore, $|G:{\bf C}_G(l)|$
is solvable. Therefore, $|G:{\bf C}_G(l)|$![]() is a prime power. If $|G:{\bf C}_G(l)|$
is a prime power. If $|G:{\bf C}_G(l)|$![]() is a $p$
is a $p$![]() -power, we are done according to case 1. As a result, $|G:{\bf C}_G(l)|$
-power, we are done according to case 1. As a result, $|G:{\bf C}_G(l)|$![]() is a $q$
is a $q$![]() -power with prime $q$
-power with prime $q$![]() distinct from $p$
distinct from $p$![]() . Moreover, ${\bf C}_G(l)^g=P^g\times K_w\leq {\bf C}_G(l)$
. Moreover, ${\bf C}_G(l)^g=P^g\times K_w\leq {\bf C}_G(l)$![]() for some $g\in G$
for some $g\in G$![]() , forcing $|G:{\bf C}_G(l)|$
, forcing $|G:{\bf C}_G(l)|$![]() is a power of $r$
is a power of $r$![]() . By [Reference Shao and Jiang24, Lemma 2.5], $l\in {\bf O}_{r,r'}(G)$
. By [Reference Shao and Jiang24, Lemma 2.5], $l\in {\bf O}_{r,r'}(G)$![]() , yielding $G\setminus N\subseteq {\bf O}_{r,r'}(G)$
, yielding $G\setminus N\subseteq {\bf O}_{r,r'}(G)$![]() . Furthermore, $G={\bf O}_{r,r'}(G)$
. Furthermore, $G={\bf O}_{r,r'}(G)$![]() , implying that $G$
, implying that $G$![]() has a normal Sylow $r$
has a normal Sylow $r$![]() -subgroup $R$
-subgroup $R$![]() .
.
Let $\widehat {G}:=G/{\bf Z}(G)$![]() . Since ${\bf C}_G(l)$
. Since ${\bf C}_G(l)$![]() is maximal in $G$
is maximal in $G$![]() and ${\bf C}_{\widehat {G}}(\widehat {l})\geq {\bf C}_G(l)/{\bf Z}(G)$
and ${\bf C}_{\widehat {G}}(\widehat {l})\geq {\bf C}_G(l)/{\bf Z}(G)$![]() , we obtain that ${\bf C}_{\widehat {G}}(\widehat {l})=\widehat {G}$
, we obtain that ${\bf C}_{\widehat {G}}(\widehat {l})=\widehat {G}$![]() or ${\bf C}_{\widehat {G}}(\widehat {l})={\bf C}_G(l)/{\bf Z}(G)$
or ${\bf C}_{\widehat {G}}(\widehat {l})={\bf C}_G(l)/{\bf Z}(G)$![]() . Note that ${\bf C}_G(l)=P^g\times K_w$
. Note that ${\bf C}_G(l)=P^g\times K_w$![]() , we conclude that ${\bf C}_{\widehat {G}}(\widehat {l})={\bf C}_G(l)/{\bf Z}(G)$
, we conclude that ${\bf C}_{\widehat {G}}(\widehat {l})={\bf C}_G(l)/{\bf Z}(G)$![]() and thus ${\bf C}_{\widehat {G}}(\widehat {l})=\widehat {P}$
and thus ${\bf C}_{\widehat {G}}(\widehat {l})=\widehat {P}$![]() is maximal in $\widehat {G}$
is maximal in $\widehat {G}$![]() . Then $\pi (\widehat {G})=\{p,\,r\}$
. Then $\pi (\widehat {G})=\{p,\,r\}$![]() , and $\widehat {P}$
, and $\widehat {P}$![]() acts on $\widehat {R}$
acts on $\widehat {R}$![]() irreducibly. Moreover, $\widehat {R}$
irreducibly. Moreover, $\widehat {R}$![]() is the minimal normal subgroup of $\widehat {G}$
is the minimal normal subgroup of $\widehat {G}$![]() , and thus $\widehat {R}$
, and thus $\widehat {R}$![]() is elementary abelian. Let $N_p=N\cap P$
is elementary abelian. Let $N_p=N\cap P$![]() . Then $\widehat {N_p}\unlhd \widehat {P}$
. Then $\widehat {N_p}\unlhd \widehat {P}$![]() . If $\widehat {N_p}\unlhd \widehat {G}$
. If $\widehat {N_p}\unlhd \widehat {G}$![]() , then $\widehat {G}/\widehat {N_p}$
, then $\widehat {G}/\widehat {N_p}$![]() is a Frobenius group. If $\widehat {N_p}\ntrianglelefteq \widehat {G}$
is a Frobenius group. If $\widehat {N_p}\ntrianglelefteq \widehat {G}$![]() , then ${\bf N}_{\widehat {G}}(\widehat {N_p})=\widehat {P}$
, then ${\bf N}_{\widehat {G}}(\widehat {N_p})=\widehat {P}$![]() , statement (1.2.3) holds.
, statement (1.2.3) holds.
Case 2. $|\pi (G/N)|\geq 2$![]() .
.
Let $\pi :=\pi (G/N)$![]() . Recall that $G/N$
. Recall that $G/N$![]() is abelian. There must exist an element $wN\in G/N$
is abelian. There must exist an element $wN\in G/N$![]() such that $\pi (wN)=\pi$
such that $\pi (wN)=\pi$![]() . Without loss, we may consider $w\in G\setminus N$
. Without loss, we may consider $w\in G\setminus N$![]() is an element with $\pi (w)=\pi$
is an element with $\pi (w)=\pi$![]() . Suppose that $w_p,\, w_q\in G\setminus N$
. Suppose that $w_p,\, w_q\in G\setminus N$![]() is the $p$
is the $p$![]() -part and the $q$
-part and the $q$![]() -part of $w$
-part of $w$![]() , respectively. By lemma 5.1, we have ${\bf C}_G(w)\leq {\bf C}_G(w_p)\cap {\bf C}_G(w_q)$
, respectively. By lemma 5.1, we have ${\bf C}_G(w)\leq {\bf C}_G(w_p)\cap {\bf C}_G(w_q)$![]() . Note that all of ${\bf C}_G(w)$
. Note that all of ${\bf C}_G(w)$![]() , ${\bf C}_G(w_p)$
, ${\bf C}_G(w_p)$![]() , and ${\bf C}_G(w_q)$
, and ${\bf C}_G(w_q)$![]() are maximal subgroups of $G$
are maximal subgroups of $G$![]() . This indicates that ${\bf C}_G(w)={\bf C}_G(w_p)={\bf C}_G(w_q)$
. This indicates that ${\bf C}_G(w)={\bf C}_G(w_p)={\bf C}_G(w_q)$![]() . In particular, ${\bf C}_G(w)$
. In particular, ${\bf C}_G(w)$![]() is abelian according to step 1. Recall that $G$
is abelian according to step 1. Recall that $G$![]() is solvable and ${\bf C}_G(w)$
is solvable and ${\bf C}_G(w)$![]() is a maximal subgroup of $G$
is a maximal subgroup of $G$![]() , indicating that $|G:{\bf C}_G(w)|=r^a$
, indicating that $|G:{\bf C}_G(w)|=r^a$![]() , where $r$
, where $r$![]() is a prime and $a>0$
is a prime and $a>0$![]() is an integer.
is an integer.
Write ${\bf C}_G(w)=K\times R_w$![]() , where $K$
, where $K$![]() is the abelian Hall $r'$
is the abelian Hall $r'$![]() -subgroup of $G$
-subgroup of $G$![]() and $R_w$
and $R_w$![]() is the Sylow $r$
is the Sylow $r$![]() -subgroup of ${\bf C}_G(w)$
-subgroup of ${\bf C}_G(w)$![]() . Let $R$
. Let $R$![]() be a Sylow $r$
be a Sylow $r$![]() -subgroup of $G$
-subgroup of $G$![]() such that $R_w< R$
such that $R_w< R$![]() . Easily, ${\bf N}_G(R_w)\gneq {\bf C}_G(w)$
. Easily, ${\bf N}_G(R_w)\gneq {\bf C}_G(w)$![]() . The maximality of ${\bf C}_G(w)$
. The maximality of ${\bf C}_G(w)$![]() yields to $R_w\unlhd G$
yields to $R_w\unlhd G$![]() . Moreover, ${\bf C}_G(w)\leq {\bf C}_G(R_w)\unlhd G$
. Moreover, ${\bf C}_G(w)\leq {\bf C}_G(R_w)\unlhd G$![]() . Again by the maximality of ${\bf C}_G(w)$
. Again by the maximality of ${\bf C}_G(w)$![]() , we get ${\bf C}_G(R_w)={\bf C}_G(w)$
, we get ${\bf C}_G(R_w)={\bf C}_G(w)$![]() or $R_w\leq {\bf Z}(G)$
or $R_w\leq {\bf Z}(G)$![]() .
.
Subcase 2.1. ${\bf C}_G(R_w)={\bf C}_G(w)$![]() .
.
In this case, ${\bf C}_G(w)\unlhd G$![]() and $|G:{\bf C}_G(w)|=r$
and $|G:{\bf C}_G(w)|=r$![]() . Furthermore, $K\unlhd G$
. Furthermore, $K\unlhd G$![]() since $K$
since $K$![]() is the Hall $r'$
is the Hall $r'$![]() -subgroup of abelian group ${\bf C}_G(w)$
-subgroup of abelian group ${\bf C}_G(w)$![]() , implying $G=K\rtimes R$
, implying $G=K\rtimes R$![]() . Notice that ${\bf C}_G(w)=K\times R_w\leq {\bf O}_{r'}(G)\times {\bf O}_{r}(G)$
. Notice that ${\bf C}_G(w)=K\times R_w\leq {\bf O}_{r'}(G)\times {\bf O}_{r}(G)$![]() . Since $G$
. Since $G$![]() is non-nilpotent and ${\bf C}_G(w)$
is non-nilpotent and ${\bf C}_G(w)$![]() is maximal, we see that $R_w={\bf O}_r(G)$
is maximal, we see that $R_w={\bf O}_r(G)$![]() with $|R:R_w|=r$
with $|R:R_w|=r$![]() .
.
Let $N_0:={\bf Z}(G){\bf O}_r(G)$![]() and $\overline {G}:=G/N_0$
and $\overline {G}:=G/N_0$![]() . Then $\overline {G}=\overline {K}\rtimes \overline {R}$
. Then $\overline {G}=\overline {K}\rtimes \overline {R}$![]() with $|\overline {R}|=r$
with $|\overline {R}|=r$![]() . Assume that there exists an $\{r,\,t\}$
. Assume that there exists an $\{r,\,t\}$![]() -element $\overline {e}\in \overline {G}$
-element $\overline {e}\in \overline {G}$![]() for some prime $t\neq r$
for some prime $t\neq r$![]() . We may assume that $e\in G\setminus N_0$
. We may assume that $e\in G\setminus N_0$![]() is an $\{r,\,t\}$
is an $\{r,\,t\}$![]() -element. Write $e=e_1e_2$
-element. Write $e=e_1e_2$![]() , where $e_1\in R\setminus N_0$
, where $e_1\in R\setminus N_0$![]() and $e_2\in K\setminus N_0$
and $e_2\in K\setminus N_0$![]() are the $r$
are the $r$![]() -part and the $t$
-part and the $t$![]() -part of $e$
-part of $e$![]() , respectively. In this case, $e_1\in {\bf C}_G(e_2)={\bf C}_G(w)$
, respectively. In this case, $e_1\in {\bf C}_G(e_2)={\bf C}_G(w)$![]() , forcing $e_1\in {\bf O}_r(G)$
, forcing $e_1\in {\bf O}_r(G)$![]() . This contradiction shows that $\overline {G}$
. This contradiction shows that $\overline {G}$![]() is a Frobenius group with abelian kernel $\overline {K}$
is a Frobenius group with abelian kernel $\overline {K}$![]() and a complement $\overline {R}$
and a complement $\overline {R}$![]() of order $r$
of order $r$![]() , statement (2.1) of the theorem holds.
, statement (2.1) of the theorem holds.
Subcase 2.2. $R_w\leq {\bf Z}(G)$![]() .
.
Recall that $w\in G\setminus N$![]() with $\pi (w)=\pi$
with $\pi (w)=\pi$![]() . We assert that $r\not \in \pi$
. We assert that $r\not \in \pi$![]() . If not, assume that $w_r\in G\setminus N$
. If not, assume that $w_r\in G\setminus N$![]() is the $r$
is the $r$![]() -part of $w$
-part of $w$![]() . Easily, $w_r\in {\bf C}_G(w)=K\times R_w$
. Easily, $w_r\in {\bf C}_G(w)=K\times R_w$![]() , forcing $w_r\in R_w\leq {\bf Z}(G)< N$
, forcing $w_r\in R_w\leq {\bf Z}(G)< N$![]() , which is a contradiction. As a result, $r\nmid |G/N|$
, which is a contradiction. As a result, $r\nmid |G/N|$![]() , leading $R\leq N$
, leading $R\leq N$![]() . Moreover, $G={\bf C}_G(w)N={\bf C}_G(w)R$
. Moreover, $G={\bf C}_G(w)N={\bf C}_G(w)R$![]() .
.
Write $\widetilde {G}:=G/{\bf Z}(G)$![]() . Then $\widetilde {G}=\widetilde {{\bf C}_G(w)}\widetilde {R}$
. Then $\widetilde {G}=\widetilde {{\bf C}_G(w)}\widetilde {R}$![]() . Easily, $\widetilde {{\bf C}_G(w)}$
. Easily, $\widetilde {{\bf C}_G(w)}$![]() is a maximal $r'$
is a maximal $r'$![]() -subgroup of $\widetilde {G}$
-subgroup of $\widetilde {G}$![]() , implying ${\bf O}_r(\widetilde {G})=\widetilde {1}$
, implying ${\bf O}_r(\widetilde {G})=\widetilde {1}$![]() or $\widetilde {R}$
or $\widetilde {R}$![]() . Assume first ${\bf O}_r(\widetilde {G})=\widetilde {1}$
. Assume first ${\bf O}_r(\widetilde {G})=\widetilde {1}$![]() . Then ${\bf O}_{r'}(\widetilde {G})>\widetilde {1}$
. Then ${\bf O}_{r'}(\widetilde {G})>\widetilde {1}$![]() since $G$
since $G$![]() is solvable. In particular, $\widetilde {K}\leq {\bf C}_{\widetilde {G}}({\bf O}_{r'}(\widetilde {G}))\leq {\bf O}_{r'}(\widetilde {G})\leq \widetilde {K}$
is solvable. In particular, $\widetilde {K}\leq {\bf C}_{\widetilde {G}}({\bf O}_{r'}(\widetilde {G}))\leq {\bf O}_{r'}(\widetilde {G})\leq \widetilde {K}$![]() since $\widetilde {K}$
since $\widetilde {K}$![]() is an abelian Hall $r'$
is an abelian Hall $r'$![]() -subgroup of $\widetilde {G}$
-subgroup of $\widetilde {G}$![]() , yielding ${\bf C}_{\widetilde {G}}({\bf O}_{r'}(\widetilde {G}))= {\bf O}_{r'}(\widetilde {G})=\widetilde {K}$
, yielding ${\bf C}_{\widetilde {G}}({\bf O}_{r'}(\widetilde {G}))= {\bf O}_{r'}(\widetilde {G})=\widetilde {K}$![]() . As a result, $K\unlhd G$
. As a result, $K\unlhd G$![]() and ${\bf C}_G(w)\unlhd G$
and ${\bf C}_G(w)\unlhd G$![]() .
.
Consequently, $\widetilde {G}=\widetilde {{\bf C}_G(w)}\rtimes \widetilde {R}$![]() . We prove that $\widetilde {G}$
. We prove that $\widetilde {G}$![]() is a Frobenius group. Suppose false, there exists an $\{r,\,t\}$
is a Frobenius group. Suppose false, there exists an $\{r,\,t\}$![]() -element $\widetilde {e}\in \widetilde {G}$
-element $\widetilde {e}\in \widetilde {G}$![]() for some prime $t\neq r$
for some prime $t\neq r$![]() . We may assume that $e$
. We may assume that $e$![]() is a $\{r,\,t\}$
is a $\{r,\,t\}$![]() -element. Write $e=e_1e_2$
-element. Write $e=e_1e_2$![]() , where $e_1\in R\setminus {\bf Z}(G)$
, where $e_1\in R\setminus {\bf Z}(G)$![]() and $e_2\in K\setminus {\bf Z}(G)$
and $e_2\in K\setminus {\bf Z}(G)$![]() are the $r$
are the $r$![]() -part and the $t$
-part and the $t$![]() -part of $e$
-part of $e$![]() , respectively. Note that $e_1\in {\bf C}_G(e_2)=K\times R_w={\bf C}_G(w)$
, respectively. Note that $e_1\in {\bf C}_G(e_2)=K\times R_w={\bf C}_G(w)$![]() . This contradiction shows that $\widetilde {G}$
. This contradiction shows that $\widetilde {G}$![]() is a Frobenius group with abelian kernel $\widetilde {{\bf C}_G(w)}$
is a Frobenius group with abelian kernel $\widetilde {{\bf C}_G(w)}$![]() . Moreover, $\widetilde {{\bf C}_G(w)}$
. Moreover, $\widetilde {{\bf C}_G(w)}$![]() is maximal in $\widetilde {G}$
is maximal in $\widetilde {G}$![]() indicates that $\widetilde {R}$
indicates that $\widetilde {R}$![]() is of order $r$
is of order $r$![]() , statement (2.1) of the theorem holds.
, statement (2.1) of the theorem holds.
Now, we consider ${\bf O}_r(\widetilde {G})=\widetilde {R}$![]() . Write $\widetilde {G}=\widetilde {R}\rtimes \widetilde {{\bf C}_G(w)}$
. Write $\widetilde {G}=\widetilde {R}\rtimes \widetilde {{\bf C}_G(w)}$![]() . Since $\widetilde {{\bf C}_G(w)}$
. Since $\widetilde {{\bf C}_G(w)}$![]() is maximal in $\widetilde {G}$
is maximal in $\widetilde {G}$![]() , we see that $\widetilde {{\bf C}_G(w)}$
, we see that $\widetilde {{\bf C}_G(w)}$![]() acts irreducibly on $\widetilde {R}$
acts irreducibly on $\widetilde {R}$![]() . By the same argument in the previous paragraph, we conclude that $\widetilde {G}$
. By the same argument in the previous paragraph, we conclude that $\widetilde {G}$![]() is a Frobenius group with kernel $\widetilde {R}$
is a Frobenius group with kernel $\widetilde {R}$![]() and complement $\widetilde {{\bf C}_G(w)}$
and complement $\widetilde {{\bf C}_G(w)}$![]() . Furthermore, $\widetilde {R}$
. Furthermore, $\widetilde {R}$![]() is a minimal normal subgroup of $\widetilde {G}$
is a minimal normal subgroup of $\widetilde {G}$![]() and thus $\widetilde {R}$
and thus $\widetilde {R}$![]() is elementary abelian by the maximality of $\widetilde {{\bf C}_G(w)}$
is elementary abelian by the maximality of $\widetilde {{\bf C}_G(w)}$![]() . Also $\widetilde {{\bf C}_G(w)}$
. Also $\widetilde {{\bf C}_G(w)}$![]() is cyclic as $\widetilde {{\bf C}_G(w)}$
is cyclic as $\widetilde {{\bf C}_G(w)}$![]() is abelian, implying that $G/N$
is abelian, implying that $G/N$![]() is cyclic, statement (2.2) of the theorem holds.
is cyclic, statement (2.2) of the theorem holds.
5. Proofs of theorems E and C
To prove theorem E and corollary 2, here we list several lemmas, which will be used in the sequel.
Lemma 5.1 Let $G$![]() be a group. If $x,\,y\in G$
be a group. If $x,\,y\in G$![]() such that $[x,\,y]=1$
such that $[x,\,y]=1$![]() and $(o(x),\,o(y))=1$
and $(o(x),\,o(y))=1$![]() , then ${\bf C}_G(xy)={\bf C}_G(x)\cap {\bf C}_G(y)$
, then ${\bf C}_G(xy)={\bf C}_G(x)\cap {\bf C}_G(y)$![]() .
.
Lemma 5.2 ([Reference Heineken15, Proposition 2])
Let $G$![]() be a non-solvable CP-group. Then there exist normal subgroups $B$
be a non-solvable CP-group. Then there exist normal subgroups $B$![]() and $C$
and $C$![]() of $G$
of $G$![]() such that $1\unlhd B\unlhd C \unlhd G$
such that $1\unlhd B\unlhd C \unlhd G$![]() , where $B$
, where $B$![]() is a 2-subgroup of $G$
is a 2-subgroup of $G$![]() , $C/B$
, $C/B$![]() is a non-abelian simple group, and $G/C$
is a non-abelian simple group, and $G/C$![]() is a $p$
is a $p$![]() -group for some prime $p$
-group for some prime $p$![]() . In particular, $G/C$
. In particular, $G/C$![]() is either cyclic or a generalized quaternion group.
is either cyclic or a generalized quaternion group.
Lemma 5.3 ([Reference Heineken15, Proposition 3])
If $G$![]() is a non-abelian simple CP-group, then $G$
is a non-abelian simple CP-group, then $G$![]() is isomorphic to one of the following groups: ${ PSL}_2(q)$
is isomorphic to one of the following groups: ${ PSL}_2(q)$![]() , for $q = 5,\, 7,\, 8,\, 9,\, 17$
, for $q = 5,\, 7,\, 8,\, 9,\, 17$![]() , ${ PSL}_3(4),\, { Sz}(8)$
, ${ PSL}_3(4),\, { Sz}(8)$![]() , or ${ Sz}(32)$
, or ${ Sz}(32)$![]() .
.
Proof of theorem E First consider $\overline {N}$![]() is nilpotent. Then $N$
is nilpotent. Then $N$![]() is also nilpotent. If there exist two distinct primes $p_1,\, p_2\in \pi (\overline {N})$
is also nilpotent. If there exist two distinct primes $p_1,\, p_2\in \pi (\overline {N})$![]() , we may take $a_1\in P_1\setminus {\bf Z}(N)$
, we may take $a_1\in P_1\setminus {\bf Z}(N)$![]() and $a_2\in P_2\setminus {\bf Z}(N)$
and $a_2\in P_2\setminus {\bf Z}(N)$![]() , where $P_1$
, where $P_1$![]() and $P_2$
and $P_2$![]() are Sylow $p_1$
are Sylow $p_1$![]() and $p_2$
and $p_2$![]() -subgroups of $N$
-subgroups of $N$![]() , respectively. By lemma 5.1, ${\bf C}_G(a_1a_2)={\bf C}_G(a_1)\cap {\bf C}_G(a_2)\leq {\bf C}_G(a_i)$
, respectively. By lemma 5.1, ${\bf C}_G(a_1a_2)={\bf C}_G(a_1)\cap {\bf C}_G(a_2)\leq {\bf C}_G(a_i)$![]() for $i=1,\, 2$
for $i=1,\, 2$![]() . As all of ${\bf C}_G(a_1a_2),\, {\bf C}_G(a_1),\, {\bf C}_G(a_2)$
. As all of ${\bf C}_G(a_1a_2),\, {\bf C}_G(a_1),\, {\bf C}_G(a_2)$![]() are maximal in $G$
are maximal in $G$![]() , we have ${\bf C}_G(a_1a_2)={\bf C}_G(a_1)={\bf C}_G(a_2)$
, we have ${\bf C}_G(a_1a_2)={\bf C}_G(a_1)={\bf C}_G(a_2)$![]() . This indicates that $P_1\leq {\bf C}_G(a_2)={\bf C}_G(a_1)$
. This indicates that $P_1\leq {\bf C}_G(a_2)={\bf C}_G(a_1)$![]() , forcing $a_1\in {\bf Z}(N)$
, forcing $a_1\in {\bf Z}(N)$![]() . This contradiction deduces that $\overline {N}$
. This contradiction deduces that $\overline {N}$![]() is a $p$
is a $p$![]() -group.
-group.
Let ${P}\in$![]() Syl$_p({N})$
Syl$_p({N})$![]() . Then $\overline {N}=\overline {P}$
. Then $\overline {N}=\overline {P}$![]() . On the contrary, ${P}$
. On the contrary, ${P}$![]() char ${N}\unlhd G$
char ${N}\unlhd G$![]() , implying $P\unlhd G$
, implying $P\unlhd G$![]() and thus $\Phi (P)\leq \Phi (G)\cap N$
and thus $\Phi (P)\leq \Phi (G)\cap N$![]() . Along with the fact that $\Phi (G)\leq {\bf C}_G(u)$
. Along with the fact that $\Phi (G)\leq {\bf C}_G(u)$![]() for any $u\in N\setminus {\bf Z}(N)$
for any $u\in N\setminus {\bf Z}(N)$![]() , we obtain that $\Phi (P)\leq {\bf C}_N(u)$
, we obtain that $\Phi (P)\leq {\bf C}_N(u)$![]() , yielding $\Phi (P)\leq {\bf Z}(N)$
, yielding $\Phi (P)\leq {\bf Z}(N)$![]() by the choice of $u$
by the choice of $u$![]() . In this case, $\overline {N}=\overline {P}=P/{\bf Z}(N)\cong (P/\Phi (P)/({\bf Z}(N)/\Phi (P))$
. In this case, $\overline {N}=\overline {P}=P/{\bf Z}(N)\cong (P/\Phi (P)/({\bf Z}(N)/\Phi (P))$![]() is elementary abelian, statement (1) of the theorem holds.
is elementary abelian, statement (1) of the theorem holds.
Now, we consider that $\overline {N}$![]() is non-nilpotent. Let $x\in N\setminus {\bf Z}(N)$
is non-nilpotent. Let $x\in N\setminus {\bf Z}(N)$![]() be an arbitrary element. Write $x=x_1\cdots x_s$
be an arbitrary element. Write $x=x_1\cdots x_s$![]() , where $x_1,\, \dots,\, x_s$
, where $x_1,\, \dots,\, x_s$![]() are distinct components of $x$
are distinct components of $x$![]() . Since $x\not \in {\bf Z}(N)$
. Since $x\not \in {\bf Z}(N)$![]() , without loss of generality, we may consider $x_1\not \in {\bf Z}(N)$
, without loss of generality, we may consider $x_1\not \in {\bf Z}(N)$![]() . By lemma 5.1, we see that ${\bf C}_G(x)={\bf C}_G(x_1)\cap \cdots \cap {\bf C}_G(x_s)\leq {\bf C}_G(x_1)$
. By lemma 5.1, we see that ${\bf C}_G(x)={\bf C}_G(x_1)\cap \cdots \cap {\bf C}_G(x_s)\leq {\bf C}_G(x_1)$![]() . Since both ${\bf C}_G(x)$
. Since both ${\bf C}_G(x)$![]() and ${\bf C}_G(x_1)$
and ${\bf C}_G(x_1)$![]() are maximal subgroups of $G$
are maximal subgroups of $G$![]() , we have ${\bf C}_G(x)={\bf C}_G(x_1)$
, we have ${\bf C}_G(x)={\bf C}_G(x_1)$![]() . Consequently, $x$
. Consequently, $x$![]() can be assumed to be a $p$
can be assumed to be a $p$![]() -element with prime $p$
-element with prime $p$![]() .
.
In the following, we distinguish the proof into two cases:
Case 1. $\overline {{\bf C}_N(v)}$![]() is an $r$
is an $r$![]() -group, for any $r$
-group, for any $r$![]() -element $v\in N\setminus {\bf Z}(N)$
-element $v\in N\setminus {\bf Z}(N)$![]() with prime $r$
with prime $r$![]() .
.
Step 1. $\overline {N}$![]() is a CP-group.
is a CP-group.
Assume false. Then there exists an element $\overline {z}\in \overline {N}$![]() of order $q^ar^b$
of order $q^ar^b$![]() , where $q,\, r\in \pi (\overline {N})$
, where $q,\, r\in \pi (\overline {N})$![]() and $a,\, b>0$
and $a,\, b>0$![]() are positive integers. By assumption, $\overline {{\bf C}_N(z^{q^a}})$
are positive integers. By assumption, $\overline {{\bf C}_N(z^{q^a}})$![]() is an $r$
is an $r$![]() -group. Notice that $\overline {z}\in \overline {{\bf C}_N(z^{q^a}})$
-group. Notice that $\overline {z}\in \overline {{\bf C}_N(z^{q^a}})$![]() , which is a contradiction because $qr\mid o(\overline {z})$
, which is a contradiction because $qr\mid o(\overline {z})$![]() .
.
Step 2. $\overline {N}$![]() is solvable.
is solvable.
Assume on the contrary that $\overline {N}$![]() is non-solvable. By lemma 5.2, $\overline {N}$
is non-solvable. By lemma 5.2, $\overline {N}$![]() has normal subgroups $\overline {B},\, \overline {C}$
has normal subgroups $\overline {B},\, \overline {C}$![]() such that $\overline {1}\unlhd \overline {B}\unlhd \overline {C }\unlhd \overline {N}$
such that $\overline {1}\unlhd \overline {B}\unlhd \overline {C }\unlhd \overline {N}$![]() , where $\overline {B}$
, where $\overline {B}$![]() is a 2-group, $\overline {C}/\overline {B}$
is a 2-group, $\overline {C}/\overline {B}$![]() is non-abelian and simple, and $\overline {N}/\overline {C}$
is non-abelian and simple, and $\overline {N}/\overline {C}$![]() is a $q_1$
is a $q_1$![]() -group for some prime $q_1$
-group for some prime $q_1$![]() , which is cyclic or generalized quaternion.
, which is cyclic or generalized quaternion.
Suppose that $\overline {B}\neq \overline {1}$![]() . Let $v\in N\setminus {\bf Z}(N)$
. Let $v\in N\setminus {\bf Z}(N)$![]() be a $q$
be a $q$![]() -element for some odd prime $q$
-element for some odd prime $q$![]() . Then ${\bf C}_G(v)$
. Then ${\bf C}_G(v)$![]() is maximal in $G$
is maximal in $G$![]() such that $B\nleq {\bf C}_G(v)$
such that $B\nleq {\bf C}_G(v)$![]() by step 1. Therefore, $G=B{\bf C}_G(v)$
by step 1. Therefore, $G=B{\bf C}_G(v)$![]() as ${\bf C}_G(v)$
as ${\bf C}_G(v)$![]() is maximal in $G$
is maximal in $G$![]() , yielding $N=B{\bf C}_N(v)$
, yielding $N=B{\bf C}_N(v)$![]() . In this case, $|\overline {N}:\overline {{\bf C}_N(v)}|=|N:{\bf C}_N(v)|=|B:{\bf C}_B(v)|$
. In this case, $|\overline {N}:\overline {{\bf C}_N(v)}|=|N:{\bf C}_N(v)|=|B:{\bf C}_B(v)|$![]() is a 2-number. This shows that $|\overline {N}|$
is a 2-number. This shows that $|\overline {N}|$![]() has exactly two prime divisors, against the fact that $\overline {N}$
has exactly two prime divisors, against the fact that $\overline {N}$![]() is non-solvable.
is non-solvable.
As a result, $\overline {B}=\overline {1}$![]() , and $\overline {C}$
, and $\overline {C}$![]() is a non-abelian simple CP-group. By lemma 5.3, $\overline {C}$
is a non-abelian simple CP-group. By lemma 5.3, $\overline {C}$![]() is one of the following groups: ${ PSL}_2(q)$
is one of the following groups: ${ PSL}_2(q)$![]() , for $q = 5,\, 7,\, 8,\, 9,\, 17$
, for $q = 5,\, 7,\, 8,\, 9,\, 17$![]() , ${ PSL}_3(4), { Sz}(8)$
, ${ PSL}_3(4), { Sz}(8)$![]() , or ${ Sz}(32)$
, or ${ Sz}(32)$![]() . Recall that $\overline {G}/{\bf C}_{\overline {G}}(\overline {C})\leq {\rm Aut}(\overline {C})$
. Recall that $\overline {G}/{\bf C}_{\overline {G}}(\overline {C})\leq {\rm Aut}(\overline {C})$![]() . As $\overline {C}\cap {\bf C}_{\overline {G}}(\overline {C})=\overline {1}$
. As $\overline {C}\cap {\bf C}_{\overline {G}}(\overline {C})=\overline {1}$![]() and $\overline {C}\times {\bf C}_{\overline {G}}(\overline {C})\unlhd \overline {G}$
and $\overline {C}\times {\bf C}_{\overline {G}}(\overline {C})\unlhd \overline {G}$![]() , we see that ${\bf C}_{\overline {G}}(\overline {C})=\overline {1}$
, we see that ${\bf C}_{\overline {G}}(\overline {C})=\overline {1}$![]() by step 1 and thus $\overline {C}\leq \overline {G}\leq {\rm Aut}(\overline {C})$
by step 1 and thus $\overline {C}\leq \overline {G}\leq {\rm Aut}(\overline {C})$![]() . Moreover, for any $z\in C\setminus {\bf Z}(N)$
. Moreover, for any $z\in C\setminus {\bf Z}(N)$![]() , we see that ${\bf C}_{\overline {G}}(\overline {z})\geq \overline {{\bf C}_G(z)}$
, we see that ${\bf C}_{\overline {G}}(\overline {z})\geq \overline {{\bf C}_G(z)}$![]() and $\overline {z}\not \in {\bf Z}(\overline {N})$
and $\overline {z}\not \in {\bf Z}(\overline {N})$![]() . Since ${\bf C}_G(z)$
. Since ${\bf C}_G(z)$![]() is maximal in $G$
is maximal in $G$![]() , we obtain that ${\bf C}_{\overline {G}}(\overline {z})=\overline {{\bf C}_G(z)}$
, we obtain that ${\bf C}_{\overline {G}}(\overline {z})=\overline {{\bf C}_G(z)}$![]() is also maximal in $\overline {G}$
is also maximal in $\overline {G}$![]() .
.
If $\overline {C}\cong { PSL}_2(5)$![]() , then $\overline {G}\leq S_5$
, then $\overline {G}\leq S_5$![]() . However, by [Reference Conway, Curtis, Norton, Parker and Wilson4], ${\bf C}_{\overline {G}}(\overline {v})$
. However, by [Reference Conway, Curtis, Norton, Parker and Wilson4], ${\bf C}_{\overline {G}}(\overline {v})$![]() is not maximal in $\overline {G}$
is not maximal in $\overline {G}$![]() for a 5-element $v\in C\setminus {\bf Z}(N)$
for a 5-element $v\in C\setminus {\bf Z}(N)$![]() , a contradiction. By the same reason, we can rule out the cases $\overline {C}\cong { PSL}_2(q)$
, a contradiction. By the same reason, we can rule out the cases $\overline {C}\cong { PSL}_2(q)$![]() , when $q= 7,\, 8,\, 9,\, 17$
, when $q= 7,\, 8,\, 9,\, 17$![]() , and ${ Sz}(8)$
, and ${ Sz}(8)$![]() or ${ Sz}(32)$
or ${ Sz}(32)$![]() . For the remaining case $\overline {C}\cong { PSL}_3(4)$
. For the remaining case $\overline {C}\cong { PSL}_3(4)$![]() , we can find an element $u\in C\setminus {\bf Z}(N)$
, we can find an element $u\in C\setminus {\bf Z}(N)$![]() with order 2 such that $\overline {{\bf C}_G(v)}$
with order 2 such that $\overline {{\bf C}_G(v)}$![]() is not maximal in $\overline {G}$
is not maximal in $\overline {G}$![]() according to [Reference Conway, Curtis, Norton, Parker and Wilson4], also a contradiction.
according to [Reference Conway, Curtis, Norton, Parker and Wilson4], also a contradiction.
Step 3. The conclusion of case 1.
Let $\overline {S}$![]() be a minimal normal subgroup of $\overline {G}$
be a minimal normal subgroup of $\overline {G}$![]() contained in $\overline {N}$
contained in $\overline {N}$![]() . Then $\overline {S}$
. Then $\overline {S}$![]() is an elementary abelian $s$
is an elementary abelian $s$![]() -group for some prime $s$
-group for some prime $s$![]() . Since $\overline {N}$
. Since $\overline {N}$![]() is non-nilpotent, there must exist an $s_1$
is non-nilpotent, there must exist an $s_1$![]() -element $a\in N\setminus {\bf Z}(N)$
-element $a\in N\setminus {\bf Z}(N)$![]() with $s_1\neq s$
with $s_1\neq s$![]() . By assumption, $\overline {{\bf C}_N(a)}$
. By assumption, $\overline {{\bf C}_N(a)}$![]() is an $s_1$
is an $s_1$![]() -subgroup, indicating that $\overline {S}\nleq \overline {{\bf C}_G(a)}$
-subgroup, indicating that $\overline {S}\nleq \overline {{\bf C}_G(a)}$![]() , and thus $S\nleq {\bf C}_G(a)$
, and thus $S\nleq {\bf C}_G(a)$![]() . Hence, $G=S{\bf C}_G(a)$
. Hence, $G=S{\bf C}_G(a)$![]() by the maximality of ${\bf C}_G(a)$
by the maximality of ${\bf C}_G(a)$![]() , yielding $\overline {N}=\overline {S} \overline {{\bf C}_N(a)}$
, yielding $\overline {N}=\overline {S} \overline {{\bf C}_N(a)}$![]() . In particular, $\overline {N}=\overline {S}\rtimes \overline {{\bf C}_N(a)}$
. In particular, $\overline {N}=\overline {S}\rtimes \overline {{\bf C}_N(a)}$![]() is a Frobenius group with complement $\overline {{\bf C}_N(a)}$
is a Frobenius group with complement $\overline {{\bf C}_N(a)}$![]() by step 1.
by step 1.
We show that $|\overline {{\bf C}_N(a)}|=s_1$![]() . For every $a_1\in {\bf C}_N(a)\setminus {\bf Z}(N)$
. For every $a_1\in {\bf C}_N(a)\setminus {\bf Z}(N)$![]() , the similar argument in the previous paragraph deduces that $\overline {N}=\overline {S}\rtimes \overline {{\bf C}_N(a_1)}$
, the similar argument in the previous paragraph deduces that $\overline {N}=\overline {S}\rtimes \overline {{\bf C}_N(a_1)}$![]() is also a Frobenius group. Since both $\overline {{\bf C}_N(a)}$
is also a Frobenius group. Since both $\overline {{\bf C}_N(a)}$![]() and $\overline {{\bf C}_N(a_1)}$
and $\overline {{\bf C}_N(a_1)}$![]() are Frobenius complement of $\overline {N}$
are Frobenius complement of $\overline {N}$![]() , and $\overline {a_1}\in \overline {{\bf C}_N(a)}\cap \overline {{\bf C}_N(a_1)}\neq \overline {1}$
, and $\overline {a_1}\in \overline {{\bf C}_N(a)}\cap \overline {{\bf C}_N(a_1)}\neq \overline {1}$![]() , we have $\overline {{\bf C}_N(a)}= \overline {{\bf C}_N(a_1)}$
, we have $\overline {{\bf C}_N(a)}= \overline {{\bf C}_N(a_1)}$![]() , forcing $\overline {{\bf C}_N(a)}$
, forcing $\overline {{\bf C}_N(a)}$![]() is abelian. By [Reference Huppert17, Theorem 5.8.7], $\overline {{\bf C}_N(a)}$
is abelian. By [Reference Huppert17, Theorem 5.8.7], $\overline {{\bf C}_N(a)}$![]() is cyclic.
is cyclic.
Let $1\overline {}\neq \overline {d}\in \overline {S}$![]() . Without loss, we assume that $d\in S\setminus {\bf Z}(N)$
. Without loss, we assume that $d\in S\setminus {\bf Z}(N)$![]() . Then ${\bf C}_G(d)$
. Then ${\bf C}_G(d)$![]() is maximal in $G$
is maximal in $G$![]() by hypothesis, forcing that $\overline {{\bf C}_G(d)}$
by hypothesis, forcing that $\overline {{\bf C}_G(d)}$![]() is maximal in $\overline {G}$
is maximal in $\overline {G}$![]() . In particular, $\overline {G}=\overline {N}\overline {{\bf C}_G(d)}$
. In particular, $\overline {G}=\overline {N}\overline {{\bf C}_G(d)}$![]() . On the contrary, $\overline {{\bf C}_G(d)}\leq {\bf C}_{\overline {G}}(\overline {d})$
. On the contrary, $\overline {{\bf C}_G(d)}\leq {\bf C}_{\overline {G}}(\overline {d})$![]() and $\overline {d}\not \in {\bf Z}(\overline {N})$
and $\overline {d}\not \in {\bf Z}(\overline {N})$![]() , we obtain that $\overline {S}\leq {\bf C}_{\overline {G}}(\overline {d})=\overline {{\bf C}_G(d)}$
, we obtain that $\overline {S}\leq {\bf C}_{\overline {G}}(\overline {d})=\overline {{\bf C}_G(d)}$![]() . In this case, $\overline {G}/\overline {S}=\overline {N}/\overline {S}\rtimes \overline {{\bf C}_G(d)}/\overline {S}$
. In this case, $\overline {G}/\overline {S}=\overline {N}/\overline {S}\rtimes \overline {{\bf C}_G(d)}/\overline {S}$![]() . The maximality of $\overline {{\bf C}_G(d)}/\overline {S}$
. The maximality of $\overline {{\bf C}_G(d)}/\overline {S}$![]() indicates that $\overline {N}/\overline {S}$
indicates that $\overline {N}/\overline {S}$![]() is a minimal normal subgroup of $\overline {G}/\overline {S}$
is a minimal normal subgroup of $\overline {G}/\overline {S}$![]() , so $\overline {N}/\overline {S}$
, so $\overline {N}/\overline {S}$![]() has prime power order. Recall that $\overline {N}/\overline {S}\cong \overline {{\bf C}_N(a)}$
has prime power order. Recall that $\overline {N}/\overline {S}\cong \overline {{\bf C}_N(a)}$![]() is cyclic. Then $|\overline {{\bf C}_N(a)}|=s_1$
is cyclic. Then $|\overline {{\bf C}_N(a)}|=s_1$![]() , as required.
, as required.
Case 2. There exists a $p$![]() -element $x\in N\setminus {\bf Z}(N)$
-element $x\in N\setminus {\bf Z}(N)$![]() such that $\overline {{\bf C}_N(x)}$
such that $\overline {{\bf C}_N(x)}$![]() is not a $p$
is not a $p$![]() -group.
-group.
Step 4. ${\bf C}_N(x)=P_x\times H_x$![]() , where $P_x\in {\rm Syl}_p({\bf C}_N(x))$
, where $P_x\in {\rm Syl}_p({\bf C}_N(x))$![]() and $H_x$
and $H_x$![]() is an abelian Hall $p'$
is an abelian Hall $p'$![]() -subgroup of ${\bf C}_N(x)$
-subgroup of ${\bf C}_N(x)$![]() .
.
Let $y\in {\bf C}_N(x)\setminus {\bf Z}(N)$![]() be an arbitrary $p'$
be an arbitrary $p'$![]() -element. By lemma 5.1, we have ${\bf C}_G(xy)={\bf C}_G(x)\cap {\bf C}_G(y)\leq {\bf C}_G(x)$
-element. By lemma 5.1, we have ${\bf C}_G(xy)={\bf C}_G(x)\cap {\bf C}_G(y)\leq {\bf C}_G(x)$![]() . Notice that ${\bf C}_G(xy)$
. Notice that ${\bf C}_G(xy)$![]() , ${\bf C}_G(x),\, {\bf C}_G(y)$
, ${\bf C}_G(x),\, {\bf C}_G(y)$![]() are all maximal in $G$
are all maximal in $G$![]() . We have ${\bf C}_G(xy)={\bf C}_G(x)={\bf C}_G(y)$
. We have ${\bf C}_G(xy)={\bf C}_G(x)={\bf C}_G(y)$![]() , yielding $y\in {\bf Z}({\bf C}_G(x))$
, yielding $y\in {\bf Z}({\bf C}_G(x))$![]() . Moreover, $y\in {\bf Z}({\bf C}_N(x))$
. Moreover, $y\in {\bf Z}({\bf C}_N(x))$![]() . As a result, ${\bf C}_N(x)=P_x\times H_x$
. As a result, ${\bf C}_N(x)=P_x\times H_x$![]() , where $P_x\in {\rm Syl}_p({\bf C}_N(x))$
, where $P_x\in {\rm Syl}_p({\bf C}_N(x))$![]() and $H_x$
and $H_x$![]() is an abelian Hall $p'$
is an abelian Hall $p'$![]() -subgroup of ${\bf C}_N(x)$
-subgroup of ${\bf C}_N(x)$![]() .
.
Step 5. ${\bf C}_N(x)\leq {\bf Z}({\bf C}_G(x))$![]() .
.
By the assumption of case 2, we see that $H_x\nleq {\bf Z}(N)$![]() . Take a $q$
. Take a $q$![]() -element $v\in H_x\setminus {\bf Z}(N)$
-element $v\in H_x\setminus {\bf Z}(N)$![]() with prime $q$
with prime $q$![]() . A similar argument as in the previous paragraph deduces that ${\bf C}_N(v)=Q_v\times K_v$
. A similar argument as in the previous paragraph deduces that ${\bf C}_N(v)=Q_v\times K_v$![]() , where $Q_v\in {\rm Syl}_q({\bf C}_N(v))$
, where $Q_v\in {\rm Syl}_q({\bf C}_N(v))$![]() and $K_v$
and $K_v$![]() is an abelian Hall $q'$
is an abelian Hall $q'$![]() -subgroup of ${\bf C}_N(v)$
-subgroup of ${\bf C}_N(v)$![]() . Notice that $x\in K_v$
. Notice that $x\in K_v$![]() and $v\in H_x$
and $v\in H_x$![]() . Then ${\bf C}_N(v)\leq {\bf C}_N(x)$
. Then ${\bf C}_N(v)\leq {\bf C}_N(x)$![]() and ${\bf C}_N(x)\leq {\bf C}_N(v)$
and ${\bf C}_N(x)\leq {\bf C}_N(v)$![]() . In particular, ${\bf C}_N(v)= {\bf C}_N(x)\leq {\bf Z}({\bf C}_G(x))$
. In particular, ${\bf C}_N(v)= {\bf C}_N(x)\leq {\bf Z}({\bf C}_G(x))$![]() .
.
Step 6. ${{\bf C}_N(x)}\cap {{\bf C}_N(y)}= {\bf Z}(N)$![]() for any $y\in N\setminus {\bf C}_N(x)$
for any $y\in N\setminus {\bf C}_N(x)$![]() .
.
Assume false. Then there exists an element $z\in ({\bf C}_N(x)\cap {\bf C}_N(y))\setminus {\bf Z}(N)$![]() . Since ${\bf C}_N(x)\leq {\bf Z}({\bf C}_G(x))$
. Since ${\bf C}_N(x)\leq {\bf Z}({\bf C}_G(x))$![]() , we see that ${\bf C}_G(z)\geq \langle {\bf C}_G(x),\, y \rangle > {\bf C}_G(x)$
, we see that ${\bf C}_G(z)\geq \langle {\bf C}_G(x),\, y \rangle > {\bf C}_G(x)$![]() . As ${\bf C}_G(x)$
. As ${\bf C}_G(x)$![]() is maximal in $G$
is maximal in $G$![]() , it follows that ${\bf C}_G(z)=G$
, it follows that ${\bf C}_G(z)=G$![]() , that is, $z\in {\bf Z}(N)$
, that is, $z\in {\bf Z}(N)$![]() , a contradiction.
, a contradiction.
Step 7. The contradiction of case 2.
By step 5, ${\bf C}_N(x)\unlhd {\bf C}_G(x)$![]() , which implies that ${\bf N}_G({\bf C}_N(x))\geq {\bf C}_G(x)$
, which implies that ${\bf N}_G({\bf C}_N(x))\geq {\bf C}_G(x)$![]() . Consequently, ${\bf N}_G({\bf C}_N(x))= {\bf C}_G(x)$
. Consequently, ${\bf N}_G({\bf C}_N(x))= {\bf C}_G(x)$![]() or ${\bf C}_N(x)\unlhd G$
or ${\bf C}_N(x)\unlhd G$![]() as ${\bf C}_G(x)$
as ${\bf C}_G(x)$![]() is maximal in $G$
is maximal in $G$![]() .
.
Assume first that ${\bf C}_N(x)\unlhd G$![]() . Then $P_x$
. Then $P_x$![]() is a normal subgroup of $G$
is a normal subgroup of $G$![]() according to step 4. Let $z\in N\setminus {\bf C}_N(x)$
according to step 4. Let $z\in N\setminus {\bf C}_N(x)$![]() be a primary element. Then ${\bf C}_G(z)$
be a primary element. Then ${\bf C}_G(z)$![]() is maximal in $G$
is maximal in $G$![]() . Moreover, $P_x\nleq {\bf C}_G(z)$
. Moreover, $P_x\nleq {\bf C}_G(z)$![]() by step 6. As a result, $G=P_x{\bf C}_G(z)$
by step 6. As a result, $G=P_x{\bf C}_G(z)$![]() , implying $N=P_x{\bf C}_N(z)$
, implying $N=P_x{\bf C}_N(z)$![]() . Furthermore, by step 6, ${\bf C}_N(x)={\bf Z}(N)P_x$
. Furthermore, by step 6, ${\bf C}_N(x)={\bf Z}(N)P_x$![]() , showing that $\overline {{\bf C}_N(x)}$
, showing that $\overline {{\bf C}_N(x)}$![]() is a $p$
is a $p$![]() -group, contrary to our assumption.
-group, contrary to our assumption.
Hence, ${\bf N}_G({\bf C}_N(x))= {\bf C}_G(x)$![]() , forcing ${\bf N}_N({\bf C}_N(x))= {\bf C}_N(x)$
, forcing ${\bf N}_N({\bf C}_N(x))= {\bf C}_N(x)$![]() . Since ${\bf N}_{\overline {G}}(\overline {{\bf C}_N(x)})\geq \overline {{\bf N}_G({\bf C}_N(x))}= \overline {{\bf C}_G(x)}$
. Since ${\bf N}_{\overline {G}}(\overline {{\bf C}_N(x)})\geq \overline {{\bf N}_G({\bf C}_N(x))}= \overline {{\bf C}_G(x)}$![]() , we get that ${\bf N}_{\overline {G}}(\overline {{\bf C}_N(x)})=\overline {G}$
, we get that ${\bf N}_{\overline {G}}(\overline {{\bf C}_N(x)})=\overline {G}$![]() or ${\bf N}_{\overline {G}}(\overline {{\bf C}_N(x)})=\overline {{\bf C}_G(x)}$
or ${\bf N}_{\overline {G}}(\overline {{\bf C}_N(x)})=\overline {{\bf C}_G(x)}$![]() . If the former holds, then ${\bf C}_N(x)\unlhd G$
. If the former holds, then ${\bf C}_N(x)\unlhd G$![]() , against our assumption. Hence, ${\bf N}_{\overline {G}}(\overline {{\bf C}_N(x)})=\overline {{\bf C}_G(x)}$
, against our assumption. Hence, ${\bf N}_{\overline {G}}(\overline {{\bf C}_N(x)})=\overline {{\bf C}_G(x)}$![]() , yielding ${\bf N}_{\overline {N}}(\overline {{\bf C}_N(x)})=\overline {{\bf C}_N(x)}$
, yielding ${\bf N}_{\overline {N}}(\overline {{\bf C}_N(x)})=\overline {{\bf C}_N(x)}$![]() .
.
We claim that for any $g\in N\setminus {\bf C}_N(x)$![]() , we always have ${\bf C}_N(x)^g\cap {\bf C}_N(x)={\bf Z}(N)$
, we always have ${\bf C}_N(x)^g\cap {\bf C}_N(x)={\bf Z}(N)$![]() . Let $d\in ({\bf C}_N(x)^g\cap {\bf C}_N(x))\setminus {\bf Z}(N)$
. Let $d\in ({\bf C}_N(x)^g\cap {\bf C}_N(x))\setminus {\bf Z}(N)$![]() . Note that ${\bf C}_N(x)\leq {\bf Z}({\bf C}_G(x))$
. Note that ${\bf C}_N(x)\leq {\bf Z}({\bf C}_G(x))$![]() . Then ${\bf C}_G(d)\geq \langle {\bf C}_G(x)^g,\, {\bf C}_G(x)\rangle$
. Then ${\bf C}_G(d)\geq \langle {\bf C}_G(x)^g,\, {\bf C}_G(x)\rangle$![]() . Since ${\bf C}_G(x)$
. Since ${\bf C}_G(x)$![]() is maximal and ${\bf C}_G(x)^g\neq {\bf C}_G(x)$
is maximal and ${\bf C}_G(x)^g\neq {\bf C}_G(x)$![]() , we have that $d\in {\bf Z}(G)$
, we have that $d\in {\bf Z}(G)$![]() and thus $d\in {\bf Z}(N)$
and thus $d\in {\bf Z}(N)$![]() , a contradiction. By [Reference Huppert17, Theorem 5.7.6], $\overline {N}$
, a contradiction. By [Reference Huppert17, Theorem 5.7.6], $\overline {N}$![]() is a Frobenius group with a complement $\overline {{\bf C}_N(x)}$
is a Frobenius group with a complement $\overline {{\bf C}_N(x)}$![]() . Write $\overline {N}=\overline {T_x}\rtimes \overline {{\bf C}_N(x)}$
. Write $\overline {N}=\overline {T_x}\rtimes \overline {{\bf C}_N(x)}$![]() , where $\overline {T_x}$
, where $\overline {T_x}$![]() is the Frobenius kernel of $\overline {N}$
is the Frobenius kernel of $\overline {N}$![]() . Let $\overline {Q} \in$
. Let $\overline {Q} \in$![]() Syl$_q(\overline {T_x})$
Syl$_q(\overline {T_x})$![]() . Note that $\overline {{\bf C}_G(x)}$
. Note that $\overline {{\bf C}_G(x)}$![]() is maximal in $\overline {G}$
is maximal in $\overline {G}$![]() . Then $\overline {G}=\overline {Q}\rtimes \overline {{\bf C}_G(x)}$
. Then $\overline {G}=\overline {Q}\rtimes \overline {{\bf C}_G(x)}$![]() by step 6. The maximality of $\overline {{\bf C}_G(x)}$
by step 6. The maximality of $\overline {{\bf C}_G(x)}$![]() indicates that $\overline {T_x}=\overline {Q}$
indicates that $\overline {T_x}=\overline {Q}$![]() is a minimal normal subgroup of $\overline {G}$
is a minimal normal subgroup of $\overline {G}$![]() . In particular, $\overline {T_x}$
. In particular, $\overline {T_x}$![]() is abelian.
is abelian.
Take $y\in T_x\setminus {\bf Z}(N)$![]() . Then $N\nleq {\bf C}_G(y)$
. Then $N\nleq {\bf C}_G(y)$![]() . The maximality of ${\bf C}_G(y)$
. The maximality of ${\bf C}_G(y)$![]() implies that $G=N{\bf C}_G(y)$
implies that $G=N{\bf C}_G(y)$![]() , and thus $\overline {G}/\overline {T_x}\cong \overline {N}/\overline {T_x} ~\overline {{\bf C}_G(y)}/\overline {T_x}$
, and thus $\overline {G}/\overline {T_x}\cong \overline {N}/\overline {T_x} ~\overline {{\bf C}_G(y)}/\overline {T_x}$![]() . Notice that $\overline {{\bf C}_G(y)}/\overline {T_x}$
. Notice that $\overline {{\bf C}_G(y)}/\overline {T_x}$![]() is a maximal subgroup of $\overline {G}/\overline {T_x}$
is a maximal subgroup of $\overline {G}/\overline {T_x}$![]() . Then $\overline {N}/\overline {T_x}$
. Then $\overline {N}/\overline {T_x}$![]() must be a minimal normal subgroup of $\overline {G}/\overline {T_x}$
must be a minimal normal subgroup of $\overline {G}/\overline {T_x}$![]() , forcing that $\overline {N}/\overline {T_x}$
, forcing that $\overline {N}/\overline {T_x}$![]() has prime power order. However, $\overline {N}/\overline {T_x}\cong \overline {{\bf C}_N(x)}$
has prime power order. However, $\overline {N}/\overline {T_x}\cong \overline {{\bf C}_N(x)}$![]() does not have prime power order, the final contradiction completes the proof.
does not have prime power order, the final contradiction completes the proof.
As an application of theorem E, here we give a new proof of theorem C.
Proof of theorem C Take $G=N$![]() in theorem E. Then $\overline {G}$
in theorem E. Then $\overline {G}$![]() is either an elementary abelian $p$
is either an elementary abelian $p$![]() -group for some prime $p$
-group for some prime $p$![]() , or $\overline {G}=\overline {P}\rtimes \overline {Q}$
, or $\overline {G}=\overline {P}\rtimes \overline {Q}$![]() is a Frobenius group, with Frobenius kernel $\overline {P}$
is a Frobenius group, with Frobenius kernel $\overline {P}$![]() and Frobenius complement $\overline {Q}$
and Frobenius complement $\overline {Q}$![]() . In particular, $\overline {P}$
. In particular, $\overline {P}$![]() is the minimal normal subgroup of $\overline {G}$
is the minimal normal subgroup of $\overline {G}$![]() and $\overline {Q}$
and $\overline {Q}$![]() is of prime order.
is of prime order.
For any $1\neq x\in P\setminus {\bf Z}(G)$![]() , ${\bf C}_G(x)$
, ${\bf C}_G(x)$![]() is maximal in $G$
is maximal in $G$![]() , which implies that $\overline {{\bf C}_G(x)}$
, which implies that $\overline {{\bf C}_G(x)}$![]() is maximal in $\overline {G}$
is maximal in $\overline {G}$![]() . Note that $\overline {G}$
. Note that $\overline {G}$![]() is a Frobenius group and $\overline {P}\leq \overline {{\bf C}_G(x)}$
is a Frobenius group and $\overline {P}\leq \overline {{\bf C}_G(x)}$![]() , it follows that $\overline {P}= \overline {{\bf C}_G(x)}$
, it follows that $\overline {P}= \overline {{\bf C}_G(x)}$![]() and $|\overline {Q}|=q$
and $|\overline {Q}|=q$![]() is a prime. Let $v\in Q\setminus {\bf Z}(G)$
is a prime. Let $v\in Q\setminus {\bf Z}(G)$![]() . Then ${\bf C}_G(v)$
. Then ${\bf C}_G(v)$![]() is maximal in $G$
is maximal in $G$![]() . Note that $Q$
. Note that $Q$![]() is abelian, we get that $\overline {{\bf C}_G(v)}=\overline {Q}$
is abelian, we get that $\overline {{\bf C}_G(v)}=\overline {Q}$![]() is maximal in $\overline {G}$
is maximal in $\overline {G}$![]() . As a result, each subgroup of $\overline {G}$
. As a result, each subgroup of $\overline {G}$![]() is contained in $\overline {P}$
is contained in $\overline {P}$![]() or $\overline {Q}^{\overline {g}}$
or $\overline {Q}^{\overline {g}}$![]() for some $\overline {g}\in \overline {G}$
for some $\overline {g}\in \overline {G}$![]() , showing that $G$
, showing that $G$![]() is a minimal non-abelian group.
is a minimal non-abelian group.
Acknowledgements
We thank the referee for his or her careful reading of the manuscript and for the constructive comments which substantially helped to improve the quality of the paper. The authors are supported by the National Natural Science Foundation of China (No. 12071181) and Natural Science Research Start-up Foundation of Recruiting Talents of Nanjing University of Posts and Telecommunications (Grant Nos. NY222090 and NY222091).