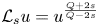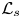1. Introduction
The study of the CR Yamabe problem began with the celebrated works of Jerison and Lee [Reference Jerison and Lee26–Reference Jerison and Lee29]. The prototypical nonlinear partial differential equation in this problem is
where $\mathscr L$![]() indicates the negative sum of squares of the left-invariant vector fields generating the horizontal space in the Heisenberg group $\mathbb {H}^n$
indicates the negative sum of squares of the left-invariant vector fields generating the horizontal space in the Heisenberg group $\mathbb {H}^n$![]() with real dimension $2n+1$
with real dimension $2n+1$![]() , whereas $Q = 2n+2$
, whereas $Q = 2n+2$![]() denotes the so-called homogeneous dimension associated with the non-isotropic group dilations. (In this paper, we always use the group law dictated by the Baker–Campbell–Hausdorff formula. When the Lie group is $\mathbb {H}^n$
denotes the so-called homogeneous dimension associated with the non-isotropic group dilations. (In this paper, we always use the group law dictated by the Baker–Campbell–Hausdorff formula. When the Lie group is $\mathbb {H}^n$![]() , or more in general a group of Heisenberg type, this choice obviously affects the expression of the horizontal Laplacian.) In the present paper, we are interested in the following nonlocal version of the above equation:
, or more in general a group of Heisenberg type, this choice obviously affects the expression of the horizontal Laplacian.) In the present paper, we are interested in the following nonlocal version of the above equation:
where the fractional parameter $s\in (0,\,1)$![]() , and $\mathscr L_s$
, and $\mathscr L_s$![]() denotes a certain pseudodifferential operator which arises in conformal CR geometry. As an application of our main result we derive sharp decay estimates of nonnegative solutions of (1.1).
denotes a certain pseudodifferential operator which arises in conformal CR geometry. As an application of our main result we derive sharp decay estimates of nonnegative solutions of (1.1).
The operator $\mathscr L_s$![]() in (1.1) was first introduced in [Reference Branson, Fontana and Morpurgo2] via the spectral formula:
in (1.1) was first introduced in [Reference Branson, Fontana and Morpurgo2] via the spectral formula:

where $\Gamma (x) = \int _0^\infty t^{x-1} {\rm e}^{-t} {\rm d}t$![]() denotes Euler gamma function. In (1.2) we have let $T = \partial _\sigma$
denotes Euler gamma function. In (1.2) we have let $T = \partial _\sigma$![]() , where for a point $g\in \mathbb {H}^n$
, where for a point $g\in \mathbb {H}^n$![]() we have indicated with $g = (z,\,\sigma )$
we have indicated with $g = (z,\,\sigma )$![]() its logarithmic coordinates. More in general, in a group of Heisenberg type $\mathbb {G}$
its logarithmic coordinates. More in general, in a group of Heisenberg type $\mathbb {G}$![]() , with logarithmic coordinates $g= (z,\,\sigma )\in \mathbb {G}$
, with logarithmic coordinates $g= (z,\,\sigma )\in \mathbb {G}$![]() , where $z$
, where $z$![]() denotes the horizontal variable and $\sigma$
denotes the horizontal variable and $\sigma$![]() the vertical one, the pseudodifferential operator $\mathscr L_s$
the vertical one, the pseudodifferential operator $\mathscr L_s$![]() is defined by the following generalization of (1.2):
is defined by the following generalization of (1.2):

where $-\Delta _\sigma$![]() is the positive Laplacian in the centre of the group, see [Reference Roncal and Thangavelu37]. Formulas (1.2) and (1.3) should be seen as the counterpart of the well-known spectral representation $\widehat {(-\Delta )^s u} = (2\pi |\xi |)^{2s} \hat u$
is the positive Laplacian in the centre of the group, see [Reference Roncal and Thangavelu37]. Formulas (1.2) and (1.3) should be seen as the counterpart of the well-known spectral representation $\widehat {(-\Delta )^s u} = (2\pi |\xi |)^{2s} \hat u$![]() , where we have denoted by $\hat f$
, where we have denoted by $\hat f$![]() the Fourier transform of a function $f$
the Fourier transform of a function $f$![]() , see [Reference Stein38, Chap. 5]. An important fact, first proved for $\mathbb {H}^n$
, see [Reference Stein38, Chap. 5]. An important fact, first proved for $\mathbb {H}^n$![]() in [Reference Frank, del Mar González, Monticelli and Tan12] using hyperbolic scattering, and subsequently generalized to any group of Heisenberg type in [Reference Roncal and Thangavelu37] using non-commutative harmonic analysis, is the following Dirichlet-to-Neumann characterization of $\mathscr L_s$
in [Reference Frank, del Mar González, Monticelli and Tan12] using hyperbolic scattering, and subsequently generalized to any group of Heisenberg type in [Reference Roncal and Thangavelu37] using non-commutative harmonic analysis, is the following Dirichlet-to-Neumann characterization of $\mathscr L_s$![]() :
:
where $U((z,\,\sigma ),\,y)$![]() is the solution to a certain extension problem from conformal CR geometry very different from that of Caffarelli–Silvestre in [Reference Caffarelli and Silvestre5]. Yet another fundamental fact, proved in [Reference Roncal and Thangavelu36, Proposition 4.1] and [Reference Roncal and Thangavelu37, Theorem 1.2] for $0< s<1/2$
is the solution to a certain extension problem from conformal CR geometry very different from that of Caffarelli–Silvestre in [Reference Caffarelli and Silvestre5]. Yet another fundamental fact, proved in [Reference Roncal and Thangavelu36, Proposition 4.1] and [Reference Roncal and Thangavelu37, Theorem 1.2] for $0< s<1/2$![]() , is the following remarkable Riesz type representation:
, is the following remarkable Riesz type representation:
where with $g = (z,\,\sigma )$![]() , we have denoted by $|g| = |(z,\,\sigma )| = (|z|^4 + 16 |\sigma |^2)^{1/4}$
, we have denoted by $|g| = |(z,\,\sigma )| = (|z|^4 + 16 |\sigma |^2)^{1/4}$![]() the non-isotropic gauge in a group of Heisenberg type $\mathbb {G}$
the non-isotropic gauge in a group of Heisenberg type $\mathbb {G}$![]() . Using the heat equation approach in [Reference Garofalo and Tralli17, Reference Garofalo and Tralli18], formula (1.4) can be extended to cover the whole range $0< s<1$
. Using the heat equation approach in [Reference Garofalo and Tralli17, Reference Garofalo and Tralli18], formula (1.4) can be extended to cover the whole range $0< s<1$![]() . In (1.4) the number $\alpha (m,\,k,\,s)>0$
. In (1.4) the number $\alpha (m,\,k,\,s)>0$![]() denotes an explicit constant depending on $s$
denotes an explicit constant depending on $s$![]() and the dimensions $m$
and the dimensions $m$![]() and $k$
and $k$![]() of the horizontal and vertical layers of the Lie algebra of $\mathbb {G}$
of the horizontal and vertical layers of the Lie algebra of $\mathbb {G}$![]() . While by (1.2), (1.3), and the classical formula $\Gamma (x+1) = x \Gamma (x)$
. While by (1.2), (1.3), and the classical formula $\Gamma (x+1) = x \Gamma (x)$![]() , it is formally almost obvious that in the limit as $s\nearrow 1$
, it is formally almost obvious that in the limit as $s\nearrow 1$![]() the operator $\mathscr L_s$
the operator $\mathscr L_s$![]() tends to the negative of the horizontal Laplacian $\mathscr L$
tends to the negative of the horizontal Laplacian $\mathscr L$![]() , we emphasize that, contrarily to an unfortunate misconception, when $\mathbb {G} = \mathbb {H}^n$
, we emphasize that, contrarily to an unfortunate misconception, when $\mathbb {G} = \mathbb {H}^n$![]() , or more in general it is of Heisenberg type, for no $s\in (0,\,1)$
, or more in general it is of Heisenberg type, for no $s\in (0,\,1)$![]() does the standard fractional power
does the standard fractional power
coincide with the pseudodifferential operator defined by the left-hand side of (1.4) (in (1.5) we have denoted by $P_t = {\rm e}^{-t\mathscr L}$![]() the heat semigroup constructed in [Reference Folland10]). Unlike their classical predecessors $(-\Delta )^s$
the heat semigroup constructed in [Reference Folland10]). Unlike their classical predecessors $(-\Delta )^s$![]() , in the purely non-Abelian setting of $\mathbb {H}^n$
, in the purely non-Abelian setting of $\mathbb {H}^n$![]() the pseudodifferential operators $\mathscr L^s$
the pseudodifferential operators $\mathscr L^s$![]() in (1.5) are not CR conformally invariant, nor they have any special geometric meaning, while the operators $\mathscr L_s$
in (1.5) are not CR conformally invariant, nor they have any special geometric meaning, while the operators $\mathscr L_s$![]() are CR conformally invariant. For these reasons, we will refer to the operator $\mathscr L_s$
are CR conformally invariant. For these reasons, we will refer to the operator $\mathscr L_s$![]() as the geometric (or conformal) fractional sub-Laplacian, even in the general setting of groups of Heisenberg type, see [Reference Frank, del Mar González, Monticelli and Tan12, Section 8.3] for relevant remarks in the remaining non-Abelian groups of Iwasawa type. Furthermore, it is not true that the fundamental solution $\mathscr E^{(s)}(z,\,\sigma )$
as the geometric (or conformal) fractional sub-Laplacian, even in the general setting of groups of Heisenberg type, see [Reference Frank, del Mar González, Monticelli and Tan12, Section 8.3] for relevant remarks in the remaining non-Abelian groups of Iwasawa type. Furthermore, it is not true that the fundamental solution $\mathscr E^{(s)}(z,\,\sigma )$![]() of $\mathscr L^s$
of $\mathscr L^s$![]() is a multiple of $|(z,\,\sigma )|^{2s-Q}$
is a multiple of $|(z,\,\sigma )|^{2s-Q}$![]() , see [Reference Garofalo and Tralli17, Theor. 5.1]. What is instead true, as proven originally by Cowling and Haagerup [Reference Cowling and Haagerup6], see also [Reference Roncal and Thangavelu36, (3.10)], and with a completely different approach based on heat equation techniques in [Reference Garofalo and Tralli17, Theor. 1.2] (the reader should also see in this respect the works [Reference Garofalo and Tralli18] and [Reference Garofalo and Tralli19]), is that the fundamental solution of the conformal fractional sub-Laplacian $\mathscr L_s$
, see [Reference Garofalo and Tralli17, Theor. 5.1]. What is instead true, as proven originally by Cowling and Haagerup [Reference Cowling and Haagerup6], see also [Reference Roncal and Thangavelu36, (3.10)], and with a completely different approach based on heat equation techniques in [Reference Garofalo and Tralli17, Theor. 1.2] (the reader should also see in this respect the works [Reference Garofalo and Tralli18] and [Reference Garofalo and Tralli19]), is that the fundamental solution of the conformal fractional sub-Laplacian $\mathscr L_s$![]() in (1.3) is given by
in (1.3) is given by
where

It is worth emphasizing here that, when $s\to 1$![]() , one recovers from (1.6) the famous formula for the fundamental solution of $-\mathscr L$
, one recovers from (1.6) the famous formula for the fundamental solution of $-\mathscr L$![]() , first found by Folland in [Reference Folland9] in $\mathbb {H}^n$
, first found by Folland in [Reference Folland9] in $\mathbb {H}^n$![]() , and subsequently generalized by Kaplan in [Reference Kaplan30] to groups of Heisenberg type. Before proceeding, we pause to notice that from the stochastic completeness and left-invariance of $P_t$
, and subsequently generalized by Kaplan in [Reference Kaplan30] to groups of Heisenberg type. Before proceeding, we pause to notice that from the stochastic completeness and left-invariance of $P_t$![]() , in any Carnot group $\mathbb {G}$
, in any Carnot group $\mathbb {G}$![]() one tautologically obtains from (1.5)
one tautologically obtains from (1.5)

where for $g\in \mathbb {G}$![]() we have defined
we have defined

with $p(g,\,t)$![]() the positive heat kernel of $-\mathscr L$
the positive heat kernel of $-\mathscr L$![]() . While in the Abelian case $\mathbb {G} = \mathbb {R}^n$
. While in the Abelian case $\mathbb {G} = \mathbb {R}^n$![]() , with Euclidean norm $|\cdot |$
, with Euclidean norm $|\cdot |$![]() , an elementary explicit calculation in (1.8), based on the knowledge that $p(x,\,t) = (4\pi t)^{-\frac n2} {\rm e}^{-\frac {|x|^2}{4t}}$
, an elementary explicit calculation in (1.8), based on the knowledge that $p(x,\,t) = (4\pi t)^{-\frac n2} {\rm e}^{-\frac {|x|^2}{4t}}$![]() , gives
, gives

and one recovers from (1.5) Riesz’ classical representation, when $\mathbb {G}$![]() is a non-Abelian Carnot group it is not true that the right-hand side of (1.8) defines a function of the gauge $|g| = |(z,\,\sigma )| = (|z|^4 + 16 |\sigma |^2)^{1/4}$
is a non-Abelian Carnot group it is not true that the right-hand side of (1.8) defines a function of the gauge $|g| = |(z,\,\sigma )| = (|z|^4 + 16 |\sigma |^2)^{1/4}$![]() . In fact, in any (non-Abelian) group of Heisenberg type the following explicit expression of (1.8) was computed in [Reference Garofalo and Tralli17, Theorem 5.1] (to obtain it, one should change $s$
. In fact, in any (non-Abelian) group of Heisenberg type the following explicit expression of (1.8) was computed in [Reference Garofalo and Tralli17, Theorem 5.1] (to obtain it, one should change $s$![]() into $-s$
into $-s$![]() in that result, see [Reference Garofalo and Tralli17, Remark 5.2])
in that result, see [Reference Garofalo and Tralli17, Remark 5.2])

where we have denoted by $F(a,\,b;c;z)$![]() the Gauss hypergeometric series. Formula (1.9) proves in particular that the function defined by (1.8) is not a function of the gauge $N(z,\,\sigma ) = (|z|^4 + 16 |\sigma |^2)^{1/4}$
the Gauss hypergeometric series. Formula (1.9) proves in particular that the function defined by (1.8) is not a function of the gauge $N(z,\,\sigma ) = (|z|^4 + 16 |\sigma |^2)^{1/4}$![]() (although it does have the expected cylindrical symmetry since it depends on $|z|^4$
(although it does have the expected cylindrical symmetry since it depends on $|z|^4$![]() and $|\sigma |^2$
and $|\sigma |^2$![]() ). If we substitute (1.9) in (1.8), and then (1.8) in (1.7), by comparing with formula (1.4), we conclude that $\mathscr L^s \not = \mathscr L_s$
). If we substitute (1.9) in (1.8), and then (1.8) in (1.7), by comparing with formula (1.4), we conclude that $\mathscr L^s \not = \mathscr L_s$![]() for every $0< s<1$
for every $0< s<1$![]() .
.
Formulas (1.4) and (1.6) motivated the results in the present work. As we have mentioned, we are interested in optimal decay estimates for nonnegative subsolutions of (1.1). In this respect, [Reference Roncal and Thangavelu36, Theorem 3.1] and [Reference Roncal and Thangavelu37, Theorem 3.7] gave the explicit form of a solution to the fractional Yamabe equation on group of Heisenberg type as a consequence of the intertwining properties of $\mathscr L_s$![]() for $0 < s < n + 1$
for $0 < s < n + 1$![]() , see also [Reference Garofalo and Tralli18] for a different approach to intertwining based on the heat equation. In the notation of [Reference Garofalo and Tralli18, Corollary 3.3], the result is that if $\mathbb {G}$
, see also [Reference Garofalo and Tralli18] for a different approach to intertwining based on the heat equation. In the notation of [Reference Garofalo and Tralli18, Corollary 3.3], the result is that if $\mathbb {G}$![]() is of Heisenberg type, and $0< s<1$
is of Heisenberg type, and $0< s<1$![]() , then for every $(z,\,\sigma )\in \mathbb {G}$
, then for every $(z,\,\sigma )\in \mathbb {G}$![]() , and $y>0$
, and $y>0$![]() one has the following intertwining identity:
one has the following intertwining identity:

Here, it might be worth clarifying for the reader that the parameter $y$![]() appearing in (1.10) is precisely the ‘extension’ variable in the parabolic counterpart of the conformal version of the extension problem discovered in [Reference Frank, del Mar González, Monticelli and Tan12]. An immediate consequence of (1.10) is that, for any real positive number $y>0$
appearing in (1.10) is precisely the ‘extension’ variable in the parabolic counterpart of the conformal version of the extension problem discovered in [Reference Frank, del Mar González, Monticelli and Tan12]. An immediate consequence of (1.10) is that, for any real positive number $y>0$![]() , the function
, the function

is a positive solution of the nonlinear equation (1.1). In this sense, we might say that functions (1.11) represent the counterpart of the so-called ‘bubbles’ from conformal geometry. We note that in the particular setting of the Heisenberg group $\mathbb {H}^n$![]() (which corresponds to the case $m = 2n$
(which corresponds to the case $m = 2n$![]() and $k=1$
and $k=1$![]() ) the function appearing in the left-hand side of (1.10) defines, up to group translations, the unique extremal of the Hardy–Littlewood–Sobolev inequalities obtained by Frank and Lieb in [Reference Frank and Lieb14]. (We emphasize that letting $s\nearrow 1$
) the function appearing in the left-hand side of (1.10) defines, up to group translations, the unique extremal of the Hardy–Littlewood–Sobolev inequalities obtained by Frank and Lieb in [Reference Frank and Lieb14]. (We emphasize that letting $s\nearrow 1$![]() one recovers from (1.11) the functions that, in the local case $s=1$
one recovers from (1.11) the functions that, in the local case $s=1$![]() , were shown to be the unique positive solutions of the CR Yamabe equation respectively in [Reference Jerison and Lee27], for the Heisenberg group $\mathbb {H}^n$
, were shown to be the unique positive solutions of the CR Yamabe equation respectively in [Reference Jerison and Lee27], for the Heisenberg group $\mathbb {H}^n$![]() , and [Reference Ivanov, Minchev and Vassilev24], for the quaternionic Heisenberg group. See also the important cited work [Reference Frank and Lieb14], and [Reference Garofalo and Vassilev20, Theor. 1.1] and [Reference Garofalo and Vassilev21] for partial results in groups of Heisenberg type.)
, and [Reference Ivanov, Minchev and Vassilev24], for the quaternionic Heisenberg group. See also the important cited work [Reference Frank and Lieb14], and [Reference Garofalo and Vassilev20, Theor. 1.1] and [Reference Garofalo and Vassilev21] for partial results in groups of Heisenberg type.)
Whether in a group of Heisenberg type $\mathbb {G}$![]() all nonnegative solutions of (1.1) are, up to left-translations, given by (1.11) presently remains a challenging open question. A first step in such problem is understanding the optimal decay of nonnegative solutions to (1.1). Keeping in mind that the number $m+2k$
all nonnegative solutions of (1.1) are, up to left-translations, given by (1.11) presently remains a challenging open question. A first step in such problem is understanding the optimal decay of nonnegative solutions to (1.1). Keeping in mind that the number $m+2k$![]() in (1.11) represents the homogeneous dimension $Q$
in (1.11) represents the homogeneous dimension $Q$![]() of the group $\mathbb {G}$
of the group $\mathbb {G}$![]() , by setting the scaling factor $y=1$
, by setting the scaling factor $y=1$![]() , we see that there exists a universal constant $C>0$
, we see that there exists a universal constant $C>0$![]() such that
such that
It is thus natural to guess that the optimal decay of all nonnegative solutions to (1.1) should be dictated by (1.6), i.e. by the fundamental solution of $\mathscr L_s$![]() . In theorem 1.2 we prove that this guess is correct.
. In theorem 1.2 we prove that this guess is correct.
To facilitate the exposition of the ideas and underline the general character of our approach, in this paper we have chosen to work in the setting of homogeneous Lie groups $\mathbb {G}$![]() with dilations $\{\delta _\lambda \}_{\lambda >0}$
with dilations $\{\delta _\lambda \}_{\lambda >0}$![]() , as in the seminal monograph of Folland and Stein [Reference Folland and Stein11]. We emphasize that such groups encompass the stratified, nilpotent Lie groups in [Reference Stein39], [Reference Folland10], and [Reference Folland and Stein11] (but they are a strictly larger class). In particular, our results include Lie groups of Iwasawa type for which (1.1) becomes significant in the case of pseudo-conformal CR and quaternionic contact geometry. We shall assume throughout that $|\cdot |$
, as in the seminal monograph of Folland and Stein [Reference Folland and Stein11]. We emphasize that such groups encompass the stratified, nilpotent Lie groups in [Reference Stein39], [Reference Folland10], and [Reference Folland and Stein11] (but they are a strictly larger class). In particular, our results include Lie groups of Iwasawa type for which (1.1) becomes significant in the case of pseudo-conformal CR and quaternionic contact geometry. We shall assume throughout that $|\cdot |$![]() is a fixed homogeneous norm in $\mathbb {G}$
is a fixed homogeneous norm in $\mathbb {G}$![]() , i.e. $g\mapsto |g|$
, i.e. $g\mapsto |g|$![]() is a continuous function on $\mathbb {G}$
is a continuous function on $\mathbb {G}$![]() which is $C^\infty$
which is $C^\infty$![]() smooth on $\mathbb {G}\setminus \{e\}$
smooth on $\mathbb {G}\setminus \{e\}$![]() , where $e$
, where $e$![]() is the group identity, $|g|=0$
is the group identity, $|g|=0$![]() if and only if $g=e$
if and only if $g=e$![]() , and for all $g\in \mathbb {G}$
, and for all $g\in \mathbb {G}$![]() we have
we have
Finally, we shall assume that the fixed norm satisfies the triangle inequality:
We stress that, according to [Reference Hebisch and Sikora23], any homogeneous group allows a norm which satisfies the triangle inequality. (It is well-known that in a group of Heisenberg type the anisotropic gauge $|g| = |(z,\,\sigma )| = (|z|^4 + 16 |\sigma |^2)^{1/4}$![]() satisfies (i)–(iii), see [Reference Cygan7].) We shall denote with
satisfies (i)–(iii), see [Reference Cygan7].) We shall denote with
the resulting open balls with centre $g$![]() and radius $R$
and radius $R$![]() .
.
For $1\le p < \infty$![]() and $0< s<1$
and $0< s<1$![]() we consider the Banach space $\mathcal {D}^{s,p}(\mathbb {G})$
we consider the Banach space $\mathcal {D}^{s,p}(\mathbb {G})$![]() defined as the closure of the space of functions $u\in \mathcal {C}^\infty _0 (\mathbb {G})$
defined as the closure of the space of functions $u\in \mathcal {C}^\infty _0 (\mathbb {G})$![]() with respect to the norm:
with respect to the norm:

We are particularly interested in the case $p=2$![]() . In this case, the Euler–Lagrange equation of (1.14) involves the following left-invariant nonlocal operator, initially defined on functions $u\in C^\infty _0(\mathbb {G})$
. In this case, the Euler–Lagrange equation of (1.14) involves the following left-invariant nonlocal operator, initially defined on functions $u\in C^\infty _0(\mathbb {G})$![]()
see [Reference Garofalo, Loiudice and Vassilev16] for a general construction of the fractional operator $\mathcal {L}_s$![]() on the Dirichlet space $\mathcal {D}^{s,2}(\mathbb {G})$
on the Dirichlet space $\mathcal {D}^{s,2}(\mathbb {G})$![]() and relevant Sobolev-type embedding results. In (1.15), and hereafter in this work, the number $Q>0$
and relevant Sobolev-type embedding results. In (1.15), and hereafter in this work, the number $Q>0$![]() represents the homogeneous dimension of $\mathbb {G}$
represents the homogeneous dimension of $\mathbb {G}$![]() associated with the group dilations $\{\delta _\lambda \}_{\lambda >0}$
associated with the group dilations $\{\delta _\lambda \}_{\lambda >0}$![]() . It is clear from (1.4) that, when $\mathbb {G}$
. It is clear from (1.4) that, when $\mathbb {G}$![]() is of Heisenberg type, the nonlocal operator $\mathcal {L}_s$
is of Heisenberg type, the nonlocal operator $\mathcal {L}_s$![]() defined using the Koranyi gauge is just a multiple of $\mathscr L_s$
defined using the Koranyi gauge is just a multiple of $\mathscr L_s$![]() in (1.3), and this provides strong enough motivation to work with (1.15). A second motivation comes from [Reference Garofalo, Loiudice and Vassilev16, Theor. 1.2], in which we prove that, if $X_1,\,\ldots,\,X_m$
in (1.3), and this provides strong enough motivation to work with (1.15). A second motivation comes from [Reference Garofalo, Loiudice and Vassilev16, Theor. 1.2], in which we prove that, if $X_1,\,\ldots,\,X_m$![]() are the left-invariant vector fields of homogeneity one with associated coordinates $x_j$
are the left-invariant vector fields of homogeneity one with associated coordinates $x_j$![]() , and the fixed homogeneous norm $|g|$
, and the fixed homogeneous norm $|g|$![]() is a spherically symmetric function of the coordinates $(x_1,\,\dots,\,x_m)$
is a spherically symmetric function of the coordinates $(x_1,\,\dots,\,x_m)$![]() , then for a function $u\in C^\infty _0(\mathbb {G})$
, then for a function $u\in C^\infty _0(\mathbb {G})$![]() we have the identities:
we have the identities:

where $\sigma _Q,\, \tau _m>0$![]() are suitable universal constants. Throughout the paper, for $0< s<1$
are suitable universal constants. Throughout the paper, for $0< s<1$![]() we let
we let
so that $2^*(s)$![]() , which is the Sobolev exponent associated with the fractional Sobolev inequality [Reference Garofalo, Loiudice and Vassilev16, Theorem 1.2]:
, which is the Sobolev exponent associated with the fractional Sobolev inequality [Reference Garofalo, Loiudice and Vassilev16, Theorem 1.2]:

and $(2^*(s))'$![]() is its Hölder conjugate. In addition to the fractional Sobolev exponent $2^*(s)$
is its Hölder conjugate. In addition to the fractional Sobolev exponent $2^*(s)$![]() , the following exponents will be used:
, the following exponents will be used:
With all this being said, we are ready to state our results. The first one concerns the nonlocal Schrödinger type equation (1.20). For the notion of subsolution to such equation, see (2.6).
Theorem 1.1 Let $\mathbb {G}$![]() be a homogeneous group. Let $u\in \mathcal {D}^{s,2}(\mathbb {G})$
be a homogeneous group. Let $u\in \mathcal {D}^{s,2}(\mathbb {G})$![]() be a nonnegative subsolution to the equation:
be a nonnegative subsolution to the equation:
Suppose the following conditions hold true:
(i) for some $t_0>r'= \frac {Q}{2s}$
 we have $V\in L^{r'}(\mathbb {G})\cap L^{t_0}(\mathbb {G})$
we have $V\in L^{r'}(\mathbb {G})\cap L^{t_0}(\mathbb {G})$ ;
;(ii) there exist $\bar R_0$
 and $K_0$
and $K_0$ so that for $R>\bar R_0$
so that for $R>\bar R_0$ we have
(1.21)\begin{equation} \int_{\{|g|>R\}} |V(g)|^{t_0}{{\rm d}g}\leq \frac{K_0}{R^{2st_0-Q}}. \end{equation}
we have
(1.21)\begin{equation} \int_{\{|g|>R\}} |V(g)|^{t_0}{{\rm d}g}\leq \frac{K_0}{R^{2st_0-Q}}. \end{equation}
Then there exists a constant $C>0$![]() , depending on $Q$
, depending on $Q$![]() , $s$
, $s$![]() , and $K_0$
, and $K_0$![]() , such that for all $g_0\in \mathbb {G}$
, such that for all $g_0\in \mathbb {G}$![]() with $|g_0|=2R_0\geq 4\bar R_0$
with $|g_0|=2R_0\geq 4\bar R_0$![]() , we have for $0< R\leq R_0$
, we have for $0< R\leq R_0$![]()
where the ‘tail’ is given by
We note that the potential $V$![]() in (1.20) is not assumed to be radial (i.e. a function of the norm $|\cdot |$
in (1.20) is not assumed to be radial (i.e. a function of the norm $|\cdot |$![]() ), or controlled by a power of $u$
), or controlled by a power of $u$![]() . Hypothesis (1.21) goes back to the work [Reference Bando, Kasue and Nakajima1], see also [Reference Vassilev42] where a similar assumption was used in the case of Schrödinger type equations modelled on the equations for the extremals to Hardy–Sobolev inequalities with polyradial symmetry. For other results about the Schrödinger equation see [Reference Frank, Lenzmann and Silvestre13]. The ‘tail’ in (1.23) appeared in [Reference Palatucci and Piccinini35] in the setting of the Heisenberg group $\mathbb {H}^n$
. Hypothesis (1.21) goes back to the work [Reference Bando, Kasue and Nakajima1], see also [Reference Vassilev42] where a similar assumption was used in the case of Schrödinger type equations modelled on the equations for the extremals to Hardy–Sobolev inequalities with polyradial symmetry. For other results about the Schrödinger equation see [Reference Frank, Lenzmann and Silvestre13]. The ‘tail’ in (1.23) appeared in [Reference Palatucci and Piccinini35] in the setting of the Heisenberg group $\mathbb {H}^n$![]() .
.
Our second result is the following theorem in which we establish the sharp asymptotic decay of weak nonnegative subsolutions to the fractional Yamabe type equation (1.1). The result applies to weak solutions of $\mathcal {L}_s u=|u|^{2^*(s)-2} u$![]() , since then $|u|$
, since then $|u|$![]() is a weak subsolution of the Yamabe type equation.
is a weak subsolution of the Yamabe type equation.
Theorem 1.2 Let $\mathbb {G}$![]() be a homogeneous group of homogeneous dimension $Q$
be a homogeneous group of homogeneous dimension $Q$![]() and $0< s<1$
and $0< s<1$![]() . If $u\in \mathcal {D}^{s,2}(\mathbb {G})$
. If $u\in \mathcal {D}^{s,2}(\mathbb {G})$![]() is a nonnegative subsolution to the nonlocal Yamabe type equation
is a nonnegative subsolution to the nonlocal Yamabe type equation
then $|\cdot |^{{Q-2s}}\,u\in L^\infty (\mathbb {G})$![]() .
.
We mention that in [Reference Brasco, Mosconi and Squassina3, Theor. 1.1] the authors established, in the setting of $\mathbb {R}^n$![]() , the sharp asymptotic behaviour of the spherically symmetric extremals for the fractional $L^p$
, the sharp asymptotic behaviour of the spherically symmetric extremals for the fractional $L^p$![]() Sobolev inequality, i.e. for the radial nonnegative solutions in $\mathbb {R}^n$
Sobolev inequality, i.e. for the radial nonnegative solutions in $\mathbb {R}^n$![]() of the equation with critical exponent
of the equation with critical exponent
where $0< s<1$![]() , $1< p<\frac {n}s$
, $1< p<\frac {n}s$![]() , see also [Reference Marano and Mosconi34]. However, both [Reference Brasco, Mosconi and Squassina3] and [Reference Marano and Mosconi34] use in a critical way the monotonicity and radial symmetry of the solutions in order to derive the asymptotic behaviour from the regularity of $u$
, see also [Reference Marano and Mosconi34]. However, both [Reference Brasco, Mosconi and Squassina3] and [Reference Marano and Mosconi34] use in a critical way the monotonicity and radial symmetry of the solutions in order to derive the asymptotic behaviour from the regularity of $u$![]() in the weak space $L^{r,\infty }$
in the weak space $L^{r,\infty }$![]() , where $r = \frac {n(p-1)}{n-sp}$
, where $r = \frac {n(p-1)}{n-sp}$![]() . As it is well-known, in the Euclidean setting one can use radially decreasing rearrangement or the moving plane method to establish monotonicity and radial symmetry of solutions to variational problems and partial differential equations. These tools are not available in Carnot groups and proving the relevant symmetries of similar problems remains a very challenging task.
. As it is well-known, in the Euclidean setting one can use radially decreasing rearrangement or the moving plane method to establish monotonicity and radial symmetry of solutions to variational problems and partial differential equations. These tools are not available in Carnot groups and proving the relevant symmetries of similar problems remains a very challenging task.
The result of theorem 1.2 does not rely on the symmetry of the solution, hence the method of proof is new even in the Euclidean setting. In order to obtain the optimal decay theorem 1.2 without relying on symmetry of the solution, we use a version of the local boundedness estimate given in theorem 1.1 and then obtain a new estimate of the tail term, which is particular for the fractional case.
In closing, we provide a brief description of the paper. In § 2 we introduce the geometric setting of the paper and the relevant definitions. We also prove proposition 2.1, a preparatory result which provides regularity in $L^p$![]() spaces for subsolutions of fractional Schrödinger equations. In § 3 we prove theorem 1.1. Finally, in § 4 we prove theorem 1.2.
spaces for subsolutions of fractional Schrödinger equations. In § 3 we prove theorem 1.1. Finally, in § 4 we prove theorem 1.2.
2. Homogeneous groups and fractional operators
This section is devoted to providing the necessary background and stating a preliminary result, proposition 2.1. Let $\mathbb {G}$![]() be a homogeneous group as defined in [Reference Folland and Stein11, Chapter 1]. In particular, $(\mathbb {G},\,\circ )$
be a homogeneous group as defined in [Reference Folland and Stein11, Chapter 1]. In particular, $(\mathbb {G},\,\circ )$![]() is a connected simply connected nilpotent Lie group. Furthermore, the exponential map $\exp :\mathfrak g\rightarrow \mathbb {G}$
is a connected simply connected nilpotent Lie group. Furthermore, the exponential map $\exp :\mathfrak g\rightarrow \mathbb {G}$![]() is a diffeomorphism of the Lie algebra $\mathfrak g$
is a diffeomorphism of the Lie algebra $\mathfrak g$![]() onto the group $\mathbb {G}$
onto the group $\mathbb {G}$![]() and $\mathfrak g$
and $\mathfrak g$![]() is endowed with a family of non-isotropic group dilations $\delta _\lambda$
is endowed with a family of non-isotropic group dilations $\delta _\lambda$![]() for $\lambda >0$
for $\lambda >0$![]() . Explicitly, there is a basis $X_j$
. Explicitly, there is a basis $X_j$![]() , $j=1,\,\dots,\,n$
, $j=1,\,\dots,\,n$![]() of the Lie algebra $\mathfrak g$
of the Lie algebra $\mathfrak g$![]() and positive real numbers $d_j$
and positive real numbers $d_j$![]() , such that,
, such that,
which, using the exponential map, define 1-parameter family of automorphisms of the group $\mathbb {G}$![]() given by $\exp \circ \delta _\lambda \circ \exp ^{-1}$
given by $\exp \circ \delta _\lambda \circ \exp ^{-1}$![]() . We will use the same notation $\delta _\lambda$
. We will use the same notation $\delta _\lambda$![]() for the group automorphisms. As customary, we indicate with
for the group automorphisms. As customary, we indicate with
the homogeneous dimension of $\mathbb {G}$![]() with respect to the nonisotropic dilations $\delta _\lambda$
with respect to the nonisotropic dilations $\delta _\lambda$![]() . We will denote with $\, {\rm d}{g}$
. We will denote with $\, {\rm d}{g}$![]() a fixed Haar measure given by the push forward of the Lebesgue measure on the Lie algebra via the exponential map, see [Reference Folland and Stein11, Proposition 1.2]. We note that this gives a bi-invariant Haar measure. Furthermore, the homogeneous dimension and the Haar measure are related by the identity $d(\delta _\lambda g)=t^Q\, {\rm d}g$
a fixed Haar measure given by the push forward of the Lebesgue measure on the Lie algebra via the exponential map, see [Reference Folland and Stein11, Proposition 1.2]. We note that this gives a bi-invariant Haar measure. Furthermore, the homogeneous dimension and the Haar measure are related by the identity $d(\delta _\lambda g)=t^Q\, {\rm d}g$![]() .
.
The polar coordinates formula for the Haar measure gives the existence of a unique Radon measure ${\rm d}\sigma (g)$![]() , such that, for $u\in L^1(\mathbb {G})$
, such that, for $u\in L^1(\mathbb {G})$![]() we have the identity, [Reference Folland and Stein11, Prop. (1.15)]:
we have the identity, [Reference Folland and Stein11, Prop. (1.15)]:
In particular, we have, see [Reference Fabes and Rivière8]:

where $\sigma _Q = Q \omega _Q$![]() , and $\omega _Q = \int _{B_1} {\rm d}g>0$
, and $\omega _Q = \int _{B_1} {\rm d}g>0$![]() .
.
2.1. The fractional operator
For $0< s<1$![]() consider the quadratic form:
consider the quadratic form:
Following [Reference Garofalo, Loiudice and Vassilev16], we let $\mathcal {D}^{s,2}(\mathbb {G})$![]() be the fractional Sobolev space defined as the closure of $C^\infty _0(\mathbb {G})$
be the fractional Sobolev space defined as the closure of $C^\infty _0(\mathbb {G})$![]() with respect to the case $p=2$
with respect to the case $p=2$![]() of the seminorm (1.14), i.e.
of the seminorm (1.14), i.e.

The infinitesimal generator of the quadratic form $\mathscr {Q}_s(u,\,\phi )$![]() is the nonlocal operator $\mathcal {L}_s$
is the nonlocal operator $\mathcal {L}_s$![]() defined in (1.15). By a weak solution of the equation $\mathcal {L}_s u =F$
defined in (1.15). By a weak solution of the equation $\mathcal {L}_s u =F$![]() we intend a function $u\in \mathcal {D}^{s,2}(\mathbb {G})$
we intend a function $u\in \mathcal {D}^{s,2}(\mathbb {G})$![]() such that for any $\phi \in C^\infty _0(\mathbb {G})$
such that for any $\phi \in C^\infty _0(\mathbb {G})$![]() one has:
one has:
Weak subsolutions are defined by requiring
for all non-negative test functions $\phi$![]() . As shown in [Reference Garofalo, Loiudice and Vassilev16, Theorem 1.1] this is equivalent to defining the fractional operator $\mathcal {L}_s u$
. As shown in [Reference Garofalo, Loiudice and Vassilev16, Theorem 1.1] this is equivalent to defining the fractional operator $\mathcal {L}_s u$![]() by formula (1.15). As we have underlined in § 1, besides the Euclidean case $\mathbb {G} = \mathbb {R}^n$
by formula (1.15). As we have underlined in § 1, besides the Euclidean case $\mathbb {G} = \mathbb {R}^n$![]() , in a Lie group of Heisenberg type, equipped with the Koranyi norm, definition (1.15) equals, up to a multiplicative constant, the fractional powers of the conformally invariant (or geometric) horizontal Laplacian defined by (1.3), see [Reference Frank, del Mar González, Monticelli and Tan12, Reference Roncal and Thangavelu37] and [Reference Garofalo and Tralli17].
, in a Lie group of Heisenberg type, equipped with the Koranyi norm, definition (1.15) equals, up to a multiplicative constant, the fractional powers of the conformally invariant (or geometric) horizontal Laplacian defined by (1.3), see [Reference Frank, del Mar González, Monticelli and Tan12, Reference Roncal and Thangavelu37] and [Reference Garofalo and Tralli17].
2.2. A preparatory result on Lebesgue space regularity
In the proof of theorem 1.1 we will need the following regularity in Lebesgue spaces involving the fractional operator (1.15). In its proof we adapt the arguments that in the local case were developed in [Reference Garofalo and Vassilev20, Lemma 10.2], [Reference Vassilev40, Theor. 4.1], and [Reference Vassilev41, Theor. 2.5], except that in the nonlocal case one has to use the Sobolev inequality (1.18), rather than the Folland–Stein embedding $\mathcal {D}^{1,2}(\mathbb {G}) \hookrightarrow L^{\frac {2Q}{Q-2}}(\mathbb {G})$![]() . As far as part (b) of proposition 2.1 is concerned, in addition to the cited references we also mention [Reference Garofalo and Lanconelli15, Sec. 4], where a similar result was proved for $L^2$
. As far as part (b) of proposition 2.1 is concerned, in addition to the cited references we also mention [Reference Garofalo and Lanconelli15, Sec. 4], where a similar result was proved for $L^2$![]() solutions, and [Reference Lanconelli and Uguzzoni32, Lemma 2.3], for a closely related result concerning the Yamabe equation on the Heisenberg group $\mathbb {H}^n$
solutions, and [Reference Lanconelli and Uguzzoni32, Lemma 2.3], for a closely related result concerning the Yamabe equation on the Heisenberg group $\mathbb {H}^n$![]() . In the local case in $\mathbb {R}^n$
. In the local case in $\mathbb {R}^n$![]() , a sharp Lorentz space result was obtained for solutions to equations modelled on Yamabe type equations, or more generally for the Euler–Lagrange equation related to the $L^p$
, a sharp Lorentz space result was obtained for solutions to equations modelled on Yamabe type equations, or more generally for the Euler–Lagrange equation related to the $L^p$![]() Sobolev inequality. This type of result originated with the work [Reference Jannelli and Solimini25], and was subsequently used to obtain the sharp $L^p$
Sobolev inequality. This type of result originated with the work [Reference Jannelli and Solimini25], and was subsequently used to obtain the sharp $L^p$![]() regularity and the asymptotic behaviour for solutions of such equations, see [Reference Vétois43, Lemma 2.2] and [Reference Brasco, Mosconi and Squassina3, Proposition 3.3]. These results were extended to Yamabe type equations in Carnot groups in [Reference Loiudice33, Theorem 11 and Proposition 3.2]. We mention that, since we work in the more general setting of a Schrödinger type equation, in proposition 2.1(b) we do not obtain a borderline $L^{r,\infty }(\mathbb {G})$
regularity and the asymptotic behaviour for solutions of such equations, see [Reference Vétois43, Lemma 2.2] and [Reference Brasco, Mosconi and Squassina3, Proposition 3.3]. These results were extended to Yamabe type equations in Carnot groups in [Reference Loiudice33, Theorem 11 and Proposition 3.2]. We mention that, since we work in the more general setting of a Schrödinger type equation, in proposition 2.1(b) we do not obtain a borderline $L^{r,\infty }(\mathbb {G})$![]() Lorentz regularity for the considered non-negative subsolutions, instead, we show that $u\in L^{q}(\mathbb {G})$
Lorentz regularity for the considered non-negative subsolutions, instead, we show that $u\in L^{q}(\mathbb {G})$![]() for $r=\frac {2^*(s)}{2}< q< \infty$
for $r=\frac {2^*(s)}{2}< q< \infty$![]() . For the statement of the next proposition, the reader should keep in mind definition (1.19) of the exponents $r$
. For the statement of the next proposition, the reader should keep in mind definition (1.19) of the exponents $r$![]() and $r'$
and $r'$![]() .
.
Proposition 2.1 Let $\mathbb {G}$![]() be a homogeneous group and suppose that $u\in \mathcal {D}^{s,2}(\mathbb {G})$
be a homogeneous group and suppose that $u\in \mathcal {D}^{s,2}(\mathbb {G})$![]() be a nonnegative subsolution to the nonlocal equation
be a nonnegative subsolution to the nonlocal equation
with $V\in L^{r'}(\mathbb {G})$![]() , i.e. for every $\phi \in C^\infty _0(\mathbb {G})$
, i.e. for every $\phi \in C^\infty _0(\mathbb {G})$![]() such that $\phi \ge 0$
such that $\phi \ge 0$![]() one has
one has
(a) We have $u\in L^q(\Omega )$
 for every $2^*(s)\ \leq \ q < \infty.$
for every $2^*(s)\ \leq \ q < \infty.$ Furthermore, for any $2^*(s)< q<\infty$
Furthermore, for any $2^*(s)< q<\infty$ there exist a constant $C_Q>0$
there exist a constant $C_Q>0$ , such that for all sufficiently large $M$
, such that for all sufficiently large $M$ for which
(2.7)\begin{equation} \left(\int_{\{|V|>M\}} V^{r'}{\rm d}g \right)^{1/r'}\leq \frac{1}{qC_Q}, \end{equation}one has
for which
(2.7)\begin{equation} \left(\int_{\{|V|>M\}} V^{r'}{\rm d}g \right)^{1/r'}\leq \frac{1}{qC_Q}, \end{equation}one has \[ \lVert u\rVert_{L^q(\mathbb{G})}\leq (qC_Q M)^{1/q}\lVert u\rVert_{\mathcal{D}^{s,2}(\mathbb{G})}. \]
\[ \lVert u\rVert_{L^q(\mathbb{G})}\leq (qC_Q M)^{1/q}\lVert u\rVert_{\mathcal{D}^{s,2}(\mathbb{G})}. \]
(b) In fact, it holds $u\in L^{q}(\mathbb {G})$
 for $r=\frac {2^*(s)}{2}< q< \infty$
for $r=\frac {2^*(s)}{2}< q< \infty$ .
.(c) If, in addition, $V\in L^{t_0}(\mathbb {G})$
 for some $t_0 > r'$
for some $t_0 > r'$ , then $u\in L^{q}(\mathbb {G})$
, then $u\in L^{q}(\mathbb {G})$ for $r=\frac {2^*(s)}{2}< q\leq \infty$
for $r=\frac {2^*(s)}{2}< q\leq \infty$ . In addition, the sup of $u$
. In addition, the sup of $u$ is estimated as follows:
\[ \lVert u\rVert_{L^\infty(\mathbb{G})} \ \leq\ C_Q \, \lVert V\rVert_{L^{t_0}(\mathbb{G})}^{\frac{t_0'r}{r-t_0'}} \, \lVert u\rVert_{L^{2^*(s)t_0'}(\mathbb{G})}, \]where $t_0'$
is estimated as follows:
\[ \lVert u\rVert_{L^\infty(\mathbb{G})} \ \leq\ C_Q \, \lVert V\rVert_{L^{t_0}(\mathbb{G})}^{\frac{t_0'r}{r-t_0'}} \, \lVert u\rVert_{L^{2^*(s)t_0'}(\mathbb{G})}, \]where $t_0'$
 is the Hölder conjugate to $t_0$
is the Hölder conjugate to $t_0$ and $C_Q$
and $C_Q$ is a constant depending on the homogeneous dimension.
is a constant depending on the homogeneous dimension.
Proof. We begin by recalling a few basic facts which are crucial for working with appropriate test functions in the weak formulation of the nonlocal equation (2.5). First, using Hölder's inequality and the definition of the homogeneous fractional Sobolev space $\mathcal {D}^{s,2}(\mathbb {G})$![]() , we can take $\phi \in \mathcal {D}^{s,2}(\mathbb {G})$
, we can take $\phi \in \mathcal {D}^{s,2}(\mathbb {G})$![]() in the weak formulation (2.6). For a globally Lipschitz function $F$
in the weak formulation (2.6). For a globally Lipschitz function $F$![]() defined on $\mathbb {R}$
defined on $\mathbb {R}$![]() and a function $u\in \mathcal {D}^{s,2}(\mathbb {G})$
and a function $u\in \mathcal {D}^{s,2}(\mathbb {G})$![]() we have from (2.3) the inequality
we have from (2.3) the inequality
hence $F\circ u\in \mathcal {D}^{s,2}(\mathbb {G})$![]() . Assuming, in addition, that $F$
. Assuming, in addition, that $F$![]() is of the form $F(t)=\int _0^t G'(\tau )^2 {\rm d}\tau$
is of the form $F(t)=\int _0^t G'(\tau )^2 {\rm d}\tau$![]() , then from Jensen's inequality we have for any nonnegative numbers $a\le b$
, then from Jensen's inequality we have for any nonnegative numbers $a\le b$![]() the inequality:
the inequality:

which gives
Applying the Sobolev inequality (1.18) to the function $G\circ u$![]() , and using (2.8), we find
, and using (2.8), we find

where in the last inequality we have used (2.6) with the choice $\phi = F\circ u$![]() as a test function.
as a test function.
For the proof of parts (a) and (c) see for example [Reference Garofalo and Vassilev20, Lemma 10.2] and [Reference Vassilev40, Theorem 4.1], but one has to use the fractional Sobolev inequality (1.18) rather than the Folland–Stein inequality. We give the proof of part (c) below taking into account also [Reference Brasco, Mosconi and Squassina3, Proposition 3.3] which dealt with the Euler–Lagrange equation of the fractional $p$![]() -Laplacian in the Euclidean setting.
-Laplacian in the Euclidean setting.
To prove (b) in proposition 2.1 we will show that for any $0<\alpha <1$![]() we have that $u\in L^{r(1+\alpha )}(\mathbb {G})$
we have that $u\in L^{r(1+\alpha )}(\mathbb {G})$![]() . From part (a) and the fact that $2^*(s)/2 < r(1+\alpha )<2r=2^*(s)$
. From part (a) and the fact that $2^*(s)/2 < r(1+\alpha )<2r=2^*(s)$![]() the claim of part (b) will be proven. The details are as follows. For $\varepsilon >0$
the claim of part (b) will be proven. The details are as follows. For $\varepsilon >0$![]() and $0<\alpha <1$
and $0<\alpha <1$![]() , consider the functions:
, consider the functions:
Notice that $F_\varepsilon$![]() is nondecreasing by definition. A simple calculation shows that
is nondecreasing by definition. A simple calculation shows that
where we have used that $\alpha <1$![]() . This shows in particular that $F'_\varepsilon (t) = G'_\varepsilon (t)^2 \le \varepsilon ^{\alpha -1}$
. This shows in particular that $F'_\varepsilon (t) = G'_\varepsilon (t)^2 \le \varepsilon ^{\alpha -1}$![]() , therefore $F_\varepsilon$
, therefore $F_\varepsilon$![]() is a globally Lipschitz function. We thus find from (2.9):
is a globally Lipschitz function. We thus find from (2.9):
In order to estimate the right-hand side in (2.11) we will use the following inequalities, which are valid for $u\ge 0$![]() :
:
The former is easily proved by noting that:
This estimate trivially gives $u F_\varepsilon (u) \le u \frac {(u+\varepsilon )^\alpha - \varepsilon ^\alpha }{\alpha }$![]() , and therefore from the definition of $G_\varepsilon$
, and therefore from the definition of $G_\varepsilon$![]() we see that the latter inequality in (2.12) does hold provided that
we see that the latter inequality in (2.12) does hold provided that
The latter inequality follows from the trivial inequality
valid for $x\geq 0$![]() and $0<\alpha <1$
and $0<\alpha <1$![]() .
.
Keeping in mind definition (1.19) of the exponents $r$![]() and $r'$
and $r'$![]() , using now in (2.11) the first inequality in (2.12) and Hölder inequality, we easily obtain for a fixed $\delta >0$
, using now in (2.11) the first inequality in (2.12) and Hölder inequality, we easily obtain for a fixed $\delta >0$![]() :
:

Next, we use the second of inequalities (2.12) to obtain the estimate:

By Lebesgue-dominated convergence one has $\int _{\{|V|\leq \delta \}}|V|^{r'}{\rm d}g\longrightarrow 0$![]() as $\delta \to 0^+$
as $\delta \to 0^+$![]() . Therefore, we can choose $\delta >0$
. Therefore, we can choose $\delta >0$![]() so small that
so small that

Combining (2.15) with (2.14) we can absorb in the left-hand side the second term in the right-hand side of (2.13), obtaining the inequality:

Notice that the hypothesis $V\in L^{r'}(\mathbb {G})$![]() and Chebyshev inequality imply that the distribution function of $V$
and Chebyshev inequality imply that the distribution function of $V$![]() satisfies for every $\delta >0$
satisfies for every $\delta >0$![]() :
:
Since $r(1+\alpha )<2r=2^*(s)$![]() , Hölder inequality thus gives
, Hölder inequality thus gives

or equivalently, recalling that $2r=2^*(s)$![]() :
:

Using (2.17), (2.18), and $r'/r=1/(1-r)$![]() in (2.16) we obtain:
in (2.16) we obtain:

Letting $\varepsilon$![]() go to 0, noting that $\lim _{\varepsilon \rightarrow 0}G_\varepsilon (u)=u^{(1+\alpha )/2}$
go to 0, noting that $\lim _{\varepsilon \rightarrow 0}G_\varepsilon (u)=u^{(1+\alpha )/2}$![]() gives:
gives:

which, taking into account also part (a), completes the proof of part (b) of proposition 2.1.
3. Proof of theorem 1.1
The proof consists of several steps detailed in the following sub-sections.
3.1. The localized fractional Sobolev inequality
The proof of theorem 1.1 will use the following version of a localized fractional Sobolev inequality. For an open set $\Omega \subset \mathbb {G}$![]() we denote by $\mathcal {D}^{s,2}(\Omega )$
we denote by $\mathcal {D}^{s,2}(\Omega )$![]() the completion of $C_0^\infty (\Omega )$
the completion of $C_0^\infty (\Omega )$![]() with respect to the norm:
with respect to the norm:

where $\tilde v$![]() denotes the extension of $v$
denotes the extension of $v$![]() to a function on $\mathbb {G}$
to a function on $\mathbb {G}$![]() , which is equal to zero outside of $\Omega$
, which is equal to zero outside of $\Omega$![]() .
.
Lemma 3.1 Let $0< s<1$![]() and $2s< Q$
and $2s< Q$![]() . There exists a constant $C=C(Q,\,s)>0$
. There exists a constant $C=C(Q,\,s)>0$![]() such that, for any ball $B_R$
such that, for any ball $B_R$![]() of radius $R$
of radius $R$![]() , $r< R$
, $r< R$![]() , and $v\in \mathcal {D}^{s,2}(B_R)$
, and $v\in \mathcal {D}^{s,2}(B_R)$![]() with $\mathrm {supp}\, v\subset B_{r }$
with $\mathrm {supp}\, v\subset B_{r }$![]() we have
we have

Proof. The proof is essentially contained in the Euclidean version [Reference Brasco and Parini4, Proposition 2.3]. We will use the trivial extension and then apply the fractional Sobolev inequality (1.18). Since $v$![]() has compact support in $B_R$
has compact support in $B_R$![]() its extension by zero on the complement of the ball is a function $\tilde v\in \mathcal {D}^{s,2}(\mathbb {G})$
its extension by zero on the complement of the ball is a function $\tilde v\in \mathcal {D}^{s,2}(\mathbb {G})$![]() . Furthermore, due to the assumption on the support of $v$
. Furthermore, due to the assumption on the support of $v$![]() , we have
, we have

In order to see the last of the above inequalities we used polar coordinates as in identity (2.2) to obtain the following inequalities, where $\sigma _Q$![]() is the area of the unit sphere:
is the area of the unit sphere:

since $|g^{-1}\cdot h|\geq |h|-r\geq |h|/2$![]() when $r< R$
when $r< R$![]() , $|g|< r$
, $|g|< r$![]() , and $|h|\geq 2R$
, and $|h|\geq 2R$![]() . Therefore, we have
. Therefore, we have

3.2. Caccioppoli inequality
We begin by stating the adaptation to our setting of the Caccioppoli inequality for the fractional $p$![]() -Laplacian in Euclidean space [Reference Brasco and Parini4]. For $\beta \geq 1$
-Laplacian in Euclidean space [Reference Brasco and Parini4]. For $\beta \geq 1$![]() and $\delta >0$
and $\delta >0$![]() define the following functions for $t\geq 0$
define the following functions for $t\geq 0$![]() :
:
For our goals, the precise value of $\delta$![]() is given in (3.9). Suppose $\Omega '\Subset \mathbb {G}$
is given in (3.9). Suppose $\Omega '\Subset \mathbb {G}$![]() and $\psi \in C ^\infty _0(\mathbb {G})$
and $\psi \in C ^\infty _0(\mathbb {G})$![]() is a positive function with supp$\, \psi \subset \Omega '$
is a positive function with supp$\, \psi \subset \Omega '$![]() . Let $u$
. Let $u$![]() be a weak nonnegative subsolution to the equation $\mathcal {L}_s u =F$
be a weak nonnegative subsolution to the equation $\mathcal {L}_s u =F$![]() with $F\in L^{(2^*(s))'}$
with $F\in L^{(2^*(s))'}$![]() . Then, we have for some constant $C=C(Q)$
. Then, we have for some constant $C=C(Q)$![]() , which is independent of $\Omega '$
, which is independent of $\Omega '$![]() , the inequality:
, the inequality:

The proof of the above formula follows from the proof of the localized Caccioppoli inequality [Reference Brasco and Parini4, Proposition 3.5] after letting $p=2$![]() , replacing the ambient space with the considered homogeneous group and using its homogeneous dimension instead of the Euclidean dimension.
, replacing the ambient space with the considered homogeneous group and using its homogeneous dimension instead of the Euclidean dimension.
We now fix $g_0\in \mathbb {G}$![]() , and for $0< r< R$
, and for $0< r< R$![]() , we take a nonnegative smooth bump function $\psi \in C ^\infty _0(\mathbb {G})$
, we take a nonnegative smooth bump function $\psi \in C ^\infty _0(\mathbb {G})$![]() such that
such that
In order to achieve (3.5) we take a cut-off function $\psi (g)=\eta (|g_0^{-1}\cdot g|)$![]() , where $\eta$
, where $\eta$![]() is a smooth bump function on the real line, such that, $\eta (t)\equiv 1$
is a smooth bump function on the real line, such that, $\eta (t)\equiv 1$![]() on $|t|\leq r$
on $|t|\leq r$![]() , $\eta \equiv 0$
, $\eta \equiv 0$![]() on $t\geq (R+r)/2$
on $t\geq (R+r)/2$![]() and for some constant $K>0$
and for some constant $K>0$![]() we have $|\eta '(t)|\leq K/(R-r)$
we have $|\eta '(t)|\leq K/(R-r)$![]() for all $t$
for all $t$![]() . Hence, for any $\rho _1,\, \rho _2\in \mathbb {R}$
. Hence, for any $\rho _1,\, \rho _2\in \mathbb {R}$![]() we have
we have
Furthermore, if we let $\rho (g)=| g^{-1}\cdot g_o|$![]() , then from the triangle inequality (1.13) it follows that $\rho$
, then from the triangle inequality (1.13) it follows that $\rho$![]() is a Lipschitz continuous function with respect to the gauge distance, with Lipschitz constant equal to 1:
is a Lipschitz continuous function with respect to the gauge distance, with Lipschitz constant equal to 1:
Therefore, for $g_j\in \mathbb {G}$![]() and $\rho _j=\rho (g_j)$
and $\rho _j=\rho (g_j)$![]() , $j=1,\,2$
, $j=1,\,2$![]() , we have
, we have
For the remainder of the proof, for any $r>0$![]() we will denote by $B_r$
we will denote by $B_r$![]() the ball $B_r(g_0)$
the ball $B_r(g_0)$![]() with the understanding that the centre is the fixed point $g_0$
with the understanding that the centre is the fixed point $g_0$![]() .
.
If $u$![]() is a nonnegative weak subsolution to
is a nonnegative weak subsolution to
then, with the above choice of $\psi$![]() and $F=Vu$
and $F=Vu$![]() , (3.4) implies the following inequality:
, (3.4) implies the following inequality:

where $u_\delta =u+\delta$![]() and $T(u;g_0,\,R)$
and $T(u;g_0,\,R)$![]() is the tail (1.23). The proof of (3.6) is contained in [Reference Brasco and Parini4, Theorem 3.8 and (3.29)], except that we have to use the Lipschitz bound in (3.5) for the term $|\psi (g)-\psi (h)|^2$
is the tail (1.23). The proof of (3.6) is contained in [Reference Brasco and Parini4, Theorem 3.8 and (3.29)], except that we have to use the Lipschitz bound in (3.5) for the term $|\psi (g)-\psi (h)|^2$![]() in (3.4).
in (3.4).
Next, we apply to inequality (3.6) the localized Sobolev inequality (3.1), with $r$![]() replaced with $(R+r)/2$
replaced with $(R+r)/2$![]() and $v$
and $v$![]() with $\psi \,u_\delta ^{(\beta +1)/2}$
with $\psi \,u_\delta ^{(\beta +1)/2}$![]() , taking into account
, taking into account
and also that by the choice of $\psi$![]() we have $\mathrm {supp}\, (\psi \,u_\delta ^{(\beta +1)/2})\Subset B_{(R+r)/2}\Subset B_R$
we have $\mathrm {supp}\, (\psi \,u_\delta ^{(\beta +1)/2})\Subset B_{(R+r)/2}\Subset B_R$![]() . As a result, we obtain:
. As a result, we obtain:

3.3. Use the assumptions on $V$
This is the core of the new argument leading to our result. By Hölder's inequality and $\mathrm {supp} \,\psi \Subset B_{(R+r)/2}$![]() , we have
, we have

where
so that
which is possible due to the assumptions in theorem 1.1. Next, we use Young's inequality $ab\leq \varepsilon \frac {a^{\kappa '}}{\kappa '}+\frac {1}{\varepsilon ^{\kappa -1}}\frac {b^\kappa }\kappa$![]() in the right-hand side of the above inequality to conclude:
in the right-hand side of the above inequality to conclude:

Hence, taking into account $\kappa '/t=2/2^*(s)$![]() , $\kappa /t_0=\frac {2s}{2st_0-Q}$
, $\kappa /t_0=\frac {2s}{2st_0-Q}$![]() and the above inequality together with the properties of $\psi$
and the above inequality together with the properties of $\psi$![]() , we obtain from (3.7) the following inequality:
, we obtain from (3.7) the following inequality:

Choosing $\varepsilon$![]() such that $\frac {C\varepsilon \beta }{\kappa '}=\frac 12$
such that $\frac {C\varepsilon \beta }{\kappa '}=\frac 12$![]() , we absorb the first term on the right-hand side in the left-hand side, and then reduce the domain of integration, taking into account that $\psi \equiv 1$
, we absorb the first term on the right-hand side in the left-hand side, and then reduce the domain of integration, taking into account that $\psi \equiv 1$![]() on $B_r$
on $B_r$![]() , which brings us to the following inequality:
, which brings us to the following inequality:

Since $u_\delta ^\beta \leq u_\delta ^{\beta +1}/\delta$![]() , the above inequality allows us to conclude:
, the above inequality allows us to conclude:

We recall that in the latter inequality we have radii $0< r< R$![]() and all balls are centred at the fixed point $g_0$
and all balls are centred at the fixed point $g_0$![]() . Suppose, in addition, that $2R_0= {|g_0|}$
. Suppose, in addition, that $2R_0= {|g_0|}$![]() and $0< R\leq R_0$
and $0< R\leq R_0$![]() . Then, we have
. Then, we have
taking into account the triangle inequality (1.13). Therefore, for $R_0\geq 2\bar R_0$![]() the decay assumption of $V$
the decay assumption of $V$![]() , cf. theorem 1.1(ii), and the above inclusions imply that for some constant $C= C(Q,\,s,\, K_0)$
, cf. theorem 1.1(ii), and the above inclusions imply that for some constant $C= C(Q,\,s,\, K_0)$![]() we have the bound
we have the bound

after using $0< R\leq R_0$![]() for the last inequality. Therefore, also observing that $R/(R-r)>1$
for the last inequality. Therefore, also observing that $R/(R-r)>1$![]() , we have proven that there exists a constant $C= C(Q,\,s,\, K_0)$
, we have proven that there exists a constant $C= C(Q,\,s,\, K_0)$![]() , such that for any $\beta \geq 1$
, such that for any $\beta \geq 1$![]() , $g_0$
, $g_0$![]() such that $R_0=\frac {|g_0|}{2}\geq \bar R_0$
such that $R_0=\frac {|g_0|}{2}\geq \bar R_0$![]() , and radii $0< r< R\leq R_0$
, and radii $0< r< R\leq R_0$![]() we have
we have

3.4. Moser's iteration
By proposition 2.1(c) we have that $u\in L^{q}(\mathbb {G})\cap L^\infty (\mathbb {G})$![]() for any $q\geq 2^*(s)/2$
for any $q\geq 2^*(s)/2$![]() , hence $u\in L^{q_0}_{loc}(\mathbb {G})$
, hence $u\in L^{q_0}_{loc}(\mathbb {G})$![]() for $q_0\geq 2$
for $q_0\geq 2$![]() . In fact, for the proof of the theorem we can assume $q_0=2$
. In fact, for the proof of the theorem we can assume $q_0=2$![]() , but the argument is valid for any $q_0\geq 2$
, but the argument is valid for any $q_0\geq 2$![]() . We also let $\beta =q_0 -1$
. We also let $\beta =q_0 -1$![]() .
.
Recalling that the exponent $r=2^*(s)/2=Q/(Q-2s)>1$![]() , see (1.19), we define the sequence
, see (1.19), we define the sequence
From (3.8) we have with $B_{r_{j}}=B(g,\,r_j)$![]() , $r_j=\frac {R}{2}(1+2^{-j})$
, $r_j=\frac {R}{2}(1+2^{-j})$![]() , $j=0,\,1,\,2,\,\dots$
, $j=0,\,1,\,2,\,\dots$![]() the inequality:
the inequality:

The definition of the tail (1.23) gives for a fixed $R\ge \bar R_0$![]() and $R/2\le r_j< R$
and $R/2\le r_j< R$![]() the inequality:
the inequality:
while a simple estimate shows

Hence, letting

we have with some constants $C_0$![]() and $C_1$
and $C_1$![]() depending on $Q$
depending on $Q$![]() and $s$
and $s$![]() the inequality:
the inequality:
Therefore, for
we have $T=2$![]() and we obtain the inequality:
and we obtain the inequality:
Therefore, recalling that $q_{j+1}=r^{j} q_0$![]() , we obtain
, we obtain

From the definitions of the exponents $r$![]() and its Hölder conjugate $r'=Q/(2s)$
and its Hölder conjugate $r'=Q/(2s)$![]() we have
we have

and

Thus, we find:

If we let $q_0=2$![]() and take into account the definition of $\delta$
and take into account the definition of $\delta$![]() we have shown that there is a constant $C_0$
we have shown that there is a constant $C_0$![]() , depending on $Q$
, depending on $Q$![]() and $s$
and $s$![]() , such that the inequality
, such that the inequality

holds for any $g_0\in \mathbb {G}$![]() with $|g_0|=2R_0\geq 2\bar R_0$
with $|g_0|=2R_0\geq 2\bar R_0$![]() and $0< R\leq R_0$
and $0< R\leq R_0$![]() , where $\bar R_0$
, where $\bar R_0$![]() is the radius in the assumptions of theorem 1.1.
is the radius in the assumptions of theorem 1.1.
3.5. Lowering the exponent
To lower the exponent in the average integral in the above inequality we follow the standard argument, see for example [Reference Giusti22, p. 223, Theorem 7.3], except that we need to account for the tail term similarly to [Reference Kuusi, Mingione and Sire31, Corollary 2.1]. In view of the eventual use of the sought estimate in obtaining the asymptotic behaviour of the solution, it is also important to keep the constant in the inequality independent of $R$![]() as in (3.10). For any $\rho >0$
as in (3.10). For any $\rho >0$![]() , let:
, let:
First, we will show the following slight modification of (3.10). There is a constant $C_1$![]() , depending on $Q$
, depending on $Q$![]() and $s$
and $s$![]() , such that, for all $g_0\in \mathbb {G}$
, such that, for all $g_0\in \mathbb {G}$![]() with $|g_0|=2R_0\geq 4\bar R_0$
with $|g_0|=2R_0\geq 4\bar R_0$![]() and $0< r< R\leq R_0$
and $0< r< R\leq R_0$![]() we have
we have

Letting $\tau =r/R$![]() , $0<\tau <1$
, $0<\tau <1$![]() , the above inequality is equivalent to showing, with the same constant $C_1$
, the above inequality is equivalent to showing, with the same constant $C_1$![]() , that we have
, that we have

We turn to the proof of (3.12). Let $g_1\in B(g_0,\,\tau R)$![]() and $\rho$
and $\rho$![]() be sufficiently small, in fact,
be sufficiently small, in fact,
so that,
Notice that by the triangle inequality we have $|g_1|\geq 2\bar R_0$![]() , which follows from $|g_0|=2R_0\geq 4\bar R_0$
, which follows from $|g_0|=2R_0\geq 4\bar R_0$![]() , cf. the line above (3.11), hence we can apply (3.10) to the ball $B(g_1,\,\rho )$
, cf. the line above (3.11), hence we can apply (3.10) to the ball $B(g_1,\,\rho )$![]() , which gives
, which gives

taking into account that by the definition of $\rho$![]() we have $R/\rho =\frac {4}{1-\tau }$
we have $R/\rho =\frac {4}{1-\tau }$![]() . We will estimate the tail term in the last line by using the tail term centred at $g_0$
. We will estimate the tail term in the last line by using the tail term centred at $g_0$![]() and radius $R$
and radius $R$![]() , and the average of $u$
, and the average of $u$![]() over the ball $B(g_0,\,R)$
over the ball $B(g_0,\,R)$![]() . For this we split the domain of integration of the integral in the formula for the tail,
. For this we split the domain of integration of the integral in the formula for the tail,
in two disjoint sets
The integral over the second of the above sets is estimated by using $h\notin B(g_1,\,\rho )$![]() , followed by Hölder's inequality, to obtain
, followed by Hölder's inequality, to obtain

where $\omega _Q$![]() is the volume of the unit gauge ball.
is the volume of the unit gauge ball.
In order to estimate the integral in the tail over $\mathbb {G}\setminus B(g_0,\,R)$![]() , we use the triangle inequality, $h\notin B(g_1,\,\rho )$
, we use the triangle inequality, $h\notin B(g_1,\,\rho )$![]() and $g_1\in B(g_0,\,\tau R)$
and $g_1\in B(g_0,\,\tau R)$![]() , which give
, which give
Hence, we have

Inequalities (3.13)–(3.15) give

since $0<1-\tau <1$![]() . The proof of (3.11) is complete.
. The proof of (3.11) is complete.
Let us note that for $r$![]() and $R$
and $R$![]() as in (3.11) satisfying, in addition, $R_0/2\leq r< R\leq R_0$
as in (3.11) satisfying, in addition, $R_0/2\leq r< R\leq R_0$![]() we have ${R}/{(R-r)}\leq 2$
we have ${R}/{(R-r)}\leq 2$![]() and
and
Therefore, inequality (3.11) implies that for all $g_0\in \mathbb {G}$![]() with $|g_0|=2R_0\geq 4\bar R_0$
with $|g_0|=2R_0\geq 4\bar R_0$![]() and $R_0/2\leq r< R\leq R_0$
and $R_0/2\leq r< R\leq R_0$![]() we have
we have

Inequality (3.17) implies, using $ab\leq \frac 12(a^2+b^2)$![]() and $R-r< R$
and $R-r< R$![]() , the inequality
, the inequality
where
Therefore, by a standard iteration argument, see for example [Reference Giusti22, p. 191, Lemma 6.1], there exists a constant $c_Q$![]() so that $M_r\leq c_Q[ {A}{(R-r)^{-Q}}+B]$
so that $M_r\leq c_Q[ {A}{(R-r)^{-Q}}+B]$![]() . Hence, for any $R_0\ge 2\bar R_0$
. Hence, for any $R_0\ge 2\bar R_0$![]() , and $g_0\in \mathbb {G}$
, and $g_0\in \mathbb {G}$![]() with $|g_0|=2R_0$
with $|g_0|=2R_0$![]() , we have
, we have

This completes the proof of theorem 1.1.
4. Proof of theorem 1.2
Recall that here we are considering a nonnegative subsolution $u$![]() to the Yamabe type equation $\mathcal {L}_s u=u^{2^*(s)-1}.$
to the Yamabe type equation $\mathcal {L}_s u=u^{2^*(s)-1}.$![]()
4.1. The optimal Lorentz space regularity
The first step is to obtain the optimal Lorentz space regularity of $u$![]() . For this we can adapt to the current setting [Reference Brasco, Mosconi and Squassina3, Propositions 3.2 and 3.3], which gives
. For this we can adapt to the current setting [Reference Brasco, Mosconi and Squassina3, Propositions 3.2 and 3.3], which gives
recalling that $r= {2^*(s)}/{2}$![]() , cf. (1.19). Notice that in the cited results from [Reference Brasco, Mosconi and Squassina3], valid in the Euclidean setting, the authors do not assume that the solution is radial, but the radial symmetry is used ultimately to obtain the rate of decay of the solution of the fractional Yamabe equation.
, cf. (1.19). Notice that in the cited results from [Reference Brasco, Mosconi and Squassina3], valid in the Euclidean setting, the authors do not assume that the solution is radial, but the radial symmetry is used ultimately to obtain the rate of decay of the solution of the fractional Yamabe equation.
For the sake of completeness and self-containment of the proof, in the setting of a homogeneous group, and right-hand side of the equation modelled on the fractional Yamabe equation, we include a proof of the sharp Lebesgue space regularity (4.1), relying on proposition 2.1. First, proposition 2.1 implies that $u\in L^{q}(\mathbb {G})\cap L^\infty (\mathbb {G})$![]() , for any $q>r=2^*(s)/2$
, for any $q>r=2^*(s)/2$![]() . Indeed, if $V=u^{2^*(s)-2}$
. Indeed, if $V=u^{2^*(s)-2}$![]() then since $u\in L^{2^*(s)}(\mathbb {G})$
then since $u\in L^{2^*(s)}(\mathbb {G})$![]() it follows that $V\in L^{r'}(\mathbb {G})$
it follows that $V\in L^{r'}(\mathbb {G})$![]() . Hence, by proposition 2.1(b) it follows $u\in L^{q}(\mathbb {G})$
. Hence, by proposition 2.1(b) it follows $u\in L^{q}(\mathbb {G})$![]() for all $q$
for all $q$![]() such that $\frac {2^*(s)}{2}< q<\infty$
such that $\frac {2^*(s)}{2}< q<\infty$![]() . Hence, part (c) gives that we also have $u\in L^{\infty }(\mathbb {G})$
. Hence, part (c) gives that we also have $u\in L^{\infty }(\mathbb {G})$![]() . Finally, we can see that $u \in L^{2^*(s)/2,\infty }(\mathbb {G})$
. Finally, we can see that $u \in L^{2^*(s)/2,\infty }(\mathbb {G})$![]() as follows. Take $F_t(u)=\min \{u,\,t\}$
as follows. Take $F_t(u)=\min \{u,\,t\}$![]() . Using the equation and the fractional Sobolev inequality we have
. Using the equation and the fractional Sobolev inequality we have
where $V=u^{2^*(s)-2}$![]() . Using first that $F_t(u)\leq t$
. Using first that $F_t(u)\leq t$![]() and then the definition of $V$
and then the definition of $V$![]() we have
we have
since $u^{2^*(s)-1}\in L^1(\mathbb {G})$![]() noting that $2^*(s)-1>2^*(s)/2$
noting that $2^*(s)-1>2^*(s)/2$![]() . Let $\mu (t)$
. Let $\mu (t)$![]() be the distribution function of $u$
be the distribution function of $u$![]() . From the definition of $F_t$
. From the definition of $F_t$![]() we have trivially:
we have trivially:
Therefore, bounding from above the left-hand side of the above inequality using (4.2) and then using (4.3) we have

which shows that $u \in L^{2^*(s)/2,\infty }(\mathbb {G})$![]() .
.
4.2. Asymptotic behaviour of the tail term
We shall reduce the problem to a question of $L^p$![]() regularity of certain truncated powers of the homogeneous norm, which we define next. For $R>0$
regularity of certain truncated powers of the homogeneous norm, which we define next. For $R>0$![]() and $\alpha >0$
and $\alpha >0$![]() , let:
, let:
Lemma 4.1 For $Q/p<\alpha$![]() the Lorentz norms of $\rho _{\alpha,R}$
the Lorentz norms of $\rho _{\alpha,R}$![]() are given by the following formulas:
are given by the following formulas:

Proof. Let $\mu (s)=\left \vert \left \{ g\mid \rho _{\alpha,R}(g)>s \right \}\right \vert$![]() be the distribution function of $\rho _{\alpha,R}$
be the distribution function of $\rho _{\alpha,R}$![]() . From the representation of the Haar measure in polar coordinates (2.2), we have
. From the representation of the Haar measure in polar coordinates (2.2), we have

The corresponding radially decreasing rearrangement is

since $s=\rho ^*(t)$![]() is determined from $\sigma _Q/Q (s^{-Q/\alpha }-R^Q )=t>0$
is determined from $\sigma _Q/Q (s^{-Q/\alpha }-R^Q )=t>0$![]() . A small calculation shows then that for some constant $C_{Q,\sigma }$
. A small calculation shows then that for some constant $C_{Q,\sigma }$![]() we have (4.5).
we have (4.5).
Next, we use the optimal Lorentz space estimate and lemma 4.1 to bound the tail.
Lemma 4.2 With the standing assumption, i.e. $u\in \mathcal {D}^{s,2}(\mathbb {G})$![]() is a nonnegative subsolution to the Yamabe type equation (1.24), we have that the tail has the following decay:
is a nonnegative subsolution to the Yamabe type equation (1.24), we have that the tail has the following decay:
with $C$![]() a constant depending on the homogeneous dimension $Q$
a constant depending on the homogeneous dimension $Q$![]() .
.
Proof. By Hölder's inequality we have
recalling the definition of $r$![]() in (1.19) and using the weak $L^{r,\infty }$
in (1.19) and using the weak $L^{r,\infty }$![]() regularity of $u$
regularity of $u$![]() that we already proved. Hence, the claim of the lemma follows by lemma 4.1 which shows that for some constant $C=C(Q)$
that we already proved. Hence, the claim of the lemma follows by lemma 4.1 which shows that for some constant $C=C(Q)$![]() we have
we have
As a consequence, taking into account that $r'=Q/(2s)$![]() we obtain (4.7).
we obtain (4.7).
4.3. The slow decay
The proof of theorem 1.2 will also use a preliminary ‘slow’ decay of the solution $u$![]() , see [Reference Zhang44, Lemma 2.1] for case of the Yamabe equation on a Riemannian manifold with maximal volume growth.
, see [Reference Zhang44, Lemma 2.1] for case of the Yamabe equation on a Riemannian manifold with maximal volume growth.
Lemma 4.3 If $u\in \mathcal {D}^{s,2}(\mathbb {G})$![]() is a nonnegative subsolution to the Yamabe type equation, then $u$
is a nonnegative subsolution to the Yamabe type equation, then $u$![]() has the slow decay $|g|^{({Q-2s})/2}u\in L^\infty (\mathbb {G})$
has the slow decay $|g|^{({Q-2s})/2}u\in L^\infty (\mathbb {G})$![]() .
.
Proof. The key to this decay is the scale invariance of the equation, i.e. the fact that
is also a subsolution to the Yamabe type equation and the scale invariance of the $\mathcal {D}^{s,2}(\mathbb {G})$![]() and the $L^{2^*(s)}(\mathbb {G})$
and the $L^{2^*(s)}(\mathbb {G})$![]() norms. In order to show the slow decay, it is then enough to show that there exist constants $\lambda _o$
norms. In order to show the slow decay, it is then enough to show that there exist constants $\lambda _o$![]() and $C$
and $C$![]() , depending only on $Q$
, depending only on $Q$![]() and $s$
and $s$![]() , and the invariant under the scaling norms, such that for all $g_0$
, and the invariant under the scaling norms, such that for all $g_0$![]() with $\lambda =|g_0|/2>\lambda _0$
with $\lambda =|g_0|/2>\lambda _0$![]() we have on the ball $B(h_0,\,1)$
we have on the ball $B(h_0,\,1)$![]() with $h_0= \delta _{\lambda ^{-1}}g_0$
with $h_0= \delta _{\lambda ^{-1}}g_0$![]() , the estimate:
, the estimate:
Indeed, (4.8) implies:

which gives the desired decay. Bound (4.8) will be seen from the local version of proposition 2.1(c) in the case $V=u_\lambda ^{2^*(s)-2}$![]() by showing that the local supremum bound is independent of $\lambda$
by showing that the local supremum bound is independent of $\lambda$![]() . To simplify the notation let $v=u_\lambda$
. To simplify the notation let $v=u_\lambda$![]() . We follow the argument in the proof of theorem 1.1 with $V=v^{2^*(s)-2}$
. We follow the argument in the proof of theorem 1.1 with $V=v^{2^*(s)-2}$![]() . Furthermore, for $\frac 12< r< R<\frac 32$
. Furthermore, for $\frac 12< r< R<\frac 32$![]() we take a bump function $\psi$
we take a bump function $\psi$![]() , so that,
, so that,
where here and for the remainder of the proof, for any $r>0$![]() we will denote by $B_r$
we will denote by $B_r$![]() the ball $B(h_0,\,r)$
the ball $B(h_0,\,r)$![]() with the understanding that the centre is $h_0$
with the understanding that the centre is $h_0$![]() .
.
In particular, we have (3.7) with $u_\delta$![]() replaced by $v_\delta$
replaced by $v_\delta$![]() , but now we can absorb the first term on the right-hand side in the left-hand side for all sufficiently large $\lambda$
, but now we can absorb the first term on the right-hand side in the left-hand side for all sufficiently large $\lambda$![]() . Indeed, applying Hölder's inequality we have
. Indeed, applying Hölder's inequality we have

Since $V=v^{2^*(s)-2}$![]() the first term can be estimated as follows:
the first term can be estimated as follows:

using the scaling property of the $L^{2^*(s)}$![]() norm and $u\in L^{2^*(s)}(\mathbb {G})$
norm and $u\in L^{2^*(s)}(\mathbb {G})$![]() . Therefore, we have the analogue of (3.8), i.e. for all $\lambda \ge \lambda _0$
. Therefore, we have the analogue of (3.8), i.e. for all $\lambda \ge \lambda _0$![]() there exists a constant $C= C(Q,\,s,\, K_0)$
there exists a constant $C= C(Q,\,s,\, K_0)$![]() , such that, the following inequality holds true:
, such that, the following inequality holds true:

A Moser type iteration argument shows then the existence of a constant $C$![]() such that for all $\lambda \ge R_0$
such that for all $\lambda \ge R_0$![]() , $h_0= \delta _{\lambda ^{-1}}g_0$
, $h_0= \delta _{\lambda ^{-1}}g_0$![]() and $|g|=2\lambda$
and $|g|=2\lambda$![]() we have the inequality
we have the inequality

after using the fractional Sobolev inequality, Hölder's inequality, (4.5), and the invariance under scalings of the $\mathcal {D}^{s,2}(\mathbb {G})$![]() and $L^{2^*(s)}(\mathbb {G})$
and $L^{2^*(s)}(\mathbb {G})$![]() norms.
norms.
4.4. Conclusion of the proof of theorem 1.2
We begin by noting that, from what we have already proved, theorem 1.1 can be applied to the potential $V=u^{2^*(s)-2}$![]() . Indeed, the slow decay of $u$
. Indeed, the slow decay of $u$![]() , cf. lemma 4.3, gives that for some constant $C$
, cf. lemma 4.3, gives that for some constant $C$![]() we have
we have
which together with (2.2) implies the needed assumptions on $V$![]() , in particular, for $t_0>r'= {Q}/{(2s)}$
, in particular, for $t_0>r'= {Q}/{(2s)}$![]() , cf. (1.19), we have
, cf. (1.19), we have

Therefore, theorem 1.1 gives that for all $g\in \mathbb {G}$![]() and $2R=|g|$
and $2R=|g|$![]() sufficiently large we have (1.22), i.e. there exists a constant $C$
sufficiently large we have (1.22), i.e. there exists a constant $C$![]() independent of $g$
independent of $g$![]() , such that
, such that
Furthermore, the weak $L^{2^*(s)/2}$![]() regularity (4.1) shows that for $r=2^*(s)/2$
regularity (4.1) shows that for $r=2^*(s)/2$![]() we have the inequality
we have the inequality
taking into account that for $1\leq p<\infty$![]() the $L^{p,1}(\mathbb {G})$
the $L^{p,1}(\mathbb {G})$![]() norm of the characteristic function of the gauge ball $B_R$
norm of the characteristic function of the gauge ball $B_R$![]() is $p|B_R|^{1/p}$
is $p|B_R|^{1/p}$![]() .
.
Now we are ready to conclude the proof of theorem 1.2 since by (4.12), (4.13), and lemma 4.2 we can claim the following estimate for all sufficiently large $2R=|g|$![]() ,
,
with a constant $C$![]() independent of $g$
independent of $g$![]() .
.
Acknowledgements
N. Garofalo is supported in part by a Progetto SID (Investimento Strategico di Dipartimento): ‘Aspects of nonlocal operators via fine properties of heat kernels’, University of Padova (2022); and by a PRIN (Progetto di Ricerca di Rilevante Interesse Nazionale) (2022): ‘Variational and analytical aspects of geometric PDEs’. He is also partially supported by a Visiting Professorship at the Arizona State University. A. Loiudice acknowledges the support of the Gruppo Nazionale per l'Analisi Matematica, la Probabilità e le loro Applicazioni (GNAMPA) of the Istituto Nazionale di Alta Matematica (INdAM); she is also supported by the National Centre on HPC, Big Data and Quantum Computing, MUR: CN00000013- CUP: H93C22000450007. D. Vassilev was partially supported by the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy, under Award Number DE-AR0001202. The views and opinions of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof.