Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-12-01T04:31:43.134Z Has data issue: false hasContentIssue false
  • English
  • Français

Elliptic transmutation I

Published online by Cambridge University Press:  14 November 2011

Robert Carroll
Robert Carroll
Affiliation:
University of Illinois at Champaign-Urbana, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Synopsis

Given 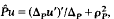and similar 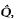, modelled on radial Laplace-Beltrami operators (ρp = 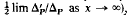, in this paper we begin the study of transmutations 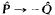which leads to elliptic equations 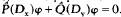Working with 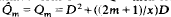and transmutations Qm → −D2 for m > −½ and −D2 → for m < −½, we obtain a transmutation formulation and derivation of many results of generalized axially symmetric potential theory in the first case and in both cases generalized Hilbert transforms (different). Canonical generalizations are then automatic using general transmutation theory.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 91 , Issue 3-4 , 1982 , pp. 315 - 334
Copyright
Copyright © Royal Society of Edinburgh 1982

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Askey, R. and Fitch, J.. Integral representations for Jacobi polynomials and some applications. J.Math. Anal. Appl. 26 (1969), 411–437.CrossRefGoogle Scholar
2Bateman, H.. Tables of integral transforms, Vol. 1 (New York: McGraw-Hill, 1954).Google Scholar
3Beltrami, E. and Wohlers, M.. Distributions and the boundary values of analytic functions (New York: Academic Press, 1966).Google Scholar
4Bers, L. and Gelbart, A.. On a class of differential equations in mechanics of continua. Quart. Appl. Math. 1 (1943), 168–188.CrossRefGoogle Scholar
5Braaksma, B. L. J.. A singular Cauchy problem and generalized translations, Int. Conf. Diff. Eqns., pp. 40–52 (New York: Academic Press, 1975).Google Scholar
6Braaksma, B. L. J. and deSnoo, H. S. V.. Generalized translation operators associated with a singular differential operator. Ordinary and partial differential equations. Dundee Conf. Lecture Notes in Mathematics 415, pp. 62–77 (Berlin: Springer, 1974).Google Scholar
7Bremerman, H.. Distributions, complex variables, and Fourier transforms (Reading Mass: Addison-Wesley, 1965).Google Scholar
8Bryčkov, Yu. and Prudnikov, A.. Integral transforms of generalized functions (Moscow: Izd. Nauka, 1977).Google Scholar
9Carmichael, R.. Cauchy integral representations of the analytic functions having ℑ′ boundary values. J. E. Mitchell Sci. Soc. 92 (1976), 87–97.Google Scholar
10Carroll, R.. Transmutation and operator differential equations. Notas de Matematica 67 (North-Holland, Amsterdam: 1979).Google Scholar
11Carroll, R.. Transmutation, generalized translation, and transform theory, I and II. Osaka J. Math., to appear.Google Scholar
12Carroll, R.. Remarks on the Gelfand-Levitan and Marčenko equations. Applicable Anal. 12 (1981), 153–157.CrossRefGoogle Scholar
13Carroll, R.. The Gelfand–Levitan and Marčenko equations via transmutation. Rocky Mountain J Math., to appear.Google Scholar
14Carroll, R.. Some remarks on the generalized Gelfand–Levitan equation. J. Math. Anal. Appl., to appear.Google Scholar
15Carroll, R.. Some remarks on singular pseudodifferential operators. Comm. Partial Differential Equations 6 (1981), 1407–1427.CrossRefGoogle Scholar
16Carroll, R.. Some inversion theorems of Fourier type. Rev. Roumaine Math. Pures Appl. to appear.Google Scholar
17Carroll, R.. Some remarks on transmutations. Applicable Anal. 9 (1979), 291–294.CrossRefGoogle Scholar
18Carroll, R.. Transmutation and separation of variables. Applicable Anal. 8 (1979), 253–263.CrossRefGoogle Scholar
19Carroll, R. and Gilbert, J.. Some remarks on transmutations, scattering theory, and special functions. Math. Annalen 258 (1981), 39–54.CrossRefGoogle Scholar
20Carroll, R. and Gilbert, J.. Scattering techniques in transmutation and some connection formulas for special functions. Proc. Japan Acad. 57 (1981), 34–37.Google Scholar
21Carroll, R. and Santosa, F.. Inverse scattering techniques in geophysics. Applicable Anal. 11 (1980), 70–81.CrossRefGoogle Scholar
22Carroll, R. and Santosa, F.. Scattering techniques for a one dimensional inverse problem in geophysics. Math. Methods Appl. Sci. 3 (1981), 145–171.CrossRefGoogle Scholar
23Carroll, R. and Santosa, F.. On complete recovery of geophysical data. Math. Methods Appl. Sci., to appear.Google Scholar
24Carroll, R. and Santos, F.. Résolution d'un problème inverse qui détermine complètement les données géophysiques, C. R. Acad. Sci. Paris 292 (1981), 23–26.Google Scholar
25Carroll, R. and Showalter, R.. Singular and degenerate Cauchy problems (New York: Academic Press, 1976).Google Scholar
26Chadan, K. and Sabatier, P.. Inverse problems in quantum scattering theory (New York: Springer, 1977).CrossRefGoogle Scholar
27Copson, E. and Erdélyi, A.. On a partial differential equation with two singular lines. Arch. Mech. Anal. 2 (1958), 76–86.CrossRefGoogle Scholar
28Dettman, J.. Related semigroups and the abstract Hilbert transform. Function theoretic methods in differential equations, pp. 94–108 (London: Pitman, 1976).Google Scholar
29Dettman, J.. Related singular problems and the generalized Hilbert transform. Proc. Roy. Soc. Edinburgh Sect A 79 (1977), 173–182.CrossRefGoogle Scholar
30Diaz, J. and Weinstein, A.. On the fundamental solutions of a singular Beltrami operator pp. 97–102Studies in Math, and Mech. (New York: Academic Press, 1954).Google Scholar
31Ditkin, V. and Prudnikov, A.. Formulaire pour le calcul opérationnel (Paris: Masson, 1967).Google Scholar
32Erdélyi, A.. Fractional integrals of generalized functions. Lecture Notes in Mathematics 457, pp. 151–170 (Berlin: Springer, 1975).Google Scholar
33Fadeev, L.. The inverse problem of quantum scattering theory. Uspehi Mat. Nauk 14 (1959), 57–119.Google Scholar
34Flensted-Jensen, M.. Paley–Wiener type theorems for a differential operator connected with symmetric spaces. Ark. Mat. 10 (1972), 143–162.CrossRefGoogle Scholar
35Flensted-Jensen, M. and Koornwinder, T.. The convolution structure for Jacobi expansions. Ark. Mat. 11 (1973), 245–262.CrossRefGoogle Scholar
36Gasymov, M.. The expansion in eigenfunctions of a nonselfadjoint second order differential operator with a singularity at zero. Proceedings of the Summer School in the Spectral Theory of Operators and the Theory of Group Representations (Baku, 1968), pp. 20–45 (Baku: Izdat ‘EUM’ 1975) (Russian).Google Scholar
37Gasymov, M.. On the eigenfunction expansion of a nonselfadjoint boundary problem for a differential equation with a singularity at zero. Dokl. Akad. Nauk SSSR 165 (1965), 261–264.Google Scholar
38Gelfand, I. and Šilov, G.. Generalized functions, Vols. 1–3Moscow: Gos. Izd. Fig. Mat. Lit., 1958).Google Scholar
39Gilbert, R.. Function theoretic methods in partial differential equations (New York: Academic Press, 1969).Google Scholar
40Heywood, P.. On a modification of the Hilbert transform. X London Math. Soc. 42 (1967), 641–645.CrossRefGoogle Scholar
41Heywood, P. and Rooney, P.. On the boundedness of Lowndes' operators. J. London Math. Soc. 10 (1975), 241–248.CrossRefGoogle Scholar
42Heywood, P.. Improved boundedness conditions for Lowndes' operators. Proc. Roy. Soc. Edinburgh Sect A 73 (1975), 291–299.CrossRefGoogle Scholar
43Huber, A.. On the uniqueness of generalized axially symmetric potentials. Ann. of Math. 60 (1954), 351–358.CrossRefGoogle Scholar
44Katrakhov, V.. Transmutation operators and pseudodifferential operators. Sibirsk. Mat. Ž. 21 (1980), 86–97.Google Scholar
45Kipriyanov, I. and Katrakhov, V.. On a class of onedimensional singular pseudodifferential operators. Mat. Sb. 104 (1977), 49–68.Google Scholar
46Kober, H.. A modification of Hilbert transforms, the Weyl integral, and functional equations. J. London Math. Soc. 42 (1967), 42–50.CrossRefGoogle Scholar
47Koornwinder, T.. A new proof of a Paley–Wiener type Theorem for the Jacobi transform. Ark. Mat. 13 (1975), 145–159.CrossRefGoogle Scholar
48Levitan, B.. The theory of generalized translation operators (Moscow: Izd. Nauka, 1973).Google Scholar
49Levitan, B.. The expansion in Bessel functions for Fourier series and integrals. Uspehi. Mat. Nauk 6 (1951), 102–143.Google Scholar
50Lions, J., Opérateurs de Delsarte et problèmes mixtes. Bull. Soc. Math. France 84 (1956), 9–95.CrossRefGoogle Scholar
51Lowndes, J.. A generalization of the Erdélyi-Kober operators. Proc. Edinburgh Math. Soc. 17 (1970), 130–148.CrossRefGoogle Scholar
52Magnus, W., Oberhettinger, F. and Soni, R.. Formulas and theorems for the special functions of mathematical physics (New York: Springer, 1966).CrossRefGoogle Scholar
53Marčenko, V.. Sturm–Liouville operators and their applications (Kiev: Izd. Nauk Dumka, 1977).Google Scholar
54McBride, A.. Fractional calculus and integral transforms of generalized functions (London: Pitman, 1979).Google Scholar
55Morse, P. and Feshbach, H.. Methods of theoretical physics (New York: McGraw-Hill, 1953).Google Scholar
56Muckenhoupt, B. and Stein, E.. Classical expansions and their relation to conjugate harmonic functions. Trans. Amer. Math. Soc. 118 (1965), 17–92.Google Scholar
57Okikiolu, G.. Aspects of the theory of bounded operators in V spaces (New York: Academic Press, 1971).Google Scholar
58Orton, M.. Hilbert transforms, Plemelj relations, and Fourier transforms of distributions. SIAMJ. Math. Anal. 4 (1973), 656–670.CrossRefGoogle Scholar
59Payne, L.. On axially symmetric flows and the method of generalized electrostatics. Quart. Appl. Math. 10 (1952), 197–204.CrossRefGoogle Scholar
60Robin, L.. Fonctions sphériques de Legendre et fonctions sphéroidales, Vols. 1–3 Paris: (Gauthier-Villars, 1957–59).Google Scholar
61Rooney, P.. On the ranges of certain fractional integrals. Canad. J. Math. 6 (1972), 1198–1216.CrossRefGoogle Scholar
62Schwartz, L.. Théorie des distributions. (Paris: Ed. “Papillon”, Hermann, 1966).Google Scholar
63Siersma, J.. On a class of singular Cauchy problems, Thesis, Groningen, 1979.Google Scholar
64Sneddon, I.. The use in mathematical physics of Erdélyi–Kober operators and of some of their generalizations. Lecture Notes in Mathematics 457, pp. 37–79 (Berlin: Springer, 1975).Google Scholar
65Sprinkuizen-Kuyper, I.. A fractional integral operator corresponding to negative powers of a second order partial differential operator. Mat. Centrum, Amsterdam, preprint 1979.Google Scholar
66Sprinkhuizen-Kuyper, I.. A fractional integral operator corresponding to negative powers of a certain second order differential operator. J. Math. Anal. Appl. 72 (1979), 674–702.CrossRefGoogle Scholar
67Staševskaya, V.. The inverse problem of spectral analysis for a differential operator with a singularity at zero. Učen. Zap. Kharkov Mat. Obšč. 25 (1957), 49–86.Google Scholar
68Volk, V.. On inversion formulas for differential operators with a singularity at x = 0. Uspehi Mat. Nauk 8 (1953), 141–151.Google Scholar
69Walker, J.. Conjugate Hankel transforms and HF theory, Thesis, Univ. of Texas, 1980.Google Scholar
70Watson, G.. Ttieory of Bessel functions (Cambridge Univ. Press, 1922).Google Scholar
71Weinstein, A.. Generalized axially symmetric potential theory. Bull. Amer. Math. Soc. 59 (1953), 20–38.CrossRefGoogle Scholar
72Weinstein, A.. On Tricomi‘s equation and generalized axially symmetric potential theory. Bull. Acad. Roy. Belg. 37 (1951), 348–358.Google Scholar
73Weinstein, A.. On axially symmetric flows. Quart. Appl. Math. 5 (1948), 429–444.CrossRefGoogle Scholar
74Weinstein, A.. Discontinuous integrals and generalized potential theory. Trans. Amer. Math. Soc. 63 (1948), 342–354.CrossRefGoogle Scholar
75Weinstein, A.. Transonic flow and generalized axially symmetric potential theory, Naval Ord. Lab., White Oak, Md., Rep. NOLR-1132, 73–82 (1950).Google Scholar
76Weinstein, A.. The singular solutions and the Cauchy problem for generalized Tricomi equations. Comm. Pure Appl. Math. 7 (1954), 105–116.CrossRefGoogle Scholar