A symmetrized conjugacy scheme for orthogonal expansions
Published online by Cambridge University Press: 18 March 2013
Abstract
We establish a symmetrization procedure in the context of general orthogonal expansions associated with a second-order differential operator L, a Laplacian. Combining with a unified conjugacy scheme from an earlier paper by Nowak and Stempak permits, using a suitable embedding, a differential-difference Laplacian 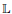 to be associated with the initially given orthogonal system of eigenfunctions of L, so that the resulting extended conjugacy scheme has the natural classical shape. This means, in particular, that the related partial derivatives decomposing
to be associated with the initially given orthogonal system of eigenfunctions of L, so that the resulting extended conjugacy scheme has the natural classical shape. This means, in particular, that the related partial derivatives decomposing 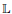 are skew-symmetric in an appropriate L2 space and they commute with Riesz transforms and conjugate Poisson integrals. The results also shed new light on the issue of defining higher-order Riesz transforms for general orthogonal expansions.
are skew-symmetric in an appropriate L2 space and they commute with Riesz transforms and conjugate Poisson integrals. The results also shed new light on the issue of defining higher-order Riesz transforms for general orthogonal expansions.
- Type
- Research Article
- Information
- Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 143 , Issue 2 , April 2013 , pp. 427 - 443
- Copyright
- Copyright © Royal Society of Edinburgh 2013
- 12
- Cited by


