Hostname: page-component-586b7cd67f-t7fkt Total loading time: 0 Render date: 2024-12-01T00:14:16.476Z Has data issue: false hasContentIssue false
  • English
  • Français

Inhomogeneous Fuchs equations and the limit cycles in a class of near-integrable quadratic systems

Published online by Cambridge University Press:  14 November 2011

Iliya D. Iliev
Iliya D. Iliev
Affiliation:
Institute of Mathematics, Bulgarian Academy of Sciences, P.O. Box 373, 1090 Sofia, Bulgaria e-mail:[email protected]
Get access Rights & Permissions [Opens in a new window]

Extract

We study the bifurcation of limit cycles in general quadratic perturbations of the particular quadratic system 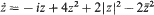which represents one of two codimension-five components in the intersection of two strata in the centre manifold, 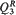and Q4. The study of limit cycles for this degenerate case requires us to investigate not the first but the second variation M2 of the displacement function. We prove that up to three limit cycles can emerge from the period annulus surrounding the centre. This implies that the cyclicity of period annuli of nearby systems in and Q4 is at most three as well. Our approach relies upon the possibility of deriving appropriate Picard–Fuchs equations satisfied by the four independent integrals included in M2.

Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 127 , Issue 6 , 1997 , pp. 1207 - 1217
Copyright
Copyright © Royal Society of Edinburgh 1997

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1Bautin, N. N.. On the number of limit cycles which appear with the variations of the coefficients from an equilibrium point of focus or center type. Amer. Math. Soc. Transl. Ser. 1 5 (1962), 396–413 (Russian original: Math. Sb. 30 (1952), 181–96).Google Scholar
2Chicone, C. and Jacobs, M.. Bifurcations of limit cycles from quadratic isochrones. J. Differential Equations 91 (1991), 268–326.CrossRefGoogle Scholar
3Dumortier, F., Roussarie, R. and Rousseau, C.. Hilbert 16th problem for quadratic vectorfields. J. Differential Equations 110 (1994), 86–133.CrossRefGoogle Scholar
4Gavrilov, L. and Horozov, E.. Limit cycles and zeroes of Abelian integrals satisfying third order. Picard-Fuchs equations. In Bifurcations of Planar Vector Fields, eds Françoise, J- P. and Roussarie, R., Lecture Notes in Mathematics 1455, 160–86 (Berlin: Springer, 1990).CrossRefGoogle Scholar
5A. van Gils, S. An inhomogeneous Picard-Fuchs equation. In Dynamics, Bifurcation and Symmetry, ed. Chossat, P., 333–41 (Dordrecht: Kluwer, 1994).CrossRefGoogle Scholar
6Guckenheimer, J., Rand, R. and Schlomiuk, D.. Degenerate homoclinic cycles in perturbations of quadratic Hamiltonian systems. Nonlinearity 2 (1989), 405–18.CrossRefGoogle Scholar
7He, Y. and Li, Ch.. On the number of limit cycles arising from perturbation of homoclinic loops of quadratic integrable systems (Preprint, Peking University, 1995).Google Scholar
8Horozov, E. and Iliev, I D.. On saddle-loop bifurcation of limit cycles in perturbations of quadratic Hamiltonian systems. J. Differential Equations 113 (1994), 84–105.CrossRefGoogle Scholar
9Horozov, E. and Iliev, I D.. On the number of limit cycles in perturbations of quadratic Hamiltonian systems. Proc. Lond. Math. Soc. 69 (1994), 198–224.CrossRefGoogle Scholar
10Horozov, E. and Iliev, I. D.. Perturbations of quadratic Hamiltonian systems with symmetry. Ann. Inst. H. Poincaré, Anal. non. linéaire 13 (1996), 17–56.CrossRefGoogle Scholar
11van. Horssen, W. T. and Kooij, R. E.. Bifurcations of limit cycles in a particular class of quadratic system with two centres. J. Differential Equations 114 (1994), 538–69.CrossRefGoogle Scholar
12Iliev, I. D.. Higher-order Melnikov functions for degenerate cubic Hamiltonians. Adv. Differential Equations 1 (1996), 689–708.CrossRefGoogle Scholar
13Iliev, I. D.. Perturbations of quadratic centers. Bull. Sci. Math, (to appear).Google Scholar
14Llibre, J., Li, Ch. and Zhi-fen, Zh.. Abelian integrals of quadratic Hamiltonian vector fields with an invariant line. Publ. Mat. 39 (1995), 355–66.Google Scholar
15Roussarie, R.. Bifurcations of planar vector fields and Hilbert's 16th problem (20 Coloquio Brasileiro de Matematica, IMPA, Rio de Janeiro, 1995).Google Scholar
16Shafer, D. S. and Zegeling, A.. Bifurcation of limit cycles from quadratic centers. J. Differential Equations 122 (1995), 48–70.CrossRefGoogle Scholar
17Zoladek, H.. Quadratic systems with center and their perturbations. J. Differential Equations 109 (1994), 223–73.CrossRefGoogle Scholar
18Żolądek, H.. The cyclicity of triangles and segments in quadratic systems. J. Differential Equations 122 (1995), 137–59.CrossRefGoogle Scholar
19Żolądek, H.. Asymptotic properties of Abelian integrals arising in quadratic systems (Preprint, University of Warsaw, 1994).Google Scholar