Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-25T02:14:05.851Z Has data issue: false hasContentIssue false
  • English
  • Français

Bifurcation sets of families of reflections on surfaces in ℝ3

Part of: Differential topology Classical differential geometry

Published online by Cambridge University Press:  14 February 2017

P. J. Giblin  and
S. Janeczko
P. J. Giblin
Affiliation:
Department of Mathematical Sciences, University of Liverpool, Liverpool L69 7ZL, UK ([email protected])
S. Janeczko
Affiliation:
Instytut Matematyczny PAN, ul. Sniadeckich 8, 00-950 Warszawa, Poland and Wydzial Matematyki i Nauk Informacyjnych, Politechnika Warszawska, Pl. Politechniki 1, 00-661 Warszawa, Poland ([email protected])
Get access Rights & Permissions [Opens in a new window]

Extract

We introduce a new affinely invariant structure on smooth surfaces in ℝ3 by defining a family of reflections in all points of the surface. We show that the bifurcation set of this family has a special structure at ‘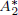 points’, which are not detected by the flat geometry of the surface. These 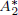points (without an associated structure on the surface) have also arisen in the study of the centre symmetry set; using our technique we are able to explain how the points are created and annihilated in a generic family of surfaces. We also present the bifurcation set in a global setting.

Keywords

affine invariantssurfacesparabolic setsbifurcation sets

MSC classification

Secondary: 53A05: Surfaces in Euclidean space 57R45: Singularities of differentiable mappings
Type
Research Article
Information
Proceedings of the Royal Society of Edinburgh Section A: Mathematics , Volume 147 , Issue 2 , April 2017 , pp. 337 - 352
Copyright
Copyright © Royal Society of Edinburgh 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)