Article contents
The Projective Leavitt Complex
Published online by Cambridge University Press: 15 August 2018
Abstract
For a finite quiver Q without sources, we consider the corresponding radical square zero algebra A. We construct an explicit compact generator for the homotopy category of acyclic complexes of projective A-modules. We call such a generator the projective Leavitt complex of Q. This terminology is justified by the following result: the opposite differential graded endomorphism algebra of the projective Leavitt complex of Q is quasi-isomorphic to the Leavitt path algebra of Qop. Here, Qop is the opposite quiver of Q, and the Leavitt path algebra of Qop is naturally 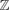 ${\open Z}$-graded and viewed as a differential graded algebra with trivial differential.
${\open Z}$-graded and viewed as a differential graded algebra with trivial differential.
- Type
- Research Article
- Information
- Proceedings of the Edinburgh Mathematical Society , Volume 61 , Issue 4 , November 2018 , pp. 1155 - 1177
- Copyright
- Copyright © Edinburgh Mathematical Society 2018
References
- 1
- Cited by


