Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Niinō, Kiyoshi
1977.
Spread relation and value distribution in an angular domain on holomorphic curves.
Kodai Mathematical Journal,
Vol. 28,
Issue. 4,
Bouvier-Durand, Michèle
Dereuddre, Jean
and
Côme, Daniel
1981.
Le réticulum endoplasmique dans le méristème radiculaire de l'embryon de Pommier (Pirus malusL.): son évolution pendant la levée de dormance au froid.
Bulletin de la Société Botanique de France. Actualités Botaniques,
Vol. 128,
Issue. 2,
p.
91.
Toda, Nobushige
1981.
Sur l’inégalité fondamentale de H. Cartan pour les systèmes de fonctions entières.
Nagoya Mathematical Journal,
Vol. 83,
Issue. ,
p.
5.


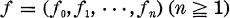 un système transcendant dans le plan
un système transcendant dans le plan 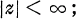 c’est-à-dire, les fonctions
c’est-à-dire, les fonctions