Hostname: page-component-78c5997874-94fs2 Total loading time: 0 Render date: 2024-11-06T07:45:05.655Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral representation of smooth functions in weight classes and its applications

Published online by Cambridge University Press:  22 January 2016

Takahide Kurokawa
Takahide Kurokawa*
Affiliation:
Department of Mathematics, College of Liberal Arts, Kagoshima University, Kagoshima 890, Japan
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let Rn be the n-dimensional Euclidean space, and for each point x =(x1,…, xn) we write .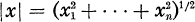

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 111 , September 1988 , pp. 1 - 11
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1988

References

[1] Burenkov, V. I., Mollifying operators with variable step and their application to approximation by infinitely differentiable functions, Nonlinear Analysis, Function Spaces and Applications Vol. 2, Teubner-texte zur Math., Leipzig, 1982, 5–37.Google Scholar
[2] Okikiolu, G. O., On inequalities for integral operators, Glasgow Math. J., 11 (1970), 126–133.CrossRefGoogle Scholar
[3] Pigolkina, T. S., The density of finite functions in weight classes, Math. Notes, 2 (1967), 518–522.CrossRefGoogle Scholar
[4] Reshetnyak, Yu. G,. The concept of capacity in the theory of functions with generalized derivatives, Siberian Math. J., 10 (1969), 818–842.CrossRefGoogle Scholar