Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-23T23:55:28.987Z Has data issue: false hasContentIssue false
  • English
  • Français

Differential operators on a hypersurface

Published online by Cambridge University Press:  22 January 2016

Balwant Singh
Balwant Singh*
Affiliation:
Tata Institute of Fundamental Research, Homi Bhabha Road, Bombay 400 005, India
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study differential operators on an affine algebraic variety, especially a hypersurface, in the context of Nakai’s Conjecture. We work over a field k of characteristic zero. Let X be a reduced affine algebraic variety over k and let A be its coordinate ring. Let 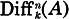be the A-module of differential operators of A over k of order ≤ n. Nakai’s Conjecture asserts that if 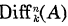is generated by 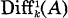for every n ≥ 2 then A is regular. In 1973 Mount and Villamayor [6] proved this in the case when X is an irreducible curve. In the general case no progress seems to have been made on the conjecture, except for a result of Brown [2], where the assertion is proved under an additional hypothesis. An interesting result proved by Becker [1] and Rego [8] says that Nakai’s Conjecture implies the Conjecture of Zariski-Lipman, which is still open in the general case and which asserts that if the module of k-derivations of A is A-projective then A is regular.

Type
Research Article
Information
Nagoya Mathematical Journal , Volume 103 , October 1986 , pp. 67 - 84
Copyright
Copyright © Editorial Board of Nagoya Mathematical Journal 1986

References

[1] Becker, J., Higher derivations and integral closure, Amer. J. Math., 100 (1978), 495–521.Google Scholar
[2] Brown, W. C., Higher derivations on finitely generated integral domains, Proc. Amer. Math. Soc, 42 (1974), 23–27.Google Scholar
[3] Cartan, H. and Eilenberg, S., Homological Algebra, Princeton Univ. Press, Princeton 1956.Google Scholar
[4] Grothendieck, A., Éléments de Géométrie Algébrique, Publ. Math. IHES, 32 (1967).Google Scholar
[5] Lipman, J., Free derivation modules on algebraic varieties, Amer. J. Math., 87 (1965), 874–898.Google Scholar
[6] Mount, K. R. and Villamayor, 0. E., On a conjecture of Y. Nakai, Osaka J. Math., 10 (1973), 325–327.Google Scholar
[7] Nakai, Y., High order derivations I, Osaka J. Math., 7 (1970), 1–27.Google Scholar
[8] Rego, C. J., Remarks on differential operators on algebraic varieties, Osaka J. Math., 14 (1977), 481–486.Google Scholar
[9] Serre, J.-P., Algèbre locale—Multiplicités, Springer-Verlag Lecture Notes in Math., No. 11, Berlin-Heidelberg-New York, 1975.Google Scholar
[10] Vigué, J.-P., Opérateurs différentiels sur les espaces analytiques, Invent, math., 20 (1973), 313–336.Google Scholar
[11] Zariski, O., Studies in equisingularity I, Amer. J. Math., 87 (1965), 507–536.Google Scholar
[12] Vigué, J.-P., Opérateurs différentiels sur les cônes normaux de dimension 2, C. R. Acad. Sc. Paris, 278, Série A, (1974), 1047–1050.Google Scholar
[13] Ishibashi, Y., Remarks on a Conjecture of Nakai, J. Algebra, 95 (1985), 31–45.Google Scholar
[14] Ishibashi, Y., Nakai’s conjecture for invariant subrings, Hiroshima Math. J., 15 (1985), 429–436.Google Scholar