Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-26T05:10:03.280Z Has data issue: false hasContentIssue false
  • English
  • Français

A CONSTRUCTION OF SURFACES WITH LARGE HIGHER CHOW GROUPS

Part of: $K$-theory in geometry Cycles and subschemes

Published online by Cambridge University Press:  16 October 2018

TOMOHIDE TERASOMA
TOMOHIDE TERASOMA*
Affiliation:
Graduate School of Mathematical Sciences, The University of Tokyo, 3-1-8 Komaba, Meguroku, Tokyo 153-8914, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we construct surfaces in 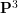$\mathbf{P}^{3}$ with large higher Chow groups defined over a Laurent power series field. Explicit elements in higher Chow group are constructed using configurations of lines contained in the surfaces. To prove the independentness, we compute the extension class in the Galois cohomologies by comparing them with the classical monodromies. It is reduced to the computation of linear algebra using monodromy weight spectral sequences.

MSC classification

Primary: 14C15: (Equivariant) Chow groups and rings; motives 19E15: Algebraic cycles and motivic cohomology 14C30: Transcendental methods, Hodge theory , Hodge conjecture
Type
Article
Information
Nagoya Mathematical Journal , Volume 236: Celebrating the 60th Birthday of Shuji Saito , December 2019 , pp. 311 - 331
Copyright
© 2018 Foundation Nagoya Mathematical Journal  

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bloch, S., Algebraic cycles and higher K -theory , Adv. Math. 61(3) (1986), 267–304.10.1016/0001-8708(86)90081-2Google Scholar
Collino, A., Müller-Stach, S. and Saito, S., On K 1 and K 2 of algebraic surfaces. Special issue in honor of Hyman Bass on his seventieth birthday. Part I , K-Theory 30(1) (2003), 37–69.Google Scholar
Müller-Stach, S. J., Constructing indecomposable motivic cohomology classes on algebraic surfaces , J. Algebraic Geom. 6(3) (1997), 513–543.Google Scholar
Peters, C. and Steenbrink, J. H. M., Mixed Hodge Structures, Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge, A Series of Modern Surveys in Mathematics, Springer, 2010.Google Scholar