Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T02:35:32.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Selection of Optimum Nonlinear Crystals for Efficient Parametric Generation and Sensitive Detection of Monochromatic ns THz Pulses

Published online by Cambridge University Press:  01 February 2011

Yujie J. Ding
Yujie J. Ding*
Affiliation:
[email protected], Lehigh University, Electrical and Computer Engineering, 19 Memorial Drive West, Bethlehem, PA, 18015, United States, (610) 758-4582, (610) 758-6279
Get access

Abstract

We report our recent progress made on the development of widely-tunable monochromatic THz sources. They have been realized based on difference-frequency generation (DFG) in GaSe, ZnGeP2, and GaP crystals, respectively. Using a GaSe crystal, the output wavelength was tuned continuously in the range from 66.5 µm to 5664 µm (from 150 cm-1 to 1.77 cm-1) with the peak power reaching 389 W. Such a high peak power corresponds to a conversion efficiency of about 0.1% (a photon conversion efficiency of 19%). A further optimization on the THz beam parameter may result in an output peak power of a few kW. Within the range of 100-250 µm the output peak powers were higher than 100 W. We have also investigated THz frequency upconversion in GaSe, ZnGeP2, and GaP crystals. Such a parametric process has a potential for detecting THz pulses at room temperature or just using a thermoelectric cooler. The minimum detectable energy per pulse was measured to be 245 pJ, which corresponds to a noise equivalent energy of 77.5 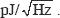. A further optimization of the process can reduce this value down to 1 .

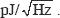Keywords

optical propertiesradiation effectsoptical
Type
Research Article
Information
MRS Online Proceedings Library (OPL) , Volume 1016: Symposium CC – Materials and Material Structures Enabling Terahertz Technology , 2007 , 1016-CC02-01
Copyright
Copyright © Materials Research Society 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Gordy, W. and Cook, R. L., Microwave molecular spectra, 3rd Ed., Wiley, NY (1984).Google Scholar
2. McClatchey, R. A., Fenn, R. W., Selby, J. E. A., Volz, F. E., and Garing, J. S., “Optical properties of the atmosphere,” in Handbook of optics, Ed. Driscoll, W. G., McGraw Hill, NY (1978).Google Scholar
3. Tomasi, C., “Vertical mass loading of aerosol particles by sun-photometric measurements,” in Optical remote sensing of air pollution, Ed. Camagni, P. and Sandroni, S., Elsevier, NY (1984).Google Scholar
4. Shi, W., Ding, Y. J., Fernelius, N., and Vodopyanov, K. L., Opt. Lett. 27, 1454 (2002).Google Scholar
5. Shi, W. and Ding, Y. J., Appl. Phys. Lett. 84, 1635 (2004).Google Scholar
6. Shi, W. and Ding, Y. J., Intern. J. High Speed Electron. Sys. 16, 589 (2006).Google Scholar
7. Shi, W. and Ding, Y. J., Optics in 2002, Optics and Photonics News, Dec. 2002, p. 57.Google Scholar
8. Shi, W. and Ding, Y. J., Appl. Phys. Lett. 83, 848 (2003).Google Scholar
9. Shi, W., Ding, Y. J., and Schunemann, P. G., Opt. Commun. 233, 183 (2004).Google Scholar
10. Shi, W. and Ding, Y. J., Opt. Lett. 30, 1030 (2005).Google Scholar
11. Ding, Y. J. and Shi, W., Sol. State Electron. 50, 1128 (2006).Google Scholar
12. Shi, W., Mu, X., Ding, Y. J., and Fernelius, N., Appl. Phys. Lett. 80, 3889 (2002).Google Scholar
13. Shi, W. and Ding, Y. J., Laser Phys. Lett. 1, 560 (2004).Google Scholar
14. Sun, H., Ding, Y. J., and Zotova, Y. B., Appl. Opt. 46, no. 19, Jul. 2007.Google Scholar
15. Sun, H., Shi, W., Fu, Z., and Ding, Y. J., and Zotova, Y. B., “Bragg reflectors and 2-D photonic crystals in the THz region,” in Terahertz for Military and Security Applications III, edited by Hwu, R. Jennifer, Woolard, Dwight L., Rosker, Mark J., Proceedings of SPIE 5790 (Bellingham, WA, 2005) 104–115.Google Scholar
16. Shi, W., Ding, Y. J., Fernelius, N., and Hopkins, F. K., Appl. Phys. Lett. 88, 101101 (2006).Google Scholar
17. Ding, Y. J. and Shi, W., Opt. Exp. 14, 8311 (2006).Google Scholar
18. Ding, Y. J., IEEE J. Sel. Top. Quantum Electron. 13, no. 3, May/June 2007.Google Scholar
19. Palik, E. D., Handbook of optical constants of solids III, Academic, NY (1998), pp. 487 & 640.Google Scholar
20. Dmitriev, V. G., Gurzadyan, G. G., and Nikogosyan, D. N., Handbook of Nonlinear Optical Crystals (Springer, Berlin, 1999), p. 168.Google Scholar
21. Mason, P. D., Jackson, D. J., and Gorton, E. K., Opt. Commun. 110, 163 (1994).Google Scholar
22. Boyd, G. D., Bridges, T. J., C. Patel, K. N., and Buehler, E., Appl. Phys. Lett. 21, 553 (1972).Google Scholar
23. Bhar, G. C., Samanta, L. K., Ghosh, D. K., and Das, S., Sov. J. Quantum Electron. 17, 860 (1987).Google Scholar
24. Zelmon, D. E., Hanning, E. A., and Schunemann, P. G., J. Opt. Soc. Amer. B 18, 1307 (2001).Google Scholar
25. Ding, Y. J. and Zotova, I. B., J. Nonl. Opt. Phys. Mats. 11, 75 (2002).Google Scholar
26. Ding, Y. J. and Shi, W., J. Nonl. Opt. Phys. & Mats. 12, 557 (2003).Google Scholar
27. Fraust, W. L. and Henry, C. H., Phys. Rev. Lett. 17, 1265 (1966).Google Scholar
28. Tanabe, T., Suto, K., Nishizawa, J., Saito, K., and Kimura, T., Appl. Phys. Lett. 83, 237 (2003).Google Scholar
29. Shi, W. and Ding, Y. J., Opt. Lett. 30, 1861 (2005).Google Scholar
30. Ding, Y. J. and Shi, W., IEEE J. Sel. Top. Quantum Electron. 12, 352 (2006).Google Scholar
31. Zotova, I. B. and Ding, Y. J., Appl. Opt. 40, 6654 (2001).Google Scholar
32. Vurgaftman, I., Meyer, J. R., and Ram-Mohan, L. R., J. Appl. Phys. 89, 5815 (2001).Google Scholar