The Atmosphere

To begin with, it will be useful to review some characteristics of our atmosphere, the gas most prominently involved in evacuation processes. The kinetic molecular theory combined two classical laws, Boyle’s Law and Charles’s Law, to produce the Ideal Gas Equation as follows:

(1) $${{n{\equals}PV} \mathord{\left/ {\vphantom {{n{\equals}PV} {RT}}} \right. \kern-\nulldelimiterspace} {RT}}$$

where n is the number of moles (one mole = 6.023 × 10²³ molecules) of gas contained in a volume V (liters) at a pressure P (Pascal) and at a temperature T (Kelvin) (K = °C + 273). The constant R has a value of 8314.4 (or 62.36 for pressures in Torr). Using this equation it is possible to calculate the number of gas molecules in a unit volume, N, a very interesting and important property of our atmosphere. The result for the atmosphere at ambient temperature (298 K = 25°C = 77°F) is

(2) $${{n{\equals}PV} \mathord{\left/ {\vphantom {{n{\equals}PV} {RT}}} \right. \kern-\nulldelimiterspace} {RT}}$$

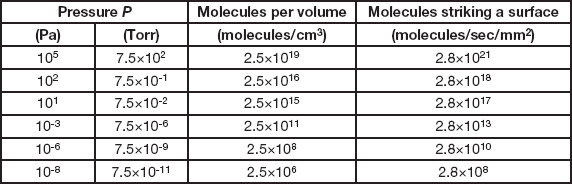
(the constant becomes 3.2 × 10¹⁹ for pressure in Torr). The order of magnitude in Equation 2 indicates that the number is very large. To emphasize this more strongly, Table 1 lists the values for the number of air molecules per cubic centimeter (not a very large volume) for a range of pressures. At atmospheric pressure (10⁵ Pa) there are twenty-five billion-billion molecules in each cubic centimeter. At 10^-6 Pa, the bottom of the high vacuum range, there are two hundred and fifty million molecules per cc, and even at 10^-8 Pa, which is well into the ultra-high vacuum range and about the best vacuum attainable in modern electron microscopes, there are still more than two million molecules per cc. So you can pump as long and as hard as you wish, but never get down to a really insignificant concentration of air molecules in your vacuum system.

Table 1 Properties of air in a vacuum at 25°C.

The kinetic molecular theory yields another very interesting and important equation, this time giving the number of molecules striking a unit area of surface at various values of temperature and pressure. For air at ambient temperature and different pressures (Pa), the equation simplifies to

(3) $${{V_{{cap}} {\equals}n_{{cap}} RT} \mathord{\left/ {\vphantom {{V_{{cap}} {\equals}n_{{cap}} RT} P}} \right. \kern-\nulldelimiterspace} P}{\equals}\left( {4.7{\times}10^{{{\minus}8}} } \right){{AP\left( {8314.4{\times}298} \right)} \mathord{\left/ {\vphantom {{AP\left( {8314.4{\times}298} \right)} P}} \right. \kern-\nulldelimiterspace} P}{\equals}{{0.12A\;{\rm liters}} \mathord{\left/ {\vphantom {{0.12A\;{\rm liters}} {{\rm sec}}}} \right. \kern-\nulldelimiterspace} {{\rm sec}}}$$

(the constant becomes 3.8 × 10¹⁸ for pressures in Torr). The numbers here are truly staggering. Each second every square millimeter of our bodies is being bombarded by nearly three thousand-billion-billion air molecules (and we are totally unaware of it). At 10^-6 Pa each square millimeter of surface inside a vacuum system is struck by nearly thirty billion molecules per second, and the number is still a substantial three hundred million at 10^-8 Pa. Air molecules are almost unimaginably small and incredibly numerous.

The Theoretical Maximum Pumping Speed

In addition to providing this interesting insight into the properties of our atmosphere, Equation 3 can be used to calculate the theoretical maximum pumping speed that a vacuum pump can develop. To aid in doing this, suppose there is a material that might be called molecular quicksand that captures every molecule that strikes it with 100 percent efficiency. Then according to this equation the number of gas molecules captured each second by a bed of this material with an area of A square millimeters will be N _cap = A(2.8 × 10¹⁶ P). Dividing by Avogadro’s number (N _A = 6.023 × 10²³ molecules per mole) will give the number of moles of gas captured per second n _cap = (4.7 × 10^-8)AP. Then using the ideal gas equation, the volume captured per second is found to be

(4) $${{V_{{cap}} {\equals}n_{{cap}} RT} \mathord{\left/ {\vphantom {{V_{{cap}} {\equals}n_{{cap}} RT} P}} \right. \kern-\nulldelimiterspace} P}{\equals}\left( {4.7{\times}10^{{{\minus}8}} } \right){{AP\left( {8314.4{\times}298} \right)} \mathord{\left/ {\vphantom {{AP\left( {8314.4{\times}298} \right)} P}} \right. \kern-\nulldelimiterspace} P}{\equals}{{0.12A\;{\rm liters}} \mathord{\left/ {\vphantom {{0.12A\;{\rm liters}} {{\rm sec}}}} \right. \kern-\nulldelimiterspace} {{\rm sec}}}$$

at ambient temperature. This is a rather interesting result, for contrary to what one might intuitively expect, the pressure cancels out. Whereas the data in Table 1 show that the number of gas molecules striking a unit area per unit time is a linear function of pressure, these calculations show that the volume of gas molecules doing so is independent of pressure.

The pumping speed of the pump serving a given vacuum system is a primary factor determining the speed of evacuation and the time required to achieve an operating vacuum. Now it is useful to remember that vacuum pumps do not suck, pull, draw, or attract gas molecules out of a vacuum system. Instead, they capture (as best they can) the gas molecules that wander into their inlet ports, under their own thermally activated motion, and return them to the surrounding atmosphere. Since the maximum number of molecules that can enter the inlet port of a pump of area A (mm²) is the same as the maximum number that would strike a bed of molecular quicksand with the same area, and since no pump can capture gas molecules more efficiently than the molecular quicksand, the equation for the theoretically maximum pumping speed is the one just derived:

(5) $$S_{{TMax}} {\equals}0.12\;A\;{\rm liters}\;{\rm per}\;{\rm second}{\rm .}$$

Since nearly all vacuum pumps have circular inlet ports, and since it is customary to use the diameter of the inlet port to specify their “size,” it is useful to express S _TMax in terms of internal flange diameter in mm, thus

(6) $$S_{{TMax}} {\equals}0.09\;D^{2} \;{\rm liters}\;{\rm per}\;{\rm second}$$

(the constant becomes 58.06 for diameters in inches). Values of S _TMax for various types of pumps of different inlet flange diameters are listed in Table 2. Here, pump diameters are those that are common to the International Standards Organization’s (ISO) system.

Table 2 Maximum pumping speeds (liters/sec) for different pump sizes and types.

S _TMax =theoretical maximum speed, S _DifPmp =speed of diffusion pump, S _TMP =speed of turbomolecular pump, and S _Ion =speed of ion pump.

Actual Pumping Speeds

Table 2 also lists the highest pumping speeds currently advertised for oil diffusion, turbomolecular, and ion pumps. These pumping speeds are a complex function of the area of a pump’s inlet, the extent to which that area is obstructed by internal structures, and the efficiency with which the pump’s mechanism captures the gas molecules that do manage to get past such obstructions. Furthermore, pumping speeds are rather difficult to measure, and different manufacturers use different methods, so the advertised values listed in Table 2 only show general trends.

Oil diffusion pumps

For inlet flanges of a given size, oil diffusion pumps provide the highest pumping speeds. The values listed in Table 2 are for pumps of “standard” design, which have barrels of uniform diameter from top to bottom. Interestingly, the VHS series of pumps introduced by the Varian Vacuum Company, which are available with inlet flanges up to 300 mm (12 inches) in diameter, are capable of achieving nearly theoretical maximum speeds. In these pumps the upper vapor jet structure is relatively small and provides little obstruction to gas molecules entering the pump. The remaining obstruction is compensated for by a bulge in the upper body of the pump, as shown schematically in Figure 1. A fractionating tube feeds high-molecular-weight oil molecules from the center of the boiler to the top jet, making it highly effective in capturing the gas molecules that reach it.

Figure 1 Schematic diagram of a Varian VHS oil diffusion pump.

Performance Characteristics

Oil diffusion pumps and turbomolecular pumps do not start to function until their backing pressure falls below about 10 Pa (10^-1 Torr), as shown in Figure 2. They reach their maximum pumping speed at about 10^-1 Pa (10^-3 Torr), and their pumping speed remains constant for lower pressures. Ion pumps require the pressure in the system to be reduced to about 10^-1 Pa (10^-3 Torr) before they start to function, and they reach their maximum speed at about 10^-4 Pa (10^-6 Torr).

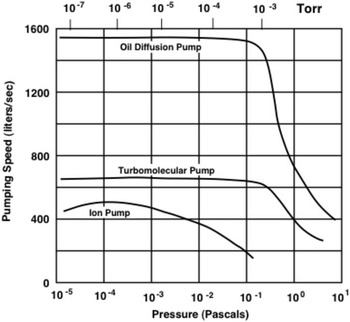
Figure 2 Variation of pumping speed with pressure for different types of high-vacuum pumps 200 mm (8”) in diameter.

Conductance and Speed of Evacuation

The parameter that is most important in describing the performance of a vacuum system is the speed of evacuation. This is defined as the rate at which gas is removed from the vacuum chamber, expressed in units of liters per second for operation in the HV and UHV ranges. If a vacuum pump is connected directly to a vacuum chamber through a well-designed valve with essentially no impedance to gas flow, then the speed of evacuation will be essentially the same as the speed of the pump. However, as is often the case, when the pump is connected to the vacuum chamber through a manifold, which may consist of a length of tubing, a valve, and possibly a liquid nitrogen trap, then these components tend to impede the flow of gas from the chamber to the pump and tend to reduce the speed of evacuation to a value considerably less than the speed of the pump. The ease with which gas molecules can flow through such components is called their conductance (the reciprocal of their impedance). For tubes with a circular cross section, the conductance can be calculated with sufficient accuracy for the present purpose using the equation

(7) $${{C_{{tube}} {\equals}\left( {0.0121\;D^{3} } \right)} \mathord{\left/ {\vphantom {{C_{{tube}} {\equals}\left( {0.0121\;D^{3} } \right)} {\left( {100\;L{\plus}0.133\;D} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {100\;L{\plus}0.133\;D} \right)}}\;\;\;{1 \mathord{\left/ {\vphantom {1 {{\rm sec}}}} \right. \kern-\nulldelimiterspace} {{\rm sec}}}$$

where D is the tube diameter in millimeters and L is its length in meters. [This equation becomes C _tube = 78 D ³ / (12 L + 1.33 D) if D is measured in inches and L in feet.]

Thus, a tube one meter long and 100 millimeters in diameter would have a conductance of a little more than 100 liters per second. Conductance values for valves, traps, and other components of pumping lines are more difficult to calculate but are usually furnished by their manufacturers. Well-designed valves usually do not impede the flow of gas appreciably, but traps and baffles do. The important point here is that the conductance C of the pumping line between the vacuum chamber and the pump can cause a very serious reduction in the speed of evacuation S _evac :

(8) $${{S_{{evac}} {\equals}\left( {CxS_{{pmp}} } \right)} \mathord{\left/ {\vphantom {{S_{{evac}} {\equals}\left( {CxS_{{pmp}} } \right)} {\left( {C{\plus}S_{{pmp}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {C{\plus}S_{{pmp}} } \right)}}\;\;\;{1 \mathord{\left/ {\vphantom {1 {{\rm sec}}}} \right. \kern-\nulldelimiterspace} {{\rm sec}}}$$

where all quantities are expressed in units of liters per second.

Figure 3 is a plot based on this equation, which shows the strong effect that the conductance of the line between the pump and the vacuum chamber has in reducing the speed of evacuation below that of the pump. For example, if the conductance of the pumping line is one-half the speed of the pump (C/S _p = 0.5), the speed of evacuation will be only about one-third the speed of the pump (S _e /S _p ~ 0.3). If the conductance equals the speed of the pump, the speed of evacuation will be half the speed of the pump. Even if the conductance could be three times the speed of the pump, the speed of evacuation would still be only three-quarters that of the pump.

Figure 3 Effect of pumping line conductance C in reducing evacuation speed S _e relative to pump speed S _p .

For example, if a 160 mm (6”) turbomolecular pump with a rated speed of 500 liters per second is attached to a vacuum chamber through a valve of negligible impedance and a one-meter length of 160 mm diameter tubing (C = 407 l/s, C/S _p = 0.8), the speed of evacuation will be a little less than one-half the speed of the pump or about 225 l/s. If the length of the tubing is reduced to one-half meter (C = 695 l/s, C/S _p = 1.4) the speed of evacuation will increase to about six-tenths the speed of the pump, or about 300 liters per second. A further reduction in the length of the pumping line will produce a further increase in speed of evacuation, and mounting the pump directly onto the vacuum chamber (again, through a well-designed valve) will increase the speed of evacuation to essentially that of the pump.

How Big Should the Pump Be?

Now the question often arises as to just how large of a pump a vacuum system should have. The answer is quite interesting, although somewhat complicated and difficult to specify exactly. Consider a bell jar 18” (460 mm) in diameter and 30” (760 mm) high, about the largest size commonly available, whose volume would be about 125 liters. Also assume the evacuation system consists of a ridiculously small oil diffusion pump with a diameter of 63 mm and a rated speed of 150 l/sec that is connected to this bell jar through a valve and a tube 63 mm in diameter and one-half meter long (C = 52 l/sec). As shown in Figure 2, oil diffusion pumps start to make significant contribution to the evacuation process when the roughing pump reduces the pressure in the system P _s to about one Pascal. At this point the pump’s speed is about one-half the rated value, or about 75 l/sec for our pump. Thus, our effective initial speed of evacuation would be about S _evac ~ (52 × 75)/(52 + 75) = 31 l/sec.

Now one characteristic of a vacuum system that is of prime importance to the operator is the rate at which it pumps down. For a system with a volume V _s and a speed of evacuation S _evac , the rate at which the pressure in the system P _s decreases is given by R _PmpDn = -(P _s /V _s )S _evac. Using this equation and these assumptions, the initial pump down rate for this bell jar system would be about R _PmpDn. = -(1/125)31 = -0.5 Pa/sec. Since the pressure in the bell jar is only 1 Pa, this suggests that this unrealistically small pumping system should be able to pump this rather large vacuum chamber down in few seconds.

Anyone who has ever operated a vacuum system knows that this is not the way it goes. What actually happens is that there is an initial rapid decrease in P _s as the high-vacuum pump starts to function and remove the free gas molecules from the system. Then the rate at which P _s decreases slows down markedly. This is because gas molecules (principally water molecules) desorb from surfaces inside the vacuum system causing a pressure increase that opposes the pump-out process and prolongs the evacuation time considerably [Reference Bigelow1]. This is particularly true if the system contains fixtures that have a lot of screws and close-fitting parts that release trapped gas molecules very slowly. The very short pump down time suggested by the above calculations is that which would be required to remove the initially free gas molecules. The actual pump down rate must take into account the rate of pressure increase produced by this gas desorption process. This is given by the rate of desorption q (Pa-liters/sec) divided by the volume of the system (that is, q / V _s l/sec). This rate of gas desorption is almost impossible to measure accurately, or even estimate for any given vacuum system, because it depends on so many different factors. Many of these are discussed in my book on Vacuum Methods in Electron Microscopy [Reference Bigelow2]. Qualitatively, however, its effect is to add a positive term to the equation for the pump down rate, which then becomes the following [Reference Bigelow1]:

(9) $${\rm R}_{{{\rm PmpDn}}} {\equals}\left( {q\,/\,V_{s} } \right){\minus}\left( {{{P_{s} } \mathord{\left/ {\vphantom {{P_{s} } {V_{s} }}} \right. \kern-\nulldelimiterspace} {V_{s} }}} \right)S_{{evac}} \;{1 \mathord{\left/ {\vphantom {1 {{\rm sec}}}} \right. \kern-\nulldelimiterspace} {{\rm sec}}}$$

where q = desorption rate, V _s = system volume, and S _evac = speed of evacuation. Thus, the performance of a vacuum system depends critically on both the speed of evacuation and the characteristics of its interior surfaces. While a very small pump could handle the free gas molecules in a very large system, it is desirable to have a large, high-speed pumping system to handle this gas-desorption problem. However, large pumps, valves, and other fixtures are very expensive, and so cost may become an overriding factor. In the end designers of vacuum systems have to compromise between producing an expensive unit with a very large pumping system that provides a short pump down time and one with a more modest, but less expensive, pumping system that may pump down somewhat more slowly. It should also be apparent that ultimately the performance of a vacuum system can be strongly affected by what is put inside it and how well its interior is kept clean and dry.

Ultimate Pressure

From the above discussion it should be apparent that both the speed of evacuation and the rate of gas desorption are important parameters in determining the performance of a vacuum system. Although this discussion has focused on the pump down rate, it is also interesting to note that these two parameters critically determine the ultimate pressure attainable in a vacuum system. This is so because the evacuation process causes the pressure P _s in the system to decrease so that ultimately the value of the second term in the above rate equation decreases to the level of the first, whereupon R _PmpDn = 0, and q = P _s S _evac . Then no further decrease in pressure will occur. The pressure that has been reached at this point is called the ultimate pressure. It is given by the simple equation P _ult = q/S _evac that involves only these two critical parameters. From this last equation, it is easy to see why ultra-high vacuum, say 10^-8 Pa, requires baking of the entire vacuum chamber to reduce q to a low value.