Introduction
The basic design of a light microscope has not changed much in the last several decades. How we use them, however, has changed dramatically and continues to evolve at a rapid rate. In part this evolution is driven by improvements in components that have allowed microscopists to approach imaging in new and creative ways. The evolution of various super-resolution approaches to microscopy, for instance, are based on radical reconceptualizations of image information collection and analysis [Reference Requejo-Isidro1]. Some new approaches have been made possible by improvements in certain microscope components. One key component that has undergone rapid evolution is the image capture system. Although we still call these systems cameras, they are a far cry from the film-based cameras with which many of us started our careers. In fact, current high-end capture devices constitute a group of hardware and software components adapted for specific types of microscopy. They have even shattered our definitions of resolution, since standard definitions of microscope resolution were based on theories that assumed the detection device would be the human eye. Many of today’s detection devices can outperform at least certain aspects of human vision by orders of magnitude. These advances in technology have provided a plethora of image capture devices and allowed new approaches to capturing image information. Super-resolution microscopy is but one of the fields that has been made possible by advances in image capture technology [Reference Small2].
Although these advances allow microscopists to ask a much wider array of questions, they also necessitate the judicious choice of systems adapted to specific needs. In this rapidly evolving field, it is very difficult to adequately review all possible choices. In general, however, image capture in the microscope can be divided into two collection schemes—one in which an entire field of view is captured simultaneously and the other where image information is collected sequentially by illuminating the specimen point-by-point and reconstructing a two-dimensional image from the individual data points. Laser scanning confocal microscopes are an example of the latter. Each approach to image data capture has distinctly different detector requirements. In this article, we will limit our discussion to simultaneous image collection systems that do not discriminate wavelengths (that is, monochrome cameras).
Materials and Methods
Digital image capture
Simultaneous image detectors are solid-state electronic devices composed of arrays of discrete photodetectors. Each detector captures photons coming from its respective area of the specimen and converts this information to an electrical signal that is proportional to the amount of light sensed by the detector. The electrical signal is converted to digital information that can be stored or displayed. There are some key points regarding this process. First, the digital information is discrete and limited. Individual values must be in whole multiples of a single quanta of information; whereas, the analog information coming in to the system can have any real number value. Thus, information is lost during the analog to digital conversion. Understanding what information is lost and knowing how to minimize the loss is a critical aspect of modern microscopy. The second key point is that the capture device is divided into discrete sensors that correspond to the pixels of the acquired image. Thus, the size of the individual discrete photodetectors helps set the limit of how small an object can be detected; more on this later.
CCD and CMOS
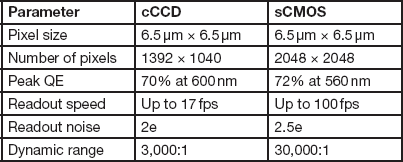
Most microscope photodetector systems have some form of charged coupled device (CCD) or complementary metal oxide semiconductor (CMOS) as the image sensor. Although there are a number of similarities, there are also dramatic differences between these two approaches [Reference Magnan3]. The CCD contains a two-dimensional array of photodiodes (Figure 1). During image capture, charge builds up in each photodiode (pixel). Image capture is then ended, and the information is read out sequentially. There are various schemes for reading out, but essentially the charge cloud of each pixel is transferred one at a time to an amplifier that measures the value of the charge and converts it to a voltage. Associated electronic devices then reduce noise, digitize the values, and output the digital value for storage in computer memory. The main drawback of the CCD design is the sequential transfer time, which limits how fast individual images can be acquired because all pixel charge transfer processes must be completed before a new image can be collected.
Figure 1 Schematic diagram of a CCD sensor with an array of photodetectors arranged geometrically. For CCDs the charge is read out sequentially one photodetector at a time, which limits the frame rate.
Cameras employing CMOS technology also have a two-dimensional array of photodetectors that convert photons to electrical charge in a manner proportional to the photon energy absorbed. However, on a CMOS chip the amplification and digitization steps happen at each individual sensor in parallel before the information is passed off the chip for storage (Figure 2). This parallel processing approach dramatically reduces the time it takes to readout image information and prepare the sensor array to capture another image. One of the trade-offs for this increased speed, however, is that there is increased pixel-to-pixel variability since each pixel has its own separate amplifier circuit.

Figure 2 Schematic diagram of a CMOS sensor. Here the charge is read out and amplified simultaneously for each individual sensor. This parallel approach allows much faster readout.
Even just five years ago, choosing between a CCD and CMOS camera was fairly simple. One chose a CCD for high resolution or a CMSO to capture rapid events. With current developments, particularly the advent of scientific CMOS (sCMOS) systems, the choice is not as clear-cut. One needs to delve deeper into the specifics of each camera system in order to match the system to your needs. Unfortunately, comparisons can be frustrating because there are so many aspects of the camera response that could be evaluated. In my experience, however, there are really only a handful of features that need to be considered in order to make a rational decision about which camera system best matches your application.
Pixel size
One of the key components to consider is the size of the individual photodetectors (pixels). This determines the spatial resolution limit of the sensor. For a given magnification, smaller pixel size allows finer image features to be captured. However, this is not the only determinant of spatial resolution. As individual pixel size gets smaller, its photon capacity (how many photons before it becomes saturated) decreases. Thus, smaller pixels typically have lower signal-to-noise ratios and lower dynamic range [Reference Chen4]. Cooling the camera below room temperature can help reduce noise in cameras with smaller pixels. Today, most high-resolution microscope cameras, cooled CCD (cCCD), and cooled sCMOS with pixel size around 6.5 µm, will provide full microscope resolution with good dynamic range and signal-to-noise characteristics [Reference Jerome5]. Table 1 compares some key attributes of recent cCCD and sCMOS cameras with a sensor size of 6.5 µm2. Recently some newer cCCD cameras have been introduced with a sensor size of 4.5 µm and reasonable signal-to-noise ratios. In general, systems using CMOS technology have a little more noise than CCD systems of equivalent sensor size. In practice, however, I have not found the difference to be very noticeable. Of course, specific tests always should be run to determine the highest spatial resolution the sensor is capable of obtaining under your specific conditions.
Table 1 Comparison of typical cooled CCD and sCMOS cameras.
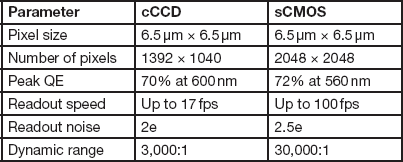
Note: sCMOS has much faster acquisition speeds and a much larger dynamic range, while the cCCD has lower read noise.
Resolution is often stated as the total number of megapixels or the pixels per inch of a system. I find these parameters much less useful than the individual pixel dimensions. Megapixels and pixels per inch do not provide the critical information regarding the smallest object in your sample that can be effectively captured. The number of megapixels is not totally useless; it does indicate how large a field of view can be captured, but it provides little information about the spatial resolution within that field of view. A pixel’s per inch value is derived from the pixel size, so you can calculate sensor size from pixels per inch and the number of pixels along one direction of the sensor. But why not just look at the sensor size directly for comparing maximum achievable spatial resolution between different camera systems?
Obviously, the microscope magnifies the image of an object onto the camera sensors. Thus, one must consider how large the image of the smallest resolvable object in the specimen has become when it is projected onto the cCCD or sCMOS photodectors. If one wants to capture the full resolution available with a particular lens, one needs to make sure that the camera chosen is capable of sampling the full resolution. Table 2 compares the effect of image magnification on the sampling of a diffraction-limited spot. All the lenses listed have a numerical aperture (NA) of 1.4 and are capable of resolving a structure about 0.2 µm in diameter. In this example, the microscope provides an additional 1.25× magnification over that of the objective lens. Thus, a 40× lens producing 50× magnification would project a 0.2 µm spot to a spot with diameter of 10 µm. The Nyquist-Shanon theorem indicates that this 10 µm diameter object would need to be sampled at least two times in the X direction and two times in the Y direction. A sensor size of 5 µm × 5 µm or less would be necessary to adequately sample this projected image. So a 6.5 µm × 6.5 µm photodetector would not capture the full diffraction-limited resolution of the lens. However, a 63× or 100× lens would project an image that was adequately sampled at greater than the Nyquist frequency.
Table 2 Magnified microscope image projected onto a 6.5 µm2 camera pixel.

Note: A 40× NA 1.4 lens on a microscope with a 1.25× magnification factor at the camera (total magnification 50×) would project a 0.2 µm object (the smallest object that can be resolved at NA 1.4) as a 10 µm diameter image on the camera. This would not be sufficiently sampled by a standard 6.5 µm × 6.5 µm photodiode. Adequate sampling is possible with the 63× and 100× objective lenses.
If your sensor size is smaller than that required to adequately sample the smallest object of interest at the Nyquist frequency (such as the 100× lens in Table 2), you can improve the signal-to-noise ratio of your image by binning the pixels. This involves combining the signal from multiple sensors into one “super pixel.” Usually this involves combining a 2 × 2 array of pixels (Figure 3). This increases the possible maximum signal by a factor of 4 but also reduces the spatial resolution by 50 percent [Reference Jerome5]. Binning of CCD pixels also allows for faster readout of the information. With CMOS systems, since the binning occurs after image readout, there is no increase in speed with binning. Most sensors developed for microscopy are equipped with the ability to bin pixels, but you should confirm this by testing the binning capability of any system before purchase.

Figure 3 Example of binning. When the full lateral resolution of a sensor array (either CCD or CMOS) is not required, the charge from several sensors can be combined into a single value. This is called binning. The yellow sensors indicate a 2 × 2 binning to create a “super” sensor. By combining the signal from 4 adjacent photosensors, the signal-to-noise ratio is increased.
Frame rate
The frame rate of a camera refers to the number of full frames that can be captured per second. Digital camera systems allow you to adjust the frame rate up to some maximum. This is where the parallel processing design of CMOS cameras clearly has an edge. Maximum frame rates for CMOS systems will be faster than for CCD systems, although some clever tricks have improved CCD frame capture rates. For both systems, however, faster frame rates mean reduced exposure time so the signal-to-noise ratio decreases as you increase the frame rate.
Quantum efficiency
Quantum efficiency (QE) is a measure of the effectiveness of the conversion of photons to charge. If every photon were converted to an electron, the QE would be 1 (100%). The quantum efficiency of a sensor is not uniform across the spectrum. Both CCD and CMOS detectors tend to have less QE at the ends of their usable wavelength ranges. Several years ago, the QE of CMOS cameras was significantly worse than for CCD systems, but the most recent CMOS designs rival the QE of CCD sensors. At their maximum, QE values are about 0.6.
Spectral response
The spectral response of the camera refers to how well specific wavelengths are detected by the sensor (Figure 4). Both CCD and high-end (scientific) CMOS sensors are sensitive to wavelengths between 400 nm and 1000 nm. However, since the quantum efficiency is not uniform across the entire spectrum, one should always check the spectral response curve of the specific system you are considering. There is usually some sensitivity in the near-infrared (NIR) range if you need to detect signals in this range. The CMOS sensors tend to be better in this range than do CCD sensors.

Figure 4 Representative response curve for a CCD photosensor. The sensor has reasonable quantum efficiency across the full visible spectrum. However, the quantum efficiency is not equivalent for all wavelengths; the peak efficiency of 73% is achieved at a wavelength of 560 nm.
Dynamic range
The dynamic range of a camera indicates how many separate and distinct gray levels the camera is capable of detecting and storing. In other words, it indicates the lowest light level the sensor can detect and how many photons a sensor can collect before it is saturated. If there is a large difference between the lowest light detectable and saturation, it is easier to discriminate subtle differences in the light coming from different areas of the specimen. A good way to think about this is if my lowest detectable level has a value of 2 and saturation is at a value of 12, then 2 defines what will be represented as black in my image and 12 as white. Between black (2) and white (12) I must divide all of the various shades of gray in my sample into only 9 levels (values 3 to 11). Thus subtle differences in shading will not be captured and stored. On the other hand, if the lowest value is 2 and the highest value is 200, I can capture and store much more subtle changes in light intensity. Therefore, the greater the dynamic range, the better the camera is at capturing small shading differences within a specimen. The dynamic range is the full well capacity of the sensor divided by the read noise. The dynamic range is often reported as a ratio. A designation of 3,000:1 would indicate a range from 1(black) to 3,000 (white). The dynamic range can also be reported as how many digital bits of information can be discriminated. A 12-bit detector will have a range of 4096:1 (212 = 4096). The dynamic range will be different at different frame capture rates, so you should compare camera systems at the frame rate you need in your experiments. Dynamic range is another area where CCD systems traditionally exceled, but sCMOS cameras now usually have much better dynamic range.
Read noise
Read noise is the inherent electronic noise in the system. The noise level of the camera is important in determining the dynamic range and also in determining how efficient the camera will be in low-light situations. Read noise goes up as frame rates increase. Thus, although sCMOS cameras are capable of frame rates as high as 100 frames per second, these rates are only useful if you have a very strong signal. For very low-light situations, a modification of the CCD approach called electron-multiplying CCD (EM-CCD) is available. In EM-CCDs the electrons from each photodetector pass through a multi-stage gain register. In each stage of the gain register, multiple electron impact ionization events increase the number of electrons so that the number of output electrons is dramatically increased. EM-CCD cameras are thus very sensitive in low-light situations. However, the photodiode size is generally larger than those of traditional cCCDs.
Dark noise
Dark noise is that generated by temperature excitation of electrons within the photodetector. Cooled CCDs reduce the dark noise by reducing the temperature. Cooled CCDs exhibit much lower dark noise than equivalent-sized sCMOS sensors. In fact, for most situations the dark noise of cCCD is negligible; not so with sCMOS. However, sCMOS manufacturers in the last few years have greatly reduced the dark noise on their chips, and we may soon see a time when sCMOS dark noise is a negligible contributor to overall readout.
Discussion
Microscope camera manufacturers are happy to provide you with a long list of specifications for their systems, especially in those areas where their specifications exceed their closest competition. However, I have found that the few parameters described above are sufficient to narrow down the potential list of cameras that would be useful for a specific purpose. Then, despite what the specifications sheet might indicate, I always compare systems on my microscopes with my specimens to make sure that the camera system is appropriate for my needs. The practical test is necessary because there is chip-to-chip variability and also because each manufacturer includes hardware and software in their camera that alters the initial photon signal collected by the photodiode. This signal processing is an integral part of the camera, but that means two cameras from different manufacturers with the same CCD or CMOS chip may have different performance.
Conclusion
Modern CCD and CMOS detectors are the sensors of choice for high-resolution microscope camera systems. Each has its unique features, and deciding which approach best meets your research needs can be daunting. In my experience, the parameters that are the most helpful for deciding if a particular camera system will meet your needs are: pixel size, frame rate, quantum efficiency, spectral response, dynamic range, and noise. In general, sCMOS systems provide faster acquisition speed and enhanced dynamic range, while cCCD systems offer better low-light sensitivity and more uniformity across the image field for cameras with the same pixel size. EM-CCD can provide even better low-light sensitivity and improved dynamic range compared to traditional cCCD systems but usually have larger pixel size. Once you have sorted out the camera specifications to find potential cameras useful for your applications, always test the cameras under your conditions to make sure the camera is appropriate to your needs.