For a beam-sensitive specimen, the spatial resolution of TEM analysis is limited by radiation damage, and it is obviously a good thing to minimize the amount of damage that occurs during a measurement. Knock-on displacement damage, which predominates in metals, can be reduced by lowering the accelerating voltage (ideally below a threshold value that depends on atomic weight and displacement energy). Ionization damage (radiolysis), which predominates in organic materials, is often ameliorated if the specimen is cooled below room temperature.

My proposal is that, whenever TEM results are presented from a beam-sensitive specimen, the microscope voltage and specimen temperature should be quoted, along with an estimate of the electron dose used to record the data. This dose (or fluence) is easily calculated as D = IT/A, where I is the incident-beam current, A is the irradiated area of specimen, and T is the recording time. The current can be measured by connecting a picoammeter to a Faraday cup at the specimen plane. Or with no specimen in the beam, the picoammeter is attached to the drift tube of an electron spectrometer or to an electrically isolated TEM screen, biased to at least +10 V to prevent emitted secondary electrons from leaving. The beam current can also be deduced from the counts in a CCD camera, if the latter is calibrated in terms of incident electrons.

An inverse measure of the radiation sensitivity of a specimen is the critical dose D _c at which observable changes occur in its image (for example, loss of crystalline structure or reduction in local thickness within the beam), in its diffraction pattern (fading of diffraction spots of rings), or in its energy-loss spectrum (a loss of fine structure due to increasing disorder, or loss of specific elements as deduced from ionization edges). These different measurements yield different values of D _c, and the critical dose depends also on whether it is based on the smallest detectable change, or on some chosen feature being reduced by a factor of e = 2.718 (sometimes called a characteristic dose), or on complete loss of that feature (giving a so-called end-point dose). However, these doses often lie within an order of magnitude (factor of 10) of each other, whereas values for different materials vary by several orders of magnitude, so accuracy is not essential and usually not achievable.

If D _c has been previously measured for a material similar to that of the specimen, the measurement dose D can be compared with that previous estimate to decide whether damage is likely to have occurred. For radiolytic damage, D _c is roughly proportional to accelerating voltage (more exactly: square of the incident-electron speed) so a correction may be needed. Also, D _c increases with decreasing specimen temperature, typically by a factor of 2–20 between 300 K and 100 K. If D _c has not been previously measured, a measurement at known temperature and accelerating voltage represents valuable information that should be quoted so that it can be added to our knowledge base, in the absence of methods for calculating critical dose.

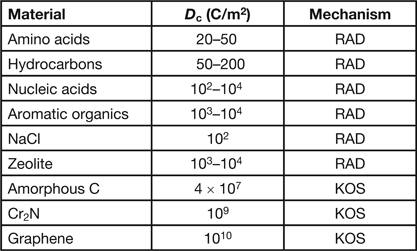
Table 1 shows the critical dose for a few organic and inorganic specimens exposed to 100 keV electrons. For knock-on sputtering, the quoted dose is for the removal of a monolayer of atoms from the beam-exit surface. Knock-on displacement of atoms within a crystal is not represented in Table 1 because it typically requires an accelerating voltage above 300 kV, although for pure Si the threshold appears to be about 220 kV.

Table 1: Typical critical dose D _c values for electron-beam damage to various materials at 100 kV accelerating voltage and for a room-temperature specimen together with the damage mechanism (RAD = radiolysis, KOS = knock-on sputtering). For further information, see [Reference Reimer and Kohl1, Reference Hobbs2, Reference Egerton3].

The concept of critical dose is based on the assumption that the damage is proportional to the energy deposited per unit volume by inelastic scattering, just as for ionization damage produced by X rays. In the X-ray community, dose is measured in Grays, where 1 Gy = 1 J/kg, and the conversion is:

$$ {\rm Grays} = ({\rm C/m}^2 )[10^6 /\lambda _{\rm i} ({\rm nm})](E_{{\rm av}} /\rho ) $$

Here λ_i (nm) is the electron mean free path for inelastic scattering, E _av is the average energy loss per inelastic collision, and ρ is the specific gravity (density in g/cm²). For 100 kV accelerating voltage and a typical organic material, λ_i ~ 100 nm, E_av ~ 35 eV and ρ ~ 1.4, so 1 C/m² is equivalent to about 0.25 MGy.

In the case of inorganic specimens, however, there is ample evidence that radiolysis depends on dose rate (current density) as well as accumulated dose. Dose-rate effects can arise because of secondary processes that follow the primary ionization, such as time-dependent diffusion or recombination (back-reaction) events.

Although knock-on damage has become troublesome, now that bright electron sources and aberration-corrected lenses can deliver current densities exceeding 10⁷ A/cm², radiolysis (where it occurs) can be a much more efficient process, as seen by the low D _c values in Table 1. In fact, the value of D _c often suggests the damage mechanism and the measures that can be taken to minimize the damage.

But are there general predictors for radiolysis? Poor electrical conductivity seems to be one, long minority-carrier lifetime another. Perhaps we cannot generalize, and everything depends on the energy-band structure of the specimen. Can time-dependent quantum mechanics be used to model radiolysis in a simple compound? Much more work needs to be done to answer such questions, and unfortunately it seems hard to get funding for such research. If so, perhaps our best hope is that this area of inquiry might appeal to retired university professors who can survive on a pittance.

But to repeat, please quote your dose, voltage, and temperature!