Calculation of Simulated STXM Spectra

We first simulated STXM spectra from a model system of trivial structure and known composition. Experimentally, STXM spectra are generated by measuring the same sample repeatedly across a range of energies. This provides an energy spectrum at each point in the material after the registration of the images. Those spectra will change from point to point according to the sample's chemical heterogeneity. Though poor image alignment can result in spectral distortions similar to what we discuss below, that step is not required for the simulation. The assumed sample consists of a semi-infinite region on the left (x < 0) consisting of one material and a semi-infinite region on the right made of another material of a different column density. Thus, the relevant characteristic of the focusing element is its knife-edge profile, which is the result of scanning the probe over the interface between a fully transparent region and one which is fully opaque. Thus, the knife-edge profile may be defined as follows:

(1)$$K( x) = \int_0^\infty {d{x}^{\prime}} \int_{-\infty }^\infty {dy{\rm PSF}( x-{x}^{\prime}, \;y) }, $$

where PSF(x,y) is the point spread function of the probe and the scan direction is taken as x. To calculate what this would be, we start with the two-dimensional Airy disk from a zone plate with a central stop, for which PSF is given by the following equation:

(2)$${\rm PSF}( r) {\kern 1pt} = {\kern 1pt} \left({\displaystyle{{2fa} \over {q( a^2-b^2) }}( {J_1( {raq}/f) -( b/a) J_1( {rbq}/f) } ) /r} \right)^2, $$

where q = 2π/λ, f is the focal length, a is the outer radius, J ₁ is the J Bessel function of order 1, and b is the inner radius. The parameters used here are a = 125 μm, b = 45 μm, energy = 300 eV, and f = 1.5 mm, which are typical among conventional STXMs using a 25 nm outer zone width optics (Rayleigh resolution of 31 nm). To get the knife-edge profile, K(x) (x is the scan direction) we integrate (numerically) twice, once to get a line profile, i.e. the intensity pattern for an infinitely narrow vertical slot, and again to sum over positions of that slot for x ∈ [0,∞). Using the well-known asymptotic form of the J Bessel function, one can show that the PSF has an asymptotic r ⁻³ +(oscillatory) form due to its sidelobes. The double integration that yields K(x) turns the distant sidelobes into an asymptotic x^{− 1} dependence, reflecting a long-range character.

In all that follows, we make the assumption made in the ptychographic theory (Guizar-Sicairos et al., Reference Guizar-Sicairos, Johnson, Diaz, Holler, Karvinen, Stadler, Dinapoli, Bunk and Menzel2014), which is that the electric field at any point ${\vec{x}}^{\,\prime}$ on the downstream surface of the sample is the product of the probe field and the sample field transmission:

(3)$$\psi ( \vec{x}, \;{\vec{x}}^{\,\prime}) = O( \vec{x}\,) P( {\vec{x}}^{\,\prime}-\vec{x}\,), $$

where $\vec{x}$ is the center position of the probe, $O( \vec{x}\,)$ is the field transmittance of the sample at point $\vec{x}$, and $P( \vec{y}\,)$ is the probe field at point $\vec{y}$. The transmitted intensity is the squared magnitude of the field:

(4)$$I( \vec{x}, \;{\vec{x}}^{\,\prime}) = T_{{\rm samp}}( {\vec{x}}^{\,\prime}) {\rm PSF}( {\vec{x}}^{\,\prime}-\vec{x}\,), $$

by definition of the PSF and T _samp = |O|². The measured transmission, $T( \vec{x}\,)$, is the integral over the sample surface of the local intensity:

(5)$$T( x) = \int {d^2{\vec{x}}^{\,\prime}T_{{\rm samp}}( {\vec{x}}^{\,\prime}) {\rm PSF}( {\vec{x}}^{\,\prime}-\vec{x}\,) } \;.$$

Now, the simulated sample we consider has a step-function transmission:

(6)$$T_{{\rm samp}}( \vec{x}\,) = \left\{{\matrix{ {T_1\;x < 0} \cr {T_2\;x \ge 0} \cr } } \right. = T_2\theta ( x) + T_1( 1-\theta ( x) ), $$

where θ(x) is the Heaviside step function and x is the component of $\vec{x}$ along the scan direction, i.e. perpendicular to the interface. Given that the PSF has circular symmetry, we can express (5) as a double integral in x and y (the direction along the interface):

(7)$$T( x) {\kern 1pt} = \int_{-\infty }^\infty {d{x}^{\prime}T_{{\rm samp}}( {x}^{\prime}) } \int_{-\infty }^\infty {d{y}^{\prime}{\rm PSF}\left({\sqrt {{( x-{x}^{\prime}) }^2 + {{y}^{\prime}}^2} } \right)} , $$

where we can take y = 0 without loss of generality. Substituting (6) into (7) and defining the PSF as normalized to have an integral of 1, we have

(8)$$\eqalign{T( x) {\kern 1pt} & = {\kern 1pt} T_1\int_0^\infty {d{x}^{\prime}\int_{-\infty }^\infty {d{y}^{\prime}{\rm PSF}\left({\sqrt {{( x-{x}^{\prime}) }^2 + {{y}^{\prime}}^2} } \right)} } \cr &+ T_2\left({1-\int_0^\infty {d{x}^{\prime}\int_{-\infty }^\infty {d{y}^{\prime}{\rm PSF}\left({\sqrt {{( x-{x}^{\prime}) }^2 + {{y}^{\prime}}^2} } \right)} } } \right)\cr & = {\kern 1pt} K( x) T_1 + ( 1-K( x) ) T_2}, $$

where K(x) is the knife-edge profile of the probe.

Adding the energy dependence, the transmission through the sample, which is assumed to be of uniform thickness, is given by the following equation:

(9)$$\eqalign{T( x, \;E) & {\kern 1pt} = {\kern 1pt} K( x) T_1( E) + ( 1-K( x) ) T_2( E) \cr & = {\kern 1pt} K( x) \exp ( -{\rm O}{\rm D}_1S_1( E) ) \cr & \quad + ( 1-K( x) ) \exp ( {-}OD_2S_2( E) ) } , $$

where S _{1, 2}(E) are the assumed spectra of the materials on either side of the interface and OD_{1, 2} their effective thicknesses. These quantities S _{1, 2}(E) are proportional to the absorption coefficients (linear or mass) of the standard substances but normalized as convenient to be dimensionless. The idea is to remove dependence on details such as sample thickness. The extracted OD is the negative natural logarithm of this. Thus, the extracted spectrum at any point is,

(10)$$S( x, \;E) {\kern 1pt} = {\kern 1pt} -{\rm ln}( T( x, \;E) ) , $$

which is fitted to

(11)$$S_{{\rm fit}}{\kern 1pt} = {\kern 1pt} A_1( x) S_1( E) + A_2( x) S_2( E), $$

with the fit done for every x. Here, A _{1, 2} are local estimates of the number of species 1,2 such that if there were no spectral blur or distortion, A _1,2 would be equal to OD_1,2. They are derived by fitting the entire OD spectrum at each point to linear combinations of reference spectra, just as one would one when analyzing actual data. Note that in this analysis, the pre-edge absorption is considered to be just as much a part of the spectra of references and “sample” as the XANES part. When fitting the simulated pixel spectra, we fit the entire energy range including the pre-edge. This is the appropriate procedure for a system assumed to consist only of the two reference materials.

For our reference spectra, S _{1, 2}(E), we used C K-edge spectra of two polymers which have been used for organic photovoltaics, PC₆₁BM and P3HT (Ulum et al., Reference Ulum, Holmes, Barr, Kilcoyne, Gong, Zhou, Belcher and Dastoor2013), scaled so that S _{1, 2} = 1 at 320 eV, an energy beyond most of the chemistry-dependent features. These spectra are shown in Figure 1.

Fig. 1. Assumed reference spectra used in modeling of PC₆₁BM (black) and P3HT (red), normalized to make intensities at 320 eV equal 1.

Experimental Comparison of Conventional and Ptychographic Spectromicroscopy

We demonstrate the spectral mixing effect experimentally by studying a two-phase material with known endmembers using both ptychography and conventional STXM. For this purpose, we chose a partially delithiated particle of LiFe²⁺PO₄ similar to one which we have studied previously. When partially delithiated, micro-plates of LiFe²⁺PO₄ have a core shell type structure with a sharp phase boundary at the interface (Boesenberg et al., Reference Boesenberg, Meirer, Liu, Shukla, Dell'anna, Tyliszczak, Chen, Andrews, Richardson and Kostecki2013; Yu et al., Reference Yu, Kim, Shapiro, Farmand, Qian, Tyliszczak, Kilcoyne, Celestre, Marchesini and Joseph2015). The outer, fully delithiated shell is Fe³⁺PO₄ and has a roughly 100 nm width, while the core phase is more mixed with regions around morphological defects showing higher degrees of delithiation. This structure is ideal for our tests because it has a sharp interface between chemically distinct phases. However, the thickness is constant across the interface, so the large spectral distortion effect shown below for the simulated system with unequal thicknesses (Fig. 3) is not expected or seen.

The STXM and ptychography measurements were conducted at beamline 7.0.1.2 (COSMIC-Imaging) of the Advanced Light Source (Celestre et al., Reference Celestre, Nowrouzi, Padmore and Shapiro2018; Shapiro et al., Reference Shapiro, Celestre, Enders, Joseph, Krishnan, Marcus, Nowrouzi, Padmore, Park and Warwick2018) using a zone plate with inner and outer radii of 47.5 and 180 μm and 45 nm outer zones. To generate end-member reference spectra, we used Iterative Target Factor Analysis (Fernandez-Garcia et al., Reference Fernandez-Garcia, Marquez Alvarez and Haller1995) to find two apparent end-member spectra, then fit each pixel to linear combinations of these spectra, Then, we classified pixels by the loadings of each component in the fit and selected clusters of pixels having similar loadings within the cluster, but with the two clusters being as spectrally different from each other as possible. This procedure resulted in one cluster of pixels within the Fe³⁺PO₄-rich shell and another occurring within the LiFe²⁺PO₄-rich interior. The averaged spectra from these clusters were taken as the end-members for this test and are shown in a subsequent section. These spectra closely resemble ones previously derived from the Fe³⁺PO₄–LiFe²⁺PO₄ system¹⁴. For brevity, we refer to these end-members as FP and LFP, even though the compositions represented are somewhat mixed. Since the thickness of the particle was uniform, the normalization of the optical densities of the two end-member spectra is the same. A test for this supposition is that the sum of loadings for pixels in the Fe³⁺PO₄- and LiFe²⁺PO₄-rich areas should be equal, and they are, to within a few percent.

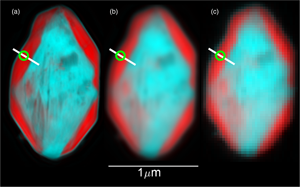
The STXM data were generated by two methods in order to confirm the effect of the PSF on the spectral content. First, conventional scanning microscopy data were generated in which total transmission is measured at each sample location by an integrating point detector. Second, for comparison, conventional image data were simulated by a convolution of high-resolution ptychographic reconstructions with the reconstructed probe. This will, in principle, generate STXM images with the same content as the conventional measurements but sampled on a high-resolution grid (5 nm pixels rather than 30 nm). For our tests of spectral distortion, we used the simulated STXM images because they are sampled on a finer grid than the actual STXM. The pixel spectra of the ptychography data were fit to sums of two end-member reference spectra, with nonnegative loading, plus a linear baseline. The results of this fit can be presented as a bicolor image, with red representing the loading of the FP end-member and cyan the LFP end-member. The STXM stack was derived by convolving each ptychographic image with the reconstructed probe function. The zone plate used had 45 nm outer zones and the probe had a diameter at a half-maximum value of 48 nm. The three versions (original ptychographic, simulated STXM, and real STXM) of the data are shown as bicolor images in Figure 4. In addition, non-ptychographic STXM was performed on the same sample, with the same zone plate in the same microscope as was used for the ptychographic stack (Fig. 4c).