Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-23T00:25:06.109Z Has data issue: false hasContentIssue false
  • English
  • Français

Localized Phonon Densities of States at Grain Boundaries in Silicon

Published online by Cambridge University Press:  16 March 2022

Peter Rez Open the ORCID record for Peter Rez [Opens in a new window] ,
Tara Boland ,
Christian Elsässer  and
Arunima Singh
Peter Rez*
Affiliation:
Department of Physics, Arizona State University, Tempe, AZ 85287-1504, USA
Tara Boland
Affiliation:
School For Engineering of Matter Transport and Energy, Arizona State University, Tempe, AZ 85287-6106, USA
Christian Elsässer
Affiliation:
Fraunhofer Institute for Mechanics of Materials IWM, Wöhlerstraße 11, 79108 Freiburg, Germany
Arunima Singh
Affiliation:
Department of Physics, Arizona State University, Tempe, AZ 85287-1504, USA
*
*Corresponding author: Peter Rez, E-mail: [email protected]
Get access

Abstract

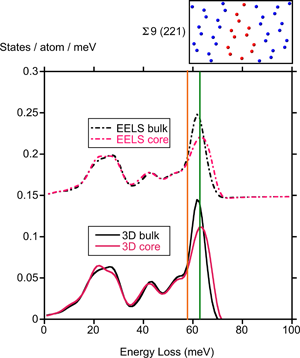
Since it is now possible to record vibrational spectra at nanometer scales in the electron microscope, it is of interest to explore whether extended defects in crystals such as dislocations or grain boundaries will result in measurable changes of the phonon densities of states (dos) that are reflected in the spectra. Phonon densities of states were calculated for a set of high angle grain boundaries in silicon. The boundaries are modeled by supercells with up to 160 atoms, and the vibrational densities of states were calculated by taking the Fourier transform of the velocity–velocity autocorrelation function from molecular dynamics simulations with larger supercells doubled in all three directions. In selected cases, the results were checked on the original supercells by comparison with the densities of states obtained by diagonalizing the dynamical matrix calculated using density functional theory. Near the core of the grain boundary, the height of the optic phonon peak in the dos at 60 meV was suppressed relative to features due to acoustic phonons that are largely unchanged relative to their bulk values. This can be attributed to the variation in the strength of bonds in grain boundary core regions where there is a range of bond lengths.

Keywords

DFT (density functional theory)EELS (electron energy-loss spectroscopy)grain boundarylocalized phononMD (molecular dynamics)
Type
Software and Instrumentation
Information
Microscopy and Microanalysis , Volume 28 , Issue 3 , June 2022 , pp. 672 - 679
Copyright
Copyright © The Author(s), 2022. Published by Cambridge University Press on behalf of the Microscopy Society of America

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ashcroft, NW & Mermin, ND (1976). Solid State Physics. Orlando, FL: Harcourt Inc.Google Scholar
Beeman, D & Alben, R (1977). Vibrational properties of amorphous semiconductors. Adv Phys 26(3), 339–361.CrossRefGoogle Scholar
de Koker, N (2009). Thermal conductivity of MgO periclase from equilibrium first principles molecular dynamics. Phys Rev Lett 103, 125902.CrossRefGoogle ScholarPubMed
Forbes, BD & Allen, LJ (2016). Modeling energy loss spectra due to phonon scattering. Phys Rev B 94, 014110.CrossRefGoogle Scholar
Forbes, BD, Martin, AV, Findlay, SD, D'Alfonso, AJ & Allen, LJ (2010). Quantum mechanical model for phonon excitation in electron diffraction and imaging using a Born-Oppenheimer approximation. Phys Rev B 82, 104103.CrossRefGoogle Scholar
Frank, W, Elsässer, C & Fahnle, M (1995). Ab initio force-constant method for phonon dispersions in alkali metals. Phys Rev Lett 74(10), 1791–1794.CrossRefGoogle ScholarPubMed
Haas, H, Wang, CZ, Ho, KM, Fahnle, M & Elsässer, C (1999). Temperature dependence of the phonon frequencies of molybdenum: A tight-binding molecular dynamics study. J Phys Condens Matter 11, 5455–5462.CrossRefGoogle Scholar
Hage, F, Kepaptsoglou, DM, Ramasse, QM & Allen, LJ (2019). Phonon spectroscopy at atomic resolution. Phys Rev Lett 122, 016103.CrossRefGoogle ScholarPubMed
Hage, FS, Radtke, G, Kepaptsoglou, DM, Lazzeri, M & Ramasse, QM (2020). Single-atom vibrational spectroscopy in the scanning transmission electron microscope. Science 367(6482), 1124.CrossRefGoogle ScholarPubMed
Hoover, WG (1985). Canonical dynamics: Equilibriium phase-space distributions. Phys Rev A 31, 1695–1197.CrossRefGoogle ScholarPubMed
Klein, ML, Martyna, GJ & Tobias, DJ (1994). Constant pressure molecular dynamics algoriths. J Chem Phys 101, 4177.Google Scholar
Kong, LT (2011). Phonon dispersion measured directly from molecular dynamics simulations. Comput Phys Commun 182(10), 2201–2207.CrossRefGoogle Scholar
Kresse, G & Furthmüller, J (1996 a). Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys Rev B 54, 11169–11186.CrossRefGoogle ScholarPubMed
Kresse, G & Furthmüller, J (1996 b). Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave set. Comput Mater Sci 6(1), 15–50.CrossRefGoogle Scholar
Kresse, G, Furthmüller, J & Hafner, J (1995). Ab initio force constant approach to phonon dispersion relations of diamond and graphite. Europhys Lett 32(9), 729–734.CrossRefGoogle Scholar
Kresse, G & Joubert, D (1999). From ultrasoft pseudopotentials to the projector augmented wave method. Phys Rev B 59(3), 1758–1775.CrossRefGoogle Scholar
Krivanek, OL, Lovejoy, TC, Delby, N, Aoki, T, Carpenter, RW, Rez, P, Soignard, E, Zhu, J, Batson, PE, Lagos, M, Egerton, RF & Crozier, PA (2014). Vibrational spectroscopy in the electron microscope. Nature 514, 209–212.CrossRefGoogle ScholarPubMed
Krivanek, OL & Maher, DM (1978). The core structure of extrinsic stacking faults in silicon. Appl Phys Lett 32, 451–453.CrossRefGoogle Scholar
Mott, AJ, Thirumuruganandham, SP, Thorpe, MF & Rez, P (2013). Fast calculation of the infrared spectra of large biomolecules. Eur Biophys J Biophys Lett 42(11–12), 795–801.CrossRefGoogle ScholarPubMed
Müser, MH & Binder, K (2001). Molecular dynamics study of the α–β transition in quartz: Elastic properties, finite size effects, and hysteresis in the local structure. Phys Chem Minerals 28(10), 746–755.Google Scholar
Nose, S (1984). A unified formulation of the constant temperature molecular dynamics method. J Chem Phys 117(1), 511–519.CrossRefGoogle Scholar
Ourmazd, A, Ahlborn, K, Ibeh, K & Honda, T (1985). Lattice and atomic structure imaging of semiconductors by high resolution transmission electron microscopy. Appl Phys Lett 47(7), 685–688.CrossRefGoogle Scholar
Perdew, JP, Burke, K & Ernzerhof, M (1996). Generalized gradient approximation made simple. Phys Rev Lett 77(18), 3865–3868.CrossRefGoogle ScholarPubMed
Plimpton, S (1995). Fast parallel algorithms for short range molecular dynamics. J Comput Phys 117(1), 1–19.CrossRefGoogle Scholar
Rez, P & Singh, A (2021). Lattice resolution of vibrational modes in the elctron microscope. Ultramicroscopy 220, 113162.CrossRefGoogle Scholar
Rohskopf, A, Seyf, HR, Gordiz, K, Tadano, T & Henry, A (2017). Empirical interatomic potentials optimized for phonon properties. Comput Mater 3, 27.CrossRefGoogle Scholar
Smith, DJ (2020). Atomic-resolution structure imaging of defects and interfaces in compound semiconductors. Prog Cryst Growth Charact Mater 66, 100498.CrossRefGoogle Scholar
Stoffers, A, Ziebarth, B, Barthel, J, Cojocaru-Miredin, O, Elsässer, C & Raabe, D (2015). Complex nanotwin substructure of an asymmetric Σ9 tilt grain boundary in a silicon polycrystal. Phys Rev Lett 115, 235502.CrossRefGoogle Scholar
Tersoff, J (1989). Modeling solid-state chemistry: Interatomic potentials for multicomponent systems. Phys Rev B 39(8), 5566–5568.CrossRefGoogle ScholarPubMed
Thomas, JA, Turney, JE, Iutzi, RM, Amon, CH & McGaughey, AJH (2010). Predicting phonon dispersion relations and lifetimes from the spectral energy density. Phys Rev B 81, 081411(R).CrossRefGoogle Scholar
Togo, A & Tanaka, I (2015). First principles calculations in materials science. Scr Mater 108, 1–5.CrossRefGoogle Scholar
Venkatraman, K, Levin, BDA, March, K, Rez, P & Crozier, PA (2019). Vibrational spectroscopy at atomic resolution with electron impact scattering. Nat Phys 15, 1237–1241.CrossRefGoogle Scholar
Wang, CZ, Chan, CT & Ho, KM (1989). Empirical tight-binding force model for molecular-dynamics simulation of Si. Phys Rev B 39(12), 8586–8592.CrossRefGoogle ScholarPubMed
Wang, CZ, Chan, CT & Ho, KM (1990). Tight-binding molecular-dynamics study of phonon anharmonic effects in silicon and diamond. Phys Rev B 42(17), 11276–11283.CrossRefGoogle ScholarPubMed
Yan, XX, Liu, CY, Gadre, CA, Gu, L, Aoki, T, Lovejoy, TC, Delby, N, Krivanek, OL, Schlom, DG, Wu, R & Pan, XQ (2021). Single-defect phonons imaged by electron microscopy. Nature 589, 65–69.CrossRefGoogle ScholarPubMed
Zeiger, PM & Rusz, J (2020). Efficient and Versatile model for vibrational STEM-EELS. Phys Rev Lett 124(2), 025501.CrossRefGoogle ScholarPubMed
Zeiger, PM & Rusz, J (2021 a). Frequency-resolved frozen phonon multislice method and its application to vibrational electron energy loss spectroscopy using parallel illumination. Phys Rev B 104, 104301.CrossRefGoogle Scholar
Zeiger, PM & Rusz, J (2021 b). Simulations of spatially and angle-resolved vibrational electron energy loss spectroscopy for a system with a planar defect. Phys Rev B 104, 094103.CrossRefGoogle Scholar
Ziebarth, B, Mrovec, M, Elsasser, C & Gumbsch, P (2015). Interstitial iron impurities at grain boundaries in silicon: A first-principles study. Phys Rev B 91, 035309.CrossRefGoogle Scholar
Supplementary material: File

Rez et al. supplementary material

Rez et al. supplementary material

Download Rez et al. supplementary material(File)
File 21.6 MB