Published online by Cambridge University Press: 26 February 2010
The object of this paper is to solve the Saint-Venant torsion problem for those cross-sections with inclusions, which are such that the z-plane boundaries involved can be mapped into concentric circles in a complex ζ-plane by the transformation
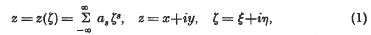
with z´(ζ) ≠ 0 or ∞ within the cross-section. We shall consider both solid and hollow inclusions having different elastic rigidities μ. In the case of the solid inclusion we have to restrict the coefficients as to be zero for all negative s, but it is an advantage to leave this restriction to the end of the analysis, since the forms of certain coefficients in the two cases differ only in this respect.