Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-23T12:59:14.890Z Has data issue: false hasContentIssue false
  • English
  • Français

Convex semi-lattices of continuous functions

Published online by Cambridge University Press:  26 February 2010

F. F. Bonsall
F. F. Bonsall
Affiliation:
Durham University, Newcastle-on-Tyne.
Get access

Extract

The purpose of this note is to settlo a question that was left incompletely solved in the author's paper [1].

Let E be a compact Hausdorff space, and C(E) the class of all continuous real-valued functions on E. A subset F of C(E) is called an upper semi-lattice (or, more briefly, is said to admit ں) if ƒ ں g ε F whenever ƒ, g ε F. A subset F of C(E) is said to be upper semi-equicontinuous (u.s.e.c.) if for every ε > 0 and s ε E there exists a neighbourhood U of s such that

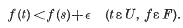
We say that F is locally u.s.e.c. if every uniformly bounded subset of F is u.s.e.c.

Type
Research Article
Information
Mathematika , Volume 7 , Issue 2 , December 1960 , pp. 113 - 116
Copyright
Copyright © University College London 1960

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1.Bonsall, F. F., “Semi-algebras of continuous functions”, Proc. London Math. Soc. (3), 10 (1960), 122–140.Google Scholar
2.Choquet, G. and Deny, J., “Ensembles semi-réticulés et ensembles réticulés de fonctions continues”, Journal de Math. Pures et Appliquées, 36 (1957), 179–189.Google Scholar