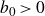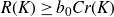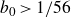1. Introduction
The ropelength of a knot K is defined as the minimum length among all knots in the ambient isotopic class of K with unit thickness [
Reference Cantarella, Kusner and Sullivan3, Reference Diao, Ernst and Jance Van Rensburg8, Reference Litherland, Simon, Durumeric and Rawdon11
]. A fundamental question in geometric knot theory asks how the ropelength R(K) of a knot K is related to Cr(K), the crossing number of K [
Reference Buck1–Reference Denne, Diao and Sullivan4, Reference Diao, Ernst, Por and Ziegler6
]. In the particular case that K is an alternating knot, a long standing conjecture, well known at least to researchers who study the ropelength problem, states that the ropelength of K is at least proportional to Cr(K). We prove that this conjecture is true. More specifically, we prove that there exists a constant
![]() $b_0 \gt 1/56$
such that
$b_0 \gt 1/56$
such that
![]() $R(K) \gt b_0Cr(K)$
for any alternating knot K.
$R(K) \gt b_0Cr(K)$
for any alternating knot K.
2. Reverse parallel links of alternating knots
Let K be a knot in
![]() $\textbf{S}^3$
. The regular neighbourhood of K on any orientable surface M embedded in
$\textbf{S}^3$
. The regular neighbourhood of K on any orientable surface M embedded in
![]() $\textbf{S}^3$
on which K lies is an annulus. Let A be such an annulus. The link formed by the boundaries
$\textbf{S}^3$
on which K lies is an annulus. Let A be such an annulus. The link formed by the boundaries
![]() $K^\prime$
,
$K^\prime$
,
![]() $K^{\prime\prime}$
of A is called a reverse parallel link of K if
$K^{\prime\prime}$
of A is called a reverse parallel link of K if
![]() $K^\prime$
,
$K^\prime$
,
![]() $K^{\prime\prime}$
are assigned opposite orientations. The linking number f between
$K^{\prime\prime}$
are assigned opposite orientations. The linking number f between
![]() $K^\prime$
and
$K^\prime$
and
![]() $K^{\prime\prime}$
when they are assigned parallel orientations is called the framing of K [
Reference Nutt12, Reference Rudolph13
]. The framing f is independent of the orientation of K and the ambient isotopy class of A in
$K^{\prime\prime}$
when they are assigned parallel orientations is called the framing of K [
Reference Nutt12, Reference Rudolph13
]. The framing f is independent of the orientation of K and the ambient isotopy class of A in
![]() $S^3$
depends only on K and the framing. Furthermore, the reverse parallel links of K are characterised by their framing numbers. That is, two reverse parallel links of K are ambient isotopic if and only if they have the same linking number. We shall denote a reverse parallel link of K with framing f by
$S^3$
depends only on K and the framing. Furthermore, the reverse parallel links of K are characterised by their framing numbers. That is, two reverse parallel links of K are ambient isotopic if and only if they have the same linking number. We shall denote a reverse parallel link of K with framing f by
![]() $\mathbb{K}_f$
following [
Reference Diao and Morton9
].
$\mathbb{K}_f$
following [
Reference Diao and Morton9
].
Let K be an alternating knot with a reduced diagram D. Let c(D) be the number of crossings in D and w(D) the writhe of D. It is known that
![]() $c(D)=Cr(K)$
is the crossing number of K. Also, all crossings of D are positive with respect to one checkerboard shading of D and are all negative with respect to the other checkerboard shading of D. Let
$c(D)=Cr(K)$
is the crossing number of K. Also, all crossings of D are positive with respect to one checkerboard shading of D and are all negative with respect to the other checkerboard shading of D. Let
![]() $v_+(D)$
be the number of regions in the shading with respect to which all crossings are positive, and
$v_+(D)$
be the number of regions in the shading with respect to which all crossings are positive, and
![]() $v_-(D)$
be the number of regions in the complementary shading with respect to which all crossings are negative, then
$v_-(D)$
be the number of regions in the complementary shading with respect to which all crossings are negative, then
![]() $v_+(D)+v_-(D)=c(D)+2$
[
Reference Kauffman10
]. The following results provide the key to solving the ropelength conjecture for alternating knots.
$v_+(D)+v_-(D)=c(D)+2$
[
Reference Kauffman10
]. The following results provide the key to solving the ropelength conjecture for alternating knots.
Theorem 2·1. [
Reference Diao and Morton9
] Let K be an alternating knot and D a reduced diagram of K. Let c(D), w(D),
![]() $v_+(D)$
and
$v_+(D)$
and
![]() $v_-(D)$
be as defined above, then the braid index of
$v_-(D)$
be as defined above, then the braid index of
![]() $\mathbb{K}_f$
, denoted by
$\mathbb{K}_f$
, denoted by
![]() $\mathbf{b}(\mathbb{K}_f)$
, is given by the following formula:
$\mathbf{b}(\mathbb{K}_f)$
, is given by the following formula:
 \begin{equation}\mathbf{b}(\mathbb{K}_f)=\left\{\begin{array}{ll}c(D)+2+a(D)-f, &\ {\rm if}\ f \lt a(D),\\[5pt] c(D)+2, &\ {\rm if}\ a(D)\le f \le b(D),\\[5pt] c(D)+2-b(D)+f, &\ {\rm if}\ f \gt b(D),\\ \end{array}\right.\end{equation}
\begin{equation}\mathbf{b}(\mathbb{K}_f)=\left\{\begin{array}{ll}c(D)+2+a(D)-f, &\ {\rm if}\ f \lt a(D),\\[5pt] c(D)+2, &\ {\rm if}\ a(D)\le f \le b(D),\\[5pt] c(D)+2-b(D)+f, &\ {\rm if}\ f \gt b(D),\\ \end{array}\right.\end{equation}
where
![]() $a(D)=-v_-(D)+w(D)$
and
$a(D)=-v_-(D)+w(D)$
and
![]() $b(D)=v_+(D)+w(D)$
. In particular,
$b(D)=v_+(D)+w(D)$
. In particular,
![]() $\mathbf{b}(\mathbb{K}_f)\ge c(D)+2$
for any f.
$\mathbf{b}(\mathbb{K}_f)\ge c(D)+2$
for any f.
Theorem 2·2. [
Reference Diao5
] Let L be an oriented link and
![]() $\mathbf{b}(L)$
be its braid index. Then
$\mathbf{b}(L)$
be its braid index. Then
![]() $\ell(L_c)\ge \mathbf{b}(L)$
where
$\ell(L_c)\ge \mathbf{b}(L)$
where
![]() $\ell(L_c)$
is the minimum length among all links in the ambient isotopic class of L that are embedded in the cubic lattice of
$\ell(L_c)$
is the minimum length among all links in the ambient isotopic class of L that are embedded in the cubic lattice of
![]() $\mathbb{R}^3$
.
$\mathbb{R}^3$
.
3. The ropelengths of alternating knots
Theorem 3·1. There exists a constant
![]() $b_0 \gt 1/56$
such that for any alternating knot K,
$b_0 \gt 1/56$
such that for any alternating knot K,
![]() $R(K)\ge b_0 Cr(K)$
.
$R(K)\ge b_0 Cr(K)$
.
Proof. Let
![]() $K_c$
be a knot on the cubic lattice that is ambient isotopic to K and has the minimum length among all lattice knots in the ambient isotopic class of K. Let
$K_c$
be a knot on the cubic lattice that is ambient isotopic to K and has the minimum length among all lattice knots in the ambient isotopic class of K. Let
![]() $\ell(K_c)$
be the length of
$\ell(K_c)$
be the length of
![]() $K_c$
, then we have
$K_c$
, then we have
![]() $R(K) \gt ({1}/{14})\ell(K_c)$
as a consequence from the proof of [
Reference Diao, Ernst and Jance Van Rensburg7
, lemma 1].
$R(K) \gt ({1}/{14})\ell(K_c)$
as a consequence from the proof of [
Reference Diao, Ernst and Jance Van Rensburg7
, lemma 1].
Now, the set
![]() $\{\textbf{x}+t(({1}/{2}, {1}/{2}, {1}/{2}): \textbf{x}\in K_c,\ 0\le t\le 1\}$
is an embedding of the annulus
$\{\textbf{x}+t(({1}/{2}, {1}/{2}, {1}/{2}): \textbf{x}\in K_c,\ 0\le t\le 1\}$
is an embedding of the annulus
![]() $\{1\le x^2+y^2\le 2:\ x, y\in \mathbb{R}\}$
into
$\{1\le x^2+y^2\le 2:\ x, y\in \mathbb{R}\}$
into
![]() $\mathbb{R}^3$
with
$\mathbb{R}^3$
with
![]() $K_c$
and
$K_c$
and
![]() $K_c^\prime=(({1}/{2}, {1}/{2}, {1}/{2}))+K_c$
as its boundary curves. Assigning
$K_c^\prime=(({1}/{2}, {1}/{2}, {1}/{2}))+K_c$
as its boundary curves. Assigning
![]() $K_c$
and
$K_c$
and
![]() $K_c^\prime$
opposite orientations yields a reverse parallel link
$K_c^\prime$
opposite orientations yields a reverse parallel link
![]() $L_c$
of K. Let
$L_c$
of K. Let
![]() $\mathbb{K}_c$
and
$\mathbb{K}_c$
and
![]() $\mathbb{K}^\prime_c$
be the lattice knots obtained from
$\mathbb{K}^\prime_c$
be the lattice knots obtained from
![]() $K_c$
and
$K_c$
and
![]() $K_c^\prime$
by scaling up with a scaling factor of 2, and let
$K_c^\prime$
by scaling up with a scaling factor of 2, and let
![]() $\mathbb{L}_c$
be the link formed by them. Notice that
$\mathbb{L}_c$
be the link formed by them. Notice that
![]() $\ell(\mathbb{L}_c)=4\ell(K_c)$
. By Theorem 2·1, we have
$\ell(\mathbb{L}_c)=4\ell(K_c)$
. By Theorem 2·1, we have
![]() $\mathbf{b}(\mathbb{L}_c)\ge Cr(K)+2$
. Then by Theorem 2·2, we have
$\mathbf{b}(\mathbb{L}_c)\ge Cr(K)+2$
. Then by Theorem 2·2, we have
![]() $\ell(K_c)\ge (Cr(K)+2)/4$
. Therefore
$\ell(K_c)\ge (Cr(K)+2)/4$
. Therefore
![]() $R(K) \gt ({1}/{14})\ell(K_c)\ge (Cr(K)+2)/56$
.
$R(K) \gt ({1}/{14})\ell(K_c)\ge (Cr(K)+2)/56$
.
Remark 3·2. The construction in the proof of [
Reference Diao, Ernst and Jance Van Rensburg7
, lemma 1] can in fact be improved to yield a better bound
![]() $R(K) \gt ({1}/{12})\ell(K_c)$
. This would allow us to improve the estimation of the constant
$R(K) \gt ({1}/{12})\ell(K_c)$
. This would allow us to improve the estimation of the constant
![]() $b_0$
to be at least
$b_0$
to be at least
![]() $1/48$
. It is certainly possible to further improve
$1/48$
. It is certainly possible to further improve
![]() $b_0$
by not using the lattice knots as a mid step.
$b_0$
by not using the lattice knots as a mid step.
Remark 3·3. Theorem 2·1 only applies to alternating knots, therefore the ropelength conjecture remains open in general for alternating links with two or more components.
Acknowledgement
The author is grateful to Hugh Morton for the key development of the theory in our joint work [ Reference Diao and Morton9 ].