Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T14:10:32.567Z Has data issue: false hasContentIssue false
  • English
  • Français

On the comparison of measure functions

Published online by Cambridge University Press:  24 October 2008

John Hawkes
John Hawkes
Affiliation:
Statistics Department, University College of Swansea, Singleton Park, Swansea SA2 8PP
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose that f and g are measure functions and that µf and µg are the corresponding Hausdorff measures. We are interested in how relationships between f and g are reflected in relationships between µf and µg and vice versa. For example, if

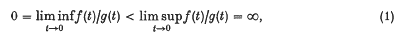
Rogers ((8), p. 80) has shown that there exists a metric space Ω which has subsets A and B with µf(A) = µg(B) = 0 and, µf(B) = µg(A) = ∞. We are more interested in what happens when the metric space in question is the real line. To get the above result we need to assume that both f and g are starshaped. This is just about a best possible result since if we assume only that f is a power of t the conclusion fails. Further-more we show that there exist measure functions f and g satisfying (1) such that µf and, µg are identical. We also consider related questions: when are, µf and, µg equivalent measures and when are they identical?

The proofs depend on the construction in Theorem 3.1 of a Cantor set having pre-scribed measure properties. Although the construction is not difficult it turns out to be quite useful to appeal to the existence of such a set. We illustrate this remark by giving a short proof of a known theorem on cartesian product sets. We also make use of these ideas in section 5 where we discuss some properties of a class of net meastues and give a partial answer to a problem posed by Billingsley.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 78 , Issue 3 , November 1975 , pp. 483 - 491
Copyright
Copyright © Cambridge Philosophical Society 1975

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Besicovitch, A. S. and Moran, P. A. P.The measure of product and cylinder sets. J. London Math. Soc. 20 (1945), 110–120.Google Scholar
(2)Billingsley, P.Ergodic theory and information (New York; John Wiley and Sons, 1965).Google Scholar
(3)Dvoretsky, A.A note on Hausdorff dimension functions. Proc. Cambridge Philos. Soc. 44 (1948), 13–16.Google Scholar
(4)Fristedt, B. E. and Pruitt, W. E.Lower functions for increasing random walks and subordinators. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 18 (1971), 167–182.Google Scholar
(5)Hawkes, J.On the potential theory of subordinators. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete (to appear).Google Scholar
(6)Horowitz, J.The Hausdorff dimension of the sample path of a subordinator. Israel J. Math. 6 (1968), 176–182.CrossRefGoogle Scholar
(7)Marstrand, J. M.The dimension of the Cartesian product sets. Proc. Cambridge Philos. Soc. 50 (1954), 198–202.Google Scholar
(8)Rogers, C. A.Hausdorff measures (Cambridge, 1970).Google Scholar