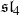1. Introduction and description of the results
To determine extensions between Verma modules in Bernstein–Gelfand–Gelfand (BGG) category
![]() $\mathcal{O}$
associated to a triangular decomposition of a semi-simple finite dimensional complex Lie algebra
$\mathcal{O}$
associated to a triangular decomposition of a semi-simple finite dimensional complex Lie algebra
![]() $\mathfrak{g}$
is a famous open problem. It was studied in, for example, [
Reference Abe1, Reference Boe7, Reference Carlin9–Reference Delorme11, Reference Dhillon and Makam13, Reference Gabber and Joseph15, Reference Mazorchuk21
]. The paper [
Reference Gabber and Joseph15
] suggested a connection between this problem and a combinatorial gadget, associated to the Weyl group of
$\mathfrak{g}$
is a famous open problem. It was studied in, for example, [
Reference Abe1, Reference Boe7, Reference Carlin9–Reference Delorme11, Reference Dhillon and Makam13, Reference Gabber and Joseph15, Reference Mazorchuk21
]. The paper [
Reference Gabber and Joseph15
] suggested a connection between this problem and a combinatorial gadget, associated to the Weyl group of
![]() $\mathfrak{g}$
, called the R-polynomials. Although not explicitly stated in [
Reference Gabber and Joseph15
], the expectation that the dimensions of the extension groups between Verma modules should be given by the coefficients of R-polynomials became known as the Gabber–Joseph conjecture. Unfortunately, in [
Reference Boe7
] it was shown that this expectation is, in general, wrong. At the present stage, there is not even a conjectural answer to this problem. Some explicit results describing the extension groups between Verma modules in special cases can be found in [
Reference Abe1, Reference Carlin9, Reference Carlin10, Reference Dhillon and Makam13, Reference Mazorchuk21
]. The main result of [
Reference Delorme11
] determines the Euler characteristic (i.e., the alternating sum) for dimensions of such extensions.
$\mathfrak{g}$
, called the R-polynomials. Although not explicitly stated in [
Reference Gabber and Joseph15
], the expectation that the dimensions of the extension groups between Verma modules should be given by the coefficients of R-polynomials became known as the Gabber–Joseph conjecture. Unfortunately, in [
Reference Boe7
] it was shown that this expectation is, in general, wrong. At the present stage, there is not even a conjectural answer to this problem. Some explicit results describing the extension groups between Verma modules in special cases can be found in [
Reference Abe1, Reference Carlin9, Reference Carlin10, Reference Dhillon and Makam13, Reference Mazorchuk21
]. The main result of [
Reference Delorme11
] determines the Euler characteristic (i.e., the alternating sum) for dimensions of such extensions.
In two recent papers [ Reference Ko, Mazorchuk and Mren19, Reference Ko, Mazorchuk and Mren20 ], written jointly with Rafael Mrden, we studied the dimensions of the first extension from a simple module to a Verma module. In the case of the special linear Lie algebra, we gave an explicit formula for this dimension, see [ Reference Ko, Mazorchuk and Mren19 ]. Outside type A the situation is more complicated. However, an explicit formula can be given in many special cases, see [ Reference Ko, Mazorchuk and Mren20 ]. These results motivated us to take a new closer look at the classical problem of extensions between Verma modules.
Our first main result, Theorem 2, explicitly determines the role that R-polynomials play in the theory of extensions between Verma modules. Category
![]() $\mathcal{O}$
admits a natural
$\mathcal{O}$
admits a natural
![]() $\mathbb{Z}$
-graded lift. Delorme’s formula mentioned above turns out to have a natural graded analogue which asserts that the coefficients of R-polynomials determine the Euler characteristic for dimensions of certain graded extensions between Verma modules. This result can be found in Section 3, see also Subsection 4·3.
$\mathbb{Z}$
-graded lift. Delorme’s formula mentioned above turns out to have a natural graded analogue which asserts that the coefficients of R-polynomials determine the Euler characteristic for dimensions of certain graded extensions between Verma modules. This result can be found in Section 3, see also Subsection 4·3.
In Section 4 we prove a number of general results about extension between graded Verma modules. Combining this additional grading with the homological grading gives a two-dimensional coordinate system (in
![]() $\mathbb{Z}^2$
) in which the potential region for non-zero graded extensions between two fixed Verma modules has the form of a triangle, see Figure 1. If the distance between the indexes of Verma modules is small, then this triangle degenerates to its included side and all extensions are indeed described by the coefficients of the R-polynomials, see Corollary 12. In fact, even in the general case, there are specific situations where graded extensions between Verma modules are given by the coefficients of the R-polynomials, see Corollary 11. In Subsection 4·2 we give several general bounds for the dimension of a fixed extension between graded Verma modules in terms of the Kazhdan–Lusztig combinatorics.
$\mathbb{Z}^2$
) in which the potential region for non-zero graded extensions between two fixed Verma modules has the form of a triangle, see Figure 1. If the distance between the indexes of Verma modules is small, then this triangle degenerates to its included side and all extensions are indeed described by the coefficients of the R-polynomials, see Corollary 12. In fact, even in the general case, there are specific situations where graded extensions between Verma modules are given by the coefficients of the R-polynomials, see Corollary 11. In Subsection 4·2 we give several general bounds for the dimension of a fixed extension between graded Verma modules in terms of the Kazhdan–Lusztig combinatorics.

Figure 1. The homomorphisms from
![]() $\Delta_x$
to
$\Delta_x$
to
![]() $\mathcal{T}_\bullet(\Delta_y)$
, and thus the extensions from
$\mathcal{T}_\bullet(\Delta_y)$
, and thus the extensions from
![]() $\Delta_x$
to
$\Delta_x$
to
![]() $\Delta_y$
, are in the dark grey region; the composition factors in
$\Delta_y$
, are in the dark grey region; the composition factors in
![]() $\mathcal{T}_\bullet(\Delta_y)$
are in the light grey region.
$\mathcal{T}_\bullet(\Delta_y)$
are in the light grey region.
Section 5 discusses a few observations about extensions between Verma modules related to the combinatorics of Bruhat order on the Weyl group. In particular, in Proposition 19 we show that graded extension between Verma modules are given by the coefficients of R-polynomials provided that the indexes of the involved Verma modules are both boolean or are both coboolean.
In Section 6 we present a number of concrete results in special cases. In particular, in Theorem 20 we show that in the Weyl type
![]() $A_3$
(i.e., for the Lie algebra
$A_3$
(i.e., for the Lie algebra
![]() $\mathfrak{sl}_4$
) all extensions between Verma modules are given by the coefficients of the R-polynomials despite the nontrivial Kazhdan–Lusztig combinatorics.
$\mathfrak{sl}_4$
) all extensions between Verma modules are given by the coefficients of the R-polynomials despite the nontrivial Kazhdan–Lusztig combinatorics.
Recall the triangle region of potential extensions between Verma modules mentioned above. It has one side included in the region and two sides that are not included. We call the extensions corresponding to the included side “expected” and the extensions corresponding to the interior of the triangle “additional”. If all extensions between two Verma modules are expected, then they are given by the coefficients of the R-polynomials. In Subsection 6·4, we use the results from [ Reference Ko, Mazorchuk and Mren19 ] to construct families of explicit non-zero additional first extensions between Verma modules in type A. In Subsection 6·5, we use the results from Subsection 6·4 to construct families of explicit non-zero additional second extensions between Verma modules in type A.
The last section of the paper, Section 7, discusses the parabolic and singular cases and the corresponding results similar to the ones that we obtain in the regular case. In particular, Theorem 31 gives a necessary condition for the graded extension algebra of Verma modules to be Koszul.
2. Preliminaries on category
 $\mathcal{O}$
$\mathcal{O}$
2·1. Category
 $\mathcal{O}$
$\mathcal{O}$
Let
![]() $\mathfrak{g}$
be a semi-simple finite dimensional complex Lie algebra with a fixed triangular decomposition
$\mathfrak{g}$
be a semi-simple finite dimensional complex Lie algebra with a fixed triangular decomposition
![]() $\mathfrak{g}=\mathfrak{n}_-\oplus \mathfrak{h}\oplus \mathfrak{n}_+$
(see [
Reference Humphreys16, Reference Moody and Pianzola25
] for details). Associated to this datum, we have the Bernstein–Gelfand–Gelfand category
$\mathfrak{g}=\mathfrak{n}_-\oplus \mathfrak{h}\oplus \mathfrak{n}_+$
(see [
Reference Humphreys16, Reference Moody and Pianzola25
] for details). Associated to this datum, we have the Bernstein–Gelfand–Gelfand category
![]() $\mathcal{O}$
. See [
Reference Bernstein, Gelfand and Gelfand4, Reference Humphreys16
].
$\mathcal{O}$
. See [
Reference Bernstein, Gelfand and Gelfand4, Reference Humphreys16
].
Simple modules in
![]() $\mathcal{O}$
are exactly the simple highest weight modules
$\mathcal{O}$
are exactly the simple highest weight modules
![]() $L(\lambda)$
, where
$L(\lambda)$
, where
![]() $\lambda\in \mathfrak{h}^*$
. For each such
$\lambda\in \mathfrak{h}^*$
. For each such
![]() $\lambda$
, we also have the corresponding:
$\lambda$
, we also have the corresponding:
-
(1) Verma module
 $\Delta(\lambda)$
;
$\Delta(\lambda)$
; -
(2) dual Verma module
 $\nabla(\lambda)$
;
$\nabla(\lambda)$
; -
(3) indecomposable projective module
 $P(\lambda)$
;
$P(\lambda)$
; -
(4) indecomposable injective module
 $I(\lambda)$
;
$I(\lambda)$
; -
(5) indecomposable tilting module
 $T(\lambda)$
.
$T(\lambda)$
.
The category
![]() $\mathcal O$
is a highest weight category with respect to the dominant order on
$\mathcal O$
is a highest weight category with respect to the dominant order on
![]() $\mathfrak{h}^*$
, where
$\mathfrak{h}^*$
, where
![]() $\Delta(\lambda)$
are the standard modules and
$\Delta(\lambda)$
are the standard modules and
![]() $\nabla(\lambda)$
are the costandard modules.
$\nabla(\lambda)$
are the costandard modules.
Consider the principal block
![]() $\mathcal{O}_0$
of
$\mathcal{O}_0$
of
![]() $\mathcal{O}$
, which is defined as the indecomposable direct summand containing the trivial
$\mathcal{O}$
, which is defined as the indecomposable direct summand containing the trivial
![]() $\mathfrak{g}$
-module L(0). Simple modules in
$\mathfrak{g}$
-module L(0). Simple modules in
![]() $\mathcal{O}_0$
are indexed by the elements of the Weyl group W of
$\mathcal{O}_0$
are indexed by the elements of the Weyl group W of
![]() $\mathfrak{g}$
. For
$\mathfrak{g}$
. For
![]() $w\in W$
, we have the corresponding simple module
$w\in W$
, we have the corresponding simple module
![]() $L_w\;:\!=\;L(w\cdot 0)$
, where
$L_w\;:\!=\;L(w\cdot 0)$
, where
![]() $w\cdot 0$
denotes the usual dot-action of the Weyl group. We similarly denote by
$w\cdot 0$
denotes the usual dot-action of the Weyl group. We similarly denote by
![]() $\Delta_w$
,
$\Delta_w$
,
![]() $\nabla_w$
,
$\nabla_w$
,
![]() $P_w$
,
$P_w$
,
![]() $I_w$
and
$I_w$
and
![]() $T_w$
the other structural modules corresponding to the weight
$T_w$
the other structural modules corresponding to the weight
![]() $w\in W$
. Then
$w\in W$
. Then
![]() $\mathcal O_0$
is highest weight with respect to the opposite of the Bruhat order on W.
$\mathcal O_0$
is highest weight with respect to the opposite of the Bruhat order on W.
We use Ext and Hom to denote extensions and homomorphisms in
![]() $\mathcal{O}$
, respectively. The simple preserving duality on
$\mathcal{O}$
, respectively. The simple preserving duality on
![]() $\mathcal{O}$
is denoted by
$\mathcal{O}$
is denoted by
![]() $\star$
.
$\star$
.
2·2. Graded category
 $\mathcal{O}$
$\mathcal{O}$
The category
![]() $\mathcal{O}_0$
admits a
$\mathcal{O}_0$
admits a
![]() $\mathbb{Z}$
-graded lift
$\mathbb{Z}$
-graded lift
![]() $\mathcal{O}_0^{\mathbb{Z}}$
, see [
Reference Soergel28
]. All structural modules in
$\mathcal{O}_0^{\mathbb{Z}}$
, see [
Reference Soergel28
]. All structural modules in
![]() $\mathcal{O}_0$
admit graded lifts (unique up to isomorphism and shift of grading). We use the following notation for the standard graded lifts of indecomposable structural modules:
$\mathcal{O}_0$
admit graded lifts (unique up to isomorphism and shift of grading). We use the following notation for the standard graded lifts of indecomposable structural modules:
-
(1) by
 ${L}_w$
the graded lift concentrated in degree 0;
${L}_w$
the graded lift concentrated in degree 0; -
(2) by
 ${\Delta}_w$
the graded lift with the top in degree 0;
${\Delta}_w$
the graded lift with the top in degree 0; -
(3) by
 ${\nabla}_w$
the graded lift with the socle in degree 0;
${\nabla}_w$
the graded lift with the socle in degree 0; -
(4) by
 ${P}_w$
the graded lift with the top in degree 0;
${P}_w$
the graded lift with the top in degree 0; -
(5) by
 ${I}_w$
the graded lift with the socle in degree 0;
${I}_w$
the graded lift with the socle in degree 0; -
(6) by
 ${T}_w$
the graded lift having the unique
${T}_w$
the graded lift having the unique
 $L_w$
subquotient in degree 0.
$L_w$
subquotient in degree 0.
We denote by
![]() $\langle k\rangle$
the functor which shifts the grading, with the convention that
$\langle k\rangle$
the functor which shifts the grading, with the convention that
![]() $\langle 1\rangle$
maps degree 0 to degree
$\langle 1\rangle$
maps degree 0 to degree
![]() $-1$
. We use ext and hom to denote extensions and homomorphisms in
$-1$
. We use ext and hom to denote extensions and homomorphisms in
![]() $\mathcal{O}_0^{\mathbb{Z}}$
, respectively. The graded version of
$\mathcal{O}_0^{\mathbb{Z}}$
, respectively. The graded version of
![]() $\star$
is also denoted by
$\star$
is also denoted by
![]() $\star$
.
$\star$
.
2·3. Bruhat order and the zeroth extensions
We recall in this subsection the graded homomorphisms between Verma modules, which is well known (see, for example, [
Reference Dixmier12
, chapter 7]). Let
![]() $\leq$
be the Bruhat order on W. Then we have
$\leq$
be the Bruhat order on W. Then we have
 \begin{equation*}\dim\hom(\Delta_x\langle a\rangle,\Delta_y\langle b\rangle ) = \begin{cases}1 &\text{if $x\geq y$ and $b-a = \ell(x)-\ell(y)$}\\0 &\text{otherwise}.\end{cases}\end{equation*}
\begin{equation*}\dim\hom(\Delta_x\langle a\rangle,\Delta_y\langle b\rangle ) = \begin{cases}1 &\text{if $x\geq y$ and $b-a = \ell(x)-\ell(y)$}\\0 &\text{otherwise}.\end{cases}\end{equation*}
Moreover, any nonzero homomorphism between Verma modules is injective. Also, the nonzero homomorphisms
![]() $L_{w_0}=\Delta_{w_0}\to \Delta_y\langle {\ell(w_0) - \ell(y)} \rangle$
, and their shifts, give the socle of the Verma modules.
$L_{w_0}=\Delta_{w_0}\to \Delta_y\langle {\ell(w_0) - \ell(y)} \rangle$
, and their shifts, give the socle of the Verma modules.
2·4. Combinatorics of category
 $\mathcal{O}_0^{\mathbb{Z}}$
$\mathcal{O}_0^{\mathbb{Z}}$
Let
![]() $\textbf{H}$
denote the Hecke algebra of W over
$\textbf{H}$
denote the Hecke algebra of W over
![]() $\mathbb{Z}[v,v^{-1}]$
in the normalisation of [
Reference Soergel30
]. It has the standard basis
$\mathbb{Z}[v,v^{-1}]$
in the normalisation of [
Reference Soergel30
]. It has the standard basis
![]() $\{H_w\,:\,w\in W\}$
and the Kazhdan–Lusztig (KL) basis
$\{H_w\,:\,w\in W\}$
and the Kazhdan–Lusztig (KL) basis
![]() $\{\underline{H}_w\,:\,w\in W\}$
. The KL polynomials
$\{\underline{H}_w\,:\,w\in W\}$
. The KL polynomials
![]() $\{p_{x,y}\,:\,x,y\in W\}$
are the entries of the transformation matrix between these two bases, that is
$\{p_{x,y}\,:\,x,y\in W\}$
are the entries of the transformation matrix between these two bases, that is
By construction, we have
![]() $p_{x,y}\in \mathbb Z[v]$
and
$p_{x,y}\in \mathbb Z[v]$
and
![]() $p_{x,y}=0$
for
$p_{x,y}=0$
for
![]() $x\not\leq y$
. When
$x\not\leq y$
. When
![]() $p_{x,y}\neq 0$
, we have
$p_{x,y}\neq 0$
, we have
![]() $\deg p_{x,y}=\ell(y)-\ell(x)$
. For
$\deg p_{x,y}=\ell(y)-\ell(x)$
. For
![]() $x,y\in W$
and
$x,y\in W$
and
![]() $k\in\mathbb{Z}$
, we denote by
$k\in\mathbb{Z}$
, we denote by
![]() $p_{x,y}^{(k)}$
the coefficient at
$p_{x,y}^{(k)}$
the coefficient at
![]() $v^k$
in
$v^k$
in
![]() $p_{x,y}$
.
$p_{x,y}$
.
Taking the Grothendieck group gives rise to an isomorphism of
![]() $\mathbb{Z}[v,v^{-1}]$
-modules as follows:
$\mathbb{Z}[v,v^{-1}]$
-modules as follows:
Here the
![]() $\mathbb{Z}[v,v^{-1}]$
-module structure on
$\mathbb{Z}[v,v^{-1}]$
-module structure on
![]() $\textrm{Gr}(\mathcal{O}_0^{\mathbb{Z}})$
is given by letting the element v act as
$\textrm{Gr}(\mathcal{O}_0^{\mathbb{Z}})$
is given by letting the element v act as
![]() $\langle -1\rangle$
. By the Kazhdan–Lusztig theorem, see [
Reference Kazhdan and Lusztig17, Reference Soergel28
], this isomorphism maps
$\langle -1\rangle$
. By the Kazhdan–Lusztig theorem, see [
Reference Kazhdan and Lusztig17, Reference Soergel28
], this isomorphism maps
![]() ${P}_w$
to
${P}_w$
to
![]() $\underline{H}_w$
, for
$\underline{H}_w$
, for
![]() $w\in W$
. In particular, we have
$w\in W$
. In particular, we have
![]() $p_{x,y}\in \mathbb Z_{\geq 0}[v]$
, where its coefficients are the multiplicities of the (graded) filtration of
$p_{x,y}\in \mathbb Z_{\geq 0}[v]$
, where its coefficients are the multiplicities of the (graded) filtration of
![]() $P_y$
by
$P_y$
by
![]() $\Delta_x$
(see Subsections 2·1, 2·2).
$\Delta_x$
(see Subsections 2·1, 2·2).
2·5. Endofunctors of
 $\mathcal{O}_0$
$\mathcal{O}_0$
The category
![]() $\mathcal{O}_0$
is equipped with the action of various families of functors, see [
Reference Andersen and Stroppel2, Reference Bernstein and Gelfand5, Reference Carlin9, Reference Humphreys16, Reference Khomenko and Mazorchuk18, Reference Mazorchuk and Stroppel24
] and references therein. For
$\mathcal{O}_0$
is equipped with the action of various families of functors, see [
Reference Andersen and Stroppel2, Reference Bernstein and Gelfand5, Reference Carlin9, Reference Humphreys16, Reference Khomenko and Mazorchuk18, Reference Mazorchuk and Stroppel24
] and references therein. For
![]() $w\in W$
, we denote by:
$w\in W$
, we denote by:
-
(1)
 $\theta_w$
the indecomposable projective endofunctor of
$\theta_w$
the indecomposable projective endofunctor of
 $\mathcal{O}_0$
sending
$\mathcal{O}_0$
sending
 $P_e$
to
$P_e$
to
 $P_w$
, see [
Reference Bernstein and Gelfand5
];
$P_w$
, see [
Reference Bernstein and Gelfand5
]; -
(2)
 $\textrm{C}_w$
the corresponding shuffling functor, see [
Reference Carlin9, Reference Mazorchuk and Stroppel24
];
$\textrm{C}_w$
the corresponding shuffling functor, see [
Reference Carlin9, Reference Mazorchuk and Stroppel24
]; -
(3)
 $\top_w$
the corresponding twisting functor, see [
Reference Andersen and Stroppel2, Reference Khomenko and Mazorchuk18
];
$\top_w$
the corresponding twisting functor, see [
Reference Andersen and Stroppel2, Reference Khomenko and Mazorchuk18
];
The action of the monoidal category
![]() $\mathcal{P}^\mathbb{Z}$
of graded projective functors on
$\mathcal{P}^\mathbb{Z}$
of graded projective functors on
![]() $\mathcal{O}_0^{\mathbb{Z}}$
categorifies the right regular
$\mathcal{O}_0^{\mathbb{Z}}$
categorifies the right regular
![]() $\textbf{H}$
-module.
$\textbf{H}$
-module.
2·6. R-polynomials
The isomorphism in (1) equips the algebra
![]() $\textbf{H}$
with the following
$\textbf{H}$
with the following
![]() $\mathbb{Z}[v,v^{-1}]$
-bases:
$\mathbb{Z}[v,v^{-1}]$
-bases:
-
(1)
 $\{H_w=[\Delta_w]\,:\,w\in W\}$
, the standard basis;
$\{H_w=[\Delta_w]\,:\,w\in W\}$
, the standard basis; -
(2)
 $\{\underline{H}_w=[P_w]\,:\,w\in W\}$
, the KL basis;
$\{\underline{H}_w=[P_w]\,:\,w\in W\}$
, the KL basis; -
(3)
 $\{[\nabla_w]\,:\,w\in W\}$
, the costandard basis;
$\{[\nabla_w]\,:\,w\in W\}$
, the costandard basis; -
(4)
 $\{[L_w]\,:\,w\in W\}$
, the dual KL basis;
$\{[L_w]\,:\,w\in W\}$
, the dual KL basis; -
(5)
 $\{[I_w]\,:\,w\in W\}$
;
$\{[I_w]\,:\,w\in W\}$
; -
(6)
 $\{[T_w]\,:\,w\in W\}$
.
$\{[T_w]\,:\,w\in W\}$
.
The R-polynomials
![]() $\{r_{x,y}\,:\,x,y\in W\}$
are defined as the entries of the transformation matrix between the standard and the costandard bases, i.e.:
$\{r_{x,y}\,:\,x,y\in W\}$
are defined as the entries of the transformation matrix between the standard and the costandard bases, i.e.:
Note that
![]() $r_{x,y}\in\mathbb{Z}[v,v^{-1}]$
, by definition. For
$r_{x,y}\in\mathbb{Z}[v,v^{-1}]$
, by definition. For
![]() $x,y\in W$
and
$x,y\in W$
and
![]() $k\in\mathbb{Z}$
, we denote by
$k\in\mathbb{Z}$
, we denote by
![]() $r_{x,y}^{(k)}$
the coefficient at
$r_{x,y}^{(k)}$
the coefficient at
![]() $v^k$
in
$v^k$
in
![]() $r_{x,y}$
.
$r_{x,y}$
.
As
![]() $\Delta_{w_0}=\nabla_{w_0}$
, we have
$\Delta_{w_0}=\nabla_{w_0}$
, we have
 \begin{equation}r_{x,w_0}=\begin{cases}1,& x=w_0;\\0,& \text{otherwise}.\end{cases}\end{equation}
\begin{equation}r_{x,w_0}=\begin{cases}1,& x=w_0;\\0,& \text{otherwise}.\end{cases}\end{equation}
For
![]() $w\in W$
and
$w\in W$
and
![]() $s\in S$
such that
$s\in S$
such that
![]() $ws>w$
, we have
$ws>w$
, we have
From this, we have the following recursive formula for R-polynomials: for
![]() $x,y\in W$
and
$x,y\in W$
and
![]() $s\in S$
such that
$s\in S$
such that
![]() $ys<y$
, we have:
$ys<y$
, we have:
 \begin{equation}r_{x,ys}=\begin{cases}r_{xs,y},& xs>x;\\r_{xs,y}+ ({v-v^{-1}})r_{x,y},& xs<x.\end{cases}\end{equation}
\begin{equation}r_{x,ys}=\begin{cases}r_{xs,y},& xs>x;\\r_{xs,y}+ ({v-v^{-1}})r_{x,y},& xs<x.\end{cases}\end{equation}
Together, (2) and (3) determine the family of R-polynomials uniquely.
Please note that our indexing of R-polynomials differs from the usual one in [
Reference Björner and Brenti6, Reference Kazhdan and Lusztig17
] by a
![]() $w_0$
-shift. For more information on R-polynomials, we refer to [
Reference Kazhdan and Lusztig17
] and [
Reference Björner and Brenti6
, section 5·3].
$w_0$
-shift. For more information on R-polynomials, we refer to [
Reference Kazhdan and Lusztig17
] and [
Reference Björner and Brenti6
, section 5·3].
2·7. Koszul and Koszul–Ringel dualities
Consider
![]() $\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$
the bounded derived category of
$\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$
the bounded derived category of
![]() $\mathcal{O}_0^{\mathbb{Z}}$
. The category
$\mathcal{O}_0^{\mathbb{Z}}$
. The category
![]() $\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$
has a famous auto-equivalence called the Koszul duality and denoted by K, see [
Reference Beilinson, Ginzburg and Soergel3, Reference Mazorchuk, Ovsienko and Stroppel23, Reference Soergel28
]. It has the following properties:
$\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$
has a famous auto-equivalence called the Koszul duality and denoted by K, see [
Reference Beilinson, Ginzburg and Soergel3, Reference Mazorchuk, Ovsienko and Stroppel23, Reference Soergel28
]. It has the following properties:
-
(1) K sends
 $P_w$
to
$P_w$
to
 $L_{w^{-1}w_0}$
;
$L_{w^{-1}w_0}$
; -
(2) K sends
 $\Delta_w$
to
$\Delta_w$
to
 $\nabla_{w^{-1}w_0}$
;
$\nabla_{w^{-1}w_0}$
; -
(3) K sends
 $L_w$
to
$L_w$
to
 $I_{w^{-1}w_0}$
;
$I_{w^{-1}w_0}$
; -
(4)
 $\textrm{K}\langle j\rangle\cong [j]\langle -j\rangle\textrm{K}$
.
$\textrm{K}\langle j\rangle\cong [j]\langle -j\rangle\textrm{K}$
.
Another famous auto-equivalence of
![]() $\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$
is its Ringel self-duality given by the derived twisting functor
$\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$
is its Ringel self-duality given by the derived twisting functor
![]() $\mathcal{L}\top_{w_0}$
, see [
Reference Soergel29
]. It has the following properties:
$\mathcal{L}\top_{w_0}$
, see [
Reference Soergel29
]. It has the following properties:
-
(1)
 $\mathcal{L}\top_{w_0}$
sends
$\mathcal{L}\top_{w_0}$
sends
 $P_w$
to
$P_w$
to
 $T_{w_0w}$
;
$T_{w_0w}$
; -
(2)
 $\mathcal{L}\top_{w_0}$
sends
$\mathcal{L}\top_{w_0}$
sends
 $T_{w}$
to
$T_{w}$
to
 $I_{w_0w}$
;
$I_{w_0w}$
; -
(3)
 $\mathcal{L}\top_{w_0}$
sends
$\mathcal{L}\top_{w_0}$
sends
 $\Delta_{w}$
to
$\Delta_{w}$
to
 $\nabla_{w_0w}$
.
$\nabla_{w_0w}$
.
The composition
![]() $\textrm{RK}\;:\!=\;(\mathcal L\top_{w_0})^{-1}\circ\textrm{K}$
of the Koszul and Ringel self-dualities results in the Koszul–Ringel self-duality. We have
$\textrm{RK}\;:\!=\;(\mathcal L\top_{w_0})^{-1}\circ\textrm{K}$
of the Koszul and Ringel self-dualities results in the Koszul–Ringel self-duality. We have
![]() $\textrm{RK}(\Delta_w)=\Delta_{w_0w^{-1}w_0}$
, and thus
$\textrm{RK}(\Delta_w)=\Delta_{w_0w^{-1}w_0}$
, and thus
![]() $\textrm{RK}^2(\Delta_w)=\Delta_w$
. Since
$\textrm{RK}^2(\Delta_w)=\Delta_w$
. Since
![]() $\{\Delta_w\}_{w\in W}$
generates
$\{\Delta_w\}_{w\in W}$
generates
![]() $\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$
, it follows that the Koszul–Ringel self-duality is an involution. It has the following properties:
$\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$
, it follows that the Koszul–Ringel self-duality is an involution. It has the following properties:
-
(1) RK sends
 $T_w$
to
$T_w$
to
 $L_{w_0w^{-1}w_0}$
;
$L_{w_0w^{-1}w_0}$
; -
(2) RK sends
 $L_w$
to
$L_w$
to
 $T_{w_0w^{-1}w_0}$
;
$T_{w_0w^{-1}w_0}$
; -
(3) RK sends
 $\Delta_w$
to
$\Delta_w$
to
 $\Delta_{w_0w^{-1}w_0}$
;
$\Delta_{w_0w^{-1}w_0}$
; -
(4) RK sends
 $\nabla_w$
to
$\nabla_w$
to
 $\nabla_{w_0w^{-1}w_0}$
.
$\nabla_{w_0w^{-1}w_0}$
.
We refer to [ Reference Mazorchuk22 ] for further details.
A concrete realisation of this self-duality is via the category
![]() $\mathscr{LC}(T)$
of linear complexes of tilting objects is in
$\mathscr{LC}(T)$
of linear complexes of tilting objects is in
![]() $\mathcal{O}_0^{\mathbb{Z}}$
. Recall that a complex
$\mathcal{O}_0^{\mathbb{Z}}$
. Recall that a complex
![]() $\mathcal{T}_\bullet$
of tilting objects is called linear provided that each summand of each
$\mathcal{T}_\bullet$
of tilting objects is called linear provided that each summand of each
![]() $\mathcal{T}_i$
has the form
$\mathcal{T}_i$
has the form
![]() $T_w\langle i\rangle$
, for some
$T_w\langle i\rangle$
, for some
![]() $w\in W$
. The essence of the Koszul–Ringel self-duality is that RK restricts to an equivalence between the categories
$w\in W$
. The essence of the Koszul–Ringel self-duality is that RK restricts to an equivalence between the categories
![]() $\mathscr{LC}(T)$
and
$\mathscr{LC}(T)$
and
![]() $\mathcal{O}_0^{\mathbb{Z}}$
where:
$\mathcal{O}_0^{\mathbb{Z}}$
where:
-
(1) the tilting module
 $T_w$
(considered as a complex) is sent to the simple module
$T_w$
(considered as a complex) is sent to the simple module
 $L_{w_0w^{-1}w_0}$
;
$L_{w_0w^{-1}w_0}$
; -
(2) the (linear!) complex of tilting modules representing
 $L_w$
is sent to the tilting module
$L_w$
is sent to the tilting module
 $T_{w_0w^{-1}w_0}$
;
$T_{w_0w^{-1}w_0}$
; -
(3) the linear tilting coresolution of
 $\Delta_w$
is sent to the module
$\Delta_w$
is sent to the module
 $\Delta_{w_0w^{-1}w_0}$
;
$\Delta_{w_0w^{-1}w_0}$
; -
(4) the linear tilting resolution of
 $\nabla_w$
is sent to the module
$\nabla_w$
is sent to the module
 $\nabla_{w_0w^{-1}w_0}$
.
$\nabla_{w_0w^{-1}w_0}$
.
We use the notation
![]() $\mathcal{T}_\bullet(L_w)$
,
$\mathcal{T}_\bullet(L_w)$
,
![]() $\mathcal{T}_\bullet(\Delta_w)$
and
$\mathcal{T}_\bullet(\Delta_w)$
and
![]() $\mathcal{T}_\bullet(\nabla_w)$
for the linear complexes of tilting modules that represent
$\mathcal{T}_\bullet(\nabla_w)$
for the linear complexes of tilting modules that represent
![]() $L_w$
,
$L_w$
,
![]() $\Delta_w$
and
$\Delta_w$
and
![]() $\nabla_w$
, for
$\nabla_w$
, for
![]() $w\in W$
, respectively.
$w\in W$
, respectively.
3. Delorme formulae
3·1. Ungraded Delorme formula
The following result is proved in [ Reference Delorme11 ].
Proposition 1. For
![]() $x,y\in W$
, we have
$x,y\in W$
, we have
Proof. First, we claim that, for any
![]() $M\in\mathcal{D}^b(\mathcal{O}_0)$
, we have the following relation in
$M\in\mathcal{D}^b(\mathcal{O}_0)$
, we have the following relation in
![]() $\textrm{Gr}(\mathcal{D}^b(\mathcal{O}_0))$
:
$\textrm{Gr}(\mathcal{D}^b(\mathcal{O}_0))$
:
Indeed, for
![]() $M=\nabla_y$
, this formula follows by combining the fact that standard and costandard modules in
$M=\nabla_y$
, this formula follows by combining the fact that standard and costandard modules in
![]() $\mathcal{O}_0$
are homologically orthogonal with the fact that
$\mathcal{O}_0$
are homologically orthogonal with the fact that
![]() $[\Delta_x]=[\Delta_x^\star]=[\nabla_x]$
, since
$[\Delta_x]=[\Delta_x^\star]=[\nabla_x]$
, since
![]() $\star$
is simple preserving. For the general M, (4) now follows using the additivity of both sides with respect to distinguished triangles and the fact that costandard modules generate
$\star$
is simple preserving. For the general M, (4) now follows using the additivity of both sides with respect to distinguished triangles and the fact that costandard modules generate
![]() $\mathcal{D}^b(\mathcal{O}_0)$
.
$\mathcal{D}^b(\mathcal{O}_0)$
.
The claim of the proposition is obtained from (4) by plugging in
![]() $M=\Delta_y$
and using that
$M=\Delta_y$
and using that
![]() $\{[\Delta_x]\,:\,x\in W\}$
is a basis in
$\{[\Delta_x]\,:\,x\in W\}$
is a basis in
![]() $\textrm{Gr}(\mathcal{D}^b(\mathcal{O}_0))$
.
$\textrm{Gr}(\mathcal{D}^b(\mathcal{O}_0))$
.
3·2. Graded Delorme formula
The following is a natural graded lift of Proposition 1. This statement explicitly explains the role which R-polynomials play in the theory of extensions between Verma modules.
Theorem 2. For
![]() $x,y\in W$
and
$x,y\in W$
and
![]() $k\in\mathbb{Z}$
, we have:
$k\in\mathbb{Z}$
, we have:
Proof. First, we claim that, for any
![]() $M\in\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$
, we have the following relation in
$M\in\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$
, we have the following relation in
![]() $\textrm{Gr}(\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}}))$
:
$\textrm{Gr}(\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}}))$
:
Indeed, for
![]() $M=\nabla_y\langle m\rangle$
, this formula follows from the fact that standard and costandard modules in
$M=\nabla_y\langle m\rangle$
, this formula follows from the fact that standard and costandard modules in
![]() $\mathcal{O}_0^{\mathbb{Z}}$
are homologically orthogonal. For the general M, (5) now follows using the additivity of both sides with respect to distinguished triangles and the fact that costandard modules generate
$\mathcal{O}_0^{\mathbb{Z}}$
are homologically orthogonal. For the general M, (5) now follows using the additivity of both sides with respect to distinguished triangles and the fact that costandard modules generate
![]() $\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$
.
$\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}})$
.
The claim of the proposition is obtained from (5) by plugging in
![]() $M=\Delta_y$
and the definition of R-polynomials, since
$M=\Delta_y$
and the definition of R-polynomials, since
![]() $[\nabla_x\langle-k\rangle]=v^k[\nabla_x]$
in
$[\nabla_x\langle-k\rangle]=v^k[\nabla_x]$
in
![]() $\textrm{Gr}(\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}}))$
.
$\textrm{Gr}(\mathcal{D}^b(\mathcal{O}_0^{\mathbb{Z}}))$
.
4. General results
4·1. General setup
For
![]() $i,j\in\mathbb{Z}$
,
$i,j\in\mathbb{Z}$
,
![]() $x,y\in W$
and
$x,y\in W$
and
![]() $k\in\mathbb{Z}_{\geq 0}$
, set
$k\in\mathbb{Z}_{\geq 0}$
, set
An ultimate goal would be to find a formula for E(x,y,i,j,k). Let us start by listing some straightforward properties:
Proposition 3. For
![]() $i,j\in\mathbb{Z}$
,
$i,j\in\mathbb{Z}$
,
![]() $x,y\in W$
and
$x,y\in W$
and
![]() $k\in\mathbb{Z}_{\geq 0}$
, we have:
$k\in\mathbb{Z}_{\geq 0}$
, we have:
-
(a)
 $E(x,y,i,j,k)=E(x,y,i+a,j+a,k)$
, for all
$E(x,y,i,j,k)=E(x,y,i+a,j+a,k)$
, for all
 $a\in\mathbb{Z}$
;
$a\in\mathbb{Z}$
; -
(b)
 $E(x,y,i,j,k)\neq 0$
implies
$E(x,y,i,j,k)\neq 0$
implies
 $x\geq y$
;
$x\geq y$
; -
(c)
 $E(x,y,i,j,k)=E(w_0x^{-1}w_0,w_0y^{-1}w_0,-i,-j,k+j-i)$
;
$E(x,y,i,j,k)=E(w_0x^{-1}w_0,w_0y^{-1}w_0,-i,-j,k+j-i)$
; -
(d)
 $E(x,y,i,j,k)=E(x^{-1},y^{-1},-i,-j,k+j-i)$
;
$E(x,y,i,j,k)=E(x^{-1},y^{-1},-i,-j,k+j-i)$
; -
(e)
 $E(x,y,i,j,k)=E(w_0y,w_0x,-j,-i,k)$
.
$E(x,y,i,j,k)=E(w_0y,w_0x,-j,-i,k)$
.
Proof. Property (a) follows from the fact that the shift of grading is an auto-equivalence. Property (b) is a usual property of standard modules in highest weight categories. Property (c) follows from Koszul–Ringel duality. Property (d) follows from property (c) since conjugation by
![]() $w_0$
corresponds to an automorphism of the Dynkin diagram, which induces a(n highest weight) auto-equivalence on
$w_0$
corresponds to an automorphism of the Dynkin diagram, which induces a(n highest weight) auto-equivalence on
![]() $\mathcal O_0$
. Property (e) follows by applying first
$\mathcal O_0$
. Property (e) follows by applying first
![]() $\mathcal{L}\top_{w_0}$
and then
$\mathcal{L}\top_{w_0}$
and then
![]() $\star$
.
$\star$
.
Due to Proposition 3(a), we can consider the case
![]() $j=0$
. We define the Laurent polynomial
$j=0$
. We define the Laurent polynomial
![]() ${\textrm{E}}_{x,y}(v,u)$
as follows:
${\textrm{E}}_{x,y}(v,u)$
as follows:
Note that
![]() ${\textrm{E}}_{x,y}(v,u)$
is a polynomial in u and a Laurent polynomial in v. In fact, in Corollary 7 below, we will see that
${\textrm{E}}_{x,y}(v,u)$
is a polynomial in u and a Laurent polynomial in v. In fact, in Corollary 7 below, we will see that
![]() ${\textrm{E}}_{x,y}(v,u)$
is also a polynomial in v.
${\textrm{E}}_{x,y}(v,u)$
is also a polynomial in v.
Here we have
![]() ${\textrm{E}}_{x,y}(v, -v^{-1})=r_{x,y}(v)$
, and Proposition 3 is expressed as follows.
${\textrm{E}}_{x,y}(v, -v^{-1})=r_{x,y}(v)$
, and Proposition 3 is expressed as follows.
Proposition 4. We have:
-
(a)
 ${\textrm{E}}_{x,y} = 0$
unless
${\textrm{E}}_{x,y} = 0$
unless
 $y\leq x$
.
$y\leq x$
. -
(b)
 ${\textrm{E}}_{x,y}(u,v) = \textrm{E}_{w_0y^{-1}w_0,w_0x^{-1}w_0}(v,u)$
.
${\textrm{E}}_{x,y}(u,v) = \textrm{E}_{w_0y^{-1}w_0,w_0x^{-1}w_0}(v,u)$
. -
(c)
 ${\textrm{E}}_{x,y}(u,v) =\textrm{E}_{y^{-1},x^{-1}}(v,u)$
.
${\textrm{E}}_{x,y}(u,v) =\textrm{E}_{y^{-1},x^{-1}}(v,u)$
. -
(d)
 ${\textrm{E}}_{x,y}(v,u)=\textrm{E}_{w_0y,w_0x}(v,u)$
.
${\textrm{E}}_{x,y}(v,u)=\textrm{E}_{w_0y,w_0x}(v,u)$
.
4·2. Bounds in terms of KL polynomials
Proposition 5. For
![]() $x,y\in W$
we have
$x,y\in W$
we have
(Note that the summand
![]() $ p_{x w_0,z w_0}(v) p_{y,z}(u)$
is zero unless
$ p_{x w_0,z w_0}(v) p_{y,z}(u)$
is zero unless
![]() $y\leq z\leq x$
.)
$y\leq z\leq x$
.)
Proof. The Koszul–Ringel duality gives
The left-hand side is, by the BGG reciprocity, equal to
![]() $[P_{w_0z^{-1} w_0}\;:\;\Delta_{w_0y^{-1} w_0}\langle -b\rangle]$
. It follows that
$[P_{w_0z^{-1} w_0}\;:\;\Delta_{w_0y^{-1} w_0}\langle -b\rangle]$
. It follows that
On the other hand, for each
![]() $z\in W$
, we have
$z\in W$
, we have
where we apply the automorphism induced by conjugation by
![]() $w_0$
in the second equality and the Ringel duality in the third equality, and thus
$w_0$
in the second equality and the Ringel duality in the third equality, and thus
Combining (9) and (8), we obtain the claimed equation.
Given
![]() $p,q\in \mathbb Z[u^{\pm1},v^{\pm1}]$
, we write
$p,q\in \mathbb Z[u^{\pm1},v^{\pm1}]$
, we write
![]() $p\leq q$
if all coefficients of
$p\leq q$
if all coefficients of
![]() $q-p$
are non-negative.
$q-p$
are non-negative.
Corollary 6. For
![]() $x,y\in W$
we have
$x,y\in W$
we have
Proof. Since the space
![]() $\operatorname{ext}^b(\Delta_x\langle b-a\rangle,\Delta_y)$
is computed as the homology of the complex
$\operatorname{ext}^b(\Delta_x\langle b-a\rangle,\Delta_y)$
is computed as the homology of the complex
![]() $\hom(\Delta_x\langle b-a \rangle [\!-\!b],\mathcal{T}_\bullet(\Delta_y))$
at the homological position 0, the claim follows from Proposition 5.
$\hom(\Delta_x\langle b-a \rangle [\!-\!b],\mathcal{T}_\bullet(\Delta_y))$
at the homological position 0, the claim follows from Proposition 5.
Corollary 7. We have
![]() ${\textrm{E}}_{x,y}\in \mathbb Z[u,v]$
. Moreover, for
${\textrm{E}}_{x,y}\in \mathbb Z[u,v]$
. Moreover, for
![]() $x\geq y$
, we have:
$x\geq y$
, we have:
-
(a)
 $\deg_u {\textrm{E}}_{x,y} = \ell(x)-\ell(y)$
;
$\deg_u {\textrm{E}}_{x,y} = \ell(x)-\ell(y)$
; -
(b)
 $\deg_v {\textrm{E}}_{x,y} = \ell(x)-\ell(y)$
;
$\deg_v {\textrm{E}}_{x,y} = \ell(x)-\ell(y)$
; -
(c)
 $\deg {\textrm{E}}_{x,y} = \ell(x)-\ell(y)$
;
$\deg {\textrm{E}}_{x,y} = \ell(x)-\ell(y)$
; -
(d) the degree of each monomial appearing in
 ${\textrm{E}}_{x,y}$
has the same parity as
${\textrm{E}}_{x,y}$
has the same parity as
 $\ell(x)-\ell(y)$
,
$\ell(x)-\ell(y)$
,
where
![]() $\deg_u,\deg_v$
denote the degrees with respect to the variables u,v, respectively. In fact, the coefficients of
$\deg_u,\deg_v$
denote the degrees with respect to the variables u,v, respectively. In fact, the coefficients of
![]() ${\textrm{E}}_{x,y}(u,v)$
at
${\textrm{E}}_{x,y}(u,v)$
at
![]() $u^{\ell(x)-\ell(y)}$
and at
$u^{\ell(x)-\ell(y)}$
and at
![]() $v^{\ell(x)-\ell(y)}$
are both 1.
$v^{\ell(x)-\ell(y)}$
are both 1.
Proof. Since
![]() $p_{w,w'}(\upsilon)\in\mathbb Z_{\geq 0}[\upsilon]$
with the parity vanishing property and
$p_{w,w'}(\upsilon)\in\mathbb Z_{\geq 0}[\upsilon]$
with the parity vanishing property and
![]() $\deg p_{w,w'} = \ell(w')-\ell(w)$
for all
$\deg p_{w,w'} = \ell(w')-\ell(w)$
for all
![]() $w,w'\in W$
with
$w,w'\in W$
with
![]() $w\leq w'$
(see Subsection 2·4), Corollary 6 provides the first statement, the inequality “
$w\leq w'$
(see Subsection 2·4), Corollary 6 provides the first statement, the inequality “
![]() $\leq$
” in all three numbered claims, and (d). To have “
$\leq$
” in all three numbered claims, and (d). To have “
![]() $=$
” in the numbered claims, it is enough to prove the last remark. But the coefficients of
$=$
” in the numbered claims, it is enough to prove the last remark. But the coefficients of
![]() ${\textrm{E}}_{x,y}(u,v)$
at
${\textrm{E}}_{x,y}(u,v)$
at
![]() $u^{\ell(x)-\ell(y)}$
and at
$u^{\ell(x)-\ell(y)}$
and at
![]() $v^{\ell(x)-\ell(y)}$
are the same by Proposition 3(c), where the former is the dimension of
$v^{\ell(x)-\ell(y)}$
are the same by Proposition 3(c), where the former is the dimension of
![]() $\hom(\Delta_x\langle {\ell(y)-\ell(x)}\rangle,\Delta_y)$
. The latter space consists of the unique inclusion between Verma modules (see Subsection 2·3), and thus has dimension one. This completes the proof.
$\hom(\Delta_x\langle {\ell(y)-\ell(x)}\rangle,\Delta_y)$
. The latter space consists of the unique inclusion between Verma modules (see Subsection 2·3), and thus has dimension one. This completes the proof.
Corollary 8. If
![]() $E(x,y,i,0,k)\neq 0$
for
$E(x,y,i,0,k)\neq 0$
for
![]() $x\geq y$
, then
$x\geq y$
, then
-
(a)
 $0\leq k\leq \ell(x)-\ell(y)$
;
$0\leq k\leq \ell(x)-\ell(y)$
; -
(b)
 $2k+\ell(y)-\ell(x)\leq i\leq k$
;
$2k+\ell(y)-\ell(x)\leq i\leq k$
; -
(c) if
 $k=0$
, then
$k=0$
, then
 $i=\ell(y)-\ell(x)$
;
$i=\ell(y)-\ell(x)$
; -
(d) if
 $k=i$
, then
$k=i$
, then
 $k=i=\ell(x)-\ell(y)$
;
$k=i=\ell(x)-\ell(y)$
; -
(e)
 $\ell(y)-\ell(x)-i$
is even.
$\ell(y)-\ell(x)-i$
is even.
Thus, each (k,i) with nonzero E(x,y,i,0,k) is in the dark grey region in Figure 1.
Proof. The claims are exactly the claims in Corollary 7 via the change of variables.
The bound given in Corollary 6 does not take into account the differentials in the complex of homomorphisms between
![]() $\Delta_y$
and
$\Delta_y$
and
![]() $\mathcal{T}_\bullet(\Delta_x)$
and can be lowered in various ways. We record one such strenghtening of the bound.
$\mathcal{T}_\bullet(\Delta_x)$
and can be lowered in various ways. We record one such strenghtening of the bound.
Proposition 9. Let
![]() $x,y\in W$
be such that
$x,y\in W$
be such that
![]() $x\geq y$
. Then, for
$x\geq y$
. Then, for
![]() $k\in\mathbb{Z}_{\geq 0}$
and
$k\in\mathbb{Z}_{\geq 0}$
and
![]() $i\in\mathbb{Z}$
such that
$i\in\mathbb{Z}$
such that
![]() $2k-i\neq \ell(x)-\ell(y)$
, we have:
$2k-i\neq \ell(x)-\ell(y)$
, we have:
Proof. Let
![]() $w\in W$
such that
$w\in W$
such that
![]() $w\geq y$
and
$w\geq y$
and
![]() $\ell(w)=\ell(y)+k$
. Via Koszul–Ringel duality, the inclusion
$\ell(w)=\ell(y)+k$
. Via Koszul–Ringel duality, the inclusion
![]() $\Delta_{w_0w^{-1}w_0}\langle k\rangle\hookrightarrow\Delta_{w_0y^{-1}w_0}$
gives an injective (component-wise) homomorphism of complexes
$\Delta_{w_0w^{-1}w_0}\langle k\rangle\hookrightarrow\Delta_{w_0y^{-1}w_0}$
gives an injective (component-wise) homomorphism of complexes
![]() $\mathcal{T}_\bullet(\Delta_w)\langle -k\rangle[k]\hookrightarrow\mathcal{T}_\bullet(\Delta_y)$
.
$\mathcal{T}_\bullet(\Delta_w)\langle -k\rangle[k]\hookrightarrow\mathcal{T}_\bullet(\Delta_y)$
.
Since each hom space between Verma modules is concentrated in one degree, any nonzero homomorphism, say
![]() $\phi\;:\;\Delta_x\langle i \rangle \to T_w=\mathcal T_0(\Delta_w)$
does not give rise to a homomorphism of complexes, that is,
$\phi\;:\;\Delta_x\langle i \rangle \to T_w=\mathcal T_0(\Delta_w)$
does not give rise to a homomorphism of complexes, that is,
![]() $d \circ \phi\neq 0$
, where d is (the restriction of) the differential in
$d \circ \phi\neq 0$
, where d is (the restriction of) the differential in
![]() $\mathcal{T}_\bullet(\Delta_w)$
.
$\mathcal{T}_\bullet(\Delta_w)$
.
Since
![]() $\mathcal{T}_\bullet(\Delta_w)\langle -k\rangle[k]$
is a subcomplex of
$\mathcal{T}_\bullet(\Delta_w)\langle -k\rangle[k]$
is a subcomplex of
![]() $\mathcal{T}_\bullet(\Delta_y)$
, we still have
$\mathcal{T}_\bullet(\Delta_y)$
, we still have
![]() $d\circ \phi\neq 0$
when d is the differential in
$d\circ \phi\neq 0$
when d is the differential in
![]() $\mathcal{T}_\bullet(\Delta_y)$
. Hence
$\mathcal{T}_\bullet(\Delta_y)$
. Hence
![]() $\phi$
does not contribute to an (appropriately shifted) extension from
$\phi$
does not contribute to an (appropriately shifted) extension from
![]() $\Delta_x$
to
$\Delta_x$
to
![]() $\Delta_y$
. The claim follows.
$\Delta_y$
. The claim follows.
4·3. The exact information given by the R-polynomials
Theorem 2 implies that the coefficient
![]() $r_{x,y}^{(i)}$
of the R-polynomial
$r_{x,y}^{(i)}$
of the R-polynomial
![]() $r_{x,y}$
has the following interpretation in terms of the dark grey triangle in Figure 1. We need to consider the integral points in the intersection of the line
$r_{x,y}$
has the following interpretation in terms of the dark grey triangle in Figure 1. We need to consider the integral points in the intersection of the line
![]() $b=i$
with the dark grey triangle (the dashed parts excluded) as given by the small black boxes in the following picture:
$b=i$
with the dark grey triangle (the dashed parts excluded) as given by the small black boxes in the following picture:

The coefficient
![]() $r_{x,y}^{(i)}$
is exactly the alternating sum of the dimensions of those extensions from (a shift of)
$r_{x,y}^{(i)}$
is exactly the alternating sum of the dimensions of those extensions from (a shift of)
![]() $\Delta_x$
to
$\Delta_x$
to
![]() $\Delta_y$
, where the top of
$\Delta_y$
, where the top of
![]() $\Delta_x$
is shifted by the coordinates of these small black boxes. Note that the dashed sides are excluded, except for the south and the east vertices of the triangle.
$\Delta_x$
is shifted by the coordinates of these small black boxes. Note that the dashed sides are excluded, except for the south and the east vertices of the triangle.
4·4. Consequences
Corollary 10. Let
![]() $\ell(x)-\ell(y)\equiv i\mod 2$
. If the intersection of the line
$\ell(x)-\ell(y)\equiv i\mod 2$
. If the intersection of the line
![]() $b=i$
with the dark grey triangle contains exactly one integral point, say
$b=i$
with the dark grey triangle contains exactly one integral point, say
![]() $(-a,b)$
, then
$(-a,b)$
, then
Proof. This follows directly from the discussion in Subsection 4·3.
Corollary 11. Let
![]() $x,y\in W$
with
$x,y\in W$
with
![]() $x\geq y$
. Then (11) holds for the following values of i:
$x\geq y$
. Then (11) holds for the following values of i:
Proof. If
![]() $i=\ell(x)-\ell(y)$
, then the intersection of
$i=\ell(x)-\ell(y)$
, then the intersection of
![]() $b=i$
with the dark grey triangle consists of the east vertex of the triangle. If
$b=i$
with the dark grey triangle consists of the east vertex of the triangle. If
![]() $i=\ell(y)-\ell(x)$
, then the intersection of
$i=\ell(y)-\ell(x)$
, then the intersection of
![]() $b=i$
with the dark grey triangle consists of the south vertex of the triangle. If
$b=i$
with the dark grey triangle consists of the south vertex of the triangle. If
![]() $i=\ell(x)-\ell(y)-2$
, then the intersection of
$i=\ell(x)-\ell(y)-2$
, then the intersection of
![]() $b=i$
with the dark grey triangle consists of the vertices
$b=i$
with the dark grey triangle consists of the vertices
![]() $(\ell(y)-\ell(x)+1,\ell(x)-\ell(y)-2)$
and
$(\ell(y)-\ell(x)+1,\ell(x)-\ell(y)-2)$
and
![]() $(\ell(y)-\ell(x)+2,\ell(x)-\ell(y)-2)$
, however, the latter one belongs to the dashed line. Similarly, if
$(\ell(y)-\ell(x)+2,\ell(x)-\ell(y)-2)$
, however, the latter one belongs to the dashed line. Similarly, if
![]() $i=\ell(y)-\ell(x)+2$
, then the intersection of
$i=\ell(y)-\ell(x)+2$
, then the intersection of
![]() $b=i$
with the dark grey triangle consists of the vertices
$b=i$
with the dark grey triangle consists of the vertices
![]() $(\!-\!1,\ell(y)-\ell(x)+2)$
and
$(\!-\!1,\ell(y)-\ell(x)+2)$
and
![]() $(0,\ell(y)-\ell(x)+2)$
, however, the latter one belongs to the dashed line.
$(0,\ell(y)-\ell(x)+2)$
, however, the latter one belongs to the dashed line.
This means that, in all four cases, we have exactly one relevant integral point. Now the claim follows from Corollary 10.
Corollary 12. Let
![]() $x,y\in W$
with
$x,y\in W$
with
![]() $x\geq y$
. If
$x\geq y$
. If
![]() $\ell(x)-\ell(y)\leq 3$
, then (11) holds.
$\ell(x)-\ell(y)\leq 3$
, then (11) holds.
4·5. Expected vs additional extensions
As illustrated in Figure 1, the proof of Proposition 5 implies that the non-zero E(x,y,i,0,k) split naturally into two types:
-
(1) The cases when
 $k={i+\ell(x)-\ell(y)}/{2}$
, i.e., the top of
$k={i+\ell(x)-\ell(y)}/{2}$
, i.e., the top of
 $\Delta_x\langle i\rangle$
lies on the solid dark grey side of the dark grey triangle. We call such cases expected.
$\Delta_x\langle i\rangle$
lies on the solid dark grey side of the dark grey triangle. We call such cases expected. -
(2) All other cases. In these cases the top of
 $\Delta_x\langle i\rangle$
belongs to the interior of the dark grey triangle. We call such cases additional.
$\Delta_x\langle i\rangle$
belongs to the interior of the dark grey triangle. We call such cases additional.
Then the discussion in Subsection 4·3 gives the following statement.
Corollary 13. If
![]() $x,y\in W$
and
$x,y\in W$
and
![]() $i\in\mathbb{Z}$
are such that all extensions between
$i\in\mathbb{Z}$
are such that all extensions between
![]() $\Delta_x\langle i\rangle$
and
$\Delta_x\langle i\rangle$
and
![]() $\Delta_y$
are known to be expected, then (11) holds.
$\Delta_y$
are known to be expected, then (11) holds.
Each non-zero element in
![]() $\textrm{ext}^k(\Delta_x\langle i\rangle,\Delta_y)$
is realised via a non-zero homomorphism from
$\textrm{ext}^k(\Delta_x\langle i\rangle,\Delta_y)$
is realised via a non-zero homomorphism from
![]() $\Delta_x\langle i\rangle$
to
$\Delta_x\langle i\rangle$
to
![]() $\mathcal{T}_{k}(\Delta_y)$
. Since the latter has a standard filtration and all non-zero morphisms between standard modules are injective, the map from
$\mathcal{T}_{k}(\Delta_y)$
. Since the latter has a standard filtration and all non-zero morphisms between standard modules are injective, the map from
![]() $\Delta_x\langle i\rangle$
to
$\Delta_x\langle i\rangle$
to
![]() $\mathcal{T}_{k}(\Delta_y)$
must be injective, in particular, it must be injective when restricted to the simple socle of
$\mathcal{T}_{k}(\Delta_y)$
must be injective, in particular, it must be injective when restricted to the simple socle of
![]() $\Delta_x\langle i\rangle$
.
$\Delta_x\langle i\rangle$
.
For expected extensions, the socle of
![]() $\Delta_x\langle i\rangle$
is on the diagonal side of the light gray triangle. This means that the homomorphism from
$\Delta_x\langle i\rangle$
is on the diagonal side of the light gray triangle. This means that the homomorphism from
![]() $\Delta_x\langle i\rangle$
to
$\Delta_x\langle i\rangle$
to
![]() $\mathcal{T}_{k}(\Delta_y)$
which realises this extension has an image inside the direct sum of all
$\mathcal{T}_{k}(\Delta_y)$
which realises this extension has an image inside the direct sum of all
![]() $T_w\langle k\rangle$
, where the sum is taken over all w such that
$T_w\langle k\rangle$
, where the sum is taken over all w such that
![]() $w\geq y$
and
$w\geq y$
and
![]() $\ell(w)=\ell(y)+k$
.
$\ell(w)=\ell(y)+k$
.
For additional extensions, the socle of
![]() $\Delta_x\langle i\rangle$
is in the interior of the light gray triangle. This means that the homomorphism from
$\Delta_x\langle i\rangle$
is in the interior of the light gray triangle. This means that the homomorphism from
![]() $\Delta_x\langle i\rangle$
to
$\Delta_x\langle i\rangle$
to
![]() $\mathcal{T}_{k}(\Delta_y)$
which realises this extension:
$\mathcal{T}_{k}(\Delta_y)$
which realises this extension:
-
(1) either induces a non-zero map to a summand of
 $\mathcal{T}_{k}(\Delta_y)$
different from the
$\mathcal{T}_{k}(\Delta_y)$
different from the
 $T_w\langle k\rangle$
as in the previous paragraph;
$T_w\langle k\rangle$
as in the previous paragraph; -
(2) or induces a non-zero map to some
 $T_w\langle k\rangle$
as in the previous paragraph, in which case the socle of this
$T_w\langle k\rangle$
as in the previous paragraph, in which case the socle of this
 $T_w\langle k\rangle$
is not simple and this induced map maps the socle of
$T_w\langle k\rangle$
is not simple and this induced map maps the socle of
 $\Delta_x\langle i\rangle$
to the socle part of
$\Delta_x\langle i\rangle$
to the socle part of
 $T_w\langle k\rangle$
which lives in a non-maximal degree.
$T_w\langle k\rangle$
which lives in a non-maximal degree.
Each of these cases is only possible in the situation when some KL-polynomials are nontrivial.
The first situation is possible only if
![]() $\mathcal{T}_{k}(\Delta_y)$
contains a summand
$\mathcal{T}_{k}(\Delta_y)$
contains a summand
![]() $T_w\langle k\rangle$
, for some
$T_w\langle k\rangle$
, for some
![]() $w\geq y$
which violates
$w\geq y$
which violates
![]() $\ell(w)=\ell(y)+k$
. Via the Koszul–Ringel duality, the fact that
$\ell(w)=\ell(y)+k$
. Via the Koszul–Ringel duality, the fact that
![]() $T_w\langle k\rangle$
is a summand of
$T_w\langle k\rangle$
is a summand of
![]() $\mathcal{T}_{k}(\Delta_y)$
means that
$\mathcal{T}_{k}(\Delta_y)$
means that
![]() $[\Delta_{w_0y^{-1}w_0}\;:\;L_{w_0w^{-1}w_0}\langle -k\rangle]\neq 0$
. The latter multiplicity is exactly the coefficient at
$[\Delta_{w_0y^{-1}w_0}\;:\;L_{w_0w^{-1}w_0}\langle -k\rangle]\neq 0$
. The latter multiplicity is exactly the coefficient at
![]() $v^k$
in the KL polynomial
$v^k$
in the KL polynomial
![]() $p_{w_0y^{-1}w_0,w_0w^{-1}w_0}$
. Since
$p_{w_0y^{-1}w_0,w_0w^{-1}w_0}$
. Since
![]() $\ell(w)\neq \ell(y)+k$
, this means that
$\ell(w)\neq \ell(y)+k$
, this means that
![]() $p_{w_0y^{-1}w_0,w_0w^{-1}w_0}$
is not trivial.
$p_{w_0y^{-1}w_0,w_0w^{-1}w_0}$
is not trivial.
The second situation is possible only if the socle of some
![]() $T_w\langle k\rangle$
, where
$T_w\langle k\rangle$
, where
![]() $w\geq y$
and
$w\geq y$
and
![]() $\ell(w)=\ell(y)+k$
, is not simple. Since the socle is a direct sum of
$\ell(w)=\ell(y)+k$
, is not simple. Since the socle is a direct sum of
![]() $L_{w_0}$
, the latter is if and only if
$L_{w_0}$
, the latter is if and only if
![]() $(T_w\;:\;\Delta_{w_0})>1$
, which is equivalent, via Koszul duality, to the polynomial
$(T_w\;:\;\Delta_{w_0})>1$
, which is equivalent, via Koszul duality, to the polynomial
![]() $p_{e,w_0w}$
being nontrivial.
$p_{e,w_0w}$
being nontrivial.
An immediate corollary of this discussion is the following.
Corollary 14. Let
![]() $y\in W$
be such that
$y\in W$
be such that
![]() $p_{w_0y^{-1}w_0,w_0w^{-1}w_0}$
and
$p_{w_0y^{-1}w_0,w_0w^{-1}w_0}$
and
![]() $p_{e,w_0w}$
are trivial, for all
$p_{e,w_0w}$
are trivial, for all
![]() $w\geq y$
. Then (11) holds for all
$w\geq y$
. Then (11) holds for all
![]() $x\in W$
such that
$x\in W$
such that
![]() $x\geq y$
.
$x\geq y$
.
Proof. By the assumption on trivial KL polynomials, the only non-zero extensions between Verma modules are those where the top of
![]() $\Delta_x\langle i\rangle$
is on the solid dark grey side of the dark grey triangle. Therefore (11) follows from Theorem 2.
$\Delta_x\langle i\rangle$
is on the solid dark grey side of the dark grey triangle. Therefore (11) follows from Theorem 2.
The assumption of Corollary 14 is satisfied for all
![]() $y\in W$
if W is of rank 2. We thus obtain the following.
$y\in W$
if W is of rank 2. We thus obtain the following.
Corollary 15. (11) holds in all cases when W has rank 2.
Remark 16. If W is of rank 2, a closed formula for the R-polynomials makes Corollary 15 more explicit. For
![]() $x,y\in W$
, letting
$x,y\in W$
, letting
![]() $d = \ell(y)-\ell(x)$
, we have
$d = \ell(y)-\ell(x)$
, we have
One way to see (12) is to directly compute the base change between the costandard and the standard bases, that is, by combining the equations
and
well known in the types of rank 2. The coefficients
![]() $1,2,\cdots,2,1$
in (12) reflect the shape of the Bruhat interval [x,y] in the dihedral group W.
$1,2,\cdots,2,1$
in (12) reflect the shape of the Bruhat interval [x,y] in the dihedral group W.
Therefore, Corollary 15 says that the graded extension between Verma modules are one dimensional in the extremes and two dimensional in the middle (along the solid dark grey side of the expected extensions). The latter result was previously obtained in [ Reference Dhillon and Makam13 , theorem 1·1].
4·6. Koszulity
Denote by
![]() $\mathscr{D}$
the full subcategory of the derived category
$\mathscr{D}$
the full subcategory of the derived category
![]() $\mathcal{D}(\mathcal{O}_0^\mathbb{Z})$
given by the objects
$\mathcal{D}(\mathcal{O}_0^\mathbb{Z})$
given by the objects
![]() $\Delta_w\langle i\rangle[j]$
, where
$\Delta_w\langle i\rangle[j]$
, where
![]() $w\in W$
and
$w\in W$
and
![]() $i,j\in\mathbb{Z}$
such that
$i,j\in\mathbb{Z}$
such that
Note that the shift put the socle of each
![]() $\Delta_w\langle i\rangle[j]$
in the “generating diagonal”
$\Delta_w\langle i\rangle[j]$
in the “generating diagonal”
![]() $i\in\{-2j,-2j+1\}$
. The group
$i\in\{-2j,-2j+1\}$
. The group
![]() $\mathbb{Z}$
acts freely on
$\mathbb{Z}$
acts freely on
![]() $\mathscr{D}$
by sending
$\mathscr{D}$
by sending
![]() $\Delta_w\langle i\rangle[j]$
to
$\Delta_w\langle i\rangle[j]$
to
![]() $\Delta_w\langle i-2m\rangle[j+m]$
, for
$\Delta_w\langle i-2m\rangle[j+m]$
, for
![]() $m\in\mathbb{Z}$
.
$m\in\mathbb{Z}$
.
Consider the category
![]() $\mathscr{D}$
-mod of finite dimensional
$\mathscr{D}$
-mod of finite dimensional
![]() $\mathscr{D}$
-modules. The objects of this category are
$\mathscr{D}$
-modules. The objects of this category are
![]() $\mathbb{C}$
-linear functors M from
$\mathbb{C}$
-linear functors M from
![]() $\mathscr{D}$
to vector spaces (over
$\mathscr{D}$
to vector spaces (over
![]() $\mathbb{C}$
) such that the sum, over all
$\mathbb{C}$
) such that the sum, over all
![]() $\texttt{i}\in \mathscr{D}$
, of the dimensions of
$\texttt{i}\in \mathscr{D}$
, of the dimensions of
![]() $\textrm{M}(\texttt{i})$
is finite. The morphisms in
$\textrm{M}(\texttt{i})$
is finite. The morphisms in
![]() $\mathscr{D}$
-mod are natural transformations of functors.
$\mathscr{D}$
-mod are natural transformations of functors.
The following results generalizes [ Reference Drozd and Mazorchuk14 , theorem 5·1] (see also Theorem 31). Theorem 20 below shows a case that is covered by Theorem 31 but not by [ Reference Drozd and Mazorchuk14 , theorem 5·1].
Theorem 17. Assume that all extensions between the Verma modules in
![]() $\mathcal{O}_0$
are expected. Then the following assertions hold:
$\mathcal{O}_0$
are expected. Then the following assertions hold:
-
(a) we have an equivalence
 $\mathcal{D}^*(\mathcal{O}_0^\mathbb{Z})\cong \mathcal{D}^*(\mathscr{D}\text{-}\textrm{mod})$
where
$\mathcal{D}^*(\mathcal{O}_0^\mathbb{Z})\cong \mathcal{D}^*(\mathscr{D}\text{-}\textrm{mod})$
where
 $*\in\{b,\uparrow,\downarrow\}$
;
$*\in\{b,\uparrow,\downarrow\}$
; -
(b) the path algebra of
 $\mathscr{D}$
is Koszul and is Koszul self-dual.
$\mathscr{D}$
is Koszul and is Koszul self-dual.
Proof. The proof essentially follows the proof of [ Reference Drozd and Mazorchuk14 , theorem 5·1].
The assumption that all extensions between the Verma modules in
![]() $\mathcal{O}_0^{\mathbb{Z}}$
are expected says exactly that
$\mathcal{O}_0^{\mathbb{Z}}$
are expected says exactly that
![]() $\mathscr{D}$
has no self-extensions (of a nonzero degree). Since
$\mathscr{D}$
has no self-extensions (of a nonzero degree). Since
![]() $\mathscr{D}$
generates
$\mathscr{D}$
generates
![]() $\mathcal{D}^b(\mathcal{O}_0^\mathbb{Z})$
, the subcategory
$\mathcal{D}^b(\mathcal{O}_0^\mathbb{Z})$
, the subcategory
![]() $\mathscr{D}$
gives rise to a tilting complex in the sense of Rickard (see [
Reference Drozd and Mazorchuk14
, subsection 2·1], where such
$\mathscr{D}$
gives rise to a tilting complex in the sense of Rickard (see [
Reference Drozd and Mazorchuk14
, subsection 2·1], where such
![]() $\mathscr{D}$
is called a tilting subset). Therefore, claim (a) follows from the Rickard-Morita Theorem (see [
Reference Drozd and Mazorchuk14
, theorem 2·1]).
$\mathscr{D}$
is called a tilting subset). Therefore, claim (a) follows from the Rickard-Morita Theorem (see [
Reference Drozd and Mazorchuk14
, theorem 2·1]).
To show claim (b), we note that the equivalence
![]() $\mathcal{D}^*(\mathcal{O}_0^\mathbb{Z})\to \mathcal{D}^*(\mathscr{D}\text{-}\textrm{mod})$
is given by
$\mathcal{D}^*(\mathcal{O}_0^\mathbb{Z})\to \mathcal{D}^*(\mathscr{D}\text{-}\textrm{mod})$
is given by
![]() $X \mapsto \textrm{Hom}_{\mathcal D^{*}(\mathcal O_0^{\mathbb{Z}})}(-,X)$
where the latter functor is restricted to
$X \mapsto \textrm{Hom}_{\mathcal D^{*}(\mathcal O_0^{\mathbb{Z}})}(-,X)$
where the latter functor is restricted to
![]() $\mathscr D$
. Since the Verma modules and the dual Verma modules are homologically orthogonal, simple objects in
$\mathscr D$
. Since the Verma modules and the dual Verma modules are homologically orthogonal, simple objects in
![]() $\mathscr{D}$
-mod correspond to dual Verma modules under the equivalence. From these we see that the quadratic dual of
$\mathscr{D}$
-mod correspond to dual Verma modules under the equivalence. From these we see that the quadratic dual of
![]() $\mathscr{D}$
consists of the dual Verma modules, with the similar shifts (the tops on the generating diagonal), and that the composition
$\mathscr{D}$
consists of the dual Verma modules, with the similar shifts (the tops on the generating diagonal), and that the composition
where the first and the third functors are from (a) and the middle functor is the simple preserving duality, agrees with the Koszul duality functor. Thus both the Koszulity and the Koszul self duality follow from [ Reference Mazorchuk, Ovsienko and Stroppel23 , theorem 30].
5. Combinatorics of Bruhat intervals
5·1. Equivalence classes of Bruhat intervals
Denote by
![]() $\mathscr{I}$
the set of all pairs
$\mathscr{I}$
the set of all pairs
![]() $(x,y)\in W^2$
such that
$(x,y)\in W^2$
such that
![]() $x\geq y$
. Each such pair (x,y) determines uniquely an interval in the Bruhat order, denoted
$x\geq y$
. Each such pair (x,y) determines uniquely an interval in the Bruhat order, denoted
![]() $[y,x]=\{z\in W\,:\, y\leq z\text{ and }z\leq x\}$
. Let
$[y,x]=\{z\in W\,:\, y\leq z\text{ and }z\leq x\}$
. Let
![]() $\sim$
denote the minimal equivalence relations on
$\sim$
denote the minimal equivalence relations on
![]() $\mathscr{I}$
that contains all
$\mathscr{I}$
that contains all
![]() $(x,y)\sim (xs,ys)$
, where
$(x,y)\sim (xs,ys)$
, where
![]() $s\in S$
is such that
$s\in S$
is such that
![]() $\ell(x)>\ell(xs)$
and
$\ell(x)>\ell(xs)$
and
![]() $\ell(y)>\ell(ys)$
, and all
$\ell(y)>\ell(ys)$
, and all
![]() $(x,y)\sim (sx,sy)$
, where
$(x,y)\sim (sx,sy)$
, where
![]() $s\in S$
is such that
$s\in S$
is such that
![]() $\ell(x)>\ell(sx)$
and
$\ell(x)>\ell(sx)$
and
![]() $\ell(y)>\ell(sy)$
.
$\ell(y)>\ell(sy)$
.
Proposition 18. If
![]() $(x,y)\sim(x',y')$
, then
$(x,y)\sim(x',y')$
, then
![]() ${\textrm{E}}_{x,y}=\textrm{E}_{x',y'}$
.
${\textrm{E}}_{x,y}=\textrm{E}_{x',y'}$
.
Proof. In case
![]() $(x',y')=(sx,sy)$
, for some
$(x',y')=(sx,sy)$
, for some
![]() $s\in S$
such that
$s\in S$
such that
![]() $\ell(x)>\ell(sx)$
and
$\ell(x)>\ell(sx)$
and
![]() $\ell(y)>\ell(sy)$
, we apply
$\ell(y)>\ell(sy)$
, we apply
![]() $\mathcal{L}\top_s$
. It sends
$\mathcal{L}\top_s$
. It sends
![]() $\Delta_{sx}$
to
$\Delta_{sx}$
to
![]() $\Delta_x$
and
$\Delta_x$
and
![]() $\Delta_{sy}$
to
$\Delta_{sy}$
to
![]() $\Delta_y$
. On top of that,
$\Delta_y$
. On top of that,
![]() $\mathcal{L}\top_s$
is a derived equivalence and thus induces the necessary isomorphisms between the extension spaces.
$\mathcal{L}\top_s$
is a derived equivalence and thus induces the necessary isomorphisms between the extension spaces.
In case
![]() $(x',y')=(xs,ys)$
, for some
$(x',y')=(xs,ys)$
, for some
![]() $s\in S$
such that
$s\in S$
such that
![]() $\ell(x)>\ell(xs)$
and
$\ell(x)>\ell(xs)$
and
![]() $\ell(y)>\ell(ys)$
, we can apply the derived equivalence
$\ell(y)>\ell(ys)$
, we can apply the derived equivalence
![]() $\mathcal{L}\textsf{C}_s$
and argue similarly to the previous paragraph. The claim follows.
$\mathcal{L}\textsf{C}_s$
and argue similarly to the previous paragraph. The claim follows.
Note that
![]() $(x,y)\sim(x',y')$
does not imply a poset isomorphism between the Bruhat intervals [y,x] and [y’,x’] in general. For example, in type
$(x,y)\sim(x',y')$
does not imply a poset isomorphism between the Bruhat intervals [y,x] and [y’,x’] in general. For example, in type
![]() $A_3$
with simple reflections r,s,t representing the following nodes of the Dynkin diagram:
$A_3$
with simple reflections r,s,t representing the following nodes of the Dynkin diagram: ![]() , we obviously have
, we obviously have
![]() $(rts,e)\sim(srts,s)$
. However, the boolean interval [e,rts] is not poset isomorphic to the interval [s,srts]. In fact, they even have different characters as graded posets.
$(rts,e)\sim(srts,s)$
. However, the boolean interval [e,rts] is not poset isomorphic to the interval [s,srts]. In fact, they even have different characters as graded posets.
5·2. Boolean and coboolean elements
Recall that an element
![]() $w\in W$
is called boolean provided it is a multiplicity-free product of simple reflections. The name is justified by the observation that the Bruhat ideal [e,w], for a boolean element w, is isomorphic, as a poset, to the poset of subsets of the set of simple reflections appearing in w.
$w\in W$
is called boolean provided it is a multiplicity-free product of simple reflections. The name is justified by the observation that the Bruhat ideal [e,w], for a boolean element w, is isomorphic, as a poset, to the poset of subsets of the set of simple reflections appearing in w.
Proposition 19. Let
![]() $x',y'\in W$
be such that
$x',y'\in W$
be such that
![]() $x'\geq y'$
.
$x'\geq y'$
.
-
(a) Assume that the equivalence class of (x’,y’) contains some (x,y) with x boolean. Then
 $\textrm{ext}^k(\Delta_{x'}\langle i\rangle,\Delta_{y'})$
is given by (11).
$\textrm{ext}^k(\Delta_{x'}\langle i\rangle,\Delta_{y'})$
is given by (11). -
(b) Assume that the equivalence class of (x’,y’) contains some (x,y) with
 $w_0y$
boolean. Then
$w_0y$
boolean. Then
 $\textrm{ext}^k(\Delta_{x'}\langle i\rangle,\Delta_{y'})$
is given by (11).
$\textrm{ext}^k(\Delta_{x'}\langle i\rangle,\Delta_{y'})$
is given by (11).
Proof. The two claims of the proposition are connected by the Ringel duality and the simple preserving duality
![]() $^\star$
, so it is enough to prove claim (b). By Proposition 18, it is enough to consider the case
$^\star$
, so it is enough to prove claim (b). By Proposition 18, it is enough to consider the case
![]() $x=x'$
and
$x=x'$
and
![]() $y=y'$
, i.e.,
$y=y'$
, i.e.,
![]() $w_0y$
is boolean. (Note that the latter is if and only if
$w_0y$
is boolean. (Note that the latter is if and only if
![]() $yw_0$
is boolean.) We claim that, in this case, all KL polynomials
$yw_0$
is boolean.) We claim that, in this case, all KL polynomials
![]() $p_{xw_0,zw_0}$
and
$p_{xw_0,zw_0}$
and
![]() $p_{y,z}$
, where
$p_{y,z}$
, where
![]() $y\leq z\leq x$
, are trivial. This and Proposition 5 proves (b).
$y\leq z\leq x$
, are trivial. This and Proposition 5 proves (b).
The claim is a well-known property of KL polynomials (see [
Reference Björner and Brenti6
, exercise 5·36.(e)]), which is proved, for example, as follows. If w is boolean, say
![]() $w=st\cdots u$
for
$w=st\cdots u$
for
![]() $s,t,\cdots,u\in S$
distinct, then the KL basis element is of the form
$s,t,\cdots,u\in S$
distinct, then the KL basis element is of the form
![]() $\underline{H}_w=\underline{H}_s\underline{H}_t\cdots \underline{H}_u$
. So all KL polynoimals
$\underline{H}_w=\underline{H}_s\underline{H}_t\cdots \underline{H}_u$
. So all KL polynoimals
![]() $p_{w',w}$
, for
$p_{w',w}$
, for
![]() $w'\leq w$
, are trivial, and so are
$w'\leq w$
, are trivial, and so are
![]() $p_{w_0w'w_0,w_0ww_0}$
. By Kazhdan–Lusztig inversion formula (see [
Reference Kazhdan and Lusztig17
, section 3]), the same is true for
$p_{w_0w'w_0,w_0ww_0}$
. By Kazhdan–Lusztig inversion formula (see [
Reference Kazhdan and Lusztig17
, section 3]), the same is true for
![]() $p_{w_0w,w_0w'}$
and
$p_{w_0w,w_0w'}$
and
![]() $p_{ww_0,w'w_0}$
. These include all
$p_{ww_0,w'w_0}$
. These include all
![]() $p_{xw_0,zw_0}$
and
$p_{xw_0,zw_0}$
and
![]() $p_{y,z}$
since
$p_{y,z}$
since
![]() $zw_0\leq yw_0$
is boolean.
$zw_0\leq yw_0$
is boolean.
6. Special cases
6·1. Type
 $A_1$
$A_1$
In type
![]() $A_1$
, we have
$A_1$
, we have
![]() $W=\{e,s\}$
. The only non-zero extension of positive degree between Verma modules is
$W=\{e,s\}$
. The only non-zero extension of positive degree between Verma modules is
![]() $\textrm{ext}^1(\Delta_s\langle 1\rangle,\Delta_e)\cong \mathbb{C}$
realised in the projective module
$\textrm{ext}^1(\Delta_s\langle 1\rangle,\Delta_e)\cong \mathbb{C}$
realised in the projective module
![]() $P_s$
. Here is the table for
$P_s$
. Here is the table for
![]() $\textrm{E}_{x,y}(v,u)$
:
$\textrm{E}_{x,y}(v,u)$
:

6·2. Type
 $A_2$
$A_2$
In type
![]() $A_2$
, we have
$A_2$
, we have
![]() $W=\{e,s,t,st,ts,w_0=sts=tst\}$
. By Corollary 15, all extensions between Verma modules in this case are given by (11) via the coefficients of R-polynomials. Here is the table for the R-polynomials in this case:
$W=\{e,s,t,st,ts,w_0=sts=tst\}$
. By Corollary 15, all extensions between Verma modules in this case are given by (11) via the coefficients of R-polynomials. Here is the table for the R-polynomials in this case:

Here is the table for E-polynomials in this case:

6·3. Type
 $A_3$
$A_3$
In type
![]() $A_3$
, the group W is generated by the simple reflections r,s,t representing the following nodes of the Dynkin diagram:
$A_3$
, the group W is generated by the simple reflections r,s,t representing the following nodes of the Dynkin diagram: ![]() . Our main result in this subsection is the following.
. Our main result in this subsection is the following.
Theorem 20. In type
![]() $A_3$
, all extensions between Verma modules in
$A_3$
, all extensions between Verma modules in
![]() $\mathcal{O}_0$
are expected and given by (11).
$\mathcal{O}_0$
are expected and given by (11).
Please note that Theorem 20 does not claim that, in type
![]() $A_3$
, we are always in the situation as described by the assumptions of Corollary 10. The claim is that, regardless whether the assumptions of Corollary 10 hold, all extensions between Verma modules are given by (11).
$A_3$
, we are always in the situation as described by the assumptions of Corollary 10. The claim is that, regardless whether the assumptions of Corollary 10 hold, all extensions between Verma modules are given by (11).
Proof. In type
![]() $A_3$
, there are two non-trivial KL-polynomials of the form
$A_3$
, there are two non-trivial KL-polynomials of the form
![]() $p_{e,w}$
, namely:
$p_{e,w}$
, namely:
This implies the following two facts:
The minimal tilting coresolution
![]() $\mathcal{T}_\bullet(\Delta_e)$
, apart from the “expected” summands
$\mathcal{T}_\bullet(\Delta_e)$
, apart from the “expected” summands
![]() $T_w\langle\ell(w)\rangle[\!-\!\ell(w)]$
, where
$T_w\langle\ell(w)\rangle[\!-\!\ell(w)]$
, where
![]() $w\in S_4$
, also has two additional summands:
$w\in S_4$
, also has two additional summands:
![]() $T_{srts}\langle 2\rangle[\!-\!2]$
and
$T_{srts}\langle 2\rangle[\!-\!2]$
and
![]() $T_{rstsr}\langle 3\rangle[\!-\!3]$
.
$T_{rstsr}\langle 3\rangle[\!-\!3]$
.

Figure 2. Dimensions of socles for summands of
![]() $\mathcal{T}_\bullet(\Delta_e)$
$\mathcal{T}_\bullet(\Delta_e)$
The following tilting modules have non-simple socle:
-
(1) the module
 $T_{s}$
, whose expected part of the socle is
$T_{s}$
, whose expected part of the socle is
 $L_{w_0}\langle -\ell(w_0s)\rangle$
, has additional socle
$L_{w_0}\langle -\ell(w_0s)\rangle$
, has additional socle
 $L_{w_0}\langle -\ell(w_0s)+2\rangle$
,
$L_{w_0}\langle -\ell(w_0s)+2\rangle$
, -
(2) the module
 $T_{rt}$
, whose expected part of the socle is
$T_{rt}$
, whose expected part of the socle is
 $L_{w_0}\langle -\ell(w_0rt)\rangle$
, has additional socle
$L_{w_0}\langle -\ell(w_0rt)\rangle$
, has additional socle
 $L_{w_0}\langle -\ell(w_0rt)+2\rangle$
.
$L_{w_0}\langle -\ell(w_0rt)+2\rangle$
.
Every
![]() $T_w$
not listed above has socle
$T_w$
not listed above has socle
![]() $L_{w_0}\langle -\ell(w_0w)\rangle$
. We can now collect the information about the socles of all tilting summands appearing in
$L_{w_0}\langle -\ell(w_0w)\rangle$
. We can now collect the information about the socles of all tilting summands appearing in
![]() $\mathcal{T}_\bullet(\Delta_e)$
in Figure 2. Here the expected hom dimension between
$\mathcal{T}_\bullet(\Delta_e)$
in Figure 2. Here the expected hom dimension between
![]() $L_{w_0}=\Delta_{w_0}$
and each
$L_{w_0}=\Delta_{w_0}$
and each
![]() $\mathcal T_i(\Delta_e)$
is marked by a circle and the additional part is marked by squares. The four additional dimensions come from the above list:
$\mathcal T_i(\Delta_e)$
is marked by a circle and the additional part is marked by squares. The four additional dimensions come from the above list:
-
(1) the additional socle of
 $T_{s}\langle 1\rangle[\!-\!1]$
gives one dimension at the point
$T_{s}\langle 1\rangle[\!-\!1]$
gives one dimension at the point
 $(\!-\!1,-2)$
;
$(\!-\!1,-2)$
; -
(2) the additional socle of
 $T_{rt}\langle 2\rangle[\!-\!2]$
gives one dimension at the point
$T_{rt}\langle 2\rangle[\!-\!2]$
gives one dimension at the point
 $(\!-\!2,0)$
;
$(\!-\!2,0)$
; -
(3) the socle of the additional summand
 $T_{srts}\langle 2\rangle[\!-\!2]$
gives one dimension at the point
$T_{srts}\langle 2\rangle[\!-\!2]$
gives one dimension at the point
 $(\!-\!2,0)$
;
$(\!-\!2,0)$
; -
(4) the socle of the additional summand
 $T_{rstsr}\langle 2\rangle[\!-\!2]$
gives one dimension at the point
$T_{rstsr}\langle 2\rangle[\!-\!2]$
gives one dimension at the point
 $(\!-\!3,2)$
.
$(\!-\!3,2)$
.
The aim is to show that no homomorphism in a square space gives rise to a nonzero homomorphism of complexes between the corresponding shifts of
![]() $L_{w_0}$
and
$L_{w_0}$
and
![]() $\mathcal{T}_\bullet(\Delta_e)$
. From this it follows that there is no additional homomorphism of complexes (i.e., no homomorphism of complexes that possibly gives an additional extension) between
$\mathcal{T}_\bullet(\Delta_e)$
. From this it follows that there is no additional homomorphism of complexes (i.e., no homomorphism of complexes that possibly gives an additional extension) between
![]() $\Delta_x$
and
$\Delta_x$
and
![]() $\mathcal{T}_\bullet(\Delta_e)$
since the latter would restrict to a homomorphism from the socle
$\mathcal{T}_\bullet(\Delta_e)$
since the latter would restrict to a homomorphism from the socle
![]() $L_{w_0}$
(see also the socle discussion in Subsection 4·5).
$L_{w_0}$
(see also the socle discussion in Subsection 4·5).
By Proposition 9, the additional socle of
![]() $T_{s}\langle 1\rangle[\!-\!1]$
does not contribute to a homomorphism of complexes from
$T_{s}\langle 1\rangle[\!-\!1]$
does not contribute to a homomorphism of complexes from
![]() $L_{w_0}\langle 1\rangle[\!-\!2]$
to
$L_{w_0}\langle 1\rangle[\!-\!2]$
to
![]() $\mathcal{T}_\bullet(\Delta_e)$
. This means that there are no additional first extensions to
$\mathcal{T}_\bullet(\Delta_e)$
. This means that there are no additional first extensions to
![]() $\Delta_e$
(this is a general fact, see [
Reference Mazorchuk21
, theorem 32]) from any Verma modules. Therefore the additional dimension 1 at the point
$\Delta_e$
(this is a general fact, see [
Reference Mazorchuk21
, theorem 32]) from any Verma modules. Therefore the additional dimension 1 at the point
![]() $(\!-\!1,-2)$
decreases the value 5 at the point
$(\!-\!1,-2)$
decreases the value 5 at the point
![]() $(\!-\!2,-2)$
by 1, resulting in the dimension 4.
$(\!-\!2,-2)$
by 1, resulting in the dimension 4.
By Koszul–Ringel duality, the fact that we have
![]() $\textrm{ext}^1(\Delta_{w_0}\langle -2\rangle,\Delta_e)=0$
implies that we have
$\textrm{ext}^1(\Delta_{w_0}\langle -2\rangle,\Delta_e)=0$
implies that we have
![]() $\textrm{ext}^3(\Delta_{w_0}\langle 2\rangle,\Delta_e)=0$
. Therefore, any homomorphism of complexes from
$\textrm{ext}^3(\Delta_{w_0}\langle 2\rangle,\Delta_e)=0$
. Therefore, any homomorphism of complexes from
![]() $\Delta_{w_0}\langle 2\rangle[\!-\!3]$
to
$\Delta_{w_0}\langle 2\rangle[\!-\!3]$
to
![]() $\mathcal{T}_\bullet(\Delta_e)$
is homotopic to zero. Since no homotopies between these two complexes are possible (as
$\mathcal{T}_\bullet(\Delta_e)$
is homotopic to zero. Since no homotopies between these two complexes are possible (as
![]() $\textrm{hom}(\Delta_{w_0}\langle 2\rangle,\mathcal{T}_2(\Delta_e))=0$
), it follows that the composition of the differential in
$\textrm{hom}(\Delta_{w_0}\langle 2\rangle,\mathcal{T}_2(\Delta_e))=0$
), it follows that the composition of the differential in
![]() $\mathcal{T}_\bullet(\Delta_e)$
homomorphism
$\mathcal{T}_\bullet(\Delta_e)$
homomorphism
![]() $\Delta_{w_0}\langle 2\rangle \to \mathcal{T}_3(\Delta_e)$
is non-zero. Therefore the only relevance of the additional dimension 1 at the point
$\Delta_{w_0}\langle 2\rangle \to \mathcal{T}_3(\Delta_e)$
is non-zero. Therefore the only relevance of the additional dimension 1 at the point
![]() $(\!-\!3,2)$
is that it decreases the value 5 at the point
$(\!-\!3,2)$
is that it decreases the value 5 at the point
![]() $(\!-\!4,2)$
by 1 resulting in 4, which is a coefficients of the R-polynomial.
$(\!-\!4,2)$
by 1 resulting in 4, which is a coefficients of the R-polynomial.
It remains to deal with the square point
![]() $(\!-\!2,0)$
. Similarly to the above, using Proposition 9, we obtain that the restriction of the differential in
$(\!-\!2,0)$
. Similarly to the above, using Proposition 9, we obtain that the restriction of the differential in
![]() $\mathcal{T}_\bullet(\Delta_e)$
to the additional socle of
$\mathcal{T}_\bullet(\Delta_e)$
to the additional socle of
![]() $T_{rt}\langle 2\rangle[\!-\!2]$
is non-zero. This takes care of one dimension at the square point
$T_{rt}\langle 2\rangle[\!-\!2]$
is non-zero. This takes care of one dimension at the square point
![]() $(\!-\!2,0)$
. The second dimension at this point corresponds to the usual (simple) socle of the additional summand
$(\!-\!2,0)$
. The second dimension at this point corresponds to the usual (simple) socle of the additional summand
![]() $T_{srts}\langle 2\rangle[\!-\!2]$
. We now argue that the image of the restriction of the differential in
$T_{srts}\langle 2\rangle[\!-\!2]$
. We now argue that the image of the restriction of the differential in
![]() $\mathcal{T}_\bullet(\Delta_e)$
to this socle component is linearly independent to the image of the restriction of the differential in
$\mathcal{T}_\bullet(\Delta_e)$
to this socle component is linearly independent to the image of the restriction of the differential in
![]() $\mathcal{T}_\bullet(\Delta_e)$
to the additional socle of
$\mathcal{T}_\bullet(\Delta_e)$
to the additional socle of
![]() $T_{rt}\langle 2\rangle[\!-\!2]$
.
$T_{rt}\langle 2\rangle[\!-\!2]$
.
Our argument is very much ad hoc, we use the explicit description of
![]() $\Delta_e$
as given in [
Reference Stroppel31
, appendix A]. From it we see that the differential in
$\Delta_e$
as given in [
Reference Stroppel31
, appendix A]. From it we see that the differential in
![]() $\mathcal{T}_\bullet(\Delta_e)$
restricts to a non-zero map from
$\mathcal{T}_\bullet(\Delta_e)$
restricts to a non-zero map from
![]() $T_{srts}\langle 2\rangle[\!-\!2]$
to
$T_{srts}\langle 2\rangle[\!-\!2]$
to
![]() $T_{sts}\langle 3\rangle[\!-\!3]$
and, at the same time, this differential restricts to the zero map from
$T_{sts}\langle 3\rangle[\!-\!3]$
and, at the same time, this differential restricts to the zero map from
![]() $T_{rt}\langle 2\rangle[\!-\!2]$
to
$T_{rt}\langle 2\rangle[\!-\!2]$
to
![]() $T_{sts}\langle 3\rangle[\!-\!3]$
. It remains to show that any non-zero map from
$T_{sts}\langle 3\rangle[\!-\!3]$
. It remains to show that any non-zero map from
![]() $T_{srts}\langle 2\rangle[\!-\!2]$
to
$T_{srts}\langle 2\rangle[\!-\!2]$
to
![]() $T_{sts}\langle 3\rangle[\!-\!3]$
is injective (i.e., does not kill the socle). Since the domain has a standard filtration and the codomain has a costandard filtration, a non-zero map from
$T_{sts}\langle 3\rangle[\!-\!3]$
is injective (i.e., does not kill the socle). Since the domain has a standard filtration and the codomain has a costandard filtration, a non-zero map from
![]() $T_{srts}\langle 2\rangle[\!-\!2]$
to
$T_{srts}\langle 2\rangle[\!-\!2]$
to
![]() $T_{sts}\langle 3\rangle[\!-\!3]$
must be a linear combination of maps lifted from some standard subquotient of
$T_{sts}\langle 3\rangle[\!-\!3]$
must be a linear combination of maps lifted from some standard subquotient of
![]() $T_{srts}\langle 2\rangle[\!-\!2]$
to some costandard subquotient of
$T_{srts}\langle 2\rangle[\!-\!2]$
to some costandard subquotient of
![]() $T_{sts}\langle 3\rangle[\!-\!3]$
. There is only one such pair which appears with correct shifts:
$T_{sts}\langle 3\rangle[\!-\!3]$
. There is only one such pair which appears with correct shifts:
![]() $\Delta_{srts}\langle 2\rangle[\!-\!2]$
for
$\Delta_{srts}\langle 2\rangle[\!-\!2]$
for
![]() $T_{srts}\langle 2\rangle[\!-\!2]$
and
$T_{srts}\langle 2\rangle[\!-\!2]$
and
![]() $\nabla_{srts}\langle 2\rangle[\!-\!2]$
for
$\nabla_{srts}\langle 2\rangle[\!-\!2]$
for
![]() $T_{sts}\langle 3\rangle[\!-\!3]$
. Therefore, a non-zero homomorphism from
$T_{sts}\langle 3\rangle[\!-\!3]$
. Therefore, a non-zero homomorphism from
![]() $T_{srts}\langle 2\rangle[\!-\!2]$
to
$T_{srts}\langle 2\rangle[\!-\!2]$
to
![]() $T_{sts}\langle 3\rangle[\!-\!3]$
is a lift of a homomorphism from
$T_{sts}\langle 3\rangle[\!-\!3]$
is a lift of a homomorphism from
![]() $\Delta_{srts}\langle 2\rangle[\!-\!2]$
to
$\Delta_{srts}\langle 2\rangle[\!-\!2]$
to
![]() $T_{sts}\langle 3\rangle[\!-\!3]$
. Since any homomorphism from a Verma module to a tilting module is injective, a non-zero map from
$T_{sts}\langle 3\rangle[\!-\!3]$
. Since any homomorphism from a Verma module to a tilting module is injective, a non-zero map from
![]() $\Delta_{srts}\langle 2\rangle[\!-\!2]$
to
$\Delta_{srts}\langle 2\rangle[\!-\!2]$
to
![]() $T_{sts}\langle 3\rangle[\!-\!3]$
is injective. Since the socles of
$T_{sts}\langle 3\rangle[\!-\!3]$
is injective. Since the socles of
![]() $T_{srts}\langle 2\rangle[\!-\!2]$
and
$T_{srts}\langle 2\rangle[\!-\!2]$
and
![]() $\Delta_{srts}\langle 2\rangle[\!-\!2]$
coincide, we get the claim.
$\Delta_{srts}\langle 2\rangle[\!-\!2]$
coincide, we get the claim.
The arguments above show that, in the category of complexes, the only homomorphisms from Verma modules to
![]() $\mathcal{T}_\bullet(\Delta_e)$
are with expected shifts. Since all
$\mathcal{T}_\bullet(\Delta_e)$
are with expected shifts. Since all
![]() $\mathcal{T}_\bullet(\Delta_y)$
are subcomplexes of
$\mathcal{T}_\bullet(\Delta_y)$
are subcomplexes of
![]() $\mathcal{T}_\bullet(\Delta_e)$
(up to some shifts in both homological and grading), it follows that the only possible extensions between Verma modules are expected extensions. The fact that they are given by (11) follows from the graded Delorme formula. This completes the proof.
$\mathcal{T}_\bullet(\Delta_e)$
(up to some shifts in both homological and grading), it follows that the only possible extensions between Verma modules are expected extensions. The fact that they are given by (11) follows from the graded Delorme formula. This completes the proof.
6·4. Some first extensions between Verma modules in type A
In this subsection we use the results of [
Reference Ko, Mazorchuk and Mren19
] to construct many additional first extensions between Verma modules in type A. We refer to [
Reference Ko, Mazorchuk and Mren19
] for the details of the facts recalled below. We assume that
![]() $W=S_n$
with the Dynkin diagram
$W=S_n$
with the Dynkin diagram
For
![]() $i,j\in\{1,2,\dots,n-1\}$
, we denote by
$i,j\in\{1,2,\dots,n-1\}$
, we denote by
![]() $\hat{w}_{i,j}$
the following element:
$\hat{w}_{i,j}$
the following element:
 $$ \hat{w}_{i,j}=\begin{cases}s_is_{i-1}\dots s_j,& j\leq i;\\s_is_{i+1}\dots s_j,& j> i.\end{cases}$$
$$ \hat{w}_{i,j}=\begin{cases}s_is_{i-1}\dots s_j,& j\leq i;\\s_is_{i+1}\dots s_j,& j> i.\end{cases}$$
Note that
![]() $\hat{w}_{i,i}=s_i$
. By construction,
$\hat{w}_{i,i}=s_i$
. By construction,
![]() $\hat{w}_{i,j}$
has left descent
$\hat{w}_{i,j}$
has left descent
![]() $s_i$
and right descent
$s_i$
and right descent
![]() $s_j$
. We also denote by
$s_j$
. We also denote by
![]() $w_{i,j}$
the element
$w_{i,j}$
the element
![]() $\hat{w}_{i,n-j}w_0$
. Dually, the element
$\hat{w}_{i,n-j}w_0$
. Dually, the element
![]() $w_{i,j}$
has left ascent
$w_{i,j}$
has left ascent
![]() $s_i$
and right ascent
$s_i$
and right ascent
![]() $s_j$
. The set
$s_j$
. The set
![]() $\{w_{i,j}\}$
is exactly the penultimate two-sided KL cell in
$\{w_{i,j}\}$
is exactly the penultimate two-sided KL cell in
![]() $S_n$
.
$S_n$
.
Each simple
![]() $L_{w_{i,j}}$
is graded multiplicity-free in
$L_{w_{i,j}}$
is graded multiplicity-free in
![]() $\Delta_e$
. In fact,
$\Delta_e$
. In fact,
![]() $[\Delta_e\;:\;L_{w_{i,j}}\langle -m\rangle]=1$
if and only if
$[\Delta_e\;:\;L_{w_{i,j}}\langle -m\rangle]=1$
if and only if
![]() $m\in\{\ell(w_{i,j}),\ell(w_{i,j})-2,\ell(w_{i,j})-4,\dots,\ell(w_{i,j})-2q_{i,j}\}$
where
$m\in\{\ell(w_{i,j}),\ell(w_{i,j})-2,\ell(w_{i,j})-4,\dots,\ell(w_{i,j})-2q_{i,j}\}$
where
Note that the ungraded multiplicity of
![]() $L_{w_{i,j}}$
in
$L_{w_{i,j}}$
in
![]() $\Delta_e$
equals
$\Delta_e$
equals
![]() $1+q_{i,j}$
.
$1+q_{i,j}$
.
Recall that an element of
![]() $S_n$
is called bigrassmannian provided that it has a unique left descent and a unique right descent (for example, all
$S_n$
is called bigrassmannian provided that it has a unique left descent and a unique right descent (for example, all
![]() $\hat{w}_{i,j}$
are bigrassmannian). There are exactly
$\hat{w}_{i,j}$
are bigrassmannian). There are exactly
![]() $1+q_{i,j}$
bigrassmannian elements in
$1+q_{i,j}$
bigrassmannian elements in
![]() $S_n$
with left descent
$S_n$
with left descent
![]() $s_i$
and right descent
$s_i$
and right descent
![]() $s_j$
. They form a chain with respect to the Bruhat order and hence are in natural bijection, denoted
$s_j$
. They form a chain with respect to the Bruhat order and hence are in natural bijection, denoted
![]() $\Phi_{i,j}$
, with the graded simple subquotients of
$\Phi_{i,j}$
, with the graded simple subquotients of
![]() $\Delta_e$
isomorphic, up to a shift, to
$\Delta_e$
isomorphic, up to a shift, to
![]() $L_{w_{i,j}}$
(ordered by increasing graded shifts). In particular, the element
$L_{w_{i,j}}$
(ordered by increasing graded shifts). In particular, the element
![]() $\hat{w}_{i,j}$
corresponds to
$\hat{w}_{i,j}$
corresponds to
![]() $L_{w_{i,j}}\langle -(\ell(w_{i,j})-2q_{i,j})\rangle$
.
$L_{w_{i,j}}\langle -(\ell(w_{i,j})-2q_{i,j})\rangle$
.
For
![]() $w\in S_n$
, denote by
$w\in S_n$
, denote by
![]() $\textbf{BM}_w$
the set of all Bruhat maximal elements in the set of all bigrassmannian elements of the Bruhat interval [e,w].
$\textbf{BM}_w$
the set of all Bruhat maximal elements in the set of all bigrassmannian elements of the Bruhat interval [e,w].
Proposition 21. Let
![]() $w\in S_n$
and let
$w\in S_n$
and let
![]() $u\in \textbf{BM}_w$
have left descent
$u\in \textbf{BM}_w$
have left descent
![]() $s_i$
and right descent
$s_i$
and right descent
![]() $s_j$
. If
$s_j$
. If
![]() $\Phi_{i,j}(u)=L_{w_{i,j}}\langle m\rangle$
and
$\Phi_{i,j}(u)=L_{w_{i,j}}\langle m\rangle$
and
![]() $w_{i,j}\geq w$
, then
$w_{i,j}\geq w$
, then
![]() $\textrm{ext}^1(\Delta_{w_{i,j}}\langle m\rangle,\Delta_{w})\neq 0$
.
$\textrm{ext}^1(\Delta_{w_{i,j}}\langle m\rangle,\Delta_{w})\neq 0$
.
Proof. Applying
![]() $\textrm{hom}({}_-, \Delta_{w})$
to the short exact sequence
$\textrm{hom}({}_-, \Delta_{w})$
to the short exact sequence
we get the exact sequence
Here
![]() $\textrm{hom}(L_{w_{i,j}}\langle m\rangle, \Delta_{w})=0$
since
$\textrm{hom}(L_{w_{i,j}}\langle m\rangle, \Delta_{w})=0$
since
![]() $w_{i,j}\neq w_0$
.
$w_{i,j}\neq w_0$
.
The above implies that the map
is an inclusion. Under the assumption
![]() $w_{i,j}\geq w$
, this map, in fact, is an isomorphism. Indeed, we even have
$w_{i,j}\geq w$
, this map, in fact, is an isomorphism. Indeed, we even have
Here the first isomorphism is a consequence of
![]() $w_{i,j}\geq w$
while the second one is given by the restriction together with the fact that the last hom-space is one-dimensional since both involved modules have isomorphic simple socle which, moreover, has multiplicity one in both modules.
$w_{i,j}\geq w$
while the second one is given by the restriction together with the fact that the last hom-space is one-dimensional since both involved modules have isomorphic simple socle which, moreover, has multiplicity one in both modules.
This implies that the map
is injective. Since
![]() $\textrm{ext}^1(L_{w_{i,j}}\langle m\rangle, \Delta_{w})\neq 0$
by [
Reference Ko, Mazorchuk and Mren19
, corollary 2], the claim follows.
$\textrm{ext}^1(L_{w_{i,j}}\langle m\rangle, \Delta_{w})\neq 0$
by [
Reference Ko, Mazorchuk and Mren19
, corollary 2], the claim follows.
We note that the non-zero extension in
![]() $\textrm{ext}^1(\Delta_{w_{i,j}}\langle m\rangle,\Delta_{w})$
produced by Proposition 21 is expected if and only if
$\textrm{ext}^1(\Delta_{w_{i,j}}\langle m\rangle,\Delta_{w})$
produced by Proposition 21 is expected if and only if
![]() $-m=\ell(w_{i,j})-\ell(w)-2$
. In all other cases, we have an additional extension.
$-m=\ell(w_{i,j})-\ell(w)-2$
. In all other cases, we have an additional extension.
Corollary 22. For
![]() $i\in\{1,2,\dots,n-1\}$
, consider the element
$i\in\{1,2,\dots,n-1\}$
, consider the element
![]() $w_{i,n-i}=s_iw_0$
. Let
$w_{i,n-i}=s_iw_0$
. Let
![]() $w\in S_n$
and let
$w\in S_n$
and let
![]() $m = 2- (\ell(w_{i,n-i})-\ell(w))$
(the expected degree of
$m = 2- (\ell(w_{i,n-i})-\ell(w))$
(the expected degree of
![]() $ext^1$
between
$ext^1$
between
![]() $\Delta_{w_{i,n-i}}$
and
$\Delta_{w_{i,n-i}}$
and
![]() $\Delta_{w}$
).
$\Delta_{w}$
).
-
(a) If
 $\Phi_{i,n-i}^{-1} (L_{w_{i,n-i}}\langle m'\rangle )\not\in BM_w$
for all
$\Phi_{i,n-i}^{-1} (L_{w_{i,n-i}}\langle m'\rangle )\not\in BM_w$
for all
 $m'\neq m$
, then we have
$m'\neq m$
, then we have  \begin{equation*}\dim\textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{i,n-i}},\Delta_{w})=\dim\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m\rangle,\Delta_{w})=|r^{({-}m)}_{w_{i,n-i},w}|.\end{equation*}
\begin{equation*}\dim\textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{i,n-i}},\Delta_{w})=\dim\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m\rangle,\Delta_{w})=|r^{({-}m)}_{w_{i,n-i},w}|.\end{equation*}
-
(b) If
 $\Phi_{i,n-i}^{-1} (L_{w_{i,n-i}}\langle m' \rangle )\in BM_w$
for some
$\Phi_{i,n-i}^{-1} (L_{w_{i,n-i}}\langle m' \rangle )\in BM_w$
for some
 $m'\neq m$
, then we have Moreover, we have
$m'\neq m$
, then we have Moreover, we have $$ \textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{i,n-i}},\Delta_{w})=\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m'\rangle,\Delta_{w})\oplus\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m\rangle,\Delta_{w}).$$
$$ \textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{i,n-i}},\Delta_{w})=\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m'\rangle,\Delta_{w})\oplus\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m\rangle,\Delta_{w}).$$
 $\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m'\rangle,\Delta_{w})\cong\mathbb{C}$
, while
$\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m'\rangle,\Delta_{w})\cong\mathbb{C}$
, while
 $\dim\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m\rangle,\Delta_{w})=|r^{({-}m)}_{w_{i,n-i},w}|$
.
$\dim\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle m\rangle,\Delta_{w})=|r^{({-}m)}_{w_{i,n-i},w}|$
.
Proof. Since
![]() $w_{i,n-i}=s_iw_0$
, we have the exact sequence
$w_{i,n-i}=s_iw_0$
, we have the exact sequence
It induces the exact sequence
By [
Reference Mazorchuk21
, theorem 32], any element in
![]() $\textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{0}}, \Delta_{w})$
is expected. By [
Reference Ko, Mazorchuk and Mren19
, corollary 2], the dimension of
$\textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{0}}, \Delta_{w})$
is expected. By [
Reference Ko, Mazorchuk and Mren19
, corollary 2], the dimension of
![]() $\textrm{Ext}^1_{\mathcal{O}}(L_{w_{i,n-i}}, \Delta_{w})$
is at most 1. This naturally splits our consideration into two cases, for the potential degree shift
$\textrm{Ext}^1_{\mathcal{O}}(L_{w_{i,n-i}}, \Delta_{w})$
is at most 1. This naturally splits our consideration into two cases, for the potential degree shift
![]() $\tilde{m}$
, namely, the cases
$\tilde{m}$
, namely, the cases
![]() $-{\tilde{m}}=\ell(w_{i,{n-i}}){-\ell(w)}-2$
and
$-{\tilde{m}}=\ell(w_{i,{n-i}}){-\ell(w)}-2$
and
![]() $-{\tilde{m}}\neq \ell(w_{i,{n-i}}){-\ell(w)}-2$
. In the first case, all first extensions are expected and thus given by (11). This is exactly claim (a).
$-{\tilde{m}}\neq \ell(w_{i,{n-i}}){-\ell(w)}-2$
. In the first case, all first extensions are expected and thus given by (11). This is exactly claim (a).
Now, assume that
![]() $-{\tilde{m}}\neq \ell(w_{i,{n-i}}){-\ell(w)}-2$
. The proof of Proposition 21 constructs an embedding from
$-{\tilde{m}}\neq \ell(w_{i,{n-i}}){-\ell(w)}-2$
. The proof of Proposition 21 constructs an embedding from
![]() $\textrm{ext}^1(L_{w_{i,n-i}}\langle {\tilde{m}}\rangle, \Delta_{w})$
to
$\textrm{ext}^1(L_{w_{i,n-i}}\langle {\tilde{m}}\rangle, \Delta_{w})$
to
![]() $\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle {\tilde{m}}\rangle, \Delta_{w})$
. We have the vanishing
$\textrm{ext}^1(\Delta_{w_{i,n-i}}\langle {\tilde{m}}\rangle, \Delta_{w})$
. We have the vanishing
![]() $\textrm{ext}^1(\Delta_{w_{0}}\langle {\tilde{m}}-1\rangle, \Delta_{w})=0$
by [
Reference Mazorchuk21
, theorem 32]. This implies that the above embedding is, in fact, an isomorphism. Now claim (b) follows from [
Reference Ko, Mazorchuk and Mren19
, corollary 2] and the observation that all expected extensions are given by (11).
$\textrm{ext}^1(\Delta_{w_{0}}\langle {\tilde{m}}-1\rangle, \Delta_{w})=0$
by [
Reference Mazorchuk21
, theorem 32]. This implies that the above embedding is, in fact, an isomorphism. Now claim (b) follows from [
Reference Ko, Mazorchuk and Mren19
, corollary 2] and the observation that all expected extensions are given by (11).
Example 23. Consider
![]() $S_{2n}$
, for
$S_{2n}$
, for
![]() $n>2$
, and
$n>2$
, and
![]() $w_{n,n}=s_nw_0$
. Let
$w_{n,n}=s_nw_0$
. Let
![]() $w=s_n$
, which is bigrassmannian. Then the socle of the module
$w=s_n$
, which is bigrassmannian. Then the socle of the module
![]() $\Delta_e/\Delta_{s_n}$
is isomorphic to the module
$\Delta_e/\Delta_{s_n}$
is isomorphic to the module
![]() $L_{w_{n,n}}\langle -(n(2n-1)-1-2(n-1))\rangle$
. Hence
$L_{w_{n,n}}\langle -(n(2n-1)-1-2(n-1))\rangle$
. Hence
![]() $\textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{i,j}},\Delta_{w})$
has the expected part of dimension
$\textrm{Ext}^1_{\mathcal{O}}(\Delta_{w_{i,j}},\Delta_{w})$
has the expected part of dimension
![]() $2n-1$
(corresponding to
$2n-1$
(corresponding to
![]() $\textrm{ext}^1(\Delta_{w_{n,n}}\langle -(n(2n-1)-3)\rangle,\Delta_{s_2})$
) and also the one-dimensional additional part
$\textrm{ext}^1(\Delta_{w_{n,n}}\langle -(n(2n-1)-3)\rangle,\Delta_{s_2})$
) and also the one-dimensional additional part
![]() $\textrm{ext}^1(\Delta_{w_{n,n}}\langle -(n(2n-1)-1-2(n-1))\rangle,\Delta_{s_n})$
.
$\textrm{ext}^1(\Delta_{w_{n,n}}\langle -(n(2n-1)-1-2(n-1))\rangle,\Delta_{s_n})$
.
6·5. Some additional higher extensions
This section presents a few ways to find additional, in the sense of Subsection 4·5, higher extensions.
We start with the first type of examples observed (in an ungraded setting) by Boe [ Reference Boe7 ] in disproving the Gabber–Joseph conjecture.
Example 24. If the coefficients
![]() $r_{x,y}^{(k)}$
do not alternate in sign, then Theorem 2 implies that there is an additional extension between
$r_{x,y}^{(k)}$
do not alternate in sign, then Theorem 2 implies that there is an additional extension between
![]() $\Delta_x$
and
$\Delta_x$
and
![]() $\Delta_y$
. (Here we cannot determine the i such that there are additional ith extensions.) Computer computation of
$\Delta_y$
. (Here we cannot determine the i such that there are additional ith extensions.) Computer computation of
![]() $r_{x,y}$
provides many such examples. We record two here:
$r_{x,y}$
provides many such examples. We record two here:
In type
![]() $D_4$
, the coefficients of
$D_4$
, the coefficients of
![]() $r_{e,w_0}$
are
$r_{e,w_0}$
are
The coefficients of
![]() $r_{e,w_0}$
in type
$r_{e,w_0}$
in type
![]() $E_7$
are
$E_7$
are
The second type of examples are also, more or less, combinatorial, this time depending on computations of KL polynomials rather than R-polynomials and using Proposition 5 rather than Theorem 2.
Example 25. Let W be of type
![]() $B_3$
with the labelling
$B_3$
with the labelling ![]() . We claim that:
. We claim that:
-
(1) either
 $\textrm{Ext}^2(\Delta_{w_0},\Delta_e)$
or
$\textrm{Ext}^2(\Delta_{w_0},\Delta_e)$
or
 $\textrm{Ext}^2(\Delta_{w_0},\Delta_{s_0})$
contains additional extensions;
$\textrm{Ext}^2(\Delta_{w_0},\Delta_{s_0})$
contains additional extensions; -
(2) either
 $\textrm{Ext}^3(\Delta_{w_0},\Delta_e)$
or
$\textrm{Ext}^3(\Delta_{w_0},\Delta_e)$
or
 $\textrm{Ext}^3(\Delta_{w_0},\Delta_{s_0})$
contains additional extensions;
$\textrm{Ext}^3(\Delta_{w_0},\Delta_{s_0})$
contains additional extensions; -
(3) either
 $\textrm{Ext}^4(\Delta_{w_0},\Delta_e)$
or
$\textrm{Ext}^4(\Delta_{w_0},\Delta_e)$
or
 $\textrm{Ext}^4(\Delta_{w_0},\Delta_{s_0})$
contains additional extensions.
$\textrm{Ext}^4(\Delta_{w_0},\Delta_{s_0})$
contains additional extensions.
A computation of KL polynomials, together with Proposition 5, shows that the dimensions of
![]() $\hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_{a}(\Delta_e)) $
and
$\hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_{a}(\Delta_e)) $
and
![]() $\hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_{a-1}(\Delta_{s_0}))$
are as in Figure 3. Recall that the embedding
$\hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_{a-1}(\Delta_{s_0}))$
are as in Figure 3. Recall that the embedding
![]() $\mathcal{T}_{\bullet-1}(\Delta_{s_0})\to \mathcal{T}_{\bullet}(\Delta_{e})$
induces an embedding
$\mathcal{T}_{\bullet-1}(\Delta_{s_0})\to \mathcal{T}_{\bullet}(\Delta_{e})$
induces an embedding
The claims additional extensions arise from the square (i.e., additional) coordinates (a,b) where the dimension difference at
![]() $(a-1,b)$
is greater than the difference at (a,b) in Figure 3. We explain the details for the details for (1). The same argument applies to the other claims.
$(a-1,b)$
is greater than the difference at (a,b) in Figure 3. We explain the details for the details for (1). The same argument applies to the other claims.

Figure 3.
![]() $\dim \hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_a(\Delta_e)) $
versus
$\dim \hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_a(\Delta_e)) $
versus
![]() $\dim \hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_{a-1}(\Delta_{s_0})) $
$\dim \hom(\Delta_{w_0}\langle b\rangle,\mathcal{T}_{a-1}(\Delta_{s_0})) $
Suppose the second extension between
![]() $\Delta_{w_0}$
and
$\Delta_{w_0}$
and
![]() $\Delta_e$
is expected. Then the map
$\Delta_e$
is expected. Then the map
is injective, where d is the (relevant restriction of) differential of
![]() $\mathcal{T}_\bullet(\Delta_e)$
. Let V be its 3-dimensional image in
$\mathcal{T}_\bullet(\Delta_e)$
. Let V be its 3-dimensional image in
![]() $\hom(\Delta_{w_0}\langle -1\rangle,\mathcal{T}_{3}(\Delta_e))$
. The embedding
$\hom(\Delta_{w_0}\langle -1\rangle,\mathcal{T}_{3}(\Delta_e))$
. The embedding
![]() $\iota$
restricts to an isomorphism
$\iota$
restricts to an isomorphism
also denoted by
![]() $\iota$
, since both spaces are of dimension 7. We obtain a 3-dimensional subspace
$\iota$
, since both spaces are of dimension 7. We obtain a 3-dimensional subspace
![]() $\iota^{-1}(V)$
in the 7-dimensional space
$\iota^{-1}(V)$
in the 7-dimensional space
![]() $\hom(\Delta_{w_0}\langle -1\rangle,\mathcal{T}_{3-1}(\Delta_{s_0}))$
which corresponds to morphisms of complexes from
$\hom(\Delta_{w_0}\langle -1\rangle,\mathcal{T}_{3-1}(\Delta_{s_0}))$
which corresponds to morphisms of complexes from
![]() $\Delta_{w_0}\langle-1\rangle$
to
$\Delta_{w_0}\langle-1\rangle$
to
![]() $\mathcal{T}_\bullet(\Delta_{s_0})$
. At most (in fact exactly) two dimensional subspace of
$\mathcal{T}_\bullet(\Delta_{s_0})$
. At most (in fact exactly) two dimensional subspace of
![]() $\iota^{-1}$
is homotopic to zero, because the dimension of at
$\iota^{-1}$
is homotopic to zero, because the dimension of at
![]() $(2,-1)$
is two. Thus the rest contributes to a nonzero element in
$(2,-1)$
is two. Thus the rest contributes to a nonzero element in
![]() $\textrm{ext}^2(\Delta_{w_0}\langle-1\rangle,\Delta_{s_0})$
which is additional.
$\textrm{ext}^2(\Delta_{w_0}\langle-1\rangle,\Delta_{s_0})$
which is additional.
Another way to construct additional extensions is to use [ Reference Ko, Mazorchuk and Mren19 ] and Subsection 6·4, as in the following proposition.
Proposition 26. In the setup of Example 23, the Yoneda product of an additional element in
![]() $\textrm{ext}^1(\Delta_{w_{n,n}}\langle -(n(2n-1)-1-2(n-1))\rangle,\Delta_{s_n})$
and an additional element in
$\textrm{ext}^1(\Delta_{w_{n,n}}\langle -(n(2n-1)-1-2(n-1))\rangle,\Delta_{s_n})$
and an additional element in
![]() $\textrm{ext}^1(\Delta_{s_n}\langle 1\rangle,\Delta_e)$
gives an additional element in
$\textrm{ext}^1(\Delta_{s_n}\langle 1\rangle,\Delta_e)$
gives an additional element in
This implies that
![]() $\textrm{ext}^2(\Delta_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle,\Delta_{e})\neq 0$
and gives an example of an additional second extension.
$\textrm{ext}^2(\Delta_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle,\Delta_{e})\neq 0$
and gives an example of an additional second extension.
Proof. From the Koszul–Ringel self-duality, it follows that the complex
![]() $\mathcal{T}_\bullet(\Delta_{s_n})[\!-\!1]\langle 1\rangle$
is a subcomplex of the complex
$\mathcal{T}_\bullet(\Delta_{s_n})[\!-\!1]\langle 1\rangle$
is a subcomplex of the complex
![]() $\mathcal{T}_\bullet(\Delta_e)$
. This inclusion corresponds precisely to an additional element in
$\mathcal{T}_\bullet(\Delta_e)$
. This inclusion corresponds precisely to an additional element in
![]() $\textrm{ext}^1(\Delta_{s_n}\langle 1\rangle,\Delta_e)$
.
$\textrm{ext}^1(\Delta_{s_n}\langle 1\rangle,\Delta_e)$
.
A non-zero element in
![]() $\textrm{ext}^1(\Delta_{w_{n,n}}\langle -(n(2n-1)-1-2(n-1))\rangle,\Delta_{s_n})$
corresponds to a non-zero homomorphism in the homotopy category of complexes from the singleton complex
$\textrm{ext}^1(\Delta_{w_{n,n}}\langle -(n(2n-1)-1-2(n-1))\rangle,\Delta_{s_n})$
corresponds to a non-zero homomorphism in the homotopy category of complexes from the singleton complex
![]() $\Delta_{w_{n,n}}[\!-\!1]\langle -(n(2n-1)-1-2(n-1))\rangle$
to
$\Delta_{w_{n,n}}[\!-\!1]\langle -(n(2n-1)-1-2(n-1))\rangle$
to
![]() $\mathcal{T}_\bullet(\Delta_{s_n})$
. Therefore, to prove the claim it is enough to show that the map from
$\mathcal{T}_\bullet(\Delta_{s_n})$
. Therefore, to prove the claim it is enough to show that the map from
![]() $\Delta_{w_{n,n}}[\!-\!2]\langle -(n(2n-1)-2(n-1))\rangle$
to
$\Delta_{w_{n,n}}[\!-\!2]\langle -(n(2n-1)-2(n-1))\rangle$
to
![]() $\mathcal{T}_\bullet(\Delta_e)$
induced by the inclusion of
$\mathcal{T}_\bullet(\Delta_e)$
induced by the inclusion of
![]() $\mathcal{T}_\bullet(\Delta_{s_n})[\!-\!1]\langle 1\rangle$
to
$\mathcal{T}_\bullet(\Delta_{s_n})[\!-\!1]\langle 1\rangle$
to
![]() $\mathcal{T}_\bullet(\Delta_e)$
is not homotopic to zero.
$\mathcal{T}_\bullet(\Delta_e)$
is not homotopic to zero.
To prove this, it is enough to show that there are no non-zero homomorphisms from
![]() $\Delta_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle$
to any indecomposable direct summand of
$\Delta_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle$
to any indecomposable direct summand of
![]() $\mathcal{T}_1(\Delta_e)$
outside of
$\mathcal{T}_1(\Delta_e)$
outside of
![]() $\mathcal{T}_0(\Delta_{s_n})[\!-\!1]\langle 1\rangle$
.
$\mathcal{T}_0(\Delta_{s_n})[\!-\!1]\langle 1\rangle$
.
These direct summands are exactly the modules
![]() $T_{s_i}\langle 1\rangle$
, where
$T_{s_i}\langle 1\rangle$
, where
![]() $i\neq n$
. Since
$i\neq n$
. Since
![]() $T_{s_i}$
is a tilting module, a non-zero homomorphism from
$T_{s_i}$
is a tilting module, a non-zero homomorphism from
![]() $\Delta_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle$
to
$\Delta_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle$
to
![]() $T_{s_i}\langle 1\rangle$
exists if and only if
$T_{s_i}\langle 1\rangle$
exists if and only if
![]() $\nabla_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle$
is a subquotient of a dual Verma flag of
$\nabla_{w_{n,n}}\langle -(n(2n-1)-2(n-1))\rangle$
is a subquotient of a dual Verma flag of
![]() $T_{s_i}\langle 1\rangle$
. Using
$T_{s_i}\langle 1\rangle$
. Using
![]() $\top_{w_0}$
, this is equivalent to
$\top_{w_0}$
, this is equivalent to
![]() $\Delta_{s_n}\langle -(n(2n-1)-2(n-1))\rangle$
being a subquotient of a dual Verma flag of
$\Delta_{s_n}\langle -(n(2n-1)-2(n-1))\rangle$
being a subquotient of a dual Verma flag of
![]() $P_{w_0s_i}\langle 1\rangle$
. By the BGG reciprocity, this is equivalent to
$P_{w_0s_i}\langle 1\rangle$
. By the BGG reciprocity, this is equivalent to
![]() $L_{w_0s_i}\langle -(n(2n-1)-2(n-1))\rangle$
being a composition subquotient of
$L_{w_0s_i}\langle -(n(2n-1)-2(n-1))\rangle$
being a composition subquotient of
![]() $\Delta_{s_n}$
.
$\Delta_{s_n}$
.
Note that
![]() $w_0s_i$
belongs to the penultimate KL-cell in the terminology of [
Reference Ko, Mazorchuk and Mren19
]. All graded simple penultimate subquotients of
$w_0s_i$
belongs to the penultimate KL-cell in the terminology of [
Reference Ko, Mazorchuk and Mren19
]. All graded simple penultimate subquotients of
![]() $\Delta_e$
are described in [
Reference Ko, Mazorchuk and Mren19
, proposition 12]. From [
Reference Ko, Mazorchuk and Mren19
, theorem 1] it follows that the socle of the module
$\Delta_e$
are described in [
Reference Ko, Mazorchuk and Mren19
, proposition 12]. From [
Reference Ko, Mazorchuk and Mren19
, theorem 1] it follows that the socle of the module
![]() $\Delta_e/(\Delta_{s_n}\langle -1\rangle)$
is the unique penultimate subquotient of of this module and that it occurs in the minimal possible degree (in
$\Delta_e/(\Delta_{s_n}\langle -1\rangle)$
is the unique penultimate subquotient of of this module and that it occurs in the minimal possible degree (in
![]() $\Delta_e$
) among all other penultimate subquotients of
$\Delta_e$
) among all other penultimate subquotients of
![]() $\Delta_e$
. It follows that any other simple subquotient of
$\Delta_e$
. It follows that any other simple subquotient of
![]() $\Delta_{s_n}$
of the form
$\Delta_{s_n}$
of the form
![]() $L_{w_0s_i}$
appears in
$L_{w_0s_i}$
appears in
![]() $\Delta_e$
in a strictly higher degree compared to the degree of the socle of
$\Delta_e$
in a strictly higher degree compared to the degree of the socle of
![]() $\Delta_e/(\Delta_{s_n}\langle -1\rangle)$
. Going back via the BGG reciprocity and the Ringel duality, we get exactly the claim that any subquotient
$\Delta_e/(\Delta_{s_n}\langle -1\rangle)$
. Going back via the BGG reciprocity and the Ringel duality, we get exactly the claim that any subquotient
![]() $\nabla_{w_{n,n}}\langle d\rangle$
of a dual Verma flag of
$\nabla_{w_{n,n}}\langle d\rangle$
of a dual Verma flag of
![]() $T_{s_i}\langle 1\rangle$
must be shifted strictly more than by
$T_{s_i}\langle 1\rangle$
must be shifted strictly more than by
![]() $-(n(2n-1)-2(n-1))$
. This completes the proof.
$-(n(2n-1)-2(n-1))$
. This completes the proof.
7. Extensions between singular and between parabolic Verma modules
We briefly discuss generalisations of the previous sections to singular and parabolic categories
![]() $\mathcal O$
.
$\mathcal O$
.
7·1. Singular blocks of
 $\mathcal{O}$
$\mathcal{O}$
Thanks to Soergel’s combinatorial description of blocks of category
![]() $\mathcal{O}$
, see [
Reference Soergel28
], it is known that every block of
$\mathcal{O}$
, see [
Reference Soergel28
], it is known that every block of
![]() $\mathcal{O}$
is equivalent to an integral (but, in general, singular) block of
$\mathcal{O}$
is equivalent to an integral (but, in general, singular) block of
![]() $\mathcal{O}$
(however, possibly, for a different Lie algebra). Therefore the complete version of the problem to describe extensions between Verma modules must address the case of singular integral blocks.
$\mathcal{O}$
(however, possibly, for a different Lie algebra). Therefore the complete version of the problem to describe extensions between Verma modules must address the case of singular integral blocks.
Let
![]() $\mathfrak{p}$
denote a parabolic subalgebra of
$\mathfrak{p}$
denote a parabolic subalgebra of
![]() $\mathfrak{g}$
containing the Borel subalgebra
$\mathfrak{g}$
containing the Borel subalgebra
![]() $\mathfrak{h}\oplus\mathfrak{n}_+$
. The subalgebra
$\mathfrak{h}\oplus\mathfrak{n}_+$
. The subalgebra
![]() $\mathfrak{p}$
is uniquely determined by a subset of simple roots, or, equivalently, by the corresponding parabolic subgroup
$\mathfrak{p}$
is uniquely determined by a subset of simple roots, or, equivalently, by the corresponding parabolic subgroup
![]() $W^{\mathfrak{p}}$
of W. Let
$W^{\mathfrak{p}}$
of W. Let
![]() $\textbf{R}^\mathfrak{p}_{\textrm{short}}$
denote the set of the shortest coset representatives in
$\textbf{R}^\mathfrak{p}_{\textrm{short}}$
denote the set of the shortest coset representatives in
![]() $W/W^{\mathfrak{p}}$
.
$W/W^{\mathfrak{p}}$
.
Let
![]() $\lambda$
be a dominant integral weight such that
$\lambda$
be a dominant integral weight such that
![]() $W^{\mathfrak{p}}$
is exactly the dot-stabilizer of
$W^{\mathfrak{p}}$
is exactly the dot-stabilizer of
![]() $\lambda$
. Consider the block
$\lambda$
. Consider the block
![]() $\mathcal{O}_\lambda$
of
$\mathcal{O}_\lambda$
of
![]() $\mathcal{O}$
containing
$\mathcal{O}$
containing
![]() $L(\lambda)$
. Then the simple objects in
$L(\lambda)$
. Then the simple objects in
![]() $\mathcal{O}_\lambda$
are
$\mathcal{O}_\lambda$
are
![]() $\{L(w\cdot\lambda)\,:\, w\in\textbf{R}^\mathfrak{p}_{\textrm{short}}\}$
. Similarly to the regular case, we also have the corresponding projective, injective, Verma, dual Verma and tilting modules and their graded versions.
$\{L(w\cdot\lambda)\,:\, w\in\textbf{R}^\mathfrak{p}_{\textrm{short}}\}$
. Similarly to the regular case, we also have the corresponding projective, injective, Verma, dual Verma and tilting modules and their graded versions.
7·2. Regular blocks of parabolic category
 $\mathcal{O}$
$\mathcal{O}$
Associated to our choice of
![]() $\mathfrak{p}$
, one also has the parabolic category
$\mathfrak{p}$
, one also has the parabolic category
![]() $\mathcal{O}^\mathfrak{p}$
introduced in [
Reference Rocha-Caridi27
]. It is defined as the full subcategory of
$\mathcal{O}^\mathfrak{p}$
introduced in [
Reference Rocha-Caridi27
]. It is defined as the full subcategory of
![]() $\mathcal{O}$
consisting of all objects, the action of
$\mathcal{O}$
consisting of all objects, the action of
![]() $U(\mathfrak{p})$
on which is locally finite.
$U(\mathfrak{p})$
on which is locally finite.
Let
![]() $\textbf{L}^\mathfrak{p}_{\textrm{short}}$
denote the set of the shortest coset representatives in
$\textbf{L}^\mathfrak{p}_{\textrm{short}}$
denote the set of the shortest coset representatives in
![]() $W^{\mathfrak{p}}\backslash W$
. Then the category
$W^{\mathfrak{p}}\backslash W$
. Then the category
![]() $\mathcal{O}_0^\mathfrak{p}$
is the Serre subcategory of
$\mathcal{O}_0^\mathfrak{p}$
is the Serre subcategory of
![]() $\mathcal{O}_0$
generated by all
$\mathcal{O}_0$
generated by all
![]() $L_w$
such that
$L_w$
such that
![]() $w\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
. We use the superscript
$w\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
. We use the superscript
![]() $\mathfrak{p}$
to denote structural objects in
$\mathfrak{p}$
to denote structural objects in
![]() $\mathcal{O}_0^\mathfrak{p}$
. In particular, for
$\mathcal{O}_0^\mathfrak{p}$
. In particular, for
![]() $w\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
, we denote by
$w\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
, we denote by
![]() $P^\mathfrak{p}_w$
the indecomposable projective cover of
$P^\mathfrak{p}_w$
the indecomposable projective cover of
![]() $L^\mathfrak{p}_w=L_w$
in
$L^\mathfrak{p}_w=L_w$
in
![]() $\mathcal{O}_0^\mathfrak{p}$
and so on. The category
$\mathcal{O}_0^\mathfrak{p}$
and so on. The category
![]() $\mathcal{O}_0^\mathfrak{p}$
inherits a graded lift from that for
$\mathcal{O}_0^\mathfrak{p}$
inherits a graded lift from that for
![]() $\mathcal{O}_0$
.
$\mathcal{O}_0$
.
7·3. Koszul–Ringel duality
For a fixed parabolic subalgebra
![]() $\mathfrak{p}$
as above and singular dominant integral
$\mathfrak{p}$
as above and singular dominant integral
![]() $\lambda$
with dot-stabilizer
$\lambda$
with dot-stabilizer
![]() $W^\mathfrak{p}$
, the combination of Koszul and Ringel dualities, together with the autoequivalence given by the conjugation with
$W^\mathfrak{p}$
, the combination of Koszul and Ringel dualities, together with the autoequivalence given by the conjugation with
![]() $w_0$
, see [
Reference Beilinson, Ginzburg and Soergel3, Reference Mazorchuk22, Reference Soergel29
], gives rise to the equivalence
$w_0$
, see [
Reference Beilinson, Ginzburg and Soergel3, Reference Mazorchuk22, Reference Soergel29
], gives rise to the equivalence
which sends
![]() $\Delta(w\cdot \lambda)$
to
$\Delta(w\cdot \lambda)$
to
![]() $\Delta^{\mathfrak{p}}_{w^{-1}}$
, where
$\Delta^{\mathfrak{p}}_{w^{-1}}$
, where
![]() $w\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$
.
$w\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$
.
In particular, this implies that
and thus the problem to determine all extensions between singular Verma modules is equivalent to the problem to detrmine all extensions between regular parabolic Verma modules.
7·4. Singular and parabolic R-polynomials
Consider the usual
![]() $\mathbb{Z}[v,v^{-1}]$
-structure on the Grothendieck group
$\mathbb{Z}[v,v^{-1}]$
-structure on the Grothendieck group
![]() $\textrm{Gr}(\mathcal{O}_\lambda^{\mathbb{Z}})$
. Similarly to the regular case, the group
$\textrm{Gr}(\mathcal{O}_\lambda^{\mathbb{Z}})$
. Similarly to the regular case, the group
![]() $\textrm{Gr}(\mathcal{O}_\lambda^{\mathbb{Z}})$
has various bases given by the classes of simple, standard, costandard, projective, injective and tilting objects.
$\textrm{Gr}(\mathcal{O}_\lambda^{\mathbb{Z}})$
has various bases given by the classes of simple, standard, costandard, projective, injective and tilting objects.
The singular R-polynomials
![]() $\{sr_{x,y}\,:\,x,y\in W\}$
are defined as the entries of the transformation matrix between the standard and the costandard bases in
$\{sr_{x,y}\,:\,x,y\in W\}$
are defined as the entries of the transformation matrix between the standard and the costandard bases in
![]() $\textrm{Gr}(\mathcal{O}_\lambda^{\mathbb{Z}})$
, i.e.:
$\textrm{Gr}(\mathcal{O}_\lambda^{\mathbb{Z}})$
, i.e.:
Note that
![]() $sr_{x,y}\in\mathbb{Z}[v,v^{-1}]$
, by definition. For
$sr_{x,y}\in\mathbb{Z}[v,v^{-1}]$
, by definition. For
![]() $x,y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$
and
$x,y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$
and
![]() $k\in\mathbb{Z}$
, we denote by
$k\in\mathbb{Z}$
, we denote by
![]() $sr_{x,y}^{(k)}$
the coefficient at
$sr_{x,y}^{(k)}$
the coefficient at
![]() $v^k$
in
$v^k$
in
![]() $sr_{x,y}$
.
$sr_{x,y}$
.
Let
![]() $w_0^\mathfrak{p}$
denotes the longest element in
$w_0^\mathfrak{p}$
denotes the longest element in
![]() $W^\mathfrak{p}$
. The connection between the usual and the singular R-polynomials is clarified by the following:
$W^\mathfrak{p}$
. The connection between the usual and the singular R-polynomials is clarified by the following:
Lemma 27. For
![]() $x,y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$
, we have
$x,y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$
, we have
Proof. Let
![]() $\theta_{\lambda}^{\textrm{on}}$
be the translation functor to the
$\theta_{\lambda}^{\textrm{on}}$
be the translation functor to the
![]() $\lambda$
-wall, that is the unique indecomposable projective functor in the sense of [
Reference Bernstein and Gelfand5
] which sends
$\lambda$
-wall, that is the unique indecomposable projective functor in the sense of [
Reference Bernstein and Gelfand5
] which sends
![]() $\Delta_e$
to
$\Delta_e$
to
![]() $\Delta_{\lambda}$
. Then
$\Delta_{\lambda}$
. Then
![]() $\theta_{\lambda}^{\textrm{on}}$
sends
$\theta_{\lambda}^{\textrm{on}}$
sends
![]() $\Delta_y$
to
$\Delta_y$
to
![]() $\Delta(y\cdot \lambda)$
. Furthermore, for
$\Delta(y\cdot \lambda)$
. Furthermore, for
![]() $y\in \textbf{R}^\mathfrak{p}_{\textrm{long}}$
and
$y\in \textbf{R}^\mathfrak{p}_{\textrm{long}}$
and
![]() $w\in W^\mathfrak{p}$
, we have
$w\in W^\mathfrak{p}$
, we have
Since
![]() $\theta_{\lambda}^{\textrm{on}}$
is exact, the claim now follows from the definitions.
$\theta_{\lambda}^{\textrm{on}}$
is exact, the claim now follows from the definitions.
Consider the usual
![]() $\mathbb{Z}[v,v^{-1}]$
-structure on the Grothendieck group
$\mathbb{Z}[v,v^{-1}]$
-structure on the Grothendieck group
![]() $\textrm{Gr}\big((\mathcal{O}_0^\mathfrak{p})^{\mathbb{Z}}\big)$
. Similarly to the regular case, the group
$\textrm{Gr}\big((\mathcal{O}_0^\mathfrak{p})^{\mathbb{Z}}\big)$
. Similarly to the regular case, the group
![]() $\textrm{Gr}\big((\mathcal{O}_0^\mathfrak{p})^{\mathbb{Z}}\big)$
has various bases given by the classes of simple, standard, costandard, projective, injective and tilting objects.
$\textrm{Gr}\big((\mathcal{O}_0^\mathfrak{p})^{\mathbb{Z}}\big)$
has various bases given by the classes of simple, standard, costandard, projective, injective and tilting objects.
The parabolic R-polynomials
![]() $\{pr_{x,y}\,:\,x,y\in W\}$
are defined as the entries of the transformation matrix between the standard and the costandard bases in
$\{pr_{x,y}\,:\,x,y\in W\}$
are defined as the entries of the transformation matrix between the standard and the costandard bases in
![]() $\textrm{Gr}\big((\mathcal{O}_0^\mathfrak{p})^{\mathbb{Z}}\big)$
, i.e.:
$\textrm{Gr}\big((\mathcal{O}_0^\mathfrak{p})^{\mathbb{Z}}\big)$
, i.e.:
Note that
![]() $pr_{x,y}\in\mathbb{Z}[v,v^{-1}]$
, by definition. For
$pr_{x,y}\in\mathbb{Z}[v,v^{-1}]$
, by definition. For
![]() $x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
and
$x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
and
![]() $k\in\mathbb{Z}$
, we denote by
$k\in\mathbb{Z}$
, we denote by
![]() $pr_{x,y}^{(k)}$
the coefficient at
$pr_{x,y}^{(k)}$
the coefficient at
![]() $v^k$
in
$v^k$
in
![]() $pr_{x,y}$
.
$pr_{x,y}$
.
As
![]() $\Delta_{w_0^\mathfrak{p}w_0}^\mathfrak{p}=\nabla_{w_0^\mathfrak{p}w_0}^\mathfrak{p}$
, we have
$\Delta_{w_0^\mathfrak{p}w_0}^\mathfrak{p}=\nabla_{w_0^\mathfrak{p}w_0}^\mathfrak{p}$
, we have
 \begin{equation}pr_{x,w_0^\mathfrak{p}w_0}=\begin{cases}1,& x=w_0^\mathfrak{p}w_0;\\0,& \text{otherwise}.\end{cases}\end{equation}
\begin{equation}pr_{x,w_0^\mathfrak{p}w_0}=\begin{cases}1,& x=w_0^\mathfrak{p}w_0;\\0,& \text{otherwise}.\end{cases}\end{equation}
For
![]() $w\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
and
$w\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
and
![]() $s\in S$
such that
$s\in S$
such that
![]() $ws\not\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
, we have
$ws\not\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
, we have
![]() $\theta_s\Delta^\mathfrak{p}_w=\theta_s\nabla^\mathfrak{p}_w=0$
. If
$\theta_s\Delta^\mathfrak{p}_w=\theta_s\nabla^\mathfrak{p}_w=0$
. If
![]() $ws\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
and
$ws\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
and
![]() $ws>w$
, then we have
$ws>w$
, then we have
From this, we have the following recursive formula for parabolic R-polynomials: For
![]() $x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
and
$x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
and
![]() $s\in S$
such that
$s\in S$
such that
![]() $ys<y$
and
$ys<y$
and
![]() $ys\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
, we have:
$ys\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
, we have:
 \begin{equation}pr_{x,ys}=\begin{cases}pr_{xs,y},& xs<x\text{ and }xs\in \textbf{L}^\mathfrak{p}_{\textrm{short}};\\pr_{xs,y}+ ({v-v^{-1}}){pr_{x,y}},& xs>x\text{ and }xs\in \textbf{L}^\mathfrak{p}_{\textrm{short}};\\-v\, pr_{x,y},& xs\not\in \textbf{L}^\mathfrak{p}_{\textrm{short}}.\end{cases}\end{equation}
\begin{equation}pr_{x,ys}=\begin{cases}pr_{xs,y},& xs<x\text{ and }xs\in \textbf{L}^\mathfrak{p}_{\textrm{short}};\\pr_{xs,y}+ ({v-v^{-1}}){pr_{x,y}},& xs>x\text{ and }xs\in \textbf{L}^\mathfrak{p}_{\textrm{short}};\\-v\, pr_{x,y},& xs\not\in \textbf{L}^\mathfrak{p}_{\textrm{short}}.\end{cases}\end{equation}
Together, (13) and (14) determine the family of parabolic R-polynomials uniquely.
Koszul–Ringel duality relates these two families of polynomials as follows:
Proposition 28. For all
![]() $x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
, we have
$x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
, we have
![]() $pr_{x,y}(v)=sr_{x^{-1},y^{-1}}(-v^{-1})$
.
$pr_{x,y}(v)=sr_{x^{-1},y^{-1}}(-v^{-1})$
.
Proof. Taking into account that the conjugation by
![]() $w_0$
is an automorphism of the Dynkin diagram, the claim of the proposition follows from the definitions using that the Koszul–Ringel duality sends
$w_0$
is an automorphism of the Dynkin diagram, the claim of the proposition follows from the definitions using that the Koszul–Ringel duality sends
![]() $\Delta(w\cdot\lambda)$
to
$\Delta(w\cdot\lambda)$
to
![]() $\Delta^\mathfrak{p}_{w_0w^{-1}w_0}$
and
$\Delta^\mathfrak{p}_{w_0w^{-1}w_0}$
and
![]() $\nabla(w\cdot \lambda)$
to
$\nabla(w\cdot \lambda)$
to
![]() $\nabla_{w_0w^{-1}w_0}^\mathfrak{p}$
and intertwines
$\nabla_{w_0w^{-1}w_0}^\mathfrak{p}$
and intertwines
![]() $[i]\langle j\rangle$
with
$[i]\langle j\rangle$
with
![]() $[i+j]\langle -j\rangle$
.
$[i+j]\langle -j\rangle$
.
7·5. Delorme formulae
Similarly to the regular case, we have both ungraded and graded versions of Delorme formulae for both, the singular and the parabolic cases, with the same proofs as for the regular case.
Proposition 29.
-
(a) For
 $x,y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$
, we have
$x,y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$
, we have  $$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{Ext}^i_{\mathcal{O}}(\Delta(x\cdot\lambda),\Delta(y\cdot\lambda))=\delta_{x,y}.$$
$$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{Ext}^i_{\mathcal{O}}(\Delta(x\cdot\lambda),\Delta(y\cdot\lambda))=\delta_{x,y}.$$
-
(b) For
 $x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
, we have
$x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
, we have  $$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{Ext}^i_{\mathcal{O}^\mathfrak{p}}(\Delta_x^\mathfrak{p},\Delta_y^\mathfrak{p})=\delta_{x,y}.$$
$$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{Ext}^i_{\mathcal{O}^\mathfrak{p}}(\Delta_x^\mathfrak{p},\Delta_y^\mathfrak{p})=\delta_{x,y}.$$
Proposition 30.
-
(a) For
 $x,y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$
and
$x,y\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$
and
 $k\in\mathbb{Z}$
, we have
$k\in\mathbb{Z}$
, we have  $$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{ext}^i(\Delta(x\cdot\lambda)\langle -k\rangle,\Delta(y\cdot\lambda))=sr_{x,y}^{(k)}.$$
$$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{ext}^i(\Delta(x\cdot\lambda)\langle -k\rangle,\Delta(y\cdot\lambda))=sr_{x,y}^{(k)}.$$
-
(b) For
 $x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
and
$x,y\in \textbf{L}^\mathfrak{p}_{\textrm{short}}$
and
 $k\in\mathbb{Z}$
, we have
$k\in\mathbb{Z}$
, we have  $$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{ext}^i_{(\mathcal{O}^\mathfrak{p})^\mathbb{Z}}(\Delta_x^\mathfrak{p}\langle -k\rangle,\Delta_y^\mathfrak{p})=pr_{x,y}^{(k)}.$$
$$ \sum_{i\geq 0}(\!-\!1)^i\dim\textrm{ext}^i_{(\mathcal{O}^\mathfrak{p})^\mathbb{Z}}(\Delta_x^\mathfrak{p}\langle -k\rangle,\Delta_y^\mathfrak{p})=pr_{x,y}^{(k)}.$$
7·6. Expected and additional extensions
Under the indexing conventions in Subsections 7·1, 7·2, the expected extensions between singular or parabolic Verma modules are the extensions in
where
![]() $2k+j = \ell(x)-\ell(y)$
. The other (nonzero) extensions are additional. If all extensions are expected, then Proposition 30 says that the dimensions of the expected ext spaces are given by the R-polynomials.
$2k+j = \ell(x)-\ell(y)$
. The other (nonzero) extensions are additional. If all extensions are expected, then Proposition 30 says that the dimensions of the expected ext spaces are given by the R-polynomials.
7·7. Koszulity
Consider the categoy
![]() $\mathcal{D}^b(\mathcal{O}_\lambda^\mathbb{Z})$
, for a dominant and integral (but not necessarily regular)
$\mathcal{D}^b(\mathcal{O}_\lambda^\mathbb{Z})$
, for a dominant and integral (but not necessarily regular)
![]() $\lambda$
. Denote by
$\lambda$
. Denote by
![]() $\mathscr{D}$
the full subcategory of
$\mathscr{D}$
the full subcategory of
![]() $\mathcal{D}(\mathcal{O}_\lambda^\mathbb{Z})$
given by the objects
$\mathcal{D}(\mathcal{O}_\lambda^\mathbb{Z})$
given by the objects
![]() $\Delta(w\cdot\lambda)\langle i\rangle[j]$
, where
$\Delta(w\cdot\lambda)\langle i\rangle[j]$
, where
![]() $w\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$
and
$w\in \textbf{R}^\mathfrak{p}_{\textrm{short}}$
and
![]() $i,j\in\mathbb{Z}$
such that
$i,j\in\mathbb{Z}$
such that
Then the same argument as Theorem 17 gives the following generalisation.
Theorem 31. Let
![]() $\lambda$
be dominant and integral. Assume that all extensions between the Verma modules in
$\lambda$
be dominant and integral. Assume that all extensions between the Verma modules in
![]() $\mathcal{O}_\lambda$
are expected. Then the following assertions hold:
$\mathcal{O}_\lambda$
are expected. Then the following assertions hold:
-
(i) We have an equivalence
 $\mathcal{D}^*(\mathcal{O}_\lambda^\mathbb{Z})\cong \mathcal{D}^*(\mathscr{D}\text{-}\textrm{mod})$
where
$\mathcal{D}^*(\mathcal{O}_\lambda^\mathbb{Z})\cong \mathcal{D}^*(\mathscr{D}\text{-}\textrm{mod})$
where
 $*\in\{b,\uparrow,\downarrow\}$
.
$*\in\{b,\uparrow,\downarrow\}$
. -
(ii) The path algebra of
 $\mathscr{D}$
is Koszul and is Koszul self-dual.
$\mathscr{D}$
is Koszul and is Koszul self-dual.
Acknowledgements
This research is partially supported by the Swedish Research Council. Examples in Subsection 6·5 were computed by SageMath. We thank the referee for helpful comments on the paper and for letting us know of [ Reference Dhillon and Makam13 ].