Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-26T07:49:18.765Z Has data issue: false hasContentIssue false
  • English
  • Français

Some formulae for the G -function

Published online by Cambridge University Press:  24 October 2008

R. K. Saxena
R. K. Saxena
Affiliation:
Department of Mathematics, University of Rajasthan, Jaipur, India*
Get access Rights & Permissions [Opens in a new window]

Extract

The object of the present note is to evaluate some integrals involving Meijer's G-function, in which the argument of the G-function contains a factor 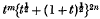where m and n are positive integers and t is the variable of integration. Two different forms of the general result have been obtained, one for m > n and the other for m < n. The value of the corresponding integral when m = n is also obtained. For the definition, properties and the behaviour of the G-function, see (2), §§ 5·3, 5·31 and (5), § 18.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 2 , April 1963 , pp. 347 - 350
Copyright
Copyright © Cambridge Philosophical Society 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Bromwich, T. J., I'A. An introduction to the theory of infinite series (Macmillan; London, 1931).Google Scholar
(2)Erdélyi, A. et al. , Higher transcendental functions, vol. I (McGraw-Hill; New York, 1953).Google Scholar
(3)Erdélyi, A. et al. , Tables of integral transforms, vol. I (McGraw-Hill; New York, 1954).Google Scholar
(4)Erdélyi, A. et al. , Tables of integral transforms, vol. II (McGraw-Hill; New York, 1954).Google Scholar
(5)Meijer, C. S., On the G-function. VI, VII. Nederl. Akad. Wetensch. Proc. 49 (1946), 936–943, 1063–1072.Google Scholar